南京大学《物理化学》练习 第二章 热力学第二定律
南京大学《物理化学》每章典型例题

南京大学《物理化学》每章典型例题第一章 热力学第一定律与热化学例题1 1mol 理想气体于27℃ 、101325Pa 状态下受某恒定外压恒温压缩到平衡,再由该状态恒容升温到97 ℃ ,则压力升到1013.25kPa 。
求整个过程的W 、Q 、△U 及△H 。
已知该气体的C V ,m恒定为20.92J •mol -1 •K -1。
解题思路:需先利用理想气体状态方程计算有关状态:(T 1=27℃, p 1=101325Pa ,V 1)→(T 2=27℃, p 2=p 外=?,V 2=?)→(T 3=97℃, p 3=1013.25kPa ,V 3= V 2)例题2水在 -5℃ 的结冰过程为不可逆过程,计算时要利用0℃ 结冰的可逆相变过程,即 H 2O (l ,1 mol ,-5℃ ,θp)H 2O (s ,1 mol ,-5℃,θp )↓△H 2 ↑△H 4H 2O (l ,1 mol , 0℃,θp )H 2O (s ,1 mol ,0℃,θp )△△∴ △H 1=△H 2+△H 3+△H 4例题3 在 298.15K 时,使 5.27 克的甲醇(摩尔质量为32克) 在弹式量热计中恒容燃烧,放出 119.50kJ 的热量。
忽略压力对焓的影响。
(1) 计算甲醇的标准燃烧焓θmc H ∆。
(2) 已知298.15K 时 H 2O(l) 和CO 2(g)的标准摩尔生成焓分别为-285.83 kJ·mol-1、-393.51 kJ·mol -1,计算CH 3OH(l)的θmfH ∆。
(3) 如果甲醇的标准蒸发焓为 35.27kJ·mol-1,计算CH 3OH(g) 的θmfH ∆。
解:(1) 甲醇燃烧反应:CH 3OH(l) +23O 2(g) → CO 2(g) + 2H 2O(l)Q V =θmcU ∆=-119.50 kJ/(5.27/32)mol =-725.62 kJ·mol -1Q p =θmcH ∆=θmcU ∆+∑RTv)g (B= (-725.62-0.5×8.3145×298.15×10-3)kJ·.mol -1=-726.86 kJ·mol -1(2)θmc H ∆=θmfH ∆(CO 2) + 2θmfH ∆(H 2O )-θmfH ∆[CH 3OH(l)]θmf H ∆[CH 3OH (l)] =θmfH ∆ (CO 2) + 2θmfH ∆(H 2O )-θmcH ∆= [-393.51+2×(-285.83)-(-726.86) ] kJ·mol -1=-238.31 kJ·mol -1(3) CH 3OH (l) →CH 3OH (g) ,θmvap ΔH=35.27 kJ·.mol -1 θmf H ∆[CH 3OH (g)] =θmfH ∆[CH 3OH (l)]+θmvapH ∆= (-38.31+35.27)kJ·.mol -1=-203.04 kJ·mol -1第二章 热力学第二定律例1. 1mol 理想气体从300K ,100kPa 下等压加热到600K ,求此过程的Q 、W 、U 、H 、S 、G 。
物理化学章节习题

第一章热力学第一定律一、单选题1) 如图,在绝热盛水容器中,浸入电阻丝,通电一段时间,通电后水及电阻丝的温度均略有升高,今以电阻丝为体系有:( )A.W =0,Q <0,∆U <0B.W <0,Q <0,∆U >0C.W <0,Q <0,∆U >0D. W <0,Q =0,∆U >02) 如图,用隔板将刚性绝热壁容器分成两半,两边充入压力不等的空气(视为理想气体),已知p右> p左,将隔板抽去后: ( )A.Q=0, W =0, ∆U =0B.Q=0, W <0, ∆U >0C.Q >0, W <0, ∆U >0D.∆U =0, Q=W ≠03)对于理想气体,下列关系中哪个是不正确的:( )A. (∂U/∂T)V=0B. (∂U/∂V)T=0C. (∂H/∂p)T=0D. (∂U/∂p)T=04)凡是在孤立孤体系中进行的变化,其∆U 和∆H 的值一定是:( )A.∆U >0, ∆H >0B.∆U =0, ∆H=0C.∆U <0, ∆H <0D.∆U =0,∆H 大于、小于或等于零不能确定。
5)在实际气体的节流膨胀过程中,哪一组描述是正确的: ( )A.Q >0, ∆H=0, ∆p < 0B.Q=0, ∆H <0, ∆p >0C.Q=0, ∆H =0, ∆p <0D.Q <0, ∆H =0, ∆p <06)如图,叙述不正确的是:( )A.曲线上任一点均表示对应浓度时积分溶解热大小B.∆H1表示无限稀释积分溶解热C.∆H2表示两浓度n1和n2之间的积分稀释热D.曲线上任一点的斜率均表示对应浓度时HCl的微分溶解热7)∆H=Q p此式适用于哪一个过程: ( )A.理想气体从101325Pa反抗恒定的10132.5Pa膨胀到10132.5sPaB.在0℃、101325Pa下,冰融化成水的水溶液C.电解CuSO4D.气体从(298K,101325Pa)可逆变化到(373K,10132.5Pa )8) 一定量的理想气体,从同一初态分别经历等温可逆膨胀、绝热可逆膨胀到具有相同压力的终态,终态体积分别为V1、V2。
物理化学2第二章热力学第二定律

物理化学2第二章热力学第二定律第二章热力学第二定律内容提要一、自发过程及其不可逆性(1)自发过程(spontaneous process ):不靠外力就能自动进行的过程。
自发过程都有确定的方向,它的逆过程绝不会自发进行。
若靠外力干涉,使原过程逆相进行,体系恢复原状,则在环境中会留下无论如何也不能消除的后果。
这种不能消除的后果就是自发过程的不可逆性。
即一切自发过程都是不可逆的。
(2)可逆过程(reversible process):可逆过程是由一连串近平衡态的微小变化组成的。
变化的动力与阻力相差无限小,因而可逆变化进行的无限缓慢。
循原过程相反方向无限缓慢变化,可使体系与环境同时恢复原状,可逆过程的后果是可以消除的。
可逆过程中,体系对环境做功最大,环境对体系做功最小。
过程在热力学上是否可逆,最终归结为过程热功的转换问题。
由于热不能完全变为功,所以凡是涉及热的过程都是不可逆的。
二、热力学第二定律的表述及公式1、Kelvin 表述:“不可能从单一热源取热使之完全变为功而不产生其它变化”。
单一热源取热使之完全变为功虽不违背热力学第一定律,但涉及热功转换现象。
此表述也可说成“第二类永动机不可能制成”。
2、Clausius 表述:“热不能自动地由低温热源传到高温热源而不发生其它变化”。
两种表述都断言:一切实际过程都是不可逆的。
3、Clausius (克劳修斯)不等式(Clausius ineauality ): d S ≥δQ/T 或T d S ≥δQ“=”适用于可逆过程,“>”适用于不可逆过程。
该不等式表示:可逆过程的热温商δQ/T 等于过程的熵变d S ;不可逆过程的热温商δQ/T 小于过程的熵变d S 。
三、熵(entropy )的定义及计算 1、熵(entropy )的定义熵是体系的性质,状态函数,以符号S 表示。
?=BA RT Q S式中,Q 为可逆过程的热,T 是可逆过程体系的温度。
2、熵的微观解释:体系任一平衡的宏观状态都与一定的微观状态数,即称混乱度相对应。
物理化学 第二章 热力学第二定律

0 任意可逆循环
T 2 QR S S2 S1 1 T
使用条件
克劳修斯不等式
T1 P1 V1 U1 H1 S1
殊 途 同 归 变 化 等
R
ΔSR =
( T
i
Qi
i
IR
)R
T2 P2 V2 U2 H2 S2 过程量
ΔSIR >
( T ?
i
Qi
i
) IR
ΔS ≥ Ti
p
绝热可逆压缩
p1 V1 T1
等温可逆膨胀
Q1
p2 V2 T1
W Q1 Q2 Q1 Q1
W
p4 V4 T2 Q2
绝热可逆膨胀
p3 V3 T2
等温可逆压缩
T1 T2 R T1
?
V
公式中 “1”—始态,“2”—终 态 (1)等温可逆膨胀: p p1 V1 T1
U 1 0 V2 Q1 W1 ( nRT 1 ln ) V1 (2)绝热可逆膨胀: Q=0 W2 = ΔU2 = nCV,m (T2 – T1)
可逆膨胀
2. Q2 W2 0
S环 Q环 T环 0 J K 1
Q环= – Q体= 0 自由膨胀为自发过程
ΔS孤= ΔS体+ΔS环 = 38.3 J K-1 > 0 3. Q3 W3 [ p2 (V2 V1 )] 恒外压膨胀为自发过程 4.988 105 (10 1) 103 4489 J
等容可逆 (变温)
WR ( pdV) V2 nR ln T T V1
T
T
nCV ,m ln
T1
T1 ,p1 ,V1
物理化学第二章 热力学第二定律2.1

风的走向
• 空气的流动形成风 • 风的流动:从高压处流向低压处
• 风的流动因磨擦将空气的势能变为 热能而散失。 • 风的逆向流动是不可能的。
电的输送
• 电流总是从电压高的一端流向电压低的 一端,即电子由电压低的一端流向电压 高的一端。
• 电子的流动须克服电路的电阻,其结果 是电能(功)转变为热能(电灯光等)。
= -ln(V4/V3)= -ln(V1/V2)
(V2/V1)-1 = (V3/V4)-1 ∴ V2/V1=V3/V4 =Rln(V1/V2)(T2-T1)=R(T2-T1)ln(V2/V1)
W= RT2ln(V1/V2)+RT1ln(V3/V4)
• 热机的效率:
热机作功与获取能量之比
• 从外界获取的热量是Q2 • =-W/Q2 • =(T2-T1)/T2 • =1-(T1/T2)
∵ I>R
T2
Q2
W’ W W ’’
Q2 R
I
Q1’
Q1
T1
• 可逆热机的效率必定等于卡诺热机的效率 • 由卡诺定理, 提高热机效率的最好方法是提高高温热 源的温度. • 将卡诺热机逆向运行便成为致冷机. • 定义致冷机效率: • =|Q1/W|=T1/(T2-T1) • 致冷的温差愈小, 其效率愈高. • 值可>1 • 热机效率 <1 (可逆及不可逆热机) • 热机的效率永远小于1, 故热不可能完全变为功. • 理论上: • →1 (T→0K)
的效率最大, 此效率与工作物质无关, 只与两热源的
温度有关, 此书的基本结论即为卡诺定理. • 卡诺当时是用热质论来证明卡诺定理的, 后来 Kelvin和Claudius对卡诺的工作进行了修正, 用热力
物理化学第二章热力学第二定律练习题及答案

第二章 热力学第二定律练习题一、判断题(说法正确否):1.自然界发生的过程一定是不可逆过程。
2.不可逆过程一定是自发过程。
3.熵增加的过程一定是自发过程。
4.绝热可逆过程的∆S = 0,绝热不可逆膨胀过程的∆S > 0,绝热不可逆压缩过程的∆S < 0。
5.为了计算绝热不可逆过程的熵变,可以在始末态之间设计一条绝热可逆途径来计算。
6.由于系统经循环过程后回到始态,∆S = 0,所以一定是一个可逆循环过程。
7.平衡态熵最大。
8.在任意一可逆过程中∆S = 0,不可逆过程中∆S > 0。
9.理想气体经等温膨胀后,由于∆U = 0,所以吸的热全部转化为功,这与热力学第二定律矛盾吗?10.自发过程的熵变∆S > 0。
11.相变过程的熵变可由T H S ∆=∆计算。
12.当系统向环境传热时(Q < 0),系统的熵一定减少。
13.一切物质蒸发时,摩尔熵都增大。
14.冰在0℃,pT H S ∆=∆>0,所以该过程为自发过程。
15.自发过程的方向就是系统混乱度增加的方向。
16.吉布斯函数减小的过程一定是自发过程。
17.在等温、等压下,吉布斯函数变化大于零的化学变化都不能进行。
18.系统由V 1膨胀到V 2,其中经过可逆途径时做的功最多。
19.过冷水结冰的过程是在恒温、恒压、不做其他功的条件下进行的,由基本方程可得∆G = 0。
20.理想气体等温自由膨胀时,对环境没有做功,所以 -p d V = 0,此过程温度不变,∆U = 0,代入热力学基本方程d U = T d S - p d V ,因而可得d S = 0,为恒熵过程。
21.是非题:⑴“某体系处于不同的状态,可以具有相同的熵值”,此话对否? ⑵“体系状态变化了,所有的状态函数都要变化”,此话对否? ⑶ 绝热可逆线与绝热不可逆线能否有两个交点?⑷ 自然界可否存在温度降低,熵值增加的过程?举一例。
⑸ 1mol 理想气体进行绝热自由膨胀,体积由V 1变到V 2,能否用公式:⎪⎪⎭⎫⎝⎛=∆12ln VV R S计算该过程的熵变?22.在100℃、p 时,1mol 水与100℃的大热源接触,使其向真空容器中蒸发成 100℃、p 的水蒸气,试计算此过程的∆S 、∆S (环)。
物理化学02章_热力学第二定律02

S体系
Qr Qsurr Qsys Q Δ S环 = = = Tsurr Tsurr Tsurr T
Δ S 总 =Δ S 体 + Δ S 环 ≥ 0
上一讲回顾
(1) 熵变的计算: 可逆过程,直接计算过程的热温商 不可逆过程,设计可逆过程计算。 (2) 等温过程,变温过程及相变过程熵变的计算 (3) 利用熵变判断过程的方向
a)恒 T 可逆 b)恒 T 不可逆 V2 V2 V2 Δ S 总 = nRTLn +(-nRLn ) Δ S 总 = nRTLn + 0 V1 V1 V1
= 0
V2 = nRTLn > 0 V1
等温过程的熵变
例: 1mol理想气体在等温下通过:(1)可逆膨胀,(2)真 空膨胀,体积增加到10倍,分别求其熵变。 解:(1)可逆膨胀
简化:
V2 P2 等 T:Δ S= nRLn =- nRLn V1 P1 T2 等 P:Δ S= CP Ln T1
T2 等 V:Δ S= CV Ln T1
变温过程的熵变
1. 先等温后等容 2. 先等温后等压 3. 先等压后等容
T2 nCV ,m dT V2 S nR ln( ) T1 V1 T T2 nC p ,m dT p1 S nR ln( ) T1 p2 T V2 p2 S nC p ,m ln( ) nCV ,m ln( ) V1 p1
S T
T2
1
nCV ,m dT T
(2) 物质的量一定的等压变温过程
S T
T2
1
nC p ,m dT T
等 P 过程:
W`=0, QP = dH = CPdT = QR
QR QP C P dT dS = = = T T T CP S )P 或 ( T T
物理化学2_热力学第二定律
∆S = ∫
T2
T1
nCV.m dT T
2.等压变温 δQR = nC p ,m dT
∆S = ∫
T2
nC p.m T
T1
dT
3.理想气体状态变化(仅有体积功 WR = −∫ p外dV = − pdV )
δQR=dU-δWR = dU + pdV = nCV,m dT + nRT
于是
dV V
∆S = ∫
Zn+CuSO 4 (aq)
ZnSO 4(aq)+Cu ∆H m *= -216.8 kJ mol -1
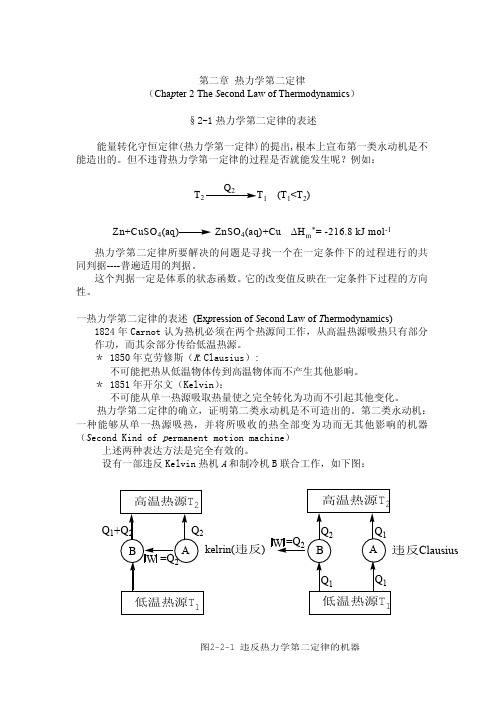
热力学第二定律所要解决的问题是寻找一个在一定条件下的过程进行的共 同判据----普遍适用的判据。 这个判据一定是体系的状态函数。它的改变值反映在一定条件下过程的方向 性。 一热力学第二定律的表述 (Expression of Second Law of Thermodynamics) 1824 年 Carnot 认为热机必须在两个热源间工作,从高温热源吸热只有部分 作功,而其余部分传给低温热源。 * 1850 年克劳修斯(R.Clausius): 不可能把热从低温物体传到高温物体而不产生其他影响。 * 1851 年开尔文(Kelvin) : 不可能从单一热源吸取热量使之完全转化为功而不引起其他变化。 热力学第二定律的确立,证明第二类永动机是不可造出的。第二类永动机: 一种能够从单一热源吸热,并将所吸收的热全部变为功而无其他影响的机器 (Second Kind of permanent motion machine) 上述两种表达方法是完全有效的。 设有一部违反 Kelvin 热机 A 和制冷机 B 联合工作,如下图:
高温热源T2
高温热源 T2
W =Q2 Q2 B Q1
南京大学《物理化学》每章典型例题讲解

第一章 热力学第一定律与热化学例题1 1mol 理想气体于27℃ 、101325Pa 状态下受某恒定外压恒温压缩到平衡,再由该状态恒容升温到97 ℃ ,则压力升到1013.25kPa 。
求整个过程的W 、Q 、△U 及△H 。
已知该气体的C V ,m 恒定为20.92J ∙mol -1 ∙K -1。
解题思路:需先利用理想气体状态方程计算有关状态: (T 1=27℃, p 1=101325Pa ,V 1)→(T 2=27℃, p 2=p 外=?,V 2=?)→(T 3=97℃, p 3=1013.25kPa ,V 3= V 2)例题2水在 -5℃ 的结冰过程为不可逆过程,计算时要利用0℃ 结冰的可逆相变过程,即H 2O (l ,1 mol ,-5℃ ,θp )(s ,1 mol ,-5℃,θp )↓△H 2 ↑△H 4H 2O (l ,1 mol , 0℃,θp ) O (s ,1 mol ,0℃,θp )∴ △H 1=△H 2+△H 3+△H 4例题3 在 298.15K 时,使 5.27 克的甲醇(摩尔质量为32克) 在弹式量热计中恒容燃烧,放出 119.50kJ 的热量。
忽略压力对焓的影响。
(1) 计算甲醇的标准燃烧焓 θm c H ∆。
(2) 已知298.15K 时 H 2O(l) 和CO 2(g)的标准摩尔生成焓分别为-285.83 kJ·mol -1、-393.51 kJ·mol -1,计算CH 3OH(l)的θm f H ∆。
(3) 如果甲醇的标准蒸发焓为 35.27kJ·mol -1,计算CH 3OH(g) 的θm f H ∆。
解:(1) 甲醇燃烧反应:CH 3OH(l) +23O 2(g) → CO 2(g) + 2H 2O(l) Q V =θm c U ∆=-119.50 kJ/(5.27/32)mol =-725.62 kJ·mol -1Q p =θm c H ∆=θm c U ∆+∑RT v)g (B= (-725.62-0.5×8.3145×298.15×10-3)kJ·.mol -1 =-726.86 kJ·mol-1(2) θm c H ∆=θm f H ∆(CO 2) + 2θm f H ∆(H 2O )-θm f H ∆ [CH 3OH(l)] θm f H ∆[CH 3OH (l)] =θm f H ∆ (CO 2) + 2θm f H ∆ (H 2O )-θm c H ∆= [-393.51+2×(-285.83)-(-726.86) ] kJ·mol -1=-238.31 kJ·mol -1(3) CH 3OH (l) →CH 3OH (g) ,θm vap ΔH= 35.27 kJ·.mol -1θm f H ∆[CH 3OH (g)] =θm f H ∆[CH 3OH (l)] +θmv ap H ∆= (-38.31+35.27)kJ·.mol-1=-203.04 kJ·mol -1第二章 热力学第二定律例1. 1mol 理想气体从300K ,100kPa 下等压加热到600K ,求此过程的Q 、W 、U 、H 、S 、G 。
《物理化学》02章_热力学第二定律

V2 V4 nRT2 ln nRT1 ln V1 V3
V2 V4 nRT2 ln nRT1 ln V1 V3 W 热机效率: V2 Q2 nRT2 ln V1
BC:绝热可逆膨胀,T2 V2-1 = T1 V3-1 DA:绝热可逆压缩, T2 V1-1 = T1 V4-1 两式相除: V2 /V1 =V3 /V4
不违背第一定律的事情是否一定能成功?
例1: 1/2O2(g)+ H2(g) H2O(l)
r H m (298.15 K) =-286KJ.mol-1
加热不能使其反向进行 例2: OH-+ H+H2O(l) 极易进行
但最终[OH-][H+]=10-14mol2.dm-6 该反应不能进行到底
§2.1 自发过程的共同特征
一.自发过程的方向和限度
自发过程:在一定环境条件下,环境不做非体积功,系
统中自动发生的过程.反之,只有环境做非体积功才 能发生的过程为非自发过程.通常所说的”过程方 向” 既是指自发过程的方向. 举例: ①.气流:高压 低压
②.传热:高温
③.扩散:高浓度
低温
低浓度
④.反应:Zn+CuSO4
对微小变化
Q dS ( )R T
B
Q SB SA S ( )R A T
二.热力学第二定律的数学表达式
对两个热源间的不可逆 循环:热温商之和小于零. Q1 T1 Q2 T2
+
<0
对任意的不可逆 循环:ຫໍສະໝຸດ ∑δQ T1 ir
<0
对不可逆循环,A
ir
B
r
A
南京大学《物理化学》考试 第二章 热力学第二定律

第二章热力学第二定律物化试卷(一)1.理想气体绝热向真空膨胀,则:(A) ΔS = 0 , W = 0 (B) ΔH = 0,ΔU = 0(C) ΔG = 0,ΔH = 0 (D) ΔU = 0,ΔG =02.熵变ΔS是: (1) 不可逆过程热温商之和 (2) 可逆过程热温商之和 (3) 与过程无关的状态函数 (4) 与过程有关的状态函数 以上说法正确的是:(A) 1,2 (B) 2,3 (C) 2 (D) 43. 理想气体经可逆与不可逆两种绝热过程:(A) 可以从同一始态出发达到同一终态(B) 从同一始态出发,不可能达到同一终态(C) 不能断定 (A)、(B) 中哪一种正确(D) 可以达到同一终态,视绝热膨胀还是绝热压缩而定4. 在标准压力,273.15 K下水凝结为冰,判断体系的下列热力学量中何者一定为零?(A) ΔU (B) ΔH (C) ΔS (D) ΔG5. 水在 100℃,标准压力下沸腾时,下列各量何者增加?(A) 熵 (B) 汽化热 (C) 吉布斯自由能 (D) 蒸气压6. 在 N2和 O2混合气体的绝热可逆压缩过程中,体系的热力学函数变化值在下列结论中正确的是:(A) ΔU = 0 (B) ΔF = 0(C) ΔS = 0 (D) ΔG = 07. 在 270 K,101.325 kPa 下,1 mol过冷水经等温等压过程凝结为同样条件下的冰,则体系及环境的熵变应为:(A) ΔS(体系)< 0 , ΔS(环境)< 0 (B) ΔS(体系)< 0 , ΔS(环境)> 0(C) ΔS(体系)> 0 , ΔS(环境)< 0 (D) ΔS(体系)> 0 , ΔS(环境)> 08. 理想气体在等温条件下,经恒外压压缩至稳定, 此变化中的体系熵变ΔS(体)及环境熵变ΔS(环)应为:(A) ΔS(体)> 0 , ΔS(环)< 0 (B)ΔS(体)< 0 , ΔS(环)> 0(C) ΔS(体)> 0 , ΔS(环)= 0 (D)ΔS(体)< 0 , ΔS(环)= 09.一个由气相变为凝聚相的化学反应,在恒温恒容下自发进行,问下列各组答案中,哪一个是正确的?(A) ΔS(体)>0, ΔS(环)<0 (B) ΔS(体)<0, ΔS(环)>0(C) ΔS(体)<0, ΔS(环)=0 (D) ΔS(体)>0, ΔS(环)=010. 在一简单的(单组分,单相,各向同性)封闭体系中,恒压只做膨胀功的条件下,吉布斯自由能值随温度升高如何变化?(A) (TG/TT)p> 0 (B) (TG/TT)p< 0(/(C) (TG/TT)p= 0 (D) 视具体体系而定11. 某气体的状态方程为p V(m) = RT +αp,其中α为大于零的常数,该气体经恒温膨胀,其热力学能:(A) 不变 (B) 增大 (C) 减少 (D) 不能确定12. 下列四个关系式中,哪一个不是麦克斯韦关系式?(A) (TT/TV)s=(TV/TS)p (B) (TT/Tp)s=(TV/TS)p(C) (TS/TV)T=(Tp/TT)v (D) (TS/Tp)T= -(TV/TT)p13. 下列各式中哪个是化学势?(A) (?T H/?T n(B))T,S, (B) (?T F/?T n(B))T,p,(C) (?T G/?T n(B))T,V, (D) (?T U/?T n(B))S,V,14. 298 K,标准压力下,有两瓶萘的苯溶液,第一瓶为 2 dm3(溶有 0.5 mol 萘), 第二瓶为 1 dm3(溶有 0.25 mol 萘),若以μ1,μ2分别表示两瓶中萘的化学势,则:(A)μ1 = 10μ2 (B)μ2= 2μ2(C) μ1 = μ2(D) μ1= 0.5μ215. 重结晶制取纯盐的过程中,析出的 NaCl 固体的化学势与母液中 NaCl 的化学势比较,高低如何?(A) 高 (B) 低 (C) 相等 (D) 不可比较16. 热力学第三定律可以表示为:(A) 在0 K 时,任何晶体的熵等于零 (B) 在0 K 时,任何完整晶体的熵等于零(C) 在0 ℃时,任何晶体的熵等于零(D) 在0 ℃时,任何完整晶体的熵等于零17.下列四种表述: (1) 等温等压下的可逆相变过程中,体系的熵变ΔS =ΔH 相变/T 相变(2) 体系经历一自发过程总有 ΔS > 0(3) 自发过程的方向就是混乱度增加的方向 (4) 在绝热可逆过程中,体系的熵变为零 两者都不正确者为:(A) (1),(2) (B) (3),(4)(C) (2),(3)(D) (1),(4)18. 在绝热条件下,用大于气筒内的压力迅速推动活塞压缩气体,此过程的熵变为:(A) 大于零 (B) 等于零 (C) 小于零 (D) 不能确定19. 在263 K的过冷水凝结成263 K的冰,则:(A) ΔS<0 (B) ΔS>0 (C) ΔS=0 (D) 无法确定20. 在标准压力和268.15 K下,冰变为水,体系的熵变ΔS体应:(A) 大于零 (B) 小于零 (C) 等于零 (D) 无法确定第二章热力学第二定律物化试卷(二)1. 2 mol H2和 2 mol Cl2在绝热钢筒内反应生成 HCl 气体,起始时为常温常压。
物理化学 第2章_热力学第二定律

所以I < R,即任何热机的效率不可能比卡诺热机的效率高。
18
卡诺定理热温商:( Clausius
5
结果环境失去功W,得到热Q ,环境是否能恢复
原状 QW ?
它们的逆过程都不能自动进行。当借助外力, 系统恢复原状后,会给环境留下不可磨灭的影响。
6
结论: 要使环境也恢复原状,必须热全部变为功而不 留下任何永久性变化。
人类经验总结: “功可以自发地全部变为热,
但热不可能全部变为功,而不留任何其它变化”。
S0(孤立系统或绝热系统): 熵增大原理
—— “在孤立系统中所发生的过程总是向着熵增大
的方向进行”
25
§2.4 熵变S的求算
一、简单状态变化
理想气体简单状 态变化
T2 V2 S nCV ,m ln + nR ln T1 V1
T2 p2 S nC p ,m ln - nR ln T1 p1
process)。
自发过程:某种变化有自动发生的趋势,一旦发生就 无需借助外力,自动进行,这种变化称为自发过程。
4
一、自发过程的共同特征
自发过程的方向性归结为热功转换的方向性。 1.理想气体自由膨胀: Q=-W=U=H=0, V>0 要使系统恢复原状,可经定温压缩过程 ( )T U=0, H=0, Q = -W, 2.热由高温物体传向低温物体: 冷冻机做功后,系统恢复原状,… 3.化学反应: Cd(s)+PbCl2(aq)=CdCl2(aq)+Pb(s) 电解使反应逆向进行,系统恢复原状,…
物理化学:第二章 热力学第二定律

此式说明:对于绝热过程,系统的熵不减少。熵增原理 即若为绝热可逆过程,S= 0,(绝热可逆过程为恒熵过程) 若为绝热不可逆过程,S>0
二、熵增加原理(principle of entropy increasing)
注意理解:自发过程为不可逆过程,但不可逆过程并 非一定为自发过程。这是因为在绝热系统中,系统与 环境无热交换,但不排斥以功的形式交换能量。 熵增原理仅能判断一过程是否为不可逆,但不能判断 是否为自发。
1mol理想气体的卡诺循环在pV 图上可以分为四步:
步骤1:等温可逆膨胀,由p1V1到p2V2(AB)
U1 0
Q1 W1
V2 V1
p
d
V
n
RT1
ln
V2 V1
所作功如AB曲线下的面积所示
p A(p1V1) Q1
B(p2V2)
V1
V2 V
卡诺循环第一步
步骤2
p A(p1V1) Q2 B(p2V2)
上解决了热机效率的极限值问题。(2)证实了热不能完 全转化为功。因为T1/T2=0不可能。
卡诺定理证明(1):
证明:(反证法)i r 不成立
假设 i热机效率大于r
高温T2
Q’2
Q2
WW i Q2' r Q2
Q2' Q2
W
i
r
W 循环净结果:
1. 两热机均恢复原态
Q’2-W Q2-W
2. 高温热源得热:
热机效率总是小于1,表明热是不能完成转化为功。
三、卡诺定理(Carnot law)
1. 在同一高温热源和同一低温热源之间工作的任意热机, 卡诺热机的效率最大,否则将违反热力学第二定律。 2.卡诺热机的效率只与两热源的温度有关,而与工作物质 无关,否则也将违反热力学第二定律。
物理化学答案——第二章-热力学第二定律

第二章 热力学第二定律 一、基本公式和基本概念 基本公式1. 热力学第二定律的数学表达式----克劳修斯不等式 ()0A B A B QS Tδ→→∆-≥∑2. 熵函数的定义 ()R QdS Tδ=, ln S k =Ω3. 熵变的计算理想气体单纯,,p V T 变化22,1122,1122,,11ln ln ln ln lnln V m p m p m V m T V S C R T V T p S C R T p V p S C C V p ∆=+∆=-∆=+理想气体定温定压混合过程ln i i iS R n x ∆=-∑封闭系统的定压过程21,d T p m T C S n T T∆=⎰封闭系统定容过程 21,d T V m T C S n T T∆=⎰可逆相变 m n H S T∆∆=标准状态下的化学反应 ,()r m Bm B BS S T θθν∆=∑定压下由1T 温度下的化学反应熵变求2T 温度下的熵变 21,21()()d T p m r m r m T C S T S T T T∆∆=∆+⎰4. 亥姆霍兹函数 A U TS ≡-5. 吉布斯函数 G H TS ≡-6. G ∆和A ∆的计算(A ∆的计算原则与G ∆相同,做相应的变换即可)定温过程G H T S ∆=∆-∆组成不变的均相封闭系统的定温过程 21d p p G V p ∆=⎰理想气体定温过程 21ln p G nRT p ∆= 7. 热力学判据熵判据:,()0U V dS ≥亥姆霍兹函数判据:,,'0(d )0T V W A =≤ 吉布斯函数判据:,,'0(d )0T p W G =≤8. 热力学函数之间的关系组成不变,不做非体积功的封闭系统的基本方程d d d d d d d d d d d d U T S p V H T S V pA S T p V G S T V p=-=+=--=-+麦克斯韦关系S VpS T Vp TT p V S T V p S S p V T S V p T ∂∂⎛⎫⎛⎫=- ⎪ ⎪∂∂⎝⎭⎝⎭⎛⎫∂∂⎛⎫= ⎪ ⎪∂∂⎝⎭⎝⎭∂∂⎛⎫⎛⎫= ⎪ ⎪∂∂⎝⎭⎝⎭⎛⎫∂∂⎛⎫=- ⎪ ⎪∂∂⎝⎭⎝⎭9. 吉布斯-亥姆霍兹方程2()pG HT T T ∆⎡⎤∂⎢⎥∆=-⎢⎥∂⎢⎥⎣⎦ 基本概念1. 热力学第二定律在研究化学或物理变化驱动力来源的过程中,人们注意到了热功交换的规律,抓住了事物的共性,提出了具有普遍意义的熵函数。
南京大学物理化学选择题答案完整版

第一章热力学第一定律及其应用物化试卷(一)1.物质的量为n的纯理想气体,该气体在如下的哪一组物理量确定之后,其它状态函数方有定值。
( )(A) p (B) V (C) T,U (D) T, p2. 下述说法哪一个正确? ( )(A) 热是体系中微观粒子平均平动能的量度 (B) 温度是体系所储存热量的量度(C) 温度是体系中微观粒子平均能量的量度 (D) 温度是体系中微观粒子平均平动能的量度3. 有一高压钢筒,打开活塞后气体喷出筒外,当筒内压力与筒外压力相等时关闭活塞,此时筒内温度将: ( )(A)不变 (B)升高 (C)降低 (D)无法判定4. 1 mol 373 K,标准压力下的水经下列两个不同过程变成373 K,标准压力下的水气, (1) 等温等压可逆蒸发, (2) 真空蒸发这两个过程中功和热的关系为: ( )(A) |W1|> |W2| Q1> Q2 (B)|W1|< |W2| Q1< Q2(C) |W1|= |W2| Q1= Q2 (D)|W1|> |W2| Q1< Q25. 恒容下,一定量的理想气体,当温度升高时热力学能将:( )(A)降低 (B)增加 (C)不变 (D)增加、减少不能确定6. 在体系温度恒定的变化中,体系与环境之间: ( )(A) 一定产生热交换 (B) 一定不产生热交换(C) 不一定产生热交换 (D) 温度恒定与热交换无关7. 一可逆热机与另一不可逆热机在其他条件都相同时,燃烧等量的燃料,则可逆热机拖动的列车运行的速度:( )(A) 较快 (B) 较慢 (C) 一样 (D) 不一定8. 始态完全相同(p1,V1,T1)的一个理想气体体系,和另一个范德华气体体系,分别进行绝热恒外压(p0)膨胀。
当膨胀相同体积之后,下述哪一种说法正确?( )(A) 范德华气体的热力学能减少量比理想气体多 (B) 范德华气体的终态温度比理想气体低(C) 范德华气体所做的功比理想气体少 (D) 范德华气体的焓变与理想气体的焓变相等9.ΔH =Qp , 此式适用于下列哪个过程:( )(A) 理想气体从106 Pa反抗恒外压105 Pa膨胀到105 Pa (B) 0℃ , 105 Pa 下冰融化成水(C) 电解 CuSO4水溶液 (D) 气体从(298 K, 105 Pa)可逆变化到(373 K, 104 Pa)10.在100℃和25℃之间工作的热机,其最大效率为: ( )(A) 100 % (B) 75 % (C) 25 % (D) 20 %11.对于封闭体系,在指定始终态间的绝热可逆途径可以有:( )(A) 一条 (B) 二条 (C) 三条 (D) 三条以上12.某理想气体的γ =C p/Cv =1.40,则该气体为几原子分子气体? ( )(A) 单原子分子气体 (B) 双原子分子气体(C) 三原子分子气体 (D) 四原子分子气体13.实际气体绝热恒外压膨胀时,其温度将: ( )(A) 升高 (B) 降低 (C) 不变 (D) 不确定14.当以5 mol H2气与4 mol Cl2气混合,最后生成2 mol HCl气。
物理化学 第二章 热力学第二定律

卡诺定理的意义:
(1)引入了一个不等号 i r ,原则上解决了热机 效率的极限值问题。 (2)证实了热不能完全转化为功,因为T1 /T2 = 0 是 不可能的。
卡诺定理(1)的证明: i r 证明:反证法 假设: i 热机效率大于 r :
高温 T2
Q’2 Q2
i
W Q
' 2
r
上式的意义:系统由状态 A 到状态 B,S有唯一的值, 等于从 A 到B 可逆过程的热温商之和。
熵的特别提醒:
(1)熵(S)是状态函数;热温商(Qr/T)是与途径 相关的概念; (2)可逆过程热温商(Qr/T)不是熵(S) ;它只 是过程熵变(ΔS)的一种量度,一种测定方法; (3)熵(S)是广度性质,具有加和性;但 Sm 是强 度性质。
这个设计就相当于热从低温热源传到高温热源而 没有发生其它变化 ---违背热力学第二定律
因此 B A
卡诺定理(2)的证明:
2. 如果A带动B,使B倒转:
高温 T2
Q’2
Q2
假设A可逆热机效率大于B
A
W
Q
' 2
B
W
Q2
A®
W W
' Q2 Q2
B®
Q2 W
Q ’2 W
卡诺定理(2)的证明:
证明: 1. 如果B带动A,使A倒转:
高温T2
Q’2
Q2
假设B可逆热机效率大于A
B
W Q
' 2
A
W Q2
B®
W W
' Q2 Q2
A®
Q2 W
Q ’2 W
低温T1
循环净结果为: 1. 两热机均恢复原态 2. 高温热源得热: Q2 Q2 3. 低温热源失热:
物理化学1.3第二章热力学第二定律

热力学的应用领域
能源转换
热力学在能源转换领域中有着广 泛的应用,如火力发电、核能发 电和太阳能发电等,涉及到热能 与其他形式的能量之间的转换。
化工生产
在化工生产过程中,热力学是必 不可少的理论基础,涉及到化学 反应过程中的热量传递和物质传
递等。
环境保护
热力学在环境保护领域中也有着 重要的应用,如烟气治理、污水 处理和大气污染控制等,涉及到
物理化学1.3第二章热力学 第二定律
目录
• 热力学第二定律的表述 • 热力学第二定律的推论 • 热力学第二定律的应用 • 热力学第二定律的微观解释 • 热力学第二定律的局限性与发展
01
热力学第二定律的表述
热力学第二定律的定义
热力学第二定律定义
热力学第二定律是描述热力系统变化方向的自然规律,它指 出在没有外界影响的情况下,自发反应总是向着能量降低的 方向进行。
熵增原理
熵增原理
熵是描述系统混乱度的物理量,根据热力学第二定律,封闭系统的熵总是增加 的,即系统总是向着更加混乱无序的方向发展。
熵与自然过程
熵增原理解释了自然过程中许多现象,例如热量自发地从高温流向低温,而不 是相反。这是因为高温物体向低温物体传递热量时,系统的熵会增加。
热力学第三定律
绝对零度不能达到
这意味着,熵与信息存在着对立的关系,即熵的增加意味着信息的减少。
在通信过程中,信息传递是有序的过程,需要消耗一定的能量和资源。 而熵的增加则意味着能量的耗散和分散,这会对通信过程产生干扰和影 响。
05
热力学第二定律的局限性与 发展
热力学第二定律的局限性
01
02
03
宏观描述
热力学第二定律主要从宏 观角度描述系统的热力学 性质,无法揭示微观分子 行为和相互作用。
南京大学_物理化学B、热力学第二定律

力,为什么两者的 ΔS 都大于零,即 ΔS2> 0,ΔS3> 0,这样的结论是否有问题? 0699 对于孤立体系中发生的实际过程,下列各式中不正确的是: (A) W = 0 (B) Q = 0 (C) ΔS > 0 (D) ΔH = 0 0700 一定量的气体在气缸内, (1) 经绝热不可逆压缩,温度升高,ΔS > 0 ; (2) 经绝热不可逆膨胀,温度降低,ΔS < 0 。 两结论对吗? 0701 熵增加原理就是隔离体系的熵永远增加。 此结论对吗? 0702 体系由平衡态 A 变到平衡态 B,不可逆过程的熵变一定大于可逆过程的熵变,对吗 ? 0703 凡是 ΔS > 0 的过程都是不可逆过程,对吗? 0704 任何气体经不可逆绝热膨胀时, 其内能和温度都要降低,但熵值增加。对吗?任何气体 如进行绝热节流膨胀,气体的温度一定降低,但焓值不变。对吗? 0705 理想气体从状态 I 经自由膨胀到状态 II,可用哪个热力学判据来判断该过程的自发性? ( ) (A) ΔH (B) ΔG (C) ΔS (D) ΔU 0706 由于热功交换的 ,而在公式中引入的 ,这对于其它过程(包括化学过 程)同样适用。因而对所有的不可逆过程就找到了一个共同的判别准则。 0707 当一个不可逆过程发生之后, 0708 牙齿的珐琅质可近似看作是由羟基–磷灰石化合物 3Ca3(PO4) Ca(OH)2 构成的。 已知羟基离子可被氟离子取代,生成 3Ca3(PO4) CaF2,可存在于牙齿构造中使对龋齿 有更大的抵抗力。如果用氟化亚锡溶液加入牙膏中,使之发生上述变化是否可能。 [298 K,CaF2(s)]=-1167 kJ·mol-1 已知:ΔfG $ m ΔfG $ [298 K,Sn(OH)2(s)]=-492 kJ·mol-1 m ΔfG $ [298 K,Ca(OH)2(s)]=-899 kJ·mol-1 m
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二章热力学第二定律
返回上一页
1. 5 mol He(g)从273.15 K和标准压力变到298.15K和压力p=10×, 求过程的ΔS。
(已知C(V,m)=3/2 R)
2. 0.10 kg 28
3.2 K的水与0.20 kg 313.2 K 的水混合,求ΔS。
设水的平均比热为
4.184kJ/(K·kg)。
3. 实验室中有一大恒温槽(例如是油浴)的温度为400 K,室温为300 K。
因恒温槽绝热不良而有4000 J的热传给空气,用计算说明这一过程是否为可逆?
4. 在298.15K的等温情况下,两个瓶子中间有旋塞连通。
开始时,一放0.2 mol O2,压力为0.2×101.325kPa,另一放0.8 mol N2,压力为0.8×101.325 kPa,打开旋塞后,两气体互相混合。
计算:
(1)终了时瓶中的压力。
(2)混合过程中的Q,W,ΔU,ΔS,ΔG;
(3)如果等温下可逆地使气体回到原状,计算过程中的Q和W。
5.(1)在298.2 K时,将1mol O2从101.325 kPa 等温可逆压缩到6×101.325 kPa,求Q,W,ΔU m,ΔH m,ΔF m,ΔG m,ΔS m,ΔS iso
(2)若自始至终用6×101.325 kPa的外压等温压缩到终态,求上述各热力学量的变化值。
6. 在中等的压力下,气体的物态方程可以写作p V(1-βp)=nRT。
式中系数β与气体的本性和温度有关。
今若在273K时,将0.5 mol O2由1013.25kPa的压力减到101.325 kPa,试求ΔG。
已知氧的β=-0.00094。
7. 在298K及下,一摩尔过冷水蒸汽变为同温同压下的水,求此过程的ΔG m。
已知298.15K时水的蒸汽压为3167Pa。
8. 将298.15K 1 mol O2从绝热可逆压缩到6×,试求Q,W,ΔU m, ΔH m, ΔF m, ΔG m, ΔS m和ΔS iso(C(p,m)=7/2 R)。
已知(298K,O2)=205.03 J/(K·mol) 。
9. 在298.15K和时,反应H2(g)+HgO(s)=Hg(l)+H2O(l) 的为195.8
J/mol。
若设计为电池,在电池
H2()|KOH(0.1 mol/kg)|HgO(s)+Hg(l)中进行上述反应,电池的电动势为0.9265 V,试求上述反应的
Δr S m和Δr G m。
10. 某一化学反应若在等温等压下(298.15K,)进行,放热40 kJ,若使该反应通过可逆电池来完成,则吸热4.0 kJ。
(1)求该化学反应的Δr S m。
(2)当该反映自发进行时(即不做电功时),求环境的熵变及总熵变。
(3)计算体系可能做的最大功。
11.一摩尔单原子理想气体始态为273 K,,计算经过下列变化后的各个ΔG m。
设该条件下气体摩尔熵为100 J/(K·mol)。
(1)恒压下体积加倍。
(2)恒容下压力加倍。
(3)恒温下压力加倍。
12.将1 mol H2O(g)在373 K下小心等温压缩,在没有灰尘情况下获得了压力为2×101.325 kPa的过热蒸汽,但不久全凝聚成液态水,请计算这凝聚过程的
ΔH m,ΔG m和ΔS m。
H2O(g,373K,2×) --> H2O(l,373K, 2×) 已知:在这条件下,水的汽化热
为46.024 kJ/mol,设气体为理想气体,水的密度为1000 kg*m-3,液体体积不受压力影响。
13.在温度为298 K,压力为下,C(金刚石)和C(石墨)的摩尔熵分别为
2.45和5.71 J/(K·mol),其燃烧热依次为-395.40和-39
3.51 kJ/mol, 又其密度分别为3513和2260 kg·m-3。
试求:
(1)在298.15K及下,石墨到金刚石的;
(2)哪一种晶形较为稳定?
(3)增加压力能否使不稳定的晶体变成稳定的晶体,如有可能,则需要加多大的压力?
14.设某气体其状态方程式为p V=RT+a p(式中a 是常数)。
求等温可逆膨胀过程中W,Q和ΔH的表示式。
15.当外压降到66.87 kPa时,水的沸点为若干度?已知(298K,H2O)为40.67 kJ/mol 。
16.溜冰鞋下面的冰刀与冰接触的地方,长度为7.62 cm,宽度为2.45× cm。
(1)若某人的体重为60 kg,试问施加于冰的压力为若干?
(2)在该压力下冰的熔点为若干?
(已知冰的融化热为6.01 kJ/mol, =273.16 K,冰的密度为920 kg·m-3, 水的密度为1000 kg·m-3 )。
17.正已烷的沸点是342.2 K,假定他服从楚顿规则,试估计298.2 K时正己烷的蒸汽压。
18.乙烯的蒸汽压与温度的关系可写作
试求乙烯在正常沸点169.3 K的蒸发热。
19.纯水蒸汽压在298.2 K时为3167.4 Pa,试问水在压力的空气中其蒸汽压为若干?
20.苯在正常沸点353K下的 =30.77 kJ/mol,今将353K及下的 1 mol C6H6(l) 向真空等温蒸发为同温同压的苯蒸汽(设为理想气体)
(1)请求计算在此过程中苯吸收的热量Q与作的功W。
(2)求苯的摩尔气化熵和摩尔气化自由能。
(3)求环境的熵变ΔS环。
(4)应用有关原理,判断上述过程是否为不可逆过程?
(5) 298 K是苯的蒸汽压为多大?。
