影像匹配的基本算法共35页
06章影像匹配基础理论与算法

6.2.2 金字塔影像相关
6.2 影像相关的谱分析
摄影测量学
将信号源发出的信号强度按频率顺序展开,使其成为频 率的函数,并考察变化规律,称为频谱分析。
对信号进行频谱分析,往往对其进行傅里叶变换,观察 其频谱幅度与频谱相位。分析软件主要为Matlab。
对于信号来说,分模拟信号与数字信号。对于模拟信号 来说,往往对其进行抽样,然后进行快速傅里叶变换 (fft),然后对其幅度(abs)和相位(angle)的图 像进行分析。对于数字信号,则可直接进行快速傅里叶 变换。
y)g 2
(x
+
x 0
,
y
+
y 0
)dxdy
−∞ −∞
放大
P2
移动
6.1.4 数字相关
摄影测量学
是根据数字影像的灰度特性,利用计算机对数 字影像进行数值计算的方式完成影像的相关。
一般是二维搜索
1972,Masry, Helava, Chapelle等引入了核线相关原理, 化二维相关为一维搜索,大大提高了相关的速度。
1 T x (t ) x (t + τ ) dt
T→∞ T 0
∫ 实用估计值 Rˆ xx ( τ ) = 1 T x ( t ) x ( t + τ ) dt T0
6.1.1 相关函数
自相关函数的性质: 1、自相关函数是偶函数
摄影测量学
R(τ) = R(−τ)
∫ R(τ ) = lim 1 T x(t)x(t +τ )dt T T →∞ 0
讲述频谱分析的主要课程:主要为电子信息与通信方向 的课程,如信号与系统,随机信号分析,数字信号处理 等
工具:频谱分析仪等工具可较为方便的观察其频谱。
图像匹配算法的简单介绍

一、图像匹配概述图像匹配技术常应用于计算机视觉识别领域中,即把两个不同的传感器或同一传感器在不同时间和条件下,从同一景物录取下来的两幅或多幅图像进行比较,找到该组图像中的共有景物,或根据所给模式在另一幅图像中寻找相应的模式。
通常,由于传感器、时间以及视角的不同,图像所获得的成像条件也不尽相同,在图像中,即使是同一物体所表现出来的光学、几何和空间等特性也会有所不同,若考虑到噪声等干扰因素,图像的差异会更大,图像匹配技术就是在这些不同之处找到它们的共同点,有这些原因造成的图像差异我们称之为图像畸变。
为解决图像畸变带来的匹配困难提出的匹配算法均是由特征空间、搜索空间、搜索策略和相似性测度这四个要素组合而成。
1.特征空间特征空间是由从标准图像和待匹配图像中提取到的可用于匹配的信息组成。
它不仅可以是图像像素的灰度值,而且也可以是点(如角点、直线交叉点、轮廓线上的局部最大曲率)、线(如边缘、轮廓)、面(区域)或者统计特征(如瞬间不变点、瞬间质心以及高层次的结构描述)。
特征空间的选取对图像匹配有着非常重要的意义,因为特种空间不仅直接关系到图像中的哪些特征对匹配算法敏感和哪些特征被匹配,而且基本上决定了匹配算法的运行速度和鲁棒性等匹配性能。
理想的特征空间应该满足以下几个条件:1)特征提取简单快捷;2)特征匹配运算量小;3)特征数据量合适;4)不受噪声、光照度等因素影响;5)对各种图像均能适用。
2.搜索空间搜索空间是指在匹配过程中对图像进行变换的方式及范围。
图像的变换范围可分为三类:全局的、局部的和位移场的。
全局变换是指整幅图像的空间变换都可以用相同的变换参数表示。
局部变换是指在图像的不同区域可以用不同的变换参数,通常的做法是在区域的关键点位置上进行参数变换,在其他位置上进行插值处理。
位移场变换是指对图像中的每一像素点独立地进行参数变换,通常使用一个连续函数来实现优化和约束。
图像有两种变换方式,分别为线性变换和非线性变换。
摄影测量学 影像匹配
vv min
仅仅认为影像灰度只存在偶然误差
n1 g1 ( x, y ) n2 g2 ( x, y )
v g1 ( x, y ) g2 ( x, y )
Photogrammetry,2004
Photogrammetry & Remote Sensing-----Surveying & Mapping Engineering
利用影像匹配获得的同名点进行相对定向
Photogrammetry & Remote Sensing-----Surveying & Mapping Engineering
主要内容:
相关系数匹配的基本原理
核线几何关系解析
最小二乘法影像匹配的原理
单点最小二乘法影像匹配 最小二乘法影像匹配精度
Photogrammetry,2004
Photogrammetry & Remote Sensing-----Surveying & Mapping Engineering
最小二乘影像匹配的数学模型
“灰度差的平方和最小”
S 2 X Y ( x1 y1 ) 2 ( x 2 y 2 ) 2 .... ( x N y N ) 2 min
同时解决“多点”影像匹配或“多片”
影像匹配
引入“粗差检测”,从而大大地提
高影像匹配的可靠性
Photogrammetry,2004
Photogrammetry & Remote Sensing-----Surveying & Mapping Engineering
1、最小二乘影像匹配原理
影像灰度的系统变形:产生影像灰度分布之间的差异。
数字影像最小二乘法匹配

vv
(g2
g2 g1 g2 2
g1 )2
(
g2 g1 g2 2
)2
g
2 2
2
g2 g1 g2 2
g2 g1
g12
vv
g12 (
g2 g1)2 g2 2
相关系数
2
(
g2 g1 )2
g1 2
g2 2
相关系数与vv的关系
1 n
2 v 2 g
信噪比 方差
SNR g v
ˆ
2 x
1 n SNR
2 v 2 g
相关系数与信噪比之间的关系
(SNR)2
1
(1 2)
ˆ
2 x
(1
n
2
)
2 v 2 g
可以得到一些很重要的结论:
影像匹配的精度与相关系数 有关,相关系数愈大则精度愈 高。它与影像窗口的“信噪比” 有关,信噪比愈大,则匹配的 精度愈高。
3.把握文章的艺术特色,理解虚词在文中的作用。
4.体会作者的思想感情,理解作者的政治理想。一、导入新课范仲淹因参与改革被贬,于庆历六年写下《岳阳楼记》,寄托自己“先天下之忧而忧,后天下之乐而乐”的政治理想。实际上,这次改革,受
到贬谪的除了范仲淹和滕子京之外,还有范仲淹改革的另一位支持者——北宋大文学家、史学家欧阳修。他于庆历五年被贬谪到滁州,也就是今天的安徽省滁州市。也是在此期间,欧阳修在滁州留下了不逊
影像匹配的精度还与影像的纹
理结构有关,即与 ( g / g) 有关。 特别 是g 当愈大,则影像匹配精
影像匹配基础理论与算法

四像元平均
九像元平均
金字塔影像层的确定方法
原始影像称第零层,第一层影像每一像素相当于零层( 原始影像称第零层,第一层影像每一像素相当于零层(l×l)l 个像素, 层影像每一像素相当于零层的( 个像素,第k层影像每一像素相当于零层的(l×l)k个像素
由影像匹配窗口大小确定金字塔影像层数
w<INT(n/lk+0.5)<l·w < 影像 长度
1 T
(τ ) =
lim
T →∞
∫
T
0
x ( t ) y ( t + τ ) dt
估计值
ˆ xy ( τ ) = 1 R T
∫
T
0
x ( t ) y ( t + τ ) dt
当x(t)=y(t)时 时 R xx ( τ ) =
自相关函数
∫
+∞ −∞
x ( t ) x ( t + τ ) dt
均值
R xx ( τ ) =
一.常见的五种基本匹配算法
同名点的确定是以匹配测度为基础 同名点的确定是以匹配测度为基础 匹配测度
G ( g ij )
数字摄影测量课件——影像匹配基础理论与算法

入变形参数, 同时按最小二乘的原则解求这些参 数。
25
§4.4 最小二乘影像匹配
1、仅考虑辐射线性畸变的最小二乘匹配—相 关系数
2、仅考虑影像相对移位的一维最小二乘匹配
26
§4.4 最小二乘影像匹配
二、单点最小二乘影像匹配
同时考虑两个影像之间的相对移位与图形变化。
7
§4.2 影像相关的谱分析
为了提高在影像匹配过程中同名匹配点命中的准确性, 特采用了金字塔二级相关。第一级是粗匹配,找到同 名点的大致位置,第二级则在第一级确定的搜索区范 围基础上继续进行精匹配,找到同名点的准确位置。
以三像元平均分频道相关技术为例(见下图)。
8
§4.3 数字影像匹配基本算法
影像相关是利用互相关函数,评价两块影像的 相似性以确定同名点。
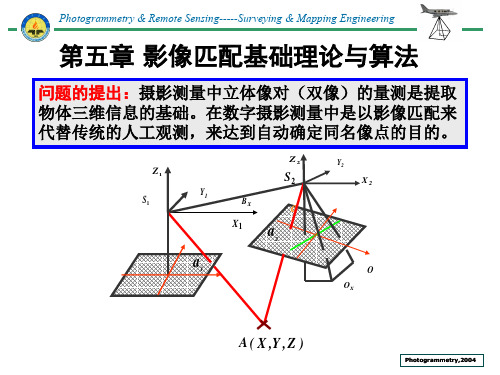
自动化立体量测的基本原理:
首先取出以待定点为中心的小区域中的影像信号,然后 取出其在另一影像中相应区域的影像信息,计算两者相 关函数,以相关函数最大值对应区域中心点为同名点。
2
§4.1 影像相关原理
一、数字相关
数字相关是利用计算机对数字影像进行数值计算 的方式完成影像的相关。即用计算机把像对数字 化后取得灰度值,用数值计算方法探求左右影像 的相似程度,完成影像相关确定同名点的位置。
点是否是最佳匹配点。
28
§4.4 最小二乘影像匹配
最小二乘影像 匹配的步骤流程图
29
§4.4 最小二乘影像匹配
三、最小二乘影像匹配的精度
(1)与相关系数有关。相关系数愈大则精度愈 高。
(2)与影像的纹理结构有关。即与 有关,当 愈大,则匹配精度愈高
30
第六章影像匹配理论与算法

( x , y )D
2 { g ( x , y ) E [ g ( x , y )]} dxdy
( x , y )D
2 { g ( x p , y q ) E [ g ( x p , y q )]} dxdy
若(p0, q0) > (p, q)( pp0, qq0), 则 p0, q0为搜索区影像相对于目标区影像的位移 参数。对于一维相关应有q 0。
1 D
( x , y )D
E[ g ( x. y )]
g ( x, y )dxdy
1 E[ g ( x p, y q)] D
( x , y )D
g( x p, y q)]dxdy
若C(p0, q0) > C(p, q)( pp0, qq0),则 p0, q0为搜索区影像相对 于目标区影像的位移参数。对于一 维相关应有q 0。
第六章 影像匹配理论与算法
第一节:影像相关的基本原理 第二节:影像相关的谱分析
第三节:影像匹配的基本算法
第四节:最小二乘法影像匹配 第五节:特征匹配
2015年1月2日 1
第一节:影像相关的基本原理 主要内容
•
相关函数 • 电子相关 • 光学相关 • 数字相关
相关原理
影像相关是利用互相关函数,评价 两块影像的相似性以确定同名点 。
相关函数的估计值即矢量X与Y的数积
R( X Y )
x
i 1
N
i
y
j
在N维空间{ y1,y2,,yN}中,R是y1, y2,,yN的线性函数
R
x
i 1
N
i
y
j
m ax
它是N维空间的一个超平面。当N=2时
医学影像处理常见算法介绍

医学影像处理常见算法介绍医学影像处理是指将医学图像通过计算机技术进行处理和分析,以研究和诊断患者的病情。
医学影像处理算法类别繁多,本文将针对常见的算法进行介绍。
一、图像增强算法图像增强算法用于提高图像的视觉效果,使图像更具有清晰度和对比度。
其中,灰度拉伸技术是最为常见的图像增强算法之一,其基本原理是通过调整图像像素的灰度级别来增强图像的对比度和亮度。
图像的灰度值是非常重要的一个指标,可以通过调整灰度值的分布范围来使图像具有更高的视觉可分性。
二、图像分割算法图像分割算法用于将医学图像中具有特定生物学意义或特征的区域单独提取出来。
其中,阈值分割是最常用的分割算法之一,其基本原理是通过设定一定的灰度值阈值,将图像中的像素分为两组,一组大于或等于阈值,另一组小于阈值。
此外,还有区域生长分割、水平线分割等算法。
三、图像配准算法图像配准算法是将不同的图像进行对齐的一种处理方法。
医学图像在不同时间、不同视角或不同成像设备下获取可能会产生不同位置或大小的误差,这时需要对图像进行配准。
其中,基于特征点匹配的配准算法是最为常用和有效的方法之一。
四、形态学处理算法形态学处理算法可以对医学图像进行腐蚀、膨胀、开操作、闭操作等处理,进而实现对图像的分割、增强等功能。
形态学变换的基本原理是通过基于结构元素进行像素运算,改变图像的形状和结构。
五、滤波算法滤波算法是用于去除图像中噪声、减少图像细节等目的的算法。
其中,中值滤波是最为常见的滤波算法之一,其基本思想是将图像中每一个像素的邻域灰度值进行排序,然后取中间值作为该像素的新灰度值。
六、特征提取算法特征提取算法是从医学图像中提取出具有特定形态、大小、密度等特点的区域或者特征点。
其中,常见的算法包括主成分分析、小波变换等。
七、神经网络算法神经网络算法可以通过对大量训练数据的学习,自动地提取出医学图像中的特征,并输出正确的医学图像诊断结果。
在医学图像文献分类、疾病诊断等方面,已经得到了广泛的应用。
第五章数字影像匹配基础

T
0
x(t ) x(t
)dt
lim 1
T
x(t)x(t )dt R( )
T T
0
二.影像相关原理
自相关函数主要性质2:
自相关函数在τ=0处取得最大值
a2 b2 2ab
x(t)x(t) x(t )x(t ) 2x(t)x(t )
均值
lim Rxy( )
1
T
x(t) y(t )dt
T T
0
估计值
Rˆxy( ) 1 T x(t) y(t )dt
T0
二.影像相关原理
当x(t)=y(t)时
自相关函数
Rxx( ) x(t) x(t )dt
均值
估计值
lim Rxx( )
T T
0
T
二.影像相关原理
自相关函数主要性质1:
令t t ,则
R( ) lim 1
T
x(t)x(t )dt
T T
0
lim 1
T
x(t )x(t)dt
T T
lim
T
1 T
0
x(t)x(t )dt
三.影像相关的谱分析
分频道相关(多级相关)
分频道可采用两像元平均、三像元平均、 四像元平均等等分若干频道的方法
1234
1
2
1
5678
3
4
2
9 10 11 12
5
6
3
1 2 3 4 5 6 7 8 9 10 11 12
1
2
(医学)图像匹配介绍

其最大的优点是能够将对整个图像进行的 各种分析转化为对图像特征的分析,从而 大大减小了图像处理过程的运算量,对灰 度变化、图像变形以及遮挡等都有较好的 适应能力。
二、图像匹配算法(SUSAN算法)
1、SUSAN算法:
SUSAN算法是一种基于灰度的角点检测算 法,Smith提出了基于USAN角点检测准则 的最小核值相似区(Smallest Univalve Seg-
二、图像匹配算法(SIFT算法)
SIFT算法特点
• SIFT特征是图像的局部特征,其对旋转、尺度 缩放、亮度变化保持不变性,对视角变化、仿 射变换、噪声也保持一定程度的稳定性。
• 独特性(Distinctiveness)好,信息量丰富,适用 于在海量特征数据库中进行快速、准确的匹配。
• 多量性,即使少数几个物体也可以产生大量 SIFT特征向量。
二、图像匹配算法(SIFT算法)
H的特征值与D的主曲率是成比例的,借用 Harris 和 Stephens (A Combined Cornerand Edge Deteetor.
一、图像匹配概述
定义一个相似性测度函数S(·),然后确定一 个最优的变换关系T,使两幅或者多幅图像 经过该空间变换后,之间的相似性达到最 大,也就是达到空间几何上的一致。
F 表示固定图像,M 表示浮动图像
一、图像匹配概述
2、图像配准的基本框架主要包括四个功能 模块: • 特征空间; • 搜索空间; • 搜索策略; • 相似性测度。
a、b、c、d、e表示圆形的掩模,十字形表示掩模的核心,黑色区域表示要 处理的图像的特征。
二、图像匹配算法(SUSAN算法)
最小二乘影像匹配

河南理工大学测绘学院遥感科学与技术系 数字摄影测量学 Digital Photogrammetry
§ 5.3 最小二乘影像匹配 [三]单点最小二乘影像匹配算法
3、误差方程的建立 v = h0 + h1 g 2 (a0 + a1 x + a2 y, b0 + b1 x + b2 y ) − g1 ( x, y )
1
2 2 2
ρ =
2
∑g ∑g
2 1
(∑ g1 g 2 ) 2
2 2
则:
ρ = 1−
∑ vv ∑g
2 1
= 1−
1 ∑ g12 ∑ vv
“相关系数最大”→“信噪比为最大” 相关系数最大” 相关系数最大 信噪比为最大” 因为没引入几何变形参数, 因为没引入几何变形参数,所以匹配结果是以 整像素为单位。 整像素为单位。
y
由于在数字影像匹配中, 由于在数字影像匹配中,灰度均是按规则格网排列的 离散阵列,且采样间隔为常数,可被视为单位长度, 离散阵列,且采样间隔为常数,可被视为单位长度,故 上式中的偏导数均用差分代替: 上式中的偏导数均用差分代替:
ɺ ɺ g y = g j (I , J ) = 1 [ g 2 ( I , J + 1) − g 2 ( I , J − 1)] 2 1 ɺ ɺ g x = g i ( I , J ) = [ g 2 ( I + 1, J ) − g 2 ( I − 1, J )] 2
在建立误差方程式时, 在建立误差方程式时,可采用以目标区中 心为坐标原点的局部坐标系。 心为坐标原点的局部坐标系。由误差方程式 建立法方程式
6-影像匹配的基本算法 (1)

分别以(xi’, yi’)与(xi”,yi”)为中心在
左右影像上取影像窗口,计算其匹配测 度,如相关系数pi。
将i的值增加1,重复(2),(3)两步,
得到ρ0,ρ1,ρ2,···ρn取其最大者ρk:
ρk= max{ρ0,ρ1,ρ2,···ρn}
还可以利用 ρ k 及其相邻的几个相关
系数拟合一抛物线,以其极值对应的 高程作为 A 点的高程,以进一步提高 精度,或以更小的高程步距在一小范 围内重复以上过程。
若S2(c0, r0) < S2(c, r),则c0, r0为搜 索区影像相对于目标区影像的位移行、列 参数。对于一维相关应有r ≡ 0。
两影像窗口灰度差的平方和即灰度向
量X与Y之差矢量
S = X −Y =(x1 − y1) +(x2 − y2) +L+(xN − yN ) =∑(xi − yi )
2 2 2 2 2 i=1 N 2
故差平方和最小等于N维空间点Y与点X 之距离最小。当N=2时,
S = ( x1 − y1 ) + ( x 2 − y 2 ) = min
2 2 2
二维平面上的一个圆 二维平面上以(x1,y2)为中心、边长为、
对角线与坐标轴平行的一个正方形
差绝对值和(差矢量分量绝对值和)
R (X ⋅Y ) =
∑
N
是y1,y2,…,yN的线性函数
R =
在N维空间{ x1,x2,…,xN}中,R
i=1
xi y
j
∑
N
x
i = 1
i
y
j
=
max
它是N维空间的一个超平面。当N=2时
R= x1yl+ x2y2
医学影像配准算法及其应用

医学影像配准算法及其应用医学影像是现代医学发展中的重要组成部分。
通过对患者体内的CT、MRI、PET等影像进行分析,医生可以快速准确地判断疾病的类型、位置和严重程度。
因此,医学影像的质量和准确度直接关系到疾病的治疗效果和患者的生存质量。
为了提高医学影像的精度和临床应用价值,医学影像配准算法应运而生。
什么是医学影像配准?医学影像配准指的是将两个或多个医学影像进行对齐,以减小对比的差异,并实现像素一一对应。
根据其所属领域的不同,医学影像配准算法可以分为结构匹配配准、功能匹配配准和多模态配准三种类型。
其中,结构匹配配准主要针对的是灰度匹配;功能匹配配准则是在结构匹配的基础上,通过比较影像内的生物学功能进行匹配;多模态配准则是将来自不同成像技术的影像进行融合,从而得到更为准确的临床诊断结果。
医学影像配准算法的实现医学影像配准可以通过手动操作和自动算法两种方式实现。
手动操作需要医生花费较长时间进行影像对齐,并且由于人类视觉的限制,无法获得较高的准确度。
因此,研究人员逐渐将自动配准算法应用到了医学影像领域。
目前,医学影像配准算法主要分为两类:基于特征点匹配的算法和基于图像互信息的算法。
特征点匹配的算法是指通过寻找匹配影像中相同的特征点对影像进行配准。
这种算法的优点是计算简单、速度快,但是它对噪声和纹理变化敏感。
基于图像互信息的算法则是通过计算影像的相似度来进行匹配。
这种算法的精度比较高,但是计算复杂度较大,需要长时间的计算。
医学影像配准应用医学影像配准主要应用于医学领域的疾病诊断、治疗和手术规划等方面。
比如,通过CT和MRI的配准,可以更加准确地定位肿瘤部位和大小,同时可以在放疗和化疗前进行影像分析,为治疗方案的制定提供依据。
在神经外科手术中,通过将MRI和CT影像结合起来,医生可以在手术中进行更加精确的定位和导航。
此外,医学影像配准还可以应用于临床研究和药物开发等方面。
结语医学影像配准算法是医学影像发展的重要组成部分。
影像匹配的基本算法共36页PPT

差绝对值和(差矢量分量绝对值和)
S(p,q)g(x,y)g(xp,yq)dxd
(x,y) D
离散灰度数据差绝对值和的计算公式为
mn
S(c,r)
gi,j gir,jc
i1 j1
若S(c0, r0) < S(c, r)( cc0, rr0),则c0, r0为搜索区影像相对于目标区影像的位移行、列 参数。对于一维相关应有r 0。
Zi=Zmin+i·Z 高程搜索步距 Z可由所要求的高程精度确定
mn
(gi,j g)(gir,jcg)
(c,r)
i1 j1
mn
mn
(gi,j g)2
(gir,jc gr,c)2
i1 j1
i1 j1
gc,r
1 m mni1
n
gir,jc
j1
g 1 m
mn i1
n
gi, j
j1
相关系数的实用公式为:
(c,r)
im 1jn 1(gi,jgir,jc)m 1n(im 1jn 1gi,j)(im 1jn 1gir,jc)
mn
C (c,r) (gi,jg)(gir,jcg)
i 1j 1
gc,r
1 m mni1
n
gir,jc
j1
g 1
mn
m i1
n
gi, j
j1
C(c0, r0) > C(c, r)( cc0, rr0)
则c0, r0为搜索区影像相对于目标区影像 的位移行、列参数
协方差函数的估计值即矢量的数积
铅垂线轨迹法(VLL-Vertical Line Locus
在物方有一条 铅垂线轨迹, 它在影像上的 投影是一直线。 就是说VLL与地 面交点A在影像 上的构像必定 位于相应的 “投影差”上。
最小二乘法影像匹配

最小二乘影像匹配的精度
最小二乘匹配算法,则可以根据 以及法方程式系数矩阵的逆矩阵, 同时求得其精度指标
x g2 g / g22
ˆ
2 x
2 0
/
g 2
2 0
1/ n 1
v2
n为目标区像元个数。由于上式右 边是的无偏估计,所以
2 0
2 v
ˆ
2 x
影像匹配的精度还与影像的纹
理结构有关,即与 ( g / g) 有关。 特别 是g 当愈大,则影像匹配精
度愈高。当
2 g
0,即目标窗口
内灰度没有变化时,则无法进行
影像匹配。
《摄影测量学》(下)第三 章
最小二乘法影像匹配
武汉大学
遥感信息工程学院 摄影测量教研室
主要内容
最小二乘法影像匹配的原理 单点最小二乘法影像匹配 最小二乘法影像匹配精度
最小二乘影像匹配
德国Ackermann教授提出了一种新 的影像匹配方法——最小二乘影像匹 配(least Squares Image Matching)
几何变形
x2 a0 a1 x a2 y y2 b0 b1 x b2 y
灰度畸变+几何变形
g1(x, y) n1(x, y) ho h1g2(a0 a1x a2 y,b0 b1x b2 y) n2(x, y)
x2
y2
经线性化后误差方程式
g2 (x)
g2 ( x
) g2(x 2
)
误差方程式可写为
v g2 x g
解得影像的相对移位
数字影像匹配方法

+
IF
IN IB
=
Z
Pmax P Y
Z0+ΔZ
ΔZ
Z0 (Approximate)
O
X
Pmin
ΔZ
Z0+ΔZ
1 n SNCC ( p, Z k ) = ∑ NCC i ( p, Z k ) n i =1
VLL基本思想
在中心投影条件下,空间任意一条铅垂线以中心投影的方式投射到影像上 仍是一条直线,该铅垂线与地面的交点在影像上的构像必定位于相应的 “投影辐射线”上。以此为基础,在立体像对上搜索相应像点,从而确定 地面高程。
对应高程为 Z k = Z min + k • ΔZ 则认为地面A点高程 Z = Z k
利用 ρ k 及其相邻的几个相关系数拟合一抛物线,以 其极值对应的高程作为A点的高程,以进一步提高精 度,或者更小的高程步距在一小范围内重复以上过 程
2 ij∈w
ij∈W
∑(f
− fW )
∑ (g
i +Δy , j +Δx
− gW )
2
相关系数越大,说明相关性越强
(Δx, Δy)为右影像窗口的偏移量
目标区 目标区
搜索区 搜索区
f ij
g ij
几何约束互相关方法(GC3)
Geometrically Constrained Cross-Correlation (Zhang Li, 2005)
2.2cm 5cm 7.5cm 10cm 15cm 20cm 50cm
305 694 1042 1389 2083 2778 6944
317/207 722/471 1082/6782 1443/942 2165/1413 2886/1884 7215/4710
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
两影像窗口灰度差绝对值和即灰度矢 量X与Y之差矢量之分量的绝对值之和
N
Sx1y1x2y2 xNyN xiyi
i 1
当N=2时,
Sx1y1x2y2 min
基于物方的影像匹配(VLL法)
影像匹配的目的是提取物体的几何 信息,确定其空间位置,
能够直接确定物体表面点空间三维 坐标的影像匹配方法得到了研究,这 些方法也被称为“地面元影像匹配”
差平方和(差矢量模)
S2(p,q)[g(x,y)g(xp,yq)]2dxd
(x,y) D
mn
S2(c,r)
(gi,j gir,jc)2
i 1 j 1
若S2(c0, r0) < S2(c, r),则c0, r0为搜 索区影像相对于目标区影像的位移行、列 参数。对于一维相关应有r 0。
两影像窗口灰度差的平方和即灰度向 量X与Y之差矢量
R( p0, q0)> R(p, q)( pp0, qq0)
若 R( p0, q0)> R(p, q)( pp0, qq0),则 p0, q0为搜索区影像相对 于目标区影像的位移参数。对于一维相 关应有q 0。
离散灰度数据对相关函数的估计公式为
mn
R(c,r)
gi,j gir,jc
i1 j1
若
i1
它是N维空间的一个超平面。当N=2时 R= x1yl+ x2y2
(X· Y)= |X| · |Y|·cos= max
|Y|cos= max
相关函数最大 (即矢量X与Y 的数积最大) 等价于矢量Y在 X上的投影最大
协方差函数(矢量投影)
C (p ,q ){ g (x ,y ) E [g (x ,y )] g (x } p ,{ y q ) E [g (x p ,y q )d ]} x
(xi x)[(ayi b)(ayb)]
i1
i1
N
(xi x)2 ( yi y)2
N
N
(xi x)2 [(ayi b)(ayb)]2
i1
i1
i1
N
(xi x)(yi y)
i1
N
N
(xi x)2 (yi y)2
i1
i1
Ya Y b
即灰度矢量经线性变换后相关 系数是不变的
mn
(gi,j g)(gir,jcg)
(c,r)
i1 j1
mn
mn
(gi,j g)2
(gir,jc gr,c)2
i1 j1
i1 j1
gc,r
1 m mni1
n
gir,jc
j1
g 1 m mn i1
n
gi, j
j1
相关系数的实用公式为:
(c,r)
im 1jn 1(gi,jgir,jc)m 1n(im 1jn 1gi,j)(im 1jn 1gir,jc)
差绝对值和(差矢量分量绝对值和)
S(p,q)g(x,y)g(xp,yq)dxd
(x,y) D
离散灰度数据差绝对值和的计算公式为mnS(c,r)
gi,j gir,jc
i1 j1
若S(c0, r0) < S(c, r)( cc0, rr0),则c0, r0为搜索区影像相对于目标区影像的位移行、列 参数。对于一维相关应有r 0。
N
S 2 X Y 2 (x 1 y 1 )2 (x 2 y 2 )2 (x N y N )2(x i y i)2 i 1
故差平方和最小等于N维空间点Y与点X 之距离最小。当N=2时,
S 2 (x 1 y 1 )2 (x 2 y 2 )2 mi
二维平面上的一个圆 二维平面上以(x1,y2)为中心、边长 为、对角线与坐标轴平行的一个正方形
N
N
C (X Y) (xix)y (jy) xiyj
i 1
i 1
C是在的投影与的长之积,因而协方差 测度等价于在上投影最大,
Cmax
在二维空间中是平行于(或E)的一条 直线
减去信号的均值等于去掉 其直流分量。因而当两影像 的灰度强度平均相差一个常 量时,应用协方差测度可不 受影响。
相关系数(矢量夹角)
(p,q)
C(p,q)
Cgg Cgg(p,q)
C gg {g(x,y)E [g(x,y)]2d }xdy
(x,y) D
C g g (p ,q ) { g (x p ,y q ) E [g (x p ,y q )2 ]d}xd
(x,y) D
若(p0, q0) > (p, q)( pp0, qq0), 则 p0, q0为搜索区影像相对于目标区影像的位移 参数。对于一维相关应有q 0。
主要内容
基于像方的匹配算法 基于物方的匹配算法 影像匹配的精度
数字影像匹配基本算法
影像匹配实质上是在两幅(或多 幅)影像之间识别同名点
常见的五种基本匹配算法
同名点的确定是以匹配测度为基础
G ( g ij )
G (gij)
相关函数(矢量数积)
R (p,q)g(x,y)g(xp,yq)dxd
(x,y) D
R(c0,r0)R(c,r)
(rr0)c, c0)
则c0, r0为搜索区影像相对于目标区影 像的位移行、列参数。对于一维相关应 有r 0。
相关函数的估计值即矢量X与Y的数积
N
R(XY)
xi yj
i1
在N维空间{ y1,y2,,yN}中,R是y1, y2,,yN的线性函数
N
R
xi yj max
mn
C (c,r) (gi,jg)(gir,jcg)
i1j1
gc,r
1 m mni1
n
gir,jc
j1
g 1 m mn i1
n
gi, j
j1
C(c0, r0) > C(c, r)( cc0, rr0)
则c0, r0为搜索区影像相对于目标区影像 的位移行、列参数
协方差函数的估计值即矢量的数积
[im 1jn 1g2i,jm 1n(im 1jn 1gi,j)2]i[m 1jn 1g2ir,jcm 1n(im 1jn 1gir,jc)2]
相关系数的估计值最大,等价于矢量X’ 与y’的夹角最小
(XY)XYco sco s
XY
XY
取值范围满足
1
相关系数是灰度线性变换的不变量
N
N
(xi x)(yi y)
(x ,y ) D
E[g(x.y)] 1
g(x,y)dxdy
D(x,y) D
E [g (xp ,yq ) ] 1 g (xp ,yq )d ] xdy D (x,y) D
若C(p0, q0) > C(p, q)( pp0, qq0),则 p0, q0为搜索区影像相 对于目标区影像的位移参数。对于 一维相关应有q 0。
