matlab 常微分方程数值解法
重要:MATLAB常微分方程(组)数值解法

Matlab常微分方程求解问题分类
边值问题:
初值问题:
• 定解附加条件在自变量 的一端
• 一般形式为: y' f (x, y)
y(a)
y0
• 初值问题的数值解法一 般采用步进法,如 Runge-Kutta法
➢ 在自变量两端均给定附加 条件
y' f (x, y)
➢ 一般形式:y(a)y1, y(b)y2
1.根据常微分方程要求的求解精度与速度要求
求解初值问题:
y
'
y
2x y
y ( 0 ) 1
(0x1)
比较ode45和ode23的求解精度和速度
ode45和ode23的比较-1
function xODE clear all clc
format long
y0 = 1; [x1,y1] = ode45(@f,[0,1],y0); [x2,y2] = ode23(@f,[0,1],y0); plot(x1,y1,'k-',x2,y2,'b--') xlabel('x') ylabel('y')
rD = k(3)*C(2)-k(5)*C(4);
rE = k(4)*C(3)+k(5)*C(4);
% Mass balances dCdt = [rA; rB; rC; rD; rE];
三个串联的CSTR等温反应器(例4-3)
function IsothermCSTRs clear all clc CA0 = 1.8; % kmol/m^3 CA10 = 0.4; % kmol/m^3 CA20 = 0.2; % kmol/m^3 CA30 = 0.1; % kmol/m^3 k = 0.5; % 1/min tau = 2; stoptime = 2.9; % min [t,y] = ode45(@Equations,[0 stoptime],[CA10 CA20 CA30],[],k,CA0,tau); disp(' Results:') disp(' t CA1 CA2 CA3') disp([t,y]) plot(t,y(:,1),'k--',t,y(:,2),'b:',t,y(:,3),'r-') legend('CA_1','CA_2','CA_3') xlabel('Time (min)') ylabel('Concentration') % -----------------------------------------------------------------function dydt = Equations(t,y,k,CA0,tau) CA1 = y(1); CA2 = y(2); CA3 = y(3); dCA1dt = (CA0-CA1)/tau - k*CA1; dCA2dt = (CA1-CA2)/tau - k*CA2; dCA3dt = (CA2-CA3)/tau - k*CA3; dydt = [dCA1dt; dCA2dt; dCA3dt];
matlab常微分方程数值解法精品PPT课件

2012
第七讲 常微分方程数值解法
内容提要
引言 欧拉近似方法 龙格-库塔(R-K)方法 MATLAB的常微分方程函数 小结
1、引言
物理学所研究的各种物质运动中,有许多物质运动的 过程是用常微分方程来描述的。
例如,质点的加速运动,简谐振动等。
F m dv dt
d2x 2x2 0
f xn1
x0
y(x), x dx
y(xn ) f y(xn ), xn h
作如下近似
yn y(xn )
得:
yn1 yn f yn , xn h
2.1.4 欧拉法误差
利用泰勒级数得:
y xn1 y(xn h)
y(xn )
hy(xn )
1 2
h2
y(xn )
y(xn )
x2 …. xn ….
y(x0) y(x1) y(x2) …. y(xn) ….
y0
y1 y2 …. yn ….
在xn节点上,微分方程可以写为
y(xn1) y(xn ) f y(xn ) , xn h
作如下近似:
yn y(tn )
则得到欧拉解法递推公式的一般形式:
yn1 yn f ( yn , xn ) h
hf
y(xn ),
xn
1 2
h2 y(xn )
作如下近似
yn y(xn )
yn1 yn f yn , xn h
局部截断误差
y
y0
dy dx
x0 x x0
y0 f ( y0 , x0 ) x x0
此切线与x=x1交点纵坐标为:
y1 y0 f ( y0 , x0 ) x1 x0
MATLAB常微分方程的数值解法

MATLAB常微分⽅程的数值解法MATLAB常微分⽅程的数值解法⼀、实验⽬的科学技术中常常要求解常微分⽅程的定解问题,所谓数值解法就是求未知函数在⼀系列离散点处的近似值。
⼆、实验原理三、实验程序1. 尤拉公式程序四、实验内容选⼀可求解的常微分⽅程的定解问题,分别⽤以上1, 4两种⽅法求出未知函数在节点处的近似值,并对所求结果与分析解的(数值或图形)结果进⾏⽐较。
五、解答1. 程序求解初值问题取n=10源程序:euler23.m:function [A1,A2,B1,B2,C1,C2]=euler23(a,b,n,y0)%欧拉法解⼀阶常微分⽅程%初始条件y0h = (b-a)/n; %步长h%区域的左边界a%区域的右边界bx = a:h:b;m=length(x);%前向欧拉法y = y0;for i=2:my(i)=y(i-1)+h*oula(x(i-1),y(i-1));A1(i)=x(i);A2(i)=y(i);endplot(x,y,'r-');hold on;%改进欧拉法y = y0;for i=2:my(i)=y(i-1)+h/2*( oula(x(i-1),y(i-1))+oula(x(i),y(i-1))+h*(oula(x(i-1),x(i-1))));B1(i)=x(i);B2(i)=y(i);endplot(x,y,'m-');hold on;%欧拉两步公式y=y0;y(2)=y(1)+h*oula(x(1),y(1));for i=2:m-1y(i+1)=y(i-1)+2*h*oula(x(i),y(i));C1(i)=x(i);C2(i)=y(i);endplot(x,y,'b-');hold on;%精确解⽤作图xx = x;f = dsolve('Dy=-3*y+8*x-7','y(0)=1','x');%求出解析解y = subs(f,xx); %将xx代⼊解析解,得到解析解对应的数值plot(xx,y,'k--');legend('前向欧拉法','改进欧拉法','欧拉两步法','解析解');oula.m:function f=oula(x,y)f=-3*y+8*x-7;2. 运算结果A1,A2为前向欧拉法在节点处的近似值,B1,B2为改进的欧拉法在节点处的近似值,C1,C2为欧拉公式法在节点处的近似值。
MATLAB应用第8章 常微分方程的数值求解
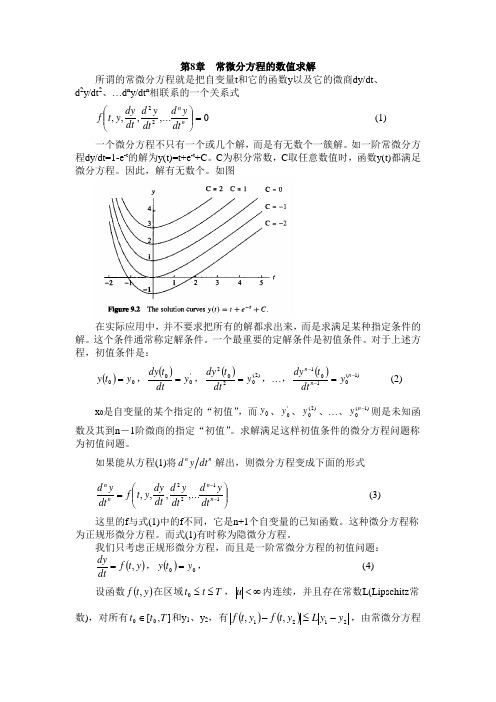
第8章 常微分方程的数值求解所谓的常微分方程就是把自变量t 和它的函数y 以及它的微商dy/dt 、d 2y/dt 2、…d n y/dt n 相联系的一个关系式0,...,,,22=⎪⎪⎭⎫ ⎝⎛n n dt y d dt y d dt dy y t f (1) 一个微分方程不只有一个或几个解,而是有无数个一簇解。
如一阶常微分方程dy/dt=1-e -t 的解为y(t)=t+e -t +C 。
C 为积分常数,C 取任意数值时,函数y(t)都满足微分方程。
因此,解有无数个。
如图在实际应用中,并不要求把所有的解都求出来,而是求满足某种指定条件的解。
这个条件通常称定解条件。
一个最重要的定解条件是初值条件。
对于上述方程,初值条件是:()00y t y =,()'00y dt t dy =,())2(0202y dt t dy =,…,())1(0101---=n n n y dt t dy (2) x 0是自变量的某个指定的“初值”,而0y 、'0y 、)2(0y 、…、)1(0-n y 则是未知函数及其到n -1阶微商的指定“初值”。
求解满足这样初值条件的微分方程问题称为初值问题。
如果能从方程(1)将n n dt y d 解出,则微分方程变成下面的形式⎪⎪⎭⎫ ⎝⎛=--1122,...,,,n n n n dt y d dt y d dt dy y t f dt y d (3) 这里的f 与式(1)中的f 不同,它是n+1个自变量的已知函数。
这种微分方程称为正规形微分方程。
而式(1)有时称为隐微分方程。
我们只考虑正规形微分方程,而且是一阶常微分方程的初值问题: ()y t f dtdy,=,()00y t y =, (4) 设函数()y t f ,在区域T t t ≤≤0,∞<u 内连续,并且存在常数L(Lipschitz 常数),对所有],[00T t t ∈和y 1、y 2,有()()2121,,y y L y t f y t f -≤-,由常微分方程理论得知,初值问题(4)在区间[t 0, T]有唯一解,且连续可微。
实验二MATLAB数值计算常微分方程(组)的求解

实验⼆MATLAB数值计算常微分⽅程(组)的求解实验⼆ MATLAB 数值计算:常微分⽅程(组)的求解⼀、实验⽬的在物理学和⼯程技术上,很多问题都可以⽤⼀个或⼀组常微分⽅程来描述,因此要解决相应的实际问题往往需要⾸先求解对应的微分⽅程。
在⼤多数情况下这些微分⽅程通常是⾮线性的或者是超越⽅程(⽐如范德堡⽅程,波导本征值⽅程等),因此往往需要使⽤计算机数值求解。
MATLAB 作为⼀种强⼤的科学计算语⾔,其在数值计算和数据的可视化⽅⾯具有⽆以伦⽐的优势。
在解决常微分⽅程问题上,MATLAB 就提供了多种可适⽤于不同场合(如刚性和⾮刚性问题)下的求解器(Solver),例如ode45,ode15s ,ode23,ode23s 等等。
本次实验将以范德堡⽅程的计算和地球卫星的运⾏轨道的仿真为例,练习使⽤MATLAB 的常微分⽅程求解器,以期达到如下⼏个⽬的:1. 熟悉常微分⽅程的求解⽅法,了解状态⽅程的概念;2. 能熟练使⽤dsolve 函数解析求解常微分⽅程;3. 能熟练运⽤ode45、ode15s 求解器分别数值求解⾮刚性和刚性常微分⽅程;4. 学习⽤求解器来绘制相图的⽅法。
⼆、实验的预备知识1.微分⽅程的概念未知的函数以及它的某些阶的导数连同⾃变量都由⼀已知⽅程联系在⼀起的⽅程称为微分⽅程。
如果未知函数是⼀元函数,称为常微分⽅程(Ordinary differential equations ,简称odes )。
n 阶常微分⽅程的⼀般形式(隐式)为:0),,",',,()(=n y y y y t F (1)其中t 为⾃变量。
如果未知函数是多元函数,成为偏微分⽅程。
联系⼀些未知函数的⼀组微分⽅程组称为微分⽅程组。
微分⽅程中出现的未知函数的导数的最⾼阶解数称为微分⽅程的阶。
若⽅程中未知函数及其各阶导数都是⼀次的,称为线性常微分⽅程,⼀般表⽰为)()(')()(1)1(1)(t b y t a y t a y t a y n n n n =++++--若上式中的系数a i (t), i =1,2,…,n 均与t ⽆关,称之为常系数。
MATLAB求解常微分方程数值解

利用MATLAB求解常微分方程数值解目录1.容简介12.Euler Method(欧拉法)求解12.1.显式Euler法和隐式Euler法22.2.梯形公式和改进Euler法32.3.Euler法实用性53.Runge-Kutta Method(龙格库塔法)求解53.1.Runge-Kutta基本原理63.2.MATLAB中使用Runge-Kutta法的函数74.使用MATLAB求解常微分方程84.1.使用ode45函数求解非刚性常微分方程84.2.刚性常微分方程95.总结9参考文献11附录121.显式Euler法数值求解122.改进Euler法数值求解123.四阶四级Runge-Kutta法数值求解134.使用ode45求解141.容简介把《高等工程数学》看了一遍,增加对数学容的了解,对其中数值解法比较感兴趣,这大概是因为在其它各方面的学习和研究中经常会遇到数值解法的问题。
理解模型然后列出微分方程,却对着方程无从下手,无法得出精确结果实在是让人难受的一件事情。
实际问题中更多遇到的是利用数值法求解偏微分方程问题,但考虑到先从常微分方程下手更为简单有效率,所以本文只研究常微分方程的数值解法。
把一个工程实际问题弄出精确结果远比弄清楚各种细枝末节更有意思,因此文章中不追求非常严格地证明,而是偏向如何利用工具实际求解出常微分方程的数值解,力求将课程上所学的知识真正地运用到实际方程的求解中去,在以后遇到微分方程的时候能够熟练运用MATLAB得到能够在工程上运用的结果。
文中求解过程中用到MATLAB进行数值求解,主要目的是弄清楚各个函数本质上是如何对常微分方程进行求解的,对各种方法进行MATLAB编程求解,并将求得的数值解与精确解对比,其中源程序在附录中。
最后考察MATLAB中各个函数的适用围,当遇到实际工程问题时能够正确地得到问题的数值解。
2.Euler Method(欧拉法)求解Euler法求解常微分方程主要包括3种形式,即显式Euler法、隐式Euler法、梯形公式法,本节容分别介绍这3种方法的具体容,并在最后对3种方法精度进行对比,讨论Euler法的实用性。
matlab数值求解常微分方程快速方法

MATLAB是一种用于科学计算和工程应用的高级编程语言和交互式环境。
它在数学建模、模拟和分析等方面有着广泛的应用。
在MATLAB 中,常微分方程的数值求解是一个常见的应用场景。
在实际工程问题中,通常需要对常微分方程进行数值求解来模拟系统的动态行为。
本文将介绍MATLAB中对常微分方程进行数值求解的快速方法。
1. 基本概念在MATLAB中,可以使用ode45函数来对常微分方程进行数值求解。
ode45是一种常用的Runge-Kutta法,它可以自适应地选取步长,并且具有较高的数值精度。
使用ode45函数可以方便地对各种类型的常微分方程进行求解,包括一阶、高阶、常系数和变系数的微分方程。
2. 函数调用要使用ode45函数进行常微分方程的数值求解,需要按照以下格式进行函数调用:[t, y] = ode45(odefun, tspan, y0)其中,odefun表示用于描述微分方程的函数,tspan表示求解的时间跨度,y0表示初值条件,t和y分别表示求解得到的时间序列和对应的解向量。
3. 示例演示为了更好地理解如何使用ode45函数进行常微分方程的数值求解,下面我们以一个具体的例子来进行演示。
考虑如下的一阶常微分方程:dy/dt = -2*y其中,y(0) = 1。
我们可以编写一个描述微分方程的函数odefun:function dydt = odefun(t, y)dydt = -2*y;按照上述的函数调用格式,使用ode45函数进行求解:tspan = [0 10];y0 = 1;[t, y] = ode45(odefun, tspan, y0);绘制出解曲线:plot(t, y);4. 高级用法除了基本的函数调用方式外,MATLAB中还提供了更多高级的方法来对常微分方程进行数值求解。
可以通过设定选项参数来控制数值求解的精度和稳定性,并且还可以对刚性微分方程进行求解。
5. 性能优化在实际工程应用中,常常需要对大规模的常微分方程进行数值求解。
常微分方程数值解与matlab

其中,r a / v
d 2 - S0 2
令: dx p, dy
d 2 x dp 2 dy dy
dy dp r 2 y 1 p p ( d 2 S 2 ) S0 0 2 2 d S 0
dy dp r 2 y 1 p p (20) 0
当 y 0 时,
x ,缉私艇不可能追赶上走私船。
dx 1 20 r y r dy 2 y 20 x(20) 0
(b)用MATLAB软件求解析解
MATLAB软件5.3以上版本提供的解常微分方程解析解的指令是 Dsolve, 完整的调用格式是: dsolve('eqn1','eqn2', ...) 其中‘eqn1’,‘eqn2’, ...是输入宗量,包括三部分: 微分方程、初始 条件、指定变量,若不指定变量,则默认小写字母t为独立变量.书P-69 微分方程的书写格式规定:当y是因变量时,用“Dny”表示y的n阶导数. 例 求微分方程
a 2) r 1 , v 1 20r r 1 r r 1 r x 20 (1 r ) y 20 (1 r ) y 2 1 r2
当 y 0 时,
x
缉私艇不可能追赶上走私船。
1 1 2 3) r 1 , x 2 20ln y 40 y
M(x,y)
d
S0
追赶方向可用方向余弦表示为:%两点形成的向量的方向余弦
cosk
S0 at xk (S0 at xk )2 ( yk )2
yk (S0 at x)2 ( yk )2
matlab在常微分方程数值解中应用

MATLAB在常微分方程数值解中的应用摘要】许多现实问题都可以通过微分方程的形式进行表示,传统解微分方程的方法有近似分析解法、表解法和图解法,这些方法需对其进行大量的假设,而使得数学模型有一定的失真,有一定的局限性。
数值解法利用计算机,使得求解更精确、效率更高,而MATLAB是一种数学软件包,有高级编程格式,使得计算结果更具有可信性,因此微分方程的求解及MATLAB在其中的应用具有实际意义。
本文对常微分方程数值解问题作进一步探讨,并应用MATLAB寸其中难解的改进Euler法和Runge-Kutta法进行编程实现,程序简洁、直观,求解速度快、方法实用性较强。
【关键词】常微分方程数值解MATLAB Euler法龙格-库塔方法ode45ode15s b5E2RGbCAPMatlab in ordinary differential equation numerical solution of application p1EanqFDPwYang Hua Zhang Lei【Abstract 】Many practical problems can be using differential equations in the form of represe ntati on, the traditi onal method of solvi ng differe ntial equati ons are similar an alysis method, table method and graphical method, these methods to carry on the large amounts of hypothesis, so that the mathematical model has certa in distort ion, have certa in limitatio n. Numerical soluti on of using a computer, make solving more accurate and more efficient, and MATLAB is a kind of mathematics software package, with adva need program ming format, maki ng calculati on result is more credibility, therefore differential equation and solution of the MATLAB in one of the application of practical significanee. This paper numerical solution of differential equation problem further discussion, and the application of MATLAB in which the difficult solution improvement Euler method and Runge - Kutta method on the programming, the program is concise, intuitive and solution speed, method of practical stronger. DXDiTa9E3d【Key words 】ordinary differential equation, numerical solution , Matlab , Euler method , Runge-Kutta method RTCrpUDGiT【引言】微分方程的概念:未知的函数以及它的某些阶的导数连同自变量都由一已知方程联系在一起的方程称为微分方程。
matlab 二阶常微分方程数值求解函数

MATLAB 二阶常微分方程数值求解函数一、MATLAB 中常微分方程的求解在科学计算领域,常微分方程是一个非常重要的数学工具,常被用于描述动态系统的演变规律。
MATLAB 作为一种功能强大的科学计算软件,提供了丰富的工具箱和函数,用于求解常微分方程。
其中,二阶常微分方程求解函数是其中的重要一部分。
二、二阶常微分方程的数值求解方法1. 常微分方程的基本概念在了解 MATLAB 中的二阶常微分方程数值求解函数之前,首先要明确常微分方程的基本概念。
常微分方程是关于未知函数及其导数的方程,而二阶常微分方程则是包含到二阶导数的方程。
通常情况下,常微分方程不易求解,因此需要借助数值求解方法进行近似求解。
2. MATLAB 中的数值求解函数在 MATLAB 中,有多种数值求解方法可用于求解二阶常微分方程,例如 ODE45、ODE23、ODE113 等。
这些函数可以根据用户输入的微分方程表达式和初始条件,使用不同的数值方法进行求解,得到相应的数值解。
三、使用 MATLAB 数值求解二阶常微分方程的示例考虑一个带有阻尼和弹簧的振动系统,其运动方程为:\[ m\frac {d^2x}{dt^2} + c\frac{dx}{dt} + kx = 0 \]其中,\( m \) 为质量,\( c \) 为阻尼系数,\( k \) 为弹簧刚度。
现在,我们可以使用 MATLAB 中的二阶常微分方程数值求解函数来求解该振动系统的运动方程。
```matlabfunction secondOrderODEExample% 定义常数m = 1; % 质量c = 0.1; % 阻尼系数k = 1; % 弹簧刚度% 定义初始条件x0 = 1; % 初位移v0 = 0; % 初速度% 定义时间范围tspan = [0 10]; % 时间范围% 定义运动方程odefun = @(t,x) [x(2); -c/m*x(2) - k/m*x(1)];% 求解微分方程[t, sol] = ode45(odefun, tspan, [x0 v0]);% 绘制位移随时间变化图figure;plot(t, sol(:,1));xlabel('Time');ylabel('Displacement');title('Displacement vs. Time');end```代码中,我们使用了 MATLAB 中的 ode45 函数来求解给定的二阶常微分方程,并绘制了位移随时间变化的图像。
matlab常微分方程初值问题的数值解法

yn+1
h = y n + [ f ( x n, y n) + f ( x n+1 , yn+1 )] 2
y ( x 2 ) ≈ y ( x 0 ) + 2 h f ( x1 , y ( x1 ))
y′( x1 ) ≈ y ( x 2 ) − y ( x0 ) 2h
y n +1 = y n −1 + 2h f (xn , y n ) n = 1, 2, ⋯ 改进欧拉法 /* modified Euler’s method */
改 进 E u le r 公 式
数值分析
数值分析
以上两组公式都使用函数f ( x , y )在某些点上的 值的线性组合来计算y( xn +1 )的近似值yn +1。 的值,为一阶方法。 Euler公式: 公式 Euler公式:每步计算一次f ( x , y )的值,为一阶方法。 改进Euler公式:需计算两次f ( x , y )的值,二阶方法。 的值,二阶方法。 改进Euler公式 Euler公式:
例 :用尤 拉公 式和 改进 的尤拉 公式 解初 值问 题 2x ' y = y− y y(0) = 1. (0 < x < 1);
数值分析
数值分析
解 : 取 步 长 h = 0 .1, 尤 拉 公 式 为 : yn+1 2 xn ). = yn + h( yn − yn
MATLAB应用第8章常微分方程的数值求解
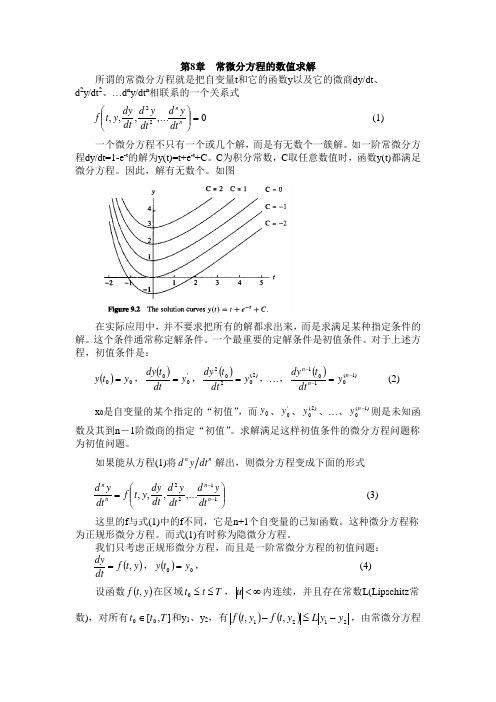
第8章 常微分方程的数值求解所谓的常微分方程就是把自变量t 和它的函数y 以及它的微商dy/dt 、d 2y/dt 2、…d n y/dt n 相联系的一个关系式0,...,,,22=⎪⎪⎭⎫ ⎝⎛n n dt y d dt y d dt dy y t f (1) 一个微分方程不只有一个或几个解,而是有无数个一簇解。
如一阶常微分方程dy/dt=1-e -t 的解为y(t)=t+e -t +C 。
C 为积分常数,C 取任意数值时,函数y(t)都满足微分方程。
因此,解有无数个。
如图在实际应用中,并不要求把所有的解都求出来,而是求满足某种指定条件的解。
这个条件通常称定解条件。
一个最重要的定解条件是初值条件。
对于上述方程,初值条件是:()00y t y =,()'00y dt t dy =,())2(0202y dt t dy =,…,())1(0101---=n n n y dt t dy (2) x 0是自变量的某个指定的“初值”,而0y 、'0y 、)2(0y 、…、)1(0-n y 则是未知函数及其到n -1阶微商的指定“初值”。
求解满足这样初值条件的微分方程问题称为初值问题。
如果能从方程(1)将n n dt y d 解出,则微分方程变成下面的形式⎪⎪⎭⎫ ⎝⎛=--1122,...,,,n n n n dt y d dt y d dt dy y t f dt y d (3) 这里的f 与式(1)中的f 不同,它是n+1个自变量的已知函数。
这种微分方程称为正规形微分方程。
而式(1)有时称为隐微分方程。
我们只考虑正规形微分方程,而且是一阶常微分方程的初值问题: ()y t f dtdy,=,()00y t y =, (4) 设函数()y t f ,在区域T t t ≤≤0,∞<u 内连续,并且存在常数L(Lipschitz 常数),对所有],[00T t t ∈和y 1、y 2,有()()2121,,y y L y t f y t f -≤-,由常微分方程理论得知,初值问题(4)在区间[t 0, T]有唯一解,且连续可微。
matlab微分方程常用数值解法

一、概述Matlab作为一种常用的科学计算软件,在微分方程的数值解法领域具有广泛的应用。
微分方程是描述自然现象中变化规律的数学工具,而数值解法则是指使用计算机进行近似求解微分方程的方法。
在Matlab 中,有多种常用的数值解法可以用来求解微分方程,例如欧拉法、改进的欧拉法、四阶龙格-库塔法等。
本文将对这些数值解法进行介绍和比较,以帮助读者更好地理解和应用微分方程求解数值方法。
二、欧拉法欧拉法是微分方程的最简单的数值解法之一,它通过离散化微分方程进行近似求解。
具体而言,对于一阶常微分方程dy/dx=f(x,y),可以利用欧拉法进行数值解。
欧拉法的基本思想是将自变量x的增量Δx分成n个小区间,然后根据微分方程的数值近似公式y(x+Δx)=y(x)+f(x,y)Δx对每个小区间进行迭代计算。
欧拉法的优点是简单易实现,但由于它是一阶的数值方法,因此对于某些微分方程求解效果可能不够准确。
三、改进的欧拉法改进的欧拉法是对欧拉法的一种改进,它通过在每个小区间内使用平均斜率来提高求解的精度。
具体而言,对于微分方程dy/dx=f(x,y),改进的欧拉法可以通过以下迭代公式进行数值求解:y(x+Δx)=y(x)+Δx/2[f(x,y)+f(x+Δx,y+Δx*f(x,y))]改进的欧拉法相比于欧拉法具有更高的数值精度,但计算量也相对增加。
四、四阶龙格-库塔法四阶龙格-库塔法是一种常用的数值微分方程求解方法,它通过四次迭代计算来获得微分方程的数值解。
具体而言,对于微分方程dy/dx=f(x,y),四阶龙格-库塔法可以用以下公式进行数值求解:k1=f(x,y)k2=f(x+Δx/2,y+Δx/2*k1)k3=f(x+Δx/2,y+Δx/2*k2)k4=f(x+Δx,y+Δx*k3)y(x+Δx)=y(x)+Δx/6*(k1+2*k2+2*k3+k4)四阶龙格-库塔法相比于欧拉法和改进的欧拉法具有更高的数值精度和稳定性,但计算量也相对较大。
第12章 MATLAB常微分方程(组)数值求解方程与方程组的数值解

ode15s求解起来效率不太高的刚性问题。
ode23t可以用来求解微分代数方程。
ode23tb 刚性
低
当方程是刚性的,并且求解要求精度不高
时可以使用。
2020/6/19
© 吴鹏, MATLAB从零到进阶.
常微分方程数值解
【例12.4-1】的结果图:
方 法 1计 算 结 果 图 1
方 法 2计 算 结 果 图 1
方 法 3计 算 结 果 图 1
0.8
0.8
0.8
0.6
0.6
0.6
0.4
0.4
0.4
0.2
0.2
0.2
0
0
0
-0.2
-0.4 0
2020/6/19
y1(t)
-0.2
y2(t)
y3(t)
-0.4
在某段时间区间内的变化来看。非刚性问题变化相对缓 慢,而刚性问题在某段时间内会发生剧烈变化,即很短 的时间内,解的变化巨大。对于刚性问题不适合用 ode45来求解,如果硬要用ode45来求解的话,达到指定 精度所耗费的时间往往会非常长 。
2020/6/19
© 吴鹏, MATLAB从零到进阶.
二、 非刚性问题举例
这些函数可以求解非刚性问题,刚性问题,隐式
微分方程,微分代数方程等初值问题,也可以求解 延迟微分方程,以及边值问题等。
2020/6/19
© 吴鹏, MATLAB从零到进阶.
二、初值问题求解函数
常微分方程数值解
1. 提供的函数
ode23, ode45, ode113, ode15s, ode23s, ode23t, ode23tb,这些函数统一 的调用格式如下:
常微分方程的数值解的matlab命令实现方法

常微分方程的数值解的matlab命令实现方法常微分方程的数值解在 MATLAB 中可以通过 ode 函数或 dsolve 函数进行求解。
其中,ode 函数可以求解一阶常微分方程,而 dsolve 函数可以求解二阶及以上的常微分方程。
下面是具体的实现方法:1. 一阶常微分方程的求解对于一阶常微分方程,可以使用 ode 函数求解。
假设我们要求解的常微分方程为:dx/dt = f(x, t)可以使用以下命令进行求解:y0 = [a, 0]; % 初值条件tspan = [0, 20]; % 时间区间[t, y] = ode45(@(t, y) odefun(t, y, a), tspan, y0); % 求解其中,odefun 函数用于定义常微分方程的解,它是一个自定义函数,其形式可以为:dy/dt = f(t, y)其中,dy 是 y 的求导,f(t, y) 是常微分方程的系数矩阵。
在 MATLAB 中,可以使用 dy[] 函数来计算 y 的求导,例如:dy = dy[](t, y);最后,使用 ode45 函数求解常微分方程的解,其中 tspan 是时间区间,y0 是初值条件。
2. 二阶常微分方程的求解对于二阶常微分方程,可以使用 dsolve 函数求解。
假设我们要求解的二阶常微分方程为:d2y/dt2 + p(t)dyy/dt + q(t)dy/dt + r(t)y = 0可以使用以下命令进行求解:syms t pqr;y0 = [a1, a2, a3]; % 初值条件[t, y] = dsolve(@(t, y) dy0(t, y), t, y0); % 求解其中,dy0 函数用于定义二阶常微分方程的解,其形式可以为:d2y/dt2 + p(t)dyy/dt + q(t)dy/dt + r(t)y = 0其中,d2y/dt2 是 y 的二阶求导,其它项是 y 的求导。
在 MATLAB 中,可以使用 dy0[] 函数来计算 y 的二阶求导。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
y0 y1 y2
yn
欧拉数值算法递推公式构造
2.1.1 差分法 差分法就是用差商近似代替微商,即
y dy x dx
代入微分方程得到:
y ( x x) y ( x) f ( y ( x), x) x y ( x x) y ( x) f ( y ( x), x)x
y1
Q(t) y(t)
y2
dy y y1 x1 x x1 dx y1 f ( y1 , x1 ) x x1
与x=x2交点纵坐标为:
tx t34 tx x x x7 t 0 1 tx 12 t 56 t6 23 x 45 t
y1 y( x1 )
y2 y1 f ( y1 , x1 ) h
xn1
y ( xn ) f y ( xn ), xn h
作如下近似
x0
f y ( x), x dx
yn y( xn )
得:
yn1 yn f yn , xn h
2.1.4 欧拉法误差
利用泰勒级数得:
y xn 1 y ( xn h) 1 2 y ( xn ) hy( xn ) h y( xn ) 2 1 2 y ( xn ) hf y ( xn ), xn h y( xn ) 2
yn 1 yn ci ki
i 1
N
k1 f ( xn , yn ) i 1 ki f ( xn ai h, yn bij k j ) j 1
四阶龙格—库塔法计算公式为:
h yn 1 yn k1 2k2 2k3 k4 6 k1 f ( xn , yn ) h h k2 f ( xn , yn k1 ) 2 2 h h k f ( x , y k ) 3 n n 2 2 2 k f ( x h, y h k ) n n 3 4
t0 t1 t2
t3 t4 t5 t6 x0 ) x1 x0 =y0 f ( y0 , x0 ) h
此切线与x=x1交点纵坐标为:
y0 y( x0 )
从(x1,y1)作曲线y(x)在 Q y (x1,y(x1))的切线的平行线, 得直线方程:
dv F m dt
d x 2 2 x 0 2 dt
简单问题可以求得解析解,多数实际问题靠数值求解。
2
一阶常微分方程(ODE )初值问题 :
ODE :Ordinary Differential Equation
dy f ( x, y ) x0 x xn dx y ( x0 ) y0
yn1 yn f ( yn , xn ) h
折线近似曲线,n增大,误差变大
2.1.3 数值积分
对微分方程作从 x0 到 x 积分得:
y( x ) y0
dy f y x , x dx x0
x
x
y x y0 f y x , x dx x0
yn y( xn )
yn1 yn h f ( xn1 , yn1 )
向后的欧拉方法(隐式方法):预报---校正法
1. 用欧拉方法预报 2. 用向后的欧拉方法校正 ① 用欧拉方法预报
y
(0) n1
yn h f ( xn , yn )
② 用向后的欧拉方法校正---迭代
对于等间隔节点
x xn1 xn h xn1 xn h
可以得到: xn y精确值 x0 x1 x2
n=0,1,2
…. …. ….
xn
…. ….
y(x0) y(x1) y(x2)
y(xn)
y近似值
y0
y1
y2
yn
….
在xn节点上,微分方程可以写为
y( xn1 ) y( xn ) f y( xn ) , x n h
整体截断误差: O(h4)
例题: y ' sin x y
y ( x0 ) 1, x0 0
time_Euler = 0.2500 time_EulerPro = 0.5000 time_RK4 = 1.0150
y
( k 1) n1
yn h f ( xn1, y )
(k ) n1
2.2.2 改进的欧拉方法 积分法求欧拉公式时,积分采用梯形近似,即得到改 进的欧拉方法。
y ( xn 1 ) y ( xn )
xn1
xn
f ( x, y )dx
h y ( xn ) f xn , y xn f xn1 , y xn 1 2
即
y y0
dy f ( x, y)dx
x0 xn1 xn
x
y( x) y0 f ( x, y)dx
x0
x
y ( xn 1 ) y ( xn )
f ( x, y )dx
y( xn ) h f xn 1 , y xn 1
向后的欧拉方法递推公式为
作如下近似:
yn y(tn )
则得到欧拉解法递推公式的一般形式:
yn1 yn f ( yn , x n ) h
具体求解过程为:
y1 y0 f ( y0 , x0 ) h y2 y1 f ( y1 , x1 ) h
y3 y2 f ( y2 , x 2 ) h
x2 x0
y0 f y ( x), x dx f y ( x), x dx
x1 x2
y ( x1 ) f y ( x1 ), x1 h
x0
x1
同样,在[x0,xn+1] ,积分采用矩形近似,得:
y ( xn 1 ) y0
在[x0,x1] ,积分采用矩形近似,得:
y ( x1 ) y0 f y ( x), x dx
x1
y0 f y ( x0 ), x0 h
x0
同样,在[x0,x2] ,积分采用矩形近似,得:
y ( x2 ) y0 f y ( x ), x dx
(0) n 1
例题: y ' sin x y
y ( x0 ) 1, x0 0
3、龙格-库塔(R-K)方法
几种方法的比较 对于一般的常微分方程:
dy f ( x, y ) dx y ( x0 ) y0
1 欧拉方法 取前一点的斜率作为平均斜率,即:
yn 1 yn k1 h k1 f ( xn , yn )
科学计算与MATLAB
主讲:唐建国 中南大学材料科学与工程学院 2012
第七讲
常微分方程数值解法
内容提要
引言 欧拉近似方法 龙格-库塔(R-K)方法 MATLAB的常微分方程函数 小结
1、引言
物理学所研究的各种物质运动中,有许多物质运动的 过程是用常微分方程来描述的。 例如,质点的加速运动,简谐振动等。
数值解法就是求y(x)在某些分立的节点 xn 上的近似值 yn,用以近似y(xn)
yn y( xn )
2、欧拉近似方法
2.1 简单欧拉(L.Euler, 1707-1783)方法。
dy f ( y, x) dx y ( x0 ) y0
欧拉数值算法就是由初值通过递推求解,递推求解 就是从初值开始,后一个函数值由前一个函数值得到。关 键是构造递推公式。
整体截断误差: O(h2)
欧拉方法(前、后)和改进的欧拉方法优点是算法简 单,但计算精度较低,不能满足实际问题求解对精度的要 求,所以使用较少。 龙格-库塔(R-K)方法就是一种精度较高的较为实用计算 常微分方程的方法。
从以上三种方法的比较,可以推测:若取多点处斜 率的加权平均作为平均斜率,精度会更高,这就是龙 格—库塔法的基本思想。
简单欧拉方法程序
function [outx,outy]=MyEuler(fun,x0,xt,y0,PointNum) %MyEuler 用前向差分的欧拉方法解微分方程 %fun 表示f(x,y) %x0,xt表示自变量的初值和终值 %y0表示函数在x0处的值,其可以为向量形式 %PointNum表示自变量在[x0,xt]上取的点数 if nargin<5 | PointNum<=0 %如果函数仅输入4个参数值,则PointNum默认值为100 PointNum=100; end if nargin<4 %y0默认值为0 y0=0; end h=(xt-x0)/PointNum;%计算步长h x=x0+[0:PointNum]'*h;%自变量数组 y(1,:) = y0(:)';%将输入存为行向量,输入为列向量形式 for k = 1:PointNum f=feval(fun,x(k),y(k,:));%计算f(x,y)在每个迭代点的值 f=f(:)'; y(k + 1,:) =y(k,:) +h*f; %对于所取的点x迭代计算y值 end outy=y; outx=x; %plot(x,y)%画出方程解的函数图
改进的欧拉方法递推公式为
h yn 1 yn f ( xn , yn ) f ( xn 1 , yn 1 ) 2
隐式方法: 预报---校正法
1. 用欧拉方法预报
2. 用改进的欧拉方法校正
计算公式为:
y yn h f ( xn , yn ) h (0) f ( x , y ) f ( x , y ) yn 1 yn n n n 1 n 1 2
