双钩打钩函数性质例题与图像详细解答
“对勾函数”的图像和性质全析

函数是高中数学中的重要内容,函数的观点和方法贯穿整个高中数学的全过程。
对勾函数是数学中一种常见而又特殊的函数,近几年高考试题中,对勾函数部分占有相当大比重。
本文通过对勾函数性质的整体分析,结合图像,运用数形结合来研究对勾函数的性质。
一、“对勾函数”的名称渊源
二、“对勾函数”的图像、性质和单调性
通过对对勾函数的图像、性质和单调性的研究,我们发现学习过的均值不等式实际就是对勾函数的参数a,b同号时的特例,等号成立时能取到最值。
当不能取到等号时就要用对勾函数的单调性来求函数的最值。
2.若a,b异号。
(1)a>0,b<0时,在定义域内是增函数,递增区间为(-∞,0)和(0,+∞)。
(2)a<0,b>0时,在定义域内是减函数,递减区间为(-∞,0)和(0,+∞)。
通过研究我们可以知道高中阶段的对勾函数的参数主要是a,b同号,求最值的应用,所以我们要熟悉对勾函数的图像、性质和单调性。
对勾函数绝对经典

对勾函数f(x)=ax+的图象与性质繁华分享对勾函数是数学中一种常见而又特殊的函数。
它在高中教材上不出现,但考试总喜欢考的函数,所以也要注意它和了解它。
(一) 对勾函数的图像对勾函数是一种类似于反比例函数的一般函数,形如f(x)=ax+(接下来写作f(x)=ax+b/x)。
当a≠0,b≠0时,f(x)=ax+b/x是正比例函数f(x)=ax与反比例函数f(x)= b/x“叠加”而成的函数。
这个观点,对于理解它的性质,绘制它的图象,非常重要。
当a,b同号时,f(x)=ax+b/x的图象是由直线y=ax与双曲线y= b/x构成,形状酷似双勾。
故称“对勾函数”,也称“勾勾函数”、“海鸥函数”。
如下图所示:a>0 b>0 a<0 b<0对勾函数的图像(ab同号)当a,b异号时,f(x)=ax+b/x的图象发生了质的变化。
但是,我们依然可以看作是两个函数“叠加”而成。
(请自己在图上完成:他是如何叠加而成的。
)对勾函数的图像(ab异号)一般地,我们认为对勾函数是反比例函数的一个延伸,即对勾函数也是双曲线的一种,只不过它的焦点和渐进线的位置有所改变罢了。
接下来,为了研究方便,我们规定a>0,b>0。
之后当a<0,b<0时,根据对称就很容易得出结论了。
(二) 对勾函数的顶点对勾函数性质的研究离不开均值不等式。
利用均值不等式可以得到:当x>0时,。
当x<0时,。
即对勾函数的定点坐标:(三) 对勾函数的定义域、值域由(二)得到了对勾函数的顶点坐标,从而我们也就确定了对勾函数的定义域、值域等性质。
(四) 对勾函数的单调性(五) 对勾函数的渐进线由图像我们不难得到:(六) 对勾函数的奇偶性对勾函数在定义域内是奇函数,利用对号函数以上性质,在解某些数学题时很简便,下面举例说明:1、求函数324222++++=x x x x y 的最小值。
yXOy=ax解:令322++=x x t ,则22)1(2≥++=x ttt t t y 112+=+= 根据对号函数tt y 1+=在(1,+∞)上是增函数及t 的取值范围,当2=t 时y 有最小值223。
对勾函数讲解与例题解析

对勾函数对勾函数:数学中一种常见而又特殊的函数。
如图一、对勾函数f(x)=ax+ 错误!未找到引用源。
的图象与性质对勾函数是数学中一种常见而又特殊的函数。
它在高中教材上不出现,但考试总喜欢考的函数,所以也要注意它和了解它。
(一) 对勾函数的图像对勾函数是一种类似于反比例函数的一般函数,形如f(x)=ax+错误!未找到引用源。
(接下来写作f(x)=ax+b/x)。
当a≠0,b≠0时,f(x)=ax+b/x是正比例函数f(x)=ax与反比例函数f(x)= b/x “叠加”而成的函数。
这个观点,对于理解它的性质,绘制它的图象,非常重要。
当a,b同号时,f(x)=ax+b/x的图象是由直线y=ax与双曲线y= b/x构成,形状酷似双勾。
故称“对勾函数”,也称“勾勾函数”、“海鸥函数”。
如下图所示:a>0 b>0 a<0 b<0对勾函数的图像(ab同号)当a,b异号时,f(x)=ax+b/x的图象发生了质的变化。
但是,我们依然可以看作是两个函数“叠加”而成。
(请自己在图上完成:他是如何叠加而成的。
)对勾函数的图像(ab异号)一般地,我们认为对勾函数是反比例函数的一个延伸,即对勾函数也是双曲线的一种,只不过它的焦点和渐进线的位置有所改变罢了。
接下来,为了研究方便,我们规定a>0,b>0。
之后当a<0,b<0时,根据对称就很容易得出结论了。
(二) 对勾函数的顶点对勾函数性质的研究离不开均值不等式。
利用均值不等式可以得到:当x>0时,错误!未找到引用源。
当x<0时,错误!未找到引用源。
即对勾函数的定点坐标:(三) 对勾函数的定义域、值域由(二)得到了对勾函数的顶点坐标,从而我们也就确定了对勾函数的定义域、值域等性质。
(四) 对勾函数的单调性(五) 对勾函数的渐进线 由图像我们不难得到: (六)对勾函数的奇偶性 :对勾函数在定义域内是奇函数, 二、均值不等式(基本不等式) 对勾函数性质的研究离不开均值不等式。
对勾函数(目前最全面的版本了吧)
对勾函数f(x)=ax+的图象与性质繁华分享对勾函数是数学中一种常见而又特殊的函数。
它在高中教材上不出现,但考试总喜欢考的函数,所以也要注意它和了解它。
(一) 对勾函数的图像对勾函数是一种类似于反比例函数的一般函数,形如f(x)=ax+(接下来写作f(x)=ax+b/x)。
当a≠0,b≠0时,f(x)=ax+b/x是正比例函数f(x)=ax与反比例函数f(x)= b/x“叠加”而成的函数。
这个观点,对于理解它的性质,绘制它的图象,非常重要。
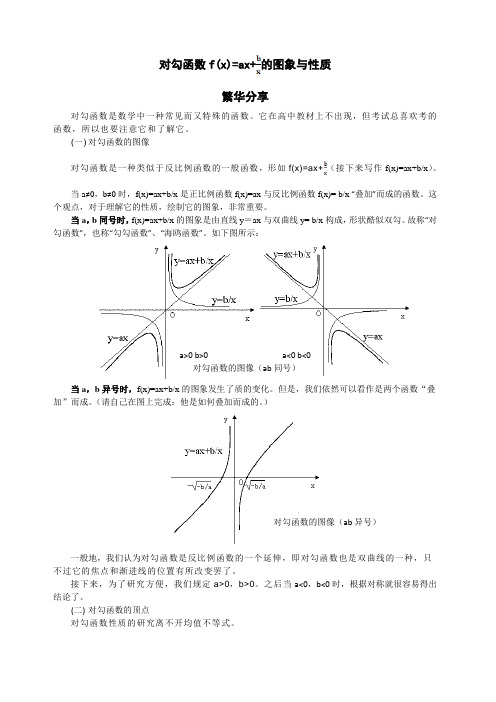
当a,b同号时,f(x)=ax+b/x的图象是由直线y=ax与双曲线y= b/x构成,形状酷似双勾。
故称“对勾函数”,也称“勾勾函数”、“海鸥函数”。
如下图所示:a>0 b>0 a<0 b<0对勾函数的图像(ab同号)当a,b异号时,f(x)=ax+b/x的图象发生了质的变化。
但是,我们依然可以看作是两个函数“叠加”而成。
(请自己在图上完成:他是如何叠加而成的。
)对勾函数的图像(ab异号)一般地,我们认为对勾函数是反比例函数的一个延伸,即对勾函数也是双曲线的一种,只不过它的焦点和渐进线的位置有所改变罢了。
接下来,为了研究方便,我们规定a>0,b>0。
之后当a<0,b<0时,根据对称就很容易得出结论了。
(二)对勾函数的顶点对勾函数性质的研究离不开均值不等式。
利用均值不等式可以得到:当x>0时,。
当x<0时,。
即对勾函数的定点坐标:(三)对勾函数的定义域、值域由(二)得到了对勾函数的顶点坐标,从而我们也就确定了对勾函数的定义域、值域等性质。
(四)对勾函数的单调性(五)对勾函数的渐进线由图像我们不难得到:(六)对勾函数的奇偶性对勾函数在定义域内是奇函数,yXOy=ax。
(完整版)“双勾函数”的性质及应用

“双勾函数”的性质及应用问题引入:求函数2y =的最小值.问题分析:将问题采用分离常数法处理得,2y ==,此时如果利用均值不等式,即2y =,等式成立的条件为==显然无实数解,所以“=”不成立,因而最小值不是2,遇到这种问题应如何处理呢?这种形式的函数又具有何特征呢?是否与我们所熟知的函数具有相似的性质呢?带着种种疑问,我们来探究一下这种特殊类型函数的相关性质.一、利用“二次函数”的性质研究“双勾函数”的性质 1.“双勾函数”的定义我们把形如()kf x x x=+(k 为常数,0k >)的函数称为“双勾函数”.因为函数()kf x x x=+(k 为常数,0k >)在第一象限的图像如“√”,而该函数为奇函数,其图像关于原点成中心对称,故此而得名.2.类比“二次函数”与“双勾函数”的图像3.类比“二次函数”的性质探究“双勾函数”的性质 (1)“二次函数”的性质①当0a >时,在对称轴的左侧,y 随着x 的增大而减小;在对称轴的右侧,y 随着x二次函数图像“双勾函数”图像的增大而增大;当2bx a=-时,函数y 有最小值244ac b a - .②当0a <时,在对称轴的左侧,y 随着x 的增大而增大;在对称轴的右侧,y 随着x的增大而减小.当2bx a=-时,函数y 有最大值244ac b a -.(2)“双勾函数”性质的探究 ①当0x >时,在x =y 随着x的增大而减小;在x =y 随着x的增大而增大;当x =y有最小值.②当0x <时,在x =y 随着x 的增大而增大;在x =y 随着x的增大而减小.当x =y有最大值-综上知,函数()f x在(,-∞和)+∞上单调递增,在[和上单调递减.下面对“双勾函数”的性质作一证明.证明:定义法.设12,x x ∈R ,且12x x <,则1212121212121212()()()()()(1)x x x x k a k k f x f x x x x x x xx x x x ---=+--==--.以下我们怎样找到增减区间的分界点呢?首先0x ≠,∴0x =就是一个分界点,另外我们用“相等分界法”,令120x x x ==,2010kx -=可得到x =因此又找到两个分界点.这样就把()f x 的定义域分为(,-∞,[,,)+∞四个区间,再讨论它的单调性.设120x x <<120x x -<,120x x >,120x x k <<, ∴120x x k -<. ∴121212121212()()()()0x x x x k k k f x f xx x x x x x ---=+--=>,即12()()f x f x >. ∴()f x 在上单调递减.同理可得,()f x 在)+∞上单调递增;在(,-∞上单调递增;在[上单调递减.故函数()f x在(,-∞和)+∞上单调递增,在[和上单调递减.性质启发:由函数()(0)kf x x k x=+>的单调性及()f x 在其单调区间的端点处取值的趋势,可作出函数()y f x =的图像,反过来利用图像可形象地记忆该函数的单调性及有关性质.此性质是求解函数最值的强有力工具,特别是利用均值不等式而等号不成立时,更彰显其单调性的强大功能.4.“二次函数”与“双勾函数”在处理区间最值问题上的类比 (1)“二次函数”的区间最值设f x ax bx c a ()()=++≠20,求f x ()在x m n ∈[],上的最大值与最小值. 分析:将f x ()配方,得对称轴方程x ba=-2, ①当a >0时,抛物线开口向上.若-∈ba m n 2[],必在顶点取得最小值,离对称轴较远端点处取得最大值; 若-∉b a m n 2[],,此时函数在[]m n ,上具有单调性,故在离对称轴x b a=-2较远端点处取得最大值,较近端点处取得最小值. ②当0a <时,抛物线开口向下.若-∈ba m n 2[],必在顶点取得最大值,离对称轴较远端点处取得最小值; 若-∉b a m n 2[],,此时函数在[]m n ,上具有单调性,故在离对称轴x b a=-2较远端点处取得最小值,较近端点处取得最大值. 以上,作图可得结论. ①当a >0时,max121()()()22()1()()()22b f m m n a f x b f n m n a ⎧-+⎪⎪=⎨⎪-<+⎪⎩如图如图,≥,;min345()()2()()()22()()2b f n n a b b f x f m n a a b f m m a ⎧->⎪⎪⎪=--⎨⎪⎪-<⎪⎩如图如图如图,,≤≤,.图1 图2 图3 图4 图5②当a <0时,max678()()2()()()22()()2b f n n a b b f x f m n a a b f m m a ⎧->⎪⎪⎪=--⎨⎪⎪-<⎪⎩如图如图如图,,≤≤,;min9101()()()22()1()()()22b f m m n a f x b f n m n a ⎧-+⎪⎪=⎨⎪-<+⎪⎩如图如图,≥,.(2)“双勾函数”的区间最值 设()(0)kf x x k x=+>,求f x ()在x m n ∈[],上的最大值与最小值. 分析:①当0x >时,其图像为第一象限部分.[]m n ,,则函数必在界点x =函数值;[]m n ,,此时函数在[]m n ,上具有单调性,故在离直线x =得最大值,较近端点处取得最小值.②当0x <时,其图像为第三象限部分.若[]m n ,,则函数必在界点x =最小值需比较两个端点处的函数值;若[]m n ,,此时函数在[]m n ,上具有单调性,故在离直线x =处取得最小值,较近端点处取得最大值.以上,作图可得结论. ①当0x >时,图7 图9图10max()(,()max{(),([,](,()(.f m n f x f m f n m n f n m ⎧>⎪⎪=⎨⎪<⎪⎩如图11)如图12)如图13)min()(,()[,](,()(.f n n f x f m n f m m ⎧>⎪⎪=⎨⎪<⎪⎩如图11)如图12)如图13)②当0x <时,max()(,()([,](,()(.f n n f x f m n f m m ⎧>⎪⎪=⎨⎪<⎪⎩,如图14)如图15),如图16)min()(,()min{(),()},[,](,()(.f m n f x f m f n m n f n m ⎧>⎪⎪=⎨⎪<⎪⎩,如图14)如图15),如图16)二、实践平台例1某化工厂生产的某种化工产品,当年产量在150吨至250吨之间时,其生产的总成本y (万元)与年产量x (吨)之间的函数关系式近似地表示为230400010x y x =-+.问:(1)年产量为多少吨时,每吨的平均成本最低?并求出最低成本;图11 图12图13图14图15图16(2)每吨平均出厂价为16万元,年产量为多少吨时,可获得最大利润?并求出最大利润.分析:将问题归结为“双勾函数”问题,利用“双勾函数”的性质,可使问题轻松获解.解:(1)由题意可知,每吨平均成本为yS x=万元. 即400014000030()301010y x S x x x x==+-=+-,因为函数在区间(0,200]上为减函数,在区间[200,)+∞上为增函数.所以当200x =时,函数400014000030()301010y x S x x x x==+-=+-有最小值为140000(200)301010200S =+-=最小(万元), 所以当年产量为200吨时,每吨的平均成本最低,最低成本为10万元.(2)设年获得总利润为Q 万元,则2211616304000(230)12901010x Q x y x x x =-=-+-=-+, 当230(150,250)x =∈,1290Q =最大,故当年产量为230吨时,可获得最大利润1290万元.评注:本题的关键是用年产量x 吨把每吨平均成本及利润表示出来,然后再求其最值,在求解最值时我们要用到“双勾函数”的单调性,记住这个结论可以简化计算过程.函数的单调性除一些理论上的应用外,它还可以灵活有效地解决现实生活中与之相关的实际问题.例2甲、乙两地相距s km ,汽车从甲地匀速行驶到乙地,速度不得超过c km/h ,已知汽车每小时的运输成本(以元为单位),由可变部分和固定部分组成;可变部分与速度v (km/h)的平方成正比,比例系数为b ,固定部分为a 元.(1)把全程运输成本y (元)表示为v (km/h)的函数,并指出这个函数的定义域.(2)为了使全程运输成本最小,汽车应以多大的速度行驶. 分析:要计算全程的运输成本s bv vabv a v s y )()(2+=+=(v <0≤c ),而已知每小时的运输成本,只需计算全程的时间,由题意不难得到全程运输成本s bv v a bv a v s y )()(2+=+=(v <0≤c ),所要解决的问题是求bv va+何时取最小值,显然要对c 的大小进行讨论,讨论的标准也就是c 与ba的大小. 解:(1)依题意知:汽车从甲地匀速行驶到乙地所用时间为sv,因此全程运输成本为s bv vabv a v s y ⋅+=+⋅=)()(2,又据题意v <0≤c ,故所求函数及其定义域分别为: )(bv vas y +⋅=,],0(c v ∈.(2)设()()aab u f v bv b v v v==+=+,∴u 在],0(b a上是减函数,在)+∞上是增函数. ①若ba≤c ,结合“双勾函数”的性质知, 当bav =时运输成本y 最小. ②若c ba>,函数在],0(c 上单调递减,所以当c v =时,全程运输成本最小. 评注:解应用题时,首先要训练读题能力,成功地完成对数学文字语言、符号语言、图形语言的理解、接受和转换,继而对题中各元素的数量关系进行加工和提炼,分清主次,并建立数学模型解决实际问题.例3(2006安徽高考)已知函数()f x 在R 上有定义,对任意实数0a >和任意实数x ,都有()()f ax af x =.(Ⅰ)证明(0)0f =;(Ⅱ)证明0()0.kx x f x hx x ⎧=⎨<⎩,≥,,其中k 和h 均为常数;(Ⅲ)当(Ⅱ)中的0k >,设1()()(0)()g x f x x f x =+>,讨论()g x 在(0)+∞,内的单调性并求最值.分析:承接第(Ⅱ)问的结论,将问题归结为“双勾函数”的单调性与函数最值的求解问题.证明:(Ⅰ)令0x =,则()()00f af =,∵0a >,∴()00f =. (Ⅱ)①令x a =,∵0a >,∴0x >,则()()2f x xf x =.假设0x ≥时,()f x kx =(k ∈R ),则()22f x kx =,而()2xf x x kx kx =⋅=,∴()()2f x xf x =,即()f x kx =成立.②令x a =-,∵0a >,∴0x <,()()2f xxf x -=-假设0x <时,()f x hx =()h R ∈,则()22f x hx -=-,而()2xf x x hx hx-=-⋅=-,∴()()2f xxf x -=-,即()f x hx =成立.∴(),0,0kx x f x hx x ≥⎧=⎨<⎩成立.(Ⅲ)当0x >时,()()()2111()k g x f x kx k x f x kx x=+=+=+, 由“双勾函数”性质知在1(0,]k 上为减函数,在1[,)k+∞上为增函数, 所以当1x k=时,min [()]2g x =. 评注:数学高考试题注重“考基础、考能力、考思想”.所以熟悉数学化归的思想,有意识地运用数学变换的方法去灵活解决有关的数学问题,将有利于强化在解决数学问题中的应变能力,有利于提高解决数学问题的思维能力和技能、技巧. 适当进行化归、转化能给人带来思维的闪光点,找到解决问题的突破口,是分析问题中思维过程的主要组成部分. 本题就是转化思想应用的一个典型,通过转化将本来抽象的问题归结到“双勾函数”区间最值的求解,让我们有一种豁然开朗的感觉.例4(2001广东高考)设计一幅宣传画,要求画面面积为4840cm 2,画面的宽与高的比为(1)λλ<,画面的上、下各留8cm 空白,左、右各留5cm 空白.怎样确定画面的高与宽尺寸,能使宣传画所用纸张面积最小?如果要求23[,]34λ∈,那么λ为何值时,能使宣传画所用纸张面积最小?分析:设定变元x ,寻找它们之间的内在联系(等量关系),选用恰当的代数式表示问题中的这种联系,建立函数模型,将问题归结为“双勾函数”区间最值问题,并运用“双勾函数”性质进行求解.解:设画面高为x cm ,宽为x λcm ,则24840x λ= 设纸张面积为S cm 2,则有2(16)(10)(1610)160S x x x x λλλ=++=+++,将2210x λ=代入上式得,58500035210(S λλ=+,(0)t t λ=>,则58()500035210()(0)S t t t t=++>,函数S 在5]8上为减函数,在5[,)8+∞上为增函数, 所以当58t =S 取最小值, 此时55(1)88λ=<,高:484088x λ==cm ,宽:588558x λ=⨯=cm .如果23[,]34λ∈,则)t ∈⊆+∞,所以函数S 在上为增函数,故当t =S 取最小值,此时23λ=. 评注:函数描述了自然界中量的依存关系,是对问题本身的数量本质特征和制约关系的一种动态刻画. 要充分重视解题过程中的推理,注意运用推理来简化运算.充分利用题目给出的信息,抽象其数学特征,建立函数关系.很明显,只有在对问题的观察、分析、判断等一系列的思维过程中,具备有标新立异、独树一帜的深刻性、独创性思维,才能构造出函数原型,达到解决问题的目的.在高考中可以利用“双勾函数”考查均值不等式、函数的单调性、函数最值等问题,其应用相当广泛,应用效果相当明显.因此也是高考中的热点和难点,倍受命题者的青睐.但只要我们能熟知“双勾函数”的性质,便不难使此类问题获解.。
对勾函数绝对经典

对勾函数f(x)=ax+的图象与性质繁华分享对勾函数是数学中一种常见而又特殊的函数。
它在高中教材上不出现,但考试总喜欢考的函数,所以也要注意它和了解它。
(一) 对勾函数的图像对勾函数是一种类似于反比例函数的一般函数,形如f(x)=ax+(接下来写作f(x)=ax+b/x)。
当a≠0,b≠0时,f(x)=ax+b/x是正比例函数f(x)=ax与反比例函数f(x)= b/x“叠加”而成的函数。
这个观点,对于理解它的性质,绘制它的图象,非常重要。
当a,b同号时,f(x)=ax+b/x的图象是由直线y=ax与双曲线y= b/x构成,形状酷似双勾。
故称“对勾函数”,也称“勾勾函数”、“海鸥函数”。
如下图所示:a>0 b>0 a<0 b<0对勾函数的图像(ab同号)当a,b异号时,f(x)=ax+b/x的图象发生了质的变化。
但是,我们依然可以看作是两个函数“叠加”而成。
(请自己在图上完成:他是如何叠加而成的。
)对勾函数的图像(ab异号)一般地,我们认为对勾函数是反比例函数的一个延伸,即对勾函数也是双曲线的一种,只不过它的焦点和渐进线的位置有所改变罢了。
接下来,为了研究方便,我们规定a>0,b>0。
之后当a<0,b<0时,根据对称就很容易得出结论了。
(二) 对勾函数的顶点对勾函数性质的研究离不开均值不等式。
利用均值不等式可以得到:当x>0时,。
当x<0时,。
即对勾函数的定点坐标:(三) 对勾函数的定义域、值域由(二)得到了对勾函数的顶点坐标,从而我们也就确定了对勾函数的定义域、值域等性质。
(四) 对勾函数的单调性(五) 对勾函数的渐进线由图像我们不难得到:(六) 对勾函数的奇偶性对勾函数在定义域内是奇函数,利用对号函数以上性质,在解某些数学题时很简便,下面举例说明:1、求函数324222++++=x x x x y 的最小值。
yXOy=ax解:令322++=x x t ,则22)1(2≥++=x ttt t t y 112+=+= 根据对号函数tt y 1+=在(1,+∞)上是增函数及t 的取值范围,当2=t 时y 有最小值223。
双勾函数的图像与性质

对勾函数:是一种类似于反比例函数的一般双 b 曲函数,是形如 f ( x ) ax ( a 0 , b 0 ) 的函 x 数。
由图像得名,又被称为“双勾函数”、“勾函 数”、"对号函数"、“双飞燕函数”等。 因函数图像和耐克商标相似,也被形象称为 “耐克函数”或“耐克曲线”。
应用举例
(3) f ( x) x3 , ( x 3) x 1
m (4) f ( x) x 在0, 1上的最小值 x源自 回顾一次函数与反比例函数
两个函数的主要性质 两个函数相加具有奇偶性吗?
链接对勾函数
b 形如 y ax (a 0, b 0)的函数图像 x
1 例:已知函数 y x x
(1) 对于x R ,求函数的值域 1 (2) 0 x 时,求y的最小值 2 1 (3) 2 x 4 时,求y的值域
练习与巩固
3 (1) f ( x) x , (o x 1) x
x 2 3x 2 (2) f ( x) , (2 x 5) x
求定义域 函数的奇偶性如何 想象函数的图像的大致趋势 函数的图像可能出现的象限 直线 的图像与整体图像存在什么关系
y ax
观察图形,思考问题
(4)值域: y ,2 ab 2 ab,
是一种类似于反比例函数的一般双曲函数是形如由图像得名又被称为双勾函数勾函数对号函数双飞燕函数等
b 形如 y ax (a 0, b 0)的函数图像 x
1 例1、已知函数 f ( x) x ,判断 f ( x)在0, 1上和1, 上的单调性 x
1 思考1:函数 f ( x) x 的奇偶性如何? x
(完整版)对勾函数详细分析

对勾函数的性质及应用、 对勾函数 y ax b (a 0,b 0) 的图像与性 x质:1. 定义域: ( ,0) (0, )2. 值域: ( , 2 ab] [2 ab, )原点呈中心对称,即 f(x) f( x) 0即 f (x) 在 x= b时,取最小值 2 ab a、 对勾函数的变形形式2. 值域: ( , 2 ab] [2 ab, )3.奇偶性:奇函数,函数图像整体呈两个 对勾”的形状,且函数图像关于4.图像在一、三象限 , 当 x 0 时, y axb2 ab (当且仅当 x b取等号), 由奇函数性质知:当x <0 时, f (x) 在 x= b时,取最大值 2 ab a 5.单调性:增区间为(,b) ,a, 减区间是( 0 ,类型一:函数 y ax b (a 0,b x 质1. 定义域: ( ,0) (0, )0)的图像与性3. 奇偶性:奇函数,函数图像整体呈两个“对勾”的形状4. 图像在二、四象限, 当x<0时,f (x)在x= b时,取最小值 2ab;当x 0时,af(x)在x= b时,取最大值 2 aba5. 单调性:增区间为(0,b),(b,0 )减区间是(b, a a a,b a)类型二:斜勾函数y ax b(ab 0)x① a 0,b 0 作图如下1. 定义域:( ,0)(0, )2. 值域:R3. 奇偶性:奇函数4. 图像在二、四象限,无最大值也无最小值.5. 单调性:增区间为(- ,0),(0,+ )② a 0,b 0 作图如下:1. 定义域:( ,0) (0, )2. 值域:R3. 奇偶性:奇函数4. 图像在二、四象限,无最大值也无最小值5. 单调性:减区间为(- ,0),(0,+ )2此类函数可变形为 f(x) ax cb ,可由对勾函数 y axc 上下平移得到 x x2练习 1.函数 f(x) x x 1 的对称中心为x类型四: 函数 f (x) x a (a 0,k 0)xk此类函数可变形为 f (x) (x k a ) k ,则 f ( x)可由对勾函数 y x a 左右平移, x k x 上下平移得到练习 1. 作函数 f(x) x 1 与 f(x) x 3 x 的草图x 2 x 22. 求函数 f (x) x 1 在 (2, )上的最低点坐标2x 4 3. 求函数 f(x) x x 的单调区间及对称中心x1a. 若 a 0 ,图像如下:1.定义域:( , ) 2. 值域:[ a 2 b ,a 2 b ]3. 奇偶性:奇函数 .4. 图像在一、三象限 . 当 x 0时, f (x) 在x b 时, 取最大值 a ,当 x<0 时, f(x)在 x= b 时,取最小值 a2 b 2 b5. 单调性:减区间为( b, ),( , b );增区间是 [ b, b]类型三函数 f(x)ax 2 bx c(ac 0)x类 型 五 : 函数 af(x) 2 xbx( )axf (x)2xa b xxb (a 0,b 0) 。
对勾函数(图像及概念)

对勾函数是一种类似于反比例函数的一般函数。
所谓的对勾函数,是形如f(x)=ax+b/x 的函数,是一种教材上没有但考试老喜欢考的函数,所以更加要注意和学习。
一般的函数图像形似两个中心对称的对勾,故名。
当x>0时,f(x)=ax+b/x 有最小值(这里为了研究方便,规定a>0,b>0),也就是当x=ab的时候。
同时它是奇函数,就可以推导出x<0时的性质。
令k=ab ,那么,增区间:{x|x≤-k}∪{x|x≥k};减区间:{x|-k≤x<0}∪{x|0<x≤k}。
由单调区间可见,它的变化趋势是:在y 轴左边,增减,在y 轴右边,减增,是两个勾。
对勾函数性质的研究离不开均值不等式。
说到均值不等式,其实也是根据二次函数得来的。
我们都知道,(a-b)2≥0,展开就是a2-2ab+b2≥0,有a2+b2≥2ab ,两边同时加上2ab ,整理得到(a+b)2≥4ab ,同时开根号,就得到了平均值定理的公式:a+b≥2ab 。
现在把ax+b/x 套用这个公式,得到ax+b/x≥2x ab =2ab ,这里有个规定:当且仅当ax=b/x 时取到最小值,解出x=ab ,对应的f(x)=2ab 。
我们再来看看均值不等式,它也可以写成这样:(a+b)/2≥ab ,前式大家都知道,是求平均数的公式。
那么后面的式子呢?也是平均数的公式,但不同的是,前面的称为算术平均数,而后面的则称为几何平均数,总结一下就是算术平均数绝对不会小于几何平均数。
这些知识点也是非常重要的。
其实用导数也可以研究对勾函数的性质。
不过首先要会负指数幂的换算,这也很简单,但要熟练掌握。
举几个例子:x 1=x-1,4/x2=4x-2。
明白了吧,x 为分母的时候可以转化成负指数幂。
那么就有f(x)=ax+xb =ax+bx-1,求导方法一样,求的的导函数为a+(-b)x-2,令f'(x)=0,计算得到b=ax2,结果仍然是x=a b ,如果需要的话算出f(x)就行了。
对勾函数绝对经典
对勾函数f(x)=ax+的图象与性质繁华分享对勾函数是数学中一种常见而又特殊的函数。
它在高中教材上不出现,但考试总喜欢考的函数,所以也要注意它和了解它。
(一) 对勾函数的图像对勾函数是一种类似于反比例函数的一般函数,形如f(x)=ax+(接下来写作f(x)=ax+b/x)。
当a≠0,b≠0时,f(x)=ax+b/x是正比例函数f(x)=ax与反比例函数f(x)= b/x“叠加”而成的函数。
这个观点,对于理解它的性质,绘制它的图象,非常重要。
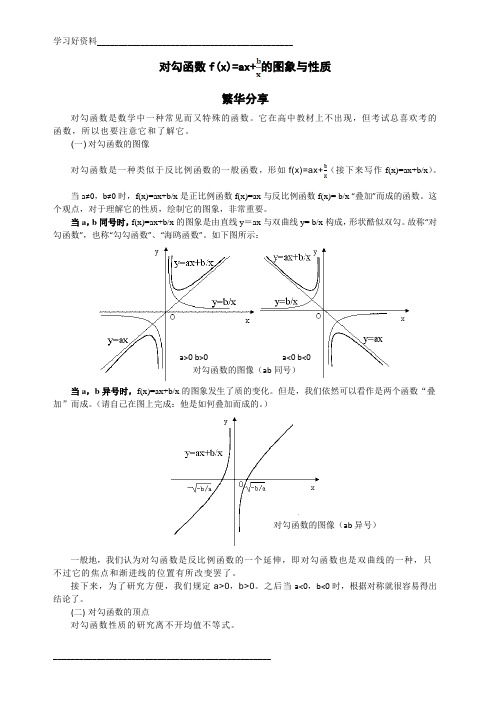
当a,b同号时,f(x)=ax+b/x的图象是由直线y=ax与双曲线y= b/x构成,形状酷似双勾。
故称“对勾函数”,也称“勾勾函数”、“海鸥函数”。
如下图所示:a>0 b>0 a<0 b<0对勾函数的图像(ab同号)当a,b异号时,f(x)=ax+b/x的图象发生了质的变化。
但是,我们依然可以看作是两个函数“叠加”而成。
(请自己在图上完成:他是如何叠加而成的。
)对勾函数的图像(ab异号)一般地,我们认为对勾函数是反比例函数的一个延伸,即对勾函数也是双曲线的一种,只不过它的焦点和渐进线的位置有所改变罢了。
接下来,为了研究方便,我们规定a>0,b>0。
之后当a<0,b<0时,根据对称就很容易得出结论了。
(二)对勾函数的顶点对勾函数性质的研究离不开均值不等式。
利用均值不等式可以得到:当x>0时,。
当x<0时,。
即对勾函数的定点坐标:(三) 对勾函数的定义域、值域由(二)得到了对勾函数的顶点坐标,从而我们也就确定了对勾函数的定义域、值域等性质。
(四) 对勾函数的单调性(五) 对勾函数的渐进线由图像我们不难得到:(六) 对勾函数的奇偶性对勾函数在定义域内是奇函数,利用对号函数以上性质,在解某些数学题时很简便,下面举例说明:1、求函数324222++++=x x x x y 的最小值。
解:令322++=x x t ,则22)1(2≥++=x ttt t t y 112+=+= yXOy=ax根据对号函数tt y 1+=在(1,+∞)上是增函数及t 的取值范围,当2=t 时y 有最小值223。
对勾函数的性质(经典实用)

对勾函数的性质(经典实用)一、定义与表达式对勾函数,也称为双曲正弦函数,其表达式为:$ f(x) =\frac{x}{\sqrt{1+x^2}} $。
这个函数的名称来源于其图像形状类似于一个对勾,即勾号“√”。
二、性质分析1. 奇偶性:对勾函数是一个奇函数,即满足 $ f(x) = f(x) $。
这意味着函数图像关于原点对称。
2. 单调性:对勾函数在定义域内($ x \in \mathbb{R} $)是单调递增的。
当 $ x $ 增大时,$ f(x) $ 也随之增大。
3. 极限性质:当 $ x $ 趋向于正无穷大或负无穷大时,$ f(x) $ 分别趋向于 1 和 1。
这可以通过计算极限 $ \lim_{x \to \infty} f(x) $ 和 $ \lim_{x \to \infty} f(x) $ 得到。
4. 导数与凹凸性:对勾函数的一阶导数为 $ f'(x) =\frac{1}{(1+x^2)^{3/2}} $。
由于导数始终大于 0,函数在整个定义域内是凹的。
这意味着函数图像在任意点处的切线都在函数图像的下方。
5. 积分性质:对勾函数的积分形式为 $ \int f(x) dx = \ln|x+\sqrt{1+x^2}| + C $,其中 $ C $ 为积分常数。
这个积分形式在对勾函数的应用中非常有用,例如在解决某些物理问题时。
6. 应用领域:对勾函数在多个领域都有应用,如物理学、工程学、统计学等。
例如,在物理学中,对勾函数可以用来描述某些非线性系统的行为;在工程学中,它可以用来解决某些优化问题;在统计学中,它可以用来构建概率密度函数。
三、结论对勾函数作为一个经典的数学工具,其性质独特且应用广泛。
理解并掌握对勾函数的性质,有助于我们在解决实际问题中更加得心应手。
对勾函数的性质(经典实用)一、定义与表达式对勾函数,也称为双曲正弦函数,其表达式为:$ f(x) =\frac{x}{\sqrt{1+x^2}} $。
对勾函数图象性质
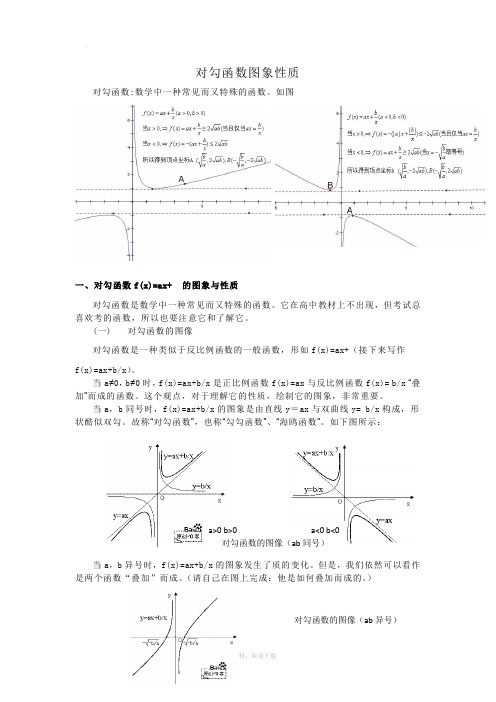
对勾函数图象性质对勾函数:数学中一种常见而又特殊的函数。
如图一、对勾函数f(x)=ax+的图象与性质对勾函数是数学中一种常见而又特殊的函数。
它在高中教材上不出现,但考试总喜欢考的函数,所以也要注意它和了解它。
(一) 对勾函数的图像对勾函数是一种类似于反比例函数的一般函数,形如f(x)=ax+(接下来写作f(x)=ax+b/x )。
当a ≠0,b ≠0时,f(x)=ax+b/x 是正比例函数f(x)=ax 与反比例函数f(x)= b/x “叠加”而成的函数。
这个观点,对于理解它的性质,绘制它的图象,非常重要。
当a ,b 同号时,f(x)=ax+b/x 的图象是由直线y =ax 与双曲线y= b/x 构成,形状酷似双勾。
故称“对勾函数”,也称“勾勾函数”、“海鸥函数”。
如下图所示:当a ,b 异号时,f(x)=ax+b/x 的图象发生了质的变化。
但是,我们依然可以看作是两个函数“叠加”而成。
(请自己在图上完成:他是如何叠加而成的。
)a>0 b>0 a<0 b<0 对勾函数的图像(ab 同号) 对勾函数的图像(ab 异号)一般地,我们认为对勾函数是反比例函数的一个延伸,即对勾函数也是双曲线的一种,只不过它的焦点和渐进线的位置有所改变罢了。
接下来,为了研究方便,我们规定a>0,b>0。
之后当a<0,b<0时,根据对称就很容易得出结论了。
(二) 对勾函数的顶点对勾函数性质的研究离不开均值不等式。
利用均值不等式可以得到:当x>0时,当且尽当时取等号 ,此时。
当x<0时,当且尽当时取等号 ,此时。
(三) 对勾函数的定义域、值域由(二)得到了对勾函数的顶点坐标,从而我们也就确定了对勾函数的定义域、值域等性质。
(四)对勾函数的单调性(五)对勾函数的渐进线(六) 对勾函数的奇偶性 :对勾函数在定义域内是奇函数,二、类对勾函数性质探讨 函数xbax y +=,在时或00==b a 为简单的单调函数,不予讨论。
对勾函数讲解与例题解析

对勾函数对勾函数:数学中一种常见而又特殊的函数。
如图一、对勾函数f(x)=ax+错误!未找到引用源。
的图象与性质对勾函数是数学中一种常见而又特殊的函数。
它在高中教材上不出现,但考试总喜欢考的函数,所以也要注意它和了解它。
(一) 对勾函数的图像对勾函数是一种类似于反比例函数的一般函数,形如f(x)=ax+错误!未找到引用源。
(接下来写作f(x)=ax+b/x )。
当a≠0,b≠0时,f(x)=ax+b/x 是正比例函数f(x)=ax 与反比例函数f(x)= b/x “叠加”而成的函数。
这个观点,对于理解它的性质,绘制它的图象,非常重要。
当a ,b 同号时,f(x)=ax+b/x 的图象是由直线y =ax 与双曲线y= b/x 构成,形状酷似双勾。
故称“对勾函数”,也称“勾勾函数”、“海鸥函数”。
如下图所示:当a ,b 异号时,f(x)=ax+b/x 的图象发生了质的变化。
但是,我们依然可以看作是两个函数“叠加”而成。
(请自己在图上完成:他是如何叠加而成的。
)一般地,我们认为对勾函数是反比例函数的一个延伸,即对勾函数也是双曲线的一种,只不过它的焦点和渐进线的位置有所改变罢了。
a>0 b>0 a<0 b<0 对勾函数的图像(ab 同号)对勾函数的图像(ab 异号)接下来,为了研究方便,我们规定a>0,b>0。
之后当a<0,b<0时,根据对称就很容易得出结论了。
(二) 对勾函数的顶点对勾函数性质的研究离不开均值不等式。
利用均值不等式可以得到:当x>0时,错误!未找到引用源。
当x<0时,错误!未找到引用源。
即对勾函数的定点坐标:(三) 对勾函数的定义域、值域由(二)得到了对勾函数的顶点坐标,从而我们也就确定了对勾函数的定义域、值域等性质。
(四) 对勾函数的单调性(五) 对勾函数的渐进线 由图像我们不难得到: (六)对勾函数的奇偶性 :对勾函数在定义域内是奇函数, 二、均值不等式(基本不等式) 对勾函数性质的研究离不开均值不等式。
双勾函数的图像与性质

两个函数的主要性质 两个函数相加具有奇偶性吗?
链接对勾函数
b 形如 y ax (a 0, b 0)的函数图像 x
求定义域 函数的奇偶性如何 想象函数的图像的大致趋势 函数的图像可能出现的象限 直线 的图像与整体图像存在什么关系
y ax
观察图形,思考问题
(4)值域: y ,2 ab 2 ab,
由图像得名,又被称为“双勾函数”、“勾函 数”、"对号函数"、“双飞燕函数”等。 因函数图像和耐克商标相似,也被形象称为 “耐克函数”或“耐克曲线”。
应用举例
1 例:已知函数 y x x
(1) 对于x R ,求函数的值域 1 (2) 0 x 时,求y的最小值 2 1 (3) 2 x 4 时,求y的值域
b 形如 y ax (a 0, b 0)的函数图像 x
1 例1、已知函数 f ( x) x ,判断 f ( x)在0, 1上和1, 上的单调性 x
1 思考1:函数 f ( x) x 的奇偶性如何? x
1 1 思考 2:函数 f ( x) x 与函数 y x以及 y 的图像有什么关系? x x
1 思考 3:可以作出函数 f ( x) x 的大致图像吗? x
b 变式 3、判断函数 f ( x) ax (a 0, b 0)在定义域上的单调性 x
b 思考:函数 f ( x) ax 与函数 y ax的图像有什么关系? x
对勾函数:是一种类似于反比例函数的一般双 b 曲函数,是形如 f ( x ) ax ( a 0 , b 0 ) 的函 x 数。
练习与巩固
3 (1) f ( x) x , (o x 1) x
