2018届高考数学-算法初步(含答案)
2018年全国各地高考数学试题及解答分类汇编大全(14 算法初步、框图)
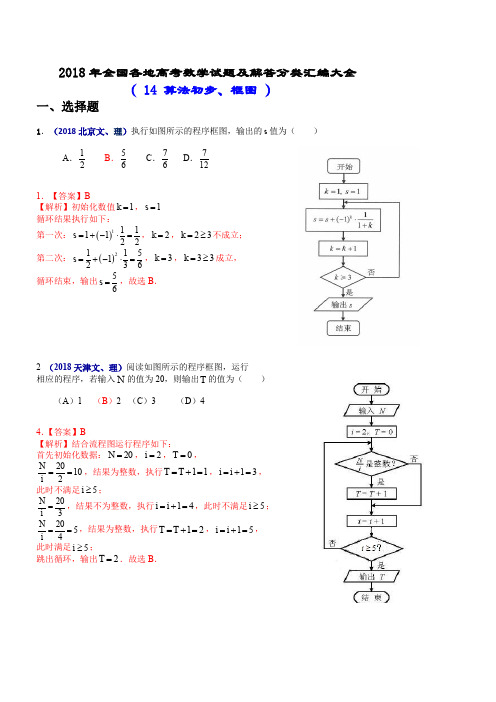
2018年全国各地高考数学试题及解答分类汇编大全( 14 算法初步、框图 )一、选择题1.(2018北京文、理)执行如图所示的程序框图,输出的s 值为( )A .12B .56C .76D .7121.【答案】B【解析】初始化数值1k =,1s = 循环结果执行如下:第一次:()1111122s =+-⋅=,2k =,23k =≥不成立;第二次:()21151236s =+-⋅=,3k =,33k =≥成立,循环结束,输出56s =,故选B .2 (2018天津文、理)阅读如图所示的程序框图,运行相应的程序,若输入N 的值为20,则输出T 的值为( )(A )1 (B )2 (C )3 (D )4 4.【答案】B【解析】结合流程图运行程序如下:首先初始化数据:20N =,2i =,0T =, 20102N i ==,结果为整数,执行11T T =+=,13i i =+=, 此时不满足5i ≥; 203N i =,结果不为整数,执行14i i =+=,此时不满足5i ≥; 2054N i ==,结果为整数,执行12T T =+=,15i i =+=, 此时满足5i ≥;跳出循环,输出2T =.故选B .3.(2018全国新课标Ⅱ文、理)为计算11111123499100S =-+-++-,设计了如图的程序框图, 则在空白框中应填入( )A .1i i =+B .2i i =+C .3i i =+D .4i i =+ 3.【答案】B【解析】由11111123499100S =-+-+⋯+-得程序框图先对奇数项累加,偶数项累加,最后再相减. 因此在空白框中应填入2i i =+,选B .二、填空1.(2018江苏)一个算法的伪代码如图所示,执行此算法,最后输出的S 的值为 ▲ .1.【答案】8【解析】由伪代码可得3I =,2S =;5I =,4S =;7I =,8S =;因为76>,所以结束循环,输出8S =.三、解答题开始0,0N T ==S N T =-S 输出1i =100i <1N N i =+11T T i =++结束是否。
江苏专用2018年高考数学总复习专题12.1算法初步试题含解析201710013147
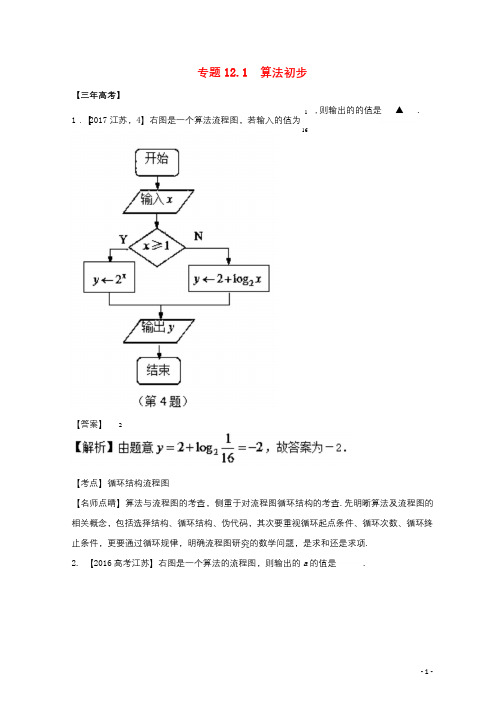
专题 12.1 算法初步【三年高考】1 1.【2017江苏,4】右图是一个算法流程图,若输入的值为16,则输出的的值是▲.【答案】2【考点】循环结构流程图【名师点睛】算法与流程图的考查,侧重于对流程图循环结构的考查.先明晰算法及流程图的 相关概念,包括选择结构、循环结构、伪代码,其次要重视循环起点条件、循环次数、循环终 止条件,更要通过循环规律,明确流程图研究的数学问题,是求和还是求项. 2. 【2016高考江苏】右图是一个算法的流程图,则输出的 a 的值是.【答案】9【解析】试题分析:第一次循环:a5,b7,第二次循环:a9,b5,此时a b,循环结束,输出的a的值是9,故答案应填:9【考点】循环结构流程图【名师点睛】算法与流程图的考查,侧重于对流程图循环结构的考查.先明晰算法及流程图的相关概念,包括选择结构、循环结构、伪代码,其次要重视循环起始条件、循环次数、循环终止条件,更要通过循环规律,明确流程图研究的数学问题,是求和还是求项.3.【2015江苏高考,4】根据如图所示的伪代码,可知输出的结果S为________.【答案】7【解析】第一次循环:S3,I4;第二次循环:S5,I7;第三次循环:S7,I10;结束循环,输出S7.【考点定位】循环结构流程图4.【2017课标3,理7】执行右图的程序框图,为使输出S的值小于91,则输入的正整数N的最小值为A.5 B.4 C.3 D.2【答案】D【考点】流程图【名师点睛】利用循环结构表示算法,一定要先确定是用当型循环结构,还是用直到型循环结构;当型循环结构的特点是先判断再循环,直到型循环结构的特点是先执行一次循环体,再判断;注意输入框、处理框、判断框的功能,不可混用;赋值语句赋值号左边只能是变量,不能是表达式,右边的表达式可以是一个常量、变量或含变量的运算式.5.【2017课标II,理8】执行右面的程序框图,如果输入的a1,则输出的S()A.2 B.3 C.4 D.5【答案】B 【解析】试题分析:阅读流程图,初始化数值 a 1,k 1,S 0循环结果执行如下:第一次: S 0 1 1,a 1,k 2 ;第二次: S 1 21,a1,k 3 ;第三次: S 13 2,a 1,k4 ;第四次: S 2 4 2,a 1,k 5 ;第五次: S 2 5 3,a 1,k6 ;第六次: S36 3,a1,k7 ;结束循环,输出 S 3 。
2018年全国各地高考数学试题及解答分类汇编大全(14算法初步、框图)

2018年全国各地高考数学试题及解答分类汇编大全(14算法初步、框图一、选择题1.【答案】B【解析】初始化数值 k =1 , s =1 循环结果执行如下:11 1第一次:s =1 ' -1, k =2 , k =2 _3不成立;2 21 2 1 5第二次:s=—+(<2'-, k =3 , k=3£3 成立,2 3 6 循环结束,输出s = 5,故选B .62 (2018天津文、理)阅读如图所示的程序框图,运行 相应的程序,若输入 N 的值为20,则输出T 的值为()(A ) 1( B ) 2 (C ) 3(D ) 44.【答案】B【解析】结合流程图运行程序如下:首先初始化数据: N =20 , i =2 , T =0 ,N=2° =10,结果为整数,执行 T 二T • 1 =1 , i =i • 1 =3 , i 2此时不满足i _5 ;N 20 N二20,结果不为整数,执行i 日,1 =4,此时不满足i 一5 ; i 3N二20=5,结果为整数,执行T 二T V =2 , i =i ・1 =5 , i 4此时满足i _5 ;跳出循环,输出T =2 .故选B .1 . (2018北京文、理) 执行如图所示的程序框图,输出的s 值为( )15 7 7 A.-B.—C.—D.— 26 6 12T=Oj= j 4 1i则在空白框中应填入 A . i =i 1 C . i =i 33.【答案】B11 +— — +一 八+ —— 3 4 99 100先对奇数项累加,偶数项累加,最后再相减. 因此在空白框中应填入i =i ,选B .1 . (2018江苏)一个算法的伪代码如图所示,执行此算法,最后输出的 S 的值为 ▲.r----------------------------------------------- 1"I:|I門::While /<6: :I 十 2:;S —2S; :End While ;| Print S\…诵了軾…1.【答案】8【解析】由伪代码可得1=3 , S=2 ; 1=5, S=4 ; 1=7, S=8;因为7 6,所以结束循环,输出S =8 .三、解答题3. (2018全国新课标n 文、理)为计算 1 1 11 1S =1 一丄•1 一丄 1-,设计了如图的程序框图,2 3 499 100填空【解析】由S =1得程序框图。
专题04 算法初步-2018年高考数学(理)母题题源系列(江苏专版)(解析版)

【母题原题1】【2018江苏,理4】一个算法的伪代码如图所示,执行此算法,最后输出的S 的值为 ▲ .点睛:本题考查伪代码,考查考生的读图能力,难度较小.【母题原题2】【2017江苏,理4】如图是一个算法流程图,若输入x 的值为116,则输出的y 的值是 ▲ .【答案】2-(第4题)【解析】由题意212log 216y =+=-,故答案为-2. 【考点】循环结构流程图 【名师点睛】算法与流程图的考查,侧重于对流程图循环结构的考查.先明晰算法及流程图的相关概念,包括选择结构、循环结构、伪代码,其次要重视循环起点条件、循环次数、循环终止条件,更要通过循环规律,明确流程图研究的数学问题,是求和还是求项.【母题原题3】【2016江苏,理6】如图是一个算法的流程图,则输出的a 的值是 ▲ .【答案】9【解析】试题分析:第一次循环:5,7a b ==,第二次循环:9,5a b ==,此时a b >,循环结束,输出的a 的值是9,故答案应填:9【考点】循环结构流程图【命题意图】 高考对本部分内容的考查以能力为主,重点考查循环结构.【命题规律】程序框图中的条件分支结构及循环结构是高考对算法考查的主要内容,常与函数求值、方程求解、不等式求解、数列求和、统计量计算等问题交汇命题;给出程序框图的全部或部分,读出其功能,执行该程序框图并求输出结果及补齐框图是高考热点.【答题模板】解答本类题目,以2018年试题为例,一般考虑如下两步:第一步:读懂流程图含义.第二步:根据题意求和或求项.【方法总结】循环结构的常考类型及解题思路(1)确定循环次数:分析进入或退出循环体的条件,确定循环次数.(2)完善程序框图:结合初始条件和输出结果,分析控制循环的变量应满足的条件或累加、累乘的变量的表达式.(3)辨析循环功能:执行程序若干次,即可判断.1.【江苏省盐城中学2018届高三全仿真模拟检测数学试题】根据如下图所示的伪代码,当输入的值为3时,输出的值为___________.【答案】9【解析】分析:分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:该程序的作用是累加,当不满足条件时退出循环,得到S的值即可.点睛:解决算法语句有三个步骤:首先通读全部语句,把它翻译成数学问题;其次领悟该语句的功能;最后根据语句的功能运行程序,解决问题.2.【江苏省苏州市2018届高三调研测试(三)数学试题】如图是一个算法的流程图,则输出的的值为__________.【答案】7【解析】分析:直接利用程序框图的循环结构求出结果.解析:在执行循环前:k=1,S=1.执行第一次循环时:S=1,k=3.执行第二次循环时:S=3,k=5.执行第三次循环时:S=15,k=7.由于S>10,输出k=7.故答案为:7.点睛:(1)条件结构中条件的判断关键是明确条件结构的功能,然后根据“是”的分支成立的条件进行判断;(2)对条件结构,无论判断框中的条件是否成立,都只能执行两个分支中的一个,不能同时执行两个分支.3.【江苏省盐城中学2018届高三考前热身2数学试卷】执行如图所示的流程图,则输出的值为____.【答案】19.点睛:本题考查了程序框图的应用问题,解题时应模拟程序框图的运行过程,以便得出正确的结论,是基础题.4.【江苏省南京师大附中2018届高三高考考前模拟考试数学试题】如图是一个算法的流程图,则输出的n 的值是______.【答案】4点睛:考查本题考查程序框图的理解和运算.需要对程序框图进行若干次执行运算,当满足跳出循环条件时输出此时n值,属基础题5.【江苏省扬州树人学校2018届高三模拟考试(四)数学试题】运行如图所示的算法流程图,输出的的值为__________.【答案】9.【解析】分析:逐次运行程序框图中的程序可得输出结果.详解:依次运行程序框图中的程序,可得①,不满足条件,继续运行;②,不满足条件,继续运行;③,不满足条件,继续运行;④,满足条件,输出9.点睛:判断程序框图的输出结果时,一般采用的方法是依次运行框图给出的程序,逐步得到输出结果即可。
2018届高考数学一轮复习精选试题算法初步与框图(解答题) Word版含答案

算法初步与框图
解答题(本大题共个小题,共分,解答应写出文字说明,证明过程或演算步骤)
.铁路托运行李,从甲地到乙地,规定每张火车票托运行李不超过公斤时,每公斤元,超过公斤时,超过部分按每公斤元计算,(不足公斤时按公斤计费),试设计一个计算某人坐火车托运行李所需费用的算法,要求画出框图,并用基本语句写出算法。
(提示:()表示取不大于的最大整数,如(),())
【答案】设此人行李重量为公斤,所需费用为(元).
输入
<
()
*
*((()
()
*
*((()
输出
.画出解不等式>(≠)的程序框图.
【答案】
.有一个光滑斜面与水平桌面成角,设有一质点在时,从斜面的顶点处开始由静止状态自由
释放,如下图所示。
如果忽略摩擦力,斜面的长度,。
求
时质点的速度。
【答案】从物理学知识知道,质点在斜面上运动时,它的加速度,当在水平面上运动时,速度为常数,且保持它在点时的速度。
从点到点的速度可由公式求出,到点时的速度为。
解题的过程是这样的:
按公式,求出当、、、…时的速度,每求出一个对应于的值后,即将与相比
较,如果,表示质点还未到达点,使再增加,再求下一个值时的值,直到时,此时
表示已越过点,此后的速度始终等于的值。
流程图如下:。
【课标通用】2018届高考数学(理)一轮课件:40-算法初步(含答案)

考点94
考点95
试做真题
高手必备 萃取高招 对点精练
3.(2017课标Ⅲ,理7)执行下面的程序框图,为使输出S的值小于91,则 输入的正整数N的最小值为( ) A.5 B.4 C.3 D.2
考点94
考点95
试做真题
高手必备 萃取高招 对点精练
【答案】 D
程序运行过程如下表所示:
S 初始状态 第 1 次循环结束 第 2 次循环结束 0 100 90 M 100 -10 1 t 1 2 3
考点94
考点95
试做真题
高手必备 萃取高招 对点精练
6.(2015课标Ⅱ,理8)下边程序框图的算法思路源于我国古代数学名 著《九章算术》中的“更相减损术”.执行该程序框图,若输入的a,b 分别为14,18,则输出的a=( )
A.0 B.2 C.4 D.14 【答案】 B 由程序框图,得(14,18)→(14,4)→(10,4)→(6,4)→(2,4) →(2,2),则输出的a=2.
考点95
试做真题
高手必备 萃取高招 对点精练
2.(2017课标Ⅱ,理8)执行下面的程序框图,如果输入的a=-1,则输出 的S=( ) A.2 B.3 C.4 D.5 【答案】 B 程序框图运行如下: a=-1,S=0,K=1,进入循环, S=0+(-1)×1=-1,a=1,K=2; S=-1+1×2=1,a=-1,K=3; S=1+(-1)×3=-2,a=1,K=4; S=-2+1×4=2,a=-1,K=5; S=2+(-1)×5=-3,a=1,K=6; S=-3+1×6=3,a=-1,K=7, 此时退出循环,输出S=3.故选B.
此时S=90<91首次满足条件,程序需在t=3时跳出循环,即N=2为 满足条件的最小值,故选D.
2018高考数学(文)分类汇编 算法初步 全国通用 Word版含解析【 高考】

第十一章 算法初步题型132 条件分支结构型算法问题2014年1.(2014四川文6)执行如图所示的程序框图,如果输入的,x y ∈R ,那么输出的S 的最大值为( ).A. B. C. D.2015年1.(2015福建文4)阅读如图所示的程序框图,运行相应的程序.若输入x 的值为1,则输出y 的值为( ).A .2 B.7 C.8 D .1281. 解析 由题意得,该程序表示分段函数2,29,2x x y x x ⎧=⎨-<⎩…,则()1918f =-=.故选C .2017年1.(2017山东卷文6)执行右侧的程序框图,当输入的的值为4时,输出的y 的值为2,则空白判断框中的条件可能为( ). A.3?x > B.4?x > C.4?x … D. 5?x …1. 解析 解法一:易知4x =不满足判断框中的条件,只有选输入x 结束输出y x ≥2?否S S开始开始结束结束开始2 ?项B 符合.故选B.解法二:输入为4,要想输出y 为2,则程序经过2log 42y ==,故判断框内填4x >.故选B.2.(2017江苏卷17)如图所示是一个算法流程图,若输入的值为116,则输出y = .2.解析 由1116x =<,得42212log 2log 2216y -=+=+=-.题型133 循环结构型算法问题2013年1. (2013安徽文3)如图所示,程序据图(算法流程图)的输出结果为( ).A. 34 B. 16 C. 1112D.25242. (2013天津文3) 阅读右边的程序框图, 运行相应的程序, 则输出n = ( ).A. B. C. D.3.(2013广东文5)执行如图1所示的程序框图,若输入的值为,则输入s =( ). A .B .a 1 ?开始结束结束开始C .D .5. (2013山东文6)执行两次右图所示的程序框图,若第一次输入的的值为 1.2-,第二次 输入的的值为1.2,则第一次,第二次输出的的值分别为( ).A. 0.2,0.2B.0.2,0.8C. 0.8,0.2D. 0.8,0.86.(2013福建文8) 阅读如图所示的程序框图,运行相应的程序,如果输入某个正整数后,输出的()10,20S ∈,那么的值为( ). A . B. C. D.7. (2013辽宁文8)执行如图所示的程序框图,若输入的8n =,则输出的S =( ).A. 49B. 67 C. 89 D. 10118. (2013重庆文5)执行如图所示的程序框图,则输出的的值是( )B = B i开始结束开始结束结束开始A. B. C. D.9. (2013湖南文12)执行如图所示的程序框图,如果输入1,2,a b ==则输出的值为 .10.(2013湖北文13)阅读如图所示的程序框图,运行相应的程序. 若输入m 的值为,则输出的结果i = .11. (2013浙江14)某程序框图如图所示,则该程序运行后输出的S = _________.2014年 1. (2014安徽文4)如图所示,程序框图(算法流程图)的输出结果是( ). A.34 B.55 C.78 D.89否是结束输出S k =k +1S=S+2kk <3?k =0,S =0开始2.(2014北京文4)执行如图所示的程序框图,输出的S 值为( ). A. B. C.7 D.153.(2014福建文4)阅读如图所示的程序框图,运行相应的程序,输出的n 的值为 ( )A. B.2 C. D. 44.(2014重庆文5) 执行如图所示的程序框图,则输出s 的值为( ).A.10B.17C.19D.36 5.(2014江西文8)阅读如图所示程序框图,运行相应的程序,则程序运行后输出的结果为( )A.7B.9C.10D.116.(2014陕西文4)根据如图所示框图,对大于的整数n ,输出的数列的通项公式是( ). A.2n a n = B.()21n a n =- C.2n n a = D.12n n a -=7.(2014湖南文7)执行如图所示的程序框图,如果输入的[]2,2t ∈-,则输出的S 属于( ).A.[]6,2--B.[]5,1--C.[]4,5-D.[]3,6-8.(2014新课标Ⅰ文9)执行如图所示的程序框图,若输入的,,a b k 分别为1,2,3,则输出的M =( ) A.203B.72C.165D.1589.(2014新课标Ⅱ文8)执行如图所示程序框图,如果输入的,x t 均为2,则输出的S =( ) A.4 B. C. D.710.(2014江苏3)如图所示是一个算法流程图,则输出的n 的值是 .11. (2014山东文11)执行如图所示的程序框图,若输入的的值为,则输出的的值为 . 12.(2014天津文11)阅读如图所示的框图,运行相应的程序,输出S 的值为________.13.(2014湖北文14)阅读如图所示的程序框图,运行相应的程序,若输入的值为,则输出S 的值为 .14.(2014辽宁文13)执行如图所示的程序框图,若输入3n =,则输出T = .当输入50时,则该程序15.(2014浙江文13)若某程序框图如图所示,运行后输出的结果i = __________.2015年输出的k =( ).1.(2015北京文5)执行如果所示的程序框图,A.3B. 4C. 5D. 6S=0,n=3输出Sn=n-1是第14题图否1题 2题 1.解析 执行程序框图,13322a =⨯=,1k =,3124a =<−−→否313224a =⨯=,2k =,3144a =<−−→否 313428a =⨯=,3k =,3184a =<−−→否3138216a =⨯=,4k =,31164a =<−−→是输出4k =.故选B.2.(2015湖南文5)执行如图所示的程序框图,如果输入3n =,则输出的S =( ).A.67 B.37 C.89 D.492.解析 由题意,输出的S 为数列()()12121n n ⎧⎫⎪⎪⎨⎬-+⎪⎪⎩⎭的前项和,即()()333111111212122121i i S i i i i ==⎛⎫==- ⎪-+-+⎝⎭∑∑1131277⎛⎫=-= ⎪⎝⎭.故选B . 3.(2015山东文11)执行如图所示的程序框图,若输入的的值为,则输出的y 的值是 .第3题图第4题图3.解析 由程序框图可知,第一次循环为,12x =<,112x =+=; 第二次循环为,22x =?,此时循环结束.则232113y =⨯+=,输出13y =. 4.(2015四川文6)执行如图所示的程序框图,输出S 的值为( ). A. B. C. 12- D. 124.解析 由程序框图可知,第一次循环为:24k =…;第二次循环为:34k =…;第三次循环为:44k =…;第四次循环为: 54k =>>.此时循环结束,5π1sin 62S ==.故输出S 的值为12.故选D. 2016年1.(2016江苏6)如图所示是一个算法的流程图,则输出a 的值是 .第1题图第2题图S=sink π6输出S结束是1.解析 ,a b2.(2016山东文11)执行如图的程序框图,若输入的值为,则输出的的值为_______. 2. 解析 按照程序框图运行程序:3,1,0n i S ===,1S =,循环,2,1i S ==,循环,3,11i S ===,退出循环,输出1S =.3.(2016北京文3)执行如图所示的程序框图,输出的值为( ). A. B. C. 27 D. 363. B 解析 开始0,0k s ==;第一次循环0,1s k ==;第二次循环1,2s k ==;第三次循环9,3s k ==,条件判断为“是”,跳出循环.所以输出的值为. 故选B.4.(2016全国丙文8)执行右面的程序框图,如果输入的4a =,6b =,那么输出的n =( ). A.3 B.4 C.5 D.64. B 解析 根据程序框图,4,6,0,0a b n s ====,执行循环: 第一次:2,4,6,6,1a b a s n =====;第二次:2,6,4,10,2a b a s n =-====;第三次:2,4,6,16,3a b a s n =====; 第四次:2,6,4,20,4a b a s n =-====;此时满足判断条件16s >,退出循环,输4n=.故选B.2017年1.(2017全国1文10)如图所示的程序框图是为了求出满足321000n n ->别填入( ).A.1000?A >和1n n =+B.1000?A >和2n n =+C.1000?A …和1n n =+D.1000?A …和2n n =+1. 10.解析 由题意选择321000n n ->,则判定框内填1000?A …,由因为选择的为偶数,所 以矩形框内填2n n =+.故选D.2.(2017全国2卷文10)执行如图所示的程序框图,如果输入的1a =-,则输出的S =( ). A .2B .3C .4D .52.解析 阅读程序框图,初始化数值1,1,0a K S =-==. 循环结果执行如下:第一次:011,1,2S a K =-=-==;第二次:121,1,3S a K =-+==-=; 第三次:132,1,4S a K =-=-==;第四次:242,1,5S a K =-+==-=; 第五次:253,1,6S a K =-=-==;第六次:363,1,7S a K =-+==-=. 结束循环,输出3S = .故选B.3.(2017全国3卷文科8)8.执行如图所示的程序框图,为使输出S 的值小于91,则输入的正整数N 的最小值为( ). A .5B .4C .3D .23.解析 第一次循环,0100S =+,10M =-,2t =;第二次循环,90S =,1M =,3t =,2N …符合,3N …不符合.故选D.评注 程序框图问题,中低难度,两次循环即可出结果,关键在于对于第一次循环中t 的值与条件的判定,易错点在于学生会忽略第一次循环中的变量必须满足条件!4.(2017北京卷文3)执行如图所示的程序框图,输出的值为( ).A.2B.32C.53D.854.解析 执行程序,0k =,1s =,3k <,成立;1k =,221s ==,3k <,成立; 2k =,21322s +==,3k <,成立; 3k =,3152332s +==,3k <,不成立,输出53s =. 故选C.题型134 含有多种结构的算法问题2013年1.(2013江西文7) 阅读如下程序框图,如果输出i=4,那么空白的判断框中应填入的条件是( ).A.8S <B. 9S <C.10S < D.11S <2016年1.(2016天津文11)阅读如图所示的程序框图,运行相应的程序,则输出S 的值为_______.1. 4 解析 第一次循环:82S n ==,;第二次循环:2,3;S n ==第三次循环:4,4S n ==. 结束循环,输出4.S =2017年1.(2017天津卷文4)阅读如图所示的程序框图,运行相应的程序,若输入N 的值为19,则输出N 的值为( ).A.0B.1C.2D.31.解析 输入N 的值为19,19不能被3整除,执行19118N =-=,“183N =…”不成立,进入循环.18能被3整除,执行1863N ==,“63N =…”不成立,进入循环.6能被3整除,执行623N ==,“23N =…”成立,输出2N =.故选C . 题型135 算法案例2015年1.(2015新课标2文)如图程序框图的算法思路源于我国古代数学名著《九章算术》中“更相减损术”.执行该程序框图,若输入的、分别为14、18,则输出的=a ( ).A. B. C. D. 141.解析 根据程序框图可知,在执行程序过程中,,的值依 次为14a =,18b =;14a =,4b =;10a =,4b =;6a =,4b =;2a =,4b =;2a =,2b =.到此有2a b ==,程序运行结束,输出a 的值为2.故选B .2016年1.(2016全国甲文9)中国古代有计算多项式值的秦九韶算法,如图是实现该算法的程序框图.执行该程序框图,若输入的2x =,2n =,依次输入的a 为2,2,,则输出的s =( ).A.7B.12C.17D.341. C 解析 第一步:0222S =⋅+=,1k =;第二步:2226S =⋅+=,2k =;第三步:26517S =⋅+=,3k =,输出17S =,故选C. 2.(2016四川文8)秦九韶是我国南宋时期的数学家,普州(现四川省安岳县)人,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法.如图所示的程序框图给出了利用秦九韶算法求多项式值的一个实例,若输入n ,x 的值分别为,2,则输出的值为( ).A.35B.20C.18D.2. C 解析程序运行如下:321i201224i10厖,,,n x v v==→==→=⨯+==→…结束循环,,,42190092018i10.=⨯+==→=⨯+==-<v i vv=故选C.输出18.。
2018年高考数学理科试题汇编-算法初步 精品
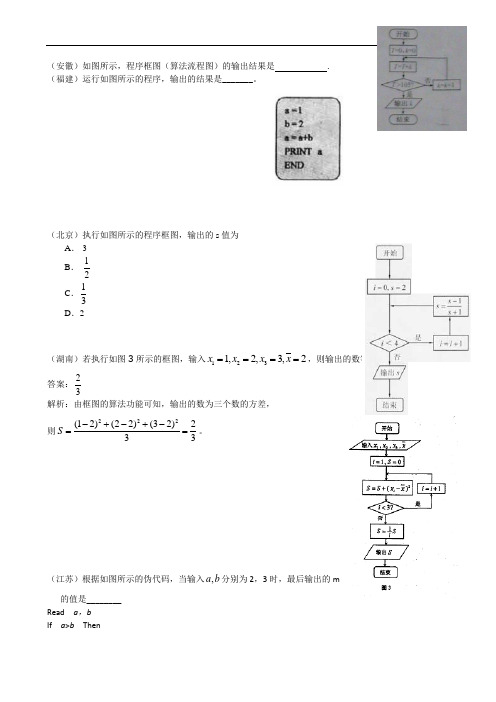
(安徽)如图所示,程序框图(算法流程图)的输出结果是 .(福建)运行如图所示的程序,输出的结果是_______。
(北京)执行如图所示的程序框图,输出的s 值为A .-3B .-12C .13D .2(湖南)若执行如图3所示的框图,输入1231,2,3,2x x x x ====,则输出的数等于 。
答案:23解析:由框图的算法功能可知,输出的数为三个数的方差,则222(12)(22)(32)233S -+-+-==。
(江苏)根据如图所示的伪代码,当输入b a ,分别为2,3时,最后输出的m的值是________Read a ,bIf a >b Thenm←aElsem←bEnd IfPrint m(辽宁)执行右面的程序框图,如果输入的n是4,则输出的P是A.8B.5C.3D.2(江西)下图是某算法程序框图,则程序运行后输出的结果是__________.10 解析:s=0,n=1;带入到解析式当中,s=0+(-1)+1=0,n=2;s=0+1+2=3, n=3;S=3+(-1)+3=5, n=4;S=5+1+4=10,此时s>9,输出。
(PS:此题实质是2018江苏理科卷第7题得翻版,同时在我们寒假题海班,理科讲义的第200页的第6题也讲过相似的。
所以童鞋们再次遇到,应该也是灰常熟悉的。
并且框图本来就是你们的拿手菜,所以最对也不觉奇怪。
)(全国新)执行右面的程序框图,如果输入的N是6,那么输出的p是(A)120 (B)720 (C)1440 (D)5040(陕西)右图中,1x ,2x ,3x 为某次考试三个评阅人对同一道题的独立评分,P 为该题的最终得分。
当1x =6,2x =9,p=8.5时,3x 等于 ( )(A)11(B)10(C)8(D)7(天津)阅读右边的程序框图,运行相应的程序,则输出i 的值为A .3B .4C .5D .6(浙江)若某程序框图如图所示,则该程序运行后输出的k 的值是 。
【精品】2018年全国高考数学试题及解答分类★★★★★(14 算法初步、框图)

【精品】2018年全国高考数学试题及解答分类★★★★★( 14 算法初步、框图 )一、选择题1.(2018北京文、理)执行如图所示的程序框图,输出的s 值为( )A .12B .56C .76D .7121.【答案】B【解析】初始化数值1k =,1s = 循环结果执行如下:第一次:()1111122s =+-⋅=,2k =,23k =≥不成立;第二次:()21151236s =+-⋅=,3k =,33k =≥成立,循环结束,输出56s =,故选B .2 (2018天津文、理)阅读如图所示的程序框图,运行相应的程序,若输入N 的值为20,则输出T 的值为( )(A )1 (B )2 (C )3 (D )4 4.【答案】B【解析】结合流程图运行程序如下:首先初始化数据:20N =,2i =,0T =, 20102N i ==,结果为整数,执行11T T =+=,13i i =+=, 此时不满足5i ≥; 203N i =,结果不为整数,执行14i i =+=,此时不满足5i ≥; 2054N i ==,结果为整数,执行12T T =+=,15i i =+=, 此时满足5i ≥;跳出循环,输出2T =.故选B .3.(2018全国新课标Ⅱ文、理)为计算11111123499100S =-+-++-,设计了如图的程序框图, 则在空白框中应填入( )A .1i i =+B .2i i =+C .3i i =+D .4i i =+ 3.【答案】B【解析】由11111123499100S =-+-+⋯+-得程序框图先对奇数项累加,偶数项累加,最后再相减. 因此在空白框中应填入2i i =+,选B .二、填空1.(2018江苏)一个算法的伪代码如图所示,执行此算法,最后输出的S 的值为 ▲ .1.【答案】8【解析】由伪代码可得3I =,2S =;5I =,4S =;7I =,8S =;因为76>,所以结束循环,输出8S =.三、解答题。
2018年高考理科数学算法初步与框图100题(含答案解析)

2018年高考理科数学算法初步与框图100题(含答案解析)1.执行如图所示的程序框图,则输出的 a=()A.1 B.﹣1 C.﹣4 D.2.阅读下边的程序框图,运行相应的程序,则输出v的值为()A.4 B.5 C.6 D.73.《九章算术》中的“两鼠穿墙”问题为“今有垣厚五尺,两鼠对穿,大鼠日一尺,小鼠也日一尺,大鼠日自倍,小鼠日自半,问何日相逢?”可用如图所示的程序框图解决此类问题.现执行该程序框图,输入的d的值为33,则输出的i的值为(A)4 (B)5 (C)6 (D)74.当向量(2,2)==-,(1,0)a cb=时,执行如图所示的程序框图,输出的i值为().A.5B.4C.3D.25.阅读如图所示的程序框图,运行相应的程序,输出的结果是().A .2B .4C .8D .166.已知如图所示的程序框图的输入值[]1,4x ∈-,则输出y 值的取值范围是( )A .[]0,2B .[]1,2-C .[]1,15-D .[]2,157.执行如图所示的程序框图,若输入的x 值为1,则输出的k 值为( ).A.3B.4C.5 D.68.执行如图所示的程序框图,输出的s值为().A.2B.32C.53D.8 59.已知某程序框图如图所示,则执行该程序后输出的结果是()A .2B .21C .﹣1D .﹣2 10.执行如图的程序框图,若输出的,则输入的整数p 的值为( )A .6B .5C .4D .3 11.执行如图所示的程序框图,输出的k 值是( )A.5 B.3 C.9 D.712.执行如图所示的程序框图,则输出的结果为()A.4 B.5 C.6 D.713.程序框图如图所示,若输入值t∈(0,3),则输出值S的取值范围是()A.(0,4)B.(0,4] C.[0,9] D.(0,3)14.如图,该程序运行后输出的结果是()A.6 B.8 C.10 D.1215.如图程序框图所示的算法来自于《九章算术》,若输入a的值为16,b的值为24,则执行该程序框图的结果为()A.6 B.7 C.8 D.916.执行如图所示的程序框图,如果输入a=3,b=2,那么输出a的值为()A.16 B.256 C.log3626 D.656117.已知某算法的程序框图如图所示,则该算法的功能是()A.求首项为1,公差为2的等差数列前2017项和B.求首项为1,公差为2的等差数列前2018项和C.求首项为1,公差为4的等差数列前1009项和D.求首项为1,公差为4的等差数列前1010项和18.《九章算术》卷五商功中有如下问题:今有刍甍,下广三丈,袤四丈,上袤二丈,无广,高一丈,问积几何.刍甍:底面为矩形的屋脊状的几何体(网格纸中粗线部分为其三视图,设网格纸上每个小正方形的边长为1丈),那么该刍甍的体积为( )A .4立方丈B .5立方丈C . 6立方丈D .12立方丈 19.某一算法程序框图如图所示,则输出的S 的值为( )A .23B . 23 C . 3D .0 20.阅读如图的程序框图,运行相应的程序,则输出的T 的值为( )A.57 B.120 C.183 D.24721.中国古代有计算多项式值的秦九韶算法,如图是实现该算法的程序框图.执行该程序框图,若输入的x=2,n=2,依次输入的a为2,2,5,则输出的s=()A.7 B.12 C.17 D.3422.阅读如图所示的程序框图,则该算法的功能是()A.计算数列{2n﹣1}前5项的和B.计算数列{2n﹣1}前6项的和C.计算数列{2n﹣1}前5项的和D.计算数列{2n﹣1}前6项的和23.某程序框图如图所示,若输入的n=10,则输出结果为()A. B.C. D.24.执行如图所示的算法,则输出的结果是()A .1B .C .D .225.执行如图所示的程序,则输出的i 的值为( )A .2B .3C .4D .526.执行右边的程序框图,若p=0.8,则输出的n=( )A.3 B.4 C.5 D.627.执行如图所示的程序框图,如果输入的N是5,那么输出的p是()A.120 B.720 C.1440 D.504028.在如下程序框图中,任意输入一次x(0≤x≤1)与y(0≤y≤1),则能输出“恭喜中奖!”的概率为()A.B.C.D.29.在如图所示的程序框图中,若函数f(x)=,则输出的结果是()A.﹣2 B.0.0625 C.0.25 D.430.若[x]表示不超过x的最大整数,执行如图所示的程序框图,则输出的S值为()A.4 B.5 C.7 D.931.某程序框图如图所示,若输入输出的n分别为3和1,则在图中空白的判断框中应填入的条件可以为()A.i≥7?B.i>7?C.i≥6?D.i<6?32.执行如图所示的程序框图,如果输入的N是10,那么输出的S是()A.2 B.﹣1 C.﹣1 D.2﹣133.执行如图所示的程序框图,输出的S值为()A.1 B.C. D.34.根据如图所示程序框图,若输入m=42,n=30,则输出m的值为()A.0 B.3 C.6 D.1235.宋元时期数学名著《算学启蒙》中有关于“松竹并生”的问题:松长五尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等.下图是源于其思想的一个程序框图,若输入的a,b 分别为5,2,则输出的n=()A.2 B.3 C.4 D.536.执行图题实数的程序框图,如果输入a=2,b=2,那么输出的a值为()A.44 B.16 C.256 D.log31637.如图所示,输入x=4程序框图(算法流程图)的输出结果是()A.3 B.4 C.5 D.838.执行如图的程序框图,则输出的S值为()A.33 B.215 C.343 D.102539.执行如图程序,输出S的值为()A.B.C.D.40.公元263年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形面积可无限逼近圆的面积,并创立了“割圆术”.利用“割圆术”刘徽得到了圆周率精确到小数点后面两位的近似值3.14,这就是著名的“徽率”.如果是利用刘徽的“割圆术”思想设计的一个程序框图,则输出n的值为()1.732≈,sin150.2588︒≈)︒≈,sin7.50.1305A.12 B.24 C.36 D.4841.执行如图的程序框图,若输出的结果是,则输入的a为()A.3 B.4 C.5 D.642.执行如图所示的程序框图(算法流程图),输出的结果是()A.9 B.121 C.130 D.1702143.如图所示的程序框图中,输出的B是()A. B.0 C.﹣D.﹣44.秦九韶是我国古代数学家的杰出代表之一,他的《数学九章》概括了宋元时期中国传统数学的主要成就.由他提出的一种多项式简化算法称为秦九韶算法:它是一种将n次多项式的求值问题转化为n个一次式的算法.即使在现代,利用计算机解决多项式的求值问题时,秦九韶算法依然是最优的算法.用秦九韶算法求多项式f(x)=4x5﹣x2+2,当x=3时的值时,需要进行的乘法运算和加法运算的次数分别为()A.4,2 B.5,2 C.5,3 D.6,245.运行如图所示的程序框图,输出的结果S=()A.14 B.30 C.62 D.12646.执行如图所示的程序框图,输出的k值为()A.3 B.4 C.5 D.647.从1,2,3,4,5,6,7,8中随机取出一个数为x,执行如图所示的程序框图,则输出的x不小于40的概率为()A.B.C.D.48.执行如图所示的程序框图,若输入三个数a=log36,b=log510,c=log714,则输出的结果为()A.log36 B.log510 C.log714 D.log2649.明朝数学家程大位将“孙子定理”(也称“中国剩余定理”)编成易于上口的《孙子歌诀》:三人同行七十稀,五树梅花廿一支,七子团圆正半月,除百零五便得知.已知正整数n被3除余2,被5除余3,被7除余4,求n的最小值.按此歌诀得算法如图,则输出n的结果为()A.53 B.54 C.158 D.26350.运行下面的程序,如果输入的n是6,那么输出的p是()A.120 B.720 C.1440 D.504051.执行如图所示的程序框图,若输出的结果是10,则判断框内m的取值范围是()A.(56,72] B.(72,90] C.(90,110] D.(56,90)52.算法如图,若输入m=210,n=119,则输出的n为()A.2 B.3 C.7 D.1153.执行如图所示的程序框图,若输入x=0,输出K的值为10,则判断框内可填入的条件是()A.x>50?B.x>90?C.x>100?D.x>200?54.宋元时期数学名著《算学启蒙》中有关于“松竹并生”的问题:松长五尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等.下图是源于其思想的一个程序框图,若输入的a,b 分别为5,2,则输出的n=()A.2 B.3 C.4 D.555.执行如图所示的程序框图,如果输入的m=168,n=112,则输出的k,m的值分别为()A.4,7 B.4,56 C.3,7 D.3,5656.执行如图所示的程序框图,若输入的a值为1,则输出的k值为()A.1 B.2 C.3 D.457.已知函数f(x)=ax3+x2在x=﹣1处取得极大值,记g(x)=.程序框图如图所示,若输出的结果S>,则判断框中可以填入的关于n的判断条件是()A.n≤2014?B.n≤2015?C.n>2014?D.n>2015?58.给出计算的值的一个程序框图如图,其中判断框内应填入的条件是()A.i>10 B.i<10 C.i>20 D.i<2059.定义[x]表示不超过x的最大整数,例如[2.11]=2,[﹣1.39]=﹣2,执行如下图所示的程序框图,则输出m的值为()A .319 B .853 C .6171D .8185 60. 秦九韶是我国南宋时期著名的数学家,普州(现四川省安岳县)人,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法.如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例,若输入x 的值为3,每次输入a 的值均为4,输出s 的值为484,则输入n 的值为( )A.6 B.5 C.4 D.361.秦九韶是我国南宋时期著名的数学家,普州(现四川省安岳县)人,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法.如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例,若输入x的值为3,每次输入a的值均为4,输出s的值为484,则输入n的值为()A.6 B.5 C.4 D.362.执行如图所示的程序框图,如果输出的S=,那么判断框内应填入的条件是()A.i<3 B.i<4 C.i<5 D.i<663.若如图框图所给的程序运行结果为S=41,则图中的判断框(1)中应填入的是()A.i>6?B.i≤6?C.i>5?D.i<5?64.如图所示,程序框图的输出值S=()A.21 B.15 C.28 D.﹣2165.若正整数N除以正整数m后的余数为n,则记为N=n(mod m),例如10=2(mod 4),下面程序框图的算法源于我国古代闻名中外的《中国剩余定理》.执行该程序框图,则输出的i等于()A.4 B.8 C.16 D.3266.如图所给的程序运行结果为S=35,那么判断框中应填入的关于k的条件是()A.k=7 B.k≤6 C.k<6 D.k>667.执行如图所示的程序框图,如果运行结果为5040,那么判断框中应填入()A.k<6?B.k<7?C.k>6?D.k>7?68.执行如图所示的程序框图,若输入a,b,c分别为1,2,0.3,则输出的结果为()A.1.125 B.1.25 C.1.3125 D.1.37569.执行如图所示的程序框图,若输出的结果是6,则判断框内m的取值范围是()A.(30,42] B.(20,30) C.(20,30] D.(20,42)70.运行图中的程序框图,若输出的结果为57,则判断框内的条件应为()A.k>4?B.k≤5?C.k>3?D.k≤4?71.执行如图的程序框图,则输出K的值为()A.98 B.99 C.100 D.10172.如图所示的程序框图描述的为辗转相除法,若输入m=5280,n=1595,则输出的m=()A.2 B.55 C.110 D.49573.执行如图所示的程序框图,若输出的k=8,则输入的k为()A.0 B.1 C.2 D.374.如果执行如图所示的程序框图,则输出的数S不可能是()A.0.7 B.0.75 C.0.8 D.0.975.如果执行如图所示的程序框图,则输出的数S不可能是()A.0.7 B.0.75 C.0.8 D.0.976.执行如图的程序框图,若程序运行中输出的一组数是(x,﹣12),则x的值为()A.27 B.81 C.243 D.72977.执行如图所示的程序框图,若输入的a,b分别为36,28,则输出的a=()A .4B .8C .12D .2078. 执行如图所示的程序框图,若输入x 的值为1,输出n 的值为N ,则在区间[﹣1,4]上随机选取一个数M ,M≥N ﹣1的概率为( )A .51 B .52 C .53 D .54 79. 阅读如图所示的程序框图,运行相应的程序,则输出i 的值为( )A.4 B.6 C.8 D.1080.执行如图所示的程序框图,若x∈[a,b],y∈[0,4],则b﹣a的最小值为()A.2 B.3 C.4 D.581.阅读如图的程序框图,运行相应的程序,输出的结果是()A .3B .717C .37D .7382.如图所示的程序框图,输出S 的值是( )A .30B .10C .15D .2183.按照如图的程序框图执行,若输出结果为31,则M 处条件可以是( )A.k>32 B.k≥16 C.k≥32 D.k<1684.运行如图所示的程序框图,若输出的点恰有3次落在直线上y=x,则判断框中可填写的条件是()A.i>8 B.i>7 C.i>6 D.i>585.执行如图所示的程序框图,任意输入一次x(0≤x≤1)与y(0≤y≤1),则能输出数对(x,y)的概率为()A.B.C.D.86.如图程序框图的算法思路源于数学名著《几何原本》中的“辗转相除法”,执行该程序框图(图中“m MOD n”表示m除以n的余数),若输入的m,n分别为495,135,则输出的m=()A.0 B.5 C.45 D.9087.我国南宋数学家秦九韶(约公元1202﹣1261年)给出了求n(n∈N*)次多项式a n x n+a n﹣x n﹣1+…+a1x+a0,当x=x0时的值的一种简捷算法.该算法被后人命名为“秦九韶算法”,例1如,可将3次多项式改写为a3x3+a2x2+a1x+a0=((a3x+a2)x+a1)x+a0,然后进行求值.运行如图所示的程序框图,能求得多项式()的值.A.x4+x3+2x2+3x+4 B.x4+2x3+3x2+4x+5C.x3+x2+2x+3 D.x3+2x2+3x+488.根据如图所示的伪代码可知,输出的结果为.89.根据如图所示的伪代码,则输出S的值为.90.阅读下列程序框图,该程序输出的结果是.91.如图是一个算法的流程图,则输出的n的值是.92.阅读右侧程序框图,则输出的数据S为__________.93.执行如图所示的程序框图,输出的S值为.94.如图程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入a,b分别为225,135,则输出的a=.95.根据如图的伪代码,输出的结果T为.96.运行如图所示的流程图,则输出的结果S是.97.根据如图所示的伪代码,输出S的值为.98.阅读下列程序框图,该程序输出的结果是.99.设a是一个各位数字都不是0且没有重复数字的三位数,将组成a的3个数字按从小到大排成的三位数记为I(a),按从大到小排成的三位数记为D(a),(例如a=746,则I(a)=467,D(a)=764)阅读如右图所示的程序框图,运行相应的程序,任意输入一个a,输出的结果b=.100.已知关于x,y的二元一次方程组无解,则a= .答案1.C【考点】程序框图.【分析】模拟程序的运行,依次写出每次循环得到的b,a,i的值,观察a的取值规律,可得当i=40时不满足条件i<40,退出循环,输出a的值为﹣4.【解答】解:模拟程序的运行,可得i=1,a=﹣4满足条件i<40,执行循环体,b=﹣1,a=﹣1,i=2满足条件i<40,执行循环体,b=﹣,a=﹣,i=3满足条件i<40,执行循环体,b=﹣4,a=﹣4,i=4满足条件i<40,执行循环体,b=﹣1,a=﹣1,i=5…观察规律可知,a的取值周期为3,由于40=3×13+1,可得:满足条件i<40,执行循环体,b=﹣4,a=﹣4,i=40不满足条件i<40,退出循环,输出a的值为﹣4.故选:C.2.C【考点】程序框图.【分析】模拟程序的运行,依次写出每次循环得到的v,i的值,当i=﹣1时不满足条件i ≥0,退出循环,输出v的值为6.【解答】解:模拟程序的运行,可得n=2,a0=1,a1=2,a2=3,v=3,i=1满足条件i≥0,执行循环体,v=5,i=0满足条件i≥0,执行循环体,v=6,i=﹣1不满足条件i≥0,退出循环,输出v的值为6.故选:C.3.C【命题意图】本小题主要考查程序框图,数列求和等基础知识;考查学生的运算求解能力及数据处理能力;考查化归与转化思想、分类与整合思想;考查数学抽象和数学运算等.【试题简析】解法一:0,0,1,1i S x y ====开始执行,然后11,11,2,2i S x y ==+==⋅⋅⋅ 111115,(124816)(1)33,32,2481632i S x y ==+++++++++<==,再执行一行,然后输出6i = 解法二:本题要解决的问题是数列求和的问题,11211111,2,,2(2)22n n n a a a n --=+=+⋅⋅⋅=+≥ 1233n a a a ++⋅⋅⋅+≥,解得n 的最小值为6.【错选原因】错选A :可能把2x x =误当成2x x =来算;错选B :当执行到5i =时,11113224816S =++++,学生估值失误,误以为会达到33或按四舍五入得到.错选D :可能先执行了1i i =+后才输出.4.Bi 0=时, 22(2)28a c ⋅=-+=,i 1=时,(2)(1)226a c ⋅=-⨯-+⨯=, i 2=时,(2)0224a c ⋅=-⨯+⨯=,i 3=时,(2)1222a c ⋅=-⨯+⨯=,i 4=时,(2)2220a c ⋅=-⨯+⨯=,此时0a c ⋅=,所以输出i 4=.故选B .5.C2S =,1n =,1S =-,2n =,12S =,4n =, 2S =,8n =输出8n =.故选C .6.B7.B0k =,156x =+=继续,1k =,6511x =+=继续,,4=,21526x =+=停止,输出k 为4,故选B .8.C解:03k =<,继续,011k =+=,1121s +==,继续, 112k =+=,21322s +==,继续, 213k =+=,3152332s +==,停业. 故选C .输出s 为53. 9.B【考点】程序框图.【分析】分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知该程序的作用是利用循环计算变量a 的值并输出,依次写出每次循环得到的a ,i 的值,当i=11时,满足条件,计算即可得解.【解答】解:程序运行过程中,各变量的值如下表示:a i 是否继续循环循环前 2 1第一圈2 是第二圈﹣1 3 是第三圈 2 4 是…第9圈 2 10 是第10圈11 是故最后输出的a值为.故选:B .10.B【考点】程序框图.【分析】分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:该程序的作用是利用循环计算满足S=+++…+=的整数p的值,并输出,结合等比数列通项公式,可得答案.【解答】解:由程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:该程序的作用是利用循环计算满足S=+++…+=的整数p的值,∵+++…+=1﹣=,故==,故p=5.故选:B.11.A【考点】程序框图.【分析】模拟程序的运行,依次写出每次循环得到的k,a,b的值,可得当a=32,b=25时满足条件a>b,退出循环,输出k的值为5.【解答】解:模拟程序的运行,可得k=1,k=3,a=8,b=9不满足条件a>b,执行循环体,k=5,a=32,b=25满足条件a>b,退出循环,输出k的值为5.故选:A.12.D【考点】程序框图.【分析】根据已知中的程序框图可得,该程序的功能是计算并输出变量i的值,模拟程序的运行过程,可得答案.【解答】解:第1次执行循环后,S=2016,i=2,不满足退出循环的条件;第2次执行循环后,S=1008,i=3,不满足退出循环的条件;第3次执行循环后,S=336,i=4,不满足退出循环的条件;第4次执行循环后,S=84,i=5,不满足退出循环的条件;第5次执行循环后,S=16.8,i=6,不满足退出循环的条件;第6次执行循环后,S=2.8,i=7,满足退出循环的条件;故输出的i值为7,故选:D.13.B【考点】程序框图.【分析】模拟执行程序框图,可得程序框图的功能是计算并输出S=的值,分类讨论即可得解.【解答】解:由程序框图可知程序框图的功能是计算并输出S=的值,∴当t∈(0,1)时,0≤3t<3;当t∈[1,3)时,4t﹣t2=4﹣(t﹣2)2∈[3,4],∴综上得:0≤S≤4.故选:B.14.C【考点】程序框图.【分析】经过观察为当型循环结构,按照循环结构进行执行,当满足执行条件时跳出循环,输出结果即可.【解答】解:模拟程序的运行,可得A=12,s=0不满足条件A≤3,执行循环体,S=2,A=10不满足条件A≤3,执行循环体,S=4,A=8不满足条件A≤3,执行循环体,S=6,A=6不满足条件A≤3,执行循环体,S=8,A=4不满足条件A≤3,执行循环体,S=10,A=2满足条件A≤3,退出循环,输出S的值为10.故选:C.15.C【考点】程序框图.。
2018年高考数学分类汇编:算法初步

训练一:2018年高考数学新课标Ⅰ卷文科数学第8题理科第7题:为计算100
1
991...4131211-
++-+-=S ,设计了如图的程序框图,则在空白框中应填入( )
A.1+=i i
B.2+=i i
C.3+=i i
D.4+=i i
本题解答:)100
1
...4121()991...3111(1001991...4131211+++-+++=-++-+-
=S 。
i N N 1+=目的求和991...3111+++;11++
=i T T 目的求和100
1
...4121+++。
两个求和计数器i 都是公差为2的等差数列⇒循环中的计算步骤为2+=i i 。
训练二:2018年高考数学北京卷文科第3题理科第3题:执行如图所示的程序框图,输出的s 值为( ) A.
21 B.65 C.67 D.12
7
本题解答:如下表所示:
所以:输出6
5=
s 。
训练三:2018年高考数学天津卷文科第4题理科第3题:阅读如图所示的程序框图,运行相应的程序,若输入N 的值为20,则输出T 的值为( )
A.1
B.2
C.3
D.4 本题解答:如下表所示:
所以:输出的2=T 。
训练四:2018年高考数学江苏卷第4题:一个算法的伪代码如图所示,执行此算法,最后输出的S 的值为 。
1←I
1←S
While 6<I 2+←I I S S 2←
End While int Pr S 本题解答:如下表所示:
所以:输出的8=S 。
