《系统工程》第四版习题解答课件
《系统工程》第四版习题解答

V
V
A
A
A
V
V
A
V
V
V
A
V
V
(A)
A
V
(V)
V
V
V
A
V
(V)
V
绘制多级递阶有向图:
23.已知下面的系统可适矩阵,分别用规范方法与实用方法建立其递阶结构模型。
(1) (2)
解:(1)规范方法:
①区域划分
1
1,5,7
1
1
2
2
2,4
2
2
3
3,5,6
3,6
3,6
4
2,4
4
4
5
5
1,3,5,6,7
5
5
6
3,5,6
系统工程第四版习题解答
第三章
21.给定描述系统基本结构的有向图,如图3-16a、b所示。要求:
(1)写出系统要素集合 及 上的二元关系集合 。
(2)建立邻接矩阵 、可达矩阵 及缩减矩阵 。
解:(2)3-16a:
规范方法:
, ,
①区域划分
1
1,2,3,4,5
1
1
2
2,3,4
1,2,5
2
3
3,4
1,2,3,5
。
②级位划分
要素集合
1
2
3
4
5
6
7
8
1
1,4
1,3
1
3
1,3,4
3
3
4
4
1,3,4,5,6,7
4
4
5
4,5
5,6,7
5
6
4,5,6,7
《系统工程》第四版习题解答

系统工程第四版习题解答第三章 系统模型与模型化21. 给定描述系统基本结构的有向图,如图3-16a 、b 所示。
要求: (1)写出系统要素集合S 及S 上的二元关系集合b R 。
(2)建立邻接矩阵A 、可达矩阵M 及缩减矩阵M '。
解:(2)3-16a : 规范方法:⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=0111000000010000010010010A ,⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=1111001000011000111011111M ,M M ='}5,4,3,2,1{)(==∏P S 。
⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=11110010000110001110111115432154321)(P M}1{},5{},2{},3{},4{,,,,)(54321==∏L L L L L P⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=11111011110011100011000011523415234)(54321L L L L L L M ③提取骨架矩阵⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=''1100011000011000011000011523415234)(54321L L L L L L M ⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=-''='01000001000001000001000001523415234)(54321L L L L L I L M A ④绘制多级递阶有向图实用方法:缩减矩阵⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=='11110010000110001110111115432154321M M⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡='11111011110011100011000011523415234)(54321L L L L L L M3-16b :规范方法:⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=000000000011100010000000001000010100A ,⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=100000111111101010000100101010111111M①区域划分φ≠=⋂=⋂}5,1{}6,5,4,2,1{}5,3,1{)()(63S A S A所以系统无法划分为两个或两个以上相互独立的区域,即}6,5,4,3,2,1{)(==∏P S 。
系统工程第四版第三章课后题答案

系统工程第三章作业02613102 徐晗P80.21. 给定描述系统基本结构的有向图,如图3-16a 、b 所示。
要求:(1)写出系统要素集合S 及S 上的二元关系集合Rb 。
(2)建立邻接矩阵A 、可达矩阵M 及缩减矩阵M ’。
解:(a) (1) 51234{S ,,,,}S S S S S =55551212334234{(S ,),(,),(,),(,),(,),(,),(,S )}b R S S S S S S S S S S S S =(2)010********00100000001110A ⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦=1100101100001100001001111A I ⎡⎤⎢⎥⎢⎥⎢⎥+=⎢⎥⎢⎥⎢⎥⎣⎦231111101110()()001100001001110A I A I M ⎡⎤⎢⎥⎢⎥⎢⎥+==+=⎢⎥⎢⎥⎢⎥⎣⎦'M M =(b)(1){1,2,3,4,5,6}S ={(1,3),(1,5),(2,4),(4,2),(4,6),(5,2),(5,1)}b R =(2) 0010*********00000010001110000000000A ⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦101010010100001000010101110010000001A I ⎡⎤⎢⎥⎢⎥⎢⎥+=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦2111010010101001000()01010111111000001A I ⎡⎤⎢⎥⎢⎥⎢⎥+=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦3411111111111001000()()0000001010101010111A I A I M ⎡⎤⎢⎥⎢⎥⎢⎥+==+=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦11110101'00100001M ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦22. 请依据图3-171P9解:1P9123456789110000001120101000113101000011400010001151001110116000001011711110111180000000119000000001P P P P P P P P P P P P P M P P P P P ⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦23. 已知下面的系统可达矩阵,分别用规范方法与实用方法建立其递阶结构模型。
系统工程第4版教学课件ppt作者汪应洛西安交通大学主编第2章 系统工程方法论

知识维(科学技术)间进程)A B C D E F G 6 5 运行阶段更新阶段知识维:指在完成上述各
阶段和各步骤所需要的各
种专业知识和管理知识。
逻辑维:每个阶段需进行的工作步骤,是运用系统工程方法进行思考、分析和解决问题应遵循的一般程序。
时间维:从规划到更新,按
时间顺序排列的SE 全过程。
“三维结构”模型
研制阶段a31a32a33a34生产阶段a41a42a43a44
代表一项具体的管理活动运行阶段a51a52a53a54
购置费
使用费保障费处置费
满意解代替最优
解,价值观方面
的重要变化。
概念模型代替
数学模型,思
路更加开阔。
《系统工程》第四版习题解答 (2)

系统工程姓名:姚德世专业班级:工程管理1107班学号:1103020724系统工程第三次作业8、假设每月招工人数MHM和实际需要人数RM成比例,招工人员的速率方程是:MHM·KL=P*RM·K,请回答以下问题:(1)K和KL的含义是什么?(2)RM是什么变量?(3)MHM、P、RM的量纲是什么?(4)(4)P的实际意义是什么?解:(1)K表示现在时间KL表示由现在时刻到未来是可的时间间隔(2)RM是速率变量(3)MHM的量纲是KL;P的量纲是RM;RM的量纲是K;(4)P的实际意义是现在之未来的增长速率。
9. 已知如下的部分DYNAMO方程:MT·K=MT·J+DT*(MH·JK-MCT·JK),MCT·KL=MT·K/TT·K,TT·K=STT*TEC·K,ME·K=ME·J*DT*(MCT·JK-ML·JK)其中:MT表示培训中的人员(人)、MH表示招聘人员速率(人/月)、MCT表示人员培训速率(人/月)、TT表示培训时间、STT表示标准培训时间、TEC表示培训有效度、ME表示熟练人员(人),ML表示人员脱离速率(人/月)。
请画出对应的SD(程)图。
MT MEMH MCT MLTTSTT TEC10. 高校的在校本科生和教师人数(S和T)是按一定的比例而相互增长的。
已知某高校现有本科生10000名,且每年以SR的幅度增加,每一名教师可引起增加本科生的速率是1人/年。
学校现有教师1500名,每个本科生可引起教师增加的速率(TR)是0.05人/年。
请用SD 模型分析该校未来几年的发展规模,要求:(1) 画出因果关系图和流(程)图;(2)写出相应的DYNAMO方程;(3)列表对该校未来3~5年的在校本科生和教师人数进行仿真计算;(4)请问该问题能否用其它模型方法来分析?如何分析?(1)解:在校本科生S教师TSTSRTRTSR STR(2)、解:L S.K=S.J+SR.JK*DT N S=10000R SR.KL=T.K*TSR C TSR=1L T.K=T.J+TR.JK*DT N T=1500R TR.KL=S.K*STR C STR=0.05 (3)解:(4)11.某城市国营和集体服务网点的规模可用SD 来研究。
《系统工程》第四版习题解答资料

7
5,7
1,7
7
所以系统可划分为两个相互独立的区域,即 。
②级位划分
要素集合
2
2
2,4
2
2
4
2,4
4
4
4
4
4
4
4
要素集合
1
1,5,7
1
1
3
3,5,6
3,6
3,6
5
5
1,3,5,6,7
5
5
6
3,5,6
3,6
3,6
7
5,7
1,7
7
1
1,7
1
1
3
3,6
3,6
3,6
3
6
3,6
3,6
3,6
6
7
7
1,7
7
4
4
5
2,3,4,5
1,5
5
所以系统无法划分为两个或两个以上相互独立的区域,即
。
②级位划分
要素集合
1
1,2,3,4,5
1
1
2
2,3,4
1,2,5
2
3
3,4
1,2,3,5
3
4
4
1,2,3,4,5ቤተ መጻሕፍቲ ባይዱ
4
4
5
2,3,4,5
1,5
5
1
1,2,3,5
1
1
2
2,3
1,2,5
2
3
3
1,2,3,5
3
3
5
2,3,5
1,5
解:设市场畅销为 ,市场滞销为 ;设产品预测畅销为 ,产品预测滞销为 ,则由已知条件: , , ,
系统工程课后答案
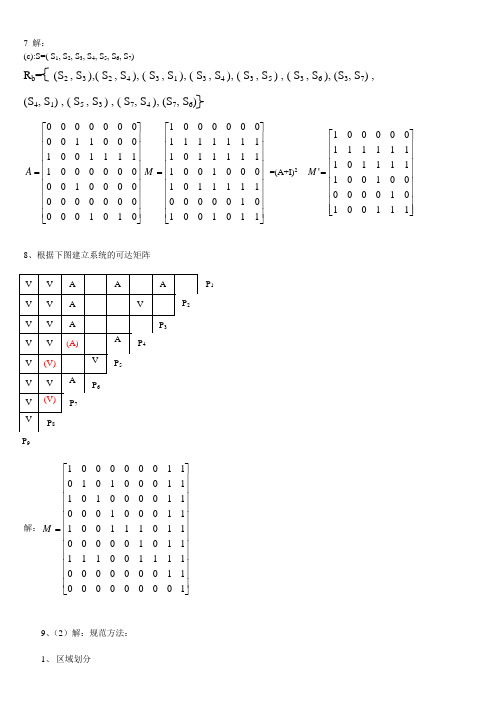
7 解:(c):S=( S 1, S 2, S 3, S 4, S 5, S 6, S 7)R b= (S 2 , S 3 ),( S 2 , S 4 ), ( S 3 , S 1 ), ( S 3 , S 4 ), ( S 3 , S 5 ) , ( S 3 , S 6 ), (S 3, S 7) , (S 4, S 1) , ( S 5 , S 3 ) , ( S 7, S 4 ), (S 7, S 6)⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=0101000000000000001000000001111100100011000000000A ⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=1101001010000011111010001001111110111111110000001M =(A+I)2 ⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=111001010000001001111101111111000001'M8、根据下图建立系统的可达矩阵解:⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=100000000110000000111100111110100000110111001110001000110000101110001010110000001M9、(2)解:规范方法:1、 区域划分因为B(S)={3,6}所以设B中元素Bu=3、Bv=6R(3)={ 1,2,3,4}、R(6)={ 2,4,5,6,7,8}R(3)∩R(6)={ 1,2、3,4} ∩{2,4,5,6,7,8} ≠φ,故区域不可分解2将满足C =R 的元素2,8挑出作为第1级 将满足C =R 的元素4挑出作为第2级 将满足C =R 的元素1,5挑出作为第3级将满足C =R 的元素3,7挑出作为第4级 将满足C =R 的元素6挑出作为第5级 将M 按分级排列:⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=110101110101011100101101000101010000110100000101000000100000000167351482M提取骨架矩阵如下:⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=010000000001001000001000000001000000010000000001000000000000000067351482'A建立其递阶结构模型如下:(1) 实用方法: (2)⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=1101100100100100100000000000067351482M建立其递阶结构模型同上。
《系统工程》第四版习题解答

系统工程第四版习题解答第三章 系统模型与模型化21. 给定描述系统基本结构的有向图,如图3-16a 、b 所示。
要求: (1)写出系统要素集合S 及S 上的二元关系集合b R 。
(2)建立邻接矩阵A 、可达矩阵M 及缩减矩阵M '。
解:(2)3-16a : 规范方法:⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=0111000000010000010010010A ,⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=1111001000011000111011111M ,M M ='}5,4,3,2,1{)(==∏P S 。
⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=11110010000110001110111115432154321)(P M}1{},5{},2{},3{},4{,,,,)(54321==∏L L L L L P⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=11111011110011100011000011523415234)(54321L L L L L L M ③提取骨架矩阵⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=''1100011000011000011000011523415234)(54321L L L L L L M ⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=-''='01000001000001000001000001523415234)(54321L L L L L I L M A ④绘制多级递阶有向图实用方法:缩减矩阵⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=='11110010000110001110111115432154321M M⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡='11111011110011100011000011523415234)(54321L L L L L L M3-16b :规范方法:⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=000000000011100010000000001000010100A ,⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=100000111111101010000100101010111111M①区域划分φ≠=⋂=⋂}5,1{}6,5,4,2,1{}5,3,1{)()(63S A S A所以系统无法划分为两个或两个以上相互独立的区域,即}6,5,4,3,2,1{)(==∏P S 。
《系统工程》第四版习题解答

系统工程第四版习题解答第三章 系统模型与模型化21. 给定描述系统基本结构的有向图,如图3-16a 、b 所示。
要求: (1)写出系统要素集合S 及S 上的二元关系集合b R 。
(2)建立邻接矩阵A 、可达矩阵M 及缩减矩阵M '。
解:(2)3-16a : 规范方法:⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=0111000000010000010010010A ,⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=1111001000011000111011111M ,M M ='①区域划分i S)(i S R)(i S A)(i S C)(i S E11,2,3,4,51 12 2,3,4 1,2,5 23 3,4 1,2,3,5 3 4 41,2,3,4,54 4 52,3,4,51,55所以系统无法划分为两个或两个以上相互独立的区域,即}5,4,3,2,1{)(==∏P S 。
⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=11110010000110001110111115432154321)(P M ②级位划分要素集合i S)(i S R)(i S A)(i S C)(i S E)(2P ∏ 0L P -11,2,3,4,5 1 1 }4{1=L2 2,3,4 1,2,5 2 33,41,2,3,534 4 1,2,3,4,5 4 4 5 2,3,4,5 1,5 5 10L L P --1 1,2,3,5 1 1 }3{2=L2 2,3 1,2,5 2 3 3 1,2,3,5 3 3 5 2,3,5 1,5 5 210L L L P --- 1 1,2,5 1 1 }2{3=L2 2 1,2,5 2 2 5 2,5 1,5 5 3210L L L L P ----1 1,5 1 1 }5{4=L5 5 1,5 5 5 43210L L L L L P -----11111}1{5=L}1{},5{},2{},3{},4{,,,,)(54321==∏L L L L L P⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=11111011110011100011000011523415234)(54321L L L L L L M ③提取骨架矩阵⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=''11000011000011000011000011523415234)(54321L L L L L L M ⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=-''='01000001000001000001000001523415234)(54321L L L L L I L M A ④绘制多级递阶有向图2第一级第二级第三级第四级第五级4153实用方法:缩减矩阵⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=='11110010000110001110111115432154321M M ⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡='11111011110011100011000011523415234)(54321L L L L L L M 2第一级第二级第三级第四级第五级41533-16b :规范方法:⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=000000000011100010000000001000010100A ,⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=100000111111101010000100101010111111M①区域划分i S)(i S R)(i S A)(i S C)(i S E11,2,3,4,5,6 1,5 1,5 2 2,4,6 1,2,4,5 2,4 3 3 1,3,5 3 3 4 2,4,6 1,2,4,5 2,4 5 1,2,3,4,5,61,5 1,5 661,2,4,5,666φ≠=⋂=⋂}5,1{}6,5,4,2,1{}5,3,1{)()(63S A S A所以系统无法划分为两个或两个以上相互独立的区域,即}6,5,4,3,2,1{)(==∏P S 。
《系统工程》第四版习题解答课件

第三章 系统模型与模型化21. 给定描述系统基本结构的有向图,如图3—16a 、b 所示。
要求: (1)写出系统要素集合S 及S 上的二元关系集合b R 。
(2)建立邻接矩阵A 、可达矩阵M 及缩减矩阵M '。
解:(2)3—16a : 规范方法:⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=0111000000010000010010010A ,⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=11110010011000111011111M ,M M ='所以系统无法划分为两个或两个以上相互独立的区域,即}5,4,3,2,1{)(==∏P S 。
⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=11110010000110001110111115432154321)(P M ②级位划分}1{},5{},2{},3{},4{,,,,)(54321==∏L L L L L P⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=11111011110011100011000011523415234)(54321L L L L L L M ③提取骨架矩阵⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=''1100011000011000011000011523415234)(54321L L L L L L M⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=-''='01000001000001000001000001523415234)(54321L L L L L I L M A实用方法:缩减矩阵⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=='1111010000110001110111115432154321M M ⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡='11111011110011100011000011523415234)(54321L L L L L L M3—16b :规范方法:⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=000000000011100010000000001000010100A ,⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=100000111111101010000100101010111111M①区域划分φ≠=⋂=⋂}5,1{}6,5,4,2,1{}5,3,1{)()(63S A S A所以系统无法划分为两个或两个以上相互独立的区域,即}6,5,4,3,2,1{)(==∏P S .⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=100000111111101010000100101010111111654321654321)(P M②级位划分}5,1{},4,2{},6,3{,,)(321==∏L L L P⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=111111111111001110001110000010000001514263514263)(321L L L L M ③提取骨架矩阵⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡='111101100010000112631263)(321L L L L M ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=''110101100010000112631263)(321L L L L M,⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=-''='010100100000000012631263)(321L L L IL M A实用方法:缩减矩阵⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡='100001001010111163216321M⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=''110101100010000112631263)(L M , 绘制多级递阶有向图:22。
系统工程课件第一章(1)

v 管理科学的发展与管理人才培养
管理科学发展的“制高点” ——系统化管理
T型人才
系统工程课件第一章(1)
导论:What
v SE是以大规模复杂系统(特 别是管理系统)为研究对象, 在系统理论、管理科学及其运 筹学、专业工程技术等学科基 础上形成的一门交叉学科。通 过学习,主要使学生掌握分析 与解决一般管理系统问题的思 想、程序和方法。
第一章 系统工程概述
系统工程的 产生、 发展 及应用
(二)系统理论的产生与发展
系统工程的研 究对象
一般系统论、控制论、信息论、 耗散结构理论、协同学及自组织理论
等是系统理论的重要内容和SE的理论基础。
。
SE的概念与 特点
系统工程课件第一章(1)
第一章 系统工程概述
系统工程的 产生、 发展 及应用
第三段
(课堂习题2)[2]
v 系统工程应用实例 [2] v (课程总结)[1]
第四段
系统工程课件第一章(1)
导论:Who/Where v Who/Where?
Who —— 学生为主体,教师为主导。 Where —— 将课堂内外的学习结合起来!
系统工程课件第一章(1)
导论:How
v How?
建议注坚重持系问统题思导1耳2考向、、说不严话许禁点3使迟平0名%用到时一,手及10次两机中%无次及途+(故扣交早期未除头退中到7接+0期扣%末除,考平三试时次)成无9绩平0时% 采用系统化3方、法不无成故绩缺。课作业一次未交及抄袭扣除
系统工程课件第一章(1)
2020/11/30
系统工程课件第一章(1)
《系统工程》课件

02
系统工程方法论
硬系统方法论
总结词
强调数学模型和定量分析的方法论
详细描述
硬系统方法论注重数学模型和定量分析在解决系统问题中的应用,通过建立精确的数学模型来描述系 统的结构和行为,并运用数学分析和优化方法来寻求最优解决方案。这种方法论在工程、物理和经济 学等领域有广泛应用。
软系统方法论
总结词
强拟、优化技术、决策分析等。
系统分析的局限性
数据获取难度大
对于某些复杂系统,难以获取完 整、准确的数据,导致分析结果 的不准确。
主观因素影响
系统分析的结果往往受到分析者 的主观因素影响,如经验、知识 背景等,可能导致结果的偏颇。
适用范围有限
系统分析方法适用于具有明确目 标、约束条件和决策变量的系统 ,对于某些模糊性、不确定性较 高的系统可能不适用。
04
系统设计
系统设计的概念和原则
概念
系统设计是根据用户需求,将系统抽 象为具体的物理结构或流程,以满足 预定目标的过程。
原则
系统设计应遵循整体性、最优化、可 靠性、可扩展性和可维护性等原则, 以确保系统能够高效、稳定地运行。
系统设计的步骤和方法
步骤
需求分析、系统规划、系统分析、系统设计、系统实施 和系统评估。
系统评价是对一个系统进行全面评估的过程,包括对其性能、效果、可行性和可 持续性等方面的评估。
目的
系统评价的目的是为了了解系统的现状,发现问题和不足,为系统的改进和创新 提供依据和支持。
系统评价的步骤和方法
步骤
确定评价目标、制定评价计划、收集 和分析数据、评估结果反馈。
方法
定性和定量评价方法,如专家评估、 问卷调查、实验法等。
系统工程的应用领域
系统工程第4版 教学PPT 作者 汪应洛 西安交通大学 主编 第1章 系统工程概述-PPT资料20页

12
一、系统的概念及特点
系统的定义:系统是由两个以上有机联系、相互作 用的要素所组成,具有特定功能、结构和环境的整体。
该定义有以下四个要点: (1)系统及其要素 (2)系统和环境 (3)系统的结构 (4)系统的功能
国际应用系统 分析研究所 (IIASA)在维也 纳成立
SE的应用开始从 工程领域进入到社会 经济领域,并发展到 了一个重要的新阶段。
70年代 VI 80年代
SE的广泛应用在国际上达到高潮
SE在国际上稳定发展、在中国的研究 与应用达到高潮
三、系统工程在中国的发展及应用
上世纪50至60年代,我国的一些研究机构和著名学 者为SE的研究与应用作了理论上的探讨、应用上的偿试 和技术方法章 系统工程方法论 第三章 系统模型与模型化 第四章 系统仿真及系统动力学方法 第五章 系统评价方法 第六章 决策分析方法 第七章 战略研究与管理 第八章 系统工程应用实例
考试 合计
学时数 4 4 8 6 6 8 4 6 2 48
第一章 系统工程概述
第一节 系统工程的产生、发展及应用 第二节 系统工程的研究对象 第三节 系统工程的概念与特点 第四节 系统工程的应用领域
一、系统的概念及特点
系统的一般属性: (1)整体性 (2)关联性 (3)环境适应性
二、系统的类型
1、自然系统与人造系统 2、实体系统与概念系统 3、动态系统和静态系统 4、封闭系统与开放系统
第三节 系统工程的概念与特点
一、系统工程的概念
定义:用定量与定性相结合的系统思想和 方法处理大型复杂系统的问题,无论是系统 的设计或组织建立,还是系统的经营管理, 都可以统一地看成是一类工程实践,统称为 系统工程。
系统工程第四版第三章课后题答案资料讲解

1 1 0 0 1
0 1 1 0 0
A I 0 0 1 1 0 0 0 0 1 0
0 1 1 1 1
1 1 1 1 1 0 1 1 1 0 (A I )2 0 0 1 1 0 (A I )3 M 0 0 0 1 0 0 1 1 1 0
M' M
(b)(1) S {1, 2,3, 4,5,6}
0 0
0 0
0 0
0 0
L1 5 0 0 1 0 0 0 0
M (L)
3 0 0 1 1 1 0 0
L2 6 0 0 1 1 1 0 0
7
0
0
1
0
0
1
0
L3 1 0 0 1 0 0 1 1
③提取骨架矩阵
E(Si ) 2
4
(P1 ) L1 {2} L2 {4}
E(Si )
(P2 )
5
L1 {5}
0 0 0 0 0 1 1
0
2
0 0
2 1 4 1
0 0
,
M
(L)
5 3 7
0 0 0
0 1
1 0
4 0 1 0 0 0 0
5 0 0 1 1 1 0
3 0 0 0 1 0 0
①区域划分
Si
R(Si )
A(Si )
1
1,5,7
1
2
2
2,4
3
3,5,6
3,6
4
2,4
4
5
5
1,3,5,6,7
6
3,5,6
3,6
7
5,7
1,7
A(S2 ) A(S5 ) {2,4} {1,3,5,6,7}
系统工程第四版第三章课后题答案

系统工程第三章作业02613102 徐晗P80.21. 给定描述系统基本结构的有向图,如图3-16a 、b 所示。
要求:(1)写出系统要素集合S 及S 上的二元关系集合Rb 。
(2)建立邻接矩阵A 、可达矩阵M 及缩减矩阵M ’。
解:(a) (1) 51234{S ,,,,}S S S S S =55551212334234{(S ,),(,),(,),(,),(,),(,),(,S )}b R S S S S S S S S S S S S =(2)010********00100000001110A ⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦=1100101100001100001001111A I ⎡⎤⎢⎥⎢⎥⎢⎥+=⎢⎥⎢⎥⎢⎥⎣⎦231111101110()()001100001001110A I A I M ⎡⎤⎢⎥⎢⎥⎢⎥+==+=⎢⎥⎢⎥⎢⎥⎣⎦'M M =(b)(1) {1,2,3,4,5,6}S ={(1,3),(1,5),(2,4),(4,2),(4,6),(5,2),(5,1)}b R =(2) 0010*********00000010001110000000000A ⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦101010010100001000010101110010000001A I ⎡⎤⎢⎥⎢⎥⎢⎥+=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦2111010010101001000()010101111110000001A I ⎡⎤⎢⎥⎢⎥⎢⎥+=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦3411111111111001000()()0000001010101010111A I A I M ⎡⎤⎢⎥⎢⎥⎢⎥+==+=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦11110101'00100001M ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦22. 请依据图3-17建立可达矩阵。
1P9解:3P9123456789110000001120101000113101000011400010001151001110116000001011711110111180000000119000000001P P P P P P P P P P P P P M P P P P P ⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦23. 已知下面的系统可达矩阵,分别用规范方法与实用方法建立其递阶结构模型。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
21.给定描述系统基本结构的有向图,如图3-16a、b所示。要求:
(1)写出系统要素集合 及 上的二元关系集合 。
(2)建立邻接矩阵 、可达矩阵 及缩减矩阵 。
解:(2)3-16a:
规范方法:
, ,
①区域划分
1
1,2,3,4,5
1
1
2
2,3,4
1,2,5
2
3
3,4
1,2,3,5
3
4
4
1,2,3,4,5
7
1
1
1
1
1
③提取骨架矩阵
,
④绘制多级递阶有向图
(2)规范方法:
①区域划分
1
1,2,4
1,3
1
2
2
1,2,3,4,5,6,7
2
2
3
1,2,3,4
3
3
4
2,4
1,3,4,5,6,7
4
5
2,4,5
5,6,7
5
6
2,4,5,6,7,8
6
6
7
2,4,5,7,8
6,7
7
8
8
6,7,8
8
8
所以系统不能划分为两个或两个以上相互独立的区域,即
x1
x2
x3
θ1
0.8
0.2
0
θ2
0.2
0.4
0.4
θ3
0
0.1
0.9
①画出该决策问题的决策树;
②确定与各种试销结果相应的贝叶斯行动;
③分析试销费用与是否试销的关系。
解:由已知条件有下表:
x1
x2
x3
θ1
0.16
0.04
0
0.2
θ2
0.06
0.12
0.12
0.3
θ3
0
0.05
0.45
0.5
0.22
0.21
补充题2某公司拟改变产品的包装,改变包装后产品的销路不能确定,公司经理的估计是:
销路差θ1
销路一般θ2
销路好θ3
概率P
0.2
0.3
0.5
销路与收益的关系如下表:
θ1
θ2
θ3
改变包装
-40
0
600
包装不变
0
0
0
为了对销路的估计更有把握,公司先在某个地区试销改变了包装的产品。根据以往的经验,试销的结果与产品在将来的实际销路中有如下关系(x1、x2、x3分别为试销为差、一般和好的事件):
解:设市场畅销为 ,市场滞销为 ;设产品预测畅销为 ,产品预测滞销为 ,则由已知条件: , , ,
有: ,
, , ,
,
, , ,
贝叶斯行动:如果市场预测结果为畅销,应该选择经营该高科技产品;若市场预测结果为滞销,则不经营。
由决策树可知,咨询公司提供信息的价值为1.13-1.1=0.03万元,因此要价超过300元不应聘请。
。
②级位划分
要素集合
1
2
3
4
5
6
7
8
1
1,4
1,3
1
3
1,3,4
3
3
4
4
1,3,4,5,6,7
4
4
5
4,5
5,6,7
5
6
4,5,6,7
6
6
7
4,5,7
6,7
7
1
1
1,3
1
1
3
1,3
3
3
5
5
5,6,7
5
5
6
5,6,7
6
6
7
5,7
6,7
7
3
3
3
3
3
6
6,7
6
6
7
7
6,7
7
7
6
6
6
6
6
③提取骨架矩阵
④绘制多级递阶有向图
TIME
0
1
2
3
4
5
S
10,000
11,500
13,500
16,075
19,325
23,378
T
1,500
2,000
2,575
3,250
4,053
5,020
11.
12.
(1)
(2) 15.
第六章决策分析
补充题1某商店拟经营一种高科技产品,若市场畅销,可以获利1万5千元;若市场滞销,将亏损5千元;若不经营,则不亏不赚。根据收集的市场销售资料,该产品畅销的概率为0.8,滞销的概率为0.2。为了降低风险,可以聘请某咨询公司进行市场调查和分析,该咨询公司对该产品畅销预测的准确率为0.95,滞销预测的准确率为0.90。画出该决策问题的决策树,并进行决策分析。
A
A
V
V
A
V
V
V
A
V
V
(A)
A
V
(V)
V
V
V
A
V
(V)
V
绘制多级递阶有向图:
23.已知下面的系统可适矩阵,分别用规范方法与实用方法建立其递阶结构模型。
(1) (2)
解:(1)规范方法:
①区域划分
1
1,5,7
1
1
2
2
2,4
2
2
3
3,5,6
3,6
3,6
4
2,4
4
4
5
5
1,3,5,6,7
5
5
6
3,5,6
3,6
(1)实用方法:
缩减矩阵
(2)实用方法:
第四章
9.已知如下的部分DYNAMO方程:
请画出对应的SD流(程)图。
10.
L S.K=S.J+SR.JK*DT
NS=10000
R SR.KL=T.K*TSR
C TSR=1
L T.K=T.J+TR.JK*DT
N T=1500
R TR.KL=S.K*STR
C STR=0.05
5
1
1,2,5
1
1
2
2
1,2,5
2
2
5
2,5
1,5
5
1
1,5
1
1
5
5
1,5
5
5
1
1
1
1
1
③提取骨架矩阵
④绘制多级递阶有向图
实用方法:
缩减矩阵
3-16b:
规范方法:
,
①区域划分
1
1,2,3,4,5,6
1,5
1,5
2
2,4,6
1,2,4,5
2,4
3
3
1,3,5
3
3
4
2,4,6
1,2,4,5
2,4
5
1,2,3,4,5,6
0.57
1.00
进一步有,
x1
x2
x3
θ1
0.7273
0.1905
0.0000
θ2
0.2727
0.5714
0.2105
θ3
0.0000
0.2381
0.7895
决策树为:
贝叶斯行动:如果试销结果为差,则不改变包装;如果试销结果为一般,则改变包装;如果试销结果为好,则改变包装。
由决策树可知,试销的价值为(抽样信息的价值)298.4-292=6.4万元,因此如果试销费用大于6.4万元则不试销,如果试销费用小于6.4万元时试销。
4
4
5
2,3,4,5
1,5
5
所以系统无法划分为两个或两个以上相互独立的区域,即
。
②级位划分
要素集合
1
1,2,3,4,5
1
1
2
2,3,4
1,2,5
2
3
3,4
1,2,3,5
3
4
4
1,2,3,4,5
4
5
2,3,4,5
1,5
5
1
1,2,3,5
1
1
2
2,3
1,2,5
2
3
3
1,2,3,5
3
3
5
2,3,5
1,5
1,5
1,5
6
6
1,2,4,5,6
6
6
所以系统无法划分为两个或两个以上相互独立的区域,即
。
②级位划分
要素集合
1
1,2,3,4,5,6
1,5
1,5
2
2,4,6
1,2,4,5
2,4
3
3
1,3,5
3
3
4
2,4,6
1,2,4,5
2,4
5
1,2,3,4,5,6
1,5
1,5
6
6
1,2,4,5,6
6
6
1
1,2,4,5
3,6
7
5,7
1,7
7
所以系统可划分为两个相互独立的区域,即 。
②级位划分
要素集合
2
2
2,4
2
2
4
2,4
4
4
4
4
4
4
4
要素集合
1
1,5,7
1
1
3
3,5,6
3,6
3,6
5
5
1,3,5,6,7
5
5
6
