普通物理第八章稳恒电流
大学物理《稳恒电流》课件

Electric Current
教学内容(1学时)
了解恒定电流产生 的条件。 了解电流密度和电 动势的概念。
2/7
【A4.15.1】恒定电流electric current
电流:单位时间通过导 体截面S 的电荷。
I dq dt
dq Senvddt
vd 为电子漂移速度的大小
S
+
+
+
+
ቤተ መጻሕፍቲ ባይዱ
+
+
I
I envdS
I S
envd
j电流密度大小
电流描述不完备!
3/7
【A4.15.2】电流密度
电流密度是描述电流分布的矢量。在导体中任意 一点的方向与正载流子在该点的流动方向相同,大小 等于通过该点并垂直于电流的单位截面的电流强度。
dI j dS jdS cos
I s j dS
dS
I +-
+ + ++Ek -
l dU l E d l E d l Ek d l 0
IR
IRi
0
全电路的欧姆定律 I
R Ri
7/7
【A4.15.5扩展】其他电阻
二极管
热敏电阻
光敏电阻
声敏电阻
8/7
宏观上稳恒电流 I I1 I2 0 I
dS j
I1 I2
S
5/7
【A4.15.4】电源电动势
6/7
电源:提供非静
电力的装置。 非静电场 Ek:能
不断分离正负电 荷使正电荷从电 源负极向正极运 动。
Ek dl
【A4.15.5】欧姆定律
稳恒电流

B
A B
电源
1. 电源:提供(产生)非静电力 Fk (非静电场 Ek Fk q )的装置(器件) (电源的正极、负极;电源内电路;电 源外电路)
2. (电源)电动势 :定量反映电源中 非静电场作功能力大小的物理量
Ek dl Ek dl B 或 Ek dl ( Ek dl 0) 外
解:由欧姆定律
I R r
i i
0
A
i
r
B
VA VB 0
r
在恒定电流的电路中,电路中电流 为零,电路两端电势差可以不为零; 电路中电流不为零,电路两端电势差 可以为零!
三.基耳霍夫定理的应用
1.电势差计 A. 当开关与标准电池接通时: (1)任选回路的 绕向方向和假设各 支路的电流方向
I R r
i i
i
2. 一段电路两端电势差(电压)
U AB VA VB i IRi Iri
(一段电路两端电势差等于电路上 各电势降落的代数和)
正负号选定规则
第二节.基尔霍夫定理 一.基尔霍夫第一定理: 节点:三条或三条以上的通电导线的会合点。 支路:两节点间的一段电路。
(3):符号规定用一句话可表示为:在绕行方向 上,电压降低则为负,电压升高则为正.
例题一:一复杂的电路中, 计算一段电路两端电势差
U AB
1 I1R1 I1r1 2 I 2 R2 I 2 r2
UCD 3 I 3 R3 I 3r3
例题二:图示 1 2 r 和 R , 求电路中电流及 U AB U A U B
0.4( A)
8稳恒电流 同济版大学物理 教学课件

将非静电力的作用效果等效成电源内存在
一个非静电性电场;
A BEK dl
单位:伏特(V )
Fk
A
Ek
Fe B
2.方向:电源内从负极到正极的方向;
----电源内电势升高的方向 8
3.当非静电力存在于整个电流回路中时
,回路中的电动势应对电源内外积分:
LE Kdl 0
----非静电性电场一定是一个非保守性电场 !
2>通过导体中任一有限截面S 的电流强度
取面元d,S 通过面元的电流强度为: S
dIjdSjd ScosjdS dS
n I
IS jdS
5
3>.稳恒电流条件
电流场中每一点的电流密度的大小和方向均不 随时间改变,各处均没有电荷的堆积与离散;
I1 I2
I1
即: j dS 0
I2
S
——电流连续性方程
6
§14-2电源 电源电动势
一.电源 电容器放电过程:正电荷
从A板经导线运动到B板, 与 B板上负电荷中和;
----只靠静电力不能形
q q
E AB
成稳恒的电流!
电源:提供非静电力的装 置----将正电荷从低电
A Fk
E Fe
B
势处移到高电势处;
7
二.电动势
1.电源电动势:在电源内部,将单位正电
荷从负极移到正极,非静电力所作的功; 并
1
2.电流密度矢量 j
对大块导体不仅需用物理量电流强度来描述, 还需建立电流密度的概念, 进一步描述电流强 度的分布;
例如:电阻法探矿
(图示)
•
•
4
1>电流密度矢量定义:
稳恒电流PPT课件

单位时间内通过任一截面的电量,表示了电路
中电流强弱的物理量。它是标量用 I 表示。
lim q dq
I
标量
t0 t dt
规定正电荷流动 的方向为正方向。
单位:库仑/秒=安培
I
(CT 1) A
它是国际单位中的基本量。
常用毫安(mA)、微安(A)
• 电流密度矢量 j
必要性:当通过任一截面的电量不均匀时,用
* 为了便于计算规定 的方向由 负极板经内电路指向正极板,即
+–
正电荷运动的方向。
单位:焦耳/库仑=(伏特)
* 越大表示电源将其它形式能量转换为电能的本
领越大。其大小与电源结构有关,与外电路无关。
参照静电力电势定义:
in Ek dl
内电路
非静电力
因为电源外部没有非静电力, 所以可写为:
K
C
0 q dq R C dt
一阶线性常系数 齐次微分方程
RC 具有时间的量纲。单位:秒
• 充电
t q 0.63q0
• 放电
t q 0.37q0
• 电容器充电图形
q
qo
q C (1 e t RC ) 0.63qo
RC大
UC (1 e t RC )
i e t RC
R
U R e t RC
0.37 R
t
相当于电容
i 短路时的电流
R
t
q
Байду номын сангаас
• 电容器放电图形 C
qo
RI
qo / e
t
q qoe t RC
UC
q0 C
e t RC
K
i qo e t RC RC
稳恒电流

b
[例]计算如图电路中的 I 和电源1的端电压 已知 1 20 V , 2 15 V R1 R2 2 ,r1 r2 0.5
1 2 解:I R1 R2 r1 r2
20 15 1A 2 2 0.5 0.5
I
r R1 1 r2 R2 2
E dl
含源电路:
b j b b Vab E dl dl Ek dl a a a
c
j ( E Ek )
1 2 I a R r c r R2 1 1 2
b
b I ( R1 R2 r1 r2 ) Ek dl Ek dl
磁力与q、v、 v与磁场方向的夹角 有关,
F qv sin
定义:
B
F qv sin
或
----磁感应强度大小
B 沿 Fmax v 方向 叠加原理 B Bi
i
Fmax B 特斯拉(T) qv
1T = 10 Gs
高斯
4
三.磁感应线(磁场线、B 线 ) B 线切向----磁场方向 B 的大小 dN
----电源内电势升高的方向
若非静电力存在于整个电流回路,
说明:
L
EK dl
----非静电场是非保守性场 电动势和电势是两个不同的物理量
电动势:与非静电力的功相联系 电势:与静电力的功相联系
三. 欧姆定律 1. 欧姆定律的微分形式
dI jdS dl dl R dS 1 dV dV jdS dS R dl
标量
高二物理竞赛课件:稳恒电流

圆周运动向心力
电子作圆周运动的角速度
当施加外磁场后,电子除受fe 作用外,还受到磁 场力fm 的作用,就引起电子运动角速度的变化。
9
电子受磁场力fm 的方向与库仑 力fe 的方向相同,即指向原子核
0
B
fm
v
磁场力大小 fm=evB=erB
Δpm
0 增加到 = 0 + ,且 满足
Ze2
4π0r 2
7
也称逆磁性,抗磁质逆磁质
磁化率m<0,相对磁导率r<1 抗磁质 与 反向
只考虑一个电量-e的电子以角速度0半径r
绕原子核作圆周运动,相当于一个圆电流。
T与0有
2 T
0
等效圆对应轨道磁矩
m总与0反向
8
电子受到的库仑力fe 的大小为
Ze 2
f e 4 0r 2
库仑力等于电子
抗磁性的产生:加外磁场后的 m 抗磁质 与 反向
单个电子的轨道磁矩 m 方向总与0反向
考虑一个电量 –e 的电子以角速度0 半径 r 绕原
子核作圆周运动,相当于一个圆电流。
0
周期 T 2
0
等效圆电流 I
e
e0
r
v
T 2
对应轨道磁矩
4
电子受到的库仑力 fe 的大小为
库仑力等于电子圆 周运动向心力 电子作圆周运动的角速度
erB
2r
2 02 20Δ
10
受磁场力与库仑力反向,
角速度将从0 减小到=0 -
0
Δpm
v
fm
B
表明磁场所引起的附加角速度总与磁场方向相同。 电子运动角速度变化必将引起轨道磁矩的变化。
轨道磁矩 变化量为
物理竞赛辅导教案稳恒电流

物理竞赛辅导教案稳恒电流辅导教案:稳恒电流一、教学目标:1.了解稳恒电流的概念;2.理解电流的定义和单位;3.掌握计算电流的方法;4.掌握串联电路和并联电路中计算电流的方法。
二、教学内容:1.稳恒电流的概念;2.电流的定义和单位;3.串联电路中的电流计算;4.并联电路中的电流计算。
三、教学过程:步骤一:导入新知识(10分钟)教师可以提问:你们能说出什么是电流吗?电流的单位是什么?请举例说明。
步骤二:学习稳恒电流的概念(15分钟)1.定义稳恒电流:稳恒电流是指在电路中,电荷在单位时间内通过特定点的数量,也就是电流表示了电荷的流动程度。
2.提示学生思考:电流的大小与电荷的量有关吗?与电流的时间有关吗?3.引导学生发现:电流与电荷的量和时间有关,电流的计算公式为I=Q/t,其中I代表电流,Q代表电荷量,t代表时间。
步骤三:学习电流的定义和单位(15分钟)1.电流的定义:电流是单位时间内通过导线横截面的电荷量,用公式I=ΔQ/Δt表示。
2.电流的单位:国际单位制中,电流的单位是安培(A),即1A等于每秒通过1库伦电荷。
步骤四:学习串联电路中的电流计算(20分钟)1.串联电路的特点:串联电路中的电流在各电器之间是相同的。
2.串联电路中的电流计算公式:根据串联电路的特点,可以利用欧姆定律计算串联电路中的电流,即I=U/R,其中I代表电流,U代表电压,R 代表电阻。
3.通过示例演练,让学生掌握串联电路中电流的计算方法。
步骤五:学习并联电路中的电流计算(20分钟)1.并联电路的特点:并联电路中的电流在各支路之间分担。
2.并联电路中的电流计算公式:根据并联电路的特点,可以利用欧姆定律和基尔霍夫定律计算并联电路中的电流。
欧姆定律:I1=U/R1,I2=U/R2,I3=U/R3基尔霍夫定律:I=I1+I2+I33.通过示例演练,让学生掌握并联电路中电流的计算方法。
步骤六:小结与拓展(10分钟)小结:通过本节课的学习,我们了解了稳恒电流的概念,掌握了电流的定义和单位,并学会了计算串联电路和并联电路中的电流。
稳恒电流1

这样的曲线称为电流线Fra bibliotek基础理论教学中心
第一节 电流的描述
二、 电流强度
形成电流的条件:
1、有可以自由移动的电荷, 2、有电场(或有电压)。
电流线形象地表示电流的分布
不能直接描述电流的强弱
单位时间内通过导体横截面积的电量,称为电流强度。
电流强度的单位是安培,简称:安(A)
1A = 103 mA = 10-6 μA
基础理论教学中心
第一节 电流的描述
电流为通过截面S 的电荷随时间的变化率
I dq dt
dq ZenvddtS
I ZenvdS
S
+
+
+
+
+
+
I
vd 为电子的迁移速度大小
迁移运动的大小与场强 的大小成正比
基础理论教学中心
第一节 电流的描述
三、电流密度 方向规定: j
该点正电荷运动方向
大小规定:等于在单位时间内过该点附近垂直于正电荷 运动方向的单位面积的电荷
j
dQ
dtdS cos
dI
dS cos
envd
dI j dS jdS cos
dS
I s j dS
I j
基础理论教学中心
第一节 电流的描述
四、 稳恒电流
单位时间内通过闭合曲面向外流出的电荷,等于此时间内
闭合曲面里电荷的减少量 .
s
j
dS
dQ dt
dQi dt
dS j
若闭合曲面 S 内 的电荷不随时间而变化,
M
(2)
vd
I nSe
5.36104 m s-1 2m h-1
普通物理学第七版 第八章 恒定电流的磁场

三、磁感应线和磁通量 1. 磁场的定性描述——磁感应线(磁感线) • 磁感线上各点的切线方向表示 此处磁场的方向 • 磁感线的疏密反映磁场的强弱
返回 退出
• 磁感应线的性质 磁感应线与闭合电流套连成无头无尾的闭合曲线 磁感应线绕行方向与电流成右手螺旋关系
返回 退出
2. 磁通量
磁通量:穿过磁场中任一给定曲面的磁感应线总数。
例:简单闭合电路
IR
a。
电路中有如图所示电流I。
Ri
绕行一周,各部分的电势变化总和为0。
。b
ε
ε UR Ui 0
ε I
R Ri
推广至多个电源和电阻组成的回路,有
I Σε j
闭合电路的欧姆定律
ΣRj ΣRij
注意式中电动势正负取值的规定。
返回 退出
例如计算如图闭合回路的电流。 I R1
Idl r2
方向:
(
Idl
r
)
各电流元产生的 dB方向各不相同,
分 解dB
垂 平直 行于 于zz轴 轴的 的ddBBz
返回 退出
由对称性,dB分量相互抵消。
B dB//
dB
sinθ
μ0 4π
Idl sinθ r2
μ0I sinθ 4πr 2
2 πR
电源把其它形式的能量转化为电势能。如化学电池、
发电机、热电偶、硅(硒)太阳能电池、核反应堆
等。
返回 退出
电动势 : ε dA dq
电动势 等于将单位正电荷从
电源负极沿内电路移到正极过
程中非静电场力做的功。
大学物理-稳恒电流-PPT

常数为 、电导率为 。试计算同轴线单位长度的
绝缘电阻。
解:方法一:用恒定电场的基本关系求解
设在同轴线内外导体间加恒定电压
U
,由于介
0
质的 0 ,介质中存在沿半径方向从内导体流向
外导体的电流。另外,内、外导体中有轴向电流,
导体中存在轴向电场 Ez ,因而漏电介质中也存在 切向电场,但 Ez E,故可忽略 Ez 。介质中任 一点处的漏电流密度为
导体内沿电流方向取一底面积为 ds 、
高为 的小柱体,显然,柱体中的
载流子 1s内都要通过截面 ds,因此
dI nq ds
由此得电流密度
j nq
5
欧姆定律的微分形式
实验表明:在电场不太强、电场变化频率不太 高的情况下,导线中的电流强度与导线两端的电 势差成正比,即
U R I
-----欧姆定律
电流密度 j 是一个矢量,其大小等于流过垂直
于电流方向的单位面积的电流强度,方向与该点正
电荷的运动方向一致。即
di j en ds
对恒定电流:
dI j en ds
3
电流密度和电流强度的关系
如果在载流导体内任取一面元 ds ,其法向方向
en 与电流密度
j
的方向成
角,则通过该面元的电流为
dI
jdS
j cosdS
j dS
I S j dS
穿过某截面的电流强度等
dI
en
于电流密度矢量穿过该截面的 通量。
dS dS
电流强度是电流密度的通量。
4
例10.5.5 讨论导体中电流密度与载流子漂移运动的 关系。
漂移运动:载流子在电场作用下的定向运动。
稳恒电流

S
稳恒电流:导体中各点的电流密度的大小和 方向不随时间变化。
电荷分布不 随时间变化
稳恒电流
稳恒电场
稳恒电流条件
S
j dS 0
单位时间从闭合面向外流出的电荷量等于单位 时间流进闭合面的电荷量。
9.1.3
欧姆定律的微分形式
一段均匀电路的 欧姆定律
U AB I R
l R S
电阻率(欧姆 米)
0
B
2 R x
2
0 IS
2 32
2当x R,即P点远离圆电流时,磁感应强度为
IS B 2x
0 3
(3)一段圆弧形载流导线在圆心处产生的磁感 应强度为
0 I 0 I B 2R 2 4R
定义:圆电流回路的磁矩
Pm ISn
S为线圈所围的面积
r
q
B
q, r
r
v
B
v
q
9.3
磁通量
恒定磁场的基本性质
dm B dS B cos dS
m
(S )
9.3.1 磁场的高斯定理
B dS
磁场高斯定理
B dS 0
S
磁场是一个无源场
9.3.2 安培环路定理
dq I I t dt
电流密度矢量
电流的方向:正电荷流 动的方向
电流在不均匀导体或大块导体中流动时, 导体中各点电流的分布不均匀。电流强度的描 述不再适用。
电流密度 矢量
dI j dS
dI
ds
ds
单位时间内通过垂直于电流方向单位面积的电量 方向: 该点电流的方向
大学物理教程课件讲义 稳恒电流的磁场

8.2 磁场 磁感应强度
图8.6 两平行载流导线间的相互作用 图8.7 通电线圈的磁极
8.2 磁场 磁感应强度
1822年,安培提出了关于磁现象起源的假设。他认为, 一切磁现象都来源于电流。物体内部任何一个分子都相当于一 个小的回路电流,称为分子电流。每一个分子电流都和一个小
N、S两极对应于分子电流的两侧,如图 8.8(a)所示。如图8.8(b)所示。如图8.8(c) 所示。
先定义载流线圈的磁矩。 若一个线度小试验线圈的面积 为ΔS,线圈中的电流为I,则 试验线圈的磁矩Pm=IΔSen,en 为线圈法线方向的单位矢量, Pm与电流方向满足右手螺旋关 系,如图8.9所示。
图8.9 载流线圈的磁矩
8.2 磁场 磁感应强度
8.3
8.3.1 电流元
在静电场中为了求任意带电 体周围某点的电场强度E,曾将带 电体先分成无限多个电荷元dq,计 算出每个电荷元在该点的电场强度 dE,再根据场的叠加原理将所有电 荷元在该点的dE叠加,即得到带电 体在该点的电场强度E.图8.10是电 流强度为I的线电流。
8.1 稳恒电流 电动势
8.1.2 电源电动势
如前所述,产生稳恒电流的条件是导体两端维持恒定不 变的电势差。然而,在静电力的作用下,正电荷将从电势高 的一端经导体流向电势低的一端,而负电荷将从电势低的一 端经导体流向电势高的一端.这一过程将会使导体两端的正、 负电荷逐渐中和,两端的电荷分布随时间逐渐减少,电势差 逐渐减小,最后均趋于零,这就破坏了稳恒电流的条件。如 图8.2(a)所示。如图8.2(b)所示。
8.5 磁场对运动电荷及载流导线的作用
利用这一特点,可以实现磁聚焦,如图8.30所示。在非 匀强磁场中,磁场越强回旋半径越小,这意味着带电粒子被 约束在一个很小的范围内做螺旋运动。当带电粒子向磁场较 强的方向做螺旋运动时,在各点所受到的磁力总可以分解出 一个与前进方向相反的分量,如图8.31所示。
第八章稳恒电流

A
IR
B
U A UB I ( R Ri )
§8-3 含源电路的欧姆定律
三、由几个电阻和电源组成的含源电路
UA UB IR
A
IR
B
在上式的应用中,为了不至于发生混乱,规定了如下的
正负号选取规则:
先任意选取沿电路的指向,写出始末端的电势差 UA-UB 。 如果通过电阻的电流方向与电路指向相同,该电阻上 电势降落取“+”号,相反则取“-”号。
(1) 1 R L
S
(2) I U R
(3) E U E
L
(4) dU U dL L
(5) P IU
(6) v
8-18 在如图所示的电路中,已知 1 2.0 V, 2 6.0 V,
3 2.0 V, R1 1.0, R2 5.0, R2 5.0 ,
R4 2.0 . 求通过电阻R2的电流的大小和方向。
2、接触电势差的大小
kT ln nA
e nB
+
A
+ +
B
+
§ 8-2 电动势
三、温差电动势
1、温电动势的形成 两种不 同的导体,互相接触,形成 闭合路,若两个接触端处于 同一温度,回路电动势为零, 若将两个接触端置于不同温 度下,则形成电势差。
2、温差电动势的大小
温差电动势的形成
1
2
k (T1 T2 ) e
ln
nA nB
§ 8-2 电动势
3、温差电动势的应用
温差电偶测温示意图 温差电堆测温示意图
§ 8-2 电动势
四、能斯特电动势
1、能斯特电动势的形成 在由半透膜相隔的溶液系中,由 于带电离子的扩散作用,在膜的两侧产生电动势。
高三物理稳恒电流

高三物理稳恒电流学科:物理教学内容:第八章 高三物理稳恒电流一、考纲要求1.产生连续电流的条件,电流强度。
B2.欧姆定律,电阻和电阻定律。
B3.电阻的串、并联、串联电路的分压作用、并联电路的分流作用。
B4.电功、电功率、串、并联电路的功率分配,焦耳定律。
B5.电源的电动势和内电阻。
闭合电路的欧姆定律,路端电压。
B6.同种电池的串联。
A7.电流、电压和电阻的测量:安培表、伏特表和欧姆表的使用、伏安法测电阻。
B 说明:要求会解简单的混联电路问题,不要求解含有电流和电动势方向相反的电路及有关电桥问题。
二、知识结构1.部分电路、电功率、电阻的连接2.闭合电路欧姆定律、电阻的测量3.直流电路的分析和运算。
三、知识点、能力点提示1.在电解液导电时,是正负离子向相反方向定向移动形成电流,在用公式I =q/t 运算电流强度时应引起注意。
2.公式R =I U 是电阻的定义式,而R=ρSL是电阻的决定式R 与U 成正比或R 与I 成反比的说法是错误的,导体的电阻大小由长度、截面积及材料决定,一旦导体给定,即使它两端的电压U =0,它的电阻仍旧照旧存在。
3.电功和电热的区别:(1)纯电阻用电器:电流通过用电器以发热为目的,例如电炉、电熨斗、电饭锅、电烙铁、白炽灯泡等。
(2)非纯电阻用电器:电流通过用电器是以转化为热能以外的形式的能为目的,发热不是目的,而是不可幸免的热能缺失,例如电动机、电解槽、给蓄电池充电、日光灯等。
在纯电阻电路中,电能全部转化为热能,电功等于电热,即W=UIt=I 2Rt=RU 2t 是通用的,没有区别,同理P=UI=I 2R=RU 2也无区别,在非纯电阻电路中,电路消耗的电能,即W=UIt分为两部分,一大部分转化为其他形式的能;另一小部分不可幸免地转化为电热Q=I 2Rt ,那个地点W=UIt 不再等于Q=I 2Rt ,应该是W=E 其他+Q ,电功就只能用W=UIt 运算,电热就只能用Q=I 2Rt 运算。
稳恒电流物理知识点

稳恒电流物理知识点稳恒电流物理学问点稳恒电流是存在于导体内部的,大小不随时间发生转变的恒定的电流,就是所谓稳恒电流。
电流场中每一点的电流强度的大小和方向均不随时间转变,下面是我整理的稳恒电流物理学问点,希望能关怀到大家!1、电流〔1〕定义:电荷的定向移动形成电流。
2〕电流的方向:规定正电荷定向移动的方向为电流的方向。
在外电路中电流由高电势点流向低电势点,在电源的内部电流由低电势点流向高电势点〔由负极流向正极〕。
2、电流强度:〔1〕定义:通过导体横截面的电量跟通过这些电量所用时间的比值,I=q/t 〔2〕在国际单位制中电流的单位是安。
1mA=10-3A,1μA=10-6A〔3〕电流强度的定义式中,假如是正、负离子同时定向移动,q应为正负离子的电荷量和。
3、电阻〔1〕定义:导体两端的电压与通过导体中的电流的比值叫导体的电阻。
〔2〕定义式:R=U/I,单位:Ω〔3〕电阻是导体本身的属性,跟导体两端的电压及通过电流无关。
4、电阻定律〔1〕内容:在温度不变时,导体的电阻R与它的长度L成正比,与它的横截面积S成反比。
〔2〕公式:R=ρL/S。
〔3〕适用条件:①粗细均匀的导线;②浓度均匀的电解液。
5、电阻率:反映了材料对电流的阻碍作用。
〔1〕有些材料的电阻率随温度升高而增大〔如金属〕;有些材料的电阻率随温度升高而减小〔如半导体和绝缘体〕;有些材料的电阻率几乎不受温度影响〔如锰铜和康铜〕。
〔2〕半导体:导电性能介于导体和绝缘体之间,而且电阻随温度的增加而减小,这种材料称为半导体,半导体有热敏特性,光敏特性,掺入微量杂质特性。
〔3〕超导现象:当温度降低到确定零度附近时,某些材料的电阻率突然减小到零,这种现象叫超导现象,处于这种状态的物体叫超导体。
6、电功和电热〔1〕电功和电功率:电流做功的实质是电场力对电荷做功。
电场力对电荷做功,电荷的电势能削减,电势能转化为其他形式的能。
因此电功W=qU=UIt,这是计算电功普遍适用的公式。
稳恒电流
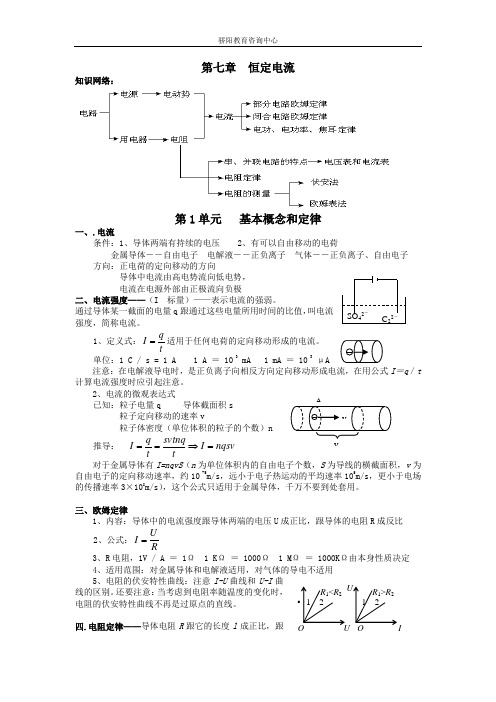
第七章 恒定电流知识网络:第1单元 基本概念和定律一、.电流条件:1、导体两端有持续的电压 2、有可以自由移动的电荷金属导体――自由电子 电解液――正负离子 气体――正负离子、自由电子 方向:正电荷的定向移动的方向导体中电流由高电势流向低电势, 电流在电源外部由正极流向负极二、电流强度——(I 标量)——表示电流的强弱。
通过导体某一截面的电量q 跟通过这些电量所用时间的比值,叫电流强度,简称电流。
1、定义式:tqI =适用于任何电荷的定向移动形成的电流。
单位:1 C / s = 1 A 1 A= 10 3mA 1 mA= 10 3μA注意:在电解液导电时,是正负离子向相反方向定向移动形成电流,在用公式I =q /t 计算电流强度时应引起注意。
2、电流的微观表达式已知:粒子电量q 导体截面积s 粒子定向移动的速率v 粒子体密度(单位体积的粒子的个数)推导: nqsv I tsvtnq t q I =⇒==对于金属导体有I=nqvS (n 为单位体积内的自由电子个数,S 为导线的横截面积,v 为自由电子的定向移动速率,约10 -5m/s ,远小于电子热运动的平均速率105m/s ,更小于电场的传播速率3×108m/s ),这个公式只适用于金属导体,千万不要到处套用。
三、欧姆定律1、内容:导体中的电流强度跟导体两端的电压U 成正比,跟导体的电阻R 成反比2、公式:RU I =3、R 电阻,1V / A = 1Ω 1 K Ω = 1000Ω 1 M Ω = 1000K Ω由本身性质决定4、适用范围:对金属导体和电解液适用,对气体的导电不适用5、电阻的伏安特性曲线:注意I-U 曲线和U-I 曲线的区别。
还要注意:当考虑到电阻率随温度的变化时,电阻的伏安特性曲线不再是过原点的直线。
四.电阻定律——导体电阻R 跟它的长度l 成正比,跟C 22-SO 42-横截面积S 成反比。
sl R ρ= (1)ρ是反映材料导电性能的物理量,叫材料的电阻率(反映该材料的性质,不是每根具体的导线的性质)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
I (nVS)(e) neVS
则电流密度的量值
J I neV S
8.2 一段电路的欧姆定律及其微分形式
一、欧姆定律
当导线的温度一定时,导线中的电流强度与导线两端 的电势差成正比,亦即
称为欧姆定律。
I U1 U2 R
R是比例系数,与导线的材料及几何形状有关,称为导线的
求介质内各点处的场强、漏电流的电流密度以及该介质的漏 电电阻值。
解:设圆柱形电容器内、外极板间的漏电总电流为I,由于
漏电电流(从内极板流向外极板)是沿径向对称分布的,而 在距离圆柱轴线r处,总电流所通过的截面积S=2πrl,所以 该处电流密度的大小应为
JI I
S 2rl
对于r—r+dr的圆柱形薄层来说,相应的电阻为
稳恒电场
电荷分布不随时间改变 但伴随着电荷的定向移动
导体内电场不为零,导 体内任意两点不等势
电场有保守性,它是 保守场,或有势场
稳恒电场的存在总要 伴随着能量的转换
例8—1 金属导体中的传导电流是由大量自由电子定向漂移
运动形成的。自由电子除了无规则的热运动外,在电场的
影响下,将沿着场强的反方向漂移设电子的电量的绝对值
I
UA
UB R
2l(U A ln
UB) rB
1000 1.10108
9.06106 A
rA
求得漏电的电流密度之值
J (U A U B ) 1 J 1.44106 1 A m2
ln rB r
r
rA
式中的r以米计,应用欧姆定律的微分形式,可求得介质中各 点处场强的大小为
E J (U A U B ) 1 1.44103 1 A m1
A q
_
FK q
dl
_ EK
dl
+–
式中 EK
FK q
表示非静电力场,数值上等于单位正电荷受
的非静电力,方向和正电荷受的非静电力的方向相同。
电动势是一个标量,其单位和电势的单位相同,为伏特 (V),其大小只取决于电源本身的性质,与电源外电路的 连接方式无关。为了使用方便,常规定电动势的方向为电 源内部电势升高的方向,也即从负极指向正极。
第八章 稳恒电流
本章主要讨论导体内形成的不随时间改变的稳恒电流。 要在导体内维持一稳恒的电流分布(电流场) ,必须在其中 建立一稳恒电场。所以我们首先说明稳恒电场与电流分布之 间的定量关系:欧姆定律的微分形式。导体内的稳恒电场虽 然有与静电场相同的性质,但它是依靠电源(例如化学电池 )来维持的。电源的作用是使稳恒电流在闭合回路中进行, 一方面电源要不断作功,将其他形式的能量转化为电能,另 一方面,电流在回路中产生热效应或以其他形式消耗电能。 因此,电路中的功能关系或能量转换关系也是本章的重点内 容—焦耳—楞次定律。
弦规律的变化时,称为正弦交流电。
二、电流密度
电流强度只能从整体上反映导体内电流的大小。当遇到电
流在粗细不均匀的导线或大块导体中流动的情况时,导体的不
同部分电流的大小和方向都可能不一样。有必要引入能够细致
描述电流分布的物理量——电流密度矢量,即需引入一个描述
空间不同点电流的大小的物理量。
dI j n
表征电源的另一个重要参量是电源的内阻r,当有电流 通过电源时,电阻r对电流也有阻碍作用,电势在r上也有
由电源的电动势ε=A/q和q=It
P I
将该式与电阻的功率P=IU相比较,可以看出ε与U相当,
事实上,当电源无内阻时,ε在数值上就等于电源的端电压 。
二、闭合电路的欧姆定律
如图所示一闭合电路,外电路中
大小: I dq dt
单位(SI):安培(A)
方向:规定为正电荷运动方向。电流强度是标量,通
常所说的电流方向是指正电荷在导体内移动的方向,
并非电流是矢量。
当I = dq/dt =常数时,即电流强度的大小和方向都不随时 间发生变化时,这种电流称为稳恒电流,也叫直流电流;当 I 随时间发生周期性变化时,称为交变电流;当I随时间作正
dI dU R
而
dI jdS
R dl
dS
E dU dl
所以
jdS Edl 1 EdS EdS dl dS
即
j E
称作欧姆定律的微分形式。它表明导体中任意一点的电流 密度与该点的电场强度成正比,且同方向。
例8—2 长度l=1.00m的圆柱形电容器,内外两个极板的半径分别
为rA=5×10-2m, rB=1×10-1 m,所充非理想电介质的电阻 率为ρ=1×109Ω·m。设两极板间所加电压UA-UB=1000v。
其电热功率为
p dQ I 2 R dt
二、焦耳——楞次定律的微分形式
电热功率密度:当导体内通有电流时,单位体积导体中每秒所放
出的热量称为热功率密度,以 表w示之。设小圆柱体的电阻率
为ρ,则它的电阻R为ρdl/dS ,又其体积为dSdl,所以,由热
功率密度的定义得
w Q (dI )2 R ( dI )2
电源有两个电极,一个叫正极,一个叫负极。电源工作
时就是靠非静电力作功不断地把正电荷从负极推向正极, 其能力的大小用电源的电动势ε来表示,其定义为:把单位 正电荷从电源的低电位(负极)推向高电位(正极)非静电力所 作的功。设电源对正电荷q施加的非静电力为Fk,则从电源
A _ FK dl
所以电源的电动势
对稳恒电流有: S j dS 0
在稳恒电流情况下,导体内电荷的分布不随时间改变。不随 时间改变的电荷分布产生不随时间改变的电场,这种电场称
稳恒电场。
l E dl 0
静电场
产生电场的电荷始终 固定不动
静电平衡时,导体内电 场为零,导体是等势体
电场有保守性,它是 保守场,或有势场
维持静电场不需要 能量的转换
为e,电子“漂移”运动速度的平均V值为 ,单位体积内自
由电子数为n。试证电流密度的J 量 n值eV
。
解: 在金属导体中,取一微小截面△S , △S的法线与电场方
向平行.通过△S的电流强度△ I,等于每秒内通过截面△S
的所有自由电子的总电量(绝对值).以△S为底面积,以V
为高作小柱体。显然,柱体内的自由电子数等于每秒内通过
R l
S 该式称为电阻定律。
当导体的横截面积不均匀或电阻率不均匀时,导体的电阻
RdRdl dS来自式中ρ是一个仅与导体材料有关的物理量,称为这种材料 的电阻率。电阻率的倒数γ(1/ ρ )称为电导率。
三、欧姆定律的微分形式
在通有电流强度I 的导体中,沿电流线方向任取一个小 圆柱体,通过的电流强度为dI,长度为dl,横戴面积为dS, 使圆柱体的轴线和它所在处的电场强度E的方向一致,面积 dS垂直于E。沿电场方向圆柱体两端的电势为U和U+dU, 圆柱体电阻为R,电流密度矢量为j。则
8.1 稳恒电流 电流密度
一、电流 电流强度
1、电流 电荷的定向移动,简称电流。
形成传导电流的条件是: ①物体中存在可以自由移动的电荷,即载流子(电子或 离子); ②存在电场。
按习惯,规定正电荷流动的方向为电流的方向。
2、电流强度
电流的强弱用电流强度来描述,其定义为:单位时间 内通过某导体横截面的电量。
dR dr dr S 2rl
对于从内到外的一系列圆柱形薄层来说,各层相应的电阻 是相互串联的,因此可求得漏电电阻值为
R dR rA dr ln rB
rB 2l r 2l rA
代入数据后,得
R 1.00 109 ln 2 1.10 108
2 1.00
按欧姆定律,求得漏电总电流
称为闭合电路的欧姆定律。
关于闭合电路的欧姆定律应注意以下几点:
(1)当R→∞时,外电路开路,I=0,此时电路上没有电流
;当R=0时,外电路短路,I=ε/r,由于一般r很小,I很大
,所以极易烧毁电源,应注意避免发生这种情况。
(2)对 IR Ir式变形可得IR+Ir-ε=0,其中IR是电压
,若将ε看作无内电阻电源的端电压,则这一关系可理解为 ,在稳恒电路中,从电路的某一点出发,绕电路一周,各个 元件的电压之和为零,这是一个很重要的结论,在分析电路 时经常用到。
电阻。R的倒数G(1/R)称为电导。在国际单位制中,电阻
的单位为欧姆(符Ω),电导的单位为西门子(符号S)。 电阻的量纲为 I 2 L2MT 3 。电导的量纲为 I 2 L2M 1T 3 。
二、电阻
一般金属导体电阻的大小与导体的材料和几何形状有 关。实验指出,对由一定材料制成的横截面均匀的导体的 电阻
I1 I2
这是稳恒电流连续性方程的另一种表达形式。
这一方程可以推广到三根或三根以上载流导线连结在一点
的情况.分别在三根载流导线中,选取横截面S1 、 S2和 S3 ,也可得连续性方程为
I1 I2 I3
四、稳恒电场
S
j
dS
dq dt
I S j dS
——电流的连续性方程
稳恒电流:导体内各处的电流密度都不随时间变化
j dS dq
s
dt
该式称为电流连续性方程。对于稳恒电流,由于I 的大小和 方向都不随时间发生变化,这样形成电流的电场就必须是 一个稳定场,产生电场的电荷就必须是一个稳定的分布, 这样对于任一闭合曲面S,必有
s j dS 0
此即为稳恒电流的连续性方程,也叫电流的稳恒条件。
如果取导体的两个截面S1和S2以及导体的侧面构成一个 闭合曲面,则由上式知,单位时间内通过S1面的电量一定等 于单位时间内通过S2的电量,即
ln rB r
r
rA
式中的r以米计,E 和J 的方向都是沿径向向外的。
8.3 电流的功和功率 焦耳—楞次定律及其微分形式
一、电流的功和功率
