高等代数习题 北大第四版 答案一到四章
高等代数第四章矩阵练习题参考答案
高等代数第四章矩阵练习题参考答案第四章矩阵习题参考答案一、判断题1.对于任意阶矩阵,,有、错、2.如果则、错、如、3.如果,则为可逆矩阵、正确、,因此可逆,且、4.设都就是阶非零矩阵,且,则得秩一个等于,一个小于、错、由可得、若一个秩等于,则该矩阵可逆,另一个秩为零,与两个都就是非零矩阵矛盾、只可能两个秩都小于、5.为阶方阵,若则错、如,有但、6.为矩阵,若则存在阶可逆矩阵及阶可逆矩阵,使正确、右边为矩阵得等价标准形,矩阵等价于其标准形、7.阶矩阵可逆,则也可逆、正确、由可逆可得,又、因此也可逆,且、8.设为阶可逆矩阵,则正确、又====、AB B A A BB A A B EA B AA A B E()(**)(*)*||*||*||||因此、由为阶可逆矩阵可得可逆,两边同时左乘式得逆可得二、选择题1.设就是阶对称矩阵,就是阶反对称矩阵,则下列矩阵中为反对称矩阵得就是(B )、(A) (B) (C) (D)(A)(D)为对称矩阵,(B)为反对称矩阵,(C)当可交换时为对称矩阵、2、设就是任意一个阶矩阵,那么( A)就是对称矩阵、(A) (B) (C) (D)3.以下结论不正确得就是( C )、(A)如果就是上三角矩阵,则也就是上三角矩阵;(B)如果就是对称矩阵,则也就是对称矩阵;(C)如果就是反对称矩阵,则也就是反对称矩阵;(D)如果就是对角阵,则也就是对角阵、4.就是矩阵, 就是矩阵, 若得第列元素全为零,则下列结论正确得就是(B )(A ) 得第行元素全等于零; (B )得第列元素全等于零; (C ) 得第行元素全等于零; (D ) 得第列元素全等于零; 5.设为阶方阵,为阶单位阵,则以下命题中正确得就是(D ) (A) (B) (C) (D)6.下列命题正确得就是(B )、 (A) 若,则 (B) 若,且,则 (C) 若,且,则 (D) 若,且,则7、就是矩阵,就是矩阵,则( B)、 (A) 当时,必有行列式; (B) 当时,必有行列式 (C) 当时,必有行列式; (D) 当时,必有行列式、为阶方阵,当时,因此,所以、 8.以下结论正确得就是( C ) (A) 如果矩阵得行列式,则; (B) 如果矩阵满足,则;(C) 阶数量阵与任何一个阶矩阵都就是可交换得; (D) 对任意方阵,有9.设就是非零得四维列向量,为得伴随矩阵,已知得基础解系为,则方程组得基础解系为( C )、(A)、 (B)、(C)、 (D)、由得基础解系为可得、因此(A),(B)中向量组均为线性相关得,而(D)显然为线性相关得,因此答案为(C)、由12341234**(,,,)(*,*,*,*)A A A A A A A O αααααααα===可得均为得解、10、设就是阶矩阵,适合下列条件( C )时,必就是可逆矩阵(A) (B) 就是可逆矩阵 (C) (B) 主对角线上得元素全为零11.阶矩阵就是可逆矩阵得充分必要条件就是( D )(A) (B) (C) (D)12.均就是阶矩阵,下列命题正确得就是( A )(A)若就是可逆矩阵,则从可推出(B)若就是可逆矩阵,则必有(C)若,则从可推出(D)若,则必有13.均就是阶矩阵,为阶单位矩阵,若,则有(C )(A)(B) (C) (D)14.就是阶方阵,就是其伴随矩阵,则下列结论错误得就是( D )(A)若就是可逆矩阵,则也就是可逆矩阵;(B)若就是不可逆矩阵,则也就是不可逆矩阵;(C)若,则就是可逆矩阵; (Ｄ)15.设就是5阶方阵,且,则( Ｄ )(A)(B) (C) (D)16.设就是得伴随阵,则中位于得元素为(Ｂ )(A) (B) (C) (D)应为得第列元素得代数余子式与得第列元素对应乘积与、17、设, ,其中就是得代数余子式,则(C )(A)就是得伴随 (B)就是得伴随 (C)就是得伴随(D)以上结论都不对18.设为方阵,分块对角阵,则 ( Ｃ )(A)(B)(C) (D)利用验证、19.已知,下列运算可行得就是( C )(A)(B) (C) (D)20.设就是两个矩阵,就是阶矩阵,那么( D )(A)(B)(C)(D)21.对任意一个阶矩阵,若阶矩阵能满足,那么就是一个( Ｃ )(A)对称阵 (B)对角阵 (C)数量矩阵 (D)得逆矩阵与任意一个阶矩阵均可交换得矩阵为数量矩阵、22.设就是一个上三角阵,且,那么得主对角线上得元素( Ｃ )(A)全为零 (B)只有一个为零（C）至少有一个为零 (D)可能有零,也可能没有零23.设,则( D )(A)(B) (C) (D)24. 设,若,则( B )(A)(B) (C) (D)25.设阶矩阵,若矩阵得秩为1,则必为(A )(A)1 (B)-1 (C)(D)矩阵得任意两行成比例、26、设为两个阶矩阵,现有四个命题:①若为等价矩阵,则得行向量组等价;②若得行列式相等,即则为等价矩阵;③若与均只有零解,则为等价矩阵;④若为相似矩阵,则与解空间得维数相同、以上命题中正确得就是( D )(A) ①, ③、(B) ②, ④、(C) ②,③、(D)③,④、当时,为相似矩阵。
高等代数北大版习题参考答案
第九章 欧氏空间1.设()ij a =A 是一个n 阶正定矩阵,而),,,(21n x x x =α, ),,,(21n y y y =β,在n R 中定义内积βαβα'A =),(,1) 证明在这个定义之下, n R 成一欧氏空间；2) 求单位向量)0,,0,1(1 =ε, )0,,1,0(2 =ε, … , )1,,0,0( =n ε，的度量矩阵；3) 具体写出这个空间中的柯西—布湿柯夫斯基不等式。
解 1)易见βαβα'A =),(是n R 上的一个二元实函数，且(1) ),()(),(αβαβαββαβαβα='A ='A '=''A ='A =，(2) ),()()(),(αβαββαβαk k k k ='A ='A =，(3) ),(),()(),(γβγαγβγαγβαγβα+='A '+'A ='A +=+，(4) ∑='A =ji j i ij y x a ,),(αααα，由于A 是正定矩阵，因此∑ji j i ij y x a ,是正定而次型，从而0),(≥αα，且仅当0=α时有0),(=αα。
2)设单位向量)0,,0,1(1 =ε, )0,,1,0(2 =ε, … , )1,,0,0( =n ε，的度量矩阵为)(ij b B =，则)0,1,,0(),()( i j i ij b ==εε⎪⎪⎪⎪⎪⎭⎫ ⎝⎛nn n n n n a a a a a aa a a212222211211)(010j ⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛ =ij a ，),,2,1,(n j i =， 因此有B A =。
4) 由定义，知∑=ji ji ij y x a ,),(βα，α==β==故柯西—布湿柯夫斯基不等式为2.在4R 中,求βα,之间><βα,(内积按通常定义)，设:1) )2,3,1,2(=α, )1,2,2,1(-=β，2) )3,2,2,1(=α, )1,5,1,3(-=β，3) )2,1,1,1(=α, )0,1,2,3(-=β。
高等代数第四版习题答案
高等代数第四版习题答案【篇一：高等代数第四章矩阵练习题参考答案】xt>一、判断题1. 对于任意n阶矩阵a，b，有a?b?a?b.错.2. 如果a2?0,则a?0.错.如a11?2?,a?0,但a?0.1?1?23. 如果a?a?e，则a为可逆矩阵.正确.a?a2?e?a(e?a)?e，因此a可逆，且a?1?a?e.4. 设a,b都是n阶非零矩阵，且ab?0，则a,b的秩一个等于n，一个小于n. 错.由ab?0可得r(a)?r(b)?n.若一个秩等于n，则该矩阵可逆，另一个秩为零，与两个都是非零矩阵矛盾.只可能两个秩都小于n.5．a,b,c为n阶方阵，若ab?ac, 则b?c.错.如a11??21??32?,b?,c，有ab?ac,但b?c.1?1?2?1?3?2?6．a为m?n矩阵，若r(a)?s,则存在m阶可逆矩阵p及n阶可逆矩阵q，使?ispaq0?0??. 0??正确.右边为矩阵a的等价标准形，矩阵a等价于其标准形.7．n阶矩阵a可逆，则a*也可逆.*?a*a?|a|e正确.由a可逆可得|a|?0，又aa.因此a*也可逆，且(a*)?1?1a. |a|8．设a,b为n阶可逆矩阵，则(ab)*?b*a*.正确.(ab)(ab)*?|ab|e?|a||b|e.又(ab)(b*a*)?a(bb*)a*?a|b|ea*?|b|aa*?|a||b|e.因此(ab)(ab)*?(ab)(b*a*).由a,b为n阶可逆矩阵可得ab可逆，两边同时左乘式ab的逆可得(ab)*?b*a*.二、选择题1．设a是n阶对称矩阵，b是n阶反对称矩阵(bt??b),则下列矩阵中为反对称矩阵的是（b ）.(a) ab?ba (b) ab?ba(c) (ab)2 (d) bab(a)(d)为对称矩阵，（b）为反对称矩阵，（c）当a,b可交换时为对称矩阵.2. 设a是任意一个n阶矩阵，那么（ a）是对称矩阵.(a) aa (b) a?a (c)a(d) a?a3．以下结论不正确的是（ c ）.(a) 如果a是上三角矩阵，则a也是上三角矩阵；(b) 如果a是对称矩阵，则 a也是对称矩阵；(c) 如果a是反对称矩阵，则a也是反对称矩阵；(d) 如果a是对角阵，则a也是对角阵.4．a是m?k矩阵, b是k?t矩阵, 若b的第j列元素全为零，则下列结论正确的是（b ）(a) ab的第j行元素全等于零；(b)ab的第j列元素全等于零；(c) ba的第j行元素全等于零； (d) ba的第j列元素全等于零；2222tt2t5．设a,b为n阶方阵，e为n阶单位阵，则以下命题中正确的是（d ）(a) (a?b)2?a2?2ab?b2(b) a2?b2?(a?b)(a?b)(c) (ab)2?a2b2 (d) a2?e2?(a?e)(a?e)6．下列命题正确的是（b ）.(a) 若ab?ac，则b?c(b) 若ab?ac，且a?0，则b?c(c) 若ab?ac，且a?0，则b?c(d) 若ab?ac，且b?0,c?0，则b?c7. a是m?n矩阵，b是n?m矩阵，则（ b）.(a) 当m?n时，必有行列式ab?0；(b) 当m?n时，必有行列式ab?0(c) 当n?m时，必有行列式ab?0；(d) 当n?m时，必有行列式ab?0.ab为m阶方阵，当m?n时，r(a)?n,r(b)?n,因此r(ab)?n?m，所以ab?0.8．以下结论正确的是（ c）(a) 如果矩阵a的行列式a?0,则a?0；(b) 如果矩阵a满足a?0，则a?0；(c) n阶数量阵与任何一个n阶矩阵都是可交换的；(d) 对任意方阵a,b，有(a?b)(a?b)?a?b9．设?1?,2?,3?,4是非零的四维列向量，a?(?1,?2,?3,?4),a*为a的伴随矩阵，222已知ax?0的基础解系为(1,0,2,0)t，则方程组a*x?0的基础解系为（ c ）.（a）?1,?2,?3.（b）?1??2,?2??3,?3??1.（c）?2,?3,?4.（d）?1??2,?2??3,?3??4,?4??1.10t由ax?0的基础解系为(1,0,2,0)可得(?1,?2,?3,?4)0,?1?2?3?0. ?2?0?因此（a），（b）中向量组均为线性相关的，而（d）显然为线性相关的，因此答案为（c）.由a*a?a*(?1,?2,?3,?4)?(a*?1,a*?2,a*?3,a*?4)?o可得?1,?2,?3,?4均为a*x?0的解.10.设a是n阶矩阵，a适合下列条件（ c ）时，in?a必是可逆矩阵nn(a) a?a (b) a是可逆矩阵 (c) a?0(b) a主对角线上的元素全为零11．n阶矩阵a是可逆矩阵的充分必要条件是（ d）(a) a?1 (b) a?0 (c) a?a (d)a?012．a,b,c均是n阶矩阵，下列命题正确的是（ a）(a) 若a是可逆矩阵，则从ab?ac可推出ba?ca(b) 若a是可逆矩阵，则必有ab?ba(c) 若a?0，则从ab?ac可推出b?c(d) 若b?c，则必有ab?ac13．a,b,c均是n阶矩阵，e为n阶单位矩阵，若abc?e，则有（c ） (a) acb?e （b）bac?e（c）bca?e (d) cba?e14．a是n阶方阵，a是其伴随矩阵，则下列结论错误的是（ d ）(a) 若a是可逆矩阵，则a也是可逆矩阵；(b) 若a是不可逆矩阵，则a也是不可逆矩阵；***t**(c) 若a?0，则a是可逆矩阵；（Ｄ）aa?a.aa*?ae?a.*15．设a是5阶方阵，且a?0，则a?（Ｄ）234n(a) a (b) a (c) a(d) a16．设a是a?(aij)n?n的伴随阵，则aa中位于(i,j)的元素为（Ｂ） (a) **?ak?1njkaki (b) ?ak?1nkjaki (c) ?ajkaik (d) ?akiakj k?1k?1nn应为a的第i列元素的代数余子式与a的第j列元素对应乘积和.a11a1na11a1n17.设a, b,其中aij是aij的代数余子式，则（c ） an1?ann???an1?ann??(a) a是b的伴随 (b)b是a的伴随(c)b是a?的伴随(d)以上结论都不对18．设a,b为方阵，分块对角阵ca0?*,则c? ( Ｃ ) ??0b?0? *?bb?0?? abb*??a*(a) c0?aa*0?(b)c??*?b??0?ba*(c)c0?aba*0?? (d) c??ab*??0利用cc*?|c|e验证.19．已知a46??135?，下列运算可行的是（ c ） ,b1?2??246?(a) a?b (b)a?b (c)ab(d)ab?ba【篇二：高等代数第4章习题解】题4.11、计算（1）(2,0,3,1)?3(0,1,2,4)?1(1,0,1,5) 2（2）5(0,1,2)?(1,1,0)?(1,1,1) 215517(1,0,1,5)?(,?3,?,?) 2222解：（1）(2,0,3,1)?3(0,1,2,4)?（2）5(0,1,2)?(1,19,0)?(1,1,1)?(0,,9) 222、验证向量加法满足交换律、结合律。
高等代数第四章及其习题答案
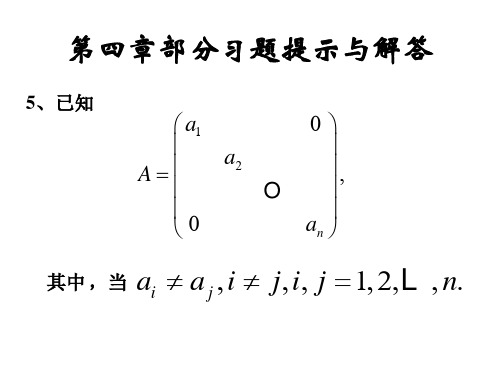
α b11
A1 0
= B1 0
β a11b11 a11β + α B1
A1 B1
，
为上三角形矩阵， 由归纳法假设知 A1 B1 为上三角形矩阵，故 AB 为上三 角形矩阵。 角形矩阵。
2）设 A = ( aij ) 为一可逆的上三角形矩阵，则 ） 为一可逆的上三角形矩阵， nn
= ε iT A j L 0 L L L 0 L a jn i 行 . L 0 L L L 0
0 M 0 a1i AEij = ( B1 , L , Bn ) ε j = Bi ε j = M ( 0, L , 0,1, 0, L , 0 ) a 0 ni M 0 0 0 = L 0 L L L 0 0 0 a1i a2 i L ani 0 L L 0 . L L L 0 L 0 0 L
T
y1 n T T 2 ( Ax) Ax = y y = ( y1 ,L, yn ) M = ∑ yi = 0, y i =1 n
从而 yi = 0, i = 1, L, n , 即 y = Ax = 0 ，由
x 的任意性知 Aε j = 0, j = 1,L , n ，其中
为数量矩阵. 为数量矩阵 级矩阵可交换， 注：因 A 与所有 n 级矩阵可交换，故 A 一定与 可交换， E i j ( i , j = 1, L , n ) 可交换，于是 AEij = Eij A.
10、已知 A为实对称矩阵 且 A2 = 0 , 不妨设 A = aij 、 为实对称矩阵, 阶矩阵， 为 n 阶矩阵， = x
T
( )
nn
高等代数(第四版)习题答案 王萼芳、石生明
3． 一元多项式的因式分解理论：主要讨论不可约多项式的基本概念与基本性质、因 式分解及其唯一性定理、三个特殊数域上的多项式分解。
4． 一元多项式的根与重根：主要讨论重因式的定义与性质、多项式的根、多项式根 的个数定理。
多元多项式则主要讨论多元多项式的基本概念、字典排列法与对称多项式。
（二）重难点归纳 本章的重点为一元多项式的概念，因式分解理论，多项式的根和对称多项式；难点为最大
解 1）由带余除法，可得 q(x) = 1 x − 7 , r(x) = − 26 x − 2
39
99
2）同理可得 q(x) = x2 + x −1, r(x) = −5x + 7
2． m, p, q 适合什么条件时，有 1） x 2 + mx −1 | x3 + px + q
高等代数北大编第1章习题参考答案
第一章多项式一、习题及参考解答1 .用g(x)除了(x),求商g(x)与余式r(x)：1 ) f (x) = x3 - 3x2 - x -1, g(x) = 3x2 - 2x +1;2 ) f(x) = x4 -2x + 5,g(x) = x2 - x + 2。
解1)由带余除法,可得q(x) =L-Z,“x) =-竺x-2 ；2)同理可得g(x) = / +x-l,r(x) = -5x + 7。
2. 〃?,PM适合什么条件时，有1 ) X2 +/?1¥-1 I X3 + px + c/ 92) x2 + nix + 11 x4 + px2 +q。
解1 )由假设,所得余式为0,即(〃 + l + 〃?2)x + (q-〃?) = O,所以当 1 + 。
时有 /+〃a-11 X* + px +g 0q _ in = 0 .2)类似可得= 于是当〃? = 0时，代入(2)可得〃=夕+ 1;q + 1 —〃一" = 0而当2- 〃 -J = 0时，代入(2)可得4 = 1 04 = ] _, 时，皆有 / + + 1 I X，+ px2 + 9。
综上所诉，当p + nr = 23 .求g(x)除f(x)的商q(x)与余式:1 ) /(x) = 2«?-5x3-8x,g(x) = x + 3 ;2) f(x) = x3-x2 - xg(x) = x-l + 2i o解[)q(x) = 2x4 - 6x3 +13x2 - 39A+ 109 ,r(x) = -327 '2)= x2 -2LV-(5+2/)r(x) = -9 + 8/ °4 .把/1(X)表示成x-%的方幕和，即表成c()+ G(X —“0)+。
2(X — X。
)~ + …+ C n(X — X。
)” + …的形式：1)/(x) = x',x()= 1 ；2) /(X)= X4-2X2+3,X0 =-2 ;3) f (x) = x4 + 2汉3 -(1 + i)x2 -3x + 7 + i,x0 =-i o解 1 ) 由综合除法，可得f(x) = l + 5(x-l) + 10(x-l)2 + 10(x-1)3+5(X-1)4 + (x-1)5 ;2 ) 由综合除法，可得X4-2X2+3=11-24(X + 2) + 22* + 2)2 -8(.r + 2)3 + (x + 2)，;3）由综合除法，可得『+2立3_（1 +82_3工+ （7 +，）= (7 + 5i)-5(x + i) + (-l-i)(x + i)2 -2i(x + i)3 + (x + i),。
高等代数北大编 第1章习题参考答案
第一章 多项式一 、习题及参考解答1． 用)(x g 除)(x f ，求商)(x q 与余式)(x r ： 1）123)(,13)(223+-=---=x x x g x x x x f ； 2）2)(,52)(24+-=+-=x x x g x x x f 。
解 1）由带余除法，可得92926)(,9731)(--=-=x x r x x q ； 2）同理可得75)(,1)(2+-=-+=x x r x x x q 。
2．q p m ,,适合什么条件时，有 1）q px x mx x ++-+32|1， 2）q px x mx x ++++242|1。
&解 1）由假设，所得余式为0，即0)()1(2=-+++m q x m p ，所以当⎩⎨⎧=-=++0012m q m p 时有q px x mx x ++-+32|1。
2）类似可得⎩⎨⎧=--+=--010)2(22m p q m p m ，于是当0=m 时，代入（2）可得1+=q p ；而当022=--m p 时，代入（2）可得1=q 。
综上所诉，当⎩⎨⎧+==10q p m 或⎩⎨⎧=+=212m p q 时，皆有q px x mx x ++++242|1。
3．求()g x 除()f x 的商()q x 与余式：1）53()258,()3f x x x x g x x =--=+； 2）32(),()12f x x x x g x x i =--=-+。
解 1）432()261339109()327q x x x x x r x =-+-+=-；2）2()2(52)()98q x x ix i r x i=--+=-+。
4．把()f x 表示成0x x -的方幂和，即表成—2010200()()...()n n c c x x c x x c x x +-+-++-+的形式：1）50(),1f x x x ==；2）420()23,2f x x x x =-+=-；3）4320()2(1)37,f x x ix i x x i x i =+-+-++=-。
高等代数习题(北大第四版)答案一到四章.docx
高等代数答案第一章多项式1 •用 g{x)除 /(.r),求商 </(.r)与余式 r(.r):1) /*(.r) = .r 3 - 3.r 2 - x-1,= 3.r 2 - 2.r +1: 2) f(x} = x 4 — 2.r+ 5,烈A ) = H -才+ 2 •解1)由带余除法，可得彳(才)=丄x--,/(.r) = - —.r--； 3 9 99 2 )同理可得久工)=X 2 + X- 1,心=-5.V+ 1 .2. m 、p 、q 适介什么条件时，冇1) x 1 + w.r-11 .t 3 + px+ q 、2) .r 2 + 7//.V+ 11 x 4 + + q o解I)由假设，所得余式为0,即(P+1 +〃小才+(0-刃) = 0,所以当+ 1 + - ° 时有才2 + my-11 x 3 + px*q° q- m- 02)类似可得(劝(2 — Q -刃?=0, j ：是当加=o 时，代入(2)可得〃=夕+ 1：而当 ［乡+ 1-p- ftl・=02-p-nr =0 时，代入(2〉可得0 = 1。
了 时,皆有 f + 〃/・丫+11 x 4 + pf + q o p + 〃厂=23. 求g(.x)除/(X )的商0⑴与余式：1) /*(.r) = Zr 5 - 5-r 3 - 8.i ,g(.r) = .r+ 3 ：2) f(x) = 一 , 一 不 g(.v)=才一 l + 2/ o0(・丫) = 2r 4 - +13” 一 39才 +109解1)；心)=-327°).(.丫) = '-2灯-(5+2/)。
/// = 0综上所诉,当 □攵.；p=q+\ -心)=-9 + 8/4. 把/(才)表示成才一兀的方幕和，即表成C Q +q(・Y-旺)+Q(才一・®)2 + ... + C…(X -X Q y+ …的形式：1) /(才)"，兀 T；2) /*(.r) = .r4 - 2.x2 + 3,x0 = -2；3) /(r) = x + 2/x一(l + /).r2一3x+ 7 + /,兀=-/«解1)由综合除法,可得/(x) = 1+ 5(x-1) + 10(r -1)2 +10(x-l)3^5(x -l)4+(r-l)5；2) 由综合除法，可得x4 -21^ + 3 = 11 - 24(.r+ 2) + 22(.r+ 2)2 -8(.r+ 2)3 + (.r+ 2)4:3) 由综介除法，可得.r4 + 2/：? - (1 + /).? -3x + (7 + z)= (7+5/)-5(x+/)4- (- 1一/比+/予-2«+/)+ (r+ // o5. 求/(貯与肌工)的最大公因式：1) /(才)=.r4 + .r5 -3, - 4才- 1£(才)=,+ , -.丫-1 ；2) /(.r) = .r4 -4.? + l,^(.r) =.? -3,r +1 ：3) f .r) - .r4 - lO.r2 + l,g(") - .r4 -心力 + 6A2 + 4/2r+ 1。
高等代数_(王萼芳_石生明_著)_课后答案__高等教育出版社
（4）不可约
（5）不可约
第二章 行列式 习题解答
1、均为偶排列
2、（1）i=8，k=3（2）i=3 k=6
3、
4、当n=4k，4k+1时为偶排列
当n=4k+2,4k+3时为奇排列
5、
6、正号
7、 ， ，
8、（1）原式= ，（2） （3）
9、解：行列式展开得一般项可表示为 ，列标 只可以在1,2,3,4,5中取不同值，故三个下标中至少有一个要取3,4,5列中一个数，从而任何一个展开式中至少要包含一个零元素，故所给行列式中每一项的乘积必为0，因此行列式只为零。
5、证：设有线性关系 则
当r=n时方程组中的未知量个数与方程个数相同，且系数行列式为一个范德蒙行列式，即
由定理得：方程组有唯一解，就是说 线性无关。
当r<n时，令
则由上面（1）的证明可知 是线性无关的。而 是 的延长向量所以 也线性无关。
6、证：由线性关系， 则
。再由题设知 线性无关，所以
解得 ，所以 线性无关
7、
证：设 是 中任意r个线性无关向量组，如果能够证明任意一个向量
都可由 线性表出就可以了。
事实上，向量组 是线性无关的，否则原向量组的秩大于r，矛盾。这说明
，再由 得任意性，即证。
8、证：有题设知 所以
，且等于r。又因为 线性无关，故而 的一个极大线性无关组。
9、
证：将所给向量组用（1）表示，它的一个极大线性五官向量组用（2）表示。
有题设由 ，所以 也就是f（1）=0，即证。
25、当n为奇数时，
当n为偶数时
27、（1）利用剩余除法试根：有一有理根：2
（2）有两个有理根： ，
北大版 线性代数第一章部分课后答案详解
习题1.2：1 .写出四阶行列式中11121314212223243132333441424344a a a a a a a a a a a a a a a a 含有因子1123a a 的项解：由行列式的定义可知，第三行只能从32a 、34a 中选，第四行只能从42a 、44a 中选，所以所有的组合只有()()13241τ-11233244a a a a 或()()13421τ-11233442a a a a ，即含有因子1123a a 的项为11233244a a a a 和11233442a a a a2. 用行列式的定义证明11121314152122232425313241425152000000000a a a a a a a a a a a a a a a a =0 证明：第五行只有取51a 、52a 整个因式才能有可能不为0，同理，第四行取41a 、42a ，第三行取31a 、32a ，由于每一列只能取一个，则在第三第四第五行中，必有一行只能取0.以第五行为参考，含有51a 的因式必含有0，同理，含有52a 的因式也必含有0。
故所有因式都为0.原命题得证.。
3.求下列行列式的值：（1）0100002;0001000n n -（2）001002001000n n-；解：（1）0100020001000n n -=()()23411n τ-123n ⨯⨯⨯⨯=()11!n n --（2）001002001000n n-=()()()()12211n n n τ---123n ⨯⨯⨯⨯=()()()1221!n n n ---4.设n 阶行列式：A=1111nn nna a a a ，B=11111212212221212n n n n n n n n nna ab a b a ba ab a b a b a -----，其中0b ≠，试证明：A=B 。
证明：B=11111212212221212n n n n n n n n nna ab a b a ba ab a b a b a -----=()()[]1212121212121n n n n s s s s n s s s s s n s s s n a b a b a b τ---∈-∑！=()()[]1212121212121()n n n n s s s s n s s s s s n s s s n a a a b b b τ---∈-∑！=()()[]12121212(1)(2)()121n n n n s s s s s s n s s s n s s s n a a a b τ-+-+-∈-∑！=()()[]121212121n n n s s s s s s n s s s n a a a τ∈-∑！=A命题得证。
高等代数__课后答案__高等教育出版社
高等代数习题答案（一至四章）第一章 多项式 习题解答1、（1）由带余除法，得17(),39q x x =-262()99r x =--（2）2()1q x x x =+-，()57r x x =-+2、（1）2100p m q m ⎧++=⎨-=⎩ ， （2）由22(2)010m p m q p m ⎧--=⎪⎨+--=⎪⎩得01m p q =⎧⎨=+⎩或212q p m =⎧⎨+=⎩。
3、（1）432()261339109,q x x x x x =-+-+()327r x =- （2）q （x ）=22(52)x ix i --+，()98r x i =--4、（1）有综合除法：2345()15(1)10(1)10(1)5(1)(1)f x x x x x x =+-+-+-+-+- （2）234()1124(2)22(2)8(2)(2)f x x x x x =-+++-+++（3）234()24(75)5()(1)()2()()f x i x i i x i i x i x i =+-++--+-+++5、（1）x+1 （2）1 （3）21x -- 6、（1）u （x ）=-x-1 ，v （x ）=x+2 （2）11()33u x x =-+，222()133v x x x =-- （3）u （x ）=-x-1, 32()32v x x x x =+--7、02u t =⎧⎨=⎩或23u t =-⎧⎨=⎩8、思路：根具定义证明证：易见d （x ）是f （x ）与g （x ）的公因式。
另设()x ϕ是f （x ）与g （x ）的任意公因式，下证()()x d x ϕ。
由于d （x ）是f （x ）与g （x ）的一个组合，这就是说存在多项式s （x ）与t （x ），使 d （x ）=s （x ）f （x ）+t （x ）g （x ）。
从而()()x f x ϕ，()()x g x ϕ，可得()()x d x ϕ。
高等代数北大编第1章习题参考答案
高等代数北大编第1章习题参考答案第一章多项式一、习题及参考解答1．用)(x g 除)(x f ，求商)(x q 与余式)(x r ： 1）123)(,13)(223+-=---=x x x g x x x x f ； 2）2)(,52)(24+-=+-=x x x g x x x f 。
解 1）由带余除法，可得92926)(,9731)(--=-=x x r x x q ； 2）同理可得75)(,1)(2+-=-+=x x r x x x q 。
2．q p m ,,适合什么条件时，有 1）q px x mx x ++-+32|1， 2）q px x mx x ++++242|1。
解 1）由假设，所得余式为0，即0)()1(2=-+++m q x m p ，所以当=-=++0012m q m p 时有q px x mx x ++-+32|1。
2）类似可得=--+=--010)2(22m p q m p m ，于是当0=m 时，代入（2）可得1+=q p ；而当022=--m p 时，代入（2）可得1=q 。
综上所诉，当??+==10q p m 或=+=212m p q 时，皆有q px x mx x ++++242|1。
3．求()g x 除()f x 的商()q x 与余式：1）53()258,()3f x x x x g x x =--=+； 2）32(),()12f x x x x g x x i =--=-+。
解 1）432()261339109()327q x x x x x r x =-+-+=-；2）2()2(52)()98q x x ix i r x i=--+=-+。
4．把()f x 表示成0x x -的方幂和，即表成2010200()()...()n n c c x x c x x c x x +-+-++-+L 的形式：1）50(),1f x x x ==；2）420()23,2f x x x x =-+=-；3）4320()2(1)37,f x x ix i x x i x i =+-+-++=-。
高等代数第四版习题答案
高等代数第四版习题答案【篇一：高等代数第四章矩阵练习题参考答案】xt>一、判断题1. 对于任意n阶矩阵a，b，有a?b?a?b.错.2. 如果a2?0,则a?0.错.如a11?2?,a?0,但a?0.1?1?23. 如果a?a?e，则a为可逆矩阵.正确.a?a2?e?a(e?a)?e，因此a可逆，且a?1?a?e.4. 设a,b都是n阶非零矩阵，且ab?0，则a,b的秩一个等于n，一个小于n. 错.由ab?0可得r(a)?r(b)?n.若一个秩等于n，则该矩阵可逆，另一个秩为零，与两个都是非零矩阵矛盾.只可能两个秩都小于n.5．a,b,c为n阶方阵，若ab?ac, 则b?c.错.如a11??21??32?,b?,c，有ab?ac,但b?c.1?1?2?1?3?2?6．a为m?n矩阵，若r(a)?s,则存在m阶可逆矩阵p及n阶可逆矩阵q，使?ispaq0?0??. 0??正确.右边为矩阵a的等价标准形，矩阵a等价于其标准形.7．n阶矩阵a可逆，则a*也可逆.*?a*a?|a|e正确.由a可逆可得|a|?0，又aa.因此a*也可逆，且(a*)?1?1a. |a|8．设a,b为n阶可逆矩阵，则(ab)*?b*a*.正确.(ab)(ab)*?|ab|e?|a||b|e.又(ab)(b*a*)?a(bb*)a*?a|b|ea*?|b|aa*?|a||b|e.因此(ab)(ab)*?(ab)(b*a*).由a,b为n阶可逆矩阵可得ab可逆，两边同时左乘式ab的逆可得(ab)*?b*a*.二、选择题1．设a是n阶对称矩阵，b是n阶反对称矩阵(bt??b),则下列矩阵中为反对称矩阵的是（b ）.(a) ab?ba (b) ab?ba(c) (ab)2 (d) bab(a)(d)为对称矩阵，（b）为反对称矩阵，（c）当a,b可交换时为对称矩阵.2. 设a是任意一个n阶矩阵，那么（ a）是对称矩阵.(a) aa (b) a?a (c)a(d) a?a3．以下结论不正确的是（ c ）.(a) 如果a是上三角矩阵，则a也是上三角矩阵；(b) 如果a是对称矩阵，则 a也是对称矩阵；(c) 如果a是反对称矩阵，则a也是反对称矩阵；(d) 如果a是对角阵，则a也是对角阵.4．a是m?k矩阵, b是k?t矩阵, 若b的第j列元素全为零，则下列结论正确的是（b ）(a) ab的第j行元素全等于零；(b)ab的第j列元素全等于零；(c) ba的第j行元素全等于零； (d) ba的第j列元素全等于零；2222tt2t5．设a,b为n阶方阵，e为n阶单位阵，则以下命题中正确的是（d ）(a) (a?b)2?a2?2ab?b2(b) a2?b2?(a?b)(a?b)(c) (ab)2?a2b2 (d) a2?e2?(a?e)(a?e)6．下列命题正确的是（b ）.(a) 若ab?ac，则b?c(b) 若ab?ac，且a?0，则b?c(c) 若ab?ac，且a?0，则b?c(d) 若ab?ac，且b?0,c?0，则b?c7. a是m?n矩阵，b是n?m矩阵，则（ b）.(a) 当m?n时，必有行列式ab?0；(b) 当m?n时，必有行列式ab?0(c) 当n?m时，必有行列式ab?0；(d) 当n?m时，必有行列式ab?0.ab为m阶方阵，当m?n时，r(a)?n,r(b)?n,因此r(ab)?n?m，所以ab?0.8．以下结论正确的是（ c）(a) 如果矩阵a的行列式a?0,则a?0；(b) 如果矩阵a满足a?0，则a?0；(c) n阶数量阵与任何一个n阶矩阵都是可交换的；(d) 对任意方阵a,b，有(a?b)(a?b)?a?b9．设?1?,2?,3?,4是非零的四维列向量，a?(?1,?2,?3,?4),a*为a的伴随矩阵，222已知ax?0的基础解系为(1,0,2,0)t，则方程组a*x?0的基础解系为（ c ）.（a）?1,?2,?3.（b）?1??2,?2??3,?3??1.（c）?2,?3,?4.（d）?1??2,?2??3,?3??4,?4??1.10t由ax?0的基础解系为(1,0,2,0)可得(?1,?2,?3,?4)0,?1?2?3?0. ?2?0?因此（a），（b）中向量组均为线性相关的，而（d）显然为线性相关的，因此答案为（c）.由a*a?a*(?1,?2,?3,?4)?(a*?1,a*?2,a*?3,a*?4)?o可得?1,?2,?3,?4均为a*x?0的解.10.设a是n阶矩阵，a适合下列条件（ c ）时，in?a必是可逆矩阵nn(a) a?a (b) a是可逆矩阵 (c) a?0(b) a主对角线上的元素全为零11．n阶矩阵a是可逆矩阵的充分必要条件是（ d）(a) a?1 (b) a?0 (c) a?a (d)a?012．a,b,c均是n阶矩阵，下列命题正确的是（ a）(a) 若a是可逆矩阵，则从ab?ac可推出ba?ca(b) 若a是可逆矩阵，则必有ab?ba(c) 若a?0，则从ab?ac可推出b?c(d) 若b?c，则必有ab?ac13．a,b,c均是n阶矩阵，e为n阶单位矩阵，若abc?e，则有（c ） (a) acb?e （b）bac?e（c）bca?e (d) cba?e14．a是n阶方阵，a是其伴随矩阵，则下列结论错误的是（ d ）(a) 若a是可逆矩阵，则a也是可逆矩阵；(b) 若a是不可逆矩阵，则a也是不可逆矩阵；***t**(c) 若a?0，则a是可逆矩阵；（Ｄ）aa?a.aa*?ae?a.*15．设a是5阶方阵，且a?0，则a?（Ｄ）234n(a) a (b) a (c) a(d) a16．设a是a?(aij)n?n的伴随阵，则aa中位于(i,j)的元素为（Ｂ） (a) **?ak?1njkaki (b) ?ak?1nkjaki (c) ?ajkaik (d) ?akiakj k?1k?1nn应为a的第i列元素的代数余子式与a的第j列元素对应乘积和.a11a1na11a1n17.设a, b,其中aij是aij的代数余子式，则（c ） an1?ann???an1?ann??(a) a是b的伴随 (b)b是a的伴随(c)b是a?的伴随(d)以上结论都不对18．设a,b为方阵，分块对角阵ca0?*,则c? ( Ｃ ) ??0b?0? *?bb?0?? abb*??a*(a) c0?aa*0?(b)c??*?b??0?ba*(c)c0?aba*0?? (d) c??ab*??0利用cc*?|c|e验证.19．已知a46??135?，下列运算可行的是（ c ） ,b1?2??246?(a) a?b (b)a?b (c)ab(d)ab?ba【篇二：高等代数第4章习题解】题4.11、计算（1）(2,0,3,1)?3(0,1,2,4)?1(1,0,1,5) 2（2）5(0,1,2)?(1,1,0)?(1,1,1) 215517(1,0,1,5)?(,?3,?,?) 2222解：（1）(2,0,3,1)?3(0,1,2,4)?（2）5(0,1,2)?(1,19,0)?(1,1,1)?(0,,9) 222、验证向量加法满足交换律、结合律。
高等代数习题(北大第四版)答案一到四章.
高等代数答案第一章多项式1．用)(x g 除)(x f ，求商)(x q 与余式)(x r ：1）123)(,13)(223+−=−−−=x x x g x x x x f ；2）2)(,52)(24+−=+−=x x x g x x x f 。
解1）由带余除法，可得92926)(,9731)(−−=−=x x r x x q ；2）同理可得75)(,1)(2+−=−+=x x r x x x q 。
2．q p m ,,适合什么条件时，有1）q px x mx x ++−+32|1，2）q px x mx x ++++242|1。
解1）由假设，所得余式为0，即0)()1(2=−+++m q x m p ，所以当⎩⎨⎧=−=++012m q m p 时有q px x mx x ++−+32|1。
2）类似可得⎩⎨⎧=−−+=−−010)2(22m p q m p m ，于是当0=m 时，代入（2）可得1+=q p ；而当022=−−m p 时，代入（2）可得1=q 。
综上所诉，当⎩⎨⎧+==1q p m 或⎩⎨⎧=+=212m p q 时，皆有q px x mx x ++++242|1。
3．求()g x 除()f x 的商()q x 与余式：1）53()258,()3f x x x x g x x =−−=+；2）32(),()12f x x x x g x x i =−−=−+。
解1）432()261339109()327q x x x x x r x =−+−+=−；2）2()2(52)()98q x x ix i r x i=−−+=−+。
4．把()f x 表示成0x x −的方幂和，即表成2010200()()...()n n c c x x c x x c x x +−+−++−+⋯的形式：1）50(),1f x x x ==；2）420()23,2f x x x x =−+=−；3）4320()2(1)37,f x x ix i x x i x i =+−+−++=−。
高等代数北大版第章习题参考答案
1. 判别下面所定义的变换那些是线性的，那些不是:4) 在 P 3 中，A (X 1，X 2,X 3) (2X 1 X 2, X 2 X 3,X 1)；5) 在 P[ X ]中，A f (x) f (x 1)； 6) 在P[ X ]中，A f(x )f(X o ),其中X 0 P 是一固定的数;7) 把复数域上看作复数域上的线性空间，A8)在P nn 中，A X=BXC 其中B,C P n n 是两个固定的矩阵.解1)当0时,是;当 0时,不是。
2)当 0时，是；当 0时，不是。
3)不是.例如当(1,0,0), k 2 时，k A ( ) (2,0,0) , A (k )(4,0,0),A (k ) k A()。
4)是•因取(y 1,y 2,y 3),有A ()= A (X 1 y 1, X 2 y 2 ,X 3 y 3)=(2X 1 2y 1 X 2 y 2 ,X 2 y= (2X 1 X 2,X 2 X 3,X 1) (2y 1=A+ A ,A (k ) A (kx 1, kx 2, kx 3)故A 是P 3上的线性变换。
5)是.因任取 f(x) P[x], g(x) P[ X],并令u(x) f (x) g(x)则A ( f (x) g(x)) = A u(x) =u(x 1) = f (x 1) g(x 1)=A f (x) + A (g(x)),再令 v( x) kf (x)则 A (kf (x)) A (v( x)) v(x 1) kf (x 1) k A ( f (x)),故A 为P[x]上的线性变换。
6)是.因任取 f (x)P[x], g(x) P[ x]则.g(x))=f(X 0) g(x 。
)A ( f (x)) A (g(x)),第七章线性变换1) 在线性空间V 中，A ,其中V 是一固定的向量;2)在线性空间V 中，A3) 在 P 3 中，A (X 1, X 2 X )其中V 是一固定的向量;(X 12 , X 2 X 3, x 3).X 3 y 3,X 1 yj y 2,y 2y 3，y 1)(2kx 1kx 2, kx 2gkxj (2kx 1kx 2, kx 2gkxjA ( f (x)A(kf (x)) kf (X0) k A(f (x))7)不是，例如取a=1,k=l，则A(ka)=-i , k( A a)=i, A^ ka) k A(a)。
高等代数北大版习题参考答案
第九章 欧氏空间1.设()ij a =A 是一个n 阶正定矩阵,而),,,(21n x x x =α, ),,,(21n y y y =β,在nR 中定义内积βαβα'A =),(,1) 证明在这个定义之下, n R 成一欧氏空间；2) 求单位向量)0,,0,1(1 =ε, )0,,1,0(2 =ε, … , )1,,0,0( =n ε，的度量矩阵；3) 具体写出这个空间中的柯西—布湿柯夫斯基不等式。
解 1)易见βαβα'A =),(是n R 上的一个二元实函数，且 (1) ),()(),(αβαβαββαβαβα='A ='A '=''A ='A =，(2) ),()()(),(αβαββαβαk k k k ='A ='A =，(3) ),(),()(),(γβγαγβγαγβαγβα+='A '+'A ='A +=+， (4)∑='A =ji j i ij y x a ,),(αααα，由于A 是正定矩阵，因此∑ji j i ij y x a ,是正定而次型，从而0),(≥αα，且仅当0=α时有0),(=αα。
2)设单位向量)0,,0,1(1 =ε, )0,,1,0(2 =ε, … , )1,,0,0( =n ε，的度量矩阵为)(ij b B =，则)0,1,,0(),()( i j i ij b ==εε⎪⎪⎪⎪⎪⎭⎫⎝⎛nn n n n n a a a a a a a a a212222211211)(010j ⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛ =ij a ，),,2,1,(n j i =， 因此有B A =。
4) 由定义，知∑=ji ji ij y x a ,),(βα，α==β==故柯西—布湿柯夫斯基不等式为2.在4R 中,求βα,之间><βα,(内积按通常定义)，设: 1) )2,3,1,2(=α, )1,2,2,1(-=β， 2) )3,2,2,1(=α, )1,5,1,3(-=β， 3))2,1,1,1(=α, )0,1,2,3(-=β。
高等代数[北大版]第1章习题参考答案解析
![高等代数[北大版]第1章习题参考答案解析](https://img.taocdn.com/s3/m/9f49e8bcf8c75fbfc77db2ad.png)
第一章 多项式1． 用)(x g 除)(x f ，求商)(x q 与余式)(x r ： 1）123)(,13)(223+-=---=x x x g x x x x f ； 2）2)(,52)(24+-=+-=x x x g x x x f 。
解 1）由带余除法，可得92926)(,9731)(--=-=x x r x x q ； 2）同理可得75)(,1)(2+-=-+=x x r x x x q 。
2．q p m ,,适合什么条件时，有 1）q px x mx x ++-+32|1， 2）q px x mx x ++++242|1。
解 1）由假设，所得余式为0，即0)()1(2=-+++m q x m p ，所以当⎩⎨⎧=-=++0012m q m p 时有q px x mx x ++-+32|1。
2）类似可得⎩⎨⎧=--+=--010)2(22m p q m p m ，于是当0=m 时，代入（2）可得1+=q p ；而当022=--m p 时，代入（2）可得1=q 。
综上所诉，当⎩⎨⎧+==10q p m 或⎩⎨⎧=+=212m p q 时，皆有q px x mx x ++++242|1。
3．求()g x 除()f x 的商()q x 与余式：1）53()258,()3f x x x x g x x =--=+； 2）32(),()12f x x x x g x x i =--=-+。
解 1）432()261339109()327q x x x x x r x =-+-+=-；2）2()2(52)()98q x x ix i r x i=--+=-+。
4．把()f x 表示成0x x -的方幂和，即表成2010200()()...()n n c c x x c x x c x x +-+-++-+L 的形式：1）50(),1f x x x ==；2）420()23,2f x x x x =-+=-；3）4320()2(1)37,f x x ix i x x i x i =+-+-++=-。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
证 由题设知 ( f ( x), g( x)) =1 ，所以存在 u(x),v(x) 使 u(x) f (x) + v(x)g (x) = 1，
从而 u(x) f (x) −v(x) f (x) +v(x) f (x) +v(x)g(x) =1，
即[u(x) − v(x)] f ( x) + v( x)[ f ( x) + g( x)] = 1 ，
所以 ( f (x), f ( x) + g( x)) =1。
同理 ( g( x), f ( x) + g( x)) =1 。
再由 12 题结论，即证 ( f ( x) g( x), f ( x) + g( x)) =1。
９．证明： ( f ( x)h( x), g( x) h( x)) = ( f( x), g( x)) h( x) ， (h( x) 的首系数为１）。
证 因为存在多项式 u(x), v( x) 使 ( f ( x), g( x)) = u( x) f ( x) + v( x) g( x) ，
所以 ( f (x), g( x)) h( x) = u( x) f( x) h( x) + v( x) g( x) h( x) ，
⎨ ⎩
p
=
q
+
1
或
⎧
⎨ ⎩
p
q =1 + m2 =
时，皆有
2
x2
+
mx
+1|
x4
+
px 2
+
q
。
3．求 g (x) 除 f (x) 的商 q(x) 与余式：
1） f (x) = 2x5 − 5x3 − 8x, g (x) = x + 3；
2） f (x) = x3 − x2 − x, g( x) = x −1 + 2i 。
q(x) = 2x4 − 6x3 +13x2 − 39x +109
解 1）
；
r (x) = −327
2） q(x) = x2 − 2ix − (5 + 2i ) 。 r (x) = −9 + 8i
4．把 f (x) 表示成 x − x0 的方幂和，即表成 c0 + c1 (x − x0 ) +c2 (x − x0 )2 + ... +cn (x −x0 )n +⋯的形式： 1） f (x) = x5 , x0 =1； 2） f (x) = x4 − 2x2 + 3, x0 = −2； 3） f (x) = x4 + 2ix3 − (1+ i )x2 − 3x + 7 + i, x0 = −i 。 解 1）由综合除法，可得 f (x) = 1+ 5(x −1) +10(x −1)2 +10(x −1)3 +5(x −1)4 +(x −1)5； 2）由综合除法，可得 x4 − 2x2 + 3 = 11− 24(x + 2) + 22(x + 2)2 − 8(x + 2)3 + (x + 2)4 ； 3） 由综合除法，可得 x4 + 2ix3 − (1+ i )x2 − 3x + (7 +i ) = (7 + 5i) − 5(x + i )+ (− 1− i )(x + i )2 − 2i (x + i )3 + (x + i )4 。 5．求 f (x) 与 g(x) 的最大公因式： 1） f (x) = x4 + x3 − 3x2 − 4x −1,g (x ) = x3 + x2 − x − 1； 2） f (x) = x4 − 4x3 +1,g (x ) = x3 − 3x2 +1； 3） f (x) = x4 −10x2 +1, g (x) = x4 − 4 2x3 + 6x2 + 4 2x + 1。 解 1） ( f ( x), g( x)) = x +1 ； 2） ( f (x), g( x)) =1； 3） ( f ( x), g( x)) = x2 − 2 2 x −1。 6．求 u(x), v( x) 使 u(x) f (x) + v(x)g (x) = ( f (x), g (x)) 。 1） f (x) = x4 + 2x3 − x2 − 4x − 2, g (x) = x4 + x3 − x2 − 2x − 2； 2） f (x) = 4x4 − 2x3 −16x2 + 5x + 9, g (x) = 2x3 − x2 − 5x + 4 ； 3） f (x) = x4 − x3 − 4x2 + 4x + 1, g (x) = x2 − x − 1。 解 1）因为 ( f ( x), g( x)) = x2 − 2 = r2( x)
13．设 f1(x),..., f m (x), g1( x),..., gn( x) 都是多项式，而且
( fi( x), g j( x)) =1 (i =1, 2,..., m; j =1, 2,..., n) 。
求证： ( f1 (x) f 2 (x)... f m (x), g1( x) g 2( x)...gn ( x)) =1 。
１０．如果 f (x), g( x) 不全为零，证明：
⎛ ⎜ ⎝
(
f
f ( x) ( x), g( x))
, (
f(
g( x) x), g(
x))
⎞ ⎟ ⎠
=1。
证 存在 u(x), v( x) 使 ( f ( x), g( x)) = u( x) f ( x) + v( x) g( x) ，
又因为 f (x), g(x) 不全为０，所以 ( f (x), g(x)) ≠ 0 ，
(u(x), v(x)) =1。
证 由上题证明类似可得结论。
12．证明：如果 ( f ( x), g( x)) =1, ( f ( x), h( x)) =1，那么 ( f ( x), g( x) h( x)) =1 。
证 由假设，存在 u1 ( x), v1 ( x) 及 u2 ( x), v2 ( x) 使
( f2( x), g1( x) g2( x)... gn( x)) =1 ................................................， ( fm (x), g1( x) g2( x)...gn ( x)) = 1
从而可得
( f1(x) f 2(x)... f m(x), g1( x) g 2( x)...gn( x)) =1 。
于是 u(x) = −q2 (x) = −x −1
。
v(x) = 1+ q1 (x )q2 (x ) = 1+1i(x + 1) = x + 2
2）仿上面方法，可得 ( f (x), g( x)) = x−1，且 u(x) = − 1 x + 1 ,v(x) = 2 x 2 − 2 x −1。
33
33
u1(x) f (x) + v1(x)g (x) = 1
（1）
u2 (x) f (x) + v2 (x)h(x) = 1
将（1）（2）两式相乘，得
（2）
[u1(x)u2(x) f (x) + v1(x)u2(x)g (x) + u1(x)v2(x)h(x)] f ( x) ， +[v1(x)v2 (x)]g( x)h( x) = 1 所以 ( f ( x), g( x) h( x)) =1 。
39
99
2）同理可得 q(x) = x 2 + x −1, r( x) = −5x + 7 。
2． m, p, q 适合什么条件时，有
1） x 2 + mx −1 | x3 + px + q ，
2） x 2 + mx + 1| x4 + px2 + q 。
解 1）由假设，所得余式为 0，即 ( p + 1 + m2 )x + (q − m) = 0，
上式说明 ( f ( x), g( x)) h( x) 是 f (x)h(x) 与 g( x)h( x) 的一个组合。
另一方面，由 ( f (x), g( x)) | f ( x) 知 ( f (x), g(x))h(x) | f ( x)h( x) ，
同理可得 ( f ( x), g( x)) h( x) | g( x) h( x) ，
高等代数答案
第一章 多项式
1． 用(x) ：
1） f (x) = x3 − 3x 2 − x −1, g(x) = 3x 2 − 2x +1；
2） f (x) = x 4 − 2x + 5, g( x) = x2 − x + 2 。
解 1）由带余除法，可得 q(x) = 1 x − 7 , r(x) = − 26 x − 2 ；
证 由于
( f1(x), g1( x)) =1 ( f1(x), g2( x)) = 1 ， .......................... ( f1(x), gn( x)) =1
反复应用第 12 题结论，可得
( f1(x), g1( x) g2 ( x)...gn ( x)) = 1，
同理可证