2010-2011第一学期《概率论与数理统计(B)》期中试题答案
概率论与数理统计试题期中考试-答案

概率论与数理统计课程期中考试考试时间:90分钟姓名:班级:学号:一、单项选择题(本大题共有5个小题,每小题4分,共20分)1,设..~(100,0.1)R V X B,1..~()2R V Yπ,且X和Y相互独立,令72+-=YXZ,则D(Z)=(D )。
A:7 B:8 C:10 D:11 2,若P(A)=1/2,P(B|A)=1/3,则P(AB)=( B )A:1/2 B: 1/3 C: 5/6 D:1/63,设X的概率密度函数为30()xke xf x-⎧>=⎨⎩其它,则=k( C )A:1/3 B:1/9 C: 3 D: 94, 如果X,Y为两个随机变量,满足COV(X,Y)=0,下列命题中正确的是( A )。
A:X,Y不相关B:X,Y相互独立C:D(XY) =D(X)+D(Y) D:D(X-Y) =D(X)-D(Y)5,在8片药中有4片是安慰剂,从中任取3片,则取到2片是安慰剂的概率为( B )A:1/4 B :3/7 C:1/2 D:6/7二、填空题(本大题共有6个小题,每空2分,共20分)4 A,B为两个随机事件,若P(A)=0.4,P(B)=0.6,P(B A)=0.2.则P(AB)= 0.4 ,P(AB)= 0.25 甲乙两人独立射击,击中目标的概率分别为0.8,0.7,现在两人同时射击同一目标,则目标被击中的概率为 0.946.若某产品平均数量为73,均方差为7,利用切比雪夫不等式估计数量在52~94之间的概率为 8/97.在8件产品中有2件次品。
从中随机抽取2次,每次抽取一件,做不放回抽取。
则两次都是正品的概率为 15/28 抽取的产品分别有一正品和一件次品的概率为 3/7 ,第二次取出的产品为次品的概率为 1/48若X~N(2,1),Y~U[1,4],X,Y互相独立,则E(X+2Y-XY+2)= 4 ,D(X-2Y+3)=49 设D(X)=D(Y)=2,0.3XY ρ=,则D(X-Y)= 2.8三、解答题(本大题共有3个小题,共32分)10(7分)病树主人外出,委托邻居浇水。
概率论2010-2011第一学期(B卷)

第 1 页共 6 页第 2 页 共 6 页4.一批产品的废品率为0.1,每次抽取1个,观察后放回去,下次再取一个,共重复3次,3次中恰有2次取到废品的概率为()。
(a) 027.0; (b) 243.0; (c) 27.0; (d) 0243.0.5.将3个不同的小球随机地放入4个杯子中去,则杯子中球的最大个数为1的概率为()。
(a)3344P ; (b)3344C ;(c) 4343P ; (d)4343C .二、计算题(共8题,第8题8分,其余每题各11分,共85分)。
1.某工厂的车床、钻床、磨床、刨床的台数之比为9:3:2:1,它们在一定时间内需修理的概率之比为1:2:3:1,当有一台机床需要修理时,求这台机床是车床的概率。
第 3 页 共 6 页2.设随机变量X 的概率密度为:⎩⎨⎧≤≤+=其他20)1()(x x k x f(1)确定k 的值;(2)求数学期望E (X )和方差D(X); (3)计算概率}10{<<X P3. 设二维随机变量(X,Y)的联合概率密度为,⎩⎨⎧<<=-其它,0,0,),(y x e y x f y求:(1) 关于X,Y 的边缘概率密度; (2) X,Y 是否相互独立; (3) 概率}1{≤+Y X P第 4 页 共 6 页4. 从大批发芽率为0.9的种子中随意抽取1000粒,试估计这1000粒种子中发芽的种子个数不低于880粒的概率(结果用)(x Φ表示)。
5.设总体X 的概率密度函数为⎩⎨⎧<<+=其他010)1()(x xx f ααn 21X ,......,X ,X 为总体X 的一个样本。
试求未知参数α的矩估计量和最大似然估计量。
第 5 页 共 6 页6.某手表厂生产的超薄女表,走时误差服从正态分布),(2σμN ,检验员随机从装配线上抽取9只进行检测,测得8.7,28.02==S x当取置信水平为95%时,求该种手表走时误差的方差2σ的置信区间。
《概率论与数理统计》考试试题B(答案)

广东白云学院2007—2008学年第二学期期末考试《概率论与数理统计》B卷参考答案及评分标准适用专业及方向: 经济管理类各专业、土木工程层次: 本科年级: 07级限时: 120分钟考试形式: 闭卷考场要求: 笔试考试形式:闭卷考场要求:笔试.(×)2. 设、为两事件, 则.(×)3. 设, 则其一定是某连续型随机变量的密度函数.(√)4. 设随机变量~N(1, 9), 则.(√)5.设, , 与相互独立, 则.二、填空题(请将正确答案填写在括号内。
每空3分,共30分), 则( 0.6 ).7.设随机变量和都服从[0,2]上的均匀分布, 则( 2 ).8. 设为两个随机事件,且已知, , ,则条件概率(0.6).则常数c=(0.1),}5.15.0{<<-XP=(0.5).10. 已知~,函数值,则=(0.9772).11. 服从参数的泊松分布, 令, 则(13), (75).12. 设三次独立试验中, 事件出现的概率相等, 若已知至少出现一次的概率等1/3 ).,则下列关系成立的是( C )A. B.C. D.15.同时抛掷3枚均匀的硬币, 则恰好有两枚正面朝上的概率为( D )A. 0.5B. 0.125C. 0.25D. 0.37516. 10张奖券中含有3张中奖的奖券,每人购买一张,则第3个购买者中奖的概率为( B )A. B. 0.3 C. D.17. 设连续型随机变量服从参数为的指数分布,若方差,则数学期望( B )A. B. C. D.18. 如果离散型随机变量相互独立,且服从参数为的泊松分布,则当充分大时,离散型随机变量( D )近似服从标准正态分布.A. B. C. D.19. 设连续型随机变量的概率密度为,则( A )A. B. C.D.四、计算题(每小题8分,共32分)(1)若事件BA,互不相容,求α; (2)若事件BA,相互独立,求α.解 (1)因为BA,互不相容,所以φ=AB, (1分)所以)()()()(BPABPBPBAP=-= (2分)而)(1)()()()(APBAPBPAPBAP-=-+=(3分)所以α=0.3 (4分)(2)因为BA,相互独立,则A与B也相互独立, (5分))())(1)(()()()()()(BPBPAPBPAPBPAPBAP+-=-+=(7分)所以α=73(8分)21. 某产品主要由三个厂家供货.甲、乙、丙三个厂家的产品分别占总数的15%,80%,5%,其次品率分别为0.02,0.01,0.03,试计算(1)从这批产品中任取一件是不合格品的概率;(2)已知从这批产品中随机地取出的一件是不合格品,问这件产品由哪个厂家生产的可能性最大?解记=A{所取一件产品是不合格品},321,,BBB分别表示”产品来自甲、乙、丙厂” (1分) 依题意有:15.0)(1=BP, 80.0)(2=BP,05.0)(3=BP02.0)(1=BAP,01.0)(2=BAP,03.0)(3=BAP (2分) (1)由全概率公式0125.0)()()(31==∑=iiiBPBAPAP (5分) (2)由贝叶斯公式24.00125.002.015.0)()()()(111=⨯==APBAPBPABP, (6分)64.00125.001.080.0)()()()(222=⨯==APBAPBPABP, (7分)12.00125.003.005.0)()()()(333=⨯==A PB A P B P A B P (8分) 22.设连续型随机变量X 的密度函数⎩⎨⎧<<=其他020)(2x Ax x ϕ,求(1)常数A ;(2))(),(X D X E .解 因为138)(202===⎰⎰∞+∞-A dx Ax dx x ϕ (2分) 所以 83=A (3分)所以 ⎪⎩⎪⎨⎧<<=其他2083)(2x xx ϕ2383)()(203===⎰⎰∞+∞-dx x dx x x X E ϕ (5分) 51283)()(20422===⎰⎰∞+∞-dx x dx x x X E ϕ (7分) 20323512)]([)()(222=⎪⎭⎫ ⎝⎛-=-=X E X E X D (8分) 23. 已知电站供电网有10000盏电灯, 夜晚每一盏灯开灯的概率都是0.7, 而假定开、关时间彼此独立, 试用切贝谢夫不等式估计夜晚同时开着的灯数在6800与7200之间的概率。
《概率论与数理统计》期中考试试题汇总,DOC

《概率论与数理统计》期中考试试题(一)一、选择题(本题共6小题,每小题2分,共12分)1.某射手向一目标射击两次,A i 表示事件“第i 次射击命中目标”,i =1,2,B 表示事件“仅第一次射击命中目标”,则B =( )A .A 1A 2B .21A AC .21A AD .21A A2345C 68.将3个球放入5个盒子中,则3个盒子中各有一球的概率为=________.9.从a 个白球和b 个黑球中不放回的任取k 次球,第k 次取的黑球的概率是=.10.设随机变量X ~U (0,5),且21Y X =-,则Y 的概率密度2f Y (y )=________.11.设二维随机变量(X ,Y )的概率密度f (x ,y )=⎩⎨⎧≤≤≤≤,y x ,其他,0,10,101则P {X +Y ≤1}=________. 12.设二维随机变量(,)X Y 的协方差矩阵是40.50.59⎛⎫ ⎪⎝⎭,则相关系数,X Y ρ=________. 13.二维随机变量(X ,Y )(1,3,16,25,0.5)N -,则X ;Z X Y =-+.(-1,31),(2,0),且取这些值的概率依次为61,a ,121,125. 求(1)a =?并写出(X ,Y )的分布律;(2)(X ,Y )关于X ,Y 的边缘分布律;问X ,Y 是否独立;(3){0}P X Y +<;(4)1X Y =的条件分布律;(5)相关系数,X Y ρ18.(8分)设测量距离时产生的随机误差X ~N (0,102)(单位:m),现作三次独立测量,记Y 为三次测量中误差绝对值大于19.6的次数,已知Φ(1.96)=0.975.(1)求每次测量中误差绝对值大于19.6的概率p ;(2)问Y 服从何种分布,并写出其分布律;求E (Y ).1取出的3件中恰有一件次品的概率为( )A .601B .457C .51D .157 2.下列选项不正确的是()A .互为对立的事件一定互斥B .互为独立的事件不一定互斥C .互为独立的随机变量一定是不相关的D .不相关的随机变量一定是独立的3.某种电子元件的使用寿命X (单位:小时)的概率密度为42100,100;()0,100,x p x x x ⎧≥⎪=⎨⎪<⎩任取一只电子元件,则它的使用寿命在150小时以内的概率为( )A .41B .31C .21D .32 4.若随机变量,X Y 不相关,则下列等式中不成立的是.A5A 6A 79.设随机变量X ~E (1),且21Y X =-,则Y 的概率密度f Y (y )=________.10.设随机变量X ~B (4,32),则{}1P X <=___________. 11.已知随机变量X 的分布函数为0,6;6(),66121,6,x x F x x x ≤-⎧⎪+⎪=-<<⎨⎪≥⎪⎩,则X 的概率密度p (x )=______________.12.设二维随机变量(,)X Y 的协方差矩阵是90.60.625⎛⎫⎪⎝⎭,则相关系数,X Y ρ=________. 13.二维随机变量(X ,Y )(2,3,9,16,0.4)N -,则X;Z X Y =-+. 14.随机变量X 的概率密度函数为,0()0,0x X e x f x x -⎧>=⎨≤⎩,Y 的概率密度函数为1,12()3Y y f y ⎧-<<⎪=⎨,,X Y 相互独立,且Z X Y =+的概率密度函数为()z f z = 试求:(1)常数α,β;(2)(X ,Y )关于X ,Y 的边缘分布律;问X ,Y 是6否独立;(3)X 的分布函数F(x);(4){1}P X Y +<;(5)1X Y =的条件分布律;(6)相关系数,X Y ρ18.(8分)设顾客在某银行窗口等待服务的时间X (单位:分钟)具有概率密度()3103x e x p x -⎧>⎪=⎨,;某顾客在窗口等待服务,若超过9分钟,他就离视机,厂方获得利润50万元,但如果因销售不出而积压在仓库里,则每一万台需支付库存费10万元,问29寸彩色电视机的年产量应定为多少台,才能使厂方的平均收益最大?《概率论与数理统计》期中试卷试题(五)一、选择题(共5题,每题2分,共计12分)1.下列选项正确的是()A.互为对立事件一定是互不相容的B.互为独立的事件一定是互不相容的C.互为独立的随机变量一定是不相关的 D.不相关的随机变量不二、填空题:(每小题2分,共18分)7.同时扔4枚均匀硬币,则至多有一枚硬币正面向上的概率为________.8.将3个球放入6个盒子中,则3个盒子中各有一球的概率为=________.89.从a 个白球和b 个黑球中不放回的任取3次球,第3次取的黑球的概率是=.10.公共汽车站每隔5分钟有一辆汽车到站,乘客到站的时刻是任意的,则一个乘客候车时间不超过3分钟的概率为 (1,2,9,16,0)N -;2Z X =-. 率密度函数51,050,0x e x x ->≤的概率密,(,)X Y 相互独立,且X Y +的概率密度函数为(z f 在某区域有一架飞机,雷达以99%的概率探测到并报警。
《概率论与数理统计》期中考试(B卷)

概率论与数理统计
期中考试 B 卷
《概率论与数理统计》期中考试(B卷)
序号:_____ 学号:____ 姓名:_____ 成绩:_____
3 1 1. (7分)某医院用某种新药医治流感,对病人进行试验,其中 的病人服此药, 的病人 4 4 不服此药,5天后有70%的病人痊愈,已知不服药的病人5天后10%有的可以治愈。 (1). 求该药的治愈率; (2). 若某病人5天后痊愈求他是服此药而痊愈的概率。 解:(1)设A = {病人服药} B = {病人痊愈}. 因 ¯ ) = P(A)P( B|A) + P(A ¯ )( BA ¯ ) = 3 × P( B|A) + 1 × 0.1 = 0.9. P( B) = P(AB) + P(AB 4 4 故该药的自愈率为P( B|A) = 0.9.′ P(AB) 27 (2)P(A| B) = = . P( B) 28 2. (10分)已知随机变量X ∼ U (−2, 5), (1). 试求方程4t2 + 4Xt + X + 2 = 0有实根的概率; (2). 求Y = |X |的概率密度。 1 7 , −2 < x < 5, 解:(1) 由已知, fX ( x) = 0, 其他 P(方程有实根) = P(判别式▽ = P{16X 2 − 16X + 2 = P{X 2} + P{X 0) 得分____ 得分____
在区域0 < y < 1, −y < x < y 内, f ( x, y) = fX ( x) fY (y), · · · · · · 1′ 因此X 与Y 不相互独立. (2)
1 P{X ≤ 1 ,Y ≥ 2 } 5 1 1 2 = . P{Y ≥ |X ≤ } = 1 2 2 7 P{ X ≤ 2 }
2011年1,4,7,10月自考《概率论与数理统计》(经管类)试题和参考答案

2011年1月全国自考概率论与数理统计(经管类)试题全国2011年4月高等教育自学考试 概率论与数理统计(经管类)试题课程代码:04183一、单项选择题(本大题共10小题,每小题2分,共20分)在每小题列出的四个备选项中只有一个是符合题目要求的,请将其代码填写在题后的括号内。
错选、多选或未选均无分。
1.设A ,B ,C 为随机事件,则事件“A ,B ,C 都不发生”可表示为( ) A .B.BC C .ABCD.2.设随机事件A 与B 相互独立,且P(A)=,P(B)=,则P(A B)=( )A . B.C . D.3.设随机变量X ~B(3,0.4),则P{X≥1}=( ) A.0.352 B.0.432 C.0.784 D.0.9364.已知随机变量X 的分布律为P{-2<X≤4 }=( )A.0.2 C.0.55 D.0.8 5.设随机变量X 的概率密度为f(x)=,则E(X),D(X)分别为 ( )A.-3,B.-3,2C.3,D.3,26.设二维随机变量(X,Y)的概率密度为f(x,y)=则常数c=( )A. B.C.2D.47.设随机变量X~N(-1,22),Y~N(-2,32),且X 与Y 相互独立,则X-Y~( )A.N(-3,-5)B.N(-3,13)C.N (1,)D.N(1,13)8.设X,Y为随机变量,D(X)=4,D(Y)=16,Cov(X,Y)=2,则XY=( )A. B.C. D.9.设随机变量X~2(2),Y~2(3),且X与Y相互独立,则( )A.2(5)B.t(5)C.F(2,3)D.F(3,2)10.在假设检验中,H0为原假设,则显著性水平的意义是( )A.P{拒绝H0| H0为真}B. P {接受H0| H0为真}C.P {接受H0| H0不真}D. P {拒绝H0| H0不真}二、填空题(本大题共15小题,每小题2分,共30分)请在每小题的空格中填上正确答案。
《概率论与数理统计》期中考试试题汇总

系数 X ,Y
18.(8 分) 设测量距离时产生的随机误差 X~N(0,102)(单位:m),现作三次独 立测量,记 Y 为三次测量中误差绝对值大于 19.6 的次数,已知Φ(1.96)=0.975.
(1)求每次测量中误差绝对值大于 19.6 的概率 p; (2)问 Y 服从何种分布,并写出其分布律;求 E(Y).
fY
( y)
1
2
, 1
y
1 , (X ,Y )
相互独立,且
Z
X
Y
的概率密度函数为
fz (z)
0, others
15. 设 随 机 变 量 X , E(X ) 3, D(X ) 1 , 则 应 用 切 比 雪 夫 不 等 式 估 计 得 3
P{| X 3|1}
三、计算题(本题共 5 小题,共 70 分)
2
D. 2
3
4.若随机变量 X ,Y 不相关,则下列等式中不成立的是
.
A. D(X Y ) DX DY
B. Cov(X ,Y ) 0
C. E(XY ) EX EY
D. D(XY ) DX DY
5.设随机变量 X 与 Y 相互独立,X 服从参数 1 为的泊松分布,Y~B(6,1 ),则 D(X-Y)=( )
pY ( y) , X 与 Y 是否独立;(4) 概率 P{Y X} , (5)求 Z X Y 的概率密度; (6)相关系数 X ,Y
20.(10 分)假定暑假市场上对冰淇淋的需求量是随机变量 X 盒,它服从区间[200, 400]上的均匀分布,设每售出一盒冰淇淋可为小店挣得 1 元,但假如销售不出而 屯积于冰箱,则每盒赔 3 元。问小店应组织多少货源,才能使平均收益最大?
《概率论与数理统计》期中考试试题汇总,DOC

《概率论与数理统计》期中考试试题(一)一、选择题(本题共6小题,每小题2分,共12分)1.某射手向一目标射击两次,A i 表示事件“第i 次射击命中目标”,i=1,2,B 表示事件“仅第一次射击命中目标”,则B=()A .A 1A 2B .21A AC .21A AD .21A A 2.某人每次射击命中目标的概率为p(0<p<1),他向目标连续射击,则第一次未中第二次命中的概率为()A .p 2B .(1-p)2C .1-2p D .p(1-p)3.已知P(A)=0.4,P(B)=0.5,且A B ,则P(A|B)=()A .0 B .0.4 C .0.8 D .14.一批产品中有5%不合格品,而合格品中一等品占60%,从这批产品中任取一件,则该件产品是一等品的概率为()A .0.2B .0.30C .0.38D .0.57 5.下列选项正确的是()A .互为对立事件一定是互不相容的B .互为独立的事件一定是互不相容的C .互为独立的随机变量一定是不相关的D .不相关的随机变量不一定是独立的6.设随机变量X 与Y 相互独立,X 服从参数2为的指数分布,Y ~B(6,21),则D(X-Y)=( ) A .1B .74C .54D .12二、填空题(本题共9小题,每小题2分,共18分)7.同时扔3枚均匀硬币,则至多有一枚硬币正面向上的概率为________.8.将3个球放入5个盒子中,则3个盒子中各有一球的概率为= ________. 9.从a 个白球和b 个黑球中不放回的任取k 次球,第k 次取的黑球的概率是= .10.设随机变量X ~U (0,5),且21Y X ,则Y 的概率密度f Y (y)=________.11.设二维随机变量(X ,Y)的概率密度 f (x,y)=,y x ,其他,0,10,101则P{X+Y ≤1}=________.12.设二维随机变量(,)X Y 的协方差矩阵是40.50.59,则相关系数,X Y = ________.13. 二维随机变量(X ,Y)(1,3,16,25,0.5)N ,则X ;Z X Y .。
2011-概率论与数理统计B答案

2011 至 2012 学年第 1 学期 考试时间: 120 分钟 课程名称: 概率论与数理统计 (B )卷 考试形式:(闭卷)年级: 10 专业: 全校相关专业 ;层次:(本)一、填空题(每小题2分,共20分) 1、0.7; 2、)16,1(N ; 3、10; 4、1,1==B A ; 5、44; 6、2720;7、 8、32,9、75,10、111-∑=n i i X n 。
二、选择题(每题2分,共20分)11、(B ); 12、(D ); 13、(D ); 14、(B ); 15、(C );16、(B );17、(A );18、(B ); 19、(A ); 20、(B ). 三、计算题(共60分)21、(8分) 解: 设 i A ={第i 次取得新球},i=1,2. (1) 设C={第二次才取得新球},有12C A A =12121464()()()(|)10915P C P A A P A P A A ===⨯=, ………2分 (2) 设事件 D = {发现其中之一是新球},E = {其中之一是新球,另一个也是新球}12121651()()()(|)1093P ED P A A P A P A A ===⨯= ………4分 121212121121()()()()1()(|)()(|)31644613310910915P D P A A P A A P A A P A P A A P A P A A =++=++=+⨯+⨯= ………6分 ()1/35(|)()13/1513P E D P E D P D ===. ………8分22、(10分)解设随机变量X 与Y 相互独立,且均服从[]0,2上的均匀分布,令U X Y =-,试求()D U 。
解:易知X 与Y 的联合密度函数为()1,,,(,)40,x y D f x y ⎧∈⎪=⎨⎪⎩其他,其中(){},02,02D x y x y =≤≤≤≤(2分)12E(U)=E X-Y 43Dx y dxdy ⎡⎤=-⋅=⎣⎦⎰⎰,(3分) ()()222212E(U )=E X-Y E X-Y 43Dx y dxdy ⎡⎤⎡⎤==-⋅=⎣⎦⎣⎦⎰⎰,(3分) ()()()2229D UE U E U =-=。
概率论与数理统计考试试卷(附答案)

概率论与数理统计考试试卷(附答案)一、选择题(共6小题,每小题5分,满分30分) 1. 事件表达式B A -的意思是 ( ) (A) 事件A 与事件B 同时发生 (B) 事件A 发生但事件B 不发生 (C) 事件B 发生但事件A 不发生(D) 事件A 与事件B 至少有一件发生2. 假设事件A 与事件B 互为对立,则事件A B ( ) (A) 是不可能事件 (B) 是可能事件 (C) 发生的概率为1(D) 是必然事件3. 已知随机变量X ,Y 相互独立,且都服从标准正态分布,则X 2+Y 2服从 ( ) (A) 自由度为1的χ2分布 (B) 自由度为2的χ2分布 (C) 自由度为1的F 分布(D) 自由度为2的F 分布4. 已知随机变量X ,Y 相互独立,X ~N (2,4),Y ~N (-2,1), 则( )(A) X +Y ~P (4) (B) X +Y ~U (2,4) (C) X +Y ~N (0,5) (D) X +Y ~N (0,3)5. 样本(X 1,X 2,X 3)取自总体X ,E (X )=μ, D (X )=σ2, 则有( ) (A) X 1+X 2+X 3是μ的无偏估计(B)1233X X X ++是μ的无偏估计(C) 22X 是σ2的无偏估计(D) 21233X X X ++⎛⎫ ⎪⎝⎭是σ2的无偏估计6. 随机变量X 服从在区间(2,5)上的均匀分布,则X 的方差D (X )的值为( ) (A) 0.25(B) 3.5(C) 0.75(D) 0.5二、填空题(共6小题,每小题5分,满分30分。
把答案填在题中横线上) 1. 已知P (A )=0.6, P (B |A )=0.3, 则P (AB )= __________2. 三个人独立地向一架飞机射击,每个人击中飞机的概率都是0.4,则飞机被击中的概率为__________3. 一个袋内有5个红球,3个白球,2个黑球,任取3个球恰为一红、一白、一黑的概率为_____4. 已知连续型随机变量,01,~()2,12,0,.x x X f x x x ≤≤⎧⎪=-<≤⎨⎪⎩其它 则P {X ≤1.5}=_______.5. 假设X ~B (5, 0.5)(二项分布), Y ~N (2, 36), 则E (2X +Y )=__________6. 一种动物的体重X 是一随机变量,设E (X )=33, D (X )=4,10个这种动物的平均体重记作Y ,则D (Y )=_____________________ _______三、有两个口袋,甲袋中盛有两个白球,一个黑球,乙袋中盛有一个白球,两个黑球。
《概率论与数理统计》期中考试试习题汇总

欢迎阅读《概率论与数理统计》期中考试试题(一)一、选择题(本题共6小题,每小题2分,共12分)1.某射手向一目标射击两次,A i 表示事件“第i 次射击命中目标”,i =1,2,B 表示事件“仅第一次射击命中目标”,则B =( )A .A 1A 2B .21A AC .21A AD .21A A2.某人每次射击命中目标的概率为p (0<p <1),他向目标连续射击,则第一次未中第二次命中的概率为( ) A .p 223.已知A .0 4率为(A .0.25A C 6.A .1- 7.8.将39.从a 10.11.12.设二维随机变量(,)X Y 的协方差矩阵是40.50.59⎛⎫⎪⎝⎭,则相关系数,X Y ρ= ________.13. 二维随机变量(X ,Y )(1,3,16,25,0.5)N -,则X;Z X Y=-+ .14. 随机变量X 的概率密度函数为51,0()50,0x X e x f x x -⎧>⎪=⎨⎪≤⎩,Y 的概率密度函数为1,11()20,Y y f y others ⎧-<<⎪=⎨⎪⎩,(,)X Y相互独立,且Z X Y =+的概率密度函数为()z f z =15. 设随机变量X , 1()3,()3E X D X ==,则应用切比雪夫不等式估计得{|3|1}P X -≥≤三、计算题(本题共5小题,共70分)16.(8分)某物品成箱出售,每箱20件,假设各箱含0,1和2件次品的概率分别是0.7,0.2和0.1,顾客在购买时,售货员随机取出一箱,顾客开箱任取4件检查,若无次品,顾客则买下该箱物品,否则退货.试求:(1) 顾客买下该箱物品的概率;(2) 现顾客买下该箱物品,问该箱物品确实17.(20求(1)a (3){P X Y +18.(8为三次(1)(2)19.(24求: (1) ;(4) 概率{P Y 20.(101.一批产品共10件,其中有2件次品,从这批产品中任取3件,则取出的3件中恰有一件次品的概率为( ) A .601 B .457 C .51 D .157 2.下列选项不正确的是( ) A .互为对立的事件一定互斥B .互为独立的事件不一定互斥C .互为独立的随机变量一定是不相关的D .不相关的随机变量一定是独立的3.某种电子元件的使用寿命X (单位:小时)的概率密度为2100,100;()0,100,x p x x x ⎧≥⎪=⎨⎪<⎩ 任取一只电子元件,则它的使用寿命在150小时以内的概率为( ) A .41 B .31 C .21 D .324.若随机变量,X Y 不相关,则下列等式中不成立的是 . A .DY DX Y X D +=+)( B. 0),(=Y X Cov C. (E 5.A .1-6.则常数x A .7.8. 将29. 10. 11. 已密度p (x 12.13. 二维随机变量(X ,Y )(2,3,9,16,0.4)N -,则X;Z X Y=-+ .14. 随机变量X 的概率密度函数为,0()0,0x X e x f x x -⎧>=⎨≤⎩,Y 的概率密度函数为1,12()30,Y y f y others⎧-<<⎪=⎨⎪⎩,,X Y 相互独立,且Z X Y =+的概率密度函数为()z f z =15. 设随机变量X,1()1,()3E X D X==,则应用切比雪夫不等式估计得{13}P X-<<≥三、计算题(本大题共5小题,共70分)16.(8分)据市场调查显示,月人均收入低于1万元,1至3万元,以及高于3万元的家庭在今后五年内有购置家用高级小轿车意向的概率分别为 0.1,0.2 和 0.7.假定今后五年内家庭月人均收入X 服从正态分布N (2, 0.82 ).试求:(1) 求今后五年内家庭有购置高级小轿车意向的概率;(2) 若已知某家庭在今后五年内有购置高级小轿车意向,求该家庭月人均收入在1至3万元的概率.17(1),Y)关问X,Y)相关18{X>9}(1)X Y的条件概率密度函数;(5)相关系数,X Yρ20.(10分)设市场上每年对某厂生产的29寸彩色电视机的需求量是随机变量X(单位:万台),它均匀分布于[10,20].每出售一万台电视机,厂方获得利润50万元,但如果因销售不出而积压在仓库里,则每一万台需支付库存费10万元,问29寸彩色电视机的年产量应定为多少台,才能使厂方的平均收益最大?《概率论与数理统计》期中试卷试题(五)一、选择题(共5题,每题2分,共计12分)1.下列选项正确的是()A .互为对立事件一定是互不相容的B .互为独立的事件一定是互不相容的C .互为独立的随机变量一定是不相关的D .不相关的随机变量不一定是独立的2. 设事件B A ,两个事件,111(),(),()2310P A P B P AB ===,则()P A B = 。
2010概率论与数理统计期中考试答案

2009年《概率论与数理统计》期中考试答案一、 填空题(每小题5分,总分40分)1、0.72、2/33、5 4、4p 2(1-p)3 5、6、a=0; b=1;c=07、1/68、4/7 二、计算题(每小题12分,总分60分) 1、 (10分)解:设A = “取出的一件是次品”; B 1 = “取出的一箱是甲厂生产的”B 2 = “取出的一箱是乙厂生产的”; B 3 = “取出的一箱是丙厂生产的”则B 1、B 2 、B 3构成一个完备事件组,而且P(B 1)=6/12, P(B 2)=4/12 ,P(B 3)=2/12 P(A/B 1)=1/18, P(A/B 2)=1/12 ,P(A/B 3)=1/6(1)由全概率公式得P(A)= P(B 1)P(A/B 1)+ P(B 2)P(A/B 2)+ P(B 3)P(A/B 3)=1/12 (2) P(B 2/ A)=22(B )(A /B )1/31/121/3()1/12P P P A ⋅==2、(10分)解:设(){}0,1,2i A i i ==取出的品中有件次品,,则246210(),iii C C P A C-=显然012,,A A A 互不相容。
所求概率为21222121212(())()1(|).()()()5P A A A P A P A A A P A A P A P A ===+3、(12分) 解: (1) 2221- 131() (1)1122A f x dx A x dx xA +∞∞==-=-=-⎰⎰A =4/3(2) 当x<1, F(x)=0)(x - =⎰∞dx x f31x x 32dt )1t 34()(F(x)2,x 12x 1x- +-=-==<≤⎰⎰∞dx x f 当1dx 0dx )1x 34(dx 0)(F(x)2,x x 2211x - =+-+==≥⎰⎰⎰⎰∞-∞dx x f 当(3) P{1.5<ξ<3}=32)134( )(21.52 1.5=-=⎰⎰dx x dx x f4、(6分)解:由已知)1,0(~N X ,则X 的概率密度为∞<<∞-=-x ex f xX 2221)(π)21()12()()(22-≤=≤+=≤=y X P y XP y Y P y F Y ;当y <1时,0)21()(2=-≤=y XP y F Y当1≥y时,22211()()(2xY y F y P XP X dx --=≤=≤≤=⎰从而122+=XY 的概率密度为110)1(21)(41≤>⎪⎩⎪⎨⎧-=--y y e y y f y Y π5、(10分)解:Y 的概率密度为,0,()0,y Y e y f y -⎧>=⎨⎩其他,则 2122{0,0}{1,2}{2},y P X X P Y Y P Y e dy e +∞--===>>=>==⎰212121{0,1}{1,2}{12},y P X X P Y Y P Y e dy ee ---===>≤=<≤==-⎰12{1,0}{1,2}{}0,P X X P Y Y P φ===≤>==11120{1,1}{1,2}{1}1,y P X X P Y Y P Y e dy e --===≤≤=≤==-⎰然后概率分布可列表给出。
概率论与数理统计期中试卷(1-4章)附答案及详解
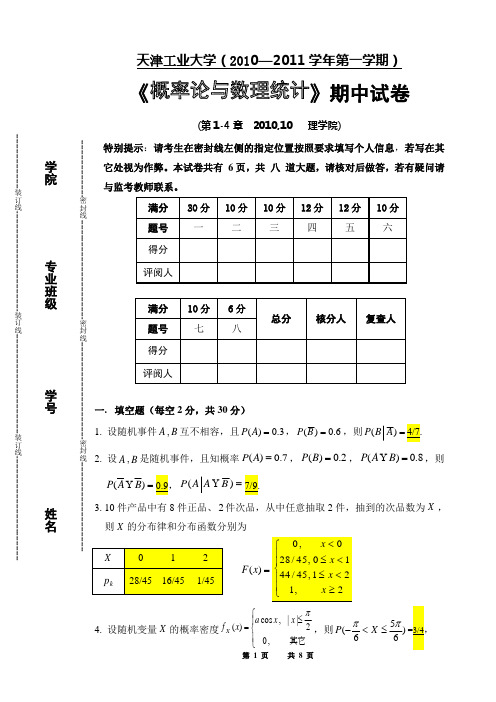
X,23π+=X Y5.设随机变量1X ,2X ,3X 相互独立,1X 在)5,1(-服从均匀分布,)2,0(~22N X,)2(~3Exp X (指数分布),记32132X X X Y +-=,则)(Y E )(Y D6. 设二维正态分布的随机变量)0,3,4,2,1( ),(22-N ~Y X ,且知8413.0)1(=Φ,则-<+)4(Y X P7. 已知随机变量X 的概率密度201()0 a bx x f x⎧+<<=⎨⎩其他, 且41)(=X E ,则a b )(X D 8. 设4.0,36)(,25)(===XY Y D X D ρ,则=+)(Y X D =-)(Y X D 二. (10分) 某车间有甲乙两台机床加工同一种零件,甲机床加工的零件数量比乙机床多一倍,甲乙机床加工零件的废品率分别为0.03,0.02. 两机床加工出的零件放在一起. 试求 (1)任取一个零件是合格品的概率;(2)任取一个零件经检验是废品,试求它是由乙机床生产的概率.解:设“从放在一起的零件中任取一件发现是甲/乙机床加工的”分别记为事件,A .A再记“从放在一起的零件中任取一件发现是废品”为事件.B 由已知得.02.0)(,03.0)(;31)(,32)(====A B P A B P A P A P …… 3’(1)由全概率公式知027.075202.03103.032)()()()()(≈=⨯+⨯=+=A B P A P A B P A P B P . …… 3’ 故任取一个零件是合格品的概率73()1()0.973.75P B P B =-=≈ …… 1’ (2)由贝叶斯公式知.4102.03103.03202.031)()()()()()()(=⨯+⨯⨯=+=A B P A P A B P A P A B P A P B A P …… 3’三. (10分)设某型号的电子元件的寿命X (单位: 小时)的分布密度为⎪⎩⎪⎨⎧>=其它,01000,1000)(2x x x f各元件在使用中损坏与否相互独立,现在从一大批这种元件中任取5只,求其中至少有一只元件的寿命大于1500小时的概率。
《概率论与数理统计》试题及答案

《概率与数理统计》B 卷姓名: 年级专业:一、 填空题(3分×5=15分)1.三个箱子中,第一箱装有4个黑球1个白球,第2箱装有3个黑球3个白球,第3个箱中装有3个黑球5个白球.现先任取一箱,再从该箱中任取一球,问这球是白球的概率为 .2. 设随机变量X 在区间[-1,2]上服从均匀分布,随机变量⎪⎩⎪⎨⎧<=>-=)0()0()0(101X X X Y ,则方差DY= .3假设事件A 和B 满足P(B|A)=1,则A 与B 的关系是_____________.4.设X,Y 是两个相互独立且均服从正态分布N ⎪⎭⎫ ⎝⎛21,0的随机变量,则随机变量Y X -的数学期望()=-Y X E ___________________.5.设随机变量X 服从参数为λ的泊松分布,且已知()()[]121=--X X E ,则λ=_________________.二、单项选择题(3分×5=15分)1.设A,B 为任意两个事件,且,0)(,>⊂B P B A 则下列选项成立的是( ).A. )|()(B A P A P <B. )|()(B A P A P ≤C. )|()(B A P A P >D. )|()(B A P A P ≥2.将一枚硬币重复掷n 次,以X 和Y 分别表示正面向上和反面向上的次数,则X 和Y 的相关系数等于( ).A. -1B. 0C. 21 D. 1 3.袋中有5个球,3个新球,2个旧球,每次取1个,无放回地抽取2次,则第2次抽到新球的概率为( ).A. 3/5B. 5/8C.2/4D. 3/104.正态总体均值已知时,对取定的样本观察值及给定的)10(<<αα ,欲求总体方差的1- α置信区间,使用的统计量服从( ).A. 标准正态分布B. t 分布C. 2x 分布D. F 分布5.若=-=⋃=⊃⊃)(,8.0)(,9.0)(,,BC A P C B P A P C A B A 则( ).A. 0.4B.0.6C. 0.7D. 0.8三、(12分)甲袋中装有3只白球和5只黑球,乙袋中装有4只白球和6只黑球,先从甲袋中取出一球放入乙袋后搅和,再从乙袋中取出一球放回甲袋,求:(1)甲袋白球数增加的概率;(2)甲袋白球数不变的概率。
厦门大学2010学年概率论与数理统计期中试卷

厦门大学 学院 2010 学年 第一学期 专业 级《 概率统计 》期中试卷考试形式:( 闭卷 )一、填空题(共 30 分,每空2分):1.事件C B A ,,中至少有一个发生可表示为 ,三个事件都发生可表示为 ,都不发生可表示为 .2.设()4.0=A P ,()3.0=B P ,()4.0=B A P Y ,则()=B A P .3.一袋中有10个球,其中3个黑球,7个白球. 每次从中任取一球,直到第3次才取到黑球的概率为 ,至少取3次才能取到黑球的概率为 .4.设随机变量X 的分布函数()⎪⎪⎩⎪⎪⎨⎧≥<≤<≤--<=31318.0114.010x x x x x F ,则X 的分布列为 .5.进行10次独立重复射击,设X 表示命中目标的次数,若每次射击命中目标的概率都是4.0,则X 服从 分布,其数学期望为 ,方差为 .6.设连续型随机变量()λe X ~,)0(>λ,则=k 时,{}412=>k X P .7.已知随机变量()2~P X ,则102-=X Y 的数学期望=EY ,方差=DY .8. 已知随机变量X 的概率密度函数为()⎩⎨⎧>-<≤≤-=2,202225.0x x x x f ,则X 服从分布,设随机变量12+=X Y ,则=EY .二、选择题(共10 分,每小题 2 分)1.设事件B A ,互不相容,且()()0,0>>B P A P ,则有 ( ) (A )()0>A B P (B )()()A P B A P =(C )()0=B A P (D )()()()B P A P AB P =2.设()x F 1与()x F 2分别为任意两个随机变量的分布函数,令()()()x bF x aF x F 21+=,则下列各组数中能使()x F 成为某随机变量的分布函数的有( )(A )52,53==b a (B )32,32==b a (C )21,23==b a (D )23,21==b a3.设随机变量X 的概率密度函数为()x f ,且()()x f x f =-,()x F 是X 的分布函数,则对任意实数a ,有( ) (A )()()dx x f a F a⎰-=-01 (B) ()()dx x f a F a⎰-=-021 (C) ()()a F a F =- (D) ()()12-=-a F a F4.如果随机变量X 的概率密度函数为()⎪⎩⎪⎨⎧<≤-<≤=其他,021,210,x x x x x f ;则{}=≤5.1X P ( )(A )()⎰⎰-+5.1112dx x xdx (B )()⎰-5.112dx x(C )()⎰-5.111dx x (D )()⎰∞--5.12dx x5.设()2,~σμN X ,且3=EX ,1=DX ,()x 0Φ为标准正态分布的分布函数,则{}=≤≤-11X P ( )(A )()1120-Φ (B )()()2400Φ-Φ (C )()()2400-Φ--Φ (D )()()4200Φ-Φ三、计算题(共 50 分,每小题 10 分)1.城乡超市销售一批照相机共10台,其中有3台次品,其余均为正品,某顾客去选购时,超市已售出2台,该顾客从剩下的8台中任意选购一台,求该顾客购到正品的概率。
安徽工业大学2010-2011学年第一学期《概率统计B》乙卷及答案

8 12 16
21.(8 分)设 X1 , X2 ,⋯, Xn 是取自总体 X 的一个样本,由
X ∼ π ( k;λ ) = λ k e−λ (k = 0,1, 2,⋯)
18. (8 分)解:设事件 A = { 老人活到 80 岁 }; B = { 老人活到 85 岁 } 则由题意有 B ⊆ A , p( A) = 0.5 , p(B) = 0.3 , -------(4 分)
故所求概率为
p(B | A) = p( AB) = p(B) = 0.3 = 3 ≈ 0.6 p( A) p( A) 0.5 5
= 0. DZ
------------- --(8 分)
20 (8 分)解:因 X1 , X2 ,…, X9 相互独立且同分布,均服从 N (0, 22 ) ,故 X1 + X 2 ∼ N (0, 22 + 22 ) = N (0, 8) ; X 3 + X4 + X5 ∼ N (0, 22 + 22 + 22 ) = N (0,12) ; X6 + X7 + X8 + X9 ∼ N (0, 22 + 22 + 22 + 22 ) = N (0,16) ----(- 3 分)
X 3
+
Y 2
⎫ ⎬ ⎭
=
1 3
EX
+
1 2
EY
=
1 3
.
-----------(2 分)
DZ
=
D
⎛ ⎜⎝
X 3
+
Y 2
⎞ ⎟⎠
=
D
⎛ ⎜⎝
X 3
⎞ ⎟⎠
+
概率论与数理统计(B卷)

(3)0.5000 (4)0.954511、设随机变量)50.0,19(~b X ,那么X 最可能取到的数值为【 】。
(1)9.5 (2)10.9 (3)10 (4)912、n X X X ,,,21 是总体X~N(2,σμ)的一个样本,)1/()(212--=∑=n X X S ni i 。
那么统计量2χ= (n-1)2S /2σ~【 】.(1))n (2χ (2))1,0(N (3))1n (2-χ (4))1n (t -13、参数θ的置信区间为【1ˆθ,2ˆθ】,且P {1ˆθ〈θ〈2ˆθ}=0.99,那么置信度为【 】. (1)0。
99 (2)99 (3)0.01 (4)不能确定14、设 X 1, X 2 …,X n 是总体X ~)(λP 的样本,则 X 1, X 2 …,X n 相互独立,且【 】 。
(1)),(~2i σμN X (2)i X ~)(λP(3))(~e i λG X (4)),0(~i λU X15、下列分布中,具备“无后效性”的分布是【 】。
(1)二项分布 (2)均匀分布 (3)指数分布 (4)泊松分布二、多项选择题(从每题后所备的5个选项中,选择至少2个正确的并将代码填题后的括号内,每题1分,本题满分5分)16、如果事件A 、B 相互独立,且P(A )=0。
40,P(B )=0.30,那么【 】。
(1)P(B A -)=0.72 (2)P (A ⋃B )=0。
58 (3)P (A —B )=0.28 (4)P(AB )=0.12 (5)P (A/B )=0。
4017、设随机变量X ~b (20,0.70),那么以下正确的有【 】.(1)EX =14 (2)X 最可能取到14和13 (3)DX = 4.2 (4))0(=X P =2070.0 (5)X 最可能取到15 18、随机变量)144,10(~N X ,那么【 】。
(1)EX =12 (2)144=DX (3)12=DX (4)12=σ (5)2/1)10()10(=<=>X P X P 19、设)25(~,)15(~22χχY X ,且X 与Y 独立,则【 】。
概率论与数理统计AB卷和答案

概率论与数理统计A 卷一、单项选择题(每小题2分,共20分)1.设A 、B 为两事件,已知P (B )=21,P (A ⋃B )=32,若事件A ,B 相互独立,则P (A )=( )A .91B .61C .31D .21 2.对于事件A ,B ,下列命题正确的是( ) A .如果A ,B 互不相容,则A ,B 也互不相容 B .如果A ⊂B ,则B A ⊂ C .如果A ⊃B ,则B A ⊃D .如果A ,B 对立,则A ,B 也对立3.每次试验成功率为p (0<p <1),则在3次重复试验中至少失败一次的概率为( ) A .(1-p )3 B .1-p 3C .3(1-p )D .(1-p )3+p (1-p )2+p 2(1-p )4.已知离散型随机变量X则下列概率计算结果正确的是( ) A .P (X =3)=0 B .P (X =0)=0 C .P (X >-1)=1D .P (X <4)=15.已知连续型随机变量X 服从区间[a ,b ]上的均匀分布,则概率P =⎭⎬⎫⎩⎨⎧+<32b a X ( )A .0B .31C .32 D .1A .(51,151)B .(151,51)C .(101,152) D .(152,101) 7.设(X ,Y )的联合概率密度为f (x ,y )=⎩⎨⎧≤≤≤≤+,,0,10,20),(其他y x y x k 则k =( )A .31B .21 C .1D .38.已知随机变量X ~N (0,1),则随机变量Y =2X +10的方差为( ) A .1 B .2 C .4D .149.设随机变量X 服从参数为0.5的指数分布,用切比雪夫不等式估计P (|X -2|≥3)≤( )A .91B .92C .31D .94 10.由来自正态总体X ~N (μ,22)、容量为400的简单随机样本,样本均值为45,则未知参数μ的置信度为0.95的置信区间是(u 0.025=1.96,u 0.05=1.645)( ) A .(44,46)B .(44.804,45.196)C .(44.8355,45.1645)D .(44.9,45.1)二、填空题(每小题2分,共30分)11.对任意两事件A 和B ,P (A -B )=______.12.袋中有4个红球和4个蓝球,从中任取3个,则取出的3个中恰有2个红球的概率为______.13.10个考签中有4个难签,有甲、乙2人参加抽签(不放回),现甲先抽,乙次之,设A ={甲抽到难签},B={乙抽到难签}.则P (B )=______.14.某地一年内发生旱灾的概率为31,则在今后连续四年内至少有一年发生旱灾的概率为______.15.在时间[]T ,0内通过某交通路口的汽车数X 服从泊松分布,且已知P (X =4)=3P (X =3),则在时间[]T ,0内至少有一辆汽车通过的概率为______.16.设随机变量X ~N (10,σ2),已知P (10<X <20)=0.3,则P (0<X <10)=______.则P {X =Y }的概率为______.18.设随机变量(X ,Y )的联合分布函数为F (x ,y )=⎩⎨⎧>>----.,00,0),1)(1(43其他y x e e y x ,则(X ,Y )关于X 的边缘概率密度f X (x )=______.19.设随机变量X ~B (8,0.5),Y=2X -5,则E (Y )=______.20.设随机变量X ,Y 的期望方差为E (X )=0.5,E (Y )=-0.5,D (X )=D (Y )=0.75,E (XY )=0,则X ,Y 的相关系数ρXY =______.21.设X 1,X 2,…,X n 是独立同分布随机变量序列,具有相同的数学期望和方差E (X i )=0,D (X i )=1,则当n 充分大的时候,随机变量Z n =∑=ni iXn11的概率分布近似服从______(标明参数).22.设X 1,X 2,…X n 为独立同分布随机变量,X i ~N (0,1),则χ2=∑=ni iX12服从自由度为______的χ2分布.23.设X l ,X 2,X 3为总体X 的样本,3214141ˆCX X X ++=μ,则C =______时,μˆ是E (X )的无偏估计. 24.设总体X 服从指数分布E (λ),设样本为x 1,x 2,…,x n ,则λ的极大似然估计λˆ=______. 25.设某个假设检验的拒绝域为W ,当原假设H 0成立时,样本(x l ,x 2,…,x n )落入W 的概率是0.1,则犯第一类错误的概率为______.三、计算题(本大题共2小题,每小题8分,共16分)26.100张彩票中有7张有奖,现有甲先乙后各买了一张彩票,试用计算说明甲、乙两人中奖的概率是否相同. 27.设随机变量X 的概率密度为⎪⎩⎪⎨⎧<≤-<≤-+=.,0,10,1,01,1)(其他x x x x x f 试求E (X )及D (X ).四、综合题(每小题12分,共24分)28.已知某种类型的电子元件的寿命X(单位:小时)服从指数分布,它的概率密度为⎪⎩⎪⎨⎧≤>=-.0,0,0,6001)(600x x ex f x某仪器装有3只此种类型的电子元件,假设3只电子元件损坏与否相互独立,试求在仪器使用的最初200小时内,至少有一只电子元件损坏的概率.29.设随机变量X ,Y 相互独立,X ~N (0,1),Y ~N (0,4),U=X +Y ,V=X -Y , 求(1)E (XY );(2)D (U ),D (V );(3)Cov(U ,V ). 五、应用题(10分)30.某食品厂对产品重量进行检测。
概率论与数理统计(B)试题及答案

概率论与数理统计(B)试题及答案陕西科技⼤学2010级试题纸课程概率论与数理统计(B )班级学号姓名1、A B C 表⽰随机事件,,A B C ⾄少有⼀个不发⽣. ()2、若()1P A =,则A 是必然事件. ()3、若2~(2,1),~(2,0.5)X N Y N -,则(0)0.5P X Y >=+. ()4、X 为随机变量,当12x x <时,则有12()()P X x P X x >≤>.. ( )5、设(,)X Y 是⼆维正态随机变量,则随机变量X 与Y 独⽴的充要条件是cov(,)0X Y =. ..( )⼆、填空题(每⼩题3分,共15分) 1、设,A B 为随机事件,()0.6P A =,()0.4P B =,()0.8P A B = ,则()P B A = .2、在区间(0,1)上随机取两个数,x y ,则关于t 的⼀元⼆次⽅程220t xt y -+=有实根的概率为 .3、设随机变量~()X P λ,且3(0)P X e -==,21Y X =-,则()D Y = .4、设随机变量~(0,1),~(2,1)X N Y N ,且X ,Y 相互独⽴,设随机变量21Z X Y =-+,则Z ~ _ .5、设随机变量X~U[1,2],由切⽐雪夫不等式可得32P X ?-≥≤??.三、选择题(每⼩题3分,共15分)1、对事件,A B ,下列命题中正确的是()A 、若,AB 互斥,则,A B 也互斥. B 、若,A B 互斥,且()0,()0P A P B >>,则,A B 独⽴.C 、若,A B 不互斥,则,A B 也不互斥D 、若,A B 相互独⽴,则,A B 也相互独⽴. 2、设随机变量X 服从正态分布2(2,)N σ,则随σ的增⼤,概率(22)P X σ-<是() A 、单调增加 B 、单调减⼩ C 、保持不变 D 、⽆法判断 3、设(,)F x y 为(,)X Y 的分布函数,则以下结论不成⽴的是()A 、0(,)1F x y ≤≤B 、 (,)1F -∞+∞=C 、(,)0F -∞+∞=D 、 (,)0F -∞-∞=4、把10本书任意地放在书架上,则其中指定的3本书放在⼀起的概率为() A 、115B 、112C 、110D 、185、若121000,...X X X 是相互独⽴的随机变量,且(1,)(1,2,,1000)i X B p i = 则下列说法中不正确的是()A 、1000111000i i X p =≈∑ B 、10001()()()i i P a X b b a =<<≈Φ-Φ∑ C 、10001~(1000,)i i X B p =∑ D、10001()i i P a X b =<<≈Φ-Φ∑四、(12分)设(,)X Y 的联合概率分布如下,求:①()()E X E Y 、②()E XY 、(,)COV X Y③Z X Y =+的概率分布.五、(10分)甲、⼄、丙三⼈同时独⽴地向某⽬标射击,命中率分别为0.3、0.2、0.5,⽬标被命中⼀发⽽被击毁的概率为0.2,⽬标被命中两发⽽被击毁的概率为0.6,⽬标被被命中三发则⼀定被击毁,求三⼈在⼀次射击中击毁⽬标的概率.六、(16分)设随机变量X 的概率密度为()2,100,10Ax f x x x ?>?=??≤?,求:①A ; ②(15)P x <; ③求X 的分布函数()F x ; ④设2Y X =,求Y 的概率密度.七、(16分)设⼆维随机变量()Y X ,的概率密度为()22,01,0,0,y e x y f x y -?≤≤>=??其它求:① (2)P Y X ≥; ②关于X 与Y 的边缘概率密度; ③X 与Y 是否独⽴?为什么?④(24)E X Y +.⼋、(6分)设X 与Y 相互独⽴,其分布函数分别为()X F x 、()Y F x .证明:随机变量X 与Y 的最⼤值max(,)U X Y =分布函数为()()X Y F u F u ?.2010级概率论与数理统计(B )试题答案⼀、√; ×; ×; ×; √ ⼆、1/3; 1/3; 12;N(-1,5); 1/6 三、D ; C ; B ; A ;B 四·(,)()()()5/144COV X Y E XY E X E Y =-=-…………………………2分五、解:设A :甲击中;B :⼄击中;C :丙击中 i D :击中i 发,(1,2,3)i =;E :击毁⽬标1()()0.47P D P ABC ABC ABC =++= 2()()0.22P D P ABC ABC ABC =+++=3()()0.03P D P ABC ==………………………………………………5分31()()()0.470.20.220.60.0310.256i i i P E P D P E D ===?+?+?=∑…………………………5分5/12EX =…………………………2分1/12EY =…………………………2分②()0E XY =…………………………2分③……………………………4分六、①2101Adx x +∞=?,则A =10 ……………………………………………4分②1521010(15)1/3P x dx x <==?……………………………………………4分③ 10,()0x F x <=210101010,()()1xxx F x f x dx dx x x -∞≥===-?…………………………4分④20,()0Y y F y <=22101020,()()()2yY y y F y P Y y P X dxx ≥=≤=≤=?20,20()[()]20/,20Y Y y f y F y y y ≤?'==?>? ………………………………… 4分七、①412021(2)24yxe P Y x dx edy -+∞--≥==………………………………… 4分②1,01()(,)0,X x f x f x y dy +∞-∞≤≤?==?其它22,0()(,)0,0y Y e y f y f x y dx y -+∞-∞>==≤??…………………………… 4分③ X 与Y 独⽴. 因为(,)()()X Y f x y f x f y = …………………………… 4分④ 11(24)2424322E X Y EX EY +=+=?+?= ……………………… 4分⼋、证明:()()(max(,))(,)U F u P U u P X Y u P X u Y u =≤=≤=≤≤………… 3分()()()()X Y P X U P Y U F u F u =≤≤= ……………………… 3 分陕西科技⼤学2011级试题纸课程概率论与数理统计(B )班级学号姓名1.设()1P AB =,则事件A 必然发⽣且事件B 必然不发⽣。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
北 京 交 通 大 学2010-2011学年第一学期《概率论与数理统计(B )》期终考试试卷(A )学院_____________ 专业___________________ 班级____________学号_______________ 姓名_____________请注意:本卷共十三大题,如有不对,请与监考老师调换试卷! 一.(满分6分)已知()P A =14,()P B A 13=,()P A B 13=,求()P A B ⋃。
解: 由概率加法公式()P ()()()A B P A P B P AB ⋃=+-由概率乘法公式()P ()()112AB P A P B A ==----2分 ()()P ()P AB B P A B 14==()P ()()()A B P A P B P AB 1115441212⋃=+-=+-= ----4分二. (满分8分)甲乙二人轮流掷一骰子,每轮掷一次,谁先掷得6点谁得胜,从甲开始掷,问甲、乙得胜的概率各为多少?解 以i A 表示事件“第i 次投掷时投掷者才得6点”.事件i A 发生,表示在前1-i 次甲或乙均未得6点,而在第i 次投掷甲或乙得6点.因各次投掷相互独立,故有.6165)(1-⎪⎭⎫⎝⎛=i i A P 因甲为首掷,故甲掷奇数轮次,从而甲胜的概率为 }{}{531 A A A P P =甲胜 +++=)()()(531A P A P A P ),(21两两不相容因 A A⎥⎥⎦⎤⎢⎢⎣⎡+⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛+= 426565161.116)6/5(11612=-=--------4分同样,乙胜的概率为}{}{642 A A A P P =乙胜 +++=)()()(642A P A P A P.1156565656153=⎥⎥⎦⎤⎢⎢⎣⎡+⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛+= .--------4分三. (满分12分)(1)已知随机变量X 的概率密度为,,21)(+∞<<-∞=-x e x f xX 求X 的分布函数.(2)已知随机变量X 的分布函数为),(x F X 另外有随机变量⎩⎨⎧≤->=,0,1,0,1X X Y 试求Y 的分布律和分布函数.解 (1)由于⎪⎪⎩⎪⎪⎨⎧+∞<≤<<∞-=-.0,21,0,21)(x e x e x f x xX当0<x 时,分布函数,212121)()(|xx x xx xX X e e dx e dx x f x F ====∞-∞-∞-⎰⎰当0≥x 时,分布函数.2112121212121)()(0x x xx x xX X e e dx e dx e dx x f x F ---∞-∞--=-+=+==⎰⎰⎰故所求分布函数为⎪⎪⎩⎪⎪⎨⎧≥-<=-.0,211,021)(x e x e x F x xX ———5分(2),21)0(}0{}1{==≤=-=X F X P Y P .21211}1{1}1{=-=-=-==Y P Y P分布律为Y -1 1k p 21 21 ——4分 分布函数为⎪⎪⎩⎪⎪⎨⎧≥<≤--<=.1,1,11,21,10)(y y y y F Y ———3分四(满分10分) 投掷一硬币直至正面出现为止,引入随机变量 =X 投掷总次数.⎩⎨⎧=.,0,1若首次投掷得到反面若首次投掷得到正面,Y(1)求X 和Y 的联合分布律及边缘分布律. (2)求条件概率}.1|2{},1|1{====X Y P Y X P解 (1)Y 的可能值是0,1,X 的可能值是.,3,2,1 }1{}1|1{}1,1{======X P X Y P Y X P .2/12/11=⨯= (因1=X 必定首次得正面,故).1}1|1{===X Y P 若1>k ,}{}|1{}1,{k X P k X Y P Y k X P ====== .0)2/1(0=⨯=k(因,1>=k X 首次得正面是不可能的,故).,3,2,0}|1{ ====k k X Y P }1{}1|0{}0,1{======X P X Y P Y X P 0)2/1(0=⨯=(因1=X 必须首次得正面,故).0}1|0{===X Y P 当1>k}{}|0{}0,{k X P k X Y P Y k X P ======,3,2),2/1(1=⨯=k k (因,1>=k X 必定首次得反面,故).1}|0{===k X Y P 综上,得),(Y X 的分布律及边缘分布律如下:XY 1 2 3 4 … }{j Y P =0 0 221 321 421 ... 21 1 21 0 0 0 (21)}{i X P = 21 221 321 421… 1 ———6分(2).12/12/1}1{}1,1{}1|1{========Y P Y X P Y X P.0}1{}2,1{}1|2{=======X P Y X P X Y P ———4分五(满分10分) 一等边三角形ROT (如下图)的边长为1,在三角形内随机地取点),(Y X Q (意指随机点),(Y X 在三角形ROT 内均匀分布).(1) 写出随机变量),(Y X 的概率密度. (2) 求点Q 的底边OT 的距离的分布密度.解 (1)因三角形ROT 的面积为4/3,故),(Y X 的概率密度为⎩⎨⎧--≤≤≤≤=.,0),1(30,30,3/4),(其他x y x y y x f ——3分(2)点),(Y X Q 到底边OT 的距离就是Y ,因而求Q 到OT 的距离的分布函数,就是求),(Y X 关于Y 的边缘分布函数,现在 ,230,32134),()(3.13/<<⎪⎪⎭⎫ ⎝⎛-==⎰-y y dx y x f y f y y Y 从而⎪⎩⎪⎨⎧<<⎪⎪⎭⎫ ⎝⎛-=.,0,230,32134)(其他y y y f Y ——4分 Y 的分布函数为⎪⎪⎪⎩⎪⎪⎪⎨⎧≥<≤-<=.23,1,230,3434,0,0)(2y y y y y y F Y ——3分六(满分8分)设随机变量),(Y X 具有概率密度⎩⎨⎧>>=+-.,0,0,0,),()1(其他y x xe y x f y x(1) 求边缘概率密度).(),(y f x f Y X (2) 求条件概率密度).|(),|(||x y f y x f X Y Y X 解 (1)当0>x 时, ,)()(0)1(x y y xy x y x X e e e dy xe x f -∞==--∞+-===⎰当0>y 时,dx xe y y xe dx xey f y x x x y x y x Y ⎰⎰∞+-∞==+-∞+-+++-==0)1(0)1(0)1(111)( .)1(1)1(22)1(+=+-=∞==+-y y xe x x y x故边缘概率密度分别是⎩⎨⎧>=-.,0,0,)(其他x e x f x X ⎪⎩⎪⎨⎧>+=.,0,0,)1(1)(2其他y y y f Y ——4分(2)条件概率密度: 当0>x 时,⎪⎩⎪⎨⎧>=-+-.,0,0,)|()1(|取其他值y y e xe x y f x y x X Y⎩⎨⎧>=-.,0,0,取其他值y y xe xy当0>y 时,⎪⎩⎪⎨⎧>+=+-.,0,0,)1/(1)|(2)1(|取其他值x x y xe y x f y x Y X⎩⎨⎧>+=+-.,0,0,)1()1(2取其他值x x e y x y x ——4分七.(满分8分)设有随机变量U 和V ,它们都仅取1,1-两个值.已知 ,2/1}1{==U P}.1|1{3/1}1|1{-=-=====U V P U V P (1)求U 和V 的联合分布密度.(2)求x 的方程02=++V Ux x 至少有一个实根的概率.(3)求x 的方程2()0xU V x U V ++++=至少有一个实根的概率.解 (1).6/1)2/1)(3/1(}1{}1|1{}1,1{========U P U V P V U P }1{}1|1{}1,1{-=-=-==-=-=U P U V P V U P.6/1)2/1)(3/1(}]1{1[)3/1(===-⨯=U P}1{}1|1{}1,1{==-==-==U P U V P V U P.3/1)2/1)(3/2(}1{}]1|1{1[=====-=U P U V P }1{}1|1{}1,1{-=⋅-====-=U P U V P V U P.3/1)2/1()3/2(}1{}]1|1{1[=⨯=-=-=-=-=U P U V PV U ,的联合分布密度为UV -1 1-1 1/6 2/6 ——4分 1 2/6 1/6(2) 方程02=++V Ux x 当且仅当在042≥-=∆V U 时至少有一实根,因而所求的概率为 .2/1}1{}04{}0{2=-==≥-=≥∆V P V U P P ——2分(3) 方程0)(2=+++++V U x V U x 当且仅当在0)(4)(2≥+-+=∆V U V U 时至少有一实根,因而所求的概率为.6/5}1,1{}1,1{}1,1{}0{=-==+=-=+-=-==≥∆V U P V U P V U P P ——2分八.(满分6分)某图书馆一天的读者人数)(~λπX ,任一读者借书的概率为p ,各读者借书与否相互独立.记一天读者借书的人数为Y ,求X 与Y 的联合分布律. 解 读者借书人数的可能值为}{}|{},{,,,2,1,0k X P k X i Y P i Y k X P X Y Y ======≤==.,,2,1,2,1,!)1(k i k k e p p i k k i k i ==-⎪⎪⎭⎫ ⎝⎛--λλ九.(满分8分)将一颗骰子掷两次,考虑事件=A “第一次掷得点数2或5”,=B “两次点数之和至少为7”,求),(),(B P A P 并问事件B A ,是否相互独立.解 将骰子掷一次共有6种等可能结果,故.3/16/2)(==A P 设以i X 表示第i 次掷出骰子的点数,则}).6({1})7({)(2121≤+-=≥+=X X P X X P B P因将骰子掷两次共有36个样本点,其中621≤+X X 有6,5,4,3,221=+X X 共5种情况,这5种情况分别含有1,2,3,4,5个样本点,故.12/712/5136/)54321(1)(=-=++++-=B P ----4分以),(21X X 记两次投掷的结果,则AB 共有(2,5),(2,6),(5,2),(5,3)(5,4),(5,5),(5,6)这7个样本点.故.36/7)(=AB P 今有).(36/7)12/7)(3/1()()(AB P B P A P ===按定义B A ,相互独立. ----4分十(满分10分) 产品的某种性能指标的测量值X 是随机变量,设X 的概率密度为⎪⎩⎪⎨⎧>=-其他.,0,0,)(221x xe x f x X 测量误差Y~U (εε,-),X ,Y 相互独立,求Z=X+Y 的概率密度)(z f Z ,并验证du e Z P u ⎰-=>εεε202/221}{解 (1)Y 的概率密度为 其他.,εεε<<-⎪⎩⎪⎨⎧=y y f Y ,0,21)( 故Z =X+Y 的概率密度为⎰+∞∞--=dx x z f x f z f Y X Z )()()( ——2分 仅当⎩⎨⎧<-<->εεx z x 0即⎩⎨⎧+<<->εεz x z x 0时上述积分的 xx=z+εO yx=z+ε图4被积函数不等于零,参考图4,即得⎪⎪⎩⎪⎪⎨⎧≥<<-=⎰⎰+--+-其他,,,,0,21,21)(2212210εεεεεεεεz dx xe z dx xe z f z z x z x Z =⎪⎪⎪⎩⎪⎪⎪⎨⎧≥-<<--+---+-其他,,,,0],[21],1[21221221221)()()(εεεεεεεεz e e z e z z z ——4分(2)⎰∞=>εεdz z f Z P Z )(}{=][21221221)()(⎰⎰∞+-∞---εεεεεdz e dz e z zε21记成[Ⅰ+Ⅱ]其中Ⅰ=⎰⎰∞-∞--=-0)(,221221du e uz e u dz z εεε令Ⅱ=⎰⎰∞-∞+--=+-εεεε2)(2121du e u z dz e u z 令 于是εε21}{=>Z P [Ⅰ+Ⅱ]=⎰-εε202121du e u——4分 1ˆx x θ=-十一.(满分6分) 解:----4分----2分}0{}0,2{}02{≥≥≤=≥≤X P X X P X X P 2,0,1357,,,,{20}.248X P X X a a a a-≤≥已知离散型随机变量的可能取值为相应的概率依次为试求概率=352224.35729248a a a a a +==++十二(满分8分)解:-----2分-----4分 -----2分CAB CB AB = ,,,.:.A B C C AB C AB AC C B AB ⊃⊃= 设随机事件满足证明,C AB ⊃由于,C A B ⊂ 故()CB A B B ⊂ 从而,AB =,CB =,ACB C AB AB == ()AC AC B B = 故ACB ACB= .CB AB =。
