小学数学《数阵图》练习题(含答案)
数阵图练习题五年级

数阵图练习题五年级数阵图练习题(五年级)在数学学习中,数阵图是一种常见的图形模型,用于表示数字之间的关系。
通过解决数阵图练习题,学生可以提高数学问题的分析和解决能力。
本文将为五年级的学生介绍一些数阵图练习题,帮助他们巩固和拓展数学知识。
练习一:数字排列请观察下面的数阵图,并回答问题。
```7 8 94 5 61 2 3```1. 数阵图中,每一行的和是多少?2. 数阵图中,每一列的和是多少?3. 数阵图中,从左上角到右下角的对角线上的和是多少?4. 数阵图中,从右上角到左下角的对角线上的和是多少?练习二:数阵图填空请根据给出的数字,将空格内的数字填入数阵图中。
```2 + 4 = 6+ 3 = 98 + 11 = ?```练习三:找规律请观察下面的数阵图,并找出其中的规律。
```1 1 1 1 12 4 8 16 323 9 27 81 2434 16 64 256 10245 25 125 625 3125```1. 数阵图中,第一行的数字有什么规律?2. 数阵图中,第二行的数字有什么规律?3. 数阵图中,第三行的数字有什么规律?4. 数阵图中,第四行的数字有什么规律?5. 数阵图中,第五行的数字有什么规律?练习四:数阵图计算请根据下面的数阵图,计算出每个圆圈中的数字。
```× 2 = 8× 5 = 35÷ 4 = 6÷ 7 = 2```结语数阵图练习题能够提高学生的数学分析和解决问题的能力。
通过观察、思考和计算,学生可以发现数字之间的规律,并运用所学的数学知识进行推理和计算。
希望以上的练习题能够帮助五年级的学生提升数学能力,取得更好的学习成果。
数阵练习题 含答案
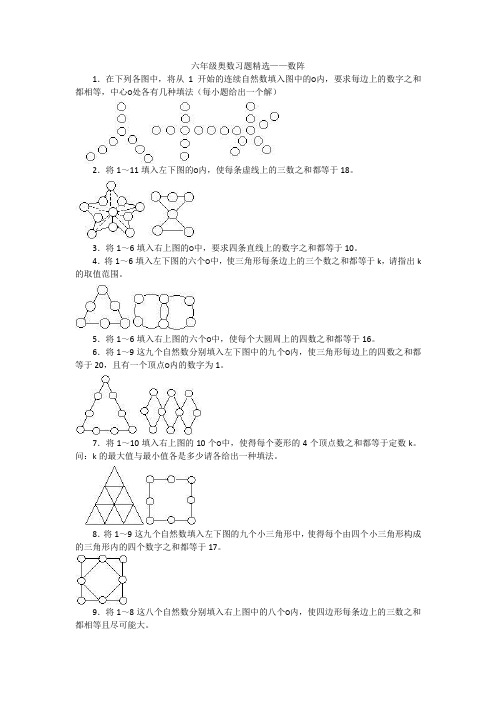
六年级奥数习题精选——数阵1.在下列各图中,将从1开始的连续自然数填入图中的○内,要求每边上的数字之和都相等,中心○处各有几种填法(每小题给出一个解)2.将1~11填入左下图的○内,使每条虚线上的三数之和都等于18。
3.将1~6填入右上图的○中,要求四条直线上的数字之和都等于10。
4.将1~6填入左下图的六个○中,使三角形每条边上的三个数之和都等于k,请指出k 的取值范围。
5.将1~6填入右上图的六个○中,使每个大圆周上的四数之和都等于16。
6.将1~9这九个自然数分别填入左下图中的九个○内,使三角形每边上的四数之和都等于20,且有一个顶点○内的数字为1。
7.将1~10填入右上图的10个○中,使得每个菱形的4个顶点数之和都等于定数k。
问:k的最大值与最小值各是多少请各给出一种填法。
8.将1~9这九个自然数填入左下图的九个小三角形中,使得每个由四个小三角形构成的三角形内的四个数字之和都等于17。
9.将1~8这八个自然数分别填入右上图中的八个○内,使四边形每条边上的三数之和都相等且尽可能大。
10.将自然数1~8填在右图的八个○内,使每个小三角形三个顶点数字之和都等于13,并且8位于大正方形的一个顶点上。
11.将1~8这八个自然数填入右图的四个圆相互分割的八个部分中,使每个圆内的三个数字之和都相等,并且这个和尽量小。
12.将自然数1~10这10个自然数分别填入左下图的10个○内,使五边形每条边上的3数之和都等于17,并且数字1位于一个顶点上。
13.将1~8填入右上图的八个○中,使小正方形的四个顶点数之和是大正方形的四个顶点数之和的两倍,并且大正方形每条边上的三个数之和都相等。
14.小明玩布阵游戏,他要用360名士兵守卫一座城池(见左下图,图中间表示城区,四周表示城墙,方格中的数表示兵力分布),要求四个角的兵力相同。
现在的兵力分布恰好每边有100名士兵,如果小明想使每边有150名士兵,那么兵力应如何分布15.有座一长方形城堡,四周有10个掩体(如右上图)。
小学数学 《数阵图》练习题(含答案)

小学数学《数阵图》练习题(含答案)数阵图问题千变万化,这一类问题要求数阵中填入了一些数以后,能保证数阵中特定关系线(或关系区域)上的数的和相等,解决这一类问题可以按以下步骤解决问题:第一步:区分数阵图中的普通点(或方格),和交叉点(方格)第二步:在数阵图的少数关键点(一般是交叉点)上设置未知数,计算各个点与该点被重复计算次数之积的和的代数式,即数阵图关系线(关系区域)上和的总和,这个和是关系线(关系区域)的个数的整数倍.第三步:判断少数关键点上可以填入的数的余数性质,并得出相应的数阵图关系线(关系区域)和.第四步:运用已经得到的信息进行尝试:数阵图还有一类题型比较少见,解决这一类问题需要理清数阵中数与数之间的相关关系,找出问题关键.(一)封闭型数阵问题【例1】(★★★)小青蛙不小心爬到一个正方形数阵图中,必须把1,2,3,4,5,6,7,8八个数字填入下图中的○内,使正方形每条边上三个数的和都等于13才能通过这个数阵图,你能帮它吗?【例2】(★★★)小乌龟被困在五个圆里面(如下图),五圆相连,每个位置的数字都是按一定规律填写的,它必须找出规律,并求出x所代表的数才能脱困,你知道该怎么办吗?24273028262218 1720x【例3】(★★★)1~9分别填入小三角形内(每个小三角形内只填一个数),要求靠近大三角形三条边的每五个数相加和相等.想一想,怎样填这些数才能使五个数的和尽可能大一些?【例4】(★★★)能否将数0,1,2,…,9分别填人下图的各个圆圈内,使得各阴影三角形的3个顶点上的数之和相等?【例5】(★★★),小熊和妈妈去外婆家要过一条河,必须要按照下面的要求填数才可以顺利通过,要求如下:20以内共有10个奇数,去掉9和15还剩八个奇数,将这八个奇数填入右图的八个○中(其中3已经填好),使得图中用箭头连接起来的四个数之和都相等.3(二)辐射型数阵【例6】(★★★)将1~7这七个数字,分别填人图中各个○内,使每条线段上的三个○内数的和相等.【例7】 (★★★)把10至20这11个数分别填入下图的各圆圈内,使每条线段上3个圆内所填数的和都相等.如果中心圆内填的数相等,那么就视为同一种填法.请写出所有可能的填法.【例8】 (★★★)左图中有三个正三角形,将1~9填入它们顶点处的九个○中,要求每个正三角形顶点的三数之和都相等,并且通过四个○的每条直线上的四数之和也相等.【例9】 (★★★)在下图的七个圆圈内各填上一个数,要求每条线上的三个数中,当中的数是两边两个数的平均数,现在已填好两个数,求x 是多少?(三)其它类型的数阵图【例10】 (★★★)在下图中的10个○内填入0~9这10个数字,使得按顺时针循环式成立:【例11】 (★★★★)将1~8这八个自然数填入左下图的空格内,使四边形组成的四个等式都成立:【例12】 (★★★★)下图包括6个加法算式,要在圆圈里填上不同的自然数,使6个算式都成立.那么最右边的圆圈中的数最少是多少?+=====----===×÷+=-+=+=1.请分别将1,2,4,6这4个数填在下图的各空白区域内,使得每个圆圈里4个数的和都等于15.2.把1~5这五个数填入下图中的○里,使每条直线上的三个数之和相等.3.把1至6分别填入下图的各方格中,使得横行3个数的和与竖列4个数的和相等.4.将1~7七个数字填入左下图的七个○内,使每个圆周和每条直线上的三个数之和都相等.5.将1~8八个数分别填入右上图的八个○内,使得图中的六个等式都成立.△代表几?37 5=== =+++++(一)封闭型数阵问题【例13】 (★★★)小青蛙不小心爬到一个正方形数阵图中,必须把1,2,3,4,5,6,7,8八个数字填入下图中的○内,使正方形每条边上三个数的和都等于13才能通过这个数阵图,你能帮它吗?75623841或84362571分析:因为每边上的和为13,那么四条边上的数字之和为13×4=52,而1+2+…+7+8=36,所以四个角上的四个数之和等于52-36=16.在1~8中选四个数,四数之和等于16,且其中相邻两个的和与任意三个的和不等于13的只有:16=1+2+6+7=1+2+5+8=1+4+5+6.经试验,只有右上图的两种填法.亮点设计:(1)求数阵问题的关键是找到关键数,也就是重复数,教会学生学会找关键数的方法是最重要的.(2)设计问题:正方形每条边之和是13,13×4=52,但是所有数的和是:1+2+…+7+8=36,为什么会出现结果不同的问题呢?仔细观察这个数阵,四条边上所有数相加的过程中四个角上的数都被重复加了一次,也就是四个角上的数是重复数,52-36=16即为这四个重复数的和. (3)强调分组法与试验法:知道了四个数的和之后,下一步就要先确定这四个数,采用分组法和试验法.分组法是将这个和根据要求拆成四个数,例如本题中要求其中相邻两个的和与任意三个的和不等于13,根据要求将16分成4个数的和:16=1+2+6+7=1+2+5+8=1+4+5+6,但是未必每一组都是合适的,这就需要采用试验法,将它们一一进行试验.(4)小结:对于封闭型的数阵,重复数基本上都是两条线相交的点,这在后面的例题中有大量体现.[前铺]将1~6六个自然数分别填入下图的○内,使三角形每边上的三数之和都等于11.614532分析:因为每边上的和为11,那么三条边上的数字之和为11×3=33,而1+2+…+5+6=21,所以三个角的三个数之和等于33-21=12,在1~6中选3个和为12的数,且其中任意两个的和不等于11,这样的组合有:12=2+4+6=3+4+5,经试验,填法见右上图.[拓展]将1~6填入左下图的六个○中,使三角形每条边上的三个数之和都等于k ,请指出k 的取值范围.654321654321654321654321k=9 k=10 k=11 k=12分析:设三角形三个顶点的数字之和为s.因为每个顶点属于两条边公有,所以把三条边的数字和加起来,等于将1至6加一遍,同时将三个顶点数字多加一遍.于是有(1+2+3+4+5+6)+s=3k,化简后为s+21=3k.由于s是三个数之和,故最小为1+2+3=6,最大为4+5+6=15,由此求出9≤k≤12.s和k有四组取值:通过试验,每组取值都对应一种填数方法(见右上图).【例14】(★★★)小乌龟被困在五个圆里面(如下图),五圆相连,每个位置的数字都是按一定规律填写的,它必须找出规律,并求出x所代表的数才能脱困,你知道该怎么办吗?242730282622181720x分析:经观察,图中所填数的规律为两个圆相交部分的数等于与它相邻两部分里的数的和的一半.比如:(26+18)÷2=22.(30+26)÷2=28.(24+30)÷2=27.所以x+18=17×2,x=16.经检验,16和24相加除以2,也恰好等于20.[拓展]找规律求xx24123082616186452分析:经观察,图中所填数的规律为两个圆相交部分的数等于与它相邻两部分里的数的差的2倍.比如:(26-18)×2=16.(30-26)×2=8.(30-24)×2=12.因为52÷2=26>24,所以x=26+24=50.经检验,(50--18)×2=64.【例15】(★★★)1~9分别填入小三角形内(每个小三角形内只填一个数),要求靠近大三角形三条边的每五个数相加和相等.想一想,怎样填这些数才能使五个数的和尽可能大一些?分析:1+2+3+4+5+6+7+8+9=45,用s表示靠近大三角形三条边的五个数的和.因为有三个小三角形所填的数在求和时只用了一次(用a,b,c来表示这三个数),其余均用了两次.于是,45×2-(a+b+c)=3 s.要使s尽可能大,只要a+b+c尽可能小.所以a+b+c=1+2+3=6,于是90-6=3 s,s=28.剩下的六个数分成三组,并且每组中两数的和是三个连续自然数,那么:4+8=12;6+7=13;5 +9=14.经过调配可得到几十种填法,右上图是填法之一.[拓展一]如图是奥林匹克的五环标志,其中a,b,c,d,e,f,g,h,i处分别填入整数1至9,如果每一个圆环内所填的各数之和都相等,那么这个相等的和最大是多少,最小是多少?ihgfedcba分析:计算五个圈内各数之和的和,其中b,d,f,h被计算了两遍,所以这个和是1+2+3+4+5+6+7+8+9+b+d+f+h,而这个和一定能被5整除,所以b,d,f,h中填入大数时能使这个和取得最大值,最大是6、7、8、9,各圆圈内的和也取得15,由于15=6+9=7+8,所以满足条件的所有数无法配成15,当和为14时可以找出满足条件的填法,所以和最大为14,当b,d,f,h取1、2、3、4时这个和取得最小值,各圆圈内的和也取得最小值11.[拓展二]有10个连续的自然数,9是其中第三大的数.现在把这10个数填到下图的10个方格中,每格内填一个数,要求图中3个2×2的正方形中的4个数之和相等.那么,这个和数的最小值是多少?分析:9是其中第三大的数,所以这10个连续自然数是2、3、4、5……9、10、11,计算三个正方形中的和的和,这个和能被3整除,其中a和b被重复计算了两次,所以2+3+……11+a+b=65+a+b=3s,当a+b=1,4,7……时,65+a+b可以被3整除,因为要取最小值,所以a+b的值越小越好,但是不可能取1与4,所以,a+b=7时,这个和取得最小值,每个正方形中的和也取得最小值(65+7)÷3=24.【例16】(★★★)能否将数0,1,2,…,9分别填人下图的各个圆圈内,使得各阴影三角形5619372481528763049分析:0+…+9=45,45-中心数=3个阴影三角形的3个顶点上的数字之和,所以中心数必须是3的倍数,只能是0,3,6,9.枚举法实验,中心数只能是3,6,答案如右上图.[拓展一]将1~10分别填入图中,使得每个小三角形3个顶点上的数字之和为图中所表示的数值.分析:先确定中间5个重复数,它们的和为(20+16+12+13+10)-(1+2+…+10)=16,所以中间5个重复数只能是1,2,3,4,6的组合.又因为有1个和为20,相应三角形上的三个数只能是4,6,10,逐一试验,答案如右上图.[拓展二]图中有大、中、小3个正方形,组成了8个三角形.现在先把1,2,3,4分别填在大正方形的4个顶点上,再把1,2,3,4分别填在中正方形的4个顶点上,最后把1,2,3,4分别填在小正方形的4个顶点上.(1)能否使8个三角形顶点上数字之和都相等?如果能,请给出填数方法;如果不能,请说明理由. (2)能否使8个三角形顶点上数字之和各不相同?如果能,给出填数方法;如果不能,请说明理由.344341222311分析:(1)不能,如果能,则8个三角形顶点和的总和应该是8的倍数,但是这个总和有三组1、2、3、4组成,其中一组数被重复计算三次,一组数被重复计算两次,一组数仅被计算一次,因此该总和的值为6×(1+2+3+4)=60,不是8的倍数,产生矛盾,因此没有任何填法使8个三角形顶点上数字之和都相等. (2)能,见右上图.【例17】 (★★★),小熊和妈妈去外婆家要过一条河,必须要按照下面的要求填数才可以顺利通过,要求如下:20以内共有个○中(其中3已经填好),使得图中用箭头连接起来的四个数之和都相等.分析:3组数都包括左右两端的数,所以每组数的中间两数之和必然相等.现在还有1、5、7、11、13、17、19七个数供选择,两两之和相等的有1+19=7+13,只有两组,淘汰这一组;还有1+17=5+13+7+11,于是得到右上图的填法.(二)辐射型数阵【例18】 (★★★)将1~7这七个数字,分别填人图中各个○内,使每条线段上的三个○内数的和相等.635412762534175243716(1) (2) (3)分析:设中心○内填a ,由于三条线上的数字和相加应是3的倍数,其中a 一共加了3次,所以1+2+3+4+5+6+7+2a=28+2a 一定是3的倍数.而28÷3—9余1,那么2a ÷3的余数应该是2,因此,a=1,4或7.(1)当a=1时,28+2=30,30÷3=10,10-1=9,除中心外,其他两数的和应是9,只要把2,3,4,5,6,7六个数按“和”是9分成三组填入相应的○内就可以了.填法如图(1) (2)当a=4时,28+8=36,36÷3=12.填法如图(2)(3)当a=7时,28+14=42,42÷3=14.填法如图(3).亮点设计:(1)建议教师首先让学生进行试做,并让学生尝试多种填法。
小学奥数:数阵图(三).专项练习及答案解析

耳tM 蚱 教学目标1 . 了解数阵图的种类2 .学会一些解决数阵图的解题方法3 .能够解决和数论相关的数阵图问题知识点拨 、数阵图定义及分类:1 .定义:把一些数字按照一定的要求,排成各种各样的图形,这类问题叫数阵图 .2 .数阵是一种由幻方演变而来的数字图 .数阵图的种类繁多,这里只向大家介绍三种数阵图:即封闭型数阵图、辐射型数阵图和复合型数阵图 ^ 3 .二、解题方法:解决数阵类问题可以采取从局部到整体再到局部的方法入手: 第一步:区分数阵图中的普通点 (或方格)和关键点(或方格);第二步:在数阵图的少数关键点(一般是交叉点)上设置未知数,计算这些关键点与相关点的 数量关系,得到关键点上所填数的范围; 第三步:运用已经得到的信息进行尝试. 这个步骤并不是对所有数阵题都适用, 很多数阵题 更需要对数学方法的综合运用.例题精讲数阵图与数论【例1】 把0—9这十个数字填到右图的圆圈内,使得五条线上的数字和构成一个等差数列,而且这个等差数列的各项之和为 55,那么这个等差数列的公差有 能的取值.【考点】数阵图与数论 【难度】3星 【题型】填空【关键词】迎春杯,三年级,初赛,第 8题【解析】设顶点分别为 A 、B G D E,有45+A +削C +D +E =55,所以A +B +C +D +E =10,所以A 、 R CH E 分别只能是0-4中的一个数字.则除之外的另外5个数(即边上的)为 45-10=35.设所形成的等差数列的首项为 a 1,公差为d .利用求和公式5(a 1 + a 1+4d ) 2=55, 得a 1+2d =11,故大于等于0+1+5=6,且为奇数,只能取 7、9或11,而对 应的公差d 分别为2、1和0.经试验都能填出来所以共有 3中情况,公差分别为2、 1、0.5-1-3-3.数阵图目地蚱_____ 种可【答案】2种可能【例2】将1~ 9填入下图的。
中,使得任意两个相邻的数之和都不是3, 5, 7的倍数.【考点】数阵图与数论【解析】根据题意可知1的两边只能是3与7; 2的两边只能是6与9; 3的两边只能是1、5 或8; 4的两边只能是7与9.可以先将3—1—7--写出来,接下来7的后面只能是4, 4的后面只能是9, 9的后面只能是2, 2的后面只能是6,可得:3—1 — 7—4 -9-2-6--,还剩下5和8两个数.由于6 8 14是7的倍数,所以接下来应该是5,这样可得:3—1—7—4 — 9—2—6 —5 —8—3.检验可知这样的填法符合题意.【答案】3 —1 — 7—4—9—2 — 6 — 5—8—3【例3】在下面8个圆圈中分别填数字1,2,3, 4, 5, 6, 7, 8(1已填出).从1开始顺时针走1步进入下一个圆圈,这个圆圈中若填n(n<8)o则从这个圆圈开始顺时针走n步进入另一个圆圈.依此下去,走7次恰好不重复地进入每个圆圈,最后进入的一个圆圈中写8 .请给出两种填法.O OO Q 0【考点】数阵图与数论【难度】4星【题型】填空【关键词】走美杯,5年级,决赛,第12题,15分【解析】按顺时针方向:1,2, 5,3, 8, 7,4, 6 或1,5,2 , 4, 8, 6, 7,3 或1,6,2,3 , 8, 5, 7, 4或1,6, 4, 2, 8, 7, 5, 3 (答对任一种给6分,总得分不超过12)由于无论如何填8都是最后一个填写,而填之前,已经走过了28步,因为28 + 8=3余4,即8永远只能在最底下的圆圈里。
三年级--数阵图 题目+答案
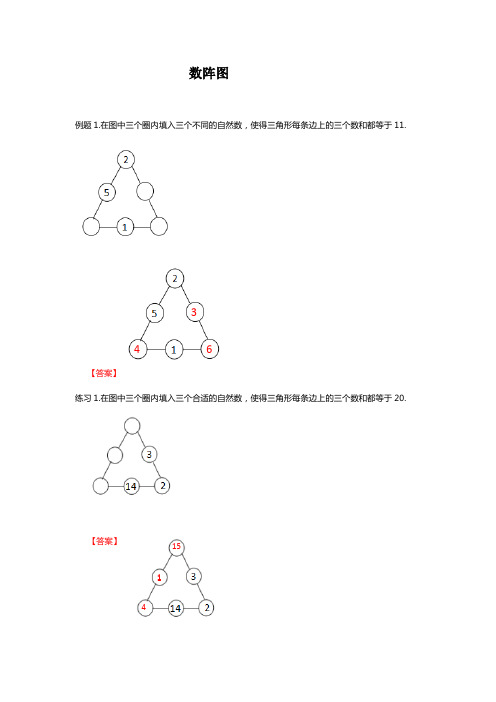
数阵图例题1.在图中三个圈内填入三个不同的自然数,使得三角形每条边上的三个数和都等于11.【答案】练习1.在图中三个圈内填入三个合适的自然数,使得三角形每条边上的三个数和都等于20.【答案】463415 1练习2.在图中三个圈内填入三个不同的自然数,使得三角形每条边上的三个数和都等于20.【答案】选做题:在图中四个圈内填入四个不同的自然数,使得每条边上的三个数和都等于14.【答案】例题2.在下图的八个圆圈中分别填入八个不同的自然数,使得正方形每条边上的三个数之和相等,现在已经填好了五个数,请你将剩下的空补充完整。
5 6491011 1697 6【答案】练习1.在下图的九个圆圈中分别填入九个不同的自然数,使得图中六条直线上的三个数之和相等,现在已经好了五个数,请你将剩下的空补充完整。
【答案】练习2.在下图的八个圆圈中分别填入八个不同的自然数,使得图中四条直线上的三个数之和相等,现在已经好了五个数,请你将剩下的空补充完整。
3 512 5694【答案】选做题.将1-9分别填入下图的圆圈内,使得图中所有三角形的三个顶点上的数之和都等于15,现已经填好了其中三个,请你在图中填出剩下的数。
【答案】8 613 10 22例题3.把1-7这七个数分别填入图中的圆圈内,使每条直线上三个圆圈内所填数之和都相等。
【答案】答案不唯一练习1.把2-8这七个数分别填入图中的圆圈内,使每条直线上三个圆圈内所填数之和都相等。
4【答案】答案不唯一练习2.把3-9这七个数分别填入图中的圆圈内,使每条直线上三个圆圈内所填数之和都相等。
【答案】答案不唯一选做题.把8-14这七个数分别填入图中的圆圈内,使每条直线上三个圆圈内所填数之和都有等于33。
【答案】例题4.把1~6填入图中的六个圆圈中,使得除了第一行外,每一个圆圈中的数都等于与它相邻的上方两个圆圈内的两数之差,其中5已经填好。
5【答案】答案不唯一练习1.把1~10填入图中的10个圆圈中(其中的两个数已经填好),使得除了第一行外,每一个圆圈中的数都等于与它相邻的上方两个圆圈内的两数之差。
数阵图练习题

数阵图练习题数阵图(Number Grid)是一种用数字组成的图形,在数学教学中常用来培养学生的逻辑思维和解题能力。
下面是一些数阵图练习题,帮助你巩固自己的数学知识和解题技巧。
1. 数阵图中的数列在数阵图中,每个数字都和相邻的数字有一定的关系。
观察下面的数阵图,并找出横向和纵向的数列规律。
```1 2 3 4 56 7 8 9 1011 12 13 14 1516 17 18 19 2021 22 23 24 25```横向数列:1, 2, 3, 4, 5纵向数列:1, 6, 11, 16, 21根据观察,我们可以得出结论:横向数列的公差为1,纵向数列的公差为5。
2. 数阵图中的数学运算在数阵图中,数字之间的运算规律也是一种常见的题型。
观察下面的数阵图,并计算出横向和纵向数学运算的结果。
```1 4 9 16 252 6 12 20 303 8 15 24 354 10 18 28 405 12 21 32 45```横向数学运算:1^2, 2^2, 3^2, 4^2, 5^2 (平方)纵向数学运算:1^2, 2^2, 3^2, 4^2, 5^2 (平方)根据观察,我们可以得出结论:横向数学运算是计算每个数字的平方,纵向数学运算也是计算每个数字的平方。
3. 数阵图中的缺失数字在数阵图中,有时候会有一些数字缺失。
观察下面的数阵图,并找出其中的缺失数字。
```3 6 9 12 1518 ? 24 27 3033 36 39 42 4548 51 ? 57 6063 66 69 ? 75```根据观察,我们可以得出结论:缺失数字分别为21、54、72。
4. 数阵图中的数学规律在数阵图中,数字之间可能会存在一些数学规律。
观察下面的数阵图,并找出其中的数学规律。
```1 123 58 13 21 34 5589 144 233 377 610987 1597? 4181 6765 10946```根据观察,我们可以得出结论:这是一个斐波那契数列的数阵图。
小学数学 《数阵图》练习题(含答案)

小学数学《数阵图》练习题(含答案)数阵图问题千变万化,这一类问题要求数阵中填入了一些数以后,能保证数阵中特定关系线(或关系区域)上的数的和相等,解决这一类问题可以按以下步骤解决问题:第一步:区分数阵图中的普通点(或方格),和交叉点(方格)第二步:在数阵图的少数关键点(一般是交叉点)上设置未知数,计算各个点与该点被重复计算次数之积的和的代数式,即数阵图关系线(关系区域)上和的总和,这个和是关系线(关系区域)的个数的整数倍.第三步:判断少数关键点上可以填入的数的余数性质,并得出相应的数阵图关系线(关系区域)和.第四步:运用已经得到的信息进行尝试:数阵图还有一类题型比较少见,解决这一类问题需要理清数阵中数与数之间的相关关系,找出问题关键.(一)封闭型数阵问题【例1】(★★★)小青蛙不小心爬到一个正方形数阵图中,必须把1,2,3,4,5,6,7,8八个数字填入下图中的○内,使正方形每条边上三个数的和都等于13才能通过这个数阵图,你能帮它吗?【例2】(★★★)小乌龟被困在五个圆里面(如下图),五圆相连,每个位置的数字都是按一定规律填写的,它必须找出规律,并求出x所代表的数才能脱困,你知道该怎么办吗?24273028262218 1720x【例3】(★★★)1~9分别填入小三角形内(每个小三角形内只填一个数),要求靠近大三角形三条边的每五个数相加和相等.想一想,怎样填这些数才能使五个数的和尽可能大一些?【例4】(★★★)能否将数0,1,2,…,9分别填人下图的各个圆圈内,使得各阴影三角形的3个顶点上的数之和相等?【例5】(★★★),小熊和妈妈去外婆家要过一条河,必须要按照下面的要求填数才可以顺利通过,要求如下:20以内共有10个奇数,去掉9和15还剩八个奇数,将这八个奇数填入右图的八个○中(其中3已经填好),使得图中用箭头连接起来的四个数之和都相等.3(二)辐射型数阵【例6】(★★★)将1~7这七个数字,分别填人图中各个○内,使每条线段上的三个○内数的和相等.【例7】 (★★★)把10至20这11个数分别填入下图的各圆圈内,使每条线段上3个圆内所填数的和都相等.如果中心圆内填的数相等,那么就视为同一种填法.请写出所有可能的填法.【例8】 (★★★)左图中有三个正三角形,将1~9填入它们顶点处的九个○中,要求每个正三角形顶点的三数之和都相等,并且通过四个○的每条直线上的四数之和也相等.【例9】 (★★★)在下图的七个圆圈内各填上一个数,要求每条线上的三个数中,当中的数是两边两个数的平均数,现在已填好两个数,求x 是多少?(三)其它类型的数阵图【例10】 (★★★)在下图中的10个○内填入0~9这10个数字,使得按顺时针循环式成立:【例11】 (★★★★)将1~8这八个自然数填入左下图的空格内,使四边形组成的四个等式都成立:【例12】 (★★★★)下图包括6个加法算式,要在圆圈里填上不同的自然数,使6个算式都成立.那么最右边的圆圈中的数最少是多少?+=====----===×÷+=-+=+=1.请分别将1,2,4,6这4个数填在下图的各空白区域内,使得每个圆圈里4个数的和都等于15.2.把1~5这五个数填入下图中的○里,使每条直线上的三个数之和相等.3.把1至6分别填入下图的各方格中,使得横行3个数的和与竖列4个数的和相等.4.将1~7七个数字填入左下图的七个○内,使每个圆周和每条直线上的三个数之和都相等.5.将1~8八个数分别填入右上图的八个○内,使得图中的六个等式都成立.△代表几?37 5=== =+++++(一)封闭型数阵问题【例13】 (★★★)小青蛙不小心爬到一个正方形数阵图中,必须把1,2,3,4,5,6,7,8八个数字填入下图中的○内,使正方形每条边上三个数的和都等于13才能通过这个数阵图,你能帮它吗?75623841或84362571分析:因为每边上的和为13,那么四条边上的数字之和为13×4=52,而1+2+…+7+8=36,所以四个角上的四个数之和等于52-36=16.在1~8中选四个数,四数之和等于16,且其中相邻两个的和与任意三个的和不等于13的只有:16=1+2+6+7=1+2+5+8=1+4+5+6.经试验,只有右上图的两种填法.亮点设计:(1)求数阵问题的关键是找到关键数,也就是重复数,教会学生学会找关键数的方法是最重要的.(2)设计问题:正方形每条边之和是13,13×4=52,但是所有数的和是:1+2+…+7+8=36,为什么会出现结果不同的问题呢?仔细观察这个数阵,四条边上所有数相加的过程中四个角上的数都被重复加了一次,也就是四个角上的数是重复数,52-36=16即为这四个重复数的和. (3)强调分组法与试验法:知道了四个数的和之后,下一步就要先确定这四个数,采用分组法和试验法.分组法是将这个和根据要求拆成四个数,例如本题中要求其中相邻两个的和与任意三个的和不等于13,根据要求将16分成4个数的和:16=1+2+6+7=1+2+5+8=1+4+5+6,但是未必每一组都是合适的,这就需要采用试验法,将它们一一进行试验.(4)小结:对于封闭型的数阵,重复数基本上都是两条线相交的点,这在后面的例题中有大量体现.[前铺]将1~6六个自然数分别填入下图的○内,使三角形每边上的三数之和都等于11.614532分析:因为每边上的和为11,那么三条边上的数字之和为11×3=33,而1+2+…+5+6=21,所以三个角的三个数之和等于33-21=12,在1~6中选3个和为12的数,且其中任意两个的和不等于11,这样的组合有:12=2+4+6=3+4+5,经试验,填法见右上图.[拓展]将1~6填入左下图的六个○中,使三角形每条边上的三个数之和都等于k ,请指出k 的取值范围.654321654321654321654321k=9 k=10 k=11 k=12分析:设三角形三个顶点的数字之和为s.因为每个顶点属于两条边公有,所以把三条边的数字和加起来,等于将1至6加一遍,同时将三个顶点数字多加一遍.于是有(1+2+3+4+5+6)+s=3k,化简后为s+21=3k.由于s是三个数之和,故最小为1+2+3=6,最大为4+5+6=15,由此求出9≤k≤12.s和k有四组取值:通过试验,每组取值都对应一种填数方法(见右上图).【例14】(★★★)小乌龟被困在五个圆里面(如下图),五圆相连,每个位置的数字都是按一定规律填写的,它必须找出规律,并求出x所代表的数才能脱困,你知道该怎么办吗?242730282622181720x分析:经观察,图中所填数的规律为两个圆相交部分的数等于与它相邻两部分里的数的和的一半.比如:(26+18)÷2=22.(30+26)÷2=28.(24+30)÷2=27.所以x+18=17×2,x=16.经检验,16和24相加除以2,也恰好等于20.[拓展]找规律求xx24123082616186452分析:经观察,图中所填数的规律为两个圆相交部分的数等于与它相邻两部分里的数的差的2倍.比如:(26-18)×2=16.(30-26)×2=8.(30-24)×2=12.因为52÷2=26>24,所以x=26+24=50.经检验,(50--18)×2=64.【例15】(★★★)1~9分别填入小三角形内(每个小三角形内只填一个数),要求靠近大三角形三条边的每五个数相加和相等.想一想,怎样填这些数才能使五个数的和尽可能大一些?分析:1+2+3+4+5+6+7+8+9=45,用s表示靠近大三角形三条边的五个数的和.因为有三个小三角形所填的数在求和时只用了一次(用a,b,c来表示这三个数),其余均用了两次.于是,45×2-(a+b+c)=3 s.要使s尽可能大,只要a+b+c尽可能小.所以a+b+c=1+2+3=6,于是90-6=3 s,s=28.剩下的六个数分成三组,并且每组中两数的和是三个连续自然数,那么:4+8=12;6+7=13;5 +9=14.经过调配可得到几十种填法,右上图是填法之一.[拓展一]如图是奥林匹克的五环标志,其中a,b,c,d,e,f,g,h,i处分别填入整数1至9,如果每一个圆环内所填的各数之和都相等,那么这个相等的和最大是多少,最小是多少?ihgfedcba分析:计算五个圈内各数之和的和,其中b,d,f,h被计算了两遍,所以这个和是1+2+3+4+5+6+7+8+9+b+d+f+h,而这个和一定能被5整除,所以b,d,f,h中填入大数时能使这个和取得最大值,最大是6、7、8、9,各圆圈内的和也取得15,由于15=6+9=7+8,所以满足条件的所有数无法配成15,当和为14时可以找出满足条件的填法,所以和最大为14,当b,d,f,h取1、2、3、4时这个和取得最小值,各圆圈内的和也取得最小值11.[拓展二]有10个连续的自然数,9是其中第三大的数.现在把这10个数填到下图的10个方格中,每格内填一个数,要求图中3个2×2的正方形中的4个数之和相等.那么,这个和数的最小值是多少?分析:9是其中第三大的数,所以这10个连续自然数是2、3、4、5……9、10、11,计算三个正方形中的和的和,这个和能被3整除,其中a和b被重复计算了两次,所以2+3+……11+a+b=65+a+b=3s,当a+b=1,4,7……时,65+a+b可以被3整除,因为要取最小值,所以a+b的值越小越好,但是不可能取1与4,所以,a+b=7时,这个和取得最小值,每个正方形中的和也取得最小值(65+7)÷3=24.【例16】(★★★)能否将数0,1,2,…,9分别填人下图的各个圆圈内,使得各阴影三角形5619372481528763049分析:0+…+9=45,45-中心数=3个阴影三角形的3个顶点上的数字之和,所以中心数必须是3的倍数,只能是0,3,6,9.枚举法实验,中心数只能是3,6,答案如右上图.[拓展一]将1~10分别填入图中,使得每个小三角形3个顶点上的数字之和为图中所表示的数值.分析:先确定中间5个重复数,它们的和为(20+16+12+13+10)-(1+2+…+10)=16,所以中间5个重复数只能是1,2,3,4,6的组合.又因为有1个和为20,相应三角形上的三个数只能是4,6,10,逐一试验,答案如右上图.[拓展二]图中有大、中、小3个正方形,组成了8个三角形.现在先把1,2,3,4分别填在大正方形的4个顶点上,再把1,2,3,4分别填在中正方形的4个顶点上,最后把1,2,3,4分别填在小正方形的4个顶点上.(1)能否使8个三角形顶点上数字之和都相等?如果能,请给出填数方法;如果不能,请说明理由. (2)能否使8个三角形顶点上数字之和各不相同?如果能,给出填数方法;如果不能,请说明理由.344341222311分析:(1)不能,如果能,则8个三角形顶点和的总和应该是8的倍数,但是这个总和有三组1、2、3、4组成,其中一组数被重复计算三次,一组数被重复计算两次,一组数仅被计算一次,因此该总和的值为6×(1+2+3+4)=60,不是8的倍数,产生矛盾,因此没有任何填法使8个三角形顶点上数字之和都相等. (2)能,见右上图.【例17】 (★★★),小熊和妈妈去外婆家要过一条河,必须要按照下面的要求填数才可以顺利通过,要求如下:20以内共有个○中(其中3已经填好),使得图中用箭头连接起来的四个数之和都相等.分析:3组数都包括左右两端的数,所以每组数的中间两数之和必然相等.现在还有1、5、7、11、13、17、19七个数供选择,两两之和相等的有1+19=7+13,只有两组,淘汰这一组;还有1+17=5+13+7+11,于是得到右上图的填法.(二)辐射型数阵【例18】 (★★★)将1~7这七个数字,分别填人图中各个○内,使每条线段上的三个○内数的和相等.635412762534175243716(1) (2) (3)分析:设中心○内填a ,由于三条线上的数字和相加应是3的倍数,其中a 一共加了3次,所以1+2+3+4+5+6+7+2a=28+2a 一定是3的倍数.而28÷3—9余1,那么2a ÷3的余数应该是2,因此,a=1,4或7.(1)当a=1时,28+2=30,30÷3=10,10-1=9,除中心外,其他两数的和应是9,只要把2,3,4,5,6,7六个数按“和”是9分成三组填入相应的○内就可以了.填法如图(1) (2)当a=4时,28+8=36,36÷3=12.填法如图(2)(3)当a=7时,28+14=42,42÷3=14.填法如图(3).亮点设计:(1)建议教师首先让学生进行试做,并让学生尝试多种填法。
小学奥数:数阵图(二).专项练习及答案解析

1. 了解数阵图的种类2. 学会一些解决数阵图的解题方法3. 能够解决和数论相关的数阵图问题.一、数阵图定义及分类:1. 定义:把一些数字按照一定的要求,排成各种各样的图形,这类问题叫数阵图.2. 数阵是一种由幻方演变而来的数字图.数阵图的种类繁多,这里只向大家介绍三种数阵图:即封闭型数阵图、辐射型数阵图和复合型数阵图. 3.二、解题方法:解决数阵类问题可以采取从局部到整体再到局部的方法入手: 第一步:区分数阵图中的普通点(或方格)和关键点(或方格); 第二步:在数阵图的少数关键点(一般是交叉点)上设置未知数,计算这些关键点与相关点的数量关系,得到关键点上所填数的范围;第三步:运用已经得到的信息进行尝试.这个步骤并不是对所有数阵题都适用,很多数阵题更需要对数学方法的综合运用.复合型数阵图【例 1】 由数字1、2、3组成的不同的两位数共有9个,老师将这9个数写在一个九宫格上,让同学选数,每个同学可以从中选5个数来求和.小刚选的5个数的和是120,小明选的5个数的和是111.如果两人选的数中只有一个是相同的,那么这个数是_____________.313233212223131211【考点】复合型数阵图 【难度】3星 【题型】填空 【关键词】迎春杯,中年级,决赛,3题 【分析】 这9个数的和:111213212223313233++++++++10203031233198=++⨯+++⨯=()()由小刚和小明选的数中只有一个是相同的,可知他们正好把这9个数全部都取到了,且有一个数取了两遍.所以他们取的数的总和比这9个数的和多出来的部分就例题精讲知识点拨教学目标5-1-3-2.数阵图是所求的数.那么,这个数是12011119833+-=.【答案】33【例 2】 如图1,圆圈内分别填有1,2,……,7这7个数。
如果6个三角形的顶点处圆圈内的数字的和是64,那么,中间圆圈内填入的数是 。
【考点】复合型数阵图 【难度】3星 【题型】填空 【关键词】希望杯,五年级,复赛,第5题,5分 【解析】 2 【答案】2【例 3】 如下图(1)所示,在每个小圆圈内填上一个数,使得每一条直线上的三个数的和都等于大圆圈上三个数的和.(1)17894【考点】复合型数阵图 【难度】3星 【题型】填空 【解析】 为叙述方便,先在每个圆圈内标上字母,如图(2),(2)a cb49817则有a+4+9=a+b+c (1)b+8+9=a+b+c (2)c+17+9=a+b+c (3) (1)+(2)+(3):(a+b+c )+56=3(a+b+c ),a+b+c=28,则 a=28-(4+9)=15,b=28-(8+9)=11,c=28-(17+9)=2解:见图.1789411215【答案】1789411215【例 4】请你将数字1、2、3、4、5、6、7填在下面图(1)所示的圆圈内,使得每个圆圈上的三个数之和与每条直线上的三个数之和相等.应怎样填?【考点】复合型数阵图【难度】3星【题型】填空【解析】为了叙述方便,将各圆圈内先填上字母,如图(2)所示.设A+B+C=A+F+G=A+D+E=B+D+F=C+E+G=k(A+B+C)+(A+F+G)+(A+D+E)+(B+D+F)+(C+E+G)=5k,3A+2B+2C+2D+2E+2F+2G=5k,2(A+B+C+D+E+F+G)+A=5k,2(1+2+3+4+5+6+7)+A=5k,56+A=5k.,因为56+A为5的倍数,得A=4,进而推出k=12,因为在1、2、3、5、6、7中,1+5+6=7+3+2=12,不妨设B=1,F=5,D=6,则C=12-(4+1)=7,G=12-(4+5)=3,E=12-(4+6)=2.,解:得到一个基本解为:(见图)7654321【答案】7654321【例 5】在左下图的每个圆圈中填上一个数,各数互不相等,每个圆圈有3个相邻(即有线段相连的圆圈)的圆圈。
小学奥数:数阵图(三).专项练习及答案解析

1.了解数阵图的种类2.学会一些解决数阵图的解题方法3.能够解决和数论相关的数阵图问题.一、数阵图定义及分类:1.定义:把一些数字按照一定的要求,排成各种各样的图形,这类问题叫数阵图.2.数阵是一种由幻方演变而来的数字图.数阵图的种类繁多,这里只向大家介绍三种数阵图:即封闭型数阵图、辐射型数阵图和复合型数阵图.3.二、解题方法:解决数阵类问题可以采取从局部到整体再到局部的方法入手:第一步:区分数阵图中的普通点(或方格)和关键点(或方格);第二步:在数阵图的少数关键点(一般是交叉点)上设置未知数,计算这些关键点与相关点的数量关系,得到关键点上所填数的范围;第三步:运用已经得到的信息进行尝试.这个步骤并不是对所有数阵题都适用,很多数阵题更需要对数学方法的综合运用.数阵图与数论【例 1】把0—9这十个数字填到右图的圆圈内,使得五条线上的数字和构成一个等差数列,而且这个等差数列的各项之和为55,那么这个等差数列的公差有种可能的取值.【考点】数阵图与数论【难度】3星【题型】填空【关键词】迎春杯,三年级,初赛,第8题【解析】设顶点分别为A、B、C 、D、E,有45+A+B+C+D+E=55,所以A+B+C+D+E=10,所以A、B、C、D、E分别只能是0-4中的一个数字.则除之外的另外5个数(即边上的)为45-10=35.设所形成的等差数列的首项为a1,公差为d.利用求和公式5(a1+a1+4d)2=55,得a1+2d=11,故大于等于0+1+5=6,且为奇数,只能取7、9或11,而对应的公差d分别为2、1和0.经试验都能填出来所以共有3中情况,公差分别为2、1、0.例题精讲知识点拨教学目标5-1-3-3.数阵图【答案】2种可能【例 2】将1~9填入下图的○中,使得任意两个相邻的数之和都不是3,5,7的倍数.【考点】数阵图与数论【难度】4星【题型】填空【解析】根据题意可知1的两边只能是3与7;2的两边只能是6与9;3的两边只能是1、5或8;4的两边只能是7与9.可以先将3—1—7--写出来,接下来7的后面只能是4,4的后面只能是9,9的后面只能是2,2的后面只能是6,可得:3—1—7—4—9—2—6--,还剩下5和8两个数.由于6814+=是7的倍数,所以接下来应该是5,这样可得:3—1—7—4—9—2—6—5—8—3.检验可知这样的填法符合题意.【答案】3—1—7—4—9—2—6—5—8—3【例 3】在下面8个圆圈中分别填数字l,2,3,4,5,6,7,8(1已填出).从1开始顺时针走1步进入下一个圆圈,这个圆圈中若填n(n≤8)。
小学数学《数阵图》练习题(含答案) (1)
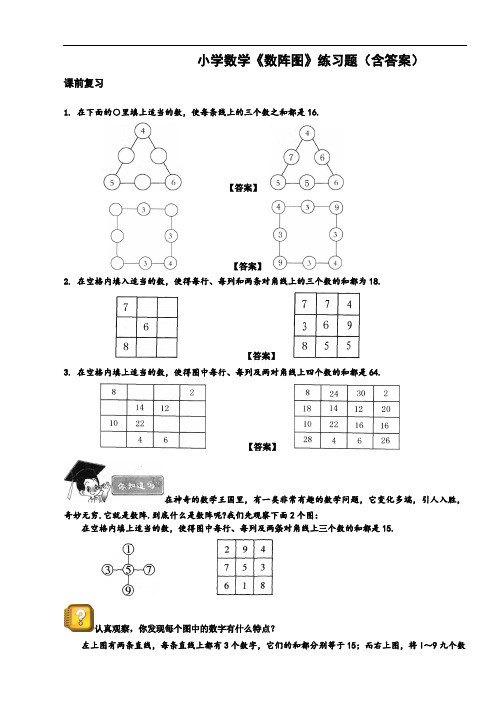
小学数学《数阵图》练习题(含答案)课前复习1.在下面的○里填上适当的数,使每条线上的三个数之和都是16.【答案】【答案】2.在空格内填入适当的数,使得每行、每列和两条对角线上的三个数的和都为18.【答案】3. 在空格内填上适当的数,使得图中每行、每列及两对角线上四个数的和都是64.【答案】在神奇的数学王国里,有一类非常有趣的数学问题,它变化多端,引人入胜,奇妙无穷.它就是数阵.到底什么是数阵呢?我们先观察下面2个图:在空格内填上适当的数,使得图中每行、每列及两条对角线上三个数的和都是15.认真观察,你发现每个图中的数字有什么特点?左上图有两条直线,每条直线上都有3个数字,它们的和都分别等于15;而右上图,将l~9九个数字排成三行、三列,每一行、每一列、每一斜行上的3个数字的和都等于15.数阵就是用数(一般指自然数)按一定的要求和规律,组成特定的形状或布成特定的阵势.它一般分为辐射型(左上图)和封闭型(右上图).要把一些数字按一定的规则填入图形中,有没有巧妙的方法来填呢?今天这节课我们就一起来学习.辐射型数阵图【例1】把1,2,3,4,5这5个数分别填入图中的圆圈内,使得横行3个数的和与竖列3个数的和都等于10.【分析】横行的三个数之和加上竖列的三个数之和,只有重叠数a被加了两次,即重叠了一次,其余各数均被加了一次.因为横行的三个数之和与竖列的三个数之和都等于10,所以(1+2+3+4+5)+a=10×2,a=5.剩下4个数中每两个数之和应该等于5,,1+4=2+3。
【例2】把4~8这五个数填入图中(已填入6),使两条直线上的三个数之和相等.【分析】方法一:把6除外,还剩4,5,7,8,这四个数,在这四个数中4+8=5+7,这样可以填出答案。
方法二:与例1不同之处是已知“重叠数”为6,而不知道两条直线上的三个数之和都等于什么数.可以先求出这个“和k”.(4+5+6+7+8)+6=k×2.K=18。
小学数学五年级《数阵图与数字谜》练习题(含答案)

《数阵图与数字谜》练习题(含答案)你还记得吗【复习1】把1~5这五个数填入右图中的○里,使每条直线上的三个数之和相等.分析:(1+2+3+4+5)+重叠数=每条直线上三数之和×2,所以,每条直线上三数之和=(15+重叠数)÷2.因为每条直线上的三数之和是整数,所以“15+重叠数”只能是偶数,重叠数只可能是1,3或5.若“重叠数”=1,则两条直线上三数之和为(15+1)÷2=8。
填法见下图(1);若“重叠数”=3,则两条直线上三数之和为(15+3)÷2=9。
填法见下图(2);若“重叠数”=5,则两条直线上三数之和为(15+5)÷2=10。
填法见下图(3).【复习2】将1~7这七个数分别填入右图的○里,使得每条直线上三个数之和与每个圆圈上的三个数之和都相等.分析:所有的数都是重叠数,中心数重叠两次,其它数重叠一次. 所以三条边及两个圆周上的所有数之和为:(1+2+…+7)×2+中心数=56+中心数.因为每条边及每个圆周上的三数之和都相等,所以这个和应该是5的倍数,再由中心数在1至7之间,所以中心数是4. 每条边及每个圆周上的三数之和等于(56+4)÷5=12.中心数是4,每边其余两数之和是12-4=8,两数之和是8的有1,7;2,6;3,5.于是得到右下图的填法.【复习3】在右图所示的竖式中,相同的汉字表示相同的数字,不同的汉字表示不同的数字。
如果:巧+解+数+字+谜=30,那么“数字谜”所代表的三位数是多少?分析:还是先看个位,5个“谜”相加的结果个位还是等于“谜”,“谜”必定是5(0显然可以排除);接着看十位,四个“字”相加再加上进位2,结果尾数还是“字”,那说明“字”只能是6;再看百位,三个“数”相加再加上进位2,结果尾数还是“数”,“数”可能是4或9;再看千位,(1)如果“数”为4,两个“解”相加再加上进位1,结果尾数还是“解”,那说明“解”只能是9;5+6+4+9=24,30-24=6,“巧”等于6与“字”等于6重复,不能;(2)如果“数”为9,两个“解”相加再加上进位2,结果尾数还是“解”,那说明“解”只能是8;5+6+9+8=28,30-28=2,可以. 所以“数字谜”代表的三位数是965.数 阵 图数阵图是将一些数按照一定要求排列而成的某种图形,有时简称数阵. 幻方是特殊的数阵图,一般地,将九个不同的数填在3×3(即三行三列)的方格中,使每行、每列、及二条对角线上的三数之和均相等,这样的3×3的数阵阵列称为三阶幻方. n 阶幻方的定义与三阶幻方相仿!【例1】 (1)将九个数填入下图(1)的九个空格中,使得任一行、任一列以及两条对角线上的三个数之和都等于定数k ,则中心方格中的数必为3k .请你说明理由! (2)将九个数填入下图(2)的空格中,使得每行、每列、每条对角线上的三个数之和都相等,则一定有:2a b e +=.请你说明理由!(3)将九个数填入下图(3)的空格中,使得每行、每列、每条对角线上的三个数之和都相等,则一定有:2a b c +=.请你说明理由!分析:(1)因为每行的三数之和都等于k ,共有三行,所以九个数之和等于3k.如右下图所示,经过中心方格的有四条虚线,每条虚线上的三个数之和都等于k ,四条虚线上的所有数之和等于4k ,其中只有中心方格中的数是“重叠数”,九个数各被计算一次后,它又被重复计算了三次.所以有:九数之和+中心方格中的数×3=4k ,3k+中心方格中的数×3=4k ,中心方格中的数=3k (2)和=3e ,a+e+b=和=3e ,所以a+b=2e ,即得:2a b e +=.(3)设中心数为d. 每行、每列、每条对角线上的三个数之和都等于3d. 由此可得右图,那么有:c +(2d -b )= a +(2d -c ),由此可得:2a b c +=. 值得注意的是,这个结论对于a 和b 并没有什么限制,可以是自然数,也可以是分数、小数;可以相同,也可以不同.【巩固】在右图的空格中填入七个自然数,使得每一行、每一列及每一条对角线上的三个数之和都等于90.分析:中心数为90÷3=30;右上角的数为(23+57)÷2=40,其它数依次可填(见右下图).【巩固】在下图的每个空格中填入个自然数,使得每一行、每一列及每条对角线上的三个数之和都相等.分析:右下角的数为(8+10)÷2=9,中心数为(5+9)÷2=7,且每行、每列、每条对角线上的三数之和都等于7×3=21.由此可得右下图的填法.【巩固】图中3×3的正方形的每一个方格内的字母都代表一个数,已知其每行、每列以及两条对角线上三个数之和都相等.若f=19,g=96.那么b是多少?分析:我们知道:g=(b+f)÷2,易得b=173.【例2】在右图的每个空格中,填入不大于12且互不相同的八个自然数,使得每行、每列、每条对角线上的三个数之和都等于21 .分析:中央一数必定是21÷3=7.从而一条对角线为8,7,6.另两个角上的数,和为14=2+12=3+11=4+10=5+9,不难验证只有3、11与4、10两种符合要求.于是填法有:【巩固】在右图的九个方格中填入不大于12且互不相同的九个自然数(其中已填好一个数),使得任一行、任一列及两条对角线上的三个数之和都等于21.分析:【例3】将1,3,5,7,9,11,13,15,17填入3×3的方格内,使其构成一个幻方. 分析:(法1):易得中心数为9,然后将剩余那么其余8个数分为4组,每组两个数的和是18,把它们分别填入图中关于中心格对称的格子内,实验可得结果,如右图. 答案不唯一,仅供参考.(法2):其实会学习的小朋友就知道理利用已经学习过的一些典型题目结果加以变形得到新题答案.事实上我们可以把结果中的幻方看作是1~9填图的幻方相应位置数字乘2减1得来的.推广开来可以知道等差数列填图的三阶幻方几乎都具有相似的形式.【前铺】将自然数1至9,分别填在右图的方格中,使得每行、每列以及两条对角线上的三个数之和都相等.分析:(法1):三行的总和=1+2+3+4+…+9=45,所以每行三个数的和是45÷3=15,所以E代表15÷3=5,由于在同一条直线的三个数之和是15,因此若某格中的数是奇数,那么与这个数在同一条直线上的另两个数的奇偶性相同.因此,四个角上的数A、C、G、I必为偶数.(否则,若A为奇数,则I为奇数.此时若B为奇数,则其余所有格亦为奇数;若B为偶数,则其余所有格亦为偶数.无论哪种情形,都与1至9中有5个奇数,4个偶数这一事实矛盾.)因此,B、D、F、H为奇数.我们不妨认为A=2(否则,可把3×3方格绕中心块旋转即能做到这一点).此时I=8.此时有两种选择:C=4或G=4.因而,G=6或C=6.其他格的数随之而定.如果把经过中心块旋转而能完全重合的两种填数法视作一种的话,一共只有两种不同的填数法:A=2,C=4或A=Z,G=4(2,4被确定位置后,其他数的位置随之而定).(法2):从法1知道中心数为5,那么其余8个数分为4组,每组两个数的和是10,把它们分别填入图中关于中心格对称的格子内,实验可得结果.这种试填的方法更易让学生接受.【拓展】如图(1)的3×3的阵列中填入了l~9的自然数,构成大家熟知的3阶幻方.现在另有一个3×3的阵列,如图(2),请选择9个不同自然数填人9个方格中,使得其中最大者为20,最小者大于5,且要求横加、竖加、对角线方式相加的3个数之和都相等.分析:①观察原表中的各数是从1~9不同的九个自然数,其中最大的数是9,最小的数是1,且横加、竖加、对角线方式相加结果相等.②根据题意,要求新制的幻方最大数为20,而9+11=20,因此,如果原表中的各数都增加11,就能符合新表中的条件了.【例4】右图是一个四阶幻方,请将其补全:分析:根据各行,各列,各对角线和相等为34,可得图(1),此时我们可以设未知数,如图(2),将一些数表示出来,进而根据和为34求得x代表9,随后得到答案,如图(3).【拓展】在图中所示方格表的每个方格内填入—个恰当的字母;可使每行、每列及两条对角线上4个方格中字母都是A、B、C、D,那么标有“*”的方格内应填的字母是什么?分析:考虑含A和*的对角线上的元素.第二行第二个元素与C同行,因此不是C,第三行第三个元素与C同列,因此也不是C,所以*代表的元素必为C.【巩固】在右图的每个方格中填入一个数字,使得每行、每列以及每条对角线上的方格中的四个数字都是1,2,3,4.分析:如下图所示,受列及对角线的限制,a处只能填1,从而b处填3;进而推知c处填4,d处填3,e处填4,……右下图为填好后的数阵图.【例5】右图是大家都熟悉的奥林匹克的五环标志. 请将1~9分别填入五个圆相互分割的九个部分,并且使每个圆环内的数字之和都相等.分析:设每个圆内的数字之和为k,则五个圆内的数字之和是5k,它等于1~9的和45,再加上两两重叠处的四个数之和. 而两两重叠处的四个数之和最小是1+2+3+4=10,最大是6+7+8+9=30,所以,5k≤45+30=75且5k≥45+10=55,即11≤k≤15 .当k=11,13,14时可得四种填法(见下图),k=12,15时无解.【前铺】将1~11填入左下图的○内,使每条虚线上的三数之和都等于18.分析:设中心数为a,由五条虚线上的数字之和得到5×18=(1+2+…+11)+4a,解得a=6. 填数方法如下图.【例6】将1~7这七个自然数分别填入右图的七个○内,使得三个大圆周上的四个数之和都等于定数,指出这个定数所有的可能取值,并给出定数为13时的一种填法.分析:设每个大圆周上的四个数之和为k(即题中的定数). 图中有一个○属于三个大圆公有,有三个○各属于两个大圆公有. 设属于三个大圆公有的○内的数为w,属于两个大圆公有的三个○内的数字之和为v.将三个大圆上的数字和相加,得到:3k=1+2+3+4+5+6+7+v+2w=28+v+2w,因为v+2w最小为11(w=1,v=2+3+4),最大为29(w=7,v=6+5+4),分别代入上式,解得13≤k≤19,即定数可以取13至19之间的整数.本题是k=13的情况,此时w=1,v=2+3+4,填法见右下图.【例7】在右图所示立方体的八个顶点上标出1~9中的八个,使得每个面上四个顶点所标数字之和都等于k,并且k不能被未标出的数整除.分析:标出的八个数是每面四个数和的2倍,是偶数,1~9和为45 ,因此未标出的数是一个奇数,在1,3,5,7,9中选一个数,并使余下八个数之和的一半不能被这个数整除,依此可知未标出的数是7.下面用余下的8个数填图,每面四个数和为:(45-7)÷2=19.如果已知某一面上四个数和为19.那么与其平行的面上四数和也必为19.因此我们只考虑有公共顶点的三个面即可.下面我们考虑以9为公共顶点的三个面.由于8,9不公面,因此8在顶点9的对顶点上,有公共点9的三个面上,每面其余三个数和为10,且每两个面有一个公共顶点.由此试验易得三个面上的数分别为:(6,3,1),(5,4,1),(3,2,5),填图如右下图.数字谜【例8】将0~9中的8个不同的数字分别用a、b、c、d、e、f、g、h替换.在替换规则+=,如上面4个式子中,“+”、“×”、下:g×g=db,g×c=bd,g×f=ef,ag b eh⨯的“=与平常算术中相应的符号意义相同,而且也是十进位制.在这种替换规则下,ca e数值等于 .分析:由g×g=db知,g≥4.若g=4,d=1,与g ×c=bd 是偶数矛盾; 若g=5,则d=2,b=5,与g ≠b 矛盾;若g=6,则d=3,b=6,与g ≠b 矛盾;若g=7,则d=4,b=9,由g×c =bd =94,得到c =4÷7=3137也不合题意; 若g=8,则d=6,b=4,由g×c =bd 46,得到c=46÷8=354,仍不合题意; 若g=9,则d=8,b=1,由g×c =bd =18,得到c=18÷9=2,再由g ×f=ef ,f=5,e=4,再由ag b eh +=,得a=e-1=3.所以23492ca e ⨯=⨯=.【例9】 在下面的加法算式中,相同的汉字表示相同的数字,不同的汉字表示不同的数字.请把下面汉字算式翻译成数字算式.分析:首先“华”=1.由于“人”≠“华”,故“人”只能是0.从百位看出. 百位没有向千位进位,即有“香”=9.看百位,知“回”比“港”大1;再看十位,可知“爱”=8,并且个位要向十位进位,即“归”+“港”=10 +“游”.因为“游”≠0,1,知“游”≥2,即“归”+“港”≥12.又“归”≠8,9,知“归”≤7,从而“港”≥5.同样,“归”也不小于5,并且由于“回”比 “港”大1,知“归”、“港”、“回”应该是5,6,7(次序未确定).容易验证,只有“归”=7,“港”=5,“回”=6符合条件,此时“游”=2,即算式为 :9567+1085=10652 .【巩固】在下面的算式中,汉字“第、十、一、届、华、杯、赛”代表1,2,3,4,5,6,7,8,9中的7个数字,不同的汉字代表不同的数字,恰使得加法算式成立.则“第、十、一、届、华、杯、赛”所代表的7个数字的和等于多少?分析:根据加法规则,“第”=1.“届”+“赛”=6或“届”+“赛”=16.若“届”+“赛”=6,只能是“届”、“赛”分别等于2或4,此时“一”+“杯”=10 只能是“一”、“杯”分别为3或7.此时“十”+“华”=9,“十”、“华’’分别只能取 (1,8),(2,7),(3,6),(4,5).但l ,2,3,4均已被取用,不能再取.所以,“届”+ “赛”=6填不出来,只能是“届”+“赛”=16.这时“届”、“赛”只能分别取9和7.这 时只能是“一”+“杯”+1=10,且“十”+“华”+1=10,也就是“一”+“杯”=9, 同时“十”+“华”=9.所以它们可以分别在(3,6),(4,5)两组中取值.因此“第、十、一、届、华、杯、赛”所代表的7个数字的和等于1+9+9+16=35.【例10】在右面的□内,各填一个合适的数字,使算式成立.分析:从被乘数个位上的□里填什么数字入手及竖式中□×6=()4,是本题的突破口.这里有两种情况:4×6=24或9×6=54,都可使□×6=()4成立.也就是说,被乘数个位上的数字可能是4,也可能是9.先考虑被乘数个位上的数字是9的可能性,因为在乘数十位上找不出任何数字与9相乘得“整十数”,所以被乘数个位上的数字不可能是9.如果被乘数个位上的数字是4,很容易推出乘数十位上的数字应是5,才能与4相乘得“整十数”.由被乘数乘以乘数十位上的5得270,也很容易推出被乘数十位上的数字是5,进而可推出其它各数字.【巩固】在□内填入适当的数字,使下列乘法竖式成立:分析:(1)17×64=1088;(2)5283×39=206037;(3)734×619=454346,被乘数是6606和4404的三位数的公约数.【例11】□内填入适当的数字,使下列竖式成立,并使商尽可能小:分析:由右式知d=8,所以c=3或8.当a=2时,由bc×a=□5□,推出c不等于3,所以c=8,故推出b=7;因为除数是两位数,它与商的各个数位的乘积都是三位数,所以商的最小可能值为262。
小学奥数:数阵图(一).专项练习及答案解析

1. 了解数阵图的种类2. 学会一些解决数阵图的解题方法3. 能够解决和数论相关的数阵图问题.一、数阵图定义及分类:1. 定义:把一些数字按照一定的要求,排成各种各样的图形,这类问题叫数阵图.2. 数阵是一种由幻方演变而来的数字图.数阵图的种类繁多,这里只向大家介绍三种数阵图:即封闭型数阵图、辐射型数阵图和复合型数阵图. 3.二、解题方法:解决数阵类问题可以采取从局部到整体再到局部的方法入手: 第一步:区分数阵图中的普通点(或方格)和关键点(或方格); 第二步:在数阵图的少数关键点(一般是交叉点)上设置未知数,计算这些关键点与相关点的数量关系,得到关键点上所填数的范围;第三步:运用已经得到的信息进行尝试.这个步骤并不是对所有数阵题都适用,很多数阵题更需要对数学方法的综合运用.模块一、封闭型数阵图【例 1】 把1~8的数填到下图中,使每个四边形中顶点的数字和相等。
【考点】复合型数阵图 【难度】3星 【题型】填空 【关键词】学而思杯,3年级,第6题 【解析】例题精讲知识点拨教学目标5-1-3-1.数阵图【答案】【例 2】 将1~8这八个自然数分别填入下图中的八个○内,使四边形每条边上的三个数之和都等于14,且数字1出现在四边形的一个顶点上.应如何填?(1)【考点】封闭型数阵图 【难度】2星 【题型】填空 【解析】 为了叙述方便,先在各圆圈内填上字母,如下图(2).由条件得出以下四个算式:(2)h gf ed c baa+b+c=14(1) c+d+e=14 (2) e+f+g=14 (3)a+h+g=14 (4)由(1)+(3),得:a+b+c+e+f+g=28,(a+b+c+d+e+f+g+h )-(d+h )=28,d+h=(1+2+3+4+5+6+7+8)-28=8,由(2)+(4),同样可得b+f=8, 又1,2,3,4,5,6,7,8中有1+7=2+6=3+5=8.又1要出现在顶点上,d+h 与b+f 只能有2+6和3+5两种填法. 又由对称性,不妨设b=2,f=6,d=3,h=5. a ,c ,e ,g 可取到1,4,7,8若a=1,则c=14-(1+2)=11,不在1,4,7,8中,不行.若c=1,则a=14-(1+2)=11,不行.若e=1,则c=14-(1+3)=10,不行.若g=1,则a=8,c=4,e=7.说明:例题为封闭型数阵,由它的分析思考过程可以看出,确定各边顶点所应填的数为封闭型数阵的解题突破口.【答案】【例 3】在如图6所示的○内填入不同的数,使得三条边上的三个数的和都是12,若A、B、C的和为18,则三个顶点上的三个数的和是。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
小学数学《数阵图》练习题(含答案)课前复习1.在下面的○里填上适当的数,使每条线上的三个数之和都是16.【答案】【答案】2.在空格内填入适当的数,使得每行、每列和两条对角线上的三个数的和都为18.【答案】3. 在空格内填上适当的数,使得图中每行、每列及两对角线上四个数的和都是64.【答案】在神奇的数学王国里,有一类非常有趣的数学问题,它变化多端,引人入胜,奇妙无穷.它就是数阵.到底什么是数阵呢?我们先观察下面2个图:在空格内填上适当的数,使得图中每行、每列及两条对角线上三个数的和都是15.认真观察,你发现每个图中的数字有什么特点?左上图有两条直线,每条直线上都有3个数字,它们的和都分别等于15;而右上图,将l~9九个数字排成三行、三列,每一行、每一列、每一斜行上的3个数字的和都等于15.数阵就是用数(一般指自然数)按一定的要求和规律,组成特定的形状或布成特定的阵势.它一般分为辐射型(左上图)和封闭型(右上图).要把一些数字按一定的规则填入图形中,有没有巧妙的方法来填呢?今天这节课我们就一起来学习.辐射型数阵图【例1】把1,2,3,4,5这5个数分别填入图中的圆圈内,使得横行3个数的和与竖列3个数的和都等于10.【分析】横行的三个数之和加上竖列的三个数之和,只有重叠数a被加了两次,即重叠了一次,其余各数均被加了一次.因为横行的三个数之和与竖列的三个数之和都等于10,所以(1+2+3+4+5)+a=10×2,a=5.剩下4个数中每两个数之和应该等于5,,1+4=2+3。
【例2】把4~8这五个数填入图中(已填入6),使两条直线上的三个数之和相等.【分析】方法一:把6除外,还剩4,5,7,8,这四个数,在这四个数中4+8=5+7,这样可以填出答案。
方法二:与例1不同之处是已知“重叠数”为6,而不知道两条直线上的三个数之和都等于什么数.可以先求出这个“和k”.(4+5+6+7+8)+6=k×2.K=18。
拓展训练把1,2,3,4,5这5个数分别填入图中的圆圈内,使得横行3个数的和与竖列3个数的和都相等.一共有多少种不同的填法?【答案】除了上面的一种填法外,还有两种方法,一共有三种不同的填法:【例3】把1,2,3,4,5,6,7这7个数分别填入右图的圆圈中,使得每条直线上的3个数的和等于12.【分析】因为图中共有3条直线,所以中心的重叠数重叠了2次,于是(1+2+3+4+5+6+7)+重叠数×2=12+12+12.重叠数就=(36-28)÷2=4.那么中间的数应该填4.剩下的6个数1,2,3,5,6,7中,2个数的和等于12-4=8的有1+7=2+6=3+5=8,答案如图.【例4】将1,2,3,4,5,6,7这7个数分别填入右图的圆圈中,使得每条直线上的3个数的和都等于10.【分析】因为图中共有3条直线,所以中心的重叠数重叠了2次,于是(1+2+3+4+5+6+7)+重叠数×2=10+10+10.重叠数就=(30-28)÷2=1.那么中间的数应该填1.剩下的6个数2,3,4,5,6,7,中,2个数的和等于10-1=9的有2+7=3+6=4+5=9.【例5】把1~7这七个数分别填入图中的各○内,使每条线段上三个○里数的和相等.一共有多少种方法?【分析】例5是例4的拓展,可以用枚举法,分别列举出不同的方法.1~7七个数的和是28,中心圆的数要多加两次.因此可得如下关系式: 28+2a=3k.用试验的方法,若a取2、3、5、6,此题无解;a取1、4、7时该数阵图成立.三种基本解法.拓展训练把1~9这9个数分别填入下图的圆圈中,使得每条直线上的3个数的和都等于15.【答案】(1+2+3+4+5+6+7+8+9)+重叠数×3=15×4,重叠数=(60-45)÷3=5.剩下的8个数1,2,3,4,6,7,8,9中,2个数的和等于15-5=10的有1+9=2+8=3+7=4+6=10,答案如图.封闭型数阵图【例6】将1,2,3,4,5,6这6个数分别填入下图中,使两个大圆上4个数的和都等于14.【分析】我们先计算出这两个重叠数的和是多少.(14+14)-(1+2+3+4+5+6)=7,在已知的6个数中,两数相加之和为7的有1与6,2与5,3与4.所以两圆的重叠数可以是1与6,2与3,3与4.这三种情况分别如下图:拓展训练把1,2,3,4,5,6,7,8这8个数分别填入下图中,使得每个大圆上的5个数的和都等于20.【答案】这两个重叠数的和是:(20+20)-(1+2+3+4+5+6+7+8)=4,在已知的8个数中,两数相加之和为4的只有1与3.20-4=16=8+6+2=7+5+4,如图:【例7】把1,2,3,4,5,6这6个数分别填入右图的6个圆圈中,使得三角形每条边上的3个数的和都等于10.【分析】我们先计算出3个重叠数的和是多少.(10+10+10)-(1+2+3+4+5+6)=9,在1~6这6个自然数中,3个数的和等于9的有(1,3,5);(1,2,6);(2,3,4).如果3个重叠数是1,2,6,那么根据每条边上3个数的和都等于10,可算出每条边中间的数,我们会发现所填数有大于6的数,同样,当重叠数是2,3,4时,会出现重复的数.当重叠数是1,3,5时,可得到符合题意的填法.如图:(不符合题意)(不符合题意)(符合题意)【例8】将1~6这六个自然数分别填入下图的六个○中,使得三角形每条边上的三个数之和都相等.还有几种不同的填法?【分析】这道题是上一题的拓展,除了上面的方法,另还有三种不同的方法.1+2+3+4+5+6=21.21+a+b+c=3k 因为每边的三数之和是整数,所以重叠数之和应是3的倍数.考虑到重叠数是1~6中的数,所以三个重叠数之和只能是6,9,12或15,对应的每条边上的三数之和就是9,10,11或12.与例6的方法类似,可得四种填法.拓展训练把4~9这6个数分别填入下图的6个圆圈中,使得三角形每条边上的3个数的和都等于21.【答案】先计算出3个重叠数的和是多少.(21+21+21)-(4+5+6+7+8+9)=24,在1~6这6个自然数中,3个数的和等于24的有7,8,9.当重叠数是7,8,9时,可得到符合题意的填法.如图:【例9】把2、3、4、5、6、7、8、9、10填入方格里,使每一横行、每一竖行、每一斜行的3个数的和都是18.【分析】每一横行、每一竖行、每一斜行3个数的和是18,那么第二列、第二行、两个斜行的总和是18+1 8+18+18=72(如图1).而2+3+4+5+6+7+8+9+10=54,72与54相差18.这是因为方格正中间的数被算了4次,即多算了3次.由于18÷3=6,所以正中间的数应填6.18—6=l2,组成12的算式有2+10=12,3+9=12,4+8=12,5+7=12,填法见图(2)通过例题分析,我们发现,填数阵不是七拼八凑就能写出答案的.而是一般先考虑正中间的数、顶角上的数.不管解哪一种数阵图,只要我们紧扣住“重复使用的数字”这一关键来进行分析,就能解决很多复杂巧妙的数阵问题.附加题(以下提供的内容,供老师参考使用)【附1】将1、2、3、4、5、6、7、8、9这9个数字分别填入图中的小圆圈里,使得每条边上4个数字的和是17.【分析】我们先计算出这三个重叠数的和是多少.(17+17+17)-(1+2+3+4+5+6+7+8+9)=6,在已知的9个数中,只有1+2+3=6,所以三个角应该填1,2,3.答案如图:【附2】把1~8这八个数分别填入图26—11中的圆内,使每条线上的三个数相加的和等于12.【分析】图形中四个角上的数各重复计算了一次.八个数的和是:1+2+3+4+5+6+ 7+8=36,36+a+b+c+d=12×4,a+b+c+d =48—36=12,这12就是四个角的四个数的和.在这八个数中有:1+2+3+6=12,因此把1,2,3,6这四个数分别填入四角的圈内.再来试算可得1+8+3=12,1+5+6=12,6+4+2=12,3+7+2=12.【附3】将1、2、3、4、5、6六个数填在图中的空灯里,使每个大圆上的四盏灯里的数相加都等于14.【分析】在这些数中,四个数的和是14的有14=6+5+2+1,14=6+4+3+1,14=5+4+3+2,根据找两个圆中相互重复的数字,我们可以得到结果,如图:【附4】将自然数1至9,分别填在下图的方格中,使得每行、每列以及两条对角线上的三个数之和都相等.【分析】方法1:此题为一三阶幻方.可按口诀"九宫者,二四为肩,六八为足,左三右七,载九履一,五居中央."填出答案.(此方法到三年级会进一步学习)方法2:按照数的分拆:三行的总和=1+2+3+4+…+9=45,所以每行三个数的和是45÷3=15.找到所有3个数和为15的情况如下: 1+5+9,1+6+8,2+4+9,2+5+8,2+6+7,3+4+8,3+5+7,4+5+6.图中E代表的数字是关键数.有4条线通过它,因此要求E出现在4个算式之中.容易找出这个数字是5.位于A、C、G、I位置的数字出现3次,它们是2、4、6、8.方法3:或者先看成辐射图.那么第二列、第二行、两个斜行的总和是15×4=60.而1+2+3+4+5+6+7+8+9=45,45+3a=60 a=5正中间的数应填5.15—5=10,组成10的算式有9+1=8+2=7+3=6+4.试验可解.练习九1. 把5,6,7,8,9这5个数填在下图的◇内,使横行、竖列3个数的和都等于( )中的数.答案:2. 将1~9填入小方格里,使横行和竖列上五个数之和相等.答案有以下7种,任写其中一种即可.3. 把10,20,30,40,50,60,70这7个数填在圆圈里,使每条直线上和每个圆周上的三个数的和都是140.答案:4. 把3、5、7、9、1 1、13、1 5这7个数分别填入图中的圆圈内,使每条直线上的3个数都等于27.答案:5.把1~6填入○里,使每个圆圈上的四个数之和都相等16.答案:6.将1~8填入○中,使得每条边上的三个数之和都等于15.答案:填数五连环小朋友们都知道,奥林匹克运动会的会标是象征着全世界人民团结奋进的主题.今天,做一个“填数五连环”游戏——每个圆环内的数之和相等,其含义是要使五大洲同等强盛起来.图上的五个圆环组成15个区域,其中5个区域里已分别填入数:10、7、1、15、8.现在,请小朋友在剩下的10个区域里分别填上一个数字,要求全部填满以后,每个圆内数相加的和必须是40.注意,供你选择的数只能在1~15之间,而且填过的数不能再用(包括10、7、1、15、8).在填数之前,可以先剪10张小纸片,把1~15的数字(除去10、7、1、15、8)分别写在每张纸片上,把纸片在圆的空白区域内移动,直到每个圆内数之和是40.。
