数学实验回归分析
简单回归分析

一、线性回归分析若是自变数与依变数都是一个,且Y 和X 呈线性关系,这就称为一元线性回归。
例如,以X 表示小麦每667m 2有效穗数,Y 表示小麦每667m 2的产量,有效穗数即属于自变数,产量即属于依变数。
在这种情形下,可求出产量依有效穗数而变更的线性回归方程。
在另一种情形下,两类变数是平行关系很难分出哪个是自变数,哪个是依变数。
例如,大豆脂肪含量与蛋白质含量的关系,依照需要确信求脂肪含量依蛋白质含量而变更的回归方程,或求蛋白质含量依脂肪含量而变更的回归方程。
回归分析要解决的问题要紧有四个方面:一是依如实验观看值成立适当的回归方程;二是查验回归方程是不是适用,或对回归方程中的回归系数的进行估量;三是对未知参数进行假设考试;四是利用成立起的方程进行预测和操纵。
(一)成立线性回归方程用来归纳两类变数互变关系的线性方程称为线性回归方程。
若是两个变数在散点图上呈线性,其数量关系可能用一个线性方程来表示。
这一方程的通式为:上式叫做y 依x 的直线回归。
其中x 是自变数,y ˆ是依变数y 的估量值,a 是x =0时的y ˆ值,即回归直线在y 轴上的截距,称为回归截距,b 是x 每增加一个单位时,y 将平均地增加(b >0时)或减少(b <0时) b 个单位数,称为回归系数或斜率(regression coefficient or slope )。
要使 能够最好地代表Y 和X 在数量上的互变关系,依照最小平方式原理,必需使将Q 看成两个变数a 与b 的函数,应该选择a 与b ,使Q 取得最小值,必需求Q 对a ,b 的一阶偏导数,且令其等于零,即得:()()⎩⎨⎧∑=∑+∑∑=∑+212xyx b x a yx b an ()()∑∑=--=-=nn Q bx a y yy Q 1min212ˆbx a y +=ˆ()1.7ˆbx a y+=由上述(1)解得:将()代入(2),那么得:()的分子 是x 的离均差与y 的离均差乘积总和,简称乘积和(sum of products ),可记为SP ,分母是x 的离均差平方和,也可记为SS x 。
数学建模-回归分析

一、变量之间的两种关系 1、函数关系:y = f (x) 。
2、相关关系:X ,Y 之间有联系,但由 其中一个不能唯一的确定另一个的值。 如: 年龄 X ,血压 Y ; 单位成本 X ,产量 Y ; 高考成绩 X ,大学成绩 Y ; 身高 X ,体重 Y 等等。
二、研究相关关系的内容有
1、相关分析——相关方向及程度(第九章)。 增大而增大——正相关; 增大而减小——负相关。 2、回归分析——模拟相关变量之间的内在 联系,建立相关变量间的近似表达式 (经验 公式)(第八章)。 相关程度强,经验公式的有效性就强, 反之就弱。
三、一般曲线性模型 1、一般一元曲线模型
y = f ( x) + ε
对于此类模型的转换,可用泰勒展开 公式,把 在零点展开,再做简单的变 f ( x) 换可以得到多元线性回归模型。 2、一般多元曲线模型
y = f ( x1 , x2源自,⋯ , xm ) + ε
对于此类模型也要尽量转化为线性模 型,具体可参考其他统计软件书,这里不 做介绍。
ˆ ˆ ˆ ˆ y = b0 + b1 x1 + ⋯ + bm x m
2、利用平方和分解得到 ST , S回 , S剩。 3、计算模型拟合度 S ,R ,R 。 (1)标准误差(或标准残差)
S =
S剩 ( n − m − 1)
当 S 越大,拟合越差,反之,S 越小, 拟合越好。 (2)复相关函数
R =
2
仍是 R 越大拟合越好。 注: a、修正的原因:R 的大小与变量的个数以及样本 个数有关; 比 R 要常用。 R b、S 和 R 是对拟合程度进行评价,但S与 R 的分 布没有给出,故不能用于检验。 用处:在多种回归模型(线性,非线性)时, 用来比较那种最好;如:通过回归方程显著性检验 得到:
spass回归分析实验报告
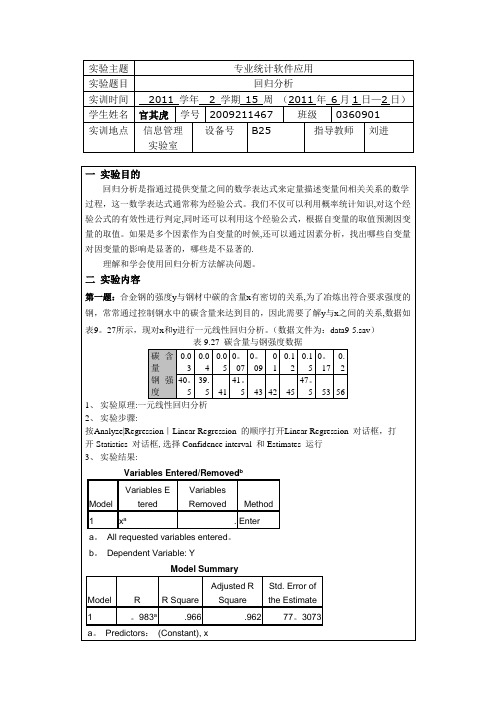
上,看哪种模型拟合效果更好从拟合优度(Rsq 即R2)来看,QUA,CUB,POW 效果较好(因为其Rsq 值较大),于是就选QUA,CUB,POW来进行。
重新进行上面的过程,只选以上三种模型。
3、实验结果:Model Summary and Parameter EstimatesDependent Variable:远视率EquationModel Summary Parameter EstimatesRSquare F df1 df2 Sig。
Constant b1 b2 b3Linear。
674 22。
7101 11 .001 74.006—4。
768Logarith mic .793 42.251 1 11 。
000 156。
773-57.574Inverse。
883 83.244 1 11 。
000 -40。
567 615.321Quadrati c .94382。
1142 10 .000 192.085-26.567。
908Cubic.959 69。
5383 9 .000 290.851—54。
7173.398 —。
069Compound。
794 42.445 1 11 .000 308。
120 .731Power.861 68.413 1 11 .000 49462.724—3。
638S .877 78.119 1 11 .000 -1。
502 37.175Growth.794 42。
4451 11 。
000 5。
730 —。
314Exponen tial .79442。
4451 11 。
000 308.120 -.314Logistic 。
794 42.445 1 11 。
000 .003 1。
369The independent variable is 年龄.分析:可以用Cubic拟合曲线图的拟合效果最好.第四题:棉花单株在不同时期的成铃数(y)与初花后天数(x)存在非线性的关系,假设这一非线性关系可用Gompertz模型表示:y=b1*exp(-b2*exp(—b3*x))。
回归分析 实验报告

回归分析实验报告1. 引言回归分析是一种用于探索变量之间关系的统计方法。
它通过建立一个数学模型来预测一个变量(因变量)与一个或多个其他变量(自变量)之间的关系。
本实验报告旨在介绍回归分析的基本原理,并通过一个实际案例来展示其应用。
2. 回归分析的基本原理回归分析的基本原理是基于最小二乘法。
最小二乘法通过寻找一条最佳拟合直线(或曲线),使得所有数据点到该直线的距离之和最小。
这条拟合直线被称为回归线,可以用来预测因变量的值。
3. 实验设计本实验选择了一个实际数据集进行回归分析。
数据集包含了一个公司的广告投入和销售额的数据,共有200个观测值。
目标是通过广告投入来预测销售额。
4. 数据预处理在进行回归分析之前,首先需要对数据进行预处理。
这包括了缺失值处理、异常值处理和数据标准化等步骤。
4.1 缺失值处理查看数据集,发现没有缺失值,因此无需进行缺失值处理。
4.2 异常值处理通过绘制箱线图,发现了一个销售额的异常值。
根据业务经验,判断该异常值是由于数据采集错误造成的。
因此,将该观测值从数据集中删除。
4.3 数据标准化为了消除不同变量之间的量纲差异,将广告投入和销售额两个变量进行标准化处理。
标准化后的数据具有零均值和单位方差,方便进行回归分析。
5. 回归模型选择在本实验中,我们选择了线性回归模型来建立广告投入与销售额之间的关系。
线性回归模型假设因变量和自变量之间存在一个线性关系。
6. 回归模型拟合通过最小二乘法,拟合了线性回归模型。
回归方程为:销售额 = 0.7 * 广告投入 + 0.3回归方程表明,每增加1单位的广告投入,销售额平均增加0.7单位。
7. 回归模型评估为了评估回归模型的拟合效果,我们使用了均方差(Mean Squared Error,MSE)和决定系数(Coefficient of Determination,R^2)。
7.1 均方差均方差度量了观测值与回归线之间的平均差距。
在本实验中,均方差为10.5,说明模型的拟合效果相对较好。
第七章 回归分析

第七章回归分析前几章所讨论的内容,其目的在于寻求被测量的最佳值及其精度。
在生产和科学实验中,还有另一类问题,即测量与数据处理的目的并不在于获得被测量的估计值,而是为了寻求两个变量或多个变量之间的内在关系,这就是本章所要解决的主要问题。
表达变量之间关系的方法有散点图、表格、曲线、数学表达式等,其中数学表达式能较客观地反映事物的内在规律性,形式紧凑,且便于从理论上作进一步分析研究,对认识自然界量与量之间关系有着重要意义。
而数学表达式的获得是通过回归分析方法完成的。
第一节回归分析的基本概念一、函数与相关在生产和科学实验中,人们常遇到各种变量。
从贬值辩证唯物主义观点来看,这些变量之间是相互联系、互相依存的,它们之间存在着一定的关系。
人们通过实践,发现变量之间的关系可分为两种类型:1.函数关系(即确定性关系)数学分析和物理学中的大多数公式属于这种类型。
如以速度v作匀速运动的物体,走过的距离s与时间t之间,有如下确定的函数关系:s=vt若上式中的变量有两个已知,则另一个就可由函数关系精确地求出。
2.相关关系在实际问题中,绝大多数情况下变量之间的关系不那么简单。
例如,在车床上加工零件,零件的加工误差与零件的直径之间有一定的关系,知道了零件直径可大致估计其加工误差,但又不能精确地预知加工误差。
这是由于零件在加工过程中影响加工误差的因素很多,如毛坯的裕量、材料性能、背吃刀量、进给量、切削速度、零件长度等等,相互构成一个很复杂的关系,加工误差并不由零件直径这一因素所确定。
像这种关系,在实践中是大量存在的,如材料的抗拉强度与其硬度之间;螺纹零件中螺纹的作用中径与螺纹中径之间;齿轮各种综合误差与有关单项误差之间;某些光学仪器、电子仪器等开机后仪器的读数变化与时间之间;材料的性能与其化学成分之间等等。
这些变量之间既存在着密切的关系,又不能由一个(或几个)变量(自变量)的数值精确地求出另一个变量(因变量)的数值,而是要通过试验和调查研究,才能确定它们之间的关系,我们称这类变量之间的关系为相关关系。
回归分析实验报告

回归分析实验报告实验报告:回归分析摘要:回归分析是一种用于探究变量之间关系的数学模型。
本实验以地气温和电力消耗量数据为例,运用回归分析方法,建立了气温和电力消耗量之间的线性回归模型,并对模型进行了评估和预测。
实验结果表明,气温对电力消耗量具有显著的影响,模型能够很好地解释二者之间的关系。
1.引言回归分析是一种用于探究变量之间关系的统计方法,它通常用于预测或解释一个变量因另一个或多个变量而变化的程度。
回归分析陶冶于20世纪初,经过不断的发展和完善,成为了数量宏大且复杂的数据分析的重要工具。
本实验旨在通过回归分析方法,探究气温与电力消耗量之间的关系,并基于建立的线性回归模型进行预测。
2.实验设计与数据收集本实验选择地的气温和电力消耗量作为研究对象,数据选取了一段时间内每天的气温和对应的电力消耗量。
数据的收集方法包括了实地观测和数据记录,并在数据整理过程中进行了数据的筛选与清洗。
3.数据分析与模型建立为了探究气温与电力消耗量之间的关系,需要建立一个合适的数学模型。
根据回归分析的基本原理,我们初步假设气温与电力消耗量之间的关系是线性的。
因此,我们选用了简单线性回归模型进行分析,并通过最小二乘法对模型进行了估计。
运用统计软件对数据进行处理,并进行了以下分析:1)描述性统计分析:计算了气温和电力消耗量的平均值、标准差和相关系数等。
2)直线拟合与评估:运用最小二乘法拟合出了气温对电力消耗量的线性回归模型,并进行了模型的评估,包括了相关系数、残差分析等。
3)预测分析:基于建立的模型,进行了其中一未来日期的电力消耗量的预测,并给出了预测结果的置信区间。
4.结果与讨论根据实验数据的分析结果,我们得到了以下结论:1)在地的气温与电力消耗量之间存在着显著的线性关系,相关系数为0.75,表明二者之间的关系较为紧密。
2)构建的线性回归模型:电力消耗量=2.5+0.3*气温,模型参数的显著性检验结果为t=3.2,p<0.05,表明回归系数是显著的。
回归分析数据

回归分析数据回归分析是一种统计方法,用于研究自变量与因变量之间的关系。
它的目的是通过建立数学模型来预测和解释因变量的变化。
在进行回归分析时,数据的收集和整理是至关重要的环节。
本文将介绍回归分析数据的搜集、整理和分析方法。
回归分析的数据搜集通常依赖于可用的数据源。
这些数据源可以是实验室实验、调查问卷、历史记录等。
为了进行回归分析,我们需要收集自变量(也称为解释变量或预测变量)和因变量(也称为被解释变量或响应变量)的数据。
自变量是用来解释因变量的变化的变量,而因变量则是我们想要预测或解释的变量。
在收集回归分析数据时,我们需要注意数据的质量和可信度。
确保数据来源可靠,并且数据收集过程中避免错误或失误的发生。
此外,还要注意数据的完整性和一致性。
如果数据不完整或存在不一致性,可能会影响回归分析的精度和可靠性。
当我们收集到回归分析所需的数据后,需要对数据进行整理和清洗。
数据整理的目的是为了使数据集合规整并符合分析的要求。
在整理数据时,我们首先要对数据进行检查,确认是否存在缺失值、异常值或离群点。
如果发现缺失值,我们可以选择删除这些缺失值,或者使用插补方法进行填充。
异常值和离群点可能是由于数据收集或记录错误造成的,我们需要审查并决定如何处理这些异常值。
数据整理后,我们还可以进行数据变换,如对数转换、标准化等操作,以满足回归分析的假设和前提条件。
完成数据整理后,我们可以开始进行回归分析。
回归分析的主要目的是找到自变量与因变量之间的关系,即建立一个数学模型来描述这种关系。
最常用的回归分析方法是线性回归分析,即通过线性方程来拟合数据。
线性回归模型可以用于预测和解释数值型因变量的变化。
此外,还有其他回归方法,如逻辑回归、多元回归等,用于不同类型的因变量和自变量。
在回归分析中,我们还需要评估模型的拟合程度和预测能力。
拟合程度可以通过计算回归系数和相关系数来衡量。
回归系数表示自变量与因变量之间的变化关系,相关系数则表示变量之间的线性相关度。
数学中各种回归分析方法总结

其主要思路是将对异常值十分敏感的经典最小二乘回归中的目标函数进行修改。
经典最小二乘回归以使误差平方和达到最小为其目标函数。
因为方差为一不稳健统计量,故最小二乘回归是一种不稳健的方法。
为减少异常点的作用,对不同的点施加不同的权重,残差小的点权重大,残差大的店权重小。
2、变系数回归地理位置加权3、偏最小二乘回归长期以来,模型式的方法和认识性的方法之间的界限分得十分清楚。
而偏最小二乘法则把它们有机的结合起来了,在一个算法下,可以同时实现回归建模(多元线性回归)、数据结构简化(主成分分析)以及两组变量之间的相关性分析(典型相关分析)。
偏最小二乘法在统计应用中的重要性体现在以下几个方面:偏最小二乘法是一种多因变量对多自变量的回归建模方法。
偏最小二乘法可以较好的解决许多以往用普通多元回归无法解决的问题。
偏最小二乘法之所以被称为第二代回归方法,还由于它可以实现多种数据分析方法的综合应用。
能够消除自变量选取时可能存在的多重共线性问题。
普通最小二乘回归方法在自变量间存在严重的多重共线性时会失效。
自变量的样本数与自变量个数相比过少时仍可进行预测。
4、支持向量回归能较好地解决小样本、非线性、高维数和局部极小点等实际问题。
传统的化学计量学算法处理回归建模问题在拟合训练样本时,要求“残差平方和”最小,这样将有限样本数据中的误差也拟合进了数学模型,易产生“过拟合”问题,针对传统方法这一不足之处,SVR采用“ε不敏感函数”来解决“过拟合”问题,即f(x)用拟合目标值yk时,取:f(x)=∑SVs(αi-α*i)K(xi,x)上式中αi和α*i为支持向量对应的拉格朗日待定系数,K(xi,x)是采用的核函数[18],x为未知样本的特征矢量,xi为支持向量(拟合函数周围的ε“管壁”上的特征矢量),SVs为支持向量的数目.目标值yk拟合在yk-∑SVs(αi-α*i)K(xi,xk)≤ε时,即认为进一步拟合是无意义的。
5、核回归核函数回归的最初始想法是用非参数方法来估计离散观测情况下的概率密度函数(pdf)。
一元线性回归分析研究实验报告

一元线性回归分析研究实验报告一元线性回归分析研究实验报告一、引言一元线性回归分析是一种基本的统计学方法,用于研究一个因变量和一个自变量之间的线性关系。
本实验旨在通过一元线性回归模型,探讨两个变量之间的关系,并对所得数据进行统计分析和解读。
二、实验目的本实验的主要目的是:1.学习和掌握一元线性回归分析的基本原理和方法;2.分析两个变量之间的线性关系;3.对所得数据进行统计推断,为后续研究提供参考。
三、实验原理一元线性回归分析是一种基于最小二乘法的统计方法,通过拟合一条直线来描述两个变量之间的线性关系。
该直线通过使实际数据点和拟合直线之间的残差平方和最小化来获得。
在数学模型中,假设因变量y和自变量x之间的关系可以用一条直线表示,即y = β0 + β1x + ε。
其中,β0和β1是模型的参数,ε是误差项。
四、实验步骤1.数据收集:收集包含两个变量的数据集,确保数据的准确性和可靠性;2.数据预处理:对数据进行清洗、整理和标准化;3.绘制散点图:通过散点图观察两个变量之间的趋势和关系;4.模型建立:使用最小二乘法拟合一元线性回归模型,计算模型的参数;5.模型评估:通过统计指标(如R2、p值等)对模型进行评估;6.误差分析:分析误差项ε,了解模型的可靠性和预测能力;7.结果解释:根据统计指标和误差分析结果,对所得数据进行解释和解读。
五、实验结果假设我们收集到的数据集如下:经过数据预处理和散点图绘制,我们发现因变量y和自变量x之间存在明显的线性关系。
以下是使用最小二乘法拟合的回归模型:y = 1.2 + 0.8x模型的R2值为0.91,说明该模型能够解释因变量y的91%的变异。
此外,p 值小于0.05,说明我们可以在95%的置信水平下认为该模型是显著的。
误差项ε的方差为0.4,说明模型的预测误差为0.4。
这表明模型具有一定的可靠性和预测能力。
六、实验总结通过本实验,我们掌握了一元线性回归分析的基本原理和方法,并对两个变量之间的关系进行了探讨。
回归分析的原理和应用

回归分析的原理和应用1. 回归分析的基本概念回归分析是一种通过建立数学模型来探究两个或多个变量之间关系的方法。
它的主要目的是了解因变量(响应变量)如何随着自变量变化而变化。
回归分析通过寻找最佳拟合线或曲线,以最小化观测值和预测值之间的差异,并预测新的观测值。
2. 简单线性回归简单线性回归是最基本的回归分析方法之一,它用于探究两个变量之间的线性关系。
在简单线性回归中,只有一个自变量和一个因变量。
该方法假定自变量和因变量之间存在线性关系,并通过最小二乘法来拟合一条直线。
拟合出的直线可以用来预测新的因变量取值。
3. 多元线性回归多元线性回归是在简单线性回归的基础上扩展出来的,它允许有多个自变量。
多元线性回归的主要思想是通过最小化残差平方和来找到最佳拟合函数。
该方法可以帮助我们探究多个自变量对因变量的影响,并进行预测和解释。
4. 回归分析的应用领域回归分析在许多领域都有广泛的应用。
以下是一些常见领域的例子:•经济学:回归分析可以用来研究经济变量之间的关系,如GDP与失业率之间的关系。
•医学研究:回归分析可以用来研究药物剂量与治疗效果之间的关系,或者研究某种特征与疾病发病率的关系。
•社会科学:回归分析可以用来研究教育水平与收入之间的关系,或者研究人口变量与犯罪率之间的关系。
•金融领域:回归分析可以用来研究股票价格与市场指数之间的关系,或者研究利率与债券价格之间的关系。
5. 回归分析的步骤进行回归分析通常需要以下步骤:1.收集数据:收集自变量和因变量的数据,可以通过实验、调查或观测等方式获取。
2.数据清洗:对收集到的数据进行清洗,包括处理缺失值、异常值和离群值等。
3.模型选择:根据研究目的和数据特点,选择合适的回归模型,如简单线性回归或多元线性回归。
4.拟合模型:使用最小二乘法或其他拟合方法,拟合出最佳的回归方程。
5.模型评估:对拟合出的模型进行评估,包括判断模型的拟合优度和统计显著性,通过残差分析检验模型的假设。
利用回归分析预测实验结果的趋势

利用回归分析预测实验结果的趋势在科学研究和实验中,预测实验结果的趋势是一项重要的任务。
回归分析作为一种常用的统计方法,可以帮助我们探索变量之间的关系,并通过数学模型预测未来的结果。
本文将介绍回归分析的基本原理和应用,以及如何利用回归分析预测实验结果的趋势。
一、回归分析的基本原理回归分析是一种统计方法,用于研究自变量与因变量之间的关系。
在回归分析中,自变量是我们想要用来预测和解释因变量的变化的变量,因变量是我们想要预测的变量。
回归分析的目标是建立一个数学模型,可以通过自变量的取值预测因变量的取值。
回归分析的基本原理是最小二乘法。
最小二乘法通过将自变量与因变量的观测值代入数学模型,计算出预测值与观测值之间的差异(残差),然后调整模型参数,使得残差的平方和最小化。
最小二乘法可以得出最优的模型参数,并基于这个模型来预测未来的结果。
二、回归分析的应用回归分析广泛应用于各个领域的科学研究和实验中。
它可以帮助我们更好地理解变量之间的关系,预测未来的趋势,并作出更合理的决策。
以下是几个常见的应用领域:1. 经济学:回归分析可以用来研究经济变量之间的关系,如GDP与通货膨胀率、利率与投资额等。
通过回归分析,我们可以预测未来的经济趋势,评估政策的效果,并制定相应的经济政策。
2. 医学研究:回归分析可以用来研究生物医学的相关性,如药物剂量与疗效、生活方式与慢性疾病的关系等。
通过回归分析,我们可以预测治疗效果,指导临床决策,并优化治疗方案。
3. 社会科学:回归分析可以用来研究社会学、心理学、教育学等领域的问题,如家庭收入对子女学业成绩的影响、领导风格对员工满意度的影响等。
通过回归分析,我们可以预测社会现象的发展趋势,为政策制定和管理提供依据。
三、利用回归分析预测实验结果的趋势在科学研究和实验中,我们经常需要通过实验数据来预测未来的趋势。
回归分析可以帮助我们利用历史数据或实验结果,建立一个模型,并用这个模型来预测未来的结果。
实验数据分析方法_回归分析

0.10
0.9877 0.9000 0.8054 0.7293 0.6694 0.6215 0.5822 0.5494 0.5214 0.4973 0.4762 0.4575 0.4409 0.4259 0.4124 0.4000 0.3887 0.3783 0.3687 0.3598 0.3233 0.2960 0.2746 0.2573 0.2428 0.2306 0.2108 0.1954 0.1829 0.1726 0.1638
上式右边第二项是回归值ŷ与平均值 y 之差的平方和,我们
称它为回归平方和,并记为U: U (y ˆ k y ) 2 ( b 0 b x k b 0 b x ) 2
k
b2 (xkx)2.
— 可以看出,回归平方和U是由于x的变化而引起的。因
此U反映了在y的总的变化中由于x和y的线性关系而引起
解之可得:
b
xkyk
xk yk N
(xk x)(yk y)
xk2N 1( xk)2
(xk x)2
b0N 1( ykb xk)ybx,
实验数据分析方法_Chap.6
8
其中 1 N
1N
xNk1xk,
y Nk1
yk.
在给定参数估计值b, b0后,可得到相应的回归方程 (或回归函数)为: yˆ b0 bx.
0.05
0.9969 0.9500 0.8783 0.8114 0.7545 0.7067 0.6664 0.6319 0.6021 0.5760 0.5529 0.5324 0.5139 0.4973 0.4821 0.4683 0.4555 0.4438 0.4329 0.4227 0.3809 0.3494 0.3246 0.3044 0.2875 0.2732 0.2500 0.2319 0.2172 0.2050 0.1946
一元线性回归分析实验报告doc

一元线性回归分析实验报告.doc一、实验目的本实验旨在通过一元线性回归模型,探讨两个变量之间的关系,即一个变量是否随着另一个变量的变化而呈现线性变化。
通过实际数据进行分析,理解一元线性回归模型的应用及其局限性。
二、实验原理一元线性回归是一种基本的回归分析方法,用于研究两个连续变量之间的关系。
其基本假设是:因变量与自变量之间存在一种线性关系,即因变量的变化可以由自变量的变化来解释。
一元线性回归的数学模型可以表示为:Y = aX + b,其中Y是因变量,X是自变量,a是回归系数,b是截距。
三、实验步骤1.数据收集:收集包含两个变量的数据集,用于建立一元线性回归模型。
2.数据预处理:对数据进行清洗、整理和标准化,确保数据的质量和准确性。
3.绘制散点图:通过散点图观察因变量和自变量之间的关系,初步判断是否为线性关系。
4.建立模型:使用最小二乘法估计回归系数和截距,建立一元线性回归模型。
5.模型评估:通过统计指标(如R²、p值等)对模型进行评估,判断模型的拟合程度和显著性。
6.模型应用:根据实际问题和数据特征,对模型进行解释和应用。
四、实验结果与分析1.数据收集与预处理:我们收集了一个关于工资与工作经验的数据集,其中工资为因变量Y,工作经验为自变量X。
经过数据清洗和标准化处理,得到了50个样本点。
2.散点图绘制:绘制了工资与工作经验的散点图,发现样本点大致呈线性分布,说明工资随着工作经验的变化呈现出一种线性趋势。
3.模型建立:使用最小二乘法估计回归系数和截距,得到一元线性回归模型:Y = 50X + 2000。
其中,a=50表示工作经验每增加1年,工资平均增加50元;b=2000表示当工作经验为0时,工资为2000元。
4.模型评估:通过计算R²值和p值,对模型进行评估。
在本例中,R²值为0.85,说明模型对数据的拟合程度较高;p值为0.01,说明自变量对因变量的影响是显著的。
实验13_回归分析
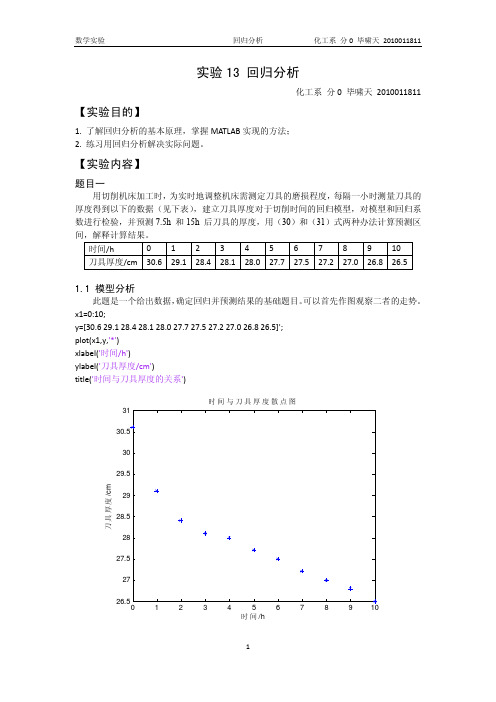
实验13 回归分析化工系 分0 毕啸天 2010011811【实验目的】1. 了解回归分析的基本原理,掌握MATLAB 实现的方法;2. 练习用回归分析解决实际问题。
【实验内容】题目一用切削机床加工时,为实时地调整机床需测定刀具的磨损程度,每隔一小时测量刀具的厚度得到以下的数据(见下表),建立刀具厚度对于切削时间的回归模型,对模型和回归系数进行检验,并预测7.5h 和15h 后刀具的厚度,用(30)和(31)式两种办法计算预测区间,解释计算结果。
1.1 模型分析此题是一个给出数据,确定回归并预测结果的基础题目。
可以首先作图观察二者的走势。
x1=0:10;y=[30.6 29.1 28.4 28.1 28.0 27.7 27.5 27.2 27.0 26.8 26.5]'; plot(x1,y,'*') xlabel('时间/h')ylabel('刀具厚度/cm')title('时间与刀具厚度的关系')时间/h刀具厚度/c m时间与刀具厚度散点图由上图可以看出,除了最初几个点偏离较大,刀具厚度y 与时间x 大致为线性关系。
因此确定回归模型为:xy 10ββ+=1.2 程序代码n=11;X=[ones(n,1),x1'];[b,bint,r,rint,s]=regress(y,X); rcoplot(r,rint)输出结果如下: b =29.545 -0.32909 bint =28.977 30.114 -0.4252 -0.23298 r =1.0545 -0.11636 -0.48727 -0.45818 -0.22909 -0.2 -0.070909 -0.041818 0.087273 0.21636 0.24545 rint =0.79381 1.3153 -1.046 0.81326 -1.3782 0.40364 -1.3873 0.47094 -1.2267 0.76848 -1.2067 0.80674 -1.0836 0.94177 -1.04 0.9564 -0.88264 1.0572 -0.70174 1.1345 -0.61524 1.1062 s =0.86957 60.002 2.8614e-005 0.19855回归结果整理成表格如下:不包含零点。
初中数学 如何进行数据的回归分析

初中数学如何进行数据的回归分析
在初中数学中,进行数据的回归分析通常是通过简单线性回归来进行的。
简单线性回归通常包括以下几个步骤:
1. 收集数据:首先,需要收集一组相关数据,通常是两组数据,一组作为自变量(x),另一组作为因变量(y)。
2. 绘制散点图:将收集到的数据绘制成散点图,以观察数据的分布情况和可能的线性关系。
3. 计算相关系数:计算自变量和因变量之间的相关系数,来衡量两组数据之间的线性关系强弱。
4. 拟合直线:利用最小二乘法,拟合一条直线来表示两组数据之间的线性关系,这条直线称为回归线。
5. 预测数值:利用回归线,可以进行数值的预测,例如根据一个自变量的数值,预测对应的因变量的数值。
这些是初中数学中常见的进行数据回归分析的步骤,希望能帮助你更好地理解。
如果有任何问题,请随时提出。
大学数学实验报告

大学数学实验报告大学数学实验报告引言:大学数学实验作为一门重要的课程,旨在培养学生的数学思维和实际应用能力。
通过实验,学生可以将抽象的数学理论与实际问题相结合,加深对数学知识的理解和掌握。
本篇报告将以三个实验为例,分别讨论数学在实际问题中的应用。
实验一:线性回归分析线性回归分析是数学中的一种重要方法,用于研究变量之间的关系。
在实验中,我们选择了一组数据集,通过对数据的分析,得到了一个线性回归模型。
通过该模型,我们可以预测未来的数据趋势,从而为决策提供依据。
实验二:优化问题求解优化问题是数学中的一个重要领域,涉及到如何找到最优解。
在实验中,我们选取了一个典型的优化问题,即如何在给定的条件下使得某个函数取得最大值或最小值。
通过使用数学建模和求解优化问题的方法,我们得到了最优解,并对结果进行了分析和解释。
实验三:概率统计分析概率统计是数学中的一个重要分支,用于研究随机事件的规律性。
在实验中,我们选择了一个实际问题,通过对数据的搜集和分析,得到了一些统计指标,如均值、方差等。
通过对这些指标的计算和解释,我们可以对实际问题进行评估和预测。
讨论:通过以上三个实验,我们可以看到数学在实际问题中的广泛应用。
线性回归分析可以帮助我们预测未来的趋势,为决策提供参考;优化问题求解可以帮助我们找到最优解,提高效率和效果;概率统计分析可以帮助我们评估风险和预测未来的可能性。
这些方法和技巧都是基于数学理论和模型的,通过对实际问题的抽象和建模,我们可以得到更准确、更可靠的结果。
结论:大学数学实验作为一门重要的课程,对培养学生的数学思维和实际应用能力起着重要的作用。
通过实验,学生可以将数学知识与实际问题相结合,提高解决问题的能力。
本篇报告以线性回归分析、优化问题求解和概率统计分析为例,讨论了数学在实际问题中的应用。
通过这些实验,我们可以看到数学的重要性和广泛应用性。
希望通过这些实验,学生能够更好地理解和掌握数学知识,为未来的学习和工作打下坚实的基础。
回归分析法

9.2.2 确定回归系数
a y b x
b
( x x)( y y ) ( x x)
i i 2 i
x 、 分别是n个x i、y i的平均值 y
1 1 x x i , y yi n n
9.2.2 确定回归系数
b
x y x
9.2 一元线性回归分析法
一元线性回归
• • • 涉及一个自变量(X)的回归 因变量y与自变量x之间为线性关系 因变量与自变量之间的关系用一条线性方 程来表示
一元线性回归模型
•
• •
描述因变量 y 如何依赖于自变量 x 和误差项 的方程称为回归模型 一元线性回归模型可表示为 y = 0 + 1 x +
i
( y
yi )( yi y) 0
( yi y ) 2 ( yi yi ) 2 ( yi y ) 2
s yy
Q U
Q-y的剩余平方和或误差平方和,U-y的回归平方和
9.2.2 确定回归系数
s 对于研究对象的给定的实际数据, yy是 确定不变的,只要能寻找一个回归方程, 使Q尽可能小(即U尽可能的大),也就是 使回归方程在总体上能尽可能近似地描述 实际变量数据。根据剩余平方和Q最小的原 则来确定回归系数,称为最小二乘原则。
相关关系的描述与测度 (散点图) (scatter diagram)
ຫໍສະໝຸດ
非线性相关
完全正线性相关
完全负线性相关
数学实验报告分析总结

数学实验报告分析总结实验目的:本次实验旨在通过分析数学实验报告的数据和结果,总结出实验中观察到的现象和得出的结论。
实验方法:本次实验采用了数学实验中常见的数据采集方法,通过实际操作和测量,收集了一系列实验数据。
然后利用数学统计分析方法对数据进行处理和分析。
实验结果:根据所收集的实验数据,我们得到了以下的实验结果:1. 实验数据显示,X变量与Y变量之间存在着强烈的正相关关系。
通过绘制X和Y的散点图,可以看到数据点呈现出明显的上升趋势,并且符合一次函数的形式。
2. 通过对数据的线性回归分析,得到了最佳拟合直线的方程为Y = aX + b。
通过计算得到的回归系数a和截距b分别为a =0.8,b = 2.5。
3. 根据回归方程的系数,可以得出结论,X变量每增加1单位,Y变量将增加0.8个单位。
而当X变量为0时,Y变量的取值为2.5。
4. 通过讨论实验数据的变异程度,我们计算出了两个变量之间的相关系数。
结果显示,相关系数为0.85,表明X和Y之间的变异程度是较为密切的。
实验分析:通过对实验数据的分析,我们得出了以上的实验结论。
根据回归分析的结果,我们发现X和Y之间存在着明显的线性关系,这为进一步的研究和预测提供了依据。
然而需要注意的是,本次实验的样本容量较小,所得结论具有一定的局限性。
为了进一步验证我们的结论,需要增加样本容量,并进行更多次的实验。
同时,在进行实验时,我们还可以采用其他的数据分析方法,如方差分析、因子分析等。
这些方法可以帮助我们深入分析数据,发现更多的规律和关系。
实验总结:通过本次数学实验,我们学习并运用了数学统计方法,对实验数据进行了分析和总结。
我们得出了X变量和Y变量之间的线性关系,并通过回归分析得到了最佳拟合直线的方程。
这次实验的结果对于进一步的研究和应用有一定的指导意义。
在实际应用中,我们可以根据回归方程预测Y变量的值,或者利用回归系数来评估X与Y之间的关系强度。
然而需要明确的是,实验结论的可靠性需要通过更多的实验数据来验证。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
x3=[587 643 635 692 1248 643 1964 1531 713 749 7895 762 2793741 625 854 716 921 595 3353];
2.4
1.85
9.8
14
25.6
7.9
1.60
3.7
6
7.5
1.7
1.78
10.3
15
37.5
14.1
16.4
3.6
7
13.0
4.3
1.76
10.5
16
36.1
14.5
1.64
3.1
8
12.8
3.7
1.76
8.7
17
39.8
14.9
1.67
1.8
9
14.6
3.9
1.75
7.4
18
44.3
15.6
1.68
表11-16
(1)若x1~x3中至多只许选择2个变量,最好的模型是什么?
(2)包含3个自变量的模型比上面的模型好吗?确定最终模型。
(3)对最终模型观察残差,有无异常点,若有,剔除后如何。
三.实验过程
先做y和xi的散点图,来大致判断自变量和因变量的关系。Matlab实现:首先在matlab中输入以下内容
x2=[6.1,6.2,6.3,8.2,9.8,10.3,10.5,8.7,7.4,6.9,5.2,4.9,4.3,3.6,3.1,1.8];
n=16;m=2;
X=[ones(n,1),x1',x2'];
[b1,bint1,r1,rint1,s1]=regress(y1',X);
subplot(2,1,1)
4.3615
[1.1197 7.6033]
R2=0.8000F=34.0024P<0.0001S2=21.8247
置信区间没有包含0,R较大,p很小。因此,模型可以是:
y=-34.0725+1.2239X1+4.3989X2
(2)将三个变量均包含进去Matlab代码如下:
n=20;
m=3;
X=[ones(n,1),x1',x2',x3'];
rcoplot(r1,rint1)
(2)对于 ,剔除第14个点后
继续剔除第七个点,得到残差及置信区间图如下:
将输出结果汇总成下表:
普通型
回归系数
回归系数估值
回归系数置信区间
107.5601
[75.3160139.8042]
-37.9283
[-57.2842-18.5723]
-3.0314
[-3.7862-2.2767]
x3=[587 643 635 692 1248 643 1964 713 749 7895 762 2793 741 625 854 716 921 595 ];
n=18;
m=2;
X=[ones(n,1),x1',x2'];
[b,bint,r,rint,s]=regress(y',X);
b,bint,s
x2=[6.1,6.2,6.3,8.2,9.8,10.3,10.5,8.7,7.4,6.9,4.9,4.3,3.6,3.1,1.8];
n=15;m=2;
X=[ones(n,1),x1',x2'];
[b1,bint1,r1,rint1,s1]=regress(y1',X);
subplot(2,1,1)
(1)对于 剔除第14、18个点后,输入代码如下:
y1=[22.1,15.4,11.7,10.3,11.4,7.5,13.0,12.8,14.6,18.9,19.3,30.1,28.2,37.5,36.1,39.8];
x1=[1.89,1.94,1.95,1.82,1.85,1.78,1.76,1.76,1.75,1.74,1.70,1.70,1.68,1.61,1.64,1.67];
[-0.0006 0.0021]
R2=0.8163F=23.6946P<0.0001S2=21.3036
如上表所示,虽然R2等量变化不大,但是β3的置信区间包含了0点,而且β1的置信区间距离0点也比较近。另外,从散点图来分析,y与x3的线性关系也不佳。因此,最终模型是y与x1,x2建立起来的模型。
(3)先观察观察模型残差Matlab代码如下:
rcoplot(r1,rint1)
继续自此基础上剔除第11个点,输入代码如下:
y1=[22.1,15.4,11.7,10.3,11.4,7.5,13.0,12.8,14.6,18.9,30.1,28.2,37.5,36.1,39.8];
x1=[1.89,1.94,1.95,1.82,1.85,1.78,1.76,1.76,1.75,1.74,1.70,1.68,1.61,1.64,1.67];
剔除之后结果如下:
回归系数
回归系数估计值
回归系数置信区间
β0
-35.5229
[-45.1435 -25.9023]
β1
1.6040
[0.7661 2.4418]
β2
3.3581
[1.1590 5.5572]
R2=0.9111F=76.9102P<0.0001S2=9.3423
同未剔除异常点前相比,β估计值改变不大,但是置信区间变短,R2和F值提高,S2值变小。而且残差中没有异常点出现。因此可认为,剔除之后模型变得更精确。最终模型可以是:y=-35.5229+1.6040x1+3.3581x2
四.实验总结
从最终的结果来看,影响犯罪率的因素是失业率与低收入。本题训练了逐步回归命令stepwise来分析多自变量情况下的变量选择问题。而且得到最优的模型还不够,还要分析残差,剔除不符的数据之后再次计算才能得到最终的模型。
题目(二)
一.实验目的
1.了解回归分析的基本原理,掌握MATLAB实现的方法;
数学实验报告
学 院:
班 级:
学 号:
姓 名:
完成日期:2016年6月24日
回归分析
题目(一)
一.实验目的
1.了解回归分析的基本原理,掌握MATLAB实现的方法.
2.练习用回归分析解决实际问题。
二.问题描述
社会学家认为犯罪与收入低、失业及人口规模有关,对20个城市的犯罪率y(每10万人中犯罪的人数)与年收入低于5000美元家庭的百分比x1、失业率x2和人口总数x3(千人)进行了调查,结果如表11-16所示。
2.练习用回归分析解决实际问题。
二.问题描述
汽车销售商认为汽车销售量与汽油价格、贷款利率有关,两种类型汽车(普通型和豪华型)18个月的调查资料如表,其中 是普通型汽车售量(千辆), 是豪华型汽车售量(千辆), 是汽油价格(元/gal), 是贷款利率(%)
(1)对普通型和豪华型汽车分别建立如下模型:
给出 的估计值和置信区间,决定系数 值及剩余方差等。
x1=[16.5 20.5 26.3 16.5 19.2 16.5 20.2 17.2 14.3 18.1 23.1 19.1 24.7 18.6 24.9 17.9 22.4 20.2 ];
x2=[6.2 6.4 9.3 5.3 7.3 5.9 6.4 4.9 6.4 6.0 7.4 5.8 8.6 6.5 8.4 6.7 8.6 8.4 ];
x2=[6.1,6.2,6.3,8.2,9.8,10.3,10.5,8.7,7.4,6.9,5.2,4.9,4.3,3.7,3.6,3.1,1.8,2.3];
n=18;m=2;
X=[ones(n,1),x1',x2'];
[b1,bint1,r1,rint1,s1]=regress(y1',X);
[b2,bint2,r2,rint2,s2]=regress(y2',X);
rcoplot(r,rint)
stepwise(x,y') %进行逐步回归
pause;
n=18;
X=[ones(n,1) x1' x2']; %由前面的逐步回归可以得到包含2个变量x1,x2时s最小[b,bi,r,ri,s]=regress(y',x);
s2=sum(r.^2)/(n-3);
b,bi,s,s2 rcoplot(r,ri) %残差分析
subplot(2,1,1)
rcoplot(r1,rint1)
subplot(2,1,2)
rcoplot(r2,rint2)
得到如下图:
在残差及置信区间的图中,有三个点的残差的置信区间不包含零点,以红色标出。残差应该服从均值为0的正态分布,可以认为这个数据是异常的,偏离了数据整体的变化趋势,给模型的有效性的精度带来不利影响,应予以剔除。剔除点后的模型求解
[b,bint,r,rint,s]=regress(y',X);
b,bint,s
结果如下表所示:
回归系数
回归系数估计值
回归系数置信区间
β0
-36.5104
[-51.4209-21.5998]
β1
1.1908
[-0.0150 2.3965]
β2
4.6840
[1.4149 7.9532]
β3
0.0008
n=20;
m=2;
X=[ones(n,1),x1',x2'];
[b,bint,r,rint,s]=regress(y',X);
