球面几何学
航海数学球面三角

• 3、球面距离: • 定理五:球面上两点间小于180度的大圆弧(劣
弧)的长是该两点间的最短球面距离,简称球面 距离。 • (1)、轴:垂直于任一圆面的球直径; • (2)、极:轴与球面相交的两点; • (3)、
1基本概念
第六章:球面三角
第一节:球面几何
练习:
(1)正方体的全面积是a,它的顶点都在球 面上,这个球的表面积是( )。 (2)球的半径为R,则它的外切正方体的 棱长为( ),内接正方体的棱长为( )。
一、 平面与球面、直线与球面的位置关系
1、平面与球的位置关系:
类比直线与圆的位置关系,来探究平面与球的位置关系。
相交、相离、相切
结论: 一个平面与球面相交,所得的交线是一个圆, 且圆心与球心的连线垂直于这一平面。 用一个平面截一个球,截面是圆面。请同学们思 考什么时候是小圆,什么时候是大圆?
2、直线与球面的位置关系:
同样,类比直线与圆的位置关系,来探究直线与球
的位置关系。
结论:
把球心O到直线L的距离记为OH, 当OH>R时,相离,直线与球没有公共点; 当OH=R时,相切,直线与球只有一个公共 点; 当OH<R时,相切,直线与球有两个公共点。 三、球幂定理
二、球面上的一些基本图形
1、大圆:当平面过球心时与球面所截成的圆最大,称
为大圆;
小圆:当平面不过球心时所截的圆称为小圆;
2、优弧、劣弧:过球面上两点一定可以作一
个大圆。(球面上两点间的距离即劣弧长) 球面上连接两点的最短路径是经过这两点的 一段大圆弧——劣弧。
欧几里得与欧几里得几何

欧几里得与欧几里得几何亚历山大里亚的欧几里得(约公元前330年—前275年),古希腊数学家,被称为“几何之父”。
他活跃于托勒密一世(公元前323年-前283年)时期的亚历山大里亚,他最著名的著作《几何原本》是欧洲数学的基础,提出五大公设,发展欧几里得几何,被广泛的认为是历史上最成功的教科书。
欧几里得也写了一些关于透视、圆锥曲线、球面几何学及数论的作品。
欧几里得是古希腊著名数学家、欧氏几何学的开创者。
欧几里得生于雅典,当时雅典就是古希腊文明的中心。
浓郁的文化气氛深深地感染了欧几里得,当他还是个十几岁的少年时,就迫不及待地想进入“柏拉图学园”学习。
他在有攀滋入学园之后,便全身心地沉潜在数学王国里。
他潜心求索,以继器粕拉图的学术为奋斗目标,除此之外,他哪儿也不去,什么也不干。
熬翻阅和研究了柏拉图的所有著作和手稿,可以说,连柏拉图的亲传攀擎也没有谁能像他那样熟悉柏拉图的学术思想、数学理论。
经过对柏拉图思想的深入探究,他得出结论:图形是神绘制的,所有一切籀象的逻辑规律都体现在图形之中。
因此,对智慧的训练,就应该从戡图形为主要研究对象的几何学开始。
他确实领悟到了柏拉图思想的要旨,并开始沿着柏拉图当年走过的道路,把几何学的研究作为自醺羽主要任务,并最终取得了世人敬仰的成就。
最早的几何学兴起于公元前7年的古埃及,后经古希腊等人传到古希腊的都城,又借毕达哥拉斯学派纂糯典。
在欧几里得以前,人们已经积累了许多几何学的知识,然黔这些知识当中,存在一个很大的缺点和不足,就是缺乏系统性。
大多数是片断、零碎的知识,公理与公理之问、证明与证明之间并没有什么很强的联系性,更不要说对公式和定理进行严格的逻辑论证和说明。
因此,随着社会经济的繁荣和发展,特别是随着农林畜牧业的发展、土地开发和利用的增多,把这些几何学知识加以条理化和系统化,成为一整套可以自圆其说、前后贯通的知识体系,已经是刻不容缓,成为科学进步的大势所趋。
欧几里得通过早期对柏拉图数学思想,尤其是几何学理论系统而周详的研究,已敏锐地察觉到了几何学理论的发展趋势。
Spheric geometry球面几何

Spheric geometry(球面几何)是几何学的一门分科。
研究球面上图形的几何学。
是古代从研究天体在天球上的“视运动”发展起来的,其中专门研究球面上三角形的性质的称为“球面三角”。
球面几何学是在二维的球面表面上的几何学,也是非欧几何的一个例子。
在平面几何中,基本的观念是点和线。
在球面上,点的观念和定义依旧不变,但线不再是“直线”,而是两点之间最短的距离,称为最短线。
在球面上,最短线是大圆的弧,所以平面几何中的线在球面几何中被大圆所取代。
同样的,在球面几何中的角被定义在两个大圆之间。
结果是球面三角学和平常的三角学有诸多不同之处。
例如:球面三角形的内角合大于180°。
对比于通过一个点至少有两条平行线,甚至无穷多条平行线的双曲面几何学,通过特定的点没有平行线的球面几何学是椭圆几何学中最简单的模式。
球面几何学在航海学和天文学都有实际且重要的用途。
球面几何学的重要关键在塑造真实投影平面,通过辨认在球面上获得正相反的对跖点(分列在边的两侧相对的点)。
在当地,投影平面具有球面几何所有的特性,但有不同的总体特性,特别是他是无定向的。
球面乃是空间中最完美匀称的曲面。
两个半径相等的球面可以用一个平移把它们叠合起来,而两个半径不相等的球面所相差者就是放大或缩小这种相似变换,由此可见本质性的球面几何可以归纳到单位半径的球面来研讨。
再者,在古典天文学的研讨中,观察星星的方向可以用单位球面上的一个点来标记它,而两个方向之间的角度(亦即方向差)则相应于单位球面上两点之间的球面距离(spherical distance) 。
这也就是为什么古希腊天文学和几何学总是合为一体的,而且古希腊的几何学家对于球面三角学(spherical trigonometry)的投入程度要远远超过他们对于平面测量学的兴趣,因为「量天的学问」才是他们所致力去理解者;它的确比丈量土地、计量财产等更引人入胜。
从现代的观点来看,球面几何乃是空间几何中蕴含在正交子群的部分,而向量几何则是空间几何中蕴含在平移子群的部分,而且两者又密切相关、相辅相成,例如向量运算都是正交协变的(orthogonal covariant),所以向量代数又是研讨球面几何的简明有力的利器。
三级学科代码表

110 数学110.11 数学史110.14 数理逻辑与数学基础110.1410 演绎逻辑学(亦称符号逻辑学) 110.1420 证明论(亦称元数学)110.1430 递归论110.1440 模型论110.1450 公理集合论110.1460 数学基础110.1499 数理逻辑与数学基础其他学科110.17 数论110.1710 初等数论110.1720 解析数论110.1730 代数数论110.1740 超越数论110.1750 丢番图逼近110.1760 数的几何110.1770 概率数论110.1780 计算数论110.1799 数论其他学科110.21 代数学110.2110 线性代数110.2115 群论110.2120 域论110.2125 李群110.2130 李代数110.2135 Kac-Moody代数110.2140 环论110.2145 模论110.2150 格论110.2155 泛代数理论110.2160 范畴论110.2165 同调代数110.2170 代数K理论110.2175 微分代数110.2180 代数编码理论110.2199 代数学其他学科110.24 代数几何学110.27 几何学110.2710 几何学基础110.2715 欧氏几何学110.2720 非欧几何学(包括黎曼几何学等) 110.2725 球面几何学110.2730 向量和张量分析110.2735 仿射几何学110.2740 射影几何学110.2745 微分几何学110.2750 分数维几何110.2755 计算几何学110.2799 几何学其他学科110.31 拓扑学110.3110 点集拓扑学110.3115 代数拓扑学110.3120 同伦论110.3125 低维拓扑学110.3130 同调论110.3135 维数论110.3140 格上拓扑学110.3145 纤维丛论110.3150 几何拓扑学110.3155 奇点理论110.3160 微分拓扑学110.3199 拓扑学其他学科110.34 数学分析110.3410 微分学110.3420 积分学110.3430 级数论110.3499 数学分析其他学科110.37 非标准分析110.41 函数论110.4110 实变函数论110.4120 单复变函数论110.4130 多复变函数论110.4140 函数逼近论110.4150 调和分析110.4160 复流形110.4170 特殊函数论110.4199 函数论其他学科110.44 常微分方程110.4410 定性理论110.4420 稳定性理论110.4430 解析理论110.4499 常微分方程其他学科110.47 偏微分方程110.4710 椭圆型偏微分方程110.4720 双曲型偏微分方程110.4730 抛物型偏微分方程110.4740 非线性偏微分方程110.4799 偏微分方程其他学科110.51 动力系统110.5110 微分动力系统110.5120 拓扑动力系统110.5130 复动力系统110.5199 动力系统其他学科110.54 积分方程110.57 泛函分析110.5710 线性算子理论110.5715 变分法110.5720 拓扑线性空间110.5725 希尔伯特空间110.5730 函数空间110.5735 巴拿赫空间110.5740 算子代数110.5745 测度与积分110.5750 广义函数论110.5755 非线性泛函分析110.5799 泛函分析其他学科110.61 计算数学110.6110 插值法与逼近论110.6120 常微分方程数值解110.6130 偏微分方程数值解110.6140 积分方程数值解110.6150 数值代数110.6160 连续问题离散化方法110.6170 随机数值实验110.6180 误差分析110.6199 计算数学其他学科110.64 概率论110.6410 几何概率110.6420 概率分布110.6430 极限理论110.6440 随机过程110.6450 马尔可夫过程110.6460 随机分析110.6470 鞅论110.6480 应用概率论110.6499 概率论其他学科110.67 数理统计学110.6710 抽样理论110.6715 假设检验110.6720 非参数统计110.6725 方差分析110.6730 相关回归分析110.6735 统计推断110.6740 贝叶斯统计110.6745 试验设计110.6750 多元分析110.6755 统计判决理论110.6760 时间序列分析110.6799 数理统计学其他学科110.71 应用统计数学110.7110 统计质量控制110.7120 可靠性数学110.7130 保险数学110.7140 统计模拟110.7199 应用统计数学其他学科110.74 运筹学110.7410 线性规划110.7415 非线性规划110.7420 动态规划110.7425 组合最优化110.7430 参数规划110.7435 整数规划110.7440 随机规划110.7445 排队论110.7450 对策论(亦称博奕论) 110.7455 库存论110.7460 决策论110.7465 搜索论110.7470 图论110.7475 统筹论110.7480 最优化110.7499 运筹学其他学科110.77 组合数学110.81 离散数学110.84 模糊数学110.87 应用数学110.99 数学其他学科。
数学中的球面几何学

数学中的球面几何学在数学中,球面几何学是一门研究球面及其相关性质的分支学科。
球面几何学广泛应用于物理学、天文学、地理学等领域,也是许多数学问题的基础。
本文将介绍球面几何学的基本概念和一些重要的定理。
一、球面的定义和基本概念球面可以看作是一个由无数个点组成的集合,这些点到中心的距离都相等。
中心是球面的一个重要属性,通常表示为O。
与球面相切的直线称为切线,它在切点处与球面相切。
球面上的一条线段称为弧,两个点之间的最短路径即为弧。
球面上还有一个重要概念是球面上的两个点之间的最短距离称为球面上的距离。
球面上的距离与平面上的距离不同,因为球面具有曲率。
二、球面的坐标系统为了描述球面上的点,我们可以使用球面坐标系统。
在球面上,我们选择以球心为原点建立坐标系。
对于任意一点P,我们可以用两个角度来确定其位置:极角和方位角。
极角表示P点与球心连线与正北方向的夹角,方位角表示P点在与极角垂直的平面上与正北方向的夹角。
球面上的距离也可以通过坐标系来计算。
给定两个点P和Q,它们的坐标分别为(θ₁, φ₁)和(θ₂, φ₂),则它们之间的距离可以通过以下公式计算:cosδ = sinθ₁sinθ₂cos(φ₁-φ₂) + cosθ₁cosθ₂其中δ表示P点和Q点之间的距离。
三、球面的面积和体积球面的面积和体积是球面几何学中的重要量度。
球面的面积公式如下:S = 4πR²其中S表示球面的面积,R表示球的半径。
球面的体积公式如下:V = (4/3)πR³其中V表示球面的体积。
四、球面几何学中的重要定理1. 定理一:球面上的内切正多边形的顶点数必为4的倍数。
2. 定理二:球面上的内切正多边形的边数受限于球的半径和所需正多边形的边数。
3. 定理三:球的表面积最小,对应于球的体积最大。
四、应用球面几何学在现实生活中具有广泛应用。
以下是一些典型的应用场景:1. 天文学:天文学家使用球面几何学来计算天体之间的距离和位置。
学科代码学科名称

学科代码学科名称110 数学110.11 数学史110.14 数理逻辑与数学基础110.141 演绎逻辑学(亦称符号逻辑学)110.142 证明论(亦称元数学)110.143 递归论110.144 模型论110.145 公理集合论110.146 数学基础110.1499 数理逻辑与数学基础其他学科110.17 数论110.171 初等数论110.172 解析数论110.173 代数数论110.174 超越数论110.175 丢番图逼近110.176 数的几何110.177 概率数论110.178 计算数论110.1799 数论其他学科110.21 代数学110.211 线性代数110.2115 群论110.212 域论110.2125 李群110.213 李代数110.2135 Kac-Moody代数110.214 环论(包括交换环与交换代数、结合环与结合代数、非结合环与非结合代数等) 110.2145 模论110.215 格论110.2155 泛代数理论110.216 范畴论110.2165 同调代数110.217 代数K理论110.2175 微分代数110.218 代数编码理论110.2199 代数学其他学科110.24 代数几何学110.27 几何学110.271 几何学基础110.2715 欧氏几何学110.272 非欧几何学(包括黎曼几何学等)110.2725 球面几何学110.273 向量和张量分析110.2735 仿射几何学110.274 射影几何学110.2745 微分几何学110.275 分数维几何110.2755 计算几何学110.2799 几何学其他学科110.31 拓扑学110.311 点集拓扑学110.3115 代数拓扑学110.312 同伦论110.3125 低维拓扑学110.313 同调论110.3135 维数论110.314 格上拓扑学110.3145 纤维丛论110.315 几何拓扑学110.3155 奇点理论110.316 微分拓扑学110.3199 拓扑学其他学科110.34 数学分析110.341 微分学110.342 积分学110.343 级数论110.3499 数学分析其他学科110.37 非标准分析110.41 函数论110.411 实变函数论110.412 单复变函数论110.413 多复变函数论110.414 函数逼近论110.415 调和分析110.416 复流形110.417 特殊函数论110.4199 函数论其他学科110.44 常微分方程110.441 定性理论110.442 稳定性理论110.443 解析理论110.4499 常微分方程其他学科110.47 偏微分方程110.471 椭圆型偏微分方程110.472 双曲型偏微分方程110.473 抛物型偏微分方程110.474 非线性偏微分方程110.4799 偏微分方程其他学科110.51 动力系统110.511 微分动力系统110.512 拓扑动力系统110.513 复动力系统110.5199 动力系统其他学科110.54 积分方程110.57 泛函分析110.571 线性算子理论110.5715 变分法110.572 拓扑线性空间110.5725 希尔伯特空间110.573 函数空间110.5735 巴拿赫空间110.574 算子代数110.5745 测度与积分110.575 广义函数论110.5755 非线性泛函分析110.5799 泛函分析其他学科110.61 计算数学110.611 插值法与逼近论110.612 常微分方程数值解110.613 偏微分方程数值解110.614 积分方程数值解110.615 数值代数110.616 连续问题离散化方法110.617 随机数值实验110.618 误差分析110.6199 计算数学其他学科110.64 概率论110.641 几何概率110.642 概率分布110.643 极限理论110.644 随机过程(包括正态过程与平稳过程、点过程等) 110.645 马尔可夫过程110.646 随机分析110.647 鞅论110.648 应用概率论110.6499 概率论其他学科110.67 数理统计学110.671 抽样理论(包括抽样分布、抽样调查等)110.6715 假设检验110.672 非参数统计110.6725 方差分析110.673 相关回归分析110.6735 统计推断110.674 贝叶斯统计(包括参数估计等)110.6745 试验设计110.675 多元分析110.6755 统计判决理论110.676 时间序列分析110.6799 数理统计学其他学科110.71 应用统计数学110.711 统计质量控制110.712 可靠性数学110.713 保险数学110.714 统计模拟110.7199 应用统计数学其他学科110.74 运筹学110.741 线性规划110.7415 非线性规划110.742 动态规划110.7425 组合最优化110.743 参数规划110.7435 整数规划110.744 随机规划110.7445 排队论110.745 对策论(亦称博奕论)110.7455 库存论110.746 决策论110.7465 搜索论110.747 图论110.7475 统筹论110.748 最优化110.7499 运筹学其他学科110.77 组合数学110.81 离散数学110.84 模糊数学110.87 应用数学110.99 数学其他学科120 信息科学与系统科学120.1 信息科学与系统科学基础学科120.101 信息论120.102 控制论120.103 系统论120.1099 信息科学与系统科学基础学科其他学科120.2 系统学120.201 混沌120.202 一般系统论120.203 耗散结构理论120.204 协同学120.205 突变论120.206 超循环论120.2099 系统学其他学科120.3 控制理论120.301 大系统理论120.302 系统辨识120.303 状态估计120.304 鲁棒控制120.3099 控制理论其他学科120.4 系统评估与可行性分析120.5 系统工程方法论120.501 系统建模120.5099 系统工程方法论其他学科120.6 系统工程120.99 信息科学与系统科学其他学科130 力学130.1 基础力学130.101 理论力学130.102 理性力学130.103 非线性力学130.104 连续介质力学130.105 摩擦学130.106 柔性多体力学130.107 陀螺力学130.108 飞行力学130.1099 基础力学其他学科130.15 固体力学130.151 弹性力学130.1515 塑性力学(包括弹塑性力学) 130.152 黏弹性、黏塑性力学130.1525 蠕变130.153 界面力学与表面力学130.1535 疲劳130.154 损伤力学130.1545 断裂力学130.155 散体力学130.1555 细观力学130.156 电磁固体力学130.1565 结构力学130.157 计算固体力学130.1575 实验固体力学130.1599 固体力学其他学科130.2 振动与波130.201 线性振动力学130.202 非线性振动力学130.203 弹性体振动力学130.204 随机振动力学130.205 振动控制理论130.206 固体中的波130.207 流体–固体耦合振动130.2099 振动与波其他学科130.25 流体力学130.2511 理论流体力学130.2514 水动力学130.2517 气体动力学130.2521 空气动力学130.2524 悬浮体力学130.2527 湍流理论130.2531 黏性流体力学130.2534 多相流体力学130.2537 渗流力学130.2541 物理–化学流体力学130.2544 等离子体动力学130.2547 电磁流体力学130.2551 非牛顿流体力学130.2554 流体机械流体力学130.2557 旋转与分层流体力学130.2561 辐射流体力学130.2564 计算流体力学130.2567 实验流体力学130.2571 环境流体力学130.2599 流体力学其他学科130.3 流变学130.35 爆炸力学130.351 爆轰与爆燃理论130.352 爆炸波、冲击波、应力波130.353 高速碰撞动力学130.3599 爆炸力学其他学科130.4 物理力学130.401 高压固体物理力学130.402 稠密流体物理力学130.403 高温气体物理力学130.404 多相介质物理力学130.405 临界现象与相变130.406 原子与分子动力学130.4099 物理力学其他学科130.45 统计力学130.5 应用力学130.99 力学其他学科140 物理学140.1 物理学史140.15 理论物理学140.151 数学物理140.152 电磁场理论140.153 经典场论140.154 相对论与引力场140.155 量子力学140.156 统计物理学140.1599 理论物理学其他学科140.2 声学140.201 物理声学140.202 非线性声学140.203 量子声学140.204 超声学140.205 水声学140.206 应用声学140.2099 声学其他学科140.25 热学140.251 热力学140.252 热物性学140.253 传热学140.2599 热学其他学科140.3 光学140.301 几何光学140.3015 物理光学140.302 非线性光学140.3025 光谱学140.303 量子光学140.3035 信息光学140.304 导波光学140.3045 发光学140.305 红外物理140.3055 激光物理140.306 应用光学140.3099 光学其他学科140.35 电磁学140.351 电学140.352 静电学140.353 静磁学140.354 电动力学140.3599 电磁学其他学科140.4 无线电物理140.401 电磁波物理140.402 量子无线电物理140.403 微波物理学140.404 超高频无线电物理140.405 统计无线电物理140.4099 无线电物理其他学科140.45 电子物理学140.451 量子电子学140.452 电子离子与真空物理140.453 带电粒子光学140.4599 电子物理学其他学科140.5 凝聚态物理学140.501 凝聚态理论140.5015 金属物理学140.502 半导体物理学140.5025 电介质物理学140.503 晶体学(包括晶体生长、晶体化学等) 140.5035 非晶态物理学140.504 液晶物理学140.5045 薄膜物理学140.505 低维物理140.5055 表面与界面物理学140.506 固体发光140.5065 磁学140.507 超导物理学140.5075 低温物理学140.508 高压物理学140.5099 凝聚态物理学其他学科140.55 等离子体物理学140.551 热核聚变等离子体物理学140.552 低温等离子体物理学140.553 等离子体光谱学140.554 凝聚态等离子体物理学140.555 非中性等离子体物理学140.5599 等离子体物理学其他学科140.6 原子分子物理学140.601 原子与分子理论140.602 原子光谱学140.603 分子光谱学140.604 波谱学140.605 原子与分子碰撞过程140.6099 原子分子物理学其他学科140.65 原子核物理学140.651 核结构140.6515 核能谱学140.652 低能核反应140.6525 中子物理学140.653 裂变物理学140.6535 聚变物理学140.654 轻粒子核物理学140.6545 重离子核物理学140.655 中高能核物理学140.6599 原子核物理学其他学科140.7 高能物理学140.701 基本粒子物理学140.702 宇宙线物理学140.703 粒子加速器物理学140.704 高能物理实验140.7099 高能物理学其他学科140.75 计算物理学140.8 应用物理学140.99 物理学其他学科150 化学150.1 化学史150.15 无机化学150.151 元素化学150.152 配位化学150.153 同位素化学150.154 无机固体化学150.155 无机合成化学150.156 无机分离化学150.157 物理无机化学150.158 生物无机化学150.1599 无机化学其他学科150.2 有机化学150.201 元素有机化学(包括金属有机化学等)150.202 天然产物有机化学150.203 有机固体化学150.204 有机合成化学150.205 有机光化学150.206 物理有机化学(包括理论有机化学、立体化学等) 150.207 生物有机化学150.2099 有机化学其他学科150.25 分析化学150.251 化学分析(包括定性分析、定量分析等)150.2515 电化学分析150.252 光谱分析150.2525 波谱分析150.253 质谱分析150.2535 热谱分析150.254 色谱分析150.2545 光度分析150.255 放射分析150.2555 状态分析与物相分析150.256 分析化学计量学150.2599 分析化学其他学科150.3 物理化学150.301 化学热力学150.3015 化学动力学(包括分子反应动力学等)150.302 结构化学(包括表面化学、结构分析等)150.3025 量子化学150.303 胶体化学与界面化学150.3035 催化化学150.304 热化学150.3045 光化学(包括超分子光化学、光电化学、激光化学、感光化学等) 150.305 电化学150.3055 磁化学150.306 高能化学(包括辐射化学、等离体化学)150.3065 计算化学150.3099 物理化学其他学科150.35 化学物理学150.4 高分子物理150.45 高分子化学150.451 无机高分子化学150.452 天然高分子化学150.453 功能高分子(包括液晶高分子化学)150.454 高分子合成化学150.455 高分子物理化学150.456 高分子光化学150.4599 高分子化学其他学科150.5 核化学150.501 放射化学150.502 核反应化学150.503 裂变化学150.504 聚变化学150.505 重离子核化学150.506 核转变化学150.507 环境放射化学150.5099 核化学其他学科150.55 应用化学150.99 化学其他学科160 天文学160.1 天文学史160.15 天体力学160.151 摄动理论160.152 天体力学定性理论160.153 天体形状与自转理论160.154 天体力学数值方法160.155 天文动力学(包括人造卫星、宇宙飞船动力学等) 160.156 历书天文学160.1599 天体力学其他学科160.2 天体物理学160.201 理论天体物理学160.202 相对论天体物理学160.203 等离子体天体物理学160.204 高能天体物理学(包括天体核物理学)160.205 实测天体物理学160.2099 天体物理学其他学科160.25 天体化学160.3 天体测量学160.301 天文地球动力学160.302 基本天体测量学160.303 照相天体测量学160.304 射电天体测量学160.305 空间天体测量学160.306 方位天文学160.307 实用天文学160.3099 天体测量学其他学科160.35 射电天文学160.351 射电天体物理学160.352 射电天文方法160.3599 射电天文学其他学科160.4 空间天文学160.401 红外天文学160.402 紫外天文学160.403 X射线天文学160.404 g射线天文学160.405 中微子天文学160.4099 空间天文学其他学科160.45 天体演化学(各层次天体形成与演化入各学科) 160.5 星系与宇宙学160.501 星系动力学160.502 星系天文学160.503 运动宇宙学160.504 星系际物质160.505 大爆炸宇宙论160.506 星系形成与演化160.507 宇宙大尺度结构起源与演化160.5099 星系与宇宙学其他学科160.55 恒星与银河系160.551 恒星物理学160.552 恒星天文学160.553 恒星形成与演化160.554 星际物质物理学160.555 银河系结构与运动160.5599 恒星与银河系其他学科160.6 太阳与太阳系160.601 太阳物理学160.602 太阳系物理学160.603 太阳系形成与演化160.604 行星物理学160.605 行星际物理学160.606 陨星学160.6099 太阳与太阳系其他学科160.65 天体生物学160.99 天文学其他学科170 地球科学170.1 地球科学史170.15 大气科学170.151 大气物理学(包括大气光学、大气声学、大气电学、云雾物理学、边界层物理学、中层物理学等)170.1515 大气化学170.152 大气探测(包括大气遥感)170.1525 动力气象学(包括数值天气预报与数值模拟等)170.153 天气学170.1535 气候学170.154 云与降水物理学170.1545 应用气象学170.1599 大气科学其他学科170.2 固体地球物理学170.201 地球动力学170.2015 地球重力学170.202 地球流体力学170.2025 地壳与地形变170.203 地球内部物理学170.2035 地声学170.2045 地电学170.205 地磁学170.2055 放射性地球物理学170.206 地震学170.2065 勘探地球物理学170.207 计算地球物理学170.2075 实验地球物理学170.2099 固体地球物理学其他学科170.25 空间物理学170.251 电离层物理学170.252 高层大气物理学170.253 磁层物理学170.254 空间物理探测170.255 空间环境学170.2599 空间物理学其他学科170.3 地球化学170.301 元素地球化学170.3015 有机地球化学170.302 放射性地球化学170.3025 同位素地球化学170.303 生物地球化学170.3035 地球内部化学170.304 同位素地质年代学170.3045 成矿地球化学170.305 勘探地球化学170.3055 实验地球化学170.3099 地球化学其他学科170.35 大地测量学170.351 地球形状学170.352 几何大地测量学170.353 物理大地测量学170.354 动力大地测量学170.355 空间大地测量学170.356 行星大地测量学170.3599 大地测量学其他学科170.4 地图学170.45 地理学170.451 自然地理学(包括化学地理学、生态地理学、地貌学、冰川学、冻土学、沙漠学、岩溶学等)170.452 人文地理学(包括区域地理、旅游地理、其他有关学科)170.4599 地理学其他学科170.5 地质学170.5011 数学地质学170.5017 动力地质学170.5021 矿物学(包括放射性矿物学)170.5024 矿床学与矿相学(包括放射性矿床学,不包括石油、天然气和煤) 170.5027 岩石学170.5031 岩土力学170.5034 沉积学170.5037 古地理学170.5041 古生物学170.5044 地层学与地史学170.5047 前寒武纪地质学170.5051 第四纪地质学170.5054 构造地质学(包括显微构造学等)170.5057 大地构造学170.5061 勘查地质学170.5064 水文地质学(包括放射性水文地质学)170.5067 遥感地质学170.5071 区域地质学170.5074 火山学170.5077 石油与天然气地质学170.5081 煤田地质学170.5084 实验地质学170.5099 地质学其他学科170.55 水文学170.551 水文物理学170.5515 水文化学170.552 水文地理学170.5525 水文气象学170.553 水文测量170.5535 水文图学170.554 湖沼学170.5545 河流学与河口水文学170.5599 水文学其他学科170.6 海洋科学170.601 海洋物理学170.6015 海洋化学170.602 海洋地球物理学170.6025 海洋气象学170.603 海洋地质学170.6035 物理海洋学170.604 海洋生物学170.6045 河口、海岸学170.605 海洋调查与监测170.6099 海洋科学其他学科170.99 地球科学其他学科180 生物学180.11 生物数学(包括生物统计学等)180.14 生物物理学180.141 生物信息论与生物控制论180.1415 生物力学(包括生物流体力学与生物流变学等) 180.142 理论生物物理学180.1425 生物声学与声生物物理学180.143 生物光学与光生物物理学180.1435 生物电磁学180.144 生物能量学180.1445 低温生物物理学180.145 分子生物物理学180.1455 空间生物物理学180.146 仿生学180.1465 系统生物物理学180.1499 生物物理学其他学科180.17 生物化学180.171 多肽与蛋白质生物化学180.1715 核酸生物化学180.172 多糖生物化学180.1725 脂类生物化学180.173 酶学180.1735 膜生物化学180.174 激素生物化学180.1745 生殖生物化学180.175 免疫生物化学180.1755 毒理生物化学180.176 比较生物化学180.1765 应用生物化学180.1799 生物化学其他学科180.21 细胞生物学180.211 细胞生物物理学180.212 细胞结构与形态学180.213 细胞生理学180.214 细胞进化学180.215 细胞免疫学180.216 细胞病理学180.2199 细胞生物学其他学科180.24 生理学180.2411 形态生理学180.2414 新陈代谢与营养生理学180.2417 心血管生理学180.2421 呼吸生理学180.2427 血液生理学180.2431 泌尿生理学180.2434 内分泌生理学180.2437 感官生理学180.2441 生殖生理学180.2444 骨骼生理学180.2447 肌肉生理学180.2451 皮肤生理学180.2454 循环生理学180.2457 比较生理学180.2461 年龄生理学180.2464 特殊环境生理学180.2467 语言生理学180.2499 生理学其他学科180.27 发育生物学180.31 遗传学180.311 数量遗传学180.3115 生化遗传学180.312 细胞遗传学180.3125 体细胞遗传学180.313 发育遗传学(亦称发生遗传学) 180.3135 分子遗传学180.314 辐射遗传学180.3145 进化遗传学180.315 生态遗传学180.3155 免疫遗传学180.316 毒理遗传学180.3165 行为遗传学180.317 群体遗传学180.3199 遗传学其他学科180.34 放射生物学180.341 放射生物物理学180.342 细胞放射生物学180.343 放射生理学180.344 分子放射生物学180.345 放射免疫学180.346 放射毒理学180.3499 放射生物学其他学科180.37 分子生物学180.41 生物进化论180.44 生态学180.441 数学生态学180.4415 化学生态学180.4425 生态毒理学180.443 区域生态学180.4435 种群生态学180.444 群落生态学180.4445 生态系统生态学180.445 生态工程学180.4499 生态学其他学科180.47 神经生物学180.471 神经生物物理学180.4715 神经生物化学180.472 神经形态学180.4725 细胞神经生物学180.473 神经生理学180.4735 发育神经生物学180.474 分子神经生物学180.4745 比较神经生物学180.475 系统神经生物学180.4799 神经生物学其他学科180.51 植物学180.511 植物化学180.5115 植物生物物理学180.512 植物生物化学180.5125 植物形态学180.513 植物解剖学180.5135 植物细胞学180.514 植物生理学180.5145 植物胚胎学180.515 植物发育学180.5155 植物遗传学180.516 植物生态学180.5165 植物地理学180.517 植物群落学180.5175 植物分类学180.518 实验植物学180.5185 植物寄生虫学180.5199 植物学其他学科180.54 昆虫学180.541 昆虫生物化学180.5415 昆虫形态学180.542 昆虫组织学180.5425 昆虫生理学180.543 昆虫生态学180.5435 昆虫病理学180.5445 昆虫行为学180.545 昆虫分类学180.5455 实验昆虫学180.546 昆虫病毒学180.5499 昆虫学其他学科180.57 动物学180.5711 动物生物物理学180.5714 动物生物化学180.5717 动物形态学180.5721 动物解剖学180.5724 动物组织学180.5727 动物细胞学180.5731 动物生理学180.5734 动物生殖生物学180.5737 动物生长发育学180.5741 动物遗传学180.5744 动物生态学180.5747 动物病理学180.5751 动物行为学180.5754 动物地理学180.5757 动物分类学180.5761 实验动物学180.5764 动物寄生虫学180.5767 动物病毒学180.5799 动物学其他学科180.61 微生物学180.611 微生物生物化学180.6115 微生物生理学180.612 微生物遗传学180.6125 微生物生态学180.613 微生物免疫学180.6135 微生物分类学180.614 真菌学180.6145 细菌学180.615 应用微生物学180.6199 微生物学其他学科180.64 病毒学180.641 病毒生物化学180.642 分子病毒学180.643 病毒生态学180.644 病毒分类学180.6499 病毒学其他学科180.67 人类学180.671 人类起源与演化学180.6715 人类形态学180.672 人类遗传学180.6725 分子人类学180.673 人类生态学180.6735 心理人类学180.674 古人类学180.6745 人种学180.675 人体测量学180.6799 人类学其他学科180.71 生物工程(亦称生物技术) 180.711 基因工程(亦称遗传工程) 180.712 细胞工程180.713 蛋白质工程180.714 酶工程180.715 发酵工程(亦称微生物工程) 180.7199 生物工程其他学科180.74 心理学180.741 心理学史180.7415 普通心理学180.742 生理心理学180.7425 认知心理学180.743 发展心理学180.7435 个性心理学180.744 缺陷心理学180.7445 比较心理学180.745 实验心理学180.7455 应用心理学180.7499 心理学其他学科180.99 生物学其他学科210 农学210.1 农业史210.2 农业基础学科210.201 农业数学210.202 农业气象学与农业气候学210.203 农业生物物理学210.204 农业生物化学210.205 农业生态学210.206 农业植物学210.207 农业微生物学210.208 植物营养学210.2099 农业基础学科其他学科210.3 农艺学210.301 作物形态学210.3015 作物生理学210.302 作物遗传学210.3025 作物生态学210.303 种子学210.3035 作物育种学与良种繁育学210.304 作物栽培学210.3045 作物耕作学210.305 作物种质资源学210.3055 农产品贮藏与加工210.3099 农艺学其他学科210.4 园艺学210.401 果树学210.402 瓜果学210.403 蔬菜学210.404 果蔬贮藏与加工210.405 茶学(包括茶加工等) 210.406 观赏园艺学210.4099 园艺学其他学科210.5 土壤学210.501 土壤物理学210.5015 土壤化学210.502 土壤地理学210.5025 土壤生物学210.503 土壤生态学210.5035 土壤耕作学210.504 土壤改良学210.5045 土壤肥料学210.505 土壤分类学210.5055 土壤调查与评价210.5099 土壤学其他学科210.6 植物保护学210.601 植物检疫学210.6015 植物免疫学210.602 植物病理学210.6025 植物药理学210.603 农业昆虫学210.6035 植物病毒学210.604 农药学210.6045 植物病虫害测报学210.605 抗病虫害育种210.6055 有害生物化学防治210.606 有害生物生物防治210.6065 有害生物综合防治210.607 杂草防治210.6075 鸟兽,鼠害防治210.6099 植物保护学其他学科210.7 农业工程210.701 农业机械学(包括农业机械制造等) 210.7015 农业机械化210.702 农业电气化与自动化210.7025 农田水利(包括灌溉工程、排水工程等) 210.703 水土保持学210.7035 农田测量210.704 农业环保工程210.7045 农业区划210.705 农业系统工程210.7099 农业工程其他学科210.99 农学其他学科220 林学220.1 林业基础学科220.101 森林气象学220.102 森林地理学220.103 森林水文学220.104 森林土壤学220.105 树木生理学220.106 森林生态学220.107 森林植物学220.1099 林业基础学科其他学科220.15 林木遗传育种学220.151 林木育种学220.152 林木遗传学220.1599 林木遗传育种学其他学科220.2 森林培育学(亦称造林学)220.25 森林经理学220.251 森林测计学220.252 森林测量学220.253 林业遥感220.254 林业信息管理220.255 林业系统工程220.2599 森林经理学其他学科220.3 森林保护学220.301 森林病理学220.302 森林昆虫学220.303 森林防火学220.3099 森林保护学其他学科220.35 野生动物保护与管理220.4 防护林学220.45 经济林学220.5 园林学220.501 园林植物学220.502 风景园林工程220.503 风景园林经营与管理220.5099 园林学其他学科220.55 林业工程220.551 森林采运学220.552 林业机械220.553 林业机械化与电气化220.554 木材学220.555 木材加工与人造板工艺学(包括家具设计与制造等)220.556 木材防腐学220.557 林产化学加工学220.5599 林业工程其他学科220.6 森林统计学220.65 林业经济学220.99 林学其他学科230 畜牧、兽医学230.1 畜牧、兽医学基础学科230.101 家畜生物化学230.102 家畜生理学230.103 家畜遗传学230.104 家畜生态学230.105 家畜微生物学230.1099 畜牧、兽医科学基础学科其他学科230.2 畜牧学230.201 家畜育种学230.2015 家畜繁殖学230.202 动物营养学230.2025 饲料学230.203 家畜饲养管理学230.2035 特种经济动物饲养学230.204 家畜行为学230.2045 家畜卫生学230.205 草原学(包括牧草学、牧草育种学、牧草栽培学、草地生态学、草地保护学等) 230.2055 畜产品贮藏与加工230.206 畜牧机械化230.2065 养禽学230.207 养蜂学230.2075 养蚕学230.208 畜牧经济学230.2099 畜牧学其他学科230.3 兽医学230.301 家畜解剖学230.3015 家畜组织胚胎学230.302 兽医免疫学230.3025 家畜病理学(亦称兽医病理学) 230.303 兽医药理学230.3035 兽医临床学230.304 兽医卫生检疫学230.3045 家畜寄生虫学230.305 家畜传染病学230.3055 家畜病毒学230.306 中兽医学230.3065 兽医器械学230.3099 兽医学其他学科230.99 畜牧、兽医学其他学科240 水产学240.1 水产学基础学科240.101 水产化学240.102 水产地理学240.103 水产生物学240.104 水域生态学240.1099 水产学基础学科其他学科240.15 水产增殖学240.2 水产养殖学240.25 水产饲料学240.3 水产保护学240.35 捕捞学240.4 水产品贮藏与加工240.45 水产工程学240.5 水产资源学240.55 水产经济学240.99 水产学其他学科310 基础医学310.11 医学生物化学310.14 人体解剖学310.141 系统解剖学310.142 局部解剖学310.1499 人体解剖学其他学科310.17 医学细胞生物学310.21 人体生理学310.24 人体组织胚胎学310.27 医学遗传学310.31 放射医学310.34 人体免疫学310.37 医学寄生虫学310.371 医学寄生虫免疫学310.372 医学昆虫学310.373 医学蠕虫学310.374 医学原虫学310.3799 医学寄生虫学其他学科310.41 医学微生物学(包括医学病毒学等)310.44 病理学310.441 病理生物学310.442 病理解剖学310.443 病理生理学310.444 免疫病理学310.445 实验病理学310.446 比较病理学310.447 系统病理学310.448 环境病理学310.4499 病理学其他学科310.47 药理学310.471 基础药理学310.472 临床药理学310.473 生化药理学310.474 分子药理学310.475 免疫药理学310.4799 药理学其他学科310.51 医学实验动物学310.54 医学心理学310.57 医学统计学310.61 生物医学工程学310.611 生物医学电子学310.612 临床工程学310.613 康复工程学310.614 生物医学测量学310.615 人工器官与生物医学材料学310.6199 生物医学工程学其他学科310.99 基础医学其他学科320 临床医学320.11 临床诊断学320.111 症状诊断学320.112 物理诊断学320.113 机能诊断学320.114 医学影像学(包括放射诊断学、同位素诊断学、超声诊断学等) 320.115 临床放射学320.116 实验诊断学320.1199 临床诊断学其他学科320.14 保健医学320.141 康复医学320.142 运动医学(包括力学运动医学等) 320.143 老年医学320.1499 保健医学其他学科320.17 理疗学320.21 麻醉学320.211 麻醉生理学320.212 麻醉药理学320.213 麻醉应用解剖学320.2199 麻醉学其他学科320.24 内科学320.241 心血管病学320.2415 呼吸病学320.242 结核病学320.2425 胃肠病学320.243 血液病学320.2435 肾脏病学320.244 内分泌学320.2445 风湿病学与自体免疫病学320.245 变态反应学320.2455 感染性疾病学320.2499 内科学其他学科320.27 外科学320.271 普通外科学320.2715 显微外科学320.272 神经外科学320.2725 颅脑外科学320.273 胸外科学320.2735 心血管外科学320.274 泌尿外科学320.2745 骨外科学320.275 烧伤外科学320.2755 整形外科学320.276 器官移植外科学320.2765 实验外科学320.2799 外科学其他学科320.31 妇产科学320.311 妇科学320.312 产科学320.313 围产医学(亦称围生医学) 320.314 助产学320.315 胎儿学320.316 妇科产科手术学320.3199 妇产科学其他学科320.34 儿科学320.41 耳鼻咽喉科学320.44 口腔医学320.441 口腔解剖生理学320.4415 口腔组织学与口腔病理学320.442 口腔材料学320.4425 口腔影像诊断学320.443 口腔内科学320.4435 口腔颌面外科学320.444 口腔矫形学320.4445 口腔正畸学320.445 口腔病预防学320.4499 口腔医学其他学科320.47 皮肤病学320.51 性医学320.54 神经病学320.57 精神病学(包括精神卫生及行为医学等) 320.61 急诊医学320.64 核医学320.67 肿瘤学320.671 肿瘤免疫学320.672 肿瘤病因学320.673 肿瘤病理学320.674 肿瘤诊断学320.675 肿瘤治疗学320.676 肿瘤预防学320.677 实验肿瘤学320.6799 肿瘤学其他学科320.71 护理学320.711 基础护理学320.712 专科护理学320.713 特殊护理学320.714 护理心理学320.715 护理伦理学320.716 护理管理学320.7199 护理学其他学科320.99 临床医学其他学科330 预防医学与卫生学330.11 营养学330.14 毒理学330.17 消毒学330.21 流行病学330.24 传染病学330.27 媒介生物控制学330.34 职业病学330.37 地方病学330.41 社会医学330.44 卫生检验学330.47 食品卫生学330.51 儿少卫生学330.54 妇幼卫生学330.57 环境卫生学330.61 劳动卫生学330.64 放射卫生学330.67 卫生工程学330.71 卫生经济学330.74 优生学330.77 健康教育学330.81 卫生管理学330.99 预防医学与卫生学其他学科340 军事医学与特种医学340.1 军事医学340.101 野战外科学340.1015 军队流行病学340.102 军事环境医学340.1025 军队卫生学340.103 军队卫生装备学340.1035 军事人机工效学340.104 核武器医学防护学340.1045 化学武器医学防护学340.105 生物武器医学防护学340.1055 激光与微波医学防护学340.1099 军事医学其他学科340.2 特种医学340.201 航空航天医学340.202 潜水医学340.203 航海医学340.204 法医学340.2099 特种医学其他学科340.99 军事医学与特种医学其他学科350 药学350.1 药物化学(包括天然药物化学等) 350.2 生物药物学350.25 微生物药物学350.3 放射性药物学350.35 药剂学350.4 药效学。
学科类词汇[资料]
![学科类词汇[资料]](https://img.taocdn.com/s3/m/6f7451e0bb0d4a7302768e9951e79b89680268e3.png)
学科类词汇科目,学科subject理科,科学science文科,艺术arts数学maths几何geometry代数algebra语文Chinese政治politics英语English历史history地理geography生物biology化学chemistry物理physics音乐music体育P.E.美术art劳技labor skill手工handwork常识general knowledge实践practice文学literature地质学geology社会学sociology哲学philosophy心理学psychology教育学pedagogy工程学engineering医学medicine农学agriculture天文学astronomy经济学economics法学law金融学,财政学finance建筑学architecture计算机科学computer science 人文学科humanities边缘学科borderline冰川学glaciology病理学pathology病理解剖学pathological病原学aetiology博物馆学museology测量学surveying测湿学psychrometry测温学thermometry测震学seismometry产科学obstetrics超声学ultrasonics板块学说plate tectonics簿记学,簿记bookkeeping材料科学materials science材料力学mechanics of materials 波动力学wave machanics词典学lexieography词汇学lexicology词汇统计学lexicostatistics弹道学ballistics内弹道学interior ballistics外弹道学exterior ballistics地球构造学geognosy地球物理学geophysics地名学toponomy地震学seismology地质学geology电磁学electromagnetics电动力学electrodynamics电工学electrical engineering电学electricity电子学electronics无线电子学radio-electronics动力学dynamics (kinetics)动物学zoology犯罪心理学criminal psychology 仿生学bionics分类学taxology符号学semiology古文字学paleography骨学osteology光学optics海洋气象学marine meteorology 海洋生物学marine biology汉学,中国学sinology航海天文学nautical astronomy 航空电子学avionics航空力学aeromechanics航空学aviation放射化学radio chemistry分析化学analytical chemistry生物化学biochemistry无机化学inorganic chemistry应用化学applized chemistry有机化学organic chemistry机器人学robotics计算机科学computer science寄生虫学parasitology价值学axiology建筑学architecture教育学pedagogy (education)教育心理学educational psychology 经济学economics静力学statics军事科学military science军事工程学military engineering考古学archaeology理科the science文科the humanities空气动力学aerodynamics空气力学aeromechanics会计学accounting矿物学mineralogy昆虫学entomology (insectology)力学mechanics动力学dynamics静力学statics流体力学fluid mechanics量子力学quantum mechanics临床学clinical medicine流行病学epidemiology伦理学ethics逻辑学logic美学aesthetics美育art education年代学chronology鸟类学ornithology农业土壤学agrology农艺学agronomy气候学climatology气体动力学aerodynamics气体力学pneumatics气象学meteorology球面几何学spherical geometry人口学demography神学theology声学acoustics声韵学phonology生态学ecology园艺学horticulture水力学hydraulics水利工程学hydraulic engineering水文学hydrology统计学statistics土壤学pedology微积分学calculus未来学futurology物理学physics地球物理学geophysics原子物理学atomic physics原子核物理学nuclear physics高能物理学high energy physics应用物理学applied physics天体物理学astrophysics力学mechanics热学heat热力学thermodynamics光学optics (photology)声学acoustics电学electricity磁学magnetism细菌学bacteriology细胞学cytology心理学psychology信息学informatics冶金学metallurgy遗传学genetics营养学nutriology语言学linguistics语源学etymology园艺学gardening运动学kinematics中药学traditional Chinese pharmacology 中医学traditional Chinese medicine主课main subject (major course)。
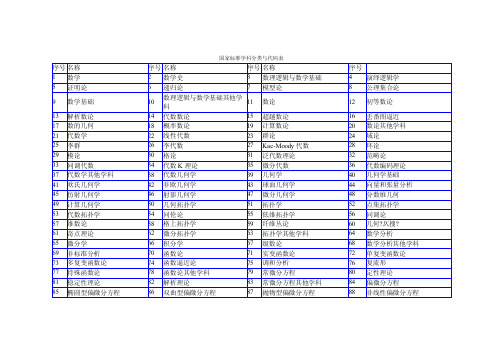
国家标准学科分类与代码表
207 弹性力学
208
210 蠕变
211 界面力学与表面力学
212
214 断裂力学
215 散体力学
216
218 结构力学
219 计算固体力学
220
222 振动与波
223 线性振动力学
224
226 随机振动力学
227 振动控制理论
228
230 振动与波其他学科
231 流体力学
232
234 气体动力学
235 空气动力学
236
238 粘性流体力学
239 多相流体力学
240
242 等离子体动力学
243 电磁流体力学
244
246 野生动物保护与管理
247 防护林学
248
250 园林植物学
251 风景园林工程
252
254 林业工程
255 森林采运学
256
258 木材学
259 木材加工与人造板工艺学 260
262 林业工程其他学科
35 微分代数 39 几何学
42 非欧几何学
43 球面几何学
46 射影几何学
47 微分几何学
50 几何拓扑学
51 拓扑学
54 同伦论 58 格上拓扑学
55 低维拓扑学 59 纤维丛论
62 微分拓扑学
63 拓扑学其他学科
66 积分学
67 级数论
70 函数论
71 实变函数论
74 函数逼近论 78 函数论其他学科
469 环境医学
470 职业病学
471 地方病学
473 卫生检验学
474 食品卫生学
475 儿少卫生学
477 环境卫生学
欧多克斯概述

欧多克斯概述1.欧多克斯生平简介:欧多克斯于公元前约400年生于奈得斯。
他是古希腊著名哲学家柏拉图的学生,欧多克斯在柏拉图学园中学习时,处境十分困难。
他的家庭很贫困,所以就只能选择住在雅典的港口比雷埃夫斯,因为这里可以找到比较便宜的的住处。
但是这样他每天往返学校就不得不走十英里。
但这些困难都没有阻挡住欧多克斯求知和学习的欲望,他在柏拉图学园毕业后到了埃及,开始进行天文学的我们今天称作研究生的学业。
后来欧多克斯在今天土耳其西北岸的锡塞克斯创办了他自己的学校,最后他把学校迁到雅典,在那里任教多年。
那时他已成为公认的很有成就的哲学家。
他再次拜访了过去的老师柏拉图,主人专为他举行了宴会。
(当公元前367年柏拉图在西西里时,欧多克斯甚至可能还是柏拉图学园的积极负责人。
)欧多克斯在几何学,天文学和医学等方面都有突出的贡献。
在这些年里,他提出了许多几何证法,后来被纳入欧几里得所总结的几何学。
他还对不能直接确定其长度和面积的图形的近似值开始进行研究,这在一百年后由阿基米德作了进一步的发展。
欧多克斯是证明一年不是整三百六十五天而是三百六十五天又六小时的第一个希腊人。
因为埃及人对此已有所了解,所以欧多克斯只不过是把这传到了希腊,而并不是他发现的。
他接受了柏拉图关于行星必须在正圆轨道上运行的观点。
然而他在观察了行星运动之后不得不承认,行星的实际运动并不是正圆轨道上的匀速运动。
为了当时所谓的“保全面子”,他是第一个试图修改柏拉图理论使之适合观察到的实际情况的人。
他认为行星在其中转动的球体的两极在另一球体中转动,而第二个球体的两极又在第三个球体中转动,以此类推。
每个球体的转动是匀速的,但各球体的转速及一球体的两极与其相挨球体两极的倾斜度总和构成行星的全部运动,而这各运动就是实际观察到的不规则运动。
就是这样,把完美的规则性来就得出观察到的不规则的不完美性。
这就保全了面子,也保全了柏拉图。
欧多克斯还画了一幅新的胜过赫克特斯的地图。
中华人民共和国国家标准GBT13745-92

中华人民共和国国家标准 GB/T 13745-92学科分类与代码(三位数字为一级学科,小数点后两位数字的为二级学科,小数点后三位数字的为三级学科)110 数学110.11 数学史110.14 数理逻辑与数学基础110.1410 演绎逻辑学110.1420 证明论110.1430 递归论110.1440 模型论110.1450 公理集合论110.1460 数学基础110.1499 数理逻辑与数学基础其他学科110.17 数论110.1710 初等数论110.1720 解析数论110.1730 代数数论110.1740 超越数论110.1750 丢番图逼近110.1760 数的几何110.1770 概率数论110.1780 计算数论110.1799 数论其他学科110.21 代数学110.2110 线性代数110.2115 群论110.2120 域论110.2125 李群110.2130 李代数110.2135 Kac-Moody代数110.2140 环论110.2145 模论110.2150 格论110.2155 泛代数理论110.2160 范畴论110.2165 同调代数110.2170 代数K理论110.2180 代数编码理论110.2199 代数学其他学科110.24 代数几何学110.27 几何学110.2710 几何学基础110.2715 欧氏几何学110.2720 非欧几何学110.2725 球面几何学110.2730 向量和张量分析110.2735 仿射几何学110.2740 射影几何学110.2745 微分几何学110.2750 分数维几何110.2755 计算几何学110.2799 几何学其他学科110.31 拓扑学110.3110 点集拓扑学110.3115 代数拓扑学110.3120 同伦论110.3125 低维拓扑学110.3130 同调论110.3135 维数论110.3140 格上拓扑学110.3145 纤维丛论110.3150 几何拓扑学110.3155 奇点理论110.3160 微分拓扑学110.3199 拓扑学其他学科110.34 数学分析110.3410 微分学110.3420 积分学110.3430 级数论110.3499 数学分析其他学科110.37 非标准分析110.41 函数论110.4110 实变函数论110.4120 单复变函数论110.4130 多复变函数论110.4140 函数逼近论110.4150 调和分析110.4160 复流形110.4170 特殊函数论110.4199 函数论其他学科110.4410 定性理论110.4420 稳定性理论110.4430 解析理论110.4499 常微分方程其他学科110.47 偏微分方程110.4710 椭圆型偏微分方程110.4720 双曲型偏微分方程110.4730 抛物型偏微分方程110.4740 非线性偏微分方程110.4799 偏微分方程其他学科110.51 动力系统110.5110 微分动力系统110.5120 拓扑动力系统110.5130 复动力系统110.5199 动力系统其他学科110.54 积分方程110.57 泛函分析110.5710 线性算子理论110.5715 变分法110.5720 拓扑线性空间110.5725 希尔伯特空间110.5730 函数空间110.5735 巴拿赫空间110.5740 算子代数110.5745 测度与积分110.5750 广义函数论110.5755 非线性泛函分析110.5799 泛函分析其他学科110.61 计算数学110.6110 插值法与逼近论110.6120 常微分方程数值解110.6130 偏微分方程数值解110.6140 积分方程数值解110.6150 数值代数110.6160 连续问题离散化方法110.6170 随机数值实验110.6180 误差分析110.6199 计算数学其他学科110.64 概率论110.6410 几何概率110.6420 概率分布110.6430 极限理论110.6440 随机过程110.6460 随机分析110.6470 鞅论110.6480 应用概率论110.6499 概率论其他学科110.67 数理统计学110.6710 抽样理论110.6715 假设检验110.6720 非参数统计110.6725 方差分析110.6730 相关回归分析110.6735 统计推断110.6740 贝叶斯统计110.6745 试验设计110.6750 多元分析110.6755 统计判决理论110.6760 时间序列分析110.6799 数理统计学其他学科110.71 应用统计数学110.7110 统计质量控制110.7120 可靠性数学110.7130 保险数学110.7140 统计模拟110.7199 应用统计数学其他学科110.74 运筹学110.7410 线性规划110.7415 非线性规划110.7420 动态规划110.7425 组合最优化110.7430 参数规划110.7435 整数规划110.7440 随机规划110.7445 排队论110.7450 对策论110.7455 库存论110.7460 决策论110.7465 搜索论110.7470 图论110.7475 统筹论110.7480 最优化110.7499 运筹学其他学科110.77 组合数学110.81 离散数学110.84 模糊数学110.87 应用数学110.99 数学其他学科120 信息科学与系统科学120.10 信息科学与系统科学基础学科120.101 信息论120.102 控制论120.103 系统论120.1099 信息科学与系统科学基础学科其他学科120.20 系统学120.2010 混沌120.2020 一般系统论120.2030 耗散结构理论120.2040 协同学120.2050 突变论120.2060 超循环论120.2099 系统学其他学科120.30 控制理论120.3010 大系统理论120.3020 系统辩识120.3030 状态估计120.3040 鲁棒控制120.3099 控制理论其他学科120.40 系统评估与可行性分析120.50 系统工程方法论120.5010 系统建模120.5099 系统工程方法论其他学科120.60 系统工程120.99 信息科学与系统科学其他学科130 力学130.10 基础力学130.1010 理论力学130.1020 理性力学130.1030 非线性力学130.1040 连续介质力学130.1050 摩擦学130.1060 柔性多体力学130.1070 陀螺力学130.1080 飞行力学130.1099 基础力学其他学科130.15 固体力学130.1510 弹性力学130.1515 塑性力学130.1520 粘弹性、粘塑性力学130.1525 蠕变130.1530 界面力学与表面力学130.1535 疲劳130.1540 损伤力学130.1545 断裂力学130.1550 散体力学130.1555 细观力学130.1560 电磁固体力学130.1565 结构力学130.1570 计算固体力学130.1575 实验固体力学130.1599 固体力学其他学科130.20 振动与波130.2010 线性振动力学130.2020 非线性振动力学130.2030 弹性体振动力学130.2040 随机振动力学130.2050 振动控制理论130.2060 固体中的波130.2070 流体—固体耦合振动130.2099 振动与波其他学科130.25 流体力学130.2511 理论流体力学130.2514 水动力学130.2517 气体动力学130.2521 空气动力学130.2524 悬浮体力学130.2527 湍流理论130.2531 粘性流体力学130.2534 多相流体力学130.2537 渗流力学130.2541 物理—化学流体力学130.2544 等离子体动力学130.2547 电磁流体力学130.2551 非牛顿流体力学130.2554 流体机械流体力学130.2557 旋转与分层流体力学130.2561 辐射流体力学130.2564 计算流体力学130.2567 实验流体力学130.2571 环境流体力学130.2599 流体力学其他学科130.30 流变学130.35 爆炸力学130.3510 爆轰与爆燃理论130.3520 爆炸波、冲击波、应力波130.3530 高速碰撞动力学130.3599 爆炸力学其他学科130.40 物理力学130.4010 高压固体物理力学130.4020 稠密流体物理力学130.4030 高温气体物理力学130.4040 多相介质物理力学130.4050 临界现象与相变130.4060 原子与分子动力学130.4099 物理力学其他学科130.45 统计力学130.50 应用力学130.99 力学其他学科140 物理学140.10 物理学史140.15 理论物理学140.1510 数学物理140.1520 电磁场理论140.1530 经典场论140.1540 相对论与引力场140.1550 量子力学140.1560 统计物理学140.1599 理论物理学其他学科140.20 声学140.2010 物理声学140.2020 非线性声学140.2030 量子声学140.2040 超声学140.2050 水声学140.2060 应用声学140.2099 声学其他学科140.25 热学140.2510 热力学140.2520 热物性学140.2530 传热学140.2599 热学其他学科140.30 光学140.3010 几何光学140.3015 物理光学140.3020 非线性光学140.3025 光谱学140.3030 量子光学140.3035 信息光学140.3040 导波光学140.3045 发光学140.3050 红外物理140.3055 激光物理140.3060 应用光学140.3099 光学其他学科140.35 电磁学140.3510 电学140.3520 静电学140.3530 静磁学140.3540 电动力学140.3599 电磁学其他学科140.40 无线电物理140.4010 电磁波物理140.4020 量子无线电物理140.4030 微波物理学140.4040 超高频无线电物理140.4050 统计无线电物理140.4099 无线电物理其他学科140.45 电子物理学140.4510 量子电子学140.4520 电子离子与真空物理140.4530 带电粒子光学140.4599 电子物理学其他学科140.50 凝聚态物理学140.5010 凝聚态理论140.5015 金属物理学140.5020 半导体物理学140.5025 电介质物理学140.5030 晶体学140.5035 非晶态物理学140.5040 液晶物理学140.5045 薄膜物理学140.5050 低维物理140.5055 表面与界面物理学140.5060 固体发光140.5065 磁学140.5070 超导物理学140.5075 低温物理学140.5080 高压物理学140.5099 凝聚态物理学其他学科140.55 等离子体物理学140.5510 热核聚变等离子体物理学140.5520 低温等离子体物理学140.5530 等离子体光谱学140.5540 凝聚态等离子体物理学140.5550 非中性等离子体物理学140.5599 等离子体物理学其他学科140.60 原子分子物理学140.6010 原子与分子理论140.6020 原子光谱学140.6030 分子光谱学140.6040 波谱学140.6050 原子与分子碰撞过程140.6099 原子分子物理学其他学科140.65 原子核物理学140.6510 核结构140.6515 核能谱学140.6520 低能核反应140.6525 中子物理学140.6530 裂变物理学140.6535 聚变物理学140.6540 轻粒子核物理学140.6545 重离子核物理学140.6550 中高能核物理学140.6599 原子核物理学其他学科140.70 高能物理学140.7010 基本粒子物理学140.7020 宇宙线物理学140.7030 粒子加速器物理学140.7040 高能物理实验140.7099 高能物理学其他学科140.75 计算物理学140.80 应用物理学140.99 物理学其他学科150 化学150.10 化学史150.15 无机化学150.1510 元素化学150.1520 配位化学150.1530 同位素化学150.1540 无机固体化学150.1550 无机合成化学150.1560 无机分离化学150.1570 物理无机化学150.1580 生物无机化学150.1599 无机化学其他学科150.20 有机化学150.2010 元素有机化学150.2020 天然产物有机化学150.2030 有机固体化学150.2040 有机合成化学150.2050 有机光化学150.2060 物理有机化学150.2070 生物有机化学150.2099 有机化学其他学科150.25 分析化学150.2510 化学分析150.2515 电化学分析150.2520 光谱分析150.2525 波谱分析150.2530 质谱分析150.2535 热谱分析150.2540 色谱分析150.2545 光度分析150.2550 放射分析150.2555 状态分析与物相分析150.2560 分析化学计量学150.2599 分析化学其他学科150.30 物理化学150.3010 化学热力学150.3015 化学动力学150.3020 结构化学150.3025 量子化学150.3030 胶体化学与界面化学150.3035 催化化学150.3040 热化学150.3045 光化学150.3050 电化学150.3055 磁化学150.3060 高能化学150.3065 计算化学150.3099 物理化学其他学科150.35 化学物理学150.40 高分子物理150.45 高分子化学150.4510 无机高分子化学150.4520 天然高分子化学150.4530 功能高分子150.4540 高分子合成化学150.4550 高分子物理化学150.4560 高分子光化学150.4599 高分子化学其他学科150.50 核化学150.5010 放射化学150.5020 核反应化学150.5030 裂变化学150.5040 聚变化学150.5050 重离子核化学150.5060 核转变化学150.5070 环境放射化学150.5099 核化学其他学科150.55 应用化学150.99 化学其他学科160 天文学160.10 天文学史160.15 天体力学160.1510 摄动理论160.1520 天体力学定性理论160.1530 天体形状与自转理论160.1540 天体力学数值方法160.1550 天文动力学160.1560 历书天文学160.1599 天体力学其他学科160.20 天体物理学160.2010 理论天体物理学160.2020 相对论天体物理学160.2030 等离子体天体物理学160.2040 高能天体物理学160.2050 实测天体物理学160.2099 天体物理学其他学科160.25 天体化学160.30 天体测量学160.3010 天文地球动力学160.3020 基本天体测量学160.3030 照相天体测量学160.3040 射电天体测量学160.3050 空间天体测量学160.3060 方位天文学160.3070 实用天文学160.3099 天体测量学其他学科160.35 射电天文学160.3510 射电天体物理学160.3520 射电天文方法160.3599 射电天文学其他学科160.40 空间天文学160.4010 红外天文学160.4020 紫外天文学160.4030 X射线天文学160.4040 r射线天文学160.4050 中微子天文学160.4099 空间天文学其他学科160.45 天体演化学160.50 星系与宇宙学160.5010 星系动力学160.5020 星系天文学160.5030 运动宇宙学160.5040 星系际物质160.5050 大爆炸宇宙论160.5060 星系形成与演化160.5070 宇宙大尺度结构起源与演化160.5099 星系与宇宙学其他学科160.55 恒星与银河系160.5510 恒星物理学160.5520 恒星天文学160.5530 恒星形成与演化160.5540 星际物质物理学160.5550 银河系结构与运动160.5599 恒星与银河系其他学科160.60 太阳与太阳系160.6010 太阳物理学160.6020 太阳系物理学160.6030 太阳系形成与演化160.6040 行星物理学160.6050 行星际物理学160.6060 陨星学160.6099 太阳与太阳系其他学科160.65 天体生物学160.99 天文学其他学科170 地球科学170.10 地球科学史170.15 大气科学170.1510 大气物理学170.1515 大气化学170.1520 大气探测170.1525 动力气象学170.1530 天气学170.1535 气候学170.1540 云与降水物理学170.1545 应用气象学170.1599 大气科学其他学科170.20 固体地球物理学170.2010 地球动力学170.2015 地球重力学170.2020 地球流体力学170.2025 地壳与地形变170.2030 地球内部物理学170.2035 地声学170.2040 地热学170.2045 地电学170.2050 地磁学170.2055 放射性地球物理学170.2060 地震学170.2065 勘探地球物理学170.2070 计算地球物理学170.2075 实验地球物理学170.2099 固体地球物理学其他学科170.25 空间物理学170.2510 电离层物理学170.2520 高层大气物理学170.2530 磁层物理学170.2540 空间物理探测170.2550 空间环境学170.2599 空间物理学其他学科170.30 地球化学170.3010 元素地球化学170.3015 有机地球化学170.3020 放射性地球化学170.3025 同位素地球化学170.3030 生物地球化学170.3035 地球内部化学170.3040 同位素地质年代学170.3045 成矿地球化学170.3050 勘探地球化学170.3055 实验地球化学170.3099 地球化学其他学科170.35 大地测量学170.3510 地球形状学170.3520 几何大地测量学170.3530 物理大地测量学170.3540 动力大地测量学170.3550 空间大地测量学170.3560 行星大地测量学170.3599 大地测量学其他学科170.40 地图学170.45 地理学170.4510 自然地理学170.4520 人文地理学170.4599 地理学其他学科170.50 地质学170.5011 数学地质学170.5014 地质力学170.5017 动力地质学170.5021 矿物学170.5024 矿床学与矿相学170.5027 岩石学170.5031 岩土力学170.5034 沉积学170.5037 古地理学170.5041 古生物学170.5044 地层学与地史学170.5047 前寒武纪地质学170.5051 第四纪地质学170.5054 构造地质学170.5057 大地构造学170.5061 勘查地质学170.5064 水文地质学170.5067 遥感地质学170.5071 区域地质学170.5074 火山学170.5077 石油与天然气地质学170.5081 煤田地质学170.5084 实验地质学170.5099 地质学其他学科170.55 水文学170.5510 水文物理学170.5515 水文化学170.5520 水文地理学170.5525 水文气象学170.5530 水文测量170.5535 水文图学170.5540 湖沼学170.5545 河流学与河口水文学170.5599 水文学其他学科170.60 海洋科学170.6010 海洋物理学170.6015 海洋化学170.6020 海洋地球物理学170.603 海洋地质学170.6035 物理海洋学170.604 海洋生物学170.6045 河口、海岸学170.605 海洋调查与监测170.6099 海洋科学其他学科170.99 地球科学其他学科180 生物学180.11 生物数学180.14 生物物理学180.1410 生物信息论与生物控制论180.1415 生物力学180.1420 理论生物物理学180.1425 生物声学与声生物物理学180.1430 生物光学与光生物物理学180.1435 生物电磁学180.1440 生物能量学180.1445 低温生物物理学180.1450 分子生物物理学180.1455 空间生物物理学180.1460 仿生学180.1465 系统生物物理学180.1499 生物物理学其他学科180.17 生物化学180.1710 多肽与蛋白质生物化学180.1715 核酸生物化学180.1720 多糖生物化学180.1725 脂类生物化学180.1730 酶学180.1735 膜生物化学180.1740 激素生物化学180.1745 生殖生物化学180.1750 免疫生物化学180.1755 毒理生物化学180.1760 比较生物化学180.1765 应用生物化学180.1799 生物化学其他学科180.21 细胞生物学180.2110 细胞生物物理学180.2120 细胞结构与形态学180.2130 细胞生理学180.2140 细胞进化学180.2150 细胞免疫学180.2199 细胞生物学其他学科180.24 生理学180.2411 形态生理学180.2414 新陈代谢与营养生理学180.2417 心血管生理学180.2421 呼吸生理学180.2424 消化生理学180.2427 血液生理学180.2431 泌尿生理学180.2434 内分泌生理学180.2437 感官生理学180.2441 生殖生理学180.2444 骨骼生理学180.2447 肌肉生理学180.2451 皮肤生理学180.2454 循环生理学180.2457 比较生理学180.2461 年龄生理学180.2464 特殊环境生理学180.2467 语言生理学180.2499 生理学其他学科180.27 发育生物学180.31 遗传学180.3110 数量遗传学180.3115 生化遗传学180.3120 细胞遗传学180.3125 体细胞遗传学180.3130 发育遗传学180.3135 分子遗传学180.3140 辐射遗传学180.3145 进化遗传学180.3150 生态遗传学180.3155 免疫遗传学180.3160 毒理遗传学180.3165 行为遗传学180.3170 群体遗传学180.3199 遗传学其他学科180.34 放射生物学180.3410 放射生物物理学180.3420 细胞放射生物学180.3430 放射生理学180.3440 分子放射生物学180.3450 放射免疫学180.3499 放射生物学其他学科180.37 分子生物学180.41 生物进化论180.44 生态学180.4410 数学生态学180.4415 化学生态学180.4420 生理生态学180.4425 生态毒理学180.4430 区域生态学180.4435 种群生态学180.4440 群落生态学180.4445 生态系统生态学180.4450 生态工程学180.4499 生态学其他学科180.47 神经生物学180.4710 神经生物物理学180.4715 神经生物化学180.4720 神经形态学180.4725 细胞神经生物学180.4730 神经生理学180.4735 发育神经生物学180.4740 分子神经生物学180.4745 比较神经生物学180.4750 系统神经生物学180.4799 神经生物学其他学科180.51 植物学180.5110 植物化学180.5115 植物生物物理学180.5120 植物生物化学180.5125 植物形态学180.5130 植物解剖学180.5135 植物细胞学180.5140 植物生理学180.5145 植物胚胎学180.5150 植物发育学180.5155 植物遗传学180.5160 植物生态学180.5165 植物地理学180.5170 植物群落学180.5175 植物分类学180.5180 实验植物学180.5185 植物寄生虫学180.5199 植物学其他学科180.5410 昆虫生物化学180.5415 昆虫形态学180.5420 昆虫组织学180.5425 昆虫生理学180.5430 昆虫生态学180.5435 昆虫病理学180.5440 昆虫毒理学180.5445 昆虫行为学180.5450 昆虫分类学180.5455 实验昆虫学180.5460 昆虫病毒学180.5499 昆虫学其他学科180.57 动物学180.5711 动物生物物理学180.5714 动物生物化学180.5717 动物形态学180.5721 动物解剖学180.5724 动物组织学180.5727 动物细胞学180.5731 动物生理学180.5734 动物生殖生物学180.5737 动物生长发育学180.5741 动物遗传学180.5744 动物生态学180.5747 动物病理学180.5751 动物行为学180.5754 动物地理学180.5757 动物分类学180.5761 实验动物学180.5764 动物寄生虫学180.5767 动物病毒学180.5799 动物学其他学科180.61 微生物学180.6110 微生物生物化学180.6115 微生物生理学180.6120 微生物遗传学180.6125 微生物生态学180.6130 微生物免疫学180.6135 微生物分类学180.6140 真菌学180.6145 细菌学180.6150 应用微生物学180.6199 微生物学其他学科180.6410 病毒生物化学180.6420 分子病毒学180.6430 病毒生态学180.6440 病毒分类学180.6499 病毒学其他学科180.67 人类学180.6710 人类起源与演化学180.6715 人类形态学180.6720 人类遗传学180.6725 分子人类学180.6730 人类生态学180.6735 心理人类学180.6740 古人类学180.6745 人种学180.6750 人体测量学180.6799 人类学其他学科180.71 生物工程180.7110 基因工程180.7120 细胞工程180.7130 蛋白质工程180.7140 酶工程180.7150 发酵工程180.7199 生物工程其他学科180.74 心理学180.7410 心理学史180.7415 普通心理学180.7420 生理心理学180.7425 认知心理学180.7430 发展心理学180.7435 个性心理学180.7440 缺陷心理学180.7445 比较心理学180.7450 实验心理学180.7455 应用心理学180.7499 心理学其他学科180.99 生物学其他学科210 农学210.10 农业史210.20 农业基础学科210.2010 农业数学210.2020 农业气象学与农业气候学210.2030 农业生物物理学210.2040 农业生物化学210.2050 农业生态学210.2060 农业植物学210.2070 农业微生物学210.2080 植物营养学210.2099 农业基础学科其他学科210.30 农艺学210.3010 作物形态学210.3015 作物生理学210.3020 作物遗传学210.3025 作物生态学210.3030 种子学210.3035 作物育种学与良种繁育学210.3040 作物栽培学210.3045 作物耕作学210.3050 作物种质资源学210.3055 农产品贮藏与加工210.3099 农艺学其他学科210.40 园艺学210.4010 果树学210.4020 瓜果学210.4030 蔬菜学210.4040 果蔬贮藏与加工210.4050 茶学210.4060 观赏园艺学210.4099 园艺学其他学科210.50 土壤学210.5010 土壤物理学210.5015 土壤化学210.5020 土壤地理学210.5025 土壤生物学210.5030 土壤生态学210.5035 土壤耕作学210.5040 土壤改良学210.5045 土壤肥料学210.5050 土壤分类学210.5055 土壤调查与评价210.5099 土壤学其他学科210.60 植物保护学210.6010 植物检疫学210.6015 植物免疫学210.6020 植物病理学210.6025 植物药理学210.6030 农业昆虫学210.6035 植物病毒学210.6040 农药学210.6045 植物病虫害测报学210.6050 抗病虫害育种210.6055 有害生物化学防治210.6060 有害生物生物防治210.6065 有害生物综合防治210.6070 杂草防治210.6075 鸟兽、鼠害防治210.6099 植物保护学其他学科210.70 农业工程210.7010 农业机械学210.7015 农业机械化210.7020 农业电气化与自动化210.7025 农田水利210.7030 水土保持学210.7035 农田测量210.7040 农业环保工程210.7045 农业区划210.7050 农业系统工程210.7099 农业工程其他学科210.99 农学其他学科220 林学220.10 林业基础学科220.1010 森林气象学220.1020 森林地理学220.1030 森林水文学220.1040 森林土壤学220.1050 树木生理学220.1060 森林生态学220.1070 森林植物学220.1099 林业基础学科其他学科220.15 林木遗传育种学220.1510 林木育种学220.1520 林木遗传学220.1599 林木遗传育种学其他学科220.20 森林培育学220.25 森林经理学220.2510 森林测计学220.2520 森林测量学220.2530 林业遥感220.2540 林业信息管理220.2550 林业系统工程220.2599 森林经理学其他学科220.30 森林保护学220.3010 森林病理学220.3020 森林昆虫学220.3030 森林防火学220.3099 森林保护学其他学科220.35 野生动物保护与管理220.40 防护林学220.45 经济林学220.50 园林学220.5010 园林植物学220.5020 风景园林工程220.5030 风景园林经营与管理220.5099 园林学其他学科220.55 林业工程220.5510 森林采运学220.5520 林业机械220.5530 林业机械化与电气化220.5540 木材学220.5550 木材加工与人造板工艺学220.5560 木材防腐学220.5570 林产化学加工学220.5599 林业工程其他学科220.60 森林统计学220.65 林业经济学220.99 林学其他学科230 畜牧、兽医科学230.10 畜牧、兽医科学基础学科230.1010 家畜生物化学230.1020 家畜生理学230.1030 家畜遗传学230.1040 家畜生态学230.1050 家畜微生物学230.1099 畜牧、兽医科学基础学科其他学科230.20 畜牧学230.2010 家畜育种学230.2015 家畜繁殖学230.2020 动物营养学230.2025 饲料学230.2030 家畜饲养管理学230.2035 特种经济动物饲养学230.2040 家畜行为学230.2045 家畜卫生学230.2050 草原学230.2055 畜产品贮藏与加工230.2060 畜牧机械化230.2065 养禽学230.2070 养蜂学230.2075 养蚕学230.2080 畜牧经济学230.2099 畜牧学其他学科230.30 兽医学230.3010 家畜解剖学230.3015 家畜组织胚胎学230.3020 兽医免疫学230.3025 家畜病理学230.3030 兽医药理学230.3035 兽医临床学230.3040 兽医卫生检疫学230.3045 家畜寄生虫学230.3050 家畜传染病学230.3055 家畜病毒学230.3060 中兽医学230.3065 兽医器械学230.3099 兽医学其他学科230.99 畜牧、兽医科学其他学科240 水产学240.10 水产学基础学科240.1010 水产化学240.1020 水产地理学240.1030 水产生物学240.1040 水域生态学240.1099 水产学基础学科其他学科240.15 水产增殖学240.20 水产养殖学240.25 水产饲料学240.30 水产保护学240.35 捕捞学240.40 水产品贮藏与加工240.45 水产工程学240.50 水产资源学240.55 水产经济学240.99 水产学其他学科310 基础医学310.11 医学生物化学310.14 人体解剖学310.1410 系统解剖学310.1420 局部解剖学310.1499 人体解剖学其他学科310.17 医学细胞生物学310.24 人体组织胚胎学310.27 医学遗传学310.31 放射医学310.34 人体免疫学310.37 医学寄生虫学310.3710 医学寄生虫免疫学310.3720 医学昆虫学310.3730 医学蠕虫学310.3740 医学原虫学310.3799 医学寄生虫学其他学科310.41 医学微生物学310.44 病理学310.4410 病理生物学310.4420 病理解剖学310.4430 病理生理学310.4440 免疫病理学310.4450 实验病理学310.4460 比较病理学310.4470 系统病理学310.4480 环境病理学310.4499 病理学其他学科310.47 药理学310.4710 基础药理学310.4720 临床药理学310.4730 生化药理学310.4740 分子药理学310.4750 免疫药理学310.4799 药理学其他学科310.51 医学实验动物学310.54 医学心理学310.57 医学统计学310.61 生物医学工程学310.6110 生物医学电子学310.6120 临床工程学310.6130 康复工程学310.6140 生物医学测量学310.6150 人工器官与生物医学材料学310.6199 生物医学工程学其他学科310.99 基础医学其他学科320 临床医学320.11 临床诊断学320.1110 症状诊断学320.1120 物理诊断学320.1140 医学影象学320.1150 临床放射学320.1160 实验诊断学320.1199 临床诊断学其他学科320.14 保健医学320.1410 康复医学320.1420 运动医学320.1430 老年医学320.1499 保健医学其他学科320.17 理疗学320.21 麻醉学320.2110 麻醉生理学320.2120 麻醉药理学320.2130 麻醉应用解剖学320.2199 麻醉学其他学科320.24 内科学320.2410 心血管病学320.2415 呼吸病学320.2420 结核病学320.2425 胃肠病学320.2430 血液病学320.2435 肾脏病学320.2440 内分泌学320.2445 风湿病学与自体免疫病学320.2450 变态反应学320.2455 感染性疾病学320.2499 内科学其他学科320.27 外科学320.2710 普通外科学320.2715 显微外科学320.2720 神经外科学320.2725 颅脑外科学320.2730 胸外科学320.2735 心血管外科学320.2740 泌尿外科学320.2745 骨外科学320.2750 烧伤外科学320.2755 整形外科学320.2760 器官移植外科学320.2765 实验外科学320.2799 外科学其他学科320.31 妇产科学320.3110 妇科学320.3120 产科学320.3130 围产医学320.3140 助产学320.3150 胎儿学320.3160 妇科产科手术学320.3199 妇产科学其他学科320.34 儿科学320.37 眼科学320.41 耳鼻咽喉科学320.44 口腔医学320.4410 口腔解剖生理学320.4415 口腔组织学与口腔病理学320.4420 口腔材料学320.4425 口腔影象诊断学320.4430 口腔内科学320.4435 口腔颌面外科学320.4440 口腔矫形学320.4445 口腔正畸学320.4450 口腔病预防学320.4499 口腔医学其他学科320.47 皮肤病学320.51 性医学320.54 神经病学320.57 精神病学320.61 急诊医学320.64 核医学320.67 肿瘤学320.6710 肿瘤免疫学320.6720 肿瘤病因学320.6730 肿瘤病理学320.6740 肿瘤诊断学320.6750 肿瘤治疗学320.6760 肿瘤预防学320.6770 实验肿瘤学320.6799 肿瘤学其他学科320.71 护理学320.7110 基础护理学320.7120 专科护理学320.7130 特殊护理学320.7140 护理心理学320.7150 护理伦理学320.7160 护理管理学320.7199 护理学其他学科320.99 临床医学其他学科330 预防医学与卫生学330.11 营养学330.14 毒理学330.17 消毒学330.21 流行病学330.24 传染病学330.27 媒介生物控制学330.31 环境医学330.34 职业病学330.37 地方病学330.41 社会医学330.44 卫生检验学330.47 食品卫生学330.51 儿少卫生学330.54 妇幼卫生学330.57 环境卫生学330.61 劳动卫生学330.64 放射卫生学330.67 卫生工程学330.71 卫生经济学330.74 优生学330.77 健康教育学330.81 卫生管理学330.99 预防医学与卫生学其他学科340 军事医学与特种医学340.10 军事医学340.1010 野战外科学340.1015 军队流行病学340.1020 军事环境医学340.1025 军队卫生学340.1030 军队卫生装备学340.1035 军事人机工效学340.1040 核武器医学防护学340.1045 化学武器医学防护学340.1050 生物武器医学防护学340.1055 激光与微波医学防护学340.1099 军事医学其他学科340.20 特种医学340.2010 航空航天医学340.2020 潜水医学340.2030 航海医学340.2040 法医学340.2099 特种医学其他学科340.99 军事医学与特种医学其他学科350 药学350.10 药物化学350.20 生物药物学350.25 微生物药物学350.30 放射性药物学350.35 药剂学350.40 药效学350.45 药物管理学350.50 药物统计学350.99 药学其他学科360 中医学与中药学360.10 中医学360.1011 中医基础理论360.1014 中医诊断学360.1017 中医内科学360.1021 中医外科学360.1024 中医骨伤科学360.1027 中医妇科学360.1031 中医儿科学360.1034 中医眼科学360.1037 中医耳鼻咽喉科学360.1041 中医口腔科学360.1044 中医老年病学360.1047 针灸学360.1051 按摩推拿学360.1054 中医养生康复学360.1057 中医护理学360.1061 中医食疗学360.1064 方剂学360.1067 中医文献学360.1099 中医学其他学科360.20 民族医学360.30 中西医结合医学360.40 中药学360.4010 中药化学360.4015 中药药理学360.4020 本草学360.4025 药用植物学360.4030 中药鉴定学360.4035 中药炮制学360.4040 中药药剂学360.4045 中药资源学360.4050 中药管理学360.4099 中药学其他学科360.99 中医学与中药学其他学科410 工程与技术科学基础学科410.10 工程数学410.15 工程控制论410.20 工程力学410.25 工程物理学410.30 工程地质学410.35 工程水文学410.40 工程仿生学410.45 工程心理学410.50 标准化科学技术410.55 计量学410.60 工程图学410.65 勘查技术410.70 工程通用技术410.7010 密封技术410.7020 粉末技术410.7030 真空技术410.7040 薄膜技术410.7050 爆破技术410.7060 包装技术410.7070 照相技术410.7080 物料搬运技术410.7099 工程通用技术其他学科410.75 工业工程学410.99 工程与技术科学基础学科其他学科420 测绘科学技术420.10 大地测量技术420.1010 大地测量定位420.1020 重力测量420.1030 测量平差420.1099 大地测量技术其他学科420.20 摄影测量与遥感技术420.2010 地物波谱学420.2020 近景摄影测量420.2030 航空摄影测量420.2040 遥感信息工程420.2099 摄影测量与遥感技术其他学科420.30 地图制图技术420.3010 地图投影学420.3020 地图设计与编绘420.3030 图形图象复制技术420.3040 地理信息系统420.3099 地图制图技术其他学科420.40 工程测量技术420.4010 地籍测量420.4020 精密工程测量420.4099 工程测量技术其他学科420.50 海洋测绘420.5010 海洋大地测量420.5015 海洋重力测量420.5020 海洋磁力测量420.5025 海洋跃层测量420.5030 海洋声速测量420.5035 海道测量420.5040 海底地形测量420.5045 海图制图420.5050 海洋工程测量420.5099 海洋测绘其他学科420.60 测绘仪器420.99 测绘科学技术其他学科430 材料科学430.10 材料科学基础学科430.1010 材料力学430.1020 相图与相变430.1030 材料的组织、结构、缺陷与性能430.1040 金属学430.1050 陶瓷学430.1060 高分子材料学430.1099 材料科学基础学科其他学科430.15 材料表面与界面430.20 材料失效与保护430.25 材料检测与分析技术430.30 材料实验430.35 材料合成与加工工艺430.40 金属材料430.4010 黑色金属及其合金430.4020 有色金属及其合金430.4030 非晶、微晶金属材料430.4040 低维金属材料430.4050 特种功能金属材料430.4099 金属材料其他学科430.45 无机非金属材料430.4510 玻璃与非晶无机非金属材料430.4520 低维无机非金属材料430.4530 人工晶体430.4540 无机陶瓷材料430.4550 特种功能无机非金属材料。
第6讲 立体几何中的交线问题(原卷版)

第6讲 立体几何中的交线问题一、单选题1.(2022·全国·高三专题练习(理))已知正方体ABCD A B C D ''''-的棱长为4,E ,F 分别为BB ',C D ''的中点,点P 在平面ABB A ''中,=PF N 在线段AE 上,则下列结论正确的个数是( )①点P 的轨迹长度为2π;①线段FP 的轨迹与平面A B CD ''的交线为圆弧;①NP ;①过A 、E 、F 作正方体的截面,则该截面的周长为103A .4 B .3 C .2 D .12.(2022·全国·高三专题练习)在正四棱锥P ABCD -中,已知2PA AB ==,O 为底面ABCD的中心,以点O 则该球的球面与侧面PCD 的交线长度为( )A B C D3.(2022·全国·高三专题练习)已知正四面体的中心与球心O 重合,正四面体的棱长为则正四面体表面与球面的交线的总长度为A.4π B . C . D .12π 4.(2022·四川成都·模拟预测(理))如图,△ABC 为等腰直角三角形,斜边上的中线AD =3,E 为线段BD 中点,将△ABC 沿AD 折成大小为2π的二面角,连接BC ,形成四面体C -ABD ,若P 是该四面体表面或内部一点,则下列说法错误的是( )A .点P 落在三棱锥E -ABC 内部的概率为12B .若直线PE 与平面ABC 没有交点,则点P 的轨迹与平面ADC 的交线长度为2C .若点P 在平面ACD 上,且满足P A =2PD ,则点P 的轨迹长度为23π D .若点P 在平面ACD 上,且满足P A =2PD ,则线段PB 长度为定值5.(2022·江苏徐州·高二期中)如图1,在正方形ABCD 中,点E 为线段BC 上的动点(不含端点),将ABE △沿AE 翻折,使得二面角B AE D --为直二面角,得到图2所示的四棱锥B AECD -,点F 为线段BD 上的动点(不含端点),则在四棱锥B AECD -中,下列说法正确的是( )A .B 、E 、C 、F 四点一定共面B .存在点F ,使得CF ∥平面BAEC .侧面BEC 与侧面BAD 的交线与直线AD 相交D .三棱锥B ADC -的体积为定值6.(2022·河南·模拟预测(理))已知正方体1111ABCD A B C D -的棱长是2,E ,F 分别是棱11B C 和1CC 的中点,点P 在正方形11BCC B (包括边界)内,当//AP 平面1A EF 时,AP 长度的最大值为a .以A 为球心,a 为半径的球面与底面1111D C B A 的交线长为( )A .2πB .πC D二、多选题7.(2022·湖南·临澧县第一中学高二阶段练习)已知正四棱柱1111ABCD A B C D -中,122CC AB ==,E 为1CC 的中点,P 为棱1AA 上的动点,平面α过B ,E ,P 三点,则( ) A .平面α⊥平面11A B EB .平面α与正四棱柱表面的交线围成的图形一定是四边形C .当P 与A 重合时,α截此四棱柱的外接球所得的截面面积为11π8D .存在点P ,使得AD 与平面α所成角的大小为π3 8.(2022·江苏·南京师大附中模拟预测)如图,圆柱的底面半径和高均为1,线段AB 是圆柱下底面的直径,点O 是下底面的圆心.线段EF 是圆柱的一条母线,且EO AB ⊥.已知平面α经过A ,B ,F 三点,将平面α截这个圆柱所得到的较小部分称为“马蹄体”.记平面α与圆柱侧面的交线为曲线C .则( )A .曲线C 是椭圆的一部分B .曲线C 是抛物线的一部分 C .二面角F AB E --的大小为4πD .马蹄体的体积为V 满足134V π<< 9.(2022·江苏·南京外国语学校模拟预测)如图,正方形ABCD -A 1B 1C 1D 1边长为1,P 是1A D 上的一个动点,下列结论中正确的是( )A .BPB .PA PC + C .当P 在直线1AD 上运动时,三棱锥1A B PC - 的体积不变D .以点B 1AB C 10.(2022·全国·高三专题练习)已知正四棱柱1111ABCD A B C D -的底面边为1,侧棱长为a ,M 是1CC 的中点,则( )A .任意0a >,1A M BD ⊥B .存在0a >,直线11AC 与直线BM 相交C .平面1A BM 与底面1111D C B A D .当2a =时,三棱锥11B A BM -外接球表面积为3π11.(2022·福建·厦门一中高二期中)在四棱锥P ABCD -中,底面ABCD 是边长为2的正方形,PA ⊥平面ABCD ,且2PA =.若点E ,F ,G 分别为棱AB ,AD ,PC 的中点,则( ) A .AG ⊥平面PBDB .直线FG 和直线AB 所成的角为4π C .当点T 在平面PBD 内,且2TA TG +=时,点T 的轨迹为一个椭圆D .过点E ,F ,G 的平面与四棱锥P ABCD -表面交线的周长为12.(2022·江苏·高三专题练习)已知在棱长为4的正方体1111ABCD A B C D -中,E 为棱BC 的中点,以点E Γ,则下列结论正确的是( )A .Γ与面11ABB AB .直线1BD 被ΓC .若点H 为Γ上的一个动点,则1HD 的最小值为8-D .Γ与截面11BDD B 13.(2022·山东省平邑县第一中学高一阶段练习)如图,在正方体1111ABCD A B C D -中,点P 为线段1B C 上一动点,则( )A .直线1BD ⊥平面11AC DB .异面直线1BC 与11A C 所成角为45︒C .三棱锥11P A DC -的体积为定值D .平面11AC D 与底面ABCD 的交线平行于11A C14.(2022·广东深圳·高三阶段练习)已知正方体1111ABCD A B C D -的棱长为1,E 为棱AD 上的动点,平面α过点E 且与平面11A DC 平行,则( )A .11B E CD ⊥B .三棱锥111E BCD -的体积为定值C .1DE 与平面11A DC 所成的角可以是3πD .平面α与底面ABCD 和侧面11CDD C 的交线长之和为15.(2022·福建三明·高一期中)《九章算术》中将底面为直角三角形且侧棱垂直于底面的三棱柱称为“堑堵”;底面为矩形,一条侧棱垂直于底面的四棱锥称之为“阳马”;四个面均为直角三角形的四面体称为“鳖膈”.如图在堑堵ABC −A 1B 1C 1中,AC ①BC ,且AA 1═AB ═2.下列说法正确的是( )A .四棱锥11B A ACC -为“阳马”、四面体11A C CB 为“鳖膈”.B .若平面1A BC 与平面111A B C 的交线为l ,且1A B 与11A B 的中点分别为M 、N ,则直线CM 、1C N 、l 相交于一点.C .四棱锥11B A ACC -体积的最大值为23.D .若F 是线段1A C 上一动点,则AF 与1A B 所成角的最大值为90︒.16.(2022·福建省福州格致中学模拟预测)中国古代数学著作《九章算术》中,记载了一种称为“曲池”的几何体,该几何体的上下底面平行,且均为扇环形(扇环是指圆环被扇形截得的部分),现有一个如图所示的曲池,它的高为2,1AA ,1BB ,1CC ,1DD 均与曲池的底面垂直,底面扇环对应的两个圆的半径分别为1和2,对应的圆心角为90°,则以下命题正确的是( )A .1AB 与1CD 成角的余弦值为45B .1A ,B ,C ,1D 四点不共面C .弧11AD 上存在一点E ,使得1BE CD ∥D .以C 23π 三、双空题17.(2022·山东临沂·三模)如图,AB 是圆锥底面圆O 的直径,圆锥的母线4PA AB ==,则此圆锥外接球的表面积为______;E 是其母线PB 的中点,若平面α过点E ,且PB ⊥平面α,则平面α与圆锥侧面的交线是以E 为顶点的抛物线的一部分,此时该抛物线的焦点F 到底面圆心O 的距离为________.四、填空题18.(2022·湖北·华中师大一附中高一期中)如图正四棱柱ABCD A B C D ''''-中,AB =2AA '=,以D 为球心,DC '为半径的球与侧面BCC B ''的交线为C E ',点P 为交线C E '上一动点,则P 从C '运动到E 时,DP 所形成的曲面面积为____________.19.(2022·河南平顶山·模拟预测(理))如图,在四面体ABCD 中,DA ,DB ,DC 两两垂直,DA DB DC ===D 为球心,1为半径作球,则该球的球面与四面体ABCD 各面交线的长度和为___.20.(2022·山东威海·高三期末)在三棱锥P ABC -中,PA ⊥平面ABC ,AC CB ⊥,4===PA AC BC .以A 为球心,表面积为36π的球面与侧面PBC 的交线长为______.21.(2022·全国·高三专题练习)在正三棱锥PABC ﹣中,侧棱PA 且侧棱PA PB PC 、、两两互相垂直,以A 为球心,2为半径的球面与正三棱锥的表面相交,则交线的长度之和为___________.22.(2022·全国·高三专题练习(文))如图,在平面四边形ABCD 中,4,120,DA DC BA BC ADC E ︒∠=====为AC 的中点,将ABC 沿AC 折起,使得4BD =,以D 为球心,DE 为半径的球与三棱锥B ADC -各面交线的长度和为___________.23.(2022·上海·高三专题练习)如图,在直三棱柱111ABC A B C -中,12AA AB BC ===,D ,E 分别为1BB ,11A C 分如中点,则过点A ,D ,E 的截面与三棱柱的侧面11BCC B 的交线的长为__________.24.(2022·全国·高三专题练习)球面几何学是几何学的一个重要分支,在航海、航空、卫星定位等面都有广泛的应用,如图,A ,B ,C 是球面上不同的大圆(大圆是过球心的平面与球面的交线)上的三点,经过这三个点中任意两点的大圆的劣弧分别为,,AB BC CA ,由这三条劣弧围成的图形称为球面ABC .已知地球半径为R ,北极为点N ,P ,Q 是地球表面上的两点若P ,Q 在赤道上,且PQ =,则球面NPQ △的面积为________;若NP PQ QN ===,则球面NPQ △的面积为________.25.(2022·陕西·西安中学二模(理))已知在圆柱12O O 内有一个球O ,该球与圆柱的上、下底面及母线均相切.过直线12O O 的平面截圆柱得到四边形ABCD ,其面积为8.若P 为圆柱底面圆弧CD 的中点,则平面PAB 与球O 的交线长为___________.26.(2022·黑龙江·哈尔滨三中模拟预测(理))正四棱锥P ABCD -中,M 为棱AB 上的点,且3PA AB AM ==,设平面P AD 与平面PMC 的交线为l ,则异面直线l 与BC 所成角的正切值为___________.27.(2022·福建福州·三模)已知正方体1111ABCD A B C D -以1A 为球心,半径为2的球面与底面ABCD 的交线的长度为___________.28.(2022·福建·厦门双十中学高一期中)如图,四棱锥P ABCD -的底面四边形ABCD 为正方形,四条侧棱PA PB PC PD ===,点E 和F 分别为棱BC 和PD 的中点.若过A 、E 、F 三点的平面与侧面PCD ,cos PDC ∠=___________.29.(2022·安徽合肥·二模(理))在正方体1111ABCD A B C D -中,E 为线段AD 的中点,设平面11A BC 与平面1CC E 的交线为l ,则直线l 与BE 所成角的余弦值为__________.30.(2022·全国·高三阶段练习)如图,圆锥底圆O 的直径长为①APB=90°,AB ,CD 是底圆的两条直径,且AB ①CD ,E 是母线PB 的中点,已知过CD 与E 的平面与圆锥侧面的交线是以E 为顶点的抛物线的一部分,则该抛物线的焦点到圆锥顶点P 的距离等于______.31.(2022·山东临沂·一模)已知正三棱台111ABC A B C -的上下底面边长分别为2和5,侧棱长为3,则以下底面的一个顶点为球心,半径为2的球面与此正三棱台的表面的交线长为______.32.(2022·全国·高三专题练习)直四棱柱1111ABCD A B C D -的所有棱长均为2,60BAD ∠=︒,以1D 1111ABCD A B C D -的侧面11 BCC B 的交线长为______.33.(2022·全国·高三专题练习)已知四面体ABCD 的所有棱长均为4,点O 满足OA OB OC OD ===,则以O ABCD 表面所得交线总长度为______.34.(2022·全国·高三专题练习)已知圆柱底面圆心分别为1O ,2O ,圆柱内有一个球,该球与圆柱的上下底面、圆柱侧面均相切,过直线12O O 的平面截圆柱得到四边形ABCD ,其面积为12,若P 为圆柱底面圆弧CD 的中点,则平面PAB 与球O 的交线长为___________. 35.(2022·河南·模拟预测(理))已知三棱锥A BCD -,5AB AD BC CD ====,8BD =,3AC =,则以点C 为球心,ABD 的交线长为______. 36.(2022·全国·高二课时练习)已知正方体1111ABCD A B C D -的棱长为2,以A 为球心,为半径的球面与平面1111D C B A 的交线长为________.。
关于欧氏几何的第5公设及非欧几何

关于欧氏几何的第5公设及非欧几何谢裕华秦敏雁施培成摘要:本文综述了由欧氏几何到非欧几何的发展历史;评述了非欧几何的思想及其伟大意义;论述了欧氏几何,罗氏几何,黎曼几何的对立统一关系。
比较了三种几何的主要特征及适用范围。
关键词:第五公设,欧氏几何,罗氏几何,黎曼几何。
一、关于Euclid的《Elements》欧几里得的《几何原本》早已失传,现存的有:1、公元四世纪末(400年左右)泰恩(Thon)的《原本》修订本。
2、18世纪在梵蒂冈图书馆发现的一个第十世纪的《原本》希腊文手抄本,可能比泰恩本更早些。
3、现代版本最早的是1482在威尼斯印刷的,依据泰恩修订本的版本。
4、现在看到的各种版本(一千多种版本)均非欧几里得手稿的传本,而是依据后人的修订本,注释本,翻译本重新整理出来的。
5、1794年法国数学家勒让德(A.M.Legendre,1752-1833)为使《几何原本》更便于教和学,曾对《原本》作了较大的修改,如删去了《原本》中的非几何部分内容,并将几何部分重新整理和编写。
把“命题”中的定理和问题加以明确区分,还把第5公设换为与它等价的平行公理;“过直线外一点,有而且只有一条直线与原直线平行”等等,编成了《新欧几里得几何原本》。
于是自19世纪开始,初等几何课本一般都是以此为兰本的改编本。
6、中国最早的汉译本是1607年(明万历35年丁未)意大利传教士利玛窦(Matteo Ricci,1552-1610)和徐光启(1562-1633)的合译本(前6卷),称之为“明译本”底本系德国人的拉丁文本15卷。
二百五十年之后,1857年,后9卷由英人伟烈亚(A.Wylie,1815-1887)和李善兰(1811-1882)合译,称之为“清译本”底本是英文版第15卷。
由于它们均系文言,并且名词,术语和现代有很大的差异,不易看懂,故现代新译本于1990年由陕西科技出版社出版。
二、关于第5公设古希腊对于数学的最杰出的贡献就是“根据公理体系来建立数学”的观念,即:一个合乎逻辑的学科,应当是由一组原始定义和原始命题(公设,公理)出发,通过演绎推理导出这一学科的其他所有命题。
球面几何学

球面几何学球面几何学是数学中一个重要的分支,它研究的是物体的弯曲和形状的变化。
《球面几何学》是一种学科,主要关注的是对圆弧形变体的研究。
它通过分析和分类球面形式的几何特征,来研究物体的表面和形状。
《球面几何学》主要被应用于探索宇宙,研究世界的地理分布,分析地球物理和地球科学等方面。
《球面几何学》的发展有着悠久的历史,早在古埃及、古希腊时就有对于球面几何学的尝试。
在古希腊,几何学家们研究了球面几何学的理论,发现它具有丰富的知识和应用,其中最有名的是欧几里得,他发现了一系列的数学定理,包括佩克莱尔定理,基督塞顿定理等。
随着科学技术的发展,《球面几何学》在现代也发挥着重要作用。
现代《球面几何学》有着多样化的应用,如地理学中的分布图,工程建设中的大型曲线结构,航空航天中的航线设计,和大气和海洋学中的活动模拟等。
《球面几何学》也在生物学,建筑学,地质学,作为一个工具进行应用。
《球面几何学》的研究也受到了越来越多的关注,我们发现,球面几何学通常与其他数学分支一起被用于描述物体的形状,并用于解释物理现象。
举例来说,物理学家们研究宇宙中空间-时间的变化,用球面几何学研究自由轨道运动,以及分析地球和其它行星的形状和弯曲度。
《面几何学》也涉及到多种数学表达式,如极坐标系,球面三角形,平面和球面的平面式,和Fubini-Study等。
这些表达式的作用是加强球面几何学的概念,提高它的表现能力,并有效地帮助研究者来分析球面几何学的问题。
综上所述,《球面几何学》是一种重要的学科,它对我们对宇宙的认知有着重要的作用,也受到越来越多的关注。
它被大量应用于空间,宇宙,地球物理学,大气学,海洋学和生物学等领域,其研究也涉及到许多数学表达式,用于加强概念,提高表现能力。
球体极角和方位角-概述说明以及解释

球体极角和方位角-概述说明以及解释1.引言1.1 概述概述:球体极角和方位角是描述一个点在球体上的位置时所使用的两个重要坐标。
极角是从球心到该点的直线与球体表面的夹角,而方位角则是该点在球体表面的投影与一个已知基准方向的夹角。
这两个角度经常在天文学、地理学、航海学等领域的定位和导航中被广泛应用。
本文将深入探讨球体极角和方位角的定义、解释以及它们在不同领域中的应用和意义。
我们将从理论基础出发,逐步展开讨论,使读者对这两个概念有更深入的理解。
1.2文章结构1.2 文章结构本文将首先对球体极角和球体方位角进行定义和解释,探讨它们的概念和特点。
接着将分别讨论它们在实际生活和科学研究中的应用和意义,探究其在不同领域中的重要性和作用。
最后,通过对球体极角和球体方位角的综合分析和比较,总结它们之间的关系和差异,展望其在未来的发展方向和应用前景,为读者提供一个全面而深入的理解和认识。
1.3 目的本文旨在深入探讨球体极角和方位角的概念、定义、应用和意义。
通过对这两个概念的详细解释和讨论,读者将能够更好地理解和应用它们在数学、物理和工程领域中的重要性。
同时,通过对球面坐标系中的极角和方位角的分析,我们也可以更清晰地理解球体在三维空间中的位置和方向,为我们的学术研究和实际工作提供更多的帮助和启发。
最终,希望本文能够为读者提供一份全面而系统的关于球体极角和方位角的参考资料,促进相关领域的学术研究和应用。
2.正文2.1 球体极角2.1.1 定义和解释球体极角是指空间中某一点到球体表面上的某一点所在的半径与球体表面的夹角。
在球坐标系中,球体极角通常用θ表示,它是从球体的正北极(顶点)到该点的连线与球体正北极的夹角。
球体的极角范围通常是0到180。
在天文学中,球体极角也有着重要的意义,比如在描述天体运动时,我们常常会用到赤道坐标系,其中的赤纬就是一种球体极角。
2.1.2 应用和意义球体极角在很多领域都有着广泛的应用,比如在航空航天领域中,飞行器的导航与定位就要用到球体极角来确定位置和方向。
北极星仰角和纬度的关系

北极星仰角和纬度的关系北极星仰角和纬度的关系北极星,又称极星、北极大星,是位于北极圈上方的最亮的恒星。
在天文学中,北极星是一个重要的参考点,特别是在航海和导航中起着至关重要的作用。
它的仰角和纬度之间存在着一定的关系,下面将详细介绍这一关系。
首先,我们需要了解一些天文基础知识。
地球自转一周的时间是24小时,而地球公转一周的时间是365.25天。
由于地球自转轴的倾斜,地球的赤道面与黄道面交角约为23.5度。
我们知道,地球上的维度是以赤道为0度,北极为90度,南极为-90度来进行度量的。
在北半球,北极星位于天空中与北极点相似的位置,并且几乎保持不动。
这是因为北极星位于地球自转轴的延长线上。
从地理学上来说,北极星的位置基本上处于北纬90度附近的位置。
而在南半球,则没有与北极星类似的明显标志星。
北极星的仰角与观察地点的纬度密切相关。
在北半球的较低纬度地区,北极星的仰角较低;而在北纬90度的北极点,北极星的仰角则达到90度。
这是因为北极星位于观察者的正上方,离地面最近。
从北极点出发,随着纬度的减小,北极星的仰角也会相应减小。
在南半球,由于没有类似的标志星,南极星被认为是南半球的“北极星”。
南极星位于南纬90度附近,其仰角的变化与北极星在北半球的变化趋势相似。
在低纬度地区,南极星的仰角较低,在南纬90度处达到最高点90度。
可以通过以下公式来计算北极星的仰角:tan α = tan(90° - φ) 其中,α是北极星的仰角,φ是观察地点的纬度。
这个公式的推导基于球面几何学。
首先,可以推到出观察者与北极星之间的连线与地球自转轴之间的夹角等于地球自转轴与观察地点的连线与地球自转轴之间的夹角。
然后,可以利用三角函数的关系,得到上述公式。
北极星的仰角与纬度之间的关系对航海和导航时起着至关重要的作用。
在没有GPS和现代导航设备的年代,航海者可以通过北极星来确定自己的纬度。
航海者只需使用一个简单的显微镜来观察北极星,并测量其仰角,然后根据上述公式就可以精确计算出自己所处的纬度。
球面几何学

4、球面二角形:也叫月形,是球面上两个有 公共直径的半大圆所夹的部分。
思考:球面二角形的面积?
球面可以看成是球面角为 的月形。
5、球面三角形
(类比平面三角形) 不在同一条直线的三点——不在同一大圆上的三点 边、顶点、内角 球面几何学中最简单、最重要的图形
三面角: 如何度量内角和边长?
6、对顶三角形
B A`
C
将上面三个等式两边相加,得
3S球面ABC S球面A`BC S球面AB`C S球面ABC` 2A B C 又∵S球面ABC S球面A`BC S球面AB`C S球面A`B`C 2R2 2 ∵ S球面ABC` S球面A`B`C 2S球面ABC 2 2A B C
BAC
2
2
, BAD
O B C
E D
2 3 , BAE 3 4
分别计算: 球面三角形 ABC、ABD、ABE的 内角和及面积
球面三角形ABC的内角和 3 = 2 球面三角形ABC的面积= 1 1 2 2r 4 2
球面三角形ABD的内角和 5 = 3
1 2 2 2r 球面三角形ABD的面积= 3 3
abeabdabc球面三角形abc的内角和?2球面三角形abc的面积?24球面三角形abd的内角和?3球面三角形abd的面积?23?2112??r5?3212??r3球面三角形abe的内角和?4球面三角形abe的面积?287?4332??r归纳出单位球面三角形的内角和公式ssccbbaa?????????猜测证明分析球面球面bsscab?abc???????2由月形的面积计算公式得球面球面assbcaabc?????2球面球面cssabc?abc?2cbacba将上面三个等式两边相加得ssbcaabc???3球面球面??ssabc球面球面??cbassabc?s球面cab?s球面?????2????2球面?c球面?cbaabcss?a???球面球面??2?2????rcbaabbca又???cbsabc????????222球面scba????即单位球面三角形的内角和公式基本概念内角和公式的推测内角和公式的证明单位球面三角形的面积公式第三节球面三角形的全等类比平面三角形的全等规定
球面上的几何

例题
如果一个球面三角形的三个角相等,则它的三条边也相 等。
球面三角形的边角关系
球面三角形的正弦定理和余弦定理
球面三角形的边角关系
球面三角形的正弦定理和余弦定理
球面三角形的边角关系
球面三角形的正弦定理和余弦定理
球面三角形的边角关系
球面三角形的正弦定理和余弦定理
证法二
第三七讲球面上的基本图形球面三角形性质球面三角形的边角关系球面三角形的正弦定理和余弦定理第三七讲球面上的基本图形球面三角形性质球面三角形的边角关系第八讲欧氏几何与非欧式几何非欧几何的诞生源于人们对欧几里得平行公理的质疑和探究这是数学史上具有划时代意义的大事它彻底改变了人们对空间乃至对数学真理性的认识从唯一的几何空间和数学真理的绝对性逐渐转向相对真理的观点也从一个侧面促进了数学观念的转变
球面几何概述
球面几何学的发展历程
早期三角学不是一门独立的学科而是依附于天文学, 是天文观测结果推算的一种方法。因而最先发展起来 的是球面三角学。
毕达哥拉斯学派却已经积累了许多球面大圆和球面三 角形的知识。
早在公元前3世纪成书的几何《原本》第十一篇“立 体几何”中,已给出了球的定义;第十二篇关于面积 和体积的命题中,用“穷竭法”证明了球(体积)之 比等于其直径的三次比。
球面三角形的边角关系
球面三角形的正弦定理和余弦定理
球面三角形的边角关系
球面三角形的正弦定理和余弦定理
球面三角形的边角关系
球面三角形的正弦定理和余弦定理
球面三角形的其它性质
定理
球面三角形两边之和大于第三边。
球面三角形的其它性质
推论
球面三角形两边之差小于第三边。
球面三角形的其它性质
著名化学家徐光宪院士总结的科研创新的条方法

著名化学家徐光宪院士总结的科研创新的16条方法国家最高科技奖得主、著名化学家徐光宪院士多年探索科研如何创新,并通过讲座等形式传递给学生后辈●知识创新都有前因后果,来龙去脉。
故而勤奋学习,建立知识框架,积累深厚基础;加上追根到底,万事逼问为什么的好奇心,就是创新的源泉。
前者是学,后者是问。
学而不问则殆,问而不学则茫。
学而问,问而思,思而行,行而果,这就是创新。
●如果你梦想要做一个科学家,那么勤奋学习就是实现你的梦想之“舟”。
但舟有快如宇航飞机,慢如蜗牛。
所以勤奋必须是高效率的勤奋,不要去做“磨擦生热”的“无用功”,更不要做“负功”。
●在科学研究中常常会遇到“山穷水尽疑无路”时,粗心大意的人很容易放过这种机遇。
只有具有敏锐眼光和扎实基础的科学家才能抓住它,取得重大的突破。
●实际的学科基础是金字塔,有比较广的知识,但是又要有塔尖,有高度,也就是你的专业知识高度。
但是一条竹竿是站不直的,所以你除了“高”,还要有一些“宽”。
多年以来,我一直在实践中探索科研如何创新的方法,总结了16条。
我可以告诉大家,我的天赋很平常,但“天道酬勤”,只要依靠勤奋,是可以取得科学成就的。
大发明家爱迪生说:天才=98%的汗水+2%的灵感。
而2%的灵感也可用勤奋来培养。
各位同学只要勤奋努力,相信都能成为出色的科学家。
1、创新与知识积累:中药铺的抽屉和知识框架创新必须先有知识积累,这是创新和继承的关系。
我幼年时常生病,生了病去看中医,到中药铺去抓药,看到中药分类归档,放在上百个抽屉里。
从那时起就模糊认识到要把学到的东西放在脑中的抽屉里,并把众多抽屉有序排列,才能记住。
以后就慢慢形成要在自已的头脑里建立知识框架的概念。
知识框架即知识文档树,建立知识文档树便于知识存贮检索、记忆、联系比较、分析归纳和创新。
2、创新链和创新树科学研究是接力赛跑,起跑点要在科学研究的前沿,要把前人的有关知识接过来。
研究生的导师很重要,他把接力赛跑的棒交给你,你就可以在科学研究的前沿起跑。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一节 平面与球面、直线与球面的位置关 系
一、平面与球的位置关系:
类比直线与圆的位置关系,来探究平面与球的位置关系。
相交、相离、相切
结论: 一个平面与球面相交,所得的交线是一个 圆,且圆心与球心的连线垂直于这一平面。
用一个平面截一个球,截面是圆面。请同 学们思考什么时候是小圆,什么时候是大 圆?
纬线
第二节 球面上的一些基本图形
1、大圆:过球心的平面在球面上的截线(直线) 小圆:不过球心的平面在球面上的截线。
2、优弧、劣弧:过球面上两点一定可以作一 个大圆。(球面上两点间的距离即劣弧长) 球面上连接两点的最短路径是经过这两点的 一段大圆弧——劣弧。
思考题:
3、球面角:记作 (类比平面中的角) 如何度量球面角?——两平面构成的二面 角。
*中小学平面几何教学综述 1.中小学数学课程中平面几何部分的内容要
求 2.中学平面几何典型例题(数学知识类、课题
学习类、信息技术应用类、实验与探究类、数学
活动类) 3.中学数学平面几何考点分析
练习:
(1)正方体的全面积是a,它的顶点都在球 面上,这个球的表面积是( )。
(2)球的半径为R,则它的外切正方体的 棱长为( ),内接正方体的棱长为( )。
4、论述:为什么相对于半径来说很小的一小 片球面可以作为一个平面来对待。
球面坐标
1、三维直角坐标系 2、球面坐标系 3、赤道坐标系 4、水平坐标系
球面坐标
设M(x,y,z)为空间一点, z
M
如果将x,y,z改用另外 三个数r, , 来表示,
r
z
则称(r, , )为点M的 O
球面坐标。
x
y
xy
P
球面三角形的内角和是定值吗?
A
球面三角形 ABC、ABD、ABE中
ABC ACB ADB AEB
2
O B
E D
C
BAC BAD BAE
探究单位球面三角形的内角和公式
A
球面三角形 ABC、ABD、ABE中
O B
E D
C
ABC ACB ADC AED
2
BAC ,BAD 2 ,BAE 3
4、球面二角形:也叫月形,是球面上两个有 公共直径的半大圆所夹的部分。
思考:球面二角形的面积?
球面可以看成是球面角为 的月形。
5、球面三角形
(类比平面三角形) 不在同一条直线的三点——不在同一大圆上的三点 边、顶点、内角 球面几何学中最简单、最重要的图形
三面角: 如何度量内角和边长?
6、对顶三角形
中学平面几何问题概述(总结)
*证明的一般思路 试误式思路: 直接式:分析法、综合法 间接式:反证法、同一法 顿悟式思路: *证明的特殊思路 面积法、向量法、复数法 (会用以上方法证题)
*几何轨迹与尺规作图
1.区别轨迹和图形 2.会用两面性证明轨迹命题 3.会按步骤解作图题(写出已知、求作,进
行分析,写出作法,证明,讨论)
直线与该直线不相交; 在球面上,大圆可视为“直线”,任意两条
“直线”(大圆)都相交,即过“直线”外一点, 没有一条“直线”与该“直线”不相交。
于是,在球面上就产生了一些与欧式平面几 何完全不同的定理。
请同学们完成专题学习报告:
提纲
1、球面上的基本图形(大圆、优弧劣弧、球面 角、球面二角形—月形、球面三角形、三面角、 对顶三角形、球极三角形、对径点、极点、 赤道圆等)
对径点:球的直径的两个端点。
A
C`
B`
B
C
A`
7、球极三角形
极点、赤道圆
性质1: 性质2:
第三节 球面三角形
一、球面三角形三边之间的关系
类比平面三角形的三边关系
二、球面等腰三角形
类比平面等腰三角形
三、球面三角形的周长
A
C`
B`
问题
平面三角形内角和为π;
B
C
A`
球面三角形内角和是多少?
2
3
4
分别计算: 球面三角形ABC、ABD、ABE的 内角和及面积
球面三角形ABC的内角和
= 3
2
球面三1 角2形rA2 BC1的 面积=
4
2
球面三角形ABD的内角和
= 5
3
球面三1 角2形r2ABD2 的面积=
3
3
球面三角形ABE的内角和
= 7
4
球面三3角形2ABrE2的面积3=
8
4
归纳出单位球面三角形的内角和公式
如何用向量的向量积证明球面上的余弦定理?
从球面上的正弦定理看球面和平面
球面上余弦定理的应用——求地球上两城市间的距离
球面上的几何学——一种新的几何学 ——一个与欧式平面几何不同的几何模型
• 研究方法:类比的思想方法
为什么平面和球面上有些不同的性质呢?
追溯根源—— 在平面上,过直线外一点,有且只有一条
球面坐标与直角坐标的关系
x r sin cos
z
M
y
r
sin
sin
OP r sin
r
z r cos
z
O
(0 r ,0 , x
y
0 2 )
A
xy
P
类比平面三角形的全等—— 规定:两个球面三角形全等是指两个图形完 全相等,即球面三角形的六个元素:三条边、 三个角分别相等。
(只能在同一球面上或半径相等的球面上讨论)
1、“边边边”判定定理
证明:
2、“边角边”判定定理 3、“角边角”判定定理 自己证明 4、“角角角”判定定理
第四节 球面三角形的边角关系
ABC S
猜测
证明
分析
由月形的面积计算公式,得
A
C`
B`
S球面ABC S球面A`BC 2A①
S球面ABC S球面AB`C 2B② S球面ABC S球面ABC` 2C③
B
C
A`
将上面三个等式两边相加,得
3S球面ABC S球面A`BC S球面AB`C S球面ABC` 2 A B C
二、直线与球面的位置关系:
同样,类比直线与圆的位置关系,来探究直线与
球的位置关系。
结论:
把球心O到直线L的距离记为OH, 当OH>R时,相离,直线与球没有公共点; 当OH=R时,相切,直线与球只有一个公共 点; 当OH<R时,相切,直线与球有两个公共点。 三、球幂定理
经线:以南极和北极为端点的半大圆
又∵ S球面ABC S球面A`BC S球面AB`C S球面A`B`C 2R 2 2
∵ S球面ABC` S球面A`B`C
2S球面ABC 2 2A B C
即
ABC S
单位球面三角形的 内角和公式
单位球面三角形的 面积公式
基本概念 内角和公式的推测 内角和公式的证明
第三节 球面三角形的全等
第九章 球面几何学
第九章 球面几何学
设想:在地球面上,从一个城市飞往另一个 城市,如何飞行距离最短?
——球面上的几何学——一种新的几何学 ——一个与欧式平面几何不同的几何模型
研究方法:类比的思想方法(?) 空间想象能力、几何直观能力
球面是空间中最完美匀称的曲面—— 两个半径相等的球面可以用平移叠合起来; 两个半径不相等的球面相差的就是放大缩小 的相似变换;
2、球面三角形与极对称三角形边角之间的关系
3、球面三角形与平面三角形的性质对比(分开列 出哪些是相同性质,哪些是不同性质)
(1)位置关系 (2)圆(球)幂定理 (3)三边之间的关系 (4)等腰三角形 (5)周长 (6)内角和 (7)内角和与面积的关系 (8)全等判定定理 (9)边角关系 (10)相似三角形 (11)两点间的距离
