svmtrain和svmpredict简介回归、分类
matlab二分类算法

matlab二分类算法二分类算法是机器学习领域中的一种常见算法,它将数据集划分为两个类别,并预测新样本属于哪一类。
MATLAB作为一种强大的数值计算和数据分析工具,提供了多种用于二分类问题的算法。
本文将介绍一些常用的MATLAB二分类算法,并说明其原理和使用方法。
一、支持向量机(Support Vector Machine,SVM)是一种非常流行的二分类算法。
其核心思想是将数据集转换为高维空间,然后找到一个超平面,使得两个类别的数据点在该超平面上的投影最大化。
在MATLAB中,可以使用fitcsvm函数来训练SVM模型,并使用predict函数进行预测。
该函数提供了多种参数配置选项,如核函数类型、惩罚系数等。
二、逻辑回归(Logistic Regression)是另一种常用的二分类算法。
它通过将线性回归模型的输出映射到一个概率值(0~1之间),然后根据阈值进行分类预测。
在MATLAB中,可以使用fitglm函数进行逻辑回归模型的训练,并使用predict函数进行预测。
fitglm函数支持多种模型配置选项,如正则化类型、损失函数类型等。
三、随机森林(Random Forest)是一种基于集成学习的二分类算法。
它由多个决策树组成,每棵树对数据集进行随机采样,并在每个节点上选择最佳的特征进行分割。
最终,通过对多棵树的结果进行投票或平均,得到最终的预测结果。
在MATLAB中,可以使用TreeBagger类来实现随机森林算法。
通过创建TreeBagger对象,设置参数并调用train函数来训练模型,然后使用predict函数进行预测。
四、神经网络(Neural Network)是一种通过模拟人脑中的神经元网络来解决问题的方法。
在二分类问题中,神经网络可以通过多个神经元和多个隐藏层构建一个复杂的模型,并通过调整权重和偏置来训练模型。
在MATLAB中,可以使用patternnet函数来创建神经网络模型,并使用train函数进行训练。
sklearn中的svm用法

sklearn中的svm用法SVM用于机器学习的模型,是一种有监督的学习算法,可以用于分类和回归问题。
在scikit-learn库中,我们可以使用sklearn.svm模块来实现SVM模型。
要使用sklearn中的svm模块,首先需要导入相应的类和函数。
下面是一些常用的类和函数:1. SVC类:用于支持向量分类。
可以根据训练数据找到一个最佳的超平面(也称为决策边界),将不同类别的样本分开。
2. SVR类:用于支持向量回归。
与SVC类似,但用于解决回归问题,预测连续的目标变量而不是分类。
3. LinearSVC类:用于线性支持向量分类。
适用于线性可分的分类问题。
4. NuSVC类:用于支持向量分类。
与SVC类似,但使用不同的参数表示支持向量。
除了上述类之外,sklearn.svm模块还提供了一些辅助函数和类,例如:1. kernel:用于指定SVM模型中使用的核函数,如线性核(linear)、多项式核(poly)、RBF核(rbf)等。
2. C:用于控制分类器的惩罚参数。
较小的C值会生成较大的间隔,但可能会导致分类误差增加。
3. gamma:在使用RBF核函数时,用于控制数据点的影响范围。
较高的gamma值会导致训练样本的影响范围更小。
接下来,我们可以使用这些类和函数来构建SVM模型并进行训练和预测。
以下是一个使用SVC类的示例:```pythonfrom sklearn import svm# 创建一个SVC分类器clf = svm.SVC(kernel='linear', C=1)# 使用训练数据进行模型拟合clf.fit(X_train, y_train)# 使用训练好的模型进行预测y_pred = clf.predict(X_test)```在上述示例中,我们使用线性核函数(kernel='linear')和惩罚参数C等于1来创建一个SVC分类器。
然后,我们使用训练数据(X_train和y_train)来进行模型拟合,并使用训练好的模型对测试数据(X_test)进行预测,预测结果存储在y_pred中。
SVM模式识别与回归软件包(LibSVM)详解
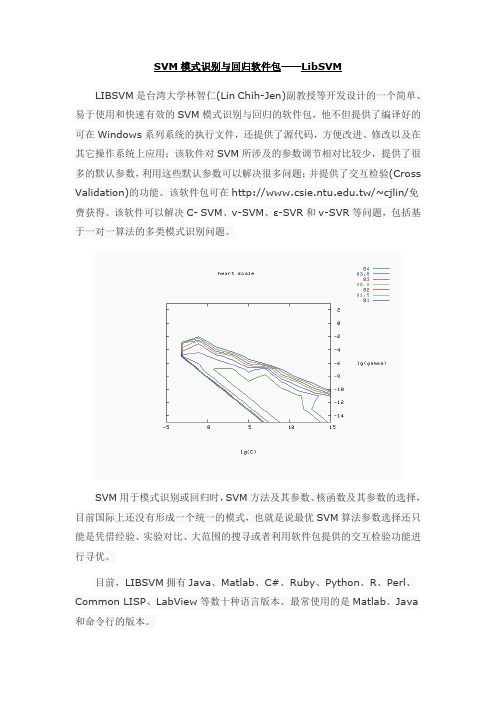
SVM模式识别与回归软件包——LibSVMLIBSVM是台湾大学林智仁(Lin Chih-Jen)副教授等开发设计的一个简单、易于使用和快速有效的SVM模式识别与回归的软件包,他不但提供了编译好的可在Windows系列系统的执行文件,还提供了源代码,方便改进、修改以及在其它操作系统上应用;该软件对SVM所涉及的参数调节相对比较少,提供了很多的默认参数,利用这些默认参数可以解决很多问题;并提供了交互检验(Cross Validation)的功能。
该软件包可在.tw/~cjlin/免费获得。
该软件可以解决C- SVM、ν-SVM、ε-SVR和ν-SVR等问题,包括基于一对一算法的多类模式识别问题。
SVM用于模式识别或回归时,SVM方法及其参数、核函数及其参数的选择,目前国际上还没有形成一个统一的模式,也就是说最优SVM算法参数选择还只能是凭借经验、实验对比、大范围的搜寻或者利用软件包提供的交互检验功能进行寻优。
目前,LIBSVM拥有Java、Matlab、C#、Ruby、Python、R、Perl、Common LISP、LabView等数十种语言版本。
最常使用的是Matlab、Java 和命令行的版本。
就要做有关SVM的报告了!由于SVM里面的有关二次优化的不是那么容易计算得到的,最起码凭借我现在的理论知识和编程能力是不能达到!幸好,现在又不少的SVM工具,他可以帮助你得到支持向量(SV),甚至可以帮助你得到预测结果,归一化数据等等。
其中SVM-light,LibSVM是比较常用的!SVM-light我们实验室有这方面的代码,而我自己就学习了下怎么使用LIBSVM(来自台湾大学林智仁)。
实验步骤如下:1:首先安装LIBSVM,这个不用多说,直接去他的官网上看:.tw/~cjlin/libsvm/index.html2:处理数据,把数据制作成LIBSVM的格式,其每行格式为:label index1:value1 index2:value2 ...其中我用了复旦的分类语料库,当然我先做了分词,去停用词,归一化等处理了3:使用svm-train.exe训练,得到****.model文件。
LIBSVM使用方法

LIBSVM1 LIBSVM简介LIBSVM是台湾大学林智仁(Lin Chih-Jen)副教授等开发设计的一个简单、易于使用和快速有效的SVM模式识别与回归的软件包,他不但提供了编译好的可在Windows 系列系统的执行文件,还提供了源代码,方便改进、修改以及在其它操作系统上应用;该软件还有一个特点,就是对SVM所涉及的参数调节相对比较少,提供了很多的默认参数,利用这些默认参数就可以解决很多问题;并且提供了交互检验(Cross -SVM回归等问题,包括基于一对一算法的多类模式识别问题。
SVM用于模式识别或回归时,SVM方法及其参数、核函数及其参数的选择,目前国际上还没有形成一个统一的模式,也就是说最优SVM算法参数选择还只能是凭借经验、实验对比、大范围的搜寻或者利用软件包提供的交互检验功能进行寻优。
ν-SVM回归和ε-SVM分类、νValidation)的功能。
该软件包可以在.tw/~cjlin/免费获得。
该软件可以解决C-SVM分类、-SVM回归等问题,包括基于一对一算法的多类模式识别问题。
SVM用于模式识别或回归时,SVM方法及其参数、核函数及其参数的选择,目前国际上还没有形成一个统一的模式,也就是说最优SVM算法参数选择还只能是凭借经验、实验对比、大范围的搜寻或者利用软件包提供的交互检验功能进行寻优。
2 LIBSVM使用方法LibSVM是以源代码和可执行文件两种方式给出的。
如果是Windows系列操作系统,可以直接使用软件包提供的程序,也可以进行修改编译;如果是Unix类系统,必须自己编译,软件包中提供了编译格式文件,我们在SGI工作站(操作系统IRIX6.5)上,使用免费编译器GNU C++3.3编译通过。
2.1 LIBSVM 使用的一般步骤:1) 按照LIBSVM软件包所要求的格式准备数据集;2) 对数据进行简单的缩放操作;3) 考虑选用RBF 核函数;4) 采用交叉验证选择最佳参数C与g;5) 采用最佳参数C与g 对整个训练集进行训练获取支持向量机模型;6) 利用获取的模型进行测试与预测。
libsvm安装方法

安装libsvm-mat(林智仁版)方法2011-10-14 10:00:33| 分类:无线视频传输仿真| 标签:|字号大中小订阅安装libsvm-mat是在MATLAB平台下使用libsvm的前提,如果没有安装好也就无法使用,在MATLAB平台下安装libsvm-mat一般有以下几个大步骤:1. 将libsvm-mat所在工具箱添加到matlab工作搜索目录(File ——》Set Path… ——》Add with Subfolders...);2. 选择编译器(mex -setup);3. 编译文件(make)。
每一步都很重要【我就不在每一步前面说这一步很重要了~】,下面我将掰饽饽说馅【一句东北俚语i.e.翔实详尽】的给大家详细说明。
1. 将libsvm-mat所在文件夹目录添加到MATLAB工作搜索目录(File ——》Set Path…——》Add with Subfolders...)这第一步很重要,如果没有将libsvm-mat所在文件夹目录正确的添加到MATLAB工作搜索目录,使用的时候就会出现??? Undefined function or variable 'XXX'.等等报错。
首先明晰一下MATLAB工作搜索目录(路径)和当前目录(路径)这两个概念:当前目录[Current Folder]是指MATLAB当前所在的路径,MATLAB菜单栏下面有一个Current Folder可以在这里进行当前所在目录的更改。
工作搜索目录(路径)是指当你使用某一个函数的时候,MATLAB可以进行搜索该函数的所有的目录集合。
注:当你使用某一个函数的时候,MATLAB首先会从当前目录搜索调用该函数,如果当前目录没有该函数,MATLAB就会从工作搜索目录按照从上到下的顺序进行搜索调用该函数,如果工作搜索目录中也没有该函数,就会给出??? Undefined function or variable 'XXX' 这个报错。
自然语言处理技术中常用的机器学习算法介绍

自然语言处理技术中常用的机器学习算法介绍自然语言处理(Natural Language Processing,NLP)是人工智能领域中研究人类语言与计算机之间交互的一门学科。
在NLP领域中,机器学习算法被广泛应用于语言模型、文本分类、命名实体识别、情感分析等任务中。
本文将介绍NLP中常用的机器学习算法,包括支持向量机(Support Vector Machine,SVM)、朴素贝叶斯(Naive Bayes)、隐马尔可夫模型(Hidden Markov Model,HMM)和递归神经网络(Recurrent Neural Network,RNN)。
支持向量机(SVM)是一种常用的监督学习算法,广泛用于文本分类、情感分析等NLP任务中。
其核心思想是将数据映射到高维空间,通过构建一个最优的超平面,来实现数据的分类。
SVM在处理小样本、非线性和高维特征等问题上具有较好的性能。
朴素贝叶斯(Naive Bayes)是一种基于概率的分类算法,常用于文本分类任务。
它基于贝叶斯定理和特征间的条件独立性假设,可以在给定训练数据的条件下,通过计算后验概率来进行分类。
朴素贝叶斯算法简单、计算效率高,并且对输入数据的特征空间进行了较弱的假设,适用于处理大规模的文本分类问题。
隐马尔可夫模型(HMM)是一种统计模型,常用于语音识别、机器翻译等NLP任务中。
HMM假设系统是一个由不可观察的隐含状态和观测到的可见状态组成的过程,通过观察到的状态序列来估计最可能的隐含状态序列。
HMM广泛应用于词性标注、命名实体识别等任务中,具有较好的效果。
递归神经网络(RNN)是一种具有记忆能力的神经网络,适用于处理序列数据,如语言模型、机器翻译等NLP任务。
RNN通过引入循环结构,可以对序列中的上下文信息进行建模。
长短期记忆网络(Long Short-Term Memory,LSTM)是RNN的一种改进,通过引入门控机制解决了传统RNN存在的长期依赖问题,更适合处理长文本和复杂语义。
svmtrain函数

svmtrain函数svmtrain函数是用于训练支持向量机(Support Vector Machine, SVM)模型的函数。
SVM是一种监督学习算法,广泛应用于分类和回归问题。
此函数在MATLAB中实现了支持向量机模型的训练过程。
```matlabsvmStruct = svmtrain(training, group);```除了上述基本语法,svmtrain函数还支持以下扩展格式来自定义SVM模型的属性:```matlabsvmStruct = svmtrain(training, group, 'PropertyName', PropertyValue, ...);```其中,`PropertyName`是属性名称,可用于设置SVM模型的各种参数,`PropertyValue`是属性值。
下面是一些常用的属性和参数,用于自定义svmtrain函数的行为:- `'KernelFunction'`:设置核函数,用于将数据映射到高维空间。
可选的核函数有线性核函数(`'linear'`)、多项式核函数(`'polynomial'`)、径向基核函数(`'rbf'`)等。
默认值为线性核函数。
- `'BoxConstraint'`:设置软间隔的约束参数C。
较大的C会使分类器更关注错误样本的数量,而较小的C会使得分类器更关注错误样本的程度。
默认值为1- `'KernelScale'`:设置径向基核函数的尺度参数。
当使用径向基核函数时,可以通过该参数控制数据点的作用范围。
默认值为1.0。
- `'KernelScale'`:设置径向基核函数的尺度参数。
当使用径向基核函数时,可以通过该参数控制数据点的作用范围。
默认值为1.0。
- `'Method'`:设置优化求解方法。
支持向量机(SVM)简述

第1 2章12.1 案例背景12.1.1 SVM概述支持向量机(Support Vector Machine,SVM)由Vapnik首先提出,像多层感知器网络和径向基函数网络一样,支持向量机可用于模式分类和非线性回归。
支持向量机的主要思想是建立一个分类超平面作为决策曲面,使得正例和反例之间的隔离边缘被最大化;支持向量机的理论基础是统计学习理论,更精确地说,支持向量机是结构风险最小化的近似实现。
这个原理基于这样的事实:学习机器在测试数据上的误差率(即泛化误差率)以训练误差率和一个依赖于VC维数(Vapnik - Chervonenkis dimension)的项的和为界,在可分模式情况下,支持向量机对于前一项的值为零,并且使第二项最小化。
因此,尽管它不利用问题的领域内部问题,但在模式分类问题上支持向量机能提供好的泛化性能,这个属性是支持向量机特有的。
支持向量机具有以下的优点:①通用性:能够在很广的各种函数集中构造函数;②鲁棒性:不需要微调;③有效性:在解决实际问题中总是属于最好的方法之一;④计算简单:方法的实现只需要利用简单的优化技术;⑤理论上完善:基于VC推广性理论的框架。
在“支持向量”x(i)和输入空间抽取的向量x之间的内积核这一概念是构造支持向量机学习算法的关键。
支持向量机是由算法从训练数据中抽取的小的子集构成。
支持向量机的体系结构如图12 -1所示。
图12-1 支持向量机的体系结构其中K为核函数,其种类主要有:线性核函数:K(x,x i)=x T x i;多项式核函数:K(x,x i)=(γx T x i+r)p,γ>0;径向基核函数:K(x,x i )=exp(-γ∥x −x i ∥2), γ>0;两层感知器核函数:K(x,x i )=tanh(γx T x i+r )。
1.二分类支持向量机C - SVC 模型是比较常见的二分类支持向量机模型,其具体形式如下:1)设已知训练集:T ={(x 1,y 1),…,(x i ,y i )}∈(X ×Y )ι其中,x i ∈X =R n ,y i ∈Y ={1,-1}( i =1,2,…,ι);x i 为特征向量。
1-6 lib-svm 经典使用 理论和介绍 工具用法 grid.py easy.py等

1/flydreamGG/archive/2009/08.aspx/flydreamGG/archive/2009/08.aspxLibSVM学习(一)——初识LibSVM 收藏LibSVM是台湾林智仁(Chih-Jen Lin) 教授2001年开发的一套支持向量机的库,这套库运算速度还是挺快的,可以很方便的对数据做分类或回归。
由于libSVM程序小,运用灵活,输入参数少,并且是开源的,易于扩展,因此成为目前国内应用最多的SVM的库。
这套库可以从.tw/~cjlin/免费获得,目前已经发展到2.89版。
下载.zip格式的版本,解压后可以看到,主要有5个文件夹和一些c++源码文件。
Java ——主要是应用于java平台;Python ——是用来参数优选的工具,稍后介绍;svm-toy ——一个可视化的工具,用来展示训练数据和分类界面,里面是源码,其编译后的程序在windows文件夹下;tools ——主要包含四个python文件,用来数据集抽样(subset),参数优选(grid),集成测试(easy), 数据检查(checkdata);windows ——包含libSVM四个exe程序包,我们所用的库就是他们,里面还有个heart_scale,是一个样本文件,可以用记事本打开,用来测试用的。
其他.h和.cpp文件都是程序的源码,可以编译出相应的.exe文件。
其中,最重要的是svm.h和svm.cpp文件,svm-predict.c、svm-scale.c和svm-train.c(还有一个svm-toy.c在svm-toy文件夹中)都是调用的这个文件中的接口函数,编译后就是windows下相应的四个exe程序。
另外,里面的README 跟FAQ 也是很好的文件,对于初学者如果E文过得去,可以看一下。
下面以svm-train为例,简单的介绍下,怎么编译:(这步很简单,也没必要,对于仅仅使用libsvm库的人来说,windows下的4个exe包已经足够了,之所以加这步,是为了那些做深入研究的人,可以按照自己的思路改变一下svm.cpp,然后编译验证)我用的是VC 6.0,新建一个控制台(win32 console application)程序,程序名叫svm-train(这个可以随意),点击OK后,选择empty。
SVM分类器的原理及应用

SVM分类器的原理及应用姓名:苏刚学号:1515063004学院:数学与计算机学院一、SVM分类器的原理SVM法即支持向量机(Support Vector Machine)法,由Vapnik等人于1995年提出,具有相对优良的性能指标。
该方法是建立在统计学习理论基础上的机器学习方法。
通过学习算法,SVM可以自动寻找出那些对分类有较好区分能力的支持向量,由此构造出的分类器可以最大化类与类的间隔,因而有较好的适应能力和较高的分准率。
该方法只需要由各类域的边界样本的类别来决定最后的分类结果。
支持向量机算法的目的在于寻找一个超平面H(d),该超平面可以将训练集中的数据分开,且与类域边界的沿垂直于该超平面方向的距离最大,故SVM法亦被称为最大边缘(maximum margin)算法。
待分样本集中的大部分样本不是支持向量,移去或者减少这些样本对分类结果没有影响,SVM法对小样本情况下的自动分类有着较好的分类结果.SVM方法是通过一个非线性映射p,把样本空间映射到一个高维乃至无穷维的特征空间中(Hilbert空间),使得在原来的样本空间中非线性可分的问题转化为在特征空间中的线性可分的问题。
简单地说,就是升维和线性化。
升维,就是把样本向高维空间做映射,一般情况下这会增加计算的复杂性,甚至会引起“维数灾难”,因而人们很少问津。
但是作为分类、回归等问题来说,很可能在低维样本空间无法线性处理的样本集,在高维特征空间中却可以通过一个线性超平面实现线性划分(或回归)。
一般的升维都会带来计算的复杂化,SVM方法巧妙地解决了这个难题:应用核函数的展开定理,就不需要知道非线性映射的显式表达式;由于是在高维特征空间中建立线性学习机,所以与线性模型相比,不但几乎不增加计算的复杂性,而且在某种程度上避免了“维数灾难”。
这一切要归功于核函数的展开和计算理论。
选择不同的核函数,可以生成不同的SVM,常用的核函数有以下4种:⑴线性核函数K(x,y)=x·y;⑵多项式核函数K(x,y)=[(x·y)+1]^d;⑶径向基函数K(x,y)=exp(-|x-y|^2/d^2);⑷二层神经网络核函数K(x,y)=tanh(a(x·y)+b);二、SVM分类器的应用2.1 人脸检测、验证和识别Osuna最早将SVM应用于人脸检测,并取得了较好的效果。
SVMs 详细介绍

SVM入门介绍1.SVM的简介支持向量机(Support Vector Machine)提出时间、人物:1995年、Cortes和Vapnik优势:它在解决小样本、非线性及高维模式识别中表现出许多特有的优势,并能够推广应用到函数拟合等其他机器学习问题中原理基础:支持向量机方法是建立在统计学习理论的VC维理论(问题的复杂程度,VC维越高,一个问题就越复杂)和结构风险最小原理基础上的,根据有限的样本信息在模型的复杂性(即对特定训练样本的学习精度Accuracy)和学习能力(即无错误地识别任意样本的能力)之间寻求最佳折衷,以期获得最好的推广能力(或称泛化能力)。
真实风险:由两部分内容刻画一是经验风险,代表了分类器在给定样本上的误差;二是置信风险,代表了我们在多大程度上可以信任分类器在未知文本上分类的结果。
小样本:并不是样本的绝对数量少(实际上,对任何算法来说,更多的样本几乎总是能带来更好的效果),而是说与问题的复杂度比起来,SVM算法要求的样本数是相对比较少的。
非线性:指SVM擅长应付样本数据线性不可分的情况,主要通过松弛变量(也有人叫惩罚变量)和核函数技术来实现,这一部分是SVM的精髓。
高维模式识别:指样本维数很高。
由于SVM 产生的分类器很简洁,用到的样本信息很少(仅仅用到那些称之为“支持向量”的样本),使得即使样本维数很高,也不会给存储和计算带来大麻烦。
2.S VM之线性分类器线性分类器,如图所示(二维空间里仅有两类样本的分类问题):图之解释:C1和C2是要区分的两个类别,中间的直线就是一个分类函数,它可以将两类样本完全分开。
一般的,如果一个线性函数能够将样本完全正确的分开,就称这些数据是线性可分的,否则称为非线性可分的。
线性函数:一维空间里→一个点,二维空间里→一条直线三维空间里→一个平面如果不关注空间的维数,这种线性函数还有一个统一的名称—超平面(Hyper Plane)!一个线性函数是一个实值函数(即函数的值是连续的实数),而我们的分类问题需要离散的输出值,例如用1表示某个样本属于类别C1,而用0表示不属于,这时只需在实值函数的基础上附加一个阈值即可,通过分类函数执行时得到的值大于还是小于这个阈值来确定类别归属。
SVM分类与回归简介ppt课件

其就是一种最简单 的支持向量机(SVM) (称为线性支持向 量机,即LSVM)
15
+1 -1
支持向量 (Support Vectors) :是 那些距离超平 面最近的点。
具有最大间隔的线 性分类器叫做最大 间隔线性分类器。
其就是一种最简单 的支持向量机(SVM) (称为线性支持向 量机,即LSVM)
R() L(y, f (x,))dP(x, y)
其中 P(x, y) 是未知的,对于不同类型的机器学习问题有不 同形式的损失函数。
4
模式识别
令训练器的输出y只有两种取值 y {0,1},并令 f (x,a),a
为指示函数集合(指示函数只有0和1两种取 值),考虑下面的损失函数:
0 若y f (x, a) L( y, f (x, a)) 1 若y f (x, a)
8
f (x, w,b) sign(w.x b)
+1 -1
如何进行数 据分类
9
+1
f (x, w,b) sign(w.x b)
-1
如何进行数 据分类
10
f (x, w,b) sign(w.x b)
+1 -1
如何进行数 据分类
11
f (x, w,b) sign(w.x b)
+1 -1
l
w i yi xi i 1
b maxi:yi 1 w*T xi mini:yi 1 w*T xi 2
21
以上所得到的最优分类函数为:
f (x) sgn{w* x b*} sgn{
l
i1 i
yi (xi x) b
}
该式只包含待分类样本与训练样本中的支持向量的内 积 运算,要解决一个特征空间中的最优线性分类问题, 我们只需要知道这个空间中的内积运算即可。
libsvm的原理及使用方法介绍

LibSVM学习目录LibSVM学习 (1)初识LibSVM (1)第一次体验libSvm (3)LibSVM使用规范 (5)1. libSVM的数据格式 (5)2. svmscale的用法 (5)3. svmtrain的用法 (6)4. svmpredict 的用法 (7)逐步深入LibSVM (7)分界线的输出 (11)easy.py和grid.py的使用 (13)1. grid.py使用方法 (13)2. easy.py使用方法 (14)参考 (16)LibSVM学习初识LibSVMLibSVM是台湾林智仁(Chih-Jen Lin's) 教授2001年开发的一套支持向量机的库,这套库运算速度还是挺快的,可以很方便的对数据做分类或回归。
由于libSVM程序小,运用灵活,输入参数少,并且是开源的,易于扩展,因此成为目前国内应用最多的SVM的库。
这套库可以从林智仁的home page上免费获得,目前已经发展到3.0版。
下载.zip格式的版本,解压后可以看到,主要有5个文件夹和一些c++源码文件。
Java ——主要是应用于java平台的源码和libsvm.jar包;Python ——是用来参数优选的工具,稍后介绍;svm-toy ——一个可视化的工具,用来展示训练数据和分类界面,里面是源码,其编译后的程序在windows文件夹下;tools ——主要包含四个python文件,用来数据集抽样(subset.py),参数优选(grid.py),集成测试(easy.py), 数据检查(checkdata.py);windows ——包含libSVM四个exe程序包,我们所用的库和程序就是它们。
其他.h和.cpp文件都是程序的源码,可以编译出相应的.exe文件。
其中,最重要的是svm.h 和svm.cpp文件,svm-predict.c、svm-scale.c和svm-train.c(还有一个svm-toy.cpp在svm-toy\qt 文件夹中)都是调用的这个文件中的接口函数,编译后就是windows下相应的四个exe程序。
支持向量机(SVM)、支持向量机回归(SVR):原理简述及其MATLAB实例

支持向量机(SVM)、支持向量机回归(SVR):原理简述及其MATLAB实例一、基础知识1、关于拉格朗日乘子法和KKT条件1)关于拉格朗日乘子法2)关于KKT条件2、范数1)向量的范数2)矩阵的范数3)L0、L1与L2范数、核范数二、SVM概述1、简介2、SVM算法原理1)线性支持向量机2)非线性支持向量机二、SVR:SVM的改进、解决回归拟合问题三、多分类的SVM1. one-against-all2. one-against-one四、QP(二次规划)求解五、SVM的MATLAB实现:Libsvm1、Libsvm工具箱使用说明2、重要函数:3、示例支持向量机(SVM):原理及其MATLAB实例一、基础知识1、关于拉格朗日乘子法和KKT条件1)关于拉格朗日乘子法首先来了解拉格朗日乘子法,为什么需要拉格朗日乘子法呢?记住,有需要拉格朗日乘子法的地方,必然是一个组合优化问题。
那么带约束的优化问题很好说,就比如说下面这个:这是一个带等式约束的优化问题,有目标值,有约束条件。
那么你可以想想,假设没有约束条件这个问题是怎么求解的呢?是不是直接 f 对各个 x 求导等于 0,解 x 就可以了,可以看到没有约束的话,求导为0,那么各个x均为0吧,这样f=0了,最小。
但是x都为0不满足约束条件呀,那么问题就来了。
有了约束不能直接求导,那么如果把约束去掉不就可以了吗?怎么去掉呢?这才需要拉格朗日方法。
既然是等式约束,那么我们把这个约束乘一个系数加到目标函数中去,这样就相当于既考虑了原目标函数,也考虑了约束条件。
现在这个优化目标函数就没有约束条件了吧,既然如此,求法就简单了,分别对x求导等于0,如下:把它在带到约束条件中去,可以看到,2个变量两个等式,可以求解,最终可以得到,这样再带回去求x就可以了。
那么一个带等式约束的优化问题就通过拉格朗日乘子法完美的解决了。
更高一层的,带有不等式的约束问题怎么办?那么就需要用更一般化的拉格朗日乘子法,即KKT条件,来解决这种问题了。
matlab逻辑回归

matlab逻辑回归逻辑回归是一种有效的机器学习方法,它的基本原理是将输入样本归类为两类样本,即正负样本,其中正样本表示正确的分类结果,而负样本则表示错误的分类结果。
matlab中提供了对应的函数能够帮助我们完成逻辑回归的任务。
1、准备工作首先,下载数据集,并从中提取出训练数据和测试数据。
这里,使用matlab的fitclinear函数,将训练数据与测试数据分为自变量(训练数据)和因变量(测试数据)。
接下来,将自变量和因变量转换为矩阵形式,同时使用matlab的svmtrain和svmpredict函数进行训练和预测。
2、数据预处理为了有助于逻辑回归的训练,需要将数据集进行预处理,包括数据标准化、数据正则化等。
最常用的数据标准化方法是均值方差归一化,matlab提供了对应的函数,可以自动将数据标准化。
另外,正则化是指在训练模型前,将训练数据的自变量进行归一化处理,以防止过拟合,matlab中使用函数normc即可实现正则化。
3、训练模型完成数据预处理后,即可使用matlab提供的fitclinear函数来训练逻辑回归模型,fitclinear函数的使用方法为:[b,dev,stats] = fitclinear(x,y,‘logistic’)其中,x为自变量,y为因变量,“logistic”参数表示使用的是logistic回归。
fitclinear函数会返回三个值:b表示回归系数,dev表示模型的偏差,stats表示模型的统计量。
4、模型预测训练完成后,我们可以使用matlab提供的predict函数进行预测,函数的使用方法为:probs = predict(b,x)其中,b是返回的回归系数,x为自变量。
predict函数返回预测值,即正负样本的概率值。
最后,为了评估模型的预测准确率,我们可以使用matlab提供的confusionmat函数来计算混淆矩阵,进而统计准确率等指标。
综上所述,matlab提供了一系列的函数,可以帮助我们轻松完成逻辑回归的训练与预测。
svm rfe原理

SVM RFE原理详解SVM RFE(Support Vector Machine Recursive Feature Elimination)是一种基于支持向量机(Support Vector Machine)的特征选择算法。
特征选择是机器学习中的重要步骤,其目的是从原始特征集合中选择出最具有代表性的特征,以提高模型的性能和泛化能力。
1. 支持向量机(SVM)支持向量机是一种监督学习算法,其主要任务是将训练数据集中的样本划分到不同的类别中。
SVM通过在特征空间中找到一个最优的超平面来实现分类任务。
超平面的选择是基于最大间隔的原则,即使得不同类别样本之间的距离最大化。
在SVM中,样本被表示为特征向量的形式,并且每个特征向量都有一个对应的类别标签。
SVM通过学习一个决策函数来进行分类,决策函数可以将新的样本点映射到特征空间,并根据其位置来预测其所属的类别。
2. 特征选择特征选择是为了降低维度,减少特征空间的复杂性,提高模型的性能和泛化能力。
在实际应用中,特征选择可以帮助我们发现最相关的特征,去除冗余和噪声特征,提高模型的解释性和可解释性。
特征选择的方法可以分为三类:过滤式(Filter)、包裹式(Wrapper)和嵌入式(Embedded)。
SVM RFE属于包裹式方法,其主要思想是将特征选择嵌入到模型训练过程中,通过迭代的方式逐步剔除不重要的特征。
3. SVM RFE算法步骤SVM RFE算法的基本步骤如下:步骤1:初始化首先,将原始特征集合作为输入,初始化SVM模型。
设定特征选择的目标维度。
步骤2:特征权重计算使用初始化的SVM模型对原始特征集合进行训练,并计算每个特征的权重。
这些权重反映了特征对模型性能的贡献程度,权重越大表示该特征越重要。
步骤3:特征剔除根据特征权重,剔除权重最小的特征。
通过剔除一个特征,得到新的特征集合。
步骤4:模型更新使用新的特征集合重新训练SVM模型,并计算特征权重。
(仅供参考)SVM模型的决策函数解析表达式

获取SVM 模型的决策函数解析表达式对于svm 模型,由于有libsvm 工具包(for matlab)或e1071安装包(for R),对于给定训练样本,很容易获取到训练之后的svm 模型,但是对于训练的svm 模型,返回的object 对象是模型的相关参数,对于模型的具体表达式并没有给出。
对于给定测试集,也很容易通过predict 函数进行预测,但对于大部分的工程应用,需要知道训练完模型之后的决策函数的解析表达式。
下文旨在分析如何通过离线训练的svm 模型获取对应的解析表达式。
本文主要针对svm 多分类问题进行剖析,且实现方法使用的是libsvm 的one-versus-one,简称OVO SVMs 或者pairwise 方法,实现工具为R ,其实matlab 实现过程更容易,在R 的e1071包实际调用的还是MATLAB 的libsvm 工具箱,如果认真阅读libsvm 中代码(svm.cpp 、svmtrain.c 、svmpredict.c ),很容易获取决策函数的解析表达式。
第一步:数据的标准化这部分内容很重要,应为如果建模数据集进行了标准化(一般svm 建模过程往往会自动完成),而测试集不进行数据的标准化,那么在后面计算内积的时候会导致很大的问题(最初对于测试集没有进行标准化,导致分类完全失真,后来通过调试发现是标准化问题),例如对于RBF 核函数,计算),exp(),(2>--=γγy x y x K 对于X(一般是训练后的标准化支撑向量)和y(测试集中的一个实例)的RBF 核内积,假设X 是标准化的数据,Y 是没有标准化的数据,这就是问题所在。
同时,对于测试集Y ,需要根据训练集X 的中心值和标准差进行标准化。
library(e1071)data(Glass,package="mlbench")##split data into a train and test setindex <-1:nrow(Glass)testindex <-sample(index,trunc(length(index)/3))testset <-Glass[testindex,]trainset <-Glass[-testindex,]svm.model <-svm(Type ~.,data =trainset,cost =100,gamma =1)#RBF 核函数使用上面的数据集,建立svm.model 模型,可以看到attributes(svm.model)svm.model$scaledsvm.model$x.scale在第一步的是时候需要根据svm 模型的svm_model$scaled 和svm_model$x.scale 两部分信息进行测试集的标准化(按列进行,每列表示一个特征)。
svmtrain函数

svmtrain函数svmtrain函数是一种机器学习算法,改算法能够用来预测数据的输出结果。
它是一种支持向量机(Support Vector Machine)算法,可以有效地处理大规模数据,并且可以在各种复杂的情况下进行有效的训练和预测工作。
SVM算法通过建立一个或多个支持向量机(SVM)模型,来依据一组已知的输入和输出样本,建立一个最优的模型,以满足特定问题的预测目标。
svmtrain函数是一种有效的SVM算法,由MATLAB库函数提供。
svmtrain函数默认采用有核函数工具,这意味着它可以快速处理非线性的训练数据。
svmtrain函数的输入有如下几种:样本特征,样本标签,核函数参数,模型参数,优化参数等等。
样本特征可以是数值型变量或者非数值型变量,样本标签是一个与样本特征相对应的输出变量;核函数参数表明svmtrain函数所采用的核函数,模型参数表示svm模型的复杂度,优化参数则表示svm模型优化所采用的算法及其参数。
当svmtrain函数得到输入参数后,就会开始训练模型,它会根据输入参数和训练数据的情况,进行支持向量机的训练,最终得出支持向量机模型,并将其保存至指定的文件路径。
训练出的模型可以通过svmclassify函数来对新的数据进行预测。
svmtrain函数是一个有效的机器学习算法,它可以有效地分类和预测比较复杂的数据,优点是训练出的模型十分准确,预测的效果也非常好,它可以应用于许多不同的领域,像医学、搜索引擎、自然语言处理、数据挖掘等,有着广泛的应用和实际意义。
总的来说,svmtrain函数是一种非常有效的机器学习算法,它可以对大规模数据进行有效的训练和预测,广泛应用于各种不同的领域,是一个相当值得研究和研发的有效算法。
matlab间隔函数

matlab间隔函数
matlab间隔函数是一种在机器学习中常用的函数,用于计算数据集中不同类别之间的间隔大小。
该函数可以帮助我们评估分类器的性能,并且可以用来选择最佳的分类边界。
在matlab中,间隔函数通常使用svmtrain和svmpredict函数来实现。
svmtrain函数用于训练支持向量机模型,而svmpredict函数用于预测新数据点的类别。
具体来说,间隔函数的计算公式如下:
间隔 = (2 / (||w||^2))
其中,w是支持向量机模型的权重向量,||w||表示其欧几里得范数。
通过计算间隔大小,我们可以确定分类器对于不同类别之间的分界线的可靠性和准确性。
如果间隔较小,则说明分类边界可能存在一定的误差,需要进一步优化模型。
如果间隔较大,则说明分类边界非常准确,并且模型具有较好的预测能力。
总之,matlab间隔函数在机器学习中具有重要的作用,可以帮助我们评估和优化分类器的性能,提高模型的预测准确性。
- 1 -。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
svmtrain和svmpredict简介
分类:SVM
本文主要介绍了SVM工具箱中svmtrain和svmpredict两个主要函数:
(1)model= svmtrain(train_label, train_matrix,
['libsvm_options']);
其中:
train_label表示训练集的标签。
train_matrix表示训练集的属性矩阵。
libsvm_options是需要设置的一系列参数,各个参数可参见《libsvm 参数说明.txt》,里面介绍的很详细,中英文都有的。
如果用
回归的话,其中的-s参数值应为3。
model:是训练得到的模型,是一个结构体(如果参数中用到-v,得到的就不是结构体,对于分类问题,得到的是交叉检验下的平均分类准确
率;对于回归问题,得到的是均方误差)。
(2)[predicted_label,
accuracy/mse,decision_values/prob_estimates]
=svmpredict(test_label, test_matrix, model,
['libsvm_options']);
其中:
test _label表示测试集的标签(这个值可以不知道,因为作预测的时候,本来就是想知道这个值的,这个时候,随便制定一个值就可以
了,只是这个时候得到的mse就没有意义了)。
test _matrix表示测试集的属性矩阵。
model 是上面训练得到的模型。
libsvm_options是需要设置的一系列参数。
predicted_label表示预测得到的标签。
accuracy/mse是一个3*1的列向量,其中第1个数字用于分类问题,表示分类准确率;后两个数字用于回归问题,第2个数字
表示mse;第三个数字表示平方相关系数(也就是说,如
果分类的话,看第一个数字就可以了;回归的话,看后两
个数字)。
decision_values/prob_estimates:第三个返回值,一个矩阵包含决策
的值或者概率估计。
对于n个预测样本、k类的问题,如果指
定“-b 1”参数,则n x k的矩阵,每一行表示这个样本分别
属于每一个类别的概率;如果没有指定“-b 1”参数,则为n
x k*(k-1)/2的矩阵,每一行表示k(k-1)/2个二分类SVM
的预测结果。
(3) 训练的参数
LIBSVM训练时可以选择的参数很多,包括:
-s svm类型:SVM设置类型(默认0)
0 —C-SVC; 1 –v-SVC; 2 –一类SVM; 3 —e-
SVR;4 —v-SVR
-t 核函数类型:核函数设置类型(默认2)
0 –线性核函数:u’v
1 –多项式核函数:(r*u’v + coef0)^degree
2 –RBF(径向基)核函数:exp(-r|u-v|^2)
3 –sigmoid核函数:tanh(r*u’v + coef0)
-d degree:核函数中的degree设置(针对多项式核函数)(默认3)-g r(gamma):核函数中的gamma函数设置(针对多项式
/rbf/sigmoid核函数)(默认1/k,k为总类别数)
-r coef0:核函数中的coef0设置(针对多项式/sigmoid核函数)((默认0)
-c cost:设置C-SVC,e -SVR和v-SVR的参数(损失函数)(默认1)
-n nu:设置v-SVC,一类SVM和v- SVR的参数(默认0.5)
-p p:设置e -SVR 中损失函数p的值(默认0.1)
-m cachesize:设置cache内存大小,以MB为单位(默认40)
-e eps:设置允许的终止判据(默认0.001)
-h shrinking:是否使用启发式,0或1(默认1)
-wi weight:设置第几类的参数C为weight*C (C-SVC中的C) (默认1)
-v n: n-fold交互检验模式,n为fold的个数,必须大于等于2
以上这些参数设置可以按照SVM的类型和核函数所支持的参数进行任意组合,如果设置的参数在函数或SVM类型中没有也不会
产生影响,程序不会接受该参数;如果应有的参数设置不正确,参数将采用默认值。
