中考真题训练 数与代数部分
2021年九年级数学中考复习分类真题训练:《数与式之 代数式》

2021年九年级数学中考复习分类真题训练:《数与式之代数式》一.列代数式1.(2020•长春)长春市净月潭国家森林公园门票的价格为成人票每张30元,儿童票每张15元.若购买m张成人票和n张儿童票,则共需花费元.二.代数式求值2.(2020•潍坊)若m2+2m=1,则4m2+8m﹣3的值是()A.4 B.3 C.2 D.1 3.(2019•贵阳)如图是一个长为a,宽为b的矩形,两个阴影图形都是一对底边长为1,且底边在矩形对边上的平行四边形.(1)用含字母a,b的代数式表示矩形中空白部分的面积;(2)当a=3,b=2时,求矩形中空白部分的面积.三.合并同类项4.(2020•通辽)下列说法不正确的是()A.2a是2个数a的和B.2a是2和数a的积C.2a是单项式D.2a是偶数四.规律型:数字的变化类5.(2020•牡丹江)一列数1,5,11,19…按此规律排列,第7个数是()A.37 B.41 C.55 D.71 6.(2020•娄底)下列各正方形中的四个数之间都有相同的规律,根据此规律,x的值为()A.135 B.153 C.170 D.189 7.(2020•云南)按一定规律排列的单项式:a,﹣2a,4a,﹣8a,16a,﹣32a,…,第n 个单项式是()A.(﹣2)n﹣1a B.(﹣2)n a C.2n﹣1a D.2n a 8.(2020•玉林)观察下列按一定规律排列的n个数:2,4,6,8,10,12,…,若最后三个数之和是3000,则n等于()A.499 B.500 C.501 D.1002 9.(2020•西藏)观察下列两行数:1,3,5,7,9,11,13,15,17,…1,4,7,10,13,16,19,22,25,…探究发现:第1个相同的数是1,第2个相同的数是7,…,若第n个相同的数是103,则n等于()A.18 B.19 C.20 D.21 10.(2020•广西)如图,某校礼堂的座位分为四个区域,前区一共有8排,其中第1排共有20个座位(含左、右区域),往后每排增加两个座位,前区最后一排与后区各排的座位数相同,后区一共有10排,则该礼堂的座位总数是.11.(2020•呼和浩特)“书法艺术课”开课后,某同学买了一包纸练习软笔书法,且每逢星期几写几张,即每星期一写1张,每星期二写2张,……,每星期日写7张,若该同学从某年的5月1日开始练习,到5月30日练习完后累积写完的宣纸总数超过120张,则可算得5月1日到5月28日他共用宣纸张数为,并可推断出5月30日应该是星期几.12.(2020•淄博)某快递公司在甲地和乙地之间共设有29个服务驿站(包括甲站、乙站),一辆快递货车由甲站出发,依次途经各站驶往乙站,每停靠一站,均要卸下前面各站发往该站的货包各1个,又要装上该站发往后面各站的货包各1个.在整个行程中,快递货车装载的货包数量最多是 个. 13.(2020•安徽)观察以下等式: 第1个等式:×(1+)=2﹣, 第2个等式:×(1+)=2﹣, 第3个等式:×(1+)=2﹣, 第4个等式:×(1+)=2﹣. 第5个等式:×(1+)=2﹣. …按照以上规律,解决下列问题: (1)写出第6个等式: ;(2)写出你猜想的第n 个等式: (用含n 的等式表示),并证明. 14.(2019•北京)小云想用7天的时间背诵若干首诗词,背诵计划如下: ①将诗词分成4组,第i 组有x i 首,i =1,2,3,4;②对于第i 组诗词,第i 天背诵第一遍,第(i +1)天背诵第二遍,第(i +3)天背诵第三遍,三遍后完成背诵,其它天无需背诵,i =1,2,3,4;第1天第2天第3天 第4天第5天 第6天 第7天 第1组 x 1x 1x 1第2组 x 2x 2x 2第3组第4组x 4 x 4x 4③每天最多背诵14首,最少背诵4首. 解答下列问题: (1)填入x 3补全上表;(2)若x 1=4,x 2=3,x 3=4,则x 4的所有可能取值为 ;(3)7天后,小云背诵的诗词最多为 首. 15.(2019•张家界)阅读下面的材料:按照一定顺序排列着的一列数称为数列,数列中的每一个数叫做这个数列的项.排在第一位的数称为第一项,记为a 1,排在第二位的数称为第二项,记为a 2,依此类推,排在第n 位的数称为第n 项,记为a n .所以,数列的一般形式可以写成:a 1,a 2,a 3,…,a n ,…. 一般地,如果一个数列从第二项起,每一项与它前一项的差等于同一个常数,那么这个数列叫做等差数列,这个常数叫做等差数列的公差,公差通常用d 表示.如:数列1,3,5,7,…为等差数列,其中a 1=1,a 2=3,公差为d =2. 根据以上材料,解答下列问题:(1)等差数列5,10,15,…的公差d 为 ,第5项是 .(2)如果一个数列a 1,a 2,a 3,…,a n …,是等差数列,且公差为d ,那么根据定义可得到:a 2﹣a 1=d ,a 3﹣a 2=d ,a 4﹣a 3=d ,…,a n ﹣a n ﹣1=d ,…. 所以a 2=a 1+da 3=a 2+d =(a 1+d )+d =a 1+2d , a 4=a 3+d =(a 1+2d )+d =a 1+3d ,……由此,请你填空完成等差数列的通项公式:a n =a 1+( )d . (3)﹣4041是不是等差数列﹣5,﹣7,﹣9…的项?如果是,是第几项?五.规律型:图形的变化类16.(2020•十堰)根据图中数字的规律,若第n 个图中出现数字396,则n =( )A .17B .18C .19D .2017.(2020•日照)用大小相同的圆点摆成如图所示的图案,按照这样的规律摆放,则第10个图案中共有圆点的个数是( )A.59 B.65 C.70 D.71 18.(2020•武汉)下列图中所有小正方形都是全等的.图(1)是一张由4个小正方形组成的“L”形纸片,图(2)是一张由6个小正方形组成的3×2方格纸片.把“L”形纸片放置在图(2)中,使它恰好盖住其中的4个小正方形,共有如图(3)中的4种不同放置方法.图(4)是一张由36个小正方形组成的6×6方格纸片,将“L”形纸片放置在图(4)中,使它恰好盖住其中的4个小正方形,共有n种不同放置方法,则n的值是()A.160 B.128 C.80 D.48 19.(2020•大庆)如图,把同样大小的黑色棋子摆放在正多边形的边上,按照这样的规律摆下去,则第20个图需要黑色棋子的个数为.参考答案一.列代数式1.解:根据单价×数量=总价得,共需花费(30m+15n)元,故答案为:(30m+15n).二.代数式求值2.解:∵m2+2m=1,∴4m2+8m﹣3=4(m2+2m)﹣3=4×1﹣3=1.故选:D.3.解:(1)S=ab﹣a﹣b+1;(2)当a=3,b=2时,S=6﹣3﹣2+1=2;三.合并同类项4.解:A.2a=a+a,即2a是2个数a的和,说法正确;B.2a是2和数a的积,说法正确;C.2a是单项式,说法正确;D.2a不一定是偶数,故原说法错误.故选:D.四.规律型:数字的变化类5.解:1=1×2﹣1,5=2×3﹣1,11=3×4﹣1,19=4×5﹣1,…第n个数为n(n+1)﹣1,则第7个数是:55.故选:C.6.解:根据规律可得,2b=18,∴b=9,∴a=b﹣1=8,∴x=2b2+a=162+8=170,故选:C.7.解:∵a=(﹣2)1﹣1a,﹣2a=(﹣2)2﹣1a,4a=(﹣2)3﹣1a,﹣8a=(﹣2)4﹣1a,16a=(﹣2)5﹣1a,﹣32a=(﹣2)6﹣1a,…由上规律可知,第n个单项式为:(﹣2)n﹣1a.故选:A.8.解:由题意,得第n个数为2n,那么2n+2(n﹣1)+2(n﹣2)=3000,解得:n=501,故选:C.9.解:第1个相同的数是1=0×6+1,第2个相同的数是7=1×6+1,第3个相同的数是13=2×6+1,第4个相同的数是19=3×6+1,…,第n个相同的数是6(n﹣1)+1=6n﹣5,所以6n﹣5=103,解得n=18.答:第n个相同的数是103,则n等于18.故选:A.10.解:因为前区一共有8排,其中第1排共有20个座位(含左、右区域),往后每排增加两个座位,所以前区最后一排座位数为:20+2(8﹣1)=34,所以前区座位数为:(20+34)×8÷2=216,因为前区最后一排与后区各排的座位数相同,后区一共有10排,所以后区的座位数为:10×34=340,所以该礼堂的座位总数是216+340=556个.故答案为:556个.11.解:∵5月1日~5月30日共30天,包括四个完整的星期,∴5月1日~5月28日写的张数为:4×=112,若5月30日为星期一,所写张数为112+7+1=120,若5月30日为星期二,所写张数为112+1+2<120,若5月30日为星期三,所写张数为112+2+3<120,若5月30日为星期四,所写张数为112+3+4<120,若5月30日为星期五,所写张数为112+4+5>120,若5月30日为星期六,所写张数为112+5+6>120,若5月30日为星期日,所写张数为112+6+7>120,故5月30日可能为星期五、六、日.故答案为:112;五、六、日.12.解:当一辆快递货车停靠在第x个服务驿站时,快递货车上需要卸下已经通过的(x﹣1)个服务驿站发给该站的货包共(x﹣1)个,还要装上下面行程中要停靠的(n﹣x)个服务驿站的货包共(n﹣x)个.根据题意,完成下表:服务驿站序号在第x服务驿站启程时快递货车货包总数1 n﹣12 (n﹣1)﹣1+(n﹣2)=2(n﹣2)3 2(n﹣2)﹣2+(n﹣3)=3(n﹣3)4 3(n﹣3)﹣3+(n﹣4)=4(n﹣4)5 4(n﹣4)﹣4+(n﹣5)=5(n﹣5)……n0由上表可得y=x(n﹣x).当n=29时,y=x(29﹣x)=﹣x2+29x=﹣(x﹣14.5)2+210.25,当x=14或15时,y取得最大值210.故答案为:210.13.解:(1)第6个等式:×(1+)=2﹣;(2)猜想的第n个等式:×(1+)=2﹣.证明:∵左边=×==2﹣=右边,∴等式成立.故答案为:×(1+)=2﹣;×(1+)=2﹣.14.解:(1)第1天第2天第3天第4天第5天第6天第7天第1组x1x1x1第2组x2x2x2第3组x3x3x3第4组x4x4x4(2)∵每天最多背诵14首,最少背诵4首,∴x1≥4,x3≥4,x4≥4,∴x1+x3≥8①,∵x1+x3+x4≤14②,把①代入②得,x4≤6,∴4≤x4≤6,∴x4的所有可能取值为4,5,6,故答案为:4,5,6;(3)∵每天最多背诵14首,最少背诵4首,∴由第2天,第3天,第4天,第5天得,x 1+x 2≤14①,x 2+x 3≤14②,x 1+x 3+x 4=14③,x 2+x 4≤14④,①+②+2③+④≤70得,x 1+x 2+x 2+x 3+2(x 1+x 3+x 4)+x 2+x 4≤70, ∴3(x 1+x 2+x 3+x 4)≤70, ∴x 1+x 2+x 3+x 4≤,∴x 1+x 2+x 3+x 4≤23,∴7天后,小云背诵的诗词最多为23首, 故答案为:23.15.解:(1)根据题意得,d =10﹣5=5; ∵a 3=15,a 4=a 3+d =15+5=20, a 5=a 4+d =20+5=25,故答案为:5;25.(2)∵a 2=a 1+da 3=a 2+d =(a 1+d )+d =a 1+2d , a 4=a 3+d =(a 1+2d )+d =a 1+3d ,……∴a n =a 1+(n ﹣1)d 故答案为:n ﹣1.(3)根据题意得,等差数列﹣5,﹣7,﹣9…的项的通项公式为:a n =﹣5﹣2(n ﹣1), 则﹣5﹣2(n ﹣1)=﹣4041, 解之得:n =2019∴﹣4041是等差数列﹣5,﹣7,﹣9…的项,它是此数列的第2019项. 五.规律型:图形的变化类(共4小题) 16.解:根据图形规律可得:上三角形的数据的规律为:2n (1+n ),若2n (1+n )=396,解得n 不为正整数,舍去; 下左三角形的数据的规律为:n 2﹣1,若n 2﹣1=396,解得n 不为正整数,舍去;下中三角形的数据的规律为:2n﹣1,若2n﹣1=396,解得n不为正整数,舍去;下右三角形的数据的规律为:n(n+4),若n(n+4)=396,解得n=18,或n=﹣22,舍去故选:B.17.解:根据图中圆点排列,当n=1时,圆点个数5+2;当n=2时,圆点个数5+2+3;当n=3时,圆点个数5+2+3+4;当n=4时,圆点个数5+2+3+4+5,…∴当n=10时,圆点个数5+2+3+4+5+6+7+8+9+10+11=4+(1+2+3+4+5+6+7+8+9+10+11)=.故选:C.18.解:观察图象可知(4)中共有4×5×2=40个3×2的长方形,由(3)可知,每个3×2的长方形有4种不同放置方法,则n的值是40×4=160.故选:A.19.解:观察图形可知:第1个图需要黑色棋子的个数为:3=1×3;第2个图需要黑色棋子的个数为:8=2×4;第3个图需要黑色棋子的个数为:15=3×5;第4个图需要黑色棋子的个数为:24=4×6;…发现规律:第n个图需要黑色棋子的个数为:n(n+2);所以第20个图需要黑色棋子的个数为:20(20+2)=440.故答案为:440.。
2019-2020年九年级数学数与代数综合练习2-九年级数学试题
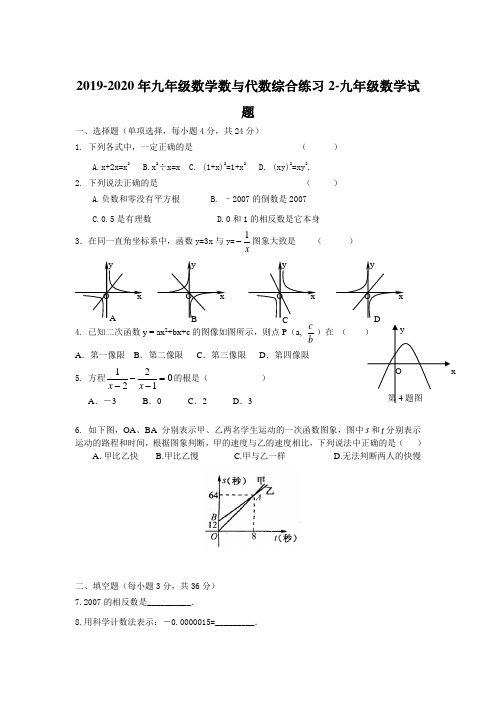
2019-2020年九年级数学数与代数综合练习2-九年级数学试题一、选择题(单项选择,每小题4分,共24分)1. 下列各式中,一定正确的是 ( )A.x+2x=x 2B.x 2÷x=x C. (1+x)2=1+x 2D. (xy)2=xy 2. 2. 下列说法正确的是 ( )A.负数和零没有平方根B. –2007的倒数是2007C.0.5是有理数D.0和1的相反数是它本身 3.在同一直角坐标系中,函数y=3x 与y=x1-图象大致是 ( )4. 已知二次函数y = ax 2+bx+c 的图像如图所示,则点P (a, bc)在 ( A .第一像限 B .第二像限 C .第三像限 D .第四像限 5. 方程01221=---x x 的根是( ) A .-3 B .0 C .2 D .36. 如下图,OA 、BA 分别表示甲、乙两名学生运动的一次函数图象,图中s 和t 分别表示运动的路程和时间,根据图象判断,甲的速度与乙的速度相比,下列说法中正确的是( )A .甲比乙快 B.甲比乙慢 C.甲与乙一样 D.无法判断两人的快慢二、填空题(每小题3分,共36分) 7.2007的相反数是__________.8.用科学计数法表示:-0.0000015=_________.9.计算:43x x ⋅=_________.10.分解因式:12-a =__________________. 11.当x =____时,分式31-x 没有意义. 12.已知函数12-=x y ,当x=1时,y=_________.13.把抛物线()22-=x y 向左平移2个单位,再向下平移1个单位,得到的解析式是_______.14.不等式3x -4≥4+2(x -2)的最小整数解是__________. 15.函数y =8632+--x x x 的自变量x 的取值范围是___________. 16.化简(m1+n 1)÷n n m +的结果是___. 17.请你写出一个5到6之间的无理数 . 18.观察下面的点阵图,探究其中的规律。
华师版中考专题《数与代数》测试题及答案

中考数学二轮专题复习卷《数与代数》一、填空题(每小题3分,共36分)1、2006的相反数是 .2、分解因式:x x 43-= .3、在等式3×□-2×□=15的两个方格内分别填入一个数使等式成立,且所填的这两个数互为相反数,则第一个方格内应填的数是 .4、方程)2(2)2)(1(+=+-x x x 的根是 .5、请你写出一个4到5之间的无理数 .6、在数轴上,与表示-1的点距离为3的点所表示的数是 .7、若代数式7322++x x 的值为8,则代数式9642-+x x 的值为 .8、如图,小红房间的窗户由6个相同的小正方形组成,上面的装饰物是两个四分之一圆,用含a 的代数式表示窗户中能射进阳光部分的面积是 .9、将抛物线22x y =向左平移1个单位,再向下平移3个单位,所得的抛物线的顶点坐标为 .10、一次函数x y -=1的图象不经过第 象限.11、等腰三角形的周长为10cm ,腰长为xcm ,底边长为ycm ,则y 与x 之间的函数关系式是 ,自变量x 的取值范围是 .12、根据指令〔s ,x 〕(其中s ≥0,0°≤x ≤180°),机器人在平面上能完成下列动作:先原地逆时针转角度x ,再朝其面对的方向沿直线行走距离s .现机器人在直角坐标系的坐标原点,且面对x 轴正方向.(1)若给机器人下了一个指令〔10,30°〕,则机器人应移到的点的坐标是 .(2)若要让机器人移到点(-6,6),则应下指令 .二、选择题(单项选择,每小题3分,共18分).13、下列计算,结果正确的是( ).(A )532a a a =+;(B )642a a a =⋅(C )236a a a =÷;(D) 832)(a a =.14、如果要使不等式组⎩⎨⎧>m <8x x 有解,则m 的取值范围是( ). (A ) m >8;(B )m ≥8;(C )m <8;(D )m ≤8.15、已知抛物线c bx x y ++=2的部分图象如图所示,若y<0,则x 的取值范围是( ).(A )-1<x <3;(B )-1<x <4;(C )x <-1或x >4;(D )x <-1或x >3.16、从一张正方形的纸片上,沿一条边剪下宽为2cm的长方形纸条,剩下的纸片为48 cm 2,则原来这张纸片的面积是( )(A )64cm 2;(B )100 cm 2;(C )121 cm 2;(D )144 cm 2.17、在“人与自然”知识竞赛中,共有25道选择题。
2024中考数学代数部分历年真题全解析

2024中考数学代数部分历年真题全解析一、方程与不等式1. 试求满足方程2x + 5 = 3x - 1的解。
解析:将方程两边的x合并到一起得到:2x - 3x = -1 - 5,化简得到-x = -6。
两边乘以-1,得到x = 6。
2. 解方程(x - 3)(2x + 4) = 0。
解析:当一个乘积为0时,至少有一个因子为0,所以(x - 3) = 0或(2x + 4) = 0。
解得x = 3或x = -2。
3. 解不等式3x + 7 < 4。
解析:将4移到不等式的左边得到3x + 7 - 4 < 0,化简得到3x + 3 < 0。
再将3移到不等式的右边得到3x < -3,最终解得x < -1。
二、函数与图像1. 表示函数y = 2x + 1的图像。
解析:根据一次函数y = kx + b的特点,我们可以知道斜率k为2,截距b为1。
所以图像是一条斜率为2的直线,在y轴上与x轴相交于点(0, 1)。
2. 求函数y = x^2 - 4x + 3的图像在x轴上的截点。
解析:当y = 0时,x^2 - 4x + 3 = 0。
将方程因式分解得到(x - 3)(x - 1) = 0。
解得x = 3或x = 1,所以图像在x轴上的截点为(3, 0)和(1, 0)。
3. 指出函数y = 2^x的一个定义域。
解析:指数函数y = a^x的定义域是(-∞, +∞),所以y = 2^x的定义域也是(-∞, +∞)。
三、平方根与平方函数1. 计算√(27 * 8)。
解析:由于27和8都是完全平方数的乘积,所以可以化简为√(3^3 * 2^3),再结合指数与根号的性质得到√(3^3 * 2^3) = 3 * 2 = 6。
2. 求解方程x^2 + 9 = 0。
解析:平方根为正数,所以方程无实数解。
3. 求函数y = (x + 2)^2的图像在x轴上的截点。
解析:当y = 0时,(x + 2)^2 = 0。
浙江省中考数学考点复习 数与代数综合测试卷-人教版初中九年级全册数学试题

, ,3,2 , ;
3 , ,2 ,3 , ;
…
若2 的位置记为(1,4),2 的位置记为(2,3),则这组数中最大的有理数的位置记为( )
A. (5,2) B. (5,3) C. (6,2) D. (6,5)
(第10题)
10. 如图,已知在平面直角坐标系xOy中,O是坐标原点,A是函数y= (x<0)图象上一点,AO的延长线交函数y= (x>0,k是不等于0的常数)的图象于点C,点A关于y轴的对称点为A′,点C关于x轴的对称点为C′,连结CC′,交x轴于点B,连结AB,AA′,A′C′.若△ABC的面积等于6,则由线段AC,CC′,C′A′,A′A所围成的图形的面积等于( )
19.原式= .∵a-1≠0,a+1≠0,a2-2a+1≠0,∴a≠±1.∴a只能取2.当a=2时,原式=5.20.6或7或8.
21.(1)400元. (2)10%.22.(1)k1=8,k2=2,b=6.
(2 )15.(3)点M(x1,y1)在第三象限,点N(x2,y2)在第一象限,理由略.23.(1)300 250 150 (2)判断:y是x的一次函数.设y=kx+b.∵当x=10时,y=300;当x=11时,y=250,∴ 解得 ∴y=-50x+800.经检验,x=13,y=150也适合上述表达式.∴y=-50x+800.(3)W=(x-8)y=(x-8)(-50x+800)=-50x2+1200x-6400=-50(x-12)2+800.∵a=-50<0,∴当x=12时,W的值最大,最大值为800,即当销售单价为12元时,每天可获得的利润最大,最大利润是800元.24.(1)由题意可得:α,β是方程-mx2+4x+2m=0的两根 ,由根与系数的关系可得:α+β= ,αβ=-2.∵ + =-2,∴ =-2,即 =-2.∴m=1.∴抛物线的函数表达式为y=-x2+4x+2.(2)存在x轴上的点M,y轴上的点N,使四边形DNME的周长最小.∵y=-x2+4x+2=-(x-2)2+6.∴抛物线的对称轴l为直线x=2,顶点D的坐标为(2,6).又∵抛物线与y轴的交点C的坐标为(0,2),点E与点C关于l对称,∴点E的坐标为(4,2).作点D关于y 轴的对称点D′,点E关于x轴的对称点E′,则点D′的坐标为(-2,6),点E′的坐标为(4,-2).连结D′E′交x轴于点M,交y轴于点N,此时四边形DNME的周长最小,为D′E′+DE,如解图所示,
初三中考数与代数测试题

临 朐 四 中初三数学中考阶段性复习测试题一、选择题1.31-的立方根是( )A .-1B .OC .1D . ±12.下列实数中是无理数的是( )A .722 B.2-2 c.5.15 D.sin450 3.据中国新闻网报道,在2014年11月17日公布的全球超级计算机500强榜单中,中国国防科技大学研制的“天河”二号超级计算机,以峰值计算速度每秒5.49亿亿次、持续计算速度每秒3.39亿亿次双精度浮点运算的优异性能位居榜首,第四次摘得全球运行速度最快的超级计算机桂冠.用科学记数法表示“5.49亿亿”,记作( )A . 5.49×1018B . 5.49×1016C . 5.49×1015D . 5.49×10144.已知实数a ,b 在数轴上的位置如图所示,下列结论错误的是( )A . |a|<1<|b|B . 1<﹣a <bC . 1<|a|<bD . ﹣b <a <﹣1 5.下列运算正确的是( )A . (﹣3mn )2=﹣6m 2n 2B . 4x 4+2x 4+x 4=6x 4C . (xy )2÷(﹣xy )=﹣xyD . (a ﹣b )(﹣a ﹣b )=a 2﹣b 26.一个几何体的三视图如右图所示,则该几何体是( )7.若代数式2)3(1-+x x 有意义,则实数x 的取值范围是( ) A.x≥一1 B .x≥一1且x≠3 C .x>-l D .x>-1且x≠38. 若不等式组⎩⎨⎧--≥+2210x x a x 无解,则实数a 的取值范围是( ) A .a≥一1 B .a<-1 C .a≤1 D.a≤-19.等腰三角形一条边的边长为3,它的另两条边的边长是关于x 的一元二次方程 x 2 -12x+k=O 的两个根,则k 的值是( )A 27B 36C 27或36D 1810.已知一次函数y 1=kx+b (k<O )与反比例函数y 2=xm (m≠O)的图象相交于A 、B 两点,其横坐标分别是-1和3,当y 1>y 2时,实数x 的取值范围是( )A .x<-l 或O<x<3B .一1<x<O 或O<x<3C .一1<x<O 或x>3D .O<x<311.如图,已知△ABC 为等边三角形,AB=2,点D 为边AB 上一点,过点D 作DE ∥AC ,交BC 于E 点;过E 点作EF ⊥DE ,交AB 的延长线于F 点.设AD=x ,△DEF 的面积为y ,则能大致反映y 与x 函数关系的图象是( )A .B .C .D .12,如图,已知正方形ABCD ,顶点A(1,3)、B(1,1)、C(3,1).规定“把正方形ABCD 先沿x 轴翻折,再向左平移1个单位”为一次变换.如此这样,连续经过2014次变换后,正方形ABCD 的对角线交点M 的坐标变为 ( )A .(—2012,2)B .(一2012,一2)C. (—2013,—2)D. (—2013,2)二、填空题13.因式分解:﹣2x 2y+12xy ﹣18y= .14.分式方程的解为 .15.如图,点A 、B 的坐标分别为(0,2),(3,4),点P 为x 轴上的一点,若点B 关于直线AP 的对称点B ′恰好落在x 轴上,则点P 的坐标为 .三、解答题16.先化简,再求值:()÷,其中x=﹣2+.17.为绿化校园,某校计划购进A、B两种树苗,共21课.已知A种树苗每棵90元,B种树苗每棵70元.设购买B种树苗x棵,购买两种树苗所需费用为y元.(1)y与x的函数关系式为:;(2)若购买B种树苗的数量少于A种树苗的数量,请给出一种费用最省的方案,并求出该方案所需费用.18.经统计分析,某市跨河大桥上的车流速度v(千米/小时)是车流密度x(辆/千米)的函数,当桥上的车流密度达到220辆/千米时,造成堵塞,此时车流速度为O千米/小时;当车流密度不超过20辆/千米时,车流速度为80千米/小时.研究表明:当20≤x≤220时,车流速度v是车流密度x的一次函数.(1)求大桥上车流密度为100辆/千米时的车流速度.(2)在交通高峰时段,为使大桥上的车流速度大于40千米/小时且小于60千米/小时时,应控制大桥上的车流密度在什么范围内?(3)车流量(辆/小时)是单位时间内通过桥上某观测点的车辆数,即:车流量=车流速度×车流密度.求大桥上车流量y的最大值.19.如图1,直线y=k1x与反比例函数y=(k≠0)的图象交于点A,B,直线y=k2x与反比例函数y=的图象交于点C,D,且k1•k2≠0,k1≠k2,顺次连接A,D,B,C,AD,BC分别交x轴于点F,H,交y轴于点E,G,连接FG,EH.(1)四边形ADBC的形状是;(2)如图2,若点A的坐标为(2,4),四边形AEHC是正方形,则k2=;(3)如图3,若四边形EFGH为正方形,点A的坐标为(2,6),求点C的坐标;(4)判断:随着k1、k2取值的变化,四边形ADBC能否为正方形?若能,求点A的坐标;若不能,请简要说明理由.。
初中中考数学试卷代数大题

一、选择题(每题5分,共25分)1. 已知二次函数y=ax^2+bx+c(a≠0)的图象与x轴交于A、B两点,且A、B两点关于y轴对称,若点A的坐标为(-2,0),则下列哪个选项是正确的?A. a=1,b=0,c=-4B. a=-1,b=0,c=-4C. a=1,b=0,c=4D. a=-1,b=0,c=42. 若m+n=5,mn=6,则m^2+n^2的值为:A. 19B. 21C. 25D. 293. 已知一元二次方程x^2-4x+3=0的两个根为α和β,则αβ+αβ^2+βα^2的值为:A. 6B. 5C. 4D. 34. 若x^2-3x+2=0的两个根为x1和x2,则x1+x2的值为:A. 3B. 2C. 1D. 05. 在等腰三角形ABC中,底边AB=AC=6,顶角A的度数为60°,则BC边上的高AD的长度为:A. 3B. 4C. 5D. 6二、填空题(每题5分,共25分)6. 若x^2-5x+6=0的两个根为x1和x2,则x1+x2的值为______,x1x2的值为______。
7. 已知一次函数y=kx+b的图象与x轴交于点A(2,0),与y轴交于点B(0,3),则该一次函数的解析式为______。
8. 若二次函数y=ax^2+bx+c(a≠0)的图象开口向上,且顶点坐标为(h,k),则a的取值范围是______。
9. 在直角坐标系中,点P(-3,4)关于x轴的对称点坐标为______。
10. 若x^2-2x+1=0的解为x1和x2,则x1^2+x2^2的值为______。
三、解答题(每题15分,共45分)11. 解一元二次方程:2x^2-5x+3=0。
12. 已知一次函数y=kx+b的图象经过点A(1,2)和B(3,-1),求该一次函数的解析式。
13. 已知二次函数y=ax^2+bx+c(a≠0)的图象开口向上,且顶点坐标为(h,k),且与x轴有两个交点,求a、b、c的取值范围。
中考数学数与式真题训练50题含参考答案

中考数学数与式真题训练50题含答案 (有理数、实数、代数、因式分解、二次根式)一、单选题1.下列各数中,是无理数的是( )A .17B C .2π D 2.下列各组单项式中,为同类项的是( ) A .3ab 2与3a 2bB .a 与1C .2bc 与3abcD .a 2b 与23a b3.下列运算正确的是( )A4±B .()3327-=C 2=D 3=4.下列运算正确的是( ) A .a 3+a 3=a 6B .(a 3)2=a 6C .(ab )2=ab 2D .2a 5·3a 5=5a 55.下列计算中,正确的是( ).A 3=-B 6=C 122= D 76.将数据72000000用科学记数法表示是( ) A .72×107B .0.72×109C .7.2×107D .7.2×1087 )AB C D8.在920,5.55,2π,133-,0.232333223332333,,123中,无理数的个数是( ) A .2B .3C .4D .59.当1<x<3 ) A .3 B .-3 C .1 D .-110在两个整数之间,下列结论正确的是( ) A .2-3之间B .3-4之间C .4-5之间D .5-6之间11.将-3-(+6)-(-5)+(-2)写成省略括号的和的形式是( )A .-3+6-5-2B .-3-6+5-2C .-3-6-5-2D .-3-6+5+212.下列结论中,不正确的是( ) A .-1<0<3 B .23>-2>-212C .-4>-3>-2D .-212>-3>-3.113.下列式子中,正确的是( )A8k =-BC )3x >D 1=-14.在31x +,3m +,23a b -,2a ,0,12-中,单项式的个数( )A .2B .3C .4D .515.代数式243x x -+的最小值为( ). A .1-B .0C .3D .516.已知边长分别为a 、b 的长方形的周长为10,面积4,则ab 2+a 2b 的值为( ) A .10B .20C .40D .8017.若x 2+mxy +4y 2是一个完全平方式,那么m 的值是( ) A .±4B .﹣2C .±2D .418.据有关部门统计,2019年“五一小长假”期间,广东各大景点共接待游客约14400000人次,将数14400000用科学记数法表示为( ) A .71.4410⨯ B .70.14410⨯C .81.4410⨯D .80.14410⨯19.在化简分式23311x x x-+--的过程中,开始出现错误的步骤是( )A .AB .BC .CD .D二、填空题 20.函数35y x =-中,自变量x 的取值范围是________. 21.在实数范围内因式分解:222ax ay -=_____. 22.把多项式24a -分解因式的结果是_____.23.14的算术平方根是_________.24.用配方法将方程2210x x +-=变为2()x a b +=的形式,则a b +=______. 25.化简2232a b a b a b--=-+__________.26.若2a b +=,3a b -=-,则22a b -=_____. 27.多项式2412xy xyz +的公因式是______. 28.计算:37-=__________.29_____.30.如图,显示的是新冠肺炎全国(含港澳台)截至4月27日20时30分,现存确诊人数数据统计结果,则昨日(4月26日)现存确诊人数是__________人.31.一种细菌半径是1.91×10-5米,用小数表示为________________米.3233.在实数范围内分解因式:-1+9a 4=____________________。
2024年中考数学真题汇编专题三 代数式及整式+答案详解

2024年中考数学真题汇编专题三 代数式及整式+答案详解(试题部分)一、单选题1.(2024·广东·中考真题)下列计算正确的是( )A .2510a a a ⋅=B .824a a a ÷=C .257a a a −+=D .()5210a a =2.(2024·四川内江·中考真题)下列单项式中,3ab 的同类项是( )A .33abB .232a bC .22a b −D .3a b3.(2024·湖北·中考真题)223x x ⋅的值是( )A .25xB .35xC .26xD .36x4.(2024·河南·中考真题)计算3···a a a a ⎛⎫ ⎪ ⎪⎝⎭个的结果是( )A .5aB .6aC .3a a +D .3a a5.(2024·浙江·中考真题)下列式子运算正确的是( )A .325x x x +=B .326x x x ⋅=C .()239x x =D .624x x x ÷=6.(2024·河北·中考真题)下列运算正确的是( )A .734a a a −=B .222326a a a ⋅=C .33(2)8a a −=−D .44a a a ÷=7.(2024·黑龙江齐齐哈尔·中考真题)下列计算正确的是( )A .224426a a a +=B .5210a a a ⋅=C .623a a a ÷=D .()224a a −=8.(2024·黑龙江牡丹江·中考真题)下列计算正确的是( )A .32622a a a ⋅=B .331(2)8a b a b −÷⨯=−C .()322a a a a a a ++÷=+D .2233a a −=9.(2024·云南·中考真题)按一定规律排列的代数式:2x ,23x ,34x ,45x ,56x ,L ,第n 个代数式是() A .2n x B .()1n n x − C .1n nx + D .()1n n x +10.(2024·云南·中考真题)下列计算正确的是( )A .33456x x x +=B .635x x x ÷=C .()327a a =D .()333ab a b =11.(2024·山东烟台·中考真题)下列运算结果为6a 的是( )A .23a a ⋅B .122a a ÷C .33a a +D .()32a 12.(2024·江苏盐城·中考真题)下列运算正确的是( )A .624a a a ÷=B .22a a −=C .326a a a ⋅=D .()235a a = 13.(2024·黑龙江牡丹江·中考真题)如图是由一些同样大小的三角形按照一定规律所组成的图形,第1个图有4个三角形.第2个图有7个三角形,第3个图有10个三角形……按照此规律排列下去,第674个图中三角形的个数是( )A .2022B .2023C .2024D .202514.(2024·江苏连云港·中考真题)下列运算结果等于6a 的是( )A .33a a +B .6a a ⋅C .28a a ÷D .()32a − 15.(2024·江苏扬州·中考真题)下列运算中正确的是( )A .222()a b a b −=−B .523a a a −=C .()235a a =D .236326a a a ⋅=16.(2024·山东威海·中考真题)下列运算正确的是( )A .5510x x x +=B .21m m n n n ÷⋅=C .624a a a ÷=D .()325a a −=−17.(2024·河北·中考真题)若a ,b 是正整数,且满足8282222222a b a a a b b b ++⋅⋅⋅+=⨯⨯⋅⋅⋅⨯个相加个相乘,则a 与b 的关系正确的是( )A .38a b +=B .38a b =C .83a b +=D .38a b =+18.(2024·四川眉山·中考真题)下列运算中正确的是( )A .2a a a −=B .23a a a ⋅=C .()325a a =D .()323626ab a b = 19.(2024·广东广州·中考真题)若0a ≠,则下列运算正确的是( )A .235a a a +=B .325a a a ⋅=C .235a a a⋅= D .321a a ÷=20.(2024·福建·中考真题)下列运算正确的是( )A .339a a a ⋅=B .422a a a ÷=C .()235a a =D .2222a a −=21.(2024·湖南·中考真题)下列计算正确的是( )A .22321a a −=B .32(0)a a a a ÷=≠C .236a a a ⋅=D .()3326a a = 22.(2024·贵州·中考真题)计算23a a +的结果正确的是( )A .5aB .6aC .25aD .26a 23.(2024·湖北武汉·中考真题)下列计算正确的是( )A .236a a a ⋅=B .()1432a a =C .()2236a a =D .()2211a a +=+ 24.(2024·黑龙江绥化·中考真题)下列计算中,结果正确的是( )A .()2139−−=B .()222a b a b +=+C 93±D .()3263x y x y −= 25.(2024·重庆·中考真题)用菱形按如图所示的规律拼图案,其中第①个图案中有2个菱形,第②个图案中有5个菱形,第③个图案中有8个菱形,第④个图案中有11个菱形,…,按此规律,则第⑧个图案中,菱形的个数是( )A .20B .21C .23D .2626.(2024·黑龙江大兴安岭地·中考真题)下列计算正确的是( )A .326a a a ⋅=B .()527a a =C .()339328a b a b −=− D .()()22a b a b a b −++=− 27.(2024·内蒙古赤峰·中考真题)下列计算正确的是( )A .235a a a +=B .222()a b a b +=+C .632a a a ÷=D .()236a a = 28.(2024·广东深圳·中考真题)下列运算正确的是( )A .()523m m −=−B .23m n m m n ⋅=C .33mn m n −=D .()2211m m −=− 29.(2024·四川广元·中考真题)下列计算正确的是( )A .336a a a +=B .632a a a ÷=C .()222a b a b +=+D .()2224ab a b =30.(2024·四川凉山·中考真题)下列运算正确的是( )A .235ab ab ab +=B .()3235ab a b =C .824a a a ÷=D .236a a a ⋅=31.(2024·江苏扬州·中考真题)1202年数学家斐波那契在《计算之书》中记载了一列数:1,1,2,3,5,……,这一列数满足:从第三个数开始,每一个数都等于它的前两个数之和.则在这一列数的前2024个数中,奇数的个数为( )A .676B .674C .1348D .135032.(2024·河北·中考真题)“铺地锦”是我国古代一种乘法运算方法,可将多位数乘法运算转化为一位数乘法和简单的加法运算.淇淇受其启发,设计了如图1所示的“表格算法”,图1表示13223⨯,运算结果为3036.图2表示一个三位数与一个两位数相乘,表格中部分数据被墨迹覆盖,根据图2中现有数据进行推断,正确的是( )A .“20”左边的数是16B .“20”右边的“□”表示5C .运算结果小于6000D .运算结果可以表示为41001025a +二、填空题33.(2024·天津·中考真题)计算86x x ÷的结果为 .34.(2024·河南·中考真题)请写出2m 的一个同类项: .35.(2024·广东广州·中考真题)如图,把1R ,2R ,3R 三个电阻串联起来,线路AB 上的电流为I ,电压为U ,则123U IR IR IR =++.当120.3R =,231.9R =,347.8R =, 2.2I =时,U 的值为 .36.(2024·上海·中考真题)计算:()324x = . 37.(2024·江西·中考真题)观察a ,2a ,3a ,4a ,…,根据这些式子的变化规律,可得第100个式子为 . 38.(2024·江苏苏州·中考真题)若2a b =+,则()2b a −= .39.(2024·四川乐山·中考真题)已知3a b −=,10ab =,则22a b += .40.(2024·广东广州·中考真题)若2250a a −−=,则2241a a −+= .41.(2024·四川成都·中考真题)若m ,n 为实数,且()2450m n +−,则()2m n +的值为 . 42.(2024·四川成都·中考真题)在综合实践活动中,数学兴趣小组对1n 这n 个自然数中,任取两数之和大于n 的取法种数k 进行了探究.发现:当2n =时,只有{}1,2一种取法,即1k =;当3n =时,有{}1,3和{}2,3两种取法,即2k =;当4n =时,可得4k =;…….若6n =,则k 的值为 ;若24n =,则k 的值为 .三、解答题43.(2024·吉林·中考真题)先化简,再求值:()()2111a a a +−++,其中3a44.(2024·陕西·中考真题)先化简,再求值:()()22x y x x y ++−,其中1x =,=2y −.45.(2024·甘肃·中考真题)先化简,再求值:()()()22222a b a b a b b ⎡⎤+−+−÷⎣⎦,其中2a =,1b =-.2024年中考数学真题汇编专题三 代数式及整式+答案详解(答案详解)一、单选题1.(2024·广东·中考真题)下列计算正确的是( )A .2510a a a ⋅=B .824a a a ÷=C .257a a a −+=D .()5210a a = 【答案】D【分析】本题主要考查了同底数幂乘除法计算,幂的乘方计算,合并同类项,熟知相关计算法则是解题的关键.【详解】解:A 、257a a a ⋅=,原式计算错误,不符合题意;B 、826a a a ÷=,原式计算错误,不符合题意;C 、253a a a −+=,原式计算错误,不符合题意;D 、()5210a a =,原式计算正确,符合题意;故选:D .2.(2024·四川内江·中考真题)下列单项式中,3ab 的同类项是( )A .33abB .232a bC .22a b −D .3a b 【答案】A【分析】本题主要考查的是同类项的定义,掌握同类项的定义是解题的关键.依据同类项的定义:所含字母相同,相同字母的次数相同,据此判断即可.【详解】解:A .是同类项,此选项符合题意;B .字母a 的次数不相同,不是同类项,故此选项不符合题意;C .相同字母的次数不相同,不是同类项,故此选项不符合题意;D .相同字母的次数不相同,不是同类项,故此选项不符合题意.故选:A . 3.(2024·湖北·中考真题)223x x ⋅的值是( )A .25xB .35xC .26xD .36x【答案】D【分析】本题主要考查单项式与单项式的乘法.运用单项式乘单项式运算法则求出结果即可判断.【详解】解:23236x x x ⋅=,故选:D .4.(2024·河南·中考真题)计算3···a a a a ⎛⎫ ⎪ ⎪⎝⎭个的结果是( ) A .5aB .6aC .3a a +D .3a a 【答案】D 【分析】本题考查的是乘方的含义,幂的乘方运算的含义,先计算括号内的运算,再利用幂的乘方运算法则可得答案.【详解】解:()()333···a a a a a a a a ==个, 故选D5.(2024·浙江·中考真题)下列式子运算正确的是( )A .325x x x +=B .326x x x ⋅=C .()239x x =D .624x x x ÷= 【答案】D【分析】本题考查了合并同类项,幂的运算,熟练掌握运算法则是解题的关键.分别利用合并同类型法则,同底数幂的乘法,幂的乘方,同底数幂的除法分别判断即可.【详解】解: A 、3x 与2x 不是同类项,不能合并,故本选项不符合题意;B 、325x x x ?,故本选项不符合题意; C 、()236x x =,故本选项不符合题意; D 、624x x x ÷=,故本选项符合题意.故选:D .6.(2024·河北·中考真题)下列运算正确的是( )A .734a a a −=B .222326a a a ⋅=C .33(2)8a a −=−D .44a a a ÷= 【答案】C【分析】本题考查整式的运算,根据合并同类项,单项式乘以单项式,积的乘方,同底数幂的除法依次对各选项逐一分析判断即可.解题的关键是掌握整式运算的相关法则.【详解】解:A .7a ,4a 不是同类项,不能合并,故此选项不符合题意;B .224326a a a ⋅=,故此选项不符合题意;C .()3328a a −=−,故此选项符合题意;D .441a a ÷=,故此选项不符合题意.故选:C .7.(2024·黑龙江齐齐哈尔·中考真题)下列计算正确的是( )A .224426a a a +=B .5210a a a ⋅=C .623a a a ÷=D .()224a a −= 【答案】D 【分析】本题考查了积的乘方、合并同类项、同底数幂相乘、除,根据运算法则逐项分析,即可作答.【详解】解:A 、22244266a a a a ≠+=,故该选项不符合题意;B 、2521010a a a a ⋅=≠,故该选项不符合题意;C 、6243a a a a ÷=≠,故该选项不符合题意;D 、()224a a −=,故该选项符合题意;故选:D8.(2024·黑龙江牡丹江·中考真题)下列计算正确的是( )A .32622a a a ⋅=B .331(2)8a b a b −÷⨯=−C .()322a a a a a a ++÷=+D .2233a a −=9.(2024·云南·中考真题)按一定规律排列的代数式:2x ,23x ,34x ,45x ,56x ,L ,第n 个代数式是( ) A .2n xB .()1n n x −C .1n nx +D .()1nn x + 【答案】D 【分析】本题考查了数列的规律变化,根据数列找到变化规律即可求解,仔细观察和总结规律是解题的关键.【详解】解:∵按一定规律排列的代数式:2x ,23x ,34x ,45x ,56x ,L , ∴第n 个代数式是()1nn x +, 故选:D .10.(2024·云南·中考真题)下列计算正确的是( )A .33456x x x +=B .635x x x ÷=C .()327a a =D .()333ab a b = 【答案】D【分析】本题考查了合并同类项、幂的乘方、积的乘方、同底数幂的除法,熟练掌握运算法则是解答的关键.利用合并同类项法则、幂的乘方运算法则、同底数幂的除法运算法则、积的乘方运算法则进行运算,并逐项判断即可.【详解】解:A 、33356x x x +=,选项计算错误,不符合题意;B 、633x x x ÷=,选项计算错误,不符合题意;C 、()326a a =,选项计算错误,不符合题意;D 、()333ab a b =,选项计算正确,符合题意;故选:D .11.(2024·山东烟台·中考真题)下列运算结果为6a 的是( )A .23a a ⋅B .122a a ÷C .33a a +D .()32a 【答案】D【分析】本题考查了同底数幂的乘法,同底数幂的除法,合并同类项,幂的乘方,解题的关键是熟练掌握以上运算法则;根据同底数幂的乘法同底数幂的除法,合并同类项,幂的乘方,运算法则计算即可【详解】A .23235a a a a +⋅==,故选项不符合题意;B . 12212210a a a a −÷==,故选项不符合题意;C .3332a a a +=,故选项不符合题意;D .()32236a a a ⨯==,故选项符合题意;故选:D .12.(2024·江苏盐城·中考真题)下列运算正确的是( )A .624a a a ÷=B .22a a −=C .326a a a ⋅=D .()235a a = 【答案】A【分析】本题考查了同底数幂乘法,合并同类项,同底数幂除法,幂的乘方等知识点,熟知相关运算法则是解本题的关键.根据同底数幂乘法,合并同类项,同底数幂除法,幂的乘方等运算法则分别计算即可得出答案.【详解】解:A 、624a a a ÷=,正确,符合题意;B 、2a a a −=,错误,不符合题意;C 、325a a a ⋅=,错误,不符合题意;D 、()236a a =,错误,不符合题意; 故选:A .13.(2024·黑龙江牡丹江·中考真题)如图是由一些同样大小的三角形按照一定规律所组成的图形,第1个图有4个三角形.第2个图有7个三角形,第3个图有10个三角形……按照此规律排列下去,第674个图中三角形的个数是( )A .2022B .2023C .2024D .2025 【答案】B 【分析】此题考查了图形的变化规律,解题的关键是根据图形的排列,归纳出图形的变化规律.根据前几个图形的变化发现规律,可用含n 的代数式表示出第n 个图形中三角形的个数,从而可求第674个图形中三角形的个数.【详解】解:第1个图案有4个三角形,即4311=⨯+,第2个图案有7个三角形,即7321=⨯+,第3个图案有10个三角形,即10331=⨯+,…,按此规律摆下去,第n 个图案有()31n +个三角形,则第674个图案中三角形的个数为:367412023⨯+=(个).故选:B .14.(2024·江苏连云港·中考真题)下列运算结果等于6a 的是( )A .33a a +B .6a a ⋅C .28a a ÷D .()32a − 【答案】C【分析】本题考查整式的运算,根据合并同类项,同底数幂的乘除法则,积的乘方和幂的乘方法则,逐一进行计算判断即可.【详解】解:A 、3332a a a +=,不符合题意;B 、67a a a ⋅=,不符合题意;C 、826a a a ÷=,符合题意;D 、()326a a −=−,不符合题意;故选:C .15.(2024·江苏扬州·中考真题)下列运算中正确的是( )A .222()a b a b −=−B .523a a a −=C .()235a a =D .236326a a a ⋅=【答案】B【分析】本题考查了乘法公式,合并同类项,幂的乘方,单项式乘法,掌握整式的运算法则是解题的关键. 【详解】解:A 、()2222a b a ab b −=−+,原选项错误,不符合题意; B 、523a a a −=,正确,符合题意; C 、()236a a =,原选项错误,不符合题意;D 、2353?26a a a =,原选项错误,不符合题意; 故选:B .16.(2024·山东威海·中考真题)下列运算正确的是( )A .5510x x x +=B .21mm n n n÷⋅= C .624a a a ÷= D .()325a a −=−【答案】C【分析】本题主要考查合并同类项、同底数幂的除法、积的乘方,根据合并同类项、同底数幂的除法、积的乘方的运算法则计算即可.【详解】A 、5552x x x +=,运算错误,该选项不符合题意; B 、223111mm n m n n n n÷⋅==,运算错误,该选项不符合题意; C 、62624a a a a −÷==,运算正确,该选项符合题意; D 、()326a a −=−,运算错误,该选项不符合题意.故选:C17.(2024·河北·中考真题)若a ,b 是正整数,且满足8282222222a b a a a b b b++⋅⋅⋅+=⨯⨯⋅⋅⋅⨯个相加个相乘,则a 与b 的关系正确的是( )A .38a b +=B .38a b =C .83a b +=D .38a b =+【答案】A【分析】本题考查了同底数幂的乘法,幂的乘方的运算的应用,熟练掌握知识点是解题的关键.由题意得:()8822a b ⨯=,利用同底数幂的乘法,幂的乘方化简即可.【详解】解:由题意得:()8822a b ⨯=,∴38222a b ⨯=, ∴38a b +=, 故选:A .18.(2024·四川眉山·中考真题)下列运算中正确的是( )A .2a a a −=B .23a a a ⋅=C .()325a a =D .()323626ab a b =【答案】B【分析】此题考查了合并同类项,同底数幂乘法,幂的乘方和积的乘方,解题的关键是掌握以上运算法则. 根据合并同类项,同底数幂乘法,幂的乘方和积的乘方运算法则进行判断即可. 【详解】解:2a 与a −不是同类项,无法合并,则A 不符合题意;23a a a ⋅=,则B 符合题意;()326a a =,则C 不符合题意;()323628ab a b =,则D 不符合题意;故选:B .19.(2024·广东广州·中考真题)若0a ≠,则下列运算正确的是( )A .235a a a+=B .325a a a ⋅=C .235a a a⋅=D .321a a ÷=20.(2024·福建·中考真题)下列运算正确的是( )A .339a a a ⋅=B .422a a a ÷=C .()235a a =D .2222a a −=【答案】B【分析】本题考查了同底数幂的乘法,同底数幂的除法,幂的乘方,合并同类项,解题的关键是掌握同底数幂的乘法,同底数幂的除法,幂的乘方,合并同类项运算法则.利用同底数幂的乘法,同底数幂的除法,幂的乘方,合并同类项计算后判断正误. 【详解】解:336a a a ⋅=,A 选项错误;422a a a ÷=,B 选项正确;()236a a =,C 选项错误;2222a a a −=,D 选项错误;故选:B .21.(2024·湖南·中考真题)下列计算正确的是( )A .22321a a −=B .32(0)a a a a ÷=≠C .236a a a ⋅=D .()3326a a =【答案】B【分析】本题考查了合并同类项,同底数幂的乘除法,积的乘方,根据以上运算法则逐项分析即可. 【详解】解:A 、22232a a a −=,故该选项不正确,不符合题意; B 、32(0)a a a a ÷=≠,故该选项正确,符合题意; C 、235a a a ⋅=,故该选项不正确,不符合题意; D 、()3328a a =,故该选项不正确,不符合题意; 故选:B .22.(2024·贵州·中考真题)计算23a a +的结果正确的是( )A .5aB .6aC .25aD .26a【答案】A【分析】本题主要考查合并同类项,根据合并同类项的法则:把同类项的系数相加,所得结果作为系数,字母和字母的指数不变即可得. 【详解】解: 235a a a +=, 故选:A .23.(2024·湖北武汉·中考真题)下列计算正确的是( )A .236a a a ⋅=B .()1432a a =C .()2236a a =D .()2211a a +=+【答案】B【分析】本题考查了完全平方公式,积的乘方,幂的乘方,同底数幂的乘法等,根据同底数幂的乘法,积的乘方,幂的乘方,完全平方公式运算法则分别判断即可. 【详解】解:A. 235a a a ⋅=,故该选项不正确,不符合题意; B. ()4312a a =,故该选项正确,符合题意;C. ()2239a a =,故该选项不正确,不符合题意; D. ()22121a a a +=++,故该选项不正确,不符合题意; 故选:B .24.(2024·黑龙江绥化·中考真题)下列计算中,结果正确的是( )A .()2139−−=B .()222a b a b +=+C 3±D .()3263x y x y −=25.(2024·重庆·中考真题)用菱形按如图所示的规律拼图案,其中第①个图案中有2个菱形,第②个图案中有5个菱形,第③个图案中有8个菱形,第④个图案中有11个菱形,…,按此规律,则第⑧个图案中,菱形的个数是( )A .20B .21C .23D .26【答案】C【分析】本题考查了图形类的规律探索,解题的关键是找出规律.利用规律求解.通过观察图形找到相应的规律,进行求解即可.【详解】解:第①个图案中有()131112+⨯−+=个菱形, 第②个图案中有()132115+⨯−+=个菱形, 第③个图案中有()133118+⨯−+=个菱形, 第④个图案中有()1341111+⨯−+=个菱形,∴第n 个图案中有()131131n n +−+=−个菱形, ∴第⑧个图案中菱形的个数为38123⨯−=, 故选:C .26.(2024·黑龙江大兴安岭地·中考真题)下列计算正确的是( )A .326a a a ⋅=B .()527a a =C .()339328a b a b −=− D .()()22a b a b a b −++=−【答案】C【分析】本题主要考查同底数幂的乘法,幂的乘方与积的乘方,平方差公式,运用相关运算法则求出各选项的结果后再进行判断即可.【详解】解:A 、3256a a a a ⋅=≠,故选项A 计算错误,此选项不符合题意; B 、()52107a a a =≠,故选项B 计算错误,此选项不符合题意;C 、()339328a b a b −=−,此选项计算正确,符合题意;D 、 ()()()()22a b a b b a b a b a −++=−+=−,故选项D 计算错误,此选项不符合题意;故选:C .27.(2024·内蒙古赤峰·中考真题)下列计算正确的是( )A .235a a a +=B .222()a b a b +=+C .632a a a ÷=D .()236a a =【答案】D【分析】此题考查了同底数幂的除法,完全平方公式,合并同类项,幂的乘方.根据同底数幂的除法法则,完全平方公式,合并同类项,幂的乘方的运算法则,可得答案. 【详解】解:A 、2a 与3a 不是同类项,不能合并,故此选项不符合题意; B 、()222222a b a ab b a b +=++≠+,故此选项不符合题意; C 、6332a a a a ÷=≠,故此选项不符合题意;D 、()236a a =,故此选项符合题意.故选:D .28.(2024·广东深圳·中考真题)下列运算正确的是( )A .()523m m −=− B .23m n m m n ⋅= C .33mn m n −= D .()2211m m −=−【答案】B【分析】本题考查了合并同类项,积的乘方,单项式乘以单项式,完全平方公式.根据单项式乘以单项式,积的乘方,完全平方公式法则进行计算即可求解. 【详解】解:A 、()2365m m m −=≠−,故该选项不符合题意;B 、23m n m m n ⋅=,故该选项符合题意;C 、33mn m n −≠,故该选项不符合题意;D 、()2221211m m m m −=−+≠−,故该选项不符合题意; 故选:B .29.(2024·四川广元·中考真题)下列计算正确的是( )A .336a a a +=B .632a a a ÷=C .()222a b a b +=+ D .()2224ab a b =【答案】D【分析】本题考查了合并同类项,同底数幂的除法,完全平方公式,积的乘方运算,正确的计算是解题的关键.根据合并同类项,同底数幂的除法,完全平方公式,积的乘方运算法则逐项分析判断即可求解. 【详解】解:A .3332a a a +=,故该选项不正确,不符合题意; B .633a a a ÷=,故该选项不正确,不符合题意; C .()222=2a b a ab b +++,故该选项不正确,不符合题意; D . ()2224ab a b =,故该选项正确,符合题意.故选:D .30.(2024·四川凉山·中考真题)下列运算正确的是( )A .235ab ab ab +=B .()3235ab a b =C .824a a a ÷=D .236a a a ⋅=【答案】A【分析】本题考查了整式的运算,根据合并同类项法则、积的乘方、同底数幂的除法和乘法分别计算即可判断求解,掌握整式的运算法则是解题的关键.【详解】解:A 、235ab ab ab +=,该选项正确,符合题意; B 、()3236ab a b =,该选项错误,不合题意;C 、826a a a ÷=,该选项错误,不合题意;D 、235a a a ⋅=,该选项错误,不合题意;故选:A .31.(2024·江苏扬州·中考真题)1202年数学家斐波那契在《计算之书》中记载了一列数:1,1,2,3,5,……,这一列数满足:从第三个数开始,每一个数都等于它的前两个数之和.则在这一列数的前2024个数中,奇数的个数为( )A .676B .674C .1348D .1350【答案】D【分析】将这一列数继续写下去,发现这列数的变化规律即可解答. 本题主要考查的是数字规律类问题,发现这列数的变化规律是解题的关键. 【详解】这一列数为:1,1,2,3,5,8,13,21,34,…可以发现每3个数为一组,每一组前2个数为奇数,第3个数为偶数. 由于202436742÷=,即前2024个数共有674组,且余2个数, ∴奇数有674221350⨯+=个. 故选:D32.(2024·河北·中考真题)“铺地锦”是我国古代一种乘法运算方法,可将多位数乘法运算转化为一位数乘法和简单的加法运算.淇淇受其启发,设计了如图1所示的“表格算法”,图1表示13223⨯,运算结果为3036.图2表示一个三位数与一个两位数相乘,表格中部分数据被墨迹覆盖,根据图2中现有数据进行推断,正确的是( )A .“20”左边的数是16B .“20”右边的“□”表示5C .运算结果小于6000D .运算结果可以表示为41001025a +则由题意得:20,5,2,mz nz ny nx a ====,∴4mznz=,即4=m n , ∴当2,1n y ==时, 2.5z =不是正整数,不符合题意,故舍; 当1,2n y ==时,则4,5,m z x a ===,如图:,A 、“20”左边的数是248⨯=,故本选项不符合题意; 、“20”右边的“□”表示4,故本选项不符合题意; a 上面的数应为4a ,如图:∴运算结果可以表示为:()1000411002541001025a a a +++=+, ∴D 选项符合题意,当2a =时,计算的结果大于6000,故C 选项不符合题意, 故选:D .二、填空题33.(2024·天津·中考真题)计算86x x ÷的结果为 . 【答案】2x【分析】本题考查同底数幂的除法,掌握同底数幂的除法,底数不变,指数相减是解题的关键. 【详解】解:862x x x ÷=, 故答案为:2x .34.(2024·河南·中考真题)请写出2m 的一个同类项: . 【答案】m (答案不唯一)【分析】本题考查的是同类项的含义,根据同类项的定义直接可得答案. 【详解】解:2m 的一个同类项为m , 故答案为:m35.(2024·广东广州·中考真题)如图,把1R ,2R ,3R 三个电阻串联起来,线路AB 上的电流为I ,电压为U ,则123U IR IR IR =++.当120.3R =,231.9R =,347.8R =, 2.2I =时,U 的值为 .【答案】220【分析】本题考查了代数式求值,乘法运算律,掌握相关运算法则,正确计算是解题关键.根据123U IR IR IR =++,将数值代入计算即可. 【详解】解:123U IR IR IR =++,当120.3R =,231.9R =,347.8R =, 2.2I =时,()20.3 2.231.9 2.247.8 2.220.331.947.8 2.2220U =⨯+⨯+⨯=++⨯=,故答案为:220.36.(2024·上海·中考真题)计算:()324x = .【答案】664x【分析】本题考查了积的乘方以及幂的乘方,掌握相关运算法则是解题关键.先将因式分别乘方,再结合幂的乘方计算即可. 【详解】解:()326464x x =,故答案为:664x .37.(2024·江西·中考真题)观察a ,2a ,3a ,4a ,…,根据这些式子的变化规律,可得第100个式子为 . 【答案】100a【分析】此题考查了单项式规律探究.分别找出系数和次数的规律,据此判断出第n 个式子是多少即可. 【详解】解:∵a ,2a ,3a ,4a ,…, ∴第n 个单项式的系数是1;∵第1个、第2个、第3个、第4个单项式的次数分别是1、2、3、4,…, ∴第n 个式子是n a . ∴第100个式子是100a . 故答案为:100a .38.(2024·江苏苏州·中考真题)若2a b =+,则()2b a −= . 【答案】4【分析】本题考查了求代数式的值,把2a b =+整体代入化简计算即可. 【详解】解:∵2a b =+, ∴()2b a − ()22b b ⎡⎤=−+⎣⎦ ()22b b =−−()22=−214=,故答案为:4.39.(2024·四川乐山·中考真题)已知3a b −=,10ab =,则22a b += . 【答案】29【分析】本题考查了完全平方公式的变形.熟练掌握完全平方公式的变形是解题的关键.根据()2222a b a b ab +=−+,计算求解即可.【详解】解:由题意知,()22222321029a b a b ab +=−+=+⨯=,故答案为:29.40.(2024·广东广州·中考真题)若2250a a −−=,则2241a a −+= . 【答案】11【分析】本题考查了已知字母的值求代数式的值,得出条件的等价形式是解题关键.由2250a a −−=,得225a a −=,根据对求值式子进行变形,再代入可得答案.【详解】解:2250a a −−=, 225a a ∴−=,()2224122125111a a a a ∴−+=−+=⨯+=, 故答案为:11.41.(2024·四川成都·中考真题)若m ,n 为实数,且()2450m n +−,则()2m n +的值为 .【答案】1【分析】本题考查非负数的性质,根据平方式和算术平方数的非负数求得m 、n 值,进而代值求解即可.【详解】解:∵()2450m n ++−=,∴40m +=,50n −=,解得4m =−,5n =,∴()()22451m n +=−+=,故答案为:1.42.(2024·四川成都·中考真题)在综合实践活动中,数学兴趣小组对1n 这n 个自然数中,任取两数之和大于n 的取法种数k 进行了探究.发现:当2n =时,只有{}1,2一种取法,即1k =;当3n =时,有{}1,3和{}2,3两种取法,即2k =;当4n =时,可得4k =;…….若6n =,则k 的值为 ;若24n =,则k 的值为 .2253++++531++++=三、解答题43.(2024·吉林·中考真题)先化简,再求值:()()2111a a a +−++,其中a44.(2024·陕西·中考真题)先化简,再求值:()()22x y x x y ++−,其中1x =,=2y −.【答案】222x y +,6【分析】本题考查了整式的混合运算以及求值.根据完全平方公式和单项式乘以多项式法则进行运算,再合并同类项,最后代入即可求解.23 【详解】解:()()22x y x x y ++−22222x xy y x xy =+++− 222x y =+;当1x =,=2y −时,原式()22212246=⨯+−=+=.45.(2024·甘肃·中考真题)先化简,再求值:()()()22222a b a b a b b ⎡⎤+−+−÷⎣⎦,其中2a =,1b =-. 【答案】2a b +,3【分析】本题主要考查了整式的化简求值,先根据平方差公式和完全平方公式去小括号,然后合并同类项,再根据多项式除以单项式的计算法则化简,最后代值计算即可.【详解】解:()()()22222a b a b a b b ⎡⎤+−+−÷⎣⎦()()22224442a ab b a b b ⎡⎤=++−−÷⎣⎦()22224442a ab b a b b =++−+÷()2422ab b b =+÷2a b =+,当2a =,1b =-时,原式()2213=⨯+−=.。
(完整版)最新数学中考试题(代数部分)
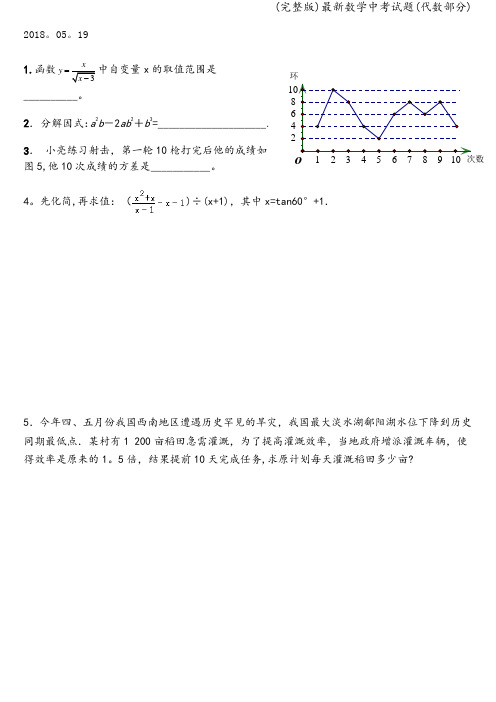
2018。
05。
19 1.函数3x y x =-中自变量x 的取值范围是__________。
2. 分解因式:a 2b -2ab 2+b 3=____________________. 3. 小亮练习射击,第一轮10枪打完后他的成绩如图5,他10次成绩的方差是___________。
4。
先化简,再求值:()÷(x+1),其中x=tan60°+1.5.今年四、五月份我国西南地区遭遇历史罕见的旱灾,我国最大淡水湖鄱阳湖水位下降到历史同期最低点.某村有1 200亩稻田急需灌溉,为了提高灌溉效率,当地政府增派灌溉车辆,使得效率是原来的1。
5倍,结果提前10天完成任务,求原计划每天灌溉稻田多少亩?环2468o6.根据规划设计,某市工程队准备在开发区修建一条长300米的盲道.铺设了60米后,由于采用新的施工方式,实际每天修建盲道的长度比原计划增加10米,结果共用了8天完成任务,该工程队改进技术后每天铺设盲道多少米?7.某商场购进一批单价为50元的商品,规定销售时单价不低于进价,每件的利润不超过40%.其中销售量y(件)与所售单价x(元)的关系可以近似的看作如图12所表示的一次函数.(1)求y与x之间的函数关系式,并求出x的取值范围;(2)设该公司获得的总利润(总利润=总销售额-总成本)为w元,求w与x之间的函数关系式。
当销售单价为何值时,所获利润最大?最大利润是多少?8.如图,小明站在窗口向外望去,发现楼下有一棵倾斜的大树,在窗口C处测得大树顶部A的俯角为45°,若已知∠ABD=60°,CD=20m,BD=16m,请你帮小明计算一下,如果大树倒在地面上,其顶端A与楼底端D的距离是多少米?(结果保留整数,参考数据:≈1.414,≈1.732).x+b的图象经过A(0,﹣2),B(1,0)两点,与反比例函数的9。
如图,一次函数y=k1图象在第一象限内的交点为M,若△OBM的面积为2.(1)求一次函数和反比例函数的表达式;(2)在x轴上是否存在点P,使AM⊥MP?若存在,求出点P的坐标;若不存在,说明理由.答案9.如图14,抛物线与x轴交于A(x1,0),B(x2,0)两点,且x1>x2,与y轴交于点C(0,4),其中x1,x2是方程x2-2x-8=0的两个根.(1)求这条抛物线的解析式;(2)点P是线段AB上的动点,过点P作PE∥AC,交BC于点E,连接CP,当△CPE的面积最大时,求点P的坐标;(3)探究:若点Q是抛物线对称轴上的点,是否存在这样的点Q,使△QBC成为等腰三角形,若存在,请直接写出所有符合条件的点Q的坐标;若不存在,请说明理由。
中考真题训练数与代数部分

中考真题训练数与代数部分一.选择题48 911. (20133的结果是【】临沂)计算11 3A .B .C .3D .【答案】 B 。
2. (20 13 威海)以下各式化简结果为无理数的是【】2 2A.2 1C. D.B.【答案】 C 。
3. (2013 枣庄)以下计算 ,正确的选项是【 A 】A.3 3B.C. 3 13 D.9 34. (2013 济宁)假如整式 x n2 5x2是对于 x 的三次三项式,那么 n 等于【 C】A . 3B . 4C .5D . 6a 12临沂)化简 a 215. (2013 2a1a 1 的结果是【 A 】A .B .C .D .22 16. (2013 泰安)化简分式 x 1x21x 1的结果是【A 】A .2B .C .D .- 2 7. (2013 淄博)以下运算错误的选项是【D 】2a ba b0.5a b 5a 10ba b b a211A . b aB .a bC . 0.2a 0.3b2a 3bD . a b b a8. (2013 滨州)对于随意实数 k ,对于 x 的方程 x 22 k 1 x k 22k 1 0的根的状况为【C 】A .有两个相等的实数根B .没有实数根C .有两个不相等的实数根D .没法确立x 2 19. (2013 淄博)假如分式 2x 2 的值为 0,则 x 的值是【 A】A . 1B . 0C .- 1D . ±12 x 310. (2013 滨州)若把不等式组x 12的解集在数轴上表示出来,则其对应的图形为【B 】A .长方形B .线段C .射线D .直线x 的方程kx21 k x 1 0,以下说法正确的选项是【 C 】 .11. (2013 潍坊)已知对于A.当时,方程无解B.当时,方程有一个实数解C.当k1时 ,方程有两个相等的实数解D.当时,方程总有两个不相等的实数解11. ( 2013 潍坊) 对于实数 x ,我们规定表示不大于 x 的 最大整数, 比如1.21 , 33, 2.53,x4若 105,则 x 的取值能够是【 C 】 . .45 C12、( 2013 德州市)如图,动点 P 从( 0,3)出发,沿所示方向运动,每当遇到矩形的边时反弹,反弹时 反射角等于入射角,当点P 第 2013 次遇到矩形的边时,点 P 的坐标为(D)A . (1, 4)B . (5,0)C . (6,4)D . ( 8,3)第 12题第13题13、( 2013 济宁市)如图,在直角坐标系中,点A 、B 的坐标分别为( 1, 4)和( 3, 0),点 的一个动点,且 A 、 B 、C 三点不在同一条直线上,当△ ABC 的周长最小时,点 C 的坐标是( DA .( 0,0)B .( 0,1)C .( 0, 2)D .( 0, 3)C 是 y 轴上)14、( 2013 莱芜市)如图,等边三角形 ABC 的边长为 3, N为形边上的动点 M 从点 A 出发,沿 A →B →C 的方向运动,抵达点 动的行程为 x , MN2=y ,则 y 对于 x 的函数图象大概为(BAC 的三平分点,三角 C 时停止.设点 M 运)A .B .C .D .215.( 2013 济南)函数 y=x +bx+c 与 y=x 的图象如下图,有以下结论: x+c < 0.此中正确的个数为()A . 1B . 2C . 3D . 416. (2013 菏泽)一条直线 y=kx+b ,此中 k+b=﹣ 5、 kb=6,那么该直线经过【 D 】A .第二、四象限B .第一、二、三象限C .第一、三象限D .第二、三、四象限17. ( 2013 年山东潍坊 3 分)设点 Ax 1 ,y 1和Bx 2 ,y 2是反比率函数图象上的两个点,当<<0 时,<,则一次函数y2xk的图象不经过的象限是【A 】 .A.第一象限B.第二象限C.第三象限D.第四象限18. ( 2013 年山东威海 3 分)如图,在平面直角坐标系中,∠AOB=90°,∠y 1 =my 2 = nOAB =30 °,反比率函数 x 的图象经过点 A ,反比率函数 x 的图象经过点 B ,则以下对于 m ,n 的关系正确的选项是【B 】m3m3A.m3nnnB. m=﹣3nC.3D.319.( 2015 烟台) 以下式子不必定建立的是( )A .aa(b 0) B. a 3a 51(a 0)C. a 24b 2(a2b)(a 2b) D. ( 2a 3 )2 4a 6bba 220. (2015 烟台)假如 x 2-x-1=(x+1)0,那么 x 的值为() A .2 或 -1 B.0或 1 C.2D. -1二.填空题x 1 m1. (2013 威海)若对于 x 的方程x5 10 2x 无解,则 m=.2.若对于 x 的分式方程的解为正数,那么字母 a 的取值范围是 .3. 分解因式: 3a212ab 12b 2.4. ( 2013 莱芜) M ( 1,a )是一次函数 y3x 2与反比率函数图象的公共点,若将一次函数y 3x 2 的图象向下平移4 个单位,则它与反比率函数图象的交点坐标为.5. (2013 年山东泰安 323246 33 分)化简:=.6、( 2013 聊城市)如图,在平面直角坐标系中,一动点从原点 O 出发,按向上,向右,向下,向右的方向不停地挪动,每挪动一个单位,获得点A1( 0, 1), A2(1, 1), A3( 1,0), A4( 2, 0),那么点A4n+1( n 为自然数)的坐标为 (用 n 表示) ( 2n , 1).三,解答题x 2 4x 2 4x1x 11. (2013 年山东烟台 6 分)先化简,再求值: x11 x,此中 x 知足 x2x 2 0 .2. (2013 年山东枣庄 m 3 5 ,此中 m 是方 程x 23x 1 08 分)先化简, 再求值:6mm 23m 2 m 2的根.13、( 2013 泰安市)如图,抛物线 y= 2 x 2+bx+c 与 y 轴交于点 C (0,﹣ 4),与 x 轴交于点 A , B ,且 B 点的坐标为( 2, 0)( 1)求该抛物线的分析式.( 2)若点 P 是 AB 上的一动点,过点 P 作 PE ∥ AC ,交 BC 于 E ,连结 CP ,求 △ PCE 面积的最大值.( 3)若点 D 为 OA 的中点,点 M 是线段 AC 上一点, 且△ OMD 为等腰三角形,求 M 点的坐标.解:( 1)把点 C ( 0,﹣ 4), B (2, 0)分别代入 y= 12 x2+bx+c中,得 ,解得∴该抛物线的分析式为 y= 1 22 x +x ﹣4.( 2)令 y=0,即 x2+x ﹣4=0,解得 x1=﹣ 4, x2=2,∴ A (﹣ 4, 0), S △ ABC=ABOC=12.设 P 点坐标为( x ,0),则 PB=2﹣ x . ∵ PE ∥ AC ,∴∠ BPE=∠ BAC ,∠ BEP=∠BCA ,∴△ PBE ∽△ ABC ,∴,即,化简得:S△ PBE=(2﹣x)2.S△ PCE=S△ PCB﹣ S△ PBE=PBOC﹣ S△ PBE=×( 2﹣ x)×4﹣( 2﹣x) 2=x2﹣ x+=(x+1) 2+3∴当 x=﹣ 1 时, S△ PCE的最大值为3.( 3)△ OMD 为等腰三角形,可能有三种情况:(I)当 DM=DO 时,如答图①所示.DO=DM=DA=2,∴∠ OAC=∠ AMD=45°,∴∠ ADM=90°,∴ M 点的坐标为(﹣2,﹣ 2);( II)当 MD=MO 时,如答图②所示.过点 M 作 MN ⊥ OD 于点 N,则点 N 为 OD 的中点,∴ DN=ON=1, AN=AD+DN=3,又△ AMN 为等腰直角三角形,∴ MN=AN=3 ,∴ M 点的坐标为(﹣ 1,﹣ 3);( III)当 OD=OM 时,∵△ OAC 为等腰直角三角形,∴点 O 到 AC 的距离为×4=,即 AC 上的点与点O 之间的最小距离为.∵> 2,∴ OD=OM 的状况不存在.综上所述,点M 的坐标为(﹣ 2 ,﹣ 2)或(﹣ 1,﹣ 3).评论:此题是二次函数综合题,考察了二次函数的图象与性质、待定系数法、相像三角形、等腰三角形等知识点,以及分类议论的数学思想.第( 2)问将面积的最值转变为二次函数的极值问题,注意此中求面积表达式的方法;第( 3 )问重在考察分类议论的数学思想,注意三种可能的情况需要一一剖析,不可以遗漏.。
[金牌原创]海南中考真题演练——数与代数.doc
![[金牌原创]海南中考真题演练——数与代数.doc](https://img.taocdn.com/s3/m/bddc4880f46527d3250ce023.png)
海南中考真题演练一一数与代数(考试时间:60分钟满分:100分)班级姓名学号—、选择题(每小题2分,共40分)在下列各题的四个备选答案中,只有一个是正确的,请把你认为正确的答案的字母代号填写在下表相应题号的方格内.1 . (2008 海南省)在 0, -2,1,L这四个数中,最小的数是()2A. 0B. -2C. 1D. 122 . (2009海南省)2的相反数是()A . 2 B. -2C.J_2D. ~23 . (2010海南省)-2的绝对值等于()A. — 21B.——2C.£2D. 24.(2008海南省)数据26000用科学记数法表示为2. 6X10",则〃的值是()A. 2B. 3C. 4D. 55.(2007海南省)参加2007年海南省初中毕业升学考试的学生达到113000人,用科学记数法表示这个人数应记作()7 8 9 10A. 113xlO3B. 11.3xl04C 1.13xlO5 D. O.113xlO66. (2007海南省)下列运算,正确的是()A 3 2 5A. a - a = aB. 2a + 3b = 5abC. +a"3 3 2 5=a D. a +a -a7 (2011海南省)不等式x-2< 0的解集是()A. x >-2B. x <-2C. x > 2 T). x <28 (2009海南省)下列各式中,与(a-b)2一定相等的是()A. a2 + 2ab + b1B. a2 -b2C. a2 +b2D. «2-2ab + b29 (2010海南省)计算— a — a的结果是()A. 0B. laC. —2aD. a~10 (2009海南省)当x = -2时,代数式x + 1的值是()A. -1B. -3C. 1D. 311. (2009海12. (2010海13 A. x>](2010海南A.3B. x > 1若分式工有意义,则X 的取值范围是X ~~1B. x<lC. x 1方程3 x - 1 = 0的根是( ) 1 1 B. - C.——3 3D .14(2009海方程x (x + l ) = 0的A . 15(2008海不等式X-1的解集是( )A. x>~l B.C. xVTD. —1VE116. (2007海一次函数y = X + 2的图象18. (2010海在反比例函 1 _ky = —— 的图象的任一支上,y 都随尤的增大而增大,则上 x的值可以是(A. -1B. 0C. 1D. 2k + 119. (2011海南省)已知点A (2,3)在反比例函数y=—的图象上,则*的值是(A. -7B. 7C. -5D. 5 式子卜1在实数范围内有意义,则x 的取值范围是( )B. x = —120. (2011海南省)海南省2010年第六次人口普查数据显示,2010年11月111零时,全省总 人口为8671518人.数据8671518用科学记数法(保留三个有效数字)表不应是( )A. 8.7 xlO 6B. 8.7 xlO 7C. 8.67 xlO 6D. 8.67 xlO 7二、填空题(每小题2分,共20分) 21. (2007海南省)分解因式:a~ -9 =22. (08 海南省)计算:(a+l )(aT )=; (09 海南省)计算:3a-2a=.A.第一象B.第二象限C.第三象限第四象D .23.(2010海南省)计算:a?杼=;(2011海南省)计算(0^)'=24.(2009海南省)“ a的2倍与1的和”用代数式表示是.25.(2008海南省)方程x2-x = 0的解是.26.(2008海南省)用同样大小的黑色棋了按下图所不的方式摆图形,按照这样的规律摆下去, 则第刀个图形需棋子枚(用含。
2020年中考数学 数与代数 提分练习(含答案)

2020年中考数学 数与代数试卷(含答案)一、单选题1.如图,在边长为2a 的正方形中央剪去一边长为()2a +的小正方形()2a >,将剩余部分剪开密铺成一个平行四边形,则该平行四边形的面积为( )A .24a +B .224a a +C .2344a a --D .242a a --2.下列计算中,结果正确的是( )A.()236aa -=- B.622a a a ÷=C.33332a a a -=3.设21,x x 是一元二次方程0322=--x x 的两根,则2221x x +=( )A.6B.8C.10D.124.解分式方程22311x x x++=-- 时,去分母后变形正确的是( ) A.()()2231x x ++=-B.()2231x x -+=-C.()223x -+=D.()()2231x x -+=- 5.若关于x 的方程1011m x x x --=-- 有增根,则m 的值是( ) A.3 B.2 C.1 D.-16.下列计算正确的是( )A .32a a a -=B .236a a a ⋅=C .236a a a ⋅=D .22(3)6a a = 7.单项式213a b π的系数和次数分别是( ) A. π3 ,3 B . -π3,3 C . -13,4 D . 13,4二、填空题8.计算()23a -的结果为________.9.()()2232x y x -⋅-=10.()()()322263221x x y x x y --⋅-+-= 。
11.约分:22121x x x --+= 12.因式分解:24520ab a -= .13.()22b +=14.计算:66642125.0⨯⨯= 15.若方程x x k x --=-133有增根,则k 。
16.若实数b a ,满足2220a ab b ++=,则b a = 。
三、计算题17.分解因式:242455m a m b -18.分解因式:()2223448a x ax +-四、解答题19.先化简,再求值:2(2)(1)(1)a a a +++-,其中34a =-20.若2248200x x y y ++++=,求xy 的值21.关于x 的一元二次方程()22230x k x k +-+=有两个不相等的实数根,αβ。
初一代数中考试题及答案

初一代数中考试题及答案一、选择题(每题3分,共30分)1. 下列哪个选项是方程2x + 3 = 7的解?A. x = 1B. x = 2C. x = 3D. x = 4答案:B2. 如果a + b = 5,那么2a + 2b等于多少?A. 10B. 8C. 6D. 4答案:A3. 计算(3x - 2) - (x + 4)的结果是?A. 2x - 6B. 2x + 2C. x - 6D. x + 2答案:A4. 一个数的3倍减去5等于10,这个数是多少?A. 5B. 7C. 3D. 2答案:B5. 下列哪个选项是不等式2x - 4 > 6的解?A. x > 5B. x > 3C. x < 5D. x < 3答案:B6. 已知x = -2是方程3x + 4 = 2x + 8的解,那么下列哪个选项是正确的?A. 方程是正确的B. 方程是错误的C. x = -2不是方程的解D. 无法确定答案:A7. 计算(2x^2 - 3x + 1) - (x^2 - 2x + 3)的结果是?A. x^2 + x - 2B. x^2 - x - 2C. x^2 - 5x + 4D. x^2 - 5x - 2答案:A8. 一个数的一半加上3等于8,这个数是多少?A. 5B. 10C. 2D. 8答案:B9. 下列哪个选项是方程x^2 - 4x + 4 = 0的解?A. x = 2B. x = -2C. x = 4D. x = -4答案:A10. 如果3a = 9,那么a的值是多少?A. 3B. 6C. 1D. 2答案:A二、填空题(每题3分,共30分)1. 方程3x - 5 = 10的解是x = ______。
答案:42. 已知a = 7,那么3a - 5 = ______。
答案:163. 计算(5x + 3) - (2x - 4) = ______。
答案:3x + 74. 一个数的4倍加上2等于18,这个数是 ______。
初中中招代数试题及答案

初中中招代数试题及答案一、选择题(每题3分,共30分)1. 下列哪个选项是方程2x+3=7的解?A. x=1B. x=2C. x=3D. x=4答案:B2. 如果一个数的平方等于9,那么这个数是?A. 3B. -3C. 3或-3D. 以上都不对答案:C3. 一个两位数,十位数字比个位数字大3,且这个两位数等于十位数字与个位数字之和的5倍,这个两位数是?A. 41B. 52C. 63D. 74答案:B4. 已知a和b互为相反数,c和d互为倒数,且a+b+c+d=10,下列哪个选项是正确的?A. ab=-1B. cd=1C. ab+cd=-1D. ab-cd=9答案:D5. 一个多项式减去3x^2+2x-5,得到-x^2+4x+7,那么原多项式是?A. 2x^2+6x+2B. 2x^2+2x+2C. 4x^2+6x+12D. 4x^2+2x+12答案:A6. 一个等差数列的前三项分别是1,3,5,那么第n项是?A. 2n-1B. 2n+1C. 2n-3D. 2n+3答案:A7. 一个等比数列的前三项分别是2,6,18,那么第四项是?A. 54B. 6C. 36D. 12答案:A8. 如果x^2-5x+6=0,那么x的值是?A. 2和3B. -2和-3C. 3和2D. -3和-2答案:A9. 一个二次函数y=ax^2+bx+c的图象开口向上,且经过点(1,0)和(-1,0),那么a的值是?A. 大于0B. 小于0C. 等于0D. 不确定答案:A10. 一个正比例函数y=kx的图象经过点(2,6),那么k的值是?A. 3B. 1.5C. 2D. 0.5答案:A二、填空题(每题3分,共15分)1. 方程3x-6=0的解是x=______。
答案:22. 一个数的立方等于-8,那么这个数是______。
答案:-23. 一个三位数,百位数字是2,十位数字是x,个位数字是x-1,且这个三位数是6的倍数,那么x的值是______。
2023北京中考数学专题训练——数与代数(4)学生版

2023北京中考数学专题训练——数与代数(4)一.选择题(共5小题)1.实数a,b,c在数轴上的对应点的位置如图所示,则正确的结论是()A.a>b B.a+b>0C.ac>0D.|a|>|c|2.广阔无垠的太空中有无数颗恒星,其中离太阳系最近的一颗恒星称为“比邻星”,它距离太阳系约4.2光年.光年是天文学中一种计量天体时空距离的长度单位,1光年约为9 500 000 000 000千米,则“比邻星”距离太阳系约为()A.4×1013千米B.4×1012千米C.9.5×1013千米D.9.5×1012千米3.点A(1,y1),B(3,y2)是反比例函数y=图象上的两点,那么y1,y2的大小关系是()A.y1>y2B.y1=y2C.y1<y2D.不能确定4.如果a2+3a+1=0,那么代数式()•的值为()A.1B.﹣1C.2D.﹣25.《西游记》的故事家喻户晓,特别是书中的孙悟空嫉恶如仇斩妖除魔大快人心.在一次降妖过程中,孙悟空念动咒语将一片树叶放大后射向妖魔.假如这个过程可以看成是在平面直角坐标系中的一次无旋转的变换,设变化前树叶尖部点A坐标为(a,b),在咒语中变化后得到对应点A'为(300a+200,300b﹣100).则变化后树叶的面积变为原来的()A.300倍B.3000倍C.9000倍D.90000倍二.填空题(共3小题)6.若在实数范围内有意义,则x的取值范围是.7.分解因式:ax2﹣25a=.8.如图,在平面直角坐标系xOy中,第一象限内的点P(x,y)与点A(2,2)在同一个反比例函数的图象上,PC⊥y轴于点C,PD⊥x轴于点D,那么矩形ODPC的面积等于.三.解答题(共5小题)9.计算|﹣5|﹣2sin60°﹣(2019﹣π)0.10.已知x=1是关于x的方程x2﹣mx﹣2m2=0的一个根,求m(2m+1)的值.11.关于x的一元二次方程x2﹣(2k﹣1)x+k2﹣1=0,其中k<0.(1)求证:方程有两个不相等的实数根;(2)当k=﹣1时,求该方程的根.12.在平面直角坐标系xOy中,直线l:y=x+b与x轴交于点A(﹣2,0),与y轴交于点B.双曲线y=与直线l交于P,Q两点,其中点P的纵坐标大于点Q的纵坐标(1)求点B的坐标;(2)当点P的横坐标为2时,求k的值;(3)连接PO,记△POB的面积为S.若,结合函数图象,直接写出k的取值范围.13.在平面直角坐标系xOy中,已知抛物线y=x2﹣mx+n.(1)当m=2时,①求抛物线的对称轴,并用含n的式子表示顶点的纵坐标;②若点A(﹣2,y1),B(x2,y2)都在抛物线上,且y2>y1,则x2的取值范围是;(2)已知点P(﹣1,2),将点P向右平移4个单位长度,得到点Q.当n=3时,若抛物线与线段PQ恰有一个公共点,结合函数图象,求m的取值范围.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
中考真题训练 数与代数部分
一.选择题
1. (2013临沂)计算
1
489
3-的结果是【 】
A .3-
B .3
C .1133-
D .11
3
3
【答案】B 。
2. (2013威海)下列各式化简结果为无理数的是【 】 A.
3
27- B.
(
)0
21
- C.
8 D.
()
2
2-
【答案】C 。
3. (2013枣庄)下列计算,正确的是【 A 】 A.
33
--=- B. 030= C. 1
33-=- D.
93=±
4. (2013济宁)如果整式n 2
x 5x 2--+是关于x 的三次三项式,那么n 等于【 C 】
A .3
B .4
C .5
D .6
5. (2013临沂)化简
2
a 121a 2a 1a 1+⎛
⎫÷+ ⎪-+-⎝⎭的结果是【 A 】 A .1a 1- B .1a 1+ C .21a 1- D .2
1
a 1+ 6. (2013泰安)化简分式
2221x 1x 1x 1⎛⎫÷+ ⎪--+⎝⎭的结果是【 A 】 A .2 B .2x 1+ C .2
x 1- D .-2
7. (2013淄博)下列运算错误的是【 D 】
A .
()
()
2
2
a b 1
b a -=- B .a b 1a b --=-+ C .0.5a b 5a 10b 0.2a 0.3b 2a 3b ++=-- D .
a b b a
a b b a --=++ 8. (2013滨州)对于任意实数k ,关于x 的方程
()22x 2k 1x k 2k 10
-+-+-=的根的情况为【 C 】
A .有两个相等的实数根
B .没有实数根
C .有两个不相等的实数根
D .无法确定
9. (2013淄博)如果分式2x 1
2x 2-+的值为0,则x 的值是【 A 】
A . 1
B .0
C .-1
D .±1
10. (2013滨州)若把不等式组2x 3x 12
-≥-⎧⎨
-≥-⎩的解集在数轴上表示出来,则其对应的图形为【 B 】
A .长方形
B .线段
C .射线
D .直线
11. (2013潍坊)已知关于x 的方程
()2kx 1k x 10
+--=,下列说法正确的是【 C 】.
A.当k 0=时,方程无解
B.当k 1=时,方程有一个实数解
C.当k 1=-时,方程有两个相等的实数解
D.当k 0≠时,方程总有两个不相等的实数解 11. (2013潍坊)对于实数x ,我们规定[
]
x 表示不大于x 的最大整数,例如[]12.1=,
[]33=,[]35.2-=-,若x 45
10+⎡⎤=⎢⎥⎣⎦,则x 的取值可以是【 C
】.A.40
B.45
C.51
D.56
12、(2013德州市)如图,动点P 从(0,3)出发,沿所示方向运动,每当碰到矩形的边时反弹,反弹时
A . (1,4)
B . (5,0)
C . (6,4)
D . (8,3)
第12题 第13题
13、(2013济宁市)如图,在直角坐标系中,点A 、B 的坐标分别为(1,4)和(3,0),点C 是y 轴上的一个动点,且A 、B 、C 三点不在同一条直线上,当△ABC 的周长最小时,点C 的坐标是(D ) A .(0,0) B .(0,1) C .(0,2) D .(0,3)
14、(2013莱芜市)如图,等边三角形ABC 的边长为3,N 为AC 的三等分点,三角形边上的动点M 从点A 出发,沿A→B→C 的方向运动,到达点C 时停止.设点M 运动的路程为x ,MN2=y ,则y 关于x 的函数图象大致为( B )
A .
B .
C .
D .
15.(2013•济南)函数y=x 2
+bx+c 与y=x 的图象如图所示,有以下结论: ①b 2﹣4c >0;②b+c+1=0;③3b+c+6=0;④当1<x <3时,x 2+(b ﹣1)x+c <0.
其中正确的个数为( )
A . 1
B . 2
C . 3
D . 4 16. (2013菏泽)一条直线y=kx+b ,其中k+b=﹣5、kb=6,那么该直线经过【 D 】 A .第二、四象限 B .第一、二、三象限 C .第一、三象限 D .第二、三、四象限
17. (2013年山东潍坊3分)设点
()
11A x ,y 和
()
22B x ,y 是反比例函数
k
y x =
图象上的两个点,当1x <2
x <0时,1y <2y ,则一次函数y 2x k =-+的图象不经过的象限是【 A 】. A.第一象限 B.第二象限 C.第三象限 D.第四象限 18. (2013年山东威海3分)如图,在平面直角坐标系中,∠AOB=90°,
∠OAB =30°,反比例函数
1m
y =
x 的图象经过点A ,反比例函数
2n y =
x 的图象经过点B ,则下列关于m ,n 的关系正确的是【 B 】
A. m 3n =-
B. m=﹣3n
C.
3m n 3=-
D. 3
m n 3=
19.(2015烟台) 下列式子不一定成立的是( ) A .
(0)a a
b b b
=≠ B. 3521(0)a a a a -⋅=≠ C. 224(2)(2)a b a b a b -=+- D. 326(2)4a a -=
20. (2015烟台) 如果x 2
-x-1=(x+1)0,
那么x 的值为( ) A .2或-1 B. 0或1 C. 2 D. -1
二.填空题
1. (2013威海)若关于x 的方程x 1m
x 5102x -=
--无解,则m= .
2.若关于x 的分式方程
的解为正数,那么字母a 的取值范围是 .
3. 分解因式:=+-2
2
12123b ab a .
4. (2013莱芜)M (1,a )是一次函数y 3x 2=+与反比例函数
k
y x =
图象的公共点,若将一次函数y 3x 2
=+的图象向下平移4个单位,则它与反比例函数图象的交点坐标为 . 5. (2013年山东泰安3分)化简:
(
)
3
232463
---- = .
6、(2013聊城市)如图,在平面直角坐标系中,一动点从原点O 出发,按向上,向右,向下,向右的方向不断地移动,每移动一个单位,得到点A1(0,1),A2(1,1),A3(1,0),A4(2,0),…那么点A4n+1(n
为自然数)的坐标为 (用n 表示) (2n ,1).
三,解答题
1. (2013年山东烟台6分)先化简,再求值:22x 4x 4x 1
x 1x 11x ⎛⎫-+-+÷ ⎪--⎝⎭,其中x 满足2x x 20+-=.
2. (2013年山东枣庄8分)先化简,再求值:2352362m m m m m -⎛⎫÷+- ⎪--⎝⎭
,其中m 是方程2x 3x 10++=的根.
3、(2013泰安市)如图,抛物线y=
1 2
x 2
+bx+c 与y 轴交于点C (0,﹣4),与x 轴交于点A ,B ,且B 点的坐标为(2,0)
(1)求该抛物线的解析式.
(2)若点P 是AB 上的一动点,过点P 作PE ∥AC ,交BC 于E ,连接CP ,求△PCE 面积的最大值.
(3)若点D 为OA 的中点,点M 是线段AC 上一点,且△OMD 为等腰三角形,求M 点的坐标.
解:(1)把点C (0,﹣4),B (2,0)分别代入y= 1
2
x2+bx+c 中,
得,解得∴该抛物线的解析式为y=
1 2
x 2
+x ﹣4. (2)令y=0,即x2+x ﹣4=0,解得x1=﹣4,x2=2,
∴A (﹣4,0),S △ABC=AB•OC=12.设P 点坐标为(x ,0),则PB=2﹣x . ∵PE ∥AC ,∴∠BPE=∠BAC ,∠BEP=∠BCA ,∴△PBE ∽△ABC ,
∴,即,化简得:S△PBE=(2﹣x)2.
S△PCE=S△PCB﹣S△PBE=PB•OC﹣S△PBE=×(2﹣x)×4﹣(2﹣x)2
=x2﹣x+=(x+1)2+3∴当x=﹣1时,S△PCE的最大值为3.
(3)△OMD为等腰三角形,可能有三种情形:(I)当DM=DO时,如答图①所示.
DO=DM=DA=2,∴∠OAC=∠AMD=45°,∴∠ADM=90°,∴M点的坐标为(﹣2,﹣2);
(II)当MD=MO时,如答图②所示.
过点M作MN⊥OD于点N,则点N为OD的中点,∴DN=ON=1,AN=AD+DN=3,
又△AMN为等腰直角三角形,∴MN=AN=3,∴M点的坐标为(﹣1,﹣3);
(III)当OD=OM时,∵△OAC为等腰直角三角形,
∴点O到AC的距离为×4=,即AC上的点与点O之间的最小距离为.
∵>2,∴OD=OM的情况不存在.综上所述,点M的坐标为(﹣2,﹣2)或(﹣1,﹣3).
点评:本题是二次函数综合题,考查了二次函数的图象与性质、待定系数法、相似三角形、等腰三角形等知识点,以及分类讨论的数学思想.第(2)问将面积的最值转化为二次函数的极值问题,注意其中求面积表达式的方法;第(3)问重在考查分类讨论的数学思想,注意三种可能的情形需要一一分析,不能遗漏.。
