2009年考研数学三真题

2009年考研数学三真题及完整解析

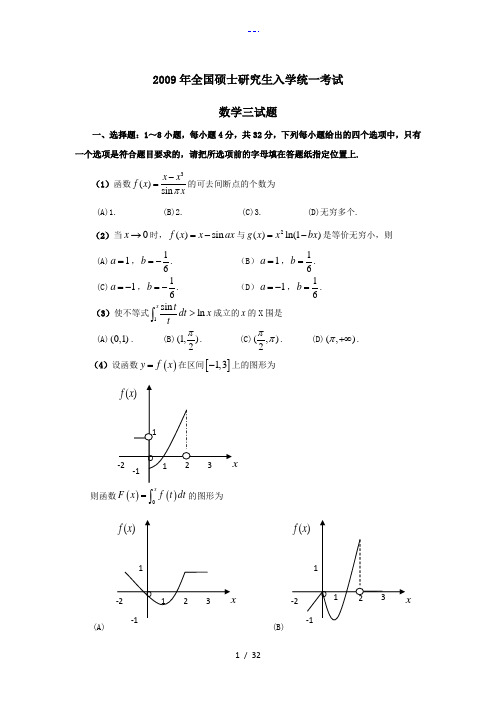
2009年全国硕士研究生入学统一考试数学三试题一、选择题：1～8小题，每小题4分，共32分，下列每小题给出的四个选项中，只有一项符合题目要求，把所选项前的字母填在题后的括号内. （1）函数3()sin x xf x xπ-=的可去间断点的个数为：（）()A .1()B . 2 ()C .3()D .无穷多个（2）当0x →时，()sin f x x ax =-与2()ln(1)g x x bx =-是等价无穷小，则（）()A .1a=，16b =-()B . 1a =，16b = ()C .1a =-，16b =-()D .1a =-，16b =（3）使不等式1sin ln xt dt x t>⎰成立的x 的范围是（）()A .(0,1)()B .(1,)2π ()C .(,)2ππ()D .(,)π+∞（4）设函数()y f x =在区间[]1,3-上的图形为：则函数()()0xF x f t dt =⎰的图形为（）()A .()B .()f x 02 3x1 -2-11()f x 0 2 3x1 -2 -11 1()f x -2 0 2 3x-1O()C .()D .（5）设,A B 均为2阶矩阵，*,A B *分别为,A B 的伴随矩阵，若||2,||3A B ==则分块矩阵 00A B⎛⎫⎪⎝⎭的伴随矩阵为（） ()A .**0320B A ⎛⎫⎪⎝⎭()B . **230B A⎛⎫⎪⎝⎭ ()C .**0320A B⎛⎫⎪⎝⎭()D .**0230A B⎛⎫⎪⎝⎭（6）设,A P 均为3阶矩阵，TP 为P 的转置矩阵，且100010002TP AP ⎛⎫ ⎪= ⎪ ⎪⎝⎭，若123122(,,),(,,)P Q ααααααα==+，则TQ A Q 为（） ()A .210110002⎛⎫ ⎪ ⎪ ⎪⎝⎭()B . 110120002⎛⎫⎪⎪ ⎪⎝⎭ ()C .200010002⎛⎫ ⎪ ⎪ ⎪⎝⎭()D .100020002⎛⎫⎪ ⎪ ⎪⎝⎭（7）设事件A 与事件B 互不相容，则（）()A .()0P A B =()B . ()()()P AB P A P B = ()C .()1()P A P B =-()D .()1P A B ⋃=（8）设随机变量X 与Y 相互独立，且X 服从标准正态分布(0,1)N ，Y 的概率分布为1{0}{1}2P Y P Y ====，记()z F Z 为随机变量Z XY =的分布函数，则函数()z F Z 的间断点个数为（）()A .()B . 1 ()C .2()D . 3二、填空题：9-14小题，每小题4分，共24分，请将答案写在答题纸指定位置上.()f x 0 2 3x1 -2-11()f x 02 3x1 -1 1（9）cos 320lim11x x e ex →-=+- .（10）设()y x z x e =+，则(1,0)z x∂=∂（11）幂级数21(1)n nnn e x n∞=--∑的收敛半径为（12）设某产品的需求函数为()Q Q P =,其对应价格P 的弹性0.2p ξ=，则当需求量为10000件时，价格增加1元会使产品收益增加元（13）设(1,1,1)T α=,(1,0,)T k β=，若矩阵T αβ相似于300000000⎛⎫⎪⎪ ⎪⎝⎭，则k = (14)设1X ，2X ,…n X 是来自二项分布总体(,)B n p 的简单随机样本，X 和2S 分别为样本均值和样本方差，记统计量2T X S =-，则E T =三、解答题：15－23小题，共94分.请将解答写在答题纸指定的位置上.解答应写出文字说明、证明过程或演算步骤.（15）（本题满分9分）求二元函数()22(,)2ln f x y x y y y =++的极值。

大学历年考研真题-2009年全国硕士研究生入学统一考试(数三)试题及答案

2009年全国硕士研究生入学统一考试数学三试题一、选择题：1～8小题，每小题4分，共32分，下列每小题给出的四个选项中，只有一个选项是符合题目要求的，请把所选项前的字母填在答题纸指定位置上.（1）函数3()sin x x f x xπ-=的可去间断点的个数为(A)1. (B)2.(C)3.(D)无穷多个.（2）当0x →时，()sin f x x ax =-与2()ln(1)g x x bx =-是等价无穷小，则(A)1a =，16b =-. （B ）1a =，16b =. (C)1a =-，16b =-. （D ）1a =-，16b =.（3）使不等式1sin ln x tdt x t>⎰成立的x 的范围是(A)(0,1).(B)(1,)2π. (C)(,)2ππ.(D)(,)π+∞.（4）设函数()y f x =在区间[]1,3-上的图形为则函数()()0xF x f t dt =⎰的图形为(A)(B)(C)(D)（5）设,A B 均为2阶矩阵，*,A B *分别为,A B 的伴随矩阵，若||2,||3A B ==，则分块矩阵O A B O ⎛⎫ ⎪⎝⎭的伴随矩阵为(A)**32O B A O ⎛⎫ ⎪⎝⎭.(B)**23OB AO ⎛⎫⎪⎝⎭. (C)**32O A B O ⎛⎫⎪⎝⎭.(D)**23OA BO ⎛⎫⎪⎝⎭. （6）设,A P 均为3阶矩阵，TP 为P 的转置矩阵，且100010002T P AP ⎛⎫ ⎪= ⎪ ⎪⎝⎭，若1231223(,,),(,,)P Q ααααααα==+，则TQ AQ 为(A)210110002⎛⎫⎪ ⎪ ⎪⎝⎭.(B)110120002⎛⎫⎪⎪ ⎪⎝⎭.(C)200010002⎛⎫ ⎪ ⎪ ⎪⎝⎭.(D)100020002⎛⎫ ⎪⎪ ⎪⎝⎭.（7）设事件A 与事件B 互不相容，则 (A)()0P AB =.(B)()()()P AB P A P B =.(C)()1()P A P B =-.(D)()1P A B ⋃=.（8）设随机变量X 与Y 相互独立，且X 服从标准正态分布(0,1)N ，Y 的概率分布为1{0}{1}2P Y P Y ====，记()z F Z 为随机变量Z XY =的分布函数，则函数()Z F z 的间断点个数为(A) 0.(B)1. (C)2. (D)3.二、填空题：9~14小题，每小题4分，共24分，请将答案写在答题纸指定位置上. （9）cos x x →= .（10）设()y xz x e =+，则(1,0)zx ∂=∂ .（11）幂级数21(1)n n nn e x n ∞=--∑的收敛半径为 . （12）设某产品的需求函数为()Q Q P =,其对应价格P 的弹性0.2p ξ=，则当需求量为10000件时，价格增加1元会使产品收益增加元.（13）设(1,1,1)T α=,(1,0,)Tk β=，若矩阵T αβ相似于300000000⎛⎫⎪ ⎪ ⎪⎝⎭，则k = .(14) 设1X ，2X ,…,m X 为来自二项分布总体(,)B n p 的简单随机样本，X 和2S 分别为样本均值和样本方差，记统计量2T X S =-，则ET = .三、解答题：15～23小题，共94分.请将解答写在答题纸指定的位置上.解答应写出文字说明、证明过程或演算步骤.（15）（本题满分9分）求二元函数()22(,)2ln f x y x y y y =++的极值. （16）（本题满分10 分）计算不定积分ln(1dx +⎰(0)x >. （17）（本题满分10 分）计算二重积分()Dx y dxdy -⎰⎰，其中22{(,)(1)(1)2,}D x y x y y x =-+-≤≥.（18）（本题满分11 分）（Ⅰ）证明拉格朗日中值定理，若函数()f x 在[],a b 上连续，在(),a b 上可导，则(),a b ξ∈，得证()'()()()f b f a f b a ξ-=-.（Ⅱ）证明：若函数()f x 在0x =处连续，在()0,,(0)σσ>内可导，且'0lim ()x f x A +→=，则'(0)f +存在，且'(0)f A +=. （19）（本题满分10 分）设曲线()y f x =，其中()f x 是可导函数，且()0f x >.已知曲线()y f x =与直线0,1y x ==及(1)x t t =>所围成的曲边梯形绕x 轴旋转一周所得的立体体积值是该曲边梯形面积值的t π倍，求该曲线的方程.（20）（本题满分11 分）设111A=111042--⎛⎫ ⎪- ⎪ ⎪--⎝⎭,1112ξ-⎛⎫⎪= ⎪ ⎪-⎝⎭.（Ⅰ）求满足21A ξξ=，231A ξξ=的所有向量2ξ，3ξ.（Ⅱ）对（Ⅰ）中的任意向量2ξ,3ξ，证明1ξ,2ξ,3ξ线性无关. （21）（本题满分11 分）设二次型2221231231323(,,)(1)22f x x x ax ax a x x x x x =++-+-.（Ⅰ）求二次型f 的矩阵的所有特征值.（Ⅱ）若二次型f 的规范形为2212y y +，求a 的值.（22）（本题满分11 分）设二维随机变量(,)X Y 的概率密度为0(,)0xe y xf x y -⎧<<=⎨⎩其他（Ⅰ）求条件概率密度()Y X f y x ；（Ⅱ）求条件概率{}11P X Y ≤≤. （23）（本题满分11分）袋中有一个红球，两个黑球，三个白球，现在放回的从袋中取两次，每次取一个，求以X 、Y 、Z 分别表示两次取球所取得的红、黑与白球的个数.（Ⅰ）求{}10P X Z ==；（Ⅱ）求二维随机变量(,)X Y 的概率分布.2009年全国硕士研究生入学统一考试数学三试题及答案解析一、选择题：1～8小题，每小题4分，共32分，下列每小题给出的四个选项中，只有一项符合题目要求，把所选项前的字母填在题后的括号内.（1）函数3()sin x x f x xπ-=的可去间断点的个数为()A .1()B . 2 ()C .3()D .无穷多个【答案】C 【解析】()3sin x x f x xπ-=则当x 取任何整数时，()f x 均无意义故()f x 的间断点有无穷多个，但可去间断点为极限存在的点，故应是30x x -=的解1,2,30,1x =±320032113211131lim lim sin cos 132lim lim sin cos 132lim lim sin cos x x x x x x x x x x x x x x x x x x x x x ππππππππππππ→→→→→-→---==--==--== 故可去间断点为3个，即0,1±（2）当0x →时，()sin f x x ax =-与2()ln(1)g x x bx =-是等价无穷小，则()A .1a =，16b =-()B . 1a =，16b = ()C .1a =-，16b =- ()D .1a =-，16b =【答案】 A【解析】2()sin ,()(1)f x x ax g x x ln bx =-=-为等价无穷小，则222200000()sin sin 1cos sin lim lim lim lim lim ()ln(1)()36x x x x x f x x ax x ax a ax a ax g x x bx x bx bx bx→→→→→---==-⋅---洛洛230sin lim 166x a ax a b b axa→==-=-⋅ 36a b ∴=- 故排除,B C 。

2009—数三真题、标准答案及解析

2009年全国硕士研究生入学统一考试数学三试题一、选择题：1～8小题，每小题4分，共32分，下列每小题给出的四个选项中，只有一个选项是符合题目要求的，请把所选项前的字母填在答题纸指定位置上.（1）函数3()sin x x f x xπ-=的可去间断点的个数为(A)1.(B)2. (C)3.(D)无穷多个.（2）当0x →时，()sin f x x ax =-与2()ln(1)g x x bx =-是等价无穷小，则(A)1a =，16b =-. （B ）1a =，16b =. (C)1a =-，16b =-. （D ）1a =-，16b =.（3）使不等式1sin ln x tdt x t>⎰成立的x 的范围是(A)(0,1).(B)(1,)2π. (C)(,)2ππ.(D)(,)π+∞.（4）设函数()y f x =在区间[]1,3-上的图形为则函数()()0xF x f t dt =⎰的图形为(A)(B)(C)(D)（5）设,A B 均为2阶矩阵，*,A B *分别为,A B 的伴随矩阵，若||2,||3A B ==，则分块矩阵O A B O ⎛⎫⎪⎝⎭的伴随矩阵为(A)**32O B A O ⎛⎫⎪⎝⎭.(B)**23OB A O ⎛⎫⎪⎝⎭.(C)**32O A BO ⎛⎫⎪⎝⎭.(D)**23O A BO ⎛⎫⎪⎝⎭. （6）设,A P 均为3阶矩阵，T P 为P 的转置矩阵，且100010002TP AP ⎛⎫ ⎪= ⎪ ⎪⎝⎭，若1231223(,,),(,,)P Q ααααααα==+，则TQ AQ 为(A)210110002⎛⎫⎪ ⎪ ⎪⎝⎭.(B)110120002⎛⎫⎪⎪ ⎪⎝⎭.(C)200010002⎛⎫ ⎪ ⎪ ⎪⎝⎭.(D)100020002⎛⎫ ⎪ ⎪ ⎪⎝⎭.（7）设事件A 与事件B 互不相容，则(A)()0P AB =.(B)()()()P AB P A P B =. (C)()1()P A P B =-.(D)()1P A B ⋃=.（8）设随机变量X 与Y 相互独立，且X 服从标准正态分布(0,1)N ，Y 的概率分布为1{0}{1}2P Y P Y ====，记()z F Z 为随机变量Z XY =的分布函数，则函数()z F Z 的间断点个数为(A) 0. (B)1. (C)2 . (D)3.二、填空题：9~14小题，每小题4分，共24分，请将答案写在答题纸指定位置上. （9）cos 0x x →= .（10）设()y xz x e =+，则(1,0)zx ∂=∂ .（11）幂级数21(1)n n nn e x n ∞=--∑的收敛半径为 . （12）设某产品的需求函数为()Q Q P =,其对应价格P 的弹性0.2p ξ=，则当需求量为10000件时，价格增加1元会使产品收益增加元.（13）设(1,1,1)T α=,(1,0,)T k β=，若矩阵Tαβ相似于300000000⎛⎫⎪ ⎪ ⎪⎝⎭，则k = .(14)设1X ，2X ,…,n X 为来自二项分布总体(,)B n p 的简单随机样本，X 和2S 分别为样本均值和样本方差，记统计量2T X S =-，则ET = .三、解答题：15～23小题，共94分.请将解答写在答题纸指定的位置上.解答应写出文字说明、证明过程或演算步骤. （15）（本题满分9分）求二元函数()22(,)2ln f x y x y y y =++的极值. （16）（本题满分10 分）计算不定积分ln(1dx +⎰(0)x >. （17）（本题满分10 分）计算二重积分()Dx y dxdy -⎰⎰，其中22{(,)(1)(1)2,}D x y x y y x =-+-≤≥. （18）（本题满分11 分）（Ⅰ）证明拉格朗日中值定理，若函数()f x 在[],a b 上连续，在(),a b 上可导，则(),a b ξ∈，得证()'()()()f b f a f b a ξ-=-.（Ⅱ）证明：若函数()f x 在0x =处连续，在()0,,(0)σσ>内可导，且'0lim ()x f x A +→=，则'(0)f +存在，且'(0)f A +=.（19）（本题满分10 分）设曲线()y f x =，其中()f x 是可导函数，且()0f x >.已知曲线()y f x =与直线0,1y x ==及(1)x t t =>所围成的曲边梯形绕x 轴旋转一周所得的立体体积值是该曲边梯形面积值的t π倍，求该曲线的方程.（20）（本题满分11 分）设111A=111042--⎛⎫ ⎪- ⎪ ⎪--⎝⎭,1112ξ-⎛⎫⎪= ⎪ ⎪-⎝⎭.（Ⅰ）求满足21A ξξ=，231A ξξ=的所有向量2ξ，3ξ.（Ⅱ）对（Ⅰ）中的任意向量2ξ,3ξ，证明1ξ,2ξ,3ξ线性无关. （21）（本题满分11 分）设二次型2221231231323(,,)(1)22f x x x ax ax a x x x x x =++-+-.（Ⅰ）求二次型f 的矩阵的所有特征值.（Ⅱ）若二次型f 的规范形为2211y y +，求a 的值.（22）（本题满分11 分）设二维随机变量(,)X Y 的概率密度为0(,)0x e y xf x y -⎧<<=⎨⎩其他（Ⅰ）求条件概率密度()Y X f y x ；（Ⅱ）求条件概率11P X Y =⎡≤≤⎤⎣⎦. （23）（本题满分11分）袋中有一个红球，两个黑球，三个白球，现在放回的从袋中取两次，每次取一个，求以X 、Y 、Z 分别表示两次取球所取得的红、黑与白球的个数. （Ⅰ）求10P X Z ⎡==⎤⎣⎦；（Ⅱ）求二维随机变量(,)X Y 的概率分布.2009年全国硕士研究生入学统一考试数学三试题解析一、选择题：1～8小题，每小题4分，共32分，下列每小题给出的四个选项中，只有一个选项是符合题目要求的，请把所选项前的字母填在答题纸指定位置上.（1）函数3()sin x x f x xπ-=的可去间断点的个数为(A)1. (B)2. (C)3.(D)无穷多个.【答案】C. 【解析】()3sin x x f x xπ-=则当x 取任何整数时，()f x 均无意义故()f x 的间断点有无穷多个，但可去间断点为极限存在的点，故应是30x x -=的解1,2,30,1x =±320032113211131lim lim sin cos 132lim lim sin cos 132lim lim sin cos x x x x x x x x x x x x x x x x x x x x x ππππππππππππ→→→→→-→---==--==--== 故可去间断点为3个，即0,1±（2）当0x →时，()sin f x x ax =-与2()ln(1)g x x bx =-是等价无穷小，则(A)1a =，16b =-. （B ）1a =，16b =. (C)1a =-，16b =-. （D ）1a =-，16b =.【答案】A.【解析】2()sin ,()(1)f x x ax g x x ln bx =-=-为等价无穷小，则222200000()sin sin 1cos sin lim lim lim lim lim ()ln(1)()36x x x x x f x x ax x ax a ax a axg x x bx x bx bx bx→→→→→---==-⋅---洛洛230sin lim 166x a ax a b b axa→==-=-⋅ 36a b ∴=- 故排除(B)、(C). 另外201cos lim3x a axbx →--存在，蕴含了1cos 0a ax -→()0x →故 1.a =排除(D).所以本题选(A).（3）使不等式1sin ln xtdt x t>⎰成立的x 的范围是 (A)(0,1).(B)(1,)2π. (C)(,)2ππ. (D)(,)π+∞.【答案】A.【解析】原问题可转化为求111sin sin 1()ln xx x tt f x dt x dt dt t t t =-=-⎰⎰⎰11sin 11sin 0x x t t dt dt t t --==>⎰⎰成立时x 的取值范围，由1sin 0tt->，()0,1t ∈时，知当()0,1x ∈时，()0f x >.故应选(A).（4）设函数()y f x =在区间[]1,3-上的图形为则函数()()0xF x f t dt =⎰的图形为(A)(B)(C)(D)【答案】D.【解析】此题为定积分的应用知识考核，由()y f x =的图形可见，其图像与x 轴及y 轴、0x x =所围的图形的代数面积为所求函数()F x ，从而可得出几个方面的特征： ①[]0,1x ∈时，()0F x ≤，且单调递减. ②[]1,2x ∈时，()F x 单调递增. ③[]2,3x ∈时，()F x 为常函数.④[]1,0x ∈-时，()0F x ≤为线性函数，单调递增. ⑤由于F(x)为连续函数结合这些特点，可见正确选项为(D).（5）设,A B 均为2阶矩阵，*,A B *分别为,A B 的伴随矩阵，若||2,||3A B ==，则分块矩阵O A B O ⎛⎫⎪⎝⎭的伴随矩阵为(A)**32O B A O ⎛⎫⎪⎝⎭.(B)**23OB A O ⎛⎫⎪⎝⎭.(C)**32O A BO ⎛⎫⎪⎝⎭.(D)**23O A BO ⎛⎫⎪⎝⎭. 【答案】B.【解析】根据CC C E *=，若111,C C C CC C*--*==分块矩阵O A B O ⎛⎫⎪⎝⎭的行列式221236O A A B B O ⨯=-=⨯=（），即分块矩阵可逆 1111661O B BO A O A O A O B B O B O B O AO A O A **---*⎛⎫ ⎪⎛⎫⎛⎫⎛⎫⎪=== ⎪ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎪⎝⎭1236132O BOB AO A O ****⎛⎫ ⎪⎛⎫== ⎪ ⎪ ⎪⎝⎭⎪⎝⎭故答案为(B).（6）设,A P 均为3阶矩阵，T P 为P 的转置矩阵，且100010002TP AP ⎛⎫ ⎪= ⎪ ⎪⎝⎭，若1231223(,,),(,,)P Q ααααααα==+，则TQ AQ 为(A)210110002⎛⎫⎪ ⎪ ⎪⎝⎭.(B)110120002⎛⎫⎪⎪ ⎪⎝⎭.(C)200010002⎛⎫ ⎪ ⎪ ⎪⎝⎭.(D)100020002⎛⎫ ⎪ ⎪ ⎪⎝⎭.【答案】A.【解析】122312312312100(,,)(,,)110(,,)(1)001Q E αααααααααα⎡⎤⎢⎥=+==⎢⎥⎢⎥⎣⎦，即： 12121212122112(1)[(1)][(1)](1)[](1)100(1)010(1)002110100100210010010110110001002001002T T TT Q PE Q AQ PE A PE E P AP E E E ===⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦（7）设事件A 与事件B 互不相容，则(A)()0P AB =.(B)()()()P AB P A P B =. (C)()1()P A P B =-.(D)()1P A B ⋃=.【答案】D.【解析】因为,A B 互不相容，所以()0P AB =(A)()()1()P AB P A B P A B ==-U U ，因为()P A B U 不一定等于1，所以(A)不正确. (B)当(),()P A P B 不为0时，(B)不成立，故排除. (C)只有当,A B 互为对立事件的时候才成立，故排除.(D)()()1()1P A B P AB P AB ==-=U ，故(D)正确.（8）设随机变量X 与Y 相互独立，且X 服从标准正态分布(0,1)N ，Y 的概率分布为1{0}{1}2P Y P Y ====，记()z F Z 为随机变量Z XY =的分布函数，则函数()z F Z 的间断点个数为（） (A) 0. (B)1. (C)2 .(D)3.【答案】 B.【解析】()()(0)(0)(1)(1)Z F z P XY z P XY z Y P Y P XY z Y P Y =≤=≤==+≤==1[(0)(1)]21[(00)(1)]2P XY z Y P XY z Y P X z Y P X z Y =≤=+≤==⋅≤=+≤=,X Y Q 独立1()[(0)()]2Z F z P x z P x z ∴=⋅≤+≤（1）若0z <，则1()()2Z F z z =Φ（2）当0z ≥，则1()(1())2Z F z z =+Φ0z ∴=为间断点，故选(B).二、填空题：9~14小题，每小题4分，共24分，请将答案写在答题纸指定位置上. （9）cos 0x x →= .【答案】32e .【解析】cos cos 10xx x x -→→=02(1cos )lim 13x e x x→-=20212lim 13x e x x →⋅=32e =. （10）设()y xz x e =+，则(1,0)zx ∂=∂ .【答案】2ln 21+. 【解析】由()xy z x e=+，故()(),01xz x x =+()''ln(1)ln(1)1ln(1)1x x x x x dz x x e e x dx x ++⎡⎤⎡⎤⎡⎤=+==++⎣⎦⎢⎥⎣⎦+⎣⎦ 代入1x =得，()ln 21,01ln 22ln 212ze x∂⎛⎫=+=+ ⎪∂⎝⎭.（11）幂级数21(1)n n nn e x n ∞=--∑的收敛半径为 . 【答案】1e. 【解析】由题意知，()210nn n e a n --=>()()()()111122122111()11111n n n n n nn n nn e e ea n n e n a n e n e e +++++⎡⎤⎛⎫--⎢⎥ ⎪⎝⎭--⎢⎥⎣⎦=⋅=⋅→→∞⎡⎤+--+⎛⎫--⎢⎥⎪⎝⎭⎢⎥⎣⎦所以，该幂级数的收敛半径为1e（12）设某产品的需求函数为()Q Q P =,其对应价格P 的弹性0.2p ξ=，则当需求量为10000件时，价格增加1元会使产品收益增加元. 【答案】8000.【解析】所求即为()QP Q P Q ''=+ 因为0.2p Q PQξ'==-，所以0.2Q P Q '=- 所以()0.20.8QP Q Q Q '=-+= 将10000Q =代入有()8000QP '=.（13）设(1,1,1)T α=,(1,0,)T k β=，若矩阵Tαβ相似于300000000⎛⎫ ⎪ ⎪ ⎪⎝⎭，则k = .【答案】2.【解析】T αβ相似于300000000⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦，根据相似矩阵有相同的特征值，得到Tαβ的特征值为3，0，0.而T αβ为矩阵Tαβ的对角元素之和，1300k ∴+=++，2k ∴=.(14)设1X ，2X ,…,n X 为来自二项分布总体(,)B n p 的简单随机样本，X 和2S 分别为样本均值和样本方差，记统计量2T X S =-，则ET = . 【答案】2np【解析】由222()(1)ET E X S E X ES np np p np =-=-=--=.三、解答题：15～23小题，共94分.请将解答写在答题纸指定的位置上.解答应写出文字说明、证明过程或演算步骤. （15）（本题满分9分）求二元函数()22(,)2ln f x y x y y y =++的极值.【解析】2(,)2(2)0x f x y x y '=+=，2(,)2ln 10y f x y x y y '=++=，故10,x y e= =. 2212(2),2,4xxyy xyf y f x f xy y''''''=+ =+ =. 则12(0,)12(2)xxef e ''=+，1(0,)0xyef ''=，1(0,)yy ef e ''=.0xxf ''>Q 而2()0xy xx yy f f f ''''''-< ∴二元函数存在极小值11(0,)f e e=-.（16）（本题满分10 分）计算不定积分ln(1dx +⎰(0)x >.t =得22212,1(1)tdtx dx t t -= =--2221ln(1ln(1)1ln(1)11111dx t d t t dt t t t =+-+=---+⎰⎰⎰而22111112()11411(1)111ln(1)ln(1)2441dt dtt t t t t t t C t =---+-++--++++⎰⎰所以2ln(1)111ln(1ln 1412(1)1ln(1.2t t dx C t t t x C ++=+-+--+=+-⎰（17）（本题满分10 分）计算二重积分()Dx y dxdy -⎰⎰，其中22{(,)(1)(1)2,}D x y x y y x =-+-≤≥. 【解析】由22(1)(1)2x y -+-≤得2(sin cos )r θθ≤+，32(sin cos )4()(cos sin )04Dx y dxdy d r r rdr πθθθθθπ+∴-=-⎰⎰⎰⎰332(sin cos )14(cos sin )034r d πθθθθθπ⎡+⎤=-⋅⎢⎥⎣⎦⎰ 2384(cos sin )(sin cos )(sin cos )34d πθθθθθθθπ=-⋅+⋅+⎰3384(cos sin )(sin cos )34d πθθθθθπ=-⋅+⎰3344438814(sin cos )(sin cos )(sin cos )3344d πππθθθθθθπ=++=⨯+⎰83=-.（18）（本题满分11 分）（Ⅰ）证明拉格朗日中值定理，若函数()f x 在[],a b 上连续，在(),a b 上可导，则(),a b ξ∈，得证()'()()()f b f a f b a ξ-=-.（Ⅱ）证明：若函数()f x 在0x =处连续，在()0,,(0)σσ>内可导，且'0lim ()x f x A +→=，则'(0)f +存在，且'(0)f A +=.【解析】（Ⅰ）作辅助函数()()()()()()f b f a x f x f a x a b aϕ-=----，易验证()x ϕ满足：()()a b ϕϕ=；()x ϕ在闭区间[],a b 上连续，在开区间(),a b 内可导，且''()()()()f b f a x f x b aϕ-=--. 根据罗尔定理，可得在(),a b 内至少有一点ξ，使'()0ϕξ=，即'()f ξ'()()0,()()()()f b f a f b f a f b a b aξ--=∴-=--（Ⅱ）任取0(0,)x δ∈，则函数()f x 满足：在闭区间[]00,x 上连续，开区间()00,x 内可导，从而有拉格朗日中值定理可得：存在()()000,0,x x ξδ∈⊂，使得()0'00()(0)x f x f f x ξ-=-……()*又由于()'lim x f x A +→=，对上式（*式）两边取00x +→时的极限可得：()()000000'''0000()00lim lim ()lim ()0x x x x x f x f f f f A x ξξξ++++→→→-====-故'(0)f +存在，且'(0)f A +=.（19）（本题满分10 分）设曲线()y f x =，其中()f x 是可导函数，且()0f x >.已知曲线()y f x =与直线0,1y x ==及(1)x t t =>所围成的曲边梯形绕x 轴旋转一周所得的立体体积值是该曲边梯形面积值的t π倍，求该曲线的方程.【解析】旋转体的体积为22()()11x x t t V f dx f dx ππ==⎰⎰曲边梯形的面积为：()1x ts f dx =⎰，则由题可知22()()()()1111x x x x t t t tV ts f dx t f dx f dx t f dx πππ=⇒=⇒=⎰⎰⎰⎰两边对t 求导可得22()()()()()()11t x t t t x t t f f dx tf f tf f dx =+⇒-=⎰⎰ V继续求导可得''2()()()()()f t f t f t tf t f t --=，化简可得'1(2())()2()12dt f t t f t f t t dy y -=⇒+=，解之得1223t c y y -=⋅+在V 式中令1t =，则2(1)(1)0,()0,(1)1f f f t f -=>∴=Q ，代入1223t cyy -=+得11,2)33c t y =∴=+.所以该曲线方程为：230y x +=.（20）（本题满分11 分）设111A=111042--⎛⎫ ⎪- ⎪ ⎪--⎝⎭,1112ξ-⎛⎫ ⎪= ⎪ ⎪-⎝⎭. （Ⅰ）求满足21A ξξ=，231A ξξ=的所有向量2ξ，3ξ.（Ⅱ）对（Ⅰ）中的任意向量2ξ,3ξ，证明1ξ,2ξ,3ξ线性无关. 【解析】（Ⅰ）解方程21A ξξ=()1111111111111,111100000211042202110000A ξ---------⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪=-→→ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪---⎝⎭⎝⎭⎝⎭()2r A =故有一个自由变量，令32x =，由0Ax =解得，211,1x x =-=求特解，令120x x ==，得31x =故21101021k ξ⎛⎫⎛⎫ ⎪ ⎪=-+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭，其中1k 为任意常数解方程231A ξξ=2220220440A ⎛⎫ ⎪=-- ⎪ ⎪⎝⎭()21111022012,2201000044020000A ξ-⎛⎫ ⎪-⎛⎫ ⎪ ⎪=--→⎪ ⎪ ⎪ ⎪-⎝⎭ ⎪⎝⎭故有两个自由变量，令231,0x x =-=，由20A x =得11x = 令230,1x x ==-，由20A x =得10x =求得特解21200η⎛⎫- ⎪ ⎪= ⎪ ⎪ ⎪⎝⎭故 3231102100010k k ξ⎛⎫-⎪⎛⎫⎛⎫ ⎪ ⎪ ⎪=-++ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭ ⎪⎝⎭，其中23,k k 为任意常数（Ⅱ）证明：由于12121212122111121112(21)()2()(21)22221k k k k k k k k k k k k k -+--=+++-+-+-+102=≠故123,,ξξξ 线性无关.（21）（本题满分11 分）设二次型2221231231323(,,)(1)22f x x x ax ax a x x x x x =++-+-.（Ⅰ）求二次型f 的矩阵的所有特征值.（Ⅱ）若二次型f 的规范形为2211y y +，求a 的值.【解析】（Ⅰ） 0101111a A a a ⎛⎫ ⎪=- ⎪ ⎪--⎝⎭0110||01()1111111aaaE A aa a a λλλλλλλλ-----=-=---+---+222()[()(1)1][0()]()[()(1)2]()[22]19(){[(12)]}24()(2)(1)a a a a a a a a a a a a a a a a a λλλλλλλλλλλλλλλλ=---+--+-=---+-=--++--=-+--=--+--123,2,1a a a λλλ∴==-=+.（Ⅱ）若规范形为2212y y +，说明有两个特征值为正，一个为0.则1) 若10a λ==，则 220λ=-< ，31λ= ，不符题意 2) 若20λ= ，即2a =，则120λ=>，330λ=>，符合3) 若30λ= ，即1a =-，则110λ=-< ，230λ=-<，不符题意综上所述，故2a =（22）（本题满分11 分）设二维随机变量(,)X Y 的概率密度为0(,)0x e y xf x y -⎧<<=⎨⎩其他（Ⅰ）求条件概率密度()Y X f y x （Ⅱ）求条件概率11P X Y =⎡≤≤⎤⎣⎦ 【解析】（Ⅰ）由0(,)0x y xe f x y -<<⎧= ⎨⎩其它得其边缘密度函数()0xx x x f x e dy xe x --== >⎰故 |(,)1(|)0()y x x f x y f y x y x f x x== << 即 |1(|)0y x y xf y x x ⎧ 0<<⎪=⎨⎪ ⎩其它（Ⅱ）[1,1][1|1][1]P X Y P X Y P Y ≤≤≤≤=≤而111011[1,1](,)12xx x x y P X Y f x y dxdy dx e dy xe dx e ---≤≤≤≤====-⎰⎰⎰⎰⎰()|,0xxyY yf y e dx e e y y+∞---+∞==-= >⎰11101[1]|110y y P Y e dy e e e ----∴ ≤==-=-+=-⎰11122[1|1]11e e P X Y e e ----∴ ≤≤==--.（23）（本题满分11分）袋中有一个红球，两个黑球，三个白球，现在放回的从袋中取两次，每次取一个，求以X 、Y 、Z 分别表示两次取球所取得的红、黑与白球的个数. ①求10P X Z ⎡==⎤⎣⎦.②求二维随机变量(,)X Y 的概率分布.【解析】（Ⅰ）在没有取白球的情况下取了一次红球，利用压缩样本空间则相当于只有1个红球，2个黑球放回摸两次，其中摸了一个红球12113324(10)9C P X Z C C ⨯∴====⋅.（Ⅱ）X ，Y 取值范围为0，1，2，故()()()()()()()()()1111332311116666111223111166661122116611221166110,0,1,0461112,0,0,136311,1,2,10910,291,20,2,20C C C C P X Y P X Y C C C C C C C P X Y P X Y C C C C C C P X Y P X Y C C C C P X Y C C P X Y P X Y ⋅⋅========⋅⋅⋅⋅========⋅⋅⋅=======⋅⋅====⋅======。

2009~2012考研数学三试题(卷)与解析

2009年全国硕士研究生入学统一考试数学三试题一、选择题：1～8小题，每小题4分，共32分，下列每小题给出的四个选项中，只有一个选项是符合题目要求的，请把所选项前的字母填在答题纸指定位置上.（1）函数3()sin x x f x xπ-=的可去间断点的个数为(A)1. (B)2.(C)3.(D)无穷多个.（2）当0x →时，()sin f x x ax =-与2()ln(1)g x x bx =-是等价无穷小，则(A)1a =，16b =-. （B ）1a =，16b =. (C)1a =-，16b =-. （D ）1a =-，16b =.（3）使不等式1sin ln x tdt x t>⎰成立的x 的X 围是(A)(0,1).(B)(1,)2π. (C)(,)2ππ.(D)(,)π+∞.（4）设函数()y f x =在区间[]1,3-上的图形为则函数()()0xF x f t dt =⎰的图形为(A)(B)(C)(D)（5）设,A B 均为2阶矩阵，*,A B *分别为,A B 的伴随矩阵，若||2,||3A B ==，则分块矩阵O A B O ⎛⎫ ⎪⎝⎭的伴随矩阵为(A)**32O B A O ⎛⎫ ⎪⎝⎭.(B)**23OB AO ⎛⎫⎪⎝⎭. (C)**32O A B O ⎛⎫⎪⎝⎭.(D)**23OA BO ⎛⎫⎪⎝⎭. （6）设,A P 均为3阶矩阵，T P 为P 的转置矩阵，且100010002TP AP ⎛⎫ ⎪= ⎪ ⎪⎝⎭，若1231223(,,),(,,)P Q ααααααα==+，则TQ AQ 为(A)210110002⎛⎫⎪ ⎪ ⎪⎝⎭.(B)110120002⎛⎫⎪⎪ ⎪⎝⎭.(C)200010002⎛⎫ ⎪ ⎪ ⎪⎝⎭.(D)100020002⎛⎫ ⎪⎪ ⎪⎝⎭.（7）设事件A 与事件B 互不相容，则 (A)()0P AB =.(B)()()()P AB P A P B =.(C)()1()P A P B =-.(D)()1P A B ⋃=.（8）设随机变量X 与Y 相互独立，且X 服从标准正态分布(0,1)N ，Y 的概率分布为1{0}{1}2P Y P Y ====，记()z F Z 为随机变量Z XY =的分布函数，则函数()Z F z 的间断点个数为(A) 0.(B)1. (C)2. (D)3.二、填空题：9~14小题，每小题4分，共24分，请将答案写在答题纸指定位置上. （9）cos x x →= .（10）设()y xz x e =+，则(1,0)zx ∂=∂ . （11）幂级数21(1)n n nn e x n ∞=--∑的收敛半径为 . （12）设某产品的需求函数为()Q Q P =,其对应价格P 的弹性0.2p ξ=，则当需求量为10000件时，价格增加1元会使产品收益增加元.（13）设(1,1,1)T α=,(1,0,)Tk β=，若矩阵T αβ相似于300000000⎛⎫⎪ ⎪ ⎪⎝⎭，则k = .(14) 设1X ，2X ,…,m X 为来自二项分布总体(,)B n p 的简单随机样本，X 和2S 分别为样本均值和样本方差，记统计量2T X S =-，则ET = .三、解答题：15～23小题，共94分.请将解答写在答题纸指定的位置上.解答应写出文字说明、证明过程或演算步骤.（15）（本题满分9分）求二元函数()22(,)2ln f x y x y y y =++的极值. （16）（本题满分10 分）计算不定积分ln(1dx +⎰(0)x >. （17）（本题满分10 分）计算二重积分()Dx y dxdy -⎰⎰，其中22{(,)(1)(1)2,}D x y x y y x =-+-≤≥.（18）（本题满分11 分）（Ⅰ）证明拉格朗日中值定理，若函数()f x 在[],a b 上连续，在(),a b 上可导，则(),a b ξ∈，得证()'()()()f b f a f b a ξ-=-.（Ⅱ）证明：若函数()f x 在0x =处连续，在()0,,(0)σσ>内可导，且'0lim ()x f x A +→=，则'(0)f +存在，且'(0)f A +=. （19）（本题满分10 分）设曲线()y f x =，其中()f x 是可导函数，且()0f x >.已知曲线()y f x =与直线0,1y x ==及(1)x t t =>所围成的曲边梯形绕x 轴旋转一周所得的立体体积值是该曲边梯形面积值的t π倍，求该曲线的方程.（20）（本题满分11 分）设111A=111042--⎛⎫ ⎪- ⎪ ⎪--⎝⎭,1112ξ-⎛⎫⎪= ⎪ ⎪-⎝⎭.（Ⅰ）求满足21A ξξ=，231A ξξ=的所有向量2ξ，3ξ.（Ⅱ）对（Ⅰ）中的任意向量2ξ,3ξ，证明1ξ,2ξ,3ξ线性无关. （21）（本题满分11 分）设二次型2221231231323(,,)(1)22f x x x ax ax a x x x x x =++-+-.（Ⅰ）求二次型f 的矩阵的所有特征值.（Ⅱ）若二次型f 的规X 形为2212y y +，求a 的值.（22）（本题满分11 分）设二维随机变量(,)X Y 的概率密度为0(,)0xe y xf x y -⎧<<=⎨⎩其他（Ⅰ）求条件概率密度()Y X f y x ；（Ⅱ）求条件概率{}11P X Y ≤≤. （23）（本题满分11分）袋中有一个红球，两个黑球，三个白球，现在放回的从袋中取两次，每次取一个，求以X 、Y 、Z 分别表示两次取球所取得的红、黑与白球的个数.（Ⅰ）求{}10P X Z ==；2009年全国硕士研究生入学统一考试数学三试题和解析一、选择题：1～8小题，每小题4分，共32分，下列每小题给出的四个选项中，只有一项符合题目要求，把所选项前的字母填在题后的括号内.（1）函数3()sin x x f x xπ-=的可去间断点的个数为：（）()A .1()B . 2 ()C .3()D .无穷多个【答案】C 【解析】()3sin x x f x xπ-=则当x 取任何整数时，()f x 均无意义故()f x 的间断点有无穷多个，但可去间断点为极限存在的点，故应是30x x -=的解1,2,30,1x =±320032113211131lim lim sin cos 132lim lim sin cos 132lim lim sin cos x x x x x x x x x x x x x x x x x x x x x ππππππππππππ→→→→→-→---==--==--== 故可去间断点为3个，即0,1±（2）当0x →时，()sin f x x ax =-与2()ln(1)g x x bx =-是等价无穷小，则（）()A .1a =，16b =-()B . 1a =，16b = ()C .1a =-，16b =- ()D .1a =-，16b =【答案】 A【解析】2()sin ,()(1)f x x ax g x x ln bx =-=-为等价无穷小，则222200000()sin sin 1cos sin lim lim lim lim lim ()ln(1)()36x x x x x f x x ax x ax a ax a ax g x x bx x bx bx bx→→→→→---==-⋅---洛洛230sin lim 166x a ax a b b axa→==-=-⋅ 36a b ∴=- 故排除,B C 。

2009-2012考研数学三试题及解析

2009年全国硕士研究生入学统一考试数学三试题一、选择题：1～8小题，每小题4分，共32分，下列每小题给出的四个选项中，只有一个选项是符合题目要求的，请把所选项前的字母填在答题纸指定位置上.（1）函数3()sin x x f x xπ-=的可去间断点的个数为(A)1. (B)2.(C)3.(D)无穷多个.（2）当0x →时，()sin f x x ax =-与2()ln(1)g x x bx =-是等价无穷小，则(A)1a =，16b =-. （B ）1a =，16b =. (C)1a =-，16b =-. （D ）1a =-，16b =.（3）使不等式1sin ln x tdt x t>⎰成立的x 的范围是(A)(0,1).(B)(1,)2π. (C)(,)2ππ.(D)(,)π+∞.（4）设函数()y f x =在区间[]1,3-上的图形为则函数()()0xF x f t dt =⎰的图形为(A)(B)()f xO 23x1-2-11()f xO 2 3x1 -2 -11 1()f x -2O 2 3x-11(C)(D)（5）设,A B 均为2阶矩阵，*,A B *分别为,A B 的伴随矩阵，若||2,||3A B ==，则分块矩阵O A B O ⎛⎫ ⎪⎝⎭的伴随矩阵为(A)**32O B A O ⎛⎫⎪⎝⎭. (B)**23OB AO ⎛⎫⎪⎝⎭. (C)**32O A BO ⎛⎫⎪⎝⎭.(D)**23OA BO ⎛⎫⎪⎝⎭. （6）设,A P 均为3阶矩阵，T P 为P 的转置矩阵，且100010002TP AP ⎛⎫ ⎪= ⎪ ⎪⎝⎭，若1231223(,,),(,,)P Q ααααααα==+，则TQ AQ 为(A)210110002⎛⎫⎪ ⎪ ⎪⎝⎭.(B)110120002⎛⎫⎪⎪ ⎪⎝⎭.(C)200010002⎛⎫ ⎪ ⎪ ⎪⎝⎭.(D)100020002⎛⎫ ⎪⎪ ⎪⎝⎭.（7）设事件A 与事件B 互不相容，则 (A)()0P AB =.(B)()()()P AB P A P B =.(C)()1()P A P B =-.(D)()1P A B ⋃=.（8）设随机变量X 与Y 相互独立，且X 服从标准正态分布(0,1)N ，Y 的概率分布为1{0}{1}2P Y P Y ====，记()z F Z 为随机变量Z XY =的分布函数，则函数()Z F z 的间断()f x O2 3x1 -2-11()f x O23x1-11点个数为(A) 0.(B)1. (C)2. (D)3.二、填空题：9~14小题，每小题4分，共24分，请将答案写在答题纸指定位置上. （9）cos 320lim11x x e e x →-=+- .（10）设()y xz x e =+，则(1,0)zx ∂=∂ . （11）幂级数21(1)n n nn e x n ∞=--∑的收敛半径为 . （12）设某产品的需求函数为()Q Q P =,其对应价格P 的弹性0.2p ξ=，则当需求量为10000件时，价格增加1元会使产品收益增加元.（13）设(1,1,1)T α=,(1,0,)Tk β=，若矩阵T αβ相似于300000000⎛⎫⎪ ⎪ ⎪⎝⎭，则k = .(14) 设1X ，2X ,…,m X 为来自二项分布总体(,)B n p 的简单随机样本，X 和2S 分别为样本均值和样本方差，记统计量2T X S =-，则ET = .三、解答题：15～23小题，共94分.请将解答写在答题纸指定的位置上.解答应写出文字说明、证明过程或演算步骤.（15）（本题满分9分）求二元函数()22(,)2ln f x y x y y y =++的极值. （16）（本题满分10 分）计算不定积分1ln(1)xdx x++⎰(0)x >. （17）（本题满分10 分）计算二重积分()Dx y dxdy -⎰⎰，其中22{(,)(1)(1)2,}D x y x y y x =-+-≤≥.（18）（本题满分11 分）（Ⅰ）证明拉格朗日中值定理，若函数()f x 在[],a b 上连续，在(),a b 上可导，则(),a b ξ∈，得证()'()()()f b f a f b a ξ-=-.（Ⅱ）证明：若函数()f x 在0x =处连续，在()0,,(0)σσ>内可导，且'0lim ()x f x A +→=，则'(0)f +存在，且'(0)f A +=.（19）（本题满分10 分）设曲线()y f x =，其中()f x 是可导函数，且()0f x >.已知曲线()y f x =与直线0,1y x ==及(1)x t t =>所围成的曲边梯形绕x 轴旋转一周所得的立体体积值是该曲边梯形面积值的t π倍，求该曲线的方程.（20）（本题满分11 分）设111A=111042--⎛⎫ ⎪- ⎪ ⎪--⎝⎭,1112ξ-⎛⎫⎪= ⎪ ⎪-⎝⎭.（Ⅰ）求满足21A ξξ=，231A ξξ=的所有向量2ξ，3ξ. （Ⅱ）对（Ⅰ）中的任意向量2ξ,3ξ，证明1ξ,2ξ,3ξ线性无关. （21）（本题满分11 分）设二次型2221231231323(,,)(1)22f x x x ax ax a x x x x x =++-+-.（Ⅰ）求二次型f 的矩阵的所有特征值.（Ⅱ）若二次型f 的规范形为2212y y +，求a 的值. （22）（本题满分11 分）设二维随机变量(,)X Y 的概率密度为0(,)0x e y x f x y -⎧<<=⎨⎩其他（Ⅰ）求条件概率密度()Y X f y x ；（Ⅱ）求条件概率{}11P X Y ≤≤. （23）（本题满分11分）袋中有一个红球，两个黑球，三个白球，现在放回的从袋中取两次，每次取一个，求以X 、Y 、Z 分别表示两次取球所取得的红、黑与白球的个数.（Ⅰ）求{}10P X Z ==；2009年全国硕士研究生入学统一考试数学三试题和解析一、选择题：1～8小题，每小题4分，共32分，下列每小题给出的四个选项中，只有一项符合题目要求，把所选项前的字母填在题后的括号内.（1）函数3()sin x x f x xπ-=的可去间断点的个数为：（）()A .1()B . 2 ()C .3()D .无穷多个【答案】C 【解析】()3s i n x x f x xπ-=则当x 取任何整数时，()f x 均无意义故()f x 的间断点有无穷多个，但可去间断点为极限存在的点，故应是30x x -=的解1,2,30,1x =±320032113211131lim lim sin cos 132lim lim sin cos 132lim lim sin cos x x x x x x x x x x x x x x x x x x x x x ππππππππππππ→→→→→-→---==--==--== 故可去间断点为3个，即0,1±（2）当0x →时，()sin f x x ax =-与2()ln(1)g x x bx =-是等价无穷小，则（）()A .1a =，16b =-()B . 1a =，16b = ()C .1a =-，16b =- ()D .1a =-，16b =【答案】 A【解析】2()sin ,()(1)f x x ax g x x ln bx =-=-为等价无穷小，则222200000()sin sin 1cos sin lim lim lim lim lim ()ln(1)()36x x x x x f x x ax x ax a ax a ax g x x bx x bx bx bx→→→→→---==-⋅---洛洛230sin lim 166x a ax a b b axa→==-=-⋅ 36a b ∴=- 故排除,B C 。

2009年数学三真题答案解析

lim e(1 cos x)
x0
1 x2
e 1 x2
lim x0
2 1 x2
3e. 2
3
3
（10）设 z (x e y )x ，则 z
.
x (1,0)
【答案】 2 ln 2 1 .
【解析】由 z x e y x ，故 z x, 0 x 1x
dz dx
x
1x
'
e xln(1x)
O
6
O 1 A A
1 B
B
O
O
6
1 2
A
1 B 3 O
O 3 A
2B
O
故答案为(B).
1 0 0
（6）设
A,
P
均为
3
阶矩阵，
PT
为
P
的转置矩阵，且
PT
AP
0
1
0
，
0 0 2
若 P (1,2,3),Q (1 2,2,3) ，则 QT AQ 为
2 1 0
(A)
1
1
0
(C)
2
B*
. O
O 2A*
(D)
3B*
. O
【答案】B.
【解析】根据 CC C E ，若 C C C 1,C 1 1 C C
O
分块矩阵
B
A
O
O
的行列式
B
A （1）22 A B 2 3 6 ，即分块矩阵可逆 O
-3-
O
B
A
O
O B
A O
O
B
A1
O
6
O A1
B
1
lim x0

09真题考研数学真题解析--数三修订版

2009年全国硕士研究生入学统一考试数学三试题一、选择题：1～8小题,每小题4分,共32分,下列每小题给出的四个选项中,只有一项符合题目要求,把所选项前的字母填在题后的括号内.1. （09年，4分）函数()3sin x x f x xπ-=的可去间断点的个数为 ( )(A ) 1. (B ) 2. (C ) 3. (D ) 无穷多个.【考查分析】本题考查间断点的定义和分类，属于间断点计算与判别的基本题型【详解】由于()3sin x x f x xπ-=,则当x 取任何整数时,()f x 均无意义,故()f x 的间断点有无穷多个,但可去间断点为极限存在的点,故应是30x x -=的解1,2,30,1x =±.320032113211131lim lim ,sin cos 132lim lim ,sin cos 132lim lim .sin cos x x x x x x x x x x x x x x x x x x x x x ππππππππππππ→→→→→-→---==--==--== 故可去间断点为3个,即1,2,30,1x =±.选C【评注】此题有相当多的考生选择（D ），认为使sin 0x π=成立的点有无穷多个，同时审题不细，没有利用()f x 的极限值以确定可去间断点的个数，故错误率较高。

2.（09年，4分）当0x →时,()sin f x x ax =-与()()2ln 1g x x bx =-是等价无穷小,则 ( )(A ) 11,6a b ==-. (B ) 11,6a b ==. (C ) 11,6a b =-=-. (D ) 11,6a b =-=.【考查分析】本题考查等价无穷小替换，洛比达法则的计算极限，属于极限计算基本题型【详解】方法1：()sin f x x ax =-与()()2ln 1g x x bx =-是0x →时的等价无穷小,则2200232000330()sin sin limlim lim ()ln(1)()sin 1cos sin lim lim lim36sin lim 1,66x x x x x x x f x x ax x axg x x bx x bx x ax a ax a axbx bx bx a ax a b ax b →→→→→→→--=-⋅---=---⎛⎫=-=-= ⎪⎝⎭等洛洛即36a b =-,故排除（B ）,（C ）.另外,201cos lim3x a axbx→--存在,蕴含了1cos 0a ax -→()0x →,故1,a =排除D. 所以本题选（A ）.方法2：由泰勒公式3331sin () (0)6ax ax a x x x ο=-+→ 3333001(1)()()6lim lim 1()111, 1 1, .66x x a x a x x f x g x bx a a b b ο→→-++⇒==-⇒=-=⇒==-因此选（A ）.【评注】求极限的问题是考试的热点和重点，洛比达法则和等价无穷小替换是常用的计算和简化的方法。

2009年考研数学三答案解析

2009年全国硕士研究生入学统一考试数学三试题及解析一、选择题：1～8小题，每小题4分，共32分，下列每小题给出的四个选项中，只有一项符合题目要求，把所选项前的字母填在题后的括号内.（1）函数3()sin x x f x xπ-=的可去间断点的个数为：（）()A .1()B . 2 ()C .3()D .无穷多个【答案】C 【解析】()3s i n x x f x xπ-=则当x 取任何整数时，()f x 均无意义故()f x 的间断点有无穷多个，但可去间断点为极限存在的点，故应是30x x -=的解1,2,30,1x =±320032113211131lim lim sin cos 132lim lim sin cos 132lim lim sin cos x x x x x x x x x x x x x x x x x x x x x ππππππππππππ→→→→→-→---==--==--== 故可去间断点为3个，即0,1±（2）当0x →时，()sin f x x ax =-与2()ln(1)g x x bx =-是等价无穷小，则（）()A .1a =，16b =-()B . 1a =，16b = ()C .1a =-，16b =- ()D .1a =-，16b =【答案】 A【解析】2()sin ,()(1)f x x ax g x x ln bx =-=-为等价无穷小，则222200000()sin sin 1cos sin lim lim lim lim lim ()ln(1)()36x x x x x f x x ax x ax a ax a ax g x x bx x bx bx bx→→→→→---==-⋅---洛洛230sin lim 166x a ax a b b axa→==-=-⋅ 36a b ∴=- 故排除,B C 。

另外201cos lim3x a axbx→--存在，蕴含了1cos 0a ax -→()0x →故 1.a =排D 。

2009考研数学三【解析版】【无水印】

2009年全国硕士研究生入学统一考试数学三试题解析一、选择题：1～8小题，每小题4分，共32分，下列每小题给出的四个选项中，只有一个选项是符合题目要求的，请把所选项前的字母填在答题纸指定位置上.（1）函数的可去间断点的个数为(A)1. (B)2.(C)3.(D)无穷多个.【答案】C. 【解析】则当取任何整数时，均无意义故的间断点有无穷多个，但可去间断点为极限存在的点，故应是的解故可去间断点为3个，即（2）当时，与是等价无穷小，则(A)，. （B ），. (C)，.（D ），. 【答案】A.【解析】为等价无穷小，则3()sin x x f x xπ-=()3sin x x f x xπ-=x ()f x ()f x 30x x -=1,2,30,1x =±320032113211131lim lim sin cos 132lim lim sin cos 132lim lim sin cos x x x x x x x x x x x x x x x x x x x x x ππππππππππππ→→→→→-→---==--==--==0,1±0x →()sin f x x ax =-2()ln(1)g x x bx =-1a =16b =-1a =16b =1a =-16b =-1a =-16b =2()sin ,()(1)f x x ax g x x ln bx =-=-故排除(B)、(C). 另外存在，蕴含了故排除(D).所以本题选(A).（3）使不等式成立的的范围是 (A). (B). (C).(D).【答案】A.【解析】原问题可转化为求成立时的取值范围，由，时，知当时，.故应选(A).（4）设函数在区间上的图形为则函数的图形为222200000()sin sin 1cos sin lim lim lim lim lim ()ln(1)()36x x x x x f x x ax x ax a ax a ax g x x bx x bx bx bx→→→→→---==-⋅---洛洛230sin lim 166x a ax a b b axa→==-=-⋅36a b ∴=-201cos lim3x a axbx →--1cos 0a ax -→()0x → 1.a =1sin ln xtdt x t>⎰x (0,1)(1,)2π(,)2ππ(,)π+∞111sin sin 1()ln xx x tt f x dt x dt dt t t t =-=-⎰⎰⎰11sin 11sin 0x x t t dt dt t t--==>⎰⎰x 1sin 0tt ->()0,1t ∈()0,1x ∈()0f x >()y f x =[]1,3-()()0xF x f t dt =⎰(A)(B)(C)(D)【答案】D.【解析】此题为定积分的应用知识考核，由的图形可见，其图像与轴及轴、所围的图形的代数面积为所求函数，从而可得出几个方面的特征：①时，，且单调递减. ②时，单调递增. ③时，为常函数.④时，为线性函数，单调递增. ⑤由于F(x)为连续函数结合这些特点，可见正确选项为(D).（5）设均为2阶矩阵，分别为的伴随矩阵，若，则分块矩阵的伴随矩阵为 ()y f x =x y0x x =()F x []0,1x ∈()0F x ≤[]1,2x ∈()F x []2,3x ∈()F x []1,0x ∈-()0F x ≤,A B *,A B *,A B ||2,||3A B ==O A B O ⎛⎫⎪⎝⎭(A). (B). (C).(D). 【答案】B.【解析】根据，若分块矩阵的行列式，即分块矩阵可逆故答案为(B).（6）设均为3阶矩阵，为的转置矩阵，且，若，则为(A).(B).(C).(D).【答案】A.**32O B A O ⎛⎫⎪⎝⎭**23O B AO ⎛⎫⎪⎝⎭**32O A BO ⎛⎫⎪⎝⎭**23O A BO ⎛⎫⎪⎝⎭CC C E *=111,C C C C C C*--*==OA BO ⎛⎫⎪⎝⎭221236O A A B B O⨯=-=⨯=（）1111661O B BO A O A O A O B B O B O B O AO A O A **---*⎛⎫ ⎪⎛⎫⎛⎫⎛⎫ ⎪=== ⎪ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎪⎝⎭1236132O BOB AO A O ****⎛⎫ ⎪⎛⎫== ⎪ ⎪ ⎪⎝⎭⎪⎝⎭,A P T P P 100010002TP AP ⎛⎫ ⎪= ⎪ ⎪⎝⎭1231223(,,),(,,)P Q ααααααα==+T Q AQ 210110002⎛⎫⎪ ⎪ ⎪⎝⎭110120002⎛⎫⎪⎪ ⎪⎝⎭200010002⎛⎫ ⎪ ⎪ ⎪⎝⎭100020002⎛⎫ ⎪ ⎪ ⎪⎝⎭【解析】，即：（7）设事件与事件B 互不相容，则(A). (B).(C).(D).【答案】D.【解析】因为互不相容，所以 (A)，因为不一定等于1，所以(A)不正确.(B)当不为0时，(B)不成立，故排除. (C)只有当互为对立事件的时候才成立，故排除. (D)，故(D)正确.（8）设随机变量与相互独立，且服从标准正态分布，的概率分布为，记为随机变量的分布函数，则函数的间断点个数为（） (A) 0.(B)1. (C)2.(D)3.【答案】 B.【解析】122312312312100(,,)(,,)110(,,)(1)001Q E αααααααααα⎡⎤⎢⎥=+==⎢⎥⎢⎥⎣⎦12121212122112(1)[(1)][(1)](1)[](1)100(1)010(1)002110100100210010010110110001002001002T T TT Q PE Q AQ PE A PE E P AP E E E ===⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦A ()0P AB =()()()P AB P A P B =()1()P A P B =-()1P A B ⋃=,A B ()0P AB =()()1()P AB P AB P AB ==-()P AB (),()P A P B ,A B ()()1()1P AB P AB P AB ==-=X Y X (0,1)N Y 1{0}{1}2P Y P Y ====()z F Z Z XY =()z F Z ()()(0)(0)(1)(1)Z F z P XY z P XY z Y P Y P XY z Y P Y =≤=≤==+≤==独立（1）若，则（2）当，则为间断点，故选(B).二、填空题：9~14小题，每小题4分，共24分，请将答案写在答题纸指定位置上. （9） .【答案】.【解析】. （10）设，则 . 【答案】. 【解析】由，故代入得，.（11）幂级数的收敛半径为 . 1[(0)(1)]21[(00)(1)]2P XY z Y P XY z Y P X z Y P X z Y =≤=+≤==⋅≤=+≤=,X Y 1()[(0)()]2Z F z P x z P x z ∴=⋅≤+≤0z <1()()2Z F z z =Φ0z ≥1()(1())2Z F z z =+Φ0z ∴=cos 0x x →=32e cos cos 10xx x x -→→=02(1cos )lim13x e x x→-=20212lim 13x e x x →⋅=32e =()y x z x e =+(1,0)zx ∂=∂2ln 21+()xy z x e=+()(),01xz x x =+()''ln(1)ln(1)1ln(1)1x x x x x dz x x e e x dx x ++⎡⎤⎡⎤⎡⎤=+==++⎣⎦⎢⎥⎣⎦+⎣⎦1x =()ln 21,01ln 22ln 212ze x∂⎛⎫=+=+ ⎪∂⎝⎭21(1)n n nn e x n ∞=--∑【答案】. 【解析】由题意知，所以，该幂级数的收敛半径为（12）设某产品的需求函数为,其对应价格的弹性，则当需求量为10000件时，价格增加1元会使产品收益增加元. 【答案】8000.【解析】所求即为因为，所以所以将代入有.（13）设,，若矩阵相似于，则 .【答案】2.【解析】相似于，根据相似矩阵有相同的特征值，得到的特征值为3，0，0.而为矩阵的对角元素之和，，.1e()210nn n e a n --=>()()()()111122122111()11111n n n n n nnn nn e e ea n n e n a n e n e e +++++⎡⎤⎛⎫--⎢⎥ ⎪⎝⎭--⎢⎥⎣⎦=⋅=⋅→→∞⎡⎤+--+⎛⎫--⎢⎥⎪⎝⎭⎢⎥⎣⎦1e()Q Q P =P 0.2p ξ=()QP Q P Q ''=+0.2p Q PQξ'==-0.2Q P Q '=-()0.20.8QP Q Q Q '=-+=10000Q =()8000QP '=(1,1,1)T α=(1,0,)T k β=T αβ300000000⎛⎫ ⎪⎪ ⎪⎝⎭k =T αβ300000000⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦T αβT αβT αβ1300k ∴+=++2k ∴=(14)设，,…,为来自二项分布总体的简单随机样本，和分别为样本均值和样本方差，记统计量，则 .【答案】【解析】由.三、解答题：15～23小题，共94分.请将解答写在答题纸指定的位置上.解答应写出文字说明、证明过程或演算步骤. （15）（本题满分9分）求二元函数的极值.【解析】，，故. . 则，，.而二元函数存在极小值.（16）（本题满分10 分）计算不定积分 .得而1X 2X n X (,)B n p X 2S 2T X S =-ET =2np 222()(1)ET E X S EX ES np np p np =-=-=--=()22(,)2ln f x y x y y y =++2(,)2(2)0x f x y x y '=+=2(,)2ln 10y f x y x y y '=++=10,x y e= =2212(2),2,4xxyy xyf y f x f xy y''''''=+ =+ =12(0,)12(2)xx ef e''=+1(0,)0xyef ''=1(0,)yyef e ''=0xxf ''>2()0xy xx yy f f f ''''''-<∴11(0,)f e e=-ln(1dx +⎰(0)x >t =22212,1(1)tdtx dx t t -= =--2221ln(1ln(1)1ln(1)11111dx t d t t dt t t t =+-+=---+⎰⎰⎰所以（17）（本题满分10 分）计算二重积分，其中.【解析】由得，.22111112()11411(1)111ln(1)ln(1)2441dt dtt t t t t t t C t =---+-++--++++⎰⎰2ln(1)111ln(1ln 1412(1)1ln(1.2t t dx C t t t x C ++=+-+--+=++⎰()Dx y dxdy -⎰⎰22{(,)(1)(1)2,}D x y x y y x =-+-≤≥22(1)(1)2x y -+-≤2(sin cos )r θθ≤+32(sin cos )4()(cos sin )04Dx y dxdy d r r rdr πθθθθθπ+∴-=-⎰⎰⎰⎰332(sin cos )14(cos sin )034r d πθθθθθπ⎡+⎤=-⋅⎢⎥⎣⎦⎰2384(cos sin )(sin cos )(sin cos )34d πθθθθθθθπ=-⋅+⋅+⎰3384(cos sin )(sin cos )34d πθθθθθπ=-⋅+⎰3344438814(sin cos )(sin cos )(sin cos )3344d πππθθθθθθπ=++=⨯+⎰83=-（18）（本题满分11 分）（Ⅰ）证明拉格朗日中值定理，若函数在上连续，在上可导，则，得证.（Ⅱ）证明：若函数在处连续，在内可导，且，则存在，且. 【解析】（Ⅰ）作辅助函数，易验证满足：；在闭区间上连续，在开区间内可导，且. 根据罗尔定理，可得在内至少有一点，使，即（Ⅱ）任取，则函数满足：在闭区间上连续，开区间内可导，从而有拉格朗日中值定理可得：存在，使得……又由于，对上式（*式）两边取时的极限可得：故存在，且.（19）（本题满分10 分）设曲线，其中是可导函数，且.已知曲线与直线及所围成的曲边梯形绕轴旋转一周所得的立体体积值是该曲边梯形面积值的倍，求该曲线的方程.【解析】旋转体的体积为()f x [],a b (),a b (),a b ξ∈()'()()()f b f a f b a ξ-=-()f x 0x =()0,,(0)σσ>'0lim ()x f x A +→='(0)f +'(0)f A +=()()()()()()f b f a x f x f a x a b aϕ-=----()x ϕ()()a b ϕϕ=()x ϕ[],a b (),a b ''()()()()f b f a x f x b aϕ-=--(),a b ξ'()0ϕξ='()f ξ'()()0,()()()()f b f a f b f a f b a b aξ--=∴-=--0(0,)x δ∈()f x []00,x ()00,x ()()000,0,x x ξδ∈⊂()0'00()(0)x f x f f x ξ-=-()*()'0lim x f x A +→=00x +→()()000000'''0000()00lim lim ()lim ()0x x x x x f x f f f f A x ξξξ++++→→→-====-'(0)f +'(0)f A +=()y f x =()f x ()0f x >()y f x =0,1y x ==(1)x t t =>x t π22()()11x x t tV f dx f dx ππ==⎰⎰曲边梯形的面积为：，则由题可知两边对t 求导可得继续求导可得，化简可得，解之得在式中令，则，代入得.所以该曲线方程为：.（20）（本题满分11 分）设,. （Ⅰ）求满足，的所有向量，. （Ⅱ）对（Ⅰ）中的任意向量,，证明,,线性无关. 【解析】（Ⅰ）解方程故有一个自由变量，令，由解得，求特解，令，得()1x ts f dx =⎰22()()()()1111x x x x t t t tV ts f dx t f dx f dx t f dx πππ=⇒=⇒=⎰⎰⎰⎰22()()()()()()11t x t t t x t tf f dx tf f tf f dx =+⇒-=⎰⎰''2()()()()()f t f t f t tf t f t --='1(2())()2()12dt f t t f t f t t dy y-=⇒+=1223t c y y -=⋅+1t =2(1)(1)0,()0,(1)1f f f t f -=>∴=1223t cyy -=+11,2)33c t y =∴=230y x =111A=111042--⎛⎫ ⎪- ⎪ ⎪--⎝⎭1112ξ-⎛⎫ ⎪= ⎪ ⎪-⎝⎭21A ξξ=231A ξξ=2ξ3ξ2ξ3ξ1ξ2ξ3ξ21A ξξ=()1111111111111,111100000211042202110000A ξ---------⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪=-→→ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪---⎝⎭⎝⎭⎝⎭()2r A =32x =0Ax =211,1x x =-=120x x ==31x =故，其中为任意常数解方程故有两个自由变量，令，由得令，由得求得特解故，其中为任意常数（Ⅱ）证明：由于故线性无关.（21）（本题满分11 分）21101021k ξ⎛⎫⎛⎫ ⎪ ⎪=-+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭1k 231A ξξ=2220220440A ⎛⎫ ⎪=-- ⎪ ⎪⎝⎭()21111022012,2201000044020000A ξ-⎛⎫ ⎪-⎛⎫⎪ ⎪=--→ ⎪ ⎪ ⎪ ⎪-⎝⎭ ⎪⎝⎭231,0x x =-=20A x =11x =230,1x x ==-20A x =10x =21200η⎛⎫- ⎪ ⎪= ⎪ ⎪ ⎪⎝⎭3231102100010k k ξ⎛⎫-⎪⎛⎫⎛⎫ ⎪⎪ ⎪=-++ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭ ⎪⎝⎭23,k k 12121212122111121112(21)()2()(21)22221k k k k k k k k k k k k k -+--=+++-+-+-+102=≠123,,ξξξ设二次型. （Ⅰ）求二次型的矩阵的所有特征值.（Ⅱ）若二次型的规范形为，求的值.【解析】（Ⅰ）.（Ⅱ）若规范形为，说明有两个特征值为正，一个为0.则1) 若，则，，不符题意 2) 若，即，则，，符合3) 若，即，则，，不符题意综上所述，故（22）（本题满分11 分）设二维随机变量的概率密度为（Ⅰ）求条件概率密度（Ⅱ）求条件概率【解析】2221231231323(,,)(1)22f x x x ax ax a x x x x x =++-+-f f 2211y y +a 0101111a A aa ⎛⎫ ⎪=- ⎪ ⎪--⎝⎭110||01()1111111aa aE A aa a a λλλλλλλλ-----=-=---+---+222()[()(1)1][0()]()[()(1)2]()[22]19(){[(12)]}24()(2)(1)a a a a a a a a a a a a a a a a a λλλλλλλλλλλλλλλλ=---+--+-=---+-=--++--=-+--=--+--123,2,1a a a λλλ∴==-=+2212y y +10a λ==220λ=-<31λ=20λ=2a =120λ=>330λ=>30λ=1a =-110λ=-<230λ=-<2a =(,)X Y 0(,)0x e y x f x y -⎧<<=⎨⎩其他()Y X f y x 11P X Y =⎡≤≤⎤⎣⎦（Ⅰ）由得其边缘密度函数故即（Ⅱ）而.（23）（本题满分11分）袋中有一个红球，两个黑球，三个白球，现在放回的从袋中取两次，每次取一个，求以、、分别表示两次取球所取得的红、黑与白球的个数. ①求.②求二维随机变量的概率分布.【解析】（Ⅰ）在没有取白球的情况下取了一次红球，利用压缩样本空间则相当于只有1个红球，2个黑球放回摸两次，其中摸了一个红球.（Ⅱ）X ，Y 取值范围为0，1，2，故0(,)0x y xe f x y -<<⎧= ⎨⎩其它0()0xx xx f x e dy xe x --== >⎰|(,)1(|)0()y x x f x y f y x y x f x x== <<|1(|)0y x y xf y x x ⎧ 0<<⎪=⎨⎪ ⎩其它[1,1][1|1][1]P X Y P X Y P Y ≤≤≤≤=≤111011[1,1](,)12xx x x y P X Y f x y dxdy dx e dy xe dx e ---≤≤≤≤====-⎰⎰⎰⎰⎰()|,0x x y Y yf y e dx e e y y+∞---+∞==-= >⎰11101[1]|110y y P Y e dy e e e ----∴ ≤==-=-+=-⎰11122[1|1]11e e P X Y e e ----∴ ≤≤==--X Y Z 10P X Z ⎡==⎤⎣⎦(,)X Y 12113324(10)9C P X Z C C ⨯∴====⋅()()()()()()()()()1111332311116666111223111166661122116611221166110,0,1,0461112,0,0,136311,1,2,10910,291,20,2,20C C C C P X Y P X Y C C C C C C C P X Y P X Y C C C C C C P X Y P X Y C C C C P X Y C C P X Y P X Y ⋅⋅========⋅⋅⋅⋅========⋅⋅⋅=======⋅⋅====⋅======。

【免积分】考研数三完整版(历年真题+答案详解)(2003-2010)真题之2009

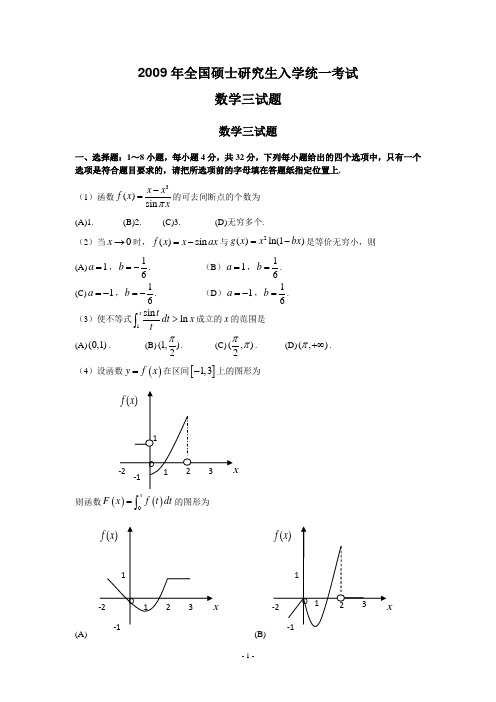
2009年全国硕士研究生入学统一考试数学三试题数学三试题一、选择题：1～8小题，每小题4分，共32分，下列每小题给出的四个选项中，只有一个选项是符合题目要求的，请把所选项前的字母填在答题纸指定位置上. （1）函数3()sin x xf x xπ-=的可去间断点的个数为(A)1.(B)2. (C)3.(D)无穷多个.（2）当0x →时，()sin f x x ax =-与2()ln(1)g x x bx =-是等价无穷小，则 (A)1a =，16b =-. （B ）1a =，16b =. (C)1a =-，16b =-. （D ）1a =-，16b =.（3）使不等式1sin ln x t dt x t>⎰成立的x 的范围是(A)(0,1).(B)(1,)2π. (C)(,)2ππ. (D)(,)π+∞.（4）设函数()y f x =在区间[]1,3-上的图形为则函数()()0x F x f t dt =⎰的图形为(A)(B)(C)(D)（5）设,A B 均为2阶矩阵，*,A B *分别为,A B 的伴随矩阵，若||2,||3A B ==，则分块矩阵O A BO ⎛⎫⎪⎝⎭的伴随矩阵为 (A)**32O B A O ⎛⎫⎪⎝⎭. (B)**23OB AO ⎛⎫⎪⎝⎭.(C)**32O A B O ⎛⎫⎪⎝⎭.(D)**23O A BO ⎛⎫⎪⎝⎭. （6）设,A P 均为3阶矩阵，TP 为P 的转置矩阵，且100010002T P A P ⎛⎫ ⎪= ⎪ ⎪⎝⎭，若1231223(,,),(,,)P Q ααααααα==+，则TQ AQ 为(A)210110002⎛⎫ ⎪ ⎪ ⎪⎝⎭. (B)110120002⎛⎫⎪⎪ ⎪⎝⎭.(C)200010002⎛⎫ ⎪ ⎪ ⎪⎝⎭.(D)100020002⎛⎫ ⎪ ⎪ ⎪⎝⎭. （7）设事件A 与事件B 互不相容，则 (A)()0P A B =.(B)()()()P AB P A P B =. (C)()1()P A P B =-.(D)()1P A B ⋃=.（8）设随机变量X 与Y 相互独立，且X 服从标准正态分布(0,1)N ，Y 的概率分布为1{0}{1}2P Y P Y ====，记()z F Z 为随机变量Z XY =的分布函数，则函数()z F Z 的间断点个数为 (A) 0. (B)1. (C)2 . (D)3.二、填空题：9~14小题，每小题4分，共24分，请将答案写在答题纸指定位置上. （9）cos 0limx x →= .（10）设()y x z x e =+，则(1,0)z x∂=∂ .（11）幂级数21(1)n nnn e x n∞=--∑的收敛半径为 .（12）设某产品的需求函数为()Q Q P =,其对应价格P 的弹性0.2p ξ=，则当需求量为10000件时，价格增加1元会使产品收益增加元.（13）设(1,1,1)T α=,(1,0,)T k β=，若矩阵T αβ相似于300000000⎛⎫⎪⎪ ⎪⎝⎭，则k = . (14)设1X ，2X ,…,n X 为来自二项分布总体(,)B n p 的简单随机样本，X 和2S 分别为样本均值和样本方差，记统计量2T X S =-，则ET = .三、解答题：15～23小题，共94分.请将解答写在答题纸指定的位置上.解答应写出文字说明、证明过程或演算步骤. （15）（本题满分9分）求二元函数()22(,)2ln f x y xy y y =++的极值.（16）（本题满分10 分）计算不定积分ln(1dx +⎰ (0)x >.（17）（本题满分10 分）计算二重积分()Dx y dxdy -⎰⎰，其中22{(,)(1)(1)2,}D x y x y y x =-+-≤≥.（18）（本题满分11 分）（Ⅰ）证明拉格朗日中值定理，若函数()f x 在[],a b 上连续，在(),a b 上可导，则(),a b ξ∈，得证()'()()()f b f a f b a ξ-=-.（Ⅱ）证明：若函数()f x 在0x =处连续，在()0,,(0)σσ>内可导，且'lim ()x f x A +→=，则'(0)f +存在，且'(0)fA +=.（19）（本题满分10 分）设曲线()y f x =，其中()f x 是可导函数，且()0f x >.已知曲线()y f x =与直线0,1y x ==及(1)x t t =>所围成的曲边梯形绕x 轴旋转一周所得的立体体积值是该曲边梯形面积值的t π倍，求该曲线的方程. （20）（本题满分11 分）设111A =111042--⎛⎫ ⎪- ⎪ ⎪--⎝⎭,1112ξ-⎛⎫ ⎪= ⎪ ⎪-⎝⎭. （Ⅰ）求满足21A ξξ=，231A ξξ=的所有向量2ξ，3ξ. （Ⅱ）对（Ⅰ）中的任意向量2ξ,3ξ，证明1ξ,2ξ,3ξ线性无关. （21）（本题满分11 分）设二次型2221231231323(,,)(1)22f x x x ax ax a x x x x x =++-+-. （Ⅰ）求二次型f 的矩阵的所有特征值.（Ⅱ）若二次型f 的规范形为2211y y +，求a 的值. （22）（本题满分11 分）设二维随机变量(,)X Y 的概率密度为0(,)0xe y xf x y -⎧<<=⎨⎩其他（Ⅰ）求条件概率密度()YXf y x ；（Ⅱ）求条件概率11P X Y =⎡≤≤⎤⎣⎦.（23）（本题满分11分）袋中有一个红球，两个黑球，三个白球，现在放回的从袋中取两次，每次取一个，求以X 、Y 、Z 分别表示两次取球所取得的红、黑与白球的个数. （Ⅰ）求10P X Z ⎡==⎤⎣⎦；（Ⅱ）求二维随机变量(,)X Y 的概率分布.2009年全国硕士研究生入学统一考试数学三试题解析一、选择题：1～8小题，每小题4分，共32分，下列每小题给出的四个选项中，只有一个选项是符合题目要求的，请把所选项前的字母填在答题纸指定位置上.（1）函数3()sin x xf x xπ-=的可去间断点的个数为(A)1. (B)2. (C)3.(D)无穷多个.【答案】C. 【解析】 ()3s i n x xf x xπ-=则当x 取任何整数时，()f x 均无意义故()f x 的间断点有无穷多个，但可去间断点为极限存在的点，故应是30x x -=的解1,2,30,1x =±3232113211131lim lim sin cos 132limlimsin cos 132limlimsin cos x x x x x x x x x xxx xxx xx xxxx ππππππππππππ→→→→→-→---==--==--==故可去间断点为3个，即0,1±（2）当0x →时，()sin f x x ax =-与2()ln(1)g x x bx =-是等价无穷小，则 (A)1a =，16b =-. （B ）1a =，16b =. (C)1a =-，16b =-. （D ）1a =-，16b =.【答案】A.【解析】2()sin ,()(1)f x x ax g x x ln bx =-=-为等价无穷小，则2222()sin sin 1cos sin limlimlimlimlim()ln(1)()36x x x x x f x x ax x ax a ax a ax g x x bx x bx bxbx→→→→→---==-⋅---洛洛23sin lim166x a ax ab baxa →==-=-⋅ 36a b ∴=- 故排除(B)、(C).另外21cos lim3x a ax bx→--存在，蕴含了1cos 0a ax -→()0x →故 1.a =排(D).所以本题选(A).（3）使不等式1sin ln xt dt x t>⎰成立的x 的范围是(A)(0,1).(B)(1,)2π. (C)(,)2ππ. (D)(,)π+∞.【答案】A.【解析】原问题可转化为求111sin sin 1()ln x x x t t f x dt x dt dt t t t =-=-⎰⎰⎰11sin 11sin 0x x t tdt dt t t--==>⎰⎰成立时x 的取值范围，由1sin 0tt->，()0,1t ∈时，知当()0,1x ∈时，()0f x >.故应选(A).（4）设函数()y f x =在区间[]1,3-上的图形为则函数()()0x F x f t dt =⎰的图形为(A)(B)(C)(D)【解析】此题为定积分的应用知识考核，由()y f x =的图形可见，其图像与x 轴及y 轴、0x x =所围的图形的代数面积为所求函数()F x ，从而可得出几个方面的特征：①[]0,1x ∈时，()0F x ≤，且单调递减. ②[]1,2x ∈时，()F x 单调递增. ③[]2,3x ∈时，()F x 为常函数.④[]1,0x ∈-时，()0F x ≤为线性函数，单调递增. ⑤由于F(x)为连续函数结合这些特点，可见正确选项为(D).（5）设,A B 均为2阶矩阵，*,A B *分别为,A B 的伴随矩阵，若||2,||3A B ==，则分块矩阵O A BO ⎛⎫⎪⎝⎭的伴随矩阵为 (A)**32O B A O ⎛⎫⎪⎝⎭. (B)**23OB AO ⎛⎫⎪⎝⎭.(C)**32O A B O ⎛⎫⎪⎝⎭.(D)**23O A BO ⎛⎫⎪⎝⎭. 【答案】B.【解析】根据CC C E *=，若111,C C C CC C*--*==分块矩阵OA B O ⎛⎫⎪⎝⎭的行列式221236O A A B BO⨯=-=⨯=（），即分块矩阵可逆1111661O B BOA OA OA OB B O BO B O AO A O A **---*⎛⎫ ⎪⎛⎫⎛⎫⎛⎫⎪=== ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎪⎝⎭1236132O B O B A O A O ****⎛⎫ ⎪⎛⎫==⎪ ⎪ ⎪⎝⎭⎪⎝⎭（6）设,A P 均为3阶矩阵，TP 为P 的转置矩阵，且100010002T P A P ⎛⎫ ⎪= ⎪ ⎪⎝⎭，若1231223(,,),(,,)P Q ααααααα==+，则T Q AQ 为(A)210110002⎛⎫ ⎪ ⎪ ⎪⎝⎭. (B)110120002⎛⎫⎪⎪ ⎪⎝⎭.(C)200010002⎛⎫ ⎪ ⎪ ⎪⎝⎭.(D)100020002⎛⎫ ⎪ ⎪ ⎪⎝⎭. 【答案】A.【解析】122312312312100(,,)(,,)110(,,)(1)01Q E αααααααααα⎡⎤⎢⎥=+==⎢⎥⎢⎥⎣⎦，即： 121212122112(1)[(1)][(1)](1)[](1)100(1)010(1)00211010010021001001011011001020102TTTTQ P E Q A Q P E A P E E P A P E E E ===⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦（7）设事件A 与事件B 互不相容，则 (A)()0P A B =.(B)()()()P AB P A P B =. (C)()1()P A P B =-.(D)()1P A B ⋃=.【答案】D.【解析】因为,A B 互不相容，所以()0P AB =(A)()()1()P A B P A B P A B ==- ，因为()P A B 不一定等于1，所以(A)不正确. (B)当(),()P A P B 不为0时，(B)不成立，故排除. (C)只有当,A B 互为对立事件的时候才成立，故排除.(D)()()1()1P A B P AB P AB ==-= ，故(D)正确.（8）设随机变量X 与Y 相互独立，且X 服从标准正态分布(0,1)N ，Y 的概率分布为1{0}{1}2P Y P Y ====，记()z F Z 为随机变量Z XY =的分布函数，则函数()z F Z 的间断点个数为（） (A) 0. (B)1. (C)2 .(D)3.【答案】 B.【解析】()()(0)(0)(1)(1)Z F z P XY z P XY z Y P Y P XY z Y P Y =≤=≤==+≤== 1[(0)(1)]21[(00)(1)]2P XY z Y P XY z Y P X z Y P X z Y =≤=+≤==⋅≤=+≤=,X Y 独立 1()[(0)()]2Z F z P x z P x z ∴=⋅≤+≤（1）若0z <，则1()()2Z F z z =Φ （2）当0z ≥，则1()(1())2Z F z z =+Φ0z ∴=为间断点，故选(B).二、填空题：9~14小题，每小题4分，共24分，请将答案写在答题纸指定位置上. （9）cos 0limx x →= .【答案】32e .【解析】cos cos 100limlimx x x x -→→=02(1cos )lim13x e x x→-=2212lim13x e xx→⋅=32e =.（10）设()y x z x e =+，则(1,0)z x∂=∂ .【答案】2ln 21+. 【解析】由()xyz x e=+，故()(),01xz x x =+()''ln(1)ln(1)1ln(1)1x x x x x dzx x e e x dx x ++⎡⎤⎡⎤⎡⎤=+==++⎣⎦⎢⎥⎣⎦+⎣⎦代入1x =得，()ln 21,01ln 22ln 212z ex∂⎛⎫=+=+ ⎪∂⎝⎭.（11）幂级数21(1)n nnn e x n∞=--∑的收敛半径为 .【答案】1e.【解析】由题意知，()210nnn e a n--=>()()()()111122122111()11111n n n n n nnnnne e ea nne n a n e n e e +++++⎡⎤⎛⎫--⎢⎥⎪⎝⎭--⎢⎥⎣⎦=⋅=⋅→→∞⎡⎤+--+⎛⎫--⎢⎥⎪⎝⎭⎢⎥⎣⎦所以，该幂级数的收敛半径为1e（12）设某产品的需求函数为()Q Q P =,其对应价格P 的弹性0.2p ξ=，则当需求量为10000件时，价格增加1元会使产品收益增加元.【答案】8000.【解析】所求即为()QP Q P Q ''=+ 因为0.2p Q P Qξ'==-，所以0.2Q P Q '=-所以()0.20.8QP Q Q Q '=-+= 将10000Q =代入有()8000QP '=.（13）设(1,1,1)T α=,(1,0,)T k β=，若矩阵Tαβ相似于300000000⎛⎫ ⎪⎪ ⎪⎝⎭，则k = . 【答案】2.【解析】Tαβ相似于30000000⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦，根据相似矩阵有相同的特征值，得到Tαβ的特征值为3，0，0.而T αβ为矩阵T αβ的对角元素之和，1300k ∴+=++，2k ∴=.(14)设1X ，2X ,…,n X 为来自二项分布总体(,)B n p 的简单随机样本，X 和2S 分别为样本均值和样本方差，记统计量2T X S =-，则ET = . 【答案】2np【解析】由222()(1)ET E X S E X ES np np p np =-=-=--=.三、解答题：15～23小题，共94分.请将解答写在答题纸指定的位置上.解答应写出文字说明、证明过程或演算步骤. （15）（本题满分9分）求二元函数()22(,)2ln f x y xy y y =++的极值.【解析】2(,)2(2)0x f x y x y '=+=，2(,)2ln 10y f x y x y y '=++=，故10,x y e= =.2212(2),2,4xxyy xyf y f x f xy y''''''=+ =+ =. 则12(0,)12(2)xxef e''=+，1(0,)0xyef ''=，1(0,)yyef e ''=.0xxf ''> 而2()0xy xx yy f f f ''''''-< ∴二元函数存在极小值11(0,)f e e=-.（16）（本题满分10 分）计算不定积分ln(1dx +⎰ (0)x >.t =得22212,1(1)tdt x dx t t -==--2221ln(1ln(1)1ln(1)11111dx t dt t dtt tt +=+-+=---+⎰⎰⎰而22111112()11411(1)111ln(1)ln(1)2441dt dttt t t t t t Ct =---+-++--++++⎰⎰所以2ln(1)111ln(1ln1412(1)1ln(1.2t t dx Ct t t x C +++=+-+--+=++-⎰（17）（本题满分10 分）计算二重积分()Dx y dxdy -⎰⎰，其中22{(,)(1)(1)2,}D x y x y y x =-+-≤≥.【解析】由22(1)(1)2x y -+-≤得2(sin cos )r θθ≤+，32(sin cos )4()(cos sin )04Dx y dxdy d r r rdr πθθθθθπ+∴-=-⎰⎰⎰⎰332(sin cos )14(cos sin )034r d πθθθθθπ⎡+⎤=-⋅⎢⎥⎣⎦⎰2384(cos sin )(sin cos )(sin cos )34d πθθθθθθθπ=-⋅+⋅+⎰3384(cos sin )(sin cos )34d πθθθθθπ=-⋅+⎰3344438814(sin cos )(sin cos )(sin cos )3344d πππθθθθθθπ=++=⨯+⎰83=-.（18）（本题满分11 分）（Ⅰ）证明拉格朗日中值定理，若函数()f x 在[],a b 上连续，在(),a b 上可导，则(),a b ξ∈，得证()'()()()f b f a f b a ξ-=-.（Ⅱ）证明：若函数()f x 在0x =处连续，在()0,,(0)σσ>内可导，且'lim ()x f x A +→=，则'(0)f +存在，且'(0)fA +=.【解析】（Ⅰ）作辅助函数()()()()()()f b f a x f x f a x a b aϕ-=----，易验证()x ϕ满足：()()a b ϕϕ=；()x ϕ在闭区间[],a b 上连续，在开区间(),a b 内可导，且''()()()()f b f a x f x b aϕ-=--.根据罗尔定理，可得在(),a b 内至少有一点ξ，使'()0ϕξ=，即 '()f ξ'()()0,()()()()f b f a f b f a f b a b aξ--=∴-=--（Ⅱ）任取0(0,)x δ∈，则函数()f x 满足：在闭区间[]00,x 上连续，开区间()00,x 内可导，从而有拉格朗日中值定理可得：存在()()000,0,x x ξδ∈⊂，使得()0'00()(0)x f x f fx ξ-=-……()*又由于()'lim x fx A +→=，对上式（*式）两边取00x +→时的极限可得：()()000000'''0()00lim lim ()lim ()0x x x x x f x f f f f A x ξξξ++++→→→-====-故'(0)f +存在，且'(0)f A +=.（19）（本题满分10 分）设曲线()y f x =，其中()f x 是可导函数，且()0f x >.已知曲线()y f x =与直线0,1y x ==及(1)x t t =>所围成的曲边梯形绕x 轴旋转一周所得的立体体积值是该曲边梯形面积值的t π倍，求该曲线的方程. 【解析】旋转体的体积为22()()11x x ttV f dx f dx ππ==⎰⎰曲边梯形的面积为：()1x ts fdx =⎰，则由题可知22()()()()1111x x x x tt tt V ts f dx t f dx f dx t f dx πππ=⇒=⇒=⎰⎰⎰⎰两边对t 求导可得22()()()()()()11t x t t t x ttf f dx tf f tf fdx =+⇒-=⎰⎰继续求导可得''2()()()()()f t f t f t tf t f t --=，化简可得'1(2())()2()12dt f t t f t f t t dyy-=⇒+=，解之得1223t c yy -=⋅+在式中令1t =，则2(1)(1)0,()0,(1)1f f f t f-=>∴= ，代入1223t c y y -=+得11,2)33c t y =∴=+.所以该曲线方程为：230y x +=.（20）（本题满分11 分）设111A =111042--⎛⎫ ⎪- ⎪ ⎪--⎝⎭,1112ξ-⎛⎫ ⎪= ⎪ ⎪-⎝⎭. （Ⅰ）求满足21A ξξ=，231A ξξ=的所有向量2ξ，3ξ. （Ⅱ）对（Ⅰ）中的任意向量2ξ,3ξ，证明1ξ,2ξ,3ξ线性无关. 【解析】（Ⅰ）解方程21A ξξ=()1111111111111,111100000211042202110000A ξ---------⎛⎫⎛⎫⎛⎫⎪⎪⎪=-→→ ⎪ ⎪ ⎪⎪ ⎪ ⎪---⎝⎭⎝⎭⎝⎭()2r A =故有一个自由变量，令32x =，由0Ax =解得，211,1x x =-= 求特解，令120x x ==，得31x =故21101021k ξ⎛⎫⎛⎫⎪ ⎪=-+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭，其中1k 为任意常数解方程231A ξξ=2220220440A ⎛⎫ ⎪=-- ⎪ ⎪⎝⎭()21111022012,2201000044020000Aξ-⎛⎫ ⎪-⎛⎫⎪ ⎪=--→ ⎪ ⎪⎪ ⎪-⎝⎭ ⎪⎝⎭故有两个自由变量，令231,0x x =-=，由20A x =得11x = 令230,1x x ==-，由20A x =得10x = 求得特解21200η⎛⎫- ⎪⎪= ⎪ ⎪ ⎪⎝⎭故 3231102100010k k ξ⎛⎫-⎪⎛⎫⎛⎫⎪⎪ ⎪=-++ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭⎪⎝⎭，其中23,k k 为任意常数（Ⅱ）证明：由于 12121212122111121112(21)()2()(21)222210k k k k k k k k k k k k k -+--=+++-+-+-+102=≠故123,,ξξξ 线性无关.（21）（本题满分11 分）设二次型2221231231323(,,)(1)22f x x x ax ax a x x x x x =++-+-. （Ⅰ）求二次型f 的矩阵的所有特征值.（Ⅱ）若二次型f 的规范形为2211y y +，求a 的值.【解析】（Ⅰ） 0101111a A a a ⎛⎫⎪=- ⎪ ⎪--⎝⎭110||01()1111111aaaE A aa a a λλλλλλλλ-----=-=---+---+222()[()(1)1][0()]()[()(1)2]()[22]19(){[(12)]}24()(2)(1)a a a a a a a a a a a a a a a a a λλλλλλλλλλλλλλλλ=---+--+-=---+-=--++--=-+--=--+--123,2,1a a a λλλ∴==-=+.（Ⅱ）若规范形为2212y y +，说明有两个特征值为正，一个为0.则1) 若10a λ==，则 220λ=-< ，31λ= ，不符题意 2) 若20λ= ，即2a =，则120λ=>，330λ=>，符合3) 若30λ= ，即1a =-，则110λ=-< ，230λ=-<，不符题意综上所述，故2a =（22）（本题满分11 分）设二维随机变量(,)X Y 的概率密度为0(,)0x e y x f x y -⎧<<=⎨⎩其他（Ⅰ）求条件概率密度()YXf y x（Ⅱ）求条件概率11P X Y =⎡≤≤⎤⎣⎦ 【解析】（Ⅰ）由0(,)0xy x e f x y -<<⎧= ⎨⎩其它得其边缘密度函数()0x x xx f x e dy xe x --== >⎰故 |(,)1(|)0()y x x f x y f y x y x f x x== <<即 |1(|)0y x y xf y x x ⎧ 0<<⎪=⎨⎪ ⎩其它（Ⅱ）[1,1][1|1][1]P X Y P X Y P Y ≤≤≤≤=≤而11111[1,1](,)12xx x x y P X Y f x y dxdy dx e dy xe dx e---≤≤≤≤====-⎰⎰⎰⎰⎰()|,0x xyY yf y e dx eey y+∞---+∞==-= >⎰1111[1]|110yyP Y edy eee----∴ ≤==-=-+=-⎰11122[1|1]11e e P X Y ee ----∴ ≤≤==--.（23）（本题满分11分）袋中有一个红球，两个黑球，三个白球，现在放回的从袋中取两次，每次取一个，求以X 、Y 、Z 分别表示两次取球所取得的红、黑与白球的个数. ①求10P X Z ⎡==⎤⎣⎦.②求二维随机变量(,)X Y 的概率分布.【解析】（Ⅰ）在没有取白球的情况下取了一次红球，利用压缩样本空间则相当于只有1个红球，2个黑球放回摸两次，其中摸了一个红球 12113324(10)9C P X Z C C⨯∴====⋅.（Ⅱ）X ，Y 取值范围为0，1，2，故 ()()()()()()()()()1111332311116666111223111166661122116611221166110,0,1,0461112,0,0,136311,1,2,10910,291,20,2,20C C C C P X Y P X Y C C C C C C C P X Y P X Y C C C C C C P X Y P X Y C CC C P X Y C C P X Y P X Y ⋅⋅========⋅⋅⋅⋅========⋅⋅⋅=======⋅⋅====⋅======。

2009年全国硕士研究生入学统一考试数学三试题

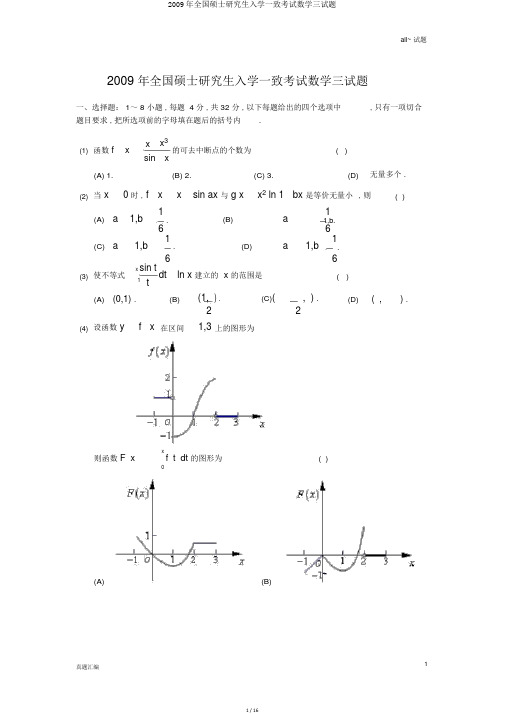
all~ 试题2009 年全国硕士研究生入学一致考试数学三试题一、选择题： 1～ 8 小题 , 每题 4 分 , 共 32 分 , 以下每题给出的四个选项中, 只有一项切合题目要求 , 把所选项前的字母填在题后的括号内.(1) 函数 f x x x3的可去中断点的个数为( ) sin x(A) 1. (B) 2. (C) 3. (D) 无量多个 .(2) 当 x 0 时, f x x sin ax 与 g x x2 ln 1 bx 是等价无量小,则( )(A) a 1,b 1(B) a1 . 1,b.6 6(C) a 1,b 1. (D) a 1,b1 6.x sin t 6(3) 使不等式dt ln x 建立的x的范围是( )1 t(A) (0,1) . (B) (1, ) . (C)( , ) . (D) ( , ) .2 2(4) 设函数 y f x 在区间1,3 上的图形为则函数 F x xf t dt 的图形为( ) 0(A)(B)all~ 试题(C)(D)(5)设 A, B 均为 2 阶矩阵 , A *,B *分别为 A, B 的陪伴矩阵 , 若 A2, B 3 , 则分块矩阵O A( )B 的陪伴矩阵为O(A)O3B *(B)O2B * .2 A *.OO 3A *(C)O3A *(D)O 2A * .2B *.3B *OO1 0 0 (6) 设 A,P 均为 3 阶矩阵 , P T 为 P 的转置矩阵 ,且 P TAP0 1 0 .0 0 2若P (1,2,3),Q (12, 2, 3),则Q TAQ 为( )21 01 1 0(A)1 1 0 . (B)1 2 0 . 0 0 2 0 0 220 01 0 0(C)0 1 0 . (D)0 2 0 .0 20 0 2(7) 设事件 A 与事件 B 互不相容 , 则( )(A) P( AB) 0 .(B)P(AB) P( A)P( B) .(C) P( A) 1 P(B) .(D)P(AU B)1 .(8) 设随机变量X 与Y 互相独立 , 且 X 听从标准正态散布N 0,1 , Y 的概率散布为P Y0 P Y 11z 为随机变量 Z XY 的散布函数 , 则函数 F Z z.记F Z2的中断点个数为( )all~ 试题(A) 0.(B) 1.(C) 2.(D) 3.二、填空题： 9-14 小题 , 每题 4 分,共24 分 . 请将答案写在答题纸指定地点上. (9)lim 3 e e cosx.x 0 1 x 21(10) 设 z ( xe y )x , 则 z_______ .x(1,0)(11) 幂级数e n ( 1)n x n 的收敛半径为______.n 1n 2(12) 设某产品的需求函数为Q Q( p) , 其对价钱 p 的弹性p0.2 , 则当需求量为 10000件时 , 价钱增添 1 元会使产品利润增添_______元 .3 0(13) 设(1,1,1)T ,(1,0, k )T . 若矩阵T相像于 0 00 , 则 k ____ .0 0(14) 设 X 1 , X 2 ,L , X m 为来自二项散布整体 B(n, p) 的简单随机样本 , X 和 S 2 分别为样本均值和样本方差 , 记统计量 TX S 2 , 则 ET_____.三、解答题： 15－ 23 小题 , 共 94 分 . 请将解答写在答题纸指定的地点上 . 解答应写出文字说明、证明过程或演算步骤 . (15)( 本题满分 9 分 )求二元函数 f ( x, y) x 2 2y 2 y ln y 的极值 .(16)( 本题满分 10 分 )计算不定积分ln 11 x dx ( x 0) .x(17)( 本题满分 10 分 )x y dxdy , 此中 Dx, yx 122x .计算二重积分y 12, yD(18)( 本题满分 11 分 )( Ⅰ ) 证明拉格朗日中值定理：若函数f x 在 a, b 上连续 , 在 (a, b) 可导 , 则存在 a,b ,使得 f b f afba .( Ⅱ ) 证明：若函数f x 在 x 0 处连续,在 0,0 内可导 , 且 lim f x A , 则x 0f 0 存在 , 且 f 0A .(19)( 本题满分 10分 )设曲线y f (x) , 此中 f (x) 是可导函数 , 且 f ( x) 0 . 已知曲线 y f ( x) 与直线y 0, x 1及 x t(t 1) 所围成的曲边梯形绕 x 轴旋转一周所得的立体体积值是该曲边梯形面积值的t 倍 , 求该曲线方程 .(20)( 本题满分 11分 )设11 1 1 A1 1 1 , 1 1422(Ⅰ)求知足 A 21, A 231 的全部向量 2, 3；( Ⅱ) 对( Ⅰ) 中的随意愿量 2, 3,证明： 1,2,3 线性没关 .(21)( 本题满分 11 分 )设二次型f x 1, x 2 , x 3 ax 12 ax 22 a 1 x 32 2x 1x 3 2x 2 x 3( Ⅰ ) 求二次型 f 的矩阵的全部特色值；( Ⅱ) 若二次型 f 的规范形为221 y2 , 求 a 的值 .y(22)( 本题满分 11 分)设二维随机变量 ( X ,Y) 的概率密度为e x , 0 y x,f ( x, y)其余 .0,(I) 求条件概率密度 f Y X ( y x) ；(II)求条件概率 P X 1Y 1.(23)( 本题满分 11 分 )袋中有 1 个红球 ,2个黑球与 3 个白球 . 现有放回地从袋中取两次, 每次取一个球 , 以X ,Y, Z 分别表示两次取球所获得的红球、黑球与白球的个数.(Ⅰ)求PX 1Z 0 ；( Ⅱ ) 求二维随机变量X , Y 的概率散布 .2009 年全国硕士研究生入学一致考试数学三试题分析一、选择题： 1～ 8 小题 , 每题 4 分 , 共 32 分 , 以下每题给出的四个选项中, 只有一项切合题目要求 , 把所选项前的字母填在题后的括号内.(1) 【答案】 (C)【分析】因为 f xx x 3 fx 均无心义 , 故 f x 的中断点有无sin , 则当 x 取任何整数时 ,x穷多个 , 但可去中断点为极限存在的点, 故应是 xx 3 0 的解 x 1,2,3 0, 1 .x x 3 lim 1 3x 21limxcos x,xsin x 0lim xx 3lim 1 3x 22 ,x1sin x x 1 cos xlim xx 3 lim 1 3x 2 2 .x1sin x x1cos x故可去中断点为 3 个, 即 x 1,2,3 0, 1 . (2) 【答案】 (A)【分析】 f xx sin ax 与 g xx 2 ln 1bx 是 x 0 时的等价无量小 , 则f ( x)limx sin ax等 lim x sin axlim2ln(1 bx) 2( bx)xg( x) x 0 x x 0 xx sin ax 洛 lim 1 a cosax 洛 lima 2 sin axlim 3 2x 0 bx x 0 3bx x 0 6bxlima 3 sin axa 3 1,6b ax6bx 0即 a 36b , 故清除 B,C.1 a cosax存在,包含了 1a cosax 0 x 0 , 故 a 1, 清除 D.此外 , lim2x 03bx所以本题选 A.(3) 【答案】 (A)【分析】原问题可转变为求xsin t dt ln x 0 建即刻 x 的取值范围 .f ( x)t1xsin txsin tx1f ( x)dt ln xdtdt1 t 1 t 1tx sin t 11 1 sin t0.1dtxdtt t由 t0,1 时, 1 sin t 0 , 知当 x0,1 时 , f ( x) 0 . 故应选 (A).t(4) 【答案】 (D)【分析】本题为定积分的应用知识查核, 由 y f ( x) 的图形能够看出 , 其图像与 x 轴及 y 轴、x x 0 所围的图形的代数面积为所求函数F (x) , 进而可得出下边几个方面的特色：① x1,0 时 , F ( x) 0为线性函数 , 单一递加；②x 0,1 时 , F (x) 0 , 且单一递减；③ x 1,2 时 , F (x) 单一递加；④ x 2,3 时 , F ( x) 为常函数；⑤ F ( x) 为连续函数 .联合这些特色 , 可见正确选项为 (D). (5) 【答案】 (B)【分析】分块矩阵O A 的队列式B OO A（ 2 2A B 2 36 ,B O 1）即分块矩阵可逆 , 且OA O A O 1OB1AB OB O BO 61 OAO1 B O 1BBO 2B66313A.O1 A OOA2A故答案为 (B). (6) 【答案】 (A)1 0 01 0 0 【分析】Q (12,2,3) (1,2,3)1 1 0P 1 1 0 , 0 0 10 0 11 0 0T0 0 1 Q T AQ P 1 1 0A P 1 1 00 0 10 0 11 1 0 1 0 0 1 0 02 1 0 0 1 0 0 1 0 1 1 0 1 1 0 . 0 0 1 0 0 2 0 0 10 0 2(7) 【答案】 (D)【分析】因为 A, B 互不相容 , 所以 P( AB )0 .(A) P( AB) P(A U B) 1 P( A U B) , 因为 P( AU B) 不必定等于 1, 所以 (A) 不正确；(B) 当 P( A), P(B) 不为 0 时, ( B) 不建立 , 故清除；(C) 只有当 A, B 互为对峙事件的时候才建立 , 故清除；(D) P(A U B) P(AB) 1 P( AB) 1 ,故(D)正确.(8) 【答案】 (B) 【分析】F Z (z) P{ XYz}P{ XY z Y 0} P{ Y 0} P{ XY z Y 1} P{ Y 1} 1 P{ XY z Y 0}1P{XYz Y 1}221 P{ X 0 z Y0}1P{Xz Y1},22因为 X ,Y 互相独立 , 所以F Z (z)1P{X 0z}1P{ X z} .212(1) 当 z 0 时 , F Z ( z)(z) ；2(2) 当 z 0时 , F Z ( z) 1 1 ( z) ,2 2所以 , z 0 为中断点 , 应选 (B).二、填空题： 9-14 小题 , 每题 4 分 , 共 24 分 . 请将答案写在答题纸指定地点上.(9) 【答案】3e 2【分析】e e cos xe(1 e cos x 1 )lim1limx21x 0 31 x 2x 0 31e(1 cosx)lim1 x 2x 03(10) 【答案】 1 2ln2e 1 x 23 lim21e .x 0x 2 23【分析】解法 1：因为 zx e yxx,0 x 1 x, 故 z ,zxe xln(1 x)e xln(1x)ln(1 x)x , x 1x y 01xall~ 试题代入 x 1, 得zeln 2ln 21 2ln2 1.x(1,0)2解法 2：因为z( x e y ) xe xln( x e y )(x e y ) xln( x e y )x ,xxxx e y故z (1 e 0) ln(1 e 0)1 2ln2 1.x (1,0)1 e 0(11)【答案】 e 1e nn【分析】由题意知 ,a n 1 0 ,n2an 1e n11 n 1n2lima nlimn2n1 nnn1e1 n 1n 2 e n 1 1limee,2nnn1e n 11e所以 , 该幂级数的收敛半径为e 1 .(12) 【答案】 8000 【分析】所求即为Qp Q p Q .因为pQ p 0.2 , 所以 Q p0.2Q , 所以 Qp0.2Q Q 0.8Q .Q将 Q 10000 代入有 Qp8000 .(13) 【答案】 230 0【分析】T相像于 0 0 0 , 依据相像矩阵有同样的特色值 , 获得T的特色值为0 03,0,0. 而 T为矩阵T的对角元素之和 , 1 k 3 0 0,k 2 .(14) 【答案】 np 2【分析】 ETE( X S 2 ) E X ES 2np np(1 p)np 2 .all~ 试题三、解答题： 15－23 小题, 共 94 分 . 请将解答写在答题纸指定的地点上 . 解答应写出文字说明、证明过程或演算步骤 . (15)( 本题满分 9 分 )【分析】f x (x, y) 2x(2 y 2 ) ,f y (x, y) 2x 2 y ln y 1.f x (x, y) 0,1 令解得独一驻点 (0, ).f y ( x, y) 0,e因为Af xx (0, 1)e1 Bf xy (0, )eCf yy (0, 1)e2(2 y 2)12(21),(0, )e 2e4xy (0, 1 ) 0,e(2 x 21 ) e,y 1)(0,e所以B 2 AC2e(212 )0,且 A 0 .e进而 f (0,1) 是 f ( x, y) 的极小值 , 极小值为 f (0, 1) 1 . ee e(16)( 本题满分 10 分 )【分析】解法 1 设 1 x1 ,t , 则 x2xt 1ln 11 x dx ln 1 t d1xt 2 1ln 1 t 1 1 dtt 2 11t 2 t 1而1 dt1 1 12 dtt 24 t 1 t 1t 1 21 t 11ln t 1 1ln t 1 2 1 C,44t 1所以all~ 试题ln 11 x ln 1 t dx 21xtx ln 1x ln 1x ln 11 ln t 1 1 C4 t 1 2t 11 x1 x 1 11xCxln1 x1x4211xx1 x 1 ln 1 x x1 x xC x 22 1 x1 x 1ln 1 xx1 x 1 x x2 C .x2221解法 21 x1 xx 11 x 1 xln 1dx x ln1xxdxxxx ln1 x 1 x1x 21 dx1 xx ln 11 x 1 x 1 x dxx2 21 xx dx u1 xu 2 12udu 2u 2 1du1 xu分部u u 2 1 ln uu 2 1 Cx 1 xln x1 x C1 xdx x ln 11x1 1 x 1 xln x1 xC即ln 1x2xx2x ln 11 x1 ln x1 x1 x x1 xCx 22x ln 11 x 1ln 1 xx1 x 1 x x2 C.x22 2(17)( 本题满分 10 分 )【分析】解法 1如右图所示 , 地区 D 的极坐标表示为0 r2(sin cos ),3 y4 .4DOxall~ 试题32(sincos )(x y)dxdy4d( r cosr sin )rdrD43 1(cosr 2(sin cos )4 sin ) r 3d43r 0438 sin )(sincos ) 3 d(cos438 3 ) 3d (siny4 (sin coscos)34D 1(2,2)8 1) 43 8 D 2(sin cos 4 .3 443解法 2 将地区 D 分红 D 1, D 2 两部分 ( 如右图 ), 此中1 2 OxD 1 x, y 12 ( x 1)2y 12 ( x 1)2 ,12 x 0 ,D 2x, y x y 12 ( x 1)2 ,0 x 2 .由二重积分的性质知x y dxdyx y dxdyx y dxdy,DD 1D 212 ( x 1)2而x y dxdy1 2dx 12 ( x 1)2( xy) dyD 10 2( x 1) 2 (x 1)2dx122 32 ( x 1)231 22 , 3x y dxdy2 1 2 ( x 1)2(xy)dydxx D 21 2 2 2( x 1) 2 ( x 1) 2dx2 01 23 24 2 (x1)22,2 3所以x y dxdyx y dxdyx y dxdy2 2 8 .DD 1D 233(18)( 本题满分 11 分 )【分析】 ( Ⅰ ) 取 F (x)f ( x)f (b) f (a) a),b (xaall~ 试题由题意知 F ( x) 在 a, b 上连续 , 在 a,b 内可导 , 且F ( a)f ( a) f (b)f (a)a)f (a),b a ( aF (b) f (b)f (b) f ( a) (b a) f (a).b a依据罗尔定理 , 存在a, b ,使得F( )f ( )f (b)f (a)0 , 即baf (b) f (a) f ( )(b a) .( Ⅱ ) 关于随意的 t (0, ) , 函数 f ( x) 在 0,t 上连续 , 在 0,t 内可导 , 由右导数定义及拉格朗日中值定理f 0lim f (t ) f 0f ( )tf ( ) , 此中0,t .t 0limtlimt 0tt因为 limf tA , 且当 t0 时 ,0 , 所以 lim f ( ) A , 故 f (0)存在 ,且t 0tf (0) A .(19)( 本题满分 10 分)【分析】解法 1 由题意知t2( x)dxt tff ( x)dx ,11 两边对 t 求导得f 2 (t ) t f (x)dx tf (t) ,1代入 t 1得 f (1) 1 或 f (1) 0 ( 舍去 ).再求导得2 f (t ) f (t) 2 f (t ) tf (t ) ,记 f (t )y , 则dt1t 1,dy 2 y1 dy1 dy1所以 ,t e2 y(e 2 ydy C ) y 2 (ydy C )y 21( 2y 23C) C2y .3y 3代入 t1, y 1 得 C1 , 进而 t2 y 1 y . 故所求曲线方程为 x 2 y1 .3333 3 yall~ 试题解法 2 同解法 1, 得2 f (t ) f (t) 2 f (t ) tf (t), f (1) 1.整理得 dy2 y.dt2 y t令yu , 则dyu tdu,tdt dt原方程变为t du3u 2u 2 ,dt2u 1分别变量得2u 1 du 1dt ,u(3 2u)t即1 1 4 du dt ,3 u 3 2u t积分得1 ln u(3 2u)2 ln Ct ,312即u 3 (3 2u) 3Ct .代入 t 1,u 1, 得 C1, 所以21t 3.u(3 2u)代入 uy化简得 y(3t 2 y) 2 1, 即 t1 2 y . 故所求曲线方程为 x 2 y1 .t3 y 3 3 3 y(20)( 本题满分 11 分 )【分析】 ( Ⅰ ) 对矩阵 ( AM 1 ) 施以初等行变换1 01 M 11 1 1 M 12211 A M 11 11 M1 0 1M22 042 M2M0 00 01 k2 21 k可求得2, 此中 k 为随意常数 .2 2 k2 2 0又 A 22 2 0 , 对矩阵 ( A 2 M 1 ) 施以初等行变换44 02 2 0 M 1 1 1 0 M12A 2 M 12 2 0 M 1 0 0 0 M 0 ,44 0 M20 0 0 M1 2a可求得3a , 此中 a,b 为随意常数 .b(Ⅱ)解法 1 由(Ⅰ)知11 k 1a2 2 21,2,31 1 k a1 0 ,2 2 22kb所以1, 2,3 线性没关 .解法2由题设可得 A 1 0 . 设存在数 k 1, k 2 , k 3 , 使得k 1 1k2 2k 3 3 0 ,①等式两头左乘A , 得 k 2 A 2 k 3 A 3 0 , 即k 2 1k 3A30 ,②等式两头再左乘A , 得 k 3 A 2 3 0 , 即 k 3 1 0 .因为 1 0 ，于是 k 3 0 , 代入②式 , 得 k 2 1 0 , 故 k 2 0 . 将 k 2 k 3 0 代入①式 , 可得k 1 0,进而1,2, 3线性没关 .(21)( 本题满分 11 分 )【分析】 ( Ⅰ ) 二次型 f 的矩阵a 0 1A 0 a1 .11 a 1因为a 0 1|EA|a 1 ( a)((a 1))( (a 2)) ,11a 1所以 A 的特色值为1a,2a 1, 3a 2 .1 0 0(Ⅱ)解法 1因为 f 的规范形为 y 12 y 22 ,所以 A 合同于0 1 0 ,其秩为 2,故0 0 0A1 2 30, 于是 a 0或 a1 或 a 2.当 a0 时 ,0, 1,2 , 此时f 的规范形为2y 21 2312,不合题意 .y当 a1 时 , 11, 20,33 , 此时 f 的规范形为 y 12 y 22 , 不合题意 . 当 a2 时 ,12,23,30 , 此时 f 的规范形为 y 12y 22 .综上可知 ,a 2 .解法 2 因为 f 的规范形为 y 12y 22 , 所以 A 的特色值有 2 个为正数 ,1 个为零 .又 a 2 a a 1, 所以 a 2 .(22)( 本题满分 11 分 )【分析】 (I)X 的概率密度xx 0,xe x , x 0, f X (x)f (x, y)dye x dy,0,x 0.0, x 0当 x0时 , Y 的条件概率密度f (x, y)1y x, f Y| X ( y | x), 0f X (x)x 其余 .0,(II) Y 的概率密度f Y ( y)f ( x, y)dxe y , y 0, 0,y0.all~ 试题P X1,Y1PX 1|Y1P Y1111xe xdyf ( x, y)dxdydx e 2 .11e y dy1ee1(23)( 本题满分 11 分)11 1【分析】 (Ⅰ )P( X1 Z 0)P{ X1,Z 0}C 2 6 3 4P{Z 0}1.) 2 9(2( Ⅱ ) 由题意知 X 与 Y 的全部可能取值均为 0,1,2.P X0,Y 0C 31 C 31 1 X 1,YC 21 C 31 1C 61 C 61 , PC 61 C 61,46P X2,Y 011,PX0,Y 1 C 21 C 21 C 31C 61 C 61 36C 61 C 61P X1,Y 1C 21 C 21 1X 2,Y10,C 61 C 61 , P9 P X0,Y 2C 21 C 21 1 ,C 61 C 619P X 1,Y 2 0,P X 2,Y 2 0,故 ( X ,Y ) 的概率散布为X12 Y0 1/4 1/6 1/36 11/3 1/9 0 21/91 ,3。

2009考研数学三真题及答案

2009考研数学三真题及答案一、选择题：1～8小题，每小题4分，共32分，下列每小题给出的四个选项中，只有一项符合题目要求，把所选项前的字母填在题后的括号内.（1）函数3()sin x x f x xπ-=的可去间断点的个数为：（）()A .1()B . 2 ()C .3()D .无穷多个（2）当0x →时，()sin f x x ax =-与2()ln(1)g x x bx =-是等价无穷小，则（）()A .1a =，16b =-()B . 1a =，16b = ()C .1a =-，16b =- ()D .1a =-，16b =（3）使不等式1sin ln x tdt x t>⎰成立的x 的范围是（） ()A .(0,1)()B .(1,)2π()C .(,)2ππ()D .(,)π+∞（4）设函数()y f x =在区间[]1,3-上的图形为：则函数()()0xF x f t dt =⎰的图形为（）()A .()B .()C .()D .（5）设,A B 均为2阶矩阵，*,A B *分别为,A B 的伴随矩阵，若||2,||3A B ==则分块矩阵00A B ⎛⎫⎪⎝⎭的伴随矩阵为（） ()A .**0320B A ⎛⎫⎪⎝⎭()B . **0230B A⎛⎫⎪⎝⎭()C .**0320A B ⎛⎫⎪⎝⎭()D .**0230A B ⎛⎫⎪⎝⎭（6）设,A P 均为3阶矩阵，TP 为P 的转置矩阵，且100010002T P AP ⎛⎫⎪= ⎪ ⎪⎝⎭，若1231223(,,),(,,)P Q ααααααα==+，则T Q AQ 为（）()A .210110002⎛⎫⎪⎪ ⎪⎝⎭()B . 110120002⎛⎫⎪⎪ ⎪⎝⎭()C .200010002⎛⎫⎪⎪ ⎪⎝⎭()D .100020002⎛⎫ ⎪⎪ ⎪⎝⎭（7）设事件A 与事件B 互不相容，则（）()A .()0P AB =()B . ()()()P AB P A P B =()C .()1()P A P B =-()D .()1P A B ⋃=（8）设随机变量X 与Y 相互独立，且X 服从标准正态分布(0,1)N ，Y 的概率分布为1{0}{1}2P Y P Y ====，记()z F Z 为随机变量Z XY =的分布函数，则函数()z F Z 的间断点个数为（）()A .()B . 1 ()C .2()D . 3二、填空题：9-14小题，每小题4分，共24分，请将答案写在答题纸指定位置上.（9）cos x x →= .（10）设()y xz x e =+，则(1,0)zx ∂=∂（11）幂级数21(1)n n nn e x n ∞=--∑的收敛半径为（12）设某产品的需求函数为()Q Q P =,其对应价格P 的弹性0.2p ξ=，则当需求量为10000件时，价格增加1元会使产品收益增加元（13）设(1,1,1)T α=,(1,0,)T k β=，若矩阵Tαβ相似于300000000⎛⎫⎪ ⎪ ⎪⎝⎭，则k =(14)设1X ，2X ,…n X 是来自二项分布总体(,)B n p 的简单随机样本，X 和2S 分别为样本均值和样本方差，记统计量2T X S =-，则ET =三、解答题：15－23小题，共94分.请将解答写在答题纸指定的位置上.解答应写出文字说明、证明过程或演算步骤.（15）（本题满分9分）求二元函数()22(,)2ln f x y x y y y =++的极值。

2009数学三试题

元.
（13）设,，若矩阵相似于，则
.
(14) 设，,…,为来自二项分布总体的简单随机样本，和分别为样
本均值和样本方差，记统计量，则
.
三、解答题：15～23小题，共94分.请将解答写在答题纸指定的位置上.解答应写出文字说明、证明过程或演算步骤.
（15）（本题满分9分）求二元函数的极值.
（16）（本题满分10 分）计算不定积分 .
2009年全国硕士研究生入学统一考试
数学三试题
一、选择题：1～8小题，每小题4分，共32分，下列每小题给出的
四个选项中，只有一个选项是符合题目要求的，请把所选项前的字母
填在答题纸指定位置上.
（1）函数的可去间断点的个数为
(A)1.
(B)2.
(C)3.
(D)
无穷多个.
（2）当时，与是等价无穷小，则
(A)，.
为，记为随机变量的分布函数，则函数的间断)3.
二、填空题：9~14小题，每小题4分，共24分，请将答案写在答题
纸指定位置上.
（9）
.
（10）设，则
.
（11）幂级数的收敛半径为
.
（12）设某产品的需求函数为,其对应价格的弹性，则当需求量为
10000件时，价格增加1元会使产品收益增加
（5）设均为2阶矩阵，分别为的伴随矩阵，若，则分块矩阵的伴随
矩阵为
(A).
(B).
(C).
(D).
（6）设均为3阶矩阵，为的转置矩阵，且，
若，则为
(A).
(B).
(C).
(D).
（7）设事件与事件B互不相容，则
(A).
(B).
(C).
(D).

2009年考研数学一、二、三真题(含详解)

O
A
O
A O
A
1
O B1
B
O
B
O
B
O
6
A1
O
O
6
1 A
A
1 B
B
6
O
O
1 2
A
1 B 3 O
O 3A
6
6
(D) a 1,b 1 6
【解析】 f x x sin ax 与 g x x2 ln 1 bx 是 x 0 时的等价无穷小,则
lim
x0
f (x) g(x)
lim
x0
x sin ax x2 ln(1 bx)
lim
x0
x sin ax x2 (bx)
lim
x0
x
sin ax bx3
,且单调递减；
0
（定积分对应的图像位于 x 轴下方）
③ x 1, 2 时, F(x) x f (t)dt 0 单调递增； 0
④ x 2,3 时, F '(x) f (x) 0 为常函数；
⑤ F (x) 为连续函数. 结合这些特点,可见正确选项为(D)
(4)
设有两个数列
an
,
bn
,若
lim
n
则 max 1k 4
Ik
(
)
D1
D2
D4
-1
D3
1
x
(A) I1
(B) I2 (C) I3 (D) I4
-1
【答案】(A)
【解析】本题利用二重积分区域的对称性及被积函数的奇偶性.令 f (x, y) y cos x ,
D2, D4 两区域关于 x 轴对称, f (x, y) y cos x f (x, y) ,即被积函数是关于 y 的奇函数, 所以 I2 I4 0 ；

2009考研数学三真题及答案解析

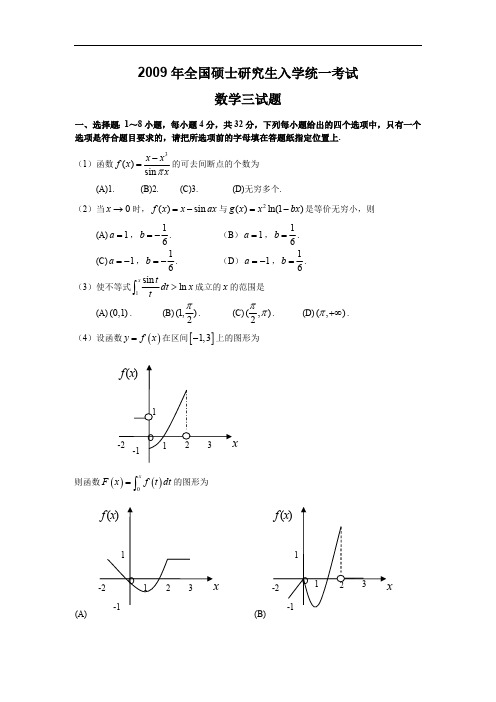
2009年全国硕士研究生入学统一考试数学三试题一、选择题：1～8小题，每小题4分，共32分，下列每小题给出的四个选项中，只有一个选项是符合题目要求的，请把所选项前的字母填在答题纸指定位置上.（1）函数的可去间断点的个数为3()sin x x f x xπ-=(A)1.(B)2.(C)3.(D)无穷多个.（2）当时，与是等价无穷小，则0x →()sin f x x ax =-2()ln(1)g x x bx =-(A)，. （B ），. 1a =16b =-1a =16b =(C)，. （D ），.1a =-16b =-1a =-16b =（3）使不等式成立的的范围是1sin ln x tdt x t>⎰x (A).(B). (C).(D).(0,1)(1,2π(,)2ππ(,)π+∞（4）设函数在区间上的图形为()y f x =[]1,3-则函数的图形为()()0xF x f t dt =⎰(A)(B)(C)(D)（5）设均为2阶矩阵，分别为的伴随矩阵，若，则分块矩,A B *,A B *,A B ||2,||3A B ==阵的伴随矩阵为O A B O ⎛⎫⎪⎝⎭(A).(B). **32O B A O ⎛⎫ ⎪⎝⎭**23OB A O ⎛⎫⎪⎝⎭(C).(D).**32O A B O ⎛⎫⎪⎝⎭**23O A BO ⎛⎫⎪⎝⎭（6）设均为3阶矩阵，为的转置矩阵，且，,A P T P P 100010002TP AP ⎛⎫ ⎪= ⎪ ⎪⎝⎭若，则为1231223(,,),(,,)P Q ααααααα==+TQ AQ (A).(B).210110002⎛⎫⎪ ⎪ ⎪⎝⎭110120002⎛⎫⎪ ⎪ ⎪⎝⎭(C). (D).200010002⎛⎫ ⎪ ⎪ ⎪⎝⎭100020002⎛⎫ ⎪ ⎪ ⎪⎝⎭（7）设事件与事件B 互不相容，则A (A). (B). ()0P AB =()()()P AB P A P B =(C).(D).()1()P A P B =-()1P A B ⋃=（8）设随机变量与相互独立，且服从标准正态分布，的概率分布为X Y X (0,1)N Y ，记为随机变量的分布函数，则函数1{0}{1}2P Y P Y ====()z F Z Z XY =()z F Z的间断点个数为(A)0.(B)1. (C)2.(D)3.二、填空题：9~14小题，每小题4分，共24分，请将答案写在答题纸指定位置上.（9）.0x →=（10）设，则.()y xz x e =+(1,0)zx ∂=∂（11）幂级数的收敛半径为 .21(1)n n nn e x n ∞=--∑（12）设某产品的需求函数为,其对应价格的弹性，则当需求量为()Q Q P =P 0.2p ξ=10000件时，价格增加1元会使产品收益增加元.（13）设,，若矩阵相似于，则.(1,1,1)T α=(1,0,)T k β=Tαβ300000000⎛⎫⎪ ⎪ ⎪⎝⎭k = (14)设，,…,为来自二项分布总体的简单随机样本，和分别为样1X 2X n X (,)B n p X 2S 本均值和样本方差，记统计量，则.2T X S =-ET =三、解答题：15～23小题，共94分.请将解答写在答题纸指定的位置上.解答应写出文字说明、证明过程或演算步骤.（15）（本题满分9分）求二元函数的极值.()22(,)2ln f x y xy y y =++（16）（本题满分10 分）计算不定积分 .ln(1dx +⎰(0)x >（17）（本题满分10 分）计算二重积分，其中.()Dx y dxdy -⎰⎰22{(,)(1)(1)2,}D x y x y y x =-+-≤≥（18）（本题满分11 分）（Ⅰ）证明拉格朗日中值定理，若函数在上连续，在上可导，则()f x [],a b (),a b ，得证.(),a b ξ∈()'()()()f b f a f b a ξ-=-（Ⅱ）证明：若函数在处连续，在内可导，且()f x 0x =()0,,(0)σσ>，则存在，且.'0lim ()x f x A +→='(0)f +'(0)f A +=（19）（本题满分10 分）设曲线，其中是可导函数，且.已知曲线与直线()y f x =()f x ()0f x >()y f x =及所围成的曲边梯形绕轴旋转一周所得的立体体积值是该曲边梯0,1y x ==(1)x t t =>x 形面积值的倍，求该曲线的方程.t π（20）（本题满分11 分）设,.111A=111042--⎛⎫ ⎪- ⎪ ⎪--⎝⎭1112ξ-⎛⎫⎪= ⎪⎪-⎝⎭（Ⅰ）求满足，的所有向量，.21A ξξ=231Aξξ=2ξ3ξ（Ⅱ）对（Ⅰ）中的任意向量,，证明,,线性无关.2ξ3ξ1ξ2ξ3ξ（21）（本题满分11 分）设二次型.2221231231323(,,)(1)22f x x x ax ax a x x x x x =++-+-（Ⅰ）求二次型的矩阵的所有特征值.f （Ⅱ）若二次型的规范形为，求的值.f 2211y y +a （22）（本题满分11 分）设二维随机变量的概率密度为(,)X Y 0(,)0xe y xf x y -⎧<<=⎨⎩其他（Ⅰ）求条件概率密度；()Y X f y x （Ⅱ）求条件概率.11P X Y =⎡≤≤⎤⎣⎦（23）（本题满分11分）袋中有一个红球，两个黑球，三个白球，现在放回的从袋中取两次，每次取一个，求以、X 、分别表示两次取球所取得的红、黑与白球的个数.Y Z （Ⅰ）求；10P X Z ⎡==⎤⎣⎦（Ⅱ）求二维随机变量的概率分布.(,)X Y 2009年全国硕士研究生入学统一考试数学三试题解析一、选择题：1～8小题，每小题4分，共32分，下列每小题给出的四个选项中，只有一个选项是符合题目要求的，请把所选项前的字母填在答题纸指定位置上.（1）函数的可去间断点的个数为3()sin x x f x xπ-=(A)1. (B)2. (C)3.(D)无穷多个.【答案】C. 【解析】()3sin x x f x xπ-=则当取任何整数时，均无意义x ()f x 故的间断点有无穷多个，但可去间断点为极限存在的点，故应是的解()f x 30x x -=1,2,30,1x =±320032113211131lim lim sin cos 132lim lim sin cos 132lim lim sin cos x x x x x x x x x x x x x x x x x x x x x ππππππππππππ→→→→→-→---==--==--==故可去间断点为3个，即0,1±（2）当时，与是等价无穷小，则0x →()sin f x x ax =-2()ln(1)g x x bx =-(A)，. （B ），. 1a =16b =-1a =16b =(C)，.（D ），.1a =-16b =-1a =-16b =【答案】A.【解析】为等价无穷小，则2()sin ,()(1)f x x ax g x x ln bx =-=-222200000()sin sin 1cos sin lim lim lim lim lim ()ln(1)()36x x x x x f x x ax x ax a ax a ax g x x bx x bx bx bx→→→→→---==-⋅---洛洛故排除(B)、(C).230sin lim 166x a ax a b b axa→==-=-⋅36a b ∴=-另外存在，蕴含了故排除(D).201cos lim3x a axbx →--1cos 0a ax -→()0x → 1.a =所以本题选(A).（3）使不等式成立的的范围是1sin ln xtdt x t>⎰x (A).(B). (C).(D).(0,1)(1,2π(,)2ππ(,)π+∞【答案】A.【解析】原问题可转化为求成立时的111sin sin 1()ln xx x tt f x dt x dt dt t t t =-=-⎰⎰⎰11sin 11sin 0x x t t dt dt t t--==>⎰⎰x 取值范围，由，时，知当时，.故应选(A).1sin 0tt->()0,1t ∈()0,1x ∈()0f x >（4）设函数在区间上的图形为()y f x =[]1,3-则函数的图形为()()0xF x f t dt =⎰(A)(B)(C)(D)【答案】D.【解析】此题为定积分的应用知识考核，由的图形可见，其图像与轴及轴、()y f x =x y 所围的图形的代数面积为所求函数，从而可得出几个方面的特征：0x x =()F x ①时，，且单调递减.[]0,1x ∈()0F x ≤②时，单调递增.[]1,2x ∈()F x ③时，为常函数.[]2,3x ∈()F x ④时，为线性函数，单调递增.[]1,0x ∈-()0F x ≤⑤由于F(x)为连续函数结合这些特点，可见正确选项为(D).（5）设均为2阶矩阵，分别为的伴随矩阵，若，则分块矩,A B *,A B *,A B ||2,||3A B ==阵的伴随矩阵为O A B O ⎛⎫⎪⎝⎭(A).(B). **32O B A O ⎛⎫ ⎪⎝⎭**23OB A O ⎛⎫⎪⎝⎭(C).(D).**32O A B O ⎛⎫⎪⎝⎭**23O A BO ⎛⎫⎪⎝⎭【答案】B.【解析】根据，若CC C E *=111,C C C CC C*--*==分块矩阵的行列式，即分块矩阵可逆O A B O ⎛⎫ ⎪⎝⎭221236O A A B B O ⨯=-=⨯=（）1111661O B BO A O A O A O B B O B O B O AO A O A**---*⎛⎫ ⎪⎛⎫⎛⎫⎛⎫ ⎪=== ⎪ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎪⎝⎭1236132O B O B AO A O ****⎛⎫⎪⎛⎫== ⎪ ⎪ ⎪⎝⎭⎪⎝⎭故答案为(B).（6）设均为3阶矩阵，为的转置矩阵，且，,A P T P P 100010002TP AP ⎛⎫ ⎪= ⎪ ⎪⎝⎭若，则为1231223(,,),(,,)P Q ααααααα==+TQ AQ (A).(B).210110002⎛⎫⎪ ⎪ ⎪⎝⎭110120002⎛⎫⎪ ⎪ ⎪⎝⎭(C). (D).200010002⎛⎫ ⎪ ⎪ ⎪⎝⎭100020002⎛⎫ ⎪ ⎪ ⎪⎝⎭【答案】A.【解析】，即：122312312312100(,,)(,,)110(,,)(1)001Q E αααααααααα⎡⎤⎢⎥=+==⎢⎥⎢⎥⎣⎦12121212122112(1)[(1)][(1)](1)[](1)100(1)010(1)002110100100210010010110110001002001002T T TT Q PE Q AQ PE A PE E P AP E E E ===⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦（7）设事件与事件B 互不相容，则A (A).(B). ()0P AB =()()()P AB P A P B =(C).(D).()1()P A P B =-()1P A B ⋃=【答案】D.【解析】因为互不相容，所以,A B ()0P AB =(A)，因为不一定等于1，所以(A)不正确.()()1()P AB P A B P A B ==- ()P A B (B)当不为0时，(B)不成立，故排除.(),()P A P B (C)只有当互为对立事件的时候才成立，故排除.,A B(D)，故(D)正确.()()1()1P A B P AB P AB ==-= （8）设随机变量与相互独立，且服从标准正态分布，的概率分布为X Y X (0,1)N Y ，记为随机变量的分布函数，则函数1{0}{1}2P Y P Y ====()z F Z Z XY =()z F Z 的间断点个数为（）(A)0.(B)1. (C)2.(D)3.【答案】 B.【解析】()()(0)(0)(1)(1)Z F z P XY z P XY z Y P Y P XY z Y P Y =≤=≤==+≤==1[(0)(1)]21[(00)(1)]2P XY z Y P XY z Y P X z Y P X z Y =≤=+≤==⋅≤=+≤=独立,X Y 1()[(0)()]2Z F z P x z P x z ∴=⋅≤+≤（1）若，则0z <1()()2Z F z z =Φ（2）当，则0z ≥1()(1())2Z F z z =+Φ为间断点，故选(B).0z ∴=二、填空题：9~14小题，每小题4分，共24分，请将答案写在答题纸指定位置上.（9）.0x →=【答案】.32e 【解析】.00x x →→=02(1cos )lim13x e x x→-=20212lim 13x e x x →⋅=32e =（10）设，则.()y xz x e =+(1,0)zx ∂=∂【答案】.2ln 21+【解析】由，故()xy z x e=+()(),01xz x x =+()''ln(1)ln(1)1ln(1)1x x x x x dz x x e e x dx x ++⎡⎤⎡⎤⎡⎤=+==++⎣⎦⎢⎥⎣⎦+⎣⎦代入得，.1x =()ln 21,01ln 22ln 212z e x∂⎛⎫=+=+ ⎪∂⎝⎭（11）幂级数的收敛半径为 .21(1)n n nn e x n ∞=--∑【答案】.1e【解析】由题意知，()210nn n e a n--=>()()()()111122122111()11111n n n n n nn n nn e e ea n n e n a n e n e e +++++⎡⎤⎛⎫--⎢⎥ ⎪⎝⎭--⎢⎥⎣⎦=⋅=⋅→→∞⎡⎤+--+⎛⎫--⎢⎥⎪⎝⎭⎢⎥⎣⎦所以，该幂级数的收敛半径为1e（12）设某产品的需求函数为,其对应价格的弹性，则当需求量为()Q Q P =P 0.2p ξ=10000件时，价格增加1元会使产品收益增加元.【答案】8000.【解析】所求即为()QP Q P Q ''=+因为，所以0.2p Q PQξ'==-0.2Q P Q '=-所以()0.20.8QP Q Q Q '=-+=将代入有.10000Q =()8000QP '=（13）设,，若矩阵相似于，则.(1,1,1)T α=(1,0,)T k β=Tαβ300000000⎛⎫ ⎪ ⎪ ⎪⎝⎭k =【答案】2.【解析】相似于，根据相似矩阵有相同的特征值，得到的特征值为T αβ300000000⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦Tαβ3，0，0.而为矩阵的对角元素之和，，.TαβT αβ1300k ∴+=++2k ∴= (14)设，,…,为来自二项分布总体的简单随机样本，和分别为样1X 2X n X (,)B n p X 2S 本均值和样本方差，记统计量，则 .2T X S =-ET =【答案】2np 【解析】由.222()(1)ET E X S E X ES np np p np =-=-=--=三、解答题：15～23小题，共94分.请将解答写在答题纸指定的位置上.解答应写出文字说明、证明过程或演算步骤.（15）（本题满分9分）求二元函数的极值.()22(,)2ln f x y xy y y =++【解析】，，故.2(,)2(2)0x f x y x y '=+=2(,)2ln 10y f x y x y y '=++=10,x y e= =.2212(2),2,4xxyy xyf y f x f xy y''''''=+ =+ =则，，.12(0,)12(2xxef e ''=+1(0,)0xyef ''=1(0,)yyef e ''=而0xxf ''> 2()0xy xx yy f f f ''''''-<二元函数存在极小值.∴11(0,)f e e=-（16）（本题满分10 分）计算不定积分 .ln(1dx+⎰(0)x >得t =22212,1(1)tdtx dx t t -= =--2221ln(1ln(1)1ln(1)11111dx t d t t dt t t t +=+-+=---+⎰⎰⎰而22111112(11411(1)111ln(1)ln(1)2441dt dtt t t t t t t C t =---+-++--++++⎰⎰所以2ln(1)111ln(1ln 1412(1)1ln(1.2t t dx C t t t x C +++=+-+--+=+++⎰（17）（本题满分10 分）计算二重积分，其中.()Dx y dxdy -⎰⎰22{(,)(1)(1)2,}D x y x y y x =-+-≤≥【解析】由得，22(1)(1)2x y -+-≤2(sin cos )r θθ≤+32(sin cos )4()(cos sin )04Dx y dxdy d r r rdr πθθθθθπ+∴-=-⎰⎰⎰⎰332(sin cos )14(cos sin )034r d πθθθθθπ⎡+⎤=-⋅⎢⎥⎣⎦⎰2384(cos sin )(sin cos )(sin cos )34d πθθθθθθθπ=-⋅+⋅+⎰3384(cos sin )(sin cos )34d πθθθθθπ=-⋅+⎰.3344438814(sin cos )(sin cos )(sin cos )3344d πππθθθθθθπ=++=⨯+⎰83=-（18）（本题满分11 分）（Ⅰ）证明拉格朗日中值定理，若函数在上连续，在上可导，则()f x [],a b (),a b ，得证.(),a b ξ∈()'()()()f b f a f b a ξ-=-（Ⅱ）证明：若函数在处连续，在内可导，且()f x 0x =()0,,(0)σσ>，则存在，且.'0lim ()x f x A +→='(0)f +'(0)f A +=【解析】（Ⅰ）作辅助函数，易验证满足：()()()()()()f b f a x f x f a x a b aϕ-=----()x ϕ；在闭区间上连续，在开区间内可导，且()()a b ϕϕ=()x ϕ[],a b (),a b .''()()()()f b f a x f x b aϕ-=--根据罗尔定理，可得在内至少有一点，使，即(),a b ξ'()0ϕξ='()f ξ'()()0,()()()()f b f a f b f a f b a b aξ--=∴-=--（Ⅱ）任取，则函数满足：在闭区间上连续，开区间内可导，0(0,)x δ∈()f x []00,x ()00,x 从而有拉格朗日中值定理可得：存在，使得()()000,0,x x ξδ∈⊂……()0'00()(0)x f x f f x ξ-=-()*又由于，对上式（*式）两边取时的极限可得：()'lim x f x A +→=00x +→()()000000'''0000()00lim lim ()lim ()0x x x x x f x f f f f A x ξξξ++++→→→-====-故存在，且.'(0)f +'(0)f A +=（19）（本题满分10 分）设曲线，其中是可导函数，且.已知曲线与直线()y f x =()f x ()0f x >()y f x =及所围成的曲边梯形绕轴旋转一周所得的立体体积值是该曲边梯0,1y x ==(1)x t t =>x 形面积值的倍，求该曲线的方程.t π【解析】旋转体的体积为22()()11x x t t V f dx f dxππ==⎰⎰曲边梯形的面积为：，则由题可知()1x ts f dx =⎰22()()()()1111x x x x t t t tV ts f dx t f dx f dx t f dxπππ=⇒=⇒=⎰⎰⎰⎰两边对t 求导可得 22()()()()()()11t x t t t x t t f f dx tf f tf f dx =+⇒-=⎰⎰继续求导可得，化简可得''2()()()()()f t f t f t tf t f t --=，解之得'1(2())()2()12dt f t t f t f t t dy y-=⇒+=1223t c y y-=⋅+在式中令，则，代入得 1t =2(1)(1)0,()0,(1)1f f f t f -=>∴= 1223t cyy -=+.11,2)33c t y =∴=所以该曲线方程为：.230y x +=（20）（本题满分11 分）设,.111A=111042--⎛⎫ ⎪- ⎪ ⎪--⎝⎭1112ξ-⎛⎫⎪= ⎪⎪-⎝⎭（Ⅰ）求满足，的所有向量，.21A ξξ=231Aξξ=2ξ3ξ（Ⅱ）对（Ⅰ）中的任意向量,，证明,,线性无关.2ξ3ξ1ξ2ξ3ξ【解析】（Ⅰ）解方程21A ξξ=()1111111111111,111100000211042202110000A ξ---------⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪=-→→ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪---⎝⎭⎝⎭⎝⎭故有一个自由变量，令，由解得，()2r A =32x =0Ax =211,1x x =-= 求特解，令，得120x x ==31x = 故，其中为任意常数21101021k ξ⎛⎫⎛⎫ ⎪ ⎪=-+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭1k解方程231Aξξ=2220220440A ⎛⎫ ⎪=-- ⎪ ⎪⎝⎭()21111022012,2201000044020000A ξ-⎛⎫ ⎪-⎛⎫ ⎪ ⎪=--→⎪ ⎪ ⎪ ⎪-⎝⎭ ⎪⎝⎭故有两个自由变量，令，由得231,0x x =-=20A x =11x =令，由得230,1x x ==-20A x =10x =求得特解21200η⎛⎫- ⎪ ⎪= ⎪ ⎪ ⎪⎝⎭故，其中为任意常数3231102100010k k ξ⎛⎫-⎪⎛⎫⎛⎫⎪ ⎪ ⎪=-++ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭ ⎪⎝⎭23,k k （Ⅱ）证明：由于12121212122111121112(21)()2((21)22221k k k k k k k k k k k k k -+--=+++-+-+-+102=≠故线性无关. 123,,ξξξ（21）（本题满分11 分）设二次型.2221231231323(,,)(1)22f x x x ax ax a x x x x x =++-+-（Ⅰ）求二次型的矩阵的所有特征值.f （Ⅱ）若二次型的规范形为，求的值.f 2211y y +a【解析】（Ⅰ） 0101111a A a a ⎛⎫ ⎪=- ⎪⎪--⎝⎭0110||01()1111111aa aE A a a a a λλλλλλλλ-----=-=---+---+222()[()(1)1][0()]()[()(1)2]()[22]19(){[(12)]}24()(2)(1)a a a a a a a a a a a a a a a a a λλλλλλλλλλλλλλλλ=---+--+-=---+-=--++--=-+--=--+--.123,2,1a a a λλλ∴==-=+（Ⅱ）若规范形为，说明有两个特征值为正，一个为0.则2212y y +1)若，则，，不符题意10a λ==220λ=-<31λ=2)若，即，则，，符合20λ=2a =120λ=>330λ=>3)若，即，则，，不符题意30λ=1a =-110λ=-<230λ=-<综上所述，故2a =（22）（本题满分11 分）设二维随机变量的概率密度为(,)X Y 0(,)0x e y xf x y -⎧<<=⎨⎩其他（Ⅰ）求条件概率密度()Y X f y x （Ⅱ）求条件概率11P X Y =⎡≤≤⎤⎣⎦【解析】（Ⅰ）由得其边缘密度函数0(,)0x y xe f x y -<<⎧= ⎨⎩其它()0xx x x f x e dy xe x --== >⎰故 |(,)1(|)0()y x x f x y f y x y x f x x== <<即|1(|)0y x y xf y x x ⎧ 0<<⎪=⎨⎪⎩其它（Ⅱ）[1,1][1|1][1]P X Y P X Y P Y ≤≤≤≤=≤而11111[1,1](,)12xxx x y P X Y f x y dxdy dx e dy xe dx e ---≤≤≤≤====-⎰⎰⎰⎰⎰()|,0x x yY yf y e dx e e y y+∞---+∞==-= >⎰11101[1]|110y y P Y e dy e e e ----∴ ≤==-=-+=-⎰.11122[1|1]11e e P X Y e e ----∴ ≤≤==--（23）（本题满分11分）袋中有一个红球，两个黑球，三个白球，现在放回的从袋中取两次，每次取一个，求以、X 、分别表示两次取球所取得的红、黑与白球的个数.Y Z ①求.10P X Z ⎡==⎤⎣⎦②求二维随机变量的概率分布.(,)X Y 【解析】（Ⅰ）在没有取白球的情况下取了一次红球，利用压缩样本空间则相当于只有1个红球，2个黑球放回摸两次，其中摸了一个红球.12113324(10)9C P X Z C C ⨯∴====⋅（Ⅱ）X ，Y 取值范围为0，1，2，故()()()()()()()()()1111332311116666111223111166661122116611221166110,0,1,0461112,0,0,136311,1,2,10910,291,20,2,20C C C C P X Y P X Y C C C C C C C P X Y P X Y C C C C C C P X Y P X Y C C C C P X Y C C P X Y P X Y ⋅⋅========⋅⋅⋅⋅========⋅⋅⋅=======⋅⋅====⋅======012 XY01/41/61/36 11/31/9021/900。

2009年数学三试题答案、解析

2009年全国硕士研究生入学统一考试数学三试题一、选择题：1~8小题，每小题8分，共32分，下列每小题给出的四个选项中，只有一项符合题目要求，把所选项前的字母填在题后的括号内。

（1）函数3()sin x x f x nx-=的可去间断点的个数为（）（A ）1 （B ）2 （C ）3 （D ）无穷多个【答案】C 【解析】3()sin x x f x xπ-=则当x 取任何整数时，()f x 均无意义故()f x 的间断点有无穷多个，但可去间断点为极限存在的点，故应是30x x -=的解1,2,30,1x =±3200131lim lim sin cos x x x x x x x ππππ→→--== 3211132lim lim sin cos x x x x x x x ππππ→→--== 3211132lim lim sin cos x x x x x x x ππππ→-→---== 故可去间断点为3个，即0，±1（2）当0x →时，()sin f x x ax =-与2()ln(1)g x x bx =-等价无穷小，则（）（A ）11,6a b ==- （B ）11,6a b ==（C ）11,6a b =-=-（D ）11,6a b =-=【解析与点评】考点：无穷小量比阶的概念与极限运算法则。

参见水木艾迪考研数学春季基础班教材《考研数学通用辅导讲义》（秦华大学出版社）例 4.67，强化班教材《大学数学强化 299》16、17 等例题。

【答案】A22220000sin sin 1cos sin lim lim lim limln(1)()36x x x x x ax x ax a x a axx bx x bx bx bx →→→→---===---- 230sin lim 166.x a ax a b b axa→==-=-36a b =-意味选项错误。

再由21cos lim 3x a axbx→-=-存在，故有1cos 0(0)a ax x -→→，故a=1，D 错误，所以选A 。

数三真题套卷09-20.pdf

目录2009年全国硕士研究生招生考试数学三试题 (2)2010年全国硕士研究生招生考试数学三试题 (6)2011年全国硕士研究生招生考试数学三试题 (10)2012年全国硕士研究生招生考试数学三试题 (14)2013年全国硕士研究生招生考试数学三试题 (18)2014年全国硕士研究生招生考试数学三试题 (22)2015年全国硕士研究生招生考试数学三试题 (26)2016年全国硕士研究生招生考试数学三试题 (31)2017年全国硕士研究生招生考试数学三试题 (36)2018年全国硕士研究生招生考试数学三试题 (40)2019年全国硕士研究生招生考试数学三试题 (44)2020年全国硕士研究生招生考试数学三试题 (48)2009年数学（三）参考答案 (52)2010年数学（三）参考答案 (54)2011年数学（三）参考答案 (56)2012年数学（三）参考答案 (58)2013年数学（三）参考答案 (59)2014年数学（三）参考答案 (61)2015年数学（三）参考答案 (63)2016年数学（三）参考答案 (64)2017年数学（三）参考答案 (66)2018年数学（三）参考答案 (68)2019年数学（三）参考答案 (70)2020年数学（三）参考答案 (71)2009年全国硕士研究生招生考试数学三试题一、选择题：1~8小题，每小题4分，共32分，下列每小题给出的四个选项中，只有一项符合题目要求，把所选项前的字母填在题后的括号内。

（1）函数3()sin x x f x xπ-=的可去间断点的个数为（）（A ）1 （B ）2 （C ）3 （D ）无穷多个（2）当0x →时，()sin f x x ax =-与2()ln(1)g x x bx =-是等价无穷小，则（）（A ）11,6a b ==-（B ）11,6a b ==（C ）11,6a b =-=- （D ）11,6a b =-=（3）使不等式1sin ln xtdt x t>⎰成立的x 的范围是（）（A ）（0，1）（B ）（1，2π）（C ）（2π，π）（D ）（π，+∞）（4）设函数()y f x =在区间[-1,3]上的图形为()f xx则函数0()()xF x f t dt =⎰为（）()A .()B .O 2 31 -1-11 O2 3 1 -2-11 oo13-1 O 2 o 1 -12()C .()D .（5）设A 、B 均为2阶矩阵，,AB **分别为A 、B 的伴随矩阵。

2009年数三

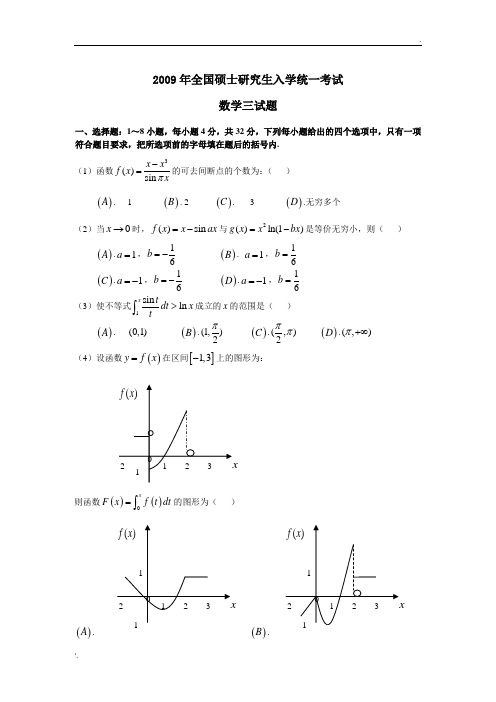
2009年全国硕士研究生入学统一考试数学三试题一、选择题：1～8小题，每小题4分，共32分，下列每小题给出的四个选项中，只有一项符合题目要求，把所选项前的字母填在题后的括号内.（1）函数3()sin x x f x xπ-=的可去间断点的个数为：（）()A .1()B . 2 ()C .3()D .无穷多个（2）当0x →时，()sin f x x ax =-与2()ln(1)g x x bx =-是等价无穷小，则（）()A .1a =，16b =-()B . 1a =，16b = ()C .1a =-，16b =- ()D .1a =-，16b = （3）使不等式1sin ln x tdt x t>⎰成立的x 的范围是（） ()A .(0,1)()B .(1,)2π()C .(,)2ππ()D .(,)π+∞（4）设函数()y f x =在区间[]1,3-上的图形为：则函数()()0xF x f t dt =⎰的图形为（）()A .()B .()C .()D .（5）设,A B 均为2阶矩阵，*,A B *分别为,A B 的伴随矩阵，若||2,||3A B ==则分块矩阵00A B ⎛⎫⎪⎝⎭的伴随矩阵为（） ()A .**0320B A ⎛⎫⎪⎝⎭()B . **0230B A⎛⎫⎪⎝⎭()C .**0320A B ⎛⎫⎪⎝⎭()D .**0230A B ⎛⎫⎪⎝⎭（6）设,A P 均为3阶矩阵，TP 为P 的转置矩阵，且100010002T P AP ⎛⎫⎪= ⎪ ⎪⎝⎭，若1231223(,,),(,,)P Q ααααααα==+，则T Q AQ 为（）()A .210110002⎛⎫⎪⎪ ⎪⎝⎭()B . 110120002⎛⎫⎪⎪ ⎪⎝⎭()C .200010002⎛⎫⎪⎪ ⎪⎝⎭()D .100020002⎛⎫ ⎪⎪ ⎪⎝⎭（7）设事件A 与事件B 互不相容，则（）()A .()0P AB =()B . ()()()P AB P A P B = ()C .()1()P A P B =-()D .()1P A B ⋃=（8）设随机变量X 与Y 相互独立，且X 服从标准正态分布(0,1)N ，Y 的概率分布为1{0}{1}2P Y P Y ====，记()z F Z 为随机变量Z XY =的分布函数，则函数()z F Z 的间断点个数为（）()A .()B . 1 ()C .2()D . 3二、填空题：9-14小题，每小题4分，共24分，请将答案写在答题纸指定位置上.（9）cos x x →= .（10）设()y xz x e =+，则(1,0)zx ∂=∂（11）幂级数21(1)n n nn e x n ∞=--∑的收敛半径为（12）设某产品的需求函数为()Q Q P =,其对应价格P 的弹性0.2p ξ=，则当需求量为10000件时，价格增加1元会使产品收益增加元（13）设(1,1,1)T α=,(1,0,)T k β=，若矩阵Tαβ相似于300000000⎛⎫⎪ ⎪ ⎪⎝⎭，则k =(14)设1X ，2X ,…n X 是来自二项分布总体(,)B n p 的简单随机样本，X 和2S 分别为样本均值和样本方差，记统计量2T X S =-，则ET =三、解答题：15－23小题，共94分.请将解答写在答题纸指定的位置上.解答应写出文字说明、证明过程或演算步骤.（15）（本题满分9分）求二元函数()22(,)2ln f x y x y y y =++的极值。