(完整版)一元二次方程知识点及其应用
(完整版)一元二次方程知识点和经典例题

一元二次方程一.基本概念定义:形如:02=++c bx ax (0≠a )的方程,叫做一元二次方程的一般式. 例题:若方程32)1(1=--+x x m m 是关于x 的一元二次方程,求m 的值.二.一元二次方程的解法(1)直接开方法: 02=+c ax , 开平方求出未知数的值:ac x -±= (2)因式分解法:0)(2=++-mn x n m x ,因式分解得:0))((=--n x m x ∴m x =1,n 2=x(3)配方法:061232=-+x x ,得:242=+x x ,∴222)2(2)2(4+=++x x 即:6)2(2=+x ∴621+-=x ,622--=x(4)公式法:解法步骤:○1先把一元二次方程化为一般式; ○2找出方程中a 、b 、c 等各项系数和常数的值;○3计算出ac b 42-的值;○4把a,b, ac b 42-的值代入公式;○5求出方程的两个根.例题:解方程: x(x+12)=8x+12解:原方程化简得:01242=-+x x ,方程中:a=1,b=4,c=-12∆=ac b 42-=(4)2-4×1×(-12)=16+48=64.∴28412644±-=⨯±-=x =42±- ∴原方程根为:21=x ,=2x -6.一元二次方程解法练习题:(1)用直接开方法解一元二次方程: ○1 (2x-1)2=7 ○222)43()43(x x -=- ○30144)3(2=--x(2)用因式分解法解一元二次方程:○11)1(3-=-x x x ○25x(x-3)=6-2x ○32(x +2)(x -1)=(x +2)(x +4)○4025)2(10)2(2=++-+x x ○542)2)(1(+=++x x x ○60)4()52(22=+--x x(3)用配方法解一元二次方程:○1x(x+4)=8x+12 ○226120x x --= ○30223)12(22=-+-+x x(4)用公式法解一元二次方程:○123520x x -+= ○5(3)(1)2x x +-=- ○112x 2-33x+130=0(5)选择适当的方法解下列方程:○122(2)9x x -= ○22299990x x +-= ○32(101)10(101)90x x +-++=○42690x x -+= ○5x(37)2x x -= ○6}113111[1()]222323x x x x ⎧--+-+=⎨⎩三.一元二次方程根的判别式1.一元二次方程根的判别式:把ac b 42-=∆叫做一元二次方程:02=++c bx ax (0≠a )的根的判别式.利用根的判别式可以不解方程判别一元二次方程跟的情况:20(1)00(2)400.b ac ∆>⇔⎧∆≥⇔⎨∆=⇔⎩∆=-∆<⇔当时方程有两个不相等的实根;当时方程有两个实数根;当时方程有两个相等的实数根;当的值小于时,即:时方程无实数根例1.不解方程判断下列方程跟的情况:(1)08822=+-x x (2)24120x x +-= (3)20232=+-x x解:(1)方程中:a=2,b=-8,c=8,∆=ac b 42-=(-8)2-4×2×8=64-64=0∵∆=0 ∴原方程有两个相等的实数根.(2)方程中:a=1,b=4,c=-12,∆=ac b 42-=(4)2-4×1×(-12)=16+48=64 ∵∆>0 ∴原方程有两个不相等的实数根.(3)方程中:a=2,b=-3,c=2,∆=ac b 42-=(-3)2-4×2×2=9-16=-7∵∆<0 ∴原方程无实数根.例2.关于x 的一元二次方程(m -1)x 2-2(m -3)x +m +2=0有实数根,求m 的取值范围.解:当m -1≠0时, 即:m 1≠时,该方程是关于x 一元二次方程.∵原方程有实数根∴0≥∆,即:Δ=[-2(m -3)]2-4(m -1)(m +2)=-28m +440≥ 解得:711≤m ∴m 的取值范围是711≤m 且m 1≠. 例3. 求证:关于x 的一元二次方程2(2)2(1)10k x k x k --+-+=(k 3)≤总有实数根. 证明:∵224=[2(1)]4(2)(1)4(3)b ac k k k k ∆=-----+=-且k 3≤,∴总有0≥∆ ∴关于x 的一元二次方程2(2)2(1)10k x k x k --+-+=(k 3)≤总有实数根.四.一元二次方程根与系数的关系1.定理:设一元二次方程02=++c bx ax (0≠a 且042≥-ac b )的两个根分别为1x 和2x ,则:ab 2x 1x -=+; a 2x 1xc =• 特别地:对于一元二次方程20x px q ++=,根与系数的关系为:12x x p +=-; 12x x q =注:○1此定理成立的前提是0∆≥.也就是说必须在方程有实..数根..时才可使用. ○2此定理在其他一些数学书籍中也叫做韦达定理。
(完整版)一元二次方程归纳总结

一元二次方程归纳总结1、一元二次方程的一般式:20 (0)ax bx c a ++=≠,a 为二次项系数,b 为一次项系数,c 为常数项。
2、一元二次方程的解法(1)直接开平方法 (也可以使用因式分解法) ①2(0)xa a =≥解为:x = ②2()(0)x a b b +=≥解为:x a += ③2()(0)ax b c c +=≥解为:ax b += ④22()()()ax b cx d a c +=+≠ 解为:()ax b cx d +=±+(2)因式分解法:提公因式分,平方公式,平方差,十字相乘法(3)公式法:一元二次方程20 (0)ax bx c a ++=≠,用配方法将其变形为:2224()24b b ac x a a -+= ①当240b ac ∆=->时,右端是正数.因此,方程有两个不相等的实根:1,22b x a-=② 当240b ac ∆=-=时,右端是零.因此,方程有两个相等的实根:1,22b x a=-③ 当240bac ∆=-<时,右端是负数.因此,方程没有实根。
注意:虽然所有的一元二次都可以用公式法来求解,但它往往并非最简单的,一定要注意方法的选用。
备注:公式法解方程的步骤:①把方程化成一般形式:一元二次方程的一般式:20 (0)ax bx c a ++=≠,并确定出a 、b 、c②求出24bac ∆=-,并判断方程解的情况。
③代公式:1,2x =3、一元二次方程的根与系数的关系法1:一元二次方程20 (0)axbx c a ++=≠的两个根为:1222b b x x a a-+-==所以:12bx x a+=+=-,221222()422(2)4b b b ac cx x a a a a a-+----⋅=⋅===定理:如果一元二次方程20 (0)axbx c a ++=≠定的两个根为12,x x ,那么:1212,b cx x x x a a+=-=法2:如果一元二次方程20 (0)axbx c a ++=≠定的两个根为12,x x ;那么2120()()0ax bx c a x x x x ++=⇔--= 两边同时除于a ,展开后可得:2212120()0b c x x x x x x x x a a++=⇔-++= 12b x x a ⇒+=-;12cx x a •=法3:如果一元二次方程20 (0)axbx c a ++=≠定的两个根为12,x x ;那么21122200ax bx c ax bx c ⎧++=⎪⎨++=⎪⎩①-②得:12bx x a+=-(余下略) 常用变形:222121212()2x x x x x x +=+-,12121211x x x x x x ++=,22121212()()4x x x x x x -=+-,12||x x -=2212121212()x x x x x x x x +=+,22111212121222212()4x x x x x x x x x x x x x x ++-+==等 练习:【练习1】若12,x x 是方程2220070xx +-=的两个根,试求下列各式的值:(1)2212x x +;(2)1211x x +;(3)12(5)(5)x x --;(4)12||x x -.【练习2】已知关于x 的方程221(1)104xk x k -+++=,根据下列条件,分别求出k 的值.(1) 方程两实根的积为5; (2) 方程的两实根12,x x 满足12||x x =.【练习3】已知12,x x 是一元二次方程24410kxkx k -++=的两个实数根.(1) 是否存在实数k ,使12123(2)(2)2x x x x --=-成立?若存在,求出k 的值;若不存在, 请您说明理由.(2) 求使12212x x x x +-的值为整数的实数k 的整数值. 4、应用题(1)平均增长率的问题:(1)n a x b += 其中:a 为基数,x 为增长率,n 表示连续增长的次数,①②b 表示增长后的数量。
(完整版)一元二次方程知识点和经典例题

一元二次方程一.基本概念定义:形如:02=++c bx ax (0≠a )的方程,叫做一元二次方程的一般式. 例题:若方程32)1(1=--+x x m m 是关于x 的一元二次方程,求m 的值.二.一元二次方程的解法(1)直接开方法: 02=+c ax , 开平方求出未知数的值:ac x -±= (2)因式分解法:0)(2=++-mn x n m x ,因式分解得:0))((=--n x m x ∴m x =1,n 2=x(3)配方法:061232=-+x x ,得:242=+x x ,∴222)2(2)2(4+=++x x 即:6)2(2=+x ∴621+-=x ,622--=x(4)公式法:解法步骤:○1先把一元二次方程化为一般式; ○2找出方程中a 、b 、c 等各项系数和常数的值;○3计算出ac b 42-的值;○4把a,b, ac b 42-的值代入公式;○5求出方程的两个根.例题:解方程: x(x+12)=8x+12解:原方程化简得:01242=-+x x ,方程中:a=1,b=4,c=-12∆=ac b 42-=(4)2-4×1×(-12)=16+48=64.∴28412644±-=⨯±-=x =42±- ∴原方程根为:21=x ,=2x -6.一元二次方程解法练习题:(1)用直接开方法解一元二次方程: ○1 (2x-1)2=7 ○222)43()43(x x -=- ○30144)3(2=--x(2)用因式分解法解一元二次方程:○11)1(3-=-x x x ○25x(x-3)=6-2x ○32(x +2)(x -1)=(x +2)(x +4)○4025)2(10)2(2=++-+x x ○542)2)(1(+=++x x x ○60)4()52(22=+--x x(3)用配方法解一元二次方程:○1x(x+4)=8x+12 ○226120x x --= ○30223)12(22=-+-+x x(4)用公式法解一元二次方程:○123520x x -+= ○5(3)(1)2x x +-=- ○112x 2-33x+130=0(5)选择适当的方法解下列方程:○122(2)9x x -= ○22299990x x +-= ○32(101)10(101)90x x +-++=○42690x x -+= ○5x(37)2x x -= ○6}113111[1()]222323x x x x ⎧--+-+=⎨⎩三.一元二次方程根的判别式1.一元二次方程根的判别式:把ac b 42-=∆叫做一元二次方程:02=++c bx ax (0≠a )的根的判别式.利用根的判别式可以不解方程判别一元二次方程跟的情况:20(1)00(2)400.b ac ∆>⇔⎧∆≥⇔⎨∆=⇔⎩∆=-∆<⇔当时方程有两个不相等的实根;当时方程有两个实数根;当时方程有两个相等的实数根;当的值小于时,即:时方程无实数根例1.不解方程判断下列方程跟的情况:(1)08822=+-x x (2)24120x x +-= (3)20232=+-x x解:(1)方程中:a=2,b=-8,c=8,∆=ac b 42-=(-8)2-4×2×8=64-64=0∵∆=0 ∴原方程有两个相等的实数根.(2)方程中:a=1,b=4,c=-12,∆=ac b 42-=(4)2-4×1×(-12)=16+48=64 ∵∆>0 ∴原方程有两个不相等的实数根.(3)方程中:a=2,b=-3,c=2,∆=ac b 42-=(-3)2-4×2×2=9-16=-7∵∆<0 ∴原方程无实数根.例2.关于x 的一元二次方程(m -1)x 2-2(m -3)x +m +2=0有实数根,求m 的取值范围.解:当m -1≠0时, 即:m 1≠时,该方程是关于x 一元二次方程.∵原方程有实数根∴0≥∆,即:Δ=[-2(m -3)]2-4(m -1)(m +2)=-28m +440≥ 解得:711≤m ∴m 的取值范围是711≤m 且m 1≠. 例3. 求证:关于x 的一元二次方程2(2)2(1)10k x k x k --+-+=(k 3)≤总有实数根. 证明:∵224=[2(1)]4(2)(1)4(3)b ac k k k k ∆=-----+=-且k 3≤,∴总有0≥∆ ∴关于x 的一元二次方程2(2)2(1)10k x k x k --+-+=(k 3)≤总有实数根.四.一元二次方程根与系数的关系1.定理:设一元二次方程02=++c bx ax (0≠a 且042≥-ac b )的两个根分别为1x 和2x ,则:ab 2x 1x -=+; a 2x 1xc =• 特别地:对于一元二次方程20x px q ++=,根与系数的关系为:12x x p +=-; 12x x q =注:○1此定理成立的前提是0∆≥.也就是说必须在方程有实..数根..时才可使用. ○2此定理在其他一些数学书籍中也叫做韦达定理。
初中数学一元二次方程知识点总结(含习题)

初中数学一元二次方程知识点总结(含习题)一元二次方程知识点的总结知识结构梳理:1、概念1) 一元二次方程含有一个未知数。
2) 未知数的最高次数是2.3) 是方程。
4) 一元二次方程的一般形式是ax²+bx+c=0.2、解法1) 因式分解法,适用于能化为(x+m)(x+n)=0的一元二次方程。
2) 公式法,即把方程变形为ax²+bx+c=0的形式,一元二次方程的解为x=[-b±√(b²-4ac)]/(2a)。
3) 完全平方式,其中求根公式是(x±a)²=b,当时,方程有两个不相等的实数根。
4) 配方法,其中求根公式是(x±a)(x±b)=0,当时,方程有两个实数根。
5) 二次函数图像法,当时,方程有没有实数根。
3、应用1) 一元二次方程可用于解某些求值题。
2) 一元二次方程可用于解决实际问题的步骤包括:列方程、化简方程、解方程、检验答案。
知识点归类:考点一:一元二次方程的定义如果一个方程通过移项可以使右边为0,而左边只含有一个未知数的二次多项式,那么这样的方程叫做一元二次方程。
一元二次方程必须同时满足以下三点:①方程是整式方程。
②它只含有一个未知数。
③未知数的最高次数是2.考点二:一元二次方程的一般形式一元二次方程的一般形式为ax²+bx+c=0,其中a、b、c分别叫做二次项系数、一次项系数、常数项。
要准确找出一个一元二次方程的二次项系数、一次项系数和常数项,必须把它先化为一般形式。
考点三:解一元二次方程的方法一元二次方程的解也叫一元二次方程的根。
解一元二次方程的方法包括因式分解法、公式法、完全平方式、配方法和二次函数图像法。
解一元二次方程有四种常用方法:直接开平方法、配方法、因式分解法和公式法。
选择哪种方法要根据具体情况而定。
直接开平方法是解形如x²=a的方程的方法,解为x=±√a。
配方法是将方程的左边加上一次项系数一半的平方,再减去这个数,使得含未知数的项在一个完全平方式里,然后用因式分解法或直接开平方法解方程。
完整版)一元二次方程(知识点考点题型总结)

完整版)一元二次方程(知识点考点题型总结)一元二次方程专题复考点一、概念一元二次方程是只含有一个未知数,且未知数的最高次数是2的整式方程。
一般表达式为ax^2+bx+c=0,其中a不等于0.关于“未知数的最高次数是2”,需要注意以下三点:一是该项系数不为0;二是未知数指数为2;三是若存在某项指数为待定系数,或系数也有待定,则需建立方程或不等式加以讨论。
典型例题:例1、下列方程中是关于x的一元二次方程的是():A。
2x^2+11x-2=0B。
ax^2+bx+c=DC。
2x=x+1变式:当k时,关于x的方程kx+2x=x+3是一元二次方程。
例2、方程m+2xm+1=0是关于x的一元一次方程,求m 的值,并写出关于x的一元一次方程。
针对练:1.方程8x^2+3mx+1=0是关于x的一元二次方程,则m的值为多少?2.若方程m-2x=0是关于x的一元一次方程,求m的值,并写出关于x的一元一次方程。
3.若方程(m-1)x+m·x=1是关于x的一元二次方程,则m 的取值范围是多少?4.若方程nx+x-2x=0是一元二次方程,则下列不可能的是():A。
m=n=2B。
m=2.n=1C。
n=2.m=1D。
m=n=1考点二、方程的解方程的解是指使方程两边相等的未知数的值。
根的概念可用于求代数式的值。
典型例题:例1、已知2y+y^2-3的值为2,则4y+2y^2+1的值为多少?例2、关于x的一元二次方程(a-2)x^2+x+a-4=0的一个根为2,求a的值。
例3、已知关于x的一元二次方程ax^2+bx+c=0的系数满足a+c=b,则此方程必有一根为多少?例4、已知a,b是方程x^2-4x+m=0的两个根,b,c是方程y^2-8y+5m=0的两个根,则m的值为多少?针对练:1.已知方程x+kx-10=0的一根是2,则k为多少?另一根是多少?2.已知关于x的方程x^2+kx-2=0的一个解与方程(x+1)/(x-1)=3的解相同,求k的值,并求方程的另一个解。
专题08一元二次方程及其应用(知识点总结+例题讲解)-2021届中考数学一轮复习

2021年中考数学专题08 一元二次方程及其应用(知识点总结+例题讲解)一、一元二次方程有关概念:1.一元二次方程定义:只含有一个未知数(一元),并且未知数的最高次数是2(二次)的整式方程,叫做一元二次方程;2.一般形式:ax2+bx+c=0;(其中a、b、c为常数,a≠0)(1)其中ax2、bx、c分别叫做二次项、一次项和常数项;(2)a、b分别称为二次项系数和一次项系数;(3)二次项系数:a≠0;(当a=0时,不含有二次项,即不是一元二次方程)3.一元二次方程必须具备三个条件:(1)必须是整式方程(等号两边都是整式);(2)必须只含有1个未知数;(3)所含未知数的最高次数是2;4.一元二次方程的解:使方程左右两边相等的未知数的值就是这个一元二次方程的解;一元二次方程的解也叫做一元二次方程的根。
【例题1】(2020秋•奉贤区期末)下列各方程中,一定是一元二次方程的是()A.1x2+1x−2=0B.ax2+bx+c=0C.(x﹣2)2=2(x﹣2)D.x2+2y=3【答案】C【解析】利用一元二次方程定义进行解答即可.解:A、含有分式,不是一元二次方程,故此选项不符合题意;B、当a=0时,不是一元二次方程,故此选项不符合题意;C、是一元二次方程,故此选项符合题意;D、含有两个未知数,不是一元二次方程,故此选项不符合题意;故选:C.【变式练习1】(2020秋•丹阳市期末)关于x的方程(m+1)x2+2mx﹣3=0是一元二次方程,则()A.m≠±1 B.m=1 C.m≠1 D.m≠﹣1【答案】D【解析】根据一元二次方程定义可得m+1≠0,再解可得答案.解:由题意得:m+1≠0,解得:m≠﹣1;故选:D.【例题2】(2020秋•郫都区期末)若x=m是方程x2+x﹣1=0的根,则m2+m+2020的值为()A.2022 B.2021 C.2019 D.2018【答案】B【解析】把x=m代入已知方程,可以求得m2+m=1,然后整体代入所求的代数式求值即可.解:∵x=m是方程x2+x﹣1=0的根,∴m2+m﹣1=0,∴m2+m=1,∴m2+m+2020=1+2020=2021.故选:B.【变式练习2】设m是方程x2﹣3x+1=0的一个实数根,则m 4+m2+1m2=8 .【答案】8【解析】利用一元二次方程的解的意义得到m2﹣3m+1=0,两边除以m得到m+1m=3,再把原式变形得到原式=m2+1+1m =(m+1m)2﹣2+1,然后利用整体代入的方法计算.解:∵m是方程x2﹣3x+1=0的一个实数根,∴m2﹣3m+1=0,∴m+1m =3,∴原式=m2+1+1m2=(m+1m)2﹣2+1=9﹣2+1=8.二、一元二次方程的解法:1.解一元二次方程的基本思想:转化思想,即把一元二次方程转化为一元一次方程来求解;2.常用方法:(1)直接开平方法:适用形式:x2=p(p≥0),(x+n)2=p或(mx+n)2=p(p≥0)的方程;(2)配方法:套用公式a2+2ab+b2=(a+b)2;a2-2ab+b2=(a-b)2将一元二次方程ax2+bx+c=0(a≠0)配方为(x+m)2=n的形式,再用直接开平方法求解;配方法解一元二次方程的一般步骤是:①将已知方程化为一般形式;②化二次项系数为1;③常数项移到右边;④方程两边都加上一次项系数的一半的平方,使左边配成一个完全平方式;变形为(x+p)2=q的形式:如果q≥0,方程的根是x=-p±q;如果q<0,方程无实根;(3)公式法:利用求根公式x=(240∆=-≥)解一元二次方程ax2+bx+c=0(a≠0);b ac(4)因式分解法:将一元二次方程通过分解因式变为(x-a)(x-b)=0的形式;进而得到x-a=0或x-b=0来求解;3.方法选择技巧:(1)若一元二次方程缺少常数项,且方程的右边为0,可考虑用因式分解法求解;(2)若一元二次方程缺少一次项,可考虑用因式分解法或直接开平方法求解; (3)若一元二次方程的二次项系数为1,且一次项的系数是偶数时或常数项非常大时,可考虑用配方法求解;(4)若用以上三种方法都不容易求解时,可考虑用公式法求解。
一元二次方程知识点总结(全章齐全)

一元二次方程知识点总结定义:两边都是整式,只含有一个未知数(一元),并且未知数的最高次数是2(二次)的方程,叫做一元二次方程.一般地,任何一个关于x的一元二次方程,经过整理,都能化成如下形式.这种形式叫做一元二次方程的一般形式.一个一元二次方程经过整理化成ax2+bx+c=0(a≠0)后,其中是二次项,是二次项系数;是一次项,是一次项系数;是常数项.注意:二次项、二次项系数、一次项、一次项系数、常数项都包括前面的符号.基本解法①直接开平方法:对于形如的方程,即一元二次方程的一边是含有未知数的一次式的平方,而另一边是一个非负数,可用直接开平方法求解。
②配方法:(1)现将已知方程化为一般形式;(2)化二次项系数为1;(3)常数项移到右边;(4)方程两边都加上一次项系数的一半的平方,使左边配成一个完全平方式;(5)变形为(x+p)2=q的形式,如果q≥0,方程的根是x=-p±√q;如果q<0,方程无实根.③公式法:(1)把一元二次方程化为一般式。
(2)确定a,b,c的值。
(3)代入中计算其值,判断方程是否有实数根。
(4)若代入求根公式求值,否则,原方程无实数根。
【小试牛刀】方程ax2+bx+c=0的根为④因式分解法·因式分解法解一元二次方程的依据:如果两个因式的积等于0,那么这两个因式至少有一个0,即:若ab=0,则a=0或b=0。
·步骤:(1)将方程化为一元二次方程的一般形式。
(2)把方程的左边分解为两个一次因式的积,右边等于0。
(3)令每一个因式都为零,得到两个一元一次方程。
(4)解出这两个一元一次方程的解,即可得到原方程的两个根。
根的判别情况判别式:b2-4ac的值x1、x2的关系根的具体值一元二次方程两根与系数的关系:。
《一元二次方程》各节知识点及典型例题

第二章 一元二次方程第一节 一元二次方程 第二节 一元二次方程的解法 第三节 一元二次方程的应用 第四节 一元二次方程根与系数的关系 五大知识点:1、一元二次方程的定义、一元二次方程的一般形式、一元二次方程的解的概念及应用2、一元二次方程的四种解法(因式分解法、开平方法和配方法、配方法的拓展运用、公式法)3、根的判别式4、一元二次方程的应用(销售问题和增长率问题、面积问题和动态问题)5、一元二次方程根与系数的关系(韦达定理)【课本相关知识点】1、一元二次方程:只含有 未知数,并且未和数的 是2,这样的整式方程叫做一元二次方程。
2、能使一元二次方程 的未知数的值叫做一元二次方程的解(或根)3、一元二次方程的一般形式:任何一个一元二次方程经过化简、整理都可以转化为 的形式,这个形式叫做一元二次方程的一般形式。
其中ax 2是 ,a 是 ,bx 是 ,b 是 ,c是常数项【典型例题】【题型一】应用一元二次方程的定义,求字母的值例1、当a 为何值时,关于x 的方程(a-1)x |a|+1+2x-7=0是一元二次方程?【题型二】一元二次方程解的应用例1、关于x 的一元二次方程(a-1)x 2+x+|a|-1=0的一个根是0,则实数a 的值为( )A .-1B .0C .-1D .-1或1例2、已知多项式ax 2-bx+c ,当x=1时,它的值是0;当x=-2时,它的值是1(1)试求a+b 的值(2)直接写出关于x 的一元二次方程ax 2+bx+c=0的一个根【题型三】一元二次方程拓展开放型题例1、已知关于x 的方程(k 2-1)x 2-(k+1)x-2=0(1)当k 取何值时,此方程为一元一次方程?并求出此方程的根(2)当k 取何值时,此方程为一元二次方程?并写出这个一元二次方程的二次项系数、一次项系数、常数项。
巩 固 练 习1、下列方程中,是一元二次方程的为( )A. x 2= -1B. 2x (x-1)+1=2x 2C. x 2+3x=2x D. ax 2+bx+c-0 2、已知关于x 的方程mx 2+(m-1)x-1=2x 2-x ,当m 取什么值时,这个方程是一元二次方程?3、若关于x 的一元二次方程(a-2)x 2是一元二次方程,则a 的取值范围是4、把方程 (x-1)2-3x (x-2)=2(x+2)+1化成一般形式,并写出它的二次项系数、一次项系数和常数项5、若a 是方程x 2-3x+1=0的一个根,求2a 2-5a-2+231a +的值 6、若关于x 的方程ax 2+bx+c=0(a ≠0)中,abc 满足a+b+c=0和a-b+c=0,则方程的根是( )A. 1,0B. -1,0C. 1,-1D. 1,27、已知x=1是一元二次方程ax 2+bx-40=0的一个解,且a ≠b ,求2222a b a b --的值【课本相关知识点】(一)1、利用因式分解的方法实现“降次”,把解一元二次方程转化为解一元一次方程的方法,叫做因式分解法。
一元二次方程知识点及考点精析

一元二次方程知识点及考点精析一、知识结构: 一元二次方程⎪⎩⎪⎨⎧*⇒韦达定理根的判别解与解法二、考点精析(1)定义:只含有一个未知数........,并且②未知数的最高次数是.........2.,这样的③整式方程....就是一元二次方程。
(2)一般表达式:)0(02≠=++a c bx ax 其中2ax 是二次项,a 叫二次项系数;bx 是一次项,b 叫一次项系数,c 是常数项。
二次项系数、一次项系数及常数项都是方程在一般形式下定义的,所以求一元二次方程的各项系数时,必须先将方程化为一般形式。
①该项系数不为“0”; ②未知数指数为“2”;③若存有某项指数为待定系数,或系数也有待定,则需建立方程或不等式加以讨论。
典型例题:例1、下列方程中是关于x 的一元二次方程的是( )A ()()12132+=+x xB 02112=-+x xC 02=++c bx axD 1222+=+x x x 变式:当k 时,关于x 的方程3222+=+x x kx 是一元二次方程。
例2、方程()0132=+++mx x m m 是关于x 的一元二次方程,则m 的值为 。
★1、方程782=x 的一次项系数是 ,常数项是 。
★2、若方程()021=--m xm 是关于x 的一元一次方程,⑴求m 的值;⑵写出关于x 的一元一次方程。
★★3、若方程()112=•+-x m x m 是关于x 的一元二次方程,则m 的取值范围是 。
★★★4、若方程nx m +x n -2x 2=0是一元二次方程,则下列不可能的是( )B.m=2,n=1C.n=2,m=1D.m=n=1⑴概念:使方程两边相等的未知数的值,就是方程的解。
⑵应用:利用根的概念求代数式的值;例1、已知322-+y y 的值为2,则1242++y y 的值为 。
例2、关于x 的一元二次方程()04222=-++-a x x a 的一个根为0,则a 的值为 。
例3、已知关于x 的一元二次方程()002≠=++a c bx ax 的系数满足b c a =+,则此方程必有一根为 。
初中数学一元二次方程知识点总结(含方法技巧归纳,易错辨析)

初中数学⼀元⼆次⽅程知识点总结(含⽅法技巧归纳,易错辨析)
考情分析⾼频考点考查频率所占分值
1.元⼆次⽅程的概念★7~12分
2.⼀元⼆次⽅程的解法★★★
3.⼀元⼆次⽅程根的判别式★★
4.⼀元⼆次⽅程根与系数的关系★
5.利⽤⼀元⼆次⽅程解决实际问题★★★
1⼀元⼆次⽅程的定义及⼀般形式
定义:等号两边都是整式,只含有⼀个未知数(⼀元),并且未知数的最⾼次数是2(⼆次)的⽅程,
叫作⼀元⼆次⽅程.
点拨
对定义的理解抓住三个条件:“⼀元”“⼆次”“整式⽅程”,缺⼀不可,同时强调⼆次项的系数不为0.
⽤公式法解⼀元⼆次⽅程的记忆⼝诀
要⽤公式解⽅程,⾸先化成⼀般式.
调整系数随其后,使其成为最简⽐.
确定参数
,计算⽅程判别式.
判别式值与零⽐,有⽆实根便得知.
若有实根套公式,若⽆实根要告之.
3因式分解法
通过因式分解,使⼀元⼆次⽅程化为两个⼀次式的乘积等于0的形式,再使这两个⼀次式分别等
于0,从⽽实现降次,这种解⼀元⼆次⽅程的⽅法叫作因式分懈法.
因式分解法体现了将⼀元⼆次⽅程“降次”转化为⼀元⼀次⽅程来解的思想,运⽤这种⽅法的步
骤:
(1)将所有项移到⽅程的左边,将⽅程的右边化为0;
(2)将⽅程左边分解为两个⼀次因式的乘积;
(3)令每个因式分别等于零,得到两个⼀元⼀次⽅程;
(4)解这两个⼀元⼀次⽅程,他们的解就是原⽅程的解.。
(完整版)一元二次方程根的判别式知识点
一元二次方程根的判别式知识点及应用1、一元二次方程ax²+bx+c=0(a≠0)的根的判别式定理:在一元二次方程ax²+bx+c=0(a≠0)中,Δ=b²4ac若△>0则方程有两个不相等的实数根若△=0则方程有两个相等的实数根若△<0则方程没有实数根2、这个定理的逆命题也成立,即有如下的逆定理:在一元二次方程ax²+bx+c=0(a≠0)中,Δ=b²4ac若方程有两个不相等的实数根,则△>0若方程有两个相等的实数根,则△=0若方程没有实数根,则△<0特别提示:(1)注意根的判别式定理与逆定理的使用区别:一般当已知△值的符号时,使用定理;当已知方程根的情况时,使用逆定理。
(2)一元二次方程ax²+bx+c=0(a≠0)(Δ=b²4ac)一、不解方程,判断一元二次方程根的情况。
例1、判断下列方程根的情况2x2+x━1=0;x2—2x—3=0;x2—6x+9=0;2x2+x+1=0二、已知一元二次方程根的情况,求方程中字母系数所满足的条件。
例2、当m为何值时关于x的方程(m—4)x2—(2m—1)x+m=0 有两个实数根?三、证明方程根的性质。
例3、求证:无论m为任何实数,关于x的方程x2+(m2+3)x+0.5(m2+2)=0恒有两个不相等的实数根。
四、判断二次三项式能否在实数范围内因式分解。
例4、当m为何值时,关于x的二次三项式mx2-2(m+2)x+(m+5)能在实数范围内因式分解。
五、判定二次三项式为完全平方式。
例5、若x2-2(k+1)x+k2+5是完全平方式,求k的值。
例6、当m为何值时,代数式(5m-1)x2-(5m+2)x+3m—2是完全平方式。
六、利用判别式构造一元二次方程。
例7、已知:(z-x)2-4(x-y)(y-z)=0(x≠y)求证:2y=x+z七、限制一元二次方程的根与系数关系的应用。
例8、已知关于x的方程x2-(k-1)x-3k-2=0的两个实数根的平方和为17,求k的值。
(完整版)一元二次方程知识点总结

一元二次方程1、一元二次方程:含有一个未知数,并且未知数的最高次数是2的整式方程叫做一元二次方程。
2、一元二次方程的一般形式:,它的特征是:等式左边十一个关)0(02≠=++a c bx ax 于未知数x 的二次多项式,等式右边是零,其中叫做二2ax 次项,a 叫做二次项系数;bx 叫做一次项,b 叫做一次项系数;c 叫做常数项。
3.一元二次方程的解法(1)直接开平方法:利用平方根的定义直接开平方求一元二次方程的解的方法叫做直接开平方法。
直接开平方法适用于解形如的一元二次方程。
根据b a x =+2)(平方根的定义可知,是b 的平方根,当时,,a x +0≥b b a x ±=+,当b<0时,方程没有实数根。
b a x ±-=(2)配方法:配方法的理论根据是完全平方公式,把公式中的a 看222)(2b a b ab a +=+±做未知数x ,并用x 代替,则有。
222)(2b x b bx x ±=+±配方法的步骤:先把常数项移到方程的右边,再把二次项的系数化为1,再同时加上1次项的系数的一半的平方,最后配成完全平方公式(3)公式法:公式法是用求根公式解一元二次方程的解的方法,它是解一元二次方程的一般方法。
一元二次方程的求根公式:)0(02≠=++a c bx ax )04(2422≥--±-=ac b aac b b x 公式法的步骤:就把一元二次方程的各系数分别代入,这里二次项的系数为a ,一次项的系数为b ,常数项的系数为c(4)因式分解法:因式分解法就是利用因式分解的手段,求出方程的解的方法,这种方法简单易行,是解一元二次方程最常用的方法。
分解因式法的步骤:把方程右边化为0,然后看看是否能用提取公因式,公式法(这里指的是分解因式中的公式法)或十字相乘,如果可以,就可以化为乘积的形式4.一元二次方程根的判别式:一元二次方程中,叫做一)0(02≠=++a c bx ax ac b 42-元二次方程的根的判别式,通常用“)0(02≠=++a c bx ax ”来表示,即∆acb 42-=∆I 当△>0时,一元二次方程有2个不相等的实数根;II 当△=0时,一元二次方程有2个相同的实数根;III 当△<0时,一元二次方程没有实数根5.一元二次方程根与系数的关系如果方程的两个实数根是,那么,)0(02≠=++a c bx ax 21x x ,ab x x -=+21。
(完整版)一元二次方程知识点及其应用

一、相关知识点1.理解并掌握一元二次方程的意义未知数个数为1,未知数的最高次数为2,整式方程,可化为一般形式; 2.正确识别一元二次方程中的各项及各项的系数(1)明确只有当二次项系数0≠a 时,整式方程02=++c bx ax 才是一元二次方程。
(2)各项的确定(包括各项的系数及各项的未知数). (3)熟练整理方程的过程3.一元二次方程的解的定义与检验一元二次方程的解 4.列出实际问题的一元二次方程二.解法1.明确一元二次方程是以降次为目的,以配方法、开平方法、公式法、因式分解法等方法为手段,从而把一元二次方程转化为一元一次方程求解;2.根据方程系数的特点,熟练地选用配方法、开平方法、公式法、因式分解法等方法解一元二次方程; 3.体会不同解法的相互的联系; 4.值得注意的几个问题:(1)开平方法:对于形如n x =2或)0()(2≠=+a n b ax 的一元二次方程,即一元二次方程的一边是含有未知数的一次式的平方,而另一边是一个非负数,可用开平方法求解. 形如n x =2的方程的解法: 当0>n 时,n x ±=; 当0=n 时,021==x x ; 当0<n 时,方程无实数根。
(2)配方法:通过配方的方法把一元二次方程转化为n m x =+2)(的方程,再运用开平方法求解。
配方法的一般步骤:①移项:把一元二次方程中含有未知数的项移到方程的左边,常数项移到方程的右边; ②“系数化1”:根据等式的性质把二次项的系数化为1; ③配方:将方程两边分别加上一次项系数一半的平方,把方程变形为n m x =+2)(的形式; ④求解:若0≥n 时,方程的解为n m x ±-=,若0<n 时,方程无实数解。
(3)公式法:一元二次方程)0(02≠=++a c bx ax 的根aac b b x 242-±-=当042>-ac b 时,方程有两个实数根,且这两个实数根不相等;当042=-ac b 时,方程有两个实数根,且这两个实数根相等,写为ab x x 221-==;当042<-ac b 时,方程无实数根.公式法的一般步骤:①把一元二次方程化为一般式;②确定c b a ,,的值;③代入ac b 42-中计算其值,判断方程是否有实数根;④若042≥-ac b 代入求根公式求值,否则,原方程无实数根。
一元二次方程知识点归纳

②销售问题;利润问题,利润=售价-成本;利润率=利润/成本×100%;
③比赛问题:
④面积问题:a.直接利用相应图形的面积公式列方程;b.将不规则图形通过割补或平移形成规则图形,运用面积之间的关系列方程.
例:方程 是关于x的一元二次方程,则方程的根为-1.
2.一元二次方程的解法
(1)直接开平方法:形如(x+m)2=n(n≥0)的方程,可直接开平方求解.
(2 )因式分解法:可化为(ax+m)(bx+n)=0的方程,用因式分解法求解.
(3)公式法:一元二次方程ax2+bx+c=0的求根公式为x= (b2-4ac≥0).
一元二次方程知识点
一、知识清单梳理
知识点一:一元二次方程及其解法
关键点拨及对应举例
1.一元二次方程的相关概念
(1)定义:只含有一个未知数=0(a≠0),其中ax2、bx、c分别叫做二次项、一次项、常数项,a、b、c分别称为二次项系数、一次项系数、常数项.
(2)解题策略:已知一元二次方程,求关于方程两根的代数式的值时,先把所求代数式变形为含有x1+x2、x1x2的式子,再运用根与系数的关系求解.
与一元二次方程两根相关代数式的常见变形:x12+x22=(x1+x2)2-2x1x2,
(x1+1)(x2+1)=x1x2+(x1+x2)+1,
等.
失分点警示
在运用根与系数关系解题时,注意前提条件时△=b2-4ac≥0.a≠0
3.根的判别式
(1)当Δ= 0时,原方程有两个不相等的实数根.
一元二次方程(知识点+考点+题型总结)

一元二次方程专题复习考点一、概念(1)定义:①只含有一个未知数........,并且②未知数的最高次数是.........2.,这样的③整式方程....就是一元二次方程。
(2)一般表达式:)0(02≠=++a c bx ax⑶难点:如何理解 “未知数的最高次数是2”:①该项系数不为“0〞;②未知数指数为“2〞;③假设存在某项指数为待定系数,或系数也有待定,那么需建立方程或不等式加以讨论。
典型例题:例1、以下方程中是关于x 的一元二次方程的是〔 〕A ()()12132+=+x x B 02112=-+xx C 02=++c bx ax D 1222+=+x x x变式:当k 时,关于x 的方程3222+=+x x kx 是一元二次方程。
例2、方程()0132=+++mx x m m是关于x 的一元二次方程,那么m 的值为 。
针对练习: ★1、方程782=x 的一次项系数是 ,常数项是 。
★2、假设方程()021=--m x m 是关于x 的一元一次方程,⑴求m 的值;⑵写出关于x 的一元一次方程。
★★3、假设方程()112=•+-x m x m 是关于x 的一元二次方程,那么m 的取值范围是 。
★★★4、假设方程nx m +x n -2x 2=0是一元二次方程,那么以下不可能的是〔 〕 A.m=n=2 B.m=2,n=1 C.n=2,m=1 D.m=n=1考点二、方程的解⑴概念:使方程两边相等的未知数的值,就是方程的解。
⑵应用:利用根的概念求代数式的值;典型例题:例1、322-+y y的值为2,那么1242++y y 的值为 。
例2、关于x 的一元二次方程()04222=-++-a x x a 的一个根为0,那么a 的值为 。
例3、关于x 的一元二次方程()002≠=++a c bx ax 的系数满足b c a =+,那么此方程必有一根为 。
例4、b a ,是方程042=+-m x x 的两个根,c b ,是方程0582=+-m y y 的两个根, 那么m 的值为 。
(完整版)一元二次方程知识点和易错点总结
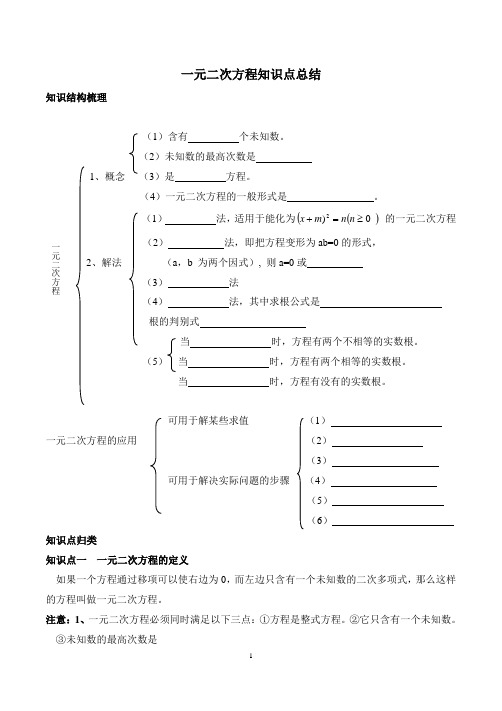
一元二次方程知识点总结知识结构梳理(1)含有 个未知数。
(2)未知数的最高次数是 1、概念 (3)是 方程。
(4)一元二次方程的一般形式是 。
(1) 法,适用于能化为)((0)2≥=+n n m x 的一元二次方程 (2) 法,即把方程变形为ab=0的形式,2、解法 (a ,b 为两个因式), 则a=0或(3) 法(4) 法,其中求根公式是 根的判别式当 时,方程有两个不相等的实数根。
(5) 当 时,方程有两个相等的实数根。
当 时,方程有没有的实数根。
可用于解某些求值 (1) 一元二次方程的应用 (2)(3)可用于解决实际问题的步骤 (4) (5)(6)知识点归类知识点一 一元二次方程的定义如果一个方程通过移项可以使右边为0,而左边只含有一个未知数的二次多项式,那么这样的方程叫做一元二次方程。
注意:1、一元二次方程必须同时满足以下三点:①方程是整式方程。
②它只含有一个未知数。
③未知数的最高次数是一元二次方程2、同时还要注意在判断时,需将方程化成一般形式。
例 下列关于x 的方程,哪些是一元二次方程?⑴3522=+x ;⑵062=-x x ;(3)5=+x x ;(4)02=-x ;(5)12)3(22+=-x x x知识点二 一元二次方程的一般形式一元二次方程的一般形式为02=++c bx ax (a ,b ,c 是已知数,0≠a )。
其中a ,b ,c 分别叫做二次项系数、一次项系数、常数项。
注意:(1)二次项、二次项系数、一次项、一次项系数,常数项都包括它前面的符号。
(2)要准确找出一个一元二次方程的二次项系数、一次项系数和常数项,必须把它先化为一般形式。
(3)形如02=++c bx ax 不一定是一元二次方程,当且仅当0≠a 时是一元二次方程。
例1 已知关于x 的方程()()021122=-+--+x m x m m 是一元二次方程时,则=m知识点三 一元二次方程的解使方程左、右两边相等的未知数的值叫做方程的解,如:当2=x 时,0232=+-x x 所以2=x 是0232=+-x x 方程的解。
完整版一元二次方程知识点总结和例题复习
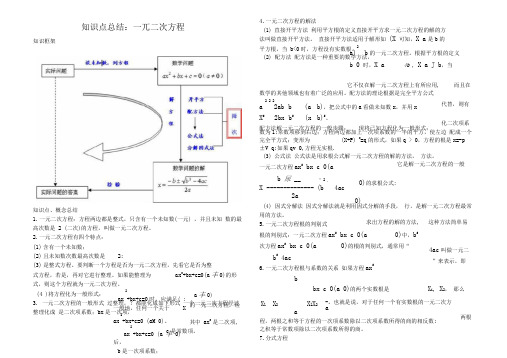
知识框架 知识点总结:一兀二次方程4. 一元二次方程的解法(1) 直接开平方法 利用平方根的定义直接开平方求一元二次方程的解的方法叫做直接开平方法。
直接开平方法适用于解形如 (X 可知,X a 是b 的平方根,当 b<0时,方程没有实数根。
(2) 配方法 配方法是一种重要的数学方法,2a) b 的一元二次方程。
根据平方根的定义b 0 时,X a4b , X a J b ,当它不仅在解一元二次方程上有所应用,而且在数学的其他领域也有着广泛的应用。
配方法的理论根据是完全平方公式2 2 2a 2ab b (a b),把公式中的a 看做未知数x ,并用x X 2 2bx b 2(x b)2。
配方法解一元二次方程的一般步骤: 现将已知方程化为一般形式;代替,则有 化二次项系知识点、概念总结 1. 一元二次方程:方程两边都是整式,只含有一个未知数(一元) ,并且未知 数的最高次数是 2 (二次)的方程,叫做一元二次方程。
2. 一元二次方程有四个特点:(1) 含有一个未知数; (2) 且未知数次数最高次数是 2; (3) 是整式方程。
要判断一个方程是否为一元二次方程,先看它是否为整 式方程,若是,再对它进行整理。
如果能整理为 ax 2+bx+c=0(a 丰0)的形 式,则这个方程就为一元二次方程。
(4 )将方程化为一般形式: 3. 一元二次方程的一般形式 过整理,?都能化成如下形式 一个一元二次方程经过整理化成 是二次项系数;bx 是一次项, 2ax +bx+c=0时,应满足( :一般地,任何一个关于 X 2ax +bx+c=0 (aM 0)。
2ax +bx+c=0 (a 丰 0)后,b 是一次项系数;a 丰0) 的一元二次方程,经其中ax 2是二次项,c 是常数项。
数为1;常数项移到右边;方程两边都加上一次项系数的一半的平方,使左边 配成一个完全平方式;变形为 (X+P) 2=q 的形式,如果q > 0,方程的根是x=-p ±V q ;如果qv 0,方程无实根.(3) 公式法 公式法是用求根公式解一元二次方程的解的方法, 方法。
(完整版)一元二次方程知识点总结

一元二次方程1. 一元二次方程的定义及一般形式:(1)等号两边都是整式,只含有一个未知数(一元),并且未知数的最高次数式2 (二次)的方程,叫做一元二次方程。
(2)一元二次方程的一般形式:ax2 bx c 0(a 0)。
其中a为二次项系数,b为一次项系数,c为常数项。
注意:三个要点,①只含有一个未知数;②所含未知数的最高次数是2;③是整式方程。
2. 一元二次方程的解法(1 )直接开平方法:形如(x a)2 b(b 0)的方程可以用直接开平方法解,两边直接开平方得x a b或者x a 、、b,x a , b。
注意:若b<0,方程无解(2)因式分解法:一般步骤如下:①将方程右边得各项移到方程左边,使方程右边为0 ;②将方程左边分解为两个一次因式相乘的形式;③令每个因式分别为零,得到两个一元一次方程;④解这两个一元一次方程,他们的解就是原方程的解。
(3)配方法:用配方法解一元二次方程ax2 bx c 0(a 0)的一般步骤①二次项系数化为1:方程两边都除以二次项系数;②移项:使方程左边为二次项与一次项,右边为常数项;③配方:方程两边都加上一次项系数一般的平方,把方程化为(x m)2 n(n 0)的形式;④用直接开平方法解变形后的方程。
注意:当n 0时,方程无解(4)公式法:一元二次方程ax2 bx c 0(a 0)根的判别式:b24ac0方程有两个不相等的实根:x b甘4/( b2 4ac 0)2af(x)的图像与x轴有两个交点0方程有两个相等的实根f(x)的图像与x轴有一个交点0方程无实根f(x)的图像与x轴没有交点3. 韦达定理(根与系数关系)我们将一元二次方程化成一般式ax2+bx+c = 0之后,设它的两个根是x i 和X2,则&和X2与方程的系数a, b, c之间有如下关系:X i+X2 = b;X i?X2 = 2a a4. 一元二次方程的应用列一元二次方程解应用题,其步骤和二元一次方程组解应用题类似①“审”,弄清楚已知量,未知量以及他们之间的等量关系;②“设”指设元,即设未知数,可分为直接设元和间接设元;③“列”指列方程,找出题目中的等量关系,再根据这个关系列出含有未知数的等式,即方程。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、相关知识点1.理解并掌握一元二次方程的意义未知数个数为1,未知数的最高次数为2,整式方程,可化为一般形式; 2.正确识别一元二次方程中的各项及各项的系数(1)明确只有当二次项系数0≠a 时,整式方程02=++c bx ax 才是一元二次方程。
(2)各项的确定(包括各项的系数及各项的未知数). (3)熟练整理方程的过程3.一元二次方程的解的定义与检验一元二次方程的解 4.列出实际问题的一元二次方程二.解法1.明确一元二次方程是以降次为目的,以配方法、开平方法、公式法、因式分解法等方法为手段,从而把一元二次方程转化为一元一次方程求解;2.根据方程系数的特点,熟练地选用配方法、开平方法、公式法、因式分解法等方法解一元二次方程; 3.体会不同解法的相互的联系; 4.值得注意的几个问题:(1)开平方法:对于形如n x =2或)0()(2≠=+a n b ax 的一元二次方程,即一元二次方程的一边是含有未知数的一次式的平方,而另一边是一个非负数,可用开平方法求解. 形如n x =2的方程的解法: 当0>n 时,n x ±=; 当0=n 时,021==x x ; 当0<n 时,方程无实数根。
(2)配方法:通过配方的方法把一元二次方程转化为n m x =+2)(的方程,再运用开平方法求解。
配方法的一般步骤:①移项:把一元二次方程中含有未知数的项移到方程的左边,常数项移到方程的右边; ②“系数化1”:根据等式的性质把二次项的系数化为1; ③配方:将方程两边分别加上一次项系数一半的平方,把方程变形为n m x =+2)(的形式; ④求解:若0≥n 时,方程的解为n m x ±-=,若0<n 时,方程无实数解。
(3)公式法:一元二次方程)0(02≠=++a c bx ax 的根aac b b x 242-±-=当042>-ac b 时,方程有两个实数根,且这两个实数根不相等;当042=-ac b 时,方程有两个实数根,且这两个实数根相等,写为ab x x 221-==;当042<-ac b 时,方程无实数根.公式法的一般步骤:①把一元二次方程化为一般式;②确定c b a ,,的值;③代入ac b 42-中计算其值,判断方程是否有实数根;④若042≥-ac b 代入求根公式求值,否则,原方程无实数根。
(因为这样可以减少计算量。
另外,求根公式对于任何一个一元二次方程都适用,其中也包括不完全的一元二次方程。
)(4)因式分解法:①因式分解法解一元二次方程的依据:如果两个因式的积等于0,那么这两个因式至少有一个为0,即:若0=ab ,则00==b a 或; ②因式分解法的一般步骤:若方程的右边不是零,则先移项,使方程的右边为零;把方程的左边分解因式;令每一个因式都为零,得到两个一元一次方程;解出这两个一元一次方程的解可得到原方程的两个解。
(5)选用适当方法解一元二次方程①对于无理系数的一元二次方程,可选用因式分解法,较之别的方法可能要简便的多,只不过应注意二次根式的化简问题。
②方程若含有未知数的因式,选用因式分解较简便,若整理为一般式再解就较为麻烦。
(6)解含有字母系数的方程(1)含有字母系数的方程,注意讨论含未知数最高项系数,以确定方程的类型;(2)对于字母系数的一元二次方程一般用因式分解法解,不能用因式分解的可选用别的方法,此时一定不要忘记对字母的取值进行讨论。
三、根的判别式1.了解一元二次方程根的判别式概念,能用判别式判定根的情况,并会用判别式求一元二次方程中符合题意的参数取值范围。
(1)∆=ac b 42-(2)根的判别式定理及其逆定理:对于一元二次方程02=++c bx ax (0≠a ) ①当⎩⎨⎧≥∆≠时00a ⇔方程有实数根;(当⎩⎨⎧>∆≠时00a ⇔方程有两个不相等的实数根;当⎩⎨⎧=∆≠时00a ⇔方程有两个相等的实数根;) ②当⎩⎨⎧<∆≠时00a ⇔方程无实数根;从左到右为根的判别式定理;从右到左为根的判别式逆定理。
2.常见的问题类型(1)利用根的判别式定理,不解方程,判别一元二次方程根的情况(2)已知方程中根的情况,如何由根的判别式的逆定理确定参数的取值范围 (3)应用判别式,证明一元二次方程根的情况②用配方法将判别式恒等变形; ③判断判别式的符号; ④总结出结论.(4)分类讨论思想的应用:如果方程给出的时未指明是二次方程,后面也未指明两个根,那一定要对方程进行分类讨论,如果二次系数为0,方程有可能是一元一次方程;如果二次项系数不为0,一元二次方程可能会有两个实数根或无实数根。
(5)一元二次方程根的判别式常结合三角形、四边形、不等式(组)等知识综合命题,解答时要在全面分析的前提下,注意合理运用代数式的变形技巧 (6)一元二次方程根的判别式与整数解的综合 (7)判别一次函数与反比例函数图象的交点问题四、一元二次方程的应用1.数字问题:解答这类问题要能正确地用代数式表示出多位数,奇偶数,连续整数等形式。
2.几何问题:这类问题要结合几何图形的性质、特征、定理或法则来寻找等量关系,构建方程,对结果要结合几何知识检验。
3.增长率问题(下降率):在此类问题中,一般有变化前的基数(a ),增长率(x ),变化的次数(n ),变化后的基数(b ),这四者之间的关系可以用公式b x a n=+)1(表示。
4.其它实际问题(都要注意检验解的实际意义,若不符合实际意义,则舍去)。
五.实际应用(1)有100米长的篱笆材料,想围成一矩形仓库,要求面积不小于600平方米,在场地的北面有一堵50米的旧墙,有人用这个篱笆围成一个长40米、宽10米的仓库,但面积只有400平方米,不合要求,问应如何设计矩形的长与宽才能符合要求呢?(2)读诗词解题(列出方程,并估算出周瑜去世时的年龄):大江东去浪淘尽,千古风流数人物,而立之年督东吴,英年早逝两位数,十位恰小个位三,个位平方与寿符,哪位学子算得准,多少年华属周瑜?(36岁)(3)已知:c b a ,,分别是ABC ∆的三边长,当0>m 时,关于x 的一元二次方程02)()(22=--++ax m m x b m x c 有两个相等的实数根,求证:ABC ∆是直角三角形。
(4)已知:c b a ,,分别是ABC ∆的三边长,求证:方程0)(222222=+-++c x a c b x b 没有实数根。
(5)当m 是什么整数时,关于x 的一元二次方程0442=+-x mx 与0544422=--+-m m mx x 的根都是整数?(1=m )(6)已知关于x 的方程02212222=-+-++mx x m x x ,其中m 为实数,(1)当m 为何值时,方程没有实数根?(2)当m 为何值时,方程恰有三个互不相等的实数根?求出这三个实数根。
答案:(1)2-<m (2)21,1±--=x .(二)一元二次方程的解法 1.开平方法解下列方程:(1)012552=-x (5,521-==x x ) (2)289)3(1692=-x (1322,135621==x x )(3)03612=+y (原方程无实根) (4)0)31(2=-m (021==m m )2.配方法解方程:(1)0522=-+x x (61±-=x ) (2)0152=++y y (2215±-=x )3.公式法解下列方程:(1)2632-=x x (333±=x ) (2)p p 3232=+ (321==p p )4.因式分解法解下列方程: (1)09412=-x (6±=x ) (2)04542=-+y y (5,921=-=y y )(3)031082=-+x x (23,4121-==x x ) (4)02172=-x x (3,021==x x )5.解法的灵活运用(用适当方法解下列方程):(1)128)72(22=-x (227±=x ) (2)222)2(212m m m m -=+-(262±=m )6.解含有字母系数的方程(解关于x 的方程):(1)02222=-+-n m mx x (n m x n m x +=-=21,)(2)124322+-=+a ax a x (1,1321+=-=a x a x )(三)一元二次方程的根的判别式 1.不解方程判别方程根的情况:(1)4x x x 732=+-(有两个不等的实数根) (2)x x 4)2(32=+ (无实数根)2.k 为何值时,关于x 的二次方程0962=+-x kx (1)有两个不等的实数根 (01≠<k k 且) (2)有两个相等的实数根 (1=k )3.已知关于x的方程m x m x -=+-1)2(42有两个相等的实数根.求m的值和这个方程的根.(21,221===x x m 或23,1021===x x m )4.若方程054)1(222=-++++a a x a x 有实数根,求:正整数a. (3,2,1===a a a )5.对任意实数m ,求证:关于x 的方程042)1(222=++-+m mx x m 无实数根.6.k 为何值时,方程0)3()32()1(2=+++--k x k x k 有实数根.7.设m 为整数,且404<<m 时,方程08144)32(222=+-+--m m x m x 有两个相异整数根,求m 的值及方程的根。
(当m =12时,方程的根为26,1621==x x ;当m =24时,方程的根为52,3821==x x )3.某商场销售一批名牌衬衫,平均每天可以售出20件,每件盈利40元,为了扩大销售增加盈利,尽快减少库存,商场决定采取适当降价措施,经调查发现,如果每件衬衫每降价1元,商场每天可多售出2件,若商场平均每天要盈利1200元,每件衬衫应降价多少元? (20元)4.已知甲乙两人分别从正方形广场ABCD 的顶点B 、C 同时出发,甲由C 向D 运动,乙由B 向C 运动,甲的速度为每分钟1千米,乙的速度每分钟2千米,若正方形广场周长为40千米,问几分钟后,两人相距102千米? (2分钟后)7.某科技公司研制一种新产品,决定向银行贷款200万元资金,用于生产这种产品,签订的合同上约定两年到期时一次性还本付息,利息为本金的8%,该产品投放市场后由于产销对路,使公司在两年到期时除还清贷款的本金和利息外,还盈余72万元,若该公司在生产期间每年比上一年资金增长的百分数相同,试求这个百分数. (20%)8.如图,东西和南北向两条街道交于O 点,甲沿东西道由西向东走, 速度是每秒4米,乙沿南北道由南向北走,速度是每秒3米,当乙通 过O 点又继续前进50米时,甲刚好通过O 点,求这两人在相距85米 时,每个人的位置。
