金属线胀系数和冰的溶解热
金属线胀系数

金属线胀系数的测定实验目的:1)学会用千分表法测量金属杆长度的微小变化2)测量金属杆的线胀系数,并判断此金属为何种金属实验仪器:实验原理:大家都知道热胀冷缩的现象,一般固体的长度或体积会随着温度的升高而膨胀,这就是固体的热膨胀。
设物体的温度改变Δt 时,其长度改变量为ΔL,如果Δt 足够小,则Δt 与ΔL 成正比,并且也与物体的原长有关系。
因此它们三个量之间有:ΔL=αL Δt式中的比例系数α称为固体的线胀系数,其物理意义是温度每升高1℃时其伸长量与它在0℃时长度的比。
设金属在0℃时的长度是L0,当温度升高为t ℃时其长度为Lt,则有:(Lt-L0)/L0=αt 即Lt=L0(1+αt)如果金属杆在温度为t1,t2时的长度分别为L1,L2,则可加热箱恒温控制仪以得到:L1=L0(1+αt1),L2=L0(1+αt2)因为L1,L2非常接近,所以得到下式:α=(L2-L1)/L0(t2-t1)由上式测得L1,L2,t1,t2就可以测得α值了。
实验过程: 1)接好电源和各个接口。
2)打开恒温控制仪,记录室温t1,再设定温度最大值,再记录此时千分表读数n1,最后按下确定键开始加热。
(实验所用金属杆0℃时长度为400mm)3)每隔5℃读一次数tn ,同时记录千分表读数n n 。
4) 将数据整理填入设计好的表格中,待处理。
实验数据记录与处理: t1=21℃L0=400mm n1=0.4012mm tn/℃ 26 3136 41 46 51 tn-t1/℃ 510 15 20 25 30 nn /mm 0.4630 0.5119 0.553 0.591 0.624 0.658 nn -n1/mm 0.062 0.111 0.152 0.19 0.223 0.26以nn-n1为横坐标,tn-t1为纵坐标作出曲线:由关系式可得直线的斜率即为:αL0,通过直线先求出斜率k 的大小,再计算α的值得α=1.975*e-5以上是通过作图法求斜率计算线胀系数α,下面通过逐差法 求线胀系数: 计数次数 12 3 4 5 ni 0.4012 0.46300.5119 0.5530 0.5912 计数次数 3 45 6 7 n(i+2) 0.5119 0.55300.5912 0.6240 0.6582 Δn 0.1107 0.09 0.0793 0.071 0.0675n n ∑∆=∆代入数据得n ∆=0.0836mm 。
初二物理金属的热膨胀计算

初二物理金属的热膨胀计算金属的热膨胀是指金属在温度变化时,由于分子间的热运动引起了体积的变化。
研究金属的热膨胀对于工程设计和材料科学至关重要。
本文将介绍金属的线膨胀和面膨胀的计算方法。
一、线膨胀的计算金属的线膨胀是指在一维方向上的长度变化。
我们可以通过以下公式来计算金属的线膨胀量:ΔL = L0 × α × ΔT其中,ΔL为长度变化量,L0为初始长度,α为线膨胀系数,ΔT为温度变化量。
线膨胀系数α是一个特定金属在每摄氏度温度变化时的长度变化比例。
不同金属有不同的线膨胀系数,可通过参考资料获得。
例如,铜的线膨胀系数为0.000016/℃,铁的线膨胀系数为0.000012/℃。
使用正确的线膨胀系数是计算线膨胀量的前提。
举例来说,假设一根铜杆的初始长度为2m,温度上升了50℃,我们可以通过以下计算求得铜杆的线膨胀量:ΔL = 2m × 0.000016/℃ × 50℃ = 0.0016m = 1.6mm所以,铜杆的长度在温度上升50℃后增加了1.6mm。
二、面膨胀的计算金属的面膨胀是指在二维平面上的面积变化。
与线膨胀类似,我们可以通过以下公式来计算金属的面膨胀量:ΔS = S0 × β × ΔT其中,ΔS为面积变化量,S0为初始面积,β为面膨胀系数,ΔT为温度变化量。
面膨胀系数β是一个特定金属在每摄氏度温度变化时的面积变化比例。
与线膨胀系数类似,不同金属有不同的面膨胀系数,可通过参考资料获得。
举例来说,假设一个铝制方板的初始面积为1m²,温度上升了100℃,我们可以通过以下计算求得铝板的面膨胀量:ΔS = 1m² × 0.000022/℃ × 100℃ = 0.0022m² = 2200cm²所以,铝板的面积在温度上升100℃后增加了2200cm²。
三、金属热膨胀的应用金属的热膨胀在工程设计和制造过程中有广泛的应用。
常用金属材料的线胀系数

常用金属材料的线胀系数线胀系数是指材料在温度变化时的长度变化率,常用于计算材料在温度变化下的热膨胀量。
线胀系数与材料的热膨胀性能密切相关,不同金属材料具有不同的线胀系数。
以下是常用金属材料的线胀系数:1.铝(Al):线胀系数为23.1×10^-6/℃,具有较高的导热性和导电性,常用于制造轻型结构和电气导线。
2.铜(Cu):线胀系数为16.6×10^-6/℃,具有良好的导电性和导热性,常用于制造电线电缆、电器和管道等。
3. 钢(Steel):线胀系数的数值因钢的类型而异,一般在10×10^-6 /℃至13×10^-6 /℃之间。
钢具有较高的强度和耐腐蚀性,广泛应用于建筑、汽车制造和机械制造等领域。
4. 不锈钢(Stainless Steel):线胀系数的数值因不锈钢的成分和类型而有所不同,一般在15×10^-6 /℃至19×10^-6 /℃之间。
不锈钢具有良好的耐腐蚀性和抗氧化性能,常用于制造厨具、化工设备和医疗器械等。
5. 镍合金(Nickel Alloy):线胀系数的数值因镍合金的成分而异,一般在11×10^-6 /℃至15×10^-6 /℃之间。
镍合金具有优异的耐高温和耐腐蚀性能,广泛应用于航空航天、石油化工和能源等领域。
6.钛(Ti):线胀系数为9.0×10^-6/℃,具有较低的密度和优良的耐腐蚀性能,常用于制造航空航天器件、医疗植入材料和化工设备等。
7.铅(Pb):线胀系数为29.2×10^-6/℃,具有较低的熔点和良好的延展性,常用于制造抗辐射材料和防护设备等。
除了上述常见金属材料外,还有许多其他金属材料的线胀系数可供参考,如铁、锌、锡、钨等。
不同材料的线胀系数可以根据实际需要在设计和工程计算中进行选择和使用,以准确计算材料在温度变化时的尺寸变化。
金属线胀系数的测定实验报告

金属线胀系数的测定实验报告金属线胀系数的测定实验报告引言:金属的热胀冷缩性质是物理学中的一个重要研究领域。
金属的线胀系数是描述金属在温度变化时长度变化的物理量。
本实验旨在通过测定不同金属的线胀系数,探究金属的热胀冷缩规律。
实验装置与方法:实验装置包括一个恒温槽、一根金属线、一个测微器和一个温度计。
首先,将金属线固定在两个支架上,保证其自由伸缩。
然后,将恒温槽中的温度调至适当的初始温度,测量金属线的初始长度。
接下来,将恒温槽中的温度逐渐升高,并记录每个温度下金属线的长度变化。
同时,使用温度计测量恒温槽中的温度。
实验结果与分析:我们选取了铜、铁和铝作为实验材料,进行了线胀系数的测定。
下表列出了实验数据:温度(℃)铜线长度(cm)铁线长度(cm)铝线长度(cm)20 10.0 10.0 10.030 10.2 10.1 10.140 10.4 10.2 10.250 10.6 10.3 10.360 10.8 10.4 10.4根据实验数据,我们可以计算出每个金属的线胀系数。
线胀系数的计算公式为:线胀系数= (ΔL / L0) / ΔT其中,ΔL为长度变化,L0为初始长度,ΔT为温度变化。
以铜为例,当温度从20℃升至30℃时,长度变化为0.2cm。
初始长度为10.0cm,温度变化为10℃。
代入公式计算得到铜的线胀系数为:线胀系数 = (0.2 / 10.0) / 10 = 0.002同样的方法可以计算出铁和铝的线胀系数。
铁的线胀系数为0.001,铝的线胀系数为0.0015。
通过比较不同金属的线胀系数,我们可以发现铝的线胀系数最大,铜次之,铁最小。
这是因为金属的线胀系数与其晶格结构和原子间的结合力有关。
铝的晶格结构较松散,原子间的结合力较弱,因此其线胀系数较大。
铜的晶格结构较紧密,原子间的结合力较强,因此其线胀系数较小。
铁的晶格结构介于铝和铜之间,因此其线胀系数处于中间水平。
结论:通过本实验,我们成功测定了铜、铁和铝的线胀系数,并比较了它们之间的差异。
金属的热膨胀系数及计算公式
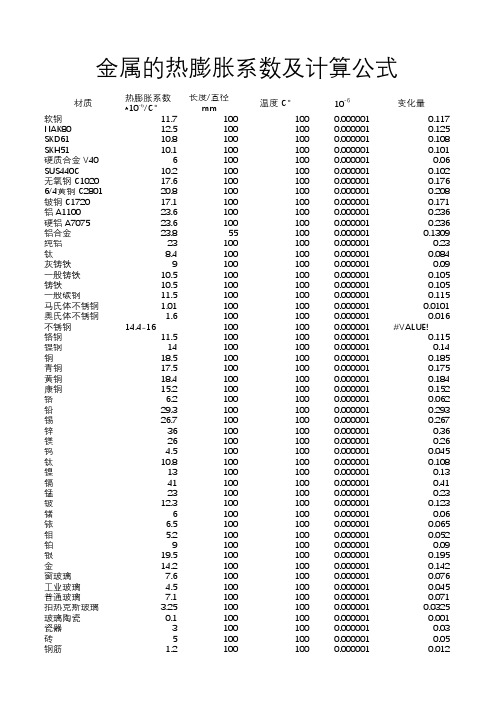
热膨胀系数*10-6/℃软钢11.71001000.0000010.117NAK8012.51001000.0000010.125SKD6110.81001000.0000010.108SKH5110.11001000.0000010.101硬质合金 V4061001000.0000010.06SUS440C10.21001000.0000010.102无氧钢 C102017.61001000.0000010.1766/4黄铜 C280120.81001000.0000010.208铍铜 C172017.11001000.0000010.171铝 A110023.61001000.0000010.236硬铝 A707523.61001000.0000010.236铝合金23.8551000.0000010.1309纯铝231001000.0000010.23钛8.41001000.0000010.084灰铸铁91001000.0000010.09一般铸铁10.51001000.0000010.105铸铁10.51001000.0000010.105一般碳钢11.51001000.0000010.115马氏体不锈钢 1.011001000.0000010.0101奥氏体不锈钢 1.61001000.0000010.016不锈钢14.4-161001000.000001#VALUE!铬钢11.51001000.0000010.115镍钢141001000.0000010.14铜18.51001000.0000010.185青铜17.51001000.0000010.175黄铜18.41001000.0000010.184康铜15.21001000.0000010.152铬 6.21001000.0000010.062铅29.31001000.0000010.293锡26.71001000.0000010.267锌361001000.0000010.36镁261001000.0000010.26钨 4.51001000.0000010.045钛10.81001000.0000010.108镍131001000.0000010.13镉411001000.0000010.41锰231001000.0000010.23铍12.31001000.0000010.123锗61001000.0000010.06铱 6.51001000.0000010.065钼 5.21001000.0000010.052铂91001000.0000010.09银19.51001000.0000010.195金14.21001000.0000010.142窗玻璃7.61001000.0000010.076工业玻璃 4.51001000.0000010.045普通玻璃7.11001000.0000010.071拍热克斯玻璃 3.251001000.0000010.0325玻璃陶瓷0.11001000.0000010.001瓷器31001000.0000010.03砖51001000.0000010.05钢筋1.21001000.0000010.012金属的热膨胀系数及计算公式材质长度/直径mm温度 ℃10-6变化量混凝土 1.0-1.51001000.000001#VALUE!水泥 6.0-141001000.000001#VALUE!花岗岩31001000.0000010.03石墨21001000.0000010.02尼龙1201001000.000001 1.2聚甲基丙烯酸甲(PMMA)(PMMA)()851001000.0000010.85聚氯乙烯(PVC)801001000.0000010.8碳纤维(HM 35 inLangsrichtung)-0.51001000.000001-0.005木头81001000.0000010.08食盐401001000.0000010.4冰 0℃1001000.0000010 1、热膨胀引起的尺寸变化计算方法例:材质为SKD61D=2、L=100mm的杆温度上升100摄氏度时的尺寸变化量为:δδ=热膨胀系数*全长*温度变化=10.8*10-6*100mm*100℃=0.108mm。
常用金属材料的线胀系数

常用金属材料的线胀系数
线胀系数是指物质在温度升高时线性膨胀的比例关系。
当温度升高时,物质分子的活动增强,导致物体的尺寸发生改变,这个现象就是热膨胀。
常见的金属材料在不同温度区间具有不同的线胀系数。
下面将介绍一些常
用金属材料的线胀系数。
1.铝(铝合金):铝和铝合金的线胀系数在常温到300℃范围内大约
为23x10^-6K^-1
2.铜(铜合金):纯铜的线胀系数在常温到300℃范围内大约为
16.5x10^-6K^-1、不同的铜合金由于合金元素的不同而有所差异。
3.镍(镍合金):镍和镍合金在常温到300℃范围内的线胀系数大约
为13.4x10^-6K^-1
4.钢:普通碳素钢的线胀系数在常温到300℃范围内大约为
11.7x10^-6K^-1、不同种类的钢可能会有细微的差异。
5.不锈钢:不锈钢的线胀系数在常温到300℃范围内大约为16x10^-
6K^-1、不同牌号的不锈钢具体数值可能会有所不同。
6.钨:钨的线胀系数在常温到300℃范围内大约为4.5x10^-6K^-1
7.铁:纯铁的线胀系数在常温到300℃范围内大约为12x10^-6K^-1
8.银:纯银的线胀系数在常温到300℃范围内大约为18x10^-6K^-1
9.铅:纯铅的线胀系数在常温到300℃范围内大约为29x10^-6K^-1
这些数值仅为近似值,实际应用时还需要考虑其他因素的影响。
此外,线胀系数还受材料的工艺处理、晶体结构等因素的影响,不同的合金成分
可能会导致不同的线胀系数。
因此,在具体的工程应用中,需要根据实际情况选择合适的金属材料和温度范围,并参考相关的资料和标准进行计算和设计。
金属材料热膨胀系数及计算公式

金属材料热膨胀系数及计算公式一、引言金属材料在受热时会发生热膨胀现象,即体积会随温度的升高而增大。
这是由于金属内部的原子和分子在受热后具有更大的运动能量,导致晶格结构发生变化,从而引起金属材料的体积膨胀。
二、热膨胀系数热膨胀系数是描述材料在温度变化下体积膨胀程度的物理量。
它表示单位温度变化时单位长度(或单位面积)的长度(或面积)变化量,通常用符号α表示。
单位一般为1/℃或1/K。
三、热膨胀系数的计算公式热膨胀系数可以通过实验测量得到,也可以通过理论计算得到。
以下是常见金属材料热膨胀系数的计算公式:1.线膨胀系数(αl):线膨胀系数是指在单位长度上的膨胀量,通常用于描述材料在长度方向上的膨胀情况。
线膨胀系数可以通过以下公式计算:αl = (ΔL / L0) / ΔT其中,ΔL为温度变化下的长度变化量,L0为初始长度,ΔT为温度变化量。
2.表膨胀系数(αA):表膨胀系数是指在单位面积上的膨胀量,通常用于描述材料在面积方向上的膨胀情况。
表膨胀系数可以通过以下公式计算:αA = (ΔA / A0) / ΔT其中,ΔA为温度变化下的面积变化量,A0为初始面积,ΔT为温度变化量。
3.体膨胀系数(αV):体膨胀系数是指在单位体积上的膨胀量,通常用于描述材料在体积方向上的膨胀情况。
体膨胀系数可以通过以下公式计算:αV = (ΔV / V0) / ΔT其中,ΔV为温度变化下的体积变化量,V0为初始体积,ΔT为温度变化量。
四、金属材料的热膨胀系数不同金属材料的热膨胀系数有所差异,下面是一些常见金属材料的热膨胀系数范围:1.铝(Al):线膨胀系数为22.2-25.5 × 10^-6/℃,表膨胀系数为69 × 10^-6/℃,体膨胀系数为71 × 10^-6/℃。
2.铜(Cu):线膨胀系数为16.6-17 × 10^-6/℃,表膨胀系数为59 × 10^-6/℃,体膨胀系数为60 × 10^-6/℃。
实验十 金属线胀系数的测定

实验十金属线胀系数的测定一、实验目的通过实验,了解金属线的胀系数测定方法,掌握线胀系数的计算方法。
二、实验原理热胀冷缩是每种物质都具有的性质,所有物质在温度变化下都会发生体积变化。
当物体温度发生变化时,由于温度感应它的分子运动状态的密度和位置的改变,使得分子间的力发生变化,从而引起物体的长度变化。
热胀系数是衡量物质温度变化下线性尺寸变化的大小的比例系数。
线胀(线性热膨胀)是指物体在温度变化下的长度变化量。
所以,通过测量金属丝在温度变化下的长度变化量,可以计算出其线胀系数。
三、实验用具1. 热力学实验台(TDE2010型)2. 电阻练测器(WY8506)3. 温度计(PWT1206型)4. 紫铜丝(φ=0.1mm)5. 不锈钢杆(φ=6mm)6. 电热板7. 耐热玻璃筒8. 相机(可选)四、实验步骤1. 实验准备选择金属丝和不锈钢杆,在电热板上加热。
使用温度计测量热源温度,并确保温度稳定在80℃左右。
同时,在耐热玻璃筒中加水,使用温度计测量水温,确保温度稳定在20℃左右。
2. 实验操作(1)将金属丝绕在不锈钢杆上,并用导线连接电阻练测器。
(2)将导线连接至热力学实验台的传感器。
(3)调整热力学实验台的控制器,使其显示热源温度与水温度。
(4)将热力学实验台中的控制器设置为线性模式,并使金属丝受到一定的压力。
(5)开启电热板,以使热源温度升高。
(6)记录金属丝长度随时间的变化情况,并使用相机或手机拍摄实验现象。
(7)重复以上步骤,记录多组数据,以验证实验结果的准确性。
1. 数据分析α = ΔL / (LΔT)其中,α表示线胀系数;ΔL表示金属丝长度的变化量;L表示原始长度;ΔT表示温度变化量。
2. 计算过程温度ΔL(mm) L(mm) ΔT(℃) α20 0 100 0 030 0.07 100 10 2.333×10-540 0.12 100 20 6×10-550 0.19 100 30 9.5×10-560 0.24 100 40 1.2×10-4因此,金属丝的平均线胀系数为:α = (2.333+6+9.5+12) ×10-5 / 4 = 7.458 ×10-5六、实验注意事项1. 在实验过程中,确保温度的稳定、可比性和精确度。
金属线胀系数的测定数据

金属线胀系数的测定数据金属的线胀系数是指金属在温度变化时单位长度的线胀量与温度变化量的比值,常用符号为α。
金属的线胀系数是帮助工程师和设计师确定在不同温度下金属材料的尺寸变化和热应力的重要参数。
测定金属线胀系数的方法有多种,下面介绍一种简单有效的方法——线胀法。
线胀法是通过测量金属材料在不同温度下的长度变化,来确定金属线胀系数的方法。
测量过程如下:1. 准备测试样品:选择与实际使用材料相同的金属样品,通常使用长条状或管状的样品。
2. 安装样品:将样品固定在测量装置上,确保样品的自由度受到限制。
3. 温度控制:通过加热或冷却装置控制样品的温度变化,通常将样品置于恒温槽中。
4. 测量长度:使用长度计等测量设备测量样品在不同温度下的长度变化。
5. 计算线胀系数:根据测得的长度变化和温度变化,应用线胀系数的定义式计算线胀系数。
线胀系数α=ΔL/ (L * ΔT)其中ΔL为长度变化,L为原始长度,ΔT为温度变化。
需要注意的是,线胀系数的测定过程中应保证实验环境的稳定和准确性,尽量排除误差。
不同金属的线胀系数不同,而同一金属在不同温度范围内线胀系数也会发生变化。
测定金属线胀系数的数据对于工程设计和材料选用都非常重要。
通过准确测定金属的线胀系数,可以更好地预测材料在不同温度下的变形和应力情况,为工程设计和材料选取提供科学依据。
对于高温工况下的材料选用和设计,金属线胀系数的测定更加重要,对保证工程的安全性和稳定性非常关键。
综上所述,通过线胀法可以测定金属的线胀系数。
这些数据对于工程设计和材料选用至关重要,能够帮助工程师和设计师预测材料在不同温度下的变形和应力情况,保证工程的安全性和稳定性。
金属线胀系数的测定--南昌大学-物理实验

金属线胀系数的测定--南昌大学-物理实验LT一、 实验原理:一般固体的体积或长度,随温度的升高而膨胀,这就是固体的热膨胀。
绝大多数固定材料,其长度是随温度的升高而增加的,这一现象称为线膨胀。
设物体的温度改变∆t 时其长度改变量为∆L ,如果∆t 足够小,则∆t 与∆L 成正比,并且也与物体原长L 成正比,因此有∆L =αL ∆t上式中比例系数α称为固体的线膨胀系数,其物理意义是温度每升高1℃时物体的伸长量与它在0℃时长度之比。
设在温度为0℃时,固体的长度为L 0,当温度升高t 时,其长度为L t ,则有(L t −L 0)/ L 0=αt即L t = L 0(1+αt )如果金属杆在温度为t 1,t 2时,其长度分别为L 1,L 2,则可得出L 1= L 0(1+αt ) L 2= L 0(1+αt )又因为L 1与L 2非常接近,所以L 1/L 2≈1,于是可得到如下结果:α=(L 2−L 1)L 1(t 2−t 1)所以,测得L 1,L 2,t 1和t 2,就可求得α值二、 实验内容和步骤:1. 接通电加热器与温控仪输入输出接口和温度传感器的航空插头。
2. 使金属杆一端与隔热顶尖紧密接触。
3. 调节千分表带绝热头的测量杆,使其刚好与金属杆的自由端接触。
4.接通恒温控制仪的电源,设定需要加热的值为65℃,按确定键开始加热,在达到设定温度后降温至室温,降温时也应读数。
注视恒温控制仪,每隔5℃读一次读数,同时读出千分表的示数,将相应的读数t 1,t 2…t n ,n 1,n 2…n n 记在表格里。
5. 显然,金属杆各时刻上升的温度是t 2-t 1,t 3-t 2,…,t n -t n−1,相应的伸长量是n 2-n 1,n 3-n 2,…,n n -n n−1,则n n -n 1=αL 1(t n -t 1)即α=(n 2−n 1)L 1(t 2−t 1)=∆nL 1∆t由此可知,线膨胀系数α是以n n -n 1为纵坐标、以t n -t 1为横坐标的实验曲线的斜率。
材料相同但粗细长度不同的两根金属线膨胀系数

材料相同但粗细长度不同的两根金属线膨胀系数金属线膨胀系数是指金属材料在温度变化时长度的增加或减少的比例关系。
对于具有相同材料但不同粗细和长度的两根金属线,它们的膨胀系数将会有所不同。
膨胀系数是一个重要的物理特性,对于工程中的温度变化有着重要的影响。
了解金属线的膨胀系数可以帮助我们预测在不同温度下线的变形情况,以避免由于温度变化而引起的不良影响。
金属材料的膨胀系数是指在每摄氏度温度变化下,它的长度变化的比例。
膨胀系数通常用α来表示,单位为1/℃(1/摄氏度)。
在不同的温度范围内,不同的金属材料会表现出不同的膨胀性能。
对于相同材料但粗细长度不同的两根金属线,其膨胀系数虽然是相同的,但由于线的粗细和长度不同,其长度变化量将会有所不同。
根据热膨胀原理,细长的金属线在温度升高时会出现更大的膨胀量,而粗短的金属线在相同温度条件下的膨胀量相对较小。
这是由于细长的金属线具有较大的表面积,能够吸收更多的热量并引起更大的膨胀。
相反,粗短的金属线由于表面积相对较小,只能吸收较少的热量从而产生较小的膨胀。
例如,我们将考虑两根金属线,一根直径较细、长度较长,另一根直径较粗、长度较短,并假设它们都是由相同的材料制成。
当这两根金属线暴露在相同的温度变化条件下时,由于细长线的表面积较大,它将吸收更多的热量并引起更大的膨胀。
相反,粗短线的表面积较小,只能吸收较少的热量从而产生较小的膨胀。
这种差异在实际应用中也非常重要。
例如,在建筑结构中,金属材料被用于支撑构件。
如果我们不考虑温度的膨胀,建筑结构可能会因为温度变化而产生应力、变形或甚至破坏。
在设计中,我们需要根据金属线的膨胀系数和长度来计算其在不同温度下的膨胀量。
通过控制线的长度和形状,我们可以在结构设计中考虑到温度变化的影响,以保证结构的安全性和可靠性。
另外,不同金属材料和合金具有不同的膨胀系数。
因此,在实际应用中,我们需要根据材料的物理特性选择合适的金属线,以满足设计和工程要求。
合金钢线膨胀系数

合金钢线膨胀系数
合金钢的线膨胀系数是指在温度变化时,单位长度的合金钢线材膨胀或收缩的程度。
合金钢的线膨胀系数一般在温度范围内是一个常数。
合金钢的线膨胀系数与温度有关,在不同的温度下线膨胀系数也会发生变化。
一般来说,合金钢的线膨胀系数随着温度的升高而增加。
根据热力学理论,合金钢的线膨胀系数可以通过测量线膨胀和温度变化的关系来确定。
实验中通常会测量合金钢在不同温度下的长度,并计算线膨胀系数。
合金钢的线膨胀系数对于工程设计和构造非常重要。
在考虑温度变化时,必须考虑合金钢线材的线膨胀系数,以避免不必要的应力和变形。
需要注意的是,合金钢的线膨胀系数与合金钢的成分和处理方式有关,因此不同类型的合金钢具有不同的线膨胀系数。
金属线胀系数的单位

金属线胀系数的单位引言金属在受热时会发生胀缩现象,这是由于温度变化引起金属原子振动强度的改变所致。
金属线胀系数是描述金属在温度变化下长度变化程度的物理量,它是衡量金属材料热膨胀性能的重要参数。
本文将介绍金属线胀系数的定义、计算方法以及相关单位。
一、金属线胀系数的定义金属线胀系数(Coefficient of linear expansion)指的是在温度升高或降低时,单位长度的金属材料长度发生的变化。
它通常用符号α表示,单位为每摄氏度(℃)。
对于一个长度为L0、温度为T0的金属材料,在温度升高ΔT后,其长度将发生变化,记作ΔL。
则金属线胀系数α可由以下公式计算得出:α = ΔL / (L0 * ΔT)其中,ΔL表示长度变化量,L0为初始长度,ΔT为温度变化量。
二、计算方法计算金属线胀系数需要知道以下几个参数:1.初始长度(L0):指在初始温度(T0)下金属材料的长度。
2.长度变化量(ΔL):指在温度变化ΔT下金属材料的长度变化量。
3.温度变化量(ΔT):指金属材料的温度变化量。
由上述参数可以得到金属线胀系数α的计算公式:α = ΔL / (L0 * ΔT)在实际应用中,可以通过以下方法来测量金属线胀系数:1.线膨胀法:将一个金属杆固定在一端,另一端放置一个游标卡尺或光电测距仪等测量工具。
然后,使金属杆受热或冷却,记录不同温度下的长度变化,通过计算得到金属线胀系数。
2.压力计法:利用压力计测量不同温度下的压力变化,再根据弹性模量和截面积等参数计算得到金属线胀系数。
三、常见单位金属线胀系数的单位通常有以下几种:1.摄氏度逆(℃⁻¹):这是最常见的单位,表示单位摄氏度温度变化引起的长度变化。
2.开尔文逆(K⁻¹):开尔文是温度的国际单位,开尔文逆也可以用来表示金属线胀系数。
3.纳米米逆(nm⁻¹):纳米是长度的国际单位,纳米米逆表示单位纳米长度变化引起的温度变化。
四、应用范围金属线胀系数在工程领域有着广泛的应用,特别是在设计和制造过程中需要考虑材料热膨胀性能时。
金属线膨胀系数与温度的关系

金属线膨胀系数与温度的关系金属线膨胀系数与温度的关系摘要:本实验主要探讨金属杆在除温度的作用下,跟所受的压力的关系,由于热胀冷缩的关系,金属杆在变化的温度下会发生膨胀,长度和体积也会发生变化。
但是,当我们加入重力的影响时,金属的膨胀现象也会发生相应的变化,然后通过千分尺测出这种变化,结合温度和重力因数,并最终得出金属杆在温度和压力的双重作用下线膨胀系数的变化情况。
关键字:金属杆;线膨胀系数;热胀冷缩;压力;物理实验1、引言:“热胀冷缩”现象是物体内部分子、原子热运动剧烈程度的外在宏观表现。
通常,随温度的变化,物体的长度和体积都会发生变化。
这种性质在工程结构的设计中,在机械和仪器的制造中,在材料的加工中,都必须加以考虑,否则将会影响到结构的稳定性和仪表的精度。
考虑不当,就会造成工程的损毁,仪表的失灵,以及加工焊接中的缺陷和失败等等。
但是,只考虑到温度的影响太过片面和局限,对于如何解决和克服这些缺陷都带来了一定程度上的限制。
因此,在这里,我要探讨一下关于在一定温度下,对金属逐渐施加重力后金属被压缩的情况,以及之间的关系。
如果当我们知道了金属的膨胀系数在不同的温度和压力下的变化情况,我们就可以根据具体的情况选择合适的金属或者设定特定的外部环境来提高金属的寿命或者性能,从而提高工程结构、机械和仪器的性能或是材料的稳定性和仪表的精确度。
2、实验方案(设计思想)本实验的主要试验仪器为FT-HX-I金属膨胀系数测定仪、千分表、游标卡尺以及多个特制的50g重的大且薄的砝码。
固体受热后其长度的增加称为线膨胀。
经验表明,在一定的温度范围内,原来长为L 的物体,受热后其伸长量⊿L与其温度的增加量⊿t近似成比例,与原长L亦成正比。
即:⊿L=ɑL⊿t。
但是如果我们加上了重量的因数就不一定了。
当我们在金属丝上施加均匀的一定程度上的重力时,试验仪器则在不停地加温改变温度,金属的膨胀系数就会受到影响。
然后我们逐渐的增加砝码的个数,增加施加在金属丝上的重力进一步加大对金属丝膨胀系数的影响,使实验的结果更加明显。
金属线胀系数的单位

金属线胀系数的单位一、引言金属线胀系数是描述金属在温度变化时长度变化的比例关系。
在工程应用中,了解金属线的胀系数是非常重要的,因为它会对结构的设计和性能产生影响。
本文将从不同角度探讨金属线胀系数的单位。
二、什么是金属线胀系数金属线胀系数,又称线膨胀系数,是指金属线在单位温度变化下的长度变化与原始长度之比。
它是一个无量纲的物理量,用来衡量金属线膨胀的程度。
金属线胀系数的单位是关键,它决定了我们如何度量金属线的胀缩。
三、常用的金属线胀系数单位1. 米/米·°C米/米·°C是最常用的金属线胀系数单位。
它表示在温度变化1摄氏度时,金属线的长度变化与原始长度之比。
这个单位适用于大多数常见的金属材料,如铁、铜、铝等。
2. 纳米/米·°C纳米/米·°C是一种更小的单位,它表示在温度变化1摄氏度时,金属线的长度变化与原始长度之比。
这个单位适用于一些特殊的金属材料,如高温合金、钨等。
3. 毫米/米·°C毫米/米·°C是一种更大的单位,它表示在温度变化1摄氏度时,金属线的长度变化与原始长度之比。
这个单位适用于一些需要更精确测量的金属线,如精密仪器的测量线。
四、金属线胀系数的影响因素金属线胀系数受多种因素的影响,包括金属的种类、温度变化范围、应力状态等。
不同金属的胀系数不同,温度变化范围越大,胀系数越大。
同时,金属线的应力状态也会影响其胀系数的大小。
五、金属线胀系数的应用金属线胀系数的应用非常广泛。
在建筑工程中,金属线胀系数的大小会影响到建筑物的伸缩缝设计;在电力工程中,金属线胀系数的大小会影响到电力线的安装和运行;在航空航天领域,金属线胀系数的大小会影响到航天器的结构设计等。
六、金属线胀系数的测量方法金属线胀系数可以通过实验测量得到。
一种常用的方法是通过测量金属线在不同温度下的长度变化来计算胀系数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
冰刚投入时,水温 高,冰熔解快,则系统 温度降低快。随着冰熔 化,冰块变小,水温降 低,冰熔解变慢,系统 温度降低变慢。
若SA=SB,则系统对外界的吸热和散热 就可以相互抵消。 这种修正方法,要求水的初温大于环 境温度(T2>θ环),末温比环境温度低 (T3<θ环),而且对初温、末温与环境 温度相差的幅度要求比较严格,在实验 中很难保证。
水初温大于环境温度约10-15℃,末温小于环境
温度。 曲线连续,时间不可间断。记好投冰的时间。 实验中要轻轻搅拌。
5、测量要点
(1)从投冰前5、6分钟开始测水温,每60S测一次。
(2)在投冰快速冷却过程中,每30S测一次, 且注意记录:A、 投物的时刻与温度; B、达到室温TR的时刻tR;
(3)水温达到最低点后继续测5、6分钟。
温度计泡入 水中的体积 热水的温度
ML Mc水 (T2 0) mc水 c铜 (m1 m2 ) V (T2 T1 )
冰的溶解热 冰全部融化为水时的温度
mc水 c铜 (m1 m2 ) V (T2 T1 ) Mc水 (T2 0) 测量公式: L
冰的熔解热的测定
熔解热概念:一定压强下晶体 开始熔解时的温度,称为该晶体 在此压强下的熔点。1克质量的 某种晶体熔解成同温度的液体所 吸收的热量,叫做该晶体的熔解 潜热,亦称熔解热。实验涉及热 平衡方程的使用。 本实验就是根据热平衡原理,用混合法来测定 冰的溶解热。
若将M克0℃的冰与m克T1 ℃的水进行混合,冰全部融化为水时的温度 为T2 ℃,内筒质量m1,比热容为c1,搅拌器的质量为m2,比热为c2,温 度计的热容为δ,若为孤立系统,根据热平衡方程Q吸=Q放,则冰的熔 解热L计算公式:
B1实验课
热学类实验 热学实验需要考虑实验的具体先后步骤,因此课 前预习很重要;另外由于各热学量与环境相关, 因此热学实验需要记录实验环境参数(温度,干 湿度,气压等)。 实验项目: 1、金属线胀系数的测定 2、冰的熔解热的测定
2014-2015学年第二学期
金属线胀系数的测定
• 主要实验内容:用光杠杆放大法对金属丝的线胀系数进行
把对热量的修正转换为对水初/末温的修正,对水初/末温没 有限制,但最好满足T2>θ环,T3<θ环。
实验内容
1. 称量质量和测量温度。 2. 记录投冰前后水温随时间的变化曲线。 投冰前每隔60秒测一个系统温度,测5-8个点。 投冰后每隔30秒测一个系统温度,测5-8个点,待末温基本稳 定读出3个数据比较合适。 3. 注意事项:
测定 。固体受热后其长度的增加称为线膨胀。在一定的 温度范围内,原长为l的物体,受热后其伸长量与l成正比, 与温度的增加量近似成正比。
主要原理为:
l l t
金属的线胀系数
数据处理:
1、计算不确定度 2、用作图法及最小二 乘法求直线率及线胀系 数,比较测量结果。
返回
实验内容和要求: 1、要求从室温测量到90度,最好每隔5度测一次望远镜中尺子
因为作图时已保证S1+S2 =S3,所以有S’=S。
因此,修正温度曲线与实际温度曲线等价。
(系统散热修正)
修正温度曲线把热交换与冰熔化分割开来。由于冰熔化变 为无限短,故没有热量交换。则:
L 1 (c水 m 水 c 铜m 筒 搅 )(T` 水 2 T` 平 3) c水 T` 平 3 c 冰 T冰 1 M冰
δq K(T θ) δt
(1)利用系统散热与吸热相互抵消的方法
T T2
根据牛顿冷却定律修正散热。温度 从T2到T3,系统与环境交换的热量:
SA SB t3
T3 t2
q K(T θ)dt K (T θ)dt K (T θ)dt
t2 t2 tθ
t3
正)
4.光杆杆常数d用游标卡尺测量五次,平面镜到望远镜标尺距离D 和金属杆初始长度l各测量一次,其误差取相应测量工具的精度 误差作为最终的误差估计。
注意事项: 1、温度计的保护,温度计上的螺丝拧紧,以免温度计掉入加温
内筒。
2、整个测量过程不能移动或触碰光杠杆。 3、注意望远镜中看到的标尺示数是在标尺0刻度的上方还是下 方,以免读数时出错。 4.加温时最高温度不应超过95摄氏度, 90摄氏度时停止加热。
6、数据处理要点
1)作T-t曲线,力求SA与SB接近相等,并作
MN、AB及CD线。 2)确定T1及T2。
3)带入公式求出溶解热
4) 与标准值比较计算百分误差(80cal/g.℃)
(2)假设冰熔化无限短来修正
T T"2 T2 S4 S1 S2 T' 3 t2 T'2 T4 S 5 S3 T3 t3 t T"3
实际温度变化是 T2''T2T4T3T3'',系统共吸收热量 相当于面积S=S2+S5-S4。
'' ' ' '' 修正温度曲线是 T2 T2T2T3T3T3 ,系统吸收热量 相当于面积S’= S3+S5-S1-S4。
M
误差公式:L M m m1 m2 V T2 T1 M T2
L M m m1 m2 V (T2 T1 ) M T2
实验系统散热的修正
虽然尽量保持系统孤立,仍不可能完全达到绝热的要求, 因此,就需要求出系统散失或吸收的热量,从而对结果进行修 正。 牛顿冷却定律:若系统温度高于环境温度,系统就要散失热 量。当温度差相当小时(小于10-15℃),散热速率与温度差 成正比,即:
的刻度,升温和降温各记录至少10个数据。
2、分别由升温和降温测的数据采用逐差法计算出金属的线胀系 数α,并与标准值比较计算百分误差(1.67×10-5/℃)。 3、做望远镜中尺子读数n和温度计读数t的n-t曲线图,曲线实 际上可由ni=Ati+B,表示,其中 A=2αLD/d.所以求出曲线的斜率
即可求出线胀系数。
