指数函数练习题(包含详细答案)
指数函数与对数函数专项训练(解析版)

指数函数与对数函数专项训练一、单选题1.(23-24高一下·云南玉溪·期末)函数()()2lg 35f x x x =-的定义域为()A .()0,∞+B .50,3⎛⎫⎪C .()5,0,3∞∞⎛⎫-⋃+ ⎪D .5,3⎛⎫+∞ ⎪【答案】C【详解】由题意知,2350x x ->,即(35)0x x ->,所以0x <或53x >.故选:C.2.(23-24高一上·云南昭通·期末)函数()327x f x x =+-的零点所在的区间是()A .()0,1B .31,2⎛⎫ ⎪⎝⎭C .3,22⎛⎫⎪D .()2,3【答案】B【详解】∵3x y =和27y x =-均在R 上单调递增,∴()327x f x x =+-在R 上单调递增;又()12f =-,327402f ⎛⎫=-> ⎪⎝⎭,∴()f x 在31,2⎛⎫ ⎪⎝⎭上有唯一的零点,故选:B.3.(23-24高一上·云南昆明·期末)滇池是云南省面积最大的高原淡水湖,一段时间曾由于人类活动的加剧,滇池水质恶化,藻类水华事件频发.在适当的条件下,藻类的生长会进入指数增长阶段.滇池外海北部某年从1月到7月的水华面积占比符合指数增长,其模型为23 1.65x y -=⨯.经研究“以鱼控藻”模式能有效控制藻类水华.如果3月开始向滇池投放一定量的鱼群后,鱼群消耗水华面积占比呈现一次函数 5.213.5y x =-,将两函数模型放在同期进行比较,如图所示.下列说法正确的是(参考数据:671.6520.2,1.6533.3≈≈)()A .水华面积占比每月增长率为1.65B .如果不采取有效措施,到8月水华的面积占比就会达到60%左右C .“以鱼控藻”模式并没有对水华面积占比减少起到作用D .7月后滇池藻类水华会因“以鱼控藻”模式得到彻底治理【答案】B【详解】对于A ,由于模型23 1.65x y -=⨯呈指数增长,故A 错误;对于B ,当8x =时,8220.63 1.605326.y -⨯==⨯≈,故B 正确;对于C ,因为鱼群消耗水华面积占比呈现一次函数 5.213.5y x =-,所以“以鱼控藻”模式对水华面积占比减少起到作用,故C 错误;对于D ,由两函数模型放在同期进行比较的图象可知,7月后滇池藻类水华并不会因“以鱼控藻”模式得到彻底治理,故D 错误.故选:B.4.(23-24高一上·云南昭通·期末)()()1log 14a f x x =-+(0a >且1a ≠)的图象恒过定点M ,幂函数()g x 过点M ,则12g ⎛⎫⎪⎝⎭为()A .1B .2C .3D .4【答案】D【详解】()()1log 14a f x x =-+,令11x -=,得2x =,()124f =,则()()1log 14a f x x =-+(0a >且1a ≠)恒过定点12,4M ⎛⎫⎪⎝⎭,设()g x x α=,则124α=,即2α=-,即()2g x x -=,∴142g ⎛⎫= ⎪⎝⎭,故选:D.5.(23-24高一下·云南楚雄·期末)已知0.320.3lo g 3,2,lo g 2a b c -===,则()A .c b a <<B .<<b c aC .<<c a bD .a b c<<【答案】A【详解】因为2log y x =在(0,)+∞上单调递增,且234<<,所以222log 2log 3log 4<<,所以21log 32<<,即12a <<,因为2x y =在R 上递增,且0.30-<,所以0.300221-<<=,即01b <<,因为0.3log y x =在(0,)+∞上单调递减,且12<,所以0.30.3log 1log 2>,所以0.3log 20<,即0c <,所以c b a <<.故选:A6.(23-24高一上·云南·期末)若()21()ln 1||f x x x =+-,设()0.3(3),(ln2),2a f b f c f =-==,则a ,b ,c 的大小关系为()A .c a b >>B .b c a >>C .a b c >>D .a c b>>【答案】D【详解】由题意知()(),00,x ∈-∞⋃+∞,由()()()21ln 1f x x f x x⎡⎤-=-+-=⎣⎦-,所以()f x 为偶函数,图象关于y 轴对称,当0x >时,由复合函数的单调性法则知()f x 随x 的增大而增大,即()0,x ∈+∞,()21()ln 1||f x x x =+-单调递增,因为()()33a f f =-=,()0.3(ln2),2b f c f ==,且00.3112222=<<=,0ln2lne 1<<=,所以0.3ln 223<<,所以()()()0.3ln223f f f <<-,即b c a <<,也就是a c b >>.故选:D7.(23-24高一下·云南·期末)设222,0()log ,0x x f x x x ⎧+≤⎪=⎨>⎪⎩,若关于x 的方程2[()](2)()20f x a f x a -++=恰有5个不同实数解,则实数a 的取值范围是()A .[]1,2B .(2,3]C .()2,+∞D .()3,+∞【答案】B【详解】方程2[()](2)()20f x a f x a -++=化为[()2][()]0f x f x a --=,解得()2f x =或()f x a =,函数()f x 在(,0]-∞上单调递增,函数值的集合为(2,3],在(0,1]上单调递减,函数值的集合为[0,)+∞,在[1,)+∞上单调递增,函数值的集合为[0,)+∞,在同一坐标系内作出直线2,y y a ==与函数()y f x =的图象,显然直线2y =与函数()y f x =的图象有两个交点,由关于x 的方程2[()](2)()20f x a f x a -++=恰有5个不同实数解,则直线y a =与函数()y f x =的图象有3个交点,此时23a <≤,所以实数a 的取值范围是(2,3].故选:B8.(23-24高一下·云南昆明·期末)若()12:lo g 11,:39a p a q --<<,则p 是q 的()条件A .充分不必要B .必要不充分C .充要D .既不充分也不必要【答案】A【详解】对于()22:log 11log 2p a -<=,则012a <-<,解得13a <<;对于1:39a q -<,则12a -<,解得3a <;因为{}|13a a <<是{}|3a a <的真子集,所以p 是q 的充分不必要条件.故选:A.二、多选题9.(23-24高一上·云南迪庆·期末)已知函数()()2ln 2f x x x =-,则下列结论正确的是()A .函数()f x 的单调递增区间是[)1,+∞B .函数()f x 的值域是RC .函数()f x 的图象关于1x =对称D .不等式()ln 3f x <的解集是()1,3-【答案】BC【详解】对于A ,当1x =时,2210x x -=-<,此时()()2ln 2f x x x =-无意义,故A 错误;对于B ,由于()22y g x x x ==-的值域为[)1,-+∞,满足()[)0,1,+∞⊆-+∞,所以函数()f x 的值域是R ,故B 正确;对于C ,由题意()()()22ln 2ln 11f x x x x ⎡⎤=-=--⎣⎦,且定义域为()(),02,-∞+∞ ,它满足()()()21ln 11f x x f x+=-=-,即函数()f x 的图象关于1x =对称,故C 正确;对于D ,由于()f x 的定义域为()(),02,-∞+∞ ,故D 错误.故选:BC.10.(23-24高一上·云南昆明·期末)已知函数2212,0()2|log ,0x x x f x x x ⎧--≤⎪=⎨⎪⎩,若1234x x x x <<<,且()()()()1234fx fx fx fx ===,则下列结论中正确的是()A .122x x +=-B .1204x x <<C .()41,4x ∈D .342x x +的取值范围是332,4⎡⎫⎪⎢⎣⎭【答案】BC【详解】作出函数2212,0()2|log ,0x x x f x x x ⎧--≤⎪=⎨⎪⎩的图像如图.对于选项A,根据二次函数的对称性知,12()224x x +=⨯=--,故A 项错误;对于选项B ,因120x x <<,由上述分析知124x x +=-,则21212120()()()42x x x x x x --<=-⋅-≤=,因12x x ≠,故有1204x x <<,即B 项正确;对于选项C ,如图,因0x ≤时,2211()2(2)2222f x x x x =--=-++≤,0x >时,2()|log |f x x =,依题意须使20|log |2x <<,由2|log |0x >得1x ≠,由2|log |2x <解得:144x <<,故有3411,144x x <<<<,即C项正确;对于选项D ,由图知2324log log x x -=,可得341x x =,故431x x =,则343322x x x x ++=,3114x <<,不妨设21,(,1)4y x x x =+∈,显然函数2y x x =+在(1,14)上单调递减,故23334x x <+<,即342x x +的取值范围是(333,4),故D 项错误.故选:BC.11.(23-24高一上·云南昆明·期末)关于函数()ln f x x x =+,以下结论正确的是()A .方程()0f x =有唯一的实数解c ,且(0,1)c ∈B .对,0,()()()x y f xy f x f y ∀>=+恒成立C .对()1212,0x x x x ∀>≠,都有()()1212f x f x x x ->-D .对12,0x x ∀>,均有()()121222f x f x x x f ++⎛⎫≤⎪【答案】AC【详解】A 选项,由于1y x =在R 上单调递增,2ln y x =在()0,∞+上单调递增,故()ln f x x x =+在定义域()0,∞+上单调递增,又()11ln 30,11033f f ⎛⎫=-<=> ⎪⎝⎭,故由零点存在性定理可得,方程()0f x =有唯一的实数解c ,且(0,1)c ∈,A 正确;B 选项,()ln f xy xy xy =+,()()ln ln ln f x f y x x y y x y xy +=+++=++,显然,0x y ∀>,由于xy 与x y +不一定相等,故()()f x f y +与()f xy 不一定相等,B 错误;C 选项,由A 选项可知,()ln f x x x =+在定义域()0,∞+上单调递增,对()1212,0x x x x ∀>≠,都有()()12120f x f x x x ->-,C 正确;D 选项,12,0x x ∀>,均有121212ln 222x xx x x x f +++⎛⎫=+ ⎪⎝⎭,()()12112212121212ln ln ln ln 22222f x f x x x x x x x x x x x x x ++++++==+=+,由于12122x x x x +≥,当且仅当12x x =时,等号成立,故1212ln ln 2x x x x +≥,即()()121222f x f x x x f ++⎛⎫≥ ⎪⎝⎭,D 错误.故选:AC 三、填空题12.(23-24高一上·云南昆明·期末)()()2,(1)29,1x a x f x x ax a x ⎧>⎪=⎨-++-≤⎪⎩是R 上的单调递增函数,则实数a 的取值范围为.【答案】[]2,5【详解】因为在R 递增,则112129a a a a a⎧⎪⎪≥⎨⎪-++-≤⎪⎩>,解得:25a ≤≤,故答案为:[]2,513.(23-24高一下·云南昆明·期末)设函数()ln(1)f x x =+,2()g x x a =-+,若曲线()y f x =与曲线()y g x =有两个交点,则实数a 的取值范围是.【答案】(0,)+∞【详解】当0x ≥时,()ln(1),f x x =+当0x <时()ln(1),f x x =-+函数图象示意图为则2()g x x a =-+与()ln (1)f x x =+有两个零点知a 的取值范围是(0,)+∞.故答案为:(0,).+∞14.(23-24高一下·云南玉溪·期末)苏格兰数学家纳皮尔(J.Napier ,1550-1617)在研究天文学的过程中,经过对运算体系的多年研究后发明的对数,为当时的天文学家处理“大数”的计算大大缩短了时间.即就是任何一个正实数N 可以表示成10(110,)n N a a n =⨯≤<∈Z ,则lg lg (0lg 1)N n a a =+≤<,这样我们可以知道N 的位数为1n +.已知正整数M ,若10M 是10位数,则M 的值为.(参考数据:0.9 1.1107.94,1012.56≈≈)【答案】8或9【详解】依题意可得910101010M ≤<,两边取常用对数可得91010lg10lg lg10M ≤<,即910lg 10M ≤<,所以0.9lg 1M ≤<,即0.91010M ≤<,又M 为正整数,所以8M =或9M =.故答案为:8或9四、解答题15.(23-24高一上·云南昆明·期末)设函数()log (3)(,10a f x x a =-+>且1)a ≠.(1)若(12)3f =,解不等式()0f x >;(2)若()f x 在[4,5]上的最大值与最小值之差为1,求a 的值.【答案】(1)10(,)3+∞(2)2a =或12a =【详解】(1)由(12)3f =可得log (123)13a -+=,解得3a =,即3()log (3)1,(3)f x x x =-+>,则()0f x >,即3log (3)10x -+>,即310,1333x x x >⎧⎪∴>⎨->⎪⎩,故不等式()0f x >的解集为10(,)3+∞;(2)由于()f x 在[4,5]上的最大值与最小值之差为1,故log 11(log 21)1a a +-+=,即log 21,2a a =∴=或12a =,即a 的值为2a =或12a =.16.(23-24高一上·云南昭通·期末)化简求值:(1)()13103420.027π4160.49--++;(2)ln22311lg125lg40.1e log 9log 1632-+++⨯.【答案】(1)8(2)9【详解】(1)()13103420.027π4160.49--++()()()1313423420.3120.7⎡⎤⎡⎤⎡⎤=-++⎣⎦⎣⎦⎣⎦0.3180.78=-++=;(2)ln22311lg125lg4lg 0.1e log 9log 1632-++++⨯3211112lg34lg2lg5lg23222lg2lg3=+-++⨯lg 5lg28=++9=.17.(23-24高一上·云南·期末)已知定义域为R 的函数()11333xx m f x +-⋅=+是奇函数.(1)求m 的值并利用定义证明函数()f x 的单调性;(2)若对于任意t ∈R ,不等式()()22620f t t f t k -+-<恒成立,求实数k 的取值范围.【答案】(1)1m =,证明见解析(2)3k <-【详解】(1)因为()f x 是奇函数,函数的定义域为R ,所以(0)0f =,所以1033m-=+,所以1m =,经检验满足()()f x f x -=-易知()11312133331x x x f x +-⎛⎫==-+ ⎪++⎝⎭设12x x <,则2112122(33)()()3(31)(31)x x x x f x f x --=++因为3x y =在实数集上是增函数,故12()()0f x f x ->.所以()f x 在R 上是单调减函数(2)由(1)知()f x 在(,)-∞+∞上为减函数.又因为()f x 是奇函数,所以()()22620f t t f t k -+-<等价于()()2262f t t f k t-<-,因为()f x 为减函数,由上式可得:2262t t k t ->-.即对一切t R ∈有:2360t t k -->,从而判别式361203k k ∆=+<⇒<-.所以k 的取值范围是3k <-.18.(23-24高一下·云南昆明·期末)已知函数1()xx f x a a ⎛⎫=- ⎪⎝⎭ (0a >且1a ≠).(1)讨论()f x 的单调性(不需证明);(2)若2a =,(ⅰ)解不等式3()2≤f x x;(ⅱ)若21()(22))2(x g f x t x x f +=-+在区间[]1,1-上的最小值为74-,求t 的值.【答案】(1)答案见解析(2)(ⅰ)(](],10,1-∞-⋃;(ⅱ)2t =-或2t =【详解】(1)若1a >,则1()()x xf x a a=-在R 上单调递增;若01a <<,则1()()x xf x a a=-在R 上单调递减.(2)(ⅰ)3()2≤f x x ,即132()022xx x --≤,设13()2()22xx g x x=--,则(1)0g =,()()g x g x -=-,所以()g x 为奇函数,当0x >时,()g x 单调递增,由()(1)g x g ≤,解得01x <≤,根据奇函数的性质,当0x <时,()(1)g x g ≤的解为1x ≤-,综上所述,3()2≤f x x的解集为(](],10,1-∞-⋃.(ⅱ)2122()2(2)2()222(22)x x x x x g x f x tf x t +--=-+=++-,令22x x m --=,因为[]1,1x ∈-,则33,22m ⎡⎤∈-⎢⎥⎣⎦,所以2()()22g x h m m tm ==++,其图象为开口向上,对称轴为m t=-的抛物线,①当32t -≤-,即32t ≥时,min 39177()()3232444h m h t t =-=-+=-=-,解得2t =.②当3322t -<-<,即3322t -<<时,222min 7()()2224h m h t t t t =-=-+=-+=-,解得1152t =,2152t =-矛盾.③当32t -≥,即32t ≤-时,min 39177()()3232444h m h t t ==++=+=-,解得2t =-.综上所述,2t =-或2t =.19.(23-24高一上·云南昆明·期末)函数()e (0)x f x mx m =-<.(1)求(1)f -和(0)f 的值,判断()f x 的单调性并用定义加以证明;(2)设0x 是函数()f x 的一个零点,当1em <-时,()02f x k >,求整数k 的最大值.【答案】(1)1(1)e f m --=+,(0)1f =,()f x 在定义域R 上单调递增,证明见解析,(2)整数k 的最大值为1-【详解】(1)1(1)e f m --=+,(0)1f =,判断()f x 在定义域R 上单调递增,证明如下:在R 上任取1x ,2x ,且12x x <,则1212121212()()e (e )(e e )()x x x x f x f x mx mx m x x -=---=---,因为12x x <,0m <,所以12e e x x <,120x x -<,0m ->,所以12e e 0x x -<,12()0m x x --<,所以1212(e e )()0x x m x x ---<,即12())0(f x f x -<,所以12()()f x f x <,所以()f x 在定义域R 上单调递增.(2)由题意得0()0f x =,即00e 0x mx -=,1em <-,则10e m +<,即0(1)0()f f x -<=,由()f x 是R 上的增函数,所以01x -<,又0(0)10()f f x =>=,所以010x -<<,0200(2)e 2x f x mx =-002e 2e x x =-,令01e (ext =∈,1),则22()2(1)1g t t t t =-=--,所以()g t 在1(e ,1)上单调递减,所以()()11g t g >=-,即0(2)1f x >-,当1em <-时,0(2)f x k >,所以1k ≤-,所以整数k 的最大值为1-.。
指数练习题及答案

指数练习题及答案指数练习题及答案指数是数学中一个非常重要的概念,广泛应用于各个领域。
在数学学习的过程中,我们经常会遇到各种关于指数的练习题。
本文将为大家提供一些常见的指数练习题及其答案,帮助大家更好地理解和掌握指数的概念和运算。
一、基础练习题1. 计算下列指数表达式的值:a) 2^3b) 5^2c) 10^0d) (-3)^4答案:a) 2^3 = 2 × 2 × 2 = 8b) 5^2 = 5 × 5 = 25c) 10^0 = 1d) (-3)^4 = (-3) × (-3) × (-3) × (-3) = 812. 化简下列指数表达式:a) 3^2 × 3^4b) (2^3)^2c) 4^3 ÷ 4^2答案:a) 3^2 × 3^4 = 3^(2+4) = 3^6b) (2^3)^2 = 2^(3×2) = 2^6c) 4^3 ÷ 4^2 = 4^(3-2) = 4^1 = 4二、进阶练习题1. 计算下列指数表达式的值:a) 2^(-2)b) 1/2^(-3)c) (1/3)^(-2)答案:a) 2^(-2) = 1/(2^2) = 1/4b) 1/2^(-3) = 2^3 = 8c) (1/3)^(-2) = (3/1)^2 = 92. 化简下列指数表达式:a) (4^2)^(-3/2)b) 2^(3/2) × 2^(-1/2)c) (2^3 × 3^2) ÷ (2^2 × 3^3)答案:a) (4^2)^(-3/2) = 4^(2×(-3/2)) = 4^(-3) = 1/(4^3) = 1/64b) 2^(3/2) × 2^(-1/2) = 2^(3/2 - 1/2) = 2^1 = 2c) (2^3 × 3^2) ÷ (2^2 × 3^3) = (2^(3-2) × 3^(2-3)) = 2^1/3^1 = 2/3三、应用练习题1. 已知一个细菌数量为100个,每小时增长50%,请问经过3小时后,细菌的数量是多少?答案:细菌数量每小时增长50%,相当于每小时增长原数量的一半。
指数函数练习题及答案

指数函数练习题及答案指数函数是高中数学中的重要内容,它在数学和科学领域中有着广泛的应用。
本文将通过一些练习题来帮助读者更好地理解指数函数的概念和运算规则,并提供相应的答案。
1. 求解指数方程:2^x = 16解:将16写成2的幂次形式,即16 = 2^4,所以原方程可以写成2^x = 2^4。
根据指数函数的性质,当底数相同时,指数相等,所以可以得到x = 4。
2. 简化指数表达式:(2^3)^4解:根据指数函数的性质,指数的乘法规则,可以将指数表达式简化为2^(3*4),即2^12。
3. 求解指数方程:3^(2x+1) = 9解:将9写成3的幂次形式,即9 = 3^2,所以原方程可以写成3^(2x+1) =3^2。
根据指数函数的性质,当底数相同时,指数相等,所以可以得到2x+1 = 2。
解方程得到x = 1/2。
4. 求解指数方程:e^x = 10解:将10写成自然对数的底数e的幂次形式,即10 = e^ln(10),所以原方程可以写成e^x = e^ln(10)。
根据指数函数的性质,当底数相同时,指数相等,所以可以得到x = ln(10)。
5. 求解指数方程:10^(2x-1) = 100解:将100写成10的幂次形式,即100 = 10^2,所以原方程可以写成10^(2x-1) = 10^2。
根据指数函数的性质,当底数相同时,指数相等,所以可以得到2x-1 = 2。
解方程得到x = 3/2。
通过以上的练习题,我们可以看到指数函数在解方程中的应用。
指数函数的特点是底数不同,函数的性质也会有所不同。
在实际问题中,指数函数可以用来描述物质的衰减、增长和变化等现象,具有很强的实用性。
除了以上的练习题,我们还可以通过绘制指数函数的图像来更好地理解其特点。
以y = 2^x为例,我们可以绘制出其图像,发现随着x的增大,y的值呈指数级增长,这是因为指数函数的增长率是逐渐加大的。
总结起来,指数函数是高中数学中的重要内容,通过练习题和图像的分析,我们可以更好地理解指数函数的概念和运算规则。
指数函数的图象和性质 专题训练卷(含答案详解)

2.1.2指数函数的图象和性质1.下列函数是指数函数的是( ).A .y =x 5B .y =4x 3C .43x y ⎛⎫= ⎪⎝⎭D .y =13x ⎛⎫- ⎪⎝⎭+2 2.函数f (x )=132a ⎛⎫- ⎪⎝⎭·a x 是指数函数,则12f ⎛⎫ ⎪⎝⎭的值为( ).A .2B .-2C .-D .3.函数||12x y -⎛⎫= ⎪⎝⎭的图象是( ).4.函数f (x )=a x (a >0且a ≠1)对于任意的实数x ,y 都有( ).A .f (xy )=f (x )f (y )B .f (xy )=f (x )+f (y )C .f (x +y )=f (x )f (y )D .f (x +y )=f (x )+f (y )5.已知f (x )=a -x (a >0且a ≠1),且f (-2)>f (-3),则a 的取值范围是( ).A .a >0B . a >1C .a <1D .0<a <16.函数y ( ).A .[0,+∞)B .[0,4]C .[0,4)D .(0,4)7.若f (x )是指数函数,且f (2)-f (1)=6,则f (x )=__________.8.已知(a 2+2a +5)3x >(a 2+2a +5)1-x ,则x 的取值范围是__________.9.函数y =的定义域是__________.10.函数y =a x (a >0且a ≠1)在区间[1,2]上的最大值比最小值大2a ,求a 的值.参考答案1. 答案: C2. 答案:D解析:∵函数f (x )是指数函数, ∴12a -3=1,a =8.∴f (x )=8x ,12182f ⎛⎫== ⎪⎝⎭3. 答案:B4. 答案:C解析:f (x +y )=a x +y =a x ·a y =f (x )·f (y ),故选C .5. 答案:D 解析:由于f (x )=a -x =1xa ⎛⎫ ⎪⎝⎭,而f (-2)>f (-3),说明f (x )是递增函数,从而11a >,0<a <1,故选D .6. 答案:C解析:∵4x >0,∴16-4x <16.∴函数y =[0,4).7. 答案:3x解析:设f (x )=a x (a >0且a ≠1),则a 2-a =6,解得a =3,即f (x )=3x .8. 答案:14⎛⎫+∞ ⎪⎝⎭,解析:对于任意实数a ,a 2+2a +5=(a +1)2+4≥4>1,故y =(a 2+2a +5)x 是递增函数,因此有3x >1-x ,即14x >. 9. 答案:(-∞,0] 解析:由21402x -⎛⎫-≥ ⎪⎝⎭,得22-x ≥22,∴2-x ≥2,x ≤0.10. 解:当a >1时,y =a x 在[1,2]上是递增函数,∴y max =f (2)=a 2,y min =f (1)=a .∴f (2)-f (1)=2a ,即a 2-a =2a .∴32a =. 当0<a <1时, y =a x 在[1,2]上是递减函数, ∴y max =f (1),y min =f (2),即f (1)-f (2)=2a ,即a -a 2=2a . ∴12a =. 综上所述,12a =或32a =.。
(完整版)指数和指数函数练习题及答案

指数和指数函数一、选择题1.(36a 9)4(63a 9)4等于()(C)a 4(A)a 16(B)a b 8(D)a -b 22.若a>1,b<0,且a +a =22,则a -a 的值等于()-b b (A)6(B)±2(C)-2(D)22x 3.函数f(x)=(a -1)在R 上是减函数,则a 的取值范围是()(A)a >1(B)a <2(C)a<2(D)1<a <4.下列函数式中,满足f(x+1)=(A)21f(x)的是( )211x -x(x+1) (B)x+ (C)2(D)224x 25.下列f(x)=(1+a )⋅a -x 是()(A)奇函数(B)偶函数(C)非奇非偶函数(D)既奇且偶函数1a 1b116.已知a>b,ab ≠0下列不等式(1)a >b ,(2)2>2,(3)<,(4)a 3>b 3,(5)()<()33a b22a b 11中恒成立的有()(A)1个(B)2个(C)3个(D)4个2x -17.函数y=x 是()2+1(A)奇函数(B)偶函数(C)既奇又偶函数(D)非奇非偶函数8.函数y=1的值域是()x 2-1(A)(-∞,1)(B)(-∞,0)⋃(0,+∞)(C)(-1,+∞)(D)(-∞,-1)⋃(0,+∞)+9.下列函数中,值域为R 的是()(A)y=512-x(B)y=(1x 11-xx)(C)y=()-1(D)y=1-223e x -e -x10.函数y=的反函数是()2(A)奇函数且在R 上是减函数(B)偶函数且在R 上是减函数++(C)奇函数且在R 上是增函数(D)偶函数且在R 上是增函数11.下列关系中正确的是()++111111(A)()3<()3<()3(B)()3<()3<()3252225111111(C)()3<()3<()3(D)()3<()3<()352252221222122112212.若函数y=3+2的反函数的图像经过P 点,则P 点坐标是()(A)(2,5)(B)(1,3)(C)(5,2)(D)(3,1)x -113.函数f(x)=3+5,则f (x)的定义域是()(A)(0,+∞)(B)(5,+∞)(C)(6,+∞)(D)(-∞,+∞)x 14.若方程a -x-a=0有两个根,则a 的取值范围是()(A)(1,+∞)(B)(0,1)(C)(0,+∞)(D)φ15.已知函数f(x)=a +k,它的图像经过点(1,7),又知其反函数的图像经过点(4,0),则函数f(x)的表达式是()x x x x (A)f(x)=2+5 (B)f(x)=5+3 (C)f(x)=3+4 (D)f(x)=4+316.已知三个实数a,b=a ,c=a a x x-1a a ,其中0.9<a<1,则这三个数之间的大小关系是()(A)a<c<b (B)a<b<c (C)b<a<c (D)c<a<bx 17.已知0<a<1,b<-1,则函数y=a +b 的图像必定不经过()(A)第一象限 (B)第二象限(C)第三象限 (D)第四象限二、填空题1.若a <ax 322,则a 的取值范围是。
指数函数及应用经典练习及答案

[基础巩固]1.下列判断正确的是( )A .2.52.5>2.53B .0.82<0.83C .π2<π 2D .0.90.3>0.90.5解析 因为函数y =0.9x 在R 上为减函数,所以0.90.3>0.90.5.答案 D2.设函数f (x )=a -|x |(a >0,且a ≠1),若f (2)=4,则( )A .f (-2)>f (-1)B .f (-1)>f (-2)C .f (1)>f (2)D .f (-2)>f (2) 解析 f (2)=a -2=4,a =12,f (x )=⎝⎛⎭⎫12-|x |=2|x |,则f (-2)>f (-1). 答案 A3.(多选)以下关于数的大小的结论正确的是( )3.(多选)以下关于数的大小的结论正确的是( )A .1.72.5<1.73B .0.8-0.1<0.8-0.2C .1.70.3<0.93.1D .⎝⎛⎭⎫13 13 >⎝⎛⎭⎫14 14解析 y =1.7x 单调递增,2.5<3,∴1.72.5<1.73,A 正确;y =0.8x 单调递减,-0.1>-0.2,∴0.8-0.1<0.8-0.2,B 正确;又1.70.3>1.70=1,0.93.1<0.90=1,∴1.70.3>0.93.1,C 错误;⎣⎡⎦⎤⎝⎛⎭⎫1313 12 =⎝⎛⎭⎫13 4 =181 , ⎣⎡⎦⎤⎝⎛⎭⎫1414 12 =⎝⎛⎭⎫14 3=164 , ∵181 <164,∴⎝⎛⎭⎫13 13 <⎝⎛⎭⎫14 14 ,D 错误. 答案 AB4.已知(a 2+a +2)x >(a 2+a +2)1-x ,则x 的取值范围是________.解析 ∵a 2+a +2=⎝⎛⎭⎫a +122+74>1, ∴y =(a 2+a +2)x 为R 上的增函数.∴x >1-x .即x >12. 答案 ⎝⎛⎭⎫12,+∞ 5.已知2x ≤⎝⎛⎭⎫14x -3,则函数y =⎝⎛⎭⎫12x 的值域为 ________________ .解析 由2x ≤⎝⎛⎭⎫14x -3,得2x ≤2-2x +6, ∴x ≤-2x +6,∴x ≤2.∴⎝⎛⎭⎫12x ≥⎝⎛⎭⎫122=14,即y =⎝⎛⎭⎫12x 的值域为⎣⎡⎭⎫14,+∞. 答案 ⎣⎡⎭⎫14,+∞6.已知函数.(1)若a =-1,求函数f (x )的单调增区间.(2)如果函数f (x )有最大值3,求实数a 的值.解析 (1)当a =-1时,令g (x )=-x 2-4x +3=-(x +2)2+7,由于g (x )在(-2,+∞)上递减,y =⎝⎛⎭⎫13x 在R 上是减函数,所以f (x )在(-2,+∞)上是增函数,即f (x )的单调增区间是(-2,+∞).(2)令h (x )=ax 2-4x +3,f (x )=⎝⎛⎭⎫13h (x ),由于f (x )有最大值3,所以h (x )应有最小值-1;因此必有⎩⎪⎨⎪⎧a >0,12a -164a=-1,解得a =1,即当f (x )有最大值3时,a 的值为1. [能力提升]7.已知函数f (x )=3x -⎝⎛⎭⎫13x ,则f (x )( )A .是奇函数,且在R 上是增函数B .是偶函数,且在R 上是增函数C .是奇函数,且在R 上是减函数D .是偶函数,且在R 上是减函数解析 因为f (x )=3x -⎝⎛⎭⎫13x ,且定义域为R ,所以f (-x )=3-x -⎝⎛⎭⎫13-x =⎝⎛⎭⎫13x -3x =-⎣⎡⎦⎤3x -⎝⎛⎭⎫13x =-f (x ),即函数f (x )是奇函数. 又y =3x 在R 上是增函数,y =⎝⎛⎭⎫13x 在R 上是减函数,所以f (x )=3x -⎝⎛⎭⎫13x 在R 上是增函数.答案 A8.若函数的值域是⎝⎛⎦⎤0,19,则f (x )的单调递增区间是________. 解析 令g (x )=ax 2+2x +3,由于f (x )的值域是⎝⎛⎦⎤0,19, 所以g (x )的值域是[2,+∞).因此有⎩⎪⎨⎪⎧a >0,12a -44a =2,解得a =1, 这时g (x )=x 2+2x +3,由于g (x )的单调递减区间是(-∞,-1],所以f (x )的单调递增区间是(-∞,-1].答案 (-∞,-1]9.已知函数,则f (x )的单调递增区间为________,值域为________.解析 令x 2-2x ≥0,解得x ≥2或x ≤0,∴f (x )的定义域为(-∞,0]∪[2,+∞),令t =x 2-2x -1,则其在(-∞,0]上递减,在[2,+∞)上递增,又y =⎝⎛⎭⎫12t 为减函数,故f (x )的增区间为(-∞,0].∵t =x 2-2x -1≥-1,∴⎝⎛⎭⎫12t ∈(0,2].故f (x )的值域为(0,2].答案 (-∞,0] (0,2]10.已知函数f (x )=a -12x +1(x ∈R ). (1)用定义证明:不论a 为何实数,f (x )在(-∞,+∞)上总为增函数.(2)若f (x )为奇函数,求a 的值.(3)在(2)的条件下,求f (x )在区间[1,5]上的最小值.解析 (1)因为f (x )的定义域为R ,任取x 1<x 2,所以f (x 1)-f (x 2)<0,即f (x 1)<f (x 2).所以不论a 为何实数,f (x )在(-∞,+∞)上总为增函数. (2)因为f (x )在R 上为奇函数,所以f (0)=0,即a -120+1=0,解得a =12. 经检验,a =12时,f (x )=12-12x +1是奇函数. (3)由(2)知,f (x )=12-12x +1, 由(1)知,f (x )在(-∞,+∞)上为增函数, 所以f (x )在区间[1,5]上的最小值为f (1).因为f (1)=12-13=16, 所以f (x )在区间[1,5]上的最小值为16. [探索创新]11.已知函数f (x )=a x (a >0且a ≠1)在[-1,1]上的最大值与最小值之差为32. (1)求实数a 的值;(2)若g (x )=f (x )-f (-x ),当a >1时,解不等式g (x 2+2x )+g (x -4)>0.解析 (1)当a >1时,f (x )max =a ,f (x )min =1a, 则a -1a =32,解得a =2, 当0<a <1时,f (x )max =1a,f (x )min =a , 则1a -a =32,解得a =12. 综上得:a =2或a =12. (2)当a >1时,由(1)知a =2,g (x )=2x -2-x 为奇函数且在R 上是增函数,所以g (x 2+2x )+g (x -4)>0⇒g (x 2+2x )>-g (x -4)=g (4-x )⇒x 2+2x >4-x ⇒x >1或x <-4.所以,原不等式的解集为{x |x >1或x <-4}.。
指数函数经典例题(答案)
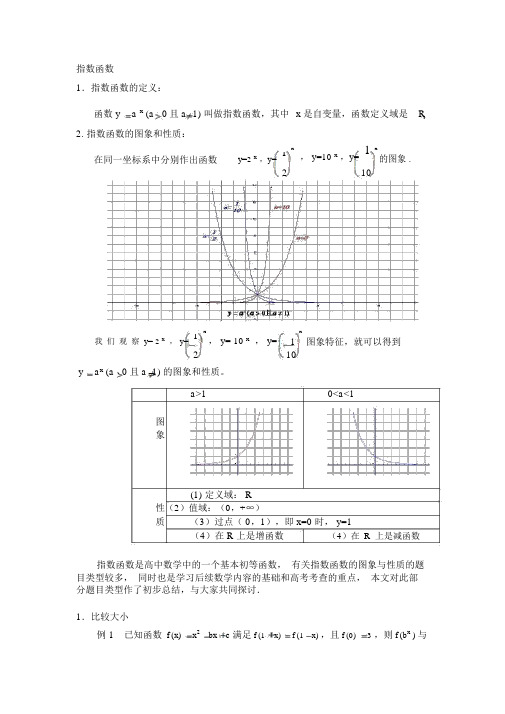
指数函数1.指数函数的定义:函数 y a x (a 0且a 1) 叫做指数函数,其中 x 是自变量,函数定义域是 R2. 指数函数的图象和性质:x , y=10 x ,y=1x在同一坐标系中分别作出函数y=2 x,y=1的图象 .2 10x x我 们 观 察 y= 2 x , y=1, y= 10 x , y=1 图象特征,就可以得到 210y a x (a 0且a 1) 的图象和性质。
a>10<a<1图象11(1) 定义域: R性(2)值域:(0,+∞) 质 (3)过点( 0,1),即 x=0 时, y=1(4)在 R 上是增函数 (4)在 R 上是减函数指数函数是高中数学中的一个基本初等函数, 有关指数函数的图象与性质的题目类型较多, 同时也是学习后续数学内容的基础和高考考查的重点, 本文对此部分题目类型作了初步总结,与大家共同探讨. 1.比较大小例 1 已知函数 f (x)x 2 bx c 满足 f (1 x) f (1 x) ,且 f (0) 3 ,则 f (b x ) 与f ( c x ) 的大小关系是_____.分析:先求 b, c 的值再比较大小,要注意b x, c x的取值是否在同一单调区间内.解:∵ f (1 x) f (1 x) ,∴函数 f ( x) 的对称轴是x 1 .故 b 2,又 f (0) 3 ,∴c 3 .∴函数 f ( x) 在∞,1 上递减,在1,∞上递增.若 x ≥ 0 ,则 3x≥ 2x≥ 1 ,∴f(3x)≥f(2x);若 x 0 ,则3x 2 x 1 ,∴f (3x) f (2x ) .综上可得 f (3x )≥ f (2x ) ,即 f (c x ) ≥ f (b x ) .评注:①比较大小的常用方法有:作差法、作商法、利用函数的单调性或中间量等.②对于含有参数的大小比较问题,有时需要对参数进行讨论.2.求解有关指数不等式例 2 已知(a22a5)3 x(a22a 5)1 x,则x的取值范围是___________.分析:利用指数函数的单调性求解,注意底数的取值范围.解:∵ a22a 5 ( a 1)24≥4 1,∴函数 y(a22a5)x在(∞,∞)上是增函数,∴ 3x 1x ,解得x 1.∴ x 的取值范围是1,∞.44评注:利用指数函数的单调性解不等式,需将不等式两边都凑成底数相同的指数式,并判断底数与 1 的大小,对于含有参数的要注意对参数进行讨论.3.求定义域及值域问题例 3求函数 y 1 6x 2的定义域和值域.解:由题意可得 16x2≥ 0 ,即 6x 2≤ 1 ,∴ x 2 ≤ 0 ,故 x ≤ 2.∴函数 f (x) 的定义域是∞,2 .令 t6x 2,则 y1t ,又∵ x≤ 2 ,∴ x 2 ≤ 0 .∴ 0 6x 2≤ 1 ,即 0 t ≤ 1 .∴ 0 ≤ 1 t 1,即 0 ≤ y 1 .∴函数的值域是01,.评注:利用指数函数的单调性求值域时,要注意定义域对它的影响.4.最值问题例 4函数y a2x2a x1(a 0且a 1)在区间[ 11],上有最大值14,则 a 的值是 _______.分析:令 t a x可将问题转化成二次函数的最值问题,需注意换元后t 的取值范围.解:令t a x,则t0 ,函数y a2 x2a x 1 可化为y(t1)2 2 ,其对称轴为t1.∴当 a 1 时,∵x11,,∴1≤ a x≤ a ,即1≤ t ≤ a .a a∴当 t a 时,y max(a1)2214.解得 a 3 或 a 5 (舍去);当 0 a 1 时,∵x11,,∴ a ≤ a x≤1,即 a ≤ t ≤1,a a1时, y max12∴ t1214 ,a a解得 a 1或 a1(舍去),∴ a 的值是 3 或1.353评注:利用指数函数的单调性求最值时注意一些方法的运用,比如:换元法,整体代入等.5.解指数方程例 5 解方程3x 232x80 .解:原方程可化为9 (3x )280 3x9 0 ,令 t3x (t0),上述方程可化为9t 280t 9 0 ,解得t9或 t1(舍去),∴ 3x9,∴ x 2 ,经检验原方程的9解是 x 2 .评注:解指数方程通常是通过换元转化成二次方程求解,要注意验根.6.图象变换及应用问题例 6 为了得到函数y 9 3x 5 的图象,可以把函数y3x的图象().A.向左平移 9 个单位长度,再向上平移 5 个单位长度B.向右平移 9 个单位长度,再向下平移 5 个单位长度C.向左平移 2 个单位长度,再向上平移 5 个单位长度D.向右平移 2 个单位长度,再向下平移 5 个单位长度分析:注意先将函数 y9 3x 5 转化为t3x 2 5 ,再利用图象的平移规律进行判断.解:∵ y 9 3x 5 3x 2 5 ,∴把函数y 3 x的图象向左平移2个单位长度,再向上平移 5 个单位长度,可得到函数y 93x 5 的图象,故选(C).评注:用函数图象解决问题是中学数学的重要方法,利用其直观性实现数形结合解题,所以要熟悉基本函数的图象,并掌握图象的变化规律,比如:平移、伸缩、对称等.习题1、比较下列各组数的大小:(1)若,比较与;(2)若,比较与;(3)若,比较与;()若,且,比较 a 与 b;4 a 与 b.()若,且,比较5解:(1)由,故,此时函数为减函数.由,故.( 2)由,故.又,故.从而.而(3)由.,因,故.又,故.从(4)应有.又因.因若,故,则.从而.又,故,这与已知,这样矛盾.(5)应有.又因.因若,且,则,故.又.从而,故,这样有,这与已知矛盾.小结:比较通常借助相应函数的单调性、奇偶性、图象来求解.2,曲线则分别是指数函数与 1 的大小关系是 ( ).,和的图象 ,(分析 : 首先可以根据指数函数单调性 , 确定, 在轴右侧令, 对应的函数值由小到大依次为 ,故应选 .小结 : 这种类型题目是比较典型的数形结合的题目 , 第(1) 题是由数到形的转化 , 第(2) 题则是由图到数的翻译 , 它的主要目的是提高学生识图 , 用图的意识 . 求最值3,求下列函数的定义域与值域 .1(1)y =2 x 3 ; (2)y=4x +2x+1+1.11解:(1) ∵ x-3 ≠0,∴ y =2 x 3 的定义域为{ x | x ∈R 且 x ≠3}. 又∵ ≠x 310,∴ 2 x 3 ≠1,1∴y =2 x 3 的值域为{ y |y>0 且 y ≠1}.(2)y = 4x +2x+1+1 的定义域为 R. ∵ 2x >0, ∴ y = 4x +2x+1+1= (2 x ) 2+2· 2x +1=x2(2 +1) >1.∴ y =4x +2x+1 +1 的值域为{ y | y>1}.4,已知-1≤x ≤2, 求函数 f(x)=3+2 ·3x+1-9 x 的最大值和最小值解:设 t=3 x, 因为 -1 ≤ x ≤ 2,所以1t 9 ,且 f(x)=g(t)=-(t-3)2+12, 故当 t=33即 x=1 时, f(x) 取最大值 12,当 t=9 即 x=2 时 f(x) 取最小值 -24 。
指数函数习题(经典含答案及详细解析)

2.函数f (x )=x 2-bx +c 满足f (1+x )=f (1-x )且A .f (b x )≤f (c x) B .f (b x )≥f (c x) lg(a x -2x-5 ≥5 [9,(9,1,,1[1,[1,,1)上的最大值比最小值大,则234x x ---+11.(2011·银川模拟)若函数y =a 2x +2a x-1(a >0且a ≠1)在x ∈[-1,1]上的最大值为14,求a 的值.的值.12.已知函数f (x )=3x ,f (a +2)=18,g (x )=λ·3ax -4x的定义域为[0,1]. (1)求a 的值;的值;(2)若函数g (x )在区间[0,1]上是单调递减函数,求实数λ的取值范围.的取值范围.指数函数答案指数函数答案1.1.解析:由解析:由a ⊗b =îïíïìa a ≤bba >b得f (x )=1⊗2x=îïíïì2xx,1x答案:答案:A A 2. 2. 解析:∵解析:∵f (1(1++x )=f (1(1--x ),∴f (x )的对称轴为直线x =1,由此得b =2. 又f (0)(0)==3,∴c =3.3.∴∴f (x )在(-∞,-∞,1)1)1)上递减,在上递减,在上递减,在(1(1(1,+∞)上递增.,+∞)上递增.,+∞)上递增.若x ≥0,则3x ≥2x ≥1,∴f (3x )≥f (2x).若x <0<0,则,则3x<2x<1<1,∴,∴f (3x)>f (2x). ∴f (3x )≥f (2x ). 答案:答案:A A3.3.解析:由于函数解析:由于函数y =|2x-1|1|在在(-∞,-∞,0)0)0)内单调递减,在内单调递减,在内单调递减,在(0(0(0,+∞)内单调递增,而函数在,+∞)内单调递增,而函数在区间区间((k -1,k +1)1)内不单调,所以有内不单调,所以有k -1<0<k +1,解得-,解得-1<1<k <1. 答案:答案:C C4. 4. 解析:由题意得:解析:由题意得:A =(1,2)(1,2),,a x -2x >1且a >2>2,由,由A ⊆B 知a x -2x>1在(1,2)(1,2)上恒成立,即上恒成立,即a x -2x -1>0在(1,2)(1,2)上恒成立,令上恒成立,令u (x )=a x -2x -1,则u ′(x )=a x ln a -2x ln2>0ln2>0,所以函数,所以函数u (x )在(1,2)(1,2)上单调递增,则上单调递增,则u (x )>u (1)(1)==a -3,即a ≥3.≥3. 答案:答案:B B5. 5. 解析:数列解析:数列解析:数列{{a n }满足a n =f (n )(n ∈N *),则函数f (n )为增函数,为增函数,注意a 8-6>(3>(3--a )×7-)×7-33,所以îïíïìa >13-a >0a8-6-a -3,解得2<a <3.答案:答案:C C6. 6. 解析:解析:f (x )<12⇔x 2-a x <12⇔x 2-12<a x ,考查函数y =a x 与y =x 2-12的图象,的图象,当a >1时,必有a -1≥12,即1<a ≤2,≤2,当0<a <1时,必有a ≥12,即12≤a <1<1,,综上,12≤a <1或1<a ≤2.≤2.答案:答案:C C7. 7. 解析:当解析:当a >1时,y =a x 在[1,2][1,2]上单调递增,故上单调递增,故a 2-a =a 2,得a =32.当0<a <1时,y =ax 在[1,2][1,2]上单调递减,故上单调递减,故a -a 2=a 2,得a =12.故a =12或32.答案:12或328. 8. 解析:分别作出两个函数的图象,通过图象的交点个数来判断参数的取值范围.解析:分别作出两个函数的图象,通过图象的交点个数来判断参数的取值范围.解析:分别作出两个函数的图象,通过图象的交点个数来判断参数的取值范围.曲线曲线||y |=2x+1与直线y =b 的图象如图所示,由图象可得:如果的图象如图所示,由图象可得:如果||y |=2x+1与直线y =b 没有公共点,则b 应满足的条件是b ∈[-1,1]1,1].. 答案:答案:[[-1,1]9. 9. 解析:如图满足条件的区间解析:如图满足条件的区间解析:如图满足条件的区间[[a ,b ],当a =-=-11,b =0或a =0,b =1时区间长度最小,最小值为1,当a =-=-11,b =1时区间长度最大,最大值为2,故其差为1. 答案:答案:1 110. 10. 解:要使函数有意义,则只需-解:要使函数有意义,则只需-x 2-3x +4≥0,即x 2+3x -4≤0,解得-4≤x ≤1.≤1. ∴函数的定义域为∴函数的定义域为{{x |-4≤x ≤1}.≤1}. 令t =-x 2-3x +4,则t =-x 2-3x +4=-=-((x +32)2+254,∴当-4≤x ≤1时,t max =254,此时x =-32,t min =0,此时x =-=-44或x =1.∴0≤t ≤254.∴0≤-x 2-3x +4≤52.∴函数y =2341()2x x ---+的值域为的值域为[[28,1]1]..+)+(≤-时,≤234()2x x ---+在,-32]-32,-32,,-32][1a,,1a ]=1a,即(1a+=13或-15(或13.。
指数函数习题及答案完整版

指数函数习题及答案Document serial number【NL89WT-NY98YT-NC8CB-NNUUT-NUT108】指数函数习题一、选择题1.定义运算ab=,则函数f(x)=12x的图象大致为( )2.函数f(x)=x2-bx+c满足f(1+x)=f(1-x)且f(0)=3,则f(b x)与f(c x)的大小关系是( )A.f(b x)≤f(c x)B.f(b x)≥f(c x)C.f(b x)>f(c x)D.大小关系随x的不同而不同3.函数y=|2x-1|在区间(k-1,k+1)内不单调,则k的取值范围是( ) A.(-1,+∞)B.(-∞,1)C.(-1,1) D.(0,2)4.设函数f(x)=ln[(x-1)(2-x)]的定义域是A,函数g(x)=lg(-1)的定义域是B,若AB,则正数a的取值范围( )A.a>3 B.a≥3C.a> D.a≥5.已知函数f(x)=若数列{a n}满足a n=f(n)(n∈N*),且{a n}是递增数列,则实数a的取值范围是( )A.[,3) B.(,3)C.(2,3) D.(1,3)6.已知a>0且a≠1,f(x)=x2-a x,当x∈(-1,1)时,均有f(x)<,则实数a 的取值范围是( )A.(0,]∪[2,+∞)B.[,1)∪(1,4]C.[,1)∪(1,2]D.(0,)∪[4,+∞)二、填空题7.函数y=a x(a>0,且a≠1)在[1,2]上的最大值比最小值大,则a的值是________.8.若曲线|y|=2x+1与直线y=b没有公共点,则b的取值范围是________.9.(2011·滨州模拟)定义:区间[x1,x2](x1<x2)的长度为x2-x1.已知函数y=2|x|的定义域为[a,b],值域为[1,2],则区间[a,b]的长度的最大值与最小值的差为________.三、解答题10.求函数y=211.(2011·银川模拟)若函数y=a2x+2a x-1(a>0且a≠1)在x∈[-1,1]上的最大值为14,求a的值.12.已知函数f(x)=3x,f(a+2)=18,g(x)=λ·3ax-4x的定义域为[0,1].(1)求a的值;(2)若函数g(x)在区间[0,1]上是单调递减函数,求实数λ的取值范围.指数函数答案1.解析:由ab=得f(x)=12x=答案:A2.解析:∵f (1+x )=f (1-x ),∴f (x )的对称轴为直线x =1,由此得b =2. 又f (0)=3,∴c =3.∴f (x )在(-∞,1)上递减,在(1,+∞)上递增. 若x ≥0,则3x ≥2x ≥1,∴f (3x )≥f (2x ). 若x <0,则3x <2x <1,∴f (3x )>f (2x ). ∴f (3x )≥f (2x ). 答案:A3.解析:由于函数y =|2x -1|在(-∞,0)内单调递减,在(0,+∞)内单调递增,而函数在区间(k -1,k +1)内不单调,所以有k -1<0<k +1,解得-1<k <1. 答案:C4.解析:由题意得:A =(1,2),a x -2x >1且a >2,由AB 知a x -2x >1在(1,2)上恒成立,即a x -2x -1>0在(1,2)上恒成立,令u (x )=a x -2x -1,则u ′(x )=a x ln a -2x ln2>0,所以函数u (x )在(1,2)上单调递增,则u (x )>u (1)=a -3,即a ≥3. 答案:B5.解析:数列{a n }满足a n =f (n )(n ∈N *),则函数f (n )为增函数, 注意a 8-6>(3-a )×7-3,所以,解得2<a <3. 答案:C6.解析:f (x )<x 2-a x <x 2-<a x ,考查函数y =a x 与y =x 2-的图象, 当a >1时,必有a -1≥,即1<a ≤2, 当0<a <1时,必有a ≥,即≤a <1, 综上,≤a <1或1<a ≤2. 答案:C7.解析:当a >1时,y =a x 在[1,2]上单调递增,故a 2-a =,得a =.当0<a <1时,y =a x 在[1,2]上单调递减,故a -a 2=,得a =.故a =或. 答案:或8.解析:分别作出两个函数的图象,通过图象的交点个数来判断参数的取值范围.曲线|y |=2x +1与直线y =b 的图象如图所示,由图象可得:如果|y |=2x +1与直线y =b 没有公共点,则b 应满足的条件是b ∈[-1,1]. 答案:[-1,1]9.解析:如图满足条件的区间[a ,b ],当a =-1,b =0或a =0,b =1时区间长度最小,最小值为1,当a =-1,b =1时区间长度最大,最大值为2,故其差为1. 答案:110.解:要使函数有意义,则只需-x 2-3x +4≥0,即x 2+3x -4≤0,解得-4≤x ≤1.∴函数的定义域为{x |-4≤x ≤1}.令t =-x 2-3x +4,则t =-x 2-3x +4=-(x +)2+,∴当-4≤x ≤1时,t max =,此时x =-,t min =0,此时x =-4或x =1. ∴0≤t ≤.∴0≤≤.∴函数y =2341()2x x --+[,1].由t =-x 2-3x +4=-(x +)2+(-4≤x ≤1)可知,当-4≤x ≤-时,t 是增函数, 当-≤x ≤1时,t 是减函数. 根据复合函数的单调性知:y =1()2[-4,-]上是减函数,在[-,1]上是增函数.∴函数的单调增区间是[-,1],单调减区间是[-4,-].11.解:令a x =t ,∴t >0,则y =t 2+2t -1=(t +1)2-2,其对称轴为t =-1.该二次函数在[-1,+∞)上是增函数.①若a >1,∵x ∈[-1,1],∴t =a x ∈[,a ],故当t =a ,即x =1时,y max =a 2+2a -1=14,解得a =3(a =-5舍去). ②若0<a <1,∵x ∈[-1,1],∴t =a x∈[a ,],故当t =,即x =-1时, y max =(+1)2-2=14. ∴a =或-(舍去). 综上可得a =3或.12.解:法一:(1)由已知得3a +2=183a =2a =log 32. (2)此时g (x )=λ·2x -4x , 设0≤x 1<x 2≤1,因为g (x )在区间[0,1]上是单调减函数,所以g (x 1)-g (x 2)=(2x 1-2x 2)(λ-2x 2-2x 1)>0恒成立,即λ<2x 2+2x 1恒成立.由于2x 2+2x 1>20+20=2,所以实数λ的取值范围是λ≤2. 法二:(1)同法一.(2)此时g (x )=λ·2x -4x ,因为g (x )在区间[0,1]上是单调减函数,所以有g ′(x )=λln2·2x -ln4·4x =ln2[-2·(2x )2+λ·2x ]≤0成立. 设2x =u ∈[1,2],上式成立等价于-2u 2+λu ≤0恒成立. 因为u ∈[1,2],只需λ≤2u 恒成立, 所以实数λ的取值范围是λ≤2.。
高一数学指数函数的图像和性质练习题(带详细答案)

指数函数练习题一.选择题2.在一致平面直角坐标系中,函数 f ( x)ax 与 g (x) a x的图像可能是()y y y y1111x o x o x o o xDA B C3.设a,b, c, d 都是不等于的正数, y a x , y b x , y c x , y d x在同一坐标系中的图像1y如下图,则a,b, c, d 的大小次序是()y b x y c xy a x y d xA.a b c dB.a b d cC.b a d cD.b a c dx 4.若1x0 ,那么以下各不等式建立的是()oA.2 x 2 x0.2xB.2x0.2 x2x C .0.2x 2 x 2 x D .2 x 2 x0.2x5 函数 f (x)(a 21) x在R上是减函数,则 a 的取值范围是()A. a1B. a2 C .a2 D.1a26.函数y1的值域是()2 x1A.(,1)B.(,0) (0,)C.(1,) D .(, 1)(0,)7.当a 1时,函数y a x1是()a x1A. 奇函数B.偶函数C.既奇又偶函数D. 非奇非偶函数8.函数y a x 2 1.(a0 且 a1) 的图像必经过点()A.(0,1)B.(1,1)C.( 2,0)D.(2,2)9.若x0是方程2x1的解,则 x0()xA.(0.1,0.2)B.(0.3,0.4)C.(0.5,0.7) D .(0.9,1)10.某厂 1998年的产值为a万元,估计产值每年以n%递加,则该厂到2010年的产值(单位:万元)是()A.a(1 n % )13B.a(1 n % )12C .a(1 n % )11D . 10 (1 n % ) 129二.填空题:1. 已知 f (x) 是指数函数,且f ( 3)5 ,则 f (3)2252. 设 0 a1,使不等式 a x 22 x 1a x 2 3x 5 建立的 x 的会合是3. 若方程 ( 1) x(1 ) xa0 有正数解,则实数 a 的取值范围是424. 函数 y (3x 1) 0 8 2x 的定义域为5. 函数 y2 x 2x的单一递加区间为三、解答题:x 11.设 0x 2 ,求函数 y 423 ? 2 x 5 的最大值和最小值。
(完整版)指数和指数函数练习题及答案(可编辑修改word版)

2 62 指数和指数函数一、选择题 1.(3 6 a 9)4( 6 3 a 9)4 等于( )(A )a 16(B )a 8(C )a 4(D )a 22. 若 a>1,b<0,且 a b+a -b=2,则 a b -a -b 的值等于( )(A ) (B ) ± 2(C )-2(D )23. 函数 f (x )=(a 2-1)x在 R 上是减函数,则 a 的取值范围是()(A ) a > 1 (B ) a < 2 (C )a< (D )1< a < 14. 下列函数式中,满足 f(x+1)= f(x)的是() 21 1 (A)(x+1)(B)x+(C)2x(D)2-x245.下列 f(x)=(1+a x )2⋅ a-x 是( )(A )奇函数 (B )偶函数(C )非奇非偶函数(D )既奇且偶函数1 1 11 1 16.已知 a>b,ab ≠ 0 下列不等式(1)a 2>b 2,(2)2a>2b,(3) < ,(4)a 3 >b 3 ,(5)( )a <( )ba b 3 3中恒成立的有( ) (A )1 个(B )2 个 (C )3 个 (D )4 个2 x - 17. 函数 y=是( )2 x+ 1 (A )奇函数(B )偶函数(C )既奇又偶函数(D )非奇非偶函数18. 函数 y=的值域是( )2 x- 1(A )(- ∞,1)(B )(- ∞, 0) ⋃ (0,+ ∞ )(C )(-1,+ ∞ ) (D )(- ∞ ,-1) ⋃ (0,+ ∞ )9. 下列函数中,值域为 R +的是( )1(A )y=5 2-xe x - e - x1(B )y=( )1-x(C )y= 3(D )y= 10. 函数 y= 的反函数是()2(A )奇函数且在 R +上是减函数(B )偶函数且在 R +上是减函数(C )奇函数且在 R +上是增函数 (D )偶函数且在 R +上是增函数11.下列关系中正确的是( )1 2 1 2 1 11 1 12 1 2(A )( ) 3 <( ) 3 <( ) 3(B )( ) 3 <( ) 3 <( ) 32 5 21 2 1 1 1 22 2 51 2 1 2 1 1(C )( ) 3 <( ) 3 <( )3 (D )( ) 3 <( ) 3 <( ) 3 5 2 25 2 22 ( 1 ) x - 1 21 -2 xx 12. 若函数 y=3+2x-1的反函数的图像经过 P 点,则 P 点坐标是()(A )(2,5) (B )(1,3) (C )(5,2) (D )(3,1)13. 函数 f(x)=3x +5,则 f -1(x)的定义域是( ) (A )(0,+ ∞ ) (B )(5,+ ∞ ) (C )(6,+ ∞ ) (D )(- ∞ ,+ ∞ )14. 若方程 a x-x-a=0 有两个根,则 a 的取值范围是( ) (A )(1,+ ∞ ) (B )(0,1) (C )(0,+ ∞ ) (D )15. 已知函数 f(x)=a x+k,它的图像经过点(1,7),又知其反函数的图像经过点(4,0),则函数 f(x)的表达式是( )(A)f(x)=2x +5 (B)f(x)=5x +3 (C)f(x)=3x+4(D)f(x)=4x+316. 已知三个实数 a,b=a a,c=a aa,其中 0.9<a<1,则这三个数之间的大小关系是()(A )a<c<b (B )a<b<c (C )b<a<c (D )c<a<b17.已知 0<a<1,b<-1,则函数 y=a x+b 的图像必定不经过( ) (A)第一象限 (B)第二象限 (C)第三象限 (D)第四象限 二、填空题31.若 a2 <a 2 ,则 a 的取值范围是 。
(完整版)指数函数及其性质习题(含答案)
指数函数及其性质习题(含答案)一、单选题的图象可能是( ) 1.在同一坐标系内,函数y=x a(a≠0)和y=ax+1aA.B.C.D.−1,若f(a)=1,则f(−a)=()2.已知函数f(x)=(e x+e−x)ln1−x1+xA.1B.−1C.3D.−33.已知函数f(x)=(x−a)(x−b)(其中a>b)的图象如图所示,则函数g(x)=a x +b的图象大致是( )A.B..C.D.4.已知a=log40.7,b=log23,c=0.20.6,则a,b,c的大小关系是( )A.c<b<a B.a<c<b C.b<a<c D.a<b<c5.函数y=a x+1−3(a>0,且a≠1)的图象一定经过的点是( )A.(0,−2)B.(−1,−3)C.(0,−3)D.(−1,−2)6.在同一坐标系中,函数y=2−x与y=−log2x的图象都正确的是()A.B.C.D .7.设a =20.5,b =0.52,c =log 20.5,则a,b,c 的大小关系为A . c >a >bB . c >b >aC . a >b >cD . b >a >c8.若01a b <<<,则b a , a b , log b a ,)A .B .C .D .9.若a ,b ,c 满足2a =3,b =log 25,3c =2,则( )A . c <a <bB . b <c <aC . a <b <cD . c <b <a二、填空题10.已知: 12a a -+=,则22a a -+=__________.11.函数()2x f x =在[]1,3-上的最小值是__________. 12.函数y=a x+2-1(a>0且a≠1)的图象恒过定点________.13.求值:2log 323−log 3427−31+log 32=__________.14.函数f(x)=(12)−x2+2x+1的单调减区间为________. 15,.16.计算:. 17.若函数()()23x f x a =-在R 上是减函数,则实数a 的取值范围是________18.已知函数()x f x a b =+ ()0,1a a >≠的定义域和值域都是[]1,0-,则b a =__________.三、解答题19.(1)计算:(−3)−(1−0.5−2)÷(338)13;(2)已知a =log 32,3b =5用a,b 表示log 3√30.20.(1)(2)已知15a a-+=,求22a a -+和.21.计算: (1))213013210.027163217---⎛⎫--+-+⋅ ⎪⎝⎭. (222.化简求值 (1) (827)23+(0.008)−23×225(2) 12523+(12)−2−(127)−13+10012+lg3+14lg9−lg √3lg81−lg2723.已知定义在R 上的函数f(x)=b−2x2x +a 是奇函数.⑴求a , b 的值,并判断函数f(x)在定义域中的单调性(不用证明);⑵若对任意的t ∈R ,不等式f(t 2−2t)+f(2t 2−k)<0恒成立,求实数k 的取值范围.24.若函数f(x)=a x −1(a >0,且a ≠1)的定义域和值域都是[0,2],求实数a 的值.25.(本小题满分10分)已知函数f(x)=log 4(4x +1)+kx(k ∈R)是偶函数.(1)求实数k 的值;(2)设g(x)=log 4(a ⋅2x +a),若f(x)= g(x)有且只有一个实数解,求实数a 的取值范围.26.计算:(1) (−338)−23+0.002−12−10(√5−2)−1+(√2−√3)0; (2)lg 5(lg 8+lg 1 000)+3lg 22+lg 16+lg 0.06. 27.已知f(x)=4x−1−2x +5,x ∈[−2,2].(1)求f(x)的值域.(2)若f(x)>3m 2+am +2对任意a ∈[−1,1]和x ∈[−2,2]都成立,求m 的取值范围.28.计算下列各式的值;(1)(2)参考答案1.B【解析】【分析】分两种情况讨论,利用函数的单调性,筛选排除即可得结果【详解】若a>0,y=x a在(0,+∞)递增,排除A,B选项,y=ax+1a递增,排除D;纵轴上截距为正数,排除C,即a>0时,不合题意;若a<0,y=x a在(0,+∞)递减,可排除C,D选项,由y=ax+1a递减可排除A,故选B.【点睛】本题通过对多个图象的选择考查函数的图象与性质,属于中档题.这类题型也是近年高考常见的命题方向,该题型的特点是综合性较强、考查知识点较多,但是并不是无路可循.解答这类题型可以从多方面入手,根据函数的定义域、值域、单调性、奇偶性、特殊点以及x→0+,x→0−,x→+∞,x→−∞时函数图象的变化趋势,利用排除法,将不合题意的选项一一排除.2.D【解析】分析:先化简f(a)=1得到(e a+e−a)ln1+a1−a=−2,再求f(−a)的值.详解:由题得(e a+e−a)ln1−a1+a −1=1,∴(e a+e−a)ln1−a1+a=2,∴−(e a+e−a)ln1+a1−a=2,∴(e a+e−a)ln1+a1−a=−2.所以f(−a)=(e−a+e a)ln1+a1−a−1=−2−1=−3.故答案为:D点睛:(1)本题主要考查函数求值和指数对数运算,意在考查学生对这些基础知识的掌握能力和运算能力.(2)解答本题的关键是整体代入求值.3.D【解析】【分析】根据二次函数的图象得到−1<b<0,a>1,继而得到g(x)=a x+b的图象经过一二三象限,问题得以解决.【详解】因为a,b 是二次函数的零点,由二次函数f (x )=(x −a )(x −b )(其中a >b )的图象可知−1<b <0,a >1, 所以g (x )=a x +b 的图象经过一二三象限,只有选项D 符合题意,故选D.【点睛】函数图象的辨识可从以下方面入手:(1)从函数的定义域,判断图象的左右位置;从函数的值域,判断图象的上下位置.(2)从函数的单调性,判断图象的变化趋势.(3)从函数的奇偶性,判断图象的对称性.(4)从函数的特征点,排除不合要求的图象4.B【解析】【分析】利用指数与对数的单调性与中间量0,1可求得三个数大小。
指数函数及其性质(含解析、答案)

A 基础练习2.1.2指数函数(1时) 1.下列函数是指数函数的是( ) A .y =-2xB .y =2x +1 C .y =2-x D .y =1x【解析】 y =2-x=⎝⎛⎭⎫12x,符合指数函数的定义,故选C.【答案】 C 2.函数y =(a -2)x 在R 上为增函数,则a 的取值范围是( )A .a>0且a ≠1B .a>3C .a<3D .2<a<3【解析】 由指数函数单调性知,底数大于1时为增函数,∴a -2>1,∴a>3,故选B. 【答案】 B 3.已知a =5-12,函数f(x)=a x ,若实数m 、n 满足f(m)>f(n),则m 、n 的大小关系为________.【解析】 ∵a =5-12∈(0,1), 故a m >a n ⇒m<n. 【答案】 m<n4.已知指数函数f(x)的图象过点(2,4),求f(-3)的值.【解析】 设指数函数f(x)=a x (a>0且a ≠1),由题意得a 2=4,∴a =2,∴f(x)=2x , ∴f(-3)=2-3=18.B 综合应用一、选择题(每小题5分,共20分) 1.函数y =a x -2+1(a>0,a ≠1)的图象必经过点( )A .(0,1)B .(1,1)C .(2,0)D .(2,2)【解析】 由于函数y =a x 经过定点(0,1),所以函数y =a x-2经过定点(2,1),于是函数y =a x -2+1经过定点(2,2).【答案】 D2.f(x)=⎝⎛⎭⎫12|x|,x ∈R ,那么f(x)是( ) A .奇函数且在(0,+∞)上是增函数 B .偶函数且在(0,+∞)上是增函数 C .奇函数且在(0,+∞)上是减函数 D .偶函数且在(0,+∞)上是减函数 【解析】因为函数f(x)= |x|= 图象如右图. 由图象可知答案显然是D. 【答案】 D3.下列四个函数中,值域为(0,+∞)的函数是( )A .y =21x B .y =2x -1C .y =2x +1D .y =⎝⎛⎭⎫122-x【解析】 在A 中,∵1x ≠0,∴21x≠1,即y =21x的值域为(0,1)∪(1,+∞).在B 中,2x -1≥0,∴y =2x -1的值域为[0,+∞). 在C中,∵2x >0,∴2x +1>1.∴y =2x +1的值域为(1,+∞). 在D 中,∵2-x ∈R ,∴y =⎝⎛⎭⎫122-x>0. ∴y =⎝⎛⎭⎫122-x 的值域为(0,+∞).故选D.【答案】 D 4.方程4x -1=116的解为( ) A .2 B .-2 C .-1 D .1 【解析】 ∵4x -1=116=4-2,∴x -1=-2,∴x =-1.故选C. 【答案】 C二、填空题(每小题5分,共10分) 5.函数y =a x -1的定义域是(-∞,0],则实数a 的取值范围为________.【解析】 由a x -1≥0,得a x ≥1=a 0,因为x ∈(-∞,0],由指数函数的性质知0<a<1.【答案】 (0,1)6.函数f(x)=⎝⎛⎭⎫13x-1,x ∈[-1,2]的值域为________.【解析】 函数y =⎝⎛⎭⎫13x 在区间[-1,2]上是减函数,所以⎝⎛⎭⎫132≤⎝⎛⎭⎫13x ≤⎝⎛⎭⎫13-1,即19≤⎝⎛⎭⎫13x ≤3, 于是19-1≤f(x)≤3-1,即-89≤f(x)≤2.【答案】 [-89,2]三、解答题(每小题10分,共20分) 7.已知函数f(x)=a x -2(x ≥0)的图象经过点⎝⎛⎭⎫4,19,其中a>0且a ≠1. (1)求a 的值;(2)求函数y =f(x)(x ≥0)的值域. 【解析】 (1)函数图象过点⎝⎛⎭⎫4,19, 所以a 4-2=19=⎝⎛⎭⎫132,∴a =13,(2)f(x)=⎝⎛⎭⎫13x -2(x ≥0), 由x ≥0,得x -2≥-2, ∴0<⎝⎛⎭⎫13x -2≤⎝⎛⎭⎫13-2=9,∴函数y =f(x)(x ≥0)的值域为(0,9]. 8.画出下列函数的图象,并说明它们是由函数f(x)=2x 的图象经过怎样的变换得到的.(1)y =2x -1;(2)y =2x +1;(3)y =2|x|; (4)y =-2x .【解析】 如图所示.y=2x-1的图象是由y=2x 的图象向右平移1个单位得到;y=2x+1的图象是由y=2x 的图象向上平移1个单位得到;y=2|x|的图象是由y=2x 的y 轴右边的图象和其关于y 轴对称的图象组成的;y=-2x 的图象与y=2x 的图象关于x 轴对称.9.(10分)函数f(x)=a x (a>0,且a ≠1)在区间[1,2]上的最大值比最小值大a2,求a的值.【解析】 (1)若a>1,则f(x)在[1,2]上递增,∴a 2-a =a 2,即a =32或a =0(舍去).(2)若0<a<1,则f(x)在[1,2]上递减, ∴a -a 2=a 2,即a =12或a =0(舍去),综上所述,所求a 的值为12或32.2.1.2指数函数(2时) A 基础练习1.已知集合M ={-1,1},N =⎩⎨⎧⎭⎬⎫x ⎪⎪12<2x +1<4,x ∈Z ,则M ∩N 等于( ) A .{-1,1} B .{-1} C .{0} D .{-1,0} 【解析】 因为N ={x|2-1<2x +1<22,x ∈Z },又函数y =2x 在R 上为增函数, ∴N ={x|-1<x +1<2,x ∈Z } ={x|-2<x<1,x ∈Z }={-1,0}. ∴M ∩N ={-1,1}∩{-1,0}={-1}.故选B.【答案】 B2.设14<⎝⎛⎭⎫14b <⎝⎛⎭⎫14a<1,那么( )A .a a <a b <b aB .a a <b a <a bC .a b <a a <b aD .a b <b a <a a【解析】 由已知及函数y =⎝⎛⎭⎫14x是R 上的减函数, 得0<a<b<1.由y =a x (0<a<1)的单调性及a<b ,得a b <a a .由0<a<b<1知0<a b <1.∵⎝⎛⎭⎫a b a <⎝⎛⎭⎫a b 0=1.∴a a <b a.故选C. 也可采用特殊值法,如取a =13,b =12.【答案】 C3.已知函数f(x)=a -12x +1,若f(x)为奇函数,则a =________.【解析】 解法1:∵f(x)的定义域为R ,又∵f(x)为奇函数,∴f(0)=0,即a -120+1=0.∴a =12.解法2:∵f(x)为奇函数,∴f(-x)=-f(x),即a -12-x +1=12x +1-a ,解得a =12.【答案】 124.函数y =2-x 2+ax -1在区间(-∞,3)内递增,求a 的取值范围.【解析】 对u =-x 2+ax -1=-⎝⎛⎭⎫x -a 22+a 24-1,增区间为⎝⎛⎦⎤-∞,a 2,∴y 的增区间为⎝⎛⎦⎤-∞,a2,由题意知3≤a2,∴a ≥6. ∴a 的取值范围是a ≥6. B 综合应用一、选择题(每小题5分,共20分) 1.设y 1=40.9,y 2=80.48,y 3=(12)-1.5,则( )A .y 3>y 1>y 2B .y 2>y 1>y 3C .y 1>y 2>y 3D .y 1>y 3>y 2 【解析】 y 1=40.9=21.8,y 2=80.48=21.44,y 3=(12)-1.5=21.5,∵y =2x 在定义域内为增函数, 且1.8>1.5>1.44, ∴y 1>y 3>y 2. 【答案】 D2.若⎝⎛⎭⎫142a +1<⎝⎛⎭⎫143-2a,则实数a 的取值范围是( )A.⎝⎛⎭⎫12,+∞B.()1,+∞ C .(-∞,1) D.⎝⎛⎭⎫-∞,12 【解析】 函数y =⎝⎛⎭⎫14x在R 上为减函数,∴2a +1>3-2a ,∴a>12.故选A.【答案】 A3.设函数f(x)定义在实数集上,它的图象关于直线x =1对称,且当x ≥1时,f(x)=3x -1,则有( )A .f(13)<f(32)<f(23)B .f(23)<f(32)<f(13)C .f(23)<f(13)<f(32)D .f(32)<f(23)<f(13)【解析】 因为f(x)的图象关于直线x =1对称,所以f(13)=f(53),f(23)=f(43),因为函数f(x)=3x -1在[1,+∞)上是增函数,所以f(53)>f(32)>f(43),即f(23)<f(32)<f(13).故选B.【答案】 B4.如果函数f(x)=(1-2a)x 在实数集R 上是减函数,那么实数a 的取值范围是( )A .(0,12)B .(12,+∞)C .(-∞,12)D .(-12,12)【解析】 根据指数函数的概念及性质求解.由已知得,实数a 应满足⎩⎪⎨⎪⎧1-2a>01-2a<1,解得⎩⎪⎨⎪⎧a<12a>0,即a ∈(0,12).故选A.【答案】 A二、填空题(每小题5分,共10分) 5.设a>0,f(x)=e x a +ae x (e>1),是R 上的偶函数,则a =________.【解析】 依题意,对一切x ∈R ,都有f(x)=f(-x),∴e x a +a e x =1ae x +ae x , ∴(a -1a )(e x -1e x )=0.∴a -1a =0,即a 2=1.又a>0,∴a =1. 【答案】 16.下列空格中填“>、<或=”. (1)1.52.5________1.53.2,(2)0.5-1.2________0.5-1.5.【解析】 (1)考察指数函数y =1.5x . 因为1.5>1,所以y =1.5x 在R 上是单调增函数.又因为2.5<3.2,所以1.52.5<1.53.2. (2)考察指数函数y =0.5x .因为0<0.5<1,所以y =0.5x 在R 上是单调减函数.又因为-1.2>-1.5,所以0.5-1.2<0.5-1.5.【答案】 <,<三、解答题(每小题10分,共20分) 7.根据下列条件确定实数x 的取值范围:a<⎝⎛⎭⎫1a 1-2x(a>0且a ≠1).【解析】 原不等式可以化为a 2x -1>a 12,因为函数y =a x (a>0且a ≠1)当底数a 大于1时在R 上是增函数;当底数a 大于0小于1时在R 上是减函数,所以当a>1时,由2x -1>12,解得x>34;当0<a<1时,由2x -1<12,解得x<34.综上可知:当a>1时,x>34;当0<a<1时,x<34.8.已知a>0且a ≠1,讨论f(x)=a -x 2+3x +2的单调性.【解析】 设u =-x 2+3x +2=-⎝⎛⎭⎫x -322+174, 则当x ≥32时,u 是减函数,当x ≤32时,u 是增函数.又当a>1时,y =a u 是增函数,当0<a<1时,y =a u 是减函数,所以当a>1时,原函数f(x)=a -x 2+3x +2在⎣⎡⎭⎫32,+∞上是减函数,在⎝⎛⎦⎤-∞,32上是增函数.当0<a<1时,原函数f(x)=a -x 2+3x +2在⎣⎡⎭⎫32,+∞上是增函数,在⎝⎛⎦⎤-∞,32上是减函数.9.(10分)已知函数f(x)=3x +3-x . (1)判断函数的奇偶性;(2)求函数的单调增区间,并证明.【解析】 (1)f(-x)=3-x +3-(-x)=3-x+3x =f(x)且x ∈R ,∴函数f(x)=3x +3-x是偶函数.(2)由(1)知,函数的单调区间为(-∞,0]及[0,+∞),且[0,+∞)是单调增区间.现证明如下:设0≤x 1<x 2,则f(x 1)-f(x 2)=3x 1+3-x 1-3x 2-2-x 2=3x 1-3x 2+13x 1-13x 2=3x 1-3x 2+3x 2-3x 13x 13x 2=(3x 2-3x 1)·1-3x 1+x 23x 1+x 2.∵0≤x 1<x 2,∴3x 2>3x 1,3x 1+x 2>1, ∴f(x 1)-f(x 2)<0,即f(x 1)<f(x 2), ∴函数在[0,+∞)上单调递增, 即函数的单调增区间为[0,+∞).。
指数函数基础训练题(含详解)

因为 ,所以 ,所以函数 是奇函数,
因为 ,且 与 均为增函数,
所以 在 上是增函数,
故选:A.
【点睛】
本题考查函数的奇偶性的判断,指数函数的单调性的应用,属于基础题.
4.A
【解析】
【分析】
找中间量0或1进行比较大小,可得结果
【详解】
,所以 ,
故选:A.
【点睛】
此题考查利用对数函数、指数函数的单调性比较大小,属于基础题
故答案为 .
【点睛】
对于形如 , 且 的指数型函数,其恒过的定点的求解方法:
先令 ,计算出 的值即为定点的横坐标,再根据 的值计算出 的值即为纵坐标,所以恒过的定点为 .
12.
【解析】
【分析】
利用指数函数 的单调性可得出 与 的大小关系.
【详解】
,所以,函数 为 上的增函数,
, .
故答案为: .
【点睛】
本题考查指数函数单调性的应用,属于基础题.
13.
【解析】
【分析】
由指数函数的单调性,将不等式化为 ,求解即可.
【详解】
,化为 ,
解得 ,
所以不等式的解集是 .
故答案为: .
【点睛】
本题考查指数不等式的解法,指数函数的单调性应用是解题的关键,属于基础题.
14.(1) (2) (3)
【解析】
【分析】
(1)化为同底数的幂的形式后,根据指数函数的单调性可得结果;
10.
【解析】
【分析】
令指数为0时,可得定点.
【详解】
当 时, ,
函数 的图象必经过 .
故答案为: .
【点睛】
本题考查指数型函数的定点问题,属于基础题.
(完整版)高一数学指数函数的图像和性质练习题(带详细答案)

指数函数练习题一.选择题:1.某种细菌在培育过程中,每 20 分钟分裂一次(一个分裂为两个) 。
经过 3 个小时,这类细菌由 1个可生殖成()A.511个B.512 个C.1023个D.1024 个2.在一致平面直角坐标系中,函数f ( x)ax 与 g (x)a x 的图像可能是()yy y y1111xoxoxoo xDABC3.设 a,b, c, d 都是不等于 1的正数, ya x , yb x , yc x , yd x 在同一坐标系中的图像yy c x如下图,则a,b, c, d 的大小次序是()y b xyaxy dxA.a b c dB.a b d cC.b ad cD.b a c dx4.若1 x 0 ,那么以下各不等式建立的是()oA.2 x 2 x 0.2xB.2x 0.2 x 2xC .0.2x 2 x 2 xD .2 x 2 x0.2 x5 函数 f (x)(a 2 1) x 在 R 上是减函数,则 a 的取值范围是()A. a 1B. a 2C .a2D.1a26.函数 y1的值域是()2 x1A.( ,1)B.(,0) (0, )C.( 1, )D .( , 1) (0, )7.当 a1 时,函数 ya x 1是()a x1A. 奇函数B.偶函数C.既奇又偶函数D. 非奇非偶函数8.函数 ya x 21.(a 0 且 a1) 的图像必经过点()A.(0,1)B.(1,1)C.( 2,0)D.(2,2)9.若 x 0 是方程 2x1 的解,则 x 0 ( )xA.(0.1,0.2)B.(0.3,0.4)C.(0.5,0.7)D.(0.9,1)10.某厂 1998 年的产值为a万元,估计产值每年以n %递加,则该厂到2010年的产值(单位:万元)是()A.a(1 n % )13B.a(1n % )12 C .a(1 n% )11 D.10(1n %)129二.填空题:1.已知f (x)是指数函数,且35f ( ),则 f (3)2252.设0 a1,使不等式a x2 2 x 1a x23x 5建立的 x 的会合是3.若方程(1) x(1) x a0 有正数解,则实数 a 的取值范围是424.函数y(3x1) 082x的定义域为5.函数y2 x2x 的单一递加区间为三、解答题:x11.设0x 2 ,求函数y42 3 ? 2 x 5 的最大值和最小值。
指数函数练习题(包含详细答案)

1.给出下列结论: ②n a n =|a |(n >1,n ∈N *,n 为偶数);④若2x =16,3y =127,则x +y =7.其中正确的是( )A .①②B .②③C .③④D .②④答案 B解析 ∵2x =16,∴x =4,∵3y =127,∴y =-3.∴x +y =4+(-3)=1,故④错.2.函数y =16-4x 的值域是( )A .[0,+∞)B .[0,4]C .[0,4)D .(0,4)答案 C3.函数f (x )=3-x -1的定义域、值域是( )A .定义域是R ,值域是RB .定义域是R ,值域是(0,+∞)C .定义域是R ,值域是(-1,+∞)D .以上都不对答案 C解析 f (x )=(13)x -1,∵(13)x >0,∴f (x )>-1.4.设y 1=40.9,y 2=80.48,y 3=(12)-1.5,则( )A .y 3>y 1>y 2B .y 2>y 1>y 3C .y 1>y 2>y 3D .y 1>y 3>y 2 答案 D解析 y 1=21.8,y 2=21.44,y 3=21.5,∵y =2x 在定义域内为增函数,∴y 1>y 3>y 2.5.函数f (x )=a x -b 的图像如图,其中a ,b 为常数,则下列结论正确的是( )A .a >1,b <0B .a >1,b >0C .0<a <1,b >0D .0<a <1,b <0 答案 D6.(2014·成都二诊)若函数f (x )=(a +1e x -1)cos x 是奇函数,则常数a 的值等于( ) A .-1B .1C .-12D.12 答案 D7.(2014·山东师大附中)集合A ={(x ,y )|y =a },集合B ={(x ,y )|y =b x +1,b >0,b ≠1},若集合A ∩B 只有一个子集,则实数a 的取值范围是( )A .(-∞,1)B .(-∞,1]C .(1,+∞)D .R 答案 B8.函数f (x )=3·4x -2x 在x ∈[0,+∞)上的最小值是( )A .-112B .0C .2D .10 答案 C解析 设t =2x ,∵x ∈[0,+∞),∴t ≥1.∵y =3t 2-t (t ≥1)的最小值为2,∴函数f (x )的最小值为2.9.已知函数f (x )=⎩⎨⎧x -1,x >0,2-|x |+1,x ≤0.若关于x 的方程f (x )+2x -k =0有且只有两个不同的实根,则实数k 的取值范围为( )A .(-1,2]B .(-∞,1]∪(2,+∞)C .(0,1]D .[1,+∞) 答案 A解析 在同一坐标系中作出y =f (x )和y =-2x +k 的图像,数形结合即可.10.函数y =2|x |的定义域为[a ,b ],值域为[1,16],当a 变化时,函数b =g (a )的图像可以是( ) 答案 B解析 函数y =2|x |的图像如图.当a =-4时,0≤b ≤4;当b =4时,-4≤a ≤0.11.若函数y =(a 2-1)x 在(-∞,+∞)上为减函数,则实数a 的取值范围是________. 答案 (-2,-1)∪(1,2)解析 函数y =(a 2-1)x 在(-∞,+∞)上为减函数,则0<a 2-1<1,解得1<a <2或-2<a <-1.12.函数y =a x 在[0,1]上的最大值与最小值的和为3,则a =________.答案 2解析 ∵y =a x 在[0,1]上为单调函数,∴a 0+a 1=3,∴a =2.13.(2014·沧州七校联考)若函数f (x )=a |2x -4|(a >0,a ≠1)满足f (1)=19,则f (x )的单调递减区间是________.答案 [2,+∞)解析 f (1)=a 2=19,a =13,f (x )=⎩⎪⎨⎪⎧ (13)2x -4,x ≥2,(13)4-2x , x <2.∴单调递减区间为[2,+∞).14.若0<a <1,0<b <1,且,则x 的取值范围是________.答案 (3,4)解析 log b (x -3)>0,∴0<x -3<1,∴3<x <4.15.若函数y =2-x +1+m 的图像不经过第一象限,则m 的取值范围是______.答案 m ≤-216.是否存在实数a ,使函数y =a 2x +2a x -1(a >0且a ≠1)在[-1,1]上的最大值是14?答案 a =3或a =13解析 令t =a x ,则y =t 2+2t -1.(1)当a >1时,∵x ∈[-1,1],∴a x ∈[1a ,a ],即t ∈[1a ,a ].∴y =t 2+2t -1=(t +1)2-2在[1a ,a ]上是增函数(对称轴t =-1<1a ).∴当t =a 时,y max =(a +1)2-2=14.∴a =3或a =-5.∵a >1,∴a =3.(2)当0<a <1时,t ∈[a ,1a]. ∵y =(t +1)2-2在[a ,1a ]上是增函数, ∴y max =(1a +1)2-2=14.∴a =13或a =-15.∵0<a <1,∴a =13.综上,a =3或a =13.17.(2011·上海)已知函数f (x )=a ·2x +b ·3x ,其中a ,b 满足a ·b ≠0.(1)若a ·b >0,判断函数f (x )的单调性;(2)若a ·b <0,求f (x +1)>f (x )时的x 的取值范围.答案 (1)a >0,b >0时,f (x )增函数;a <0,b <0时,f (x )减函数(2)a <0,b >0时,x >log 1.5⎝ ⎛⎭⎪⎫-a 2b ;a >0,b <0时,x <log 1.5⎝ ⎛⎭⎪⎫-a 2b 解析 (1)当a >0,b >0时,任意x 1,x 2∈R ,x 1<x 2,∴f (x 1)-f (x 2)<0,∴函数f (x )在R 上是增函数.当a <0,b <0时,同理,函数f (x )在R 上是减函数.(2)f (x +1)-f (x )=a ·2x +2b ·3x >0.当a <0,b >0时,⎝ ⎛⎭⎪⎫32x >-a 2b ,则x >log 1.5⎝ ⎛⎭⎪⎫-a 2b ; 当a >0,b <0时,⎝ ⎛⎭⎪⎫32x <-a 2b ,则x <log 1.5⎝ ⎛⎭⎪⎫-a 2b .18.已知函数f (x )=-2x2x +1. (1)用定义证明函数f (x )在(-∞,+∞)上为减函数;(2)若x ∈[1,2],求函数f (x )的值域;(3)若g (x )=a 2+f (x ),且当x ∈[1,2]时g (x )≥0恒成立,求实数a 的取值范围.答案 (1)略 (2)[-45,-23] (3)a ≥85(2)∵f (x )在(-∞,+∞)上为减函数,∴f (x )的值域为[-45,-23].(3)当x ∈[1,2]时,g (x )∈[a 2-45,a 2-23].∵g (x )≥0在x ∈[1,2]上恒成立,∴a 2-45≥0,∴a ≥85.。
高中数学:指数函数的概念练习及答案

高中数学:指数函数的概念练习及答案指数函数的概念1.下列函数中,是指数函数的是( )A.y=2·3xB.y=3x+1C.y=3xD.y=x32.下列以x为自变量的函数中,是指数函数的是( )A.y=(-5)xB.y=e x(e≈2.71828)C.y=-5xD.y=πx+23.函数y=(a2-5a+5)ax是指数函数,则有( )A.a=1或a=4B.a=1C.a=4D.a>0,且a≠14.若函数f(x)=(a-3)·a x是指数函数,则f(2)的值为( )A.4B.8C.2D.165.函数y=(m-2)x是指数函数,则m的取值范围是________.待定系数法求指数函数解析式6.指数函数y=a x的图象经过点(2,16),则a的值是( )A.B.C.2D.47.已知指数函数的图象经过点(-1,2),则指数函数的解析式为________.8.已知f(x)是指数函数,且f(1+)·f(1-)=9,则f(2+)·f(2-)的值为________.9.若指数函数f(x)的图象过点(1,),则f(-2)=________.指数函数的求值10.已知指数函数f(x)=a x(a>0,且a≠1)的图象过点(3,8),则a2.5与a2.3的大小为( )A.a2.5=a2.3B.a2.5<a2.3C.a2.5>a2.3D.无法确定11.已知f(x)=2x+2-x,若f(a)=3,则f(2a)等于( )A.5B.7C.9D.1112.已知函数f(x)=则f[f(-4)]等于( )A.-4B.-C.4D.613.给出函数f(x)=,则f(-1)=________.14.若f(2x-1)=3x-2x,则f(4)=________.指数函数的实际应用15.设f(x)=则f(f(-2))等于( )A.-1B.C.D.16.某种细菌经60分钟培养,可繁殖为原来的2倍,且知该细菌的繁殖规律为y=10e kt,其中k为常数,t 表示时间(单位:小时),y表示细菌个数,10个细菌经过7小时培养,细菌能达到的个数为( ) A.640B.1280C.2560D.512017.某环保小组发现某市生活垃圾年增长率为b,2009年该市生活垃圾量为a吨,由此可以预测2019年垃圾量为( )A.a(1+10b)吨B.a(1+9b)吨C.a(1+b)10吨D.a(1+b)9吨18.某种计算机病毒是通过电子邮件进行传播的,如果某台计算机感染上这种病毒,那么它就会在下一轮病毒发作时传播一次病毒,并感染其它20台未感染病毒的计算机.现有一台计算机被第一轮病毒感染,问被第4轮病毒感染的计算机有( )台.A.60B.400C.8000D.16000019.一种产品的成本是a元,在今后的n年内,计划成本每年比上一年降低p%,则成本随着年数变化的函数关系式是( )A.a(1-p%)n(n∈N*)B.a(p%)n(n∈N*)C.a(1-p)n%(n∈N*)D.a(1-np%)(n∈N*)20.据报道,全球变暖,使北冰洋冬季冰盖面积在最近50年内减少了5%,如果按此规律,设2000年的冬季冰盖面积为m,从2000年起,经过x年后冬季冰盖面积y与x的函数关系是( )A.y=·mB.y=(1-)·mC.y=0.9550·x·mD.y=(1-0.0550·x)·m21.某医药研究所开发一种新药,据监测,如果成人按规定的剂量服用该药,服药后每毫升血液中的含药量y(μg)与服药后的时间t(h)之间近似满足如图所示的曲线.其中OA是线段,曲线段AB是函数y=k·at(t ≥1,a>0,k,a是常数)的图象.(1)写出服药后每毫升血液中含药量y关于时间t的函数关系式;(2)据测定:每毫升血液中含药量不少于2(μg)时治疗有效,假若某病人第一次服药为早上6:00,为保持疗效,第二次服药最迟是当天几点钟?(3)若按(2)中的最迟时间服用第二次药,则第二次服药后在过3h,该病人每毫升血液中含药量为多少μg?(精确到0.1μg)答案1.下列函数中,是指数函数的是( )A.y=2·3xB.y=3x+1C.y=3xD.y=x3【答案】C【解析】形如y=ax(a>0,a≠1)的函数为指数函数,y=2·3x的3x系数不为1,y=3x+1的指数不是x,y=x2是幂函数,只有y=3x符合指数函数定义.故选C.2.下列以x为自变量的函数中,是指数函数的是( )A.y=(-5)xB.y=e x(e≈2.71828)C.y=-5xD.y=πx+2【答案】B3.函数y=(a2-5a+5)ax是指数函数,则有( )A.a=1或a=4B.a=1C.a=4D.a>0,且a≠1【答案】C【解析】∵函数y=(a2-5a+5)ax是指数函数,∴解得a=4.故选C.4.若函数f(x)=(a-3)·a x是指数函数,则f(2)的值为( ) A.4B.8C.2D.16【答案】D【解析】∵函数f(x)是指数函数,∴a-3=1,∴a=4.∴f(x)=4x,f(2)=42=16.5.函数y=(m-2)x是指数函数,则m的取值范围是________.【答案】m>2且m≠3【解析】根据指数函数的定义,y=ax中的底数a规定a>0且a≠1. 故此m-2>0且m-2≠1.所以m>2且m≠3.6.指数函数y=a x的图象经过点(2,16),则a的值是( )A.B.C.2D.4【答案】D【解析】指数函数y=ax(a>0且a≠1),将(2,16)代入,得16=a2,解得a=4,所以y=4x,故选D.7.已知指数函数的图象经过点(-1,2),则指数函数的解析式为________.【答案】y=()x【解析】设指数函数的解析为:y=ax(a>0,且a≠1),∵函数的图象经过(-1,2)点,∴2=a-1,∴a=,∴指数函数的解析式为y=()x,故答案为y=()x.8.已知f(x)是指数函数,且f(1+)·f(1-)=9,则f(2+)·f(2-)的值为________.【答案】81【解析】∵f(x)是指数函数,∴设f(x)=ax(a>0且a≠1),∵f(1+)·f(1-)=9,∴·=a2=9,即a=3.∴f(2+)·f(2-)=·=34=81,故答案为81.9.若指数函数f(x)的图象过点(1,),则f(-2)=________.【答案】4【解析】设指数函数为f(x)=ax(a>0且a≠1),将(1,)代入得=a1,解得a=,所以f(x)=()x,则f(-2)=()-2=4.故答案为4.10.已知指数函数f(x)=a x(a>0,且a≠1)的图象过点(3,8),则a2.5与a2.3的大小为( ) A.a2.5=a2.3B.a2.5<a2.3C.a2.5>a2.3D.无法确定【答案】C【解析】∵指数函数f(x)=ax(a>0,且a≠1)的图象过点(3,8),∴a3=8,解得a=2.∴f(x)=2x,且在R上单调递增,∴22.3<22.5.故选C.11.已知f(x)=2x+2-x,若f(a)=3,则f(2a)等于( )A.5B.7C.9D.11【答案】B【解析】由f(a)=3,得2a+2-a=3,两边平方得,22a+2-2a+2=9,即22a+2-2a=7,∴f(2a)=7.选B项.12.已知函数f(x)=则f[f(-4)]等于( )A.-4B.-C.4D.6【答案】C【解析】f[f(-4)]=f[()-4]=f(16)==4.13.给出函数f(x)=,则f(-1)=________.【答案】9【解析】f(-1)=f(1)=f(3)=32=9.14.若f(2x-1)=3x-2x,则f(4)=________.【答案】21【解析】令2x-1=4,得x=3,将其代入f(2x-1)=3x-2x,得f(4)=33-2×3=21.15.设f(x)=则f(f(-2))等于( )A.-1B.C.D.【答案】C【解析】因为f(-2)=2-2=,所以f(f(-2))=f()=1-=1-=,故答案选C.16.某种细菌经60分钟培养,可繁殖为原来的2倍,且知该细菌的繁殖规律为y=10e kt,其中k为常数,t 表示时间(单位:小时),y表示细菌个数,10个细菌经过7小时培养,细菌能达到的个数为( ) A.640B.1280C.2560D.5120【答案】B【解析】设原来的细菌数为a.由题意可得,在函数y=10e kt中,当t=1时,y=2a.∴2a=10e k即e k=.当a=10时,e k=2,y=10e kt=10·2t,若t=7,则可得此时的细菌数为y=10×27=1280,故选B.17.某环保小组发现某市生活垃圾年增长率为b,2009年该市生活垃圾量为a吨,由此可以预测2019年垃圾量为( )A.a(1+10b)吨B.a(1+9b)吨C.a(1+b)10吨D.a(1+b)9吨【答案】C【解析】2009年该市生活垃圾量为a吨,所以2010年产生的垃圾量是a(1+b)吨,2011年产生的垃圾量是a(1+b)(1+b)=a(1+b)2吨,…由此可以预测2019年垃圾量为a(1+b)10吨.故选C.18.某种计算机病毒是通过电子邮件进行传播的,如果某台计算机感染上这种病毒,那么它就会在下一轮病毒发作时传播一次病毒,并感染其它20台未感染病毒的计算机.现有一台计算机被第一轮病毒感染,问被第4轮病毒感染的计算机有( )台.A.60B.400C.8000D.160000【答案】C【解析】由题意可得,每一轮感染的计算机数量构成以1为首项,以20为公比的等比数列,故第4轮病毒感染的计算机数量为1×203=8000台,故选C.19.一种产品的成本是a元,在今后的n年内,计划成本每年比上一年降低p%,则成本随着年数变化的函数关系式是( )A.a(1-p%)n(n∈N*)B.a(p%)n(n∈N*)C.a(1-p)n%(n∈N*)D.a(1-np%)(n∈N*)【答案】A【解析】设成本经过x年降低到y元,第一年为y=a(1-p%),第二年为y=a(1-p%)(1-p%)=a(1-p%)2,第三年为y=a(1-p%)(1-p%)(1-p%)=a(1-p%)3,…则随着年数n变化的函数关系式是y=a(1-p%)n(n∈N*).故选A.20.据报道,全球变暖,使北冰洋冬季冰盖面积在最近50年内减少了5%,如果按此规律,设2000年的冬季冰盖面积为m,从2000年起,经过x年后冬季冰盖面积y与x的函数关系是( )A.y=·mB.y=(1-)·mC.y=0.9550·x·mD.y=(1-0.0550·x)·m【答案】A【解析】设北冰洋冬季冰盖面积的年平均变化率为p,则p50=0.95,∴p=,∴设2000年的冬季冰盖面积为m,从2000年起,经过x年后冬季冰盖面积y与x的函数关系是:y=·m. 故选A.21.某医药研究所开发一种新药,据监测,如果成人按规定的剂量服用该药,服药后每毫升血液中的含药量y(μg)与服药后的时间t(h)之间近似满足如图所示的曲线.其中OA是线段,曲线段AB是函数y=k·at(t ≥1,a>0,k,a是常数)的图象.(1)写出服药后每毫升血液中含药量y关于时间t的函数关系式;(2)据测定:每毫升血液中含药量不少于2(μg)时治疗有效,假若某病人第一次服药为早上6:00,为保持疗效,第二次服药最迟是当天几点钟?(3)若按(2)中的最迟时间服用第二次药,则第二次服药后在过3h,该病人每毫升血液中含药量为多少μg?(精确到0.1μg)【答案】(1)当0≤t<1时,y=8t;当t≥1时,把A(1,8)、B(7,1)代入y=kat,得解得故y =(2)设第一次服药后最迟过t小时服第二次药,则解得t=5,即第一次服药后5h服第二次药,也即上午11:00服药.(3)第二次服药3h后,每毫升血液中含第一次服药后的剩余量为:y1=8()8=μg,含第二次服药量为:y2=8()3=4μg,所以此时两次服药剩余的量为+4≈4.7μg,故该病人每毫升血液中的含药量为4.7μg.11/11。
指数和指数函数练习题及答案

指数和指数函数专题 9.24一、选择题 1.(369a )4(639a )4等于( )(A )a16(B )a8(C )a4(D )a 22.若a>1,b<0,且a b+a -b=22,则a b-a -b的值等于( )(A )6 (B )±2 (C )-2 (D )23.函数f (x )=(a 2-1)x在R 上是减函数,则a 的取值范围是( ) (A )1>a (B )2<a (C )a<2 (D )1<2<a4.下列函数式中,满足f(x+1)=21f(x)的是( ) (A)21(x+1) (B)x+41 (C)2x (D)2-x5.下列f(x)=(1+a x )2xa-⋅是( )(A )奇函数 (B )偶函数 (C )非奇非偶函数 (D )既奇且偶函数6.已知a>b,ab 0≠下列不等式(1)a 2>b 2,(2)2a>2b,(3)ba 11<,(4)a 31>b 31,(5)(31)a <(31)b中恒成立的有( )(A )1个 (B )2个 (C )3个 (D )4个7.函数y=1212+-x x 是( )(A )奇函数 (B )偶函数 (C )既奇又偶函数 (D )非奇非偶函数 8.函数y=121-x的值域是( ) (A )(-1,∞) (B )(-,∞0)⋃(0,+∞) (C )(-1,+∞) (D )(-∞,-1)⋃(0,+∞) 9.下列函数中,值域为R +的是( ) (A )y=5x-21(B )y=(31)1-x (C )y=1)21(-x (D )y=x21-10.函数y=2xx e e --是( )(A )奇函数且在R +上是减函数 (B )偶函数且在R +上是减函数(C )奇函数且在R +上是增函数 (D )偶函数且在R +上是增函数 11.下列关系中正确的是( )(A )(21)32<(51)32<(21)31 (B )(21)31<(21)32<(51)32(C )(51)32<(21)31<(21)32 (D )(51)32<(21)32<(21)3112.若函数y=3+2x-1的图像经过定点P 点,则P 点坐标是( )(A )(2,5) (B )(1,3) (C )(5,2) (D )(3,1)13.某厂1998年的产值为a 万元,预计产值每年以n %递增,则该厂到2010年的产值(单位:万元)是( ) n a A +1(.%13) n a B +1(.%12) n a C +1(.%11) n D -1(910.%12) 14.若方程a x-x-a=0有两个根,则a 的取值范围是( ) (A )(1,+∞) (B )(0,1) (C )(0,+∞) (D )φ 15.已知三个实数a,b=a a,c=aaa ,其中0.9<a<1,则这三个数之间的大小关系是( )(A )a<c<b (B )a<b<c (C )b<a<c (D )c<a<b16.已知0<a<1,b<-1,则函数y=a x+b 的图像必定不经过( )(A)第一象限 (B)第二象限 (C)第三象限 (D)第四象限 二、填空题 1.若a 23<a2,则a 的取值范围是 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.给出下列结论:
②n
a n=|a|(n>1,n∈N*,n为偶数);
④若2x=16,3y=1
27,则x+y=7.
其中正确的是()
A.①②B.②③C.③④D.②④答案 B
解析
∵2x=16,∴x=4,∵3y=1
27,∴y=-3.
∴x+y=4+(-3)=1,故④错.
2.函数y=16-4x的值域是() A.[0,+∞) B.[0,4] C.[0,4) D.(0,4) 答案 C
3.函数f(x)=3-x-1的定义域、值域是() A.定义域是R,值域是R
B.定义域是R,值域是(0,+∞)
C.定义域是R,值域是(-1,+∞)
D.以上都不对
答案 C
解析f(x)=(1
3)
x-1,
∵(13)x >0,∴f (x )>-1.
4.设y 1=40.9,y 2=80.48,y 3=(12)-1.5,则( )
A .y 3>y 1>y 2
B .y 2>y 1>y 3
C .y 1>y 2>y 3
D .y 1>y 3>y 2
答案 D
解析 y 1=21.8,y 2=21.44,y 3=21.5,
∵y =2x 在定义域内为增函数,∴y 1>y 3>y 2.
5.函数f (x )=a x -b 的图像如图,其中a ,b 为常数,则下列结论正确的是( )
A .a >1,b <0
B .a >1,b >0
C .0<a <1,b >0
D .0<a <1,b <0
答案 D
6.(2014·成都二诊)若函数f (x )=(a +
1e x -1)cos x 是奇函数,则常数a 的值等于( )
A .-1
B .1
C .-12
D.12 答案 D
7.(2014·山东师大附中)集合A ={(x ,y )|y =a },集合B ={(x ,y )|y =b x +1,b >0,b ≠1},若集合A ∩B 只有一个子集,则实数a 的取值范围是( )
A .(-∞,1)
B .(-∞,1]
C .(1,+∞)
D .R 答案 B
8.函数f (x )=3·4x -2x 在x ∈[0,+∞)上的最小值是( )
A .-112
B .0
C .2
D .10
答案 C 解析 设t =2x ,∵x ∈[0,+∞),∴t ≥1.
∵y =3t 2-t (t ≥1)的最小值为2,
∴函数f (x )的最小值为2.
9.已知函数f (x )=⎩⎨⎧
x -1,x >0,2-|x |+1,x ≤0.
若关于x 的方程f (x )+2x -k =0有且只有两个不同的实根,则实数k 的取值范围为( )
A .(-1,2]
B .(-∞,1]∪(2,+∞)
C .(0,1]
D .[1,+∞) 答案 A
解析 在同一坐标系中作出y =f (x )和y =-2x +k 的图像,数形结合即可.
10.函数y =2|x |的定义域为[a ,b ],值域为[1,16],当a 变化时,函数b =g (a )的图像可以是( )
答案 B
解析 函数y =2|x |的图像如图.
当a =-4时,0≤b ≤4;当b =4时,-4≤a ≤0.
11.若函数y =(a 2-1)x 在(-∞,+∞)上为减函数,则实数a 的取值范围是
________.
答案 (-2,-1)∪(1,2)
解析 函数y =(a 2-1)x 在(-∞,+∞)上为减函数,则0<a 2-1<1,解得1<a <2或-2<a <-1.
12.函数y =a x 在[0,1]上的最大值与最小值的和为3,则a =________. 答案 2
解析 ∵y =a x 在[0,1]上为单调函数,
∴a 0+a 1=3,∴a =2.
13.(2014·沧州七校联考)若函数f (x )=a |2x -4|(a >0,a ≠1)满足f (1)=19,则f (x )
的单调递减区间是________.
答案 [2,+∞)
解析 f (1)=a 2=19,a =13,
f (x )=⎩⎪⎨⎪⎧ (13)2x -4,
x ≥2,(13)4-2x , x <2.
∴单调递减区间为[2,+∞).
14.若0<a <1,0<b <1,且
,则x 的取值范围是________. 答案 (3,4)
解析 log b (x -3)>0,∴0<x -3<1,∴3<x <4.
15.若函数y =2-x +1+m 的图像不经过第一象限,则m 的取值范围是______. 答案 m ≤-2
16.是否存在实数a ,使函数y =a 2x +2a x -1(a >0且a ≠1)在[-1,1]上的最大值是14?
答案 a =3或a =13
解析 令t =a x ,则y =t 2+2t -1.
(1)当a >1时,∵x ∈[-1,1],
∴a x ∈[1a ,a ],即t ∈[1a ,a ].
∴y =t 2+2t -1=(t +1)2-2在[1a ,a ]上是增函数(对称轴t =-1<1a ).
∴当t =a 时,y max =(a +1)2-2=14.
∴a =3或a =-5.∵a >1,∴a =3.
(2)当0<a <1时,t ∈[a ,1a
]. ∵y =(t +1)2-2在[a ,1a ]上是增函数,
∴y max =(1a +1)2-2=14.
∴a =13或a =-15.∵0<a <1,∴a =13.
综上,a =3或a =13.
17.(2011·上海)已知函数f (x )=a ·2x +b ·3x ,其中a ,b 满足a ·b ≠0.
(1)若a ·b >0,判断函数f (x )的单调性;
(2)若a ·b <0,求f (x +1)>f (x )时的x 的取值范围.
答案 (1)a >0,b >0时,f (x )增函数;a <0,b <0时,f (x )减函数
(2)a <0,b >0时,x >log 1.5⎝ ⎛⎭⎪⎫-a 2b ;a >0,b <0时,x <log 1.5⎝ ⎛⎭
⎪⎫-a 2b 解析 (1)当a >0,b >0时,任意x 1,x 2∈R ,x 1<x 2,
∴f (x 1)-f (x 2)<0,∴函数f (x )在R 上是增函数.
当a <0,b <0时,同理,函数f (x )在R 上是减函数.
(2)f (x +1)-f (x )=a ·2x +2b ·3x >0.
当a <0,b >0时,⎝ ⎛⎭⎪⎫32x >-a 2b ,则x >log 1.5⎝ ⎛⎭
⎪⎫-a 2b ; 当a >0,b <0时,⎝ ⎛⎭⎪⎫32x <-a 2b ,则x <log 1.5⎝ ⎛⎭
⎪⎫-a 2b . 18.已知函数f (x )=-2x
2x +1
. (1)用定义证明函数f (x )在(-∞,+∞)上为减函数;
(2)若x ∈[1,2],求函数f (x )的值域;
(3)若g (x )=a 2+f (x ),且当x ∈[1,2]时g (x )≥0恒成立,求实数a 的取值范围.
答案 (1)略 (2)[-45,-23] (3)a ≥85
(2)∵f (x )在(-∞,+∞)上为减函数,
∴f (x )的值域为[-45,-23].
(3)当x ∈[1,2]时,g (x )∈[a 2-45,a 2-23].
∵g (x )≥0在x ∈[1,2]上恒成立,
∴a 2-45≥0,∴a ≥85.。
