框架梁内力调整例题
结构内力计算分析案例

结构内力计算分析案例以下是一个关于结构内力计算分析的案例,以帮助读者更好地理解该过程。
案例:栋多层住宅楼的楼板结构受力分析和计算。
1.结构描述:该楼为一栋钢筋混凝土框架结构的多层住宅楼,楼高5层,每层高度为3米。
楼板采用承重梁和板的形式,梁间距为6米,梁宽为0.3米。
2.受力分析:根据力学原理,梁和板在受力作用下会产生内力。
梁的受力情况分为竖向和横向两个方向:-竖向受力:竖向受力主要包括自重、活载和楼层间的等分荷载。
自重一般按照材料密度计算,活载是指居住者的活动荷载,楼层间的等分荷载指的是各个楼层产生的附加荷载。
-横向受力:横向受力主要包括风荷载和地震荷载。
这些荷载会通过墙体和梁传递到结构内部。
3.内力计算:根据受力分析结果,可以进行结构内力的计算。
具体计算方法有两种:静力分析和弹性力学方法。
-静力分析:这是一种通过平衡受力和力矩的方法进行计算的方法。
根据平衡条件,可以得到各个构件的内力。
-弹性力学方法:这是一种通过应力和应变的关系进行计算的方法。
根据材料力学性质和结构的几何形状,可以计算出各个构件的内力。
4.结果分析和验证:计算得到的结构内力结果需要进行分析和验证。
主要包括两个方面:构件强度和位移。
-构件强度:计算得到的内力和构件的截面尺寸一起,可以判断构件是否满足强度要求。
如果内力超过了构件材料的承载力,需要进行加固。
-位移:根据结构内力和材料的弹性模量,可以计算出结构的位移。
结构的位移应该满足设计的要求,如果超过了预定的限值,需要进行刚度调整。
总结:结构内力计算分析是工程的关键环节,其目的是保证结构的安全性和可靠性。
通过对不同构件的受力分析和力学计算,可以得到结构的内力结果,并进行分析和验证。
这样可以确保结构的设计和施工符合规范,并达到预期的使用寿命和性能要求。
框架结构内力位移计算算例

结构力学课程大作业——多层多跨框架结构内力及位移计算班级学号姓名华中科技大学土木工程与力学学院年月日结构力学课程大作业——多层多跨框架结构内力与位移计算一、任务1、计算多层多跨框架结构在荷载作用下的弯矩和结点位移。
2、计算方法要求:(1)用迭代法、D 值法、反弯点法及求解器计算框架结构在水平荷载作用下的弯矩,并用迭代法的结果计算其结点位移。
(2)用迭代法、分层法、二次力矩分配法及求解器计算框架结构在竖向荷载作用下的弯矩,并用迭代法的结果计算其结点位移。
3、分析近似法产生误差的原因。
二、计算简图及基本数据本组计算的结构其计算简图如图1所示,基本数据如下。
混凝土弹性模量:723.010/h E kN m =⨯构件尺寸:柱:底 层:23040b h cm ⨯=⨯其它层:23030b h cm ⨯=⨯ 梁:边 梁:22560b h cm ⨯=⨯中间梁:22530b h cm ⨯=⨯ 水平荷载:'15P F kN =,30P F kN =(见图2)竖向均布恒载:17/q kN m 顶= 21/q kN m 其它=(见图8) 图1各构件的线刚度:EIi L =,其中312b h I ⨯=边 梁:33410.250.6 4.51012I m -⨯==⨯F 7311 3.010 4.510225006EI i kN m L -⨯⨯⨯===⋅ 中间梁: 34420.250.3 5.6251012I m -⨯==⨯ 7422 3.010 5.6251067502.5EI i kN m L -⨯⨯⨯===⋅ 底层柱: 33440.30.4 1.61012I m -⨯==⨯ 7344 3.010 1.61096005EI i kN m L -⨯⨯⨯===⋅ 其它层柱:34430.30.3 6.751012I m -⨯==⨯ 7433 3.010 6.75106136.43.3EI i kN m L -⨯⨯⨯===⋅ 三、水平荷载作用下的计算 (一)用迭代法计算1、计算各杆的转角分配系数ikμ' 转角分配系数计算公式:()2ikikiki i i μ'=-∑结点“1”:12225000.3932(6136.422500)μ'=-=-⨯+156136.40.1072(6136.422500)μ'=-=-⨯+结点“2”:21225000.3182(67506136.422500)μ'=-=-⨯++图2232(67506136.422500)⨯++266136.40.0872(67506136.422500)μ'=-=-⨯++由于该结构是对称结构,因此结点“3”的分配系数应该等于结点“2”的,结点“4”的分配系数应该与结点“1”的相等,所以本题只需计算1、2、5、6、9、10、13、14、17、18结点的分配系数。
框架施工图—内力分析及侧移计算(建筑构造)

(2) 侧移刚度d的确定 侧移刚度d表示柱上下两端有单位侧移时在柱中产生的 剪力。根据假定(1),梁柱线刚度之比无穷大,则各 柱端转角为零,由结构力学的两端无转角但有单位水平 位移时杆件的杆端剪力方程,柱的侧移刚度d可写成:
V 12 i
d= =
c
D
h2
EI
i=
c
h
内力分析及侧移计算
(3)同层各柱剪力的确定
(5
柱端弯矩确定以后,根据节点平衡条件可确定梁的弯矩。
对于边柱节点(图(a)),有Mb=Mc1+Mc2 对于中柱节点(图1(b))
Mb1=ib1/(ib1+ib2)(Mc1+Mc2 Mb2=ib2/(ib1+ib2)(Mc1+Mc2)
内力分析及侧移计算
如图所示,从框架中任取一柱AB,根据转角位移方
内力分析及侧移计算
分层法
认为某层框架梁上的荷载只给本层梁及与本层梁相连的框架产 生剪力和弯矩
进行弯矩分配后叠加,叠加后的不平衡弯矩再分配但不传递
内力分析及侧移计算
2 框架在水平荷载作用下内力的近似计算——反弯点法和D值法
A 反弯点法 反弯点法基本假定: (1) 在进行各柱间的剪力分配时,假定梁与柱的线
(2) 在确定各柱的反弯点位置时,假定除底层柱以
多层多跨框架所受水平荷载主要是风荷载及水平 地震作用。一般可简化为作用在框架节点上的集中 荷载,其弯矩图如图(a)所示。它的特点是,各杆的 弯矩图都是直线形,每杆都有一个零弯矩点,称为 反弯点。框架在水平荷载作用下的变形情况如图(b) 所示
内力分析及侧移计算
程,柱两端剪力为:
V
=
12ic h2
6ic h
框架结构抗震设计例题

抗震计算设计(框架内力计算)
6.2 按分层法或弯矩二次分配法计算内力 活荷载、恒载分别计算
6.3 叠合成整体框架弯矩图,不平衡弯矩再 分配一次
6.4 计算梁端剪力,及剪力图 6.5 柱子轴力,及轴力图
抗震计算设计(框架内力计算)
• 竖向荷载作用下的梁端弯矩调幅
调幅系数:0.8-0.85
M0:按简支梁 计算的跨中
柱网布置要简单规整贯通
(2)结构水平承重体系(楼屋面结构布置) 现浇钢筋混凝土楼屋面:肋梁楼盖 (单向板、双向板) 井式楼盖 (双向板)
梁板布置要传力明确、简洁,美观经济
概念设计(结构布置方案)
3.构件截面尺寸估算(以肋梁楼盖为例)
3.1 板的厚度 (1)按施工条件控制的最小厚度
类别 屋盖 楼盖 民用建筑 工业建筑 阳台、雨篷的根部
两种方法都要考虑填充墙的影响。uT顶点位移法:Gi
T1 = 1.7ψ T uT = 1.7(0.6 ~ 0.7) uT
uT:结构顶点假想位移
抗震计算设计(框架内力计算)
7.6 确定地震参数 (P40)
(1)确定特征周期Tg 根据建筑场地类别和地震分组,查表3-2得特征周期Tg。
(2)取结构阻尼系数ζ=0.05
(1)框架柱截面可按轴心受压估算。
①近似地取静荷载(10-15)kN/m2,填充墙较少时取小值。
②轴力N =负荷面积×层数×单位面积上的荷载。 即: N = 1.2恒+1.4活
③柱子的截面Ac由下式计算(Ac=b×h ):
(1.2 ~ 1.4) N = ϕ ( fc Ac + f y′As′ ) = 1.0( fc Ac + 0.01 f y′Ac )
① |M|max及相应的N,V ② Nmax及相应的M,V ③ Nmin 及相应的M,V
框架结构的内力和位移计算(精)

假定: (1)平面结构假定; (2)忽略柱的轴向变形; (3)D值法考虑了结点转角, 假定同层结点转角相等
2019/3/19
27
D 值法
计算方法 1、D值——修正抗侧刚度的计算 水平荷载作用下,框架不仅有侧移, 且各结点有转角,设杆端有相对位 移 ,转角 、 ,转角 1 2 位移方程为:
2019/3/19
22
反弯点法
2、剪力的计算 根据假定1:
V1 j d1 j j
Vij d ij j
Vij , d ij
——第j层第I根柱的剪力及其抗侧刚度
第j层总剪力
V pj
Vpj V1 j V2 j Vmj
2019/3/19 23
反弯点法
V1 j
第j层各柱剪力为
M ( z) N B
M(z)——上部水平荷载对坐标Z力矩总和 B——两边柱轴线间的距离
N
2019/3/19 44
柱轴向变形产生的侧移
N j
任意水平荷载下柱轴向变形产生的第j层处侧移 把框架连续化,根据单位荷载法:
2 ( NN / EA)dz
N j 0
Hj
N ( H j z) / B
框架结构的内力和位移计算荷载和设计要求51计算简图计算简图计算简图计算简图计算简图52竖向荷载作用下的近似计算方法分层法分层法分层法分层法力学知识回顾分层法计算过程构件弯矩图53水平荷载作用下内力近似计算方法反弯点法反弯点法弯点法反弯点法反弯点法反弯点法反弯点法反弯点法54水平荷载作用下内力近似计算方法d55水平荷载作用下侧移的近似计算梁柱刚度比k中柱
2019/3/19
9
计算简图
二、结构构件的截面抗弯刚度 考虑楼板的影响,框架梁的截面抗弯刚度应适当提高 现浇钢筋混凝土楼盖: 中框架:I=2I0 边框架:I=1.5I0 装配整体式钢筋混凝土楼盖: 截面形式选取: 框架梁跨中截面: 中框架:I=1.5 I0 T型截面 边框架:I=1.2 I0 框架梁支座截面: 装配式钢筋混凝土楼盖: 矩形截面 中框架:I=I0 边框架:I=I0 注:I0为矩形截面框架梁的截面惯性矩
第四章 框架结构内力计算

4、计算和确定梁、柱弯矩分配系数。 按修正后的刚度计算各结点周围杆件的杆 端分配系数。 5、按力矩分配法计算单层梁、柱弯矩。 6、将每个单层框架的计算结果按相应部分迭 加起来便得到原框架的计算结果,即柱的弯矩 取相邻两个单元中同一柱对应弯矩之和,而梁 的弯矩直接采用。
四、计算例题
作业2
3.2 水平荷载下内力的近似计算—反弯点法
d
i 1
m
V pj
ij
4、柱端弯矩的确定 M j V jY j 柱下端弯矩 柱上端弯矩 M j V j (h j Yj )
5、梁端弯矩的确定 M ml (M mt M m1b ) 对于边柱 ibl 对于中柱
M ml ( M mt M m1b ) M mr ibl ibr ibr ( M mt M m1b ) ibl ibr
第3章 框架结构的内力和位移计算
3.1 竖向荷载下内力的近似计算—分层法 3.2 水平荷载下内力的近似计算—反弯点法 3.3 水平荷载下内力的近似计算—D值法 3.4 水平荷载作用下侧移的近似计算
3.1 竖向荷载下内力近似计算—分层法
一、竖向荷载 自重、活荷、雪荷载及施工检修荷载等。 二、分层法的基本假设 1、忽略侧移的影响; 2、忽略每层梁的竖向荷载对其它各层梁 的影响。 三、分层法计算要点 1、将N层框架划分成N个单层框架,柱 端假定为固端, 用力矩分配法计算。
三、柱的侧移刚度D 12ic D 2 h
—为柱侧移刚度修正系数,表示梁柱刚 度比对柱侧移刚度的影响。
四、剪力计算 有了D值后,与反弯点法类似,计算各柱分 配的剪力 Dij Vij V pj Dij 五、确定柱反弯点高度比 影响柱反弯点高度的主要因素是柱上下端的 约束条件。
内力组合及内力调整

7 内力组合及内力调整7.1内力组合各种荷载情况下的框架内力求得后,根据最不利又是可能的原则进行内力组合。
当考虑结构塑性内力重分布的有利影响时,应在内力组合之前对竖向荷载作用下的内力进行增幅。
分别考虑恒荷载和活荷载由可变荷载效应控制的组合和由永久荷载效应控制的组合,并比较两种组合的内力,取最不利者。
由于构件控制截面的内力值应取自支座边缘处,为此,进行组合前,应先计算各控制截面处的(支座边缘处的)内力值。
1)、在恒载和活载作用下,跨间max M 可以近似取跨中的M 代替,在重力荷载代表值和水平地震作用下,跨内最大弯矩max M 采用解析法计算:先确定跨内最大弯矩max M 的位置,再计算该位置处的max M 。
当传到梁上的荷载为均布线荷载或可近似等效为均布线荷载时,按公式7-1计算。
计算方式见图7-1、7-2括号内数值,字母C 、D 仅代表公式推导,不代表本设计实际节点标号字母。
2max182M M M ql +≈-右左 且满足2max 116M ql = (7-1) 式中:q ——作用在梁上的恒荷载或活荷载的均布线荷载标准值;M 左、M 右——恒载和活载作用下梁左、右端弯矩标准值;l ——梁的计算跨度。
2)、在重力荷载代表值和地震作用组合时,左震时取梁的隔离体受力图,见图7-1所示, 调幅前后剪力值变化,见图7-2。
图7-1 框架梁内力组合图图7-2 调幅前后剪力值变化图中:GC M 、GD M ——重力荷载作用下梁端的弯矩; EC M 、CD M ——水平地震作用下梁端的弯矩C R 、D R ——竖向荷载与地震荷载共同作用下梁端支座反力。
左端梁支座反力:()C 1=2GD GC EC ED ql R M M M M l--++;由0M ddx=,可求得跨间max M 的位置为:1C /X R q = ; 将1X 代入任一截面x 处的弯矩表达式,可得跨间最大弯矩为: 弯矩最大点位置距左端的距离为1X ,1=/E X R q ;()101X ≤≤; 最大组合弯矩值:2max 1/2GE EF M qX M M =-+;当10X <或11X >时,表示最大弯矩发生在支座处,取1=0X 或1=X l ,最大弯矩组合设计值的计算式为:2max C 11/2GE EF M R X qX M M =--+; 右震作用时,上式中的GE M 、EF M 应该反号。
框架结构例题讲解

PMCAD模块的使用一、框架结构设计例题本建筑为5层框架结构,抗震设防烈度为7度,二类场地,框架抗震等级为3级,周期折减系数取0.7,按一组计算。
基本风压0.4kN/m2,地面粗糙度类别为C类,梁、板、柱的混凝土等级均为C30,梁、柱主筋选HRB400,箍筋选HPB235,板筋选HPB235。
框架梁端弯矩调幅系数为0.85,结构重要性系数为1。
1~五层的结构层高分别为5.5m(从基础顶面算起)、3.0m、3.0m、3.0m、3.0m。
各层采用现浇混凝土板,板厚取100mm。
对于框架结构,非受力墙起分割空间作用,在PMCAD建模时不要布置非受力墙,而应将墙重转化为梁间荷载在荷载输入中布置。
大厅、电梯间处的次梁和交叉梁的某些次梁应作主梁输入,卫生间有门洞的墙下不布置二级次梁,做现浇带处理。
具体楼面恒载、活载,梁间恒载按《建筑荷载规范》中的规定取值,或经过计算得出的结果。
结构标准层:结构标准层1、结构标准层2、结构标准层3、结构标准层4。
荷载标准层:荷载标准层1、荷载标准层2、荷载标准层3、荷载标准层4。
楼层组合:1个标准层1+荷载标准层1(层高5.5m);2个标准层2+荷载标准层2(层高3.0m);1个标准层3+荷载标准层3(层高3.0m);1个标准层4+荷载标准层4(层高3.0m)。
主菜单1—建筑模型与荷载输入*定义第1结构标准层**建立网格*轴线输入,正交轴网,轴网输入开间:6000,跨度:10,添加进深:5400,跨度1,添加进深:2100,跨度1,添加进深:5400,跨度1,添加基点:左下,转角:0,确定用光标在屏幕选择一点*轴线命名*轴线命名[Tab],用光标点取起始轴,用光标点取终止轴。
若不需要标轴线,用光标点取不标的轴线,[Esc]用光标点取两个方向的轴线,分别命名。
*构件定义**柱定义*构件定义,柱定义按照设计要求,分别定义柱子的截面类型,材料类别,点取确定。
例如:400mm×400mm*梁定义*(没有特殊情况全部按主梁布置,次梁也按主梁布置)定义梁的截面尺寸(梁宽、梁高),材料类别,点取确定。
内力组合及内力调整

7 内力组合及内力调整7.1内力组合各种荷载情况下的框架内力求得后,根据最不利又是可能的原则进行内力组合。
当考虑结构塑性内力重分布的有利影响时,应在内力组合之前对竖向荷载作用下的内力进行增幅。
分别考虑恒荷载和活荷载由可变荷载效应控制的组合和由永久荷载效应控制的组合,并比较两种组合的内力,取最不利者。
由于构件控制截面的内力值应取自支座边缘处,为此,进行组合前,应先计算各控制截面处的(支座边缘处的)内力值。
1)、在恒载和活载作用下,跨间max M 可以近似取跨中的M 代替,在重力荷载代表值和水平地震作用下,跨内最大弯矩max M 采用解析法计算:先确定跨内最大弯矩max M 的位置,再计算该位置处的max M 。
当传到梁上的荷载为均布线荷载或可近似等效为均布线荷载时,按公式7-1计算。
计算方式见图7-1、7-2括号内数值,字母C 、D 仅代表公式推导,不代表本设计实际节点标号字母。
2max182M M M ql +≈-右左 且满足2max 116M ql = (7-1) 式中:q ——作用在梁上的恒荷载或活荷载的均布线荷载标准值;M 左、M 右——恒载和活载作用下梁左、右端弯矩标准值;l ——梁的计算跨度。
2)、在重力荷载代表值和地震作用组合时,左震时取梁的隔离体受力图,见图7-1所示, 调幅前后剪力值变化,见图7-2。
图7-1 框架梁内力组合图图7-2 调幅前后剪力值变化图中:GC M 、GD M ——重力荷载作用下梁端的弯矩; EC M 、CD M ——水平地震作用下梁端的弯矩C R 、D R ——竖向荷载与地震荷载共同作用下梁端支座反力。
左端梁支座反力:()C 1=2GD GC EC ED ql R M M M M l--++;由0M ddx=,可求得跨间max M 的位置为:1C /X R q = ; 将1X 代入任一截面x 处的弯矩表达式,可得跨间最大弯矩为: 弯矩最大点位置距左端的距离为1X ,1=/E X R q ;()101X ≤≤; 最大组合弯矩值:2max 1/2GE EF M qX M M =-+;当10X <或11X >时,表示最大弯矩发生在支座处,取1=0X 或1=X l ,最大弯矩组合设计值的计算式为:2max C 11/2GE EF M R X qX M M =--+; 右震作用时,上式中的GE M 、EF M 应该反号。
毕业设计指导书(框架结构设计)-内力计算及组合

计算杆件固端弯矩时应带符号,杆端弯矩一律以顺时针方向为正,如图3-6。
图 3-6 杆端及节点弯矩正方向
1)横梁固端弯矩:
(1)顶层横梁
自重作用:
板传来的恒载作用:
(2)二~四层横梁
自重作用:
板传来的恒载作用:
2)纵梁引起柱端附加弯矩:(本例中边框架纵梁偏向外侧,中框架纵梁偏向内侧)
顶层外纵梁
相交于同一点的多个杆件中的某一杆件,其在该节点的弯矩分配系数的计算过程为:
(1)确定各杆件在该节点的转动刚度
杆件的转动刚度与杆件远端的约束形式有关,如图3-1:
(a)杆件在节点A处的转动刚度
(b)某节点各杆件弯矩分配系数
图 3-1 A节点弯矩分配系数(图中 )
(2)计算弯矩分配系数μ
(3)相交于一点杆件间的弯矩分配
(3)求某柱柱顶左侧及柱底右侧受拉最大弯矩——该柱右侧跨的上、下邻层横梁布置活荷载,然后隔跨布置,其它层按同跨隔层布置(图3-4c);
当活荷载作用相对较小时,常先按满布活荷载计算内力,然后对计算内力进行调整的近似简化法,调整系数:跨中弯矩1.1~1.2,支座弯矩1.0。
(a)(b) (c)
图 3-4 竖向活荷载最不利布置
∑Mik/l
V1/A=gl/2+u-∑Mik/l
M=gl/2*l/4+u*1.05-MAB-V1/A*l/2
4
21.9
4.08
2.25
6
12.24
41.06
-30.54
2.55
50.75
-60.24
3
16.61
4.08
2.25
6
12.24
31.14
一榀框架计算-内力计算

第8章 一榀框架计算8.7框架内力计算框架结构承受的荷载主要有恒载、活载、风荷载、地震作用。
其中恒载、活载为竖向荷载,风荷载和地震为水平作用。
手算多层多跨框架结构的内力和侧移时,采用近似方法。
求竖向荷载作用下的内力采用分层法,求水平荷载作用下的内力采用反弯点法、D 值法。
在计算各项荷载作用下的效应时,一般按标准值进行计算,然后进行荷载效应组合。
8.7.2框架内力计算1。
恒载作用下的框架内力 (1)计算简图将图8-12(a )中梁上梯形荷载折算为均布荷载。
其中a=1。
8m ,l=6.9m ,=1800/69000.26a α==,顶层梯形荷载折算为均布荷载值:232312+=120.26+0.2621.31=18.8kN m q αα-⨯-⨯⨯()(),顶层总均布荷载为18.8+4.74=23.54kN m 。
其他层计算方法同顶层,计算值为21.63kN m 。
中间跨只作用有均布荷载,不需折算。
由于该框架为对称结构,取框架的一半进行简化计算,计算简图见8-19。
(2)弯矩分配系数节点A 1:101044 1.18 4.72A A A A S i ==⨯=111144 1.33 5.32A B A B S i ==⨯=12120.940.94 1.61 5.796A A A A S i =⨯=⨯⨯=()0.622 1.3330.84415.836AS =++=∑1010 4.720.29815.836A A A A AS S μ===∑图8-19 恒载作用下计算简图(括号内数值为梁柱相对线刚度)1111 5.320.33615.836A B A B AS S μ===∑1212 5.7960.36615.836A A A A AS S μ===∑ 节点B 1:11112 1.12 2.24B D B D S i ==⨯=18.076BS =∑1111 5.320.29418.076B A B A BS S μ===∑1010 4.720.32118.076B B B B BS S μ===∑ 1212 5.7960.32118.076B B B B BS S μ===∑1111 2.240.12418.076B D B D BS S μ===∑节点A 2:()210.94 1.610.4170.94 1.610.776 1.33A A μ⨯⨯==⨯⨯++230.940.7760.20113.91A A μ⨯⨯==224 1.330.38213.91A B μ⨯==节点B 2:224 1.330.3294 1.330.94 1.61+0.940.7762 1.12B A μ⨯==⨯+⨯⨯⨯⨯+⨯210.94 1.610.35916.15B B μ⨯⨯==212 1.120.13916.15B C μ⨯==230.940.7760.17316.15B B μ⨯⨯==节点A 3 、A 4、A 5与A 2相同B 3、B 4、B 5与B 2相同。
竖向荷载作用下框架结构的内力计算
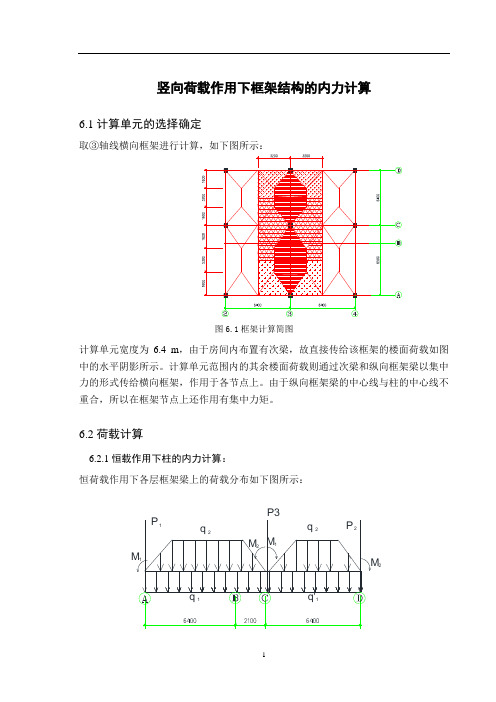
竖向荷载作用下框架结构的内力计算6.1计算单元的选择确定取③轴线横向框架进行计算,如下图所示:图6.1框架计算简图计算单元宽度为6.4 m,由于房间内布置有次梁,故直接传给该框架的楼面荷载如图中的水平阴影所示。
计算单元范围内的其余楼面荷载则通过次梁和纵向框架梁以集中力的形式传给横向框架,作用于各节点上。
由于纵向框架梁的中心线与柱的中心线不重合,所以在框架节点上还作用有集中力矩。
6.2荷载计算6.2.1恒载作用下柱的内力计算:恒荷载作用下各层框架梁上的荷载分布如下图所示:2图6.2恒荷载作用下各层框架梁上的荷载分布图(1)、对于顶层屋面,q1、q1'代表横梁自重,为均布荷载形式。
q1=0.3×0.75×25=5.625kN/mq1'=0.3×0.75×25=5.625kN/mq2为屋面板传给横梁的梯形荷载。
q2=5.29×3.2=16.928kN/mP1、P2分别由边纵梁、中纵梁直接传给柱的恒载,它包括主梁自重、次梁自重、楼板重等重力荷载,计算如下:P1=6.4*0.3*0.75*25+8.5/2*0.25*0.6*25+5.29*3.2*1.6+(5.3+8.5)*1.6*5.29/4=108.223KN P2=6.4*0.3*0.75*25+6.4/2*0.25*0.6*25+5.29*3.2*1.6 +(3.2+6.4)*1.6*5.29/4=95.398KN P3=6.4*0.3*0.75*25+(8.5+6.4)*0.5*0.25*0.6*25+5.29*3.2*1.6*2++(3.2+6.4)*1.6*5.29/4= 190.64KN集中力矩M1=P1e1=108.223×(0.6 -0.3)/2=16.23kN·mM2=P2e2=147.23×(0.6 -0.3)/2=14.31kN·m(2)、对于3层,包括梁自重和其上横墙自重,为均布荷载,其它荷载的计算方法同第顶层。
竖向荷载作用下框架结构采用分层法进行内力计算举例

竖向荷载作用下框架结构采用分层法进行内力计算举例
例,某8层框架,底层层高5.0m ,其余层层高3.2 m ,各层横梁竖向均布荷载为12kN/m ,各层梁柱的相对线刚度如下图所示,用分层法计算此框架在竖向荷载作用下的弯矩。
梁柱相对线刚度图
解:分层法采用力矩分配法计算,具体过程见以下各图,各杆的分配系数写在方框内。
带*号的数值是固端弯矩,各结点均分配两次,次序为先两边结点,后中间结点。
固端弯矩分配时要变号,弯矩传递不变号。
梁端弯矩传递系数为1/2,顶层和中间层各柱远端弯矩等于各柱近梁端弯矩的1/3(即传递系数为1/3),底层各柱远端弯矩等于各柱近梁端弯矩的1/2(即传递系数为1/2)。
最下一行数字为分配后各杆端弯矩。
12
-2
ql M =均载固, Fe M -=集中荷载固, 集中荷载均载梁固端M M M +=
顶层框架力矩分配过程
顶层弯矩图
中间层框架力矩分配过程
中间层弯矩图
底层框架力矩分配过程
底层弯矩图
各层柱端弯矩叠加,不平衡弯矩可再进行一次分配,得到框架弯矩总图(略)。
梁剪力可采用结构力学取脱离体的方法。
某框架顶层受荷图
完成顶层框架力矩分配过程。
框架结构内力及位移计算

第一节 高层建筑结构计算的基本假定
高层建筑是一个复杂的空间结构,它不仅平面形状多变,立面体型也各种各样,而且结 构型式和结构体系均各不相同,高层建筑中,有框架、剪力墙和筒体等竖向抗侧力结构,又 有水平放置的楼板将它们连为整体;同时高层建筑的实际荷载也是很复杂的,钢筋混凝土结 构又会有开裂、屈服等现象,并不是弹性匀质材料。因此要对这种高次超静定、多种结构型 式组合在一起的空间结构进行精确的内力和位移计算是十分困难的,在设计计算时,就必须 作出一些简化假定,以便简化计算。
面形状复杂,抗侧力结构又斜向布置时,就需要经过计算才能确定主轴方向。
四、框架结构计算方法分类
框架在结构力学中称为刚架,刚架的内力和位移计算方法很多,通常有精确法(如力法
和位移法)、渐近法(如力矩分配法、迭代法和无剪力分配法)和近似法(分层法、反弯点
法和 D 值法)三种。
精确法计算假定少,较为接近实际状况,但需建立大型的代数方程组,一般均利用计算 机进行求解;渐近法通常是利用一般的数学运算,使解答逐步趋于正确值,渐近法的优点是: 运算简单,方法易于掌握,当计算精度达到应用要求时,即可停止计算,故渐近法兼有近似 法和精确法的功能,渐近法的缺点是在数值计算中,不能包含变量,故不能研究某些量改变 时对结构的影响;近似法对结构引入较多的假定,忽略了一些次要因素,进行简化计算,其 概念清楚、计算简单、易于掌握、精确度也足够。
V = 12ic δ h2
因此,柱的侧移刚度为:
d = V = 12ic δ h2
ic
=
EI h
图 14 柱剪力与水平位移的关系
上两式中:V 为柱剪力; δ 为柱层间位移; h 为层高; EI 为柱抗弯刚度; ic 为柱线刚度。 侧移刚度 d 的物理意义是柱上下两端相对有单位侧移时柱中产生的剪力。 设同层各柱剪力为V1,V2 ,L,Vi ,L, 根据层剪力平衡,有:
混凝土框架结构分层法计算框架内力

分层法近似计算框架内力2010-07-03 08:53:43| 分类:默认分类|字号大中小订阅将框架结构划分为平面框架后,按照楼板的支承方式计算由楼盖传到框架上的荷载,即按照框架的承荷面积计算竖向荷载。
图24-4(a)所示为框架上的可能出现的竖向荷载形式,可能是均布荷载,或者是三角形或梯形分布荷载,如有次梁,则还有集中荷载。
在柱上作用的集中力是另一方向的梁传来的荷截,当这个集中力作用在柱截面重心轴上时,只产生柱轴力。
多层多跨框架在一般竖向荷载作用下侧移是很小的,可按照无侧移框架的计算方法进行内力分析。
由影响线理论及精确分析可知,各层荷载对其他层杆件的内力影响不大。
因此,可将多层框架简化为多个单层框架,并且用力矩分配法求解杆件内力,这种分层计算法是一种近似的内力计算法。
如图24-4(a)所示的三层框架分成如图24-4(b)所示的三个单层框架分别计算。
分层计算所得的梁弯矩即为最终弯矩;每一根柱都同时属于上、下两层,必须将上、下两层所得的同一根柱子的内力叠加,才能得到该柱的最终内力。
用力矩分配法计算各单层框架内力的要点如下,具体计算见例24-1。
(1)框架分层后,各层柱高及梁跨度均与原结构相同,把柱的远端假定为固端。
图24-4 竖向荷载下分层计算简图(2)各层梁上竖向荷载与原结构相同,计算竖向荷载在梁端的固端弯矩。
(3)计算梁柱线刚度及弯矩分配系数。
梁柱的线刚度分别为,,、分别为梁、柱截面惯性矩,、分别为梁跨度与层高。
计算梁截面的惯性矩时,应考虑楼板的影响,现浇楼板的有效作用宽度可取楼板厚度的6倍(梁每侧),设计时也可按下式近似计算有现浇楼板的梁截面惯性矩:式中,为由矩形截面计算得到的截面惯性矩。
除底层柱外,其他各层柱端并非固定端,分层计算时假定它为固端,因而除底层柱以外的其他柱子的线刚度乘以0.9修正系数(底层柱不修正),在计算每个节点周围各杆件为刚度分配系数时,用修正以后的柱线刚度计算。
(4)计算传递系数。
三种方法计算框架水平作用下的内力(D值法,反弯点法,门架法)

C 9.08E+4
21.88
35.01
D 2.38E+4
24.99
42.48
E 4.64E+4 94000 98.7 48.72 1.7
82.82 77.49 81.65 69.40 77.49
F 2.38E+4 1
A
24.99 24.99
42.48 82.47
B
48.72 3.3 160.78
C
24.99
令 i左边梁 为 1.0,梁柱的相对线刚度如图 4 所示。
图.4 梁柱相对线刚度
(3)求修正的反弯点高度(图 5)
图.5 修正的反弯点高度图
反弯点高度比的修正:
y = y0 + y1 + y2 + y3 A、B、C 轴柱的反弯点高度的计算如表 3、表 4 和表 5 所示。
表 3 A 轴框架柱反弯点位置、D 值的计算
=
12
53
= 4.64 ×10 4 kN / m
其余各层边柱:
D余边柱
= 12EI h3
12 × 3.25 ×107 × 1 × 0.55 × 0.553
=
12
3.23
= 9.08 ×104 kN / m
其余各层中柱:
D余中柱
= 12EI h3
12 × 3.25 ×107 × 1 × 0.65 × 0.653
4
3.20 0.56 0.45
0
0
0
0.45 1.44 0.219 90758 19876
3
3.20 0.56 0.480 Nhomakorabea0
0
0.48 1.54 0.219 90758 19876
04 水平荷载作用下框架结构的内力及变形计算

水平荷载作用下框架结构的计算
反弯点法
在确定柱的侧向刚度时,反弯点法假定各 柱上、下端都不产生转动,即认为梁柱线刚 度比为无限大。将趋近于无限大代入D值法 的公式,可得 c =1。因此,由式可得反弯 点法的柱侧向刚度,并用D0表示为:
D0
12ic h2
4 水平荷载作用下框架结构内力和侧移的近似计算
zH
q( y)dy( y B
z)
4 水平荷载作用下框架结构内力和侧移的近似计算
水平荷载作用下框架结构的计算
2
3
V0 H 3 EAB2
uN
1
4
V0 H 3 EAB2
11 30
V0 H 3 EAB2
(顶点集中荷载) (均匀分布荷载) (倒三角分布荷载)
V0 是水平外荷载在框架底面产生的总剪力。
Vi
Dij
j 1
该式即为层间剪力Vi在各柱间的分配公式,它适 用于整个框架结构同层各柱之间的剪力分配。可见, 每根柱分配到的剪力值与其侧向刚度成比例。
4 水平荷载作用下框架结构内力和侧移的近似计算
水平荷载作用下框架结构的计算
( 4)柱的反弯点高度比y
反弯点高度示意图
框架各柱的反弯点高度比y可用下式表示:
y = yn + y1 + y2 + y3
4 水平荷载作用下框架结构内力和侧移的近似计算
水平荷载作用下框架结构的计算
柱的反弯点高度比y
式中:yn表示标准反弯点高度比,可 由附表查得;
y1表示上、下层横梁线刚度变 化时反弯点高度比的修正值; y2、y3表示上、下层层高变化 时反弯点高度比的修正值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
框架梁内力组合例题
某跨AB ,q 1=1.2恒=19.89kN/m ,q 2=1.2(恒+0.5活)=18.576 kN/m
A
B q 2
1、活载的内力是在屋面取雪载的情况下计算出来的。
2、为便于施工(钢筋不要太密)及考虑框架梁端塑性变形内力重分布,通常对竖向荷载作用下的梁端负弯矩进行调幅,调幅系数可取0.8~0.9。
上表中恒载和活载两列中的弯矩为经过调幅的弯矩,即内力图中的弯矩乘0.85。
3、弯矩以梁上侧受拉为负。
一、支座A 用来配筋的弯矩的选取和弯矩值调整:
①A 支座负弯矩最大值为-390.12,将这个支座中心处的弯矩换算为支座边缘控制截面的弯矩:
54.305425.003.19912.390-=⨯+-=A M
其中199.03为上表中的剪力值,0.425=2
55.07.0-为边支座中心与支座边的距离 ②将弯矩值乘承载力抗震调整系数RE γ,梁取0.75(抗规5.4.2)
54.30575.0⨯=A RE M γ=229.16(229.16为配筋所使用的弯矩值)
关于RE γ的说明:在进行抗震验算时,采用的材料承载力设计值并不是材料在地
震作用下的承载力设计值,而是各规范规定的材料承载力,材料抗震承载力要比各规范规定的材料承载力高,故需要以承载力抗震调整系数来考虑,考虑抗震承载力调整系数还有经济性方面的考虑。
二、支座B 用来配筋的弯矩的选取和弯矩值调整:
①B 支座负弯矩最大值为-350.337,将这个支座中心处的弯矩换算为支座边缘控制截面的弯矩
18.28027.045.200337.350-=⨯+-=B M ,其中2
7.0为中柱边长的一半 ②B RE M γ
三、求跨间最大正弯矩
将下面的图用求解器计算,求跨间最大正弯矩。
①1.2(恒载+0.5活载)+1.3左震
350.337
260.74
q 2
q 1=1.2恒=19.89kN/m ,q 2=1.2(恒+0.5活)=18.576 kN/m
②1.2(恒载+0.5活载)+1.3右震
③1.0(恒载+0.5活载)+1.3左震
q 1=1.0恒,q 2
=1.0(恒+0.5活)
④1.0(恒载+0.5活载)+1.3右震
q 2
226.07
上面四种情况中求出的跨间最大正弯矩中的最大值乘承载力抗震调整系数RE γ即用来配筋的弯矩。
也有可能跨间最大正弯矩出现在第二种组合的支座弯矩中。
比如左震时为271.519,右震时为226.07,取左震的271.519。
四、剪力计算:
左震16.26-=A V ,45.200=B V 计算支座边缘处弯矩:
62.249425.016.2674.260=⨯-=A M 右震03.199=A V ,74.24-=B V 计算支座边缘处弯矩:
11.2062
7.074.24773.214=⨯-=B M 249.62+280.18=529.8
305.54+206.11=511.65
529.8大于511.65
抗震设计时,梁端剪力设计值按下式调整 ()重力V l M M V n B A Vb ++=/η
1.1=Vb η 梁端剪力增大系数
8.529=B A M M +
n l =4.625 为净跨
83.7528.1625.48.1625.42121=⎪⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛-+⨯+⨯q q V =重力 因此84.201=V
梁斜截面受剪承载力按84.20185.0⨯=V RE γ计算。
