《等腰直角三角形中的常用模型》
(完整版)等腰直角三角形中的常用模型

等腰直角三角形中的常用模型模型一:一条直线(不与三角形的边重合)过等腰直角三角形的直角顶点(1)以原等腰直角三角形的两直角边为对应斜边,必定可以构造一对全等的直角三角形:例1.如图:Rt ΔABC 中,∠BAC =90º,AB =AC ,点D 是BC 上任意一点,过B 作BE ⊥AD 于点E ,过C 作CF ⊥AD 于点F 。
(1)求证:BE-CF=EF ;(2)若D 在BC 的延长线上(如图(2)),(1)中的结论还成立吗?若不成立,请写出新的结论并证明。
1.如图1,等腰Rt △ABC 中,AB=CB ,∠ABC =90º,点P 在线段BC 上(不与B 、C 重合),以AP 为腰长作等腰直角△P AQ ,QE ⊥AB 于E ,连CQ 交AB 于M 。
(1)求证:M 为BE 的中点(2)若PC=2PB ,求MBPC的值(2)以原等腰直角三角形的两直角边为对应直角边,必定可以构造一对全等的直角三角形:3、如图:Rt ΔABC 中,∠BAC =90º,AB =AC ,点D 是BC 上任意一点,过B 作BE ⊥AD 于点E ,交AC 于点G ,过C 作CF ⊥AC 交AD 的延长线与于点F 。
(1)求证:BG=AF ;(2)若D 在BC 的延长线上(如图(2)),(1)中的结论还成立吗?若不成立,请写出新的结论并证明。
变式1:如图,在R t △ABC 中,∠ACB =45º,∠BAC =90º,AB=AC ,点D 是AB 的中点,AF ⊥CD 于H 交BC 于F ,BE ∥AC 交AF 的延长线于E ,求证:BC 垂直且平分DE .G G B ACD E F (2)(1)FE D C B AF DAA(2)FEDC A A B C DE F (1)(2)(3)(1)DD EEC C EC A AAB变式2:等腰Rt △ABC 中,AC=AB ,∠BAC =90°,点D 是AC 的中点,AF ⊥BD于点E ,交BC 于点F ,连接DF ,求证:∠1=∠2。
等腰直角三角形中的常见模型

中考复习专题1 姓名:等腰直角三角形中的常用模型【复习说明】1.本节课针对成都市中考中A卷20题(10分)以及B卷5道填空题之一(4分)可能出现的题目;2.本节课涉及三个模型,分析思考时要注意不同状态的辅助线添加方式以及对应的证明方式.【涉及知识点回顾】——等腰直角三角形的几何特征①角的特征: ___________________________________________________________________________②边的特征: ___________________________________________________________________________ 模型一:一条直线(不与三角形的边重合)过等腰直角三角形的直角顶点★(1)以原等腰直角三角形的两直角边为对应斜边,必能构造一对全等的直角三角形:C【例1】【A卷20题前两问】如图:Rt A ABC中,N BAC=90°, AB=AC,点D是BC上任意一点,过B作BE±AD于点E,过C作CF±AD于点F.(1)若D在线段BC上(如图(1)),求证:BE-CF=EF;(2)若D在BC的延长线上(如图(2)), (1)中的结论还成立吗?若成立,请说明理由;若不成立,请写出新的结论并证明.【课堂练习1】【B卷填空】如图,等腰RtA ABC中,AB=CB,N ABC=90°,点P在线段BC上(不与B、C重合),以AP为腰作等腰直角4PAQ, QE±AB于E ,连CQ交AB于M.若BPPC则上的值为.MB★(2)以原等腰直角三角形的两直角边为对应直角边,必能构造一对全等的直角三角形:・如何构造:【例2I A卷20题前两问】如图:Rt A ABC中,N BAC=90°, AB=AC, 点D是BC上任意一点,过B作BE±AD于点E,交AC于点G, 过C作CF±AC交AD的延长线与于点F.(1)若D在线段BC上(如图(1)),求证:BG=AF;(2)若D在BC的延长线上(如图(2)), (1)中的结论还成立吗?若成立,请说明理由;若不成立,请写出新的结论并证明.【课堂练习2】【B卷填空】等腰Rt A ABC中,AC=AB,N BAC= 90°,点D、E是AC上两点,且AD=CE, AF±BD于点G,交BC于点F,连接FE并延长,交BD延长线于H.若N ABD=21°, 求N H的度数为°.模型二:等腰直角三角形与另一个直角三角形共斜边★等腰直角三角形与另一个直角三角形有公共斜边,必能以两腰为斜边构造全等三角形・如何构造:•有何特点:【例3】【B 卷填空】等腰Rt A ABC 中,AC=AB , /BAC =90°,±BE 于。
《等腰直角三角形中的常用模型》
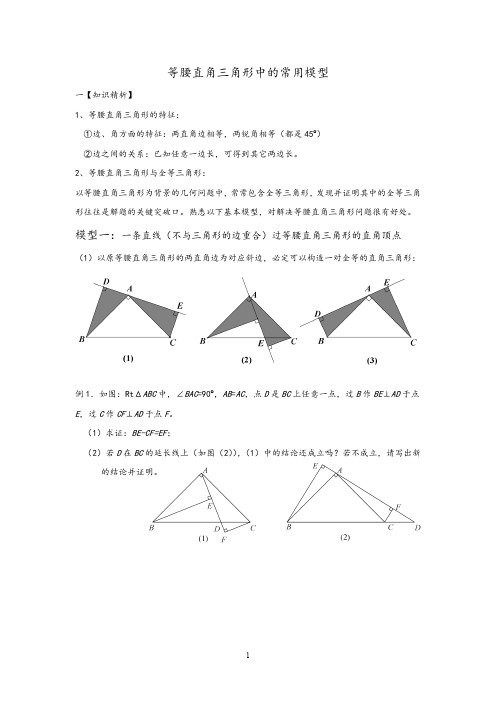
等腰直角三角形中的常用模型一【知识精析】1、等腰直角三角形的特征:①边、角方面的特征:两直角边相等,两锐角相等(都是45º)②边之间的关系:已知任意一边长,可得到其它两边长。
2、等腰直角三角形与全等三角形:以等腰直角三角形为背景的几何问题中,常常包含全等三角形,发现并证明其中的全等三角形往往是解题的关键突破口。
熟悉以下基本模型,对解决等腰直角三角形问题很有好处。
模型一:一条直线(不与三角形的边重合)过等腰直角三角形的直角顶点(1)以原等腰直角三角形的两直角边为对应斜边,必定可以构造一对全等的直角三角形:例1.如图:RtΔABC中,∠BAC=90º,AB=AC,点D是BC上任意一点,过B作BE⊥AD于点E,过C作CF⊥AD于点F。
(1)求证:BE-CF=EF;(2)若D在BC的延长线上(如图(2)),(1)中的结论还成立吗?若不成立,请写出新的结论并证明。
2.如图1,等腰Rt△ABC 中,AB=CB ,∠ABC =90º,点P 在线段BC 上(不与B、C 重合),以AP 为腰长作等腰直角△PAQ ,QE ⊥AB 于E ,连CQ 交AB 于M 。
(1)求证:M 为BE 的中点(2)若PC=2PB,求MBPC的值(2)以原等腰直角三角形的两直角边为对应直角边,必定可以构造一对全等的直角三角形:3、如图:RtΔABC 中,∠BAC =90º,AB =AC ,点D 是BC 上任意一点,过B 作BE ⊥AD 于点E ,交AC 于点G ,过C 作CF ⊥AC 交AD 的延长线与于点F 。
(1)求证:BG=AF ;(2)若D 在BC 的延长线上(如图(2)),(1)中的结论还成立吗?若不成立,请写出新的结论并证明。
变式1:如图,在R t△ABC中,∠ACB=45º,∠BAC=90º,AB=AC,点D是AB的中点,AF⊥CD 于H交BC于F,BE∥AC交AF的延长线于E,求证:BC垂直且平分DE.变式2:等腰Rt△ABC中,AC=AB,∠BAC=90°,点D是AC的中点,AF⊥BD于点E,交BC 于点F,连接DF,求证:∠1=∠2。
等腰直角三角形模型、三垂直模型

精彩文档45°45°C BA D CB A题型一:等腰直角三角形模型思路导航等腰直角三角形数学模型思路:⑴利用特殊边特殊角证题(AC=BC 或904545︒︒°,,).如图1; ⑵常见辅助线为作高,利用三线合一的性质解决问题.如图2; ⑶补全为正方形.如图3,4.图1 图2图3 图4全等三角形的经典模型(一)ABCOMN AB COMN典题精练【例1】 已知:如图所示,Rt △ABC 中,AB =AC ,90BAC ∠=°,O 为BC 的中点,⑴写出点O 到△ABC 的三个顶点A 、B 、C 的距离的关系(不要求证明)⑵如果点M 、N 分别在线段AC 、AB 上移动,且在移动中保持 AN =CM .试判断△OMN 的形状,并证明你的结论. ⑶如果点M 、N 分别在线段CA 、AB 的延长线上移动,且在移动中保持AN =CM ,试判断⑵中结论是否依然成立,如果是请给出证明. 【解析】 ⑴OA =OB =OC⑵连接OA ,∵OA =OC 45∠=∠=BAO C ° AN =CM ∴△ANO ≌△CMO∴ON =OM∴∠=∠NOA MOC∴90∠+∠=∠+∠=︒NOA BON MOC BON ∴90∠=︒NOM∴△OMN 是等腰直角三角形⑶△ONM 依然为等腰直角三角形,证明:∵∠BAC =90°,AB =AC ,O 为BC 中点 ∴∠BAO =∠OAC =∠ABC =∠ACB =45°, ∴AO =BO =OC ,∵在△ANO 和△CMO 中,AN CM BAO C AO CO =⎧⎪∠=∠⎨⎪=⎩∴△ANO ≌△CMO (SAS ) ∴ON =OM ,∠AON =∠COM , 又∵∠COM -∠AOM =90°, ∴△OMN 为等腰直角三角形.【例2】 两个全等的含30,60角的三角板ADE 和三角板ABC ,如图所示放置,,,E A C 三点在一条直线上,连接BD ,取BD 的中点M ,连接ME ,MC .试判断EMC △的形状,并说明理由.【解析】EMC △是等腰直角三角形. 证明:连接AM .由题意,得,90,90.DE AC DAE BAC DAB =∠+∠=∠= ∴DAB △为等腰直角三角形. ∵D M M B =, MEDCBA ABCOM NMEDCBA精彩文档FE DCBANM 12A B CDE F312A BCDEF 3∴,45MA MB DM MDA MAB ==∠=∠=. ∴105MDE MAC ∠=∠=,∴ED M △≌CAM △.∴,EM MC DME AMC =∠=∠.又90EMC EMA AMC EMA DME ∠=∠+∠=∠+∠=. ∴CM EM ⊥,∴EMC △是等腰直角三角形.【例3】 已知:如图,ABC △中,AB AC =,90BAC ∠=°,D 是AC 的中点,AF BD ⊥于E ,交BC 于F ,连接DF . 求证:ADB CDF ∠=∠. 【解析】 证法一:如图,过点A 作AN BC ⊥于N ,交BD 于M .∵AB AC =,90BAC ∠=°, ∴345DAM ∠=∠=°.∵45C ∠=°,∴3C ∠=∠.∵AF BD ⊥,∴190BAE ∠+∠=°∵90BAC ∠=°,∴290BAE ∠+∠=°. ∴12∠=∠.在ABM △和CAF △中, 123AB AC C ∠=∠⎧⎪=⎨⎪∠=∠⎩∴ABM CAF △≌△.∴AM CF =. 在ADM △和CDF △中, AD CD DAM C AM CF =⎧⎪∠=∠⎨⎪=⎩∴ADM CDF △≌△. ∴ADB CDF ∠=∠.证法二:如图,作CM AC ⊥交AF 的延长线于M . ∵AF BD ⊥,∴3290∠+∠=°, ∵90BAC ∠=°, ∴1290∠+∠=°, ∴13∠=∠.在ACM △和BAD △中, 1390AC ABACM BAD ∠=∠⎧⎪=⎨⎪∠=∠=⎩° ∴ACM BAD △≌△.∴M ADB ∠=∠,AD CM = ∵AD DC =,∴CM CD =. 在CMF △和CDF △中,P CB A PC B AD 45=⎧⎪∠=∠=⎨⎪=⎩CF CF MCF DCF CM CD ° ∴CMF CDF △≌△.∴M CDF ∠=∠ ∴ADB CDF ∠=∠.【例4】 如图,等腰直角ABC △中,90AC BC ACB =∠=,°,P 为ABC △内部一点,满足 PB PC AP AC ==,,求证:15BCP ∠=︒.【解析】 补全正方形ACBD ,连接DP ,易证ADP △是等边三角形,60DAP ∠=︒,45BAD ∠=︒, ∴15BAP ∠=︒,30PAC ∠=︒,∴75∠=︒ACP , ∴15BCP ∠=︒.【探究对象】等腰直角三角形添补成正方形的几种常见题型 在解有关等腰直角三角形中的一些问题,若遇到不易解决或解法比较复杂时,可将等腰直角三角形引辅助线转化成正方形,再利用正方形的一些性质来解,常常可以起到化难为易的效果,从而顺利地求解。
列举构造等腰三角形4种常用方法模型

列举构造等腰三角形4种常用方法模型
1. 构造等腰三角形的一个底角:
已知等腰三角形的一个底角,我们可以使用圆规和直尺来构造等腰三角形的另一条底边和另一个底角。
2. 利用中垂线构造等腰三角形:
已知线段的中点,我们可以使用中垂线性质来构造等腰三角形。
3. 利用平行线构造等腰三角形:
已知一条直线和该直线外的一点,我们可以使用平行线性质来构造等腰三角形。
4. 利用角平分线性质构造等腰三角形:
已知一个角的角平分线,我们可以使用角平分线性质来构造等腰三角形。
关于两个等腰三角形的三个重要的几何模型之间的异同以及当三角形为等腰直角三角形时的特殊证法

关于两个等腰三角形的三个重要的几何模型之间的异同以及当三角形为等腰直角三角形时的特殊证法------手拉手、婆罗摩笈多模型、脚拉脚初中阶段,关于两个等腰三角形的问题,十分常见.我们可以归纳为大三类,为了介绍方便,分别取名为“手拉手模型、婆罗摩笈多模型、脚拉脚模型”.1.1 手拉手模型:两个等腰三角形的顶角顶点重合,且顶角相等.按逆时针顺序,把位置相同的底角顶点相连.简记为:共顶点,同顶角,左手拉左手.如图,两个等腰三角形△ABE 和△ACD ,∠BAE=∠CAD ,且AB=AE ,AC=AD ,连接BD ,CE.结论:(1)△ABD ≌△AEC ;(2)∠α+∠BOC=180°(位置相同的底角顶点相连,所成夹角等于顶角) ;(3)OA 平分∠BOC(第三边的交点与顶点连线平分第三边的夹角).证明:(1)由AB=AE ,AC=AD ,∠BAD=∠CAE ,易得△ABD ≌△AEC.(2) 因为△ABD ≌△AEC ,所以∠CEA=∠DBA ,又∠EOA+∠OEA=∠EAB+∠DBA ,所以∠OEA=∠α.(3)第3问的证明很巧妙,只需过A 点作BD ,CE 的垂线段.因为△ABD ≌△AEC ,所以对应边的高也相等.再由角平分线的判定,从而得到OA 平分∠BOC.1.2 手拉手模型的特殊情况:当两个等腰三角形是等腰直角三角形时,而且隐藏在正方形中,如下:变式1.如图,两个正方形ABCD 与DEFG ,连结CE AG ,,二者相交于点H .问:(1)CDE ADG ∆≅∆是否成立?(2)AG 是否与CE 相等?(3)AG 与CE 之间的夹角为多少度?(4)HD 是否平分AHE ∠?解析:(1)由,,,DC DA ADG CDE DG DE =∠=∠=得.)(≌△△SAS CDE ADG 由.CE AG CDE ADG =∴≌△△(2) 设AG 与CD 相较于点P ,由GAD ECD CDE ADG ∠=∠∴≌△△又.90H CE AG CDA CHA APD GAD CPG ECD 于点⊥∴︒=∠=∠∴∠+∠=∠+∠(3) 过D 点作AG DM ⊥于M 点,EC DN ⊥于N 点DN DM CDE ADG =∴≌△△HD ∴平分.AHE ∠2.1婆罗摩笈多模型:两个等腰三角形的顶角顶点重合,且顶角互补。
浙教版八年级数学上册腰直角三角形中的常用模型
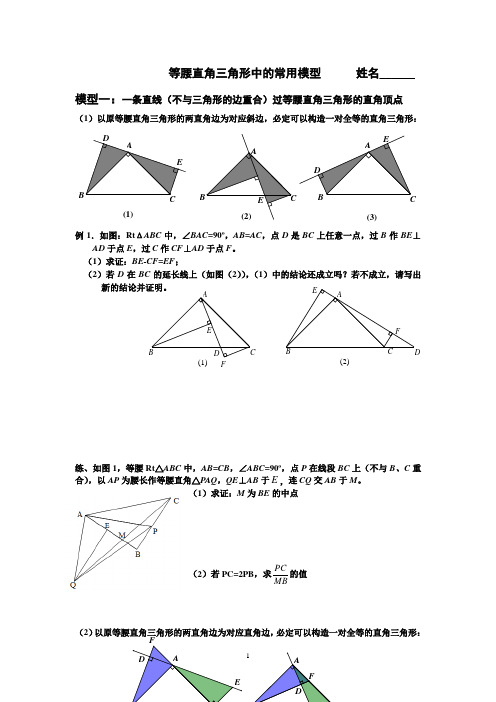
等腰直角三角形中的常用模型 姓名______ 模型一:一条直线(不与三角形的边重合)过等腰直角三角形的直角顶点(1)以原等腰直角三角形的两直角边为对应斜边,必定可以构造一对全等的直角三角形:例1.如图:Rt ΔABC 中,∠BAC =90º,AB =AC ,点D 是BC 上任意一点,过B 作BE ⊥AD 于点E ,过C 作CF ⊥AD 于点F 。
(1)求证:BE-CF=EF ;(2)若D 在BC 的延长线上(如图(2)),(1)中的结论还成立吗?若不成立,请写出新的结论并证明。
练、如图1,等腰Rt △ABC 中,AB=CB ,∠ABC =90º,点P 在线段BC 上(不与B 、C 重合),以AP 为腰长作等腰直角△PAQ ,QE ⊥AB 于E ,连CQ 交AB 于M 。
(1)求证:M 为BE 的中点(2)若PC=2PB ,求MB PC 的值(2)以原等腰直角三角形的两直角边为对应直角边,必定可以构造一对全等的直角三角形: (2)(3)(1)DD EE C C E C A B B A A B F(2)F E D C B A A B C D E F (1)例2、如图:Rt ΔABC 中,∠BAC =90º,AB =AC ,点D 是BC 上任意一点,过B 作BE ⊥AD 于点E ,交AC 于点G ,过C 作CF ⊥AC 交AD 的延长线与于点F 。
(1)求证:BG=AF ;(2)若D 在BC 的延长线上(如图(2)),(1)中的结论还成立吗?若不成立,请写出新的结论并证明。
变式1:如图,在R t △ABC 中,∠ACB =45º,∠BAC =90º,AB=AC ,点D 是AB 的中点,AF ⊥CD 于H 交BC 于F ,BE ∥AC 交AF 的延长线于E ,求证:BC 垂直且平分DE .变式2:等腰Rt △ABC 中,AC=AB ,∠BAC =90°,点D 是AC 的中点,AF ⊥BD 于点E ,G G B A C D E F (2)(1)F E D C B A交BC 于点F ,连接DF ,求证:∠1=∠2。
八上数学 小专题(十二) 等腰直角三角形常见的解题模型

【变式】 将第 3 题中的“∠AEB=45°”改为“∠AEC=135°”, 第 3 题中的结论还成立吗?并说明理由.
解:第 3 题中的结论仍然成立. 理由:如图,过点 A 作 AF⊥AE,交 CE 的延长线于点 F, 则∠BAE=90°+∠CAE=∠CAF. ∵∠AEC=135°, ∴∠AEF=45°. ∴△AEF 为等腰直角三角形,AE=AF.
模型二 等腰直角三角形+8 字模型中有两直角,常用截长补短若 BE⊥CE, 则有∠1=∠2.常通过在 BE 上取点 F,使得 BF=CE⇒△ABF≌△ACE.
2.如图,△ABC 为等腰直角三角形,∠BAC=90°,AB=AC, D 是 AC 上一点.若 CE⊥BD 于点 E,连接 AE.求证:∠AEB=45°.
证明:在 BE 上截取 BF=CE, 连接 AF. 易证∠ABF=∠ACE, △ABF≌△ACE(SAS), 得等腰 Rt△AFE, ∴∠AEB=45°.
模型二变式 等腰直角三角形及 8 字模型中只有一个直角,过等 腰直角三角形的顶点作垂线构造直角
如图,已知等腰 Rt△ABC,∠AEB=45°,常过点 A 作 AF⊥AE, 则∠FAE=90°,∠1=∠2.
4.如图,在平面直角坐标系中,A(2,0),B(0,1),AC 由 AB 绕 点 A 顺时针旋转 90°而得,则点 C 的坐标为 (3,2).
2020年秋人教版 八年级上册数学 同步课时训练
模型一 等腰直角三角形+斜边的中点→连接直角顶点和斜边中 点
如图,在等腰 Rt△ABC 中,D 为斜边的中点,则连接 AD⇒AD= BD=DC,∠B=∠DAF=45°.常结合已知条件证△BDE≌△ADF 或 △ADE≌△CDF 得出相关结论.
1.如图,在△ABC 中,∠A=90°,AB=AC,D 为 BC 的中点, E,F 分别是 AB,AC 上的点,且 BE=AF.求证:△DEF 为等腰直角 三角形.
《等腰直角三角形中的常用模型》

等腰直角三角形中的常用模型一【知识精析】1、等腰直角三角形的特征:①边、角方面的特征:两直角边相等,两锐角相等(都是45º) ②边之间的关系:已知任意一边长,可得到其它两边长。
2、等腰直角三角形与全等三角形:以等腰直角三角形为背景的几何问题中,常常包含全等三角形,发现并证明其中的全等三角形往往是解题的关键突破口。
熟悉以下基本模型,对解决等腰直角三角形问题很有好处。
模型一:一条直线(不与三角形的边重合)过等腰直角三角形的直角顶点(1)以原等腰直角三角形的两直角边为对应斜边,必定可以构造一对全等的直角三角形:例1.如图:Rt ΔABC 中,∠BAC =90º,AB =AC ,点D 是BC 上任意一点,过B 作BE ⊥AD 于点E ,过C 作CF ⊥AD 于点F 。
(1)求证:BE-CF=EF ;(2)若D 在BC 的延长线上(如图(2)),(1)中的结论还成立吗?若不成立,请写出新的结论并证明。
如图1,等腰Rt △ABC 中,AB=CB ,∠ABC =90º,点P 在线段BC 上(不与B 、C 重合),以AP 为腰长作等腰直角△PAQ ,QE ⊥AB 于E ,连CQ 交AB 于M 。
(1)求证:M 为BE 的中点(2)若PC=2PB ,求MBPC的值(3)(1)(2)F ED C B AA B C DE F (1)(2)以原等腰直角三角形的两直角边为对应直角边,必定可以构造一对全等的直角三角形:3、如图:Rt ΔABC 中,∠BAC =90º,AB =AC ,点D 是BC 上任意一点,过B 作BE ⊥AD 于点E ,交AC 于点G ,过C 作CF ⊥AC 交AD 的延长线与于点F 。
(1)求证:BG=AF ;(2)若D 在BC 的延长线上(如图(2)),(1)中的结论还成立吗?若不成立,请写出新的结论并证明。
变式1:如图,在R t △ABC 中,∠ACB =45º,∠BAC =90º,AB=AC ,点D 是AB 的中点,AF ⊥CD于H 交BC 于F ,BE ∥AC 交AF 的延长线于E ,求证:BC 垂直且平分DE .变式2:等腰Rt △ABC 中,AC=AB ,∠BAC =90°,点D 是AC 的中点,AF ⊥BD 于点E ,交BC于点F ,连接DF ,求证:∠1=∠2。
等腰直角三角形中的常用模型
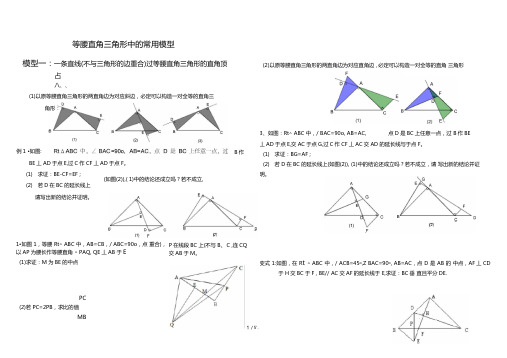
等腰直角三角形中的常用模型模型一:一条直线(不与三角形的边重合)过等腰直角三角形的直角顶占八、、(1)以原等腰直角三角形的两直角边为对应斜边,必定可以构造一对全等的直角三角形: B 作(2)以原等腰直角三角形的两直角边为对应直角边,必定可以构造一对全等的直角 三角形:点D 是BC 上任意一点,过 B 作BE例1 •如图: BE 丄AD 于点E,过C 作CF 丄AD 于点F 。
(1) 求证:BE-CF=EF ;(2) 若D 在BC 的延长线上请写出新的结论并证明。
(如图(2)),( 1)中的结论还成立吗?若不成立,(2)1•如图 1,等腰 Rt△ ABC 中,AB=CB ,/ ABC=90o ,点 重合),以AP 为腰长作等腰直角 △ PAQ, QE 丄AB 于E (1)求证:M 为BE 的中点 P 在线段BC 上(不与B 、C ,连CQ 交AB 于M 。
PC (2)若PC=2PB ,求比的值 MB/ 5'.3、如图:Rt △ ABC 中,/ BAC=90o, AB=AC,丄AD 于点E,交AC 于点G,过C 作CF 丄AC 交AD 的延长线与于点 F 。
(1) 求证:BG=AF ;(2) 若D 在BC 的延长线上(如图(2)), (1)中的结论还成立吗?若不成立,请 写出新的结论并证明。
(2)变式 1:如图,在 R t △ ABC 中,/ ACB=45o ,Z BAC=90o , AB=AC ,点 D 是 AB 的 中点,AF 丄CD于H 交BC 于F , BE// AC 交AF 的延长线于 E,求证:BC 垂 直且平分DE.于D ,连接AD ,求证:/ ADB = 45例 1:等腰 Rt △ ABC 中,AC=AB , / BAC = 90°, E 是 AC 上一点,过 C 作 CD 丄 BE变式2 :等腰 Rt △ ABC 中,AC=AB , / BAC = 90°,点 D 是AC 的中点,AF 丄BD于点E ,交BC 于点F ,连接DF ,求证:/ 1 = / 2。
(基础版)等腰直角三角形中的基本模型

基础版)等腰直角三角形中的基本模型等腰直角三角形是一种特殊的三角形,具有两条边长度相等且与底边垂直的特点。
对于等腰直角三角形,我们可以有一些基本模型来帮助我们理解和解决相关问题。
1.基本定义等腰直角三角形具有以下特点:两条边的长度相等,称为腰;底边与两条腰垂直相交,形成一个直角。
2.边长关系设等腰直角三角形的腰长为 *a*,底边长为 *b*。
由勾股定理可知:a^2 + a^2 = b^2*,即 *2a^2 = b^2*;则 *a = \sqrt{\frac{b^2}{2}}*。
3.高的计算等腰直角三角形的高即为顶点到底边的垂直距离。
根据几何关系可知,高等于腰的一半,即高 *h* 和腰 *a* 的关系为:h = \frac{a}{2}*。
4.面积计算等腰直角三角形的面积可以通过底边长和高的关系来计算,即面积 *S* 和底边长 *b*、高 *h* 的关系为:S = \frac{b \cdot h}{2}*。
5.例题解析例题 1已知等腰直角三角形的底边长为 8 cm,求其面积。
解析:根据高的计算公式,高 *h* 等于底边长的一半,即 *h =\frac{8}{2} = 4*。
代入面积公式可得:S = \frac{8 \cdot 4}{2} = 16*。
所以,等腰直角三角形的面积为 16 平方厘米。
例题 2已知等腰直角三角形的腰长为 6 cm,求其底边长和面积。
解析:根据边长关系公式,底边长 *b* 等于 *a* 的平方根的两倍,即*b = 2 \cdot \sqrt{\frac{6^2}{2}} = 12*。
代入面积公式可得:S = \frac{12 \cdot \frac{6}{2}}{2} = 18*。
所以,等腰直角三角形的底边长为 12 厘米,面积为 18 平方厘米。
6.总结等腰直角三角形是一种特殊的三角形,在解题过程中可以利用基本定义、边长关系、高的计算和面积计算等基本模型来求解相关问题。
通过掌握这些基本模型,我们可以更好地理解和应用等腰直角三角形的概念和性质。
等腰直角三角形中的常用模型
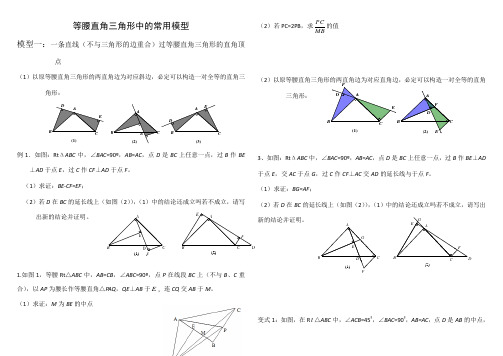
等腰直角三角形中的常用模型模型一:一条直线(不与三角形的边重合)过等腰直角三角形的直角顶点(1)以原等腰直角三角形的两直角边为对应斜边,必定可以构造一对全等的直角三角形:例1.如图:Rt ΔABC 中,∠BAC =90º,AB =AC ,点D 是BC 上任意一点,过B 作BE⊥AD 于点E ,过C 作CF ⊥AD 于点F 。
(1)求证:BE-CF=EF ;(2)若D 在BC 的延长线上(如图(2)),(1)中的结论还成立吗若不成立,请写出新的结论并证明。
1.如图1,等腰Rt △ABC 中,AB=CB ,∠ABC =90º,点P 在线段BC 上(不与B 、C 重合),以AP 为腰长作等腰直角△PAQ ,QE ⊥AB 于E ,连CQ 交AB 于M 。
(1)求证:M 为BE 的中点(2)若PC=2PB ,求MBPC的值(2)以原等腰直角三角形的两直角边为对应直角边,必定可以构造一对全等的直角三角形:3、如图:Rt ΔABC 中,∠BAC =90º,AB =AC ,点D 是BC 上任意一点,过B 作BE ⊥AD 于点E ,交AC 于点G ,过C 作CF ⊥AC 交AD 的延长线与于点F 。
(1)求证:BG=AF ;(2)若D 在BC 的延长线上(如图(2)),(1)中的结论还成立吗若不成立,请写出新的结论并证明。
变式1:如图,在R t △ABC 中,∠ACB =45º,∠BAC =90º,AB=AC ,点D 是AB 的中点,GG BACDEF(2)(1)F EDCBADEF FED (2)(1)CCABBA(2)FEDC B AAB C D E F(1)(2)(3)(1)DDEECEAAABAF⊥CD于H交BC于F,BE∥AC交AF的延长线于E,求证:BC垂直且平分DE.变式2:等腰Rt△ABC中,AC=AB,∠BAC=90°,点D是AC的中点,AF⊥BD于点E,交BC于点F,连接DF,求证:∠1=∠2。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 / 6等腰直角三角形中的常用模型一【知识精析】1、等腰直角三角形的特征:①边、角方面的特征:两直角边相等,两锐角相等(都是45º) ②边之间的关系:已知任意一边长,可得到其它两边长。
2、等腰直角三角形与全等三角形:以等腰直角三角形为背景的几何问题中,常常包含全等三角形,发现并证明其中的全等三角形往往是解题的关键突破口。
熟悉以下基本模型,对解决等腰直角三角形问题很有好处。
模型一:一条直线(不与三角形的边重合)过等腰直角三角形的直角顶点 (1)以原等腰直角三角形的两直角边为对应斜边,必定可以构造一对全等的直角三角形:例1.如图:Rt ΔABC 中,∠BAC =90º,AB =AC ,点D 是BC 上任意一点,过B 作BE ⊥AD 于点E ,过C 作CF ⊥AD 于点F 。
(1)求证:BE-CF=EF ;(2)若D 在BC 的延长线上(如图(2)),(1)中的结论还成立吗?若不成立,请写出新的结论并证明。
如图1,等腰Rt △ABC 中,AB=CB ,∠ABC =90º,点P 在线段BC 上(不与B 、C 重合),以AP 为腰长作等腰直角△PAQ ,QE ⊥AB 于E ,连CQ 交AB 于M 。
(1)求证:M 为BE 的中点 (2)若PC=2PB ,求MBPC 的值(2)(3)(1)D DEECE CABBAAB(2)F ED C B AAB C DE F (1)2 / 6 (2)以原等腰直角三角形的两直角边为对应直角边,必定可以构造一对全等的直角三角形:3、如图:Rt ΔABC 中,∠BAC =90º,AB =AC ,点D 是BC 上任意一点,过B 作BE ⊥AD 于点E ,交AC 于点G ,过C 作CF ⊥AC交AD 的延长线与于点F 。
(1)求证:BG=AF ;(2)若D 在BC 的延长线上(如图(2)),(1)中的结论还成立吗?若不成立,请写出新的结论并证明。
变式1:如图,在R t △ABC 中,∠ACB =45º,∠BAC =90º,AB=AC,点D 是AB 的中点,AF ⊥CD 于H 交BC 于F ,BE ∥AC 交AF 的延长线于E ,求证:BC 垂直且平分DE .变式2:等腰Rt △ABC 中,AC=AB ,∠BAC =90°,点D 是AC的中点,AF ⊥BD 于点E ,交BC 于点F ,连接DF ,求证:∠1=∠2。
变式3:等腰Rt △ABC 中,AC=AB ,∠BAC =90°,点D 、E 是AC 上两点且AD=CE ,AF ⊥BD 于点G ,交BC 于点F 连接DF ,求证:∠1=∠2。
模型二:等腰直角三角形与另一个直角三角形共斜边等腰直角三角形与另一个直角三角形有公共斜边,一定可以以两腰为对应边构造全等三角形例1:等腰Rt △ABC 中,AC=AB ,∠BAC =90°,E 是AC 上一D EFFED(2)(1)CCABBAABCDEF(2)(1)FED CBAGGBACDEF (2)(1)FE DCBA3 / 6点,过C 作CD ⊥BE 于D ,连接AD ,求证:∠ADB =45°。
变式1:等腰Rt △ABC 中,AC=AB ,∠BAC =90°,E 是AC 上一点,点D 为BE 延长线上一点,且∠ADC =135°求证:BD ⊥DC 。
变式2:等腰Rt △ABC 中,AC=AB ,∠BAC =90°,BE 平分∠ABC 交AC 于E ,过C 作CD ⊥BE 于D ,DM ⊥AB 交BA 的延长线于点M ,(1)求BC AB BM +的值;(2)求AB BC AM -的值。
模型三:两个等腰直角三角形共一个顶点(1)两个等腰直角三角形共直角顶点,必定含一对全等三角形: 例1、如图1,△ABC 、△BEF 都是等腰直角三角形,∠ABC =∠BEF =90º,连接AF 、CF ,M 是AF 的中点,连ME ,将△BEF 绕点B 旋转。
猜想CF 与EM 的数量关系并证明;(2)两个等腰直角三角形共锐角顶点且直角开口方向相同,必定含一对相似三角形:(3)两个等腰直角三角形共锐角顶点且直角开口方向相反,必定可利用平移构造含一对全等三角形:ABC DE A B C DEEDCBA(1)(2)(3)EDCA(3)FEDC BA(2)FF(1)ABCDE图(1)MFEBCAA D E(2)AB E EDB A(1)4 / 6A FBDEC如图,△ABC 和△EBD 都是等腰直角三角形,∠BAC =∠BED =90º。
把DE 平移到CF ,使E 与C 重合,连接AE 、AF ,则△AEB 与△AFC 全等(关键是利用平行证明∠ABE =∠ACF )例.如图:两个直角三角形ABC 、ADE 的顶点A 重合,P 是线段BD 的中点,连PC 、PE 。
(1)如图1,若∠BAC =∠DAE =45°,当A 、C 、D 在同一直线上时,线段PC 、PE 的关系是;(2)如图2、3,将⊿BAC 绕A 旋转α度,(1)中的结论是否仍然成立?任意选择一个证明你的结论。
三【巩固练习】1.如图,在ABC Rt ∆中,AC AB =,∠︒=90BAC ,D 、E 为BC 上两点,∠︒=45DAE ,F 为ABC ∆外一点,且FB ⊥BC ,AE FA ⊥,则下列结论:①BF CE =;②222DE CE BD =+;③EF AD S ADE ⋅=∆41;④2222AE BE CE =+,其中正确的是A 、①②③④B 、①②④C 、①③④D 、②③2.已知:Rt ⊿ABC 中,AB=AC ,∠BAC =90°,若O 是BC 的中点,以O 为顶点作∠MON ,交AB 、AC 于点M 、N 。
(1)若∠MON =90°(如图1),求证:①OM=ON ;②BM 2+CN 2=MN 2;图1NMO CBA图1PED C BA A BC D EP 图2ABCDEP 图35 / 6(2)若∠MON =45°(如图2),求证:①AM+MN =CN ;3、如图,在平面直角坐标系中,△AOB 为等腰直角三角形,A (4,4)。
(1)若C 为x 轴正半轴上一动点,以AC 为直角边作等腰直角△ACD ,∠ACD=90°,连OD ,求∠AOD 的度数;(2)过A 作y 轴的垂线交y 轴于E ,F 为x 轴负半轴上一点,G 在EF 的延长线上,以EG 为直角边作等腰Rt △EGH ,过A 作x 轴垂线交EH 于点M ,连FM ,等式1=-OFFMAM 是否成立?若成立,请证明;若不成立,说明理由。
4.在△ABC 和△DCE 中,AB =AC ,DC =DE ,∠BAC =∠EDC =90°,点E 在AB 上,连AD ,DF ⊥AC 于点F 。
试探索AE 、AF 、AC 的数量关系;并求出∠DAC 的度数。
5.如图:等腰Rt △ABC 和等腰Rt △EDB ,AC=BC ,DE=BD ,∠ACB=∠EDB =90°,E 为AB 是一点,P 为AE 的中点。
⑴连接PC ,PD ;则PC ,PD 的位置关系是;数量关系是;并证明你的结论。
⑵当E 在线段AB 上变化时,其它条件不变,作EF ⊥BC 于F ,连接PF ,试判断△PCF 的形状;在点E 运动过程中,△PCF图2NMO CBAFADBCE(2)6 / 6是否可为等边三角形?若可以,试求△ACB 与△EDB 的两直角边之比。
6(2013年湖南常德10分)已知两个共一个顶点的等腰Rt △ABC ,Rt △CEF ,∠ABC=∠CEF=90°,连接AF ,M 是AF 的中点,连接MB 、ME .(1)如图1,当CB 与CE 在同一直线上时,求证:MB ∥CF ; (2)如图1,若CB=a ,CE=2a ,求BM ,ME 的长; (3)如图2,当∠BCE=45°时,求证:BM=ME .7、如图,在平面直角坐标系中,A (4,0),B (0,4)。
点N 为OA 上一点,OM ⊥BN 于M ,且∠ONB=45°+∠MON 。
(1)求证:BN 平分∠OBA ; (2)求BNMNOM 的值; (3)若点P 为第四象限内一动点,且∠APO =135°,问AP 与BP 是否存在某种确定的位置关系?请证明你的结论。
8.已知:PA =2,PB =4,以AB 为直角边作等腰直角三角形ABD ,且P 、D 两点在直线AB 的两侧.(1)如图,当∠APB =45°时,求AB 及PD 的长;(2)当∠APB 变化,且其它条件不变时,求PD 的最大值及相应∠APB 的大小.。
