a2013年第十八届华杯赛决赛小高年级(A)卷-试题及解析word版
2013高年级华杯赛决赛A卷答案

解答. 用右图代替题目中的 2 1 小长方形. 因为题目所给的小长方形上下不对称, 所以同一 个小长方形在拼成的上下对称的正方形中, 不会既在上半部分也在下半部分. 这样, 就可以 只考虑上半部分的不同情形. 1) 相邻的空白格在第一行最左边或最右边. 因为要排除旋转相同的, 所以只考虑相邻 空白格在最右边的情况, 有下图所示的 2 种图形,
12. 答案:不能
解答. 设放的最小自然数为 a , 则放的最大自然数为 a 23 . 于是这 24 个数的和为
A 12(2a 23).
假设可能, 设每个正方形边上的数之和为 S . 因为共有 5 个正方形, 这些和的和为 5S . 因为每个数在这些和中出现两次, 所以有
5S 2 A.
1 1 y 1.5 1.5 y 1.5 4.5 1.5 . 3 6
整理上式得
5 4 y 1.5 6.75 , 6
4 y 5.5 ,
y 1.375 (千米).
综合 1) 和 2) 的讨论, 小虎的船最多离租船处 1.375 千米.
由上面的等式可得, (1)
9 (u1 u 2 u 2010 223 r ) 3r 9 (v1 v 2 v 2012 223 s) 5 s ,
(2)
9 ( w1 w2 w2013 223 t ) 6 t 9 (v1 v 2 v 2012 223 s) 5 s ,
“华杯赛”官网四大类网络课程 √ 专题讲座 √ 赛前串讲 √ 真题详解 √ 月月练讲解
第 2 页 共 5 页
客服电话:400 650 0888 记最小的 16 个数的和为 B , 则 B 8(2a 15) . 下面分两种情形讨论: (1) 若B S , 则
华杯赛小学高年级试卷合集(18-21)A3

初赛试卷 A(小学高年级组)试题 一、选择题
第十九届华罗庚杯少儿数学邀请赛
初赛试卷 A(小学高年级组)试题
1、平面上的四条直线将平面分割成八个部分,则这四条直线中至多有( A.0 B.2 C.3 D.4
5、右图 ABCD 是平行四边形,M 是 DC 的中点,E 和 F 分别位于 AB 和 AD 上,且 EF 平行于 BD,若三角形 MDF 的面积等于 5 平方厘米,则三角形 CEB 的面积等于 ( )平方厘米。 A.5 B.10 C.15 D.20
6、如图所示,AF=7cm,DH=4cm,BG=5cm,AE=1cm。若正方形 ABCD 内的四边形 EFGH 的面积为 78cm²,则正方形 的边长为( A.10 二、填空题 7、五名选手 A、B、C、D、E 参加“好声音”比赛,五个人站成一排集体亮相。他们胸 前有每人的选手编号牌,5 个编号之和等于 35。已知站在 E 右边的选手的编号和为 13;站在 D 右边的选 )cm。 B.11 C.12 D.13
10、 圣诞老人有 36 个同样的礼物,分别装在 8 个袋子中。 已知 8 个袋子中的礼物的个数 至少为 1 且各不相同。现要从中选出一些袋子,将选出的袋子中的所有礼物平均分给 8 个小朋友,恰好分完(每个小朋友至少分得一个礼物),那么,共 种不同的选择。
第二十一届华罗庚杯少儿数学邀请赛 第二十届华罗庚杯少儿数学邀请赛 一、选择题 1、现在从甲、乙、丙、丁四个人中选出两个人参加一项活动。规定:如果甲去,那么乙也去;如果丙不去, 那么乙也不去;如果丙去,那么丁不去。最后去参加活动的两个人是( A.甲、乙 B.乙、丙 C.甲、丙 ) A. 2017 B. 2016 C. 2015 D. 2014 初赛试卷 A(小学高年级组)试题 一、选择题 1. 算式 的计算结果中含有(
2020年第十八届华杯赛决赛小高年级(A)卷-试题及解析word版

总分第十八届华罗庚金杯少年邀请赛决赛试题A(小学高年级组)(时间2013年4月20日10:00~11:30)一、填空题(每小题10分,共80分)1.计算:19×0.125+281×81-12.5=________.解析:原式=(19+281-100)×0.125=200×0.125=252.农谚‘逢冬数九’讲的是,从冬至之日起,每九天分为一段,依次称之为一九,二九,……,九九,冬至那天是一九的第一天.2012年12月21日是冬至,那么2013年的元旦是________九的第________天.解析:31-21+1+1=12,12÷9=1…3,2013年的元旦是二九的第3天.3.某些整数分别被119977553,,,除后,所得的商化作带分数时,分数部分分别是92725232,,,,则满足条件且大于1的最小整数是________.解析:设整数为A,分别被119977553,,,除后,所得的商分别为A A A A 911795735,,,;)1(911921911)1(7972179)1(5752157)1(3532135-++=-++=-++=-++=A A A A A A A A ,,,显然,当A-1是[3,5,7,9]的时候满足题意。
所以A-1=315,A=316。
4.如右图,在边长为12厘米的正方形ABCD 中,以AB 为底边作腰长为10厘米的等腰三角形PAB .则三角形PAC 的面积等于________平方厘米.解析:过P点做PE⊥AB,由于三角形PAB为等腰三角形,所以AE=EB=6cm。
根据勾股定理:PE 2=102-62=64=82,所以PE=8cm。
S△PAB=12×8÷2=48cm 2,S△PCB=12×6÷2=36cm 2,S△PAC=48+36-12×12÷2=12cm 2。
第18届华杯赛决赛真题答案(小高组a卷)
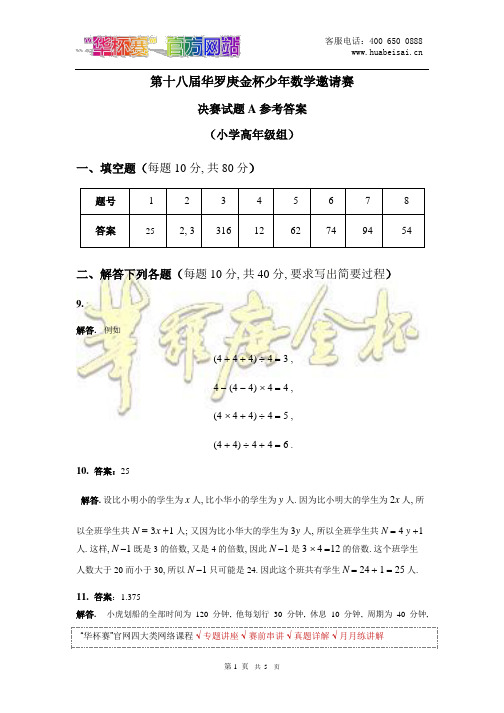
第十八届华罗庚金杯少年数学邀请赛决赛试题 A 参考答案(小学高年级组)一、填空题(每题 10 分, 共 80 分)题号 1 2 3 4 5 6 7 8答案25 2, 3 316 12 62 74 94 54二、解答下列各题(每题 10 分, 共 40 分, 要求写出简要过程)9.解答.例如(4 + 4 + 4) ÷ 4 = 3 ,4 - (4 - 4) ⨯ 4 = 4 ,(4 ⨯ 4 + 4) ÷ 4 = 5 ,(4 + 4) ÷ 4 + 4 = 6 .10.答案:25解答. 设比小明小的学生为x人,比小华小的学生为y人.因为比小明大的学生为2x人,所以全班学生共 N =3x +1人;又因为比小华大的学生为3y人,所以全班学生共N=4y+1人. 这样, N-1既是 3 的倍数, 又是 4 的倍数, 因此N-1是3⨯4=12的倍数. 这个班学生人数大于 20 而小于 30, 所以N-1只可能是 24. 因此这个班共有学生N=24+1=25人.11.答案:1.375解答.小虎划船的全部时间为120分钟,他每划行30分钟,休息10分钟,周期为40分钟, “华杯赛”官网四大类网络课程√专题讲座√赛前串讲√真题详解√月月练讲解所以一共可分为 3 个 30 分钟划行时间段, 有 3 个 10 分钟休息划船时, 顺水的船速与逆水的船速之比为 4.5:1.5=3:1. 因为小虎要把船划到离租船处尽可能远, 他在划船的过程中只能换一次划船的方向, 而且是在尽可能远处. 分两种情况讨论.1)开始向下游划船, 设最远离租船处x千米. 因为回到租船处是逆水, 所以小虎只有 110 分钟可用. 由于划船时顺流速度是逆流速度的 3 倍, 所以用在向下游划船的时间不能超过半小时. 另外两次休息时间只能用在返程, 在休息期间内船向下游漂流了13⨯1.5 , 所以⎛ 1 ⎫x ÷4.5+ x + ⨯1.5⎪ ÷1.5 = 1.5 .3⎝ ⎭整理上式得x +3x +1.5=6.75,4x= 5.25,x =1.3125(千米).2)开始向上游划, 设最远离租船处y千米. 小虎可用 120 分钟, 有两次休息时间用在向上游. 所以⎛ 1 ⎫ ⎛ 1 ⎫y + ⨯1.5⎪ ÷1.5 + y - ⨯1.5⎪ ÷ 4.5 = 1.5 .3 6⎝ ⎭ ⎝ ⎭整理上式得4 y+5 ⨯1.5 = 6.75 , 4 y= 5.5 , y =1.375(千米).6综合 1) 和 2) 的讨论, 小虎的船最多离租船处 1.375 千米.12.答案:不能解答. 设放的最小自然数为a,则放的最大自然数为a+23.于是这24个数的和为A= 12(2a+ 23).假设可能, 设每个正方形边上的数之和为S . 因为共有5个正方形, 这些和的和为5S . 因为每个数在这些和中出现两次, 所以有5S= 2A.“华杯赛”官网四大类网络课程√专题讲座√赛前串讲√真题详解√月月练讲解记最小的 16 个数的和为B , 则B=8(2a+15) . 下面分两种情形讨论:(1)若 B ≤ S ,则S = 2 A = 24 (2a+ 23) ≥ 8(2a+15) , 9.8a+110.4 ≥16a+120 ,5 5不存在自然数 a 使得不等式成立.(2)情形 B > S 也是不可能的,因为此时不可能选择最大正方形边上的16个数使得这16 个数的和等于S .三、解答下列各题(每题 15 分, 共 30 分, 要求写出详细过程)13.答案:5解答. 用右图代替题目中的2⨯1小长方形.因为题目所给的小长方形上下不对称,所以同一个小长方形在拼成的上下对称的正方形中, 不会既在上半部分也在下半部分. 这样, 就可以只考虑上半部分的不同情形.1)相邻的空白格在第一行最左边或最右边. 因为要排除旋转相同的, 所以只考虑相邻空白格在最右边的情况, 有下图所示的 2 种图形,2)相邻的空白格在第一行中间. 去掉旋转重合的, 有下图所示的 3 种图形,所有不同的图形为 5 种.14.答案:6036“华杯赛”官网四大类网络课程√专题讲座√赛前串讲√真题详解√月月练讲解解答. 令n = a1+ a2++ a2010 = b1 + b2 + + b2012 = c1 + c2 ++ c2013 ,其中, 所有的a i数字和相同, 所有的b j数字和相同, 所有的c k数字和相同. 两个自然数数字的和相同, 则它们除以 9 的余数相同, 即a i = 9u i + r, i =1, 2, , 2010,bj = 9v j + s, j =1, 2, , 2012,c k = 9w k + t, k =1, 2, , 2013.则n= 9 ⨯ (u1+u2+ +u2010 ) + 2010⨯r= 9 ⨯ (v1+v2+ +v2012 ) + 2012⨯s (1)= 9 ⨯ (w1+w2+ +w2013 ) + 2013⨯t,由上面的等式可得,9 ⨯ (u1+u2++ u2010 + 223 ⨯ r) + 3r = 9 ⨯ (v1 + v2 ++ v2012 + 223 ⨯ s) + 5 ⨯ s ,(2)9 ⨯ (w1+w2++ w2013 + 223 ⨯ t) + 6 ⨯ t = 9 ⨯ (v1 + v2 ++ v2012 + 223 ⨯ s) + 5 ⨯ s ,(3) 由 (2) 可以得出s是 3 的倍数, 只能是 0, 3 或 6. 下面三种情况讨论:1)s =0.此时,对j=1, 2,, 2012 ,因为b j=9v j的数字和不为零,所以v j≥1. 则n =9⨯(v1+ v2++ v2012 ) ≥ 9 ⨯ 2012 = 18108 .2)s =6.此时“华杯赛”官网四大类网络课程√专题讲座√赛前串讲√真题详解√月月练讲解客服电话:400 650 0888 n =9(v1+ v2++ v2012 ) + 2012 ⨯ 6 ≥ 12072 .3)s =3,此时n= 9(v1+v2+ +v2012 ) + 2012 ⨯ 3 ≥ 6036 .可以取 r =2, t =1.而6036 = 3 + 3 + + 3 = 2 + 2 + + 2 +11 +11 + +112012 个x 个y 个=10 +10 + +10 +1 +1 + +1.=m 个n 个下面计算 x, y 与 m, n,⎧x + y =2010, ⎨ ⎧m + n =2013,⎨⎩10m+n= 6 0 3,6即6036 = 2⨯1786 +11⨯224 =10⨯447 +1566 = 3⨯2012.最终, 满足条件的最小自然数是 6036.“华杯赛”官网四大类网络课程√专题讲座√赛前串讲√真题详解√月月练讲解第 5 页共5页。
第18届华杯赛初赛试题解答(高小A)

第十八届华罗庚金杯少年邀请赛初赛试题A(小学高年级组)(时间2013年3月23日10:00~11:00)一、选择题(每题10分,满分60分,以下每题的四个选项中,仅有一个是正确的,请将表示正确答案的英文字母写在每题的圆括号内。
)1.2012.25×2013.75-2010.25×2015.75=()。
A.5 B.6 C.7 D.8解析:巧算问题原式=(2010.25+2)×(2015.75-2)-2010.25×2015.75=2015.75×2-2010.25×2-4=7所以选C。
2.2013年的钟声敲响了, 小明哥哥感慨地说: 这是我有生以来第一次将要渡过一个没有重复数字的年份。
已知小明哥哥出生的年份是19的倍数, 那么2013年小明哥哥的年龄是()岁。
A.16 B.18 C.20 D.22解析:简单数论。
从1990年~2012年,年份中都有重复数字,其中是19的倍数的数只有1900+95=1995,2012—1995=18(岁),所以选B。
3.一只青蛙8点从深为12米的井底向上爬, 它每向上爬3米, 因为井壁打滑, 就会下滑1米, 下滑1米的时间是向上爬3米所用时间的三分之一。
8点17分时, 青蛙第二次爬至离井口3米之处, 那么青蛙从井底爬到井口时所花的时间为()分钟。
A.22 B.20 C.17 D.16解析:周期问题。
下滑1米的时间是向上爬3米所用时间的三;爬一米和滑一米的时间相同,以爬三米,滑一米为一个周期;(3-1)×3+3=9m,青蛙第一次爬至离井口3米之处,(3-1)×4+1=9m,青蛙第二次爬至离井口3米之处,此时,青蛙爬了4个周期加1米,用时17分钟,所以青蛙每爬1m或滑1m所用时间为1分钟。
(12—3)÷(3-1)=4…1,青蛙从井底爬到井口经过5个周期,再爬2m,用时5×(3+1)+2=22分钟,选A。
第18届华杯赛决赛小中组卷及参考答案

第十八届华罗庚金杯少年数学邀请赛决赛(A)卷【小中组】一、填空题(每小题10分,共80分)1.计算:(2014×2014+2012)-2013×2013=________.2.将长方形的纸片ABCD按右图的方式折叠后压平,使三角形DCF落在三角形DEF的位置,顶点E恰落在边AB上.已知∠1=20°,那么∠2是________度.3.鸡兔同笼,共有40个头,兔脚的数目比鸡脚的数目的10倍少8只,那么兔有________只.4.第一次操作将图a左下角的正方形分为四个小正方形,见图b;第二次操作再将图b左下角的小正方形分为四个更小的正方形,见图c;这样继续下去,当完成第六次操作时,得到的图形中共有________个正方形.图a图b图c5.右面的加法竖式中,相同的汉字代表1至9中的相同数字,而不同的汉字代表不同的数字.则竖式中的“数学”所表示的两位数共有________个.6.大小两个正方体积木粘在一起,构成右图所示的立体图形,其中小积木的下底面的四个顶点,恰好是大积木的上底面各边的中点.如果大积木的棱长为2,那么这个立体图形的表面积是________.7.某班学生人数大于20而小于30,其中女同学的人数是男同学的2倍.全班报名参加“华杯赛”的人数是未报名人数的3倍少1人.这个班有学生________名.8.见右图,图形内的数字分别表示所在的矩形或三角形的面积,那么阴影三角形的面积为________.二、简答题(每小题15分,共60分,要求写出简要过程)9.用4个数码4和一些加、减、乘、除号和小括号,写出值分别等于2、3、4、5、6的五个算式.10.右图是U,V,W,X四辆不同类型的汽车每百千米的耗油量.如果每辆车都有50升油,那么这四辆车最多可行驶的路程总计是多少千米?11.某商店卖出一支钢笔的利润是9元,一个小熊玩具的进价为2元.一次,商家采取“买4支钢笔赠送一个小熊玩具”的打包促销,共获利润1922元.问这次促销最多卖出了多少支钢笔?12.编号从1到10的10个白球排成一行,现按照如下方法涂红色:1)涂2个球;2)被涂色的2个球的编号之差大于2,求不同的涂色方法有多少种?第十八届华罗庚金杯少年数学邀请赛决赛(A )卷参考答案【小中组】一、填空题(每小题10分,共80分)1.解析:【知识点】运算律,平方差公式原式6039201240272012)20132014()20132014(20122013201422=+=+-⨯+=+-=2.解析:【知识点】平面几何o 201=∠=∠CDF ,DCF ∠与CDF ∠互余,则o o o 702090=-=∠DFC ,o 70=∠=∠DFC DFE ,o o o o 4070701802=--=∠。
【数学】第十八届华杯赛初赛试卷_小学高年级组

第十八届华罗庚金杯少年数学邀请赛初赛试卷C (小学高年级组) 第十八届华罗庚金杯少年数学邀请赛 初赛试卷C (小学高年级组) ( 时间: 2013 年3月23日8:00 ~ 9:00) 一、选择题 (每小题 10 分, 满分60分. 以下每题的四个选项中, 仅有一个是正确的, 请将表示正确答案的英文字母写在每题的圆括号内. ) 1. 如果m n =+⨯⨯20122014201420132013(其中m 与n 为互质的自然数), 那么m +n 的值是( ). (A )1243 (B )1343 (C )4025 (D )4029 2. 甲、乙、丙三位同学都把25克糖放入100克水中混合成糖水, 然后他们又分别做了以下事情: 最终,( )得到的糖水最甜. (A )甲 (B )乙 (C )丙 (D )乙和丙 3. 一只青蛙8点从深为12米的井底向上爬, 它每向上爬3米, 因为井壁打滑, 就会下滑1米, 下滑1米的时间是向上爬3米所用时间的三分之一. 8点17分时, 青蛙第二次爬至离井口3米之处, 那么青蛙从井底爬到井口时所花的时间为( )分钟. (A )22 (B )20 (C )17 (D )16 4. 已知正整数A 分解质因数可以写成235A αβγ=⨯⨯, 其中α、β、γ 是自然数. 如果A 的二分之一是完全平方数, A 的三分之一是完全立方数, A 的五分之一是某个自然数的五次方, 那么++αβγ的最小值是( ).(A )10 (B )17 (C )23 (D )31装订线总分第十八届华罗庚金杯少年数学邀请赛初赛试卷C(小学高年级组)5.今有甲、乙两个大小相同的正三角形, 各画出了一条两边中点的连线. 如图, 甲、乙位置左右对称, 但甲、乙内部所画线段的位置不对称. 从图中所示的位置开始, 甲向右水平移动, 直至两个三角形重叠后再离开. 在移动过程中的每个位置, 甲与乙所组成的图形中都有若干个三角形. 那么在三角形个数最多的位置, 图形中有()个三角形.(A)9 (B)10 (C)11 (D)126.从1~11这11个整数中任意取出6个数, 则下列结论正确的有()个.①其中必有两个数互质;②其中必有一个数是其中另一个数的倍数;③其中必有一个数的2倍是其中另一个数的倍数.(A)3 (B)2 (C)1 (D)0二、填空题(每小题 10 分, 满分40分)7.有四个人去书店买书, 每人买了4本不同的书, 且每两个人恰有2本书相同, 那么这4个人至少买了_______种书.8.每天, 小明上学都要经过一段平路AB、一段上坡路BC和一段下坡路CD (如右图). 已知AB:BC:CD = 1:2:1, 并且小明在平路、上坡路、下坡路上的速度比为3:2:4. 如果小明上学与放学回家所用的时间比是n(其中m与m n是互质的自然数),那么m+n的值是.9.黑板上有11个1, 22个2, 33个3, 44个4. 做以下操作: 每次擦掉3个不同的数字,并且把没擦掉的第四种数字多写2个. 例如: 某次操作擦掉1个1, 1个2, 1个3, 那就再写上2个4. 经过若干次操作后, 黑板上只剩下3个数字, 而且无法继续进行操作, 那么最后剩下的三个数字的乘积是.10.如右图, 正方形ABCD被分成了面积相同的8个三角形, 如果DG = 5, 那么正方形ABCD面积是.。
第十八届华杯赛总决赛试题

第十八届华杯赛总决赛试题——必答题A 组试题必答题A1左下图是一个等腰梯形,上底和两腰的长度是2,下底长度是4;右下图是一个正六角星形,面积和等腰梯形的面积相等,问:正六角星形的周长是多少?必答题A2将1,2,3,4分别填入下面的方格中,使得等式+2× +3× +4×=22成立,那么第一个方格填的数与第四个方格填的数之积是多少?必答题A3右图的三角形ABC 中,D ,E 分别是所在边的中点,BC=6MN ,三角形GMN 的面积等于3平方厘米。
求三角形ABC 的面积。
等腰梯形正六角星形100以内仅能分解为两个不同质数之积的自然数共有多少个?必答题A5梯形ABCD 中,腰AD=10厘米,梯形的面积为70平方厘米。
则由腰BC 的中点M 到直线AD 的距离为多少厘米?必答题A6某植物园计划在如图所示的A ,B ,C ,D ,E ,五个地块栽种四种不同颜色的郁金香,每个地块内的郁金香必须同色。
相同的(有公共边界的)地块的郁金香不能同色,不相邻的地块可以同色。
问共有多少种不同的栽种方案?必答题A7如图所示,已知△ABC ,△ACD ,△ADE ,△AEF 都是等腰直角三角形,若它们的总面积是30平方厘米,求AB+AD+AF 的长。
EDC B A黑板上写有数字1到9.请你擦掉其中的几个数字,使得剩下的数字的两两相乘积中,个位出现由0到9这十个数字,你从黑板上最多能擦掉几个数字?第十八届华杯赛总决赛试题——必答题B组试题必答题B1在100至200之间有三个连续的自然数,其中最小的能被3整除,中间的能被5整除,最大的能被7整除。
写出这样的三个连续自然数。
必答题B2边长分别为6厘米和8厘米的两张正方形纸板,放在一个边长为10厘米的大正方形内,大正方形内未被两小正方形纸板盖住的部分的面积最小值是多少平方厘米?必答题B3自然数n是两个质数的乘积,它的包含1但不包含n的所有因数的和等于100,那么n=?必答题B4如图,三角形ABC中,∠ACB=90°,AC=1cm,AB=2cm.以B为中心,将三角形ACB顺时针旋转,使得点A落在边CB的延长线上A1点,此时点C落在点C1的位置。
2013年第十八届华杯赛决赛小高年级(A)卷-试题及解析word版

第十八届华罗庚金杯少年邀请赛决赛试题A (小学高年级组)(时间2013年4月20日10:00~11:30)一、填空题(每小题 10分, 共80分)1.计算: 19×0.125+281×81-12.5=________. 解析:原式=(19+281-100)×0.125=200×0.125=252.农谚‘逢冬数九’讲的是, 从冬至之日起, 每九天分为一段, 依次称之为一九, 二九, ……, 九九, 冬至那天是一九的第一天. 2012年12月21日是冬至, 那么2013年的元旦是________九的第________天.解析:31-21+1+1=12,12÷9=1…3,2013年的元旦是二九的第3天.3.某些整数分别被119977553,,,除后, 所得的商化作带分数时, 分数部分分别是92725232,,,, 则满足条件且大于1的最小整数是________.解析:设整数为A, 分别被119977553,,,除后, 所得的商分别为A A A A 911795735,,,; )1(911921911)1(7972179)1(5752157)1(3532135-++=-++=-++=-++=A A A A A A A A ,,,显然,当A-1是[3,5,7,9]的时候满足题意。
所以A-1=315,A=316。
4.如右图, 在边长为12厘米的正方形ABCD 中, 以AB 为底边作腰长为10厘米的等腰三角形PAB . 则三角形PAC 的面积等于________平方厘米.解析:过P 点做PE ⊥AB,由于三角形PAB 为等腰三角形,所以AE=EB=6cm 。
根据勾股定理:PE 2=102-62=64=82,所以PE=8cm 。
S △PAB=12×8÷2=48cm 2,S △PCB=12×6÷2=36cm 2,S △PAC=48+36-12×12÷2=12 cm 2。
第18届华杯赛决赛小高组(A)、(B)卷试题及参考答案

8.用“学”和“习”代表两个不同的数字,四位数“学学学学”与“习习习习”的积是一个七位数,且它的个位和 百万位数字与“学”所代表的数字相同,那么“学习”所能代表的两位数共有_______个.
7.设 n 是小于 50 的自然数,那么使得 4n+5 和 7n+6 有大于 1 的公约数的所有 n 的可能值之和为________. 8.由四个完全相同的正方体堆积成如右图所示的立体,则立体的表面上(包括底面)所有黑点的总数至 少是________.
二、解答下列各题(每题 10 分,共 40 分要求写出简要过程) 9.用四个数字 4 和一些加、减、乘、除号和括号,写出四个分别等于 3,4,5 和 6 的算式.
6.解析:【知识点】立体几何 求出小积木的棱长即可,如图所示:
小积木的棱长是直角三角形的斜边长度,小积木一个面的面积为12 22 5 ,大积木一个面的面积为 32 9 ,立体图形的表面积为: S 9 5 5 5 (9 5) 74 7.解析:【知识点】数论,余数,因数
设 4n 5 和 7n 6 的公约数为 k ,则 (4n 5) k 为整数,(7n 6) k 也为整数,为了作差消去 n ,前者 乘 7,后者乘 4,则[7(4n 5) 4(7n 6)] k 11 k 为整数,因为 k 1,则11 k 为整数时,只能是 k 11, 即 4n 5 和 7n 6 的公约数为 11; 又因为[(7n 6) (4n 5)] 11为整数,则 3n 1 为整数,
第十八届华杯赛·小学高年级组·武汉

【分析】 原式
2.
3.
4.
5.
【考点】勾股定理 【答案】 110 【分析】 直角边有 101 条,斜边有 9 条,一共 110 条. 【考点】计数 【答案】 B 【分析】 和是 12,有 1 种;和是 10 有 1 种;和是 8,有 2 种;和是 6 有 2 种;和是 4, 有 1 种,一共 7 种,选 B. 【考点】完全平方数 【答案】 9 【分析】 5ab 4 是完全平方数,那么这个数末位是 2 或 8,在判断首位只能是 7,验证 722 5184 满足,那么 a b 9 【考点】容斥 【答案】 140 【分析】 5,8 40 个一周期,去的时候一共标记 40 个,回来时标记 25 个,重复标记 5 个,没有被标记的一共有 200 40 25 5 140 个.
一、填空题 1. 【考点】计算 【答案】2013
2012 2013 2007 2014 2013 . 2007 2012 2014 【考点】扶梯问题 【答案】36 2 【分析】 小孩的速度: 60 90 (米/秒) ,自动扶梯的速度是: 60 60 1 (米/秒) , 3 2 需要: 60 1 36 (秒) 3 【考点】行程 【答案】 3 : 40 【分析】 骑车 A:10 分钟共走 3 千米,骑车 B:10 分钟走 40 千米,速度比等于路程 比是 3 : 40 . 【考点】比例应用题 【答案】20 5 4 【分析】 猴大:猴二:猴三= 5 : 4 : 4 45 : 20 :16 ,则猴二为 9 9 20 29 45 16 20 .
A G F E
B
D
C
11. 影院正在放映《玩具总动员》 、 《冰河世纪》 、 《怪物史莱克》 、 《齐天大圣》四部动漫电影, 票价分别为 50 元、55 元、60 元、65 元。来影院的观众至少看一场,至多看两场。因 时间关系《冰河世纪》与《怪物史莱克》不能观看,若今天必有 200 人看电影所花的钱 一样多,则影院今天至少接待观众多少人?
第十八届“华罗庚金杯”少年数学邀请赛决赛试卷(小中组a卷)

2013年第十八届“华罗庚金杯”少年数学邀请赛决赛试卷(小中组A卷)一、填空题(每小题10分,共80分)1.(10分)计算:(2014×2014+2012)﹣2013×2013 .2.(10分)将长方形的纸片ABCD按右图的方式折叠后压平,使三角形DCF 落在三角形DEF的位置,顶点E恰落在边AB上.已知∠1=22°,那么∠2是度.3.(10分)鸡兔同笼,共有40个头,兔脚的数目比鸡脚的数目的10倍少8只,那么兔有只.4.(10分)第一次操作将图a左下角的正方形分为四个小正方形,见图b;第二次操作再将图b左下角的小正方形分为四个更小的正方形,见图c;这样继续下去,当完成第六次操作时,得到的图形中共有个正方形.5.(10分)如图加法竖式中,相同的汉字代表1至 9中的相同数字,而不同的汉字代表不同的数字.则竖式中的“数学”所表示的两位数共有个.6.(10分)大小两个正方体积木粘在一起,构成如图所示的立体图形,其中小积木的下底面的四个顶点,恰好是大积木的上底面各边的中点.如果大积木的棱长为2,那么这个立体图形的表面积是.7.(10分)某班学生人数大于20而小于30,其中女同学的人数是男同学的2倍.全班报名参加“华杯赛”的人数是未报名人数的3倍少1人.这个班有学生名.8.(10分)如图,图形内的数字分别表示所在的矩形或三角形的面积,那么阴影三角形的面积为.二、简答题(每小题15分,共60分,要求写出简要过程)9.(15分)用四个数字4和一些加、减、乘、除号和括号,写出四个分别等于3、4、5和6的算式.10.(15分)如图是U,V,W,X四辆不同类型的汽车每百千米的耗油量.如果每辆车都有50升油,那么这四辆车最多可行驶的路程总计是多少千米?11.(15分)某商店卖出一支钢笔的利润是9元,一个小熊玩具的进价为2元.一次商家采取“买4支钢笔赠送一个小熊玩具”的打包促销,共获利润1922元.问这次促销最多卖出了多少支钢笔?12.(15分)编号从1到10的10个白球排成一行,现按照如下方法涂红色:(1)涂2个球;(2)被涂色的2个球的编号之差大于2.那么不同的涂色方法有多少种?2013年第十八届“华罗庚金杯”少年数学邀请赛决赛试卷(小中组A卷)参考答案与试题解析一、填空题(每小题10分,共80分)1.(10分)计算:(2014×2014+2012)﹣2013×2013 6039 .【分析】把2014看作2013+1,把2012看作2013﹣1,进行简算即可.【解答】解:(2014×2014+2012)﹣2013×2013=[(2013+1)×(2013+1)+(2013﹣1)]﹣2013×2013=(2013+1)×(2013+1)+2013﹣1﹣2013×2013=2013×2013+2013+2013+1+2013﹣1﹣2013×2013=(2013×2013﹣2013×2013)+(1﹣1)+(2013+2013+1+2013)=6039.故答案为:6039.2.(10分)将长方形的纸片ABCD按右图的方式折叠后压平,使三角形DCF 落在三角形DEF的位置,顶点E恰落在边AB上.已知∠1=22°,那么∠2是44 度.【分析】由题意可知:因为是翻折,∠CFD应该和∠EFD相等,又因∠DEF 等于90°,∠1=22°,于是利用三角形的内角和定理即可求出∠DFE的度数,又因∠CFD和∠EFD和∠2构成了一个平角,平角是180°,据此即可求出∠2的度数.【解答】解:因为翻折,∠CFD=∠EFD=90°﹣22°=68°,∠2=180°﹣68°﹣68°=44°.故答案为:44.3.(10分)鸡兔同笼,共有40个头,兔脚的数目比鸡脚的数目的10倍少8只,那么兔有33 只.【分析】设兔有x只,则鸡有(40﹣x)只,根据脚的倍数关系:兔脚的数=鸡脚的数×10倍+8只,可列方程解答即可.【解答】解:设兔有x只,则鸡有(40﹣x)只,根据脚的倍数关系可列方程:4x+8=10×2×(40﹣x)4x+8=800﹣20xx=33答:兔子有33只.故答案为:33.4.(10分)第一次操作将图a左下角的正方形分为四个小正方形,见图b;第二次操作再将图b左下角的小正方形分为四个更小的正方形,见图c;这样继续下去,当完成第六次操作时,得到的图形中共有29 个正方形.【分析】图a有5个正方形,以后每次操作将一个正方形数目变成四个小正方形,每次增加4个正方形.所以答案为5+6×4=29.【解答】解:5+6×4=29.故答案为:29.5.(10分)如图加法竖式中,相同的汉字代表1至 9中的相同数字,而不同的汉字代表不同的数字.则竖式中的“数学”所表示的两位数共有 3 个.【分析】根据“学+学+学”没有进位,可知“学”只有3种可能.“学”=1,“学习”=17,“数学”=51;“学”=2,“学习”=24,“数学”=72;“学”=3,“学习”=31,“数学”=93.竖式中的“数学”所表示的两位数共有3个.【解答】解:根据题干分析可得:所以数学表示的两位数是51或72或93,一共有3个.答:竖式中的“数学”所表示的两位数共有 3个.故答案为:3.6.(10分)大小两个正方体积木粘在一起,构成如图所示的立体图形,其中小积木的下底面的四个顶点,恰好是大积木的上底面各边的中点.如果大积木的棱长为2,那么这个立体图形的表面积是32 .【分析】如图,因为小积木的下底面的四个顶点,恰好是大积木的上底面各边的中点,所以大正方体一个面的面积是小正方体一个面的面积的2倍.因此,这个立体图形的表面积是大正方体的表面积加上小正方体四个面的面积.据此解答.【解答】解:6×2×2+4×(2×2÷2)=24+4×2=24+8=32.答:这个立体图形的表面积是32.故答案为:32.7.(10分)某班学生人数大于20而小于30,其中女同学的人数是男同学的2倍.全班报名参加“华杯赛”的人数是未报名人数的3倍少1人.这个班有学生27 名.【分析】女同学的人数是男同学的2倍,所以全班人数是3的倍数,全班人数只能是21,24,27;全班报名参加“华杯赛”的人数是未报名人数的3倍少1人,所以全班人数加1人,是4的倍数;检验的全班人数为27人.【解答】解:根据分析知:全班人数是3的倍数,全班人数只能是21,24,27;全班报名参加“华杯赛”的人数是未报名人数的3倍少1人,所以全班人数加1人,是4的倍数;检验的全班人数为27人.故答案为:27.8.(10分)如图,图形内的数字分别表示所在的矩形或三角形的面积,那么阴影三角形的面积为9 .【分析】如下图所示:OA×OC=30,OD×OF=12,将两个式子的等号的两边分别相乘,得出OA×OC×OD×OF=30×12,而OC×OD=10×2=20,由此得出OA×OF,进而求出阴影三角形的面积.【解答】解:因为OA×OC=30,OD×OF=12,所以OA×OC×OD×OF=30×12=360.又因为OC×OD=10×2=20,所以OA×OF=360÷20=18.所以S△AGF=GF•AG=OA•OF=×18=9;答:阴影三角形的面积为9.故答案为:9.二、简答题(每小题15分,共60分,要求写出简要过程)9.(15分)用四个数字4和一些加、减、乘、除号和括号,写出四个分别等于3、4、5和6的算式.【分析】因为12÷4=3,4+4+4=12,所以可以写成(4+4+4)÷4=3;因为4×(4﹣4)=0,4﹣0=4,所以可以写成4﹣(4﹣4)×4=4;因为4×5=20,20÷4=5,所以可以写成(4×4+4)÷4=5;因为2+4=6,(4+4)÷4=2,所以可以写成(4+4)÷4+4=6.【解答】解:(4+4+4)÷4=3;4﹣(4﹣4)×4=4;(4×4+4)÷4=5;(4+4)÷4+4=6;10.(15分)如图是U,V,W,X四辆不同类型的汽车每百千米的耗油量.如果每辆车都有50升油,那么这四辆车最多可行驶的路程总计是多少千米?【分析】根据统计图所提供的信息,可以看出每种车每百千米的耗油量,用50(升)除以每种车的百千米耗油量(升),就是每种车行驶的路程,把四辆车行驶的路程相加即可.【解答】解:(50÷20+50÷25+50÷5+50÷10)×100=(2.5+2+10+5)×100=19.5×100=1950(千米)答:这四辆车最多可行驶的路程总计是1950千米.11.(15分)某商店卖出一支钢笔的利润是9元,一个小熊玩具的进价为2元.一次商家采取“买4支钢笔赠送一个小熊玩具”的打包促销,共获利润1922元.问这次促销最多卖出了多少支钢笔?【分析】根据题意,“买4支钢笔赠送一个小熊玩具”这样卖4支钢笔实得利润9×4﹣2=34元,要这次促销钢笔卖出最多,则要求尽量打包销售.由此可以求出1922是34的多少倍就是打包卖出多少个4支,进而求出最多卖出多少支钢笔.据此解答.【解答】解析:要这次促销钢笔卖出最多,则要求尽量打包销售.1922÷(4×9﹣2)=1922÷34=56(倍)…18(元);18÷9=2(支);56×4+2=224+2=226(支).答:这次促销最多卖出了226支钢笔.12.(15分)编号从1到10的10个白球排成一行,现按照如下方法涂红色:(1)涂2个球;(2)被涂色的2个球的编号之差大于2.那么不同的涂色方法有多少种?【分析】本题采用枚举法,令被涂色的第一个球的编号小于第二个球的编号,由于8+2=10,要使编号之差大于2,所以第二个球编号最大是7,那么第一个球可以是1~7号中的任意一个,由此进行逐个情况讨论,最后再把各种情况的种数相加即可.【解答】解:第一个球涂1号,则另一个球可涂4~10;有7种不同的情况;第一个球涂2号,则另一个球可涂5~10;有6种不同的情况;第一个球涂3号,则另一个球可涂6~10;有5种不同的情况;第一个球涂4号,则另一个球可涂7~10;有4种不同的情况;第一个球涂5号,则另一个球可涂8~10;有3种不同的情况;第一个球涂6号,则另一个球可涂9~10;有2种不同的情况;第一个球涂7号,则另一个球可涂10;有1种不同的情况;所以,不同的涂色方法有:7+6+5+4+3+2+1=28(种).答:不同的涂色方法有28种.声明:试题解析著作权属菁优网所有,未经书面同意,不得复制发布日期:2019/5/7 10:52:49;用户:小学奥数;邮箱:pfpxxx02@;学号:20913800第11页(共11页)。
第十八届“华罗庚金杯”少年数学邀请赛初赛试卷(小高组a卷)

2013年第十八届“华罗庚金杯”少年数学邀请赛初赛试卷(小高组A卷)一、选择题(每题10分,满分60分,以下每题的四个选项中,仅有一个是正确的,请将表示正确答案的英文字母写在每题的圆括号内.)1.(10分)2012.25×2013.75﹣2010.25×2015.75=()A.5 B.6 C.7 D.82.(10分)2013年的钟声敲响了,小明哥哥感慨地说:这是我有生以来第一次将要渡过一个没有重复数字的年份.已知小明哥哥出生的年份是19的倍数,那么2013年小明哥哥的年龄是()岁.A.16 B.18 C.20 D.223.(10分)一只青蛙8点从深为12米的井底向上爬,它每向上爬3米,因为井壁打滑,就会下滑1米,下滑1米的时间是向上爬3米所用时间的三分之一.8点17分时,青蛙第二次爬至离井口3米之处,那么青蛙从井底爬到井口时所花的时间为()分钟.A.22 B.20 C.17 D.164.(10分)一个盒子里有黑棋子和白棋子若干粒,若取出一粒黑子,则余下的黑子数与白子数之比为9:7,若放回黑子,再取出一粒白子,则余下的黑子数与白子数之比为7:5,那么盒子里原有的黑子数比白子数多()个.A.5 B.6 C.7 D.85.(10分)图ABCD是平行四边形,M是DC的中点,E和F分别位于AB和AD上,且EF平行于BD.若三角形MDF的面积等于5平方厘米,则三角形CEB的面积等于()平方厘米.A.5 B.10 C.15 D.206.(10分)水池A和B同为长3米,宽2米,深1.2米的长方体.1号阀门用来向A池注水,18分钟可将无水的A池注满; 2号阀门用来从A池向B池放水,24分钟可将A池中满池水放入B池.若同时打开1号和2号阀门,那么当A池水深0.4米时,B池有()立方米的水.A.0.9 B.1.8 C.3.6 D.7.2二、填空题(每小题10分,满分40分)7.(10分)小明、小华、小刚三人分363张卡片,他们决定按年龄比来分.若小明拿7张,小华就要拿6张;若小刚拿8张,小明就要拿5张.最后,小明拿了张;小华拿了张;小刚拿了张.8.(10分)某公司的工作人员每周都工作5天休息2天,而公司要求每周从周一至周日,每天都至少有32人上班,那么该公司至少需要名工作人员.9.(10分)图中,AB是圆O的直径,长6厘米,正方形BCDE的一个顶点E 在圆周上,∠ABE=45°.那么圆O中非阴影部分的面积与正方形BCDE 中非阴影部分面积的差等于平方厘米(取π=3.14)10.(10分)圣诞老人有36个同样的礼物,分别装在8个袋子中.已知8个袋子中礼物的个数至少为1且各不相同.现要从中选出一些袋子,将选出的袋子中的所有礼物平均分给8个小朋友,恰好分完(每个小朋友至少分得一个礼物).那么,共有种不同的选择.2013年第十八届“华罗庚金杯”少年数学邀请赛初赛试卷(小高组A卷)参考答案与试题解析一、选择题(每题10分,满分60分,以下每题的四个选项中,仅有一个是正确的,请将表示正确答案的英文字母写在每题的圆括号内.)1.(10分)2012.25×2013.75﹣2010.25×2015.75=()A.5 B.6 C.7 D.8【分析】把2012.25看作2010.25+2,2015.75看作2013.75+2,原式变为(2010.25+2)×2013.75﹣2010.25×(2013.75+2),进一步计算为2×2013.75﹣2010.25×2,再运用乘法分配律简算.【解答】解:2012.25×2013.75﹣2010.25×2015.75,=(2010.25+2)×2013.75﹣2010.25×(2013.75+2),=2010.25×2013.75+2×2013.75﹣2010.25×2013.75﹣2010.25×2,=2×2013.75﹣2010.25×2,=(2013.75﹣2010.25)×2,=3.5×2,=7;故选:C.2.(10分)2013年的钟声敲响了,小明哥哥感慨地说:这是我有生以来第一次将要渡过一个没有重复数字的年份.已知小明哥哥出生的年份是19的倍数,那么2013年小明哥哥的年龄是()岁.A.16 B.18 C.20 D.22【分析】从1990年~2012年,年份中都有重复数字,其中是19的倍数的数只有1900+95=1995,然后用2013﹣1995,解答即可.【解答】解:从1990年~2012年,年份中都有重复数字,其中是19的倍数的数只有1900+95=1995,2013﹣1995=18(岁);故选:B.3.(10分)一只青蛙8点从深为12米的井底向上爬,它每向上爬3米,因为井壁打滑,就会下滑1米,下滑1米的时间是向上爬3米所用时间的三分之一.8点17分时,青蛙第二次爬至离井口3米之处,那么青蛙从井底爬到井口时所花的时间为()分钟.A.22 B.20 C.17 D.16【分析】下滑1米的时间是向上爬3米所用时间的3倍;爬1米和滑1米的时间相同,以爬3米,滑1米为一个周期;(3﹣1)×3+3=9m,青蛙第一次爬至离井口3米之处,(3﹣1)×4+1=9m,青蛙第二次爬至离井口3米之处,此时,青蛙爬的路程为(3+1)×4+1=17米,即4个周期加1米,用时17分钟,所以青蛙每爬1m或滑1m所用时间为1分钟;(12﹣3)÷(3﹣1)=4…1,青蛙从井底爬到井口经过5个周期,再爬2m,用时5×(3+1)+2;解答即可.【解答】解:以爬3米,滑一米为一个周期;(3﹣1)×3+3=9m,青蛙第一次爬至离井口3米之处,(3﹣1)×4+1=9m,青蛙第二次爬至离井口3米之处,此时,青蛙爬了4个周期加1米,用时17分钟,所以青蛙每爬1m或滑1m所用时间为1分钟;(12﹣3)÷(3﹣1)=4…1,青蛙从井底爬到井口经过5个周期,再爬2m,用时5×(3+1)+2=22分钟;故选:A.4.(10分)一个盒子里有黑棋子和白棋子若干粒,若取出一粒黑子,则余下的黑子数与白子数之比为9:7,若放回黑子,再取出一粒白子,则余下的黑子数与白子数之比为7:5,那么盒子里原有的黑子数比白子数多()个.A.5 B.6 C.7 D.8【分析】我们运用比例进行解答,设白子有x个,黑子是x+1.用黑子的个数与白子的个数减去1个的比是7:5,列方程进行解答即可.【解答】解:设白子有x个,黑子是x+1.(x+1):(x﹣1)=7:5,x×5+5=7x﹣7,6x+5=7x﹣7,x=12,x×=12×,x=21;黑子的个数:x=21+1=28;28﹣21=7(个);故选:C.5.(10分)图ABCD是平行四边形,M是DC的中点,E和F分别位于AB和AD上,且EF平行于BD.若三角形MDF的面积等于5平方厘米,则三角形CEB的面积等于()平方厘米.A.5 B.10 C.15 D.20【分析】连接FC,DE,FB,在梯形FBCD中,有S△FDB和S△FDC等底等高,所以面积相等;在梯形EBCD中,有S△EDB和S△EBC等底等高,所以面积相等;在梯形FEBD中,有S△FDB和S△EDB等底等高,所以面积相等;所以可得S△FDC =S△EBC,又因为M是DC的中点,根据高一定时,三角形的面积与底成正比例的性质,所以S△EBC=2×5=10cm2.【解答】解:如图,连接FC,DE,FB,在梯形FBCD中,有S△FDB=S△FDC,在梯形EBCD中,有S△EDB=S△EBC,在梯形FEBD中,有S△FDB=S△EDB,所以S△FDC=S△EBC,因为M是DC的中点,所以S△EBC=2×5=10(平方厘米).则S△EBC=10平方厘米,答:三角形EBC的面积是10平方厘米.故选:B.6.(10分)水池A和B同为长3米,宽2米,深1.2米的长方体.1号阀门用来向A池注水,18分钟可将无水的A池注满; 2号阀门用来从A池向B池放水,24分钟可将A池中满池水放入B池.若同时打开1号和2号阀门,那么当A池水深0.4米时,B池有()立方米的水.A.0.9 B.1.8 C.3.6 D.7.2【分析】根据题意,设水池A和B的容积为“1”,1号阀门A池每分钟进水效率,2号阀门B池每分钟进水效率,A池每分钟放水效率也是,同时打开1号和2号阀门,则A池每分钟进水效率为,B池每分钟进水效率.A池水深0.4米,则A池进水0.4÷1.2=,需要时间分钟,B池进水24×=1,所以B池有水3×2×1.2=7.2m3.【解答】解:设水池A和B的容积为“1”,同时打开1号和2号阀门,则A池每分钟进水效率为:,A池水深0.4米,则A池进水:0.4÷1.2=,需要时间:分钟,B池进水:24×=1,所以B池有水:3×2×1.2=7.2(立方米).故选:D.二、填空题(每小题10分,满分40分)7.(10分)小明、小华、小刚三人分363张卡片,他们决定按年龄比来分.若小明拿7张,小华就要拿6张;若小刚拿8张,小明就要拿5张.最后,小明拿了105 张;小华拿了90 张;小刚拿了168 张.【分析】根据题意,可知小明的张数:小华的张数=7:6,小明的张数:小刚的张数=5:8,进而把这两个比写成连比,即小明的张数:小华的张数:小刚的张数=(7×5):(6×5):(8×7)=35:30:56;再根据“小明、小华、小刚三人分363张卡片”,也即要分配的总量为363,是按照35:30:56进行分配的,从而按照比例分配的方法求解.【解答】解:小明的张数:小华的张数:小刚的张数为:(7×5):(6×5):(8×7)=35:30:56,小明拿的张数:363×=105(张),小华拿的张数:363×=90(张),小明拿的张数:363×=168(张).答:小明拿了105张;小华拿了90张;小刚拿了168张.故答案为:105,90,168.8.(10分)某公司的工作人员每周都工作5天休息2天,而公司要求每周从周一至周日,每天都至少有32人上班,那么该公司至少需要45 名工作人员.【分析】根据题意,该公司一周总上班人次至少为32×7=224(人次),把它看做224个元素,而每人每周上5次,把它看做5个抽屉,考虑最值:224÷5=44(名)…4名,所以至少需要44+1=45人.【解答】解:根据题干分析可得:32×7÷5=44(名)…4名,44+1=45(名),答:那么该公司至少需要45名工作人员.故答案为:45.9.(10分)图中,AB是圆O的直径,长6厘米,正方形BCDE的一个顶点E 在圆周上,∠ABE=45°.那么圆O中非阴影部分的面积与正方形BCDE 中非阴影部分面积的差等于10.26 平方厘米(取π=3.14)【分析】连接EO,圆O中非阴影部分的面积﹣正方形BCDE中非阴影部分面积=(圆O中非阴影部分的面积+阴影部分面积)﹣(正方形BCDE中非阴影部分面积+阴影部分面积)=S圆﹣S正.然后,根据,∠ABE=45°可得正方形的边长等于圆的半径,进而推导出BE2=r2=(6÷2)2×2,再根据前面的关系式代入数据解答即可.【解答】解:如图,连接EO,S正=EB×EB=EO2+BO2=(6÷2)2×2=18cm2所以圆O中非阴影部分的面积与正方形BCDE中非阴影部分面积的差:π×(6÷2)2﹣18=10.26(平方厘米);答:圆O中非阴影部分的面积与正方形BCDE中非阴影部分面积的差等于10.26平方厘米.故答案为:10.26.10.(10分)圣诞老人有36个同样的礼物,分别装在8个袋子中.已知8个袋子中礼物的个数至少为1且各不相同.现要从中选出一些袋子,将选出的袋子中的所有礼物平均分给8个小朋友,恰好分完(每个小朋友至少分得一个礼物).那么,共有31 种不同的选择.【分析】36个同样的礼物装在8个袋子中,每个袋子礼物的个数至少为1且各不相同,而1+2+3+…+8=(1+8)×8÷2=36,明确8个袋子分别装的礼物数是1~8.根据题意要求选出袋子里装的礼物数为8的倍数,分情况枚举即可.【解答】解:如果每人分1个礼物:8=<8=1+7=2+6=3+5=1+2+5=1+3+4,6种;如果每人分2个礼物:16=1+7+8=2+6+8=3+5+8=3+6+7=4+5+7=1+2+5+8=1+2+6+7=1+3+4+8=1+3+5+7=1+4+5+6=2+3+4+7=2+3+5+6 =1+2+3+4+6,共13种;如果每人分3个礼物,拆分24,与拆分36﹣24=12是一样的.12=4+8=5+7=1+3+8=1+4+7=1+5+6=2+3+7=2+4+6=3+4+5=1+2+3+6=1+2+4+5,共10种;如果每人分4个礼物,同理拆分36﹣32=44=4=1+3,共2种;所以,共有6+13+10+2=31种不同的选择.故答案为:31.声明:试题解析著作权属菁优网所有,未经书面同意,不得复制发布日期:2019/5/7 10:56:29;用户:小学奥数;邮箱:pfpxxx02@;学号:20913800第11页(共11页)。
第18届“华杯赛”笔试决赛小学高年级组试题C及参考答案

三、解答下列各题(每题 15 分, 共 30 分, 要求写出详细过程)
13. 答案:
1 4
14. 答案: 10
第 1 页
共 3 页
小数 0. a b c 化成最简分数后, 分子有________不同情况. 8. 由四个完全相同的正方体堆积成如右图所示的立体 , 则立
体的表面上(包括底面)所有黑点的总数至少是________.
二、解答下列各题(每题 10 分, 共 40 分, 要求写出简要过程)
9. 右图中, 大正方形的周长比小正方形的周长多 80 厘米, 阴影部 分的面积为 880 平方厘米. 那么, 大正方形的面积是多少平方 厘米? 10. 某高中根据入学考试成绩确定了录取分数线, 录取了四分之一的考生. 所有 被录取者的成绩平均分比录取分数线高 10 分, 所有没有被录取的平均分比 录取分数线低 26 分, 所有考生的平均成绩是 70 分. 那么录取分数线是多少? 11. 设 n 是小于 50 的自然数, 求使得 3n+5 和 5n+4 有大于 1 的公约数的所有 n. 12. 一次数学竞赛中, 参赛各队每题的得分只有 0 分, 3 分和 5 分三种可能. 比赛 结束时, 有三个队的总得分之和为 32 分. 若任何一个队的总得分都可能达到 32 分, 那么这三个队的总得分共有多少种不同的情况?
2. 农谚 ‘逢冬数九’ 讲的是, 从冬至之日起, 每九天分为一段, 依次称之为一九, 二九, ……, 九九, 冬至那天是一九的第一天. 2012 年 12 月 21 日是冬至, 那 么 2013 年 2 月 3 日是________九的第________天. 3. 最简单分数
2013年第十八届华罗庚金杯少年数学邀请赛小高组ABC试卷及详解

第十八届华罗庚金杯少年数学邀请赛初赛试题A(小学高年级组)第十八届华罗庚金杯少年数学邀请赛初赛试题C (小学高年级组)(时间: 2013 年3月23日)一、选择题 (每小题 10 分, 满分60分. 以下每题的四个选项中, 仅有一个是正确的, 请将表示正确答案的英文字母写在每题的圆括号内.)1. 如果mn =+⨯⨯20122014201420132013(其中m 与n 为互质的自然数), 那么m +n 的值是( ). (A )1243 (B )1343 (C )4025 (D )4029解答:B 。
在考试中,选择恰当的方法很重要。
这道题,看到这道题后,我第一个想法就是归纳。
2222315=+、2231422=+、2244537=+、2255648=+、写完前三个,发现第二个算式很不和谐,又写出了第四个,仔细一想,原来第二个可以写成2233426=+,规律找到了,分子是原式中分子部分的一个因数,分母比分子大3!答案一定是20132016,很简单,第一题是很容易的年份题,等等,年份2013这个数是我们非常熟悉的,2013=3×11×61,是3的倍数,那么加3不还是3的倍数么?可以约分,所以最后的答案是20136712016672=所以选B ! 如果本题需要详细的过程,那么用规纳的方法是不合适的,因为这是不完全归纳法,你这么知道前几个适用的情况下,最后的2013也适用呢,所以最正确的方法是这样思考:如果这道题直接计算,分别算出分子分母,然后必然需要一个约分的过程(从选项可以看出),那么就太麻烦了,如果不计算出最后结果就可以约分,是件好事儿,那么转化分子还是转化分母呢?我们都知道,当分子分母都是乘法的形式,是比较好约分的,所以要转化分母,要在分母中“凑”出2013.具体过程是这样的:201320132014(20131)2012201320132014201320142012201320132014201320132201320132013671,2013(20142)2016672⨯=⨯++⨯=⨯++⨯=⨯+⨯⨯===⨯+原式 6716721343.m n +=+=这个题做完了,很容易得分的一道题,也是容易马虎的一个题,如果不仔细读题,忽略了“m 与n 为互质的自然数”,那么就容易把答案写成D 。
2013年第十八届华杯复赛小学高年级组A卷(含解析)

62
8
9
10
11
12
13
(4 4 4) 4 3
4 (4 4) 4 4
54
25
1.375 不能
5
(4 4 4) 4 5
4 (4 4) 4 6
参考解析
一、填空题(每小题 10 分,满分 80 分) 1.计算:19 0.125 281 1 12.5 _______.
14.不为零的自然数 n 既是 2010 个数字和相同的自然数之和,也是 2012 个数字和相同的自 然数之和,还是 2013 个数字和相同的自然数之和,那么 n 最小是多少?
3 / 11
第十八届华罗庚金杯少年数学邀请赛 决赛试卷 A(小学高年级组) 参考答案
1
2
3
4
5
6
25
2,3
316
153
12
10.小明与小华同在小六(1)班,该班学生人数介于 20 和 30 之间,且每个人的出生日期均 不相同.小明说:“本班比我大的人数是比我小的人数的两倍”小华说:“本班比我大的 人数是比我小的人数的的三倍”,问这个班有多少名学生?
11.小虎周末到公园划船,九点从租船处出发,计划不超过十一点回到租船处.已知,租船 处在河的中游,河道笔直,河水流速 1.5 千米/小时; 划船时,船在静水中的速度是 3 千米/小时,每划船半小时,小虎就要休息十分钟让船顺水漂流.问: 小虎的船最远可 以离租船处多少千米?
5 7 9 11
35
2 , 2 ,则满足条件且大于 1 的最小整数是_______. 79
【考点】数论——余数+周期问题
【难度】☆☆☆
4 / 11
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第十八届华罗庚金杯少年邀请赛 决赛试题A (小学高年级组)
(时间2013年4月20日10:00~11:30)
一、填空题(每小题 10分, 共80分) 1.计算: 19×0.125+281×
8
1
-12.5=________. 解析:原式=(19+281-100)×0.125
=200×0.125 =25
2.农谚‘逢冬数九’讲的是, 从冬至之日起, 每九天分为一段, 依次称之为一九, 二九, ……, 九九, 冬至那天是一九的第一天. 2012年12月21日是冬至, 那么2013年的元旦是________九的第________天.
解析:31-21+1+1=12,12÷9=1…3,2013年的元旦是二九的第3天.
3.某些整数分别被119977553,,,除后, 所得的商化作带分数时, 分数部分分别是9
2725232,,,, 则满足条件且大于1的最小整数是________.
解析:设整数为A, 分别被119977553,,,除后, 所得的商分别为
A A A A 9
11
795735,,,;
)1(9
11
921911)1(7972179)1(5752157)1(3532135-++=-++=-++=-++=A A A A A A A A ,,,显然,当A-1是[3,5,7,9]的时候满足题意。
所以A-1=315,A=316。
4.如右图, 在边长为12厘米的正方形ABCD 中, 以AB 为底边作腰长为10厘米的等腰三角形PAB . 则三角形PAC 的面积等于________平方厘米.
解析:过P 点做PE ⊥AB,由于三角形PAB 为等腰三角形,所以AE=EB=6cm 。
根据勾股定理:PE 2=102-62=64=82
,所以PE=8cm 。
S △PAB=12×8÷2=48cm 2,S △PCB=12×6÷2=36cm 2
,
S △PAC=48+36-12×12÷2=12 cm 2。
5.有一筐苹果, 甲班分, 每人3个还剩11个; 乙班分, 每人4个还剩10个; 丙班分, 每人5个还剩12个. 那么这筐苹果至少有________个.
解析:11≡2(mod3)=2;10≡2(mod4)=2;12≡5(mod5)=2,所以苹果数除以3,4,5都余2, [3,4,5]=60, 这筐苹果至少有60+2=62个.
6.两个大小不同的正方体积木粘在一起, 构成右图所示的立体图形, 其中, 小积木的粘贴面的四个顶点分别是大积木的粘贴面各边的一个三等分点.如果大积木的棱长为3, 则这个立体图形的表面积为________.
解析:如图所示,四个三角形面积都是1×2÷2=1,
所以小积木一个面的面积是32
-1×4=5。
这个立体图形的表面积为大积木的表面积加上小积木四个面的面积。
所以面积为6×32
+4×5=74。
7.设n
是小于50
的自然数, 那么使得4n +5和7n +6有大于1
的公约数的所有n 的可能值之和为 .
E
解析:设4n+5和7n+6大于1的公约数为A,则A∣(4n+5),A∣(7n+6)。
(4n+5)×7,(7n+6)×4
相减消去n,则差能被11整除,(4n+5)×7-(7n+6)×4=11,11是质数,所以A只能是11。
(4n+5),(7n+6)都是11的倍数,为了分别找出所有的n,2×(4n+5)-(7n+6)=n+4,11∣(n+4),所以n=7,18,29,40。
所以答案为7+18+29+40=94。
8.由四个完全相同的正方体堆积成如右图所示的立体, 则立体的表面上(包
括底面)所有黑点的总数至少是________.
解析:将黑点数转化为1,2,3,4,5,6,根据图可知,2与4,6,3,1相邻,则2与5
相对,4与6,1相邻,则4与3相对,1与6相对。
最左边的正方体左右两个面上是1和6,可以重叠6;
最右边的正方体重叠6;
最上面的正方体重叠5;
正中间左右两个面一起重叠7,上面重叠6。
所以正方体重叠面上的黑点最多是7+6+5+6+6=30,
立体的表面上所有黑点的总数至少是4×7×3—30=54。
二、解答下列各题(每题10分, 共40分, 要求写出简要过程)
9.用四个数字4和一些加、减、乘、除号和括号, 写出四个分别等于3, 4, 5和6的算式.
解析:(4+4+4)÷4=3,4+(4-4)÷4=4,(4×4+4)÷4=5,4+(4+4)÷4=6
10.小明与小华同在小六(1)班, 该班学生人数介于20和30之间, 且每个人的出生日期均不相同. 小明说: “本班比我大的人数是比我小的人数的两倍”, 小华说: “本班比我大的人数是比我小的人数的三倍”. 问这个班有多少名学生?
解析:根据小明,小华的话可知:六(1)班人数-1是3的倍数,也是4的倍数。
[3,4]=12,所以这个班有12×2+1=25名学生
11.小虎周末到公园划船, 九点从租船处出发, 计划不超过十一点回到租船处. 已知, 租船处在河的中游, 河道笔直, 河水流速1.5千米/小时; 船在静水中的速度是3千米/小时, 划船时, 每
划船半小时, 小虎就要休息十分钟让船顺水漂流. 问: 小虎的船最远可以离租船处多少千米? 解析:V顺:V逆:V水=4.5:1.5:1.5=3:1:1;注意逆水速度等于静水速度。
小虎每划船半小时,就要休息十分钟让船顺水漂流,120÷(30+10)=3,小虎休息三次,则船顺水漂流30分钟,则逆水时间里面有30分钟要和他抵消,相当于船没有动。
在剩下120-30-30=60分钟里要船能回到租船处,则逆水时间和顺水时间为V顺:V逆=3:1,所以顺水时间为60÷(3+1)=15分钟。
注意小虎的船最远可以离租船处,还需加上船顺水漂流10分钟的路程,
所以答案为:4.5×15÷60+1.5×10÷60=1.375km
12.由四个相同的小正方形拼成右图. 能否将连续的24个自然数分别放在图中所示的24个黑点处
(每处放一个, 每个数只使用一次), 使得图中所有正方形边上所放的数之和都
相等? 若能, 请给出一个例子; 若不能, 请说明理由.
解析:设这24个连续自然数为a,a+1,a+2,…,a+23。
注意:图中有五个正方形,五个正方形上共有16+4×8=48,仔细分析,每个数重
复用了2次。
假设能使得图中所有正方形边上所放的数之和都相等,且设这个和为A。
则有(a+a+1+a+2+…+a+23)×2=48a+552=5A
48≡3(mod5),552≡2(mod5),要48a+552是5的倍数,则48a除以5余3,即a要是5的倍数多1,不妨设a=5b+1,48a+552=48×5b+48+552=240b+600,所以A=48b+120
我们再来看大正方形上的16个数,即使是这24个数中最小的16个,它们的和是
5b+1+5b+2+5b+3+…5b+16=80b+136> A=48b+120
所以不能使得图中所有正方形边上所放的数之和都相等。
三、解答下列各题(每小题 15分,共30分,要求写出详细过程)
13.用八个右图所示的2×1的小长方形可以拼成一个4×4的正方形. 若一个拼成的正方形图形经过旋转与另一个拼成的正方形图形相同, 则认为两个拼成的正方形相同. 问: 在所有可能拼成的正方形图形中, 上下对称、第一行有两个空白小方格且空白小方格相
?
代替
因为的正方形图形中, 上下对称,而所给图形上下不对称(第二层,第三层只能横拼,不能竖拼),所以只需考虑一、二层2×4的长方形。
分两个空白正方形在三、四列(两个空白正方形在一、二列旋转可得到两个空白正方形在三、四列的情况)和两个空白正方形在二、三列两种情况。
所以答案为五种。
14.不为零的自然数n ,既是2010个数字和相同的自然数之和, 也是2012个数字和相同的自然数之和, 还是2013个数字和相同的自然数之和, 那么n 最小是多少?
解析:数论。
根据题意有n=2010A=2012B=2013C 。
能把数字和和数联系起来的数是能被3或9整除的数。
明白一个结论,求一个数能否被3或9整除, 将这个数按数位截成若干个数或拆成若干个数,若若干个数的和能被3或9整除,则这个数能被3或9整除。
例:求12346789101112…2013能否被9整除,只需求1+2+…+2013的和能否被9整除。
显然2010,2013都是3的倍数,则n 是3的倍数,2012B 是3的倍数。
根据非零自然数,B 最小为3,则n 最小为6036。
检验:x+y=2010 3x+12y=6036,x=2008,y=2(数字和也可以为2) c+d=2013 10c+d=6036 c=447,d=1566(数字和等于2和3没有可能) 6036=2012×3=2008×3+12×2 =10×447+1566×1 总数n 最小值为6036.。
