算法与程序框图习题课

合集下载

高中数学《算法---程序框图》典型例题练习(含答案)

高中数学《算法---程序框图》典型例题练习（含答案）算法与程序框图在高考中常以小题出现，难度不大，主要考察循环结构。

在处理这类问题时关键在于计算的准确。

一、基础知识：读框图时，要抓住“看头，审尾，记过程”这三点1、看头：观察框图中变量的个数，以及赋予的初始值2、审尾：强调细致的“审查”循环结束时，变量所取到的最后一个值，这也是易错点3、记过程：为了保证计算的准确，在读取框图的过程中，可详细记录循环体中每经过一个步骤，变量取值的变化情况，以便于在跳出循环时能快速准确得到输出变量的值二、典型例题：例1：执行下图所示的程序框图，若输入2x =，则输出y 的值为 .思路：通过框图的判断语句可知y 关于x 的函数为：2321,01,012,1x x y x x x x x −<⎧⎪=+≤<⎨⎪+≥⎩，所以当2x =时，322212y =+⋅=答案：12例2：阅读右边的程序框图，运行相应的程序，则输出的值为（）A ．3B ．4C ．5D ．6思路：循环的流程如下：① 1,2i a ==② 2,5i a ==③ 3,16i a ==④ 4,65i a ==i循环终止，所以4i =答案：B例3：某程序框图如图所示，若输出的57S =，则判断框内为（）A. 4?k >B. 5?k >C. 6?k >D. 7?k >思路：循环的流程如下：① 2,4k S ==② 3,11k S ==③ 4,26k S ==④ 5,57k S ==所以应该在此时终止，所以填入4?k >答案：A例4：执行右面的程序框图，如果输入的N 是6，那么输出的p 是（）A. 120B. 720C. 1440D. 5040思路：循环的流程如下：① 1p =② 2,2k p ==③ 3,6k p ==④ 4,24k p ==⑤ 5,120k p ==⑥ 6,720k p ==答案：B例5：右图是一个算法的流程图，则输出S 的值是______ 第4题思路：循环的流程如下： ① 1123S =+=② 22,327n S ==+=③ 33,7215n S ==+=④ 44,15231n S ==+=⑤ 55,31263n S ==+=循环结束，所以63S =答案：63S =例6：执行如图所示的程序框图，若输出i 的值为2，则输入x 的最大值是( )A ．5B ．6C ．22D ．33思路：因为输出的2i =，说明只经过了一次循环。

《算法与程序框图》习题课片段与点评

蒺一霪爹
《法与程序框图》算
执教者：南平第一中学点评者：南平第一中学吴恬影陈登福
星
．．．
Ｌ
呈
一、
教材背景
师：他们做得都对吗？
生：对！
算法是高中课标新增内容，其中的程序内容初中教材没有涉及，学生在现实生活中也没有体验，学生
往盒子Ｓ中加入盒子ｉ中已有的小球，后盒子中再然加一个小球。这样的话，第１圈运行完后，ＳＯＩ＝＋，ｉ１，相当于这时盒子Ｓ中有１个小球，盒子ｉ中＝＋１有２个小球，那么第２圈运行完后Ｓ＝＋Ｉ２，ｉ２１＝＋
细微的差别，生的框图出乎教师的意料。
学生们开始埋头做了起来。
２８辐教４９０．止０７
生：表ｌ第ｌ圈００１好像有错吧。这表格怎＝＋
么填啊？
有学生得出结果。
生不对，那样的话最后输出的是Ｓ＝＋＋＋１２３
师：那么，这两个框图都能表示Ｉ２３＋＋＋… ＋１００
的算法吗？
的三个基本逻辑结构、画程序框图的基本规则，本课要求学生进一步理解算法，通过模仿、操作、探索，
经历通过设计程序框图解决问题的过程，学会灵活、

12.1 算法与程序框图练出高分(含答案解析)

§12.1算法与程序框图A组专项基础训练(时间：35分钟，满分：57分)一、选择题(每小题5分，共20分)1．算法共有三种逻辑结构，即顺序结构、条件结构、循环结构，下列说法正确的是() A．一个算法只能含有一种逻辑结构B．一个算法最多可以包含两种逻辑结构C．一个算法必须含有上述三种逻辑结构D．一个算法可以含有上述三种逻辑结构中的任一种答案 D解析在一个算法中，可出现顺序结构、条件结构、循环结构三种结构中的任一种．2．已知一个算法：(1)m＝a.(2)如果b<m，则m＝b，输出m；否则执行第3步．(3)如果c<m，则m＝c，输出m.如果a＝3，b＝6，c＝2，那么执行这个算法的结果是() A．3 B．6 C．2 D．m答案 C解析当a＝3，b＝6，c＝2时，依据算法设计，执行后，m＝a＝3<b＝6，c＝2<a＝3＝m，∴c＝2＝m，即输出m的值为2，故选C.3．(2012·天津)阅读如图所示的程序框图，运行相应的程序，当输入x的值为－25时，输出x的值为()A．－1 B．1C．3 D．9答案 C解析当x＝－25时，|x|>1，所以x＝25－1＝4>1，x＝4－1＝1>1不成立，所以输出x＝2×1＋1＝3.4． (2012·北京)执行如图所示的程序框图，输出的S 值为 ( )A ．2B ．4C ．8D ．16答案 C解析当k ＝0时，满足k <3，因此S ＝1×20＝1；当k ＝1时，满足k <3，因此S ＝1×21＝2；当k ＝2时，满足k <3，因此S ＝2×22＝8；当k ＝3时，不满足k <3，因此输出S ＝8. 二、填空题(每小题5分，共15分)5．某算法的程序框图如图所示，则输出量y 与输入实数x 满足的关系式是________．答案 y ＝⎩⎪⎨⎪⎧2x，x ≤1x －2，x >1解析由题意知，程序框图表达的是一个分段函数y ＝⎩⎪⎨⎪⎧2x，x ≤1x －2，x >1. 6．如图是求12＋22＋32＋…＋1002的值的程序框图，则正整数n ＝________.答案 100解析第一次判断执行后，i ＝2，s ＝12；第二次判断执行后，i ＝3，s ＝12＋22，而题目要求计算12＋22＋…＋1002，故n ＝100.7． (2012·广东)执行如图所示的程序框图，若输入n 的值为8，则输出s 的值为________．答案 8解析当i ＝2，k ＝1时，s ＝1×(1×2)＝2；当i ＝4，k ＝2时，s ＝12×(2×4)＝4；当i ＝6，k ＝3时，s ＝13×(4×6)＝8；当i ＝8时，i <n 不成立，输出s ＝8. 三、解答题(共22分)8． (10分)任意给定3个正实数，设计一个算法，判断以这3个正实数为三条边边长的三角形是否存在，并画出这个算法的程序框图．解算法如下：第一步，输入3个正实数a ，b ，c .第二步，判断a ＋b >c ，b ＋c >a ，c ＋a >b 是否同时成立．若是，则存在这样的三角形；否则，不存在这样的三角形．程序框图：9．(12分)某工种按工时计算工资，每月总工资＝每月劳动时间(小时)×每小时工资，从总工资中扣除10%作公积金，剩余的为应发工资，当输入劳动时间和每小时工资数时，试编写一个算法输出应发工资，画出程序框图．解算法如下：第一步，输入每月劳动时间t和每小时工资a；第二步，求每月总工资y＝每月劳动时间t×每小时工资a；第三步，求应发工资z＝每月总工资y×(1－10%)；第四步，输出应发工资z.程序框图如图：B组专项能力提升(时间：25分钟，满分：43分)一、选择题(每小题5分，共15分)1．(2011·天津)阅读下边的程序框图，运行相应的程序，则输出的i的值为()A ．3B ．4C ．5D ．6答案 B解析 i ＝1时，a ＝2；i ＝2时，a ＝5；i ＝3时，a ＝16；当i ＝4时，a ＝65>50.即条件a >50成立，所以输出的i 的值为4.2． (2012·课标全国)如果执行如图所示的程序框图，输入正整数N (N ≥2)和实数a 1，a 2，…，a N ，输出A ，B ，则( )A ．A ＋B 为a 1，a 2，…，a N 的和 B.A ＋B 2为a 1，a 2，…，a N 的算术平均数C ．A 和B 分别是a 1，a 2，…，a N 中最大的数和最小的数D ．A 和B 分别是a 1，a 2，…，a N 中最小的数和最大的数答案 C解析由于x ＝a k ，且x >A 时，将x 值赋给A ，因此最后输出的A 值是a 1，a 2，…，a N 中最大的数；由于x ＝a k ，且x <B 时，将x 值赋给B ，因此最后输出的B 值是a 1，a 2，…，a N 中最小的数．3．如图，若依次输入的x 分别为56π、π6，相应输出的y 分别为y 1、y 2，则y 1、y 2的大小关系是( )A ．y 1＝y 2B ．y 1>y 2C ．y 1<y 2D ．无法确定答案 C解析由程序框图可知，当输入的x 为5π6时，sin 5π6>cos 5π6成立，所以输出的y 1＝sin5π6＝12；当输入的x 为π6时，sin π6>cos π6不成立，所以输出的y 2＝cos π6＝32，所以y 1<y 2. 二、填空题(每小题5分，共15分)4． (2012·浙江)若某程序框图如图所示，则该程序运行后输出的T 的值是________．答案1120解析由程序框图可知，当T ＝1，i ＝1时， T ＝Ti ＝1，i ＝2，不满足i >5；T ＝T i ＝12，i ＝3，不满足i >5；T ＝T i ＝16，i ＝4，不满足i >5；T ＝T i ＝124，i ＝5，不满足i >5；T ＝T i ＝1120，i ＝6，满足i >5.输出T ＝1120.5． (2011·安徽)如图所示，程序框图(流程图)的输出结果是________．答案 15解析由T ＝T ＋k 可知T 是一个累加变量，原题实质为求1＋2＋3＋…＋k 的和，其和为k (k ＋1)2.令k (k ＋1)2≤105，得k ≤14.故当k ＝15时，T ＝1＋2＋3＋…＋15＝120>105，此时输出k ＝15.6．执行如图所示的程序框图，输出的A 为________．答案 2 047解析本题计算的是递推数列a 0＝1，a n ＋1＝2a n ＋1 (n ＝0,1,2，…)的第11项，{a n ＋1}是首项为2，公比为2的等比数列，故a 10＋1＝211，故a 10＝2 047.三、解答题7．(13分)给出以下10个数：5,9,80,43,95,73,28,17,60,36.要求把大于40的数找出来并输出．试画出该问题的算法程序框图．解程序框图如下：。

数学算法和程序框图试题答案及解析

数学算法和程序框图试题答案及解析1.运行如图所示的程序，若结束时输出的结果不小于3，则的取值范围为（）A．B．C．D．【答案】D【解析】第一次运行后,第二次运行后,第三次运行后,此时,停止循环,则,即.2.一个算法的程序框图如右图所示，若该程序输出的P位于区间内，则判断框内应填入的条件是（）A．B．C．D．【答案】C【解析】因为第一次循环，第二次循环，第三次循环，第四次循环，第五次循环，第六次循环，此时应结束循环，所以判断框中应填选C.【考点】程序框图3.执行如图所示的程序框图,输出的S值为时，则输入的的值为（）A．B．C．D．【答案】D【解析】在程序执行过程中，的值依次为；；；，程序结束，输出的S值为．故，即．【命题意图】本题考查程序框图基础知识，意在考查学生基本运算能力和逻辑推理能力. 4.已知函数y＝，写出求该函数函数值的算法及程序框图．【答案】见解析【解析】算法如下：第一步，输入x．第二步，如果x>0，则y＝－2；如果x＝0，则y＝0；如果x<0，则y＝2．第三步，输出函数值y．相应的程序框图如图所示．5.设计算法求＋＋＋…＋的值，并画出程序框图．【答案】见解析【解析】算法如下：第一步，令S＝0，i＝1；第二步，若i≤2 011成立，则执行第三步；否则，输出S，结束算法；第三步，S＝S＋；第四步，i＝i＋1，返回第二步．程序框图：6.根据下列算法语句, 当输入x为60时, 输出y的值为（）A．25B．30C．31D．61【答案】C【解析】,故选择C。

解答要注意条件的运用和判断。

【考点】本题考查算法程序，重点突出对条件语句的考查．是容易题。

7.如果执行右边的程序框图，输入正整数N(N≥2)和实数a1，a2，…，aN，输出A，B，则()A．A＋B为a1，a2，…，aN的和B．为a1，a2，…，aN的算术平均数C．A和B分别是a1，a2，…，aN中最大的数和最小的数D．A和B分别是a1，a2，…，aN中最小的数和最大的数【答案】C【解析】由程序框图可知，当x>A时，A＝x；当x≤A且x<B时，B＝x，所以A是a1，a2，…，a N 中的最大数，B是a1，a2，…，aN中的最小数．故选C．8.执行如图所示的程序框图，则输出的S值是()A．－1B．C．D．4【答案】A【解析】本小题主要考查程序框图的应用．解题的突破口为分析i与6的关系．当i＝1时，S＝＝－1；当i＝2时，S＝＝；当i＝3时，S＝＝；当i＝4时，S＝＝4；当i＝5时，S＝＝－1；当i＝6时程序终止，故而输出的结果为－1．9.程序框图如图所示，则该程序运行后输出的值是________．【答案】【解析】本题主要考查算法的程序框图及其应用．当i＝1时，T＝＝1，而i＝1＋1＝2，不满足条件i>5；接下来，当i＝2时，T＝，而i＝2＋1＝3，不满足条件i>5；接下来，当i＝3时，T ＝＝，而i＝3＋1＝4，不满足条件i>5；接下来，当i＝4时，T＝＝，而i＝4＋1＝5，不满足条件i>5；接下来，当i＝5时，T＝＝，而i＝5＋1＝6，满足条件i>5；此时输出T ＝，故应填．10.某程序框图如图所示，现将输出值依次记为：若程序运行中输出的一个数组是则数组中的（）A．32B．24C．18D．16【答案】A【解析】解:运行第一次,输出 , , ,运行第二次,输出运行第三次,输出运行第四次,输出运行第五次,输出运行第六次,输出所以选A．11.若如图所示的程序框图输出的S是30，则在判断框中M表示的“条件”应该是( ) A．B．C．D．【答案】B【解析】首先执行程序到,则应该填,故选B．12.某程序框图如图所示，若，则该程序运行后，输出的的值为（）A．33B．31C．29D．27【答案】B【解析】若，，则；；满足条件继续，；不满足条件，输出，结束．13.执行程序框图，则输出的S是（）A．5040B．4850C．2450D．2550【答案】C【解析】由程序框图分析可知：第一次循环：第二次循环：第三次循环：…，当时循环结束，此时，故输出的结果为2450，选C．14.某程序框图如图所示，该程序运行后输出的值是（）A．63B．31C．27D．15【答案】A【解析】程序框图运行如下：15.某程序框图如图所示，则该程序运行后输出的值为．【答案】7【解析】开始时，，进入循环，；，继续循环，；，继续循环，；，跳出循环，故．16.执行如图所示的算法流程图，则最后输出的等于．【答案】63【解析】第一次循环，第二次循环，第三次循环，第四次循环，第六次循环，终止循环，输出．17.若某程序框图如右图所示，则该程序运行后输出的值为．【答案】8【解析】，不满足是奇数，，不满足；，不满足是奇数，，不满足；，满足是奇数，，不满足；，不满足是奇数，，不满足；，不满足是奇数，，不满足；，不满足是奇数，，不满足；，不满足是奇数，，满足，输出．18.在下图算法框图中，若输入，程序运行的结果那么判断框中应填入的关于的判断条件是（）A．B．C．D．【答案】B．【解析】由，而输出，由程序框图使用列举法可得：，，结束算法，输出，因此判断框内条件应为“”故选B．【命题意图】本题考查定积分，算法框图中的顺序结构，条件结构、循环结构以及相应语句等基础知识，意在考查分析问题、解决问题的能力、基本运算能力及推理能力．19.对任意函数，，可按如图构造一个数列发生器，记由数列发生器产生数列{}．若定义函数，且输入，则数列{}的项构成的集合为（）A．B．C．D．【答案】C【解析】∵的定义域，把代入可得，把代入可得，把代入可得，因为，所以数列只有三项：，，．【命题意图】本题考查程序框图基础知识，意在考查学生基本运算能力和运算能力.20.如图所示,程序框图（算法流程图）的输出结果是，那么判断框中应填入的关于的判断条件是（）A．B．C．D．【答案】B【解析】经分析，此时满足题意，循环终止，故选B．【命题意图】本题主要考程序框图和循环结构等基础知识，意在考查学生是否理解和认识，并能利用程序框图解决问题的能力．。

北师大版高中数学必修3课后习题答案

第一章算法初步 1．1算法与程序框图练习（P5） 1、算法步骤：第一步，给定一个正实数r .第二步，计算以r 为半径的圆的面积2S r π=.第三步，得到圆的面积S .2、算法步骤：第一步，给定一个大于1的正整数n .第二步，令1i =.第三步，用i 除n ，等到余数r .第四步，判断“0r =”是否成立. 若是，则i 是n 的因数；否则，i 不是n 的因数.第五步，使i 的值增加1，仍用i 表示.第六步，判断“i n >”是否成立. 若是，则结束算法；否则，返回第三步.练习（P19）算法步骤：第一步，给定精确度d ，令1i =.第二步，i 位的不足近似值，赋给a ；小数点后第i 位的过剩近似值，赋给b . 第三步，计算55bam =-.第四步，若m d <，则得到5a；否则，将i 的值增加1，仍用i 表示.返回第二步. 第五步，输出5a.程序框图：习题1.1 A 组（P20）1、下面是关于城市居民生活用水收费的问题.为了加强居民的节水意识，某市制订了以下生活用水收费标准：每户每月用水未超过7 m 3时，每立方米收费1.0元，并加收0.2元的城市污水处理费；超过7m 3的部分，每立方收费1.5元，并加收0.4元的城市污水处理费. 设某户每月用水量为x m 3，应交纳水费y 元，那么y 与x 之间的函数关系为 1.2,071.9 4.9,7x x y x x ≤≤⎧=⎨->⎩我们设计一个算法来求上述分段函数的值.算法步骤：第一步：输入用户每月用水量x .第二步：判断输入的x 是否不超过7. 若是，则计算 1.2y x =；若不是，则计算 1.9 4.9y x =-.第三步：输出用户应交纳的水费y .程序框图：2、算法步骤：第一步，令i =1，S=0.第二步：若i ≤100成立，则执行第三步；否则输出S. 第三步：计算S=S+i 2.第四步：i = i +1，返回第二步.程序框图：3、算法步骤：第一步，输入人数x ，设收取的卫生费为m 元.第二步：判断x 与3的大小. 若x >3，则费用为5(3) 1.2m x =+-⨯；若x ≤3，则费用为5m =.第三步：输出m .程序框图：B 组 1、算法步骤：第一步，输入111222,,,,,a b c a b c ..第二步：计算21121221b c b c x a b a b -=-.第三步：计算12211221a c a c y ab a b -=-.第四步：输出,x y .程序框图：2、算法步骤：第一步，令n=1第二步：输入一个成绩r，判断r与6.8的大小. 若r≥6.8，则执行下一步；若r<6.8，则输出r，并执行下一步.第三步：使n的值增加1，仍用n表示.第四步：判断n与成绩个数9的大小. 若n≤9，则返回第二步；若n>9，则结束算法.程序框图：说明：本题在循环结构的循环体中包含了一个条件结构.1．2基本算法语句练习（P24） 123练习（P29） 12、本程序的运行过程为：输入整数x . 若x 是满足9<x <100的两位整数，则先取出x 的十位，记作a ，再取出x 的个位，记作b ，把a ，b 调换位置，分别作两位数的个位数与十位数，然后输出新的两位数. 如输入25，则输出52. 34、4练习（P32）12习题1.2 A组（P33）1、1(0)0(0)1(0)x xy xx x-+<⎧⎪==⎨⎪+>⎩23、程序：习题1.2 B组（P33）1、程序：23、 4、1．3算法案例练习（P45） 1、（1）45；（2）98；（3）24；（4）17. 2、2881.75.3、2200811111011000=（），820083730=（）习题1.3 A 组（P48） 1、（1）57；（2）55. 2、21324.3、（1）104；（2）7212（）（3）1278；（4）6315（）.4、习题1.3 B 组（P48）1、算法步骤：第一步，令45n =，1i =，0a =，0b =，0c =.第二步，输入()a i .第三步，判断是否0()60a i ≤<. 若是，则1a a =+，并执行第六步. 第四步，判断是否60()80a i ≤<. 若是，则1b b =+，并执行第六步. 第五步，判断是否80()100a i ≤≤. 若是，则1c c =+，并执行第六步. 第六步，1i i =+. 判断是否45i ≤. 若是，则返回第二步.第七步，输出成绩分别在区间[0,60),[60,80),[80,100]的人数,,a b c .2、如“出入相补”——计算面积的方法，“垛积术”——高阶等差数列的求和方法，等等.第二章复习参考题A组（P50）1、（1）程序框图：程序：1、（2）程序框图：程序：INPUT “x=”；x IF x<0 THENy=0ELSEIF x<1 THENy=1ELSEy=xEND IFEND IFPRINT “y=”；y ENDINPUT “x=”；x IF x<0 THENy=（x＋2）＾2 ELSEIF x=0 THENy=4ELSEy=（x－2）＾2 END IFEND IFPRINT “y=”；y END2、见习题1.2 B组第1题解答. 34、程序框图：程序：5、（1）向下的运动共经过约199.805 m （2）第10次着地后反弹约0.098 m （3）全程共经过约299.609 m 第二章复习参考题B 组（P35）1、 2、 INPUT “n=”；n i=1 S=0WHILE i<=n S=S+1／i i=i+1 WENDPRINT “S=”；S ENDi=100 sum=0 k=1 WHILE k<=10 sum=sum+i i=i ／2 k=k+1 WEND PRINT “（1）”；sum PRINT “（2）”；i PRINT “（3）”；2*sum －100 ENDINPUT “n=”；n IF n MOD 7=0 THENPRINT “Sunday ”3、算法步骤：第一步，输入一个正整数x 和它的位数n . 第二步，判断n 是不是偶数，如果n 是偶数，令2nm =;如果n 是奇数，令12n m -=. 第三步，令1i =第四步，判断x 的第i 位与第(1)n i +-位上的数字是否相等. 若是，则使i 的值增加1，仍用i 表示；否则，x 不是回文数，结束算法.第五步，判断“i m >”是否成立. 若是，则n 是回文数，结束算法；否则，返回第四步.第二章统计 2．1随机抽样练习（P57）抽样调查的好处是可以节省人力、物力和财力，可能出现的问题是推断的结果与实际情况之间有误差. 如抽取的部分个体不能很好地代表总体，那么我们分析出的结果就会有偏差.2、（1）抽签法：对高一年级全体学生450人进行编号，将学生的名字和对应的编号分别写在卡片上，并把450张卡片放入一个容器中，搅拌均匀后，每次不放回地从中抽取一张卡片，连续抽取50次，就得到参加这项活动的50名学生的编号.（2）随机数表法：第一步，先将450名学生编号，可以编为000,001， (449)第二步，在随机数表中任选一个数. 例如选出第7行第5列的数1（为了便于说明，下面摘取了附表的第6～10行）.16 22 77 94 39 49 54 43 54 82 17 37 93 23 78 87 35 20 96 43 84 26 34 91 6484 42 17 53 31 57 24 55 06 88 77 04 74 47 67 21 76 33 50 25 83 92 12 06 7663 01 63 78 59 16 95 55 67 19 98 10 50 71 75 12 86 73 58 07 44 39 52 38 7933 21 12 34 29 78 64 56 07 82 52 42 07 44 38 15 51 00 13 42 99 66 02 79 5457 60 86 32 44 09 47 27 96 54 49 17 46 09 62 90 52 84 77 27 08 02 73 43 28第三步，从选定的数1开始向右读，得到一个三位数175，由于175<450，说明号码175在总体内，将它取出；继续向右读，得到331，由于331<450，说明号码331在总体内，将它取出；继续向右读，得到572，由于572>450，将它去掉. 按照这种方法继续向右读，依次下去，直到样本的50个号码全部取出，这样我们就得到了参加这项活动的50名学生.3、用抽签法抽取样本的例子：为检查某班同学的学习情况，可用抽签法取出容量为5的样本. 用随机数表法抽取样本的例子：部分学生的心理调查等.抽签法能够保证总体中任何个体都以相同的机会被选到样本之中，因此保证了样本的代表性.4、与抽签法相比，随机数表法抽取样本的主要优点是节省人力、物力、财力和时间，缺点是所产生的样本不是真正的简单样本.练习（P59）1、系统抽样的优点是：（1）简便易行；（2）当对总体结构有一定了解时，充分利用已有信息对总体中的个体进行排队后再抽样，可提高抽样调查；（3）当总体中的个体存在一种自然编号（如生产线上产品的质量控制）时，便于施行系统抽样法.系统抽样的缺点是：在不了解样本总体的情况下，所抽出的样本可能有一定的偏差.2、（1）对这118名教师进行编号；（2）计算间隔1187.37516k==，由于k不是一个整数，我们从总体中随机剔除6个样本，再来进行系统抽样. 例如我们随机剔除了3,46,59,57,112,93这6名教师，然后再对剩余的112位教师进行编号，计算间隔7k=；（3）在1～7之间随机选取一个数字，例如选5，将5加上间隔7得到第2个个体编号12，再加7得到第3个个体编号19，依次进行下去，直到获取整个样本.3、由于身份证（18位）的倒数第二位表示性别，后三位是632的观众全部都是男性，所以这样获得的调查结果不能代表女性观众的意见，因此缺乏代表性.练习（P62）1、略2、这种说法有道理，因为一个好的抽样方法应该能够保证随着样本容量的增加，抽样调查结果会接近于普查的结果. 因此只要根据误差的要求取相应容量的样本进行调查，就可以节省人力、物力和财力.3、可以用分层抽样的方法进行抽样. 将麦田按照气候、土质、田间管理水平的不同而分成不同的层，然后按照各层麦田的面积比例及样本容量确定各层抽取的面积，再在各层中抽取个体（这里的个体是单位面积的一块地）. 习题2.1 A 组（P63）1、产生随机样本的困难：（1）很难确定总体中所有个体的数目，例如调查对象是生产线上生产的产品. （2）成本高，要产生真正的简单随机样本，需要利用类似于抽签法中的抽签试验来产生非负整值随机数.（3）耗时多，产生非负整数值随机数和从总体中挑选出随机数所对的个体都需要时间.2、调查的总体是所有可能看电视的人群.学生A 的设计方案考虑的人数是：上网而且登录某网址的人群，那些不能上网的人群，或者不登录某网址的人群就被排除在外了. 因此A 方案抽取的样本的代表性差.学生B 的设计方案考虑的人群是小区内的居民，有一定的片面性. 因此B 方案抽取的样本的代表性差.学生C 的设计方案考虑的人群是那些有电话的人群，也有一定的片面性. 因此C 方案抽取的样本的代表性.所以，这三种调查方案都有一定的片面性，不能得到比较准确的收视率. 3、（1）因为各个年级学习任务和学生年龄等因素的不同，影响各年级学生对学生活动的看法，所以按年级分层进行抽样调查，可以得到更有代表性的样本.（2）在抽样的过程中可能遇到的问题如敏感性问题：有些学生担心提出意见对自己不利；又如不响应问题：由于种种原因，有些学生不能发表意见；等等. （3）前面列举的两个问题都可能导致样本的统计推断结果的误差.（4）为解决敏感性问题，可以采用阅读与思考栏目“如何得到敏感性问题的诚实反应”中的方法设计调查问卷；为解决不响应问题，可以事先向全体学生宣传调查的意义，并安排专人负责发放和催收调查问卷，最大程度地回收有效调查问卷. 4、将每一天看作一个个体，则总体由365天组成. 假设要抽取50个样本，将一年中的各天按先后次序编号为0～364天用简单随机抽样设计方案：制作365个号签，依次标上0～364. 将号签放到容器内充分搅拌均匀，从容器中任意不放回取出50个号签. 以签上的号码所对应的那些天构成样本，检测样本中所有个体的空气质量. 用系统抽样设计抽样方案：先通过简单随机抽样方法从365天中随机抽出15天，再把剩下的350天重新按先后次序编号为0～349. 制作7个分别标有0～7的号签，放在容器中充分搅拌均匀. 从容器中任意取出一个号签，设取出的号签的编号为a ，则编号为7(050)a k k +≤<所对应的那些天构成样本，检测样本中所有个体的空气质量.显然，系统抽样方案抽出的样本中个体在一年中排列的次序更规律，因此更好实施，更受方案的实施者欢迎.5、田径队运动员的总人数是564298+=（人），要得到28人的样本，占总体的比例为27.于是，应该在男运动员中随机抽取256167⨯=（人），在女运动员中随机抽取281612-=（人）.这样我们就可以得到一个容量为28的样本.6、以10为分段间隔，首先在1～10的编号中，随机地选取一个编号，如6，那么这个获奖者奖品的编号是：6,16,26,36,46.7、说明：可以按年级分层抽样的方法设计方案. 习题2.1 B 组（P64）1、说明：可以按年级分层抽样的方法设计方案，调查问卷由学生所关心的问题组成.例如：（1）你最喜欢哪一门课程？（2）你每月的零花钱平均是多少？（3）你最喜欢看《新闻联播》吗？（4）你每天早上几点起床？（5）你每天晚上几点睡觉？要根据统计的结果和具体的情况解释结论,主要从引起结论的可能原因及结论本身含义来解释.2、说明：这是一个开放性的题目，没有一个标准的答案. 2．2用样本估计总体练习（P71）1、说明：由于样本的极差为364.41362.51 1.90-=，取组距为0.19，将样本分为10组. 可以按照书上的方法制作频率分布表、频率分布直观图和频率折线图.2、说明：此题目属于应用题，没有标准的答案.3、茎叶图为：由该图可以看出30名工人的日加工零件个数稳定在120件左右. 练习（P74）这里应该采用平均数来表示每一个国家项目的平均金额，因为它能反应所有项目的信息. 但平均数会受到极端数据2000万元的影响，所以大多数项目投资金额都和平均数相差比较大. 练习（P79）1、甲乙两种水稻6年平均产量的平均数都是900，但甲的标准差约等于23.8，乙的标准差约等于41.6，所以甲的产量比较稳定.2、（1）平均重量496.86x ≈，标准差 6.55s ≈.（2）重量位于(,)x s x s -+之间有14袋白糖，所占的百分比约为66.67％. 3、（1）略. （2）平均分19.25x ≈，中位数为15.2，标准差12.50s ≈.这些数据表明这些国家男性患该病的平均死亡率约为19.25，有一半国家的死亡率不超过15.2，15.2x >说明存在大的异常数据，值得关注. 这些异常数据使标准差增大. 习题2.2 A 组（P81）。

12算法与程序框图习题课精品PPT课件

(3)每一步的明确性和有效性 (确定与可行性)
(4)每一步具有顺序性 (顺序性)
图形符号
条件C
名称
功能
开始/终止框表示程序的开
始和结束
表示数据的输入
输入/输出框
或输出
处理框判断框
表示数据作某种处理
表示程序将根据条件 C来选择执行路径
流线连接符
表示程序执行的流向
连接程序框图的两部分
程序框图有以下三种不同的逻辑结构：
2、框图表示
语句1 语句2
问(1)中填什么？
二、选择结构
表示程序的执行步骤出现了分支，它需要根据某一特定的条件选择其中的一个分支执行。
常见的选择结构可以用程序框图表示为下面两种形式：
条件?
Y
语句1
N
语句2
N 条件?
Y
语句1
周一下雨吗？
请标注上Y和N
去上学
去秋游
把流程图补充完整
a>b?
N
Y
讲师：XXXXXX XX年XX月XX日
输入a=21，b=32，c=75，求最后a、b、c输出是多少？
开始输入a,b,c
x=a a=c c=b b=x 输出a,b,c 结束
a=21,b=32,c=75, x=21, a=75, c=32, b=21.
(变形)输入a=21，b=32，c=75，求最后a、b、c输出是多少？
开始输入a,b,c
计数器n=0
S1
N<=100? N Y
跳绳一次
大课间未结束？ N
Y 练习投篮
n n+1
S1
执行如图所示的程序框图，则输出的 S 的值是(
)

课时作业13：§13.4 算法与程序框图

§13.4 算法与程序框图基础送分提速狂刷练一、选择题1．执行如图所示的程序框图，如果输入n ＝3，则输出的S ＝( )A.67B.37C.89D.492．如图所示的程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”．执行该程序框图，若输入的a ，b 分别为14,18，则输出的a ＝( )A ．0B ．2C ．4D ．143．如图所示的程序框图，若输入x ，k ，b ，p 的值分别为1，－2,9,3，则输出的x 值为( )A ．－29B ．－5C ．7D ．194．执行下面的程序框图，如果输入的N ＝10，那么输出的S ＝( )A ．1＋12＋13＋…＋110B ．1＋12！＋13！＋…＋110！C ．1＋12＋13＋…＋111D ．1＋12！＋13！＋…＋111！5．执行如图所示的程序框图，则输出的结果为( )A ．7B ．9C ．10D ．116．执行下面的程序框图，如果输入的a ＝4，b ＝6，那么输出的n ＝( )A ．3B ．4C ．5D ．67．执行如图所示的程序框图，则输出的S ＝( )A.32 B. 3 C ．－32D ．0 8．我们可以用随机数法估计π的值，如图所示的程序框图表示其基本步骤(函数RAND 是产生随机数的函数，它能随机产生(0,1)内的任何一个实数)，若输出的结果为521，则由此可估计π的近似值为( )A ．3.119B ．3.126C ．3.132D ．3.1519．已知函数f (x )＝ax 3＋12x 2在x ＝－1处取得极大值，记g (x )＝1f ′(x ).执行如图所示的程序框图，若输出的结果S >20162017，则判断框中可以填入的关于n 的判断条件是( )A ．n ≤2016?B ．n ≤2017?C ．n >2016?D ．n >2017?10．执行如图所示的程序框图，输出的S 的值为( )A ．log 210－1B ．2log 23－1 C. 92D ．611．下边程序框图的功能是求出16＋16＋16＋16＋16的值，则框图中①、②两处应分别填写的是( )A ．i ≥1，aB ．i ≥1，a －6C ．i >1，aD ．i >1，a －612．给出30个数：1,2,4,7,11，…，要计算这30个数的和，现已给出了该问题的程序框图如图所示，那么框图中判断框①处和执行框②处应分别填入( )A．i≤30？；p＝p＋i－1 B．i≤31？；p＝p＋i＋1C．i≤31？；p＝p＋i D．i≤30？；p＝p＋i二、填空题13．定义n！＝1×2×3×…×n，如图是求10！的程序框图，其中k为整数，则k＝________.14．秦九韶算法是中国南宋时期的数学家秦九韶提出的一种多项式简化算法，如图所示的程序框图表示用秦九韶算法求5次多项式f(x)＝a5x5＋a4x4＋a3x3＋a2x2＋a1x＋a0当x＝x0(x0是任意实数)时的值的过程，若输入a0＝2，a1＝－5，a2＝6，a3＝－4，a4＝7，a5＝2，x0＝3，则输出的v的值为________．15．随机抽取某中学甲、乙两个班各10名同学，测量他们的身高获得身高数据的茎叶图如图，在样本的20人中，记身高在[150,160)，[160,170)，[170,180)，[180,190]的人数依次为A1，A2，A3，A4.如图是统计样本中身高在一定范围内的人数的算法框图．若图中输出的S＝18，则判断框应填________．16．执行如图所示的程序框图，当①是i<6时，输出的S值为________；当①是i<2018时，输出的S值为________．参考答案基础送分提速狂刷练一、选择题 1．【答案】 B【解析】当输入n ＝3时，输出S ＝11×3＋13×5＋15×7＝12⎝⎛⎭⎫1－13＋13－15＋15－17＝37.故选B. 2．【答案】 B【解析】开始：a ＝14，b ＝18，第一次循环：a ＝14，b ＝4；第二次循环：a ＝10，b ＝4；第三次循环：a ＝6，b ＝4；第四次循环：a ＝2，b ＝4；第五次循环：a ＝2，b ＝2.此时，a ＝b ，退出循环，输出a ＝2.故选B. 3．【答案】 D【解析】程序执行过程如下：n ＝1，x ＝－2×1＋9＝7； n ＝2，x ＝－2×7＋9＝－5； n ＝3，x ＝－2×(－5)＋9＝19； n ＝4>3，终止循环，输出x ＝19. 故选D. 4．【答案】 B【解析】 T ＝1，S ＝1，k ＝2； T ＝12，S ＝1＋12，k ＝3；T ＝12×3，S ＝1＋12＋12×3，k ＝4；T ＝14！，S ＝1＋12！＋13！＋14！，k ＝5；……；T ＝110！，S ＝1＋12！＋13！＋…＋110！，k ＝11>10，输出S ，故选B.5．【答案】 B【解析】 i ＝1，s ＝1×13≤0.1，否；i ＝3，s ＝13×35＝15≤0.1，否；i ＝5，s ＝15×57＝17≤0.1，否；i ＝7，s ＝17×79＝19≤0.1，否；i ＝9，s ＝19×911＝111≤0.1，是，输出i ＝9，故选B. 6．【答案】 B【解析】第一次循环：a ＝2，b ＝4，a ＝6，s ＝6，n ＝1；第二次循环：a ＝－2，b ＝6，a ＝4，s ＝10，n ＝2；第三次循环：a ＝2，b ＝4，a ＝6，s ＝16，n ＝3；第四次循环：a ＝－2，b ＝6，a ＝4，s ＝20，n ＝4. 结束循环，输出n 的值为4，故选B. 7．【答案】 A【解析】由程序框图得S ＝sin π3＋sin 2π3＋sin 3π3＋sin 4π3＋sin 5π3＋sin 6π3＋sin 7π3＋…＋sin 2017π3.由正弦函数的周期性，得S ＝sin π3＝32，故选A.8．【答案】 B【解析】在空间直角坐标系Oxyz 中，不等式组⎩⎪⎨⎪⎧0<x <1，0<y <1，0<z <1，表示的区域是棱长为1的正方体区域，相应区域的体积为13＝1；不等式组⎩⎪⎨⎪⎧0<x <1，0<y <1，0<z <1，x 2＋y 2＋z 2<1表示的区域是棱长为1的正方体区域内的18球形区域，相应区域的体积为18×4π3×13＝π6，因此π6≈5211000，即π≈3.126，故选B. 9．【答案】 B【解析】 f ′(x )＝3ax 2＋x ，则f ′(－1)＝3a －1＝0，解得a ＝13，g (x )＝1f ′(x )＝1x 2＋x ＝1x (x ＋1)＝1x －1x ＋1，g (n )＝1n －1n ＋1，则S ＝1－12＋12－13＋…＋1n －1n ＋1＝1－1n ＋1＝nn ＋1，因为输出的结果S >20162017，分析可知判断框中可以填入的判断条件是“n ≤2017？”，故选B.10．【答案】 B【解析】 S ＝3，i ＝1，i ≤7成立； S ＝3＋log 221，i ＝2，i ≤7成立； S ＝3＋log 221＋log 232＝3＋log 2⎝⎛⎭⎫21× 32 ＝3＋log 23， i ＝3，i ≤7成立； S ＝3＋log 23＋log 243＝3＋log 2⎝⎛⎭⎫3× 43＝3＋log 24，i ＝4，i ≤7成立；……；S ＝3＋log 28，i ＝8，i ≤7不成立，退出循环，S ＝log 2(3＋log 28)＝log 2⎝⎛⎭⎫3＋32＝log 292＝2log 23－1，故选B. 11．【答案】 D【解析】程序框图是计算16＋16＋16＋16＋16的值，则利用累积加，则第一个处理框应为i >1，然后计算i 是自减1个，i ＝i －1，第二空输出结果a －6.故选D. 12．【答案】 D【解析】由于要计算30个数的和，故循环要执行30次，由于循环变量的初值为1，步长为1，故终值应为30，即①中应填写“i ≤30？”；又由第1个数是1；第2个数比第1个数大1即1＋1＝2；第3个数比第2个数大2即2＋2＝4；第4个数比第3个数大3即4＋3＝7；故②中应填写p ＝p ＋i .故选D. 二、填空题 13．【答案】 11【解析】因为10！＝1×2×…×10，所以判断框内的条件为“i <11？”，故k ＝11. 14．【答案】 986【解析】执行程序框图，输入a 0＝2，a 1＝－5，a 2＝6，a 3＝－4，a 4＝7，a 5＝2，x 0＝3，经过第1次循环得v ＝13，n ＝2；经过第2次循环得v ＝35，n ＝3；经过第3次循环得v ＝111，n ＝4；经过第4次循环得v ＝328，n ＝5；经过第5次循环得v ＝986，n ＝6，退出循环．故输出的v 的值为986.15．【答案】 i <5？(或i ≤4？)【解析】由于i 从2开始，也就是统计大于或等于160的所有人数，于是就要计算A 2＋A 3＋A 4，因此，判断框应填i <5？或i ≤4？. 16．【答案】 5 2017【解析】当①是i <6时，当i ＝1时，a 1＝cos π2＋1＝1，S ＝1；当i ＝2时，a 2＝cos 2π2＋1＝0，S ＝1；当i ＝3时，a 3＝cos 3π2＋1＝1，S ＝1＋1＝2；当i ＝4时，a 4＝cos 4π2＋1＝2，S ＝2＋2＝4；当i ＝5时，a 5＝cos 5π2＋1＝1，S ＝4＋1＝5；当i ＝6时，a 6＝cos 6π2＋1＝0，S ＝5＋0＝5.此时不满足条件，输出S ＝5.当①是i <2018时，因为a i ＝cos i π2＋1的周期为4，所以a 1＋a 2＋a 3＋a 4＝4，所以S ＝a 1＋a 2＋…＋a 2018＝504(a 1＋a 2＋a 3＋a 4)＋a 2017＋a 2018＝504×4＋a 1＋a 2＝2017.。

算法语句与程序框图(高三复习、教案、习题含答案)

第一章算法初步第1课时算法与程序框图【知识梳理】1．算法的概念算法具有确定性、有效性、有限性等特征．算法设计与一般意义上的解决问题不同，它是对一类问题的一般解法的抽象与概括，主要借助一般的问题解决方法，又要包括此类问题的所有情形．它往往是把问题的解决划分为若干个可执行的步骤，有时甚至是重复多次，但最终都必须在有限个步骤之内完成．（1）用数学语言描述算法解决问题的过程大体可分为三步：第一步，明确问题的性质，分析题意．我们将问题简单地分为数值问题和非数值问题，不同类型的问题可以有针对性地采用不同的方法进行处理．第二步，建立问题的描述模型．对于数值型问题，可以建立数学模型，通过数学语言来描述问题．对于非数值型问题，我们可以建立过程模型，通过过程模型来描述问题．第三步，设计、确立算法．对于数值型问题，我们可以采用数值分析的方法进行处理，数值分析中有许多现成的固定算法，我们可以直接使用．当然我们也可以根据问题的实际情况设计算法．对于非数值型问题，根据过程模型分析算法并进行处理，也可以选择一些成熟的办法进行处理，如排序、递推等．（2）算法设计应注意：①与解决问题的一般方法有联系，从中提炼出算法；②将解决问题的过程分为若干个可执行步骤；③引入有关的参数或变量对算法步骤加以表达；④用最简练的语言将各个步骤表达出来；⑤算法的执行要在有限步内完成．2．程序框图程序框图又称流程图，是一种用___________、___________及___________来表示算法的图形．程序框图是人们用来描述算法步骤的形象化的方法．在程序框图中，一个或几个程序框的组合表示算法中的一个步骤；带有方向箭头的流程线将程序框连接起来，表示算法步骤的执行顺序．另外，程序框内还要有必要的文字说明．构成程序框图的图形符号、名称及其功能如下表：说明：一个完整的程序框图一定会包含终端框（用于表示一个算法的开始和结束），处理框（赋值、计算，算法中处理数据需要的算式、公式等）和流程线．3．算法的三种基本逻辑结构通常一个算法只能由三种基本逻辑结构构成，这三种基本逻辑结构分别是：顺序结构、条件结构和循环结构．（1）顺序结构顺序结构是由若干个___________的步骤组成的．这是任何一个算法都离不开的基本结构．顺序结构可以用程序框图表示为顺序结构是最简单的算法结构，语句与语句之间，框与框之间是按从上到下的顺序进行的，其中A和B两个框是依次执行的，只有在执行完A框所指定的操作后，才能接着执行B框所指定的操作，顺序结构各步骤之间不能随便调换，调换后可能会使算法不能运行或错误．（2）条件结构在一个算法中，经常会遇到一些条件的判断，算法的流程根据___________有不同的流向．条件结构就是处理这种过程的结构．条件结构对应的程序框图如图所示：（1）（2）注意：①无论条件是否成立，图（1）中只能执行“步骤A”框或“步骤B”框，但不可以既执行“步骤A”又执行“步骤B”，也不可以“步骤A”和“步骤B”都不执行；“步骤A”和“步骤B”中可以有一个是空的，如图（2）所示．②在利用条件结构画程序框图时，必须清楚判断的条件是什么，条件判断后分别对应着什么样的结果．（3）循环结构在一些算法中，要求___________同一操作的结构称为循环结构．即从算法某处开始，按照一定的条件反复执行某些步骤．反复执行的步骤称为循环体．循环结构有两种形式：直到型循环结构和当型循环结构．①直到型循环结构直到型循环结构可以用程序框图表示为：这个循环结构有如下特征：在执行了一次循环体后，对条件进行判断，如果条件不满足，就继续执行循环体，直到条件满足时终止循环．②当型循环结构当型循环结构可以用程序框图表示为：这个循环结构有如下特征：在每次执行循环体前，先对控制循环的条件进行判断，当条件满足时，执行循环体，否则终止循环．4．程序框图的画法在用自然语言表述一个算法后，可以画出程序框图，用顺序结构、条件结构和循环结构来表示这个算法．这样表示的算法清楚、简练，便于阅读和交流．设计一个算法的程序框图通常要经过以下步骤：第一步，用自然语言表述算法步骤.第二步，确定每一个算法步骤所包含的逻辑结构，并用相应的程序框图表示，得到该步骤的程序框图.第三步，将所有步骤的程序框图用流程线连接起来，并加上终端框，得到表示整个算法的程序框图.注意：流程线不要忘记画箭头，因为它是反映流程执行先后次序的，若不画出箭头，则难以判断各框的执行顺序．【参考答案】1.某一类问题；2.程序框流程线文字说明；3．（1）依次执行（2）条件是否成立（3）反复执行【重难点强化】1．算法的概念常见的设计算法的问题有解方程（组）问题、直接应用数学公式求解的问题、筛选问题、实际生活问题等，设计算法时要注意：（1）认真分析问题，联系解决此问题的一般数学方法；（2）综合考虑此类问题中可能涉及的各种情况；（3）将解决问题的过程划分为若干个步骤．【例1】已知直角三角形两直角边长为a，b，求斜边长c的一个算法分下列三步：①计算c=a，b的值；③输出斜边长c的值；其中正确的顺序是A．①②③B．②③①C．①③②D．②①③【答案】D【解析】由算法规则得：第一步：输入直角三角形两直角边长a，b的值，第二步：计算c第三步：输出斜边长c的值；这样，就是求斜边长c的一个算法．故选D．【点睛】算法是解决某一类问题的精确描述，这就要求我们在写算法时应简练、清晰，并善于分析任何可能出现的情况，体现出思维的严密性和完整性．【例2】下列关于算法的理解正确的是A．算法等同于解法B．任何问题都可以运用算法解决C．按照算法一步步执行，在有限步之后，总能得出结果D．解决某一个具体问题时，算法不同，结果也不同【答案】C2．顺序结构与顺序结构相关的问题一般是利用公式求解问题．在使用顺序结构书写程序框图时，（1）要注意各种框图符号的正确使用；（2）要先赋值，再运算，最后输出结果．【例3】将两个数a=2017，b=2018交换，使得a=2018，b=2017，下面语句正确一组是A．B．C．D．【答案】B【解析】先把b的值赋给中间变量c，这样c=2018，再把a的值赋给变量b，这样b=2017，把c的值赋给变量a，这样a=2018．故选B．【例4】已知函数f（x）=x2–3x+2，请设计一个算法，画出算法的程序框图，求f（3）+f（–1）的值．【点睛】画顺序结构的程序框图问题，不仅要遵循程序框图的画图原则，而且要看要求的量需要根据哪些条件求解，需要的条件必须先输入，或将已知的条件全部输入，求出未知的量．3．条件结构凡是需要先根据条件作出判断，然后再决定进行哪一个步骤的问题，在画程序框图时，必须引入判断框，采用条件结构，有时会需要多个判断框，至于判断框内的内容是没有固定顺序的．【例5】一算法的程序框图如图所示，若输出的12y=，则输入的x可能为A．–1 B．1 C．1或5 D．–1或1【答案】B【点睛】（1）对于求分段函数的函数值的程序框图画法：如果是分两段的函数，只需引入一个判断框；如果是分三段的函数，需要引入两个判断框；依此类推．至于判断框内的内容是没有顺序的．（2）判断框内的内容可以不唯一，但判断框内的内容一经改变，其相应的处理框等内容均要有所改变．【例6】阅读程序框图，如果输出的函数值在区间1142⎡⎤⎢⎥⎣⎦，内，则输入的实数x的取值范围是A．（–∞，–2] B．[–2，–1] C．[–1，2] D．[2，+∞）【答案】B【解析】分析程序中各变量、各语句的作用，再根据流程图所示的顺序，可知：该程序的作用是计算分段函数f（x）=[]()()222222x xx⎧∈-⎪⎨∈-∞-+∞⎪⎩，，，，，的函数值．又∵输出的函数值在区间1142⎡⎤⎢⎥⎣⎦，内，∴11242x<<，解得x∈[–2，–1]．故选B．4．循环结构如果算法问题中涉及的运算进行了许多次重复的操作，且先后参与运算的数之间有相同的变化规律，就可以引入变量(我们称之为循环变量)，构成循环结构．循环结构中常用的几个变量：①计数变量：即计数器，用来记录执行循环体的次数，如1n n=+．=+，1i i②累加变量：即累加器，用来计算数据之和，如S S i=+．③累乘变量：即累乘器，用来计算数据之积，如P P i=*．在程序框图中，一般要根据实际情况先给这些变量赋初始值．一般情况下，计数变量的初始值为1，累加变量的初始值为0，累乘变量的初始值为1．【例7】阅读如图的程序框图．若输入n=5，则输出k的值为A．2 B．3 C．4 D．5【答案】B【例8】已知流程图如图所示，该程序运行后，为使输出的b值为16，则循环体的判断框内①处应填A．2 B．3 C．4 D．5【答案】B【习题训练】1．早上从起床到出门需要洗脸刷牙（5 min）、刷水壶（2 min）、烧水（8 min）、泡面（3 min）、吃饭（10 min）、听广播（8 min）几个步骤，从下列选项中选出最好的一种算法A．第一步洗脸刷牙、第二步刷水壶、第三步烧水、第四步泡面、第五步吃饭、第六步听广播B．第一步刷水壶、第二步烧水同时洗脸刷牙、第三步泡面、第四步吃饭、第五步听广播C．第一步刷水壶、第二步烧水同时洗脸刷牙、第三步泡面、第四步吃饭同时听广播D．第一步吃饭同时听广播、第二步泡面、第三步烧水同时洗脸刷牙、第四步刷水壶2．我们已学过的算法有求解一元二次方程的求根公式，加减消元法求二元一次方程组的解，二分法求函数的零点等，对算法的描述有：①对一类问题都有效；②算法可执行步骤必须是有限的；③算法可以一步一步地进行，每一步都有确切的含义；④是一种通法，只要按部就班地做，总能得到结果．以上对算法的描述正确的有A．1个B．2个C．3个D．4个3．表示“根据给定条件判断”的符号是A B C D4．下面的程序框图是顺序结构的是5．如图所示的程序框图表示的算法意义是A．边长为3，4，5的直角三角形面积B．边长为3，4，5的直角三角形内切圆面积C．边长为3，4，5的直角三角形外接圆面积D．以3，4，5为弦的圆面积6．如图所示的程序框图是已知直角三角形两直角边a，b求斜边c的算法，其中正确的是7．根据所给的程序框图，如图所示，输出的结果是A ．3B ．1C ．2D ．08．下列说法：①条件结构是最简单的算法结构；②顺序结构就是按照程序语句运行的自然顺序，依次地执行顺序；③条件结构可以根据设定的条件，控制语句流程，有选择地执行不同的语句序列．其中正确的说法是 A ．①②B ．①③C ．②③D ．①②③9．求下列函数的函数值的算法中需要用到条件结构的是 A ．f （x ）＝x 2－1B ．f （x ）＝2x ＋1C ．f （x ）＝⎩⎪⎨⎪⎧x 2＋1x >1，x 2－1x ≤1.D ．f （x ）＝2x10．如右图所示的程序框图，其功能是A ．输入a ，b 的值，按从小到大的顺序输出它们的值B ．输入a ，b 的值，按从大到小的顺序输出它们的值C ．求a ，b 的最大值D ．求a ，b 的最小值 11．直到型循环结构对应的框图为12．如右图所示的程序框图中，循环体是A ．①B ．②C ．③D ．②③13．阅读如图框图，运行相应的程序，则输出i的值为A．3 B．4 C．5 D．6 14．下面程序框图表示的算法的运行结果是________．15．若R＝8，则如图所示的程序框图运行后的结果为a＝________．16．试写一个解三元一次方程组12,3316,2x y z x y z x y z ++=⎧⎪--=⎨⎪--=-⎩①②③的算法．17．已知半径为r 的圆的周长公式为C ＝2πr ，当r ＝10时，写出计算圆的周长的一个算法，并画出程序框图．18．如下算法：第一步，输入x 的值；第二步，若x ≥0，则y ＝x ；第三步，否则，y ＝x 2；第四步，输出y 的值，若输出的y 值为9，则x 的值是 A ．3B ．－3C ．3或－3D ．－3或919．给出下列程序框图：若输出的结果为2，则①处的执行框内应填的是A ．x ＝2B ．b ＝2C ．x ＝1D ．a ＝520．下面的程序框图能判断任意输入的数的奇偶性．其中判断框中的条件是 A ．？B ．？C ．？D ．？x 0m =0x =1x =1m =21．某程序框图如图所示，现输入如下四个函数，则可以输出的函数是A ．()2f x x =B ．()1f x x=C ．()e x f x =D ．()3f x x x =+22．执行如图所示的程序框图，若输出的n ＝7，则输入的整数K 的最大值是A ．18B ．50C ．78D ．30623．执行如图所示的程序框图，输出的S 值为A ．1B ．23C ．1321D ．61098724．执行如图所示的程序框图，输出的结果为A．（－2，2）B．（－4，0）C．（－4，－4）D．（0，－8）25．执行如图所示的程序框图，输出的S值为A．1 B．3 C．7 D．1526．阅读如图所示的程序框图，运行相应的程序，输出的n的值为A．1 B．2 C．3 D．427．如图给出的是计算12＋14＋16＋18＋…＋1100的一个程序框图，其中判断框内应填入的条件是A ．i ＜50？B ．i ＞50?C ．i ＜25?D ．i ＞25?28．一个算法的程序框图如图所示，当输入的x 值为3时，输出y 的值恰好是13，则“①”处的关系式是A ．y ＝x 3B ．y ＝3－xC ．y ＝3xD ．y ＝x 1329．如图是求长方体的体积和表面积的一个程序框图，补充完整，横线处应填_____________．30．已知函数()()2log 2,22,x x y x x ⎧⎪=⎨-<⎪⎩图中表示的是给定x 的值，求其对应的函数值y 的程序框图．①处应填写_____________；②处应填写_____________．【习题训练答案】1.【答案】C2.【答案】D3.【答案】A4.【答案】A5.【答案】B6.【答案】C7.【答案】C8.【答案】C9.【答案】C 10.【答案】C 11.【答案】B 12.【答案】B 13.【答案】B 14.【答案】6 6【解析】由题意得P ＝5＋6＋72＝9，S ＝9×4×3×2＝63＝66．15.【答案】4【解析】由R ＝8得b ＝R2＝2，a ＝2b ＝4． 16.【答案】略． 17.【答案】详见解析．【解析】算法如下：第一步，令r ＝10．第二步，计算C ＝2πr ．第三步，输出C ．程序框图如图：18.【答案】D 19.【答案】C 20.【答案】D 21.【答案】A 22.【答案】C 23.【答案】C 24.【答案】B 25.【答案】C 26.【答案】B 27.【答案】B 28.【答案】C【解析】当x ＝3时，∵x ＞0，由x ＝x －2，得x ＝1；再用x ＝x －2，得x ＝－1；而当x ＝－1时，3x ＝13． 29.【答案】【解析】根据题意，长方体的长、宽、高应从键盘输入，故横线处应填写输入框．30.【答案】2?x < 2log y x =【解析】框图中的①就是分段函数关系式两种形式的判断条件，故填写“2?x <”．②就是该函数的另一段表达式2log y x =．【点睛】求分段函数函数值的程序框图的画法：如果是分两段的函数，只需要引入一个判断框；如果是分三段的函数，需要引入两个判断框，依此类推，至于判断框内的内容是没有顺序的．第2课时算法与程序框图【知识梳理】1．五种基本算法语句任何一种程序设计语言中都包含五种基本的算法语句，分别它们是___________、___________、___________、___________、和___________．2．输入语句输入语句与程序框图中的___________对应，以BASIC语言为例，其一般格式为：INPUT “提示内容”；变量其中，“提示内容”一般是提示用户输入什么样的信息．输入语句的作用是输入提示内容要求的相应信息或值，计算机每次都把新输入的值赋给变量．3．输出语句输出语句与程序框图中的___________对应，以BASIC语言为例，其一般格式为：PRINT “S ”；S输出语句的作用是输出算法的信息(表达式)．输出语句的功能是在计算机的屏幕上输出常量、变量的值和系统信息．4．赋值语句赋值语句与程序框图中表示赋值的处理框对应，以BASIC语言为例，其一般格式为：___________赋值语句的作用是将表达式所代表的值赋给变量．判断赋值语句正确与否的两个步骤：（1）看格式，看是否满足“变量=表达式”的格式．（2）看内容，看赋值号是否超过了一个，即看是否进行了代数式的计算．5．条件语句条件语句与程序框图中的___________相对应．条件语句主要有两种，分别是“___________”语句和“___________”语句．（1）IF—THEN—END IF语句计算机在执行如图所示的条件语句时，首先对IF后的条件进行判断，如果(IF)条件符合，那么(THEN)执行语句体，否则执行END IF之后的语句．（2）IF—THEN—ELSE—END IF语句当计算机执行如图所示的条件语句时，首先对IF后的条件进行判断，如果(IF)条件符合，那么(THEN)执行语句体1，否则(ELSE)执行语句体2．学.科网注意：①当判断语句的两个出口只有一个需要执行其他语句时，使用“IF—THEN—END IF”语句；当判断语句的两个出口都需要执行其他语句时，使用“IF—THEN—ELSE—END IF”语句．②“条件”可以是复合条件，此时应用AND加以连接．③END IF是“出口”，是条件语句的结束符号，在书写程序时不要漏掉．6．循环语句循环语句与程序框图中的循环结构相对应．一般程序设计语言中都有__________和__________两种循环语句结构．（1）直到型(UNTIL)语句当计算机遇到UNTIL语句时，先执行一次DO和UNTIL之间的循环体，再对UNTIL后的条件进行判断．如果条件不符合，继续执行循环体；然后再检查上述条件，如果条件仍不符合，再次执行循环体，直到条件符合时为止．这时，计算机将不执行循环体，直接跳到UNTIL语句后，接着执行UNTIL语句之后的语句．如图所示：（2）当型(WHILE)语句当计算机遇到WHILE语句时，先判断条件的真假，如果条件符合，就执行WHILE和WEND之间的循环体；然后再检查上述条件，如果条件仍符合，再次执行循环体，这个过程反复进行，直到某一次条件不符合为止．这时，计算机将不执行循环体，直接跳到WEND语句后，接着执行WEND之后的语句．如图所示：学&科网应用循环语句编写程序时需注意：①循环语句中的循环变量一般要设初始值．②在循环过程中需要有“结束”的语句，程序中最忌“死循环”．【重难点强化】1．输入语句、输出语句、赋值语句（1）输入语句可以给多个变量赋值，其格式为：INPUT “提示内容1，提示内容2，提示内容3，…”；变量1，变量2，变量3，…（2）输出语句具有计算功能．（3）对于赋值语句，①在代数中A＝B与B＝A是等效的两个等式，而在赋值语句中则是两个不同的赋值过程．②“＝”左边必须是变量，右边可以是常量、变量或算式．③一个语句只能给一个变量赋值，不能对几个变量连续赋值，但可以辗转赋值．④可给一个变量多次赋值，但只保留最后一次所赋的值．【例1】下列语句正确的是①输入语句INPUT x ②输入语句INPUT “A，B，C”；a，b，c③输出语句PRINT A+B=C ④赋值语句3=A．A．①③B．②③C．②④D．①②【答案】D【解析】根据输入语句的一般格式知：①②正确；输出语句不具有赋值或执行功能，③错误；④赋值语句应改为A=3，④错误．故选D．学科*网【例2】下列程序语句正确的是A．输出语句PRINT A=4 B．输入语句INPUT x=3C．赋值语句A=A*A+A–3 D．赋值语句55=a【答案】C2．条件语句条件语句可实现算法中的条件结构，当计算机处理按条件判断后的不同情况时，就需要用到条件语句．如求分段函数的函数值等，往往要用到条件语句，有时甚至要用到条件语句的嵌套．在有些较为复杂的算法中，有时需要对按条件执行的某一语句(特别是ELSE后的语句)继续按照另一个要求进行判断，这时可以再利用一个条件语句进行判断，这就形成了条件语句的嵌套．条件语句的嵌套是条件结构嵌套的实现和表达．一般形式如下：IF 条件1 THEN语句体1ELS EIF 条件2 THEN语句体2ELSE语句体3END IFEND IF【例3】如图所示的程序是计算函数y=f（x）函数值的程序，若输入的x的值为4，则输出的y值为A．17 B．3 C．–3 D．–17【答案】C【例4】下列关于条件语句的叙述，正确的是A．条件语句中必须有if、else和end B．条件语句中可以没有endC．条件语句中可以没有else，但必须有end D．条件语句中可以没有else及没end【答案】C【解析】条件语句是处理条件分支逻辑结构的算法语句．表示形式有2种：①IF–THEN–ELSE格式：执行时，先对IF后的条件进行判断，若条件符合，执行语句1，否则执行语句2．②IF–THEN格式：执行时，先对IF后的条件进行判断，若条件符合，执行THEN后的语句，否则结束条件语句，执行其他语句．所以条件语句中可以没有else，但必须有end．故选C．3．循环语句WHILE语句与UNTIL语句两种循环语句的联系与区别：（1）联系：两种语句都可以实现计算机反复执行循环体的目的，只是表达形式不同．一般来讲，WHILE 语句与UNTIL语句可以相互转化．（2）区别：①直到型循环语句是先执行（循环体），后判断（条件），而当型循环语句是先判断（条件），后执行（循环体）．②直到型循环语句是条件不满足时执行循环体，条件满足时结束循环；而当型循环语句是当条件满足时执行循环体，不满足时结束循环．③直到型循环结构至少执行一次循环体，而当型循环结构可能一次也不执行循环体．④在设计程序时，一般说来，这两种语句用哪一种都可以，但在某种限定条件下，有时用WHILE语句较好，有时用UNTIL语句较好．【例5】执行下列程序后，输出的i的值是A．5 B．6 C．10 D．11【答案】D4．混淆WHILE 语句与UNTIL 语句【例6】编写程序计算98246++⋅⋅⋅++的值．【解析】【错解一】程序如下：【错解二】程序如下：【分析】错解一中WEND 应与WHILE 对应；错解二中DO 与LOOP UNTIL 对应，另外，i=i+1应为i=i+2．【正解一】程序如下：【正解二】程序如下：【习题训练】1．对赋值语句的描述正确的是①可以给变量提供初值；②可以将表达式的值赋给变量；③可以给一个变量重复赋值；④不能给同一个变量重复赋值．A．①②③B．①②C．②③④D．①②④2．执行‘PRINT “3+5=”；3+5’的输出结果是A．3+5=3+5 B．3+5=8 C．8=3+5 D．8=83．下列程序的输出结果是A．10 B．15 C．25 D．54．阅读下面的程序，判断程序执行后的结果是A．6，9 B．9，6 C．6，12 D．9，95．在设计求函数2,2()1,2266,2x xf x x xx x⎧>⎪=--<≤⎨⎪-≤-⎩的值的程序中不可能用到的算法语句为A．输入语句B．条件语句C．输出语句D．循环语句6．根据下列算法语句，当输入x为60时，输出y的值为A．25 B．30 C．31D．617．读下面的程序：该程序的作用是A．计算9个数的和B．计算9个数的平均数C．计算10个数的和D．计算10个数的平均数8．以下程序运行后的输出结果为i=1WHILE i<8i=i+2S=2*i+3i=i–1WENDPRINT SENDA．17 B．19 C．21 D．239．下列给出的输入、输出语句正确的是①输入语句：INPUT a；b；c ②输入语句：INPUT x=3③输出语句：PRINT A=4 ④输出语句：PRINT 20，3*2A．①②B．②③C．③④D．④10．执行图程序中，若输出y的值为2，则输入x的值为__________．11．下面是用程序语句表示的一个问题的算法，试根据其画出程序框图．12．下列正确的语句的个数是①输入语句：INPUT a+2 ②赋值语句：x=x–5 ③输出语句：PRINT M=2A．0 B．1 C．2 D．313．阅读下面的程序，然后判断程序执行后的结果是A．5 B．15 C．11 D．14 14．若下面的程序运行之后输出的值为16，那么输入的值x应该是A．3或3-B．5-C．5或3-D．5或5-15．阅读下面的程序：程序运行的结果是A．3B．3 4C．3 4 5D．3 4 5 616．下面为一个求50A．i>50 B．i<50 C．i>=50 D．i<=50 17．如图程序的输出结果为__________181920．下列程序运行的结果是【习题训练答案】17．【答案】（7，10）18．【答案】4，1 19．【答案】7 20．【答案】64。

1.1.2程序框图与算法的基本逻辑结构习题课全面版

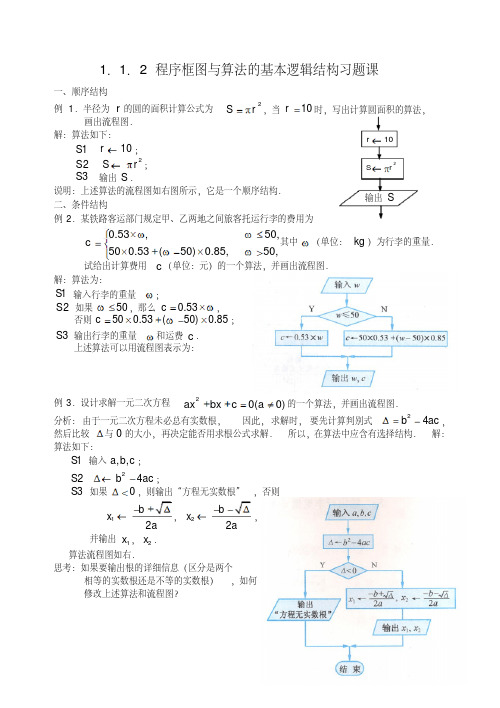
1．1．2 程序框图与算法的基本逻辑结构习题课一、顺序结构例1．半径为r 的圆的面积计算公式为2Sr ，当10r时，写出计算圆面积的算法，画出流程图．解：算法如下：1S 10r ；2S 2Sr ；3S 输出S ．说明：上述算法的流程图如右图所示，它是一个顺序结构．二、条件结构例2．某铁路客运部门规定甲、乙两地之间旅客托运行李的费用为0.53,50,500.53(50)0.85,50,c其中（单位：kg ）为行李的重量．试给出计算费用c （单位：元）的一个算法，并画出流程图．解：算法为：1S 输入行李的重量；2S 如果50，那么0.53c，否则500.53(50)0.85c ；3S 输出行李的重量和运费c ．上述算法可以用流程图表示为：例3．设计求解一元二次方程20(0)axbx c a 的一个算法，并画出流程图．分析：由于一元二次方程未必总有实数根，因此，求解时，要先计算判别式24b ac ，然后比较与0的大小，再决定能否用求根公式求解．所以，在算法中应含有选择结构．解：算法如下：1S 输入,,a b c ；2S 24b ac ；3S 如果0，则输出“方程无实数根”，否则12b x a，22b x a，并输出1x ，2x ．算法流程图如右．思考：如果要输出根的详细信息（区分是两个相等的实数根还是不等的实数根），如何修改上述算法和流程图？输出S2Sr10r例4．设计一个求任意数的绝对值的算法，并画出流程图．解：1S 输入任意实数x ；2S 若0x ，则y x ；否则y x ；3S 输出y ．算法流程图如右．三、循环结构例5．设计一个计算10个数平均数的算法，并画出流程图．分析：由于需要依次输入10个数，并计算它们的和，因此，需要用一个循环结构，并用一个变量存放数的累加和。

在求出10个数的总和后，再除以10，就得到10个数的平均数。

解：1S 0S； {使0S } 2S 1I ； {使1I }3S 输入G ； {输入一个数} 4S S S G ； {求S G ，其和仍放在变量S 中}5S 1I I ； {使I 的值增加1} 6S 如果10I ，转3S ， {如果10I ，退出循环}7S 10S A ； {将平均数10S存放到A 中} 8S 输出A 。

1.1 算法与程序框图习题课

1.执行如图所示的程序框图，输出的S值为（
）
A. 2
B .4
C.8
D. 16
解:根据程序框图可得: 当k=0时，S 1 20 1；当k=1时，S 1 21 2；当k=2时， S 2 22 8；循环结束，当k=3时，不满足k<3，输出的S为8，故选C.
2. 如图所示,程序框图(算法流程图)的输出结果是（ B ） A. 3 B .4 C.5 D. 8
所以输出的是－4.
5.若某程序框图如图所示，则该程序运行后输出的值是__________ 解:根据程序框图可得:
1 第一次运算为 T , i 1； 1
1 第二次运算为 T , i 2； 1 2
1 第三次运算为 T , i 3； 1 2 3 1 第四次运算为 T , i 4； 1 2 3 4 1 第五次运算为 T , i 5； 1 2 3 4 5 1 1 T . 第六次运算不满足条件，输出 1 2 3 4 5 120
4.如果执行如图3所示的程序框图，输入,输入x=－1,n=3,则输出的数 S= .
解:根据程序框图可得: 输入x=－1,n=3,，执行过程如下：
i 2 : S 6 2 1 3; i 1 : S 3(1) 1 1 5;
i 0 : S 5(1) 0 1 4;
解:根据程序框图可得:
2 = 1；当i=1时，S 24 2 2 当i=2时，S = ； 2 ( 1) 3
3 当i=3时，S = ； 2 2 2 3 2 当i=4时，S =4; 3 2 2 2 S = 1；当i=5时， 24 2
解:根据程序框图可得:

1.1 算法与程序框图习题课

结束
3：
P15习题1—1（B）（3）：
开始
输入 x
y 2x
输出 y
结束
（4）：开始
输入 x
y asin x cosx
输出 y
结束
四种图框类型输入、输出框
处理框判断框起止框
算法的三种基本逻辑结构和框图表示
顺序结构
条件分支结构
循环结构
A
Yp N
B
A
B
N
p
Y
A
P14练习A
1：
开始 S=0,i=1
i 10 N
Y
S=S+i i=i+1
输出S 结束
P14练习A
2：
开始 S=0,i=1
N
i 10
Y
S=S+1/i
i=i+1
加班工作时间工资t、p1、p2 计算t=60-40=20
计算p1=40×8=320
计算p2=20×10=200
计算总工资 p3=p1+p2=520 计算净得工资 p=p3×0.9=468
输出p
结束
P15习题1—1（A） 3：
设两位小数为a.bc ，其
中a, b, c 都为整数，且
0 b 9,0 c 9 .
《复习课》
算法与程序框框图表示
顺序结构条件分支结构
循环结构
算法
可以理解为由基本运算及规定的运算顺序所构成的完整的解题步骤，或
者看成按照要求设计好的有限的确切
的计算序列，并且这样的步骤或序列
能够一类问题解决.
自然语言、数学语言、形式语言、框图。
程序框图用一些通用图形符号构成一张图来表示算法，这种图称作程序框图（简称框图）.

必修三算法与程序框图讲义及达标题

算法与程序框图1．算法的含义与程序框图(1)算法：算法是指按照一定规则解决某一类问题的明确和有限的步骤．(2)程序框图：程序框图又称流程图，是一种用程序框、流程线及文字说明来表示算法的图形．2.[做一做]1．在程序框图中，算法的一个步骤到另一个步骤的连接用( ) A ．连接点 B ．判断框C ．流程线 D ．处理框解析：选C.带有方向箭头的流程线将程序框连接起来． 2．(2015·福建福州模拟)执行如图所示的程序框图，若输入x ＝0.1，则输出的m 的值是( )A ．0B ．0.1C ．1D ．－1解析：选A.当x ＝0.1时，m ＝lg 0.1＝－1，因为－1<0，执行m ＝m ＋1＝－1＋1＝0，将0赋给m ，输出的m 的值是0.1．辨明两个易误点(1)易混淆处理框与输入框，处理框主要是赋值、计算，而输入框只是表示一个算法输入的信息． (2)易忽视循环结构中必有条件结构，其作用是控制循环进程，避免进入“死循环”，是循环结构必不可少的一部分．2．识别三种结构的关系顺序结构是每个算法结构都含有的，而对于循环结构有重复性，条件结构具有选择性没有重复性，并且循环结构中必定包含一个条件结构，用于确定何时终止循环体，循环结构和条件结构都含有顺序结构． [做一做] 3．(2014·高考北京卷)执行如图所示的程序框图，输出的S 值为( )A ．1B ．3C ．7D ．15 解析：选C.程序框图运行如下：k ＝0<3，S ＝0＋20＝1，k ＝1<3；S ＝1＋21＝3，k ＝2<3；S ＝3＋22＝7，k ＝3.输出S ＝7. 4．阅读如图所示的程序框图，若输出的y ＝1，则输入的x 的值可能是( )A ．±2和2B ．－2和2C ．± 2D ．2解析：选C.由程序框图可知，当x >2时，log 2x ＝1⇒x ＝2，舍去；当x ≤2时，x 2－1＝1，x ＝±2.考点一顺序结构与条件结构(2013·高考课标全国卷Ⅰ)执行如图所示的程序框图，如果输入的t ∈[－1，3]，则输出的s 属于( )A ．[－3，4]B ．[－5，2]C ．[－4，3]D ．[－2，5][解析] 由程序框图得分段函数s ＝⎩⎪⎨⎪⎧3t ，t <1，4t －t 2，t ≥1.所以当－1≤t <1时，s ＝3t ∈[－3，3)；当1≤t ≤3时，s ＝4t －t 2＝－(t －2)2＋4，所以此时3≤s ≤4.综上函数的值域为[－3，4]，即输出的s 属于[－3，4]．[答案] A若本例的判断框中的条件改为“t ≥1？”，则输出的s 的范围是________．解析：由程序框图得分段函数s ＝⎩⎪⎨⎪⎧3t ，t ≥1，4t －t 2，t <1.所以当1≤t ≤3时，s ＝3t ∈[3，9]，当－1≤t <1时，s ＝4t －t 2＝－(t －2)2＋4，所以此时－5≤s <3.综上函数的值域为[－5，9]，即输出的s 属于[－5，9]．答案：[－5，9][规律方法] 应用顺序结构和条件结构的注意点 (1)顺序结构顺序结构是最简单的算法结构，语句与语句之间、框与框之间是按从上到下的顺序进行的． (2)条件结构利用条件结构解决算法问题时，重点是判断框，判断框内的条件不同，对应的下一图框中的内容和操作要相应地进行变化，故要重点分析判断框内的条件是否满足．1.(2015·辽宁省大连市高三模拟)执行如图所示的程序框图，若输入的x ∈[0，2π]，则输出y的取值范围是( )A ．[0，1]B ．[－1，1]C ．[－22，1] D ．[－1，22] 解析：选C.根据程序框中判断框内的条件，得知y 为sin x ，cos x 中的较大值．在同一个坐标系中画出y ＝sin x ，y ＝cos x 的图象，可知y 的取值范围为[－22，1]．考点二循环结构(高频考点)循环结构是高考命题的一个热点问题，多以选择题、填空题的形式呈现，试题难度不大，多为容易题或中档题．高考对循环结构的考查主要有以下三个命题角度： (1)由框图求输出的结果； (2)完善程序框图；(3)由程序框图及输出结果，求输入的值．(1)(2014·高考重庆卷)执行如图所示的程序框图，若输出k 的值为6，则判断框内可填入的条件是( )A ．s >12B ．s >35C ．s >710D ．s >45(2)(2014·高考辽宁卷)执行如图所示的程序框图，若输入x ＝9，则输出y ＝________.(3)(2014·高考山东卷)执行如图所示的程序框图，若输入的x 的值为1，则输出的n 的值为________．[解析] (1)第一次执行循环：s ＝1×910＝910，k ＝8，s ＝910应满足条件；第二次执行循环：s ＝910×89＝810，k ＝7，s ＝810应满足条件，排除选项D ；第三次执行循环：s ＝810×78＝710，k ＝6，正是输出的结果，故这时程序不再满足条件，结束循环，而选项A 和B 都满足条件，故排除A 和B ，故选C.(2)x ＝9时，y ＝93＋2＝5，|y －x |＝|5－9|＝4<1不成立；x ＝5，y ＝53＋2＝113，|y －x |＝⎪⎪⎪⎪113－5＝43<1不成立；x ＝113，y ＝119＋2＝299，|y －x |＝⎪⎪⎪⎪299－113＝49<1成立，输出y ＝299. (3)由x 2－4x ＋3≤0，解得1≤x ≤3.当x ＝1时，满足1≤x ≤3，所以x ＝1＋1＝2，n ＝0＋1＝1；当x ＝2时，满足1≤x ≤3，所以x ＝2＋1＝3，n ＝1＋1＝2；当x ＝3时，满足1≤x ≤3，所以x ＝3＋1＝4，n ＝2＋1＝3；当x ＝4时，不满足1≤x ≤3，所以输出n ＝3.[答案] (1)C (2)299(3)3[规律方法] 利用循环结构表示算法的步骤：利用循环结构表示算法，第一要先确定是利用当型循环结构，还是利用直到型循环结构；第二要选择准确的表示累计的变量；第三要注意在哪一步开始循环，满足什么条件不再执行循环体．2.(1)(2015·山西省四校联考)如图所示的程序框图的输出结果为( )A.2 0142 015B.12 015C.2 0152 016D.12 016 (2)如图，在算法框图的判断框中，若输出S 的值为120，则判断框内可填入________．(3)(2015·沈阳市教学质量监测)有如图所示的程序框图，则该程序框图表示的算法的功能是( )A ．输出使1×2×4×…×n ≥2 015成立的最小整数nB ．输出使1×2×4×…×n ≥2 015成立的最大整数nC ．输出使1×2×4×…×n ≥2 015成立的最大整数n ＋2D ．输出使1×2×4×…×n ≥2 015成立的最小整数n ＋2解析：(1)本框图是对{1i （i ＋1）}的求和，所以S ＝11×2＋12×3＋…＋12 015×2 016＝1－12 016＝2 0152 016.(2)120＝1×2×3×4×5，所以当i ＝1，2，3，4，5时执行，判断框内可填入“i <6？”．(3)依题意与题中的程序框图可知，该程序框图表示的算法的功能是输出使1×2×4×…×n ≥2 015成立的最小整数n ＋2.答案：(1)C (2)i <6？ (3)D考点三基本算法语句(1)(2013·高考陕西卷)60时，输出y 的值为( )A ．25B ．30C ．31D ．61(2)设计一个计算1×3×5×7×9×11×13的算法，下面给出了程序的一部分，则在①处不能填入的数是( )A ．13B ．13.5C ．14D ．14.5[解析] (1)该语句的分段函数y ＝⎩⎪⎨⎪⎧0.5x ，x ≤50，25＋0.6（x －50），x >50，当x ＝60时，y ＝25＋0.6×(60－50)＝31.∴输出y 的值为31.(2)若填13，当i ＝11＋2＝13时，不满足条件，终止循环，因此得到的是1×3×5×7×9×11的计算结果，故不能填13，但填的数字只要超过13且不超过15均可保证终止循环时，得到的是1×3×5×7×9×11×13的计算结果．[答案] (1)C (2)A[规律方法] 1.输入语句的要求(1)输入语句要求输入的值是具体的常量．(2)提示内容提示用户输入的是什么信息，必须加双引号，提示内容“原原本本”地在计算机屏幕上显示，提示内容与变量之间要用分号隔开． 2．输出语句的要求(1)表达式是算法和程序要求输出的信息．(2)提示内容提示用户要输出的是什么信息，必须加双引号，提示内容和表达式要用分号分开． (3)输出语句可以一次完成输出多个表达式的功能，不同的表达式之间可用“，”分隔；输出语句还可以是“提示内容1”；表达式1，“提示内容2”；表达式2，“提示内容3”；表达式3，…的形式，例如，PRINT “a ，b ，c ”；a ，b ，c ；PRINT “a ”；a ，“b ”；b ，“c ”；c .3.(1)下列程序执行后输出的结果是________．(2)根据如图所示的程序，最后输出的m 的值为________．解析：(1)程序反映出的算法过程为i ＝11⇒S ＝11×1，i ＝10； i ＝10⇒S ＝11×10，i ＝9； i ＝9⇒S ＝11×10×9，i ＝8；i ＝8<9退出循环，执行“PRINT S ”．故S ＝990.(2)由程序可知，m 为a ，b 中的较大值，故最后输出的m 值为3. 答案：(1)990 (2)3交汇创新——算法与不等式的交汇给出一个如图所示的程序框图，若要使输入的x 值与输出的y 值相等，则这样的x 值个数是( )A ．1B ．2C ．3D ．4解析：选C.由程序框图得到如下分段函数：y ＝⎩⎪⎨⎪⎧x 2，x ≤2，2x －3，2<x ≤5，1x ，x >5.当x ≤2时，y ＝x 2＝x ，解得x 1＝0，x 2＝1；当2<x ≤5时，y ＝2x －3＝x ，解得x ＝3；当x >5时，y ＝1x ＝x ，解得x ＝±1(舍去)，故x 可为0，1，3.达标训练题1．(2015·济南市模拟)若某程序框图如图所示，则该程序运行后输出的值是( )A ．2B ．3C ．4D ．5 解析：选C.逐次运行的结果是n ＝3，i ＝2；n ＝4，i ＝3；n ＝2，i ＝4.故输出的值是4. 2．(2015·太原市模拟试题)如图是一算法的程序框图，若输出结果为S ＝720，则在判断框中应填入的条件是( )A ．k ≤6?B ．k ≤7?C ．k ≤8?D ．k ≤9?解析：选B.第一次执行循环，得到S ＝10，k ＝9；第二次执行循环，得到S ＝90，k ＝8，第三次执行循环，得到S ＝720，k ＝7.此时满足条件，故选B. 3．(2014·高考课标全国卷Ⅰ)执行下面的程序框图，若输入的a ，b ，k 分别为1，2，3，则输出的M ＝( )A.203B.165C.72D.158 解析：选D.当n ＝1时，M ＝1＋12＝32，a ＝2，b ＝32；当n ＝2时，M ＝2＋23＝83，a ＝32，b ＝83；当n ＝3时，M ＝32＋38＝158，a ＝83，b ＝158；n ＝4时，终止循环．输出M ＝158.4．某程序框图如图所示，若该程序运行后输出的值是95，则( )A ．a ＝4B ．a ＝5C ．a ＝6D ．a ＝7 解析：选A.该程序框图的功能为计算1＋11×2＋12×3＋…＋1a （a ＋1）＝2－1a ＋1的值，由已知输出的值为95，可知当a ＝4时2－1a ＋1＝95.故选A. 5．已知实数x ∈[2，30]，执行如图所示的程序框图，则输出的x 不小于103的概率为( )A.514B.914C.59D.49 解析：选B.由程序框图可知，经过3次循环跳出，设输入的初始值为x ＝x 0，则输出的x ＝2[2(2x 0＋1)＋1]＋1≥103，∴8x 0≥96，即x 0≥12，故输出的x 不小于103的概率为P ＝30－1230－2＝1828＝914.6．(2015·东北三校联考)已知某算法的程序框图如图所示，若输入x ＝7，y ＝6，则输出的有序数对为( )A．(13，14) B．(12，13) C．(14，13) D．(13，12)解析：选A.执行程序框图得，n＝1，x＝6＋1＝7，y＝8；n＝2，x＝y＋1＝9，y＝10；n＝3，x＝y＋1＝11，y＝12；n＝4，x＝y＋1＝13，y＝14；n＝5，循环结束，输出(13，14)，故选A.7．(2015·合肥二检)执行如图所示的程序框图，输出的所有值之和是________．解析：列举几项，发现输出的x开始为1，每次递增2，去掉x是3的倍数的那些数，最后可得输出的所有值之和为1＋5＋7＋11＋13＋17＋19＝73.答案：738．图1是某高三学生进入高中三年来的数学考试成绩茎叶图，第1次到第14次的考试成绩依次记为A1，A2，…，A14.图2是统计茎叶图中成绩在一定范围内考试次数的一个程序框图．那么输出的结果是________．解析：从程序框图可知，该图是统计成绩大于或等于90分的考试次数．从茎叶图可知输出的结果为10.答案：109．(2015·贵州省六校第一次联考)如图，x1，x2，x3为某次考试三个评阅人对同一道题的独立评分，p为该题的最终得分，当x1＝6，x2＝9，p＝9.5时，x3等于()A．10 B．9 C．8 D．7解析：选A.x1＝6，x2＝9，|x1－x2|＝3，|x3－6|<|x3－9|不成立，取x1＝x3⇒x3＋9＝9.5×2⇒x3＝10. 10．(2015·成都模拟)已知某算法的程序框图如图所示，若将输出的(x，y)值依次记为(x1，y1)，(x2，y2)，…，(x n，y n)，…(1)若程序运行中输出的一个数组是(9，t)，求t的值；(2)程序结束时，共输出(x，y)的组数为多少？解：(1)由程序框图知，当x＝1时，y＝0，当x＝3时，y＝－2；当x＝9时，y＝－4，所以t＝－4.(2)当n＝1时，输出一对，当n＝3时，又输出一对，…，当n＝2015时，输出最后一对，共输出(x，y)的组数为1008.。

程序框图(流程图)习题课(含参考答案)

程序框图习题课参考答案一、会读流程图1.如图（1）为循环体中的__当型__循环，它换成另外一种__直到型__循环的框图.2.写出如图(2)的算法功能__求乘积为624的相邻两个偶数__.3.指出程序框图的运算结果: 当箭头指向①处时,输出sum=__5_；指向②处时,输出sum=__15__.4.观察所给程序框图,写出它所表示的函数.5.如图所示是某一算法的程序框图，根据该框图指出这一算法的功能. 求和201614121++++= S 二、会写流程图（一）、条件结构练习1. 设计一个求任意数的绝对值的算法,并画出程序框图.⎪⎩⎪⎨⎧≤<≤<≤=)100005000(,50)5000100(,01.0)100(,1x x x xy2. 画出一个求3个实数中最小数的程序框图.3. 闰年是指年份能被4整除但不能被100整除,或者能被400整除的年份.编写一个程序框图,判断输入的年份是否为闰年.（二）循环结构练习关注易错点：①关注变量的初始值，理解两种变量的意义：计数变量（循环变量、步进变量）和累加（累乘）变量。

②关注“S=S+i ”和“i=i+1”先后顺序的影响（初始值的影响、循环次数的影响、输出结果的影响）。

③判断条件是否具备“=”。

④当型与直到型分别是什么时候继续循环，什么时候结束循环。

怎样改为当型循环？误右侧程序框图是否有错的最小正整数求满足?,1021.16222n n >+++左图1应该输出1-i ，左图2应该初始化为1=S2. 已知30021≤+++i ，画出求解i 的最大值的过程的程序框图如右图. 问题：输出处横线应该填__2-i _.变1：若改为sum<300, 输出处横线应该填__1-i _.变2：若改变i=i+1与sum=sum+i 的顺序，输出处横线应该填__1-i _.（初始化要改为1=sum ）变3：在变2的条件下，要输出i ，判断框内应该填_ sum<300_.3. 设计一个求1+2+4+7+…+46的算法,并画出相应的程序框图.见左侧（变差数列的设计）4. 课本P20页B 组第2题.（略）。

课时作业6：13.4 算法与程序框图

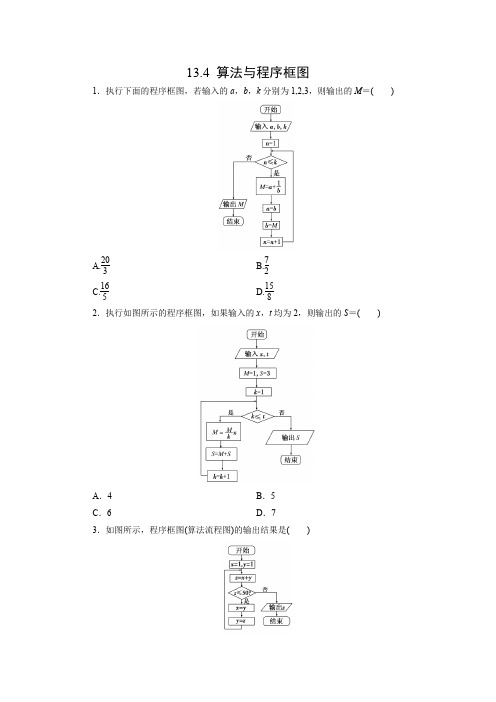
13.4 算法与程序框图1．执行下面的程序框图，若输入的a ，b ，k 分别为1,2,3，则输出的M ＝( )A.203B.72C.165D.1582．执行如图所示的程序框图，如果输入的x ，t 均为2，则输出的S ＝( )A ．4B ．5C ．6D ．73．如图所示，程序框图(算法流程图)的输出结果是( )A．34 B．55C．78 D．894．阅读如图所示的程序框图，运行相应的程序，输出的n的值为()A．1 B．2C．3 D．45．执行如图所示的程序框图，输出的S值为()A．1 B．3C．7 D．156．执行如图所示的程序框图，若输入的x的值为1，则输出的n的值为________．7．如图是一个算法流程图，则输出的n的值是________．8．若某程序框图如图所示，当输入50时，则该程序运行后输出的结果是________．9．执行如图所示的程序框图，若输入n＝3 ，则输出T＝________.10．阅读如图所示的框图，运行相应的程序，输出S的值为________．11.阅读如图所示的程序框图，运行相应的程序，若输入n的值为9，则输出S的值为________ .12．下图是一个算法的流程图，则输出的n的值是________．答案1．【解析】选D 第一次循环：M ＝32，a ＝2，b ＝32，n ＝2；第二次循环：M ＝83，a ＝32，b ＝83，n ＝3；第三次循环：M ＝158，a ＝83，b ＝158，n ＝4，则输出M ＝158，选D. 2．【解析】选D k ＝1≤2，执行第一次循环，M ＝11×2＝2，S ＝2＋3＝5，k ＝1＋1＝2；k＝2≤2，执行第二次循环，M ＝22×2＝2，S ＝2＋5＝7，k ＝2＋1＝3；k ＝3>2，终止循环，输出S ＝7.故选D.3．【解析】选B 执行该程序框图(算法流程图)可得x ＝1，y ＝1，z ＝2；x ＝1，y ＝2，z ＝3；x ＝2，y ＝3，z ＝5；x ＝3，y ＝5，z ＝8；x ＝5，y ＝8，z ＝13；x ＝8，y ＝13，z ＝21；x ＝13，y ＝21，z ＝34；x ＝21，y ＝34，z ＝55，跳出循环．4．【解析】选B 当n ＝1时，21>12成立，当n ＝2时，22>22不成立，所以输出n ＝2，故选B.5．【解析】选C 列表如下：故输出的S 值是7. 6．【解析】12－4×1＋3≤0，x ＝2，n ＝1；22－4×2＋3≤0，x ＝3，n ＝2；32－4×3＋3≤0，x ＝4，n ＝3,42－4×4＋3＞0，跳出循环，此时输出n 的值，故输出的n 的值为3.【答案】3 7．【解析】该流程图共运行5次，各次2n 的值分别是2,4,8,16,32，所以输出的n 的值是5.【答案】5 8．【解析】S ＝0，i ＝1；S ＝1，i ＝2；S ＝4，i ＝3；S ＝11，i ＝4；S ＝26，i ＝5；S ＝57，i ＝6，此时S >n ，所以输出的结果为6.【答案】69．【解析】输入n＝3，则i＝0，S＝0，T＝0，i≤n成立，故i＝1，S＝0＋1＝1，T＝0＋1＝1，此时i＝1≤n成立，故i＝2，S＝1＋2＝3，T＝1＋3＝4，此时i＝2≤n成立，故i＝3，S ＝3＋3＝6，T＝4＋6＝10，此时i＝3≤n成立，故i＝4，S＝6＋4＝10，T＝10＋10＝20，此时i＝4≤n不成立，故输出T＝20.【答案】2010．【解析】S＝0，n＝3，第1次运行，S＝0＋(－2)3＝－8，n＝2，不满足条件；第2次运行，S＝－8＋(－2)2＝－8＋4＝－4，n＝1，满足条件，跳出循环，输出S的值为－4.【答案】－411.【解析】S＝(21＋22＋…＋29)＋(1＋2＋…＋9)＝210－2＋45＝1 024＋43＝1 067.【答案】1 06712．【解析】本题考查算法的基本概念及流程图的运算法则，意在考查学生的逻辑推理能力及对循环结构的理解．算法流程图执行过程如下：n＝1，a＝2，a<20；n＝2，a＝8，a<20; n＝3，a＝26，a>20，输出n＝3.【答案】3。

算法与程序框图例题

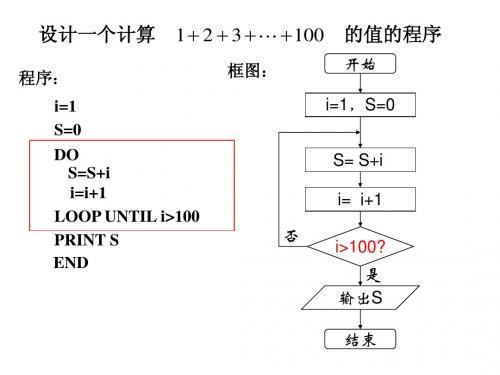
y=x
y=1
y=0
输出 y
结束
利用循环结构寻找特定的数
【例】写出求1＋2＋3＋…＋n＞20 000的最小正整数n的算法，并画出相应的算法框图． [思路探索] 解答本题可利用累加求和的循环结构解决，或应用公式采用循环结构解决．
解法一算法为：第一步，令n＝0， S＝0. 第二步，n＝n＋1. 第三步，S＝S＋n. 第四步，如果S＞20 000，则输出n，否则，执行第二步．该算法的框图如图所示：
设计一个计算 1 2 3
程序：
i 100 的值的程序
开始
i=1，S=0 否
框图：
i=1 S=0 WHILE i<100 S=S+i i=i+1 WEND PRINT i-2 END
s<100? 是 S= S+i
i= i+1
输出i-2
结束
开始
i=1，S=0 否
框图：
i=1 S=0 WHILE i<=100 S=S+i i=i+1 WEND PRINT S END
i<=100? 是 S= S+i
i= i+1
输出S
结束
例.画程序框图, 对于输入的x值, 输出相应的y值.
开始
输入x
x<0? 否 0≤x<1? 否是
程序框图
是
0( x 0) y 1(0 x 1) x ( x 1)
设计一个计算程序：1 Nhomakorabea 3
框图：
100
的值的程序
开始 i=1，S=0 S= S+i i= i+1

算法与程序框图习题附答案

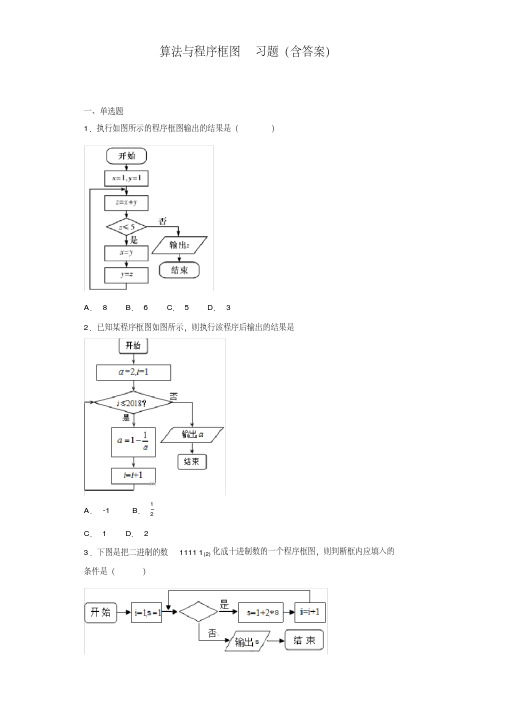
试写出给定自变量
x + 1, x < 0,
x,求函数值 y 的算法 .
x2 2x x 2
27．求函数 y={
的值的程序框图如图所示 .
2x 2
(1) 指出程序框图中的错误，并写出算法； (2) 重新绘制解决该问题的程序框图，并回答下面提出的问题． ① 要使输出的值为正数，输入的 x 的值应满足什么条件？ ② 要使输出的值为 8，输入的 x 值应是多少？ ③ 要使输出的 y 值最小，输入的 x 值应是多少？
(2) 写出 A、B 两点经此程序框图执行运算后的对应点方向上的投影 . 21 ．按右图所示的程序框图操作：
A0，B0 的坐标，并求出 OA0 在 OB0
( Ⅰ ) 写出输出的数所组成的数集．
( Ⅱ ) 如何变更 A 框内的赋值语句，使得根据这个程序框图所输出的数恰好是数列
2n 的
前 7 项？ ( Ⅲ ) 如何变更 B 框内的赋值语句，使得根据这个程序框图所输出的数恰好是数列
A． 18 B． 41 C． 88 D． 183 9．执行图 1 所示的程序框图，则 S 的值为，，
图1
A． 16 C． 64
B． 32 D． 128
二、填空题 10 ．我国南北朝时期的数学家张丘建是世界数学史上解决不定方程的第一人，他在《张
丘建算经》中给出一个解不定方程的百鸡问题，问题如下：鸡翁一，值钱五，鸡母一，
循环次数； (5) 要注意各个框的顺序 ,（ 6）在给出程序框图求解输出结果的试题中只要按照
程序框图规定的运算方法逐次计算，直到达到输出条件即可
.
6． D 【解析】【分析】
根据程序框图进行运行，得到不满足条件的取值，即可得到结论．【详解】

算法与程序框图习题课

高中数学《算法---程序框图》典型例题练习(含答案)

《算法与程序框图》习题课片段与点评

12.1 算法与程序框图 练出高分(含答案解析)

数学算法和程序框图试题答案及解析

北师大版高中数学必修3课后习题答案

12算法与程序框图习题课精品PPT课件

课时作业13：§13.4 算法与程序框图

算法语句与程序框图(高三复习、教案、习题含答案)

1.1.2程序框图与算法的基本逻辑结构习题课全面版

1.1 算法与程序框图习题课

1.1 算法与程序框图习题课

必修三 算法与程序框图 讲义及达标题

最新人教版高中数学必修3第一章《算法与程序框图》课后训练(第2课时)

程序框图(流程图)习题课(含参考答案)

课时作业6：13.4 算法与程序框图

算法与程序框图例题

算法与程序框图习题附答案

12.1 算法与程序框图练出高分(含答案解析)

必修三算法与程序框图讲义及达标题