2.25阴影部分面积及周长的专题(较难)
阴影部分求面积及周长(含答案)

【史上最全小学求暗影部分面积专题—含答案】小学及小升初温习专题-圆与求暗影部分面积----完全答案在最后面目的:经由过程专题温习,增强学生对于图形面积盘算的灵巧应用.并加深对面积和周长概念的懂得和区分.面积求解大致分为以下几类:c重难点:不雅察图形的特色,依据图形特色选择适合的办法求解图形的面积.能灵巧应用所学过的根本的平面图形的面积求暗影部分的面积.例2.正方形面积是7平方厘米,求暗影部分的面积.例1.求暗影部分的面积.(单位:厘米)(单位:厘米)例3.求图中暗影部分的面积.(单位:厘例4.求暗影部分的面积.(单位:厘米)米)例5.求暗影部分的面积.(单位:厘米) 例6.如图:已知小圆半径为2厘米,大圆半径是小圆的3倍,问:空白部分甲比乙的面积多若干厘米?例7.求暗影部分的面积.(单位:厘米)例8.求暗影部分的面积.(单位:厘米)例9.求暗影部分的面积.(单位:厘米)例10.求暗影部分的面积.(单位:厘米)例11.求暗影部分的面积.(单位:厘米)例12.求暗影部分的面积.(单位:厘米)例13.求暗影部分的面积.(单位:厘米)例14.求暗影部分的面积.(单位:厘米)例15.已知直角三角形面积是12平方厘米,求暗影部分的面积.例16.求暗影部分的面积.(单位:厘米)例17.图中圆的半径为5厘米,求暗影部分的面积.(单位:厘米)例18.如图,在边长为6厘米的等边三角形中挖去三个同样的扇形,求暗影部分的周长.例19.正方形边长为2厘米,求暗影部分的面积.例20.如图,正方形ABCD的面积是36平方厘米,求暗影部分的面积.例21.图中四个圆的半径都是1厘米,求暗影部分的面积.例22.如图,正方形边长为8厘米,求暗影部分的面积.例23.图中的4个圆的圆心是正方形的4个极点,,它们的公共点是该正方形的中间,假如每个圆的半径都是1厘米,那么暗影部分的面积是若干?例24.如图,有8个半径为1厘米的小圆,用他们的圆周的一部分连成一个花瓣图形,图中的黑点是这些圆的圆心.假如圆周π率取3.1416,那么花瓣图形的的面积是若干平方厘米?例25.如图,四个扇形的半径相等,求暗影部分的面积.(单位:厘米)例26.如图,等腰直角三角形ABC和四分之一圆DEB,AB=5厘米,BE=2厘米,求图中暗影部分的面积.例27.如图,正方形ABCD的对角线AC=2厘米,扇形ACB是以AC为直径的半圆,扇形DAC是以D为圆心,AD为半径的圆的一部分,求暗影部分的面积.例28.求暗影部分的面积.(单位:厘米)例29.图中直角三角形ABC 的直角三角形的直角边AB=4厘米,BC=6厘米,扇形BCD地点圆是以B为圆心,半径为BC的圆,∠CBD=,问:暗影部分甲比乙面积小若干?例30.如图,三角形ABC是直角三角形,暗影部分甲比暗影部分乙面积大28平方厘米,AB=40厘米.求BC的长度.例31.如图是一个正方形和半圆所构成的图形,个中P 为半圆周的中点,Q为正方形一边上的中点,求暗影部分的面积.例32.如图,大正方形的边长为6厘米,小正方形的边长为4厘米.求暗影部分的面积.例33.求暗影部分的面积.(单位:厘米)例34.求暗影部分的面积.(单位:厘米)例35.如图,三角形OAB是等腰三角形,OBC是扇形,OB=5厘米,求暗影部分的面积.触类旁通★巩固演习【专1】下图中,大小正方形的边长分离是9厘米和5厘米,求暗影部分的面积.【专1-1】.右图中,大小正方形的边长分离是12厘米和10厘米.求暗影部分面积.【专1-2】.求右图中暗影部分图形的面积及周长.【专2】已知右图暗影部分三角形的面积是5平方米,求圆的面积.【专2-1】已知右图中,圆的直径是2厘米,求暗影部分的面积.【专2-2】求右图中暗影部分图形的面积及周长.【专2-3】求下图中暗影部分的面积.(单位:厘米)【专3】求下图中暗影部分的面积.【专3-1】求右图中暗影部分的面积.【专3-2】求右图中暗影部分的面积.【专3-3】求下图中暗影部分的面积.完全答案例1解:这是最根本的办法:圆面积减去等腰直角三角形的面积,×-2×1=1.14(平方厘米)例2解:这也是一种最根本的办法用正方形的面积减去圆的面积.设圆的半径为 r,因为正方形的面积为7平方厘米,所以=7,所以暗影部分的面积为:7-=7-例3解:最根本的办法之一.用四个圆构成一个圆,用正方形的面积减去圆的面积,所以暗影部分的面积:2×2-π=0.86平方厘米.例4解:同上,正方形面积减去圆面积, 16-π()=16-4π例5解:这是一个用最经常应用的办法解最罕有的题,为便利起见,我们把暗影部分的每一个小部分称为“叶形”,是用两个圆减去一个正方形,π(别的:此题还可以算作是1题中暗影部分的8倍.例6解:两个空白部分面积之差就是两圆面积之差(全加上暗影部分)π-π()=100.48平方厘米(注:这和两个圆是否订交.交的情形若何无关)例7解:正方形面积可用(对角线长×对角线长÷2,求)所以暗影面积为:π÷4-12.5=7.125平方厘米(注:以上几个题都可以直接用图形的差来求,无需割.补.增.减变形)例8解:右面正方形上部暗影部分的面积,等于左面正方形下部空白部分面积,割补今后为圆,所以暗影部分面积为:π(例9解:把右面的正方形平移至左边的正方形部分,则暗影部分合成一个长方形,所以暗影部分面积为:2×3=6平方厘米例10解:同上,平移阁下两部分至中央部分,则合成一个长方形,所以暗影部分面积为2×1=2平方厘米(注: 8.9.10三题是简略割.补或平移)例11解:这种图形称为环形,可以用两个齐心圆的面积差或差的一部分来求.(π -π)×=例12.解:三个部分拼成一个半圆面积.π(例13解: 连对角线后将"叶形"剪开移到右上面的空白部分,凑成正方形的一半.所以暗影部分面积为:8×8÷2=32平方厘米例14解:梯形面积减去圆面积,(4+10)×4-π=28-4π=15.44平方厘米 . 例15.剖析: 此题比上面的题有必定难度,这是"叶形"的一个半.解: 设三角形的直角边长为r,则=12,=6圆面积为:π÷2=3π.圆内三角形的面积为12÷2=6,暗影部分面积为:(3π-6)×例16解:[π+π-π] =例17解:上面的暗影部分以AB为轴翻转后,全部暗影部分成为梯形减去直角三角形,或两个小直角三角形AED.BCD面积和.例18解:暗影部分的周长为三个扇形弧,拼在一路为一个半圆弧,例19解:右半部分上面部分逆时针,下面部分顺时针扭转到左半部分,构成一个矩形.所以面积为:1×2=2平方厘米例20解:设小圆半径为r,4=36, r=3,大圆半径为R,=2=18,将暗影部分经由过程迁移转变移在一路构成半个圆环,所以面积为:π(-例21.解:把中央部分分成四等分,分离放在上面圆的四个角上,补成一个正方形,边长为2厘米,所以面积为:2×2=4平方厘米例22解法一: 将左边上面一块移至右边上面,补上空白,则左边为一三角形,右边一个半圆.暗影部分为一个三角形和一个半圆面积之和. π(解法二: 补上两个空白为一个完全的圆.所以暗影部分面积为一个圆减去一个叶形,叶形面积为:π()÷2-4×4=8π-16所以暗影部分的面积为:π(例23解:面积为4个圆减去8个叶形,叶形面积为:π-1×1=π-1所以暗影部分的面积为:4π-8(π-1)=8平方厘米例24剖析:衔接角上四个小圆的圆心构成一个正方形,各个小圆被切去个圆,这四个部分正好合成3个整圆,而正方形中的空白部分合成两个小圆.解:暗影部分为大正方形面积与一个小圆面积之和.例25剖析:四个空白部分可以拼成一个以2为半径的圆.所以暗影部分的面积为梯形面积减去圆的面积,4×(4+7)÷2-π例26解: 将三角形CEB以B为圆心,逆时针迁移转变90度,到三角形ABD地位,暗影部分成为三角形ACB面积减去个小圆面积,为: 5×5÷2-π例27解: 因为2==4,所以=2以AC为直径的圆面积减去三角形ABC面积加上弓形AC面积,π-2×2÷4+[π÷4-2]=π-1+(π-1)例28解法一:设AC中点为B,暗影面积为三角形ABD面积加弓形BD的面积,弓形面积为:[π解法二:右上面空白部分为小正方形面积减去小圆面积,其值为:5×5-π=25-π暗影面积为三角形ADC减去空白部分面积,为:10×5÷2-(25-π)=例29.解: 甲.乙两个部分同补上空白部分的三角形后合成一个扇形BCD,一个成为三角形ABC,此两部分差即为:π×-例30.解:两部分同补上空白部分后为直角三角形ABC,一个为半圆,设BC长为X,则40X÷2-π÷2=28例31.解:连PD.PC转换为两个三角形和两个弓形,两三角形面积为:△APD面积+△QPC面积=两弓形PC.PD面积为:π-5×5所以暗影部分的面积为:37.5+π-25=51.75平方厘例32解:三角形DCE的面积为:×4×10=20平方厘米梯形ABCD的面积为:(4+6)×4=20平方厘米从而知道它们面积相等,则三角形ADF面积等于三角形EBF面积,暗影部分可补成圆ABE的面积,其面积为:π米例33.解:用大圆的面积减去长方形面积再加上一个以2为半径的圆ABE面积,为(π+π)-6=×13π-6例34解:两个弓形面积为:π-3×4÷2=π-6暗影部分为两个半圆面积减去两个弓形面积,成果为π+π-(π-6)=π(4+-)+6=6平方厘米例35解:将两个同样的图形拼在一路成为圆减等腰直角三角形[π÷4-×5×5]÷2=(π-触类旁通★巩固演习-answer【专1】(5+9)×5÷2+9×9÷2-(5+9)×5÷2=40.5(平方厘米)【专1-1】(10+12)×10÷×12×12÷4-(10+12)×10÷2=113.04(平方厘米)【专1-2】面积:6×(6÷×(6÷2)×(6÷2)÷2=3.87(平方厘米)×6÷2+6+(6÷2)×2=21.42(厘米)【专2】2r×r÷2=5 即r×r=5×5=15.7(平方厘米)【专2-1】×(2÷2)×(2÷2)-2×2÷2=1.14(平方厘米)【专2-2】×6×6÷×(6÷2)×(6÷2)÷2=14.13 (平方厘米)周长:2××6÷×6÷2+6=24.84 (厘米)【专2-3】(6+4)×4÷2-(4××4×4÷4)=16.56(平方厘米)【专3】6×3-3×3÷2=13.5(平方厘米)【专3-1】8×(8÷2)÷2=16(平方厘米)【专3-2】×4×4÷4-4×4÷2=4.56(平方厘米)【专3-3】5×5÷2=12.5(平方厘米)。
阴影部分求面积及周长(含答案)

【史上最全小学求阴影部分面积专题—含答案】小学及小升初复习专题-圆与求阴影部分面积----完整答案在最后面目标:通过专题复习,加强学生对于图形面积计算的灵活运用。
并加深对面积和周长概念的理解和区分。
面积求解大致分为以下几类:c重难点:观察图形的特点,根据图形特点选择合适的方法求解图形的面积。
能灵活运用所学过的基本的平面图形的面积求阴影部分的面积。
例1.求阴影部分的面积。
(单位:厘米)例2.正方形面积是7平方厘米,求阴影部分的面积。
(单位:厘米)例3.求图中阴影部分的面积。
(单位:厘米) 例4.求阴影部分的面积。
(单位:厘米)例5.求阴影部分的面积。
(单位:厘米) 例6.如图:已知小圆半径为2厘米,大圆半径是小圆的3倍,问:空白部分甲比乙的面积多多少厘米?例7.求阴影部分的面积。
(单位:厘米)例8.求阴影部分的面积。
(单位:厘米)例9.求阴影部分的面积。
(单位:厘米)例10.求阴影部分的面积。
(单位:厘米)例11.求阴影部分的面积。
(单位:厘米)例12.求阴影部分的面积。
(单位:厘米)例13.求阴影部分的面积。
(单位:厘米)例14.求阴影部分的面积。
(单位:厘米)例15.已知直角三角形面积是12平方厘米,求阴影部分的面积。
例16.求阴影部分的面积。
(单位:厘米)例17.图中圆的半径为5厘米,求阴影部分的面积。
(单位:厘米) 例18.如图,在边长为6厘米的等边三角形中挖去三个同样的扇形,求阴影部分的周长。
例19.正方形边长为2厘米,求阴影部分的面积。
例20.如图,正方形ABCD的面积是36平方厘米,求阴影部分的面积。
例21.图中四个圆的半径都是1厘米,求阴影部分的面积。
例22.如图,正方形边长为8厘米,求阴影部分的面积。
例23.图中的4个圆的圆心是正方形的4个顶点,,它们的公共点是该正方形的中心,如果每个圆的半径都是1厘米,那么阴影部分的面积是多少?例24.如图,有8个半径为1厘米的小圆,用他们的圆周的一部分连成一个花瓣图形,图中的黑点是这些圆的圆心。
阴影部分求面积及周长(含答案)
*创作编号:BG7531400019813488897SX*创作者:别如克*【史上最全小学求阴影部分面积专题—含答案】小学及小升初复习专题-圆与求阴影部分面积----完整答案在最后面目标:通过专题复习,加强学生对于图形面积计算的灵活运用。
并加深对面积和周长概念的理解和区分。
面积求解大致分为以下几类:c重难点:观察图形的特点,根据图形特点选择合适的方法求解图形的面积。
能灵活运用所学过的基本的平面图形的面积求阴影部分的面积。
例1.求阴影部分的面积。
(单位:厘米) 例2.正方形面积是7平方厘米,求阴影部分的面积。
(单位:厘米)例3.求图中阴影部分的面积。
(单位:厘米)例4.求阴影部分的面积。
(单位:厘米)例5.求阴影部分的面积。
(单位:厘米)例6.如图:已知小圆半径为2厘米,大圆半径是小圆的3倍,问:空白部分甲比乙的面积多多少厘米?例7.求阴影部分的面积。
(单位:厘米)例8.求阴影部分的面积。
(单位:厘米)例9.求阴影部分的面积。
(单位:厘米)例10.求阴影部分的面积。
(单位:厘米)例11.求阴影部分的面积。
(单位:厘米)作编号:BG7531400019813488897SX 作者:别如克*例12.求阴影部分的面积。
(单位:厘米)例13.求阴影部分的面积。
(单位:厘米)例14.求阴影部分的面积。
(单位:厘米)例15.已知直角三角形面积是12平方厘米,求阴影部分的面积。
例16.求阴影部分的面积。
(单位:厘米)例17.图中圆的半径为5厘米,求阴影部分的面积。
(单位:厘米) 例18.如图,在边长为6厘米的等边三角形中挖去三个同样的扇形,求阴影部分的周长。
例19.正方形边长为2厘米,求阴影部分的面积。
例20.如图,正方形ABCD的面积是36平方厘米,求阴影部分的面积。
例21.图中四个圆的半径都是1厘米,求阴影部分的面积。
例22.如图,正方形边长为8厘米,求阴影部分的面积。
例23.图中的4个圆的圆心是正方形的4个顶点,,它们的公共点是该正方形的中心,如果每个圆的半径都是1厘米,那么阴影部分的面积是多少?例24.如图,有8个半径为1厘米的小圆,用他们的圆周的一部分连成一个花瓣图形,图中的黑点是这些圆的圆心。
阴影部分求面积及周长(含答案)

【史上最全小学求阴影部分面积专题—含答案】小学及小升初复习专题-圆与求阴影部分面积----完整答案在最后面目标:通过专题复习,加强学生对于图形面积计算的灵活运用。
并加深对面积和周长概念的理解和区分。
面积求解大致分为以下几类:c重难点:观察图形的特点,根据图形特点选择合适的方法求解图形的面积。
能灵活运用所学过的基本的平面图形的面积求阴影部分的面积。
例1.求阴影部分的面积。
(单位:厘米)例2.正方形面积是7平方厘米,求阴影部分的面积。
(单位:厘米)例3.求图中阴影部分的面积。
(单位:厘米) 例4.求阴影部分的面积。
(单位:厘米)例5.求阴影部分的面积。
(单位:厘米) 例6.如图:已知小圆半径为2厘米,大圆半径是小圆的3倍,问:空白部分甲比乙的面积多多少厘米?例7.求阴影部分的面积。
(单位:厘米)例8.求阴影部分的面积。
(单位:厘米)例9.求阴影部分的面积。
(单位:厘米)例10.求阴影部分的面积。
(单位:厘米)例11.求阴影部分的面积。
(单位:厘米)例12.求阴影部分的面积。
(单位:厘米)例13.求阴影部分的面积。
(单位:厘米)例14.求阴影部分的面积。
(单位:厘米)例15.已知直角三角形面积是12平方厘米,求阴影部分的面积。
例16.求阴影部分的面积。
(单位:厘米)例17.图中圆的半径为5厘米,求阴影部分的面积。
(单位:厘米) 例18.如图,在边长为6厘米的等边三角形中挖去三个同样的扇形,求阴影部分的周长。
例19.正方形边长为2厘米,求阴影部分的面积。
例20.如图,正方形ABCD的面积是36平方厘米,求阴影部分的面积。
例21.图中四个圆的半径都是1厘米,求阴影部分的面积。
例22.如图,正方形边长为8厘米,求阴影部分的面积。
例23.图中的4个圆的圆心是正方形的4个顶点,,它们的公共点是该正方形的中心,如果每个圆的半径都是1厘米,那么阴影部分的面积是多少?例24.如图,有8个半径为1厘米的小圆,用他们的圆周的一部分连成一个花瓣图形,图中的黑点是这些圆的圆心。
椭圆的周长与面积求阴影部分较难

椭圆的周长与面积求阴影部分较难
椭圆是一个具有特殊形状的几何图形,其周长和面积是椭圆的
基本属性。
本文将讨论如何求解椭圆的周长和面积,并且针对其中
的一个难点——求解椭圆阴影部分的周长和面积,提供一些简单的
策略。
椭圆周长的求解
椭圆的周长是指椭圆上所有点到椭圆中心的距离之和。
其求解
公式为:
$$C = \pi(a+b)$$
其中,$a$ 是椭圆的长半轴长度,$b$ 是椭圆的短半轴长度,$\pi$ 是圆周率。
椭圆面积的求解
椭圆的面积是指椭圆内部所包围的区域的大小。
其求解公式为:
$$A = \pi ab$$
其中,$a$ 是椭圆的长半轴长度,$b$ 是椭圆的短半轴长度,$\pi$ 是圆周率。
求解椭圆阴影部分的周长和面积
要求解椭圆阴影部分的周长和面积,我们可以采用以下简单的策略:
1. 首先,确定椭圆的长半轴和短半轴长度以及阴影部分所在的位置。
2. 根据给定的条件,计算出阴影部分所占的角度。
若阴影部分不是一个完整的扇形,则需要计算出相应的角度范围。
3. 根据所得到的角度范围,可以利用椭圆周长和面积的求解公式,计算出阴影部分的周长和面积。
请注意,在实际操作中,可能需要将角度转换为弧度进行计算。
还要确保所用的椭圆周长和面积公式适用于给定的椭圆参数。
以上是求解椭圆的周长和面积以及椭圆阴影部分的周长和面积
的简单策略。
根据具体问题的不同,可能需要进一步的数学推导和
计算。
希望这些信息能对你的研究和研究有所帮助。
参考文献:。
六年级正确解答阴影部分(不规则 )的面积与周长研讨问题

为了消除这种迁移带来的负面影响,我们加强了对比, 引导学生观察、对比:
发现:割补后,面积不变,周长变了。
在求阴影部分的周长时,不能随意的使 用转化的方法,而是应该根据周长的概 念,明确一个图形的周长是一个封闭的 图形,是一个图形一周的长度,会用手 比划,知道是从哪到哪。
4.练习对比--搜集题型,方法指导。 (1)齐出。求阴影部分的面积和周长同时出现。 (2)比划。用手比划面积是指哪部分,周长是从哪到 哪。 (3)列关系式。如
2.求阴影部分的周长和面积,发现了什么?
2cm
最后,欢迎大家 提出问题, 共同研讨
一、我们的问题: 如何引导学生正确解答阴影部分 (不规则 )的面积与周长?
二、提出的原因分析: 1.教材方面,小学阶段,对平面图形的面 积、周长的知识都已学完,这部分内容 可以看成是对这些知识的综合运用,也 为中学学习垫定基础。
2.学生出现错误,特别是求周长错误率 高,错误的类型有: (1)割补后计算周长 (2)周长与面积混淆做 (3)数据使用错误
三、出错原因:
1.面积、周长概念不清晰,模糊,没 有真正理解概念,或混淆。 2.求阴影部分的周长时,受到求面积 时割补的负迁移的影响。 3.图形间的关系理不清,不清楚给出 的数据如何使用
四、对策:
1. 概念对比----加强辨析。 2.关系对比--加强沟通。 3.方法对比---消除负迁移。
4.练习对比--搜集题型,方法指导。
四、对策: 1. 概念对比----加强辨析。 这个问题的出现,提醒了大家,在教 学面积、周长概念时要多对比。特别 是不规则图形的周长,要学生能够熟 练地用手指出,这样为后面的学习扫 除障碍。
2.关系对比--加强沟通
是以长方形的面积 为基础,将平行四边形利用割补法,转化 成长方形后求平行四边形面积的,同样三 角形、梯形、圆的面积求法也都利用了转 化的思想,给学生的印象较深刻,知识的 学习懂的迁移是好事,但有时却会产生负 迁移,这就给学习带来了不利,割补法对 面积来说,原、新图形面积不变,而周长 经过割补后发生了变化,在求阴影部分周 长时,基本是不可取的。
阴影部分求面积及周长(含答案)

阴影部分求面积及周长(含答案)LT【史上最全小学求阴影部分面积专题—含答案】小学及小升初复习专题-圆与求阴影部分面积----完整答案在最后面目标:通过专题复习,加强学生对于图形面积计算的灵活运用。
并加深对面积和周长概念的理解和区分。
面积求解大致分为以下几类:c重难点:观察图形的特点,根据图形特点选择合适的方法求解图形的面积。
能灵活运用所学过的基本的平面图形的面积求阴影部分的面积。
例 1.求阴影部分的面积。
(单位:厘米) 例2.正方形面积是7平方厘米,求阴影部分的面积。
(单位:厘米)例3.求图中阴影部分的面积。
(单位:厘米) 例4.求阴影部分的面积。
(单位:厘米)例5.求阴影部分的面积。
(单位:厘米) 例6.如图:已知小圆半径为2厘米,大圆半径是小圆的3倍,问:空白部分甲比乙的面积多多少厘米?例7.求阴影部分的面积。
(单位:厘米)例8.求阴影部分的面积。
(单位:厘米)例9.求阴影部分的面积。
(单位:厘米)例10.求阴影部分的面积。
(单位:厘米)例12.求阴影部分的面积。
(单位:厘米)例14.求阴影部分的面积。
(单位:厘米)例16.求阴影部分的面积。
(单位:厘米)例18.如图,在边长为6厘米的等边三角形中挖去三个同样的扇形,求阴影部分的周长。
例20.如图,正方形ABCD的面积是36平方厘米,求阴影部分的面积。
例22. 如图,正方形边长为8厘米,求阴影部分的面积。
例24.如图,有8个半径为1厘米的小圆,用他们的圆周的一部分连成一个花瓣图形,图中的黑点是这些圆的圆心。
如果圆周π率取3.1416,那么花瓣图形的的面积是多少平方厘米?例25.如图,四个扇形的半径相等,求阴影部分的面积。
(单位:厘米) 例26.如图,等腰直角三角形ABC和四分之一圆DEB,AB=5厘米,BE=2厘米,求图中阴影部分的面积。
例27.如图,正方形ABCD的对角线AC=2厘米,扇形ACB是以AC为直径的半圆,扇形DAC是以D为圆心,AD为半径的圆的一部分,求阴影部分的面积。
阴影部分面积及周长的专题(较难)

阴影部分面积的专题阴影部分的面积的方法:一、相加法:这种方法是将不规则图形分解转化成几个基本规则图形,分别计算它们的面积,然后相加求出整个图形的面积.例如,右图中,要求整个图形的面积,只要先求出上面半圆的面积,再求出下面正方形的面积,然后把它们相加就可以了。
二、相减法:这种方法是将所求的不规则图形的面积看成是若干个基本规则图形的面积之差.例如,右图,若求阴影部分的面积,只需先求出正方形面积再减去里面圆的面积即可。
三、直接求法:这种方法是根据已知条件,从整体出发直接求出不规则图形面积.如下页右上图,欲求阴影部分的面积,通过分析发现它是一个底2,高4的三角形,就可以直接求面积了。
四、重新组合法:这种方法是将不规则图形拆开,根据具体情况和计算上的需要,重新组合成一个新的图形,设法求出这个新图形面积即可.例如,欲求右图中阴影部分面积,可以把它拆开使阴影部分分布在正方形的4个角处,这时采用相减法就可求出其面积了。
五、辅助线法:这种方法是根据具体情况在图形中添一条或若干条辅助线,使不规则图形转化成若干个基本规则图形,然后再采用相加、相减法解决即可.如右图,右图中大小正方形的边长分别是9厘米和5厘米,求阴影部分的面积.此题虽然可以用相减法解决,但不如添加一条辅助线后用直接法作更简便。
六、割补法:这种方法是把原图形的一部分切割下来补在图形中的另一部分使之成为基本规则图形,从而使问题得到解决.例如,如右图,欲求阴影部分的面积,只需把右边弓形切割下来补在左边,这样整个阴影部分面积恰是正方形面积的一半.七、平移法:这种方法是将图形中某一部分切割下来平行移动到一恰当位置,使之组合成一个新的基本规则图形,便于求出面积.例如,如上页最后一图,欲求阴影部分面积,可先沿中间切开把左边正方形内的阴影部分平行移到右边正方形内,这样整个阴影部分恰是一个正方形。
八、旋转法:这种方法是将图形中某一部分切割下来之后,使之沿某一点或某一轴旋转一定角度贴补在另一图形的一侧,从而组合成一个新的基本规则的图形,便于求出面积.例如,欲求上图(1)中阴影部分的面积,可将左半图形绕B点逆时针方向旋转180°,使A与C重合,从而构成如右图(2)的样子,此时阴影部分的面积可以看成半圆面积减去中间等腰直角三角形的面积.九、对称添补法:这种方法是作出原图形的对称图形,从而得到一个新的基本规则图形.原来图形面积就是这个新图形面积的一半.例如,欲求右图中阴影部分的面积,沿AB在原图下方作关于AB为对称轴的对称扇形ABD.弓形CBD的面积的一半就是所求阴影部分的面积。
阴影部分求面积及周长(含答案)

【史上最全小学求阴影部分面积专题—含答案】之司秆蘸矗创作小学及小升初复习专题-圆与求阴影部分面积----完整答案在最后面目标:通过专题复习,加强学生对于图形面积计算的灵活运用。
并加深对面积和周长概念的理解和区分。
面积求解大致分为以下几类:c重难点:观察图形的特点,根据图形特点选择合适的方法求解图形的面积。
能灵活运用所学过的基本的平面图形的面积求阴影部分的面积。
例2.正方形面积是7平方厘米,求阴影部分的面积。
例1.求阴影部分的面积。
(单位:厘米)(单位:厘米)例3.求图中阴影部分的面积。
(单位:厘例4.求阴影部分的面积。
(单位:厘米)米)例5.求阴影部分的面积。
(单位:厘米) 例6.如图:已知小圆半径为2厘米,大圆半径是小圆的3倍,问:空白部分甲比乙的面积多多少厘米?例7.求阴影部分的面积。
(单位:厘米)例8.求阴影部分的面积。
(单位:厘米)例9.求阴影部分的面积。
(单位:厘米)例10.求阴影部分的面积。
(单位:厘米)例11.求阴影部分的面积。
(单位:厘米)例12.求阴影部分的面积。
(单位:厘米)例13.求阴影部分的面积。
(单位:厘米)例14.求阴影部分的面积。
(单位:厘米)例15.已知直角三角形面积是12平方厘米,求阴影部分的面积。
例16.求阴影部分的面积。
(单位:厘米)例17.图中圆的半径为5厘米,求阴影部分的面积。
(单位:厘米)例18.如图,在边长为6厘米的等边三角形中挖去三个同样的扇形,求阴影部分的周长。
例19.正方形边长为2厘米,求阴影部分的面积。
例20.如图,正方形ABCD的面积是36平方厘米,求阴影部分的面积。
例21.图中四个圆的半径都是1厘米,求阴影部分的面积。
例22.如图,正方形边长为8厘米,求阴影部分的面积。
例23.图中的4个圆的圆心是正方形的4个顶点,,它们的公共点是该正方形的中心,如果每个圆的半径都是1厘米,那么阴影部分的面积是多少?例24.如图,有8个半径为1厘米的小圆,用他们的圆周的一部分连成一个花瓣图形,图中的黑点是这些圆的圆心。
阴影部分求面积及周长(含答案)

【史上最全小学求阴影部分面积专题—含答案】小学及小升初复习专题-圆与求阴影部分面积----完整答案在最后面目标:通过专题复习,加强学生对于图形面积计算的灵活运用。
并加深对面积和周长概念的理解和区分。
面积求解大致分为以下几类:c重难点:观察图形的特点,根据图形特点选择合适的方法求解图形的面积。
能灵活运用所学过的基本的平面图形的面积求阴影部分的面积。
例1.求阴影部分的面积。
例2.正方形面积是7平方厘米,求阴影部分的面积。
(单位:厘米)(单位:厘米)例3.求图中阴影部分的面积。
(单位:厘米) 例4.求阴影部分的面积。
(单位:厘米)例5.求阴影部分的面积。
(单位:厘米) 例6.如图:已知小圆半径为2厘米,大圆半径是小圆的3倍,问:空白部分甲比乙的面积多多少厘米?例7.求阴影部分的面积。
(单位:厘米)例8.求阴影部分的面积。
(单位:厘米)例9.求阴影部分的面积。
(单位:厘米)例10.求阴影部分的面积。
(单位:厘米)例11.求阴影部分的面积。
(单位:厘米)例12.求阴影部分的面积。
(单位:厘米)例13.求阴影部分的面积。
(单位:厘米)例14.求阴影部分的面积。
(单位:厘米)例16.求阴影部分的面积。
(单位:厘米) 例15.已知直角三角形面积是12平方厘米,求阴影部分的面积。
例17.图中圆的半径为5厘米,求阴影部分的面积。
(单位:厘米) 例18.如图,在边长为6厘米的等边三角形中挖去三个同样的扇形,求阴影部分的周长。
例19.正方形边长为2厘米,求阴影部分的面积。
例20.如图,正方形ABCD的面积是36平方厘米,求阴影部分的面积。
例21.图中四个圆的半径都是1厘米,求阴影部分的面积。
例22.如图,正方形边长为8厘米,求阴影部分的面积。
例23.图中的4个圆的圆心是正方形的4个顶点,,它们的公共点是该正方形的中心,如果每个圆的半径都是1厘米,那么阴影部分的面积是多少?例24.如图,有8个半径为1厘米的小圆,用他们的圆周的一部分连成一个花瓣图形,图中的黑点是这些圆的圆心。
小升初复习:阴影部分求面积及周长含答案
【史上最全小学求阴影部分面积专题—含答案】小学及小升初复习专题-圆与求阴影部分面积----完整答案在最后面目标:通过专题复习,加强学生对于图形面积计算的灵活运用。
并加深对面积和周长概念的理解和区分。
面积求解大致分为以下几类:c重难点:观察图形的特点,根据图形特点选择合适的方法求解图形的面积。
能灵活运用所学过的基本的平面图形的面积求阴影部分的面积。
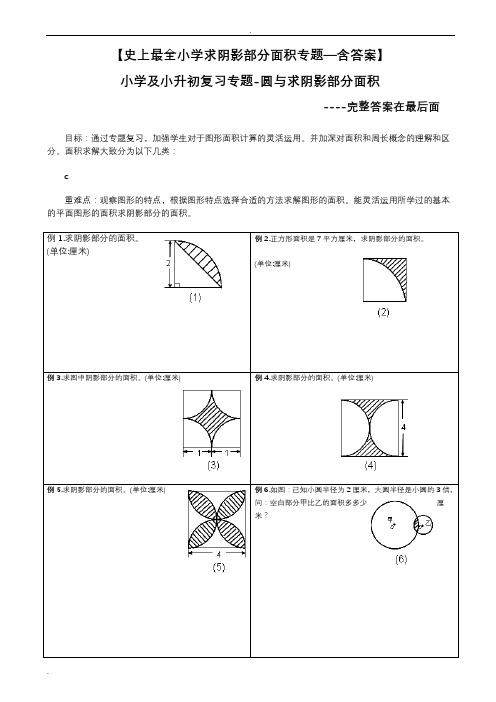
例1.求阴影部分的面积。
(单位:厘米)例2.正方形面积是7平方厘米,求阴影部分的面积。
(单位:厘米)例3.求图中阴影部分的面积。
(单位:厘米) 例4.求阴影部分的面积。
(单位:厘米)例5.求阴影部分的面积。
(单位:厘米) 例6.如图:已知小圆半径为2厘米,大圆半径是小圆的3倍,问:空白部分甲比乙的面积多多少厘米?例7.求阴影部分的面积。
(单位:厘米)例8.求阴影部分的面积。
(单位:厘米)例9.求阴影部分的面积。
(单位:厘米)例10.求阴影部分的面积。
(单位:厘米)例11.求阴影部分的面积。
(单位:厘米)例12.求阴影部分的面积。
(单位:厘米)例13.求阴影部分的面积。
(单位:厘米)例14.求阴影部分的面积。
(单位:厘米)例15.已知直角三角形面积是12平方厘米,求阴影部分的面积。
例16.求阴影部分的面积。
(单位:厘米)例17.图中圆的半径为5厘米,求阴影部分的面积。
(单位:厘米) 例18.如图,在边长为6厘米的等边三角形中挖去三个同样的扇形,求阴影部分的周长。
例19.正方形边长为2厘米,求阴影部分的面积。
例20.如图,正方形ABCD的面积是36平方厘米,求阴影部分的面积。
例21.图中四个圆的半径都是1厘米,求阴影部分的面积。
例22.如图,正方形边长为8厘米,求阴影部分的面积。
例23.图中的4个圆的圆心是正方形的4个顶点,,它们的公共点是该正方形的中心,如果每个圆的半径都是1厘米,那么阴影部分的面积是多少?例24.如图,有8个半径为1厘米的小圆,用他们的圆周的一部分连成一个花瓣图形,图中的黑点是这些圆的圆心。
多边形的周长与面积求阴影部分较难

多边形的周长与面积求阴影部分较难多边形的周长和面积是数学中常见的概念,但对于求解多边形阴影部分的周长和面积,可能会稍显复杂。
本文将介绍一个简单的方法来解决这个问题。
多边形的周长求解求解多边形的周长是计算多边形边长之和的过程。
首先,需要知道多边形的各个边的长度,然后将这些边长相加即可得到多边形的周长。
对于简单的多边形,这个过程较为简单。
然而,在求解多边形阴影部分的周长时,我们需要注意阴影部分的形状是否规则。
如果阴影部分是规则多边形,那么可以直接应用相应规则多边形的周长公式。
如果阴影部分是非规则形状,我们可以将其视为由多个规则多边形组成的复杂形状,分别计算每个规则多边形的周长,然后将这些周长相加得到总周长。
多边形的面积求解求解多边形的面积是计算多边形内部区域的面积的过程。
对于简单的多边形,可以应用相应的面积公式进行计算。
对于多边形阴影部分的面积求解,也需要注意阴影部分的形状是否规则。
如果阴影部分是规则多边形,可以直接应用相应规则多边形的面积公式。
如果阴影部分是非规则形状,我们可以将其分割成多个规则多边形,计算每个规则多边形的面积,然后将这些面积相加得到总面积。
简单方法求解多边形阴影部分的周长和面积对于比较复杂的多边形阴影部分,我们可以采用简单方法来求解。
首先,我们可以将阴影部分分割成多个较为简单的形状,如矩形、三角形等。
然后,分别计算每个简单形状的周长和面积,并将它们相加得到多边形阴影部分的周长和面积。
这种方法适用于大多数情况下,并且不会牵涉到复杂的数学推导和推算。
然而,对于特殊情况下的阴影部分,可能需要应用更加复杂的数学方法来求解。
在具体应用时,我们可以根据实际情况选择最适合的方法来求解多边形阴影部分的周长和面积,确保结果的准确性和可信度。
***以上是关于多边形的周长与面积求阴影部分较难的文档内容。
希望对您有所帮助!。
梯形的周长与面积求阴影部分较难

梯形的周长与面积求阴影部分较难概述梯形是一个常见的几何形状,它有两条平行的边和两条不平行的边。
在求解梯形的周长和面积时,我们通常要考虑到阴影部分的存在。
本文将讨论如何求解梯形的周长和面积,并介绍如何处理阴影部分。
周长的求解梯形的周长可以通过将所有边的长度相加而得到。
对于一个梯形,假设上底的长度为$AB$,下底的长度为$CD$,左斜边的长度为$AD$,右斜边的长度为$BC$,那么梯形的周长可以表示为$AB+BC+CD+AD$。
面积的求解梯形的面积可以通过以下公式求解:$$A = \frac{{(AB+CD) \times H}}{2}$$其中,$A$表示梯形的面积,$AB$和$CD$表示上底和下底的长度,$H$表示梯形的高度。
需要注意的是,梯形的高度通常是从上底到下底的垂直距离。
处理阴影部分当梯形中有阴影部分时,我们需要将阴影部分的面积从总面积中减去,以得到真实的梯形面积。
处理阴影部分的方法通常是根据具体情况而定。
如果阴影部分是一个简单的几何形状(例如矩形或三角形),我们可以通过求解阴影部分的面积,并将其从总面积中减去来得到梯形的真实面积。
如果阴影部分变化复杂,难以直接计算其面积,我们可以考虑使用数值方法或近似方法来估算阴影部分的面积。
例如,可以将梯形分解为更小的几何形状,对每个小形状求解面积,然后将它们相加。
结论梯形的周长可以通过将所有边长相加而得到,而梯形的面积可以通过公式$A = \frac{{(AB+CD) \times H}}{2}$求解。
当梯形中存在阴影部分时,我们需要根据具体情况采取相应的求解方法,将阴影部分的面积从总面积中减去,以得到真实的梯形面积。
请注意,本文只提供了梯形的基本周长和面积求解方法,并提出了处理阴影部分的一般思路。
具体情况下,应根据实际问题和具体形状进行适当的调整和求解。
以上就是关于梯形的周长与面积求解以及处理阴影部分的较难部分的内容。
希望对您有所帮助!。
阴影部分求面积及周长练习集(完整答案)

阴影部分求⾯积及周长练习集(完整答案)⼩学及⼩升初复习专题-圆与求阴影部分⾯积----完整答案在最后⾯⽬标:通过专题复习,加强学⽣对于图形⾯积计算的灵活运⽤。
并加深对⾯积和周长概念的理解和区分。
⾯积求解⼤致分为以下⼏类:1、从整体图形中减去局部;2、割补法,将不规则图形通过割补,转化成规则图形。
重难点:观察图形的特点,根据图形特点选择合适的⽅法求解图形的⾯积。
能灵活运⽤所学过的基本的平⾯图形的⾯积求阴影部分的⾯积。
) 例18.如图,在边长为6厘⽶的等边三⾓形中挖去三个同样个圆的圆⼼是正⽅形的4个顶点,,它们的⼀个花瓣图圆⼼。
图形的的⾯例29.图中直⾓三⾓形ABC的直⾓三⾓形的直⾓边AB=4厘⽶,BC=6厘⽶,扇形BCD所在圆是以B为圆⼼,半径为BC的圆,∠CBD=,问:阴影部分甲⽐⼄⾯积⼩多少?举⼀反三★巩固练习【专1 】下图中,⼤⼩正⽅形的边长分别是9厘⽶和5厘⽶,求阴影部分的⾯积。
【专1-1】.右图中,⼤⼩正⽅形的边长分别是12厘⽶和10厘⽶。
求阴影部分⾯积。
【专1-2】. 求右图中阴影部分图形的⾯积及周长。
【专2】已知右图阴影部分三⾓形的⾯积是5平⽅⽶,求圆的⾯积。
【专2-1】已知右图中,圆的直径是2厘⽶,求阴影部分的⾯积。
【专2-2】求右图中阴影部分图形的⾯积及周长。
【专2-3】求下图中阴影部分的⾯积。
(单位:厘⽶)【专3】求下图中阴影部分的⾯积。
【专3-1】求右图中阴影部分的⾯积。
【专3-2】求右图中阴影部分的⾯积。
【专3-3】求下图中阴影部分的⾯积。
例1解:这是最基本的⽅法:圆⾯积减去等腰直⾓三⾓形的⾯积,×-2×1=1.14(平⽅厘⽶)例2解:这也是⼀种最基本的⽅法⽤正⽅形的⾯积减去圆的⾯积。
设圆的半径为r ,因为正⽅形的⾯积为7平⽅厘⽶,所以=7,所以阴影部分的⾯积为:7-=7-×7=1.505平⽅厘⽶例3解:最基本的⽅法之⼀。
⽤四个圆组成⼀个圆,⽤正⽅形的⾯积减去圆的⾯积,所以阴影部分的⾯积:2×2-π=0.86平⽅厘⽶。
小升初——求阴影部分面积及周长(带答案)

【史上最全小学求阴影部份面积专题—含谜底】之马矢奏春创作时间:二O二一年七月二十九日小学及小升初复习专题-圆与求阴影部份面积----完整谜底在最后面目标:通过专题复习,加强学生对图形面积计算的灵活运用.并加深对面积和周长概念的理解和区分.面积求解年夜致分为以下几类:1、从整体图形中减去局部;2、割补法,将不规则图形通过割补,转化陈规则图形.重难点:观察图形的特点,根据图形特点选择合适的方法求解图形的面积.能灵活运用所学过的基本的平面图形的面积求阴影部份的面积.例1.求阴影部份的面积. (单元:厘米)例2.正方形面积是7平方厘米,求阴影部份的面积.(单元:厘米)积.(单元:厘米)例5.求阴影部份的面积.(单元:厘米)例6.如图:已知小圆半径为2厘米,年夜圆半径是小圆的3倍,问:空白部份甲比乙的面积多几多厘米?例7.求阴影部份的面积.(单元:厘米)例8.求阴影部份的面积.(单元:厘米)例9.求阴影部份的面积.(单元:厘米)例10.求阴影部份的面积.(单元:厘米)例11.求阴影部份的面积.(单元:厘米)例12.求阴影部份的面积.(单元:厘米)元:厘米)米,求阴影部份的面积.例16.求阴影部份的面积.(单元:厘米)例17.图中圆的半径为5厘米,求阴影部份的面积.(单元:厘米) 例18.如图,在边长为6厘米的等边三角形中挖去三个同样的扇形,求阴影部份的周长.例19.正方形边长为2厘米,求阴影部份的面积.例20.如图,正方形ABCD的面积是36平方厘米,求阴影部份的面积.例21.图中四个圆的半径都是1厘米,求阴影部份的面积. 例22. 如图,正方形边长为8厘米,求阴影部份的面积.例23.图中的4个圆的圆心是正方形的4个极点,,它们的公共点是该正方形的中心,如果每例24.如图,有8个半径为1厘米的小圆,用他们的圆周的一部份连成一个花瓣图形,图中的个圆的半径都是1厘米,那么阴影部份的面积是几多?黑点是这些圆的圆心.如果圆周π率取3.1416,那么花瓣图形的的面积是几多平方厘米?例25.如图,四个扇形的半径相等,求阴影部份的面积.(单元:厘米) 例26.如图,等腰直角三角形ABC和四分之一圆DEB,AB=5厘米,BE=2厘米,求图中阴影部份的面积.例27.如图,正方形ABCD的对角线AC=2厘米,扇形ACB是以AC为直径的半圆,扇形DAC是以D为圆心,AD为半径的圆的一部份,求阴影部份的面积.例28.求阴影部份的面积.(单元:厘米)例29.图中直角三角形ABC的直角三角形的直角边AB=4厘米,BC=6厘米,扇形BCD所在圆是以B为圆心,半径为BC的圆,∠CBD=,问:阴影部份甲比乙面积小几多?例30.如图,三角形ABC是直角三角形,阴影部份甲比阴影部份乙面积年夜28平方厘米,AB=40厘米.求BC的长度.例31.如图是一个正方形和半圆所组成的图形,其中P为半圆周的中点,Q为正方形一边上的中点,求阴影部份的面积.例32.如图,年夜正方形的边长为6厘米,小正方形的边长为4厘米.求阴影部份的面积.例33.求阴影部份的面积.(单元:厘米) 例34.求阴影部份的面积.(单元:厘米)例35.如图,三角形OAB是等腰三角形,OBC是扇形,OB=5厘米,求阴影部份的面积.完整谜底例1解:这是最基本的方法:圆面积减去等腰直角三角形的面积,×-2×1=1.14(平方厘米)例2解:这也是一种最基本的方法用正方形的面积减去圆的面积.设圆的半径为 r,因为正方形的面积为7平方厘米,所以=7,所以阴影部份的面积为:7-=7-例3解:最基本的方法之一.用四个圆组成一个圆,用正方形的面积减去圆的面积, 所以阴影部份的面积:2×2-π=0.86平方厘米.例4解:同上,正方形面积减去圆面积, 16-π()=16-4π=3.44平方厘米例5解:这是一个用最经常使用的方法解最罕见的题,为方便起见,我们把阴影部份的每一个小部份称为“叶形”,是用两个圆减去一个正方形, 例6解:两个空白部份面积之差就是两圆面积之差(全加上阴影部份)π-π()=100.48平方厘米(注:这和两个圆是否相交、交的情况π()×2-16=8π-16=9.12平方厘米另外:此题还可以看成是1题中阴影部份的8倍.如何无关)例7解:正方形面积可用(对角线长×对角线长÷2,求)正方形面积为:5×5÷2=12.5所以阴影面积为:π÷4-12.5=7.125平方厘米(注:以上几个题都可以直接用图形的差来求,无需割、补、增、减变形)例8解:右面正方形上部阴影部份的面积,即是左面正方形下部空白部份面积,割补以后为圆,所以阴影部份面积为:π(例9解:把右面的正方形平移至左边的正方形部份,则阴影部份合成一个长方形, 所以阴影部份面积为:2×3=6平方厘米例10解:同上,平移左右两部份至中间部份,则合成一个长方形,所以阴影部份面积为2×1=2平方厘米(注: 8、9、10三题是简单割、补或平移)例11解:这种图形称为环形,可以用两个同心圆的面积差或差的一部份来求.(π -π)×=例12. 解:三个部份拼成一个半圆面积.π()÷2=14.13平方厘米例13解: 连对角线后将"叶形"剪开移到右上面的空白部份,凑成正方形的一半.所以阴影部份面积为:8×8÷2=32平方厘米例14解:梯形面积减去圆面积,(4+10)×4-π=28-4π=15.44平方厘米 .例15. 分析: 此题比上面的题有一定难度,这是"叶形"的一个半.解: 设三角形的直角边长为r,则=12,=6圆面积为:π÷2=3π.圆内三角形的面积为12÷2=6,阴影部份面积为:(3π-6)×例16解:[π+π-π] =π(116-36)=40π=125.6平方厘米例19解:右半部份上面部份逆时针,下面部份顺时针旋转到左半部份,组成一个矩形.所以面积为:1×2=2平方厘米例20解:设小圆半径为r,4=36, r=3,年夜圆半径为R,=2=18,将阴影部份通过转动移在一起构成半个圆环,所以面积为:π(-例21.解:把中间部份分成四等分,分别放在上面圆的四个角上,补成一个正方形,边长为2厘米,所以面积为:2×2=4平方厘米例22解法一: 将左边上面一块移至右边上面,补上空白,则左边为一三角形,右边一个半圆.阴影部份为一个三角形和一个半圆面积之和.π()÷2+4×4=8π+16=41.12平方厘米解法二: 补上两个空白为一个完整的圆.所以阴影部份面积为一个圆减去一个叶形,叶形面积为:π()÷2-4×4=8π-16 所以阴影部份的面积为:π(例23解:面积为4个圆减去8个叶形,叶形面积为:π-1×1=π-1所以阴影部份的面积为:4π-8(π-1)=8平方厘米例24分析:连接角上四个小圆的圆心构成一个正方形,各个小圆被切去例25分析:四个空白部份可以拼成一个以2为半径的圆.所以阴影部份的面积为梯形面积减去圆的面积,4×(4+7)÷2-π例26解: 将三角形CEB以B为圆心,逆时针转动90度,到三角形ABD位置,阴影部份成为三角形ACB面积减去个小圆面积,为: 5×5÷2-π例27解: 因为2==4,所以=2 以AC为直径的圆面积减去三角形ABC面积加上弓形AC面积,π-2×2÷4+[π÷4-2]=π-1+(π-1)=π-2=1.14平方厘米例28解法一:设AC中点为B,阴影面积为三角形ABD面积加弓形BD的面积,三角形ABD的面积为:5×5÷2=12.5弓形面积为:[π÷2-5×5]÷2=7.125所以阴影面积为:12.5+7.125=19.625平方厘米解法二:右上面空白部份为小正方形面积减去小圆面积,其值为:5×5-π=25-π阴影面积为三角形ADC减去空白部份面积,为:10×5÷2-(25-π)=π=19.625平方厘米例29. 解: 甲、乙两个部份同补上空白部份的三角形后合成一个扇形BCD,一个成为三角例30. 解:两部份同补上空白部份后为直角三角形ABC,一个为半圆,设BC长为X,则40X÷2-π形ABC,此两部份差即为:π×-例31.解:连PD、PC转换为两个三角形和两个弓形,两三角形面积为:△APD面积+△QPC面积=(5×10+5×5)=37.5两弓形PC、PD面积为:π-5×5所以阴影部份的面积为:37.5+π-25=51.75平方厘米例32解:三角形DCE的面积为:×4×10=20平方厘米梯形ABCD的面积为:(4+6)×4=20平方厘米从而知道它们面积相等,则三角形ADF面积即是三角形EBF面积,阴影部份可补成圆ABE的面积,其面积为:π÷4=9π=28.26平方厘米例33.解:用年夜圆的面积减去长方形面积再加上一个以2为半径的圆ABE面积,为(π+π)-6 =例34解:两个弓形面积为:π-3×4÷2=π-6阴影部份为两个半圆面积减去两个弓形面积,结果为π+π-(π-6)=π(4+-)+6=6平方厘米例35解:将两个同样的图形拼在一起成为圆减等腰直角三角形[π÷4-×5×5]÷2=(π-时间:二O二一年七月二十九日。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
阴影部分面积的专题
阴影部分的面积的方法:
一、相加法:这种方法是将不规则图形分解转化成几个基本规则图形,分别计算它们的面积,然后相加求出整个图形的面积.例如,右图中,要求整个图形的面积,只要先求出上面半圆的面积,再求出下面正方形的面积,然后把它们相加就可以了。
二、相减法:这种方法是将所求的不规则图形的面积看成是若干个基本规则图形的面积之差.例如,右图,若求阴影部分的面积,只需先求出正方形面积再减去里面圆的面积即可。
三、直接求法:这种方法是根据已知条件,从整体出发直接求出不规则图形面积.如下页右上图,欲求阴影部分的面积,通过分析发现它是一个底2,高4的三角形,就可以直接求面积了。
四、重新组合法:这种方法是将不规则图形拆开,根据具体情况和计算上的需要,重新组合成一个新的图形,设法求出这个新图形面积即可.例如,欲求右图中阴影部分面积,可以把它拆开使阴影部分分布在正方形的4个角处,这时采用相减法就可求出其面积了。
五、辅助线法:这种方法是根据具体情况在图形中添一条或若干条辅助线,使不规则图形转化成若干个基本规则图形,然后再采用相加、相减法解决即可.如右图,右图中大小正方形的边长分别是9厘米和5厘米,求阴影部分的面积.此题虽然可以用相减法解决,但不如添加一条辅助线后用直接法作更简便。
六、割补法:这种方法是把原图形的一部分切割下来补在图形中的另一部分使之成为基本规则图形,从而使问题得到解决.例如,如右图,欲求阴影部分的面积,只需把右边弓形切割下来补在左边,这样整个阴影部分面积恰是正方形面积的一半.
七、平移法:这种方法是将图形中某一部分切割下来平行移动到一恰当位置,使之组合成一个新的基本规则图形,便于求出面积.例如,如上页最后一图,欲求阴影部分面积,可先沿中间切开把左边正方形
内的阴影部分平行移到右边正方形内,这样整个阴影部分恰是一个正方形。
八、旋转法:这种方法是将图形中某一部分切割下来之后,使之沿某一点或某一轴旋转一定角度贴补在另一图形的一侧,从而组合成一个新的基本规则的图形,便于求出面积.例如,欲求上图(1)中阴影部分的面积,可将左半图形绕B点逆时针方向旋转180°,使A与C 重合,从而构成如右图(2)的样子,此时阴影部分的面积可以看成半圆面积减去中间等腰直角三角形的面积.
九、对称添补法:这种方法是作出原图形的对称图形,从而得到一个新的基本规则图形.原来图形面积就是这个新图形面积的一半.例如,欲求右图中阴影部分的面积,沿AB在原图下方作关于AB为对称轴的对称扇形ABD.弓形CBD的面积的一半就是所求阴影部分的面积。
十、重叠法:这种方法是将所求的图形看成是两个或两个以上图形的重叠部分,然后运用“容斥原理”(SA∪B=SA+SB-SA∩B)解决。
例如,欲求右图中阴影部分的面积,可先求两个扇形面积的和,减去正方形面积,因为阴影部分的面积恰好是两个扇形重叠的部分.
求阴影部分的面积的课前练习
1、如下图,正方形ABCD的边长为6厘米,△ABE、△ADF与四边形AECF的面积彼此相等,求三角形AEF的面积.
2、如下图,甲、乙两图形都是正方形,它们的边长分别是10厘米和12厘米.求阴影部分的面积。
3、如下图,梯形ABCD的面积是45平方米,高6米,△AED的面积是5平方米,BC=10米,求阴影部分面积。
4、如下图,正方形ABCD的边长为4厘米,分别以B、D为圆心以4厘米为半径在正方形内画圆,求阴影部分面积。
5、矩形ABCD中,AB=6厘米,BC=4厘米,扇形ABE半径AE=6厘米,扇形CBF的半CB=4厘米,求阴影部分的面积。
6、如右图,直角三角形ABC中,AB是圆的直径,且AB=20厘米,如果阴影(Ⅰ)的面积比阴影(Ⅱ)的面积大7平方厘米,求BC长。
7、如右图,两个正方形边长分别是10厘米和6厘米,求阴影部分的面积。
专题练习:(图形)
1、求阴影部分面积:(单位:米)
12cm
20
30
2、求下列各图形的周长和面积:(单位:分米)
阴影部分面积专题练习
(单位:厘米)
2、右图中,O为圆心,OC垂直于AB,三角形ABC的面积是36平方厘米,求阴影部分的面积。
3、下图中长方形的长是6厘米,宽是5厘米,求阴影部分的面积。
4、如图长方形的面积是45平方厘米,宽是5厘
米,求阴影部分的面积。
5、如图,两个大小不等的正方形拼成一个图形,
已知小正方形的边长是4厘米,阴影部分的面积
是30平方厘米,求空白部分的面积是多少?
6、将直角三角形ABC向右平移6厘米,再向下平移1.5厘米,得到一个图形如图,已知三角形的底边BC长16厘米,求阴影部分的面积。
7、如图,半圆的直径为20厘米,已知阴影A比阴影B的面积少27平方厘米,求MN的长是多少?
8.一个长方形(如图),被两条直线分成四个长方形,其中三个
面积分别是20平方米、25平方米和30平方米。
阴影部分的面积
是多少?。
