结构力学_第九章_作业参考答案
结构力学课后习题答案

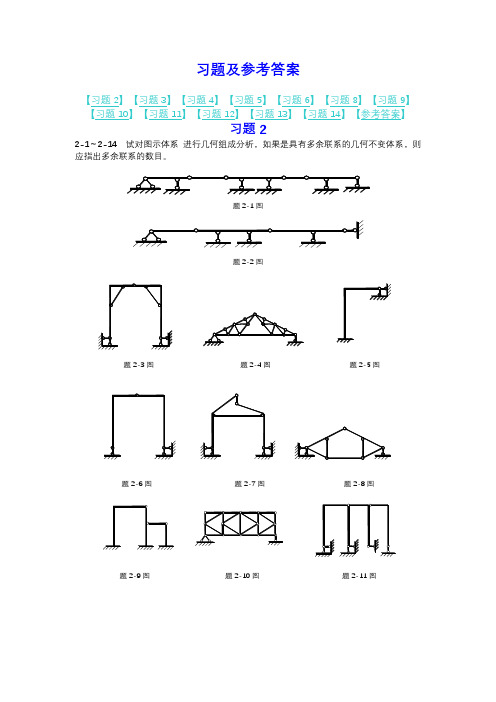
习题及参考答案【习题2】【习题3】【习题4】【习题5】【习题6】【习题8】【习题9】【习题10】【习题11】【习题12】【习题13】【习题14】【参考答案】习题22-1~2-14试对图示体系进行几何组成分析,如果是具有多余联系的几何不变体系,则应指出多余联系的数目。
题2-1图题2-2图题2-3图题2-4图题2-5图题2-6图题2-7图题2-8图题2-9图题2-10图题2-11图题2-12图 题2-13图 题2-14图习题33-1 试作图示多跨静定梁的M 及Q 图。
(b)(a)20kN40kN20kN/m40kN题3-1图3-2 试不计算反力而绘出梁的M 图。
(b)5kN/m40kN(a)题3-2图习题44-1 作图示刚架的M 、Q 、N 图。
(c)(b)(a)20kN /m2kN /m题4-1图4-2 作图示刚架的M 图。
P(e)(d)(a)(b)(c)20k N /m4kN题4-2图4-3 作图示三铰刚架的M 图。
(b)(a)题4-3图4-4 作图示刚架的M 图。
(a)题4-4图4-5 已知结构的M 图,试绘出荷载。
(b)(a)题4-5图4-6 检查下列刚架的M 图,并予以改正。
(e)(g)(h)P(d)(c)(a)(b)(f)题4-6图习题55-1 图示抛物线三铰拱轴线方程x x l lfy )(42-=,试求D 截面的内力。
题5-1图5-2 带拉杆拱,拱轴线方程x x l lfy )(42-=,求截面K 的弯矩。
C题5-2图 题5-3图5-3 试求图示带拉杆的半圆三铰拱截面K 的内力。
习题66-1 判定图示桁架中的零杆。
(c)(b)题6-1图6-2 用结点法计算图示桁架中各杆内力。
(b)题6-2 图6-3 用截面法计算图示桁架中指定各杆的内力。
(b)题6-3图6-4 试求图示组合结构中各链杆的轴力并作受弯杆件的M 、Q 图。
(a)题6-4图6-5 用适宜方法求桁架中指定杆内力。
(c)(b)(a)题6-6图习题88-1 试作图示悬臂梁的反力V B 、M B 及内力Q C 、M C 的影响线。
结构力学课后习题答案
习题及参考答案【习题2】【习题3】【习题4】【习题5】【习题6】【习题8】【习题9】【习题10】【习题11】【习题12】【习题13】【习题14】【参考答案】习题22-1~2-14试对图示体系进行几何组成分析,如果是具有多余联系的几何不变体系,则应指出多余联系的数目。
题2-1图题2-2图题2-3图题2-4图题2-5图题2-6图题2-7图题2-8图题2-9图题2-10图题2-11图题2-12图 题2-13图 题2-14图习题33-1 试作图示多跨静定梁的M 及Q 图。
题3-1图3-2 试不计算反力而绘出梁的M 图。
题3-2图习题44-1 作图示刚架的M 、Q 、N 图。
题4-1图4-2 作图示刚架的M 图。
(b)(a)20kN40kN20kN/m40kN(b)5kN/m40kN(a)(c)(b)(a)题4-2图4-3 作图示三铰刚架的M 图。
题4-3图4-4 作图示刚架的M 图。
题4-4图4-5 已知结构的M 图,试绘出荷载。
P(e)(d)(a)(b)(c)/4kN(b)(a)(a)(b)(a)题4-5图4-6 检查下列刚架的M 图,并予以改正。
题4-6图习题55-1 图示抛物线三铰拱轴线方程,试求D 截面的内力。
题5-1图5-2 带拉杆拱,拱轴线方程,求截面K 的弯矩。
题5-2图 题5-3图5-3 试求图示带拉杆的半圆三铰拱截面K 的内力。
习题66-1 判定图示桁架中的零杆。
(e)(g)(h)P(d)(c)(a)(b)(f)x x l l fy )(42-=x x l lfy )(42-=C题6-1图6-2 用结点法计算图示桁架中各杆内力。
题6-2 图6-3 用截面法计算图示桁架中指定各杆的内力。
题6-3图6-4 试求图示组合结构中各链杆的轴力并作受弯杆件的M 、Q 图。
题6-4图6-5 用适宜方法求桁架中指定杆内力。
(c)(b)(b)(b)(a)题6-6图习题88-1 试作图示悬臂梁的反力V B 、M B 及内力Q C 、M C 的影响线。
结构力学习题及答案

构造力学习题第2章平面体系的几何组成分析2-1~2-6 试确定图示体系的计算自由度。
题2-1图题2-2图题2-3图题2-4图题2-5图题2-6图2-7~2-15 试对图示体系进展几何组成分析。
假设是具有多余约束的几何不变体系,那么需指明多余约束的数目。
题2-7图题2-8图题2-9图题2-10图题2-11图题2-12图题2-13图题2-14图题2-15图题2-16图题2-17图题2-18图题2-19图题2-20图题2-21图2-11=W2-1 9-W=2-3 3-W=2-4 2-W=2-5 1-W=2-6 4-W=2-7、2-8、2-12、2-16、2-17无多余约束的几何不变体系2-9、2-10、2-15具有一个多余约束的几何不变体系2-11具有六个多余约束的几何不变体系2-13、2-14几何可变体系为2-18、2-19 瞬变体系2-20、2-21具有三个多余约束的几何不变体系第3章静定梁和静定平面刚架的内力分析3-1 试作图示静定梁的内力图。
〔a〕〔b〕(c) (d)习题3-1图3-2 试作图示多跨静定梁的内力图。
〔a〕〔b〕(c)习题3-2图3-3~3-9 试作图示静定刚架的内力图。
习题3-3图习题3-4图习题3-5图习题3-6图习题3-7图习题3-8图习题3-9图3-10 试判断图示静定构造的弯矩图是否正确。
(a)(b)(c)(d)局部习题答案3-1〔a 〕m kN M B ⋅=80〔上侧受拉〕,kN F RQB 60=,kN F L QB 60-=〔b 〕m kN M A ⋅=20〔上侧受拉〕,m kN M B ⋅=40〔上侧受拉〕,kN F RQA 5.32=,kN F L QA 20-=,kN F LQB 5.47-=,kN F R QB 20=(c)4Fl M C =〔下侧受拉〕,θcos 2F F L QC =3-2 (a)0=E M ,m kN M F ⋅-=40〔上侧受拉〕,m kN M B ⋅-=120〔上侧受拉〕〔b 〕m kN M RH ⋅-=15(上侧受拉),m kN M E ⋅=25.11〔下侧受拉〕〔c 〕m kN M G ⋅=29(下侧受拉),m kN M D ⋅-=5.8(上侧受拉),m kN M H ⋅=15(下侧受拉) 3-3 m kN M CB ⋅=10〔左侧受拉〕,m kN M DF ⋅=8〔上侧受拉〕,m kN M DE ⋅=20〔右侧受拉〕 3-4 m kN M BA ⋅=120〔左侧受拉〕3-5 m kN M F ⋅=40〔左侧受拉〕,m kN M DC ⋅=160〔上侧受拉〕,m kN M EB ⋅=80(右侧受拉) 3-6 m kN M BA ⋅=60〔右侧受拉〕,m kN M BD ⋅=45〔上侧受拉〕,kN F QBD 46.28=3-7 m kN M C ⋅=70下〔左侧受拉〕,m kN M DE ⋅=150〔上侧受拉〕,m kN M EB ⋅=70(右侧受拉) 3-8 m kN M CB ⋅=36.0〔上侧受拉〕,m kN M BA ⋅=36.0〔右侧受拉〕 3-9 m kN M AB ⋅=10〔左侧受拉〕,m kN M BC ⋅=10〔上侧受拉〕 3-10 〔a 〕错误 〔b 〕错误 〔c 〕错误 〔d 〕正确第4章 静定平面桁架和组合构造的内力分析4-1 试判别习题4-1图所示桁架中的零杆。
结构力学课后解答:第9章__超静定结构的实用计算方法与概念分析

习 题9-2解:设EI=6,则5.1,1==BC AB i i 53.05.13145.1347.05.131414=⨯+⨯⨯==⨯+⨯⨯=BC BA μμ结点 A BC 杆端 AB BA BC 分配系数 固端 0.47 0.53 绞支 固端弯矩 -60 60 -30 0 分配传递 -7.05 -14.1 -15.9 0 最后弯矩-67.0545.9-45.9()()()逆时针方向215.216005.6721609.4522131m KN EI EI m M m M i AB AB BA BA B ⋅-=⎥⎦⎤⎢⎣⎡+---=⎥⎦⎤⎢⎣⎡---=θ(b)解:设EI=9,则3,31,1====BE BD BC AB i i i i12.0141333331316.0141333331436.01413333333=⨯+⨯+⨯+⨯⨯==⨯+⨯+⨯+⨯⨯==⨯+⨯+⨯+⨯⨯==BC BA BE BD μμμμ结点 A BC杆端 AB BA BC BD BE 分配系数 固端 0.16 0.12 0.36 0.36 绞支 固端弯矩0 45 -90 0 分配传递 3.6 7.2 5.4 16.216.20 最后弯矩 3.6 7.25.461.2 -73.8()()()顺时针方向22.1606.32102.732131m KN EI EI m M m M i AB AB BA BA B ⋅=⎥⎦⎤⎢⎣⎡---=⎥⎦⎤⎢⎣⎡---=θ9-3 (a) 解:B为角位移节点设EI=8,则1==BC AB i i ,5.0==BC BA μμ 固端弯矩()m KN l b l Pab M BA ⋅=⨯⨯⨯⨯=+=4882124432222 m KN l M BC ⋅-=⋅+-=582621892 结点力偶直接分配时不变号结点 A BC 杆端 AB BA BC 分配系数 铰接 0.5 0.5 固端弯矩 0 48 -58 12 分配传递0 50 50 5 5 12 最后弯矩103-312(b) 解:存在B 、C 角位移结点设EI=6,则1===CD BC AB i i i73741413145.0141414==⨯+⨯⨯==⨯+⨯⨯==BC CB BC BA μμμμ固端弯矩:mKN M M M m KN M m KN M CDCB BC BA AB ⋅-=⨯+⨯-===⋅-=⋅-=14021808640080802结点 A BC杆端 AB BA BC CB CD 分配系数 固结 0.5 0.5 4/7 3/7 固端弯矩-80 80 0 0 -140 分配传递-20 -40 -40 -2047.5 91.4 68.6 -11.4 -22.8 -22.8 -11.4 3.25 6.5 4.9 -0.82-1.63-1.63-0.820.6 0.45 最后弯矩-112.2215.57-15.4866.28-66.05(c) 解:B 、C 为角位移结点51411,5441454414,51411=+==+==+==+=CD CBBC BA μμμμ固端弯矩:mKN M mKN M mKN M mKN M mKN M mKN M DC CD CB BC BA AB ⋅-=⨯-=⋅-=⨯-=⋅=⨯=⋅-=⨯-=⋅=⨯=⋅=⨯=10065242003524501252450125241283424646424222222结点 A BCD 杆端 AB BA BC CB CD 滑动 分配系数 滑动 0.2 0.8 0.8 0.2 -100固端弯矩64 128 -50 50 -200 分配传递15.6 -15.6 -62.4 -31.272.48 144.96 36.24 -36.24 14.5 -14.5 -58 -29 11.6 23.2 5.8 -5.8 2.32-2.32-9.28-4.643.7 0.93 -0.93 最后弯矩96.4295.58-95.6157.02-157.03-142.9796.42(d) 解:11313141413114131414145.0141414=⨯+⨯+⨯⨯===⨯+⨯+⨯⨯===⨯+⨯⨯=DBDE DCCD CA μμμμμ 固端弯矩:mKN M mKN M ED DE ⋅=⋅-=⨯-=383812422 结点 A CD E 杆端 AC CA CD DC DB DE ED 分配系数 固结 0.5 0.5 4/11 3/11 4/11 固结 固端弯矩0 0 0 0 0 -2.67 2.67 分配传递-5 -10 -10 -546/33 92/33 69/33 92/33 46/33 -0.35 - 23/33- 23/33-0.35 0.127 0.096 0.127 0.064 最后弯矩-5.35-10.7-9.3-2.442.190.254.12(e) 解:当D 发生单位转角时:()()2414-=⨯⨯=m EI K Y C 则())假设12(441==⨯=-m EI EIM DC73,74,3716,379,371216,12,16,9,12=====∴=====∴EB ED DE DA DC DE EB DE DA DC S S S S S μμμμμ 结点D EB 杆端 DC DA DE ED EB BE 分配系数 12/37 9/37 16/37 4/7 3/7 固结 固端弯矩0 0 -9 9 0 0 分配传递-2.57 -5.14 -3.86 -1.93 3.75 2.81 5 -2.5 -0.72 -1.43 -1.07 -0.54 0.230.18 0.31 0.16 最后弯矩3.982.99-6.985-5-2.47(f) 解:截取对称结构为研究对象。
《结构力学习题集》(下)-结构的动力计算习题及答案

第九章 结构的动力计算一、判断题:1、结构计算中,大小、方向随时间变化的荷载必须按动荷载考虑。
2、仅在恢复力作用下的振动称为自由振动。
3、单自由度体系其它参数不变,只有刚度EI 增大到原来的2倍,则周期比原来的周期减小1/2。
4、结构在动力荷载作用下,其动内力与动位移仅与动力荷载的变化规律有关。
5、图示刚架不计分布质量和直杆轴向变形,图a 刚架的振动自由度为2,图b 刚架的振动自由度也为2。
6、图示组合结构,不计杆件的质量,其动力自由度为5个。
7、忽略直杆的轴向变形,图示结构的动力自由度为4个。
8、由于阻尼的存在,任何振动都不会长期继续下去。
9、设ωω,D 分别为同一体系在不考虑阻尼和考虑阻尼时的自振频率,ω与ωD 的关系为ωω=D 。
二、计算题:10、图示梁自重不计,求自振频率ω。
l l /411、图示梁自重不计,杆件无弯曲变形,弹性支座刚度为k ,求自振频率ω。
l /2l /212、求图示体系的自振频率ω。
l l0.5l 0.513、求图示体系的自振频率ω。
EI = 常数。
ll 0.514、求图示结构的自振频率ω。
l l15、求图示体系的自振频率ω。
EI =常数,杆长均为l 。
16、求图示体系的自振频率ω。
杆长均为l 。
17、求图示结构的自振频率和振型。
l /2l /2l /18、图示梁自重不计,W EI ==⨯⋅2002104kN kN m 2,,求自振圆频率ω。
B2m2m19、图示排架重量W 集中于横梁上,横梁EA =∞,求自振周期ω。
EIEIW20、图示刚架横梁∞=EI 且重量W 集中于横梁上。
求自振周期T 。
EIEIWEI 221、求图示体系的自振频率ω。
各杆EI = 常数。
a aa22、图示两种支承情况的梁,不计梁的自重。
求图a 与图b 的自振频率之比。
l /2l/2(a)l /2l /2(b)23、图示桁架在结点C 中有集中重量W ,各杆EA 相同,杆重不计。
求水平自振周期T 。
结构力学课后习题答案

习题及参考答案【习题2】【习题3】【习题4】【习题5】【习题6】【习题8】【习题9】【习题10】【习题11】【习题12】【习题13】【习题14】【参考答案】习题22-1~2-14试对图示体系进行几何组成分析,如果是具有多余联系的几何不变体系,则应指出多余联系的数目。
题2-1图题2-2图题2-3图题2-4图题2-5图题2-6图题2-7图题2-8图题2-9图题2-10图题2-11图题2-12图 题2-13图 题2-14图习题33-1 试作图示多跨静定梁的M 及Q 图。
(b)(a)20kN40kN20kN/m40kN题3-1图3-2 试不计算反力而绘出梁的M 图。
(b)5kN/m40kN(a)题3-2图习题44-1 作图示刚架的M 、Q 、N 图。
(c)(b)(a)20kN /m2kN /m题4-1图4-2 作图示刚架的M 图。
P(e)(d)(a)(b)(c)20k N /m4kN题4-2图4-3 作图示三铰刚架的M 图。
(b)(a)题4-3图4-4 作图示刚架的M 图。
(a)题4-4图4-5 已知结构的M 图,试绘出荷载。
(b)(a)题4-5图4-6 检查下列刚架的M 图,并予以改正。
(e)(g)(h)P(d)(c)(a)(b)(f)题4-6图习题55-1 图示抛物线三铰拱轴线方程x x l lfy )(42-=,试求D 截面的内力。
题5-1图5-2 带拉杆拱,拱轴线方程x x l lfy )(42-=,求截面K 的弯矩。
C题5-2图 题5-3图5-3 试求图示带拉杆的半圆三铰拱截面K 的内力。
习题66-1 判定图示桁架中的零杆。
(c)(b)题6-1图6-2 用结点法计算图示桁架中各杆内力。
(b)题6-2 图6-3 用截面法计算图示桁架中指定各杆的内力。
(b)题6-3图6-4 试求图示组合结构中各链杆的轴力并作受弯杆件的M 、Q 图。
(a)题6-4图6-5 用适宜方法求桁架中指定杆内力。
(c)(b)(a)题6-6图习题88-1 试作图示悬臂梁的反力V B 、M B 及内力Q C 、M C 的影响线。
华工网院结构力学随堂练习答案

结构力学随堂练习1. 在图示体系中,视为多余联系的三根链杆应是:(C)A。
5、6、9B.5、6、7C。
3、6、8D.1、6、7。
2。
联结三个刚片的铰结点,相当的约束个数为:(C )A.2个B.3个C.4个D.5个。
3. 图示体系为:( B )A.几何不变无多余约束B.几何不变有多余约束C.几何常变D.几何瞬变4. 图示体系为:( A )A.几何不变无多余约束B.几何不变有多余约束C.几何常变D.几何瞬变问题解析:5。
图示体系是:( B )A.无多余联系的几何不变体系B.有多余联系的几何不变体系C.几何可变体系D.瞬变体系6. 图示体系为几何不变体系,且其多余联系数目为:(D )A.1B.2C.3D.47。
图示体系内部几何组成分析的正确结论是:( D )A。
几何不变且有两个多余联系B.几何不变且有一个多余联系C。
几何不变且无多余联系D。
几何瞬变体系8。
图示体系的几何组成为:( C )A.几何不变,无多余约束B.几何不变,有多余约束C.瞬变体系D.常变体系9。
图示体系的几何组成为:( A )A.几何不变,无多余约束B.几何不变,有多余约束C.瞬变体系D.常变体系10.图示体系是几何不变体系。
(×)11。
图示体系按三刚片法则分析,三铰共线,故为几何瞬变体系。
( ×)12。
图示体系为几何瞬变。
(×)13。
在图示体系中,去掉其中任意两根支座链杆后,所余下部分都是几何不变的。
(×)14.图示体系为几何可变体系。
(×)15。
图示体系是几何不变体系。
(×)16。
图示体系是几何不变体系。
( ×)第三章静定结构的内力计]1。
静定结构在支座移动时,会产生:(C )A。
内力B.应力C。
刚体位移D。
变形.2。
静定结构有变温时:( C )A.无变形,无位移,无内力B。
有变形,有位移,有内力C。
有变形,有位移,无内力D.无变形,有位移,无内力。
3。
图示两桁架结构杆AB的内力分别记为和。
结构力学第九章薄壁杆件扭转 28页

§9-2 薄壁杆件的自由扭转
作业2、3、5
考试
考试题型: (1)选择填空 (2)判断题(不要解释理由,只要判断对错)
以上两项共54分,可能会增加题量,减小每题的分值 (3)计算题(基本运算)46分 计算题比作业题目简单,运算量小 重点在后面章节,与材料力学重复率低的章节 试验报告+作业=平时分 考试时计算题先把关键公式写下
§9-1 概述
§9-1 概述
§9-1 概述
§9-1 概述
§9-1 概述
如果薄壁杆件受到扭矩作用,由于存在支座或其 他约束,扭转时不能自由变形,则这种扭转称为约束 扭转。薄壁杆件约束扭转时,各横截面的翘曲程度是 不相同的,这将引起相邻两截面间纵向纤维的长度改 变,于是横截面上除了有扭转而引起的剪应力之外, 还有因翘曲而产生的正应力。由于翘曲正应力在横截 面上分布不均匀,就会导致薄壁杆件发生弯曲,并伴 随产生弯曲剪应力。这样,薄壁杆件约束扭转时,截 面上就存在二次剪应力。二次剪应力又将在截面上形 成一个附加扭矩,称之为二次扭矩,于是杆件截面上 的扭矩就等于自由扭转扭矩与二次扭矩之和。由此可 见,薄壁杆件约束扭转是比较复杂的。
壁截面(图9-1a,b,c)和闭口薄壁截面(图9-1d,e,f)
两类。闭口截面又分为单闭室(图9-1d,e)和多闭室
(图9-1f)两种。
§9-1 概述
除薄壁圆管外,薄壁杆件通常是非圆截面杆件。 材料力学中已经指出,非圆截面杆件在扭转变形后, 杆件的截面已不再保持为平面,而是变为曲面,这种 现象称为翘曲。
qds dA o
x tb b
a ta
b ds
dx
§9-2 薄壁杆件的自由扭转
btb atad x 0
或
qbtbata (9-7)
结构力学作业参考-知识归纳整理

知识归纳整理结构力学课程作业答案第一章 绪论1、按照不同的构造特征和受力特点,平面杆件结构可分为哪几类?平面杆件结构根据其组成特征和受理特点可以分成如下几种类型梁、(刚架) 、( 桁架)、拱以及组合结构。
2、何为静定结构和超静定结构?从几何构造分析的角度看,结构必须是几何不变体系。
根据多余约束 n ,几何不变体系又分为: 有多余约束( n > 0)的几何不变体系——超静定结构;无多余约束( n = 0)的几何不变体系——静定结构。
从求解内力和反力的想法也可以以为:静定结构:凡只需要利用静力平衡条件就能计算出结构的全部支座反力和杆件内力的结构。
超静定结构:若结构的全部支座反力和杆件内力,不能惟独静力平衡条件来确定的结构。
3、土建、水利等工程中的荷载,根据其不同的特征,主要有哪些分类?第二章 平面结构的几何组成分析作业题:1、何为平面体系的几何组成分析?按照机械运动及几何学的观点,对平面结构或体系的组成事情举行分析,称为平面体 系的几何组成分析。
2、何为几何不变体系?何为几何可变体系?几何不变体系—若不思量材料的应变,体系的位置和形状不会改变。
几何可变体系—若不思量材料的应变,体系的位置和形状是可以改变的。
3、几何组成分析的目的是什么?1)保证结构的几何不变性,以确保结构能承受荷载和维持体系平衡.2)判别某一体系是否为几何不变,从而决定它能否作为结构.3)研究几何不变体系的组成规则,以保证所设计的结构是几何不变体系,从而能承受荷载而维持平衡.4)根据体系的几何组成分析,正确区分静定结构和超静定结构,从而挑选适当的计算想法进行结构的反力和内力计算.5)经过几何组成分析,明确结构的构成特点,从而挑选结构受力分析的顺序以简化计算.4、何为一具体系的自由度?知悉体系计算自由度的公式。
求知若饥,虚心若愚。
5、试对下图所示体系举行几何组成分析。
1图图3图4 6、试求图示各体系的计算自由度数W。
千里之行,始于足下。
李廉锟《结构力学》笔记和课后习题(含考研真题)详解-第9章 渐近法【圣才出品】

9.1 复习笔记【知识框架】【重点难点归纳】一、力矩分配法(见表9-1-1) ★★★★图9-1-1二、无剪力分配法(见表9-1-2) ★★表9-1-2 无剪力分配法表9-1-3 剪力分配法9.2 课后习题详解复习思考题1.什么是转动刚度?什么是分配系数?为什么一刚结点处各杆端的分配系数之和等于1?答:(1)转动刚度的定义杆端的转动刚度是指当杆件的近端转动单位角时,在该近端产生的弯矩。
(2)分配系数的定义分配系数是指结点某一杆端的劲度系数与该结点处所有杆端的劲度系数的比值。
(3)刚结点处各杆端的分配系数之和等于1的原因:因为分配系数的计算公式,在刚节点处各杆端分配系数之和应为1ijij n ijj S Sμ==∑111n ij j ij n ijj SSμ====∑∑2.单跨超静定梁的劲度系数和传递系数与杆件的线刚度有何关系?答:单跨超静定梁的劲度系数不仅与杆件线刚度i=EI/l相关,而且与杆件另一端(又称远端)的支承情况有关;传递系数与杆件的线刚度无关,只与远端支承形式有关。
3.图9-2-1所示三个单跨梁,仅B端约束不同。
它们的劲度系数S AB和传递系数C AB 是否相同,为什么?图9-2-1答:不考虑杆件轴向变形,(a)、(b)、(c)三个单跨梁的劲度系数均相同,即S AB=4i,其中i为杆件的线刚度;(a)、(b)、(c)三个图的传递系数均相同,即C AB=0.5。
因为虽然B端约束表面上形式各异,但在不考虑杆件轴向变形的条件下,(a)、(b)、(c)三个单跨梁在B端的最终约束效果上均可以当成固定端来处理。
若考虑杆件轴向变形,(a)、(c)的劲度系数相同,(b)远端可在水平向自由收缩,A端转到相同的转角需要的力更小,因此劲度系数略小于(a)、(c)。
4.什么是不平衡力矩?如何计算不平衡力矩?为什么要将它反号才能进行分配?答:(1)不平衡力矩的定义不平衡力矩是指在附加约束结点处各固端弯矩所不能平衡的差额。
结构力学第九章习题及参考答案(7-12)

9-7试求图示等截面单跨梁的极限荷载。
梁的截面为矩形b ×h=5 cm×20 cm,s σ=235 Mpa 。
解 根据弯矩图形状,很容易判断,形成机构说,塑性铰出现在B 、D 两点,故()Pu u u 22u e Pu 11335cm 20cm 235MPa 4704kN F l M M M bh F l l l lσ-=⨯⨯====习题9-7图9-8试求图示等截面单跨梁的极限荷载。
解:梁变成机构时,任意截面的弯矩为3u23u u 11()66d ()110d 6231166M x qlx qx M l M x ql qx x x l M ql q M q l =--=-===--=9-9试求图示等截面超静定梁的极限荷载。
解: 第一跨变成机构时,()()11Pu u Pu u 181.56m 2(kN)49F M F M ⨯⨯==第二跨变成机构时,()()22Pu u Pu u 16m 1.5(kN)4F M F M ⨯⨯==极限弯矩为()2Pu Pu u (kN)F F M ==习题9-8图9-10试求图示等截面连续梁的极限弯矩。
解: 第一跨变成机构时,()211u u 1320kN/m 6m 60kNm 82M M ⨯⨯==()()()()()()()()()()2u11u u 211111u u u uu 1122u u 212u 11()22d ()1110d 221111112222211822361.92kNm 2xM x qlx qx M lM M x ql qx M x l x l qlM M M M ql l q l l M ql ql l ql M M ql ql M ql =--=--==-⎛⎫⎛⎫⎛⎫=----- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭=-+-== 第二跨变成机构时,()()()222u u 1120kN/m 6m 40kN 6m 275kNm 84M M ⨯⨯+⨯⨯==第三跨变成机构时,()()33u u 1332080kN 8m kNm 106.7kNm 423M M ⨯⨯=== 极限弯矩为()3u u 106.7kNm M M ==9-11试求图示阶形柱的极限荷载。
结构力学课后习题答案

习题及参考答案【习题2】【习题3】【习题4】【习题5】【习题6】【习题8】【习题9】【习题10】【习题11】【习题12】【习题13】【习题14】【参考答案】习题22-1~2-14试对图示体系进行几何组成分析,如果是具有多余联系的几何不变体系,则应指出多余联系的数目。
题2-1图题2-2图题2-3图题2-4图题2-5图题2-6图题2-7图题2-8图题2-9图题2-10图题2-11图题2-12图 题2-13图 题2-14图习题33-1 试作图示多跨静定梁的M 及Q 图。
(b)(a)20kN10kN40kN20kN/m40kN题3-1图3-2 试不计算反力而绘出梁的M 图。
(b)5kN/m40kN(a)题3-2图习题44-1 作图示刚架的M 、Q 、N 图。
(c)(b)(a)20kN /m2kN /m题4-1图4-2 作图示刚架的M 图。
P(e)(d)(a)(b)(c)20k N /m4kN题4-2图4-3 作图示三铰刚架的M 图。
(b)(a)题4-3图4-4 作图示刚架的M 图。
(a)题4-4图4-5 已知结构的M 图,试绘出荷载。
(b)(a)题4-5图4-6 检查下列刚架的M 图,并予以改正。
(e)(g)(h)P(d)(c)(a)(b)(f)题4-6图习题55-1 图示抛物线三铰拱轴线方程x x l l fy )(42-=,试求D 截面的内力。
题5-1图5-2 带拉杆拱,拱轴线方程x x l lfy )(42-=,求截面K 的弯矩。
C题5-2图 题5-3图5-3 试求图示带拉杆的半圆三铰拱截面K 的内力。
习题66-1 判定图示桁架中的零杆。
(c)(b)题6-1图6-2 用结点法计算图示桁架中各杆内力。
(b)题6-2 图6-3 用截面法计算图示桁架中指定各杆的内力。
(b)题6-3图6-4 试求图示组合结构中各链杆的轴力并作受弯杆件的M 、Q 图。
(a)题6-4图6-5 用适宜方法求桁架中指定杆内力。
(c)(b)(a)P题6-6图习题88-1 试作图示悬臂梁的反力V B 、M B 及内力Q C 、M C 的影响线。
结构力学第九章 薄壁杆件扭转

§9-2 薄壁杆件的自由扭转
沿整个截面积分可得总扭矩为:
M s 2qA
式中A——闭口截面壁厚中心线所围的总面积。从 而沿截面的剪流为:
Ms q t 2A
(9-8)
再来推导扭率和扭矩常数计算公式。若从薄壁杆 件中取出长度为dx的微段,其受扭矩Ms作用产生的扭 角为dφ,则扭矩所做的功为:求扭转惯性矩 剪流300400
§9-2 薄壁杆件的自由扭转
作业2、3、5
考试
考试题型: (1)选择填空 (2)判断题(不要解释理由,只要判断对错) 以上两项共54分,可能会增加题量,减小每题的分值 (3)计算题(基本运算)46分 计算题比作业题目简单,运算量小 重点在后面章节,与材料力学重复率低的章节 试验报告+作业=平时分 考试时计算题先把关键公式写下
q t
(9-6)
称q为剪流。现在来确定q沿截面的变化规律。图 9-3b所示的为一个变厚度单元,由于自由扭转时截面 上无正应力,即轴向力为零,所以有: y a (图9-3) a b ta ds h a b qds tb dA o x b ds
dx
§9-2 薄壁杆件的自由扭转
btb a ta dx 0
薄壁截面视其壁厚中心线是否封闭而分为开口薄 壁截面(图9-1a,b,c)和闭口薄壁截面(图9-1d,e,f) 两类。闭口截面又分为单闭室(图9-1d,e)和多闭室 (图9-1f)两种。
§9-1 概述
除薄壁圆管外,薄壁杆件通常是非圆截面杆件。 材料力学中已经指出,非圆截面杆件在扭转变形后, 杆件的截面已不再保持为平面,而是变为曲面,这种 现象称为翘曲。 薄壁杆件扭转分为自由扭转和约束扭转两种。 如果一根等截面杆件仅在两端受到扭矩作用,并 不受任何约束,扭转时可以自由变形,则这种扭转就 称为自由扭转。非圆截面薄壁杆件自由扭转时,其横 截面虽将发生翘曲,但由于扭转不受阻碍,所以各横 截面的翘曲程度都相同。因此,杆件上平行于杆轴的 直线在变形后长度不变且仍为直线;杆件各横截面上 没有正应力而只有扭转引起的剪应力。
结构力学课后习题答案

结构力学课后习题答案(总23页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--习题及参考答案【习题2】【习题3】【习题4】【习题5】【习题6】【习题8】【习题9】【习题10】【习题11】【习题12】【习题13】【习题14】【参考答案】习题22-1~2-14试对图示体系进行几何组成分析,如果是具有多余联系的几何不变体系,则应指出多余联系的数目。
题2-1图题2-2图题2-3图题2-4图题2-5图题2-6图题2-7图题2-8图题2-9图题2-10图题2-11图题2-12图 题2-13图 题2-14图习题33-1 试作图示多跨静定梁的M 及Q 图。
(b)(a)20kN10kN40kN20kN/m40kN题3-1图3-2 试不计算反力而绘出梁的M 图。
(b)5kN/m40kN(a)题3-2图习题44-1 作图示刚架的M 、Q 、N 图。
(c)(b)(a)/20kN /m2kN /m题4-1图4-2 作图示刚架的M 图。
P(e)(d)(a)(b)(c)20k N /m4kN题4-2图4-3 作图示三铰刚架的M 图。
(b)(a)题4-3图4-4 作图示刚架的M 图。
(a)题4-4图4-5 已知结构的M 图,试绘出荷载。
(b)(a)题4-5图4-6 检查下列刚架的M 图,并予以改正。
(e)(g)(h)P(d)(c)(a)(b)(f)题4-6图习题55-1 图示抛物线三铰拱轴线方程x x l lfy )(42-=,试求D 截面的内力。
题5-1图5-2 带拉杆拱,拱轴线方程x x l lf y )(42-=,求截面K 的弯矩。
C题5-2图 题5-3图5-3 试求图示带拉杆的半圆三铰拱截面K 的内力。
习题66-1 判定图示桁架中的零杆。
(c)(b)题6-1图6-2 用结点法计算图示桁架中各杆内力。
(b)题6-2 图6-3 用截面法计算图示桁架中指定各杆的内力。
(b)题6-3图6-4 试求图示组合结构中各链杆的轴力并作受弯杆件的M 、Q 图。
工程力学课后答案第9章

第9章平面体系的几何组成分析习题.【解】若上部结构与地基之间的连接比较多(N4),能够考虑先将上部结构中的某•刚片与地基连成一个大刚片。
然后,在考虑这个大刚片与上部其它杆件的连接。
本例中,上部结构与地基之间用4个约束连接。
杆件ABE与地基之间用钗A和一根不同过该絞的链杆B相连,组成几何不变体系,且没有多余约束。
所以,能够将杆件ABE与地基看成一个没有多余约束的大刚片。
杆件FCD用三根既不相互平行又不相交于一点的链杆(链杆EF、链杆C、链杆D)与这个大刚片相连,组成一个更大的几何不变体系,且没有多余约束。
杆件ABE与地基之间用平行链杆A和一根不同过该絞的链杆B相连,组成几何不变体系,且没有多余约束。
将杆件ABE与地基看成一个没有多余约束的大刚片。
杆件FCD用三根既不相互平行又不相交于一点的链杆(链杆EF、链杆C、链杆D)与这个大刚片相连,组成一个更大的几何不变体系,且没有多余约束。
-I*羡诊为习题(C)图若上部结构中有皎接三角形,能够考虑将这些三角形看成刚片,然后在进行分析。
刚片I与地基组成•个没有多余约束的大刚片。
这个大刚片与刚片II用三根既不相互平行又不相交于一点的链杆相连,组成一个更大的几何不变体系,且没有多余约束。
习题(d)图将扩大的三角形看成刚片。
先分析一部分:左边的刚片与地基组成一个大刚片ABCD。
增加二元体:在大刚片ABCD上增加二元体DE杆和链杆E,组成一个更大的刚片。
此刚片与刚片GH1F由三根延长线交于H点的链杆(杆件CG、杆件FE、链杆1)相连。
故,体系为瞬变体系。
若上部结构与地基之间用三个约束连接,且符合几何不变体系的组成规律,能够只分析上部结构。
上部结构的分析结论就是整个体系的分析结论。
若折杆只用两个较与其它物体相连,能够将折杆看成是连接两个钗的直杆。
去掉二元体。
剩下部分为两个刚片用两个钗连接,为几何不变体系,且有一个多余约束。
故,整体体系也为几何不变体系,且有一个多余约束。
结构力学题库第九章力矩分配法习题解答

1、清华5-6 试用力矩分配法计算图示连续梁,并画其弯矩图和剪力图。
C清华V图M(kN解:(1)计算分配系数:320.632440.4324BABABA BCBCBCBA BCs is s i is is s i iμμ⨯===+⨯+⨯⨯===+⨯+⨯(2)计算固端弯矩:固端弯矩仅由非结点荷载产生,结点外力偶不引起固端弯矩,结点外力偶逆时针为正直接进行分配。
3360667.51616FABFBAMPlM=⨯⨯===⋅kN m(3)分配与传递,计算列如表格。
(4)叠加固端弯矩和分配弯矩或传递弯矩,得各杆端的最后弯矩,作弯矩图如图所示。
(5)根据弯矩图作剪力图如图所示。
0153027.60153032.63517.58.756AB BA AB AB AB BA BA BA BC CB BC CB M M V V l M M V V l M M V V l ++=-=-=++=-=--=+--==-=-=5kN 5kN kN2、利用力矩分配法计算连续梁,并画其弯矩图和剪力图。
4m1m2m2m原结构简化结构·解:(1)计算分配系数:,4,34BA BC BA BC EIi i i S i S i =====令 430.4290.5714343BC BA BA BC BA BC BA BC s s iis s i is s i iμμ======++++(2)计算固端弯矩:CD 杆段剪力和弯矩是静定的,利用截面法将外伸段从C 处切开,让剪力直接通过支承链杆传给地基,而弯矩暴露成为BC 段的外力偶矩,将在远端引起B 、C 固端弯矩。
22204101088154102020828F FAB BA F F BCCB Pl M M ql m M M ⨯=-=-=-⋅⋅⨯=-+=-+=-⋅=⋅kN m,=kN m kN m,kN m(3)分配与传递,计算列如表格。
(4)叠加固端弯矩和分配弯矩或传递弯矩,得各杆端的最后弯矩,作弯矩图如图所示。
结构力学章节习题及参考答案
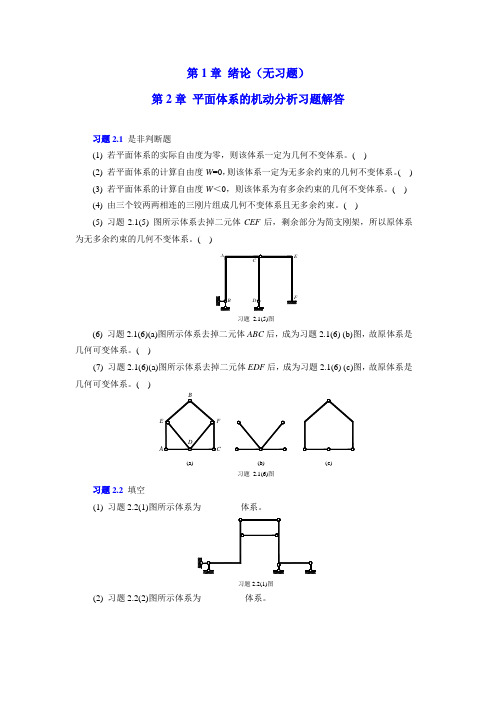
第1章绪论(无习题)第2章平面体系的机动分析习题解答习题2.1是非判断题(1) 若平面体系的实际自由度为零,则该体系一定为几何不变体系。
( )(2) 若平面体系的计算自由度W=0,则该体系一定为无多余约束的几何不变体系。
( )(3) 若平面体系的计算自由度W<0,则该体系为有多余约束的几何不变体系。
( )(4) 由三个铰两两相连的三刚片组成几何不变体系且无多余约束。
( )(5) 习题2.1(5) 图所示体系去掉二元体CEF后,剩余部分为简支刚架,所以原体系为无多余约束的几何不变体系。
( )习题2.1(5)图(6) 习题2.1(6)(a)图所示体系去掉二元体ABC后,成为习题2.1(6) (b)图,故原体系是几何可变体系。
( )(7) 习题2.1(6)(a)图所示体系去掉二元体EDF后,成为习题2.1(6) (c)图,故原体系是几何可变体系。
()(a)(b)(c)习题2.1(6)图习题2.2填空(1) 习题2.2(1)图所示体系为_________体系。
习题2.2(1)图(2) 习题2.2(2)图所示体系为__________体系。
习题2-2(2)图(3) 习题 2.2(3)图所示4个体系的多余约束数目分别为_______、________、__________、__________。
习题2.2(3)图(4) 习题2.2(4)图所示体系的多余约束个数为___________。
习题2.2(4)图(5) 习题2.2(5)图所示体系的多余约束个数为___________。
习题2.2(5)图(6) 习题2.2(6)图所示体系为_________体系,有_________个多余约束。
习题2.2(6)图(7) 习题2.2(7)图所示体系为_________体系,有_________个多余约束。
习题2.2(7)图习题2.3对习题2.3图所示各体系进行几何组成分析。
(a)(b)(c)(d)(e)(f)(h)(g)(i)(j)(k)(l)习题2.3图第3章 静定梁与静定刚架习题解答习题3.1 是非判断题(1) 在使用内力图特征绘制某受弯杆段的弯矩图时,必须先求出该杆段两端的端弯矩。
结构力学1-9章答案
①中无弯矩。
②取半结构:
基本结构为:
M图整体结构M图
(b)
(c)
解:根据对称性,考虑1/4结构:
基本结构为:
1
1
M
(d)
解:取1/4结构:
q
基本结构为:
q
X2
X1
1
1
1 1
M
(e)
(f)
(BEH杆弯曲刚度为2EI,其余各杆为EI)
取1/2结构:
= +
①②②中弯矩为0。
考虑①:反对称荷载作用下,取半结构如下:
解:基本结构为:
(c)
解:基本结构为:
(d)
解:基本结构为:
6-6试用力法求解图示超静定桁架,并计算1、2杆的内力。设各杆的EA均相同。
(a) (b)
题6-6图
6-7试用力法计算图示组合结构,求出链杆轴力并绘出M图。
(a)
解:基本结构为:
(b)
6-8试利用对称性计算图示结构,并绘出M图。
(a)
解:
原结构= +
同济大学朱慈勉结构力学第3章习题答案
3-2试作图示多跨静定梁的弯矩图和剪力图。
(a)
(b)
(c)
(d)
3-3试作图示刚架的内力图。
(a)
(b)
(c)
(d)
(e)
(f)
3-4试找出下列各弯矩图形的错误之处,并加以改正。
(a)
(b)
(c)
(d)
(e)
(f)
3-5试按图示梁的BC跨跨中截面的弯矩与截面B和C的弯矩绝对值都相等的条件,确定E、F两铰的位置。
(5)结构刚度方程
解得:
8-8试利用对称性用先处理法分析图示刚架并作出M、FQ图。忽略杆件的轴向变形。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
截面
DA
AD
AB
BA
BE
分配 系数 固端 弯矩
0.333
0.667
0.4
0.2
第一次
12←
24
12
第二次 -2←
-4
-8
→-4
第三次
0.8←
1.6
0.8
第四次 -0.13← -0.26
-0.54 →-0.27
第五次
0.05←
0.11
0.05
最终 弯矩
-2.13
-0.02 -4.28
-0.03 4.28
1/4 结构
3
华南农业大学 水利与土木工程学院(College of water conservancy and Civil Engineering, SCAU)
9-12 试计算图示空腹梁弯矩,绘制 M 图。 E = 常数
解:
截面
AB
BA
BC
CB
CD
CE
EC
分配 系数 固端 弯矩
0.856
0.143
0.143
0.856
0
1
1
0
1
第一次
0.286← -0.286 -1.714
0
第二次
-1.101 -0.185 →-0.185
第三次
0.026
0.159
0
第四次
最终
弯矩
-1.101
1.101
0.555 -1.555
1
注:表中弯矩× Fl 12
1/4 结构
4
0.0588 -18.75
第一次
-1.47←
1.47
第二次
18.96
1.26
→-1.26
第三次
-0.07←0.07 19.03
0 -19.03
-18.47
CD 0.8824 22.06
1.11 23.17
CE 0.0588 -6.25 1.47
0.07
-4.7
EC
-6.25 →-1.47 →-0.07 -7.79
EF FE
0.6
-4
4
0.8 →0.4
0.62 →0.31
0.06 →0.03 2.52 4.71
1
华南农业大学 水利与土木工程学院(College of water conservancy and Civil Engineering, SCAU)
9-6 试用力矩分配法计算图示刚架,绘制 M 图。 E = 常数
3
-8
8 -5.33 2.69
2.64 2.36 →1.18 0.27← 0.53
-1.03
→
←
-2.06 -2.06 -1.03
0.54 0.49 →0.24 0.22← 0.41
-0.11 ←
-0.22
-0.22
→ -0.11
0.06 0.05
0.05
6.24 -6.24 7.14 -7.12 2.54
→-0.02 21.42
12.85
BC 0.4 -60 24
1.6
0.11
-34.29
CB 60 →12 →0.8
72.8
2
结构力学 第九章 习题 参考答案
9-12 试计算图示空腹梁弯矩,绘制 M 图。 E = 常数
解:
截面
AB
BA
BC
CB
分配 系数 固端 弯矩
0.9375
0.0625 -18.75
结构力学 第九章 习题 参考答案
结构力学 第九章习题 参考答案
TANG Gui-he
9-4 图示连续梁 EI = 常数 ,试用力矩分配法计算其杆端弯矩,绘制 M 图。
解:
截面 A BA BC
分配 系数 固端 弯矩
6 -6
第一次
第二次
第三次
第四次
最终
弯矩 0 6
-6
CB CD DC DE ED
0.529 0.471 0.5 0.5 0.4
