相交线与平行线测试题
平行线与相交线单元测试题

平行线与相交线单元测试题一、选择题(每题2分,共10分)1. 平行线的定义是什么?A. 永远不会相交的直线B. 相交于一点的直线C. 垂直于同一条直线的直线D. 相交于一个点但角度不同的直线2. 如果两条直线相交,它们的角度和是多少度?A. 90度B. 180度C. 360度D. 45度3. 以下哪项不是平行线的性质?A. 平行线在任何地方都不相交B. 平行线之间的距离处处相等C. 平行线可以相交D. 通过平行线之一可以画出无数条平行线4. 两条平行线被第三条直线所截,所形成的内错角的特点是?A. 内错角相等B. 内错角互补C. 内错角和为90度D. 内错角和为180度5. 同位角的定义是什么?A. 两条平行线被第三条直线所截,同侧的角B. 两条直线相交形成的角C. 两条平行线被第三条直线所截,异侧的角D. 两条直线相交形成的同侧角二、填空题(每题2分,共10分)6. 当两条直线相交时,它们形成的角中,____角相等。
7. 如果两条直线相交,且其中一个角是90度,则这两条直线是____。
8. 平行线之间的距离在任何地方都是____。
9. 两条平行线被第三条直线所截,同旁内角的和是____。
10. 如果两条直线相交,且其中一个角是锐角,则这个角的对顶角是____。
三、判断题(每题1分,共5分)11. 平行线永远不会相交。
()12. 垂直线是相交线的一种特殊形式。
()13. 两条平行线之间的夹角总是90度。
()14. 同旁内角互补,即它们的和为180度。
()15. 如果两条直线相交形成的角是钝角,那么这个角的对顶角是锐角。
()四、简答题(每题5分,共10分)16. 解释什么是“对应角”,并给出一个例子。
17. 描述如何使用三角板来测量两条直线是否平行。
五、计算题(每题5分,共10分)18. 如果两条平行线被一条直线所截,形成的内错角分别为40度和140度,请计算同旁内角的度数。
19. 在一个直角三角形中,如果一个锐角是30度,求另一个锐角的度数。
相交线与平行线单元测试题(含答案)

相交线与平行线一、选择题(本大题共8小题,每小题只有一个正确选项,每小题3分,共24分)1.在下面各图中,∠1与∠2是对顶角的是()A.B.C.D.2.如图,直线a、b相交于点O,若∠1=30°,则∠2等于()A.60°B.30°C.140°D.150°3.如图,直线a,b相交于点O,若∠1=40°,则∠2=()A.40°B.50°C.60°D.140°4.如图,点P在直线l外,点A,B在直线l上,PA=3,PB=7,点P到直线l的距离可能是()A.2 B.4 C.7 D.85.如图,直线a∥b,∠1=50°,则∠2的度数为()A.40°B.50°C.55°D.60°6.如图,工人师傅用角尺画出工件边缘AB的垂线a和b,得到a∥b.理由是()A.连接直线外一点与直线上各点的所有线段中,垂线段最短B.在同一平面内,垂直于同一条直线的两条直线互相平行C.在同一平面内,过一点有一条而且仅有一条直线垂直于已知直线D.经过直线外一点,有且只有一条直线与这条直线平行7.如图,已知ON丄a,OM丄a,所以OM与ON重合的理由是()A.两点确定一条直线B.经过一点有且只有一条线段垂直于己知直线C.过一点只能作一条垂线D.垂线段最短8.如图,直线AB∥CD,∠A=70°,∠E=30°,则∠C等于()A.30°B.40°C.60°D.70°二、填空题(本大题共6小题,每小题3分,共18分)9.如图所示,在铁路旁边有一李庄,现要建一火车站,为了使李庄人乘火车最方便(即距离最近),请你在铁路旁选一点来建火车站(位置已选好),说明理由:.10.如图,已知O是直线AB上一点,∠1=30°,OD平分∠BOC,则∠2=.11.如图,直线AB、CD相交于点O,EO⊥AB,∠AOC=25°。
七年级下册地理相交线和平行线测试题

七年级下册地理相交线和平行线测试题一、选择题1. 在地理上,经线是指连接 __A__。
A. 两极的虚线B. 东西两极的实线C. 东西之间的实线D. 东北、东南、西北、西南之间的实线2. 下列哪些线是地图上的纵线 __C__。
A. 赤道线B. 天空线C. 经线D. 纬线3. 世界由多少个纬线构成 __B__。
A. 1个B. 180个C. 360个D. 720个4. 经线和纬线在地球上形成了一种 __D__。
A. 直线关系B. 弧线关系C. 分叉关系D. 网格关系5. 在地理上,纬线是指连接 __C__。
A. 北极的实线B. 南极的虚线C. 东西两极的实线D. 东西之间的实线二、判断题1. 世界地图上的纬线和经线是相交的。
__X__2. 纬线是指连接东西两极的线。
__X__3. 地图上的经线比纬线多。
__X__三、填空题1. 地理上经线的最大称号是 __经线的圈__2. 纬线的最大称号是 __纬线的圈__四、简答题1. 解释纬线和经线的作用。
答:纬线和经线在地理上主要用来确定地球的位置和导航。
纬线垂直于经线,横跨地球表面,并表示地球表面的纬度。
纬线以赤道为基准,南北分布,帮助人们确定地球上不同地区的纬度。
而经线则是连接地球两极的线,纵向分布,辅助人们确定地球上不同地点的经度。
2. 世界地图上的纬线和经线为什么被称为相交线和平行线?答:纬线和经线在地球上形成了网格状的关系。
纬线相互平行,以赤道为基准,平行地包围着地球。
而经线则从一个极点穿过另一个极点,在地球上形成相交的关系。
这种相交和平行的关系使纬线和经线分别被称为相交线和平行线。
人教版数学七年级下册 第五章《相交线与平行线》测试试题(含答案)

第五章《相交线与平行线》测试题一、单选题(每小题只有一个正确答案)1.在下图中,∠1,∠2是对顶角的图形是( )A .B .C .D .2.已知1∠与2∠互为补角,1120∠=︒,则2∠的余角的度数为( )A .30°B .40︒C .60︒D .120︒3.如图,不能判断12//l l 的条件是( )A .13∠=∠B .24180∠+∠=︒C .45∠=∠D .23∠∠=4.下列图案中,可以利用平移来设计的图案是( )A .B .C .D .5.如图所示,有下列五种说法:①∠1和∠4是同位角;②∠3和∠5是内错角;③∠2和∠6旁内角;④∠5和∠2是同位角;⑤<1和∠3是同旁内角;其中正确的是( )A .①②③④B .①②③④C .①②③④⑤D .①②④⑤6.如图,点E 在AD 的延长线上,下列条件中能判断BC∥AD 的是( )A .∠3=∠4B .∠A +∠ADC =180° C .∠1=∠2D .∠A =∠57.如图,计划把河水引到水池A 中,可以先引AB ⊥CD ,垂足为B ,然后沿AB 开渠,则能使所开的渠最短,这样设计的依据是( )A .垂线段最短B .两点之间,线段最短C .两点确定一条直线D .两点之间,直线最短8.如图,已知AB CD ∥,BE 平分ABC ∠,150CDE ∠=︒,则C ∠=( )A .105︒B .120︒C .130︒D .150︒9.命题:①对顶角相等;②垂直于同一条直线的两条直线平行;③相等的角是对顶角;④同位角相等.其中错误的有( )A .1个B .2个C .3个D .4个10.如图,若∠1=∠2,则下列选项中可以判定AB ∥CD 的是( )A .B .C .D .11.将一个矩形纸片按如图所示折叠,若∠1=40°,则∠2的度数是( )A .40°B .50°C .60°D .70°12.如图,若AB∥CD,CD∥EF,那么∠BCE=( )A .∠1+∠2B .∠2-∠1C .180°-∠1+∠2D .180°-∠2+∠1二、填空题13.如图,直线,AB CD 相交于点O ,OA 平分EOC ∠,:2:3EOC EOD ∠∠=,则BOD ∠=________°.14.如图,直线AB 、CD 相交于点O ,OE AB ⊥于点O ,且50COE ∠=︒,则BOD ∠=________.15.小泽在课桌上摆放了一副三角板,如图所示,得到________∥________,依据是________.16.如图,一条公路两次转弯后,和原来的方向相同.如果第一次的拐角∠A 的度数为130°,第二次拐角∠B 的度数为______.三、解答题17.如图,1∠和2∠互为补角,A D ∠=∠,求证://AB CD .请根据条件进行推理,得出结论,并在括号内注明理由.证明:∵1∠和2∠互为补角(已知),∴12180∠+∠=︒(补角定义).又1CGD ∠=∠( ),∴2180CGD ∠+∠=︒(等量代换).∴//AE ( ).又∵A D ∠=∠(已知),∴D ∠=∠ .( )∴//AB CD .( ).18.如图,OA ⊥OB ,OC ⊥OD ,∠BOC =28°,求∠AOD 的度数.19.已知:如图,在△ABC 中,CD ⊥AB 于点D ,E 是AC 上一点且∠1+∠2=90°.求证:DE ∥BC .20.如图,∠ADC=∠ABC,BE 、DF 分别平分∠ABC、∠ADC、且∠1=∠2.(1)求证:AB∥CD.(2)求证:∠A=∠C.21.如图,已知,A ADE C E ∠=∠∠=∠.(1)若3,EDC C ∠=∠求C ∠的度数;(2)求证://BE CD .22.如图所示,已知//,80,140AB DE ABC CDE ︒︒∠=∠=,求BCD ∠的度数.23.如图,已知∠A = ∠C,∠E=∠F,试说明AB∥CD.参考答案1.B2.A3.D4.D5.D6.C7.A8.B9.C10.D11.D12.D13.36 14.40︒ 15.AC ∥DF 内错角相等 两直线平行 16.130°17. 证明:∵1∠和2∠互为补角(已知),∴12180∠+∠=︒(补角定义).又1CGD ∠=∠( 对顶角相等 ),∴2180CGD ∠+∠=︒(等量代换).∴//AE FD ( 同旁内角互补,两直线平行 ).又∵A D ∠=∠(已知),∴D ∠=∠ BFD .( 两直线平行,同位角相等 )∴//AB CD .( 内错角相等,量直线平行 ).18. 解:∵OC ⊥OD ,∠BOC =28°,∴∠BOD =90BOC ︒-∠=62°,∵OA ⊥OB ,∴∠AOB =90°,∴∠AOD =∠BOD +∠AOB =62°+90°=152°.19. 解:证明:∵CD ⊥AB (已知),∴∠1+∠3=90°(垂直定义).∵∠1+∠2=90°(已知),∴∠3=∠2(同角的余角相等).∴DE ∥BC (内错角相等,两直线平行).20. 证明:(1)∵BE、DF 平分∠ABC、∠ADC ∴112322ABC ADC ,∠=∠∠=∠ ∵∠ABC=∠ADC,∴∠2=∠3∵∠1=∠2,∴∠1=∠3,∴AB∥CD;(2)由(1)得AB∥CD∴∠A+∠ADC=180°,∠C+∠ABC=180°∵∠ADC=∠ABC,∴∠A=∠C.21.解:(1)A ADE∠=∠Q,∴,//ED AC∴∠+∠=︒.180EDC CQ,∠=∠EDC C3∴∠+∠=︒,3180C C∴∠=︒;45C(2)A ADE∠=∠Q,∴,//ED AC∴∠=∠.ABE E∠=∠Q,C E∴∠=∠,ABE C∴.//BE CD22.解:延长ED交BC于M.因为AB∥DE,∠ABC=80°,所以∠BMD=∠ABC=80°,因为∠CDE =140°,所以∠MDC=180°-140°=40°.在△CDM中,∠BMD=∠C+∠MDC,所以∠BCD =∠BMD-∠MDC=80°-40°=40°.23.证明:∵∠E=∠F,∴AE∥CF,∴∠A=∠ABF,∵∠A=∠C,∴∠ABF=∠C,∴AB∥CD.。
相交线与平行线单元测试题含答案

相交线与平行线单元测试题含答案相交线与平行线单元测试题一、选择题1、下列说法正确的是() A. 相交的两条直线一定有一个交点 B. 同位角相等 C. 两直线平行,对角线一定相等 D. 相等的两个角一定是对顶角2、以下不能说明直线AB与CD平行的是() A. AB//CD,A与B在同一方向,C与D在同一方向 B. $\angle 3 = \angle 4$ C. $\angle A = \angle C$ D. $\angle A + \angle B = 180^{\circ}$,$\angleC + \angleD = 180^{\circ}$3、下列说法正确的是() A. 过一点有且只有一条直线与已知直线平行 B. 两直线平行,同位角相等 C. 内错角相等,两直线平行 D. 如果两条直线都与第三条直线平行,那么这两条直线也互相平行4、下列说法正确的是() A. 两条直线被第三条直线所截,同位角相等 B. 相等的两个角是对顶角 C. 两直线平行,同旁内角互补 D. 互补的两个角不一定是邻补角5、下列说法正确的是() A. 同位角相等 B. 互补的角是邻补角 C. 两直线平行,同旁内角相等 D. 两直线平行,内错角相等二、填空题1、同一平面内,如果两条直线都与第三条直线平行,那么这两条直线互相________,简述为________.2、两直线平行,同位角________;两直线平行,内错角________;两直线平行,同旁内角________.3、两条直线的位置关系有________、________.4、若三条直线两两相交,则共有________个交点.5、在同一平面内,若两直线都垂直于第三条直线,那么这两条直线________.6、如图所示,若$\angle A + \angle B = 180^{\circ}$,$\angle A = \angle D$,则$\angle B =$________.7、如图所示,若$\angle A = \angle B$,则$\angle C =$________.8、如图所示,若$\angle A + \angle B = 90^{\circ}$,$\angle B + \angle C = 90^{\circ}$,则$\angle A =$________.9、若一个角的两边分别和另一个角的两边分别平行,则这两个角的关系是________.10、如图所示,若AB//CD,则$\angle A + \angle B + \angle C=$________.三、解答题1、已知两条平行线被第三条直线所截,则形成的同位角的数量是多少?这些同位角还具有什么性质?2、利用所给图形探究规律。
人教版七年级数学下册第五章相交线与平行线单元检测卷(共6套)
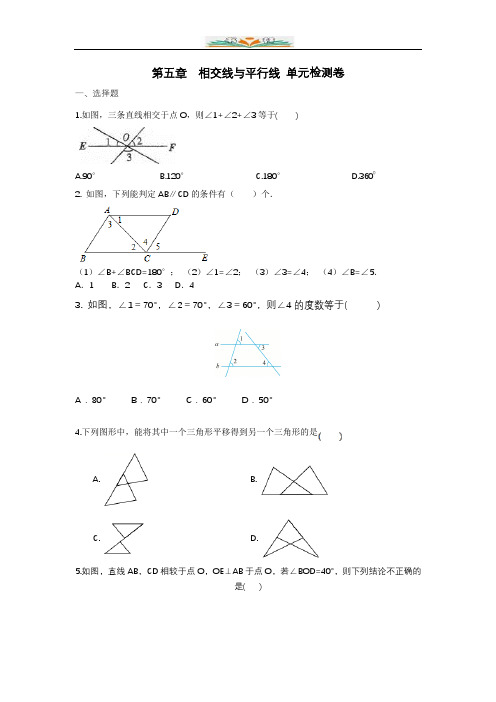
第五章相交线与平行线单元检测卷一、选择题1.如图,三条直线相交于点O,则∠1+∠2+∠3等于( )A.90°B.120°C.180°D.36002. 如图,下列能判定AB∥CD的条件有()个.(1)∠B+∠BCD=180°;(2)∠1=∠2;(3)∠3=∠4;(4)∠B=∠5.A.1 B.2 C.3 D.43. 如图,∠1=70°,∠2=70°,∠3=60°,则∠4的度数等于( )A.80°B.70°C.60°D.50°4.下列图形中,能将其中一个三角形平移得到另一个三角形的是A. B.C. D.5.如图,直线AB,CD相较于点O,OE⊥AB于点O,若∠BOD=40°,则下列结论不正确的是( )A.∠AOC=40°B.∠COE=130°C.∠EOD=40°D.∠BOE=90°6.如图,直线a,b被c,d所截,且a∥b,则下列结论中正确的是( )A.∠1=∠2 C.∠3+∠4=180°B.∠3=∠4 D.∠1+∠4=180°7.如图,点A在直线BG上,AD∥BC,AE平分∠GAD,若∠CBA=80°,则( )A.60°B.50°C.40°D.30°8.下列各图中,∠1与∠2互为邻补角的是( )9.对于图中标记的各角,下列条件能推理得到a∥b的是()A.∠1=∠2 B.∠2=∠4 C.∠3=∠4 D.∠1+∠4=18010.下列说法正确的是( )A.一个角的补角一定比这个角大B.一个角的余角一定比这个角小C.一对对顶角的两条角平分线必在同一条直线上D.有公共顶点并且相等的两个角是对顶角二、填空题11.如图,直线AB,CD相交于点O, EO⊥AB于点O,∠EOD=50°,则∠BOC的度数为______.12. 如图是由五个形状、大小完全相同的三角形组成的图案,三角形的三个角分别为36°,72°,72°,则图中共有_____对平行线.13.如图,,则的度数等于14.如图,点0是直线AB上一点平分,图中与互余的角有______ .图中与互补的角有______ .15. 说明命题“x>-4,则x2>16”是假命题的一个反例可以是x=____________.16.如图,现要从村庄A修建一条连接公路PQ的最短小路,过点A作AH⊥PQ于点H,沿AH修建公路,则这样做的理由是三、解答题17.如图,直线AB,CD 相交于点O,∠AOD=3∠BOD+20°.(1)求∠BOD的度数;(2)以O为端点引射线OE,OF ,射线OE平分∠BOD,且∠EOF= 90°,求∠BOF的度数.18.已知:如图,AB∥CD,∠1=∠2,∠3=∠4.(1)求证:AD∥BE;(2)若∠B=∠3=2∠2,求∠D的度数.19.如图,D,E,F是线段AB的四等分点.(1)过点D画DH∥BC交于点H,过点E画EG∥BC交AC于点G,过点F画FM∥BC交AC 于点M;(2)量出线段AH,HG,GM,MC的长度,你有什么发现?(3)量出线段HD,EG,FM,BC的长度,你又有什么发现?20.请写出命题“两直线平行,同位角相等”的题设和结论:题设:,结论:.21.观察下图,寻找对顶角:(1)如图1,图中共有对对顶角(2)如图2,图中共有对对顶角(3)如图3,图中共有对对顶角(4)若有n条直线相交于一点,则可形成多少对对顶角?22.如图,已知直线AB∥DF,∠D+∠B=180°.(1)试说明DE∥BC;(2)若∠AMD=75°,求∠AGC的度数.【若缺失公式、图片现象属于系统读取不成功,文档内容齐全完整,请放心下载。
相交线与平行线测试题

相交线与平行线测试题一、选择题1. 以下哪一条不是相交线的特征?A. 相交线在平面内相交于一点B. 相交线可以是曲线C. 相交线相交后形成4个角D. 相交线相交后,对角线相等2. 平行线的定义是什么?A. 永远不会相交的直线B. 相交于一点但不是直线C. 相交于两点的直线D. 永远不会相交的曲线3. 以下哪个条件不能保证两直线平行?A. 同位角相等B. 内错角相等C. 同旁内角互补D. 两条直线相交4. 如果两条直线相交,它们可以形成多少个角?A. 1个B. 2个C. 4个D. 无数个5. 平行线的性质中,以下哪一项是错误的?A. 平行线之间的距离处处相等B. 平行线永远不会相交C. 平行线可以是曲线D. 平行线相交于无穷远处二、填空题6. 两条直线相交所形成的角中,如果两个角是内错角,那么这两个角的关系是________。
7. 如果两条直线相交,其中一个角是锐角,那么它的对角是________。
8. 平行线的性质之一是,如果两条平行线被一条横截线所截,那么同位角相等,内错角相等,同旁内角的和为________。
9. 两条平行线之间的距离是指________。
10. 如果两条直线是平行的,那么它们之间的夹角是________。
三、简答题11. 解释“内错角”和“同旁内角”的定义,并给出它们在平行线中的性质。
12. 描述如何使用“同位角”来证明两条直线是平行的。
13. 如果两条直线相交,它们形成的角有哪些可能的组合?请列举所有情况。
四、计算题14. 在平面直角坐标系中,直线L1的方程为 y = 2x + 3,直线L2的方程为 y = -x + 5。
求这两条直线的交点坐标。
15. 如果两条平行线在y轴上的距离为5,且一条直线的方程为 y =3x + 7,求另一条平行线的方程。
五、证明题16. 给定两条直线AB和CD,已知AB平行于CD,且AB与CD之间的距离为10。
如果AB上的点E到CD的距离为8,求点E到与AB平行且与CD相交的直线的距离。
相交线与平行线经典测试题含答案

【点睛】
本题综合考查了平行线的判定及性质.
5.如图,AB∥CD,AE平分∠CAB交CD于点E,若∠C=50°,则∠AED=()
A.65°B.115°C.125°D.130°
【答案】B
【解析】
试题分析:∵AB∥CD,∴∠C+∠CAB=180°,∵∠C=50°,∴∠CAB=180°﹣50°=130°,∵AE平分∠CAB,∴∠EAB=65°,∵AB∥CD,∴∠EAB+∠AED=180°,∴∠AED=180°﹣65°=115°,故选B.
∴∠1=60°,
故选:B.
【点睛】
此题考查平行线的性质,三角板的知识,熟记性质是解题的关键.
8.如图, , ,则 ()
A. B. C. D.
【答案】C
【解析】
【分析】
首先证明a∥b,再根据两直线平行同位角相等可得∠3=∠6,再根据对顶角相等可得∠4.
【详解】
解:∵∠1+∠5=180°,∠1+∠2=180°,
B、∵∠3=∠4,∴AB∥CD(内错角相等,两直线平行),故B能判断;
C、∵∠ABD=∠BDC,∴AB∥CD(内错角相等,两直线平行),故C能判断;
D、∵∠ABC+∠BCD=180°,∴AB∥CD(同旁内角互补,两直线平行),故D能判断,
故选A.
【点睛】
本题考查了平行线的判定.掌握同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行是解题的关键.
【详解】
解:∵AB=AC,∠A=36°,
∴∠ABC=∠C=72°,
∵BD平分∠ABC,
∴∠ABD=∠DBC=36°,
∴∠BDC=180°﹣36°﹣72°=72°,
相交线与平行线单元测试题

相交线与平行线单元测试题一、选择题(每题2分,共20分)1. 下列说法中,正确的是:A. 经过直线外一点,有且只有一条直线与已知直线平行B. 经过直线外一点,有且只有一条直线与已知直线相交C. 经过直线外一点,可以画无数条直线与已知直线平行D. 经过直线外一点,可以画无数条直线与已知直线相交2. 如果两直线相交,那么它们相交所成的角是:A. 锐角B. 直角C. 钝角D. 任意角3. 两条直线被第三条直线所截,如果同侧的内错角相等,那么这两条直线:A. 平行B. 相交C. 垂直D. 无法判断4. 平行线的性质中,下列说法不正确的是:A. 平行线之间的距离处处相等B. 平行线永不相交C. 两条平行线可以确定一个平面D. 平行线之间的夹角是锐角5. 对于两条平行线,下列说法正确的是:A. 它们之间的距离在任何地方都是相同的B. 它们可以相交C. 它们之间的夹角可以是任意角D. 它们可以确定一个平面二、填空题(每题2分,共10分)6. 如果两条直线相交成直角,则称这两条直线互相______。
7. 两条直线相交,如果其中一个角是锐角,则其他三个角分别是______。
8. 平行线之间的距离是指______。
9. 两条直线相交所成的角中,最大的角是______。
10. 如果两条直线被第三条直线所截,那么内错角相等的条件是这两条直线______。
三、判断题(每题1分,共10分)11. 两条直线相交所成的角都是锐角。
()12. 平行线在任何地方的距离都是相等的。
()13. 两条直线相交,形成的对顶角相等。
()14. 两条平行线之间的夹角是直角。
()15. 如果两条直线被第三条直线所截,同位角相等,则这两条直线平行。
()四、简答题(每题5分,共20分)16. 解释什么是“同位角”、“内错角”和“同旁内角”,并说明它们在判断两条直线是否平行时的作用。
17. 描述如何使用直角三角板来检验两条直线是否平行。
18. 给出两条直线相交的几何图形,并说明如何确定它们相交所成的角的大小。
相交线与平行线测试题及答案

相交线与平行线测试题及答案1. 单选题:在平面上,两条互相垂直的直线称为()。
A. 平行线B. 垂直线C. 相交线D. 对称线答案:B. 垂直线2. 单选题:下面哪种说法是正确的?A. 平行线永远不会相交B. 相交线永远不会平行C. 平行线和相交线可以同时存在D. 平行线和相交线不能同时存在答案:C. 平行线和相交线可以同时存在3. 多选题:判断下列述句是否正确。
1) 平行线没有交点。
2) 相交线可以有无数个交点。
3) 两条垂直线的交点一定是直角。
A. 正确的有1)、2)、3)B. 正确的有1)、3)C. 正确的有2)、3)D. 正确的只有3)答案:B. 正确的有1)、3)4. 填空题:两条互相垂直的直线所成的角度为()度。
答案:90度5. 判断题:两条平行线的夹角为180度。
答案:错误6. 判断题:两条相交直线一定不平行。
答案:正确7. 计算题:已知直线L1与直线L2互相垂直,L1的斜率为2,过点(1,3)的直线L2的斜率为()。
答案:-1/28. 计算题:已知直线L1过点(1,2)且斜率为3/4,直线L2与L1平行且过点(3,5),求直线L2的斜率。
答案:3/49. 解答题:请解释什么是相交线和平行线,并举例说明。
答案:相交线是指两条直线或线段在平面上有唯一一点相交。
例如,在平面上有两条直线,一条通过点A和点B,另一条通过点C和点D,如果点A与点C不重合并且点B与点D不重合,则这两条直线相交于点E。
平行线是指在平面上没有任何交点的两条直线。
例如,在平面上有一条直线通过点A和点B,另一条直线通过点C和点D,如果两条直线没有任何一点相交,则这两条直线是平行线。
10. 解答题:如何通过直线的斜率来判断两条直线是否平行或垂直?答案:两条直线平行的充要条件是它们的斜率相等,即斜率相同的两条直线是平行线。
两条直线垂直的充要条件是它们的斜率的乘积为-1,即斜率之积为-1的两条直线是垂直线。
总结:在平面几何中,相交线是指两条直线或线段在平面上有唯一一点相交,平行线是指在平面上没有任何交点的两条直线。
相交线与平行线单元测试题

相交线与平行线单元测试题一、选择题(每题2分,共10分)1. 两条直线在同一平面内,且不相交,这两条直线叫做平行线。
以下哪项描述不正确?A. 平行线在任何情况下都不会相交B. 平行线之间的距离处处相等C. 平行线可以无限延伸D. 平行线可以相交2. 根据平行线的性质,以下哪个命题是正确的?A. 同位角相等B. 内错角相等C. 同旁内角互补D. 以上都是3. 如果两条直线相交成30度角,那么这两条直线的对顶角是:A. 30度B. 60度C. 90度D. 120度4. 已知直线AB与CD相交于点O,那么OA与OB的关系是:A. OA=OBB. OA垂直于OBC. OA平行于OBD. 无法确定5. 在平面几何中,以下哪个条件不能判定两直线平行?A. 同位角相等B. 内错角相等C. 同旁内角互补D. 两直线没有交点二、填空题(每题2分,共10分)6. 如果两条直线相交所构成的同位角不相等,则这两条直线_________。
7. 平行于同一条直线的两条直线_________。
8. 两条直线相交,如果其中一个角是直角,则这两条直线_________。
9. 如果直线a与直线b相交,且a垂直于直线b,则直线a与直线b所成的角是_________度。
10. 两条平行线被第三条直线所截,同旁内角的度数之和为_________。
三、判断题(每题1分,共5分)11. 两条直线相交所形成的角中,对顶角相等。
()12. 平行线的性质可以推出同位角相等,内错角相等,同旁内角互补。
()13. 如果两条直线相交,那么它们一定在某一点相交。
()14. 两条直线相交所形成的角中,邻角互补。
()15. 平行线之间的距离处处相等,这是平行线的一个性质。
()四、简答题(每题5分,共10分)16. 解释什么是“相交线”,并给出相交线的基本性质。
17. 解释什么是“平行线”,并说明平行线的性质有哪些。
五、解答题(每题15分,共15分)18. 在平面直角坐标系中,已知直线L1: y = 2x + 3 和直线L2: y = -x + 5,请判断这两条直线是否平行或相交,并给出证明。
七年级数学下册第五章《相交线与平行线》测试卷-人教版(含答案)

七年级数学下册第五章《相交线与平行线》测试卷-人教版(含答案)三总分题号一二19 20 21 22 23 24分数一、选择题(每题3分,共30分)1.下列四个图案中,可能通过如图平移得到的是()A.B.C.D.2.下列说法正确的是()A.直线AB和直线BA是同一条直线 B.直线是射线的2倍C.射线AB与射线BA是同一条射线 D.三条直线两两相交,有三个交点3.下列各图中,∠1=∠2一定成立的是()A.B.C.D.4.如图,直线BC,DE相交于点O,AO⊥BC于点O.OM平分∠BOD,如果∠AOE =50°,那么∠BOM的度数()A.20°B.25°C.40°D.50°5.如图,在铁路旁有一李庄,现要建一火车站,为了使李庄人乘车最方便,请你在铁路线上选一点来建火车站,应建在()A.A点B.B点C.C点D.D点6.如图,点P在直线L外,点A,B在直线l上,PA=3,PB=7,点P到直线l 的距离可能是()A.2 B.4 C.7 D.87.如图所示,∠1和∠2不是同位角的是()A.①B.②C.③D.④8.如图所示,同位角共有()A.6对B.8对C.10对D.12对9.下列说法正确的有()个.①不相交的两条直线是平行线;②在同一平面内,两条不相交的线段是平行线;③过一点可以而且只可以画一条直线与已知直线平行;④如果一条直线与两条平行线中的一条平行,那么它与另一条直线也互相平行.A.1 B.2 C.3 D.410.如图,a∥b,M、N分别在a,b上,P为两平行线间一点,那么∠1+∠2+∠3=()A .180°B .360°C .270°D .540°二、填空题(每题3分,共24分)11.把命题“等角的补角相等”改写成“如果…那么…”的形式是______. 12.如图所示,12//l l ,点A ,E ,D 在直线1l 上,点B ,C 在直线2l 上,满足BD 平分ABC ∠,BD CD ⊥,CE 平分DCB ∠,若136BAD =︒∠,那么AEC ∠=___________.13.把一个直角三角板(90GEF ∠=︒,30GFE ∠=︒)如图放置,已知AB ∥CD ,AF 平分BAE ∠,则AEG ∠=_____________14.如图,点E 在BC 延长线上,四个条件中:①13∠=∠;②25180+=︒∠∠,③4∠=∠B ;④B D ∠=∠;⑤180D BCD ∠+∠=︒,能判断//AB CD 的是______.(填序号).15.如图,已知12//l l ,直线l 分别与12,l l 相交于,C D 两点,现把一块含30角的直角三角中尺按如图所示的位置摆放.若1130∠=︒,则2∠=___________.16.如图,∠AEM=∠DFN=a,∠EMN=∠MNF=b,∠PEM=12∠AEM,∠MNP=12∠FNP,∠BEP,∠NFD的角平分线交于点I,若∠I=∠P,则a和b的数量关系为_____(用含a的式子表示b).17.如图所示,将△ABC沿BC边平移得到△A1B1C1,若BC1=8,B1C=2,则平移距离为.18.如图,△ABC的边长AB =3 cm,BC=4 cm,AC=2 cm,将△ABC沿BC方向平移a cm(a<4 cm),得到△DEF,连接AD,则阴影部分的周长为_______cm.三.解答题(共46分)19.(7分)如图,直线l1,l2,l3相交于点O,∠1=40°,∠2=50°,求∠3的度数.20.(7分)已知:如图,AB∥CD,CD∥EF.求证:∠B+∠BDF+∠F=360°.21.(8分)如图,直线DE与∠ABC的边BC相交于点P,现直线AB,DE被直线BC所截,∠1与∠2.∠1与∠3,∠1与∠4分别是什么角?22.(8分)如图,已知∠1+∠2=180°,∠3=∠B.(1)试判断DE与BC的位置关系,并说明理由.(2)若DE平分∠ADC,∠2=3∠B,求∠1的度数.23.(8分)图1,点E在直线AB上,点F在直线CD上,EG⊥FG.(1)若∠BEG+∠DFG=90°,请判断AB与CD的位置关系,并说明理由;(2)如图2,在(1)的结论下,当EG⊥FG保持不变,EG上有一点M,使∠MFG=2∠DFG,则∠BEG与∠MFG存在怎样的数量关系?并说明理由;(3)如图2,若移动点M,使∠MFG=n∠DFG,请直接写出∠BEG与∠MFG的数量关系.24.(8分)已知,E、F分别是直线AB和CD上的点,AB∥CD,G、H在两条直线之间,且∠G=∠H.(1)如图1,试说明:∠AEG=∠HFD;(2)如图2,将一45°角∠ROS如图放置,OR交AB于E,OS交CD于F,设K为SO上一点,若∠BEO=∠KEO,EG∥OS,判断∠AEG,∠GEK的数量关系,并说明理由;(3)如图3,将∠ROS=(n为大于1的整数)如图放置,OR交AB于E,OS交CD于F,设K为SO上一点,连接EK,若∠AEK=n∠CFS,则=.参考答案一、选择题: 题号 1 2 3 4 5 6 7 8 9 10 答案 CACAAACCDB二、填空题:11.如果两个角是等角的补角,那么它们相等. 12.146° 13.30°解:∵AB ∥CD ,AF 平分∠BAE , ∴∠BAF=∠EAF=∠AFE , 又∵∠GFE=30°,∴∠BAF=∠EAF=30°,即∠BAE=60°, ∴∠AEF=180°-60°=120°, 又∵∠GEF=90°,∴∠AEG=120°-90°=30°, 14.②③解:①∵∠1=∠3,∴AD ∥BC ;②∵∠2+∠5=180°,∵∠5=∠AGC ,∴∠2+∠AGC=180°,∴AB ∥DC ; ③∵∠4=∠B ,∴AB ∥DC ; ④∠B=∠D 无法判断出AD ∥BC ; ⑤∵∠D+∠BCD=180°,∴AD ∥BC . 15.20︒如图,∵121130,l l ∠=︒∥, ∴50CDB ∠=︒, ∵30ADB ∠=︒,∴2503020CDB ADB ∠=∠-∠=︒-︒=︒.16.如图1,ABCD是长方形纸带(AD∥BC),∠DEF=18°,将纸带沿EF折叠成图2,再沿BF折叠成图3,则图3中的∠CFE的度数是126°.【分析】在图1中,由AD∥BC,利用“两直线平行,内错角相等”可得出∠BFE的度数,由折叠的性质可知,在图3中∠BFE处重叠了三次,进而可得出∠CFE+3∠BFE=180°,再代入∠BFE的度数即可求出结论.【解答】解:在图1中,AD∥BC,∴∠BFE=∠DEF=18°.由折叠的性质可知,在图3中,∠BFE处重叠了三次,∴∠CFE+3∠BFE=180°,∴∠CFE=180°﹣3×18°=126°.故答案为:126°.17.解:∵△ABC沿BC边平移得到△A1B1C1,∴BC=B1C1,BB1=CC1,∵BC1=8,B1C=2,∴BB1=CC1=,即平移距离为3,故答案为:3.18.180;3;内错角相等,两直线平行;两直线平行,同位角相等三.解答题:19.解:∵∠1=40°,∠2=50°,∴∠5=∠1=40°,∠4=∠2=50°,∴∠3=180°﹣∠5﹣∠4=180°﹣40°﹣50°=90°.20.证明:∵AB∥CD(已知)∴∠B+∠BDC=180°(两直线平行,同旁内角互补)∵CD∥EF(已知)∴∠CDF+∠F=180°(两直线平行,同旁内角互补)∴∠B+∠BDC+∠CDF+∠F=360°,∵∠BDF=∠BDC+∠CDF(已知)∴∠B+∠BDF+∠F=360°.21.解:∵直线AB,DE被直线BC所截,∴∠1与∠2是同旁内角,∠1与∠3是内错角,∠1与∠4是同位角.22.解:(1)如图1,作直线GH交AB于M,交CD于Q,∵AB∥CD,∴∠BMG=∠FQH,∵∠EGH=∠GHF,∴∠AEG=∠EGH﹣∠BMG=∠FHG﹣∠FQH=∠HFD;(2)∠GEK﹣2∠AEG=45°,如图2,延长KO交AB于M,∵EG∥MS,∴∠AEG=∠EMF,∠GEK=∠OKE,设∠OEM=α,则∠OEK=2α,∠OME=45°﹣α,∴∠OKE=180°﹣∠MEK﹣∠OME=135°﹣2α,∵EG∥OS,∴∠GEK=∠OKE=135°﹣2α,∴∠AEG=180°﹣∠GEK﹣∠MEK=180°﹣135°+2α﹣3α=45°﹣α,即∠GEK﹣2∠AEG=45°.(3)作OH∥AB,∵AB∥CD,∴OH∥CD,如图3,∵AB∥OH,∴∠OEB=∠EOH,又∵OH∥CD,∴∠FOH=∠OFD,又∵∠OFD=∠CFS=∠AEK,而∠EOH+∠HOF=,∴∠EOH =﹣∠AEK,即180°﹣n∠EOH=∠AEK,又∵∠OEK+∠AEK+∠EOH=180°,∴∠OEK+180°﹣n∠EOH+∠EOH=180°,∴∠OEK=(n﹣1)∠EOH,∴,又∵∠EOH=∠BEO,∴.故答案为:.。
相交线与平行线经典测试题附答案

17.如图,直线 被直线 所截, ,则 的大小是()
A. B. C. D.
【答案】A
【解析】
【分析】
先根据对顶角相等得到 ,再根据平行线的判定得到a∥b,再根据平行线的性质得到 即可得到答案.
∴∠1=180°-∠3=50°,
∵∠2-∠1=15°,
∴∠2=15°+∠1=65°;
故答案为D.
【点睛】
本题考查角的运算,邻补角的性质,比较简单.
2.如图,直线 , ,如果 , , ,那么点 到直线 的距离为()
A. B. C. D.无法确定
【答案】A
【解析】
【分析】
根据点到直线的距离是指垂线段的长度,根据AB⊥AC,得出点C到直线AB的距离为AC.
【详解】
解:由∠EOD+∠OBF=∠COB+∠OBF=180°可知EC∥BF,结合CE是角平分线可得∠ECB=∠ACE=∠CBF,再由EC∥BF可得∠ACE=∠F=∠G,则由三角形内角和定理可得∠GDC=∠CBF.综上所得,∠ECB=∠ACE=∠CBF=∠F=∠G=∠GDC,共有5个与∠ECB相等的角,
【详解】
解: 标记为如下图所示,
∵ 是对顶角,
∴ (对顶角相等),
又∵ ,
∴ ,
∴a∥b(同旁内角互补,两直线平行),
∴ (两直线平行,内错角相等),
∴ ,
故A为答案.
【点睛】
本题主要考查了对顶角的性质(对顶角相等)、直线平行的判定(同旁内角互补,两直线平行)、直线平行的性质(两直线平行,内错角相等),能灵活运用所学知识是解题的关键..
相交线与平行线测试20题

第五章 相交线与平行线班级 姓名 得分一、选择题(3分×7=21分)1、 如图 点E 在AC 延长线上,下列条件中能判断AB ∥CD 的是 ( )A 、 ∠3=∠4B 、 ∠1=∠2C 、 ∠D=∠DCED 、 ∠D+∠ACD=1802、 如图a ∥b ,∠3=1080,则∠1的度数是 ( )A 、 720B 、 800C 、 820D 、 1083、 下列说法正确的是 ( )A 、 a 、b 、c 是直线,且a ∥b, b ∥c,则a ∥cB 、 a 、b 、c 是直线,且a ⊥b, b ⊥c ,则a ⊥cC 、 a 、b 、c 是直线,且a ∥b, b ⊥c 则a ∥cD 、 a 、b 、c 是直线,且a ∥b, b ∥c ,则a ⊥c4、如图由AB ∥CD ,可以得到 ( )A 、∠1=∠2B 、∠2=∠3C 、∠1=∠4D 、∠3=∠45、如图B ∥CD ∥EF ,那么∠BAC+∠ACE+∠CEF= ( )A 、1800B 、 2700C 、 3600D 、5406、下列命题中,错误的是 ( ) A 、邻补角是互补的角 B 、互补的角若相等,则此两角是直角 C 、两个锐角的和是锐角 D 、一个角的两个邻补角是对顶角7、图中,与∠1 成同位角的个数是 ( )A 、 2个 B、3个 C、 4个 D、 5个二、填空题(8、11、12、13、14每题3分共25分)8、如图一个弯形管道ABCD的拐角∠ABC=1200,∠BCD=600,这时说管道AB∥CD,是根据9、如图直线AB、CD、EF相交于点O,是∠AOC的邻补角是 ,∠DOA的对顶角是 ,若∠AOC=500,则∠BOD=0,∠COB= 0第(1)题4321E D CB A 第(2)题b a 31第(4)题4321D C B A 第(5)题F E DC B A L2L 1c 第(7)题b a1D CD 1C 1B 1A 1C O ED B Aba 432110、如图所示的长方体,用符号表示下列棱的位置关系:A 1B 1 AB AA 1 AB 1,A 1D 1C 1D 1 AD BC11、如图直线,a ∥b,∠1=540,则∠2= 0,∠3= 0,∠4= 0。
初中数学相交线与平行线经典测试题附答案

A. B. C. D.
【答案】B
【解析】
【分析】
由 可得∠ABE+∠CEB=180°,∠BED= ,即∠CEB=130°,由 可得 ,设 =k,则∠CEF=6k,∠FEB=7k,可得∠FEB=70°,可得∠DEF=∠FEB+∠BED=120°;又由 可得 =∠DEF即可解答.
故选:B.
【点睛】
此题考查平行线的性质和判定,平行线公理及推论,能熟记知识点的内容是解题的关键.
5.如图,直线a∥b,直线 分别交a,b于点A,C,∠BAC的平分线交直线b于点D,若∠1=50°,则∠2的度数是
A.50°B.70°C.80°D.110°
【答案】C
【解析】
【分析】
根据平行线的性质可得∠BAD=∠1,再根据AD是∠BAC的平分线,进而可得∠BAC的度数,再根据补角定义可得答案.
考点:平行线的性质.
9.如图,下列条件中能判定 的是( )
A. B.
C. D.
【答案】C
【解析】
【分析】
对于A,∠EDC=∠EFC不是两直线被第三条直线所截得到的,据此进行判断;
对于B、D,∠AFE=∠ACD,∠1=∠2是EF和BC被AC所截得到的同位角和内错角,据此进行判断;
对于C,∠3=∠4这两个角是AC与DE被EC所截得到的内错角,据此进行判断.
【详解】
∠EDC=∠EFC不是两直线被第三条直线所截得到的,因而不能判定两直线平行;
∠AFE=∠ACD,∠1=∠2是EF和BC被AC所截得到的同位角和内错角,因而可以判定EF∥BC,但不能判定DE∥AC;
∠3=∠4这两个角是AC与DE被EC所截得到的内错角,可以判定DE∥AC.
相交线与平行线测试题及答案难

相交线与平行线测试题及答案难一、选择题1. 在同一平面内,两条直线的位置关系是()。
A. 相交或平行B. 相交或重合C. 平行或重合D. 相交、平行或重合答案:D2. 如果两条直线都与第三条直线平行,那么这两条直线的关系是()。
A. 相交B. 平行C. 重合D. 不确定答案:B3. 两条直线相交成90度角,这两条直线是()。
A. 相交线B. 垂直线C. 平行线D. 异面直线答案:B二、填空题4. 如果两条直线都与第三条直线相交,且交角相等,则这两条直线()。
答案:平行5. 在平面几何中,如果两条直线不相交,则它们被称为()。
答案:平行线三、判断题6. 两条平行线被第三条直线所截,同位角相等。
()答案:正确7. 垂直于同一直线的两条直线一定平行。
()答案:错误四、解答题8. 已知直线AB与直线CD相交于点O,且∠AOB=90°,求证:AB⊥CD。
证明:因为∠AOB=90°,所以AB与CD相交成直角,根据垂直的定义,AB⊥C D。
9. 若直线m平行于直线n,直线n平行于直线p,求证:直线m平行于直线p。
证明:根据平行公理,如果两条直线都与第三条直线平行,那么这两条直线也互相平行。
因此,直线m平行于直线p。
五、综合题10. 在平面直角坐标系中,直线l1的方程为y=2x+3,直线l2的方程为y=-x+5,求证:l1与l2相交。
证明:首先,我们可以将两个方程联立求解。
\begin{cases}y = 2x + 3 \\y = -x + 5\end{cases}将第一个方程中的y代入第二个方程,得到:2x + 3 = -x + 5解得:x = 1将x=1代入任意一个方程求得y,例如第一个方程:y = 2(1) + 3 = 5因此,l1与l2的交点为(1,5),所以l1与l2相交。
11. 已知直线l1平行于直线l2,直线l2平行于直线l3,求证:直线l1平行于直线l3。
证明:根据平行公理,如果两条直线都与第三条直线平行,那么这两条直线也互相平行。
相交线与平行线测试题

相交线与平行线测试题姓名一、选择(每小题4分,共40分)1、在同一平面内,两条直线的位置关系可能是()A、相交或平行B、相交或垂直C、平行或垂直D、不能确定2、如图,下列说法错误的是()A、∠A与∠C是同旁内角B、∠1与∠3是同位角C、∠2与∠3是内错角D、∠3与∠B是同旁内角第2题图第3题图第4题图3、如图,AB∥DE,∠1=∠2,则AE与DC的位置关系是()A、相交B、平行C、垂直D、不能确定4、如图,直线a,b都与c相交,由下列条件能推出的是()①②③④A.① B.①② C.①②③ D.①②③④5、下列角的平分线中,互相垂直的是()A.平行线的同旁内角的平分线 B.平行线的同位角的平分线C.平行线的内错角的平分线 D.对顶角的平分线6、下面4个命题中正确的是()A、相等的两个角是对顶角B、和等于90 º的两个角互为余角C、如果∠1+∠2+∠3 =180º,那么∠1,∠2,∠3互为补角D、一个角的补角一定大于这个角7、点P为直线l外一点,点A,B,C为直线l上三点,PA=4 cm,PB=5 cm,PC=2 cm,则点P到直线l的距离为( )A、4 cmB、2 cmC、小于2 cmD、不大于2 cm8、一辆汽车在公路上行驶,两次拐弯后,仍在原来的方向平行行驶,那么这两个拐弯的角度可能是( )A.先向左转130°,再向左转50°B.先向左转50°,再向右转50°C.先向左转50°,再向右转40°D.先向左转50°,再向左转40°9、如图,已知AB CD //,∠α等于( )A. 75B.80 C .85 D.95 A B120° α25°C D第9题图 第10题图10、如图,把一块含有45°角的直角三角板的两个顶点放在直尺的对边上.如果∠1=20°,那么∠2的度数是( )A.30°B.25°C.20°D.15°二、填空(每小题4分,共24分)11、如图,直线AB 、CD 相交于点E ,DF ∥AB ,若∠AEC=1000,则∠D 的度数等于 .12、如图所示,用直尺和三角尺作平行线AB ∥CD,其中的道理是__________________________________.ABCD EF第1题图 第2题图13、下列语句是有关几何作图的叙述.①以O 为圆心作弧;②延长射线AB 到点C ;③作∠AOB ,使∠AOB=∠1;④作直线AB ,使AB=a ⑤过三角形ABC 的顶点C 作它的对边AB 的平行线.其中正确的有 .(填序号即可)14、两个互为余角的角的差是30°,则这两角中较小的角的补角是______. AB C D EO第5题图 第6题图 15、如图,直线AB 、CD 相交于点O ,OE ⊥AB ,O 为垂足,如果∠EOD=38 o,则∠AOC= 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
相交线与平行线
2 .一辆汽车在笔直的公路上行驶,两次拐弯后, 仍在原来的方向上平行前进, 那么两次拐弯的
角度是(
)
(1)摆动的钟摆。
(2)在笔直的公路上行驶
的汽车。
(3)随风摆动的旗帜。
(4)摇动
的大绳。
(5)汽车玻璃上雨刷的运动。
(6
)
从楼顶自由落下的球(球不旋转)。
10.如图,直线 AB 、CD 相交于点 O , OE 丄AB ,
O 为垂足,如果/ EOD = 38°,则/ AOC
11.如图,AC 平分/ DAB ,/ 1 = / 2。
填空:因 为AC 平分/
DAB ,所以/ 1 = _______________________ 。
所 以/ 2 = __________ 。
所以 AB // __________ 。
三、做一做(本题 10分)
12 .已知三角形 ABC 、点D ,过点D 作三角形 ABC 平移后的
图形。
6.下列说法中正确的是( )
A .有且只有一条直线垂直于已知直线。
B .从直线外一点到这条直线的垂线段,叫做 这点到这条直线的距离。
C .互相垂直的两条直线一定相交。
D .直线c 外一点A 与直线c 上各点连接而成
1. (时间:45分钟 满分:100分) 姓名 __________________ 、选择题(每小题 4分,共24 分) 下面
四个图形中,/ 个数是( A . 0 B . 与/2是对顶角的图形的 的所有线段中,最短线段的长是 3cm ,则 点A 到直线c 的距离是3cm 。
二、填空题(每小题 4分,共20分) 1
7 .两个角的两边两两互相平行,且一个角的
等
2
1 于另一个角的 -,则这两个角的度数分别 3 为 ________________________ 。
8.猜谜语(打本章两个几何名称)。
剩下十分钱 ______________ ;两牛相斗 ____________ 。
9 .下面生活中的物体的运动情况可以看成平移的
A . 第
一 次右拐
50°, 第二次左拐 130°。
B . 第一
次左拐 50°, 第二次右拐
50°。
C . 第一
次左拐 50°, 第二次左拐
130°。
D . 第一
次右拐 50°, 第二次右拐
50°。
冋一平面内的四条直线满足
a 丄
b , b 丄
c , c ±
d ,
则下列式子成立的是( )
A .a // b
B . b 丄
d
C .a 丄d
D . b // c
交于'
不同三点时, 对顶角有 n 对,则
m 与n
的关. H. /
系是( )
A . m = n
B . m > n
C .m v n
D . m + n = 10
5.如图, 若 m / n , / 1 =
105 ° ,则/2=
( )
A . 55 °60 ° C . 65 ° D . 75°
(第10题图)
(第11题图)
4.三条直线两两相交于同一点时,
对顶角有m 对,
四、算一算(本题 10分)
13.如图,AD 是/ EAC 的平分线,AD // BC ,/
B = 30 °,你能算出/ EAD 、/ DA
C 、/ C 的
度数吗? 六、实际应用:(本大题两小题,共 24分)
15•
结合本班实际,画出班级的简易平面图形,找 出其中的垂线和平行线。
(本题11分)
16•如图,有两堵墙,要测量地面上所形成的/ AOB 的度数,但
人又不能进入围墙,只能站在墙外。
如何测量(运用本章
知识)?(本题 13分)
五、想一想(每空 3分,共12分)
14.如图,EF // AD ,/ 1 = / 2,/ BAC = 70 °。
将求/ AGD 的过程填写
完整。
因为EF // AD ,所以 / 2 = ____________ 。
又因为/ 1 = / 2,所以/ 1 = / 3。
所以
AB // ___________ 。
所以/ BAC + ____________ = 180。
又因为/ BAC = 70°,所以/
AGD
A
14.本题考查学生对平行线的性质和特征的应用及它们之间的区别,使学生获得一些研究问题的方法和经验,发展思维能力。
附:命题意图及参考答案
(一)命题意图
一、选择题
1.考查学生对对顶角概念的理解,加深学生对平面图形的认识和感受。
2.考查学生对平行线的条件的理解及形象思维的能力。
3.考查学生对数学知识的理解和思维的深刻性。
4.考查学生对对顶角概念的深刻理解及思维的灵活性。
5.考查学生对平行线性质掌握情况。
6.考查学生对垂直知识的掌握情况,提高学生运用基础知识解决问题的能力。
二、填空题
7.考查学生的计算能力。
8.本题通过猜谜引发学生对有关数学概念的思考。
9.本题让学生认识平移在现实生活中的应用。
10.本题考查学生的计算能力。
11.本题意在教会学生使用数学语言有条理地表达思考的过程。
六、实际应用
本题意在提高学生应用数学的意识,体会数学的价值。
设置探索题与开发题,可以暴露学生的思维过程,能深化学生的思维品质,发展学生的逻辑思维和创造性思维能力。
(二)参考答案
1.B
2.B
3.C
4.A
5.D
6.D
7.72°,108°
8.余角,对顶角
9.(2)和(6)
10.52°,128°
11./ BAC,/ BAC , CD。
12 .略
13.30°,30 °,30°
14./ 3,DG,/ AGD ,110°
15 .略
16.延长AO与BO,测/ AOB的对顶角。
三、做一做
12.考查学生对平移作图的掌握情况,提高学生动手动脑能力。
四、算一算
13.本题意在引导学生体会数学知识之间的联系, 感受数学的整体性,不断丰富解决问题的策略,提高解题能力。
五、想一想。
