小学数学求阴影部分面积经典题目汇总
小学六年级阴影部分面积专题复习经典例题(含答案)

小学六年级阴影部分面积专题复习经典例题(含答案)欢迎下载研究必备资料, 本文主要涉及组合图形的面积计算。
以下是各题的解答和点评:1.求如图阴影部分的面积。
(单位: 厘米)分析: 阴影部分的面积等于梯形的面积减去直径为4厘米的半圆的面积。
利用梯形和半圆的面积公式代入数据即可解答。
解答: $(4+6)\times4\div2\div2-3.14\times2^2=10-6.28=3.72$(平方厘米)。
答案: 阴影部分的面积是3.72平方厘米。
点评:组合图形的面积一般都是转化到已知的规则图形中利用公式计算, 这里考查了梯形和圆的面积公式的灵活应用。
2.如图, 求阴影部分的面积。
(单位: 厘米)分析:根据图形可以看出, 阴影部分的面积等于正方形的面积减去4个扇形的面积。
正方形的面积等于(10×10)100平方厘米, 4个扇形的面积等于半径为(10÷2)5厘米的圆的面积。
解答: 扇形的半径是: $10\div2=5$(厘米);$10\times10-3.14\times5\times5=100-78.5=21.5$(平方厘米)。
答案: 阴影部分的面积为21.5平方厘米。
点评:组合图形的面积计算需要注意各部分之间的关系, 特别是涉及到圆形时需要注意半径的计算。
3.求如图阴影部分面积。
(单位: 厘米)解答:该题缺少图形, 无法回答。
4.求出如图阴影部分的面积: 单位: 厘米。
解答:该题缺少图形, 无法回答。
5.求如图阴影部分的面积。
(单位: 厘米)解答:该题缺少图形, 无法回答。
6.求如图阴影部分面积。
(单位: 厘米)解答:该题缺少图形, 无法回答。
7.计算如图中阴影部分的面积。
单位: 厘米。
解答:该题缺少图形, 无法回答。
8.求阴影部分的面积。
单位: 厘米。
解答:该题缺少图形, 无法回答。
9.如图是三个半圆, 求阴影部分的周长和面积。
(单位: 厘米)分析: 阴影部分可以看成是两个半圆和一个矩形组成的, 可以分别计算各部分的周长和面积再相加。
小学六年级-阴影部分面积-专题复习-典型例题(含答案)

阴影部分面积专题例1.求阴影部分的面积。
(单位:厘米)解:这是最基本的方法:圆面积减去等腰直角三角形的面积,×-2×1=1.14(平方厘米)例2.正方形面积是7平方厘米,求阴影部分的面积。
(单位:厘米)解:这也是一种最基本的方法用正方形的面积减去圆的面积。
设圆的半径为r,因为正方形的面积为7平方厘米,所以=7,所以阴影部分的面积为:7-=7-×7=1.505平方厘米例3.求图中阴影部分的面积。
(单位:厘米)解:最基本的方法之一。
用四个圆组成一个圆,用正方形的面积减去圆的面积,所以阴影部分的面积:2×2-π=0.86平方厘米。
例4.求阴影部分的面积。
(单位:厘米)解:同上,正方形面积减去圆面积,16-π()=16-4π=3.44平方厘米例5.求阴影部分的面积。
(单位:厘米)解:这是一个用最常用的方法解最常见的题,为方便起见,我们把阴影部分的每一个小部分称为“叶形”,是用两个圆减去一个正方形,π()×2-16=8π-16=9.12平方厘米另外:此题还可以看成是1题中阴影部分的8倍。
例6.如图:已知小圆半径为2厘米,大圆半径是小圆的3倍,问:空白部分甲比乙的面积多多少厘米?解:两个空白部分面积之差就是两圆面积之差(全加上阴影部分)π-π()=100.48平方厘米(注:这和两个圆是否相交、交的情况如何无关)例7.求阴影部分的面积。
(单位:厘米) 解:正方形面积可用(对角线长×对角线长÷2,求)正方形面积为:5×5÷2=12.5所以阴影面积为:π÷4-12.5=7.125平方厘米(注:以上几个题都可以直接用图形的差来求,无需割、补、增、减变形) 例8.求阴影部分的面积。
(单位:厘米)解:右面正方形上部阴影部分的面积,等于左面正方形下部空白部分面积,割补以后为圆,所以阴影部分面积为:π()=3.14平方厘米例9.求阴影部分的面积。
小学五年级数学求阴影部分面积习题

小学五年级数学求阴影部分面积习题1、三角形ABC的面积是24平方厘米,AE=BC=8厘米,CD=4厘米,求阴影部分面积。
2、正方形ABCD的周长是48厘米,已知AE的长度是EB的3倍,求阴影部分面积。
3、如图,一个直角梯形的上底是10厘米,下底是6厘米,面积是40平方厘米,把它分成一个平行四边形和直角三角形后,三角形的面积是多少平方厘米。
4、下面直角梯形的面积是49平方分米,求阴影部分的面积。
5、求整个图形的面积。
(单位:厘米)6、下图所示梯形,如果它的上底增加4厘米,面积就增加18平方厘米,这梯形原来的面积是多少平方厘米?7、求下面图形中阴影部分的面积。
(单位:厘米)8、下图由大小不等的两个正方形拼成,小正方形的边长是6厘米,阴影部分面积是60 厘米,求图中空白部分的面积。
9、求正方形中阴影部分的面积。
10、在下图中,已知平行四边形ABED的面积是30平方厘米,BE长6厘米,EC长4厘米。
求梯形ABCD的面积。
11、图中空白部分是一个面积为30平方厘米的平行四边形,求阴影部分面积。
12、如图:在直角梯形ABCD中,AB=4分米。
CD=9分米,空白部分面积为10平方分米,求阴影部分面积。
13、求阴影部分的面积(单位:厘米):14、图中三角形DEC的面积是平方米,AD=米,AB=2米。
求平行四边形CDFG中阴影部分的面积。
15、如图,在梯形ABCD中,CD=4厘米,AB=2DC,AECD为平行四边形,已知梯形面积为66平方厘米,求阴影部分面积。
16、图中三角形ABC的面积是24平方厘米,AE=BC=8厘米,CD=4厘米,求阴影部分的面积。
17、图中空白部分是一个面积为30平方厘米的平行四边形,求阴影部分面积。
18、图中,阴影部分的面积是56平方厘米,BD=14厘米,求梯形ABCD 的面积。
19、梯形ABCD面积是96平方厘米,AB=6厘米,中位线EF=12厘米,求阴影部分面积。
20、求这个组合图形的面积。
小学五年级数学求阴影部分面积习题

小学五年级数学求阴影部分面积习题1、三角形ABC的面积是24平方厘米,AE=BC=8厘米,CD=4厘米,求阴影部分面积。
2、正方形ABCD的周长是48厘米,已知AE的长度是EB的3倍,求阴影部分面积。
3、如图,一个直角梯形的上底是10厘米,下底是6厘米,面积是40平方厘米,把它分成一个平行四边形和直角三角形后,三角形的面积是多少平方厘米。
4、下面直角梯形的面积是49平方分米,求阴影部分的面积。
5、求整个图形的面积。
(单位:厘米)6、下图所示梯形,如果它的上底增加4厘米,面积就增加18平方厘米,这梯形原来的面积是多少平方厘米?7、求下面图形中阴影部分的面积。
(单位:厘米)8、下图由大小不等的两个正方形拼成,小正方形的边长是6厘米,阴影部分面积是60 厘米,求图中空白部分的面积。
9、求正方形中阴影部分的面积。
10、在下图中,已知平行四边形ABED的面积是30平方厘米,BE长6厘米,EC长4厘米。
求梯形ABCD的面积。
11、图中空白部分是一个面积为30平方厘米的平行四边形,求阴影部分面积。
12、如图:在直角梯形ABCD中,AB=4分米。
CD=9分米,空白部分面积为10平方分米,求阴影部分面积。
13、求阴影部分的面积(单位:厘米):14、图中三角形DEC的面积是2.7平方米,AD=4.4米,AB=2米。
求平行四边形CDFG中阴影部分的面积。
15、如图,在梯形ABCD中,CD=4厘米,AB=2DC,AECD为平行四边形,已知梯形面积为66平方厘米,求阴影部分面积。
16、图中三角形ABC的面积是24平方厘米,AE=BC=8厘米,CD=4厘米,求阴影部分的面积。
17、图中空白部分是一个面积为30平方厘米的平行四边形,求阴影部分面积。
18、图中,阴影部分的面积是56平方厘米,BD=14厘米,求梯形ABCD的面积。
19、梯形ABCD面积是96平方厘米,AB=6厘米,中位线EF=12厘米,求阴影部分面积。
20、求这个组合图形的面积。
小学数学六年级圆的阴影面积与周长100道经典题型

小学数学六年级圆的阴影面积与周长100道经典题型六年级圆的阴影面积与周长100道经典题型1.求阴影部分的面积。
(单位:厘米)2.正方形面积是7平方厘米,求阴影部分的面积。
(单位:厘米)3.求图中阴影部分的面积。
(单位:厘米)4.求阴影部分的面积。
(单位:厘米)5.求阴影部分的面积。
(单位:厘米)6.如图:已知小圆半径为2厘米,大圆半径是小圆的3倍,问:空白部分甲比乙的面积多多少厘米?7.求阴影部分的面积。
(单位:厘米)8.求阴影部分的面积。
(单位:厘米)9.求阴影部分的面积。
(单位:厘米)10.求阴影部分的面积。
(单位:厘米)11.求阴影部分的面积。
(单位:厘米)12.求阴影部分的面积。
(单位:厘米)13.求阴影部分的面积。
(单位:厘米)14.求阴影部分的面积。
(单位:厘米)15.已知直角三角形面积是12平方厘米,求阴影部分的面积。
16.求阴影部分的面积。
(单位:厘米)17.图中圆的半径为5厘米,求阴影部分的面积。
(单位:厘米)18.求阴影部分的面积。
(单位:厘米)19.正方形边长为2厘米,求阴影部分的面积。
20.如图,正方形ABCD的面积是36平方厘米,求阴影部分的面积。
21.如图,正方形边长为8厘米,求阴影部分的面积。
22.求阴影部分的面积。
23.求阴影部分的周长与面积。
24.求阴影部分的周长与面积。
25.求阴影部分的周长与面积。
26.求阴影部分的周长与面积。
27.求阴影部分的周长与面积。
28.求阴影部分的周长与面积。
29.求阴影部分的面积。
30.求阴影部分的面积。
31.正方形面积是7平方厘米,求阴影部分的面积和周长。
(单位:厘米)32.求图中阴影部分的面积和周长。
(单位:厘米)33.求图中阴影部分的面积和周长。
(单位:厘米)34.求图中阴影部分的面积和周长。
(单位:厘米)35.求图中阴影部分的面积和周长。
(单位:厘米)36.求图中阴影部分的面积和周长。
(单位:厘米)37.求图中阴影部分的面积和周长。
小学五年级数学求阴影部分面积习题

g si nt he i rb ei n ga re go od fo rs o 1、下图中,已知阴影部分面积使30平方厘米,AB =15厘米,求图形空白部分的总面积。
2、 右图,一个长方形和一个三角形重叠在一起,已知三角形ADE 的面积比长方形ABCD 的面积小4平方厘米,求CE 的长。
3、 如图,求直角梯形中阴影部分的面积。
(单位:厘米) 4、 阴影部分面积是40平方米,求空白部分面积。
(单位:米)i ng si nt he i rb ei n ga re go od fo rs o 6、 右图,ABCD 只直角梯形,已知AE =EF =FD ,AB 为6厘米,BC 为10厘米,阴影部分面积为6平方厘米。
求直角梯形ABCD 的面积。
7、 下图是由一个三角形和一个梯形组成,已知三角形的面积是1平方分米,求这个图形的面积。
(单位:分米) 8、如图,平行四边形面积240平方厘米,求阴影部分面积。
9、下图ABCD 是梯形,它的面积是140平方厘米,已知AB =15厘米,DC =5厘米。
求阴g si nt he i rb ei n ga re go od fo rs o 10、 求右面图形的面积(单位:厘米) 11、如图,求长方形中的梯形面积。
(单位:厘米) 12、求下图阴影部分的面积(单位:厘米)13、求梯形的面积。
(单位:厘米)h i ng si nt he i rb ei n ga re go od fo rs o 14、如图,已知梯形ABCD 的面积为37.8平方厘米,BE 长7厘米,EC 长4厘米,求平行四边形ABED 的面积。
15、求空白部分面积。
(单位:厘米) 16、如图,已知平行四边形ABCD 中,阴影部分面积为72平方厘米,求三角形BCD 的面积。
17、求梯形中阴影部分的面积。
(单位:cm )g si nt he i rb ei n ga re go od fo rs o 18、下图,ABCD 是一个等腰梯形,ADFE 是边长为4厘米的正方形,CF =2厘米,求阴影部分的面积。
小学五年级数学求阴影部分面积习题

小学五年级数学求阴影部分面积习题1、三角形ABC的面积是24平方厘米,AE=BC=8厘米,CD=4厘米,求阴影部分面积。
2、正方形ABCD的周长是48厘米,已知AE的长度是EB的3倍,求阴影部分面积。
3、如图,一个直角梯形的上底是10厘米,下底是6厘米,面积是40平方厘米,把它分成一个平行四边形和直角三角形后,三角形的面积是多少平方厘米。
4、下面直角梯形的面积是49平方分米,求阴影部分的面积。
5、求整个图形的面积。
(单位:厘米)6、下图所示梯形,如果它的上底增加4厘米,面积就增加18平方厘米,这梯形原来的面积是多少平方厘米?7、求下面图形中阴影部分的面积。
(单位:厘米)8、下图由大小不等的两个正方形拼成,小正方形的边长是6厘米,阴影部分面积是60 厘米,求图中空白部分的面积。
9、求正方形中阴影部分的面积。
10、在下图中,已知平行四边形ABED的面积是30平方厘米,BE长6厘米,EC长4厘米。
求梯形ABCD的面积。
11、图中空白部分是一个面积为30平方厘米的平行四边形,求阴影部分面积。
12、如图:在直角梯形ABCD中,AB=4分米。
CD=9分米,空白部分面积为10平方分米,求阴影部分面积。
13、求阴影部分的面积(单位:厘米):14、图中三角形DEC的面积是2.7平方米,AD=4.4米,AB=2米。
求平行四边形CDFG中阴影部分的面积。
15、如图,在梯形ABCD中,CD=4厘米,AB=2DC,AECD为平行四边形,已知梯形面积为66平方厘米,求阴影部分面积。
16、图中三角形ABC的面积是24平方厘米,AE=BC=8厘米,CD=4厘米,求阴影部分的面积。
17、图中空白部分是一个面积为30平方厘米的平行四边形,求阴影部分面积。
18、图中,阴影部分的面积是56平方厘米,BD=14厘米,求梯形ABCD 的面积。
19、梯形ABCD面积是96平方厘米,AB=6厘米,中位线EF=12厘米,求阴影部分面积。
20、求这个组合图形的面积。
(完整)小学六年级-阴影部分面积-专题-复习-经典例题(含答案)-推荐文档

小升初阴影部分面积专题1. 求如图阴影部分的面积. (单位: 厘米)2. 如图, 求阴影部分的面积. (单位: 厘米)3. 计算如图阴影部分的面积. (单位: 厘米)4. 求出如图阴影部分的面积: 单位: 厘米.5. 求如图阴影部分的面积. (单位: 厘米)6. 求如图阴影部分面积. (单位: 厘米)7. 计算如图中阴影部分的面积. 单位: 厘米.8. 求阴影部分的面积. 单位: 厘米.9. 如图是三个半圆, 求阴影部分的周长和面积. (单位: 厘米)10. 求阴影部分的面积. (单位: 厘米)11. 求下图阴影部分的面积. (单位: 厘米)12. 求阴影部分图形的面积. (单位: 厘米)13. 计算阴影部分面积(单位: 厘米).14. 求阴影部分的面积. (单位: 厘米)15. 求下图阴影部分的面积: (单位: 厘米)16. 求阴影部分面积(单位: 厘米).17. (2012•长泰县)求阴影部分的面积. (单位: 厘米)☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆参考答案与试题解析1. 求如图阴影部分的面积. (单位: 厘米)考点组合图形的面积;梯形的面积;圆、圆环的面积. 1526356分析阴影部分的面积等于梯形的面积减去直径为4厘米的半圆的面积, 利用梯形和半圆的面积公式代入数据即可解答.解答解: (4+6)×4÷2÷2﹣3.14×÷2,=10﹣3.14×4÷2,=10﹣6.28,=3.72(平方厘米);答:阴影部分的面积是3.72平方厘米.答: 阴影部分的面积是3.72平方厘米.答:阴影部分的面积是3.72平方厘米.点评组合图形的面积一般都是转化到已知的规则图形中利用公式计算, 这里考查了梯形和圆的面积公式的灵活应用.2. 如图, 求阴影部分的面积. (单位: 厘米)考点组合图形的面积. 1526356分析根据图形可以看出:阴影部分的面积等于正方形的面积减去4个扇形的面积.正方形的面积等于(10×10)100平方厘米, 4个扇形的面积等于半径为(10÷2)5厘米的圆的面积, 即:3.14×5×5=78.5(平方厘米).解答解: 扇形的半径是:10÷2,=5(厘米);10×10﹣3.14×5×5,100﹣78.5,=21.5(平方厘米);答:阴影部分的面积为21.5平方厘米.答: 阴影部分的面积为21.5平方厘米.答:阴影部分的面积为21.5平方厘米.点评解答此题的关键是求4个扇形的面积, 即半径为5厘米的圆的面积.3. 计算如图阴影部分的面积. (单位: 厘米)考点组合图形的面积. 1526356分析分析图后可知, 10厘米不仅是半圆的直径, 还是长方形的长, 根据半径等于直径的一半, 可以算出半圆的半径, 也是长方形的宽, 最后算出长方形和半圆的面积, 用长方形的面积减去半圆的面积也就是阴影部分的面积.解答解: 10÷2=5(厘米),长方形的面积=长×宽=10×5=50(平方厘米),半圆的面积=πr2÷2=3.14×52÷2=39.25(平方厘米),阴影部分的面积=长方形的面积﹣半圆的面积,=50﹣39.25,=10.75(平方厘米);答:阴影部分的面积是10.75.答: 阴影部分的面积是10.75.答:阴影部分的面积是10.75.点评这道题重点考查学生求组合图形面积的能力, 组合图形可以是两个图形拼凑在一起, 也可以是从一个大图形中减去一个小图形得到;像这样的题首先要看属于哪一种类型的组合图形, 再根据条件去进一步解答.4. 求出如图阴影部分的面积: 单位: 厘米.考点组合图形的面积. 1526356专题平面图形的认识与计算.分析由题意可知:阴影部分的面积=长方形的面积﹣以4厘米为半径的半圆的面积, 代入数据即可求解.解答解: 8×4﹣3.14×42÷2,=32﹣25.12,=6.88(平方厘米);答:阴影部分的面积是6.88平方厘米.答: 阴影部分的面积是6.88平方厘米.答:阴影部分的面积是6.88平方厘米.点评解答此题的关键是:弄清楚阴影部分的面积可以由哪些图形的面积和或差求出.5. 求如图阴影部分的面积. (单位: 厘米)考点圆、圆环的面积. 1526356分析由图可知, 正方形的边长也就是半圆的直径, 阴影部分由4个直径为4厘米的半圆组成, 也就是两个圆的面积, 因此要求阴影部分的面积, 首先要算1个圆的面积, 然后根据“阴影部分的面积=2×圆的面积”算出答案.解答解: S=πr2=3.14×(4÷2)2=12.56(平方厘米);阴影部分的面积=2个圆的面积,=2×12.56,=25.12(平方厘米);答:阴影部分的面积是25.12平方厘米.答: 阴影部分的面积是25.12平方厘米.答:阴影部分的面积是25.12平方厘米.点评解答这道题的关键是重点分析阴影部分是由什么图形组成的, 再根据已知条件去计算.6. 求如图阴影部分面积. (单位: 厘米)考点长方形、正方形的面积;平行四边形的面积;三角形的周长和面积. 1526356分析图一中阴影部分的面积=大正方形面积的一半﹣与阴影部分相邻的小三角形的面积;图二中阴影部分的面积=梯形的面积﹣平四边形的面积, 再将题目中的数据代入相应的公式进行计算.解答解: 图一中阴影部分的面积=6×6÷2﹣4×6÷2=6(平方厘米);图二中阴影部分的面积=(8+15)×(48÷8)÷2﹣48=21(平方厘米);答:图一中阴影部分的面积是6平方厘米, 图二中阴影部分的面积是21平方厘米.答:图一中阴影部分的面积是6平方厘米,图二中阴影部分的面积是21平方厘米.答: 图一中阴影部分的面积是6平方厘米,图二中阴影部分的面积是21平方厘米.答:图一中阴影部分的面积是6平方厘米,图二中阴影部分的面积是21平方厘米.点评此题目是组合图形, 需要把握好正方形、三角形、梯形及平行四边形的面积公式, 再将题目中的数据代入相应的公式进行计算.7. 计算如图中阴影部分的面积. 单位: 厘米.考点组合图形的面积. 1526356分析由图意可知:阴影部分的面积= 圆的面积, 又因圆的半径为斜边上的高, 利用同一个三角形的面积相等即可求出斜边上的高, 也就等于知道了圆的半径, 利用圆的面积公式即可求解.解答解: 圆的半径: 15×20÷2×2÷25,=300÷25,=12(厘米);阴影部分的面积:×3.14×122,= ×3.14×144,=0.785×144,=113.04(平方厘米);答:阴影部分的面积是113.04平方厘米.答: 阴影部分的面积是113.04平方厘米.答:阴影部分的面积是113.04平方厘米.点评此题考查了圆的面积公式及其应用, 同时考查了学生观察图形的能力.8. 求阴影部分的面积. 单位: 厘米.考点组合图形的面积;三角形的周长和面积;圆、圆环的面积. 1526356分析(1)圆环的面积等于大圆的面积减小圆的面积, 大圆与小圆的直径已知, 代入圆的面积公式, 从而可以求出阴影部分的面积;(2)阴影部分的面积=圆的面积﹣三角形的面积, 由图可知, 此三角形是等腰直角三角形, 则斜边上的高就等于圆的半径, 依据圆的面积及三角形的面积公式即可求得三角形和圆的面积, 从而求得阴影部分的面积.(2)阴影部分的面积=圆的面积﹣三角形的面积,由图可知,此三角形是等腰直角三角形,则斜边上的高就等于圆的半径,依据圆的面积及三角形的面积公式即可求得三角形和圆的面积,从而求得阴影部分的面积.(2)阴影部分的面积=圆的面积﹣三角形的面积,由图可知,此三角形是等腰直角三角形,则斜边上的高就等于圆的半径,依据圆的面积及三角形的面积公式即可求得三角形和圆的面积,从而求得阴影部分的面积.解答解: (1)阴影部分面积:3.14×﹣3.14×,=28.26﹣3.14,=25.12(平方厘米);(2)阴影部分的面积:3.14×32﹣×(3+3)×3,=28.26﹣9,=19.26(平方厘米);答:圆环的面积是25.12平方厘米, 阴影部分面积是19.26平方厘米.答:圆环的面积是25.12平方厘米,阴影部分面积是19.26平方厘米.答: 圆环的面积是25.12平方厘米,阴影部分面积是19.26平方厘米.答:圆环的面积是25.12平方厘米,阴影部分面积是19.26平方厘米.点评此题主要考查圆和三角形的面积公式, 解答此题的关键是找准圆的半径.9. 如图是三个半圆, 求阴影部分的周长和面积. (单位: 厘米)考点组合图形的面积;圆、圆环的面积. 1526356专题平面图形的认识与计算.分析观察图形可知:图中的大半圆内的两个小半圆的弧长之和与大半圆的弧长相等, 所以图中阴影部分的周长, 就是直径为10+3=13厘米的圆的周长, 由此利用圆的周长公式即可进行计算;阴影部分的面积=大半圆的面积﹣以10÷2=5厘米为半径的半圆的面积﹣以3÷2=1.5厘米为半径的半圆的面积, 利用半圆的面积公式即可求解.解答解: 周长: 3.14×(10+3),=3.14×13,=40.82(厘米);面积: ×3.14×[(10+3)÷2]2﹣×3.14×(10÷2)2﹣×3.14×(3÷2)2,= ×3.14×(42.25﹣25﹣2.25),= ×3.14×15,=23.55(平方厘米);答:阴影部分的周长是40.82厘米, 面积是23.55平方厘米.答:阴影部分的周长是40.82厘米,面积是23.55平方厘米.答: 阴影部分的周长是40.82厘米,面积是23.55平方厘米.答:阴影部分的周长是40.82厘米,面积是23.55平方厘米.点评此题主要考查半圆的周长及面积的计算方法, 根据半圆的弧长=πr, 得出图中两个小半圆的弧长之和等于大半圆的弧长, 是解决本题的关键.10. 求阴影部分的面积. (单位: 厘米)考点圆、圆环的面积. 1526356分析先用“3+3=6”求出大扇形的半径, 然后根据“扇形的面积”分别计算出大扇形的面积和小扇形的面积, 进而根据“大扇形的面积﹣小扇形的面积=阴影部分的面积”解答即可.解答解: r=3, R=3+3=6, n=120,,=,=37.68﹣9.42,=28.26(平方厘米);答:阴影部分的面积是28.26平方厘米.答: 阴影部分的面积是28.26平方厘米.答:阴影部分的面积是28.26平方厘米.点评此题主要考查的是扇形面积计算公式的掌握情况, 应主要灵活运用.11. 求下图阴影部分的面积. (单位: 厘米)考点组合图形的面积. 1526356分析先求出半圆的面积3.14×(10÷2)2÷2=39.25平方厘米, 再求出空白三角形的面积10×(10÷2)÷2=25平方厘米, 相减即可求解.解答解: 3.14×(10÷2)2÷2﹣10×(10÷2)÷2=39.25﹣25=14.25(平方厘米).答:阴影部分的面积为14.25平方厘米.答: 阴影部分的面积为14.25平方厘米.答:阴影部分的面积为14.25平方厘米.点评考查了组合图形的面积, 本题阴影部分的面积=半圆的面积﹣空白三角形的面积.12. 求阴影部分图形的面积. (单位: 厘米)考点组合图形的面积. 1526356分析求阴影部分的面积可用梯形面积减去圆面积的, 列式计算即可.解答解: (4+10)×4÷2﹣3.14×42÷4,=28﹣12.56,=15.44(平方厘米);答:阴影部分的面积是15.44平方厘米.答: 阴影部分的面积是15.44平方厘米.答:阴影部分的面积是15.44平方厘米.点评解答此题的方法是用阴影部分所在的图形(梯形)面积减去空白图形(扇形)的面积, 即可列式解答.13. 计算阴影部分面积(单位: 厘米).考点组合图形的面积. 1526356专题平面图形的认识与计算.分析如图所示, 阴影部分的面积=平行四边形的面积﹣三角形①的面积, 平行四边形的底和高分别为10厘米和15厘米, 三角形①的底和高分别为10厘米和(15﹣7)厘米, 利用平行四边形和三角形的面积公式即可求解.解答解: 10×15﹣10×(15﹣7)÷2,=150﹣40,=110(平方厘米);答:阴影部分的面积是110平方厘米.答: 阴影部分的面积是110平方厘米.答:阴影部分的面积是110平方厘米.点评解答此题的关键是明白:阴影部分的面积不能直接求出, 可以用平行四边形和三角形的面积差求出.14. 求阴影部分的面积. (单位: 厘米)考点梯形的面积. 1526356分析如图所示, 将扇形①平移到扇形②的位置, 求阴影部分的面积就变成了求梯形的面积, 梯形的上底和下底已知, 高就等于梯形的上底, 代入梯形的面积公式即可求解.解答解: (6+10)×6÷2,=16×6÷2,=96÷2,=48(平方厘米);答:阴影部分的面积是48平方厘米.答: 阴影部分的面积是48平方厘米.答:阴影部分的面积是48平方厘米.点评此题主要考查梯形的面积的计算方法, 关键是利用平移的办法变成求梯形的面积.15. 求下图阴影部分的面积: (单位: 厘米)考点组合图形的面积. 1526356分析根据三角形的面积公式:S=ah, 找到图中阴影部分的底和高, 代入计算即可求解.解答解: 2×3÷2=6÷2=3(平方厘米).答:阴影部分的面积是3平方厘米.答: 阴影部分的面积是3平方厘米.答:阴影部分的面积是3平方厘米.点评考查了组合图形的面积, 本题组合图形是一个三角形, 关键是得到三角形的底和高.16. 求阴影部分面积(单位: 厘米).考点组合图形的面积. 1526356分析由图意可知:阴影部分的面积=梯形的面积﹣圆的面积, 梯形的上底和高都等于圆的半径, 上底和下底已知, 从而可以求出阴影部分的面积.解答解: (4+9)×4÷2﹣3.14×42×,=13×4÷2﹣3.14×4,=26﹣12.56,=13.44(平方厘米);答:阴影部分的面积是13.44平方厘米.答: 阴影部分的面积是13.44平方厘米.答:阴影部分的面积是13.44平方厘米.点评解答此题的关键是明白:梯形的下底和高都等于圆的半径, 且阴影部分的面积=梯形的面积﹣圆的面积.17. (2012•长泰县)求阴影部分的面积. (单位: 厘米)考点组合图形的面积. 1526356分析由图可知, 阴影部分的面积=梯形的面积﹣半圆的面积.梯形的面积= (a+b)h, 半圆的面积= πr2, 将数值代入从而求得阴影部分的面积.解答解: ×(6+8)×(6÷2)﹣×3.14×(6÷2)2= ×14×3﹣×3.14×9,=21﹣14.13,=6.87(平方厘米);答:阴影部分的面积为6.87平方厘米.答: 阴影部分的面积为6.87平方厘米.答:阴影部分的面积为6.87平方厘米.点评考查了组合图形的面积, 解题关键是看懂图示, 把图示分解成梯形, 半圆和阴影部分, 再分别求出梯形和半圆的面积.。
(完整版)小学五年级数学求阴影部分面积习题
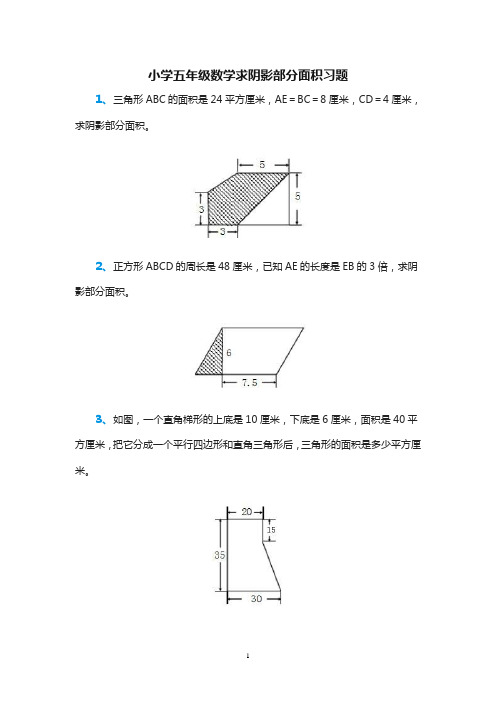
小学五年级数学求阴影部分面积习题1、三角形ABC的面积是24平方厘米,AE=BC=8厘米,CD=4厘米,求阴影部分面积。
2、正方形ABCD的周长是48厘米,已知AE的长度是EB的3倍,求阴影部分面积。
3、如图,一个直角梯形的上底是10厘米,下底是6厘米,面积是40平方厘米,把它分成一个平行四边形和直角三角形后,三角形的面积是多少平方厘米。
4、下面直角梯形的面积是49平方分米,求阴影部分的面积。
5、求整个图形的面积。
(单位:厘米)6、下图所示梯形,如果它的上底增加4厘米,面积就增加18平方厘米,这梯形原来的面积是多少平方厘米?7、求下面图形中阴影部分的面积。
(单位:厘米)8、下图由大小不等的两个正方形拼成,小正方形的边长是6厘米,阴影部分面积是60 厘米,求图中空白部分的面积。
9、求正方形中阴影部分的面积。
10、在下图中,已知平行四边形ABED的面积是30平方厘米,BE长6厘米,EC长4厘米。
求梯形ABCD的面积。
11、图中空白部分是一个面积为30平方厘米的平行四边形,求阴影部分面积。
12、如图:在直角梯形ABCD中,AB=4分米。
CD=9分米,空白部分面积为10平方分米,求阴影部分面积。
13、求阴影部分的面积(单位:厘米):14、图中三角形DEC的面积是2.7平方米,AD=4.4米,AB=2米。
求平行四边形CDFG中阴影部分的面积。
15、如图,在梯形ABCD中,CD=4厘米,AB=2DC,AECD为平行四边形,已知梯形面积为66平方厘米,求阴影部分面积。
16、图中三角形ABC的面积是24平方厘米,AE=BC=8厘米,CD=4厘米,求阴影部分的面积。
17、图中空白部分是一个面积为30平方厘米的平行四边形,求阴影部分面积。
18、图中,阴影部分的面积是56平方厘米,BD=14厘米,求梯形ABCD 的面积。
19、梯形ABCD面积是96平方厘米,AB=6厘米,中位线EF=12厘米,求阴影部分面积。
20、求这个组合图形的面积。
小学五年级数学求阴影部分面积习题

小学五年级数学求阴影部分面积习题1、三角形ABC的面积是24平方厘米,AE=BC=8厘米,CD=4厘米,求阴影部分面积。
2、正方形ABCD的周长是48厘米,已知AE的长度是EB的3倍,求阴影部分面积。
3、如图,一个直角梯形的上底是10厘米,下底是6厘米,面积是40平方厘米,把它分成一个平行四边形和直角三角形后,三角形的面积是多少平方厘米。
4、下面直角梯形的面积是49平方分米,求阴影部分的面积。
5、求整个图形的面积。
(单位:厘米)|6、下图所示梯形,如果它的上底增加4厘米,面积就增加18平方厘米,这梯形原来的面积是多少平方厘米7、求下面图形中阴影部分的面积。
(单位:厘米)8、下图由大小不等的两个正方形拼成,小正方形的边长是6厘米,阴影部分面积是60 厘米,求图中空白部分的面积。
9、求正方形中阴影部分的面积。
10、在下图中,已知平行四边形ABED的面积是30平方厘米,BE长6厘米,EC长4厘米。
求梯形ABCD的面积。
\11、图中空白部分是一个面积为30平方厘米的平行四边形,求阴影部分面积。
12、如图:在直角梯形ABCD中,AB=4分米。
CD=9分米,空白部分面积为10平方分米,求阴影部分面积。
13、求阴影部分的面积(单位:厘米):…14、图中三角形DEC的面积是平方米,AD=米,AB=2米。
求平行四边形CDFG中阴影部分的面积。
15、如图,在梯形ABCD中,CD=4厘米,AB=2DC,AECD为平行四边形,已知梯形面积为66平方厘米,求阴影部分面积。
16、图中三角形ABC的面积是24平方厘米,AE=BC=8厘米,CD=4厘米,求阴影部分的面积。
17、图中空白部分是一个面积为30平方厘米的平行四边形,求阴影部分面积。
18、图中,阴影部分的面积是56平方厘米,BD=14厘米,求梯形ABCD的面积。
19、梯形ABCD面积是96平方厘米,AB=6厘米,中位线EF=12厘米,求阴影部分面积。
20、求这个组合图形的面积。
100例小学数学图形中阴影部分的面积附答案
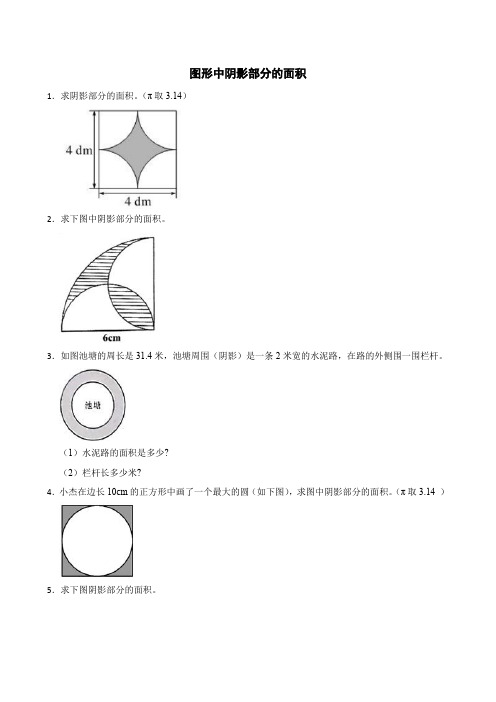
图形中阴影部分的面积1.求阴影部分的面积。
(π取3.14)2.求下图中阴影部分的面积。
3.如图池塘的周长是31.4米,池塘周围(阴影)是一条2米宽的水泥路,在路的外侧围一围栏杆。
(1)水泥路的面积是多少?(2)栏杆长多少米?4.小杰在边长10cm的正方形中画了一个最大的圆(如下图),求图中阴影部分的面积。
(π取3.14 )5.求下图阴影部分的面积。
6.求图中阴影部分的面积.(单位:厘米)7.求阴影部分的面积。
(单位:厘米)8.求下图阴影部分的面积。
(单位:分米)9.求下图中阴影部分的面积。
(单位:米)10.如下图,求阴影部分的面积。
11.求下图阴影部分的面积.(单位:厘米)12.求出下图阴影部分的面积。
13.下图中三个圆的周长都是25.12厘米,不用测量。
计算图中阴影部分的总面积。
14.计算图中阴影部分的面积.(单位:厘米)15.求各图中阴影部分的面积.(单位:cm)(1)(2)16.求阴影部分的面积。
17.求下列图形阴影部分的面积。
(单位:厘米,π≈3.14)(1)(2)18.求下面图形阴影部分的周长和面积。
19.计算如图中阴影部分的面积.20.甲、乙两图中正方形的面积都是40cm2,阴影部分的面积哪一块大?大多少?21.求下图中阴影部分的面积。
(单位:m)(1)(2)22.求阴影部分的面积。
(1)(2)23.求阴影部分的面积。
24.求阴影部分的面积。
25.如图:圆的直径是6dm,阴影部分的面积是多少?26.计算阴影部分的周长和面积27.求下图中阴影部分的面积。
(1)R=10cm,r=4cm (2)28.计算阴影部分的周长和面积29.求阴影部分的周长。
(单位:cm)30.下图中,正方形的边长是4cm,求阴影部分的面积。
31.在半径为4厘米的圆中有两条直线垂直相交(如图),比较该图中阴影部分的面积与空白部分面积的大小,谁大?大多少?32.分别以直角三角形ABC的三条边为直径画了三个半圆,得到下图。
求阴影部分面积-小学数学专项-(答案、例题)(9页)答案和例题在一起

1、下图是一个圆柱体,如果把它的高截短3厘米,它的表面积减少94.2平方厘米。
这个圆柱体积减少多少立方厘米?÷÷÷(厘米)94=2.5142.33.32=⨯⨯(立方厘米)145.235352、一根底面直径是2分米、长是2米的圆木,要锯成横截面是最大的正方形的方木,需要锯下多少木料?2=⨯(立方分米)÷⨯402022()8.62⨯÷⨯(立方分米).32=22014262=8.-(立方分米)22408.3、一个底面积是125.6平方米的圆柱形蓄水池,容积是314立方米。
如果再深挖0.5米,水池容积是多少立方米?125=6.+⨯(立方米)3148.3765.01、如图所示,求图中阴影部分的面积。
(单位:分米,π取3.14)①5.28505.782101041101014.3=-=÷⨯-⨯⨯⨯ ②76.1324.5064418814.388=-=⨯⨯⨯-⨯2、如图所示,正方形ABCD 的边长为4 厘米,分别以B 、D 为圆心,以4厘米为半径在正方形内画圆,求阴影部分面积。
(π取3)56.4856.12244414414.3=-=÷⨯-⨯⨯⨯3、计算阴影部分的面积。
(单位:cm )25.14251025514.3=÷⨯-÷⨯⨯4、求出如图阴影部分的面积。
(单位:cm )5+8=13(cm) 5×5×÷2=12.5(cm 2) (5+13)×5÷2-12.5=32.5(cm 2)【例题1】已知如图,三角形ABC 的面积为8平方厘米,AE =ED ,BD=32BC ,求阴影部分的面积。
连接DF ,三角形ABC 的面积=5倍三角形DFC 的面积2.3258=⨯÷(平方厘米)变式1-1:如图,AE =ED ,BC=3BD ,S △ABC =30平方厘米。
求阴影部分的面积。
小学五年级数学求阴影部分面积习题
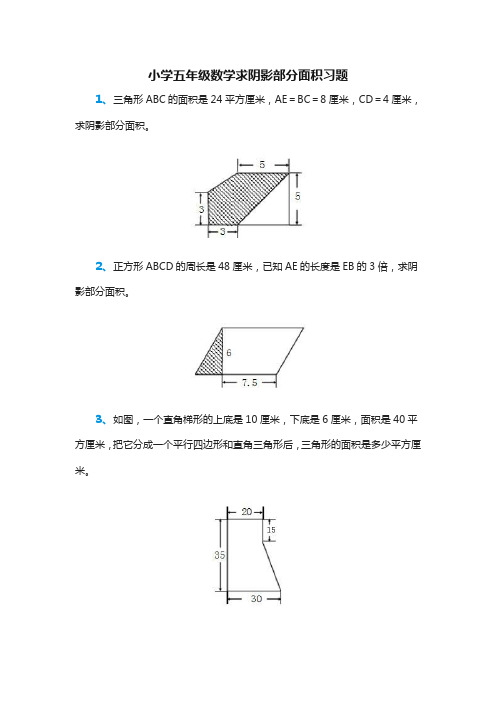
小学五年级数学求阴影部分面积习题1、三角形ABC的面积是24平方厘米,AE=BC=8厘米,CD=4厘米,求阴影部分面积。
2、正方形ABCD的周长是48厘米,已知AE的长度是EB的3倍,求阴影部分面积。
3、如图,一个直角梯形的上底是10厘米,下底是6厘米,面积是40平方厘米,把它分成一个平行四边形和直角三角形后,三角形的面积是多少平方厘米。
4、下面直角梯形的面积是49平方分米,求阴影部分的面积。
5、求整个图形的面积。
(单位:厘米)6、下图所示梯形,如果它的上底增加4厘米,面积就增加18平方厘米,这梯形原来的面积是多少平方厘米?7、求下面图形中阴影部分的面积。
(单位:厘米)8、下图由大小不等的两个正方形拼成,小正方形的边长是6厘米,阴影部分面积是60 厘米,求图中空白部分的面积。
9、求正方形中阴影部分的面积。
10、在下图中,已知平行四边形ABED的面积是30平方厘米,BE长6厘米,EC长4厘米。
求梯形ABCD的面积。
11、图中空白部分是一个面积为30平方厘米的平行四边形,求阴影部分面积。
12、如图:在直角梯形ABCD中,AB=4分米。
CD=9分米,空白部分面积为10平方分米,求阴影部分面积。
13、求阴影部分的面积(单位:厘米):14、图中三角形DEC的面积是2.7平方米,AD=4.4米,AB=2米。
求平行四边形CDFG中阴影部分的面积。
15、如图,在梯形ABCD中,CD=4厘米,AB=2DC,AECD为平行四边形,已知梯形面积为66平方厘米,求阴影部分面积。
16、图中三角形ABC的面积是24平方厘米,AE=BC=8厘米,CD=4厘米,求阴影部分的面积。
17、图中空白部分是一个面积为30平方厘米的平行四边形,求阴影部分面积。
18、图中,阴影部分的面积是56平方厘米,BD=14厘米,求梯形ABCD 的面积。
19、梯形ABCD面积是96平方厘米,AB=6厘米,中位线EF=12厘米,求阴影部分面积。
20、求这个组合图形的面积。
小学阴影面积试题及答案

小学阴影面积试题及答案1. 题目:计算下列图形的阴影部分面积。
答案:阴影部分面积为15平方厘米。
2. 题目:下图中,长方形的长为8厘米,宽为5厘米,求阴影部分的面积。
答案:阴影部分面积为20平方厘米。
3. 题目:一个正方形的边长为6厘米,其内有一个半径为2厘米的圆,求阴影部分的面积。
答案:阴影部分面积为18平方厘米。
4. 题目:一个平行四边形的底为10厘米,高为6厘米,其内有一个底为4厘米,高为3厘米的三角形,求阴影部分的面积。
答案:阴影部分面积为36平方厘米。
5. 题目:一个半圆形的直径为10厘米,求阴影部分的面积。
答案:阴影部分面积为25π平方厘米。
6. 题目:一个梯形的上底为4厘米,下底为6厘米,高为5厘米,其内有一个底为3厘米,高为4厘米的三角形,求阴影部分的面积。
答案:阴影部分面积为10平方厘米。
7. 题目:一个圆形的半径为7厘米,其内有一个半径为3厘米的圆,求阴影部分的面积。
答案:阴影部分面积为153π平方厘米。
8. 题目:一个三角形的底为8厘米,高为6厘米,其内有一个底为4厘米,高为3厘米的三角形,求阴影部分的面积。
答案:阴影部分面积为12平方厘米。
9. 题目:一个长方形的长为10厘米,宽为7厘米,其内有一个直径为6厘米的圆,求阴影部分的面积。
答案:阴影部分面积为49平方厘米。
10. 题目:一个等腰三角形的底为10厘米,高为8厘米,其内有一个底为5厘米,高为4厘米的三角形,求阴影部分的面积。
答案:阴影部分面积为20平方厘米。
