常用符号表
常用数学符号大全

常用数学符号大全数学,作为一门精确而又充满逻辑的学科,有着丰富多样的符号来表达各种数学概念和运算。
这些符号就像是数学世界的语言,让数学的表达更加简洁、准确和高效。
下面就让我们一起来了解一些常用的数学符号吧!一、基本运算符号1、加号(+):用于表示两个或多个数相加的运算。
例如:2 + 3 = 5。
2、减号():表示减法运算,如 5 2 = 3。
3、乘号(×或):指示乘法操作,比如 2 × 3 = 6 或者 2 3 = 6。
4、除号(÷或/):用于表示除法运算,像 6 ÷ 2 = 3 或者 6 / 2 = 3。
二、关系符号1、等于号(=):表明左右两边的量相等,比如 2 + 3 = 5 。
2、大于号(>):表示左边的量大于右边的量,例如 5 > 3 。
3、小于号(<):与大于号相反,意味着左边的量小于右边的量,像 3 < 5 。
4、大于等于号(≥):表示左边的量大于或等于右边的量,例如 5 ≥ 3 。
5、小于等于号(≤):表示左边的量小于或等于右边的量,比如 3 ≤ 5 。
三、集合符号1、属于(∈):如果一个元素属于某个集合,就用这个符号表示。
例如,若集合 A ={1, 2, 3},2 ∈ A 。
2、不属于(∉):与属于相反,如果一个元素不属于某个集合,就用这个符号。
比如 4 ∉ A 。
3、并集(∪):表示两个集合中所有元素组成的新集合。
例如,集合 A ={1, 2, 3},集合 B ={3, 4, 5},则 A ∪ B ={1, 2, 3, 4, 5} 。
4、交集(∩):表示两个集合中共同元素组成的集合。
比如,集合 A ={1, 2, 3},集合 B ={2, 3, 4},则A ∩ B ={2, 3} 。
四、代数符号1、未知数(通常用 x、y、z 等表示):在方程中代表需要求解的值。
例如,在方程 2x + 3 = 7 中,x 就是未知数。
2、系数(用数字与未知数相乘的数字):比如在式子 5x 中,5 就是系数。
常用符号一览

═║╒╓╔╕╖╗╘╙╚╛╜╝╞╟╠╡╢╣╤╥╦╧╨╩╪╫╬╳
╔ ╗╝╚ ╬ ═ ╓ ╩┠┨┯┷┏┓┗┛┳⊥﹃﹄┌╭╮╯╰
箭头符号↑返回顶部
↑ ↓ ← →↖↗↙↘↔ ↕➻➼➽➸➳➺➻➴➵➶➷➹▶➩➪➫➬➭➮➯➱➲➾➔➘➙➚➛➜➝➞➟➠➡➢➣➤➥➦➧➨↚↛↜↝↞↟↠↠↡↢↣↤↤↥↦↧↨⇄⇅⇆⇇⇈⇉⇊⇋⇌⇍⇎⇏⇐⇑⇒⇓⇔⇖⇗⇘⇙⇜↩↪↫↬↭↮↯↰↱↲↳↴↵↶↷↸↹↺↻↼↽↾↿⇀⇁⇂⇃⇞⇟⇠⇡⇢⇣⇤⇥⇦⇧⇨⇩⇪
注音码↑返回顶部
ァアィイゥウェエォオカガキギクグケゲコゴサザシジスズセゼソゾタダチヂッツヅテデトドナニヌネノハバパヒビピフブプヘベペホボポマミムメモャヤュユョヨラリルレロヮワヰヱヲンヴヵヶ
绘表符号↑返回顶部
─━│┃┄┅┆┇┈┉┊┋┌┍┎┏┐┑┒┓└┕┖┗┘┙┚┛
├┝┞┟┠┡┢┣┤┥┦┧┨┩┪┫┬┭┮┯┰┱┲┳┴┵┶┷┸┹┺┻
∷∶∫∮∝∞∧∨∑ ∏∪∩∈∵∴⊥∥∠⌒⊙√ ∟⊿㏒㏑% ‰
特殊符号↑返回顶部
·⊙①?◎Θ⊙●○¤㊣㈱@の■□★☆◆◇◣◢◤◥▲△▼▽⊿◢
▂▃▄▅▆▇█▉▊▋▌▍▎▏■ ▓回□〓≡
↑↓→←↘↙♀♂┇┅‖$ @ * & #※卍卐∞Ψ §∮№⌒*
░ ▒▣▤▥▦▧▨▩▪ ▫ ▬◆◇◈◎●◐◑☉☎☏☜☞☺ ☻ ☼ ♠♡♢♣♤♥ ♦♧♨♩♪ ♫♬♭♯
编号&序号↑返回顶部
①②③④⑤⑥⑦⑧⑨⑩㈠㈡㈢㈣㈤㈥㈦㈧㈨㈩№
⑴⑵⑶⑷⑸⑹⑺⑻⑼⑽⑾⑿⒀⒁⒂⒃⒄⒅⒆⒇
⒈⒉⒊⒋⒌⒍⒎⒏⒐⒑⒒⒓⒔⒕⒖⒗⒘⒙⒚⒛
ⅠⅡⅢⅣⅤⅥⅦⅧⅨⅩⅪⅫⅰⅱⅲⅳⅴⅵⅶⅷⅸⅹ
⑪⑫⑬⑭⑮⑯⑰⑱⑲⑳ⓐⓑⓒⓓⓔⓕⓖⓗⓘⓙⓚⓛⓜⓝⓞⓟⓠⓡⓢⓣⓤⓥⓦⓧⓨⓩ
数学符号↑返回顶部
常用标点符号与特殊符号大全

常用标点符号与特殊符号大全*标点符号 : 。
,、;:?!…-·ˉˇ¨‘\'“”々~‖∶"'`|〃〔〕〈〉《》「」『』.〖〗【】()[]{}*数字序号 :ⅠⅡⅢⅣⅤⅥⅦⅧⅨⅩⅪⅫ㈠㈡㈢㈣㈤㈥㈦㈧㈨㈩⑴⑵⑶⑷⑸⑹⑺⑻⑼⑽①②③④⑤⑥⑦⑧⑨⑩⑾⑿⒀⒁⒂⒃⒄⒅⒆⒇①②③④⑤⑥⑦⑧⑨⑩№一二三四五六七八九十⑴⑵⑶⑷⑸⑹⑺⑻⑼⑽⑾⑿⒀⒁⒂⒃⒄⒅⒆⒇⒈⒉⒊⒋⒌⒍⒎⒏⒐⒑⒒⒓⒔⒕⒖⒗⒘⒙⒚⒛ⅠⅡⅢⅣⅤⅥⅦⅧⅨⅩⅪⅫⅰⅱⅲⅳⅴⅵⅶⅷⅸⅹ*数学符号 :≈≡≠=≤≥<>≮≯∷±+-×÷/∫∮∝∞∧∨∑∏∪∩∈∵∴⊥∥∠⌒⊙≌∽√*单位符号 :°′″$£¥‰%℃¤¢○一二三四五六七八九十百千万亿兆吉太拍艾分厘毫微零壹贰叁肆伍陆柒捌玖拾佰仟*制表符 :┌┍┎┏┐┑┒┓─┄┈├┝┞┟┠┡┢┣│┆┊┬┭┮┯┰┱┲┳┼┽┾┿╀╁╂╃*特殊符号 :§№☆★○●◎◇◆□■△▲※→←↑↓〓#&@\^_&@\^*希腊字母 :αβγδεζηθικλμνξοπρστυφχψωΑΒΓΔΕΖΗΘΙΚΛΜΝΞΟΠΡΣΤΥΦΧΨΩ*俄文字母 :абвгдеёжзийклмнопрстуфхцчшщъыьэюяАБВГДЕЁЖЗИЙКЛМНОПРСТУФХЦЧШЩЪЫЬЭЮЯ*注音符号 :ㄅㄉㄓㄚㄞㄢㄦㄆㄊㄍㄐㄔㄗㄧㄛㄟㄣㄇㄋㄎㄑㄕㄘㄨㄜㄠㄤㄈㄏㄒㄖㄙㄩㄝㄡㄥ*拼音符号 :āáǎàōóǒòêēéěèīíǐìūúǔùǖǘǚǜü*日文平假名 :ぁぃぅぇぉかきくけこんさしすせそたちつってとゐなにぬねのはひふへほゑまみむめもゃゅょゎをあいうえおがぎぐげござじずぜぞだぢづでどぱぴぷぺぽぼびぶべぼらりるれろやゆよわ*日文片假名 :ァィゥヴェォカヵキクケヶコサシスセソタチツッテトヰンナニヌネノハヒフヘホヱマミムメモャュョヮヲアイウエオガギグゲゴザジズゼゾダヂヅデドパピプペポバビブベボラリルレロヤユヨワ]レロヤユヨワ*重量单位 :㎎㎏㎜㎝㎞㎡㏄㏎㏑*注册标志:(注意:这两个符号不能直接粘贴复制,请复制代码然后插在网页内)® 网页代码 ® ©网页代码 ©*补充符号 :常用标点符号用法简表名称符号用法说明举例句号。
电工常用50个电气符号

电工常用50个电气符号以下是电工常用100个电气符号:电流表PA 电压表PV有功电度表PJ 无功电度表PJR频率表PF 相位表PPA最大需量表(负荷监控仪) PM 功率因数表PPF有功功率表PW 无功功率表PR无功电流表PAR 声信号HA光信号HS 指示灯HL红色灯HR 绿色灯HG黄色灯HY 蓝色灯HB白色灯HW 连接片XB插头XP 插座XS端子板XT 电线,电缆,母线W直流母线WB 插接式(馈电)母线WIB 电力分支线WP 照明分支线WL应急照明分支线WE 电力干线WPM照明干线WLM 应急照明干线WEM滑触线WT 合闸小母线WCL控制小母线WC 信号小母线WS闪光小母线WF 事故音响小母线WFS预告音响小母线WPS 电压小母线WV事故照明小母线WELM 避雷器F熔断器FU 快速熔断器FTF 跌落式熔断器FF 限压保护器件FV 电容器 C 电力电容器CE正转按钮SBF 反转按钮SBR停止按钮SBS 紧急按钮SBE试验按钮SBT 复位按钮SR限位开关SQ 接近开关SQP手动控制开关SH 时间控制开关SK 液位控制开关SL 湿度控制开关SM 压力控制开关SP 速度控制开关SS 温度控制开关,辅助开关ST 电压表切换开关SV 电流表切换开关SA 整流器U可控硅整流器UR 控制电路有电源的整流器VC 变频器UF 变流器UC逆变器UI 电动机M异步电动机MA 同步电动机MS直流电动机MD 绕线转子感应电动机MW 鼠笼型电动机MC 电动阀YM电磁阀YV 防火阀YF排烟阀YS 电磁锁YL跳闸线圈YT 合闸线圈YC气动执行器YPA,YA 电动执行器YE 发热器件(电加热) FH 照明灯(发光器件) EL 空气调节器EV 电加热器加热元件EE 感应线圈,电抗器L 励磁线圈LF消弧线圈LA 滤波电容器LL电阻器,变阻器R 电位器RP热敏电阻RT 光敏电阻RL。
常用的特殊符号大全

常用的特殊符号大全特殊符号是我们在日常书写和表达中经常使用的,它们可以用来表示特定的意义、注释或者增加文本的可读性。
下面是一些常见的特殊符号的大全:1. 标点符号:- 句号(.):用于句子的结束。
- 逗号(,):用于分隔句子中的短语或列表项。
- 分号(;):用于分隔较长的独立子句或列举项。
- 冒号(:):用于引导解释、说明或列举。
- 感叹号(!):用于表示强烈的情感或惊讶。
- 问号(?):用于表示疑问或询问。
2. 引号:- 双引号(''):用于引用直接的对话、引文或特定的词语。
- 单引号(''):用于引用间接的对话或特定的词语。
3. 括号:- 圆括号(()):用于插入补充说明或解释的内容。
- 方括号([]):用于引用或注释文本。
- 大括号({}):用于表示集合、分组或约束条件。
4. 运算符:- 加号(+):用于表示加法运算。
- 减号(-):用于表示减法运算。
- 乘号(×):用于表示乘法运算。
- 除号(÷):用于表示除法运算。
- 等号(=):用于表示相等关系。
- 大于号(>)和小于号(<):用于表示大小关系。
- 百分号(%):用于表示百分比。
5. 特殊符号:- 版权符号():用于表示版权所有。
- 注册商标符号():用于表示商标注册。
- 电话号码符号():用于表示电话联系方式。
- 心形符号():用于表示爱或喜欢。
- 笑脸符号():用于表示愉快或开心的表情。
- 禁止符号():用于表示禁止或不允许。
这些是一些常见的特殊符号的大全,它们在我们的书写和表达中起到了重要的作用。
熟练地使用这些符号能够让我们的文本更加丰富多样,增强交流的效果。
常用数学符号大全

常用数学符号大全点击查看>>数学实用工具:数学符号大全1、几何符号ⅷⅶ△2、代数符号ⅴⅸⅹ~ⅵ?3、运算符号如加号(+),减号(-),乘号(×或·),除号(÷或/),两个集合的并集(?),交集(?),根号(ⅳ),对数(log,lg,ln),比(:),微分(dx),积分(?),曲线积分(?)等。
4、集合符号ⅰ5、特殊符号ⅲπ(圆周率)6、推理符号|a| ??△ⅶ±??ⅰ?↖↗↘↙ⅷⅸⅹ&; §←↑→↓??↖↗ΓΔΘΛΞΟΠΣΦΧΨΩαβγδεδεζηθικλμνπξζηυθχψωⅠ Ⅱ Ⅲ Ⅳ Ⅴ Ⅵ Ⅶ Ⅷ Ⅸ Ⅹ Ⅺ Ⅻⅰ ⅱ ⅲ ⅳ ⅴ ⅵ ⅶ ⅷ ⅸ ⅹⅰⅱⅲ?ⅳⅴⅵ? ⅶ?ⅷⅸⅹ⊕??℃指数0123:o1237、数量符号如:i,2+i,a,x,自然对数底e,圆周率π。
8、关系符号如“=”是等号,“?”是近似符号,“?”是不等号,“>”是大于符号,“<”是小于符号,“?”是大于或等于符号(也可写作“?”),“?”是小于或等于符号(也可写作“?”),。
“? ”表示变量变化的趋势,“?”是相似符号,“?”是全等号,“ⅷ”是平行符号,“?”是垂直符号,“ⅴ”是成正比符号,(没有成反比符号,但可以用成正比符号配倒数当作成反比)“ⅰ”是属于符号,“??”是“包含”符号等。
9、结合符号如小括号“()”中括号“[]”,大括号“{}”横线“—”10、性质符号如正号“+”,负号“-”,绝对值符号“| |”正负号“±”11、省略符号如三角形(△),直角三角形(Rt△),正弦(sin),余弦(cos),x的函数(f (x)),极限(lim),角(ⅶ),因为,(一个脚站着的,站不住)所以,(两个脚站着的,能站住)总和(ⅲ),连乘(ⅱ),从n 个元素中每次取出r个元素所有不同的组合数(C(r)(n) ),幂(A,Ac,Aq,x^n)等。
电工仪表的常用符号表格

电工仪表的常用符号以下是电工仪表的常用符号及其含义:1.电流表 PA2.电压表 PV3.有功电度表 PJ4.无功电度表 PJR5.频率表 PF6.相位表 PPA7.最大需量表(负荷监控仪) PM8.功率因数表 PPF9.有功功率表 PW10.无功功率表 PR11.无功电流表 PAR12.声信号 HA13.光信号 HS14.指示灯 HL15.红色灯 HR16.绿色灯 HG17.黄色灯 HY18.蓝色灯 HB19.白色灯 HW20.连接片 XB21.插头 XP22.插座 XS23.端子板 XT24.电线,电缆,母线 W25.直流母线 WB26.插接式(馈电)母线 WIB27.电力分支线 WP28.照明分支线 WL29.应急照明分支线 WE30.电力干线 WPM31.照明干线 WLM32.应急照明干线 WEM33.滑触线 WT34.合闸小母线 WCL35.控制小母线 WC36.信号小母线 WS37.闪光小母线 WF38.事故音响小母线 WFS39.预告音响小母线 WPS40.电压小母线 WV41.事故照明小母线 WELM42.避雷器 F43.熔断器 FU44.快速熔断器 FTF45.跌落式熔断器 FF46.限压保护器件 FV47.电容器 C48.电力电容器 CE49.正转按钮 SBF50.反转按钮 SBR51.停止按钮 SBS52.紧急按钮 SBE53.试验按钮 SBT54.复位按钮 SR55.限位开关 SQ56.接近开关 SQP57.手动控制开关 SH58.时间控制开关 SK59.液位控制开关 SL60.压力控制开关 SP。
57个常用速记符号

常用速记符号大于〉小于V小于或等于秋于或等于麦等于、意味着二不等于黑约等于嚨憾、悲哀;高兴、荣兴(错误、否、不、否定XE确、对、好、肯定A不同意N同意Y 上升、增加f下降、减少J强、好+更强、更好++弱、差—更弱、更差一一因为•••所以二优秀★属于?胜利V问题、疑问?和、与&结论是=>促进、发展/国家口国与国口/ □原因—导致、结果T对立、冲突><波折VV会议、会面。
进入n接触、交往X 分歧丄非常、十分重要**坚持苇关键!奇观!有关@替换为s但是与••…比较而言//空洞贸表厶口译笔记的功能是:第一、具有辅助短时记忆的作用,避免遗忘漏失。
第二、透过图像、版面与符号的交错运用,笔记具有语段逻辑分析与保存的功能,能将语篇的段落整理清楚并保存一段时间。
笔记是口译讯息整理与保存的工具,运用这项工具时必须先了解到底笔记的内容是什么。
缩减练习中已经提到,建立新架构的必要讯息是5W1H「六何」(何人、何事、何时、何地、何物、如何)。
再加上,数字与专有名词就是了。
在讯息内容之外,还要进一步掌握的就是讯息内容之间的关系。
讯息关系内容说明方法运用段落的顺序显示出语篇或语意的段落画线或排列表示逻辑的关系祝贺、谢词、欢迎、感想运用笔记符号表示强弱的程度表达状语等修饰词,如「极为」、「少许」、「经常」、「偶而」等在右上角用1-2个+ -!?等表示变化的情形升高、降低、波动、剧变运用V> 等表示一、做口译笔记时的注意事项1. 口译笔记应记要点,切忌求记“全”。
口译笔记是记忆的延伸或补充,不应也不必取代记忆。
口译笔记的主要内容是概念、命题、名称、数字、组织机构和逻辑关系(如大小、先后、正反、上下、升降、因果关系等),笔记单位以表达意群的词语和符号为主。
2. 口译笔记求快求精,但不可潦草。
3. 口译笔记可使用来源语,也可使用目标语,也可以双语兼用。
只要有利于口译的准确性和流利性,不必拘泥于某种文字或符号。
常用化学元素符号表
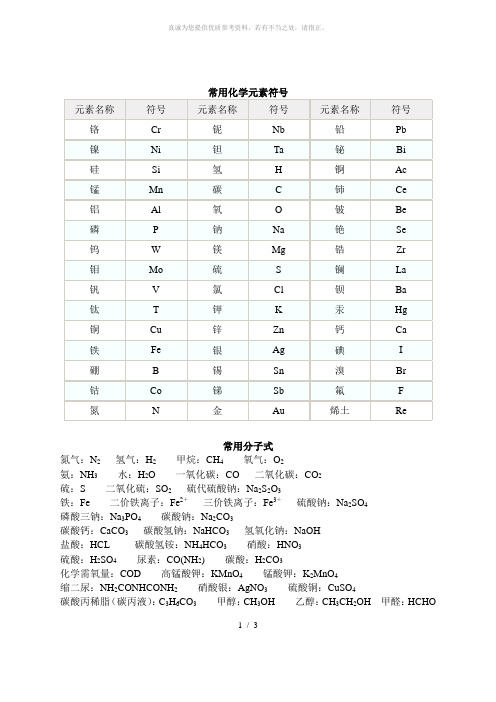
常用分子式氮气:N2氢气:H2甲烷:CH4氧气:O2氨:NH3水:H2O 一氧化碳:CO 二氧化碳:CO2硫:S 二氧化硫:SO2硫代硫酸钠:Na2S2O3铁:Fe 二价铁离子:Fe2+三价铁离子:Fe3+硫酸钠:Na2SO4磷酸三钠:Na3PO4碳酸钠:Na2CO3碳酸钙:CaCO3碳酸氢钠:NaHCO3氢氧化钠:NaOH盐酸:HCL 碳酸氢铵:NH4HCO3硝酸:HNO3硫酸:H2SO4尿素:CO(NH2) 碳酸:H2CO3化学需氧量:COD 高锰酸钾:KMnO4锰酸钾:K2MnO4缩二尿:NH2CONHCONH2硝酸银:AgNO3硫酸铜:CuSO4碳酸丙稀脂(碳丙液):C3H6CO3甲醇:CH3OH 乙醇:CH3CH2OH 甲醛:HCHO1 / 3一甲氨:NH2CH3二甲氨:NH(CH3)2 三甲氨:N(CH3)3三氧化二铝:AL2O3三氧化二铁:Fe2O3 氧化铜:CuO 氯化钠:NaCL一、初中化学常见混合物的重要成分1、空气:氮气(N2)和氧气(O2)2、水煤气:一氧化碳(CO)和氢气(H2)3、煤气:一氧化碳(CO)4、天然气:甲烷(CH4)5、石灰石/大理石:(CaCO3)6、生铁/钢:(Fe)7、木炭/焦炭/炭黑/活性炭:(C)8、铁锈:(Fe2O3)二、初中化学常见物质俗称1、氯化钠(NaCl):食盐2、碳酸钠(Na2CO3) :纯碱,苏打,口碱3、氢氧化钠(NaOH):火碱,烧碱,苛性钠4、氧化钙(CaO):生石灰5、氢氧化钙(Ca(OH)2):熟石灰,消石灰6、二氧化碳固体(CO2):干冰7、氢氯酸(HCl):盐酸8、碱式碳酸铜(Cu2(OH)2CO3):铜绿9、硫酸铜晶体(CuSO4 .5H2O):蓝矾,胆矾10、甲烷(CH4):沼气11、乙醇(C2H5OH):酒精12、乙酸(CH3COOH):醋酸13、过氧化氢(H2O2):双氧水14、汞(Hg):水银15、碳酸氢钠(NaHCO3):小苏打三、物质的除杂1、CO2(CO):把气体通过灼热的氧化铜,2、CO(CO2):通过足量的氢氧化钠溶液3、H2(水蒸气):通过浓硫酸/通过氢氧化钠固体4、CuO(C):在空气中(在氧气流中)灼烧混合物5、Cu(Fe) :加入足量的稀硫酸6、Cu(CuO):加入足量的稀硫酸7、FeSO4(CuSO4): 加入足量的铁粉2 / 38、NaCl(Na2CO3):加入足量的盐酸9、NaCl(Na2SO4):加入足量的氯化钡溶液10、NaCl(NaOH):加入足量的盐酸11、NaOH(Na2CO3):加入足量的氢氧化钙溶液12、NaCl(CuSO4):加入足量的氢氧化钡溶液13、NaNO3(NaCl):加入足量的硝酸银溶液14、NaCl(KNO3):蒸发溶剂15、KNO3(NaCl):冷却热饱和溶液。
常用单位符号表
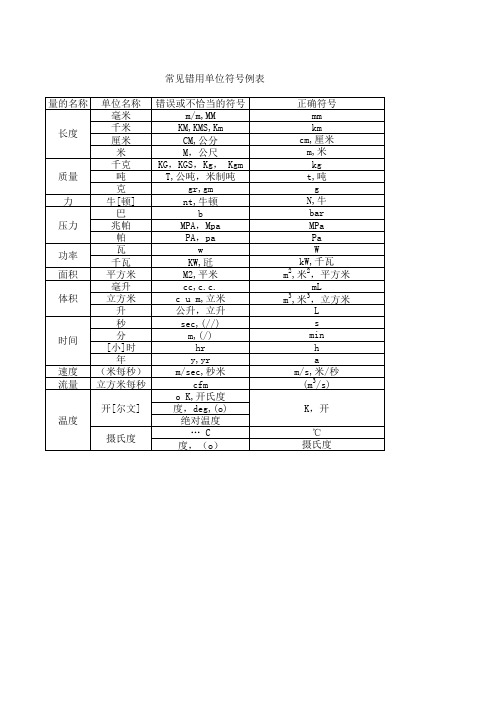
质量 力 压力 功率 面积 体积
ห้องสมุดไป่ตู้
时间 速度 流量
温度
常见错用单位符号例表 量的名称 长度 单位名称 错误或不恰当的符号 毫米 m/m,MM 千米 KM,KMS,Km 厘米 CM,公分 米 M,公尺 千克 KG,KGS,Kg, Kgm 吨 T,公吨,米制吨 克 gr,gm 牛[顿] nt,牛顿 巴 b 兆帕 MPA,Mpa 帕 PA,pa 瓦 w 千瓦 KW,瓩 平方米 M2,平米 毫升 cc,c.c. 立方米 c u m,立米 升 公升,立升 秒 sec,(//) 分 m,(/) [小]时 hr 年 y,yr (米每秒) m/sec,秒米 立方米每秒 cfm o K,开氏度 开[尔文] 度,deg,(o) 绝对温度 … C 摄氏度 度,(o) 正确符号 mm km cm,厘米 m,米 kg t,吨 g N,牛 bar MPa Pa W kW,千瓦 m2,米2,平方米 mL 3 3 m ,米 ,立方米 L s min h a m/s,米/秒 (m3/s) K,开 ℃ 摄氏度
常用的标点符号

“到底去还是不去?我的小姑奶奶。 ”
这是一个倒装句, “我的小姑奶奶”是全句的主语。凡是倒装问句,问号应置于句末, 才能准确表达出疑问或反间的语气。不能一看到发问便加问号。
3.分句之间用顿号
“浦东展开了翅膀,她是那样欢快、昂扬、奋发、正在向辉煌的明天飞去。 ”
这里实际上有三个分句,在第二个分句和第三个分句之间,应用逗号而不是顿号。 “欢
d.伟大的东西总是围以辉煌的光彩,辉煌的光彩就会激起虚荣心, 而虚荣心又很容易引 起激动或我们心目中的激动;谁要是为名利的恶魔所诱惑,他就不能保持理智,就会依 照不可抗拒的力量所指引给他的方向扑去。
4引号的用法有:a.引用,b.特定称谓,c.强调,d.讽刺,e否定。请在句后括号中填 写相应用法的字母序号。
接号连接汉语拼音时占半个字格,而在公路、铁路等交通部门标识运行起讫点时,占两 格。
5、着重号和专名号都放在文字的下边,不单独占格。
五、标点符号专项训练
1下列句子使用问号有错误的一句是:()
a.延安的革命传统结出了丰硕之果,有谁不万分欣喜呢
b.只有古柏知道这昔日的野岭荒山,恶水险川,是怎样变成了今天的繁华世界
⑵分号(;)表示复句内部并列分句间的Байду номын сангаас顿。例如:
使用分号应注意几点:
1单句排比,要求气势贯通,一般用逗号,不用分号。例如:
2并列关系句,分句较短的用逗号,不用分号。例如:
⑶顿号(、)
顿号表示句子内部最小的停顿,常用在并列的词或词组之间。例如:
a、并列词语中如果有连词“和”“及”“与”“或”“或者”等就不必用顿号。
1、七种点号书写时紧挨着文字,放在文字右边偏下,占一格。
2、引号、括号、书名号都用在文字前后,占一格。这三种标号的前半边不可以出现在
电气工程常用符号对照表

电气工程常用符号对照表电气工程常用符号对照表旨在为电气工程师提供准确、简洁的符号解释,以便在工作中准确使用和理解电气图纸和文档。
以下是一些常见的电气工程符号及其解释:1.电源与传输AC:交流电(Alternating Current)AC:交流电(Alternating Current)AC:交流电(Alternating Current)DC:直流电(Direct Current)DC:直流电(Direct Current)DC:直流电(Direct Current)V:电压(Voltage)V:电压(Voltage)V:电压(Voltage)I:电流(Current)I:电流(Current)I:电流(Current)R:电阻(Resistance)R:电阻(Resistance)R:电阻(Resistance)L:电感(Inductance)L:电感(Inductance)L:电感(Inductance)C:电容(Capacitance)C:电容(Capacitance)C:电容(Capacitance)GND:地(Ground)GND:地(Ground)GND:地(Ground)2.电源设备发电机(Generator)发电机(Generator)发电机(Generator)电动机(Motor)电动机(Motor)电动机(Motor)蓄电池(Battery)蓄电池(Battery)蓄电池(Battery)变压器(Transformer)变压器(Transformer)变压器(Transformer)3.连接元件导线(Wire)导线(Wire)导线(Wire)开关(Switch)开关(Switch)开关(Switch)插座(Outlet)插座(Outlet)插座(Outlet)继电器(Relay)继电器(Relay)继电器(Relay)开关断路器(Circuit Breaker)开关断路器(Circuit Breaker)开关断路器(Circuit Breaker)保险丝(Fuse)保险丝(Fuse)保险丝(Fuse)接线柱(Terminal Block)接线柱(Terminal Block)接线柱(Terminal Block)4.灯具与灯泡灯具(Luminaire)灯具(Luminaire)灯具(Luminaire)荧光灯(Fluorescent Light)荧光灯(Fluorescent Light)荧光灯(Fluorescent Light)LED灯(LED Light)LED灯(LED Light)LED灯(LED Light)霓虹灯(Neon Light)霓虹灯(Neon Light)霓虹灯(Neon Light)照明支路(Lighting Circuit)照明支路(Lighting Circuit)照明支路(Lighting Circuit)5.传感器温度传感器(___)温度传感器(___)温度传感器(___)湿度传感器(Humidity Sensor)湿度传感器(Humidity Sensor)湿度传感器(Humidity Sensor)压力传感器(Pressure Sensor)压力传感器(Pressure Sensor)压力传感器(Pressure Sensor)光敏传感器(Light Sensor)光敏传感器(Light Sensor)光敏传感器(Light Sensor)烟雾传感器(Smoke Sensor)烟雾传感器(Smoke Sensor)烟雾传感器(Smoke Sensor)6.控制元件按钮(Button)按钮(Button)按钮(Button)指示灯(Indicator Light)指示灯(Indicator Light)指示灯(Indicator Light)继电器(Relay)继电器(Relay)继电器(Relay)计时器(Timer)计时器(Timer)计时器(Timer)编码器(Encoder)编码器(Encoder)编码器(Encoder)触摸屏(Touchscreen)触摸屏(Touchscreen)触摸屏(Touchscreen)7.电机与控制电机(Motor)电机(Motor)电机(Motor)驱动器(Driver)驱动器(Driver)驱动器(Driver)变频器(Inverter)变频器(Inverter)变频器(Inverter)PLC:可编程逻辑控制器(Programmable Logic Controller)PLC:可编程逻辑控制器(Programmable Logic Controller)PLC:可编程逻辑控制器(Programmable Logic Controller)HMI:人机界面(Human Machine Interface)HMI:人机界面(Human Machine Interface)HMI:人机界面(Human Machine Interface)8.测量与仪表电压表(Voltmeter)电压表(Voltmeter)电压表(Voltmeter)电流表(Ammeter)电流表(Ammeter)电流表(Ammeter)频率表(Frequency Meter)频率表(Frequency Meter)频率表(Frequency Meter)功率表(Power Meter)功率表(Power Meter)功率表(Power Meter)示波器(Oscilloscope)示波器(Oscilloscope)示波器(Oscilloscope)9.接线方法并联(Parallel)并联(Parallel)并联(Parallel)串联(Series)串联(Series)串联(Series)10.保护与安全接地保护(Grounding n)接地保护(Grounding n)接地保护(Grounding n)过压保护(___)过压保护(___)过压保护(___)漏电保护(Ground ___)漏电保护(Ground ___)漏电保护(Ground ___)过载保护(___)过载保护(___)过载保护(___)短路保护(Short ___)短路保护(Short ___)短路保护(Short ___)以上是一些常见的电气工程符号及其解释,希望本文档能帮助您更好地理解和使用电气工程符号。
常用电器仪表符号大全

电流表PA电压表PV有功电度表PJ无功电度表PJR频率表PF相位表PPA最大需量表(负荷监控仪) PM 功率因数表PPF有功功率表PW无功功率表PR无功电流表PAR声信号HA光信号HS指示灯HL红色灯HR绿色灯HG黄色灯HY蓝色灯HB白色灯HW连接片XB 插头XP插座XS端子板XT电线,电缆,母线W直流母线WB插接式(馈电)母线WIB 电力分支线WP照明分支线WL应急照明分支线WE电力干线WPM照明干线WLM应急照明干线WEM滑触线WT合闸小母线WCL控制小母线WC信号小母线WS闪光小母线WF事故音响小母线WFS 预告音响小母线WPS 电压小母线WV事故照明小母线WELM 避雷器F熔断器FU快速熔断器FTF跌落式熔断器FF限压保护器件FV电容器C电力电容器CE正转按钮SBF反转按钮SBR停止按钮SBS紧急按钮SBE试验按钮SBT复位按钮SR限位开关SQ接近开关SQP手动控制开关SH时间控制开关SK液位控制开关SL湿度控制开关SM压力控制开关SP速度控制开关SS温度控制开关,辅助开关ST 电压表切换开关SV 电流表切换开关SA整流器U可控硅整流器UR控制电路有电源的整流器VC 变频器UF变流器UC逆变器UI电动机M异步电动机MA同步电动机MS直流电动机MD绕线转子感应电动机MW鼠笼型电动机MC电动阀YM电磁阀YV防火阀YF排烟阀YS电磁锁YL跳闸线圈YT合闸线圈YC气动执行器YPA,YA电动执行器YE发热器件(电加热)FH 照明灯(发光器件) EL 空气调节器EV电加热器加热元件EE 感应线圈,电抗器L励磁线圈LF消弧线圈LA滤波电容器LL电阻器,变阻器R电位器RP热敏电阻RT光敏电阻RL压敏电阻RPS接地电阻RG放电电阻RD启动变阻器RS频敏变阻器RF限流电阻器RC 光电池,热电传感器B压力变换器BP温度变换器BT速度变换器BV时间测量传感器BT1,BK 液位测量传感器BL温度测量传感器BH,BM辅助文名称字符号A 电流A 模拟ACA 交流自动AUTACC 加速ADD 附加ADJ 可调AUX 辅助ASY 异步BBRK 制动BK 黑BL 蓝BW 向后C 控制CW 顺时针CCW 逆时针D 延时(延迟)D 差动D 数字D 降DC 直流DEC 减E 接地EM 紧急F 快速FB 反馈FW 正,向前GN 绿H 高IN 输入INC 增IND 感应L 左L 限制L 低LA 闭锁M 主M 中M 中间线MMAN 手动N 中性线OFF 断开ON 接通(闭合)OUT 输出P 压力P 保护PE 保护接地PEN 保护接地与中性线共用PU 不接地保护R 记录R 右R 反RD 红色RRST 复位RES 备用RUN 运转S 信号ST 启动SSET 置位、定位SAT 饱和STE 步进STP 停止SYN 同步T 温度T 时间TE 无噪音(防干扰)接地V 真空V 速度V 电压WH 白YE 黄。
新华字典 常用标点符号简表

新华字典中常用的标点符号包括:
1. 句号 (。
):用于句子结束,表示句子完整、结束。
2. 逗号 (,):用于分隔列举的成分或句子中短暂停顿的地方。
3. 问号 (?):用于疑问句末尾,表示疑问。
4. 叹号 (!):用于感叹句末尾,表示强调、感叹或惊讶。
5. 顿号 (、):用于列举成分时,表示并列关系。
6. 分号 (;):用于分隔句子成分,比逗号分割的成分更独立。
7. 冒号 (:):用于引出例证、解释、总结或说明的部分。
8. 引号 (‘’、“”):用于引用文字、表示说话内容或特
殊含义。
9. 括号 (()【】{}等):用于括注、解释、补充说明等。
10. 破折号 (—):用于连接具有密切关系的词语、短语或句子。
11. 省略号 (…):用于表示省略、暂停、未完待续等意思。
12. 书名号 (《》):用于标注书籍、作品的名称。
13. 着重号 (‘’):用于强调、标识或注释。
这些标点符号在书写中起着不同的作用,有助于表达句子的逻辑关系、停顿、强调等。
Excel表格最常用的37种符号,帮你整理齐了!

Excel表格最常用的37种符号,帮你整理齐了!Excel表格最常用的37种符号,帮你整理齐了!一、公式中常用符号:表示一个单元格区域,如A1:B10+ - * / 加减乘除运算符> 大于号>= 大于等于号<><=><> 不等于号,如=IF(A1<>'销售部',,)^数字乘方运算,如2^3结果8。
^(1/数字) 开方运算 8^(1/3)结果为2& 文本连续符,如 'A'& 1 结果为 A1* 通配符表示任意字符多个字符通配符,表示单个任意字符{数字} 常量数组{公式} 数组公式标志,在公式后按Ctrl + shift + Enter后在公式两端自动添加的。
$ 绝对引用符号,可以在复制公式时防止行号或列标发生变动,如A&1公式向下复制时,1不会变成2,3..如果不加$则会变化!工作表和单元格的隶属关于,如表格sheet1的单元格A1,表示为 Sheet1!A1Excel表格最常用的37种符号,帮你整理齐了!二、自定义格式中的符号0 单个数字占位符,如果0的位数大于数字个数,会用0补齐,如123设置格式00000, 会显示成 00123# 单个数字占位符,和0区别是不会补位! 强制显示它后面的字符\ 作用同 ![ ] 设置条件,如 [>100][红色] 大于100的数字显示红色yyyy 4位年d 日m 月aaa 星期代码,只显示大写数字aaaa 星期代码,显示星期+大写数字ddd 星期代码,英文简写dddd 星期代码,英文全称mmm 英文短月份mmmm 英文月份完整单词h 小时[h] 显示大于24小时的数字m 分种s 秒* 用*后的字符补齐位置,让字符长度填满单元格_ 添加一个空格和_后的字符宽度相等@ 文本占位符,可以显示单元格的文本内容,如爱你设置@@后可以显示为爱你爱你Excel表格最常用的37种符号,帮你整理齐了!。
高中数学常用符号表

高中数学常用符号表1. 基本运算符号加法:+减法:乘法:×(中文)、(英文)除法:÷(中文)、/(英文)平方根:√立方根:³√指数:^(英文)2. 比较符号大于:>小于:<大于等于:≥小于等于:≤等于:=不等于:≠3. 集合符号属于:∈不属于:∉空集:∅并集:∪交集:∩补集:A'4. 函数符号函数:f(x)值域:f(x) ∈ D定义域:x ∈ D反函数:f^(1)(x)极限:lim(x→a) f(x) 5. 三角函数符号正弦:sin余弦:cos正切:tan余切:cot正割:sec余割:csc6. 对数符号对数:log自然对数:ln以10为底的对数:lg 7. 概率与统计符号总体:N样本:n平均数:μ样本平均数:x̄标准差:σ样本标准差:s方差:Var协方差:Cov相关系数:ρ8. 微积分符号导数:f'(x)积分:∫微分:d9. 矩阵符号矩阵:A转置:A^T矩阵乘法:A×B矩阵加法:A+B矩阵减法:AB矩阵的逆:A^(1) 10. 其他符号无穷大:∞虚数单位:i平行:∥垂直:⊥交集:∩并集:∪1. 集合论符号集合的元素个数:|A|子集:A⊆B真子集:A⊊B交集:A∩B并集:A∪B差集:A\B 或 AB对称差:A⊕B2. 数列与级数符号数列:{a_n}级数:∑等差数列:a_n = a_1 + (n1)d等比数列:a_n = a_1 r^(n1)数列的极限:lim(n→∞) a_n 3. 几何符号点:A线段:AB线:l平面:α角:∠ABC三角形:△ABC四边形:ABCD圆:⊙O弧:⌒扇形:扇ABO直线与平面的夹角:∠Al平面与平面的夹角:∠αβ坐标系:Oxyz点的坐标:(x, y)直线的斜率:k直线的截距:b圆的半径:r圆的直径:d球的半径:R球的直径:D向量:a→向量的模:|a→|向量的点积:a→·b→向量的叉积:a→×b→5. 复数符号复数:a + bi实部:Re(z)虚部:Im(z)复数的模:|z|复数的共轭:z复数的辐角:θ6. 排列组合符号排列:A(n, k)组合:C(n, k)阶乘:n!数列的通项公式:a_n = f(n)数列的前n项和:S_n等差数列的前n项和:S_n = n/2 (a_1 + a_n)等比数列的前n项和:S_n = a_1 (1 r^n) / (1 r)(r ≠ 1)2. 几何符号三角形的周长:P三角形的面积:S三角形的内角和:180°圆的周长:C圆的面积:A球的表面积:A球的体积:V3. 解析几何符号直线的方程:y = mx + b圆的方程:(x a)^2 + (y b)^2 = r^2椭圆的方程:(x h)^2/a^2 + (y k)^2/b^2 = 1双曲线的方程:(x h)^2/a^2 (y k)^2/b^2 = 1抛物线的方程:y = ax^2 + bx + c4. 复数符号复数的指数形式:z = r(cosθ + isinθ)复数的极坐标形式:z = r∠θ复数的欧拉公式:e^(iθ) = cosθ + isinθ排列的个数:P(n, k) = n! / (n k)!组合的个数:C(n, k) = n! / [k!(n k)!]二项式系数:C(n, k) = (n choose k)6. 概率与统计符号概率:P(A)条件概率:P(A|B)独立事件:P(A∩B) = P(A)P(B)互斥事件:P(A∪B) = P(A) + P(B)期望值:E(X)方差:Var(X)标准差:σ正态分布:N(μ, σ^2)。
常用数学符号读法大全

常⽤数学符号读法⼤全 数学中有很多运算⽤希腊字母来表⽰,这些字母通⽤性很强,往往⽤来表⽰分类标⽰、数学运算符,物理或化学中也经常应⽤。
但有些⽐较复杂,好多同学不会读,下⾯就是⼩编给⼤家带来的数学符号读法,希望能帮助到⼤家!下⾯就将常⽤列表如下: ⼤写⼩写英⽂注⾳国际⾳标注⾳中⽂注⾳ Αα alpha alfa 阿⽿法 Ββ beta beta 贝塔 Γγ gamma gamma 伽马 Δ δ deta delta 德⽿塔 Εε epsilon epsilon 艾普西隆 Ζζ zeta zeta 截塔 Ηη eta eta 艾塔 Θθ theta θita 西塔 Ιι iota iota 约塔 Κκ kappa kappa 卡帕 ∧λ lambda lambda 兰姆达 Μ µ mu miu 缪 Νν nu niu 纽 Ξξ xi ksi 可塞 Οο omicron omikron 奥密可戎 ∏π pi pai 派 Ρρ rho rou 柔 ∑ σ sigma sigma 西格马 Ττ tau tau 套 Υυ upsilon jupsilon ⾐普西隆 Φφ phi fai 斐 Χχ chi khai 喜 Ψψ psi psai 普西 Ωω omega omiga 欧⽶伽 · 数学符号: (1)数量符号:如:i,2+i,a,x,⾃然对数底e,圆周率π。
(2)运算符号:如加号(+),减号(-),乘号(×或·),除号(÷或/),两个集合的并集(∪),交集(∩),根号(√),对数(log,lg,ln),⽐(:),微分(dx),积分(∫)等。
(3)关系符号:如“=”是等号,“≈”是近似符号,“≠”是不等号,“>”是⼤于符号,“<”是⼩于符号,“→”表⽰变量变化的趋势,“∽”是相似符号,“≌”是全等号,“∥”是平⾏符号,“⊥”是垂直符号,“∝”是反⽐例符号,“∈”是属于符号,“C”或“C下⾯加⼀横”是“包含”符号等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
普通逻辑符号
1.⇒实质蕴涵读作“如果.. 那么” , A ⇒ B 意味着如果 A 为真,则 B 也为真;如果 A 为假,则对 B 没有任何影响。
例子:x = 2 ⇒x2 = 4 为真,但x2 = 4 ⇒x = 2 一般为假(因为x可以是−2)
2.→ 可能意味着同⇒一样的意思(这个符号也可以指示函数的域和陪域;参见数学符号表)。
范畴为命题逻辑
3.⊃蕴涵,可能意味着同⇒一样的意思(这个符号也可以指示超集)。
范畴为命题逻辑,例子:A⊃B⇔A→B
4.⇔, ↔实质等价,当且仅当。
A ⇔ B 意味着 A 为真如果 B 为真,和 A 为假如果 B 为假。
5.¬逻辑否定非, 陈述¬A 为真,当且仅当 A 为假。
穿过其他算符的斜线同于在它, 例子:¬(¬A)⇔ A,x ≠y ⇔¬(x = y) ,
6.˜逻辑否定,非,穿过其他算符的斜线同于在它前面放置的"¬"。
例子:~A⇔Ā⇔-A⇔¬A
7.∧逻辑合取“与”如果A与B二者都为真,则陈述A∧ B为真;否则为假。
例子:n< 4 ∧n>2 ⇔n= 3 当n是自然数的时候。
A·B⇔A&B⇔A∧B⇔A和B
8.∨逻辑析取“或”如果A或B或二者均为真陈述,则A∨B为真;如果二者都为假,则陈述为假。
例子:n≥ 4∨n≤ 2⇔n≠ 3 当n是自然数的时候。
9.⊕、⊻,范畴为命题逻辑、布尔代数、“异或”陈述A⊕ B为真,在要么 A 要么 B 但不是二
者为真的时候为真。
A⊻B意思相同。
例子:(¬A) ⊕ A总是真,A⊕ A总是假。
10.∀全称量词“对于所有;对于任何;对于每个”谓词逻辑,∀x: P(x) 意味着所有的x都使P(x) 都为真。
例子:∀n∈ N: n2≥ n.
(x)F(x)⇔∀xF(x),∧xF(x)
11.∃存在量词“存在着”谓词逻辑,∃x: P(x) 意味着有至少一个x使P(x) 为真。
例子:∃n∈ N: n是偶数。
(∃x)F(x)⇔∃xF(x),∨xF(x)
12.∃!唯一量词“精确的存在一个”谓词逻辑,∃! x: P(x) 意味着精确的有一个x使P(x) 为真。
例子:∃! n∈ N: n+ 5 = 2n.
13.:= , :⇔,≡,定义“被定义为”范畴为所有地方。
x := y或x≡ y意味着x被定义为y的另一个名字(但要注意≡ 也可以意味着其他东西,比如全等)。
P :⇔Q意味着P被定义为逻辑等价于Q。
例子:cosh x:= (1/2)(exp x+ exp (−x))
A XOR B:⇔ (A∨B) ∧¬(A∧B)
14.()优先组合,范畴为所有地方。
优先进行括号内的运算。
例子:(8/4)/2 = 2/2 = 1, 而8/(4/2) = 8/2 = 4。
15.├推论, 命题逻辑, 谓词逻辑x├ y意味着y推导自x。
例子:A→ B├ ¬B→ ¬A
等值:A≡B⇔A↔B
常用符号
概念符号:φ直径;∞无穷大,自然常数e,温度℃
Αα阿尔法角度;系数
Ββ贝塔磁通系数;角度;系数
Γγ伽马电导系数(小写)
Δδ德尔塔变动;密度;屈光度
Εε伊普西龙对数之基数
Ζζ截塔系数;方位角;阻抗;相对粘度;原子序数
Ηη艾塔磁滞系数;效率(小写)
Θθ西塔温度;相位角
Ιι约塔微小,一点儿
Κκ卡帕介质常数
∧λ兰布达波长(小写);体积
Μμ缪磁导系数;微(千分之一);放大因数(小写)
Νν纽磁阻系数
Ξξ克西
Οο奥密克戎
∏π派圆周率=圆周÷直径=3.1416
Ρρrou 电阻系数(小写)
∑σ西格马总和(大写),表面密度;跨导(小写)
Ττ套时间常数
Υυ宇普西龙位移
Φφ佛爱磁通;角
Χχ西
Ψψ普西角速;介质电通量(静电力线);角
Ωω欧米伽欧姆(大写);角速(小写);角
大小比较符号:|x| x绝对值;≥大于等于;≤小于等于;≡恒等于或同余;≯不大于;≮不小于;>>远远大于号;<<远远小于号;≠不等于;≈是近似符号;“~”几何表示相似;“≌”几何表示全等;∥平行符号;⊥垂直符号
运算符号:+加号;-减号;×或·乘号;÷或/除号;√根号;^幂;对数(log,lg,ln);a:b a比b;floor(x) 上取整函数;ceil(x) 下取整函数;x mod y数论求余数;x - floor(x) 小数部分;dx微分;∫积分;曲线积分∮;极限(lim);连乘(∏);阶乘(!);从n个元素中每次取出r个元素所有不同的组合数(C(r)(n) );x的函数f(x) ;∝成正比符号;总和(∑);三角函数(cos,sin。
);绝对值符号“| |”等等∪并集;∩交集;→表示变量变化的趋势
关系符号:∈是属于符号;⊆包括;⊇被包括;因为(∵);所以(∴);和&
⊂包括,⊃被包括
优先秩序符号:大括号{};中括号[];小括号(),连接符号—
图形符号:三角形△;直角三角形Rt△;⊙圆;角度∠;弧⌒
性质符号:正号“+”,负号“-”,正负号“±”
其他不常用得未收录,必然现代物理,数学比较深层的。
