绘制贝塞尔曲线正弦波
bezier曲线绘制算法

bezier曲线绘制算法
摘要:
1.贝塞尔曲线简介
2.贝塞尔曲线的计算方法
3.贝塞尔曲线的应用
4.贝塞尔曲线的优缺点
正文:
贝塞尔曲线是一种以四个控制点定义的平滑曲线,它具有很好的局部性和全球性,广泛应用于计算机图形学、动画设计等领域。
计算贝塞尔曲线的方法有多种,其中比较常见的是使用de Casteljau 算法。
该算法通过计算两个分段贝塞尔曲线的交点,来求解原始贝塞尔曲线上的点。
具体来说,假设我们有四个控制点A、B、C、D,我们首先计算出AB、BC 两条线段的贝塞尔曲线,然后求解这两条贝塞尔曲线的交点P,接着以P 为控制点,计算出PB、PC 两条线段的贝塞尔曲线,最后求解这两条贝塞尔曲线与AC 的交点,该交点即为所求的贝塞尔曲线上的点。
贝塞尔曲线的应用非常广泛,例如在计算机图形学中,它可以用于绘制任意形状的曲线,还可以用于控制物体的动画运动路径;在计算机辅助设计中,它可以用于精确控制设计曲线的形状,提高设计的准确性和效率。
贝塞尔曲线的优点在于其具有很好的局部性和全球性,可以很好地描述出各种复杂的曲线形状。
同时,贝塞尔曲线的计算方法相对简单,易于实现和控制。
然而,贝塞尔曲线也存在一些缺点,例如其计算过程中需要处理复杂的数
学运算,对计算机的计算能力有一定的要求。
此外,贝塞尔曲线的控制点数量较多,调整起来比较麻烦,需要一定的技巧和经验。
总的来说,贝塞尔曲线是一种重要的曲线描述方法,其在计算机图形学、动画设计等领域有着广泛的应用。
绘制Bezier曲线编程及说明

绘制Bezier曲线编程及说明整体方案:(1)单击鼠标左键绘制控制点(不超过10个顶点),并自动连接为控制多边形。
(2)单击鼠标右键确定绘制Bezier曲线完毕。
(3)绘制时鼠标显示坐标。
(4)点击控制点可以改变Bezier曲线形状。
(5)可以使用鼠标或者键盘输入坐标绘制Bezier曲线。
关键技术:最小二乘法,曲线拟合,MFC框架编程Bezier曲线编程算法:// JjbView.cpp : implementation of the CJjbView class//#include "stdafx.h"#include "Jjb.h"#include "JjbDoc.h"#include "JjbView.h"#ifdef _DEBUG#define new DEBUG_NEW#undef THIS_FILEstatic char THIS_FILE[] = __FILE__;#endif/////////////////////////////////////////////////////////////////////////////// CJjbViewIMPLEMENT_DYNCREATE(CJjbView, CView)BEGIN_MESSAGE_MAP(CJjbView, CView)//{{AFX_MSG_MAP(CJjbView)ON_COMMAND(ID_BEZIER, OnBezier)ON_WM_LBUTTONDOWN()ON_WM_LBUTTONUP()ON_WM_MOUSEMOVE()ON_WM_RBUTTONDOWN()//}}AFX_MSG_MAP// Standard printing commandsON_COMMAND(ID_FILE_PRINT, CView::OnFilePrint)ON_COMMAND(ID_FILE_PRINT_DIRECT, CView::OnFilePrint)ON_COMMAND(ID_FILE_PRINT_PREVIEW, CView::OnFilePrintPreview) END_MESSAGE_MAP()/////////////////////////////////////////////////////////////////////////////// CJjbView construction/destructiondouble J(int n,int i);double C(int n,int i);double N(double u,int n);int JieCheng(int n);//构造函数CJjbView::CJjbView(){// TODO: add construction code herem_bIsChoosed=false;m_bStopDraw=false;m_bMakeSure=false;m_eChooseType=Bezier;while (m_vInputPoint.size()!=0){m_vInputPoint.pop_back();}while (m_vControlPoint.size()!=0){m_vControlPoint.pop_back();}while (m_vXiShu.size()!=0){m_vXiShu.pop_back();}}//析构函数CJjbView::~CJjbView(){while (m_vInputPoint.size()!=0){m_vInputPoint.pop_back();}while (m_vControlPoint.size()!=0){m_vControlPoint.pop_back();}while (m_vXiShu.size()!=0){m_vXiShu.pop_back();}}BOOL CJjbView::PreCreateWindow(CREATESTRUCT& cs) //定义窗口{// TODO: Modify the Window class or styles here by modifying// the CREATESTRUCT csreturn CView::PreCreateWindow(cs);}/////////////////////////////////////////////////////////////////////////////// CJjbView drawing// 刷新时绘图void CJjbView::OnDraw(CDC* pDC){CJjbDoc* pDoc = GetDocument();ASSERT_V ALID(pDoc);// TODO: add draw code for native data hereGetClientRect(&rect);if (m_eMouseStatus==MouseMove&&m_bStopDraw==false){m_vInputPoint.push_back(m_cMovePoint);}CString str;CClientDC d(this);int i;if(m_bIsChoosed==true){if (m_bStopDraw==false){str.Format(" X=%d,y=%d ]",m_cMovePoint.x,m_cMovePoint.y);d.TextOut(m_cMovePoint.x+10,m_cMovePoint.y+10,str);}switch(m_eChooseType)//菜单选择{case Bezier: //选择后的窗口状态str.Format("Bezier曲线,点击右键表示确定,移动节点改变形状。
贝塞尔曲线绘制原理

贝塞尔曲线绘制原理
《贝塞尔曲线绘制原理》
嘿,大家好呀!今天咱来聊聊贝塞尔曲线绘制原理。
你知道吗,我有一次特别有趣的经历,就和这贝塞尔曲线有关呢。
那时候我正在电脑前捣鼓一些图形绘制,就想着能不能自己画出一条特别好看的曲线来。
我就开始各种尝试啊,一会儿这样画,一会儿那样画,可就是画不出我想要的那种效果。
然后我就开始研究起贝塞尔曲线了。
哎呀,这一研究才发现,原来它就像是一个魔法一样。
它通过一些控制点来决定曲线的形状,就好像我在牵着一条线跳舞,我可以通过调整那些控制点的位置,让这条曲线变得或弯曲或平缓,就跟我指挥似的,特别有意思。
比如说,我把一个控制点往这边挪一点,哇,曲线立马就有变化了;再把另一个控制点往那边移一点,嘿,曲线又不一样了。
我就感觉自己像是一个曲线魔法师,在创造着属于我自己的独特曲线呢。
慢慢地,我掌握了贝塞尔曲线的绘制窍门,能画出各种漂亮的形状啦。
我发现它真的太神奇了,就这么几个控制点,就能创造出无穷无尽的曲线变化。
现在每次我看到那些漂亮的贝塞尔曲线图形,我就会想起我那次捣鼓的经历,还真是有趣呢。
这就是贝塞尔曲线绘制原理呀,真的很神奇,很值得我们去探索和玩味哟!哈哈!。
贝塞尔工具的应用详解
贝塞尔工具的应用详解By;QQ932525422贝塞尔工具是创建完美图形最常用的工具之一,它构造路径的方法比较适合长期性的绘图作业及要求精度较高的绘图任务。
在使用“贝塞尔”工具绘图之前,首选应了解有关“贝塞尔曲线”的概念。
法国数学家“贝塞尔”在工作中发现,任何一条曲线都可以通过与它相切的控制柄两端的点的位置来定义。
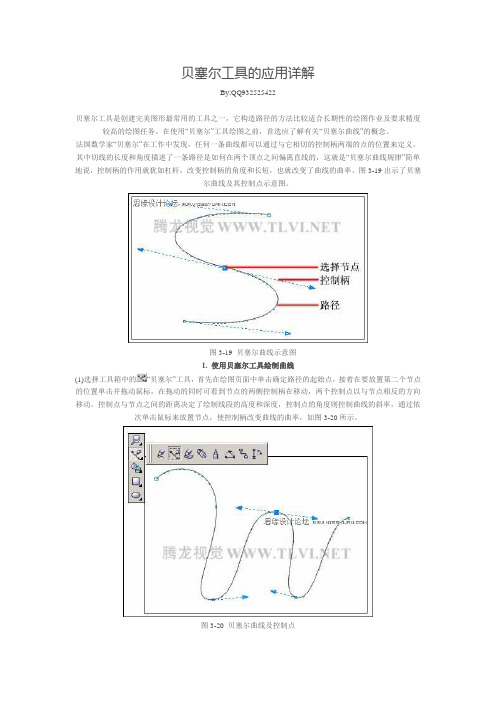
其中切线的长度和角度描述了一条路径是如何在两个顶点之间偏离直线的,这就是“贝塞尔曲线规律”简单地说,控制柄的作用就犹如杠杆,改变控制柄的角度和长短,也就改变了曲线的曲率。
图3-19出示了贝塞尔曲线及其控制点示意图。
图3-19 贝塞尔曲线示意图1. 使用贝塞尔工具绘制曲线(1)选择工具箱中的“贝塞尔”工具,首先在绘图页面中单击确定路径的起始点,接着在要放置第二个节点的位置单击并拖动鼠标,在拖动的同时可看到节点的两侧控制柄在移动,两个控制点以与节点相反的方向移动。
控制点与节点之间的距离决定了绘制线段的高度和深度,控制点的角度则控制曲线的斜率,通过依次单击鼠标来放置节点,使控制柄改变曲线的曲率,如图3-20所示。
图3-20 贝塞尔曲线及控制点提示:当确定控制点位置时按住键,可以使控制点以15度的增量变化。
(2)参照图3-21所示绘制路径,接着使用“形状”工具,对绘制的路径节点进行调整。
然后通过按下键,将其放到所有字母图形下面,并填充为白色,轮廓宽度为2mm。
图3-21 绘制曲线技巧:在使用“贝塞尔”工具绘制曲线拖动其控制柄时,加按键盘上的键,可使节点变为“尖突节点”;若加按键,则可使节点变为“平滑节点”;按住键可以移动最后创建节点的位置。
2. 使用贝塞尔工具绘制直线(1)接下来使用“贝塞尔”工具,在绘图页面中单击确定起始点的位置,然后移动鼠标到下一个节点的位置再次单击创建直线,参照图3-22所示,绘制封闭路径并填充颜色。
提示:在使用“贝塞尔”工具绘制曲线的同时,在其属性栏中单击“自动闭合曲线”按钮,可将曲线闭合。
实验六 3D编程及Bezier曲线绘制

实验七 3D编程及Bezier曲线曲面绘制一、实验目的1.3D编程:熟悉视点观察函数的设置和使用;熟悉投影变换函数的设置和使用;熟悉基本3D 图元的绘制2.了解OpenGL绘制Bezier曲线的方法二、实验环境硬件要求:PC机,主流配置,最好为独立显卡,显存512M以上。
软件环境:操作系统:Windows XP。
语言开发工具:VC6.0。
三、实验要求:按照实验内容做实验,保留所作步骤效果截图或演示程序,当场检查,现场计分四、实验内容1.3D编程3D Cube.cpp 为一静止3D立方体,3D Cube2.cpp 为正交投影下的旋转3D立方体,按下鼠标可实现不同方向的旋转。
分析3D编程代码与程序结构。
图7-1 静止立方体效果图图7-2 旋转立方体效果图图7-3 旋转茶壶和圆环效果图1.让静止的立方体绕Z轴不停旋转2.修改视点,目标点不变,观看显示效果3. 修改目标点,视点不动,观看显示效果4. 视点与目标点同时修改,观看显示效果5. 视点与目标点不变,修改观察体大小,观看显示效果6. 将正交投影观察体改为透视投影观察体,并设置其大小,观察显示效果7. 将立方体替换为茶壶,观看显示效果.选做2.Bezier曲线绘制BezierCurve.cpp为绘制bezier曲线的源程序,仔细研读源程序,并作如下修改1).改变控制点,观察曲线和曲面形状的变化,控制点起什么作用?2).改写bezier.cpp,增加控制点数目,修改控制点位置,使之成为空间封闭曲线,写出修改的关键代码及注释(TIPS:OpenGLBezier曲线绘制方法最多只能有8个控制点)3).根据bezier曲线的性质,改写程序,使之成为两段曲线光滑连接。
每段曲线用不同颜色表示,并画出控制点。
图7-2·Bezier曲线绘制效果五、函数参考(一)3D编程1.视点设置函数void gluLookAt(GLdouble eyex, GLdouble eyey,GLdouble eyez,GLdouble atx,GLdouble aty,GLdouble atz,GLdouble upx,GLdouble upy,GLdouble upz)给出矩阵作用于当前矩阵,定义相机位置和方向视点:eyex, eyey, eyez目标点:atx,aty,atz相机向上方向:upx,upy,upz如果不引用该函数,则eyex=0,eyey=0,eyez=0,atx=0,aty=0,atz=-1,Upx=0,upy=1,upz=0此函数放在display函数中调用参考坐标系:世界坐标系2.正交投影变换设置函数. void glOrtho(GLdouble left,GLdouble right,GLdouble bottom,GLdouble top,GLdouble near,GLdouble far),建立正交投影矩阵,定义一个正平行观察体。
VC实现贝塞尔曲线绘制

VC实现贝塞尔曲线绘制摘要:本文主要通过对Bezier曲线的几何图形的进一步理解,探讨其具体的控制方法,结合具体绘制实际分析理论描述对控制点计算理解的偏差,统一了认识;结合曲线绘制函数PolyBezier()具体的要求,实现VC环境下简单的曲线绘制方法研究。
关键词:贝塞尔曲线;PolyBezier;曲线连续性1贝塞尔曲线描述贝赛尔曲线的每一个顶点都有两个控制点,用于控制在该顶点两侧的曲线的弧度。
所以本函数的顶点数组的记录方式是:控制点+顶点+控制点+控制点+顶点+控制点+……。
所以两个顶点之间的曲线是由两个顶点以及两个顶点之间的控制点来决定的。
一条贝塞尔样条由4个定义点定义:两个端点和两个控制点。
2曲线的绘制方法2.1PolyBezier函数PolyBezier函数用于画贝赛尔样条曲线,原型:BOOL PolyBezier (HDC,hdc,CONST POINT *lppt,DWORD cPoints);参数:hdc:指定的设备环境句柄。
Lppt:POINT结构数组的指针,包括了样条端点和控制点的坐标、其顺序是起点的坐标、起点的控制点的坐标、终点的控制点的坐标和终点的坐标。
cPoints:指明数组中的点的个数。
本文中绘制曲线主要用到这个函数。
2.2一阶连续性图1所示为一段Bezier曲线经过p0、p1两个端点,要绘制经过它们的曲线需要再确定k1、K2两个控制点,这条曲线最终是由p0、k1、k2、p1四个点决定。
图2为经过p0、p1(p2)、p3的一段连续曲线,可以看出,它是由p0-p1及p2-p3两段曲线组成,连续的贝塞尔曲线会把前一个终止点当作起始点:即p1=p2。
要绘制如图2所示曲线,关键在于确定k0、k1、k2、k3四个控制点方法,一般是根据两段曲线连续(即一阶连续性:两个相邻曲线段在交点处有相同的一阶导数)条件来得出。
总的来说,就是k0p0 连线即为曲线在p0处切线,k1p1连线为p1处切线,k24p2为p2处切线,k3p3为p3处切线,两段曲线连续必然要求k1p1与k2p2在一条线上。
CAD中的贝塞尔曲线 绘制与编辑的技巧方法

CAD中的贝塞尔曲线:绘制与编辑的技巧方法CAD软件中的贝塞尔曲线是一种常用的绘图工具,可以用于绘制平滑曲线或形状。
掌握绘制和编辑贝塞尔曲线的技巧方法,对于设计师和工程师来说非常重要。
首先,让我们了解一下贝塞尔曲线的基本概念。
贝塞尔曲线由若干个控制点组成,这些控制点决定了曲线的形状。
曲线的起点和终点是通过起点和终点控制点来确定的。
中间的控制点则用来控制曲线的形状。
在CAD软件中绘制贝塞尔曲线的方法如下:1. 打开CAD软件,并选择“绘图”工具栏中的“曲线”选项。
2. 在绘图区域中选择“贝塞尔曲线”工具。
3. 依次点击起点、终点和若干个控制点,以确定曲线的形状。
4. 点击“完成”或按下回车键,完成贝塞尔曲线的绘制。
绘制贝塞尔曲线时,可以在曲线的起点和终点之间添加更多的控制点,以获得更复杂的曲线形状。
在添加控制点时,可以使用“插入点”工具来调整曲线的弯曲程度。
编辑贝塞尔曲线的方法如下:1. 选中需要编辑的贝塞尔曲线。
2. 在CAD软件的工具栏中选择“编辑”选项。
3. 在“编辑”菜单中选择“贝塞尔曲线”工具。
4. 根据需要,调整曲线的起点、终点和控制点的位置。
可以通过拖拽、调整控制点的弯曲程度等方式来编辑曲线。
除了基本的绘制和编辑技巧外,还有一些高级的贝塞尔曲线技巧可以帮助您更好地应用该工具:1. 操作序列的调整:可以通过修改控制点的位置来调整贝塞尔曲线的形状。
如果需要调整曲线上某一点的位置,可以先选中该点,再进行调整。
2. 对称性控制:可以通过选择贝塞尔曲线上的某一点,并在对称轴上添加相应的控制点来实现对称形状的绘制。
3. 钳制控制:可以调整控制点的位置,使得曲线在某些点上通过。
4. 文字与路径:可以将文字对齐到贝塞尔曲线上,使其沿曲线呈现弯曲效果,从而实现更多样化的设计效果。
绘制和编辑贝塞尔曲线是CAD软件中的一项基本技能,它可以帮助我们创建平滑的曲线或复杂的形状,提高设计工作的效率和质量。
通过掌握上述技巧和方法,您将能够更灵活地运用贝塞尔曲线,实现您的设计目标。
bezier曲线绘制算法

bezier曲线绘制算法贝塞尔曲线绘制算法贝塞尔曲线是一种常用于计算机图形学中的数学曲线,具有平滑弯曲的特性。
通过控制点的位置和数量,可以绘制出各种形状的曲线,如圆弧、曲线等。
本文将介绍贝塞尔曲线绘制算法的基本原理和实现方法。
1. 贝塞尔曲线的基本概念贝塞尔曲线由两个或多个控制点决定,通过这些控制点的位置,可以确定曲线的形状和轨迹。
其中,起始点和结束点称为锚点,而其他点称为控制点。
贝塞尔曲线的形状由控制点之间的插值和权重决定,权重决定了每个控制点对曲线形状的影响程度。
2. 二次贝塞尔曲线绘制算法二次贝塞尔曲线由三个点决定,分别是起始点P0、控制点P1和结束点P2。
绘制二次贝塞尔曲线的算法如下:(1) 将曲线分为若干个线段,每段用t从0到1进行插值。
(2) 根据插值参数t,计算控制点P0、P1和P2在x和y轴上的值。
(3) 绘制连接P0和P1的线段,连接P1和P2的线段。
3. 三次贝塞尔曲线绘制算法三次贝塞尔曲线由四个点决定,分别是起始点P0、控制点P1、P2和结束点P3。
绘制三次贝塞尔曲线的算法如下:(1) 将曲线分为若干个线段,每段用t从0到1进行插值。
(2) 根据插值参数t,计算控制点P0、P1、P2和P3在x和y轴上的值。
(3) 绘制连接P0和P1的线段,连接P1和P2的线段,以及连接P2和P3的线段。
4. 高阶贝塞尔曲线的绘制算法除了二次和三次贝塞尔曲线,还存在更高阶的贝塞尔曲线。
对于n 阶贝塞尔曲线,需要n+1个点来确定。
其绘制算法与二次和三次贝塞尔曲线类似,通过插值参数t来计算各个控制点的值,并连接相邻控制点。
5. 贝塞尔曲线的应用贝塞尔曲线在计算机图形学中有广泛的应用,常用于绘制平滑曲线、图形变形、字体设计等方面。
在计算机动画、游戏开发等领域,贝塞尔曲线的应用也非常广泛。
贝塞尔曲线是一种常用于计算机图形学中的数学曲线,通过控制点的位置和数量,可以绘制出各种形状的曲线。
本文介绍了贝塞尔曲线的基本概念,以及二次、三次和高阶贝塞尔曲线的绘制算法。
贝齐尔曲面绘制.doc

目录1 绪论 (1)1.1贝齐尔曲面的介绍 (1)1.2贝齐尔曲面的应用 (2)2 贝齐尔曲面设计 (3)2.1 贝齐尔曲面定义 (3)2.2 贝齐尔曲面性质 (4)2.3 贝齐尔曲面算法 (5)2.4 程序设计步骤 (5)2.4.1 Bezier曲面的生成 (5)2.4.2 绘制网格曲面 (6)2.4.3 绘制一个填充曲面 (8)2.4.4 三次贝齐尔曲面 (9)2.5 主程序 (10)3 总结 (20)参考文献 (21)致谢 (22)1 绪论1.1贝齐尔曲面的介绍到了70年代,法国雷诺汽车公司的工程师贝齐尔(Bezier)创造出一种适用于几何体外形设计的新的曲线表示法。
这种方法的优越性在于:对于在平面上随手勾画出的一个多边形(称为特征多边形),只要把其顶点坐标输入计算机,经过不到一秒钟的计算,绘图机就会自动画出同这个多边形很相像、又十分光滑的一条曲线。
这种方法被人们称为贝齐尔(Bezier)方法(以下统称为Bezier方法)。
贝齐尔曲线的形状是通过一组多边折线(也称为贝齐尔控制多边形)的各顶点惟一地定义出来的。
在该多边折线的各顶点中,只有第一点和最后一点在曲线上,其余的顶点则用来定义曲线的形状。
图1-1列举了一些Bezier多边折线和相应的Bezier曲线的形状关系。
图1-1 Bezier线曲线和曲面是计算机图形学中研究的重要内容之一,他们在实际工作中有着广泛的应用。
例如,实验数据的曲线表示,设计、优化的曲面表示等。
为了外形美观和物理性能最佳,汽车飞机等的外型设计十分重要。
由于实际问题不断对曲线和曲面提出新的要求,近几十年来,曲线和曲面理论及其应用得到了很大的发展。
1963年,波音飞机公司的Ferguson将曲线曲面表示成参数矢量形式,并用3次参数曲线来构造组合曲线,用4个角点的位置矢量及其两个方向的切向矢量来构造3次曲面。
1964年,麻省理工学院的coons用封闭的曲线的4条边界定义一个曲面。
贝塞尔曲线详解

贝塞尔曲线详解“贝塞尔工具” 是所有绘图类软件中最为重要的工具之一。
“贝塞尔工具”可以创建比手绘工具更为精确的直线和对称流畅的曲线。
对于大多数用户而言,“贝塞尔工具”提供了最佳的绘图控制和最高的绘图准确度。
为使广大图形软件初学用户能了解“贝塞尔工具”的应用,本人这里以CorelDRAW这款软件为例,详细地剖析“贝塞尔工具”的使用方法。
“贝塞尔”是CorelDRAW中的称谓,在Photoshop、Illustrator、InDesign、QuarkXPress 等软件中,称之为“钢笔工具”,虽然名称不一样,但作用是一致的,大家可以触类旁通,参照了解。
1、绘制线段利用“贝塞尔工具”绘制线段的方式和“手绘工具”一样,能绘制直线、斜线。
按住Ctrl 键即限制水平、垂直或呈角度绘制线段,不同的是“贝塞尔工具”可以连续地绘制多段线段。
以图01为例:先在屏幕某个位置单击鼠标以指定起始点,然后将鼠标移向(不必要按住不放)红圈1处单击指定第一个线段的终止点(在绘制多段线时,此终止点同时也为下一线段的起始点),然后继续将鼠标移向经圈2处单击,完成第二线段的绘制;以此类推,鼠标不断地在新的位置点击,就不断地产生新的线段。
图片如下:如果是绘制封闭的对象,“贝塞尔工具”的绘制过程是:如图02所示,在红圈1处单击鼠标以指定起始点,然后移动鼠标在红圈2处单击,即绘制出一条线段;保持工具不变,继续将鼠标移向红圈3、红圈4、红圈5处单击,最后移向红圈1处,在起始点上单击鼠标完成闭合操作,一个多边形就完成了。
图片如下:2、认识贝塞尔曲线“贝塞尔曲线”由节点连接而成的线段组成的直线或曲线,每个节点都有控制点,允许修改线条的形状。
贝塞尔曲线由一个或多个直线段或曲线段组成,如图03,以节点标记路径段的端点。
在曲线段上,每个选中的节点显示一条或两条方向线,方向线以方向点结束。
方向线和方向点的位置决定曲线段的大小和形状,移动这些因素将改变曲线的形状。
贝塞尔曲线的连接与制作

贝塞尔曲线的连接与制作
贝塞尔曲线,又称贝兹曲线或贝济埃曲线,一般的矢量图形软件通过它来精确画出曲线,贝兹曲线由线段与节点组成,节点是可拖动的支点,线段像可伸缩的皮筋,在绘图工具上看到的钢笔工具就是来做这种矢量曲线的。
当然在一些比较成熟的位图软件中也有贝塞尔曲线工具,如PhotoShop 等。
在Flash4中还没有完整的曲线工具,而在Flash5里面已经提供出贝塞尔曲线工具。
问题
如图这些绿色的点我们希望用光滑的曲线连接它们。
解决方案
大致思路就是先算出相邻原始点的中点,在把相邻中点连成的线段平移到对应的原始点,以平移后的中点作为控制点,相邻原始点为起始点画贝塞尔曲线,这样就保证了连接处的光滑。
而贝塞尔曲线本身是光滑的,所以就把这些原始点用光滑曲线连起来了。
实验结果
看起来连接的还是比较光滑的。
贝塞尔曲线

详细内容定义贝塞尔曲线(B6zier curve),又称贝兹曲线或贝济埃曲线,是应用于二维图形应用程序的数学曲线。
曲线的定义有四个点:起始点、终止点(也称锚点)以及两个相互分离的中间点,滑动两个中间点,贝塞尔曲线的形状会发生变化。
依据四个位置任意的点坐标可绘制出一条光滑曲线[1]。
对于N次的贝塞尔曲线:设Δbj=bj+1-bj时,有旋转矩阵M,使得:Δbj=MjΔb0i=0…,n-1当t∈[0,1]时,对于任意单位向量,矩阵M满足:则这条曲线是由一系列控制点bi定义的A级贝塞尔曲线。
此时,旋转矩阵M满足以下两个条件:1)矩阵MT+M-2I和MTM-I的特征值必均为非负。
这里I为一个单位矩阵。
2)矩阵M必映射到单位球体外的任一点。
即:M的奇异值δ1,δ2应不小于1。
若旋转矩阵M是由旋转角θ<π/2和一个尺度因子s组成,则满足下列条件:的矩阵M被称为A级矩阵。
由A级矩阵即可产生A级贝塞尔曲线。
特性贝塞尔曲线是一种非常自由的曲线,通过改变其控制点的位置和权重就能改变线条的形状。
相对于传统的直线和圆弧相组合来表达曲线的方式,这是一个巨大的提高。
汽车设计中的曲面形状比较复杂,直线和圆弧不能满足其形状变化的要求。
贝塞尔曲线非常自由,我们可以通过改变控制点来改变线条的形状,有着非常良好的交互性,非常适合汽车曲面设计[2]。
贝塞尔曲线数学原理①线性贝塞尔曲线。
给定两点P0、P,线性贝塞尔曲线只是一条两点之间的直线。
这条线由下式给出:B(t)=P0+(Pl—Po)t=(1-t)Po+tPl,t∈[0,1]且其等同于线性插值。
②二次方贝塞尔曲线。
给定三点Po、P、P:,二次方贝塞尔曲线由函数B(t)表示:B(t)=(1-t)2Po+2t(1-t)P1+tzp2,t∈[0,1]③三次方贝塞尔曲线。
Po、P、P、P3四个点在平面或在三维空间中定义了三次方贝塞尔曲线。
曲线起始于P。
走向P,并从P2的方向来到3。
一般不会经过P,或P2,这两个点只是在那里提供方向资讯。
绘制贝塞尔曲线正弦波

3.层次原理图之间的切换
注意: 1.掌握从总图切换到方块电路图对立
的子图的方法。 2.掌握从子图切换到总图的方法。
4.3 产 生 报 表
4.3.1 生成网络表文件
生成网络表文件的方法可以执行菜单 命令【Design】/【Create Netlist】,将会 出现如图4-21所示的网络表对话框。
4.3.2 生成元件列表文件
元件列表主要包括元件的名称、序号、封 装形式。这样可以对原理图中的所有元件 有一个详细的清单,以便检查,校对。
Margins(设置页边距) Scale(设置缩放比例) Preview(预览) Vector Font Option(向量字体选项) 其他项目设置
4.4.2 打印输出
设置好打印机后用户就可以打印输出了。 用 户 可 以 执 行 菜 单 命 令 【File】/ 【Print】,或者在设置打印机的对话框 中单击【Print】按钮,程序就会按照上 述设置进行打印。
4.3.4 其他报表文件
还可以生成该设计的所有内部文件的列表, 生成的方法可以执行菜单命令【Reports】 /【Design Hierarchy】,之后会生成后缀 为*.rep的文件并在当前的窗口中自动打开。 在该设计系统中可以看到如图4-35所示的 文件。
还可以执行【Reports】/【Cross Reference】生成如图4-36所示的*.xrf文件。
1.添加文字标注 2.添加文本框
4.2.3 给原理图添加图片
1.原理图的编辑 2.图件的选择
(1)逐个选择图件 (2)用鼠标框选择一组图件 (3)用菜单命令选择图件
计算机图形学——绘制Bezier曲线

计算机图形学实验报告专业:信息与计算科学班级: 1002班学号: **********姓名: ****实验目的:(1)掌握直线的参数表示法。
(2)掌握德卡斯特里奥算法的几何意义。
(3)掌握绘制二维Bezier曲线的方法。
实验要求:(1)使用鼠标左键绘制个数为10以内的任意控制点,使用直线连接构成控制多边形。
(2)使用鼠标右键绘制Bezier曲线。
(3)在状态栏显示鼠标的位置坐标。
(4)B ezier曲线使用德卡斯特里奥算法绘制。
实验算法:Bezier曲线的分割递推德卡斯特里奥算法给定空间n+1个点P i(i=0,1,2,…,n)及参数t,有P r i(t)=(1-t)P1-r i(t)+t P1-r1i+(t)式中,r=1,2,…,n;i=0,1,…,n-r;t∈[0,1]。
且规定当r=0时,P0i(t)=P i, P n0(t)是在曲线上具有参数t的点。
德卡斯特里奥算法的基础就是在矢量−−→−PP10上选择一个点P,使得P点划分矢量−−→−PP10为|PP0|:|PP1|=t:1-t,给定点P0、P1的坐标以及t的值,点P的坐标为P=P0+t(P1-P0)=(1-t)P0+tP1。
式中,t∈[0,1]。
定义贝塞尔曲线的控制点编号为P r i,其中,r表示迭代次数。
德卡斯特里奥证明了,当r=n时,P n0表示Bezier曲线上的点。
函数功能介绍1.德卡斯特里奥函数:long CMy12View::DeCasteliau(double t,long *p){double P[N_MAX_POINT][N_MAX_POINT];int n=CtrlPNum-1;for(int k=0;k<=n;k++){P[0][k]=p[k];}for(int r=1;r<=n;r++){for(int i=0;i<=n-r;i++){P[r][i]=(1-t)*P[r-1][i]+t*P[r-1][i+1];}}return(long(P[n][0]));}函数功能介绍:此函数为德卡斯特里奥算法函数。
bezier曲线绘制算法

bezier曲线绘制算法贝塞尔曲线绘制算法贝塞尔曲线是一种常用于图形设计和计算机图形学中的数学曲线。
它根据给定的控制点,通过插值计算得出平滑曲线。
这种曲线有着良好的平滑度和逼真度,在二维和三维图形的绘制中被广泛使用。
本文将介绍贝塞尔曲线的绘制算法及其应用。
一、贝塞尔曲线的基本原理贝塞尔曲线的绘制基于控制点的位置和权重来计算曲线上的点。
以二次贝塞尔曲线为例,需要三个控制点P0、P1和P2。
曲线上的任意一点P(t)的坐标可以通过以下公式计算:P(t) = (1-t)^2 * P0 + 2 * t * (1-t) * P1 + t^2 * P2其中,t为参数,取值范围为[0,1]之间。
当t=0时,P(t)为起点P0;当t=1时,P(t)为终点P2。
通过调整t的取值,可以得到不同位置的曲线上的点。
二、绘制贝塞尔曲线的算法绘制贝塞尔曲线的一种常用算法是利用递归和二项式展开来计算曲线上的点。
具体步骤如下:1. 确定控制点的数量和位置:根据需要绘制的曲线类型(二次、三次等),确定控制点的数量。
同时,确定每个控制点的具体位置。
2. 递归计算插值点:根据递推公式,计算参数t对应位置的插值点。
对于二次贝塞尔曲线,计算公式为P(t) = (1-t)^2 * P0 + 2 * t * (1-t) * P1+ t^2 * P2。
对于每个t值,计算出对应的插值点坐标。
3. 绘制曲线:连接计算得到的插值点,绘制出平滑曲线。
三、贝塞尔曲线的应用贝塞尔曲线由于其良好的平滑性和可控性,在图形设计和计算机图形学中得到广泛的应用。
下面介绍几个常见的应用领域。
1. 二维图形设计:贝塞尔曲线可以用于绘制二维图形和路径,如绘制平滑的曲线、绘制字体的曲线路径等。
通过调整控制点的位置和权重,可以绘制出各种形状的曲线和路径。
2. 三维图形建模:在三维图形建模中,贝塞尔曲线可用于绘制曲线型的三维物体,如飞机机翼的曲线形状、车辆车身的流线型等。
通过调整控制点的位置和权重,可以创建复杂的曲面。
coreldraw9中怎样画正弦曲线

coreldraw9中怎样画正弦曲线、波浪线
办法是:
1、单击贝慈曲线工具,先在空白页面上单击一点,然后按Ctrl键单击另一端点画一根水平直线。
2、选取节点编辑工具(或者按F10),框选两端的节点(是框选:按F10后点左键不
放拖动鼠标框住这条直线)。
这时属性上面后出现符号(+ -),单击属性栏上的“+”图标,为直线增加正中间的节点。
再按“+”图标,可无限增加二分节点。
效果如下:
3、利用Shift键(还是F10的状态),每隔一个节点选中节点。
按住Ctrl键同时向上垂直拖动节点。
如下:
4、框选所有节点-单击(转换直线为曲线)-再单击(使节点平滑),将节点属性改为对称。
效果如下:
完成。
贝塞尔曲线基本用法

贝塞尔曲线基本⽤法使⽤UIBezierPath可以创建基于⽮量的路径,此类是Core Graphics框架关于路径的封装。
使⽤此类可以定义简单的形状,如椭圆、矩形或者有多个直线和曲线段组成的形状等。
UIBezierPath是CGPathRef数据类型的封装。
如果是基于⽮量形状的路径,都⽤直线和曲线去创建。
我们使⽤直线段去创建矩形和多边形,使⽤曲线去创建圆弧(arc)、圆或者其他复杂的曲线形状。
1.使⽤UIBezierPath画图步骤:2.创建⼀个UIBezierPath对象3.调⽤-moveToPoint:设置初始线段的起点4.添加线或者曲线去定义⼀个或者多个⼦路径5.改变UIBezierPath对象跟绘图相关的属性。
如,我们可以设置画笔的属性、填充样式等UIBezierPath创建⽅法介绍1.UIBezierPath类提供了哪些创建⽅式,这些都是⼯⼚⽅法,直接使⽤即可。
+ (instancetype)bezierPath;+ (instancetype)bezierPathWithRect:(CGRect)rect;+ (instancetype)bezierPathWithOvalInRect:(CGRect)rect;+ (instancetype)bezierPathWithRoundedRect:(CGRect)rectcornerRadius:(CGFloat)cornerRadius;+ (instancetype)bezierPathWithRoundedRect:(CGRect)rectbyRoundingCorners:(UIRectCorner)cornerscornerRadii:(CGSize)cornerRadii;+ (instancetype)bezierPathWithArcCenter:(CGPoint)centerradius:(CGFloat)radiusstartAngle:(CGFloat)startAngleendAngle:(CGFloat)endAngleclockwise:(BOOL)clockwise;+ (instancetype)bezierPathWithCGPath:(CGPathRef)CGPath;2.下⾯我们⼀个⼀个地介绍其⽤途。
贝塞尔工具的使用技巧

贝塞尔工具的使用技巧“贝塞尔工具” 是所有绘图类软件中最为重要的工具之一。
“贝塞尔工具”可以创建比手绘工具更为精确的直线和对称流畅的曲线。
对于大多数用户而言,“贝塞尔工具”提供了最佳的绘图控制和最高的绘图准确度。
为使广大图形软件初学用户能了解“贝塞尔工具”的应用,本人这里以CorelDRAW这款软件为例,详细地剖析“贝塞尔工具”的使用方法。
“贝塞尔”是CorelDRAW中的称谓,在Photoshop、Illustrator、InDesign、QuarkXPress等软件中,称之为“钢笔工具”,虽然名称不一样,但作用是一致的,大家可以触类旁通,参照了解。
1、绘制线段利用“贝塞尔工具”绘制线段的方式和“手绘工具”一样,能绘制直线、斜线。
按住Ctrl键即限制水平、垂直或呈角度绘制线段,不同的是“贝塞尔工具”可以连续地绘制多段线段。
以图01为例:先在屏幕某个位置单击鼠标以指定起始点,然后将鼠标移向(不必要按住不放)红圈1处单击指定第一个线段的终止点(在绘制多段线时,此终止点同时也为下一线段的起始点),然后继续将鼠标移向经圈2处单击,完成第二线段的绘制;以此类推,鼠标不断地在新的位置点击,就不断地产生新的线段。
图片如下:此主题相关图片如下:如果是绘制封闭的对象,“贝塞尔工具”的绘制过程是:如图02所示,在红圈1处单击鼠标以指定起始点,然后移动鼠标在红圈2处单击,即绘制出一条线段;保持工具不变,继续将鼠标移向红圈3、红圈4、红圈5处单击,最后移向红圈1处,在起始点上单击鼠标完成闭合操作,一个多边形就完成了。
图片如下:此主题相关图片如下:2、认识贝塞尔曲线“贝塞尔曲线”由节点连接而成的线段组成的直线或曲线,每个节点都有控制点,允许修改线条的形状。
贝塞尔曲线由一个或多个直线段或曲线段组成,如图03,以节点标记路径段的端点。
在曲线段上,每个选中的节点显示一条或两条方向线,方向线以方向点结束。
方向线和方向点的位置决定曲线段的大小和形状,移动这些因素将改变曲线的形状。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
4.5.2 层次原理图的设计方法
层次原理图的设计方法通常有两种, 一种是自顶向下的设计方法,一种是自底 向上的设计方法。
1.自顶向下设计
用自顶向下设计时,首先建立一张总 图(Mastபைடு நூலகம்r Schematic)。
层次原理总图的设计过程。
1.放置方块电路图 2.对方块电路图属性进行设置 3.用同样的方法完成其他方块
执行菜单命令【Report】/【Bill of Material】。
3种列表元件定义格式分别为:Protel 格式,文件后缀名为*.bom;电子表格可 调用格式,文件后缀名为*.csv;Protel99 的表格格式,文件后缀名为*.xls。
4.3.3 生成电气规则测试报告
执行菜单命令 【Tools】/【ERC…】
4.4 原理图的打印
4.4.1 设置打印机
要想打印出Protel 99 SE环境下的原 理图,首先要设置打印机,设置打印机的 方法为执行菜单命令【File】/【Setup Printer】。或者直接在主工具栏中单击按 钮。之后,会弹出打印机设置对话框,如 图4-37所示。
Select Printer (选择打印机) Batch Type (选择输出的目标图形文件) Color (设置输出颜色)
4.3 产 生 报 表
4.3.1 生成网络表文件
生成网络表文件的方法可以执行菜单 命令【Design】/【Create Netlist】,将会 出现如图4-21所示的网络表对话框。
4.3.2 生成元件列表文件
元件列表主要包括元件的名称、序号、封 装形式。这样可以对原理图中的所有元件 有一个详细的清单,以便检查,校对。
电路的绘制
4.放置方块电路的端口的
按钮设置端口的属性
5.将具有电气连接关系的方
块电路端口用导线或总线连接 起来,也就是绘制导线。
6.把总图中的每一个方块电
路对应的层次原理图子图绘制 出来。
2.自底向上设计
先设计出下层模块的原理图,再由这 些原理图产生方块电路,进而产生上层原 理图。这样层层向上组织,最后生成总图。
1.绘制多边形
执行绘制多边形命令的方法有下面的3种。
执 行 菜 单 命 令 【Place】/【Drawing Tools】/【Polygons】。
单击画图形工具栏上的用于画多边形的 按钮。
按快捷键【Alt】+【P】/【D】/ 【P】。
2.绘制椭圆弧
椭圆的边界即为椭圆弧线。当椭圆的X轴 半径和Y半径相等时,椭圆弧线即变成圆 弧。
4.3.4 其他报表文件
还可以生成该设计的所有内部文件的列表, 生成的方法可以执行菜单命令【Reports】 /【Design Hierarchy】,之后会生成后缀 为*.rep的文件并在当前的窗口中自动打开。 在该设计系统中可以看到如图4-35所示的 文件。
还可以执行【Reports】/【Cross Reference】生成如图4-36所示的*.xrf文件。
单击画图形工具栏上的用于画贝塞尔曲 线按钮。
按快捷键【Alt】+【P】/【D】/【B】。
执行命令后,同样出现十字光标。按 【Tab】键弹出设置贝塞尔曲线参数的对 话框,如图4-9所示。
4.2.2 给原理图添加文字
为了读图方便,原理图中最好能够添加文 字说明,添加文字的方法通常有两种,下 面来分别介绍。
1.添加文字标注 2.添加文本框
4.2.3 给原理图添加图片
1.原理图的编辑 2.图件的选择
(1)逐个选择图件 (2)用鼠标框选择一组图件 (3)用菜单命令选择图件
3.图件的排列和对齐
图件排列和对齐的方式有左对齐、右 对齐、水平中心对齐、顶端对齐、底端对 齐、垂直中心对齐、水平匀布和垂直匀布 等8种方式。相应的菜单命令均在菜单 【Edit】/【Align】中,如图4-19所示。
打印时会出现如图4-41所示的对话 框。
4.5 关于层次原理图
4.5.1 概念
在前面的内容中已经提到过层次图。 其实,层次图就是要把整个设计项目分成 若干原理图表达。为了达到这一目的,必 须建立一些特殊的图形符号、概念来表示 各张原理图之间的连接关系。
在绘制层次图时常用的不同于一般原理图 的按钮有如下几个。 是层次图中用于画方块电路的按钮 是用于画方块电路图端口的按钮 是用来画I/O端口的按扭
例如,要绘制一个半径为30mil的半 圆,就应该选择用于画椭圆弧线的按钮, 会出现如图4-4所示的光标。
3.绘制圆弧 4.绘制贝塞尔曲线
正弦波、抛物线等曲线可用贝塞尔曲 线(Bezier Curve)来实现。可用如下 3种方法来实现。
执 行 菜 单 命 令 【Place】/【Drawing Tools】/【 Bezier】。
4.1 完成原理图设计
4.1.1 回到原理图设计
编辑环境
4.1.2 在原理图中添加
自己制作的元件
4.2 美化原理图
4.2.1 画图形工具 (Drawing
Tools)介绍
在前面的内容中,都没有用上画图形的工 具。主要是因为这些工具只是起标注的作 用,并不代表任何电气意义。
图4-1所示的就是画图形的工具栏,下面就 来逐个介绍一下各个按钮的功能。
(1)绘制好底层模块,把需要与其 他模块相连的端口用I/O端口的形式画出 。
(2)在设计数据库中建立一个新的 原理图文件 。
(3)执行菜单命令【Design】/ 【Create Symbol From Sheet】, 选择 模块文件。
(4) 选择是否转换端口输入/输 出方向。
(5)对方块图属性进行修改。
Margins(设置页边距) Scale(设置缩放比例) Preview(预览) Vector Font Option(向量字体选项) 其他项目设置
4.4.2 打印输出
设置好打印机后用户就可以打印输出了。 用 户 可 以 执 行 菜 单 命 令 【File】/ 【Print】,或者在设置打印机的对话框 中单击【Print】按钮,程序就会按照上 述设置进行打印。
