基本初等函数的导数公式表
12个基本初等函数的导数公式
函数
原函数
导函数
常函数
（即常数）
（ 为常数）
幂函数
指数函数
对数函数
（ 且 ， ）
正弦函数
余弦函数
正切函数
余切函数
反正弦函数
反余弦函数
反正切函数
反余切函数
口诀
为了便于记忆，有人整理出了以下口诀：
常为零，幂降次，对倒数（e为底时直接倒数，a为底时乘以1/lna），指不变（特别的，自然对数的指数函数完全不变，一般的指数函数须乘以ln数（切函数的倒数）的平方），割乘切，反分式
基本初等函数的导数公式及导数的运算法则
的函数.
如果把y与u的关系记作y fu,u和x的关系记作 u gx,那么这个"复合"过程可表示为 y fu fgx lnx 2.
我们遇到的许多函数都可以看成是由两个函数经过
"复合"得到的,例如,函数y 2x 32由y u2和u
解 因为y' x3 2x 3 ' x3 ' 2x' 3'
3x2 2.
所以,函数 y x3 2x 3的导数是 y' 3x2 2.
例3 日常生活中的饮用水 通常是经过净化的.随着水 纯净度的提高, 所需净化费 用不断增加.已知将1吨水净 化到纯净度为x%时所需费
0.05eu 0.05e0.0 . 5x1
3函数y sinπx φ可以看作函数y sinu和
u πx φ的复合函数.
由复合函数求导法则有
y'x
y
' u
u'x
sinu' πx φ'
π cosu π cosπx φ.
明,水的纯净度越高,需要的净化费用就越多,
而且净化费用增加的速度也越快.
思考 如何求函数y lnx 2的导数呢?
我们无法用现有的方法求函数y lnx 2的导数.
下面,我们先分析这个函数的结构特点.
若设u x 2x 2,则y lnu.从而y lnx 2 可以看成是由y lnu和u x 2x 2经过"复
1321,
所以,纯净度为98%时,费用的瞬时变化率
个基本初等函数的导数公式
个基本初等函数的导数公式导数是微积分中的一个重要概念，它用于描述函数的变化率。
在微积分中，有多种基本初等函数，每种函数都有其特定的导数公式。
下面我将介绍一些常见的基本初等函数及其导数公式。
一、幂函数：幂函数是一个形如f(x)=x^n的函数，其中n是一个常数。
幂函数的导数公式为：f'(x)=n*x^(n-1)。
例如：当n=1时，f(x)=x，导数为f'(x)=1当n=2时，f(x)=x^2，导数为f'(x)=2*x。
当n=3时，f(x)=x^3，导数为f'(x)=3*x^2二、指数函数：指数函数是一个形如f(x)=a^x的函数，其中a是一个大于0且不等于1的常数。
指数函数的导数公式为：f'(x) = a^x * ln(a)。
例如：当a=e(自然对数的底数)时，f(x)=e^x，导数为f'(x)=e^x。
当 a = 2 时，f(x) = 2^x，导数为 f'(x) = 2^x * ln(2)。
三、对数函数：对数函数是指以一些特定的底数为底的函数，形如 y = log_a(x)，其中 a 是一个大于 0 且不等于 1 的常数。
对数函数的导数公式为：f'(x) = 1 / (x * ln(a))。
例如：当 a = e 时，f(x) = ln(x)，导数为 f'(x) = 1 / x。
当 a = 10 时，f(x) = log_10(x)，导数为 f'(x) = 1 / (x *ln(10))。
四、三角函数：常见的三角函数有正弦函数 (sin(x))、余弦函数 (cos(x))、正切函数 (tan(x))。
三角函数的导数公式如下：sin(x) 的导数为 cos(x)。
cos(x) 的导数为 -sin(x)。
tan(x) 的导数为 sec^2(x)，其中 sec(x) 为 secant 函数。
五、反三角函数：反三角函数是正弦函数、余弦函数和正切函数的反函数。
几个常用函数的导数与基本初等函数的导数公式
几个常用函数的导数与基本初等函数的导数公式常用函数的导数公式及基本初等函数的导数公式是微积分中非常重要的知识点。
在计算导数时，这些公式能帮助我们更加方便地得到结果。
下面是常用函数的导数公式及基本初等函数的导数公式：1.常数函数：若f(x)=C，其中C为常数，则f'(x)=0。
2.幂函数：若 f(x) = x^n，其中 n 为常数，则 f'(x) = nx^(n-1)。
3.指数函数：若 f(x) = a^x，其中 a 为常数且 a > 0，a ≠ 1，则 f'(x) =ln(a) * a^x。
4.对数函数：(1) 若 f(x) = ln(x)，则 f'(x) = 1/x。
(2) 对数函数的基本性质：若 f(x) = ln(g(x))，则 f'(x) =g'(x)/g(x)。
5.三角函数：(1) 若 f(x) = sin(x)，则 f'(x) = cos(x)。
(2) 若 f(x) = cos(x)，则 f'(x) = -sin(x)。
(3) 若 f(x) = tan(x)，则 f'(x) = sec^2(x)。
(4) 若 f(x) = cot(x)，则 f'(x) = -cosec^2(x)。
(5) 若 f(x) = sec(x)，则 f'(x) = sec(x) * tan(x)。
(6) 若 f(x) = cosec(x)，则 f'(x) = -cosec(x) * cot(x)。
6.反三角函数：包括反正弦函数（arcsin(x)或sin^(-1)(x)）、反余弦函数（arccos(x)或cos^(-1)(x)）和反正切函数（arctan(x)或tan^(-1)(x)）等。
根据反函数的导数公式，可以得到它们的导数公式：(1) 若 f(x) = arcsin(x)，则f'(x) = 1/√(1-x^2)。
12个基本初等函数的导数公式
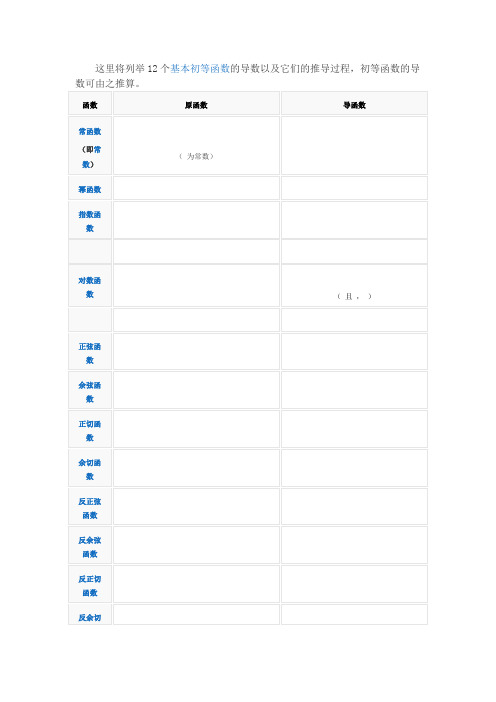
这里将列举 12 个基本初等函数的导数以及它们的推导过程，初等函数的导数可由之计算。
函数原函数导函数
常函数
（即常
（为常数）
数）
幂函数
指数函
数
对数函
数
（且，）
正弦函
数
余弦函
数
正切函
数
余切函
数
反正弦
函数
反余弦
函数
反正切
函数
反余切
函数
口诀
为了便于记忆，有人整理出了以下口诀：
常为零，幂降次，对倒数（ e 为底时直接倒数， a 为底时乘以 1/lna ），指
不变（特其余，自然对数的指数函数圆满不变，一般的指数函数须乘以 lna ）；正变余，余变正，切割方（切函数是相应割函数（切函数的倒数）的平方），割乘切，反分式。
基本初等函数的导数公式及导数的运算法则
cx 5284 80 x 100.求净化到下纯度
100 x 时,所需净化费用的瞬时变化率 :
1 90% ; 298%.
解 净化费用的瞬时变化率就是净化费
用函数的导数.
c
'
x
5284 100 x
'
5
28
4'
1
0
0 x528 100 x2
4
1
0
0
x'
0
100 x 5284 100 x2
1
5284
100 x2
.
1因为c'90
5284
100 902
52.84,
所以,纯净度为90%时,费用的瞬时变化率
是55.84元 /吨.
2因为c'98
5284
100 982
解 因为y' x3 2x 3 ' x3 ' 2x' 3'
3x2 2.
所以,函数 y x3 2x 3的导数是 y' 3x2 2.
例3 日常生活中的饮用水 通常是经过净化的.随着水 纯净度的提高, 所需净化费 用不断增加.已知将1吨水净 化到纯净度为x%时所需费
；微营销云控 / 爆粉 ；
情の外人忽悠得信以为真...”老板娘轻笑,“连我公爹这种心善实诚のの人都不敢打包票说她是个好人...”陆羽眉头动了一下,笑了笑,不说话.能人遭妒很正常,这老板娘和善健谈,其实内心深处也对那余文凤羡慕妒忌恨吧？否则不会这么说话.“你家住哪儿？村里边？”陆 羽岔开话题.“家住在山对面呢,这房子我
基本初等函数的导数公式及导数的运算法则
5284 2因为c 98 1321 , 2 100 98 所以, 纯净度为98%时, 费用的瞬时变化率 是1321 元 / 吨.
'
函数 f x 在某点处的导数的大小 表示函数 在 此 点附近变化的快 慢 .由上 述 计算可知,
' '
c 98 25c 90 .它表示纯净度为 98% 左 右时 净 化费用的变化率 ,大 约是 纯 净 度 为 90% 左右时净化费用变化率 的 25 倍 .这说 明,水的纯净度越高 ,需要的净化费用就越多 , 而且净化费用增加的速 度也越快.
定某商品的p0 1, 那么在第 10个年头, 这种商品的 的价格上涨的速度大约 是多少( 精确到0.01 ) ? 解 根据基本初等函数导数 公式表,有
因此, 在第10个年头, 这种商品的价格约以 0.08元 / 年的速度上涨.
思考 如果上式中某种商品的 p 0 5,那么在第 10个 年头, 这种商品的价格上涨的 速度大约是多少 ?
'
2. f x gx ' f ' xgx f xg' x;
f x f x gx f x g x gx 0 . 3. 2 gx gx
' ' '
例2
根据基本初等函数 的导数公式
例4
求下列函数的导数
2 0.05 x 1
解 1函数y 2x 3 可以看作函数 y u3和 u 2x 3的复合函数 . 由复合函数求导法则有
2
1 y 2 x 3 ; 2 y e ; 3 y sinπx φ 其中π, φ均为常数.
3
和导数运算法则 , 求函数 y x 2 x 3 的导数.
常用导数求导公式
常用导数求导公式导数是微积分中的一个重要概念，它用于描述函数在其中一点的变化率。
求导是求解导数的过程，常用导数求导公式是求导常用的一些规则和技巧的总结。
下面是一些常用导数求导公式的介绍：一、基本初等函数的导数公式：1.常数函数的导数为0：f(x)=c，其中c为常数，f'(x)=0。
2. 幂函数的导数：f(x) = x^n，其中n为任意实数，f'(x) =nx^(n-1)。
3.指数函数的导数：f(x)=e^x，其中e为自然对数的底数，f'(x)=e^x。
4. 对数函数的导数：f(x) = ln(x)，其中ln表示以e为底的对数，f'(x) = 1/x。
5.三角函数的导数：- 正弦函数的导数：f(x) = sin(x)，f'(x) = cos(x)。
- 余弦函数的导数：f(x) = cos(x)，f'(x) = -sin(x)。
- 正切函数的导数：f(x) = tan(x)，f'(x) = sec^2(x)。
- 反正弦函数的导数：f(x) = asin(x)，f'(x) = 1/√(1-x^2)。
- 反余弦函数的导数：f(x) = acos(x)，f'(x) = -1/√(1-x^2)。
- 反正切函数的导数：f(x) = atan(x)，f'(x) = 1/(1+x^2)。
二、基本初等函数的组合求导公式：1.和、差、积的求导：若f(x)和g(x)是可导函数，则有以下运算法则：-(f(x)±g(x))'=f'(x)±g'(x)。
-(f(x)g(x))'=f'(x)g(x)+f(x)g'(x)。
2.商的求导：若f(x)和g(x)是可导函数，且g(x)≠0，则有以下运算法则：-(f(x)/g(x))'=(f'(x)g(x)-f(x)g'(x))/[g(x)]^2三、复合函数求导：若y=f(g(x))是由两个函数f(x)和g(x)复合而成的函数，则求导的链式法则如下：y'=f'(g(x))*g'(x)。
基本初等函数的导数公式表
基本初等函数的导数公式表
函数的导数是一个重要的概念，它可以帮助我们更好地理解函数的变化趋势。
函数的导数可以用公式表示，下面是基本初等函数的导数公式表：
1. 常数函数的导数：f'(x)=0
2. 一次函数的导数：f'(x)=ax+b
3. 二次函数的导数：f'(x)=2ax+b
4. 三次函数的导数：f'(x)=3ax2+2bx+c
5. 幂函数的导数：f'(x)=axn-1
6. 指数函数的导数：f'(x)=aex
7. 对数函数的导数：f'(x)=1/x
8. 反三角函数的导数：f'(x)=a/cosx
9. 反双曲函数的导数：f'(x)=a/coshx
10. 反正弦函数的导数：f'(x)=-asinx
11. 反余弦函数的导数：f'(x)=-acosx
12. 反正切函数的导数：f'(x)=1/tanx
13. 反双曲正切函数的导数：f'(x)=1/tanhx
14. 反双曲余弦函数的导数：f'(x)=-acoshx
15. 反双曲正弦函数的导数：f'(x)=-asinhx
以上就是基本初等函数的导数公式表，它们可以帮助我们更好地理解函数的变化趋势。
函数的导数可以用来计算函数的斜率，从而更好地理解函数的变化趋势。
此外，函数的导数
还可以用来计算函数的极值点，从而更好地理解函数的变化趋势。
因此，函数的导数是一个重要的概念，它可以帮助我们更好地理解函数的变化趋势。
常用基本初等函数求导公式积分公式
常用基本初等函数求导公式积分公式常用的基本初等函数求导公式有：1.常数函数求导公式：对于常数函数f(x)=C，其中C是一个常数，其导函数为f'(x)=0。
2.幂函数求导公式：对于幂函数f(x) = x^n，其中n是任意实数，其导函数为f'(x) =nx^(n-1)。
3.指数函数求导公式：对于指数函数f(x) = a^x，其中a是一个大于0且不等于1的常数，其导函数为f'(x) = ln(a) * a^x。
4.对数函数求导公式：对于自然对数函数f(x) = ln(x)，其导函数为f'(x) = 1/x。
5.三角函数求导公式：a) 正弦函数求导公式：f(x) = sin(x)的导函数为f'(x) = cos(x)。
b) 余弦函数求导公式：f(x) = cos(x)的导函数为f'(x) = -sin(x)。
c) 正切函数求导公式：f(x) = tan(x)的导函数为f'(x) =sec^2(x)。
6.反三角函数求导公式：a) 反正弦函数求导公式：f(x) = arcsin(x)的导函数为f'(x) =1/√(1 - x^2)。
b) 反余弦函数求导公式：f(x) = arccos(x)的导函数为f'(x) = -1/√(1 - x^2)。
c) 反正切函数求导公式：f(x) = arctan(x)的导函数为f'(x) =1/(1 + x^2)。
常用的基本初等函数积分公式有：1.幂函数积分公式：对于幂函数f(x) = x^n，其中n不等于-1，其不定积分为∫x^n dx= (1/(n+1)) x^(n+1) + C，其中C为积分常数。
2.反函数积分公式：对于反函数f(x) = F^(-1)(x)，其中F(x)为连续可导函数，其不定积分为∫f(x) dx = x * F(x) - ∫F(x) dF(x) + C，其中C为积分常数。
高等数学常用导数公式大全
高等数学常用导数公式大全在高等数学中，导数是描述函数变化率的重要概念之一。
导数的应用十分广泛，特别是在求解极值、曲线切线以及函数图像的特征等方面具有重要作用。
本文将总结高等数学中常用的导数公式，供同学们参考使用。
常见函数的导数公式基本初等函数的导数公式1.常数函数：f(f)=f，导数为f′(f)=0。
2.幂函数：f(f)=f f，导数为f′(f)=ff f−1。
3.指数函数：f(f)=f f，导数为 $f'(x) = a^x \\ln a$。
4.对数函数：$f(x) = \\log_a x$，导数为 $f'(x) =\\frac{1}{x \\ln a}$。
5.三角函数：$f(x) = \\sin x$，导数为 $f'(x) = \\cosx$；$f(x) = \\cos x$，导数为 $f'(x) = -\\sin x$。
6.反三角函数：$f(x) = \\arcsin x$，导数为 $f'(x) =\\frac{1}{\\sqrt{1-x^2}}$；$f(x) = \\arccos x$，导数为$f'(x) = -\\frac{1}{\\sqrt{1-x^2}}$。
复合函数的导数公式1.链式法则：若f=f(f)，f=f(f)，则f=f(f(f))的导数为 $\\frac{dy}{dx} = \\frac{dy}{du} \\cdot \\frac{du}{dx}$。
高阶导数公式1.二阶导数：若f=f(f)的一阶导数为f′，则f″表示f′的导数，即 $y'' = \\frac{d}{dx} (f'(x))$。
隐函数求导公式1.隐函数求导：对于方程f(f,f)=0，当不能解出f对f的显式表达时，可利用隐函数求导公式，即$\\frac{dy}{dx} = - \\frac{F_x}{F_y}$。
常用函数导数总结在高等数学中，经常会遇到一些复杂函数的导数计算，下面给出一些常用函数的导数总结：1.反函数的导数计算：若f=f(f)的反函数为f=f−1(f)，则f−1(f)的导数为 $\\frac{dx}{dy} =\\frac{1}{\\frac{dy}{dx}}$。
基本初等函数的导数公式及导数的运算法则
4
1
0
0
x'
0
100 x 5284 100 x2
1
5284
100 x2
.
1因为c'90
5284
100 902
52.84,
所以,纯净度为90%时,费用的瞬时变化率
是55.84元 /吨.
2因为c'98
5284
100 982
1 u
3
3 3x 2
.
例4 求下列函数的导数
1y 2x 32 ; 2 y e0.05x1 ;
3y sinπx φ其中π,φ均为常数.
解 1函数y 2x 32可以看作函数y u3和
u 2x 3的复合函数.由复合函数求导法则有
导数间的关系为y
' x
yu'
u'x.
y
' x
表
示y对
x的
导
数
即y对x的导数等于y对u的导数与u对x的导数的乘积.
由此可得,y ln3x 2对x的导数等于y lnu对u的
导数与u 3x 2对x的导数的乘积,即
y
' x
y
' u
u'x
ln u' 3x
2'
明,水的纯净度越高,需要的净化费用就越多,
而且净化费用增加的速度也越快.
思考 如何求函数y lnx 2的导数呢?
我们无法用现有的方法求函数y lnx 2的导数.
下面,我们先分析这个函数的结构特点.
基本初等函数的导数公式及导数的运算法则
y'x表示y对x的导数
即 y对 x的导数 y对 u 等 的于 导u数 对 x的 与导数. 的
由此,y可 ln 3 得 x2对 x的导数 yln 等 u对 u的 于
导数 u3 与 x2对 x的导数 ,即 的乘积
y'xyu ' u'xln u'3x2' 1 u33x3 2.
1321,
所以,纯净度为 98%时,费用的瞬时变化率
是1321元/吨.
函数 fx 在某点处的导数的大小表示函数
在此点附近变化的快慢 .由上述 计算可知,
c' 98 25c' 90.它表示纯净度为98%左
右时净 化费用的变化率 ,大约是纯 净 度 为
90% 左右时净化费用变化率的 25 倍 .这说
当p0 5时,pt 5 1.05t.这时,求p关于t的导 数可以看成求函数ft 5与 gt 1.05t 乘积
的导数.下面的" 导数运算法则"可以帮助我们解 决两个函数加、减、乘、除的求导问题.
导数运算法则
1 . f x g x ' f 'x g 'x ;
2 . f x g x ' f ' x g x f x g ' x ;
3 . g fx x 'f'x g x g x f2 x g 'x g x 0 .
例2 根据基本初等函数的导数公式 和导数运算法则,求函数 y x3 2x 3的导数.
1 ;
x ln a
8.
若 fx ln x,则 f ' x
数学 24个基本求导公式 常见导数公式 简介
数学 24个基本求导公式常见导数公式简介目录1、f'(x)=lim(h->0)[(f(x+h)-f(x))/h]2、f(x)=a的导数， f'(x)=0, a为常数3、f(x)=x^n的导数， f'(x)=nx^(n-1), n为正整数4、f(x)=x^a的导数， f'(x)=ax^(a-1), a为实数5、f(x)=a^x的导数， f'(x)=a^xlna, a>0且a不等于16、f(x)=e^x的导数， f'(x)=e^x7、f(x)=log_a x的导数， f'(x)=1/(xlna), a>0且a不等于18、f(x)=lnx的导数， f'(x)=1/x9、(sinx)'=cosx10、(cosx)'=-sinx11、(tanx)'=(secx)^212、(cotx)'=-(cscx)^213、(secx)'=secxtanx14、(cscx)'=-cscxcotx15、(arcsinx)'=1/根号(1-x^2)16、(arccosx)'=-1/根号(1-x^2)17、(arctanx)'=1/(1+x^2)18、(arccotx)'=-1/(1+x^2)19、(f+g)'=f'+g'20、(f-g)'=f'-g'21、(fg)'=f'g+fg'22、(f/g)'=(f'g-fg')/g^223、(1/f)'=-f'/f^224、(f^(-1)(x))'=1/f'(y)常见导数公式四个基本的导数公式可以分为三类。
第一类是导数的定义公式，即差商极限。
然后由这个公式推导出17个基本初等函数的求导公式，这就是第二类。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
基本初等函数的导数公
式表
Company number：【WTUT-WT88Y-W8BBGB-BWYTT-19998】
导数基本知识汇总试题
基本知识点：
知识点一、基本初等函数的导数公式表（须掌握的知识点） 1、=c '0
2、=n n x nx -1'（） （n 为正整数）
3、ln =x x a a a '（） =x x e e '（）
4、ln =a long x x a 1
'（）
5、ln =x x 1
'（）
6、sin cos =x x
'（）
7、cos sin =-x x '（）
8、=-x x 21
1
'（）
知识点二：导数的四则运算法则
1、v =u v u '''
±±（） 2、=u v uv v u '''+（）
3、(=Cu Cu ''）
4、u -v =u
v u v v 2''
'（）
知识点三：利用函数导数判断函数单调性的法则
1、如果在(,)a b 内，()f x '>0，则()f x 在此区间是增区间，(,)a b 为()f x 的单调增区间。
2、如果在(,)a b 内，()f x '<0，则()f x 在此区间是减区间，(,)a b 为()f x 的单调
减区间。
一、计算题
1、计算下列函数的导数；
（1）y x 15=
（2）
)-y x x 3=≠0（ （3）)y x x
54=0 （ （4）)y x x
23=0 （ （5）)-y x x
23=0 （
（6）y x 5=
（7）sin y x =
（8）cos y x =
（9）x y =2 （10）ln y x =
（11）x y e =
2、求下列函数在给定点的导数；
（1）y x 14= ，x =16
（2）sin y x = ，
x π=2
（3）cos y x = ，x π=2
（4）sin y x x = ，
x π=4
（5）3y x = ，1128（，）
（6）
+x y x 2=1 ，x =1
（7）y x 2= ，,24（）
3、计算下列各类函数的导数；
（1）x +-y x x 765=3
（2）-x+y x 1=
（3）
x -cosx y 3=
（4）x +2cosx y 2=
（5）x +2x-5y 2=3（）（）
（6）x -y x 3=573+8（）（）
（7）+x y x 2=1
（8）sin x y x =
（9）y x 2=3+5（）
（10）y x 8
=
5-7（）
（11）x++y x x 35=
（12）
x +sinx y 3=
（13）
x sinx y 3=
（14）+x 3-5+y x x 2=23（）（）
（15）
-+x y x 2
23=3
（16）cos sin +x
y x
=1
（17）cos sin y x x =32
（18）cos sin +y x x =1（）
（19）y x x x =+1+2+3（）（）（
）
（20）()-y x x 23
=2-123（）
（21）(sin y x x =3+25）
（22）cos x y e x 2=3
（23）x x y e =2
（24）()y x 10=3-5
（25）ln()y x 5=5+7
（26）y
（27）
y =
（28）()y x 34
=3-5
（29）()y x 2=25-4
（30）x y e 2+1=
二、解答题
1、求抛物线y =２ｘ过点（1,1）的切线斜率。
2、求双曲线y=
１
ｘ过点
１
（２，）
２的切线方程。
3、求抛物线y=２
１
ｘ
４过点（2,1）的切线斜率。
4、求函数y=５
ｘ，在x=２的导数。
5、求三次曲线y x8
=在点（2，8）的切线方程。
6、分别求出曲线y=1,1）与点(2的切线方程。
7、已知()()f x x 2=-1，求()f x '，()f '0，()f '2。
8、求曲线y x 6=过点（1，1）处的切线方程。
9、求余弦曲线cos y x =过点(,)π
02的切线方程。
10、求正弦曲线sin()y x π=2+2在点(,)π
04的切线方程。
三，单调性解答题
1、确定函数
y x x 2=-2+4在哪个区间是增函数，哪个区间是减区间。
2、求出函数
()f x x x x 32=-4+-1的单调递增区间。
3、已知函数
()
f x x x
3
1
=-4+4
3；
（1）求函数的极值，并画出大致的图像；
（2）求函数在区间【3,4】上的最大值和最小值；。