中考数学折叠问题压轴题专项训练,初中折叠翻折问题的经典题型,历年中考折叠问题真题及答案解析

合集下载

中考数学专题复习专题33 中考几何折叠翻折类问题(教师版含解析)

中考专题33 中考专题几何折叠翻折类问题1.轴对称(折痕)的性质：(1)成轴对称的两个图形全等。

(2)对称轴与连结“对应点的线段”垂直。

(3)对应点到对称轴的距离相等。

(4)对应点的连线互相平行。

也就是不管是轴对称图形还是两个图形关于某条直线对称，对称轴都是任何一对对应点所连线段的垂直平分线.对称的图形都全等.2.折叠或者翻折试题解决哪些问题(1)求角度大小；(2)求线段长度；(3)求面积；(4)其他综合问题。

3.解决折叠问题的思维方法(1)折叠后能够重合的线段相等，能够重合的角相等，能够重合的三角形全等，折叠前后的图形关于折痕对称，对应点到折痕的距离相等。

(2)折叠类问题中，如果翻折的直角，那么可以构造三垂直模型，利用三角形相似解决问题。

(3)折叠类问题中，如果有平行线，那么翻折后就可能有等腰三角形，或者角平分线。

这对解决问题有很大帮助。

(4)折叠类问题中，如果有新的直角三角形出现，可以设未知数，利用勾股定理构造方程解决。

(5)折叠类问题中，如果折痕经过某一个定点，往往用辅助圆解决问题。

一般试题考查点圆最值问题。

(6)折叠后的图形不明确，要分析可能出现的情况，一次分析验证可以利用纸片模型分析。

【经典例题1】(2020年•哈尔滨)如图，在Rt△ABC中，∠BAC＝90°，∠B＝50°，AD⊥BC，垂足为D，△ADB与△ADB'关于直线AD对称，点B的对称点是点B'，则∠CAB'的度数为( )A．10°B．20°C．30°D．40°【标准答案】A【答案剖析】由余角的性质可求∠C＝40°，由轴对称的性质可得∠AB'B＝∠B＝50°，由外角性质可求解．∵∠BAC＝90°，∠B＝50°，∴∠C＝40°，∵△ADB与△ADB'关于直线AD对称，点B的对称点是点B'，∴∠AB'B＝∠B＝50°，∴∠CAB'＝∠AB'B﹣∠C＝10°。

2024年中考数学压轴突破【几何中的折叠】题型汇编(解析版)

几何中的折叠问题一、单选题1如图，在菱形ABCD中，AD=5，tan B=2，E是AB上一点，将菱形ABCD沿DE折叠，使B、C的对应点分别是B 、C ，当∠BEB =90°时，则点C 到BC的距离是()A.5+5B.25+2C.6D.35【答案】D【分析】过C作CH⊥AD于H，C 作C F⊥AD于F，HD=5，HC=25，再由折叠证明∠BED=∠B ED=135°，∠EDC=∠EDC =45°，△CHD≌△DFC ，C F= HD=5，【C作CH⊥AD于H，C 作C F⊥AD于F，由已知AD=5，tan B=2，=2，∴CD=5，tan∠CDH=HCHD∴设HD=x，HC=2x，∴在Rt△HDC中HC2+HD2=CD2，2x2+x2=52，解得x=5，∴HD=5，HC=25，由折叠可知∠BED=∠B ED，∠EDC=∠EDC ，CD=C D∵∠BEB =90°，∴∠BED=∠B ED=135°，∵AB∥DC，∴∠EDC=180°-∠BED=45°，∴∠EDC=∠EDC =45°∴∠CDC =90°∵∠CHD =∠C AD =90°，∴∠CDH +C DF =90°，∵∠CDH +∠HCD =90°，∴∠C DF =∠HCD ，∴△CHD ≌△DFC ，∴C F =HD =5，∴点C 到BC 的距离是C F +CH =5+25=35．故选：D ．【点睛】本题考查了全等三角形的性质和判定、菱形的性质、图形的折叠以及正切定义的应用，解答关键是根据折叠的条件推出∠BED =∠B ED =135°．2如图，将△ABC 折叠，使AC 边落在AB 边上，展开后得到折痕l 与BC 交于点P ，且点P 到AB 的距离为3cm ，点Q 为AC 上任意一点，则PQ 的最小值为()A.2cmB.2.5cmC.3cmD.3.5cm【答案】C【分析】由折叠可得：PA 为∠BAC 的角平分线，根据垂线段最短即可解答．【详解】解：∵将△ABC 折叠，使AC 边落在AB 边上，∴PA 为∠BAC 的角平分线，∵点Q 为AC 上任意一点，∴PQ 的最小值等于点P 到AB 的距离3cm ．故选C ．【点睛】本题主要考查了折叠的性质、角平分线的性质定理等知识点，掌握角平分线上的点到两边距离相等是解答本题的关键．3如图，在▱ABCD 中，BC =8,AB =AC =45，点E 为BC 边上一点，BE =6，点F 是AB 边上的动点，将△BEF 沿直线EF 折叠得到△GEF ，点B 的对应点为点G ，连接DE ，有下列4个结论：①tan B =2；②DE =10；③当GE ⊥BC 时，EF =32；④若点G 恰好落在线段DE 上时，则AF BF=13．其中正确的是()A.①②③B.②③④C.①③④D.①②④【答案】D【分析】过点A 作AH ⊥BC 于点H ，利用三线和一以及正切的定义，求出tan B ，即可判断①；过点D 作DK ⊥BC 于点K ，利用勾股定理求出DE ，判断②；过点F 作FM ⊥BC 于点M ，证明△EMF 为等腰直角三角形，设EM =FM =x ，三角函数求出BM 的长，利用BE =BM +EM ，求出x 的值，进而求出EF 的长，判断③；证明△AND ∽△CNE ，推出∠ENC =∠ECN ，根据折叠的性质，推出EF ∥CA ，利用平行线分线段成比例，即可得出结论，判断④．【详解】解：①过点A 作AH ⊥BC 于点H ，∵BC =8,AB =AC =45，∴BH =12BC =4，∴AH =AB 2-BH 2=8，∴tan B =AHBH=2；故①正确；②过点D 作DK ⊥BC 于点K ，则：四边形AHKD 为矩形，∴DK =AH =8，HK =AD =BC =8，∵BE =6，∴CE =2，∵CH =12BC =4，∴CK =4，∴EK =CE +CK =6，∴DE =EK 2+DK 2=10；故②正确；③过点F 作FM ⊥BC 于点M ，∵GE ⊥BC ，∴∠BEG =90°，∵翻折，∴∠BEF =∠GEF =45°，∴∠EFM =∠BEF =45°，∴EM =FM ，设EM =FM =x ，∵tan B =FMBM =2，∴BM =12FM =12x ，∴BE =BM +EM =12x +x =6，∴x =4，∴EM =FM =4，∴EF =2EM =42；故③错误；④当点G 恰好落在线段DE 上时，如图：设AC 与DE 交于点N ，∵▱ABCD ，∴AD ∥BC ，∴△AND ∽△CNE ，∴EN DN =CE AD=28=14，∴EN DE =15，∴EN =15DE =2=CE ，∴∠ENC =∠ECN ，∴∠BEN =∠ENC +∠ECN =2∠ECN ，∵翻折，∴∠BEN =2∠BEF ，∴∠BEF =∠ECN ，∴EF ∥AC ，∴AF BF =CE BE=26=13；故④正确，综上：正确的是①②④；故选D ．【点睛】本题考查平行四边形的折叠问题，同时考查了解直角三角形，相似三角形的判定和性质，等腰三角形的判定和性质，勾股定理．本题的综合性强，难度较大，是中考常见的压轴题，熟练掌握相关性质，添加合适的辅助线，构造特殊三角形，是解题的关键．4如图，AB 是⊙O 的直径，点C 是⊙O 上一点，将劣弧BC 沿弦BC 折叠交直径AB 于点D ，连接CD ，若∠ABC =α0°<α<45° ，则下列式子正确的是()A.sin α=BCABB.sin α=CD ABC.cos α=AD BDD.cos α=CD BC【答案】B【分析】连AC ，由AB 是⊙O 的直径，可知∠ACB =90°，由折叠，AC和CD所在的圆为等圆，可推得AC =CD ，再利用正弦定义求解即可．【详解】解：连AC ，∵AB 是⊙O 的直径，∴∠ACB =90°，由折叠，AC 和CD所在的圆为等圆，又∵∠CBD =∠ABC ，∴AC和CD所对的圆周角相等，∴AC=CD，∴AC =CD ，在Rt △ACB 中，sin α=AC AB =CDAB，故选：B ．【点睛】本题考查圆周角定理和圆心角、弦、弧之间的关系以及正弦、余弦定义，解答关键是通过折叠找到公共的圆周角推出等弦．5如图，在平面直角坐标系中，OA 在x 轴正半轴上，OC 在y 轴正半轴上，以OA ，OC 为边构造矩形OABC ，点B 的坐标为8,6 ，D ，E 分别为OA ，BC 的中点，将△ABE 沿AE 折叠，点B 的对应点F 恰好落在CD 上，则点F 的坐标为()A.3213,3013B.3013,3213C.3013,2013D.2013,3013【答案】A【分析】先求得直线CD 的解析式，过点F 作FM ⊥CE 于点M ，过点F 作FN ⊥OC 于点N ，设点F m ,-32m +6 ，在Rt △EMF 中，再利用勾股定理得到关于m 的方程，解方程即可．【详解】解：∵点B 的坐标为8,6 ，四边形OABC 是矩形，D ，E 分别为OA ，BC 的中点，∴C 0,6 ，D 4,0 ，E 4,6 ，由折叠的性质可得：EF =BE =4，设直线CD 的解析式为y =kx +b ，则6=b 4k +b =0 ，解得：k =-32b =6，∴直线CD 的解析式为y =-32x +6，过点F 作FM ⊥CE 于点M ，过点F 作FN ⊥OC 于点N ，设点F m,-32m+6，则MF=CN=6--32m+6=32m，EM=4-m，在Rt△EMF中，EM2+MF2=EF2，∴4-m2+32m2=42，解得：m=3213或m=0(不合题意，舍去)，当m=3213时，y=-32×3213+6=3013，∴点F的坐标为3213,30 13，故选：A．【点睛】本题是一次函数与几何综合题，考查了求一次函数解析式，勾股定理，翻折的性质，矩形的性质，中点的性质，熟练掌握知识点并灵活运用是解题的关键．6综合与实践课上，李老师让同学们以矩形纸片的折叠为主题开展数学活动．如图，将矩形纸片ABCD对折，折痕为EF，再把点A折叠在折痕EF上，其对应点为A ，折痕为DP，连接A B，若AB=2，BC =3，则tan∠A BF的值为()A.33B.3 C.32D.12【答案】A【分析】先证明EF=AB=CD=2，CF=BF=DE=32，∠DEA=90°，∠A FB=90°，AD=A D=3，可得A E=A D2-DE2=32，AF=2-32=12，再利用正切的定义求解即可.【详解】解：∵矩形纸片ABCD对折，折痕为EF，AB=2，BC=3，∴EF=AB=CD=2，CF=BF=DE=32，∠DEA=90°，∠A FB=90°，由折叠可得：AD=A D=3，∴A E=A D2-DE2=32，∴A F=2-32=12，∴tan ∠A BF =1232=33.故选A【点睛】本题考查的是轴对称的性质,矩形的性质,勾股定理的应用,求解锐角的正切,熟记轴对称的性质是解本题的关键.7如图，矩形ABCD 中，AB =2，BC =3，P 是边BC 中点，将顶点D 折叠至线段AP 上一点D ，折痕为EF ，此时，点C 折叠至点C ．下列说法中错误的是()A.cos ∠BAP =45B.当AE =53时，D E ⊥AP C.当AE =18-65时，△AD E 是等腰三角形 D.sin ∠DAP =45【答案】C【分析】根据矩形的性质，直角三角形的性质，三角函数，勾股定理，折叠的性质计算判断即可．【详解】∵矩形ABCD 中，AB =2，BC =3，P 是边BC 中点，∴BP =12BC =32，∠B =90°，∴AP =AB 2+BP 2=22+32 2=52，∴cos ∠BAP =AB AP=252=45，故A 正确；∵矩形ABCD ，∴AD ∥BC ，∴∠DAP =∠APB ，∴sin ∠DAP =sin ∠APB =cos ∠BAP =45，故D 正确；设DE =D E =x ，根据题意，得AE =AD -DE =3-x ，sin ∠DAP =45，∵D E ⊥AP ，∴sin ∠DAP =D E AE=x 3-x =45，解得x =43，∴AE =AD -DE =3-x =53，故B 正确；当D E =AE 时，∴x =3-x ，解得x =32；此时D ,A 重合，三角形不存在，不符合题意；当D E =AD 时，过点D 作D N ⊥AD 于点N ，则AN =NE ；∵矩形ABCD ，∴AD ∥BC ，∴∠DAP =∠APB ，∴cos ∠DAP =cos ∠APB =3252=35，设DE =D E =x ，根据题意，得AE =AD -DE =3-x ，D E =AD =x ，∴AN AD=AN x =35，解得AN =35x ；∴AE =AD -DE =3-x =2AN =65x ，解得x =1511；∴AE =65×1511=1811；当AE =AD 时，过点D 作D H ⊥AD 于点H ，设DE =D E =x ，根据题意，得AE =AD =AD -DE =3-x ，∴D H =AD sin ∠DAP =453-x ，AH =AD cos ∠DAP =353-x ，∴HE =AE -AH =3-x -353-x =253-x ，根据勾股定理，得HE 2+D H 2=D E 2，∴253-x 2+453-x2=x 2解得x =65-12；∴AE =3-x =15-65；综上所述，AE =15-65或AE =1811，故C 错误，故选C ．【点睛】本题考查了矩形的性质，直角三角形的性质，三角函数，勾股定理，折叠的性质，熟练掌握三角函数，勾股定理，矩形的性质，折叠的性质是解题的关键．8如图，AB 为半圆O 的直径，点O 为圆心，点C 是弧上的一点，沿CB 为折痕折叠BC交AB 于点M ，连接CM ，若点M 为AB 的黄金分割点(BM >AM )，则sin ∠BCM 的值为()A.5-12B.5+12C.5-14D.12【答案】A【分析】过点M作MD⊥CB，垂足为D，延长MD交半⊙O于点M′，连接CM ，BM′，根据折叠的性质可得：∠CMB=∠CM′B，BC⊥MM′，从而可得∠BDM=90°，再根据黄金分割的定义可得BMAB =5-12，然后利用直径所对的圆周角是直角可得∠ACB=90°，从而证明A字模型相似三角形△DBM∽△CBA，进而利用相似三角形的性质可得DMAC=BMAB=5-12，最后根据圆内接四边形对角互补以及平角定义定义可得：∠A=∠AMC，从而可得CA=CM，再在Rt△CDM中，利用锐角三角函数的定义进行计算，即可解答．【详解】解：过点M作MD⊥CB，垂足为D，延长MD交半⊙O于点M′，连接CM ，BM′，由折叠得：∠CMB=∠CM′B，BC⊥MM′，∴∠BDM=90°，∵点M为AB的黄金分割点(BM>AM)，∴BMAB =5-12，∵AB为半圆O的直径，∴∠ACB=90°，∴∠ACB=∠MDB，∵∠DBM=∠CBA，∴△DBM∽△CBA，∴DMAC =BMAB=5-12，∵四边形ACM′B是半⊙O的内接四边形，∴∠A+∠CM′B=180°，∵∠AMC+∠CMB=180°，∠CMB=∠CM′B，∴∠A=∠AMC，∴CA=CM，在Rt△CDM中，sin∠BCM=DMCM=DMAC=5-12．故选：A．【点睛】本题考查了相似三角形的判定与性质，黄金分割，解直角三角形，翻折变换(折叠问题)，圆周角定理，根据题目的已知条件并结合图形添加适当的辅助线是解题的关键．二、填空题9如图，将一张矩形纸片ABCD折叠，折痕为EF，折叠后，EC的对应边EH经过点A，CD的对应边HG交BA的延长线于点P．若PA=PG，AH=BE，CD=3，则BC的长为．【答案】43【分析】本题考查了矩形与折叠问题，全等三角形的判定和性质，勾股定理．连接PF ，设BC =2x ，AH =BE=a ，证明Rt △PAF ≌Rt △PGF HL ，求得FA =FG =FD =x ，由折叠的性质求得BE =12x ，在Rt △ABE中，利用勾股定理列式计算，即可求解．【详解】解：连接PF ，设BC =2x ，AH =BE =a ，由矩形的性质和折叠的性质知FG =FD ，∠G =∠FAP =90°，AB =CD =3，AD =BC ，∵PA =PG ，PF =PF ，∴Rt △PAF ≌Rt △PGF HL ，∴FA =FG =FD =12AD =12BC =x ，由矩形的性质知：AD ∥BC ∴∠AFE =∠FEC ，折叠的性质知：∠FEA =∠FEC ，∴∠FEA =∠AFE ，∴AE =FA =x ，由折叠的性质知EC =EH =AE +AH =x +a ，∴BC =BE +EC =a +x +a =2x ，∴a =12x ，即BE =12x ，在Rt △ABE 中，AB 2+BE 2=AE 2，即32+12x 2=x 2，解得x =23，∴BC =2x =43，故答案为：4310如图，在矩形ABCD 中，AB =3，AD =6，M 为AD 的中点，N 为BC 边上一动点，把矩形沿MN 折叠，点A ，B 的对应点分别为A ，B ，连接AA '并延长交射线CD 于点P ，交MN 于点O ，当N 恰好运动到BC 的三等分点处时，CP 的长为．【答案】1或5【分析】分两种情况：①当CN =2BN 时．过点N 作NG ⊥AD 于点G ，则四边形ABNG 为矩形；②当BN =2CN 时，过点N 作NG ⊥AD 于点G ，则四边形ABNG 为矩形，根据矩形的性质得GM =AM -AG =1.再由折叠的性质可得∠AOM =90°，然后根据相似三角形的判定与性质可得答案．【详解】解：①当CN =2BN 时．如图1，过点N 作NG ⊥AD 于点G ，则四边形ABNG 为矩形，∴NG =AB =3，AG =BN =2．∵M 为AD 的中点，∴AM =3，∴GM =AM -AG =1．由折叠A 与A 对应，∴∠AOM =90°，∵∠MAO +∠APD =90°，∠MAO +∠AMO =90°，∴∠AMO =∠APD ，即∠GMN =∠APD ．又∵∠NGM =∠ADP =90°，∴△ADP ∽△NGM ，∴NG AD=GM DP =12，解得DP =2，∴CP =CD -DP =1．②当BN =2CN 时，如图2，过点N 作NG ⊥AD 于点G ，则四边形ABNG 为矩形，∴NG =AB =3，AG =BN =4．∵M 为AD 的中点，∴AM =3，∴GM =AG -AM =1．由折叠A 与A 对应，∴∠AOM =90°∠MAO +∠AMO =90°，∠MAO +∠APD =90°，∴∠AMO =∠APD ，即∠GMN =∠APD ．又∠ADP =∠NGM =90°，∴△ADP ∽△NGM ，∴NG AD=GM DP =12，解得DP =2，∴CP =CD +DP =5．综上，CP 的长为1或5．故答案为：1或5．【点睛】此题考查的是翻折变换-折叠问题、矩形的性质，正确作出辅助线是解决此题的关键．11如图，DE 平分等边△ABC 的面积，折叠△BDE 得到△FDE ,AC 分别与DF ,EF 相交于G ,H 两点．若DG =m ,EH =n ，用含m ,n 的式子表示GH 的长是．【答案】m 2+n 2【分析】先根据折叠的性质可得S △BDE =S △FDE ，∠F =∠B =60°，从而可得S △FHG =S △ADG +S △CHE ，再根据相似三角形的判定可证△ADG ∽△FHG ,△CHE ∽△FHG ，根据相似三角形的性质可得S △ADG S △FHG =DG GH2=m 2GH 2，S △CHE S △FHG =EH GH 2=n 2GH 2，然后将两个等式相加即可得．【详解】解：∵△ABC 是等边三角形，∴∠A =∠B =∠C =60°，∵折叠△BDE 得到△FDE ，∴△BDE ≌△FDE ，∴S △BDE =S △FDE ，∠F =∠B =60°=∠A =∠C ，∵DE 平分等边△ABC 的面积，∴S 梯形ACED =S △BDE =S △FDE ，∴S △FHG =S △ADG +S △CHE ，又∵∠AGD =∠FGH ,∠CHE =∠FHG ，∴△ADG ∽△FHG ,△CHE ∽△FHG ，∴S △ADG S △FHG =DG GH 2=m 2GH 2，S △CHE S △FHG =EH GH 2=n 2GH 2，∴S △ADG S △FHG +S △CHE S △FHG =m 2+n 2GH 2=S △ADG +S △CHE S △FHG =1，∴GH 2=m 2+n 2，解得GH =m 2+n 2或GH =-m 2+n 2(不符合题意，舍去)，故答案为：m 2+n 2．【点睛】本题考查了等边三角形的性质、折叠的性质、相似三角形的判定与性质等知识点，熟练掌握相似三角形的判定与性质是解题关键．12在矩形ABCD 中，点E 为AD 边上一点(不与端点重合)，连接BE ，将矩形ABCD 沿BE 折叠，折叠后点A 与点F 重合，连接并延长EF ，BF 分别交BC ，CD 于G ，H 两点.若BA =6，BC =8，FH =CH ，则AE 的长为．【答案】92【分析】连接GH ，证明Rt △FHG ≅Rt △CHG (HL )，可得FG =CG ，设FG =CG =x ，在Rt △BFG 中，有62+x 2=(8-x )2，可解得CG =FG =74，知BG =254，由矩形ABCD 沿BE 折叠，折叠后点A 与点F 重合，得∠AEB =∠FEB ，可得∠FEB =∠EBG ，EG =BG =254，故EF =EG -FG =92，从而得到AE =92．【详解】连接GH ，如图：∵四边形ABCD 是矩形，∴∠A =∠C =90°，∵将矩形ABCD 沿BE 折叠，折叠后点A 与点F 重合，∴BF =AB =6,AE =EF ,∠BFE =∠A =90°，∴∠GFH =90°=∠C ，∵GH =GH ,FH =CH ，∴Rt △FHG ≅Rt △CHG (HL )，∴FG =CG ，设FG =CG =x ，则BG =BC -CG =8-x在Rt △BFG 中，BF 2+FG 2=BG 2∴62+x 2=(8-x )2，解得：x =74，∴CG =FG =74，∴BG =8-x =25x，∵将矩形ABCD 沿BE 折叠，折叠后点A 与点F 重合，∴∠AEB =∠FEB ，∵AD ⎳BC ，∴∠AEB =∠EBG ，∴∠FEB =∠EBG ，∴EG =BG =254，∴AE =92，故答案为：92．【点睛】本题考查矩形中的翻折变换，涉及三角形全等的判定与性质，勾股定理及应用，掌握相关知识是解题的关键．13如图，在矩形ABCD 中，AD =23，CD =6，E 是AB 的中点，F 是线段BC 上的一点，连接EF ，把△BEF 沿EF 折叠，使点B 落在点G 处，连接DG ，BG 的延长线交线段CD 于点H ．给出下列判断：①∠BAC =30°；②△EBF ∽△BCH ；③当∠EGD =90°时，DG 的长度是23 ④线段DG 长度的最小值是21-3；⑤当点G 落在矩形ABCD 的对角线上，BG 的长度是3或33；其中正确的是．(写出所有正确判断的序号)【答案】①②③【分析】利用正切函数的定义即可判断①正确；利用同角的余角相等推出∠HBC =∠BEF ，可判断②正确；推出点D 、G 、F 三点共线，证明Rt △EAD ≌Rt △EGD HL ，可判断③正确；当点D 、G 、E 三点共线，线段DG 长度的最小值是21-3，由于F 是线段BC 上的一点，不存在D 、G 、E 三点共线，可判断④不正确；证明△BGE 是等边三角形，可判断⑤．【详解】解：连接AC ，∵矩形ABCD 中，AD =23，CD =6，∴tan ∠ACD =AD CD=236=33，∴∠ACD =30°，∴∠BAC =30°，故①正确；由折叠的性质知EF 是BG 的垂直平分线，∴∠HBC +∠BFE =90°=∠BEF +∠BFE ，∴∠HBC =∠BEF ，∴△EBF ∽△BCH ，故②正确；由折叠的性质知∠EGF =∠ABC =90°，∵∠EGD =90°，∴点D 、G 、F 三点共线，连接DE ，在Rt △EAD 和Rt △EGD 中，AE =BE =EG ，DE =DE ，∴Rt △EAD ≌Rt △EGD HL ，∴DG =AD =23，故③正确；∵AE =BE =EG ，∴点A 、G 、B 都在以E 为圆心，3为半径的圆上，DE =23 2+32=21，∴当点D 、G 、E 三点共线，线段DG 长度的最小值是21-3，但F 是线段BC 上的一点，∴D 、G 、E 三点不可能共线，故④不正确；当点G 落在矩形ABCD 的对角线AC 上时，由折叠的性质知BE =EG ，∵E 是AB 的中点，由①知∠BAC =30°，∴BE =EG =EA ，∠BAC =∠EGA =30°，∴∠BEG =∠BAC +∠EGA =60°，∴△BGE 是等边三角形，∴BG 的长度是3；由于F 是线段BC 上的一点，则点G 不会落在矩形ABCD 的对角线BD 上，故⑤不正确；综上，①②③说法正确，故答案为：①②③．【点睛】本题考查了矩形与折叠问题，正切函数，相似三角形的判定，勾股定理等知识，解答本题的关键是明确题意，找出所求问题需要的条件．14如图，将矩形ABCD沿BE折叠，点A与点A 重合，连接EA 并延长分别交BD、BC于点G、F，且BG=BF．(1)若∠AEB=55°，则∠GBF=；(2)若AB=3，BC=4，则ED=．【答案】40°/40度5-10/-10+5【分析】(1)先证明∠DEF=180°-2×55°=70°，∠BFG=∠DEF=70°，利用BG=BF，可得答案；(2)如图，过F作FQ⊥AD于Q，可得CF=DQ，FQ=CD=3，同理可得：∠BGF=∠BFG，∠DEG=∠BFG，而∠DGE=∠BGF，则∠DEG=∠DGE，设DE=DG=x，而BD=32+42=5，则BG=BF=5-x，CF=4-5-x=1，再求解EF=12+32=10，由折叠可得：A E=AE=4 =x-1，EQ=x-x-1-x，AF=10-4+x，利用cos∠BFA=cos∠FEQ，再建立方程求解即可．【详解】解：(1)∵∠AEB=55°，结合折叠可得：∠AEB=∠A EB=55°，∴∠DEF=180°-2×55°=70°，∵矩形ABCD，∴AD∥BC，∴∠BFG=∠DEF=70°，∵BG=BF，∴∠BGF=∠BFG=70°；∴∠GBF=180°-2×70°=40°；故答案为：40°．(2)如图，过F作FQ⊥AD于Q，∴四边形FCDQ是矩形，则CF=DQ，FQ=CD=3，同理可得：∠BGF=∠BFG，∠DEG=∠BFG，而∠DGE=∠BGF，∴∠DEG=∠DGE，∴设DE=DG=x，∵矩形ABCD，AB=3，BC=4，∴BD=32+42=5，∴BG=BF=5-x，∴CF=4-5-x=x-1，∴EQ=x-x-1=1，∴EF=12+32=10，由折叠可得：A E=AE=4-x，∴AF =10-4+x，∵∠QEF=∠BFA ，∴cos∠BFA =cos∠FEQ，∴EQEF=A FBF，∴110=10-4+x5-x，解得：x=5-10，经检验符合题意；∴DE=5-10．故答案为：5-10．【点睛】本题考查的是轴对称的性质，矩形的性质与判定，勾股定理的应用，锐角三角函数的应用，等腰三角形的判定与性质，熟练的利用以上知识解题是关键．三、解答题15综合与实践课上，老师让同学们以“正方形的折叠”为主题开展实践活动．(1)操作判断操作一：如图(1)，正方形纸片ABCD，点E是BC边上(点E不与点B，C重合)任意一点，沿AE折叠△ABE到△AFE，如图(2)所示；操作二：将图(2)沿过点F的直线折叠，使点E的对称点G落在AE上，得到折痕MN，点C的对称点记为H，如图(3)所示；操作三：将纸片展平，连接BM，如图(4)所示．根据以上操作，回答下列问题：①B，M，N三点(填“在”或“不在”)一条直线上；②AE和BN的位置关系是，数量关系是；③如图(5)，连接AN，改变点E在BC上的位置，(填“存在”或“不存在”)点E，使AN平分∠DAE．(2)迁移探究苏钰同学将正方形纸片换成矩形纸片ABCD，AB=4，BC=6，按照(1)中的方式操作，得到图(6)或图(7)．请完成下列探究：①当点N在CD上时，如图(6)，BE和CN有何数量关系？并说明理由；②当DN的长为1时，请直接写出BE的长．【答案】(1)①在，②AE⊥BN，相等；③不存在；(2)①BECN =23，理由见解析；②BE=2或165．【分析】(1)①E的对称点为E ，BF⊥EE ，MF⊥EE ，即可判断；②由①AE⊥BN，由同角的余角相等得∠BAE=∠CBN，由AAS可判定△ABE≌△BCN，由全等三角形的性质即可得证；③由AAS可判定△DAN≌△MAN，由全等三角形的性质得AM=AD，等量代换得AB=AM，与AB>AM矛盾，即可得证；(2)①由(1)中的②可判定△ABE∽△BCN，由三角形相似的性质即可求解；②当N在CD上时，△ABE∽△BCN，由三角形相似的性质即可求解；当N在AD上时，同理可判定△ABE∽△NAB，由三角形相似的性质即可求解．【详解】(1)解：①E的对称点为E ，∴BF⊥EE ，MF⊥EE ，∴B、F、M共线，故答案为：在；②由①知：B、F、M共线，N在FM上，∴AE⊥BN，∴∠AMB=90°，∴∠ABM+∠BAE=90°，∵四边形ABCD是正方形，∴∠ABC=∠BCN=90°，AB=BC，∴∠CBN+∠ABM=90°，∴∠BAE=∠CBN，在△ABE和△BCN中，∠BAE=∠CBN ∠ABC=∠BCN AB=BC，∴△ABE≌△BCN(AAS)，∴AE=BN，故答案为：相等；③不存在，理由如下：假如存在，∵AN平分∠DAE，∴∠DAN=∠MAN，∵四边形ABCD是正方形，AM⊥BN，∴∠D=∠AMN=90°，在△DAN和△MAN中，∠D=∠AMN∠DAN=∠MAN AN=ANN∴△DAN≌△MAN(AAS)，∴AM=AD，∵AD=AB，∴AB=AM，∵AB是Rt△ABM的斜边，∴AB>AM，∴AB =AM 与AB >AM 矛盾，故假设不成立，所以答案为：不存在；(2)解：①BE CN=23，理由如下：由(1)中的②得：∠BAE =∠CBN ，∠ABE =∠C =90°，∴△ABE ∽△BCN ，∴BE CN =AB BC=23；②当N 在CD 上时，CN =CD -DN =3，由①知：△ABE ∽△BCN ，∴BE CN =AB BC =23，∴BE =23CN =2，当N 在AD 上时，AN =AD -DN =5，∵∠BAE =∠CBN =∠ANB ，∠ABE =∠BAN =90°，∴△ABE ∽△NAB ，∴BE AB =AB AN ，∴BE 4=45，∴BE =165，综上所述：BE =2或165．【点睛】本题考查了折叠的性质，矩形的性质，正方形的性质，全等三角形的判定及性质，三角形相似的判定及性质，掌握相关的判定方法及性质，“十字架”典型问题的解法是解题的关键．16在矩形ABCD 中，AD =2AB =8，点P 是边CD 上的一个动点，将△BPC 沿直线BP 折叠得到△BPC ．(1)如图1，当点P 与点D 重合时，BC ′与AD 交于点E ，求BE 的长度；(2)当点P 为CD 的三等分点时，直线BC ′与直线AD 相交于点E ，求DE 的长度；(3)如图2，取AB 中点F ，连接DF ，若点C ′恰好落在DF 边上时，试判断四边形BFDP 的形状，并说明理由．【答案】(1)BE 的长度为5；(2)DE 的长度为113或83;(3)四边形BFDP 是平行四边形(理由见解析)【分析】本题利用了折叠的知识(折叠后的两个图形全等)以及矩形的性质(矩形的对边相等，对角相等)，以及平行四边形的判定有关知识．(1)利用矩形性质和折叠的性质可推出BE=DE，设BE=x,则DE=x,AE=8-x,利用勾股定理建立方程求解即可得出答案；(2)设DE=m,则AE=m+8，设BE交CD于G，可证得△AEB∽△CBG，得出CGAB =BCAE，即CG4=8m+8，求得CG=32m+8，分两种情况：当PC=13CD=43时，当PC=23CD=83时，分别添加辅助线构造相似三角形，利用相似三角形性质建立方程求解即可得出答案；(3)由中点定义可得AF=BF，过点C 作C M∥AD交AB于点M，过点F作FN⊥BC 于点N，由矩形性质和翻折的性质可得∠C BP=∠CBP=12∠C BC，可证得△FC M∽△FDA，得出FMAF=C MAD，再证得△BFN∽△BC M，进而推出FM=FN，利用角平分线的判定定理可得∠BC F=∠MC F=12∠BC M推出∠BC F=∠C BP，再由平行线的判定定理可得DF∥BP，运用平行四边形的判定定理即可证得四边形BFDP是平行四边形．【点睛】点睛片段【详解】(1)解：∵AD=2AB=8，∴AB=4，∵四边形ABCD是矩形，∴∠A=90°，AD∥BC，∴∠ADB=∠DBC，由折叠得：∠DBC=∠DBC ，∴∠ADB=∠DBC ，即∠EDB=∠EBD，∴BE=DE，设BE=x，则DE=x，AE=8-x，在Rt△ABE中，AE2+AB2=BE2，∴(8-x)2+42=x2，解得：x=5，∴BE的长度为5；(2)设DE=m，则AE=m+8，设BE交CD于G，∵四边形ABCD是矩形，∴BC=AD=8，CD=AB=4，AD∥BC，∠A=∠BCG=90°，∴∠AEB=∠CBG，∴△AEB∽△CBG，∴CG AB =BCAE，即CG4=8m+8，∴CG=32m+8，当PC=13CD=43时，BP=BC2+PC2=82+432=4373，连接CC ，过点C 作C H⊥CD于点H，如图，∵将△BPC沿直线BP折叠得到△BPC ，∴CC ⊥BP，△BPC ≌△BPC，∴S四边形BCPC =2S△BPC，∴1BP⋅CC =2×1BC⋅PC，即12×4373CC =2×12×8×43，∴CC =163737，∵∠C CH +∠BPC =90°，∠PBC +∠BPC =90°，∴∠C CH =∠PBC ，∵∠CHC =∠BCP =90°，∴△CC H ∽△BPC ，∴C H PC =CH BC =CC BP ，即CH 43=CH 8=1637374373，∴C H =1637，CH =9637，∵∠C HG =∠EDG =90°，∴C H ∥AE ，∴∠GC ′H =∠AEB ，∴△C GH ∽△EBA ，∴GH AB =C H AE ，即GH 4=1637m +8，∴GH =6437(m +8)，∵CH +GH =CG ，∴9637+6437(m +8)=32m +8，解得：m =113，经检验，m =113是该方程的解，∴DE =113；当PC =23CD =83时，BP =BC 2+PC 2=82+83 2=8103，连接CC ，过点C 作C H ⊥CD 交CD 的延长线于点H ，作C G ⊥AD 于点G ，如图，同理可得：CC =8105，同理△CC H ∽△BPC ，∴C H PC =CH BC =CC BP ，即CH 83=CH 8=81058103，∴C H =85，CH =245，∴DH =CH -CD =245-4=45，∵∠HDG =∠H =∠C GD =90°，∴四边形DGC H 是矩形，∴C G =DH =45，DG =C H =85，∵∠C GE =∠A =90°，∠C EG =∠BEA ，∴△C EG ∽△BEA ，∴EG AE =C G AB =454=15，∴AE =5EG ，∵AE +EG =AG =AD -DG =8-85=325，∴5EG +EG =325，∴EG =1615，∴DE =DG +EG =85+1615=83，综上所述，DE 的长度为113或83；(3)四边形BFDP 是平行四边形，理由如下：∵点F 是AB 的中点，∴AF =BF ，过点C 作C M ∥AD 交AB 于点M ，过点F 作FN ⊥BC 于点N ，如图，则∠FC M =∠ADF ，∵四边形ABCD 是矩形，∴AD ∥BC ,AB ∥CD ，∴C M ∥BC ，∴∠BC M =∠C BC ，由翻折得：∠C BP =∠CBP =12∠C BC ，BC =BC =8，∵C M ∥AD ，∴△FC M ∽△FDA ，∴FM AF =C M AD ，∴FM BF =C MBC ，∵∠BNF =∠BMC =90°，∠FBN =∠C BM ，∴△BFN ∼△BC M∴FN BF =C MBC ，∴FM BF =FN BF ，∴FM =FN ，又∵FM ⊥C M ，FN ⊥C B ，∴∠BC F =∠MC F =12∠BC M ，∴∠BC F =∠C BP ，∴DF ∥BP ，∴四边形BFDP 是平行四边形．17矩形ABCD 中，AB =6，AD =8，点E 为对角线AC 上一点，过点E 作EF ⊥AD 于点F ，EG ⊥AC 交边BC 于点G ，将△AEF 沿AC 折叠得△AEH ，连接HG ．(1)如图1，若点H 落在边BC 上，求证：AH =CH ；(2)如图2，若A ，H ，G 三点在同一条直线上，求HG 的长；(3)若△EHG 是以EG 为腰的等腰三角形，求EF 的长．【答案】(1)见解析(2)HG =94(3)EF =103或4【分析】(1)根据矩形的性质和翻折的性质证明∠ACH =∠HAC ，即可解决问题；(2)结合(1)的方法AG =CG ，解Rt △AEG ，Rt △HEG 分别求得EG ,HG ；(3)当△EHG 是以EG 为腰的等腰三角形时，分两种情况：①当EG =EH ，②当EG =HG ，结合(2)的方法，利用全等三角形的判定与性质和相似三角形的判定与性质即可解决问题．【详解】(1)∵四边形ABCD 是矩形，∴AD ∥BC ．∴∠DAE =∠ACH .∵△AHE 由△AFE 折叠得到，∴∠HAC =∠DAE ，∴∠HAC =∠ACH ，∴AH =CH ；(2)∵矩形ABCD 中，AB =6,AD =8．∴AC =10.当A ，H ，G 三点在同一条直线上时，∠EHG =90°．同(1)可得AG =CG ．又∵EG ⊥AC ，∴AE =12AC =5．∵∠AEH +∠HEG =90°，∠AEH +∠HAE =90°，∴∠HEG =∠HAC =∠CAD ．∵在Rt △AEG 中，tan ∠EAG =EG AE =34，∴EG =34AE =154．∵在Rt △HEG 中，sin ∠HEG =HG EG =35，∴HG =35EG =94．(3)①若EH =EG ，如图3①设EF =EH =EG =x ，∵EF ⊥AD ，∴EF ∥CD ，∴△AEF ∽△ACD ，∴AE AC =AF AD =EF CD ∴AE 10=AF 8=x 6∴AE =53x ,AF =43x ，∴AH =AF =43x ，∵∠AHE =∠CEG =90°，∠HAE =∠GCE ，EH =EH ，∴△AHE ≌△CGE AAS ，∴AH =CE ，∴43x =10-53x ，∴x =103∴EF =103．②若HG =GE ，如图3②．(图3②)过点G 作GM ⊥HE ，设EF =a ,∵EC =10-53a ，∵∠AHE =∠CEG =90°，∠HAE =∠GCE ，∴△AHE ∽△CGE ，∴EG =34EC =3410-53a =152-54a ，∵∠GME =∠EHA ，∠MGE =90°-∠MEG =∠HAE ，∴△MGE ∽△HEA ，∴ME AH =EG AE ，∵AH AE =AD AC =45，∴AH =45AE ，∴ME =45EG =45152-54a =6-a ，∴HE =2ME =12-2a =EF ，∴12-2a =a ，∴a =4，∴EF =4，综上，EF =103或4．【点睛】本题考查了矩形的性质，解直角三角形，全等三角形的判定与性质，相似三角形的判定与性质，勾股定理，等腰三角形的性质，翻折的性质，解决本题的关键是综合运用以上知识．18综合与实践【问题情境】数学活动课上，老师准备了若干张正方形纸片ABCD，组织同学们进行折纸探究活动．【初步尝试】把正方形对折，折痕为EF，然后展开，沿过点A与点E所在的直线折叠，点B落在点B 处，连接 B C，如图1，请直接写出∠AEB 与∠ECB 的数量关系．【能力提升】把正方形对折，折痕为EF，然后展开，沿过点A与BE上的点G所在的直线折叠，使点B落在EF上的点P处，连接PD，如图2，猜想∠APD的度数，并说明理由．【拓展延伸】在图2的条件下，作点A关于直线CP的对称点A ，连接PA ，BA ，AC，如图3，求∠PA B的度数．【答案】初步尝试：∠AEB =∠ECB ；能力提升：猜想：∠APD=60°，理由见解析；拓展延伸：∠PA B=15°【分析】初步尝试：连接BB ，由折叠的性质可知，BE=CE，BE=BE ，∠AEB=∠AEB ，BB ⊥AE，根据等边对等角的性质和三角形内角和定理，得出∠BB C=90°，推出AE∥CB ，即可得出答案；能力提升：根据正方形的性质和折叠的性质，易证△AFP≌△DFP SAS，从而证明△APD是等边三角形，即可得到答案；拓展延伸：连接A C、AA ，由(2)得△APD是等边三角形，进而得出∠PDC=30°，再结合等边对等角的性质和三角形内角和定理，求得∠PAC=15°，∠ACP=30°，由对称性质得：AC=A C，∠ACP=∠A CP=30°，证明△AA B≌△CA B SSS，得到∠CA B=30°，再由∠CA P=∠CAP=15°，即可求出∠PA B的度数．【详解】解：初步尝试：∠AEB =∠ECB ，理由如下：如图，连接BB ，由折叠的性质可知，BE=CE，BE=BE ，∠AEB=∠AEB ，BB ⊥AE，∴BE=CE=BE ，∴∠EBB =∠EB B，∠ECB =∠EB C，∵∠EBB +∠EB B+∠EB C+∠ECB =2∠EB B+∠EB C=180°，∴∠BB C=90°，即BB ⊥CB ，∴AE∥CB ，∴∠AEB=∠ECB ，∴∠AEB =∠ECB ；解：能力提升：猜想：∠APD=60°，理由如下：理由：∵四边形ABCD是正方形，∴AB=AD，∠ADC=90°，由折叠性质可得：AF =DF ，EF ⊥AD ，AB =AP ，在△AFP 和△DFP 中，AF =DF∠AFP =∠DFP =90°FP =FP，∴△AFP ≌△DFP SAS ，∴AP =PD ，∴AP =AD =PD ，∴△APD 是等边三角形，∴∠APD =60°；解：拓展延伸：如图，连接A C 、AA ，由(2)得△APD 是等边三角形，∴∠PAD =∠PDA =∠APD =60°，AP =DP =AD ，∵∠ADC =90°，∴∠PDC =30°，又∵PD =AD =DC ，∴∠DPC =∠DCP =12×180°-30° =75°，∠DAC =∠DCA =45°，∴∠PAC =∠PAD -∠DAC =60°-45°=15°，∠ACP =∠DCP -∠DCA =75°-45°=30°，由对称性质得：AC =A C ，∠ACP =∠A CP =30°，∴∠ACA =60°，∴△ACA 是等边三角形，在△AA B 与△CA B 中，A A =A CA B =A B AB =BC，∴△AA B ≌△CA B SSS ，∴∠AA B =∠CA B =12∠AA C =30°，又∵∠CA P =∠CAP =15°，∴∠PA B =∠CA B -∠CA P =15°．【点睛】本题考查了折叠的性质，等腰三角形的判定和性质，三角形内角和定理，正方形的性质，全等三角形的判定和性质，等边三角形的判定和性质等知识，作辅助线构造全等三角形是解题关键．19综合与实践数学活动课上，数学老师以“矩形纸片的折叠”为课题开展数学活动：将矩形纸片ABCD 对折，使得点A ，D 重合，点B ，C 重合，折痕为EF ，展开后沿过点B 的直线再次折叠纸片，点A 的对应点为点N ，折痕为BM ． (1)如图(1)若AB =BC ，则当点N 落在EF 上时，BF 和BN 的数量关系是，∠NBF 的度数为．思考探究：(2)在AB=BC的条件下进一步进行探究，将△BMN沿BN所在的直线折叠，点M的对应点为点M ．当点M 落在CD上时，如图(2)，设BN，BM 分别交EF于点J，K．若DM =4，请求出三角形BJK的面积．开放拓展：(3)如图(3)，在矩形纸片ABCD中，AB=2，AD=4，将纸片沿过点B的直线折叠，折痕为BM，点A的对应点为点N，展开后再将四边形ABNM沿BN所在的直线折叠，点A的对应点为点P，点M的对应点为点M ，连接CP，DP，若PC=PD，请直接写出AM的长．(温馨提示：12+3=2-3，12+1=2-1)【答案】(1)BF=12BN，60°(2)2+2(3)4-23【分析】(1)根据折叠的性质得：AB=BN，BF=CF=12BC，根据直角三角形的性质可得∠BNF=30°，由直角三角形的两锐角互余可得结论；(2)由折叠得：BM=BM ，证明Rt△ABM≌Rt△CBM (HL)，可知AM=CM ，∠ABM=∠CBM ，得△BFJ是等腰直角三角形，再证明四边形ABCD是正方形，分别计算BF=FJ=12BC=2+2，JK=2，由三角形面积公式可得结论；(3)如图(3)，过点P作PG⊥BC于G，PH⊥CD于H，根据等腰三角形的三线合一可得DH=CH=12CD=12AB=1，由折叠的性质和矩形的性质可得PG=CH=1，BN=BP=AB=2，∠NBP=∠ABN，设PL=x，则M L=2x，M P=3x，根据NL=233=NM +M L，列方程可解答．【详解】(1)解：由折叠得：AB=BN，BF=CF，∠BFN=90°，∵AB=BC，∴BF=12BN，∴∠BNF=30°，∴∠NBF=90°-30°=60°，故答案为：BF=12BN，60°；(2)由折叠得：BM=BM ，∵四边形ABCD是矩形，∴∠A=∠C=90°，∵AB=BC，∴Rt△ABM≌Rt△CBM (HL)，∴AM=CM ，∠ABM=∠CBM ，∴∠ABM=∠MBN=∠NBM =∠CBM ，∴∠FBJ=45°，∴△BFJ是等腰直角三角形，∵四边形ABCD是矩形，AB=BC，∴矩形ABCD是正方形，∴AD=CD，∠D=90°，∴DM=DM =4，∴MM =42，∵AM=MN=M N=CM ，∴CM =22，∴BC =CD =4+22，∴BF =FC =2+2，∵FK ∥CM ，∴BK =KM ，∴FK =12CM =2，∵△BFJ 是等腰直角三角形，∴BF =FJ =12BC =2+2，∴JK =2+2-2=2，∴S △BJK =12⋅JK ⋅BF =12×2×(2+2)=2+2；(3)如图，过点P 作PG ⊥BC 于G ，PH ⊥CD 于H ，∵PC =PD ，∴DH =CH =12CD =12AB =1，∵∠PGC =∠PHC =∠BCH =90°，∵四边形PGCH 是矩形，∴PG =CH =1，由折叠得：BN =BP =AB =2，∠NBP =∠ABN ，Rt △BPG 中，∠PBG =30°，∴∠ABN =∠NBP =90°-30°2=30°，延长NM ，BP 交于L ，Rt △BNL 中，BN =2，∠NBL =30°，∴NL =2×33=233，Rt △M PL 中，∠M LP =90°-30°=60°，∴∠PM L =30°，设PL =x ，则M L =2x ，M P =3x ，∵NL =233=NM +M L ，∴3x +2x =233，∴x =433-2，∴AM =3x =3×433-2 =4-23．【点睛】本题是四边形的综合题，考查了折叠的性质，含30°角的直角三角形的性质，矩形的性质和判定，正方形的判定和性质，三角函数等知识，掌握折叠的性质和正确作辅助线是解题的关键，题目具有一定的综合性，比较新颖．20综合与实践综合与实践课上，老师带领同学们以“矩形和平行四边形的折叠”为主题开展数学活动．(1)操作判断如图1，先用对折的方式确定矩形ABCD 的边AB 的中点E ，再沿DE 折叠，点A 落在点F 处，把纸片展平，延长DF ，与BC 交点为G ．。

中考数学折叠,旋转问题专题含答案

【经典例题1】如图，CD是⊙O的直径，AB是⊙O的弦，AB⊥CD，垂足为G，OG：OC＝3：5，AB＝8．（1）求⊙O的半径；（2）点E为圆上一点，∠ECD＝15°，将沿弦CE翻折，交CD于点F，求图中阴影部分的面积．【解析】（1）连接AO，如右图1所示，∵CD为⊙O的直径，AB⊥CD，AB＝8，∴AG＝＝4，∵OG：OC＝3：5，AB⊥CD，垂足为G，∴设⊙O的半径为5k，则OG＝3k，∴（3k）2+42＝（5k）2，解得，k＝1或k＝﹣1（舍去），∴5k＝5，即⊙O的半径是5；（2）如图2所示，将阴影部分沿CE翻折，点F的对应点为M，∵∠ECD＝15°，由对称性可知，∠DCM＝30°，S阴影＝S弓形CBM，连接OM，则∠MOD＝60°，∴∠MOC＝120°，过点M作MN⊥CD于点N，∴MN＝MO•sin60°＝5×，∴S阴影＝S扇形OMC﹣S△OMC＝＝，即图中阴影部分的面积是：．练习1-1如图，在⊙O中，点C在优弧上，将弧沿BC折叠后刚好经过AB 的中点D，连接AC，CD．则下列结论中错误的是（）A．AC＝CD B．+＝C．OD⊥AB D．CD平分∠ACB 【解析】A、过D作DD'⊥BC，交⊙O于D'，连接CD'、BD'，由折叠得：CD＝CD'，∠ABC＝∠CBD'，∴AC＝CD'＝CD，故①正确；B、∵AC＝CD'，∴，由折叠得：，∴＝，故②正确；C、∵D为AB的中点，∴OD⊥AB，故③正确；D、延长OD交⊙O于E，连接CE，∵OD⊥AB，∴∠ACE＝∠BCE，∴CD不平分∠ACB，故④错误；故选：D．练习1-2如图，AB是⊙O的弦，点C在上，点D是AB的中点．将在沿AC 折叠后恰好经过点D，若⊙O的半径为2，AB＝8．则AC的长是（）A．6B．C．2D．4【解析】如图，延长BO交⊙O于E，连接AE，OA，OD，OC，BC，作CH⊥AB 于H．∵AD＝DB，∴OD⊥AB，∴∠ADO＝90°，∵OA＝2，AD＝DB＝4，∴OD＝＝2，∵BE是直径，∴∠BAE＝90°，∵AD＝DB，EO＝OB，∴OD∥AE，AE＝2OD＝4，∴AE＝AD，∴＝，∴＝，∴∠CAE＝∠CAH＝45°，∴∠BOC＝2∠CAB＝90°，∴BC＝OC＝2，∵CH⊥AB，∴∠CAH＝∠ACH＝45°，∴AH＝CH，设AH＝CH＝x，则BH＝8﹣x，在Rt△BCH中，∵CH2+BH2＝BC2，∴x2+（8﹣x）2＝（2）2，∴x＝6或2（舍弃），在Rt△ACH中，∵AC＝，∴AC＝6．故选：A．练习1-3在扇形AOB中，∠AOB＝75°，半径OA＝12，点P为AO上任一点（不与A、O重合）．（1）如图1，Q是OB上一点，若OP＝OQ，求证：BP＝AQ．（2）如图2，将扇形沿BP折叠，得到O的对称点O'．①若点O'落在上，求的长．②当BO'与扇形AOB所在的圆相切时，求折痕的长．（注：本题结果不取近似值）【解析】（1）证明：∵BO＝AO，∠O＝∠O，OP＝OQ，∴△BOP≌△AOQ（SAS）．∴BP＝AQ．（2）解：①如图1，点O'落在上，连接OO'，∵将扇形沿BP折叠，得到O的对称点O'，∴OB＝O'B，∵OB＝OO'，∴△BOO'是等边三角形，∴∠O'OB＝60°．∵∠AOB＝75°，∴∠AOO'＝15°．∴的长为．②BO'与扇形AOB所在的圆相切时，如图2所示，∴∠OBO'＝90°．∴∠OBP＝45°．过点O作OC⊥BP于点C，∵OA＝OB＝12，∠COB＝∠OBP＝45°，∴．又∵∠AOB＝75°，∠COB＝45°，∴∠POC＝30°，∴．∴．∴折痕的长为．旋转类【经典例题2】如图1，在锐角△ABC中，AB=5，AC=42，∠ACB=45∘. 计算：求BC的长；操作：将图1中的△ABC绕点B按逆时针方向旋转，得到△A1BC1.如图2，当点C1在线段CA的延长线上时。

中考数学中的旋转翻折类问题专项训练经典汇编(共30题)

中考数学中的旋转翻折类问题专项训练经典汇编（共30题）1．阅读下面材料．小炎遇到这个一个问题：如图1，点E、F分别在正方形ABCD的边BC、CD上，∠EAF ＝45°，连接EF，则EF＝BE+DF，试说明理由．小炎是这样思考的：要想解决这个问题，首先应想办法将这些分散的线段相对集中，她先尝试了翻折、旋转、平移的方法，最后发现线段AB、AD是共点并且相等的，于是找到解决问题的方法．她的方法是将△ABE绕着点A逆时针旋转90°得到△ADG，再利用全等的知识解决这个问题（如图2）．参考小炎同学思考问题的方法，解决下列问题：（1）写出小炎的推理过程；（2）如图3，四边形ABCD中，AB＝AD，∠BAD＝90°，点E、F分别在边BC、CD 上，∠EAF＝45°，若∠B、∠D都不是直角，则当∠B与∠D满足于关系时，仍有EF＝BE+DF；（3）如图4，在△ABC中，∠BAC＝90°，AB＝AC，点D、E均在边BC上，且∠DAE ＝45°，若BD＝1，EC＝2，求DE的长．2．如图1，把△ABC沿直线BC平移线段BC的长度，得到△ECD；如图2，以BC为轴，把△ABC沿BC翻折180°，可以得到△DBC；如图3，以点A为中心，把△ABC旋转180°，可以得到△AED．像这样，其中一个三角形是由另一个三角形按平移、翻折、旋转等方法得到的，这种只改变位置，不改变形状、大小的图形变换，叫做三角形的全等变换．回答下列问题：（1）在图4中，可以使△ABE通过平移、翻折、旋转中的哪一种方法得到△ADF？（2）图中线段BE与DF相等吗？为什么？3．阅读材料并解答问题：探究：小明遇到这样一个问题：如图1，在正方形ABCD，点E、F分别为BC、CD边上的点，且∠EAF＝45°，求证：BE+DF＝EF．小明是这样思考的：要想解决这个问题，首先应想办法将这些分散的线段集中到同一条线段上．他先后尝试了平移、翻折、旋转的方法，发现通过旋转可以解决此问题．他的方法是将△ADF绕点A顺时针旋转90°得到△ABG（如图1），此时GE即是BE+DF．请回答：在图1中，∠GAF的度数是．理解：如图2，已知Rt△ABC中，∠ACB＝90°，AC＝BC，点D、E在斜边AB上，且∠DCE＝45°，请写出AD、DE、BE三条线段之间的数量关系，并证明．应用：如图3，正方形ABCD中，△AMN的顶点M、N分别在BC、CD边上，AH⊥MN，且AH＝AB，连接BD分别交AM、AN于点E，若MH＝2，NH＝3，DF＝2，求AH、EF的长．4．阅读下面材料：小炎遇到这样一个问题：如图1，点E、F分别在正方形ABCD的边BC，CD上，∠EAF ＝45°，连接EF，则EF＝BE+DF，试说明理由．小炎是这样思考的：要想解决这个问题，首先应想办法将这些分散的线段相对集中．她先后尝试了翻折、旋转、平移的方法，最后发现线段AB，AD是共点并且相等的，于是找到解决问题的方法．她的方法是将△ABE绕着点A逆时针旋转90°得到△ADG，再利用全等的知识解决了这个问题（如图2）．参考小炎同学思考问题的方法，解决下列问题：（1）如图3，四边形ABCD中，AB＝AD，∠BAD＝90°点E，F分别在边BC，CD上，∠EAF＝45°．若∠B，∠D都不是直角，则当∠B与∠D满足关系时，仍有EF＝BE+DF；（2）如图4，在△ABC中，∠BAC＝90°，AB＝AC，点D、E均在边BC上，且∠DAE ＝45°，若BD＝1，EC＝2，求DE的长．5．如图，在正方形ABCD中，E为AD的中点，F是BA延长线上一点，AF＝AB．（1）图中的全等三角形是哪一对？（2）在图中，可以通过平移、翻折、旋转中哪一种方法，使△ABE变换到△ADF的位置？（3）图中线段BE与DF之间有怎样的关系？为什么？6．已知点E是△ABC内部一点．将△ABE沿BE翻折，点A落在BC上的点F′处．（1）如图1，若∠BAC﹣80°，∠C﹣40°，EF∥AC．求∠BEF的度数；（2）如图2，若∠C＝2∠BAE，请说明．（3）如图3．连接AF，若AE⊥BC，∠ABC﹣70°，∠C＝40°，将△BEF绕点B顺时针方向旋转一个角度α（0＜α＜180°）得到ΔBE1F1，则在这个旋转过程中，当E1F1与△AFC的某一边垂直时，直接写出旋转角α的度数．7．如图1，在Rt△ABC中，∠A＝90°，AB＝21，AC＝28，点D为BC边上一点，过点作DE⊥AB于点E，作DF⊥AC于点F，且DE＝DF．（1）求证：四边形AEDF为正方形；（2）如图2，将△CDF沿DF翻折，得△GDF，DG交AB于点H，求证：DH＝DB；（3）将（2）中的△BDH绕点D逆时针旋转α（0°＜α＜180°）得△B′DH′（点B的对应点为B′，点H的对应点为H′，连接GH′，CB′，点M为线段GH′的中点，连接DM．当△B′DC为直角三角形时，直接写出线段DM的长．8．如图，在等边△ABC中，AD⊥BC于点D，E为线段AD上一动点（不与A，D重合），连接BE，CE，将CE绕点C顺时针旋转60°得到线段CF，连接AF．（1）如图1，求证：∠CBE＝∠CAF；（2）如图2，连接BF交AC于点G，连接DG，EF，EF与DG所在直线交于点H，求证：EH＝FH；（3）如图3，连接BF交AC于点G，连接DG，EG，将△AEG沿AG所在直线翻折至△ABC所在平面内，得到△APG，将△DEG沿DG所在直线翻折至△ABC所在平面内，得到△DQG，连接PQ，QF．若AB＝4，直接写出PQ+QF的最小值．9．在Rt△ABC中，∠ABC＝90°，过B点作BE⊥AC于点E，点D为线段AC的中点，连接BD．（1）如图1，AB＝2，AC＝6，求ED的长度；（2）如图2，将线段DB绕着点D逆时针旋转45°得到线段DG，此时DG⊥AC，连接BG，点F为BG的中点，连接EF，求证：BC＝2EF；（3）如图3，∠ACB＝30°，AB＝3，点P是线段BD上一点，连接AP，将△APB沿AP 翻折到同一平面内得到△APB'，连接CB′，将线段绕点CB′顺时针旋转60°得线段CQ，连接BQ，当BQ最小时，直接写出△BCQ的面积．10．如图，CD为△ABC的中线，以CD为直角边在其右侧作直角△CDE，CD⊥DE，BC与DE交于点F，∠E＝30°．（1）如图1，若CF＝EF＝5，求CD的长；（2）如图2，若将BC绕点C逆时针旋转120°得CG，连接AG、AE，探究AG、AE的数量关系，并说明理由；（3）如图3，若∠ACB＝90°，AC＝2，．直线CE上有一点M，连接MF，将△CFM沿着MF翻折至△ABC所在的平面内得到△NFM．取NF的中点P，连接AP，当AP最小时，请直接写出△APB的面积．11．已知△ABC为等边三角形，D是边AB上一点，连接CD，点E为CD上一点，连接BE．（1）如图1，延长BE交AC于点F，若∠ABF＝15°，．求AF的长；（2）如图2，将△BEC绕点C顺时针旋转60°到△AGC，延长BC至点H，使得CH＝BD，连接AH交CG于点N，猜想线段CE，GN，DE之间存在的数量关系，并证明你的猜想；（3）如图3，AB＝8，点H是BC上一点，且BD＝2CH，连接DH，点K是AC上一点，CK＝AD，连接DK，BK，将△BKD沿BK翻折到△BKQ，连接CQ，当△ADK的周长最小时，直接写出△CKQ的面积．12．在边长为8的等边三角形ABC中，D为BC的中点，E，F分别为AC、AD上任意一点，连接EF，将线段EF绕点E顺时针旋转60°得到线段EG，连接FG交AC于点N，连接AG．（1）如图1，点E与点C重合，且GF的延长线过点B，证明：四边形AFEG是菱形；（2）如图2，EF的延长线交AB于点M，当AM+MF＝AE时，求∠EAG的度数；（3）如图3，E为AC的中点，连接BE，H为直线BC上一动点，连接EH，将△BEH 沿EH翻折至△ABC所在平面内，得到△B′EH，连接B′G，直接写出线段B′G长度的最小值．13．在△ABC中，∠ACB＝90°，AC＝BC，D是AC边上一动点，连接BD．（1）如图1，在平面内将线段DC绕点C顺时针旋转90°得到线段CK，点F为BC边上一点，连接AF交BD于M，连接AK．若∠CAF＝2∠DBA，AF＝8，AK＝10，求CF的长；（2）如图2，在平面内将线段DB绕点B顺时针旋转一定角度得到线段BE，连接AE交BC于G，连接DE，若∠CDE＝∠DBA，猜想线段AD，CG的数量关系，并证明你的猜想；（3）在（2）的条件下，将△CDB沿BD直线BD翻折至△ABC所在平面内得到△BDC1，连接AC1，若AC＝2+，在点D运动过程中，当线段AC1取得最小值时，请直接写出△ABE与四边形BCDC1重叠部分的面积．14．在△ABC中，∠BAC＝90°，AB＝AC，点D为BC边上一动点，连接AD，将AD绕着D点逆时针方向旋转90°得到DE，连接AE．（1）如图1，AH⊥BC，点D恰好为CH中点，AE与BC交于点G，若AB＝4，求AE 的长度；（2）如图2，DE与AB交于点F，连接BE，在BA延长线上有一点P，∠PCA＝∠EAB，求证：AB＝AP+BD；（3）如图3，DE与AB交于点F，且AB平分∠EAD，点M为线段AF上一点，点N为线段AD上一点，连接DM，MN，点K为DM延长线上一点，将△BDK沿直线BK翻折至△BDK所在平面内得到△BQK，连接DQ，在M，N运动过程中，当DM+MN取得最小值，且∠DKQ＝45°时，请直接写出的值．15．在平面直角坐标系中，已知点A（4，0），点B（0，3）．点P从点A出发，以每秒1个单位的速度向右平移，点Q从点B出发，以每秒2个单位的速度向右平移，又P、Q 两点同时出发．（1）连接AQ，当△ABQ是直角三角形时，则点Q的坐标为；（2）当P、Q运动到某个位置时，如果沿着直线AQ翻折，点P恰好落在线段AB上，求这时∠AQP的度数；（3）若将AP绕点A逆时针旋转，使得P落在线段BQ上，记作P'，且AP'∥PQ，求此时直线PQ的解析式．16．（1）特殊发现如图1，正方形BEFG与正方形ABCD的顶点B重合，BE、BG分别在BC、BA边上，连接DF，则有：①＝；②直线DF与直线AG所夹的锐角等于度；（2）理解运用将图1中的正方形BEFG绕点B逆时针旋转，连接DF、AG．①如图2，（1）中的结论是否仍然成立？请说明理由；②如图3，若D、F、G三点在同一直线上，且过AB边的中点O，BE＝4，直接写出AB的长；（3）拓展延伸如图3，点P是正方形ABCD的AB边上一动点（不与A、B重合），连接PC，沿PC将△PBC翻折到△PEC位置，连接DE并延长，与CP的延长线交于点F，连接AF，若P A ＝3PB，则的值是否是定值？请说明理由．17．已知：如图①，在矩形ABCD中，AB＝8，AD＝6，连接AC，将△ABC沿AC翻折，使B点落在E点处，连接EC、AE，AE交DC于F点．（1）求DF的长．（2）若将△CEF沿着射线CA方向平移，设平移的距离为m（平移距离指点C沿CA方向所经过的线段长度）．当点F平移到线段AD上时，如图②，求出相应的m的值．（3）如图③，将△CEF绕点C逆时针旋转一个角a（0°＜a＜∠ECB），记旋转中的△CEF为△CE'F'，过E'作E'G⊥AD于G点，在旋转过程中，当△DCE'为等腰三角形时，求出线段E'G的长度．18．已知矩形ABCD中，AB＝2，BC＝m，点E是边BC上一点，BE＝1，连接AE．（1）沿AE翻折△ABE使点B落在点F处．①连接CF，若CF∥AE，求m的值；②连接DF，若≤DF≤，求m的取值范围．（2）△ABE绕点A顺时针旋转得△AB1E1，点E1落在边AD上时旋转停止．若点B1落在矩形对角线AC上，且点B1到AD的距离小于时，求m的取值范围．19．如图，四边形OABC是一张放在平面直角坐标系中的长方形纸片，O为原点，点A在x 轴的正半轴上，点C在y轴的正半轴上，点B的坐标为（10，8），在OC边上取一点D，将纸片沿AD翻折，使点O落在BC边上的点E处．（1）求CE和OD的长；（2）求DE所在直线的解析式；（3）若直线y＝kx+b与直线DE的比例系数相等，当它与矩形OABC有公共点时，请直接写出b的取值范围．20．如图1，将△ABC纸片沿中位线EH折叠，使点A对称点D落在BC边上，再将纸片分别沿等腰△BED和等腰△DHC的底边上的高线EF，HG折叠，折叠后的三个三角形拼合形成一个矩形，类似地，对多边形进行折叠，若翻折后的图形恰能拼合成一个无缝隙、无重叠的矩形，这样的矩形称为叠合矩形．（1）将▱ABCD纸片按图2的方式折叠成一个叠合矩形AEFG，则操作形成的折痕分别是线段、，S矩形AEFG：S▱ABCD＝；（2）▱ABCD纸片还可以按图3的方式折叠成一个叠合矩形EFGH，若EF＝9，EH＝12，求AD的长；（3）如图4，四边形ABCD纸片满足AD∥BC，AD＜BC，AB⊥BC，AB＝12，CD＝13，小明把该纸片折叠，得到叠合正方形，请你帮助画出叠合正方形的示意图，并直接写出AD、BC的长．（写出一种即可）21．如图1，在平面直角坐标系xOy中，直线y＝﹣x+8分别交x轴、y轴于A、B两点，已知点C（3，0），点D是线段AB上的一个动点．（1）判断△ABO的形状；（2）OD+CD的最小值为；（3）如图2，点P为y轴正半轴上一点，连接BC、PC，若∠BCP与△ABC中的一个角相等，求点P的坐标；（4）如图3，将△ACD沿CD翻折，点A恰好落在y轴上的点A′处，求此时点D的坐标．22．在等腰△ABC中，AB＝BC，高AD，BE所在的直线相交于点F，将△ACD沿直线AD 翻折，点C的对称点C′落在直线BC上，连接FC′．（1）如图1，当∠ABC＝45°时，①求证：BF＝AC；②求∠FC′D的度数．（2）当∠ABC＝135°时，补全图2，并求证：C′F∥AB．23．如图1，在平面直角坐标系中，点A坐标为（6，3），过点A作AB⊥x轴，交x轴于点B，点P是x轴上一动点，将△ABP沿直线AP翻折，使得点B落在点B'处，点E是翻折后AB'延长后与y轴的交点．（1）若点E的坐标为（0，3），则点P坐标为；（2）如图2，若点E的坐标为（0，），直线AE与x轴交于点F．①求点F的坐标；②求直线AP的函数关系式．24．如图，在矩形ABCD中，E是BC边上的一个动点，沿着AE翻折△ABE，使点B落在点F处，AB＝2，BC＝AB．（1）当点E运动到点C时，求CF的长；（2）当FC∥AE时，试判断E是否为BC的中点？并说明理由；（3）当点F在矩形ABCD内部，且DF＝CD时，求BE的长．25．如图，在平面直角坐标系中，四边形OABC的边OC在x轴上，OA在y轴上，O为坐标原点，AB∥OC，线段OA，AB的长分别是方程x2﹣9x+20＝0的两个根（OA＜AB），延长CB交y轴于点H，＝．（1）求点B，C的坐标；（2）P为OA上一点，Q为OC上一点，OQ＝5，将△POQ翻折，使点O落在AB上的点O'处，双曲线y＝的一分支过点O′，求k的值；（3）在（2）的条件下，M为坐标轴上一点，在平面内是否存在点N，使以O'，Q，M，N为顶点四边形为矩形？若存在，请直接写出点N的坐标；若不存在，请说明理由．26．如图1，在正方形ABCD中，E为边BC上一点（不与点B、C重合），垂直于AE的一条直线MN分别交AB、AE、CD于点M、P、N．（1）求证AE＝MN；（2）如图2，若垂足P恰好为AE的中点，连接BD，交MN于点Q，连接EQ，并延长交边AD于点F．求∠AEF的度数；（3）如图3，若该正方形ABCD边长为10，将正方形沿着直线MN翻折，使得BC的对应边B′C′恰好经过点A，过点A作AG⊥MN，垂足分别为G，若AG＝6，请直接写出AC′的长．27．如图1，矩形的边OA在x轴上，边OC在y轴上，点B的坐标为（6，8）．D是AB边上一点（不与点A、B重合），将△BCD沿直线CD翻折，使点B落在点E处．（1）求直线AC所表示的函数的表达式；（2）如图2，当点E恰好落在矩形的对角线AC上时，求点D的坐标；（3）如图3，当以O、E、C三点为顶点的三角形是等腰三角形时，求△OEA的面积．28．已知在平行四边形ABCD中，AB≠BC，将△ABC沿直线AC翻折，点B落在点E处，AD与CE相交于点O，连接DE．（1）如图1，求证：AC∥DE；（2）如图2，如果∠B＝90°，AB＝，BC＝，求△OAC的面积；（3）如果∠B＝30°，AB＝2，当△AED是直角三角形时，求BC的长．29．如图，矩形ABCD中，已知AB＝6．BC＝8，点E是射线BC上的一个动点，连接AE 并延长，交射线DC于点F．将△ABE沿直线AE翻折，点B的对应点为点B'．（1）如图1，若点E为线段BC上一点，延长AB'交CD于点M，求证：AM＝FM；（2）如图2，若点B'恰好落在对角线AC上，求的值；（3）若＝，求∠DAB'的正弦值．30．如图1，四边形ABCD是矩形，点O位于对角线BD上，将△ADE，△CBF分别沿DE、BF翻折，点A，点C都恰好落在点O处．（1）求证：∠EDO＝∠FBO；（2）求证：四边形DEBF是菱形：（3）如图2，若AD＝2，点P是线段ED上的动点，求2AP+DP的最小值．。

中考折叠问题(原创)

05月26日教案+习题中考折叠问题1、中考中折叠问题每年必考。

有时出现在选择填空，有时候出现在压轴题。

2、折叠对象有三角形、矩形、正方形、梯形等；3、考查问题有求折点位置、求折线长、折纸边长周长、求重叠面积、求角度、判断线段之间关系等；4、解题时，灵活运用轴对称性质和背景图形性质。

5、轴对称性质——①折线是对称轴，折线两边图形全等②对应点连线垂直对称轴③对应边平行或交点在对称轴上。

ABC 的边AB 、BC 上，将△BDE 沿直线DE 翻折，使点B 落在B 1处，DB 1、EB 1分别交边AC 于点F 、G ．若∠ADF=80°，则∠CGE= ．例2．（2011·贺州）把一张矩形纸片ABCD 按如图方式折叠，使顶点B 和顶点D 重合，折痕为EF ．若BF ＝4，FC ＝2，则∠DEF 的度数是_ ．例3．（2011昭通，8，3）如图所示，将矩形纸片ABCD 折叠，使点D 与点B 重合，点C 落在点处，折痕为EF ，若，那么∠ABE 的度数为 ____________C '︒='∠125C EF ABC EF A’D (B )例4. 如图，在矩形ABCD 中，点E 在AB 边上，沿CE 折叠矩形ABCD ，使点B 落在AD 边上的点F 处，若AB=4，BC=5，则tan ∠AFE 的值为（） A ．43 B.35C ．34 D ．45例5.如图．将正方形纸片ABCD 折叠，使边AB 、CB 均落在对角线BD 上，得折痕BE 、BF ，则∠EBF 的大小为 ( ) A.15° B.30° C. 45° D.60°例6、（2011•广元）如图，M 为矩形纸片ABCD 的边AD 的中点，将纸片沿BM 、CM 折叠，使点A 落在A 1处，点D 落在D 1处．若∠A 1MD1=40°，则∠BMC 的度数为．例1、（2011•河北）如图，在△ABC 中，∠C=90°，BC=6，D ，E 分别在 AB 、AC 上，将△ABC 沿DE 折叠，使点A 落在点A ′处，若A ′为CE 的中点，则折痕DE 的长为（）A 、B 、2C 、3D 、4例2.如图所示，已知在三角形纸片ABC 中，BC =3， 6AB =， ∠BCA=90°在AC 上取一点E ，以BE 为折痕，使AB 的一部分与BC 重合，A 与BC 延长线上的点D 重合，则 D Ｅ的长度为 () A.6B.3C.D.例3、（2011•衡阳）如图所示，在△ABC 中，∠B=90°，AB=3，AC=5，将△ABC 折叠，使点CA E DCFC'BAC D与点A 重合，折痕为DE ，则△ABE 的周长为．例4．如图，矩形纸片ABCD 中，已知AD =8，折叠纸片使AB 边与对角线AC 重合，点B 落在点F 处，折痕为AE ，且EF =3，则AB 的长为( )A .3B .4C .5D .6 例5、（2011•泸州）如图，在Rt △ABC 中，∠ABC=90°，∠C=60°，方向翻折过去，使点C 落在BA 上的点C ′，折痕为BE ，则EC 的长度是（ A 、 B 、 C 、 D 、例6．将长8 cm ，宽4 cm 的矩形纸片ABCD 折叠，使点A 与C 重合，则折痕EF 的长等于 cm ．例7.如图，点O 是矩形ABCD 的中心，E 是AB 上的点，沿CE 折叠后，点B 恰好与点O 重合，若BC=3，则折痕CE 的长为（）（A ）（B ）（C ）（D ）6例8、（2011•潼南县）如图，在△ABC 中，∠C=90°，点D 在AC 上，将△BCD 沿着直线BD 翻折，使点C 落在斜边AB 上的点E 处，DC=5cm ，则点D 到斜边AB 的距离是 cm ．例9、（2011•巴彦淖尔）如图，AD 是△ABC 的中线，∠ADC=60°，BC=6，把△ABC 沿直线AD 折叠，点C 落在C ′处，连接BC ′，那么BC ′的长为．例10．将一块直角三角形纸片ABC 折叠，使点A 与点C 重合，展开后平铺在桌面上（如图所示）．若∠C ＝90°，BC ＝8cm ，则折痕DE 的长度是 cm ．例11、（2011•天水）如图，有一矩形纸片ABCD ，AB=8，AD=6．将纸片折叠，使得AD 边落322323B C在AB 边上，折痕为AE ，再将△AED 沿DE 向右翻折，AE 与BC 的交点为F ，则CF 的长为（）A 、6B 、4C 、2D 、1例12．如图，在矩形纸片ABCD 中，AB ＝2cm ，点E 在BC 上，且AE ＝CE ．若将纸片沿AE 折叠，点B 恰好与AC 上的点B 1重合，则AC ＝cm ． ABC 中，∠C=90°，BC=6cm ，AC=8cm ，按图中所示方法将△BCD 沿BD 折叠，使点C 落在AB 边的C ′点，那么△ADC ′的面积是．例1.如图，正方形ABCD 中，AB ＝6，点E 在边CD 上，且CD ＝3DE 。

中考数学折叠专项训练试题（含答案）

中考数学折叠专项训练试题（含答案）中考数学折叠专项训练试题附参考答案一．选择题（共9小题）1．（2013?贵港）如图，在矩形ABCD中，点E是AD的中点，∠EBC的平分线交CD于点F，将△DEF沿EF折叠，点D恰好落在BE 上M点处，延长BC、EF交于点N．有下列四个结论：①DF=CF；②BF⊥EN；③△BEN是等边三角形；④S△BEF=3S△DEF．其中，将正确结论的序号全部选对的是（）A．①②③B．①②④C．②③④D．①②③④考点：翻折变换（折叠问题）；等边三角形的判定；矩形的性质．专题：压轴题．分析：由折叠的性质、矩形的性质与角平分线的性质，可证得CF=FM=DF；易求得∠BFE=∠BFN，则可得BF⊥EN；易证得△BEN是等腰三角形，但无法判定是等边三角形；易求得BM=2EM=2DE，即可得EB=3EM，根据等高三角形的面积比等于对应底的比，即可求得答案．解答：解：∵四边形ABCD是矩形，∴∠D=∠BCD=90°，DF=MF，由折叠的性质可得：∠EMF=∠D=90°，即FM⊥BE，CF⊥BC，∵BF平分∠EBC，∴CF=MF，∴DF=CF；故①正确；∵∠BFM=90°﹣∠EBF，∠BFC=90°﹣∠CBF，∴∠BFM=∠BFC，∵∠MFE=∠DFE=∠CFN，∴∠BFE=∠BFN，∵∠BFE+∠BFN=180°，∴∠BFE=90°，即BF⊥EN，故②正确；∵在△DEF和△CNF中，，∴△DEF≌△CNF（ASA），∴EF=FN，∴BE=BN，但无法求得△BEN各角的度数，∴△BEN不一定是等边三角形；故③错误；∵∠BFM=∠BFC，BM⊥FM，BC⊥CF，∴BM=BC=AD=2DE=2EM，∴BE=3EM，∴S△BEF=3S△EMF=3S△DEF；故④正确．故选B．点评：此题考查了折叠的性质、矩形的性质、角平分线的性质以及全等三角形的判定与性质．此题难度适中，注意掌握数形结合思想的应用．2．如图，将矩形ABCD的一个角翻折，使得点D恰好落在BC边上的点G处，折痕为EF，若EB为∠AEG的平分线，EF和BC的延长线交于点H．下列结论中：①∠BEF=90°；②DE=CH；③BE=EF；④△BEG和△HEG的面积相等；⑤若，则．以上命题，正确的有（）A．2个B．3个C．4个D．5个考点：翻折变换（折叠问题）．专题：压轴题．分析：①根据平角的定义，折叠的性质和角平分线的性质即可作出判断；②根据折叠的性质和等腰三角形的性质可知DE≠CH；③无法证明BE=EF；④根据角平分线的性质，等腰三角形的性质和三角形中线的性质可得△BEG和△HEG的面积相等；⑤过E点作EK⊥BC，垂足为K．在RT△EKG中利用勾股定理可即可作出判断．解答：解：①由折叠的性质可知∠DEF=∠GEF，∵EB为∠AEG的平分线，∴∠AEB=∠GEB，∵∠AED=180°，∴∠BEF=90°，故正确；②可证△EDF∽△HCF，DF＞CF，故DE≠CH，故错误；③只可证△EDF∽△BAE，无法证明BE=EF，故错误；④可证△GEB，△GEH是等腰三角形，则G是BH边的中线，∴△BEG和△HEG的面积相等，故正确；⑤过E 点作EK ⊥BC ，垂足为K ．设BK=x ，AB=y ，则有y 2+（2y ﹣2x ）2=（2y ﹣x ）2，解得x 1=y （不合题意舍去），x 2=y ．则，故正确．故正确的有3个．故选B ．点评：本题考查了翻折变换，解答过程中涉及了矩形的性质、勾股定理，属于综合性题目，解答本题的关键是根据翻折变换的性质得出对应角、对应边分别相等，然后分别判断每个结论，难度较大，注意细心判断．3．（2012?遵义）如图，矩形ABCD 中，E 是AD 的中点，将△ABE 沿BE 折叠后得到△GBE ，延长BG 交CD 于F 点，若CF=1，FD=2，则BC 的长为（）A ．3B ．2C ．2D ．2考点：翻折变换（折叠问题）．专题：压轴题．分析：首先过点E 作EM ⊥BC 于M ，交BF 于N ，易证得△ENG ≌△BNM （AAS ），MN 是△BCF 的中位线，根据全等三角形的性质，即可求得GN=MN ，由折叠的性质，可得BG=3，继而求得BF 的值，又由勾股定理，即可求得BC 的长．解答：解：过点E 作EM ⊥BC 于M ，交BF 于N ，∵四边形ABCD 是矩形，∴∠A=∠ABC=90°，AD=BC ，∵∠EMB=90°，∴四边形ABME 是矩形，∴AE=BM ，由折叠的性质得：AE=GE ，∠EGN=∠A=90°，∴EG=BM ，∵∠ENG=∠BNM ，∴△ENG ≌△BNM （AAS ），∴NG=NM ，∴CM=DE ，∵E 是AD 的中点，∴AE=ED=BM=CM ，∵EM ∥CD ，∴BN ：NF=BM ：CM ，∴BN=NF，∴NM=CF=，∴NG=，∵BG=AB=CD=CF+DF=3，∴BN=BG﹣NG=3﹣=，∴BF=2BN=5，∴BC===2．故选B．点评：此题考查了矩形的判定与性质、折叠的性质、三角形中位线的性质以及全等三角形的判定与性质．此题难度适中，注意辅助线的作法，注意数形结合思想的应用．4．如图，两个正方形ABCD和AEFG共顶点A，连BE，DG，CF，AE，BG，K，M分别为DG和CF的中点，KA的延长线交BE于H，MN⊥BE于N．则下列结论：①BG=DE 且BG⊥DE；②△ADG和△ABE的面积相等；③BN=EN，④四边形AKMN为平行四边形．其中正确的是（）A．③④B．①②③C．①②④D．①②③④考点：正方形的性质；全等三角形的判定；平行四边形的判定．专题：证明题．分析：充分利用三角形的全等，正方形的性质，平行四边形的性质依次判断所给选项的正误即可．解答：解：由两个正方形的性质易证△AED≌△AGB，∴BG=DE，∠ADE=∠ABG，∴可得BG与DE相交的角为90°，∴BG⊥DE．①正确；如图，延长AK，使AK=KQ，连接DQ、QG，∴四边形ADQG是平行四边形；作CW⊥BE于点W，FJ⊥BE于点J，∴四边形CWJF是直角梯形；∵AB=DA，AE=DQ，∠BAE=∠ADQ，∴△ABE≌△DAQ，∴∠ABE=∠DAQ，∴∠ABE+∠BAH=∠DAQ+∠BAH=90°．∴△ABH是直角三角形．易证：△CWB≌△BHA，△EJF≌△AHE；∴WB=AH，AH=EJ，∴WB=EJ，又WN=NJ，∴WN﹣WB=NJ﹣EJ，∴BN=NE，③正确；∵MN是梯形WGFC的中位线，WB=BE=BH+HE，∴MN=（CW+FJ）=WC=（BH+HE）=BE；易证：△ABE≌△DAQ（SAS），∴AK=AQ=BE，∴MN∥AK且MN=AK；四边形AKMN为平行四边形，④正确．S△ABE=S△ADQ=S△ADG=S?ADQG，②正确．所以，①②③④都正确；故选D．点评：当出现两个正方形时，一般应出现全等三角形．图形较复杂，选项较多时，应用排除法求解．5．（2012?资阳）如图，在△ABC中，∠C=90°，将△ABC沿直线MN翻折后，顶点C恰好落在AB边上的点D处，已知MN∥AB，MC=6，NC=，则四边形MABN的面积是（）A．B．C．D．考点：翻折变换（折叠问题）．专题：压轴题．分析：首先连接CD，交MN于E，由将△ABC沿直线MN翻折后，顶点C恰好落在AB边上的点D处，即可得MN⊥CD，且CE=DE，又由MN∥AB，易得△CMN∽△CAB，根据相似三角形的面积比等于相似比的平方，相似三角形对应高的比等于相似比，即可得，又由MC=6，NC=，即可求得四边形MABN的面积．解答：解：连接CD，交MN于E，∵将△ABC沿直线MN翻折后，顶点C恰好落在AB边上的点D 处，∴MN⊥CD，且CE=DE，∴CD=2CE，∵MN∥AB，∴CD⊥AB，∴△CMN∽△CAB，∴，∵在△CMN中，∠C=90°，MC=6，NC=，∴S△CMN=CM?CN=×6×2=6，∴S△CAB=4S△CMN=4×6=24，∴S四边形MABN=S△CAB﹣S△CMN=24﹣6=18．故选C．点评：此题考查了折叠的性质、相似三角形的判定与性质以及直角三角形的性质．此题难度适中，解此题的关键是注意折叠中的对应关系，注意数形结合思想的应用．6．如图，D是△ABC的AC边上一点，AB=AC，BD=BC，将△BCD沿BD折叠，顶点C 恰好落在AB边的C′处，则∠A′的大小是（）A．40°B．36°C．32°D．30°考点：翻折变换（折叠问题）．分析：连接C'D，根据AB=AC，BD=BC，可得∠ABC=∠ACB=∠BDC，然后根据折叠的性质可得∠BCD=∠BC'D，继而得出∠ABC=∠BCD=∠BDC=∠BDC'=∠BC'D，根据四边形的内角和求出各角的度数，最后可求得∠A的大小．解答：解：连接C'D，∵AB=AC，BD=BC，∴∠ABC=∠ACB=∠BDC，∵△BCD沿BD折叠，顶点C恰好落在AB边的C′处，∴∠BCD=∠BC'D，∴∠ABC=∠BCD=∠BDC=∠BDC'=∠BC'D，∵四边形BCDC'的内角和为360°，∴∠ABC=∠BCD=∠BDC=∠BDC'=∠BC'D==72°，∴∠A=180°﹣∠ABC﹣∠ACB=36°．故选B．点评：本题考查了折叠的性质，解答本题的关键是掌握翻折前后的对应角相等，注意本题的突破口在于得出∠ABC=∠BCD=∠BDC=∠BDC'=∠BC'D，根据四边形的内角和为360°求出每个角的度数．7．（2012?舟山）如图，已知△ABC中，∠CAB=∠B=30°，AB=2，点D在BC边上，把△ABC沿AD翻折使AB与AC重合，得△AB′D，则△ABC与△AB′D重叠部分的面积为（）A．B．C．3﹣D．考点：翻折变换（折叠问题）．专题：压轴题．分析：首先过点D作DE⊥AB′于点E，过点C作CF⊥AB，由△ABC中，∠CAB=∠B=30°，AB=2，利用等腰三角形的性质，即可求得AC的长，又由折叠的性质，易得∠CDB′=90°，∠B′=30°，B′C=AB′﹣AC=2﹣2，继而求得CD与B′D的长，然后求得高DE的长，继而求得答案．解答：解：过点D作DE⊥AB′于点E，过点C作CF⊥AB，∵△ABC中，∠CAB=∠B=30°，AB=2，∴AC=BC，∴AF=AB=，∴AC===2，由折叠的性质得：AB′=AB=2，∠B′=∠B=30°，∵∠B′CD=∠CAB+∠B=60°，∴∠CDB′=90°，∵B′C=AB′﹣AC=2﹣2，∴CD=B′C=﹣1，B′D=B′C?cos∠B′=（2﹣2）×=3﹣，∴DE===，∴S阴影=AC?DE=×2×=．故选A．点评：此题考查了折叠的性质，等腰三角形的性质、直角三角形的性质以及特殊角的三角函数问题．此题难度适中，注意掌握辅助线的作法，注意数形结合思想的应用，注意掌握折叠前后图形的对应关系．8．（2013?定海区模拟）如图，已知△ABC中，∠CAB=∠B=30°，AB=，点D在BC 边上，把△ABC沿AD翻折，使AB与AC重合，得△AED，则BD的长度为（）A．B．C．D．考点：翻折变换（折叠问题）．分析：作CF⊥AB于点F，利用三线合一定理即可求得BF的长，然后证明△CDE是直角三角形，BD=x，则CD=DE=2﹣x，利用三角函数即可得到关于x的方程，解方程即可求解．解答：解：作CF⊥AB于点F．∵∠CAB=∠B∴AC=BC，∴BF=AB=，在直角△BCF中，BC==2，在△CDE中，∠E=∠B=30°，∠ECD=∠CAB+∠B=60°，DE=BD，∴∠CDE=90°，设BD=x，则CD=DE=2﹣x，在直角△CDE中，tanE===tan30°=，解得：x=3﹣．故选B．点评：本题考查了图形的折叠，以及三线合一定理、三角函数，正确理解折叠的性质，找出图形中相等的线段、相等的角是关键．9．（2013?绥化）如图，在Rt△ABC中，∠C=90°，AC=，BC=1，D在AC上，将△ADB 沿直线BD翻折后，点A落在点E处，如果AD⊥ED，那么△ABE的面积是（）A．1B．C．D．考点：翻折变换（折叠问题）．专题：压轴题．分析：先根据勾股定理计算出AB=2，根据含30度的直角三角形三边的关系得到∠BAC=30°，在根据折叠的性质得BE=BA=2，∠BED=∠BAD=30°，DA=DE，由于AD⊥ED得BC∥DE，所以∠CBF=∠BED=30°，在Rt△BCF中可计算出CF=，BF=2CF=，则EF=2﹣，在Rt△DEF中计算出FD=1﹣，ED=﹣1，然后利用S△ABE=S△ABD+S△BED+S△ADE=2S△ABD+S△ADE计算即可．解答：解：∵∠C=90°，AC=，BC=1，∴AB==2，∴∠BAC=30°，∵△ADB沿直线BD翻折后，点A落在点E处，∴BE=BA=2，∠BED=∠BAD=30°，DA=DE，∵AD⊥ED，∴BC∥DE，∴∠CBF=∠BED=30°，在Rt△BCF中，CF==，BF=2CF=，∴EF=2﹣，在Rt△DEF中，FD=EF=1﹣，ED=FD=﹣1，∴S△ABE=S△ABD+S△BED+S△ADE=2S△ABD+S△ADE=2×BC?AD+AD?ED=2××1×（﹣1）+×（﹣1）（﹣1）=1．故选A．点评：本题考查了折叠问题：折叠前后两图形全等，即对应线段相等；对应角相等．也考查了勾股定理和含30度的直角三角形三边的关系．。

专题18 折叠问题-中考数学压轴题精品专题练(第二期)

一、选择题1．（2017四川省乐山市，第10题，3分）如图，平面直角坐标系xOy 中，矩形OABC 的边OA 、OC 分别落在x 、y 轴上，点B 坐标为（6，4），反比例函数x y 6=的图象与AB 边交于点D ，与BC 边交于点E ，连结DE ，将△BDE 沿DE 翻折至△B 'DE 处，点B '恰好落在正比例函数y =kx 图象上，则k 的值是（）A ．52-B ．211-C ．51-D ．241- 2．（2017四川省内江市，第11题，3分）如图，在矩形AOBC 中，O 为坐标原点，OA 、OB 分别在x 轴、y 轴上，点B 的坐标为（0，33），∠ABO =30°，将△ABC 沿AB 所在直线对折后，点C 落在点D 处，则点D 的坐标为（）A ．（32，332）B ．（2，332）C ．（332，32）D ．（32，3﹣332） 3．（2017江苏省无锡市，第10题，3分）如图，△ABC 中，∠BAC =90°，AB =3，AC =4，点D 是BC 的中点，将△ABD 沿AD 翻折得到△AED ，连CE ，则线段CE 的长等于（）A ．2B ．54C ．53D ．754．（2017浙江省台州市，第10题，4分）如图，矩形EFGH 的四个顶点分别在菱形ABCD 的四条边上，BE =BF ，将△AEH ，△CFG 分别沿边EH ，FG 折叠，当重叠部分为菱形且面积是菱形ABCD 面积的116时，则AE EB为（）A ． 53B ．2C ． 52D ．4 5．（2017衢州，第9题，3分）如图，矩形纸片ABCD 中，AB =4，BC =6，将△ABC 沿AC 折叠，使点B 落在点E 处，CE 交AD 于点F ，则DF 的长等于（）A ． 53B ． 35C ． 37D ． 45 6．（2017湖南省长沙市，第12题，3分）如图，将正方形ABCD 折叠，使顶点A 与CD 边上的一点H 重合（H 不与端点C ，D 重合），折痕交AD 于点E ，交BC 于点F ，边AB 折叠后与边BC 交于点G ．设正方形ABCD 的周长为m ，△CHG 的周长为n ，则mn 的值为（）A ．22B ．21 C ．215 D ．随H 点位置的变化而变化7．（2016内蒙古包头市）如图，直线243y x=+与x轴、y轴分别交于点A和点B，点C、D分别为线段AB、OB的中点，点P为OA上一动点，PC+PD值最小时点P的坐标为（）A．（﹣3，0）B．（﹣6，0）C．（32-，0）D．（52-，0）8．（2016内蒙古呼伦贝尔市，第6题，3分）将点A（3，2）向左平移4个单位长度得点A′，则点A′关于y轴对称的点的坐标是（）A．（﹣3，2）B．（﹣1，2）C．（1，﹣2）D．（1，2）9．（2016内蒙古呼伦贝尔市，第12题，3分）如图，Rt△ABC中，AB=9，BC=6，∠B=90°，将△ABC折叠，使A点与BC的中点D重合，折痕为PQ，则线段BQ的长度为（）A．53B．52C．4D．510．（2016天津市）如图，把一张矩形纸片ABCD沿对角线AC折叠，点B的对应点为B′，AB′与DC相交于点E，则下列结论一定正确的是（）A．∠DAB′=∠CAB′B．∠ACD=∠B′CD C．AD=AE D．AE=CE 11．（2016四川省南充市）如图，对折矩形纸片ABCD，使AB与DC重合得到折痕EF，将纸片展平；再一次折叠，使点D落到EF上点G处，并使折痕经过点A，展平纸片后∠DAG的大小为（）A．30°B．45°C．60°D．75°12．（2016四川省资阳市）如图，矩形ABCD与菱形EFGH的对角线均交于点O，且EG∥BC，将矩形折叠，使点C与点O重合，折痕M N恰好过点G若AB=6，EF=2，∠H=120°，则DN的长为（）A．32B．632+C．63-D．236-13．（2016四川省雅安市）如图，在矩形ABCD中，AD=6，AE⊥BD，垂足为E，ED=3BE，点P、Q分别在BD，AD上，则AP+PQ的最小值为（）A．22B．2C．23D．3314．（2016山东省威海市）如图，在矩形ABCD中，AB=4，BC=6，点E为BC的中点，将△ABE沿AE折叠，使点B落在矩形内点F处，连接CF，则CF的长为（）A．95B．125C．165D．18515．（2016山东省枣庄市）如图，△ABC的面积为6，AC=3，现将△ABC沿AB所在直线翻折，使点C落在直线AD上的C′处，P为直线AD上的一点，则线段BP的长不可能是（）A．3B．4C．5.5D．1016．（2016山东省济宁市）如图，在4×4正方形网格中，黑色部分的图形构成一个轴对称图形，现在任意选取一个白色的小正方形并涂黑，使黑色部分的图形仍然构成一个轴对称图形的概率是（）A．613B．513C．413D．31317．（2016山东省聊城市）如图，把一张矩形纸片ABCD沿EF折叠后，点A落在CD边上的点A′处，点B落在点B′处，若∠2=40°，则图中∠1的度数为（）A．115°B．120°C．130°D．140°18．（2016广西百色市）如图，正△ABC的边长为2，过点B的直线l⊥AB，且△ABC与△A′BC′关于直线l对称，D为线段BC′上一动点，则AD+CD的最小值是（）A．4B．32C．23D．2319．（2016广西钦州市）如图，把矩形纸片ABCD沿EF翻折，点A恰好落在BC边的A′处，若AB3，∠EF A=60°，则四边形A′B′EF的周长是（）A ．133+B ．33+C ．43+D ．53+20．（2016江苏省南通市）平面直角坐标系xOy 中，已知A （﹣1，0）、B （3，0）、C （0，﹣1）三点，D （1，m ）是一个动点，当△ACD 的周长最小时，△ABD 的面积为（）A ．13B ．23C ．43D ．8321．（2016江苏省宿迁市）如图，把正方形纸片ABCD 沿对边中点所在的直线对折后展开，折痕为M N ，再过点B 折叠纸片，使点A 落在M N 上的点F 处，折痕为BE ．若AB 的长为2，则F M 的长为（）A ．2B ．3C ．2D ．122．（2016江苏省苏州市）矩形OABC 在平面直角坐标系中的位置如图所示，点B 的坐标为（3，4），D 是OA 的中点，点E 在AB 上，当△CDE 的周长最小时，点E 的坐标为（）A ．（3，1）B ．（3，43）C ．（3，53） D ．（3，2） 23．（2016江苏省镇江市）如图，在平面直角坐标系中，坐标原点O 是正方形OABC 的一个顶点，已知点B 坐标为（1，7），过点P （a ，0）（a ＞0）作PE ⊥x 轴，与边OA 交于点E （异于点O 、A ），将四边形ABCE 沿CE 翻折，点A ′、B ′分别是点A 、B 的对应点，若点A ′恰好落在直线PE 上，则a 的值等于（）A．54B．43C．2D．324．（2016海南省）如图，AD是△ABC的中线，∠ADC=45°，把△ADC沿着直线AD对折，点C落在点E的位置．如果BC=6，那么线段BE的长度为（）A．6B．62C．23D．3225．（2016浙江省台州市）小红用次数最少的对折方法验证了一条四边形丝巾的形状是正方形，她对折了（）A．1次B．2次C．3次D．4次26．（2016浙江省温州市）如图，一张三角形纸片ABC，其中∠C=90°，AC=4，BC=3．现小林将纸片做三次折叠：第一次使点A落在C处；将纸片展平做第二次折叠，使点B落在C处；再将纸片展平做第三次折叠，使点A落在B处．这三次折叠的折痕长依次记为a，b，c，则a，b，c的大小关系是（）A．c＞a＞b B．b＞a＞c C．c＞b＞a D．b＞c＞a27．（2016浙江省湖州市）如图1，在等腰三角形ABC中，AB=AC=4，BC=7．如图2，在底边BC上取一点D，连结AD，使得∠DAC=∠ACD．如图3，将△ACD沿着AD所在直线折叠，使得点C落在点E处，连结BE，得到四边形ABED．则BE的长是（）A．4B．174C．32D．2528．（2016浙江省舟山市）把一张圆形纸片按如图所示方式折叠两次后展开，图中的虚线表示折痕，则BC 的度数是（）A．120°B．135°C．150°D．165°29．（2016湖北省咸宁市）已知菱形OABC在平面直角坐标系的位置如图所示，顶点A（5，0），OB=45，点P是对角线OB上的一个动点，D（0，1），当CP+DP最短时，点P的坐标为（）A．（0，0）B．（1，12）C．（65，35）D．（107，57）30．（2016福建省莆田市）如图，在△ABC中，∠ACB=90°，AC=BC=4，将△ABC折叠，使点A落在BC 边上的点D处，EF为折痕，若AE=3，则sin∠BFD的值为（）A．13B．223C．24D．3531．（2016贵州省遵义市）如图，正方形ABCD的边长为3，E、F分别是AB、CD上的点，且∠CFE=60°，将四边形BCFE沿EF翻折，得到B′C′FE，C′恰好落在AD边上，B′C′交AB于点G，则GE的长是（）A ．334-B ．425-C ．423-D ．523-32．（2016湖北省鄂州市）如图，菱形ABCD 的边AB =8，∠B =60°，P 是AB 上一点，BP =3，Q 是CD 边上一动点，将梯形APQD 沿直线PQ 折叠，A 的对应点A ′．当CA ′的长度最小时，CQ 的长为（）A ．5B ．7C ．8D ．13233．（2016福建省龙岩市）如图，在周长为12的菱形ABCD 中，AE =1，AF =2，若P 为对角线BD 上一动点，则EP +FP 的最小值为（）A ．1B ．2C ．3D ．434．（2016贵州省毕节市）如图，正方形ABCD 的边长为9，将正方形折叠，使顶点D 落在BC 边上的点E 处，折痕为GH ．若BE ：EC =2：1，则线段CH 的长是（）A ．3B ．4C ．5D ．635．（2016黑龙江省牡丹江市）如图，在平面直角坐标系中，A （﹣8，﹣1），B （﹣6，﹣9），C （﹣2．﹣9），D （﹣4，﹣1）．先将四边形ABCD 沿x 轴翻折，再向右平移8个单位长度，向下平移1个单位长度后，得到四边形A 1B 1C 1D 1，最后将四边形A 1B 1C 1D 1，绕着点A 1旋转，使旋转后的四边形对角线的交点落在x 轴上，则旋转后的四边形对角线的交点坐标为（）A ．（4，0）B ．（5，0）C ．（4，0）或（﹣4，0）D ．（5，0）或（﹣5，0）36．（2015常州）将一张宽为4cm 的长方形纸片（足够长）折叠成如图所示图形，重叠部分是一个三角形，则这个三角形面积的最小值是（）A ．338cm 2B ．8cm 2C ．3316cm 2 D ．16cm 2 37．（2015贵港）在平面直角坐标系中，若点P （m ，m ﹣n ）与点Q （﹣2，3）关于原点对称，则点M （m ，n ）在（）A ．第一象限B ．第二象限C ．第三象限D ．第四象限38．（2015庆阳）在如图所示的平面直角坐标系中，△OA 1B 1是边长为2的等边三角形，作△B 2A 2B 1与△OA 1B 1关于点B 1成中心对称，再作△B 2A 3B 3与△B 2A 2B 1关于点B 2成中心对称，如此作下去，则△B 2n A 2n +1B 2n +1（n 是正整数）的顶点A 2n +1的坐标是（）A ．（4n ﹣13）B ．（2n ﹣13）C ．（4n +13D ．（2n +13）39．（2015桂林）如图，在△ABC中，AB=10，AC=8，BC=12，AD⊥BC于D，点E、F分别在AB、AC边上，把△ABC沿EF折叠，使点A与点D恰好重合，则△DEF的周长是（）A．14B．15C．16D．1740．（2015南宁）如图，AB是⊙O的直径，AB=8，点M在⊙O上，∠MA B=20°，N是弧M B的中点，P 是直径AB上的一动点．若M N=1，则△P M N周长的最小值为（）A．4B．5C．6D．741．（2015北海）如图，在矩形OABC中，OA=8，OC=4，沿对角线OB折叠后，点A与点D重合，OD与BC交于点E，则点D的坐标是（）A．（4，8）B．（5，8）C．（245，325）D．（225，365）42．（2015攀枝花）如图，在边长为2的等边△ABC中，D为BC的中点，E是AC边上一点，则BE+DE 的最小值为．二、填空题43．（2017四川省成都市，第25题，4分）如图1，把一张正方形纸片对折得到长方形ABCD，再沿∠ADC 的平分线DE折叠，如图2，点C落在点C′处，最后按图3所示方式折叠，使点A落在DE的中点A′处，折痕是FG，若原正方形纸片的边长为6cm，则FG= cm．44．（2017四川省达州市，第16题，3分）如图，矩形ABCD中，E是BC上一点，连接AE，将矩形沿AE 翻折，使点B落在CD边F处，连接AF，在AF上取点O，以O为圆心，OF长为半径作⊙O与AD相切于点P．若AB=6，BC=33，则下列结论：①F是CD的中点；②⊙O的半径是2；③AE=92CE；④32S阴影．其中正确结论的序号是．45．（2017山东省潍坊市，第18题，3分）如图，将一张矩形纸片ABCD的边BC斜着向AD边对折，使点B落在AD边上，记为B′，折痕为CE，再将CD边斜向下对折，使点D落在B′C边上，记为D′，折痕为CG，B′D′=2，BE=13BC．则矩形纸片ABCD的面积为．46．（2017广东省，第16题，4分）如图，矩形纸片ABCD中，AB=5，BC=3，先按图（2）操作：将矩形纸片ABCD沿过点A的直线折叠，使点D落在边AB上的点E处，折痕为AF；再按图（3）操作，沿过点F的直线折叠，使点C落在EF上的点H处，折痕为FG，则A、H两点间的距离为．47．（2017南宁，第16题，3分）如图，菱形ABCD的对角线相交于点O，AC=2，BD=23，将菱形按如图方式折叠，使点B与点O重合，折痕为EF，则五边形AEFCD的周长为．48．（2017江苏省连云港市，第16题，3分）如图，已知等边三角形OAB与反比例函数kyx（k＞0，x＞0）的图象交于A、B两点，将△OAB沿直线OB翻折，得到△OCB，点A的对应点为点C，线段CB交x轴于点D，则BDDC的值为．（已知sin15°=62）49．（2017江西省，第12题，3分）已知点A（0，4），B（7，0），C（7，4），连接AC，BC得到矩形AOBC，点D的边AC上，将边OA沿OD折叠，点A的对应边为A'．若点A'到矩形较长两对边的距离之比为1：3，则点A'的坐标为．50．（2017河南省，第15题，3分）如图，在Rt△ABC中，∠A=90°，AB=AC，BC2+1，点M，N分别是边BC，AB上的动点，沿MN所在的直线折叠∠B，使点B的对应点B′始终落在边AC上，若△MB′C 为直角三角形，则BM的长为．51．（2017浙江省宁波市，第18题，4分）如图，在菱形纸片ABCD中，AB=2，∠A=60°，将菱形纸片翻折，使点A落在CD的中点E处，折痕为FG，点F，G分别在边AB，AD上，则cos∠EFG的值为．52．（2017湖北省武汉市，第15题，3分）如图，在△ABC中，AB=AC=23，∠BAC=120°，点D、E都在边BC上，∠DAE=60°．若BD=2CE，则DE的长为．53．（2017湖北省襄阳市，第16题，3分）如图，在△ABC中，∠ACB=90°，点D，E分别在AC，BC上，且∠CDE=∠B，将△CDE沿DE折叠，点C恰好落在AB边上的点F处．若AC=8，AB=10，则CD的长为．54．（2017贵州省贵阳市，第15题，4分）如图，在矩形纸片ABCD中，AB=2，AD=3，点E是AB的中点，点F是AD边上的一个动点，将△AEF沿EF所在直线翻折，得到△A′EF，则A′C的长的最小值是．55．（2017辽宁省营口市，第17题，3分）在矩形纸片ABCD中，AD=8，AB=6，E是边BC上的点，将纸片沿AE折叠，使点B落在点F处，连接FC，当△EFC为直角三角形时，BE的长为．56．（2017辽宁省锦州市，第15题，3分）如图，正方形ABCD中，AB=2，E是CD中点，将正方形ABCD 沿AM折叠，使点B的对应点F落在AE上，延长MF交CD于点N，则DN的长为．57．（2017重庆，第18题，4分）如图，正方形ABCD中，AD=4，点E是对角线AC上一点，连接DE，过点E作EF⊥ED，交AB于点F，连接DF，交AC于点G，将△EFG沿EF翻折，得到△EFM，连接DM，交EF于点N，若点F是AB的中点，则△EMN的周长是．58．（2017重庆B，第18题，4分）如图，正方形ABCD中，AD=4，点E是对角线AC上一点，连接DE，过点E作EF⊥ED，交AB于点F，连接DF，交AC于点G，将△EFG沿EF翻折，得到△EFM，连接DM，交EF于点N，若点F是AB的中点，则△EMN的周长是．59．（2017青海省西宁市，第20题，2分）如图，将▱ABCD沿EF对折，使点A落在点C处，若∠A=60°，AD=4，AB=6，则AE的长为．60．（2016云南省曲靖市）如图，在矩形ABCD中，AD=10，CD=6，E是CD边上一点，沿AE折叠△ADE，使点D恰好落在BC边上的F处，M是AF的中点，连接B M，则sin∠AB M= ．61．（2016吉林省）在三角形纸片ABC中，∠C=90°，∠B=30°，点D（不与B，C重合）是BC上任意一点，将此三角形纸片按下列方式折叠，若EF的长度为a，则△DEF的周长为（用含a的式子表示）．62．（2016宁夏）如图，Rt△AOB中，∠AOB=90°，OA在x轴上，OB在y轴上，点A，B的坐标分别为（3，0），（0，1），把Rt△AOB沿着AB对折得到Rt△AO′B，则点O′的坐标为63．（2016四川省内江市）如图所示，已知点C（1，0），直线y=﹣x+7与两坐标轴分别交于A，B两点，D，E分别是AB，OA上的动点，则△CDE周长的最小值是．64．（2016山东省东营市）如图，折叠矩形ABCD的一边AD，使点D落在BC边的点F处，已知折痕AE=55cm，且tan∠EFC=34，那么矩形ABCD的周长为cm．65．（2016山东省临沂市）如图，将一矩形纸片ABCD折叠，使两个顶点A，C重合，折痕为FG．若AB=4，BC=8，则△ABF的面积为．66．（2016山东省德州市）如图，半径为1的半圆形纸片，按如图方式折叠，使对折后半圆弧的中点M与圆心O重合，则图中阴影部分的面积是．67．（2016山东省日照市）如图，△ABC是一张直角三角形纸片，∠C=90°，两直角边AC=6cm、BC=8cm，现将△ABC折叠，使点B与点A重合，折痕为EF，则tan∠CAE= ．68．（2016山东省济南市）如图1，在矩形纸片ABCD中，AB=83AD=10，点E是CD中点，将这张纸片依次折叠两次；第一次折叠纸片使点A与点E重合，如图2，折痕为M N，连接M E/NE；第二次折叠纸片使点N与点E重合，如图3，点B落到B′处，折痕为HG，连接HE，则tan∠EHG= ．69．（2016山东省青岛市）如图，以边长为20cm的正三角形纸板的各顶点为端点，在各边上分别截取4cm 长的六条线段，过截得的六个端点作所在边的垂线，形成三个有两个直角的四边形．把它们沿图中虛线剪掉，用剩下的纸板折成一个底为正三角形的无盖柱形盒子，则它的容积为cm3．70．（2016广东省）如图，矩形ABCD中，对角线AC=23，E为BC边上一点，BC=3BE，将矩形ABCD 沿AE所在的直线折叠，B点恰好落在对角线AC上的B′处，则AB= ．71．（2016广西南宁市）如图，在4×4正方形网格中，有3个小正方形已经涂黑，若再涂黑任意一个白色的小正方形（每一个白色的小正方形被涂黑的可能性相同），使新构成的黑色部分的图形是轴对称图形的概率是．72．（2016广西河池市）如图的三角形纸片中，AB=AC，BC=12cm，∠C=30°，折叠这个三角形，使点B 落在AC的中点D处，折痕为EF，那么BF的长为cm．73．（2016江苏省淮安市）如图，在Rt△ABC中，∠C=90°，AC=6，BC=8，点F在边AC上，并且CF=2，点E为边BC上的动点，将△CEF沿直线EF翻折，点C落在点P处，则点P到边AB距离的最小值是．74．（2016江苏省盐城市）如图，已知菱形ABCD的边长2，∠A=60°，点E、F分别在边AB、AD上，若将△AEF沿直线EF折叠，使得点A恰好落在CD边的中点G处，则EF= ．75．（2016河北省）如图，已知∠AOB=7°，一条光线从点A出发后射向OB边．若光线与OB边垂直，则光线沿原路返回到点A，此时∠A=90°-7°=83°．当∠A＜83°时，光线射到OB边上的点A1后，经OB反射到线段AO上的点A2，易知∠1=∠2．若A1A2⊥AO，光线又会沿A2→A1→A原路返回到点A，此时∠A=__ ___°．……若光线从点A发出后，经若干次反射能沿原路返回到点A，则锐角∠A的最小值=___ ____°．76．（2016江苏省苏州市）如图，在△ABC中，AB=10，∠B=60°，点D、E分别在AB、BC上，且BD=BE=4，将△BDE沿DE所在直线折叠得到△B′DE（点B′在四边形ADEC内），连接AB′，则AB′的长为．77．（2016江苏省连云港市）如图1，将正方形纸片ABCD对折，使AB与CD重合，折痕为EF．如图2，展开后再折叠一次，使点C与点E重合，折痕为GH，点B的对应点为点M，E M交AB于N．若AD=2，则M N= ．78．（2016河南省）如图，已知AD∥BC，AB⊥BC，AB=3，点E为射线BC上一个动点，连接AE，将△ABE 沿AE折叠，点B落在点B′处，过点B′作AD的垂线，分别交AD，BC于点M，N．当点B′为线段M N 的三等分点时，BE的长为．79．（2016浙江省绍兴市）如图，矩形ABCD中，AB=4，BC=2，E是AB的中点，直线l平行于直线EC，且直线l与直线EC之间的距离为2，点F在矩形ABCD边上，将矩形ABCD沿直线EF折叠，使点A恰好落在直线l上，则DF的长为．80．（2016浙江省金华市）如图，Rt△ABC纸片中，∠C=90°，AC=6，BC=8，点D在边BC上，以AD为折痕△ABD折叠得到△AB′D，AB′与边BC交于点E．若△DEB′为直角三角形，则BD的长是．81．（2016湖北省黄冈市）如图，在矩形ABCD中，点E、F分别在边CD、BC上，且DC=3DE=3a．将矩形沿直线EF折叠，使点C恰好落在AD边上的点P处，则FP= ．82．（2016贵州省黔东南州）如图，在平面直角坐标系xOy中，矩形OABC的边OA、OC分别在x轴和y 轴上，OC=3，OA=26，D是BC的中点，将△OCD沿直线OD折叠后得到△OGD，延长OG交AB于点E，连接DE，则点G的坐标为．83．（2016湖北省随州市）如图，直线y=x+4与双曲线kyx（k≠0）相交于A（﹣1，a）、B两点，在y轴上找一点P，当PA+PB的值最小时，点P的坐标为．84．（2016湖南省张家界市）如图，将矩形ABCD沿GH对折，点C落在Q处，点D落在E处，EQ与BC相交于F．若AD=8cm，AB=6cm，AE=4cm．则△EBF的周长是cm．85．（2016甘肃省天水市）如图，把矩形纸片OABC放入平面直角坐标系中，使OA、OC分别落在x轴、y轴上，连接OB，将纸片OABC沿OB折叠，使点A落在点A′的位置，若OB=5，tan∠BOC=12，则点A′的坐标为．86．（2016重庆市）正方形ABCD中，对角线AC，BD相交于点O，DE平分∠ADO交AC于点E，把△ADE 沿AD翻折，得到△ADE′，点F是DE的中点，连接AF，BF，E′F．若AE=2．则四边形ABFE′的面积是．87．（2016重庆市）如图，在正方形ABCD中，AB=6，点E在边CD上，DE=13DC，连接AE，将△ADE沿AE翻折，点D落在点F处，点O是对角线BD的中点，连接OF并延长OF交CD于点G，连接BF，BG，则△BFG的周长是．88．（2016黑龙江省齐齐哈尔市）如图，在边长为2的菱形ABCD 中，∠A =60°，点M 是AD 边的中点，连接M C ，将菱形ABCD 翻折，使点A 落在线段CM 上的点E 处，折痕交AB 于点N ，则线段EC 的长为．89．（2016黑龙江省龙东地区）如图，M N 是⊙O 的直径，M N =4，∠A M N =40°，点B 为弧AN 的中点，点P 是直径M N 上的一个动点，则PA +PB 的最小值为．90．（2015宜宾）如图，一次函数的图象与x 轴、y 轴分别相交于点A 、B ，将△AOB 沿直线AB 翻折，得△ACB ．若C （32，32），则该一次函数的解析式为．91．（2015达州）如图，将矩形ABCD 沿EF 折叠，使顶点C 恰好落在AB 边的中点C ′上，点D 落在D ′处，C ′D ′交AE 于点M ．若AB =6，BC =9，则A M 的长为．三、解答题92．（2017吉林省，第26题，10分）《函数的图象与性质》拓展学习片段展示：【问题】如图①，在平面直角坐标系中，抛物线24(2)3y a x =--经过原点O ，与x 轴的另一个交点为A ，则a = ．【操作】将图①中抛物线在x 轴下方的部分沿x 轴折叠到x 轴上方，将这部分图象与原抛物线剩余部分的图象组成的新图象记为G ，如图②．直接写出图象G 对应的函数解析式．【探究】在图②中，过点B （0，1）作直线l 平行于x 轴，与图象G 的交点从左至右依次为点C ，D ，E ，F ，如图③．求图象G 在直线l 上方的部分对应的函数y 随x 增大而增大时x 的取值范围．【应用】P 是图③中图象G 上一点，其横坐标为m ，连接PD ，PE ．直接写出△PDE 的面积不小于1时m 的取值范围．93．（2017四川省达州市，第25题，12分）如图1，点A 坐标为（2，0），以OA 为边在第一象限内作等边△OAB ，点C 为x 轴上一动点，且在点A 右侧，连接BC ，以BC 为边在第一象限内作等边△BCD ，连接AD 交BC 于E ．（1）①直接回答：△OBC 与△ABD 全等吗？②试说明：无论点C 如何移动，AD 始终与OB 平行；（2）当点C 运动到使AC 2=AE •AD 时，如图2，经过O 、B 、C 三点的抛物线为y 1．试问：y 1上是否存在动点P ，使△BEP 为直角三角形且BE 为直角边？若存在，求出点P 坐标；若不存在，说明理由；（3）在（2）的条件下，将y 1沿x 轴翻折得y 2，设y 1与y 2组成的图形为M ，函数33y x m =+的图象l与M 有公共点．试写出：l 与M 的公共点为3个时，m 的取值．94．（2017德州，第23题，10分）如图1，在矩形纸片ABCD 中，AB =3cm ，AD =5cm ，折叠纸片使B 点落在边AD 上的E 处，折痕为PQ ，过点E 作EF ∥AB 交PQ 于F ，连接BF ．（1）求证：四边形BFEP 为菱形；（2）当点E在AD边上移动时，折痕的端点P、Q也随之移动；①当点Q与点C重合时（如图2），求菱形BFEP的边长；②若限定P、Q分别在边BA、BC上移动，求出点E在边AD上移动的最大距离．95．（2017山东省淄博市，第23题，9分）如图，将矩形纸片ABCD沿直线MN折叠，顶点B恰好与CD 边上的动点P重合（点P不与点C，D重合），折痕为MN，点M，N分别在边AD，BC上，连接MB，MP，BP，BP与MN相交于点F．（1）求证：△BFN∽△BCP；（2）①在图2中，作出经过M，D，P三点的⊙O（要求保留作图痕迹，不写做法）；②设AB=4，随着点P在CD上的运动，若①中的⊙O恰好与BM，BC同时相切，求此时DP的长．96．（2017山西省，第22题，12分）综合与实践背景阅读早在三千多年前，我国周朝数学家商高就提出：将一根直尺折成一个直角，如果勾等于三，股等于四，那么弦就等于五，即“勾三，股四，弦五”．它被记载于我国古代著名数学著作《周髀算经》中．为了方便，在本题中，我们把三边的比为3：4：5的三角形称为（3，4，5）型三角形．例如：三边长分别为9，12，15或32,42,523，4，5）型三角形．用矩形纸片按下面的操作方法可以折出这种类型的三角形．实践操作如图1，在矩形纸片ABCD中，AD=8cm，AB=12cm．第一步：如图2，将图1中的矩形纸片ABCD沿过点A的直线折叠，使点D落在AB上的点E处，折痕为AF，再沿EF折叠，然后把纸片展平．第二步：如图3，将图2中的矩形纸片再次折叠，使点D与点F重合，折痕为GH，然后展平，隐去AF．第三步：如图4，将图3中的矩形纸片沿AH折叠，得到△AD′H，再沿AD′折叠，折痕为AM，AM与折痕EF 交于点N ，然后展平．问题解决（1）请在图2中证明四边形AEFD 是正方形．（2）请在图4中判断NF 与ND ′的数量关系，并加以证明．（3）请在图4中证明△AEN 是（3，4，5）型三角形．探索发现（4）在不添加字母的情况下，图4中还有哪些三角形是（3，4，5）型三角形？请找出并直接写出它们的名称．97．（2017广西桂林市，第26题，12分）已知抛物线214y ax bx =+-（a ≠0）与x 轴交于点A （﹣1，0）和点B （4，0）．（1）求抛物线1y 的函数解析式；（2）如图①，将抛物线1y 沿x 轴翻折得到抛物线2y ，抛物线2y 与y 轴交于点C ，点D 是线段BC 上的一个动点，过点D 作DE ∥y 轴交抛物线1y 于点E ，求线段DE 的长度的最大值；（2）在（2）的条件下，当线段DE 处于长度最大值位置时，作线段BC 的垂直平分线交DE 于点F ，垂足为H ，点P 是抛物线2y 上一动点，⊙P 与直线BC 相切，且S ⊙P ：S △DFH =2π，求满足条件的所有点P 的坐标．98．（2017广西贵港市，第26题，10分）已知，在Rt △ABC 中，∠ACB =90°，AC =4，BC =2，D 是AC 边上的一个动点，将△ABD 沿BD 所在直线折叠，使点A 落在点P 处．（1）如图1，若点D 是AC 中点，连接PC ．①写出BP ，BD 的长；②求证：四边形BCPD 是平行四边形．（2）如图2，若BD =AD ，过点P 作PH ⊥BC 交BC 的延长线于点H ，求PH 的长．99．（2017江苏省宿迁市，第25题，10分）如图，在平面直角坐标系xOy 中，抛物线223y x x =--交x 轴于A ，B 两点（点A 在点B 的左侧），将该抛物线位于x 轴上方曲线记作M ，将该抛物线位于x 轴下方部分沿x 轴翻折，翻折后所得曲线记作N ，曲线N 交y 轴于点C ，连接AC 、BC ．（1）求曲线N 所在抛物线相应的函数表达式；（2）求△ABC 外接圆的半径；（3）点P 为曲线M 或曲线N 上的一动点，点Q 为x 轴上的一个动点，若以点B ，C ，P ，Q 为顶点的四边形是平行四边形，求点Q 的坐标．100．（2017江苏省宿迁市，第26题，10分）如图，在矩形纸片ABCD 中，已知AB =1，BC =3，点E 在边CD 上移动，连接AE ，将多边形ABCE 沿直线AE 翻折，得到多边形AB ′C ′E ，点B 、C 的对应点分别为点B ′、C ′．（1）当B ′C ′恰好经过点D 时（如图1），求线段CE 的长；（2）若B ′C ′分别交边AD ，CD 于点F ，G ，且∠DAE =22.5°（如图2），求△DFG 的面积；（3）在点E 从点C 移动到点D 的过程中，求点C ′运动的路径长．101．（2017浙江省绍兴市，第24题，14分）如图1，已知□ABCD ，AB ∥x 轴，AB =6，点A 的坐标为（1，-4），点D 的坐标为（-3，4），点B 在第四象限，点P 是□ABCD 边上一个动点．（1）若点P 在边BC 上，PD =CD ，求点P 的坐标．（2）若点P 在边AB 、AD 上，点P 关于坐标轴对称的点Q ，落在直线1y x =-上，求点P 的坐标．（3）若点P 在边AB ，AD ，CD 上，点G 是AD 与y 轴的交点，如图2，过点P 作y 轴的平行线PM ，过点G 作x 轴的平行线GM ，它们相交于点M ，将△PGM 沿直线PG 翻折，当点M 的对应点落在坐标轴上时，求点P 的坐标（直接写出答案）．102．（2017金华，第23题，10分）如图1，将△ABC 纸片沿中位线EH 折叠，使点A 对称点D 落在BC 边上，再将纸片分别沿等腰△BED 和等腰△DHC 的底边上的高线EF ，HG 折叠，折叠后的三个三角形拼合形成一个矩形，类似地，对多边形进行折叠，若翻折后的图形恰能合成一个无缝隙，无重叠的矩形，这样的矩形称为叠合矩形．（1）将▱ABCD 纸片按图2的方式折叠成一个叠合矩形AEFG ，则操作形成的折痕分别是线段，；S 矩形AE S ▱ABCD = ．（2）如图4，四边形ABCD 纸片满足AD ∥BC ，AD ＜BC ，AB ⊥BC ，AB =8，CD =10，小明把该纸片折叠，得到叠合正方形，请你帮助画出叠合正方形的示意图，并求出AD 、BC 的长．103．（2017辽宁省盘锦市，第26题，14分）如图，直线y =﹣2x +4交y 轴于点A ，交抛物线212y x bx c =++ 于点B （3，﹣2），抛物线经过点C （﹣1，0），交y 轴于点D ，点P 是抛物线上的动点，作PE ⊥DB 交DB 所在直线于点E ．（1）求抛物线的解析式；（2）当△PDE 为等腰直角三角形时，求出PE 的长及P 点坐标；（3）在（2）的条件下，连接PB ，将△PBE 沿直线AB 翻折，直接写出翻折点后E 的对称点坐标．104．（2017辽宁省葫芦岛市，第26题，14分）如图，抛物线22y ax x c =-+（a ≠0）与x 轴、y 轴分别交于点A ，B ，C 三点，已知点A （﹣2，0），点C （0，﹣8），点D 是抛物线的顶点．（1）求抛物线的解析式及顶点D 的坐标；（2）如图1，抛物线的对称轴与x 轴交于点E ，第四象限的抛物线上有一点P ，将△EBP 沿直线EP 折叠，使点B 的对应点B '落在抛物线的对称轴上，求点P 的坐标；（3）如图2，设BC 交抛物线的对称轴于点F ，作直线CD ，点M 是直线CD 上的动点，点N 是平面内一点，当以点B ，F ，M ，N 为顶点的四边形是菱形时，请直接写出点M 的坐标．105．（2017辽宁省辽阳市，第26题，14分）如图1，抛物线213y x bx c =++经过A （3-0）、B （0，﹣2）两点，点C 在y 轴上，△ABC 为等边三角形，点D 从点A 出发，沿AB 方向以每秒2个单位长度的速度向终点B 运动，设运动时间为t 秒（t ＞0），过点D 作DE ⊥AC 于点E ，以DE 为边作矩形DEGF ，使点F 在x 轴上，点G 在AC 或AC 的延长线上．（1）求抛物线的解析式；（2）将矩形DEGF 沿GF 所在直线翻折，得矩形D 'E 'GF ，当点D 的对称点D '落在抛物线上时，求此时点D '的坐标；（3）如图2，在x 轴上有一点M （23，0），连接BM 、CM ，在点D 的运动过程中，设矩形DEGF 与四边形ABMC 重叠部分的面积为S ，直接写出S 与t 之间的函数关系式，并写出自变量t 的取值范围． 106．（2017黑龙江省龙东地区，第28题，10分）如图，矩形AOCB 的顶点A 、C 分别位于x 轴和y 轴的正半轴上，线段OA 、OC 的长度满足方程15130x y -+-=（OA ＞OC ），直线y =kx +b 分别与x 轴、y 轴交于M 、N 两点，将△BCN 沿直线BN 折叠，点C 恰好落在直线MN 上的点D 处，且tan ∠CBD =34．（1）求点B 的坐标；（2）求直线BN 的解析式；（3）将直线BN 以每秒1个单位长度的速度沿y 轴向下平移，求直线BN 扫过矩形AOCB 的面积S 关于运动的时间t （0＜t ≤13）的函数关系式．107．（2017黑龙江省龙东地区，第28题，10分）如图，矩形AOCB 的顶点A 、C 分别位于x 轴和y 轴的正半轴上，线段OA 、OC 的长度满足方程15130x y --=（OA ＞OC ），直线y =kx +b 分别与x 轴、y 轴交于M 、N 两点，将△BCN 沿直线BN 折叠，点C 恰好落在直线MN 上的点D 处，且tan ∠CBD =34．（1）求点B 的坐标；（2）求直线BN 的解析式；（3）将直线BN 以每秒1个单位长度的速度沿y 轴向下平移，求直线BN 扫过矩形AOCB 的面积S 关于运动的时间t （0＜t ≤13）的函数关系式．108．（2017湖南省娄底市，第26题，10分）如图，抛物线2y ax bx c =++与x 轴交于两点A （﹣4，0）和B （1，0），与y 轴交于点C （0，2），动点D 沿△ABC 的边AB 以每秒2个单位长度的速度由起点A 向终点B 运动，过点D 作x 轴的垂线，交△ABC 的另一边于点E ，将△ADE 沿DE 折叠，使点A 落在点F 处，设点D 的运动时间为t 秒．（1）求抛物线的解析式和对称轴；（2）是否存在某一时刻t ，使得△EFC 为直角三角形？若存在，求出t 的值；若不存在，请说明理由；（3）设四边形DECO 的面积为s ，求s 关于t 的函数表达式．109．（2016新疆）如图，▱ABCD 中，AB =2，AD =1，∠ADC =60°，将▱ABCD 沿过点A 的直线l 折叠，使点D 落到AB 边上的点D ′处，折痕交CD 边于点E ．（1）求证：四边形BCED ′是菱形；（2）若点P 时直线l 上的一个动点，请计算PD ′+PB 的最小值．。

中考数学专题训练：图形的折叠问题(附参考答案)

中考数学专题训练：图形的折叠问题（附参考答案）1．如图，在平面直角坐标系中，矩形ABCD的边AD＝5，OA∶OD＝1∶4，将矩形ABCD沿直线OE折叠到如图所示的位置，线段OD1恰好经过点B，点C落在y轴的点C1处，则点E的坐标是( )A．(1，2) B．(－1，2)C．(√5－1，2) D．(1－√5，2)2．如图，将矩形纸条ABCD折叠，折痕为EF，折叠后点C，D分别落在点C′，D′处，D′E与BF交于点G.已知∠BGD′＝30°，则∠α的度数是( )A．30°B．45°C．74°D．75°3．如图，在矩形ABCD中，AB＝2，BC＝2√5，E是BC的中点，将△ABE沿直线AE翻折，点B落在点F处，连接CF，则cos ∠ECF的值为( )A．23B．√104C．√53D．2√554．把一张矩形纸片ABCD按如图所示方法进行两次折叠，得到等腰直角三角形BEF.若BC＝1，则AB的长度为( )A．√2B．√2+12C．√5+12D．435．如图，在Rt△ABC中，∠ACB＝90°，AC＝4，BC＝3，点D，E分别在AB，AC 上，连接DE，将△ADE沿DE翻折，使点A的对应点F落在BC的延长线上．若FD平分∠EFB，则AD的长为( )A．259B．258C．157D．2076．如图，在Rt△ABC中，∠C＝90°，CA＝CB＝3，点D在边BC上．将△ACD沿AD折叠，使点C落在点C′处，连接BC′，则BC′的最小值为__________．7．如图，在Rt△ABC纸片中，∠ACB＝90°，CD是边AB上的中线，将△ACD沿CD折叠，当点A落在点A′处时，恰好CA′⊥AB.若BC＝2，则CA′＝_______．8．如图，点E在矩形ABCD的边CD上，将△ADE沿AE折叠，点D恰好落在边BC 上的点F处．若BC＝10，sin ∠AFB＝45，则DE＝_____．9．如图，在扇形AOB中，点C，D在AB⏜上，将CD⏜沿弦CD折叠后恰好与OA，OB 相切于点E，F.已知∠AOB＝120°，OA＝6，则EF⏜的度数为________；折痕CD 的长为_______．10．如图，在矩形ABCD中，AB＝5，AD＝4，M是边AB上一动点(不含端点)，将△ADM沿直线DM对折，得到△NDM.当射线CN交线段AB于点P时，连接DP，则△CDP的面积为______；DP的最大值为_______．11．如图，在矩形ABCD中，AB＝2，AD＝√7，动点P在矩形的边上沿B→C→D →A运动．当点P不与点A，B重合时，将△ABP沿AP对折，得到△AB′P，连接CB′，则在点P的运动过程中，线段CB′的最小值为_________．12．如图，DE平分等边三角形ABC的面积，折叠△BDE得到△FDE，AC分别与DF，EF相交于G，H两点．若DG＝m，EH＝n，用含m，n的式子表示GH的长是______．13．如图，在Rt△ABC中，∠ABC＝90°，CD平分∠ACB交AB于点D，过点D作DE∥BC交AC于点E，将△DEC沿DE折叠得到△DEF，DF交AC于点G.若AGGE ＝73，则tan A＝______．14．如图，在等边三角形ABC中，过点C作射线CD⊥BC，点M，N分别在边AB，BC上，将△ABC沿MN折叠，使点B落在射线CD上的点B′处，连接AB′，已知AB＝2.给出下列四个结论：①CN＋NB′为定值；②当BN＝2NC时，四边形BMB′N为菱形；③当点N与C重合时，∠AB′M＝18°；④当AB′最短时，MN＝7√21.20其中正确的结论是__________．(填序号)15．将一个矩形纸片OABC放置在平面直角坐标系中，点O(0，0)，点A(3，0)，点C(0，6)，点P在边OC上(点P不与点O，C重合)，折叠该纸片，使折痕所在的直线经过点P，并与x轴的正半轴相交于点Q，且∠OPQ＝30°，点O的对应点O′落在第一象限．设OQ＝t.(1)如图1，当t＝1时，求∠O′QA的大小和点O′的坐标；(2)如图2，若折叠后重合部分为四边形，O′Q，O′P分别与边AB相交于点E，F，试用含有t的式子表示O′E的长，并直接写出t的取值范围；(3)若折叠后重合部分的面积为3√3，则t的值可以是__________________________________________．(请直接写出两个不同．．．．的值即可)16．如图，已知△ABC，AB＝AC，BC＝16，AD⊥BC，∠ABC的平分线交AD于点E，且DE＝4.将∠C沿GM折叠使点C与点E恰好重合．下列结论正确的有________．(填序号)①BD＝8；②点E到AC的距离为3；③EM＝103；④EM∥AC.17．综合与实践课上，老师让同学们以“正方形的折叠”为主题开展数学活动，有一位同学操作过程如下：操作一：对折正方形纸片ABCD，使AD与BC重合，得到折痕EF，把纸片展平；操作二：在AD上选一点P，沿BP折叠，使点A落在正方形内部点M处，把纸片展平，连接PM，BM，延长PM交CD于点Q，连接BQ.(1)如图1，当点M在EF上时，∠EMB＝________；(填度数)(2)改变点P在AD上的位置(点P不与点A，D重合)如图2，判断∠MBQ与∠CBQ 的数量关系，并说明理由．参考答案1.D 2．D 3．C 4．A 5．D6. 3√2－3 7．2√3 8．5 9．60°4√6 10．10 2√511．－2 12．√m2+n2 13．3√7714．①②④15．(1)∠O′QA＝60°点O′的坐标为(32，√32)(2)O′E＝3t－6，其中t的取值范围是2<t<3 (3)3或103(答案不唯一，满足3≤t<2√3即可) 16．①④17．(1)30°(2)∠MBQ＝∠CBQ，理由略。

中考复习专题折叠压轴题(无答案)

中考专题：折叠问题折叠型问题是近年中考的热点问题，通常是把某个图形按照给定的条件折叠，通过折叠前后图形变换的相互关系来命题。

折叠型问题立意新颖，变幻巧妙，对培养学生的识图能力及灵活运用数学知识解决问题的能力非常有效。

图形折叠问题中题型的变化比较多，主要有以下几点：1．图形的翻折部分在折叠前和折叠后的形状、大小不变，是全等形；2．图形的翻折部分在折叠前和折叠后的位置关于折痕成轴对称；3．将长方形纸片折叠，三角形是否为等腰三角形；4．解决折叠问题时，要抓住图形之间最本质的位置关系，从而进一步发现其中的数量关系；5．充分挖掘图形的几何性质，将其中的基本的数量关系，用方程的形式表达出来，并迅速求解，这是解题时常用的方法之一。

折叠问题数学思想：(1)思考问题的逆向(反方向)，(2)从一般问题的特例人手，寻找问题解决的思路；(3)把一个复杂问题转化为解决过的基本问题的转化与化归思想；(4)归纳与分类的思想(把折纸中发现的诸多关系归纳出来，并进行分类)；(5)从变化中寻找不变性的思想.用“操作”、“观察”、“猜想”、“分析”的手段去感悟几何图形的性质是学习几何的方法。

折叠问题主要有以下题型：题型1：动手问题此类题目考查学生动手操作能力，它包括裁剪、折叠、拼图，它既考查学生的动手能力，又考查学生的想象能力，往往与面积、对称性质联系在一起．题型2：证明问题动手操作的证明问题，既体现此类题型的动手能力，又能利用几何图形的性质进行全等、相似等证明．题型3：探索性问题此类题目常涉及到画图、测量、猜想证明、归纳等问题，它与初中代数、几何均有联系．此类题目对于考查学生注重知识形成的过程，领会研究问题的方法有一定的作用，也符合新课改的教育理论。

典型例题一．折叠后求度数例1．将一张长方形纸片按如图所示的方式折叠，BC、BD为折痕，则∠CBD的度数为（）A．600B．750C．900D．950练习1．如图，把一个长方形纸片沿EF折叠后，点D、C分别落在D′、C′的位置，若∠EFB ＝65°，则∠AED′等于（）A．50°B．55°C．60°D．65°2．把一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G，D、C分别在M、N的位置上，若∠EFG=55°，则∠1=_______°，∠2=_______°A3. 用一条宽相等的足够长的纸条，打一个结，如图（1）所示，然后轻轻拉紧、压平就可以得到如图（2）所示的正五边形ABCDE ，其中∠BAC ＝度。

2022年九年级数学中考折叠问题--压轴题

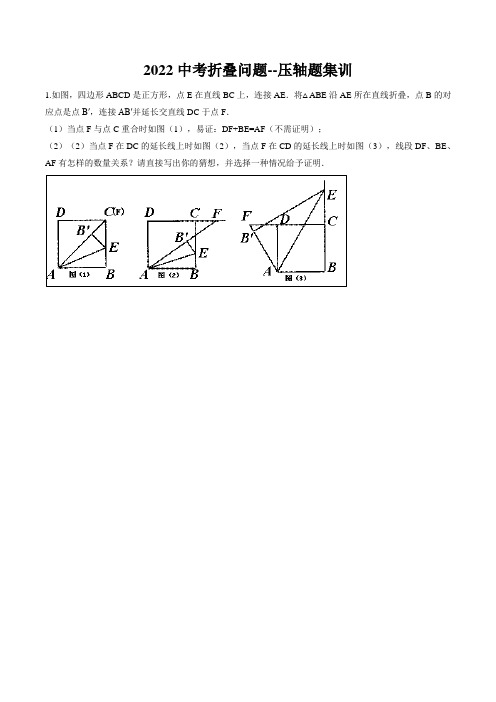
2022中考折叠问题--压轴题集训1.如图，四边形ABCD是正方形，点E在直线BC上，连接AE．将△ABE沿AE所在直线折叠，点B的对应点是点B′，连接AB′并延长交直线DC于点F．（1）当点F与点C重合时如图（1），易证：DF+BE=AF（不需证明）；（2）（2）当点F在DC的延长线上时如图（2），当点F在CD的延长线上时如图（3），线段DF、BE、AF有怎样的数量关系？请直接写出你的猜想，并选择一种情况给予证明．2、数学活动：在综合与实践活动课上，老师让同学们以“三角形纸片的折叠、旋转”为主题开展数学活动，探究线段长度的有关问题.动手操作：如图1，在直角三角形纸片ABC 中，∠BAC＝90°，AB＝6，AC＝8.将三角形纸片ABC 进行以下操作：第一步：折叠三角形纸片ABC 使点C 与点A 重合，然后展开铺平，得到折痕DE；第二步：将△ABC 沿折痕DE 展开，然后将△DEC 绕点D 逆时针方向旋转得到△DFG，点E，C 的对应点分别是点F，G，射线GF 与边AC 交于点M(点M 不与点A 重合)，与边AB交于点N，线段DG 与边AC 交于点P.数学思考：（1）求DC 的长；（2）在△DEC 绕点D 旋转的过程中，试判断MF 与ME 的数量关系，并证明你的结论；问题解决：（3）在△DEC 绕点D 旋转的过程中，探究下列问题：①如图2，当GF∥BC 时，求AM 的长；②如图3，当GF 经过点B 时，AM 的长为③当△DEC 绕点D 旋转至DE 平分∠FDG 的位置时，试在图4 中作出此时的△DFG 和射线GF，并直接写出AM 的长（要求：尺规作图，不写作法，保留作图痕迹，标记出所有相应的字母）3.如图，已知一个直角三角形纸片ACB ，其中∠ACB =90°，AC =4，BC =3，E 、F 分别是AC 、AB 边上点，连接EF ．（1）图①，若将纸片ACB 的一角沿EF 折叠，折叠后点A 落在AB 边上的点D 处，且使S 四边形ECBF =3S △EDF ，求AE 的长；（2）如图②，若将纸片ACB 的一角沿EF 折叠，折叠后点A 落在BC 边上的点M 处，且使M F ∥CA ． ①试判断四边形AE M F 的形状，并证明你的结论； ②求EF 的长；（3）如图③，若FE 的延长线与BC 的延长线交于点N ，CN =1，CE =47，求AFBF 的值．4．如图1，四边形的对角线相交于点，，，，.（1）填空：与的数量关系为；（2）求的值；（3）将沿翻折，得到（如图2），连接，与相交于点.若，求的长.5.Rt△ABC中，∠ACB＝90°，AC＝3，BC＝7，点P是边AC上不与点A、C重合的一点，作PD∥BC交AB 边于点D．（1）如图1，将△APD沿直线AB翻折，得到△AP'D，作AE∥PD．求证：AE＝ED；（2）将△APD绕点A顺时针旋转，得到△AP'D'，点P、D的对应点分别为点P'、D'，①如图2，当点D'在△ABC内部时，连接P′C和D'B，求证：△AP'C∽△AD'B；②如果AP：PC＝5：1，连接DD'，且DD'＝√2AD，那么请直接写出点D'到直线BC的距离．6．如图1和图2，AB是⊙O的直径，AB＝10，C是⊙O上的一点，将沿弦BC翻折，交AB于点D．（1）若点D与圆心O重合，直接写出∠B的度数；（2）设CD交⊙O于点E，若CE平分∠ACB，①求证：△BDE是等腰三角形；②求△BDE的面积；（3）将图1中的沿直径AB翻折，得到图2，若点F恰好是翻折后的的中点，直接写出∠B的度数．7．如图1，AB是⊙O的直径，AB＝10，C是⊙O上的一点，将弧BC沿弦BC翻折，交AB于点D，连接CD并延长，交⊙O于点E，连接BE．（1）当AD＝2时，BE的长是．（2）当点D位于线段OA上时（不与点A重合），设∠ABC＝a，则a的取值范围是．（3）当∠ABC＝15°时，点D和点O的距离是．（4）如图2，设所在圆的圆心是O′，当BE与⊙O′相切时，求BE的长．8．如图1，将长为10的线段OA绕点O旋转90°得到OB，点A的运动轨迹为，P是半径OB上一动点，Q是上的一动点，连接PQ．（1）当∠POQ＝度时，PQ有最大值，最大值为．（2）如图2，若P是OB中点，且QP⊥OB于点P，求的长；（3）如图3，将扇形AOB沿折痕AP折叠，使点B的对应点B′恰好落在AO的延长线上，求阴影部分面积．（4）如图4，将扇形OAB沿PQ折叠，使折叠后的弧QB′恰好与半径OA相切，切点为C，若OP＝6，求点O到折痕PQ的距离．9．如图1，半圆的直径AB长为6，点C在AB上，以BC为一边向半圆内部作一正方形BCDE，连接AD 并延长交半圆于F点，连接BF．设BC的长为x（0＜x＜3），AF的长为y，（1）求y与x的函数关系式；（2）当x＝2时，①求BF的长；②如图2，若将弧AF沿直线AF翻折与直径AB交于点G，试求AG的长．10.如图，四边形ABCD为一个矩形纸片，AB＝3，BC＝2，动点P自D点出发沿DC方向运动至C点后停止，△ADP以直线AP为轴翻折，点D落到点D1的位置，设DP＝x，△AD1P与原纸片重叠部分的面积为y.(1)如图1，当x为何值时，直线AD1过点C?(2)如图2，当x为何值时，直线AD1过BC的中点E?(3)求出y与x的函数表达式．11.如图1，将△ABC纸片沿中位线EH折叠，使点A的对称点D落在BC边上，再将纸片分别沿等腰△BED和等腰△DHC的底边上的高线EF，HG折叠，折叠后的三个三角形拼合形成一个矩形．类似地，对多边形进行折叠，若翻折后的图形恰能拼成一个无缝隙、无重叠的矩形，这样的矩形称为叠合矩形．(1)将▱ABCD纸片按图2的方式折叠成一个叠合矩形AEFG，则操作形成的折痕分别是线段，；S矩形AEFG∶S▱ABCD＝；(2)▱ABCD纸片还可以按图3的方式折叠成一个叠合矩形EFGH，若EF＝5，EH＝12，求AD的长；(3)如图4，四边形ABCD纸片满足AD∥BC，AD<BC，AB⊥BC，AB＝8，CD＝10.小明把该纸片折叠，得到叠合正方形．请你帮助画出叠合正方形的示意图，并求出AD，BC的长．12.早在三千多年前，我国周朝数学家商高就提出：将一根直尺折成一个直角，如果勾等于三，股等于四，那么弦就等于五，即“勾三，股四，弦五”．它被记载于我国古代著名数学著作《周髀算经》中．为了方便，在本题中，我们把三边的比为3∶4∶5的三角形称为(3，4，5)型三角形．例如：三边长分别为9，12，15或32，42，52的三角形就是(3，4，5)型三角形．用矩形纸片按下面的操作方法可以折出这种类型的三角形．实践操作如图1，在矩形纸片ABCD中，AD＝8 cm，AB＝12 cm.第一步：如图2，将图1中的矩形纸片ABCD沿过点A的直线折叠，使点D落在AB上的点E处，折痕为AF，再沿EF折叠，然后把纸片展平．第二步：如图3，将图2中的矩形纸片再次折叠，使点D与点F重合，折痕为GH，然后展平，隐去AF.第三步：如图4，将图3中的矩形纸片沿AH折叠，得到△AD′H，再沿AD′折叠，折痕为AM，AM 与折痕EF交于点N，然后展平．问题解决(1)请在图2中证明四边形AEFD是正方形；(2)请在图4中判断NF与ND′的数量关系，并加以证明；(3)请在图4中证明△AEN是(3，4，5)型三角形．探索发现(4)在不添加字母的情况下，图4中还有哪些三角形是(3，4，5)型三角形？请找出并直接写出它们的名称．。

中考数学压轴题---《与折叠有关的计算》题型讲解

中考数学压轴题---《与折叠有关的计算》题型讲解1、（2020•青岛）如图，将矩形ABCD折叠，使点C和点A重合，折痕为EF，EF与AC交于点O．若AE＝5，BF＝3，则AO的长为（）A．B．C．2D．4【答案】C【解答】解：∵矩形ABCD，∴AD∥BC，AD＝BC，AB＝CD，∴∠EFC＝∠AEF，由折叠得，∠EFC＝∠AFE，∴∠AFE＝∠AEF，∴AE＝AF＝5，由折叠得，FC＝AF，OA＝OC，∴BC＝3+5＝8，在Rt△ABF中，AB＝＝4，在Rt△ABC中，AC＝＝4，∴OA＝OC＝2，故选：C．2、如图，在△ABC纸片中，∠B＝30°，AB＝AC＝，点D在AB上运动，将纸片沿CD折叠，得到点B的对应点B′（D在A点时，点D的对应点是本身），则折叠过程对应点B′的路径长是（）A．3B．6C．πD．2π【答案】C【解答】解：过点A作AE⊥BC于点E，∵∠B＝30°，AB＝AC＝，∴BE＝AB cos∠B＝，∴BC＝2BE＝3，由折叠的性质可得：∠BCB''＝2∠ACB＝60°，∴B′的路径长＝＝π．故选：C．3、（2022•宜宾）如图，在矩形纸片ABCD中，AB＝5，BC＝3，将△BCD沿BD折叠到△BED位置，DE交AB于点F，则cos∠ADF的值为（）A．B．C．D．【答案】C【解答】解：∵四边形ABCD是矩形，∴∠A＝90°，AB∥CD，AD＝BC＝3，AB＝CD＝5，∴∠BDC＝∠DBF，由折叠的性质可得∠BDC＝∠BDF，∴∠BDF＝∠DBF，∴BF＝DF，设BF＝x，则DF＝x，AF＝5﹣x，在Rt△ADF中，32+（5﹣x）2＝x2，∴x＝，∴cos∠ADF＝，故选：C．4、（2022•毕节市）矩形纸片ABCD中，E为BC的中点，连接AE，将△ABE沿AE折叠得到△AFE，连接CF．若AB＝4，BC＝6，则CF的长是（）A．3B．C．D．【答案】D【解答】解：连接BF，交AE于O点，∵将△ABE沿AE折叠得到△AFE，∴BE＝EF，∠AEB＝∠AEF，AE垂直平分BF，∵点E为BC的中点，∴BE＝CE＝EF＝3，∴∠EFC＝∠ECF，∵∠BEF＝∠ECF+∠EFC，∴∠AEB＝∠ECF，∴AE∥CF，∴∠BFC＝∠BOE＝90°，在Rt△ABE中，由勾股定理得，AE＝＝，∴BO＝＝，∴BF＝2BO＝，在Rt△BCF中，由勾股定理得，CF＝＝＝，故选：D．5、（2022•湖州）如图，已知BD是矩形ABCD的对角线，AB＝6，BC＝8，点E，F分别在边AD，BC上，连结BE，DF．将△ABE沿BE翻折，将△DCF沿DF翻折，若翻折后，点A，C分别落在对角线BD上的点G，H处，连结GF．则下列结论不正确的是（）A．BD＝10B．HG＝2C．EG∥FH D．GF⊥BC 【答案】D【解答】解：∵四边形ABCD是矩形，∴∠A＝90°，BC＝AD，∵AB＝6，BC＝8，∴BD＝＝＝10，故A选项不符合题意；∵将△ABE沿BE翻折，将△DCF沿DF翻折，点A，C分别落在对角线BD上的点G，H处，∴AB＝BG＝6，CD＝DH＝6，∴GH＝BG+DH﹣BD＝6+6﹣10＝2，故B选项不符合题意；∵四边形ABCD是矩形，∴∠A＝∠C＝90°，∵将△ABE沿BE翻折，将△DCF沿DF翻折，点A，C分别落在对角线BD上的点G，H处，∴∠A＝∠BGE＝∠C＝∠DHF＝90°，∴EG∥FH．故C选项不符合题意；∵GH＝2，∴BH＝DG＝BG﹣GH＝6﹣2＝4，设FC＝HF＝x，则BF＝8﹣x，∴x2+42＝（8﹣x）2，∴x＝3，∴CF＝3，∴，又∵，∴，若GF⊥BC，则GF∥CD，∴，故D选项符合题意．故选：D．6、（2021•天津）如图，在△ABC中，∠BAC＝120°，将△ABC绕点C逆时针旋转得到△DEC，点A，B的对应点分别为D，E，连接AD．当点A，D，E在同一条直线上时，下列结论一定正确的是（）A．∠ABC＝∠ADC B．CB＝CD C．DE+DC＝BC D．AB∥CD【答案】D【解答】解：由旋转的性质得出CD＝CA，∠EDC＝∠BAC＝120°，∵点A，D，E在同一条直线上，∴∠ADC＝60°，∴△ADC为等边三角形，∴∠DAC＝60°，∴∠BAD＝60°＝∠ADC，∴AB∥CD，故选：D．7、（2022•滨州）正方形ABCD的对角线相交于点O（如图1），如果∠BOC绕点O按顺时针方向旋转，其两边分别与边AB、BC相交于点E、F（如图2），连接EF，那么在点E由B到A的过程中，线段EF的中点G经过的路线是（）A．线段B．圆弧C．折线D．波浪线【答案】A【解答】解：建立如图平面直角坐标系，设正方形ABCD的边长为1，∵四边形ABCD是正方形，∴∠OAE＝∠OBF＝45°，OA＝OB，∵∠AOB＝∠EOF＝90°，∴∠AOE＝∠BOF，∴△AOE≌△BOF（ASA），∴AE＝BF，设AE＝BF＝a，则F（a，0），E（0，1﹣a），∵EG＝FG，∴G（a，﹣a），∴点G在直线y＝﹣x+上运动，∴点G的运动轨迹是线段，故选：A．8、（2022•眉山）如图，四边形ABCD为正方形，将△EDC绕点C逆时针旋转90°至△HBC，点D，B，H在同一直线上，HE与AB交于点G，延长HE与CD的延长线交于点F，HB＝2，HG＝3．以下结论：①∠EDC＝135°；②EC2＝CD•CF；③HG＝EF；④sin∠CED＝．其中正确结论的个数为（）A．1个B．2个C．3个D．4个【答案】D【解答】解：∵△EDC旋转得到△HBC，∴∠EDC＝∠HBC，∵ABCD为正方形，D，B，H在同一直线上，∴∠HBC＝180°﹣45°＝135°，∴∠EDC＝135°，故①正确；∵△EDC旋转得到△HBC，∴EC＝HC，∠ECH＝90°，∴∠HEC＝45°，∴∠FEC＝180°﹣45°＝135°，∵∠ECD＝∠ECF，∴△EFC∽△DEC，∴，∴EC2＝CD•CF，故②正确；设正方形边长为a，∵∠GHB+∠BHC＝45°，∠GHB+∠HGB＝45°，∴∠BHC＝∠HGB＝∠DEC，∵∠GBH＝∠EDC＝135°，∴△GBH∽△EDC，∴，即，∵△HEC是等腰直角三角形，∴，∵∠GHB＝∠FHD，∠GBH＝∠HDF＝135°，∴△HBG∽△HDF，∴，即，解得：EF＝3，∵HG＝3，∴HG＝EF，故③正确；过点E作EM⊥FD交FD于点M，∴∠EDM＝45°，∵ED＝HB＝2，∴，∴，∵∠DEC+∠DCE＝45°，∠EFC+∠DCE＝45°，∴∠DEC＝∠EFC，∴，故④正确综上所述：正确结论有4个，故选：D．9、（2022•单县一模）如图，将边长为8cm的正方形ABCD折叠，使点D落在AB边的中点E处，折痕为FH，点C落在Q处，EQ与BC交于点G，则△EBG 的周长是cm．【答案】16【解答】解：设EF＝x，∵EF＝DF，∴DF＝x，则AF＝8﹣x；而AE＝4，由勾股定理得：x2＝42+（8﹣x）2，解得：x＝5；AF＝8﹣5＝3；∠GEF＝∠D＝90°，∠A＝∠B＝90°，∴∠AEF+∠AFE＝∠AEF+∠BEG，∴∠AFE＝∠BEG；∴△AEF∽△BGE，∴＝＝，∴EG＝＝，BG＝＝，∴△EBG的周长＝++4＝16．故答案为16．10、如图，在矩形ABCD中，AB＝3，BC＝5，点P在CD边上，联结AP．如果将△ADP沿直线AP翻折，点D恰好落在线段BC上，那么的值为．【答案】【解答】解：如图：∵将△ADP沿直线AP翻折，点D恰好落在线段BC上的D'，∴AD'＝AD＝5，PD＝PD'，∠AD'P＝∠D＝90°，在Rt△ABD'中，BD'＝＝＝4，∴CD'＝BC﹣BD'＝5﹣4＝1，设CP＝x，则PD＝PD'＝3﹣x，在Rt△CPD'中，CD'2+CP2＝PD'2，∴12+x2＝（3﹣x）2，解得x＝，∴CP＝，PD＝，∴S△ADP＝AD•PD＝×5×＝，S四边形ABCP＝S矩形ABCD﹣S△ADP＝3×5﹣＝，∴＝＝，故答案为：．11、（2022•铜仁市）如图，在边长为2的正方形ABCD中，点E为AD的中点，将△CDE沿CE翻折得△CME，点M落在四边形ABCE内．点N为线段CE 上的动点，过点N作NP∥EM交MC于点P，则MN+NP的最小值为．【答案】【解答】解：作点P关于CE的对称点P′，由折叠的性质知CE是∠DCM的平分线，∴点P′在CD上，过点M作MF⊥CD于F，交CE于点G，∵MN+NP＝MN+NP′≥MF，∴MN+NP的最小值为MF的长，连接DG，DM，由折叠的性质知CE为线段DM的垂直平分线，∵AD＝CD＝2，DE＝1，∴CE＝＝，∵CE×DO＝CD×DE，∴DO＝，∴EO＝，∵MF⊥CD，∠EDC＝90°，∴DE∥MF，∴∠EDO＝∠GMO，∵CE为线段DM的垂直平分线，∴DO＝OM，∠DOE＝∠MOG＝90°，∴△DOE≌△MOG，∴DE＝GM，∴四边形DEMG为平行四边形，∵∠MOG＝90°，∴四边形DEMG为菱形，∴EG＝2OE＝，GM＝DE＝1，∴CG＝，∵DE∥MF，即DE∥GF，∴△CFG∽△CDE，∴，即，∴FG＝，∴MF＝1+＝，∴MN+NP的最小值为；方法二：同理方法一得出MN+NP的最小值为MF的长，DO＝，∴OC＝＝，DM＝2DO＝，∵S△CDM＝DM•OC＝CD•MF，即×＝2×MF，∴MF＝，∴MN+NP的最小值为；故答案为：。

中考数学中考最后压轴题训练---折叠旋转问题

一．折叠类【1 】1. （13江苏徐州卷）在平面直角坐标系中,已知矩形ABCD 中,边2AB =,边1AD =,且AB .AD 分离在x 轴.y 轴的正半轴上,点A 与坐标原点重合．将矩形折叠,使点A 落在边DC 上,设点A '是点A 落在边DC 上的对应点．（1）当矩形ABCD 沿直线12y x b =-+折叠时（如图1）,求点A '的坐标和b 的值;（2）当矩形ABCD 沿直线y kx b =+折叠时,①求点A '的坐标（用k 暗示）;求出k 和b 之间的关系式; ② 假如我们把折痕地点的直线与矩形的地位分为如图2.3.4所示的三种情况,请你分离写出每种情况时k 的取值规模．（将答案直接填在每种情况下的横线上）（——当如图1.2折叠时,求D A '的取值规模？）k 的取值规模是; k 的取值规模是;k 的取值规模是;[解] （1）如图答5,设直线12y x b =-+与OD 交于点E ,与OB 交于点F ,贯穿连接A O ',则OE = b ,OF = 2b ,设点A '的坐标为（a ,1）因为90DOA A OF ''∠+∠=︒,90OFE A OF '∠+∠=︒, 所以DOA OFE '∠=∠,所以△DOA '∽△OFE ．所以DA DO OE OF '=,即12a b b =,所以12a =．所以点A '的坐标为（12,1）．贯穿连接A E ',则A E OE b '==．在R t △DEA '中,依据勾股定理有222A E A D DE ''=+ ,即2221()(1)2b b =+-,解得58b =．（2）如图答6,设直线y kx b =+与OD 交于点E ,与OB 交于点F ,贯穿连接A O ',则OE = b ,bOF k =-,设点A '的坐标为（a ,1）．因为90DOA A OF ''∠+∠=︒,90OFE A OF '∠+∠=︒．所以DOA OFE '∠=∠,所以△DOA '∽△OFE ．所以DA DOOE OF'=,即1a b b k=-,所以a k =-．所以A '点的坐标为（k -,1）．贯穿连接A E ',在Rt △DEA '中,DA k '=-,1DE b =-,A E b '=．因为222A E A D DE ''=+,所以222()(1)b k b =-+-．所以212k b +=．在图答6和图答7中求解参照给分．（3）图13﹣2中：21k -≤≤-; 图13﹣3中：1-≤k≤2-+图13﹣4中：20k -≤[点评]这是一道有关折叠的问题,重要考核一次函数.四边形.类似形等常识,试题中贯串了方程思惟和数形结合的思惟,请留意领会.2. （13广西钦州卷）如图,在平面直角坐标系中,矩形OABC 的极点O 为原点,E 为AB 上一点,把CBE △沿CE 折叠,使点B 正好落在OA 边上的点D 处,点AD ，的坐标分离为(50)，和(30)，．（1）求点C的坐标;（2）求DE地点直线的解析式;（3）设过点C的抛物线22(0)y x c b=+<与直线BC的另一个交点为M,问在该抛物线上是否消失点G,使得CMG△为等边三角形．若消失,解释来由．[解] （1）依据题意,得53CD CB OA OD====，,90COD=∠,4OC∴=．∴点C的坐标是(04)，;（2）4AB OC==,设AE x=,则4DE BE x==-,532AD OA OD=-=-=,在Rt DEA△中,222DE AD AE=+．222(4)2x x∴-=+．解之,得32x=,即点E的坐标是352⎛⎫⎪⎝⎭，．设DE地点直线的解析式为y kx b=+,30352k bk b+=⎧⎪∴⎨+=⎪⎩，，解之,得3494kb⎧=⎪⎪⎨⎪=-⎪⎩，．DE∴地点直线的解析式为3944y x=-;（3）点(04)C ，在抛物线22y x c =++上,4c ∴=．即抛物线为224y x =++．假设在抛物线224y x =++上消失点G ,使得CMG △为等边三角形,依据抛物线的对称性及等边三角形的性质,得点G 必定在该抛物线的极点上．设点G 的坐标为()m n ，,224m ∴=-=-⨯,22424)323428b n ⨯⨯--==⨯,即点G 的坐标为232348b ⎛⎫-- ⎪ ⎪⎝⎭，．设对称轴x =CB 交于点F ,与x 轴交于点H ．则点F 的坐标为4⎛⎫⎪⎪⎝⎭． 00b m <∴>，,点G 在y 轴的右侧,CF m ==2232334488b b FH FG -==-=，．2CM CG CF ===∴在Rt CGF △中,222CG CF FG =+,222238b ⎛⎛⎛⎫=+ ⎪ ⎝⎭⎝⎭⎝⎭．解之,得2(0)b b =-<．．42m ∴=-=,2323582b n -==． ∴点G 的坐标为522⎛⎫⎪ ⎪⎝⎭，．∴在抛物线224(0)y x b =++<上消失点G 52⎫⎪⎪⎝⎭，,使得CMG △为等边三角形．[点评]这是一道以折叠为布景的分解型压轴题,分解性较强,这类试题在各地中考题中消失的频率不小,本题中第1.2小题只需依据折叠的基赋性质结合函数常识即可得解,第3小题是探讨型问题,是一道检测学生才能的好题.3（13湖北咸宁卷）如图,OABC 是一张放在平面直角坐标系中的矩形纸片,O 为原点,点A 在x 轴的正半轴上,点C 在y 轴的正半轴上,53OA OC ==，．（1）在AB 边上取一点D ,将纸片沿OD 翻折,使点A 落在BC 边上的点E 处,求点D ,E 的坐标;（2）若过点D E ，的抛物线与x 轴订交于点(50)F -，,求抛物线的解析式和对称轴方程; （3）若（2）中的抛物线与y 轴交于点H ,在抛物线上是否消失点P ,使PFH △的心坎在坐标轴．．．上？若消失,求出点P 的坐标,若不消失,请解释来由．（4）若（2）中的抛物线与y 轴订交于点H ,点Q 在线段OD 上移动,作直线HQ ,当点Q 移动到什么地位时,O D ，两点到直线HQ 的距离之和最大？请直接写出此时点Q 的坐标及直线HQ 的解析式．4. .(14台州市)24．如图,四边形OABC坐标系中的矩形纸片,点A 在x 轴上,点C 在y 轴上,折叠,使点B 落在边OA 的点D 处．已知折叠CE =3tan 4EDA ∠=．（1）断定OCD △与ADE △是否类似？请解释来由; （2）求直线CE 与x 轴交点P 的坐标;题）（3）是否消失过点D 的直线l ,使直线l .直线CE 与x 轴所围成的三角形和直线l .直线CE 与y 轴所围成的三角形类似？假如消失,请直接写出其解析式并画出响应的直线;假如不消失,请解释来由．解：（1）OCD △与ADE △类似．来由如下：由折叠知,90CDE B ∠=∠=°,1290∠+∠=∴°,13902 3.∠+∠=∴∠=∠，又90COD DAE ∠=∠=∵°,OCD ADE ∴△∽△．（2）3tan 4AE EDA AD ∠==∵,∴设3AE t =,则4AD t =．由勾股定理得5DE t =．358OC AB AE EB AE DE t t t ==+=+=+=∴．由（1）OCD ADE △∽△,得OC CDAD DE=, 845t CDt t=∴, 10CD t =∴．在DCE △中,222CD DE CE +=∵,222(10)(5)t t +=∴,解得1t =．83OC AE ==∴，,点C 的坐标为(08)，, 点E 的坐标为(103)，, 设直线CE 的解析式为y kx b =+,1038k b b +=⎧⎨=⎩，∴，解得128k b ⎧=-⎪⎨⎪=⎩，，（第24题图2）182y x =-+∴,则点P 的坐标为(160)，．（3）知足前提的直线l 有2条：212y x =-+,212y x =-．如图2：精确画出两条直线． 5. (14宁德市)26. 已知：矩形纸片ABCD 中,26AB =厘米,18.5BC =厘米,点E 在AD 上,且6AE =厘米,点P 是AB 边上一动点．按如下操纵：步调一,折叠纸片,使点P 与点E 重合,睁开纸片得折痕MN （如图1所示）; 步调二,过点P 作PT AB ⊥,交MN 地点的直线于点Q ,衔接QE （如图2所示）（1）无论点P 在AB 边上任何地位,都有PQ QE （填“>”.“=”.“<”号）; （2）如图3所示,将纸片ABCD 放在直角坐标系中,按上述步调一.二进行操纵： ①当点P 在A 点时,PT 与MN 交于点11Q Q ，点的坐标是（,）; ②当6PA =厘米时,PT 与MN 交于点22Q Q ，点的坐标是（,）;③当12PA =厘米时,在图3中画出MN PT ，（不请求写画法）,并求出MN 与PT 的交点3Q 的坐标;（3）点P 在活动进程,PT 与MN 形成一系列的交点123Q Q Q ，，，…不雅察.猜测：浩瀚的交点形成的图象是什么？并直接写出该图象的函数表达式．解: （1）PQ QE =．C B图1图3CE图2（2）①(03)，;②(66)，． ③绘图,如图所示．解：办法一：设MN 与EP 交于点F ．在Rt APE △中,PE ==∵12PF PE ==∴390Q PF EPA ∠+∠=∵°,90AEP EPA ∠+∠=°,3Q PF AEP ∠=∠∴．又390EAP Q FP ∠=∠=∵°, 3Q PF PEA ∴△∽△．3Q P PFPE EA=∴． 315PE PFQ P EA==·∴． 3(1215)Q ∴，．办法二：过点E 作3EG Q P ⊥,垂足为G ,则四边形APGE 是矩形．6GP =∴,12EG =．设3Q G x =,则336Q E Q P x ==+．在3Rt Q EG △中,22233EQ EG Q G =+∵． 222(6)12x x +=+∴．9x =∴．3125Q P =∴． 3(1215)Q ∴，．（3）这些点形成的图象是一段抛物线．函数关系式：213(026)12y x x =+≤≤． 6. (14日照市)24. 如图,直线EF 将矩形纸片ABCD 分成面积相等的两部分,E .F 分离与BC 交于点E ,与AD 交于点F （E ,F 不与极点重合）,设AB=a,AD=b,BE=x ．(Ⅰ)求证：AF=EC ;(Ⅱ)用铰剪将纸片沿直线EF 剪开后,再将纸片ABEF 沿AB 对称翻折,然后平移拼接在梯形ECDF 的下方,使一底边重合,直腰落在边DC 的延伸线上,拼接后,下方的梯形记作EE′B′C .（1）求出直线EE ′分离经由原矩形的极点A 和极点D 时,所对应的 x ︰b 的值;（2）在直线EE ′经由原矩形的一个极点的情况下,衔接B E′,直线BE ′与EF 是否平行？你若认为平行,请赐与证实;你若认为不服行,请你解释当a 与b 知足什么关系时,它们垂直？解: (Ⅰ)证实：∵AB=a ,AD=b ,BE=x ,S 梯形ABEF =S 梯形CDFE ． ∴21a (x +AF )=21a (EC +b -AF ), ∴2AF =EC +(b -x )．又∵EC ＝b -x ,∴2AF =2EC ,即AF=EC ;(Ⅱ)（1）当直线EE′经由原矩形的极点D 时,如图（一）, ∵EC ∥E ′B ′, ∴B E EC ''=BD DC'. 由EC ＝b -x ,E ′B ′=EB =x ,DB ′=DC +CB ′=2a , 得aax x b 2=-, ∴x ︰b =32;当直线E′E 经由原矩形的极点A 时,如图（二）, 在梯形AE ′B ′D 中,∵EC ∥E ′B ′,点C 是DB ′的中点, ∴CE =21(AD + E ′B ′),即b -x ＝21（b ＋x ）, ∴x ︰b =31．(2) 如图（一）, 当直线EE′ 经由原矩形的极点D 时,BE ′∥EF ．证实：衔接BF ． ∵FD ∥BE , FD =BE ,∴四边形FBED 是平行四边形, ∴FB ∥DE , FB =DE ,又∵EC ∥E ′B ′, 点C 是DB ′的中点, ∴DE =EE ′,∴FB ∥EE ′, FB = EE ′,∴四边形BE ′EF 是平行四边形 ∴BE ′∥EF ．如图（二）, 当直线EE′ 经由原矩形的极点A 时,显然BE ′与EF 不服行,设直线EF 与BE′交于点G .过点E ′作E ′M ⊥BC 于M , 则E ′M =a .．∵x ︰b =31, ∴EM =31BC =31b ．若BE′与EF 垂直,则有∠GBE +∠BEG =90°,又∵∠BEG ＝∠FEC ＝∠MEE ′, ∠MEE ′+∠ME ′E =90°, ∴∠GBE =∠ME ′E .在R t △BME ′中,tan ∠E ′BM = tan ∠GBE =BM M E '=b a32．在R t △EME ′中,tan ∠ME ′E =M E EM '=ab31,∴b a 32＝a b 31．又∵a ＞0,b ＞0,=ba32, ∴当=ba32时,BE′与EF 垂直. 7. (14荆门市)28. 如图1,在平面直角坐标系中,有一张矩形纸片OABC ,已知O (0,0),A (4,0),C (0,3),点P 是OA 边上的动点(与点O .A 不重合)．现将△P AB 沿PB 翻折,得到△PDB ;再在OC 边上拔取恰当的点E ,将△POE 沿PE 翻折,得到△PFE ,并使直线PD .PF 重合．(1)设P (x ,0),E (0,y ),求y 关于x 的函数关系式,并求y 的最大值;(2)如图2,若翻折后点D 落在BC 边上,求过点P .B .E 的抛物线的函数关系式;(3)在(2)的情况下,在该抛物线上是否消失点Q ,使△PEQ 是以PE 为直角边的直角三角形？若不消失,解释来由;若消失,求出点Q 的坐标．解：(1)由已知PB 等分∠APD ,PE 等分∠OPF ,且PD .PF 重合,则∠BPE =90°．∴∠OPE ＋∠APB =90°．又∠APB ＋∠ABP =90°,∴∠OPE =∠PBA ． ∴Rt △POE ∽Rt △BP A ． ∴PO BA OE AP =．即34x y x =-．∴y =2114(4)333x x x x -=-+(0＜x ＜4)．且当x =2时,y 有最大值13．图2图1(2)由已知,△P AB .△POE 均为等腰三角形,可得P (1,0),E (0,1),B (4,3)．设过此三点的抛物线为y =ax 2＋bx ＋c ,则1,0,164 3.c a b c a b c =⎧⎪++=⎨⎪++=⎩∴1,23,21.a b c ⎧=⎪⎪⎪=-⎨⎪=⎪⎪⎩y =213122x x -+． (3)由(2)知∠EPB =90°,即点Q 与点B 重应时知足前提．直线PB 为y =x －1,与y 轴交于点(0,－1)．将PB 向上平移2个单位则过点E (0,1), ∴该直线为y =x ＋1．由21,131,22y x y x x =+⎧⎪⎨=-+⎪⎩得5,6.x y =⎧⎨=⎩∴Q(5,6)．故该抛物线上消失两点Q (4,3).(5,6)知足前提．8. (14湖北省孝感市)25.在我们进修过的数学教科书中,有一个数学活动,其具体操纵进程是：第一步：半数矩形纸片ABCD ,使AD 与BC 重合,得到折痕EF ,把纸片睁开（如图1）; 第二步：再一次折叠纸片,使点A 落在EF 上,并使折痕经由点B ,得到折痕BM ,同时得到线段BN （如图2）.（图1）（图2）请解答以下问题：（1）如图2,若延伸MN 交BC 于P ,△BMP 是什么三角形？请证实你的结论．（2）在图2中,若AB=a ,BC=b,a .b 知足什么关系,才干在矩形纸片ABCD 上剪出相符（1）中结论的三角形纸片BMP ？（3）设矩形ABCD 的边AB =2,BC =4,并树立如图3所示的直角坐标系. 设直线BM '为y kx =,当M BC '∠=60°时,求k 的值.此时,将△ABM ′沿BM ′折叠,点A 是否落在EF 上（E.F 分离为AB.CD 中点）？为什么？（图3）解：（1）△BMP 是等边三角形. 证实：贯穿连接AN ∵EF 垂直等分AB ∴AN = BN由折叠知 AB = BN∴AN = AB = BN ∴△ABN 为等边三角形 ∴∠ABN =60°∴∠PBN =30°又∵∠ABM =∠NBM =30°,∠BNM =∠A =90° ∴∠BPN =60°∠MBP =∠MBN +∠PBN =60° ∴∠BMP =60°∴∠MBP =∠BMP =∠BPM =60° ∴△BMP 为等边三角形 .（2）要在矩形纸片ABCD 上剪出等边△BMP ,则BC ≥BP在Rt △BNP 中, BN = BA =a ,∠PBN =30°∴BP =cos30a∴b ≥cos30a ∴a ≤23b .∴当a ≤23b 时,在矩形上能剪出如许的等边△BMP . （3）∵∠M ′BC =60°∴∠ABM ′=90°－60°=30°在Rt △ABM ′中,tan ∠ABM ′=AM AB '∴tan30°=2AM '∴AM ′∴M ′,2).代入y =kx 中 ,得k设△ABM ′沿BM ′折叠后,点A 落在矩形ABCD 内的点为A ' 过A '作A 'H ⊥BC 交BC 于H .∵△A 'BM ′≌△ABM ′∴A BM ''∠=ABM '∠=30°,A 'B = AB =2∴A BH MBH''∠=∠－A BM ''∠=30°. 在Rt △A 'BH 中,A 'H =12A 'B =1 ,BH=3 ∴()3,1A '∴A '落在EF 上.(图2) (图3)9. (14广东省茂名市)25. 如图,已知平面直角坐标系xoy 中,有一矩形纸片OABC ,O 为坐标原点,AB x ∥轴, B （3）,现将纸片按如图折叠,AD ,DE 为折痕,30OAD ∠=︒．折叠后,点O 落在点1O ,点C 落在点1C ,并且1DO 与1DC 在统一向线上．（1）求折痕AD 地点直线的解析式; （2）求经由三点O ,1C ,C 的抛物线的解析式;（3）若⊙P 的半径为R ,圆心P 在（2）的抛物线上活动, ⊙P 与两坐标轴都相切时,求⊙P 半径R 的值．解：(第25题图)C DOA BEO 1C 1 xy30OA OAD =∠=︒．∴tan 3013OD OA =︒==,∴(()010A D ，，．设直线AD 的解析式为y kx b =+．把A ,D 坐标代入上式得：b k b ⎧=⎪⎨+=⎪⎩,解得：k b ⎧=⎪⎨=⎪⎩,折痕AD地点的直线的解析式是y = （2）过1C 作1C F OC ⊥于点F ,由已知得160ADO ADO ∠=∠=︒,∴160C DC ∠=︒．又DC ＝3－1＝2,∴12DC DC ==．∴在1Rt C DF △中,111sin 2sin60C F DC C DF =∠=⨯︒1112DF DC ==,∴(1C ,罢了知()3,0C ．法一：设经由三点O ,C 1,C 的抛物线的解析式是()3y ax x =-点(12C 在抛物线上,∴()223a -=∴a =∴()23222y x x x x =--=-+为所求法二：设经由三点O ,C 1,C 的抛物线的解析式是2,(0)y ax bx c a =++≠．把O ,C 1,C 的坐标代入上式得:042930c a b c a b c =⎧⎪++=⎨⎪++=⎩解得0a b c ⎧=⎪⎪=⎨⎪=⎪⎩∴2y x x =为所求．（3）设圆心(),P x y ,则当⊙P 与两坐标轴都相切时,有y x =±．由y x =,得2x x x =,解得10x =（舍去）,233x =-．由y x =-,得2x x x +=-解得10x =（舍去）,23x =． ∴所求⊙P的半径3R =-或3R =+ 10. (14重庆市) 28．已知,在Rt △OAB 中,∠OAB ＝900,∠BOA ＝300,AB ＝2.若以O 为坐标原点,OA 地点直线为x 轴,树立如图所示的平面直角坐标系,点B 在第一象限内.将Rt △OAB 沿OB 折叠后,点A 落在第一象限内的点C 处.（1）求点C 的坐标;（2）若抛物线bx ax y +=2（a ≠0）经由C.A 两点,求此抛物线的解析式;（3）若抛物线的对称轴与OB 交于点D,点P 为线段DB 上一点,过P 作y 轴的平行线,交抛物线于点M.问：是否消失如许的点P,使得四边形CDPM 为等腰梯形？若消失,请求出此时点P 的坐标;若不消失,请解释来由.注：抛物线c bx ax y ++=2（a ≠0）的极点坐标为⎪⎪⎭⎫⎝⎛--a b ac ，a b 4422,对称轴公式为abx 2-=解: （1）过点C 作CH ⊥x 轴,垂足为H∵在Rt △OAB 中,∠OAB ＝900,∠BOA ＝300,AB ＝2 ∴OB ＝4,OA ＝32由折叠知,∠COB ＝300,OC ＝OA ＝32 ∴∠COH ＝600,OH ＝3,CH ＝3 ∴C 点坐标为（3,3）（2）∵抛物线bx ax y +=2（a ≠0）经由C （3,3）.A （32,0）两点∴()()⎪⎩⎪⎨⎧+=+=b a b a 3232033322解得：⎩⎨⎧=-=321b a∴此抛物线的解析式为：x x y 322+-=（3）消失.因为x x y 322+-=的极点坐标为（3,3）即为点CMP ⊥x 轴,设垂足为N,PN ＝t ,因为∠BOA ＝300,所以ON ＝3t ∴P （3t ,t ）作PQ ⊥CD,垂足为Q,ME ⊥CD,垂足为E把t x ⋅=3代入x x y 322+-=得：t t y 632+-=∴ M （3t ,t t 632+-）,E （3,t t 632+-）同理：Q （3,t ）,D （3,1）要使四边形CDPM 为等腰梯形,只需CE ＝QD 即()16332-=+--t t t ,解得：341=t ,12=t （舍） ∴ P 点坐标为（334,34） ∴ 消失知足前提的点P,使得四边形CDPM 为等腰梯形,此时P 点的坐为（334,34）11. （15山东青岛）24．（本小题满分12分）已知：如图①,在Rt ACB △中,90C ∠=,4cm AC =,3cm BC =,点P 由B 动身沿BA 偏向向点A 匀速活动,速度为1cm/s;点Q 由A 动身沿AC 偏向向点C 匀速活动,速度为2cm/s;衔接PQ ．若设活动的时光为(s)t （02t <<）,解答下列问题：（1）当t 为何值时,PQ BC ∥？（2）设AQP △的面积为y （2cm ）,求y 与t 之间的函数关系式;（3）是否消失某一时刻t ,使线段PQ 正好把Rt ACB △的周长和面积同时等分？若消失,求出此时t 的值;若不消失,解释来由;（4）如图②,衔接PC ,并把PQC △沿QC 翻折,得到四边形PQP C ',那么是否消失某一时刻t ,使四边形PQP C '为菱形？若消失,求出此时菱形的边长;若不消失,解释来由．12. （15浙江湖州）24．（本小题12分）已知：在矩形AOBC 中,4OB =,3OA =．分离以OB OA ，地点直线为x 轴和y 轴,树立如图所示的平面直角坐标系．F 是边BC 上的一个动点（不与B C ，重合）,过F 点的反图①比例函数(0)ky k x=>的图象与AC 边交于点E ．（1）求证：AOE △与BOF △的面积相等;（2）记OEF ECF S S S =-△△,求当k 为何值时,S 有最大值,最大值为若干？（3）请摸索：是否消失如许的点F ,使得将CEF △沿EF 半数后,C 点正好落在OB 上？若消失,求出点F 的坐标;若不消失,请解释来由．（15浙江湖州24题解析）24．（本小题12分）（1）证实：设11()E x y ，,22()F x y ，,AOE △与FOB △的面积分离为1S ,2S , 由题意得11k y x =,22k y x =．1111122S x y k ∴==,2221122S x y k ==． 12S S ∴=,即AOE △与FOB △的面积相等．（2）由题意知：E F ，两点坐标分离为33kE ⎛⎫ ⎪⎝⎭，,44k F ⎛⎫ ⎪⎝⎭，, 1111432234ECF S EC CF k k ⎛⎫⎛⎫∴==-- ⎪⎪⎝⎭⎝⎭△, 11121222EOF AOE BOF ECF ECF ECF AOBC S S S S S k k S k S ∴=---=---=--△△△△△△矩形11112212243234OEF ECF ECF S S S k S k k k ⎛⎫⎛⎫∴=-=--=--⨯-- ⎪⎪⎝⎭⎝⎭△△△2112S k k ∴=-+．当161212k =-=⎛⎫⨯- ⎪⎝⎭时,S 有最大值．131412S -==⎛⎫⨯- ⎪⎝⎭最大值．（3）解：设消失如许的点F ,将CEF △沿EF 半数后,C 点正好落在OB 边上的M 点,过点E 作EN OB ⊥,垂足为N ．由题意得：3EN AO ==,143EM EC k ==-,134MF CF k ==-, 90EMN FMB FMB MFB ∠+∠=∠+∠=,EMN MFB ∴∠=∠．又90ENM MBF ∠=∠=,ENM MBF ∴△∽△．EN EM MB MF∴=,11414312311331412k k MB k k ⎛⎫-- ⎪⎝⎭∴==⎛⎫-- ⎪⎝⎭, 94MB ∴=． 222MB BF MF +=,222913444k k ⎛⎫⎛⎫⎛⎫∴+=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,解得218k =．21432k BF ∴==． ∴消失相符前提的点F ,它的坐标为21432⎛⎫⎪⎝⎭，．13（15浙江衢州）24.(本题14分)已知直角梯形纸片OABC 在平面直角坐标系中的地位如图所示,四个极点的坐标分离为O(0,0),A(10,0),B(8,32),C(0,32),点T 在线段OA 上(不与线段端点重合),将纸片折叠,使点A 落在射线AB 上(记为点A ′),折痕经由点T,折痕TP 与射线AB 交于点P,设点T 的横坐标为t,折叠后纸片重叠部分(图中的暗影部分)的面积为S; (1)求∠OAB 的度数,并求当点A ′在线段AB 上时,S 关于t 的函数关系式;(2)当纸片重叠部分的图形是四边形时,求t 的取值规模;(3)S 消失最大值吗？若消失,求出这个最大值,并求此时t 的值;若不消失,请解释来由.（15浙江衢州24题解析）24.(本题14分)解：(1)∵A,B 两点的坐标分离是A(10,0)和B(8,32),∴381032OAB tan =-=∠,∴︒=∠60OAB当点A ´在线段AB 上时,∵︒=∠60OAB ,TA=TA ´, ∴△A ´TA 是等边三角形,且A T TP '⊥, ∴)t 10(2360sin )t 10(TP -=︒-=,)t 10(21AT 21AP P A -===', ∴2TPA )t 10(83TP P A 21S S -=⋅'=='∆, 当A ´与B 重应时,A T=AB=460sin 32=︒, 所以此时10t 6<≤.(2)当点A ´在线段AB 的延伸线,且点P 在线段AB(不与B 重合)上时, 纸片重叠部分的图形是四边形(如图(1),个中E 是TA ´与CB 的交点),(3)S 消失最大值○1当10t 6<≤时,2)t 10(83S -=, 在对称轴t=10的左边,S 的值跟着t 的增大而减小,∴当t=6时,S 的值最大是32.○2当6t 2<≤时,由图○1,重叠部分的面积EB A TP A S S S '∆'∆-=∵△A ´EB 的高是︒'60sin B A , ∴23)4t 10(21)t 10(83S 22⨯----=34)2t (83)28t 4t (8322+--=++-=当t=2时,S 的值最大是34;○3当2t 0<<,即当点A ´和点P 都在线段AB 的延伸线是(如图○2,个中E 是TA ´与CB 的交点,F 是TP 与CB 的交点),∵ETF FTP EFT ∠=∠=∠,四边形ETAB 是等腰形,∴EF=ET=AB=4, ∴3432421OC EF 21S =⨯⨯=⋅=综上所述,S 的最大值是34,此时t 的值是2t 0≤<.14 15浙江绍兴）24．将一矩形纸片OABC 放在平面直角坐标系中,(00)O ，,(60)A ，,(03)C ，．动点Q 从点O 动身以每秒1个单位长的速度沿OC 向终点C 活动,活动23秒时,动点P 从点A 动身以相等的速度沿AO 向终点O 活动．当个中一点到达终点时,另一点也停滞活动．设点P 的活动时光为t （秒）．（1）用含t 的代数式暗示OP OQ ，;（2）当1t =时,如图1,将OPQ △沿PQ 翻折,点O 正好落在CB 边上的点D 处,求点D 的坐标;AT COF（3）贯穿连接AC ,将OPQ △沿PQ 翻折,得到EPQ △,如图2．问：PQ 与AC 可否平行？PE 与AC 可否垂直？若能,求出响应的t 值;若不克不及,解释来由．（15浙江绍兴24题解析）24．（本题满分14分）解：（1）6OP t =-,23OQ t =+．（2）当1t =时,过D 点作1DD OA ⊥,交OA 于1D ,如图1, 则53DQ QO ==,43QC =, 1CD ∴=,(13)D ∴，．（3）①PQ 能与AC 平行．若PQ AC ∥,如图2,则OP OAOQ OC=, 即66233t t -=+,149t ∴=,而703t ≤≤, 149t ∴=．②PE 不克不及与AC 垂直．图1图1（第24题图）若PE AC ⊥,延伸QE 交OA 于F ,如图3,则23335t QF OQ QFAC OC +==．23QF t ⎫∴=+⎪⎭．EF QF QE QF OQ ∴=-=- 2233t t ⎫⎛⎫=+-+⎪ ⎪⎭⎝⎭21)1)3t =+．又Rt Rt EPF OCA △∽△,PE OCEF OA∴=, 63261)3t t -∴=⎛⎫+ ⎪⎝⎭,3.45t ∴≈,而703t ≤≤,t ∴不消失．15. （15浙江宿迁24题解析）24．如图,在矩形ABCD 中,9AB =,AD =,点P 是边BC 上的动点（点P 不与点B ,点C 重合）,过点P 作直线PQ BD ∥,交CD 边于Q 点,再把PQC △沿着动直线PQ 半数,点C 的对应点是R 点,设CP 的长度为x ,PQR △与矩形ABCD 重叠部分的面积为y ．（1）求CQP ∠的度数;（2）当x 取何值时,点R 落在矩形ABCD 的AB 边上？（3）①求y 与x 之间的函数关系式;②当x 取何值时,重叠部分的面积等于矩形面积的727？二．扭转类1. （15湖南常德26题）如图9,在直线l 上摆放有△ABC 和直角梯形DEFG ,且CD ＝6㎝;在△ABC 中：∠C ＝90O ,∠A ＝300,AB ＝4㎝;在直角梯形DEFG 中：EF//DG,∠DGF ＝90O ,DG ＝6㎝,DE ＝4㎝,∠EDG ＝600.解答下列问题：（1）扭转：将△ABC 绕点C 顺时针偏向扭转900,请你在图中作出扭转后的对应图形 △A 1B 1C,并求出AB 1的长度;（2）翻折：将△A 1B 1C 沿过点B 1且与直线l 垂直的直线翻折,得到翻折后的对应图形 △A 2B 1C 1,试剖断四边形A 2B 1DE 的外形？并解释来由;（3）平移：将△A 2B 1C 1沿直线l 向右平移至△A 3B 2C 2,若设平移的距离为ｘ,△A 3B 2C 2与直角梯形重叠部分的面积为ｙ,当ｙ等于△ABC 面积的一半时,ｘ的值是若干？（15湖南常德26题解析）解：（1）在△ABC 中由已知得：BC=2,AC ＝AB×cos30°=32,∴AB 1=AC+C B 1=AC+CB=322 .……………………………………2分AC DG图9(2)四边形A 2B 1DE 为平行四边形.来由如下：∵∠EDG ＝60°,∠A 2B 1C 1＝∠A 1B 1C ＝∠ABC ＝60°,∴A 2B 1∥DE又A 2B 1＝A 1B 1＝AB ＝4,DE ＝4,∴A 2B 1＝DE,故结论成立.………………4分（3）由题意可知： S △ABC =3232221=⨯⨯, ① 当20<≤x 或10≥x 时,ｙ＝0此时重叠部分的面积不会等于△ABC 的面积的一半……………5分②当42<≤x 时,直角边B 2C 2与等腰梯形的下底边DG 重叠的长度为DC 2=C 1C 2-DC 1=（ｘ－2）㎝,则ｙ＝()()()222323221-=--x x x , 当ｙ=21S △ABC = 3时,即()32232=-x , 解得22-=x （舍）或22+=x .∴当22+=x 时,重叠部分的面积等于△ABC 的面积的一半.③当84<≤x 时,△A 3B 2C 2完整与等腰梯形重叠,即32=y ……………7分 ④当108<≤x 时,B 2G=B 2C 2-GC 2=2－(x －8)=10-x则ｙ＝()()()210231031021x x x -=-⋅-, 当ｙ=21S △ABC = 3时,即()310232=-x , 解得210-=x ,或210+=x (舍去).∴当210+=x 时,重叠部分的面积等于△ABC 的面积的一半.………9分由以上评论辩论知,当22+=x 或210+=x 时, 重叠部分的面积等于△ABC 的面积的一半.………10分2. （广西玉林卷）在矩形ABCD 中,4AB =,2BC =,认为A 坐标原点,AB 地点的直线为x 轴,树立直角坐标系．然后将矩形ABCD 绕点A 逆时针扭转,使点B 落在y 轴的E 点上,则C 和D 点依次落在第二象限的F 点上和x 轴的G 点上（如图）．（1）求经由B E G ，，三点的二次函数解析式;（2）设直线EF 与（1）的二次函数图象订交于另一点H ,试求四边形EGBH 的周长．（3）设P 为（1）的二次函数图象上的一点,BP EG ∥,求P 点的坐标． [解] （1）解：由题意可知,4AE AB ==,2AG AD BC ===．(40)B ，∴,(04)E ，,(20)G -，．设经由B E G ，，三点的二次函数解析式是(2)(4)y a x x =+-．把(04)E ，代入之,求得12a =-． 3分 ∴所求的二次函数解析式是：211(2)(4)422y x x x x =-+-=-++．（2）解：由题意可知,四边形AEFG 为矩形．FH GB ∴∥,且6GB =．∵直线4y =与二次函数图象的交点H 的坐标为(24)H ，, 2EH =∴．G ∵与B E ，与H 关于抛物线的对称轴对称,BH EG ===∴． ∴四边形EGBH 的周长262=++⨯8=+．BP EG ∵∥,::AB AG AM AE =∴,即4:2:4AM =．8AM =∴,于是(08)M -，．设直线BM 的解析式为y kx b =+．把(40)B ，,(08)M -，代入之,得408.k b b +=⎧⎨=-⎩，解得28.k b =⎧⎨=-⎩，28y x =-∴．结合一次,二次函数解析式构成方程组2281 4.2y x y x x =-⎧⎪⎨=-++⎪⎩，解得620x y =-⎧⎨=-⎩，或40.x y =⎧⎨=⎩，（此组数为B 点坐标）∴所求的P 点坐标为(620)P -，．解法2：过P 作PN x ⊥轴于N ．由BP EG ∥,得EGB PBN ∠=∠．设所求P 点的横坐标为(0)a a <,则纵坐标为214(0)2a a a -++<． tan PN PBN NB ∠=∵,4tan 22AE EGB AG ∠===, 2PN AENB AG==∴． 4NB NA AB a =+=-∴,22114422PN a a a a ⎛⎫=--++=-- ⎪⎝⎭,214224a a a--=-∴．解之,得6a =-或4a =．经磨练可知,6a =-是原方程的根;4a =是原方程的增根,故应舍去．当6a =-时,22114(6)642022a a -++=-⨯--+=． ∴所求的P 点坐标为(620)P -，． [点评]此题的分解性较强,考核的常识点较多,但是解法较多,使试题的切入点也较多,很轻易入题.3. (14南京市) 27．在平面内,先将一个多边形以点O 为位似中间放大或缩小,使所得多边形与原多边形对应线段的比为k ,并且原多边形上的任一点P ,它的对应点P '在线段OP 或其延伸线上;接着将所得多边形以点O 为扭转中间,逆时针扭转一个角度θ,这种经由和扭转的图形变换叫做扭转类似变换,记为()O k θ，,个中点O 叫做扭转类似中间,k 叫做类似比,θ叫做扭转角．（1）填空：①如图1,将ABC △以点A 为扭转类似中间,放大为本来的2倍,再逆时针扭转60,得到ADE △,这个扭转类似变换记为A （,）;②如图2,ABC △是边长为1cm 的等边三角形,将它作扭转类似变换)A ,得到ADE △,则线段BD 的长为cm ;（2）如图3,分离以锐角三角形ABC 的三边AB ,BC ,CA 为边向外作正方形ADEB ,BFGC ,CHIA ,点1O ,2O ,3O 分离是这三个正方形的对角线交点,试分离应用12AO O △与ABI △,CIB △与2CAO △之间的关系,应用扭转类似变换的常识解释线段12O O 与2AO 之间的关系．解：（1）①2,60; ②2;（2）12AO O △经由扭转类似变换)A ,得到ABI △,此时,线段12O O 变成线段BI ; CIB △经由扭转类似变换45C ⎫⎪⎪⎝⎭,得到2CAO △,此时,线段BI 变成线段1AO ． 2212⨯=,454590+=, 122O O AO ∴=,122O O AO ⊥．4. （15湖北恩施）六.(本大题满分12分)ＣＡDE图1ＡBＣDE图2ＥＤＢＦＧＣＨＡＩ3O1O2O图324. 如图11,在统一平面内,将两个全等的等腰直角三角形ABC 和AFG 摆放在一路,A 为公共极点,∠BAC =∠AGF =90°,它们的斜边长为2,若∆ABC 固定不动,∆AFG 绕点A 扭转,AF .AG 与边BC 的交点分离为D .E (点D 不与点B 重合,点E 不与点C 重合),设BE =m,CD =n. （1）请在图中找出两对类似而不全等的三角形,并拔取个中一对进行证实. （2）求m 与n 的函数关系式,直接写出自变量n 的取值规模.（3）以∆ABC 的斜边BC 地点的直线为x 轴,BC 边上的高地点的直线为y 轴,树立平面直角坐标系(如图12).在边BC 上找一点D ,使BD =CE ,求出D 点的坐标,并经由过程盘算验证BD 2＋CE 2=DE 2.（4）在扭转进程中,(3)中的等量关系BD 2＋CE 2=DE 2是否始终成立,若成立,请证实,若不成立,（15湖北恩施24题解析）六.(本大题满分12分)24. 解:(1)∆ABE ∽∆DAE , ∆ABE ∽∆DCA 1分 ∵∠BAE =∠BAD +45°,∠CDA =∠BAD +45° ∴∠BAE =∠CDA 又∠B =∠C =45° ∴∆ABE ∽∆DCA 3分 (2)∵∆ABE ∽∆DCA ∴CDBACA BE由依题意可知CA =BA =2 ∴nm 22∴m=n25分自变量n 的取值规模为1<n<2. 6分 (3)由BD =CE 可得BE =CD ,即m=n ∵m=n2 ∴m=n=2 ∵OB =OC =21BC =1 ∴OE =OD =2－1 ∴D (1－2, 0) 7分∴BD =OB －OD =1-(2－1)=2－2=CE , DE =BC －2BD =2-2(2－2)=22－2∵BD 2＋CE 2=2 BD 2=2(2－2)2=12－82, DE 2=(22－2)2= 12－82∴BD 2＋CE 2=DE 28分 (4)成立 9分证实:如图,将∆ACE 绕点A 顺时针扭转90°至∆ABH 的地位,则CE =HB ,AE =AH , ∠ABH =∠C =45°,扭转角∠EAH =90°.衔接HD ,在∆EAD 和∆HAD 中∵AE =AH , ∠HAD =∠EAH -∠F AG =45°=∠EAD , AD∴∆EAD ≌∆HAD ∴DH =DE又∠HBD =∠ABH +∠ABD =90°∴BD 2+HB 2=DH 2 即BD 2＋CE 2=DE 2 12分5.（15湖北武汉）（本题答案暂缺）25.（本题 12分）如图 1,抛物线y=ax2-3ax+b 经由A （-1,0）,C （3,2）两点,与y 轴交于点D,与x 轴交于另一点B.（1）求此抛物线的解析式;（2）若直线y=kx-1（k≠0）将四边形ABCD 面积二等分,求k 的值;（3）如图2,过点 E （1,-1）作EF ⊥x 轴于点F,将△AEF 绕平面内某点扭转 180°后得△MNQ （点M,N,Q 分离与点 A,E,F 对应）,使点M,N 在抛物线上,求点M,N 的坐标.（15湖北武汉25题解析）25.⑴213222y x x =-++;⑵43k =;⑶M （3,2）,N （1,3） 6. （15江苏淮安）（本题答案暂缺）28．(本小题14分)如图所示,在平面直角坐标系中．二次函数y=a(x-2)2-1图象的极点为P,与x 轴交点为 A.B,与y 轴交点为C ．贯穿连接BP 并延伸交y 轴于点D. (1)写出点P 的坐标;(2)贯穿连接AP,假如△APB 为等腰直角三角形,求a 的值及点C.D 的坐标;(3)在(2)的前提下,贯穿连接BC.AC.AD,点E(0,b)在线段CD(端点C.D 除外)上,将△BCD 绕点E 逆时针偏向扭转90°,得到一个新三角形．设该三角形与△ACD 重叠部分的面积为S,依据不合情况,分离用含b 的代数式暗示S ．选择个中一种情况给出解答进程,其它情况直接写出成果;断定当b 为何值时,重叠部分的面积最大?写出最大值．7. （15江苏徐州）（本题答案暂缺）28.如图1,一副直角三角板知足AB ＝BC,AC ＝DE,∠ABC ＝∠DEF ＝90°,∠EDF ＝30°【操纵】将三角板DEF 的直角极点E 放置于三角板ABC 的斜边AC 上,再将三角板．．．．DEF ．．．绕．点．E ．扭转．．,并使边DE 与边AB 交于点P,边EF 与边BC 于点Q 【探讨一】在扭转进程中, （1）如图2,当CE1EA＝时,EP 与EQ 知足如何的数目关系？并给出证实. （2）如图3,当CE2EA＝时EP 与EQ 知足如何的数目关系？,并解释来由. （3）依据你对（1）.（2）的探讨成果,试写出当CEEA＝m 时,EP 与EQ 知足的数目关系式为_________,个中m 的取值规模是_______(直接写出结论,不必证实)【探讨二】若,AC ＝30cm,持续PQ,设△EPQ 的面积为S(cm 2),在扭转进程中：（1） S 是否消失最大值或最小值？若消失,求出最大值或最小值,若不消失,解释来由. （2）跟着S 取不合的值,对应△EPQ 的个数有哪些变更？不出响应S 值的取值规模.（15山东青岛24题解析）24．（本小题满分12分）FC(E)A(D)Q PDEFCBAQPDEFCBA解：（1）在Rt△ABC 中,522=+=AC BC AB ,由题意知：AP = 5－t ,AQ = 2t , 若PQ ∥BC ,则△APQ ∽△ABC ,∴=AC AQ AB AP, ∴5542t t -=, ∴710=t ．3′（2）过点P 作PH ⊥AC 于H ． ∵△APH ∽△ABC , ∴=BC PH AB AP, ∴=3PH 55t-,∴t PH 533-=, ∴t t t t PH AQ y 353)533(221212+-=-⨯⨯=⨯⨯=．6′ （3）若PQ 把△ABC 周长等分, 则AP+AQ=BP+BC+CQ ．∴)24(32)5(t t t t -++=+-, 解得：1=t ．若PQ 把△ABC 面积等分,则ABC APQ S S ∆∆=21, 即－253t ＋3t =3． ∵ t =1代入上面方程不成立,∴不消失这一时刻t ,使线段PQ 把Rt △ACB 的周长和面积同时等分．9′ （4）过点P 作PM ⊥AC 于Ｍ,PN ⊥BC 于N ,若四边形PQP ′ C 是菱形,那么PQ ＝PC ． ∵PM ⊥AC 于M , ∴QM=CM ．图①B∵PN ⊥BC 于N,易知△PBN ∽△ABC ．∴AB BPAC PN =, ∴54t PN =, ∴54tPN =, ∴54t CM QM ==, ∴425454=++t t t , 解得：910=t ．∴当910=t 时,四边形PQP ′ C 是菱形．此时37533=-=t PM , 9854==t CM ,在Rt△PMC 中,9505816494922=+=+=CM PM PC , ∴菱形PQP ′ C 边长为9505．12′ 7.（15山东枣庄）25．(本题满分1０分)把一副三角板如图甲放置,个中90ACB DEC ==∠∠,45A =∠,30D =∠,斜边6cm AB =,7cm DC =．把三角板DCE 绕点C 顺时针扭转15°得到△D 1CE 1（如图乙）．这时AB 与CD 1订交于点O ,与D 1E 1订交于点F ．（1）求1OFE ∠的度数; （2）求线段AD 1的长;（3）若把三角形D 1CE 1绕着点C 顺时针再扭转30°得△D 2CE 2,这时点B 在△D 2CE 2的内部.外部.照样边上？解释来由．BN（甲）ACE DBB（乙）AE 1CD 1OF（15山东枣庄25题解析）25．(本题满分10分) 解：（1）如图所示,315∠=,190E ∠=,∴1275∠=∠=． ………………………………1分又45B ∠=,∴114575120OFE B ∠=∠+∠=+=． ………3分（2）1120OFE ∠=,∴∠D 1FO =60°．1130CD E ∠=,∴490∠=．4分又AC BC =,6AB =,∴3OA OB ==．90ACB ∠=,∴116322CO AB ==⨯=．5分又17CD =,∴11734OD CD OC =-=-=．在1Rt AD O △中,15AD ===．6分（3）点B 在22D CE △内部．7分来由如下：设BC （或延伸线）交22D E 于点P ,则2153045PCE ∠=+=．在2Rt PCE △中,2CP ==…………9分3CB =<,即CB CP <,∴点B 在22D CE △内部． ……………10分 815浙江金华）（本题答案暂缺）24. (本题12分) 如图1,在平面直角坐标系中,己知ΔAOB 是等边三角形,点A 的坐标是(0,4),点B 在第一象限,点P 是x 轴上的一个动点,贯穿连接AP,并把ΔAOP 绕着点A 按逆时针偏向扭转.使边AO 与AB 重合.得到ΔABD.（1）求直线AB 的解析式;（2）当点P 活动到点（3,0）时,求此时DP的长及点D 的坐标;（3）是否消失点P,使ΔOPD 的面积等于43,若消失,请求出相符前提的点P 的坐标;若不消失,请解释来由.1EC A 19. （15辽宁沈阳26题）（本题14分）26．如图所示,在平面直角坐标系中,矩形ABOC 的边BO 在x 轴的负半轴上,边OC 在y 轴的正半轴上,且1AB =,OB =矩形ABOC绕点O 按顺时针偏向扭转60后得到矩形EFOD ．点A 的对应点为点E ,点B 的对应点为点F ,点C 的对应点为点D ,抛物线2y ax bx c =++过点A E D ，，．（1）断定点E 是否在y 轴上,并解释来由; （2）求抛物线的函数表达式;（3）在x 轴的上方是否消失点P ,点Q ,使以点O B P Q ，，，为极点的平行四边形的面积是矩形ABOC 面积的2倍,且点P 在抛物线上,若消失,请求出点P ,点Q 的坐标;若不消失,请解释来由．（15辽宁沈阳26题解析）解：（1）点E 在y 轴上1分来由如下：衔接AO ,如图所示,在Rt ABO △中,1AB =,BO =2AO ∴=1sin 2AOB ∴∠=,30AOB ∴∠= 由题意可知：60AOE ∠=306090BOE AOB AOE ∴∠=∠+∠=+=点B 在x 轴上,∴点E 在y 轴上．3分（2）过点D 作DM x ⊥轴于点M1OD =,30DOM ∠=。

中考数学几何图形折叠试题典题及解答

中考数学几何图形折叠试题典题及解答一、题目描述：下面是一道关于几何图形折叠的中考数学试题，请根据给出的图形进行折叠并回答相关问题。

二、题目内容：以下是一些典型的几何图形折叠试题，供同学们考试复习参考。

1. 长方形折叠在平面上给出一张长方形纸片，长为12厘米，宽为6厘米。

折叠该长方形纸片，使得长方形的两个对边重叠，然后再剪掉重叠部分。

请问最后得到的图形是什么？计算它的周长和面积。

解答：将长方形纸片对折，让两条边相重合。

然后沿着重合的边将多余的部分剪掉。

最后得到的图形是一个等边三角形。

它的周长为36厘米（等边三角形的三条边长相等，每条边长为12厘米），面积为36平方厘米（等边三角形的面积公式为：面积=（边长^2）×(根号3)/4）。

2. 圆形折叠给出一张半径为8厘米的圆形纸片，折叠该圆形纸片使得圆心与边上的一点重合，然后再剪掉重叠部分。

请问最后得到的图形是什么？计算它的周长和面积。

解答：将圆形纸片对折，使得圆心与边上的一点重合。

然后沿着重合的边将多余的部分剪掉。

最后得到的图形是一个等腰三角形。

它的周长为2πr+2r（其中r为圆的半径，即8厘米），面积为（r^2）×π（等腰三角形的面积公式为：面积=（底边×高）/2，这里的底边等于2r）。

3. 正方形折叠给出一张边长为10厘米的正方形纸片，折叠该正方形纸片使对边重叠，然后再剪掉重叠部分。

请问最后得到的图形是什么？计算它的周长和面积。

解答：将正方形纸片对折，使得对边重叠。

然后沿着重合的边将多余的部分剪掉。

最后得到的图形是一个等腰梯形。

它的周长为2a+2b（其中a和b分别为梯形的上、下底边，都等于10厘米），面积为（（a+b）×h）/2（等腰梯形的面积公式为：面积=（上底+下底）×高/2，这里的高等于10厘米）。

4. 直角三角形折叠给出一张直角三角形纸片，已知直角边长为5厘米，斜边长为8厘米。

折叠该直角三角形纸片，使直角边重叠，然后再剪掉重叠部分。

中考数学压轴题(六)折叠问题

折叠问题折叠对象有三角形、矩形、正方形、梯形等；考查问题有求折点位置、求折线长、折纸边长周长、求重叠面积、求角度、判断线段之间关系等；解题时，灵活运用轴对称性质和背景图形性质。

轴对称性质-----折线是对称轴、折线两边图形全等、对应点连线垂直对称轴、对应边平行或交点在对称轴上。

压轴题是由一道道小题综合而成，常常伴有折叠；解压轴题时，要学会将大题分解成一道道小题；那么多作折叠的选择题填空题，很有必要。

1、（2009年浙江省绍兴市）如图，D E ，分别为ABC △的AC ，BC 边的中点，将此三角形沿DE 折叠，使点C 落在AB 边上的点P 处．若48CDE ∠=°，则APD ∠等于（）A ．42°B ．48°C ．52°D ．58°2、（2009湖北省荆门市）如图，Rt △ABC 中，∠ACB =90°，∠A =50°，将其折叠，使点A 落在边CB 上A ′处，折痕为CD ，则A DB '∠=（）A ．40°B ．30°C ．20°D ．10°3、（2009年日照市）将三角形纸片（△ABC ）按如图所示的方式折叠，使点B 落在边AC 上，记为点B ′，折痕为EF ．已知AB ＝AC ＝3，BC ＝4，若以点B ′，F ，C 为顶点的三角形与△ABC 相似，那么BF 的长度是．4、（2009年衢州）在△ABC 中，AB =12，AC =10，BC =9，AD 是BC 边上的高.将△ABC 按如图所示的方式折叠，使点A 与点D 重合，折痕为EF ，则△DEF 的周长为A ．9.5B ．10.5C ．11D ．15.55、（2009泰安）如图，在Rt △ABC 中，第2题图 A 'B D A C（第18题图）A CB ∠ACB=90°，∠A ＜∠B ，沿△ABC 的中线CM 将△CMA 折叠，使点A 落在点D 处，若CD 恰好与MB 垂直，则tanA 的值为．6、(2009年上海市)在Rt ABC △中，903BAC AB M ∠==°，，为边BC 上的点，联结AM （如图3所示）．如果将ABM △沿直线AM 翻折后，点B 恰好落在边AC 的中点处，那么点M 到AC 的距离是．7、(2009宁夏) 如图：在Rt ABC △中，90ACB ∠=°，CD 是AB 边上的中线，将ADC △沿AC 边所在的直线折叠，使点D 落在点E 处，得四边形ABCE ．求证：EC AB ∥．8、（2009年清远）如图，已知一个三角形纸片ABC ，BC 边的长为8，BC 边上的高为6，B ∠和C ∠都为锐角，M 为AB 一动点（点M 与点A B 、不重合），过点M 作MN BC ∥，交AC 于点N ，在AMN △中，设MN 的长为x ，MN 上的高为h ．（1）请你用含x 的代数式表示h ．（2）将AMN △沿MN 折叠，使AMN △落在四边形BCNM 所在平面，设点A 落在平面的点为1A ，1A MN △与四边形BCNM 重叠部分的面积为y ，当x 为何值时，y 最大，最大值为多少？9、（2009恩施市）如图，在ABC △中，9010A BC ABC ∠==°，，△的面积为25，点D 为AB 边上的任意一点（D 不与A 、B 重合），过点D 作DE BC ∥，交AC 于点E ．设DE x =，以DE 为折线将BC NM AA图3 BMC EC B A DADE △翻折（使ADE △落在四边形DBCE 所在的平面内），所得的A DE '△与梯形DBCE 重叠部分的面积记为y ．（1）用x 表示ADE △的面积；（2）求出05x <≤时y 与x 的函数关系式；（3）求出510x <<时y 与x 的函数关系式；（4）当x 取何值时，y 的值最大？最大值是多少？提示：相似、二次函数10、（2009年天津市）已知一个直角三角形纸片OAB ，其中9024AOB OA OB ∠===°，，．如图，将该纸片放置在平面直角坐标系中，折叠该纸片，折痕与边OB 交于点C ，与边AB 交于点D ．（Ⅰ）若折叠后使点B 与点A 重合，求点C 的坐标；提示：画出图形，图中性质△ACD ≌△BCD,△BDC ∽△BOA,BC=AC（Ⅱ）若折叠后点B 落在边OA 上的点为B '，设OB x '=，OC y =，试写出y 关于x 的函数解析式，并确定y 的取值范围；提示：画图，△COB ＇中由勾股定理得出函数关系式，由x 取值范围确定y 范围。

中考数学压轴题(六)折叠问题

（第18题图）MAC B 折叠问题折叠对象有三角形、矩形、正方形、梯形等；考查问题有求折点位置、求折线长、折纸边长周长、求重叠面积、求角度、判断线段之间关系等；解题时，灵活运用轴对称性质和背景图形性质。

轴对称性质-----折线是对称轴、折线两边图形全等、对应点连线垂直对称轴、对应边平行或交点在对称轴上。

压轴题是由一道道小题综合而成，常常伴有折叠；解压轴题时，要学会将大题分解成一道道小题；那么多做折叠的选择题填空题，很有必要。

1、（2009年浙江省绍兴市）如图，D E ，分别为ABC △的AC ，BC 边的中点，将此三角形沿DE 折叠，使点C 落在AB 边上的点P 处．若48CDE ∠=°，则APD ∠等于（） A ．42° B ．48° C ．52° D ．58°2、（2009湖北省荆门市）如图，Rt △ABC 中，∠ACB =90°，∠A =50°，将其折叠，使点A 落在边CB 上A ′处，折痕为CD ，则A DB '∠=（） A ．40° B ．30° C ．20° D ．10°3、（2009年日照市）将三角形纸片（△ABC ）按如图所示的方式折叠，使点B 落在边AC 上，记为点B ′，折痕为EF ．已知AB ＝AC ＝3，BC ＝4，若以点B ′，F ，C 为顶点的三角形与△ABC 相似，那么BF 的长度是．4、（2009年衢州）在△ABC 中，AB =12，AC =10，BC =9，AD 是BC 边上的高.将△ABC 按如图所示的方式折叠，使点A 与点D 重合，折痕为EF ，则△DEF 的周长为 A ．9.5 B ．10.5 C ．11 D ．15.5第4题图第5题图第6题图 5、（2009泰安）如图，在Rt △ABC 中，∠ACB=90°，∠A ＜∠B ，沿△ABC 的中线CM 将△CMA 折叠，使点A 落在点D 处，若CD 恰好与MB 垂直，则tanA 的值为．6、(2009年上海市)在Rt ABC △中，903BAC AB M ∠==°，，为边BC 上的点，联结AM （如图3所示）．如果将ABM △沿直线AM 翻折后，点B 恰好落在边AC 的中点处，那么点M 到AC 的距离是．7、(2009宁夏) 如图：在Rt ABC △中，90ACB ∠=°，CD 是AB 边上的中线，将ADC △沿AC 边所在的直线折叠，使点D 落在点E 处，得四边形ABCE ．求证：EC AB ∥．第2题图A 'BDAC E C 第3题图A 图3B M C8、（2009年清远）如图，已知一个三角形纸片ABC ，BC 边的长为8，BC 边上的高为6，B ∠和C ∠都为锐角，M 为AB 一动点（点M 与点A B 、不重合），过点M 作MN BC ∥，交AC 于点N ，在AMN △中，设MN 的长为x ，MN 上的高为h ．（1）请你用含x 的代数式表示h ．（2）将AMN △沿MN 折叠，使AMN △落在四边形BCNM 所在平面，设点A 落在平面的点为1A ，1A MN △与四边形BCNM 重叠部分的面积为y ，当x 为何值时，y 最大，最大值为多少？9、（2009恩施市）如图，在ABC △中，9010A BC ABC ∠==°，，△的面积为25，点D 为AB 边上的任意一点（D 不与A 、B 重合），过点D 作DE BC ∥，交AC 于点E ．设DE x =，以DE 为折线将ADE △翻折（使ADE △落在四边形DBCE 所在的平面内），所得的A DE '△与梯形DBCE 重叠部分的面积记为y ．（1）用x 表示ADE △的面积；（2）求出05x <≤时y 与x 的函数关系式；（3）求出510x <<时y 与x 的函数关系式；（4）当x 取何值时，y 的值最大？最大值是多少？提示：相似、二次函数10、（2009天津）已知一个直角三角形纸片OAB ，其中9024AOB OA OB ∠===°，，．如图，将该纸片放置在平面直角坐标系中，折叠该纸片，折痕与边OB 交于点C ，与边AB 交于点D ．（Ⅰ）若折叠后使点B 与点A 重合，求点C 的坐标；提示：画出图形，图中性质△ACD ≌△BCD,△BDC ∽△BOA,BC=ACB C N M AE A 'D BC AB CA（Ⅱ）若折叠后点B 落在边OA 上的点为B '，设OB x '=，OC y =，试写出y 关于x 的函数解析式，并确定y 的取值范围；提示：画图，△COB ＇中由勾股定理得出函数关系式，由x 取值范围确定y 范围。

【全文】中考第三轮专题复习-折叠中的数学问题(

若AB=8cm，AD=10cm，你能求出EF的长吗？
A
D
首先关注哪个三角形?
O E
Rt△CEF
B
F
C
没有变动的Rt△CEF
A
A B
D
E
折叠
FC
实质
轴对称F
D
E
轴对称性质：
由折叠可得： 1.△AFE≌△ADE

2.AE是DF的中垂线
1.图形的全等性：重合部分是全等图形，对应边角相等。
2.点的对称性：对称点连线被对称轴垂直平分。
图 39－3
第39讲┃ 操作探究题
解：连接 CE，则 CE＝AE，设 AE＝x，则 DE＝4－x. 在 Rt△CDE 中，CE2＝DE2＋DC2，所以 x2＝(4－x)2＋32，解得 x＝285，即 CE＝285. 在 Rt△ABC 中，AC＝ AB2＋BC2＝ 32＋42＝5，由题意知：AO＝CO＝A2C＝52，所以在 Rt△CEO 中，EO＝ CE2－CO2＝185. ∵AD∥BC，∴∠EAO＝∠ACF.
A
O
F
B
（1）操作1：将矩形ABCD沿对角线AC折叠（如图1），猜想重叠部分是什么图形？并验证你的猜想。
连结BE与AC有什么位置关系？
E
A
FD
B 图1
（2）操作2：折叠矩形ABCD，让点B落 A
在对角线AC上（如图2），若AD=4，
AB=3，请求出线段CE的长度。
F
C
D
B
E
C
图2
3．如图 39－3，在矩形 ABCD 中，AB＝3，BC＝4，将矩形折叠，使点 C 与 A 点重合，求折痕 EF 的长．
解决的方法：

中考数学折叠问题压轴题专项训练,初中折叠翻折问题的经典题型,历年中考折叠问题真题及答案解析

中考数学专题复习 专题33 中考几何折叠翻折类问题(教师版含解析)

2024年中考数学压轴突破【几何中的折叠】题型汇编(解析版)

中考数学折叠,旋转问题专题含答案

中考数学中的旋转翻折类问题专项训练经典汇编(共30题)

中考折叠问题(原创)

中考数学折叠专项训练试题（含答案）

专题18 折叠问题-中考数学压轴题精品专题练(第二期)

中考数学专题训练：图形的折叠问题(附参考答案)

中考复习专题折叠压轴题(无答案)

2022年九年级数学中考折叠问题--压轴题

中考数学压轴题---《与折叠有关的计算》题型讲解

中考数学中考最后压轴题训练---折叠旋转问题

中考数学几何图形折叠试题典题及解答

中考数学压轴题(六)折叠问题

中考数学压轴题(六)折叠问题

【全文】中考第三轮专题复习-折叠中的数学问题(

中考数学专题复习专题33 中考几何折叠翻折类问题(教师版含解析)