三视图及其表面积体积
高考数学一轮复习-81-空间几何体的三视图-直观图-表面积与体积课件-新人教A

=172a2.所以 S 球=4πR2=4π×172a2=73πa2.
(2)这个几何体是一个圆台被轴截面割出来的一半.
根据图中数据可知圆台的上底面半径为 1,下底面半径为 2,高为 3,母线长为 2,几何体的表面积是两个半圆的面 积、圆台侧面积的一半和轴截面的面积之和,故这个几何 体的表面积为 S=12π×12+12π×22+12π×(1+2)×2+12 ×(2+4)× 3=112π+3 3. 答案 (1)B (2)112π+3 3
可能是圆柱,排除选项C;又由俯视图可知,该几何体
不可能是棱柱或棱台,排除选项A,B,故选D.
(2)如图,在原图形OABC中, 应有 OD=2O′D′=2×2 2 =4 2(cm), CD=C′D′=2 cm. ∴OC= OD2+CD2 = (4 2)2+22=6(cm), ∴OA=OC, 故四边形 OABC 是菱形. 答案 (1)D (2)C
诊断自测
1.判断正误(在括号内打“√”或“×”) 精彩PPT展示
(1)有两个面平行,其余各面都是平行四边形的几何体是
棱柱.
(×)
(2)有一个面是多边形,其余各面都是三角形的几何体是
棱锥.
( ×)
(3)正方体、球、圆锥各自的三视图中,三视图均相同.
(×)
(4)圆柱的侧面展开图是矩形.
(√)
2.(2014·福建卷)某空间几何体的正视图是三角形,则该几
(2)画出坐标系 x′O′y′,作出△OAB 的 直观图 O′A′B′(如图).D′为 O′A′的中 点.易知 D′B′=12DB(D 为 OA 的中点), ∴S△O′A′B′=12× 22S△OAB= 42× 43a2= 166a2.
立体几何三视图及体积表面积的求解
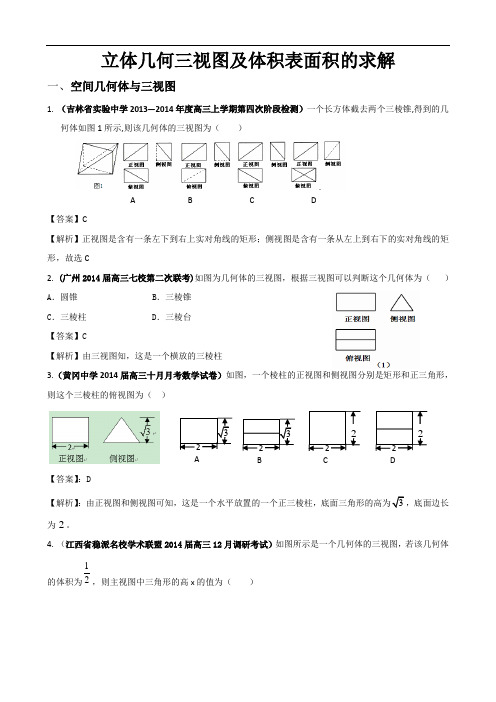
立体几何三视图及体积表面积的求解一、空间几何体与三视图1. (吉林省实验中学2013—2014年度高三上学期第四次阶段检测)一个长方体截去两个三棱锥,得到的几何体如图1所示,则该几何体的三视图为( )A B C D【答案】C【解析】正视图是含有一条左下到右上实对角线的矩形;侧视图是含有一条从左上到右下的实对角线的矩形,故选C2. (广州2014届高三七校第二次联考)如图为几何体的三视图,根据三视图可以判断这个几何体为( ) A .圆锥B .三棱锥C .三棱柱D .三棱台【答案】C【解析】由三视图知,这是一个横放的三棱柱3.(黄冈中学2014届高三十月月考数学试卷)如图,一个棱柱的正视图和侧视图分别是矩形和正三角形,则这个三棱柱的俯视图为( )【答案】:D【解析】为。
4. (江西省稳派名校学术联盟2014届高三12月调研考试)如图所示是一个几何体的三视图,若该几何体的体积为,则主视图中三角形的高x 的值为( )212 2A32B32 C22 D2A. B. C. 1 D.【答案】C 【解析】5.(石家庄2014届高三第一次教学质量检测)用一个平面去截正方体,有可能截得的是以下平面图形中的 .(写出满足条件的图形序号)(1)正三角形 (2)梯形 (3)直角三角形 (4)矩形 【答案】(1)(2)(4) 【解析】6.(黄冈中学2014届高三十月月考数学试卷)一个底面是等腰直角三角形的直棱柱,侧棱长与底面三角形的腰长相等,其体积为4,它的三视图中俯视图如右图所示,侧视图是一个矩形,则这个矩形的对角线长为 .【答案】123432【解析】:设底面的等腰直角三角形的腰长为,则侧棱长也为,则,解得,则其,宽为。
二、空间几何体的体积和表面积1.(湖北省黄冈中学2014届高三数学(文)期末考试)某空间组合体的三视图如图所示,则该组合体的体积为()A .48 B .56 C .64 D .72【答案】C【解析】该组合体由两个棱柱组成,上面的棱柱体积为24540创=,下面的棱柱体积为46124创=,故组合体的体积为642.(四川省泸州市2014届高三数学第一次教学质量诊断性考试)一个几何体的三视图如图所示,其中俯视图是菱形,则该几何体的侧面积为( ) A .B .C .D .a a 3142V a ==2a =2=3. (2014年福建宁德市普通高中毕业班单科质量检查)一个几何体的三视图如图所示,则该几何体的侧面积为()A.8+B.10C.8+.123. (承德市联校2013-2014年第一学期期末联考)把边长为2的正方形ABCD沿对角线BD折起,连结AC,得到三棱锥C-ABD,其正视图、俯视图均为全等的等腰直角三角形(如图所示),则其侧视图的面积为()A.32B.12C.1 D.22【答案】B【解析】由两个视图可以得到三棱锥如图:其侧视图的面积即t R ACEV的面积,由正方形的边长为2得==1AE CE,故侧视图面积为125.(安徽省六校教育研究会2014届高三2月联考)某三棱椎的三视图如图所示,该三棱锥的四个面的面积中,最大的面积是()(A) (B)(C)(D)8【答案】D【解析】由三视图可得三棱锥如图所示:底面是边长为4的正三角形,AD BDC ^平面,故四个面的面积中,最大的面积是ABC V 的面积为142创4. (宁夏银川一中2014届高三年级月考)如图是一个几何体的三视图,正视图和侧视图均为矩形,俯视图中曲线部分为半圆,尺寸如图,则该几何体的全面积为( )A .2+3.2+2.8+5.6+3【答案】A【解析】由三视图可知,该几何体是半个圆柱和侧棱垂直于底面的三棱柱组成的组合体,该几何体的表面积.5. (湖南省2014届高三第五次联考数学)已知三棱锥的三视图如图所示,则它的外接球表面积为( ) A. 16pB. 4pC. 8pD. 2pπ+π+π+π+1212(1)2S ππ=⨯⨯++32π=+7.(西安铁一中2014届高三11月模拟考试试题)一个几何体的三视图如图所示,则其外接球的表面积是( )A. B.【答案】B【解析】由三视图知:该几何体为长方体,长方体的棱长分别为3、4、5,所以长方体的体对角线为,所以外接球的半径为,所以外接球的表面积为。
2023年高考数学一轮复习点点练26空间几何体的三视图与直观图表面积与体积含解析理

第八单元立体几何考情分析多以两小一大的形式出现,每年必考,分值为17~22分.重点考查几何体的三视图问题、几何体的表面积与体积、空间线面位置关系,用向量法计算空间角,其中与球有关的接(切)问题是考查的难点.对于空间向量的应用,空间直角坐标系的建立是否合理是解决有关问题的关键,有时所给空间图形不规则——没有三条互相垂直的直线,不利于空间直角坐标系的建立,另外,探索性问题中动点坐标的设法及有关计算是难点.点点练26空间几何体的三视图与直观图、表面积与体积一基础小题练透篇1.[2022·山东济宁检测]已知水平放置的△ABC按“斜二测画法”得到如图所示的直观图,其中B′O′=C′O′=1,A′O′=32,那么原△ABC的面积是( )A.3B.22C.32D.342.[2021·江西吉安联考]某几何体的三视图如图所示,其中网格纸上小正方形的边长为1,则该几何体中,最长的棱的长度为( )A.3B.32C.33D.63.[2022·四川成都七中高三期中]已知一个几何体的三视图如图,则它的表面积为( )A .3πB .4πC.5πD.6π4.[2021·衡水模拟]已知正三棱锥S ABC 的三条侧棱两两垂直,且侧棱长为2,则此三棱锥的外接球的表面积为( )A .πB.3πC.6πD.9π5.[2022·云南大理模拟预测]一个几何体的三视图如图所示,则这个几何体的体积为( )A .43πB.2πC.πD.83π 6.[2021·江苏海安高级月考]三棱锥A BCD 中,∠ABC =∠CBD =∠DBA =60°,BC =BD =1,△ACD 的面积为114,则此三棱锥外接球的表面积为( ) A .4πB.16πC.163πD.323π7.[2022·四川省南充市白塔模拟]如图所示,网格纸上小正方形的边长为1,粗线画出的是某个多面体的三视图,若该多面体的所有顶点都在球C 的表面上,则球C 的表面积是( )A .8πB.12πC.16πD.32π 8.有一块多边形的菜地,它的水平放置的平面图形的斜二测直观图是直角梯形(如图所示),∠ABC =45°,AB =AD =1,DC ⊥BC ,则这块菜地的面积为________.9.[2022·湘豫名校联考]在四面体ABCD 中,AB =CD =5,AD =BC =13,AC =BD =10,则此四面体的体积为________.二能力小题提升篇1.[2022·深圳市高三调研]已知圆柱的底面半径为2,侧面展开图为面积为8π的矩形,则该圆柱的体积为( )A .8πB.4πC.83πD.2π2.[2022·浙江省高三测试]如图是用斜二测画法画出的∠AOB 的直观图∠A ′O ′B ′,则∠AOB 是( )A .锐角B .直角C .钝角D .无法判断3.[2022·河南省洛阳市高三调研]大约于东汉初年成书的我国古代数学名著《九章算术》中,“开立圆术”曰:置积尺数,以十六乘之,九而一,所得开立方除之,即立圆径.“开立圆术”实际是知道了球的体积V ,利用球的体积,求其直径d 的一个近似值的公式:d =3169V ,而我们知道,若球的半径为r ,则球的体积V =43πr 3,则在上述公式d =3169V 中,相当于π的取值为( )A.3B .227C .278D .1694.[2021·云南省曲靖市高三二模]如图,在水平地面上的圆锥形物体的母线长为12,底面圆的半径等于4,一只小虫从圆锥的底面圆上的点P 出发,绕圆锥侧面爬行一周后回到点P 处,则小虫爬行的最短路程为( )A .123B .16C .24D .24 35.[2022·江西省兴国县高三月考]已知三棱锥P ABC 中,PA ⊥平面ABC ,AB ⊥AC ,AB =AC =2,且三棱锥P ABC 外接球的表面积为36π.则PA =________.6.[2022·广东七校第二次联考]在四棱锥P ABCD 中,四边形ABCD 是边长为2a 的正方形,PD ⊥底面ABCD ,且PD =2a ,若在这个四棱锥内放一个球,则该球半径的最大值为________.三高考小题重现篇1.[2021·山东卷]已知圆锥的底面半径为2,其侧面展开图为一个半圆,则该圆锥的母线长为( )A .2B.2 2 C .4D.4 22.[2021·全国甲卷]在一个正方体中,过顶点A 的三条棱的中点分别为E ,F ,G .该正方体截去三棱锥A EFG 后,所得多面体的三视图中,正视图如图所示,则相应的侧视图是( )3.[2021·全国甲卷]已知一个圆锥的底面半径为6,其体积为30π,则该圆锥的侧面积为________.4.[2021·全国甲卷]已知A,B,C是半径为1的球O的球面上的三个点,且AC⊥BC,AC=BC=1,则三棱锥OABC的体积为( )A.212B.312C.24D.345.[2020·山东卷]已知直四棱柱ABCD-A1B1C1D1的棱长均为2,∠BAD=60°.以D1为球心,5为半径的球面与侧面BCC1B1的交线长为________.6.[2019·全国卷Ⅱ]中国有悠久的金石文化,印信是金石文化的代表之一.印信的形状多为长方体、正方体或圆柱体,但南北朝时期的官员独孤信的印信形状是“半正多面体”(图1).半正多面体是由两种或两种以上的正多边形围成的多面体.半正多面体体现了数学的对称美.图2是一个棱数为48的半正多面体,它的所有顶点都在同一个正方体的表面上,且此正方体的棱长为1.则该半正多面体共有________个面,其棱长为________.四经典大题强化篇1.在三棱柱ABCA1B1C1中,侧面AA1C1C⊥底面ABC,AA1=A1C=AC=AB=BC=2,且点O 为AC的中点.(1)证明:A1O⊥平面ABC;(2)求三棱锥C1ABC的体积.2.已知点P,A,B,C是半径为2的球面上的点,PA=PB=PC=2,∠ABC=90°,点B 在AC上的射影为D,求三棱锥P-ABD体积的最大值.点点练26 空间几何体的三视图与直观图、表面积与体积一 基础小题练透篇1.答案:A解析:由题图可知原△ABC 的高AO =3,BC =B ′C ′=2,∴S △ABC =12·BC ·OA =12×2×3= 3.2.答案:C解析:由三视图还原几何体,可得该几何体可看作如图所示的棱长为3的正方体中,以A ,B ,C ,D 为顶点的三棱锥,其最长的棱为BD ,且BD =32+32+32=3 3.3.答案:B解析:由三视图可知,该几何体是圆锥和半球拼接成的组合体,且圆锥的底面圆和半球的大圆面半径相同,底面圆的半径r =1,圆锥的母线长l =(3)2+1=2,记该几何体的表面积为S ,故S =12(2πr )l +12×4πr 2=4π.4.答案:C解析:正三棱锥的外接球即是棱长为2的正方体的外接球,所以外接球的直径2R =(2)2+(2)2+(2)2=6,所以4R 2=6,外接球的表面积4πR 2=6π.5.答案:A解析:根据三视图可知几何体是由有公共的底面的圆锥和圆柱体的组合体,由三视图可知,圆锥的底面半径为1,高为1,圆柱的底面半径为1,高为1,所以组合体的体积为13π×12×1+π×12×1=4π3.6.答案:A解析:∵BC =BD =1,∠CBD =60°,∴CD =1,又AB =AB ,∠ABC =∠DBA =60°,BC =BD ,∴△ABC ≌△ABD ,则AC =AD ,取CD 中点E ,连接AE ,又由△ACD 的面积为114,可得△ACD 的高AE =112,则可得AC =AD =3,在△ABC 中,由余弦定理AC 2=AB 2+BC 2-2AB ·BC ·cos60°,∴3=AB 2+1-2×AB ×1×12,解得AB =2,则AC 2+BC 2=AB 2,可得∠ACB =90°,∴∠ADB=90°,∴AC ⊥BC ,AD ⊥BD ,根据球的性质可得AB 为三棱锥外接球的直径,则半径为1, 故外接球的表面积为4π×12=4π.7.答案:A解析:由三视图可还原几何体为从长、宽均为2,高为2的长方体中截得的四棱锥S ABCD ,则四棱锥S ABCD 的外接球即为长方体的外接球, ∴球C 的半径R =122+2+4=2,∴球C 的表面积S =4πR 2=8π. 8.答案:2+22解析:如图1,在直观图中,过点A 作AE ⊥BC ,垂足为E .在Rt△ABE 中,AB =1,∠ABE =45°,∴BE =22.又四边形AECD 为矩形,AD =EC =1,∴BC =BE +EC =22+1,由此还原为原图形如图2所示,是直角梯形A ′B ′C ′D ′.在梯形A ′B ′C ′D ′中,A ′D ′=1,B ′C ′=22+1,A ′B ′=2. ∴这块菜地的面积S =12(A ′D ′+B ′C ′)·A ′B ′=12×⎝ ⎛⎭⎪⎫1+1+22×2=2+22.9.答案:2解析:设四面体ABCD 所在的长方体的长、宽、高分别为a ,b ,c ,则⎩⎪⎨⎪⎧a 2+b 2=5,a 2+c 2=13,b 2+c 2=10,得⎩⎪⎨⎪⎧a =2,b =1,c =3,所以四面体ABCD 的体积V =abc -13×12abc ×4=13abc =2.二 能力小题提升篇1.答案:A解析:设圆柱的高为h ,则2π×2×h =8π⇒h =2,所以圆柱的体积为π×22×2=8π.2.答案:C解析:根据斜二测画法规则知,把直观图∠A ′O ′B ′还原为平面图,如图所示:所以∠AOB 是钝角. 3.答案:C解析:由d =3169V 得V =916·(2r )3=43·278r 3,比较V =43πr 3,相当于π的取值为278. 4.答案:A解析:如图,设圆锥侧面展开扇形的圆心角为θ,则由题可得2π×4=12θ,则θ=2π3,在Rt△POP ′中,OP =OP ′=12,则小虫爬行的最短路程为PP ′=122+122-2×12×12×⎝ ⎛⎭⎪⎫-12=12 3.5.答案:27解析:由PA ⊥平面ABC ,AB ⊥AC ,将三棱锥补成长方体,它的对角线是其外接球的直径,∵三棱锥外接球的表面积为36π,设外接球的半径为R ,则4πR 2=36π,解得R =3∴三棱锥外接球的半径为3,直径为6,∵AB =AC =2,∴22+22+PA 2=62,∴PA =27.6.答案:(2-2)a解析:方法一 由题意知,球内切于四棱锥P ABCD 时半径最大.设该四棱锥的内切球的球心为O ,半径为r ,连接OA ,OB ,OC ,OD ,OP ,则V P -ABCD =V O -ABCD +V O -PAD +V O -PAB +V O -PBC +V O -PCD ,即13×2a ×2a ×2a =13×⎝ ⎛⎭⎪⎫4a 2+2×12×2a ×2a +2×12×2a ×22a ×r ,解得r =(2-2)a .方法二 易知当球内切于四棱锥P -ABCD ,即与四棱锥P -ABCD 各个面均相切时,球的半径最大.作出相切时的侧视图如图所示,设四棱锥P -ABCD 内切球的半径为r ,则12×2a ×2a=12×(2a +2a +22a )×r ,解得r =(2-2)a . 三 高考小题重现篇1.答案:B解析:设圆锥的母线长为l ,由于圆锥底面圆的周长等于扇形的弧长,则πl =2π×2,解得l =2 2.2.答案:D解析:根据题目条件以及正视图可以得到该几何体的直观图,如图,结合选项可知该几何体的侧视图为D.3.答案:39π解析:设该圆锥的高为h ,则由已知条件可得13×π×62×h =30π,解得h =52,则圆锥的母线长为h 2+62=254+36=132,故该圆锥的侧面积为π×6×132=39π. 4.答案:A解析:如图所示,因为AC ⊥BC ,且AC =BC =1,所以AB 为截面圆O 1的直径,且AB = 2.连接OO 1,则OO 1⊥面ABC ,OO 1=1-⎝ ⎛⎭⎪⎫AB 22=1-⎝ ⎛⎭⎪⎫222=22,所以三棱锥O ABC 的体积V =13S △ABC ×OO 1=13×12×1×1×22=212. 5.答案:2π2解析:如图,连接B 1D 1,易知△B 1C 1D 1为正三角形,所以B 1D 1=C 1D 1=2.分别取B 1C 1,BB 1,CC 1的中点M ,G ,H ,连接D 1M ,D 1G ,D 1H ,则易得D 1G =D 1H =22+12=5,D 1M ⊥B 1C 1,且D 1M = 3.由题意知G ,H 分别是BB 1,CC 1与球面的交点.在侧面BCC 1B 1内任取一点P ,使MP =2,连接D 1P ,则D 1P =D 1M 2+MP 2=(3)2+(2)2=5,连接MG ,MH ,易得MG =MH =2,故可知以M 为圆心,2为半径的圆弧GH 为球面与侧面BCC 1B 1的交线.由∠B 1MG =∠C 1MH =45°知∠GMH =90°,所以GH 的长为14×2π×2=2π2. 6.答案:26 2-1 解析:依题意知,题中的半正多面体的上、下、左、右、前、后6个面都在正方体的表面上,且该半正多面体的表面由18个正方形,8个正三角形组成,因此题中的半正多面体共有26个面.注意到该半正多面体的俯视图的轮廓是一个正八边形,设题中的半正多面体的棱长为x ,则22x +x +22x =1,解得x =2-1,故题中的半正多面体的棱长为2-1. 四 经典大题强化篇1.解析:(1)证明:因为AA 1=A 1C ,且O 为AC 的中点,所以A 1O ⊥AC ,又平面AA 1C 1C ⊥平面ABC ,平面AA 1C 1C ∩平面ABC =AC ,且A 1O ⊂平面AA 1C 1C ,∴A 1O ⊥平面ABC .(2)∵A 1C 1∥AC ,A 1C 1⊄平面ABC ,AC ⊂平面ABC ,∴A 1C 1∥平面ABC ,即C 1到平面ABC 的距离等于A 1到平面ABC 的距离.由(1)知A 1O ⊥平面ABC ,且A 1O =AA 21 -AO 2=3,∴VC 1-ABC =VA 1-ABC =13S △ABC ·A 1O =13×12×2×3×3=1. 2.解析:设点P 在平面ABC 上的射影为G ,如图,由PA =PB =PC =2,∠ABC =90°,知点P 在平面ABC 上的射影G 为△ABC 的外心,即AC 的中点.设球的球心为O ,连接PG ,则O 在PG 的延长线上.连接OB ,BG ,设PG =h ,则OG =2-h ,所以OB 2-OG 2=PB 2-PG 2,即4-(2-h )2=4-h 2,解得h =1,则AG =CG = 3.设AD =x ,则GD =x -AG =x -3,BG =3,所以BD =BG 2-GD 2=-x 2+23x ,所以S △ABD =12AD ·BD =12-x 4+23x 3. 令f (x )=-x 4+23x 3,则f ′(x )=-4x 3+63x 2.由f ′(x )=0,得x =0或x =332,易知当x =332时,函数f (x )取得最大值24316,所以(S △ABD )max =12×934=938.又PG =1,所以三棱锥P -ABD 体积的最大值为13×938×1=338.。
高考数学(文)《立体几何》专题复习

(2)两个平面垂直的判定和性质
✓ 考法5 线面垂直的判定与性质
1.证明直线 与平面垂直 的方法
2.线面垂直 的性质与线 线垂直
(1)判定定理(常用方法): 一条直线与一个平面内的两条相交直线都垂直,则该直线
与此平面垂直.判定定理中的两条相交直线必须保证“在平面 内相交”这一条件. (2)性质: ①应用面面垂直的性质(常用方法):若两平面垂直,则在一 个平面内垂直于交线的直线必垂直于另一个平面,是证明线 面垂直的主要方法; ②(客观题常用)若两条平行直线中的一条垂直于一个平面, 则另一条也垂直于这个平面.
64
65
✓ 考法4 面面平行的判定与性质
1.证明平面 与平面平行 的常用方法 2.空间平行关系 之间的转化
66
✓ 考法3 面面平行的判定与性质
1.证明平面 与平面平行 的常用方法
这是立体几何中证明平行关系常用的思路,三 种平行关系的转化可结合下图记忆
2.空间平行关系 之间的转化
67
68
600分基础 考点&考法
定义 判定方法
2.等角定理
判定定理 反证法 两条异面直线所成的角
✓ 考法2 异面直线所成的角
常考形式
直接求 求其三角函数值
常用方法
作角
正弦值 余弦值 正切值
证明 求值 取舍
55
56
57
58
600分基础 考点&考法
➢ 考点46 线面、面面平行的判定与性质 ✓ 考法3 线面平行的判定与性质 ✓ 考法4 面面平行的判定与性质
1.计算有关 线段的长
2.外接球、内切 球的计算问题
观察几何体的特征 利用一些常用定理与公式 (如正弦定理、余弦定理、勾股定理、 三角函数公式等) 结合题目的已知条件求解
三视图课件

B
A. 32 B. 16 16 2 C. 48 D. 16 32 2
5.2010湖南高考
4
6. (2007宁夏理•8) 已知某个几何体的三视图 如下,根据图中标出的尺寸(单位:cm), 可得这个几何体的体积是( B)
24
柱体
夯实基础 1.棱柱 (1)定义:有两个面互相平行,而且夹在这两个平行 平面间的每相邻两个面的交线都 互相平行,由这些面所 围成的多面体叫做棱柱. 稳固根基
(如图)
1° 球面被经过球心的平面截得的圆叫做大圆. 2° 不过球心的截面截得的圆叫做球的小圆.
(3)球面距离: 1° 定义:在球面上两点之间的最短距离,就是经过这 两点的 大圆 在这两点间的一段 劣弧 的长度, 这个弧长 叫做两点的球面距离. 2° 地球上的经纬线 当把地球看作一个球时, 经线是球面上从北极到南极 的半个大圆,纬线是与地轴垂直的平面与球面的交线,其 中赤道是一个大圆,其余纬线都是一个小圆.
5.球的概念与性质 (1)定义: 半圆绕它的直径所在直线旋转所成的曲面叫 做球面,球面所围成的几何体叫做球.球面也可以看作空 间中到定点的距离等于定长的点的集合. (2)球的截面性质 ①用一个平面去截球,截面是圆面.
②球心到截面的距离 d 与球的半径 R 及截面的半径 r,有下面的关系:
r= R2-d2
空间几何体的结构、三 视图和直观图、表面积 和体积
椎体
2
2.棱锥及其分类 (1)定义: 有一个面是多边形, 其余各面是 有一个公共顶点 的三 角形.由这些面所围成的几何体叫做棱锥. (2)正棱锥 如果棱锥的底面是正多边形, 顶点在过底面中心且与 底面垂直的直线上,则这个棱锥叫做正棱锥.
正棱锥的性质: ①各侧棱相等, 各侧面都是全等的等腰三角形. 这些 等腰三角形的高叫做棱锥的斜高. ②棱锥的高、 斜高和斜高在底面内的射影组成一个直 角三角形; 棱锥的高、 侧棱和侧棱在底面内的射影也组成 一个直角三角形.
2019数学(理)二轮精选讲义专题五 立体几何 第一讲空间几何体的三视图、表面积与体积 含答案

专题五立体几何第一讲空间几何体的三视图、表面积与体积考点一空间几何体的三视图与直观图1.三视图的排列规则俯视图放在正(主)视图的下面,长度与正(主)视图的长度一样,侧(左)视图放在正(主)视图的右面,高度与正(主)视图的高度一样,宽度与俯视图的宽度一样.即“长对正、高平齐、宽相等”.2.原图形面积S与其直观图面积S′之间的关系S′=错误!S。
[对点训练]1.(2018·全国卷Ⅲ)中国古建筑借助榫卯将木构件连接起来.构件的凸出部分叫榫头,凹进部分叫卯眼,图中木构件右边的小长方体是榫头.若如图摆放的木构件与某一带卯眼的木构件咬合成长方体,则咬合时带卯眼的木构件的俯视图可以是()[解析]两个木构件咬合成长方体时,小长方体(榫头)完全嵌入带卯眼的木构件,易知俯视图可以为A.故选A。
[答案]A2.(2018·河北衡水中学调研)正方体ABCD-A1B1C1D1中,E 为棱BB1的中点(如图),用过点A,E,C1的平面截去该正方体的上半部分,则剩余几何体的左视图为()[解析]过点A,E,C1的截面为AEC1F,如图,则剩余几何体的左视图为选项C中的图形.故选C。
[答案]C3.(2018·江西南昌二中模拟)一个几何体的三视图如图所示,在该几何体的各个面中,面积最小的面的面积为()A.8 B.4 C.4错误!D.4错误![解析]由三视图可知该几何体的直观图如图所示,由三视图特征可知,P A⊥平面ABC,DB⊥平面ABC,AB⊥AC,P A=AB =AC=4,DB=2,则易得S△P AC=S△ABC=8,S△CPD=12,S梯形ABDP =12,S△BCD=错误!×4错误!×2=4错误!,故选D。
[答案]D4.如图所示,一个水平放置的平面图形的直观图是一个底角为45°,腰和上底长均为1的等腰梯形,则该平面图形的面积为________.[解析]直观图的面积S′=错误!×(1+1+错误!)×错误!=错误!.故原平面图形的面积S=错误!=2+错误!.[答案]2+错误看到三视图,想到常见几何体的三视图,进而还原空间几何体.(2)看到平面图形直观图的面积计算,想到斜二侧画法,想到原图形与直观图的面积比为错误!.由三视图还原到直观图的3步骤(1)根据俯视图确定几何体的底面.(2)根据正(主)视图或侧(左)视图确定几何体的侧棱与侧面的特征,调整实线和虚线所对应的棱、面的位置.(3)确定几何体的直观图形状.考点二空间几何体的表面积与体积1.柱体、锥体、台体的侧面积公式(1)S柱侧=ch(c为底面周长,h为高);(2)S锥侧=错误!ch′(c为底面周长,h′为斜高);(3)S台侧=错误!(c+c′)h′(c′,c分别为上下底面的周长,h′为斜高).2.柱体、锥体、台体的体积公式(1)V柱体=Sh(S为底面面积,h为高);(2)V锥体=错误!Sh(S为底面面积,h为高);(3)V台=错误!(S+错误!+S′)h(不要求记忆).3.球的表面积和体积公式S表=4πR2(R为球的半径),V球=43πR3(R为球的半径).[对点训练]1.(2018·浙江卷)某几何体的三视图如图所示(单位:cm),则该几何体的体积(单位:cm3)是()A.2 B.4 C.6 D.8[解析]由三视图可知该几何体是直四棱柱,其中底面是直角梯形,直角梯形上,下底边的长分别为1 cm,2 cm,高为2 cm,直四棱柱的高为2 cm.故直四棱柱的体积V=1+22×2×2=6 cm3.[答案]C2.(2018·哈尔滨师范大学附中、东北师范大学附中联考)某几何体的三视图如图所示,其中正视图是半径为1的半圆,则该几何体的表面积是()A.错误!+2B.错误!+2C.错误!+3 D。
2020届高考数学(理)课标版二轮课件:重难考点专题三第1讲 空间几何体的三视图、表面积与体积

为 7 ,SA与圆锥底面所成角为45°.若△SAB的面积为5 15,则该圆锥的侧面积
8
为
.
答案 40 2 π
解析 因为母线SA与圆锥底面所成的角为45°,所以圆锥的轴截面为等腰直
角三角形.设底面圆的半径为r,则母线长l= 2 r.在△SAB中,cos∠ASB= 7 ,所以
8
sin∠ASB= 15 .因为△SAB的面积为5 15,即 1 SA·SBsin∠ASB=1 · 2 r·2 r×
A.20π C.28π
B.24π D.32π
答案 C 由三视图知圆锥的高为2 3,底面半径为2,则圆锥的母线长为4,所
以圆锥的侧面积为 1 ×4π×4=8π.圆柱的底面积为4π,圆柱的侧面积为4×4π=
2
16π,从而该几何体的表面积为8π+16π+4π=28π,故选C.
2.(2018课标全国Ⅱ,16,5分)已知圆锥的顶点为S,母线SA,SB所成角的余弦值
BC=3,AA1=5.设△ABC内切圆半径为r,则S△ABC=
1 2
×3×4=
1 2
×(3+4+5)r,解得r=1,
所以内切球最大半径为1,直径为2,由AA1=5得,最多可加工出2个球.
2.(2019洛阳联考)已知球O与棱长为4的正四面体的各棱相切,则球O的体积 为( A )
A.8 2 π
3
B.8 3 π
在△ACD中,AD⊥CD,S△ACD= 5 ;
2
在△BCD中,BD⊥CD,S△BCD=1 ,
2
所以表面积为 3 + 2 + 5 .故选A.
2
2
命题角度二 空间几何体的体积
1.(2018课标全国Ⅱ文,16,5分)已知圆锥的顶点为S,母线SA,SB互相垂直,SA与
人教版九年级数学下册第3课时 由三视图确定几何体的表面积或体积

2. 如图是一个几何体的三视图,则这个几何体
的A侧.18面cm积2 是( A )
B.20cm2
C. 18 6
3 4
10 2
2
cm
D. 18
75 2
3
解析:由三视图可得,几何体是三棱柱,几何体的侧面积 是三个矩形的面积和,矩形的长为3cm,宽为2cm,∴侧面 积为3×3×2=18cm2.
=
300
240
1 2
=36000(cm2
)
S侧面面积= 300 200=60000(cm2 )
S帐篷表面积=36000 +60000 =96000(cm2)
课堂小结
由三视图确定几何体的表面积或体积,一般步骤为: ① 想象:根据各视图想象从各个方向看到的几何体形状; ② 定形:综合确定几何体(或实物原型)的形状; ③ 展开图:画出展开图,求展开面积。
由三视图描述实物形状,画出物体表面展开图
由三视图确定几何体的表面积或是体积, 首先要确定该几何体的形状。
1.根据下列几何体的三视图,画出它们的展开图。
(1)
(2)
(3)
典例解析
例1 某工厂要加工一批密封罐,设计者给出了密封
罐的三视图,请你按照三视图确定制作每个密封罐所
需钢板的面积.
50
100 50
第3课时 由三视图确定几何体的 表面积或体积
R·九年级下册
复习导入
由三视图描述几何体(或实物原型),一般先根据各视图想象从 各个方向看到的几何体形状, 然后综合起来确定几何体(或实物原 型)的形状, 再根据三视图“长对正、高平齐、宽相等”的关系, 确定轮廓线的位置,以及各个方向的尺寸.
高中数学必修二 空间几何体的三视图如何求其表面积和体积

高中数学必修二空间几何体的三视图如何求其表面积和体积【教学目标】一、知识目标熟练掌握已知空间几何体的三视图如何求其表面积和体积。
二、能力目标先介绍由空间三视图求其表面积和体积,然后引导学生讨论和探讨问题。
三、德育目标1.通过空间几何体三视图的应用,培养学生的创新精神和探究能力。
2.通过研究性学习,培养学生的整体性思维。
【教学重点】观察、实践、猜想和归纳的探究过程。
【教学难点】如何引导学生进行合理的探究。
【教学方法】电教法、讲述法、分析推理法、讲练法【教学用具】多媒体、实物投影仪【教学过程】[投影]本节课的教学目标1.熟练掌握已知空间几何体的三视图如何求其表面积和体积。
【学习目标完成过程】一、复习提问1.如何求空间几何体的表面积和体积(例如:球、棱柱、棱台等)?2.三视图与其几何体如何转化?二、新课讲解[设置问题]例1:(如下图1),这是一个奖杯的三视图,试根据奖杯的三视图计算出它的表面积和体积(尺寸如图1,单位:cm,π取314,结果精确到1cm3)。
[提出问题]1.空间几何体的表面积和体积分别是什么?2.怎样运用柱体、锥体、台体、球体的表面积与体积的公式计算几何体的表面积和体积?[学生思考、总结板书]空间几何体的表面积是几何体表面的面积,它表示几何体表面的大小,体积是几何体所占空间的大小;先将直观图的各个要素弄清楚,然后再代公式进行计算。
[承转过渡]求空间几何体的表面积是将几何体的各个面的面积相加求得;求体积是将几何体各个部分的体积相加求得,那请同学们动脑筋想一想,假设没有给出几何体的直观图,只是给出一个几何体的三视图,我们怎样解决求该几何体的表面积和体积?在例1有没有给出几何体的直观图?[学生讨论、总结板书]例1没有直接给出几何体的直观图,只是给出实物几何体的三视图,要求该几何体的表面积和体积,应首先将该三视图转化为几何体的直观图,然后弄清给出直观图的各个要素,再代公式进行计算。
[设问]请问例1的三视图转化为实物几何体是由那几个部分构成?怎样求出该几何体的表面积和体积?[讨论、板书]该实物几何体是由一个球体、一个四棱柱和一个四棱台构成;应先分别求出一个球体、一个四棱柱和一个四棱台的表面积和体积。
高中数学 专题1.立体几何(立体图形的三视图、表面积、体积及外接球)
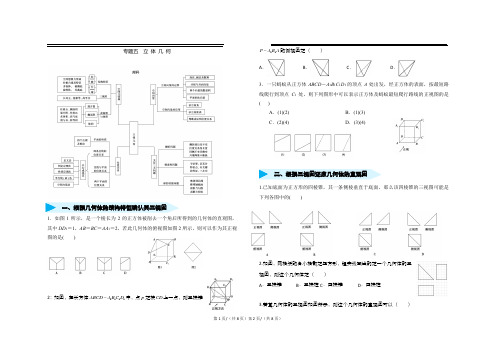
专题五 立 体 几 何1.如图1所示,是一个棱长为2的正方体被削去一个角后所得到的几何体的直观图,其中DD 1=1,AB =BC =AA 1=2,若此几何体的俯视图如图2所示,则可以作为其正视图的是( )2:如图,在长方体1111ABCD A B C D -中,点P 是棱CD 上一点,则三棱锥11P A B A -的侧视图是( )A .B .C .D .3.一只蚂蚁从正方体ABCD -A 1B 1C 1D 1的顶点A 处出发,经正方体的表面,按最短路线爬行到顶点C 1处,则下列图形中可以表示正方体及蚂蚁最短爬行路线的正视图的是( )A .(1)(2)B .(1)(3)C .(2)(4)D .(3)(4)1.已知底面为正方形的四棱锥,其一条侧棱垂直于底面,那么该四棱锥的三视图可能是下列各图中的( )2.如图,网格纸的各小格都是正方形,粗实线画出的是一个几何体的三视图,则这个几何体是( ) A .三棱锥 B .三棱柱C .四棱锥 D .四棱柱3.若某几何体的三视图如图所示,则这个几何体的直观图可以( )二、根据三视图还原几何体的直观图一、根据几何体的结构特征确认其三视图A.B.C.D.1.如图是一个空间几何体的正视图和俯视图,则它的侧视图为()A.B.C.D.2.(2018·南宁一模)一个简单几何体的正视图、侧视图如图所示,则其俯视图可能是( )①长、宽不相等的长方形;②正方形;③圆;④椭圆.A.①②B.①④C.②③D.③④3.一个几何体的三视图中,正视图和侧视图如图所示,则俯视图不可以为()A.B.C.D.4.中国古代数学名著《九章算术》中,将底面是直角三角形的直棱柱称为“堑堵”.已知“堑堵”的正视图和俯视图如图所示,则该“堑堵”的侧视图的面积为()A.18 6 B.18 3 C.18 2 D.27221.如图所示,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则该几何体的表面积为()A.5π18+B.6π18+C.8π6+D.10π6+2.如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则该几何体的表面积为()A.8+3π B.8+4πC.8+5π D.8+6π3.(2017·全国卷Ⅰ,7)某多面体的三视图如图所示,其中正视图和左视图都由正方形和等腰直角三角形组成,正方形的边长为2,俯视图为等腰直角三角形.该多面体的各个面中有若干个是梯形,这些梯形的面积之和为( ) A.10B.12C.14D.164..如图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的表面积为( )A.20πB.24πC.28πD.32π三、已知几何体的三视图中某两个视图,确定另外一种视图四、根据几何体的三视图计算表面积五、根据几何体的三视图计算体积1.(2019·江苏卷)如图,长方体ABCD-A1B1C1D1的体积是120,E为CC1的中点,则三棱锥EBCD的体积是_______2.(2017·山东卷,13)由一个长方体和两个14圆柱体构成的几何体的三视图如下,则该几何体的体积为。
专题 由三视图求表面积和体积

由三视图求表面积和体积一、方法与技巧二、常见几何体1.(2016•益阳模拟)若某空间几何体的三视图如图所示,则该几何体的表面积是()A.60 B.54 C.48 D.24【解答】解:由三视图知:几何体是一个侧面向下放置的直三棱柱,侧棱长为4,底面三角形为直角三角形,直角边长分别为3,4,斜边长为5.∴几何体的表面积S=S棱柱侧+S底面=(3+4+5)×4+2××3×4=48+12=60.故选:A.2.(2016•凉山州模拟)一个棱锥的三视图如图所示,则这个棱锥的体积是()A.6 B.12 C.24 D.36【解答】解:由已知的三视图可得该棱锥是以俯视图为底面的四棱锥其底面长和宽分别为3,4,棱锥的高是3故棱锥的体积V=Sh=×3×4×3=12故选B3.(2016•衡水校级一模)已知一个几何体的三视图如图所示,则该几何体的体积为()A.B.C.27﹣3πD.18﹣3π【解答】解:由三视图可知,该几何体为放到的直四棱柱,且中间挖去半个圆柱,由三视图中的数据可得:四棱柱的高为3,底面为等腰梯形,梯形的上、下底边分别为2、4,高为2,圆柱的高为3,圆柱底面的半径都是1,∴几何体的体积V==,故选:B.4.(2016•广元二模)一个多面体的三视图分别是正方形、等腰三角形和矩形,其尺寸如图,则该多面体的体积为()A.48cm3B.24cm3C.32cm3D.28cm3【解答】解:由三视图可知该几何体是平放的直三棱柱,高为4,底面三角形一边长为6,此边上的高为4 体积V=Sh==48cm3故选A5.(2016•江门模拟)一个几何体的三视图及其尺寸如下,则该几何体的表面积为()A.12πB.15πC.24πD.36π【解答】解:由三视图可知该几何体为一个圆锥,底面直径为6,母线长为5,底面圆的面积S1=π×()2=9π.侧面积S2=π×3×5=15π,表面积为S1+S2=24π.故选C.6.(2016•安康二模)一空间几何体的三视图如图所示,则该几何体的体积为()A.B.C.D.【解答】解:三视图复原的几何体是三棱锥,底面是底边长为2,高为2的等腰三角形,三棱锥的一条侧棱垂直底面,高为2.三棱锥的体积为:==.故选D.7.(2016•杭州模拟)某几何体的三视图如图所示,则该几何体的体积为()A.B.C.D.【解答】解:该几何体为三棱柱与三棱锥的组合体,如右图,三棱柱的底面是等腰直角三角形,其面积S=×1×2=1,高为1;故其体积V1=1×1=1;三棱锥的底面是等腰直角三角形,其面积S=×1×2=1,高为1;故其体积V2=×1×1=;故该几何体的体积V=V1+V2=;故选:A.8.(2016•呼伦贝尔一模)一个几何体的三视图如图所示,其中正视图和侧视图是腰长为4的两个全等的等腰直角三角形.若该几何体的体积为V,并且可以用n个这样的几何体拼成一个棱长为4的正方体,则V,n的值是()A.V=32,n=2 B.C.D.V=16,n=4【解答】解:由三视图可知,几何体为底面是正方形的四棱锥,所以V=,边长为4的正方体V=64,所以n=3.故选B9.(2016•广东模拟)一空间几何体的三视图如图所示,则该几何体的体积为()A.12 B.6 C.4 D.2【解答】解:由三视图知,几何体是一个四棱锥,四棱锥的底面是一个直角梯形,直角梯形的上底是1,下底是2,垂直于底边的腰是2,一条侧棱与底面垂直,这条侧棱长是2,∴四棱锥的体积是=2,故选D.10.(2016•延边州模拟)如图,水平放置的三棱柱的侧棱长和底边长均为2,且侧棱AA1⊥面A1B1C1,正视图是正方形,俯视图是正三角形,该三棱柱的侧视图面积为()A.B.C. D.4【解答】解:由题意知三棱柱的侧视图是一个矩形,矩形的长是三棱柱的侧棱长,宽是底面三角形的一条边上的高,在边长是2的等边三角形中,底边上的高是2×=,∴侧视图的面积是2.故选A.11.(2016•江西校级一模)如图是一个无盖器皿的三视图,正视图、侧视图和俯视图中的正方形边长为2,正视图、侧视图中的虚线都是半圆,则该器皿的表面积是()A.π+24 B.π+20 C.2π+24 D.2π+20【解答】解:该器皿的表面积可分为两部分:去掉一个圆的正方体的表面积s1和半球的表面积s2,s1=6×2×2﹣π×12=24﹣π,s2==2π,故s=s1+s2=π+24故选:A.12.(2016•太原二模)某几何体的三视图如图所示,图中的四边形都是边长为2的正方形,两条虚线互相垂直,则该几何体的体积是()A.B.C.D.【解答】解:由三视图知原几何体是一个棱长为2的正方体挖去一四棱锥得到的,该四棱锥的底为正方体的上底,高为1,如图所示:所以该几何体的体积为23﹣×22×1=.故选A.13.(2016•太原校级二模)某几何体的三视图如图所示,则该几何体中,面积最大的侧面的面积为()A.B.C.D.3【解答】解:由三视图可知,几何体的直观图如图所示,平面AED⊥平面BCDE,四棱锥A﹣BCDE的高为1,四边形BCDE是边长为1的正方形,则S△AED==,S△ABC=S△ADE==,S△ACD==,故选:B.14.(2016•河西区模拟)如图是某几何体的三视图,其中正视图是腰长为2的等腰三角形,俯视图是半径为1的半圆,则该几何体的体积是()A.B. C.D.【解答】解:由三视图知几何体的直观图是半个圆锥,又∵正视图是腰长为2的等腰三角形∴r=1,h=∴故选:D.15.(2016•岳阳二模)一个几何体的三视图如图所示,已知这个几何体的体积为,则h=()A.B.C. D.【解答】解:三视图复原的几何体是底面为边长5,6的矩形,一条侧棱垂直底面高为h,所以四棱锥的体积为:,所以h=.故选B.16.(2016•汉中二模)一个四棱锥的底面为正方形,其三视图如图所示,则这个四棱锥的体积是()A.1 B.2 C.3 D.4【解答】解:由题设及图知,此几何体为一个四棱锥,其底面为一个对角线长为2的正方形,故其底面积为=2由三视图知其中一个侧棱为棱锥的高,其相对的侧棱与高及底面正方形的对角线组成一个直角三角形由于此侧棱长为,对角线长为2,故棱锥的高为=3此棱锥的体积为=2故选B.17.(2016•榆林一模)某三棱锥的三视图如图所示,该三棱锥的体积为()A.80 B.40 C.D.【解答】解:由三视图可知该几何体是如图所示的三棱锥:PO⊥平面ABC,PO=4,AO=2,CO=3,BC⊥AC,BC=4.从图中可知,三棱锥的底是两直角边分别为4和5的直角三角形,高为4,体积为V=.故选D.18.(2016•揭阳一模)已知某空间几何体的三视图如图所示,则该几何体的体积是48.【解答】解:由三视图可知原几何体如图所示,可看作以直角梯形ABDE为底面,BC为高的四棱锥,由三棱锥的体积公式可得V=××(2+6)×6×6=48,故答案为:48.三、常见几何体的组合体19.(2016•佛山模拟)已知某几何体的三视图如图所示,其中,正(主)视图,侧(左)视图均是由三角形与半圆构成,俯视图由圆与内接三角形构成,根据图中的数据可得此几何体的体积为()A.B.C. D.【解答】解:由三视图可得该几何体的上部分是一个三棱锥,下部分是半球,所以根据三视图中的数据可得:V=××=,故选C.20.(2016•乐山模拟)一个几何体的三视图如图所示,则此几何体的体积是()A.112 B.80 C.72 D.64【解答】解:由三视图可知,此几何体是由一个棱柱和一个棱锥构成的组合体,棱柱的体积为4×4×4=64;棱锥的体积为×4×4×3=16;则此几何体的体积为80;故选B.四、常见几何体的切割体21.(2016•茂名一模)若某几何体的三视图(单位:cm)如图所示,则该几何体的体积等于()A.10cm3B.20cm3C.30cm3D.40cm3【解答】解:由三视图知几何体为三棱柱削去一个三棱锥如图:棱柱的高为5;底面为直角三角形,直角三角形的直角边长分别为3、4,∴几何体的体积V=×3×4×5﹣××3×4×5=20(cm3).故选B.22.(2016•威海一模)一个棱长为2的正方体沿其棱的中点截去部分后所得几何体的三视图如图示,则该几何体的体积为()A.7 B.C.D.【解答】解:依题意可知该几何体的直观图如图示,其体积为正方体的体积去掉两个三棱锥的体积.即:,故选D.23.(2016•张掖校级模拟)某几何体的三视图如图所示,则该几何体的体积为26【解答】解:由三视图知几何体为为三棱柱,去掉一个三棱锥的几何体,如图:三棱柱的高为5,底面是直角边为4,3,去掉的三棱锥,是底面是直角三角形直角边为4,3,高为2的三棱锥.∴几何体的体积V==26.故答案为:26.24.(2016•商洛模拟)已知一个几何体的三视图是三个全等的边长为l的正方形,如图所示,则该几何体的体积为()A.B.C.D.【解答】解:该几何体是正方体削去一个角,体积为1﹣=1﹣=.故选:D.25.(2016•银川校级一模)如图,网格纸上小正方形的边长为1,粗线画出的是一正方体被截去一部分后所得几何体的三视图,则被截去部分的几何体的表面积为54+18.【解答】解:由三视图可知正方体边长为6,截去部分为三棱锥,作出几何体的直观图如图所示:∴被截去的几何体的表面积S=+×(6)2=54+18.故答案为54+18.26.(2016•哈尔滨校级二模)一个空间几何体的三视图如图所示,则这个几何体的体积为.【解答】解:根据已知中的三视图,可得几何体的直观图如下图所示:该几何是由一个以俯视图为底面的四棱锥,切去两个棱锥所得的组合体,四棱柱的体积为:×(2+4)×4×4=48,四棱锥F﹣EHIJ的体积为:×(2+4)×4×2=8,中棱锥F﹣HGJ的体积为:=,故组合体的体积V=,故答案为:4.(2011•北京模拟)已知一个几何体的三视图如所示,则该几何体的体积为()A.6 B.5.5 C.5 D.4.5【考点】由三视图求面积、体积.【分析】由三视图知几何体是一个长方体割去两个三棱锥,三棱锥的底面是一个底面面积可以做出,高是3,做出截去得到三棱锥的体积,长方体的体积也可以做出.【解答】解:由三视图知几何体是一个长方体割去两个三棱锥,三棱锥的底面是一个底面面积是×1×1=,高是3,∴截去得到三棱锥的体积是2××=1,长方体的体积是3×2×1=6∴几何体的体积是6﹣1=5故选C.。
高考数学立体几何专题1空间立体几何的三视图、表面积和体积

专题1空间立体几何的三视图、表面积和体积【考点点击】1.以选择、填空题形式考查空间位置关系的判断,及文字语言、图形语言、符号语言的转换,难度适中;2.以熟悉的几何体为背景,考查多面体或旋转体的侧面积、表面积和体积计算,间接考查空间位置关系的判断及转化思想等,常以三视图形式给出几何体,辅以考查识图、用图能力及空间想象能力,难度中等.3.几何体的三视图与表(侧)面积、体积计算结合;【重点知识】一、空间几何体1.柱体、锥体、台体、球的结构特征名称几何特征棱柱①有两个面互相平行(底面可以是任意多边形);②其余各面都是平行四边形,并且每相邻两个四边形的公共边互相平行棱锥①有一个面是多边形(底面);②其余各面是有公共顶点的三角形.棱台①底面互相平行;②所有侧棱延长后交于一点(即原棱锥的顶点)圆柱①有两个互相平行的圆面(底面);②有一个侧面是曲面(母线绕轴旋转一周形成的),且母线与底面垂直圆台①底面互相平行;②有一个侧面是曲面,可以看成母线绕轴旋转一周形成的球①有一个曲面是球面;②有一个球心和一条半径长R,球是一个几何体(包括内部),可以看成半圆以它的直径所在直线为旋转轴旋转一周形成的2.柱体、锥体、台体、球的表面积与体积名称体积表面积棱柱V棱柱=Sh(S为底面积,h为高)S棱柱=2S底面+S侧面棱锥V棱锥=13Sh(S为底面积,h为高)S棱锥=S底面+S侧面棱台V棱台=13h(S+SS′+S′)S棱台=S上底+S下底+S侧面圆柱V圆柱=πr2h(r为底面半径,h为高)S圆柱=2πrl+2πr2(r为底面半径,l为母线长)圆锥V圆锥=13πr2h(r为底面半径,h为高)S圆锥=πrl+πr2(r为底面半径,l为母线长)圆台V圆台=13πh(r2+rr′+r′2)S圆台=π(r+r′)l+πr2+πr′2球V球=43πR3(R为球的半径)S球=4πR2(R为球的半径)3.空间几何体的三视图和直观图(1)空间几何体的三视图三视图的正视图、侧视图、俯视图分别是从物体的正前方、正左方、正上方看到的物体轮廓线的正投影围成的平面图形,三视图的画法规则为“长对正、高平齐、宽相等”.(2)空间几何体的直观图空间几何体直观图的画法常采用斜二测画法.用斜二测画法画平面图形的直观图规则为“轴夹角45°(或135°),平行长不变,垂直长减半”.4.几何体沿表面某两点的最短距离问题一般用展开图解决;不规则几何体求体积一般用割补法和等积法求解;三视图问题要特别留意各种视图与观察者的相对位置关系.【考点分析】考点一空间几何体的结构【例1】已知正三棱锥PABC ,点P ,A ,B ,C 都在半径为3的球面上,若PA ,PB ,PC 两两相互垂直,则球心到截面ABC 的距离为________.【答案】33【解析】正三棱锥PABC 可看作由正方体PADCBEFG 截得,如图所示,PF 为三棱锥PABC 的外接球的直径,且PF ⊥平面ABC.设正方体棱长为a ,则22,2,1232=====BC AC AB a a ,3223222221=⨯⨯⨯=∆ABC S ,由,PAC B ABC P V V --=得222213131⨯⨯⨯⨯=⋅∆ABC S h ,所以332=h 因此球心到平面ABC 得距离为33考点二三视图、直观图【例2】下图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的表面积为()(A )20π(B )24π(C )28π(D )32π【答案】C【解析】由题意可知,圆柱的侧面积为12π2416πS =⋅⋅=,圆锥的侧面积为2π248πS =⋅⋅=,圆柱的底面面积为23π24πS =⋅=,故该几何体的表面积为12328πS S S S =++=,故选C.【例3】某三棱锥的三视图如图所示,则该三棱锥的表面积是()A .2+5B .4+5C .2+25D .5【答案】C【解析】该三棱锥的直观图如图所示:过D 作DE ⊥BC ,交BC 于E ,连接AE ,则BC =2,EC =1,AD =1,ED =2,ABCABD ACD BCD S S S S S ∆∆∆∆+++=表5225221152115212221+=⨯⨯+⨯⨯+⨯⨯+⨯⨯=考点三几何体的表面积【例4】长方体的长、宽、高分别为3,2,1,其顶点都在球O 的球面上,则球O 的表面积为【答案】14π.【解析】球的直径是长方体的体对角线,所以222232114,4π14π.R S R =++===【例5】如图,某几何体的三视图是三个半径相等的圆及每个圆中两条相互垂直的半径.若该几何体的体积是328π,则它的表面积是()(A )17π(B )18π(C )20π(D )28π【答案】A【解析】该几何体直观图如图所示:是一个球被切掉左上角的81,设球的半径为R ,则32834873ππ=⨯=R V ,解得R 2=,所以它的表面积是87的球面面积和三个扇形面积之和πππ172413248722=⨯⨯+⨯⨯=S 故选A .考点四几何体的体积【例6.】已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为()A .πB .3π4C .π2D .π4【答案】B【解析】绘制圆柱的轴截面如图所示,由题意可得:11,2AC AB ==,结合勾股定理,底面半径2213122r ⎛⎫=-= ⎪⎝⎭,由圆柱的体积公式,可得圆柱的体积是2233ππ1π24V r h ⎛==⨯⨯= ⎝⎭,故选B.考点五与球的组合体问题纵观近几年高考对于组合体的考查,重点放在与球相关的外接与内切问题上.要求学生有较强的空间想象能力和准确的计算能力,才能顺利解答.从实际教学来看,这部分知识是学生掌握最为模糊,看到就头疼的题目.分析原因,除了这类题目的入手确实不易之外,主要是学生没有形成解题的模式和套路,以至于遇到类似的题目便产生畏惧心理.本文就高中阶段出现这类问题加以类型的总结和方法的探讨.【例7】棱长为1的正方体1111ABCD A B C D -的8个顶点都在球O 的表面上,E F ,分别是棱1AA ,1DD 的中点,则直线EF 被球O 截得的线段长为()A .22B .1C .212+D .2解:由题意可知,球为正方体的外接球.平面11AA DD 截面所得圆面的半径12,22AD R ==11EF AA DD ⊂ 面,∴直线EF 被球O 截得的线段为球的截面圆的直径22R =.【例8】正四棱柱1111ABCD A B C D -的各顶点都在半径为R 的球面上,则正四棱柱的侧面积有最值,为.【例9】在正三棱锥S ABC -中,M N 、分别是棱SC BC 、的中点,且AM MN ⊥,若侧棱23SA =,则正三棱锥S ABC -外接球的表面积是.解:如图,正三棱锥对棱相互垂直,即,AC SB ⊥又,,,.SB MN MN AC MN AM MN SAC ∴⊥⊥∴⊥∥又平面于是,,,SB SAC SB SA SB SC ⊥∴⊥⊥平面从而.SA SC ⊥此时正三棱锥S ABC -的三条侧棱互相垂直并且相等,故将正三棱锥补形为正方体.球的半径23,3,436.2R SA R S R ππ=∴=∴==【例10】一个几何体的三视图如图所示,其中主视图和左视图是腰长为1的两个全等的等腰直角三角形,则该几何体的外接球的表面积为()A .12πB .C .3πD .【答案】C【解析】把原来的几何体补成以DA DC DP 、、为长、宽、高的长方体,原几何体四棱锥与长方体是同一个外接球,2=R l ,=2R ,234434S R πππ==⨯=球.【例11】在三棱锥P -ABC 中,PA =,侧棱PA 与底面ABC 所成的角为60°,则该三棱锥外接球的体积为()A .πB.3π C.4πD.43π解:如图所示,过P 点作底面ABC 的垂线,垂足为O ,设H 为外接球的球心,连接,,AH AO 因60,PAO PA ∠== 故2AO =,32PO =又△AHO 为直角三角形,222,,AH PH r AH AO OH ==∴=+22233344(),1,1.2233r r r V ππ∴=+-∴=∴=⨯=【例12】矩形ABCD 中,4,3,AB BC ==沿AC 将矩形ABCD 折成一个直二面角B ACD --,则四面体ABCD 的外接球的体积是()A.π12125 B.π9125C.π6125D.π3125解:由题意分析可知,四面体ABCD 的外接球的球心落在AC 的中点,此时满足,OA OD OB OC ===522AC R ∴==,343V R π=1256π=.【总结归纳】1个特征——三视图的长度特征“长对正,宽相等,高平齐”,即正视图和侧视图一样高,正视图和俯视图一样长,侧视图和俯视图一样宽。
空间几何体的三视图、表面积及体积
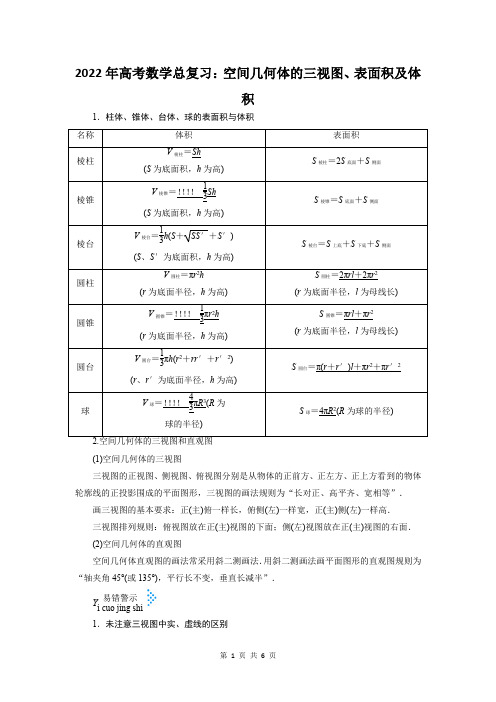
2022年高考数学总复习:空间几何体的三视图、表面积及体积1.柱体、锥体、台体、球的表面积与体积(1)空间几何体的三视图三视图的正视图、侧视图、俯视图分别是从物体的正前方、正左方、正上方看到的物体轮廓线的正投影围成的平面图形,三视图的画法规则为“长对正、高平齐、宽相等”.画三视图的基本要求:正(主)俯一样长,俯侧(左)一样宽,正(主)侧(左)一样高.三视图排列规则:俯视图放在正(主)视图的下面;侧(左)视图放在正(主)视图的右面.(2)空间几何体的直观图空间几何体直观图的画法常采用斜二测画法.用斜二测画法画平面图形的直观图规则为“轴夹角45°(或135°),平行长不变,垂直长减半”.Y易错警示i cuo jing shi1.未注意三视图中实、虚线的区别在画三视图时应注意看到的轮廓线画成实线,看不到的轮廓线画成虚线.2.不能准确分析组合体的结构致误对简单组合体表面积与体积的计算要注意其构成几何体的面积、体积是和还是差.3.台体可以看成是由锥体截得的,此时截面一定与底面平行.4.空间几何放置的方式不同时,对三视图可能会有影响.1.(2018·全国卷Ⅲ,3)中国古建筑借助榫卯将木构件连接起来,构件的凸出部分叫榫头,凹进部分叫卯眼,图中木构件右边的小长方体是榫头.若如图摆放的木构件与某一带卯眼的木构件咬合成长方体,则咬合时带卯眼的木构件的俯视图可以是( A )[解析]选A.由直观图可知选A.2.(文)(2018·全国卷Ⅰ,5)已知圆柱的上、下底面的中心分别为O1,O2,过直线O1O2的平面截该圆柱所得的截面是面积为8的正方形,则该圆柱的表面积为( B ) A.122π B.12πC.82π D.10π[解析]截面面积为8,所以高h=22,底面半径r=2,所以该圆柱表面积S=π·(2)2·2+2π·2·22=12π.(理)(2018·全国卷Ⅰ,7)某圆柱的高为2,底面周长为16,其三视图如图所示,圆柱表面上的点M在正视图上的对应点为A,圆柱表面上的点N在侧视图上的对应点为B,则在此圆柱侧面上,从M到N的路径中,最短路径的长度为( B )A.217 B.25C.3 D.2[解析]选B.将三视图还原为圆柱,M,N的位置如图1所示,将侧面展开,最短路径为M,N连线的距离,所以MN=42+22=2 5.3.(2018·浙江卷,3)某几何体的三视图如图所示(单位:cm),则该几何体的体积(单位:cm 3)是( C )A .2B .4C .6D .8[解析] 选C . 由三视图可知,该几何体是底面为直角梯形的直四棱柱,底面面积S =(1+2)×22=3,高h =2,所以V =Sh =6.4.(2018·北京卷,5)某四棱锥的三视图如图所示,在此四棱锥的侧面中,直角三角形的个数为( C )A .1B .2C .3D .4[解析] 选C .将四棱锥三视图转化为直观图,如图,侧面共有4个三角形,即△P AB ,△PBC ,△PCD ,△P AD , 由已知,PD ⊥平面ABCD ,又AD ⊂平面ABCD ,所以PD ⊥AD ,同理PD ⊥CD ,PD ⊥AB , 所以△PCD ,△P AD 是直角三角形.因为AB ⊥AD ,PD ⊥AB ,PD ,AD ⊂平面P AD ,PD ∩AD =D , 所以AB ⊥平面P AD ,又P A ⊂平面P AD , 所以AB ⊥P A ,△P AB 是直角三角形. 因为AB =1,CD =2,AD =2,PD =2,所以P A =PD 2+AD 2=22,PC =PD 2+CD 2=22, PB =P A 2+AB 2=3,在梯形ABCD 中,易知BC =5,△PBC 三条边长为22,3,5,△PBC 不是直角三角形. 综上,侧面中直角三角形个数为3.5.(文)(2018·全国卷Ⅰ,10)在长方体ABCD A 1B 1C 1D 1中,AB =BC =2,AC 1与平面BB 1C 1C 所成的角为30°,则该长方体的体积为( C )A .8B .6 2C .8 2D .83[解析]选C .如图,连接AC 1和BC 1,因为AB ⊥平面BB 1C 1C ,AC 1与平面BB 1C 1C 所成角为30°,所以∠AC 1B =30°, 所以AB BC 1=tan30°,BC 1=23,所以CC 1=22,所以V =2×2×22=8 2.(理)(2018·全国卷Ⅲ,10)设A ,B ,C ,D 是同一个半径为4的球的球面上四点,△ABC 为等边三角形且其面积为93,则三棱锥D ABC 体积的最大值为( B )A .12 3B .18 3C .24 3D .543[解析] 设△ABC 的边长为a ,则S △ABC =12a 2sin C =34a 2=93,解得a =6,如图所示,当点D 在底面上的射影为三角形ABC 的中心H 时,三棱锥D ABC 的体积最大,设球心为O ,则在直角三角形AHO 中,AH =23×32×6=23,OA =R =4,则OH=OA 2-AH 2=16-12=2,所以DH =2+4=6,所以三棱锥D ABC 的体积最大值为V =13S △ABC ×DH =13×93×6=18 3. 6.(文)(2018·天津卷,11)如图,已知正方体ABCD A 1B 1C 1D 1的棱长为1,则四棱锥A 1BB 1D 1D 的体积为13.[解析] 连接A 1C 1,交B 1D 1于O 1点,依题意得A 1O 1⊥平面BB 1D 1D ,即A 1O 1为四棱锥A 1BB 1D 1D 的高,且A 1O 1=22,而四棱锥A 1BB 1D 1D 的底面为矩形,其面积为2,所以四棱锥A 1BB 1D 1D 的体积V =13Sh =13×2×22=13.(理)(2018·天津卷,11)已知正方体ABCD A 1B 1C 1D 1的棱长为1,除面ABCD 外,该正方体其余各面的中心分别为点E ,F ,G ,H ,M (如图),则四棱锥M EFGH 的体积为112.[解析] 依题意得:该四棱锥M EFGH 为正四棱锥,其高为正方体棱长的一半,即为12,正方形EFGH 的边长为22,其面积为12,所以四棱锥M EFGH 的体积V M EFGH =13Sh =13×12×12=112. 7.(2018·全国卷Ⅱ,16)已知圆锥的顶点为S ,母线SA ,SB 所成角的余弦值为78,SA 与圆锥底面所成角为45°,若△SAB 的面积为515,则该圆锥的侧面积为402π.[解析] 如图:设SA =SB =l ,底面圆半径为r ,因为SA 与圆锥底面所成角为45°,所以l =2r ,在△SAB 中,AB 2=SA 2+SB 2-2SA ·SB ·cos ∠ASB =12r 2,AB =22r ,AB 边上的高为(2r )2-⎝⎛⎭⎫24r 2=304r ,△SAB 的面积为515, 所以12·22r ·304r =515,解得r =210,所以该圆锥的侧面积为πrl =π2r 2=402π.8.(2017·全国卷Ⅰ,16)已知三棱锥S -ABC 的所有顶点都在球O 的球面上,SC 是球O 的直径.若平面SCA ⊥平面SCB ,SA =AC ,SB =BC ,三棱锥S -ABC 的体积为9,则球O 的表面积为36π.[解析] 如图,连接OA ,OB .由SA =AC ,SB =BC ,SC 为球O 的直径,知OA ⊥SC ,OB ⊥SC .由平面SCA ⊥平面SCB ,平面SCA ∩平面SCB =SC ,OA ⊥SC ,知OA ⊥平面SCB . 设球O 的半径为r ,则OA =OB =r ,SC =2r , ∴三棱锥S -ABC 的体积V =13×(12SC ·OB )·OA =r 33,即r 33=9, ∴r =3,∴S 球表=4πr 2=36π.。
【高考数学】第三部分_重点板块_专题三立体几何:第1讲空间几何体的三视图、表面积及体积
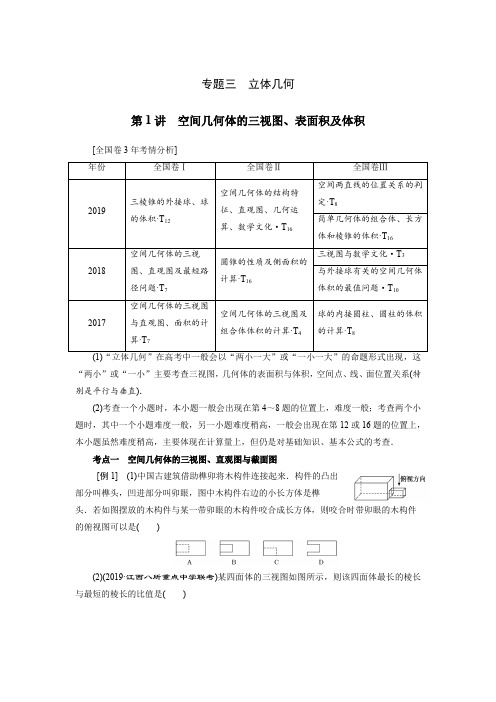
专题三立体几何第1讲空间几何体的三视图、表面积及体积[全国卷3年考情分析]年份全国卷Ⅰ全国卷Ⅱ全国卷Ⅲ2019三棱锥的外接球、球的体积·T12空间几何体的结构特征、直观图、几何运算、数学文化·T16空间两直线的位置关系的判定·T8简单几何体的组合体、长方体和棱锥的体积·T16 2018空间几何体的三视图、直观图及最短路径问题·T7圆锥的性质及侧面积的计算·T16三视图与数学文化·T3与外接球有关的空间几何体体积的最值问题·T10 2017空间几何体的三视图与直观图、面积的计算·T7空间几何体的三视图及组合体体积的计算·T4球的内接圆柱、圆柱的体积的计算·T8“两小”或“一小”主要考查三视图,几何体的表面积与体积,空间点、线、面位置关系(特别是平行与垂直).(2)考查一个小题时,本小题一般会出现在第4~8题的位置上,难度一般;考查两个小题时,其中一个小题难度一般,另一小题难度稍高,一般会出现在第12或16题的位置上,本小题虽然难度稍高,主要体现在计算量上,但仍是对基础知识、基本公式的考查.考点一空间几何体的三视图、直观图与截面图[例1](1)中国古建筑借助榫卯将木构件连接起来.构件的凸出部分叫榫头,凹进部分叫卯眼,图中木构件右边的小长方体是榫头.若如图摆放的木构件与某一带卯眼的木构件咬合成长方体,则咬合时带卯眼的木构件的俯视图可以是()(2)(2019·江西八所重点中学联考)某四面体的三视图如图所示,则该四面体最长的棱长与最短的棱长的比值是()A .52B .2C .355D .32(3)(2018·全国卷Ⅰ)已知正方体的棱长为1,每条棱所在直线与平面α所成的角都相等,则α截此正方体所得截面面积的最大值为( )A .334B .233C .324D .321.(2018·全国卷Ⅰ)某圆柱的高为2,底面周长为16,其三视图如图所示.圆柱表面上的点M 在正视图上的对应点为A ,圆柱表面上的点N 在左视图上的对应点为B ,则在此圆柱侧面上,从M 到N 的路径中,最短路径的长度为( )A .217B .25C .3D .22.已知球O 是正三棱锥A BCD 的外接球,BC =3,AB =23,点E 在线段BD 上,且BD =3BE ,过点E 作球O 的截面,则所得截面中面积最小的截面圆的面积是________.考点二 几何体的表面积与体积 题型一 求空间几何体的表面积[例2] (1)《九章算术》是我国古代内容极为丰富的数学名著,书中提到了一种名为“刍甍”的五面体,如图所示,四边形ABCD 为矩形,棱EF ∥AB .若此几何体中,AB =4,EF =2,△ADE 和△BCF 都是边长为2的等边三角形,则该几何体的表面积为( )A .83B .8+83C .62+23D .8+62+23(2)我国古代数学名著《算法统宗》中有如下问题:“今有倚壁外角堆米,下周九十尺,高十二尺.”其意思为:在屋外墙角处堆放米(其三视图如图所示),米堆底部的弧长为90尺,米堆的高为12尺.圆周率约为3.若将此堆米用草席盖上,则此草席的面积至少约为(计算结果保留整数,如544≈23,550≈23)( )A .250平方尺B .990平方尺C .1 035平方尺D .518平方尺题型二 求空间几何体的体积[例3] (1)(2019·天津高考)已知四棱锥的底面是边长为2的正方形,侧棱长均为 5.若圆柱的一个底面的圆周经过四棱锥四条侧棱的中点,另一个底面的圆心为四棱锥底面的中心,则该圆柱的体积为________.(2)(2019·江西省五校协作体试题)某几何体的三视图如图所示,正视图是一个上底为2,下底为4的直角梯形,俯视图是一个边长为4的等边三角形,则该几何体的体积为______.1.(2019·重庆市学业质量调研)已知某几何体的三视图如图所示,则该几何体的体积为( )A.323 B .643C.1283 D .16032.已知一个底面是菱形、侧面是矩形的四棱柱,侧棱长为5,菱形的对角线的长分别是9和15,则这个棱柱的侧面积是( )A .3034B .6034C .3034+135D .1353.已知直四棱柱ABCD A 1B 1C 1D 1的所有棱长都是1,∠ABC =60°,AC ∩BD =O ,A 1C 1∩B 1D 1=O 1,点H 在线段OB 1上,OH =3HB 1,点M 是线段BD 上的动点,则三棱锥M C 1O 1H 的体积的最小值为________.考点三 与球有关的切、接问题 题型一 外接球[例4] (2019·全国卷Ⅰ)已知三棱锥P ABC 的四个顶点在球O 的球面上,P A =PB =PC ,△ABC 是边长为2的正三角形,E ,F 分别是P A ,AB 的中点,∠CEF =90°,则球O 的体积为( )A .86πB .46πC .26πD .6π题型二 内切球[例5] 已知一个平放的各棱长为4的三棱锥内有一个小球O (重量忽略不计),现从该三棱锥顶端向内注水,小球慢慢上浮,当注入的水的体积是该三棱锥体积的78时,小球与该三棱锥各侧面均相切(与水面也相切),则小球的表面积等于( )A.7π6 B .4π3C.2π3 D .π2题型三 与球有关的最值问题[例6] (2018·全国卷Ⅲ)设A ,B ,C ,D 是同一个半径为4的球的球面上四点,△ABC 为等边三角形且其面积为93,则三棱锥D ABC 体积的最大值为( )A .123B .183C .243D .5431.已知圆锥的高为3,底面半径为3,若该圆锥的顶点与底面的圆周都在同一个球面上,则这个球的体积等于( )A .83πB .323πC .16πD .32π2.(2019·福建五校第二次联考)已知直三棱柱ABC A 1B 1C 1的6个顶点都在球O 的球面上,若AB =3,AC =4,AB ⊥AC ,AA 1=12,则球O 的直径为______.3.已知四棱锥S ABCD 的所有顶点在同一球面上,底面ABCD 是正方形且球心O 在此平面内,当四棱锥的体积取得最大值时,其表面积等于16+163,则球O 的体积为______.4.已知某几何体的三视图如图所示,则该几何体的体积等于( )A .2π+4B .4π+2 C.2π3+4 D .4π3+8【课后专项练习】A 组一、选择题1.如图是一个空间几何体的正视图和俯视图,则它的侧视图为( )2.(2019·福州市质量检测)棱长为1的正方体ABCD A 1B 1C 1D 1木块的直观图如图所示,平面α过点D 且平行于平面ACD 1,则该木块在平面α内的正投影面积是( )A.3 B .323C.2D .13.已知矩形ABCD ,AB =2BC ,把这个矩形分别以AB ,BC 所在直线为轴旋转一周,所成几何体的侧面积分别记为S 1,S 2,则S 1与S 2的比值等于( )A.12 B .1 C .2D .44.设球O 是正方体ABCD A 1B 1C 1D 1的内切球,若平面ACD 1截球O 所得的截面面积为6π,则球O 的半径为( )A.32 B .3 C.32D .35.(2019·武汉市调研测试)如图,在棱长为1的正方体ABCD A 1B 1C 1D 1中,M 为CD 的中点,则三棱锥A BC 1M 的体积VA BC 1M =( )A.12 B .14C.16 D .1126.(2019·武汉市调研测试)如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,则该几何体的体积为( )A.23π B .43πC .2πD .25π7.在三棱锥A BCD 中,侧棱AB ,AC ,AD 两两垂直,△ABC ,△ACD ,△ADB 的面积分别为22,32,62,则该三棱锥的体积为( ) A. 6 B .66 C .6 D .268.已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为( )A .πB .3π4C.π2 D .π49.若一个球与四面体的六条棱都相切,则称此球为四面体的棱切球.已知正四面体的棱长为2,则它的棱切球的体积为( )A .3π54B .π6C .π3D .3π210.已知点A ,B ,C ,D 均在球O 上,AB =BC =3,AC =3.若三棱锥D ABC 体积的最大值为334,则球O 的表面积为( )A .36πB .16πC .12πD .163π11.已知一个半径为7的球中有一个各条棱长都相等的内接正三棱柱,则正三棱柱的体积是( )A .18B .16C .12D .812.(2019·福州市质量检测)如图,以棱长为1的正方体的顶点A 为球心,以2为半径作一个球面,则该正方体的表面被球面所截得的所有弧长之和为( )A.3π4 B .2π C.3π2 D .9π4二、填空题13.(2019·长春市质量监测(一))已知一所有棱长都是2的三棱锥,则该三棱锥的体积为______.14.已知正方体ABCD A 1B 1C 1D 1的棱长为1,除面ABCD 外,该正方体其余各面的中心分别为点E ,F ,G ,H ,M (如图),则四棱锥M EFGH 的体积为______.15.古人采取“用臼舂米”的方法脱去稻谷的外壳,获得可供食用的大米,用于舂米的“臼”多用石头或木头制成.一个“臼”的三视图如图所示,则凿去部分(看成一个简单的组合体)的体积为______.16.已知三棱锥P ABC 的四个顶点都在球O 的表面上,P A ⊥平面ABC ,AB ⊥BC ,且P A =8.若平面ABC 截球O 所得截面的面积为9π,则球O 的表面积为______.B 组1.(2019·合肥市第二次质量检测)如图,正方形网格纸中的实线图形是一个多面体的三视图,则该多面体各表面所在平面互相垂直的有( )A .2对B .3对C .4对D .5对2.在棱长为3的正方体ABCD A 1B 1C 1D 1中,P 在线段BD 1上,且BP PD 1=12,M 为线段B 1C 1上的动点,则三棱锥M PBC 的体积为( )A .1B .32C.92 D .与M 点的位置有关3.已知正方体ABCD A 1B 1C 1D 1的体积为1,点M 在线段BC 上(点M 异于B ,C 两点),点N 为线段CC 1的中点,若平面AMN 截正方体ABCD A 1B 1C 1D 1所得的截面为四边形,则线段BM 的取值范围为( )A.⎝⎛⎦⎤0,13 B .⎝⎛⎦⎤0,12 C.⎣⎡⎭⎫12,1 D .⎣⎡⎦⎤12,234.已知直三棱柱ABC A 1B 1C 1的侧棱长为6,且底面是边长为2的正三角形,用一平面截此棱柱,与侧棱AA 1,BB 1,CC 1分别交于三点M ,N ,Q ,若△MNQ 为直角三角形,则该直角三角形斜边长的最小值为( )A .22B .3C.23D.45.(2019·郑州市第二次质量预测)在△ABC中,已知AB=23,BC=26,∠ABC=45°,D是边AC上的一点,将△ABD沿BD折叠,得到三棱锥ABCD,若该三棱锥的顶点A在底面BCD上的射影M在线段BC上,设BM=x,则x的取值范围是() A.(0,23)B.(3,6)C.(6,23)D.(23,26)6.如图,在正三棱柱ABCA1B1C1中,D为棱AA1的中点.若AA1=4,AB=2,则四棱锥BACC1D的体积为________.7.已知在正四棱锥SABCD中,SA=63,那么当该棱锥的体积最大时,它的高为________.8.(2019·河南八市重点高中联盟测评改编)已知一个高为1的三棱锥,各侧棱长都相等,底面是边长为2的等边三角形,则三棱锥的表面积为________,若三棱锥内有一个体积为V 的球,则V的最大值为________.。
利用三视图求几何体的表面积和体积

6
5
由三视图求几何体的体积和表面积的思路
1、由三视图确定几何体的形状 (1)由俯视图确定几何体的底面 (2)根据正视图或侧视图确定几何体侧棱与侧面特征,调整 实线和虚线所对应的棱、面的位置 (3)确定几何体直观图形状 2、由题目中的数据进行代入公式求解
布置作业:
《优化设计》p22-基础巩固3,4,6,7 P24例2,变式训练2, P25-基础巩固7,9
积等于
.
解析:该几何体如图所示,挖去的圆锥的母线长为
62 22 2 10
则圆锥的侧面积等于 4 10 圆柱的侧面积为2π×2×6=24π,圆柱的一个底面面 积为 22 4 ,所以组合体的表面积
为 4 10 24 4 4 10 28 .
答案: 4 10 28
题型二:三视图有关的体积计算
1 3Байду номын сангаас
(S
SS' S')h
题型一:三视图有关面积计算
例1.已知一个几何体的三视图如图所示,则这个几何体的表面积为( )
A.72 B.66 C.60 D.30
解析:由所给三视图可知该几何体为一个三棱柱,且底面为
直角三角形,直角边长分别为3和4,斜边长为5,三棱柱的高为5,
如图所示,所以表面积为
2
温故知新
1、三视图
画三视图的三大原则
正俯一样长,正侧一样高,侧俯一样宽
温故知新
面积
圆柱的表面积:S圆柱 2r(r l) 圆锥的表面积:S圆锥 r(r l) 圆台的表面积:S圆台 (r 2 r'2 rl r'l)
体积
柱体的体积:V柱 Sh
锥体的体积:V锥
1 Sh 3
台体的体积:V台
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三视图及其表面积体积一、选择题1.一只蚂蚁从正方体1111ABCD A B C D 的顶点A 处出发,经正方体的表面,按最短路线爬行到达顶点1C 位置,则下列图形中可以表示正方体及蚂蚁最短爬行路线的正视图是( )A.①②B.①③C.③④D.②④2.一个几何体的三视图如图所示,其中正视图和侧视图是腰长为2的两个全等的等腰直角三角形,则该几何体的外接球的表面积是( )A .38B .π34C .π12D .π338 3.某空间几何体的三视图如图所示,该空间几何体的体积是( )A.320 B. 10 C. 340 D. 3504.已知某锥体的正视图和侧视图如图,其体积为233,则该锥体的俯视图可以是( )A .B .C .D .5.若某几何体的三视图如图所示,其中俯视图是个半圆,则该几何体的表面积为( )A.π23B.3+πC.323+πD.325+π 6.已知一几何体的三视图如图所示,俯视图由一个直角三角形与一个半圆组成,则该几何体的体积为( )A .126+πB .246+πC .1212+πD .1224+π 7.某空间几何体的三视图中,有一个是正方形,则该空间几何体不可能是( ) A .圆柱 B .圆锥 C .棱锥 D .棱柱8.一个机器零件的三视图如图所示,其中俯视图是一个半圆内切于边长为2的正方形,则该机器零件的体积为A .8π3+B .8π23+ C .8π83+ D .8π163+ 9.某几何体的三视图如图所示,图中的四边形都是边长为2的正方形,两条虚线互相垂直,则该几何体的体积是( )A .320 B .316C .68π-D .38π-10.一个三棱锥的三视图如图所示,则该三棱锥的表面积为( )A .22514++B .16214+C .8214+D .814+11.已知某几何体的三视图如图所示,则该几何体的表面积为( )A.16B.26C.32D.252034+12.某空间几何体的三视图中,有一个是正方形,则该空间几何体不可能是( ) A .圆柱 B .圆锥 C .棱锥 D .棱柱13.已知某棱锥的三视图如图所示,则该棱锥的表面积为( )A .25+B .532+C .522+ D .35+ 14.已知几何体的三视图及其尺寸如图(单位:cm ),则该几何体的表面积和体积分別为( )A.2324,12cm cm ππ B.2315,12cm cm ππC.2324,36cm cm ππ D.以上都不正确15.正方体ABCD ﹣A 1B 1C 1D 1中E 为棱BB 1的中点(如图),用过点A ,E ,C 1的平面截去该正方体的上半部分,则剩余几何体的左视图为( )A. B . C . D .16.如果一个几何体的三视图如图所示,主视图与左视图是边长为2的正三角形、俯视图轮廓为正方形,(单位:cm ),则此几何体的表面积是( )A .82cmB .432cmC .122cmD .443 2cm17.已知某三棱锥的三视图如图所示,则该三棱锥的体积为( )A .8B .24C .325 D .96518.三棱锥S ﹣ABC 及其三视图中的正视图和侧视图如图所示,则棱SB 的长为( )俯视图主视图 左视图A .211B .163C .38D .4219.一个几何体的三视图形状都相同、大小均相等,那么这个几何体不可以是( ) A .球 B .三棱锥 C .正方体 D .圆柱 20.一块石材表示的几何体的三视图如图所示,将该石材切削、打磨,加工成球,则能得到的最大球的半径等于( )A.1B.2C.3D.4 21.利用斜二测画法得到的: ①三角形的直观图是三角形;②平行四边形的直观图是平行四边形; ③正方形的直观图是正方形; ④菱形的直观图是菱形. 以上结论正确的是( )A .①②B .①C .③④D .①②③④ 评卷人 得分二、解答题22.已知平面五边形ADCEF 是轴对称图形(如图1),BC 为对称轴,AD ⊥CD ,AD=AB=1,3CD BC ==,将此五边形沿BC 折叠,使平面ABCD ⊥平面BCEF ,得到如图2所示的空间图形,对此空间图形解答下列问题.(1)证明:AF ∥平面DEC ;(2)求二面角E AD B --的余弦值.23.一个几何体的三视图如图所示(单位长度为:cm )(1)求该几何体的体积; (2)求该几何体的表面积. 评卷人 得分三、填空题24.已知正ABC ∆的边长为a ,那么的平面直观图C B A '''∆的面积为 .参考答案1.D 【解析】试题分析:最短距离是正方体侧面展开图,即矩形111ABCC B A A 的对角线1AC (经过1BB )、或矩形11ABCC D DA 的对角线1AC (经过CD ),故视图为②④.考点:最短距离. 2.C 【解析】试题分析:由三视图可知该几何体为四棱锥,底面为正方形,边长为2,有一侧棱垂直于底面,侧棱为2,因此外切球直径为233r ∴=2412S r ππ∴==考点:三视图与几何体体积 3.C 【解析】试题分析:此几何体是 三棱锥,底面是直角三角形面积为104521=⨯⨯=S ,三棱锥的高是4,所以几何体的体积34041031=⨯⨯=V ,故选C. 考点:三视图4.C 【解析】试题分析:选项C 的体积1123223323V =⨯⨯⨯⨯=,故选C. 考点:1、三视图;2、锥体的体积.【方法点晴】本题主要考查三视图和锥体的体积,计算量较大,属于中等题型.应注意把握三个视图的尺寸关系:主视图与俯视图长应对正(简称长对正),主视图与左视图高度保持平齐 (简称高平齐),左视图与俯视图宽度应相等(简称宽相等),若不按顺序放置和不全时,则应注意三个视图名称.此外本题应注意掌握锥体的面积公式. 5.C 【解析】试题分析: 由三视图可知该几何体为一个半圆锥,即由一个圆锥沿中轴线切去一半面得112322S =⨯⨯+ 1321322πππ⨯+⨯⨯=+,故选C.考点:1、三视图;2、表面积.【方法点晴】本题主要考查三视图和表面积,计算量较大,属于中等题型.应注意把握三个视图的尺寸关系:主视图与俯视图长应对正(简称长对正),主视图与左视图高度保持平齐 (简称高平齐),左视图与俯视图宽度应相等(简称宽相等),若不按顺序放置和不全时,则应注意三个视图名称.此外本题应注意掌握球 和锥体的表面积公式. 6.A 【解析】试题分析:由三视图可知,该几何体为一组合体,它由半个圆柱和一个底面是直角三角形的直棱柱组成,故该几何体的体积2112324361222V ππ=⨯⨯⨯+⨯⨯⨯=+,故选A. 考点:1.三视图;2.多面体与旋转体的体积.7.B 【解析】试题分析:当棱锥和棱柱分别为正四棱锥和正四棱柱时,会出现正方形;圆柱的横截面为长方形,当其底面直径和高相等时,就是正方形;对于圆锥,三视图可能出现的有:圆、三角形.所以选B . 考点:三视图. 8.A【解析】此几何体为组合体,下面是正方体,上面是球的41,且球的半径为1,所以体积314π222π18433V =⨯⨯+⨯⨯=+,故选A.9.A【解析】试题分析:由三视图知原几何体是一个棱长为2的正方体挖去一四棱锥得到的,该四棱锥的底为正方体的上底,高为1,如图所示,∴该几何体的体积为3203481231223=-=⨯⨯-,故选A .考点:由三视图求面积、体积.10.C 【解析】试题分析:由三视图作出三棱锥的直观图,如图, ,ABC ADC ∆∆是全等的直角三角形, 0==90ABC ADC ∠∠,==543,2ABC AD BC +==,故12332ABC ADC S S ∆∆==⨯⨯=,在Rt BCD ∆中, 2BC CD ==,0=90BCD ∠,所以12222BCD S ∆=⨯⨯=,在ABD ∆中, AB AD =,高927AE =-=,所以1227142BAD S ∆=⨯⨯=,故表面积为所以33214814+++=+,选D.考点:由三视图求表面积.11.C 【解析】试题分析:由图可知,该几何体为三棱锥,直观图故下图所示,由图可知,表面积为111145343454322222ABC ACD BCD ABD S S S S ∆∆∆∆+++=⋅⋅+⋅⋅+⋅⋅+⋅⋅=.54345BDCA考点:三视图. 12.B 【解析】试题分析:当棱锥和棱柱分别为正四棱锥和正四棱柱时,会出现正方形;圆柱的横截面为长方形,当其底面直径和高相等时,就是正方形;对于圆锥,三视图可能出现的有:圆、三角形.所以选A . 考点:三视图. 13.D 【解析】试题分析:根据三视图可知,几何体是一条侧棱垂直于底面的四棱锥,底面是边长为1的正方形,如下图所示,该几何体的四个侧面均为直角三角形,侧面积11=2(1512)=2+522S ⋅⋅⋅+⋅⋅侧,底面积=1S 底,所以该几何体的表面积为35S =+,故选D.考点:三视图与表面积. 【易错点睛】本题考查三视图与表面积,首先应根据三视图还原几何体,需要一定的空间想象能力,另外解本题时,也可以将几何体置于正方体中,这样便于理解、观察和计算.根据三视图求表面积一定要弄清点、线、面的平行和垂直关系,能根据三视图中的数据找出直观图中的数据,从而进行求解,考查学生空间想象能力和计算能力. 14.A 【解析】试题分析:根据三视图可知该几何体是圆锥,其底面半径为3r =,母线长为5,高为224h l r =-=,所以该几何体的表面积为215S rl cm ππ==,体积为231123V r h cm ππ==,故选A.考点:三视图与几何体的表面积与体积.【方法点晴】本题主要考查了三视图与几何体的表面积与体积,属于中档题.三视图往往需要根据三个视图还原几何体,该几何体为圆锥,这是解题的关键,根据三视图的规则,主俯同长,左俯同宽,主左同高,据此可知圆锥的底面半径为3r =,母线长5l =,根据轴截面可得圆锥的高h ,根据圆锥的表面积和体积公式求解即可. 15.C 【解析】试题分析:过点1,,C E A 的平面截去该正方体的上半部分后,剩余部分的直观图如图,则该几何体的左视图为C.所以C 选项是正确的.考点:三视图. 16.C 【解析】试题分析:由已知可得:该几何体是一个四棱锥,侧高和底面的棱长均为2,故此几何体的表面积2122242212S cm =⨯+⨯⨯⨯=,故选:C .考点:棱柱、棱锥、棱台的体积;由三视图求面积、体积.17.C【解析】试题分析:由三视图知,该几何体是一个以俯视图为底面的三棱锥,底面面高C.考点:1、三棱锥的三视图书馆2、三棱锥的体积.【方法点睛】解答此类问题的关键是由多面体的三视图想象出空间几何体的形状并画出其直观图.三视图中“正侧一样高、正俯一样长、俯侧一样宽”,因此,可以根据三视图的形状及相关数据推断出原几何图形中的点、线、面之间的位置关系及相关数据.18.D【解析】试题分析:由已知中的三视图可得SC⊥平面ABC,且底面△ABC为等腰三角形,在△ABC中AC=4,AC故BC=4,在Rt△SBC中,由SC=4,可得考点:简单空间图形的三视图19.D【解析】试题分析:球的三视图都是圆,如果是同一点出发的三条侧棱两两垂直,并且长度相等的三棱锥的三视图是全等的等腰直角三角形,正方体的三视图可以是正方形,但圆柱的三视图中有两个视图是矩形,有一个是圆,所以圆柱不满足条件,故选D.考点:三视图20.B【解析】试题分析:由三视图可知,这是一个三棱柱,内切球在正视图的投影是正视图的内切圆,设其半径为r,根据三角考点:几何体的内切球.21.A【解析】试题分析:由斜二测画法的规则可知:根据平行性不变,所以①正确;根据平行性不变,所以②是正确的;正方形的直观图是平行四边形,所以③错误;因为平行与y轴的线段长度减半,平行于x轴的线段长度不变,所以④是错误的,故选A.考点:斜二测画法.22.见解析【解析】(1)如图,过D作DG⊥BC于点G,连接GE,因为BC为对称轴,所以AB⊥BC,则有AB∥DG,又AB⊂平面ABF,所以DG∥平面ABF,同理EG∥平面ABF.又DG∩EG=G,所以平面DGE∥平面ABF.又平面AFED∩平面ABF=AF,平面AFED∩平面DGE=DE,所以AF∥DE,又DE⊂平面DEC,所以AF∥平面DEC.(2)如图,过G作GH⊥AD于点H,连接HE.由(1)知EG⊥BC,又平面ABCD⊥平面BCEF,平面ABCD∩平面BCEF=BC,所以EG⊥平面ABCD,所以EG⊥AD.又EG∩HG=G,所以AD⊥平面EHG,则AD⊥HE,则∠EHG即为二面角E AD B--的平面角.由AD⊥CD,AD=AB=1G为BC因为EGH△为直角三角形,所以则二面角E AD B--的余弦值为23.(1(2【解析】试题分析:(1)由图知该几何体是一个上面是正四棱锥,下面是一个正方体的组合体.由此求得几何体的体积为(2)正方体部分一共5个面,面积是44580⨯⨯=.试题解析:(1)由图知该几何体是一个上面是正四棱锥,下面是一个正方体的组合体.且正四棱锥的底面边长为4,四棱锥的高为2,(2考点:三视图,立体几何求表面积和体积.24【解析】试题分析:如图所示是实际图形和直观图,在图中作C D A B''''⊥,垂足为D ',则考点:斜二测画法.【方法点晴】本题主要考查斜二测画法,属于中等题型.应注意以下步骤:取O 点为原点,以水平方向的直线为x 轴,竖直方向的直线为y 轴,取任一点'O ,画出相应的'x 轴、'y 轴,使'''45x O y ∠=o .(1)在已知图形中,取互相垂直的x 轴和y 轴,两轴相交于点O ,画直观图时,把它们画成对应的'x 和'y 轴,两轴相交于点'O ,且使'''45x O y ∠=o (或0135),它们确定的平面表示水平面;(2)在已知图形中平行于x 轴、y 轴的线段,在直观图中分别画成平行于'x 轴或'y 轴的线段;(3)在已知图形中平行于x 轴的线段,在直观图中保持长度不变;平行于y 轴的线段,长度为原来的一半;(4)如需第三维则在已知图形中平行于z 轴的线段,在直观图中保持长度不变.。
