期末模拟试卷A答案
2022——2023学年浙江省杭州市七年级下学期期末语文模拟试卷AB卷(含答案)

2022-2023学年浙江省杭州市七年级下册期末语文模拟试卷(A卷)一、语文知识及运用1.下列加点字注音全部正确....的一项是()A.妥帖.(tiē)蒙.胧(méng)累.赘(lěi)颠沛.流离(pèi)B.修葺.(qì)稠.密(chóu)炽.热(zhì)五脏.六腑(zàng)C.吟.唱(yín)鲁莽.(mǎng)遨.游(áo)悲天悯.人(mǐn)D.俯瞰.(kàn)点缀.(zhuì)矜.持(jīn)忧心忡.忡(cōng)2.根据拼音将汉字工整地写在下边田字格中。
村zhài_____外竹林环绕,掩映于连绵的翠绿之中,每当日落山头,那shùn_____息的景色,美不胜收。
走近一座座竹楼,可以发现周围的陈设都是原生态取材制作的,门口是竹编的鱼篓,家中是由数百根竹miè_____编织而成的桌椅。
竹林清幽,溪水潺潺,烟雨蒙蒙,如诗如画。
3.下列加点词语使用错误....的一项是()A.杜甫的一生正如大唐由盛而衰的命运般崎岖多舛,但他忧国忧民、悲天悯人....的情怀令后世敬重,被尊为“诗圣”。
B.古镇上这棵黄桷树,树身粗大,树根盘虬卧龙....般延伸开去;树叶很密,枝条宽广如撑起的一把大伞。
C.6月19日,神舟十四号飞行乘组在轨驻留满两周。
他们调试好了通信链路后,地面终于收到终端的信号,航天员们如卸千钧重负....。
D.小唐和同学约好今天晚上一起去参加合唱排练。
八点钟小唐不期而至....,准时到达了约定地点。
4.下列各句中,没有语病....的一项是()A.杨绛先生出身于民国的名门望族,她学贯中西,著述丰硕,成就非凡,享誉海内外。
B.不仅谷爱凌是滑雪天才,而且是斯坦福学霸,她理应是我们学习的榜样。
C.随着直播间“东方甄选”的出圈,让不少观众网友感慨现在没点文化都不敢来带货了。
D.时隔16年,中国女足再次问鼎世界杯,其原因是女足有强大的意志力的缘故。
《财政与税收》最新期末考试模拟试卷A(含)参考答案

最新《财政与税收》期末考试模拟试卷AB卷A(含)参考答案1、我国进入新时代之后,对公共财政的功能定位是:财政是国家治理的()。
A、财力保障B、制度保障C、基础和重要支柱D、特殊调控方式2、我国养老保险和医疗保险采取的筹资模式是:()。
A、完全社会统筹B、完全积累制C、现收现付制D、社会统筹与个人账户相结合3、以下哪一项不是公债的主要功能()。
A、弥补财政赤字B、筹集建设资金C、调节经济运行D、调节收入分配4、目前以纳税人实际缴纳的增值税、消费税税额为计税依据的税种是()。
A、城镇土地使用税B、土地增值税C、城市维护建设税D、资源税5、关于单式预算与复试预算的表述,不正确的是()。
A、单式预算区分了各项财政收支的经济性质B、单式预算的优点是整体性强C、复式预算是表现为两个或两个以上的预算表格D、复试预算打破了预算的完整性原则和传统的收支平衡观念6、党的十九大提出,市场在资源配置中起什么作用()。
A、基础性B、决定性C、重要性D、关键性7、下列说法正确的是()。
A、实行市场经济的国家,政府投资在社会投资总额中所占的比重较大B、在实行计划经济的国家,政府投资所占比重较小C、发达国家中政府投资占社会总投资的比重较大D、欠发达国家和中等发达国家的政府投资占社会总投资的比重较大8、税收占国民生产总值的比率是()。
A、企业税收负担率B、个人税收负担率C、宏观税收负担率D、广义税收负担率9、以下对财政平衡的认识,错误的是()。
A、财政平衡是相对的、大体的平衡,而非绝对的平衡。
B、财政平衡有动态和静态平衡之分。
C 、财政平衡是宏观经济总体平衡的必然要求。
D、财政平衡有真假之分,有中央预算平衡和地方预算平衡之别。
10、就赤字口径而言,在把年度债务收支记入正常财政收支范围,仍然收不抵支而形成的差额,称为()。
A 、硬赤字B、软赤字C 、预算赤字D、决算赤字11、按照欧盟国家《马斯特里赫特条约》规定的“入围限制标准”,适度赤字水平的参考值是赤字率不超过()。
2013-2014第二学期模拟电子技术期末试卷A详细答案

2013 - 2014学年第二学期 《模拟电子技术》期末试卷(A )姓名: 学号: 专业班级:__________()一、 填空(本题共8小题,每空1分, 总计20分)得分 判卷人1. PN 结的伏安特性方程 i =I S (e U/UT-1),表明PN 结呈现 单向 导电性。
2. 放大电路中,已知三极管三个电极的对地电位为 U A = -9V ,U B = -6.2V ,U C = -6V ,则该三极管是 锗PNP 型三极管,A 为 集电极 ;B 为 基 极 ;C 为 发射 极。
3. 对于下图所示的电压跟随器,其输出电压与输入电压的关系是 u o =u i ,输入电阻趋于 零 ;输出电阻趋于 无穷大 ,该电路是 电压串联 类型反馈电路(反馈组态)。
4.多级放大电路与各单级放大电路比较,多级放大电路压增益大,单级放大电路 通頻带宽。
5.双端输入、双端输出差动放大电路如下所示,已知 静态时V O =V C1-V C2=0,设差模电压增益|A VD |=100,共模电压增益A VC =0,V i1=10mV ,V i2=5mV ,则差模输入电压V id 为 5mV ,共模输入电压V ic 为 7.5mV ,输出电压|V o |= 0.5V 。
6.所示放大电路中引入的反馈组态是电流串联负反馈。
该反馈能稳定电路的输出电__流_。
7.场效应管(FET )用于放大时,应工作在 恒流 区。
8.为了稳定放大器的静态工作点,应引入 直流 负反馈;为了稳定放大器的交流性能,应引入 交流 负反馈。
v o +-R L R 1v ii o A二、选择题(共10小题,每题1分,总计10分)1. 在杂质半导体中,多数载流子的浓度主要取决于 [ C ]A.温度 B.掺杂工艺的类型C.杂质浓度 D.晶体中的缺陷2.滞回比较器有2个阈值电压,因此在输入电压从足够低逐渐增大到足够高的过程中,其输出状态将发生次跃变。
[ A ]A. 1B. 2C. 3D. 03.当稳压管在正常稳压工作时,其两端施加的外部电压的特点为。
部编版七年级语文下册期末模拟试卷(附答案及解析)

部编版七年级语文下册期末模拟试卷(附答案及解析)(满分120分时间150分钟)一、积累与运用(27分)1.补出下列句子中的空缺部分。
(8分)①________________,惟解漫天作雪飞。
(韩愈《晚春》)②可怜夜半虚前席________________。
(李商隐《贾生》)③当你遭遇困境时,千万不要放弃,因为困境中往往蕴藏着希望,正如陆游《游山西村》所说,“________________,________________”。
④唐朝杜牧在《泊秦淮》中借月亮创设了一种朦胧凄清的意境,这两句诗是________________,________________。
⑤王安石《登飞来峰》中表达了锐意进取的精神和高瞻远瞩的气概的句子是:________________,________________。
【答案】杨花榆荚无才思不问苍生问鬼神山重水复疑无路柳暗花明又一村烟笼寒水月笼沙夜泊秦淮近酒家不畏浮云遮望眼自缘身在最高层【解析】此题考查的是名句的默写。
需要注意“杨”“苍”“笼”“沙”“近”的书写,理解型默写③抓关键词“困境中往往蕴藏着希望”,④的关键词是“朦胧凄清的意境”,⑤题抓关键词“锐意进取的精神和高瞻远瞩的气概”。
2.给下列句中加点的字注音,根据拼音写上相应的汉字。
(2分)(1)我似乎遇着了一个霹雳,全体都震悚( )了起来。
(2)我出于对他的尊敬,想不直接动笔,只提一些商酌( )性的意见。
(3)船舱鼓鼓的,又像一个忍俊不jīn( )的笑容,就要绽开似的。
(4)他们可以坐在挺huò( )亮的屋子里,泡上一壶茶,守住一个小火炉……【答案】 sǒng zhuó禁豁【解析】(1)震悚:sǒng,身体因为恐惧或者过度兴奋而颤动。
(2)商酌:zhuó,商量斟酌。
(3)忍俊不jīn:忍俊不禁,忍不住要发笑。
注意下半部分不要写错。
(4)huò亮:豁亮,宽敞明亮。
书写时注意右半部分。
部编版2020-2021学年下学期六年语文期末模拟试卷(A卷)(含答案)

[考试时间:90分钟 满分:100分]一、看拼音,写词语。
(8分)yàn hu ì zh àn f àng qi ū y ǐn bō li qiāng b ì zh ēng r óng m ǎ y ǐ nóng ch óu二、下面读音完全正确的一组是( )。
(2分)A.增添( zh ēng ti ān) 间断( ji ān du àn) 寺院( s ì yu àn)B.粉碎( f ěn su ì) 缘故( yu án g ù) 徘徊( p ái hu í)C.忧郁( y ōu y ù) 解除( ji ě ch ú) 僻静( p ì j ìng)D.恐怖( k ōng b ù) 抽屉( ch ōu t ì) 军阀( j ūn f á)三、比一比,再组词。
(6分)阶( ) 褐( )价( ) 渴( ) 芥( ) 遏( )四、把下列词语补充完整,并解释所填的字。
(6分)前所未( )与世隔( ) 无( )于事跃跃( )试 天( )海角 万象( )新五、判断下列句子使用的修辞手法,写在后面括号里。
(4分)1.古老的威尼斯沉沉地入睡了。
( )2.桂子花开,十里飘香。
( )2020-2021学年度第二学期期末教学质量检测六年级语文试卷3.“腊七腊八,冻死寒鸦”,这是一年里最冷的时候。
()4.春风吹绿了小草,吹醒了青蛙,吹皱了河水。
()六、毕业之际,如果为伙伴写毕业赠言,下面不适合引用的一项是()。
(2分)A.芝麻开花——节节高B.百尺竿头——更进一步C.欲穷千里目,更上一层楼D.一鼓作气,再而衰,三而竭七、先将下列诗词补充完整,再完成练习。
(10分,每空1分)A.今夜月明人尽望,___________?B.__________,寒食东风御柳斜。
2022-2023学年江西省吉安市三年级下册数学期末模拟试卷(A卷B卷)含解析

2022-2023学年江西省吉安市三年级下册数学期末模拟试卷(A卷)一、计算(29分)1.(6分)口算3.8﹣2.9= 2.5+1.5=745+196=490÷7=0×36=930÷3=0+126=25×40=355÷9≈281÷4≈30×40=480﹣210=2.(14分)用竖式计算,带※的要验算※416÷427×2232×58360÷3※87×69359÷73.(9分)脱式计算320+12×27840÷4×3312÷(300﹣296)二、填空题(每空1分,共29分)4.(2分)十六点八五写作 ,20.03读作 .5.(2分)物体的表面或封闭图形的大小就是它们的 .边长1分米的正方形纸可以剪成 个边长1厘米的小正方形.6.(3分)74×25的积的最高位是 位;728÷8的商是 位数;50×40积的末尾有 个零.7.(1分)在平行四边形、长方形、三角形中, 形一定是轴对称图形.8.(3分)今年是2019年,全年共有 天,闰年有 天,闰年的第一季度有 天.9.(6分)2年= 月3日= 时5时= 分17平方分米= 平方3米= 分米2厘米= 米厘米10.(2分)正方形周长12厘米,边长是 厘米,面积是 平方厘米.11.(4分)把24时计时法或普通计时法表示下面的时刻早上8时 .下午4时 .22时 .19时 .12.(4分)(1)一张电话卡的面积大约是40 .(2)教室长8 ,宽6 ,面积是 .13.(2分)□59÷6要使商是两位数,□里最大可以填 ,要使商是三位数,□里最小可以填 .三、判断题(对的打“√”,错的打“×”。
)(每题1分,共5分)14.(1分)所有的整数一定比小数小. (判断对错).15.(1分)小红的爸爸是4月31日从北京出差回来了. (判断对错).16.(1分)边长4厘米的正方形周长和面积相等. .(判断对错)17.(1分)54×80 与540×8 的计算结果相同. .(判断对错)18.(1分)23时15分就是11时15分. .(判断对错)四、选一选(把正确的答案序号填在括号里).(每题1分,共5分)19.(1分)第一小组100米跑的成绩分别是16.7秒,17.5秒,16.58秒,16.08秒,他们中跑的最快的是( )A.16.7B.17.5C.16.58D.16.0820.(1分)一个正方形的边长是12米,它的面积是( )平方米.A.144B.48C.2421.(1分)如图分成了甲、乙两部分,这两部分的( )A.周长和面积都相等B.周长相等、面积不相等C.周长和面积都不相等22.(1分)用小数表示1元7角等于( )元.A.17B.1.7C.1.0723.(1分)中华人民共和国是1949年10月1日成立的,到今年为止已经成立了( )周年.A.60B.50C.70五、操作.(1题画图每个1分,计算每个1分,共4分;2题每小题4分;共8分)24.(4分)在如图的方格纸上画出面积是16平方厘米的长方形和正方形,并计算它们的周长.25.(4分)下面是四个组球队一个赛季的进球个数.组名甲乙丙丁个数9568(1)根据上表,完成下面的条形统计图.(2)从表格中你发现了什么?六、解决问题.(2题8分,其它每题4分,共24分)26.(4分)世界遗产大会召开期间,新城花园小学三年级107名学生去公园,公园门票每张9元,带900元钱买门票够不够?27.(8分)一个长方形的花圃,长60米,宽30米,要在花圃周围围一圈篱笆,需要篱笆多少米?如果每平方米栽2棵月季花,一共可以栽多少棵月季花?28.(4分)一辆汽车上午10:30从甲地出发,下午7:30到达乙地,这辆汽车平均每小时行46千米,甲乙两地相距多少千米?29.(4分)张林要练习打乒乓球,一支乒乓球拍7.8元,一个乒乓球1.5元,张林带了10元钱买了一支球拍和一个乒乓球,应找回多少钱?30.(4分)超市有960个鸡蛋,每盒装6个,每箱装5盒,求一共能装多少箱?答案与试题解析一、计算(29分)1.(6分)(2019春•庆云县期末)口算3.8﹣2.9= 2.5+1.5=745+196=490÷7=0×36=930÷3=0+126=25×40=355÷9≈281÷4≈30×40=480﹣210=【考点】21:整数的加法和减法;25:整数的乘法及应用;27:整数的除法及应用;2C:数的估算;2J:小数的加法和减法.【专题】11:计算题.【分析】根据整数、小数加减乘除法的计算方法以及整数除法的估算方法进行计算.解:3.8﹣2.9=0.9 2.5+1.5=4745+196=941490÷7=700×36=0930÷3=3100+126=12625×40=1000355÷9≈40281÷4≈7030×40=1200480﹣210=270【点评】口算时,注意运算符号和数据,然后再进一步计算.2.(14分)(2019春•庆云县期末)用竖式计算,带※的要验算※416÷427×2232×58360÷3※87×69359÷7【考点】25:整数的乘法及应用;27:整数的除法及应用.【专题】11:计算题.【分析】根据整数乘除法的计算方法进行计算,注意验算方法的选择.解:※416÷4=10427×22=59432×58=1856360÷3=120※87×69=6003359÷7=51 (2)【点评】考查了整数乘除法的笔算,根据各自的计算方法进行计算,注意验算方法的选择.3.(9分)(2019春•庆云县期末)脱式计算320+12×27840÷4×3312÷(300﹣296)【考点】2B:整数四则混合运算.【专题】421:运算顺序及法则.【分析】(1)先算乘法,再算加法;(2)按照从左到右的顺序计算;(3)先算减法,再算除法.解:(1)320+12×27=320+324=644(2)840÷4×3=210×3=630(3)312÷(300﹣296)=312÷4=78【点评】本题考查了简单的四则混合运算,计算时先理清楚运算顺序,根据运算顺序逐步求解即可.二、填空题(每空1分,共29分)4.(2分)(2019春•庆云县期末)十六点八五写作 16.85 ,20.03读作 二十点零三 .【考点】1E:小数的读写、意义及分类.【专题】412:小数的认识.【分析】小数的写法:整数部分按整数的写法来写,小数点写在个位右下角,小数部分依次写出每一个数位上的数字;根据小数的读法:整数部分按整数的读法来读,小数点读作点,小数部分要依次读出每个数位的数字.解:十六点八五写作16.85,20.03读作二十点零三;故16.85,二十点零三.【点评】本题主要考查小数的写法和读法,注意小数部分的读写方法.5.(2分)(2019春•庆云县期末)物体的表面或封闭图形的大小就是它们的 面积 .边长1分米的正方形纸可以剪成 100 个边长1厘米的小正方形.【考点】A5:长方形、正方形的面积.【专题】461:平面图形的认识与计算.【分析】根据面积的意义,物体的表面或封闭图形的大小就是它们的面积.根据正方形的面积公式:s=a2,分别求出边长1分米、1厘米的正方形的面积,再根据平方分米与平方厘米之间的进率,把平方分米换算成平方厘米.解:物体的表面或封闭图形的大小就是它们的面积.1×1=1(平方分米),1×1=1(平方厘米),1平方分米=100平方厘米.故面积,100.【点评】此题考查的目的是理解面积的意义,掌握面积单位之间的进率及换算方法.6.(3分)(纳雍县期末)74×25的积的最高位是 千 位;728÷8的商是 两 位数;50×40积的末尾有 3 个零.【考点】25:整数的乘法及应用;27:整数的除法及应用.【专题】421:运算顺序及法则.【分析】用74乘上25求出积,再判断积的位数;计算728÷8先用除数试除被除数的前一位数,不够除,就看被除数的前两位数,商的最高位是十位,据此解答即可.根据因数末尾有零的整数乘法计算法则可知,计算50×40时,可先计算5×4=20,然后再在20后加上50、40后边的两个零,即50×40=2000,积是4位数,积的末尾有三个零.解:74×25=1850,所以74×25的积的最高位是千位;728÷8,因为被除数的最高位是7,小于除数8,不够除,所以要用被除数的前两位去除,所以商最高位在十位上,商是两位数;计算50×40时,可先计算5×4=20,然后再在20后加上50、40后边的两个零,即50×40=2000,积是4位数,积的末尾有3个零.故千,两,3.【点评】此题考查整数的除法及应用,解决此题的关键是用除数试除被除数的前一位数,不够除,就看被除数的前两位数,除到那一位,就把商商到那一位的上面;整数末尾有0的乘法:可以先把0前面的数相乘,然后看各因数的末尾一共有几个0,就在乘得的数的末尾添写几个0.7.(1分)(2019春•庆云县期末)在平行四边形、长方形、三角形中, 长方 形一定是轴对称图形.【考点】B6:轴对称图形的辨识.【专题】463:图形与变换.【分析】根据轴对称图形的意义:如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴;据此解答.解:根据轴对称图形的意义可知:在平行四边形、长方形、三角形中,只有长方形沿一条直线对折后,直线两旁的部分能完全重合,所以长方形是轴对称图形;故长方.【点评】判断是不是轴对称图形的关键是找出对称轴,图形两部分沿对称轴折叠后能完全重合.8.(3分)(2019春•庆云县期末)今年是2019年,全年共有 365 天,闰年有 366 天,闰年的第一季度有 91 天.【考点】44:年、月、日及其关系、单位换算与计算;4I:平年、闰年的判断方法.【专题】442:质量、时间、人民币单位.【分析】用2019除以4,首先判断2019年是闰年还是平年,平年和闰年的区别:平年二月有28天闰年二月有29天,所以平年是365天,闰年是366天;1月和3月都是大月有31天,再加上2月29天即可得解.解:2019÷4=504…3,不是4的倍数,所以2019年是平年,全年365天;闰年全年有366天闰年第一季度有:31+31+29=91(天)答:今年是2019年,全年共有365天.闰年有366天,闰年的第一季度有91天.故365;366;91.【点评】此题考查了年、月、日及其关系、单位换算与计算,以及平年、闰年的判定方法.9.(6分)(2019春•庆云县期末)2年= 24 月3日= 72 时5时= 300 分3米= 10 分米2厘米= 0.02 米17平方分米= 1700 平方厘米【考点】43:时、分、秒及其关系、单位换算与计算;44:年、月、日及其关系、单位换算与计算;4A:长度的单位换算;4C:面积单位间的进率及单位换算.【专题】441:长度、面积、体积单位;442:质量、时间、人民币单位.【分析】根据进率,年化成月需要乘进率12;日化成时需乘进率24;时化成分需要乘进率60;平方分米化成平方厘米乘进率100.米化成分米乘进率10;厘米化成米除以进率100.解:2年=24月3日=72时5时=300分3米=30分米2厘米=0.02米17平方分米=1700平方厘米故24;72;300;1700;30;0.02.【点评】此题考查名数的换算,把高级单位的名数换算成低级单位的名数,就乘单位间的进率,把低级单位的名数换算成高级单位的名数,就除以单位间的进率.10.(2分)(2019春•庆云县期末)正方形周长12厘米,边长是 3 厘米,面积是 9 平方厘米.【考点】A2:正方形的周长;A5:长方形、正方形的面积.【专题】461:平面图形的认识与计算.【分析】根据正方形的周长公式可得:正方形的边长=周长÷4,据此再利用正方形的面积=边长×边长即可解答.解:12÷4=3(厘米)3×3=9(平方厘米)答:这个正方形的边长是3厘米,面积是9平方厘米.故3,9.【点评】此题主要考查正方形的周长与面积公式的计算应用11.(4分)(2019春•庆云县期末)把24时计时法或普通计时法表示下面的时刻早上8时 8时 .下午4时 16时 .22时 晚上10时 .19时 下午7时 .【考点】43:时、分、秒及其关系、单位换算与计算.【专题】442:质量、时间、人民币单位.【分析】(1)早上8时改写成24时计时法,去掉“早上”即可;(2)下午4时改写成24时计时法,去掉“下午”加上12即可;(3)22时改写成普通计时法,用22减去12,再在前面加上“晚上”即可;(4)19时改写成普通计时法,用19减去12,然后前面加上“下午”即可.解:(1)早上8时=8时(2)下午4时=16时(3)22时=晚上10时(4)19时=下午7时故8时;16时;晚上10时;下午7时.【点评】主要考查普通计时法与24时计时法的改写.解答此题的关键是弄清楚:在进行计时法的转换时,什么时候加12,什么时候减12,什么时候保持不变.12.(4分)(2019春•庆云县期末)(1)一张电话卡的面积大约是40 平方厘米 .(2)教室长8 米 ,宽6 米 ,面积是 48平方米 .【考点】41:根据情景选择合适的计量单位;49:长度及长度的常用单位;4B:面积和面积单位.【专题】441:长度、面积、体积单位.【分析】根据生活经验、对长度单位,面积单位和数据大小的认识,可知计量一张电话卡的面积用“平方厘米”做单位;计量教室长用“米”作单位,计量教室宽用“米”作单位;计量面积用“平方米”作单位,据此解答即可.解:(1)一张电话卡的面积大约是40平方厘米;(2)教室长8米,宽6米,面积是48平方米.故平方厘米;米、米,48平方米.【点评】此题考查根据情景选择合适的计量单位,要注意联系生活实际、计量单位和数据的大小,灵活的选择.13.(2分)(2019春•庆云县期末)□59÷6要使商是两位数,□里最大可以填 5 ,要使商是三位数,□里最小可以填 6 .【考点】27:整数的除法及应用.【专题】421:运算顺序及法则.【分析】算式囗59÷6,被除数为三位数,除数为6,根据整数除法的运算法则可知,要使商是两位数,则应使囗中的数小于除数6;要使商是三位数,则应使囗中的数大于或等于除数6,所以囗里最小能填6.解:□59÷6要使商是两位数,那么□里面的数就要<6,可以是1,2,3,4,5,最大可以填5;要使商是三位数,那么□里面的数就要≥6,可以是6,7,8,9,最小是6.故5;6.【点评】掌握除数是一位数的除法法则是解决问题的关键.三、判断题(对的打“√”,错的打“×”。
2022——2023学年吉林省长春市高一下学期化学期末模拟试卷AB卷(含答案)

2022-2023学年吉林省长春市高一下册化学期末模拟试卷(A 卷)可能用到的相对原子质量:H-1C-12N-14O-16Na-23Mg-24Al-27Cl-35.5Mn-55Fe-56Cu-64Zn-65一、选一选(本题包括22小题,每小题2分,共44分.每题只有一个选项符合题意)1.化学与社会、生产、生活密切相关。
下列说法没有正确....的是()A.推广使用新能源汽车,可以有效减少氮的氧化物排放B.推广使用燃煤脱硫技术,可减少SO 2对空气的污染C.从海水中提取物质都必须通过化学反应才能实现D.废旧电池中的汞、镉、铅等重金属元素对土壤和水源会造成污染2.下列关于农药和肥料的说确的是()A.草木灰含有K 2CO 3,可作为钾肥使用B.含磷化合物都可以作为磷肥直接使用C.氮肥只能通过人工合成而得到D.农药都对人体无害,可以大量使用农药3.下列说法没有正确....的是()A.金刚石和C 60互为同素异形体B.CH 3—CH 2OH 和CH 3—O—CH 3互为同分异构体C.32He 和42He 互为同位素D.分子式为C 4H 10的物质为纯净物4.下列叙述中正确的是()A.乙烯、氯乙烯、聚乙烯均可使酸性高锰酸钾溶液褪色B.聚合物可由32CH CH CH =和22CH CH =加聚制得C.分馏、干馏都是物理变化,裂化、裂解都是化学变化D.纤维素、聚乙烯、光导纤维都属于高分子化合物5.如图所示是几种常见的化学电源示意图,下列有关说法没有正确....的是()A.化学电源是将化学能转化为电能的实用装置B.干电池示意图所对应的电池属于二次电池C.铅蓄电池充电时PbO2(正极)应与外接电源正极相连D.氢氧燃料电池是一种具有应用前景的绿色电源6.下列事实与带点物质表现出的性质(括号中)对应关系没有正确....的是()A.蔗糖与浓硫酸...反应有黑色物质生成(脱水性)B.常温下,铁遇浓硫酸...发生钝化(强氧化性)...、浓硝酸C.SO..2能使含有酚酞的氢氧化钠溶液褪色(漂白性)D.久置的浓硝酸...,颜色略显黄色(没有稳定性)7.鉴别淀粉、蛋白质、葡萄糖水溶液,依次可分别使用的试剂和对应的现象正确的是()A.碘水,变蓝色;浓硝酸,变黄色;新制的Cu(OH)2,砖红色沉淀B.浓硝酸,变黄色;新制的Cu(OH)2,砖红色沉淀;碘水,变蓝色C.新制的Cu(OH)2,砖红色沉淀;碘水,变蓝色;浓硝酸,变黄色D.碘水,变蓝色;新制的Cu(OH)2,砖红色沉淀;浓硝酸,变黄色8.下列反应中,属于加成反应的是()A.CH4错误!C+2H2B.CH3—CH3+2Cl2错误!CH2Cl—CH2Cl+2HClC.C3H8+5O2错误!3CO2+4H2OD.CH3CH==CH2+Br2―→CH3CHBrCH2Br9.具有相同官能团的有机物化学性质相似,据此判断对HOCH2CH=CHCH2COOH的叙述没有正...确.的是()A.分子中有3种官能团B.能分别与乙醇、乙酸在一定条件下发生酯化反应C.与溴的四氯化碳溶液和酸性高锰酸钾溶液褪色的原理相同D.1mol该有机分子与足量钠反应能产生2g H210.下面是部分矿物资源的利用及产品流程,有关说确的是()A.可用电解AlCl3的方法制备金属铝B.生产铝、铜、高纯硅及玻璃过程中都涉及氧化还原反应C.黄铜矿冶炼铜时,副产物SO2可用于生产硫酸,FeO可作冶炼铁的原料D.由石英制玻璃的原理可知,硅酸的酸性比碳酸强11.下表中,对陈述Ⅰ、Ⅱ的正确性判断都正确的是()选项陈述Ⅰ陈述Ⅱ判断A 硝酸铵和碱石灰共热用于实验室制备NH3铵盐与碱能发生复分解反应Ⅰ对,Ⅱ错B 向浓盐酸中加入浓硫酸可制备氯化氢气体浓盐酸易挥发,浓硫酸与水作用放出大量的热Ⅰ对,Ⅱ对C 硫单质在纯氧中燃烧有少量SO3生成在纯氧中硫单质部分被氧化为SO3Ⅰ对,Ⅱ对D Cu能与浓HNO3反应由于Cu具有还原性,浓HNO3具有氧化性,在任何条件下生成的气体一定是NO2Ⅰ对,Ⅱ对12.某同学设计如图所示实验,探究反应中的能量变化。
北师大版2022——2023学年五年级下学期数学期末调研模拟试卷AB卷(含答案)

【北师大版】2022-2023学年五年级下学期数学期末调研模拟试卷(A卷)一、选择题(满分16分)1.足球有x个,篮球比足球的6倍还多1个,篮球有()个。
A.6x+1B.6x-1C.6÷3+1D.(6-1)÷32.8.7+7.6-8.7+7.6=().A.0B.15.2C.7.63.从正面观察,所看到的图形是()。
A.B.C.4.林叔叔开了一家超市,11月前5天的营业额分别是501元、503元、498元、495元、499元。
估计林叔叔家超市11月的总营业额大约是()元。
A.1500B.10000C.12000D.150005.三角形的两条边长分别是6cm和8cm,第三条边长度有()种可能。
(取整厘米数)A.9B.10C.116.“一本书126页,看了3天后,还剩下45页,_______?”张明将问题中的未知数设为x,列出方程:453126x+=。
从方程中可以看出他要解决的问题是()。
A.一共有多少页B.这3天,平均每天看多少页C.看了多少页D.剩下的还要几天才能看完7.一支铅笔0.5元,3支一共要用()元。
A.3.5元B.1.5元C.15元8.下图中的点M所在的位置可以用小数()表示。
A.0.6B.1.4C.1.6D.2.4二、填空题(满分16分)9.在尺子上找出下面各长度的位置,用箭头标出来,然后在下面的括号里用分数表示。
10.写出下面的数量关系式:奶奶的岁数是64岁,妈妈和我的岁数合起来与奶奶岁数相同.__________________________________________11.有两根小棒分别是7cm和9cm,下图中________可以和它俩拼成一个三角形.12.按要求搭一搭,再填空。
(1)用三个正方体,从正面看有3个正方体,从左面看只有1个正方体,从上面看也是3个正方体,这个图形是()号图形。
(2)用三个正方体,从正面看有3个正方体,从左面看是2个正方体,从上面看是2个正方体,这个图形是()号图形。
全国通用2022-2023学年五年级下册数学期末真题模拟试卷(A卷)含解析

全国通用2022-2023学年五年级下册数学期末真题模拟试卷(A卷)一.选一选(共8小题)1.(2022•双桥区)下面各数中没有能化成有限小数的是()A.B.C.D.2.(2022春•合肥期末)乐乐和哥哥、爸爸三人同时从逍遥津公园回家,哥哥骑共享单车用了0.6小时,爸爸带着乐乐乘坐公交车用了小时。
下面说确的是()A.哥哥先到家B.爸爸和乐乐先到家C.三人同时到家3.(2022•潮州)一个由8个完全相同的小正方体组成的大正方体,如果在大正方体的表面涂上红色,那么三面涂红色的小正方体有()个。
A.6B.12C.8D.14.(2022春•岷县月考)一间长9m、宽6m、高3m的教室,要粉刷它的四壁和房顶(门、窗和黑板没有粉刷),已知门、窗和黑板的面积是15.4m2,求粉刷的面积。
列式正确的是()A.9×6×2+9×3×2+6×3×2﹣15.4B.9×6+9×3×2+6×3×2﹣15.4C.9×6×2+9×3+6×3×2﹣15.45.(2022•河西区)芳芳步行千米用小时,照这样计算,她步行1千米用()小时.A.B.C.D.6.(2021春•河西区期末)男生有a人,女生比男生的2倍多1人,女生有()人。
A.2a+1B.2a﹣1C.(a﹣1)÷2D.a÷2﹣1 7.(2021春•河西区期末)书店在学校的东偏南30°,还可以说成书店在学校的()A.南偏东30°方向B.南偏东60°方向C.西偏北60°方向D.西偏北30°方向8.(2019春•简阳市期末)根据12比x的3倍少8,列出的方程错误的是()A.12=3x﹣8B.3x=12+8C.3x+8=12二.填空题(共6小题)9.(2022春•福鼎市期末)++++,这个算式再加上,结果等于1。
2022——2023学年山东省菏泽市七年级下学期期末语文模拟试卷AB卷(含答案)

2022-2023学年山东省菏泽市七年级下册期末语文模拟试卷(A卷)一、积累与运用(20分)1.阅读下面文字,完成后面的问题。
与春夏相比,这山上不变的是松柏。
一出别墅..的后门,就有十几株两抱之粗的苍松直通天穹。
树干粗粗壮壮,溜光挺直,直到树梢尽头才伸出几根虬劲的枝,枝上挂着束束松针,该怎样绿还是怎样绿。
树皮在寒风中(chéng xiàn)出紫红色,像壮汉的脸。
这时太阳从东方冉冉升起,走到松枝间却寂然不动了。
我徘徊..于树下又斜倚在石上,看着这红日绿松,心中清静安闲,觉得胸若虚谷、头悬明镜、人山一体。
此时我只感到山的(wēié)与松的伟岸,冬日香山就只剩下这两样东西了。
(1)给这段文字中加着重号的词语注音。
别墅....徘徊(2)根据这段文字中的注音写出相应的词语。
chéng xiàn wēié2.在下列横线上填写出相应的句子。
(1)黄梅时节家家雨,。
(赵师秀《约客》)(2)李玉同学刚升人初中,经过一段时间的学习,他感觉学习没有什么困难,于是学习有些松懈。
请你用《过松源晨炊漆公店》中的两句诗告诫他:,。
(3)李商隐《贾生》中表现汉文帝似乎诚意十足,贾生才华横溢的句子是:,。
(4)《陋室铭》中以工整的句式写陋室主人交往之雅的句子是:,。
3.下列选项中对文学、文化常识表述不正确的一项是()。
A.古代文人表述自己的志向和情操时,往往不采用直白的方式,而是以物为喻,写得比较含蓄,这叫做“托物言志”,例如《陋室铭》《爱莲说》均是托物言志的名文。
B.鲁迅,浙江绍兴人,原名周树人,是中国现代文学的奠基人,其代表作有小说集《呐喊》《彷徨》,散文集《朝花夕拾》,散文诗集《野草》。
“鲁迅”是他1918年发表《狂人日记》时所用的笔名。
C.杜甫是唐代大诗人,他的诗作在总体上反映了唐王朝由盛而衰的变化过程,号称“诗仙”。
D.刘禹锡,字梦得,河南洛阳人,唐朝时期文学家,有“诗豪”之称,诗文俱佳,涉猎题材广泛,与柳宗元并称“刘柳”。
(小升初)全国通用2023年语文期末模拟试卷(卷一卷二)2套含答案

D.智 致 质 制 治 至
4.( )是传说中农业和医药的发明者。
A.黄帝
B.燧人氏
C.仓颉
D.神农氏
5.把多义词的正确解释的序号写在括号里。(2%)
绚丽异常中异的正确解释是( ):
A 没有同的 B 分开 C 另外的,别的 D 特别的
6.《一年级大个子二年级小子个》中,在寻找正也的过程中,秋代是沿着( )找到正也的。
A.询问路人
B.正也留下的花朵
C.正也留下的脚印
7.下列诗句的作者姓氏按音序排列,正确的一项是( )。
第 7页/总 14页
①夜静春山空 ②南望王师又一年 ③唯见长江天际流 ④乡村四月闲人少
A.③②①④
B.③②④①
C.②③④①
D.②③①④
二、书写 8.根据拼音写字词。
我望
的老师身体
,永远快乐。
三、填 空 题 9.默写古诗。 夜书所见 叶绍翁 萧萧梧叶送寒声, ______________。 知有__________, _________一灯明。 10.在横线上填上恰当的汉字,使之搭配成词语。
写,让我们感受到榕树旺盛的生命力。
D.“即使是蒙蒙细雨的夜晚,也有一只两只萤火虫,闪着朦胧的微光在飞行。”这里的动态
描写,让我们看到了夏天夜晚时的独特画面。
7.下列句子中没有是比喻句的一项是( )
A.因为我早听到闰土这名字,而且知道他和我仿佛年纪,闰月生的,五行缺土,所以他的父
亲叫_____
líng lóng_____
xiāo_____毁
zào_____声
13.解释下面加点字词的意思。 (1)默而识之,学而没有厌.,诲人没有倦。(_________)
试卷第 2页,总 4页
2020-2021学年浙江省杭州市高一下期末模拟数学试卷及答案A-精品试题

最新浙江省杭州市高一(下)期末数学试卷一、选择题(共25小题,每小题2分,满分55分)1.函数f(x)=的定义域是()A.[1,+∞)B.(1,+∞)C.(0,1)D.[0,1]2.函数f(x)=sin2x,x∈R的一个对称中心是()A.(,0)B.(,0)C.(,0)D.(,0)3.设向量=(m,2)(m≠0),=(n,﹣1),若∥,则=()A.B.﹣C.2 D.﹣24.函数f(x)=lnx+x﹣2的零点位于区间()A.(0,1)B.(1,2)C.(2,3)D.(3,4)5.已知幂函数f(x)=kxα(k∈R,α∈R)的图象过点(,),则k+α=()A.B.1 C.D.26.在区间(﹣1,1)上单调递增且为奇函数的是()A.y=ln(x+1)B.y=xsinx C.y=x﹣x3D.y=3x+sinx7.若向量=﹣2,||=4,||=1,则向量,的夹角为()A.B.C.D.8.设函数f(x)=x2+ax,a∈R,则()A.存在实数a,使f(x)为偶函数B.存在实数a,使f(x)为奇函数C.对于任意实数a,f(x)在(0,+∞)上单调递增D.对于任意实数a,f(x)在(0,+∞)上单调递减9.若偶函数f(x)在区间(﹣∞,0]上单调递减,且f(7)=0,则不等式(x﹣1)f(x)>0的解集是()A.(﹣∞,﹣1)∪(1,+∞)B.(﹣∞,﹣7)∪(7,+∞)C.(﹣7,1)∪(7,+∞)D.(﹣7,1]∪(7,+∞)A.2 B.﹣2 C.±2 D.11.函数f(x)=sin2x与函数g(x)=2x的图象的交点的个数是()A.1 B.3 C.5 D.712.设a=log2π,b=logπ,c=π﹣2,则()A.a>b>c B.b>a>c C.a>c>b D.c>b>a13.函数y=cos2x﹣sin2x的图象可以由函数y=cos2x+sin2x的图象经过下列哪种变换得到()A.向右平移B.向右平移πC.向左平移D.向左平移π14.函数f(x)=ln(x2+1)的图象大致是()A.B.C. D.15.设函数f(x)=min{2,|x﹣2|},其中min|a,b|=.若函数y=f(x)﹣m有三个不同的零点x1,x2,x3,则x1+x2+x3的取值范围是()A.(2,6﹣2)B.(2,+1)C.(4,8﹣2)D.(0,4﹣2)16.设M是△ABC边BC上任意一点,N为AM上一点且AN=2NM,若,则λ+μ=()A.B.C.1 D.17.计算:=()A.B.C.D.﹣18.若函数f(x)=x2﹣2x+1在区间[a,a+2]上的最小值为4,则a的取值集合为()A.[﹣3,3] B.[﹣1,3] C.{﹣3,3} D.[﹣1,﹣3,3]19.若不等式|ax+1|≤3的解集为{x|﹣2≤x≤1},则实数a=()A.1 B.2 C.3 D.420.如图,己知||=5,||=3,∠AOB为锐角,OM平分∠AOB,点N为线段AB的中点,=x+y,若点P在阴影部分(含边界)内,则在下列给出的关于x、y的式子中,①x≥0,y≥0;②x﹣y≥0;③x﹣y≤0;A.①②④B.①③④C.①③⑤D.②⑤21.设不等式4x﹣m(4x+2x+1)≥0对于任意的x∈[0,1]恒成立,则实数m的取值范围是()A.(﹣∞,] B.[] C.[] D.[,+∞)22.设O为△ABC的外心(三角形外接圆的心),若=||2,则=()A.1 B.C.2 D.23.设函数f(x)=.若方程f(x)=1有3个不同的实数根,则实数a的取值范围是()A.(1,+∞)B.{﹣1}∪(1,+∞)C.(﹣∞,﹣1)D.(﹣∞,﹣1)∪(1,+∞)24.函数的值域为()A.[1,] B.[1,] C.[1,] D.[1,2]25.在△ABC中,BC=6,若G,O分别为△ABC的重心和外心,且=6,则△ABC的形状是()A.锐角三角形B.钝角三角形C.直角三角形D.上述三种情况都有可能二、填空题(共5小题,每小题3分,满分15分)26.若函数f(x)=2sin(ωx)(ω>0)的最小正周期为,则ω= .27.设tanx=2,则cos2x﹣2sinxcosx= .28.计算:log89log32﹣lg4﹣lg25= .29.已知A、B、C是单位圆上三个互不相同的点,若||=||,则的最小值是.30.若函数f(x)=﹣﹣a存在零点,则实数a的取值范围是.三、解答题(共3小题,满分30分)31.已知向量,如图所示.(Ⅰ)作出向量2﹣(请保留作图痕迹);(Ⅱ)若||=1,||=2,且与的夹角为45°,求与的夹角的余弦值.32.设α是三角形的一个内角,且sin()=cos().(Ⅰ)求tan2α的值;(Ⅱ)求函数f(x)=4sinxcosxcos2α+cos2xsin2α﹣1的最大值.33.设函数f(x)=(x﹣2)||x|﹣a|,a>0.(Ⅰ)当a=3时,求f(x)的单调递增区间;(Ⅱ)求f(x)在[﹣3,3]上的最小值.参考答案与试题解析一、选择题(共25小题,每小题2分,满分55分)1.函数f(x)=的定义域是()A.[1,+∞)B.(1,+∞)C.(0,1)D.[0,1] 【考点】函数的定义域及其求法.【专题】函数的性质及应用.【分析】根据函数成立的条件即可求函数的定义域.【解答】解:要使函数有意义,则x﹣1≥0,即x≥1,故函数的定义域为[1,+∞),故选:A【点评】本题主要考查函数的定义域的求解,要求熟练掌握常见函数成立的条件.2.函数f(x)=sin2x,x∈R的一个对称中心是()A.(,0)B.(,0)C.(,0)D.(,0)【考点】正弦函数的图象.【专题】三角函数的图像与性质.【分析】由条件利用余弦函数的图象的对称性求得函数的对称中心,从而得出结论.【解答】解:对于函数f(x)=sin2x,x∈R,令2x=kπ,k∈z,求得x=,故函数的对称中心为(,0),k∈z,故选:D.【点评】本题主要考查余弦函数的图象的对称性,属于基础题.3.设向量=(m,2)(m≠0),=(n,﹣1),若∥,则=()A.B.﹣C.2 D.﹣2【考点】平面向量共线(平行)的坐标表示.【专题】计算题;平面向量及应用.【分析】根据两向量平行的坐标表示,列出方程,求出m的值.【解答】解:∵向量=(m,2)(m≠0),=(n,﹣1),且∥,∴﹣1m﹣2n=0∴=﹣.故选:B.【点评】本题考查了平面向量的坐标运算问题,是基础题目.4.函数f(x)=lnx+x﹣2的零点位于区间()A.(0,1)B.(1,2)C.(2,3)D.(3,4)【考点】函数零点的判定定理.【专题】函数的性质及应用.【分析】求导函数,确定函数f(x)=lnx+x﹣2单调增,再利用零点存在定理,即可求得结论.【解答】解:求导函数,可得f′(x)=+1,∴函数f(x)=lnx+x﹣2单调增∵f(1)=ln1+1﹣2=﹣1<0,f(2)=ln2>0∴函数在(1,2)上有唯一的零点故选:B.【点评】本题考查函数的零点,解题的关键是确定函数的单调性,利用零点存在定理进行判断.5.已知幂函数f(x)=kxα(k∈R,α∈R)的图象过点(,),则k+α=()A.B.1 C.D.2【考点】幂函数的概念、解析式、定义域、值域.【专题】函数的性质及应用.【分析】根据幂函数f(x)的定义与性质,求出k与α的值即可.【解答】解:∵幂函数f(x)=kxα(k∈R,α∈R)的图象过点(,),∴k=1,=,∴α=﹣;∴k+α=1﹣=.故选:A.【点评】本题考查了幂函数的定义与性质的应用问题,是基础题.6.在区间(﹣1,1)上单调递增且为奇函数的是()A.y=ln(x+1)B.y=xsinx C.y=x﹣x3D.y=3x+sinx【考点】函数单调性的判断与证明;函数奇偶性的判断.【专题】函数的性质及应用.【分析】利用奇偶函数的定义判断奇偶性,再确定函数的单调性,即可得到结论【解答】解:对于A,函数不是奇函数,在区间(﹣1,1)上是增函数,故不正确;对于B,函数是偶函数,故不正确;对于C,函数是奇函数,因为y′=1﹣3x2,所以函数在区间(﹣1,1)不恒有y′>0,函数在区间(﹣1,1)上不是单调递增,故不正确;对于D,以y=3x+sinx是奇函数,且y′=3+cosx>0,函数在区间(﹣1,1)上是单调递增,故D正确【点评】本题考查函数单调性与奇偶性的结合,正确运用定义是关键7.若向量=﹣2,||=4,||=1,则向量,的夹角为()A.B.C.D.【考点】平面向量数量积的运算.【专题】平面向量及应用.【分析】根据平面向量的数量积公式求向量的夹角.【解答】解:由已知向量=﹣2,||=4,||=1,则向量,的夹角的余弦值为:,由向量的夹角范围是[0,π],所以向量,的夹角为;故选:A.【点评】本题考查了利用平面向量的数量积公式求向量的夹角;熟记公式是关键.8.设函数f(x)=x2+ax,a∈R,则()A.存在实数a,使f(x)为偶函数B.存在实数a,使f(x)为奇函数C.对于任意实数a,f(x)在(0,+∞)上单调递增D.对于任意实数a,f(x)在(0,+∞)上单调递减【考点】函数奇偶性的性质;函数单调性的性质.【专题】函数的性质及应用.【分析】根据偶函数、奇函数的定义,二次函数的单调性即可判断每个选项的正误.【解答】解:A.a=0时,f(x)=x2为偶函数,∴该选项正确;B.若f(x)为奇函数,f(﹣x)=x2﹣ax=﹣x2﹣ax;∴x2=0,x≠0时显然不成立;∴该选项错误;C.f(x)的对称轴为x=;当a<0时,f(x)在(0,+∞)没有单调性,∴该选项错误;【点评】考查偶函数、奇函数的定义,以及二次函数单调性的判断方法.9.若偶函数f(x)在区间(﹣∞,0]上单调递减,且f(7)=0,则不等式(x﹣1)f(x)>0的解集是()A.(﹣∞,﹣1)∪(1,+∞)B.(﹣∞,﹣7)∪(7,+∞)C.(﹣7,1)∪(7,+∞)D.(﹣7,1]∪(7,+∞)【考点】奇偶性与单调性的综合.【专题】函数的性质及应用.【分析】根据函数奇偶性和单调性之间的关系,将不等式进行转化即可.【解答】解:∵偶函数f(x)在区间(﹣∞,0]上单调递减,且f(7)=0,∴f(x)在区间[0,+∞)上单调递增,且f(﹣7)=f(7)=0,即f(x)对应的图象如图:则不等式(x﹣1)f(x)>0等价为:或,即或,即x>7或﹣7<x<1,故选:C【点评】本题主要考查不等式的求解,利用函数奇偶性和单调性的性质是解决本题的关键.10.函数f(x)=asin2x+cos2x,x∈R的最大值为,则实数a的值为()A.2 B.﹣2 C.±2 D.【考点】两角和与差的正弦函数.【分析】通过辅助角公式,化简函数为一个角的一个三角函数的形式,通过函数的最大值求出a.【解答】解:函数f(x)=asin2x+cos2x=sin(2x+φ),其中tanφ=,…(2分)因为函数f(x)=asin2x+cos2x的最大值为,∴=,解得a=±2.故选:C.…(4分)【点评】本题主要考查了正弦函数的单调性,考查了计算能力,属于基础题.11.函数f(x)=sin2x与函数g(x)=2x的图象的交点的个数是()A.1 B.3 C.5 D.7【考点】正弦函数的图象.【专题】三角函数的图像与性质.【分析】在同一个坐标系中分别画出函数f(x)=sin2x与函数g(x)=2x的图象,数形结合可得它们的图象的交点个数.【解答】解:在同一个坐标系中分别画出函数f(x)=sin2x与函数g(x)=2x的图象,如图所示,结合图象可得它们的图象的交点个数为1,故选:A.【点评】本题主要考查正弦函数的图象特征,体现了数形结合的数学思想,属于基础题.12.设a=log2π,b=logπ,c=π﹣2,则()A.a>b>c B.b>a>c C.a>c>b D.c>b>a【考点】对数值大小的比较.【专题】函数的性质及应用.【分析】根据对数函数和幂函数的性质求出,a,b,c的取值范围,即可得到结论.【解答】解:log2π>1,logπ<0,0<π﹣2<1,即a>1,b<0,0<c<1,∴a>c>b,故选:C【点评】本题主要考查函数值的大小比较,利用对数函数和幂函数的性质是解决本题的关键,比较基础.13.函数y=cos2x﹣sin2x的图象可以由函数y=cos2x+sin2x的图象经过下列哪种变换得到()A.向右平移B.向右平移πC.向左平移D.向左平移π【考点】函数y=Asin(ωx+φ)的图象变换.【专题】三角函数的图像与性质.【分析】根据函数y=cos2x+sin2x=sin(2x+),y=cos2x﹣sin2x=sin(),利用y=Asin(ωx+φ)的图象变化规律,可得结论.【解答】解:∵y=cos2x+sin2x=sin(2x+),y=cos2x﹣sin2x=sin(),又∵y=sin[2(x﹣)+]=sin(2x﹣)=﹣sin(π+﹣2x)=sin(),∴函数y=cos2x+sin2x的图象向右平移可得函数y=cos2x﹣sin2x的图象.故选:A.【点评】本题主要考查两角和差的正弦公式,y=Asin(ωx+φ)的图象变化规律,属于基础题.14.函数f(x)=ln(x2+1)的图象大致是()A.B.C. D.【专题】函数的性质及应用.【分析】∵x2+1≥1,又y=lnx在(0,+∞)单调递增,∴y=ln(x2+1)≥ln1=0,函数的图象应在x轴的上方,在令x取特殊值,选出答案.【解答】解:∵x2+1≥1,又y=lnx在(0,+∞)单调递增,∴y=ln(x2+1)≥ln1=0,∴函数的图象应在x轴的上方,又f(0)=ln(0+1)=ln1=0,∴图象过原点,综上只有A符合.故选:A【点评】对于函数的选择题,从特殊值、函数的性质入手,往往事半功倍,本题属于低档题.15.设函数f(x)=min{2,|x﹣2|},其中min|a,b|=.若函数y=f(x)﹣m有三个不同的零点x1,x2,x3,则x1+x2+x3的取值范围是()A.(2,6﹣2)B.(2,+1)C.(4,8﹣2)D.(0,4﹣2)【考点】函数零点的判定定理.【专题】函数的性质及应用.【分析】先比较2与|x﹣2|的大小以确定f(x)的解析式,然后结合函数的图象即可判断符合条件的m的范围,求出x1,x2,x3,的值从而求出x1+x2+x3的取值范围.【解答】解:令y=f(x)﹣m=0,得:f(x)=m,由2≥|x﹣2|可得x2﹣8x+4≤0,解可得4﹣2≤x≤4+2,当4﹣2≤x≤4+2时,2≥|x﹣2|,此时f(x)=|x﹣2|当x>4+2或0≤x<4﹣3时,2<|x﹣2|,此时f(x)=2,其图象如图所示,,∵f(4﹣2)=2﹣2,由图象可得,当直线y=m与f(x)图象有三个交点时m的范围为:0<m<2﹣2,不妨设0<x1<x2<2<x3,则由2=m得x1=,由|x2﹣2|=2﹣x2=m,得x2=2﹣m,由|x3﹣2|=x3﹣2=m,得x3=m+2,+x2+x3=+2﹣m+m+2=+4,∴x1当m=0时,+4=4,m=2﹣2时,+4=8﹣2,+x2+x3<8﹣2.∴4<x1故选:C.【点评】本题以新定义为载体,主要考查了函数的交点个数的判断,解题的关键是结合函数的图象.16.设M是△ABC边BC上任意一点,N为AM上一点且AN=2NM,若,则λ+μ=()A.B.C.1 D.【考点】平面向量的基本定理及其意义.【专题】平面向量及应用.【分析】利用平面向量基本定理,用、表示出、,从而得出结论.【解答】解:如图所示,∵M是△ABC边BC上任意一点,设=m+n,∴则m+n=1,又∴AN=2NM,∴=,∴==m+n=λ+μ,∴λ+μ=(m+n)=.故选:B.【点评】本题考查了平面向量基本定理的应用问题,解题的关键是用、表示出向量,属于基础题.17.计算:=()A.B.C.D.﹣【考点】三角函数中的恒等变换应用.【专题】计算题;三角函数的求值.【分析】利用诱导公式,倍角公式,同角三角函数关系式将所求式子转化为10°角的正弦函数值,即可得解.【解答】解:===.故选:A.【点评】本题主要考查了诱导公式,倍角公式,同角三角函数关系式的应用,属于基础题.18.若函数f(x)=x2﹣2x+1在区间[a,a+2]上的最小值为4,则a的取值集合为()A.[﹣3,3] B.[﹣1,3] C.{﹣3,3} D.[﹣1,﹣3,3]【考点】二次函数在闭区间上的最值.【专题】函数的性质及应用.【分析】配方法得到函数的对称轴为x=1,将对称轴移动,讨论对称轴与区间[a,a+2]的位置关系,合理地进行分类,从而求得函数的最小值【解答】解:∵函数f(x)=x2﹣2x+1=(x﹣1)2,对称轴x=1,∵区间[a,a+2]上的最小值为4,=f(a)=(a﹣1)2=4,a=﹣1(舍去)或a=3,∴当1≤a时,ymin当a+2≤1时,即a≤﹣1,y min=f(a+2)=(a+1)2=4,a=1(舍去)或a=﹣3,当a<a<a+2时,y min=f(1)=0≠4,故a的取值集合为{﹣3,3}.故选:C.【点评】配方求得函数的对称轴是解题的关键.由于对称轴所含参数不确定,而给定的区间是确定的,这就需要分类讨论.利用函数的图象将对称轴移动,合理地进行分类,从而求得函数的最值,当然应注意若求函数的最大值,则需按中间偏左、中间偏右分类讨论19.若不等式|ax+1|≤3的解集为{x|﹣2≤x≤1},则实数a=()A.1 B.2 C.3 D.4【考点】绝对值不等式的解法.【专题】不等式的解法及应用.【分析】由题意可得﹣3≤ax≤2,即﹣2≤x≤1,由此可得a的值.【解答】解:由题意可得,不等式|ax+1|≤3,即﹣3≤ax+1≤3,即﹣4≤ax≤2,即﹣2≤x≤1,∴a=2,故选:B.【点评】本题主要考查绝对值不等式的解法,属于基础题.20.如图,己知||=5,||=3,∠AOB为锐角,OM平分∠AOB,点N为线段AB的中点,=x+y,若点P在阴影部分(含边界)内,则在下列给出的关于x、y的式子中,①x≥0,y≥0;②x﹣y≥0;③x﹣y≤0;④5x﹣3y≥0;⑤3x﹣5y≥0.满足题设条件的为()A.①②④B.①③④C.①③⑤D.②⑤【考点】向量的线性运算性质及几何意义.【专题】平面向量及应用.【分析】利用向量共线定理,及三角形法则,将向量表示出来,的系数对应等于x,y.由此即可解题【解答】解:设线段OP与AB的交点为C,则由向量共线定理知:存在实数λ,,其中λ>0,∴==,∵共线,∴存在实数μ,使得,∵N为AB的中点,∴μ'又∵||=5,||=3,OM平分∠AOB,∴由正弦定理知,AM=BM∴AC≤AM=AB,故,∴==∴x=λ(1﹣μ),y=λμ,∴x≥0,y≥0;∴x﹣y=λ(1﹣2μ)≤0;∴5x﹣3y=λ(5﹣8μ)≥0.故选:B.【点评】本题主要考察了平面向量的共线定理以及向量的三角形法则,并涉及到了正弦定理,难度较大,属于难题.21.设不等式4x﹣m(4x+2x+1)≥0对于任意的x∈[0,1]恒成立,则实数m的取值范围是()A.(﹣∞,] B.[] C.[] D.[,+∞)【考点】指数函数综合题.【专题】计算题;函数思想;综合法;函数的性质及应用.【分析】把已知不等式变形,分离参数m,然后结合指数式的值域,利用配方法求得的范围得答案.【解答】解:由4x﹣m(4x+2x+1)≥0,得m(4x+2x+1)≤4x,即m≤=,∵x∈[0,1],∴∈[,1],则∈[],∴∈[],则m.故选:A.【点评】本题考查恒成立问题,考查了分离变量法,训练了利用配方法求函数的最值,是中档题.22.设O为△ABC的外心(三角形外接圆的心),若=||2,则=()A.1 B.C.2 D.【考点】平面向量数量积的运算.【专题】平面向量及应用.【分析】利用三角形的外心,得到,,两式平方相减化简,得到2,又=||2,得到AB,AC的关系【解答】解:因为O是三角形的外心,所以,,,两式平方相减得2,即2,又=||2,所以2,所以;故选:B.【点评】本题考查了三角形外心性质以及向量数量积等运算;考查学生的运算能力;属于中档题.23.设函数f(x)=.若方程f(x)=1有3个不同的实数根,则实数a的取值范围是()A.(1,+∞)B.{﹣1}∪(1,+∞)C.(﹣∞,﹣1)D.(﹣∞,﹣1)∪(1,+∞)【考点】根的存在性及根的个数判断.【专题】计算题;作图题;函数的性质及应用.【分析】当x<0时,由f(x)=x2=1得x=﹣1;从而可得,当0≤x≤π时,方程sin2x=有2个不同的解;作函数y=sin2x,(0≤x≤π)的图象,结合图象求解即可.【解答】解:当x<0时,f(x)=x2=1,解得,x=﹣1;∵方程f(x)=1有3个不同的实数根,∴当0≤x≤π时,方程f(x)=1可化为asin2x=1;显然可知a=0时方程无解;故方程可化为sin2x=,且有2个不同的解;作函数y=sin2x,(0≤x≤π)的图象如下,结合图象可得,0<<1或﹣1<<0;解得,a∈(﹣∞,﹣1)∪(1,+∞);故选D.【点评】本题考查了分段函数的应用及方程的根与函数的图象的交点的应用,同时考查了数形结合的思想应用,属于中档题.24.函数的值域为()A.[1,] B.[1,] C.[1,] D.[1,2]【考点】函数的值域.【专题】综合题;压轴题;转化思想;综合法.【分析】先求出函数的定义域,观察发现,根号下两个数的和为1,故可令则问题可以转化为三角函数的值域问题求解,易解【解答】解:对于f(x),有3≤x≤4,则0≤x﹣3≤1,令,则=∵,∴.函数的值域为[1,2]故选D【点评】本题考查求函数的值域,求解的关键是观察到问题可以转化为三角函数求解,注意本题转化的依据,两数的和为1,此是一个重要的可以转化为三角函数的标志,切记.25.在△ABC中,BC=6,若G,O分别为△ABC的重心和外心,且=6,则△ABC的形状是()A.锐角三角形B.钝角三角形C.直角三角形D.上述三种情况都有可能【考点】平面向量数量积的运算.【专题】平面向量及应用.【分析】在△ABC中,G,O分别为△ABC的重心和外心,取BC的中点为D,连接AD、OD、GD,运用重心和外心的性质,运用向量的三角形法则和中点的向量形式,以及向量的平方即为模的平方,可得2﹣=﹣36,又BC=6,则有||=||2+||2,运用勾股定理逆定理即可判断三角形的形状.【解答】解:在△ABC中,G,O分别为△ABC的重心和外心,取BC的中点为D,连接AD、OD、GD,如图:则OD⊥BC,GD=AD,∵,,由=6,则()==﹣()=6,即﹣()()=6,则,又BC=6,则有||=||2+||2,即有C为直角.则三角形ABC为直角三角形.故选:C.【点评】本题考查向量的数量积的性质和运用,主要考查向量的三角形法则和向量的平方即为模的平方,运用勾股定理逆定理判断三角形的形状.二、填空题(共5小题,每小题3分,满分15分)26.若函数f(x)=2sin(ωx)(ω>0)的最小正周期为,则ω= 4 .【考点】三角函数的周期性及其求法.【专题】计算题;三角函数的图像与性质.【分析】由三角函数的周期性及其求法可得T==,即可解得ω的值.【解答】解:由三角函数的周期性及其求法可得:T==,解得:ω=4.故答案为:4.【点评】本题主要考查了三角函数的周期性及其求法,属于基本知识的考查.27.设tanx=2,则cos2x﹣2sinxcosx= ﹣.【考点】同角三角函数基本关系的运用.【专题】三角函数的求值.【分析】原式分母看做“1”,利用同角三角函数间的基本关系化简,把tanx的值代入计算即可求出值.【解答】解:∵tanx=2,∴原式====﹣,故答案为:﹣【点评】此题考查了同角三角函数基本关系的运用,熟练掌握基本关系是解本题的关键.28.计算:log89log32﹣lg4﹣lg25= .【考点】对数的运算性质.【专题】函数的性质及应用.【分析】根据对数的运算性质计算即可.【解答】解:log89log32﹣lg4﹣lg25=log23log32﹣lg100=﹣2=﹣,故答案为:【点评】本题考查了对数的运算性质,属于基础题.29.已知A、B、C是单位圆上三个互不相同的点,若||=||,则的最小值是.【考点】平面向量数量积的运算.【专题】平面向量及应用.【分析】如图所示,取=(1,0),不妨设B(cosθ,sinθ),(θ∈(0,π)).由于,可得C(cosθ,﹣sinθ).再利用数量积运算、二次函数的单调性、余弦函数的单调性即可得出.【解答】解:如图所示,取=(1,0),不妨设B(cosθ,sinθ),(θ∈(0,π)).∵,∴C(cosθ,﹣sinθ).∴=(cosθ﹣1,sinθ)(cosθ﹣1,﹣sinθ)=(cosθ﹣1)2﹣sin2θ=,当且仅当,即时,上式取得最小值.即的最小值是﹣.故答案为:﹣.【点评】本题考查了数量积运算、二次函数的单调性、余弦函数的单调性,考查了推理能力和计算能力,属于难题.30.若函数f(x)=﹣﹣a存在零点,则实数a的取值范围是(﹣1,1).【考点】函数零点的判定定理.【专题】计算题;数形结合;函数的性质及应用.【分析】化简a=﹣,从而利用其几何意义及数形结合的思想求解.【解答】解:由题意得,a=﹣=﹣;表示了点A(﹣,)与点C(3x,0)的距离,表示了点B(,)与点C(3x,0)的距离,如下图,结合图象可得,﹣|AB|<﹣<|AB|,即﹣1<﹣<1,故实数a的取值范围是(﹣1,1).故答案为:(﹣1,1).【点评】本题考查了数形结合的思想应用.三、解答题(共3小题,满分30分)31.已知向量,如图所示.(Ⅰ)作出向量2﹣(请保留作图痕迹);(Ⅱ)若||=1,||=2,且与的夹角为45°,求与的夹角的余弦值.【考点】向量的线性运算性质及几何意义.【专题】平面向量及应用.【分析】(I)运用向量的加减运算的几何性质求解绘画,(II)根据向量的运算得出==,=利用夹角得出cosθ=,求解即可.【解答】解:(I)先做出2,再作出,最后运用向量的减法得出2,如图表示红色的向量,(II)设,的夹角θ,∵||=1,||=2,且与的夹角为45°∴=1×2×cos45°=,∴==,=,()=1﹣4=﹣3,cosθ=====.【点评】本题考察了平面向量的加减运算,数量积,向量的模的计算,属于向量的典型的题目,难度不大,计算准确即可.32.设α是三角形的一个内角,且sin()=cos().(Ⅰ)求tan2α的值;(Ⅱ)求函数f(x)=4sinxcosxcos2α+cos2xsin2α﹣1的最大值.【考点】三角函数的最值;两角和与差的余弦函数;两角和与差的正弦函数.【专题】三角函数的求值.【分析】(Ⅰ)花间条件可得tanα=﹣,求得α的值,可得tan2α的值.(Ⅱ)利用三角恒等变换化简函数f(x)的解析式,再利用正弦函数的值域求得它的最大值.【解答】解:(Ⅰ)∵sin()=cos(),∴2sinαcos+2cosαsin=cosαcos+sinαsin,化简可得sinα+cosα=0,即tanα=﹣.又α是三角形的一个内角,可得α=,故tan2α=tan=tan=.(Ⅱ)求函数f(x)=4sinxcosxcos2α+cos2xsin2α﹣1=2sin2xcos+cos2xsin﹣1=﹣sin2x﹣cos2x﹣1=﹣sin(2x+θ)﹣1,故当sin(2x+θ)=﹣1时,f(x)取得最大值为﹣1.【点评】本题主要考查三角恒等变换,根据三角函数的值求角,正弦函数的值域,属于中档题.33.设函数f(x)=(x﹣2)||x|﹣a|,a>0.(Ⅰ)当a=3时,求f(x)的单调递增区间;(Ⅱ)求f(x)在[﹣3,3]上的最小值.【考点】分段函数的应用.【专题】分类讨论;函数的性质及应用;不等式的解法及应用.【分析】(Ⅰ)当a=3时,f(x)=(x﹣2)||x|﹣3|,对x讨论,去掉绝对值,再由二次函数的对称轴和单调性,即可得到所求增区间;(Ⅱ)对x讨论,去绝对值,再对a讨论,分0<a≤2,2<a<3时,3≤a<8,a≥8,结合对称轴和区间[﹣3,3]的关系,即可得到最小值.【解答】解:(Ⅰ)当a=3时,f(x)=(x﹣2)||x|﹣3|,当x≥3时,f(x)=(x﹣2)(x﹣3)=x2﹣5x+6在[3,+∞)递增;当0<x<3时,f(x)=(x﹣2)(3﹣x)=﹣x2+5x﹣6在(0,]递增;当﹣3<x≤0时,f(x)=(x﹣2)(x+3)=x2+x﹣6在[﹣,0]递增;当x≤﹣3时,f(x)=(x﹣2)(﹣x﹣3)=﹣x2﹣x﹣6在(﹣∞,﹣3]递增.综上可得,f(x)的增区间为(﹣∞,﹣3],[﹣,],[3,+∞).(Ⅱ)f(x)=,(1)若0<a≤2,则f(x)min=min{f(﹣3),f(0)}=min{﹣5|3﹣a|,﹣2a},当﹣5|3﹣a|=﹣2a,解得a=或a=5,即当0<a≤2时,f(x)min=﹣5(3﹣a);(2)若2<a<3时,f(x)min=min{f(﹣3),f()}=min{﹣5|3﹣a|,﹣},当﹣5|3﹣a|=﹣,解得a=10﹣12∈(2,3),即f(x)min=,(3)若﹣a≤﹣3<,即3≤a<8时,f(x)min=f(﹣)=﹣,(4)若≤﹣3,则a≥8,f(x)min=f(﹣3)=15﹣5a.综上可得,f(x)min=.【点评】本题考查分段函数的单调性和最值求法,注意讨论对称轴和区间的关系,运用分类讨论的思想方法是解题的关键.。
人教版四年级下册数学语文英语期末模拟试卷及数语答案A

人教版四年级下册数学语文英语期末模拟试卷及数语答案AStandardization of sany group #QS8QHH-HHGX8Q8-GNHHJ8-HHMHGN#人教版小学数四年级下学期期末模拟试卷〖100分钟完卷〗一“神机”妙算:(41%) 1.直接写出得数:(8分)+ = 150×6= += +=×100= 60×50= 287- 199= ×125×8=1 - = 927÷9= 60÷100= ×99+= ×99≈ ×≈ ÷≈ ++=2.列竖式计算(第③题要验算):(7分)① + ② – ③ –3.求未知数X :(8分)X ÷70= 140 X ×25 = 400 + X =30 X – =4.用你喜欢的方法计算:(12分) ① +++ ② ③ 57×101 - 57④ (520 + 480)÷50×4 ⑤ 400-(1300÷65+35) ⑥ 60-()+5.列式并计算:(6分)① 用39与41的和,去除585与265的差, ② 5292除以36的商,和1470与1386商是多少 的差相乘,积是多少二.对号“入座”:(17%)1.第五次人口普查结果公布:中国总人口达到十二亿九千五百三十三万人,写作( )人,改写成以“万”为单位的数是( )人,省略“亿”后面尾数约是( )人。
2.由5个百、2个一、8个百分之一组成的数,写作( ),读作 ( ),表示( )。
3.改成三位小数是( ),这是根据小数的( )。
4.9.9549保留整数约是( ),精确到十分位约是( ),保留两位小数约是( )。
5.在〇里填上“>”、“<”或“=”。
〇 〇 公顷 〇 7900平方米6.平方米=( ) 平方分米 1小时40分=( )分 米=( )米( ) 厘米 吨=( )吨( )千克 7.把下面各数按从小到大顺序排列:8.把扩大100倍是( ); 把缩小( )倍是。
人教版2022——2023学年小学三年级下册数学期末专项提升模拟试卷AB卷(含答案)

【人教版】2022-2023学年小学三年级下册数学期末专项提升模拟试卷(A 卷)一、选一选1.下面的算式中,得数小于2400的是()。
A .7842⨯B .5325⨯C .4962⨯2.小明从学校出来往西走300米,再往北走100米,就到了家,小明家在学校的()。
A .东南方B .南方C .西3.2088年的季度有()天.A .89B .90C .914.9□×6□的积是()位数.A .三B .四C .三或四5.正方形的边长4米,它的周长与面积()。
A .周长>面积B .周长<面积C .无法比较D .周长=面积6.从红、黄、白、绿、黑五个颜色球中,任意选出两个球装进纸箱中,至多可有()种没有重复的方法。
A .12B .11C .10D .87.学校食堂运来84千克大米,吃了6天正好吃完。
用84÷6计算的是()。
A .平均每天吃多少千克B .还剩多少千克C .5天吃多少千克8.“0.6元6角”,比较大小,在○里应填的符号是()A.>B.<C.=D.÷二、填空题9.69□÷3的商是()位数,如果商的个位是0,□里可以填()。
时,他先算________,再在积的末尾添写________个0,积是________。
10.小明在口算154011.早晨,你面对太阳时,你的后面是()面,右面是()面。
12.红红买一条毛巾花了19.4元,丽丽买一条毛巾花了7.8元,红红买的毛巾比丽丽贵()元,她们买毛巾一共花了()元。
13.周长是48分米的正方形,如果它的边长扩大到原来的2倍,那么它的周长是()分米,面积是()平方分米。
14.今年7月1日是中国100周岁生日,这个月在()季度,这个月共有()星期零()天。
15.一个周长是8分米的正方形,如果它的边长扩大到原来的3倍,那么它的周长变成()分米,面积变成()平方分米。
16.计算42-36÷6时,应先算()法,计算结果是();计算(42-36)÷6时,应先算()法,计算结果是()。
2023-2024学年八年级第一学期语文期末模拟试卷(一)(含解析)

2023-2024学年第一学期八年级语文期末模拟试卷(一)一、基础知识(共8题;共41分)1.(13分)请运用所积累的知识,完成问题。
时不可失。
必须在敌人援军到达之前把桥占领。
于是再一次征求志愿人员。
红军战士一个个站出来愿意冒生命危险,于是在报名的人中最后选了三十个人。
他们身上背了毛瑟枪和手榴弹,马上就爬到沸腾的河流上去了,紧紧地抓住了铁索一步一抓地前进。
红军机枪向敌军碉堡开火,子弹都飞迸在桥头堡上。
敌军也以机枪回报,jū击手向着在河流上空摇晃地向他们慢慢爬行前进的红军射击。
第一个战士中了弹掉到了下面的急流中,接着又有第二个,第三个。
但是别的人越来越爬近到桥中央桥上的木板对这些敢死队起了一点保护作用,敌人的大部分子弹都迸了开去,或者落在对岸的悬崖上。
(1)(3分)给加点的字注音,根据拼音写出相应的汉字。
①沸腾②飞迸③jū击手(2)(3分)下列短语的结构类型与“慢慢爬行”相同的一项是()A.战士中弹B.河流上空C.抓住铁索D.慷慨激昂(3)(3分)选文描写了激烈的战斗场景,下列诗句中没有写到战争的一项是()A.万里长征人未还B.醉卧沙场君莫笑C.猎马带禽归D.都护在燕然(4)(4分)以上文段节选自美国记者(人名)创作的长篇纪实作品《红星照耀中国》本书曾易名为《》。
选文再现的历史事件是文中“红军战士”的精神感人至深。
2.(3分)下列句子加点成语使用有误的一项是()A.逛了一天公园,回家后我已经筋疲力尽了。
B.这次考试班上只有肖东同学没及格,他可真是鹤立鸡群呀。
C.当敌人冲进大厅的时候,只见他正襟危坐,那副处变不惊、视死如归的气节真让人敬佩!D.雷锋精神应该继续继承发扬,这一点无可置疑。
3.(3分)下列病句的修改不正确的一项是()A.2016年,中国对世界经济增长的贡献率超过30%多,是世界经济增长的压舱石。
(语意重复,应删去“超过”或“多”)B.在著名物理学家霍金的首条中国微博中表示,希望与中国网友分享生活趣事和工作心得。
全国通用2022-2023学年五年级下学期数学期末调研模拟试卷AB卷(含解析)
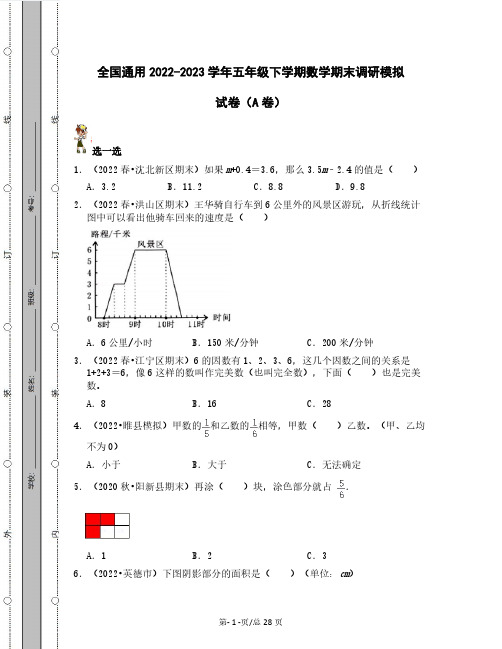
试卷(A卷)1.(2022春•沈北新区期末)如果m+0.4=3.6,那么3.5m﹣2.4的值是( )A.3.2B.11.2C.8.8D.9.82.(2022春•洪山区期末)王华骑自行车到6公里外的风景区游玩,从折线统计图中可以看出他骑车回来的速度是( )A.6公里/小时B.150米/分钟C.200米/分钟3.(2022春•江宁区期末)6的因数有1、2、3、6,这几个因数之间的关系是1+2+3=6,像6这样的数叫作完美数(也叫完全数),下面( )也是完美数。
A.8B.16C.284.(2022•睢县模拟)甲数的和乙数的相等,甲数( )乙数。
(甲、乙均不为0)A.小于B.大于C.无法确定5.(2020秋•阳新县期末)再涂( )块,涂色部分就占.6.(2022•英德市)下图阴影部分的面积是( )(单位:cm)A.9.42cm2B.14.13cm2C.18.84cm2D.28.26cm27.(2022春•合阳县期末)下图中每个小方格代表1平方厘米,下面三个图形面积大小排列顺序正确的是( )A.③>②>①B.②>①>③C.③>①>②D.①>③>②填一填8.(2022春•通许县期末)估计下列图形中, 图形的周长最长, 图形的面积最大。
A.B.C.9.(2022•巩义市)如图,圆的周长是31.4cm,圆的半径是 cm,正方形的周长是 cm,阴影部分的面积是 cm2。
10.(2021春•慈溪市期末)m比m短 m,m比 m短m。
11.(2022春•盐城期末)一个分数,它的分子缩小2倍,分母扩大2倍后得,原来的分数是 .12.(2022春•江宁区期末)如图,大正方形中的三个涂色图形的周长和是60厘米。
大正方形的面积是 平方厘米。
若用N个这样的大正方形拼一个长方形,这个长方形周长的厘米数是 。
(填“奇数”或“偶数”)13.(2021春•灵武市期末)如图是某商场2020年下半年的销售情况统计图。
衬衫 月份销售量最低;两种服装 月份销售量相差最多,相差 件。
2022——2023学年北京市西城区八年级上册数学期末专项突破模拟卷AB卷(含答案)

2022-2023学年北京市西城区八年级上册数学期末专项突破模拟卷(A 卷)一、选一选(每小题只有一个选项符合题意,请将你认为正确的选项字母填入下表相应空格内,每小题3分,共30分)1.下面各式中正确的是A.m n mn a a a ⋅= B.2m m ma a a +=C.()()nmmna a = D.()mmab ab =2.下列“数字”图形中,有且仅有一条对称轴的是()A. B. C. D.3.设一个正方形的边长为a cm ,若边长增加3cm ,则新正方形的面积增加了A.9cm 2B.6a cm 2C.(6a +9)cm 2D.无法确定4.下式等式从左到右的变形,属于因式分解的是()A.()()22a b a b a b +-=-;B.()21+4+41a a a a +=+;C.()()311x x x x x -=-+;D.2111x x x x x ⎛⎫++=++⎪⎝⎭.5.已知2264x kxy y ++是一个完全平方式,则k 的值是()A.8B.8± C.16D.16±6.若a ≠b ,下列各式中没有能成立的是A.22()()a b a b +=-- B.()()()()a b a b b a b a +-=+-C.22()()n na b b a -=- D.33()()a b b a +=+7.若(x ﹣3)(x +4)=x 2+px +q ,那么p 、q 的值是()A.p =1,q =﹣12B.p =﹣1,q =12C.p =7,q =12D.p =7,q =﹣128.如图,直线是一条河,A 、B 是两个新农村定居点.欲在l 上的某点处修建一个水泵站,由水泵站直接向A 、B 两地供水.现有如下四种管道铺设,图中实线表示铺设的供水管道,则铺设管道最短的是()A. B. C. D.9.如图,Rt △ABC 中,∠C=90°,∠B=45°,AD 是∠CAB 的平分线,DE ⊥AB 于E ,AB=a ,CD=m ,则AC 的长为()A.2mB.a-mC.aD.a+m10.用10米长的铝合金做成一个长方形的窗框(如图),设长方形窗框的横条长度为x 米,则长方形窗框的面积为A.()10x x -平方米B.()103x x -平方米C.352x x ⎛⎫-⎪⎝⎭平方米 D.3102x x ⎛⎫-⎪⎝⎭平方米二、填空题(共5个小题,每小题3分,共15分)11.计算:﹣a 11÷(﹣a )6•(﹣a )5=_____________.12.计算:24(1)(25)(25)x x x ⨯+-+-=_________.13.因式分解:()224a b b --=______.14.若点M (2,a +3)与点N (2,2a ﹣15)关于x 轴对称,则a 2+3=_____________.15.如图,P 是△ABC 的∠ABC 和∠ACB 的外角的平分线的交点,若∠A =90°,则∠P =_____________.三、解答题(共8个小题,共75分,解答应写出必要的文字说明、证明过程或演算步骤)16.化简下列多项式:(1)2(1)(41)(21)x x x +---(2)(223)(223)a b a b +--+(3)若2530x y +-=,求432x y ⋅的值.(4)先化简,再求值:(2x ﹣1)2﹣(3x +1)(3x ﹣1)+5x (x ﹣1),其中x =﹣2.17.分解因式(1)4x 3﹣16xy 2(2)3a 2+6ab +3b 218.已知2246130x yx y +-++=,求2269x xy y -+的值.19.通过学习,同学们已经体会到灵活运用乘法公式使整式的乘法运算方便、快捷.相信通过对下面材料的学习、探究,会使你大开眼界,并获得成功的喜悦.例:用简便方法计算:195205⨯.解:195205⨯,()20052005=-+①,222005=-②,39975=.(1)例题求解过程中,第②步变形是利用___________(填乘法公式的名称).(2)用简便方法计算:91110110001⨯⨯⨯.20.如图,方格纸中每个小正方形的边长都是1,ABC 的三个顶点都在格点上.()1画ABC 关于直线MN 的对称图形111(A B C 没有写画法);()2求ABC 的面积;21.阅读下面的解答过程,求y 2+4y +8的最小值.解:y 2+4y +8=y 2+4y +4+4=(y +2)2+4≥4,∵(y +2)2≥0即(y +2)2的最小值为0,∴y 2+4y +8的最小值为4.仿照上面的解答过程,求m 2+m +4的最小值和4﹣x 2+2x 的值.22.已知正整数a 、b 、c 满足没有等式22243a b c +++≤98ab b c ++,求a 、b 、c 的值.23.如图,△ABC 是等边三角形,点D 在AC 上,点E 在BC 的延长线上,且BD =DE .(1)若点D 是AC 的中点,如图1,求证:AD =CE(2)若点D 没有是AC 的中点,如图2,试判断AD 与CE 的数量关系,并证明你的结论:(提示:过点D 作DF ∥BC ,交AB 于点F )2022-2023学年北京市西城区八年级上册数学期末专项突破模拟卷(A 卷)一、选一选(每小题只有一个选项符合题意,请将你认为正确的选项字母填入下表相应空格内,每小题3分,共30分)1.下面各式中正确的是A.m n mn a a a ⋅= B.2m m ma a a +=C.()()nmmna a = D.()mmab ab =【正确答案】C【详解】A. m n mn a a a ⋅=,原式计算错误,故本选项错误;B.m a 和n a 没有是同类项,没有能合并;C.()m n a =()n m a ,计算正确,故本选项正确;D.()m m ab ab =,原式计算错误,故本选项错误.故选C.2.下列“数字”图形中,有且仅有一条对称轴的是()A. B. C. D.【正确答案】A【详解】A 轴对称图形,一条对称轴;B 没有是轴对称图形;C 是轴对称图形,有两条对称轴;D 是轴对称图形,有两条对称轴.故选A.考点:轴对称图形.3.设一个正方形的边长为a cm ,若边长增加3cm ,则新正方形的面积增加了A.9cm 2B.6a cm 2C.(6a +9)cm 2D.无法确定【正确答案】C【详解】解:根据题意得:(a +3)2−a 2=a 2+6a +9−a 2=(6a +9)cm 2,∴新正方形的面积增加了(6a +9)cm 2故选:C .本题考查了整式的混合运算,先由题意表示出增加后新正方形的边长,分别求出原正方形与新正方形的面积,相减即可得到增加的面积.4.下式等式从左到右的变形,属于因式分解的是()A.()()22a b a b a b +-=-;B.()21+4+41a a a a +=+;C.()()311x x x x x -=-+; D.2111x x x x x ⎛⎫++=++⎪⎝⎭.【正确答案】C【分析】根据因式分解是把一个多项式转化成几个整式积的形式,可得答案.【详解】A.是整式的乘法,故A 错误;B.没把一个多项式转化成几个整式积的形式,故B 错误;C.把一个多项式转化成几个整式积的形式,故C 正确;D.没把一个多项式转化成几个整式积的形式,故D 错误;故选C.此题考查因式分解的意义,解题关键在于掌握运算法则5.已知2264x kxy y ++是一个完全平方式,则k 的值是()A.8B.8± C.16D.16±【正确答案】D【分析】两个完全平方式:222,a ab b ±+本题的特点可得:218,k =±⨯⨯从而可得答案.【详解】解:()222264=8x kxy y x kxy y++++,2264x kxy y ++是一个完全平方式,21816,k ∴=±⨯⨯=±故选D本题考查的是完全平方式的应用,掌握利用完全平方式的特点求解参数的值是解本题的关键.6.若a ≠b ,下列各式中没有能成立的是A.22()()a b a b +=-- B.()()()()a b a b b a b a +-=+-C.22()()nn a b b a -=- D.33()()a b b a +=+【正确答案】B【详解】A.(a+b)²=a²+2ab+b²,(−a−b)²=[−(a+b)]²=a²+2ab+b ²,故本选项错误;B.(a+b)(a−b)=22a b -,(b+a)(b+a)=b²−a ²,故本选项正确;C.2()n a b -和2()n b a -相等,故本选项错误;D.33()()a b b a +=+,故本选项错误;故选B.7.若(x ﹣3)(x +4)=x 2+px +q ,那么p 、q 的值是()A.p =1,q =﹣12B.p =﹣1,q =12C.p =7,q =12D.p =7,q =﹣12【正确答案】A【详解】试题分析:此题可以将等式左边展开和等式右边对照,根据对应项系数相等即可得到p 、q 的值.由于(x-3)(x+4)=x 2+x-12=x 2+px+q ,则p=1,q=-12.故选A .考点:多项式乘多项式的法则8.如图,直线是一条河,A 、B 是两个新农村定居点.欲在l 上的某点处修建一个水泵站,由水泵站直接向A 、B 两地供水.现有如下四种管道铺设,图中实线表示铺设的供水管道,则铺设管道最短的是()A. B. C. D.【正确答案】D【分析】利用轴对称的性质,通过等线段代换,将所求路线长转化为两定点之间的距离.【详解】解:作点A 关于直线的对称点A ',连接BA '交直线l 于一点,根据两点之间,线段最短,可知选项D 铺设的管道最短.故选:D本题考查了最短问题、解题的关键是理解题意,灵活运用所学知识解决问题,属于中考常考题型.9.如图,Rt △ABC 中,∠C=90°,∠B=45°,AD 是∠CAB 的平分线,DE ⊥AB 于E ,AB=a ,CD=m ,则AC 的长为()A.2mB.a-mC.aD.a+m【正确答案】B【详解】:∵AD 是∠CAB 的平分线,DE ⊥AB ,∠C=90°,∴CD=DE ,在Rt △ACD 和Rt △AED 中,AD ADCD DE ⎧⎨⎩==,∴Rt △ACD ≌Rt △AED (HL ),∴AC=AE ,∵∠B=45°,DE ⊥AB ,∴△BDE 是等腰直角三角形,∴BE=DE=m ,∵AE=AB-BE=a-m ,∴AC=a-m .故选B .10.用10米长的铝合金做成一个长方形的窗框(如图),设长方形窗框的横条长度为x 米,则长方形窗框的面积为A.()10x x -平方米B.()103x x -平方米C.352x x ⎛⎫-⎪⎝⎭平方米 D.3102x x ⎛⎫-⎪⎝⎭平方米【正确答案】C【详解】由题意得,窗框的竖条长为:12(10−3x)=5−32x ,所以,长方形窗框的面积为x(5−32x).故选C.二、填空题(共5个小题,每小题3分,共15分)11.计算:﹣a 11÷(﹣a )6•(﹣a )5=_____________.【正确答案】a 10【详解】11651165116510()()()a a a a a a a a -+-÷-⋅-=-÷⋅-==,故答案为10a 12.计算:24(1)(25)(25)x x x ⨯+-+-=_________.【正确答案】8x 29+【详解】原式=224(21)(425)x x x ++--=224x 8x 44x 25++-+=8x+4+25=8x+29,故答案为8x+29.13.因式分解:()224a b b --=______.【正确答案】()()3a b a b -+【分析】利用平方差公式进行因式分解.【详解】解:()()()()()224223a b b a b b a b b a b a b --=-+--=+-.故答案是:()()3a b a b -+.本题考查因式分解,解题的关键是掌握因式分解的方法.14.若点M (2,a +3)与点N (2,2a ﹣15)关于x 轴对称,则a 2+3=_____________.【正确答案】19【详解】试题分析:根据纵坐标互为相反数列式求得a 的值,代入所给代数式求值即可.试题解析:∵点M (2,a+3)与点N (2,2a-15)关于x 轴对称,∴a+3+2a-15=0,解得a=4,∴a 2+3=19.考点:1.关于x 轴、y 轴对称的点的坐标;2.代数式求值.15.如图,P 是△ABC 的∠ABC 和∠ACB 的外角的平分线的交点,若∠A =90°,则∠P =_____________.【正确答案】45°【详解】根据三角形的外角性质,∠ACE=∠A+∠ABC ,∠PCE=∠P+∠PBC ,∵BP 平分∠ABC ,CP 是△ABC 的外角的平分线,∴∠PBC=12∠ABC,∠PCE=12∠ACE ,∴∠P+12∠ABC=12(∠A+∠ABC),∴∠A=2∠P ,∵∠A=90°,∴∠P=45°故答案为45°点睛:本题考查了三角形内角和定理,三角形的外角性质,根据三角形的一个外角等于与它没有相邻的两个内角的和列式表示出∠ACE 和∠PCE ,再根据角平分线的定义表示出∠PBC 和∠PCE ,然后整理求出∠A=2∠P ,再代入进行计算即可得解.三、解答题(共8个小题,共75分,解答应写出必要的文字说明、证明过程或演算步骤)16.化简下列多项式:(1)2(1)(41)(21)x x x +---(2)(223)(223)a b a b +--+(3)若2530x y +-=,求432x y ⋅的值.(4)先化简,再求值:(2x ﹣1)2﹣(3x +1)(3x ﹣1)+5x (x ﹣1),其中x =﹣2.【正确答案】(1)72x -(2)2244129a b b -+-(3)8;(4)20.【详解】(1)先利用多项式的乘法计算,再运用完全平方公式计算即可;(2)利用平方差公式计算即可;(3)利用幂的乘方,同底数幂的乘法的逆运算计算即可;(4)原式利用平方差公式,完全平方公式,以及单项式乘以多项式法则计算得到最简结果,把x 的值代入计算即可求出值.本题解析:(1)()()()214121x x x +---=2244144172x x x x x x -+--+-=-,(2)原式=[][]222(22)3(22)3(22)94849a b a b a b a ab b +-++=+-=++-,(3)∵2x+5y=3,∴原式=2525253(2)(2)22228x y x y x y +⋅=⋅===,(4)解(2x ﹣1)2﹣(3x+1)(3x ﹣1)+5x (x ﹣1)=4x 2﹣4x+1﹣9x 2+1+5x 2﹣5x=﹣9x+2,当x=﹣2时,原式=﹣9×(﹣2)+2=20.17.分解因式(1)4x 3﹣16xy 2(2)3a 2+6ab +3b 2【正确答案】(1)4x(x+2y)(x ﹣2y);(2)3(a+b)2.【详解】分析:(1)直接提取公因式4x ,再利用平方差公式分解因式得出答案;(2)直接提取公因式3,再利用完全平方公式分解因式得出答案;本题解析:解:(1)4x 3﹣16xy 2=4x (x 2﹣4y 2)=4x(x+2y)(x ﹣2y);(2)3a 2+6ab+3b 2=3(a 2+2ab+b 2)=3(a+b)2;18.已知2246130x yx y +-++=,求2269x xy y -+的值.【正确答案】121【详解】∵x²+y²−4x+6y+13=(x−2)²+(y+3)²=0,∴x−2=0,y+3=0,即x=2,y=−3,则原式=(x−3y)²=11²=121.本题考查了因式分解-运用公式法,非负数的性质:偶次方,已知等式左边利用完全平方公式变形,利用非负数的性质求出x与y的值,代入原式计算即可得到结果.19.通过学习,同学们已经体会到灵活运用乘法公式使整式的乘法运算方便、快捷.相信通过对下面材料的学习、探究,会使你大开眼界,并获得成功的喜悦.⨯.例:用简便方法计算:195205⨯,解:195205()=-+①,2005200522=-②,2005=.39975(1)例题求解过程中,第②步变形是利用___________(填乘法公式的名称).⨯⨯⨯.(2)用简便方法计算:91110110001101-.【正确答案】(1)平方差公式;(2)8【分析】(1)因为这两个二项式中有一项完全相同,另一项互为相反数,所以利用平方差公式;(2)首先将原式变形为:(10﹣1)(10+1)(100+1)(10000+1),再利用平方差公式依次计算即可求得答案.【详解】(1)平方差公式;(2)9×11×101×10001,=(10﹣1)(10+1)(100+1)(10000+1),=(100﹣1)(100+1)(10000+1),=(10000﹣1)(10000+1),101-.=8考查了平方差公式的应用.注意平方差公式:(1)两个两项式相乘;(2)有一项相同,另一项互为相反数,熟记公式是解题的关键.的三个顶点都在格点上.20.如图,方格纸中每个小正方形的边长都是1,ABC()1画ABC 关于直线MN 的对称图形111(A B C 没有写画法);()2求ABC 的面积;【正确答案】(1)作图见解析;(2)作图见解析;()8.5.【详解】分析:(1)根据轴对称的性质画出△A1B1C1即可;(2)过点A 作AE 垂直CB 的延长线与点E ,则线段AE 即为所求;(3)利用矩形的面积减去三个顶点上三角形的面积即可.本题解析;解:(1)如图所示:(2)如图所示:(3)S △ABC =4×5﹣12×1×4﹣12×1×4﹣12×3×5=8.5.21.阅读下面的解答过程,求y 2+4y +8的最小值.解:y 2+4y +8=y 2+4y +4+4=(y +2)2+4≥4,∵(y +2)2≥0即(y +2)2的最小值为0,∴y 2+4y +8的最小值为4.仿照上面的解答过程,求m 2+m +4的最小值和4﹣x 2+2x 的值.【正确答案】154;5【分析】多项式配方后,根据完全平方式恒大于等于0,即可求出最小值;多项式配方后,根据完全平方式恒大于等于0,即可求出值.【详解】解:(1)m 2+m+4=(m+12)2+154,∵(m+12)2≥0,∴(m+12)2+154≥154.则m 2+m+4的最小值是154;()224215x x x -+=--+,∵()21x --≤0,∴()215x --+≤5,∴值是5.本题考查了配方法的应用,熟练掌握完全平方公式是解决本题的关键.22.已知正整数a 、b 、c 满足没有等式22243a b c +++≤98ab b c ++,求a 、b 、c 的值.【正确答案】3a =,6b =,4c =.【详解】分析:由已知条件构造完全平方公式,得()()222136424a b b c ⎛⎫-+-+- ⎪⎝⎭≤0,然后由非负数的性质求解.本题解析:解:∵22243a b c +++≤98ab b c ++,∴22221392781644a ab b b bc c -++-++-+≤0,∴()()222136424a b b c ⎛⎫-+-+- ⎪⎝⎭≤0,又∵212a b ⎛⎫- ⎪⎝⎭≥0,()2364b -≥0,()24c -≥0,∴()()222136424a b b c ⎛⎫-+-+- ⎪⎝⎭≥0,∴()()222136424a b b c ⎛⎫-+-+- ⎪⎝⎭=0,∴102a b -=,60b -=,40c -=,∴3a =,6b =,4c =.23.如图,△ABC是等边三角形,点D在AC上,点E在BC的延长线上,且BD=DE.(1)若点D是AC的中点,如图1,求证:AD=CE(2)若点D没有是AC的中点,如图2,试判断AD与CE的数量关系,并证明你的结论:(提示:过点D作DF∥BC,交AB于点F)【正确答案】(1)证明见解析;(2)AD=CE,证明见解析.【分析】(1)求出∠E=∠CDE,推出CD=CE,根据等腰三角形性质求出AD=DC,即可得出答案;(2)过D作DF∥BC,交AB于F,证△BFD≌△DCE,推出DF=CE,证△ADF是等边三角形,推出AD=DF,即可得出答案.【详解】(1)证明:∵△ABC是等边三角形,∴∠ABC=∠ACB=60°,AB=AC=BC,∵D为AC中点,∴∠DBC=30°,AD=DC,∵BD=DE,∴∠E=∠DBC=30°∵∠ACB=∠E+∠CDE,∴∠CDE=30°=∠E,∴CD=CE,∵AD=DC,∴AD=CE;(2)AD=CE,如图2,过D作DF∥BC,交AB于F,则∠ADF=∠ACB=60°,∵∠A=60°,∴△AFD是等边三角形,∴AD=DF=AF,∠AFD=60°,∴∠BFD=∠DCE=180°﹣60°=120°,∵DF∥BC,∴∠FDB=∠DBE=∠E,在△BFD和△DCE中FDB E BFD DCEBD DE∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△BFD≌△DCE,∴CE=DF=AD,即AD=CE.本题考查了全等三角形的判定与性质,利用了等边三角形的判定与性质,全等三角形的判定与性质,解决本题的关键是作出辅助线,构建全等三角形.2022-2023学年北京市西城区八年级上册数学期末专项突破模拟卷(B卷)一、选一选(每题3分,共24分)1.下面图案中是轴对称图形的有()A .1个B.2个C.3个D.4个2.在△ABC 中,∠A =70°,∠B =55°,则△ABC 是()A.钝角三角形B.等腰三角形C.等边三角形D.等腰直角三角形3.在ABC ∆和A B C '''∆中,,AB A B AC A C =='''',高AD A D ''=,则C ∠和C '∠的关系是()A.相等B.互补C.相等或互补D.以上都没有对4.如图,ABC 中,AB AC =,D 是BC 中点,下列结论中没有正确的是()A.B C ∠=∠B.AD BC⊥ C.AD 平分BAC∠ D.2AB BD=5.由下列条件没有能判定ABC 为直角三角形的是()A.A B C =∠+∠∠B.::1:3:2A B C ∠∠∠=C .111,,345a b c === D.2()()b c b c a +-=6.在一个直角三角形中,若斜边的长是13,一条直角边的长为12,那么这个直角三角形的面积是()A.30B.40C.50D.607.下列说法中正确的是()A.两个直角三角形全等B.两个等腰三角形全等C.两个等边三角形全等D.两条直角边对应相等的直角三角形全等8.已知正方形①、②在直线上,正方形③如图放置,若正方形①、②的面积分别为81cm 2和144cm 2,则正方形③的边长为()A.225cmB.63cmC.50cmD.15cm二、填空题(每题2分,共20分)9.如果等腰三角形的底角是50°,那么这个三角形的顶角的度数是___________10.直角三角形的两条直角边分别是9和12,则斜边是___________11.如图,在Rt ABC ∆中,90ACB D ∠=︒,为斜边AB 的中点,AC =6cm,BC =8cm ,则CD 的长为___________cm.12.如图,在ABC 中,AB AC =,点D 为BC 中点,35BAD ∠=︒,则C ∠的度数为_____.13.已知等腰三角形的周长为15cm ,其中一边长为7cm ,则底边长为__________.14.甲、乙两人同时从同一地点出发,甲往北偏东60°的方向走了12km ,乙往南偏东30°的向走了5km ,这时甲、乙两人相距___________km15.如图,△ABC 中,∠C =90°,AB 的垂直平分线交BC 于点D ,如果∠B =20°,则∠CAD =_____________16.如图,Rt ABC ∆中,90,8,3C AC BC ∠=︒==,,,AE AC P Q ⊥分别是,AC AE 上动点,且PQ AB =,当AP =_______时,才能使ABC ∆和PQA ∆全等.17.如图,有一块直角三角形纸片,两直角边AC =6cm ,BC =8cm ,现将直角边AC 沿直线AD 对折,使它落在斜边AB 上,且与AE 重合,CD 的长为______.18.如图,90MON ∠=︒,已知ABC ∆中,5,6AC BC AB ===,ABC ∆的顶点,A B 分别在边,OM ON 上,当点B 在边ON 上运动时,点A 随之在边OM 上运动,ABC ∆的形状保持没有变,在运动过程中,点C 到点O 的距离为____________.三、解答题(共56分)19.如图,在正方形网格上有一个△DEF.(1)作△DEF 关于直线HG 的轴对称图形;(2)作△DEF 的EF 边上的高;(3)若网格上的最小正方形边长为1,求△DEF 的面积.20.如图,OA ⊥OB ,OA =45海里,OB =15海里,有一海岛位于O 点,我国海监船在点B 处发现有一没有明国籍的渔船,自A 点出发沿着AO 方向匀速驶向海岛O ,我国海监船立即从B 处出发以相同的速度沿某直线去拦截这艘渔船,结果在点C 处截住了渔船.(1)请用直尺和圆规作出C 处的位置;(2)求我国海监船行驶的航程BC 的长.21.如图,AD 是BAC ∠的平分线,点E 在AB 上,且,//AE AC EF BC =交AC 于点F .试说明:EC 平分DEF ∠.22.已知:如图,在ABC ∆中,90,,ACB AC BC D ∠=︒=是AB 的中点,点E 在AC 上,点F 在BC 上,且AE CF =.(1)求证:,DE DF DE DF =⊥;(2)若AC =2,求四边形DECF 的面积.23.如图,在ABC ∆中,90,,BAC AB AC BD ∠=︒=平分ABC ∠,CE BD ⊥于点E .(1)求ECD ∠的度数.(2)求证.2BD EC=24.如图,已知ABC ∆中,90,,,BAC AB AC D E ∠=︒=是BC 边上的点,将ABD ∆绕点A 旋转,得到ACD ∆'.(1)当45DAE ∠=︒时,求证.DE D E='(2)在(1)的条件下,猜想2BD ,2DE ,2CE 有怎样的数量关系,并说明理由.25.如图,已知点D 为OB 上的一点,请用直尺和圆规按下列要求进行作图,保留作图痕迹.(1)作∠AOB 的平分线OC ;(2)在OC 上取一点P ,使得OP=a ;(3)爱动脑筋的小刚仔细观察后,进行如下操作:在边OA 上取一点E ,使得PE =PD ,这时他发现∠OEP 与∠ODP 之间存在一定的数量关系,请写出∠OEP 与∠ODP 的数量关系,并说明理由.26.通过类比联想、引申拓展研究典型题目,可达到解一题知一类的目的.下面是一个案例,请补充完整.原题:如图1,点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,连接EF,则EF=BE+DF,试说明理由.(1)思路梳理∵AB=CD,∴把△ABE绕点A逆时针旋转90°至△ADG,可使AB与AD重合.∵∠ADC=∠B=90°,∴∠FDG=180°,点F、D、G共线.根据,易证△AFG≌,得EF=BE+DF.(2)类比引申如图2,四边形ABCD中,AB=AD,∠BAD=90°,点E、F分别在边BC、CD上,∠EAF=45°.若∠B、∠D都没有是直角,则当∠B与∠D满足等量关系时,仍有EF=BE+DF.(3)联想拓展如图3,在△ABC中,∠BAC=90°,AB=AC,点D、E均在边BC上,且∠DAE=45°.猜想BD、DE、EC应满足的等量关系,并写出推理过程.2022-2023学年北京市西城区八年级上册数学期末专项突破模拟卷(B 卷)一、选一选(每题3分,共24分)1.下面图案中是轴对称图形的有()A.1个B.2个C.3个D.4个【正确答案】B【分析】根据轴对称图形的概念:如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,找出轴对称图形的个数即可.【详解】解:各图案中,是轴对称图形的有:第(1)第(2)个,共2个.故选B.本题考查了轴对称图形,解题的关键是熟练的掌握轴对称图形的概念.2.在△ABC 中,∠A =70°,∠B =55°,则△ABC 是()A.钝角三角形B.等腰三角形C.等边三角形D.等腰直角三角形【正确答案】B【详解】解:∵在△ABC 中,∠A =70°,∠B =55°,∴∠C =180°﹣∠A ﹣∠B =55°,∴∠B =∠C ,∴△ABC 是等腰三角形.故选:B .本题考查了三角形的内角和,等腰三角形的判定,熟记三角形的内角和是解题的关键.3.在ABC ∆和A B C '''∆中,,AB A B AC A C =='''',高AD A D ''=,则C ∠和C '∠的关系是()A.相等B.互补C.相等或互补D.以上都没有对【正确答案】C【详解】试题解析:当∠C ′为锐角时,如图1所示,∵AC=A′C′,AD=A′D′,AD ⊥BC ,A′D′⊥B′C′,∴Rt △ADC ≌Rt △A′D′C′,∴∠C=∠C′;当∠C 为钝角时,如图3所示,∵AC=A′C′,AD=A′D′,AD ⊥BC ,A′D′⊥B′C′,∴Rt △ACD ≌Rt △A′C′D′,∴∠C=∠A′C′D′,∴∠C+∠A′C′B′=180°.故选C.4.如图,ABC 中,AB AC =,D 是BC 中点,下列结论中没有正确的是()A.B C∠=∠ B.AD BC ⊥ C.AD 平分BAC ∠ D.2AB BD=【正确答案】D【分析】利用三线合一的性质对每一个选项进行验证从而求解.【详解】解:∵△ABC 中,AB =AC ,D 是BC 中点,∴∠B =∠C ,(故A 正确)AD ⊥BC ,(故B 正确)∠BAD =∠CAD (故C 正确)无法得到AB =2BD ,(故D 没有正确).故选:D .此题主要考查了等腰三角形的性质,本题关键熟练运用等腰三角形的三线合一性质.5.由下列条件没有能判定ABC 为直角三角形的是()A.A B C =∠+∠∠B.::1:3:2A B C ∠∠∠=C.111,,345a b c === D.2()()b c b c a +-=【正确答案】C【分析】由勾股定理的逆定理,只要验证两小边的平方和等于最长边的平方或角是否是90°即可.【详解】A 、∵∠A+∠B=∠C ,∴∠C=90°,故是直角三角形,正确;B 、∵∠A :∠B :∠C=1:3:2,∴∠B=36×180°=90°,故是直角三角形,正确;C 、∵(13)2+(14)2≠(15)2,故没有能判定是直角三角形;D 、∵(b+c )(b-c )=a 2,∴b 2-c 2=a 2,即a 2+c 2=b 2,故是直角三角形,正确.故选C .本题考查勾股定理的逆定理的应用.判断三角形是否为直角三角形,已知三角形三边的长,只要利用勾股定理的逆定理加以判断即可.6.在一个直角三角形中,若斜边的长是13,一条直角边的长为12,那么这个直角三角形的面积是()A.30B.40C.50D.60【正确答案】A=5.则直角三角形的面积是12×12×5=30.故选A .7.下列说法中正确的是()A.两个直角三角形全等B.两个等腰三角形全等C.两个等边三角形全等D.两条直角边对应相等的直角三角形全等【正确答案】D【详解】试题解析:A 、两个直角三角形只能说明有一个直角相等,其他条件没有明确,所以没有一定全等,故本选项错误;B 、两个等腰三角形,腰没有一定相等,夹角也没有一定相等,所以没有一定全等,故本选项错误;C 、两个等边三角形,边长没有一定相等,所以没有一定全等,故本选项错误;D 、它们的夹角是直角相等,可以根据边角边定理判定全等,正确.故选D .8.已知正方形①、②在直线上,正方形③如图放置,若正方形①、②的面积分别为81cm 2和144cm 2,则正方形③的边长为()A.225cmB.63cmC.50cmD.15cm【正确答案】D【详解】试题解析:∵四边形①、②、③都是正方形,∴∠EAB=∠EBD=∠BCD=90°,BE=BD ,∴∠AEB+∠ABE=90°,∠ABE+∠DBC=90°,∴∠AEB=∠CBD .在△ABE 和△CDB 中,EAB BCD AEB CBD BE DB ∠∠⎧⎪∠∠⎨⎪⎩===,∴△ABE ≌△CDB (AAS ),∴AE=BC ,AB=CD .∵正方形①、②的面积分别81cm 2和144cm 2,∴AE 2=81,CD 2=144.∴AB 2=63.在Rt △ABE 中,由勾股定理,得BE 2=AE 2+AB 2=81+144=225,∴BE=15.故选D .二、填空题(每题2分,共20分)9.如果等腰三角形的底角是50°,那么这个三角形的顶角的度数是___________【正确答案】80°【详解】试题解析:180°-50°×2=180°-100°=80°.故这个三角形的顶角的度数是80°.10.直角三角形的两条直角边分别是9和12,则斜边是___________【正确答案】15【详解】试题解析:由一个直角三角形的两条直角边分别是9和12,.11.如图,在Rt ABC ∆中,90ACB D ∠=︒,为斜边AB 的中点,AC =6cm,BC =8cm ,则CD 的长为___________cm.【正确答案】5【详解】试题解析:由勾股定理得,=10cm ,∵∠ACB=90°,D 为斜边AB 的中点,∴CD=12AB=12×10=5cm .12.如图,在ABC 中,AB AC =,点D 为BC 中点,35BAD ∠=︒,则C ∠的度数为_____.【正确答案】55°【分析】由等腰三角形的三线合一性质可知∠BAC=70°,再由三角形内角和定理和等腰三角形两底角相等的性质即可得出结论.【详解】解:AB=AC,D为BC中点,∴AD是∠BAC的平分线,∠B=∠C,∵∠BAD=35°,∴∠BAC=2∠BAD=70°,∴∠C=12(180°-70°)=55°.故55°.本题考查的是等腰三角形的性质,熟知等腰三角形三线合一的性质是解答此题的关键.13.已知等腰三角形的周长为15cm,其中一边长为7cm,则底边长为__________.【正确答案】1cm或7cm【分析】分7cm是腰或底边两种情况进行讨论.【详解】解:当底为7cm时,此时腰长为4cm和4cm,满足三角形的三边关系;当腰为7cm时,此时另一腰为7cm,则底为1cm,满足三角形的三边关系;所以底边长为1cm或7cm.本题考查的是等腰三角形的性质,在解答此题时要注意进行分类讨论,没有要漏解.14.甲、乙两人同时从同一地点出发,甲往北偏东60°的方向走了12km,乙往南偏东30°的向走了5km,这时甲、乙两人相距___________km【正确答案】13【详解】试题解析:如图所示,∵甲往北偏东60°的方向走了12km ,乙往南偏东30°的向走了5km ,∴∠AOB=90°,∴2222125OA OB ++=13(km ).15.如图,△ABC 中,∠C =90°,AB 的垂直平分线交BC 于点D ,如果∠B =20°,则∠CAD =_____________【正确答案】50°【详解】∵DE 是AB 的垂直平分线,∴AD =BD ,∴∠BAD =∠B =20°,∵∠C =90°,∴∠CAD =180°-20°×2-90°=180°-40°-90°=50°,故50°.本题考查了线段垂直平分线的性质、等腰三角形的判定与性质及三角形内角和定理;解决本题的关键是利用线段的垂直平分线性质得到相应的角相等,然后根据三角形的内角和求解.16.如图,Rt ABC ∆中,90,8,3C AC BC ∠=︒==,,,AE AC P Q ⊥分别是,AC AE 上动点,且PQ AB =,当AP =_______时,才能使ABC ∆和PQA ∆全等.【正确答案】3或8【详解】试题解析:分为两种情况:①当AP=3时,∵BC=3,∴AP=BC ,∵∠C=90°,AE ⊥AC ,∴∠C=∠QAP=90°,∴在Rt △ABC 和Rt △QAP 中,AB PQ BC AP⎧⎨⎩==∴Rt △ABC ≌Rt △QAP (HL ),②当AP=8时,∵AC=8,∴AP=AC ,∵∠C=90°,AE ⊥AC ,∴∠C=∠QAP=90°,∴在Rt △ABC 和Rt △QAP 中,AB PQ AC AP⎧⎨⎩==∴Rt △ABC ≌Rt △QAP (HL ),故答案为3或8.17.如图,有一块直角三角形纸片,两直角边AC =6cm ,BC =8cm ,现将直角边AC 沿直线AD 对折,使它落在斜边AB 上,且与AE 重合,CD 的长为______.【正确答案】3cm【分析】由勾股定理求得AB =10cm ,然后由翻折的性质求得BE =4cm ,设DC =xcm ,则BD =(8-x )cm ,DE =x cm ,在△BDE 中,利用勾股定理列方程求解即可.【详解】解:∵在Rt △ABC 中,两直角边AC =6cm ,BC =8cm ,22226810AB AC BC cm ∴=+=+=().由折叠的性质可知:DC =DE ,AC =AE =6cm ,∠DEA =∠C =90°,∴BE =AB -AE =10-6=4(cm ),∠DEB =90°,设DC =x cm ,则BD =(8-x )cm ,DE =x cm ,在Rt △BED 中,由勾股定理得:BE 2+DE 2=BD 2,即42+x 2=(8-x )2,解得:x =3.故答案为3cm .本题主要考查的是翻折变换以及勾股定理的应用,一元方程的解法,熟练掌握翻折的性质和勾股定理是解题的关键.18.如图,90MON ∠=︒,已知ABC ∆中,5,6AC BC AB ===,ABC ∆的顶点,A B 分别在边,OM ON 上,当点B 在边ON 上运动时,点A 随之在边OM 上运动,ABC ∆的形状保持没有变,在运动过程中,点C 到点O 的距离为____________.【正确答案】7【详解】试题解析:如图,取AB 的中点D ,连接CD .∵AC=BC=5,AB=6.∵点D 是AB 边中点,∴BD=12AB=3,∴222253BC BD --=4;连接OD ,OC ,有OC≤OD+DC ,当O 、D 、C 共线时,OC 有值,值是OD+CD ,又∵△AOB 为直角三角形,D 为斜边AB 的中点,∴OD=12AB=3,∴OD+CD=3+4=7,即OC=7.三、解答题(共56分)19.如图,在正方形网格上有一个△DEF.(1)作△DEF 关于直线HG 的轴对称图形;(2)作△DEF 的EF 边上的高;(3)若网格上的最小正方形边长为1,求△DEF 的面积.【正确答案】(1)作图见解析;(2)作图见解析;(3)3.【分析】(1)分别得出对应点位置进而得出答案;(2)利用钝角三角形高线作法得出答案;(3)利用三角形面积求法得出答案.【详解】解:(1)如图所示,△DEF 关于直线HG 的轴对称图形为△D′E′F′;(2)如图所示,DH即为所求;(3)S△DEF=12×3×2=3.此题主要考查了作图--轴对称变换和三角形面积求法,关键是确定组成图形的对应点位置.20.如图,OA⊥OB,OA=45海里,OB=15海里,有一海岛位于O点,我国海监船在点B处发现有一没有明国籍的渔船,自A点出发沿着AO方向匀速驶向海岛O,我国海监船立即从B 处出发以相同的速度沿某直线去拦截这艘渔船,结果在点C处截住了渔船.(1)请用直尺和圆规作出C处的位置;(2)求我国海监船行驶的航程BC的长.【正确答案】(1)见详解;(2)BC=25海里【分析】(1)连接AB,然后作AB的垂直平分线,交OA于一点C,则点C即为所求;(2)由(1)可设AC=BC=x,则有OC=45-x,然后根据勾股定理可求解.【详解】解:(1)连接AB,分别以点A、B为圆心,大于AB长的一半为半径画弧,交于两点,然后连接这两个点,交OA于点C,则C即为所求;如图所示:(2)连接BC,如图所示:由(1)及OB=15海里,OA=45海里,可设AC=BC=x ,则有OC=45-x ,在Rt △BOC 中,222BC OB OC =+,即()2221545x x =+-,解得:25x =,即BC=25海里.本题主要考查垂直平分线的性质及勾股定理,熟练掌握垂直平分线的性质定理及勾股定理是解题的关键.21.如图,AD 是BAC ∠的平分线,点E 在AB 上,且,//AE AC EF BC =交AC 于点F .试说明:EC 平分DEF ∠.【正确答案】证明见解析.【分析】先根据SAS 证明△ACD ≌△AED ,再根据全等三角形的性质得到CD =ED ,由等腰三角形的性质和平行线的性质可得∠DEC =∠FEC ,从而得出结论.【详解】证明:∵AD 平分∠BAC ,∴∠BAD =∠CAD ,在△ACD 与△AED 中,∵AE AC BAD CAD AD AD =⎧⎪∠=∠⎨⎪=⎩,∴△ACD ≌△AED (SAS ),∴CD =ED ,∴∠DEC =∠DCE ,∵EF ∥BC ,∴∠FEC =∠DCE ,∴∠DEC =∠FEC ,∴CE 平分∠DEF .本题考查的是三角形全等的判定与性质,角平分线的定义,掌握以上知识是解题的关键.22.已知:如图,在ABC ∆中,90,,ACB AC BC D ∠=︒=是AB 的中点,点E 在AC 上,点F 在BC 上,且AE CF =.(1)求证:,DE DF DE DF =⊥;(2)若AC =2,求四边形DECF 的面积.【正确答案】(1)证明见解析;(2)1.【分析】(1)首先可判断△ABC 是等腰直角三角形,连接CD ,再证明BD =CD ,∠DCF =∠A ,根据全等三角形的判定易得到△ADE ≌△CDF ,继而可得出结论;(2)根据全等可得S △AED =S △CFD ,进而得到S 四边形CEDF =S △ADC ,然后再利用三角形的中线平分三角形的面积可得答案.【详解】解:(1)证明:如图,连接CD .因为AC BC =,90ACB ∠=︒所以ABC ∆是等腰直角三角形所以45A B ∠=∠=︒。
国家开放大学《数学思想与方法》期末复习题参考答案(可下载编辑)

国家开放大学《数学思想与方法》期末复习题参考答案模拟试卷A卷一、填空题(每题3分,共30分)1.算法的有效性是指(如果使用该算法从它的初始数据出发,能够得到这一问题的正确解)2.数学的研究对象大致可以分成两大类:(数量关系,空间形式)3.所谓数形结合方法,就是在研究数学问题时,(由数思形、见形思数、数形结合考虑问题)的一种思想方法。
4.推动数学发展的原因主要有两个:(实践的需要,理论的需要),数学思想方法的几次突破就是这两种需要的结果。
5.古代数学大体可分为两种不同的类型:一种是崇尚逻辑推理,以《几何原本》为代表;一种是长于计算和实际应用,以(《九章算术》)为典范。
6.匀速直线运动的数学模型是(一次函数)。
7.数学的统一性是客观世界统一性的反映,是数学中各个分支固有的内在联系的体现,它表现为(数学的各个分支相互渗透和相互结合)的趋势。
8.不完全归纳法是根据(对某类事物中的部分对象的分析),作出关于该类事物的一般性结论的推理方法。
9.学生理解或掌握数学思想方法的过程一般有三个主要阶段:(潜意识阶段、明朗化阶段、深刻理解阶段)10.在实施数学思想方法教学时,应该注意三条原则:(化隐为显原则、循序渐进原则、学生参与原则)二、判断题(每题4分,共20分。
在括号里填上是或否)1.计算机是数学的创造物,又是数学的创造者。
(是)2.抽象得到的新概念与表述原来的对象的概念之间一定有种属关系。
(否)3.一个数学理论体系内的每一个命题都必须给出证明。
(否)4.贯穿在整个数学发展历史过程中有两个思想,一是公理化思想,一是机械化思想。
(是)5.提出一个问题的猜想是解决这个问题的终结。
(否)三、简答题(每题10分,共50分)1.为什么说《几何原本》是一个封闭的演绎体系?参考答案:(1)因为在《几何原本》中,除了推导时所需要的逻辑规则外,每个定理的证明所采用的论据均是公设、公理或前面已经证明过的定理,并且引入的概念(除原始概念)也基本上是符合逻辑上对概念下定义的要求,原则上不再依赖其它东西。
(完整版)六年级下册期末数学模拟试卷A卷及解析

(完整版)六年级下册期末数学模拟试卷A卷及解析一、选择题1.一个零件长2毫米,画在设计图上长是20厘米,这幅设计图的比例尺是().A.1:10 B.1:100 C.100:12.一个长6cm、宽4cm、高12cm的牛奶盒装满牛奶,明明不小心洒了一些(图中空白部分),洒出()mL牛奶。
(纸盒厚度忽略不计)A.36 B.72 C.1443.小刚16小时走了12千米,他每走1千米,需多少小时?正确的算式是()A.16÷12B.16×12C.12÷164.一个三角形三个内角度数的比是5:3:1,这个三角形是()。
A.钝角三角形B.直角三角形C.等腰三角形5.用几个相同的小正方体拼成甲、乙两个图形,比较它们的表面积,结果是()。
A.表面积一样大B.甲的表面积大C.乙的表面积大D.无法比较6.用5个小正方体搭成一个立体图形,从正面看是,从右面看是,从上面看是,这个立体图形是()。
A.B.C.D.7.在“某班男生人数是女生人数的45”中,以下说法错误的是()。
A.女生人数是单位“1”B.女生比男生人数多1 5C.男生人数占全班人数的49D.男生比女生人数少158.一个圆柱的侧面展开图是一个正方形,这个圆柱底面直径与高的比是()。
A.1∶4πB.1∶πC.1∶1 D.1∶29.一件毛衣原价120元,降价了15后又提价15,现在的价格比原价().A.高了B.低了C.一样10.如下图,甲是直角三角形,乙是平行四边形,丙是直角梯形,则甲、乙、丙三个图形的面积之比是()。
A .2:5:3B .1:5:3C .1:5:4D .2:5:4二、填空题11.34m =(________)cm ;12dm 3=(________)cm 3;45分钟=(________)小时。
12.观察下图,直线上的点A 用分数表示是(______),再添上(______)个它的分数单位后就变成了最小的合数。
13.40千克是50千克的(______)%;40千克比50千克少(______)%。
部编版六年级下册语文期末模拟试卷(A)(含答案)

2020-2021学年度第二学期期末教学质量检测六年级语文试卷[考试时间:90分钟满分:100分]题号一二三四五六七八总分得分一、看拼音,写词语(8分)chóu yuàn tiào wànɡ qǐ yuán yōnɡ dàiwǎ lán làn yònɡ cì wèi dànɡ yànɡ二、选择题(10分)1.下列词语中画线字读音完全正确的一组是( )A.粗糙(zāo) 召唤(zhào) 肖像(xiāo) 前仆后继(pū)B.奔丧(sāng) 晕船(yùn) 逮捕(pǔ) 风号浪吼(háo)C.要挟(xié) 嫉妒(jì) 悄然(qiǎo) 斩钉截铁(zǎn)D.气氛(fēn) 飘拂(fú) 运载(zài) 抓耳挠腮(náo)2.下列各组词语中书写全部正确的一组是( )A.标新立异马革裹尸别出新裁悬灯结彩B.驷马难追舍本逐末不容置疑风华正茂C.匪夷所思无源无故邯郸学步有惊无险D.腾云驾雾美味家肴应接不遐人声鼎沸3.下列句子没有语病的一项是( )A.良好的心态是我们在竞赛中能否取得成功的重要因素。
B.老师应该培养学生善于观察、善于思考、善于创造的水平。
C.一部好的电影可以给你带来许多教益,甚至可以影响你的一生。
D.气象小组的同学每天都记录并收听当天的天气预报。
4.对下列句子所用的修辞手法辨别不正确的一项是()A.有喜有忧,有笑有泪,有花有果,有香有色,这就是养花的乐趣。
(排比)B.就在这鸟儿勇敢的叫喊声里,乌云听出了欢乐。
(拟人)C.弯弯的月儿小小的船,小小的船儿两头尖。
(比喻)D.我从乡下来到京城里,一转眼六年了。
(夸张)5.有一副对联,它的上联是:梅花无意分春色,它的下联是()A.明月有心许秋声B.流水有心唱秋风C.柳絮含情传风情D.白雪怎能掩傲骨6.“晓看红湿处,花重锦官城”中的“锦官城”指的是( )A.北京B.杭州C.成都D.重庆7.“冬天到了,春天还会远吗?”这句话是下列哪位诗人说的?( )A.徐志摩B.席勒C.舒婷D.雪莱8.文学名著《水浒传》栩栩如生地塑造了梁山好汉形象,下列书中人物与绰号对应有误的一项是( )A.青面兽杨志B.浪里白条燕青C.小李广花荣D.及时雨宋江9.下列文言文句子朗读停顿不正确的一项是()A.思/援弓缴/而射之。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
南京财经大学
成人教育模拟试题(A卷)
一、判断题(判断对错,每小题1分,共15分)
1. 公共财政是与市场经济相适应的一种财政类型,是市场经济国家通行的财政制度。
(对)
2. 财政职能是指财政本身所具有的内在功能,它是财政本质的反映,具有客观必然性。
(对)
3.外部性是指一些厂商的行为在给别人造成损害时给予补偿或给别人带来受益的同时得到回报。
(错)
4.充分就业是指所有有工作能力又要求工作的人都能得到一个有一定工资报酬的工作机会。
(错)
5.一个商品或一项服务是否具有公共性以及是否需要公共部门来提供是固定的。
(错)
6.国有资产收益主要是指政府通过对工商金融资产的经营或凭借对这些资产的所有权所获得的利润、租金、股息、红利、资金占用费等收入的总称。
(错)
7.政府投资并不意味着完全的无偿拨款。
(对)
8.社会产品价值中,M是新创造价值中归社会支配的剩余产品价值,它是公共收入的唯一来源。
(错)9.税收的强制性是指税收的征收依据的是国家的政治权力,政府征税与是否占有生产资料有直接联系。
(错)
10.地方财政在国家财政体系中处于主导地位,地方财政收入占全国财政收入的比重一般在60%以上。
(错)
11. 现代市场经济国家可以通过税收、公债等手段调节资源在公共部门和私人部门之间的配置结构。
(对)
12. 转移性支出过程使政府资金转移到领受者手中,它只是资金使用权的转移,对分配产生直接影响。
(对)
13.货币国债和实物国债是将国债按发行载体分类。
(错)
14.政府预算是政府的经济活动在财政上的集中体现。
(错)
15.适度分权的税权划分模式的代表国家是德国。
(错)
二、名词解释(每小题3分,共15分)
1. 市场失灵:是指市场无法有效率地分配商品和劳务的情况。
2. 基尼系数:是指20世纪意大利经济学家基尼根据洛伦兹曲线得出的判断分配平等程度的指标。
3. 购买性支出:是政府作为一般的市场主体,按照等价交换的原则在市场上购买商品与劳务的支出。
4.非税收入:指税收和政府债务收入以外的收入。
5. 国债依存度:是指政府偿债能力的指标是采用当年国债发行数占中央财政支出的比重。
三、简答题(每小题5分,共40分)
1.全额累进税率与超额累进税率的区别:全额累进税率与超额累进税率按照量能纳税的原则设计的,但两者又有不同的特点。
首先,全额累进税率的累进程度高,超额累进税率的累进程度低,在税率级次和比例相同时,前者的负担重,后者的负担轻;其次,在所得额级距的临界点处,全额累进会出现税额增长超过所得额增长的不合理情况,超额累进则不存在这种问题;再次,全额累进税率在计算上简便,超额累进税率计算复杂。
2.财政投融资的基本特征。
①财政投融资是一种政府投入资本金的政策性融资②财政投融资的目的性很强,范围有严格限制③计划性与市场机制相结合④财政投融资的管理由国家设立的专门机构—政策性金融机构负责统筹管理经营⑤财政投融资的预算管理比较灵活
3.影响公共收入规模的因素: 1、经济发展水平;2、技术创新和变迁的能力;3、收入分配政策和分配制度;4、价格总水平;5、公共财政收入制度;6、其他特殊因素。
4.税收中性的含义。
一是国家征税使社会所付出的代价以税款为限,尽可能不给纳税人或社会带来其他的额外损失或负担;二是国家征税应避免对市场经济正常运行的干扰,特别是不能使税收超越市场机制而成为资源配置的决定因素。
5.蒂布特的“以足投票”理论:在《地方公共支出的纯粹理论》一书中的六大假设条件下,蒂布特构建了一个地方政府模型,他认为人们通过在社区间的充分流动,选择公共产品与税收的组合使自己效用最大化的社区政府,社区只有有效地提供人们需要的公共产品,否则,人们会迁移到能更好地满足他们偏好的社区,这样,社区间的竞争将使资源能够有效配置,实现帕累托最优,从而达到社会福利的最大化。
这就是所谓的“以足投票”理论。
6. 财政补贴的特点。
①政策性。
财政补贴的政策性导源于财政补贴的依据,即一定时期国家的政策。
②可控性。
财政补贴是国家可以直接控制的经济手段,具有可控性。
③特定性。
实施财政补贴的依据是国家一定时期的特定政策,因此,财政补贴的对象、范围、数量以及要发挥的作用和要求达到的效果也是特定的。
④灵活性。
国家可以根据形势的变化和新的政策要求,适时地调整和修正财政补贴。
⑤时效性。
财政补贴的时效性取决于国家政策的时效性。
7.政府扶贫工作制度创新的内容。
1、确定于国际贫困线接近的贫困人口标准制度。
2、尽快规范财政转移支付制度,保证区域性扶贫开发的资金投入。
3、建立和完善扶贫奖惩于激励制度。
4、积极推行小额信贷制度。
5、努力扩大报账制度的覆盖范围。
8. 财政转移支付制度的目标。
1、实现社会公平是政府间转移支付制度的终极目标。
2、实现经
济相对均衡发展是政府间转移支付制度的基本目标。
3、实现各级政府财政能力和公共服务水平的均等化是政府间转移支付制度的直接目标。
四、论述题(15分)
什么是财政的资源配置职能?财政实现资源配置职能的手段与机制有哪些?
答:财政的资源配置职能是指政府通过财政收支以及相应的财产税收政策,调整和引导现有经济资源的流向和流量,以达到资源的优化配置和充分利用,实现最大的经济效益和社会效益的功能。
财政实现资源配置职能的手段与机制有:1、在妥善处理政府和市场的关系、明确界定政府职能的前提下,科学确定社会公共需要的基本范围,合理确定财政收支的总体规模和结构,实现财政总体规模控制和资源的战略性优化配置,提高总体配置和运作效率。
2、合理安排政府投资的规模与结构,优化政府投资性支出的配置效率。
政府投资规模主要指预算内投资在社会总投资中所占的比重,表明政府集中的投资对社会总投资的调节力度。
预算内投资和保证重点建设在产业结构中起着重要的作用。
3、提高财政资源配置本身的效率。
提高财政自身资源配置效率的关键是要做好财政支出行为的成本收益分析和投入产出分析,注重财政资源配置的绩效。
五、案例分析题(15分)
案例资料:
财政预算,是国家机关、团体和事业单位等对于未来一定时期内的收入和支出的计划。
每年“两会”,财政部部长所作的预算报告,都是代表们锁定的“焦点”。
政府预算是一本政府公开的“财务大账”:过去的一年收了多少钱?钱投到哪里去了?今年的钱该怎么用?这些钱是不是“取之于民,用之于民”,每年都要接受人大代表的监督和审查。
然而,长期以来,由于财政预算编制较粗,“外行看不懂,内行看不清”,预算的透明度不高,造成了很多部门预算游离在人大监督范围之外。
同样,在预算执行方面也不尽如人意,缺乏有效的监督制约办法。
对每年人代会批准的财政预算,执行随意性大。
由于预算资金没有落实到具体的项目上,造成了执行难的问题。
往往部门申请多、找领导批条子多、临时性支出多,变成“一年预算,预算一年”,然后再报人大常委会做出调整预算的决议。
为此,在近年各地的人代会上,代表对财政预算的监督力度明显加大。
如广东省十届人大二次会议上,代表们对预算中“拨2000万元给机关幼儿园”、“事业单位的行政编制外人员每人每年补贴3.2万元”等提出了质疑。
浙江、四川等省的预算报告也明显加厚,列支项目也更加详尽,以利于人大代表的监督。
问题分析:
1.政府预算的本质什么?
答:政府预算的本质是政府预算是一种权力制衡的工具。
2.为保证政府预算的科学性应坚持什么原则?
答:保证政府预算的科学性应坚持以下原则:1、完整性。
这就是要求政府的预算包括政府全年的全部预算收支项目,完整地反映政府全部的财政收支活动,不允许有预算外的其他财政收支。
2、统一性。
这就是要求预算收支按照统一的程序来编制,任何单位的收支都要以总额列入预算,不应当只列入收支相抵后的净额。
3、年度性。
要求政府预算按年度编制,预算中要列明全年的预算收支,并进行对比。
不容许预算收支有跨年度的规定。
4、可靠性。
这就是要求编制预算时,正确地估计各项预算收支数字,对各项收支的性质必须明确的区分。
5、公开性。
预算属于公开性的法律文件,所以其内容必须明确,以便于社会公众能了解、审查政府如何支配纳税人的钱,并进行监督使用。
