matlab第三章答案
MATLAB基础及其应用教程-周开利-邓春晖课后答案,第三章
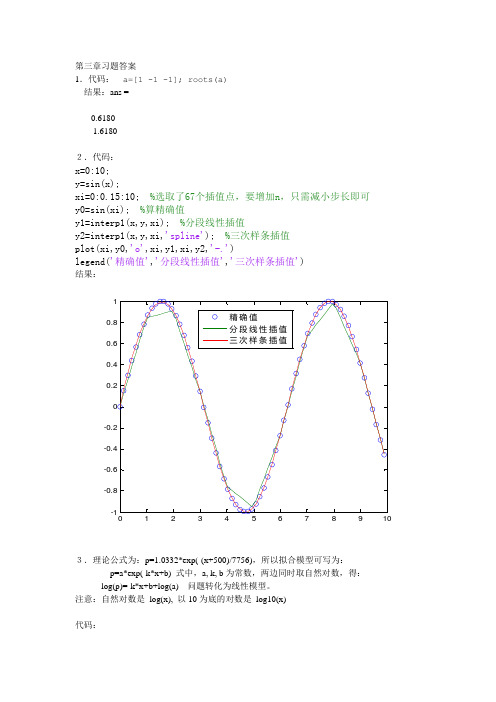
第三章习题答案1.代码:a=[1 -1 -1]; roots(a)结果:ans =-0.61801.61802.代码:x=0:10;y=sin(x);xi=0:0.15:10; %选取了67个插值点,要增加n,只需减小步长即可y0=sin(xi); %算精确值y1=interp1(x,y,xi); %分段线性插值y2=interp1(x,y,xi,'spline'); %三次样条插值plot(xi,y0,'o',xi,y1,xi,y2,'-.')legend('精确值','分段线性插值','三次样条插值')结果:3.理论公式为:p=1.0332*exp(-(x+500)/7756),所以拟合模型可写为:p=a*exp(-k*x+b) 式中,a, k, b为常数,两边同时取自然对数,得:log(p)=-k*x+b+log(a)问题转化为线性模型。
注意:自然对数是log(x), 以10为底的对数是log10(x)代码:clear;x=[0 300 600 1000 1500 2000];p=[0.9689 0.9322 0.8969 0.8519 0.7989 0.7491];lnp=log(p); %转化为 p 的自然对数值,模型转化为线性模型pk=polyfit(x,lnp,1); % 线性拟合,得到模型的斜率pk(1)和常数pk(2) 模型为: p=exp(pk(1)*x)*exp(pk(2))xi=0:50:2000;p0=1.0332*exp(-(xi+500)/7756); %理论值p1=exp(pk(1)*xi+pk(2)); %拟合模型值p2=interp1(x,p,xi,'spline'); %三次样条插值plot(x,p,'p',xi,p0,xi,p1,'--',xi,p2,'-.');legend('测量值','理论值','拟合值','三次样条值');format long % 数据显示格式为15位有效数字x2=0:200:2000 % 取10个点,比较差异pp1=1.0332*exp(-(x2+500)/7756) %理论值pp2=exp(pk(1)*x2+pk(2)) % 拟合值pp3=interp1(x,p,x2,'spline') % 样条插值err1=sum(abs(pp2-pp1).^2) % 拟合值的误差绝对值总和err2=sum(abs(pp3-pp1).^2) % 样条值的误差绝对值总和结果:0200400600800100012001400160018002000从图像上,都符合得很好,但很难看出差异。
matlab第三章答案

matlab第三章答案第1题:从键盘输入一个3位数,将它反向输出。
如输入639输出936、n1=fix(n/100);n2=rem(fix(n/10),10);n3=rem(n,10);m=n3*100+n2*10+n1;disp(m)请输入一个三位数:489984第2题:输入一个百分制成绩,要求输出成绩等级A、B、C、D、E。
其中90~100分为A,80~89分为B、70~79分为C、60~69分为D,60分以下为E。
要求:(1)分别用if语句与switch语句实现。
(2)输入百分制成绩后要判断成绩得合理性,对不合理得成绩应输出错信息。
If语句:>> s=input('请输入成绩分数:');if s>=90&s<=100disp('A');elseif s>=80&s<=89disp('B');elseif s>=70&s<=79disp('C');elseif s>=60&s<=69disp('D');elseif s>=0&s<60disp('E');elsedisp('false');end请输入成绩分数:89BSwitch语句:>> s=input('请输入成绩分数:');switch fix(s/10)case {9,10}disp('A');case {8}disp('B');case {7}disp('C');case {6}disp('D');case {5,4,3,2,1,0}disp('E');otherwisedisp('false');end请输入成绩分数:88B第3题输入20个数,求其中最大数与最小数。
数字信号处理Matlab练习第三章-080802084朱桂香

1.编写一个Matlab程序,用一个N点的复数离散傅里叶变换计算两个长度为N的实数序列的N点离散傅里叶变换,并将结果同直接使用两个N点离散傅里叶变换得到的结果进行比较。
n=0:11; %设定n的范围x1=cos(pi/6.*n); %给定序列x1[n]x2=(4/5).^n; %给定序列x2[n]w1=x1+1i*x2; %由序列x1[n]和x2[n]组成复数序列w1[n]w2=x1-1i*x2; %序列w1[n]的共轭序列w2[n]figure,subplot(2,1,1),stem(n,x1); %指定位置1,绘制序列x1[n]xlabel('n'); %设定序列x1[n]的横轴标注和纵轴标注ylabel('x1[n]');subplot(2,1,2),stem(n,x2); %指定位置2,绘制序列x2[n]xlabel('n'); %设定序列x2[n]的横轴标注和纵轴标注ylabel('x2[n]');figure,subplot(4,1,1),stem(abs(w1)); %指定位置1,绘制序列w1[n]幅度谱xlabel('n'); %设定横轴标注,纵轴标注和标题ylabel('magnitude');title('W1的幅度谱');subplot(4,1,2),stem(angle(w1)); %指定位置2,绘制序列w1[n]相位谱xlabel('n'); %设定横轴标注,纵轴标注和标题ylabel('phase');title('W1的相位谱');subplot(4,1,3),stem(abs(w2)); %指定位置3,绘制序列w2[n]幅度谱xlabel('n'); %设定横轴标注,纵轴标注和标题ylabel('magnitude');title('W2的幅度谱');subplot(4,1,4),stem(angle(w2)); %指定位置4,绘制序列w2[n]相位谱xlabel('n'); %设定横轴标注,纵轴标注和标题ylabel('phase');title('W2的相位谱');X1=fft(x1); %求序列x1[n]的离散傅里叶变换X1(k)X2=fft(x2); %求序列x2[n]的离散傅里叶变换X2(k)W1=fft(w1); %求序列w1[n]的离散傅里叶变换W1(k)W2=fft(w2); %求序列w2[n]的离散傅里叶变换W2(k)Y1=(1/2)*(W1+W2); %由W1(k)和W2(k)来求X1(k)Y2=(1/(2*1i))*(W1-W2); %由W1(k)和W2(k)来求X2(k)figure,subplot(2,1,1),stem(abs(X1)); %指定位置1,绘制|X1(k)|xlabel('k'); %设定横轴标注和纵轴标注ylabel('|X1(k)|');subplot(2,1,2),stem(abs(Y1)); %指定位置2,绘制|Y1(k)|xlabel('k'); %设定横轴标注和纵轴标注ylabel('|Y1(k)|');figure,subplot(2,1,1),stem(abs(X2)); %指定位置1,绘制|X2(k)|xlabel('k'); %设定横轴标注和纵轴标注ylabel('|X2(k)|');subplot(2,1,2),stem(abs(Y2)); %指定位置2,绘制|Y2(k)|xlabel('k'); %设定横轴标注和纵轴标注 ylabel('|Y2(k)|');结果图:nx 1[n]024681012nx 2[n ]图1 序列x1[n]和x2[n]02468101212nm a g n i t u d eW1的幅度谱24np h a s eW1的相位谱02468101212nm a g n i t u d eW2的幅度谱024681012-4-20np h a s e图2 w1和w2的幅度谱和相位谱图246k|X 1(k )|246k|Y 1(k )|图3 两种计算X1(k)的方法比较024681012246k|X 2(k )|024681012246k|Y 2(k )|图4 两种计算X2(k)的方法比较2.编写一个Matlab 程序,用两个N 点的复数离散傅里叶变换计算一个长度为2N 的实数序列的2N 点离散傅里叶变换,并将结果同直接使用一个2N 点离散傅里叶变换得到的结果进行比较。
matlab课后习题答案第三章

第3章数值数组及其运算习题3及解答1 要求在闭区间]2,0[ 上产生具有10个等距采样点的一维数组。
试用两种不同的指令实现。
〖目的〗●数值计算中产生自变量采样点的两个常用指令的异同。
〖解答〗%方法一t1=linspace(0,2*pi,10)%方法二t2=0:2*pi/9:2*pi %要注意采样间距的选择,如这里的2*pi/9.t1 =Columns 1 through 70 0.6981 1.3963 2.0944 2.7925 3.4907 4.1888 Columns 8 through 104.88695.58516.2832t2 =Columns 1 through 70 0.6981 1.3963 2.0944 2.7925 3.4907 4.1888 Columns 8 through 104.88695.58516.28322 由指令rng('default'),A=rand(3,5)生成二维数组A,试求该数组中所有大于0.5的元素的位置,分别求出它们的“全下标”和“单下标”。
〖目的〗●数组下标的不同描述:全下标和单下标。
●sub2ind, int2str, disp的使用。
●随机发生器的状态控制:保证随机数的可复现性。
〖解答〗rng('default')A=rand(3,5)[ri,cj]=find(A>0.5);id=sub2ind(size(A),ri,cj);ri=ri';cj=cj';disp(' ')disp('大于0.5的元素的全下标')disp(['行号 ',int2str(ri)])disp(['列号 ',int2str(cj)])disp(' ')disp('大于0.5的元素的单下标')disp(id')A =0.8147 0.9134 0.2785 0.9649 0.95720.9058 0.6324 0.5469 0.1576 0.48540.1270 0.0975 0.9575 0.9706 0.8003大于0.5的元素的全下标行号 1 2 1 2 2 3 1 3 1 3列号 1 1 2 2 3 3 4 4 5 5大于0.5的元素的单下标1 2 4 5 8 9 10 12 13 153 采用默认全局随机流,写出产生长度为1000的“等概率双位(即取-1,+1)取值的随机码”程序指令,并给出 -1码的数目。
(完整版)第3章MATLAB矩阵处理_习题答案

3
B.y=cond(A) D.y=norm(A)
1.建立 3 阶幺矩阵的命令是
。ones(3)
2.设 A 为 2×3 矩阵,则用 zeros(size(A))建立的矩阵是
行
列的
矩阵。2,3,零
3.将 3 阶魔方矩阵主对角线元素加 10,命令是
。10*eye(3)+magic(3)
4.
可以用来描述矩阵的性能,它越接近于
D.B=diag(tril(A))
7.在 MATLAB 中定义 A=randn(5,4,3,2),则下列关于 A 的操作中正确的是(
)。D
A.y=eig(A)
B.y=reshape(A,[4 3 6 7])
C.y=cond(A)
D.y=sin(A)
8.在命令行窗口中分别输入下列命令,对应输出结果正确的是(
7 8 9
10 11 12
,
B
10
7
4
1
11 8 5 2
12
3
9
,
C
6
6
9
3
12
2 5 8 11
1
4
7
10
第 1 题: (1)
a=1:12;
A=reshape(a,3,4)
(2)
B=rot90(A)
(3)
C=rot90(A,-1) 3.用矩阵求逆法求线性方程组的解。
4
x1
3x1
2x2 x3 x2 2x3
)。 C
A.命令 x=[-2:2]',结果 x=[-2 -1 0 1 2]
B.命令 x=zeros(1,2);x>0,结果 ans=1
C.命令 y=diag(eye(3),1)&#,2),结果 ans=[-5.0501 1.2311]
MATLAB第三章

第三章微积分问题的计算机求解一、实验内容:题目1.试求出如下极限。
①limx→∞(3x +9x )1/ x,②lim x→∞[(x+2)x+2(x+3)x+3 ]/(x+5)2x+5【分析】:该题为单变量函数的极限。
极限问题可以用limit()函数直接求出。
要注意该函数的调用格式为:L=limit(fun,x,x0)(求极限),L=limit(fun,x,x0,’left’或’right’)(求极限)。
还需注意一开始要对函数的字符进行申明。
【解答】:(1)输入如下语句:>> syms x;f=(3^x+9^x)^(1/x);L=limit(f,x,inf)语句运行后显示如下:L =9(2)输入如下语句:>>syms x;f=(x+2)^(x+2)*(x+3)^(x+3)/(x+5)^(2*x+5);>> L=limit(f,x,inf)语句运行后显示如下:L =exp(-5)题目2.试求下面的双重极限。
①lim x→−1y→2 (x2y+xy3)/(x+y) 3,②limx→0 y→0 xy /√(xy+1)−1,③limx→0y→0 [1−cos(x2+y2)]/(x2+y2)e x2+y2。
【分析】:该题为多变量函数的极限问题。
他可以用嵌套使用limit()函数来解决。
在MATLAB上可以用L=limit(limit(f,x,x0),y,y0)或者L=limit(f,y,y0),x,x0)来解决。
其思想是所有的先关于X求导,再所有的关于y求导。
【解答】:(1)输入如下语句:>> syms x y>> f=(x^2*y+x*y^3)/(x+y)^3;>> L=limit(limit(f,x,-1),y,2)语句运行后显示如下:L =-6(2)输入如下语句:>> syms x yf=(x*y)/(sqrt(x*y+1)-1);L=limit(limit(f,x,0),y,0)按ENTER键,语句运行后显示如下:L =2(3)输入如下语句:>> syms x yf=(1-cos(x^2+y^2))/(sqrt(x^2+y^2)*exp(x^2+y^2));L=limit(limit(f,x,0),y,0)按ENTER键,语句运行后显示如下:L =题目3.求出下面函数的导数。
MATLAB语言与控制系统仿真_参考题答案_第3章

3.5 MATLAB 绘图实训3.5.1 实训目的1.学会MATLAB 绘图的基本知识;2.掌握MATLAB 子图绘制、图形注释、图形编辑等基本方法;3.学会通过MATLAB 绘图解决一些实际问题;4.练习二维、三维绘图的多种绘图方式,了解图形的修饰方法;5.学会制作简单的MATLAB 动画。
图3-46 炮弹发射示意图3.5.2 实训内容1. 炮弹发射问题〔1炮弹发射的基础知识炮弹以角度α射出的行程是时间的函数,可以分解为水平距离)(t x 和垂直距离)(t y 。
)cos()(0αtv t x = %水平方向的行程; 205.0)sin()(gt tv t y -=α %垂直方向的行程;其中,0v 是初速度;g 是重力加速度,为9.82m/s ;t 是时间。
〔2炮弹发射程序举例:分析以下程序以及图3-47各个图形的实际意义。
a=pi/4; v0=300; g=9.8;t=0:0.01:50; x=t*v0*cos<a>;y=t*v0*sin<a>-0.5*g*t.^2;subplot<221>;plot<t,x>;grid;title<‘时间-水平位移曲线'>; subplot<222>;plot<t,y>;grid;title<‘时间-垂直位移曲线'>; subplot<223>;plot<x,y>;grid;title<‘水平位移-垂直位移曲线'>; subplot<224>;plot<y,x>;grid;title<‘垂直位移-水平位移曲线'>; 图3-4745角发射曲线 〔3编程解决炮弹发射问题①假设在水平地面上以垂直于水平面的角度向上发射炮弹,即发射角90=α,假设初速度分别为[310,290,270]m/s,试绘制时间-垂直位移曲线,编程求取最高射程;绘图要求:◆ 标题设为"炮弹垂直发射问题";◆ 在图上通过添加文本的方式表明初速度; ◆ 在x 轴标注"时间";◆ 在y 轴上标注"垂直距离"; ◆ 添加网格线;◆ 将310m/s 的曲线改为线粗为2的红色实线; ◆ 将290m/s 的曲线改为线粗为3的绿色点划线;◆ 将270m/s 的曲线改为线粗为2的蓝色长点划线;a=pi/2; v1=310; g=9.8;t=0:0.01:50; x1=t*v1*cos<a>;y1=t*v1*sin<a>-0.5*g*t.^2;plot<t,y1>;grid; title<'炮弹垂直发射问题'>; xlabel<'时间'>; ylabel<'垂直距离'>; hold on; v2=290;x2=t*v2*cos<a>;y2=t*v2*sin<a>-0.5*g*t.^2; plot<t,y2>; v3=270;x3=t*v3*cos<a>;y3=t*v3*sin<a>-0.5*g*t.^2; plot<t,y3>;zgsc=[max<y1>; max<y2>; max<y3>] %三次发射的最高射程 运行结果如下: zgsc =1.0e+003 * 4.9031 4.29083.7194最高射程分别为:4903.1米,4290.8米,3719.4米。
matlab程序设计第三章课后习题答案资料

m a t l a b程序设计第三章课后习题答案1. p138 第6题在同一坐标轴中绘制下列两条曲线并标注两曲线交叉点。
>> t=0:0.01:pi;>> x1=t;>> y1=2*x1-0.5;>> x2=sin(3*t).*cos(t);>> y2=sin(3*t).*sin(t);>> plot(x1,y1,'r-',x2,y2,'g-')>> axis([-1,2,-1.5,1])>> hold on>> s=solve('y=2*x-0.5','x=sin(3*t)*cos(t)','y=sin(3*t)*sin(t)');>> plot(double(s.x),double(s.y),'*');截图:p366 第4题绘制极坐标曲线,并分析对曲线形状的影响。
function [ output_args ] = Untitled2( input_args )%UNTITLED2 Summary of this function goes here% Detailed explanation goes heretheta=0:0.01:2*pi;a=input('请输入a的值:');b=input('请输入b的值:');n=input('请输入n的值:');rho=a*sin(b+n*theta);polar(theta,rho,'k');end下面以a=1,b=1,n=1的极坐标图形为基础来分析a、b、n的影响。
对a的值进行改变:对比发现a只影响半径值的整倍变化对b的值进行改变:对比发现b的值使这个圆转换了一定的角度对n的值进行改变:对比发现当n>=2时有如下规律1、当n为整数时,图形变为2n个花瓣状的图形2、当n为奇数时,图形变为n个花瓣状的图形分别让n为2、3、4、5同时改变b和n的值,对比发现图形变为2n个花瓣状,并且还旋转了一定角度1 绘制sin(x)曲线,通过句柄修改曲线的颜色,要求:a)生成曲线的同时,获取句柄,再修改颜色;>> x=0:pi/50:2*pi;>> y=sin(x);>> h=plot(x,y)h =174.0101>> set(h,'color','r');截图如下:b)先生成曲线,然后再获取句柄,再完成颜色修改。
matlab答案第三章

第三章1.写出完成下列操作的命令。
(1)建立3阶单位矩阵A 。
(2)建立5x6随机矩阵A ,其元素为[100,200]范围内的随机整数。
(3)产生均值为1,方差为0.2的500个正态分布的随机数。
(4)产生和A 同样大小的幺矩阵。
(5)将矩阵A 对角线的元素加30。
答:(1)A=eye(3)(2) A=100+100*rand(5,6)(3)A=1+sqrt(0.2)*randn(10,50) (4)B=ones(size(A)) (5)A+30*eye(size(A))2.建立一个方阵A ,求A 的逆矩阵和A的行列式的值,并验证A 与A -1是互逆的。
答:B=inv(A) ;A 的逆矩阵 C=det(A) ;A 的行列式的值 D=A*B E=B*AD=E=同阶单位矩阵 因此A 与A -1是互逆的。
3.求下面线性方程组的解。
⎪⎩⎪⎨⎧=+=+-=-+8312102322421321321x x x x x x x x 答:A=[4 2 -1;3 -1 2;12 3 0]; b=[2;10;8]; x=inv(A)*b x =-6.0000 26.6667 27.33334.求下列矩阵的秩、迹、条件数。
(1)⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--=901511250324153211A (2) ⎥⎦⎤⎢⎣⎡-=2149.824343.0B 答: (1)rank(A) ;秩 ans =4cond(A) ;条件数 ans =11.1739trace(A) ;迹 ans =16 (2)略5.求矩阵A 的特征值和相应的特征向量。
⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=225.05.025.0115.011A 答:A=[1 1 0.5;1 1 0.25;0.5 0.25 2] A =1.0000 1.0000 0.5000 1.0000 1.0000 0.2500 0.5000 0.25002.0000 [V,D]=eig(A) V =0.7212 0.4443 0.5315 -0.6863 0.5621 0.4615 -0.0937 -0.6976 0.7103 D =-0.0166 0 0 0 1.4801 0 0 0 2.5365。
Matlab第三章习题答案

Matlab第三章习题答案第三章3.5计算多项式乘法()()222254x x x x ++++>> a=[1 2 2];>> b=[1 5 4];>> c=conv(a,b)c =1 7 16 18 8poly2sym(c)ans =x^4 + 7*x^3 + 16*x^2 + 18*x + 83.6计算多项式的除法()()3231368/4x x x x ++++ >> a=[3 13 6 8];>> b=[1 4];>> [q r]=deconv(a,b)q =3 1 2r =0 0 0 0>> poly2sym(q)ans =3*x^2 + x + 23.8求多项式4324121459x x x x --++的微分和积分(1)微分:>> a=[4 -12 -14 5 9];>> b=polyder(a)b =16 -36 -28 5>> poly2sym(b)ans =16*x^3 - 36*x^2 - 28*x + 5(2)积分:polyint(a)ans =0.8000 -3.0000 -4.6667 2.5000 9.00000 >> poly2sym(ans)ans =(4*x^5)/5 - 3*x^4 - (14*x^3)/3 + (5*x^2)/2 + 9*x3.9求代数⽅程32349x x x +-+=0的解。
>> [x]=solve('x^3+3*x^2-4*x+9')x =- 7/(3*(15/2 - (108^(1/2)*4703^(1/2))/108)^(1/3)) - (15/2 -1/108*108^(1/2)*4703^(1/2))^(1/3) - 17/(6*(15/2 - (108^(1/2)*4703^(1/2))/108)^(1/3)) + (15/2 -(108^(1/2)*4703^(1/2))/108)^(1/3)/2 - (3^(1/2)*i*(7/(3*(15/2 -(108^(1/2)*4703^(1/2))/108)^(1/3)) - (15/2 - 1/108*108^(1/2)*4703^(1/2))^(1/3)))/2 - 1 7/(6*(15/2 - (108^(1/2)*4703^(1/2))/108)^(1/3)) + (15/2 -(108^(1/2)*4703^(1/2))/108)^(1/3)/2 + (3^(1/2)*i*(7/(3*(15/2 -(108^(1/2)*4703^(1/2))/108)^(1/3)) - (15/2 - 1/108*108^(1/2)*4703^(1/2))^(1/3)))/2 – 1 3.10求线性⽅程组223430x xy y x x ?++=??-+=??的解 eqn1='x^2+x*y+y=3';>> eqn2='x^2-4*x+3=0';[x,y]=solve(eqn1,eqn2)x =13y =1-3/23.11求微分⽅程64dy y x dx=+的通解。
信号与系统_MATLAB_实验_课后习题答案
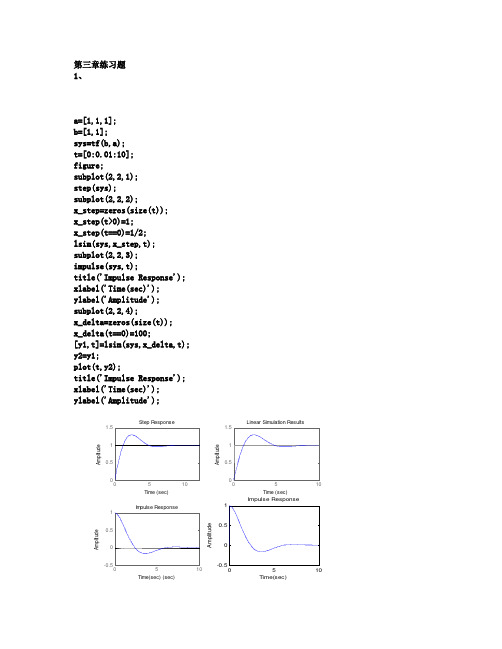
第三章练习题 1、a=[1,1,1]; b=[1,1]; sys=tf(b,a); t=[0:0.01:10]; figure;subplot(2,2,1); step(sys);subplot(2,2,2);x_step=zeros(size(t)); x_step(t>0)=1; x_step(t==0)=1/2; lsim(sys,x_step,t); subplot(2,2,3); impulse(sys,t);title('Impulse Response'); xlabel('Time(sec)'); ylabel('Amplitude'); subplot(2,2,4);x_delta=zeros(size(t)); x_delta(t==0)=100;[y1,t]=lsim(sys,x_delta,t); y2=y1;plot(t,y2);title('Impulse Response'); xlabel('Time(sec)'); ylabel('Amplitude');00.511.5Step ResponseTime (sec)A m p l i t u d eLinear Simulation ResultsTime (sec)A m p l i t u d e-0.500.51Impulse ResponseTime(sec) (sec)A m p l i t u d eImpulse ResponseTime(sec)A m p l i t u d e2、函数int1如下:function [F,tF]=int1(f,tf,a)T=tf(2)-tf(1);F=zeros(size(tf)); tF=zeros(size(tf));tF=tf;for n=1:length(tf)-1;F(n+1)=F(n)+T*f(n);end验证如下:t=[-1:0.01:4];e=zeros(size(t));e=(t>-1/2&t<1);[z,zz]=intl(e,t,-1);figure;plot(zz,z);第四章练习题1、T1=1;N1=10000; t1=linspace(0,T1-T1/N1,N1)';f1=1-2*t1;OMG=32*pi;K1=100;omg=linspace(-OMG/2,OMG/2-OMG/K1,K1)';X1=T1/N1*exp(-j*kron(omg,t1.'))*f1;fs1=OMG/2/pi/K1*exp(j*kron(t1,omg.'))*X1;T2=5;N2=10000;t2=linspace(0,T2-T2/N2,N2)';fs2=0*t2;f2=sawtooth(t2*2*pi,0);X2=T2/N2*exp(-j*kron(omg,t2.'))*f2;fs2=fs2+OMG/2/pi/K1*exp(j*kron(t2,omg.'))*X2;figure;subplot(2,2,1);plot(omg,abs(X1),'r');xlabel('Frequency'),ylabel('Amplitude')title('单个锯齿周期幅频特性曲线');subplot(2,2,2);plot(t1,fs1,'r');xlabel('Time'),ylabel('Amplitude')title('Function after recovered');subplot(2,2,3);plot(omg,abs(X2),'r');xlabel('Frequency'),ylabel('Amplitude')title('五个锯齿周期幅频特性曲线');subplot(2,2,4);plot(t2,fs2,'r');xlabel('Time'),ylabel('Function after recovered')title('Function after recovered');-100-5005000.20.40.60.8FrequencyA m p l i t u d e单个锯齿周期幅频特性曲线00.51-1-0.500.51TimeA m p l i t u d eFunction after recovered-100-5005000.511.52FrequencyA m p l i t u d e五个锯齿周期幅频特性曲线246-2-1012TimeF u n c t i o n a f t e r r e c o v e r e dFunction after recovered2、fsana 函数如下:function F=fsana(t,f,N); omg1=2*pi/(max(t)-min(t)); k=[-N:N]';F=1/length(t)*exp(-j*kron(k*omg1,t.'))*f; fssyn 函数如下:function f=fssyn(F,t)omg1=2*pi/(max(t)-min(t)); N=floor(length(F)/2); k=[-N:N];f=exp(j*kron(t,k*omg1))*F; 验证如下: clc clearclose allT1=1;N1=256; t=linspace(0,T1-T1/N1,N1)'; f=1-2*t;subplot(3,1,1); plot(t,f);title('验证原函数') N=25;F1=fsana(t,f,N); subplot(3,1,2); stem(abs(F1),'s');title('前N 项傅立叶级数系数幅度曲线') f2=fssyn(F1,t) ;subplot(3,1,3); plot(t,f2);xlabel('time[s]'),ylabel('Amplitude'); title('傅立叶逆变换后时域函数');00.10.20.30.40.50.60.70.80.91-101验证原函数00.20.4前N 项傅立叶级数系数幅度曲线00.10.20.30.40.50.60.70.80.91-202time[s]A m p l i t u d e傅立叶逆变换后时域函数第五章练习题1、(a) Residue计算a1=[1,5,6];b1=[4,5];[r1,p1,k1]=residue(b1,a1); t=[0:0.01:10];e1=zeros(size(t));for n=1:size(r1);e1=e1+r1(n)*exp(p1(n)*t); end;figure;subplot(1,2,1);plot(t,e1);title('residue计算');xlabel('t/s');ylabel('u/v');lism仿真sys1=tf([4,5],[1,5,6]);t=[0:0.01:10];delta=zeros(size(t));delta(t==0)=100;h1=lsim(sys1,delta,t); subplot(1,2,2);plot(t,h1);title('lism仿真');xlabel('t/s');ylabel('u/v');Residue计算和lism仿真结果相同(b)Residue计算t=[0,0.01,10];delta=zeros(size(t));delta(t==0)=100;e2=sin(t);figure;subplot(2,1,1);plot(t,e2);title('residue计算');xlabel('t/s');ylabel('u/v');lism仿真sys1=tf([1,0,2],[1,0,1]);t=[0:0.01:10];delta=zeros(size(t));delta(t==0)=100;h2=lism(sys1,delta,t); subplot(2,1,2);plot(h,t2);axis([0,10,-1,1]);title('lism仿真');xlabel('t/s');ylabel('u/v');Residue计算和lism仿真结果相同2、S=isstable(sys)函数:Function s=isstable(sys);X=ploe(sys);S=1;For n=1:Size(x)If x(n)>0S=0;break;End;End;稳定系统:Sys=tf(1,[1,2]);S=isstable(sys);S=1不稳定系统:Sys=tf(1,[1,-2]);S=isstable(sys);S=第七章练习题1、a=[1,0.5,-0.2,-0.1]; b=[1,-0.3];n=[0:10]';[hi,t]=impz(b,a,n); subplot(1,2,1);stem(n,hi);u=(n>=0);hn=filter(b,a,u); subplot(1,2,2);stem(n,hn);2、n1=[0:9]';n2=[10:19]';x1=(n1>=0);x2=-(n2>=10);a1=[1,-0.2,-0.1];a2=[1,-0.2,0.5];b=[1,0.01];[y1,wf1]=filter(b,a1,x1,[0,1]); [y2,wf2]=filter(b,a2,x2,wf1); stem(n1,y1);hold on;stem(n2,y2);。
matlab程序设计第三章课后习题答案
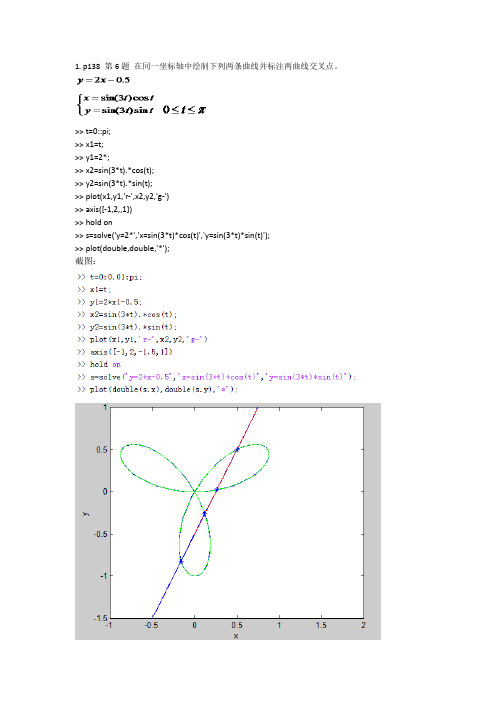
1. p138 第6题在同一坐标轴中绘制下列两条曲线并标注两曲线交叉点。
>> t=0::pi;>> x1=t;>> y1=2*;>> x2=sin(3*t).*cos(t);>> y2=sin(3*t).*sin(t);>> plot(x1,y1,'r-',x2,y2,'g-')>> axis([-1,2,,1])>> hold on>> s=solve('y=2*','x=sin(3*t)*cos(t)','y=sin(3*t)*sin(t)');>> plot(double,double,'*');截图:p366 第4题绘制极坐标曲线,并分析对曲线形状的影响。
function [ output_args ] = Untitled2( input_args )%UNTITLED2 Summary of this function goes here% Detailed explanation goes heretheta=0::2*pi;a=input('请输入a的值:');b=input('请输入b的值:');n=input('请输入n的值:');rho=a*sin(b+n*theta);polar(theta,rho,'k');end下面以a=1,b=1,n=1的极坐标图形为基础来分析a、b、n的影响。
对a的值进行改变:对比发现a只影响半径值的整倍变化对b的值进行改变:对比发现b的值使这个圆转换了一定的角度对n的值进行改变:对比发现当n>=2时有如下规律1、当n为整数时,图形变为2n个花瓣状的图形2、当n为奇数时,图形变为n个花瓣状的图形分别让n为2、3、4、5同时改变b和n的值,对比发现图形变为2n个花瓣状,并且还旋转了一定角度1 绘制sin(x)曲线,通过句柄修改曲线的颜色,要求:a)生成曲线的同时,获取句柄,再修改颜色;>> x=0:pi/50:2*pi;>> y=sin(x);>> h=plot(x,y)h =>> set(h,'color','r');截图如下:b)先生成曲线,然后再获取句柄,再完成颜色修改。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(2)循环结构
n=input('请输入一个数:')
s=1;
for i=1:n
s=s*(i+1)*(i+1)/(i*(i+2));
end
s
向量运算
n=input('请输入一个数:');
a=2:2:2*n;
b=1:2:(2*n-1);
c=3:2:(2*n+1);
e=(a.*a)./(b.*c);
y=e.*e;
f=A(1);
for i=1:20;%还可用A=input('ENTER A:');
m=A(i);
if m<f;
f=m;
end
end
end
A=input('ENTER A:');
a=max(A);
b=min(A);
a
b
第4题
y= ,当a取-3.0、-2.9、-2.8、、2.8、2.9、3.0时,求各点的函数值。要求分别用顺序结构和循环结构实现。
a=a+0.1;
end
y
第5题
当n分别取100、1000、10000时,求下列各式的值:
(1)
循环结构:
n=input('请输入一个数:');
sum=0;
for i=1:n
sum=sum+1/(i*i);
end
sum
向量运算
n=input('请输入一个数:')
a=1:1:n;
b=1:1:n;
y=sum(1./(a.*b));
(2)
function f=factor1(n)
a=1:1:n;
b=2:1:(n+1);
f=sum(a.*b);
end
y=factor1(40)/(factor1(30)+factor1(20));
思考题
2(1)2.*N (2)1/2.*N(3)1./N(4)1./(N.*N)
4.(1)循环结构
n=input('请输入一个数:')
y=y+1/(4^i);
end
y
向量运算:
n=input('请输入一个数:');
a=1:1:n;
y=sum(1./(4.^a));
y
第1题:
从键盘输入一个3位数,将它反向输出。如输入639输出936.
n1=fix(n/100);
n2=rem(fix(n/10),10);
n3=rem(n,10);
m=n3*100+n2*10+n1;
disp(m)
请输入一个三位数:489
984
第2题:
输入一个百分制成绩,要求输出成绩等级A、B、C、D、E。其中90~100分为A,80~89分为B、70~79分为C、60~69分为D,60分以下为E。
1循序结构
A=[1 2 3 4 5 6 7 23 32 12 53 1 23 53 5 235 31 8888 33 3 21];%还可用A=input('ENTER A:');
min=A(1);
max=A(1);
for i=1:19
if A(i+1)>max
max=A(i+1);
end
if A(i+1)<min
disp('A');
case {8}
disp('B');
case {7}
disp('C');
case {6}
disp('D');
case {5,4,3,2,1,0}
disp('E');
otherwise
disp('falБайду номын сангаасe');
end
请输入成绩分数:88
B
第3题
输入20个数,求其中最大数和最小数。要求分别用循环结构和调用MATLAB的max函数、min函数来实现。
y
n=input('请输入一个数:');
y=1;
a=2:2:2*n;
b=1:2:(2*n-1);
c=3:2:(2*n+1);
y=prod((a.*a)./(b.*c));
y
第6题
建立5x6矩阵,要求输出矩阵第n行元素。当n值超过矩阵的行数时,自动转为输出矩阵最后一行元素,并给出出错信息。
A=[1,2,3,4,5,6;2,3,4,5,6,7;3,4,5,6,7,8;4,5,6,7,8,9;5,6,7,8,9,0];
n=input('需要输出矩阵的行数:');
if n>0 & n<6
disp(A(n,:));
else
disp(A(5,:));disp('false!');
end
第7题
(1)
function f=factor(n)
f=n+10*log(n^2+5);
end
y=factor(40)/(factor(30)+factor(20));
顺序结构
a=-3.0:0.1:3.0;
y=(exp(0.3*a)-exp(-0.3*a))/2.*sin(a+0.3)+log((0.3+a)/2);
y
循环结构
a=-3.0;
while a<=3.0
y=(exp(0.3*a)-exp(-0.3*a))/2.*sin(a+0.3)+log((0.3+a)/2)
要求:(1)分别用if语句和switch语句实现。
(2)输入百分制成绩后要判断成绩的合理性,对不合理的成绩应输出错信息。
If语句:
>> s=input('请输入成绩分数:');
if s>=90&s<=100
disp('A');
elseif s>=80&s<=89
disp('B');
elseif s>=70&s<=79
y=0;
for i=1:n
y=y+(-1)^(i-1)/(2*i-1);
end
y
向量运算
n=input('请输入一个数:');
a=1:4:(4*n-3);
b=-3:-4:-(4*n-1);
y=sum(1./a+1./b);
y
4(2)
循环结构:
n=input('请输入一个数:');
y=0;
for i=1:n
min=A(i+1);
end
end
max
min
结果:
max =
8888
min =
1
2调用matlab函数
funtion f=max(A)
f=A(1);
for i=1:20;
m=A(i);%还可用A=input('ENTER A:');
if m>f;
f=m;
end
end
end
funtion f=min(A)
disp('C');
elseif s>=60&s<=69
disp('D');
elseif s>=0&s<60
disp('E');
else
disp('false');
end
请输入成绩分数:89
B
Switch语句:
>> s=input('请输入成绩分数:');
switch fix(s/10)
case {9,10}
