《积分变换》复习卷
【复变函数与积分变换期末复习题】含大题答案

复习题2一.单项选择题1.函数),(),()(y x iv y x u z f +=在点000iy x z +=处连续的充要条件是()(A)),(y x u 在),(00y x 处连续(B)),(y x v 在),(00y x 处连续(C)),(y x u 和),(y x v 在),(00y x 处连续(D)),(),(y x v y x u +在),(00y x 处连续2.设C z ∈且1=z ,则函数zz z z f 1)(2+-=的最小值为()(A)3-(B)2-(C)1-(D)13.函数)(z f 在点z 可导是)(z f 在点z 解析的()(A)充分不必要条件(B)必要不充分条件(C)充分必要条件(D)既非充分条件也非必要条件4.下列命题中,正确的是()(A)设y x ,为实数,则1)cos(≤+iy x (B)若0z 是函数)(z f 的奇点,则)(z f 在点0z 不可导(C)若v u ,在区域D 内满足柯西-黎曼方程,则iv u z f +=)(在D 内解析(D)若)(z f 在区域D 内解析,则)(z if 在D 内也解析5.设1:1=z c 为负向,3:2=z c 正向,则=⎰+=dz z zc c c 212sin ()(A)iπ2-(B)0(C)iπ2(D)iπ46.设c 为正向圆周2=z ,则=-⎰dz z zc2)1(cos ()(A)1sin -(B)1sin (C)1sin 2i π-(D)1sin 2i π7.设c 为从原点沿x y =2至i +1的弧段,则=+⎰cdz iy x )(2()(A)i6561-(B)i 6561+-(C)i 6561--(D)i6561+8.复变函数1)(-=z e z f 在复平面上()(A)无可导点(B)有可导点,但不解析(C)仅在零点不解析(D)处处解析9.使得22z z =成立的复数z 是()(A)不存在的(B)唯一的(C)纯虚数(D)实数10.设z 为复数,则方程i z z +=+2的解是()(A)i +-43(B)i +43(C)i -43(D)i --4311.ii 的主值为()(A)0(B)1(C)2πe(D)2eπ-12.ze 在复平面上()(A)无可导点(B)有可导点,但不解析(C)有可导点,且在可导点集上解析(D)处处解析13.设z z f sin )(=,则下列命题中,不正确的是()(A))(z f 在复平面上处处解析(B))(z f 以π2为周期(C)2)(iziz e e z f --=(D))(z f 是无界的14.设c 为从原点沿x y =2至i +1的弧段,则=+⎰cdz iy x )(2()(A)i 6561-(B)i 6561+-(C)i 6561--(D)i 6561+15.设c 为不经过点1与1-的正向简单闭曲线,则dz z z zc⎰+-2)1)(1(为()(A)2iπ(B)2i π-(C)0(D)(A)(B)(C)都有可能16.设1:1=z c 为负向,3:2=z c 正向,则=⎰+=dz zzc c c 212sin ()(B)i π2-(B)0(C)iπ2(D)iπ417.设()()F f t F ω=⎡⎤⎣⎦则()0sin F f t t ω=⎡⎤⎣⎦().A .()()00j2F F ωωωω+--⎡⎤⎣⎦B.()()00j2F F ωωωω++-⎡⎤⎣⎦C.()()0012F F ωωωω+--⎡⎤⎣⎦D.()()0012F F ωωωω++-⎡⎤⎣⎦18.设()()F f t F ω=⎡⎤⎣⎦则()()1F t f t -=⎡⎤⎣⎦().A .()()F F ωω'- B.()()F F ωω'--C.()()j F F ωω'- D.()()j F F ωω'--19.积分=-⎰=231091z dz z z ()(A)0(B)i π2(C)10(D)5i π20.积分21sin z z zdz ==⎰()(A)0(B)61-(C)3i π-(D)iπ-21.复数ii+=1z 位于复平面第()象限.A .一B .二C .三D .四22.下列等式成立的是().A .Lnz Lnz 77=;B .)1arg()1(r =g A ;C .112=i;D .)z z Re(z z =。
复变函数积分变换复习卷及答案

复变函数复习卷及参考答案一、填空题1、复数1z i =+的三角表示式=2(cossin )44i pp+;复指数表示式=42ie p 。
2、复数()13z i =+的z =2;23Argz k pp =+;arg 3z p=;13z i =-。
3、62111i i i -æö==-ç÷+èø。
10125212131i i i i i +-=+-=-。
4、()()31123513253x y i x i y i x y +=ì++-=-Þí-=-î,求解方程组可得,45,1111x y -==。
5、()()231,f z z z =-+则()61f i i ¢-=--。
6、()n3L i -ln 226i k i pp =-+;ln()ie 12i p=+。
7、()(2)1321,(13)2ik i iiee i p p p -++==+。
8、32282(cossin)33k k i p pp p++-=+;0,1,2k =。
1224(4)2i i -==±。
9、1sin 2e e i i --=;221cos ()22i e e pp p -=+;10 、21024z dzz z ==++ò ;1212z dz i z p ==-ò 。
11、设31cos ()zf z z -=,则0z =是(一级极点);31cos 1Re [,0]2z s z -=。
1()s i n f z z=,0z =是本性奇点。
二、判断下列函数在何处可导?何处解析?在可导处求出导数。
(1)()22f z x iy=+;解:22,,2,0,0,2u u v v u x v y x y xyxy¶¶¶¶======¶¶¶¶,一阶偏导连续,因此当,x y y x u v u v ==-时,即x y =时可导,在z 平面处处不解析。
成人高考数学复变函数与积分变换考核试卷

D. L{sin(at)} = a/(s²+a²)
()
6.对于傅里叶变换,以下表述正确的是()
A.傅里叶变换是一种积分变换
B.傅里叶变换可以将时域信号转换为频域信号
C.傅里叶变换具有线性性质
D. A、B、C都正确
()
7.以下关于复变函数积分变换的表述,正确的是()
B. f(z)在z=0处的解析延拓与f(z)在z=0处的解析性质有关
C. f(z)在z=0处的解析延拓的收敛域与f(z)在z=0处的解析性质有关
D. A、B、C都正确
()
16.以下关于积分变换的表述,正确的是()
A.积分变换是一种线性变换
B.积分变换可以解决微分方程初值问题
C.积分变换可以简化计算过程
8.拉普拉斯变换可以解决微分方程的初值问题。()
9.在复变函数中,任何连续函数的积分都是路径无关的。()
10. Z变换是复变函数积分变换的一种,常用于控制理论。()
五、主观题(本题共2小题,每题10分,共20分)
1. (10分)请说明复变函数解析的概念,并给出两个解析函数的例子。
2. (10分)请解释傅里叶级数的概念,并说明其在信号处理中的应用。
A.函数在整个复平面上解析
B.函数在一个单连通区域内解析
C.函数在一个多连通区域内解析,但积分路径不包围任何奇点
D.函数在一个多连通区域内解析,积分路径包围了奇点
()
13.以下哪些是复变函数的应用领域?()
A.量子力学
B.电路分析
C.流体力学
D.数论
()
14.关于积分变换的性质,以下哪些是正确的?()
复变函数与积分变换五套试题及答案

复变函数与积分变换试题(一)一、填空(3分×10)1.的模 ,幅角 。
)31ln(i --2.-8i 的三个单根分别为: ,,。
3.Ln z 在 的区域内连续。
4.的解极域为:。
z z f =)(5.的导数。
xyi y x z f 2)(22+-==')(z f 6.。
=⎥⎦⎤⎢⎣⎡0,sin Re 3z z s 7.指数函数的映照特点是:。
8.幂函数的映照特点是:。
9.若=F [f (t )],则= F 。
)(ωF )(t f )][(1ω-f 10.若f (t )满足拉氏积分存在条件,则L [f (t )]=。
二、(10分)已知,求函数使函数为解析函222121),(y x y x v +-=),(y x u ),(),()(y x iv y x u z f +=数,且f (0)=0。
三、(10分)应用留数的相关定理计算⎰=--2||6)3)(1(z z z z dz四、计算积分(5分×2)1.⎰=-2||)1(z z z dz2. C :绕点i 一周正向任意简单闭曲线。
⎰-c i z z3)(cos 五、(10分)求函数在以下各圆环内的罗朗展式。
)(1)(i z z z f -=1.1||0<-<i z 2.+∞<-<||1i z 六、证明以下命题:(5分×2)(1)与构成一对傅氏变换对。
)(0t t -δo iwt e -(2))(2ωπδ=⎰∞+∞-ω-dt e t i 七、(10分)应用拉氏变换求方程组满足x (0)=y (0)=z (0)=0的解y (t )。
⎪⎩⎪⎨⎧='+=+'+='++'0401z y z y x z y x 八、(10分)就书中内容,函数在某区域内解析的具体判别方法有哪几种。
复变函数与积分变换试题答案(一)一、1., 2.-i 2i -i22942ln π+ππk arctg 22ln 32+-333.Z 不取原点和负实轴 4. 空集5.2z 6.07.将常形域映为角形域8.角形域映为角形域9.10.⎰∞+∞-ωωπωωd e F i )(21⎰∞+-0)(dte tf st 二、解:∵∴(5分)yu x x v ∂∂-=-=∂∂xuy y v ∂∂==∂∂c xy u +=cxy y x i z f ++⎪⎭⎫ ⎝⎛+-=222121)(∵f (0)=0c =0(3分)∴(2分)222222)2(2)(2)(z ixyi y x i y x i xy z f -=+--=--=三、解:原式=(2分)⎥⎦⎤⎢⎣⎡--∑=k k z z z z s i ,)3)(1(1Re 2621π01=z 12=z (2分)⎥⎦⎤⎢⎣⎡---=∑=k k z z z z s i ,)3)(1(1Re 2643π33=z ∞=4z 2312(3,)3)(1(1Re 66⨯=⎥⎦⎤⎢⎣⎡--分)z z z s =0⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⋅--=⎥⎦⎤⎢⎣⎡∞--0,1)31)(11(11Re 2,)3)(1(1Re 266z z z z s z z z s 分)(∴原式=(2分) =23126⨯⨯i πi 63π-四、1.解:原式(3分)z 1=0z 2=1⎥⎦⎤⎢⎣⎡-π=∑=k k z z z s i ,)1(1Re 221=0(2分)]11[2+-=i π2.解:原式=iz z i=''=s co !22πi z z i =-π=)(cos i i cos π-=1ich π-五、1.解:ni z z f ∑∞⎪⎫⎛--⋅=⋅⋅=⋅=1111111111)(分)(分)(分)((2分)11)(--∞=-=∑n n n i z in nn i z i )(1-=∑∞-=2.解:⎪⎭⎫⎝⎛-+⋅-=-+⋅-=i z i i z i z i i z z f 11)(11)(1)(11)(2分)(分)((1分)(2分)nn i z i i z ∑∞=⎪⎭⎫ ⎝⎛---=02)(120)(11+∞=-=∑n n n i z i 20)(--∞=-=∑n n n i z i 六、1.解:∵(3分)∴结论成立0)(0t i e t t ti t i e dt e t t ωωωδ-==--∞+∞-=-⎰(2)解:∵(2分)1)(2210==ωπδπ=ωω-ω-∞+∞-⎰t i t i e dw e ∴与1构成傅氏对)(2w πδ∴(2分))(2ωπδω=-∞+∞-⎰dt e t i 七、解:∵(3分)⎪⎪⎩⎪⎪⎨⎧=+=++=++)3(0)(4)()2(0)()()()1(1)()()(s sZ s Y s Z s sY s X S s sZ s Y s sX S (2)-(1):∴(3分)⎪⎭⎫ ⎝⎛-⋅-=s s s Y 111)(2⎪⎭⎫ ⎝⎛++--=--=1111211112s s s s s s ∴cht e e t Y t t -=--=-121211)(八、解:①定义;②C-R 充要条件Th ;③v 为u 的共扼函数10分复变函数与积分变换试题(二)一、填空(3分×10)1.函数f (z )在区域D 内可导是f (z )在D 内解析的()条件。
积分变换试卷A

华南理工大学 广州汽车学院 2007——2008学年度第一学期期末考试 《积分变换》 试卷A 考生注意:1.考前请将密封线内各项填写清楚; 2.本试卷共四个大题,满分100分,考试时间120分钟; 3.所有答案应直接写在试卷上。
一.利用定义求下列函数的Fourier 变换(本大题共2小题,每小题5分,共10分) 1.4,02,()0,t f t ≤≤⎧=⎨⎩其它; 2.sin ,,()0,.t t f t t ππ⎧<⎪=⎨>⎪⎩二.利用性质求下列函数的Fourier 变换(本大题共4小题,每小题5分,共20分)1.()();n f t u t t = 2.()()sin 2;t f t u t e t -=3.2()sin ;f t t t = 4.()()sin().4t f t t e t πδ=+三.证明(本大题共1小题,每小题7分, 共7分) 设()[()]F F f t ω=,证明:0001[()cos ](()()).2F f t t F F ωωωωω=-++四.求下列函数的卷积(本大题共1小题,每小题8分,共8分)sin ,02,()(),()0,.t t t f t e u t g t π-≤≤⎧==⎨⎩其它五.利用Fourier 变换解下列积分方程(本大题共1小题,每小题7分, 共7分) 0sin ()cos .t g td t ωωω+∞=⎰ 六.利用定义求下列函数的Laplace 变换(本大题共2小题,每小题5分,共10分) 1.1,03,()0,3t t f t t +≤≤⎧=⎨>⎩; 2.sin ,0,(),.t t f t t t ππ≤≤⎧=⎨>⎩七.利用性质求下列函数的Laplace 变换(本大题共4小题,每小题5分,共20分)1.4()3()2;t f t u t e =- 2.2()();t f t e t δ-=+3.()1;at f t e -=- 4.2()sin 2.f t t t =八.求下列像函数的Laplace 逆变换(本大题共2小题,每小题5分,共10分) 1.41();F s ω= 2.1().(2)F s s ω=+九.求解下列微分方程(本大题共1小题,每小题8分, 共8分)'sin ,(0) 1.x x t x +==-。
复变函数与积分变换考试试卷

复变函数与积分变换考试试卷一. 填空题(每空 5 分,共 25 分)1.设100i)(1z +=,则Imz = 。
2.方程lnz=i 3π的解为 。
3.)21(421lim z zi x +++→=_______________________________________。
4.导函数xv i x u x f ∂∂+∂∂=)('在区域D 内解析的充要条件为_________。
5.函数)Re()Im()(z z z x f -=仅在点z=____________________处可导。
二.选择题(每题 5 分,共 25 分)1.复数i 218-2116z =的辐角为 ( ) A.arctan 21 B .-arctan 21 C .π-arctan 21 D .π+arctan 21 2. 方程|z+2-3i|=2所代表的曲线( )A.中心为2-3i ,半径为2的圆周B. 中心为-2+3i ,半径为2的圆周C. 中心为-2+3i ,半径为2的圆周D. 中心为2-3i ,半径为2的圆周3. 复数)2(tan πθπθ i z -=的三角表示式是( ) A.⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+θπθπθ2sin 2cos sec i B.⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+θπθπθ23sin 23cos sec i C.-⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+θπθπθ23sin 23cos sec i D.-⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+θπθπθ2sin 2cos sec i 4. 若函数在复平面内处处解析,那么实常数a=( )A.0B.1C.2D. -25.设f(z)=sinz,则下列命题中,不正确的是( )A. f(z)在复平面上处处解析B.f(z)以 π2为周期C.2e f(z)iz ize --= D.|f(z)|是无界的 三.计算题(每题10 分,共 50 分)1.设)22(2)(22xy x i y y x z f ++--=,写出f(z)关于z 的表达式。
积分变换A卷参考答案

8.已知 的Fourier变换是 ,则 .
9. .
10.函数 的Laplace变换是 .
三、计算题。(每小题10分,共70分)
11.设 的Fourier变换为 ,求 .
解由频域微分性质得 (5分)
由线性性质可得 (10分)
12.若 ,求
解 (4分)
2.若 的Fourier变换为 ,则 的Fourier变换为(D)
A. B. C. D.
3.下列函数中不存在Laplace变换的是(A)
A. B. C. D.
4.下面的式子中不正确的是(C)
A. B. C. D.
5. 的Laplace为(B)
A. B. C. D.
二、填空题。(每小题3分,共15分)
试题
2018年~2019年第二学期
课程名称:积分变换专业年级:
考生学号:考生姓名:
试卷类型:A卷√B卷□考试方式:开卷□闭卷√
……………………………………………………………………………………………………………………
一、单项选择题。(每小题3分,共15分)
1.函数 的Fourier变换为(B)
A. B. C. D.
(10分)
13.设函数 (1)求 (2)求 .
解: (3分) (6分)
根据对称性质,有 (10分)
14.设 ,求 的Laplace变换.
解:由于 ,故由线性性质和延迟性质得(4分)
(10分)
解法二 (4分)
(10分)
15.已知 ,求 .
解:因为 (5分)
所以 (10分)
解法二 (5分)
(10分)
16.利用Laplace变换计算积分 .
解:由于 ,根据像函数的积分性质得(3分)
积分变换复习题解答

积分变换复习题解答一、求下列函数的付氏变换1、设(),0,00,⎩⎨⎧<≥=-t t e t f t β求()[]()[]()[]t f F t f F t f F -+'',1,解:()()()2117152F f t j F f t j ωωβω---''==⎡⎤⎡⎤⎣⎦⎣⎦+()()11415(1)11j j F f t eF f t ej ωωβω---⋅-+==⎡⎤⎡⎤⎣⎦⎣⎦+()()1212151F f t F j ωβω----=-=⎡⎤⎣⎦-2、()()()()1151141722111122{[]}{}itj j F e u t F u t eF u t e j ωωωωωωωωπδωω-----⋅-⋅=+=+=+⎡⎤⎡⎤-=-==+⎡⎤⎢⎥⎣⎦⎣⎦⎣⎦()2(1)11(1)j e j ωπδωω-+⎡⎤=++⎢⎥+⎣⎦3、[]()()112000sin F t j ωωδωωδωω-=+--⎡⎤⎣⎦4、()()()55114173351353j j F u t F u t e F u t e j ωωπδωω----⎡⎤⎡⎤⎛⎫-=-==+⎡⎤⎡⎤ ⎪⎢⎥⎢⎥⎣⎦⎣⎦⎝⎭⎣⎦⎣⎦5、()()()()()1181721122d d d F tu t j F u t j F u t j j d d d j πδωπδωωωωωω--⎡⎤'===+=-+⎡⎤⎡⎤⎡⎤⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦6、()()()()()114118111j j j j F t eF t e j F t e j j e ωωωωδδωδωω---⋅---''-===⋅=⎡⎤⎡⎤⎡⎤⎣⎦⎣⎦⎣⎦7、()()()()1111111[11]cos F t t F t t t δδπδδππ-++-=++-=⎡⎤⎡⎤⎣⎦⎣⎦8、()110323itF e πδω-⎡⎤=-⎣⎦二、计算:1、()127sin sin 0332t t dt ππδ-+∞-∞⎛⎫⎛⎫-=-= ⎪ ⎪⎝⎭⎝⎭⎰2、128sin sin 42242t t dt ππππδ-+∞-∞⎛⎫⎛⎫⎛⎫-+=+= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎰三、求卷积:1、设()(),0,00,,0,00,221⎩⎨⎧<≥=⎩⎨⎧<≥=--t t e t f t t e t f t t 求:()()t f t f 21*解:0t <时:12()()0f t f t *=0t ≥时:()()()22212120()()tttt tt t f t f t f f t d e ed ee d e e ττττττττ------*=-===-⎰⎰⎰212,0()()0,0t te e tf t f t t --⎧-≥∴*=⎨<⎩2、设()()212,0,0,0,00,0t t t t f t f t t t ≥⎧≥⎧==⎨⎨<<⎩⎩,求:()()t f t f 21* 解:0t <时:12()()0f t f t *=0t ≥时:()()()24121201()()12ttf t f t f f t d t d t ττττττ*=-=-=⎰⎰ 412,0()()120,0t t f t f t t ⎧≥⎪∴*=⎨⎪<⎩四、求下列函数的拉氏变换: 1、219126333222255[sin5][sin5]5(3)5ts s s s L e t L t s s ---=-=-===+-+ 2、()(1)1221[cos2][cos2]12t ts L et e L e t e s ---+=⋅=⋅++同上题3、()()()(){}22221521812422222222231442[2]1[2][]ss s d d d L t u t L u t e L u t e e ds ds ds s s s s -------⎧⎫⎛⎫-=--==⋅=++⎨⎬ ⎪⎩⎭⎝⎭4、()222511[521]2ts L e t t e s s sδ-+-++=+++- 5、[]272822211sin sin cos cos sin sin cos 444221121s s L t L t t L t t s s s πππ--⎡⎤-⎛⎫⎡⎤⎡⎤-=-=-=-= ⎪⎢⎥⎢⎥⎢⎥+++⎝⎭⎣⎦⎣⎦⎣⎦6、(){}21312191271122[cos2]1[cos2]{[cos2]}2tts s s s d d d sL te t L e t L t ds dsds s -----=-=-⎧⎫=-=-=-⎨⎬+⎩⎭()22222123(1)225d s s s ds s s s ⎧⎫---=-=⎨⎬-+⎩⎭-+ 7、⎥⎦⎤⎢⎣⎡t t L 2sin []21712822sin 2arctan arctan 2222ss s s sL t ds ds s π---+∞+∞+∞====-+⎰⎰ 8、⎥⎦⎤⎢⎣⎡⎰-tt tdt e L 023sin []()21621912622221113sin3sin323t s s L e t L t s ss s -----=+⎡⎤==⋅=⋅⎣⎦++9、20t t e e dt t --+∞-⎰21722000111ln ln 2122t ts L e e ds ds s s s --+∞+∞--+∞+⎛⎫⎡⎤=-=-== ⎪⎣⎦+++⎝⎭⎰⎰10、设()5,122,24,0,4t f t t t ≤<⎧⎪=≤<⎨⎪≥⎩试用单位阶跃函数及延迟了的单位阶跃函数表示()t f ,并求[])(t f L 。
复变函数与积分变换期末考试复习题及参考答案-高起本

《复变函数与积分变换》复习题一、判断题1、cos z 与sin z 在复平面内有界. ( )2、若{}n z 收敛,则{Re }n z 与{Im }n z 都收敛. ( )3、若函数()f z 在0z 处解析,则它在该点的某个邻域内可以展开为幂级数. ( )4、若()f z 在区域D 内解析,且'()0f z ,则()f z C (常数).( )5、若()f z 在区域D 内解析, 则对D 内任一简单闭曲线C ()0Cf z dz .( )6、若()f z 在0z 的某个邻域内可导,则函数()f z 在0z 解析. ( )7、若{}n z 收敛,则{Re }n z 与{Im }n z 都收敛. ( )8、若()f z 在区域D 内解析,且'()0f z ,则()f z C (常数).( )9、若0z 是()f z 的m 阶零点,则0z 是1/()f z 的m 阶极点. ( )10、若0lim ()zz f z 存在且有限,则0z 是函数()f z 的可去奇点.( )二、选择题 1.arg13i ( )A.-3π B.3πC.32πD.3n 2π+2 2.2z 在0z 复平面上( )A.不连续B.可导C.不可导D.解析3.设z xyi ,则下列函数为解析函数的是( )A.22()2f z x y xyB.()f z x iyC. ()2f z x i yD.()2f z xiy7.0z 是3sin zz 的极点,其阶数为( ) A.1 B.2 C.3 D.410.整数0k 则Res[cot ,]z =( )A.1kB.0C.1kD.k11、设复数1cossin33z i ,则arg z ( )A.-3B.6C.3D.2312、2w z 将z 平面上的实轴映射为w 平面的( )A.非负实轴B.实轴C.上半虚轴D.虚轴13、下列说法正确的是( )。
积分变换复习卷

《积分变换》复习卷一、单项选择题1.复数z=1625825-i 的辐角为( )BA.arctan 12B.-arctan 12C.π-arctan 12D. π+arctan 122.方程Rez 2=1所表示的平面曲线为( )D A.圆B.直线C.椭圆D.双曲线3.复数z=--355(cos sin )ππi 的三角表示式为( )C A.-+34545(cos sin )ππiB.34545(cos sin )ππ-iC. 34545(cos sin )ππ+iD.--34545(cos sin )ππi3.复数e 3+i 所对应的点在( )A A.第一象限 B.第二象限 C.第三象限D.第四象限4.积分路线C 是由点z=-1到z=1的上半单位圆周,则z z dz C+⎰12等于( )CA.2+πiB.2-πiC.--2πiD.-+2πi5.函数w=z 2把Z 平面上的扇形区域:0<argz<π3,0<|z|<2映射成W 平面上的区域( )AA.0<argw<23π,0<|w|<4 B.0<argw<π3,0<|w|<4 C.0<argw<23π,0<|w|<2D.0<argw<π3,0<|w|<2 6.设C 为正向圆周|z+1|=2,n 为正整数,则积分dz z i n C()-+⎰1等于( )CA.1B.2πiC.0D.12πi7.设函数f z e d z()=⎰ξξξ0,则f(z)等于( )DA.ze z +e z +1B.ze z +e z -1C.-ze z +e z -1D.ze z -e z +18.级数()!()!n n z n n+=∞∑120的收敛半径为( )D A.0 B.1 C.2D.+∞9.幂级数z n n n -=∞∑11!的收敛区域为( )B A.0<|z|<+∞ B.|z|<+∞ C.0<|z|<1D.|z|<110.z=-1是函数cot ()πzz +14的( )C A.3阶极点 B.4阶极点 C.5阶极点D.6阶极点11.下列影射中,把角形域0<argz<π4保角映射成单位圆内部|w|<1的为( )C A.w=z z 4411+- B.w=z z 4411-+ C.w=z i z i44-+D.w=z i z i44+-12.设Q(z)在点z=0处解析,f(z)=Q z z z ()()-1,则Res[f(z),0]等于( )B A.Q(0)B.-Q(0)C.'Q ()0D.-'Q ()013.映射w=z 2+2z 在下列区域中每一点的伸缩率都大于1的是( )A A.|z+1|>12B.|z+1|<12C.|z|>12D.|z|<12二、填空题11.复数z=4+48i 的模|z|= .8 12.设z=e 2+i ,则argz= .113.方程Rez 2=1所表示的平面曲线为 .双曲线14.复数z=--355(cos sin )ππi 的三角表示式为 .34545(cos sin )ππ+i15.设z=cosi ,则Imz= .0 16.f(z)=z 2的可导处为 .017.积分路线C 是由点z=-1到z=1的上半单位圆周,则z z dz C+⎰12等于 .--2πi18.函数f(z)在正向简单闭曲线C 所包围的区域D 内解析,在C 上连续,且z=a 为D 内任一点,n 为正整数,则积分f z z a dz n C()()-+⎰1等于 .2πi n f a n !()()19.设C 为正向圆周|z|=1,则积分dzz C ||⎰等于 .020.f(z)=1111115zz z [()]+++⋅⋅⋅++在点z=0处的留数为 .6 21.方程lnz=π3i 的解为 . 3),31(21πi e i 或+22.设C 为正向圆周|z -i|=12,则积分e z z i dz z Cπ()-=⎰2. -+2ππ()i23.级数n n z nn n !=∞∑1的收敛半径为 . e 三、计算题24.=x 2+2xy -y 2的共轭调和函数v(x,y),并使v(0,0)=1.解: ∂∂∂∂u x x y uyx y =+=-2222,,由C -R 条件,有∂∂∂∂v y u x =,∂∂∂∂v x uy=-,∴ v vydy x y dy xy y x ==+=++⎰⎰∂∂ϕ()()2222. 再由∂∂ϕ∂∂v x y x x y uy=+'=-+=-222(), 得'=-=-+ϕϕ(),(),x x x x C 22于是 ∴ v=2xy+y 2-x 2+C. 由v(0,0)=1, 得C=1. 故v=2xy+y 2-x 2+1.25.积分I=z zz dz C+⎰||的值,其中C 为正向圆周|z|=2.解:z z z dz zdz i i d CC +==⋅+-⎰⎰⎰||Re cos (cos sin )12222θθθθππ=4i (cos ).1240+=⎰θθππd i26.函数f(z)=e d z-⎰ζζ20在点z=0处的泰勒级数,并指出其收敛区域.解:因为f ˊ(z)=ez -2=()!()!(||)-=-<+∞=∞=∞∑∑z n n z z nn n n n2021, 所以由幂级数在收敛圆内逐项求积性质,得 f(z)='=-++=∞∑⎰f d n z n n n n z()()!ζζ12121(||z <+∞). 27.设Z 平面上的区域为D :|z+i|>2,|z -i|<2,试求下列保角映射: (1)w 1=f 1(z)把D 映射成W 1平面上的角形域D 1:π4<argw 1<34π;(2)w 2=f 2(w 1)把D 1映射成W 2平面上的第一象限D 2:0<argw 2<π2; (3)w=f 3(w 2)把D 2映射成W 平面的上半平面G :Imw>0; (4)w=f(z)把D 映射成G. 28.留数求积分I=cos x x x dx 42109+++∞⎰的值.解:在上半平面内,f(z)=e z z iz()()2219++有一阶极点z=i 和z=3i.∵I=121912192222cos ()()Re()()xx x dx e x x dx ix++=++-∞+∞-∞+∞⎰⎰=12223Re{Re [(),]Re [(),]},ππi s f z i i s f z i + Res[f(z),i]=116ei, Res[f(z),3i]=-1483e i,∴ I e e =-π483132().29.面上的区域为D :|z+i|>2,|z -i|<2,试求下列保角映射: (1)w 1=f 1(z)把D 映射成W 1平面上的角形域D 1:π4<argw 1<34π;(2)w 2=f 2(w 1)把D 1映射成W 2平面上的第一象限D 2:0<argw 2<π2; (3)w=f 3(w 2)把D 2映射成W 平面的上半平面G :Imw>0; (4)w=f(z)把D 映射成G.解:(1)由||||z i z i +=-=⎧⎨⎪⎩⎪22 解得交点z 1=1,z 2=-1. 设w 1=z z -+11,则它把D 映射成W 1平面上的D 1:ππ4341<<arg .w(2)设w 2=e w i -π41,则它把D 1映射成W 2平面上的第一象限D 2:022<<arg .w π(3)设w=w 22,则它把D 2映射成W 平面的上半平面G :Imw>0. (4)w=()().ez z i z z i -⋅-+=--+π4221111。
上海交通大学数学物理方法-积分变换试题

8.
像函数 F ( )
9.
已 知 某 函 数 f( t ) 的 傅 里 叶 变 换 为 F ( )
[( 2) ( 3)], 则
f (t )
1 2it [e e 3it ] 2 2 3t 3 p 1 e 2t 的拉普拉斯逆变换为 e 5 5 p p 6
6.
设解析函数 f (z ) u(x ,y )
iv(x ,y ) 的实部 u(x ,y ) 是以下拉普拉斯方程的边值
u xx u yy 0, 问题 u(0,y ) 2y ,u(1,y ) 0 的解. u(x ,0) 0,u(x ,1) 2(x 1)
一、 单项选择题
1. 设 f ( t) (A)
te 3t sin 2t ,则拉普拉斯变换 L[f (t )] 为(A)
(B)
4(P 3) ; [(P 3)2 4]2
(P 3) ; [(P 3)2 4]2
(C)
4(P 3) ; (P 3)2 4
(D)
4P . [P 4]2
(B)
(A)
1 (1 i ) 1
2
1 (1 i )2 1 1 (1 i )2 1
(C)
1 (1 i ) 1
2
(D)
5.
设函数 f ( t )的拉普拉斯变换 L[f (t )]
F ( p ),则以下公式不正确的是(C)
( B)
(A) f (t )
2
2.利用拉普拉斯变换的性质,实积分
0
te at sin btdt(a 0) 的值为(C)
( B)
复变函数与积分变换复习题

复变函数与积分变换复习题复习题第一套一、选择题1、满足不等式Im z >1且z <2的所有点z 构成的集合是()A 有界单连通域B 无界单连通域C 有界复连通域D 无界复连通域2、函数23)(z z f =在点0=z 处是( )A 解析的B 可导的C 不可导的D 既不解析也不可导3、下列命题中,正确的是( )A 设,x y 为实数,则1)cos(≤+iy xB 若0z 是函数)(z f 的奇点,则()f z 在点0z 不可导C 若,u v 在区域D 内满足柯西-黎曼方程,则()f z u iv =+在D 内解析D 若)(z f 在区域D 内解析,则)(z if 在D 内也解析4、设01q <<,则幂级数20n n n q z ∞=∑的收敛半径R =( ) A q B 1qC 0D +∞ 5、函数1()1F s s =-的拉氏逆变换为() A 1t - B t e -C jt eD te 6、z =∞是函数3232z z z ++的( ) A 可去奇点 B 一级极点C 二级极点D 本性奇点7、映射3w z =在0z i =处的旋转角为( )A 0 B2π C π .D 2π- 8、级数1!nn i n ∞=∑ ( )A 绝对收敛B 条件收敛C 发散D 无法判断9、将单位圆内部变成单位圆内部的分式线性映射为()A 00i z z w e z z φ--=- B 001i z z w e z z φ--=+ C 001i z z w e z z φ--=- D 001i z z w e z z φ-+=-10、将点1,,1z i =-分别映射为点,1,0w =∞-的分式线性变换为()A 11z w z +=- B 11z w z+=-C 211i z w e zπ+=- D 211i z w e z π+=-二、填空题1、13i --的幅角的主值为。
2、(1)Ln i -= 。
积分变换试题
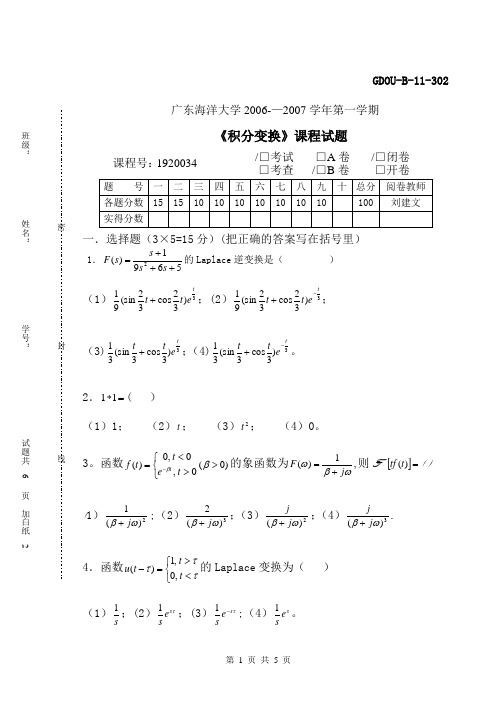
广东海洋大学2006-—2007学年第一学期《积分变换》课程试题课程号: 1920034/□ 考试□ A 卷/□ 闭卷□ 考查/□ B 卷□ 开卷一.选择题(3×5=15分)(把正确的答案写在括号里)1.5691)(2+++=s s s s F 的Laplace 逆变换是( ) (1)3)32cos 32(sin 91te t t +;(2)3)32cos 32(sin 91te t t -+;(3)3)3cos 3(sin 31t e t t +;(4)3)3cos 3(sin 31te t t -+。
2.=*11( )(1)1; (2)t ; (3)2t ; (4)0。
3。
函数)0(0,0,0)(>⎩⎨⎧><=-ββt e t t f t的象函数为,1)(ωβωj F +=则F []=)(t tf ( ) (1)2)(1ωβj +;(2)3)(2ωβj +;(3)2)(ωβj j +;(4)3)(ωβj j+. 4.函数⎩⎨⎧<>=-τττt t t u ,0,1)(的Laplace 变换为( ) (1)s1;(2)τs e s1;(3)τs e s-1;(4)s e s1。
班级:姓名:学号:试题共 6页加白纸 2张密封线GDOU-B-11-3025.已知L []22cos ks skt +=,则L []=-kt e at sin ( ) (1)22)(k a s s ++;(2)22)(k a s a s +++;(3)22)(k a s s ++;(4)22)(k a s k++二.填空题(3×5=15分)1.若)(t f 为无穷可微函数,则⎰∞+∞-='dt t f t )()(δ( ) 2.若),(2)(ωπδω=F 则=)(t f ( ) 3.若=)(ωF F [])(t f ,则=ωωd dF )(( ) 4.已知L []22sin k s kkt +=,则L []=kt t sin ( )5.已知F [])(1)(ωπδω+=j t u ,F []1)(=t δ,则F []=t sgn ( ) 三.求积分⎰∞+-032sin tdt te t 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《积分变换》复习卷一、单项选择题(本大题共10小题,每小题3分,共30分) 1.复数z=1625825-i 的辐角为( )B A.arctan12B.-arctan12C.π-arctan 12D. π+arctan 122.复数z=--355(cos sin )ππi 的三角表示式为( )C A.-+34545(cos sin )ππi B.34545(cos sin )ππ-i C. 34545(cos sin )ππ+iD.--34545(cos sin )ππi3.复数e 3+i所对应的点在( )A A.第一象限 B.第二象限 C.第三象限D.第四象限4.函数w=z 2把Z 平面上的扇形区域:0<argz<π3,0<|z|<2映射成W 平面上的区域( )AA.0<argw<23π,0<|w|<4 B.0<argw<π3,0<|w|<4 C.0<argw<23π,0<|w|<2D.0<argw<π3,0<|w|<25.设C 为正向圆周|z+1|=2,n 为正整数,则积分dz z i n C()-+⎰1等于( )CA.1B.2πiC.0D.12πi6.设函数f z e d z()=⎰ξξξ0,则f(z)等于( )DA.ze z +e z +1B.ze z +e z -1C.-ze z +e z -1D.ze z -e z +17.幂级数z n n n -=∞∑11!的收敛区域为( )BA.0<|z|<+∞B.|z|<+∞C.0<|z|<1D.|z|<18.z=-1是函数cot ()πz z +14的( )C A.3阶极点 B.4阶极点 C.5阶极点D.6阶极点9.设Q(z)在点z=0处解析,f(z)=Q z z z ()()-1,则Res[f(z),0]等于( )B A.Q(0)B.-Q(0)C.'Q ()0D.-'Q ()010.映射w=z 2+2z 在下列区域中每一点的伸缩率都大于1的是( )A A.|z+1|>12B.|z+1|<12C.|z|>12D.|z|<12二、填空题(本大题共10小题,每小题3分,共30分) 11.复数z=4+48i 的模|z|= .8 12.设z=e 2+i ,则argz= .113.方程Rez 2=1所表示的平面曲线为 .双曲线 14.设z=cosi ,则Imz= .015.积分路线C 是由点z=-1到z=1的上半单位圆周,则z zdz C+⎰12等于 .--2πi16.函数f(z)在正向简单闭曲线C 所包围的区域D 内解析,在C 上连续,且z=a 为D 内任一点,n 为正整数,则积分f z z a dz n C()()-+⎰1等于 .2πi n f a n !()()17.设C 为正向圆周|z|=1,则积分dzz C ||⎰等于 .018.方程lnz=π3i 的解为 . 3),31(21πi e i 或+19.设C为正向圆周|z -i|=12,则积分e z z i dz z Cπ()-=⎰2. -+2ππ()i20.级数n nz nn n !=∞∑1的收敛半径为 . e三、计算题(本大题共4小题,每小题10分,共40分) 21.=x 2+2xy -y 2的共轭调和函数v(x,y),并使v(0,0)=1. 解:∂∂∂∂u x x y u yx y =+=-2222,, 由C -R 条件,有∂∂∂∂v y u x =,∂∂∂∂v x uy=-,∴ v vydy x y dy xy y x ==+=++⎰⎰∂∂ϕ()()2222. 再由∂∂ϕ∂∂v x y x x y uy=+'=-+=-222(),得'=-=-+ϕϕ(),(),x x x x C 22于是 ∴ v=2xy+y 2-x 2+C. 由v(0,0)=1, 得C=1. 故v=2xy+y 2-x 2+1.22.函数f(z)=ed z -⎰ζζ20在点z=0处的泰勒级数,并指出其收敛区域.解:因为f ˊ(z)=ez -2=()!()!(||)-=-<+∞=∞=∞∑∑z n n z z nn n n n2021, 所以由幂级数在收敛圆内逐项求积性质,得 f(z)='=-++=∞∑⎰f d n z n n n n z()()!ζζ12121(||z <+∞).23.留数求积分I=cos x x x dx 42109+++∞⎰的值.解:在上半平面内,f(z)=e z z iz()()2219++有一阶极点z=i 和z=3i.∵I=121912192222cos ()()Re()()xx x dx e x x dx ix++=++-∞+∞-∞+∞⎰⎰=12223Re{Re [(),]Re [(),]},ππi s f z i i s f z i +Res[f(z),i]=116ei, Res[f(z),3i]=-1483e i,∴ I e e =-π483132().24.面上的区域为D :|z+i|>2,|z -i|<2,试求下列保角映射: (1)w 1=f 1(z)把D 映射成W 1平面上的角形域D 1:π4<argw 1<34π;(2)w 2=f 2(w 1)把D 1映射成W 2平面上的第一象限D 2:0<argw 2<π2;(3)w=f 3(w 2)把D 2映射成W 平面的上半平面G :Imw>0; (4)w=f(z)把D 映射成G. 解:(1)由||||z i z i +=-=⎧⎨⎪⎩⎪22解得交点z 1=1,z 2=-1.设w 1=z z -+11,则它把D 映射成W 1平面上的D 1:ππ4341<<arg .w (2)设w 2=ew i -π41,则它把D 1映射成W 2平面上的第一象限D 2:022<<arg .w π(3)设w=w 22,则它把D 2映射成W 平面的上半平面G :Imw>0. (4)w=()().ez z i z z i -⋅-+=--+π4221111****************学院继续教育学院《积分变换》期终试卷(B 卷)班级 *********** 姓名 学号 得分一、单项选择题(本大题共20小题,每小题2分,共40分) 1.方程Rez 2=1所表示的平面曲线为( )D A.圆B.直线C.椭圆D.双曲线2.设z=cosi ,则( )A A.Imz=0 B.Rez=π C.|z|=0D.argz=π3.w=Ln(1-i),则Imw 等于( )BA.-π4B.2401k k ππ-=±⋅⋅⋅,,,C.π4D.2401k k ππ+=±⋅⋅⋅,,,4.函数f(z)在正向简单闭曲线C 所包围的区域D 内解析,在C 上连续,且z=a 为D 内任一点,n 为正整数,则积分f z z a dz n C()()-+⎰1等于( )DA.211πin f a n ()!()()++ B.2πin f a !() C.2πif a n ()()D.2πi n f a n !()()5.C 为正向圆周|z|=1,则积分dzz C ||⎰等于( )AA.0B.2πiC.2πD.-2π6.积分路线C 是由点z=-1到z=1的上半单位圆周,则z z dz C+⎰12等于( )CA.2+πiB.2-πiC.--2πiD.-+2πi7.π3是函数f(z)=sin()z z --ππ33的( )B A.一阶极点 B.可去奇点C.一阶零点D.本性奇点8.级数()!()!n n z n n+=∞∑120的收敛半径为( )D A.0 B.1 C.2D.+∞9.下列积分中,积分值不为零的是( )D A.()z z dz C323++⎰,其中C 为正向圆周|z -1|=2B.e dz z C⎰,其中C 为正向圆周|z|=5C.zzdz C sin ⎰,其中C 为正向圆周|z|=1 D.cos zz dz C -⎰1,其中C 为正向圆周|z|=210.下列影射中,把角形域0<argz<π4保角映射成单位圆内部|w|<1的为( )C A.w=z z 4411+- B.w=z z 4411-+ C.w=z i z i44-+D.w=z i z i44+-二、填空题(本大题共10空,每空2分,共20分)11.z=(1+i)100,则Imz= .0 12.复数z=1625825-i 的辐角为 .-arctan 1213.复数z=--355(cos sin )ππi 的三角表示式为 .34545(cos sin )ππ+i 14.复数e 3+i 所对应的点在 .第一象限15.函数w=z 2把Z 平面上的扇形区域:0<argz<π3,0<|z|<2映射成W 平面上的区域 .0<argw<23π,0<|w|<416.设C 为正向圆周|z+1|=2,n 为正整数,则积分dz z i n C()-+⎰1等于 .017.f(z)=z 2的可导处为 .018.为正向圆周|z|=1,则()1zz dz C+=⎰ . 4πi19.为正向圆周|ξ|=2,f(z)=sinπζζζ3-⎰z d C,其中|z|<2,则'=f ()1 . ππππ23233i i ,cos或⋅20.f(z)=1111115zz z [()]+++⋅⋅⋅++在点z=0处的留数为 .6 三、计算题(本大题共4小题,每小题10分,共40分) 21.积分I=z zz dz C +⎰||的值,其中C 为正向圆周|z|=2.解:z z z dz zdz i i d CC +==⋅+-⎰⎰⎰||Re cos (cos sin )12222θθθθππ=4i (cos ).1240+=⎰θθππd i22.积分I=e z i z i dz zCπ()()-+⎰223的值,其中C 为正向圆周|z -1|=3.解:因在C 内f(z)=e z i z i zπ()()-+223有二阶极点z=i ,所以f z dz i ddzz i f z z i C()!lim[()()]=-→⎰212π =232323ππππi ez i ez i z iz z lim[()()]→+-+=ππ1612().-+i 23.利用留数求积分I=cos x x x dx 420109+++∞⎰的值.解:在上半平面内,f(z)=e z z iz()()2219++有一阶极点z=i 和z=3i.∵I=121912192222cos ()()Re()()xx x dx e x x dx ix++=++-∞+∞-∞+∞⎰⎰=12223Re{Re [(),]Re [(),]},ππi s f z i i s f z i + Res[f(z),i]=116ei, Res[f(z),3i]=-1483e i,∴ I ee =-π483132().24.设Z 平面上的区域为D :|z+i|>2,|z -i|<2,试求下列保角映射: (1)w 1=f 1(z)把D 映射成W 1平面上的角形域D 1:π4<argw 1<34π;(2)w 2=f 2(w 1)把D 1映射成W 2平面上的第一象限D 2:0<argw 2<π2;(3)w=f 3(w 2)把D 2映射成W 平面的上半平面G :Imw>0; (4)w=f(z)把D 映射成G. 解:(1)由||||z i z i +=-=⎧⎨⎪⎩⎪22解得交点z 1=1,z 2=-1.设w 1=z z -+11,则它把D 映射成W 1平面上的D 1:ππ4341<<arg .w (2)设w 2=ew i -π41,则它把D 1映射成W 2平面上的第一象限D 2:022<<arg .w π(3)设w=w 22,则它把D 2映射成W 平面的上半平面G :Imw>0. (4)w=()().ez z i z z i -⋅-+=--+π4221111。
