第5章课后习题参考答案

合集下载

基础会计学第5_6章课后复习题与参考答案

《基础会计学》第五章课后习题及参考答案第五章记账载体作业一：一，单项选择题1．日记账按分类用途属于（）A序时账簿 B备查账簿 C分类账簿 D联合账簿2．活页式账簿主要适用于（）A特种日记账 B总分类账簿 C普通日记账 D明细分类账簿3．特种日记账的账页格式有（）A三栏式和多栏式 B两栏式 C三栏式 D多栏式4．下列适用多栏式明细分类账簿的是（）A应付账款 B财务费用 C实收资本 D库存商品5．某会计人员根据记账凭证登账时，误将400元计为4000元，更正这种记账错误的方法是（）A红字冲销法 B补充登记法 C划线更正法 D以上三种任意一种都可以二，多项选择题1．账簿按其外表形式分类，可分为（）A序时账簿 B订本式账簿 C活页式账簿 D卡片式账簿2．会计账簿应具备的基本要素有（）A封面 B扉页 C账页 D封底3．下列会计凭证中，可以作为登记现金日记账的依据的是（）A现金收款凭证 B现金付款凭证 C现金支票存根 D银行存款付款凭证4．明细分类账可以根据（）登记A记账凭证 B原始凭证 C科目汇总表 D汇总原始凭证4．数量金额式明细账的账页格式适用于（）A产成品明细账 B生产成本明细账 C材料明细账 D应付账款明细账5．下列错误中，可以用红字冲销法更正的有（）A结账后发现的一切登记错误 B发现记账凭证中会计科目和金额都有错误，并且已经登记入账C发现记账凭证中所记会计科目有错，并已登记入账D在结账前发现记账凭证无误，但账簿记录中文字或数字过账错误。

三，判断题1．账簿是企业设置的全部账户的总称（）2．序时账簿、分类账簿、备查账簿是按账簿的外表形式作的分类。

（）3．备查账簿是和序时账簿以及分类账簿一样必须设置的。

（）4．企业出纳人员除了负责货币资金收付业务，还要登记现金和银行存款日记账和总账。

（）5．结账是在月终把某一月份发生的经济业务全部登记入账，计算和记录本期发生额和期末余额。

（）四，名词解释账簿序时账簿分类账簿五，简答题1．设置会计账簿有哪些作用？2．简述划线更正法的适用围和更正程。

第五章微机原理课后习题参考答案

习题五一. 思考题⒈半导体存储器主要分为哪几类？简述它们的用途和区别。

答：按照存取方式分，半导体存储器主要分为随机存取存储器RAM（包括静态RAM和动态RAM）和只读存储器ROM（包括掩膜只读存储器，可编程只读存储器，可擦除只读存储器和电可擦除只读存储器）。

RAM在程序执行过程中，能够通过指令随机地对其中每个存储单元进行读\写操作。

一般来说，RAM中存储的信息在断电后会丢失，是一种易失性存储器；但目前也有一些RAM 芯片，由于内部带有电池，断电后信息不会丢失，具有非易失性。

RAM的用途主要是用来存放原始数据，中间结果或程序，与CPU或外部设备交换信息。

而ROM在微机系统运行过程中，只能对其进行读操作，不能随机地进行写操作。

断电后ROM中的信息不会消失，具有非易失性。

ROM通常用来存放相对固定不变的程序、汉字字型库、字符及图形符号等。

根据制造工艺的不同，随机读写存储器RAM主要有双极型和MOS型两类。

双极型存储器具有存取速度快、集成度较低、功耗较大、成本较高等特点，适用于对速度要求较高的高速缓冲存储器；MOS型存储器具有集成度高、功耗低、价格便宜等特点，适用于内存储器。

⒉存储芯片结构由哪几部分组成？简述各部分的主要功能。

答：存储芯片通常由存储体、地址寄存器、地址译码器、数据寄存器、读\写驱动电路及控制电路等部分组成。

存储体是存储器芯片的核心，它由多个基本存储单元组成，每个基本存储单元可存储一位二进制信息，具有0和1两种状态。

每个存储单元有一个唯一的地址，供CPU访问。

地址寄存器用来存放CPU访问的存储单元地址，该地址经地址译码器译码后选中芯片内某个指定的存储单元。

通常在微机中，访问地址由地址锁存器提供，存储单元地址由地址锁存器输出后，经地址总线送到存储器芯片内直接进行译码。

地址译码器的作用就是用来接收CPU送来的地址信号并对它进行存储芯片内部的“译码”，选择与此地址相对应的存储单元，以便对该单元进行读\写操作。

数理经济学第5章课后题答案

第五章习题答案1．求下面等式约束最优化问题可能的极值点，要求写出一阶必要条件并求解由一阶必要条件构成的方程组。

（1）164..),(max 212121=+=x x t s x x x x f ，（2）32..),(min max 222122121=+=x x t s x x x x f or（3）11..),(min max 22=+=+=y x y x t s xy y x f or 和解：（1）首先写出拉格朗日函数：121212(,,)(164)L x x x x x x λλ=+--将L 对1x ，2x 和λ分别求偏导数可得：1221120401640x x L x L x L x x λλλ=-=⎧⎪=-=⎨⎪=--=⎩ 解得128, 2x x **==，2λ*=，此时16f =。

则点(8,2)为目标函数的驻点，且在该点处约束条件满足约束规格。

（2）首先写出拉格朗日函数：222121212(,,)(32)L x x x x x x λλ=+--\将L 对1x ，2x 和λ分别求偏导数可得：12121212221224020320x x L x x x L x x L x x λλλ=-=⎧⎪=-=⎨⎪=--=⎩ 解得121, 1x x **==，12λ*=，此时1f =；或者121, 1x x **==-，12λ*=-，此时1f =-；或者121, 1x x **=-=，12λ*=，此时1f =；或者121, 1x x **=-=-，12λ*=-，此时1f =-。

则点(1,1)、(1,1)-、(1,1)-和(1,1)--为目标函数的驻点，且在这些点处约束条件满足约束规格。

（3）首先写出拉格朗日函数：221212(,,,)(1)(1)L x y xy x y x y λλλλ=+--+--将L 对x ，y ，1λ和2λ分别求偏导数可得：1212122220201010x yL y x L x y L x y L x y λλλλλλ=--=⎧⎪=--=⎪⎨=--=⎪⎪=--=⎩ 解得111,0,2x y λ***===-2,1λ*=，此时0f =；或者110,1,2x y λ***===- ，21λ*=，此时0f =。

概率论与数理统计第五章课后习题及参考答案

概率论与数理统计第五章课后习题及参考答案1．用切比雪夫不等式估计下列各题的概率．(1)废品率为03.0，1000个产品中废品多于20个且少于40个的概率；(2)200个新生儿中，男孩多于80个而少于120个的概率(假设男孩和女孩的概率均为5.0)．解：(1)设X 为1000个产品中废品的个数，则X ～)1000,03.0(B ，有30)(=X E ，1.29)(=X D ，由切比雪夫不等式，得)3040303020()4020(-<-<-=<<X P X P )103010(<-<-=X P )1030(<-=X P 709.0101.2912=-≥．(2)设X 为200个新生儿中男孩的个数，则X ～)200,5.0(B ，有100)(=X E ，50)(=X D ，由切比雪夫不等式，得)10012010010080()12080(-<-<-=<<X P X P )2010020(<-<-=X P )20100(<-=X P 87205012=-≥．2．一颗骰子连续掷4次，点数总和记为X ，估计)1810(<<X P ．解：设i X 为该骰子掷第i 次出现的点数，则61)(==k X P i ，6,,2,1 =i ，6,,2,1 =k ．27)654321(61)(=+++++=i X E ，691)654321(61)(2222222=+++++=i X E ，35)]([)()(22=-=i i i X E X E X D ，4,3,2,1=i ．因为4321X X X X X +++=，且1X ，2X ，3X ，4X 相互独立，故有14)(=X E ，335)(=X D ．由切比雪夫不等式，得)1418141410()1810(-<-<-=<<X P X P )4144(<-<-=X P )414(<-=X P 271.0433512=-≥．3．袋装茶叶用及其装袋，每袋的净重为随机变量，其期望值为100g ，标准差为10g ，一大盒内装200袋，求一盒茶叶净重大于5.20kg 的概率．解：设i X 为一袋袋装茶叶的净重，X 为一盒茶叶的净重，由题可知∑==2001i i X X ，100)(=i X E ，100)(=i X D ，200,,2,1 =i ．因为1X ，2X ，…，200X 相互独立，则20000)()(2001==∑=i i X E X E ，20000)()(2001==∑=i i X D X D ．)()(20500)()(()20500(2001X D X E X D X E X P X P i i ->-=>∑=)1020020000205001020020000(⋅->⋅-=X P )2251020020000(>⋅-=X P 由独立同分布的中心极限定理，1020020000⋅-X 近似地服从)1,0(N ，于是0002.0)5.3(1)2251020020000(=Φ-≈>⋅-X P ．4．有一批建筑用木桩，其80%的长度不小于3m ．现从这批木桩中随机取出100根，试问其中至少有30根短于3m 的概率是多少？解：设X 为100根木桩中短于3m 的根数，则由题可知X ～)2.0,100(B ，有20)(=X E ，16)(=X D ，由棣莫弗—拉普拉斯定理，得)30(1)30(<-=≥X P X P )42030(1)()((1-Φ-=-Φ-=X D X E X 0062.0)5.2(1=Φ-=．5．某种电器元件的寿命服从均值为100h 的指数分布．现随机选取16只，设它们的寿命是相互独立的．求这16只元件寿命总和大于1920h 的概率．解：设i X 为第i 只电器元件的寿命，由题可知i X ～)01.0(E ，16,,2,1 =i ，且1X ，2X ，…，16X 相互独立，则100)(=i X E ，10000)(=i X D ．记∑==161i i X X ，则1600)()(161==∑=i i X E X E ，160000)()(161==∑=i i X D X D ．))()(1920)()(()1920(X D X E X D X E X P X P ->-=>)400160019204001600(->-=X P )8.04001600(>-=X P ，由独立同分布的中心极限定理，1600-X 近似地服从)1,0(N ，于是2119.0)8.0(1)8.04001600(=Φ-=>-X P ．6．在数值计算中中，每个数值都取小数点后四位，第五位四舍五入(即可以认为计算误差在区间]105,105[55--⨯⨯-上服从均匀分布)，现有1200个数相加，求产生的误差综合的绝对值小于03.0的概率．解：设i X 为每个数值的误差，则i X ～)105,105(55--⨯⨯-U ，有0)(=i X E ，1210)(8-=i X D ，1200,,2,1 =i ．从而0)()(12001==∑=i i X E X E ，61200110)()(-===∑i i X D X D ．由独立同分布的中心极限定理，X 近似地服从)10,0(6-N ，于是)03.0(<X P ))()(03.0)()((X D X E X D X E X P -≤-=12101200003.0121012000(44--⋅-≤⋅-=X P 9974.01)3(2=-Φ=．7．某药厂断言，该厂生产的某药品对医治一种疑难的血液病治愈率为8.0．医院检验员任取100个服用此药的病人，如果其中多于75个治愈，就接受这一断言，否则就拒绝这一断言．(1)若实际上此药对这种病的治愈率是8.0，问接受这一断言的概率是多少？(2)若实际上此药对这种病的治愈率是7.0，问接受这一断言的概率是多少？解：设X 为100个服用此药的病人中治愈的个数，(1)由题可知X ～)8.0,100(B ，则80)(=X E ，16)(=X D ，由棣莫弗—拉普拉斯定理，得)75(1)75(≤-=>X P X P 48075(1))()((1-Φ-=-Φ-=X D X E X 8944.0)25.1(=Φ=．(2)由题可知X ～)7.0,100(B ，则70)(=X E ，21)(=X D ，由棣莫弗—拉普拉斯定理，得)75(1)75(≤-=>X P X P 217075(1)()((1-Φ-=-Φ-=X D X E X 1379.0)09.1(1=Φ-=．8．一射手在一次射击中，所得环数的分布律如下表：X678910P 05.005.01.03.05.0求：(1)在100次射击中环数介于900环与930环之间的概率是多少？(2)超过950环的概率是多少？解：设X 为100次射击中所得的环数，i X 为第i 次射击的环数，则∑==1001i i X X ，15.9)(=i X E ，95.84)(2=i X E ，2275.1)]([)()(22=-=i i i X E X E X D ，100,,2,1 =i ．由1X ，2X ，…，100X 相互独立，得915)()(1001==∑=i i X E X E ，75.122)()(1001==∑=i i X D X D ．由独立同分布的中心极限定理，75.122915-X 近似地服从)1,0(N ，于是(1))930900(≤≤X P ))()(930)()()()(900(X D X E X D X E X X D X E P -≤-≤-=75.12291593075.12291575.122915900(-≤-≤-=X P )75.1221575.122915(≤-=X P 823.01)35.1(2=-Φ≈．(2))950(>X P ))()(950)()((X D X E X D X E X P ->-=75.122915950)()((->-=X D X E X P 001.0)1.3(1=Φ-≈．9．设有30个电子元件1A ，2A ，…，30A ，其寿命分别为1X ，2X ，…，30X ，且且都服从参数为1.0=λ的指数分布，它们的使用情况是当i A 损坏后，立即使用1+i A (29,,2,1 =i )．求元件使用总时间T 不小于350h 的概率．解：由题可知i X ～)1.0(E ，30,,2,1 =i ，则10)(=i X E ，100)(=i X D ．记∑==301i i X T ，由1X ，2X ，…，30X 相互独立，得300)()(301==∑=i i X E T E ，3000)()(301==∑=i i X D T D ．))()(350)()(()350(T D T E T D T E T P T P ->-=>30103003503010300(⋅->⋅-=T P )91.03010300(>⋅-≈T P ，由独立同分布的中心极限定理，3010300⋅-T 近似地服从)1,0(N ，于是1814.0)91.0(1)91.03010300(=Φ-=>⋅-T P ．10．大学英语四级考试，设有85道选择题，每题4个选择答案，只有一个正确．若需要通过考试，必须答对51道以上．试问某学生靠运气能通过四级考试的概率有多大？解：设X 为该学生答对的题数，由题可知X ～41,85(B ，则25.21)(=X E ，9375.15)(=i X D ，85,,2,1 =i ．由棣莫弗—拉普拉斯中心极限定理，近似地有9375.1525.21-X ～)1,0(N ，得)8551(≤≤X P ))()(85)()()()(51(X D X E X D X E X X D X E P -≤-≤-=)9375.1525.21859375.1525.219375.1525.2151(-≤-≤-=X P 0)45.7()97.15(=Φ-Φ=．即学生靠运气能通过四级考试的概率为0．。

自动控制原理及其应用课后习题第五章答案

40 20 0 -20 -20dB/dec 10 1 2ωc -40dB/dec -60dB/dec 40 -40dB/dec
ω
20 0 -20
10 ωc
1
2 -20dB/dec
ω
-60dB/dec
10 ≈1 ω2 0.5 c
ω c=4.5
5 ≈1 ω c=7.9 ω 0.01 c3
第五章习题课 (5-17)
-20
低频段曲线：低频段曲线： 20lgK=20dB φ (ω ) 0 ω1=5 ω2=15 -90 相频特性曲线：相频特性曲线： -180 -270 φ ( )= -90o ω ω=0 φ ( )= -270o ω ω=∞
-60dB/dec
ω
第五章习题课 (5-2)
10(s+0.2) 1.33(5s+1) (5) G(s)= s2(s+0.1)(s+15)=s2(10s+1)(0.67s+1) 解：低频段曲线：低频段曲线： 20lgK=2.5dB
第五章习题课 (5-7)
5-7 已知奈氏曲线，p为不稳定极点个数，已知奈氏曲线，为不稳定极点个数为不稳定极点个数， υ为积分环节个数，试判别系统稳定性。为积分环节个数，试判别系统稳定性。 Im υ=2 (b) p=0 (a) p=0 Im υ=0
ω=0 Re -1 0 ω=0+ -1 0 ω=0 Re
第五章习题课 (5-1)
5-1(1) 已知单位负反馈系统开环传递函数，已知单位负反馈系统开环传递函数，当输入信号r(t)=sin(t+30o)，试求系统的稳态当输入信号，输出。输出。 10 G(s)=(s+1) 10 解： φ(s)= (s+11) 10 = 10 = 10 ω A( )= 2 2 112+1√ 122 =0.905 √ 11 +( ) √ ω φ ( )=-tg-1ω =-tg-1 1 =-5.2o ω 11 11 cs(t)=0.9sin(t+24.8o)

第五章课后习题答案

5.10 假设对指令Cache 的访问占全部访问的75%；而对数据Cache 的访问占全部访问的25%。

Cache 的命中时间为1个时钟周期，失效开销为50 个时钟周期，在混合Cache 中一次load 或store 操作访问Cache 的命中时间都要增加一个时钟周期，32KB 的指令Cache 的失效率为0.39%，32KB 的数据Cache 的失效率为4.82%，64KB 的混合Cache 的失效率为1.35%。

又假设采用写直达策略，且有一个写缓冲器，并且忽略写缓冲器引起的等待。

试问指令Cache 和数据Cache 容量均为32KB 的分离Cache 和容量为64KB 的混合Cache 相比，哪种Cache 的失效率更低？两种情况下平均访存时间各是多少？解：（1）根据题意，约75%的访存为取指令。

因此，分离Cache 的总体失效率为：（75%×0.15%）＋（25%×3.77%）＝1.055%；容量为128KB 的混合Cache 的失效率略低一些，只有0.95%。

（2）平均访存时间公式可以分为指令访问和数据访问两部分：平均访存时间＝指令所占的百分比×（读命中时间＋读失效率×失效开销）＋数据所占的百分比×（数据命中时间＋数据失效率×失效开销）所以，两种结构的平均访存时间分别为：分离Cache 的平均访存时间＝75%×（1＋0.15%×50）＋25%×（1＋3.77%×50）＝（75%×1.075）＋（25%×2.885）＝1.5275混合Cache 的平均访存时间＝75%×（1＋0.95%×50）＋25%×（1＋1＋0.95%×50）＝（75%×1.475）＋（25%×2.475）＝1.725因此，尽管分离Cache 的实际失效率比混合Cache 的高，但其平均访存时间反而较低。

第五章课后习题及答案

第五章中学生的情绪管理一、理论测试题（一）单项选择题1．（）是人各种感觉、思想和行为的一种综合的心理和生理状态，是对外界刺激所产生的心理反应，以及附带的生理反应，如喜、怒、哀、乐等。

A．情绪B．情感C．心情D．态度2．（）是指人或动物面对现实的或想象中的危险、自己厌恶的事物等产生的处于惊慌与紧急的状态。

A．快乐B．愤怒C．恐惧D．悲哀3．小华即将上考场，感觉心跳加速，有点微微出汗，这属于情绪的（）。

A．外部表现B．主观体验C．生理唤醒D．认知活动4．下列不属于基本情绪的是（）。

A．快乐B．焦虑C．恐惧D．悲哀5．王悦接到高考录取通知书已经十多天了，仍心情愉悦，往常觉得平淡的事也能让她很高兴，这种情绪状态属于（）。

A．激情B．心境C．应激6.“情急生智”所描述的一种情绪状态是（）。

A．心境B．理智C．应激D．激情7．“忧者见之则忧，喜者见之则喜”，这是受一个人的（）影响所致。

A．激情B．心境C．应激D．热情8．（）是一种猛烈、迅疾和短暂的情绪，类似于平时说的激动。

A．快乐B．应激C．心境D．激情9．狂喜、恐惧的情绪状态属于（）。

A．激情B．热情C．应激D．心境10．学生临考的怯场属于（）。

A．应激B．心境C．激情D．热情11．车祸、地震、水灾等突如其来的灾难引起的情绪体验是（）。

A．心境B．激情C．应激12．晓东在解决了困扰他许久的数学难题后出现的喜悦感属于（）。

A．道德感B．理智感C．美感D．效能感13．求知欲属于（）。

A．道德感B．理智感C．美感D．应激14．“先天下之忧而忧，后天下之乐而乐”是（）。

A．道德感B．理智感C．美感D．热情15．当同学们获悉本班取得学校合唱比赛第一名的成绩时欣喜若狂。

他们的情绪状态属于（）。

A．心境B．激情C．应激D．热情16．当人们遇到突然出现的事件或意外发生危险时，为了应付这类瞬息万变的紧急情境，就得果断地采取决定。

这种情况属于（）。

A．激情B．应激C．快乐D．心境17．（）用因素分析的方法，提出人类具有8～11种基本情绪，它们是兴趣、惊奇、痛苦、厌恶、愉快、愤怒、恐惧、悲伤、害羞、轻蔑、自罪感。

现代通信原理第5章课后习题及答案

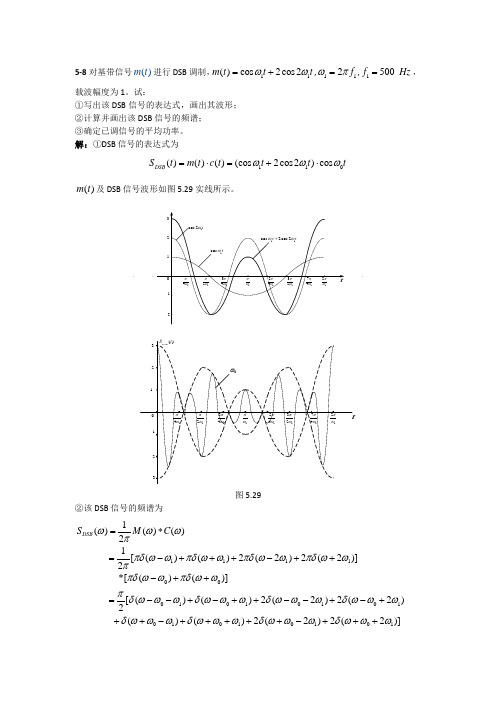
5-8对基带信号()m t 进行DSB 调制，11()cos 2cos2m t t t ωω=+,112f ωπ=,1500f Hz = ，载波幅度为1。

试：①写出该DSB 信号的表达式，画出其波形； ②计算并画出该DSB 信号的频谱； ③确定已调信号的平均功率。

解：①DSB 信号的表达式为110()()()(cos 2cos2)cos DSB S t m t c t t t t ωωω=⋅=+⋅()m t 及DSB 信号波形如图5.29实线所示。

图5.29②该DSB 信号的频谱为111100*********()()()21[()()2(2)2(2)]2*[()()][()()2(2)2(2)2(DSB S M C ωωωππδωωπδωωπδωωπδωωππδωωπδωωπδωωωδωωωδωωωδωωωδωω=∗ =−+++−++ −++ =−−+−++−−+−+ ++01010101)()2(2)2(2)]ωδωωωδωωωδωωω−+++++−+++频谱图如图5.30所示图5.30③已调信号的平均功率为221122111111111()21(cos 2cos 2)2cos 4cos cos 24cos 2(1cos 2)2(cos3cos )2(1cos 4)12.5 1.252DSB fBP P m t t t t t t tt t t t Wωωωωωωωωωω===+ ++ +++++ ==××1=211= 22 5-9 设SSB 发射机被一正弦信号()m t 调制，1()5cos m t t ω=，112f ωπ=，1500f Hz = ，载波幅度为1。

试：①计算()m t 的希尔伯特变换ˆ()mt ； ②确定下边带SSB 信号的表达式； ③确定SSB 信号的均方根（rms ）值； ④确定SSB 信号的峰值； ⑤确定SSB 信号的平均功率。

解：①1()5cos m t t ω=，其傅里叶变换为11()5[()()]M ωπδωωδωω=−++其希尔伯特变换的频谱为ˆ()sg n ()()Mj M j ωωωπδωωδωω11=−⋅ =5[(+)−(−)]因此，m(t)的希尔伯特变换为1ˆ()[()]5sin m t m t t ω==H②下边带SSB 信号的表达式为00101001ˆ()()co s ()sin 5cos cos 5sin sin 5cos[()]SSB S t m t t m t t t t t t t ωωωωωωωω=+ =⋅+⋅ =− ③以下边带SSB 信号为例，有SSB rms = ==④由下边带SSB 信号表达式可知，信号峰值为 max ()|5SSB S t =⑤SSB 信号平均功率为 225()12.52SSBSSB P S t W === 5-17已知幅度调制信号()AM S t 的总功率为200kW ，调制信号()f t 的最高频率 5 m f kHz =，载波频率810 o f kHz =，边带功率为40kW ，信道中噪声的双边功率谱密度，系统采用包络检波解调。

王孝玲《教育统计学》第五章课后练习题超详细解答步骤

考试科目物理化学数学总和
标准分数甲生 -3 0.67 0.92 -1.41 乙生 2 -0.67 -0.08 1.25
在团体中的位置（在改分数之下的人数比例）甲生 0.00135 0.74857 0.82121 乙生 0.97725 0.25143 0.46812
5
总平均
-0.47
0.416667
18（人）
226（人）
11 （人）
18（人）
6
13. 答：首先，通过人数比例计算每个等级的所占面积；其次，寻找每个面积对应的中位数来代表等级的数量化分数教师甲（人等级优良中差极差总和数） 10 20 5 5 0 40 甲比率（人数比例） 0.25 0.5 0.125 0.125 0 本组 1/2 至 Z=0 的面积 0.375 0 0.3125 0.4375 中位数 1.15 0 -0.89 -1.53 -
7. 答： (1) 直接查表 (2) P(2.8)-P(0.5)= 0.49744 – 0.19146=0.30598 (3) 直接查绝对值 (4) P(-1.5)+P(1.8)=0.43319+0.46407=0.89726 (5) P(-1.8)-P(-0.5)= 0.46407-0.19146=0.27261 (6) P(-2.5)+P(0.8)=0.49379+0.28814=0.78193 8. 答： (1) 直接查绝对值 (2) 直接查表 (3) P(Z)=0.5-0.2=0.3 ~ 0.29955 Y=0.28034 (4) P(Z)=0.8/2=0.4 ~ 0.39973 Y=0.17585
本组 1/2 至 Z=0 的
中位数

第5章-经营决策分析习题

D．单位的产品总成本为400元
三、判断题
1、相关成本与无关成本的区分并不是绝对的（）
2、专门生产某种产品的专用设备折旧费，保险费属于该产品的专属成本（）
3、差量分析法一般仅适用于两个方案之间的比较（）
4、如果一项资产只能用于某一职能，则不会产生机会成本（）
5、机会成本是一项实际指出，应登记入账（）
6、在任何情况下，边际成本都与变动成本一致（）
要求：（1）分别计算完全成本法下的单位产品生产成本和成本加成率指标；
（2）分别计算变动成本法下的单位产品成本和成本成定价法确定目标售价。
第五章习题参考答案
一、单选题
1-5 DBAAB
6-10 CCAAC
11-14BCDC
二、多选题
1、ABCD
（4）条件同（3），但企业也可以采纳用剩余生产能力自制15000个零件甲，其余全部外购的方式。
3、某企业生产过程中需要的零件甲的年需要量不确定。企业可以选择外购或自制该零件：其中自制零件方案需增添专业设备两台，每台价值100000元，使用期限5年，假定没有残值，按直线法进行折旧，每年为40000元，另外单位变动成本为58元；外购单价为60元。要求：判断该厂应自制还是外购零甲。
7、沉没成本是现在发生的，无法由现在或将来的任何决策所改变的成本（）
8、联合成本是由多个产品或部门共同负担的成本，因此属于相关成本，决策时应考虑（）
四、计算题
1、某企业生产ABC三种产品，有关资料如下，
项目
A
B
C
合计
销售量
1000
1200
1800
单位售价
900
700
500
单位变动成本
700
580

第5章课后习题参考答案

}
printf("一行字符中字母#和a出现的次数分别是%d，%d\n ",num1,num2);
}
6、从键盘输入一个正整数，统计该数的位数，如输入1234，输出4，输入0，输出1
#include<stdio.h>
void main()
{
int n,m,num=0;
printf("请输入一个正整数n：");
}
ave=sum/num2;
printf("负数个数num1=%d，正数的平均值ave=%.2f\n",num1,ave);
}
2、sum=2+5+8+11+14+…，输入正整数n，求sum的前n项和。
#include<stdio.h>
void main()
{
int i,n,sum=0;
#include<stdio.h>
void main()
{
char ch;
int num1=0,num2=0;
printf("请输入一行字符：\n");
while((ch=getchar())!='\n')
{
if(ch=='#') num1++;
if(ch=='a') num2++;
#include<stdio.h>
void main()
{
int x,y,z,num=0;
for(x=1;x<=9;x++)

第5章 0~3岁婴幼儿动作指导活动的设计与组织【课后习题及参考答案】

第五章0~3岁婴幼儿动作指导活动的设计与组织【课后习题及参考答案】1.在设计0~3岁婴幼儿动作指导活动的目标时，有哪些注意事项？答：①目标设计要兼顾适宜性与发展性。

①目标设计要考虑带养人的需求。

①目标设计要具体、明确、具有可操作性。

①目标在陈述时应考量主体、动词及程度等因素。

2.请针对10月龄宝宝的站立动作，分别设计两个指导活动。

答：活动1：晃一晃活动目标：锻炼宝宝站立的能力以及发展平衡感，增进亲子感情。

活动准备：柔软的地垫。

活动过程：1.开始环节（1）解释：“今天这个活动主要是锻炼宝宝站立的能力以及宝宝的平衡感，同时在欢快的儿歌中，孩子也会感到情绪愉悦，以增进和爸爸妈妈的感情。

”（2）导入：“宝宝，我们一起来玩一个晃一晃的游戏吧！”（3）示范：教师和玩偶娃娃面对面站好或站在玩偶娃娃的身后，用手扶住玩偶娃娃的腋下，帮助玩偶娃娃站稳，用缓慢有节奏的声音念儿歌，并配合做相应的动作。

儿歌《晃一晃》晃一晃，晃一晃，晃到空中追云朵（轻轻左右摇晃宝宝，再把宝宝举高）。

晃一晃，晃一晃，晃到水面捞小鱼（轻轻左右摇晃宝宝，再把宝宝放低转一圈，让宝宝站立在地垫上）。

晃一晃，晃一晃，亲亲宝贝长高了（轻轻左右摇晃宝宝，再把宝宝微微抛高后接住，再放低，让宝主站立在地垫上）。

2.主体环节家长带领孩子一起做摇啊摇的游戏，教师巡回观察指导。

提示家长动作幅度不要太大，避免宝宝感到不安和害怕。

3.结束环节（1）教师对家长再次强调此次动作训练的指导要点（即示范环节里的内容），并对今天孩子的表现与家长的指导做适当的点评。

（2）鼓励家长回家后可以换其他儿歌继续进行训练。

（3）和孩子温柔地拥抱告别。

活动2：扶着走活动目标：锻炼宝宝走步能力与平衡能力。

活动准备：圆形的体操圈。

活动过程：1.开始环节（1）解释：“今天这个活动可以让宝宝借助一定的外力，慢慢练习走步的能力，并在这个过程中逐渐学会控制自己身体的平衡。

”（2）导入：“宝宝，快看，今天老师给你们带来了一个好玩的体操圈，快看看老师是怎么跟它玩的，一会儿也邀请你们来和它一起玩哦。

《电磁场与电磁波》课后习题解答(第五章)

《电磁场与电磁波》课后习题解答(第五章)————————————————————————————————作者：————————————————————————————————日期：习题及参考答案5.1 一个点电荷 Q 与无穷大导体平面相距为d ，如果把它移动到无穷远处，需要作多少功？解：用镜像法计算。

导体面上的感应电荷的影响用镜像电荷来代替，镜像电荷的大小为-Q ，位于和原电荷对称的位置。

当电荷Q 离导体板的距离为x 时，电荷Q 受到的静电力为2)2(042x Q F επ-=静电力为引力，要将其移动到无穷远处，必须加一个和静电力相反的外力2)2(042x Q f επ=在移动过程中，外力f 所作的功为d Q d dx dx Q dx f 016220162επεπ=⎰∞⎰∞= 当用外力将电荷Q 移动到无穷远处时，同时也要将镜像电荷移动到无穷远处，所以，在整个过程中，外力作的总功为dq8/2επ。

也可以用静电能计算。

在移动以前，系统的静电能等于两个点电荷之间的相互作用能：d Q d Q Q d Q Q q q W 082)2(04)(21)2(042122211121επεπεπϕϕ-=-+-=+=移动点电荷Q 到无穷远处以后，系统的静电能为零。

因此，在这个过程中，外力作功等于系统静电能的增量，即外力作功为dq8/2επ。

5．2 一个点电荷放在直角导体内部（如图5-1），求出所有镜像电荷的位置和大小。

解：需要加三个镜像电荷代替导体面上的感应电荷。

在（-a ，d ）处，镜像电荷为-q ，在（错误！链接无效。

）处，镜像电荷为q ，在（a ，-d ）处，镜像电荷为-q 。

图5-1 5．3 证明：一个点电荷q 和一个带有电荷Q 、半径为R 的导体球之间的作用力为]2)22(2[04R D DRq D D qR Q q F --+=επ其中D 是q 到球心的距离（D ＞R ）。

证明：使用镜像法分析。

机械设计基础第5章课后习题参考答案

第五章5-1 齿轮传动的最基本要求是什么？齿廓的形状符合什么条件才能满足上述要求？答：齿轮传动最基本要求是其瞬时转速比（或传动比）要恒定不变；如果采用的齿廓曲线能使两齿廓在任何位置啮合时，其公法线都通过中心连线上的定点P，则其任何瞬时传动比都为定值。

5-2 简单叙述齿廓啮合基本定律。

答：两齿轮转动角速度比（传动比i12）等于其中心连线O1O2被齿廓啮合点的公法线分成的两段的反比，即i12=ω1/ω2=O2N2/O1N1=O2P/O1P。

5-3 分度圆和节圆，压力角和啮合角有何区别？答：以齿轮转动中心（O1、O2）为圆心，过节点P所作的圆称为节圆，在节点P处圆周速度相等，且节圆是在啮合传动时存在，对于单个齿轮并不存在节圆；而分度圆是人为假想的一个圆，齿轮上模数和压力角均为标准值的圆，分度圆对于单个的齿轮是存在的。

当两个标准齿轮在标准中心距间啮合时，节圆与分度圆重合。

压力角是相对分度圆而言的，指齿轮分度圆处法线与速度方向之间所夹的锐角，而啮合角是相对于节圆而言的，指节圆的公切线与啮合线N1N2之间所夹的锐角，一对标准齿轮在标准中心距间啮合传动时，其啮合角α’等于分度圆压力角α；而对非标准中心距啮合传动时，啮合角与压力角关系是：a’*cosα’=a*cosα，其中a是标准中心距，a’是实际啮合中心距。

5-5 某直齿圆柱齿轮传动的小齿轮已丢失，但已知与之相配的大齿轮为标准齿轮，其齿数Z2=52，齿顶圆直径d a2=135mm，标准安装中心距a=112.5mm。

试求丢失的小齿轮的齿数、模数、分度圆直径、齿顶圆直径，齿根圆直径。

答：由公式d a2=d2+2h a=(z2+2h a*)m，且由于是标准齿轮，齿顶高系数h a*=1代入数值，可得模数m=2.5 mm，即小齿轮模数也为2.5 mm标准中心距a=(d1+d2)/2=m(z1+z2)/2代入数值，可得小齿轮齿数Z1=38，分度圆直径d1=mz1=95mm齿顶圆直径d a1=d1+2h a=(z1+2h a*)m=(38+2*1)*2.5=100mm齿根圆直径d f1=d1-2h f=(z1-2h a*-2 c*)m=(38-2*1-2*0.25)*2.5=88.75mm5-7 当α=20o的正常齿渐开线标准齿圆柱齿轮的齿根圆和基圆相重合时，其齿数应为多少？又若齿数大于求出的数值，则基圆和齿根圆哪一个大？答：对于正常齿渐开线标准圆柱齿轮，齿顶高系数h a*=1，顶隙系数c*=0.25齿根圆直径d f=d-2h f=(z-2h a*-2 c*)m基圆直径d b=dcosα=mzcosα联立上述两公式，可求z=41.45，取整z=42此外，d f/d b=(z-2h a*-2 c*)m/ mzcosα=(z-2.5)/zcosα由于压力角α不变，由上述公式可知，若齿数大于求出的数值，则d f/d b＞1，因此齿根圆大。

第5章课后习题参考答案

第五章习题参考答案3．给定一个单位立方体，一个顶点在(0，0，0)，相对的另一个顶点在(1，1，1)，过这两个顶点连接一条直线，将单位立方体绕该直线旋转θ角，试导出变换矩阵。

解答：需进行以下复合变换：⑴绕Z轴旋转-45。

角，变换矩阵为：/220 0T1= 2/20 00 1 00 0 1⑵绕Y轴旋转2)角，变换矩阵为：/30 30T2= 0 1 0 030 300 0 0 1⑶绕X轴旋转θ角，变换矩阵为：1 0 0 0T3= 0 cosθs i nθ00 -sinθc o sθ00 0 0 1⑷绕Y轴旋转2)角，变换矩阵为：/30 30T4= 0 1 0 030 300 0 0 1⑸绕Z 轴旋转45。

角，变换矩阵为：/2/20 0 T5= 2/20 0 0 0 1 00 0 0 1 故最后的变换矩阵为： T=T1T2T3T4T5=1/32/3cos θ+ 1/3/3s i n1/3c o s θθ+- 1/3/3s i n 1/3c o s θθ-- 0 1/33sin 1/3cos θθ-- 1/32/3c o s θ+ 1/3/3s i n1/3c o s θθ+- 01/33sin 1/3cos θθ+- 1/3/3s i n1/3c o s θθ-- 1/32/3c o s θ+ 00 0 0 1 6．编程绘制第5题中三棱锥的正等轴测和正二测图。

同上类似，只是变换矩阵改为T 正等=0.70700.40800.70700.4080000.816001-⎡⎤⎢⎥--⎢⎥⎢⎥⎢⎥⎣⎦和T 正二=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡---1000943.0000312.00354.00118.00935.07．编程绘制第5题中三棱锥的斜等测和斜二测投影图。

同上类似，变换矩阵改为：T 斜等=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-1001000707.00707.00001T斜二=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-1001000354.00354.000018．编程绘制第5题中三棱锥的立体一点、二点和三点透视图。

大学物理课后习题答案第五章

第五章机械波5．1 已知一波的波动方程为y = 5×10-2sin(10πt – 0.6x ) (m)．（1）求波长、频率、波速及传播方向；（2）说明x = 0时波动方程的意义，并作图表示． [解答]（1）与标准波动方程比较得：2π/λ= 0.6，因此波长为：λ = 10.47(m)；圆频率为：ω = 10π，频率为：v =ω/2π = 5(Hz)；波速为：u = λ/T = λv = 52.36(m·s -1)．且传播方向为x 轴正方向．（2）当x = 0时波动方程就成为该处质点的振动方程： y = 5×10-2sin10πt = 5×10-2cos(10πt – π/2)，振动曲线如图．5．2 一平面简谐波在媒质中以速度为u = 0.2m·s -1沿x 轴正向传播，已知波线上A 点（x A = 0.05m ）的振动方程为(m)．试求：（1）简谐波的波动方程；（2）x= -0.05m 处质点P 处的振动方程．[解答]（1）简谐波的波动方程为：；即= 0.03cos[4π(t – 5x ) + π/2]．（2）在x = -0.05m 处质点P 点的振动方程为：y = 0.03cos[4πt + π + π/2]= 0.03cos(4πt - π/2)．5．3已知平面波波源的振动表达式为(m)．求距波源5m 处质点的振动方程和该质点与波源的位相差．设波速为2m·s -1．[解答]振动方程为：，位相差为 Δφ = 5π/4(rad)．5．4有一沿x 轴正向传播的平面波，其波速为u = 1m·s -1，波长λ = 0.04m ，振幅A = 0.03m ．若以坐标原点恰在平衡位置而向负方向运动时作为开始时刻，试求：（1）此平面波的波动方程；（2）与波源相距x = 0.01m 处质点的振动方程，该点初相是多少？ [解答]（1）设原点的振动方程为：y 0 = A cos(ωt + φ)，其中A = 0.03m ．由于u = λ/T ，所以质点振动的周期为：T = λ/u = 0.04(s)，圆频率为：ω = 2π/T = 50π．当t = 0时，y 0 = 0，因此cos φ = 0；由于质点速度小于零，所以φ = π/2．原点的振动方程为：y 0 = 0.03cos(50πt + π/2)，平面波的波动方程为：= 0.03cos[50π(t – x ) + π/2)．（2）与波源相距x = 0.01m 处质点的振动方程为：y = 0.03cos50πt ．该点初相φ = 0．5．5一列简谐波沿x 轴正向传播，在t 1 = 0s ，t 2 = 0.25s 时刻的波形如图所示．试求：（1）P 点的振动表达式；2cos()xy A t πωλ=-0.03cos(4)2A y t ππ=-cos[()]Ax x y A t uωϕ-=-+0.050.03cos[4()]0.22x y t ππ-=--20 6.010sin2y t π-=⨯26.010sin()2xy t u π-=⨯-50.06sin()24t ππ=-0.03cos[50()]2x y t u ππ=-+（2）波动方程；（3）画出O 点的振动曲线．[解答]（1）设P 点的振动方程为y P = A cos(ωt + φ)，其中A = 0.2m ．在Δt = 0.25s 内，波向右传播了Δx = 0.45/3 = 0.15(m)，所以波速为u = Δx/Δt = 0.6(m·s -1)．波长为：λ = 4Δx = 0.6(m)，周期为：T = λ/u = 1(s)，圆频率为：ω = 2π/T = 2π．当t = 0时，y P = 0，因此cos φ = 0；由于波沿x 轴正向传播，所以P 点在此时向上运动，速度大于零，所以φ = -π/2．P 点的振动表达式为：y P = 0.2cos(2πt - π/2)．（2）P 点的位置是x P = 0.3m ，所以波动方程为．（3）在x = 0处的振动方程为y 0 = 0.2cos(2πt + π/2)，曲线如图所示．5．6 如图所示为一列沿x 负向传播的平面谐波在t = T /4时的波形图，振幅A 、波长λ以及周期T 均已知．（1）写出该波的波动方程；（2）画出x = λ/2处质点的振动曲线；（3）图中波线上a 和b 两点的位相差φa – φb 为多少？[解答]（1）设此波的波动方程为：，当t = T /4时的波形方程为：．在x = 0处y = 0，因此得sin φ = 0，解得φ = 0或π．而在x = λ/2处y = -A ，所以φ = 0．因此波动方程为：．（2）在x = λ/2处质点的振动方程为：，曲线如图所示．（3）x a = λ/4处的质点的振动方程为； x b = λ处的质点的振动方程为．波线上a 和b 两点的位相差φa – φb = -3π/2．0.2cos[2()]2P x x y t u ππ-=--100.2cos(2)32t x πππ=-+cos[2()]t xy A T πϕλ=++cos(2)2xy A ππϕλ=++sin(2)xA πϕλ=-+cos 2()t x y A T πλ=+cos(2)cos 2t t y A A T Tπππ=+=-cos(2)2a t y A T ππ=+cos(22)b ty A Tππ=+图5.55．7 已知波的波动方程为y = A cosπ(4t – 2x )（SI ）．（1）写出t = 4.2s 时各波峰位置的坐标表示式，并计算此时离原点最近的波峰的位置，该波峰何时通过原点？（2）画出t = 4.2s 时的波形曲线．[解答]波的波动方程可化为：y = A cos2π(2t – x )，与标准方程比较，可知：周期为T = 0.5s ，波长λ = 1m ．波速为u = λ/T = 2m·s -1．（1）当t = 4.2s 时的波形方程为 y = A cos(2πx – 16.8π)= A cos(2πx – 0.8π)．令y = A ，则cos(2πx – 0.8π) = 1，因此 2πx – 0.8π = 2k π，(k = 0, ±1, ±2,…)，各波峰的位置为x = k + 0.4，(k = 0, ±1, ±2,…)．当k = 0时的波峰离原点最近，最近为：x = 0.4(m)．通过原点时经过的时间为：Δt = Δx/u = (0 – x )/u = -0.2(s)，即：该波峰0.2s 之前通过了原点．（2）t = 0时刻的波形曲线如实线所示．经过t = 4s 时，也就是经过8个周期，波形曲线是重合的；再经Δt = 0.2s ，波形向右移动Δx = u Δt = 0.4m ，因此t = 4.2s 时的波形曲线如虚线所示．[注意]各波峰的位置也可以由cos(2πx – 16.8π) = 1解得，结果为x = k + 8.4，(k = 0, ±1, ±2,…)，取同一整数k 值，波峰的位置不同．当k = -8时的波峰离原点最近，最近为x = 0.4m ．5．8一简谐波沿x 轴正向传播，波长λ = 4m ，周期T = 4s ，已知x = 0处的质点的振动曲线如图所示．（1）写出时x = 0处质点的振动方程；（2）写出波的表达式；（3）画出t = 1s 时刻的波形曲线．[解答]波速为u = λ/T = 1(m·s -1)．（1）设x = 0处的质点的振动方程为y = A cos(ωt + φ)，其中A = 1m ，ω = 2π/T = π/2．当t = 0时，y = 0.5，因此cos φ = 0.5，φ = ±π/3．在0时刻的曲线上作一切线，可知该时刻的速度小于零，因此φ = π/3．振动方程为：y = cos(πt /2 + π/3)．（2）波的表达式为：．（3）t = 1s 时刻的波形方程为，波形曲线如图所示．5．9在波的传播路程上有A 和B 两点，都做简谐振动，B 点的位相比A 点落后π/6，已知A 和B 之间的距离为2.0cm ，振动周期为2.0s ．求波速u 和波长λ．cos[2()]t x y A T πϕλ=-+cos[2()]t xy A T πϕλ=-+cos[()]23t x ππ=-+5cos()26y x ππ=-图5.8[解答]设波动方程为：，那么A 和B 两点的振动方程分别为：，．两点之间的位相差为：，由于x B – x A = 0.02m ，所以波长为：λ = 0.24(m)．波速为：u = λ/T = 0.12(m·s -1)． 5．10 一平面波在介质中以速度u = 20m·s -1沿x 轴负方向传播．已知在传播路径上的某点A 的振动方程为y = 3cos4πt ．（1）如以A 点为坐标原点，写出波动方程；（2）如以距A 点5m 处的B 点为坐标原点，写出波动方程；（3）写出传播方向上B ，C ，D 点的振动方程． [解答]（1）以A 点为坐标原点，波动方程为．（2）以B 点为坐标原点，波动方程为．（3）以A 点为坐标原点，则x B = -5m 、x C = -13m 、x D = 9m ，各点的振动方程为，，．[注意]以B 点为坐标原点，求出各点坐标，也能求出各点的振动方程．5．11 一弹性波在媒质中传播的速度u = 1×103m·s -1，振幅A = 1.0×10-4m ，频率ν= 103Hz ．若该媒质的密度为800kg·m -3，求：（1）该波的平均能流密度；（2）1分钟内垂直通过面积S = 4×10-4m 2的总能量． [解答]（1）质点的圆频率为：ω = 2πv = 6.283×103(rad·s -1)，波的平均能量密度为：= 158(J·m -3)，平均能流密度为：= 1.58×105(W·m -2)．（2）1分钟内垂直通过面积S = 4×10-4m 2的总能量为：E = ItS = 3.79×103(J)．5．12一平面简谐声波在空气中传播，波速u = 340m·s -1，频率为500Hz ．到达人耳时，振幅A = 1×10-4cm ，试求人耳接收到声波的平均能量密度和声强？此时声强相当于多少分贝？已知空气密度ρ = 1.29kg·m -3．[解答]质点的圆频率为：ω = 2πv = 3.142×103(rad·s -1)，声波的平均能量密度为：= 6.37×10-6(J·m -3)， cos[2()]t xy A T πϕλ=-+cos[2()]AA x ty A T πϕλ=-+cos[2()]BB x ty A Tπϕλ=-+2(2)6BAx x πππλλ---=-3cos 4()3cos(4)5x x y t t u πππ=+=+3cos 4()Ax x y t u π-=+3cos(4)5x t πππ=+-3cos 4()3cos(4)BB x y t t u πππ=+=-33cos 4()3cos(4)5C C x y t t u πππ=+=-93cos 4()3cos(4)5D D x y t t u πππ=+=+2212w A ρω=I wu =2212w A ρω=图5.10平均能流密度为：= 2.16×10-3(W·m -2)，标准声强为：I 0 = 1×10-12(W·m -2)，此声强的分贝数为：= 93.4(dB)．5．13 设空气中声速为330m·s -1．一列火车以30m·s -1的速度行驶，机车上汽笛的频率为600Hz ．一静止的观察者在机车的正前方和机车驶过其身后所听到的频率分别是多少？如果观察者以速度10m·s -1与这列火车相向运动，在上述两个位置，他听到的声音频率分别是多少？[解答]取声速的方向为正，多谱勒频率公式可统一表示为，其中v S 表示声源的频率，u 表示声速，u B 表示观察者的速度，u S 表示声源的速度，v B 表示观察者接收的频率．（1）当观察者静止时，u B = 0，火车驶来时其速度方向与声速方向相同，u S = 30m·s -1，观察者听到的频率为= 660(Hz)．火车驶去时其速度方向与声速方向相反，u S = -30m·s -1，观察者听到的频率为= 550(Hz)．（2）当观察者与火车靠近时，观察者的速度方向与声速相反，u B = -10m·s -1；火车速度方向与声速方向相同，u S = 30m·s -1，观察者听到的频率为= 680(Hz)．当观察者与火车远离时，观察者的速度方向与声速相同，u B = 10m·s -1；火车速度方向与声速方向相反，u S = -30m·s -1，观察者听到的频率为= 533(Hz)． [注意]这类题目涉及声速、声源的速度和观察者的速度，规定方向之后将公式统一起来，很容易判别速度方向，给计算带来了方便．5．14．一声源的频率为1080Hz ，相对地面以30m·s -1速率向右运动．在其右方有一反射面相对地面以65m·s -1的速率向左运动．设空气中声速为331m·s -1．求：（1）声源在空气中发出的声音的波长；（2）反射回的声音的频率和波长．[解答]（1）声音在声源垂直方向的波长为：λ0 = uT 0 = u /ν0 = 331/1080 = 0.306(m)；在声源前方的波长为：λ1 = λ0 - u s T 0 = uT 0 - u s T 0 = (u - u s )/ν0 = (331-30)/1080 = 0.2787(m)；在声源后方的波长为：λ2 = λ0 + u s T 0 = uT 0 + u s T 0 = (u + u s )/ν0= (331+30)/1080 = 0.3343(m)．（2）反射面接收到的频率为 = 1421(Hz)．将反射面作为波源，其频率为ν1，反射声音的频率为= 1768(Hz)．I wu =010lgIL I =BB S Su u u u νν-=-33060033030B S S u u u νν==--33060033030B S S u u u νν==-+3301060033030B B S S u u u u νν-+==--3301060033030B B S S u u u u νν--==-+1033165108033130B Su u u u νν++==⨯--`11331142133165B u u u νν==⨯--反射声音的波长为=0.1872(m)．或者= 0.1872(m)． [注意]如果用下式计算波长=0.2330(m)，结果就是错误的．当反射面不动时，作为波源发出的波长为u /ν1 = 0.2330m ，而不是入射的波长λ1．5.15S 1与S 2为两相干波源，相距1/4个波长，S 1比S 2的位相超前π/2．问S 1、S 2连线上在S 1外侧各点的合成波的振幅如何？在S 2外侧各点的振幅如何？[解答]如图所示，设S 1在其左侧产生的波的波动方程为，那么S 2在S 1左侧产生的波的波动方程为，由于两波源在任意点x 产生振动反相，所以合振幅为零．S 1在S 2右侧产生的波的波动方程为，那么S 2在其右侧产生的波的波动方程为，由于两波源在任意点x 产生振动同相，所以合振幅为单一振动的两倍．5.16两相干波源S 1与S 2相距5m ，其振幅相等，频率都是100Hz ，位相差为π；波在媒质中的传播速度为400m·s -1，试以S 1S 2连线为坐标轴x ，以S 1S 2连线中点为原点，求S 1S 2间因干涉而静止的各点的坐标．[解答]如图所示，设S 1在其右侧产生的波的波动方程为，那么S 2在其左侧产生的波的波动方程为．两个振动的相差为Δφ = πx + π，当Δφ = (2k + 1)π时，质点由于两波干涉而静止，静止点为x = 2k ， k 为整数，但必须使x 的值在-l /2到l /2之间，即-2.5到2.5之间．当k = -1、0和1时，可得静止点的坐标为：x = -2、0和2(m)．5.17设入射波的表达式为，`1111331651421BBu u u uλννν--=-==`1`13311768uλν==`111650.27871768Bu λλν=-=-1cos[2()]t xy A T πϕλ=++2/4cos[2()]2t x y A T λππϕλ-=++-cos[2()]t xA T πϕπλ=++-1cos[2()]t xy A T πϕλ=-+2/4cos[2()]2t x y A T λππϕλ-=-+-cos[2()]t xA T πϕλ=-+1/2cos[2()]x l y A t u πνϕ+=-+5cos(2)24A t x πππνϕ=-+-2/2cos[2()]x l y A t u πνϕπ-=+++cos(2)24A t x πππνϕ=++-1cos 2()t xy A T πλ=+S 1 S 2S 12在x = 0处发生反射，反射点为一自由端，求：（1）反射波的表达式；（2）合成驻波的表达式．[解答]（1）由于反射点为自由端，所以没有半波损失，反射波的波动方程为．（2）合成波为y = y 1 + y 2，将三角函数展开得，这是驻波的方程．5.18两波在一很长的弦线上传播，设其表达式为：，，用厘米、克、秒（cm,g,s ）制单位，求：（1）各波的频率，波长、波速；（2）节点的位置；（3）在哪些位置上，振幅最大？[解答]（1）两波可表示为：，，可知它们的周期都为：T = 0.5(s)，频率为：v = 1/T = 2(Hz)；波长为：λ = 200(cm)；波速为：u = λ/T = 400(cm·s -1)．（2）位相差Δφ = πx /50，当Δφ = (2k + 1)π时，可得节点的位置x = 50(2k + 1)(cm)，(k = 0，1，2，…)．（3）当Δφ = 2k π时，可得波腹的位置x = 100k (cm)，(k = 0，1，2，…)．2cos 2()t xy A T πλ=-222coscosy A x t Tππλ=1 6.0cos(0.028.0)2y x t π=-2 6.0cos(0.028.0)2y x t π=+1 6.0cos 2()0.5200t x y π=-2 6.0cos 2()0.5200t x y π=+。

基础物理学第五章(静电场)课后习题答案

第五章静电场思考题5-1 根据点电荷的场强公式2041rqE ⋅=πε，当所考察的点与点电荷的距离0→r 时，则场强∞→E ，这是没有物理意义的。

对这个问题该如何解释？答:当时,对于所考察点来说,q 已经不是点电荷了,点电荷的场强公式不再适用.5-2 0FE q =与02014q E r r πε=⋅两公式有什么区别和联系？答：前式为电场（静电场、运动电荷电场）电场强度的定义式，后式是静电点电荷产生的电场分布。

静电场中前式是后一式的矢量叠加，即空间一点的场强是所有点电荷在此产生的场强之和。

5-3 如果通过闭合面S 的电通量e Φ为零，是否能肯定面S 上每一点的场强都等于零？答：不能。

通过闭合面S 的电通量e Φ为零，即0=⋅⎰SS d E，只是说明穿入、穿出闭合面S的电力线条数一样多，不能讲闭合面各处没有电力线的穿入、穿出。

只要穿入、穿出，面上的场强就不为零，所以不能肯定面S 上每一点的场强都等于零。

5-4 如果在闭合面S 上，E 处处为零，能否肯定此闭合面一定没有包围净电荷？答：能肯定。

由高斯定理∑⎰=⋅内qS d E S1ε，E 处处为零，能说明面内整个空间的电荷代数和0=∑内q，即此封闭面一定没有包围净电荷。

但不能保证面内各局部空间无净电荷。

例如，导体内有一带电体，平衡时导体壳内的闭合高斯面上E 处处为零0=∑内q，此封闭面包围的净电荷为零，而面内的带电体上有净电荷，导体内表面也有净电荷，只不过它们两者之和为零。

5-5 电场强度的环流lE dl ⋅⎰表示什么物理意义？0lE dl⋅=⎰表示静电场具有怎样的性质？答：电场强度的环流lE dl ⋅⎰说明静电力是保守力，静电场是保守力场。

0lE dl⋅=⎰表示静电场的电场线不能闭合。

如果其电场线是闭合曲线，我们就可以将其电场线作为积分回路，由于回路上各点沿环路切向，得⎰≠⋅Ll d E 0，这与静电场环路定理矛盾，说明静电场的电场线不可能闭合。

《统计学概论》第五章课后练习题答案

《统计学概论》第五章课后练习题答案一、思考题1．什么叫时间序列，构成时间序列的基本要素有哪些？P1212．序时平均数与一般平均数有何异同？P1273．时间数列与时点数列有哪些区别？P124－1254．环比增长速度与定基增长速度之间有什么关系？P1365．什么是平均发展速度？说说水平法和累计法计算平均发展速度的基本思路，各在什么情况下选用？P1386．测定长期趋势有哪些常用的方法？测定的目的是什么？P1367．实际中如何根据时间序列的发展变化的数列特征来判断合适的趋势方程形式？P1458．影响时间序列指标数值大小的因素有哪些？这些因素共同作用的理论模型有哪些？P140二、判断题1．时间序列也称动态数列，它是变量数列的一种形式。

（×）【解析】时间序列是数列，而变量数列是静态数列。

2．时间数列和时点数列属于总量指标时间序列。

（√）3．所谓序时平均数是指将同一总体的不同时期的平均数按时间先后顺序排列起来。

（×）【解析】序时平均数是将不同时期的发展水平加以平均而得到的平均数。

4．间隔相等的时期数列计算平均发展水平时，应用首末折半法。

（×）【解析】间隔相等的时点数列计算平均发展水平时，应用首末折半法。

5．平均增长速度等于各期环比增长速度连乘积开n次方。

（×）【解析】平均发展速度等于各期环比发展速度连乘积开n次方，平均增长速度=平均发展速度－1（或100%）6．两个相邻时期的定基发展速度之比等于相应的环比发展速度。

（√）7．用移动平均法测定长期趋势时，移动平均项数越多越好。

（×）【解析】移动平均法所取项数的多少，应视资料的特点而定。

8．某一时间序列有25年的数据，若采用五项移动平均，则修匀后的数列缺少4项数据。

（√）9．如果时间序列是年度数据，则不存在季节变动。

（√）10．用相同方法拟合趋势方程时，t的取值不同，则得到的趋势方程也不同，但趋势预测值不变。

（√）三、单项选择题1．时间序列的构成要素是（）。

第5章课后习题参考答案

基础会计学第5_6章课后复习题与参考答案

第五章微机原理课后习题参考答案

数理经济学第5章课后题答案

概率论与数理统计第五章课后习题及参考答案

自动控制原理及其应用课后习题第五章答案

第五章课后习题答案

第五章 课后习题及答案

现代通信原理 第5章 课后习题及答案

王孝玲《教育统计学》第五章课后练习题超详细解答步骤

第5章-经营决策分析习题

第5章课后习题参考答案

第5章 0~3岁婴幼儿动作指导活动的设计与组织【课后习题及参考答案】

《电磁场与电磁波》课后习题解答(第五章)

机械设计基础第5章 课后习题参考答案

第5章课后习题参考答案

大学物理课后习题答案第五章

基础物理学第五章(静电场)课后习题答案

《统计学概论》第五章课后练习题答案

第五章课后习题及答案

现代通信原理第5章课后习题及答案

机械设计基础第5章课后习题参考答案