硬盘整数分区计算器在线工具 (NTFS FAT32)
磁盘精灵DiskGenius使用图文教程常用功能

磁盘精灵DiskGenius使用图文教程-常用功能DiskGenius是一款磁盘分区及数据恢复软件;支持对GPT磁盘使用GUID分区表的分区操作;除具备基本的建立分区、删除分区、格式化分区等磁盘管理功能外,还提供了强大的已丢失分区恢复功能快速找回丢失的分区、误删除文件恢复、分区被格式化及分区被破坏后的文件恢复功能、分区备份与分区还原功能、复制分区、复制硬盘功能、快速分区功能、整数分区功能、检查分区表错误与修复分区表错误功能、检测坏道与修复坏道的功能;提供基于磁盘扇区的文件读写功能;支持VMware、 Virtual PC、 VirtualBox虚拟硬盘文件格式;支持IDE、SCSI、SATA等各种类型的硬盘,及各种U盘、USB移动硬盘、存储卡闪存卡;支持 FAT12/FAT16/FAT32/NTFS/EXT3文件系统;以上就是DiskGenius的官方简介,很强大的一款磁盘工具,玩电脑必备现在我们来截图讲解一下;本文由教程整理发布一、分区;创建分区之前首先要确定准备创建的分区类型;有三种分区类型,它们是“主分区”、“扩展分区”和“逻辑分区”;主分区是指直接建立在硬盘上、一般用于安装及启动操作系统的分区;由于分区表的限制,一个硬盘上最多只能建立四个主分区,或三个主分区和一个扩展分区;扩展分区是指专门用于包含逻辑分区的一种特殊主分区;可以在扩展分区内建立若干个逻辑分区;逻辑分区是指建立于扩展分区内部的分区;没有数量限制;如果要建立主分区或扩展分区,请首先在结构图上选择要建立分区的空闲区域以灰色显示;如果要建立逻辑分区,要先选择扩展分区中的空闲区域以绿色显示;然后点击工具栏“新建分区”按钮,或依次选择“分区 - 建立新分区”菜单项,也可以在空闲区域上点击鼠标右键,然后在弹出的菜单中选择“建立新分区”菜单项;程序会弹出“建立分区”对话框;然后在弹出的对话框里面选择“分区类型”,“分区大小”,“确定”即可完成分区;DiskGenius 有很多高级设置,比如“对其到扇区的整数倍”,“选择柱面”……对于某些采用了大物理扇区的硬盘,比如4KB物理扇区的西部数据“高级格式化”硬盘,其分区应该对齐到物理扇区个数的整数倍,否则读写效率会下降;此时,应该勾选“对齐到下列扇区数的整数倍”并选择需要对齐的扇区数目;柱面选项可以跳过坏扇区,如果需要,配合其他工具来检测坏道所在的扇区之后,跳过它DiskGenius的快速分区功能是整盘分区,所以在当前磁盘运行了系统的时候是无法执行的,需要重启到DOS版的DiskGenius才可以操作;如果你有两个硬盘,那第二块硬盘就是用DiskGenius来快速分区;问你是否重启,确定重启之后,“快速分区”划分出来的分区,除了使用“剩余容量”的分区以外,其它均为“整数分区”,即在Windows的资源管理器中显示为“整数”大小,看起来更美观;二、恢复丢失或被合并的分区此功能在DiskGenius的帮助文档里面有详细的介绍,以下以一个真实经历来讲解一下应用;有一次给一个美女教师装Win7,不知道怎么的,就遇到了如下的情况:1. 打开电脑,发现E、F盘不见了;身上冒冷汗啊,上面可有好多教学的资料啊,美女不杀了我才怪;2. 请出DiskGenius 一探究竟,发现丢失的两个盘被合成一个空闲空间了,见下图中绿条;于是选中绿条,并从工具里点击搜索已丢失分区表;3. 找到一个100G的分区,但不是我想要的,忽略;4.又找到一个400G的分区,但是还是不是我想要的,继续忽略;5. 再找到一个400G的分区,并且立即看见了这个区的文件,发现这正是我丢失的分区之一;毫不犹豫的点了保留;6. 继续,又发现一个399.5G 的分区,可惜的是不是我想到的,继续忽略;7. 哈哈,又来一个399.5G 的分区,我又看见了我熟悉的文件,正是我丢失分区之一,立马保留;8. 丢失的两个分区完全已经完全找到,点击菜单工具栏上硬盘——保存更改;9. 退出DiskGenius ,最好再重启一下电脑;然后,打开的我电脑,哈哈,丢失的分区回家了,欢迎; 至此,已丢失的2个分区完美恢复,耗时不要3分钟;写在最后:说起来这次磁盘合并算是不幸中的万幸,这次只是丢失了文件的分区表;按以上的步骤毫不费力的把它们找回来了;不要急于保留分存表,可以前前后后多试几次,只到找到你认为最符合丢失分区容量大小的才保留,这个动作可以重复来,只要你不保存分区表就不会写数据到硬盘;回忆上次我碰到的另一起分区合并事件,就比这起严重的多;当时也是找到了想要的分区表,但并不像现在这样立马就能看见里面的文件,里面显示空荡荡的;如果你也遇上这样的情况, 也不用太担心;步骤还是和上面做法一样,先查找丢失的分区,将找到的最接近你分区容量的分区保留,再保存分存表;然后选中丢失的分区,点击恢复文件,选择误格式化后的文件恢复,然后开始,切记不要将恢复文件保存在丢失分区的硬盘上,最好恢复到外置硬盘或新添加一块硬盘来存放恢复文件;然后就慢慢的等他查找恢复,直到全部完成;DiskGenius Pro 32位绿色专业版下载路径:本文参考资料护卫神技术频道:.转载请注明出处;。
DiskGenius(硬盘修复工具)

DiskGen ius是一款硬盘分区及数据维护软件。
它具有操作直观简便的特点,从最初的DOS 版起就深受用户好评。
新版主要功能:1、支持基本的分区建立、删除、隐藏等操作。
建立新分区时可指定详细参数;2、支持IDE、SCSI、SA TA等各种类型的硬盘。
支持U盘、USB硬盘、存储卡(闪存卡);3、支持FAT12、FA T16、FA T32、NTFS文件系统;4、可以快速格式化FAT12、FA T16、FA T32、NTFS分区。
格式化时可设定簇大小、支持NTFS文件系统的压缩属性;5、可浏览包括隐藏分区在内的任意分区内的任意文件,包括通过正常方法不能访问的文件。
可通过直接读磁盘扇区的方式读取文件、强制删除文件;6、支持盘符的分配及删除;7、支持已删除文件的恢复、分区误格式化后的文件恢复。
成功率较高;8、增强的已丢失分区恢复功能,恢复过程中,可即时显示搜索到的分区参数及分区内的文件。
搜索完成后,可在不保存分区表的情况下恢复分区内的文件;9、可将整个分区备份到一个镜像文件中,可在必要时(如分区损坏)恢复。
支持在Wind ows运行状态下备份系统盘;10、支持分区复制操作。
并提供“全部复制”、“按结构复制”、“按文件复制”等三种复制方式,以满足不同需求;11、支持硬盘复制功能。
同样提供与分区复制相同的三种复制方式;12、支持VMWar e虚拟硬盘文件(“。
vmdk”文件)。
打开虚拟硬盘文件后,即可像操作普通硬盘一样操作虚拟硬盘;13、可在不启动VM Ware虚拟机的情况下从虚拟硬盘复制文件、恢复虚拟硬盘内的已删除文件(包括格式化后的文件恢复)等。
硬盘修复工具软件简介DiskGen ius(硬盘修复工具)是一款硬盘分区及数据维护软件。
DiskGen ius(硬盘修复工具)具有操作直观简便的特点,从最初的DOS版起就深受用户好评。
磁盘精灵DiskGenius使用图文教程—常用功能

磁盘精灵D i s k G e n i u s 使用图文教程—常用功能Document number:NOCG-YUNOO-BUYTT-UU986-1986UT磁盘精灵DiskGenius使用图文教程-常用功能DiskGenius是一款磁盘分区及数据恢复软件。
支持对GPT磁盘(使用GUID分区表)的分区操作。
除具备基本的建立分区、删除分区、格式化分区等磁盘管理功能外,还提供了强大的已丢失分区恢复功能(快速找回丢失的分区)、误删除文件恢复、分区被格式化及分区被破坏后的文件恢复功能、分区备份与分区还原功能、复制分区、复制硬盘功能、快速分区功能、整数分区功能、检查分区表错误与修复分区表错误功能、检测坏道与修复坏道的功能。
提供基于磁盘扇区的文件读写功能。
支持VMware、VirtualPC、VirtualBox虚拟硬盘文件格式。
支持IDE、SCSI、SATA等各种类型的硬盘,及各种U盘、USB移动硬盘、存储卡(闪存卡)。
支持FAT12/FAT16/FAT32/NTFS/EXT3文件系统。
以上就是DiskGenius的官方简介,很强大的一款磁盘工具,玩电脑必备!现在我们来截图讲解一下。
(本文由教程整理发布)一、分区。
创建分区之前首先要确定准备创建的分区类型。
有三种分区类型,它们是“主分区”、“扩展分区”和“逻辑分区”。
主分区是指直接建立在硬盘上、一般用于安装及启动操作系统的分区。
由于分区表的限制,一个硬盘上最多只能建立四个主分区,或三个主分区和一个扩展分区;扩展分区是指专门用于包含逻辑分区的一种特殊主分区。
可以在扩展分区内建立若干个逻辑分区;逻辑分区是指建立于扩展分区内部的分区。
没有数量限制。
如果要建立主分区或扩展分区,请首先在结构图上选择要建立分区的空闲区域(以灰色显示)。
如果要建立逻辑分区,要先选择扩展分区中的空闲区域(以绿色显示)。
然后点击工具栏“新建分区”按钮,或依次选择“分区-建立新分区”菜单项,也可以在空闲区域上点击鼠标右键,然后在弹出的菜单中选择“建立新分区”菜单项。
DiskGen图文教程

Disk Genius V2.0 Beta 0219,它是一款完全的国产免费软件,虽是一款基于纯DOS的软件却拥有完全的简体中文界面,整个软件的大小也总共只有149k,非常便于携带。
本文将从实际应用入手,对这款软件的几个典型应用进行讲解,并对硬盘及硬盘分区的知识做一个介绍,希望通过本文的介绍能让大家用好这款软件,并用它来解决一些实际应用中遇到的问题应用一,直观的进行硬盘分区新买电脑的用户往往对于分区这种比较底层的操作感到陌生与害怕,以至于叫装机人员草草把自己的硬盘分为几个相等大小的分区了事,但往往在日后的应用中由于硬盘分区的不合理造成很多的不便。
其实给新硬盘分区也并不是很困难的操作,下面的文字将介绍如何用Disk Genius进行磁盘的分区,相信您看过之后完全可以代上张装有Disk Genius的盘,根据需要想好硬盘空间的分配方案,在装机时自己动手来为自己的硬盘进行合理的分区。
作为一款磁盘分区及管理软件,分区这个功能是必不可少的,它与其他大多数分区软件相比最大的一个特点就是直观,让我们来看看它的界面(图1,图2),从图中可以看到右边是一个仿Windows的窗体,左边是一个柱状的硬盘空间显示条,通过在它上面选择我们可以一目了然的看到硬盘各个分区的大小及分区类型。
下面我们进行实际的分区操作,一台新电脑里的新硬盘都是没有分区的,在运行Disk Genius时你会看到和图1类似的画面,整个灰色的柱状的硬盘空间显示条表示硬盘上没有任何的分区,而分完区之后的硬盘将会有类似于图2的画面。
1.建立主分区想从硬盘引导系统那么硬盘上至少需要有一个主分区,所以建立主分区就是我们的第一步。
在界面里按Alt键将调出菜单,选择分区菜单里面的“新建分区”,此时会要求你输入主分区的大小,一般来说主分区用于操作系统的安装,不宜分得太大,确定之后软件会询问是否建立DOS FAT分区,如果选择“是”那么软件会根据你刚刚天写的分区的小进行设置,小于640M时该分区将被自动设为FAT16格式,而大于640M时分区则会自动设为FAT32格式。
gpt硬盘分区整数计算

GPT硬盘分区的整数计算方法主要涉及到分区的起始位置和分区的大小。
1. 分区的大小:以扇区为单位进行计算,每个扇区的大小通常为512字节,但也可以是其他大小如4096字节。
因此,分区的大小应该是扇区数乘以每个扇区的大小。
2. 分区的起始位置:GPT分区的起始位置(偏移量)是以LBA (Logical Block Addressing)地址表示的。
LBA地址是从硬盘开始处计算的块编号,每个块的大小通常为512字节。
因此,分区的起始位置应该是以LBA地址表示的。
另外,硬盘整数分区计算方法一般算法:分区大小=(分区大小-1)×4+1024×分区大小。
如果按照硬盘分区整数G计算公式X-1)*4+1024*X=Y,其中X就是你想要得到的整数分区的数值,单位是G,Y是你分区时应该输入的数字,单位是M。
例如,40GB=(40-1)×4+1024×40=41116MB。
以上信息仅供参考,如果还有疑问,建议咨询专业人士。
Windows磁盘空间占用分析工具-WizTree

WizTree作用
WizTree树状分析图
WizTree特点
获取网址
WizTree作用
平时我们电脑用久了,产生很多文件,导致盘符空间不足,但是不知道那些文件占用比较多,这就需要磁盘空间分析工具-WizTree来分析文件占用情况
WizTree树状分析图
选中C盘,点击“扫描”按钮,它可以快速扫描并分析你的电脑C硬中文件和文件夹,并以可视化块状的方式展示使用情况。
这样你就很方便找到占用磁盘空间大的文件。
WizTree特点
1. 支持多种硬件类型:如NTFS、FAT、FAT32、网络等,也支持外接的移动硬盘、U盘等存储设备;
2. 支持模糊查询与选中文件删除;
3. 选中的文件信息可以导出到 CSV文件或复制到剪贴板,也可以转储 MFT文件到电脑中。
获取网址
WizTree磁盘空间占用分析工具。
NTFS格式整数分区的公式与参数

分区分成整数,其实这是一个很无聊的问题。
很多时候大家分区完成以后总是显示X.99G,这样对于有洁癖的人或者是完美主义者来说是很不爽的。
通常的的算法说是 M=(G-1)*4+1024*G得到填写多少M。
实际上这个算法并不准确。
下面是使用这种算法分区以后NTFS格式的显示。
今日一个朋友告诉我一个比较准确的算法:硬盘一般有255磁头,63扇区,故每柱面大小为:512byte×255×63=8225280bytes =7.84423828125 M如果要分4G,那么要4x1024M=4096M需要柱面数为4096÷7.84423828125=522.166取整数既为523个柱面应分M数为523x7.84423828125=4102.53662109375M不管小数点后面几位都进1,也就是4103M,windows就认为是4.00G了。
这个方法NTFS和FAT32通用。
于是我马上拿新硬盘进行测试,是不是很整齐呢。
听说一位仁兄为了验证上面的算法的准确性格式坏硬盘一个。
大家也可以试试。
顺便送一个刚才写了的小脚本给大家计算整数分区。
(IE only)运行代码框[Ctrl+A 全部选择提示:你可先修改部分代码,再按运行]精确的算法如下:硬盘一般有255磁头,63扇区,故每柱面大小为:512byte x 255 x 63=8225280bytes =7.84423828125 M如果要分4G,那么要4x1024M=4096M需要柱面数为4096÷7.84423828125=522.166取整数既为523个柱面应分M数为523x7.84423828125=4102.53662109375M不管小数点后面几位都进1,也就是4103M,windows就认为是4.00G了。
这个方法NTFS和FAT32通用。
这样太复杂了,还要一个个去算。
我已经都算好了,相信大多数人可以找到自己想要的答案!1G=1028M2G=2056M3G=3075M4G=4103M5G=5123M6G=6150M7G=7170M8G=8198M9G=9217M10G=1024M11G=11265M12G=12292M13G=13320M14G=14340M15G=15367M16G=16387M17G=17415M19G=19462M 20G=20482M 21G=21509M 22G=22529M 23G=23557M 24G=24584M 25G=25604M 26G=26623M 27G=27651M 28G=28679M 29G=29699M 30G=30726M35G=35841M 40G=40963M 45G=46085M 50G=51508M 55G=56322M 60G=61444M 65G=66567M 70G=71603M 75G=76803M 80G=81926M90G=92162M 95G=97285M 100G=102406M 105G=107521M 110G=112644M 115G=117766M 120G=12888M 125G=128003M 130G=133125M 135G=138247M 140G=143362M 145G=148484M 150G=153606M 155G=158721M 160G=163843M 165G=168965M 170G=174088M 175G=179202M 180G=184324M 185G=189447M 190G=194561M 195G=199683M 200G=204806M210G=215042M 215G=220165M 220G=225287M 225G=230401M 230G=235524M 235G=240646M 240G=245768M 245G=250883M 250G=256005M 255G=261127M 260G=266242M 265G=271364M 270G=276486M 275G=281601M 280G=286723M 285G=291845M 290G=296968M 295G=302082M 300G=307204M一些个性数字168G=172040M88G=90115M66G=67586M666G=681986M360G=368648M365G=373763M888G=909320M一切都结束了................。
硬盘整数分区计算器和公式下载,附Win7系统盘整数分区方法

硬盘整数分区计算器和公式下载,附Win7系统盘整数分区方法要想吧分区显示为整数,可没有那么简单,下面我就为大家详细分析硬盘分区容量显示之谜:1. 硬盘厂商为了换算方便,是按照千进制来计算硬盘容量的,一块1TB的硬盘实际容量是1,000,000,000,000Bit=976,562,500KB=953,674MB=931GB左右,分区后实际可用容量会更小;2. 操作系统实际计算硬盘容量是按照1024进制,由此导致实际可用容量小于标称容量,硬盘容量越大,“损失”的容量也越大;3. 电脑当中实际显示的分区大小,既不是按照硬盘厂商的设计也不是操作系统的设计,而是另有误差。
原因就是硬盘在分区和格式化之后还会在硬盘上占用一定的空间用来存储磁盘结构和数据位置等信息;4. 对于FAT32分区,每1024字节可用容量会使用4字节用于存储磁盘结构和数据存储位置等信息,但分区中第一GB可用容量却不占用额外的存储容量,因此FAT32整数分区公式为:应分配MB数=(分区GB数-1)×4+1024×分区GB数5. 对于NTFS分区,原理更加复杂。
NTFS分区的最小容量单位不可能精确到1MB,而是柱面大小。
硬盘一般有255磁头,63扇区,故每柱面大小为:512bitx255x63=8225280bit =7.84423828125MB如果要分10GB,那么应当是10x1024MB=10240MB实际需要柱面数为10240÷7.84423828125=1305.4柱面只可能算整数,即1306个柱面这样实际应分MB数为1306x7.84423828125=10244.575MB不管小数点后面几位都进1,也就是10245MB,这样系统才能认成是10.0GB了上面的计算方法太过复杂,原理大家了解一些就行了,真正操作时如果还用公式+计算器慢慢换算,那就效率太低了。
现在已经有人为我们设计了简单方便的硬盘整数分区计算器,支持FAT32和NTFS两种格式:如果是给WIn7分系统盘的话,它会自动预留100MB的隐藏分区,因此在输入分区容量的时候,必须把计算器的数值+100,非系统分区则不需要附件:文件名:硬盘整数分区计算器.rar下载次数:7158文件类型:application/octet-stream文件大小: 10.85 K上传时间:8/5/2009 10:39:42 AM。
DiskGenius硬盘分区工具使用图文

DiskGenius硬盘分区工具使用图文应用一,直观的进行硬盘分区新买电脑的用户往往对于分区这种比较底层的操作感到陌生与害怕,以至于叫装机人员草草把自己的硬盘分为几个相等大小的分区了事,但往往在日后的应用中由于硬盘分区的不合理造成很多的不便。
其实给新硬盘分区也并不是很困难的操作,下面的文字将介绍如何用Disk Genius进行磁盘的分区,相信您看过之后完全可以代上张装有Disk Genius的盘,根据需要想好硬盘空间的分配方案,在装机时自己动手来为自己的硬盘进行合理的分区。
作为一款磁盘分区及管理软件,分区这个功能是必不可少的,它与其他大多数分区软件相比最大的一个特点就是直观,让我们来看看它的界面(图1,图2),从图中可以看到右边是一个仿Windows的窗体,左边是一个柱状的硬盘空间显示条,通过在它上面选择我们可以一目了然的看到硬盘各个分区的大小及分区类型。
1.jpg2.jpg下面我们进行实际的分区操作,一台新电脑里的新硬盘都是没有分区的,在运行Disk Genius时你会看到和图1类似的画面,整个灰色的柱状的硬盘空间显示条表示硬盘上没有任何的分区,而分完区之后的硬盘将会有类似于图2的画面。
1.建立主分区想从硬盘引导系统那么硬盘上至少需要有一个主分区,所以建立主分区就是我们的第一步。
在界面里按Alt键将调出菜单,选择分区菜单里面的“新建分区”,此时会要求你输入主分区的大小,一般来说主分区用于操作系统的安装,不宜分得太大,确定之后软件会询问是否建立DOS FAT分区,如果选择“是”那么软件会根据你刚刚天写的分区的小进行设置,小于640M时该分区将被自动设为FAT16格式,而大于640M时分区则会自动设为FAT32格式。
如果选择了“否”软件将会提示你手工填写一个系统标志,并在右边窗体的下部给出一个系统标志的列表供用户参考和填写,确定之后主分区的建立就完成了(图3),主分区就是我们将来的C:盘。
3.jpg2.建立扩展分区和逻辑分区在建立了主分区之后就要接着建立扩展分区和在扩展分区上面的逻辑分区,首先我们建立扩展分区,我们先在柱状硬盘空间显示条上选定未分配的灰色区域,然后按Alt选择菜单栏里分区下的“建扩展分区”如图4,之后会有提示要求你输入建的扩展分区的大小,通常情况下我们应该将所有的剩余空间都建立为扩展分区,所以这里可以直接按回车确定。
Diskgen使用说明
硬盘分区软件diskgen使用说明应用一:直观的进行硬盘分区新买电脑的用户往往对于分区这种比较底层的操作感到陌生与害怕,以至于叫装机人员草草把自己的硬盘分为几个相等大小的分区了事,但往往在日后的应用中由于硬盘分区的不合理造成很多的不便。
其实给新硬盘分区也并不是很困难的操作,下面的文字将介绍如何用Disk Genius进行磁盘的分区,相信您看过之后完全可以代上张装有Disk Genius的盘,根据需要想好硬盘空间的分配方案,在装机时自己动手来为自己的硬盘进行合理的分区。
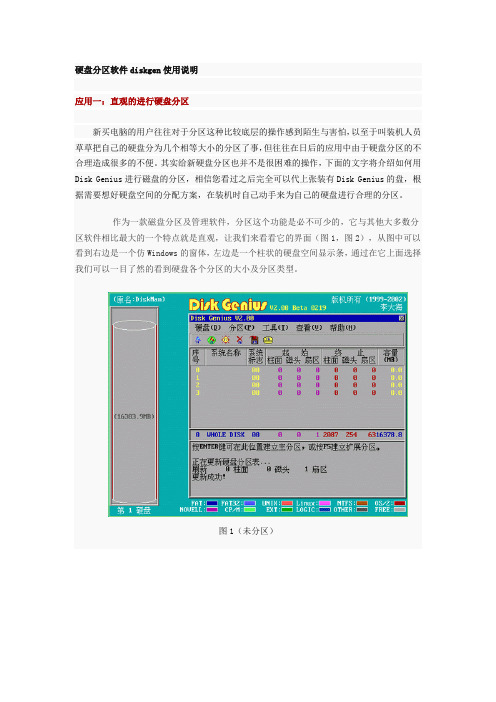
作为一款磁盘分区及管理软件,分区这个功能是必不可少的,它与其他大多数分区软件相比最大的一个特点就是直观,让我们来看看它的界面(图1,图2),从图中可以看到右边是一个仿Windows的窗体,左边是一个柱状的硬盘空间显示条,通过在它上面选择我们可以一目了然的看到硬盘各个分区的大小及分区类型。
图1(未分区)图2(已分区)下面我们进行实际的分区操作,一台新电脑里的新硬盘都是没有分区的,在运行Disk Genius时你会看到和图1类似的画面,整个灰色的柱状的硬盘空间显示条表示硬盘上没有任何的分区,而分完区之后的硬盘将会有类似于图2的画面。
1.建立主分区想从硬盘引导系统那么硬盘上至少需要有一个主分区,所以建立主分区就是我们的第一步。
在界面里按Alt键将调出菜单,选择分区菜单里面的“新建分区”,此时会要求你输入主分区的大小,一般来说主分区用于操作系统的安装,不宜分得太大,确定之后软件会询问是否建立DOS FAT分区,如果选择“是”那么软件会根据你刚刚天写的分区的小进行设置,小于640M时该分区将被自动设为FAT16格式,而大于640M时分区则会自动设为FAT32格式。
如果选择了“否”软件将会提示你手工填写一个系统标志,并在右边窗体的下部给出一个系统标志的列表供用户参考和填写,确定之后主分区的建立就完成了(图3),主分区就是我们将来的C:盘。
图32.建立扩展分区和逻辑分区在建立了主分区之后就要接着建立扩展分区和在扩展分区上面的逻辑分区,首先我们建立扩展分区,我们先在柱状硬盘空间显示条上选定未分配的灰色区域,然后按Alt 选择菜单栏里分区下的“建扩展分区”如图4,之后会有提示要求你输入建的扩展分区的大小,通常情况下我们应该将所有的剩余空间都建立为扩展分区,所以这里可以直接按回车确定。
如何对硬盘进行整数分区的计算方法.

装系统或重装系统时,总是为硬盘容量不是整数发愁,原来是自己的计算方法不对,那么,如何通过正确计算对硬盘进行整数分区呢?下面的文章对您一定有所帮助硬盘整数分区计算方法一般算法:分区大小=(分区大小-1×4+1024×分区大小如果按照硬盘分区整数G计算公式:(X-1*4+1024*X=Y 其中X就是你想要得到的整数分区的数值,单位是G,Y是你分区时应该输入的数字,单位是M,比如40GB=(40-1×4+1024×40=41116MB 按照这样的计算方法:5G=5136MB10G=10276MB15G=15416MB20G=20556MB30G=30836MB40G=41116MB30G以内,输入上面的数据,如10G你输入10276,在Windows资源管理器里面显示的刚好10.00GB,而在管理工具-磁盘管理界面显示就是10.04GB,如果是40G你输入41116,那么在Windows资源管理器里面显示的刚好40.01GB。
因此上面的计算公式还不是很准确。
最精确硬盘分区的算法如下(来自网络搜索:硬盘一般有255磁头,63扇区,故每柱面大小为:512byte x 255 x 63=8225280bytes =7.84423828125 MB如果要分40GB,那么要40x1024MB=40960MB需要柱面数为40960÷7.84423828125=5221.66取整数既为5222个柱面应分M数为5222x7.84423828125=40962.6123046875MB不管小数点后面几位都进1,也就是40963MB,windows就认为是40GB了。
这个方法NTFS和FAT32通用。
下面附10GB到200GB整10GB递增的精确计算结果:10GB = 10245MB20GB = 20482MB30GB = 30726MB40GB = 40963MB50GB = 51208MB60GB = 61444MB70GB = 71681MB80GB = 81926MB90GB = 92162MB100GB = 102407MB110GB = 112644MB120GB = 122888MB130GB = 133125MB140GB = 143362MB150GB = 153606MB160GB = 163843MB170GB = 174088MB180GB = 184324MB190GB = 194561MB此精确分区结果,在管理工具-磁盘管理界面,和Windows资源管理器里面显示的是整数,10G就是10.00GB,20G就是20.00GB,40G就是40.00GB。
gpt硬盘分区整数计算

gpt硬盘分区整数计算硬盘分区是指将物理硬盘划分为若干逻辑驱动器的过程。
在进行硬盘分区时,我们通常需要进行一些整数计算,以确定分区的大小、位置以及剩余空间等。
首先,我们需要了解硬盘的基本单位——扇区(Sector)。
扇区是硬盘上最小的存储单位,一般为512字节。
硬盘分区的大小通常以扇区数表示。
硬盘分区的大小可以根据需求进行计算。
如果我们知道想要分区的大小(以字节为单位),可以通过以下公式将其转换为扇区数:扇区数 = 分区大小 / 512例如,如果我们想要创建一个大小为1GB(1073741824字节)的分区,将其转换为扇区数:扇区数 = 1073741824 / 512 = 2097152扇区确定分区位置时,我们需要考虑已有分区的大小以及空间占用。
如果我们知道某个分区的起始位置和大小,可以通过以下公式计算其结束位置:结束位置(扇区数)= 起始位置(扇区数)+ 分区大小(扇区数)- 1例如,如果某个分区起始于第2048扇区,大小为8388608扇区:结束位置 = 2048 + 8388608 - 1 = 8388607扇区从而确定了分区的结束位置。
另外,我们还可以进行一些整数计算来了解硬盘分区的剩余空间。
通常,剩余空间可以通过以下公式计算:剩余空间(字节) = 总容量(字节) - 已使用空间(字节)如果我们已知总容量和已使用空间的扇区数,可以通过以下公式计算剩余空间的扇区数:剩余扇区数 = 总扇区数 - 已使用扇区数这些整数计算可以帮助我们在进行硬盘分区时确定大小、位置以及剩余空间等关键参数。
在实际操作中,还需要考虑到文件系统的格式化、磁盘容量单位的转换等因素。
总的来说,硬盘分区的整数计算涉及到分区大小的转换、分区位置的确定以及剩余空间的计算。
通过合理的整数计算,我们可以更好地进行硬盘分区的规划和管理。
硬盘整数分区计算方法

10G=10276MB
15G=15416MB
20G=20556MB
30G=30836MB
40G=41116MB
30G以内,输入上面的数据,如10G你输入10276,在Windows资源管理器里面显示的刚好10.00GB,而在管理工具-磁盘管理界面显示就是10.04GB,如果是40G你输入41116,那么在Windows资源管理器里面显示的刚好40.01GB。
80GB = 81926MB
90GB = 92162MB
100GB = 102407MB
110GB = 112644MB
120GB = 122888MB
130GB = 133125MB
140GB = 143362MB
150GB = 153606MB
160GB = 163843MB
硬盘整数分区计算方法
一般算法
(来自按照硬盘分区整数G计算公式X-1)*4+1024*X=Y 其中X就是你想要得到的整数分区的数值,单位是G,Y是你分区时应该输入的数字,单位是M,
比如40GB=(40-1)×4+1024×40=41116MB 按照这样的计算方法:
需要柱面数为40960÷7.84423828125=5221.66
取整数既为5222个柱面
应分M数为5222x7.84423828125=40962.6123046875MB
不管小数点后面几位都进1,也就是40963MB,windows就认为是40GB了。
这个方法NTFS和FAT32通用。
170GB = 174088MB
180GB = 184324MB
190GB = 194561MB
硬盘分区整G整数法(从1g到200g最精确的整数分区

硬盘分区整G整数法(从1g到200g最精确的整数分区硬盘分区整G整数法(从1g到200g最精确的整数分区)(转)整数分区通常的算法是M=(G-1)X4+1024*G,M为分区时输入的大小.比如我们所需要的分区为10G,则(10-1)X4+1024X10,结果为10276M,实际上这种算法并不准确。
硬盘一般有255磁头,63扇区(此处待考证,一般没那么多的磁头,但后面的结果还是正确的),故每柱面大小为:512byte x 255 x 63=8225280bytes =7.84423828125 M如果要分4G,那么要4×1024M=4096M需要柱面数为4096÷7.84423828125=522.166取整数既为523个柱面应分M数为523×7.84423828125=4102.53662109375M不管小数点后面几位都进1,也就是4103M,windows就认为是4.00G了。
(此处有疑问,为何4103M但windows却识别为整G)这个方法NTFS和FAT32通用。
从1g到200g最精确的整数分区1G : 1028M2G : 2056M3G : 3075M4G : 4103M5G : 5123M6G : 6150M7G : 7170M8G : 8198M9G : 9217M10G : 10245M15G : 15367M20G : 20482M25G : 25604M30G : 30726M 35G : 35841M 40G : 40963M 45G : 46085M 50G : 51208M 55G : 56322M 60G : 61444M 65G : 66567M 70G : 71681M 75G : 76803M 80G : 81926M 85G : 87048M 90G : 92162M 95G : 97285M 100G : 102407M 110G : 112644M 120G : 122888M 130G : 133125M 140G : 143362M 150G : 153606M 160G : 163843M 170G : 174088M 180G : 184324M 190G : 194561M 200G : 204806M。
DISKGEN图解教程_好用的硬盘工具

现在可供选用的硬盘分区工具软件很多,但基本上都是“外国货”,只有被誉为分区小超人的DISKMAN是地地道道的国货。
DISKMAN以其操作直观简便的特点为菜鸟级电脑用户所喜爱,但在近两年的时间里,DISKMAN的版本一直停留在V1.2,总不见作者推出升级版本,不免让人为它担心。
现在,2.0版本的DISKMAN终于出现了,仍然是免费软件,只是名子改成了Disk Genius。
经过近两年的潜心“修炼”,Disk Genius的“功力”确实不可当日而语,它不仅提供了基本的硬盘分区功能(如建立、激活、删除、隐藏分区),还具有强大的分区维护功能(如分区表备份和恢复、分区参数修改、硬盘主引导记录修复、重建分区表等);此外,它还具有分区格式化、分区无损调整、硬盘表面扫描、扇区拷贝、彻底清除扇区数据等实用功能。
虽然Disk Genius功能更强大了,但它的身材依然“苗条”,只有区区143KB。
一、硬盘分区未建立分区的硬盘空间(即自由空间)在分区结构图中显示为灰色,只有在硬盘的自由空间才能新建分区。
如图1。
分区参数表格的第0~3 项分别对应硬盘主分区表的四个表项,而将来新建立的第4、5、6…以后的项分别对应逻辑盘D、E、F…等。
当硬盘只有一个DOS主分区和扩展分区时(利用FDISK进行分区的硬盘一般都是这样的),“第0项”表示主分区(逻辑盘C)的分区信息,“第1项”表示扩展分区的信息,“第2、第3项”则全部为零,不对应任何分区,所以无法选中。
笔者曾在某网站论坛上发现一张有关DISKMAN疑问的帖子,询问有没有办法将分区参数表格中全部为零的“第2项、第3项”删除掉,这当然是不可能的,发帖者显然对硬盘分区知识缺乏了解。
想真正弄懂分区参数表格中各项的意义,必须了解硬盘分区表链结构,建议有兴趣的朋友多找一些相关资料看看。
图1:未建立分区的新硬盘1 建立主分区想从硬盘引导系统,那么硬盘上至少需要有一个主分区,所以建立主分区就是我们的第一步。
gpt硬盘分区整数计算

gpt硬盘分区整数计算GPT(全局磁盘分区表)是一种用来对硬盘进行分区的标准,它的出现使得硬盘分区更加灵活和高效。
在进行GPT硬盘分区时,我们经常会遇到整数计算的问题,这种计算是非常常见且基础的。
在本文中,我将向大家介绍GPT硬盘分区整数计算的方法和技巧。
首先,我们需要了解GPT硬盘分区的基本概念。
GPT硬盘可以被分成多个分区,每个分区都有一个唯一的标识符GUID(全球唯一标识符)。
在进行分区时,我们需要考虑两个关键参数:起始扇区和大小。
起始扇区是指一个分区在硬盘上的起始位置,它用扇区号来表示。
一个扇区通常为512字节大小,因此起始扇区的值是一个整数,代表了该分区在硬盘上的偏移位置。
大小参数表示了一个分区的大小,它同样用扇区数量来表示。
我们可以通过计算扇区的数量来确定分区的大小,这个计算也需要用到整数。
在进行GPT硬盘分区时,我们需要先确定所有分区的大小和起始位置,然后再进行整数计算。
下面给出了一个简单的分区示例,以帮助大家更好地理解整数计算的方法。
假设有一块1TB大小的硬盘,我们准备将其分为三个分区:分区A 占据前10%的空间,分区B占据中间50%的空间,分区C占据剩余的40%的空间。
首先,我们需要计算每个分区的大小。
根据硬盘的总大小和各分区所占比例,我们可以得出分区A的大小为1TB * 10% = 100GB,分区B的大小为1TB * 50% = 500GB,分区C的大小为1TB * 40% = 400GB。
注意,在进行计算时,我们需要将百分比转化为实际数值。
接下来,我们需要确定每个分区的起始扇区。
根据硬盘的总扇区数和各分区所占比例,我们可以得出分区A的起始扇区为0,分区B的起始扇区为总扇区数的10%,分区C的起始扇区为总扇区数的60%。
同样地,我们需要将百分比转化为实际数值。
在最后进行整数计算时,我们需要将浮点数结果转化为整数。
对于分区B的起始扇区,假设总扇区数为10000,计算得到的起始扇区为10000 * 10% = 1000。
DiskGenius分区教程

DiskGenius是一款磁盘管理及数据恢复软件。
支持对GPT磁盘(使用GUID分区表)的分区操作。
除具备基本的建立分区、删除分区、格式化分区等磁盘管理功能外,还提供了强大的已丢失分区恢复功能(快速找回丢失的分区)、误删除文件恢复、分区被格式化及分区被破坏后的文件恢复功能、分区备份与分区还原功能、复制分区、复制硬盘功能、快速分区功能、整数分区功能、检查分区表错误与修复分区表错误功能、检测坏道与修复坏道的功能。
提供基于磁盘扇区的文件读写功能。
支持VMWare虚拟硬盘文件格式。
支持IDE、SCSI、SATA 等各种类型的硬盘,及各种U盘、USB移动硬盘、存储卡(闪存卡)。
支持FAT12/FAT16/FAT32/NTFS/EXT3文件系统。
DiskGenius 软件主界面DiskGenius的主界面由三部分组成。
分别是:硬盘分区结构图、分区目录层次图、分区参数图。
如下图所示:其中,硬盘分区结构图用不同的颜色显示了当前硬盘的各个分区。
用文字显示了分区卷标、盘符、类型、大小。
逻辑分区使用了网格表示,以示区分。
用绿色框圈示的分区为“当前分区”。
用鼠标点击可在不同分区间切换。
结构图下方显示了当前硬盘的常用参数。
通过点击左侧的两个“箭头”图标可在不同的硬盘间切换。
分区目录层次图显示了分区的层次及分区文件夹的树状结构。
通过点击可切换当前硬盘、当前分区。
也可点击文件夹以在右侧显示文件夹的文件列表。
分区参数图在上方显示了“当前硬盘”各个分区的详细参数(起止位置、名称、容量等),下方显示了当前所选择的分区的详细信息。
为了方便区分不同类型的分区,本软件将不同类型的分区,用不同的颜色显示。
每种类型分区使用的颜色是固定的。
如FAT32分区用蓝色显示、NTFS分区用棕色显示等等。
“分区目录层次图”及“分区参数图”中的分区名称也用相应类型的颜色区分。
各个视图中的分区颜色是一致的。
“当前硬盘”是指当前选择的硬盘。
“当前分区”则是指当前选择的分区。
windows分区exfat整数计算

windows分区exfat整数计算Windows分区是指将硬盘或固态硬盘划分为多个逻辑存储区域的过程,在Windows操作系统中,常用的文件系统有FAT32、NTFS和exFAT。
本文将重点介绍exFAT文件系统在Windows分区中的整数计算特性。
exFAT是指“Extended File Allocation Table”(扩展文件分配表)的缩写,是一种由微软公司开发的文件系统。
相比于FAT32和NTFS,exFAT具有更高的兼容性和更好的性能,特别适用于移动存储设备,如U盘和SD卡。
在Windows分区中使用exFAT文件系统进行整数计算时,我们可以利用Windows操作系统提供的计算器应用程序。
计算器应用程序是Windows的一个标准工具,可以进行多种数学运算,包括整数计算。
使用计算器应用程序进行整数计算非常简单。
首先,打开计算器应用程序,可以通过在Windows搜索栏中输入“计算器”来找到它。
然后,在计算器界面上选择“标准”模式,这样就可以进行整数计算了。
在进行整数计算时,我们可以使用计算器应用程序提供的各种功能,例如加法、减法、乘法和除法。
只需在计算器界面上点击相应的按钮或者使用键盘上的对应按键,就可以输入数字和操作符进行计算。
计算器还提供了括号功能,可以使用括号来改变计算的优先级。
除了基本的整数计算功能,计算器还提供了一些高级的功能,如取余、开方和幂运算等。
这些功能对于一些特殊的整数计算需求非常有用。
除了计算器应用程序,Windows操作系统还提供了其他一些工具和功能,可以用于整数计算。
例如,命令行界面提供了一些内置的命令和工具,可以进行简单的整数计算。
另外,Windows还支持各种编程语言,如C++和Python,可以使用这些编程语言进行复杂的整数计算。
需要注意的是,在进行整数计算时,我们需要遵循整数的运算规则,比如整数相除会得到整数结果。
如果需要得到精确的计算结果,可以使用浮点数进行计算。
