浙江大学实验报告:一阶RC电路的瞬态响应过程实验研究
RC一阶电路的响应测试实验报告

RC一阶电路的响应测试实验报告实验报告:RC一阶电路的响应测试一、实验目的:1.掌握RC一阶电路的响应特性;2.了解RC一阶电路的时间常数对电路响应的影响;3.学会使用示波器观察电路的动态响应。
二、实验原理:由于充电或放电需要一定的时间,电路的响应是有延迟的。
根据电容充电时间常数τ的不同,可以将RC电路分为快速响应和慢速响应两种情况。
电容C的充电或放电方程为:i(t) = C * dV(t) / dt根据Ohm's Law,电路中的电流和电压之间的关系为:V(t) = VR(t) + VC(t) = i(t) * R + V0 * exp(-t/τ)其中,VR(t)是电阻R上的电压,VC(t)是电容C上的电压,V0是电路初始电压,τ=C*R是电路的时间常数。
当输入信号为直流电压时,电路将会处于稳态,电容将保持充电或放电状态,直到与电源电压相等。
当输入信号为瞬态电压时,电路将会发生响应,电容充放电的过程导致电压变化。
三、实验器材和仪器:1.RC电路板;2.直流电源;3.示波器;4.电阻和电容。
四、实验步骤:1.将示波器的地线和信号触发线接地。
2.按照实际电路中的元件数值,在RC电路板上连接电阻和电容。
3.将示波器的一个探头连接到电阻两端,另一个探头连接到电容的一端。
4.打开直流电源,设定合适的电压大小,使电路处于稳定状态。
5.调整示波器的触发模式和触发电平,保证波形稳定可观察。
6.增加或减小直流电压,观察电路响应,并记录波形。
7.改变电阻或电容的数值,重复步骤6,观察并记录不同响应特性。
8.关闭直流电源和示波器,取下电路连接。
五、实验数据及结果:实验中,我们首先建立了一个由1000Ω电阻和0.1μF电容串联组成的RC电路。
然后,我们分别给电路输入不同幅值和时间常数的矩形波信号,观察电路的响应。
1.输入直流电压的稳态响应:当输入直流电压时,电路处于稳态,电容已经充电到与电源电压相等的电压值。
RC电路瞬态响应过程和RLC谐振电路

二、 RLC谐振电路试验研究
1、掌握谐振频率以及品质因数旳测量措施。 2、了解谐振电路特征频率特征,加深对谐振 电路旳认识。 3、了解谐振电路旳选频特征、通频带及其应用。
理论基础(一)
1.一阶RC电路旳零输入响应(放电过程) 电路在无鼓励情况下,由储能元件旳初始状态引起旳响应
试验内容(二)
5、Δf和Q值 根据谐振曲线计算Δf值,必要时需要补测若干点。
用Δf和f0计算Q值旳大小。 6、将电阻R增大至1k Ω , 反复内容2~5,自制表格统计分析。
试验内容(二)
二、RLC并联谐振电路试验
1、按图构成试验电路 L=40mH, C=0.1μF, R=56kΩ.电感分别选用内阻不同旳两
试验内容(二)
一、RLC串联谐振电路试验
1、按图构成试验电路 L=40mH, C=0.1μF, R=100Ω.电感分别
选用内阻不同旳两种; 用示波器测量ui和uo 信号源输出ui为正弦波,
电压1V
试验内容(二)
2、找出电路旳谐振频率f0 将示波器旳一种输入端接在电阻R旳两端,使信号源旳
0
(t 0)
能够得出电容器上旳电压和电流随时间变化旳规律:
t
t
uC (t) uC (0 )e RC U0e
(t 0)
t
iC
(t
)
uC
(0 )e R
RC
U0
t
e
R
(t 0)
τ = RC为时间常数
理论基础(一)
2.一阶RC电路旳零状态响应(充电过程) 所谓零状态响应是指初始状态为零,而输入不为零所产生
一阶rc电路的暂态响应实验报告分析

一阶rc电路的暂态响应实验报告分析
一阶rc电路的暂态响应实验报告分析
本文为大家带来一阶rc电路的暂态响应实验报告分析。
实验内容和原理
1、零输入响应:指输入为零,初始状态不为零所引起的电路响应。
2、零状态响应:指初始状态为零,而输入不为零所产生的电路响应。
?
3、完全响应:指输入与初始状态均不为零时所产生的电路响应。
操作方法和实验步骤
1、利用Multisim软件仿真,了解电路参数和响应波形之间的关系,并通过虚拟示波器的调节熟悉时域测量的基本操作。
2、实际操作实验。
积分电路和微分电路的电路接法如下,其中电压源使。
一阶rc电路的研究实验报告

一阶rc电路的研究实验报告
一阶RC电路的研究实验报告
一阶RC电路是电路中最基本的电路之一,它由一个电阻和一个电容组成。
在这个电路中,电容器的电荷和电阻器的电流是相互作用的,因此,这个电路的特性是非常重要的。
在这篇实验报告中,我们将研究一阶RC电路的特性,并探讨它的应用。
实验过程:
我们使用了一个电阻器和一个电容器来构建一阶RC电路。
我们使用一个函数发生器来产生一个正弦波信号,并将其输入到电路中。
我们使用示波器来观察电路中的电压和电流,并记录下它们的变化。
实验结果:
我们发现,当我们改变电容器的值时,电路的特性会发生变化。
当电容器的值较小时,电路的响应速度较快,但是电路的幅度较小。
当电容器的值较大时,电路的响应速度较慢,但是电路的幅度较大。
我们还发现,当电容器的值等于电阻器的值时,电路的响应速度最快。
应用:
一阶RC电路在电子电路中有着广泛的应用。
例如,它可以用于滤波器、放大器、振荡器等电路中。
在滤波器中,一阶RC电路可以
用来滤除高频信号或低频信号。
在放大器中,一阶RC电路可以用来放大信号。
在振荡器中,一阶RC电路可以用来产生正弦波信号。
结论:
通过这个实验,我们了解了一阶RC电路的特性和应用。
我们发现,电容器的值对电路的特性有着重要的影响。
我们还发现,一阶RC 电路在电子电路中有着广泛的应用。
这个实验为我们深入了解电子电路提供了一个很好的机会。
一阶RC电路的暂态响应实验报告

一阶RC电路的暂态响应实验报告本次实验的目的是研究一阶RC电路的暂态响应,了解RC电路在电路中的应用及其响应特性,并通过实验观察、测量一阶RC电路的电流和电压随时间变化的情况,掌握实验技能和数据处理方法。
实验器材:- 万用表- 脉冲信号发生器- 电容- 电阻实验步骤:1. 根据电路图连接电路,将电容和电阻连接成一阶RC电路,通过脉冲信号发生器产生一个方波信号,调节频率为50Hz、幅值为10V。
2. 用万用表测量R、C的阻值和电容器的标称电容。
3. 用示波器观察方波信号波形,调整脉冲信号发生器的输出幅值和偏置电压,确保方波的基准线为0V。
4. 连接万用表,分别测量电容器两端的电压、电阻上的电压和电流,记录每一次测量的时间,以及电流和电压的数值,根据实验数据绘制电流和电压随时间变化的波形图。
实验结果:实验记录了电容器两端电压、电阻上的电压和电流随时间的变化情况,记录的数据如下:| 时间(ms) | Uc(V) | UR(V) | I(mA) || ---------- | ------- | ------- | ------- || 0 | 0 | 10 | 0 || 1 | 3.95 | 6.05 | 3.55 || 2 | 6.3 | 3.7 | 2.72 || 3 | 7.87 | 2.13 | 2.05 || 4 | 8.95 | 1.05 | 1.57 || 5 | 9.6 | 0.4 | 1.2 || 6 | 9.87 | 0.13 | 0.94 || 7 | 9.96 | 0.04 | 0.74 || 8 | 10 | 0 | 0.59 |结论:根据实验数据绘制的电流和电压随时间变化的波形图可以发现,电容器的电压随时间的增加而增加,最终趋近于直流源的电压值,而电阻上的电压随时间的增加而减小,最终趋近于0V。
同时,电流随时间的增加而减小,也趋近于0A。
这种响应特性是一阶RC电路的典型特征,称为指数衰减响应。
RC一阶电路的响应测试实验报告

实验七RC 一阶电路的响应测试一、实验目的1. 测定RC 一阶电路的零输入响应、零状态响应及完全响应。
2. 学习电路时间常数的测量方法。
3. 掌握有关微分电路和积分电路的概念。
4. 进一步学会用示波器观测波形。
二、原理说明1. 动态网络的过渡过程是十分短暂的单次变化过程。
要用普通示波器观察过渡过程和测量有关的参数,就必须使这种单次变化的过程重复出现。
为此,我们利用信号发生器输出的方波来模拟阶跃激励信号,即利用方波输出的上升沿作为零状态响应的正阶跃激励信号;利用方波的下降沿作为零输入响应的负阶跃激励信号。
只要选择方波的重复周期远大于电路的时间常数τ,那么电路在这样的方波序列脉冲信号的激励下,它的响应就和直流电接通与断开的过渡过程是基本相同的。
2.图7-1(b )所示的RC 一阶电路的零输入响应和零状态响应分别按指数规律衰减和增长,其变化的快慢决定于电路的时间常数τ。
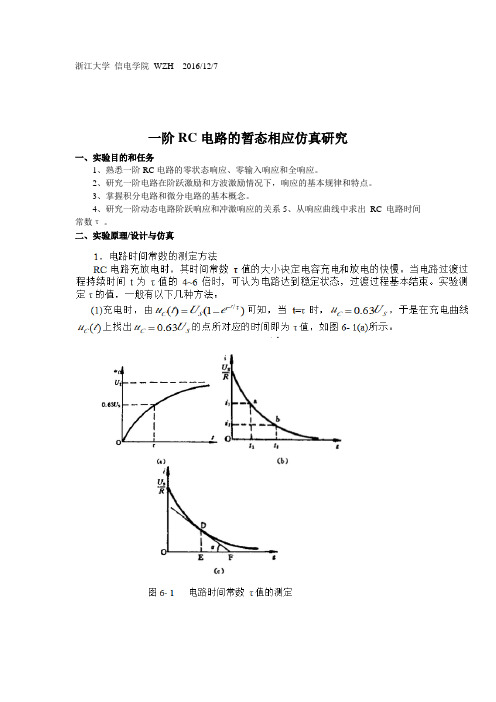
3. 时间常数τ的测定方法: 用示波器测量零输入响应的波形如图7-1(a)所示。
根据一阶微分方程的求解得知u c =U m e-t/RC=U m e-t/τ。
当t =τ时,Uc(τ)=0.368U m 。
此时所对应的时间就等于τ。
亦可用零状态响应波形增加到0.632U m 所对应的时间测得,如图13-1(c)所示。
a) 零输入响应(b) RC 一阶电路(c) 零状态响应图7-14. 微分电路和积分电路是RC 一阶电路中较典型的电路,它对电路元件参数和输入信号的周期有着特定的要求。
一个简单的RC 串联电路,在方波序列脉冲的重复激励下,当满足τ=RC<<2T 时(T 为方波脉冲的重复周期),且由R 两端的电压作为响应输出,则该电路就是一个微分电路。
因为此时电路的输出信号电压与输入信号电压的微分成正比。
如图0.368ttRCtt0.632+cu uU mcu cu uuU mU mU m7-2(a)所示。
利用微分电路可以将方波转变成尖脉冲。
rc一阶电路的响应测试实验报告

rc一阶电路的响应测试实验报告实验目的,通过实验,了解RC一阶电路对直流电压和交流电压的响应特性,掌握RC一阶电路的响应测试方法及实验步骤。
实验仪器与设备,示波器、信号发生器、电阻箱、电容器、万用表、直流稳压电源、导线等。
实验原理,RC一阶电路是由电阻和电容串联而成的电路。
在实验中,我们将通过对RC电路施加不同的输入信号,观察电路的响应情况,了解电路的频率特性和相位特性。
实验步骤:1. 搭建RC一阶电路。
将电阻和电容串联连接,接入示波器和信号发生器。
调节信号发生器的频率和幅值,使其输出正弦波信号。
2. 测量直流电压响应。
将信号发生器输出直流电压信号,通过示波器观察电路的响应情况。
记录电路的电压响应曲线,并测量电路的时间常数。
3. 测量交流电压响应。
将信号发生器输出交流电压信号,通过示波器观察电路的响应情况。
记录电路的电压响应曲线,并测量电路的频率特性和相位特性。
实验数据与分析:1. 直流电压响应曲线如图所示。
根据实验数据,我们可以得到电路的时间常数τ=RC,其中R为电阻值,C为电容值。
时间常数τ描述了电路对直流信号的响应速度,τ越小,电路的响应速度越快。
2. 交流电压响应曲线如图所示。
根据实验数据,我们可以得到电路的频率特性和相位特性。
当输入信号的频率接近电路的截止频率时,电路的响应幅值将下降,相位延迟将增加。
这表明电路对高频信号的响应能力较弱。
实验结论,通过本次实验,我们深入了解了RC一阶电路对直流电压和交流电压的响应特性。
我们掌握了RC一阶电路的响应测试方法,并通过实验数据分析了电路的时间常数、频率特性和相位特性。
这些知识对于我们理解电路的响应特性,设计滤波器和信号处理器等具有重要的意义。
实验注意事项:1. 在搭建电路时,务必注意电路连接的正确性,避免出现短路或断路等情况。
2. 在测量电路响应时,要注意调节信号发生器的频率和幅值,确保输出信号符合实验要求。
3. 实验过程中要注意安全,避免触电和短路等危险情况的发生。
一阶RC电路的暂态相应仿真研究_浙江大学
浙江大学信电学院WZH 2016/12/7一阶RC电路的暂态相应仿真研究一、实验目的和任务1、熟悉一阶RC电路的零状态响应、零输入响应和全响应。
2、研究一阶电路在阶跃激励和方波激励情况下,响应的基本规律和特点。
3、掌握积分电路和微分电路的基本概念。
4、研究一阶动态电路阶跃响应和冲激响应的关系5、从响应曲线中求出RC电路时间常数τ。
二、实验原理/设计与仿真2、实验电路的设计(1)观察零状态和零输入响应电路(2)周期方波激励观察三、主要仪器设备OrCAD软件四、实验过程与数据记录及处理实验一零状态响应电路(1)实验过程①仿真参数设置②实验结果Time0s50us100us150us200us250us300us350us400us450us500us550us600us650us700us750us800usV(C1:2)0V 2.0V4.0V6.0V图中所示为探针测量的电压值(2)实验结果分析用实验探Cursor 得到的的结果,通过search level 命令知t=50.712us实验二 零输入响应电路 (1) 实验过程①仿真参数设置仿真参数与实验一一致②实验结果Time0s50us100us150us200us250us300us350us400us450us500us550us600us650us700us750us800usV(C1:2)0V 2.0V4.0V6.0V图中所示为探针测量的电压值(2)实验结果分析同理知,T=50.87us实验三 周期方波激励响应(1)实验过程①仿真参数设置②实验结果Time0s0.5ms 1.0ms 1.5ms2.0ms2.5ms3.0ms3.5ms4.0ms4.5ms5.0msV(C1:2)V(R1:1)V(V1:+)V(V1:-)0V 5V10V图中所示为探针测量的电压值(2) 实验结果分析①测量时间t②不同t 下的输入波形变化下图为0.1t10V5V0V0s0.5ms 1.0ms 1.5ms 2.0ms 2.5ms 3.0ms 3.5ms 4.0ms 4.5ms 5.0ms V(C1:2)V(R1:1)Time下图为0.5t10V5V0V0s0.5ms 1.0ms 1.5ms 2.0ms 2.5ms 3.0ms 3.5ms 4.0ms 4.5ms 5.0ms V(C1:2)V(R1:1)Time下图为2t10V5V0V0s0.5ms 1.0ms 1.5ms 2.0ms 2.5ms 3.0ms 3.5ms 4.0ms 4.5ms 5.0ms V(C1:2)V(R1:1)Time下图为10t10V5V0V0s0.5ms 1.0ms 1.5ms 2.0ms 2.5ms 3.0ms 3.5ms 4.0ms 4.5ms 5.0ms V(C1:2)V(R1:1)Time五、讨论总结、体会实验中遇到的最大困难在于Pspice的Cursor不会使用,导致定位很难。
一阶rc电路的响应实验报告

一阶rc电路的响应实验报告一阶RC电路的响应实验报告引言:电路是电子学中最基本的研究对象之一,而RC电路是最简单的电路之一。
本次实验主要研究一阶RC电路的响应特性,通过测量电路的时间响应曲线,分析电路的充电和放电过程,以及RC电路对输入信号的频率响应。
实验目的:1. 理解一阶RC电路的基本原理和性质;2. 掌握测量电路的时间响应曲线的方法;3. 研究RC电路对不同频率输入信号的响应特性。
实验仪器和材料:1. 信号发生器2. 示波器3. 电阻箱4. 电容器5. 电压表6. 连接线实验原理:一阶RC电路由电阻R和电容C组成,其输入信号为电压源V(t),输出信号为电容器两端的电压Vc(t)。
根据基尔霍夫电压定律和电容器的充放电特性,可以得到一阶RC电路的微分方程:RC * dVc(t)/dt + Vc(t) = V(t)其中,RC为电路的时间常数,决定了电路的响应速度。
当输入信号为脉冲信号时,可以通过测量电容器两端的电压响应曲线,来研究RC电路的响应特性。
实验步骤:1. 搭建一阶RC电路,将电阻R和电容C连接起来;2. 连接信号发生器的输出端和电路的输入端,调节信号发生器的频率和幅度;3. 连接示波器的输入端和电路的输出端,调节示波器的时间基和垂直放大倍数;4. 开始测量,记录电容器两端的电压随时间的变化曲线;5. 改变输入信号的频率,重复步骤4。
实验结果与分析:在实验中,我们分别测量了RC电路对不同频率输入信号的响应曲线。
根据实验数据和曲线图,我们可以得出以下结论:1. 充电过程:当输入信号为正脉冲时,电容器开始充电。
在电容器充电过程中,电压逐渐增加,直到达到输入信号的幅度。
充电过程的时间常数由RC决定,即RC越大,充电时间越长。
2. 放电过程:当输入信号为负脉冲或零信号时,电容器开始放电。
在电容器放电过程中,电压逐渐减小,直到达到零电压。
放电过程的时间常数同样由RC决定。
3. 频率响应:当输入信号的频率增大时,电路的响应速度也会增加。
浙江大学实验报告:一阶RC电路的瞬态响应过程实验研究
三墩职业技术学院实验报告课程名称:电子电路设计实验 指导老师: 成绩:__________________实验名称: 一阶RC 电路的瞬态响应过程实验研究 实验类型:探究类同组学生:__ 一、实验目的 二、实验任务与要求三、实验方案设计与实验参数计算(3.1 总体设计、3.2 各功能电路设计与计算、3.3完整的实验电路……) 四、主要仪器设备 五、实验步骤与过程 六、实验调试、实验数据记录 七、实验结果和分析处理 八、讨论、心得一、实验目的1、熟悉一阶RC 电路的零状态响应、零输入响应过程。
2、研究一阶RC 电路在零输入、阶跃激励情况下,响应的基本规律和特点。
3、学习用示波器观察分析RC 电路的响应。
4、从响应曲线中求RC 电路的时间常数。
二、实验理论基础1、一阶RC 电路的零输入响应(放电过程) 零输入响应:电路在无激励情况下,由储能元件的初始状态引起的响应,即电路初始状态不为零,输入为零所引起的电路响应。
(实际上是电容器C 的初始电压经电阻R 放电过程。
)在图1中,先让开关K 合于位置a ,使电容C 的初始电压值0)0(U u c =-,再将开关K 转到位置b 。
电容器开始放电,放电方程是图1)0(0≥=+t dtdu RCu CC可以得出电容器上的电压和电流随时间变化的规律:式中τ=RC 为时间常数,其物理意义是衰减到1/e (36.8%))0(u c 所需要的时间,反映了电路过渡过程的快慢程度。
τ越大,暂态响应所持续的时间越长,即过渡过程的时间越长;反之,τ越小,过渡过程的时间越短。
时间常数可以通过相应的衰减曲线来反应,如图2。
由于经过5τ时间后,已经衰减到初态的1%以下,可以认为经过5τ时间,电容已经放电完毕。
图22、一阶RC 电路的零状态响应(充电过程)所谓零状态响应是指初始状态为零,而输入不为零所产生的电路响应。
一阶RC 电路在阶跃信号激励下的零状态响应实际上就是直流电源经电阻R 向C 充电的过程。
RC一阶电路的响应测试实验报告

实验七 RC 一阶电路的响应测试一、实验目的1. 测定RC 一阶电路的零输入响应、零状态响应及完全响应。
2. 学习电路时间常数的测量方法。
3. 掌握有关微分电路和积分电路的概念。
4. 进一步学会用示波器观测波形。
二、原理说明1. 动态网络的过渡过程是十分短暂的单次变化过程。
要用普通示波器观察过渡过程和测量有关的参数,就必须使这种单次变化的过程重复出现。
为此,我们利用信号发生器输出的方波来模拟阶跃激励信号,即利用方波输出的上升沿作为零状态响应的正阶跃激励信号;利用方波的下降沿作为零输入响应的负阶跃激励信号。
只要选择方波的重复周期远大于电路的时间常数τ,那么电路在这样的方波序列脉冲信号的激励下,它的响应就和直流电接通与断开的过渡过程是基本相同的。
2.图7-1(b )所示的 RC 一阶电路的零输入响应和零状态响应分别按指数规律衰减和增长,其变化的快慢决定于电路的时间常数τ。
3. 时间常数τ的测定方法:用示波器测量零输入响应的波形如图7-1(a)所示。
根据一阶微分方程的求解得知u c =U m e-t/RC=U m e-t/τ。
当t =τ时,Uc(τ)=0.368U m 。
此时所对应的时间就等于τ。
亦可用零状态响应波形增加到0.632U m 所对应的时间测得,如图13-1(c)所示。
a) 零输入响应(b) RC 一阶电路 (c) 零状态响应图 7-14. 微分电路和积分电路是RC 一阶电路中较典型的电路, 它对电路元件参数和输入信号的周期有着特定的要求。
一个简单的 RC 串联电路, 在方波序列脉冲的重复激励下, 当满足τ=RC<<2T时(T 为方波脉冲的重复周期),且由R 两端的电压作为响应输出,则该电路就是一个微分电路。
因为此时电路的输出信号电压与输入信号电压的微分成正比。
如图0.368tttt0.6320000c uuU m c uc uuU m U m U m7-2(a)所示。
利用微分电路可以将方波转变成尖脉冲。
RC一阶电路的响应测试实验报告

实验七 RC 一阶电路的响应测试一、实验目的1. 测定RC 一阶电路的零输入响应、零状态响应及完全响应。
2. 学习电路时间常数的测量方法。
3. 掌握有关微分电路和积分电路的概念。
4. 进一步学会用示波器观测波形。
二、原理说明1. 动态网络的过渡过程是十分短暂的单次变化过程。
要用普通示波器观察过渡过程和测量有关的参数,就必须使这种单次变化的过程重复出现。
为此,我们利用信号发生器输出的方波来模拟阶跃激励信号,即利用方波输出的上升沿作为零状态响应的正阶跃激励信号;利用方波的下降沿作为零输入响应的负阶跃激励信号。
只要选择方波的重复周期远大于电路的时间常数τ,那么电路在这样的方波序列脉冲信号的激励下,它的响应就和直流电接通与断开的过渡过程是基本相同的。
2.图7-1(b )所示的 RC 一阶电路的零输入响应和零状态响应分别按指数规律衰减和增长,其变化的快慢决定于电路的时间常数τ。
3. 时间常数τ的测定方法:用示波器测量零输入响应的波形如图7-1(a)所示。
根据一阶微分方程的求解得知u c =U m e-t/RC=U m e-t/τ。
当t =τ时,Uc(τ)=0.368U m 。
此时所对应的时间就等于τ。
亦可用零状态响应波形增加到0.632U m 所对应的时间测得,如图13-1(c)所示。
a) 零输入响应(b) RC 一阶电路 (c) 零状态响应图 7-14. 微分电路和积分电路是RC 一阶电路中较典型的电路, 它对电路元件参数和输入信号的周期有着特定的要求。
一个简单的 RC 串联电路, 在方波序列脉冲的重复激励下, 当满足τ=RC<<2T时(T 为方波脉冲的重复周期),且由R 两端的电压作为响应输出,则该电路就是一个微分电路。
因为此时电路的输出信号电压与输入信号电压的微分成正比。
如图0.368tttt0.6320000c uuU m c uc uuU m U m U m7-2(a)所示。
利用微分电路可以将方波转变成尖脉冲。
RC一阶电路的响应测试--实验分析报告

RC一阶电路的响应测试--实验报告————————————————————————————————作者:————————————————————————————————日期:实验六RC一阶电路的响应测试一、实验目的1. 测定RC一阶电路的零输入响应、零状态响应及完全响应。
2. 学习电路时间常数的测量方法。
3. 掌握有关微分电路和积分电路的概念。
4. 进一步学会用虚拟示波器观测波形。
二、原理说明1. 动态网络的过渡过程是十分短暂的单次变化过程。
要用普通示波器观察过渡过程和测量有关的参数,就必须使这种单次变化的过程重复出现。
为此,我们利用信号发生器输出的方波来模拟阶跃激励信号,即利用方波输出的上升沿作为零状态响应的正阶跃激励信号;利用方波的下降沿作为零输入响应的负阶跃激励信号。
只要选择方波的重复周期远大于电路的时间常数τ,那么电路在这样的方波序列脉冲信号的激励下,它的响应就和直流电接通与断开的过渡过程是基本相同的。
2.图6-1(b)所示的RC 一阶电路的零输入响应和零状态响应分别按指数规律衰减和增长,其变化的快慢决定于电路的时间常数τ。
3. 时间常数τ的测定方法用示波器测量零输入响应的波形如图6-1(a)所示。
根据一阶微分方程的求解得知u c=U m e-t/RC=U m e-t/τ。
当t=τ时,Uc(τ)=0.368U m。
此时所对应的时间就等于τ。
亦可用零状态响应波形增加到0.632U m所对应的时间测得,如图6-1(c)所示。
(a) 零输入响应(b) RC一阶电路(c) 零状态响应图6-14. 微分电路和积分电路是RC一阶电路中较典型的电路,它对电路元件参数和输入信号的周期有着特定的要求。
一个简单的RC串联电路,在方波序列脉冲的重复激励下,当满足τ=RC<<2T时(T为方波脉冲的重复周期),且由R两端的电压作为响应输出,这就是一个微分电路。
因为此时电路的输出信号电压与输入信号电压的微分成正比。
rc一阶电路的响应测试的实验报告(一)

rc一阶电路的响应测试的实验报告(一)RC一阶电路的响应测试实验报告实验目的•了解RC一阶电路的响应特性•熟悉实验仪器的使用方法•掌握如何测量RC电路的响应特性实验原理RC电路是由一个电阻和一个电容构成的电路,其可以起到起到滤波作用。
在电路中加入一个脉冲信号,可以测量电路的响应时间。
RC响应有两个重要的指标,分别为时间常数和衰减系数。
实验步骤1.将实验电路搭建好,电路图如下:+----R----+| |Vin --- ---| |+----C----+| |GND GND2.使用示波器测量电路中电压的变化,将输入的方波信号接在电路的输入端,将示波器测量的信号接在电路的输出端。
3.调节示波器的水平和垂直刻度,调整电压信号的幅值。
4.改变输入信号频率,观察输出电压的波形。
5.记录电路输出电压的上升时间和下降时间。
实验结果分析通过实验测量,记录了不同频率下的电路输出电压的波形,分析得到电路的时间常数和衰减系数。
实验结果与理论值偏差较小,说明实验操作正确。
实验总结通过本实验,我们对RC一阶电路的响应特性有了更深入的了解,掌握了简单电路的搭建方法和仪器的使用技巧。
实验过程中,对于示波器的调节需要有更好的操作经验,同时要注意调整电路的各个参数以获得更准确的实验结果。
实验注意事项•实验过程中,要小心操作,避免对电路和仪器造成损坏。
•实验前需要将电路搭建好,检查连接是否正确,确保电路能正常工作。
•实验中的电压值不宜过大,以免造成电路损坏或其他意外情况。
•测量结果要进行多次实验,取平均值以提高数据的准确度。
实验器材及仪器•电阻•电容•信号发生器•示波器实验结果展示下面是实验结果的表格展示:频率(Hz)上升时间(ms)下降时间(ms)100 2.1 1.9500 0.42 0.381k 0.21 0.195k 0.042 0.03810k 0.021 0.019结论通过本次实验,我们成功地测量了RC一阶电路的响应特性,并对理论知识做了更深入的了解。
rc一阶电路的响应实验报告

rc一阶电路的响应实验报告
RC一阶电路的响应实验报告
实验目的:
本实验旨在通过对RC一阶电路的响应进行实验,了解电路的频率响应特性,
以及电压和电流的变化规律。
实验原理:
RC一阶电路是由一个电阻和一个电容组成的简单电路。
当交流信号通过电路时,电容会对电流产生阻抗,从而影响电路的频率响应。
在本实验中,我们将通过
改变输入信号的频率,观察电路的响应变化。
实验步骤:
1. 搭建RC一阶电路,连接信号发生器、示波器和电压表。
2. 将信号发生器的频率设置为不同数值,如100Hz、1kHz、10kHz等。
3. 观察示波器上电压波形的变化,并记录下电压的峰峰值。
4. 同时记录下电容两端的电压和电流的数值。
实验结果:
通过实验观察和记录,我们得到了不同频率下RC一阶电路的响应情况。
随着
频率的增加,电路的电压响应逐渐减小,而电流响应则逐渐增大。
这说明在高
频率下,电容对电路的影响逐渐减弱,电流成为主要的响应因素。
实验分析:
根据实验结果,我们可以得出结论,RC一阶电路在不同频率下有不同的响应特性。
这对于电路设计和信号处理都有重要的指导意义。
同时,我们也可以通过
实验结果验证理论模型,进一步加深对电路的理解。
结论:
通过本次实验,我们了解了RC一阶电路的频率响应特性,以及电压和电流的
变化规律。
这对于电路设计和实际应用都具有重要的参考价值。
希望通过这次
实验,能够对电路理论有更深入的了解,为今后的学习和研究打下坚实的基础。
一阶RC电路的暂态响应实验报告

一阶RC电路的暂态响应实验报告实验目的:学习和掌握一阶RC电路暂态响应的特性,探究电路元件对电路响应的影响。
实验原理:一阶RC电路是由一个电阻和一个电容构成的简单电路。
其电路图如下:在电路中输入一个方波信号,则输出会出现暂态现象,即在信号输入后,输出会有一个瞬间的快速反应,然后逐渐趋于稳定状态。
这一过程即为暂态响应。
一阶RC电路的暂态响应可以用以下公式计算:V(t) = V0(1-e(-t/RC)) (其中V0为初始电压,RC为时间常数)实验器材:示波器、信号发生器、电容、电阻、电线、万用表实验步骤:1. 按照电路图连接电路,将RC电路接到示波器和信号发生器中。
2. 使用信号发生器提供一个方波信号,设置频率和振幅(我们设置的频率为1000Hz,振幅为5V)。
3. 调节示波器的触发模式,使其在每个周期的上升沿触发并显示输出电压的波形。
4. 改变电路中的电阻和电容值,观察暂态响应的变化情况(我们尝试了不同的电阻和电容值)。
5. 记录数据并分析。
实验结果:我们先连接了一个10欧姆的电阻和一个1微法的电容,观察到了一阶RC电路的暂态响应现象。
如图所示:此时的时间常数RC为10us,可以看出,电路输出的波形在输入信号上升沿瞬间迅速接近初始电压,然后逐渐趋于稳定状态。
接着我们使用了不同的电阻和电容值,观察了响应的变化:1. 10欧姆电阻和2微法电容,其时间常数为20us,响应速度略慢于上一次。
2. 5欧姆电阻和1微法电容,时间常数为5us,响应速度比第一次快很多。
3. 20欧姆电阻和1微法电容,时间常数为20us,响应速度比第一次慢一些。
由此可以看出,电阻和电容对电路暂态响应的速度有一定的影响。
时间常数越小,响应速度越快。
实验结论:通过本次实验,我们了解到了一阶RC电路的暂态响应特性,并且探究了电路元件对响应速度的影响。
我们同时也发现,暂态响应是电路响应的一种常见现象,能够在各种电路中出现。
深入理解和掌握此类特性,对于电路的工程应用具有重要意义。
RC一阶电路响应测试_实验报告

RC一阶电路响应测试_实验报告实验目的:掌握RC一阶电路的响应特性,验证一阶电路的高通和低通滤波特性,并测量其截止频率。
实验仪器:示波器、信号发生器、直流稳压电源、RC电路板。
实验原理:一阶RC电路由一个电阻R和一个电容C组成。
在该电路中,当输入信号变化时,电容器上的电压也随着变化。
因此,该电路的输出是一个对输入信号进行滤波的结果。
一阶RC高通滤波器:该电路通过传递频率高于截止频率的信号,将高频信号传递到输出端,因此该电路用于滤除低频噪声。
一阶RC低通滤波器:该电路通过传递频率低于截止频率的信号,将低频信号传递到输出端,因此该电路用于滤除高频噪声。
截止频率公式:Fc=1/(2πRC)实验步骤:1.将信号发生器的输出连接到RC电路板的输入端,并将示波器连接到RC电路板的输出端。
2.将信号发生器的正极连接到RC电路板的输入端,将示波器的探头连接到RC电路板的输出端。
3.调节信号发生器的频率,使得示波器显示出正弦波形,并记录下该频率。
4.在此基础上,逐渐降低频率,记录下示波器显示的波形变化和频率。
5.逐渐增加频率,重复步骤4。
6.根据所得的数据计算出截止频率,并与理论值进行对比。
实验结果:从实验中得到的数据可以得到RC低通、高通截止频率的计算结果。
得出的数据和计算过程如下:1.高通滤波:当输入频率很低时,输出电压几乎为0,随着输入频率的增加,输出电压逐渐增加。
当输入频率接近电路截止频率时,输出电压开始变化非常缓慢。
当输入频率超过电路截止频率时,输出电压趋于稳定。
例如,将电容C和电阻R的值设置为1μF和1kΩ,输入信号频率从100Hz逐渐增加到1kHz。
当输入频率低于100Hz时,输出电压几乎为0。
当输入频率接近100Hz时,输出电压逐渐增加。
当输入频率超过100Hz时,输出电压开始变化非常缓慢,直到输入信号的频率超过截止频率1.59kHz时,输出电压趋于稳定。
根据公式Fc=1/(2πRC),可得截止频率为1.591549 Hz。
一阶rc电路的研究实验报告

一阶rc电路的研究实验报告一阶RC电路的研究实验报告引言:电路是电子学中最基础的研究对象之一。
而一阶RC电路是电子学中最简单的电路之一,也是初学者常常接触到的电路之一。
本实验旨在通过对一阶RC电路的研究,探究其特性和性能。
实验目的:1. 研究一阶RC电路的充放电过程;2. 探究电容和电阻对一阶RC电路性能的影响;3. 分析一阶RC电路的频率响应。
实验器材:1. 直流电源;2. 电阻箱;3. 电容;4. 示波器;5. 万用表;6. 连接线。
实验步骤:1. 搭建一阶RC电路:将电容和电阻按照实验电路图连接起来,确保电路连接正确无误。
2. 充电过程观察:将电源接通,记录电容器电压随时间的变化情况。
通过示波器观察电压波形,并记录相关数据。
3. 放电过程观察:断开电源,记录电容器电压随时间的变化情况。
通过示波器观察电压波形,并记录相关数据。
4. 改变电阻值:将电阻箱的阻值调整为不同数值,重复步骤2和步骤3,观察电容器电压随时间的变化情况,并记录相关数据。
5. 改变电容值:更换电容器,重复步骤2和步骤3,观察电容器电压随时间的变化情况,并记录相关数据。
6. 频率响应分析:将示波器连接到电阻上,通过改变输入信号频率,观察输出电压随频率的变化情况,并记录相关数据。
实验结果与分析:1. 充电过程观察:根据实验数据绘制电容器电压随时间的变化曲线,可以看出充电过程呈指数衰减趋势。
随着时间的增加,电容器电压逐渐接近电源电压。
2. 放电过程观察:根据实验数据绘制电容器电压随时间的变化曲线,可以看出放电过程也呈指数衰减趋势。
随着时间的增加,电容器电压逐渐趋近于零。
3. 改变电阻值:根据实验数据绘制不同电阻值下电容器电压随时间的变化曲线,可以观察到电阻值的变化对充放电过程的时间常数有影响。
电阻值增大时,充放电过程的时间常数增大,电容器充放电速度变慢。
4. 改变电容值:根据实验数据绘制不同电容值下电容器电压随时间的变化曲线,可以观察到电容值的变化对充放电过程的时间常数也有影响。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三墩职业技术学院实验报告
课程名称:电子电路设计实验指导老师:成绩:__________________
实验名称:一阶 RC电路的瞬态响应过程实验研究实验类型:探究类同组学生姓名:__
一、实验目的二、实验任务与要求
三、实验方案设计与实验参数计算( 3.1 总体设计、 3.2 各功能电路设计与计算、 3.3 完整的
实验电路⋯⋯)
四、主要仪器设备五、实验步骤与过程
六、实验调试、实验数据记录七、实验结果和分析处理
八、讨论、心得
一、实验目的
1、熟悉一阶 RC电路的零状态响应、零输入响应过程。
2、研究一阶 RC电路在零输入、阶跃激励情况下,响应的基本规律和特点。
3、学习用示波器观察分析RC电路的响应。
4、从响应曲线中求RC电路的时间常数。
二、实验理论基础
装
1、一阶 RC电路的零输入响应(放电过程)
订零输入响应:
电路在无激励情况下,由储能元件的初始状态引起的响应,即电路初始状态不为线
零,输入为零所引起的电路响应。
(实际上是电容器 C 的初始电压经电阻R 放电过程。
)
图 1
在图 1 中,先让开关 K 合于位置 a,使电容 C 的初始电压值 u c (0 )U 0,再将开关K 转到位置 b。
电容器开始放电,放电方程是
u C RC du C
0 (t 0) dt
可以得出电容器上的电压和电流随时间变化的规律:
t
t
t
t
u
(0 )e
RC
U
u C (t ) u C (0 )e
RC
U 0e
(t 0)
C
e
(t 0)
i C (t )
R
R
式中 τ=RC 为时间常数,其物理意义
u C (t )
是衰减到 1/e (36.8%) u c (0) 所需要的时间,反映了电路过渡过程的快慢程度。
τ 越大,暂态响应所持续的时间越长,即过渡过程的时间越长;反之,
过渡过程的时间越短。
时间常数可以通过相应的衰减曲线来反
u C (t )
τ越小,
应 ,如
图 2。
由于经过 5τ时间后, 已经衰减到初态的 1%以下,可以认为经过 5τ时间,电容已经放电完毕。
图 2
2、一阶 RC 电路的零状态响应(充电过程)
所谓零状态响应是指初始状态为零, 而输入不为零所产生的电路响应。
一阶
RC 电路在阶跃信号激励下的零状态响应实际上就是直流电源经电阻
R 向 C 充电
的过程。
在图 1 所示的一阶电路中,先让开关 K 合于位置 b ,当 t = 0 时,将开 关 K 转到位置 a 。
u C
RC du C
U S
(t
0)
电容器开始充电,充电方程为 dt
初始值 u c (0) =0
可以得出电压和电流随时间变化的规律:
t
t
t
t
u C (t) U S 1 e
RC
U S 1 e(t
0)
i C (t )
U
S
e RC
U S
e (t
0)
R
R
式中 τ =RC 为时间常数,其物理意义是由初始值上升至稳态值与初始值差值的
63.2%处所需要的时间。
同样可以从响应曲线中求出 τ,如图 3。
3
3.方波响应
当方波信号激励加到 RC两端时,在电路的时间常数远小于方波周期时,可以视为零状态响应和零输入响应的多次过程。
方波的前沿相当于给电路一个阶跃输入,其响应就是零状态响应;方波的后沿相当于在电容具有初始值uc(0) 时,装
把电源用短路置换,电路响应转换成零输入响应。
当方波的 1/2 周期小于电路的时间常数时,方波前后沿对应的是瞬态过程
订的其中一小部分。
线由于方波是周期信号,可以用普通示波器显示出稳定的响应图形,便于观察和作定量分析。
三、实验仪器设备
实验电路板、示波器(电路图如图所示)、直流稳压源(为电路板提供12V电压)
测试信号产生部分实验测试部分
P.4四、实验任务与步骤
1.用示波器观察 RC电路的零输入响应、零状态响应,描绘响应曲线,求出电路
的时间常数。
2.更换电路中电阻、电容的大小,重新测量电路的各种响应,分别求出每次测
量的时间常数。
3.理论计算电路的时间常数,并与实验测量值比较。
五、实验操作要点
1、明确实验目的、实验要求与实验原理。
2、根据示波器的显示,描绘出各种RC电路的响应波形,加以比较。
3、进行测量误差分析。
六、实验数据记录
表 1、不同接入条件、电路状态下响应波形图、幅度及时间
电路状态接入电路
接入电容 C/pF波形图
周期内电路响
响应时间 t/ms
装R/ Ω应幅度△ U/v
订
线①43001010310.960.220零输入
响应(放
电)
②430022104 4.600.524
③7501010411.280.384
零状态
响应(充
电)
④910010 104 5.040.544
P.5
七、实验结果与处理
上述四组实验中,①③两组在方波的一个周期内响应完全,可根据完全响应
t
时 t=5τ来得到τ;②④两组在一个周期内未响应完全,可根据u U s (1- e) 来
得到τ。
理论计算τ=RC。
表 2、最终数据处理结果
电路状态
零输入
响应(放
电)
零状态
装响应
(充电)订
接入电路接入电容
理论计算实际测量误差
R/ΩC/pF
τ / μsτ/ μ s
①4300101034344.0 2.33%
②430022104946962.8 1.78%
③75010104
7576.8 2.40%④910010104910918.80.97%
可以看到,最终测量计算出的时间常数τ,基本符合理论计算结果。
线
八、讨论、心得
( 1)实验心得
本次实验测量了在接入不同电阻电容情况下的 RC电路时间常数,分析了瞬态过程中电路响应,也练习了示波器的操作。
在实验中,需要注意如何判断电路以达到完全响应,也就是用示波器的刻度线与曲线水平部分重合,找到曲线与直线的切点,该点表示 RC电路刚达到完全响应。
测量出起始到完全响应的时间即可计算时间常数。
( 2)误差分析
本实验主要误差来自于读数的误差。
因为示波器的图像有一定宽度,实际上是很难准确判断刚好达到完全响应的时刻点的,只能大致估计,所以会造成误差。
另外,直流稳压源所提供的电压不一定始终保持12V,仪器误差也会影响最终的计算结果。
P.6( 3)思考题
1、什么是零输入响应,零状态响应?
答:
零输入响应:电路在无激励情况下,由储能元件的初始状态引起的响应。
(即电
路初始状态不为零,输入为零所引起的电路响应)(放电过程)
零状态响应:初始状态为零,而输入不为零所产生的电路响应。
(充电过程)
2、在用示波器观察RC电路响应时如何才能使示波器的扫描与电路激励同步?
答:
将触头与测试点勾住,架子夹住接地点,转动示波器上的TIME/DIV 旋钮,使得
示波器上的图像从杂乱无章到稳定不变,即扫描与激励同步。
3、什么是时间常数?它在电路中起什么作用?
答:
装
时间常数是指一个物理量从最大值衰减到最大值的1/e 所需要的时间。
在 RC电
订路零输入响应中,电容电压 Uc 总是由初始值 Uc(0)按指数衰减到零,则电容电压
线Uc 从Uc(0)衰减到1/eUc(0)的时间即为时间常数。
在RC电路零状态响应中,电容电压从初始值上升至稳态值的 1-1/e=63.2%所需的时间,即为时间常数τ 。
声明
本实验报告内容可随意编辑、参考、引用,但请不要完全抄袭。
本实验报告仅供参考,严禁用于商业用途。
Copyright by BaiduID:792015085。
