实验四 图像增强
图像增强实验

图像增强实验图像的增强⼀. 实验⽬的1. 熟悉直⽅图的计算和显⽰;2. 熟悉通过算术运算进⾏图像增强的⽅法;3. 熟悉运⽤直⽅图变换进⾏图像增强的原理。
⼆. 实验原理1. 直⽅图在数字图像处理中,⼀种最简单和最有⽤的⼯具是直⽅图,它概括了⼀幅图像的灰度级内容。
(1)函数:imhist(I,n)功能:显⽰指定图像的直⽅图。
语法格式:Imhist(I,n)Imhist(X,map)*counsts,x+=imhist(…)说明:I为输⼊图像,n为指定的灰度级数⽬,默认值为256。
Imhist(X,map)计算和显⽰索引⾊图像为X的直⽅图,map为调⾊板。
*counsts,x+=imhist(…)返回直⽅图数据向量counts 或相应的⾊彩值向量x。
(2)函数:imadjust功能:将图像的灰度值映像为⼀个新的数值范围。
语法格式:J=imsdjust(I,[low_in high_in],[low_out high_out],gamma)newmap=imadjust(map,[low high],[bottom top],gamma) 说明:I是输⼊图像矩阵,J是经过直⽅图变换后的输出图像矩阵。
Low_in参数和high_in参数分别⽤来指定输⼊图像需要映像的灰度范围,参数Low_out和high_out指定输出图像所在的灰度范围。
newmap=imadjust(map,[low high],[bottom top],gamma)命令是调整索引⾊图像的调⾊板map。
此时若[low high]和[bottom top]都是2×3矩阵,就根据它们的值分别调整R、G、B三个分量。
不管I属于哪⼀类,此处指定的强度值的范围均为[1,0]。
如果I是unint8,则会将⽤户指定的值乘以255,然后将得到的结果作为实际的强度使⽤。
如果I是unint16,则会乘以65536。
Gamma是⼀个可选参数。
⼀般来说灰度间的映像是直线,但是通过调整gamma参数可以使其变为⾮线性的映像。
图像增强实验报告

图像增强实验报告图像增强实验报告引言:图像增强是数字图像处理中的重要技术之一,它可以通过改变图像的亮度、对比度、色彩等参数,使图像更加清晰、细节更加突出。
本实验旨在探究不同图像增强方法对图像质量的影响,并比较它们的效果。
一、实验目的通过实验比较不同的图像增强方法,包括直方图均衡化、拉普拉斯算子增强、灰度变换等,对图像质量的影响,了解各种方法的优缺点,为实际应用提供参考。
二、实验步骤1. 实验准备:准备一组包含不同场景、不同光照条件下的图像样本,以及实验所需的图像处理软件。
2. 直方图均衡化:将图像的直方图进行均衡化,使得图像的像素值分布更加均匀,从而提高图像的对比度和亮度。
3. 拉普拉斯算子增强:使用拉普拉斯算子对图像进行边缘增强,突出图像的细节和纹理。
4. 灰度变换:通过调整图像的灰度级别,改变图像的亮度和对比度,使图像更加清晰明亮。
5. 实验结果分析:对比不同图像增强方法处理后的图像,分析它们在视觉效果上的差异,并根据实验结果评估各种方法的优劣。
三、实验结果与讨论在本次实验中,我们选择了一张室内拍摄的暗淡图像作为样本进行增强处理。
首先,我们对该图像进行了直方图均衡化处理。
结果显示,通过直方图均衡化,图像的亮度和对比度得到了明显的提升,细节也更加清晰可见。
然而,由于直方图均衡化是全局处理,可能会导致图像的局部细节过于突出,从而影响整体视觉效果。
接下来,我们采用了拉普拉斯算子增强方法。
通过对图像进行边缘增强,图像的纹理和细节得到了突出展示。
然而,拉普拉斯算子增强也存在一定的局限性,对于噪声较多的图像,可能会导致边缘增强过程中出现伪影和锯齿现象。
最后,我们尝试了灰度变换方法。
通过调整图像的灰度级别,我们改变了图像的亮度和对比度,使图像的细节更加突出。
与直方图均衡化相比,灰度变换方法更加灵活,可以根据实际需求对图像进行个性化的调整。
综合对比三种图像增强方法的实验结果,我们可以得出以下结论:直方图均衡化适用于对整体亮度和对比度进行提升的场景;拉普拉斯算子增强适用于突出图像的边缘和纹理;灰度变换方法可以根据实际需求对图像进行个性化调整。
ERDAS实验报告
遥感实验四图像增强和利用监督分类提取地类信息一、实验目的根据任务分配表获取自己所需要的数据源,应用ERDAS和ArcGIS软件将本人所分配城市范围内城镇用地和水域面积进行统计并作对比, 并制作城市土地变化图。
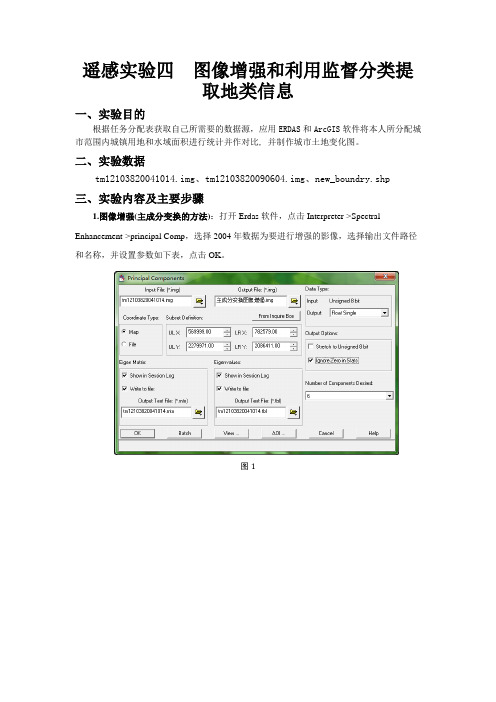
二、实验数据tm12103820041014.img、tm12103820090604.img、new_boundry.shp三、实验内容及主要步骤1.图像增强(主成分变换的方法):打开Erdas软件,点击Interpreter->Spectral Enhancement->principal Comp,选择2004年数据为要进行增强的影像,选择输出文件路径和名称,并设置参数如下表,点击OK。
图1图22.裁剪(AOI视图裁剪方法):点击Data Prep->Subset Image,弹出Subset对话框,选择要输入和输出的文件路径和名称,打开视图窗口,加载new_boundry.shp,点击合肥市所在区域,点击AOI->Copy Selection to AOI,点击Subset对话框中的AOI按钮,选择Viewer,点击OK。
图3 图4图63.监督分类i点击Classifier->Signature Editor,弹出Signature Editor对话框,点击视图窗口AOI->Tools。
利用按钮在裁剪的图上勾选出感兴趣区域,点击按钮添加到Signature Editor对话框中。
添加9个水域的感兴趣区域后,选择所有添加的记录,点击Signature Editor对话框将上面的记录归结为一类,并命名为water,点击Edit->Delete,删除选中的记录。
同理,选择出绿地和城镇的分类信息。
点击File->Save as,存储为*sig格式的分类信息文件。
ii点击Classifier->Supervised Classification,选择要进行分类的图像和分类后的图像名称和路径,选择之前做好的*sig格式分类信息文件导入,点击OK。
数字图像处理实验 频域图像增强

数字图像处理实验报告实验四频域图像增强1、实验目的• 1.熟悉傅里叶变换的基本性质;• 2.热练掌握FFT方法及应用;• 3.通过实验了解二维频谱的分布特点;• 4.通过本实验掌握利用MATLAB编程实现数字图像的傅立叶变换及滤波锐化和复原处理;• 5.了解理想、巴特沃兹、高斯等不同滤波器的结构及滤波效果。
2、实验步骤•1.调入实验一获得的图像,对这幅图像做FFT并显示其频谱;•2.对上幅图像做离散余弦变换并显示其频谱;•3.将离散余弦变换应用于图像压缩。
3、实验源码对这幅图像做FFT并显示其频谱B=imread('test.bmp')imshow(B)F=fft2(B)S=abs(F)imshow(S,[])对上幅图像做离散余弦变换并显示其频谱i=imread('test.bmp')i=im2double(i)T=dctmtx(8)B=blkproc(i,[8,8],'P1*x*P2',T,T)imshow(B)将离散余弦变换应用于图像压缩(压缩后的图像有点失真,但不影响视觉效果,图像数据量缩小了)mask=[1 1 1 1 0 0 0 01 1 1 0 0 0 0 01 1 0 0 0 0 0 01 0 0 0 0 0 0 00 0 0 0 0 0 0 00 0 0 0 0 0 0 0]B2=blkproc(B,[8,8],'P1*x',mask)i2=blkproc(B2,[8,8],'P1*x*P2',T,T)subplot(1,2,1),imshow(i);title('原图')subplot(1,2,2),imshow(i2);title('离散余弦变换压缩')4、实验截图实验一获得的图像图像做FFT并显示其频谱做离散余弦变换并显示其频谱将离散余弦变换应用于图像压缩5、实验小结付里叶变换在计算图像的卷积中有很大应用。
实验四 彩色增强技术

实验四 彩色增强技术一、实验目的:1、熟悉伪彩色增强原理和方法,掌握伪彩色增强技术及其应用。
2、熟悉真彩色图像增强的方法和步骤,提高学生彩色图像处理能力。
二、 实验原理伪彩色增强是把黑白图像的各个不同灰度级变换成不同的彩色。
1、密度分割法密度分割或称强度分割法是伪彩色增强中最简单的一种,使用多分层技术。
具体过程如下:做若干个平行于xy 坐标的平面,那么每个平面与函数f (x ,y )相交,这样就把f (x ,y )表示的连续灰度分成若干级别,分层数可根据需要的精度加以任意设置。
然后可以根据下面的关系分配颜色: f (x ,y )=C kC k 是与切割平面定义的第k 个区间Rk 相关的颜色。
2、空间域灰度——彩色变换合成法这是一种更常用、更有效的伪彩色增强法。
处理过程如图1所示。
它是根据色度学原理,将原图像的灰度分段经过红、绿、蓝三种不同的变换,变成三基色分量,然后便可以合成一幅彩色图像。
彩色的含量由变换函数的形状而定。
典型的变换函数如图2所示,其中图(a )(b )(c )分别为红、绿、蓝三种变换函数,(d )是把三种变换函数画在同一坐标系。
由图可见,灰度为不同值时,通过变换将由三基色混合成不同的色调。
彩色合成图1 灰度——彩色变换过程3、真彩色增强真彩色增强处理的对象不是一幅灰度图像,而是一幅自然彩色图像或是同一景物的多光谱图像,是从彩色到彩色的一种转换。
彩色增强的目的:一个是变换图像的色彩,引起人们的特别关注;另一个是由于人眼对不同颜色的灵敏度不同,使景物呈现与人眼色觉相匹配的颜色,以提高人眼对目标的分辨率。
选择合适的变换函数,映射出新的彩色空间。
将RGB 转换为HSI模型,然后对其亮度、色度等信息增强,再返回RGB模式。
三、 实验内容1、MATLAB 中彩色图像的表示方法图像处理工具将彩色图像当作索引图像或RGB 图像。
(1) RGB 图像:M ×N ×3的数组,每个像素有红、绿、兰三个分量组成。
图像增强__实验报告

深圳大学实验报告课程名称: 数字图像处理实验项目名称: 图像增强学院: 信息工程学院专业: 通信工程****: ***报告人: 学号: 班级: 1班实验时间: 2015、04、09实验报告提交时间: 2015、05、21教务处制[1] 简述直方图均衡化原理答:直方图均衡化的基本思想就是对原始图像中的像素灰度做某种映射变换,使变换后的图像灰度的概率密度就是均匀分布的,即变换后图像就是一幅灰度均匀分布的图像,这意味着图像灰度的动态范围得到了增加,从而可提高图像的对比度。
[2] 对给定的两幅灰度数字图像(可以用MATLAB自带的图像文件)进行如下处理:a、对原图像进行直方图均衡化处理,同屏显示处理前后图像及其直方图,比较异同,并回答为什么数字图像均衡化后其直方图并非完全均匀分布。
答:代码实现如下:A = imread('1、jpg');I=rgb2gray(A);[height,width] = size(I);figuresubplot(221)imshow(I)%显示原始图像subplot(222)imhist(I)%显示原始图像直方图%进行像素灰度统计;s = zeros(1,256);%统计各灰度数目,共256个灰度级for i = 1:heightfor j = 1: widths(I(i,j) + 1) = s(I(i,j) + 1) + 1;%对应灰度值像素点数量增加一 endend%计算灰度分布密度p = zeros(1,256);for i = 1:256p(i) = s(i) / (height * width * 1、0);end%计算累计直方图分布c = zeros(1,256);c(1) = p(1);for i = 2:256c(i) = c(i - 1) + p(i);end%累计分布取整,将其数值归一化为1~256c = uint8(255 、* c + 0、5);%对图像进行均衡化for i = 1:heightfor j = 1: widthI(i,j) = c(I(i,j)+1);endendsubplot(223)imshow(I)%显示均衡化后的图像subplot(224)imhist(I)%显显示均衡化后的图像的直方图进行灰度均衡化的公式有很多,只要满足两个关键的条件就行了。
实验四、图像增强

实验四、图像增强一、实验目的1掌握灰度直方图的概念及其计算方法;2熟练掌握直力图均衡化和直方图规定化的计算过程;3熟练掌握空域滤波中常用的平滑和锐化滤波器;4掌握色彩直方图的概念和计算方法5利用MATLAB程序进行图像增强。
二、实验原理图像增强是指按特定的需要突出一幅图像中的某些信息,同时,削弱或去除某些不需要的信息的处理方法。
其主要目的是处理后的图像对某些特定的应用比原来的图像更加有效。
图像增强技术主要有直方图修改处理、图像平滑化处理、图像尖锐化处理和彩色处理技术等。
本实验以直方图均衡化增强图像对比度的方法为主要内容,其他方法同学们可以在课后自行联系。
直方图是多种空间域处理技术的基础。
直方图操作能有效地用于图像增强。
除了提供有用的图像统计资料外,直方图固有的信息在其他图像处理应用中也是非常有用的,如图像压缩与分割。
直方图在软件中易于计算,也适用于商用硬件设备,因此,它们成为了实时图像处理的一个流行工具。
直方图是图像的最基本的统计特征,它反映的是图像的灰度值的分布情况。
直方图均衡化的目的是使图像在整个灰度值动态变化范围内的分布均匀化,改善图像的亮度分布状态,增强图像的视觉效果。
灰度直方图是图像预处理中涉及最广泛的基本概念之一。
图像的直方图事实上就是图像的亮度分布的概率密度函数,是一幅图像的所有象素集合的最基本的统计规律。
直方图反映了图像的明暗分布规律,可以通过图像变换进行直方图调整,获得较好的视觉效果。
直方图均衡化是通过灰度变换将一幅图像转换为另一幅具有均衡直方图,即在每个灰度级上都具有相同的象素点数的过程。
处理后的图像直方图分布更均匀了,图像在每个灰度级上都有像素点。
从处理前后的图像可以看出,许多在原始图像中看不清楚的细节在直方图均衡化处理后所得到的图像中都变得十分清晰。
三、实验步骤1.显示一幅图像的直方图和经过均衡化处理过的图像直方图,进行观察对比。
相应的代码:x1=imread('lenna.bmp'); %读原图x2=rgb2gray(x1); %转换为灰度图像imshow(x2);figure,imhist(x2);x3=histeq(x2);%均衡化figure,imshow(x3);显示的结果:直方图:均衡化后的图像:2.给一幅图像分别加入高斯噪声和椒盐噪声,使用中值滤波(窗口3*3, 5*5)对其进行平滑,显示平滑结果,并进行观察对比。
实验四 图像增强处理

实验三图像增强处理一、实习目的和要求·了解什么是遥感图像解译,了解遥感图像解译的目的,根据不同的应用目的能够选择不同的方法增强解译效果;·学习图像增强的方法,能够对不同应用目的的图像进行不同的增强效果,达到解译效果;·知道ERDAS软件中图像增强处理主要分成三部分:空间、辐射、光谱增强,了解空间、辐射、光谱分辨率的概念并有直观的概念;·理解各种图像增强方法的原理,熟练掌握用ERDAS软件进行增强的操作步骤;要求能够独立完成各种增强处理;·了解图像解译的基本原理,能够通过ERDAS软件进行简单的图像解译,达到分析图像应用图像的目的;·掌握变化监测的原理并能够通过软件分析和应用变化监测;·了解地形分析和傅里叶变换的原理能够使用遥感软件进行分析;·了解归纳分析和区域特征的原理,会使用这几种方法,掌握代数运算的原理了解在图像处理中的实际应用;·了解图像投影变换的原理以及方法;·了解傅里叶变换的方法以及原理和应用;二、实验原理·当一幅图像的目视效果不太好,或则有用的信息突出不够时,就需要对图像进行增强处理,图像增强的目的是为了提高图像质量和突出所需信息,有利于分析判读或作进一步处理;·图像空间增强是利用象元自身及其周围象元的灰度值进行运算,达到增强目的主要有卷积增强、非定向边缘增强、纹理分析、锐化处理、自适应滤波等;·图像辐射增强处理时对单个象元的灰度值进行变换达到图像增强的目的,主要有直方图均衡化、直方图匹配、亮度反转、降噪处理、去条带处理等;·图像光谱增强处理是基于多波段数据对每个象元的灰度值进行变换达到增强,主要方法有主成分变换、主成分逆变换、缨帽变换、色彩变换、指数变换等;·变化监测是根据两个时期的遥感图像来计算其差异,系统可以根据您所定义的阈值来表明重点变化区域,并输出两个分析结果图像,其一是图像变化文件,其二是主要变化区域文件。
实验四 图像增强和滤波实验

实验四图像增强和滤波实验实验报告一.实验目的掌握基本的图像增强方法,观察图像增强的效果,加深对灰度直方图的理解。
掌握基本的图像滤波方法,观察图像滤波的效果。
二.实验仪器PC机(安装Windows98、Windows2000或者Windows XP或以上),Matlab软件。
三.实验原理1.直方图1)灰度直方图灰度直方图表示数字图像中每一灰度级出现的频数(该灰度级的像素数与图像的总像素数之比)。
2)直方图均衡化直方图均衡化的基本思想是把原始图像的直方图变换成在整个灰度级范围内均匀分布的形式,这样就增加了象素灰度值的动态范围,从而达到了增强图像整体对比度的效果。
2.均值滤波算法也称线性滤波,主要思想为邻域平均法,即用几个像素灰度的平均值来代替每个像素的灰度。
有效抑制加性噪声,但容易引起图像模糊,可以对其进行改进,主要避开对景物边缘的平滑处理。
3.中值滤波中值滤波是基于排序统计理论的一种能有效抑制噪声的非线性空间滤波方法。
原理:利用一个含有奇数个像素的滑动窗口,将窗口中心像素点的灰度值用窗口内各点灰度的中值代替。
四.实验内容对给定的灰度的数字图像(cameraman.tif,rice.tif,pout.tif)进行如下处理:1)统计原图像的灰度直方图,并利用直方图均衡化处理进行图像增强,同屏显示处理前后图像以及灰度直方图,比较异同,并回答数字图像均衡化后其直方图分布情况。
2)利用图像调整函数(直接灰度调整方法)进行图像增强,同屏显示处理前后图像及其灰度直方图,比较异同,并回答数字图像均衡化后其直方图分布情况。
3)利用函数IMNOISE,在图像(LENA256.BMP)上分别叠加高斯噪声(gaussian)和椒盐噪声(salt & peppers)(不同的噪声方差),对比高斯低通滤波器,均值滤波器和中值滤波的性能。
五.实验代码im=imread('cameraman.tif'); %此处将图片换成rice.png和pout.tif再做两次figure(1);subplot(2,2,1);imshow(im);title('原始图像');subplot(2,2,2);imhist(im,64);title('直方图');subplot(2,2,3);im2=histeq(im,64);imshow(im2);title('均衡化后的图像');subplot(2,2,4);imhist(im2);title('均衡化后的直方图');im3=imadjust(im);figure(2);subplot(2,2,1)imshow(im)title('原始图像');subplot(2,2,2);imhist(im,64);title('直方图');subplot(2,2,3);imshow(im3);title('imadjust函数调整后的图像');subplot(2,2,4);imhist(im3,64);title('调整后的直方图');im0=imread('pout.tif')im4=imnoise(im0,'gaussian');im5=imnoise(im0,'salt & pepper');figure(3);subplot(1,3,1)imshow(im0)title('原始图像');subplot(1,3,2);imshow(im4);title('加入高斯噪声后的图像');subplot(1,3,3);imshow(im5);title('加入椒盐噪声后的图像');H1=fspecial('gaussian');H2=fspecial('average');im_gaussian=imfilter(im4,H1); %im4换成im5再试一次im_average=imfilter(im4,H2); %im4换成im5再试一次im_med=medfilt2(im4);figure(4);subplot(2,2,1)imshow(im4)title('加入高斯噪声后的图像'); %im4换成im5后原图为“加入椒盐噪声后的图像”subplot(2,2,2);imshow(im_gaussian);title('高斯低通滤波后的图像 ');subplot(2,2,3);imshow(im_average);title('均值滤波后的图像');subplot(2,2,4);imshow(im_med);title('中值滤波后的图像');六.实验图像原始图像1000200030004000直方图100200均衡化后的图像5001000均衡化后的直方图100200原始图像1000200030004000直方图100200imadjust 函数调整后的图像0100020003000调整后的图像的直方图100200原始图像均衡化后的图像01000200030004000直方图1002005001000均衡化后的直方图100200原始图像imadjust 函数调整后的图像01000200030004000直方图1002000100020003000调整后的图像的直方图100200原始图像020004000直方图100200均衡化后的图像50010001500均衡化后的直方图100200原始图像020004000直方图100200imadjust 函数调整后的图像0100020003000调整后的图像的直方图100200原始图像加入高斯噪声后的图像加入椒盐噪声后的图像对加入高斯噪声的图像进行滤波处理:加入高斯噪声后的图像高斯低通滤波后的图像均值滤波后的图像中值滤波后的图像对加入椒盐噪声的图像进行滤波处理:加入椒盐噪声后的图像高斯低通滤波后的图像均值滤波后的图像中值滤波后的图像滤波原理的理解:1.均值滤波:就是给定一个目标像素模板,其中包括了以目标像素为中心周围的8个像素,即去掉目标像素,再用模板中的全体像素的平均值来代替原来像素值。
遥感数据图像处理实验四、图像增强处理

遥感数据图像处理实验四、图像增强处理实验四、图像增强实验内容:1. 空间增强处理(Spatial Enhancement)2. 辐射增强处理(Radiometric Enhancement)1.空间增强处理(Spatial Enhancement)⼀、⾮定向边缘增强(Non-directional Edge)(以c:\program files\ imagine 8.4\examples\lanier.img为例)⾮定向边缘增强应⽤两个⾮常通⽤的滤波器(Sobel滤波器和Prewitt滤波器),⾸先通过两个正交卷积算⼦(Horizontal算⼦和Vertical算⼦)分别对遥感图像进⾏边缘探测,然后将两个正交结果进⾏平均化处理。
⾮定向边缘增强具体操作过程如下:ERDAS IMAGINE 8.4图标⾯板菜单条:Main→Image Interpreter(或单击ERDAS IMAGINE 8.4图标⾯板⼯具条“Interpreter”图标)→打开Image Interpreter对话框→选择Spatial Enhancement→打开Spatial Enhancement对话框→选择Non-directional Edge→打开Non-directional Edge对话框在Non-directional Edge对话框中需要⾊置下列参数:→Input File(确定输⼊⽂件):lanier.img→Output File(定义输出⽂件):non-direct.img→Coordinate Type(⽂件坐标类型):Map→Subset Definition(处理范围确定):ULX,ULY;LRX,LRY(缺省状态为整个图像范围)→Output Data Type(输出数据类型):Unsigned 8 bit→Filter Selection(滤波器选择):Sobel→选定Ignore Zero in Stats(输出数据统计时忽略零值)→单击OK按钮(关闭Non-directional Edge对话框,执⾏⾮定向边缘增强)⼆、纹理分析(以c:\program files\ imagine 8.4\examples\lanier.img为例)纹理分析通过在⼀定的窗⼝内进⾏⼆次变异分析(2nd-order Variance)或三次⾮对称分析(3rd-order Skewness),使图像的纹理结构得到增强,操作的关键是窗⼝⼤⼩(Window Size)的确定和操作函数(Operator)的定义。
光电图像处理实验报告(图像增强)

电子科技大学实验报告学生姓名: XXX学号: XXXXXXXXXX指导教师: XXX日期: 2010年3月25日一、实验室名称: 光电楼327机房二、实验项目名称: 图像增强三、实验原理:图像在生成、获取、传输等过程中,受照明光源性能、成像系统性能、通道带宽和噪声等因素的影响,造成对比度偏低、清晰度下降、并引入干扰噪声。
因此,图像增强的目的,就是改善图像质量,获得更适合于人眼观察、或者对后续计算机处理、分析过程更有利的图像。
图像增强是有选择地突出某些对人或计算机分析有意义的信息,抑制无用信息,提高图像的使用价值。
1、对数与指数变换提高对比度(1) 对数变换,低灰度区扩展,高灰度区压缩。
(2) 指数变换,高灰度区扩展,低灰度区压缩。
对合适的图像选择对数变换或者指数变换,均可提高图像对比度。
cb y x f a y x g ln ]1),(ln[),(++=1),(]),([-=-a y x f c b y x g2、中值滤波中值滤波法是把邻域内所有像素按灰度顺序排列,然后取中间值作为中心像素的输出。
中值滤波可以有效的去除椒盐噪声。
四、实验目的:1、熟练掌握各种灰度域变换的图像增强原理及方法;2、熟悉直方图均衡化和直方图规格化的原理及方法;3、了解空域滤波中常用的平滑和锐化滤波器;4、熟悉和掌握利用Matlab 工具进行图像的读、写、显示及基本的图像处理步骤;5、利用Matlab 工具进行图像增强处理。
五、实验内容:1、读取一幅低对比度图像,分别对其进行对数变换与指数变换。
进行变换前,应根据需要分别选取合适的指数和对数函数(即确定a、b、c 等调节因子),画出指数和变换曲线。
程序设计及处理过程中,要求在同一窗口中分别显示原始图像、变换结果及其直方图。
2、读取一幅含有椒盐噪声的被污染图像,并对其进行中值滤波处理。
要求在同一窗口中显示原始图像及中值滤波的结果。
(选作内容)六、实验器材(设备、元件):计算机,Matlab软件七、实验步骤:1、对数与指数变换提高对比度⑴打开计算机,从计算机中选择一幅对比度较低的图像作为原始图像。
实验四图像增强

实验四-图像增强信息工程学院实验报告课程名称:数字图像处理班级: 姓名: 学号:一、实验目的1.了解图像增强的目的及意义,加深对图像增强的感性认识,巩固所学理论知识。
2. 掌握图像空域增强算法的基本原理。
3. 掌握图像空域增强的实际应用及MATLAB 实现。
4. 掌握频域滤波的概念及方法。
5. 熟练掌握频域空间的各类滤波器。
6.掌握怎样利用傅立叶变换进行频域滤波。
7. 掌握图像频域增强增强的实际应用及MATLAB 实现。
二、实验步骤及结果分析1. 基于幂次变换的图像增强 程序代码:clear all ; close all ;I{1}=double(imread('fig534b.tif')); I{1}=I{1}/255;figure,subplot(2,4,1);imshow(I{1},[]);hold on I{2}=double(imread('room.tif')); I{2}=I{2}/255;subplot(2,4,5);imshow(I{2},[]);hold on for m=1:2 Index=0;for lemta=[0.5 5] Index=Index+1;F{m}{Index}=I{m}.^lemta;subplot(2,4,(m-1)*4+Index+1),imshow(F{m}{Index},[]) end end成 绩:指导老师(签名):执行结果:图1 幂次变换增强结果实验结果分析:由实验结果可知,当r<1时,黑色区域被扩展,变的清晰;当r>1时,黑色区域被压缩,变的几乎不可见。
2.直方图规定化处理程序代码:clear allclcclose all%0.读图像I=double(imread('lena.tiff'));subplot(2,4,1);imshow(I,[]);title('原图')N=32;Hist_image=hist(I(:),N);Hist_image=Hist_image/sum(Hist_image);Hist_image_cumulation=cumsum(Hist_image);%累计直方图subplot(245);stem(0:N-1,Hist_image);title('原直方图');%1.设计目标直方图Index=0:N-1;%正态分布直方图Hist{1}=exp(-(Index-N/2).^2/N);Hist{1}=Hist{1}/sum(Hist{1});Hist_cumulation{1}=cumsum(Hist{1});subplot(242);stem([0:N-1],Hist{1});title('规定化直方图1');%倒三角形状直方图Hist{2}=abs(2*N-1-2*Index);Hist{2}=Hist{2}/sum(Hist{2});Hist_cumulation{2}=cumsum(Hist{2});subplot(246);stem(0:N-1,Hist{2});title('规定化直方图2');%2. 规定化处理Project{1}=zeros(N);Project{2}=zeros(N);Hist_result{1}=zeros(N);Hist_result{2}=zeros(N);for m=1:2Image=I;%SML 处理(SML,Single Mapping Law 单映射规则 for k=1:NTemp=abs(Hist_image_cumulation(k)-Hist_cumulation{m});[Temp1,Project{m}(k)]=min(Temp); end%2.2 变换后直方图 for k=1:NTemp=find(Project{m}==k); if isempty(Temp) Hist_result{m}(k)=0; elseHist_result{m}(k)=sum(Hist_imag e(Temp)); end endsubplot(2,4,(m-1)*4+3); stem(0:N-1,Hist_result{m}); title(['变换后的直方图',num2str(m)]); %2.3结果图 Step=256/N; for K=1:NIndex=find(I>=Step*(k-1)&I<Step *k);Image(Index)=Project{m}(k); endsubplot(2,4,(m-1)*4+4),imshow(I mage,[]);title(['变换后的结果图',num2str(m)]); end执行结果:原图0.020.040.060.080.100.020.040.060.080.100.020.040.060.08规定化直方图220400.050.10.150.2变换后的直方图1变换后的结果图1020400.020.040.060.080.10.12变换后的直方图2变换后的结果图2图2 直方图规定化实验结果分析:由实验结果可知,采用直方图规定化技术后,原图的直方图逼近规定化的直方图,从而有相应的变换后的结果图1和变换后的结果图2。
实验四 图像增强

1.直接灰度变换>> clear all;>> I=imread('peppers.png');>> colormap;imshow(I);>> j=imadjust(I,[0 1],[1 0],1.5);>> figure;subimage(j)效果如图a 原始图像b 灰度倒置后的图像2.直方均衡化>> I=imread('forest.tif');J=histeq(I);>> figure,imshow(I)>> figure,imshow(J)>> figure,imhist(I,64)>> figure,imhist(J,64)效果如图a 原始图像b原始图像均衡后c直方均衡前 d 直方均衡后3.相关拉伸>> I=imread('pout.tif');J=adapthisteq(I);>> figure,imshow(I)>> figure,imshow(J)>> figure,imhist(J,64)效果如图a原始图像b处理后的图像C处理后的直方图4.Wiener滤波中值滤波(1)wiener滤波实现降噪过程>> clear all>> I=imread('lena.bmp');>> figure,imshow(I)>> K1=wiener2(I,[3,3]);K2=wiener2(I,[5,5]);K3=wiener2(I,[7,7]);>> figure,imshow(K1);>> figure,imshow(K2);>> figure,imshow(K3);效果如图a原始图像 b 3*3wiener滤波C 5*5wiener滤波 d 7*7wiener滤波(2)含有椒盐噪声的图像实现中值滤波处理过程>> clear all>> I=imread('lena.bmp');>> figure,imshow(I)>> I1=imnoise(I,'salt&pepper',0.06);>> I1=imnoise(I,'salt & pepper',0.06);>> K1=medfilt2(I,[3,3]);K2=medfilt2(I,[5,5]);K3=medfilt2(I,[7,7]);>> figure,imshow(K1);>> figure,imshow(K2);>> figure,imshow(K3);效果如图a原始图像 b 3*3模板中值滤波c 5*5模板中值滤波d 7*7模板中值滤波5.线性锐化sobel滤波(1)调用filter()函数和fspecial()函数实现线性锐化>> clear all>> I1=imread('lena.bmp');>> I1=double(I1);>> h1=fspecial('laplacian');>> I2=filter2(h1,I1);>> figure,imshow(I1,[]);>> I3=I1-I2;>> figure,imshow(I3,[]);效果如图a原始图像 b 处理后的图像(2)利用Sobel算子对图像滤波>> clear all>> I=imread('eight.tif');>> H=fspecial('sobel');>> figure,imshow(I);>> J=filter2(H,I);>> figure,imshow(J);效果如图a原始图像 b 进行sobel算子后的效果6.频域低通滤波高通滤波(1)频率低通滤波>> clear all>> [I,map]=imread('lena.bmp');noisy=imnoise(I,'gaussian',0.01);>> [M,N]=size(I);>> F=fft2(noisy);>> fftshift(F);>> Dcut=100;D0=150;D1=250;>> for u=1:Mfor v=1:ND(u,v)=sqrt(u^2+v^2);BUTTERH(u,v)=1/(1+(sqrt(2)-1)*(D(u,v)/Dcut)^2);EXPOTH(u,v)=exp(log(1/sqrt(2))*(D(u,v)/Dcut)^2);if D(u,v)<D0THPFH(u,v)=1;elseif D(u,v)<=D1THPFH(u,v)=(D(u,v)-D1)/(D0-D1);elseTHPFH(u,v)=0;endendend>> BUTTERG=BUTTERH.*F;>> BUTTERfiltered=ifft2(BUTTERG);>> EXPOTG=EXPOTH.*F;>> EXPOTfiltered=ifft2(EXPOTG);>> THPFG=THPFH.*F;>> THPFfiltered=ifft2(THPFG);>> figure,imshow(noisy);>> figure,imshow(BUTTERfiltered,map);>> figure,imshow(EXPOTfiltered,map);>>figure,imshow(THPFfiltered,map);效果如图a原始图像b巴特沃斯低通滤波后的图像C指数低通滤波后的图像d梯形低通滤波后的图像(2)高通滤波>> clear all>> [I,map]=imread('lena.bmp');noisy=imnoise(I,'gaussian',0.01);>> [M,N]=size(I); F=fft2(noisy);>> fftshift(F);>> Dcut=100;D0=250;D1=150;>> for u=1:Mfor v=1:ND(u,v)=sqrt(u^2+v^2);BUTTERH(u,v)=1/(1+(sqrt(2)-1)*(D(u,v)/Dcut)^2);EXPOTH(u,v)=exp(log(1/sqrt(2))*(D(u,v)/Dcut)^2);if D(u,v)<D1THPFH(u,v)=0;elseif D(u,v)<=D0THPFH(u,v)=(D(u,v)-D1)/(D0-D1);elseTHPFH(u,v)=1;endendend>> BUTTERG=BUTTERH.*F;BUTTERfiltered=ifft2(BUTTERG);>> EXPOTG=EXPOTH.*F;EXPOTfiltered=ifft2(EXPOTG);>> THPFG=THPFH.*F;THPFfiltered=ifft2(THPFG);>> figure,imshow(noisy);>> figure,imshow(BUTTERfiltered,map);>> figure,imshow(EXPOTfiltered,map);>> figure,imshow(THPFfiltered,map);效果如图a加入高斯噪声后的图像b巴特沃斯高通滤波后的图像C指数高通滤波后的图像d梯形高通滤波后的图像。
图像增强实验

一、实验目的1、了解图像增强的目的及意义,加深对图像增强的感性认识,巩固所学理论知识。
2、学会对图像直方图的分析。
3、掌握直接灰度变换的图像增强方法。
4、掌握直方图均衡化。
5、采用均值滤波、中值滤波实现图像平滑。
6、采用梯度方法、拉普拉斯算子、Sobel 算子和 Prewitt 算子实现图像锐化。
二、实验原理及知识点图像增强是指按特定的需要突出一幅图像中的某些信息,同时,消弱或去除某些不需要的信息的处理方法。
其主要目的是处理后的图像对某些特定的应用比原来的图像更加有效。
图像增强技术主要有直接灰度尺度变换、直方图修改处理、图像平滑化处理、图像尖锐化处理等。
1、 灰度变换灰度变换是图像增强的一种重要手段,它常用于改变图象的灰度范围及分布,是图象数字化及图象显示的重要工具。
在实际应用中,为了突出图像中感兴趣的研究对象,常常要求局部扩展拉伸某一范围的灰度值,或对不同范围的灰度值进行不同的拉伸处理。
若假定原图像f(x, y)的灰度范围为[a, b ],希望变换后图像 g(x, y)的灰度范围扩展至[c, d ],则线性变换可表示为:g (x , y )= [ f (x , y ) − a ] + c2、 直方图变换直方图是图像的最基本的统计特征,它反映的是图像的灰度值的分布情况。
直方图均衡化的目的是使图像在整个灰度值动态变化范围内的分布均匀化,改善图像的亮度分布状态,增强图像的视觉效果。
直方图均衡化是通过灰度变换将一幅图像转换为另一幅具有均衡直方图,即在每个灰度级上都具有相同的象素点数的过程。
依据定义,在离散形式下, 用 r k 代表离散灰度级,用 p r (r k )代表 p r (r ),并且有下式成立:ab c d --P r(r k)=n k0 ≤r k≤ 1 k= 0,1,2,L,l−1 n式中:n k为图像中出现r k级灰度的像素数,n是图像像素总数,而n k/n即为频数。
k nj ks k= T (r k)=∑=∑ p r(r j) 0≤ r j≤1 k =0,1,L,l −1nj =0j =03、空域滤波空域滤波是在图像空间中借助模板对图像进行领域操作,处理图像每一个像素的取值都是根据模板对输入像素相应领域内的像素值进行计算得到的。
实验4_图像增强(辐射与空间增强)

Equalization:直方图均衡拉伸,使设定灰度范围内的像元数量大 致相等。
Square Root:平方根拉伸,计算输入图像的平方根,然后对设定 灰度范围内的像元进行线性拉伸。
Arbitrary:自定义拉伸和直方图匹配,可在输出直方图自由绘制 直方图形状,或者与另一个图像的直方图进行匹配。
5、空间增强
图像增强
张洋
QQ:332954604
Email:kymgoal@ kymgoal@
1、图像增强
图像增强是为了突出相关的专题信息,提高 图像的视觉效果,使分析者更容易的识别像增强一般分为辐射(光谱)增强和空间增 强。
3、辐射增强-对比度增强
Stretch_Type菜单功能: Linear:线性拉伸,设置拉伸区间后将拉伸区间内的值线性变换 到0-255的区间。 Piecewise Linear:分段线性拉伸,可通过鼠标中键在输入直方图 中的转换函数(初始为一条直线)上放置几个点进行交互式拉伸, 对各点之间的部分按对应的变换函数进行线性拉伸。 Gaussian:高斯拉伸,设定拉伸区间后按照高斯函数对图像进行 拉伸。
辐射增强是对地物的光谱特征,如像元的对 比度,波段间的亮度比等进行增强和转换。 空间增强主要是针对图像的空间特征,考虑 像元即周围像元亮度间的关系,使图像的空 间几何特征如边缘、形状、大小等突出或削 减。
2、辐射增强-波段比
3、辐射增强-对比度增强
对比度增强拉伸是将图像的亮度值范围进行 拉伸或压缩,从而提高图像全部或部分的对 比度,将输入图像中的数值输出成计算机的 显示值。 ENVI实现: 图像上右键-Interactive stretching或主图像 窗口中Enhance-Interactive stretching 通过选择Stretch_Type中的拉伸选项进行操 作。
图像增强的实验报告

图像增强的实验报告图像增强的实验报告引言:图像增强是数字图像处理领域中的一项重要任务。
通过改善图像的质量和清晰度,图像增强可以使我们更好地观察和分析图像中的细节。
本实验旨在探索图像增强的不同方法,并评估它们在不同场景下的效果。
实验设计:为了比较不同的图像增强方法,我们选择了一组具有不同特征的图像作为实验对象。
这些图像包括自然风景、人像和低对比度图像。
我们将使用以下三种方法进行图像增强:直方图均衡化、自适应直方图均衡化和增强对比度自适应拉伸。
实验步骤:1. 直方图均衡化:直方图均衡化是一种常用的图像增强方法,它通过重新分布图像的像素值来增强对比度。
我们首先将图像转换为灰度图像,然后计算灰度直方图。
接下来,我们使用累积分布函数对直方图进行均衡化,使得图像中的像素值分布更加均匀。
最后,我们将均衡化后的图像转换回原始图像的颜色空间。
2. 自适应直方图均衡化:直方图均衡化在某些情况下可能会导致图像的局部细节丢失。
为了解决这个问题,我们使用自适应直方图均衡化方法。
在这种方法中,我们将图像分成许多小区域,并对每个区域的直方图进行均衡化。
通过这种方式,我们可以保留图像的局部特征,并增强整体对比度。
3. 增强对比度自适应拉伸:增强对比度自适应拉伸是一种简单而有效的图像增强方法。
它通过将图像的像素值映射到一个更大的范围来增强对比度。
我们首先计算图像的平均亮度和标准差,然后使用以下公式对图像进行拉伸:enhanced_pixel = (pixel - mean) * (max_stretch / std) + mean其中,pixel是原始图像中的像素值,mean是图像的平均亮度,std是图像的标准差,max_stretch是拉伸的最大范围。
实验结果:我们将三种图像增强方法应用于不同类型的图像,并进行了对比分析。
结果显示,直方图均衡化方法在某些情况下可以显著增强图像的对比度,特别是对于低对比度图像。
然而,它可能会导致图像的噪声增加和细节丢失。
图像处理实验报告——图像增强-推荐下载

对图像进行平滑处理,可以处理高斯噪声,但是很带来图像的边缘细节模糊。
对于具有对称特性的算子,conv2和imfilter处理的图像效果是一样的,非对称的算子,处理的效果一般不样。
对图像进行锐化处理,会得到图像的边缘部分,变化小部分对应的灰度值较小。
10、总结及心得体会:总结:通过本次的图像增强实验了解了图像的最基本的像素级的操作,对图像的变换有了一定的了解,同时增加了自己对数字图像的了解。
心得体会:一些看起来很简单的图像处理,要自己编程进行实现比不是一件很简单的事,所以对于理论要多加以实践才能更好地掌握。
11、对本实验过程及方法、手段的改进意见:如果对现有的某些简单的函数进行限制使用,要求学生自己编写,可以很大程度的增强学生的编程能力。
报告评分:指导教师签字:图1 线性拉伸变换原图和结果图图2 线性拉伸变换灰度变换曲线)图像的非线性灰度变换(指数变换)图3 指数拉伸变换原图和结果图图4 对数拉伸变换灰度变换曲线)图像的非线性灰度变换(中值滤波)图5 中值滤波原图和结果图)光电图像的空域平滑处理像像像像像像像像像像像像图7 算子的3D图)光电图像的空域高通滤波图8 平滑处理原图、加噪图和结果图图9 算子的3D图)数字图像的线性灰度变换%拉伸到15到230clc,close all,clear all;remax=230;remin=15;y=imread('cloud_24bitgry.jpg');y=rgb2gray(y);subplot(1,2,1),imshow(y);y=double(y);title('原始图像');ymax=max(max(y));ymin=min(min(y));[a,b]=size(y);%灰度变换程序for m=1:a;for n=1:b;result_image(m,n)=(remax-remin)/(ymax-ymin)*(y(m,n)-ymin)+remin;endendresult_image=uint8(result_image);subplot(1,2,2),imshow(result_image); imwrite(result_image,'灰度线性变换.jpg','jpg');%保存图像title('灰度变换图像');o=[]for x=1:255;if x<ymin;k=remin;elseif x>ymax;k=remax;elsek=(remax-remin)/(ymax-ymin)*(x-ymin)+remin;endo=[o,k];end%画变换曲线图x=1:255;figure,plot(x,o);title('灰度变换曲线');xlabel('f(x,y)'),ylabel('g(x,y)');(2)图像的非线性灰度变换(指数变换)%灰度对数变换clc,close all,clear all;imb=1.56;ima=13;imc=0.05;y=imread('Einstein.jpg');y=rgb2gray(y);subplot(1,2,1),imshow(y);title('原始图像'); y=double(y);[a,b]=size(y);%对数变换程序for m=1:a;for n=1:b;result_image(m,n)=imb^(imc*(y(m,n)-ima))-1;endendsubplot(1,2,2),imshow(result_image,[]);titl e('变换图像');imwrite(uint8(result_image),'灰度对数变换. jpg','jpg');%保存图像u=[];for x=0:255;o=imb^(imc*(x-ima))-1;u=[u,o];endx=0:255;figure(),plot(x,u);title('对数变换曲线'); xlabel('f(x,y)'),ylabel('g(x,y)');(3)图像的非线性灰度变换(中值滤波)%灰度对数变换clc,close all,clear all;imb=1.56;ima=13;imc=0.05;y=imread('lowlight_spn24.jpg');y=rgb2gray(y);subplot(1,2,1),imshow(y);title('原始图像'); [a,b]=size(y);%中值滤波变换程序o=y;for m=2:a-1;for n=2:b-1;O=[y(m-1,n-1),y(m,n-1),y(m+1,n-1),y(m-1,n),y(m,n),y(m+1,n),y(m-1,n+1),y(m,n+1),y(m+1,n+1)];o(m,n)=median(O);endendsubplot(1,2,2),imshow(o);title('滤波图像');(4)光电图像的空域平滑处理%平滑去噪clc,close all,clear all;y=imread('Einstein.jpg');y=rgb2gray(y);subplot(2,2,1),imshow(y),title('原始图像'); y=imnoise(y,'gauss',0.002);%加噪声subplot(2,2,2),imshow(y);title('加噪图像'); y=double(y);h1=1/273*[1,4,7,4,7;4,16,26,16,4;7,26,41,26,7;4,16,26,16,4;1,4,7,4,1];M=conv2(y,h1);%卷积处理图像subplot(2,2,3),imshow(uint8(M));title('卷积去噪图像');M=imfilter(y,h1);subplot(2,2,4),imshow(uint8(M));title('函数去噪图像');x=-9:10;y=-9:10;h1=imresize(h1,4,'bilinear');[X,Y]=meshgrid(x,y);figure,surfc(X,Y,h1);(5)光电图像的空域高通滤波% 图像锐化程序clc,close all,clear all;y=imread('Einstein.jpg');y=rgb2gray(y);subplot(1,3,1),imshow(y),title('原始图像'); y=double(y);h1=[-1,0,1;-1,0,1;-1,0,1];sum(sum(h1))M=conv2(y,h1);%卷积处理图像subplot(1,3,2),imshow(uint8(M));title('卷积锐化图像');M=imfilter(y,h1);subplot(1,3,3),imshow(uint8(M));title('图像锐化图像');x=-5:6;y=-5:6;h1=imresize(h1,4,'bilinear');[X,Y]=meshgrid(x,y);figure,surfc(X,Y,h1);。
图像增强技术实验报告

图像增强技术实验报告
近年来,随着数字图像处理技术的快速发展,图像增强技术在各个
领域得到了广泛的应用。
本实验旨在探究图像增强技术的原理和方法,通过实际操作加深对该技术的理解和掌握。
首先,在本实验中我们使用了常见的图像增强技术包括灰度拉伸、
直方图均衡化、滤波等方法。
针对不同的图像特点和需求,我们选择
了不同的增强方法进行处理,并分析比较它们的效果和适用场景。
在实验过程中,我们首先对原始图像进行了灰度拉伸处理,通过拉
伸灰度范围来增强图像的对比度,使得图像中的细节更加清晰。
接着,我们运用直方图均衡化技术,将图像的像素分布均匀化,从而提高了
图像的整体亮度和细节展现。
同时,我们还尝试了一些滤波方法,如
均值滤波、中值滤波等,来去除图像中的噪声和平滑图像。
通过实验数据分析,我们发现不同的图像增强方法在处理不同类型
的图像时会产生不同的效果。
比如对于对比度较低的图像,灰度拉伸
和直方图均衡化能够取得比较好的增强效果;而对于受到噪声干扰的
图像,则需要采用滤波方法进行去噪处理。
综合以上实验结果,我们深入探讨了图像增强技术的优缺点以及适
用范围。
图像增强技术在医疗影像、航空航天、安防监控等领域具有
广泛的应用前景,在实际应用中需要根据图像特点和需求选择合适的
增强方法,以达到最佳的效果。
通过本次实验,我们对图像增强技术有了更深入的了解,并在实践中提升了我们的技术水平和解决问题的能力。
希望今后能够进一步拓展应用领域,将图像增强技术发挥到更大的作用,为社会发展和人类福祉做出更大的贡献。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
信息工程学院实验报告课程名称:数字图像处理Array实验项目名称:实验四图像增强实验时间:班级:姓名:学号:一、实验目的1.了解图像增强的目的及意义,加深对图像增强的感性认识,巩固所学理论知识。
2. 掌握图像空域增强算法的基本原理。
3. 掌握图像空域增强的实际应用及MATLAB实现。
4. 掌握频域滤波的概念及方法。
5. 熟练掌握频域空间的各类滤波器。
6.掌握怎样利用傅立叶变换进行频域滤波。
7. 掌握图像频域增强增强的实际应用及MATLAB实现。
二、实验步骤及结果分析1. 基于幂次变换的图像增强程序代码:clear all;close all;I{1}=double(imread('fig534b.tif'));I{1}=I{1}/255;figure,subplot(2,4,1);imshow(I{1},[]);hold onI{2}=double(imread('room.tif'));I{2}=I{2}/255;subplot(2,4,5);imshow(I{2},[]);hold onfor m=1:2Index=0;for lemta=[0.5 5]Index=Index+1;F{m}{Index}=I{m}.^lemta;subplot(2,4,(m-1)*4+Index+1),imshow(F{m}{Index},[])endend执行结果:图1 幂次变换增强结果实验结果分析:由实验结果可知,当r<1时,黑色区域被扩展,变的清晰;当r>1时,黑色区域被压缩,变的几乎不可见。
2.直方图规定化处理程序代码:clear allclcclose all%0.读图像I=double(imread('lena.tiff'));subplot(2,4,1);imshow(I,[]);title('原图')N=32;Hist_image=hist(I(:),N);Hist_image=Hist_image/sum(Hist_image);Hist_image_cumulation=cumsum(Hist_image);%累计直方图subplot(245);stem(0:N-1,Hist_image);title('原直方图');%1.设计目标直方图Index=0:N-1;%正态分布直方图Hist{1}=exp(-(Index-N/2).^2/N);Hist{1}=Hist{1}/sum(Hist{1});Hist_cumulation{1}=cumsum(Hist{1});subplot(242);stem([0:N-1],Hist{1});title('规定化直方图1');%倒三角形状直方图Hist{2}=abs(2*N-1-2*Index);Hist{2}=Hist{2}/sum(Hist{2});Hist_cumulation{2}=cumsum(Hist{2});subplot(246);stem(0:N-1,Hist{2});title('规定化直方图2');%2. 规定化处理Project{1}=zeros(N);Project{2}=zeros(N);Hist_result{1}=zeros(N);Hist_result{2}=zeros(N);for m=1:2Image=I;%SML处理(SML,Single Mapping Law单映射规则for k=1:NTemp=abs(Hist_image_cumulation(k)-Hist_cumulation{m});[Temp1,Project{m}(k)]=min(Temp);end%2.2 变换后直方图for k=1:NTemp=find(Project{m}==k);if isempty(Temp)Hist_result{m}(k)=0;elseHist_result{m}(k)=sum(Hist_image(T emp));endendsubplot(2,4,(m-1)*4+3);stem(0:N-1,Hist_result{m}); title(['变换后的直方图',num2str(m)]);%2.3结果图Step=256/N;for K=1:NIndex=find(I>=Step*(k-1)&I<Step*k) ;Image(Index)=Project{m}(k);endsubplot(2,4,(m-1)*4+4),imshow(Imag e,[]);title(['变换后的结果图',num2str(m)]);end执行结果:原图规定化直方图2变换后的直方图1变换后的结果图1变换后的直方图2变换后的结果图2图2 直方图规定化实验结果分析:由实验结果可知,采用直方图规定化技术后,原图的直方图逼近规定化的直方图,从而有相应的变换后的结果图1和变换后的结果图2。
3.灰度图像常用平常、锐化滤波程序代码:clear all ; close all ;%0.原图I=double(imread('lena.tiff')); subplot(2,4,1);imshow(I,[]);title('原图');%1.均值低通滤波H=fspecial('average',5); F{1}=double(filter2(H,I)); subplot(2,4,2);imshow(F{1},[]);tit le('均值低通滤波');%2.gaussian 低通滤波H=fspecial('gaussian',7,3); F{2}=double(filter2(H,I)); subplot(2,4,3);imshow(F{2},[]);tit le('高斯低通滤波');%3.增强图像=原图-均值低通滤波F{3}=2*I-F{1};subplot(2,4,4);imshow(uint8(F{3}),[]);title('原图-均值低通滤波'); %4.增强图像=原图-高斯低通滤波 F{4}=2*I-F{2};subplot(2,4,5);imshow(uint8(F{4}),[]);title('原图-高斯低通滤波'); %5.'prewitt'边缘算子增强 H=fspecial('prewitt'); F{5}=uint8(I+filter2(H,I)); subplot(2,4,6);imshow(F{5},[]);tit le('prewitt 边缘算子增强'); %6.'soble'边缘算子增强 H=fspecial('sobel'); F{6}=uint8(I+filter2(H,I)); subplot(2,4,7);imshow(F{6},[]);tit le('sobel 边缘算子增强');执行结果:原图均值低通滤波高斯低通滤波原图-均值低通滤波原图-高斯低通滤波prewitt 边缘算子增强sobel 边缘算子增强图3 灰色图像平滑、锐化实验结果分析:由实验结果可知,均值和高斯滤波都使原图模糊,而采用原图减去低通滤波图像方法、prewitt 算子、sobel 算子都可以增强图像边缘。
4. 频率域滤波:对于给定图像+噪声,使用不同的频域滤波器对图像进行滤波处理。
(1)用Butterworth 低通滤波器实现图像信号的滤波运算。
程序代码:clear all ; close all ;%(a)读入并显示图像electric.tif ; I=imread('electric.tif');subplot(2,3,1),imshow(I);title('原图像');%(b)利用imnoise 命令在图electric.tif 上加入高斯(gaussian) 噪声;J=imnoise(I,'gaussian',0,0.01); subplot(2,3,2),imshow(J);title('加入高斯噪声的图像');%(c)用Butterworth 低通滤波器实现图像信号的滤波运算,变换不同的截止频率d I1=fftshift(fft2(J)); [m,n]=size(I1);N=2;d1=30;d2=50;d3=70;d4=90; n1=floor(m/2);n2=floor(n/2); for i=1:m for j=1:nd=sqrt((i-n1)^2+(j-n2)^2); H1=1/(1+(d/d1)^(2*N)); H2=1/(1+(d/d2)^(2*N)); H3=1/(1+(d/d3)^(2*N));H4=1/(1+(d/d4)^(2*N)); I3(i,j)=H1*I1(i,j); I5(i,j)=H2*I1(i,j); I7(i,j)=H3*I1(i,j); I9(i,j)=H4*I1(i,j); end endI3=ifftshift(I3); I4=real(ifft2(I3)); I5=ifftshift(I5); I6=real(ifft2(I5)); I7=ifftshift(I7); I8=real(ifft2(I7)); I9=ifftshift(I9); I10=real(ifft2(I9));subplot(2,3,3),imshow(I4,[]),title ('Butterworth 低通滤波器d1=30'); subplot(2,3,4),imshow(I6,[]),title ('Butterworth 低通滤波器d2=50'); subplot(2,3,5),imshow(I8,[]),title ('Butterworth 低通滤波器d3=70'); subplot(2,3,6),imshow(I10,[]),titl e('Butterworth 低通滤波器d4=90');执行结果:原图像加入高斯噪声的图像Butterworth 低通滤波器d1=30Butterworth 低通滤波器d2=50Butterworth 低通滤波器d3=70Butterworth 低通滤波器d4=90图4 Butterworth 低通滤波器滤波结果实验结果分析:由实验结果可知,采用Butterworth低通滤波器对加噪声的图像进行滤波运算,滤波器的截止频率d越小,滤波后的图像越模糊。
