自动检测算法
城市快速路交通事件自动检测分析与算法设计

先 对 实 时 交 通 流数 据 行 预 处 理 , 后通 过 事 件 检 而
测算 法判 断事 件 是否发 生 。一 旦计算 结果 为事件
道 路大约 6 %的拥 挤是 由诸如 事故 、车辆 抛锚等 0 随机 事 件 引起 的【。交通 事件 是 影 响道 路交 通运 1 ]
行效 率和 安全 性 的首要 因素 ,而 当今交术 》2 1 机 0 0年第 4期
交通 波 动 的影 响而 产 生 的噪 声进行 滤 波 处理 ,去
掉原 始数 据 中 的噪声和 高频成 分 ,减 少 误报 率 ;
() 消 除 噪 声 的 同 时 对 原 始 数 据 进 行 初 步 2在
算法 的报 警 率在 一 定 范 围里 ,可根 据 实 际情况 进
频繁 发生及 其产 生后 果 的 日益 严重 性 已经成 为世
界各 大城 市共 同面 临的严 峻挑 战 , 由其 导致 的延
误增加 、安 全性 降低 、成本 耗 费 巨大 等诸 多 问题 日渐成 为 困扰人们 日常生活 的难 题 。而快速 发现
果 是 一个 误 警 的话 , 会 浪 费救援 资源 , 则 影响 同时 发 生 的其 它事 件 的处 理和 降低 有 关人 员对AI D系
2 算 法 的 设 计
21 一 级报警 .
由 于在 一 级 报 警 模 块 中 要 实 现 的功 能 有 两
个:
时变性 、非 线性 等特 征 ,单从某 个 时间或 空 间或 是完全 从理论 上推 导某 种规 律来 描述 交通流 ,不
() 由于检 测器 故 障 、通信 系统 故障或 随机 1对
中 图分 类 号 :U4 1 1 T 2 7 文 献标 识 码 :A 文 章 编 号 : 17 —4 0 (000 一O 8 4 9. P 7 3 6 2 8 l2 1)4 3 —0
自动驾驶车辆的目标检测与跟踪算法

自动驾驶车辆的目标检测与跟踪算法1. 引言随着人工智能和计算机视觉技术的不断发展,自动驾驶成为了汽车行业的一个热门领域。
自动驾驶车辆需要具备实时地感知和识别周围道路环境中的各种物体,其中最基本的就是目标检测与跟踪算法。
本文将介绍自动驾驶车辆中常用的目标检测与跟踪算法,并分析其优缺点。
2. 目标检测算法目标检测算法是自动驾驶车辆中的核心技术之一,其主要功能是识别道路上的各种目标物体,如车辆、行人、信号灯等。
目前,常用的目标检测算法主要有以下几种:2.1 卷积神经网络(CNN)卷积神经网络是目标检测中最为常用的算法之一。
它通过多层卷积和池化操作提取图像的特征,并通过全连接层进行分类。
CNN的优点是能够自动学习和提取图像特征,因此具有较高的准确率。
然而,CNN的计算量较大,在实时性方面存在一定的挑战。
2.2 支持向量机(SVM)支持向量机是一种二分类模型,其主要思想是通过找到一个最优超平面将不同类别的数据分离开。
在目标检测中,可以将SVM应用于特征提取和分类。
SVM的优点是在小样本情况下仍具有较好的表现,并且对于异常点的鲁棒性较强。
但SVM算法相对复杂,需要大量的计算资源。
2.3 区域卷积神经网络(R-CNN)R-CNN是一种基于区域的目标检测算法,其主要思想是先生成一系列候选框,然后对每个候选框应用CNN进行特征提取和分类。
R-CNN算法的优点是能够对目标进行定位,并且检测准确率较高。
但R-CNN算法的缺点是速度较慢,不适用于实时应用。
3. 目标跟踪算法目标跟踪算法是自动驾驶车辆中的另一个重要技术,其主要功能是在连续的图像序列中追踪目标物体的位置和运动。
以下是目标跟踪中常用的算法:3.1 卡尔曼滤波(Kalman Filter)卡尔曼滤波是一种用于状态估计和滤波的算法,其基本思想是通过融合预测和观测结果来估计目标的状态。
在目标跟踪中,可以将目标的位置和速度作为状态量进行估计。
卡尔曼滤波算法的优点是计算简单,适用于实时应用。
目标检测常用算法

目标检测常用算法目标检测是计算机视觉领域中的一个重要任务,其目的是在图像或视频中准确地识别和定位特定对象。
在实际应用中,目标检测可以广泛应用于自动驾驶、安防监控、智能家居等领域。
本文将介绍目标检测常用算法,包括传统的基于特征工程的算法和现代的基于深度学习的算法。
一、传统的基于特征工程的算法1. Haar特征分类器Haar特征分类器是一种基于AdaBoost算法的目标检测算法。
它通过对图像中不同区域进行Haar特征提取,并采用AdaBoost算法训练分类器来实现目标检测。
Haar特征包括边缘、线性、对角线等几种类型,通过计算不同类型Haar特征之间的差异来提取图像中不同物体的区分度。
2. HOG+SVMHOG+SVM是一种基于支持向量机(SVM)和方向梯度直方图(HOG)特征提取方法的目标检测算法。
HOG是一种有效地描述图像纹理和形状信息的方法,它将图像划分成小块,并计算每个小块内的梯度方向和大小,然后将这些信息组合成一个特征向量。
SVM是一种经典的二分类器,通过学习样本数据的特征和标签之间的关系来实现分类。
3. SURFSURF是一种基于加速稳健特征(Speeded Up Robust Feature)算法的目标检测算法。
它通过对图像进行尺度空间分析和兴趣点提取,并计算每个兴趣点周围区域的局部特征描述子,来实现目标检测。
SURF算法具有较好的旋转不变性和尺度不变性,能够适应不同角度和大小的物体检测。
二、现代的基于深度学习的算法1. R-CNNR-CNN是一种基于深度卷积神经网络(CNN)的目标检测算法。
它通过对图像进行区域提取,并将每个区域输入到CNN中进行特征提取和分类。
R-CNN采用了候选区域提取方法来减少计算量,同时使用了多任务损失函数来优化模型性能。
2. Faster R-CNNFaster R-CNN是一种快速区域卷积神经网络(Fast R-CNN)和RPN (Region Proposal Network)相结合的目标检测算法。
一种多链路状态自动检测及快速切换算法研究

断 开状况 , 同时还没 有 较 好 的 自动 链 路 切换 算 法 将
应 用切换 到 新 的链 路 上 去 。文献 [ ] 述 了在 操作 4描
系统层 面实现的链路切换 的方法 , 它没 有实 现链 路 可
靠性 的判 决 , 同时也较难通 知上层应用 。文献 [ 6 5— ]
1 算 法 总体 方 案
第3 2卷 第 3期 21 0 2年 6月
南 京 邮 电 大 学 学 报 ( 自 然 科 学 版 ) Junl f aj gU i ri f ot a dT l o m nct n( a r cec ) ora o ni nv syo P s n e cm u i i s N t a Si e N n e t s e ao ul n
不进行 任何 人为 操作 , 上层 应 用 及 系 统 并 不会 自动 选 择 另外一 条连 接链 路 , 即使 另 外 一 条链 路 显 示 在
线 , 其 中就涉及 到路 由 划 转 的 问题 。即使 当前 这
息 中存 在 “ U N N ” R N I G 关键 字 , 则没有 。 否
L n n a : 太 网 硬 件 地 址 e : c:6: e: d a i k e c p以 e e 7 c c :c i e 地 址 :7 2 .3 .8 广 播 :7 2 .3 2 5 掩 码 : nt 1 2. 1 1 4 2 1 2. 1 1 4. 5 i e 6 地 址 : f B : 2 c: 6 f f c c a / 4 S o e: i k nt e 0 : O 7 f : e O: d c 6 c p L n U RACS UNN UTCS P BO DA T R N If H L IA T i 刖 :5e 10 跃 点 数 : l
Ku频段卫星通信信号自适应检测算法

第54卷 第4期2021年4月通信技术Communications Technology Vol.54 No.4Apr. 2021·786·文献引用格式:李成,白园,陈飞. Ku 频段卫星通信信号自适应检测算法[J].通信技术,2021,54(4):786-791.LI Cheng, BAI Yuan, CHEN Fei. A Self-adaptive Detection Algorithm for Ku-band SatelliteCommunication Signals [J].Communications Technology,2021,54(4):786-791.doi:10.3969/j.issn.1002-0802.2021.04.002Ku 频段卫星通信信号自适应检测算法*李 成,白 园,陈 飞(中国电子科技集团公司第三十研究所,四川 成都 610041)摘 要:通过对Ku 频段通信卫星电磁频谱的分析,提出了一种无须人工干预的自适应检测算法。
算法基于信号功率谱平滑拼接的统计特性,结合噪声估计与能量检测迭代策略,实现对Ku 频段卫星通信信号的自适应检测。
仿真结果表明,算法能够在较低的信噪比下达到较好的检测性能。
此外,该算法实时性好、且通用性好,更能满足实际工程实现的需要。
关键词:频谱拼接;频域平滑;噪声估计;自适应检测中图分类号:TN918 文献标识码:A 文章编号:1002-0802(2021)-04-0786-06A Self-adaptive Detection Algorithm for Ku-band SatelliteCommunication SignalsLI Cheng, BAI Yuan, CHEN Fei(No.30 Institute of CETC ,Chengdu Sichuan 610041,China )Abstract: Through the analysis of the electromagnetic spectrum of Ku-band communication satellites, a self-adaptive detection algorithm without human intervention is proposed. The algorithm is based on the statistical characteristics of smooth splicing of signal power spectrum, combined the noise estimation and an iterative strategy for energy detection, to realize adaptive detection of Ku-band satellite communication signals. Simulation results indicate that the proposed algorithm can achieve better performance at low SNR. In addition, the algorithm has good real-time performance and good general purpose, which can meet the needs of practical engineering implementation.Keywords: spectrum splicing; frequency domain smoothing; noise estimation; self-adaptive detection0 引 言近年来,卫星通信以其频谱资源丰富、支持宽带信号传输、覆盖广、受地理条件限制小等优点,逐渐在军民领域都占有不可替代的重要地位。
恒虚警与自动检测报告
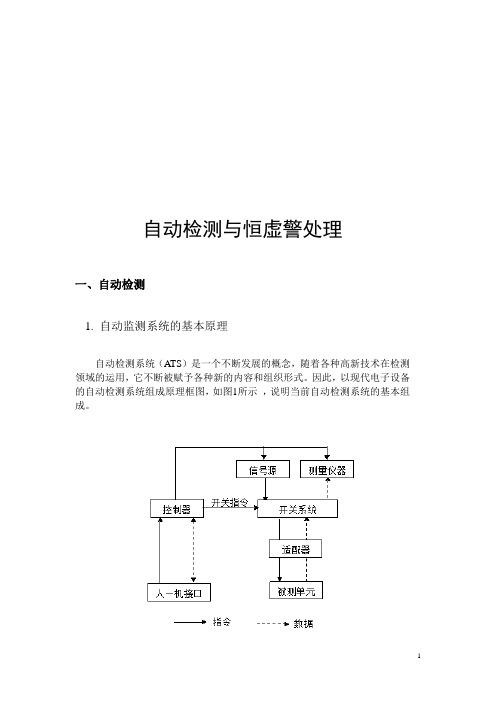
自动检测与恒虚警处理一、自动检测1. 自动监测系统的基本原理自动检测系统(ATS)是一个不断发展的概念,随着各种高新技术在检测领域的运用,它不断被赋予各种新的内容和组织形式。
因此,以现代电子设备的自动检测系统组成原理框图,如图1所示,说明当前自动检测系统的基本组成。
图一自动检测系统原理图图中表明,当前的自动检测系统,通常包括以下几个部分。
(1)控制器:控制器是自动检测系统的核心,它由计算机构成。
其功能是管理检测周期,控制数据流向,接收检测结果,进行数据处理,检查读数是否在误差范围内,进行故障诊断,并将检测结果送到显示器或打印机。
控制器是在检测程序的作用下,对检测周期内的每一步骤进行控制,从而完成上述功能的。
(2)励信号源:激励信号源是主动式检测系统必不可少的组成部分.其功能是向被测单元(UUT)提供检测所需的激励使号。
根据各种UUT的不同要求,激励装置的形式也不同,如交直流电源、函数发生器、D/A变换器、频率合成器、微波源等。
(3)测量仪器:测量仪器的功能是检测UUT的输出信号.根据检测的不同要求,测量仪器的形式也不同,如数字式多用表,频率计,A/D变换器及其它类型的检测仪器等。
(4)开关系统:开关系统的功能是控制UUT和自动检测系统中有关部件间的信号通道。
即控制激励信号输入UUT,和UUT的被测信号输往测量装置的信号通道。
(5)适配器:适配器的功能是实现UUT与自动检测系统之间的信号连接。
(6)人机接口:人机接口的功能是实现操作员和控制器的双向通信。
常见的形式为,操作员用键盘或开关向控制器输人信息,控制器将检测结果及操作提示等有关信息送到显示器显示。
显示器的类型有阴极射线管(CRT)显示器、液晶(LCD)显示器、发光二级管(LED)显示器或灯光显示装置等。
当需要打印检测结果时,人机接口内应配备打印机。
(7)检测程序:自动检测系统是在检测程序的控制下进行性能检测和故障诊断的。
检测程序完成人机交互、仪器管理和驱动、检测流程控制、检测结果的分析处理和输出显示、故障诊断等,是自动检测系统的重要组成部分。
电池阴阳极X射线自动检测装置的算法设计

作者简 介:蔡杰 (9 3 ) 16 一 ,女 ,辽 宁丹东人 ,教授 ,研究 方向 :自动化及计算机应用技术。
Hale Waihona Puke 池 图片所 包含 的区域很 大 ,所 以在 进行 检测 时必 须 要 对 需要 进行 检 测 的区域 做小 范 围的框定 ,以便设
置检 测线 。
检测线 的设置参数应该提前设置,根据设定的 参数值 ,装置 软件 自动 画出检测线 ,并为后来 的 “ 尺寸 测量 ” 做准 备 。工 业摄 像 机 采集 到 的图片 中 手 机 电池 阴 阳极 边界 是否 清晰对 检测 线 的划定 至关 重要 。 因此 , 初 的 图像 处 理 步骤 是 图片 的边 缘 锐 最 化 。装置的图片锐化方法使用的是拉普拉斯算子的 锐化方法 , 设原始图像每个点的灰度值为 i ) 其 , , 中i 『 别 代 表 点 的行 和 列 , 原 图F坐 标 为 和- 分 对 (,) i/的点 对行 方 向的灰 度微 分为 : . , )= ( +1 )一 △ i f . i , √) 厂
电池 电极 射 线 检 测 的算 法 部 分 主 要 是 靠 边 缘 提取 算 法 进 行 划 定 边 缘 ,从 而 提 取 出 电池 阴 阳
极 。当边缘模糊 的时候 ,边缘提取算法一般会造成 划线 弯 曲 j ,因此 现 阶段 光 物 标 边 缘 划 定 主要 运 用 回归算 法 和 网络算法 等 技术 ,同时小 波变 换检
量。其 中的核心部分为检测线设置 ,文章给 出了 检测线设置条件和设置的基本算法。通过工业 实验证 明, 该方法对于电池 阴阳极距 离检测等方面有 良好的效果 ,在 x射线检测中有着广泛的发展前景。 关键 词 :电池检 测装 置 ;参差 距 离;灰 度 ;梯度 中 图分类 号 : 文 献标 志码 :A 文章 编号 :17 4 3 ( 0 2 3— 15— 2 6 3— 9 9 2 1 )0 0 8 0
基于排序方差的非参量自动删除检测算法

t e u h a k fp 来自e ft e t s e l o l s e s Th e f r n e o h e e to l o i m s h n s ms t e r n s o u s so h e t c l fa l we p . s e p ro ma c ft e d t c in a g r h i t
( 军 航 空 工程 学 院 ,山东 烟 台 2 4 0 ) 海 6 0 1
摘 要 :为 了增 强 广 义 符 号 ( s 检 测 算 法 在 多 目标 环 境 中的 检 测 性 能 , 于 自动 删 除 单 元 平 均 ( C G) 基 A —
c 检 测 算 法 和 GS统 计 量 提 出 了一 种 新 的 非 参 量 检 测 算 法 ( G ) 它 的前 沿和 后 沿 均 采 用 A C 检 测 算 A) AC S , C A
( ACCA ) a S i e e t d. I a st um w o ACCA o a s i a i s a hec oieofr fr n e c l, nd G spr s n e tt ke he s oft l c le tm ton st h c e e e c e l
Ab ta t I o de o i p o hede e to e f m a eofG S de e to l ort n m uli e t r ta s r c : n r rt m r vet t c in p ror nc t c i n a g ihm i tpl— a ge n—
大 的 性 能 改善 。
关 键 词 : 参 量 ;广 义 符 号 统计 量 ; 自动 删 除 单 元 平 均 ; 序 数 据 方差 非 排
中图 分 类 号 : N9 7 5 T 5. 1 文献标识码 : A 文 章 编 号 : 6 22 3 ( 0 2 0 — 2 10 1 7 — 3 7 2 1 ) 30 8 — 5
全自动条形码检测及定位算法优化

全自动条形码检测及定位算法优化随着条形码在商业和物流领域的广泛应用,全自动条形码检测及定位算法的优化成为当今亟待解决的问题之一。
本文将探讨条形码检测及定位算法的基本原理,并介绍当前主流的优化方法和可能面临的挑战。
一、算法原理全自动条形码检测及定位算法的基本原理是通过计算机视觉技术来检测并定位图像中的条形码。
主要步骤包括图像预处理、条形码检测、条形码定位和校验等。
1. 图像预处理:图像预处理是为了提取有价值的信息,包括去噪、灰度化和增强等。
去噪可以采用平滑滤波和边缘保留滤波等方法,消除图像中的噪声。
灰度化将彩色图像转化为灰度图像,简化后续处理。
增强可以通过直方图均衡化、对比度增强等技术,使得条形码更加清晰。
2. 条形码检测:条形码检测是通过采用特定的图像处理算法来判断图像中是否存在条形码。
常见的方法包括基于边缘检测的方法、基于颜色分割的方法和基于模板匹配的方法。
边缘检测方法通过检测图像中的边缘来判断是否存在条形码。
颜色分割方法则是通过提取条形码的颜色信息来判断是否存在条形码。
模板匹配方法则是利用预先定义的模板图像与待检测图像进行匹配。
3. 条形码定位:条形码定位是为了准确地确定条形码的位置和姿态。
常见的方法包括基于边缘检测的方法、霍夫变换的方法和形态学处理的方法。
边缘检测方法通过检测图像中的条形码边缘来准确确定位置。
霍夫变换方法则是通过检测直线的方法来定位条形码。
形态学处理方法则是利用形态学操作来定位条形码。
4. 校验:校验是为了确保条形码的正确性,主要包括条形码类型的识别和条形码数据的解码。
条形码类型的识别可以通过匹配已知的条形码类型的模板来实现。
条形码数据的解码可以通过扫描条形码的条形数据,然后根据对应字符集进行解码。
二、优化方法为了提高全自动条形码检测及定位算法的准确性和效率,研究者们提出了一系列优化方法,主要包括以下几种。
1. 深度学习方法:深度学习方法是近年来在图像处理领域广泛应用的方法,可以有效提高条形码检测和定位的准确性。
印刷板钻孔机自动检测钻孔算法研究

马 庆 功 ( 常 州 大学信 息 中心 , 江苏 常州 2 1 3 1 6 4 )
摘
要
随 着 电子 产 品 向轻 薄短 小 、 高功 能化 、 高 密度 化 、 高可靠性 、 低 成 本 化 方 向发 展 , 促使 P CB制 造 中 的 关键 设备 P CB钻
孔机也向高速、 高精 度 、 高稳 定 、 低 成 本 方 向 发展 。 所 运 用 的 算 法基 本 保 留传 统 H OU GH 变 换 的优 点 , 并 且 对 图像 场景 中 的 干扰 不敏 感 , 在 圆周 残 缺 不 全 的 情 况 下 仍 能 进行 正确 检 测 。
op me nt , t o pr o mo t e t h e k e y e qui pmen t i n t h e PCB m a nu f ac t u r i n g P CB dr i l l i n g mac hi ne wi t h t h e hi gh-s pe ed, h i gh a c cu r ac y, hi gh s t abi l i t y, l ow c os t d ev e l o pm e n t di r ec t i on . T he b as i c al g or i t h m u s e d i n t hi s pa per r e t a i n t h e ad v an t ag es o f t r a di t i o na l HOUGH t r an s f Or m, an d t he i n t er f e r e n ce o f t h e i m ag e s c en e i s no t s en s i t i ve , i n t h e ca s e o f i n co m pl e t e ci r c l e s t i l l co r r ec t l y de —
aoi检测原理

aoi检测原理
AOI(自动光学检测)是一种利用光学设备进行电子元件、印
刷电路板(PCB)和其他光学组装的自动检测技术。
其主要原理是通过摄像仪和光源对待检测物体表面进行扫描,然后通过计算机算法对采集到的图像进行分析和处理,从而实现快速、高精度的检测。
AOI检测主要包括以下步骤:
1. 目标定位:通过电脑辅助设计(CAD)数据或已知的特征,确定待检测物体的位置和方向。
这可以通过在AOI系统中预
先加载CAD数据或使用计算机视觉算法(如边缘检测、阈值
处理等)来实现。
2. 光学扫描:使用高分辨率的摄像仪和恰当的光源对待检测物体进行扫描。
光源的选择根据被检测物体的表面特性和缺陷类型而定。
扫描可以是单向的,也可以是多方向的,以确保对整个物体表面的覆盖。
3. 图像采集:摄像仪将扫描到的图像传输到计算机中进行采集和存储。
为了提高检测效果,图像采集的速度和分辨率需要根据被检测物体的特性进行优化。
4. 图像分析与缺陷检测:采集到的图像通过计算机视觉算法进行分析。
这些算法可以包括边缘检测、图像过滤、颜色分析、形状匹配等。
通过设定合适的阈值和规则,算法可以检测出图像中的缺陷,如焊点缺失、焊盘变形、元件位置偏移等。
5. 缺陷分类和报警:检测到的缺陷根据其类型和严重程度进行分类,并根据预设的标准判定是否报警。
报警通常以声音、光信号或计算机界面的形式呈现,以便操作人员能够及时采取措施修复缺陷,并确保产品质量。
总之,AOI检测利用光学设备和计算机视觉算法实现对待检测物体进行快速、精确的缺陷检测,广泛应用于电子制造、PCB 生产、半导体等行业中。
道路巡检检测算法

道路巡检检测算法一、概述道路巡检检测算法是一种用于自动检测和识别道路状况、车辆、行人和交通违规行为的计算机视觉算法。
通过实时分析道路监控视频,该算法能够自动识别道路破损、障碍物、交通违规、车辆违章停车、交通拥堵以及路标和行人流量等关键信息,有助于提高道路交通安全和效率。
二、道路破损检测道路破损检测是道路巡检检测算法的重要功能之一。
该算法利用图像处理和计算机视觉技术,自动检测和分类道路表面的各种破损类型,如裂缝、坑洼、修补区等。
通过分析路面纹理、颜色和形状等信息,算法能够准确地识别出道路破损的位置和程度,为道路维护和修复提供及时的信息。
三、障碍物识别障碍物识别是道路巡检检测算法的另一项重要功能。
该算法能够实时检测道路上的各种障碍物,如车辆、行人、动物、施工区域等。
通过分析视频流中的动态物体和静态物体的运动轨迹和速度,算法能够准确地识别出障碍物的位置、大小和运动状态,及时发现潜在的安全隐患,提高道路交通的安全性。
四、交通违规检测交通违规检测是道路巡检检测算法的重要应用之一。
该算法通过分析视频流中的车辆轨迹和行为,能够自动检测各种交通违规行为,如闯红灯、超速、逆行等。
通过识别车辆特征和运动状态,算法能够准确地检测出交通违规行为,为交通管理部门提供及时的信息,有效遏制交通违法行为。
五、车辆违章停车检测车辆违章停车是常见的交通问题之一,也是道路巡检检测算法的重要应用之一。
该算法通过分析视频流中的车辆位置和运动状态,能够自动检测车辆违章停车行为。
通过识别车辆特征和停车行为模式,算法能够准确地检测出违章停车的位置和时间,为交通管理部门提供及时的信息,有效遏制车辆违章停车行为。
六、交通拥堵分析交通拥堵是城市交通中的常见问题之一,也是道路巡检检测算法的重要应用之一。
该算法通过分析视频流中的车辆轨迹和密度等信息,能够实时监测道路交通拥堵状况。
通过识别拥堵区域和拥堵程度,算法能够为交通管理部门提供及时的信息,优化交通流量分布,缓解交通拥堵问题。
自动警戒圈的目标检测算法

( mp t n i er ol e J i nv ri , im n3 1 2 , hn ) Co ue E gn e l g , i iesy X a e 6 0 1 C ia r C e me U t ( vg t nC l g , i i ies , a n3 1 2 , hn ) Na iai ol e J o e me Unv r t Xi i y me 6 0 1 C ia
it frn eo en i . x r n h w ta te a o tm a e ue n ojc eet g o aa A P ne eec ft os E pi r h e e met so t l r s h h gi h cn b sd i bet d t i frdr R A s c n /
t e t bet i u ma c e i l T e grh o s’ne mpe p r in, n l r o t edt t g od t j s na t t rc ce h o tm dent edc l o a o s adft s u e i c e oc o iat r . l l a i o xe t i e t h c e n
l 引言
随着海 运事业的蓬勃发展 ,船舶也朝着多样化 、
大型化 、智 能化发展 。尽管现代化船舶都装备 了各种 通信设备 ,先进 的定位导航设备 以及 自动驾驶仪等 ,
拟和 自动雷达标绘仪模拟 。
其中雷达模拟包 括在 稳定的相对运动模式和海、 陆稳 定的真运动模式上操作:模仿天气 、潮流、海流、
关键词 :雷J/ P 2 AR A模拟器 ;回波;二值 图像 ; 目标检 测;区域生长  ̄
T eA g rtm f jcs tcini tmaiAlr ice h loi o etDeet Auo t et rl h Ob o n c C
基于机器视觉的自动检测系统研究

基于机器视觉的自动检测系统研究自动检测系统是机器视觉领域中一项重要的研究内容。
它利用计算机视觉技术和机器学习算法,实现对图像和视频中目标物体的自动识别和检测。
本文将就基于机器视觉的自动检测系统展开研究,并探讨其研究方向、应用领域以及挑战与发展趋势。
一、研究方向1. 目标检测算法:目标检测算法是自动检测系统的核心。
目前,常用的目标检测算法包括传统的特征提取与分类方法,以及基于卷积神经网络(CNN)的深度学习方法。
传统方法常使用的包括Haar特征、SIFT特征等,而深度学习方法以Faster R-CNN、YOLO、SSD等为代表。
对这些方法进行深入研究,改进其准确度和泛化能力,是这一方向的主要研究内容。
2. 数据集构建与标注:高质量的数据集对于训练和评估自动检测系统至关重要。
构建标准化、多样性的数据集,并进行准确的标注,可以提高系统的检测效果。
此外,数据集的美观性、实时性等因素也需要考虑,使得系统能适应不同的应用场景。
3. 硬件优化:实时性是自动检测系统在实际应用中的一个重要指标。
因此,对硬件平台的优化尤为关键。
GPU、FPGA等硬件加速技术的研究与应用,可以大幅提高系统的实时性和检测效果。
同时,优化算法与硬件平台之间的配合,也是这一方向的研究重点。
二、应用领域自动检测系统在许多领域中有着广泛的应用,以下是几个典型的应用领域:1. 自动驾驶:自动驾驶是近年来的热门领域之一。
自动检测系统在自动驾驶领域中可以用于路况感知、障碍物检测、行人识别等功能。
通过实时地对周围环境进行检测,自动驾驶系统可以做出更加准确和安全的决策。
2. 安防监控:自动检测系统在安防监控领域中能够实现对特定区域中异常行为的自动检测,如人员聚集、异常目标等。
通过及时发现异常情况,并进行报警和处理,可以提高安全性和防范能力。
3. 工业生产:自动检测系统在工业生产中可以用于产品的质量检测、缺陷检测等方面。
通过实时地对产品进行检测,可以提高生产效率和质量,降低成本,并减少人工检测带来的不稳定性。
目标检测经典算法

目标检测经典算法目标检测是计算机视觉领域的重要问题之一。
其任务是在图像中定位出物体的位置并且给出对应的类别。
在实际应用中,目标检测技术广泛应用于自动驾驶、智能安防、工厂产线等多个领域。
目前,目标检测算法已经达到了极高的精度和速度,并且还在不断地进行改进和优化。
下面将介绍目标检测的一些经典算法。
一、基于图像区域提取的目标检测算法基于图像区域提取的目标检测算法与分类器密切相关。
其基本思想是首先在图像中生成一些可能包含物体的区域,然后对这些图像区域进行分类来确定物体的类别。
这类算法包括Selective Search、EdgeBoxes 等。
1. Selective SearchSelective Search是基于启发式搜索的目标检测算法。
其可以在不同尺度和分辨率下生成大量的候选区域。
具体来说,它使用类似于人类视觉系统的方式来不断地合并相邻的像素,直到整个图像被分成了一组连通的区域。
然后,使用其他算法来筛选出可能包含物体的候选区域,并且对这些候选区域进行分类。
2. EdgeBoxesEdgeBoxes算法是一种基于边缘的目标检测算法。
其使用边缘检测算法来检测出图像中的边缘,并且利用这些边缘来提取可能包含物体的候选区域。
与Selective Search不同,EdgeBoxes可以生成高质量的大型目标框,并且具有高效的性能。
二、基于深度学习的目标检测算法基于深度学习的目标检测算法是目前最为流行和高精度的算法。
这类算法通过训练深度神经网络来完成目标检测任务。
其中最著名的算法包括Faster R-CNN、YOLO、SSD等。
1. Faster R-CNNFaster R-CNN算法是一种基于区域提取网络(RPN)的目标检测算法。
其使用RPN来产生候选框,并且使用RoI池化层将候选框缩放为固定大小的特征图,然后输入到全连接层进行分类和位置回归。
2. YOLOYOLO算法(You Only Look Once)是一种单阶段目标检测算法。
基于数学形态学的快速糖尿病视网膜病变自动检测方法

图 3 示) 佳。 所 更
病灶候选 区域 ;运用数学形态学获取 精确 的病灶轮 廓 , 而 从
法 。
() z中面积大于一定数值且 亮度最大 的区域 即为视盘 3夕
P , 将分割结果显示在原 图上 的效果见 图 4 。
2 基于数学形态学 的 E s自动检测算法 X
由于 E s X 边缘清晰 ,亮度较高 , 与背景具有 较为 明显 的 对 比度 ,因此 ,首先利用数学形态学 结合大 津法 阈值 分割 快 速 提取 出视盘 , 在此基础上得 到病灶候 选 区域 ; 然后 利用 形
() 1利用 大津法对 , 进行阈值分割 , P ; r 得
() P 进行二值形态 学开运算 , 掉小面 积 区域 ,得 2对 去
P ; 2
点 非常适合应用于与视觉信息相关 的信 息处理与分 析 ,因此
对 于糖 网病 灶一 E s的 自动检 测 ,选 择 使用 数 学形 态 学 方 X
(E 005 ) B 2 16 2 资助
作者简介 : 高玮玮 , 9 5 1 8 年生 , 南京航空航天大学机 电学 院博士研究生
e a : w 0 0 0 3 @s a cr - i g w 3 2 2 4 i .o m l n n
第 3期
光谱 学与光谱分析 2 1 2 视 盘分割算法 ..
一
() 1
其中 表示膨胀运算 , B表 示大 小为 s的形 态结 构元 素 B,
T表 示 阈值 分 割 。
基于深度置信网络Otsu混合模型的自动云检测算法

遥感数据数量和种类的增加以及对云检测精确度要求的不断 提高ꎬ固定阈值方法已经无法满足要求ꎮ 动态阈值相对于固 定阈值具有更好的灵活性、适应性以及可扩展性ꎬ出现了一些 自动分割或自动阈值云检测方法[3 -4] 取代原有的固定阈值方 法ꎬ 但是总体来说ꎬ目前已有的动态阈值方法自动化程度仍 然较低ꎬ很难满足云检测的需要ꎮ 另一类传统云检测方法主 要是根据云的纹理、形状、灰度等物理特征来进行分类ꎮ 支持 向量 机 ( Support Vector Machineꎬ SVM ) [5] 、 Bag ̄of ̄Words 模 型[6] 、贝叶斯时空算法[7] 以及逐步求精算法[8] 等分类算法在 云检测方面得到了较好的应用ꎬ 但是依据云的物理特征进行 分类时ꎬ计算量大且较为复杂ꎬ需要的数据种类也较多ꎮ 近年 来ꎬ一些新兴的智能方法开始应用于云检测领域ꎬ主要是利用 深度学习神经网络( Neural Networkꎬ NN) 进行分类[9 - 10] ꎬ综 合多种算法模型也成为新的趋势[11 - 13] ꎮ 新兴的智能云检测 方法相对传统检测方法自动化程度得到了一定的提升ꎬ但是 泛化能力相对较弱ꎬ尤其在数据受冰雪影响较大时ꎬ检测结果 会产生较大偏差ꎮ
关键词:深度学习ꎻ云检测ꎻ深度置信网络ꎻ最大类间方差法ꎻ高级甚高分辨率辐射计 中图分类号:TP317. 4 文献标志码:A
Automatic cloud detection algorithm based on deep belief network ̄Otsu hybrid model
QIU Meng YIN Haoyu CHEN Qiang LIU Yingjian∗
舶舶AIS轨迹异常的自动检测与修复算法

>: 2 h 2 0 4 G F : 2 5 A b v 0 2 1 Mk . 0 2 F
1 5: 3 8: 1 O! AI VDM , 1, 1 , , B, B 6: VW v h 3 0 1 53 8 : 1 0 4 1 3 7 7 1 7 7 l 2 2 3 . 8 5 7 5 5 2 。 W. 0 . 0 0 0 8 5 3 。 N 7 6 . 8
t o t h e a b n o r m i t y o f A I S t r a j e c t o y .T r h r o u g h i n — d e p t h a n a l y s i s o f a l a r g e a mo u n t o f A I S d a t a ,t h i s p a p e r i d e n t i i f e s s e v e r a l
船舶 自动识别 系统 ( A u t o m a t i c I d e n t i i f c a t i o n S y s —
t e n, A I S ) 数 据 中蕴含 着 大 量 船 舶信 息 , 可 通 过 提 取 这 些信 息 了解 船舶 的航 行 状 态 , 将 其 应用 到船 舶 避
a n d t h e t i me o f a s h i p,a r e v a l u a b l e f o r s h i p s a i l i n g s t a t e a n a l y s i s ,ma i r t i me t r a f f i c l f o w p r e d i c t i o n,a n d ma ri t i me a c c i d e n t
a n a l y s i s .Ho we v e r,d u e t o t h e i nt e r f e r e n c e s o f s o me f a c t o r s,t he r e s o me t i me s e x i s t e r r o r s i n t h e c o l l e c t e d AI S da t a,l e a di n g
深度学习算法在自动化检测中的使用教程

深度学习算法在自动化检测中的使用教程随着人工智能技术的不断发展,深度学习算法作为其中的重要组成部分,已经开始在自动化检测领域展示出强大的应用潜力。
本文将为您详细介绍深度学习算法在自动化检测中的使用方法和步骤。
一、深度学习算法简介深度学习是机器学习领域中的一个重要分支,在过去的几年里取得了惊人的发展。
它模仿人脑神经网络的工作原理,通过训练数据来提取特征并进行模式识别。
深度学习算法的优势在于其可以自动学习、处理大量的非结构化数据,并且具备较强的泛化能力。
二、深度学习算法在自动化检测中的应用1. 数据准备在开始使用深度学习算法进行自动化检测之前,首先需要准备好相关的数据。
这些数据应该包括正常和异常情况下的实例,以便让算法能够学习并识别出异常情况。
2. 构建模型在深度学习算法中,神经网络是最常用的模型之一。
在进行自动化检测时,可以使用不同种类的神经网络模型,例如卷积神经网络(CNN)、长短期记忆网络(LSTM)等。
根据实际情况,选择适合的模型进行构建。
3. 特征提取提取有效的特征是深度学习算法的核心任务之一。
深度学习算法可以根据输入数据自动学习并提取最相关的特征。
通过合适的特征提取方法,可以大幅提高自动化检测的准确性和效果。
4. 模型训练在准备好数据并构建好模型后,下一步就是进行模型的训练。
模型训练过程包括将数据输入到模型中,并通过反向传播算法来调整模型参数,使其输出结果与真实结果尽可能接近。
训练过程需要大量的计算资源和时间,通常需要在GPU上进行加速。
5. 模型评估训练完成后,需要对模型进行评估以验证其性能。
评估过程可以使用一些常见的指标,如精确度、召回率、F1值等,来评估模型的准确度和鲁棒性。
如果模型表现不佳,可以通过调整参数或者采用其他优化方法来改进模型。
6. 模型部署在模型训练和评估完成后,可以将模型部署到实际的自动化检测系统中。
部署过程包括将训练好的模型保存到文件中,并根据实际需求,将其嵌入到自动化检测系统中,以实现实时检测和预测。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
③只要适当改变软件滤波器的滤波程序和运 算参数,即可改变滤波特性,这对于低频脉 冲于扰、随机噪声特别有效。
滤波方法
5.1.1 程序判断法
5.1.2中位值滤波法 5.1.3 算术平均滤波法 5.1.4 递推平均滤波法 5.1.5 加权递推平均滤波法 5.1.6 一阶惯性滤波法 5.1.7 复合滤波法
在采用硬件方法时要确定RC网络滤波器有大 的时间常数和多高精度。而一阶惯性滤波算 法是一种以数字形式通过算法来实现的动态 RC滤波方法.
一阶惯性滤波算法的实现
y (1 a) yn a y
n
n1
a Tf T T f
为未经滤波的第n 次采样值
滤波时间常数和采 样周期
5.1.7 复合滤波法
常把前面所介绍的两种以上的方法结合 起来使用,形成复合滤波。 达到更好的 滤波效果。
故加权速推平均滤波算法适用于有较大纯滞 后时间常数的对象和采样周期较短的系统。 而对于纯滞后时间常数较小、采样周期较长、 缓慢变化的信号,则不能迅速反应系统当前 所受干扰的严重程度,滤波效果差。
5.1.6 一阶惯性滤波法
在模拟量输入通道等硬件电路中,常用一阶 惯性RC模拟滤波器来抑制干扰。一阶惯性 滤波算法对周期性干扰具有良好的抑制作用, 适用于波动频繁的参数滤波,其不足之处是 带来了相位滞后,灵敏度低。同时,它不能 滤除频率高于采样频率二分之一(称为奈奎 斯特频率)的干扰信号。
算术平均滤波程序只需要注意两点:时间和 存储容量
5.1.4 递推平均滤波法
应用:实时系统中,要求数据计算速率高。 递推平均滤波法是把N个测量数据看成一个
队列,队列的长度固定为N,每进行一次新的 测量,把测量结果放在队尾,而扔掉原来队 首的一个数据,这样在队列中始终有N个“最 新”数据。 计算滤波值时,只要把队列中的N个数据进行 算术平均,就可得到新的滤波值。这样每进 行一次测量,就可计算得到一个新的平均滤 波值,这种滤波算法称为递推平均滤波法。 N为递推平均项数 的选择:参考工程经验 。
常常要从系统的实际精度要求出发,用 逼近法来降低一个已知非线性特性函数
的次数,以简化数学模型。便于计算和
处理。
具体方法
1.代数插值法 2.非线性校正 3.最小二乘法 4Leabharlann 最佳一致逼近法(1)线性插值
线性插值就是最常用的直线方程校正法
线性插值是在一组数据(xi,yi)中选取两个 有代表性的点(xo,yo),(x1,y1),然 后根据插值原理,求出插值方程 :
5.2.1 系统误差的模型校正法(非线性 校正)
5.2.2 系统误差的标准数据校正法 5.2.3 系统零位误差和增益误差的校正方
法
5.2.4 传感器温度误差的校正方法
5.2.1 系统误差的模型校正法 (非线性校正)
在某些情况下,对系统误差进行理论分 析和数学处理,可以建立起系统误差模 型。一旦有了模型,就可以确定校正系 统误差的算法和表达式。
y y 扰,并视后一次采样值
n 为非法值,应予剔除.
作废后,
n
y y 可以用
替代
n1
n。
参数 最大 变化 速度
5.1.2中位值滤波法
对被测参数连续采样(n次奇数次)一 系列值之后,对采样值按照大小排队, 取中间值作为本次采样值。
注意适用范围:被测参数缓慢变化
5.1.3 算术平均滤波法
算术平均滤波就是连续取几个采样值进行算 术平均。
算术平均滤波法适用于对一般具有随机干扰
的信号进行滤波。这种信号的特点是有一个 平均值,信号在某一数值范围附近做上下波 动,在这种情况下,仅取一个采样值作为依 据来显示是不准确的。
算术平均滤波法对信号的平滑程度完全取决 于N值,当N值较大时,平滑度高,但灵敏度 低;当N值较小时,平滑度低,但灵敏度高。
5.2 消除系统误差的软件算法
系统误差是指在相同条件下,多次测量同一 量时其大小和符号保持不变或按一定规律变 化的误差。
系统误差不能依靠概率统计方法来消除或消 弱,不像抑制随机干扰那样能导出一些普遍 适用的处理方法,而只能针对某一具体情况 在测量技术上采取一定的措施。
通常都采用离线处理的方法来确定校正算法 和数学表达式,在线测量时则利用此校正算 式对系统误差做出修正。
P1 ( X
)
x x1 x0 x1
y0
x x0 x1 x0
y1
a1x
a0
对于非线性程度严重或测量范围较宽的非线 性特性,采用上述直线校正方程进行校正, 往往很难满足仪器的精度要求。 采用
5.2.2 系统误差的标准数据校 正法
5.3量程自动切换及标度变换
5.3.1量程自动切换 5.3.2 标度变换
5.1.5 加权递推平均滤波法
为了增加新采样数据在速推平均中的比重, 以提高系统对当前采样值中所受干扰的灵敏 度,可采用加权选推平均滤波算法。它是递 推平均滤波算法的改进,即不同时刻的数据 加以不同的权,通常越接近现时刻的数据, 权取得越大。
常系数C0,C1,```,CN-1的选取有多种方法,其 中最常用的是加权系数法。
表示相邻两个采样
5.1.1 程序判断法
值之差最大可能的 变化范围
程序判断法又称限幅滤波 关键问题:a 的选择=T*Vmax
限幅滤波是一种十分有效的方法,其基本方法是通过比较相邻
y y (n 和 n-1 时刻)的两个采样值 和 ,如果它们的差值
n
n1
过大,超出了参数可能的最大变化范围,则认为发生了随机干
第5章 自动检测算法
原来靠硬件电路难以实现的信号 处理问题得以解决,从而克服和 弥补了包括传感器在内的各个测 量环节中硬件本身的缺陷或弱点,
提高了系统的综合性能。
自动检测算法的主要功能
随机误差的克服(数字滤波) 系统误差的消除 量程自动切换 工程量变换等
5.1 数字滤波技术
①数字滤波无需硬件,只是一个计算过程, 因此可靠性高,不存在阻抗匹配问题。尤其 是数字滤波可以对频率很高或很低的信号进 行滤波,这是模拟滤波器所不及的。
