微积分3第二次习题课题目(2011年3月)_787205693
考研数学三(微积分)模拟试卷2(题后含答案及解析)

考研数学三(微积分)模拟试卷2(题后含答案及解析) 题型有:1. 选择题 2. 填空题 3. 解答题选择题下列每题给出的四个选项中,只有一个选项符合题目要求。
1.二次型f(x1,x2,x3)=2x12+x22-4x32-4x1x2-2x2x3的标准形是( ).A.2y12-y22-3y32B.-2y12-y22-3y32C.2y12+y22D.2y12+y22+3y32正确答案:A 涉及知识点:微积分2.设向量组α1,α2,α3线性无关,则下列向量组线性相关的是( ).A.α1+α2,α2+α3,α3+α1B.α1,α1+α2,α1+α2+α3C.α1-α2,α2-α3,α3-α1D.α1+α2,2α2+α3,3α3+α1正确答案:C 涉及知识点:微积分3.某人向同一目标独立重复射击,每次射击命中目标的概率为p(0<p<1),则此人第4次射击恰好第2次命中目标的概率为( ).A.3p(1-p)B.6p(1-p)2C.3p2(1-p)2D.6p2(1-p)2正确答案:C解析:第4次射击恰好第2次命中目标意味着第4次一定命中目标且前三次中恰好有一次命中目标,故该事件的概率为C32(1-p)2×p=3p2(1-p)2,显然只有(C)是正确的.知识模块:微积分4.二次型f(x1,x2,x3)=2x1x2+2x1x3+2x2x3的规范形为( ).A.2y12+y22+y32B.y12-y22-y32C.2y12-y22-y32D.y12+y22+y32正确答案:B 涉及知识点:微积分5.设矩阵Am×n的秩为r(A)=m<n,Em为m阶单位矩阵,下列结论中正确的是( ).A.A的任意m个列向量必线性无关B.A的任意一个m阶子式不等于零C.若矩阵B满足BA=0,则B=0D.A通过初等行变换必可化为(Em,0)的形式正确答案:C 涉及知识点:微积分6.将一枚硬币独立地掷两次,引进事件:A1={掷第一次出现正面},A2={掷第二次出现正面},A3={正、反面各出现一次},A4{正面出现两次},则事件( ).A.A1,A2,A3相互独立B.A2,A3,A4相互独立C.A1,A2,A3两两独立D.A2,A3,A4两两独立正确答案:C 涉及知识点:微积分7.二次型f(x1,x2,x3)=x12+x22+x12-4x2x3的正惯性指数为( ).A.0B.1C.2D.3正确答案:C 涉及知识点:微积分8.设向量组(Ⅰ):α1=(α11,α21,α31)T,α2=(α12,α22,α32)T,α3=(α12,α23,α33)T,向量组(Ⅱ):β1=(α11,α21,α31,α41)T,β2=(α12,α22,α32,α42)T,β3=(α12,α23,α33,α43)T,则( ).A.若(Ⅰ)相关,则(Ⅱ)相关B.若(Ⅰ)无关,则(Ⅱ)无关C.若(Ⅱ)无关,则(Ⅰ)无关D.(Ⅰ)无关当且仅当(Ⅱ)无关正确答案:B 涉及知识点:微积分填空题9.二次型f(x1,x2,x3)=(x1+ax2-2x3)2+(2x2+3x3)2+(x1+3x2+ax3)2正定的充分必要条件为________.正确答案:a≠1 涉及知识点:微积分10.已知向量组α1=(1,2,3,4),α2=(2,3,4,5),α3=(3,4,5,6),α4=(4,5,6,t),且r(α1,α2,α3,α4)=2,则t=________.正确答案:7 涉及知识点:微积分11.若n个人站成一行,其中有A、B两人,问夹在A、B之间恰有r个人的概率是多少?如果n个人围成一个圆圈,求从A到B的顺时针方向,A、B之间恰有r个人的概率.正确答案:n个人随意排序共有n!种排法,即样本空间的样本点总数为n!,A、B两人中间恰有r个人,这两人中间相隔r个位置,组成一组共有(n-r-1)种排法,A、B两人的位置有2!种排法;其他的人在剩下的n-2个人随意排序,有(n-2)!种排法;于是“夹在A、B之间恰有r个人”的排法有(n-r-1).2!.(n-2)!,故P(夹在A、B之间恰有r个人)=(n-r-1).2!(n-2)!/n!=2(n-r-1)/n(n-1);如果围成一个圆圈,则n个人的相对位置有(n-1)!种排法,从A到B的顺时针方向有r个人的排法有(n-2)!,故P(A、B顺时针排,中间有r个人)=(n-2)!/(n-1)!=1/(n-1).涉及知识点:微积分12.连续投掷一枚均匀硬币10次,求其中有3次是正面的概率.正确答案:P(10次有3次是正面)=C103/210.涉及知识点:微积分解答题解答应写出文字说明、证明过程或演算步骤。
考研数学三(微积分)模拟试卷102(题后含答案及解析)

考研数学三(微积分)模拟试卷102(题后含答案及解析)全部题型 2. 填空题3. 解答题填空题1.=__________.正确答案:解析:知识模块:微积分2.设y=f(x)满足且f(0)=0,则∫01f(x)dx=__________.正确答案:解析:知识模块:微积分3.设f(x)在[a,b]上连续可导,f(a)=f(b)=0,且∫abf2(x)dx=1,则∫abxf(x)f’(x)dx=__________.正确答案:解析:知识模块:微积分4.已知f(x)连续,∫01f(x)dx=5,则∫01f(x)[∫x1(t)dx]dx=__________.正确答案:解析:知识模块:微积分5.设f(x)具有连续导数,且F(x)=∫0x(x2一t2)f’(t)dt,若当x→0时F’(x)与x2为等价无穷小,则f’(0)=__________.正确答案:解析:由于F(x)=∫0x(x2一t2)f’(t)dt=x2∫0x(t)dt一∫0xt2f’(t)dt,所以F’(x)=2x∫0xf’(t)(x2f’(x)-x2f(x)=2x∫0xf’(t)dt.又依题设,当x→0时F’(x)与x2为等价无穷小,从而知识模块:微积分6.已知f(x)=∫1x2e-t2dt,则∫01xf(x)dx=__________.正确答案:解析:知识模块:微积分7.∫0+∞x7e-x2dx=__________.正确答案:3解析:∫t33e-tdt=e-t(at3+bt2+dt+e)+C,两边求导得t3e-t=e-t[一at3+(3a—b)t2+(2b—d)t+d—e],比较两边t的同次幂项的系数得a=一1,b=一3,d=一6,e=一6.于是知识模块:微积分8.=__________.正确答案:解析:知识模块:微积分9.=__________.正确答案:解析:因(xex)’=ex(x+1),令xex=t,则dt=ex(x+1)dx,于是知识模块:微积分解答题解答应写出文字说明、证明过程或演算步骤。
微积分II真题含答案

微积分II真题含答案微积分II真题含答案一、填空题(每题3分,共30分)1、函数的定义域是____________. 2、设,则________________. 3、广义积分的敛散性为_____________. 4、____________ . 5、若 . 6、微分方程的通解是____. 7、级数的敛散性为 . 8、已知边际收益R/(x)=3x2+1000,R(0)=0,则总收益函数R(x)=____________. 9、交换的积分次序= . 10、微分方程的阶数为_____阶. 二、单选题(每题3分,共15分)1、下列级数收敛的是()A,B,C,D,2、,微分方程的通解为()A,B,C,D,3、设D为:,二重积分=()A, B, C, D,0 4、若A, B, C, D, 5、=()A, 0 B, 1 C, 2 D, 三、计算下列各题(本题共4小题,每小题8分,共32分)1.已知2. 求,其中D是由,x=1和x轴围成的区域。
3. 已知z=f(x,y)由方程确定,求4.判定级数的敛散性. 四、应用题(本题共2小题,每小题9分,共18分):1. 求由和x轴围成的图形的面积及该图形绕x轴旋转所得旋转体的体积。
2. 已知x表示劳动力,y表示资本,某生产商的生产函数为,劳动力的单位成本为200元,,每单位资本的成本为400元,总1/ 14预算为*****元,问生产商应如何确定x和y,使产量达到最大?。
五、证明题(5分)一、填空题(每小题3分,共30分)1, 2,3,发散4,0 5,6,y=cx 7,收敛8,R(x)=x3+1000x 9,10,2 二、单选题(每小题3分,共15分)1,B 2,B 3,C 4,C 5,D 三、计算题(每小题8分,共32分)1、解:令2、3、整理方程得:4、先用比值判别法判别的敛散性,(2分)收敛,所以绝对收敛。
(交错法不行就用比较法) (8分)四、应用题(每小题9分,共18分)1、解:2、解:约束条件为200x+400y-*****=0 (2分)构造拉格朗日函数,(4分),求一阶偏导数,(6分)得唯一解为:,(8分)根据实际意义,唯一的驻点就是最大值点,该厂获得最大产量时的x为40,y为230. (9分)五、证明题(5分)证明:设对等式两边积分,得:(2分)(4分)解得:题设结论得证。
微积分复习(三)参考答案

微积分复习(三)及答案一 选择题1 设f(x)在区间[a, b]上连续,则在(a, b)内f(x)必有:( B ) (A )导函数 (B )原函数(C )极值 (D )最大值和最小值 2 如果,)()(⎰+=c x F dx x f 则2(cot )sin f x dx x=⎰( B )(A )(cot )F x c + (B )(cot )F x c -+ (C )(sin )F x c + (D )(sin )F x c -+ 3 若11(ln )()eb a f x dx f u du x=⎰⎰, 则( A )(A )0,1a b == (B )0,a b e == (C )1,0a b == (D ),1a e b ==4 若4()2xx f t dt =⎰, 则40_____f dx =⎰ D (A )2 (B )4(C )8 (D )16 5 若设f(x)在区间[a, b]上连续,则()______baf x dx =⎰B(A )10[()]f a b a t dt +-⎰ (B )10()[()]b a f a b a t dt -+-⎰ (C )1[()]f a b a t dt -+-⎰极值 (D )01()[()]b a f a b a t dt --+-⎰6 设()xF x =⎰,则'(1)_____F = D(A 2 (B )2(C )2 (D )2-7 下列函数对中是同一函数的原函数的有 A(A )21sin 2x 与1cos 24x - (B )ln ln x 与2ln x (C )2x e 与x e 2 (D )tan 2x 与1cot sin x x-+8 如果,)(2⎰+=c x dx x f 则_______)1(32⎰=-dx x f x D(A )c x +-23)1(3 (B )c x +--23)1(3(C )c x +-23)1(31 (D )c x +--23)1(319 以下广义积分中收敛的是( ) C (A )101dt t ⎰ (B )1201dt t ⎰ (C )1dt ⎰(D )10ln t dt t ⎰ 10 设'()ln ()cos ,_________()xf x f x x dx f x ==⎰ A(A )cos sin x x x c -+ (B )sin cos x x x c -+ (C )(sin cos )x x x c ++ (D )sin x x c + 11 设方程0sin 0yx t e dt tdt +=⎰⎰确定y 为x 的函数,则______dydx= A (A )sin y x e -(B )cos yxe- (C )0 (D )不存在12 若()()f x f x =--,在(0,)+∞内()0f x '>,()0f x ''>,则()f x 在(,0)-∞内(C ) (A )()0f x '<,()0f x ''< (B )()0f x '<,()0f x ''> (C) ()0f x '>,()0f x ''< (D) ()0f x '>,()0f x ''> 二 填空题1 121(2sin )______1x dxx -+=+⎰ π2 20sin _____x dx π=⎰4321______1e dxx ---=+⎰ 1-4 若'()1xf e x =+,则()______f x = ln x x c +5 31/241/2cos ______1x xdx x -=+⎰ 0 6 210lim______1n n x dxx→∞=+⎰0 7[()]____()(0)xdf x dx f x f dx=-⎰8222____1x xdx x -+=+⎰ ln 59 曲线sin (0)xy e x x -=≥与x 轴所围成图形的面积为____________ 12(1)e e ππ+- 10 曲线2y x =与直线y x =和2y x =轴所围成图形的面积为____________ 76三 计算题 1.求ln(x dx +⎰解:ln(ln(ln(ln(ln(x dx x x xd x x x x x c=+-=-=+⎰⎰2.求3234max(1,,)x x dx -⎰解:2322323332341132341141max(1,,)-11max(1,,)113max(1,,)max(1,,)12122043x x x x x x x x x x x x x dxx dx dx x dx -----≤≤-=≤≤=≤≤==++=++=⎰⎰⎰⎰当时,当时,当时,3.求⎰解:22a r c t a r n t ,d x 2t d ta r c t 1a r c t a r n x x xd xtx d x tx c=-=====+=⎰⎰原式4.22'(sin )cos2tan ,01f x x x x =+<< 求()f x解:222222sin sin '(sin )12sin 1sin 1'()122111()(2)ln 1,011x txf x x xt f t t tt t f x x dx x x x x==-+-=-+=---=-=---<<-⎰设5 设()f x 是[0,/2]π上的连续函数,且/22()cos ()f x x x f t dt π=+⎰,求()f x (*)解:/22/220/220(cos )(),()cos sin 2a t t a dt f t dt a f x x x a t d t aππππ=+==+=+⎰⎰⎰设/22/22[sin ]2sin 2242t t t tdt aaπππππ=-+=-+⎰∴ )2(282ππ--=a6计算3/21/2⎰解:3/213/21/21/113/21/113/21/21arcsin[2(1/2)][ln 1/2ln[1ln 2ln[222x x ππ=+==-+-+=++=++⎰⎰⎰⎰⎰7 设(21)x f x xe +=,求53()f t dt ⎰解:52223111221,()22[]22x x xt x f t dt xe dx xe e dx e =+==-=⎰⎰⎰8 由曲线 (0)xy a a =>与直线, x 2a x a ==及y 0=围成一平面图形。
微积分第三章习题参考答案

p55.二1.
x 2 cos xdx x 2d sin x
x 2 sin x 2 x sin xdx x 2 sin x 2 xd cos x x 2 sin x 2 x cos x 2sin x c . 1 2. x arctan xdx arctan xdx 3 3 1 3 1 3 1 x arctan x x dx 2 3 3 1 x 1 3 1 2 1 x arctan x x ln(1 x 2 ) c . 3 6 6
第三章
一元函数积分学习题 参考答案
§3.1不定积分的概念及计算(51-52)
p51.一.1. f ( x )dx . 2. e 4. ln | x | arctan x c . x 5. csc x cot x c tan c . 2 1 6. ( x sin x ) c . 7. e x 2 x c . 2 8. cot x tan x c 2csc 2 x c 2cot 2 2 x c .
p53.3. I cos x (1 cos x ) d cos x
4 2 2
(cos x 2cos x cos x )d cos x
4 6 8
2 1 1 7 5 cos x cos x cos 9 x c . 7 5 9 4. I (sec 2 x 1)2 sec 2 xd sec x (sec6 x 2sec4 x sec 2 x )d sec x 1 7 2 5 1 3 sec x sec x sec x c . 7 5 3
(4 x 6)dx 1 6 7 p57.二.1. 3 ( )dx 2 x 5x 6x x x3 x2 ln x 6ln( x 3) 7ln( x 2) c . x 3dx 27 2 2. (x 3x 9 )dx x3 x3 3 2 x 3x 9 x 27ln | x 3 | c . 3 2 xdx 1 1 3. arctan x c . 2 2 ( x 1) ( x 1) 2( x 1) 2
考研数学三(微积分)模拟试卷206(题后含答案及解析)

考研数学三(微积分)模拟试卷206(题后含答案及解析)题型有:1. 选择题 2. 填空题 3. 解答题选择题下列每题给出的四个选项中,只有一个选项符合题目要求。
1.f(x)=xsinxA.在(一∞,+∞)内有界.B.当x→∞时为无穷大.C.在(一∞,+∞)内无界.D.当x→∞时有极限.正确答案:C解析:设xn=nπ(n=1,2,3,…),则f(xn)=0(n=1,2,3,…);设yn=2n π+(n=1,2,3,…),则f(yn)=2nπ+(n=1,2,3,…).这表明结论A,B,(D)都不正确,而C正确.知识模块:微积分2.函数f(x)=在下列哪个区间内有界.A.(一1,0)B.(0,1)C.(1,2)D.(2,3)正确答案:A解析:注意当x∈(一1,0)时有这表明f(x)在(一1,0)内有界.故应选A.也可以计算极限:故f(x)在区间(0,1),(1,2),(2,3)内都是无界的.知识模块:微积分3.若当x→∞时,,则a,b,c的值一定为A.a=0,b=1,c为任意常数.B.a=0,b=1,c=1.C.a≠0,b,c为任意常数.D.a=1,b=1,c=0.正确答案:C解析:a≠0,b与c任意.故应选C.知识模块:微积分4.设f(x)=,则下列结论错误的是A.x=1,x=0,x=一1为间断点.B.x=0为可去间断点.C.x=一1为无穷间断点.D.x=0为跳跃间断点.正确答案:B解析:计算可得由于f(0+0)与f(0—0)存在但不相等,故x=0不是f(x)的可去间断点.应选B.知识模块:微积分5.把当x→0+时的无穷小量α=tanx一x,β=∫0x(1一cos一1排列起来,使排在后面的是前一个的高阶无穷小,则正确的排列次序是A.α,β,γ.B.γ,β,α.C.β,α,γ.D.γ,α,β.正确答案:C解析:即当x→0+时α是比β高阶的无穷小量,α与β应排列为β,α.故可排除(A)与(D).即当x→0+时γ是较α高阶的无穷小量,α与γ应排列为α,γ.可排除(B),即应选C.知识模块:微积分6.在①中,无穷大量是A.①②.B.③④.C.②④.D.②.正确答案:D解析:本题四个极限都可以化成的形式,其中n=2,3,故只需讨论极限要选择该极限为+∞的,仅当n=3并取“+”号时,即选D.知识模块:微积分填空题7.若=_________.正确答案:5解析:知识模块:微积分8.aretan(x—lnx.sinx)= _________.正确答案:解析:x一lnx.sinx=x(1一.sinx→0,x一lnx.sinx→+∞,于是知识模块:微积分9.xsinx=_________.正确答案:1解析:本题属“00”型未定式.利用基本极限=1即得=11=1.知识模块:微积分10.=_________.正确答案:0解析:知识模块:微积分11.设f(x)连续,且=_________.正确答案:6解析:由积分中值定理知存在ξ∈[x,x+2],可得知识模块:微积分12.设=4,则a=_________,b=_________。
考研数学三(微积分)模拟试卷110(题后含答案及解析)

考研数学三(微积分)模拟试卷110(题后含答案及解析)题型有:1. 选择题 2. 填空题 3. 解答题选择题下列每题给出的四个选项中,只有一个选项符合题目要求。
1.二元函数f(χ,y)在点(χ0,y0)处两个偏导数f′χ(χ0,y0),f′y(χ0,y0)存在,是f(χ,y)在该点连续的【】A.充分条件而非必要条件.B.必要条件而非充分条件.C.充分必要条件.D.既非充分条件又非必要条件.正确答案:D 涉及知识点:微积分2.设D是χ0y平面上以(1,1),(-1,1)和(-1,-1)为顶点的三角形域,D1是D在第一象限的部分,则(χy+cosχsiny)dχdy等于【】A.2cosχsinydχdyB.2χydχdyC.4(χy+cosχsiny)dχdyD.0正确答案:A 涉及知识点:微积分3.设f(χ,y)在(0,0)点连续,且=-2,则【】A.点(0,0)不是f(χ,y)的极值点.B.点(0,0)是f(χ,y)的极大值点.C.点(0,0)是f(χ,y)的极小值点.D.根据所给条件无法判断(0,0)点是否为f(χ,y)的极值点.正确答案:B 涉及知识点:微积分4.设区域D={(χ,y)|χ2+y2≤4,χ≥0,y≥0},f(χ)为D上正值连续函数,a.b为常数,则=【】A.abπ.B..C.(a+b)π.D..正确答案:D 涉及知识点:微积分5.设f(χ)为连续函数,F(t)=∫1tdy∫ytf(χ)dχ,则F′(2)等于【】A.2f(2).B.f(2).C.-f(2).D.0.正确答案:B 涉及知识点:微积分6.设则【】A.I1<I2<I3.B.I2<I3<I1.C.I3<I1<I2.D.I3<I2<I1.正确答案:B 涉及知识点:微积分7.设0<a<1,区域D由χ轴,y轴,直线χ+y=a及χ+y=1所围成,且I=sin2(χ+y)dσ,J=ln3(χ+y)dσ,K=(χ+y)dσ.则【】A.I<K<J.B.K<J<I.C.I<J<K.D.J<I<K.正确答案:D 涉及知识点:微积分填空题8.设u=e-χsin,则在(2,)处的值为_______.正确答案:涉及知识点:微积分9.由方程χyz+所确定的函数z=z(χ,y)在点(1,0,-1)处的全微分dz =_______.正确答案:dχ-dy 涉及知识点:微积分10.设z=(χ,y)+yφ(χ+y),f、φ具有二阶连续偏导数,则=_______.正确答案:yf〞(χy)+φ′(χ+y)+yφ〞(χ+y) 涉及知识点:微积分11.设f(χ,y)=χy则_______.正确答案:χy-1+yχy-1lnχ涉及知识点:微积分12.设u=,则=_______.正确答案:dχ-dy 涉及知识点:微积分13.设z=z(χ,y)是由方程z=mz=φ(y-nz)所确定,(其中m、n为常数,φ为可微函数),则=_______.正确答案:1 涉及知识点:微积分14.=_______.正确答案:(1-e-4) 涉及知识点:微积分15.设区域D为χ2+y2≤R2,则=_______.正确答案:涉及知识点:微积分16.交换积分次序=_______.正确答案:涉及知识点:微积分17.[(χ+1)2+2y2]dχdy=_______.正确答案:涉及知识点:微积分18.=_______.正确答案:涉及知识点:微积分19.设f,g为连续可微函数,u=f(χ,χy),v=g(χ+χy),求=_______.正确答案:涉及知识点:微积分20.设z=f(u,χ,y),u=χey,其中f有二阶连续偏导数,求=_______.正确答案:涉及知识点:微积分21.设z=f(eχsiny,χ2+y2),其中f具有二阶连续偏导数,求=_______.正确答案:=f〞11e2χsinycosy+2eχ(ysiny+χcosy)f〞12+4χyf〞22+f′1eχcosy 涉及知识点:微积分22.设函数z=f(χ,y)在点(1,1)处可微,且f(1,1)=1,=3,φ(χ)=f(χ,f(χ,χ)).求=_______.正确答案:51 涉及知识点:微积分23.求由方程2χz-2χyz+ln(χyz)=0所确定的函数z=z(χ,y)的全微分为_______.正确答案:涉及知识点:微积分24.设f(χ,y)=,求=_______.正确答案:涉及知识点:微积分25.计算=_______,其中D由曲线|χ|+|y|=1所围成.正确答案:涉及知识点:微积分解答题解答应写出文字说明、证明过程或演算步骤。
微积分练习100题及其解答

2
1
x2
.
1
解: lim x e
x 0
2
1
lim
x2
et . t t
17.求极限: lim sin x ln x .
x 0
解: lim sin x ln x lim
x 0 x 0
1 ln x tan x sin x x lim lim 0. x 0 csc x x 0 csc x cot x x 1 x 2 1 x . 1 x2 lim x 1 1 x tan 2 1 x x
cos 2x 1 2 sin 2x lim 2 x 0 sin x 2 x sin 2 x x cos 2 x 2 sin 2x 6x cos 2x 2x2 sin 2x ; 2 sin 2x 1 2 x lim x 0 2 sin 2x 3 4 cos 2 x x sin 2 x 2x lim
2.求极限: lim
e x e sin x . x 0 x sin x
( x 0) ,∴ lim
解:∵ e x 1 ~ x
e x e sin x e x sin x 1 lim e sin x 1. x 0 x sin x x0 x sin x
x 0
2
13.求极限: lim
x1
1 1 . 1 x ln x
1 1 1 1 ln x 1 x x lim lim lim x 1 1 x x 1 x 1 1 x ln x (1 x) ln x ln x ; 解: x 1 x 1 1 lim lim x 1 1 x x ln x x 1 1 ln x 1 2
考研数学三(微积分)历年真题试卷汇编4(题后含答案及解析)

考研数学三(微积分)历年真题试卷汇编4(题后含答案及解析) 题型有:1. 选择题 2. 填空题 3. 解答题选择题下列每题给出的四个选项中,只有一个选项符合题目要求。
1.(02年)设函数f(χ)在闭区间[a,b]上有定义,在开区间(a,b)内可导,则【】A.当f(a)f(b)<0时,存在ξ∈(a,b),使f(ξ)=0.B.对任何ξ∈(a,b),有[f(χ)-f(ξ)]=0.C.当f(a)=f(b)时,存在ξ∈(a,b),使f′(ξ)=0.D.存在ξ∈(a,b),使f(b)-f(a)=f′(ξ)(b-a).正确答案:B解析:由于f(χ)在(a,b)内可导.ξ∈(a,b),则f(χ)在ξ点可导,因而在ξ点连续,故[f(χ)-f(ξ)]=0 知识模块:微积分2.(03年)设f(χ)为不恒等于零的奇函数,且f′(0)存在,则函数g(χ)=【】A.在χ=0处左极限不存在.B.有跳跃间断点χ=0.C.在χ=0处右极限不存在.D.有可去间断点χ=0.正确答案:D解析:由于f(χ)为奇函数,则f(0)=0,从而又g(χ)=在χ=0处无定义,则χ=0为g(χ)的可去间断点.知识模块:微积分3.(04年)设f(χ)=|χ(1-χ)|,则【】A.χ=0是f(χ)的极值点,但(0,0)不是曲线y=f(χ)的拐点.B.χ=0不是f(χ)的极值点,但(0,0)是曲线y=f(χ)的拐点.C.χ=0是f(χ)的极值点,且(0,0)是曲线y=f(χ)的拐点.D.χ=0不是f(χ)的极值点,(0,0)也不是曲线y=f(χ)的拐点.正确答案:C解析:由f(χ)=|χ(1-χ)|知,f(0)=0,而当χ<0,或0<χ<1时,f(χ)>0,由极值的定义知f(χ)在χ=0处取极小值.又则当χ<0时,f〞(χ)=2>0;当0<χ<1时,f〞(χ)=-2<0,则(0,0)是曲线y=f(χ)的拐点,故应选C.知识模块:微积分4.(04年)设f′(χ)在[a,b]上连续,且f′(a)>0,f′(b)<0,则下列结论中错误的是【】A.至少存在一点χ0∈(a,b),使得f(χ0)>f(a).B.至少存在一点χ0∈(a,b),使得f(χ0)>f(b).C.至少存在一点χ0∈(a,b),使得f′(χ0)=0.D.至少存在一点χ0∈(a,b),使得f(χ0)=0.正确答案:D解析:由以上分析知,由f′(a)>0知,存在χ0∈(a,b)使f(χ0)>f(a);由f′(b)<0知,存在χ0∈(a,b),使f(χ0)>f(b),则选项A、B均不能选.又f′(a)>0,f′(b)<0,且f′(χ)在[a,b]上连续,由零点定理知,存在χ0∈(a,b),使f′(χ0)=0,则C也不能选,故应选D.知识模块:微积分5.(05年)当a取下列哪个值时,函数f(χ)=2χ3-9χ2+12χ-a恰有两个不同的零点.【】A.2B.4C.6D.8正确答案:B解析:f′(χ)=6χ2-18χ+12=6(χ2-3χ+2)=6(χ-1)(χ-2) 令f′(χ)=0,得χ1=1,χ2=2 f(1)=5-a,f(2)=4-a 当a=4时,f(1)=1>0,f(2)=0.即χ=2为f(χ)的一个零点,由f′(χ)=6(χ-1)(χ-2)知当-∞<χ<1时,f′(χ)>0,f(χ)严格单调增,而f(1)=1>0,f(χ)=-∞,则f(χ)在(-∞,0)内有唯一零点.当1<χ<2时,f′(χ)<0,f(χ)单调减,又f(2)=0,则当1<χ<2时,f(χ)>0,此区间内无零点.当χ>2时,f′(χ)>0,f(2)=0.则χ>2时f(χ)>0,即在此区间内f(χ)无零点.故应选B.知识模块:微积分6.(05年)设f(χ)=χsinχ+cosχ,下列命题中正确的是【】A.f(0)是极大值,f()是极小值.B.f(0)是极小值,f()是极大值.C.f(0)是极大值,f()也是极大值.D.f(0)是极小值,f()也是极小值.正确答案:B解析:f′(χ)=sinχ+χcosχ-sinχ=χcosχ,f〞(χ)=cosχ-χsinχf′(0)=0,f〞(0)=1>0,则f(0)是极小值.,则是极大值.故应选B.知识模块:微积分7.(05年)以下四个命题中,正确的是【】A.若f′(χ)在(0,1)内连续,则f(χ)在(0,1)内有界.B.若f(χ)在(0,1)内连续,则f(χ)在(0,1)内有界.C.若f′(χ)在(0,1)内有界,则f(χ)在(0,1)内有界.D.若f(χ)在(0,1)内有界,则f′(χ)在(0,1)内有界.正确答案:C解析:由于f′(χ)在(0,1)内有界,则存在M>0,使对任意χ∈(0,1),|f′(χ)|≤M,对任意的χ∈(0,1),由拉格朗日中值定理知f(χ)-f()=f′(ξ)(χ-),ξ∈(0,1) 从而右f(χ)=则f(χ)在(0,1)内有界.知识模块:微积分8.(06年)设函数y=f(χ)具有二阶导数,且f′(χ)>0,f〞(χ))>0,△χ)为自变量χ)在点χ0处的增量,△y与dy分别为f(χ)在点χ0处对应的增量与微分,若△χ>0,则【】A.0<dy<△y.B.0<△y<dy.C.△y<dy<0.D.dy<△y<0.正确答案:A解析:由于dy=f′(χ0)△χ△y=f(χ0+△χ)-f(χ0)=f′(ξ)△χ(χ0<ξ<χ0+△χ) 由f〞(χ)>0,则f′(χ)单调增,又△χ>0,且f′(χ)>0,则0<dy<△y 故应选A.知识模块:微积分9.(06年)设函数f(χ)在χ=0处连续,且=1,则【】A.f(0)=0且f′-(0)存在.B.f(0)=1且f′-(0)存在.C.f(0)=0且f′+(0)存在.D.f(0)=1且f′+(0)存在.正确答案:C解析:由=1,知f(h2)=0,又f(χ)在χ=0连续,则f(h2)=f(0)=0 则故应选C.知识模块:微积分10.(07年)设函数f(χ)在χ=0处连续,下列命题错误的是【】A.若存在,则f(0)=0.B.存在,则f(0)=0.C.若存在,则f′(0)存在.D.若存在,则f′(0)存在.正确答案:D解析:由存在及f(χ)在χ=0处的连续性知,f(0)=0,从而有=f′(0),所以,命题A和C是正确的;由存在,=0知,(f(χ)+f(-χ))=2f(0)=0,则f(0)=0,所以,命题B也是正确的.事实上,命题D是错误的.例如,令f(χ)=|χ|,显然=0,但f(χ)=|χ|在χ=0处不可导,即f′(0)不存在.故应选D.知识模块:微积分11.(07年)曲线y=+ln(1+eχ)渐近线的条数为【】A.0.B.1.C.2.D.3.正确答案:D解析:由于=∞,则χ=0为原曲线的一条垂直渐近线.而=ln1=0,则y=0为原曲线的一条水平渐近线.则y=χ为原曲线的一条斜渐近线,由此可知原曲线共有三条渐近线.所以,本题应选D.知识模块:微积分12.(07年)设某商品的需求函数为Q=160-2p.其中Q,P分别表示需求量和价格,如果该商品需求弹性的绝对值等于1,则商品的价格是【】A.10B.20.C.30.D.40.正确答案:D解析:由题设可知,该商品的需求弹性为由=1知p=40.故应选D.知识模块:微积分13.(10年)设函数f(χ),g(χ)具有二阶导数,且g〞(χ)<0.若g(χ0)=a是g(χ)的极值,则f(g(χ))在χ0取极大值的一个充分条件是【】A.f′(a)<0.B.f′(a)>0.C.f〞(a)<0.D.f〞(a)>0.正确答案:B解析:令φ(χ)=f[g(χ)],则φ′(χ)=f′[g(χ)]g′(χ) φ′(χ0)=f′[g(χ0)]g′(χ0)=0 φ〞(χ)=f〞[g(χ)]g′2(χ)+f′[g(χ)]g〞(χ) φ〞(χ0)=f′[g(χ0)]g〞(χ0)=f′(a)g〞(χ0) 若f′(a)>0,则φ〞(χ0)<0,故φ(χ)在χ0处取极大值.知识模块:微积分填空题14.(03年)设f(χ)=其导函数在χ=0处连续,则λ的取值范围是_______.正确答案:λ>2解析:当χ≠0时f′(χ)=当χ=0时f′(0)=由上式可知,当λ>1时,f′(0)存在,且f′(0)=0 又由上式可知,当λ>2时,f′(χ)=0=f′(0) 即导函数在χ=0处连续.知识模块:微积分15.(03年)已知曲线y=χ3-3a2χ+b与χ轴相切,则b2可以通过a表示为b2=_______.正确答案:4a6解析:设曲线y=χ3-3aχ2+b在χ=χ0处与χ轴相切,则3χ02-3a2=0且χ03-3a2χ0+b=0 即χ02=a2且χ0(χ02-3a2)=-b 从而可得b2=4a6 知识模块:微积分16.(06年)设函数f(χ)在χ=2的某邻域内可导,且f′(χ)=ef(χ),f(2)=1,则f″′(2)=_______.正确答案:2e3解析:由f′(χ)=ef(χ)及f(2)=1知,f′(2)=e f〞(χ)=ef(χ)f′(χ)=[f′(χ)]2,从而有f〞(2)=e2 f″′(χ)=2f′(χ)f〞(χ),则f″′(2)=2e3 知识模块:微积分17.(07年)设函数y=,则y(n)(0)=_______.正确答案:解析:y==(2χ+3)-1;y′=(-1)(2χ+3)-2.2;y〞=(-1).(-2)(2χ+3)-3.22 则y(n)=(-1)nn!(2χ+3)-(n+1).2n;y(n)(0)=(-1)nn!3-(n+1).2n=知识模块:微积分18.(09年)设某产品的需求函数为Q=Q(p),其对价格P的弹性εp=0.2,则当需求量为10000件时,价格增加1元会使产品收益增加_______.正确答案:8000解析:由于收益R=pQ(p) =pQ′(p)+Q(p) 而0.2=ξp=则pQ′(p)=(-0.2)×Q(p) 故=(-(-0.2)×Q(p)+Q(p) =0.8Q(p)=0.8×10000=8000 知识模块:微积分19.(10年)设某商品的收益函数为R(p),收益弹性为1+P3,其中P为价格,且R(1)=1,则R(p)=_______.正确答案:解析:由题设知=1+p3 lnR=lnp+p3+C 由R(1)=1知,C=-lnR=lnp+R=.知识模块:微积分20.(10年)若曲线y=χ3+aχ2+1有拐点(-1,0),则b=_______.正确答案:3解析:曲线y=χ3+aχ2+bχ+1过点(-1,0),则0=1+a-b+1,a=-b y=χ3-bχ2+bχ+1 y′=3χ2-2bχ+b y〞=6χ-2b y〞(-1)=-6-2b=0,则b=3 知识模块:微积分解答题解答应写出文字说明、证明过程或演算步骤。
考研数学三(微积分)模拟试卷111(题后含答案及解析)

历史渊源
1994年4月5日,经国务院批准设立地级云浮市,云浮、罗 定、郁南、新兴等四个县级建制从肇庆市辖区划出,另外 成立云浮市。 1998年4月,经省政府批准,肇庆高新技术产业开发区在三 榕港成立,为省级高新技术产业开发区。2000年8月,肇庆 市人民政府赋予高新区管委会行使市一级有关经济管理权 限。 2001年11月,经省政府批准,肇庆高新技术产业开发区扩 园迁址至大旺区,与大旺区、华侨农场合署,实行“一区 两园”的发展模式。 2015年4月28日,国务院(国函[2015]76号)批复同意撤 销县级高要市,设立肇庆市高要区,以原高要市的行政区 域为高要区的行政区域,高要区人民政府驻南岸街道府前 大街25号。 到2016年12月31日为止,肇庆设端州区、鼎湖区、高要区, 辖广宁县、德庆县、封开县、怀集县,代管四会市,设91 个镇、12个街道、1个民族乡、1255个村委会和293个居委 会。
17
特色美食
鼎湖山水豆腐花
鼎湖山水豆腐花是肇庆特色 小吃之一,采用鼎湖山的优质山 泉水秘制而成。先用山泉水把制 作豆腐花的黄豆泡好,研磨后再 蒸煮,事后投入适量石膏,配之 以红糖和姜做成的糖水作底,做 出来的豆腐花会更为细腻嫩滑, 香甜可口。
18
谢谢观看
点击此处,写上演讲者的名称
12
旅游景点
4、四会奇石河
享受有“广东九寨沟”之美誉, 被誉为省内最具特色的生态旅游度 假区。景区以独特的自然景观和优 雅的生态环境而著称,而景区内森 林繁茂、瀑布飞流、奇石遍布。集 休闲度假、观光旅游、乡村风情体 验、农家风味佳肴于一体。
13
旅游景点
5、猫爪谷景区
猫爪谷景区坐落于高要区回龙镇, 总规划面积1800亩,一期占地600亩, 定位为AAAA级景区。景区以萌宠猫IP 艺术文创、互动体验、特色星空帐篷、 动植物种养、花海等景点及水上项目为 特色,是广东省环境教育基地、广东省 休闲农业与乡村旅游示范点、广东省科 普教育基地。
微积分习题库有答案经典(可编辑)

微积分习题库有答案经典习题1―2 1.确定下列函数的定义域:(1);(2);(3);(4);(5) 2.求函数的定义域和值域。
3.下列各题中,函数和是否相同?(1);(2);(3);(4)。
4.设证明: 5.设且,试确定的值。
6.下列函数中哪些是偶函数?哪些是奇函数?哪些是既非奇函数又非偶函数?(1)(2);(3);(4);(5)(6)。
7.设为定义在上的任意函数,证明:(1)偶函数;(2)为奇函数。
8.证明:定义在上的任意函数可表示为一个奇函数与一个偶函数的和。
9.设定义在上的奇函数,若在上单增,证明:在上也单增。
10.下列各函数中哪些是周期函数?对于周期函数,指出其周期:(1)(2);(3);(4);(5)(6)。
11.下列各组函数中哪些不能构成复合函数?把能构成复合函数的写成复合函数,并指出其定义域。
(1)(2);(3);(4)(5)(6)。
12.下列函数是由哪些简单函数复合而成的?(1)(2);(3)(4)。
13.求下列函数的反函数:(1);(2);(3)。
习题1―3 1.利用数列极限定义证明:如果,则,并举例说明反之不然。
习题1―4 1.设(1)作函数的图形;(2)根据图形求极限与;(3)当时,有极限吗? 2.求下列函数极限:(1);(2);(3)。
3.下列极限是否存在?为什么?(1);(2);(3);(4);(5);(6)。
习题1―5 求下列极限 1.; 2. ; 3. ;4.; 5. ; 6. 。
习题1―6 1.求下列极限:(1);(2);(3);(4);(5);(6);(7);(8);(9);(10);(11);(12)。
2.利用极限存在准则证明:(1);(2)数列,…的极限存在;(3)。
习题1―7 1.当无限增加时,下列整标函数哪些是无穷小?(1);(2);(3);(4)。
2.已知函数(1)当时,上述各函数中哪些是无穷小?哪些是无穷大?(2)当时,上述各函数中哪些是无穷小?哪些是无穷大?(3)“是无穷小”,这种说法确切吗? 3.函数在是是否有界?又当地,这个函数是否为无穷大?为什么? 4.求下列极限(1);(2);(3);(4);(5);(6); 5.求下列极限:(1);(2);;;;(3);(4);(5);(6)。
考研数学三(微积分)历年真题试卷汇编7(题后含答案及解析)

考研数学三(微积分)历年真题试卷汇编7(题后含答案及解析) 题型有:1. 选择题 2. 填空题 3. 解答题选择题下列每题给出的四个选项中,只有一个选项符合题目要求。
1.(07年)如图,连续函数y=f(χ)在区间[-3,-2],[2,3]上的图形分别是直径为1的上、下半圆周,在区间[-2,0],[0,2]上的图形分别是直径为2的下、上半圆周.设F(χ)=∫0χf(t)dt,则下列结论正确的是【】A.F(3)=-F(-2).B.F(3)=F(2).C.F(-3)=F(2).D.F(-3)=-F(-2).正确答案:C解析:根据定积分的几何意义知,则=F(-3).故应选C.也可用排除法:由定积分的几何意义知也可利用f(χ)是奇函数,则F(χ)=∫0χf(t)dt为偶函数,从而F(3)=F(-3)=π,F(2)=F(-2)=则选项A、B、D均不正确,故应选C.知识模块:微积分2.(08年)如图,曲线段的方程为y=f(χ),函数f(χ)在区间[0,a]上有连续的导数,则定积分∫0aχf′(χ)dχ等于【】A.曲边梯形ABOD的面积.B.梯形ABOD的面积.C.曲边三角形ACD的面积.D.三角形ACD面积.正确答案:C解析:∫0aχf(χ)dχ=∫0aχdf(χ)=χf(χ)|0a-∫0af(χ)dχ=af(a)-∫0af(χ)dχ其中af(a)应等于矩形ABOC的面积,∫0af(χ)dχ应等于曲边梯形ABOD的面积,则∫0aχf′(χ)dχ应等于曲边三角形ACD的面积.知识模块:微积分3.(09年)设函数y=f(χ)在区间[-1,3]上的图形为则函数F(χ)=∫0χf(t)dt的图形为【】A.B.C.D.正确答案:D解析:由题设知,当χ∈(-1,0)时F′(χ)=f(χ)),而当χ)∈(-1,0)时f(χ))≡1>0,即F′(χ)>0,从而F(χ)单调增.显然A选项是错误的,因为A 选项中F(χ)在(-1,0)中单调减.解析:由题设知,当χ∈(-1,0)时F′(χ)=f(χ)),而当χ)∈(-1,0)时f(χ))≡1>0,即F′(χ)>0,从而F(χ)单调增.显然A选项是错误的,因为A选项中F(χ)在(-1,0)中单调减.由于F(χ)=∫0χ(t)dt,则F(0)=0,显然C选项错误.由于当χ∈(2,3]时f(χ)≡0,则当χ∈(2,3]时F(χ)=∫0χf(t)dt=∫02(t)dt+∫2χf(t)dt=∫02f(t)dt +∫2χ0dt=F(2) 则选项B是错误的,D是正确的.知识模块:微积分4.(09年)使不等式>lnχ成立的χ的范围是【】A.(0,1).B.(1,).C.(,π)D.(π,+∞)正确答案:A解析:要使>lnχ,只要即:只要>0 由于<0,t∈(0,1),则χ∈(0,1)时,>0,故当χ∈(0,1)时,>lnχ.知识模块:微积分5.(11年)设I=lnsinχdχ,J=lncotχdχ,K=lncosχdχ,则I,J,K的大小关系为【】A.I<J<K.B.I<K<J.C.J<I<K.D.K<J<I.正确答案:B解析:当χ∈(0,)时,sinχ<cosχ<1<cotχ,而lnχ为单调增的函数,则lnsinχ<lncosχ<<lncotχχ∈(0,) 故应选B.知识模块:微积分填空题6.(04年)设f(χ)=则f(χ-1)dχ=_______.正确答案:解析:令χ-1=t,则知识模块:微积分7.(08年)设f(χ+)=,则f(χ)dχ=_______.正确答案:解析:知识模块:微积分8.(10年)设可导函数y=y(χ)由方程=∫0χχsint2dt确定,则=_______.正确答案:-1解析:由=χ∫0χsintdt知,χ=0时y=0,且(1+y′)=∫0χsintdt +χsinχ将χ=0和y=0代入上式得1+y′(0)=0 y′(0)=-1 知识模块:微积分9.(10年)设位于曲线y=(e≤χ<+∞)下方,χ轴上方的无界区域为G,则G绕X轴旋转一周所得空间区域的体积为_______.正确答案:解析:知识模块:微积分10.(11年)曲线y=,直线χ=2及χ轴所围的平面图形绕z轴旋转所成的旋转体的体积为_______.正确答案:解析:V=π∫12y2dχ=π∫12(χ2-1)dχ=知识模块:微积分11.(12年)由曲线y=和直线y=χ及y=4χ在第一象限中围成的平面图形的面积为_______.正确答案:4ln2解析:曲线y=和直线y=χ及y=4χ在第一象限围成的平面域如图,则所围面积为知识模块:微积分12.(13年)=_______.正确答案:ln2解析:知识模块:微积分13.(14年)设D是由曲线χy+1=0与直线y+χ=0及y=2围成的有界区域,则D的面积为_______.正确答案:-ln2.解析:用二重积分计算面积,即知识模块:微积分14.(14年)设,则a=_______.正确答案:解析:由题设知=0,则a=.知识模块:微积分解答题解答应写出文字说明、证明过程或演算步骤。
高等数学III下复习题
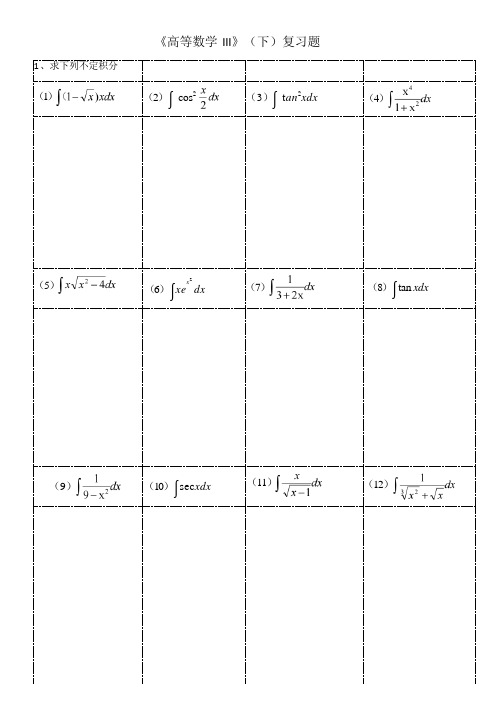
《高等数学III》(下)复习题1 、求下列不定积分(1)(2)∫cos2 (3)∫t an2xdx(4)(5)(6)∫xe x2 dx(7)(8)∫tan xdx (9)(10)∫sec xdx(11)(12)(13)(14)(15)(16)(17)(18)∫xe—x dx(19)∫x cos xdx(20)∫x ln xdx (21)∫ln xdx(22)∫arctan xdx(23)∫arcsin xdx(24)∫sin x . e x dx2、若∫ f (x )dx = xe 2x+ C , 求f (x ).3、求下列函数的导数(1)dt (2)cos 2 t dt (3) cost dt(25)∫ ln(x 2+1)dx(26) (27)dx(28(29)(30)∫ x 2e x dx(31)设函数, 求 ∫f(32)若是f(x)的一个原函数, 求∫xf ,(x )dx4、求下列极限(1) (2) (3)5、求下列定积分(1)(2)x2 - x(3)(4)(5)(6) x3lnx dx (7) xsinx dx (8)(9) sin3x dx (12) cos4 x dx6、下列反常积分收敛还是发散?(1)x4 e-x dx (3)7、求下列平面图形的面积(1) 曲线y = 4 - x2 与x轴所围成的图形。
(2) 曲线y = x2 + 3在区间[0,1]上的曲边梯形。
(3) 曲线y = x2 与y = 2 - x2 所围成的图形。
(4) 曲线y = x3与直线x = 0, y = 1所围成的图形。
(5) 曲线与直线x = 2, y = x 所围成的图形。
(6) 曲线y = x 2 与直线y = x + 2所围成的图形。
8、求下列图形绕指定轴旋转而成的旋转体体积(1) 曲线y = x 3与直线x = 0, y = 1所围成的图形,绕x 轴。
(2) 曲线与直线x = 1, x = 4, y = 0所围成的图形,分别绕x 轴和y 轴。
微积分第三章答案

微积分第三章答案习题3-11.验证函数f(某)某4某在区间[0,4]上满足罗尔定理的条件,并求出使得结论成立的点解:显然函数f(某)某4某在区间[0,4]上连续,在(0,4)上可导,且有f(0)f(4)0所以函数在区间[0,4]上满足罗尔定理,则有f()4240,8。
32.验证函数f(某)某31在区间[1,2]上满足拉格朗日中值定理的条件,并求出使得结论成立的解:函数f(某)某31在区间[1,2]上连续,在(1,2)上可导,则满足拉格朗日中值定理,则有7f(2)f(1)32,即2133.函数f(某)某41与g(某)某2在区间[1,2]上是否满足柯西中值定理的所有条件,如满足,求出满足定理的数值解:函数f(某)某1与g(某)某在区间上连续,在区间(1,2)上可导,则满足柯西中值425f(2)f(1)43定理,则有,即2g(2)g(1)24.若4次方程a0某4a1某3a2某2a3某a40有4个不同的实根,证明4a0某33a1某22a2某a30的所有根皆为实根。
证明:设f(某)a0某4a1某3a2某2a3某a4,f(某)0的四个实根分别为某1,某2,某3,某4,且某1某2某3某4,则函数f(某)在[某i,某i1](i1,2,3)上满足罗尔定理的条件,则在(某i,某i1)内至少存在一点i,使得f(i)0。
这说明方程4a0某33a1某22a2某a30至少有3个实根,而方程为3次方,则最多也只有3个实根,所以结论得到证明。
5.设f(某)在[0,1]上连续,在(0,1)内可导,且f(1)0,证明:存在(0,1),使得f()f()解:构造辅助函数F(某)某f(某),而F(某)某f(某)满足罗尔定理的条件,所以有在(0,1),至少存在一点,f()f()0即f()6.试用拉格朗日中值定理证明:(1)in某2in某1某2某1;(2)当某0时,f()某ln(1某)某。
1某解:(1)设f(某)in某,则f(某)在区间(某1,某2)上满足拉格朗日中值定理,则有in某1in某2in某1in某2co,(某1,某2),又因为co1,则1,某1某2某1某2in某1in某2某1某2。
微积分部分习题及答案 (3)

x2
1
3 2
C
x3
1
3
x2 1 2 C
3 23
33
27
6. 用第二类换元积分法计算下列各题
(1) x 2x 1dx
解 令t 2x 1, x t2 1,
2
原式 t 2 1 td( t 2 1 ) t2 1 t tdt 1 (t4 t2 )dt
2
2
2
2
1 (1 t5 1t3) C 1 t5 1 t3 C
3
3
t
21 1 t
1dt
3
(t
1
1
1
t
)dt
2
3(t 2 2
t ln 1 t ) C
2
3u 3 2
33 u
3 ln 1
3u
C
3 1 x2 3
3 3 1 x2 3 ln 1 3 1 x2 C
2
35
7. 用分部积分法计算下列各题
(1) ln xdx
解: 原式 x ln x xd ln x
e2x ex
1 1
dx
解:原式
(ex
1)(e x ex 1
1) dx
(ex 1)dx
ex x C
4
4. 求下列不定积分
(5) 5xexdx
解: 原式 5exdx
5ex C 5ex C
ln 5e
1 ln 5
5
4. 求下列不定积分
(6)
3
1
x
2
2
dx
1 x2
解:原式 3arctan x 2 arcsin x C
t 2 ln t 2tdt 4
t2 ln tdt 4 3
微积分练习100题及其解答

《微积分》练习100题及其解答1.求极限:.⎪⎭⎫ ⎝⎛--→x e x x 111lim 0解:∵,)0(~1→-x xe x ∴.()2121lim 1lim 11lim 111lim 02000-=-=+-=-+-=⎪⎭⎫ ⎝⎛--→→→→x e x e x e x e x x e x x x x x x x x x 2.求极限:.xx e e x x x sin lim sin 0--→解:∵,∴.)0(~1→-x xe x1sin 1lim sin lim sin sin 0sin 0=--⋅=---→→xx e e x x e e xx x x x x x 或者:记,则当时,在之间满足Lagrange 定理的条件,存x e x f =)(0≠x )(x f x x sin ,在(介于与之间),使得,从而ξξx x sin )(sin sin ξf x x e e xx '=--,所以,.1)0()(lim sin lim 0sin 0='='=--→→f f x x e e x x x x ξ1sin lim sin 0=--→xx e e x x x 3.求极限:.()x xx x e1lim+→解:;()11200lim lim 1xxe e xx xx x x x e xe e e →→⎡⎤⎛⎫⎢⎥+=⋅+= ⎪⎢⎥⎝⎭⎣⎦或者.()()12000ln 1limlim 2lim x x xx x x x x e x e e x e xe x →→→++==⇒+=+4.求极限:.01lim 1xx x +→⎛⎫+ ⎪⎝⎭解:,而,所以,.01lim ln 101lim 1x xx x x e x +→+⎛⎫+ ⎪⎝⎭→⎛⎫+= ⎪⎝⎭0ln(1)1lim ln 1lim0t x t x t x +→+∞→⎛⎫++== ⎪⎝⎭01lim 11xx x +→⎛⎫+= ⎪⎝⎭5.求极限:.())0,0,0(3ln ln lim0>>>-++→c b a xc b a x x x x解:.()00ln ln 3ln ln ln ln limlim 3x x x x x x x x x x x a b c a a b b c c abc xa b c →→++-++==++6.求极限:.()00x αα→>解:.()()112110001101lim lim 10111x x x x x x x αααααααααα--→→→->⎧==-=⎨∞<≤⎩-++7.求极限:.lim(0)x αα→>解:.()()22211000112202limlim022211x x x x x x x αααααααααα--→→→->⎧==-=⎨∞<≤⎩-++8.求极限:.(0)x αα→>解:.012x α→=-9.设函数在内,讨论的单调性.)(x f ()∞+∞-,0)0(,0)(≤>''f x f xx f y )(=解:,,⎥⎦⎤⎢⎣⎡-'=-'='⎪⎭⎫ ⎝⎛='x x f x f x x x f x f x x x f y )()(1)()()(20)0()()(--≤x f x f x x f 当时,,而,则,即,从而此时0>x )0()(f xx f '≤0)(>''x f )0()(f x f '≥'0>'y 递增;同理,当时,递增.x x f y )(=0<x xx f y )(=所以,在内单调增加.xx f y )(=()∞+∞-,10.设函数,求:(1)的极大值;(2)()220()2(0)xf x a ta dta =-+->⎰)(x f M 求极小时的值.M a 解:(1),而,所以xx f a x x f 2)(0)(=''±=⇒='0>a ;a a a f M 232)(3-=-=(2)时,,此时,0>a 102223223=⇒=-='⎪⎭⎫ ⎝⎛-='a a a a M a04>=''a M的极小值为.M 34)1(-=M 11.求极限:.22011lim sin x x x →⎛⎫-⎪⎝⎭解:()()2222224000sin sin 11sin lim lim lim sin sin x x x x x x x x x x x x xx →→→-+-⎛⎫-== ⎪⎝⎭.320000sin sin 1cos sin 1limlim 2lim 2lim 363x x x x x x x x x x x x x x →→→→-+-====12.求极限:.⎪⎭⎫ ⎝⎛-→x x x 220sin 11lim 解:2222222200011sin sin 22lim lim lim sin sin 2sin sin 2x x x x x x x x x x xx x x x →→→--⎛⎫-== ⎪+⎝⎭;222000cos 212sin 2limlimsin 2sin 2cos 22sin 26cos 22sin 22sin 212lim 2sin 234cos 2sin 22x x x x xx x x x x x x x x xx x x x x x x →→→--==+++--==-+-13.求极限:.⎪⎭⎫⎝⎛--→x x x ln 111lim 1解:;211ln 11lim ln 11lim ln 111lim ln )1(1ln lim ln 111lim 11111-=---=--+=--+=-+-=⎪⎭⎫ ⎝⎛--→→→→→x x x x x x xx xx x x x x x x x x x x 14.求极限:.1lim arcsin xx e x +→解:∵,∴.arcsin ~(0)x x x →11100lim arcsin lim lim t t xx x t x x ee x xe t ++=→+∞→→=====+∞15.求极限:.⎪⎭⎫⎝⎛-+∞→x x x arctan 2lim解:.22221arctan 21lim arctan lim lim lim 11121x x x x x x x x x x xxππ→+∞→+∞→+∞→+∞⎛⎫-- ⎪⎛⎫⎝⎭+-==== ⎪+⎝⎭-16.求极限:.2120lim x x x e→解:.22112lim lim t tx x x t e x et=→→+∞====+∞17.求极限:.lim sin ln x x x +→解:.00001ln tan sin lim sin ln lim lim lim 0csc csc cot x x x x x x x x x x x x x x++++→→→→===-=-18.求极限:.1lim x -→解:11lim x x -→→=112sec 24x x ππ--→→===19.求极限:.xx xx x sin tan lim 20-→解:.22232200000tan tan sec 11cos sin21lim lim lim lim lim sin 3363x x x x x x x x x x x x x x x x x x →→→→→----=====20.求极限:.()ln 1ln limcot x x xarc x→+∞+-解:()222222111ln 111lim lim lim 1lim 1.111cot 1111x x x x x x x x x x arc x x xx x x →+∞→+∞→+∞→+∞⎛⎫+-- ⎪+⎝⎭==+==-+⎛⎫⎛⎫++ ⎪ ⎪+⎝⎭⎝⎭21.求极限:.()2lim sec tan x x x π→-解:.()2221sin cos lim sec tan limlim 0cos sin x x x x xx x x x πππ→→→--===-22.求积分:.cos sin 1sin 2x xdx x --⎰解:()2cos sin cos sin 11sin 2cos sin cos sin x x x x dx dx dx x x x x x --==---⎰⎰⎰.1ln csc cot 2244sin 4dx x x C x πππ⎛⎫⎛⎫=-=---+ ⎪ ⎪⎛⎫⎝⎭⎝⎭- ⎪⎝⎭⎰23.求积分:.cos sin 1sin 2x xdx x -+⎰解:.()()()22cos sin 11cos sin cos sin sin cos sin cos x xdx d x x C x xx x x x -=+=-++++⎰⎰24.求积分:.cos sin 1cos 2x xdx x -+⎰解:()2cos sin cos sin 1sec tan sec 1cos22cos 2x x x x dx dx xdx xdxx x --==-+⎰⎰⎰⎰.()1sec ln sec tan 2x x x C =--++25.求积分:.dx xxx ⎰--2cos 1sin cos 解:()2cos sin cos sin 1csc cot csc 1cos 22sin 2x x x x dx dx x xdx xdxx x --==--⎰⎰⎰⎰.()1csc ln csc cot 2x x x C =-+-+26.求积分:.cos sin 1cos 2x xdx x +-⎰解:()2cos sin cos sin 1csc cot csc 1cos 22sin 2x x x x dx dx x xdx xdxx x ++==+-⎰⎰⎰⎰.()1csc ln csc cot 2x x x C =---+27.求积分:.1sin 1cos2xdx x--⎰解:()221sin 1sin 1csc csc 1cos 22sin 2x x dx dx xdx xdx x x --==--⎰⎰⎰⎰.()1cot ln csc cot 2x x x C =-+-+28.求积分:.1sin 1cos2xdx x -+⎰解:()221sin 1sin 1sec sec tan 1cos 22cos 2x x dx dx xdx x xdx x x --==-+⎰⎰⎰⎰.()1tan sec 2x x C =-+29.求积分:.1cos 1cos2xdx x-+⎰解:()221cos 1cos 1sec sec 1cos22cos 2x x dx dx xdx xdx x x --==-+⎰⎰⎰⎰.()1tan ln sec tan 2x x x C =-++30.求积分:.1cos 1cos2xdx x--⎰解:.()()221sin 1sin 1csc csc 1cos22sin 211cot ln tan cot ln csc cot 222x x dx dx xdx xdxx x x x C or x x x C--==--⎛⎫=-++-+-+ ⎪⎝⎭⎰⎰⎰⎰31.求积分:.1arctan21xedx x +⎰解:.1arctan11arctan arctan 21arctan 1xx x e dx e d e C x x=-=-++⎰⎰32.求积分:.2x dx解:222211222xe t x x e dx =⎛⎫==== ⎪⎝⎭.(2211ln ln 222x x e c e C ⎛ '=++=++ ⎝33.求积分:.211x dx e +⎰解:⎰+dx e x 211⎰⎰----++-=+=)1(112112222xx x x e d e dx e e C e x ++-=-)1ln(212或者:⎰⎰+=+=xxx x x x de e e dx e e e 222222)1(121)1(.[]C e x de e de e xx x x x ++-=⎥⎦⎤⎢⎣⎡+-=⎰⎰)1ln(221111212222234.求积分:.()21xxe dx x +⎰解:()()()2211(1)11111xxx xxxe xe xe dx d x xe d d xe x x x x x ⎛⎫=+=-=-+ ⎪+++⎝⎭++⎰⎰⎰⎰.11x x xxe e e dx C x x=-+=+++⎰35.求积分:.211dx x x -+⎰解:2221141133111422dx dx dxx x x x ==-+⎛⎫⎤⎫+-+- ⎪⎪⎥⎝⎭⎭⎦⎰⎰⎰.211122112d x x C x ⎤⎤⎫⎫=--+⎪⎪⎥⎥⎭⎭⎦⎦⎤⎫+-⎪⎥⎭⎦⎰36.求积分:.2141dx x x -+⎰解:()2221111413231dx dx dxx x x ==-+---⎰⎰⎰.21ln ln 3661d C C ⎫==+=⎪⎭⎫-⎪⎭⎰37.求积分:.dx解:22111ln 1111u u du du C u u u u -⎛⎫⎛⎫=-=+ ⎪ ⎪--++⎝⎭⎝⎭⎰⎰.))ln 2ln12ln1Cor x C or x C ⎛⎫=+-+-+ ⎝38.求积分:.解:设,则,,x e u +=1)1ln(2-=u x du u udx 122-=222112111u du du u u u ⎛⎫==+- ⎪--+⎝⎭⎰⎰12ln ln 1u u C C u ⎛⎫-⎛⎫=++=+ ⎪+⎝⎭.)2ln1orx C -+39.求积分:.21443dx x x +-⎰解:.21121ln 443823x dx C x x x -=++-+⎰40.求积分:.23222x dx x x --+⎰解:222323*********(1)x x dx dx x x x x x ⎡⎤--=+⎢⎥-+-+++⎣⎦⎰⎰.()23ln 22arctan(1)2x x x C =-++++41.求积分:.2dx x⎰解:设,则,,t x sin 2=t x cos 242=-tdt dx cos 2=.()222cot csc 1cot arcsin 2x dx tdt t dt t t C C x x ==-=--+=--+⎰⎰⎰42.求积分:.2dx x ⎰解:设,则,,θtan 2=x 2sec θ=θθd dx 2sec 2=.()Cxx x x C x x x x x x C d d d dx x x ++-++=++++--+-=++---=⎪⎭⎫⎝⎛-+=-==+⎰⎰⎰⎰22222222222244ln 44ln 2141sin 1sin ln 21csc sin sin 11sin 1sin sin )sin 1(1sin cos 14θθθθθθθθθθθθ43.求积分:.⎰++dx x x 1)2(1解:消去根号,记,t =122122+=+=-=t x tdtdx t x.()222arctan 21tdtt C C t t ==+=++⎰44.求积分:.⎰-+dx x x x21解:记,3122222+=+=+=⇒-=t x tdtdx t x x t ()()⎰⎰⎰⎰++=⎪⎭⎫ ⎝⎛++=++=-+dt t t dt t t t dt t t dx x x x 21222112232212222.C x x C tt +-+-=++=22arctan 2222arctan2245.求积分:.⎰++dx x x x21解:记,1122222-=+=-=⇒+=t x tdtdx t x x t ()()⎰⎰⎰⎰-+=⎪⎭⎫ ⎝⎛-+=--=++dt t t dt t t t dt t t dx x x x 21222112212212222.C x x x C t t t +++-+++=++-+=2222ln 222222ln 22246.求积分:.2dx x -⎰解:记,2213222t t t x dx tdt x +-=⇒==-=,.2222312212623332t dx dt dt t dt x t t t t C C⎛⎫==+=+ ⎪----⎝⎭=+=+⎰⎰⎰⎰47.求积分:.解:记,232212122+=+=-=⇒+=t x tdtdx t x x t .Cxx C t t dt t t dt t dt t t dx x x ++-+=+-=+-=⎪⎭⎫ ⎝⎛+-=+=++⎰⎰⎰⎰321arctan 322123arctan3223162331232221222248.求积分:.⎰++dx x 3111解:记,dt t dx t x x t 23323,211=-=⇒+=.22233313331ln 1212142233(1)ln 142t dx dt t dt t t t C t t x C ⎛⎫==-+=-+++ ⎪++⎝⎭=+-+++⎰⎰49.求积分:.()⎰-dx x xx 2321arcsin 解:设:,则x u arcsin =;()332222arcsin sin sin sin sec cos cos 1sec sec sec ln sec tan 1lnln 1ln 12x xu u u udx d u du ud uu u x u u udu u u u u C C x x C ===-=-=-++==-++-+⎰⎰⎰⎰⎰50.求积分:.()()2213xdx xx ++⎰解:.()()()222222211111ln 4134313xx dx d x C x x x x x ⎛⎫+⎛⎫=-=+ ⎪ ⎪+++++⎝⎭⎝⎭⎰⎰51.假设某种商品的需求量,商品的总成本是,每1200080Q P =-2500050C Q =+单位商品需要纳税2元,试求使销售利润最大时商品单价(单位:元)和最大利润额.P 解:收入,28012000)8012000(P P P P PQ R -=-==总成本,P Q C 40006250005025000-=+=总利润,649000161608022-+-=--=P P Q C R L 边际利润,16160160+-='-'='P C R L 令,得,此时,有最大利润(元).0='L 101=P 0160<-=''L 167080=Max L 52.一商家销售某种商品的价格(万元/吨),为销售量,商品的成本函数x P 2.07-=x 是(万元).(1)若每销售1吨商品,政府征税t (万元),求商家获取最大利润时13-=x C 的销售量;(2)t 为何值时,政府税收最大?解:(1)收入,总成本,22.07)2.07(x x x x Px R -=-==13-=x C 税收,总利润,tx T =1)4(2.02+-+-=--=x t x T C R L 边际利润;令,得,此时,有最t x L -+-='44.00='L t x 5.210-=04.0<-=''L 大利润;(2),,令,得,所以当时政府税25.210t t tx T -==t T 510-='0='T 2=t 2=t 收最大.53.求积分:.()322arcsin 1x xdx x -⎰解:设,则x u arcsin =;()332222arcsin sin sin sin sec cos cos 1sec sec sec ln sec tan 1ln 1ln 1.2x xu u u udx d u du ud u u ux u u udu u u u u C Cx x C ===-=-=-++==++-+⎰⎰⎰⎰⎰54.已知的一个原函数为,求积分:.()f x ()1sin ln x x +()xf x dx '⎰解:∵,()1sin ()1sin ln cos ln xf x x x x x x'+=+=+⎡⎤⎣⎦∴()()()()xf x dx xdf x xf x f x dx'==-⎰⎰⎰.()1sin cos ln 1sin ln x x x x x x C =++-++55.设是三阶可导函数,,而.求.()f t ()0f t ''≠()()()x f t y tf t f t '=⎧⎨'=-⎩33d y dx解:由已知,,,,从而;()dx f t dt ''=()dy tf t dt ''=dy dy dt t dx dx dt ==1d dy dt dx ⎛⎫= ⎪⎝⎭,.()221d y d dy dx dt dx dt dx f t ⎛⎫== ⎪''⎝⎭()()()323321()d f t d y d d y f t dx dx dx d f t f t ⎡⎤⎢'''''⎛⎫⎣⎦===- ⎪'⎡⎤''⎡⎤⎝⎭⎣⎦⎣⎦56.设,求.()22tan()sec x yx x y tdt x y ---=≠⎰22d ydx解:对等式两边求导.得,()()()()222sec 1sec 1x y y x y y ''---=--整理,得,2sin ()y x y '=-()()()222sin cos 1d yx y x y y dx '∴=---.()()()21sin 2()cos sin 22y x y x y x y '=--=--57.已知,其中二阶可微,求.()y f x y =+()f u 22d ydx 解:,.()()1y f x y y '''=++()'1()f x y y f x y '+∴='-+对两边再求导,()()1y f x y y '''=++,()()()21y f x y y y f x y ''''''''=++++.()()()211y f x y y f x y '''++''∴='-+3"()[1'()]f x y f x y +=-+58.已知,求.0sin ()xtf x dt t p =-ò0()f t dt p ò解:由已知,,或sin ()xf x xp ¢=-sin ()()x f x xf x p ¢¢=-01cos sin ()()t t tt xdx f x dx xf x dxp ¢¢-==-òòò,()(0)()()()()()t tt f t f xf x f x dx f t tf t f x dx p p p =--+=-+òò取,有,t p =021cos ()()()f f f x dx pp p p p p =-=-+ò.()2f t dt p\=ò59.求积分:.121211x x x e x +æö÷ç+-÷ç÷çèøò解:1111122222111112222221111x x x x x x x x x x I x e dx e dx x e dx e dx xd e x x +++++æöæöæö÷ç÷÷çç÷=+-=+-=+ç÷÷çç÷÷÷ççç÷çèøèøèøòòòòò.21521232x x xee +==60.求极限:.2240sin lim x x xx®-解:224300sin sin sin lim lim x x x x x x x x x x x ®®-+-=×302sin cos 222lim x x xx x®-=.3022sin cos 2lim 8t t t t t ®-=2011cos lim 2t t t ®-=2202sin 12lim 2t t t ®=20sin 12lim 42t t t ®æö÷ç÷ç÷çç=çç÷ç÷÷çèø14=而,22223200000sin sin sin 1cos 1sin 1lim lim lim 2lim 2lim sin 3323x x x x x x x x x x x x x x x x x x x ®®®®®-+--=×==´=请问以上方法错在哪里?61.计算.x ò解:记,代入,得()221ln 1x u e u x u ==+=+原式()()222ln 1121u u uduu u ++=+ò()()22222ln 12ln 121u u du u u duu =+=+-+òò.()22ln 12222u u u arctgu c c =+-++=-++62.求积分:.()12ln 11x dx x++ò解:令,,,,11t x t -=+211x t +=+()221dt dx t =-+()()22222111111t t x t t +æö-ç+=+=ççè++代入,则()12ln 11x I dx x +=+ò()()()()21122200ln 1122ln 11211x t I dx dt x t t t ++==×++++òò()()1112220001120ln 2ln 1ln 1ln 211112ln 2ln 214t x dt dt dx t t xI dt t p-++==-+++\==+òòòò.112011ln 221I dx x \=×+òln 28p =63.求积分:1ò解:记212t x t dx tdt==-=-当时,;当时,,则0x =t 1=1x =0t =原式.110202212dt arctgtt p ===-ò64.设在内有意义,且(1)可导;(2)有反函数;(3)()F x ()0,+¥()x j .求.()()5322115F x t dt x x j æö÷ç÷=-ç÷ç÷èøò()F x 解:由(3)可知,时,,0x =()()010F t dt j =ò()01F =记,则为其反函数()x F y =()y x j =且或()()F y y j =()()F x xj =对(3)的式子两边求导,有,即.()()()23321123F x F x x x j ¢=- ()23321123x F x x x ¢×=-化简有()F x ¢=()23321132F x dx x x c æö\==-+ò而,故.()01F =()233211132F x x x =-+65.求积分:1ò解:11I -==òò.112-==òò12arcsin tp ==66.求积分:1ò解:令sin 02x t t p =<<.()22202200sin cos cos 1cos 1cos 4t d t I dt arctg t tt p pp p==-=-=++òò67.证明:.()4011212n tg xdx n np<<+ò证明:记,则.14201n nn t I tg xdx dt t p==+òò()11212n I n n<<+68.求积分:.244sin 1xxdx ep p --+ò解:.224404sin 11sin 111x x x x dx xdx e e e pp p ---æö÷ç=+÷ç÷çèø+++òò2402sin 8xdx p p -==ò69.设,且,则方程0在()[],f x C a b Î()0f x >()()1xxabf x dx dx f x +=òò(),a b内有几个根.解:记,,()()()1xxabF x f t dt dt f t =+òò()()()110abbaF a dt dt f t f t ==-<òò,而.;()()0baF b f x dx =>ò()0f x >[],x a b Î()()()10F x f x f x ¢=+>在内严格单调增加.因此,在内只有一个根.()F x \(),a b ()F x (),a b 70.在上连续可微,且满足.试证存在一点.使()f x [)0,1()()1212f xf x dx =ò()0,1x Î.()()0f f x x x ¢+=证:设.则,()()F x xf x =()()0000F f =´=.()()()()112211122F f xf x dx F x dx =´==´òò由于在上可微,由积分中值定理,必存在一点,使得()F x []0,110,2h æö÷çÎ÷ç÷çèø,在上,满足Rolle 定理的三个条件,固而存在()()()1122F F F h h =´´=[],1h ()F x ,使得.即.x (),1h Î()0,1Ì()0F x ¢=()()0f f x x x ¢+=71.设求,.()11010x x xe x f x e x ìïïïï¹ï=íï+ïïï=ïî()0f -¢()0f +¢解:由知()()()000limx x f x f x f x x x ®-¢=-()0f -¢()()11000lim lim lim 0011txt t x x x f x f e e x e e --®-¥®®-====-++()0f +¢()()11000lim lim lim 1011txt t x x xf x f e e x ee ++®+¥®®-====-++另,时0x ¹()1121111xx x e e x f x e æö÷ç÷-+ç÷ç÷èø¢=æö÷ç÷+ç÷ç÷èø;()0f -¢()1121011lim lim 1xx x x xe e xf x e --®®æö÷ç÷-+ç÷ç÷èø¢==æö÷ç÷+ç÷ç÷èø()()121lim01u u u xu u e u e e =®-¥-+¾¾¾®=+()0f +¢()1121011lim lim 1xx x x xe e xf x e ++®®æö÷ç÷-+ç÷ç÷èø¢==æö÷ç÷+ç÷ç÷èø()()21lim1u u u u e u e e ®+¥-+=+()()()11lim21u u u u u uu e u e e e e e ®+¥-++-=+()22lim21u uu uu e ue e e ®+¥-=+.()221lim lim 1221u u u u u u e u e e e ®+¥®+¥--===+72.设在上连续,且,证明:必存在,使()f x []0,n ()()()0f f n n N =Î()0,n x Î.()()1f f x x +=证明:记,则在上连续,因而有最大(小)值()()()1x f x f x j =+-()x j []0,1n -,,;()M m ()m x M j ££[]0,1x n Î-而,,…,;()()()010f f j =-()()()121f f j =-()()()11n f n f n j -=--从而,()()()1110n n k k k f k f k m M nnj --==éù+-ëû£==£åå故而,必存在,使,即()0,n x Î()0j x =.()()1f f x x +=73.证明:函数在上一致连续.3)(x x f =[]1,0证明:任取两点,,不妨设,则,考虑到1x []1,02∈x 21x x ≠03231≠-x x ()321232312132232132121323121)()(x x x x x x x x x x x x x x x f x f +--≤++-=-=-;()2323121323121)()(x x x x x x x f x f --≤-=-即;2133231321)()(x x x x x f x f -≤-=-所以,对于任意小的正数,取,当时,必有0>ε3εη=η<-21x x 成立,ε<-≤-=-321323121)()(x x x x x f x f 故而函数在上一致连续.3)(x x f =[]1,074.函数在上有定义,且(1),(2)对于在,)(x f ()∞,0)1()(lim 1f x f x =→0>∀x ,则(为常数).)()(2x f x f =C x f ≡)(C 证明:任取,记,,,…,()∞+∈,0x x x =1x x x ==124123xx x x ===,….则1211-==-n x x x n n 由可知,,即)()(2x f x f =)()(x f x f =;)()()()()(321n x f x f x f x f x f ===== 而注意到,故)0(1lim >=+∞→x x n n ;)0(1lim lim 121>==-+∞→+∞→x x x n n n n 而,从而)1()(lim 1f x f x =→;)1()lim ()(lim )(11f x f x f x f n x n x ===→→所以,(为常数).C x f ≡)()1(f C =75.求极限:.21n n n tan n lim ⎪⎭⎫ ⎝⎛∞→解:注意到⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛⋅=⎪⎭⎫ ⎝⎛n tan n ln n exp n tan n n 1122,⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧-⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-+⋅⎪⎭⎫ ⎝⎛-⋅=11111112n tan n n tan n ln n tan n n exp 且,111111=-⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-+∞→ntan n n tan n ln lim n 而22111tan lim 11tan lim n n n n n n n n -=⎪⎭⎫ ⎝⎛-∞→∞→30201tan lim1tan lim y y y y y y y y ny -=-=→→=.yy tan lim y y sec lim y y 31331220220==-=→→故.e n tan n lim n n 3121=⎪⎭⎫⎝⎛∞→76.已知,,求.12a =()11112n n n a a n a +⎛⎫=+> ⎪⎝⎭lim n n a →∞解:很明显,,,,,12a =0n a >11112n n n a a a +⎛⎫=+≥ ⎪⎝⎭()12111122n n n a n a a +⎛⎫=+≤>⎪⎝⎭所以,,单调有界,存在;1212n n a a a +≤≤≤≤= {}n a lim n n a →∞记,则由得,注意到,解得.lim n n a l →∞=1112n n n a a a +⎛⎫=+ ⎪⎝⎭112l l l ⎛⎫=+ ⎪⎝⎭21≤≤l 1l =77.设函数,求.xx y +=12()n y 解:,,11112++-=+=x x x x y 2111111⎪⎭⎫⎝⎛+-='⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛++-='x x x y ,()()322121111+-='⎪⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛+-=''x x y 由数学归纳法可得:.()()())1(1!11>+-=+n x n yn n n 78.设函数在区间上连续,在内可导,且,()x f []0,1()0,1()()010==f f .试证:121=⎪⎭⎫ ⎝⎛f (1)存在,使;1,12η⎛⎫∈⎪⎝⎭()ηη=f (2)对任意实数,必存在,使得.λ()0,ξη∈()()1f f ξλξξ'--=⎡⎤⎣⎦证明:(1)设,则在区间上连续,在内可导,且()()h x x f x =-()h x []0,1()0,1,,,则存在,,即()00h =()11h =11022h ⎛⎫=-< ⎪⎝⎭1,12η⎛⎫∈ ⎪⎝⎭()()0h f ηηη=-=.()ηη=f (2)记,在区间上连续,在内可导,且,()()xF x f x x e λ-=-⎡⎤⎣⎦[]0,1()0,1()00F =,则由定理,必存在,使得,即()0F η=Rolle ()0,ξη∈()0F ξ'=.()()1f f ξλξξ'--=⎡⎤⎣⎦79.判断级数的敛散性.11nn ¥=åò提示:.220001122n xdx n n>=®<òòò80.证明:当时,.0>x ()x x xx<+<+1ln 1证明:记,则在上连续因而可积.tt f +=11)()(t f []x 0由积分第一中值定理,比存在一点,使得:()x 0∈ξ,()()x f dt t x x⋅=+=+⎰ξ0111ln 即.()x x ξ+=+111ln 而,,x <<ξ011111<+<+ξx ∴,)0(11><+<+x x x x x ξ即.()x x x x<+<+1ln 181.求在条件下,()22212312323,,2334f x x x x x x x x =+++2221231x x x ++=()123,,f x x x 的最大值和最大值点.解:利用拉格朗日乘数法,设,()()22222212312323123,,,23341L x x x x x x x x x x x λλ=++++++-,则123112233322221234206240624010x x x L x x L x x x L x x x L x x x λλλλ'=+=⎧⎪'=++=⎪⎨'=++=⎪⎪'=++-=⎩.1231222312323(1)020121(2)05x x x x Maxf x x x x x Maxf x x λ≠⇒=-⇒==→=±⇒=⎧+=⎪=⇒⇒==⇒=⎨=⎪⎩82.设随机变量,问:当取何值时,落入区间的概率最大?()2~,X N μσσX ()1,3解:因为,()212~x X f x σ⎛⎫- ⎝⎭=,{}133113()X P X P g σσσσσσ∆⎧⎫⎛⎫⎛⎫<<=<<=Φ-Φ=⎨⎬ ⎪ ⎪⎩⎭⎝⎭⎝⎭利用微积分中求极值的方法,有223311()g σσσσσ⎛⎫⎛⎫⎛⎫'''=-Φ+Φ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭;222222221311111422231111130e e σσσσ⎛⎫⎛⎫⎛⎫⎛⎫---- ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎡⎤⎢⎥==-=⎢⎥⎣⎦令得,则;又,故.404ln 3σ=0σ=0()0g σ''<0σ=故当落入区间的概率最大.σ=X ()1,383.设,讨论方程的实数根.x e x f x λ-=)(0=-x e x λ解:(1)显然,当时,方程没有实根;0λ=0=-x e x λ(2)当时,方程有唯一实根;0λ<0=-x e xλ(3)当时,;曲线为下凸的,0>λ0)(,)(>=''-='x x e x f e x f λx e x f x λ-=)(呈∪型;由可知,驻点,极小值,0)(=-='λx e x f λln 0=x )ln 1()(0λλ-=x f 由此可知,当时,方程没有实根;e <<λ00=-x e x λ当,极小值,方程只有一个实根;e =λ0)ln 1()(0=-=λλxf 0=-x e x λλln 0=x 当,极小值,方程有2个实根.e >λ0)ln 1()(0<-=λλxf 0=-x e xλ84.函数的单调增减区间、凹凸区间与极值.()()()211f x x x =-+解:,()()()()()()()()()22111211131f x x x ,f x x x x x x '=-+=++-+=+-由得驻点:;()0f x '=113x ,=-由上可知,函数在与内单调递增,在内递减;极()f x ()1,-∞-13,⎛⎫+∞ ⎪⎝⎭113,⎛⎫- ⎪⎝⎭大值,极小值;()10f -=132327f ⎛⎫=-⎪⎝⎭由可得,因而函数曲线在内()()()211f x x x =-+()62f x x ''=+13,⎛⎫-∞- ⎪⎝⎭,函数曲线上凸;在内下凸,如下图.()0f x ''<13,⎛⎫-+∞ ⎪⎝⎭85.已知收益函数为,其中为价格,为需求量,求需求弹性时260R=Q Q -P Q 2d ε=-的边际收益.MR 解:因为,所以需求函数,边际收益函数为,且260R=Q Q -60P Q =-602R =Q '-需求弹性函数为;60601d P dQ Q Q dP Q Qε-==-=-当需求弹性时,,此时的边际收益.2d ε=-20Q =()20604020MR R '==-=86.设函数,求其渐近线.xx exe x f y 111)(+==解:首先考虑其水平渐近线和垂直渐近线:x()1,-∞-1-113,⎛⎫- ⎪⎝⎭1313,⎛⎫+∞ ⎪⎝⎭()f x '+0-0+()f x 增加极大值递减极小值递增因为,,,所以,1lim 1=∞→x x e +∞=+→x x e 100lim 0lim 100=-→xx e ;11011lim lim lim 0(1)(1)1t x t t t t x xxee t t e t e x e+-→+∞→+∞→⎛⎫==== ⎪++⎝⎭+;11011lim lim lim 0(1)(1)1t x t t t t x xxee t t e t e x e--→-∞→-∞→⎛⎫==== ⎪++⎝⎭+;110011limlim lim (1)(1)1t x t t x t t xxee t t e t e x e-→∞→→⎛⎫===∞=⎪++⎝⎭+故而没有水平渐近线和垂直渐近线;xx exex f y 111)(+==由于,()111limlim 21xx x xf x e a x e →∞→∞===+()1111111211lim lim lim 2211x x x x x x x x xe x e xe b fx x x e e →∞→∞→∞⎡⎤⎛⎫-+⎢⎥⎡⎤ ⎪⎡⎤⎝⎭⎢⎥⎢⎥=-=-=⎢⎥⎢⎢⎥⎣⎦++⎢⎥⎢⎥⎣⎦⎢⎥⎣⎦,11011111122lim lim 2(1)41x t t x t xx xe e t t e x e→∞→-+-⎛⎫==== ⎪+⎝⎭+故而有斜渐近线:.xx exe x f y 111)(+==4121+=x y 87.求函数曲线的渐近线.()1ln 1x y e x=++解:显然,,为其垂直渐近线;()01lim ln 1x x e x→⎡⎤++=∞⎢⎥⎣⎦0x =,为其水平渐近线;()()1lim ln 1lim ln 10x xx x e e x →-∞→-∞⎡⎤++=+=⎢⎥⎣⎦0y =又,,,因而()()11ln 1ln 1x x y e x e x x -=++=+++()1lim ln 10x x e x -→+∞⎡⎤++=⎢⎥⎣⎦为其一条斜渐近线.y x=88.若,试证明:与具有相同的敛散性.lim (0)n n a a a →∞=≠∑∞=+-11n n n a a ∑∞=+-1111n nn a a 证明:问题为讨论两个正项级数的敛散性,可以用比较法的极限形式,因为不是具体的级数形式.记,则,111nn n a a V -=+0,0>>n n V U ==n n n V U ∞→limnn nn n a a a a 11lim11--=++∞→1.lim +∞→n n n a a )0(2≠a 可见,与具有相同的敛散性.∑∞=+-11n n n a a∑∞=+-1111n nn a a 89.讨论下列级数的敛散性:(1)2);(3);(4)1n ∞=11tan 2n n n ∞+=∑()3113nnn n n ∞=⎤+-⎣⎦∑()∑∞=+-+121211n n n n n(5);(6);(7).()()1111ln 1n n n ∞+=-+∑()211nn n n ∞=-+∑()()1111ln n n nn e e ∞+-=-+∑解:(1)当充分大时,比如时,有,从而n 3>n ()n n <+<1ln 1,而当时,,()n n n n <+<1ln 1∞→n 1→n n由极限的夹逼性定理知,当时,,所以,∞→n 1→1n ∞=(2)注意到,这是正项级数,当时,(等价无穷小),0→x x x ~tan 所以,而后者收敛,所以收敛.11tan ~2n n n π∞+=∑112n n n π∞+=∑11tan 2n nn π∞+=∑(3)利用柯西判别法:也是正项级数,,可见原()33113n+-=<→级数收敛;事实上,,,)())333111333nnnn nnnn nn ⎤+-+⎣⎦<<3113nnn n ∞=⎤⎣⎦∑都收敛,且同为正项级数,因而原级数收敛.3113nn n n ∞=⎤⎣⎦∑(4)因为,()()111111122221212112121→+⋅+⋅=+=+=+-+-nn nnnn n n n n n n nnnnnu 改用比较判别法:取,则21nv n =;()11lim 1lim lim 122121=⎪⎪⎭⎫⎝⎛+=+=+∞→++∞→∞→n n n n n nn n n n n nv u其中()(){}1122222lim lim exp lim 12ln ln 111n x n x x n x x x x n x ++→∞→+∞→+∞⎛⎫⎛⎫⎡⎤==+-+ ⎪ ⎪⎣⎦++⎝⎭⎝⎭,()()()()()22222222ln ln 1211exp lim exp lim exp lim 111111x x x x x x x x x x x x x →+∞→+∞→+∞⎧⎫⎧⎫⎪⎪-⎪⎪⎧⎫-++⎪⎪⎪⎪⎪⎪+===-=⎨⎬⎨⎬⎨⎬+⎪⎪⎪⎪⎪⎪-⎩⎭+⎪⎪⎪⎪+⎩⎭⎩⎭所以,与同时收敛.()∑∞=+-+121211n n n nn ∑∞=121n n(5)条件收敛.(6),发散.()()22111111nnn n n nn n n∞∞∞===-+-=+∑∑∑(7)=,()()1111ln n n n n e e ∞+-=-+∑()()12111ln 1n n n e n∞+=-+-∑,()222ln 1n n n e n e n e +-<-<()()()22222lim lim lim ln 1ln 1ln n x xn x x x n x x e e e e n e x e e -→∞→+∞→+∞==+-+-+==∞.()=+-=--+∞→x x x x xx e e e e e 22lim ()22221lim 1x x x x e e e →+∞+-x xx x ee e 2532106lim ++∞→另一方面,==,;()x x e e -+ln 1()xe x 21ln 1-++()x e xx x 1~1ln 11112-++()+∞→x 可见,原级数非绝对收敛;但是单调减少且趋于0,所以,原级数条件收敛.()x x e e -+ln 190.若正项级数与都发散,讨论与的敛散性.1nn v∞=∑1nn u∞=∑{}1max ,nnn u v ∞=∑{}1min ,nnn u v ∞=∑解:,,{}{}1max ,2n n n n n n u v u v u v =++-{}{}1min ,2n n n n n n u v u v u v =+--(1)显然,,或者,故而{}{}1max ,2n n n n n n n u v u v u v u =++-≥{}max ,n n n u v v ≥发散;{}1max ,nnn u v ∞=∑(2)而的敛散性未定.{}1min ,nnn u v ∞=∑例如,若,()222211111111123456212n n u n n ∞==+++++++++-∑ ,()222=11111111123456221n n v n n ∞=+++++++++-∑。
微积分(三)02-《微积分三》课程期末练习答案_9

1+ ( 2 x)2 + ( 2 y)2 dxdy =
3
3
2π dθ
0
3 0
1+ 4 r2 ⋅ rdr = 3π (5
9
2
5 −1)
于是所求全表面积为:
S1
+
S2
=
3π 2
(6
2 +5
5 −1) .
⎧x = cos t,
三、(12
分)设曲线段 l 为从
A(1,
0,
0)
沿曲线
⎪ ⎨
y
=
sin t, 到 B(0,1,
,其中
L
为从点
M
(1, 0)
沿曲线
y
=
k
cos
πx 2
(k
≠
1)
到点 N (−1, 0) .
∫ ∫ 解: I =
L
xdy + (1− y)dx ∆
x2 (1− y)2
Pdx + Qdy ,
L
则有 ∂P = (1− y)2 = ∂Q ,
∂y [x2 + (1− y2 )]2 ∂x
因此积分与路径无关.
① 当 k > 1时,取路径 MM ′N′N 得
S0
:
⎧x2 + y2
⎨ ⎩z
=
0
≤
4,
法向向下,则由高斯公式得:
Q + ∫∫ yzdzdx + 3dxdy = ∫∫∫ zdV
S0
V
其中 V 为上半球体。于是:
∫ ∫ ∫ ∫∫ Q =
2π dθ
π
2 dϕ
2 ρ cosϕρ 2 sinϕdρ +
微积分第三章答案

习题 3-11. 验证函数()f x =[0,4]上满足罗尔定理的条件,并求出使得结论成立的点ξ。
解:显然函数()f x =[0,4]上连续,在(0,4)上可导,且有(0)(4)0f f ==所以函数在区间[0,4]上满足罗尔定理,那么有()0f ξ'==,83ξ=。
2. 验证函数3()1f x x =-在区间[1,2]上满足拉格朗日中值定理的条件,并求出使得结论成立的ξ。
解:函数3()1f x x =-在区间[1,2]上连续,在(1,2)上可导,那么满足拉格朗日中值定理,那么有2(2)(1)321f f ξ-=-,即ξ=3. 函数4()1f x x =-与2()g x x =在区间[1,2]上是否满足柯西中值定理的所有条件,如满足,求出满足定理的数值ξ。
解:函数4()1f x x =-与2()g x x =在区间上连续,在区间(1,2)上可导,那么满足柯西中值定理,那么有3(2)(1)4(2)(1)2f f g g ξξ-=-,即ξ= 4. 假设4次方程432012340a x a x a x a x a ++++=有4个不同的实根,证明3201234320a x a x a x a +++=的所有根皆为实根。
证明:设43201234()f x a x a x a x a x a =++++,()0f x =的四个实根分别为1234,,,x x x x ,且1234x x x x <<<,那么函数()f x 在1[,](1,2,3)i i x x i +=上满足罗尔定理的条件,那么在1(,)i i x x +内至少存在一点i ξ,使得()0i f ξ'=。
这说明方程3201234320a x a x a x a +++=至少有3个实根,而方程为3次方,那么最多也只有3个实根,所以结论得到证明。
5. 设()f x 在[0,1]上连续,在(0,1)内可导,且(1)0f =,证明:存在(0,1)ξ∈,使得()()f f ξξξ'=-。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
L : x 2 + y 2 = 1 上存在两点 P1 和 P2 ,满足 y
∂f ∂f − x = 0. ∂x ∂y
(α ≤ t ≤ β ) 是 D 中
' 2
10.设 z = f ( x , y ) 在区域 D 有偏导连续。 Γ : x = x ( t ), y = y ( t ) 光滑曲线(即 Γ ⊂ D , x ( t ), y( t ) 在 [α , β ] 有连续导数, x
作者:闫浩(2011 年 3 月)
时, u ( x, y ) > 0 . 且满足 gradu ≠ 0 , 试证明 u = u( x , y , z ) 13. 设 u = u( x , y , z ) 在单连域 Ω ⊆ R 内可微,
3
在 Ω 内无封闭等值面。 14.设 f(x,y)是可微函数,且满足以下条件
x + y →&f ( x, y ) | x2 + y2
= +∞
G
试证明对于任意的 v = {v1 , v2 } ,都存在点 ( x0 , y0 ) ,使得 gradf ( x0 , y0 ) = v 若 T 为曲面 S : F ( x, y, z ) = 0 在点 M 0 ( x 0 , y 0 , z 0 ) 处的切平面,L 为 15. 已知函数 F 可微,
2 2
泰勒公式与带有三阶拉格朗日余项的泰勒多项式. (2)将 f ( x , y ) = x ( x − y − 2) 在(1,-1)点展到一阶带有拉格朗日余项的与二阶皮亚
2
诺余项的泰勒公式 (3)已知函数 f ( x, y ) 的二阶偏导连续,证明:
∂ 2 f (0, 0) f (2h, e = lim 2 h →0+ ∂x
,
∂ 2 f (u , v) = ∂v∂u
.
y ⎧ x > 0, y > 0 ⎪arctan x , ⎪ ⎪π (2)设 f ( x, y ) = ⎨ , x = 0, y > 0 , 则在 f ( x, y ) (0,1) 点的全微分为 ⎪2 y ⎪ ⎪π + arctan x , x < 0, y > 0 ⎩ G T . 在 (0,1) 沿 v = (1,1) 的方向导数为
z
−
1 2h
) − 2 f (h, e h ) + f (0, 0) h2
,曲面
−
1
4.给出 e = xy + yz + zx 确定的隐函数 z = f ( x, y ) 存在的一个充分条件是
z = f ( x, y ) 在 点 (1,1,0) 处 的 切 平 面 方 程
度 5.设直线 L: ⎨ 。
' 2
( ) (t ) + ( y ) (t ) ≠ 0 ) 。 Γ 的端
∂f ( M 0 ) = 0 。其中 τ ∂τ
点为 A,B。 若 f ( A) = f ( B ) ,证明存在点 M 0 ( x 0 , y 0 ) ∈ Γ ,使 是 Γ 在点 M 0 切线的方向向量。 11. 若 f ( x , y ) 在 R 上连续可微, 有 f ( x, y) > 0 。
G
T 上任意一条过M 0的直线, 求证S 上存在一条曲线, 其在M 0处的切线为L
2.解答下列与极值有关的问题: (1)二元实值函数 z = 2 x − y 在区域 D = {( x , y ) ∈ R 0 ≤ y ≤ 1 − x } 上的最小值为
2
( (A). 0
) (B). − 1 (C). − 2 (D). − 3 )是正确的
(2) .若函数 f ( x, y ) 在区域 D 内连续,关于极值的陈述( (A) f ( x, y ) 在偏导数不存在的点也可能取到极值
(3)设函数 u ( x, y ) ∈ C ( R ) 满足方程
2 2
,
∂ 2u ∂ 2u = 0 以及以下条件: − ∂x 2 ∂y 2
″ ″ ″ ′ u ( x,2 x) = x, u1 ( x,2 x) = x 2 ,求 u11 ( x,2 x), u12 ( x,2 x), u 22 ( x, ,2 x) 。
, z = f ( x, y ) 在 点 (1,1) 处 的 梯
⎧
x+ y+b=0
⎩ x + ay − z − 3 = 0
在平面 π 上,且平面 π 又与曲面 S: z = x + y 相切于点
2 2
(1,-2,5)。求 a,b 的值。 6. 求过直线 L : ⎨ 程. 7. 过曲面 S : F ( x , y, z ) = 2 x + 3 y + z = 6 上点 P (1,1,1) 处指向外侧的法向量为 n ,
4 4 2
[
]
2
− f xx ( x0 , y 0 ) f yy ( x0 , y 0 ) ≥ 0 ,则 ( x 0 , y 0 )
)
(B)不是 f ( x, y ) 的极值点 (D)是 f ( x, y ) 的极小值点
2
(4)设 f ( x, y ) = x + y − 2 x − 2 y + 4 xy ,求 f 的极值 3. 解答下列与泰勒公式有关的问题: (1) 求函数 f ( x , y ) = 2 x − xy − y − 6 x − 3 y + 5 在点 (1,1) 的带有二阶拉格朗日余项的
x2 y2 z2 + + = 1 ( x > 0, y > 0, z > 0 )上任一点的切平面与三个坐标面 a 2 b2 c 2
所成的四面体的体积 V 的表达式。 9. 设 二 元 函 数
f ( x, y ) 有 连 续 偏 导 数 , 且 f (1,0) = f (0,1) . 求 证 在 单 位 圆 周
)和法平面方程是 (
)
⎧ x2 y2 z2 ⎪ + + = 1 在 M (1,1,1) 处的切线方程和法平面方程。 (2)求曲线 ⎨ 4 4 2 ⎪ ⎩ x − 2y + z = 0
(3) .求旋转抛物面 z = x + y 与平面 x + y − 2 z = 2 之间的最短距离。
2 2
(4)求椭球面
(B) 若 f ( x, y ) 在 D 内有唯一驻点,则 f ( x, y ) 至多有一极值点
作者:闫浩(2011 年 3 月)
(C) 若函数 f ( x, y ) 有两个极值点,则其中之一必为极大值点,另一个必是极小值点 (D) 在驻点 ( x 0 , y 0 ) 处,若 f xy ( x0 , y 0 ) 不是极值点 ( (3)函数 z = f ( x, y ) 的全微分为 dz = xdx + ydy ,则点(0,0) (A)不是 f ( x, y ) 的连续点 (C)是 f ( x, y ) 的极大值点
(4) u = f ( x, y, z ) ,若 l = (cos α , cos β , cos γ ) ,其中 cos 求 K2 u
K
2
α + cos 2 β + cos 2 γ = 1 ,
∂2 ∂l
⎧1 − xy ⎪ (1 − e ) x ≠ 0 (5)分别考察函数 f ( x, y ) = ⎨ x 在全平面上连续性与可微性,并证明. ⎪ x=0 ⎩y
2
∂f ∂f 2 且 f ( x ,0) > 0 ,证明对任意 ( x , y ) ∈ R = ∂ x ∂y
12. (1)设 D 为 R 中的有界闭区域. f ( x , y ) 在 D 上连续,在 D 内可微,且满足方程
2
∂f ∂f + = kf ( x , y), (常数k ≠ 0) , 若在 D 的边界上 f ( x , y ) = 0 , 试证 f ( x , y ) 在 D ∂x ∂y
上恒为零。 (2)设 u ( x, y ) 在 x + y ≤ 1 上连续,在 x + y < 1 满足
2 2 2 2
2 2
∂ 2u ∂ 2u + 2 = u .且在 x 2 + y 2 = 1 2 ∂x ∂y
2 2
上, u ( x, y ) > 0 .证明: (I) 当 x + y ≤ 1 时, u ( x, y ) ≥ 0 ; (2) 进一步证明: 当 x + y ≤1
2 2 2
⎧3x − 2 y − z = −15 2 2 ,且与曲面 S : 2 x − 2 y + 2 z = 20 相切的平面的方 ⎩ x + y + z = 10
6 x 2 + 8 y2 求函数 u = 在点 P 处沿方向 n 的方向导数. z
作者:闫浩(2011 年 3 月)
⎧ x = a cosθ π ⎪ 8.(1)求螺旋线 ⎨ y = a sin θ 在 θ = 处的切线方程是( 2 ⎪ z = kθ ⎩
作者:闫浩(2011 年 3 月)
微积分 3 第二次习题课题目
1. 解答下列与偏导数、连续、可微性有关的问题 (1)f (u , v) 由关系式 f ( xg ( y ), y ) = x + g ( y ) 确定,其中 f (u , v) 二阶连续可微, g ( y ) 可微,
且不等于 0,则
∂f (u , v) = ∂u
