专题四_二次函数的图像与性质
九年级数学 二次函数y=ax2bxc(a≠0)的图像与性质(知识讲解1)Word版含解析

专题2.12 二次函数y=ax2+bx+c(a≠0)的图像与性质(知识讲解1)-2021-2022学年九年级数学下册基础知识专项讲练(北师大版)专题2.12 二次函数y=ax²+bx+c(a≠0)的图象与性质(知识讲解1) 【学习目标】1.会用描点法画二次函数2(0)y ax bx c a =++≠的图象;会用配方法将二次函数2y ax bx c =++的解析式写成2()y a x h k =-+的形式;2.通过图象能熟练地掌握二次函数2y ax bx c =++的性质;3.经历探索2y ax bx c =++与2()y a x h k =-+的图象及性质紧密联系的过程,能运用二次函数的图象和性质解决简单的实际问题,深刻理解数学建模思想以及数形结合的思想. 【要点梳理】要点一、二次函数2(0)y ax bx c a =++≠与2(1)(0)y a x t k a =-+≠之间的相互关系 1.顶点式化成一般式从函数解析式2()y a x h k =-+我们可以直接得到抛物线的顶点(h ,k),所以我们称2()y a x h k =-+为顶点式,将顶点式2()y a x h k =-+去括号,合并同类项就可化成一般式2y ax bx c =++. 2.一般式化成顶点式 22222()()()22b b b b y ax bx c a x x c a x x c a a a a ⎡⎤=++=++=++-+⎢⎥⎣⎦224()24b ac b a x a a-=++.对照2()y a x h k =-+,可知2b h a =-,244ac b k a-=.∴抛物线2y ax bx c =++的对称轴是直线2b x a =-,顶点坐标是24(,)24b ac b a a--. 特别说明:1.抛物线2y ax bx c =++的对称轴是直线2b x a =-,顶点坐标是24(,)24b ac b a a--,可以当作公式加以记忆和运用.2.求抛物线2y ax bx c =++的对称轴和顶点坐标通常用三种方法:配方法、公式法、代入法,这三种方法都有各自的优缺点,应根据实际灵活选择和运用.要点二、二次函数2(0)y ax bx c a =++≠的图象的画法 1.一般方法:列表、描点、连线; 2.简易画法:五点定形法. 其步骤为:(1)先根据函数解析式,求出顶点坐标和对称轴,在直角坐标系中描出顶点M ,并用虚线画出对称轴.(2)求抛物线2y ax bx c =++与坐标轴的交点,当抛物线与x 轴有两个交点时,描出这两个交点A 、B 及抛物线与y 轴的交点C ,再找到点C 关于对称轴的对称点D ,将A 、B 、C 、D 及M 这五个点按从左到右的顺序用平滑曲线连结起来. 特别说明:当抛物线与x 轴只有一个交点或无交点时,描出抛物线与y 轴的交点C 及对称点D ,由C 、M 、D 三点可粗略地画出二次函数图象的草图;如果需要画出比较精确的图象,可再描出一对对称点A 、B ,然后顺次用平滑曲线连结五点,画出二次函数的图象, 要点三、二次函数2(0)y ax bx c a =++≠的图象与性质 1.二次函数2(0)y ax bx c a =++≠图象与性质2.二次函数2(0)y ax bx c a =++≠图象的特征与a 、b 、c 及b2-4ac 的符号之间的关系要点四、求二次函数2(0)y ax bx c a =++≠的最大(小)值的方法如果自变量的取值范围是全体实数,那么函数在顶点处取得最大(或最小)值,即当2b x a =-时,244ac b y a-=.特别说明:如果自变量的取值范围是x1≤x≤x2,那么首先要看2ba-是否在自变量的取值范围x1≤x≤x2内,若在此范围内,则当2b x a =-时,244ac b y a-=,若不在此范围内,则需要考虑函数在x1≤x≤x2范围内的增减性,如果在此范围内,y 随x 的增大而增大,则当x =x2时,22y bx c ++;当x =x1时,211y ax bx c =++,如果在此范围内,y 随x 的增大而减小,则当x =x1时,2max 11y ax bx c =++;当x =x2时,2min 22y ax bx c =++,如果在此范围内,y 值有增有减,则需考察x =x1,x =x2,2bx a=-时y 值的情况. 特别说明: 【典型例题】类型一、二次函数2(0)y ax bx c a =++≠化为顶点式1.已知抛物线2y x bx c =-++经过点A (3,0),B (﹣1,0). (1)求抛物线的解析式; (2)求抛物线的顶点坐标. 举一反三: 【变式1】2.用配方法把二次函数y=12x 2–4x+5化为y=a(x+m)2+k 的形式,再指出该函数图象的开口方向、对称轴和顶点坐标. 【变式2】3.已知二次函数2y x 4x 3=-+.()1用配方法将其化为2y a(x h)k =-+的形式;()2在所给的平面直角坐标系xOy 中,画出它的图象.【变式3】4.已知二次函数y =﹣2x 2+bx +c 的图象经过点A (0,4)和B (1,﹣2). (1)求此抛物线的解析式;(2)求此抛物线的对称轴和顶点坐标; (3)设抛物线的顶点为C ,试求∴CAO 的面积. 类型二、画二次函数2(0)y ax bx c a =++≠的图象5.已知:二次函数243y x x =++ (1)求出该函数图象的顶点坐标; (2)在所提供的网格中画出该函数的草图.举一反三: 【变式1】6.已知二次函数y =﹣x 2+4x .(1)写出二次函数y =﹣x 2+4x 图象的对称轴;(2)在给定的平面直角坐标系中,画出这个函数的图象(列表、描点、连线); (3)根据图象,写出当y <0时,x 的取值范围. 【变式2】7.已知二次函数y =12x 2﹣x ﹣32. (1)在平面直角坐标系内,画出该二次函数的图象; (2)根据图象写出:①当x 时,y >0; ②当0<x <4时,y 的取值范围为 .【变式3】8.已知抛物线22232(0)y ax ax a a =--+≠. (1)求这条抛物线的对称轴;(2)若该抛物线的顶点在x 轴上,求其解析式;(3)设点()1,P m y ,()23,Q y 在抛物线上,若12y y <,求m 的取值范围. 类型三、二次函数2(0)y ax bx c a =++≠的性质9.把抛物线21:23C y x x =++先向右平移4个单位长度,再向下平移5个单位长度得到抛物线2C .(1)直接写出抛物线2C 的函数关系式;(2)动点(),6P a -能否在拋物线2C 上?请说明理由;(3)若点()()12,,,A m y B n y 都在抛物线2C 上,且0m n <<,比较12,y y 的大小,并说明理由. 举一反三: 【变式1】10.在平面直角坐标系xOy 中,关于x 的二次函数2y x px q +=+的图象过点(1,0)-,(2,0).(1)求这个二次函数的表达式;(2)求当21x -≤≤时,y 的最大值与最小值的差;(3)一次函数(2)2y m x m =-+-的图象与二次函数2y x px q +=+的图象交点的横坐标分别是a 和b ,且3a b <<,求m 的取值范围. 【变式2】11.如图,已知抛物线y=x 2-2x -3与x 轴交于A 、B 两点.(1)当0<x <3时,求y 的取值范围;(2)点P 为抛物线上一点,若S △PAB =10,求出此时点P 的坐标.【变式3】12.已知抛物线2y ax bx c =++,如图所示,直线1x =-是其对称轴,()1确定a ,b ,c ,24b ac =-的符号;()2求证:0a b c -+>;()3当x 取何值时,0y >,当x 取何值时0y <.类型四、二次函数的图象及各项的系数13.如图,抛物线y=﹣x2+(m﹣1)x+m与y轴交于点(0,3).(1)m的值为________;(2)当x满足________时,y的值随x值的增大而减小;(3)当x满足________时,抛物线在x轴上方;(4)当x满足0≤x≤4时,y的取值范围是________.举一反三:【变式1】14.已知二次函数y=ax2+bx+c的图象如图所示,给出下列结论:∴abc>0;∴a﹣b+c<0;∴2a+b﹣c<0;∴4a+2b+c>0,∴若点(﹣23,y1)和(73,y2)在该图象上,则y1>y2.其中正确的结论是_____(填入正确结论的序号)类型五、一次函数、二次函数图象的综合判断15.如图,已知直线y=-2x+m与抛物线y=ax2+bx+c相交于A,B两点,且点A(1,4)为抛物线的顶点,点B在x轴上.(1)求m 的值; (2)求抛物线的解析式;(3)若点P 是x 轴上一点,当∴ABP 为直角三角形时直接写出点P 的坐标. 举一反三: 【变式1】16.已知二次函数()2229y mx m x m =++++.()1如果二次函数的图象与x 轴有两个交点,求m 的取值范围;()2如图,二次函数的图象过,点()4,0A ,与y 轴交于点B ,直线AB 与这个二次函数图象的对称轴交于点P ,求点P 的坐标.【变式2】17.如图所示,已知直线y=12-x 与抛物线y=2164x -+交于A 、B 两点,点C 是抛物线的顶点.(1)求出点A 、B 的坐标; (2)求出∴ABC 的面积;(3)在AB 段的抛物线上是否存在一点P ,使得∴ABP 的面积最大?若存在,请求出点P 的坐标;若不存在,请说明理由.参考答案:1.(1)2y x 2x 3=-++(2)(1,4)【详解】解:(1)∴抛物线2y x bx c =-++经过点A (3,0),B (-1,0), ∴抛物线的解析式为;()()y x 3x 1=--+,即2y x 2x 3=-++, (2)∴抛物线的解析式为()22y x 2x 3x 14=-++=--+, ∴抛物线的顶点坐标为:(1,4).(1)根据抛物线2y x bx c =-++经过点A (3,0),B (﹣1,0),直接由交点式得出抛物线的解析式.(2)将抛物线的解析式化为顶点式,即可得出答案.2.抛物线的开口向上,对称轴是直线x =4,顶点坐标是(4,-3). 【分析】用配方法把一般式化为顶点式,根据二次函数的性质解答即可. 【详解】解:∵y =12x 2-4x +5=12(x -4)2-3,∴抛物线的开口向上,对称轴是直线x =4,顶点坐标是(4,-3).【点睛】本题考查的是二次函数的三种形式,正确利用配方法把一般式化为顶点式是解题的关键.3.(1)2(x 2)1--;(2)见解析.【分析】(1)利用配方法把二次函数解析式化成顶点式即可; (2)利用描点法画出二次函数图象即可.【详解】解:()21y x 4x 3=-+=222x 4x 223-+-+ =2(x 2)1--()22y (x 2)1=--,∴顶点坐标为()2,1-,对称轴方程为x 2=.函数二次函数2y x 4x 3=-+的开口向上,顶点坐标为()2,1-,与x 轴的交点为()3,0,()1,0, ∴其图象为:故答案为(1)2(x 2)1--;(2)见解析.【点睛】本题考查二次函数的配方法,用描点法画二次函数的图象,掌握配方法是解题的关键.4.(1)y =﹣2x 2﹣4x +4;(2)对称轴为直线x =﹣1,顶点坐标为(﹣1,6);(3)∴CAO 的面积为2.【分析】(1)利用待定系数法把A (0,4)和B (1,﹣2)代入y =﹣2x 2+bx +c 中,可以解得b ,c 的值,从而求得函数关系式即可; (2)利用配方法求出图象的对称轴和顶点坐标;(3)由(2)可得顶点C 的坐标,再根据三角形的面积公式即可求出△CAO 的面积. 【详解】解:(1)把A (0,4)和B (1,﹣2)代入y =﹣2x 2+bx +c ,得:24212c b c =⎧⎨-⨯++=-⎩,解得:44b c =-⎧⎨=⎩, 所以此抛物线的解析式为y =﹣2x 2﹣4x +4; (2)∴y =﹣2x 2﹣4x +4 =﹣2(x 2+2x )+4 =﹣2[(x +1)2﹣1]+4 =﹣2(x +1)2+6,∴此抛物线的对称轴为直线x =﹣1,顶点坐标为(﹣1,6); (3)由(2)知:顶点C (﹣1,6), ∴点A (0,4),∴OA =4, ∴S △CAO =12OA •|xc |=12×4×1=2,即△CAO 的面积为2.故答案为(1)y =﹣2x 2﹣4x +4;(2)对称轴为直线x =﹣1,顶点坐标为(﹣1,6);(3)△CAO 的面积为2.【点睛】本题考查了用待定系数法求二次函数的解析式,二次函数解析式的三种形式,二次函数的性质以及三角形的面积,难度适中.正确求出函数的解析式是解题的关键. 5.(1) (-2,-1);(2)见解析【分析】(1)将二次函数化为顶点式即可得出顶点坐标; (2)利用五点法画二次函数的图象即可.【详解】(1)243y x x =++化为顶点式为2(2)1y x =+- 则该函数图象的顶点坐标为(2,1)--;(2)先求出自变量x 在4,3,2,1,0----处的函数值,再列出表格 当4x =-和0x =时,3y =当3x =-和=1x -时,2(1)4(1)30y =-+⨯-+= 当2x =-时,1y =- 列出表格如下:由此画出该函数的草图如下:【点睛】本题考查了二次函数的顶点式、画二次函数的图象,掌握函数图象的画法是解题关键.6.(1)对称轴是过点(2,4)且平行于y轴的直线x=2;(2)见解析;(3)x<0或x>4.【详解】试题分析:(1)把一般式化成顶点式即可求得;(2)首先列表求出图象上点的坐标,进而描点连线画出图象即可.(3)根据图象从而得出y<0时,x的取值范围.试题解析:(1)∴y=-x2+4x=-(x-2)2+4,∴对称轴是过点(2,4)且平行于y轴的直线x=2;(2)列表得:描点,连线.(3)由图象可知,当y<0时,x的取值范围是x<0或x>4.7.(1)见解析;(2)①x<﹣1或x>3;②﹣2≤y<52.【分析】(1)先把解析式配成顶点式得到抛物线的顶点坐标为(1,2);再分别求出抛物线与坐标轴的交点坐标,然后利用描点法画二次函数图象;(2)∴利用函数图象写出抛物线在x轴上方所对应的自变量的范围即可;∴先确定x=4时,y=52,然后利用函数图象写出当0<x<4时对应的函数值的范围.【详解】解:(1)∴y=12(x﹣1)2﹣2,∴抛物线的对称轴为直线x=1,顶点坐标为(1,2);当x=0时,y=12x2﹣x﹣32=﹣32,则抛物线与y轴交点坐标为(0,﹣32)当y =0时,12 x 2﹣x ﹣32=0,解得x 1=﹣1,x 2=3,抛物线与x 轴的交点坐标为(﹣1,0)、(3,0), 如图,(2)∴当x <﹣1或x >3时,y >0; ∴当0<x <4时,﹣2≤y <52;故答案为x <﹣1或x >3;﹣2≤y <52.【点睛】本题考查了抛物线与x 轴的交点:把求二次函数y =ax 2+bx +c (a ,b ,c 是常数,a ≠0)与x 轴的交点坐标问题转化解关于x 的一元二次方程即可求得交点横坐标.也考查了二次函数的性质.8.(1)1x =;(2)233322y x x =-+或221y x x =-+-;(3)当a >0时,13m -<<;当a <0时,1m <-或3m >.【分析】(1)将二次函数化为顶点式,即可得到对称轴;(2)根据(1)中的顶点式,得到顶点坐标,令顶点纵坐标等于0,解一元二次方程,即可得到a 的值,进而得到其解析式;(3)根据抛物线的对称性求得点Q 关于对称轴的对称点,再结合二次函数的图象与性质,即可得到m 的取值范围.【详解】(1)∴22232y ax ax a =--+, ∴22(1)32y a x a a =---+, ∴其对称轴为:1x =.(2)由(1)知抛物线的顶点坐标为:2(1,23)a a --,∴抛物线顶点在x 轴上, ∴2230a a --=, 解得:32a =或1a =-, 当32a =时,其解析式为:233322y x x =-+, 当1a =-时,其解析式为:221y x x =-+-, 综上,二次函数解析式为:233322y x x =-+或221y x x =-+-. (3)由(1)知,抛物线的对称轴为1x =, ∴()23,Q y 关于1x =的对称点为2(1,)y -, 当a >0时,若12y y <, 则-1<m <3;当a <0时,若12y y <, 则m <-1或m >3.【点睛】本题考查了二次函数对称轴,解析式的计算,以及根据二次函数的图象性质求不等式的取值范围,熟知相关计算是解题的关键.9.(1)2(3)3y x =--;(2)不在,见解析;(3)12y y >,见解析【分析】(1)先求出抛物线1C 的顶点坐标,再根据向右平移横坐标加,向下平移纵坐标减求出平移后的抛物线的顶点坐标即可;(2)根据抛物线2C 的顶点的纵坐标为3-,即可判断点()6P a -,不在拋物线2C 上; (3)根据抛物线2C 的增减性质即可解答.【详解】(1)抛物线221:23(1)2C y x x x =++=++,∴抛物线1C 的顶点坐标为(﹣1,2),根据题意,抛物线2C 的顶点坐标为(-1+4,2-5),即(3,﹣3), ∴抛物线2C 的函数关系式为:2(3)3y x =--; (2)动点P 不在抛物线2C 上. 理由如下:∴抛物线2C 的顶点为()3,3-,开口向上, ∴抛物线2C 的最低点的纵坐标为3-. ∴63P y =-<-,∴动点P 不在抛物线2C 上; (3)12y y >. 理由如下:由(1)知抛物线2C 的对称轴是3x =,且开口向上, ∴在对称轴左侧y 随x 的增大而减小. ∴点()()12,,,A m y B n y 都在抛物线2C 上,且03m n <<<, ∴12y y >.【点睛】本题考查了二次函数图象与几何变换,二次函数图象上点的坐标特征,熟练掌握平移的规律“左加右减,上加下减”以及熟练掌握二次函数的性质是解题的关键. 10.(1)2y x x 2=--;(2)254;(3)1m <. 【分析】(1)利用待定系数法将点(1,0)-,(2,0)代入解析式中解方程组即可; (2)根据(1)中函数关系式得到对称轴12x =,从而知在21x -≤≤中,当x=-2时,y 有最大值,当12x =时,y 有最小值,求之相减即可; (3)根据两函数相交可得出x 与m 的函数关系式,根据有两个交点可得出∆>0,根据根与系数的关系可得出a ,b 的值,然后根据3a b <<,整理得出m 的取值范围. 【详解】解:(1)∴2y x px q +=+的图象过点(1,0)-,(2,0),∴10420p q p q -+=⎧⎨++=⎩解得12p q =-⎧⎨=-⎩ ∴2y x x 2=--(2)由(1)得,二次函数对称轴为12x =∴当21x -≤≤时,y 的最大值为(-2)2-(-2)-2=4,y 的最小值为21192224⎛⎫--=- ⎪⎝⎭ ∴y 的最大值与最小值的差为925444⎛⎫--= ⎪⎝⎭;(3)由题意及(1)得()2222y m x my x x ⎧=-+-⎨=--⎩整理得()()2340x m x m ----=即()(1)40x x m +--=⎡⎤⎣⎦∴一次函数(2)2y m x m =-+-的图象与二次函数2y x px q +=+的图象交点的横坐标分别是a 和b ,∴()()23440m m ∆=-+-> 化简得210250m m -+> 即()250m -> 解得m≠5∴a ,b 为方程()(1)40x x m +--=⎡⎤⎣⎦的两个解 又∴3a b << ∴a=-1,b=4-m 即4-m>3 ∴m<1综上所述,m 的取值范围为1m <.【点睛】本题考查了利用待定系数法求二次函数解析式,二次函数图象的性质,根与系数的关系等知识.解题的关键是熟记二次函数图象的性质. 11.(1) ﹣4≤y <0;(2) P 点坐标为(﹣2,5)或(4,5)【详解】分析:(1)、首先将抛物线配成顶点式,然后根据x 的取值范围,从而得出y 的取值范围;(2)、根据题意得出AB 的长度,然后根据面积求出点P 的纵坐标,根据抛物线的解析式求出点P 的坐标.详解:(1)∴抛物线的解析式为y=x 2﹣2x ﹣3,∴y=x 2﹣2x ﹣3=(x ﹣1)2﹣4, ∴顶点坐标为(1,﹣4),由图可得当0<x <3时,﹣4≤y <0. (2)当y=0时,x 2﹣2x ﹣3=0, 解得:x 1=-1 x 2=3 ∴A (﹣1,0)、B (3,0), ∴AB=4.设P (x ,y ),则S △PAB =AB•|y|=2|y|=10, ∴|y|=5, ∴y=±5. ∴当y=5时,x 2﹣2x ﹣3=5,解得:x 1=﹣2,x 2=4, 此时P 点坐标为(﹣2,5)或(4,5); ∴当y=﹣5时,x 2﹣2x ﹣3=﹣5,方程无解; 综上所述,P 点坐标为(﹣2,5)或(4,5).点睛:本题主要考查的是二次函数的性质,属于基础题型.求函数值取值范围时,一定要注意自变量的取值范围是否是在对称轴的一边.12.(1)0a <,0b <,0c >,240b ac =->;(2)详见解析;(3)当31x -<<时,0y >;当3x <-或1x >时,0y <.【分析】(1)根据开口方向确定a 的符号,根据对称轴的位置确定b 的符号,根据抛物线与y 轴的交点确定c 的符号,根据抛物线与x 轴交点的个数确定b 2-4ac 的符号; (2)根据图象和x=-1的函数值确定a -b+c 与0的关系; (3)抛物线在x 轴上方时y >0;抛物线在x 轴下方时y <0. 【详解】()1∵抛物线开口向下, ∴0a <, ∵对称轴12bx a=-=-, ∴0b <,∵抛物线与y 轴的交点在x 轴的上方, ∴0c >,∵抛物线与x 轴有两个交点, ∴240b ac =->;()2证明:∵抛物线的顶点在x 轴上方,对称轴为1x =-,∴当1x =-时,0y a b c =-+>;()3根据图象可知,当31x -<<时,0y >;当3x <-或1x >时,0y <.【点睛】本题考查了二次函数图象与系数的关系,解题的关键是熟练的掌握二次函数图象与系数的关系.13.(1)3;(2)x >1;(3)-1<x <3;(4)-5≤y ≤4 【分析】根据函数的图象和性质即可求解.【详解】解:(1)将(0,3)代入y =﹣x 2+(m ﹣1)x +m 得,3=m , 故答案为3;(2)m =3时,抛物线的表达式为y =﹣x 2+2x +3, 函数的对称轴为直线x =2ba-=1, ∴﹣1<0,故抛物线开口向下,当x >1时,y 的值随x 值的增大而减小, 故答案为x >1;(3)令y =﹣x 2+2x +3,解得x =﹣1或3, 从图象看,当﹣1<x <3时,抛物线在x 轴上方; 故答案为﹣1<x <3;(4)当x =0时,y =3;当x =4时,y =﹣x 2+2x +3=﹣5, 而抛物线的顶点坐标为(1,4),故当x 满足0≤x ≤4时,y 的取值范围是﹣5≤y ≤4, 故答案为﹣5≤y ≤4.【点睛】本题主要考查二次函数的图像与性质及系数的关系,熟练掌握二次函数的图像与性质及系数的关系是解题的关键. 14.∴∴∴【详解】解:∴抛物线开口向下, ∴a <0,∴对称轴在y 轴右边, ∴b >0,∴抛物线与y 轴的交点在x 轴的上方, ∴c >0,∴abc <0,故∴错误;∴二次函数y =ax 2+bx +c 图象可知,当x =﹣1时,y <0,∴a ﹣b +c <0,故∴正确;∴二次函数图象的对称轴是直线x =1,c >0, ∴2b a-=1, ∴2a +b =0,∴2a +b <c ,∴2a +b ﹣c <0,故∴正确;∴二次函数y =ax 2+bx +c 图象可知,当x =2时,y >0,∴4a +2b +c >0,故∴正确;∴二次函数图象的对称轴是直线x =1,∴抛物线上x =23-时的点与当x =83时的点对称, ∴x >1,y 随x 的增大而减小,∴y 1<y 2,故∴错误;故答案为∴∴∴.【点睛】本题考查了二次函数的图象与系数的关系,要熟练掌握,解答此题的关键是要明确:∴二次项系数a 决定抛物线的开口方向和大小:当a >0时,抛物线向上开口;当a <0时,抛物线向下开口;∴一次项系数b 和二次项系数a 共同决定对称轴的位置:当a 与b 同号时(即ab >0),对称轴在y 轴左; 当a 与b 异号时(即ab <0),对称轴在y 轴右.(简称:左同右异)∴常数项c 决定抛物线与y 轴交点. 抛物线与y 轴交于(0,c ).15.(1)m =6;(2)y =﹣x 2+2x +3;(3)点P 的坐标为(7,0)或(1,0).【分析】(1)将点A 坐标代入y=-2x+m ,即可求解;(2)y=-2x+6,令y=0,则x=3,故点B (3,0),则二次函数表达式为:y=a (x -1)2+4,将点B 的坐标代入上式,即可求解;(3)分∴BAP=90°、∴AP (P′)B=90°两种情况,求解即可.【详解】解:(1)将点A 坐标代入y =﹣2x+m 得:4=﹣2+m ,解得:m =6;(2)y =﹣2x+6,令y =0,则x =3,故点B (3,0),则二次函数表达式为:y =a (x ﹣1)2+4,将点B 的坐标代入上式得:0=a (3﹣1)2+4,解得:a =﹣1,故抛物线的表达式为:y =﹣(x ﹣1)2+4=﹣x 2+2x+3;(3)∴当∴BAP =90°时,直线AB 的表达式为:y =﹣2x+6,则直线PB 的表达式中的k 值为12,设直线PB 的表达式为:y =12x+b ,将点A 的坐标代入上式得:4=12×1+b , 解得:b =72, 即直线PB 的表达式为:y =12x+72, 当y =0时,x =﹣7,即点P (7,0);∴当∴AP (P′)B =90°时,点P′(1,0);故点P 的坐标为(7,0)或(1,0).【点睛】本题考查的是二次函数综合运用,涉及到一次函数的基本知识,要注意类讨论,避免遗漏,本题较为简单.16.(1)45m <且0m ≠;(2)P 点坐标为()1,6. 【分析】解:(1)根据题意得0m ≠且()24(2)490m m m =+-⋅+>;(2)先求二次函数的解析式,再求抛物线的对称轴,用待定系数法求直线AB 的解析式,再求AB 与对称轴的交点P.【详解】解:()1根据题意得0m ≠且()24(2)490m m m =+-⋅+>, 所以45m <且0m ≠; ()2把()4,0A 代入()2229y mx m x m =++++得()168290m m m ++++=,解得1m =-,所以抛物线解析式为2228(1)9y x x x =-++=--+,所以抛物线的对称轴为直线1x =,当0x =时,2288y x x =-++=,则()0,8B ,设直线AB 的解析式为y kx b =+,把()4,0A ,()0,8B 代入得{408k b b +==,解得{28k b =-=,所以直线AB 的解析式为28y x =-+,当1x =时,286y x =-+=,所以P 点坐标为()1,6.【点睛】本题考核知识点:二次函数与一次函数. 解题关键点:理解二次函数图象的交点问题.17.(1)点A 、B 的坐标分别为:(6,﹣3),(﹣4,2);(2)30;(3)当a =1时,∴ABP 的面积最大,此时点P 的坐标为(1,234). 【分析】(1)由直线1y x 2=-与抛物线21y x 64=-+交于A 、B 两点,可得方程211x x 624-=-+,解方程即可求得点A 、B 的坐标;(2)首先由点C 是抛物线的顶点,即可求得点C 的坐标,又由S △ABC =S △OBC +S △OAC 即可求得答案;(3)首先过点P 作PD∴OC ,交AB 于D ,然后设21P a,a 64⎛⎫-+ ⎪⎝⎭,即可求得点D 的坐标,可得PD 的长,又由S △ABP =S △BDP +S △ADP ,根据二次函数求最值的方法,即可求得答案.【详解】解:(1)∴直线1y x 2=-与抛物线21y x 64=-+交于A 、B 两点, ∴211x x 624-=-+, 解得:x =6或x =﹣4,当x =6时,y =﹣3,当x =﹣4时,y =2,∴点A 、B 的坐标分别为:(6,﹣3),(﹣4,2);(2)∴点C 是抛物线的顶点.∴点C 的坐标为(0,6),∴S △ABC =S △OBC +S △OAC =12×6×4+12×6×6=30;(3)存在.过点P 作PD∴OC ,交AB 于D ,设P(a ,﹣14a 2+6), 则D(a ,﹣12a), ∴PD =﹣14a 2+6+12a , ∴S △ABP =S △BDP +S △ADP =12×(﹣14a 2+6+12a)×(a+4)+12×(﹣14a 2+6+12a)×(6﹣a)=25125(a 1)44--+ (﹣4<a <6), ∴当a =1时,∴ABP 的面积最大,此时点P 的坐标为(1,234).【点睛】此题考查了二次函数与一次函数的交点问题,三角形面积的求解以及二次函数的最值问题等知识.此题综合性很强,难度较大,解题的关键是方程思想与数形结合思想的应用.。
二次函数的图象和性质(解析版)

第04讲 二次函数的图象和性质(重点题型方法与技巧)目录类型一:二次函数的定义 类型二:二次函数的图象与性质 类型三:二次函数的解析式 类型四:二次函数的平移问题类型一:二次函数的定义函数y =ax 2+bx +c 为二次函数的前提条件是a ≠0.在解二次函数的相关问题时,一定不能忽视“二次项系数不为0”这一隐含条件,尤其是二次项系数含字母的二次函数,应特别注意.典型例题例题1.(2022·浙江丽水·九年级期中)下列函数中,是二次函数的是( ) A .y =21x +x +1 B .y =x 2-(x +1)2C .y =-12x 2+3x +1 D .y =3x +1【答案】C 【详解】A. y =21x +x +1,不是二次函数,故该选项不正确,不符合题意; B. y =x 2-(x +1)221x ,不是二次函数,故该选项不正确,不符合题意;C. y =-12x 2+3x +1,是二次函数,故该选项正确,符合题意;D. y =3x +1,不是二次函数,故该选项不正确,不符合题意; 故选C点评:例题1考查了二次函数的定义,掌握二次函数的定义是解题的关键.根据二次函数的定义逐项分析即可,二次函数的定义:一般地,形如2y ax bx c =++(a b c 、、是常数,0a ≠)的函数,叫做二次函数.例题2.(2022·安徽宿州·九年级期末)如果()()221y m x m x =-+-是关于x 的二次函数,则m 的取值范围是( )A .1m ≠B .2m ≠C .2m ≠且1m ≠D .全体实数【答案】B【详解】∵()()221y m x m x =-+-是关于x 的二次函数,∴20m -≠, ∴2m ≠, 故选B .点评:例题2主要考查了二次函数的定义,正确把握二次函数的定义是解题的关键.例题3.(2022·全国·九年级课时练习)下列实际问题中的y 与x 之间的函数表达式是二次函数的是( ) A .正方体集装箱的体积3m y ,棱长x mB .小莉驾车以108km h 的速度从南京出发到上海,行驶x h ,距上海y kmC .妈妈买烤鸭花费86元,烤鸭的重量y 斤,单价为x 元/斤D .高为14m 的圆柱形储油罐的体积3m y ,底面圆半径x m 【答案】D【详解】A.由题得:3y x =,不是二次函数,故此选项不符合题意; B.由题得:108y x =,不是二次函数,故此选项不符合题意; C.由题得:86y x=,不是二次函数,故此选项不符合题意; D.由题得:214y x π=,是二次函数,故此选项符合题意. 故选:D .点评:例题3考查二次函数的定义,形如2(0)y ax bx c a =++≠的形式为二次函数,掌握二次函数的定义是解题的关键.根据题意,列出关系式,即可判断是否是二次函数.例题4.(2021·广西南宁·九年级期中)若12m y x x -=+是关于x 的二次函数,则m =_______ 【答案】3【详解】解:∵函数12m y x x -=+是关于x 的二次函数, ∴12m -=, 解得:3m =. 故答案为:3.点评:例题4考查了二次函数的定义,一般地,形如y=ax2+bx+c (a 、b 、c 是常数,a≠0)的函数,叫做二次函数.例题5.(2021·北京市宣武外国语实验学校九年级期中)某工厂今年八月份医用防护服的产量是50万件,计划九月份和十月份增加产量,如果月平均增长率为x ,那么十月份医用防护服的产量y (万件)与x 之间的函数表达式为______. 【答案】()2501=+y x【详解】解:十月份医用防护服的产量y (万件)与x 之间的函数表达式为 ()2501=+y x故答案为:()2501=+y x点评:例题5考查的是列二次函数关系式,掌握“两次变化后的量=原来量⨯(1+增长率)2”是解本题的关键.某工厂今年八月份医用防护服的产量是50万件,月平均增长率为x ,则九月份的产量为()501x +万件,十月份医用防护服的产量为()2501x +万件,从而可得答案.例题6.(2021·全国·九年级专题练习)已知函数()()221y m m x mx m =-+++,m 是常数.()1若这个函数是一次函数,求m 的值;()2若这个函数是二次函数,求m 的值.【答案】(1)1m =;()20m ≠且1m ≠.【详解】(1)依题意得200m m m ⎧-=⎨≠⎩∴010m m m ==⎧⎨≠⎩或 ∴1m =;()2依题意得20m m -≠,∴0m ≠且1m ≠.点评:例题6主要考查了一次函数及二次函数的定义,关键是掌握一次函数y=kx+b 的定义条件是:k 、b 为常数,k≠0,自变量次数为1;二次函数y=ax2+bx+c 的定义条件是a≠0,b 、c 为常数,自变量的最高次数是2.同类题型演练1.(2022·全国·九年级单元测试)下列函数中,是二次函数的是( )A .2832y x x =++B .81y x =+C .8y x=D .28y x =【答案】A【详解】A 、2832y x x =++是二次函数,符合题意; B 、81y x =+是一次函数,不合题意; C 、8y x=是反比例函数,不合题意; D 、28y x =不是二次函数,不合题意; 故选A .2.(2021·河南·油田十中九年级阶段练习)若函数()1334m y m x x -=++-是二次函数,则m 的值为( )A .-3B .3或-3C .3D .2或-2【答案】C【详解】解:∵函数()1334m y m x x -=++-是二次函数,∴12m -=且m +3≠0, 解得:m =3, 故选:C .3.(2022·全国·九年级课时练习)下列实际问题中,可以看作二次函数模型的有( )①正常情况下,一个人在运动时所能承受的每分钟心跳的最高次数b 与这个人的年龄a 之间的关系为b =0.8(220-a );②圆锥的高为h ,它的体积V 与底面半径r 之间的关系为V =13πr 2h (h 为定值);③物体自由下落时,下落高度h 与下落时间t 之间的关系为h =12gt 2(g 为定值);④导线的电阻为R ,当导线中有电流通过时,单位时间所产生的热量Q 与电流I 之间的关系为Q =RI 2(R 为定值). A .1个 B .2个C .3个D .4个【答案】C【详解】形如y=ax 2+bx+c (a 、b 、c 是常数且a≠0)的函数是二次函数,由二次函数的定义可得②③④是二次函数,故选C .4.(2022·全国·九年级课时练习)已知函数y =(m ﹣2)x 2+mx ﹣3(m 为常数). (1)当m _______时,该函数为二次函数; (2)当m _______时,该函数为一次函数. 【答案】 ≠2 =2【详解】解:(1)∵函数y =(m ﹣2)x 2+mx ﹣3为二次函数, ∴m ﹣2≠0, ∴m ≠2.( 2 )∵函数y =(m ﹣2)x 2+mx ﹣3为一次函数, ∴m ﹣2=0,m ≠0, ∴m =2.故答案为:(1)≠2;(2)=25.(2021·山东滨州·九年级期中)某商店从厂家以每件21元的价格购进一批商品,该商店可以自行定价,若每件商品的售价为x 元,则可卖出()35010x -件,那么卖出商品所赚钱y 元与售价x 元之间的函数关系为________.【答案】2105607350y x x =-+-【详解】解:由题意得:每件商品的盈利为:()21x -元, 所以:()()2135010y x x =--2102103507350x x x =-++-2105607350x x =-+-故答案为:2105607350y x x =-+-6.(2022·全国·九年级课时练习)根据下面的条件列出函数解析式,并判断列出的函数是否为二次函数: (1)如果两个数中,一个比另一个大5,那么,这两个数的乘积p 是较大的数m 的函数;(2)一个半径为10cm 的圆上,挖掉4个大小相同的正方形孔,剩余的面积S (cm 2)是方孔边长x (cm )的函数;(3)有一块长为60m 、宽为40m 的矩形绿地,计划在它的四周相同的宽度内种植阔叶草,中间种郁金香,那么郁金香的种植面积S (cm 2)是草坪宽度a (m )的函数. 【答案】(1)p = m 2﹣5m ,是二次函数 (2)S =100π﹣4x 2,是二次函数(3)S =4a 2﹣200a +2400;是二次函数【详解】(1)解:这两个数的乘积p 与较大的数m 的函数关系为:p =m (m ﹣5)=m 2﹣5m ,是二次函数; (2)解:剩余的面积S (cm 2)与方孔边长x (cm )的函数关系为:S =100π﹣4x 2,是二次函数;(3)解:郁金香的种植面积S (cm 2)与草坪宽度a (m )的函数关系为:S =(60﹣2a )(40﹣2a )=4a 2﹣200a +2400,是二次函数;7.(2019·湖北·黄州区宝塔中学九年级阶段练习)已知函数()()24323mm y m x m x +-=++++(其中0x ≠).()1当m 为何值时,y 是x 的二次函数?()2当m 为何值时,y 是x 的一次函数?【答案】()1当m 为2时,y 是x 的二次函数;()2当m 为3-117-±121-±y 是x 的一次函数.【详解】()1根据题意得30m +≠且242m m +-=,解得2m =, 即当m 为2时,y 是x 的二次函数;()2当30m +=时,即3m =-时,y 是x 的一次函数;当240m m +-=且20m +≠时,y 是x 的一次函数,解得117m -±=; 当241m m +-=且320m m +++≠时,y 是x 的一次函数,解得121m -±=; 即当m 为3-117-±121-±时,y 是x 的一次函数. 类型二:二次函数的图象与性质二次函数的解析式中,a 决定抛物线的形状和开口方向,h 、k 仅决定抛物线的位置.若两个二次函数的图象形状完全相同且开口方向相同,则它们的二次项系数a 必相等.典型例题例题1.(2022·浙江湖州·九年级期末)对于二次函数y =x 2-4x -1的图象,下列叙述正确的是( ) A .开口向下B .对称轴为直线x =2C .顶点坐标为(-2,-5)D .当x ≥2时,y 随x 增大而减小【答案】B【详解】解:∵224125y x x x =--=--(), ∴该函数图象开口向上,对称轴为直线2x =,顶点坐标为(2,-5), ∴当2x ≥时,y 随x 的增大而增大,故选项B 符合题意, 故选:B .点评:例题1考查二次函数的图象和性质,解答本题的关键是明确题意,利用二次函数的性质解答. 例题2.(2021·天津市晟楷中学九年级阶段练习)抛物线()2235y x =--的顶点坐标是( ) A .(3,5)-- B .(3,5)- C .(3,5)- D .(3,5)【答案】C【详解】解:抛物线()2235y x =--的顶点坐标是()3,5-,故选:C .点评:例题2考查了求抛物线的顶点坐标,解题的关键是熟练掌握抛物线的顶点坐标的求法.例题3.(2022·甘肃·张掖市第一中学九年级期末)如图所示的二次函数2y ax bx c =++的图象中,刘星同学观察得出了下面四条信息:(1)240b ac ->;(2)c >1;(3)20a b -<;(4)0a b c ++<.你认为其中错误的有( )A .2个B .3个C .4个D .1个【答案】D【详解】解:(1)根据图示知,该函数图象与x 轴有两个交点, ∴240b ac ∆=->; 故本选项正确;(2)由图象知,该函数图象与y 轴的交点在点(0,1)以下, ∴1c <;故本选项错误; (3)由图示,知对称轴12bx a=->-;又函数图象的开口方向向下, ∴0a <,∴2b a -<-,即20a b -<, 故本选项正确;(4)根据图示可知,当x =1,即0y a b c =++<,∴0a b c ++<;故本选项正确;综上所述,其中错误的是(2),共有1个; 故选:D .点评:例题3主要考查二次函数图象与二次函数系数之间的关系,会利用对称轴的范围求2a 与b 的关系,以及二次函数与方程之间的转换,根的判别式的熟练运用是解题的关键.由抛物线与x 轴交点情况判断24b ac -与0的关系,由抛物线与y 轴的交点判断c 与1的关系,然后根据对称轴及a 的范围推理2a b -的符号,根据当x =1的函数值判断a b c ++的符号.例题4.(2022·全国·九年级专题练习)若点A (﹣1,y 1)、B (1,y 2)、C (4,y 3)为二次函数y =﹣x 2+4x +5的图象上的三点,则y 1,y 2,y 3的大小关系是____(用“>”号连接). 【答案】y 2>y 3>y 1【详解】解:∵二次函数y =﹣x 2+4x +5中a =﹣1, ∴函数图象开口向下,∵y =﹣x 2+4x +5=﹣(x ﹣2)2+9, ∴函数的对称轴为直线x =2,∵A (﹣1,y 1)、B (1,y 2)、C (4,y 3),∴A 点到对称轴的距离为3,B 点到对称轴的距离为1,C 点到对称轴的距离为2, ∴y 2>y 3>y 1, 故答案为:y 2>y 3>y 1.点评:例题4考查了二次函数的图象性质,由解析式求出对称轴是解题关键.求出函数的对称轴为直线x =2,由于函数开口向下,则函数图象上的点离对称轴越远所对应的函数值越小,由此即可求解. 例题5.(2021·福建漳州·模拟预测)已知抛物线25y x bx =-++与x 轴交于A ,B 两点. (1)若抛物线的对称轴是直线x =2. ①求抛物线的解析式;②对称轴上是否存在一点P ,使点B 关于直线OP 的对称点B '恰好落在对称轴上.若存在,请求出点P 的坐标;若不存在,请说明理由.(2)当b ≥4,0≤x ≤2时,函数y 的最大值满足5≤y ≤13,求b 的取值范围. 【答案】(1)①245y x x =-++;②存在,点P (2,217)或P (2,2217-) (2)4≤b ≤6【详解】(1)解:①抛物线25y x bx =-++的对称轴为直线()212b bx =-=⨯-,抛物线的对称轴是直线x =2, ∴22b=,解得b =4, ∴抛物线的解析式为245y x x =-++; ②存在.理由如下:抛物线的对称轴与x 轴交于点C ,若点P 在x 轴上方,点B 关于OP 对称的点B '在对称轴上,连结OB ′、PB ,则OB '=OB ,PB '=PB ,如图所示:对于245y x x =-++,令y =0,则2450x x -++=,即2450x x --=, 解得125,1x x ==-, ∴A (﹣1,0),B (5,0), ∴OB '=OB =5,∴在Rt B OC '∆中,90B CO '∠=︒,5,2OB OC '==,则22225221B C B O OC ''--= ∴(21B ',设点P (2,m ),由22BP B P '=,得()2222921mm +=-,即(22921m m +=,解得217m =, ∴P (2221), 同理,当点P 在x 轴下方时,P (2,221, 综上所述,点P (2,2217)或P (2,217-; (2)解:∵抛物线25y x bx =-++的对称轴为直线2bx =, ∴当b ≥4时,22bx =≥, ∵抛物线开口向下,在对称轴左边,y 随x 的增大而增大, ∴当0≤x ≤2时,取x =2,y 有最大值,即y =﹣4+2b +5=2b +1,∵5≤y≤13,∴5≤2b+1≤13,解得2≤b≤6,又∵b≥4,∴4≤b≤6.点评:例题5考查二次函数的综合应用,涉及到二次函数的图像与性质,勾股定理的应用,轴对称性质,二次函数最值问题,二次函数增减性应用等知识点,解题的关键是熟练掌握二次函数的图像与性质、轴对称性质等相关知识,灵活运用数形结合思想、分类讨论思想解决问题.(1)①根据抛物线的对称轴公式即可求出解析式;②如图,若点P在x轴上方,点B关于OP对称的点B'在对称轴上,连接OB′、PB,根据轴对称的性质得到OB'=OB,PB'=PB,求出点B的坐标,利用勾股定理得到B′(2,21),再根据PB'=PB,列出方程解答,同理得到点P在x轴下方时的坐标即可;(2)当b≥4时,确定对称轴的位置,再结合开口方向,确定当0≤x≤2时,函数的增减性,从而得到当x=2时,函数取最大值,再根据函数值y的最大值满足5≤y≤13,列出不等式解答即可.同类题型演练1.(2022·全国·九年级课时练习)下列关于二次函数y=2x2的说法正确的是()A.它的图象经过点(-1,-2)B.它的图象的对称轴是直线x=2C.当x<0时,y随x的增大而增大≤≤2时,y有最大值为8,最小值为0D.当-1x【答案】D【详解】解:二次函数y=2x2,当x=-1时,y=2,故它的图象不经过点(-1,-2),故选项A不合题意;二次函数y=2x2的图象的对称轴是直线y轴,故选项B不合题意;当x<0时,y随x的增大而减小,故选项C不合题意;二次函数y=2x2,在-1≤x≤2的取值范围内,当x=2时,有最大值8;当x=0时,y有最小值为0,故选项D 符合题意;故选:D.2.(2021·江苏·南通市八一中学九年级阶段练习)抛物线2314y x的顶点坐标是()A.(1,4)B.(1,﹣4)C.(﹣1,4)D.(﹣1,﹣4)【详解】解:根据题意得:抛物线2314y x 的顶点坐标是(﹣1,﹣4).故选:D3.(2021·福建·平潭翰英中学九年级期中)二次函数y =ax 2+bx +c (a ≠0)的图象如图,给出下列四个结论:①4ac ﹣b 2<0;②4a +c <2b ;③3b +2c <0;④m (am +b )+b <a (m ≠﹣1),其中正确结论的个数是( )A .①②B .①③④C .②③④D .①④【答案】B【详解】解:∵函数图象与x 轴有两个交点, ∴方程ax 2+bx +c =0有两个不相等的实数根, ∴b 2−4ac >0, ∴4ac −b 2<0, 故①正确;∵函数图象与x 轴的一个交点的横坐标在0至1之间, ∴函数图象与x 轴的另一个交点的横坐标在-2至-3之间, 由图象可知:当x =−2时,y >0, ∴4a −2b +c >0, ∴4a +c >2b , 故②错误; ∵12ba-=-, ∴b =2a ,∵当x =1时,y <0, ∴a +b +c <0,∴102b bc ++<,3b +2c <0,∵由函数图象可知x =−1时,该二次函数取得最大值, ∴a −b +c >am 2+bm +c (m ≠−1), ∴m (am +b )<a −b , 故④正确;∴正确的有①③④三个, 故选:B .4.(2021·黑龙江·肇源县第五中学九年级期中)已知抛物线21y x x =--与经过点(m ,1),则代数式m ²-m +2019的值为_____. 【答案】2021【详解】解:∵抛物线2=1y x x +-经过点(,1)P m ∴21=1m m --,即22m m -=∴²2019m m -+=2+2019=2021. 故答案为:2021.5.(2022·全国·九年级课时练习)已知点A (-1,y 1),B (2 ,y 2),C (5,y 3)在二次函数y =x 2﹣6x +c 的图象上,则y 1, y 2, y 3的大小关系是_____________ (按照从小到大用<连接). 【答案】231y y y <<【详解】解:∵二次函数y =x 2-6x +c 中a =1>0, ∴抛物线开口向上,有最小值. ∵63221b x a -=-=-=⨯, ∴离对称轴水平距离越远,函数值越大, ∵3(1)5332-->->-, ∴231y y y <<; 故答案为:231y y y <<.6.(2022·福建三明·九年级期末)平面直角坐标系中,抛物线221y x ax a -++-=(a 为常数)的顶点为A . (1)当抛物线经过点(1,2),求抛物线的函数表达式;(2)求顶点A 的坐标(用含字母a 的代数式表示),判断顶点A 是在x 轴上方还是下方,并说明理由; (3)当x ≥0时,抛物线221y x ax a -++-=(a 为常数)的最高点到直线y =3a 的距离为5,求a 的值. 【答案】(1)241y x x =-+-(2)()2,1a a a -+,顶点A 在x 轴上方,理由见解析(3)222+-1【详解】(1)解:当抛物线221y x ax a -++-=(a 为常数)经过点(1,2), ∴2121a a =-++-, 整理得2a =.将2a =代入221y x ax a -++-=中, ∴抛物线的函数表达式为241y x x =-+-;(2)解:∵抛物线221y x ax a -++-=(a 为常数)的顶点为A , ∴()2221b ax a a =-=-=⨯-, 将x a =代入221y x ax a -++-=中, 得到222211y a a a a a =-++-=-+,∴顶点为A 的坐标为()2,1a a a -+;顶点A 在x 轴上方,理由如下:∵2213124a a a ⎛⎫-+=-+ ⎪⎝⎭,2102a ⎛⎫-≥ ⎪⎝⎭,∴2314a a -+≥, ∴顶点A 在x 轴上方.(3)解:由(2)可知,抛物线221y x ax a -++-=的对称轴为x a =,顶点坐标为()2,1a a a -+,①当0a >时,对称轴在y 轴右侧,如图所示,∵x ≥0时图象的最高点是顶点()2,1a a a -+,且最高点到直线y =3a 的距离为5,∴2135a a a -+-=,即2415a a -+=,若2415a a -+=,解得12222,222a a =+=-(不合题意,舍去), 若2415a a -+=-,()222a -=-,原方程无解; ②当0a =时,对称轴是y 轴,如图所示,∵x ≥0时图象的最高点是顶点0,1,最高点到直线y =3a 的距离不可能为5, ∴此种情况不存在;③当0a <时,对称轴在y 轴左侧,如图所示,∵x ≥0时图象的最高点是()0,1a -,且最高点到直线y =3a 的距离为5, ∴135a a --=,解得1a =-. 综上所述,a 的值为222+或-1.类型三:二次函数的解析式用待定系数法可求出二次函数的解析式,确定二次函数一般需要三个独立条件,根据不同条件选择不同的设法:(1)设一般式:y =ax 2+bx +c (a ≠0),若已知条件是图象上的三个点,则设所求二次函数为y =ax 2+bx +c ,将已知条件代入解析式,得到关于a ,b ,c 的三元一次方程组,解方程组求出a ,b ,c 的值,解析式便可得出. (2)设顶点式:y =a (x -h )2+k ,若已知二次函数图象的顶点坐标或对称轴方程与最大值(或最小值),设所求二次函数为y =a (x -h )2+k ,将已知条件代入,求出待定系数,最后将解析式化为一般形式.(3)设交点式:y =a (x -x 1)(x -x 2)(a ≠0),若已知二次函数图象与x 轴的两个交点的坐标为(x 1,0),(x 2,0),设所求二次函数为y =a (x -x 1)(x -x 2),将第三个点的坐标(m ,n )(其中m ,n 为已知数)或其他已翻条件代入,求出待定系数a ,最后将解析式化为一般形式.典型例题例题1.(2021·江苏·九年级专题练习)已知二次函数的图象的顶点是(1,2)-,且经过点(0,5)-,则二次函数的解析式是( ). A .23(1)2y x =-+- B .23(1)2y x =+- C .23(1)2y x =--- D .23(1)2=--y x【答案】C【详解】解:设该抛物线解析式是:y =a (x -1)2﹣2(a ≠0). 把点(0,-5)代入,得 a (0-1)2﹣2=-5, 解得a=-3.故该抛物线解析式是23(1)2y x =---. 故答案选:C点评:例题1主要考查了待定系数法求抛物线的解析式,难度不大,需要掌握抛物线的顶点式. 例题2.(2020·内蒙古·乌海市海南区教育局教研室九年级期中)若抛物线的顶点为点(2,3)且抛物线经过点(3,1),那么抛物线解析式是( ) A .y=4(x -2)2 -3 B .y=-2(x -2)2+3C .y=-2(x -2)2-3D .y= -225(x -2)2+3 【答案】B【详解】∵抛物线的顶点为(2,3), ∴设抛物线的解析式为y=a (x -2)2+3, ∵经过点(3,1), ∴代入得:1=a (3-2)2+3, 解得:a=-2, 即y=-2(x -2)2+3, 故选B .点评:例题2考查了求抛物线的解析式的应用,解题的关键是注意抛物线解析式的设法.设抛物线的解析式为y=a (x-2)2+3,把点(3,1)代入得出1=a (3-2)2+3,求出a 即可.例题3.(2020·吉林·九年级阶段练习)将二次函数2y x x =+的图象沿x 轴翻折后,所得图象的函数解析式是( ) A .2y x x =+ B .2y x xC .2y x x =-+D .2y x x =--【答案】D【详解】∵2211()24y x x x =+=+-,∴二次函数2y x x =+的图象顶点坐标为(-12,-14),∴将二次函数2y x x =+的图象沿x 轴翻折后,所得图象的顶点坐标为(-12,14),且图形开口方向相反,开口大小相等,故a=1,∴翻折后图象的函数解析式为2211()24x y x x =-++=--,故选:D.点评:例题3考查翻折的性质,求函数解析式,将二次函数的一般形式化为顶点式.先求出二次函数2y x x =+的图象顶点坐标,利用翻折得到所得函数的顶点坐标为(-12,14),a=1,由此得到函数的解析式. 例题4.(2022·湖北襄阳·九年级期末)已知一个二次函数的图象开口向上,顶点坐标为()0,5-,那么这个二次函数的解析式可以是________.(只需写一个). 【答案】25y x =-(答案不唯一)【详解】解:∵二次函数的图象开口向上, ∴二次函数()()20=-+≠y a x h k a 中0a >, ∵顶点坐标为()0,5-,∴这个二次函数的解析式可以是25y x =- 故答案为:25y x =-(答案不唯一)点评:例题4主要考查了待定系数法求函数解析式,熟练掌握抛物线的顶点式是解题的关键.根据二次函数的图象开口向上,可得0a >,再由顶点坐标为()0,5-,即可求解例题5.(2022·河南新乡·九年级期末)小刚在用描点法画抛物线C 1:2y ax bx c =++时,列出了下面的表格:x … 0 1 2 3 4 … y…36763…请根据表格中的信息,写出抛物线C 1的解析式:______. 【答案】243y x x =-++【详解】解:把(0,3)(1,6)(2,7)代入y =ax 2+bx +c 中得: 36427c a b c a b c ⎧⎪++⎨⎪++⎩===, 解得:143a b c -⎧⎪⎨⎪⎩===,∴抛物线C 1的解析式为:y =-x 2+4x +3, 故答案为:y =-x 2+4x +3.点评:例题5考查了二次函数的性质,待定系数法求二次函数解析式,解题的关键是准确熟练地进行计算. 例题6.(2022·河北·保定市清苑区北王力中学九年级期末)在下图的平面直角坐标系中,已知抛物线22y x mx =-与x 轴的一个交点为A (4,0).(1)求抛物线的表达式及顶点B 的坐标;(2)将05x ≤≤时函数的图象记为G ,点P 为G 上一动点,求P 点纵坐标的取值范围;(3)在(2)的条件下,若经过点C (4,-4)的直线0y kx b k =+≠()与图象G 有两个公共点,结合图象直接写出b 的取值范围.【答案】(1)24y x x =-,B (2,-4) (2)45P y -≤≤ (3)40b -<≤【详解】(1)解:∵A (4,0)在抛物线22y x mx =-上 ∴1680m -=,解得2m =.∴24y x x =-,即()224y x =-- ∴顶点坐标为B (2,-4). (2)解:如图所示, 当2x =时,y 有最小值-4; 当5x =时,y 有最大值5∴点P 纵坐标的P y 的取值范围是45P y -≤≤.(3)解:如图所示: b 的取值范围为−4<b ≤0,直线0y kx b k =+≠()与图象G 有两个公共点.点评:例题6主要考查了二次函数的解析式的求法和与几何图形结合的综合能力的培养.关键是利用数形结合的思想把代数和几何图形结合起来.(1)根据待定系数法可求抛物线的表达式及顶点D 的坐标;(2)根据二次函数的增减性和对称性可求P 点纵坐标P y 的取值范围; (3)先画出函数图象,再结合图象写出b 的取值范围.同类题型演练1.(2022·全国·九年级专题练习)已知抛物线与二次函数y =2x 2的图象的开口大小相同,开口方向相反,且顶点坐标为(﹣1,2021),则该抛物线对应的函数表达式为( ) A .y =﹣2(x ﹣1)2 +2021B .y =2(x ﹣1)2 +2021C .y =﹣2(x +1)2+2021D .y =2(x +1)2+2021【答案】C【详解】解:∵抛物线的顶点坐标为(﹣1,2021), ∴设抛物线的解析式为y =a (x +1)2+2021,∵抛物线y =a (x +1)2+2021与二次函数y =2x 2的图象的开口大小相同,开口方向相反, ∴a =﹣2,∴抛物线的解析式为y =﹣2(x +1)2+2021. 故选:C .2.(2022·全国·九年级专题练习)抛物线()()213y x x =+-关于y 轴对称后所得到的抛物线解析式为( ) A .()()213y x x =-+- B .()()213y x x =-- C .()()213y x x =-+ D .()()213y x x =--+【答案】C【详解】∵拋物线()()()2213=2-1-8y x x x =+-,∴顶点坐标为(1,-8),关于y 轴对称后顶点坐标为(-1,-8),且开口向上, ∴该抛物线的解析式为()()()221-823-1y x x x =+=+; 故选:C .3.(2021·江苏·九年级专题练习)已知点()2,3在抛物线22y ax ax c =-+上,则下列四个点中,一定也在该抛物线上的是( ) A .()0,3 B .()0,3-C .()3,2D .()2,3--【答案】A【详解】解:将点(2,3)代入抛物线22y ax ax c =-+, 可得y=c=3, ∴223y ax ax =-+. 当x=0时,y=c=3;当x=3时,y=9a -6a+3=3a+3; 当x=-2时,y=4a+4a+3=8a+3;故(0,3)一定在该抛物线上, 故选:A .4.(2021·山东·威海市实验中学九年级期末)抛物线2y ax bx =+经过点A (2,0),该抛物线顶点在直线2y x =-+上,则该抛物线解析式为______. 【答案】22y x x =-+【详解】∵抛物线2y ax bx =+经过点()0,0 ,A (2,0), ∴顶点横坐标为1, ∵顶点在直线y =-x +2上, ∴y =-1+2=1, ∴顶点坐标(1,1),∵y =ax 2+bx 过点A (2,0),(1,1),∴1420a b a b +=⎧⎨+=⎩,∴12a b =-⎧⎨=⎩,∴22y x x =-+. 故答案为:22y x x =-+.5.(2022·全国·九年级专题练习)如图1,在平面直角坐标系xOy 中,抛物线y =ax 2+bx +c 与x 轴分别相交于A 、B 两点,与y 轴相交于点C ,下表给出了这条抛物线上部分点(x ,y )的坐标值:x … ﹣1 0 1 2 3 … y…343…则这条抛物线的解析式为_______. 【答案】2y x 2x 3=-++【详解】根据表格可得到点(-1,0)、(0,3)、(3,0) 设抛物线的解析式为(1)(3)y a x x =+- 将(0,3)代入解析式得33a =- 解得1a =-∴解析式为2(1)(3)23y x x x x =-+-=-++故答案为:2y x 2x 3=-++.6.(2021·黑龙江·肇源县第五中学九年级期中)如图,抛物线2y ax bx c =++(a ≠0)与直线y =x +1相交于A (-1,0),B (4,n )两点,且抛物线经过点C (5,0).(1)求抛物线的解析式;(2)点P 是直线AB 上方抛物线上的一个动点(不与点A 、点B 重合),过点P 作直线PD ⊥x 轴于点D ,交直线AB 于点E ,设点P 的横坐标为m .①求线段PE 长的最大值,并求此时P 点坐标;②是否存在点P 使BEC △为等腰三角形?若存在,请直接写出m 的值;若不存在,请说明理由. 【答案】(1)245y x x =-++ (2)①PE 有最大值254,点P 的坐标为335,24⎛⎫⎪⎝⎭;②存在,413或0或34 【详解】(1)解:由题意,抛物线2y ax bx c =++的解析式可化为(1)(5)y a x x =+-, 将点()4,B n 代入直线1y x =+ 得:415n =+=,将点(4,5)B 代入(1)(5)y a x x =+- 得:(41)(45)5a +⨯-=, 解得1a =-,则抛物线的解析式为2(1)(5)45y x x x x =-+-=-++, 即245y x x =-++;(2)①由题意:设2(,45)P m m m -++,(,1)E m m +, 点P 在点E 的上方,则()2223254513424PE m m m m m m =-++-+=-++=-⎫ ⎪⎭+⎛⎝-∵ -1<0∴当m =32时,PE 有最大值,最大值为254当m =32时,235454m m -++=,此时点P 的坐标为(32,354);②存在,m 的值为4130或34.(4,5),(5,0),(,1)B C E m m +,222(54)(05)26BC ∴=-+-=,2222(4)(15)2(4)BE m m m =-++-=-,22222(5)(10)(5)(1)CE m m m m =-++-=-++,由等腰三角形的定义,分以下三种情况:(ⅰ)当BC BE =时,BEC △为等腰三角形,则22BC BE =,即22(4)26m -=, 解得413m =413m =(ⅰ)当BC CE =时,BEC △为等腰三角形,则22BC CE =,即22(5)(1)26m m -++=, 解得0m =或4m =(舍去);(ⅰ)当BE CE =时,BEC △为等腰三角形,则22BE CE =,即2222(4)(5)(1)m m m -=-++,解得34m =;综上,m 的值为4130或34.类型四:二次函数的平移问题(1)抛物线在平移的过程中,a 的值不发生变化,变化的只是顶点的位置,且与平移方向有关. (2)涉及抛物线的平移时,首先将表达式转化为顶点式y =a (x -h )2+k 的形式.(3)抛物线的移动主要看顶点的移动,y =ax 2的顶点是(0,0),y =ax 2+k 的顶点是(0,k ),y =a (x -h )2的顶点是(h ,0),y =a (x -h )2+k 的顶点是(h ,k ).我们只需在坐标系中画出这几个顶点,即可轻松地看出平移的方向.(4)抛物线的平移口诀:自变量加减左右移,函数值加减上下移.典型例题例题1.(2021·黑龙江·兰西县第三中学九年级期中)将抛物线2y x 向右平移2个单位,再向上平移1个单位,所得抛物线相应的函数表达式是( )A .2(2)1y x =++B .2(2)1y x =+-C .22()1y x =-+D .2(2)1y x =--【答案】C 【详解】∵抛物线2y x 的顶点坐标为(0,0),∴2yx 向右平移2个单位,再向上平移1个单位后的图象的顶点坐标为(2,1),∴得到新抛物线的解析式是22()1y x =-+, 故选:C .点评:例题1考查了二次函数图象与几何变换:由于抛物线平移后的形状不变,故a 不变,所以求平移后的抛物线解析式通常可利用两种方法:一是求出原抛物线上任意两点平移后的坐标,利用待定系数法求出解析式;二是只考虑平移后的顶点坐标,即可求出解析式.例题2.(2022·内蒙古赤峰·九年级期末)将抛物线()2325y x =++向下平移1个单位,再向右平移两个单位后的顶点坐标是( ) A .(-4,4) B .(0,4) C .(0,6) D .(-4,-6)【答案】B【详解】解:将抛物线()2325y x =++向下平移1个单位,再向右平移两个单位后的解析式为: ()232251,y x =+-+- 即234,y x =+∴抛物线的顶点坐标为:()0,4, 故选:B点评:例题2考查二次函数图象的平移,解题关键是掌握二次函数图象的平移规律,掌握二次函数的顶点式.例题3.(2021·湖北·襄阳市樊城区青泥湾中学九年级阶段练习)要得到抛物线22(4)1y x =-+,可以将抛物线22y x =( )A .向左平移4个单位长度,再向上平移1个单位长度B .向左平移4个单位长度,再向下平移1个单位长度C .向右平移4个单位长度,再向上平移1个单位长度D .向右平移4个单位长度,再向下平移1个单位长度 【答案】C【详解】解:∵y =2(x -4)2+1的顶点坐标为(4,1),y =2x 2的顶点坐标为(0,0), ∴将抛物线y =2x 2向右平移4个单位,再向上平移1个单位,可得到抛物线y =2(x -4)2+1.故选:B .点评:例题3考查了二次函数图象与几何变换,解答时注意抓住点的平移规律和求出关键点顶点坐标. 例题4.(2022·天津滨海新·九年级期末)抛物线()223y x =+-可以由抛物线2y x 先向左平移2个单位,再向下平移___________个单位得到的. 【答案】3 【详解】解:抛物线2y x 向左平移2个单位,向下平移3个单位得到的函数图象的解析式为:()223y x =+-. 故答案为:3.点评:例题4考查的是二次函数的图象平移变换,熟知函数图象平移变换的法则是解答此题的关键. 例题5.(2022·江苏·九年级专题练习)已知抛物线2(1)y a x h =-+,经过点(0,3)-和(3,0). (1)求a 、h 的值;(2)将该抛物线向上平移2个单位长度,再向右平移1个单位长度,得到新的抛物线,直接写出新的抛物线相应的函数表达式. 【答案】(1)14a h =⎧⎨=-⎩;(2)242y x x =-+【详解】(1)解:将点(0,3)-和(3,0)代入抛物线2(1)y a x h =-+得:22(01)3(31)0a h a h ⎧-+=-⎨-+=⎩解得:14a h =⎧⎨=-⎩,∴1a =,4h =-;(2)解:∵原函数的表达式为:2(1)4y x =--,向上平移2个单位长度,再向右平移1个单位长度,得∴平移后的新函数表达式为:22(11)42=42y x x x =---+-+即242y x x =-+;点评:例题5考查了待定系数法确定解析式,顶点式的函数平移,口诀:“左加右减,上加下减”,正确的计算和牢记口诀是解题的关键同类题型演练1.(2021·福建·平潭翰英中学九年级期中)将抛物线y = x 2先向左平移5个单位,再向下平移4个单位,得到新抛物线的解析式是( ) A . y =()25x +-4 B . y =()25x ++4 C . y =()25x --4 D . y =()25x -+4【答案】A。
二次函数的图像与性质(含答案)

九年级数学竞赛专题 ---二次函数的图像与性质一、内容概述二次函数有丰富的内容,下面从四个方面加以总结1.定义: 形如函数2(0)y ax bx c a =++≠称为二次函数,对实际问题二次函数也有定义域.2.图像二次函数的图像为抛物线,一般作二次函数图像,取五个点,先确定顶点的横坐标,再以它为中心向左、向右对称取点.3.性质 对2(0)y ax bx c a =++≠的图像来讲,(1)开口方向:当0a >时,抛物线开口向上;当0a <时,抛物线开口向下。
(2)对称轴方程:2bx a=-(3)顶点坐标:24,24b ac b a a ⎛⎫-- ⎪⎝⎭(4)抛物线与坐标轴的交点情况: 若240bac -<,则抛物线与x 轴没有交点;若240b ac -=,则抛物线与x 轴有一个交点;若240b ac ->,则抛物线与x 轴有两个交点,分别为,;另外,抛物线与y 轴的交点为()0,c .(5)抛物线在x a=(6)y 与x 的增减关系:当0a >,2b x a >-时,y 随x 的增大而增大,2bx a <-时,y 随x 的增大而减小;当0a <,2b x a >-时,y 随x 的增大而减小,2bx a<-时,y 随x 的增大而增大.(7)最值:当0a >时,y 有最小值,当2b x a =-时,244ac b y a -最小值=;当0a <时,y 有最大值,当2b x a =-时,244ac b y a-最大值=(8)若抛物线与x 轴两交点的横坐标为1x 、2x (12x x <),则:当0a >时,12x x x <<时,0y <;12x x x x <>或时,0y >;当0a<时,12x x x <<时,0y >;12x x x x <>或时,0y <.4.求解析式抛物线的解析式常用的有三种形式:(1)一般式:2(0)y ax bx c a =++≠(2)顶点式:2()(0)y a x h k a =-+≠,其中(,)h k 是抛物线的顶点坐标。
人教版九年级数学上册专题四二次函数的图象性质与系数的关系同步测试及答案【2020精品】

二次函数的图象性质与系数的关系 [见A 本P22] (教材P47习题22.2第6题)下列情形时,如果a >0,抛物线y =ax 2+bx +c 的顶点在什么位置。
(1)方程ax 2+bx +c =0有两个不等的实数根;(2)方程ax 2+bx +c =0有两个相等的实数根;(3)方程ax 2+bx +c =0无实数根;如果a <0呢?解:a >0,抛物线开口向上:(1)抛物线与x 轴相交(有两个交点),抛物线的顶点在x 轴下方.(2)抛物线与x 轴相切(只有一个交点),抛物线的顶点在x 轴上.(3)抛物线与x 轴无交点,抛物线的顶点在x 轴上方.a <0,抛物线开口向下:(1)抛物线与x 轴相交(有两个交点),抛物线的顶点在x 轴上方.(2)抛物线与x 轴相切(只有一个交点),抛物线的顶点在x 轴上.(3)抛物线与x 轴无交点,抛物线的顶点在x 轴下方.已知二次函数y =-x 2+3x -35,当自变量x 取m 时对应的函数值大于0,设自变量x 分别取m -3,m +3时对应的函数值为y 1,y 2,则( D )A .y 1>0,y 2>0B .y 1>0,y 2<0C .y 1<0,y 2>0D .y 1<0,y 2<0如图1,二次函数y =ax 2+bx +c (a ≠0)的图象与x 轴交于A ,B 两点,与y 轴交于C 点,且对称轴为x =1,点B 坐标为(-1,0).则下面的四个结论:①2a +b =0;②4a -2b +c <0;③ac >0;④当y <0时,x <-1或x >2.其中正确的个数是( B )图1A .1B .2C .3D .4函数y =x 2+bx +c 与y =x 的图象如图3所示,有以下结论:①b 2-4c >0;②b +c +1=0;③3b +c +6=0;④当1<x <3时,x 2+(b -1)x +c <0.其中正确的个数是( B )图2A .1B .2C .3D .4二次函数y =ax 2+bx +c (a ≠0)的图象如图4所示:图3(1)判断a ,b ,c 及b 2-4ac 的符号;(2)若|OA |=|OB |,求证:ac +b +1=0.解:(1)由图象知:开口向上,∴a>0,对称轴-b2a>0,∴b<0,与y轴交于负半轴,∴c<0,与x轴有两个交点,∴Δ=b2-4ac>0;(2)∵|OA|=|OB|,且|OB|=|c|=-c,∴ax2+bx+c=0有一根为c,从而ac2+bc+c=0,又∵c≠0,∴ac+b+1=0.。
上册微专题四二次函数图象的性质与系数的关系人教版九年级数学全一册完美课件

上册 微专题四 二次函数图象的性质与系数的关系- 2020秋 人教版 九年级 数学全 一册课 件(共1 7张PPT )
上册 微专题四 二次函数图象的性质与系数的关系- 2020秋 人教版 九年级 数学全 一册课 件(共1 7张PPT )
由图象知对称轴 x=-2ba>-1,得2ba<1.由 a<0,结合不等式的性质可得 b>2a, 即 2a<b,故③错误;
上册 微专题四 二次函数图象的性质与系数的关系- 2020秋 人教版 九年级 数学全 一册课 件(共1 7张PPT )
[2019·鄂州]二次函数 y=ax2+bx+c 的图象如图 4 所示,对称轴是直线 x=1.下列结论:①abc<0;②3a+c>0;③(a+c)2-b2<0;④a+b≤m(am+b)(m 为 实数).其中正确结论的个数为( C )
上册 微专题四 二次函数图象的性质与系数的关系- 2020秋 人教版 九年级 数学全 一册课 件(共1 7张PPT )
上册 微专题四 二次函数图象的性质与系数的关系- 2020秋 人教版 九年级 数学全 一册课 件(共1 7张PPT )
[2019·娄底]二次函数 y=ax2+bx+c 的图象如图 3 所示,下列结论中正
上册 微专题四 二次函数图象的性质与系数的关系- 2020秋 人教版 九年级 数学全 一册课 件(共1 7张PPT )
③由于抛物线与 x 轴有两个交点, ∴Δ=b2-4ac>0,故③正确; ④由图象可知 x=1 时,y=a+b+c<0,故④正确; ⑤当 x>-2ba时,y 随着 x 的增大而增大,故⑤错误. 故选 C.
上册 微专题四 二次函数图象的性质与系数的关系- 2020秋 人教版 九年级 数学全 一册课 件(共1 7张PPT )
二次函数的图象和性质(含详细参考答案10页)

2013年中考数学专题复习 二次函数的图象和性质【基础知识回顾】一、 二次函数的定义:一般地如果y= (a 、b 、c 是常数a ≠0)那么y 叫做x 的二次函数名师提醒: 二次函数y=kx 2+bx+c(a ≠0)的结构特征是:1、等号左边是函数,右边是 关 于 自 变 量x 的 二 次 式,x 的 最 高 次 数 是 , 按 一次排列2、强调二次项系数a 0二、二次函数的同象和性质:1、二次函数y=kx 2+bx+c(a ≠0)的同象是一条 ,其定点坐标为 对称轴式2、在抛物y=kx 2+bx+c(a ≠0)中:(1)当a>0时,y 口向 ,当x<-2ba 时,y 随x 的增大而 ,当x 时,y 随x 的增大而增大,(2)当a<0时,开口向 当x<-2ba时,y 随x 增大而增大,当x 时,y 随x 增大而减小.名师提醒:注意几个特殊形式的抛物线的特点1、y=ax 2 ,对称轴 定点坐标2、y= ax 2+k ,对称轴 定点坐标 3、y=a(x-h) 2对称轴 定点坐标4、y=a(x-h) 2 +k 对称轴 定点坐标三、二次函数同象的平移名师提醒:二次函数的平移本质可看作是定点问题的平移,固然要掌握整抛物线的平移,只要关键的顶点平移即可四、二次函数y= ax 2+bx+c 的同象与字母系数之间的关系:a:开口方向 向上则a 0,向下则a 0 |a |越大,开口越 b:对称轴位置,与a 联系一起,用 判断b=0时,对称轴是 c:与y 轴的交点:交点在y 轴正半轴上,则c 0负半轴上则c 0,当c=0时,抛物点过 点名师提醒:在抛物线y= ax 2+bx+c 中,当x=1时,y= 当x=-1时y= ,经常根据对应的函数值判考a+b+c 和a-b+c 的符号【重点考点例析】考点一:二次函数图象上点的坐标特点例1 (2012•常州)已知二次函数y=a (x-2)2+c (a >0),当自变量x3、0时,对应的函数值分别:y1,y2,y3,,则y1,y2,y3的大小关系正确的是()A.y3<y2<y1B.y1<y2<y3C.y2<y1<y3D.y3<y1<y2对应训练1.(2012•衢州)已知二次函数y=12-x2-7x+152,若自变量x分别取x1,x2,x 3,且0<x1<x2<x3,则对应的函数值y1,y2,y3的大小关系正确的是()A.y1>y2>y3B.y1<y2<y3C.y2>y3>y1D.y2<y3<y1考点二:二次函数的图象和性质例2 (2012•咸宁)对于二次函数y=x2-2mx-3,有下列说法:①它的图象与x轴有两个公共点;②如果当x≤1时y随x的增大而减小,则m=1;③如果将它的图象向左平移3个单位后过原点,则m=-1;④如果当x=4时的函数值与x=2008时的函数值相等,则当x=2012时的函数值为-3.其中正确的说法是.(把你认为正确说法的序号都填上)考点:二次函数的性质;二次函数图象与几何变换;抛物线与x轴的交点.对应训练2.(2012•河北)如图,抛物线y1=a(x+2)2-3与y2=12(x-3)2+1交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B,C.则以下结论:①无论x取何值,y2的值总是正数;②a=1;③当x=0时,y2-y1=4;④2AB=3AC;其中正确结论是()A.①② B.②③ C.③④ D.①④考点三:抛物线的特征与a、b、c的关系例3 (2012•玉林)二次函数y=ax2+bx+c(a≠0)的图象如图所示,其对称轴为x=1,有如下结论:①c<1;②2a+b=0;③b2<4ac;④若方程ax2+bx+c=0的两根为x1,x2,则x1+x2=2,则正确的结论是()A.①② B.①③ C.②④ D.③④对应训练3.(2012•重庆)已知二次函数y=ax2+bx+c(a≠0)的图象如图所示对称轴为x=12-.下列结论中,正确的是()A.abc>0 B.a+b=0 C.2b+c>0 D.4a+c<2b考点四:抛物线的平移例4 (2012•桂林)如图,把抛物线y=x2沿直线y=x平移2个单位后,其顶点在直线上的A处,则平移后的抛物线解析式是()A.y=(x+1)2-1 B.y=(x+1)2+1C.y=(x-1)2+1 D.y=(x-1)2-1对应训练4.(2012•南京)已知下列函数①y=x2;②y=-x2;③y=(x-1)2+2.其中,图象通过平移可以得到函数y=x2+2x-3的图象的有(填写所有正确选项的序号).【聚焦中考】1.(2012•泰安)二次函数y=a(x+m)2+n的图象如图,则一次函数y=mx+n的图象经过()A.第一、二、三象限 B.第一、二、四象限C.第二、三、四象限 D.第一、三、四象限2.(2012•济南)如图,二次函数的图象经过(-2,-1),(1,1)两点,则下列关于此二次函数的说法正确的是()A.y的最大值小于0 B.当x=0时,y的值大于1C.当x=-1时,y的值大于1 D.当x=-3时,y的值小于03.(2012•菏泽)已知二次函数y=ax2+bx+c的图象如图所示,那么一次函数y=bx+c和反比例函数ayx在同一平面直角坐标系中的图象大致是A. B. C. D.4.(2012•泰安)设A(-2,y1),B(1,y2),C(2,y3)是抛物线y=-(x+1)2+a上的三点,则y1,y2,y3的大小关系为()A.y1>y2>y3B.y1>y3>y2C.y3>y2>y1D.y3>y1>y25.(2012•烟台)已知二次函数y=2(x-3)2+1.下列说法:①其图象的开口向下;②其图象的对称轴为直线x=-3;③其图象顶点坐标为(3,-1);④当x<3时,y随x的增大而减小.则其中说法正确的有()A.1个 B.2个 C.3个 D.4个6.(2012•日照)二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出下列结论:①b2-4ac>0;②2a+b<0;③4a-2b+c=0;④a:b:c=-1:2:3.其中正确的是()A.①② B.②③ C.③④ D.①④7.(2012•泰安)将抛物线y=3x2向上平移3个单位,再向左平移2个单位,那么得到的抛物线的解析式为()A.y=3(x+2)2+3 B.y=3(x-2)2+3 C.y=3(x+2)2-3 D.y=3(x-2)2-38.(2012•潍坊)许多家庭以燃气作为烧水做饭的燃料,节约用气是我们日常生活中非常现实的问题.某款燃气灶旋转位置从0度到90度(如图),燃气关闭时,燃气灶旋转的位置为0度,旋转角度越大,燃气流量越大,燃气开到最大时,旋转角度为90度.为测试燃气灶旋转在不同位置上的燃气用量,在相同条件下,选择燃气灶旋钮的5个不同位置上分别烧开一壶水(当旋钮角度太小时,其火力不能够将水烧开,故选择旋钮角度x度的范围是18≤x≤90),记录相关数据得到下表:旋钮角度(度)20 50 70 80 90所用燃气量(升)73 67 83 97 115(1)请你从所学习过的一次函数、反比例函数和二次函数中确定哪种函数能表示所用燃气量y 升与旋钮角度x度的变化规律?说明确定是这种函数而不是其它函数的理由,并求出它的解析式;(2)当旋钮角度为多少时,烧开一壶水所用燃气量最少?最少是多少?(3)某家庭使用此款燃气灶,以前习惯把燃气开到最大,现采用最节省燃气的旋钮角度,每月平均能节约燃气10立方米,求该家庭以前每月的平均燃气量.【备考真题过关】一、选择题1.(2012•白银)二次函数y=ax2+bx+c的图象如图所示,则函数值y<0时x的取值范围是()A.x<-1 B.x>3 C.-1<x<3 D.x<-1或x>32.(2012•兰州)二次函数y=ax2+bx+c(a≠0)的图象如图所示,若|ax2+bx+c|=k(k≠0)有两个不相等的实数根,则k的取值范围是()A.k<-3 B.k>-3 C.k<3 D.k>33.(2012•德阳)设二次函数y=x2+bx+c,当x≤1时,总有y≥0,当1≤x≤3时,总有y≤0,那么c的取值范围是()A.c=3 B.c≥3 C.1≤c≤3 D.c≤34.(2012•北海)已知二次函数y=x2-4x+5的顶点坐标为()A.(-2,-1) B.(2,1)C.(2,-1) D.(-2,1)5.(2012•广元)若二次函数y=ax2+bx+a2-2(a、b为常数)的图象如图,则a的值为()A.1 B.2 C.-2 D.-26.(2012•西宁)如同,二次函数y=ax2+bx+c的图象过(﹣1,1)、(2,﹣1)两点,下列关于这个二次函数的叙述正确的是()A.当x=0时,y的值大于1B.当x=3时,y的值小于0C.当x=1时,y的值大于1D.y的最大值小于06.(2012•巴中)对于二次函数y=2(x+1)(x-3),下列说法正确的是()A.图象的开口向下 B.当x>1时,y随x的增大而减小C.当x<1时,y随x的增大而减小 D.图象的对称轴是直线x=-17.(2012•天门)已知二次函数y=ax2+bx+c的图象如图所示,它与x轴的两个交点分别为(-1,0),(3,0).对于下列命题:①b-2a=0;②abc<0;③a-2b+4c <0;④8a+c>0.其中正确的有()A.3个 B.2个 C.1个 D.0个8.(2012•乐山)二次函数y=ax2+bx+1(a≠0)的图象的顶点在第一象限,且过点(-1,0).设t=a+b+1,则t值的变化范围是()A.0<t<1 B.0<t<2 C.1<t<2 D.-1<t<19.(2012•扬州)将抛物线y=x2+1先向左平移2个单位,再向下平移3个单位,那么所得抛物线的函数关系式是()A.y=(x+2)2+2 B.y=(x+2)2-2C.y=(x-2)2+2 D.y=(x-2)2-210.(2012•宿迁)在平面直角坐标系中,若将抛物线y=2x2-4x+3先向右平移3个单位长度,再向上平移2个单位长度,则经过这两次平移后所得抛物线的顶点坐标是()A.(-2,3) B.(-1,4) C.(1,4) D.(4,3)11.(2012•陕西)在平面直角坐标系中,将抛物线y=x2-x-6向上(下)或向左(右)平移m个单位,使平移后的抛物线恰好经过原点,则|m|的最小值为()A.1 B.2 C.3 D.6二、填空题12.(2012•玉林)二次函数y=-(x-2)2+94的图象与x轴围成的封闭区域内(包括边界),横、纵坐标都是整数的点有个(提示:必要时可利用下面的备用图画出图象来分析).13.(2012•长春)在平面直角坐标系中,点A是抛物线y=a(x-3)2+k与y轴的交点,点B是这条抛物线上的另一点,且AB∥x轴,则以AB为边的等边三角形ABC的周长为.14.(2012•孝感)二次函数y=ax2+bx+c(a,b,c是常数,a≠0)图象的对称轴是直线x=1,其图象的一部分如图所示.对于下列说法:①abc<0;②a-b+c<0;③3a+c<0;④当-1<x<3时,y>0.其中正确的是(把正确的序号都填上).15.(2012•苏州)已知点A(x1,y1)、B(x2,y2)在二次函数y=(x-1)2+1的图象上,若x1>x2>1,则y1y2(填“>”、“<”或“=”).16.(2012•成都)有七张正面分别标有数字-3,-2,-1,0,l,2,3的卡片,它们除数字不同外其余全部相同.现将它们背面朝上,洗匀后从中随机抽取一张,记卡片上的数字为a,则使关于x的一元二次方程x2-2(a-1)x+a (a-3)=0有两个不相等的实数根,且以x为自变量的二次函数y=x2-(a2+1)x-a+2的图象不经过点(1,0)的概率是.17.(2012•上海)将抛物线y=x2+x向下平移2个单位,所得抛物线的表达式是.18.(2012•宁波)把二次函数y=(x-1)2+2的图象绕原点旋转180°后得到的图象的解析式为.19.(2012•贵港)若直线y=m (m为常数)与函数y=的图象恒有三个不同的交点,则常数m的取值范围是.19.(2012•广安)如图,把抛物线y=12x2平移得到抛物线m,抛物线m经过点A(-6,0)和原点O(0,0),它的顶点为P,它的对称轴与抛物线y=12x2交于点Q,则图中阴影部分的面积为.三、解答题20.(2012•柳州)已知:抛物线y=34(x-1)2-3.(1)写出抛物线的开口方向、对称轴;(2)函数y有最大值还是最小值?并求出这个最大(小)值;(3)设抛物线与y轴的交点为P,与x轴的交点为Q,求直线PQ的函数解析式.21.(2012•佛山)规律是数学研究的重要内容之一.初中数学中研究的规律主要有一些特定的规则、符号(数)及其运算规律、图形的数值特征和位置关系特征等方面.请你解决以下与数的表示和运算相关的问题:(1)写出奇数a用整数n表示的式子;(2)写出有理数b用整数m和整数n表示的式子;(3)函数的研究中,应关注y随x变化而变化的数值规律(课本里研究函数图象的特征实际上也是为了说明函数的数值规律).下面对函数y=x2的某种数值变化规律进行初步研究:xi0 1 2 3 4 5 …yi0 1 4 9 16 25 …y i+1﹣yi1 3 5 7 9 11 …由表看出,当x的取值从0开始每增加1个单位时,y的值依次增加1,3,5…请回答:①当x的取值从0开始每增加个单位时,y的值变化规律是什么?②当x的取值从0开始每增加个单位时,y的值变化规律是什么?【重点考点例析】考点一:二次函数图象上点的坐标特点例1 解:∵二次函数y=a(x-2)2+c(a>0),∴该抛物线的开口向上,且对称轴是x=2.∴抛物线上的点离对称轴越远,对应的函数值就越大,∵x取0时所对应的点离对称轴最远,x取2时所对应的点离对称轴最近,∴y3>y2>y1.故选B.1.(2012•衢州)解:∵二次函数y=12-x2-7x+152,∴此函数的对称轴为:x=2ba-=7712()2--=-⨯-,∵0<x1<x2<x3,三点都在对称轴右侧,a<0,∴对称轴右侧y随x的增大而减小,∴y1>y2>y3.故选:A.考点二:二次函数的图象和性质例2 (2012•咸宁)解:①∵△=4m2-4×(-3)=4m2+12>0,∴它的图象与x轴有两个公共点,故本选项正确;②∵当x≤1时y随x 的增大而减小,∴函数的对称轴x=-22m --≥1在直线x=1的右侧(包括与直线x=1重合),则22m--≥1,即m ≥1,故本选项错误;③将m=-1代入解析式,得y=x 2+2x-3,当y=0时,得x 2+2x-3=0,即(x-1)(x+3)=0,解得,x 1=1,x 2=-3,将图象向左平移3个单位后不过原点,故本选项错误;④∵当x=4时的函数值与x=2008时的函数值相等,∴对称轴为x=420082+=1006,则22m--=1006,m=1006,原函数可化为y=x 2-2012x-3,当x=2012时,y=20122-2012×2012-3=-3,故本选项正确.故答案为①④(多填、少填或错填均不给分). 对应训练2.(2012•河北)解:①∵抛物线y 2=12(x-3)2+1开口向上,顶点坐标在x 轴的上方,∴无论x 取何值,y 2的值总是正数,故本小题正确;②把A (1,3)代入,抛物线y 1=a (x+2)2-3得,3=a (1+2)2-3,解得a=23,故本小题错误;③由两函数图象可知,抛物线y 1=a (x+2)2-3过原点,当x=0时,y 2=12(0-3)2+1=112,故y 2-y 1=112,故本小题错误;④∵物线y 1=a (x+2)2-3与y 2=12(x-3)2+1交于点A (1,3),∴y 1的对称轴为x=-2,y 2的对称轴为x=3,∴B (-5,3),C (5,3)∴AB=6,AC=4,∴2AB=3AC ,故本小题正确.故选D . 考点三:抛物线的特征与a 、b 、c 的关系例3 (2012•玉林)解:由抛物线与y 轴的交点位置得到:c >1,选项①错误;∵抛物线的对称轴为x=2ba-=1,∴2a+b=0,选项②正确;由抛物线与x 轴有两个交点,得到b 2-4ac >0,即b2>4ac ,选项③错误;令抛物线解析式中y=0,得到ax 2+bx+c=0,∵方程的两根为x 1,x 2,且2b a -=1,及b a -=2,∴x 1+x 2=ba-=2,选项④正确,综上,正确的结论有②④.故选C 对应训练3.(2012•重庆)解:A 、∵开口向上,∴a >0,∵与y 轴交与负半轴,∴c <0,∵对称轴在y 轴左侧,∴2ba-<0,∴b >0,∴abc <0,故本选项错误;B 、∵对称轴:x=2b a -=12-,∴a=b ,故本选项错误;C 、当x=1时,a+b+c=2b+c <0,故本选项错误;D 、∵对称轴为x=12-,与x 轴的一个交点的取值范围为x1>1,∴与x 轴的另一个交点的取值范围为x 2<-2,∴当x=-2时,4a-2b+c <0,即4a+c <2b ,故本选项正确.故选D . 考点四:抛物线的平移例4 (2012•桂林)解:∵A 在直线y=x 上,∴设A (m ,m ),∵OA=2,∴m 2+m 2=(2)2,解得:m=±1(m=-1舍去),m=1,∴A (1,1),∴抛物线解析式为:y=(x-1)2+1,故选:C . 对应训练4.(2012•南京)解:原式可化为:y=(x+1)2-4,由函数图象平移的法则可知,将函数y=x 2的图象先向左平移1个单位,再向下平移4个单位即可得到函数y=(x+1)2-4,的图象,故①正确;函数y=(x+1)2-4的图象开口向上,函数y=-x 2;的图象开口向下,故不能通过平移得到,故②错误;将y=(x-1)2+2的图象向左平移2个单位,再向下平移6个单位即可得到函数y=(x+1)2-4的图象,故③正确.故答案为:①③.【聚焦中考】1.解:∵抛物线的顶点在第四象限,∴-m >0,n <0,∴m <0,∴一次函数y=mx+n 的图象经过二、三、四象限,故选C . 2.解:A 、由图象知,点(1,1)在图象的对称轴的左边,所以y 的最大值大于1,不小于0;故本选项错误;B 、由图象知,当x=0时,y 的值就是函数图象与y 轴的交点,而图象与y 轴的交点在(1,1)点的左边,故y <1;故本选项错误;C 、对称轴在(1,1)的右边,在对称轴的左边y 随x 的增大而增大,∵-1<1,∴x=-1时,y 的值小于x=-1时,y 的值1,即当x=-1时,y 的值小于1;故本选项错误;D 、当x=-3时,函数图象上的点在点(-2,-1)的左边,所以y 的值小于0;故本选项正确.故选D . 3.解:∵二次函数图象开口向下,∴a <0,∵对称轴x=2ba-<0,∴b <0,∵二次函数图象经过坐标原点,∴c=0,∴一次函数y=bx+c 过第二四象限且经过原点,反比例函数ay x=位于第二四象限,纵观各选项,只有C 选项符合.故选C . 4.解:∵函数的解析式是y=-(x+1)2+a ,如右图,∴对称轴是x=-1,∴点A 关于对称轴的点A ′是(0,y 1),那么点A ′、B 、C 都在对称轴的右边,而对称轴右边y 随x 的增大而减小,于是y 1>y 2>y 3.故选A .5.解:①∵2>0,∴图象的开口向上,故本小题错误;②图象的对称轴为直线x=3,故本小题错误;③其图象顶点坐标为(3,1),故本小题错误;④当x <3时,y 随x 的增大而减小,正确;综上所述,说法正确的有④共1个.故选A . 6.解:由二次函数图象与x 轴有两个交点,∴b 2-4ac >0,选项①正确;又对称轴为直线x=1,即2ba-=1,可得2a+b=0(i ),选项②错误;∵-2对应的函数值为负数,∴当x=-2时,y=4a-2b+c <0,选项③错误;∵-1对应的函数值为0,∴当x=-1时,y=a-b+c=0(ii ),联立(i )(ii )可得:b=-2a ,c=-3a ,∴a :b :c=a :(-2a ):(-3a )=-1:2:3,选项④正确,则正确的选项有:①④.故选D . 7.A8.解:(1)若设y=kx+b (k ≠0),由7320 6750k b k b =+⎧⎨=+⎩,解得1577k b ⎧=-⎪⎨⎪=⎩,所以y=15-x+77,把x=70代入得y=65≠83,所以不符合;若设k y x =(k ≠0),由73=20k ,解得k=1460,所以y=1460x,把x=50代入得y=29.2≠67,所以不符合;若设y=ax 2+bx+c , 则由7340020 67250050 83490070a b c a b c a b c =++⎧⎪=++⎨⎪=++⎩,解得1 508 597a b c ⎧=⎪⎪⎪=-⎨⎪=⎪⎪⎩,所以y=150x 2-85x+97(18≤x ≤90),把x=80代入得y=97,把x=90代入得y=115,符合题意.所以二次函数能表示所用燃气量y 升与旋钮角度x 度的变化规律; (2)由(1)得:y=150x 2-85x+97=150(x-40)2+65,所以当x=40时,y 取得最小值65.即当旋钮角度为40°时,烧开一壶水所用燃气量最少,最少为65升;(3)由(2)及表格知,采用最节省燃气的旋钮角度40度比把燃气开到最大时烧开一壶水节约用气115-65=50(升) 设该家庭以前每月平均用气量为a 立方米,则由题意得:50115a=10,解得a=23(立方米),即该家庭以前每月平均用气量为23立方米.【备考真题过关】1.C 2.D 解:根据题意得:y=|ax 2+bx+c|的图象如右图:所以若|ax 2+bx+c|=k (k ≠0)有两个不相等的实数根,则k >3,故选D .3.B 解:∵当x ≤1时,总有y ≥0,当1≤x ≤3时,总有y ≤0,∴函数图象过(1,0)点,即1+b+c=0①,∵当1≤x ≤3时,总有y ≤0,∴当x=3时,y=9+3b+c ≤0②,①②联立解得:c ≥3,故选B . 4.B 5.C6.解:由图可知,当x >﹣1时,函数值y 随x 的增大而减小,A 、当x=0时,y 的值小于1,故本选项错误;B 、当x=3时,y 的值小于0,故本选项正确;C 、当x=1时,y 的值小于1,故本选项错误;D 、y 的最大值不小于1,故本选项错误.6.C 解:二次函数y=2(x+1)(x-3)可化为y=2(x-1)2-8的形式,A 、∵此二次函数中a=2>0,∴抛物线开口向上,故本选项错误;B 、∵由二次函数的解析式可知,此抛物线开口向上,对称轴为x=1,∴当x >1时,y 随x 的增大而增大,故本选项错误;C 、∵由二次函数的解析式可知,此抛物线开口向上,对称轴为x=1,∴当x <1时,y 随x 的增大而减小,故本选项正确; D 、由二次函数的解析式可知抛物线对称轴为x=1,故本选项错误.故选C . 7.B 解:根据图象可得:a >0,c <0,对称轴:2bx a=->0,①∵它与x 轴的两个交点分别为(-1,0),(3,0),∴对称轴是x=1,∴2ba-=1,∴b+2a=0,故①错误;②∵a >0,∴b <0,∵c <0,∴abc >0,故②错误;③∵a-b+c=0,∴c=b-a ,∴a-2b+4c=a-2b+4(b-a )=2b-3a ,又由①得b=-2a ,∴a-2b+4c=-7a <0,故此选项正确;④根据图示知,当x=4时,y >0,∴16a+4b+c >0,由①知,b=-2a ,∴8a+c >0;故④正确;故正确为:③④两个.8.B 解:∵二次函数y=ax 2+bx+1的顶点在第一象限,且经过点(-1,0),∴易得:a-b+1=0,a <0,b >0,由a=b-1<0得到b <1,结合上面b >0,所以0<b <1①,由b=a+1>0得到a >-1,结合上面a <0,所以-1<a <0②,∴由①②得:-1<a+b <1,且c=1,得到0<a+b+1<2,∴0<t <2.故选:B . 9.B 10.D 11.B 解:当x=0时,y=-6,故函数与y 轴交于C (0,-6),当y=0时,x 2-x-6=0,即(x+2)(x-3)=0,解得x=-2或x=3,即A (-2,0),B (3,0);由图可知,函数图象至少向右平移2个单位恰好过原点,故|m|的最小值为2. 二、填空题12.7 解:∵二次项系数为-1,∴函数图象开口向下,顶点坐标为(2,94),当y=0时,-(x-2)2+94=0,解得x 1=12,得x 2=72.可画出草图为:(右图)图象与x 轴围成的封闭区域内(包括边界),横、纵坐标都是整数的点有7个,为(2,0),(2,1),(2,2),(1,0),(1,1),(3,0),(3,1).13.解:∵抛物线y=a (x-3)2+k 的对称轴为x=3,且AB ∥x 轴,∴AB=2×3=6,∴等边△ABC 的周长=3×6=18.故答案为:18. 14.①②③ 解:根据图象可得:a <0,c >0,对称轴:x=2b a -=1,2b a=-1,b=-2a ,∵a <0, ∴b >0,∴abc <0,故①正确;把x=-1代入函数关系式y=ax 2+bx+c 中得:y=a-b+c ,由图象可以看出当x=-1时,y <0,∴a-b+c <0,故②正确;∵b=-2a ,∴a-(-2a )+c <0,即:3a+c <0,故③正确;由图形可以直接看出④错误.故答案为:①②③. 15.y 1>y 2 解:由二次函数y=(x-1)2+1可,其对称轴为x=1,∵x1>x2>1,∴两点均在对称轴的右侧,∵此函数图象开口向上,∴在对称轴的右侧y 随x 的增大而增大∵x1>x2>1,∴y1>y2.故答案为:>. 16.37解:∵x 2-2(a-1)x+a (a-3)=0有两个不相等的实数根,∴△>0,∴[-2(a-1)]2-4a (a-3)>0,∴a >-1,将(1,0)代入y=x 2-(a 2+1)x-a+2得,a 2+a-2=0,解得(a-1)(a+2)=0,a 1=1,a 2=-2.可见,符合要求的点为0,2,3.∴P=3 7 .故答案为37. 17.y=x 2+x-2 18.y=-(x+1)2-2 解:二次函数y=(x-1)2+2顶点坐标为(1,2),绕原点旋转180°后得到的二次函数图象的顶点坐标为(-1,-2),所以,旋转后的新函数图象的解析式为y=-(x+1)2-2.故答案为:y=-(x+1)2-2.18 解:分段函数y=的图象如图:故要使直线y=m (m 为常数)与函数y=的图象恒有三个不同的交点,常数m 的取值范围为0<m <2,故答案为:0<m <2.19.272解:如图,过点P 作PM ⊥y 轴于点M ,∵抛物线平移后经过原点O 和点A (-6,0),∴平移后的抛物线对称轴为x=-3,得出二次函数解析式为:y=12(x+3)2+h ,将(-6,0)代入得出:0=12(-6+3)2+h ,解得:h=92-,∴点P 的坐标是(-3,92-),根据抛物线的对称性可知,阴影部分的面积等于矩形NPMO 的面积,∴S=|-3|×|92-|=272.故答案为:272.三、解答题20.解:(1)抛物线y=34(x-1)2-3,∵a=34>0,∴抛物线的开口向上,对称轴为x=1; (2)∵a=34>0,∴函数y 有最小值,最小值为-3; (3)令x=0,则y=34(0-1)2-3=94-,所以,点P 的坐标为(0,94-),令y=0,则34(x-1)2-3=0,解得x 1=-1,x 2=3,所以,点Q 的坐标为(-1,0)或(3,0),当点P (0,94-),Q (-1,0)时,设直线PQ 的解析式为y=kx+b ,则940b k b ⎧=-⎪⎨⎪-+=⎩,解得9494kb⎧=-⎪⎪⎨⎪=-⎪⎩,所以直线PQ的解析式为y=94-x94-,当P(0,94-),Q(3,0)时,设直线PQ的解析式为y=mx+n ,则9430nm n⎧=-⎪⎨⎪+=⎩,解得3494mn⎧=⎪⎪⎨⎪=-⎪⎩,所以,直线PQ的解析式为y=34x94-,综上所述,直线PQ的解析式为y=94-x94-或y=34x94-.3.(2012•佛山)解:(1)n是任意整数,则表示任意一个奇数的式子是:2n+1;(2)有理数b=(n≠0);(3)①当x=0时,y=0,当x=时,y=,当x=1时,y=1,当x=时,y=.故当x的取值从0开始每增加个单位时,y的值依次增加、、…②当x=0时,y=0,当x=时,y=,当x=时,y=,当x=时,y=,故当x的取值从0开始每增加个单位时,y的值依次增加、、…。
专题4二次函数的图象和性质4(含解析)

专题4 二次函数的图象和性质3一、单选题(共6小题)1.将抛物线y=x2向右平移两个单位,再向下平移4个单位,所得抛物线是()A.y=(x+2)2+4 B.y=(x﹣2)2﹣4 C.y=(x﹣2)2+4 D.y=(x+2)2﹣42.抛物线y=3(x+1)2+1的顶点所在象限是()A.第一象限B.第二象限C.第三象限D.第四象限3.抛物线C1向右平移4个单位长度后与抛物线C2重合,若(﹣1,3)在抛物线C1上,则下列点中,一定在抛物线C2上的是()A.(3,3)B.(3,﹣1)C.(﹣1,7)D.(﹣5,3)4.如图是二次函数y=ax2+bx+c图象的一部分,其对称轴为x=﹣1,且过点(﹣3,0),下列说法:其中说法正确的是()①abc<0;②2a﹣b=0;③4a+2b+c<0;④若(﹣5,y1),(3,y2)是抛物线上两点,则y1>y2A.①②B.②③C.①②④D.②③④5.已知二次函数y=﹣x2+mx+m(m为常数),当﹣2≤x≤4时,y的最大值是15,则m的值是()A.﹣10和6 B.﹣19和C.6和D.﹣19和66.定义符号min{a,b}的含义为:当a≥b时min{a,b}=b;当a<b时min{a,b}=a.如:min{1,﹣3}=﹣3,min{﹣4,﹣2}=﹣4.则min{﹣x2+1,﹣x}的最大值是()A.B.C.1 D.0二、填空题(共8小题)7.抛物线y=2x2﹣mx+3的对称轴是直线x=1,则m的值为.8.已知抛物线的对称轴是x=n,若该抛物线与x轴交于(1,0),(3,0)两点,则n的值为.9.如图,△ABC中,∠ABC=90°,AB=6,BC=8,O为AC的中点,过O作OE⊥OF,OE、OF分别交射线AB、BC于E、F,则EF的最小值为.10.如图,抛物线y=ax2+bx与直线y=mx+n相交于点A(﹣3,﹣6),B(1,﹣2),则关于x的方程ax2+bx=mx+n的解为﹣.11.若将抛物线y=﹣x2+1先向右平移1个单位长度,再向上平移2个单位长度,则所得抛物线的函数解析式为﹣﹣.12.抛物线y=ax2+bx+c(a≠0)的部分图象如图所示,与x轴的一个交点坐标为(4,0),抛物线的对称轴是直线x=1,下列结论:①abc>0;②2a+b=0;③方程ax2+bx+c=3有两个不相等的实数根;④抛物线与x轴的另一个交点坐标为(﹣2,0),其中正确的结论有.13.已知抛物线y=﹣x2+bx+c经过(﹣1,a)和(3,a)两点,则a﹣c=﹣.14.如图,抛物线y=x2在第一象限内经过的整数点(横坐标、纵坐标都为整数的点)依次为A1,A2,A3…A n,将抛物线y=x2沿直线L:y=x向上平移,得到一系列抛物线,且满足下列条件:①抛物线的顶点M1,M2,M3,…M n都在直线L:y=x上;②抛物线依次经过点A1,A2,A3…A n,则顶点M2020的坐标为.三、解答题(共6小题)15.用配方法求抛物线y=2x2﹣4x﹣5的顶点坐标.16.已知二次函数的图象过三个点(﹣1,0),(3,0),(1,﹣8).(1)用你认为最简便的方法求函数的解析式;(2)将图象向右平移2个单位时,求所得图象的函数解析式.17.抛物线y=ax2﹣2ax与x轴正半轴交于B、C为顶点,且点C的纵坐标为2.(1)求此抛物线的解析式;(2)点P为抛物线上一点,且△OPC是以OC为直角边的直角三角形,求点P的坐标.18.已知二次函数y=ax2+bx+c中,函数y与自变量x的部分对应值如表:x…﹣10123…y…105212…(1)求该二次函数的表达式;(2)当y>5时,x的取值范围是.19.如图抛物线y=x2+bx﹣c经过直线y=x﹣3与坐标轴的两个交点A,B,与x轴交于另一点C,抛物线的顶点为D.(1)求此抛物线的解析式;(2)求S△ACD的面积.20.已知抛物线y=x2﹣mx+c与x轴交于点A(x1,0)B(x2,0),与y轴交于点C(0,c).若△ABC为直角三角形,求c的值.专题4 二次函数的图象和性质3参考答案一、单选题(共6小题)1.【分析】先确定出原抛物线的顶点坐标,然后根据向右平移横坐标加,向下平移纵坐标减求出新图象的顶点坐标,然后写出即可.【解答】解:抛物线y=x2的顶点坐标为(0,0),向右平移2个单位,再向下平移4个单位后的图象的顶点坐标为(2,﹣4),所以,所得图象的解析式为y=(x﹣2)2﹣4,故选:B.【点评】本题主要考查的是函数图象的平移,根据平移规律“左加右减,上加下减”利用顶点的变化确定图形的变化是解题的关键.2.【分析】根据抛物线y=3(x+1)2+1,可以写出该抛物线的顶点坐标,从而可以得到顶点在第几象限.【解答】解:∵抛物线y=3(x+1)2+1,∴该抛物线的顶点是(﹣1,1),在第二象限,故选:B.【点评】本题考查二次函数的性质,解答本题的关键是明确题意,利用二次函数的性质解答.3.【分析】直接利用平移的性质得出(﹣1,3)平移后对应点进而得出答案.【解答】解:∵抛物线C1向右平移4个单位长度后与抛物线C2重合,(﹣1,3)在抛物线C1上,∴当(﹣1,3)向右平移4个单位时,得到(3,3),故(3,3)一定在抛物线C2上.故选:A.【点评】此题主要考查了二次函数与几何变换,正确掌握平移规律是解题关键.4.【分析】由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.【解答】解:①函数对称轴在y轴右侧,则ab>0,c<0,故abc<0,正确,符合题意;②函数的对称轴x=﹣=﹣1,即b=2a,故2a﹣b=0正确,符合题意;③函数的对称轴为:x=﹣1,且过点(﹣3,0),则另外一个交点为:(1,0),故当x=2时,y=4a+2b+c>0,故原答案错误,不符合题意;④函数的对称轴为:x=﹣1,而点(﹣5,y1)和(3,y2)与对称轴等间隔,故y1=y2,故原答案错误,不符合题意;故选:A.【点评】本题考查的是二次函数图象与系数的关系,要求学生熟悉函数的基本性质,能熟练求解函数与坐标轴的交点及顶点的坐标等.5.【分析】根据题意和二次函数的性质,利用分类讨论的方法可以求得m的值,从而可以解答本题.【解答】解:∵二次函数y=﹣x2+mx+m=﹣(x﹣)2++m,∴当<﹣2时,即m<﹣4,∵当﹣2≤x≤4时,y的最大值是15,∴当x=﹣2时,﹣(﹣2)2﹣2m+m=15,得m=﹣19;当﹣24时,即﹣4≤m≤8时,∵当﹣2≤x≤4时,y的最大值是15,∴当x=时,+m=15,得m1=﹣10(舍去),m2=6;当>4时,即m>8,∵当﹣2≤x≤4时,y的最大值是15,∴当x=4时,﹣42+4m+m=15,得m=(舍去);由上可得,m的值是﹣19或6;故选:D.【点评】本题考查二次函数的性质、二次函数的最值,解答本题的关键是明确题意,利用二次函数的性质解答.6.【分析】理解min{a,b}的含义就是取二者中的较小值,画出函数图象草图,利用函数图象的性质可得结论.【解答】解:在同一坐标系xOy中,画出函数二次函数y=﹣x2+1与正比例函数y=﹣x的图象,如图所示.设它们交于点A、B.令﹣x2+1=﹣x,即x2﹣x﹣1=0,解得:x=或,∴A(,),B(,).观察图象可知:①当x≤时,min{﹣x2+1,﹣x}=﹣x2+1,函数值随x的增大而增大,其最大值为;②当<x<时,min{﹣x2+1,﹣x}=﹣x,函数值随x的增大而减小,其最大值为;③当x≥时,min{﹣x2+1,﹣x}=﹣x2+1,函数值随x的增大而减小,最大值为.综上所示,min{﹣x2+1,﹣x}的最大值是.故选:A.【点评】本题考查了二次函数与正比例函数的图象与性质,充分理解定义min{a,b}和掌握函数的性质是解题的关键.二、填空题(共8小题)7.【分析】根据抛物线y=2x2﹣mx+3的对称轴是直线x=1,可以求得m的值,本题得以解决.【解答】解:∵抛物线y=2x2﹣mx+3的对称轴是直线x=1,∴1=﹣,解得,m=4,故答案为:4.【点评】本题考查二次函数的性质,解答本题的关键是明确抛物线的对称轴是直线x=﹣.8.【分析】利用抛物线与x轴的交点为对称轴,从而得到抛物线的对称轴方程.【解答】解:∵抛物线与x轴交于(1,0),(3,0)两点,∴抛物线的对称轴为直线=2.即n的值为2.故答案为2.【点评】本题考查了抛物线与x轴的交点:把求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x 轴的交点坐标问题转化解关于x的一元二次方程即可求得交点横坐标.也考查了二次函数的性质.9.【分析】首先过点O作OM⊥AB于点M,作ON⊥BC于点N,易得四边形OMBN是矩形,可得△AOM∽△ACB,△CON∽△CAB,又由AB=6,BC=8,O为AC的中点,可求得OM与ON的长,然后由勾股定理求得MN的长,又由垂线段最短,可得当OE与OM重合,即EF与MN重合时,EF最短,求得答案.【解答】解:过点O作OM⊥AB于点M,作ON⊥BC于点N,∵∠ABC=90°,∴四边形OMBN是矩形,∴OM∥BC,ON∥AB,∴△AOM∽△ACB,△CON∽△CAB,∴OM:BC=OA:AC,ON:AB=OC:AC,∵O为AC的中点,∴OM=BC=×8=4,ON=AB=×6=3,∴MN==5,由垂线段最短,可得当OE与OM重合,即EF与MN重合时,EF最短,∴EF的最小值为5.故答案为:5.【点评】此题考查了相似三角形的判定与性质、勾股定理以及垂线段最短的知识.此题难度适中,注意掌握数形结合思想的应用.10.【分析】关于x的方程ax2+bx=mx+n的解为抛物线y=ax2+bx与直线y=mx+n交点的横坐标.【解答】解:∵抛物线y=ax2+bx与直线y=mx+n相交于点A(﹣3,﹣6),B(1,﹣2),∴关于x的方程ax2+bx=mx+n的解为x1=﹣3,x2=1.故答案为x1=﹣3,x2=1.【点评】本题考查了抛物线与x轴的交点:把求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x 轴的交点坐标问题转化解关于x的一元二次方程即可求得交点横坐标.也考查了二次函数的性质.11.【分析】利用二次函数图象的平移规律,左加右减,上加下减得出答案.【解答】解:∵抛物线y=﹣x2+1向右平移1个单位长度,∴平移后解析式为:y=﹣(x﹣1)2+1,∴再向上平移2个单位长度所得的抛物线解析式为:y=﹣(x﹣1)2+3.故答案为:y=﹣(x﹣1)2+3.【点评】此题主要考查了二次函数与几何变换,正确记忆图形平移规律是解题关键.12.【分析】由图可知a<0,由已知可得对称轴x=1=﹣,b=﹣2a>0,函数与y轴的交点c>0;①abc<0;②b+2a=0;③函数与y轴交点坐标纵坐标c>3,则方程ax2+bx+c=3有两个不相等的实数根;④由函数的对称性,与x轴的一个交点坐标为(4,0),另一个交点为(﹣2,0);【解答】解:由图可知a<0,∴对称轴x=1=﹣,∴b=﹣2a>0,函数与y轴的交点c>0,①∵abc<0;①错误;②b=﹣2a,∴b+2a=0;②正确;③∵函数与y轴交点c>3,∴x=1时,y>3∴直线y=3与抛物线有两个交点,∴方程ax2+bx+c=3有两个不相等的实数根;③正确;④由函数的对称性,与x轴的一个交点坐标为(4,0),∴另一个交点为(﹣2,0);④正确;故答案为②③④;【点评】本题考查二次函数的图象及性质;熟练掌握二次函数图象及性质,能够通过函数图象提取信息是解题的关键.13.【分析】根据已知抛物线y=﹣x2+bx+c经过(﹣1,a)和(3,a)两点求出抛物线的对称轴,求出b的值,再把点(﹣1,a)代入,即可求出答案.【解答】解:∵抛物线y=﹣x2+bx+c经过(﹣1,a)和(3,a)两点,∴抛物线的对称轴是直线x==1,即﹣=1,解得:b=2,即y=﹣x2+bx+c=﹣x2+2x+c,把(﹣1,a)代入得:a=﹣1﹣2+c,即a﹣c=﹣3,故答案为:﹣3.【点评】本题考查了二次函数图象上点的坐标特征和二次函数的性质,能根据点的坐标特点求出抛物线的对称轴是解此题的关键.14.【分析】根据抛物线的解析式结合整数点的定义,找出点A n的坐标为(n,n2),设点M n的坐标为(a,a),则以点M n为顶点的抛物线解析式为y=(x﹣a)2+a,由点A n的坐标利用待定系数法,即可求出a值,将其代入点M n的坐标即可得出结论.【解答】解:∵抛物线y=x2在第一象限内经过的整数点(横坐标、纵坐标都为整数的点)依次为A1,A2,A3,…,A n,…,∴点A n的坐标为(n,n2).设点M n的坐标为(a,a),则以点M n为顶点的抛物线解析式为y=(x﹣a)2+a,∵点A n(n,n2)在抛物线y=(x﹣a)2+a上,∴n2=(n﹣a)2+a,解得:a=2n﹣1或a=0(舍去),∴M n的坐标为(2n﹣1,2n﹣1),∴M2020的坐标为(4039,4039).故答案为:(4039,4039).【点评】本题考查了二次函数图象与几何变换、一次函数图象上点的坐标特征以及待定系数法求二次函数解析式,根据点A n的坐标利用待定系数法求出a值是解题的关键.三、解答题(共6小题)15.【分析】运用配方法把二次函数的一般式化为顶点式,根据二次根式的性质求出抛物线的顶点坐标.【解答】解:y=2x2﹣4x﹣5=2(x﹣1)2﹣7,则抛物线y=2x2﹣4x﹣5的顶点坐标为(1,﹣7).【点评】本题考查的是二次函数的三种形式,正确运用配方法把二次函数的一般式化为顶点式是解题的关键.16.【分析】(1)设二次函数的解析式为y=a(x+1)(x﹣3),然后代入(1,﹣8)用待定系数法即可求得.(2)可根据二次函数图象左加右减,上加下减的平移规律进行解答.【解答】解:(1)设二次函数的解析式为y=a(x+1)(x﹣3),由于抛物线的图象经过(1,﹣8),则有:﹣8=a(1+1)(1﹣3),解得a=2.∴二次函数的解析式为y=2(x+1)(x﹣3)=2x2﹣4x﹣6.(2)由y=2x2﹣4x﹣6=2(x﹣1)2﹣8,图象向右平移2个单位得的函数解析式是y=2(x﹣1﹣2)2﹣8即y=2x2﹣12x+10.【点评】主要考查的是用待定系数法求二次函数解析式的方法以及函数图象的平移,用平移规律“左加右减,上加下减”直接代入函数解析式求得平移后的函数解析式.17.【分析】(1)先把y=ax2﹣2ax配成顶点式,然后根据顶点的纵坐标为2求出a的值,即可得到抛物线解析式;(2)根据抛物线上点的坐标特征设P点坐标为(x,﹣2x2+4x),再利用两点间的距离公式得到OP2=x2+(﹣2x2+4x)2,PC2=(x﹣1)2+(﹣2x2+4x﹣2)2,再分类讨论:当∠PCO=90°时,根据勾股定理得OC2+PC2=OP2;当∠POC=90°时,根据勾股定理OC2+PO2=CP2,然后分别得到x的一元二次方程,解方程求出x即可得到满足条件的P点坐标.【解答】解:(1)∵y=a(x﹣1)2﹣a,∴顶点C的坐标为(1,﹣a),而C的纵坐标为2,∴﹣a=2,解得a=﹣2,∴抛物线解析式为y=﹣2x2+4x;(2)设P点坐标为(x,﹣2x2+4x),而C(1,2),则OC2=12+22=5,OP2=x2+(﹣2x2+4x)2,PC2=(x﹣1)2+(﹣2x2+4x﹣2)2,当∠PCO=90°时,OC2+PC2=OP2,即5+(x﹣1)2+(﹣2x2+4x﹣2)2=x2+(﹣2x2+4x)2,整理得4x2﹣9x+5=0,解得x1=1(舍去),x2=,此时P点坐标为(,);当∠POC=90°时,OC2+PO2=CP2,即5+x2+(﹣2x2+4x)2=(x﹣1)2+(﹣2x2+4x﹣2)2,整理得4x2﹣9x=0,解得x1=0(舍去),x2=,此时P点坐标为(,﹣),综上所述,满足条件的P点坐标为(,)或(,﹣).【点评】本题考查了抛物线与x轴的交点:二次函数y=ax2+bx+c(a,b,c是常数,a≠0)的交点与一元二次方程ax2+bx+c=0根之间的关系,△=b2﹣4ac决定抛物线与x轴的交点个数.也考查了两点间的距离公式和勾股定理.18.【分析】(1)根据表格中的数据可以求得二次函数的解析式;(2)观察表格求出抛物线的对称轴,确定开口方向,利用二次函数的对称性判断出x=4时,y=5,然后写出y>5时,x的取值范围即可.【解答】解:(1)由表格可知,抛物线经过(1,2)、(3,2),∴对称轴为直线x==2,∴抛物线的顶点为(2,1),设函数为y=a(x﹣2)2+1.∵函数的图象经过点(0,5),∴5=a×(﹣2)2+1.解得a=1.∴该二次函数的表达式为y=(x﹣2)2+1(或y=x2﹣4x+5);(2)由所给数据可知当x=2时,y有最小值1,∴二次函数的对称轴为x=2.∴x=4时,y=5,∴当y>5时,对应的x的范围为x<0或x>4,故答案为x<0或x>4.【点评】本题考查用待定系数法求二次函数解析式、二次函数的性质,解题的关键是正确分析表中的数据.19.【分析】(1)根据一次函数的解析式求出A、B点坐标,再代入抛物线解析式即可;(2)求出C点坐标,确定AC长,再根据抛物线解析式求出顶点D坐标,则面积可求.【解答】解:(1)当x=0时,y=x﹣3=﹣3,∴B(0,﹣3);当y=0时,x=3,∴A(3,0).∵抛物线y=x2+bx﹣c经过A、B两点,∴,解得b=﹣2.所以抛物线的解析式为y=x2﹣2x﹣3.(2)根据0=x2﹣2x﹣3,解得x=﹣1或3,∴C(﹣1,0).∴AC=4.抛物线的顶点坐标为(1,﹣4),所以S△ACD的面积为.【点评】本题主要考查用待定系数法求函数解析式、抛物线与x轴交点、二次函数的性质.20.【分析】△ABC为直角三角形,则只有∠ACB一种情况,证明∠BCO=∠CAB,tan∠BCO=tan∠CAB,则OC2=OA•OB,即可求解.【解答】解:△ABC为直角三角形,则只有∠ACB一种情况,连接BC,∵∠BCO+∠ACO=90°,∠ACO+∠OAC=90°,∴∠BCO=∠CAB,tan∠BCO=tan∠CAB,则OC2=OA•OB,而OA•OB=﹣x1x2=2c=c2,解得:c=0或﹣2(舍去0),故c=﹣2.【点评】本题考查的是抛物线与x轴的交点,关键是确定∠ACB=90°,用解直角三角形的方法确定OC2=OA•OB,即可求解.。
小专题(四) 二次函数图象信息题归类

小专题(四) 二次函数图象信息题归类小专题(四)二次函数图象信息题归类抛物线y=ax2+bx+c的图象与字母系数a,b,c 之间的关系:(1)当a>0时,开口向上;当a<0时,开口向下.(2)若对称轴在y轴的左侧,则a,b同号;若对称轴在y轴的右侧,则a,b异号.(3)若抛物线与y轴的正半轴相交,则c>0;若抛物线与y轴的负半轴相交,则c<0;若抛物线经过原点,则c=0.(4)当x=1时,y=ax2+bx+c=a+b+c;当x=-1时,y=ax2+bx+c=a-b+c;当x=2时,y=ax2+bx+c=4a+2b+c;当x=-2时,y=ax2+bx+c=4a-2b+c,…(5)当对称轴x=1时,2a+b=0;当对称轴x=-1时,2a-b=0;判断2a+b大于或者等于0,看对称轴与1的大小关系;判断2a-b大于或者等于0,看对称轴与-1的大小关系.(6)当b2-4ac>0时,抛物线与横轴有两个交点;当b2-4ac=0时,抛物线与横轴有一个交点;当b2-4ac<0时,抛物线与横轴没有交点.A.b≥5B.b≥1或b≤-14C.b≥2D.1≤b≤25.二次函数y=ax2+bx+c的图象如图所示,则下列解析式不正确的是(C)A.a<0B.abc>0C.a+b+c>0D.b2-4ac>06.如图,二次函数y=ax2+bx+c=0(a≠0)的图象与x轴正半轴相交于A,B两点,与y轴相交于点C,对称轴为直线x=2,且OA=OC,则下列结论:①abc>0;②9a+3b+c<0;③-1<c<0;④关于x的方.其中正确的结程ax2+bx+c=0(a≠0)有一个根为-1a论有(C)A.1个B.2个C.3个D.4个7.(恩施中考)抛物线y1=ax2+bx+c与直线y2=mx+n的图象如图所示,下列判断中:①abc<0;②a+b+c>0;③5a-c=0;④当x<12或x>6时,y 1>y 2,其中正确的个数为(C )A.1B.2C.3D.4 类型3 利用二次函数图象求二次函数解析式8.如图,一个二次函数的图象经过A ,B ,C 三点,点A的坐标是(-1,0),点C 的坐标是(0,5),且OA ∶OB=1∶4,则这个二次函数的解析式是 y=-54x 2+154x+5 . 类型4 利用二次函数图象求一元二次方程的根9.(苏州中考)已知二次函数y=x 2-3x+m (m 为常数)的图象与x 轴的一个交点为(1,0),则关于x 的一元二次方程x 2-3x+m=0的两实数根是(B )A.x 1=1,x 2=-1B.x 1=1,x 2=2C.x 1=1,x 2=0D.x 1=1,x 2=310.若二次函数y=ax2+bx+c(a<0)的图象如图所示,且关于x的方程ax2+bx+c=k有两个不相等的实根,则常数k的取值范围是(D)A.0<k<4B.-3<k<1C.k<-3或k>1D.k<4类型5利用二次函数图象解不等式11.二次函数y=x2-x-2的图象如图所示,则不等式x2-x-2<0的解集是(C)A.x<-1B.x>2C.-1<x<2D.x<-1或x>212.如图,二次函数y1=ax2+bx+c与一次函数y2=kx 的图象交于点A和原点O,点A的横坐标为-4,点A和点B关于抛物线的对称轴对称,点B的横坐标为1,则满足0<y1<y2的x的取值范围是(A)A. -4<x<-3B.-4<x<0C.-3<x<0D.-4<x<113.如图是二次函数y=-x2+2x+4的图象,使y≤1成立的x的取值范围是x≤-1或x≥3.14.如图,二次函数y=(x+2)2+m的图象与y轴交于点C,点B在抛物线上,且与点C关于抛物线的对称轴对称,已知一次函数y=kx+b的图象经过该二次函数图象上的点A(-1,0)及点B.(1)求二次函数与一次函数的解析式;(2)根据图象,写出满足(x+2)2+m≥kx+b的x的取值范围.解:(1)二次函数的解析式为y=(x+2)2-1=x2+4x+3,一次函数的解析式为y=-x-1.(2)x≤-4或x≥-1.。
二次函数图像和性质

y
b c x1 x2 , x1 x2 a a
对称轴
AB=|x1-x2|= | a |
x x2 x 1 2
o
x
x1 x2 x 2
y
x1x2>0, 点A,点B在原点同侧
x1 x2 0, 原点右侧
x1 x2 0,原点左侧
x1x2<0,点A,点B在原点两侧 x1 x2 0, BO AO
2 4.当m= -1 时,y=(m+2)xm +3m+2是二次函数,
二.二次函数的图象及性质
a的符号 图象
开口方向 对称轴
a>0
a<0
x
开口向上
b 2a 4ac b 2 b ( , ) 4a 2a b x 当 2a 时,y x
开口向下
b 2a 4ac b 2 b ( , ) 4a 2a x
y=a(x-h)2 y=a(x-h)2+k
抛物线y=ax2向左 直线X=h (h,0) (h<0)、向右(h>0) 平移|h|个单位, 向上 (k>0)、向下(k<0) 直线X=h (h,k) 平移|k|个单位后,可以得 到抛物线y=a(x-h)2+k 。
a 越大,开口越小.
a 越小,开口越大.
做一做: 1 2 y 2 y x , x 1. 已知函数 2 的图象如图所示。 抛物线①②③④ 分别对应哪个函数?
3.已知抛物线y=ax2+2x+c 经过点(-1,0)、(0,3) (2)x取何值时,y 随 x 的增大而增大; x取何值时,抛物线在 x 轴的上方; x取何值时,y 随 x 的增大而减小且 y <0。 (3)利用图象求方程 ax2+2x+c=-5 解。
二次函数专题复习讲义

二次函数专题复习专题一:二次函数的图象与性质本专题涉及二次函数概念,二次函数的图象性质,抛物线平移后的表达式等.试题多以填空题、选择题为主,也有少量的解答题出现.考点1.二次函数图象的对称轴和顶点坐标二次函数的图象是一条抛物线,它的对称轴是直线x=-2b a ,顶点坐标是-2b a,244ac b a -.例1 已知,在同一直角坐标系中,反比例函数5y x=与二次函数22y x x c =-++的图像交于点(1)A m -,. 1求m 、c 的值;2求二次函数图像的对称轴和顶点坐标. 考点2.抛物线与a 、b 、c 的关系抛物线y=ax 2+bx+c 中,当a>0时,开口向上,在对称轴x=-2ba的左侧y 随x 的增大而减小,在对称轴的右侧,y 随x 的增大而增大;当a<0时,开口向下,在对称轴的右侧,y 随x 的增大而增大,在对称轴的右侧,y 随x 的增大而减小.例2 已知2y ax bx =+的图象如图1所示,则y ax b =-的图象一定过A .第一、二、三象限B .第一、二、四象限C .第二、三、四象限D .第一、三、四象限考点3、二次函数的平移当k>0k<0时,抛物线y=ax 2+ka ≠0的图象可由抛物线y=ax 2向上或向下平移|k|个单位得到;当h>0h<0时,抛物线y=ax-h 2a ≠0的图象可由抛物线y=ax 2向右或向左平移|h|个单位得到. 例3 把抛物线y=3x 2向上平移2个单位,得到的抛物线是=3x+22=3x-22=3x 2+2 =3x 2-2 专题练习11.对于抛物线y=13-x 2+103x 163-,下列说法正确的是A.开口向下,顶点坐标为5,3B.开口向上,顶点坐标为5,3C.开口向下,顶点坐标为-5,3D.开口向上,顶点坐标为-5,3 2.若抛物线y=x 2-2x+c 与y 轴的交点为0,-3,则下列说法不正确的是 A.抛物线开口向上 B.抛物线的对称轴是x=1 C.当x=1时,y 的最大值为-4 D.抛物线与x 轴交点为-1,0,3,03.将二次函数y=x 2的图象向左平移1个单位长度,再向下平移2个单位长度后,所得图象的函数表达式是________. 4.小明从上图2所示的二次函数2y ax bx c =++的图象中,观察得出了下面五条信息:①0c <;②0abc >;③0a b c -+>;④230a b -=;⑤40c b ->,你认为其中正确信息的个数有_______.填序号专题复习二:二次函数表达式的确定图1图2本专题主要涉及二次函数的三种表示方法以及根据题目的特点灵活选用方法确定二次函数的表达式.题型多以解答题为主.考点1.根据实际问题模型确定二次函数表达式例1、如图1,用一段长为30米的篱笆围成一个一边靠墙墙的长度不限的矩形菜园ABCD ,设AB 边长为x 米,则菜园的面积y 单位:米2与x 单位:米的函数关系式为 不要求写出自变量x 的取值范围.考点2.根据抛物线上点的坐标确定二次函数表达式1.若已知抛物线上三点的坐标,则可用一般式:y=ax 2+bx+ca ≠0;2.若已知抛物线的顶点坐标或最大小值及抛物线上另一个点的坐标,则可用顶点式:y=ax-h 2+ka ≠0; 3.若已知抛物线与x 轴的两个交点坐标及另一个点,则可用交点式:y=ax-x 1x-x 2a ≠0. 例2 已知抛物线的图象以A-1,4为顶点,且过点B2,-5,求该抛物线的表达式.例3 已知一抛物线与x 轴的交点是A-2,0、B1,0,且经过点C2,8.1求该抛物线的解析式; 2求该抛物线的顶点坐标.专项练习21.由于世界金融危机的不断蔓延,世界经济受到严重冲击.为了盘活资金,减少损失,某电器商场决定对某种电视机连续进行两次降价.若设平均每次降价的百分率是x,降价后的价格为y 元,原价为a 元,则y 与x 之间的函数表达式为 =2ax-1 =2a1-x =a1-x 2=a1-x22.如图2,在平而直角坐标系xOy 中,抛物线y=x 2+bx+c 与x 轴交于A 、B 两点,点A 在x 轴负半轴,点B 在x 轴正半轴,与y 轴交于点C,且tan∠ACO=12,CO=BO,AB=3,则这条抛物线的函数解析式是 . 3.对称轴平行于y 轴的抛物线与y 轴交于点0,-2,且x=1时,y=3;x=-1时y=1, 求此抛物线的关系式.4.推理运算:二次函数的图象经过点(03)A -,,(23)B -,,(10)C -,.1求此二次函数的关系式; 2求此二次函数图象的顶点坐标;3填空:把二次函数的图象沿坐标轴方向最少..平移 个单位,使得该图象的顶点在原点. 专题三:二次函数与一元二次方程的关系本专题主要涉及根据二次函数的图象求一元二次方程的近似根,由图象判断一元二次方程根的情况,由一元二次方程根的情况判断抛物线与x 轴的交点个数等,题型主要填空题、选择题和解答题. 考点1.根据二次函数的自变量与函数值的对应值,确定方程根的范围一元二次方程ax 2+bx+c=0就是二次函数y=ax 2+bx+c 当函数y 的值为0时的情况.ABC D图1菜园墙图2例1 根据下列表格中二次函数y=ax 2+bx+c 的自变量x 与函数值y 的对应值,判断方程ax 2+bx+c=0a ≠0,a,b,c,为常数的一个解x 的范围是A.6 6.17x << B.6.17 6.18x << C.6.18 6.19x <<D.6.19 6.20x <<考点2.根据二次函数的图象确定所对应的一元二次方程的根.二次函数y=ax 2+bx+c 的图象与x 轴的交点有三种情况:有两个交点、一个交点、没有交点;当二次函数y=ax 2+bx+c 的图象与x 轴有交点时,交点的横坐标就是当y=0时自变量x 的值,即一元二次方程ax 2+bx+c=0的根.例2 已知二次函数y=-x 2+3x+m 的部分图象如图1所示,则关于x 的一元二次方程-x 2+3x+m=0的解为________. 考点3.抛物线的交点个数与一元二次方程的根的情况当二次函数y=ax 2+bx+c 的图象与x 轴有两个交点时,则一元二次方程ax 2+bx+c=0的实数根;当二次函数y=ax 2+bx+c 的图象与x 轴有一个交点时,则一元二次方程ax 2相等的实数根;当二次函数y=ax 2+bx+c 的图象与x 轴没有交点时,则一元二次方程ax 2实数根.反之亦然.例3 在平面直角坐标系中,抛物线21y x =-与x 轴的交点的个数是专项练习31.抛物线y=kx 2-7x-7的图象和x 轴有交点,则k 的取值范围是________.2.已知二次函数22y x x m =-++的部分图象如图2所示,则关于x 的一元二次方程220x x m -++=的解为 .3.已知函数2y ax bx c =++的图象如图3所示,那么关于x 的方程220ax bx c +++= 的根的情况是A.无实数根B.有两个相等实数根C.有两个异号实数根D.有两个同号不等实数根4. 二次函数2(0)y ax bx c a =++≠的图象如图4所示,根据图象解答下列问题:1写出方程20ax bx c ++=的两个根.2写出不等式20ax bx c ++>的解集.3写出y 随x 的增大而减小的自变量x 的取值范围.4若方程2ax bx c k ++=有两个不相等的实数根,求k 的取值范围.图2专题四:利用二次函数解决实际问题本专题主要涉及从实际问题中建立二次函数模型,根据二次函数的最值解决实际问题,能根据图象学习建立二次函数模型解决实际问题.解决实际问题的基本思路:1理解问题;2分析问题中的变量和常量;3用函数表达式表示出它们之间的关系;4利用二次函数的有关性质进行求解;5检验结果的合理性,对问题加以拓展等.例1某商场将进价为2000元的冰箱以2400元售出,平均每天能售出8台,为了配合国家“家电下乡”政策的实施,商场决定采取适当的降价措施.调查表明:这种冰箱的售价每降低50元,平均每天就能多售出4台.1假设每台冰箱降价x元,商场每天销售这种冰箱的利润是y元,请写出y与x之间的函数表达式;不要求写自变量的取值范围2商场要想在这种冰箱销售中每天盈利4800元,同时又要使百姓得到实惠,每台冰箱应降价多少元3每台冰箱降价多少元时,商场每天销售这种冰箱的利润最高最高利润是多少专题训练41.小李想用篱笆围成一个周长为60米的矩形场地,矩形面积S单位:平方米随矩形一边长x单位:米的变化而变化.1求S与x之间的函数关系式,并写出自变量x的取值范围;2当x是多少时,矩形场地面积S最大最大面积是多少2.某旅行社有客房120间,每间客房的日租金为50元,每天都客满.旅社装修后要提高租金,经市场调查发现,如果每间客房的日租金每增加5元时,则客房每天出租数就会减少6间,不考虑其他因素,旅社将每间客房的日租金提高到多少元时,客房日租金的总收入最高3.一座拱桥的轮廓是抛物线型如图1所示,拱高6m,跨度20m,相邻两支柱间的距离均为5m.1将抛物线放在所给的直角坐标系中如图2所示,求抛物线的解析式;2求支柱EF的长度;3拱桥下地平面是双向行车道正中间是一条宽2m的隔离带,其中的一条行车道能否并排行驶宽2m、高3m的三辆汽车汽车间的间隔忽略不计请说明你的理由.x图1。
(完整版)二次函数图像与性质专题复习
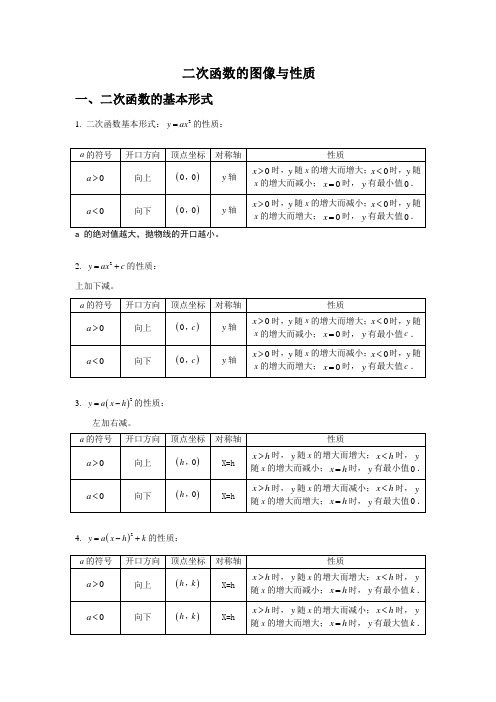
二次函数的图像与性质 一、二次函数的基本形式1. 二次函数基本形式:2y ax =的性质:2. 2y ax c =+的性质: 上加下减。
3. ()2y a x h =-的性质:左加右减。
4. ()2y a x h k =-+的性质:二、二次函数图象的平移1. 平移步骤:方法一:⑴ 将抛物线解析式转化成顶点式()2y a x h k =-+,确定其顶点坐标()h k ,; ⑵ 保持抛物线2y ax =的形状不变,将其顶点平移到()h k ,处,具体平移方法如下:【或左(h <0)】向右(h >0)【或左(h 平移|k|个单位2. 平移规律在原有函数的基础上“h 值正右移,负左移;k 值正上移,负下移”. 概括成八个字“左加右减,上加下减”. 方法二:⑴c bx ax y ++=2沿y 轴平移:向上(下)平移m 个单位,c bx ax y ++=2变成m c bx ax y +++=2(或m c bx ax y -++=2)⑵c bx ax y ++=2沿轴平移:向左(右)平移m 个单位,c bx ax y ++=2变成c m x b m x a y ++++=)()(2(或c m x b m x a y +-+-=)()(2)三、二次函数()2y a x h k =-+与2y ax bx c =++的比较从解析式上看,()2y a x h k =-+与2y ax bx c =++是两种不同的表达形式,后者通过配方可以得到前者,即22424b ac b y a x a a -⎛⎫=++ ⎪⎝⎭,其中2424b ac b h k a a -=-=,. 四、二次函数2y ax bx c =++图象的画法五点绘图法:利用配方法将二次函数2y ax bx c =++化为顶点式2()y a x h k =-+,确定其开口方向、对称轴及顶点坐标,然后在对称轴两侧,左右对称地描点画图.一般我们选取的五点为:顶点、与y 轴的交点()0c ,、以及()0c ,关于对称轴对称的点()2h c ,、与x 轴的交点()10x ,,()20x ,(若与x 轴没有交点,则取两组关于对称轴对称的点). 画草图时应抓住以下几点:开口方向,对称轴,顶点,与x 轴的交点,与y 轴的交点.五、二次函数2y ax bx c =++的性质1. 当0a >时,抛物线开口向上,对称轴为2bx a =-,顶点坐标为2424b ac b a a ⎛⎫-- ⎪⎝⎭,.当2b x a <-时,y 随x 的增大而减小;当2b x a >-时,y 随x 的增大而增大;当2bx a=-时,y 有最小值244ac b a-.2. 当0a <时,抛物线开口向下,对称轴为2bx a =-,顶点坐标为2424b ac b a a ⎛⎫-- ⎪⎝⎭,.当2b x a <-时,y 随x 的增大而增大;当2b x a >-时,y 随x 的增大而减小;当2bx a=-时,y 有最大值244ac b a-.六、二次函数解析式的表示方法1. 一般式:2y ax bx c =++(a ,b ,c 为常数,0a ≠);2. 顶点式:2()y a x h k =-+(a ,h ,k 为常数,0a ≠);3. 两根式:12()()y a x x x x =--(0a ≠,1x ,2x 是抛物线与x 轴两交点的横坐标). 注意:任何二次函数的解析式都可以化成一般式或顶点式,但并非所有的二次函数都可以写成交点式,只有抛物线与x 轴有交点,即240b ac -≥时,抛物线的解析式才可以用交点式表示.二次函数解析式的这三种形式可以互化.七、二次函数的图象与各项系数之间的关系1. 二次项系数a二次函数2y ax bx c =++中,a 作为二次项系数,显然0a ≠.⑴ 当0a >时,抛物线开口向上,a 的值越大,开口越小,反之a 的值越小,开口越大; ⑵ 当0a <时,抛物线开口向下,a 的值越小,开口越小,反之a 的值越大,开口越大.总结起来,a 决定了抛物线开口的大小和方向,a 的正负决定开口方向,a 的大小决定开口的大小. 2. 一次项系数b在二次项系数a 确定的前提下,b 决定了抛物线的对称轴. ⑴ 在0a >的前提下,当0b >时,02ba-<,即抛物线的对称轴在y 轴左侧; 当0b =时,02ba-=,即抛物线的对称轴就是y 轴; 当0b <时,02ba->,即抛物线对称轴在y 轴的右侧.⑵ 在0a <的前提下,结论刚好与上述相反,即 当0b >时,02ba->,即抛物线的对称轴在y 轴右侧; 当0b =时,02ba-=,即抛物线的对称轴就是y 轴; 当0b <时,02ba-<,即抛物线对称轴在y 轴的左侧. 总结起来,在a 确定的前提下,b 决定了抛物线对称轴的位置.ab 的符号的判定:对称轴abx 2-=在y 轴左边则0>ab ,在y 轴的右侧则0<ab ,概括的说就是“左同右异” 总结:3. 常数项c⑴ 当0c >时,抛物线与y 轴的交点在x 轴上方,即抛物线与y 轴交点的纵坐标为正; ⑵ 当0c =时,抛物线与y 轴的交点为坐标原点,即抛物线与y 轴交点的纵坐标为0; ⑶ 当0c <时,抛物线与y 轴的交点在x 轴下方,即抛物线与y 轴交点的纵坐标为负. 总结起来,c 决定了抛物线与y 轴交点的位置. 总之,只要a b c ,,都确定,那么这条抛物线就是唯一确定的.二次函数解析式的确定:根据已知条件确定二次函数解析式,通常利用待定系数法.用待定系数法求二次函数的解析式必须根据题目的特点,选择适当的形式,才能使解题简便.一般来说,有如下几种情况:1. 已知抛物线上三点的坐标,一般选用一般式;2. 已知抛物线顶点或对称轴或最大(小)值,一般选用顶点式;3. 已知抛物线与x 轴的两个交点的横坐标,一般选用两根式;4. 已知抛物线上纵坐标相同的两点,常选用顶点式.八、二次函数图象的对称二次函数图象的对称一般有五种情况,可以用一般式或顶点式表达 1. 关于x 轴对称2y ax bx c =++关于x 轴对称后,得到的解析式是2y ax bx c =---;()2y a x h k =-+关于x 轴对称后,得到的解析式是()2y a x h k =---;2. 关于y 轴对称2y ax bx c =++关于y 轴对称后,得到的解析式是2y ax bx c =-+;()2y a x h k =-+关于y 轴对称后,得到的解析式是()2y a x h k =++;3. 关于原点对称2y ax bx c =++关于原点对称后,得到的解析式是2y ax bx c =-+-; ()2y a x h k =-+关于原点对称后,得到的解析式是()2y a x h k =-+-; 4. 关于顶点对称(即:抛物线绕顶点旋转180°)2y ax bx c =++关于顶点对称后,得到的解析式是222b y ax bx c a=--+-;()2y a x h k =-+关于顶点对称后,得到的解析式是()2y a x h k =--+.5. 关于点()m n ,对称 ()2y a x h k =-+关于点()m n ,对称后,得到的解析式是()222y a x h m n k =-+-+-根据对称的性质,显然无论作何种对称变换,抛物线的形状一定不会发生变化,因此a 永远不变.求抛物线的对称抛物线的表达式时,可以依据题意或方便运算的原则,选择合适的形式,习惯上是先确定原抛物线(或表达式已知的抛物线)的顶点坐标及开口方向,再确定其对称抛物线的顶点坐标及开口方向,然后再写出其对称抛物线的表达式.二次函数图像参考:十一、2-32y=-2x 2y=3(x+4)22y=3x2y=-2(x-3)2【例题精讲】一、一元二次函数的图象的画法 【例1】求作函数64212++=x x y 的图象 【例2】求作函数342+--=x x y 的图像。
二次函数专题讲解含答案
二次函数专题专题必要性:高考中的很多题,往往最后都能转化为二次函数、一元二次方程和一元二次不等式问题,因此二次函数贯穿整个高考中,需深度掌握。
一、二次函数的定义:形如(a≠0,a,b,c为常数)的函数为二次函数.二、二次函数的性质:(1)二次函数y=ax2 (a≠0)的图象是一条抛物线,其顶点是原点,对称轴是y轴;当a>0时,抛物线开口向上,顶点是最低点;当a<0时,抛物线开口向下,顶点是最高点;函数(2)二次函数的图象是一条抛物线.顶点为(-,),对称轴;函数抛物线开口向上,并向上无限延伸抛物线开口向下,并向下无限延伸三、二次函数的三种表现形式1)一般式:2)顶点式:;3)两根式: 其中、是二次函数的与轴的两个交点的横坐标,此时二次函数的对称轴为直线. 注意:任何二次函数的解析式都可以化成一般式或顶点式,但并非所有的二次函数都可以写成交点式,只有抛物线与x 轴有交点,即240b ac -≥时,抛物线的解析式才可以用交点式表示.二次函数解析式的这三种形式可以互化.四、二次函数根的由来——配方法 第一步:提公因式。
看二次项的系数是否为1,若系数不为1,则要先把系数提公因式,使二次项的系数变成1;若系数是1,就可以直接进行配方。
如:函数2246y x x =++的二次项2(0)y ax bx c a =++≠2()(0),)y a x h k a h k =-+≠此时二次函数的顶点坐标为(12()()y a x x x x =--1x 2x x 122x x x +=系数是2,因此不能直接配方,要先把2提出来,即:22(23)y x x =++。
第二步:配方。
配方的方法是:二次项以及一次项保持不变,在常数项上加上一次项系数一半的平方,同时,为了保持原式不变,加上了一个什么数,就要减去一个相同的数;如:222222[2()()3]22y x x =++-+第三步:整理配方的前三项可以组成一个完全平方式,再把常数项算出最后的结果即 可,如:22[(1)13]y x =+-+ , 即:22(1)4y x =++ 。
武汉中考复习:二次函数的图像与性质(15题)

专题四:二次函数的图像与性质(中考15题)1.二次函数y =ax 2+bx +c (a ≠0)的部分图象如图,图象过点(﹣1,0),对称轴为直线x =2,下列结论:①4a +b =0;②9a +c >3b ;③4a +2b ≥am 2+bm (m 为任意实数);④当x >﹣1时,y 的值随x 值的增大而增大;⑤若(−12,y 1),(133,y 2)是抛物线上两点,则y 1<y 2,⑥若点B (m ,y 1),C (4﹣m ,y 2)在此函数图象上,则y 1=y 2.其中正确的结论有 (填序号).第1题图 第2题图 第5题图2.如图,二次函数y =ax 2+bx +c (a ≠0)的图象与x 轴交于A (﹣1,0),对称轴为直线x =1,与y 轴的交点B 在(0,2)和(0,3)之间(不包括这两个点),下列结论:①当﹣1<x <3时,y >0;②﹣1<a <﹣.③当m ≠1时,a +b >m (am +b );④b 2﹣4ac =15a 2.其中正确的结论的序号 .3.抛物线y =ax 2+bx +c 经过点(﹣1,0),对称轴为直线x =2,与y 轴的交点在(0,﹣2)与(0,﹣3)之间(不包括这两点).下列结论:①a +b +c <0;②若点M (0.5,y 1)、N (2.5,y 2)在图象上,则y 1<y 2;③若m 为任意实数,则a (m 2﹣4)+b (m ﹣2)≥0;④﹣24≤5(a +b +c )<﹣16.其中正确结论的序号为 .4.在平面直角坐标系中,二次函数y =ax 2+bx +c (a ≠0)的图象与轴的交点分别(﹣3,0),(1,0),且函数与y 轴交点在(0,﹣1)的下方,现给以下结论:①abc <0:②关于方程a (x 2﹣1)+b (x ﹣1)+c =0始终有两个不相等的实数解;③当﹣2≤x ≤3时,y 的取值范围是﹣≤y ≤6b ;则上述说法正确的是 .(填序号)5.如图,二次函数y =ax 2+bx +c (a ≠0)的图象与x 轴交于A 、B 两点,与y 轴交于点C ,且OA =OC ,对称轴为直线x =1,则下列结论:①abc <0;②a +12b +14c =0;③当m <﹣1时,关于x 的方程ax 2+bx +c +m =0无实根;④ac ﹣b +1=0;⑤OA •OB =c a ,⑥2+c 是关于x 的一元二次方程ax 2+bx +c =0的一个根.其中正确的结论有 (填序号).6.二次函数y =ax 2+bx +c 的部分图象如图所示,对称轴为,与x 轴负半轴交点在(﹣4,0)与(﹣3,0)之间,以下结论:①3a ﹣b =0;②b 2﹣4ac >0;③5a ﹣2b +c >0;④4b +3c >0.其中一定正确的是 (填序号).7.如图,抛物线y =﹣x 2+2x +m +1(m 为常数)交y 轴于点A ,与x 轴的一个交点在2和3之间,顶点为B.以下结论:①抛物线y=﹣x2+2x+m+1与直线y=m+2有且只有一个交点;②若点M(﹣2,y1)、点N(,y2)、点P(2,y3)在该函数图象上,则y1<y2<y3;③将该抛物线向左平移2个单位,再向下平移2个单位,所得抛物线解析式为y=﹣(x+1)2+m;④点A关于直线x=1的对称点为C,点D、E分别在x轴和y轴上,当m=1时,四边形BCDE周长的最小值为.其中一定正确的是(填序号).第6题图第7题图第8题图8.二次函数y=ax2+bx+c(a≠0)的图象经过点(﹣2,0),(x0,0),0<x0<1,与y轴正半轴相交,且交点在(0,1)的上方,下列结论:①2a<b;②(a+c)2<b2;③a(m2﹣1)+b(m+1)≤0(m 为任意实数);④b>2a+.其中一定成立的结论的序号是.9.二次函数y=ax2+bx+c的图象如图所示,给出下列结论:①abc>0;②3a﹣c>0;③若﹣1<m<n <1,则m+n<﹣;④<16,其中正确的序号是.10.如图,二次函数y=ax2+bx+c(a≠0)的图象经过点(1,2),且与x轴交点的横坐标分别为x1、x2,其中﹣1<x1<0,1<x2<2.下列结论:①﹣a<b<﹣2a;②b2+8a>4ac;③a<﹣1;④方程ax2+(b+c﹣2)x=0的解为x1=0,x2=1.其中正确的是.第9题图第10题图第11题图11.抛物线y=ax2+bx+c(a,b,c是常数,a≠0)的顶点坐标是(﹣2,3),与x轴的一个交点在点(﹣4,0)和点(﹣3,0)之间,其部分图象如图所示,下列结论:①4a﹣b=0;②关于x的方程ax2+bx+c=2有两个不相等实数根;③c≤3a.其中正确的序号是.12.二次函数y =ax 2+bx +c (a 、b 、c 为常数,a ≠0)中的x 与y 的部分对应值如下表:x ﹣3 01 y 4 4 n当n <0时,下列结论:①abc <0;②当x >﹣1时,y 的值随x 值的增大而减小;③a <﹣1;④n >4a ;⑤当n =−43时,关于x 的不等式ax 2+(b +43)x +c <0的解集为x <﹣3或x >1.其中一定正确的是 (填序号即可).13.二次函数y =ax 2+bx +c (a ,b ,c 是常数,a ≠0)的自变量x 与函数值y 的部分对应值如表: x … ﹣2 ﹣1 01 2 … y =ax 2+bx +c …t m ﹣2 ﹣2 n … 且当x =时,与其对应的函数值y >0,下列结论:①abc >0;②﹣2和3是关于x 的方程ax 2+bx +c=t 的两个根;③0<m +n <;④4a +c >n +2b ;其中,正确结论的是 . 14.二次函数y =ax 2+bx +c (a ,b ,c 为常数,a ≠0)中的x 与y 的部分对应值如表:x…… ﹣3 ﹣2 ﹣1 0 t …… y …… 0 m n m0 …… 下列结论中一定正确的有 .(填序号即可)①9a ﹣3b +c =0;②t =1;③关于x 的一元二次方程a (x ﹣1)2+bx +c =2a 的解是x 1=﹣2,x 2=2;④若方程ax 2+bx +c =p 有两个实数根x 1,x 2,则二次函数y =a (x ﹣x 1)(x ﹣x 2)+p 与x 轴的交点坐标是(﹣1,0),(3,0).15.定义[a 、b 、c ]为二次函数y =ax 2+bx +c (a ≠0)的特征数,下面给出特征数为[2m ,1﹣m ,﹣1﹣m ]的函数的一些结论:①当m =﹣3时,函数图象的顶点坐标是(,);②当m >0时,函数图象截x 轴所得的线段长度大于;③当m <0时,函数在x >时,y 随x 的增大而减小;④当m ≠0时,函数图象经过同一个点,正确的结论是 .16.已知,抛物线y =﹣x 2+mx +m (其中m 是常数).下列结论:①无论m 取何实数,它都经过定点P (﹣1,﹣1);②它的顶点在抛物线y =x 2+2x 上运动;③当它与x 轴有唯一交点时,m =0;④当x <﹣1时,﹣x 2+mx +m <x .其中一定正确的是 (填序号即可).17.二次函数y =(m +1)x 2﹣2mx +m ﹣2的图象与x 轴有两个交点(x 1,0)和(x 2,0),下列结论:①该函数图象过点(1,﹣1);②当m =0时,二次函数与坐标轴的交点所围成的三角形面积是2;③若该函数的图象开口向下,则m 的取值范围为﹣2<m <﹣1;④当m >0,且﹣2≤x ≤﹣1时,y 的最大值为(9m +2).其中一定正确的是 (填序号即可).18.已知二次函数y=ax2+bx+c(a>0,c<0)的图象经过点(,m),(3,n),与x轴交于点A(x1,0),点B(x2,0)(点A在点B的左侧).若7a+3b+2c=0,则有下列结论:①m<0,n>0;②x1+x2<;③<x2<3.其中一定正确的是(填序号即可).19.已知抛物线y=ax2+bx+c(a,b,c为常数,且a≠0)的图象如图所示,下列结论:①b>a;②若﹣1<m<n<1,则m+n<﹣;③3|a|+|c|<2|b|.其中一定正确的是(填序号即可).第19题图第20题图第21题图20.数学课上老师出了这样一道题:如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣2,与x轴的一个交点在(﹣3,0)和(﹣4,0)之间,其部分图象如图所示,请同学们据此写出正确结论,每写对一个结论得20分,写错一个结论倒扣10分;小涛得到了如下结论:①c>0;②4a﹣b=0;③﹣3a+c>0;④4a﹣2b≥at2+bt(t为实数);⑤点(﹣3,y1),(﹣5,y2),(0,y3)是该抛物线的点,则y1>y3>y2.则小涛此题得分为21.如图,直线y=kx+b(k≠0)与抛物线y=ax2(a≠0)交于A,B两点,且点A的横坐标是﹣2,点B的横坐标是3,则以下结论:①抛物线y=ax2(a≠0)的图象的顶点一定是原点;②x>0时,直线y=kx+b(k≠0)与抛物线y=ax2(a≠0)的函数值都随着x的增大而增大;③AB的长度可以等于5;④△OAB有可能成为等边三角形;⑤当﹣3<x<2时,ax2+kx<b,其中一定正确的是(填序号即可).22.在平面直角坐标系xOy中,抛物线y=mx2﹣2mx+m﹣3与x轴交于点A、B.下列结论:①m的取值范围是m>0;②抛物线的顶点坐标为(1,﹣3);③若线段AB上有且只有5个点的横坐标为整数,则m的取值范围是<m≤;④若抛物线在﹣3<x<0这一段位于x轴下方,在5<x<6这一段位于x轴上方,则m的值为.其中一定正确的是(填序号即可).23.已知抛物线y=ax2+bx+c(a≠0)与x轴交于点A(﹣1,0),对称轴为直线x=1,与y轴的交点B在(0,3)和(0,4)之间(包含这两个点).有下列结论:①abc<0;②关于x的方程ax2+bx+c =2a有两个不等的实数根;③﹣≤a≤﹣1.其中一定正确的是(填序号即可).。
2019年初升高数学衔接辅导之二次函数y=ax2+bx+c的图像和性质(含答案)

04二次函数y =ax 2+bx +c 的图像和性质高中必备知识点1:二次函数图像的伸缩变换问题 函数y =ax 2与y =x 2的图象之间存在怎样的关系? 为了研究这一问题,我们可以先画出y =2x 2,y =12x 2,y =-2x 2的图象,通过这些函数图象与函数y =x 2的图象之间的关系,推导出函数y =ax 2与y =x 2的图象之间所存在的关系. 先画出函数y =x 2,y =2x 2的图象. 先列表:再描点、连线,就分别得到了函数y =x 2,y =2x 2的图象(如图2-1所示),从图2-1我们可以得到这两个函数图象之间的关系:函数y =2x 2的图象可以由函数y =x 2的图象各点的纵坐标变为原来的两倍得到.同学们也可以用类似于上面的方法画出函数y =12x 2,y =-2x 2的图象,并研究这两个函数图象与函数y =x 2的图象之间的关系. 通过上面的研究,我们可以得到以下结论:二次函数y =ax 2(a ≠0)的图象可以由y =x 2的图象各点的纵坐标变为原来的a 倍得到.在二次函数y =ax 2(a ≠0)中,二次项系数a 决定了图象的开口方向和在同一个坐标系中的开口的大小.典型考题【典型例题】二次函数的图象如图所示,有下列结论:①;②;③;④,其中正确的结论个数是A.1个B.2 个C.3 个D.4 个【变式训练】下列说法错误的是( )A.二次函数y=-2x2中,当x=0时,y有最大值是0B.二次函数y=4x2中,当x>0时,y随x的增大而增大C.在三条抛物线y=2x2,y=-0.5x2,y=-x2中,y=2x2的图象开口最大,y=-x2的图象开口最小D.不论a是正数还是负数,抛物线y=ax2(a≠0)的顶点一定是坐标原点【能力提升】抛物线y=x2,y=﹣3x2,y=﹣x2,y=2x2的图象开口最大的是()A.y=x2B.y=﹣3x2C.y=﹣x2D.y=2x2高中必备知识点2:二次函数图像的平移变换函数y =a (x +h )2+k 与y =ax 2的图象之间存在怎样的关系?同样地,我们可以利用几个特殊的函数图象之间的关系来研究它们之间的关系.同学们可以作出函数y =2(x +1)2+1与y =2x 2的图象(如图2-2所示),从函数的同学我们不难发现,只要把函数y =2x 2的图象向左平移一个单位,再向上平移一个单位,就可以得到函数y =2(x +1)2+1的图象.这两个函数图象之间具有“形状相同,位置不同”的特点.类似地,还可以通过画函数y =-3x 2,y =-3(x -1)2+1的图象,研究它们图象之间的相互关系.通过上面的研究,我们可以得到以下结论:二次函数y =a (x +h )2+k (a ≠0)中,a 决定了二次函数图象的开口大小及方向;h 决定了二次函数图象的左右平移,而且“h 正左移,h 负右移”;k 决定了二次函数图象的上下平移,而且“k 正上移,k 负下移”.由上面的结论,我们可以得到研究二次函数y =ax 2+bx +c (a ≠0)的图象的方法:由于y =ax 2+bx +c =a (x 2+b x a )+c =a (x 2+b x a+224b a )+c -24b a224()24b b aca x a a-=++, 所以,y =ax 2+bx +c (a ≠0)的图象可以看作是将函数y =ax 2的图象作左右平移、上下平移得到的,于是,二次函数y =ax 2+bx +c (a ≠0)具有下列性质:(1)当a >0时,函数y =ax 2+bx +c 图象开口向上;顶点坐标为24(,)24b ac b a a--,对称轴为直线x =-2ba;当x <2b a -时,y 随着x 的增大而减小;当x >2b a -时,y 随着x 的增大而增大;当x =2ba-时,函数取最小值y =244ac b a -.(2)当a <0时,函数y =ax 2+bx +c 图象开口向下;顶点坐标为24(,)24b ac b a a--,对称轴为直线x =-2ba;当x <2b a -时,y 随着x 的增大而增大;当x >2b a -时,y 随着x 的增大而减小;当x =2ba-时,函数取最大值y =244ac b a -.典型考题【典型例题】如图,已知抛物线C 1:y =﹣x 2+4,将抛物线C 1沿x 轴翻折,得到抛物线C 2(1)求出抛物线C 2的函数表达式;(2)现将抛物线C 1向左平移m 个单位长度,平移后得到的新抛物线的顶点为M ,与x 轴的交点从左到右依次为A ,B ;将抛物线C 2向右也平移m 个单位长度,平移后得到的新抛物线的顶点为N ,与x 轴交点从左到右依次为D ,E .在平移过程中,是否存在以点A ,N ,E ,M 为顶点的四边形是矩形的情形?若存在,请求出此时m 的值;若不存在,请说明理由.【变式训练】如图,抛物线轴的负半轴相交于点,将抛物线平移得到抛物线相交于点,直线于点,且.(1)求点的坐标;(2)写出一种将抛物线平移到抛物线的方法;(3)在轴上找点,使得的值最小,求点的坐标.【能力提升】已知抛物线y=﹣x2+bx+c经过点B(﹣1,0)和点C(2,3).(1)求此抛物线的函数表达式;(2)如果此抛物线上下平移后过点(﹣2,﹣1),试确定平移的方向和平移的距离.专题验收测试题1.抛物线y=ax2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表:从上表可知,下列说法正确的有多少个①抛物线与x轴的一个交点为(﹣2,0);②抛物线与y轴的交点为(0,6);③抛物线的对称轴是直线x=;④抛物线与x轴的另一个交点为(3,0);⑤在对称轴左侧,y随x增大而减少.A.2 B.3 C.4 D.52.如图,一条抛物线与x轴相交于A(x1,0)、B(x2,0)两点(点B在点A的右侧),其顶点P在线段MN上移动,M、N的坐标分别为(﹣1,2)、(1,2),x1的最小值为﹣4,则x2的最大值为()A.6 B.4 C.2 D.﹣23.如图,已知抛物线y=x2+bx+c与直线y=x交于(1,1)和(3,3)两点,现有以下结论:①b2﹣4c>0;②3b+c+6=0;③当x2+bx+c>2x时,x>2;④当1<x<3时,x2+(b﹣1)x+c<0,其中正确的序号是()A.①②④B.②③④C.②④D.③④4.定义运算“※”为:a※b=,如:1※(﹣2)=﹣1×(﹣2)2=﹣4.则函数y=2※x 的图象大致是()A.B.C.D.5.若抛物线y=ax2+2ax+4a(a>0)上有A(32,y1)、B(2,y2)、C(32,y3)三点,则y1、y2、y 3的大小关系为( ). A .y 1<y 2<y 3B .y 1<y 3<y 2C .y 3<y 1<y 2D .y 2<y 3<y 16.下列函数是二次函数的是( ). A .y =2x B .y =1x+x C .y =x +5D .y =(x +1)(x ﹣3)7.下列对二次函数2y x x =-的图象的描述,正确的是( ) A .经过原点 B .对称轴是y 轴 C .开口向下D .在对称右侧部分是向下的8.已知函数y =(x ﹣a )(x ﹣b )(其中a >b )的图象如图所示,则函数y =ax +b 的图象大致是( )A .B .C .D .9.如图,已知抛物线y =ax 2+bx +c 经过点(﹣1,0),以下结论:①2a +b >0;②a +c <0;③4a +2b +c >0;④b 2﹣5a 2>2a c .其中正确的是( )A .①②B .③④C .②③④D .①②③④10.二次函数y =ax 2+bx +c (a ≠0)的大致图象如图所示,顶点坐标为(﹣2,﹣9a ),下列结论:①abc >0;②4a +2b +c >0;③5a ﹣b +c =0;④若方程a (x +5)(x ﹣1)=﹣1有两个根x 1和x 2,且x 1<x 2,则﹣5<x 1<x 2<1;⑤若方程|ax 2+bx +c |=2有四个根,则这四个根的和为﹣4.其中正确的结论有( )A .2个B .3个C .4个D .5个11.如图,与抛物线y =x 2﹣2x ﹣3关于直线x =2成轴对称的函数表达式为______.12.已知关于x 的一元二次方程ax 2+bx +c =5的一个根是2,且二次函数y =ax 2+bx +c 的对称轴是直线x =2,则抛物线y =ax 2+bx +c 的顶点坐标为_____.13.二次函数21212y x x =-+ 中,二次项系数为____,一次项是____,常数项是___ 14.如图,二次函数y =ax 2+bx +c (a ≠0).图象的顶点为D ,其图象与x 轴的交点A 、B 的横坐标分别为﹣1、3,与y 轴负半轴交于点C .下面三个结论:①2a +b =0;②a +b +c >0;③只有当12a =时,△ABD 是等腰直角三角形;那么,其中正确的结论是_____.(只填你认为正确结论的序号)15.把二次函数y=x2+2x+3的图象向左平移1个单位长度,再向下平移1个单位长度,就得到二次函数____的图象.16.已知当2≤x≤3时,关于x的多项式x2﹣2kx+k2﹣k﹣1(k为大于2的常数)有最小值﹣2,则常数k的值为___.17.已知二次函数y=a(x-m)2-a(x-m)(a,m为常数,且a≠0).(1)求证:不论a与m为何值,该函数的图象与x轴总有两个公共点;(2)设该函数的图象与x轴的两个交点为A(x1,0),B(x2,0),且x12+x22=25,求m的值;(3)设该函数的图象的顶点为C,与x轴交于A,B两点,且△ABC的面积为1,求a的值.18.如图,抛物线y=﹣x2+bx+c经过A(﹣1,0),B(3,0)两点,且与y轴交于点C,点D是抛物线的顶点,抛物线对称轴DE交x轴于点E,连接B D.(1)求经过A,B,C三点的抛物线的函数表达式;(2)点P是线段BD上一点,当PE=PC时,求点P的坐标.19.如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(﹣2,0),B(4,0),与直线y=32x﹣3交于点C(0,﹣3),直线y=32x﹣3与x轴交于点D.(1)求该抛物线的解析式(2)点P是抛物线上第四象限上的一个动点连接PC,PD,当△PCD的面积最大时,求点P的坐标;(3)将抛物线的对称轴向左平移3个长度单位得到直线l,点E是直线l上一点,连接OE,BE,若直线l上存在使sin∠BEO最大的点E,请直接写出满足条件的点E的坐标;若不存在,请说明理由.20.已知抛物线y=ax2+bx+2经过A(﹣1,0),B(2,0),C三点.直线y=mx+12交抛物线于A,Q两点,点P是抛物线上直线AQ上方的一个动点,作PF⊥x轴,垂足为F,交AQ于点N.(1)求抛物线的解析式;(2)如图①,当点P运动到什么位置时,线段PN=2NF,求出此时点P的坐标;(3)如图②,线段AC的垂直平分线交x轴于点E,垂足为D,点M为抛物线的顶点,在直线DE上是否存在一点G,使△CMG的周长最小?若存在,请求出点G的坐标;若不存在,请说明理由.21.现有一次函数y=mx+n和二次函数y=mx2+nx+1,其中m≠0,(1)若二次函数y=mx2+nx+1经过点(2,0),(3,1),试分别求出两个函数的解析式.(2)若一次函数y=mx+n经过点(2,0),且图象经过第一、三象限.二次函数y=mx2+nx+1经过点(a,y1)和(a+1,y2),且y1>y2,请求出a的取值范围.(3)若二次函数y=mx2+nx+1的顶点坐标为A(h,k)(h≠0),同时二次函数y=x2+x+1也经过A点,已知﹣1<h<1,请求出m的取值范围.22.如图,在直角坐标系中,直线y=13x+1与x轴、y轴的交点分别为A、B,以x=﹣1为对称轴的抛物线y=﹣x2+bx+c与x轴分别交于点A、C.(1)求抛物线的解析式;(2)若点P是第二象限内抛物线上的动点,设抛物线的对称轴l与x轴交于一点D,连接PD,交AB于E,求出当以A、D、E为顶点的三角形与△AOB相似时点P的坐标;(3)若点Q在第二象限内,且tan∠AQD=2,线段CQ是否存在最小值?如果存在直接写出最小值,如果不存在,请说明理由.专题04二次函数y=ax2+bx+c的图像和性质高中必备知识点1:二次函数图像的伸缩变换问题函数y=ax2与y=x2的图象之间存在怎样的关系?为了研究这一问题,我们可以先画出y =2x 2,y =12x 2,y =-2x 2的图象,通过这些函数图象与函数y =x 2的图象之间的关系,推导出函数y =ax 2与y =x 2的图象之间所存在的关系. 先画出函数y =x 2,y =2x 2的图象. 先列表:再描点、连线,就分别得到了函数y =x 2,y =2x 2的图象(如图2-1所示),从图2-1我们可以得到这两个函数图象之间的关系:函数y =2x 2的图象可以由函数y =x 2的图象各点的纵坐标变为原来的两倍得到.同学们也可以用类似于上面的方法画出函数y =12x 2,y =-2x 2的图象,并研究这两个函数图象与函数y =x 2的图象之间的关系. 通过上面的研究,我们可以得到以下结论:二次函数y =ax 2(a ≠0)的图象可以由y =x 2的图象各点的纵坐标变为原来的a 倍得到.在二次函数y =ax 2(a ≠0)中,二次项系数a 决定了图象的开口方向和在同一个坐标系中的开口的大小.典型考题【典型例题】二次函数的图象如图所示,有下列结论:①;②;③;④,其中正确的结论个数是A.1个B.2 个C.3 个D.4 个【答案】C【解析】由图象可得,,,故错误,当时,,故正确,当时,,由得,,则,得,故正确,,得,故正确,故选:C.【变式训练】下列说法错误的是( )A.二次函数y=-2x2中,当x=0时,y有最大值是0B.二次函数y=4x2中,当x>0时,y随x的增大而增大C.在三条抛物线y=2x2,y=-0.5x2,y=-x2中,y=2x2的图象开口最大,y=-x2的图象开口最小D.不论a是正数还是负数,抛物线y=ax2(a≠0)的顶点一定是坐标原点【答案】C【解析】A、a=-2<0,抛物线开口向下,当x=0时,y有最大值是0,故该选项正确;B、二次函数y=4x2中,当x>0时,y随x的增大而增大,故该选正确;C、因为|2|>|-1|>|-0.5|,所以,y=2x2的图象开口最小,y=-0.5x2的图象开口最大,故该选错误;D、不论a是正数还是负数,抛物线y=ax2(a≠0)的顶点一定是坐标原点,故该选正确.故选C.【能力提升】抛物线y=x2,y=﹣3x2,y=﹣x2,y=2x2的图象开口最大的是()A.y=x2B.y=﹣3x2C.y=﹣x2D.y=2x2【答案】A【解析】∵二次函数中|a|的值越小,则函数图象的开口也越大,又∵,∴抛物线y=x2,y=﹣3x2,y=﹣x2,y=2x2的图象开口最大的是y=x2,故选A.高中必备知识点2:二次函数图像的平移变换函数y=a(x+h)2+k与y=ax2的图象之间存在怎样的关系?同样地,我们可以利用几个特殊的函数图象之间的关系来研究它们之间的关系.同学们可以作出函数y=2(x+1)2+1与y=2x2的图象(如图2-2所示),从函数的同学我们不难发现,只要把函数y=2x2的图象向左平移一个单位,再向上平移一个单位,就可以得到函数y=2(x +1)2+1的图象.这两个函数图象之间具有“形状相同,位置不同”的特点.类似地,还可以通过画函数y =-3x 2,y =-3(x -1)2+1的图象,研究它们图象之间的相互关系.通过上面的研究,我们可以得到以下结论:二次函数y =a (x +h )2+k (a ≠0)中,a 决定了二次函数图象的开口大小及方向;h 决定了二次函数图象的左右平移,而且“h 正左移,h 负右移”;k 决定了二次函数图象的上下平移,而且“k 正上移,k 负下移”.由上面的结论,我们可以得到研究二次函数y =ax 2+bx +c (a ≠0)的图象的方法:由于y =ax 2+bx +c =a (x 2+b x a )+c =a (x 2+b x a+224b a )+c -24b a224()24b b aca x a a-=++, 所以,y =ax 2+bx +c (a ≠0)的图象可以看作是将函数y =ax 2的图象作左右平移、上下平移得到的,于是,二次函数y =ax 2+bx +c (a ≠0)具有下列性质:(1)当a >0时,函数y =ax 2+bx +c 图象开口向上;顶点坐标为24(,)24b ac b a a--,对称轴为直线x =-2ba;当x <2b a -时,y 随着x 的增大而减小;当x >2b a -时,y 随着x 的增大而增大;当x =2ba-时,函数取最小值y =244ac b a -.(2)当a <0时,函数y =ax 2+bx +c 图象开口向下;顶点坐标为24(,)24b ac b a a--,对称轴为直线x =-2ba;当x <2b a -时,y 随着x 的增大而增大;当x >2b a -时,y 随着x 的增大而减小;当x =2ba-时,函数取最大值y =244ac b a -.典型考题【典型例题】如图,已知抛物线C 1:y =﹣x 2+4,将抛物线C 1沿x 轴翻折,得到抛物线C 2(1)求出抛物线C 2的函数表达式;(2)现将抛物线C 1向左平移m 个单位长度,平移后得到的新抛物线的顶点为M ,与x 轴的交点从左到右依次为A ,B ;将抛物线C 2向右也平移m 个单位长度,平移后得到的新抛物线的顶点为N ,与x 轴交点从左到右依次为D ,E .在平移过程中,是否存在以点A ,N ,E ,M 为顶点的四边形是矩形的情形?若存在,请求出此时m 的值;若不存在,请说明理由.【答案】(1)y =x 2﹣4(2)当m =3时,以点A ,N ,E ,M 为顶点的四边形是矩形 【解析】(1)∵抛物线C 1的顶点为(0,4), ∴沿x 轴翻折后顶点的坐标为(0.﹣4),∴抛物线C 2的函数表达式为y =x 2﹣4;(2)存在连接AN ,NE ,EM ,MA ,依题意可得:M (﹣m ,4),N (m ,﹣4),∴M,N关于原点O对称OM=ON,原C1、C2抛物线与x轴的两个交点分别(﹣2,0),(2,0),∴A(﹣2﹣m,0),E(2+m,0),∴A,E关于原点O对称,∴OA=OE∴四边形ANEM为平行四边形,∴AM2=22+42=20,ME2=(2+m+m)2+42=4m2+8m+20,AE2=(2+m+2+m)2=4m2+16m+16,若AM2+ME2=AE2,∴20+4m2+8m+20=4m2+16m+16,解得m=3,此时△AME是直角三角形,且∠AME=90,∴当m=3时,以点A,N,E,M为顶点的四边形是矩形.【变式训练】如图,抛物线轴的负半轴相交于点,将抛物线平移得到抛物线相交于点,直线于点,且.(1)求点的坐标;(2)写出一种将抛物线平移到抛物线的方法;(3)在轴上找点,使得的值最小,求点的坐标.【答案】(1)A(-2,0),B(3,5),C(8,10);(2)先将向右平移5个单位,再向上平移5个单位得到;(3)P(0,).【解析】(1)M1:y=x2-4与x轴的负半轴相交于点A,∴A(-2,0),∵AB=BC,C(8,m),∴,设AB直线解析式为y=kx+b,∵y=x2-4与相交于点A和B,∴m=10,∴B(3,5),C(8,10);(2)∵抛物线M1平移得到抛物线M2,∴a=1,∵B(3,5),C(8,10)在抛物线y=x2+bx+c上,∴y=x2-10+26=(x-5)2+1,由M1平移得到抛物线M2先向右平移5个单位长度,再向上平移5个单位长度;(3)作点B关于y轴的对称点B',连接CB'与y轴的交点即为P,∴B'(-3,5),设直线B'C的直线解析式为y=mx+n,.【能力提升】已知抛物线y=﹣x2+bx+c经过点B(﹣1,0)和点C(2,3).(1)求此抛物线的函数表达式;(2)如果此抛物线上下平移后过点(﹣2,﹣1),试确定平移的方向和平移的距离.【答案】(1)y=﹣x2+2x+3;(2)将抛物线向上平移4个单位.【解析】(1)把B(﹣1,0)和点C(2,3)代入y=﹣x2+bx+c得,解得,所以抛物线解析式为y=﹣x2+2x+3;(2)把x=﹣2代入y=﹣x2+2x+3得y=﹣4﹣4+3=﹣5,点(﹣2,﹣5)向上平移4个单位得到点(﹣2,﹣1),所以需将抛物线向上平移4个单位.专题验收测试题1.抛物线y=ax2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表:从上表可知,下列说法正确的有多少个①抛物线与x轴的一个交点为(﹣2,0);②抛物线与y轴的交点为(0,6);③抛物线的对称轴是直线x=;④抛物线与x轴的另一个交点为(3,0);⑤在对称轴左侧,y随x增大而减少.A.2 B.3 C.4 D.5【答案】C【解析】的对称性,逐一判断.【详解】根据图表,抛物线与x轴的一个交点为(﹣2,0),∴①正确;根据图表,抛物线与y轴交与(0,6),②正确;∵抛物线经过点(0,6)和(1,6),∴对称轴为x=,∴③正确;设抛物线经过点(x,0),∴x=解得:x=3∴抛物线一定经过(3,0),④正确;在对称轴左侧,y随x增大而增大,∴⑤错误,故选C.2.如图,一条抛物线与x轴相交于A(x1,0)、B(x2,0)两点(点B在点A的右侧),其顶点P在线段MN上移动,M、N的坐标分别为(﹣1,2)、(1,2),x1的最小值为﹣4,则x2的最大值为()A.6 B.4 C.2 D.﹣2【答案】B【解析】由题意可知,当P在M点时,x1有最小值﹣4,∵M的坐标分别为(﹣1,2),∴x2=2;∴x2与对称轴的距离是3;当P在N点时,x2有最大值,∵N的坐标分别为(1,2),∴x2的最大值为4.故选B.3.如图,已知抛物线y=x2+bx+c与直线y=x交于(1,1)和(3,3)两点,现有以下结论:①b2﹣4c>0;②3b+c+6=0;③当x2+bx+c>2x时,x>2;④当1<x<3时,x2+(b﹣1)x+c<0,其中正确的序号是()A.①②④B.②③④C.②④D.③④【答案】C【解析】∵函数y=x2+bx+c与x轴无交点,∴b2﹣4ac<0;∴b2﹣4c<0故①不正确;当x=3时,y=9+3b+c=3,即3b+c+6=0;故②正确;把(1,1)(3,3)代入y=x2+bx+c,得抛物线的解析式为y=x2﹣3x+3,当x=2时,y=x2﹣3x+3=1,y=2x=1,抛物线和双曲线的交点坐标为(2,1)第一象限内,当x>2时,x2+bx+c>2x;或第三象限内,当x<0时,x2+bx+c>2x;故③错误;∵当1<x<3时,二次函数值小于一次函数值,∴x2+bx+c<x,∴x2+(b﹣1)x+c<0.故④正确;故选:C.4.定义运算“※”为:a※b=,如:1※(﹣2)=﹣1×(﹣2)2=﹣4.则函数y=2※x 的图象大致是()A.B.C.D.【答案】C【解析】解:y=2※x=,当x>0时,图象是y=对称轴右侧的部分;当x<0时,图象是y=对称轴左侧的部分,所以C选项是正确的.5.若抛物线y=ax2+2ax+4a(a>0)上有A(32,y1)、B(2,y2)、C(32,y3)三点,则y1、y2、y3的大小关系为( ).A.y1<y2<y3B.y1<y3<y2C.y3<y1<y2D.y2<y3<y1【答案】B【解析】解:抛物线的对称轴是x=﹣1,开口向上,且与x轴无交点,∴与对称轴距离越近的点对应的纵坐标越小.A、B、C三点与对称轴距离按从小到大顺序是A、C、B,∴y1<y3<y2,故选:B.6.下列函数是二次函数的是( ).A .y =2xB .y =1x +xC .y =x +5D .y =(x +1)(x ﹣3)【答案】D【解析】解:A 、y =2x ,是一次函数,故此选项错误;B 、y =1x +x ,不是整式,故此选项错误;C 、y =x +5,是一次函数,故此选项错误;D 、y =(x +1)(x ﹣3),是二次函数,故此选项正确.故选:D .7.下列对二次函数2y x x =-的图象的描述,正确的是()A .经过原点B .对称轴是y 轴C .开口向下D .在对称右侧部分是向下的【答案】A【解析】解:A 、当x =0时,y =x 2﹣x =0,∴抛物线经过原点,选项A 正确;B 、∵122ba -=, ∴抛物线的对称轴为直线12x =,选项B 不正确;C 、∵a =1>0,∴抛物线开口向上,选项C 不正确;D 、∵a >0,抛物线的对称轴为直线12x =, ∴当12x >时,y 随x 值的增大而增大,选项D 不正确.故选:A .8.已知函数y=(x﹣a)(x﹣b)(其中a>b)的图象如图所示,则函数y=ax+b的图象大致是()A.B.C.D.【答案】C【解析】解:∵y=(x﹣a)(x﹣b)=x2﹣(a+b)x+ab,∵抛物线的开口向上知二次项系数>0,与y轴的交点为在y轴负半轴上,∴ab<0,∵对称轴在y轴的右侧,二次项系数大于0,∴﹣(a+b)>0.∴a+b<0,∵a>b,∴a>0,b<0,∴y=ax+b的图象是C选项,故选:C.9.如图,已知抛物线y=ax2+bx+c经过点(﹣1,0),以下结论:①2a+b>0;②a+c<0;③4a+2b+c >0;④b2﹣5a2>2a c.其中正确的是( )A .①②B .③④C .②③④D .①②③④【答案】B【解析】 解:由图象可知a <0,0<﹣2b a <1, ∴b <﹣2a ,∴2a +b <0,所以①错误; ∵﹣2b a>0,a <0, ∴b >0,当x =﹣1时,y 1=a ﹣b +c =0,∴a +c =b >0,所以②错误;∵当x =2时,y >0,∴4a +2b +c >0﹣﹣﹣﹣②,所以③正确;∵过(﹣1,0),代入得a ﹣b +c =0,∴b 2﹣2ac ﹣5a 2=(a +c )2﹣2ac ﹣5a 2=c 2﹣4a 2=(c +2a )(c ﹣2a )又∵4a +2b +c >04a +2(a +c )+c >0即2a +c >0①∵a <0,∴c >0则c ﹣2a >0②由①②知(c +2a )(c ﹣2a )>0,所以b 2﹣2ac ﹣5a 2>0,即b 2﹣5a 2>2ac ,所以④正确. 故选:B .10.二次函数y =ax 2+bx +c (a ≠0)的大致图象如图所示,顶点坐标为(﹣2,﹣9a ),下列结论:①abc >0;②4a +2b +c >0;③5a ﹣b +c =0;④若方程a (x +5)(x ﹣1)=﹣1有两个根x 1和x 2,且x 1<x 2,则﹣5<x 1<x 2<1;⑤若方程|ax 2+bx +c |=2有四个根,则这四个根的和为﹣4.其中正确的结论有( )A .2个B .3个C .4个D .5个【答案】A【解析】 解:∵抛物线的开口向上,则a >0,对称轴在y 轴的左侧,则b >0,交y 轴的负半轴,则c <0,∴abc <0,所以①结论错误;∵抛物线的顶点坐标(﹣2,﹣9a ), ∴﹣b 2a -=﹣2,244ac b a-=﹣9a , ∴b =4a ,c =﹣5a ,∴抛物线的解析式为y =ax 2+4ax ﹣5a ,∴4a +2b +c =4a +8a ﹣5a =7a >0,所以②结论正确,5a ﹣b +c =5a ﹣4a ﹣5a =﹣4a <0,故③结论错误,∵抛物线y =ax 2+4ax ﹣5a 交x 轴于(﹣5,0),(1,0),∴若方程a (x +5)(x ﹣1)=﹣1有两个根x 1和x 2,且x 1<x 2,则﹣5<x 1<x 2<1,正确,故结论④正确,若方程|ax 2+bx +c |=1有四个根,设方程ax 2+bx +c =1的两根分别为x 1,x 2,则122x x +=﹣2,可得x 1+x 2=﹣4,设方程ax 2+bx +c =1的两根分别为x 3,x 4,则342x x +=﹣2,可得x 3+x 4=﹣4,所以这四个根的和为﹣8,故结论⑤错误,故选:A .11.如图,与抛物线y =x 2﹣2x ﹣3关于直线x =2成轴对称的函数表达式为______.【答案】y =(x ﹣3)2﹣4【解析】解:y =x 2﹣2x ﹣3的顶点是(1,﹣4),(1,﹣4)关于x =2的对称点是(3,﹣4),y =x 2﹣2x ﹣3关于直线x =2成轴对称的函数表达式为y =(x ﹣3)2﹣4,故答案为:y =(x ﹣3)2﹣4.12.已知关于x 的一元二次方程ax 2+bx +c =5的一个根是2,且二次函数y =ax 2+bx +c 的对称轴是直线x =2,则抛物线y =ax 2+bx +c 的顶点坐标为_____.【答案】(2,5)【解析】解:∵二次函数y =ax 2+bx +c 的对称轴是直线x =2,方程ax 2+bx +c =5的一个根是2,∴当x =2时,y =ax 2+bx +c =5,∴抛物线的顶点坐标是(2,5).故答案为:(2,5).13.二次函数21212y x x =-+ 中,二次项系数为____,一次项是____,常数项是___ 【答案】12 -2x , 1 【解析】∵y =ax 2+bx +c (a ,b ,c 是常数且a ≠0).在一般形式中ax 2叫二次项,bx 叫一次项,c 是常数项.其中a ,b ,c 分别叫二次项系数,一次项系数,常数项∴21212y x x =-+ 中,二次项系数为12,一次项是-2x ,常数项是1. 故答案是:12; -2x;1. 14.如图,二次函数y =ax 2+bx +c (a ≠0).图象的顶点为D ,其图象与x 轴的交点A 、B 的横坐标分别为﹣1、3,与y 轴负半轴交于点C .下面三个结论:①2a +b =0;②a +b +c >0;③只有当12a =时,△ABD 是等腰直角三角形;那么,其中正确的结论是_____.(只填你认为正确结论的序号)【答案】①③【解析】解:①∵图象与x 轴的交点A ,B 的横坐标分别为﹣1,3,∴AB =4,∴对称轴x =﹣b 2a =1, 即2a +b =0.故选项正确;②由抛物线的开口方向向上可推出a >0,而﹣b 2a=1, ∴b <0,∵对称轴x =1,∴当x =1时,y <0,∴a +b +c <0.故选项错误;③要使△ABD 为等腰直角三角形,必须保证D 到x 轴的距离等于AB 长的一半; D 到x 轴的距离就是当x =1时y 的值的绝对值.当x =1时,y =a +b +c ,即|a +b +c |=2,∵当x=1时y<0,∴a+b+c=﹣2,又∵图象与x轴的交点A,B的横坐标分别为﹣1,3,∴当x=﹣1时y=0,即a﹣b+c=0,x=3时y=0,即9a+3b+c=0,解这三个方程可得:b=﹣1,a=12,c=﹣32,故选项正确.故答案为:①③.15.把二次函数y=x2+2x+3的图象向左平移1个单位长度,再向下平移1个单位长度,就得到二次函数____的图象.【答案】y=(x+2)2+1或y=x2+2x+5.【解析】∵y=x2+2x+3=(x+1)2+2,∴抛物线y=x2+2x+3先向左平移1个单位,再向下平移1个单位,平移后的函数关系式是:y=(x+2)2+1或y=x2+2x+5.故答案为:y=(x+2)2+1或y=x2+2x+5.16.已知当2≤x≤3时,关于x的多项式x2﹣2kx+k2﹣k﹣1(k为大于2的常数)有最小值﹣2,则常数k的值为___.【答案】4.【解析】解:x2﹣2kx+k2﹣k﹣1=(x﹣k)2﹣k﹣1(k>2),①当2<k≤3时,当x=k时取最小值,∴﹣k﹣1=﹣2,∴k=2,不合题意;②当k>3时,当x=3时取最小值,∴9﹣6k+k2﹣k﹣1=﹣2,∴k=4或2.5,∵k>3,∴k=4;综上,k=4;故答案为:4.17.已知二次函数y=a(x-m)2-a(x-m)(a,m为常数,且a≠0).(1)求证:不论a与m为何值,该函数的图象与x轴总有两个公共点;(2)设该函数的图象与x轴的两个交点为A(x1,0),B(x2,0),且x12+x22=25,求m的值;(3)设该函数的图象的顶点为C,与x轴交于A,B两点,且△ABC的面积为1,求a的值.【答案】(1)证明见解析;(2)m的值为-4或3;(3)a的值是±8.【解析】(1)证明:令y=0,a(x-m)2-a(x-m)=0,△=(-a)2-4a×0=a2,∵a≠0,∴a2>0,∴不论a与m为何值,该函数的图象与x轴总有两个公共点;(2)解:y=0,则a(x-m)2-a(x-m)=a(x-m)(x-m-1)=0,解得x1=m,x2=m+1,∵x12+x22=25,∴m2+(m+1)2=25,解得m1=-4,m2=3.故m的值为-4或3;(3)解:∵x1=m,x2=m+1,∴AB=(m+1)-m=1,y=a(x-m)2-a(x-m)=a(x-m-12)2-4a,△ABC的面积=12×1×|-4a|=1,解得a=±8.故a的值是±8.18.如图,抛物线y=﹣x2+bx+c经过A(﹣1,0),B(3,0)两点,且与y轴交于点C,点D是抛物线的顶点,抛物线对称轴DE交x轴于点E,连接B D.(1)求经过A,B,C三点的抛物线的函数表达式;(2)点P是线段BD上一点,当PE=PC时,求点P的坐标.【答案】(1)y=﹣x2+2x+3;(2)点P的坐标为(2,2).【解析】解:(1)∵抛物线y=﹣x2+bx+c经过A(﹣1,0),B(3,0)两点,∴10930b cb c--+=⎧⎨-++=⎩,解得23bc=⎧⎨=⎩,∴所求的抛物线的函数表达式为y=﹣x2+2x+3;(2)如图,连接PC,PE.抛物线的对称轴为x=222(1)ba-=-⨯-=1.当x=1时,y=4,∴点D的坐标为(1,4).设直线BD的解析式为y=kx+b,则4 30 k bk b+=⎧⎨+=⎩,解得26kb=-⎧⎨=⎩.∴直线BD的解析式为:y=2x+6,设点P的坐标为(x,﹣2x+6),又C(0,3),E(1,0),则PC2=x2+(3+2x﹣6)2,PE2=(x﹣1)2+(﹣2x+6)2,∵PC=PE,∴x2+(3+2x﹣6)2=(x﹣1)2+(﹣2x+6)2,解得,x=2,则y =﹣2×2+6=2, ∴点P 的坐标为(2,2).19.如图,在平面直角坐标系中,抛物线y =ax 2+bx +c (a ≠0)与x 轴交于点A (﹣2,0),B (4,0),与直线y =32x ﹣3交于点C (0,﹣3),直线y =32x ﹣3与x 轴交于点D . (1)求该抛物线的解析式(2)点P 是抛物线上第四象限上的一个动点连接PC ,PD ,当△PCD 的面积最大时,求点P 的坐标;(3)将抛物线的对称轴向左平移3个长度单位得到直线l ,点E 是直线l 上一点,连接OE ,BE ,若直线l 上存在使sin ∠BEO 最大的点E ,请直接写出满足条件的点E 的坐标;若不存在,请说明理由.【答案】(1)233384y x x =--;(2)P (3,﹣815);(3)点E 的坐标为(﹣2,)或(﹣2,﹣. 【解析】解:(1)用交点式函数表达式得:y =a (x +2)(x ﹣4)=a (x 2﹣2x ﹣8),即﹣8a =﹣3,解得:a =38, 则函数的表达式为:233384y x x =--;(2)y =32x ﹣3,令y =0,则x =2,即点D (2,0),连接OP ,设点P (x ,233384x x --), S △PCD =S △PDO +S △PCO ﹣S △OCD =22133113272(3)323(3)2842288x x x x ⨯-+++⨯⨯-⨯⨯=--+, ∵﹣38<0,∴S △PCD 有最大值, 此时点P (3,﹣815); (3)如图,经过点O 、B 的圆F 与直线l 相切于点E ,此时,sin ∠BEO 最大,过圆心F 作HF ⊥x 轴于点H ,则OH =12OB =2=OA ,OF =EF =4,∴HF =,过点E 的坐标为(﹣2,﹣;同样当点E 在x 轴的上方时,其坐标为(﹣2,;故点E 的坐标为(﹣2,2,﹣).20.已知抛物线y =ax 2+bx +2经过A (﹣1,0),B (2,0),C 三点.直线y =mx +12交抛物线于A ,Q 两点,点P 是抛物线上直线AQ 上方的一个动点,作PF ⊥x 轴,垂足为F ,交AQ 于点N .(1)求抛物线的解析式;(2)如图①,当点P运动到什么位置时,线段PN=2NF,求出此时点P的坐标;(3)如图②,线段AC的垂直平分线交x轴于点E,垂足为D,点M为抛物线的顶点,在直线DE上是否存在一点G,使△CMG的周长最小?若存在,请求出点G的坐标;若不存在,请说明理由.【答案】(1)y=﹣x2+x+2;(2)点P的坐标为(12,94);(3)在直线DE上存在一点G,使△CMG的周长最小,此时G(﹣38,1516).【解析】(1)∵抛物线y=ax2+bx+2经过A(﹣1,0),B(2,0),∴将点A和点B的坐标代入得:204220a ba b-+=⎧⎨++=⎩,解得a=﹣1,b=1,∴抛物线的解析式为y=﹣x2+x+2.(2)直线y=mx+12交抛物线与A、Q两点,把A(﹣1,0)代入解析式得:m=12,∴直线AQ的解析式为y=12x+12.设点P的横坐标为n,则P(n,﹣n2+n+2),N(n,12n+12),F(n,0),∴PN=﹣n2+n+2﹣(12n+12)=﹣n2+12n+32,NF=12n+12.∵PN=2NF,即﹣n2+12n+32=2×(12n+12),解得:n=﹣1或12.当n=﹣1时,点P与点A重合,不符合题意舍去.∴点P的坐标为(12,94).(3)∵y=﹣x2+x+2,=﹣(x﹣12)2+94,∴M(12,94).如图所示,连结AM交直线DE与点G,连结CG、CM此时,△CMG的周长最小.设直线AM的函数解析式为y=kx+b,且过A(﹣1,0),M(12,94).根据题意得:1924k bk b-+=⎧⎪⎨+=⎪⎩,解得3232kb⎧=⎪⎪⎨⎪=⎪⎩.∴直线AM的函数解析式为y=32x+32.∵D为AC的中点,∴D(﹣12,1).设直线AC的解析式为y=kx+2,将点A的坐标代入得:﹣k+2=0,解得k=2,∴AC的解析式为y=2x+2.设直线DE的解析式为y=﹣12x+c,将点D的坐标代入得:14+c=1,解得c=34,∴直线DE的解析式为y=﹣12x+34.将y=﹣12x+34与y=32x+32联立,解得:x=﹣38,y=1516.∴在直线DE上存在一点G,使△CMG的周长最小,此时G(﹣38,1516).21.现有一次函数y=mx+n和二次函数y=mx2+nx+1,其中m≠0,(1)若二次函数y=mx2+nx+1经过点(2,0),(3,1),试分别求出两个函数的解析式.(2)若一次函数y=mx+n经过点(2,0),且图象经过第一、三象限.二次函数y=mx2+nx+1经过点(a,y1)和(a+1,y2),且y1>y2,请求出a的取值范围.(3)若二次函数y=mx2+nx+1的顶点坐标为A(h,k)(h≠0),同时二次函数y=x2+x+1也经过A 点,已知﹣1<h <1,请求出m 的取值范围. 【答案】(1)y =x ﹣2,y =12-x 2+32+1;(2)a <12;(3)m <﹣2或m >0. 【解析】(1)将点(2,0),(3,1),代入一次函数y =mx +n 中,0213m nm n =+⎧⎨=+⎩, 解得12m n =⎧⎨=-⎩,∴一次函数的解析式是y =x ﹣2,再将点(2,0),(3,1),代入二次函数y =mx 2+nx +1,04211931m n m n =++⎧⎨=++⎩, 解得1232m n ⎧=-⎪⎪⎨⎪=⎪⎩,∴二次函数的解析式是213122y x =-++. (2)∵一次函数y =mx +n 经过点(2,0), ∴n =﹣2m ,∵二次函数y =mx 2+nx +1的对称轴是x =n 2m-, ∴对称轴为x =1,又∵一次函数y =mx +n 图象经过第一、三象限, ∴m >0, ∵y 1>y 2, ∴1﹣a >1+a ﹣1, ∴a <12. (3)∵y =mx 2+nx +1的顶点坐标为A (h ,k ), ∴k =mh 2+nh +1,且h =n 2m-,又∵二次函数y=x2+x+1也经过A点,∴k=h2+h+1,∴mh2+nh+1=h2+h+1,∴11 hm=-+,又∵﹣1<h<1,∴m<﹣2或m>0.22.如图,在直角坐标系中,直线y=13x+1与x轴、y轴的交点分别为A、B,以x=﹣1为对称轴的抛物线y=﹣x2+bx+c与x轴分别交于点A、C.(1)求抛物线的解析式;(2)若点P是第二象限内抛物线上的动点,设抛物线的对称轴l与x轴交于一点D,连接PD,交AB于E,求出当以A、D、E为顶点的三角形与△AOB相似时点P的坐标;(3)若点Q在第二象限内,且tan∠AQD=2,线段CQ是否存在最小值?如果存在直接写出最小值,如果不存在,请说明理由.【答案】(1)y=﹣x2﹣2x+3;(2)点P的坐标是(﹣1,4)或(﹣2,3);(3)存在,CQ【解析】解:(1)∵直线y=13x+1与x轴交点为A,∴点A的坐标为(﹣3,0),∵抛物线的对称轴为x=﹣1,∴点C的坐标为(1,0),∵抛物线y=﹣x2+bx+c与x轴分别交于点A、C,。
二次函数的图像和性质

二次函数的图像和性质一、二次函数的一般形式二次函数是一种形式为f(x)=ax2+bx+c的函数,其中a、b、c是实数且a eq0。
二、二次函数的图像1.抛物线二次函数的图像是一条抛物线。
当a>0时,抛物线开口朝上;当a<0时,抛物线开口朝下。
2.判别法利用二次函数的判别式 $\\Delta = b^2 - 4ac$ 的正负性可以确定二次函数的图像开口方向和与x轴的交点情况。
3.最值点二次函数的顶点为抛物线的最值点,当a>0时,最小值在顶点处取得;当a<0时,最大值在顶点处取得。
顶点的横坐标为 $-\\frac{b}{2a}$,纵坐标为 $f\\left(-\\frac{b}{2a}\\right)$。
三、二次函数的性质1.对称轴二次函数的对称轴为直线 $x = -\\frac{b}{2a}$,即抛物线关于对称轴对称。
2.单调性当a>0时,二次函数在对称轴左侧递增,在对称轴右侧递减;当a<0时,二次函数在对称轴左侧递减,在对称轴右侧递增。
3.零点二次函数的零点为方程f(x)=0的解,可以利用求根公式 $x = \\frac{-b \\pm \\sqrt{b^2 - 4ac}}{2a}$ 求得。
4.图像的平移如f(x)=a(x−ℎ)2+k,其中(ℎ,k)为平移后的顶点坐标,抛物线上下平移,方向与a的正负有关。
四、应用二次函数在几何、物理、经济等领域有着广泛的应用。
例如几何问题中的抛物线轨迹、物体自由落体运动方程、经济学中的成本、收益关系等均可用二次函数描述。
结语二次函数作为高中数学中重要的函数类型,在图像和性质上有着独特的表现,通过对其图像和性质的深入理解,可以更好地应用于解决实际问题。
希望本文的介绍能帮助读者更好地掌握二次函数的知识。
专题讲解—二次函数的性质4

二次函数的图像和性质知识点一:二次函数平移问题:1. (2012•鄂州)把抛物线y=x 2+bx+4的图象向右平移3个单位,再向上平移2个单位,所得到的图象的解析式为y=x 2﹣2x+3,则b 的值为( ) A . 2B . 4C . 6D . 82. (2011•攀枝花)在同一平面内下列4个函数;①y=2(x+1)2﹣1;②y=2x 2+3;③y=﹣2x 2﹣1;④2112y x =-的图象不可能由函数y=2x 2+1的图象通过平移变换得到的函数是 .(把你认为正确的序号都填写在横线上)3. (2010•徐州)平面直角坐标系中,若平移二次函数y=(x ﹣2009)(x ﹣2010)+4的图象,使其与x 轴交于两点,且此两点的距离为1个单位,则平移方式为( ) A . 向上平移4个单位B . 向下平移4个单位C . 向左平移4个单位D . 向右平移4个单位4. (2011•桂林)在平面直角坐标系中,将抛物线y=x 2+2x+3绕着它与y 轴的交点旋转180°,所得抛物线的解析式是( ) A 、y=-(x+1)2+2 B 、y=-(x-1)2+4 C 、y=-(x-1)2+2 D 、y=-(x+1)2+45. 把抛物线y=x 2-2x-3绕点A (3,0)旋转180°后所得的抛物线解析式是6. 抛物线y=-(x-L )(x-3-k)+L 与抛物线y=(x-3)2+4关于原点对称,L+k= .知识点二:多个函数图像在同一坐标系共存问题: 1. 二次函数y=ax 2+bx+c 的图像如图,反比例函数y =ax与正比例函数y =(b +c )x 在同一坐标系中的大致图像可能是( )2. 抛物线c bx ax y ++=2图像如图所示,则一次函数24b ac bx y +--=与反比例函数 xc b y ++=a 在同一坐标系内的图像大致为( )知识点三:二次函数通过图像与系数a ,b ,c 的关系抛物线开口抛物线对称轴抛物线与坐标轴交点a >0,开口向上 a <0,开口向下│a │越大,开口越小 直线x=-b/2a当a 、b 同号时,对称轴在y 轴左侧; 当a 、b 异号时,对称轴在y 轴右侧;与y 轴交点坐标(0,c ),当c =0时,抛物线过原点。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题四 二次函数的图像与性质(一)【知识梳理】1.一般地,形如_______的函数叫做二次函数,当a_______ ,b________时,是一次函数. 2.二次函数y =ax 2+bx +c 的图象是_______,对称轴是_______,顶点坐标是_______. 3.抛物线的开口方向由a 确定,当a>0时,开口_______;当a<0时,开口_______;越大,开口越_______.4.抛物线与y 轴的交点坐标为_______.当c>0时,与y 轴的_______半轴有交点;当c<0时,与y 轴的_______半轴有交点;当c =0时,抛物线过________. 5.若a_______0,当x =2ba -时,y 有最小值,为_______; 若a_______0,当x =2ba-时,y 有最大值,为_______.6.当a>0时,在对称轴的左侧,y 随x 的增大而_______,在对称轴的右侧,y 随x 的增大而_______;当a<0时,在对称轴的左侧,y 随x 的增大而_______,在对称轴的右侧.y 随x 的增大而_______.7.当m>0时,二次函数y =ax 2的图象向_______平移_______个单位得到二次函数y =a (x +m)2的图象;当k>0时,二次函数y =ax 2的图象向_______平移_______个单位得到二次函数y =ax 2+k 的图象.平移的口诀:左“+”右 “-”;上“+”下“-”. 【考点例析】考点一 二次函数的有关概念例1已知二次函数y =x 2-4x +5的顶点坐标为 ( ) A .(-2,-1) B .(2,1) C .(2,-1)D (-2,1)考点二 抛物线的平移例2 将抛物线y =3x 2向上平移3个单位,再向左平移2个单位,那么得到的抛物线的解析式为 ( ) A .y =3(x +2)2+3B .y =3(x -2)2+3C .y =3(x +2)2-3D .y =3(x -2)2-3考点三 同一坐标系下二次函数与其他函数图象的共存问题例3 在同一坐标系中°一次函数y =ax +1与二次函数y =x 2+a 的图象可能是( )考点四利用二次函数的增减性比较坐标大小例4设A(-2,y1),B(1,y2),C(2,y3)是抛物线y=-(x+1)2+m上的三点,则y1、y2、y3的大小关系为( )A.y1>y2>y3B.y1>y3>y2C.y3>y2>y1D.y2>y1>y3【反馈练习】1.抛物线y=-2x2+1的对称轴是( )A.直线y=12B.直线x=-12C.y轴D.直线x=22.已知二次函数y=2(x-3)2+1,下列说法:①其图象的开口向下;②其图象的对称轴为直线x=-3;③其图象的顶点坐标为(3,-1);④当x<3时,y随x的增大而减小.其中说法正确的有( )A.1个B.2个C.3个D.4个3.抛物线y=(x+2)2-3可以由抛物线y=x2平移得到,则下列平移过程正确的是( ) A.先向左平移2个单位,再向上平移3个单位B.先向左平移2个单位,再向下平移3个单位C.先向右平移2个单位,再向下平移3个单位D.先向右平移2个单位,再向上平移3个单位4.将抛物线y=x2+x向下平移2个单位.所得新抛物线的解析式是________.5.已知点A(x1,y1)、B(x2,y2)在二次函数y=(x-1)2+1的图象上,若x1>x2>1,则y1_______y2.二次函数的图像与性质(二)1.二次函数解析式的求法:(1)若给出抛物线上三点,通常可设一般式:________(a≠0).(2)若给宝抛物线的顶点坐标或对称轴与最值,通常可设顶点式:________(a≠0),其中点(h,k)为顶点,对称轴为直线x=h.(3)若给出抛物线与x轴的两个交点(x1,0)、(x2,0)及其他一个条件,通常可设交点式:_______(a≠0).其中x1,x2是抛物线与x轴的交点的横坐标.2.对于二次函数y=ax2+bx+c(a≠0),当给定y的值时,二次函数可转化为一元二次方程,所以我们可ax2+bx+c=_______.3.当b2-4ac>0时,方程ax2+bx+c=0(a≠0)有两个不相等的实数根,则二次函数y=ax2+bx+c的图象与x轴有_______交点.4.当b2-4ac=0时,方程ax2+bx+c=0(a≠0)有两个相等的实数根,则二次函数y =ax2+bx+c的图象与x轴有_______交点.5.当b2-4ac-<0时,方程ax2+bx+c=0(a≠0)没有实数根,则二次函数y=ax2+bx+c的图象与x轴_______交点.【考点例析】考点一二次函数的各项系数与图象之间的关系例1 已知二次函数y=ax2+bx+c=0(a≠0)的图象如图所示,现有下列结论:①abc>0;②b2-4ac<0;③4a-2+c<0;④b=-2a,其中结论正确的是( ) A.①③B.③④C.②③D.①④考点二求二次函数的解析式例2 (1)任选以下三个条件中的一个,求二次函数y=ax2+bx+c的解析式.①y随x变化的部分数值规律如下表:②有序数对(-1,0)、(1,4)、(3,0)满足y=ax2+bx+c;③已知函数y=ax2+bx+c的图象的一部分(如图).(2)直接写出(1)中二次函数y=ax2+bx+c的三个性质.考点三利用图象求一元二次方程的解例3二次函数y=ax2+bx的图象如图,若一元二次方程ax2+bx+m=0有实数根.则m的最大值为( )A.-3 B.3 C.-6 D.9考点四二次函数图象与坐标轴的交点个数例4抛物线y=-3x2-x+4与坐标轴的交点的个数是( )A.3 B.2 C.1 D.0考点五二次函数图象与不等式的关系例5如图是二次函数y=ax2+bx+c的部分图象,由图象可知不等式ax2+bx+c<0的解集是( )A.-1<x<5 B.x>5C.x<-1且x>5 D.x<-1或x>5【反馈练习】1.已知抛物线y=x3-x-1,与x轴的一个交点为(m,0),则代数式m2-m+2011的值为( )A.2009 B.2012 C.2011 D.20102.二次函数y=a(x+m)2+n的图象如图,则一次函数y=mx+n的图象经过( ) A.第一、二、三象限B.第一、二、四象限C.第二、三、四象限D.第一、三、四象限,下列结3.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为直线x=-12论中,正确的是( )A.abc>0 B.a+b=0C.2b+c>0 D.4a+c<2b4.若抛物线y=ax2+bx+c的顶点是A(2,1),且经过点B(1,0),则抛物线的函数关系式为_______.5.如图,在平面直角坐标系中,边长为2的正方形OA BC的顶点A、C分别在x轴、y 轴的正半轴上,二次函数y=-2x2+bx+c的图象经过B、C两点.3(1)求该二次函数的解析式;(2)结合函数的图象探索:当y>0时x的取值范围.课后练习1.(2017四川省攀枝花市)二次函数2=++(a≠0)的图象如图所示,则下列命y ax bx c题中正确的是()A.a>b>cB.一次函数y=ax +c的图象不经第四象限C.m(am+b)+b<a(m是任意实数)D.3b+2c>02.(2017四川省阿坝州)如图,抛物线2=++(a≠0)的对称轴为直线x=1,y ax bx c与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:①4ac<b2;②方程20++=的两个根是x1=﹣1,x2=3;ax bx c③3a+c>0④当y>0时,x的取值范围是﹣1≤x<3⑤当x<0时,y随x增大而增大其中结论正确的个数是()A.4个B.3个C.2个D.1个3.(2017贵州省黔南州)二次函数2=++的图象如图所示,以下结论:①abc>y ax bx c0;②4ac<b2;③2a+b>0;④其顶点坐标为(12,﹣2);⑤当x<12时,y随x的增大而减小;⑥a+b+c>0正确的有()A.3个B.4个C.5个D.6个4.(2017辽宁省盘锦市)如图,抛物线2y ax bx c=++与x轴交于点A(﹣1,0),顶点坐标(1,n),与y轴的交点在(0,3),(0,4)之间(包含端点),则下列结论:①abc>0;②3a+b<0;③﹣43≤a≤﹣1;④a+b≥am2+bm(m为任意实数);⑤一元二次方程2ax bx c n++=有两个不相等的实数根,其中正确的有()A.2个B.3个C.4个D.5个5.(2017四川省资阳市)如图,抛物线2y ax bx c=++(a≠0)的顶点和该抛物线与y轴的交点在一次函数y=kx+1(k≠0)的图象上,它的对称轴是x =1,有下列四个结论:①abc<0,②13a<-,③a=-k,④当0<x<1时,ax+b>k,其中正确结论的个数是()A.4 B.3 C.2 D.16.(2017四川省广元市)已知二次函数2y ax bx c=++的图象如图所示,有下列结论:①abc<0;②a+c>b;③3a+c<0;④a+b>m(am+b)(其中m≠1),其中正确的结论有.7.(2017山东省莱芜市)二次函数2y ax bx c=++(a<0)图象与x轴的交点A、B的横坐标分别为﹣3,1,与y轴交于点C,下面四个结论:①16a﹣4b+c<0;②若P(﹣5,y1),Q(52,y2)是函数图象上的两点,则y1>y2;③a=﹣13c;④若△ABC是等腰三角形,则b=27.其中正确的有(请将结论正确的序号全部填上)8.(2017贵州省黔西南州)如图,图中二次函数解析式为2y ax bx c=++(a≠0)则下列命题中正确的有(填序号)①abc>0;②b2<4ac;③4a﹣2b+c>0;④2a+b>c.9.(2017辽宁省锦州市)如图,二次函数2y ax bx c=++的图象与y轴正半轴相交,其顶点坐标为(12,1),下列结论:①abc>0;②a=b;③a=4c﹣4;④方程21ax bx c++=有两个相等的实数根,其中正确的结论是.(只填序号即可).。
