小学奥数知识讲解第十五讲 最短路线问题
最短路径问题PPT课件

A
·
C′ C
B
·
l
B′
问题1 归纳
B A
l
解决实 际问题
B
A
C
l
B′
抽象为数学问题 用旧知解决新知
B
A
C
l
联想旧知
A
C
l
B
尝试应用:
1.如图,直线l是一条河,P、Q是两个村庄.欲在l上的某处修建
一个水泵站,向P、Q两地供水,现有如下四种铺设方案,图中
实线表示铺设的管道,则所需要管道最短的是( D )
A
·
l C
B′
问题3 你能用所学的知识证明AC +BC最短吗? 证明:如图,在直线l 上任取一点C′(与点C 不
重合),连接AC′,BC′,B′C′.
由轴对称的性质知,
BC =B′C,BC′=B′C′. ∴ AC +BC
= AC +B′C = AB′, AC′+BC′
= AC′+B′C′. 在△AB′C′中,
从图中的A 地出发,到一条笔直的河边l 饮马,然 后到B 地.到河边什么地方饮马可使他所走的路线全程 最短?
B A
l
将A,B 两地抽象为两个点,将河流l 抽象为一条直 线.
·B A·
l
你能用自己的语言说明这个问题的意思, 并把它抽象为数学问题吗?
(1)从A 地出发,到河流l边 饮马,然后到B 地;
AM+NB+MN.
问题3:还有其他的方法选两点M,N,使得 AM+MN+NB的和最小吗?试一试。
a
b
A
M
N
B
问题2 归纳
解决实 际问题
《最短路径问题》PPT课件教学

你能要自己的语言重新描述一下问题吗? C是l上一个动点, 当点C在l的什么位置时,AC+BC最小?
探究 如图,点A,B 在直线l 的同侧,点C 是直线上的一个动点,当点C 在l 的什么位置时,AC 与CB 的和最小?
一开始的时候我们就讨论过点A,B在直线异侧的情况, 你还记得是怎么做的吗? 连接两点,交点就是所求 同侧的情况也能直连接两点吗?不行
拓广探索
在纸上画五个点,使任意三个点组成的三角形都 是等腰三角形 . 这五个点应该怎样画?
拓广探索
如图,△ABC 是等边三角形,BD 是中线,延长BC 至 E,使CE =CD . 求证DB =DE .
拓广探索
如图,△ABC 是等腰三角形,AC =BC,△BDC 和△ACE 分别为等边三角形,AE 与BD 相较于F,连接CF 并延长 ,交AB 于点G . 求证:G 为AB 的中点 .
复习巩固
如图,在△ABC 中,∠ABC =50°,∠ACB =80°,延长 CB至D,使DB =BA,延长BC 至E,使CE =CA,连接 AD,AE .求∠D,∠E,∠DAE 的度数 .
复习巩固 如图,AD =BC,AC=BD,求证:△EAB 是等腰三角形 .
复习巩固
综合应用
试确定如图所示的正多边形的对称轴的条数,一般地 ,一个正n边形有多少条对称轴?
综合应用
如图,从图形Ι 到图形Ⅱ是进行了平移还是轴对称?如果 是轴对称,找出对称轴;如果是平移,是怎样平移?
综合应用
如图,AD是△ABC 的角平分线,DE,DF 分别是△ABD 和△ACD的高 . 求证:AD 垂直平分EF .
综合应用
如图,在等边三角形 ABC 的三边上,分别取点D,E,F ,使AD =BE =CF . 求证△DEF 是等边三角形 .
《最短路径问题》PPT课件

A
a 3、连接PA,PB,由对称轴 的性质知,PA= P1A,
P1
PB=P2B
∴先到点A处吃草,再到点B
处饮水,最后回到营地,
这时的放牧路线总路程最
短,即 (PB+BA+AP)min
• 证明:
P2
b ∵ PA1+A1B1+B1P
B1 B
.P
河
= P1A1+A1B1+B1P2 > P1A+AB+BP2
前面和右面
D D1
③
A 1 A1
C1
2
4
B1
AC1 =√52+22 =√29
左面和上面
• 1、如图是一个长方体木块,已知 AB=5,BC=3,CD=4,假设一只蚂蚁 在点A处,它要沿着木块侧面爬到点D 处,则蚂蚁爬行的最短路径是 7 4 。
D
4
C
A
5
B3
• 2、现要在如图所示的圆柱体侧面A点 与B点之间缠一条金丝带(金丝带的宽 度忽略不计),圆柱体高为6cm,底面 圆周长为16cm,则所缠金丝带长度的 最小值为 10cm 。
在河上建一座桥MN,桥造在何处才能使从A到B
的路径最短?(假设河的两岸是平行的直线,桥
要与河垂直)
.A M
作法: 1、将点B沿垂直与河岸的方
向平移一个河宽到E
N
2、. E连接AE交河对岸与点M,则
.点BM为建桥的位置,MN为 所建的桥。
A C
M ND E
B
• 证明: ∵ AC+CD+DB = AC+CD+CE = AC+CE+CD > AE+CD = AM+ME+CD = AM+NB+MN ∴ AC+CD+DB > AM+NB+MN
四年级下册数学讲义-奥数讲练: 最短路线问题
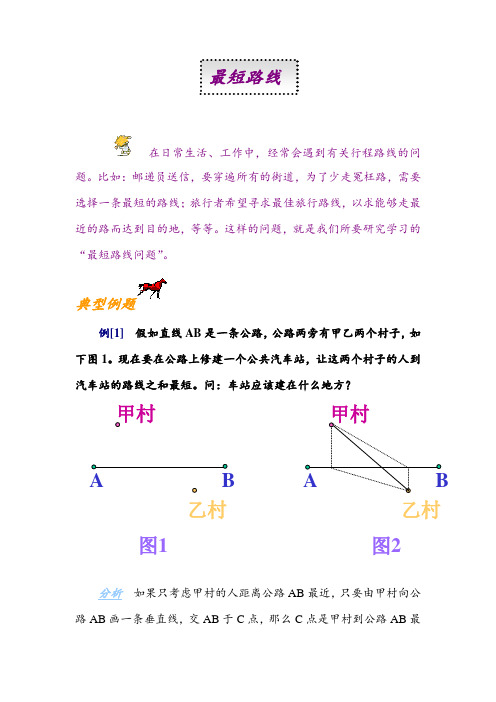
在日常生活、工作中,经常会遇到有关行程路线的问题。
比如:邮递员送信,要穿遍所有的街道,为了少走冤枉路,需要选择一条最短的路线;旅行者希望寻求最佳旅行路线,以求能够走最近的路而达到目的地,等等。
这样的问题,就是我们所要研究学习的“最短路线问题”。
典型例题例[1] 假如直线AB 是一条公路,公路两旁有甲乙两个村子,如下图1。
现在要在公路上修建一个公共汽车站,让这两个村子的人到汽车站的路线之和最短。
问:车站应该建在什么地方?分析 如果只考虑甲村的人距离公路AB 最近,只要由甲村向公路AB 画一条垂直线,交AB 于C 点,那么C 点是甲村到公路AB 最甲村 乙村AB 甲村乙村 图1图2最短路线近的点,但是乙村到C点就较远了。
反过来,由乙村向公路AB画垂线,交AB于D点,那么D点是乙村到公路AB最近的点。
但是这时甲村到公路AB的D点又远了。
因为本题要求我们在公路AB上取的建站点,能够兼顾甲村和乙村的人到这个车站来不走冤枉路(既路程之和最短),根据我们的经验:两个地点之间走直线最近,所以,只要在甲村乙村间连一条直线,这条直线与公路AB交点P,就是所求的公共汽车站的建站点了(图2)。
解用直线把甲村、乙村连起来。
因为甲村乙村在公路的两侧,所以这条连线必与公路AB有一个交点,设这个交点为P,那么在P 点建立汽车站,就能使甲村乙村的人到汽车站所走的路程之和最短。
例[2] 一个邮递员投送信件的街道如图3所示,图上数字表示各段街道的千米数。
他从邮局出发,要走遍各街道,最后回到邮局。
问:走什么样的路线最合理?全程要走多少千米?3分析选择最短的路线最合理。
那么,什么路线最短呢?一笔画路线应该是最短的。
邮递员从邮局出发,还要回到邮局,按一笔画问题,就是从偶点出发,回到偶点。
因此,要能一笔把路线画出来,必须途径的各点全是偶点。
但是图中有8个奇点,显然邮递员要走遍所有街道而又不走重复的路是不可能的。
要使邮递员从邮局出发,仍回到邮局,必须使8个奇点都变成偶点,就是要考虑应在哪些街道上重复走,也就是相当于在图上添哪些线段,能使奇点变成偶点。
六年级奥数最短路线

最短路线一、学习目标:通过最短路线的学习,体会转化的数学思想。
二、基础知识:最短路线通常的最短路线问题是以“平面内连结两点的线中,直线段最短”为原则引伸出来的。
在求最短路线时,常常先用“对称”的方法化成两点之间的最短距离问题。
利用对称性把折线化成易求的直线段,所以这种方法也叫做化直法,其他还有旋转法、翻折法等。
有时所求最短路线位于凸多面体的不同平面上,需将它们展开在同一平面上。
三、例题解析:例1:如图,A、B两个学校在公路的两侧.想在这两校的附近的公路上建一个汽车站,要求车站到两个学校的距离之和最小,应该把车站建在哪里?解:例2:如图,A、B两个学校都在公路的同侧.想在这两校的附近的公路上建一个汽车站,要求车站到两个学校的距离之和最小,应该把车站建在哪里?解:练一练:如下图,侦察员骑马从A地出发,去B地取情报.在去B地之前需要先饮一次马,如果途中没有重要障碍物,那么侦察员选择怎样的路线最节省时间,请你在图中标出来。
并说明做法。
解:例3:少先队一小队组织一次有趣的赛跑比赛,规则是从A点出发(见下图),跑到墙边,用手触摸墙壁,然后跑到B点.接着,离B点再次跑到墙边手触摸墙壁后,跑到C点.问选择怎样的路线最节省时间,请你在图中标出来。
分析:实际上是两个最短路线问题。
解:例4:在河中有A、B两岛(如下图),六年级一班组织一次划船比赛,规则要求船从A岛出发,必须先划到甲岸,又到乙岸,再到B岛,最后回到A岛,试问应选择怎样的路线才能使路程最短?解:例5:如图13—6,河流EF与公路FD所夹的角是一个锐角,某公司A在锐角EFD内.现在要在河边建一个码头,在公路边修建一个仓库,工人们从公司出发,先到河边的码头卸货,再把货物转运到公路边的仓库里去,然后返回到A处,问仓库、码头各应建在何处,使工人们所行的路程最短。
解:例6:A、B两个村子,中间隔了一条小河,现在要在小河上架一座桥,使它垂直于河岸。
请你在河两岸选择合适的架桥地点。
奥数 最短距离

最短路线例1.下图是从学校到邮局经过的所有马路,问从学校到邮局共有几条最短路线?思路分析:为了便于叙述,在各交叉点上标出字母.要想从家到学校走的路程最短,就不能走回头路,这道题中,最短也要走长方形ACGI的一个长和一个宽.为保证走得路线最短,只能向下和向右走.如果我们一条一条地数,可以发现共有以下六条路线最短:A→B→C→F→I;A→D→G→H→I;A→B→E→F→I;A→D→E→F→I;A→B→E→H→I;A→D→E→H→I;但如果按上述方法找,难免发生重复遗漏的路线.下面我们观察一下,看看是否有规律可循.①从A点出发向下或向右走只能到达B、D两点,到B点有一种走法,到D点同样只有一种走法,所以在B点、D点处各标角码1,表示从A点到此点的最近走法只有1种.②从B点可以向右走到达C点,因为从A到C的最短路线也仅有1条,所以角码为1.从B点向下可到E点,另外从D点到达E点的距离也最短,所以E点角标角码2.如图所示.继续做下去,我们会发现,每一个小格右下角的数正好是这个小格右上角与左下角的数的和,这个和就是从出发点A到I点所有最短路线的条数.例2.一个邮递员投送信件,街道如图所示,图上的数字表示各段街道的公里数.他从邮局出发,走遍各街道,最后回到邮局,怎样走路线最合理?思路分析:由于街道是含8个奇点的图形,所以,不可能不重复地走遍所有街道,为了保证邮递员从邮局出发再回到邮局,图形中8个奇点都应变为偶点.即将奇点两两相配对用线连结,有很多连法,下图仅列出了三种情形:添加的路线的里程分别是:(1)3×4=12(公里)(2)3×2+2×2=10(公里)(3)2×4=8(公里)由此可见邮递员按图(3)的路线走,重复的路最少,最合理.全程共走:3×6+1×4+2×8+2×4=46(公里)例3.小刚家和小明家之间各条道路的示意图,请问要从小刚家到小明家,最近路线有几条?思路分析:要求从小刚家到小明家的最近路线有几条,就是要求从小刚家到小明家的最短路线.把各交点标上字母,如下图.这道题和前面例1有所不同,要格外注意由哪两点的和来确定另一点的.①由A→B,A→C各有1种走法,可以确定A→D有1+1=2(种)走法.②由A→I有1种走法,A→D有2种走法,可以确定A→J有1+2=3(种)走法.③由A→M有1种走法,A→J有3种走法,可以确定A→N有1+3=4(种)走法.④A→E有2种走法,A→J有3种走法,A→K有2+3=5(种)走法.⑤A→E有2种走法,A→G有2种走法,A→H与2+2=4(种)走法.⑥A→K有5种走法,A→H有4种走法,A→L有5+4=9(种)走法.⑦A→N有4种走法,A→K有5种走法,A→O有4+5=9(种)走法.⑧A→O有9种走法,A→L有9种走法,A→L上有9种走法,A→P有9+9=18(种)走法.。
小学奥数-最短路线

最短路线
1、请你画出从小明家去图书馆的最短路线,并说出理由。
2、一只小蚂蚁想从下图中的点A爬到对边BC。
沿怎样的路线爬行需要的时间最少?在图中画一画。
3、如图,三角形ABC的三条边AB,AC,BC分别表示三条公路。
在D点处有一名士兵接到一个紧急任务,需要他先到达BC公路,然后再到达AB公路。
他怎样走才能以最短的时间完成任务呢?在图中画出路线。
(假设士兵的速度一定)
4、如图,三角形ABC的三条边AB,AC,BC分别表示三条公路。
在D处有一个村庄,现准备修一条通往公路的小路,在图中画出最短的小路。
5、一只小蚂蚁想从下图中的点A爬到对边CD。
你能帮它开辟一条最短的路线,使它尽快到达吗?在图中画一画。
6、一个邮递员投送信件的街道如下图所示,你能帮他设计一条最短路线,使自己从邮局出发,走遍每一条街道并回到邮局吗?
7、如右图,每个小方格的边长是1厘米,一条贪吃的蛇从左下角出发,沿着格线爬行,如果它想吃掉图中的3个“”,最少要爬多远?请你画出路线。
8、下图是一个公园的平面图,A点是出入口,B,C,D,E,F,G,H,I,J是各个景点,你能帮游客设计一条最短路线,使他从出入口出发,走遍每一条路后,最终回到出入口吗?。
最短路线问题 技巧解析

最短路线问题技巧解析最值问题遵循一个原则:“平面内连结两点的线中,直线段最短”如果研究问题的限制条件允许已知的两点在同一平面内,那么所求的最短路线是线段;如果它们位于凸多面体的不同平面上,而允许走的路程限于凸多面体表面,那么所求的最短路线是折线段;如果它们位于圆柱和圆锥面上,那么所求的最短路线是曲线段;但允许上述哪种情况,它们都有一个共同点:当研究曲面仅限于可展开为平面的曲面时,例如圆柱面、圆锥面和棱柱面等,将它们展开在一个平面上,两点间的最短路线则是连结两点的直线段.在求最短路线时,一般先用“对称”的方法化成两点之间的最短距离问题,而两点之间直线段最短,从而找到所需的最短路线.其中也体现了数学中的转化思想。
1、A、B两个村子,中间隔了一条小河(如下图),现在要在小河上架一座小木桥,使它垂直于河岸.请你在河的两岸选择合适的架桥地点,使A、B两个村子之间路程最短.分析因为桥垂直于河岸,所以最短路线必然是条折线,直接找出这条折线很困难,于是想到要把折线化为直线.由于桥的长度相当于河宽,而河宽是定值,所以桥长是定值.因此,从A点作河岸的垂线,并在垂线上取AC等于河宽,就相当于把河宽预先扣除,找出B、C两点之间的最短路线,问题就可以解决.解:如上图,过A点作河岸的垂线,在垂线上截取AC的长为河宽,连结BC交河岸于D 点,作DE垂直于河岸,交对岸于E点,D、E两点就是使两村行程最短的架桥地点.即两村的最短路程是AE+ED+DB.2、如下图,侦察员骑马从A地出发,去B地取情报.在去B地之前需要先饮一次马,如果途中没有重要障碍物,那么侦察员选择怎样的路线最节省时间,请你在图中标出来.解:要选择最节省时间的路线就是要选择最短路线.作点A关于河岸的对称点 A′,即作 AA′垂直于河岸,与河岸交于点C,且使AC=A′C,连接A′B交河岸于一点P,这时 P点就是饮马的最好位置,连接 PA,此时 PA+PB就是侦察员应选择的最短路线.证明:设河岸上还有异于P点的另一点P′,连接P′A,P′B, P′A′.∵P′A+P′B=P′A′+P′B>A′B=PA′+PB=PA+PB,而这里不等式 P′A′+P′B>A′B成立的理由是连接两点的折线段大于直线段,所以PA+PB是最短路线.此例利用对称性把折线APB化成了易求的另一条最短路线即直线段A′B,所以这种方法也叫做化直法,其他还有旋转法、翻折法等.看下面例题.3、长方体ABCD—A′B′C′D′中,AB=4,A′A=2′,AD=1,有一只小虫从顶点D′出发,沿长方体表面爬到B点,问这只小虫怎样爬距离最短?(见图(1))解:因为小虫是在长方体的表面上爬行的,所以必需把含D′、B两点的两个相邻的面“展开”在同一平面上,在这个“展开”后的平面上 D′B间的最短路线就是连结这两点的直线段,这样,从D′点出发,到B点共有六条路线供选择.①从D′点出发,经过上底面然后进入前侧面到达B点,将这两个面摊开在一个平面上(上页图(2)),这时在这个平面上D′、B间的最短路线距离就是连接D′、B两点的直线段,它是直角三角形ABD′的斜边,根据勾股定理,D′B2=D′A2+AB2=(1+2)2+42=25,∴D′B=5.②容易知道,从D′出发经过后侧面再进入下底面到达B点的最短距离也是5.③从D′点出发,经过左侧面,然后进入前侧面到达B点.将这两个面摊开在同一平面上,同理求得在这个平面上D′、B两点间的最短路线(上页图(3)),有:D′B2=22+(1+4)2=29.④容易知道,从D′出发经过后侧面再进入右侧面到达B点的最短距离的平方也是29.⑤从D′点出发,经过左侧面,然后进入下底面到达B点,将这两个平面摊开在同一平面上,同理可求得在这个平面上D′、B两点间的最短路线(见图),D′B2=(2+4)2+12=37.⑥容易知道,从D′出发经过上侧面再进入右侧面到达B点的最短距离的平方也是37.比较六条路线,显然情形①、②中的路线最短,所以小虫从D′点出发,经过上底面然后进入前侧面到达B点(上页图(2)),或者经过后侧面然后进入下底面到达B点的路线是最短路线,它的长度是5个单位长度.利用例2、例3中求相邻两个平面上两点间最短距离的旋转、翻折的方法,可以解决一些类似的问题,例如求六棱柱两个不相邻的侧面上A和B两点之间的最短路线问题(下左图),同样可以把A、B两点所在平面及与这两个平面都相邻的平面展开成同一个平面(下右图),连接A、B成线段AP1P2B,P1、P2是线段AB与两条侧棱线的交点,则折线AP1P2B就是AB 间的最短路线.圆柱表面的最短路线是一条曲线,“展开”后也是直线,这条曲线称为螺旋线.因为它具有最短的性质,所以在生产和生活中有着很广泛的应用.如:螺钉上的螺纹,螺旋输粉机的螺旋道,旋风除尘器的导灰槽,枪膛里的螺纹等都是螺旋线,看下面例题.4、景泰蓝厂的工人师傅要给一个圆柱型的制品嵌金线,如下左图,如果将金线的起点固定在A点,绕一周之后终点为B点,问沿什么线路嵌金线才能使金线的用量最少?解:将上左图中圆柱面沿母线AB剪开,展开成平面图形如上页右图(把图中的长方形卷成上页左图中的圆柱面时,A′、B′分别与A、B重合),连接AB′,再将上页右图还原成上页左图的形状,则AB′在圆柱面上形成的曲线就是连接AB且绕一周的最短线路.圆锥表面的最短路线也是一条曲线,展开后也是直线.请看下面例题.5、有一圆锥如下图,A、B在同一母线上,B为AO的中点,试求以A为起点,以B为终点且绕圆锥侧面一周的最短路线.解:将圆锥面沿母线AO剪开,展开如上右图(把右图中的扇形卷成上图中的圆锥面时,A′、B′分别与A、B重合),在扇形中连AB′,则将扇形还原成圆锥之后,AB′所成的曲线为所求.6、如下图,在圆柱形的桶外,有一只蚂蚁要从桶外的A点爬到桶内的B点去寻找食物,已知A点沿母线到桶口C点的距离是12厘米, B点沿母线到桶口 D点的距离是8厘米,而C、D两点之间的(桶口)弧长是15厘米.如果蚂蚁爬行的是最短路线,应该怎么走?路程总长是多少?分析我们首先想到将桶的圆柱面展开成矩形平面图(下图),由于B点在里面,不便于作图,设想将BD延长到F,使DF=BD,即以直线CD为对称轴,作出点B的对称点F,用F代替B,即可找出最短路线了.解:将圆柱面展成平面图形(上图),延长BD到F,使DF=BD,即作点B关于直线CD 的对称点F,连结AF,交桶口沿线CD于O.因为桶口沿线CD是 B、F的对称轴,所以OB=OF,而A、F之间的最短线路是直线段AF,又AF=AO+OF,那么A、B之间的最短距离就是AO+OB,故蚂蚁应该在桶外爬到O点后,转向桶内B点爬去.延长AC到E,使CE=DF,易知△AEF是直角三角形,AF是斜边,EF=CD,根据勾股定理,AF2=(AC+CE)2+EF2 =(12+8)2+152=625=252,解得AF=25.即蚂蚁爬行的最短路程是25厘米.7、如图一只壁虎要从一面墙壁α上A点,爬到邻近的另一面墙壁β上的B点捕蛾,它可以沿许多路径到达,但哪一条是最近的路线呢?解:我们假想把含B点的墙β顺时针旋转90°(如下页右图),使它和含A点的墙α处在同一平面上,此时β转过来的位置记为β′,B点的位置记为B′,则A、B′之间最短路线应该是线段AB′,设这条线段与墙棱线交于一点P,那么,折线4PB就是从A点沿着两扇墙面走到B点的最短路线.证明:在墙棱上任取异于P点的P′点,若沿折线AP′B走,也就是沿在墙转90°后的路线AP′B′走都比直线段APB′长,所以折线APB是壁虎捕蛾的最短路线.由此例可以推广到一般性的结论:想求相邻两个平面上的两点之间的最短路线时,可以把不同平面转成同一平面,此时,把处在同一平面上的两点连起来,所得到的线段还原到原始的两相邻平面上,这条线段所构成的折线,就是所求的最短路线.8、在河中有A、B两岛(如下图),六年级一班组织一次划船比赛,规则要求船从A 岛出发,必须先划到甲岸,又到乙岸,再到B岛,最后回到A岛,试问应选择怎样的路线才能使路程最短?解:如上图,分别作A、B关于甲岸线、乙岸线的对称点A′和B′,连结A′、B′分别交甲岸线、乙岸线于E、F两点,则A→E→F→B→A是最短路线,即最短路程为:AE+EF+FB+BA.证明:由对称性可知路线A→E→F→B的长度恰等于线段A′B′的长度.而从A岛到甲岸,又到乙岸,再到B岛的任意的另一条路线,利用对称方法都可以化成一条连接A′、B′之间的折线,它们的长度都大于线段 A′B′,例如上图中用“·—·—·”表示的路线A→E′→F′→B的长度等于折线AE′F′B的长度,它大于A′B′的长度,所以A→E→F→B→A 是最短路线.。
数学最短路径问题讲解

数学最短路径问题讲解数学中的最短路径问题是一个经典的优化问题,主要涉及在图或网络中找到两个节点之间的最短路径。
这类问题在日常生活和工程中有着广泛的应用,如交通路线规划、网络路由、电路设计等。
最短路径问题的常用算法有Dijkstra算法和Bellman-Ford算法。
Dijkstra算法适用于没有负权重的图,它从源节点开始,逐步找到离源节点最近的节点,直到找到目标节点。
Bellman-Ford算法则可以处理包含负权重的图,它通过不断地松弛边的权重来找到最短路径。
下面以一个简单的例子来解释最短路径问题:假设我们有一个有向图,其中节点表示城市,边表示道路,边的权重表示两城市之间的距离。
我们要找出从城市A到城市B的最短路径。
首先,我们需要理解最短路径的含义。
最短路径是指从一个节点到另一个节点经过的边的权重之和最小的路径。
如果存在负权重的边,我们需要找到一个路径,使得经过的边的权重之和加上起点的权重(如果起点有权重)最小。
在解决最短路径问题时,我们可以使用图论中的一些基本概念,如路径、权重、源节点、目标节点等。
路径是指从一个节点到另一个节点经过的一系列边,权重是指路径上边的权重之和。
源节点是指我们开始寻找最短路径的节点,目标节点是指我们要找到最短路径的终点。
最短路径问题的求解方法通常包括贪心算法和动态规划。
贪心算法是指每一步都选择当前看起来最优的选择,希望这样的局部最优选择能够导致全局最优解。
动态规划则是将问题分解为若干个子问题,并从子问题的最优解逐步推导出原问题的最优解。
在实际应用中,我们还需要考虑一些特殊情况,如图中存在负权重的环、图中存在负权重的边等。
对于这些情况,我们需要使用特定的算法来处理,如Bellman-Ford算法或Floyd-Warshall算法等。
总之,最短路径问题是一个经典的的问题,它的求解方法有很多种。
在实际应用中,我们需要根据具体情况选择合适的算法来处理最短路径问题。
最短路径问题课件ppt

·B A·
l
探索新知
追问2 你能用自己的语言说明这个问题的意思, 并把它抽象为数学问题吗?
(1)从A 地出发,到河边l 饮马,然后到B 地; (2)在河边饮马的地点有无穷多处,把这些地点与A,
B 连接起来的两条线段的长度之和,就是从A 地 到饮马地点,再回到B 地的路程之和;
若直线l 上任意一点(与点 C 不重合)与A,B 两点的距离 和都大于AC +BC,就说明AC + BC 最小.
A
·
C′ C
B
·
l
B′
探索新知
追问2 回顾前面的探究过程,我们是通过怎样的 过程、借助什么解决问题的?
A
·
C′ C
B
·
l
B′
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
(Ⅰ)两点在一条直线异侧
已知:如图,A,B在直线L的两侧, 在L上求一点P,使得PA+PB最小。
连接AB,线段AB与直线L的交点P ,就是所求。
P
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
思考???
为什么这样做就能得到最短距 离呢?
根据:两点之间线段最短.
引入新知
引言: 前面我们研究过一些关于“两点的所有连线中,线 段最短”、“连接直线外一点与直线上各点的所有线段 中,垂线段最短”等的问题,我们称它们为最短路径问 题.现实生活中经常涉及到选择最短路径的问题,本节 将利用数学知识探究数学史中著名的“将军饮马问题”.
最短路径问题归纳总结

最短路径问题归纳总结本文介绍了数学中的最短路径问题,该问题是图论研究中的一个经典算法问题,旨在寻找图中两结点之间的最短路径。
具体的算法形式包括确定起点的最短路径问题、确定终点的最短路径问题、确定起点终点的最短路径问题和全局最短路径问题。
其中,“将军饮马”、“造桥选址”和“费马点”是该问题的原型。
解决该问题需要涉及知识包括“两点之间线段最短”、“垂线段最短”、“三角形三边关系”、“轴对称”和“平移”等。
在解题思路方面,可以通过找对称点实现“折”转“直”,近两年出现“三折线”转“直”等变式问题考查。
本文还列举了十二个基本问题,包括确定起点的最短路径问题、确定终点的最短路径问题、确定起点终点的最短路径问题、全局最短路径问题、将军饮马、造桥选址等。
对于每个问题,本文都给出了详细的作法和图形原理,以及需要用到的知识原理。
问题6】给定直线m和直线n,求在它们上面的两个点M和N,使得XXX的值最小。
根据垂线段最短的原理,将点A向右平移a个长度得到A',作A'关于直线m的对称点A'',连A''B,交直线MN于点M,直线NB于点N,使得MN⊥m且MN=a。
则AM+MN+BN的最小值为A''B+MN。
在直线l上求两点M、N(M在左),使MN=a,并使AM+MN+NB的值最小。
将N点向左平移a个单位得到M。
问题7】给定两条直线l1和l2,求在它们上面的两个点A和B,使得PA+AB的值最小。
根据垂线段最短的原理,作点P关于l1的对称点P',作P'B⊥l2于B,交l2于A。
则PA+AB的最小值为线段P'B的长。
在l1上求点A,在l2上求点B,使PA+AB值最小。
问题8】给定两条直线l1和l2,求在它们上面的两个点A和B,使得AM+MN+NB的值最小。
根据两点之间线段最短的原理,作点A关于l2的对称点A',作点B关于l1的对称点B',连A'B'交l2于M,交l1于N。
小学数学典型应用题之最短路线问题

小学数学典型应用题之最短路线问题一、含义在日常生活和工作中,经常会遇到有关行程路线的问题。
比如:邮递员送信,要穿遍所有的街道,为了少走冤枉路,需要选择一条最短的路线;旅行者希望寻求最佳旅行路线,以求能够走最近的路而达到目的地等等。
这样的问题,就是所要学习的“最短路线问题”。
二、解题思路和方法(1)两点之间线段最短。
(2)尽量不走回头路和重复路,这样的话才能做到省时省力。
三、例题例题(一):一只蚂蚁在长方形格纸上的A点,它想去B点玩,但是不知走哪条路最近。
小朋友们,你能给它找到几条这样的最短路线呢?解析一:(1)从A点走到B点,不论怎样走,最短也要走长方形AHBD的一个长与一个宽。
(2)因此在水平方向上,所有线段的长度和应等于AD;在竖值方向上,所有线段的长度和应等于DB。
(3)这样我们走的这条路线才是最短路线,为了保证这一点,我们就不应该走“回头路”,只能向右和向下走。
(4)因此所有的最短路线为:A→C→D→G→B 、A→C→F→G→B、A→E→F →G→B;A→C→F→l →B、A→E→F→l→B、A→E→H→l→B。
解析二:(1)看C点∶只有从A到C的这一条路线。
同样道理:从A到D、从A到E、从A到H也都只有一条路线。
我们把数字“1"分别标在C、D、E、H 这四个点上。
(2)看F点:从A点出发到F,可以是A→C→F,也可以是A→E→F,共有两种走法。
那么我们在F点标上数字"2"(2=1+1)。
(3)看G点:从A→G有三种走法,即A→C→D→G、A→C→F→G、A→E→F →G,在G点标上数字"3"(3=1+2)。
(4)看I点:共有三种走法,即A→C→F→l、A→E→F→l、A→E→H→l,在Ⅰ点标上"3”(3=1+2)。
(5)看B点:从上向下走是G→B,从左向右走是l→B,那么从出发点A→B 有六种走法,即A→C→D→G→B、A→C→F→G→B、A→E→F→G→B、A→C→F→l →B、A→E→F→l→B、A→E→H→l→B ,在B点标上"6"( 6=3+3 )。
小学奥数最短路线问题(有答案)

小学六年级奥数教案—运筹学初步本讲主要讲统筹安排问题、排队问题、最短路线问题、场地设置问题等。
这些都是人们日常生活、工作中经常碰到的问题,怎样才能把它们安排得更合理,多快好省地办事,就是这讲涉及的问题。
当然,限于现有的知识水平,我们仅仅是初步探索一下。
1.统筹安排问题例1星期天妈妈要做好多事情。
擦玻璃要20分钟,收拾厨房要15分钟,洗脏衣服的领子、袖口要10分钟,打开全自动洗衣机洗衣服要40分钟,晾衣服要10分钟。
妈妈干完所有这些事情最少用多长时间?分析与解:如果按照题目告诉的几件事,一件一件去做,要95分钟。
要想节约时间,就要想想在哪段时间里闲着,能否利用闲着的时间做其它事。
最合理的安排是:先洗脏衣服的领子和袖口,接着打开全自动洗衣机洗衣服,在洗衣服的40分钟内擦玻璃和收拾厨房,最后晾衣服,共需60分钟(见下图)。
例1告诉我们,当有许多事要做时,科学地安排好先后顺序,就能用较少的时间完成较多的事情。
2.排队问题例2理发室里有甲、乙两位理发师,同时来了五位顾客,根据他们所要理的发型,分别需要10,12,15,20和24分钟。
怎样安排他们的理发顺序,才能使这五人理发和等候所用时间的总和最少?最少要用多少时间?分析与解:一人理发时,其他人需等待,为使总的等待时间尽量短,应让理发所需时间少的人先理。
甲先给需10分钟的人理发,然后15分钟的,最后24分钟的;乙先给需12分钟的人理发,然后20分钟的。
甲给需10分钟的人理发时,有2人等待,占用三人的时间和为(10×3)分;然后,甲给需 15分钟的人理发,有 1人等待,占用两人的时间和为(15×2)分;最后,甲给需 24分钟的人理发,无人等待。
甲理发的三个人,共用(10×3+15×2+24)分,乙理发的两个人,共用(12×2+20)分。
总的占用时间为(10×3+15×2+24)+(12×2+20)=128(分)。
小学三年级奥数最短路线问题(下学期教案)

小学三年级奥数最短路线问题(下学期教案) -CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN小学三年级奥数最短最短路线问题(下学期教案)在日常工作、生活和娱乐中,经常会遇到有关行程路线的问题.在这一讲里,我们主要解决的问题是如何确定从某处到另一处最短路线的条数。
例1 下图4—1中的线段表示的是汽车所能经过的所有马路,这辆汽车从A走到B处共有多少条最短路线?分析为了叙述方便,我们在各交叉点都标上字母.如图4—2.在这里,首先我们应该明确从A到B的最短路线到底有多长?从A点走到B点,不论怎样走,最短也要走长方形AHBD的一个长与一个宽,即AD+DB.因此,在水平方向上,所有线段的长度和应等于AD;在竖直方向上,所有线段的长度和应等于DB.这样我们走的这条路线才是最短路线.为了保证这一点,我们就不应该走“回头路”,即在水平方向上不能向左走,在竖直方向上不能向上走.因此只能向右和向下走。
有些同学很快找出了从A到B的所有最短路线,即:A→C→D→G→B A→C→F→G→BA→C→F→I→B A→E→F→G→BA→E→F→I→B A→E→H→I→B通过验证,我们确信这六条路线都是从A到B的最短路线.如果按照上述方法找,它的缺点是不能保证找出所有的最短路线,即不能保证“不漏”.当然如果图形更复杂些,做到“不重”也是很困难的。
现在观察这种题是否有规律可循。
1.看C点:由A、由F和由D都可以到达C,而由F→C是由下向上走,由D→C是由右向左走,这两条路线不管以后怎样走都不可能是最短路线.因此,从A 到C只有一条路线。
同样道理:从A到D、从A到E、从A到H也都只有一条路线。
我们把数字“1”分别标在C、D、E、H这四个点上,如图4—2。
2.看F点:从上向下走是C→F,从左向右走是E→F,那么从A点出发到F,可以是A→C→F,也可以是A→E→F,共有两种走法.我们在图4—2中的F点标上2数字“2”.2=1+1.第一个“1”是从A→C的一种走法;第二个“1”是从A→E的一种走法。
奥数最短路线标数法

奥数最短路线标数法
奥数最短路线标数法是指一种求解最短路径问题的算法,它可以用于求解有向图、无向图和带权图的最短路径问题。
该算法的主要思想是利用标记来记录图中每个节点的最短路径,并通过不断更新标记的方式逐步优化路径,最终得到最短路径。
具体来说,该算法的步骤如下:
1. 初始化:对于所有节点v,将其标记设为无穷大,起点s的标记设为0。
2. 标记更新:对于每个节点v,将所有从起点s到v的路径长度与v 的标记进行比较,若存在一条路径可以缩短v的标记,则更新v的标记为该路径长度。
3. 路径选择:按照已标记节点的顺序,依次选择未标记节点中标记最小的节点,将其标记为已标记,重复执行上述标记更新和路径选择的步骤,直到所有节点都被标记为止。
4. 路径提取:根据标记,倒推从终点t到起点s的最短路径,并输出路径长度和路径本身。
奥数最短路线标数法的优点是可以处理带负权图的最短路径问题,即
便存在负权回路也能够判断出来。
同时,该算法具有较高的效率,时
间复杂度为O(n^2)。
当然,奥数最短路线标数法也存在一些缺点。
首先,由于其中涉及到
大量的节点间比较和标记更新,算法的空间复杂度较高,可能会消耗
较多的内存空间。
其次,由于路径选择过程中仅有一个方向,并不能
有效处理有多个起点和终点的情形。
总的来说,奥数最短路线标数法是一种实用性较强的最短路径算法,
可以在多种情况下解决最短路径问题。
但在选择算法时,还需要结合
具体问题的特点进行综合考虑,选择最合适的算法才能取得最佳效果。
小学奥数最短路线问题

小学六年级奥数教案—运筹学初步本讲主要讲统筹安排问题、排队问题、最短路线问题、场地设置问题等。
这些都是人们日常生活、工作中经常碰到的问题,怎样才能把它们安排得更合理,多快好省地办事,就是这讲涉及的问题。
当然,限于现有的知识水平,我们仅仅是初步探索一下。
1.统筹安排问题例1星期天妈妈要做好多事情。
擦玻璃要20分钟,收拾厨房要15分钟,洗脏衣服的领子、袖口要10分钟,打开全自动洗衣机洗衣服要40分钟,晾衣服要10分钟。
妈妈干完所有这些事情最少用多长时间?分析与解:如果按照题目告诉的几件事,一件一件去做,要95分钟。
要想节约时间,就要想想在哪段时间里闲着,能否利用闲着的时间做其它事。
最合理的安排是:先洗脏衣服的领子和袖口,接着打开全自动洗衣机洗衣服,在洗衣服的40分钟内擦玻璃和收拾厨房,最后晾衣服,共需60分钟(见下图)。
例1告诉我们,当有许多事要做时,科学地安排好先后顺序,就能用较少的时间完成较多的事情。
2.排队问题例2理发室里有甲、乙两位理发师,同时来了五位顾客,根据他们所要理的发型,分别需要10,12,15,20和24分钟。
怎样安排他们的理发顺序,才能使这五人理发和等候所用时间的总和最少?最少要用多少时间?分析与解:一人理发时,其他人需等待,为使总的等待时间尽量短,应让理发所需时间少的人先理。
甲先给需10分钟的人理发,然后15分钟的,最后24分钟的;乙先给需12分钟的人理发,然后20分钟的。
甲给需10分钟的人理发时,有2人等待,占用三人的时间和为(10×3)分;然后,甲给需 15分钟的人理发,有 1人等待,占用两人的时间和为(15×2)分;最后,甲给需 24分钟的人理发,无人等待。
甲理发的三个人,共用(10×3+15×2+24)分,乙理发的两个人,共用(12×2+20)分。
总的占用时间为(10×3+15×2+24)+(12×2+20)=128(分)。
小学奥数知识讲解 第十五讲 最短路线问题

典型例题
为使8个奇点变成偶点,我们可以用下面的4种方法走重复的路
图4
典型例题
图4中添虚线的地方,就是重复走的路线。
重复走的路程分别为:(a)3×4=12(千米)
(b)3×2+2×2=10(千米)
(c)2×4=8(千米)
(d)3×2+4×2=14(千米)
当然,重复走的路程最短,总路程就最短。
图4
从上面的计算不难找出最合理的路线了。
典型例题
分析:如果只考虑甲村的人距离公路AB最近,只要由 甲村向公路AB画一条垂直线,交AB于C点,那么C点 是甲村到公路AB最近的点,但是乙村到C点就较远了。 反过来,由乙村向公路AB画垂线,交AB于D点,那么 D点是乙村到公路AB最近的点。但是这时甲村到公路 AB的D点又远了。因为本题要求我们在公路AB上取的 建站点,能够兼顾甲村和乙村的人到这个车站来不走 冤枉路(既路程之和最短),根据我们的经验:两个 地点之间走直线最近,所以,只要在甲村乙村间连一 条直线,这条直线与公路AB交点P,就是所求的公共 汽车站的建站点了(图2)。
解:邮递员应按图4(c)所示的路线走,这条路重复的路程最短, 所以最合理。全程为: (1+2+4+2+1)×2+3×6+2×4 =20+18+8 =46(千米)
典型例题
例3:图5中的线段表示的是小明从家到学校所能经过的所有街道。小明 上学走路的方向都是向东或向南,因为他不想偏离学校的方向而走冤枉 路。那么小明从家到学校可以有多少条不同的路线?
图5
典型例题
分析:为了叙述的方便,我们在各交叉点标上字母(见图 6)。
图6
我们从小明家出发,顺序往前推。由于从小明家到A、B、C、D各处都是 沿直线行走,所以都只有一种走法。我们分别在交叉点处标上“1”。而从小明 家到E处,就有先到A或先到D的两种走法,正好是两个对角上标的数1+1的 和。从小明家到F点,则有3条路线,又正好是两个对角上标的数1+2的和。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
在日常生活、工作中,经常会遇到有关行程路线的问
题。
比如:邮递员送信,要穿遍所有的街道,为了少走冤枉路,需要选择一条最短的路线;旅行者希望寻求最佳旅行路线,以求能够走最近的路而达到目的地,等等。
这样的问题,就是我们所要研究学习的“最短路线问题”。
典型例题
例[1] 假如直线AB 是一条公路,公路两旁有甲乙两个村子,如下图1。
现在要在公路上修建一个公共汽车站,让这两个村子的人到汽车站的路线之和最短。
问:车站应该建在什么地方?
分析 如果只考虑甲村的人距离公路AB 最近,只要由甲村向公
路AB 画一条垂直线,交AB 于C 点,那么C 点是甲村到公路AB 最
甲乙
乙图1
图
2
近的点,但是乙村到C点就较远了。
反过来,由乙村向公路AB画垂线,交AB于D点,那么D点是乙村到公路AB最近的点。
但是这时甲村到公路AB的D点又远了。
因为本题要求我们在公路AB上取的建站点,能够兼顾甲村和乙村的人到这个车站来不走冤枉路(既路程之和最短),根据我们的经验:两个地点之间走直线最近,所以,只要在甲村乙村间连一条直线,这条直线与公路AB交点P,就是所求的公共汽车站的建站点了(图2)。
解用直线把甲村、乙村连起来。
因为甲村乙村在公路的两侧,所以这条连线必与公路AB有一个交点,设这个交点为P,那么在P 点建立汽车站,就能使甲村乙村的人到汽车站所走的路程之和最短。
例[2] 一个邮递员投送信件的街道如图3所示,图上数字表示各段街道的千米数。
他从邮局出发,要走遍各街道,最后回到邮局。
问:走什么样的路线最合理?全程要走多少千米?
3
分析选择最短的路线最合理。
那么,什么路线最短呢?一笔画路线应该是最短的。
邮递员从邮局出发,还要回到邮局,按一笔画问
题,就是从偶点出发,回到偶点。
因此,要能一笔把路线画出来,必须途径的各点全是偶点。
但是图中有8个奇点,显然邮递员要走遍所有街道而又不走重复的路是不可能的。
要使邮递员从邮局出发,仍回到邮局,必须使8个奇点都变成偶点,就是要考虑应在哪些街道上重复走,也就是相当于在图上添哪些线段,能使奇点变成偶点。
如果有不同的添法,就还要考虑哪一种添法能使总路程最短。
为使8个奇点变成偶点,我们可以用图4的4种方法走重复的路
图4中添虚线的地方,就是重复走的路线。
重复走的路程分别为: (a )
3×4=12(千米) (b ) 3×2+2×2=10(千米) (c ) 2×4=8(千米) (d ) 3×2+4×2=14(千米)
3
3
3
3
( a )
( b )
( c )
( d )
图4
当然,重复走的路程最短,总路程就最短。
从上面的计算不难找出最合理的路线了。
解 邮递员应按图4(c )所示的路线走,这条路重复的路程最短,所以最合理。
全程为: (1+2+4+2+1)×2+3×6+2×4 =20+18+8 =46(千米)
例[3] 图5中的线段表示的是小明从家到学校所能经过的所有街道。
小明上学走路的方向都是向东或向南,因为他不想偏离学校的方向而走冤枉路。
那么小明从家到学校可以有多少条不同的路线?
分析 为了叙述的方便,我们在各交叉点标上字母(见图6)。
学校
小明家
A B F E
F D E
F
我们从小明家出发,顺序往前推。
由于从小明家到A 、B 、C 、D 各处都是沿直线行走,所以都只有一种走法。
我们分别在交叉点处标上“1”。
而从小明家到E 处,就有先到A 或先到D 的两种走法,正好是两个对角上标的数1+1的和。
从小明家到F 点,则有3条路线,又正好是两个对角上标的数1+2的和。
标在各交叉点的数,就是依次顺序推出的到各交叉点能有多少种不同的路线的数。
从中我们可以看出,每个格内上右角与下左角两个对角上的数的和,正好等于下右角上的数。
解 从小明家到学校有13条不同的路线。
如图7所示。
图7
学校
H M
N
K。
