矩形的性质
《矩形的性质》课件

矩形的周长和面积计算
周长公式
矩形的周长是两倍长和两倍宽 的和。
面积公式
矩形的面积是长乘以宽。
实例演示
通过几个例子演示如何计算矩 形的周长和面积。
矩形的性质和推导
同位角和内角和
矩形中同位角互相相等,内角和为360度。
对角线关系
矩形的对角线相互垂直。中点连线长为矩形面积开根号两次。
《矩形的性质》PPT课件
欢迎来到《矩形的性质》课件!在这个课程中,我们将深入探讨矩形的定义、 特征、周长和面积计算、性质和推导、应用和联系。让我们一起开始吧!
矩形的定义和特征
1 矩形的定义
矩形是一种四边形,有四个内角为直角,且对边相等。
2 边长关系
矩形的相邻两边长度相等,对边长度也相等。
3 对角线性质
矩形与其他几何图形的联系
正方形和长方形
正方形是一种特殊的矩形,长方形是一种分类 的矩形。
平行四边形和菱形
平行四边形有一组对边平行,菱形在矩形的基 础上增加了对边相等的特性。
总结
1 矩形是一种特殊的四边形
它有许多有趣的性质和应用。
2 学习矩形有助于理解几何图形
并对工程、建筑和计算机图形学有所帮助。
矩形的面积性质
在周长一定的情况下,矩形的面积最大。
矩形的应用和实例
1
建筑设计中的矩形
许多建筑设计基于矩形的特点:平整、稳定、便于构造。
2
计算机图形学中的矩形
由于矩形方便处理,许多2D和3D计算机图形学软件使用矩形来表示图形。
3
矩形与数学方程的关系
许多数学方程中包含矩形,如直角坐标系和平面直角坐标系。
矩形的性质和判定

矩形的性质和判定矩形的性质和判定定义:一个有一个直角的平行四边形被称为矩形。
性质:1.矩形的四个角都是直角。
2.矩形的对角线相互平分且相等。
3.矩形是中心对称图形和轴对称图形,有两条对称轴。
4.矩形的面积为长乘宽。
判定:1.有一个角是直角的平行四边形是矩形。
2.有三个角是直角的四边形是矩形。
3.对角线相等的平行四边形是矩形。
4.对角线相等且互相平分的四边形是矩形。
矩形与平行四边形的区别与联系:相同点:1.两组对边分别平行。
2.两组对边分别相等。
3.两组对角分别相等。
4.对角线相互平分。
区别:1.有一个角是直角的平行四边形是矩形。
2.对角线相互平分且相等。
例题精讲:考点1:矩形的性质例1:在矩形ABCD中,BE=CF,求证:AF=DE。
例2:在矩形ABCD中,BE=DF,求证:△ABE≌△CDF。
例3:在矩形ABCD中,AB=2,且AOB=60°,求对角线AC的长。
考点2:矩形的判定例4:在△ABC中,AB=AC,D为BC中点,四边形ABDE是平行四边形,求证:四边形ADCE是矩形。
例5:在平行四边形ABCD中,E是CD的中点,△ABE是等边三角形,求证:四边形ABCD是矩形。
例6:在平行四边形ABCD中,AQ、BN、CN、DQ分别是DAB、ABC、BCD、CDA的平分线,AQ与BN交于P,CN与DQ交于M,证明:四边形PQMN是矩形。
变式5】在三角形ABC中,AB=AC,AD是BC边上的高,AF是∠BAC的外角平分线,DE∥AB交AF于点E。
可以证明四边形ADCE是矩形。
变式6】在图11中,已知E是四边形ABCD中BC边的中点,连接AE并延长AE交DC的延长线于点F。
(1) 可以证明△ABE≌△FCE。
(2) 连接AC、BF,如果∠AEC=2∠ABC,可以证明四边形ABFC是矩形。
课堂训练】1、矩形具有对边相等和对角线互相平分的性质。
2、正确的个数是6个。
3、不一定正确的是B、AC=BDC。
矩形的判定和性质
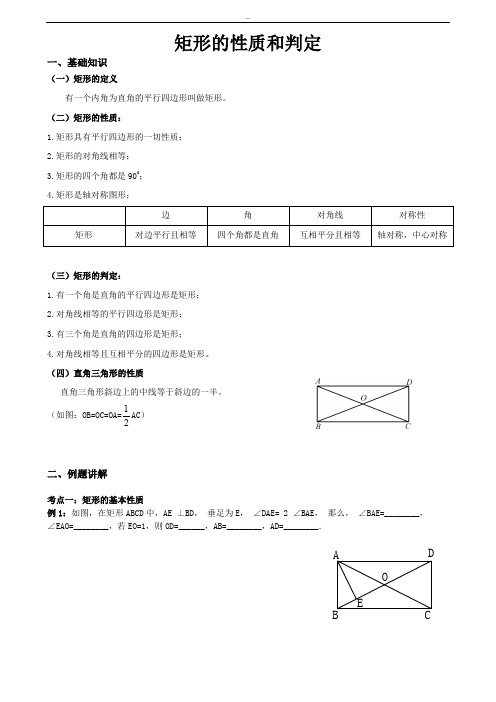
矩形的性质和判定一、基础知识(一)矩形的定义有一个内角为直角的平行四边形叫做矩形。
(二)矩形的性质:1.矩形具有平行四边形的一切性质;2.矩形的对角线相等;3.矩形的四个角都是900; 4.矩形是轴对称图形;边 角 对角线 对称性 矩形对边平行且相等四个角都是直角互相平分且相等轴对称,中心对称(三)矩形的判定:1.有一个角是直角的平行四边形是矩形;2.对角线相等的平行四边形是矩形;3.有三个角是直角的四边形是矩形;4.对角线相等且互相平分的四边形是矩形。
(四)直角三角形的性质直角三角形斜边上的中线等于斜边的一半。
(如图:OB=OC=OA=21AC )二、例题讲解考点一:矩形的基本性质例1:如图,在矩形ABCD 中,AE•⊥BD ,•垂足为E ,•∠DAE=•2•∠BAE ,•那么,•∠BAE=________, ∠EAO=________,若EO=1,则OD=______,AB=________,AD=________.AEDCBO练习 1:矩形ABCD中, ,对角线AC与BD相交于点O,BC的长为6,△OBC的周长是15,求矩形的对角线的长度.练习2:如图,在矩形ABCD中,CE⊥BD,E为垂足,∠DCE∶∠ECB=3∶1,求∠ACD.例2:如图,矩形ABCD被两条对角线分成四个小三角形,如果四个小三角形的周长的和是86cm,对角线长是13cm,那么矩形的周长是多少?练习1:矩形ABCD中, ,对角线AC与BD相交于点O,已知矩形ABCD的面积是12cm2,AB=4cm,求矩形的对角线长。
例3:如图,在矩形ABCD 中,相邻两边AB 、BC 分别长15cm 和25cm ,内角∠BAD 的角平分线与边BC 交于点E .试求BE 与CE 的长度.练习1:如图,在矩形ABCD 中,E 是边AD 上的一点.试说明△BCE 的面积与矩形ABCD 的面积之间的关系.例4:(2009年广西钦州)已知:如图1,在矩形ABCD 中,AF =BE .求证:DE =CF ;ADCB 图1F E练习1:如图,矩形ABCD 中,E 为AD 中点,∠BEC 为直角,矩形ABCD 的周长是20,求AD 、AB 的长。
矩形的性质与判定 八年级

PHD C B A 矩形的性质与判定【知识要点:】1.矩形的定义:有一个角是直角的平行四边形是矩形(矩形是特殊的平行四边形)。
2.矩形的性质:矩形具有平行四边形的所有性质。
(1)角:四个角都是直角。
(2)对角线:互相平分且相等。
3.矩形的判定: (1)有一个角是直角的平行四边形。
(2)对角线相等的平行四边形。
(3)有三个角是直角的四边形。
4.矩形的对称性:矩形是中心对称图形,对角线的交点是它的对称中心;矩形是轴对称图形,对称轴有2条,是经过对角线的交点且垂直于矩形一边的直线。
5.矩形的周长和面积:矩形的周长=)(2b a + 矩形的面积=长⨯宽=ab (b a ,为矩形的长与宽)【经典例题:】例1、如图,矩形ABCD 中,E 为AD 上一点,EF ⊥CE 交AB 于F ,若DE=2,矩形ABCD 的周长为16,且CE=EF ,求AE 的长.例2、 如图, 在矩形ABCD 中, AP=DC, PH=PC, 求证: PB 平分∠CBH. 例3、已知:如图所示,矩形ABCD 中,E 是BC 上的一点,且AE=BC ,︒=∠15EDC . 求证:AD=2AB .例4、已知:如图,平行四边形ABCD 的四个内角的平分线分别相交于点E ,F ,G ,H ,求证:四边形EFGH 是矩形。
例5、已知:如图,四边形ABCD 是由两个全等的正三角形ABD 和BCD 组成的,M 、N•分别为BC 、AD 的中点.求证:四边形BMDN 是矩形.A BECD例6、如图,已知在四边形ABCD 中,AC DB 交于O ,E 、F 、G 、H 分别是四边的中点, 求证:四边形EFGH 是矩形.练习题:1.判断一个四边形是矩形,下列条件正确的是( )A .对角线相等B .对角线垂直C .对角线互相平分且相等D .对角线互相垂直且相等。
2.矩形具有而一般的平行四边形不一定具有的特征是( )。
A .对角相等 B. 对边相等 C .对角线相等 D. 对角线互相平分 3.在下列图形性质中,矩形不一定具有的是( )A .对角线互相平分且相等B .四个角相等C .是轴对称图形D .对角线互相垂直平分4.矩形的两边长分别为10cm 和15cm ,其中一个内角平分线分长边为两部分,这两部分分别为( )A .6cm 和9cmB .5cm 和10cmC .4cm 和11cmD .7cm 和8cm5.在矩形ABCD 中, 对角线交于O 点,AB=0.6, BC=0.8, 那么△AOB 的面积为 ; 周长为 .6.一个矩形周长是12cm, 对角线长是5cm, 那么它的面积为 .7.矩形的两条对角线的夹角是60°,一条对角线与矩形短边的和为15,那么矩形对角线的长为 ,短边长为 .8.矩形的两邻边分别为4㎝和3㎝,则其对角线为 ㎝,矩形面积为 cm 2. 9.若矩形的一条对角线与一边的夹角是40°,则两条对角线相交所成的锐角是 . 10.矩形的对角线相交所成的钝角为120°,矩形的短边长为5 cm ,则对角线之长为 cm 。
矩形的性质和判定

矩形的性质和判定基础知识点1、矩形的性质和判定:定 义矩 形有一个内角是直角的平行四边形。
性质边对边平行,对边相等。
角 四个角相等,都是直角。
对角线互相平分,相等。
判定有一个角是直角的平行四边形是矩形。
有三个角是直角的四边形是矩形。
对角线相等的平行四边形是矩形。
2、在直角三角形中,斜边的中线等于斜边的一半。
3、矩形是轴对称图形,对称轴是对边中点的连线所在的直线。
例题剖析例1、 已知矩形ABCD 中,AB=2BC ,点E 在边DC 上,且AE=AB ,求∠EBC 的度数.【变式练习】矩形ABCD 中,AC 与BD 交于O 点,BE ⊥AC 于E ,CF ⊥BD 于F ,•求证:BE=CF .【变式练习】在矩形ABCD 中,AC ,BD 是对角线,过顶点C 作BD•的平行线与AB 的延长线相交于点E ,求证:△ACE 是等腰三角形.例2、折叠矩形ABCD 纸片,先折出折痕BD ,再折叠使A 落在对角线BD 上A ′位置上,折痕为DG ,AB=2,BC=1。
求AG 的长。
GA`DCBA【变式练习】如图,将矩形ABCD 沿对角线BD 折叠,使点C 落在F 的位置,BF 交AD 于E ,AD=8,AB=4,求△BED 的面积。
EDC BAF例3、在△ABC中,∠ABC=90°,BD是△ABC的中线,延长BD到E,•使DE=BD,连结AE,CE,求证:四边形ABCE是矩形.【变式练习】在△ABC中,AB=AC,D为BC中点,四边形ABDE是平行四边形。
求证:四边形ADCE是矩形。
例4、已知:如图,在△ABC中,AB=AC,点D为BC中点,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E.求证:四边形ADCE为矩形.【变式练习】(2011•青岛)在▱ABCD中,E、F分别是AB、CD的中点,连接AF、CE.(1)求证:△BEC≌△DFA;(2)连接AC ,当CA=CB 时,判断四边形AECF 是什么特殊四边形?并证明你的结论【变式练习】E 为□ABCD 外一点,AE ⊥CE,BE ⊥DE ,求证:□ABCD 为矩形例5、□ABCD 中,AE 、BF 、CG 、DH 分别是各内角的平分线,E 、F 、G 、H 为它们的交点, 求证:四边形EFGH 的矩形。
矩形的特征与性质

矩形的特征与性质矩形是几何形状中最常见的一种,它具有许多独特的特征和性质。
在本文中,我们将探讨矩形的定义、性质和一些相关的定理。
通过对矩形进行全面的了解,我们可以更好地理解它在几何学中的重要性。
矩形的定义矩形是一种四边形,其四个内角都是直角(90度)。
也就是说,它的四条边互相垂直,并且长度相等。
矩形的两条对边是平行的,所以矩形也是一个平行四边形。
矩形的特征除了上述的定义特征外,矩形还具有以下的特征:1. 对角线相等:矩形的两条对角线相等长,并且彼此垂直交叉于中心点。
这个特征使得矩形具有一些独特性质和定理,如下文将要讨论的。
2. 中心对称性:矩形是关于其中心点对称的,也就是说,如果从矩形的中心点沿着任意方向画一条直线,那么这条直线将把矩形分为两个完全相同的部分。
3. 尺寸关系:矩形的宽度和长度差异明显,其中宽度较小,长度较大。
这种特点使得矩形可以用来表示各种比例和尺寸关系。
矩形的性质除了上述的特征外,矩形还具有以下的性质和定理:1. 面积:矩形的面积可以通过将宽度乘以长度来计算。
即面积 = 宽度 ×长度。
2. 周长:矩形的周长可以通过将宽度和长度乘以2然后相加来计算。
即周长 = 2 × (宽度 + 长度)。
3. 对角线:矩形的两条对角线相等长,可以通过勾股定理得知其长度。
即对角线长度= √(宽度² + 长度²)。
4. 正方形:当矩形的宽度和长度相等时,矩形就变成了正方形。
正方形是一种特殊的矩形,它具有所有矩形的性质和特征,同时还具有对边相等的特点。
矩形的定理1. 矩形的内角和定理:矩形的内角和为360度。
由于矩形的每个内角都是直角(90度),所以四个内角之和为360度。
2. 矩形的对角线定理:矩形的两条对角线相等。
这是因为矩形的对角线可以看作是通过矩形的中心点的垂直交叉线,由对角线的定义可知,对角线相等。
3. 矩形的对角线互相垂直定理:矩形的两条对角线互相垂直。
矩形的性质与判定

矩形的周长计算与性质
矩形的周长计算:
• 两倍的长加上两倍的宽 • 对角线的和
矩形的周长性质:
• 周长大于等于零 • 周长是一个常数
矩形在实际问题中的应用案例
建筑设计中的矩形框架:
• 节省材料 • 结构稳定
电子元件中的矩形封装:
• 方便安装 • 散热性能好
04
矩形与其他图形的关系与转化
矩形与平行四边形的关系与转化
矩形的性பைடு நூலகம்与判定
CREATE TOGETHER
DOCS
01
矩形的定义与基本性质
矩形的定义及其几何特征
矩形的定义:
• 有四个角都是直角的四边形 • 对边平行且相等
矩形的几何特征:
• 对边平行且相等 • 四个角都是直角 • 对角线相等且互相平分
矩形的实际应用:
• 建筑设计中的矩形框架 • 电子元件中的矩形封装
• 矩形可以通过对角线平移转化为正方形 • 正方形可以通过对角线折叠转化为矩形
矩形与长方形的关系与转化
矩形与长方形的关系:
• 矩形是长方形的一种特殊情况 • 长方形是特殊的矩形
矩形与长方形的转化:
• 矩形可以通过对角线平移转化为长方形 • 长方形可以通过对角线折叠转化为矩形
05
矩形在几何解题中的策略与方法
矩形的对边平行且相等
矩形的对边平行且相等的性质:
• 对角线互相平分 • 对角线相等
矩形的对边平行:
• 同一列的边平行 • 同一行的边平行
矩形的对边相等:
• 同一列的边相等 • 同一行的边相等
矩形的四个角都是直角
矩形的角:
• 四个角都是直角 • 直角的角度为90度
矩形的直角性质:
矩形定义、性质、判定

矩形定义、性质、判定
•矩形:
是一种平面图形,矩形的四个角都是直角,同时矩形的对角线相等,而且矩形所在平面内任一点到其两对角线端点的距离的平方和相等。
•矩形的性质:
1.矩形的4个内角都是直角;
2.矩形的对角线相等且互相平分;
3.矩形所在平面内任一点到其两对角线端点的距离的平方和相等;
4.矩形既是轴对称图形,也是中心对称图形(对称轴是任何一组对边中点的连线),它至少有两条对称轴。
对称中心是对角线的交点。
5.矩形是特殊的平行四边形,矩形具有平行四边形的所有性质
6.顺次连接矩形各边中点得到的四边形是菱形
•矩形的判定:
①定义:有一个角是直角的平行四边形是矩形
②定理1:有三个角是直角的四边形是矩形
③定理2:对角线相等的平行四边形是矩形
④对角线互相平分且相等的四边形是矩形
矩形的面积:S矩形=长×宽=ab。
•黄金矩形:
宽与长的比是(√5-1)/2(约为0.618)的矩形叫做黄金矩形。
黄金矩形给我们一协调、匀称的美感。
世界各国许多著名的建筑,为取得最佳的视觉效果,都采用了黄金矩形的设计。
如希腊的巴特农神庙等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《矩形的性质》导学案
设计人: 阚家中学 岳素娟
学习目标:
1.探索并掌握矩形的有关性质,感受定理的由来。
2.进一步培养学生的分析、综合的思考方法,及表达书写能力.发展学生演绎推理能力。
学习重点: 矩形的定义及其性质定理。
学习难点: 灵活运用矩形的性质定理解决矩形的有关问题。
课前预习学案
预习导学:(预习课本P13-15回答下列问题)
1.矩形定义:__________________________________叫做矩形(通常也叫_________). 2. 归纳矩形的性质:
⑴具有平行四边形的一切性质。
⑵矩形性质定理1: ____________________________. ⑶矩形性质定理2:____________________________. 3.直角三角形斜边上的中线等于_____________的一半.
课中实施学案
一、自主学习:(脑筋越用越灵活!)
探究1:矩形的四个角都是直角 (口述证明过程 ) 探究2:矩形的对角线相等
已知:如图,
求证: 证明: 探究3:
问题一 如图 ,矩形ABCD ,对角线相交于O ,观 察平行四边形的对角线所分成的三角形, 由性质2,你会发现有以下相等关系: AO=___=___=____=
21___=2
1
___.
C
问题二 将目光锁定在Rt △ABC 中,你能发现直角三角形有什么特殊的性质吗?
二、性质运用:(动手动脑,勤于思考)
1、合作交流:生自学课本第15页例1,探讨另一种解法。
(提示:用直角三角形中,30度的锐角所对的直角边等于斜边的一半来解) 解:
2、变式训练:
变式1:本题若将“∠BOC=120°”改为“∠BOC ∶∠BOA =2∶1”,你能求出BD 的长吗?
变式2:本题若将“∠BOC=120°”改为“AC=2AB ”,你能获得有关这个矩形的哪些结论?
三、知识巩固:(学数学是为了用数学!)
1.下列说法错误的是( ).
A 、矩形的对角线互相平分
B 、矩形的对角线相等
C 、有一个角是直角的四边形是矩形
D 、有一个角是直角的平行四边形叫做矩形 2.矩形的对角线把矩形分成的三角形中全等三角形一共有( ). A 、2对 B 、4对 C 、6对 D 、8对
3.已知矩形的一条对角线长为10cm ,两条对角线的一个交角为120°,则矩形的边长分别为_________cm , cm , cm , cm .
三、课堂小结:(今天的知识,要今天掌握!)
本节课你有哪一些收获?有哪些易错点与易混点?(同位交流)
对自己说我学会了______________________________。
对同学说,容易混淆的知识点有:_____________________ 对大家说,还有疑惑点有:____________________。
(让大家帮你解决。
)
四、当堂检测:(相信你一定能行!)
1.矩形的两条对角线的夹角为60°,对角线长为15cm ,较短边的长为( ). (A)12cm (B)10cm (C)7.5cm (D)5cm
2. 在矩形ABCD 中,对角线AC ,BD 相交于点O ,若对角线AC=10cm ,•边BC=•8cm ,•则△
ABO 的周长为________. 3.矩形ABCD 被两条对角线分成四个小三角形,如果△AOD 周长比△AOB 周长大4cm , 矩形ABCD 的周长为20cm ,求AB 、AD 的长。
课后延伸学案
1.如图,EF 过矩形对角线的交点O ,且分别交ABCD 于EF , 那么阴影部分的面积是矩形ABCD 面积的( ) A .
51 B .41 C .31 D .10
3 2.在矩形ABCD 中, ∠AOB =120°,AD =3,则AC 为( ) A . 1.5 B . 3 C . 6 D . 9
3.直角三角形斜边上的高与中线分别是5和6,则它的面积是_______________.
4.已知:如图,E 为矩形ABCD 内一点,且EB=EC 。
求证:
EA=ED.
5.已知:如图,在□ABCD中,AE⊥BD,CF⊥BD,垂足分别为E、F,G、H分别是AD、BC 的中点。
求证:EG =FH, EG∥FH.
6..已知:如图,△ABC中,BD⊥AC于D,CE⊥AB于E,点M、N分别是BC、DE的中点.
求证:MN⊥DE
B。
