第6章 树和二叉树 作业
数据结构-习题-第六章-树

数据结构-习题-第六章-树和二叉树E F D G A B / + + * - C * 第六章 树和二叉树一、选择题1.已知一算术表达式的中缀形式为 A+B*C-D/E ,后缀形式为ABC*+DE/-,其前缀形式为( )A .-A+B*C/DE B. -A+B*CD/EC .-+*ABC/DE D. -+A*BC/DE【北京航空航天大学 1999 一、3 (2分)】2.算术表达式a+b*(c+d/e )转为后缀表达式后为( )【中山大学 1999 一、5】A .ab+cde/*B .abcde/+*+C .abcde/*++D .abcde*/++ 3. 设有一表示算术表达式的二叉树(见下图), 它所表示的算术表达式是( )【南京理工大学1999 一、20(2分)】A. A*B+C/(D*E)+(F-G)B.(A*B+C)/(D*E)+(F-G)C. (A*B+C)/(D*E+(F-G ))D.A*B+C/D*E+F-G4. 设树T 的度为4,其中度为1,2,3和4的结点个数分别为4,2,1,1 则T 中的叶子数为( )A .5B .6C .7D.8【南京理工大学 2000 一、8 (1.5分)】5. 在下述结论中,正确的是()【南京理工大学 1999 一、4 (1分)】①只有一个结点的二叉树的度为0; ②二叉树的度为2;③二叉树的左右子树可任意交换;④深度为K的完全二叉树的结点个数小于或等于深度相同的满二叉树。
A.①②③ B.②③④ C.②④ D.①④6. 设森林F对应的二叉树为B,它有m个结点,B的根为p,p的右子树结点个数为n,森林F中第一棵树的结点个数是()A.m-n B.m-n-1 C.n+1 D.条件不足,无法确定【南京理工大学2000 一、17(1.5分)】7. 树是结点的有限集合,它( (1))根结点,记为T。
其余结点分成为m(m>0)个((2))的集合T1,T2,…,Tm,每个集合又都是树,此时结点T称为Ti的父结点,Ti称为T的子结点(1≤i≤m)。
第六章 树和二叉树 作业

以数据集{2 以数据集{2,5,7,9,13}为权值构造一棵 {2, 13}为权值构造一棵 huffman树 并计算其带权路径长度。 huffman树,并计算其带权路径长度。
2 5 7 9 36 14 22 13
7
7
9
13
2
5
WPL=(2+5)*3+(7+9+13)*2=79
t)
//释放左子树 //释放左子树 //释放右子树 //释放右子树 //释放根节点 //释放根节点
已知一棵二叉树的中序序列为cbedahgijf, 已知一棵二叉树的中序序列为cbedahgijf,后序 序列为cedbhjigfa, 序列为cedbhjigfa,画出该二叉树的先序线索二 叉树。 叉树。 a 中序:c 中序:c b e d a h g i j f 后序:c 后序:c e d b h j i g f a 先序:abcdefghij 先序:abcdefghij
编写一个将二叉树中每个结点的左右孩子交换的算法 分析:采用递归的方式求解。当二叉树的左右孩子之一 分析:采用递归的方式求解。 不空时,将左右孩子交换, 不空时,将左右孩子交换,然后再分别递归处理左右 子树。 子树。
void exchange( BiTree &t) { BiTree m ; if ( !t->lchild||!t->rchild) !t->lchild||!t{ m=tm=t->lchild ; t->lchild =t->rchild; t=tt->rchild=m; exchange(texchange(t->lchild) ; exchange(texchange(t->rchild) ; } }
第6章_数据结构习题题目及答案_树和二叉树_参考答案

一、基础知识题6.1设树T的度为4,其中度为1,2,3和4的结点个数分别为4,2,1,1,求树T中的叶子数。
【解答】设度为m的树中度为0,1,2,…,m的结点数分别为n0, n1, n2,…, nm,结点总数为n,分枝数为B,则下面二式成立n= n0+n1+n2+…+nm (1)n=B+1= n1+2n2 +…+mnm+1 (2)由(1)和(2)得叶子结点数n0=1+即: n0=1+(1-1)*4+(2-1)*2+(3-1)*1+(4-1)*1=86.2一棵完全二叉树上有1001个结点,求叶子结点的个数。
【解答】因为在任意二叉树中度为2 的结点数n2和叶子结点数n0有如下关系:n2=n0-1,所以设二叉树的结点数为n, 度为1的结点数为n1,则n= n0+ n1+ n2n=2n0+n1-11002=2n0+n1由于在完全二叉树中,度为1的结点数n1至多为1,叶子数n0是整数。
本题中度为1的结点数n1只能是0,故叶子结点的个数n0为501.注:解本题时要使用以上公式,不要先判断完全二叉树高10,前9层是满二叉树,第10层都是叶子,……。
虽然解法也对,但步骤多且复杂,极易出错。
6.3 一棵124个叶结点的完全二叉树,最多有多少个结点。
【解答】由公式n=2n0+n1-1,当n1为1时,结点数达到最多248个。
6.4.一棵完全二叉树有500个结点,请问该完全二叉树有多少个叶子结点?有多少个度为1的结点?有多少个度为2的结点?如果完全二叉树有501个结点,结果如何?请写出推导过程。
【解答】由公式n=2n0+n1-1,带入具体数得,500=2n0+n1-1,叶子数是整数,度为1的结点数只能为1,故叶子数为250,度为2的结点数是249。
若完全二叉树有501个结点,则叶子数251,度为2的结点数是250,度为1的结点数为0。
6.5 某二叉树有20个叶子结点,有30个结点仅有一个孩子,则该二叉树的总结点数是多少。
《数据结构》习题汇编06第六章树和二叉树试题

第六章树和二叉树试题一、单项选择题1.树中所有结点的度等于所有结点数加()。
A. 0B. 1C. -1D. 22.在一棵树中,()没有前驱结点。
A. 分支结点B. 叶结点C. 根结点D. 空结点3.在一棵二叉树的二叉链表中,空指针域数等于非空指针域数加()。
A. 2B. 1C. 0D. -14.在一棵具有n个结点的二叉树中,所有结点的空子树个数等于()。
A. nB. n-1C. n+1D. 2*n5.在一棵具有n个结点的二叉树的第i层上(假定根结点为第0层,i大于等于0而小于等于树的高度),最多具有()个结点。
A. 2iB. 2i+1C. 2i-1D. 2n6.在一棵高度为h(假定根结点的层号为0)的完全二叉树中,所含结点个数不小于()。
A. 2h-1B. 2h+1C. 2h-1D. 2h7.在一棵具有35个结点的完全二叉树中,该树的高度为()。
假定空树的高度为-1。
A. 5B. 6C. 7D. 88.在一棵具有n个结点的完全二叉树中,分支结点的最大编号为()。
假定树根结点的编号为0。
A. ⎣(n-1)/2⎦B. ⎣n/2⎦C. ⎡n/2⎤D. ⎣n/2⎦ -19.在一棵完全二叉树中,若编号为i的结点存在左孩子,则左子女结点的编号为()。
假定根结点的编号为0A. 2iB. 2i-1C. 2i+1D. 2i+210.在一棵完全二叉树中,假定根结点的编号为0,则对于编号为i(i>0)的结点,其双亲结点的编号为()。
A. ⎣(i+1)/2⎦B. ⎣(i-1)/2⎦C. ⎣i/2⎦D. ⎣i/2⎦-111.在一棵树的左子女-右兄弟表示法中,一个结点的右孩子是该结点的()结点。
A. 兄弟B. 子女C. 祖先D. 子12.在一棵树的静态双亲表示中,每个存储结点包含()个域。
A. 1B. 2C. 3D. 413.已知一棵二叉树的广义表表示为a (b (c), d (e ( , g (h) ), f ) ),则该二叉树的高度为()。
数据结构习题第6章

第6章树和二叉树一、选择题1.不含任何结点的空树()。
A. 是一棵树B. 是一棵二叉树C. 是一棵树也是一棵二叉树;D. 既不是树也不是二叉树2. 一棵有n个结点的树的所有结点的度数之和为()。
A. n-1B. nC. n+1D. 2n3. 在二叉树中某一个结点的深度为3,高度为4,则该树的高度是()。
A. 5B. 6C. 7D. 84. 设高度为h的二叉树中只有度为0和度为2的结点,则该树的结点数至多为()。
A. 2h-1B. 2h+1C. 2h-1D. 2h+15. 设高度为h的二叉树中只有度为0和度为2的结点,则该树的结点数至少为()。
A. 2h-1B. 2h+1C. 2h-1D. 2h+16. 高度为h的满二叉树中有n个结点,其中有m个叶结点,则正确的等式是()。
A. h+m=nB. h+m=2nC. m=h-1D. n=2h-17.二叉树是非线性数据结构,所以()。
A. 它不能用顺序存储结构存储B. 它不能用链式存储结构存储C. 顺序存储结构和链式存储结构都能存储D. 顺序存储结构和链式存储结构都不能使用8. 一棵完全二叉树有25个叶结点,则该树最少有()个结点。
A. 48B. 49C. 50D. 519. 假设一个三叉树的结点数为36,则该树的最小高度为()。
A. 2B. 3C. 4D. 510. 设二叉树有n个结点,则二叉链表中非空指针数为()。
A. n-1B. nC. n+1D. 2n11. 先序序列和中序序列正好相反的二叉树是()。
A. 完全二叉树B. 满二叉树C. 左单枝树D. 右单枝树12. 后序序列和中序序列正好相反的二叉树是()。
A. 完全二叉树B. 满二叉树C. 左单枝树D. 右单枝树13.把一棵树转换为二叉树后,这棵二叉树的形态是()。
A. 唯一的B. 有多种C. 有多种,但根结点都没有左孩子D. 有多种,但根结点都没有右孩子14. 将一棵树T转换为孩子—兄弟链表表示的二叉树H,则T的后根序遍历是H 的()。
第6章树和二叉树习题

第六章 树和二叉树一、选择题1.算术表达式a+b*(c+d/e )转为后缀表达式后为( B )A .ab+cde/*B .abcde/+*+C .abcde/*++ 2. 设有一表示算术表达式的二叉树(见下图),它所表示的算术表达式是( C )A. A*B+C/(D*E)+(F-G)B. (A*B+C)/(D*E)+(F-G)C. (A*B+C)/(D*E+(F-G ))D. A*B+C/D*E+F-G3. 设树T 的度为4,其中度为1,2,3和4的结点个数别离为4,2,1,1 则T 中的叶子数为( D )A .5B .6C .7D .84. 在下述结论中,正确的是( D )①只有一个结点的二叉树的度为0; ②二叉树的度为2; ③二叉树的左右子树可任意互换;④深度为K 的完全二叉树的结点个数小于或等于深度相同的满二叉树。
A .①②③B .②③④C .②④D .①④5. 设丛林F 对应的二叉树为B ,它有m 个结点,B 的根为p,p 的右子树结点个数为n,丛林F 中第一棵树的结点个数是( A )A .m-nB .m-n-1C .n+1D .条件不足,无法确信6.若一棵二叉树具有10个度为2的结点,5个度为1的结点,则度为0的结点个数是( B )A .9B .11C .15D .不确信7.设丛林F 中有三棵树,第一,第二,第三棵树的结点个数别离为M1,M2和M3。
与丛林F 对应的二叉树根结点的右子树上的结点个数是( D )。
A .M1B .M1+M2C .M3D .M2+M38.一棵完全二叉树上有1001个结点,其中叶子结点的个数是( E )A.250 B.500 C.254 D.505 E.以上答案都不对9. 有关二叉树下列说法正确的是( B )A.二叉树的度为2 B.一棵二叉树的度能够小于2C.二叉树中至少有一个结点的度为2 D.二叉树中任何一个结点的度都为210.二叉树的第I层上最多含有结点数为(C )A.2I B.2I-1-1 C.2I-1D.2I -111. 一个具有1025个结点的二叉树的高h为( C )A.11 B.10 C.11至1025之间D.10至1024之间12.一棵二叉树高度为h,所有结点的度或为0,或为2,则这棵二叉树最少有( B )结点A.2h B.2h-1 C.2h+1 D.h+113. 一棵树高为K的完全二叉树至少有( C )个结点A.2k–1 B. 2k-1–1 C. 2k-1 D. 2k14.对二叉树的结点从1开始进行持续编号,要求每一个结点的编号大于其左、右小孩的编号,同一结点的左右小孩中,其左小孩的编号小于其右小孩的编号,可采纳( C )顺序的遍历实现编号。
数据结构 第六章 树和二叉树作业及答案

第六章树和二叉树作业一、选择题(每题2分,共24分)。
1. 一棵二叉树的顺序存储情况如下:树中,度为2的结点数为( C )。
A.1 B.2 C.3 D.42. 一棵“完全二叉树”结点数为25,高度为(B )。
A.4 B.5 C.6 D.不确定3.下列说法中,(B )是正确的。
A. 二叉树就是度为2的树B. 二叉树中不存在度大于2的结点C. 二叉树是有序树D. 二叉树中每个结点的度均为24.一棵二叉树的前序遍历序列为ABCDEFG,它的中序遍历序列可能是(B )。
A. CABDEFGB. BCDAEFGC. DACEFBGD. ADBCFEG5.线索二叉树中的线索指的是(C )。
A.左孩子 B.遍历 C.指针 D.标志6. 建立线索二叉树的目的是(A )。
A. 方便查找某结点的前驱或后继B. 方便二叉树的插入与删除C. 方便查找某结点的双亲D. 使二叉树的遍历结果唯一7. 有 D )示意。
A.B.C.D.8. 一颗有2046个结点的完全二叉树的第10层上共有(B )个结点。
A. 511B. 512C. 1023D. 10249. 一棵完全二叉树一定是一棵(A )。
A. 平衡二叉树B. 二叉排序树C. 堆D. 哈夫曼树10.某二叉树的中序遍历序列和后序遍历序列正好相反,则该二叉树一定是( C )的二叉树。
A .空或只有一个结点B .高度等于其结点数C .任一结点无左孩子D .任一结点无右孩子11.一棵二叉树的顺序存储情况如下:1 2 3 4 5 6 7 8 9 10 11 12 13 14 15A B C D E 0 F 0 0 G H 0 0 0 X结点D 的左孩子结点为( D )。
A .EB .C C .FD .没有12.一棵“完全二叉树”结点数为25,高度为( B )。
A .4B .5C .6D .不确定二、填空题(每空3分,共18分)。
1. 树的路径长度:是从树根到每个结点的路径长度之和。
对结点数相同的树来说,路径长度最短的是 完全 二叉树。
数据结构课后习题(第6章)

【课后习题】第6章树和二叉树网络工程2010级()班学号:姓名:一、填空题(每空1分,共16分)1.从逻辑结构看,树是典型的。
2.设一棵完全二叉树具有999个结点,则此完全二叉树有个叶子结点,有个度为2的结点,有个度为1的结点。
3.由n个权值构成的哈夫曼树共有个结点。
4.在线索化二叉树中,T所指结点没有左子树的充要条件是。
5.在非空树上,_____没有直接前趋。
6.深度为k的二叉树最多有结点,最少有个结点。
7.若按层次顺序将一棵有n个结点的完全二叉树的所有结点从1到n编号,那么当i为且小于n时,结点i的右兄弟是结点,否则结点i没有右兄弟。
8.N个结点的二叉树采用二叉链表存放,共有空链域个数为。
9.一棵深度为7的满二叉树有___ ___个非终端结点。
10.将一棵树转换为二叉树表示后,该二叉树的根结点没有。
11.采用二叉树来表示树时,树的先根次序遍历结果与其对应的二叉树的遍历结果是一样的。
12.一棵Huffman树是带权路径长度最短的二叉树,权值的外结点离根较远。
二、判断题(如果正确,在对应位置打“√”,否则打“⨯”。
每题0.5分,共5分)1.对于一棵非空二叉树,它的根结点作为第一层,则它的第i层上最多能有2i-1个结点。
2.二叉树的前序遍历并不能唯一确定这棵树,但是,如果我们还知道该二叉树的根结点是那一个,则可以确定这棵二叉树。
3.一棵树中的叶子结点数一定等于与其对应的二叉树中的叶子结点数。
4.度≤2的树就是二叉树。
5.一棵Huffman树是带权路径长度最短的二叉树,权值较大的外结点离根较远。
6.采用二叉树来表示树时,树的先根次序遍历结果与其对应的二叉树的前序遍历结果是一样的。
7.不存在有偶数个结点的满二叉树。
8.满二叉树一定是完全二叉树,而完全二叉树不一定是满二叉树。
9.已知二叉树的前序遍历顺序和中序遍历顺序,可以惟一确定一棵二叉树;10.已知二叉树的前序遍历顺序和后序遍历顺序,不能惟一确定一棵二叉树;三、单项选择(请将正确答案的代号填写在下表对应题号下面。
数据结构习题第六章树和二叉树

第六章 树和二叉树一、选择题1.已知一算术表达式的中缀形式为 A+B*C-D/E ,后缀形式为ABC*+DE/-,其前缀形式为( )A .-A+B*C/DE B. -A+B*CD/E C .-+*ABC/DE D.-+A*BC/DE【北京航空航天大学 1999 一、3 (2分)】2.算术表达式a+b*(c+d/e )转为后缀表达式后为( )【中山大学 1999 一、5】A .ab+cde/*B .abcde/+*+C .abcde/*++D 3. 设有一表示算术表达式的二叉树(见下图),它所表示的算术表达式是( ) 【南京理工大学1999 一、20(2分)】 A. A*B+C/(D*E)+(F-G) B. (A*B+C)/(D*E)+(F-G) C. (A*B+C)/(D*E+(F-G )) D. A*B+C/D*E+F-G 4. 设树T 的度为4,其中度为1,2,3和4的结点个数分别为4,2,1,1 则T 中的叶子数为( )A .5B .6C .7D .8【南京理工大学 2000 一、8 (1.5分)】5. 在下述结论中,正确的是( )【南京理工大学 1999 一、4 (1分)】①只有一个结点的二叉树的度为0; ②二叉树的度为2; ③二叉树的左右子树可任意交换;④深度为K 的完全二叉树的结点个数小于或等于深度相同的满二叉树。
A .①②③B .②③④C .②④D .①④6. 设森林F 对应的二叉树为B ,它有m 个结点,B 的根为p,p 的右子树结点个数为n,森林F 中第一棵树的结点个数是( )A .m-nB .m-n-1C .n+1D .条件不足,无法确定 【南京理工大学2000一、17(1.5分)】7. 树是结点的有限集合,它( (1))根结点,记为T 。
其余结点分成为m (m>0)个((2))的集合T1,T2, …,Tm ,每个集合又都是树,此时结点T 称为Ti 的父结点,Ti 称为T的子结点(1≤i ≤m )。
《数据结构》习题集:第6章 树和二叉树

第6章树和二叉树一、选择题1.有一“遗传”关系,设x是y的父亲,则x可以把它的属性遗传给y,表示该遗传关系最适合的数据结构是( D )A、向量B、树C、图D、二叉树2.树最适合用来表示( B )A、有序数据元素B、元素之间具有分支层次关系的数据C、无序数据元素D、元素之间无联系的数据3.树B 的层号表示为1a,2b,3d,3e,2c,对应于下面选择的( C )A、1a(2b(3d,3e),2c)B、a(b(D,e),c)C、a(b(d,e),c)D、a(b,d(e),c)4.对二叉树的结点从1 开始连续编号,要求每个结点的编号大于其左、右孩子的编号,同一结点的左右孩子中,其左孩子的编号小于其右孩子的编号,则可采用( B )次序的遍历实现二叉树的结点编号。
A、先序B、中序C、后序D、从根开始按层次遍历5.按照二叉树的定义,具有3 个结点的二叉树有(C )种。
A、3B、4C、5D、66.在一棵有n个结点的二叉树中,若度为2的结点数为n2,度为1的结点数为n1,度为0的结点数为n0,则树的最大高度为(),其叶结点数为();树的最小高度为(),其叶结点数为();若采用链表存储结构,则有()个空链域。
log+1 C、log2n D、nA、n/2B、⎣⎦n2E、n0+n1+n2F、n1+n2G、n2+1H、1I、n+1 J、n1K、n2L、n1+17.对一棵满二叉树,m 个树叶,n 个结点,深度为h,则( D )A、n=m+hB、h+m=2nC、m=h-1D、n=2h-18.设高度为h 的二叉树中只有度为0 和度为2 的结点,则此类二叉树中所包含的结点数至少为( A ),至多为(D )。
A、2hB、2h-1C、2h-1D、2h-19.在一棵二叉树上第5 层的结点数最多为(B)(假设根结点的层数为1)A、8B、16C、15D、3210.深度为5 的二叉树至多有( C )个结点。
A、16B、32C、31D、1011.一棵有124 个叶结点的完全二叉树,最多有(B )个结点A、247B、248C、249D、25012.含有129 个叶子结点的完全二叉树,最少有( B )个结点A、254B、255C、256D、25713.假定有一棵二叉树,双分支结点数为15,单分支结点数为30,则叶子结点数为( D )个。
数据结构与算法第六章课后答案第六章 树和二叉树
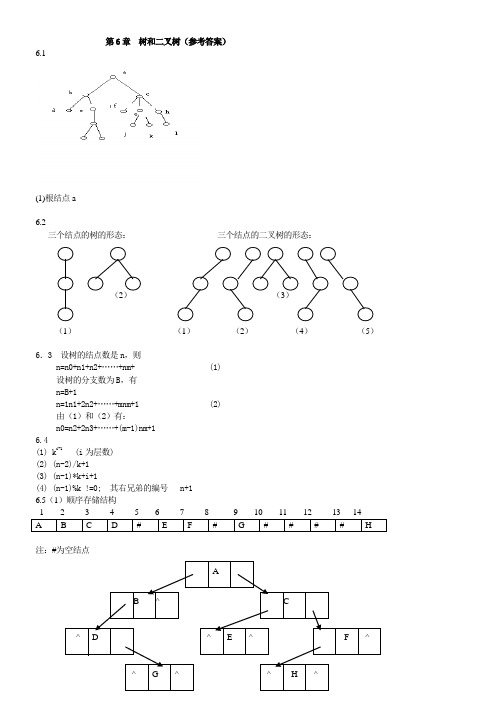
第6章 树和二叉树(参考答案)6.1(1)根结点a6.2三个结点的树的形态: 三个结点的二叉树的形态:(1) (1) (2) (4) (5)6.3 设树的结点数是n ,则n=n0+n1+n2+……+nm+ (1)设树的分支数为B ,有n=B+1n=1n1+2n2+……+mnm+1 (2)由(1)和(2)有:n0=n2+2n3+……+(m-1)nm+16.4(1) k i-1 (i 为层数)(2) (n-2)/k+1(3) (n-1)*k+i+1(4) (n-1)%k !=0; 其右兄弟的编号 n+16.5(1)顺序存储结构注:#为空结点6.6(1) 前序 ABDGCEFH(2) 中序 DGBAECHF(3) 后序 GDBEHFCA6.7(1) 空二叉树或任何结点均无左子树的非空二叉树(2) 空二叉树或任何结点均无右子树的非空二叉树(3) 空二叉树或只有根结点的二叉树6.8int height(bitree bt)// bt是以二叉链表为存储结构的二叉树,本算法求二叉树bt的高度{ int bl,br; // 局部变量,分别表示二叉树左、右子树的高度if (bt==null) return(0);else { bl=height(bt->lchild);br=height(bt->rchild);return(bl>br? bl+1: br+1); // 左右子树高度的大者加1(根) }}// 算法结束6.9void preorder(cbt[],int n,int i);// cbt是以完全二叉树形式存储的n个结点的二叉树,i是数// 组下标,初始调用时为1。
本算法以非递归形式前序遍历该二叉树{ int i=1,s[],top=0; // s是栈,栈中元素是二叉树结点在cbt中的序号 // top是栈顶指针,栈空时top=0if (n<=0) { printf(“输入错误”);exit(0);}while (i<=n ||top>0){ while(i<=n){visit(cbt[i]); // 访问根结点if (2*i+1<=n) s[++top]=2*i+1; //若右子树非空,其编号进栈i=2*i;// 先序访问左子树}if (top>0) i=s[top--]; // 退栈,先序访问右子树} // END OF while (i<=n ||top>0)}// 算法结束//以下是非完全二叉树顺序存储时的递归遍历算法,“虚结点”用‘*’表示void preorder(bt[],int n,int i);// bt是以完全二叉树形式存储的一维数组,n是数组元素个数。
数据结构第六章作业及答案

3、试分别画出具有3个结点的树和3个结点的二叉树 的所有不同形态。 4、对右图所示的二叉树求出 A 以下的遍历序列: B C (1)先序序列 D E F (2)中序序列 (3)后序序列 G H 5、假设一棵二叉树的先序序列为 EBADCFHGIKJ 和 中序序列为 ABCDEFGHIJK。请画出该树,并给 出后序序列。 6、假设一棵二叉树的中序序列为 DCBGEAHFIJK和 后序序列为 DCEGBFHKJIA 。请画出该树,并给 出先序序列。
2
7、将以下森林转换成二叉树。
A
B
C
D
E F G J I
H
L K
3
8、画出和下列二叉树相应的森林。
(a)
A
(b) (c)
A B C
(d)
A B C B C D B
(e)
A
C E F
A
G
J
H
K M
I
4
第六章作业解答 1、(1) M、N、D、L、F、J、K是叶子结点
(2) C是结点G的双亲 (3) A、C是结点G的祖先 (4) I、M、N是结点E的子孙 (5) 树的深度是5 2、(1)二叉树与树的区别: 二叉树的一个结点至多有2个子树,树则不然; 二叉树的一个结点有左、右之分,而树则没有此要求 (2)一棵度为2的树有2个分支,没有左、右之分, 一棵二叉树也可以有2个分支,但有左、右之分, 且左、右不能交换。 3、具有3个结点的树的形态为:
C D
E
F
K
7
7、解:转换后的二叉树为:
A B C D E F G J K I L H
8
8、解:转换后的森林为: (a) (b) (c)
A A B A B C
数据结构第六章树和二叉树习题及答案

习题六树和二叉树一、单项选择题1.以下说法错误的是 ( )A.树形结构的特点是一个结点可以有多个直接前趋B.线性结构中的一个结点至多只有一个直接后继C.树形结构可以表达(组织)更复杂的数据D.树(及一切树形结构)是一种"分支层次"结构E.任何只含一个结点的集合是一棵树2.下列说法中正确的是 ( )A.任何一棵二叉树中至少有一个结点的度为2B.任何一棵二叉树中每个结点的度都为2C.任何一棵二叉树中的度肯定等于2D.任何一棵二叉树中的度可以小于23.讨论树、森林和二叉树的关系,目的是为了()A.借助二叉树上的运算方法去实现对树的一些运算B.将树、森林按二叉树的存储方式进行存储C.将树、森林转换成二叉树D.体现一种技巧,没有什么实际意义4.树最适合用来表示 ( )A.有序数据元素 B.无序数据元素C.元素之间具有分支层次关系的数据 D.元素之间无联系的数据5.若一棵二叉树具有10个度为2的结点,5个度为1的结点,则度为0的结点个数是()A.9 B.11 C.15 D.不确定6.设森林F中有三棵树,第一,第二,第三棵树的结点个数分别为M1,M2和M3。
与森林F 对应的二叉树根结点的右子树上的结点个数是()。
A.M1 B.M1+M2 C.M3 D.M2+M37.一棵完全二叉树上有1001个结点,其中叶子结点的个数是()A. 250 B. 500 C.254 D.505 E.以上答案都不对8. 设给定权值总数有n 个,其哈夫曼树的结点总数为( )A.不确定 B.2n C.2n+1 D.2n-19.二叉树的第I层上最多含有结点数为()A.2I B. 2I-1-1 C. 2I-1 D.2I -110.一棵二叉树高度为h,所有结点的度或为0,或为2,则这棵二叉树最少有( )结点A.2h B.2h-1 C.2h+1 D.h+111. 利用二叉链表存储树,则根结点的右指针是()。
A.指向最左孩子 B.指向最右孩子 C.空 D.非空12.已知一棵二叉树的前序遍历结果为ABCDEF,中序遍历结果为CBAEDF,则后序遍历的结果为()。
数据结构课后习题答案第六章

欢迎下载
6
-
9.已知信息为“ ABCD BCD CB DB ACB ”,请按此信息构造哈夫曼树,求出每一字符的最优编码。 10. 己知中序线索二叉树采用二叉链表存储结构,链结点的构造为:
_,双分支结点的个数为 ____, 3 分支结点的个数为 ____, C 结点的双亲结点为 ____ ,其孩子结点为 ____。
5. 一棵深度为 h 的满 k 叉树有如下性质:第 h 层上的结点都是叶子结点,其余各层上的每个结点都有
k 棵非空子树。
如果按层次顺序(同层自左至右)从 1 开始对全部结点编号,则:
7.二叉树的遍历分为 ____ ,树与森林的遍历包括 ____。 8.一棵二叉树的第 i(i>=1) 层最多有 ____ 个结点;一棵有 n(n>0) 个结点的满二叉树共有 ____ 个叶子和 ____个非终端结点。
9.在一棵二叉树中,假定双分支结点数为 5 个,单分支结点数为 6 个,则叶子结点为 ____个。
A. 逻辑 B.逻辑和存储 C.物理 D.线性 19.由权值分别是 8,7, 2, 5 的叶子结点生成一棵哈夫曼树,它的带权路径长度为
A. 23 B. 37 C. 46 D. 43 20.设 T 是哈夫曼树,具有 5 个叶结点,树 T 的高度最高可以是 ( )。
A.2 B . 3 C. 4 D. 5
()
6.在叶子数目和权值相同的所有二叉树中,最优二叉树一定是完全二叉树。
()
7.由于二叉树中每个结点的度最大为 2,所以二叉树是一种特殊的树。 8.二叉树的前序遍历序列中,任意一个结点均处在其子树结点的前面。
第6章 树和二叉树的作业

第6章树和二叉树
一、基础知识题
1.在结点个数为n(n>1)的各棵树中,高度最小的树的高度是多少?它有多少个叶结点?多少个分支结点?高度最大的树的高度是多少?它有多少个叶结点?多少个分支结点?
2.试分别画出具有3个结点的树和3个结点的二叉树的所有不同形态。
3.如果一棵树有n1个度为1的结点,有n2个度为2的结点,…,n m个度为m 的结点,试问有多少个度为0的结点?试推导之。
4.试分别找出满足以下条件的所有二叉树:
(1)二叉树的前序序列与中序序列相同;
(2)二叉树的中序序列与后序序列相同;
(3)二叉树的前序序列与后序序列相同。
5.填空题
(1)对于一棵具有n个结点的树,该树中所有结点的度数之和为。
(2)假定一棵三叉树的结点个数为50,则它的最小高度为,最大高度为。
(3)一棵高度为h的四叉树中,最多含有结点。
(4)在一棵三叉树中,度为3的结点数有2个,度为2的结点数有1个,度为1的结点数为2个,那么度为0的结点数有个。
(5)一棵高度为5的满二叉树中的结点数为个,一棵高度为3的满四叉树中的结点数为个。
(6)在一棵二叉树中,假定度为2的结点有5个,度为1的结点有6个,则叶子结点数有个。
(7)对于一棵含有40个结点的理想平衡树,它的高度为。
(8)若对一棵二叉树从0开始进行结点编号,并按此编号把它顺序存储到一堆数组a中,即编号为0的结点存储到a[0]中,其余类推,则a[i]元素的左子女结点为,右子女结点为,双亲结点(i≥1)为。
第6章 树和二叉树 作业

第6章树和二叉树作业1、假设在树中,结点x是结点y的双亲时,用(x,y)来表示树边。
已知一棵树的树边集合为{ (e,i), (b,e), (b,d), (a,b), (g,j), (c,g), (c,f), (h,l), (c,h), (a,c) } ,用树型表示法表示该树,并回答下列问题:①哪个是根结点? 哪些是叶子结点? 哪个是g的双亲? 哪些是g的祖先? 哪些是g的孩子? 那些是e的子孙? 哪些是e的兄弟? 哪些是f 的兄弟?②b和n的层次各是多少? 树的深度是多少? 以结点c为根的子树的深度是多少?2、一棵深度为h的满k叉树有如下性质:第h层上的结点都是叶子结点,其余各层上每个结点都有k棵非空子树。
如果按层次顺序(同层自左至右)从1开始对全部结点编号,问:①各层的结点数是多少?②编号为i的结点的双亲结点(若存在)的编号是多少?③编号为i的结点的第j个孩子结点(若存在)的编号是多少?④编号为i的结点的有右兄弟的条件是什么? 其右兄弟的编号是多少?3、设有如图6-27所示的二叉树。
①分别用顺序存储方法和链接存储方法画出该二叉树的存储结构。
②写出该二叉树的先序、中序、后序遍历序列。
4、已知一棵二叉树的先序遍历序列和中序遍历序列分别为ABDGHCEFI和GDHBAECIF,请画出这棵二叉树,然后给出该树的后序遍历序列。
5、设一棵二叉树的中序遍历序列和后序遍历序列分别为BDCEAFHG 和DECBHGFA ,请画出这棵二叉树,然后给出该树的先序序列。
6、已知一棵二叉树的中序遍历序列和后序遍历序列分别为dgbaekchif 和gdbkeihfca,请画出这棵二叉树对应的中序线索树和后序线索树。
7、以二叉链表为存储结构,请分别写出求二叉树的结点总数及叶子结点总数的算法。
8、设图6-27所示的二叉树是森林F所对应的二叉树,请画出森林F。
9、设有一棵树,如图6-28所示。
①请分别用双亲表示法、孩子表示法、孩子兄弟表示法给出该树的存储结构。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第6章树和二叉树作业
1、假设在树中,结点x是结点y的双亲时,用(x,y)来表示树边。
已知一棵树的树边集合为{ (e,i), (b,e), (b,d), (a,b), (g,j), (c,g), (c,f), (h,l), (c,h), (a,c) } ,用树型表示法表示该树,并回答下列问题:
①哪个是根结点? 哪些是叶子结点? 哪个是g的双亲? 哪些是g的祖先? 哪些是g的孩子? 那些是e的子孙? 哪些是e的兄弟? 哪些是f 的兄弟?
②b和n的层次各是多少? 树的深度是多少? 以结点c为根的子树的深度是多少?
2、一棵深度为h的满k叉树有如下性质:第h层上的结点都是叶子结点,其余各层上每个结点都有k棵非空子树。
如果按层次顺序(同层自左至右)从1开始对全部结点编号,问:
①各层的结点数是多少?
②编号为i的结点的双亲结点(若存在)的编号是多少?
③编号为i的结点的第j个孩子结点(若存在)的编号是多少?
④编号为i的结点的有右兄弟的条件是什么? 其右兄弟的编号是多少?
3、设有如图6-27所示的二叉树。
①分别用顺序存储方法和链接存储方法画
出该二叉树的存储结构。
②写出该二叉树的先序、中序、后序遍历序
列。
4、已知一棵二叉树的先序遍历序列和中序遍
历序列分别为ABDGHCEFI和
GDHBAECIF,请画出这棵二叉树,然后给
出该树的后序遍历序列。
5、设一棵二叉树的中序遍历序列和后序遍历序列分别为BDCEAFHG 和DECBHGFA ,请画出这棵二叉树,然后给出该树的先序序列。
6、已知一棵二叉树的中序遍历序列和后序遍历序列分别为dgbaekchif 和gdbkeihfca,请画出这棵二叉树对应的中序线索树和后序线索树。
7、以二叉链表为存储结构,请分别写出求二叉树的结点总数及叶子结点总数的算法。
8、设图6-27所示的二叉树是森林F所对应的二叉树,请画出森林F。
9、设有一棵树,如图6-28
所示。
①请分别用双亲表示法、孩
子表示法、孩子兄弟表示法
给出该树的存储结构。
②请给出该树的先序遍历
序列和后序遍历序列。
③请将这棵树转换成二叉
树。
10、设给定权值集合
w={3,5,7,8,11,12} ,请构造
关于w的一棵huffman树,并求其加权路径长度WPL 。
11、假设用于通信的电文是由字符集{a, b, c, d, e, f, g, h}中的字符构成,这8个字符在电文中出现的概率分别为{0.07, 0.19, 0.02, 0.06, 0.32,
0.03, 0.21, 0.10} 。
①请画出对应的huffman树(按左子树根结点的权小于等于右子树根结点的权的次序构造)。
②求出每个字符的huffman编码。
