高频电子线路(第二版)课件 第五章
高频电子线路 非线性电路基本分析方法

iC1
i0
1 ez
,
iC 2
i0
1 ez
如图所示为归一化电流iC1/ i0 、iC2/ i0与z值的
关系曲线。在 z 1 的范围内,可近似看成线
性关系,即:
iC1 gm0v1, iC2 gm0v1
其中
gm0
iC1 v1
iC 2 v1
称为放大器的跨导。
由电路的对称性可得差
分放大器的输出电压为:
的电导值随时间变化,所以该电路也称为时变 电导(时变电阻)电路。
由于v2(t)具有周期性,而根据S(t)的表达式, 可得它具有与v2(t)相同的周期性,S(t)与v2(t)的
周期皆为T0=2/2。
因此,可将S(t)展开成傅里叶级数:
S (t )
1 2
n1
4 (1)n1
(2n 1)
cos(2n
(2) 折线分析法
前面介绍的幂级数分析法一般要取至少三项 以上,会增加计算复杂度。为此引入折线分 析法以简化分析。
以晶体管的转移特性为 例,其工作曲线AOC 可用两条直线段AB和 BC来近似,即:
ic
ic 0 gc (vB VBZ
)
(vB VBZ ) (vB VBZ )
VBZ为特性曲线折线化后 的截止电压,gc为跨导。
即不满足迭加性原理,这也是非线性元件和 非线性电路的一个重要特点。
二、非线性电路分析方法 ➢ 用解析法来分析非线性电路时,需要知道非
线性曲线的数学表达式。在没有或无法获得 准确的数学表达式时,必须选取某些函数来 近似表示或替代这些非线性关系。下面介绍 几种常见的非线性电路分析方法:
(1) 幂级数分析法 对于非线性元件的特性函数i=f(v),如果f(v) 的各阶导数存在,可将非线性函数f(v)展开 成幂级数的形式:i a0 a1v a2v2 a3v3
高频电子线路(第五章 高频功率放大器)

高频功率放大器和低频功率放大器的共同 特点都是输出功率大和效率高。
7
(3)高频功率放大器的种类
谐振功率放大器(学习重点)
特点是负载是一个谐振回路,功率放大增益可
以很大,一般用于末级; 不易于自动调谐。
宽带功率放大器(了解即可)
特点是负载是传输线变压器,可在很宽的频带
工作状态 甲类 乙类 甲乙类 丙类 丁类 半导通角 c=180° c=90° 90° <c<180° c<90° 开关状态 理想效率 50% 78.5% 50%<h<78.5% h>78.5% 负 载 电阻 推挽,回路 推挽 选频回路 选频回路 应 用 低频 低频,高频 低频 高频 高频
90%~100%
由于这种周期性的能量补充,所以振荡回路能维持振 荡。当补充的能量与消耗的能量相等时,电路中就建立起 动态平衡,因而维持了等幅的正弦波振荡。
34
问题二:半流通角θc通常多大合适?
如果θc取值过大,趋向甲类放大器,则效率 太低; 如果θc取值过小,效率虽然提高了,但输出 功率的绝对值太小(因为iC脉冲太低); 这是一对矛盾,根据实验折中,人们通常 取
gC (vB VBZ )(当vB VBZ )
外部电路关系:
vB VBB Vbm cos t
v C V CC V cm cos t
31
(4)对2个问题的解释
问题一(可能会引起同学们困惑的问题)
为什么iC的波形时有时无,而输出的波形vo却能
是连续的?
问题二(有的题目已知条件不给θc,而解题 中又需要θc )
通过LC回路,滤去无用分量,只留下 Icm1cosωt分量
高频电子线路最新版课后习题解答第五章 正弦波振荡器习题解答

思考题与习题5.1 振荡器是一个能自动将直流电源提供的能量能量转换成交流能量的转换电路,所以说振荡器是一个能量转换器。
5.2 振荡器在起振初期工作在小信号甲类线性状态,因此晶体管可用小信号微变等效电路进行简化,达到等幅振荡时,放大器进入丙类工作状态。
5.3 一个正反馈振荡器必须满足三个条件:起振条件、平衡条件、稳定条件(3)正弦波振荡器的振幅起振条件是;T=A k f >1相位起振条件是2f T A k n ϕϕϕπ=+=;正弦波振荡器的振幅平衡条件是:T=A k f =1,相位平衡条件是:2f T A k n ϕϕϕπ=+=;正弦波振荡器的振幅平衡状态的稳定条件是:0i iAiV V T V =∂<∂,相位平衡状态的稳定条件是:0oscT ωωϕω=∂<∂。
5.4 LC 三点式振荡器电路组成原则是与发射极相连接的两个电抗元件必须性质相同,而不与发射极相连接的电抗元件与前者必须性质相反,且LC 回路满足0ce be cb x x x ++=的条件。
5.5 从能量的角度出发,分析振荡器能够产生振荡的实质。
解:LC 振荡回路振荡在进行电能、磁能相互转换的过程中的能量损耗,由正反馈网络提供补偿,将直流电源提供的直流能量转换为交流输出。
5.6 为何在振荡器中,应保证振荡平衡时放大电路有部分时间工作在截止状态,而不是饱和状态?这对振荡电路有何好处? 解:之所以将振荡平衡时放大电路有部分时间工作在截止状态,而不是饱和状态是因为在截止状态集电极电流小,功率损耗低。
这样可以保证振荡管安全工作。
5.7 若反馈振荡器满足起振和平衡条件,则必然满足稳定条件,这种说法是否正确?为什么?解:不正确。
因为满足起振条件和平衡条件后,振荡由小到大并达到平衡。
但当外界因素(温度、电源电压等)变化时,平衡条件受到破坏。
若不满足稳定条件,振荡起就不会回到平衡状态,最终导致停振。
5.8 分析图5.2.1(a)电路振荡频率不稳定的具体原因?解:电路振荡频率不稳定的具体原因是晶体管的极间电容与输入、输出阻抗的影响,电路的工作状态以及负载的变化,再加上互感耦合元件分布电容的存在,以及选频回路接在基极回路中,不利于及时滤除晶体管集电极输出的谐波电流成分,使电路的电磁干扰大,造成频率不稳定。
高频电子线路上课ppt

还原
所传送信息
3. 传输信道(无线信道、有线信道)
下面主要介绍无线信道
电磁波谱
无线电波、红外线、可见光、紫外线、X射线、γ射线都是电 磁波,按波长或频率的不同顺序排列起来,称做电磁波谱. 可见光 无线电波 微波 红外线 X射线 紫外线 射线 f/HZ /m
104 106 108 1010 1012 1014 1016 1018 -4 10-6 10-8 10-10 104 102 100 10-2 10
本书涉及的频率范围:几百kHz ~ 几百MHz 例:300KHz~300MHz 对应波长 1000m ~1m
无线电频谱
课程性质:
电子、通信类专业的重要专业基础课。 与相关课程之间的关系:
先修课程:电路分析、模拟电子线路、信号与系统。 电路(是基础) 模拟电子线路(低频电路) 信号与系统(分析工具)
100~1000m
300~3000KHz
中频 (MF)
高频 (HF)
地波,天波
广播,通信, 导航
广播, 中距离通信 移动通信,电视广播, 调频广播,雷达导,航 等 通信,中继通信,卫星 通信,电视广播,雷达 中继通信,雷达,卫星 通信 微波通信,雷达
10~100m
3~30MHz
天波,地波
1~10m
30~300MHz
信 道 解 码
同 步
保 密 解 码
压 缩 解 码
信 宿
信源编码
噪 声
信源解码
发送端
接收端
数字通信系统模型
(3)按传输媒介(信道)的物理特征可分为: 有线通信系统和无线通信系统
有线(包括光纤)通信系统——利用导线(光导 纤维) 传送信息; 无线通信系统——利用电磁波传送信息; 在无线模拟通信系统中,信道便是指自由空间。
(完整版)高频电子线路第5章习题答案

第5章 振幅调制、振幅解调与混频电路5.1 已知调制信号()2cos(2π500)V,u t t Ω=⨯载波信号5()4cos(2π10)V,c u t t =⨯令比例常数1a k =,试写出调幅波表示式,求出调幅系数及频带宽度,画出调幅波波形及频谱图。
[解] 5()(42cos 2π500)cos(2π10)AM u t t t =+⨯⨯54(10.5cos 2π500)cos(2π10)V t t =+⨯⨯20.5,25001000Hz 4a m BW ===⨯= 调幅波波形和频谱图分别如图P5.1(s)(a)、(b)所示。
5.2 已知调幅波信号5[1cos(2π100)]cos(2π10)V o u t t =+⨯⨯,试画出它的波形和频谱图,求出频带宽度BW 。
[解] 2100200Hz BW =⨯=调幅波波形和频谱图如图P5.2(s)(a)、(b)所示。
5.3已知调制信号3[2cos(2π210)3cos(2π300)]Vu t t Ω=⨯⨯+⨯,载波信号55cos(2π510)V,1c a u t k =⨯⨯=,试写出调辐波的表示式,画出频谱图,求出频带宽度BW 。
[解] 35()(52cos2π2103cos2π300)cos2π510c u t t t t =+⨯⨯+⨯⨯⨯3555353555(10.4cos2π2100.6cos2π300)cos2π5105cos2π510cos2π(510210)cos2π(510210)1.5cos2π(510300) 1.5cos2π(510300)(V)t t tt t t t t t =+⨯⨯+⨯⨯⨯=⨯⨯+⨯+⨯+⨯-⨯+⨯++⨯- 3max 222104kHz BW F =⨯=⨯⨯=频谱图如图P5.3(s)所示。
5.4 已知调幅波表示式6()[2012cos(2π500)]cos(2π10)V u t t t =+⨯⨯,试求该调幅波的载波振幅cm U 、调频信号频率F 、调幅系数a m 和带宽BW 的值。
第五章 频谱的线性搬移

有用分量
2a2u1u2 a2U1U 2 cos 1 2 t a2U1U 2 cos 1 2 t
第 5章
16
频谱搬移通过提取两个信号的和频与差频实现。实现理想乘法 运算,减少无用组合频率数目和强度是重要目标。 (1)从非线性器件的特性考虑:选用具有平方律特性的场效应管; 选择器件工作特性接近平方律的区域。 (2)从电路考虑,采用平衡等措施,抵消无用分量,加强有用分量。 (3)从输入信号大小考虑,限制输入信号振幅,减小高阶项强度。
第五章 频谱的线性搬移电路
5.1 非线性电路的分析方法 5.2 二极管电路 5.3 差分对电路 5.4 其它频谱线性搬移电路
信息科学技术学院 电子信息科学与技术系
高频电子线路
第 5章
1
概述
频谱搬移电路:将输入信号进行频谱变换,获得具有所需 频谱的输出信号,分为线性搬移电路和非线性搬移电路。 线性搬移电路:频谱搬移前后的频率分量的比例关系不变。 例如:幅度调制与解调,混频电路等。
u1
非线性 器 件 u2
滤波器
滤除无 用分量
n
uo
有用 信号
信号i f u
a u
n 0 n
1
u2 包含频率组合分量为:
p ,q p1 q2
经滤波器滤除无用分量后,有用频率分量(和频与差频分量)为
1,1 1 2 ,此时p=q=1
该频率分量由二个信号的二次乘积项/交叉项产生:
f U Q u1 u2
式中, u 为加在非线性器件上的电压,其中 UQ 为 静态工作点, 用泰勒级数将上式在静态工作点UQ展开:
i a0 a1 u1 u2 a2 u1 u2 an u1 u2
高频电子线路_第5章5_1 PPT课件
7)角度调制:频谱搬移时没有线性对应关系,称为非线性
角度调制。(频率调制与解调电路)
2020/11/12
8)已调波:经调制后的高频振荡波。 9)解调:从已调信号中取出原来的信息。
也称检波电路。 10)混频:把已调信号的载频变成另一个载频的电路
= U c m 1 m a c o s t c o s (c t)
k U a m = a
U 2020/11/12
m cm
ma称调幅系数或调幅度。 它表示载波振幅受调制信号控制的程度。
utU m cos t
uctU cm cosω ct
uAMt
调幅波的特点:
=Ucm1macostcos(ct)
2020/11/12
根据频谱的不同特点,频谱变换电路可分为线性变换 和非线性变换两大类。
线性变换的作用是将输入信号的频谱进行不失真地搬 迁,如振幅的调制与解调电路、混频电路等。
非线性变换的作用是将输入信号的频谱进行特定的变 换,如角度的调制与解调电路等。
本章学习振幅的调制与解调电路、混频电路等。
2020/11/12
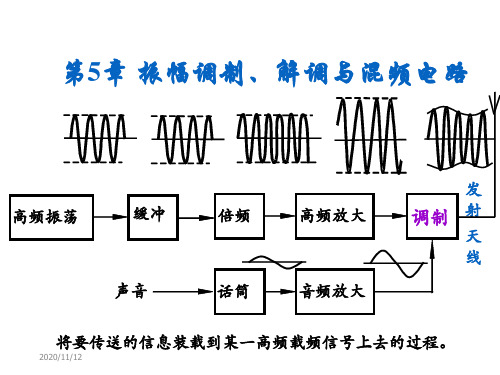
第5章 振幅调制、解调与混频电路
高频振荡
缓冲
声音
倍频 话筒
高频放大 音频放大
发
调制 射
天
线
将要传送的信息装载到某一高频载频信号上去的过程。
2020/11/12
一、调制的原因
从切实可行的天线出发 为使天线能有效地发送和接收电磁波,天线的
几何尺寸必须和信号波长相比拟,一般不宜短于1/4 波长。 音频信号: 20Hz~20kHz 波长:15 ~15000 km
调幅的原则: 高频载波的振幅随调制信号成线性关系。
高频电子线路第章共100页

此时式5.2.1式变为
A f
A 1 AF
5.2.2
当其 AF 1 时,就会产生自激振荡。其
振幅条件为:|A F |1
相位条件为:arA g F AF2nn0, 1, 2, ...
要使振荡器能够起振,在刚接通电源后,| AF |1,当达
到平衡时,| AF |1。这就是振荡器振幅平衡条件。
由5.5.3和5.5.4式,归结起来,Xbe和Xce性质相同;Xcb 和Xce、Xbe性质相反。这就是三点式振荡器的相位判据。也 可以这样来记忆,与发射极相连接的两个电抗性质相同,另
一个电抗则性质相反。
5.5.2 电容三点式振荡器——考毕兹振荡器
图所示电路是电容三点式的典型电路。LC回路的三个 端点分别与三个电极相连,且Xce和Xbe为容抗,Xcb为感抗。 故属电容反馈三点式振荡器,又称考毕兹振荡器。
参数的交流振荡信号的装置。和放大器一样也是能量转换
器。它与放大器的区别在于,不需要外加信号的激励,其输
出信号的频率,幅度和波形仅仅由电路本身的参数决定。 低频正弦振荡器
振荡器 分类
正弦振荡 高频正弦振荡器
微波振荡器 矩形波振荡器
非正弦波振荡器 三角波振荡器
锯齿波振荡器
应用范围:在发射机、接收机、测量仪器(信号发生 器)、计算机、医疗、仪器乃至电子手表等许多方面振荡器 都有着广泛的应用。
率、振幅平衡条件和起振条件。
5.4 互感耦合振荡器
互感耦合振荡器 振荡器分类 石英晶体振荡器
电感反馈振荡器 基本型 三点式振荡器
电容反馈振荡器 克拉泼振荡器
5.4.1 单管互感耦合振荡器
西勒振荡器
互感耦合振荡器(或变压器反馈振荡器)又称为调谐型振
高频电子线路完整章节课件

作用是将输入的高频载波信号和低频调制信号 变换成高频已调信号,并以足够大的功率输送 到天线,然后辐射到空间;
高频功率放大器与调幅器:
1
把话筒变换的音频信号放大到一定的幅度,以实现一定的调制度。
低频放大器:
3
话筒(拾音器):
输入变换器,它的作用是把声音信源转变成电信号,称为音频信号,即基带信号或调制信号;
01
04
02
03
无线电波的基本特点
非线性电路的基本概念
通信与通信系统
本课程的主要内容及特点
通信与通信系统
通信系统: 用电信号(或光信号)传输信号的系统 称为通信系统,也称电信系统。
通信系统的组成: 一般通信系统由输入、输出变换器,发 送、接收设备和信道等组成。
1.1、通信与通信系统
无线通信系统组成框图
1.1、通信与通信系统
各部分作用 信息源:提供需要传送的信息; 输入变换器:将信息源(图像、声音等)的信息变换成电信号,把该信号称为基带信号; 发射机:将基带信号进行某种处理,并以足够的功率送入信道,以实现有效的传送,其中最主要的处理为调制,调制后的信号称为已调信号,或已调波;
小 结
5
高频电子线路的典型应用是通信系统;
通信系统由发射设备、接收设备和传输媒介三部分组成;
电信号的发射与接收的关键是调制与解调;
高放、混频、本振、调制、解调等相关知识是本课程要解决的问题;
了解无线电信号所具有的基本特点是必备的基本知识。
5
课堂练习一
1.如果广播电台发射的信号频率为
高频电子线路
高等教育出版社,胡宴如、耿苏燕主编
课程性质:理论联系实践,突出重点,重应用,强调物理概念,强调工程实践。
高频电子线路第5章习题参考答案

高频电子线路习题参考答案
2 2 U1 U 3 U1 U 3 3a 3 cos(21 3 )t cos(21 3 )t 4 4 2 U 2 U1 U 3 U1 3 cos(23 1 )t cos(23 1 )t 4 4 2 U2U3 U2U3 2 cos(22 3 )t cos(22 3 )t 4 4 2 U2U2 U3U2 3 cos(23 2 )t cos(23 2 )t 4 4
答5-2 能出现50 kHz和 350 kHz的频率成分,因为在u2项中将会 出现以下2次谐波和组合频率分量。 200 kHz-150 kHz=50 kHz 200 kHz+150 kHz=350 kHz
2x200 kHz=400 kHz
2x150 kHz=300 kHz
高频电子线路习题参考答案
5-3 一非线性器件的伏安特性为 gDu u 0 i 0 u 0 式中,u=EQ+ul+u2=EQ+U1COSω1t+U2COSω2t。若U1 很小,满足线性时变条件,则在EQ=-U2/2时,求出时变电导 gm(t)的表示式。 解5-3,根据已知条件,
高频电子线路习题参考答案
设一个开关函数 1 K(w 2 t) 0 2 2 2n 2 t 2n 3 3 2 4 2n 2 t 2n 3 3
将 K(2 t)进行展开为富式级数为 K(2 t) 2 2 2n 2 3 sin cos n2t cos 2t 3 1 n 3 3 3 3 3 cos 22t cos 42t cos 52t ...... 2 4 5
a 2 U1U 3 cos( 1 3 )t U1U 3 cos( 1 3 )t a 2 U 3 U 2 cos(3 2 )t U 3 U 2 cos( 3 2 )t
高频电子线路第5章ppt课件

载波uc
已调波uAM
振荡器
倍频
高频 放大器
调制
话筒
调制信号 放大器 调制信号 uΩ
无线电通信发射机的组成框图
3
5.1.1 普通调幅波
所谓调制,就是使幅度、频率、或相位随调制信号 的大小而线性变化的过程。分别称为振幅调制、频率调 制或相位调制,简称调幅、调频和调相。
解调是调制的相反过程,即从已调波信号中恢复原 调制信号的过程。与调幅、调频和调相相对应,有振幅 解调、频率解调和相位解调,简称检波、鉴频和鉴相。
u A M =U cm (1+M acosΩ t)cosω ct
=U cm cosω ct+M a 2 U cm cos(ω c+Ω )t+M a 2 U cm cos(ω c-Ω )t
载波分量
上边带分量
下边带分量
电 压 振 幅
U Ωm
调幅波的频谱图
U cm
MaUcm / 2
MaUcm / 2
0Ω
ω c - Ω ω c ωc + Ω
过调幅失真
Ma >1
8
U m (t)= U c m (1+ M a c o sΩ t)
U m m ax=U cm (1+M a) Um m in=Ucm(1-M a)
包络的振幅为:
Um=Umm ax2 -Umm in=UcmM a
调制度
包络振幅
Ma 载波振幅
Um Ucm
9
3. AM调幅波的频谱及带宽
ω
u A M = U c m (1 + M a c o s Ω t)c o s ω c t
= U c m c o s ω c t+ M a 2 U c m c o s ( ω c + Ω ) t+ M a 2 U c m c o s ( ω c -Ω ) t
《高频电子线路》PPT课件

uo(t)
uΩ(t)
Δuc
uo(t)=uΩ(t)+UDC
包含了直流及低频调制分量。
峰值包络检波器的应用型输出电路
+ (a) ui
-
VD
Cd
+
+UDC -
+
C uo R
RL uΩ
-
-
(b)
+ ui
-
VD
Rφ
+
C uo R Cφ
-
t
UDC t
+ UDC -
图(a):电容Cd的隔直作用,直流分量UDC被隔离,输出信号为解调恢复后 的原调制信号uΩ,一般常作为接收机的检波电路。 图(b):电容Cφ的旁路作用,交流分量uΩ(t)被电容Cφ旁路,输出信号为直 流分量UDC,一般可作为自动增益控制信号(AGC信号)的检测电路。
rd C R
②对高频载波信号uc来说,电容C的容抗
1 R ,电容C相当于短
cC
路,起到对高频电流的旁路作用,即滤除高频信号。
理想情况下,RC低通滤波网络所呈现的阻抗为分析
+ uD -
当输入信号ui(t)为调幅波时,那么载波正半 +
周时二极管正向导通,输入高频电压通过二 ui
☺调幅解调的分类
振幅调制
AM调 制DSB调制
SSB调制
包络检波 解调
同步检波
峰值包络检波 平均包络检波 叠加型同步检波 乘积型同步检波
☺调幅解调的方法
1. 包络检波
调幅波
t 调幅波频谱
非线形电路
ωc-Ω ωc ωc+Ω ω
低通滤波器
包络检波输出
t 输出信号频谱
高频电子线路第五章(new)PPT课件

界
-
49
各变量对功放工作状态影响的总结 功放在过压和欠压工作状态的一个重要特点
-
50
解:1)
-
51
-
52
5.5 高频功率放大器的电路组成
要使高频功放正常工作,在其输入和输出端需接 有直流通路和交流通路: ➢ 直流馈电线路:为晶体管各级提供合适的偏置及能
量功率; ➢ 交流匹配网络:使高频交
流信号能有效地进行传输。
高频与射频线路
第五章 高频功率放大器
-
1
学习内容
➢ 掌握高频功率放大器的工作原理;
➢ 掌握高频功率放大器的折线近似分析法;
➢ 掌握高频功率放大器的电路组成原则与匹 配网络的计算;
➢ 了解倍频器的工作原理。
-
2
5.1 概述
高效率输出 高功率输出
话 筒
音频 放大器
调制器
变频器
激励放大
输出功 率放大
载波 振荡器
低频区:
中频区:
β0
高频区:
故高频区或中频区的分析和
计算是相当困难,本节将从低
频区的静态特性来解析晶体管
的高频功放的工作原理。-
6
高频放大器的工作状态:
+
-
+ +- -
-
+
功放基本电路
-
7
iC
iC
VBB
VBZ
vB
0
0
-
8
Class-A Amplifier
0
0
甲类放大器工作状态
-
9
Class-B Amplifier
证放大器传输到负载的
功率最大,即它起着匹
高频电路第五章课件

(5―6)
1 1 22 1 [[Cmm/ / 1 C 利用三角变换,变为22 Cnn cos(n 2kk))xx ] Ckk cos(n 2 ] 2nn nn 2 kk 0 0 cosnn xx cos 11 (5―8) ( 1) i bnU1ncos n1t 1 22( nn 1) 1 n 0 Cnn cos(n 2kk))xx Ckk cos( n 2 2nn 1 kk0 2 1 0 可见,输出信号中出现了输入信号频率的基波及各次 谐波分量。
Department of P.&E.I.S
高频电子线路
非线性函数的级数展开分析法
从上面分析可见,只有一个输入信号时,只能获得 该信号频率的基波及其谐波分量,不能获得任意频率 的信号,若要实现频谱在频域上的任意搬移,还需要 另外一个频率的信号。
非线性 器 件 u2
u1
滤波器
uo
Department of P.&E.I.S
高频电子线路
非线性函数的级数展开分析法
在实际应用中应尽量减少无用的组合频率分量的数目 和幅度,一般可从以下三个方面考虑: (3)从输入信号的大小考虑。如减小u1、u2的振幅, 以便有效地减小高阶相乘项及其产生的组合频率分量 的幅度。
Department of P.&E.I.S
高频电子线路
(二) 线性时变电路分析法
考虑u1和u2都是余弦信号,u1=U1cosω1t, u2=U2cosω2t,时 变偏置电压EQ(t)=EQ+U2cosω2t 为一周期性函数, 故I0(t)、 g(t)也必为周期性函数, 可用傅里叶级数展开,得
I 0 (t ) f (EQ U2 cos2t ) I00 I 01 cos2t I 02 cos22t ...
关于高频电子线路5课件

可见单频调制的双边带调幅波只有 c 。
图5-5 双边带调幅波的波形
首页
上一页 下一页
退出
第一节 概述
(二)单边带调幅波(SSB) 1、数学表示式
u ( t ) U m 'c o s (c ) t 或 u ( t ) U m 'c o s (c ) t
则普通调幅波的数学表示式为 u (t) U c m ( 1 m a c o s t)c o sc t
其中
ma
K aU m U cm
称为调幅指数(调幅度)
首页
上一页 下一页
退出
第一节 概述
(三)普通调幅波的波形
1.图5-1是单频调制普通调幅波的波形图。已调波振幅的
包络形状与调制信号一样,是不失真调幅。
首页
上一页 下一页
退出
第一节 概述
四、抑制载波的双边带调幅信号和单边带调幅信号
(一)抑制载波的双边带调幅波(DSB)
1、数学表示式 u ( t ) u ( t ) u c ( t ) U m c o s t U c m c o s c t U m c o s t c o s c t 2、波形
振幅 U
' m
(t)
为
Um ' (t)UcmKau(t)
则普通调幅波的数学表示式为 u ( t) U m '( t) c o sc t [ U c m K a u ( t) ] c o sc t
Байду номын сангаас
若 u(t)U mcos t时 ,根据定义
U m '( t ) U c m K a U m c o s t U c m ( 1 K U a U c m m c o s t ) U c m ( 1 m a c o s t )
高频电路复习课件chapter5-8

上、下边频的平均功率均为
AM波的平均功率为载波功率与两个边带功率之和
Department of P.&E.I.S
高频电子线路
振幅调制电路
低电平调幅电路
+ u uD VD - iD i + H(j) uuAM (t) o - uc 0
若滤波回路的中心频率为fc ,带宽为2F,则经滤波 后的输出电压即为普通调幅(AM)信号。
mUc Uc
ma =
Umax - Umin Umax + Umin
0 (c) u A M(t)
调幅度ma≤1。
0
m=1 t
Department of P.&E.I.S
高频电子线路
常数 调幅波的频谱 (a)
uc
m m u AM (t ) U C cos ct U C cos(c + )t × C cos(A M )t U u uc 2 2
n 0
若作用在非线性器件上的两个电压均为余弦信号,即 u1 =U1cosω1t,u2 =U2cosω2t,则输出电流i中将包含由下 1 列通式表示的无限多个频率组合分量 1 cos( x y ) cos x cos y cos( x y )
p q
2 p1 q2
( x y)3 x3 3x 2 y 3xy2 y3
Department of P.&E.I.S
高频电子线路
第六章
振幅调制、解调及混频
本 章 要 点
调幅波的概念、数学表达式、波形、频谱、带 宽和功率关系 包络检波器的原理及其失真现象 混频的概念及工作原理
混频干扰的分类及特点
BW 2 F 20 kHz
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
I 0 (t ) f ( EQ U 2 cos 2t ) I 00 cos 2t I 02 cos 2t (5-15) g (t ) f ( EQ U 2 cos 2t ) g 0 cos 2t g 2 cos 2t
(5-16)
例如:若作用在非线性器件上的两个电压均为余弦信
号,即u1=U1cosω1t, u2=U2cosω2t,利用式(5-7)和三角函 数的积化和差公式
1 1 cos x cos y cos(x y ) cos(x+y ) 2 2 i
p q
(5-9)
C
p ,q
cos(p 1 q 2 )t
n 0
(5-8)
由(5-8)式可得:
(1) 单一频率信号作用于非线性电路时,其输出除包含原 来频率成分外,还有其多次谐波成分。 (2) 如果在其输出端加一窄带滤波器,可作为倍频电路。 (3) 若要使输出包含任意所需有频率成分(即在输出有任
意频率成分),不能在非线性电路输入端只输入一个单
一频率信号来完成。
(5-17)
(5-18)
也可从式(5-11)中获得
I 0k
n 0
2
n 2 C2 n k a2 n kU 2 n k 1 , 2 n k 1
1
k 0,1, 2, k 0,1, 2,
g k 1
n 0
nk n 2 (2n k ) 2 n k 2 C2 n k a2 n kU 2 n k 1 , 2
n 0
(5-2)
式中,an(n=0,1,2,…)为各次方项的系数,由下式确定:
1 d n f (u ) an n ! du n
n m0
u EQ
1 n f ( EQ ) n!
(5-3)
m m (u1 u2 )n Cn u1n mu2
(5-4)
式中,Cmn=n!/m!(n-m)!为二项式系数,故
的(为什么?),因此要实现频谱搬移,必须使用非线性电 路,在非线性电路中,其核心是非线性器件。
线性电路的分析方法在非线性电路中是不适用的,它有
其特有的分析方法,主要有级数展开发和时变参数分析法等。
一、非线性函数的级数展开分析法
1、非线性函数的泰勒级数 非线性器件的伏安特性,可用下面的非线性函数来 表示:
频率分量为
变电路的输出信号的频率分量仅有(5-10) 中p为0和1、q为任意的组合分量。没有q为任意、p大于1的 各组合分量(即与级数展开分析法相比,减少了一些频率成 分,请同学们思考为什么?)。
例5-1 一个晶体二极管,用指数函数逼近它的伏安特性, 即: u u
i I e ( eVT 1) I s eVT
在线性时变工作状态下,上式可表示为
(5-21)
i I 0 (t ) g (t )u1
设u2=U2cos2t,式中:
EQ u2
(5-22)
I 0 (t ) I s e
VT
I Q e x2 cos2t
(5-23)
di g (t ) du
u1
线性时变 器 件 u2
滤波器
uo
图5-3 线性时变电路完成频谱的搬移
5.2
二极管电路
二极管频率搬移电路的特点:电路简单、工作频带宽
等。 一、 单二极管电路 单二极管电路的原理电路如图5-4所示,输入信号u1 和控制信号(参考信号)u2 相加作用在非线性器件二极 管上。图中用传输函数为H(j)的滤波器取出所需信号。 通常u2>>u1,且u2>0.5V,即二极管工作在大信号状态。
以上各次方项,则该式化简为:
i f ( EQ u2 ) f ( EQ u2 )u1
(5-13)
即有
i I 0 (t ) g (t )u1
(5-14)
由上式可见,就非线性器件的输出电流与输入电压的关 系上看类似于线性系统,但其系数却是时变的。 2、线性时变参数分析法的应用 下面,考虑u1 和u2 都是余弦信号,u1 =U1cosω1t,u2 = U2cosω2t,则时变偏置电压EQ(t)=EQ+U2cosω2t,为一周期 性函数,故I0(t)、g(t)也必为周期性函数,可用傅里叶 级数展开,得:
3、同时输入两个信号
u1 非线性 器 件 u2
图5-2 非线性电路完成频谱的搬移
滤波器
uo
为了便于区别,u1称为输入信号,为要处理的信号,通 常占据一定带宽,u2 称为参考信号或控制信号,通常为单一
频率成分信号(通常频谱搬移电路中有f2>>f1)。
由式(5-5)可得,此时除包含两个输入信号成分外,还包 括各种乘积项u1 n-m u2 m
A、从非线性器件的特性考虑,使其非线性接近平方律特性。 B、从电路考虑,如采用多个电路组合成平衡电路,以抵消 部分无用成分。 C、从两个输入信号的大小配合上考虑。
二、 线性时变电路分析法 1、线性时变参数分析法的原理
对式(5-1)在EQ+u2上对u1用泰勒级数展开,有
i f ( EQ u1 u2 ) 1 f ( EQ u2 ) f ( EQ u2 )u1 f ( EQ u2 )u12 2! 1 (n) f ( EQ u2 )u1n (5-11) n!
0
fc
f
0
f (b)
0
fc
f
图5-1 频谱搬移电路 (a)频谱的线性搬移;(b)频谱的非线性搬移
5.1 非线性电路的分析方法
我们知道,在频谱搬移电路中,输出信号的频率成分与 输入信号的频率成分不同,因此,要实现频谱搬移,要求电 路必须能够产生新的频率成分。
根据我们所学知识,线性电路是不能产生新的频率成分
UQ UT
u EQ u2
Is e VT
IQ UT
EQ u2 VT
gQ e x2 cos 2t
(5-24)
其中,Q I s e 、 x2 U I T
UQ
、 gQ
分别是晶体二极管的静态
工作电流、归一化的参考信号振幅和静态工作点上的电导。
而: e
x2 cos 2t
0 ( x2 ) 2 n ( x2 ) cos n 2t
VD + - + - u1
iD + H(j) uo -
u2
图5-4 单二极管电路
忽略输出电压u。对回路的反作用, 这样,加在二极
管两端的电压uD为:
uD u1 u2
(5-28)
由于二极管工作在大信号状态,主要工作在截止区和 导通区,此时二极管的伏安特性可近似用折线近似。
折线的斜率为gD,此时二极管可等效为一个受控开关,
控制电压就是uD。有
g DuD iD 0
uD Vp uD V p
(5-29)
i
i
1 gD= r D
i gD
0
u u
0 Vp
u
0
u
t gD (1/rD )
(a) S uc (d) g D (t)
(b)
(c)
图5-5 二极管伏安持性的折线近似
由前已知,U2>>U1,而uD=u1+u2,可进一步认为二极
与式(5-5)相对应,有
2 f ( EQ u2 ) an u2 n 0 n f ( EQ u2 ) nan u2 1 n 1 m n f ( EQ u2 ) 2! Cn 2anu2 2 n 2
(5-12)
若u1足够小,可以忽略式(5-11)中u1的二次方及其
两个展开式的系数可直接由傅里叶系数公式求得
1 I 00 f ( EQ U 2 cos 2t )d2t 2 1 I k 1 f ( EQ U 2 cos 2t ) cos k 2td 2t k 1, 2,3,
1 g0 f ( EQ U 2 cos 2t )d2t 2 1 g k f ( EQ U 2 cos 2t ) cos k 2td 2t k 1, 2,3,
(5-10)
p , q p 1 q 2
通常,把p+q称为组合分量的阶数。
其频率分量产生的规律是: (1) 凡是p+q为偶数的组合分量,均由幂级数中n为偶 数且大于等于p+q的各次方项产生的; (2) 凡是p+q为奇数的组合分量,均由幂级数中n为奇 数且大于等于p+q的各次方项产生的。
第5章 频谱的线性搬移电路
5.1 非线性电路的分析方法 5.2 二极管电路 5.3 差分对电路 5.4 其它频谱线性搬移电路
频谱搬移的概念:频谱搬移电路是通信系统最基本的单元电 路之一,主要完成将信号频谱从一个位置搬移至另一个位置。 频谱搬移的分类:频谱的线性搬移和非线性搬移两大类。
0
f (a)
管的通断主要由u2控制,可得
g D uD iD 0
u2 Vp u2 Vp
(5-30)
一般情况下,Vp较小,有U2>>Vp,可令Vp=0(也可在 电路中加一固定偏置电压Eo,用以抵消Vp,在这种情况下, uD=Eo+u1+u2),式(5-30)可进一步写为
i
m0
m0
n
m m anCn u1n mu2
(5-5)
下面分别进行分析。
2、只输入一个余弦信号时
先来分析一种最简单的情况。令u2=0,即只有一个输入信 号,且令u1=U1cosω1t,代入式(5-2),有:
i anu1n anU1n cos n 1t
n 0 n 0
