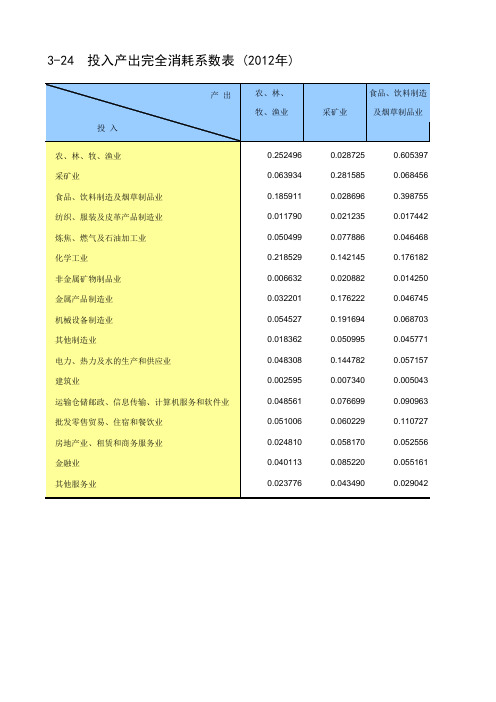
投入产出完全消耗系数表2012年

信息传输、软件和信息技术服务业消耗情况分析

信息传输、软件和信息技术服务业消耗情况分析摘要本文基于贵州省投入产出表对信息传输、软件和信息技术服务业进行分析，以找出与它关联性较强的部门，并着力发展。

结果表明，此部门生产过程所需要其他部门投入的中间产品较少，即其独立性较强；第二产业中的制造业，电力、热力、燃气及水生产和供应业等部门对于信息传输、软件和信息技术服务业部门的消耗较大，这些部门的发展受信息传输、软件和信息技术服务业部门的约束较大。

关键词信息传输、软件和信息技术服务业；完全消耗；投入产出表The Analysis of consumption between Information transfer software and information technology services and other sectors——Based on the input and output table of Guizhou Province in 2012Cao Gaigai（Statistics and Mathematics，Yunnan University of Finance and Economics，Kunming 650221，China）Abstract Based on the input-output table of Guizhou Province，this paper analyzes the information transfer software and information technology services to find out the department with strong correlation and focus on the development. The results show that the production process in this sector requires less intermediate products in other departments，，that is，its independence is strong. The manufacturing industry and the power and heat gas and water production and supply industries in the second industry，has a higher cost on it. That is to say，the development of these sectors is constrained by information transfer software and information technology services.Key words Information transfer、software and information technology services；Complete Consumption；Input-output Table引言电子商务、大数据、云计算的蓬勃发展无一不证明了信息时代的来临，贵州省的信息产业整体呈现快速发展，《贵州省数字经济发展规划（2017-2020年）》中指出“2016年，通信服务业业务总量796.6亿元、软件和信息技术服务收入210亿元，分别同比增长65.8%和35%”；但同时也存在一些问题，“信息化整体水平在全国排名第20位，数字生活指数排名全国第30位，处于靠后水平”，可见，着力发展贵州省的信息产业具有必要性。

2012年投入产出表标准版

金融业
其他服务业
0.025889 0.042101 0.024046 0.024338 0.032726 0.051585 0.007682 0.044134 0.069857 0.076155 0.030502 0.014641 0.088552 0.081747 0.203071 0.106385 0.043055
0.031580 0.874537 0.035253 0.020166 0.146960 0.156803 0.025879 0.138634 0.172357 0.044447 0.134765 0.007780 0.087071 0.066040 0.057908 0.085875 0.039763
0.043156 0.448619 0.039611 0.030892 0.126663 0.183352 0.045463 0.752445 0.203368 0.131530 0.184374 0.008470 0.107876 0.079373 0.064544 0.110967 0.049203
0.605397 0.068456 0.398755 0.017442 0.046468 0.176182 0.014250 0.046745 0.068703 0.045771 0.057157 0.005043 0.090963 0.110727 0.052556 0.055161 0.029042
纺织、服装及皮革产品制造业 Nhomakorabea炼焦、燃气及石油加工业化学工业
非金属矿物制品业
金属产品制造业
机械设备制造业
0.311343 0.096438 0.121872 0.823868 0.058602 0.363341 0.011463 0.059580 0.094243 0.050821 0.091189 0.006366 0.096023 0.151472 0.060289 0.067205 0.034357

投入产出模型中的经济分析（直接消耗系数等）

投⼊产出模型中的经济分析（直接消耗系数等）⼀、直接消耗系数与直接消耗系数矩阵（⼀）直接消耗、间接消耗与完全消耗的涵义及关系1、直接消耗 P872、间接消耗 P893、完全消耗=直接消耗+全部间接消耗 P894、三者的关系图以炼钢⽣产的钢材对电⼒的消耗为例。

（⼆）直接消耗系数的经济意义 P87直接消耗系数，记为（i,j=1,2,3…n）它是指在⽣产经营过程中第j产品（或产业）部门的单位总产出所直接消耗的第i产品部门货物或服务的价值量。

（三）直接消耗系数的计算公式及⽰例 P87⽤第j产品（或产业）部门的总投⼊去除该产品（或产业）部门⽣产经营中所直接消耗的第i产品部门的货物或服务的价值量⽤公式表⽰为：（i,j=1,2,3…n）⽰例以P82表3-2资料为例。

（请同学上来计算）（四）直接消耗系数矩阵 P87将各产品（或产业）部门的直接消耗系数⽤表的形式表现出来，就是直接消耗系数表或直接消耗系数矩阵，通常⽤字母A表⽰。

计算公式为：（五）⼏点结论（可以让学⽣来总结）1、2、的个数是产品部门数⽬的平⽅3、反映各产品部门之间⽣产技术的直接联系程度4、作为中间产品和总产品之间的媒介变量5、作为计算完全消耗系数的基础数据⼆、完全消耗系数与完全消耗系数矩阵（⼀）完全消耗系数的经济意义及与直接消耗系数的关系 P89完全消耗系数，记为（i,j=1,2,3…n）是指第j产品部门每提供⼀个单位最终使⽤时，对第i产品部门货物或服务的直接消耗和间接消耗（全部消耗）之和。

直接消耗系数相对于总产品⽽⾔，说明中间产品与总产品之间的数量关系；完全消耗系数则相对于最终产品⽽⾔，说明中间产品与最终产品之间的数量关系。

（⼆）完全消耗系数及矩阵的计算公式 P89-90将各产品部门的完全消耗系数⽤表的形式表现出来，就是完全消耗系数表或完全消耗系数矩阵，通常⽤字母B表⽰。

1、以上图来说明公式的推导 P89（i，j=1，2，…，n）等式两端同时左加⼀个单位矩阵I，再同时左乘以（I-A）得：（I-A）（I+B）=（I-A）（）==当m趋于⽆穷⼤时，等式右端为单位矩阵，则有：2、以下图来说明公式的推导等式两端同时右乘得：（三）完全消耗系数矩阵的计算⽅法1、初等⾏变换2、求逆矩阵的⽅法3、⽤EXCEL软件的计算步骤第⼀步：启运EXCEL，并输⼊矩阵A；第⼆步：根据EXCEL的计算功能，计算出（I-A）；第三步：⽤⿏标单击EXCEL的帮助菜单，并选择“micrsoft excel 帮助（H） F1“第四步：输⼊lotus后，单击“搜索”后，再单击“通过转成lotus1-2-3的帮助”，再单击“详细说明”第五步：对出现的对话框选“数据”后，再选“矩阵”，如求逆则选“颠倒”，求矩阵相乘则选“乘”即可。

2012全国42部门投入产出表

3735163 1136 106789 314552 4666538 6040828 721695 329158 3097463 141017 1600028 774047 46847 386460 39353 22870 200132 73957 144931419 18494463 8160547 5462175 10440151 4255 30 31 32 33 34 35 36 37 38 39 40 41 42 TII VA001 VA002 VA003 VA004 TVA TI
8886566 7776 33769 81428 13186515 10845115 792683 879315 11048752 12124 308011 5160072 1286354 764823 114015 66256 36387 348595 370625314 529963186 -28956569 22581542 0 523588159 894213473
造纸印刷和文教体育用品 10 12898294 2736766 0 0 503503 1495091 11373077 1446707 5022960 76522829 988991 36412826 829418 19294523 2119092 897949 1669522 64279 636951 1257454 65097 401633 6925720 152612
8905198 3753 107429 580945 3117414 5247797 834777 236129 10603858 53665 4741396 1844466 95821 1363474 162690 67826 242117 58835 114130877 56420753 23043287 9607792 21879658 110951490 225082366

投入产出表

投入产出表
Ð Ö ä ¼ ¶ Í ë È
Ò² » ú þ² ¶ ú ý² È ú Ï¼ º Æ Û¾ Õ É ö Ô V Ó ¼ M µ Ö º Ï¼ Æ × Ü² úÖ µ
× Ü ×Ö î Õ£ ¨¹ ÊÓ Ã£ ©º Ï¼ Æ ú ² ÓÃ ¾ ñ « ¹¹ ² ¹ Ì× Ê ¿ â´ æ ¾ »³ ö ³ »² Ò ú ¶ þ² ú È ý² ú º Ï¼ Æ Ï û· Ñ û Ï· Ñ Ð Î³ É Ô ö¼ Ó Ú ¿ º Ï¼ Æ ö 950 4068 120 5138 2547 60 780 540 20 3947 9085 1950 23140 2100 27190 7782 80 6300 610 300 15072 42262 441 3480 931 4852 1971 2730 320 -20 5001 9853 3341 30688 3151 37180 12300 2870 7400 1150 300 24020 61200 150 1260 210 1620 4804 4714 4682 14200 790 5600 1810 8200 5744 11574 6702 24020 9085 42262 9853 61300 Ð¼ Ö ä² úÆ ·¨ £û Ïº Ä£ ©
《国民经济核算》
作者：张裕民
第三章
投入产出核算
一、投入产出表二、直接消耗系数
三、完全消耗系数
一、投入产出表的基本原理
（一）投入产出表的概念：中间投入（中间消耗）１、投入最初投入（要素投入）中间产出（中间产品）２、产出最终产出（最终产品）
3.投入产出表的概念：
是根据国民经济各部门生产中的投入来源和使用去向纵横交叉组成的一张棋盘式平衡表，揭示了国民经济各部门间的相互依存、相互制约的数量关系。

我国信息和通讯技术产业的投入产出分析——基于2012年中国投入产出表

我国信息和通讯技术产业的投入产出分析蒋训林广东外语外贸大学南国商学院——基于2012年中国投入产出表摘　要：本文以2012年中国42部门投入产出表为基础，把国民经济整合成包括第一产业、剔除信息和通讯技术产业的第二产业、剔除信息和通讯技术产业的第三产业以及信息和通讯技术产业在内的四个部门。

根据此四部门投入产出表，分析信息和通讯技术产业的各种产业波及特性。

关键词：信息和通讯技术产业　投入产出　产业波及目前，我国电子商务的发展如火如荼，互联网金融也异军突起，以阿里巴巴、腾讯、京东商城为杰出代表的互联网企业为我国的经济增长注入了新的动力和活力。

不难看出，信息和通讯技术（ICT）产业的发展，一方面推动了产业结构的优化升级，另一方面通过改造传统产业，提高其劳动和资本产出效率，促进经济增长的集约化。

本文采用投入产出分析法，来研究ICT产业的投入、产出经济绩效和产业波及效应，探讨ICT产业对经济增长的作用。

一、数据处理2015年底公布的2012年中国42部门投入产出表是目前最新的全国投入产出表，本文以该投入产出表为分析对象，将整个国民经济整合成第一产业、剔除ICT产业的第二产业、剔除ICT产业的第三产业、ICT产业四个部门。

2012年全国投入产出表并没有具体指明ICT产业，通过对该表42个部门进行分析，发现表中的通信设备、计算机和其它电子设备（行业代码20）以及信息传输、软件和信息技术服务（行业代码32）这两大类产业可归为ICT产业。

二、信息和通讯技术产业的中间需求和中间投入分析中间需求是指某产业的产出在经济活动中被其它产业（包括该产业本身）使用和消耗的总和，而中间投入是指某产业在经济活动中从其它产业（包括该产业本身）得到的投入之和。

中间需求率是指各产业的中间需求和该产业的总需求之比，中间投入率是各产业的中间投入与总投入之比。

从表一可看出，ICT产业的中间需求率和中间投入率都偏高，均超过了50%。

中间需求率越高的产业，其产出用做其它产业原材料的成分就越大，就越具有基础产业的特点。

(整理)投入产出表的直接消耗系数和完全消耗系数概念及其计算方法

投入产出表的主要系数投入产出系数是进行投入产出分析的重要工具。

投入产出系数包括直接消耗系数、完全消耗系数、感应度系数、影响力系数和各种诱发系数。

由于直接消耗系数和完全消耗系数是最基本的投入产出系数，这里只介绍直接消耗系数和完全消耗系数的定义和计算方法。

1、直接消耗系数直接消耗系数，也称为投入系数，记为a ij(i,j=1,2,…,n),它是指在生产经营过程中第j产品(或产业)部门的单位总产出所直接消耗的第i产品部门货物或服务的价值量，将各产品(或产业)部门的直接消耗系数用表的形式表现就是直接消耗系数表或直接消耗系数矩阵，通常用字母A表示。

直接消耗系数的计算方法为：用第j产品(或产业)部门的总投入X j去除该产品部门(或产业)生产经营中所直接消耗的第i产品部门的货物或服务的价值量x ij,用公式表示为:a ij=x ij/X j (i,j=1,2,…,n)直接消耗系数体现了列昂惕夫模型中生产结构的基本特征，是计算完全消耗系数的基础。

它充分揭示了国民经济各部门之间的技术经济联系，即部门之间相互依存和相互制约关系的强弱，并为构造投入产出模型提供了重要的经济参数。

从直接消耗系数的定义和计算方法可以看出，直接消耗系数的取值范围在0≦a ij ＜1之间，a ij 越大，说明第j 部门对第i 部门的直接依赖性越强；a ij 越小，说明第j 部门对第i 部门的直接依赖性越弱；a ij =0则说明第j 部门对第i 部门没有直接的依赖关系。

2、完全消耗系数完全消耗系数是指第j 产品部门每提供一个单位最终使用时，对第i 产品部门货物或服务的直接消耗和间接消耗之和。

将各产品部门的完全消耗系数用表的形式表现出来，就是完全消耗系数表或完全消耗系数矩阵，通常用字母Ｂ表示。

完全消耗系数的计算公式为：...111111++++=∑∑∑∑∑∑======kj sk ts n t n s n k it kj sk n s n k is kj n k ik ij ij a a a a a a a a a a b（i,j=1,2,…,n）式中的第一项ij a 表示第j 产品部门对第i 产品部门的直接消耗量；式中的第二项kj n k ik a a ∑=1表示第j 产品部门对第i 产品部门的第一轮间接消耗量；式中的第三项kj sk n s n k is a a a ∑∑==11为第二轮间接消耗量；式中的第四项kj sk ts n t n s n k it a a a a ∑∑∑===111为第三轮间接消耗量；依此类推，第n+1项为第n 轮间接消耗量。

完全消耗系数

23
定理7.2.5 如果第j部门最终需求增加 y j，而
其他部门的最终需求不变，那么部门总产出
X的增量为
X y j B j e j

其中 X x1 x2 xn , B j b1 j b2 j bnj , e j 为单位坐标向量。证明由定理7.2.4知 B E A E ，将此
X E A Y
1
0.63 0.09 0.09 235 400 1 0.17 0.59 0.095 125 300 0.4455 0.1 0.085 0.58 210 350
即三个车间的总产值分别为400，300，350。
16
定理7.2.2 方程(E-D)X=Z的系数矩阵E-D是可逆
的。证明因
n n n E D diag1 ai1 1 ai 2 1 ain i 1 i 1 i 1
1 aij 0 j 1,2,, n ，故由性质7.2.2知，
1
关系代入方程(7-19)，得
24
X E A Y B E Y BY Y
1
由定理假设，部门最终需求增量
Y 0,,0, y j ,0,,0 y j e j
于是

X BY Y By j e j y j e j
y j Be j y j e j y j B j e j
消耗系数矩阵
0.25 0.10 0.10 A 0.20 0.20 0.10 0.10 0.10 0.20 直接消耗系数 aij i, j 1,2,, n 具有下面重
要性质：
性质7.2.1 0 aij 1 i, j 1,2,, n 性质7.2.2

投入产出表的直接消耗系数及完全消耗系数计算方法(练习)

0.104570.096260.012181000.214640.547540.213130100.048540.082340.09449001
0.104570.447770.013210.046140.547540.049690.04476
0.35319
0.09449
MINVERSE(P3:R5-l3:n5)-P3:R5在中国，季度GDP 以生产法为基础进行核算，年度GDP 采用生产法和支出法这两种方法进行核算。

直接消耗系数矩阵=中间使用矩阵的行/总产出
直接消耗系数(支出法)生产法核算公式：GDP=总产出－中间投入
收入法核算公式：GDP=劳动者报酬+生产税净额+固定资产折旧+营业盈余支出法核算公式：GDP=最终消费支出+资本形成总额+货物和服务净出口完全消耗系数矩阵=(单位矩阵-直接消耗系数矩阵)的逆矩直接消耗系数矩阵=中间使用矩阵的列/总产出
直接消耗系数(收入法)
单位矩阵
0.184900.266380.078640.61851 1.448080.58453
0.119760.236900.16172
MINVERSE(P3:R5-L8:N10)-P3:R50.18490 1.239180.085280.13296 1.448080.136280.11043
1.01612
0.16172
完全消耗系数（支出法）净出口=出口-进口完全消耗系数（收入法）利润税金=生产税净额+营业盈余求逆矩阵函数：MINVERSE
的逆矩阵-单位矩阵。

国民经济核算—投入产出表

RAS法绘制2014年全国的投入产出表一、调查方法选择在中国，逢2、逢7年份编制基准年国家投入产出表，因2012 年的投入产出表数据缺失，故采用2007年作为基准年对2014年进行估算。

二、数据查阅由国家统计局官网公布的2014年年度数据，我们可以得到：（1）2014年各部门总产出：农业总产出为102226.09亿；工业总产出为1094646.50亿；第三产业部门增加值为306038.2亿，与总产出的比例为48.1%。

（2）2014年各部门中间投入合计：第一产业102226.09-58336.1=43889.99 亿；第二产业1094646.50-271764.5=822882 亿；第三产业（306038.2/48.1%）*（107730/255768）=267991.49 亿。

（3）2014年各部门中间使用合计：最终消费328311.2亿；固定资本形成总额为283017.6亿；净出口为17462.9亿。

再假定最终使用的产品结构不变，利用2007年的结构推出2014年的中间使用，第一产业为102226.09亿，第二产业为1094646.5亿，第三产业为636254.05亿。

二、运用RAS法进行估计(1) 如表所示不断重复，进入迭代程序，直到行比例与列比例都非常接近1,即同时满足行、列约束为止，如上表所示，此条件已经满足。

(2) 利用2007年结构推出2014年的最终使用与进口矩阵(3) 利用2007年结构推出2014年的最初投入(4) 得到投入产出表最终使用中间使用第一产业第二产业第三产业第一产业14485.5965951.9515923.71990361 第二产业16665.7743938.91186369.2726669 合计 2014总消费14固定资本形成总4出合计 2014进口误差2014总228653.4665207.8014H3D3.183A721 产岀3787.41341864.8102226.1 中间投入 )798557.655 259354.1252924497536107153427672.510946474.12830171813911755240120422698363.21833127 第三产业12738.612923991.13875698.4^4282301100.08 18455.6726983.8225982.9481.55B8825.6S625 合计 _______________ ___________________________ 劳动者报酬832.46223169.O22421939.460S355.1 43889.99 822882 267991.4913476328311.2 固定资产折旧35899&90.052S7903.722E229.99 生产税净2989.86134421.09358418.23183402.6 营业盈余 082118.245222012.2H89587.8 最初投入增加值 59920.59254898.41340273.63595575.5 总投入 102226.09094646.5 636254.05833127四、投入产出表的相关分析(1)影响分析①投入产出表在国内生产总值核算中的作用：投入产出表反映生产过程中货物和服务的生产成本以及生产的货物和服务的分配去向。

投入产出表的直接消耗系数及完全消耗系数计算方法练习

0.104570.096260.012181000.214640.547540.213130100.048540.082340.09449001
0.104570.447770.013210.046140.547540.049690.04476
0.35319
0.09449
MINVERSE(P3:R5-l3:n5)-P3:R5在中国，季度GDP 以生产法为基础进行核算，年度GDP 采用生产法和支出法这两种方法进行核算。

直接消耗系数矩阵=中间使用矩阵的行/总产出
直接消耗系数(支出法)生产法核算公式：GDP=总产出－中间投入
收入法核算公式：GDP=劳动者报酬+生产税净额+固定资产折旧+营业盈余支出法核算公式：GDP=最终消费支出+资本形成总额+货物和服务净出口完全消耗系数矩阵=(单位矩阵-直接消耗系数矩阵)的逆矩直接消耗系数矩阵=中间使用矩阵的列/总产出
直接消耗系数(收入法)
单位矩阵
0.184900.266380.078640.61851 1.448080.58453
0.119760.236900.16172
MINVERSE(P3:R5-L8:N10)-P3:R50.18490 1.239180.085280.13296 1.448080.136280.11043
1.01612
0.16172
完全消耗系数（支出法）净出口=出口-进口完全消耗系数（收入法）利润税金=生产税净额+营业盈余求逆矩阵函数：MINVERSE
的逆矩阵-单位矩阵。

投入产出表的主要系数

投入产出表的主要系数投入产出系数是进行投入产出分析的重要工具。

投入产出系数包括直接消耗系数、完全消耗系数、感应度系数、影响力系数和各种诱发系数。

由于直接消耗系数和完全消耗系数是最基本的投入产出系数，这里只介绍直接消耗系数和完全消耗系数的定义和计算方法。

1、直接消耗系数直接消耗系数，也称为投入系数，记为a ij(i,j=1,2,…,n),它是指在生产经营过程中第j产品(或产业)部门的单位总产出所直接消耗的第i产品部门货物或服务的价值量，将各产品(或产业)部门的直接消耗系数用表的形式表现就是直接消耗系数表或直接消耗系数矩阵，通常用字母A表示。

直接消耗系数的计算方法为：用第j产品(或产业)部门的总投入X j去除该产品部门(或产业)生产经营中所直接消耗的第i产品部门的货物或服务的价值量x ij,用公式表示为:a ij=x ij/X j (i,j=1,2,…,n)直接消耗系数体现了列昂惕夫模型中生产结构的基本特征，是计算完全消耗系数的基础。

它充分揭示了国民经济各部门之间的技术经济联系，即部门之间相互依存和相互制约关系的强弱，并为构造投入产出模型提供了重要的经济参数。

从直接消耗系数的定义和计算方法可以看出，直接消耗系数的取值范围在0≦a ij ＜1之间，a ij 越大，说明第j 部门对第i 部门的直接依赖性越强；a ij 越小，说明第j 部门对第i 部门的直接依赖性越弱；a ij =0则说明第j 部门对第i 部门没有直接的依赖关系。

2、完全消耗系数完全消耗系数是指第j 产品部门每提供一个单位最终使用时，对第i 产品部门货物或服务的直接消耗和间接消耗之和。

将各产品部门的完全消耗系数用表的形式表现出来，就是完全消耗系数表或完全消耗系数矩阵，通常用字母Ｂ表示。

完全消耗系数的计算公式为：...111111++++=∑∑∑∑∑∑======kj sk ts n t n s n k it kj sk n s n k is kj n k ik ij ij a a a a a a a a a a b（i,j=1,2,…,n）式中的第一项ij a 表示第j 产品部门对第i 产品部门的直接消耗量；式中的第二项kj n k ik a a ∑=1表示第j 产品部门对第i 产品部门的第一轮间接消耗量；式中的第三项kj sk n s n k is a a a ∑∑==11为第二轮间接消耗量；式中的第四项kj sk ts n t n s n k it a a a a ∑∑∑===111为第三轮间接消耗量；依此类推，第n+1项为第n 轮间接消耗量。

2012年中国投入产出直接消耗系数表

畜牧产品 0.10190 0.00001 0.07923 0.00001 0.00117 0.00003 0.00000 0.00000 0.00000 0.00000 0.00000 0.03578 0.23750 0.00088 0.00000 0.00000 0.00065 0.00000 0.00000 0.00000 0.00000 0.00000 0.00002 0.00000 0.00000 0.00000 0.00000 0.00000 0.00000 0.00000 0.00000 0.00001 0.00000 0.00001 0.00001 0.00000 0.00000 0.00000 0.00324 0.00000 0.00000 0.00000 0.00001 0.00000 0.00000 0.00000 0.00000 0.01051 0.00000 0.00000
渔产品 0.02936 0.00070 0.00086 0.04096 0.02754 0.00013 0.00000 0.00000 0.00000 0.00003 0.00000 0.01138 0.16166 0.00213 0.00000 0.00000 0.00434 0.00000 0.00000 0.00000 0.00000 0.00000 0.00012 0.00003 0.00000 0.00001 0.00000 0.00000 0.00000 0.00003 0.00000 0.00000 0.00000 0.00049 0.00058 0.00013 0.00048 0.00002 0.01866 0.00000 0.00000 0.00008 0.00010 0.00000 0.00006 0.00001 0.00002 0.00215 0.00289 0.00020

投入产出表的直接消耗系数和完全消耗系数概念及其计算方法

投入产出表的直接消耗系数和完全消耗系数概念及其计算方法投入产出表的主要系数投入产出系数是进行投入产出分析的重要工具。

投入产出系数包括直接消耗系数、完全消耗系数、感应度系数、影响力系数和各种诱发系数。

由于直接消耗系数和完全消耗系数是最基本的投入产出系数，这里只介绍直接消耗系数和完全消耗系数的定义和计算方法。

1、直接消耗系数直接消耗系数，也称为投入系数，记为a(i,j=1,2,…,n),它是指在生产经营过程中第j产品(或产ij业)部门的单位总产出所直接消耗的第i产品部门货物或服务的价值量，将各产品(或产业)部门的直接消耗系数用表的形式表现就是直接消耗系数表或直接消耗系数矩阵，通常用字母A表示。

直接消耗系数的计算方法为:用第j产品(或产业)部门的总投入X去除该产品部门(或产业)生产经营中所直接消耗j的第i产品部门的货物或服务的价值量x,用公式表示为: ija=x/X(i,j=1,2,…,n) ijijj直接消耗系数体现了列昂惕夫模型中生产结构的基本特征，是计算完全消耗系数的基础。

它充分揭示了国民经济各部门之间的技术经济联系，即部门之间相互依存和相互制约关系的强弱，并为构造投入产出模型提供了重要的经济参数。

从直接消耗系数的定义和计算方法可以看出，直接消耗aaijij系数的取值范围在0?,1之间，越大，说明第j部门aij对第i部门的直接依赖性越强;越小，说明第j部门对第aiji部门的直接依赖性越弱;=0则说明第j部门对第i部门没有直接的依赖关系。

2、完全消耗系数完全消耗系数是指第j产品部门每提供一个单位最终使用时，对第i产品部门货物或服务的直接消耗和间接消耗之和。

将各产品部门的完全消耗系数用表的形式表现出来，就是完全消耗系数表或完全消耗系数矩阵，通常用字母,表示。

完全消耗系数的计算公式为:nnnnnnb,a，aa，aaa，aaaa，...ijijikkjisskkjittsskkj,,,,,,k,1s,,11kt,,,111sk(i,j=1,2,…,n)aij式中的第一项表示第j产品部门对第i产品部门的直naa,ikkj,1k接消耗量;式中的第二项表示第j产品部门对第i产nnaaa,,isskkj,,11sk品部门的第一轮间接消耗量;式中的第三项为第二nnnaaaa,,,ittsskkj,,,111tsk轮间接消耗量;式中的第四项为第三轮间接消耗量;依此类推，第n+1项为第n轮间接消耗量。

12年投入产出分析系数计算

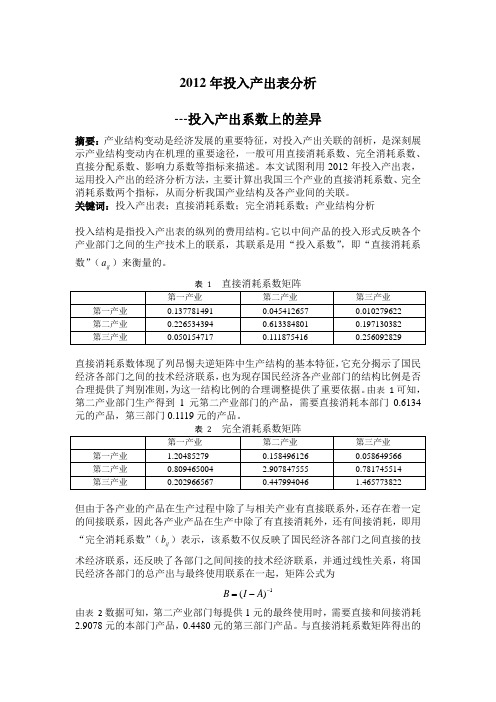
2012年投入产出表分析---投入产出系数上的差异摘要：产业结构变动是经济发展的重要特征，对投入产出关联的剖析，是深刻展示产业结构变动内在机理的重要途径，一般可用直接消耗系数、完全消耗系数、直接分配系数、影响力系数等指标来描述。

本文试图利用2012年投入产出表，运用投入产出的经济分析方法，主要计算出我国三个产业的直接消耗系数、完全消耗系数两个指标，从而分析我国产业结构及各产业间的关联。

关键词：投入产出表；直接消耗系数；完全消耗系数；产业结构分析投入结构是指投入产出表的纵列的费用结构。

它以中间产品的投入形式反映各个产业部门之间的生产技术上的联系，其联系是用“投入系数”，即“直接消耗系a）来衡量的。

数”（ij直接消耗系数体现了列昂惕夫逆矩阵中生产结构的基本特征，它充分揭示了国民经济各部门之间的技术经济联系，也为现存国民经济各产业部门的结构比例是否合理提供了判别准则，为这一结构比例的合理调整提供了重要依据。

由表1可知，第二产业部门生产得到1元第二产业部门的产品，需要直接消耗本部门0.6134元的产品，第三部门0.1119元的产品。

但由于各产业的产品在生产过程中除了与相关产业有直接联系外，还存在着一定的间接联系，因此各产业产品在生产中除了有直接消耗外，还有间接消耗，即用b）表示，该系数不仅反映了国民经济各部门之间直接的技“完全消耗系数”（ij术经济联系，还反映了各部门之间间接的技术经济联系，并通过线性关系，将国民经济各部门的总产出与最终使用联系在一起，矩阵公式为1()=-B I A-由表2数据可知，第二产业部门每提供1元的最终使用时，需要直接和间接消耗2.9078元的本部门产品，0.4480元的第三部门产品。

与直接消耗系数矩阵得出的结果相比，都可得出第二产业部门的产品主要依靠本部门和第三部门提供的产品，但其差异在于对产业内部结构关联的程度范围分析，后者（完全消耗系数）更具体地计算了一次性间接消耗、二次性间接消耗等间接消耗系数，深刻地反映一个部门的生产与本部门发生的经济数量联系，因此它比直接消耗系数能更本质、更全面地反映部门内部和部门之间的技术经济联系，其经济意义在于在实际生活中，第二产业部门的实际生产消耗对本部门和第三部门有较大的依存关系。

投入产出完全消耗系数表2012年

信息传输、软件和信息技术服务业消耗情况分析

2012年投入产出表 标准版

投入产出模型中的经济分析（直接消耗系数等）

2012全国42部门投入产出表

投入产出表

我国信息和通讯技术产业的投入产出分析——基于2012年中国投入产出表

(整理)投入产出表的直接消耗系数和完全消耗系数概念及其计算方法

完全消耗系数

投入产出表的直接消耗系数及完全消耗系数计算方法(练习)

国民经济核算—投入产出表

投入产出表的直接消耗系数及完全消耗系数计算方法练习

投入产出表的主要系数

2012年中国投入产出直接消耗系数表

投入产出表的直接消耗系数和完全消耗系数概念及其计算方法

12年投入产出分析系数计算

2012年投入产出表标准版