初三数学难题集锦
初三数学上册经典难题

初三数学上册经典难题1、一元二次方程()0122=+++m x m mx 有实数根,则m 的取值范围是( )A 、 41-≥m B 、 41-≥m 且0≠m C 、41-≤m D 、41-≤m 且0≠m 2、已知,x+y=-5,xy=3,则yxyx y x+的结果是( ) A 32 B -32 C 23 D -233、(本题8分)如图,四边形ABCD 内接与⊙O ,BD 是直径,AE ⊥CD 于E ,DA 平分∠BDE(1) 求证:AE 是⊙O 的切线;(2)若∠DBC=30°,DE=1㎝,求BD 的长 4、(本题10分)如图,以直角坐标系的原点O 为圆心作⊙O ,点W 、N 是⊙O 上的两点,M(-1,2),N(2,1)(1) 试在x 轴上找点P 使PM+PN 最小,求出P 点的坐标 (2)若在坐标系中另有一直线AB,A(10,0),点B 在y 轴上,∠BAO =30°,⊙O 以0.2个单位/秒的速度沿x 轴正方向运动,问圆在运动过程中与该直线相交的时间有多长?5、下列语句中不正确的个数有( )①相等的圆心角所对的弧相等;②平分弦的直径垂直于弦;③圆是轴对称图形,任何一条直径都是它的对称轴;④半圆是弧。
A 、1个B 、2个C 、3个D 、4个 6、已知圆锥的底面半径为3cm ,母线长为9cm ,C 为母线 PB 的中点,在圆锥的侧面上,从A 到C 的最短距离为 ; 7、(7分)已知a ()a bab b a++b=-8,ab=8,化简求值:8、(本小题满分10分)如图,AB 是⊙O 的直径,C 为圆周上一点,过点C 的直线MN 满 足∠MCA=∠CBA ,(1)求证:直线MN 是⊙O 的切线;(2)过点A 作 AD ⊥MN 于点D ,交⊙O 于点E ,已知AB=6,BC=3,求阴影部分的面积。
9.若关于x 的一元二次方程0962=+-x kx 有两个不相等的实数根,则k 的取值范围( ).A.k <1B.k ≠0C.k <1且k ≠0D.k >1 10.如图,圆内接ABC △中,4===BC AC AB ,OD 、OE 为O ⊙的半径,0120=∠DOE ,请问:当DOE ∠绕着O 点旋转时,这两条半径与ABC △的两条边围成的图形(图中阴影部分)面积是( ) A.34 B.32 C. 334 D. 不能确定11.如图,圆O 与圆P 相交,EA 过圆心P 交圆于C ,连心线PO交于圆O 于点D ,已知∠BCA=36°,则∠EDB= .12. 如图,在平面直角坐标系中有一正方形AOBC,反比例函数k y x=经过正方形AOBC 对角线的交点,半径为(422-)的圆内切于△ABC ,则k 的值为________..13.(本题满分8分)如图,已知直线PA 交⊙0于A 、B 两点,AE 是⊙0的直径.点C 为⊙0上一点,且AC 平分∠PAE ,过C 作CD ⊥PA ,垂足为D ; (1)求证:CD 为⊙0的切线;(2)若DC+DA=6,⊙0的直径为l0,求AB 的长度.14. (本题满分12分)已知:如图,在直角坐标系xoy 中,点A (6,0),点B 在第一象限且△OAB 为正三角形,△OAB 的外接圆交y 轴的正半轴于点C ,过点C 的圆的切线交x 轴于点D .(1)求B 、C 两点的坐标; (2)求直线CD 的函数解析式;(3)设E 、F 分别是线段AB 、AD 上的两个动点,且EF 平分四边形ABCD 的周长.试探究:当点E 运动到什么位置时,△AEF 的面积为427.第22题图第24题BC DAEFH 15. 已知扇形的弧长为2Л,半径为4,则此扇形的面积为( ) A.8π B.6π C. 5π D.16、如果关于x 的一元二次方程22110kx k x -++=x+1=0有两个不相等的实数根,那么k 的取值范围是 A .12k <B .1k <且0k ≠C .1122k -≤<D .1122k -≤<且0k ≠ 17.如图,O 是正△ABC 内一点,OA =3,OB =4,OC =5,将线段BO 以点B 为旋转中心逆时针旋转60°得到线段BO ′,下列结论:①△BO ′A 可以由△BOC 绕点B 逆时针旋转60°得到;②点O 与O ′的距离为4;③∠AOB =150°;④S 四边形AOBO ′633=+.其中正确结论的个数A .1B .2C .3D .418、(本小题满分10分)已知21,x x 是一元二次方程02)6(2=++-a ax x a 的两个实数根.(1)是否存在实数a ,使22114x x x x +=+-成立?若存在,求出a 的值;若不存在,请你说明理由;(2)求使)1)(1(21++x x 为负整数的实数a 的整数值.19、(本小题满分12分)如图,已知正方形ABCD 的边长为5,且∠EAF =45,把∆ABE 绕点A 逆时针旋转90o,落在∆ADG 的位置.(1)请在图中画出∆ADG .(2)证明:∠GAF =45. (3)求点A 到EF 的距离AH .20、(本小题满分12分)如图,已知△ABC 是等边三角形.(1)将△ABC绕点A逆时针旋转角θ(0°<θ<180°),得到△ADE,BD和EC所在直线相交于点O.aθ①如图,当 =20°时,△ABD与△ACE是否全等?(填“是”或“否”),∠BOE= 度;②当△ABC旋转到如图b所在位置时,求∠BOE的度数;(2)如图c,在AB和AC上分别截取点B′和C′,使AB=3AB′, AC=3AC′,连接B′C′,将△AB′C′绕点A逆时针旋转角θ(0°<θ<180°),得到△ADE,BD和EC所在直线相交于点O,请利用图c探索∠BOE的度数,直接写出结果,不必说明理由.21.已知n8是整数,则正整数n的最小值为A. 1B. 2C. 4D. 822. 下列语句中不正确的有()①相等的圆心角所对的弧相等②平分弦的直径垂直于弦③圆是轴对称图形,任何一条直径都是它的对称轴④长度相等的两条弧是等弧OADBCHA.3个B.2个C.1个D.以上都不对23.同圆中,两条弦长分别为a 和b ,它们的弦心距分别为c 和d ,若c >d ,则有( )A.a >bB.a <bC.a =bD.不能确定24. 在半径为R 的圆中,一条弧长为l 的弧所对的圆心角为( )A. l R 180π度B. R l π180度C. 180Rlπ度 D.Rlπ180度25.如图所示,△ABC 按顺时针方向转动一个角度后成为为△C B A '',则图中旋转中心是 , ∠ACA ′=26. .(6)已知:如图8,△ABC 中,AC =BC ,以BC 为直径的⊙O交AB 于点D ,过点D 作DE ⊥AC 于点E ,交BC 的延长线于点F .求证:(1)AD =BD ; (2)DF 是⊙O 的切线.27. (10)已知:如图△ABC 内接于⊙O ,OH ⊥AC 于H ,过A 点的切线与OC 的延长线交于点D ,∠B =30°,OH=5 3 .请求出: (1)∠AOC 的度数;(2)劣弧AC 的长(结果保留π); (3)线段AD 的长(结果保留根号).AA ’BB ’C500 第17题FEDCBAO28下列根式2xy ,8,2ab ,35xy ,x y +,12中最简二次根式的个数是 ( ) A. 2个 B. 3个 C. 4个 D. 5个 29、化简二次根式1()a b a b--- ,()a b ∠正确的是 ( )A .b a - B. a b - C. -b a - D. -a b -30、如果1是关于x 的方程x 2 +2kx -3k 2= 0的根,则k 的值( )A.1B. 1或13-C. -1或13D. 13-或1331.下列说法正确的是( )①平分弦的直径,必平分弦所对的两条弧. ②圆的切线垂直于圆的半径.③三角形的外心到三角形的三个顶点的距离相等。
初三数学难题集锦

初三数学难题集锦初中数学难题集锦1.(本小题满分10分)如图,AB 为⊙O 的直径,点C 在⊙O 上,过点C 作⊙O 的切线交AB 的延长线于点D ,已知∠D =30°.⑴求∠A 的度数;⑵若点F 在⊙O 上,CF ⊥AB ,垂足为E ,CF =34,求图中阴影部分的面积.2.(本小题满分10分)已知抛物线2y ax bx =+(a ≠0)的顶点在直线112y x =--上,且过点A (4,0).⑴求这个抛物线的解析式;⑵设抛物线的顶点为P ,是否在抛物线上存在一点B ,使四边形OPAB 为梯形?若存在,求出点B 的坐标;若不存在,请说明理由.⑶设点C (1,-3),请在抛物线的对称轴确定一点D ,使AD CD -的值最大,请直接写出点D 的坐标.3.(本小题满分12分)已知在梯形ABCD 中,AB ∥DC ,且AB =40cm ,AD =BC =20cm ,∠ABC =120°.点P 从点B 出发以1cm/s 的速度沿着射线BC 运动,点Q 从点C 出发以2cm/s 的速度沿着线段CD 运动,当点Q 运动到点D 时,所有运动都停止. 设运动时间为t 秒.⑴如图1,当点P 在线段BC 上且△CPQ ∽△DAQ 时,求t 的值;⑵在运动过程中,设△APQ 与梯形ABCD 重叠部分的面积为S ,求S 关于t 的函数关系式,并写出自变量t 的取值范围;图1QPD CB A参考答案1.(本小题满分10分)⑴解:连结OC,∵CD切⊙O于点C,∴∠OCD=90°.(1分)∵∠D=30°,∴∠COD=60°. …………………(2分)∵OA=OC,∴∠A=∠ACO=30°. ………………(4分)⑵∵CF⊥直径AB,CF=34,∴CE=(5分)∴在Rt△OCE中,OE=2,OC=4. ……………………(6分)∴2BOC60483603Sππ扇形==,EOC122S??=…………………………(8分)∴EOCBOCS S Sπ阴影扇形8=-=-3 …………………………………………………(10分) 2.(本小题满分10分)⑴∵抛物线过点(0,0)、(4,0),∴抛物线的对称轴为直线2x=. ………………………………………………………(1分) ∵顶点在直线112y x=--上,∴顶点坐标为(2,-2). …………………………(3分)故设抛物线解析式为2(2)2y a x=--,∵过点(0,0),∴12a=,∴抛物线解析式为2122y x x=-………………………(5分)⑵当AP∥OB时,如图,∠BOA=∠OAP=45°,过点B作BH⊥x轴于H,则OH=BH.设点B(x,x),故2122x x x=-,解得x=6或x=0(舍去)…………………………(6分)∴B(6,6). …………………………………………………………………………(7分)当OP∥AB时,同理设点B(4-x,x)故21(4)2(4)2x x x =---,解得x =6或x =0(舍去),∴B (-2,6) .……(8分)⑶D (2,-6).………………………………………………………………………………(10分)3.(本小题满分12分)解:⑴如图1,分别过点作AM ⊥CD 于M ,BN ⊥CD 于N ,∵BC =20,∠C =180°-∠ABC =60°,∴CN =10=DM ,BN =103,∴CD =60.∵△CPQ ∽△DAQ ,∴CP CQDA DQ=,∴20220602t tt=--,∴110t =,260t =(不合题意),∴t =10.………(5分)图1 图2⑵当点P 在线段BC 上时,如图2,过P 作FG ⊥CD 于G ,交AB 延长线于F. ∴PF =32t ,PG =3(20)2t -,∴11032ABPSAB PF t ==,13(20)22CPQS CQ PG t t ==-, ADQ CPQ ABP ABCD S SSS S =梯形---=5003-1602)1032t ?(- H图1QP D C BA M N图1Q P D C B A F G(20)t --220400)t t -+. (020t <≤)(8分) 当点P 在线段BC 的延长线上时,如图3,过P 作PH ⊥AB 于H ,则设AP 与CD 交于点E ,∵EC PC AB PB=,∴40800t EC t -=, ∴QE =CQ -CE =2240800t t t-+.∴y =310800402212?+-?tt t =tt t )40020(3102+-.(2030t <≤) ………………………………………(12分)。
初中数学好题难题集锦(含答案解析)

初三下学期数学好题难题集锦一、分式:1、如果abc=1,求证++=1.2、已知+=,则+等于多少?3、一个圆柱形容器的容积为V立方米,开始用一根小水管向容器内注水,水面高度达到容器高度一半后,改用一根口径为小水管2倍的大水管注水.向容器中注满水的全过程共用时间t分.求两根水管各自注水的速度.4、(2009•邵阳)已知M=、N=,用“+”或“﹣”连接M、N,有三种不同的形式,M+N、M﹣N、N﹣M,请你任取其中一种进行计算,并简求值,其中x:y=5:2.二、反比例函数:5、一张边长为16cm正方形的纸片,剪去两个面积一定且一样的小矩形得到一个“E”图案如图1所示.小矩形的长x(cm)与宽y(cm)之间的函数关系如图2所示:(1)求y与x之间的函数关系式;(2)“E”图案的面积是多少?(3)如果小矩形的长是6≤x≤12cm,求小矩形宽的范围.6、(2009•邵阳)如图是一个反比例函数图象的一部分,点A(1,10),B(10,1)是它的端点.(1)求此函数的解析式,并写出自变量x的取值范围;(2)请你举出一个能用本题的函数关系描述的生活实例.7、如图,⊙A和⊙B都与x轴和y轴相切,圆心A和圆心B都在反比例函数的图象上,则图中阴影部分的面积等于_________.8、(2009•郴州)如图1,已知正比例函数和反比例函数的图象都经过点M(﹣2,﹣1),且P(﹣1,﹣2)为双曲线上的一点,Q为坐标平面上一动点,PA垂直于x轴,QB垂直于y 轴,垂足分别是A、B.(1)写出正比例函数和反比例函数的关系式;(2)当点Q在直线MO上运动时,直线MO上是否存在这样的点Q,使得△OBQ与△OAP 面积相等如果存在,请求出点的坐标,如果不存在,请说明理由;(3)如图2,当点Q在第一象限中的双曲线上运动时,作以OP、OQ为邻边的平行四边形OPCQ,求平行四边形OPCQ周长的最小值.9、如图,在平面直角坐标系中,直线AB与y轴和x轴分别交于点A、点B,与反比例函数y在第一象限的图象交于点c(1,6)、点D(3,x).过点C作CE上y轴于E,过点D 作DF上X轴于F.(1)求m,n的值;(2)求直线AB的函数解析式.三、勾股定理:10、清朝康熙皇帝是我国历史上对数学很有兴趣的帝王.近日,西安发现了他的数学专著,其中有一文《积求勾股法》,它对“三边长为3、4、5的整数倍的直角三角形,已知面积求边长”这一问题提出了解法:“若所设者为积数(面积),以积率六除之,平方开之得数,再以勾股弦各率乘之,即得勾股弦之数”.用现在的数学语言表述是:“若直角三角形的三边长分别为3、4、5的整数倍,设其面积为S,则第一步:=m;第二步:=k;第三步:分别用3、4、5乘以k,得三边长”.(1)当面积S等于150时,请用康熙的“积求勾股法”求出这个直角三角形的三边长;(2)你能证明“积求勾股法”的正确性吗请写出证明过程.11、(2009•温州)一张等腰三角形纸片,底边长15cm,底边上的高长22.5cm.现沿底边依次从下往上裁剪宽度均为3cm的矩形纸条,如图所示.已知剪得的纸条中有一张是正方形,则这张正方形纸条是()A、第4张B、第5张C、第6张D、第7张12、(2009•茂名)如图,甲,乙两楼相距20米,甲楼高20米,小明站在距甲楼10米的A 处目测得点A与甲,乙楼顶B、C刚好在同一直线上,若小明的身高忽略不计,则乙楼的高度是_________米.13、(2009•恩施州)恩施州自然风光无限,特别是以“雄、奇、秀、幽、险”著称于世.著名的恩施大峡谷(A)和世界级自然保护区星斗山(B)位于笔直的沪渝高速公路X同侧,AB=50km、B到直线X的距离分别为10km和40km,要在沪渝高速公路旁修建一服务区P,向A、B两景区运送游客.小民设计了两种方案,图(1)是方案一的示意图(AP与直线X 垂直,垂足为P),P到A、B的距离之和S1=PA+PB,图(2)是方案二的示意图(点A关于直线X的对称点是A',连接BA'交直线X于点P),P到A、B的距离之和S2=PA+PB.(1)求S1、S2,并比较它们的大小;(2)请你说明S2=PA+PB的值为最小;(3)拟建的恩施到张家界高速公路Y与沪渝高速公路垂直,建立如图(3)所示的直角坐标系,B到直线Y的距离为30km,请你在X旁和Y旁各修建一服务区P、Q,使P、A、B、Q组成的四边形的周长最小.并求出这个最小值.14、(2009•重庆)已知:如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,DE⊥AC于点F,交BC于点G,交AB的延长线于点E,且AE=AC.(1)求证:BG=FG;(2)若AD=DC=2,求AB的长.四、四边形:15、(2008•佛山)如图,△ACD、△ABE、△BCF均为直线BC同侧的等边三角形.(1)当AB≠AC时,证明四边形ADFE为平行四边形;(2)当AB=AC时,顺次连接A、D、F、E四点所构成的图形有哪几类?直接写出构成图形的类型和相应的条件.16、(2008•山西)如图,已知△ABC是等边三角形,D、E分别在边BC、AC上,且CD=CE,连接DE并延长至点F,使EF=AE,连接AF、BE和CF.(1)请在图中找出一对全等三角形,用符号“≌”表示,并加以证明;(2)判断四边形ABDF是怎样的四边形,并说明理由;(3)若AB=6,BD=2DC,求四边形ABEF的面积.17、(2008•资阳)如图,在△ABC中,∠A,∠B的平分线交于点D,DE∥AC交BC于点E,DF∥BC交AC于点F.(1)点D是△ABC的_________心;(2)求证:四边形DECF为菱形.18、(2008•哈尔滨)在矩形ABCD中,点E是AD边上一点,连接BE,且∠ABE=30°,BE=DE,连接BD.点P从点E出发沿射线ED运动,过点P作PQ∥BD交直线BE于点Q.(1)当点P在线段ED上时(如图1),求证:BE=PD+PQ;(2)若BC=6,设PQ长为x,以P、Q、D三点为顶点所构成的三角形面积为y,求y与x 的函数关系式(不要求写出自变量x的取值范围);(3)在②的条件下,当点P运动到线段ED的中点时,连接QC,过点P作PF⊥QC,垂足为F,PF交对角线BD于点G(如图2),求线段PG的长.19、(2008•常州)如图,这是一张等腰梯形纸片,它的上底长为2,下底长为4,腰长为2,这样的纸片共有5张.打算用其中的几张来拼成较大的等腰梯形,那么你能拼出哪几种不同的等腰梯形?分别画出它们的示意图,并写出它们的周长.20、(2008•常州)已知:如图,在矩形ABCD中,E、F分别是边BC、AB上的点,且EF=ED,EF⊥ED.求证:AE平分∠BAD.21、(2008•潍坊)如图,矩形纸片ABCD中,AB=8,将纸片折叠,使顶点B落在边AD的E点上,BG=10.(1)当折痕的另一端F在AB边上时,如图.求△EFG的面积;(2)当折痕的另一端F在AD边上时,如图.证明四边形BGEF为菱形,并求出折痕GF 的长.22、(2008•新疆)(1)请用两种不同的方法,用尺规在所给的两个矩形中各作一个不为正方形的菱形,且菱形的四个顶点都在矩形的边上.(保留作图痕迹)(2)写出你的作法.23、(2008•海南)如图,P是边长为1的正方形ABCD对角线AC上一动点(P与A、C不重合),点E在射线BC上,且PE=PB.(1)求证:①PE=PD;②PE⊥PD;(2)设AP=x,△PBE的面积为y.①求出y关于x的函数关系式,并写出x的取值范围;②当x取何值时,y取得最大值,并求出这个最大值.24、(2008•义乌市)如图1,四边形ABCD是正方形,G是CD边上的一个动点(点G与C、D不重合),以CG为一边在正方形ABCD外作正方形CEFG,连接BG,DE.我们探究下列图中线段BG、线段DE的长度关系及所在直线的位置关系:(1)①猜想如图1中线段BG、线段DE的长度关系及所在直线的位置关系;②将图1中的正方形CEFG绕着点C按顺时针(或逆时针)方向旋转任意角度α,得到如图2,如图3情形.请你通过观察、测量等方法判断①中得到的结论是否仍然成立,并选取图2证明你的判断;(2)将原题中正方形改为矩形(如图4﹣6),且AB=a,BC=b,CE=ka,CG=kb(a≠b,k >0),第(1)题①中得到的结论哪些成立,哪些不成立?若成立,以图5为例简要说明理由;(3)在第(2)题图5中,连接DG、BE,且a=3,b=2,k=,求BE2+DG2的值.五、几何:25、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .(初二)26、已知:如图,P 是正方形ABCD 内点,∠PAD =∠PDA =150. 求证:△PBC 是正三角形.(初二)27、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)28、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC的延长线交MN 于E 、F .求证:∠DEN =∠F .A P C DB A F G CEBO D D 2 C 2B 2 A 2D 1 C 1 B 1C B DA A 1 BF29、已知:△ABC 中,H 为垂心(各边高线的交点),O(1)求证:AH =2OM ; (2)若∠BAC =600,求证:AH =AO .(初二)30、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 引圆的两条直线,交圆于B 、C 及D 、E ,直线EB 及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二)31、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q . 求证:AP =AQ .(初二)32、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.33、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)34、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .(初二)35、设P 是正方形ABCD 一边BC 上的任一点,PF ⊥AP ,CF 平分∠DCE .求证:PA =PF .(初二)36、如图,PC 切圆O 于C ,AC 为圆的直径,PEF 为圆的割线,AE 、AF 与直线PO 相交于B 、D .求证:AB =DC ,BC =AD .(初三)E37、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,PC =5. 求:∠APB 的度数.(初二)38、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA .求证:∠PAB =∠PCB .(初二)39、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD .(初三)40、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二)41、设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC ,求证:≤L <2.42、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.43、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a ,求正方形的边长.44、如图,△ABC 中,∠ABC =∠ACB =800,D 、E 分别是AB 、AC 上的点,∠DCA =300,∠EBA =200,求∠BED 的度数.APCB ACBPDEDCB A A CBPD五、数据的分析:45、(2005•南平)为了帮助贫困失学儿童,宿迁市团委发起“爱心储蓄”活动,鼓励学生将自己的压岁钱和零花钱存入银行,定期一年,到期后取回本金,而把利息捐赠给贫困失学儿童.某中学共有学生1200人,图1是该校各年级学生人数比例分布的扇形统计图,图2是该校学生人均存款情况的条形统计图.(1)求该学校的人均存款数;(2)已知银行一年定期存款的年利率是2.25%(“爱心储蓄”免收利息税),且每351元能提供给1位失学儿童一年的基本费用,那么该学校一学年能够帮助多少位失学儿童?46、(2005•河北)如图是连续十周测试甲、乙两名运动员体能训练情况的折线统计图.教练组规定:体能测试成绩70分以上(包括70分)为合格.(1)请根据图中所提供的信息填写右表:(2)请从下面两个不同的角度对运动员体能测试结果进行判断:①依据平均数与成绩合格的次数比较甲和乙,_________的体能测试成绩较好;②依据平均数与中位数比较甲和乙,_________的体能测试成绩较好.③依据折线统计图和成绩合格的次数,分析哪位运动员体能训练的效果较好.47、(2005•重庆)如图所示,A、B两个旅游点从2001年至2005年“五•一”的旅游人数变化情况分别用实线和虚线表示.根据图中所示解答以下问题:(1)B旅游点的旅游人数相对上一年,增长最快的是哪一年?(2)求A、B两个旅游点从2001到2005年旅游人数的平均数和方差,并从平均数和方差的角度,用一句话对这两个旅游点的情况进行评价;(3)A旅游点现在的门票价格为每人80元,为保护旅游点环境和游客的安全,A旅游点的最佳接待人数为4万人,为控制游客数量,A旅游点决定提高门票价格.已知门票价格x(元)与游客人数y(万人)满足函数关系y=5﹣.若要使A旅游点的游客人数不超过4万人,则门票价格至少应提高多少?答案与评分标准一、分式:1、如果abc=1,求证++=1.考点:分式的混合运算。
初三奥赛数学难题汇总(附答案)

如图,在直角坐标系中,以点A(3,0)为圆心,以32为半径的圆与x 轴交于B 、C 两点,与y 轴交于D 、E 两点. (1)求D 点坐标.(2)若B 、C 、D 三点在抛物线c bx ax y ++=2上,求这个抛物线的解析式. (3)若⊙A 的切线交x 轴正半轴于点M ,交y 轴负半轴于点N ,切点为P ,∠OMN=30º,试判断直线MN 是否经过所求抛物线的顶点?说明理由.28、(12分)某企业有员工300人,生产A 种产品,平均每人每年可创造利润m 万元(m 为大于零的常数)。
为减员增效,决定从中调配x 人去生产新开发的B 种产品,根据评估,调配后,继续生产A 种产品的员工平均每人每年创造的利润可增加20%,生产B 种产品的员工平均每人每年可创造利润1.54m 万元。
(1)调配后,企业生产A 种产品的年利润为_________万元,企业生产B 种产品的年利润为_________万元(用含x 和m 的代数式表示)。
若设调配后企业全年总利润为y 万元,则y 与x 之间的关系式为y =____________。
(2)若要求调配后,企业生产A 种产品的年利润不小于调配前企业年利润的54,生产B 种产品的年利润大于调配前企业年利润的一半,应有哪几种调配方案 ?请设计出来,并指出其中哪种方案全年总利润最大(必要时,运算过程可保留3个有效数字)。
(3)企业决定将(2)中的年最大总利润(设m =2)继续投资开发新产品。
现有6种产品可供选择(不得重复投资同一种产品)各产品所需资金及所获年利润如下表:如果你是企业决策者,为使此项投资所获年利润不少于145万元,你可以投资开发哪些产品?请写出两种投资方案。
25.解:(1)连结AD ,得OA=3,AD=23 ……………………1分∴OD =3, D(0,-3) ………………………………………………2分(2)由B (-3,0),C (33,0),D (0,-3)三点在抛物线c bx ax y ++=2上, (3)分得 ⎪⎩⎪⎨⎧=-++=+-=c c b a c b a 333270330 解得 ⎪⎪⎪⎩⎪⎪⎪⎨⎧-=-==333231c b a ………………………………5分x∴3332312--=x x y …………………………………………………………6分 (3)连结AP ,在Rt △APM 中,∠PMA==30º,AP=23 ∴AM =43, M (53,0) …………………………7分5333530tan =⋅=︒⋅=MO ON ∴N (0,-5) ……………………………………………8分 直线MN 解析式为:533-=x y 抛物线顶点坐标为(3,-4) ………………………………9分∵45333533-=-⨯=-x ∴抛物线顶点在直线MN 上. ……………………………10分28、解:(1)m x %)201()300(+⋅-,mx 54.1,mx m x y 54.1%)201)(300(++-=(2)由题意得⎪⎪⎩⎪⎪⎨⎧⨯>⨯≥+-mmx m m x 3002154.130054%)201(0300(解得773197<x ≤100。
中考数学难题归纳

一.选择题(共3小题)1.(1998•南京)若双曲线的两个分支在第二、四象限内,则抛物线y=kx2﹣2x+k2的图象大致是图中的( )大致是图中的(A.B.C.D.2.如图,∠AOD=90°,OA=OB=BC=CD,那么下列结论成立的是(,那么下列结论成立的是( )OCA B B.△OAB∽△ODA A.△OAB∽△OCA C.△BAC∽△BDA D.以上结论都不成立.以上结论都不成立3.(2012•绵阳)已知△ABC中,∠C=90°,tanA=,D是AC上一点,∠CBD=∠A,则sin∠ABD=()A.B. C.D.二.填空题(共11小题)4.(2012•黄石)“数学王子”高斯从小就善于观察和思考.在他读小学时就能在课堂上快速地计算出1+2+3+…+98+99+100=5050,今天我们可以将高斯的做法归纳如下:,今天我们可以将高斯的做法归纳如下:令S=1+2+3+…+98+99+100 ①S=100+99+98+…+3+2+1 ②①+②:有2S=(1+100)×100 解得:S=5050 请类比以上做法,回答下列问题:请类比以上做法,回答下列问题:若n为正整数,3+5+7+…+(2n+1)=168,则n=_________.5.如图,在平面直角坐标系中,点A的坐标是(10,0),点B的坐标为(8,0),点C,D在以OA为直的坐标为 _________.径的半圆M上,且四边形OCDB是平行四边形,则点C的坐标为6.如图,⊙O的半径是5cm,P是⊙O外一点,PO=8cm,∠P=30°,则AB=_________cm.7.(2000•甘肃)如图,AB 是半圆的直径,直线MN 切半圆于C ,CM ⊥MN ,BN ⊥MN ,如果AM=a ,BN=b ,那么半圆的半径是那么半圆的半径是 _________ .8.已知双曲线y=与直线y=相交于A ,B 两点.第一象限上的点M (m ,n )(在A 点左侧)是双曲线y=上的动点.过点B 作BD ∥y 轴交x 轴于点D .过N (0,﹣n )作NC ∥x 轴交双曲线y=于点E ,交BD于点C .若B 是CD 的中点,四边形OBCE 的面积为4,则直线CM 的解析式为的解析式为 _________ .9.如图,M 为双曲线y=上的一点,过点M 作x 轴、y 轴的垂线,分别交直线y=﹣x+m 于D 、C 两点,若直线y=﹣x+m 与y 轴、x 轴分别交于点A 、B ,则AD •BC 的值为的值为 _________ .10.如图,正方形ABCD 的对角线AC 、BD 相交于点O ,E 是BC 的中点,DE 交AC 于F ,若DE=6,则EF 等于等于 _________ .11.(2012•金山区二模)金山区二模)如图,如图,如图,已知已知AD 为△ABC 的角平分线,DE ∥AB 交AC 于E ,如果,那么=_________ .12.如图,在△ABC中,D、E是BC的三等分点,M是AC的中点,BM交AD、AE于G、H,则BG:GH:HM=_________.13.(2013•上海)如图,在△ABC中,AB=AC,BC=8,tanC=,如果将△ABC沿直线l翻折后,点B落在边AC的中点处,直线l与边BC交于点D,那么BD的长为的长为 _________.14.(2013•芦淞区模拟)在Rt△ABC中,∠ACB=90°,CD⊥AB于点D.已知AC=,BC=2,那么sin∠ACD= _________.三.解答题(共9小题)15.已知:如图,△ABC内接于圆,AD⊥BC于D,弦BH⊥AC于E,交AD于F.求证:FE=EH.16.把抛物线y=x2+bx+c向右平移3个单位,再向下平移2个单位,所得图象的解析式是y=x2﹣3x+5,求b,c的值.的值.17.(2003•海南)已知抛物线y=ax2+bx+c开口向下,并且经过A(0,1)和M(2,﹣3)两点.)两点.,求此抛物线的解析式;(1)若抛物线的对称轴为直线x=﹣1,求此抛物线的解析式;的取值范围;(2)如果抛物线的对称轴在y轴的左侧,试求a的取值范围;的值.(3)如果抛物线与x轴交于B、C两点,且∠BAC=90°,求此时a的值.18.(2000•杭州)已知一个正三角形和一个正六边形的周长相等,求它们的面积的比值.杭州)已知一个正三角形和一个正六边形的周长相等,求它们的面积的比值. 19.(原创题)如图所示,扇形OAB从图①无滑动旋转到图②,再由图②到图③,∠O=60°,OA=1.点所运动的路径长;(1)求O点所运动的路径长;围成的面积.(2)O点走过路径与直线L围成的面积.20.(2013•重庆)重庆) 已知:如图,抛物线y=x 2+2x ﹣3与x 轴的交点为A 、B 两点,与y 轴交于点C ,直线AC 与抛物线交于A 、C 两点.两点.如图,的y=ax 2+bx+c (a ≠0)与x 轴相交于A 、B 两点,其中点A 的坐标为(﹣3,0).(1)求点B 的坐标.的坐标.(2)在抛物线的对称轴x=﹣1上是否存在一点P ,使得△BCP 为等腰三角形,若存在,直接写出点P 的坐标;若不存在,说明理由.标;若不存在,说明理由.(3)若点Q 在直线AC 下方的抛物线上,且S △QOC =2S △BOC ,求点Q 的坐标.的坐标.21.(2014•徐州模拟)如图,已知抛物线y=﹣x 2+2x+1﹣m 与x 轴相交于A 、B 两点,与y 轴相交于点C ,其中点C 的坐标是(0,3),顶点为点D ,连接CD ,抛物线的对称轴与x 轴相交于点E .(1)求m 的值;的值;(2)求∠CDE 的度数;的度数;(3)在抛物线对称轴的右侧部分上是否存在一点P ,使得△PDC 是等腰三角形?如果存在,求出符合条件的点P 的坐标;如果不存在,请说明理由.的坐标;如果不存在,请说明理由.22.(2006•锦州)如图,在平面直角坐标系中,在平面直角坐标系中,四边形四边形OABC 为菱形,为菱形,点点C 的坐标为(4,0),∠AOC=60°,垂直于x 轴的直线l 从y 轴出发,沿x 轴正方向以每秒1个单位长度的速度运动,设直线l 与菱形OABC的两边分别交于点M 、N (点M 在点N 的上方).(1)求A 、B 两点的坐标;两点的坐标;(2)设△OMN 的面积为S ,直线l 运动时间为t 秒(0≤t ≤6),试求S 与t 的函数表达式;的函数表达式;(3)在题(2)的条件下,t 为何值时,S 的面积最大?最大面积是多少?的面积最大?最大面积是多少?23.(2007•济宁)如图,先把一矩形ABCD 纸片对折,设折痕为MN ,再把B 点叠在折痕线上,得到△ABE ,过B 点折纸片使D 点叠在直线AD 上,得折痕PQ .(1)求证:△PBE ∽△QAB ;(2)你认为△PBE和△BAE相似吗?如果相似给出证明,如不相似请说明理由;相似吗?如果相似给出证明,如不相似请说明理由;上?为什么?(3)如果沿直线EB折叠纸片,点A是否能叠在直线EC上?为什么?2南京)若双曲线的两个分支在第二、四象限内,则抛物线A.B.C.D.考点:二次函数的图象;反比例函数的性质.分析:的符号判断抛物线的开口方向及对称轴. 根据双曲线的图象位置可知k<0;再根据k的符号判断抛物线的开口方向及对称轴.解答:解:∵双曲线的两个分支在第二、四象限内,即k<0,抛物线开口向下,∴抛物线开口向下,对称轴x=﹣=<0,对称轴在y轴的左边.故选A.本题考查了反比例函数图象的性质和二次函数系数与抛物线形状的关系.点评:本题考查了反比例函数图象的性质和二次函数系数与抛物线形状的关系.A.△OAB∽△OCA B.△OAB∽△ODA C.△BAC∽△BDA D.以上结论都不成立上结论都不成立考点:相似三角形的判定.专题:常规题型.常规题型.根据已知及相似三角形的判定进行分析,从而得到答案.分析:根据已知及相似三角形的判定进行分析,从而得到答案.解答:解:∵∠AOD=90°,设OA=OB=BC=CD=x ∴AB=x,AC=x,AD=x,OC=2x,OD=3x,BD=2x ∴,,∴∴△BAC∽△BDA 故选C.点评:此题考查了相似三角形的判定:①如果两个三角形的三组对应边的比相等,那么这两个三角形相似;如果两个三角形的三组对应边的比相等,那么这两个三角形相似;如果两个三角形的两条对应边的比相等,且夹角相等,那么这两个三角形相似;②如果两个三角形的两条对应边的比相等,且夹角相等,那么这两个三角形相似;如果两个三角形的两个对应角相等,那么这两个三角形相似.③如果两个三角形的两个对应角相等,那么这两个三角形相似.3.(2012•绵阳)已知△ABC中,∠C=90°,tanA=,D是AC上一点,∠CBD=∠A,则sin∠ABD=()A.B.C.D.考点:相似三角形的判定与性质;勾股定理;锐角三角函数的定义.压轴题.专题:压轴题.分析:作DE⊥AB于点E,根据相等的角的三角函数值相等即可得到===,设CD=1,则可以求得AD的长,然后利用勾股定理即可求得DE、AE的长,则BE可以求得,根据同角三角函数之间的关系即可求解.解答:解:作DE⊥AB于点E.∵∠CBD=∠A,∴tanA=tan∠CBD====,设CD=1,则BC=2,AC=4,∴AD=AC﹣CD=3,在直角△ABC中,AB===2,在直角△ADE中,设DE=x,则AE=2x,∵AE2+DE2=AD2,∴x2+(2x)2=9,解得:x=,则DE=,AE=.∴BE=AB﹣AE=2﹣=,∴tan∠DBA==,∴sin∠DBA=.故选:A.本题考查了三角函数的定义,以及勾股定理,正确理解三角函数就是直角三角形中边的比值是关键.点评:本题考查了三角函数的定义,以及勾股定理,正确理解三角函数就是直角三角形中边的比值是关键.n=12.考点:有理数的混合运算.压轴题;规律型.专题:压轴题;规律型.根据题目提供的信息,列出方程,然后求解即可.分析:根据题目提供的信息,列出方程,然后求解即可.解答:解:设S=3+5+7+…+(2n+1)=168①,则S=(2n+1)+…+7+5+3=168②,①+②得,2S=n(2n+1+3)=2×168,整理得,n2+2n﹣168=0,即(n﹣12)(n+14)=0,解得n1=12,n2=﹣14(舍去).故答案为:12.点评:本题考查了有理数的混合运算,读懂题目提供的信息,表示出这列数据的和并列出方程是解题的关键.的坐标为 (1,3).的坐标为考点:垂径定理;勾股定理;平行四边形的性质.计算题.专题:计算题.分析:过点M作MF⊥CD于点F,则CF=CD=4,过点C作CE⊥OA于点E,由勾股定理可求得MF的长,从而的坐标.得出OE的长,然后写出点C的坐标.解答:解:∵四边形OCDB是平行四边形,B(8,0),∴CD∥OA,CD=OB=8 过点M作MF⊥CD于点F,则CF=CD=4 过点C作CE⊥OA于点E,∵A(10,0),∴OE=OM﹣ME=OM﹣CF=5﹣4=1.连接MC,则MC=OA=5 ∴在Rt△CMF中,由勾股定理得∴点C的坐标为(1,3)本题考查了勾股定理、垂径定理以及平行四边形的性质,是基础知识要熟练掌握.点评:本题考查了勾股定理、垂径定理以及平行四边形的性质,是基础知识要熟练掌握.6.如图,⊙O的半径是5cm,P是⊙O外一点,PO=8cm,∠P=30°,则AB=6cm.考点:垂径定理;含30度角的直角三角形;勾股定理.的长,再解直角三角形并根据垂径定理即可求出.分析:首先作出辅助线,求出OD的长,再解直角三角形并根据垂径定理即可求出.解答:解:如图:作OD⊥AB于D,连接OB,因为∠P=30°所以OD=PO=×8=4cm 在直角三角形ODB中,BD===3cm 根据垂径定理,BD=AD,则AB=2BD=2×3=6cm.,根据垂径定理解答.点评:解答此题的关键是作出辅助线OD,根据垂径定理解答.7.(2000•甘肃)如图,AB是半圆的直径,直线MN切半圆于C,CM⊥MN,BN⊥MN,如果AM=a,BN=b,那么半圆的半径是 .半圆的半径是考点:梯形中位线定理;切线的性质.分析:根据切线的性质,只需连接OC.根据切线的性质定理以及平行线等分线段定理得到梯形的中位线,再根据梯形的中位线定理进行计算即可.梯形的中位线定理进行计算即可.解答:解:连接OC,则OC⊥MN.∴OC∥AM∥BN,又OA=OB,则MC=NC.根据梯形的中位线定理,得该半圆的半径是.点评:此题主要是根据切线的性质定理和平行线等分线段定理,发现梯形的中位线,进而熟练运用梯形的中位线定理求解.定理求解.8.已知双曲线y=与直线y=相交于A,B两点.第一象限上的点M(m,n)(在A点左侧)是双曲线y=上的动点.过点B作BD∥y轴交x轴于点D.过N(0,﹣n)作NC∥x轴交双曲线y=于点E,交BD于点C.若B是CD的中点,四边形OBCE的面积为4,则直线CM的解析式为的解析式为 y=.考点:反比例函数与一次函数的交点问题.动点型.专题:动点型.根据一次函数和反比例函数的性质及点的坐标和解析式的关系解答.分析:根据一次函数和反比例函数的性质及点的坐标和解析式的关系解答.解答:解:设B点坐标为(x1,﹣),代入y=x得,﹣=x1,x1=﹣2n;∴B点坐标为(﹣2n,﹣).因为BD∥y轴,所以C点坐标为(﹣2n,﹣n).因为四边形ODCN的面积为2n•n=2n2,三角形ODB,三角形OEN的面积均为,四边形OBCE的面积为4.则有2n2﹣k=4﹣﹣﹣①;又因为2n•=k,即n2=k﹣﹣﹣②②代入①得,4=2k﹣k,解得k=4;则解析式为y=;又因为n2=4,故n=2或n=﹣2.M在第一象限,n>0;将M(m,2)代入解析式y=,得m=2.故M点坐标为(2,2);C(﹣4,﹣2);设直线CM解析式为y=kx+b,则,解得∴一次函数解析式为:y=x+.点评:解答本题要明确两个关系:(1)双曲线中,xy=k;(2)S△DBO=|k|.9.如图,M为双曲线y=上的一点,过点M作x轴、y轴的垂线,分别交直线y=﹣x+m于D、C两点,若直线y=﹣x+m与y轴、x轴分别交于点A、B,则AD•BC的值为的值为 2.考点:反比例函数综合题.综合题.专题:综合题.分析:作CE⊥x轴于E,DF⊥y轴于F,如图所示,根据直线y=﹣x+m,表示出A与B坐标,可得出三角形OAB 为等腰直角三角形,进而确定出三角形ADF与三角形CEB都为等腰直角三角形,设M(a,b),代入反比的值.例解析式得到ab=,CE=b,DF=a,表示出AD与BC,即可求出AD•BC的值.解答:解:作CE⊥x轴于E,DF⊥y轴于F,如图,,如图,对于y=﹣x+m,令x=0,得到y=m;令y=0,得到x=m,∴A(0,m),B(m,0),为等腰直角三角形,∴△OAB为等腰直角三角形,都是等腰直角三角形,∴△ADF与△CEB都是等腰直角三角形,设M(a,b),则ab=,CE=b,DF=a,∴AD=DF=a,BC=CE=b,∴AD•BC=a•b=2ab=2.故答案为:2.点评:此题属于反比例函数综合题,涉及的知识有:等腰直角三角形的性质,坐标与图形性质,反比例函数的性质,以及矩形的性质,熟练掌握等腰直角三角形的性质是解本题的关键.质,以及矩形的性质,熟练掌握等腰直角三角形的性质是解本题的关键.10.如图,正方形ABCD的对角线AC、BD相交于点O,E是BC的中点,DE交AC于F,若DE=6,则EF等于等于 2.考点:相似三角形的判定与性质;正方形的性质.分析:因为四边形ABCD是正方形,E是BC中点,所以CE=AD,由相似三角形的判定定理得出△CEF∽△ADF,再根据相似三角形的对应边成比例可得出.再根据相似三角形的对应边成比例可得出.中点,解答:解:∵四边形ABCD是正方形,E是BC中点,∴CE=AD,∵AD∥BC,∴∠ADF=∠DEC,∠AFD=∠EFC,∴△CEF∽△ADF,∴=,∴,即,解得EF=2,故答案为2.点评:本题考查的是相似三角形的判定与性质及正方形的性质,先根据题意判断出△CEF∽△ADF,再根据相似三角形的对应边成比例进行解答是解答此题的关键.形的对应边成比例进行解答是解答此题的关键.11.(2012•金山区二模)如图,已知AD为△ABC的角平分线,DE∥AB交AC于E,如果,那么=.考点:相似三角形的判定与性质;等腰三角形的判定与性质.分析:的值. 根据角平分线的定义,平行线的性质易证EA=ED,△CED∽△CAB,从而求得的值.的角平分线,解答:解:∵AD为△ABC的角平分线,∴∠BAD=∠EAD,∵DE∥AB,∴△CED∽△CAB,∠BAD=∠EDA.∴∠EDA=∠EAD,∴EA=ED,∵=,∴ED:EC=2:3,∴=ED:EC=2:3.故答案为:.点评:本题主要考查了相似三角形的判定与性质,相似三角形的对应边对应成比例,同时考查了角平分线的定义.12.如图,在△ABC中,D、E是BC的三等分点,M是AC的中点,BM交AD、AE于G、H,则BG:GH:HM= 5:3:2.考点:平行线分线段成比例;三角形中位线定理.分析:首先过点M作MK∥BC,交AD,AE分别于K,N,由M是AC的中点与D、E是BC的三等分点,根据平行线分线段成比例定理,即可求得MN=NK=BD=DE=EC,然后根据比例的性质,即可求得BG:GH:HM的值.的值.解答:解:法一:过点M作MK∥BC,交AD,AE分别于K,N,∵M是AC的中点,的中点,∴=,的三等分点,∵D、E是BC的三等分点,∴BD=DE=EC,∴MN=NK,∵=,=1,∴MH=BH,MG=BG,设MH=a,BH=4a,BG=GM=,∴GH=GM﹣MH=,∴BG:GH:HM=::a=5:3:2.故答案为:5:3:2.点评:此题考查了平行线分线段成比例定理与比例的性质.此题难度适中,解题的关键是注意辅助线的作法,注意数形结合思想的应用.意数形结合思想的应用.13.(2013•上海)如图,在△ABC中,AB=AC,BC=8,tanC=,如果将△ABC沿直线l翻折后,点B落在边AC的长为 .的中点处,直线l与边BC交于点D,那么BD的长为考点:翻折变换(折叠问题).压轴题.专题:压轴题.即可.分析:首先根据已知得出△ABC的高以及B′E的长,利用勾股定理求出BD即可.解答:解:过点A作AQ⊥BC于点Q,∵AB=AC,BC=8,tanC=,∴=,QC=BQ=4,∴AQ=6,的中点处,∵将△ABC沿直线l翻折后,点B落在边AC的中点处,过B′点作B′E⊥BC于点E,∴B′E=AQ=3,∴=,∴EC=2,设BD=x,则B′D=x,∴DE=8﹣x﹣2=6﹣x,∴x2=(6﹣x)2+32,解得:x=,直线l与边BC交于点D,那么BD的长为:.故答案为:.点评:此题主要考查了翻折变换的性质以及勾股定理和锐角三角函数关系,根据已知表示出DE的长是解题关键.AC=,ACD=.考点:解直角三角形.分析:在直角△ABC中,根据勾股定理即可求得AB,而∠B=∠ACD,即可把求sin∠ACD转化为求sinB.解答:解:在直角△ABC中,根据勾股定理可得:AB===3.∵∠B+∠BCD=90°,∠ACD+∠BCD=90°,∴∠B=∠ACD.∴sin∠ACD=sin∠B==.本题考查了解直角三角形中三角函数的应用,要熟练掌握好边角之间的关系.点评:本题考查了解直角三角形中三角函数的应用,要熟练掌握好边角之间的关系.考点:圆周角定理.证明题.专题:证明题.分析:首先连接AH,由AD⊥BC,BH⊥AC与∠AFE=∠BFD,即可得∠EAF=∠FBD,又由圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,即可得∠HAC=∠HBC,即可得∠HAE=∠F AE,则可用ASA证得△AEF≌△AEH,继而证得FE=EH.解答:证明:连接AH,∵AD⊥BC,BH⊥AC,∴∠FDB=∠AEF=90°,∵∠AFE=∠BFD,∴∠EAF=∠FBD,∵∠HAC=∠HBC,∴∠HAE=∠EAF,∵BH⊥AC,∴∠AEF=∠AEH=90°,中,在△AEF和△AEH中,∴△AEF≌△AEH(ASA),∴FE=EH.点评:此题考查了圆周角定理、直角三角形的性质、全等三角形的判定与性质.此题难度适中,解题的关键是准确作出辅助线,掌握在同圆或等圆中,同弧或等弧所对的圆周角相等定理的应用.确作出辅助线,掌握在同圆或等圆中,同弧或等弧所对的圆周角相等定理的应用.16.把抛物线y=x2+bx+c向右平移3个单位,再向下平移2个单位,所得图象的解析式是y=x2﹣3x+5,求b,c的值.值.考点:二次函数图象与几何变换.分析:先求出y=x2﹣3x+5的顶点坐标,再根据“左加右减”求出平移前的抛物线的顶点坐标,然后利用顶点式解析式写出,整理成二次函数的一般形式,再根据对应项系数相等解答.式写出,整理成二次函数的一般形式,再根据对应项系数相等解答.解答:解:∵y=x2﹣3x+5=(x﹣)2+,∴y=x2﹣3x+5的顶点坐标为(,),个单位,∵向右平移3个单位,向下平移2个单位,∴平移前的抛物线的顶点的横坐标为﹣3=﹣,纵坐标为+2=,∴平移前的抛物线的顶点坐标为(﹣,),∴平移前的抛物线为y=(x+)2+=x2+3x+7,∴b=3,c=7.点评:本题考查了二次函数的图象与几何变换,根据两个函数图象的顶点坐标确定平移方法更简便,要注意知道平移后的顶点坐标求平移前的顶点坐标的方法.平移后的顶点坐标求平移前的顶点坐标的方法.17.(2003•海南)已知抛物线y=ax2+bx+c开口向下,并且经过A(0,1)和M(2,﹣3)两点.)两点.,求此抛物线的解析式;(1)若抛物线的对称轴为直线x=﹣1,求此抛物线的解析式;的取值范围;(2)如果抛物线的对称轴在y轴的左侧,试求a的取值范围;的值.(3)如果抛物线与x轴交于B、C两点,且∠BAC=90°,求此时a的值.考点:二次函数综合题.压轴题.专题:压轴题.分析:(1)可将A、M的坐标代入抛物线的解析式中,用a替换掉b、c的值,再根据抛物线的对称轴为﹣1,即可求出a的值,也就确定了抛物线的解析式.的值,也就确定了抛物线的解析式.的取值范围. (2)抛物线的对称轴在y轴左侧,即抛物线对称轴方程小于0,由此可得出a的取值范围.(3)可设出B、C的坐标,如果∠BAC=90°,在直角三角形BAC中,可根据射影定理得出OA2=OC•OB,的值.据此可得出a的值.解答:解:将A、M的坐标代入抛物线的解析式中有:的坐标代入抛物线的解析式中有:,解得:∴抛物线的解析式为y=ax2﹣(2+2a)x+1.(1)∵x=﹣=﹣1,∴=﹣1,解得a=﹣.∴抛物线的解析式为y=﹣x2﹣x+1.(2)由题意知:x=﹣<0,即﹣<0;抛物线开口向下,∵抛物线开口向下,∴a<0 ∴1+a>0,且a<0 ∴﹣1<a<0.(3)设B(x1,0),C(x2,0),x1<x2;∵x1x2=,且a<0.轴正半轴;∴x1x2<0,即B在x轴负半轴,C在x轴正半轴;∴OB=﹣x1,OC=x2.∵∠BAC=90°,,根据射影定理可得:在直角三角形BAC中,AO⊥BC,根据射影定理可得:OA2=OB•OC=﹣x1•x2=1,即﹣=1,a=﹣1.本题主要考查了抛物线对称轴解析式、二次函数与一元二次方程的关系、韦达定理等知识.点评:本题主要考查了抛物线对称轴解析式、二次函数与一元二次方程的关系、韦达定理等知识.18.(2000•杭州)已知一个正三角形和一个正六边形的周长相等,求它们的面积的比值.杭州)已知一个正三角形和一个正六边形的周长相等,求它们的面积的比值.考点:正多边形和圆.分析:根据正多边形的面积等于周长与边心距的乘积的一半,所以只需根据它们的周长计算其边心距;在由正多边形的半径、边心距和边长组成的直角三角形中,根据锐角三角函数的概念可以分别求得它们的边心距,再进一步计算其面积,从而得到其比值.再进一步计算其面积,从而得到其比值..根据题意,得解答:解:设它们的周长是1.根据题意,得正三角形的边长是,正六边形的边长是.则正三角形的边心距是,正六边形的边心距是.则正三角形的面积是,正六边形的面积是.则它们的面积比是2:3.点评:熟悉正多边形的面积公式:正多边形的面积等于周长与边心距的乘积的一半.能够根据由半径、边心距和半边组成的直角三角形,运用锐角三角函数进行计算.半边组成的直角三角形,运用锐角三角函数进行计算.19.(原创题)如图所示,扇形OAB从图①无滑动旋转到图②,再由图②到图③,∠O=60°,OA=1.点所运动的路径长;(1)求O点所运动的路径长;围成的面积.(2)O点走过路径与直线L围成的面积.考点:扇形面积的计算;弧长的计算.本题一共转动了三次,关键是分析每一次转动的圆心角和半径,然后利用弧长公式求.分析:本题一共转动了三次,关键是分析每一次转动的圆心角和半径,然后利用弧长公式求.解答:解:(1)运动路径第一段弧长=,第二段路径为线段长为,第三段路径为,即O在L上运动路径为.)围成面积,(2)围成面积,S1=.本题的难点是第二次,实际上就是扇形的弧长,其它二次则简单.点评:本题的难点是第二次,实际上就是扇形的弧长,其它二次则简单.20.(2013•重庆)重庆) 已知:如图,抛物线y=x2+2x﹣3与x轴的交点为A、B两点,与y轴交于点C,直线AC与抛两点.物线交于A、C两点.如图,的y=ax2+bx+c(a≠0)与x轴相交于A、B两点,其中点A的坐标为(﹣3,0).的坐标.(1)求点B的坐标.(2)在抛物线的对称轴x=﹣1上是否存在一点P,使得△BCP为等腰三角形,若存在,直接写出点P的坐标;若不存在,说明理由.存在,说明理由.的坐标.(3)若点Q在直线AC下方的抛物线上,且S△QOC=2S△BOC,求点Q的坐标.考点:二次函数综合题.压轴题.专题:压轴题.分析:(1)由抛物线y=ax2+bx+c的对称轴为直线x=﹣1,交x轴于A、B两点,其中A点的坐标为(﹣3,0),点的坐标;根据二次函数的对称性,即可求得B点的坐标;(2)①a=1时,先由对称轴为直线x=﹣1,求出b的值,再将B(1,0)代入,求出二次函数的解析式为y=x2+2x ﹣3,得到C点坐标,然后设P点坐标为(x,x2+2x﹣3),根据S△POC=4S△BOC列出关于x的方程,解方程的坐标;求出x的值,进而得到点P的坐标;②先运用待定系数法求出直线AC的解析式为y=﹣x﹣3,再设Q点坐标为(x,﹣x﹣3),则D点坐标为(x,x2+2x﹣3),然后用含x的代数式表示QD,根据二次函数的性质即可求出线段QD长度的最大值.长度的最大值.解答:解:(1)∵对称轴为直线x=﹣1的抛物线y=ax2+bx+c(a≠0)与x轴相交于A、B两点,两点,对称,∴A、B两点关于直线x=﹣1对称,∵点A的坐标为(﹣3,0),∴点B的坐标为(1,0);(2)①a=1时,∵抛物线y=x2+bx+c的对称轴为直线x=﹣1,∴=﹣1,解得b=2.将B(1,0)代入y=x2+2x+c,得1+2+c=0,解得c=﹣3.则二次函数的解析式为y=x2+2x﹣3,∴抛物线与y轴的交点C的坐标为(0,﹣3),OC=3.设P点坐标为(x,x2+2x﹣3),∵S△POC=4S△BOC,∴×3×|x|=4××3×1,∴|x|=4,x=±4.当x=4时,x2+2x﹣3=16+8﹣3=21;当x=﹣4时,x2+2x﹣3=16﹣8﹣3=5.∴点P的坐标为(4,21)或(﹣4,5);)代入,②设直线AC的解析式为y=kx+t,将A(﹣3,0),C(0,﹣3)代入,得,解得,即直线AC的解析式为y=﹣x﹣3.设Q点坐标为(x,﹣x﹣3)(﹣3≤x≤0),则D点坐标为(x,x2+2x﹣3),QD=(﹣x﹣3)﹣(x2+2x﹣3)=﹣x2﹣3x=﹣(x+)2+,∴当x=﹣时,QD有最大值.点评:此题考查了待定系数法求二次函数、一次函数的解析式,二次函数的性质以及三角形面积、线段长度问题.此题难度适中,解题的关键是运用方程思想与数形结合思想.题难度适中,解题的关键是运用方程思想与数形结合思想.21.(2014•徐州模拟)如图,已知抛物线y=﹣x2+2x+1﹣m与x轴相交于A、B两点,与y轴相交于点C,其中点C的坐标是(0,3),顶点为点D,连接CD,抛物线的对称轴与x轴相交于点E.(1)求m的值;的值;的度数;(2)求∠CDE的度数;(3)在抛物线对称轴的右侧部分上是否存在一点P,使得△PDC是等腰三角形?如果存在,求出符合条件的点P的坐标;如果不存在,请说明理由.坐标;如果不存在,请说明理由.考点:二次函数综合题.综合题.专题:综合题.的值. 分析:(1)由于抛物线的解析式中只有一个未知数m,因此只需将C点的坐标代入抛物线中即可求出m的值.(2)此题可首先表示出抛物线的顶点式,就可以求出D点的坐标,然后过C点作DE的垂线CF,在△DCF的度数;中根据C、D、F三点的坐标求出DF和CF长度相等,得出∠CDE的度数;的坐标. (3)利用二次函数的对称性可求出,以及利用线段垂直平分线的性质求出P的坐标.解答:(1)∵抛物线过点C(0,3)∴1﹣m=3 ∴m=﹣2 (2)由(1)可知该抛物线的解析式为y=﹣x2+2x+3=﹣(x﹣1)2+4 ∴此抛物线的对称轴x=1 抛物线的顶点D(1,4)过点C作CF⊥DE,则CF∥OE ∴F(1,3)所以CF=1,DF=4﹣3=1 ∴CF=DF 又∵CF⊥DE ∴∠DFC=90°∴∠CDE=45°)存在.(3)存在.的对称点时,①延长CF交抛物线于点P1,则CP1∥X轴,所以P1正好是C点关于DE的对称点时,有DC=DP1,得出P1点坐标(2,3);由y=﹣x2+2x+3得,D点坐标为(1,4),对称轴为x=1.②若以CD为底边,则PD=PC,,根据两点间距离公式,设P点坐标为(x,y),根据两点间距离公式,得x2+(3﹣y)2=(x﹣1)2+(4﹣y)2,即y=4﹣x.)在抛物线上,又∵P点(x,y)在抛物线上,∴4﹣x=﹣x2+2x+3,即x2﹣3x+1=0,,应舍去;解得:x=,<1,应舍去;∴x=,∴y=4﹣x=则P2点坐标(,).∴符合条件的点P坐标为(,)和(2,3).点评:此题主要考查了二次函数的对称性,以及等腰三角形的判定方法和垂直平分线的性质等知识,题目综合性较强,是中考中热点题型.较强,是中考中热点题型.22.(2006•锦州)如图,在平面直角坐标系中,四边形OABC为菱形,点C的坐标为(4,0),∠AOC=60°,垂直于x轴的直线l从y轴出发,沿x轴正方向以每秒1个单位长度的速度运动,设直线l与菱形OABC的两边分别交于点M、N(点M在点N的上方).两点的坐标;(1)求A、B两点的坐标;的函数表达式;(2)设△OMN的面积为S,直线l运动时间为t秒(0≤t≤6),试求S与t的函数表达式;(3)在题(2)的条件下,t为何值时,S的面积最大?最大面积是多少?的面积最大?最大面积是多少?。
初三数学中考难题总结

初三数学中考难题总结1.如图1所示,四边形ABCD 中,M ,N 分别为AB ,CD 的中点,且AD=BC ,延长MN ,AD 交与E 点,延长BC ,MN 交与F 点。
求证:∠DEN =∠F .ABCDMNF E图 12.如图2平行四边形ABCD 中,AB=5,BC=10,BC 边上的高AM=4,E 为BC 边上的一个动点,且不与B ,C 两点重合,过E 作AB 的垂线,垂足为F ,FE 与DC 的延长线交与G ,连接DE ,DF 。
(1)求证:BE*CG=BF*CE 。
(2)当点E 在BC 上运动时,三角形BEF 和三角形CEG 的周长之间有什么关系?并说明理由。
(3)设BE 为x ,三角形DEF 的面积为y ,求出y 与x 之间的函数关系式,并求出x 为什么值得时候,y 有最大值,最大值为多少?DCBA F MEG图 23.在数学工具中,三角板经常用到,如图3.1所示,将三角板ABC与三角板DEF摆放在一起,A与D重合,C与E重合,然后将三角板DEF的一个直角顶点放在边AC上,如图3.2所示,旋转一定角度,使DE与AB边交与P,DF与AC边交与Q,若CE:AE=1:1,连接PQ,判定三角形EPQ的形状,并说明理由。
A,DB C,EFD F CAB QPE图3.1图3.24.如图4所示,在梯形ABCD中,AB//CD,AB=7,CD=1,AD=BC=5,点M,N分别在AD,BC上移动,保持MN//AB,ME垂直AB于E,NF垂直于AB于F。
(1)求梯形ABCD的面积。
(2)求四边形MEFN面积的最大值。
(3)试判断MEFN能否为正方形,若能,求出面积,若不能,说明理由。
D CA BE FM N图 45.如图5所示,AB 是半圆O 上的直径,E 是 ⌒BC 的中点,OE 交弦BC 于点D ,过点C 作⊙O 切线交OE 的延长线于点F. 已知BC=8,DE=2. ⑴求⊙O 的半径;⑵求CF 的长;⑶求tan ∠BAD 的值。
初中数学难题精选(附问题详解)
3、设P是正方形ABCD一边BC上的任一点,PF⊥AP,CF平分∠DCE.
求证:PA=PF.(初二)
4、如图,PC切圆O于C,AC为圆的直径,PEF为圆的割线,AE、AF与直线PO相交于B、D.求证:AB=DC,BC=AD.(初三)
经典难题(四)
1、已知:△ABC是正三角形,P是三角形内一点,PA=3,PB=4,PC=5.
经典难题(一)
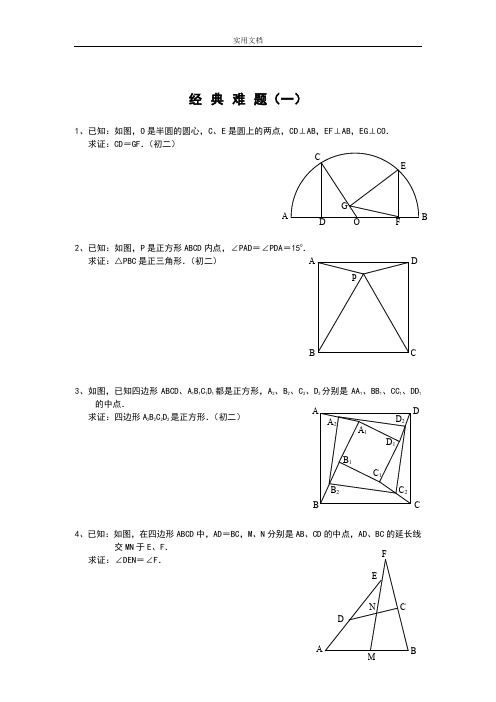
1、已知:如图,O是半圆的圆心,C、E是圆上的两点,CD⊥AB,EF⊥AB,EG⊥CO.
求证:CD=GF.(初二)
2、已知:如图,P是正方形ABCD内点,∠PAD=∠PDA=150.
求证:△PBC是正三角形.(初二)
3、如图,已知四边形ABCD、A1B1C1D1都是正方形,A2、B2、C2、D2分别是AA1、BB1、CC1、DD1的中点.
2、设MN是圆O外一直线,过O作OA⊥MN于A,自A引圆的两条直线,交圆于B、C及D、E,直线EB及CD分别交MN于P、Q.
求证:AP=AQ.(初二)
3、如果上题把直线MN由圆外平移至圆内,则由此可得以下命题:
设MN是圆O的弦,过MN的中点A任作两弦BC、DE,设CD、EB分别交MN于P、Q.
求证:AP=AQ.(初二)
经典难题(四)
1.顺时针旋转△ABP 600,连接PQ,则△PBQ是正三角形。
可得△PQC是直角三角形。
所以∠APB=1500。
2.作过P点平行于AD的直线,并选一点E,使AE∥DC,BE∥PC.
可以得出∠ABP=∠ADP=∠AEP,可得:
AEBP共圆(一边所对两角相等)。
可得∠BAP=∠BEP=∠BCP,得证。
经典难题(一)
1.如下图做GH⊥AB,连接EO。由于GOFE四点共圆,所以∠GFH=∠OEG,
九年级上册数学难题及其解答

九年级上册数学难题及其解答一、一元二次方程相关(5题)1. 已知关于x的一元二次方程x^2-(2k + 1)x + k^2+k = 0。
- 求证:方程有两个不相等的实数根。
- 若ABC的两边AB、AC的长是这个方程的两个实数根,第三边BC的长为5。
当ABC是等腰三角形时,求k的值。
- 解答:- 对于一元二次方程ax^2+bx + c = 0(a≠0),判别式Δ=b^2-4ac。
在方程x^2-(2k + 1)x + k^2+k = 0中,a = 1,b=-(2k + 1),c=k^2+k。
- Δ=(2k + 1)^2-4(k^2+k)- =4k^2+4k + 1-4k^2-4k- =1>0,所以方程有两个不相等的实数根。
- 由一元二次方程x^2-(2k + 1)x + k^2+k = 0,根据韦达定理x_1+x_2=-(b)/(a),x_1x_2=(c)/(a),可得x_1+x_2=2k + 1,x_1x_2=k^2+k。
- 因为ABC是等腰三角形,BC = 5,设AB=x_1,AC = x_2。
- 当AB=BC = 5或AC = BC = 5时,把x = 5代入方程x^2-(2k + 1)x +k^2+k = 0得:- 25-5(2k + 1)+k^2+k = 0- 25-10k - 5+k^2+k = 0- k^2-9k + 20 = 0- (k - 4)(k - 5)=0- 解得k = 4或k = 5。
- 当k = 4时,原方程为x^2-9x+20 = 0,解得x_1=5,x_2=4,三角形三边为5,5,4,满足三角形三边关系。
- 当k = 5时,原方程为x^2-11x + 30 = 0,解得x_1=5,x_2=6,三角形三边为5,5,6,满足三角形三边关系。
2. 若关于x的一元二次方程mx^2-(3m - 1)x+2m - 1 = 0,其根的判别式的值为1,求m的值及该方程的根。
- 解答:- 对于一元二次方程ax^2+bx + c = 0(a≠0),判别式Δ=b^2-4ac。
初中数学难题精选(附答案)
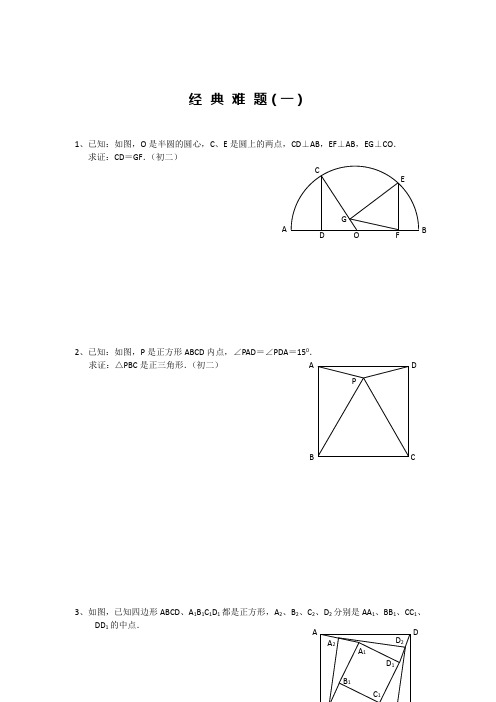
经典难题(一)1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .(初二)2、已知:如图,P 是正方形ABCD 内点,∠PAD =∠PDA =150.求证:△PBC 是正三角形.(初二)3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.A P CDBAFGCE BODD 2 A 2D 1C 1B 1DA A 1求证:四边形A2B2C2D2是正方形.(初二)4、已知:如图,在四边形ABCD中,AD=BC,M、N分别是AB、CD的中点,AD、BC的延长线交MN于E、F.Array求证:∠DEN=∠F.B经典难题(二)1、已知:△ABC中,H为垂心(各边高线的交点),O为外心,且(2)若∠BAC=600,求证:AH=AO.(初二)2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自AD 、E ,直线EB 及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二)3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q .求证:AP =AQ .(初二)F 4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.经典难题(三)1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F . 求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .(初二)3、设P 是正方形ABCD 一边BC 上的任一点,PF ⊥AP ,CF 平分∠DCE .求证:PA =PF .(初二)4、如图,PC 切圆O 于C ,AC 为圆的直径,PEF 为圆的割线,AE 、AF 与直线PO 相交于B 、D .求证:AB =DC ,BC =AD .(初三)经典难题(四)1、已知:△ABC是正三角形,P是三角形内一点,PA=3,PB=4,PC=5.求:∠APB的度数.(初二)Array 2、设P是平行四边形ABCD内部的一点,且∠PBA=∠PDA.求证:∠PAB=∠PCB.(初二)3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD .4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二)经典难题(五)1、设P是边长为1的正△ABC内任一点,L=PA+PB+PC,求证:≤L<2.2、已知:P是边长为1的正方形ABCD内的一点,求PA+PB+PC的最小值.3、P为正方形ABCD内的一点,并且PA=a,PB=2a,PC=3a,求正方形的边长.4、如图,△ABC中,∠ABC=∠ACB=800,D、E分别是AB、ACEBA=200,求∠BED的度数.经典难题(一)1.如下图做GH⊥AB,连接EO。
中考数学经典难题集锦

经典难题(一)1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .(初二)2、已知:如图,P 是正方形ABCD 内点,∠PAD =∠PDA =150. 求证:△PBC 是正三角形.(初二)3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC的延长线交MN 于E 、F .求证:∠DEN =∠F .经典难题(二)A P C DB A F G CE BO D D 2 C 2B 2 A 2D 1 C 1 B 1C B DA A 1 BF1、已知:△ABC 中,H 为垂心(各边高线的交点),O(1)求证:AH =2OM ; (2)若∠BAC =600,求证:AH =AO .(初二)2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 及D 、E ,直线EB及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二)3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q . 求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.经典难1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F . 求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F . 求证:AE =AF .(初二)3、设P 是正方形ABCD 一边BC 上的任一点,PF ⊥AP ,CF 平分∠DCE . 求证:PA =PF .(初二)4、如图,PC 切圆O 于C ,AC 为圆的直径,PEF 为圆的割线,AE 、AF 与直线PO 相交于B 、D .求证:AB =DC ,BC =AD .经典难题(四)1、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,PC =5.求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA . 求证:∠PAB =∠PCB .(初二)3、Ptolemy (托勒密)定理:设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD . (初三)4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二)经典难题(五)1、设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC ,求证:1≤L <中考数学经典难题集锦2.2、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.3、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a4、如图,△ABC 中,∠ABC=∠ACB =800,D 、E 分别是AB 、AC 上的点,∠EBA =200,求∠BED 的度数.。
九年级数学难题精选(有答案)

一、如图,已知抛物线y=﹣x2+bx+c与一直线相交于A(﹣1,0),C(2,3)两点,与y轴交于点N,其顶点为D.(1)抛物线及直线AC的函数关系式;(2)设点M(3,m),求使MN+MD的值最小时m的值;(3)若抛物线的对称轴与直线AC相交于点B,E为直线AC上的任意一点,过点E作EF ∥BD交抛物线于点F,以B,D,E,F为顶点的四边形能否为平行四边形?若能,求点E 的坐标;若不能,请说明理由;(4)若P是抛物线上位于直线AC上方的一个动点,求△APC的面积的最大值.解:(1)由抛物线y=﹣x2+bx+c过点A(﹣1,0)及C(2,3)得,,解得,故抛物线为y=﹣x2+2x+3又设直线为y=kx+n过点A(﹣1,0)及C(2,3)得,解得故直线AC为y=x+1;(2)作N点关于直线x=3的对称点N',则N'(6,3),由(1)得D(1,4),故直线DN'的函数关系式为y=﹣x+,当M(3,m)在直线DN'上时,MN+MD的值最小,则m=﹣×=;(3)由(1)、(2)得D(1,4),B(1,2)∵点E在直线AC上,设E(x,x+1),①当点E在线段AC上时,点F在点E上方,则F(x,x+3),∵F在抛物线上,∴x+3=﹣x2+2x+3,解得,x=0或x=1(舍去)∴E(0,1);②当点E在线段AC(或CA)延长线上时,点F在点E下方,则F(x,x﹣1)由F在抛物线上∴x﹣1=﹣x2+2x+3解得x=或x=∴E(,)或(,)综上,满足条件的点E为E(0,1)、(,)或(,);(4)方法一:过点P作PQ⊥x轴交AC于点Q;过点C作CG⊥x轴于点G,如图1设Q(x,x+1),则P(x,-x2+2x+3)∴PQ=(-x2+2x+3)-(x﹣1)=-x2+x+2又∵S△APC=S△APQ+S△CPQ=PQ·AG=(-x2+x+2)×3=-(x﹣)2+∴面积的最大值为.二、已知:直角梯形OABC中,BC∥OA,∠AOC=90°,以AB为直径的圆M交OC于D、E,连结AD、BD、BE。
初中几何动点最值问题难题集锦

初中几何动点最值问题难题集锦初中几何动点最值问题是初中数学中的一道难题类型。
动点最值问题考察动点在几何形状内运动时,某一量的最大值或最小值的求解方法。
下面是一些初中几何动点最值问题的难题集锦。
1.【问题描述】在一个矩形ABCD中,点P动态地沿着矩形的边移动,求线段AP的最长长度。
【解答】假设矩形ABCD的边长为a和b(a<b),点P动态地沿着矩形的边移动。
我们可以观察到,当点P处于矩形的顶点A或D时,线段AP的长度为a;当点P处于矩形的顶点B或C时,线段AP的长度为b。
因此,线段AP的最长长度为b。
2.【问题描述】在一个圆形O内,点P动态地沿着圆的周长移动,求线段OP的最长长度。
【解答】设圆的半径为r,点P动态地沿着圆的周长移动。
根据三角形的性质,可以知道线段OP的长度最长时,点P应该位于圆的周长上的与点O相对的点,即直径上的点。
因此,线段OP的最长长度为2r。
3.【问题描述】在一个正方形ABCD内,点P动态地沿着正方形的边移动,求线段BP的最长长度。
【解答】设正方形ABCD的边长为a,点P动态地沿着正方形的边移动。
由于线段BP的长度等于点P距离B点的距离,所以线段BP的最长长度为正方形的对角线长度,即√2a。
4.【问题描述】在一个等腰直角三角形ABC中,点P动态地沿着三角形的边移动,求线段AP的最长长度。
【解答】设等腰直角三角形ABC的等腰边长为a,点P动态地沿着三角形的边移动。
可以观察到,当点P处于顶点B或C 时,线段AP的长度为a;当点P处于顶点A时,线段AP的长度为0。
因此,线段AP的最长长度为a。
5.【问题描述】在一个梯形ABCD中,点P动态地沿着梯形的边移动,求线段CP的最长长度。
【解答】设梯形ABCD的上底长为a,下底长为b(a>b),点P动态地沿着梯形的边移动。
可以观察到,当点P处于梯形的底端点C或顶端点D时,线段CP的长度为0;当点P处于梯形的上底端点A时,线段CP的长度为ab。
(完整)初中数学难题集锦

.(9分)如图8,禁渔期间,我渔政船在A处发现正北方向B处有一艘可疑船只,测得A,B两处距离为200海里,可疑船只正沿南偏东45°方向航行.我渔政船迅速沿北偏东30°方向前去拦截,经历4小时刚好在C处将可疑船只拦截.求该可疑船只航行的平均速度(结果保留根号).如图,禁止捕鱼期间,某海上稽查队在某海域巡逻,上午某一时刻在A处接到指挥部通知,在他们东北方向距离12海里的B处有一艘捕鱼船,正在沿南偏东75°方向以每小时10海里的速度航行,稽查队员立即乘坐巡逻船以每小时14海里的速度沿北偏东某一方向出发,在C处成功拦截捕鱼船,求巡逻船从出发到成功拦截捕鱼船所用的时间.10.(2016南充)如图,正五边形的边长为2,连接对角线AD,BE,C E,线段AD分别与B E和C E相交于点M,N.给出下列结论:①∠AM E=108°;②A N2=AM·AD;③;④.其中正确结论的个数是()A.1个B.2个C.3个D.4个[2015·四川南充]关于x的一元二次方程x2+2mx+2n=0有两个整数根且乘积为正,关于y 的一元二次方程y2+2ny+2m=0同样也有两个整数根且乘积为正,给出三个结论:①这两个方程的根都负根;②(m﹣1)2+(n﹣1)2≥2;③﹣1≤2m﹣2n≤1,其中正确结论的个数是()A. 0个B. 1个C. 2个D. 3个解:①两个整数根且乘积为正,两个根同号,由韦达定理有,x1•x2=2n>0,y1•y2=2m>0,y1+y2=﹣2n<0,x1+x2=﹣2m<0,这两个方程的根都为负根,①正确;②由根判别式有:△=b2﹣4ac=4m2﹣8n≥0,△=b2﹣4ac=4n2﹣8m≥0,∵4m2﹣8n≥0,4n2﹣8m≥0,∴m2﹣2n≥0,n2﹣2m≥0,m2﹣2m+1+n2﹣2n+1=m2﹣2n+n2﹣2m+2≥2,(m﹣1)2+(n﹣1)2≥2,②正确;③由根与系数关系可得2m﹣2n=y1y2+y1+y2=(y1+1)(y2+1)﹣1,由y1、y2均为负整数,故(y1+1)•(y2+1)≥0,故2m﹣2n≥﹣1,同理可得:2n﹣2m=x1x2+x1+x2=(x1+1)(x2+1)﹣1,得2n﹣2m≥﹣1,即2m﹣2n≤1,故③正确.[2015·四川南充]如图,正方形ABCD的边长为1,以AB为直径作半圆,点P是CD中点,BP与半圆交于点Q,连结PQ,给出如下结论:①DQ=1;②=;③S△PDQ=;④cos∠ADQ=,其中正确结论是(填写序号)解:正确结论是①②④.提示:①连接OQ,OD,如图1.易证四边形DOBP是平行四边形,从而可得DO∥BP.结合OQ=OB,可证到∠AOD=∠QOD,从而证到△AOD≌△QOD,则有DQ=DA=1.故①正确;②连接AQ,如图2.则有CP=,BP==.易证Rt△AQB∽Rt△BCP,运用相似三角形的性质可求得BQ=,则PQ=﹣=,∴=.故②正确;③过点Q作QH⊥DC于H,如图3.易证△PHQ∽△PCB,运用相似三角形的性质可求得QH=,∴S△DPQ=DP•QH=××=.故③错误;④过点Q作QN⊥AD于N,如图4.易得DP∥NQ∥AB,根据平行线分线段成比例可得==,则有=,解得:DN=.由DQ=1,得cos∠ADQ==.故④正确.综上所述:正确结论是①②④.(2014?天津)已知二次函数y=ax2+bx+c(a≠0)的图象如图,且关于x的一元二次方程ax2+bx+c-m=0没有实数根,有下列结论:①b2-4ac>0;②abc<0;③m>2.其中,正确结论的个数是()A.0B.1C.2D.3••①∵二次函数y=ax2+bx+c与x轴有两个交点,∴b2-4ac>0,故①正确;②∵抛物线的开口向下,∴a<0,∵抛物线与y轴交于正半轴,∴c>0,∵对称轴x=-b2a•>0,∴ab<0,∵a<0,∴b>0,∴abc<0,故②正确;③∵一元二次方程ax2+bx+c-m=0没有实数根,∴y=ax2+bx+c和y=m没有交点,由图可得,m>2,故③正确.故选:D..(2015•四川攀枝花第10题3分)如图,在菱形ABCD中,AB=BD,点E、F分别是AB、AD上任意的点(不与端点重合),且AE=DF,连接BF与DE相交于点G,连接CG与BD相交于点H.给出如下几个结论:①△AED≌△DFB;②S四边形BCDG=CG2;③若AF=2DF,则BG=6GF;④CG与BD一定不垂直;⑤∠BGE的大小为定值.其中正确的结论个数为()解答:解:①∵ABCD为菱形,∴AB=AD,∵AB=BD,∴△ABD为等边三角形,∴∠A=∠BDF=60°,又∵AE=DF,AD=BD,∴△AED≌△DFB,故本选项正确;②∵∠BGE=∠BDG+∠DBF=∠BDG+∠GDF=60°=∠BCD,即∠BGD+∠BCD=180°,∴点B、C、D、G四点共圆,∴∠BGC=∠BDC=60°,∠DGC=∠DBC=60°,∴∠BGC=∠DGC=60°,过点C作CM⊥GB于M,CN⊥GD于N(如图1),则△CBM≌△CDN(AAS),∴S四边形BCDG=S四边形CMGN,S四边形CMGN=2S△CMG,∵∠CGM=60°,∴GM=CG,CM=CG,∴S四边形CMGN=2S△CMG=2××CG×CG=CG2,故本选项错误;③过点F作FP∥AE于P点(如图2),∵AF=2FD,∴FP:AE=DF:DA=1:3,∵AE=DF,AB=AD,∴BE=2AE,∴FP:BE=FP:=1:6,∵FP∥AE,∴PF∥BE,∴FG:BG=FP:BE=1:6,即BG=6GF,故本选项正确;④当点E,F分别是AB,AD中点时(如图3),由(1)知,△ABD,△BDC为等边三角形,∵点E,F分别是AB,AD中点,∴∠BDE=∠DBG=30°,∴DG=BG,在△GDC与△BGC中,,∴△GDC≌△BGC,∴∠DCG=∠BCG,∴CH⊥BD,即CG⊥BD,故本选项错误;⑤∵∠BGE=∠BDG+∠DBF=∠BDG+∠GDF=60°,为定值,故本选项正确;综上所述,正确的结论有①③⑤,共3个,故选B.•如图,矩形ABCD的边长AD=3,AB=2,E为AB的中点,F在边BC上,且BF=2FC,AF分别与DE、DB相交于点M,N,则MN的长为()A.B.C.D.•B【考点】相似三角形的判定与性质;矩形的性质.【分析】过F作FH⊥AD于H,交ED于O,于是得到FH=AB=2,根据勾股定理得到AF===2,根据平行线分线段成比例定理得到OH=AE=,由相似三角形的性质得到= =,求得AM=AF=,根据相似三角形的性质得到==,求得AN=AF=,即可得到结论.【解答】解:过F作FH⊥AD于H,交ED于O,则FH=AB=2∵BF=2FC,BC=AD=3,∴BF=AH=2,FC=HD=1,∴AF===2,∵OH∥AE,∴==,∴OH=AE=,∴OF=FH﹣OH=2﹣=,∵AE∥FO,∴△AME∽FMO,∴==,∴AM=AF=,∵AD∥BF,∴△AND∽△FNB,∴==,∴AN=AF=,∴MN=AN﹣AM=﹣=,故选B.(2014•扬州)已知矩形ABCD的一条边AD=8,将矩形ABCD折叠,使得顶点B落在CD边上的P 点处.(1)如图1,已知折痕与边BC交于点O,连结AP、OP、OA.①求证:△OCP∽△PDA;②若△OCP与△PDA的面积比为1:4,求边AB的长;(2)若图1中的点P恰好是CD边的中点,求∠OAB的度数;(3)如图2,在(1)的条件下擦去折痕AO、线段OP,连结BP.动点M在线段AP上(点M与点P、A不重合),动点N在线段AB的延长线上,且BN=PM,连结MN交PB于点F,作ME⊥BP于点E.试问当点M、N在移动过程中,线段EF的长度是否发生变化?若变化,说明理由;若不变,求出线段EF的长度.24.在数学活动课上,老师要求学生在5×5的正方形ABCD网格中(小正方形的边长为1)画直角三角形,要求三个顶点都在格点上,而且三边与AB或AD都不平行.画四种图形,并直接写出其周长(所画图象相似的只算一种).【考点】作图—相似变换.【分析】在图1中画等腰直角三角形;在图2、3、4中画有一条直角边为,另一条直角边分别为3,4,2的直角三角形,然后计算出四个直角三角形的周长.【解答】解:如图1,三角形的周长=2+;如图2,三角形的周长=4+2;如图3,三角形的周长=5+;如图4,三角形的周长=3+.•如图,在平面直角坐标系中,点O为坐标原点,直线l与抛物线y=mx2+nx相交于A(1,3),B(4,0)两点.(1)求出抛物线的解析式;(2)在坐标轴上是否存在点D,使得△ABD是以线段AB为斜边的直角三角形?若存在,求出点D的坐标;若不存在,说明理由;(3)点P是线段AB上一动点,(点P不与点A、B重合),过点P作PM∥OA,交第一象限内的抛物线于点M,过点M作MC⊥x轴于点C,交AB于点N,若△BCN、△PMN的面积S△BCN、S△PMN满足S△BCN=2S△PMN,求出的值,并求出此时点M的坐标.•【解答】解:(1)∵A(1,3),B(4,0)在抛物线y=mx2+nx的图象上,∴,解得,∴抛物线解析式为y=﹣x2+4x;(2)存在三个点满足题意,理由如下:当点D在x轴上时,如图1,过点A作AD⊥x轴于点D,∵A(1,3),∴D坐标为(1,0);当点D在y轴上时,设D(0,d),则AD2=1+(3﹣d)2,BD2=42+d2,且AB2=(4﹣1)2+(3)2=36,∵△ABD是以AB为斜边的直角三角形,∴AD2+BD2=AB2,即1+(3﹣d)2+42+d2=36,解得d=,∴D点坐标为(0,)或(0,);综上可知存在满足条件的D点,其坐标为(1,0)或(0,)或(0,);(3)如图2,过P作PF⊥CM于点F,∵PM∥OA,∴Rt△ADO∽Rt△MFP,∴==3,∴MF=3PF,在Rt△ABD中,BD=3,AD=3,∴tan∠ABD=,∴∠ABD=60°,设BC=a,则CN=a,在Rt△PFN中,∠PNF=∠BNC=30°,∴tan∠PNF==,∴FN=PF,∴MN=MF+FN=4PF,∵S△BCN=2S△PMN,∴a2=2××4PF2,∴a=2PF,∴NC=a=2PF,∴==,∴MN=NC=×a=a,∴MC=MN+NC=(+)a,∴M点坐标为(4﹣a,( +)a),又M点在抛物线上,代入可得﹣(4﹣a)2+4(4﹣a)=(+)a,解得a=3﹣或a=0(舍去),OC=4﹣a=+1,MC=2+,∴点M的坐标为(+1,2+).•如图,在边长为4的正方形ABCD中,P是BC边上一动点(不含B、C两点),将△ABP沿直线AP翻折,点B落在点E处;在CD上有一点M,使得将△CMP沿直线MP翻折后,点C落在直线PE上的点F处,直线PE交CD于点N,连接MA,NA.则以下结论中正确的有(写出所有正确结论的序号)①△CMP∽△BPA;②四边形AMCB的面积最大值为10;③当P为BC中点时,AE为线段NP的中垂线;④线段AM的最小值为2;⑤当△ABP≌△ADN时,BP=4﹣4.•【解答】解:∵∠APB=∠APE,∠MPC=∠MPN,∵∠CPN+∠NPB=180°,∴2∠NPM+2∠APE=180°,∴∠MPN+∠APE=90°,∴∠APM=90°,∵∠CPM+∠APB=90°,∠APB+∠PAB=90°,∴∠CPM=∠PAB,∵四边形ABCD是正方形,∴AB=CB=DC=AD=4,∠C=∠B=90°,∴△CMP∽△BPA.故①正确,设PB=x,则CP=4﹣x,∵△CMP∽△BPA,∴=,∴CM=x(4﹣x),∴S四边形AMCB= [4+x(4﹣x)]×4=﹣x2+2x+8=﹣(x﹣2)2+10,∴x=2时,四边形AMCB面积最大值为10,故②正确,当PB=PC=PE=2时,设ND=NE=y,在RT△PCN中,(y+2)2=(4﹣y)2+22解得y=,∴NE≠EP,故③错误,作MG⊥AB于G,∵AM==,∴AG最小时AM最小,∵AG=AB﹣BG=AB﹣CM=4﹣x(4﹣x)=(x﹣1)2+3,∴x=1时,AG最小值=3,∴AM的最小值==5,故④错误.∵△ABP≌△ADN时,∴∠PAB=∠DAN=22.5°,在AB上取一点K使得AK=PK,设PB=z,∴∠KPA=∠KAP=22.5°∵∠PKB=∠KPA+∠KAP=45°,∴∠BPK=∠BKP=45°,∴PB=BK=z,AK=PK=z,∴z+z=4,∴z=4﹣4,∴PB=4﹣4故⑤正确.故答案为①②⑤.如图,在Rt△ABC中,,AC的垂直平分线分别与AC,BC及AB的延长线相交于点D,E,F,且.⊙O是△BEF的外接圆,的平分线交EF于点G,交⊙O于点H,连接BD,FH.(1)求证:△ABC≌△EBF;(2)试判断BD与⊙O的位置关系,并说明理由;(3)若,求的值.正确答案为:(1)证明:∵∠ABC=90°,∴∠EBF=90°,∵DF⊥AC,∴∠ADF=90°,∴∠C+∠A=∠A+∠AFD=90°,∴∠C=∠BFE,在△ABC与△EBF中,,∴△ABC≌△EBF;(2)解:BD与⊙O相切,如图1,连接OB ,理由:∵OB=OF,∴∠OBF=∠OFB,∵∠ABC=90°,AD=CD,∴BD=CD,∴∠C=∠DBC,∵∠C=∠B FE,∴∠DBC=∠OBF,∵∠CBO+∠OBF=90°,∴∠DBC+∠CBO=90°,∴∠DBO=90°,∴BD与⊙O相切;(3)如图2,连接CF,HE,∵∠CBF=90°,BC=BF,∴CF=BF,∵DF垂直平分AC,∴AF=CF=AB+BF=1+BF=BF,∴BF=,∵△ABC≌△EBF,∴BE=AB=1,∴EF=,∵BH平分∠CBF,∴∴EH=FH,∴△EHF是等腰直角三角形,∴HF=EF=,∵∠EFH=∠HBF=45°,∠BHF=∠BHF,∴△BHF∽△FHG,∴,∴.。
初三数学难题精选答案及讲解

1、如果将点P 绕定点M 旋转180°后与点Q 重合,那么称点P 与点Q 关于点M 对称,定点M 叫做对称中心。
此时,M 是线段PQ 的中点。
如图,在平面直角坐标系中,△ABO 的顶点A ,B ,O 的坐标分别为(1,0),(0,1),(0,0)。
点列P 1,P 2,P 3,…中的相邻两点都关于△ABO 的一个顶点对称:点P 1与点P 2关于点A 对称,点P 2与点P 3关于点B 对称,点P 3与点P 4关于点O 对称,点P 4与点P 5关于点A 对称,点P 5与点P 6关于点B 对称,点P 6与点P 7关于点O 对称…对称中心分别是A ,B ,O ,A ,B ,O ,…,且这些对称中心依次循环。
已知点P 1的坐标是(1,1),则点P 2017的坐标为 。
解:P 2的坐标是(1,-1),P 2017的坐标是(1,-1)。
理由:作P 1关于A 点的对称点,即可得到P 2(1,-1),P 3(-1,3),P 4(1,-3),P 5(1,3),P 6(-1,-1),又回到原来P 1的坐标,P 7(-1,-1);由此可知,每6个点为一个周期,作一次循环,2017÷6=336…1,循环了336次后又回到了原来P 1的坐标,故P 2017的坐标与P 1的坐标一样为(1,1)。
点评:此题主要考查了平面直角坐标系中中心对称的性质,以及找规律问题,根据已知得出点P 的坐标每6个一循环是解题关键.2、如图①,已知△ABC 是等边三角形,点E 在线段AB 上,点D 在直线BC 上,且DE=EC ,将△BCE 绕点C 顺时针旋转60°至△ACF ,连接EF 。
试证明:AB=DB+AF 。
【类比探究】(1)如图②,如果点E 在线段AB 的延长线上,其它条件不变,线段AB 、DB 、AF 之间又有怎样的数量关系?请说明理由。
(2)如果点E 在线段BA 的延长线上,其他条件不变,请在图③的基础上将图形补充完整,并写出AB ,DB ,AF 之间数量关系,不必说明理由。
初中数学难题精选(附答案)

经典难题(一)1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .(初二)2、已知:如图,P 是正方形ABCD 点,∠PAD =∠PDA =150. 求证:△PBC 是正三角形.(初二)3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC 的延长线交MN 于E 、F .求证:∠DEN =∠F .A P C DB A FG CE B O D D 2 C 2B 2 A 2 D 1C 1 B 1C B DA A 1BF经典难题(二)1、已知:△ABC 中,H 为垂心(各边高线的交点),O 为外心,且OM ⊥BC 于M . (1)求证:AH =2OM ; (2)若∠BAC =600,求证:AH =AO .(初二)2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 引圆的两条直线,交圆于B 、C 与D 、E ,直线EB 与CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二)3、如果上题把直线MN 由圆外平移至圆,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q . 求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.经典难题(三)1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .(初二)3、设P 是正方形ABCD 一边BC 上的任一点,PF ⊥AP ,CF 平分∠DCE .求证:PA =PF .(初二)4、如图,PC 切圆O 于C ,AC 为圆的直径,PEF 为圆的割线,AE 、AF 与直线PO 相交于B 、D .求证:AB =DC ,BC =AD .(初三)经典难题(四)1、已知:△ABC 是正三角形,P 是三角形一点,PA =3,PB =4,PC =5.求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 部的一点,且∠PBA =∠PDA . 求证:∠PAB =∠PCB .(初二)3、设ABCD 为圆接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD .(初三)4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二)经典难题(五)1、设P 是边长为1的正△ABC 任一点,L =PA +PB +PC ,求证:≤L <2.2、已知:P 是边长为1的正方形ABCD 的一点,求PA +PB +PC 的最小值.3、P 为正方形ABCD 的一点,并且PA =a ,PB =2a ,PC =3a ,求正方形的边长.APCB ACBPDA CBPD4、如图,△ABC中,∠ABC=∠ACB=800,D、E分别是AB、AC DCA=300,∠EBA =200,求∠BED的度数.经典难题(一)1.如下图做GH⊥AB,连接EO。
初三数学超难试题及答案

初三数学超难试题及答案一、选择题(每题3分,共30分)1. 下列哪个选项是二次函数的一般形式?A. y = ax^2 + bx + cB. y = ax^3 + bx^2 + cx + dC. y = ax^2 + bx + c + dD. y = ax^2 + bx + c - d答案:A2. 如果一个圆的半径为5,那么它的面积是多少?A. 25πB. 50πC. 75πD. 100π答案:B3. 一个等腰三角形的两边长分别为6和8,那么它的周长是多少?A. 20B. 22C. 24D. 26答案:C4. 以下哪个选项是不等式x > 2的解?A. x = 1B. x = 2C. x = 3D. x = 0答案:C5. 一个数的平方根是它本身的数是?A. 0B. 1C. -1D. 以上都是答案:D6. 一个三角形的内角和是多少度?A. 90°B. 180°C. 270°D. 360°答案:B7. 以下哪个选项是方程2x - 3 = 7的解?A. x = 5B. x = 3C. x = 2D. x = 4答案:A8. 一个正数的倒数是?A. 比它小的数B. 比它大的数C. 0D. 1除以这个数答案:D9. 以下哪个选项是方程x^2 - 5x + 6 = 0的解?A. x = 2B. x = 3C. x = 6D. x = 9答案:A10. 一个数的立方根是它本身的数是?A. 0B. 1C. -1D. 以上都是答案:D二、填空题(每题4分,共20分)11. 一个数的绝对值是它本身,那么这个数是______。
答案:非负数12. 如果一个角的补角是120°,那么这个角是______。
答案:60°13. 一个数的相反数是-5,那么这个数是______。
答案:514. 一个直角三角形的两直角边长分别为3和4,那么它的斜边长是______。
答案:515. 如果一个数的平方是25,那么这个数是______。
(易错题精选)初中数学图形的相似难题汇编

(易错题精选)初中数学图形的相似难题汇编一、选择题1.已知正方形ABCD的边长为5,E在BC边上运动,DE的中点G,EG绕E顺时针旋转90°得EF,问CE为多少时A、C、F在一条直线上()A.35B.43C.53D.34【答案】C【解析】【分析】首先延长BC,做FN⊥BC,构造直角三角形,利用三角形相似的判定,得出Rt△FNE∽Rt△ECD,再利用相似比得出12.52NE CD==,运用正方形性质,得出△CNF是等腰直角三角形,从而求出CE.【详解】解:过F作BC的垂线,交BC延长线于N点,∵∠DCE=∠ENF=90°,∠DEC+∠NEF=90°,∠NEF+∠EFN=90°,∴∠DEC=∠EFN,∴Rt△FNE∽Rt△ECD,∵DE的中点G,EG绕E顺时针旋转90°得EF,∴两三角形相似比为1:2,∴可以得到CE=2NF,12.52NE CD==∵AC平分正方形直角,∴∠NFC=45°,∴△CNF是等腰直角三角形,∴CN=NF,∴2255.3323 CE NE==⨯=故选C.【点睛】此题主要考查了旋转的性质与正方形的性质以及相似三角形的判定等知识,求线段的长度经常运用相似三角形的知识解决,同学们应学会这种方法.2.如果两个相似正五边形的边长比为1:10,则它们的面积比为()A .1:2B .1:5C .1:100D .1:10【答案】C【解析】 根据相似多边形的面积比等于相似比的平方,由两个相似正五边形的相似比是1:10,可知它们的面积为1:100.故选:C .点睛:此题主要考查了相似三角形的性质:相似三角形的面积比等于相似比的平方.3.如图,四边形ABCD 内接于O e ,AB 为直径,AD CD =,过点D 作DE AB ⊥于点E ,连接AC 交DE 于点F .若3sin 5CAB ∠=,5DF =,则AB 的长为( )A .10B .12C .16D .20【答案】D【解析】【分析】 连接BD ,如图,先利用圆周角定理证明ADE DAC ∠=∠得到5FD FA ==,再根据正弦的定义计算出3EF =,则4AE =,8DE =,接着证明ADE DBE ∆∆∽,利用相似比得到16BE =,所以20AB =.【详解】解:连接BD ,如图,AB Q 为直径,90ADB ACB ∴∠=∠=︒,AD CD =Q ,DAC DCA ∴∠=∠,而DCA ABD ∠=∠,DAC ABD ∴∠=∠,DE AB ∵⊥,90ABD BDE ∴∠+∠=︒,而90ADE BDE ∠+∠=︒,ABD ADE ∴∠=∠,ADE DAC ∴∠=∠,5FD FA ∴==,在Rt AEF ∆中,3sin 5EF CAB AF ∠==Q , 3EF ∴=, 22534AE ∴=-=,538DE =+=, ADE DBE ∠=∠Q ,AED BED ∠=∠,ADE DBE ∴∆∆∽,::DE BE AE DE ∴=,即8:4:8BE =,16BE ∴=,41620AB ∴=+=.故选:D .【点睛】本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.推论:半圆(或直径)所对的圆周角是直角,90︒的圆周角所对的弦是直径.也考查了解直角三角形.4.如图,在x 轴的上方,直角∠BOA 绕原点O 按顺时针方向旋转.若∠BOA 的两边分别与函数1y x=-、2y x =的图象交于B 、A 两点,则∠OAB 大小的变化趋势为( )A .逐渐变小B .逐渐变大C .时大时小D .保持不变【答案】D【解析】【分析】 如图,作辅助线;首先证明△BEO ∽△OFA ,,得到BE OE OF AF =;设B 为(a ,1a-),A 为(b ,2b ),得到OE=-a ,EB=1a-,OF=b ,AF=2b ,进而得到222a b =,此为解决问题的关键性结论;运用三角函数的定义证明知tan ∠2为定值,即可解决问题.【详解】解:分别过B和A作BE⊥x轴于点E,AF⊥x轴于点F,则△BEO∽△OFA,∴BE OE OF AF=,设点B为(a,1 a-),A为(b,2b),则OE=-a,EB=1a-,OF=b,AF=2b,可代入比例式求得222a b=,即222ab=,根据勾股定理可得:OB=22221OE EB aa+=+,OA=22224OF AF bb+=+,∴tan∠OAB=2222222212244baOB a bOAb bb b++==++=222214()24bbbb++=22∴∠OAB大小是一个定值,因此∠OAB的大小保持不变.故选D【点睛】该题主要考查了反比例函数图象上点的坐标特征、相似三角形的判定等知识点及其应用问题;解题的方法是作辅助线,将分散的条件集中;解题的关键是灵活运用相似三角形的判定等知识点来分析、判断、推理或解答.5.如图所示,在正方形ABCD中,G为CD边中点,连接AG并延长交BC边的延长线于E 点,对角线BD交AG于F点.已知FG=2,则线段AE的长度为()A.6 B.8 C.10 D.12【答案】D【解析】分析:根据正方形的性质可得出AB∥CD,进而可得出△ABF∽△GDF,根据相似三角形的性质可得出AF ABGF GD==2,结合FG=2可求出AF、AG的长度,由CG∥AB、AB=2CG可得出CG为△EAB的中位线,再利用三角形中位线的性质可求出AE的长度,此题得解.详解:∵四边形ABCD为正方形,∴AB=CD,AB∥CD,∴∠ABF=∠GDF,∠BAF=∠DGF,∴△ABF∽△GDF,∴AF ABGF GD==2,∴AF=2GF=4,∴AG=6.∵CG∥AB,AB=2CG,∴CG为△EAB的中位线,∴AE=2AG=12.故选D.点睛:本题考查了相似三角形的判定与性质、正方形的性质以及三角形的中位线,利用相似三角形的性质求出AF的长度是解题的关键.6.如图,正方形OABC的边长为6,D为AB中点,OB交CD于点Q,Q是y=kx上一点,k的值是()A.4 B.8 C.16 D.24【答案】C【解析】【分析】延长根据相似三角形得到:1:2BQ OQ =,再过点Q 作垂线,利用相似三角形的性质求出QF 、OF ,进而确定点Q 的坐标,确定k 的值.【详解】解:过点Q 作QF OA ⊥,垂足为F ,OABC Q 是正方形,6OA AB BC OC ∴====,90ABC OAB DAE ∠=∠=︒=∠,D Q 是AB 的中点,12BD AB ∴=, //BD OC Q ,OCQ BDQ ∴∆∆∽, ∴12BQ BD OQ OC ==, 又//QF AB Q ,OFQ OAB ∴∆∆∽, ∴22213QF OF OQ AB OA OB ====+, 6AB =Q , 2643QF ∴=⨯=,2643OF =⨯=, (4,4)Q ∴,Q 点Q 在反比例函数的图象上,4416k ∴=⨯=,故选:C .【点睛】本题考查了待定系数法求反比例函数、相似三角形的性质和判定,利用相似三角形性质求出点Q 的坐标是解决问题的关键.7.如图,点A在双曲线y═kx(x>0)上,过点A作AB⊥x轴,垂足为点B,分别以点O和点A为圆心,大于12OA的长为半径作弧,两弧相交于D,E两点,作直线DE交x轴于点C,交y轴于点F(0,2),连接AC.若AC=1,则k的值为()A.2 B.3225C.43D.252+【答案】B【解析】分析:如图,设OA交CF于K.利用面积法求出OA的长,再利用相似三角形的性质求出AB、OB即可解决问题;详解:如图,设OA交CF于K.由作图可知,CF垂直平分线段OA,∴OC=CA=1,OK=AK,在Rt△OFC中,22=5OF OC+∴255,∴OA=455,由△FOC∽△OBA,可得OF OC CFOB AB OA==,∴215455 OB AB==,∴OB=85,AB=45,∴A(85,45),∴k=32 25.故选B.点睛:本题考查作图-复杂作图,反比例函数图象上的点的坐标特征,线段的垂直平分线的性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.8.如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上.已知纸板的两条直角边40DE cm=,20EF cm=,测得边DF离地面的高度 1.5AC m=,8CD m=,则树高AB是()A.4米B.4.5米C.5米D.5.5米【答案】D【解析】【分析】利用直角三角形DEF和直角三角形BCD相似求得BC的长后加上小明的身高即可求得树高AB.【详解】解:∵∠DEF=∠BCD-90°∠D=∠D∴△ADEF∽△DCB∴BC DC EF DE=∴DE=40cm=0.4m,EF-20cm=0.2m,AC-1.5m,CD=8m∴80.20.4BC=解得:BC=4∴AB=AC+BC=1.5+4=5.5米故答案为:5.5.【点睛】本题考查了相似三角形的应用,解题的关键是从实际问题中整理出相似三角形的模型。
初中数学难题试题及答案

初中数学难题试题及答案1. 已知函数f(x) = 2x^2 - 4x + 3,求f(x)的最小值。
答案:首先求导数f'(x) = 4x - 4,令f'(x) = 0,解得x = 1。
将x = 1代入原函数,得到f(1) = 2(1)^2 - 4(1) + 3 = 1。
因此,f(x)的最小值为1。
2. 一个数列的前三项为1, 2, 3,从第四项开始,每一项是前三项的和。
求数列的第10项。
答案:数列的前几项为1, 2, 3, 6, 11, 20, 37, 68, 125, 230。
因此,数列的第10项为230。
3. 一个圆的半径为5,求圆内接正方形的面积。
答案:圆内接正方形的对角线等于圆的直径,即10。
设正方形的边长为a,则对角线与边长的关系为a^2 + a^2 = 10^2,解得a = 5√2。
因此,正方形的面积为(5√2)^2 = 50。
4. 已知三角形ABC中,∠A = 30°,∠B = 45°,求∠C的度数。
答案:根据三角形内角和定理,三角形的内角和为180°。
因此,∠C = 180° - ∠A - ∠B = 180° - 30° - 45° = 105°。
5. 计算(2x - 3)(x + 4)的展开式。
答案:根据多项式乘法法则,(2x - 3)(x + 4) = 2x^2 + 8x - 3x - 12 = 2x^2 + 5x - 12。
6. 一个长方体的长、宽、高分别为2cm、3cm和4cm,求其体积。
答案:长方体的体积计算公式为V = 长× 宽× 高,所以V = 2cm × 3cm × 4cm = 24cm³。
7. 一个等差数列的前三项为2, 5, 8,求第10项。
答案:等差数列的通项公式为an = a1 + (n - 1)d,其中a1为首项,d为公差。
(完整)初中数学难题集锦

.(9分)如图8,禁渔期间,我渔政船在A处发现正北方向B处有一艘可疑船只,测得A,B两处距离为200海里,可疑船只正沿南偏东45°方向航行.我渔政船迅速沿北偏东30°方向前去拦截,经历4小时刚好在C处将可疑船只拦截.求该可疑船只航行的平均速度(结果保留根号).如图,禁止捕鱼期间,某海上稽查队在某海域巡逻,上午某一时刻在A处接到指挥部通知,在他们东北方向距离12海里的B处有一艘捕鱼船,正在沿南偏东75°方向以每小时10海里的速度航行,稽查队员立即乘坐巡逻船以每小时14海里的速度沿北偏东某一方向出发,在C处成功拦截捕鱼船,求巡逻船从出发到成功拦截捕鱼船所用的时间.10.(2016南充)如图,正五边形的边长为2,连接对角线AD,BE,C E,线段AD分别与B E和C E相交于点M,N.给出下列结论:①∠AM E=108°;②A N2=AM·AD;③;④.其中正确结论的个数是()A.1个B.2个C.3个D.4个[2015·四川南充]关于x的一元二次方程x2+2mx+2n=0有两个整数根且乘积为正,关于y 的一元二次方程y2+2ny+2m=0同样也有两个整数根且乘积为正,给出三个结论:①这两个方程的根都负根;②(m﹣1)2+(n﹣1)2≥2;③﹣1≤2m﹣2n≤1,其中正确结论的个数是()A. 0个B. 1个C. 2个D. 3个解:①两个整数根且乘积为正,两个根同号,由韦达定理有,x1•x2=2n>0,y1•y2=2m>0,y1+y2=﹣2n<0,x1+x2=﹣2m<0,这两个方程的根都为负根,①正确;②由根判别式有:△=b2﹣4ac=4m2﹣8n≥0,△=b2﹣4ac=4n2﹣8m≥0,∵4m2﹣8n≥0,4n2﹣8m≥0,∴m2﹣2n≥0,n2﹣2m≥0,m2﹣2m+1+n2﹣2n+1=m2﹣2n+n2﹣2m+2≥2,(m﹣1)2+(n﹣1)2≥2,②正确;③由根与系数关系可得2m﹣2n=y1y2+y1+y2=(y1+1)(y2+1)﹣1,由y1、y2均为负整数,故(y1+1)•(y2+1)≥0,故2m﹣2n≥﹣1,同理可得:2n﹣2m=x1x2+x1+x2=(x1+1)(x2+1)﹣1,得2n﹣2m≥﹣1,即2m﹣2n≤1,故③正确.[2015·四川南充]如图,正方形ABCD的边长为1,以AB为直径作半圆,点P是CD中点,BP与半圆交于点Q,连结PQ,给出如下结论:①DQ=1;②=;③S△PDQ=;④cos∠ADQ=,其中正确结论是(填写序号)解:正确结论是①②④.提示:①连接OQ,OD,如图1.易证四边形DOBP是平行四边形,从而可得DO∥BP.结合OQ=OB,可证到∠AOD=∠QOD,从而证到△AOD≌△QOD,则有DQ=DA=1.故①正确;②连接AQ,如图2.则有CP=,BP==.易证Rt△AQB∽Rt△BCP,运用相似三角形的性质可求得BQ=,则PQ=﹣=,∴=.故②正确;③过点Q作QH⊥DC于H,如图3.易证△PHQ∽△PCB,运用相似三角形的性质可求得QH=,∴S△DPQ=DP•QH=××=.故③错误;④过点Q作QN⊥AD于N,如图4.易得DP∥NQ∥AB,根据平行线分线段成比例可得==,则有=,解得:DN=.由DQ=1,得cos∠ADQ==.故④正确.综上所述:正确结论是①②④.(2014?天津)已知二次函数y=ax2+bx+c(a≠0)的图象如图,且关于x的一元二次方程ax2+bx+c-m=0没有实数根,有下列结论:①b2-4ac>0;②abc<0;③m>2.其中,正确结论的个数是()A.0B.1C.2D.3••①∵二次函数y=ax2+bx+c与x轴有两个交点,∴b2-4ac>0,故①正确;②∵抛物线的开口向下,∴a<0,∵抛物线与y轴交于正半轴,∴c>0,∵对称轴x=-b2a•>0,∴ab<0,∵a<0,∴b>0,∴abc<0,故②正确;③∵一元二次方程ax2+bx+c-m=0没有实数根,∴y=ax2+bx+c和y=m没有交点,由图可得,m>2,故③正确.故选:D..(2015•四川攀枝花第10题3分)如图,在菱形ABCD中,AB=BD,点E、F分别是AB、AD上任意的点(不与端点重合),且AE=DF,连接BF与DE相交于点G,连接CG与BD相交于点H.给出如下几个结论:①△AED≌△DFB;②S四边形BCDG=CG2;③若AF=2DF,则BG=6GF;④CG与BD一定不垂直;⑤∠BGE的大小为定值.其中正确的结论个数为()解答:解:①∵ABCD为菱形,∴AB=AD,∵AB=BD,∴△ABD为等边三角形,∴∠A=∠BDF=60°,又∵AE=DF,AD=BD,∴△AED≌△DFB,故本选项正确;②∵∠BGE=∠BDG+∠DBF=∠BDG+∠GDF=60°=∠BCD,即∠BGD+∠BCD=180°,∴点B、C、D、G四点共圆,∴∠BGC=∠BDC=60°,∠DGC=∠DBC=60°,∴∠BGC=∠DGC=60°,过点C作CM⊥GB于M,CN⊥GD于N(如图1),则△CBM≌△CDN(AAS),∴S四边形BCDG=S四边形CMGN,S四边形CMGN=2S△CMG,∵∠CGM=60°,∴GM=CG,CM=CG,∴S四边形CMGN=2S△CMG=2××CG×CG=CG2,故本选项错误;③过点F作FP∥AE于P点(如图2),∵AF=2FD,∴FP:AE=DF:DA=1:3,∵AE=DF,AB=AD,∴BE=2AE,∴FP:BE=FP:=1:6,∵FP∥AE,∴PF∥BE,∴FG:BG=FP:BE=1:6,即BG=6GF,故本选项正确;④当点E,F分别是AB,AD中点时(如图3),由(1)知,△ABD,△BDC为等边三角形,∵点E,F分别是AB,AD中点,∴∠BDE=∠DBG=30°,∴DG=BG,在△GDC与△BGC中,,∴△GDC≌△BGC,∴∠DCG=∠BCG,∴CH⊥BD,即CG⊥BD,故本选项错误;⑤∵∠BGE=∠BDG+∠DBF=∠BDG+∠GDF=60°,为定值,故本选项正确;综上所述,正确的结论有①③⑤,共3个,故选B.•如图,矩形ABCD的边长AD=3,AB=2,E为AB的中点,F在边BC上,且BF=2FC,AF分别与DE、DB相交于点M,N,则MN的长为()A.B.C.D.•B【考点】相似三角形的判定与性质;矩形的性质.【分析】过F作FH⊥AD于H,交ED于O,于是得到FH=AB=2,根据勾股定理得到AF===2,根据平行线分线段成比例定理得到OH=AE=,由相似三角形的性质得到= =,求得AM=AF=,根据相似三角形的性质得到==,求得AN=AF=,即可得到结论.【解答】解:过F作FH⊥AD于H,交ED于O,则FH=AB=2∵BF=2FC,BC=AD=3,∴BF=AH=2,FC=HD=1,∴AF===2,∵OH∥AE,∴==,∴OH=AE=,∴OF=FH﹣OH=2﹣=,∵AE∥FO,∴△AME∽FMO,∴==,∴AM=AF=,∵AD∥BF,∴△AND∽△FNB,∴==,∴AN=AF=,∴MN=AN﹣AM=﹣=,故选B.(2014•扬州)已知矩形ABCD的一条边AD=8,将矩形ABCD折叠,使得顶点B落在CD边上的P 点处.(1)如图1,已知折痕与边BC交于点O,连结AP、OP、OA.①求证:△OCP∽△PDA;②若△OCP与△PDA的面积比为1:4,求边AB的长;(2)若图1中的点P恰好是CD边的中点,求∠OAB的度数;(3)如图2,在(1)的条件下擦去折痕AO、线段OP,连结BP.动点M在线段AP上(点M与点P、A不重合),动点N在线段AB的延长线上,且BN=PM,连结MN交PB于点F,作ME⊥BP于点E.试问当点M、N在移动过程中,线段EF的长度是否发生变化?若变化,说明理由;若不变,求出线段EF的长度.24.在数学活动课上,老师要求学生在5×5的正方形ABCD网格中(小正方形的边长为1)画直角三角形,要求三个顶点都在格点上,而且三边与AB或AD都不平行.画四种图形,并直接写出其周长(所画图象相似的只算一种).【考点】作图—相似变换.【分析】在图1中画等腰直角三角形;在图2、3、4中画有一条直角边为,另一条直角边分别为3,4,2的直角三角形,然后计算出四个直角三角形的周长.【解答】解:如图1,三角形的周长=2+;如图2,三角形的周长=4+2;如图3,三角形的周长=5+;如图4,三角形的周长=3+.•如图,在平面直角坐标系中,点O为坐标原点,直线l与抛物线y=mx2+nx相交于A(1,3),B(4,0)两点.(1)求出抛物线的解析式;(2)在坐标轴上是否存在点D,使得△ABD是以线段AB为斜边的直角三角形?若存在,求出点D的坐标;若不存在,说明理由;(3)点P是线段AB上一动点,(点P不与点A、B重合),过点P作PM∥OA,交第一象限内的抛物线于点M,过点M作MC⊥x轴于点C,交AB于点N,若△BCN、△PMN的面积S△BCN、S△PMN满足S△BCN=2S△PMN,求出的值,并求出此时点M的坐标.•【解答】解:(1)∵A(1,3),B(4,0)在抛物线y=mx2+nx的图象上,∴,解得,∴抛物线解析式为y=﹣x2+4x;(2)存在三个点满足题意,理由如下:当点D在x轴上时,如图1,过点A作AD⊥x轴于点D,∵A(1,3),∴D坐标为(1,0);当点D在y轴上时,设D(0,d),则AD2=1+(3﹣d)2,BD2=42+d2,且AB2=(4﹣1)2+(3)2=36,∵△ABD是以AB为斜边的直角三角形,∴AD2+BD2=AB2,即1+(3﹣d)2+42+d2=36,解得d=,∴D点坐标为(0,)或(0,);综上可知存在满足条件的D点,其坐标为(1,0)或(0,)或(0,);(3)如图2,过P作PF⊥CM于点F,∵PM∥OA,∴Rt△ADO∽Rt△MFP,∴==3,∴MF=3PF,在Rt△ABD中,BD=3,AD=3,∴tan∠ABD=,∴∠ABD=60°,设BC=a,则CN=a,在Rt△PFN中,∠PNF=∠BNC=30°,∴tan∠PNF==,∴FN=PF,∴MN=MF+FN=4PF,∵S△BCN=2S△PMN,∴a2=2××4PF2,∴a=2PF,∴NC=a=2PF,∴==,∴MN=NC=×a=a,∴MC=MN+NC=(+)a,∴M点坐标为(4﹣a,( +)a),又M点在抛物线上,代入可得﹣(4﹣a)2+4(4﹣a)=(+)a,解得a=3﹣或a=0(舍去),OC=4﹣a=+1,MC=2+,∴点M的坐标为(+1,2+).•如图,在边长为4的正方形ABCD中,P是BC边上一动点(不含B、C两点),将△ABP沿直线AP翻折,点B落在点E处;在CD上有一点M,使得将△CMP沿直线MP翻折后,点C落在直线PE上的点F处,直线PE交CD于点N,连接MA,NA.则以下结论中正确的有(写出所有正确结论的序号)①△CMP∽△BPA;②四边形AMCB的面积最大值为10;③当P为BC中点时,AE为线段NP的中垂线;④线段AM的最小值为2;⑤当△ABP≌△ADN时,BP=4﹣4.•【解答】解:∵∠APB=∠APE,∠MPC=∠MPN,∵∠CPN+∠NPB=180°,∴2∠NPM+2∠APE=180°,∴∠MPN+∠APE=90°,∴∠APM=90°,∵∠CPM+∠APB=90°,∠APB+∠PAB=90°,∴∠CPM=∠PAB,∵四边形ABCD是正方形,∴AB=CB=DC=AD=4,∠C=∠B=90°,∴△CMP∽△BPA.故①正确,设PB=x,则CP=4﹣x,∵△CMP∽△BPA,∴=,∴CM=x(4﹣x),∴S四边形AMCB= [4+x(4﹣x)]×4=﹣x2+2x+8=﹣(x﹣2)2+10,∴x=2时,四边形AMCB面积最大值为10,故②正确,当PB=PC=PE=2时,设ND=NE=y,在RT△PCN中,(y+2)2=(4﹣y)2+22解得y=,∴NE≠EP,故③错误,作MG⊥AB于G,∵AM==,∴AG最小时AM最小,∵AG=AB﹣BG=AB﹣CM=4﹣x(4﹣x)=(x﹣1)2+3,∴x=1时,AG最小值=3,∴AM的最小值==5,故④错误.∵△ABP≌△ADN时,∴∠PAB=∠DAN=22.5°,在AB上取一点K使得AK=PK,设PB=z,∴∠KPA=∠KAP=22.5°∵∠PKB=∠KPA+∠KAP=45°,∴∠BPK=∠BKP=45°,∴PB=BK=z,AK=PK=z,∴z+z=4,∴z=4﹣4,∴PB=4﹣4故⑤正确.故答案为①②⑤.如图,在Rt△ABC中,,AC的垂直平分线分别与AC,BC及AB的延长线相交于点D,E,F,且.⊙O是△BEF的外接圆,的平分线交EF于点G,交⊙O于点H,连接BD,FH.(1)求证:△ABC≌△EBF;(2)试判断BD与⊙O的位置关系,并说明理由;(3)若,求的值.正确答案为:(1)证明:∵∠ABC=90°,∴∠EBF=90°,∵DF⊥AC,∴∠ADF=90°,∴∠C+∠A=∠A+∠AFD=90°,∴∠C=∠BFE,在△ABC与△EBF中,,∴△ABC≌△EBF;(2)解:BD与⊙O相切,如图1,连接OB ,理由:∵OB=OF,∴∠OBF=∠OFB,∵∠ABC=90°,AD=CD,∴BD=CD,∴∠C=∠DBC,∵∠C=∠B FE,∴∠DBC=∠OBF,∵∠CBO+∠OBF=90°,∴∠DBC+∠CBO=90°,∴∠DBO=90°,∴BD与⊙O相切;(3)如图2,连接CF,HE,∵∠CBF=90°,BC=BF,∴CF=BF,∵DF垂直平分AC,∴AF=CF=AB+BF=1+BF=BF,∴BF=,∵△ABC≌△EBF,∴BE=AB=1,∴EF=,∵BH平分∠CBF,∴∴EH=FH,∴△EHF是等腰直角三角形,∴HF=EF=,∵∠EFH=∠HBF=45°,∠BHF=∠BHF,∴△BHF∽△FHG,∴,∴.。
中考数学难题汇总

C'E D C B AP D C BAGF E DCB A 1.已知:如图,梯形ABCD 中,AD ∥BC ,90B ∠=︒,4AD AB ==,7BC =,点E 在BC 边上,将△CDE 沿DE 折叠,点C 恰好落在AB 边上的点'C 处.(1)求'C DE ∠的度数; (2)求△'C DE 的面积.2.已知,如图,梯形ABCD 中,AD ∥BC ,∠A =90°,∠C =45°,BE ⊥DC 于E ,BC =5,AD :BC =2:5. 求ED 的长.3在△ABC 中,AC=BC ,∠ACB=90°,AB=6,过点C 作射线CP ∥AB ,在射线CP 上截取CD=2,联结AD ,求AD 的长.4.在梯形ABCD 中,AB ∥CD ,BD ⊥AD ,BC =CD ,∠A =60°,(1)求∠CBD 的度数; (2)求下底AB 的长.5.已知:如图,在□ABCD 中,∠ADC 、∠DAB 的平分线DF 、AE 分别与线段BC 相交于点F 、E ,DF 与AE 相交于点G . (1)求证:AE ⊥DF ;(2)若AD =10,AB =6,AE =4,求DF 的长.6.已知:如图,在直角梯形ABCD 中,AD ∥BC,∠A=90°,∠C=45°,上底AD = 8,AB=12,CD 边的垂直平分线交BC 边于点G ,且交AB 的延长线于点E ,求AE 的长.A BCD GFEDCBA7.如图,在矩形ABCD 中,AB =5,BC =4,将矩形ABCD 翻折,使得点B 落在CD 边上的点E 处,折痕AF 交BC 于点F ,求FC 的长.EDA BC8.已知, 点P 是∠MON 的平分线上的一动点,射线P A 交射线OM 于点A ,将射线P A 绕点P 逆时针 旋转交射线ON 于点B ,且使∠APB +∠MON =180°. (1)利用图1,求证:P A =PB ;(2)若∠MON =60°,OB =2,射线AP 交ON 于点D ,且满足且PBD ABO ∠=∠, 请借助图2补全图形,并求OP 的长.9.(本题满分4分)(1)如图①两个正方形的边长均为3,求三角形DBF 的面积.(2)如图②,正方形ABCD 的边长为3,正方形CEFG 的边长为1, 求三角形DBF 的面积. (3)如图③,正方形ABCD 的边长为a ,正方形CEFG 的边长为b ,求三角形DBF 的面积.从上面计算中你能得到什么结论.图1TNMBPOA 图2TN M B P O AC10.(本小题满分7分) 已知:等边三角形ABC(1) 如图1,P 为等边△ABC 外一点,且∠BPC=120°. 试猜想线段BP 、PC 、AP 之间的数量关系,(2)如图2,P 为等边△ABC 内一点,且∠APD=120求证:PA+PD+PC >BD11.已知:如图,在四边形ABCD 中, AD =B C ,∠A 、∠B 均为锐角.(1) 当∠A=∠B 时,则C D 与A B 的位置关系是CD AB ,大小关系是CD AB ; (2) 当∠A>∠B 时,(1)中C D 与A B 的大小关系是否还成立, 证明你的结论.12.已知:△ABC 和△ADE 都是等腰直角三角形,∠ABC =∠ADE =90°,点M 是CE 的中点,连接BM .(1)如图①,点D 在AB 上,连接DM ,并延长DM 交BC 于点N ,可探究得出BD 与BM 的数量关系为 ;(2)如图②,点D 不在AB 上,(1)中的结论还成立吗?如果成立,请证明;如果不成立,说明理由.CB B D CBA 图①图②C'E D C B AEB CDA 1.已知:如图,梯形ABCD 中,AD ∥BC ,90B ∠=︒,4AD AB ==,7BC =,点E 在BC 边上,将△CDE 沿DE 折叠,点C 恰好落在AB 边上的点'C 处.(1)求'C DE ∠的度数; (2)求△'C DE 的面积. .解:(1) 过点D 作DF BC ⊥于F . ∵ AD BC , 90B ∠=︒, AD AB =, ∴ 四边形ABFD 是正方形.∴4DF BF AB === , 3FC = --------1分 在Rt DFC ∆中,2222435CD DF FC =+=+= ∴ '5C D =∵ AD FD =,90A DFC ∠=∠=︒, 'C D CD = ∴ 'AC D FCD ∆≅∆∴ 'ADC FDC ∠=∠ , '3AC FC == ----------------------------------2分 ∴ ''''90ADF ADC C DF FDC C DF C DC ∠=∠+∠=∠+∠=∠=︒ ∵ 'C DE CDE ∠=∠ ∴ '45C DE ∠=︒-----------------------------3分 (2) 设 EC x = , 则7BE x =- ,'C E x = ∵'3AC = ∴'1BC =在Rt 'BEC ∆中 22(7)1x x -+= 解方程,得 257x = ∴ '11255014722777C DE CDE S S EC DF ∆∆==⋅=⨯⨯== ---------------5分2.已知,如图,梯形ABCD 中,AD ∥BC ,∠A =90°,∠C =45°, BE ⊥DC 于E ,BC =5,AD :BC =2:5. 求ED 的长.解:作DF ⊥BC 于F ,EG ⊥BC 于G. …………………………1分 ∵∠A =90°,AD ∥BC ∴ 四边形ABFD 是矩形. ∵ BC =5,AD :BC =2:5.∴ AD=BF=2. ………………………………………..2分 ∴ FC=3.在Rt △DFC 中, ∵ ∠C =45°, ∴ DC=23.…………………………………………3分 在Rt △BEC 中,P D C BA∴ EC =225……………………………………………….……………………………....4分 ∴ DE =2222523=-……………………………………………………………….5分3在△ABC 中,AC=BC ,∠ACB=90°,AB=6,过点C 作射线CP ∥AB ,在射线CP 上截取CD=2,联结AD ,求AD 的长.解:过点D 作DE ⊥AB 于E ,过点C 作CF ⊥AB 于F ,则DE ∥CF ∵CP ∥AB ,∴四边形DEFC 是矩形---------------------------------------1分 ∵在△ABC 中,AC=BC ,∠ACB=90°,AB=6,CD=2 ∴AF=CF=12AB=3 ---------------------------------------2分 ∴EF=CD=2,DE=CF=3 --------------------------------------3分∴AE=1 --------------------------------------4分 在△ADE 中,∠AED=90°,DE =3,AE=1 ∴----------------------------5分4.在梯形ABCD 中,AB ∥CD ,BD ⊥AD ,BC =CD ,∠A =60°,BC =2cm . (1)求∠CBD 的度数; (2)求下底AB 的长.解:∵AD BD ⊥, ∴︒=∠90ADB . ∵︒=∠60A ,∴︒=∠30ABD .………………………………1分 ∵AB ∥CD ,∴︒=∠=∠30CBD ABD .……………………2分 ∵BC=CD,∴︒=∠=∠30CBD CDB . ……………………3分 ∴︒=∠60ABC .ABCD FE P D CBAG F ED CB A∴ABCA∠=∠.∴梯形ABCD是等腰梯形.…………………4分∴AD=BC=2.在中,︒=∠90ADB,︒=∠30ABD,∴AB=2AD=4. ………………………………5分5.已知:如图,在□ABCD中,∠ADC、∠DAB的平分线DF、AE分别与线段BC相交于点F、E,DF与AE相交于点G.(1)求证:AE⊥DF;(2)若AD=10,AB=6,AE=4,求DF的长.:(1)在□ABCD中,AB DC∥,∴∠ADC+∠DAB=180°.DF、AE分别是∠ADC、∠DAB的平分线,∴12ADF CDF ADC∠=∠=∠,12DAE BAE DAB∠=∠=∠.∴1()902ADF DAE ADC DAB∠+∠=∠+∠=︒.∴90AGD∠=︒.∴AE⊥DF.…………………………………………………………………2分(2)过点D作DH AE∥,交BC的延长线于点H,则四边形AEHD是平行四边形,且FD⊥DH.∴DH=AE=4,EH=AD=10.在□ABCD中,AD BC∥,∴∠ADF=∠CFD,∠DAE=∠BEA.∴∠CDF=∠CFD,∠BAE=∠BEA.∴DC=FC,AB=EB.在□ABCD中,AD=BC=10,AB=DC=6,∴CF=BE=6,BF=BC-CF=10-6=4.∴FE=BE-BF=6-4=2.…………………………………………………3分∴FH= FE+EH= 12.………………………………………………………4分6.已知:如图,在直角梯形ABCD中,AD∥BC,∠A=90°,∠C=45°,上底AD = 8,AB=12,CD边的垂直平分线交BC边于点G,且交AB的延长线于点E,求AE的长.解:联结DG………………………………………1分∵EF是CD的垂直平分线∴DG=CG………………………………………2分GFEDCBAHGF EDCBA∴∠GDC =∠C , 且∠C =45° ∴∠DGC=90°∵AD ∥BC,∠A=90° ∴∠ABC=90°∴四边形ABGD 是矩形………………………………………3分 ∴BG=AD=8∴∠FGC =∠BGE =∠E= 45°∴BE=BG=8 ………………………………………4分 ∴AE=AB+BE=12+8=20………………………………………5分7.如图,在矩形ABCD 中,AB =5,BC =4,将矩形ABCD 翻折,使得点B 落在CD 边上的点E 处,折痕AF 交BC 于点F ,求FC 的长.E:由题意,得AE=AB=5,AD=BC=4,EF=BF. …………………………………… 1分在Rt △ADE 中,由勾股定理,得DE=3. …………………………………… 2分 在矩形ABCD 中,DC=AB=5.∴CE=DC-DE=2. ………………………………………………………………… 3分 设FC=x ,则EF=4-x.在Rt △CEF 中,()22242x x -=+. .…………………………………………… 4分 解得23=x . ………5分 即FC=23.8.已知, 点P 是∠MON 的平分线上的一动点,射线P A 交射线OM 于点A ,将射线P A 绕点P 逆时针 旋转交射线ON 于点B ,且使∠APB +∠MON =180°. (1)利用图1,求证:P A =PB ;(2)若∠MON =60°,OB =2,射线AP 交ON 于点D ,且满足且PBD ABO ∠=∠, 请借助图2补全图形,并求OP 的长.N图2B(1)在OB 上截取OD =OA ,连接PD ,∵OP 平分∠MON , ∴∠MOP =∠NOP . 又∵OA =OD ,OP =OP ,∴△AO P ≌△DO P . ……………1分 ∴P A =PD ,∠1=∠2.∵∠APB +∠MON =180°, ∴∠1+∠3=180°. ∵∠2+∠4=180°, ∴∠3=∠4. ∴PD =PB .∴P A =PB . …………… 2分 (2)作BE ⊥OP 交OP 于E ,∵∠AOB =600,且OP 平分∠MON , ∴∠1=∠2=30°.∵∠AOB +∠APB =180°, ∴∠APB =120°. ∵P A =PB ,∴∠5=∠6=30°. ∵∠3+∠4=∠7,∴∠3+∠4=∠7=(180°-30°)÷2=75°. ∵在Rt △OBE 中,∠3=600,OB =2∴∠4=150,OE =3,BE =1 ∴∠4+∠5=450,∴在Rt △BPE 中,EP =BE =1∴OP =13+ …………… 8分9.(本题满分4分)(1)如图①两个正方形的边长均为3,求三角形DBF 的面积.(2)如图②,正方形ABCD 的边长为3,正方形CEFG 的边长为1, 求三角形DBF 的面积. (3)如图③,正方形ABCD 的边长为a ,正方形CEFG 的边长为b ,求三角形DBF 的面积.7612435ECAOPBM NTD 1234AO PBMNT(1)92 92………………………(2分) (2)22a …………(2分)结论是:三角形DBF 的面积的大小只与a 有关, 与b 无关. (没写结论也不扣分)从上面计算中你能得到什么结论.10.(本小题满分7分) 已知:等边三角形ABC(2) 如图1,P 为等边△ABC 外一点,且∠BPC=120°. 试猜想线段BP 、PC 、AP 之间的数量关系,(2)如图2,P 为等边△ABC 内一点,且∠APD=120°.求证:PA+PD+PC >BD猜想:AP=BP+PC ------------------------------1分 (1)证明:延长BP 至E ,使PE=PC ,联结CE ∵∠BPC=120°∴∠CPE=60°,又PE=PC ∴△CPE 为等边三角形∴CP=PE=CE ,∠PCE=60° ∵△ABC 为等边三角形 ∴AC=BC ,∠BCA=60°CB CB P DB ∴∠ACB=∠PCE ,∴∠ACB+∠BCP=∠PCE+∠BCP 即:∠ACP=∠BCE∴△ACP ≌△BCE∴AP=BE --------------------------------- ------------------------------------------2分 ∵BE=BP+PE∴AP=BP+PC ------------------------------------ ---------------------------------------- 3分(2)方法一:在AD 外侧作等边△AB ′D ---------------------------------------------------------- 4分 则点P 在三角形ADB ′外∵∠APD=120°∴由(1)得PB ′=AP+PD 在△PB ′C 中,有PB ′+PC >CB ′,∴PA+PD+PC >CB ′ ∵△AB ′D 、△ABC 是等边三角形 ∴AC=AB ,AB ′=AD ,∠BAC=∠DA B ′=60°∴∠BAC+∠CAD=∠DAB ′+∠CAD即:∠BAD=∠CAB ′ ∴△AB ′C ≌△ADB∴C B ′=BD ------------------------------------------------------------------------ 6分 ∴PA+PD+PC >BD ------------------------------------------------------------------------- 7分方法二:延长DP 到M 使PM=PA ,联结AM 、BM ∵∠APD=120°,∴△APM 是等边三角形, -----------------------------4分∴AM=AP ,∠PAM=60° ∴DM=PD+PA ------------------------------5分∵△ABC 是等边三角形 ∴AB=AC ,∠BAC=60° ∴△AMB ≌△APC∴BM=PC ---------------------------------------------------------------------------------6分 在△BDM 中,有DM + BM >BD ,∴PA+PD+PC >BD ----------------------------------------------------------------------------7分11.已知:如图,在四边形ABCD 中, AD =B C ,∠A 、∠B 均为锐角.(3) 当∠A=∠B 时,则C D 与A B 的位置关系是CD AB ,大小关系是CD AB ; (4) 当∠A>∠B 时,(1)中C D 与A B 的大小关系是否还成立, 证明你的结论.)答:如图1,D CBA M P D CB ACD ∥AB ,C D <A B . …………2分(2)答:C D <A B 还成立. …………3分证法1:如图2,分别过点D 、B 作BC 、C D 的平行线,两线交于F 点.∴ 四边形DCBF 为平行四边形.∴.,FB DC BC FD ==∵ AD =B C ,∴ AD =FD . …………4分 作∠ADF 的平分线交A B 于G 点,连结GF . ∴ ∠ADG =∠FDG . 在△ADG 和△FDG 中⎪⎩⎪⎨⎧=∠=∠=,,,DG DG FDG ADG FD AD ∴ △ADG ≌△FDG .∴ AG =FG . …………5分 ∵在△BFG 中,BF BG FG >+.∴ .DC BG AG >+ …………6分 ∴ DC <A B . …………7分证法2:如图3,分别过点D 、B 作A B 、AD 的平行线,两线交于F 点.∴ 四边形DABF 为平行四边形.∴ .,BF AD AB DF ==∵ A D =B C , ∴ B C =BF .作∠CBF 的平分线交DF 于G 点,连结C G . 以下同证法112.已知:△ABC 和△ADE 都是等腰直角三角形,∠ABC =∠ADE =90°,点M 是CE 的中点,连接BM .(1)如图①,点D 在AB 上,连接DM ,并延长DM 交BC 于点N ,可探究得出BD 与BM 的数量关系为 ;(2)如图②,点D 不在AB 上,(1)中的结论还成立吗?如果成立,请证明;如果不成立,说明理由.MECBAD解:(1)BD=2BM. ……………………………………………………………………………2分图①图②NMDECABABCD E F(2)结论成立.证明:连接DM ,过点C 作CF ∥ED ,与DM 的延长线交于点F ,连接BF , 可证得△MDE ≌△MFC.………………………………… 3分 ∴DM=FM, DE=FC. ∴AD=ED=FC.作AN ⊥EC 于点N. 由已知∠ADE=90°,∠ABC=90°, 可证得∠1=∠2, ∠3=∠4.……………………………4分 ∵CF ∥ED ,∴∠1=∠FCM.∴∠BCF=∠4+∠FCM =∠3+∠1=∠3+∠2=∠BAD.∴△BCF ≌△BAD. …………………………………………………………………………5分 ∴BF=BD ,∠5=∠6.∴∠DBF=∠5+∠ABF=∠6+∠ABF=∠ABC=90°.∴△DBF 是等腰直角三角形. ………………………………………………………………6分 ∵点M 是DF 的中点,则△BMD 是等腰直角三角形.∴BD=2BM. …………………………………7分 (说明:以上答案仅供参考,若有不同解法,只要过程和解法都正确,可相应给分.)13.(海淀)如图,在梯形ABCD 中,AD ∥BC ,∠B=60°,∠ADC=105°,AD =6,且AC ⊥AB ,求AB 的长.14丰台.已知:如图,在四边形ABFC 中,ACB ∠=90°,BC 的垂直平分线EF 交BC 于点D,交AB 于点E,且CF=AE.(1) 求证:四边形BECF 是菱形;(2) 当A ∠的大小为多少度时,四边形BECF 是正方形?A DCBDC BA ABC DA B CD15.如图,梯形ABCD 中, AD //BC , ∠ABC =45︒ , ∠ADC =120︒ , AD =DC , AB =22, 求BC的长.16西城.已知:在梯形ABCD 中,AD ∥BC ,∠B=45°,∠BAC=105°,AD =CD =4.求BC 的长.17.已知:在△ABC 中,BC=a ,AC=b ,以AB 为边作等边三角形ABD. 探究下列问题:(1)如图1,当点D 与点C 位于直线AB 的两侧时,a=b=3,且∠ACB=60°,则CD= ;(2)如图2,当点D 与点C 位于直线AB 的同侧时,a=b=6,且∠ACB=90°,则CD= ;(3)如图3,当∠ACB 变化,且点D 与点C 位于直线AB 的两侧时,求 CD 的最大值及相应的∠ACB 的度数.图1 图2 图318. 朝阳(本小题8分)DC B A图① 图② (1) 已知:如图①,Rt △ABC 中,∠ACB=90°,AC=BC ,点D 、E 在斜边AB 上,且∠DCE=45°. 求证:线段DE 、AD 、EB 总能构成一个直角三角形; (2)已知:如图②,等边三角形ABC 中,点D 、E 在边AB 上,且∠DCE=30°,请你找出一个条件,使线段DE 、AD 、EB 能构成一个等腰三角形,并求出此时等腰三角形顶角的度数;19崇文.(本小题满分8分)在等边ABC ∆的两边AB 、AC 所在直线上分别有两点M 、N ,D 为ABC 外一点,且︒=∠60MDN ,︒=∠120BDC ,BD=DC. 探究:当M 、N 分别在直线AB 、AC 上移动时,BM 、NC 、MN 之间的数量关系及AMN ∆的周长Q 与等边ABC ∆的周长L 的关系.图1 图2 图3(I )如图1,当点M 、N 边AB 、AC 上,且DM=DN 时,BM 、NC 、MN 之间的数量关系是 ; 此时=LQ;(II)如图2,点M、N边AB、AC上,且当DM≠DN时,猜想(I)问的两个结论还成立吗?写出你的猜想并加以证明;(III)如图3,当M、N分别在边AB、CA的延长线上时,若AN=x,则Q= (用x、L表示).20.海淀.在课外小组活动时,小慧拿来一道题(原问题)和小东、小明交流.原问题:如图1,已知△ABC, ∠ACB=90︒, ∠ABC=45︒,分别以AB、BC为边向外作△ABD与△BCE, 且DA=DB, EB=EC,∠ADB=∠BEC=90︒,连接DE交AB于点F.探究线段DF与EF的数量关系.小慧同学的思路是:过点D作DG⊥AB于G,构造全等三角形,通过推理使问题得解.小东同学说:我做过一道类似的题目,不同的是∠ABC=30︒,∠ADB=∠BEC=60︒.小明同学经过合情推理,提出一个猜想,我们可以把问题推广到一般情况.请你参考小慧同学的思路,探究并解决这三位同学提出的问题:(1)写出原问题中DF与EF的数量关系;(2)如图2,若∠ABC=30︒,∠ADB=∠BEC=60︒,原问题中的其他条件不变,你在ABC DEF (1)中得到的结论是否发生变化?请写出你的猜想并加以证明;(3)如图3,若∠ADB =∠BEC =2∠ABC , 原问题中的其他条件不变,你在(1)中得到的结论是否发生变化?请写出你的猜想并加以证明.图1 图2 图313.(海淀)如图,在梯形ABCD 中,AD ∥BC ,∠B=60°,∠ADC=105°,AD =6,且AC ⊥AB ,求AC 的长. 解:过点D 作DE ⊥AC 于点E ,则∠AED =∠DEC =90°.………….……………………1分 ∵ AC ⊥AB ,∴ ∠BAC =90°. ∵ ∠B =60°,∴ ∠ACB =30°.∵ AD ∥BC ,∴ ∠DAC =∠ACB =30°.………….……………………2分∴ 在Rt △ADE 中,DE =12AD =3,AE =,∠ADE =60°. ….………3分 ∵ ∠ADC=105°,∴ ∠EDC =45°.∴ 在Rt △CDE 中, CE =DE =3.…………….……………………………4分∴ AC =AE +CE =3.14丰台.已知:如图,在四边形ABFC 中,ACB ∠=90°,BC 的垂直平分线EF 交BC 于点D,交AB 于点E,且CF=AE.(3) 求证:四边形BECF 是菱形;BECAD FDACE FBEFCBAD ADCB ADCBEAB CDEF(4) 当A ∠的大小为多少度时,四边形BECF 是正方形?⑴∵ EF 垂直平分BC,∴CF=BF,BE=CE ,∠BDE=90° …………………………1’又∵ ∠ACB=90°∴EF ∥AC∴E 为AB 中点, 即BE=AE ………………………………2’ ∵CF=AE ∴CF=BE∴CF=FB=BE=CE …………………………………………3’ ∴四边形是BECF 菱形. …………………………………4’ ⑵当∠A= 45°时,四边形是BECF 是正方形. …………5’15.如图,梯形ABCD 中, AD //BC , ∠ABC =45︒ , ∠ADC =120︒ , AD =DC , AB =22, 求BC的长.16西城.已知:在梯形ABCD 中,AD ∥BC ,∠B=45°,∠BAC=105°,AD =CD =4.求BC 的长.作AE ∥DC 交BC 于点E ,AF ⊥BC 于点F (如图2). ······································· 1分∵AD ∥BC ,∴四边形ADCE 是平行四边形. ······················································ 2分 ∵AD=CD ,∴四边形ADCE 是菱形. ∴ AE=EC =CD=AD =4. ······················ 3分 ∴∠EAC =∠ACB ,∵∠B=45°,∠BAC=105°,∴∠ACB=180°-∠B -∠BAC=30°.∴∠AEB =∠EAC +∠ACB =60°.在Rt △AEF 中,221==AE EF ,323==EF AF . ··························· 4分 DC B AD AB C E F 图2DC BA ABC DA B CD在Rt △ABF 中,32==BF AF .∴BC =BF +EF +EC =326+.························································ 5分17.已知:在△ABC 中,BC=a ,AC=b ,以AB 为边作等边三角形ABD. 探究下列问题:(1)如图1,当点D 与点C 位于直线AB 的两侧时,a=b=3,且∠ACB=60°,则CD= ;(2)如图2,当点D 与点C 位于直线AB 的同侧时,a=b=6,且∠ACB=90°,则CD= ;(3)如图3,当∠ACB 变化,且点D 与点C 位于直线AB 的两侧时,求 CD 的最大值及相应的∠ACB 的度数.图1 图2 图318. 朝阳(本小题8分)图① 图② (1) 已知:如图①,Rt △ABC 中,∠ACB=90°,AC=BC ,点D 、E 在斜边AB 上,且∠DCE=45°. 求证:线段DE 、AD 、EB 总能构成一个直角三角形; (2)已知:如图②,等边三角形ABC 中,点D 、E 在边AB 上,且∠DCE=30°,请你找出一个条件,使线段DE 、AD 、EB 能构成一个等腰三角形,并求出此时等腰三角形顶角的度数;(1)证明:如图①,∵∠ACB=90°,AC=BC,∴∠A=∠B=45°.以CE为一边作∠ECF=∠ECB,在CF上截取CF=CB,则CF=CB=AC. 图①连接DF、EF,则△CFE≌△CBE. ………………………………………………1分∴FE=BE,∠1=∠B=45°.∵∠DCE=∠ECF+∠DCF=45°,∴∠DCA+∠ECB=45°.∴∠DCF=∠DCA.∴△DCF≌△DCA. ……………………………………………………………2分∴∠2=∠A=45°,DF=AD.∴∠DFE=∠2+∠1=90°.∴△DFE是直角三角形.又AD=DF,EB=EF,∴线段DE、AD、EB总能构成一个直角三角形. ……………………………4分(2)当AD=BE时,线段DE、AD、EB能如图②,与(1)类似,以CE为一边,作∠ECF=∠ECB,在CF上截取CF=CB,可得△CFE≌△CBE,△DCF≌△DCA.∴AD=DF,EF=BE.图②∴∠DFE=∠1+∠2=∠A+∠B=120°. ……………………………………5分若使△DFE为等腰三角形,只需DF=EF,即AD=BE.∴当AD=BE时,线段DE、AD、EB能构成一个等腰三角形. ……………6分且顶角∠DFE为120°.19崇文.(本小题满分8分)在等边ABC ∆的两边AB 、AC 所在直线上分别有两点M 、N ,D 为ABC 外一点,且︒=∠60MDN ,︒=∠120BDC ,BD=DC. 探究:当M 、N 分别在直线AB 、AC 上移动时,BM 、NC 、MN 之间的数量关系及AMN ∆的周长Q 与等边ABC ∆的周长L 的关系.图1 图2 图3(I )如图1,当点M 、N 边AB 、AC 上,且DM=DN 时,BM 、NC 、MN 之间的数量关系是 ; 此时=LQ; (II )如图2,点M 、N 边AB 、AC 上,且当DM ≠DN 时,猜想(I )问的两个结论还成立吗?写出你的猜想并加以证明;(III ) 如图3,当M 、N 分别在边AB 、CA 的延长线上时, 若AN=x ,则Q= (用x 、L 表示).解:(I )如图1, BM 、NC 、MN 之间的数量关系 BM+NC=MN .此时32=L Q . (II )猜想:结论仍然成立.证明:如图,延长AC 至E ,使CE=BM ,连接DE .CD BD =,且 120=∠BDC .∴ 30=∠=∠DCB DBC .又ABC ∆是等边三角形,∴90MBD NCD ∠=∠=.在MBD ∆与ECD ∆中:⎪⎩⎪⎨⎧=∠=∠=DC BD ECD MBD CE BM∴≅∆MBD ECD ∆(SAS) . ∴DM=DE, CDE BDM ∠=∠∴ 60=∠-∠=∠MDN BDC EDN在MDN ∆与EDN ∆中:⎪⎩⎪⎨⎧=∠=∠=DN DN EDN MDN DE DM ∴≅∆MDN EDN ∆(SAS) ∴MN=NE=NC+BMAMN ∆的周长Q=AM+AN+MN=AM+AN+(NC+BM)=(AM+BM)+(AN+NC) =AB+AC =2AB而等边ABC ∆的周长L=3AB∴3232==AB AB L Q . (III )如图3,当M 、N 分别在AB 、CA 的延长线上时,若AN=x ,则Q= 2x +L 32(用x 、L 表示).25.怀柔如图1,在△ABC 中,∠ACB 为锐角.点D 为射线BC 上一动点,连接AD ,以AD 为一边且在AD 的右侧作正方形ADEF . 解答下列问题:(1)如果AB=AC ,∠BAC=90º.①当点D 在线段BC 上时(与点B 不重合),如图2,线段CF 、BD 之间的位置关系为 ,数量关系为 .②当点D 在线段BC 的延长线上时,如图3,①中的结论是否仍然成立,为什么?A B C D E F图1 图2 FE D C B AF E D C B A 图3(2)①如果AB=AC ,∠BAC≠90º,点D 在射线BC 上运动.在图4中同样作出正方形ADEF ,你发现(1)问中的结论是否成立?不用说明理由;②如果∠BAC=90º,AB≠AC ,点D 在射线BC 上运动.在图5中同样作出正方形ADEF ,你发现(1)问中的结论是否成立?不用说明理由; 答:(3)要使(1)问中CF ⊥BC 的结论成立,试探究:△ABC 应满足的一个..条件,(点C 、F 重合除外)?画出相应图形(画图不写作法),并说明理由;(1)①CF 与BD 位置关系是 垂 直、数量关系是相 等;……1分②当点D在BC的延长线上时①的结论仍成立(如图3).由正方形ADEF得AD=AF ,∠DAF=90º.∵∠BAC=90º,∴∠DAF=∠BAC ,∴∠DAB=∠FAC.又AB=AC ,∴△DAB≌△FAC.∴CF=BD.∠ACF=∠ABD.∵∠BAC=90º,AB=AC ,∴∠ABC=45º,∴∠ACF=45º,∴∠BCF=∠ACB+∠ACF= 90º.即CF⊥BD.……………3分(2)①画出图形(如图4),判断:(1)中的结论不成立.②画出图形(如图5),判断:(1)中的结论不成立.……4分(3)当∠BCA=45º时,CF⊥BD(如图6).理由是:过点A作AG⊥AC交BC于点G,∴AC=AG.可证:△GAD≌△CAF∴∠ ACF=∠AGD=45º .∠BCF=∠ACB+∠ACF= 90º.即CF⊥BD.…………………………………5分图620.海淀.在课外小组活动时,小慧拿来一道题(原问题)和小东、小明交流.原问题:如图1,已知△ABC, ∠ACB=90︒, ∠ABC=45︒,分别以AB、BC为边向外作△ABD与△BCE, 且DA=DB, EB=EC,∠ADB=∠BEC=90︒,连接DE交AB于点F.探究线段DF与EF的数量关系.小慧同学的思路是:过点D作DG⊥AB于G,构造全等三角形,通过推理使问题得解.小东同学说:我做过一道类似的题目,不同的是∠ABC =30︒,∠ADB =∠BEC =60︒. 小明同学经过合情推理,提出一个猜想,我们可以把问题推广到一般情况. 请你参考小慧同学的思路,探究并解决这三位同学提出的问题: (1)写出原问题中DF 与EF 的数量关系;(2)如图2,若∠ABC =30︒,∠ADB =∠BEC =60︒,原问题中的其他条件不变,你在 (1)中得到的结论是否发生变化?请写出你的猜想并加以证明;(3)如图3,若∠ADB =∠BEC =2∠ABC , 原问题中的其他条件不变,你在(1)中得到的结论是否发生变化?请写出你的猜想并加以证明.图1 图2 图3解: (1)DF= EF . ………………………………………………………………1分 (2)猜想:DF= FE .证明:过点D 作DG ⊥AB 于G , 则∠DGB =90︒. ∵ DA =DB , ∠ADB =60︒.∴ AG =BG , △DBA 是等边三角形. ∴ DB =BA .∵ ∠ACB =90︒ , ∠ABC =30︒,∴ AC =21AB =BG . …………………………………………………………2分 ∴ △DBG ≌△BAC .∴ DG =BC . ……………………………………………………3分 ∵ BE=EC , ∠BEC =60︒ , ∴ △EBC 是等边三角形. ∴ BC =BE , ∠CBE =60︒.∴ DG = BE , ∠ABE =∠ABC +∠CBE =90︒ . ∵ ∠DFG =∠EFB , ∠DGF =∠EBF , ∴ △DFG ≌△EFB .∴ DF= EF . ……………………………………………………4分(3)猜想:DF= FE .证法一:过点D 作DH ⊥AB 于H , 连接HC , HE , HE 交CB 于K , 则∠DHB =90︒. ∵ DA =DB ,∴ AH =BH , ∠1=∠HDB .∵ ∠ACB =90︒, ∴ HC =HB .BECAD FDACE FBEFCBAD K H BFECAD 2431∵ EB =EC , HE =HE ,∴ △HBE ≌△HCE . ……………………………5分 ∴ ∠2=∠3, ∠4=∠BEH . ∴ HK ⊥BC .∴ ∠BKE =90︒. ……………………………6分 ∵ ∠ADB =∠BEC =2∠ABC , ∴ ∠HDB =∠BEH =∠ABC .∴ ∠DBC =∠DBH +∠ABC =∠DBH +∠HDB =90︒,∠EBH =∠EBK +∠ABC =∠EBK +∠BEK =90︒. ∴ DB //HE , DH //BE .∴ 四边形DHEB 是平行四边形.∴ DF =EF . ………………………………………………………………………7分 证法二:分别过点D 、E 作DH ⊥AB 于H , EK ⊥BC 于K , 连接HK , 则∠DHB =∠EKB =90︒.∵ ∠ACB =90︒,∴ EK //AC .∵ DA =DB , EB =EC ,∴ AH =BH , ∠1=∠HDB ,CK =BK , ∠2=∠BEK .∴ HK //AC . ∴ 点H 、K 、E 在同一条直线上. …………………5分D A CE F B H K 12。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
⑵在运动过程中,设△APQ与梯形ABCD重叠部分的面积为S,求S关于t的函数关系式,并写出自变量t的取值范围;
参考答案
1.(本小题满分10分)
⑴解:连结OC,∵CD切⊙O于点C,∴∠OCD=90°.………………………………(1分)
∵∠D=30°,∴∠COD=60°.…………………(2分)
初中数学难题集锦组题:韩松
1.(本小题满分10分)
如图,AB为⊙O的直径,点C在⊙O上,过点C作⊙O的切线交AB的延长线于点D,已知∠D=30°.
⑴求∠A的度数;
⑵若点F在⊙O上,CF⊥AB,垂足为E,CF= ,求图中阴影部分的面积.
2.先阅读下面材料,然后解答问题:(本小题满分10分)
【材料一】:如图⑴,直线l上有 、 两个点,若在直线l上要确定一点P,且使点P到点 、 的距离之和最小,很明显点P的位置可取在 和 之间的任何地方,此时距离之和为 到 的距离.
∵OA=OC,∴∠A=∠ACO=30°.………………(4分)
⑵∵CF⊥直径AB,CF= ,∴CE= ,…………(5分)
∴在Rt△OCE中,OE=2,OC=4.……………………(6分)
∴ , .…………………………(8分)
∴ …………………………………………………(10分)
2.先阅读下面材料,然后解答问题:(本小题满分10分)
⑵当AP∥OB时,
如图,∠BOA=∠OAP=45°,过点B作BH⊥x轴于H,则OH=BH.
设点B(x,x),故 ,解得x=6或x=0(舍去)…………………………(6分)
∴B(6,6).…………………………………………………………………………(7分)
当OP∥AB时,同理设点B(4-x,x)
故 ,解得x=6或x=0(舍去),∴B(-2,6).……(8分)
⑶如图2,,△ABC中,∠ABC=90°,以AC为一边向形外作菱形ACEF,D为菱形ACEF的中心,连结BD,当BD平分∠ABC时,判断四边形ACEF为何种特殊的四边形?请说明理由. 若此时AB=3,BD= ,求BC的长.
6.(本小题满分12分)
已知在梯形ABCD中,AB∥DC,且AB=40cm,AD=BC=20cm,∠ABC=120°.点P从点B出发以1cm/s的速度沿着射线BC运动,点Q从点C出发以2cm/s的速度沿着线段CD运动,当点Q运动到点D时,所有运动都停止.设运动时间为t秒.
根据图象进行以下探究:
⑴请在图①中标出A地的位置,并作简要的文字说明;
⑵求图②中M点的坐标,并解释该点的实际意义.
⑶在图②中补全甲车的函数图象,求甲车到A地的距离 与行驶时间x的函数关系式.
⑷A地设有指挥中心,指挥中心及两车都配有对讲机,两部对讲机在15千米之内(含15千米)时能够互相通话,求两车可以同时与指挥中心用对讲机通话的时间.
所以点M表示乙车1.2小时到达A地.…(4分)
⑶甲车的函数图象如图所示.…………(5分)
当 时, ;…………(6分)
当 时,Байду номын сангаас.…………(7分)
⑷由题意得 ,得 ; ,得 .
∴ …………………………………………………………………………(9分)
∴两车同时与指挥中心通话的时间为 小时.…………………………(10分)
4.(本小题满分10分)
已知抛物线 (a≠0)的顶点在直线 上,且过点A(4,0).
⑴求这个抛物线的解析式;
⑵设抛物线的顶点为P,是否在抛物线上存在一点B,使四边形OPAB为梯形?若存在,求出点B的坐标;若不存在,请说明理由.
⑶设点C(1,-3),请在抛物线的对称轴确定一点D,使 的值最大,请直接写出点D的坐标.
如图⑵,直线l上依次有 、 、 三个点,若在直线l上要确定一点P,且使点P到点 、 、 的距离之和最小,不难判断,点P的位置应取在点 处,此时距离之和为 到 的距离.(想一想,这是为什么?)
不难知道,如果直线l上依次有 、 、 、 四个点,同样要确定一点P,使它到各点的距离之和最小,则点P应取在点 和 之间的任何地方;如果直线l上依次有 、 、 、 、 五个点,则相应点P的位置应取在点 的位置.
【问题二】:现要求 的最小值,
根据问题一的解答思路,可知当x值为时,上式有最小值为.
3.(本小题满分10分)
如图①,一条笔直的公路上有A、B、C三地,B、C两地相距 150 千米,甲、乙两辆汽车分别从B、C两地同时出发,沿公路匀速相向而行,分别驶往C、B两地.甲、乙两车到A地的距离 、 (千米)与行驶时间x(时)的关系如图②所示.
⑶D(2,-6).………………………………………………………………………………(10分)
【材料二】:数轴上任意两点a、b之间的距离可以表示为 .
【问题一】:若已知直线l上依次有点 、 、 、……、 共25个点,要确定一点P,使它到已知各点的距离之和最小,则点P的位置应取在;
若已知直线l上依次有点 、 、 、……、 共50个点,要确定一点P,使它到已知各点的距离之和最小,则点P的位置应取在.
5.(本小题满分12分)
定义:只有一组对角是直角的四边形叫做损矩形,连结它的两个非直角顶点的线段叫做这个损矩形的直径.
⑴如图1,损矩形ABCD,∠ABC=∠ADC=90°,则该损矩形的直径是线段.
⑵在线段AC上确定一点P,使损矩形的四个顶点都在以P为圆心的同一圆上(即损矩形的四个顶点在同一个圆上),请作出这个圆,并说明你的理由.友情提醒:“尺规作图”不要求写作法,但要保留作图痕迹.
问题一:点 处…………(3分)点 和 之间的任何地方………(6分)
问题二:48…………(8分)1225………(10分)
3.(本小题满分10分)
⑴A地位置如图所示.使点A满足AB∶AC=2∶3.………………………………(2分)
⑵乙车的速度150÷2=75千米/时,
,∴M(1.2,0)………………(3分)
4.(本小题满分10分)
⑴∵抛物线过点(0,0)、(4,0),
∴抛物线的对称轴为直线 .………………………………………………………(1分)
∵顶点在直线 上,∴顶点坐标为(2,-2).…………………………(3分)
故设抛物线解析式为 ,
∵过点(0,0),∴ ,∴抛物线解析式为 ………………………(5分)
