平面向量的线性运算

合集下载

平面向量的线性运算知识点总结

平面向量的线性运算知识点总结平面向量是数学中的重要概念之一，它们具有方向和大小，并且可以进行线性运算。

本文将对平面向量的线性运算相关知识进行总结，包括加法、数乘和线性组合三个方面。

一、平面向量的加法平面向量的加法是指将两个向量合成为一个新向量的运算。

具体而言，设有两个向量A和B，它们的加法运算符号为"＋"，则其加法公式为：A +B = (Aₓ + Bₓ, Aᵧ + Bᵧ)其中，Aₓ和Aᵧ分别表示向量A在坐标系中的x轴和y轴上的分量，Bₓ和Bᵧ分别表示向量B在坐标系中的x轴和y轴上的分量。

需要注意的是，向量的加法满足交换律和结合律。

即：A +B = B + A(A + B) + C = A + (B + C)二、平面向量的数乘数乘是指将向量与一个实数相乘得到一个新向量的运算。

具体而言，设有一个向量A和一个实数k，它们的数乘运算符号为"·"，则其数乘公式为：k·A = (k·Aₓ, k·Aᵧ)其中，Aₓ和Aᵧ分别表示向量A在坐标系中的x轴和y轴上的分量。

数乘的运算法则如下：1. 若k>0，则k·A的方向与A的方向相同。

2. 若k<0，则k·A的方向与A的方向相反。

3. 若k=0，则k·A的方向为零向量。

4. |k·A| = |k|·|A|三、平面向量的线性组合线性组合是指将多个向量按一定比例相加得到一个新向量的运算。

具体而言，设有n个向量A₁、A₂、...、Aₙ和n个实数k₁、k₂、...、kₙ，它们的线性组合公式为：k₁A₁ + k₂A₂ + ... + kₙAₙ线性组合的运算法则如下：1. 线性组合的次序不影响结果，即k₁A₁ + k₂A₂ + ... + kₙAₙ =kₙAₙ + ... + k₂A₂ + k₁A₁。

2. 向量的线性组合满足数乘与加法的结合律，即k₁(A₁ + A₂) =k₁A₁ + k₁A₂。

典型例题：平面向量的线性运算

平面向量的线性运算例1一辆汽车从A点出发向西行驶了100公里到达B点，然后又改变方向向西偏北050走了200公里到达C点，最后又改变方向，向东行驶了100公里到达D点。

（1）作出向量AB，BC，CD；（2）求AD。

分析：解答本题应首先确立指向标，然后再根据行驶方向确定出有关向量，进而求解。

解析：（1）如图所示。

（2）由题意易知，AB与CD方向相反，故AB与CD共线。

又AB CD=，∴在四边形ABCD中，//=，AB CD且AB CD∴四边形ABCD为平行四边形。

故200==（公里）。

AD BC评注：准确画出向量的方法是先确定向量的起点，再确定向量的方向，然后根据向量的大小确定向量的终点。

例2化简：()()---。

AB CD AC BD分析：该例为一基础题目，可有多种解法。

解法1：原式AB CD AC BD=--+=+++()()AB DC CA BD=+++AB BD DC CA=+=0AD DA评注：该解法是将向量减法转化为加法进行化简的。

解法2：原式AB CD AC BD=--+=()-DC DB-()AB AC=CB BC+=0评注：本解法是利用AB AC CB-=进行化简的。

-=，DC DB BC解法3：设O为平面内任意一点，则有原式AB CD AC BD=--+=-----+-OB OA OD OC OC OA OD OB()()()()=--+-++-OB OA OD OC OC OA OD OB=0评注：本解法是利用MN ON OM=-关系进行化简的。

例3对于下列各种情况，各向量的终点的集合分别是什么图形（1）把所有单位向量的起点平行移动到同一点P ；（2）把平行于直线l 的所有单位向量的起点平行移动到直线l 的点P ；（3）把平行于直线l 的所有向量的起点平行移动到直线l 的点P 。

分析：数学中的向量是自由向量，可以重新选择起点进行平移，只要平移前后两个向量相等即可。

解析：（1）是以P 点为圆心，以1个单位长为半径的圆；（2）是直线l 上与P 的距离为1个单位长的两个点；（3）是直线l 。

平面向量的线性运算与应用

平面向量的线性运算与应用在数学中，平面向量是一个具有大小和方向的量，常用箭头表示，用于表示平面上的物理量或几何概念。

平面向量的线性运算是指对向量进行加减和标量乘法的操作。

同时，平面向量的线性运算在许多应用中是非常重要和有用的。

一、平面向量的定义和表示平面向量由其大小和方向共同确定，通常用a→表示。

其中，大小称为向量的模，记作|a→|，方向可以用与向量平行的线段来表示。

在笛卡尔坐标系中，可以用坐标表示平面向量。

例如，向量a→可以用(ai, aj)来表示。

二、平面向量的线性运算1. 向量的加法平面向量的加法是指两个向量按照相同的方向进行相加。

设向量a→=(a1, a2)，向量b→=(b1, b2)，则向量a→+b→=(a1+b1, a2+b2)。

2. 向量的减法平面向量的减法是指两个向量按照相反的方向进行相减。

设向量a→=(a1, a2)，向量b→=(b1, b2)，则向量a→-b→=(a1-b1, a2-b2)。

3. 向量的标量乘法平面向量的标量乘法是指向量与一个标量的乘积。

设向量a→=(a1, a2)，标量k，则向量ka→=(ka1, ka2)。

三、平面向量的应用平面向量的线性运算在许多数学和物理问题中都有广泛的应用。

1. 平面几何问题在平面几何问题中，平面向量的线性运算常常用于判断点、线、圆等的位置关系，计算长度和面积等。

例如，可以利用向量的加法和减法判断线段的平行性和垂直性；可以使用向量的模计算线段的长度；可以利用向量的叉乘计算三角形的面积等。

2. 力学问题在力学中，平面向量的线性运算被广泛应用于描述物体的受力情况。

根据牛顿第二定律，物体所受的合力等于物体的质量乘以加速度，可以用平面向量的标量乘法表示。

同时，可以使用平面向量的加法和减法来计算多个力的合力，从而描述物体的运动状态。

3. 电磁学问题在电磁学中，平面向量的线性运算同样起着重要的作用。

例如，可以使用平面向量的加法和减法来计算电场的合成和分解；可以利用平面向量的叉乘来计算电磁感应产生的力和磁场等。

平面向量的线性运算

平面向量的线性运算平面向量是解决平面几何问题的重要工具。

平面向量之间可以进行线性运算，包括加减法、数量乘法和应用特殊运算规则的向量乘法。

本文将详细介绍平面向量的线性运算及其应用。

一、平面向量的基本概念在平面直角坐标系中，向量由两个有序实数对表示，分别表示向量在 x 轴和 y 轴上的分量。

设向量 a 的分量为 (a1, a2)，则向量 a 可表示为 a = a1i + a2j，其中 i 和 j 分别是 x 轴和 y 轴的单位向量。

二、平面向量的加法设有两个平面向量 a = a1i + a2j， b = b1i + b2j，其和为 c = (a1 +b1)i + (a2 + b2)j。

向量的加法满足交换律、结合律和零向量的存在性。

三、平面向量的减法设有两个平面向量 a = a1i + a2j， b = b1i + b2j，其差为 c = (a1 - b1)i + (a2 - b2)j。

向量的减法也满足交换律和结合律。

四、平面向量的数量乘法设有平面向量 a = a1i + a2j，实数 k，k与向量 a 的数量积为 k * a =ka1i + ka2j。

数量乘法满足结合律、分配律和对数乘法的分布律等性质。

五、平面向量的线性运算应用1. 向量共线与平行若有两个非零向量 a 和 b，当且仅当存在实数 k，使得 a = kb，称向量 a 和 b 共线。

若向量 a 和 b 共线且方向相同或相反，则称向量 a 和b 平行。

2. 向量的线性组合设有向量组 a1, a2, ..., an，其中每个向量的形式为 ai = ai1i + ai2j。

对于任意给定的实数 k1, k2, ..., kn，向量 b = k1a1 + k2a2 + ... + knan 称为向量组 a1, a2, ..., an 的线性组合。

3. 向量的共面性若存在不全为零的实数 k1, k2, k3，使得 k1a1 + k2a2 + k3a3 = 0，称向量组 a1, a2, a3 共面。

平面向量的概念及线性运算

平面向量的概念及线性运算
一、平面向量的线性运算（三角形重心问题）
例 1、在△ABC 中，D、E 分别为 BC，AC 边上的中点，G 为 BE 上一点，且 GB=2GE，设
AB a ， AC b ，试用 a ， b 表示 AD ， AG 。
变式 1：（2007 年高考北京卷）已知 O 是△ABC 所在平面内一点，D 为 BC 边中点，且
2OA OB OC 0 ，那么（
A、 AO OD
） C、 AO 3OD D、 2 AO OD ）
B、 AO 2OD
变式 2：G 为△ABC 内一点，且满足 GA GB GC 0 ,则 G 为△ABC 的（ A、外心 B、内心 C、垂心 D、重心
变式 3：若 OA OB OC 0 ，且 OA OB OC ，则△ABC 是
D、
4 3 a b 5 5
AB AC m AM 成立，则 m=
A、5 B、4 C、3 D、2 变式 6：在△ABC 中，点 D 在边 AB 上，CD 平分∠ACB，若 CB a ， CA b ， a 1 ，
b 2 ，则 CD =（
A、 a
） B、
1 3
2 b 3
2 1 a b 3 3
C、
3 4 a b 5 5
三角形；
变式 4 ：设 G 是 ABC 的重心， a, b, c 分别是角 A, B, C 的对边，若
3 aGA bGB cGC 0 则角 A （ 3 A、 90 B、 60
） C、 45

D、 30

变式 5 ：已知 △ ABC 和点 M 满足 MA MB MC 0 ，若存在实数 m 使得

2024年中考重点之平面向量的线性运算

2024年中考重点之平面向量的线性运算一、平面向量的定义与表示平面向量是指在平面内具有大小和方向的量，一般表示为箭头形式。

通常用有序数对表示平面向量，如AB表示起点为A、终点为B的平面向量。

二、平面向量的加法平面向量的加法满足以下运算规律：1. 交换律：AB+CD=CD+AB2. 结合律：(AB+CD)+EF=AB+(CD+EF)3. 平移性质：向量的平移不影响其大小和方向，即若P、Q为平面上两点，则PQ=QR，其中R为PQ的平移向量。

三、平面向量的数乘平面向量的数乘是指一个向量与一个实数相乘的运算。

设k为实数，AB为平面向量，则kAB为平面向量，其大小为|k|·|AB|，方向与AB相同（k>0）或相反（k<0）。

四、平面向量的线性运算平面向量的线性运算包括加法和数乘。

根据向量运算规律，我们可以得出以下结论：1. 乘法分配律：k(AB+CD)=kAB+kCD，(k+m)AB=kAB+mAB，其中k、m为实数。

2. 结合律：k(mAB)=(km)AB，其中k、m为实数。

3. 零向量：0AB=O，其中O为原点。

4. 相反向量：(-1)AB=-AB。

五、平面向量的应用平面向量的线性运算在几何学和物理学中有广泛的应用，尤其是解决平面几何问题和力学问题时。

其中一些常见的应用包括：1. 平面向量的模运算：通过向量的数乘和加法，我们可以求解平面向量的模和方向角。

2. 平面向量的共线与垂直判定：设有两个非零向量AB和CD，若存在实数k，使得CD=kAB，则称向量CD与向量AB共线；若CD·AB=0，则称向量CD与向量AB垂直。

3. 平面向量的平行判定：设有两个非零向量AB和CD，若存在实数k，使得CD=kAB或CD=k(-AB)，则称向量CD与向量AB平行。

4. 向量的投影：向量的投影是指将一个向量沿另一个向量的方向分解的过程，用于求解向量的分解与合成问题。

5. 平面向量的线性方程组：由平面向量的线性运算性质，我们可以建立平面向量的线性方程组，用于求解几何和物理问题。

平面向量的线性运算

平面向量的线性运算线性运算是以向量和矩阵进行操作的数学运算方法，它可以引发出许多更复杂的数学原理和研究结果。

线性运算可以在各种学科中应用，例如线性系统的分析和解析，图论，资源分配，Modal和语义计算等等。

一、定义线性运算是一种数学方法，用来处理平面向量。

它基于直线，计算两个向量之间的关系。

在数学上，从点到点之间有一条路径，称为一条直线，线性运算可以用来描述这条直线上起点和终点之间的空间特征。

二、实现方式1、向量乘法：向量乘法是两个向量相乘，以计算它们之间的关系。

2、矩阵乘法：矩阵乘法是两个矩阵相乘，它可以用来揭示一种向量的多重关系。

3、矩阵分解：矩阵分解是把一个大的矩阵分解为多个子矩阵，用来求解一组向量关系问题。

4、向量累加：向量累加是两个向量加起来，用来表示向量之间关系的变化。

5、根据相反关系：根据相反关系，把两个平面向量的起点和终点的关系，反转过来，以计算出新的关系。

三、应用1、线性代数：高等数学中的线性代数中，线性运算涉及到线性方程，矩阵，特征值，线性空间等等基本概念，也常常被用来分析线性系统，解析图论问题，和解决资源分配问题等等。

2、机器学习：机器学习中，线性运算被用来表示各种模型，用来对数据集或者特征分析，例如线性回归，逻辑斯谛回归，支持向量机等等。

3、信号处理：在信号处理中，线性运算可以用来表示信号的变换和处理，例如傅里叶变换，滤波器，卷积，离散余弦变换等等。

4、语言处理：线性运算也可以被用来处理自然语言，例如用于语法分析的实体矩阵，或者模糊语义的语义码表。

四、总结线性运算是以向量和矩阵进行操作的数学运算方法，可以应用于多种学科，也可以用来理解多重关系，分析和解决资源分配问题。

它可以引发出许多更复杂的数学原理和研究结果，已被广泛应用于模型表示，信号处理和语义计算等领域。

(完整版)平面向量的线性运算

ABabbaa a O =−→−OBA B O B a abb=−→−OB a +b ABAa +b向量的线性运算（一）1.向量的加法向量的加法：求两个向量和的运算叫做向量的加法。

表示：→--AB −→−+BC =→--AC ．规定：零向量与任一向量a ，都有00a a a +=+=．【注意】：两个向量的和仍旧是向量（简称和向量）作法：在平面内任意取一点O ，作→--OA =a →--→--OB =→--OA +→--AB a +b2.向量的加法法则（1）共线向量的加法：同向向量反向向量（2）不共线向量的加法几何中向量加法是用几何作图来定义的，一般有两种方法，即向量加法的三角形法则（“首尾相接，首尾连”）和平行四边形法则（对于两个向量共线不适应）。

三角形法则：根据向量加法定义得到的求向量和的方法，称为向量加法的三角形法则。

表示：→--AB −→−+BC=→--AC ．平行四边形法则：以同一点A 为起点的两个已知向量a ，b 为邻边作平行四边形ABCD ，则以A 为起点的对角线→--AC 就是a 与b 的和，这种求向量和的方法称为向量加法的平行四边形法则。

如图，已知向量a 、b 在平面内任取一点A ，作→--AB =a ，=−→−BC b ，则向量−→−AC 叫做a与b 的和，记作a +b ，即a +b +=−→−AB =−→−BC −→−AC【说明】：教材中采用了三角形法则来定义，这种定义，对两向量共线时同样适用，当向量不共线时，向量加法的三角形法则和平行四边形法则是一致的特殊情况：探究：（1）两相向量的和仍是一个向量；（2）当向量a 与b 不共线时，a +b 的方向不同向，且|a +b |<|a |+|b |; （3）当a 与b 同向时，则a +b 、a 、b 同向，且|a +b |=|a |+|b |,当a 与b 反向时，若|a |>|b |,则a +b 的方向与a 相同，且|a +b |=|a |-|b |；若|a |<|b |,则a +b 的方向与b 相同，且|a +b |=|b |-|a |.（4）“向量平移”：使前一个向量的终点为后一个向量的起点，可以推广到n 个向量连加3.向量加法的运算律（1）向量加法的交换律：a +b =b +a（2）向量加法的结合律：(a +b ) +c =a +(b +c ) 证明：如图：使=−→−AB a , =−→−BC b , =−→−CD c 则(a +b )+c =−→−AC +=−→−CD −→−AD ，a + (b +c )=−→−AB −→−+BD −→−=AD ,∴(a +b )+c =a +(b +c )从而，多个向量的加法运算可以按照任意的次序、任意的组合来进行例如：()()()()a b c d b d a c +++=+++；[()]()a b c d e d a c b e ++++=++++．例题：例1. O 为正六边形的中心，作出下列向量：（1）−→−OA +−→−OC （2）−→−BC +−→−FE （3）−→−OA +−→−FE例2．如图，一艘船从A 点出发以h km /32的速度向垂直于对岸的方向行驶，同时水aaab bba +ba +b ABC ABCD三角形法则平行四边形法则的流速为h km /2，求船实际航行的速度的大小与方向。

平面向量的线性运算(解析版)

专题一平面向量的线性运算1．向量的线性运算首尾相接指向终点起点重合指向对顶点起点重合指向被减向量2．多边形法则一般地，首尾顺次相接的多个向量的和等于从第一个向量起点指向最后一个向量终点的向量，即A 1A 2→＋A 2A 3→＋A 3A 4→＋…＋A n －1A n ＝A 1A n →，特别地，一个封闭图形，首尾连接而成的向量和为零向量．3．平面向量基本定理定理：如果e 1，e 2是同一平面内的两个不共线向量，那么对于这一平面内的任意向量a ，存在唯一的一对实数λ1，λ2，使a ＝λ1e 1＋λ2e 2，其中，不共线的向量e 1，e 2叫作表示这一平面内所有向量的一组基底，记为{e 1，e 2}．4．“爪”子定理形式1：在△ABC 中，D 是BC 上的点，如果|BD |＝m ，|DC |＝n ，则AD →＝m m ＋n AC →＋n m ＋n AB →，其中AD →，AB →，AC →知二可求一．特别地，若D 为线段BC 的中点，则AD →＝12(AC →＋AB →)．形式2：在△ABC 中，D 是BC 上的点，且BD →＝λBC →，则AD →＝λAC →＋(1－λ)AB →，其中AD →，AB →，AC →知二可求一．特别地，若D 为线段BC 的中点，则AD →＝12(AC →＋AB →)．形式1与形式2中AC →与AB →的系数的记忆可总结为：对面的女孩看过来(歌名，原唱任贤齐) 考点一向量的线性运算C 形式1C形式2【方法总结】利用平面向量的线性运算把一个向量表示为两个基向量的一般方法向量AD →＝f (AB →，AC →)的确定方法(1)在几何图形中通过三点共线即可考虑使用“爪”子定理完成向量AD →用AB →，AC →的表示．(2)若所给图形比较特殊(正方形、矩形、直角梯形、等边三角形、等腰三角形或直角三角形等)，则可通过建系将向量坐标化，从而得到AD →＝f (AB →，AC →)与AD →＝g (AB →，AC →)的方程组，再进行求解．【例题选讲】[例1](1)(2015·全国Ⅰ)设D 为△ABC 所在平面内一点，BC →＝3CD →，则( ) A ．AD →＝－13AB →＋43AC → B ．AD →＝13AB →－43AC →C ．AD →＝43AB →＋13AC → D ．AD →＝43AB →－13AC →答案 A 解析 AD →＝AC →＋CD →＝AC →＋13BC →＝AC →＋13(AC →－AB →)＝43AC →－13AB →＝－13AB →＋43AC →，故选A ．(2) (2014·全国Ⅰ)设D ，E ，F 分别为△ABC 的三边BC ，CA ，AB 的中点，则EB →＋FC →＝( ) A ．AD → B ．12AD → C ．BC →D ．12BC →答案 A 解析 EB →＋FC →＝12(AB →＋CB →)＋12(AC →＋BC →)＝12(AB →＋AC →)＝AD →，故选A ．(3) (2018·全国Ⅰ)在△ABC 中，AD 为BC 边上的中线，E 为AD 的中点，则EB →＝( ) A ．34AB →－14AC → B ．14AB →－34AC → C ．34AB →＋14AC → D ．14AB →＋34AC →答案 A 解析 ∵E 是AD 的中点，∴EA →＝－12AD →，∴EB →＝EA →＋AB →＝－12AD →＋AB →，又知D 是BC 的中点，∴AD →＝12(AB →＋AC →)，因此EB →＝－14(AB →＋AC →)＋AB →＝34AB →－14AC →．(4)如图，在△ABC 中，点D 在BC 边上，且CD ＝2DB ，点E 在AD 边上，且AD ＝3AE ，则用向量AB →，AC →表示CE →为( )A ．29AB →＋89AC → B ．29AB →－89AC → C ．29AB →＋79AC →D ．29AB →－79AC →答案 B 解析由平面向量的三角形法则及向量共线的性质可得CE →＝AE →－AC →＝13AD →－AC →＝13(AB →＋13BC →)－AC →＝13⎣⎡⎦⎤AB →＋13(AC →－AB →)－AC →＝29AB →－89AC →． (5)如图所示，下列结论正确的是( )①PQ →＝32a ＋32b ；②PT →＝32a －b ；③PS →＝32a －12b ；④PR →＝32a ＋b ．A ．①②B ．③④C ．①③D ．②④答案 C 解析 ①根据向量的加法法则，得PQ →＝32a ＋32b ，故①正确；②根据向量的减法法则，得PT→＝32a －32b ，故②错误；③PS →＝PQ →＋QS →＝32a ＋32b －2b ＝32a －12b ，故③正确；④PR →＝PQ →＋QR →＝32a ＋32b －b ＝32a ＋12b ，故④错误，故选C ． (6)如图所示，在△ABO 中，OC →＝14OA →，OD →＝12OB →，AD 与BC 相交于M ，设OA →＝a ，OB →＝b ．则用a和b 表示向量OM →＝___________．答案 OM ＝17a ＋37b 解析设OM ＝m a ＋n b ，则AM ＝OM －OA ＝m a ＋n b －a ＝(m －1)a ＋n b ．AD ＝OD －OA ＝12OB －OA ＝－a ＋12b ．又∵A 、M 、D 三点共线，∴AM 与AD 共线．∴存在实数t ，使得AM ＝t AD ，即(m －1)a ＋n b ＝t ⎝⎛⎭⎫－a ＋12b ．∴(m －1)a ＋n b ＝－t a ＋12t b ．∴⎩⎪⎨⎪⎧m －1＝－t ，n ＝t 2，消去t得，m －1＝－2n ，即m ＋2n ＝1．①．又∵CM ＝OM －OC ＝m a ＋n b －14a ＝⎝⎛⎭⎫m －14a ＋n b ，CB ＝OB －OC ＝b －14a ＝－14a ＋b ．又∵C 、M 、B 三点共线，∴CM 与CB 共线．∴存在实数t 1，使得CM ＝t 1CB ，∴⎝⎛⎭⎫m －14a ＋n b ＝t 1⎝⎛⎭⎫－14a ＋b ，∴⎩⎪⎨⎪⎧m －14＝－14t 1，n ＝t 1.消去t 1得，4m ＋n ＝1，②．由①②得m ＝17，n ＝37，∴OM ＝17a ＋37b ．另解因为A ，M ，D 三点共线，所以OM →＝λ1OD →＋(1－λ1)OA →＝12λ1b ＋(1－λ1)a ，①，因为C ，M ，B三点共线，所以OM →＝λ2OB →＋(1－λ2)OC →＝λ2b ＋(1－λ24)a ，②，由①②可得⎩⎨⎧12λ1＝λ2，1－λ1＝1－λ24，解得⎩⎨⎧λ1＝67，λ2＝37.故OM →＝17a ＋37b ．(7)在平行四边形ABCD 中，AC 与BD 相交于点O ，点E 是线段OD 的中点，AE 的延长线与CD 交于点F ，若AC →＝a ，BD →＝b ，则AF →＝( )A ．14a ＋12bB ．23a ＋13bC ．12a ＋14bD ．13a ＋23b答案 B 解析如图，根据题意，得AB →＝12AC →＋12DB →＝12(a －b )，AD →＝12AC →＋12BD →＝12(a ＋b )．令AF →＝tAE →，则AF →＝t (AB →＋BE →)＝t ⎝⎛⎭⎫AB →＋34 BE → ＝t 2a ＋t 4b ．由AF →＝AD →＋DF →，令DF →＝sDC →，又AD →＝12(a ＋b )，DF →＝s2a －s 2b ，所以AF →＝s ＋12a ＋1－s2b ，所以⎩⎨⎧t 2＝s ＋12，t 4＝1－s2，解方程组得⎩⎨⎧s ＝13，t ＝43，把s 代入即可得到AF →＝23a ＋13b ，故选B ．另解如图，AF →＝AD →＋DF →，由题意知，DE ∶BE ＝1∶3＝DF ∶AB ，故DF →＝13AB →，则AF →＝12a ＋12b ＋13 (12a －12b )＝23a ＋13b ．(8)在平行四边形ABCD 中，E ，F 分别是BC ，CD 的中点，D E 交AF 于H ，记AB →，BC →分别为a ，b ，则AH →＝( )A ．25a －45bB ．25a ＋45bC ．－25a ＋45bD ．－25a －45b答案 B 解析如图，过点F 作BC 的平行线交DE 于G ，则G 是DE 的中点，且GF →＝12EC →＝14BC →，∴GF →＝14AD →，易知△AHD ∽△FHG ，从而HF →＝14AH →，∴AH →＝45AF →，AF →＝AD →＋DF →＝b ＋12a ，∴AH →＝45⎝⎛⎭⎫b ＋12a ＝25a ＋45b ，故选B ．(9)如图，在直角梯形ABCD 中，AB ＝2AD ＝2DC ，E 为BC 边上一点，BC →＝3EC →，F 为AE 的中点，则BF →＝( )A ．23AB →－13AD → B ．13AB →－23AD →C ．－23AB →＋13AD → D ．－13AB →＋23AD →答案 C 解析 BF →＝BA →＋AF →＝BA →＋12AE →＝－AB →＋12(AD →＋12AB →＋CE →)＝－AB →＋12(AD →＋12AB →＋13CB →)＝－AB →＋12AD →＋14AB →＋16(CD →＋DA →＋AB →)＝－23AB →＋13AD →．(10)如图，已知AB 是圆O 的直径，点C ，D 是半圆弧的两个三等分点，AB ＝a ，AC ＝b ，则AD 等于( )A ．a －12bB ．12a －bC ．a ＋12bD ．12a ＋b答案 D 解析连接CD ，由点C ，D 是半圆弧的三等分点，得CD ∥AB 且CD →＝12AB →＝12a ，所以AD →＝AC →＋CD →＝b ＋12a ．【对点训练】1．已知O ，A ，B 是平面上的三个点，直线AB 上有一点C ，满足2AC →＋CB →＝0，则OC →等于( ) A ．2OA →－OB → B ．－OA →＋2OB →C ．23OA →－13OB →D ．－13OA →＋23OB →1．答案 A 解析由2AC →＋CB →＝0得2OC →－2OA →＋OB →－OC →＝0，故OC →＝2OA →－OB →． 2．如图，在△ABC 中，点D 是BC 边上靠近B 的三等分点，则AD →等于( )A ．23AB →－13AC → B ．13AB →＋23AC → C ．23AB →＋13AC →D ．13AB →－23AC →2．答案 C 解析由平面向量的三角形法则，得AD →＝AB →＋BD →．又因为点D 是BC 边上靠近B 的三等分点，所以AD →＝AB →＋13BC →＝AB →＋13(AC →－AB →)＝23AB →＋13AC →．3．在△ABC 中，AB →＝c ，AC →＝b ，若点D 满足BD →＝2DC →，若将b 与c 作为基底，则AD →等于( ) A ．23b ＋13c B ．35c －23b C ．23b －13c D ．13b ＋23c3．答案 A 解析 ∵BD →＝2DC →，∴AD →－AB →＝2(AC →－AD →)，∴AD →－c ＝2(b －AD →)，∴AD →＝13c ＋23b ．4．如图所示，在△ABC 中，若BC →＝3DC →，则AD →＝( )A ．23AB →＋13AC → B ．23AB →－13AC → C ．13AB →＋23AC →D ．13AB →－23AC →4．答案 C 解析 AD →＝CD →－CA →＝13CB →－CA →＝13(AB →－AC →)＋AC →＝13AB →＋23AC →．故选C ．5．设D ，E ，F 分别为△ABC 三边BC ，CA ，AB 的中点，则DA →＋2EB →＋3FC →＝( ) A ．12AD → B ．32AD → C ．12AC → D ．32AC →5．答案 D 解析因为D ，E ，F 分别为△ABC 三边BC ，CA ，AB 的中点，所以DA →＋2EB →＋3FC →＝12(BA →＋CA →)＋2×12(AB →＋CB →)＋3×12×(AC →＋BC →)＝12BA →＋AB →＋CB →＋32BC →＋32AC →＋12CA →＝12AB →＋12BC →＋AC →＝12AC →＋AC →＝32AC →．6．已知点M 是△ABC 的边BC 的中点，点E 在边AC 上，且EC →＝2AE →，则EM →＝( ) A ．12AC →＋13AB → B ．12AC →＋16AB → C ．16AC →＋12AB → D ．16AC →＋32AB →6．答案 C 解析如图，∵EC →＝2AE →，∴EM →＝EC →＋CM →＝23AC →＋12CB →＝23AC →＋12(AB →－AC →)＝12AB →＋16AC →．7．在△ABC 中，P ，Q 分别是边AB ，BC 上的点，且AP ＝13AB ，BQ ＝13BC ．若AB →＝a ，AC →＝b ，则PQ →＝( )A ．13a ＋13bB ．－13a ＋13bC ．13a －13bD ．－13a －13b7．答案 A 解析 PQ →＝PB →＋BQ →＝23AB →＋13BC →＝23AB →＋13(AC →－AB →)＝13AB →＋13AC →＝13a ＋13b ，故选A ．8．已知D ，E ，F 分别为△ABC 的边BC ，CA ，AB 的中点，且BC →＝a ，CA →＝b ，给出下列命题：①AD →＝12a －b ；②BE →＝a ＋12b ；③CF →＝－12a ＋12b ；④AD →＋BE →＋CF →＝0．其中正确命题的序号为________．8．答案 ②③④ 解析 BC →＝a ，CA →＝b ，AD →＝12CB →＋AC →＝－12a －b ，BE →＝BC →＋12CA →＝a ＋12b ，CF →＝12(CB →＋CA →)＝12(－a ＋b )＝－12a ＋12b ，所以AD →＋BE →＋CF →＝－b －12a ＋a ＋12b ＋12b －12a ＝0．所以正确命题的序号为②③④．9．(多选)在△ABC 中，D ，E ，F 分别是边BC ，CA ，AB 的中点，AD ，BE ，CF 交于点G ，则( ) A ．EF →＝12CA →－12BC → B ．BE →＝－12BA →＋12BC → C ．AD →＋BE →＝FC → D ．GA →＋GB →＋GC →＝09．答案 CD 解析如图，因为点D ，E ，F 分别是边BC ，CA ，AB 的中点，所以EF →＝12CB →＝－12BC →，故A 不正确；BE →＝BC →＋CE →＝BC →＋12CA →＝BC →＋12(CB →＋BA →)＝BC →－12BC →－12AB →＝－12AB →＋12BC →，故B 不正确；FC →＝AC →－AF →＝AD →＋DC →＋F A →＝AD →＋12BC →＋F A →＝AD →＋FE →＋F A →＝AD →＋FB →＋BE →＋F A →＝AD →＋BE →，故C正确；由题意知，点G 为△ABC 的重心，所以AG →＋BG →＋CG →＝23AD →＋23BE →＋23CF →＝23×12(AB →＋AC →)＋23×12(BA→＋BC →)＋23×12(CB →＋CA →)＝0，即GA →＋GB →＋GC →＝0，故D 正确．故选CD ．10．如图所示，在△ABC 中，D ，F 分别是AB ，AC 的中点，BF 与CD 交于点O ，设AB →＝a ，AC →＝b ，则用a ，b 表示向量AO →为____________．10．答案 AO →＝13(a ＋b ) 解析由D ，O ，C 三点共线，可设DO →＝k 1DC →＝k 1(AC →－AD →)＝k 1⎝⎛⎭⎫b －12a ＝－12k 1a ＋k 1b (k 1为实数)，同理，可设BO →＝k 2BF →＝k 2(AF →－AB →)＝k 2⎝⎛⎭⎫12b －a ＝－k 2a ＋12k 2b (k 2为实数)，①，又BO →＝BD →＋DO →＝－12a ＋⎝⎛⎭⎫－12k 1a ＋k 1b ＝－12(1＋k 1)a ＋k 1b ，②，所以由①②，得－k 2a ＋12k 2b ＝－12(1＋k 1)a BCA EF G＋k 1b ，即12(1＋k 1－2k 2)a ＋⎝⎛⎭⎫12k 2－k 1b ＝0．又a ，b 不共线，所以⎩⎨⎧12(1＋k 1－2k 2)＝0，12k 2－k 1＝0，解得⎩⎨⎧k 1＝13，k 2＝23.所以BO →＝－23a ＋13b ．所以AO →＝AB →＋BO →＝a ＋⎝⎛⎭⎫－23a ＋13b ＝13(a ＋b )．另解因为B ，O ，F 三点共线，所以AO →＝λ1AB →＋(1－λ1)AF →＝λ1a ＋12(1－λ1)b ，①，因为D ，O ，C 三点共线，所以AO →＝λ2AC →＋(1－λ2)AD →＝λ2b ＋12(1－λ2)a ，②，由①②可得⎩⎨⎧12(1－λ1)＝λ2，λ1＝1－λ22，解得⎩⎨⎧λ1＝13，λ2＝13.故AO →＝13(a ＋b )．11．如图，正方形ABCD 中，点E 是DC 的中点，点F 是BC 的一个三等分点，那么EF 等于( )A ．12AB －13AD B ．14AB ＋12ADC ．13AB ＋12DAD ．12AB －23AD11．答案 D 解析在△CEF 中，有EF →＝EC →＋CF →．因为点E 为DC 的中点，所以EC →＝12DC →．因为点F为BC 的一个三等分点，所以CF →＝23CB →．所以EF →＝12DC →＋23CB →＝12AB →＋23DA →＝12AB →－23AD →，故选D ．12．如图，在平行四边形ABCD 中，E 为DC 边的中点，且AB →＝a ，AD →＝b ，则BE →＝( )A ．12b －aB ．12a －bC ．－12a ＋bD ．12b ＋a12．答案 C 解析 BE →＝BA →＋AD →＋12DC →＝－a ＋b ＋12a ＝b －12a ，故选C ．13．在平行四边形ABCD 中，AB ＝a ，AD ＝b ，AN ＝3NC ，M 为BC 的中点，则MN ＝____________．(用a ，b 表示)13．答案－14a ＋14b 解析由AN →＝3NC →得，AN →＝34AC →＝34(a ＋b )，AM →＝a ＋12b ，所以MN →＝AN →－AM →＝34(a＋b )－⎝⎛⎭⎫a ＋12b ＝－14a ＋14b ． 14．在平行四边形ABCD 中，AB →＝e 1，AC →＝e 2，NC →＝14AC →，BM →＝12MC →，则MN →＝_________．(用e 1，e 2表示)14．答案－23e 1＋512e 2 解析如图，MN →＝CN →－CM →＝CN →＋2BM →＝CN →＋23BC →＝－14AC →＋23(AC →－AB →)＝－14e 2＋23(e 2－e 1)＝－23e 1＋512e 2．15．在平行四边形ABCD 中，E ，F 分别是BC ，CD 的中点，DE 交AF 于H ，记AB →，BC →分别为a ，b ，则AH →＝( )A ．25a －45bB ．25a ＋45bC ．－25a ＋45bD ．－25a －45b15．答案 B 解析设AH →＝λAF →，DH →＝μDE →．而DH →＝DA →＋AH →＝－b ＋λAF →＝－b ＋λ⎝⎛⎭⎫b ＋12a ，DH →＝μDE →＝ μ⎝⎛⎭⎫a －12b ．因此，μ⎝⎛⎭⎫a －12b ＝－b ＋λ⎝⎛⎭⎫b ＋12a ．由于a ，b 不共线，因此由平面向量的基本定理，得⎩⎨⎧μ＝12λ，－12μ＝－1＋λ.解之得λ＝45，μ＝25．故AH →＝λAF →＝λ⎝⎛⎭⎫b ＋12a ＝25a ＋45b ．16．在梯形ABCD 中，AB →＝3DC →，则BC →＝( )A ．－23AB →＋AD → B ．－23AB →＋43AD →C ．－13AB →＋23AD → D ．－23AB →－AD →16．答案 A 解析因为在梯形ABCD 中，AB →＝3DC →，所以BC →＝BA →＋AD →＋DC →＝－AB →＋AD →＋13AB →＝－23AB →＋AD →，故选A ．考点二根据向量线性运算求参数【方法总结】利用平面向量的线性运算求参数的一般方法向量方程AD →＝xAB →＋yAC →中x ，y 的确定方法(1)在几何图形中通过三点共线即可考虑使用“爪”子定理完成向量的表示，进而确定x ，y ． (2)若所给图形比较特殊(正方形、矩形、直角梯形、等边三角形、等腰三角形或直角三角形等)，则可通过建系将向量坐标化，从而得到关于x ，y 的方程组，再进行求解．(3)若题目中某些向量的数量积已知，则对于向量方程AD →＝xAB →＋yAC →，可考虑两边对同一向量作数量积运算，从而得到关于于x ，y 的方程组，再进行求解．(4)对于求x ＋y 的值的有关问题可考虑平面向量的等和线定理法，见《平面向量特训之满分必杀篇》第一讲平面向量的等和线．【例题选讲】[例1](1)如图，在△OAB 中，P 为线段AB 上的一点，OP →＝xOA →＋yOB →，且BP →＝2P A →，则( )A ．x ＝23，y ＝13B ．x ＝13，y ＝23C ．x ＝14，y ＝34D ．x ＝34，y ＝14答案 A 解析由题意知OP →＝OB →＋BP →，又BP →＝2P A →，所以OP →＝OB →＋23BA →＝OB →＋23(OA →－OB →)＝23OA →＋13OB →，所以x ＝23，y ＝13． (2)(2013·江苏)设D ，E 分别是△ABC 的边AB ，BC 上的点，AD ＝12AB ，BE ＝23BC ．若DE →＝λ1AB →＋λ2AC→(λ1，λ2为实数)，则λ1＋λ2的值为________．答案 12 解析由题意，得DE →＝DB →＋BE →＝12AB →＋23BC →＝12AB →＋23(AC →－AB →)＝－16AB →＋23AC →，则λ1＝－16，λ2＝23，即λ1＋λ2＝12．(3)如图，在△ABC 中，点D 在线段BC 上，且满足BD ＝12DC ，过点D 的直线分别交直线AB ，AC 于不同的两点M ，N ，若AM →＝mAB →，AN →＝nAC →，则( )A ．m ＋n 是定值，定值为2B ．2m ＋n 是定值，定值为3C ．1m ＋1n 是定值，定值为2D ．2m ＋1n是定值，定值为3答案 D 解析法一：如图，过点C 作CE 平行于MN 交AB 于点E ．由AN →＝nAC →可得AC AN ＝1n ，所以AE EM ＝AC CN ＝1n －1，由BD ＝12DC 可得BM ME ＝12，所以AM AB ＝n n ＋n －12＝2n 3n －1，因为AM →＝mAB →，所以m ＝2n 3n －1，整理可得2m ＋1n＝3．故选D ．法二：因为M ，D ，N 三点共线，所以AD →＝λAM →＋(1－λ)·AN →．又AM →＝mAB →，AN →＝nAC →，所以AD →＝λmAB →＋(1－λ)·nAC →．又BD →＝12DC →，所以AD →－AB →＝12AC →－12AD →，所以AD →＝13AC →＋23AB →．比较系数知λm ＝23，(1－λ)n＝13，所以2m ＋1n＝3，故选D ． (4)如图，在△ABC 中，AD →＝23AC →，BP →＝13BD →，若AP →＝λAB →＋μAC →，则λ＋μ的值为( )A ．89B ．49C ．83D ．43答案 A 解析 AP →＝AB →＋BP →＝AB →＋13BD →＝AB →＋13(AD →－AB →)＝23AB →＋13×23AC →＝23AB →＋29AC →．因为AP →＝λAB →＋μAC →，所以λ＝23，μ＝29，则λ＋μ＝23＋29＝89．(5)已知在Rt △ABC 中，∠BAC ＝90°，AB ＝1，AC ＝2，D 是△ABC 内一点，且∠DAB ＝60°，设AD →＝λAB →＋μAC →(λ，μ∈R )，则λμ＝( )A ．233B ．33C ．3D ．23答案 A 解析如图，以A 为原点，AB 所在直线为x 轴，AC 所在直线为y 轴建立平面直角坐标系，则B 点的坐标为(1，0)，C 点的坐标为(0，2)，因为∠DAB ＝60°，所以设D 点的坐标为(m ，3m )(m ≠0)．AD →＝(m ，3m )＝λAB →＋μAC →＝λ(1，0)＋μ(0，2)＝(λ，2μ)，则λ＝m ，且μ＝32m ，所以λμ＝233．(6)如图，在△ABC 中，设AB →＝a ，AC →＝b ，AP 的中点为Q ，BQ 的中点为R ，CR 的中点为P ，若AP →＝m a ＋nb ，则m ＋n ＝________．答案 67 解析根据已知条件得，BQ →＝AQ →－AB →＝12AP →－AB →＝12(m a ＋n b )－a ＝⎝⎛⎭⎫m 2－1a ＋n 2b ，CR →＝BR →－BC →＝12BQ →－AC →＋AB →＝12⎣⎡⎦⎤⎝⎛⎭⎫m 2－1a ＋n 2b －b ＋a ＝⎝⎛⎭⎫m 4＋12a ＋⎝⎛⎭⎫n 4－1b ，∴QP →＝m 2a ＋n 2b ，RQ →＝⎝⎛⎭⎫m 4－12a ＋n 4b ，RP →＝－⎝⎛⎭⎫m 8＋14a ＋⎝⎛⎭⎫12－n 8b ．∵RQ →＋QP →＝RP →，∴⎝⎛⎭⎫3m 4－12a ＋3n 4b ＝⎝⎛⎭⎫－m 8－14a ＋⎝⎛⎭⎫12－n 8b ，∴⎩⎨⎧3m 4－12＝－m 8－14，3n 4＝12－n 8，解得⎩⎨⎧m ＝27，n ＝47，故m ＋n ＝67．(7)如图所示，点P 在矩形ABCD 内，且满足∠DAP ＝30°，若|AD →|＝1，|AB →|＝3，AP →＝mAD →＋nAB →(m ，n ∈R )，则mn等于( )A ．13B ．3C ．33D ．3答案 B 解析如图，过点P 作P E ⊥AB 于点E ，作PF ⊥AD 于点F ，则结合图形及题设得AP →＝AF →＋AE →＝mAD →＋nAB →，所以可得|AF →|＝m ，|PF →|＝|AE →|＝3n ．又∠DAP ＝30°，在Rt △APF 中，t a n ∠F AP ＝t a n 30°＝|PF →||AF →|＝33，则33＝3n m ，化简得m n ＝3．故选B ．优解：如图所示，假设点P 在矩形的对角线BD 上，由题意易知|DB →|＝2，∠ADB ＝60°，又∠DAP ＝30°，所以∠DP A ＝90°．由|AD →|＝1，可得|DP →|＝12＝14|DB →|，从而可得AP →＝AD →＋DP →＝AD →＋14DB →＝AD →＋14(AB →－AD →)＝34AD →＋14AB →．又AP →＝mAD →＋n AB →，所以m ＝34，n ＝14，则m n＝3．故选B ．(8)在平行四边形ABCD 中，点E 和F 分别是边CD 和BC 的中点．若AC →＝λAE →＋μAF →，其中λ，μ∈R ，则λ＋μ＝__________．答案 43 解析选择AB →，AD →作为平面向量的一组基底，则AC →＝AB →＋AD →，AE →＝12AB →＋AD →，AF →＝AB →＋12AD →，又AC →＝λAE →＋μAF →＝⎝⎛⎭⎫12λ＋μAB →＋⎝⎛⎭⎫λ＋12μAD →，于是得⎩⎨⎧12λ＋μ＝1，λ＋12μ＝1，即⎩⎨⎧λ＝23，μ＝23，故λ＋μ＝43．(9)如图，在直角梯形ABCD 中，DC →＝14AB →，BE →＝2EC →，且AE →＝rAB →＋sAD →，则2r ＋3s ＝( )A ．1B ．2C ．3D ．4答案 C 解析根据图形，由题意可得AE →＝AB →＋BE →＝AB →＋23BC →＝AB →＋23(BA →＋AD →＋DC →)＝13AB →＋23(AD →＋DC →)＝13AB →＋23⎝⎛⎭⎫AD →＋14AB →＝12AB →＋23AD →．因为AE →＝rAB →＋sAD →，所以r ＝12，s ＝23，则2r ＋3s ＝1＋2＝3，故选C ．优解：如图，建立平面直角坐标系xAy ，依题意可设点B (4m ，0)，D (3m ，3h )，E(4m ，2h )，其中m ＞0，h ＞0．由AE →＝rAB →＋sAD →，得(4m ，2h )＝r (4m ，0)＋s (3m ，3h )，∴⎩⎪⎨⎪⎧4m ＝4mr ＋3ms 2h ＝3hs ，解得⎩⎨⎧r ＝12，s ＝23.∴2r ＋3s ＝3．(10) (2017·江苏)如图，在同一个平面内，向量OA →，OB →，OC →的模分别为1，1，2，OA →与OC →的夹角为α，且tan α＝7，OB →与OC →的夹角为45°．若OC →＝mOA →＋nOB →(m ，n ∈R )，则m ＋n ＝__________．答案 3 解析以O 为坐标原点，OA 所在直线为x 轴建立平面直角坐标系，则A (1，0)，由tan α＝7，α∈⎝⎛⎭⎫0，π2，得sin α＝752，cos α＝152，设C (x C ，y C )，B (x B ，y B )，则x C ＝|OC →|cos α＝2×152＝15，y C ＝|OC →|sin α＝2×752＝75，即C ⎝⎛⎭⎫15，75．又cos(α＋45°)＝152×12－752×12＝－35，sin(α＋45°)＝45，则x B＝|OB →|cos(α＋45°)＝－35，y B ＝|OB →|sin(α＋45°)＝45，即B ⎝⎛⎭⎫－35，45，由OC →＝mOA →＋nOB →，可得⎩⎨⎧15＝m －35n ，75＝45n ，解得⎩⎨⎧m ＝54，n ＝74，所以m ＋n ＝54＋74＝3．【对点训练】1．在△ABC 中，已知D 是AB 边上一点，若AD →＝2DB →，CD →＝13CA →＋λCB →，则λ＝________．1．答案 23 解析由图知CD →＝CA →＋AD →，①．CD →＝CB →＋BD →，②．且AD →＋2BD →＝0．①＋②×2得：3CD →＝CA →＋2CB →，∴CD →＝13CA →＋23CB →，∴λ＝23．2．如图所示，在△ABC 中，D 为BC 边上的一点，且BD ＝2DC ，若AC →＝mAB →＋nAD →(m ，n ∈R )，则m －n ＝________．2．答案－2 解析由于BD ＝2DC ，则BC →＝－3CD →，其中BC →＝AC →－AB →，CD →＝AD →－AC →，那么BC →＝－ 3CD →可转化为AC →－AB →＝－3(AD →－AC →)，可以得到－2AC →＝－3AD →＋AB →，即AC →＝－12AB →＋32AD →，则m ＝－12，n ＝32，那么m －n ＝－12－32＝－2． 3．已知△ABC 中，点D 在BC 边上，且CD →＝2DB →，CD →＝rAB →＋sAC →，则r ＋s 的值是( ) A ．23 B ．43C ．－3D ．03．答案 D 解析 ∵DB →＝AB →－AD →，∴CD →＝AB →－DB →－AC →＝AB →－12CD →－AC →，∴32CD →＝AB →－AC →，∴CD →＝23AB →－23AC →．又CD →＝rAB →＋sAC →，∴r ＝23，s ＝－23，∴r ＋s ＝0，故选D ． 4．在锐角△ABC 中，CM →＝3MB →，AM →＝xAB →＋yAC →(x ，y ∈R )，则x y＝________．4．答案 3 解析由题设可得AM →＝CM →－CA →＝34CB →＋AC →＝34(AB →－A C →)＋AC →＝34AB →＋14AC →，则x ＝34，y＝14．故xy＝3．5．在△ABC 中，点M ，N 满足AM →＝2MC →，BN →＝NC →．若MN →＝xAB →＋yAC →，则x ＝________，y ＝______． 5．答案 12 －16 解析 MN →＝MC →＋CN →＝13AC →＋12CB →＝13AC →＋12(AB →－AC →)＝12AB →－16AC →＝xAB →＋yAC →，∴x＝12，y ＝－16．6．如图所示，在△ABC 中，点O 是BC 的中点．过点O 的直线分别交直线AB 、AC 于不同的两点M 、N ，若AB →＝mAM →，AC →＝nAN →，则m ＋n 的值为________．6．答案 2 解析 ∵O 是BC 的中点，∴AO →＝12(AB →＋AC →)．又∵AB →＝mAM →，AC →＝nAN →，∴AO →＝m 2AM →＋n2AN →．∵M ，O ，N 三点共线，∴m 2＋n 2＝1．则m ＋n ＝2．7．已知点G 是△ABC 的重心，过G 作一条直线与AB ，AC 两边分别交于M ，N 两点，且AM →＝xAB →，AN →＝yAC →，则xy x ＋y的值为( )A ．12B ．13C ．2D ．37．答案 B 解析由已知得M ，G ，N 三点共线，∴AG →＝λAM →＋(1－λ)AN →＝λxAB →＋(1－λ)yAC →．∵ 点G 是△ABC 的重心，∴AG →＝23×12(AB →＋AC →)＝13·(AB →＋AC →)，∴⎩⎨⎧λx ＝13，(1－λ)y ＝13，即⎩⎨⎧λ＝13x，1－λ＝13y，得13x＋13y ＝1，即1x ＋1y ＝3，通分变形得，x ＋y xy ＝3，∴xy x ＋y ＝13． 8．如图所示，AD 是△ABC 的中线，O 是AD 的中点，若CO →＝λAB →＋μAC →，其中λ，μ∈R ，则λ＋μ的值为 ( )A ．－12B ．12C ．－14D ．148．答案 A 解析由题意知，CO →＝12(CD →＋CA →)＝12×⎝⎛⎭⎫12CB →＋CA →＝14(AB →－AC →)＋12CA →＝14AB →－34AC →，则λ＝ 14，μ＝－34，故λ＋μ＝－12． 9．如图，在△ABC 中，AN →＝13NC →，P 是BN 上的一点，若AP →＝mAB →＋211AC →，则实数m 的值为________．9．答案311 解析设BP →＝kBN →，k ∈R ．因为AP →＝AB →＋BP →＝AB →＋kBN →＝AB →＋k (AN →－AB →)＝AB →＋k (14AC →－AB →) ＝(1－k )AB →＋k 4AC →，且AP →＝mAB →＋211AC →，所以1－k ＝m ，k 4＝211，解得k ＝811，m ＝311．10．在△ABC 中，AN →＝14NC →，若P 是直线BN 上的一点，且满足AP →＝mAB →＋25AC →，则实数m 的值为( )A ．－4B ．－1C ．1D ．410．答案 B 解析根据题意设BP →＝nBN →(n ∈R )，则AP →＝AB →＋BP →＝AB →＋nBN →＝AB →＋n (AN →－AB →)＝AB →＋n (25AC →－AB →)＝(1－n )AB →＋n 5AC →．又AP →＝mAB →＋25AC →，∴⎩⎪⎨⎪⎧1－n ＝m ，n 5＝25，解得⎩⎪⎨⎪⎧n ＝2，m ＝－1. 11．在△ABC 中，M 为边BC 上任意一点，N 为AM 的中点，AN →＝λAB →＋μAC →，则λ＋μ的值为( )A ．12B ．13C ．14D ．111．答案 A 解析设BM →＝tBC →，则AN →＝12AM →＝12(AB →＋BM →)＝12AB →＋12BM →＝12AB →＋t 2BC →＝12AB →＋t 2(AC →－AB →)＝⎝⎛⎭⎫12－t 2AB →＋t 2AC →，∴λ＝12－t 2，μ＝t 2，∴λ＋μ＝12，故选A ． 12．在△ABC 中，AB ＝2，BC ＝3，∠ABC ＝60°，AD 为BC 边上的高，O 为AD 的中点，若AO →＝λAB →＋μBC →，则λ＋μ等于( )A ．1B ．12C ．13D ．2312．答案 D 解析 ∵AD →＝AB →＋BD →＝AB →＋13BC →，∴2AO →＝AB →＋13BC →，即AO →＝12AB →＋16BC →．故λ＋μ＝12＋16＝23．13．在△ABC 中，D 为三角形所在平面内一点，且AD →＝13AB →＋12AC →．延长AD 交BC 于E ，若AE →＝λAB →＋μAC →，则λ－μ的值是________．13．答案－15 解析设AE →＝xAD →，∵AD →＝13AB →＋12AC →，∴AE →＝x 3AB →＋x 2AC →．由于E ，B ，C 三点共线，∴x 3＋x 2＝1，x ＝65．根据平面向量基本定理，得λ＝x 3，μ＝x 2．因此λ－μ＝x 3－x 2＝－x 6＝－15． 14．如图，正方形ABCD 中，E 为DC 的中点，若AE →＝λAB →＋μAC →，则λ＋μ的值为( )A ．12B ．－12C ．1D ．－114．答案 A 解析由题意得AE →＝AD →＋12AB →＝BC →＋AB →－12AB →＝AC →－12AB →，∴λ＝－12，μ＝1，∴λ＋μ＝12，故选A ．15．如图所示，正方形ABCD 中，M 是BC 的中点，若AC →＝λAM →＋μBD →，则λ＋μ＝( )A ．43B ．53C ．158D ．215．答案 B 解析因为AC →＝λAM →＋μBD →＝λ(AB →＋BM →)＋μ(BA →＋AD →)＝λ (AB →＋12AD →)＋μ(－AB →＋AD →)＝(λ－μ) AB →＋⎝⎛⎭⎫12λ＋μAD →，且AC →＝AB →＋AD →，所以⎩⎪⎨⎪⎧λ－μ＝1，12λ＋μ＝1，得⎩⎨⎧λ＝43，μ＝13，所以λ＋μ＝53，故选B ．16．如图所示，矩形ABCD 的对角线相交于点O ，E 为AO 的中点，若DE →＝λAB →＋μAD →(λ，μ为实数)，则λ2＋μ2等于( )A ．58B ．14C ．1D ．51616．答案 A 解析 DE →＝12DA →＋12DO →＝12DA →＋14DB →＝12DA →＋14(DA →＋AB →)＝14AB →－34AD →，所以λ＝14，μ＝－34，故λ2＋μ2＝58，故选A ．17．如图，直线EF 与平行四边形ABCD 的两边AB ，AD 分别交于E ，F 两点，且与对角线AC 交于点K ，其中，AE →＝25AB →，AF →＝12AD →，AK →＝λAC →，则λ的值为______．17．答案 29 解析 ∵AE →＝25AB →，AF →＝12AD →，∴AB →＝52AE →，AD →＝2AF →．由向量加法的平行四边形法则可知，AC →＝AB →＋AD →，∴AK →＝λAC →＝λ(AB →＋AD →)＝λ(52AE →＋2AF →)＝52λAE →＋2λAF →，∵E ，F ，K 三点共线，∴52λ＋2λ＝1，∴λ＝29． 18．如图，在平行四边形ABCD 中，AC ，BD 相交于点O ，E 为线段AO 的中点．若BE →＝λBA →＋μBD →(λ，μ∈R )，则λ＋μ等于( )A ．1B ．34C ．23D ．1218．答案 B 解析 ∵E 为线段AO 的中点，∴BE →＝12BA →＋12BO →＝12BA →＋12×12BD →＝12BA →＋14BD →＝λBA →＋μBD →，∴λ＋μ＝12＋14＝34．19．一直线l 与平行四边形ABCD 中的两边AB ，AD 分别交于点E ，F ，且交其对角线AC 于点M ，若AB →＝2AE →，AD →＝3AF →，AM →＝λAB →－μAC →(λ，μ∈R )，则52μ－λ＝( )A ．－12B ．1C ．32D ．－319．答案 A 解析 AM →＝λAB →－μAC →＝λAB →－μ(AB →＋AD →)＝(λ－μ)AB →－μAD →＝2(λ－μ)AE →－3μAF →．因为E ，M ，F 三点共线，所以2(λ－μ)＋(－3μ)＝1，即2λ－5μ＝1，∴52μ－λ＝－12．20．如图，在平行四边形ABCD 中，E ，F 分别为边AB ，BC 的中点，连接CE ，DF ，交于点G ．若CG →＝λCD →＋μCB →(λ，μ∈R )，则λμ＝________．20．答案 12解析由题意可设CG →＝xCE →(0<x <1)，则CG →＝x (CB →＋BE →)＝x ⎝⎛⎭⎫CB →＋12CD →＝x 2CD →＋xCB →．因为 CG →＝λCD →＋μCB →，CD →与CB →不共线，所以λ＝x 2，μ＝x ，所以λμ＝12．21．如图，在直角梯形ABCD 中，AB ∥DC ，AD ⊥DC ，AD ＝DC ＝2AB ，E 为AD 的中点，若CA →＝λCE →＋μDB →(λ，μ∈R )，则λ＋μ的值为( )A ．65B ．85C ．2D ．8321．答案 B 解析建立如图所示的平面直角坐标系，则D (0，0)．不妨设AB ＝1，则CD ＝AD ＝2，所以C (2，0)，A (0，2)，B (1，2)，E (0，1)，∴CA →＝(－2，2)，CE →＝(－2，1)，DB →＝(1，2)，∵CA →＝λCE →＋μDB →，∴(－2，2)＝λ(－2，1)＋μ(1，2)，∴⎩⎪⎨⎪⎧－2λ＋μ＝－2，λ＋2μ＝2，解得⎩⎨⎧λ＝65，μ＝25，则λ＋μ＝85．22．在梯形ABCD 中，已知AB ∥CD ，AB ＝2CD ，M ，N 分别为CD ，BC 的中点．若AB →＝λAM →＋μAN →，则λ＋μ的值为( )A ．14B ．15C ．45D ．5422．答案 C 解析法一：连接AC (图略)，由AB →＝λAM →＋μAN →，得AB →＝λ·12(AD →＋AC →)＋μ·12(AC →＋AB →)，则⎝⎛⎭⎫μ2－1AB →＋λ2AD →＋⎣⎡⎭⎫λ2＋μ2AC →＝0，得⎝⎛⎭⎫μ2－1AB →＋λ2AD →＋⎣⎡⎭⎫λ2＋μ2 [AD →＋12AB →]＝0，得⎝⎛⎭⎫14λ＋34μ－1AB →＋⎝⎛⎭⎫λ＋μ2AD →＝0．又AB →，AD →不共线，所以由平面向量基本定理得⎩⎨⎧14λ＋34μ－1＝0，λ＋μ2＝0，解得⎩⎨⎧λ＝－45，μ＝85.所以λ＋μ＝45．法二：因为AB →＝AN →＋NB →＝AN →＋CN →＝AN →＋(CA →＋AN →)＝2AN →＋CM →＋MA →＝2AN →－14AB →－AM →，所以AB →＝85AN →－45AM →，所以λ＋μ＝45．法三：根据题意作出图形如图所示，连接MN 并延长，交AB 的延长线于点T ，由已知易得AB ＝45AT ，所以45AT →＝AB →＝λAM →＋μAN →，因为T ，M ，N 三点共线，所以λ＋μ＝45．23．已知|OA →|＝1，|OB →|＝3，OA →·OB →＝0，点C 在∠AOB 内，且OC →与OA →的夹角为30°，设OC →＝mOA →＋nOB →(m ，n ∈R )，则mn的值为( )A ．2B ．52C ．3D ．423．答案 C 解析 ∵OA →·OB →＝0，∴OA →⊥OB →，以OA →所在直线为x 轴，OB →所在直线为y 轴建立平面直角坐标系(图略)，OA →＝(1，0)，OB →＝(0，3)，OC →＝mOA →＋nOB →＝(m ，3n )．∵tan 30°＝3n m ＝33，∴m＝3n ，即mn＝3，故选C ．考点三根据向量线性运算求参数的取值范围(最值) 【方法总结】向量线性运算求参数的取值范围(最值)问题的2种求解方法(1)几何法：即临界位置法，结合图形，确定临界位置的动态分析求出范围．(2)代数法：即目标函数法，将参数表示为某一个变量或两个变量的函数，建立函数关系式，再利用三角函数有界性、二次函数或基本不等式求最值或范围．【例题选讲】[例1](1)已知在△ABC 中，点D 满足2BD →＋CD →＝0，过点D 的直线l 与直线AB ，AC 分别交于点M ，N ，AM →＝λAB →，AN →＝μAC →．若λ>0，μ>0，则λ＋μ的最小值为________．答案3＋223 解析连接AD ．因为2BD →＋CD →＝0，所以BD →＝13BC →，AD →＝AB →＋BD →＝AB →＋13BC →＝AB →＋13(AC →－AB →)＝23AB →＋13AC →．因为D ，M ，N 三点共线，所以存在x ∈R ，使AD →＝xAM →＋(1－x )AN →，则AD →＝xλAB →＋(1－x )μAC →，所以xλAB →＋(1－x )μAC →＝23AB →＋13AC →，所以xλ＝23，(1－x )μ＝13，所以x ＝23λ，1－x ＝13μ，所以23λ＋13μ＝1，所以λ＋μ＝13(λ＋μ)⎝⎛⎭⎫2λ＋1μ＝13⎝⎛⎭⎫3＋2μλ＋λμ≥3＋223，当且仅当λ＝2μ时等号成立，所以λ＋μ的最小值为3＋223．(2)如图，圆O 是边长为23的等边三角形ABC 的内切圆，其与BC 边相切于点D ，点M 为圆上任意一点，BM →＝xBA →＋yBD →(x ，y ∈R )，则2x ＋y 的最大值为( )A ．2B ．3C ．2D ．22答案 C 解析方法一如图，连接DA ，以D 点为原点，BC 所在直线为x 轴，DA 所在直线为y 轴，建立如图所示的平面直角坐标系．设内切圆的半径为r ，则圆心为坐标(0，r )，根据三角形面积公式，得12×l △ABC ×r ＝12×AB ×AC ×sin 60°(l △ABC 为△ABC 的周长)，解得r ＝1．易得B (－3，0)，C (3，0)，A (0，3)，D (0，0)，设M (cos θ，1＋sin θ)，θ∈[0，2π)，则BM →＝(cos θ＋3，1＋sin θ)，BA→＝(3，3)，BD →＝(3，0)，故BM →＝(cos θ＋3，1＋sin θ)＝(3x ＋3y ,3x )，故⎩⎨⎧cos θ＝3x ＋3y －3，sin θ＝3x －1，则⎩⎨⎧x ＝1＋sin θ3，y ＝3cos θ3－sin θ3＋23，所以2x ＋y ＝3cos θ3＋sin θ3＋43＝23sin ⎝⎛⎭⎫θ＋π3＋43≤2．当θ＝π6时等号成立．故2x ＋y 的最大值为2．方法二因为BM →＝xBA →＋yBD →，所以|BM →|2＝3(4x 2＋2xy ＋y 2)＝3[(2x ＋y )2－2xy ]．由题意知，x ≥0，y ≥0，|BM →|的最大值为(23)2－(3)2＝3，又(2x ＋y )24≥2xy ，即－(2x ＋y )24≤－2xy ，所以3×34(2x ＋y )2≤9，得2x ＋y ≤2，当且仅当2x ＝y ＝1时取等号．(3) (2017·全国Ⅲ)在矩形ABCD 中，AB ＝1，AD ＝2，动点P 在以点C 为圆心且与BD 相切的圆上．若AP →＝λAB →＋μAD →，则λ＋μ的最大值为( )A ．3B ．22C ．5D ．2答案 A 解析建立如图所示的直角坐标系，则C 点坐标为(2，1)．设BD 与圆C 切于点E ，连接CE ，则CE ⊥BD ．因为CD ＝1，BC ＝2，所以BD ＝12＋22＝5，EC ＝BC ·CD BD ＝25＝255，所以P 点的轨迹方程为(x －2)2＋(y －1)2＝45．设P (x 0，y 0)，则⎩⎨⎧x 0＝2＋255cos θ，y 0＝1＋255sin θ(θ为参数)，而AP →＝(x 0，y 0)，AB →＝(0，1)，AD →＝(2，0)．因为AP →＝λAB →＋μAD →＝λ(0，1)＋μ(2，0)＝(2μ，λ)，所以μ＝12x 0＝1＋55cos θ，λ＝y 0＝1＋255sin θ．两式相加，得λ＋μ＝1＋255sin θ＋1＋55cos θ＝2＋sin(θ＋φ)≤3⎝⎛⎭⎫其中sin φ＝55，cos φ＝255，当且仅当θ＝π2＋2k π－φ，k ∈Z 时，λ＋μ取得最大值3．故选A ．(4)如图，在扇形OAB 中，∠AOB ＝π3，C 为弧AB 上的一个动点，若OC →＝xOA →＋yOB →，则x ＋3y 的取值范围是________．答案 [1，3] 解析设扇形的半径为1，以OB 所在直线为x 轴，O 为坐标原点建立平面直角坐标系(图略)，则B (1,0)，A ⎝⎛⎭⎫12，32，C (cos θ，sin θ)⎝⎛⎭⎫其中∠BOC ＝θ，0≤θ≤π3．则OC →＝(cos θ，sin θ)＝x ⎝⎛⎭⎫12，32＋y (1,0)，即⎩⎨⎧x2＋y ＝cos θ，32x ＝sin θ，解得x ＝23sin θ3，y ＝cos θ－3sin θ3，故x ＋3y ＝23sin θ3＋3cos θ－3sin θ＝3cos θ－33sin θ，0≤θ≤π3．令g (θ)＝3cos θ－33sin θ，易知g (θ)＝3cos θ－33sin θ在⎣⎡⎦⎤0，π3上单调递减，故当θ＝0时，g (θ)取得最大值为3，当θ＝π3时，g (θ)取得最小值为1，故x ＋3y 的取值范围为[1,3]．【对点训练】1．在△ABC 中，点D 在线段BC 的延长线上，且BC →＝3CD →，点O 在线段CD 上(与点C ，D 不重合)，若AO →＝xAB →＋(1－x )AC →，则x 的取值范围是( )A ．⎝⎛⎭⎫0，12B ．⎝⎛⎭⎫0，13C ．⎝⎛⎭⎫－12，0D ．⎝⎛⎭⎫－13，0 1．答案 D 解析设CO →＝yBC →，∵AO →＝AC →＋CO →＝AC →＋yBC →＝AC →＋y (AC →－AB →)＝－yAB →＋(1＋y )AC →．∵BC →＝3CD →，点O 在线段CD 上(与点C ，D 不重合)，∴y ∈⎝⎛⎭⎫0，13，∵AO →＝xAB →＋(1－x )AC →，∴x ＝－y ，∴x ∈⎝⎛⎭⎫－13，0． 2．在△ABC 中，点D 满足BD →＝DC →，当点E 在线段AD 上移动时，若AE →＝λAB →＋μAC →，则t ＝(λ－1)2＋μ2的最小值是________．2．答案 12 解析因为BD →＝DC →，所以AD →＝12AB →＋12AC →．又AE →＝λAB →＋μAC →，点E 在线段AD 上移动，所以AE →∥AD →，则12λ＝12μ，即λ＝μ⎝⎛⎭⎫0≤λ≤12．所以t ＝(λ－1)2＋λ2＝2λ2－2λ＋1＝2⎝⎛⎭⎫λ－122＋12．当λ＝12时，t 的最小值是12．3．如图所示，在△ABC 中，点O 是BC 的中点，过点O 的直线分别交直线AB ，AC 于不同的两点M ，N ，若AB →＝mAM →，AC →＝nAN →，则mn 的最大值为__________．3．答案解析因为点O 是BC 的中点，所以AO →＝12(AB →＋AC →)．又因为AB →＝mAM →，AC →＝nAN →，所以AO →＝m 2AM →＋n 2AN →．又因为M ，O ，N 三点共线，所以m 2＋n2＝1，即m ＋n ＝2，所以mn ≤⎝⎛⎭⎫m 2＋n 22＝1，当且仅当m ＝n ＝1时，等号成立，故mn 的最大值为14．在锐角三角形ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，点O 为△ABC 的外接圆的圆心，A ＝π3，且AO →＝λAB →＋μAC →，则λμ的最大值为________．4．答案 19 解析 ∵△ABC 是锐角三角形，∴O 在△ABC 的内部，∴0<λ<1,0<μ<1．由AO →＝λ(OB →－OA →)＋μ(OC →－OA →)，得(1－λ－μ)AO →＝λOB →＋μOC →，两边平方后得，(1－λ－μ)2AO →2＝(λOB →＋μOC →)2＝λ2OB →2＋μ2OC →2＋2λμOB →·OC →，∵A ＝π3，∴∠BOC ＝2π3，又|AO →|＝|BO →|＝|CO →|．∴(1－λ－μ)2＝λ2＋μ2－λμ，∴1＋3λμ＝2(λ＋μ)，∵0<λ<1,0<μ<1，∴1＋3λμ≥4λμ，设λμ＝t ，∴3t 2－4t ＋1≥0，解得t ≥1(舍)或t ≤13，即λμ≤13⇒λμ≤19，∴λμ的最大值是19．5．在矩形ABCD 中，AB ＝5，BC ＝3，P 为矩形内一点，且AP ＝52，若AP →＝λAB →＋μAD →(λ，μ∈R )，则 5λ＋3μ的最大值为______． 5．答案102解析建立如图所示的平面直角坐标系，设P (x ，y )，B (5，0)，C (5，3)，D (0，3)．∵ AP ＝52，∴x 2＋y 2＝54．点P 满足的约束条件为⎩⎪⎨⎪⎧0≤x ≤5，0≤y ≤3，x 2＋y 2＝54，∵AP →＝λAB →＋μAD →(λ，μ∈R )，∴(x ，y )＝λ(5，0)＋μ(0，3)，∴⎩⎨⎧x ＝5λ，y ＝3μ，∴x ＋y ＝5λ＋3μ．∵x ＋y ≤2(x 2＋y 2)＝2×54＝102，当且仅当x ＝y 时取等号，∴5λ＋3μ的最大值为102．6．平行四边形ABCD 中，AB ＝3，AD ＝2，∠BAD ＝120°，P 是平行四边形ABCD 内一点，且AP ＝1，若 AP →＝xAB →＋yAD →，则3x ＋2y 的最大值为________．6．答案 2 解析 |AP →|2＝(xAB →＋yAD →)2＝9x 2＋4y 2＋2xy ×3×2×⎝⎛⎭⎫－12＝(3x ＋2y )2－3(3x )·(2y )≥(3x ＋2y )2－34 (3x ＋2y )2＝14(3x ＋2y )2．又|AP →|2＝1，因此14(3x ＋2y )2≤1，故3x ＋2y ≤2，当且仅当3x ＝2y ，即x ＝13，y ＝12时，3x ＋2y 取得最大值2．7．在直角梯形ABCD 中，∠A ＝90°，∠B ＝30°，AB ＝23，BC ＝2，点E 在线段CD 上，若AE →＝AD →＋μAB →，则μ的取值范围是________．7．答案 ⎣⎡⎦⎤0，12 解析由题意可求得AD ＝1，CD ＝3，所以AB →＝2DC →．∵点E 在线段CD 上，∴DE →＝ λDC → (0≤λ≤1)．∵AE →＝AD →＋DE →，又AE →＝AD →＋μAB →＝AD →＋2μDC →＝AD →＋2μλDE →，∴2μλ＝1，即μ＝λ2．∵0≤λ≤1，∴0≤μ≤12，即μ的取值范围是⎣⎡⎦⎤0，12． 8．如图所示，A ，B ，C 是圆O 上的三点，线段CO 的延长线与BA 的延长线交于圆O 外的一点D ，若OC →＝mOA →＋nOB →，则m ＋n 的取值范围是________．8．答案 (－1，0) 解析由题意得，OC →＝kOD →(k ＜0)，又|k |＝|OC →||OD →|＜1，∴－1＜k ＜0．又∵B ，A ，D 三点共线，∴OD →＝λOA →＋(1－λ)OB →，∴mOA →＋nOB →＝kλOA →＋k (1－λ)OB →，∴m ＝kλ，n ＝k (1－λ)，∴m ＋n ＝k ，从而m ＋n ∈(－1，0)．9．给定两个长度为1的平面向量OA →和OB →，它们的夹角为90°，如图所示，点C 在以O 为圆心的圆弧AB ︵上运动，若OC →＝xOA →＋yOB →，其中x ，y ∈R ，则x ＋y 的最大值是( )A ．1B ．2C ．3D ．29．答案 B 解析因为点C 在以O 为圆心的圆弧AB ︵上，所以|OC →|2＝|xOA →＋yOB →|2＝x 2＋y 2＋2xyOA →·OB →＝ x 2＋y 2，∴x 2＋y 2＝1，则2xy ≤x 2＋y 2＝1．又(x ＋y )2＝x 2＋y 2＋2xy ≤2，故x ＋y 的最大值为2． 10．给定两个长度为1的平面向量OA 和OB ，它们的夹角为2π3．如图所示，点C 在以O 为圆心的圆弧AB 上运动．若OC ＝x OA ＋y OB ，其中x ，y ∈R ，则x ＋y 的最大值为________．．10．答案 2 解析以O 为坐标原点，OA →所在的直线为x 轴建立平面直角坐标系，如图所示，则A (1，0)，B (－12，32)，设∠AOC ＝α(α∈[0，2π3])，则C (cos α，sin α)，由OC →＝xOA →＋yOB →，得1cos 2sin x y y αα⎧=-⎪⎪⎨⎪=⎪⎩，所以x ＝cos α＋33sin α，y ＝233sin α，所以x ＋y ＝cos α＋3sin α＝2sin(α＋π6)，又α∈[0，2π3]，所以当α＝π3时，x ＋y 取得最大值2．。

平面向量的线性运算课件

A
2b
a
b
b
a
O
[类似题]已知非零向量e1和e2不共线，如果 AB e1 e2 ,
BC 2e1 8e2 ,CD 3 e1 e2 , 证明：ABD三点共线.
2.[逆向使用]已知非零向量e1和e2不共线，欲使ke1 e2和
e1 ke2共线，确定实数k的值.
3.[课本例题 ]如图，平行四边形 ABCD 的两条对角线相交于点 M，且 AB a, AD b，用a, b表示MA, MB, MC , MD.
完毕课本84页练习
平面对量旳线性运算
——向量旳减法运算
预备知识：相反向量
类比实数旳相反数旳概率，定义相反向量：
与a长度相等，方向相反旳向量，叫做a旳相反向
量，记作-a ; -a与a互为相反向量
要求：零向量旳相反向量仍是零向量
所以: 1、-(-a)=a；2、a+(-a)=(-a)+a=0；
3、
a=-b，b=-a，a+b=0
1.已知a,
b是两个非零向量,下列说法正确的有
概念辨析
_____ .
(1) 2a的方向与5a的方向相反，且 2a的模是5a的模的 2 ； 5
(2)a b与（b a）是一对相反向量；
(3)若a, b不共线，则 a( 0)与b不共线；
2.下列说法正确的个数是 _______
(1)若 a 0，则 0；(2)若 0，则 a 0；
探究：
问题：已知OA和OB不共线，AC t AB(t R), 试用OA和OB表示OC .
特例：对于OC (1 t)OA tOB,当t 1 时，你知道其几何意义吗？ 2
中点公式向量表示法： C为AB中点，则OC OA OB 2

平面向量的线性运算

平面向量的线性运算在数学中，平面向量是向量的一种，它在平面内具有长度和方向，可以用有向线段表示。

平面向量之间可以进行线性运算，包括加法和数乘。

本文将详细介绍平面向量的线性运算及其性质。

一、平面向量的定义平面向量是指具有大小和方向的向量，它们通常用加粗的小写字母表示，如a、a等。

平面向量可以用有向线段表示，线段的起点表示向量的起点，线段的方向表示向量的方向，线段的长度表示向量的大小。

二、平面向量的加法平面向量的加法是指将两个向量相加得到一个新的向量。

设有两个平面向量a和a，它们的加法定义为：a + a = a + a这意味着向量的加法满足交换律，顺序不影响结果。

加法的几何解释为将两个向量的起点相连，然后将它们的箭头相连，新向量的起点与第一个向量的起点相同，终点与第二个向量的终点相同。

三、平面向量的数乘平面向量的数乘是指将一个向量与一个实数相乘得到一个新的向量。

设有一个平面向量a和一个实数a，它们的数乘定义为：aa = aa数乘有以下性质：1. 数乘满足结合律：(aa)a = a(aa)，其中a和a为实数。

2. 数乘满足分配律：(a + a)a = aa + aa，其中a和a为实数。

3. 数乘满足分配律：a(a + a) = aa + aa，其中a为实数，a和a为平面向量。

四、线性组合线性组合是指将一组向量与一组实数相乘并求和得到一个新的向量。

设有a个平面向量a₁、a₂、...、aa和a个实数a₁、a₂、...、aa，它们的线性组合定义为：a₁a₁ + a₂a₂ + ... + aaaa线性组合是向量加法和数乘的联合运算，这个概念在线性代数中具有重要的应用。

五、线性运算的性质1. 交换律：向量加法满足交换律，即a + a = a + a。

2. 结合律：向量加法满足结合律，即(a + a) + a = a + (a + a)，其中a、a和a为平面向量。

3. 分配律：向量加法和数乘满足分配律，即a(a + a) = aa + aa，(a + a)a = aa + aa，其中a、a为实数，a和a为平面向量。

认识简单的平面向量向量的线性运算与位置关系

认识简单的平面向量向量的线性运算与位置关系平面向量是数学中的重要概念，它在几何学、物理学等多个领域中都有广泛应用。

本文将着重介绍平面向量的线性运算和位置关系，帮助读者更好地理解和运用向量的相关知识。

一、平面向量的定义和表示方法在平面上，向量可以用有序数对表示。

设有两个点A(x₁, y₁)和B(x₂, y₂)，向量AB可以表示成(a, b)，其中a = x₂ - x₁，b = y₂ - y₁。

这里(a, b)称为向量的坐标表示。

二、向量的线性运算向量的线性运算包括向量的加法和数乘两种运算。

1. 向量的加法设有两个向量A(a₁, a₂)和B(b₁, b₂)，则它们的和可以表示为C(a₁ + b₁, a₂ + b₂)。

向量的加法满足交换律和结合律，即A + B = B + A，(A + B) + C = A + (B + C)。

2. 向量的数乘设有一个向量A(a₁, a₂)和一个数k，向量A的数乘可以表示为kA(ka₁, ka₂)。

向量的数乘满足分配律，即k(A + B) = kA + kB，(k +l)A = kA + lA，k(lA) = (kl)A。

三、向量的位置关系向量的位置关系包括共线、平行和垂直三种情况。

1. 共线向量若两个非零向量A和B在同一直线上或反向同一直线上，则称它们为共线向量。

共线向量具有如下性质：- 若A和B共线，则存在一个实数k，使得A = kB。

- 若A和B同向共线，则k为正数；若A和B反向共线，则k为负数。

2. 平行向量若两个非零向量A和B的方向相同或相反，则称它们为平行向量。

平行向量具有如下性质：- 若A和B平行，则存在一个实数k，使得A = kB。

- 若A和B同向平行，则k为正数；若A和B反向平行，则k为负数。

3. 垂直向量若两个非零向量A和B的数量积为0，则称它们为垂直向量。

即A·B = 0。

垂直向量具有如下性质：- 若A和B垂直，则它们不共线。

- 若A和B分别是x轴和y轴的单位向量，则A和B垂直。

平面向量的线性运算

平面向量的线性运算平面向量是平面上的有向线段，可以进行各种线性运算，包括加法、减法、数乘、内积和外积。

本文将详细介绍平面向量的线性运算。

一、平面向量的定义平面向量是平面上具有大小和方向的有向线段，通常用箭头表示，例如，向量AB用→AB表示，A为向量的起点，B为向量的终点。

平面向量可以表示为(a, b)，其中a和b分别表示向量在x轴和y轴上的投影。

二、平面向量的加法设有平面向量→AB和→CD，它们的和向量为→AD=→AB+→CD。

向量的加法满足交换律，即→AB+→CD=→CD+→AB。

加法运算的几何解释是将向量→CD以→AB为起点进行平移，得到以A为起点，D为终点的向量→AD。

三、平面向量的减法设有平面向量→AB和→CD，它们的差向量为→AC=→AB-→CD。

向量的减法满足非交换律，即→AB-→CD≠→CD-→AB。

减法运算的几何解释是将向量→CD以→AB的起点为终点进行平移，得到以A为起点，C为终点的向量→AC。

四、平面向量的数乘对于平面向量→AB，实数k，k×→AB为平面向量的数乘。

数乘的结果是一个新的平面向量，它的长度为原向量的长度乘以数乘系数k，方向与原向量相同（当k>0时），或相反（当k<0时）。

五、平面向量的内积两个向量→AB和→CD的内积记作→AB·→CD，它等于向量→AB在→CD上的投影长度与→CD的模长之积，即|→AB|×|→CD|×cosθ，其中θ为→AB和→CD的夹角。

内积运算满足交换律，即→AB·→CD=→CD·→AB；和分配律，即(→AB+→CD)·→EF=→AB·→EF+→CD·→EF。

内积运算可以用来判断两个向量是否垂直，当且仅当向量的内积为0时，它们垂直。

六、平面向量的外积两个向量→AB和→CD的外积记作→AB×→CD，它是一个新的向量，它的模长等于两个向量构成的平行四边形的面积，方向垂直于所构成平行四边形的平面，并按右手法则确定。

平面向量的线性运算

平面向量的线性运算在数学中，平面向量是一个有大小和方向的量。

它可以表示为一个箭头，并且可以用坐标表示。

平面向量的线性运算是指对平面向量进行加法和数乘的操作。

一、平面向量的加法平面向量的加法是指将两个向量的对应分量相加，得到一个新的向量。

如果有两个向量A和B，它们的坐标分别为(Ax, Ay)和(Bx, By)，则它们的加法可以表示为：A +B = (Ax + Bx, Ay + By)例如，如果有向量A(2, 3)和向量B(1, -2)，则它们的加法运算为：A +B = (2 + 1, 3 + (-2)) = (3, 1)二、平面向量的数乘平面向量的数乘是指一个向量与一个实数相乘的操作。

如果有一个向量A和一个实数k，则它们的数乘可以表示为：kA = (kAx, kAy)例如，如果有向量A(2, 3)和实数k = 2，则它们的数乘运算为：2A = (2 × 2, 2 × 3) = (4, 6)三、平面向量的线性运算平面向量的线性运算是指对向量加法和数乘进行组合运算。

如果有两个向量A和B，以及两个实数k和m，则它们的线性运算可以表示为：kA + mB = (kAx + mBx, kAy + mBy)例如，如果有向量A(2, 3)、向量B(1, -2)和实数k = 2，m = 3，则它们的线性运算为：2A + 3B = (2 × 2 + 3 × 1, 2 × 3 + 3 × (-2)) = (7, 0)四、平面向量的性质平面向量的线性运算具有以下性质：1. 交换律：A + B = B + A2. 结合律：(A + B) + C = A + (B + C)3. 分配律：k(A + B) = kA + kB4. 结合分配律：(k + m)A = kA + mA这些性质使得平面向量的线性运算更加方便和灵活，可以简化运算过程并推导出更多的结论。

总结：平面向量的线性运算包括加法和数乘两种操作。

平面向量的概念与线性运算知识点

平面向量的概念与线性运算知识点平面向量是二维空间中的量，可以看作是带有方向和长度的箭头。

它通常用有序数对表示，即(x,y)。

其中，x称为向量的横坐标，y称为向量的纵坐标。

平面向量可以进行很多运算，其中包括线性运算，即向量的加法和数乘。

1.向量的加法：向量的加法定义为：对于两个向量A=(a₁,a₂)和B=(b₁,b₂)，它们的和定义为C=(a₁+b₁,a₂+b₂)。

加法满足以下性质：-交换律：A+B=B+A-结合律：(A+B)+C=A+(B+C)-零向量：对于任意向量A，存在一个零向量0，使得A+0=0+A=A2.向量的数乘：向量的数乘定义为：对于一个向量A=(a₁,a₂)和一个实数k，它们的数乘定义为B=(ka₁, ka₂)。

数乘满足以下性质：- 结合律：k*(l*A) = (kl)*A-1的作用：1*A=A-0的作用：0*A=0除了加法和数乘外，还可以进行向量的减法和向量的数量积。

3.向量的减法：向量的减法定义为：对于两个向量A=(a₁,a₂)和B=(b₁,b₂)，它们的差定义为C=(a₁-b₁,a₂-b₂)。

减法满足以下性质：-A-A=04.向量的数量积：向量的数量积（也称为内积、点积）定义为：对于两个向量A=(a₁,a₂)和B=(b₁,b₂)，它们的数量积定义为a₁b₁+a₂b₂。

用符号表示为A·B。

数量积的性质：-交换律：A·B=B·A-结合律：(kA)·B=A·(kB)=k(A·B)-分配律：A·(B+C)=A·B+A·C向量的数量积还可以通过向量的坐标和向量的夹角来求得：A·B = ，A，，B，cosθ其中，A，和，B，分别表示向量A和向量B的长度，θ表示向量A和向量B之间的夹角。

除了上述基本概念和运算外，还有一些与平面向量相关的重要知识点，如向量的模、单位向量、向量的垂直和平行关系、共线与共点等等。

平面向量的线性运算

平面向量的线性运算平面向量是解析几何中的重要概念，它不仅可以表示方向和大小，还可以进行各种运算。

其中，线性运算是指向量之间基于线性关系进行的运算，包括向量的加法、减法和数量乘法。

下面将详细介绍这些线性运算。

1. 向量的加法向量的加法是指将两个向量相加得到一个新的向量。

设有向量A和向量A，它们的加法运算是指将向量A的终点与向量A的起点重合，将向量A的终点与此位置的终点相连接得到一个新的向量A。

表示为：A = A + A。

2. 向量的减法向量的减法是指将一个向量减去另一个向量得到一个新的向量。

设有向量A和向量A，它们的减法运算是指将向量A取反后与向量A进行加法运算，即A = A - A，等价于A = A + (-A)。

3. 数量乘法数量乘法是指将一个向量与一个实数相乘得到一个新的向量。

设有向量A和实数A，它们的数量乘法运算是指将向量A拉长或缩短，与实数A的绝对值成正比。

当A > 0时，方向与原向量相同；当A < 0时，方向与原向量相反。

表示为：AA。

在进行向量的线性运算时，需要特别注意以下几点：1. 矢量的起点和终点在进行向量的线性运算时，需要明确矢量的起点和终点。

起点表示向量的起始位置，终点表示向量的结束位置。

2. 向量的方向向量的方向是指从起点指向终点的方向。

加法和减法运算中，可以通过将向量的起点重合来确定新向量的方向。

3. 向量的大小向量的大小是指向量的长度或模。

表示为 |A|，可以通过勾股定理来计算：|A| = √(A²+A²)，其中A和A分别为向量的水平和垂直分量。

4. 向量的单位向量单位向量是指长度为1的向量。

可以通过将向量除以它的模来得到单位向量。

表示为：A = A/|A|。

5. 向量的平行和垂直性向量A与向量A平行等价于A = AA（A为实数），向量A与向量A垂直等价于A ·A = 0（·表示向量的数量积）。

通过以上介绍，我们了解了平面向量的线性运算和相关概念。

平面向量的线性运算

平面向量的线性运算平面向量是平面上的有向线段，具有大小和方向，可以进行线性运算。

本文将介绍平面向量的加法、减法、数量乘法以及其他相关的线性运算。

一、平面向量的加法平面向量的加法满足以下性质：1. 交换律：对于任意两个向量a和b，a+b=b+a。

2. 结合律：对于任意三个向量a、b和c，(a+b)+c=a+(b+c)。

3. 零向量：对于任意向量a，存在一个特殊的向量0，称为零向量，满足a+0=a。

4. 相反向量：对于任意向量a，存在一个特殊的向量-b，称为a的相反向量，满足a+(-a)=0。

二、平面向量的减法平面向量的减法可以看作是向量加上其相反向量的过程。

即，对于任意向量a和b，a-b=a+(-b)。

三、平面向量的数量乘法平面向量的数量乘法即将一个向量乘以一个实数。

具体来说，对于任意向量a和实数k，ka是一个新的向量，满足以下性质：1. 数量乘法的结合律：对于任意向量a和实数k、l，(kl)a=k(la)。

2. 数量乘法与向量加法的分配律：对于任意向量a和实数k、l，(k+l)a=ka+la。

3. 数量乘法与实数加法的分配律：对于任意向量a和实数k、l，(k+l)a=ka+la。

4. 数量乘法与实数乘法的分配律：对于任意向量a和实数k、l，(kl)a=k(la)。

四、线性组合线性组合是指将若干个向量按照一定比例进行加法和数量乘法运算得到的向量。

具体来说，对于给定的向量a1、a2、...、an和实数k1、k2、...、kn，线性组合为k1a1+k2a2+...+knan。

五、平面向量的点积平面向量的点积也称为数量积或内积。

对于任意向量a和b，其点积记作a·b，满足以下性质：1. 交换律：对于任意向量a和b，a·b=b·a。

2. 分配律：对于任意向量a、b和c，(a+b)·c=a·c+b·c。

3. 结合律：对于任意向量a和b以及实数k，(ka)·b=k(a·b)=a·(kb)。

平面向量线性运算

A
变式一：求线段 BO 的比值
BN
N
O
C
B
M
例2：ABC中，BO CO，过O的直线与AB或延长线交于点M ,过O的直线与AC或延长线交于点N, AM m AB, AN n AC,求 1 1 的值
mn
C M
O
A
B
N
变式一：ABC中，BO BC，过O的直线与AB或延长线
交于点M ,过O的直线与AC或延长线交于点N, AM m AB,
若Q是BCD内部包括边界一动点，且 AQ m AB n ADm, n R
则m 2n
D
C
Q
P
A
E
B
链接高考：2013浙江理17.
设e1, e2为单位向量，非零向量b xe1 ye2 , x, y R.
若e1,
e2的夹角为6
，则
x b
的最大值等于
2015浙江理15）设e1、e2是空间单位向量，e1 e2
1 2
,b e1
2,
be2
5 ,x, y R, b 2
xe1
ye2
b x0 e1 y0 e2 , x0, y0 R
则求x0，y0 , b
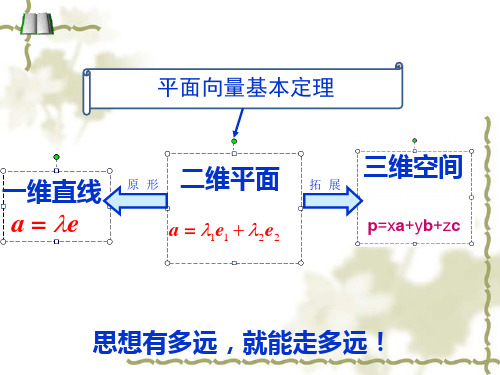
平面向量基本定理
一维直线
a = e
原形二维平面
a = 1e1 2e2
三维空间
拓展
p=xa+yb+zc
思想有多远，就能走多远！
引例、如图，平行四边形ABCD的对角线AC和BD相交于点 M，AB a , AD b，试用基底a、b表示AC、BD
D
C
A
B
例1：如图，ABC中，点M是BC的中点，点N在AC上，且AN 3NC, AM与BN相交于点Oቤተ መጻሕፍቲ ባይዱ设CA a,CB b, 用a, b表示向量CO