模拟试题与答案九
九年级数学期末模拟精品测试题及答案,精品3套

(第2题)(第3题)(第6题)九年级数学期末模拟精品测试题及答案,精品3套九年级上全册精品试卷(满分:150分)一、选择题。
(本题共10个小题,每小题4分,共40分)1、2010上海世博会刚刚圆满闭幕,下列各图是选自历届世博会徽中的图案,其中是中心对称图形的是()A、 B、 C、 D、2、如图,AB与⊙O切于点B,AO=6cm,AB=4cm,则⊙O•的半径为()A、、、cm3、图中∠BOD的度数是()A、55°B、110°C、125° D.150°4、若x<0,则xxx2-的结果是()A.0 B.-2 C.0或-2 D.25、下列各式中,最简二次根式是()A、32B、22+a C、a8 D、23a6、我们知道,“两点之间线段最短”,“直线外一点与直线上各点连线的所有线段中,垂线段最短”在此基础上,人们定义了点与点的距离,•点到直线的距离.类似地,如图,若P是⊙O外一点,直线PO交⊙O 于A、B两点,PC•切⊙O于点C,则点P到⊙O的距离是()A、线段PO的长度B、线段PA的长度C、线段PB的长度 D、线段PC的长度7、下列命题错误..的是()A、经过三个点一定可以作圆B、三角形的外心到三角形各顶点的距离相等C、同圆或等圆中,相等的圆心角所对的弧相等D、经过切点且垂直于切线的直线必经过圆心8、如图,△COD是△AOB绕点O顺时针方向旋转40°后所得的图形,点C恰好在AB上,(第8题)(第14题)(第15题)(第16题)∠AOD =90°,则∠B 的度数是( )A 、500B 、400C 、450D 、6009、已知一元二次方程230x px ++=的一个根为3-,则p 的值为( )A .1B .2C .3D .410、若m,n 是方程020102=--x x 的两根,则代数式)20102()20102(22++-⨯--n n m m 的值为( ).A .-2010 B.2010 C.0 D.1二、填空题。
九年级文言文模拟语文综合试题带答案

九年级文言文模拟语文综合试题带答案一、文言文1.阅读下面的文字,回答问题。
【甲】侍中、侍郎郭攸之、费祎、董允等,此皆良实,志虑忠纯,是以先帝简拔以遗陛下。
愚以为宫中之事,事无大小,悉以咨之,然后施行,必能裨补阙漏,有所广益。
将军向宠,性行淑均,晓畅军事,试用于昔日,先帝称之曰能,是以众议举宠为督。
愚以为营中之事,悉以咨之,必能使行阵和睦,优劣得所。
(节选自诸葛亮《出师表》)【乙】高祖①曰:“吾所以有天下者何?项氏所以失天下者何?”高起②等对曰:“陛下使人攻城略③地,所降下者因以予之,与天下④同利也。
项羽妒贤嫉能,战胜而不予人功,得地而不予人利,此所以失天下也。
”高祖曰:“运筹帷幄之中,决胜千里之外,吾不如子房⑤;镇国家,抚百姓,吾不如萧何;连⑥百万之军,战必胜,吾不如韩信。
此三杰,吾能用之。
项羽有一范增而不能用,此其所以为我擒也。
”(节选自《史记·高祖本纪》,有删改)【注】①高祖:指汉高祖刘邦。
②高起:高祖臣子。
③略:攻占。
④天下:这里指刘邦的部属。
⑤子房:西汉谋士张良。
⑥连:率领。
(1)解释下列划线词在文中的意思。
①事无大小,悉以咨之悉:________②性行淑均,晓畅军事晓:________③战胜而不予人功予:________(2)把下面的句子翻译成现代汉语。
①先帝称之曰能,是以众议举宠为督。
①项羽有一范增而不能用,此其所以为我擒也。
(3)下面对【甲】【乙】两个文段理解不正确的一项是( )A.【甲】文中诸葛亮两次提到“先帝”是希望刘禅谨记先帝遗志,谨遵先帝安排,言辞恳切,拳拳之心,溢于言表。
B.【乙】文中,司马迁通过对话描写,将高祖取胜与项羽失败进行对比,刻画了高祖睿智英明的形象。
C.【甲】文中诸葛亮向刘禅举荐郭攸之、费祎、董允等管理“营中”之事,向宠管理“宫中”之事,安排得十分细致周到。
D.【乙】文中高祖非常有自知之明,他能够很清晰地认识到张良、萧何、韩信各自的长处,并让他们各得其所。
教师资格证考试《小学综合素质》备考模拟试题及答案(九)

教师资格证考试《小学综合素质》备考模拟试题及答案(九) 1.某幼儿园把小学一年级的语文、数学知识作为内容,有违()。
A.幼儿身心发展的互补性B.幼儿身心发展的稳定性C.幼儿身心发展的个别差异性D.幼儿身心发展的顺序性2.以下哪个选项不是我国现代作曲家冼星海的作品( )A.《黄河》B.《到敌人后方去》C.《义勇军进行曲》D.《在太行山上》3.音乐欣赏的关键是()。
A.听B.唱C.想D.说4.教师获取报酬主要通过工资报酬、福利待遇和()来体现。
B.政治地位C.有偿家教D.教师节5.战国时期最有实力的七个诸侯国家被称为“战国七雄”,他们分别是( )。
A.齐、魏、越、秦、晋、韩、赵B.齐、楚、燕、赵、秦、韩、魏C.齐、秦、越、赵、燕、韩、魏D.齐、赵、越、秦、鲁、韩、魏6.法国大作家雨果曾经说过,“人类没有任何一种重要的思想不被建筑艺术写在石头上”。
建筑如同石头写就的史书一般,记载着人类社会从远古产生一直发展到现在的全部经历,带给我们一把打开历史之门的钥匙。
以下你认为正确的是()。
A.故宫的宫殿建筑,是全世界规模最宏大、保存最完好的古代皇宫建筑群之一,也是中国古代建筑水平最高的杰作B.欧洲宫殿建筑的第一典范是卢浮宫,被人称为“立体的诗篇,凝固的画卷”C.沙特尔大教堂高耸入云的建筑结构和形式是典型的拜占庭式建筑D.17世纪意大利兴起的“洛可可”建筑风格讲究“不规则的造型和奢华的装饰”7.下列文学作品属于浪漫主义风格的是()。
A.《茅屋为秋风所破歌》B.《望庐山瀑布》D.《新婚别》8.为适应科学知识的加速增长和人的持续发展要求而逐渐形成的教育思想和教育制度称为()。
A.终身教育B.普通教育C.职业教育D.义务教育9.(2021年上半年真题)百老汇是美国的一条大街,由于集中了著名的影剧院、音乐厅、夜总会等娱乐场所,因此百老汇成为了美国戏院业和娱乐业的代称。
其所在的城市是()。
A.华盛顿B.洛杉矶C.纽约D.费城10.小学生高某在学校组织的校外活动中不慎受伤。
广东省东莞市2023-2024学年九年级上册期末数学模拟试题(附答案)

广东省东莞市2023-2024学年九年级上学期期末数学模拟试题说明:1.全卷共6页,满分为120分,考试时间为120分钟。
2.答题必须用黑色字迹钢笔或签字笔作答,答案必须写在答题卷各题目的指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液。
不按以上要求作答的答案无效。
3.考生必须保持答题卷的整洁。
考试结束后,将试题卷和答题卷一并交回。
一.选择题(共10题,每小题3分,共30分)1.方程的二次项系数和一次项系数分别为()。
22310x x --=A.和 B.和 C.2和 D.2和322x 3x -22x 3x 3-2.“福禄寿喜”图是中华传统祥云图纹,以下四个图案是中心对称图形的是()A. B. C. D.3.一个不透明的袋子中只有4个黑球和2个白球,这些球除颜色外无其他差别,随机从袋子中一次摸出3个球,下列事件中是不可能事件的是()。
A.3个球都是黑球B.3个球都是白球C.3个球中有黑球D.3个球中有白球4.二次函数的图象可由的图象()。
()2212y x =-+22y x =A.向左平移1个单位,再向下平移2个单位得到B.向左平移1个单位,再向上平移2个单位得到C.向右平移1个单位,再向下平移2个单位得到D.向右平移1个单位,再向上平移2个单位得到5.如图,在平面直角坐标系中,的顶点为,,。
以点O OAB △()0,0O ()6,4A -()3,0B -为位似中心,在第四象限内作与的位似比为的位似图形,则点C 坐标为OAB △12OCD △()。
A. B. C. D.()3,2-()2,1-33,22⎛⎫- ⎪⎝⎭3,12⎛⎫- ⎪⎝⎭6.如图,在中,点C 是上一点,若,则的度数为()。
O e ¶AB 126AOB ∠=︒C ∠A.127°B.117°C.63°D.54°7.为积极响应国家“双减”政策,某市推出名师公益大课堂,为学生提供线上线下免费辅导,据统计第一批公益课受益学生2万人次,第三批公益课受益学生2.42万人次。
人教版九年级化学中考模拟试题及参考答案

人教版九年级化学中考模拟试题(考试时间:60分钟 满分:60分)请注意:1.本试卷分选择题和非选择题两部分。
2.所有试题的答案均须填写在答题纸上,答案写在试卷上无效。
可能用到的相对原子质量:H-1 C-12 O-16 Na-23 Mg-24 S-32 Fe-56 Cu-64 Zn-65第一部分 选择题(共20分)第1~10题,每小题只有一个选项符合题意。
每小题1分,共10分。
1.2019年3月,姜堰区中小学开展了“打赢蓝天保卫战”活动。
下列行动不利于“保卫蓝天”的是A .尽量低碳出行B .露天焚烧垃圾C .使用清洁能源D .积极植树造林2.下列属于化学变化的是A .工业制氧气B .盐酸挥发C .石油分馏D .粮食酿醋 3.下图为“中国节能”标志的是A B C D4.下列物质的用途利用其物理性质的是 A .干冰用于人工降雨 B .铁粉用作食品吸氧剂C .氧气用于医疗供氧D .小苏打治疗胃酸过多5.下列实验操作正确的是A .移走蒸发皿B .溶解固体C .加入大理石D .检查装置的气密性 6.下列物质属于纯净物的是A .酒精B .不锈钢C .矿泉水D .加碘盐 7.下列说法正确的是A .铜绿加热后颜色变红,并生成有刺激性气味的气体B .空气中二氧化碳含量增加,导致了酸雨的形成C .洗洁精有乳化作用,可用于洗去碗筷上的油污D .活性炭可将硬水软化 8.下列有关化学用语表示正确的是液柱上升A .两个亚铁离子:2Fe 3+B .氧分子:OC .保持二氧化碳化学性质的最小微粒:CO 2D .钠原子的结构示意图: 9A .2O 3FeCl 2B .Na 2CO 3 NaCl NaNO 3C . C CO CO 2D . H 2O 2 O 2 SO 310.下列对主题知识的归纳,完全正确的一组是第11~15题,每题有一个或两个选项符合题意。
多选、错选均不得分,少选得1分。
每小题2分,共10分。
11.氨催化氧化是制硝酸的主要反应之一。
最新九年级语文中考模拟试题附答案

2022-2023学年九年级语文中考模拟测试题一、知识与运用。
1.(6分)阅读下面的文字,完成问题。
站在历史的海岸漫溯那一道道历史的沟渠:楚大夫沉吟泽畔..,九死不悔;魏武帝扬鞭东指,壮心不已;陶渊明悠然南山,饮酒采菊……他们选择了永恒。
(纵然/无论)谄媚....魂归关西,也要扬声边塞尽扫..污蔑,蒙蔽..视听,也不随其流扬其波,①;马革裹尸狼烟,②;一身清苦终日难饱,也愿怡然..自乐、躬耕陇亩....,③。
有多少人愿选择清贫,选择质朴,选择刚健........平息了壮志,阿谀逢迎..?物欲横流(淌尽/流尽)了血汗,歌舞生平迎合了庸人。
选择永恒,需要“威武不能屈”的大丈夫精神,“金弋..志向,“要..铁马去”的慷慨留清白在人间”的高洁。
需要用今生无悔的选择(铸就/造就)春秋的华盖与乐章,虽九死而犹未悔!(1)文中加点字词的注音和字形,全都正确的一项是A.漫溯.(shuò)怡然歌舞生平B.蒙蔽.(bì)刚健阿谀逢迎C.谄.(chán)媚慷慨躬耕陇亩D.泽畔.(pàn)金弋马革裹尸(2)依次选用文中括号里的词语,最恰当的一项是A.无论流尽造就B.纵然淌尽造就C.无论淌尽铸就D.纵然流尽铸就(3)文中三处横线上填入语句,衔接最恰当的一项是A.①这是豪壮的选择②这是执着的选择③这是高雅的选择B.①这是执着的选择②这是豪壮的选择③这是高雅的选择C.①这是高雅的选择②这是执着的选择③这是豪壮的选择D.①这是执着的选择②这是高雅的选择③这是豪壮的选择2.(2分)下列各句中标点符号使用正确的一项是()A.他的节奏、他的理念,超越了大多数人,所以容易产生争议;有争议,说明受关注;有争议,说明他人气旺。
B.他说他的改变来自学校温暖的关怀:“让我感激的是老师们对我那么好,现在我对学校很有感情,因为我在这里能够时时感到成长的力量。
”小杰说。
C.身体温暖,微循环才会正常,所以清早起来第一口食物最好选择温热的,应该享用热稀饭、热黑米粥、热牛奶、热豆浆和芝麻糊……再配着吃蔬菜、面包、三明治、水果。
人教版九年级化学中考模拟试题及参考答案

初三化学测试可能用到的相对原子质量H1C12N14O16Na23Ca40第一部分选择题1.下列做法中,不符合...“低碳”理念的是BA.公交出行B.浪费纸张C.节约用电D.道路绿化2.下列物质在氧气中燃烧,火星四射,生成黑色固体的是AA.铁丝B.硫粉C.蜡烛D.红磷3.地壳中含量最多的金属元素是CA.O B.Si C.Al D.Fe 4.下列图标表示“禁止燃放鞭炮”的是AA B C D 5.为保证实验安全,下列操作合理的是DA.加热时试管口对着自己或他人B.加热后的试管,立即用冷水冲洗干净C.用完酒精灯后,用嘴吹灭D.加热时试管内液体体积不超过试管容积的1/36.下列属于化石燃料的是DA.太阳能B.潮汐能C.地热能D.石油7.下列物质属于氧化物的是CA.N2B.CaCO3C.P2O5D.NaCl 8.下列实验操作正确的是DA.称量氯化钠B.倾倒液体C.点燃酒精灯D.读取液体体积9.下列物质的化学式书写不正确...的是AA.氧化铝AlO B.碳酸钙CaCO3C.氢氧化钙Ca(OH)2D.氧气O210.下列符号能表示2个氢分子的是DA.2H B.2H+C.H2O D.2H211.能闻到花香的原因是CA .分子的质量很小B .分子间有间隔C .分子在不断运动D .分子由原子构成12.下列属于纯净物的是DA .空气B .澄清石灰水C .天然水D .五氧化二磷13.钛被称为“航空金属”,国产C919大飞机的钛合金用量达到9.3%。
已知一种钛原子核内有22个质子和26个中子,该原子的核外电子数为AA .22B .26C .48D .414.电解水实验装置如右图所示。
下列说法不正确...的是A A .a 中收集到的气体是氢气B .b 中收集到的气体可以燃烧C .水不是由一种元素组成的D .水在通电条件下可以分解成氢气和氧气15.下列关于CaCO 3CaO+CO 2↑的说法正确的是DA .反应中CaCO 3和CO 2的质量比为1:1B .反应中原子种类发生了改变C .反应中元素种类没有发生改变D .CaCO 3中的氧元素全部转化到CO 2中依据金属的性质回答16-19题。
九年级历史模拟试题及答案

九年级历史模拟试题及答案九年级历史模拟试题选择题1.小王同学在学习某一阶段的中国历史时,列了该阶段朝代发展的顺序,正确的是A.秦朝西汉东汉三国B.秦朝西汉新朝东汉C.西汉秦朝东汉三国D.新朝秦朝西汉东汉2.下面是某校七年级的同学在学习某一主题时,根据收集的信息判断他们学习的主题是A.中华文明的起源B.国家的产生和社会变革C.繁荣与开放的社会D.统一的多民族国家的巩固和发展3.对于现在的中日钓鱼岛争端,有专家评论说:“面对中国的崛起,日本的危机感剧增。
日本想借钓鱼岛问题联合美国发动对中国的战争,以第三次打断中国的现代化进程。
”这位专家眼中的日本“第二次打断中国的现代化进程”应该是指①甲午中日战争②逼迫袁世凯签订“二十一条” ③20世纪三四十年代的全面侵华战争A.①B.②C.③D.①②③4.浙江奉化溪口雪窦山,为张学良将军幽禁生活的第一站。
院落中将军塑像的底座上,刻有周恩来题写的“千古功臣”四个大字。
称张学良为中华民族的“千古功臣”,最主要的原因是A.抓住了中国共产党的老对手蒋介石B.邀请中国共产党参加谈判C.最终促成了抗日民族统一战线的初步形成D.停止向红军进攻6.有一段发言是这样写的:“我以无可言状的悲怆追忆那血腥的风雨,我以颤抖的手抚摸那30万亡灵的冤魂,我以赤子之心刻下这苦难民族的伤痛。
我祈求,我期望,古老民族的觉醒,精神的觉醒”。
这段发言应放置在哪个纪念馆门前A.侵华日军南京大屠杀遇难同胞纪念馆B.台儿庄战役纪念馆C.中国人民抗日战争纪念馆D.上海淞沪抗战纪念馆7.世界文明发源地大都起源于大河流域,也有起源海洋的。
下列文明起源于海洋的是A.古代希腊B.古代埃及C.古代印度D.古代中国8.罗马共和国时期没有君主,国家的最高官职是A.元老B.元首C.元帅D.执政官9.峨眉山是佛教名山,是我们宣传乐山的城市名片。
世界三大宗教是①佛教②__③道教④伊斯兰教A.①②③B.②③④C.①②④D.①③④10.分析下可知三角贸易对欧洲最大的影响是:A.丧失了上亿精壮人口B.获得了大量的劳动力C.获取了美洲大量土地D.促进了欧洲资本主义的发展11.恩格斯说:“意大利是一个典型的国家,自从现代世界的曙光在那里升起的那个时代以来,它产生过许多伟大人物。
2023年九年级语文中考模拟试题附答案

2022-2023学年九年级语文中考模拟测试题一、基础知识积累。
1.(3分)下列句子中字音、字形全部正确的一项是()A.你只会感到更高邈.(miǎo)、深远,并让凄冷的雨滴,去纯净你的灵魂,而且一定会瑶望一场秋雨后将出现的一个更净美、开阔的大地。
B.耳朵里有不可捉摸的声响,极远的又是极近的,极洪大的又是极细切的,像春蚕在咀嚼.(jáo)桑叶,像野马在平原上奔弛,像山泉在呜咽,像波涛在澎湃。
C.每逢骤雨猝.(cù)至,这两位物理学家就匆忙把设备搬进棚屋,大开着门窗让空气流通,以便继续工作,而不至于因烟窒息。
D.名人强.词夺理(qiáng),叫作雄辩,凡人就是狡辩;名人跟人握握手,叫作平易进人,凡人就是巴结别人了。
2.(3分)下列句子中加点的成语,使用不正确的一项是()A.在迈向民族伟大复兴中国梦的征程中,唯有法治的保驾护航....,我们才能“蹄疾走日月,步稳度关山”。
B.望眼欲穿....漫天的星辰,鲜花和掌声在不远处起落,也许一切都只能这样,也许此生就茫然的活着,也许一片沙漠,还落一场霜雪,我会期待生命的春风来过,太久夙愿会开出灿烂花朵,永不凋落。
C.教师应注意引导学生认识郑和下西洋的历史局限,这样才有助于学生全面、正确、公允地评价郑和,避免因评价偏颇,而潜滋暗长....的虚骄之气对学生思想的侵害。
D.美国媒体在竞争剧烈的情况下,不得不顺应人们寻找刺激的倾向,而政治人物也使出浑身解数....的本领,以求脱颖而出。
3.(3分)下列句子有语病的一项是()A.任何一种文明的发展都是与其他文明碰撞、交流、融合的过程,完全封闭的环境不可能带来文明的进步,只会导致文明的衰落。
B.在遭受强烈地震海啸后,印尼面临着饮用水、食品、帐篷等物资短缺,基础设施损坏严重,救援工作很难展开。
C.我们只有继承和发扬长征精神,才能把新时代的长征之路走得坚定,走得稳健,走得昂首阔步。
D.近年来,我校围绕“让阅读成为习惯,让书香溢满校园”这一主题,让师生通过阅读增加文化底蕴,通过经典诵读让孩子学会做人,让书香伴随师生成长。
最新九年级中考数学模拟试题 及答案 (1)
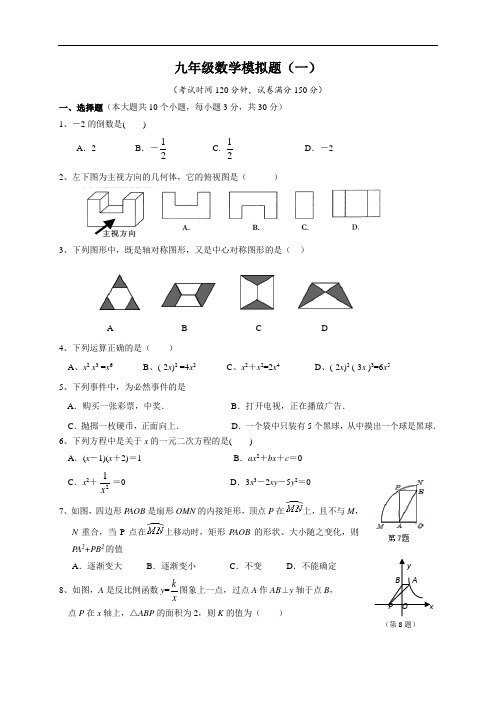
九年级数学模拟题(一)(考试时间120分钟,试卷满分150分)一、选择题(本大题共10个小题,每小题3分,共30分)1、-2的倒数是()A.2 B.-21C.21D.-22、左下图为主视方向的几何体,它的俯视图是()3、下列图形中,既是轴对称图形,又是中心对称图形的是()A B C D4、下列运算正确的是()A、x2x3 =x6B、(-2x)2 =4x2C、x2+x2=2x4D、(-2x)2 (-3x )3=6x55、下列事件中,为必然事件的是A.购买一张彩票,中奖.B.打开电视,正在播放广告.C.抛掷一枚硬币,正面向上.D.一个袋中只装有5个黑球,从中摸出一个球是黑球.6、下列方程中是关于x的一元二次方程的是()A.(x-1)(x+2)=1 B.ax2+bx+c=0C.x2+21x=0 D.3x3-2xy-5y2=07、如图,四边形P AOB是扇形OMN的内接矩形,顶点P在上,且不与M,N重合,当P点在上移动时,矩形P AOB的形状、大小随之变化,则P A2+PB2的值A.逐渐变大B.逐渐变小C.不变D.不能确定8、如图,A是反比例函数y=xk图象上一点,过点A作AB⊥y轴于点B,点P在x轴上,△ABP的面积为2,则K的值为()(第8题)ABP xyOA .1B .2C .3D .49、某学校用420元钱到商场去购买“84”消毒液,经过还价,每瓶便宜0.5元,结果比用原价多买了20瓶,求原价每瓶多少元?若设原价每瓶x 元,则可列出方程为 ( )A .205.0420420=--x x B .204205.0420=--x x C .5.020420420=--x x D .5.042020420=--xx10、已知二次函数2y ax bx c =++ ()0a ≠ 的图像,如图所示,有下列5个结论: ⑴0abc >; ⑵b a c <+;⑶420a b c ++>;⑷23c b <;⑸()a b m am b +>+,()1m ≠的实数.其中,正确结论的个数为( )A .4B .3C .2D .1二、填空题(本大题共8个小题,每小题3分,共24分) 11、要使式子aa 2+有意义,则a 的取值范围为_________. 12、根据新网上海6月1日电:世博会开园一个月来,客流平稳,累计到当晚19时,参观者已超过8000000人次,试用科学记数法表示8000000= .13、若m 2-5m +2=0,则2m 2-10m +2012= .14、如图,四边形ABCD 内接于⊙O ,若∠BOD =138°,则它的一个外角∠DCE 等于 .15、如图,一块含有30°角的直角三角板ABC ,在水平桌面上绕点C 按顺时针方向旋转到C B A ''的位置.若BC 的长为15cm ,那么顶点A •从开始到结束所经过的路径长为 ㎝.16、如图,等边三角形ABC 中,D 、E 分别为AB 、BC 边上的两动点,且总使AD =BE ,AE 与CD 交于点F ,AG ⊥CD 于点G ,则FGAF = __________.17、如图,把一个半径为12cm 的圆形硬纸片等分成三个扇形,用其中一个扇形制作成一个圆锥形纸筒的侧面(衔接处无缝隙且不重叠),则圆锥底面半径等于 cm .18、在直角坐标系中,直线y =x +1与y 轴交于点A 1, 按 如图方式作正方形A 1B 1C 1O 、A 2B 2C 2C 1、A 3B 3C 3C 2…, 点A 1、A 2、A 3…在直线y =x +1上,点C 1、C 2、C 3…在 x 轴上,图中阴影部分三角形的面积从左到右依次记 为S 1、S 2、S 3、…S n ,则S n 的值为____________ (用含n 的代数式表示,n 为正整数).三、解答题(本大题共2个题,第19题10分,第20题12分,共22分)19、先化简,再求值:4441x 1122++-÷x x x )--(,其中1311+⎪⎭⎫ ⎝⎛=-x20、如图,在平面直角坐标系中,已知点(42)B ,,BA x ⊥轴于A .(1)画出将△OAB 绕原点旋转180°后所得的△OA 1B 1,并写出 点A 1、B 1的坐标;(2)将△OAB 平移得到△O 2A 2B 2,点A 的对应点是A 2,点B 的对应点B 2的坐标为(22)-,在坐标系中作出△O 2A 2B 2,并写出点O 2、A 2的坐标;(3)△OA 1B 1与△O 2A 2B 2成中心对称吗?若是,找出对称中心,并写出对称中心的坐标.四、解答题(本大题共2个题,每题10分,共20分)21、有A 、B 两个黑布袋,A 布袋中有两个完全相同的小球,分别标有数字1和2,B 布袋中有三个完全相同的小球,分别标有数字-l ,-2和-3.小强从A 布袋中随机取出一个小球,记录其标有的数字为a ,再从B 布袋中随机取出一个小球,记录其标有的数字为b ,这样就确定点Q 的一个坐标为OxAB11 y(a,b).⑴用列表或画树状图的方法写出点Q的所有可能坐标;⑵求点Q落在直线y=x-3上的概率、22、数学兴趣小组想利用所学的知识了解某广告牌的高度,已知CD=2m,经测量,得到其它数据如图所示.其中∠CAH=30°,∠DBH=60°,AB=10m.请你根据以上数据计算GH的长.(3≈1.73要求结果精确到0.1m)五、解答题(本大题共12分)23、如图,以Rt△ABC的直角边AB为直径作⊙O,交斜边AC于点D,点E为OB的中点,连接CE并延长交⊙O于点F,点F恰好落在的中点,连接AF并延长与CB的延长线相交于点G,连接OF.(1)求证:OF=BG;(2)若AB=4,求DC的长.六、解答题(本大题14分)24、某书店正在销售一种课外读本,进价12元/本,售价20元/本,为了促销,书店决定凡是一次购买10本以上的客户,每多买一本,售价就降低0.10元,但最低价为16元/本.(1)客户一次至少买多少本,才能以最低价购买?(2)写出当一次购买x本时(x>10),书店利润y(元)与购买量x(本)之间的函数关系式;(3)在销售过程中,书店发现卖出50本比卖出46本赚的钱少,为了使每次的销售均能达到多卖出就多获利,在其他促销条件不变的情况下,最低价应确定为多少元/本?请说明理由.七、解答题(本大题14分)ll l25、已知,在△ABC中,AB=AC.过A 点的直线a从与边AC重合的位置开始绕点A按顺时针方向旋转角θ,直线a交BC边于点P(点P不与点B、点C重合),△BMN的边MN始终在直线a上(点M在点N的上方),且BM=BN,连接CN.(1)当∠BAC=∠MBN=90°时,①如图a,当θ=45°时,∠ANC的度数为;②如图b,当θ≠45°时,①中的结论是否发生变化?说明理由;(2)如图c,当∠BAC=∠MBN≠90°时,请直接写出∠ANC与∠BAC之间的数量关系,不必证明.八、解答题(本大题14分)26、如图,Rt△ABO的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,O为坐标原点,A、B两点的坐标分别为(﹣3,0)、(0,4),抛物线y=x2+bx+c经过点B,且顶点在直线x=上.(1)求抛物线对应的函数关系式;(2)若把△ABO沿x轴向右平移得到△DCE,点A、B、O的对应点分别是D、C、E,当四边形ABCD是菱形时,试判断点C和点D是否在该抛物线上,并说明理由;(3)若M点是CD所在直线下方该抛物线上的一个动点,过点M作MN平行与y轴交CD于点N.设点M的横坐标为t,MN的长度为,求与t之间的函数关系式,并求取最大值时,点M的坐标。
徐州市中考数学模拟试卷(九)含答案解析

江苏省徐州市中考数学模拟试卷(九)一、选择题(共8小题,每题4分,满分32分;每小题只有一个正确的选项,请在答题卡的相应位置填涂)1.﹣5的相反数是()A.﹣5 B.5 C.D.﹣2.地球绕太阳公转的速度约是110000千米/时,将110000用科学记数法表示为()A.11×104B.1.1×104C.1.1×105D.0.11×1063.如图所示某几何体的三视图,则这个几何体是()A.三棱锥B.圆柱C.球D.圆锥4.下列计算正确的是()A.x4•x4=x16B.(a3)2=a5C.(ab2)3=ab6D.a+2a=3a5.下列命题中,假命题是()A.对顶角相等 B.三角形两边的和小于第三边C.菱形的四条边都相等D.多边形的外角和等于360°6.某工厂现在平均每天比原计划多生产50台机器,现在生产600台所需时间与原计划生产450台机器所需时间相同.设原计划平均每天生产x台机器,根据题意,下面所列方程正确的是()A. =B. = C. = D. =7.如图,在正方形ABCD的外侧,作等边三角形ADE,AC、BE相交于点F,则∠BFC为()A.45° B.55°C.60°D.75°8.如图,已知直线y=﹣x+2分别与x轴,y轴交于A,B两点,与双曲线y=交于E,F两点,若AB=2EF,则k的值是()A.﹣1 B.1 C.D.二、填空题(本大题共有10小题.每小题3分,共30分.不需要写出解答过程,请把答案直接写在答题卡的相应位置上)9.分解因式:ma+mb=.10.若5件外观相同的产品中有1件不合格,现从中任意抽取1件进行检测,则抽到不合格产品的概率是.11.计算:( +1)(﹣1)=.12.△ABC中,已知∠A=60°,∠B=80°,则∠C的外角的度数是°.13.已知OC是∠AOB的平分线,点P在OC上,PD⊥OA,PE⊥OB,垂足分别为点D、E,PD=10,则PE的长度为.14.代数式有意义时,x应满足的条件为.15.若(m﹣1)2+=0,则m+n的值是.16.如图,在▱ABCD中,DE平分∠ADC,AD=6,BE=2,则▱ABCD的周长是.17.如图,在Rt△ABC中,∠ACB=90°,点D,E分别是边AB,AC的中点,延长BC到点F,使CF=BC.若AB=10,则EF的长是.18.将四根长度相等的细木条首尾相接,用钉子钉成四边形ABCD,转动这个四边形,使它形状改变,当∠B=90°时,如图1,测得AC=2,当∠B=60°时,如图2,AC=.三、解答题(本大题共有10小题,共86分.请在答题卡指定区域作答,解答时应写出文字说明、证明过程或演算步骤)19.(1)计算: +()0+|﹣1|;(2)先化简,再求值:(x+2)2+x(2﹣x),其中x=.20.(1)解方程:2x2+4x﹣1=0;(2)解不等式:5x﹣2≤3x,并在数轴上表示解集.21.如图,点E、F在BC上,BE=FC,AB=DC,∠B=∠C.求证:∠A=∠D.22.如图,在边长为1个单位长度的小正方形所组成的网格中,△ABC的顶点均在格点上.①sinB的值是;②画出△ABC关于直线l对称的△A1B1C1(A与A1,B与B1,C与C1相对应).连接AA1,BB1,并计算梯形AA1B1B的面积.23.设中学生体质健康综合评定成绩为x分,满分为100分,规定:85≤x≤100为A级,75≤x≤85为B级,60≤x≤75为C级,x<60为D级.现随机抽取福海中学部分学生的综合评定成绩,整理绘制成如下两幅不完整的统计图,请根据图中的信息,解答下列问题:(1)在这次调查中,一共抽取了名学生,α=%;(2)补全条形统计图;(3)扇形统计图中C级对应的圆心角为度;(4)若该校共有2000名学生,请你估计该校D级学生有多少名?24.现有A,B两种商品,买2件A商品和1件B商品用了90元,买3件A商品和2件B商品用了160元.(1)求A,B两种商品每件各是多少元?(2)如果小亮准备购买A,B两种商品共10件,总费用不超过350元,但不低于300元,问有几种购买方案,哪种方案费用最低?25.如图,轮船从点A处出发,先航行至位于点A的南偏西15°且与点A相距100km的点B处,再航行至位于点B的北偏东75°且与点B相距200km的点C处.(1)求点C与点A的距离(精确到1km);(2)确定点C相对于点A的方向.(参考数据:≈1.414,≈1.732)26.如图,在△ABC中,∠B=45°,∠ACB=60°,AB=3,点D为BA延长线上的一点,且∠D=∠ACB,⊙O为△ACD的外接圆.(1)求BC的长;(2)求⊙O的半径.27.如图1,点O在线段AB上,AO=2,OB=1,OC为射线,且∠BOC=60°,动点P以每秒2个单位长度的速度从点O出发,沿射线OC做匀速运动,设运动时间为t秒.(1)当t=秒时,则OP=,S△ABP=;(2)当△ABP是直角三角形时,求t的值;(3)如图2,当AP=AB时,过点A作AQ∥BP,并使得∠QOP=∠B,求证:AQ•BP=3.28.如图,抛物线y=(x﹣3)2﹣1与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,顶点为D.(1)求点A,B,D的坐标;(2)连接CD,过原点O作OE⊥CD,垂足为H,OE与抛物线的对称轴交于点E,连接AE,AD,求证:∠AEO=∠ADC;(3)以(2)中的点E为圆心,1为半径画圆,在对称轴右侧的抛物线上有一动点P,过点P作⊙E 的切线,切点为Q,当PQ的长最小时,求点P的坐标,并直接写出点Q的坐标.江苏省徐州市中考数学模拟试卷(九)参考答案与试题解析一、选择题(共8小题,每题4分,满分32分;每小题只有一个正确的选项,请在答题卡的相应位置填涂)1.﹣5的相反数是()A.﹣5 B.5 C.D.﹣【考点】相反数.【专题】常规题型.【分析】根据相反数的定义直接求得结果.【解答】解:﹣5的相反数是5.故选:B.【点评】本题主要考查了相反数的性质,只有符号不同的两个数互为相反数,0的相反数是0.2.地球绕太阳公转的速度约是110000千米/时,将110000用科学记数法表示为()A.11×104B.1.1×104C.1.1×105D.0.11×106【考点】科学记数法—表示较大的数.【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.【解答】解:将110000用科学记数法表示为1.1×105.故选C.【点评】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.3.如图所示某几何体的三视图,则这个几何体是()A.三棱锥B.圆柱C.球D.圆锥【考点】由三视图判断几何体.【分析】根据一个空间几何体的主视图和俯视图都是三角形,可判断该几何体是锥体,再根据左视图的形状,即可得出答案.【解答】解:∵几何体的主视图和俯视图都是三角形,∴该几何体是一个锥体,∵俯视图是一个圆,∴该几何体是一个圆锥;故选D.【点评】本题考查的知识点是三视图,如果有两个视图为三角形,该几何体一定是锥,如果有两个矩形,该几何体一定柱,其底面由第三个视图的形状决定.4.下列计算正确的是()A.x4•x4=x16B.(a3)2=a5C.(ab2)3=ab6D.a+2a=3a【考点】幂的乘方与积的乘方;合并同类项;同底数幂的乘法.【专题】计算题.【分析】根据同底数幂相乘,底数不变指数相加,幂的乘方,底数不变指数相乘,积的乘方,先把积的每一个因式分别乘方,再把所得到幂相乘,合并同类项,即把同类项的系数相加,所得结果作为系数,字母和字母的指数不变.对各小题计算后利用排除法求解.【解答】解;A、x4•x4=x8,故A错误;B、(a3)2=a6,故B错误;C、(ab2)3=a2b6,故C错误;D、a+2a=3a,故D正确.故选:D.【点评】本题主要考查了同底数幂相乘,幂的乘方的性质,积的乘方的性质,合并同类项,熟练掌握运算性质并理清指数的变化是解题的关键.5.下列命题中,假命题是()A.对顶角相等 B.三角形两边的和小于第三边C.菱形的四条边都相等D.多边形的外角和等于360°【考点】命题与定理.【分析】分别利用对顶角的性质、三角形的三边关系、菱形的性质及多边形的外角和对四个选项分别判断后即可确定正确的选项.【解答】解:A、对顶角相等,正确,是真命题;B、三角形的两边之和大于第三边,错误,是假命题;C、菱形的四条边都相等,正确,是真命题;D、多边形的外角和为360°,正确,为真命题,故选:B.【点评】本题考查了命题与定理的知识,解题的关键是熟知对顶角的性质、三角形的三边关系、菱形的性质及多边形的外角和定理,属于基础知识,难度较小.6.某工厂现在平均每天比原计划多生产50台机器,现在生产600台所需时间与原计划生产450台机器所需时间相同.设原计划平均每天生产x台机器,根据题意,下面所列方程正确的是()A. =B. = C. = D. =【考点】由实际问题抽象出分式方程.【分析】设原计划平均每天生产x台机器,则实际平均每天生产(x+50)台机器,根据题意可得,现在生产600台所需时间与原计划生产450台机器所需时间相同,据此列方程即可.【解答】解:设原计划平均每天生产x台机器,则实际平均每天生产(x+50)台机器,由题意得, =.故选B.【点评】本题考查了由实际问题抽象出分式方程,解答本题的关键是读懂题意,设出未知数,找出合适的等量关系,列方程.7.如图,在正方形ABCD的外侧,作等边三角形ADE,AC、BE相交于点F,则∠BFC为()A.45° B.55°C.60°D.75°【考点】正方形的性质;等腰三角形的性质;等边三角形的性质.【分析】根据正方形的性质及全等三角形的性质求出∠ABE=15°,∠BAC=45°,再求∠BFC.【解答】解:∵四边形ABCD是正方形,∴AB=AD,又∵△ADE是等边三角形,∴AE=AD=DE,∠DAE=60°,∴AB=AE,∴∠ABE=∠AEB,∠BAE=90°+60°=150°,∴∠ABE=(180°﹣150°)÷2=15°,又∵∠BAC=45°,∴∠BFC=45°+15°=60°.故选:C.【点评】本题主要是考查正方形的性质和等边三角形的性质,本题的关键是求出∠ABE=15°.8.如图,已知直线y=﹣x+2分别与x轴,y轴交于A,B两点,与双曲线y=交于E,F两点,若AB=2EF,则k的值是()A.﹣1 B.1 C.D.【考点】反比例函数图象上点的坐标特征;一次函数图象上点的坐标特征;等腰直角三角形.【专题】压轴题.【分析】作FH⊥x轴,EC⊥y轴,FH与EC交于D,先利用一次函数图象上点的坐标特征得到A (2,0),B(0,2),易得△AOB为等腰直角三角形,则AB=OA=2,所以EF=AB=,且△DEF为等腰直角三角形,则FD=DE=EF=1;设F点坐标为(t,﹣t+2),则E点坐标为(t+1,﹣t+1),根据反比例函数图象上点的坐标特征得到t(﹣t+2)=(t+1)•(﹣t+1),解得t=,这样可确定E点坐标为(,),然后根据反比例函数图象上点的坐标特征得到k=×.【解答】解:作FH⊥x轴,EC⊥y轴,FH与EC交于D,如图,A点坐标为(2,0),B点坐标为(0,2),OA=OB,∴△AOB为等腰直角三角形,∴AB=OA=2,∴EF=AB=,∴△DEF为等腰直角三角形,∴FD=DE=EF=1,设F点横坐标为t,代入y=﹣x+2,则纵坐标是﹣t+2,则F的坐标是:(t,﹣t+2),E点坐标为(t+1,﹣t+1),∴t(﹣t+2)=(t+1)•(﹣t+1),解得t=,∴E点坐标为(,),∴k=×=.故选:D.【点评】本题考查了反比例函数图象上点的坐标特征:反比例函数y=(k为常数,k≠0)的图象是双曲线,图象上的点(x,y)的横纵坐标的积是定值k,即xy=k.二、填空题(本大题共有10小题.每小题3分,共30分.不需要写出解答过程,请把答案直接写在答题卡的相应位置上)9.分解因式:ma+mb=m(a+b).【考点】因式分解-提公因式法.【专题】因式分解.【分析】这里的公因式是m,直接提取即可.【解答】解:ma+mb=m(a+b).故答案为:m(a+b)【点评】本题考查了提公因式法分解因式,公因式即多项式各项都含有的公共的因式.10.若5件外观相同的产品中有1件不合格,现从中任意抽取1件进行检测,则抽到不合格产品的概率是.【考点】概率公式.【分析】根据不合格品件数与产品的总件数比值即可解答.【解答】解:∵在5个外观相同的产品中,有1个不合格产品,∴从中任意抽取1件检验,则抽到不合格产品的概率是:.故答案为:.【点评】本题主要考查概率公式,如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=.11.计算:( +1)(﹣1)=1.【考点】二次根式的乘除法;平方差公式.【专题】计算题.【分析】两个二项式相乘,并且这两个二项式中有一项完全相同,另一项互为相反数.就可以用平方差公式计算.结果是乘式中两项的平方差(相同项的平方减去相反项的平方).【解答】解:( +1)(﹣1)=.故答案为:1.【点评】本题应用了平方差公式,使计算比利用多项式乘法法则要简单.12.△ABC中,已知∠A=60°,∠B=80°,则∠C的外角的度数是140°.【考点】三角形的外角性质.【分析】根据三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解.【解答】解:∵∠A=60°,∠B=80°,∴∠C的外角=∠A+∠B=60°+80°=140°.故答案为:140.【点评】本题考查了三角形的一个外角等于与它不相邻的两个内角的和的性质,熟记性质是解题的关键.13.已知OC是∠AOB的平分线,点P在OC上,PD⊥OA,PE⊥OB,垂足分别为点D、E,PD=10,则PE的长度为10.【考点】角平分线的性质.【分析】根据角平分线上的点到角的两边距离相等可得PE=PD.【解答】解:∵OC是∠AOB的平分线,PD⊥OA,PE⊥OB,∴PE=PD=10.故答案为:10.【点评】本题考查了角平分线上的点到角的两边距离相等的性质,熟记性质是解题的关键,作出图形更形象直观.14.代数式有意义时,x应满足的条件为x≠±1.【考点】分式有意义的条件.【分析】根据分式有意义,分母等于0列出方程求解即可.【解答】解:由题意得,|x|﹣1≠0,故答案为:x≠±1.【点评】本题考查了分式有意义的条件,从以下三个方面透彻理解分式的概念:(1)分式无意义⇔分母为零;(2)分式有意义⇔分母不为零;(3)分式值为零⇔分子为零且分母不为零.15.若(m﹣1)2+=0,则m+n的值是﹣1.【考点】非负数的性质:算术平方根;非负数的性质:偶次方.【分析】根据非负数的性质列式求出m、n的值,然后代入代数式进行计算即可得解.【解答】解:由题意得,m﹣1=0,n+2=0,解得m=1,n=﹣2,所以m+n=1+(﹣2)=﹣1.故答案为:﹣1.【点评】本题考查了非负数的性质:几个非负数的和为0时,这几个非负数都为0.16.如图,在▱ABCD中,DE平分∠ADC,AD=6,BE=2,则▱ABCD的周长是20.【考点】平行四边形的性质;等腰三角形的判定与性质.【分析】根据角平分线的定义以及两直线平行,内错角相等求出∠CDE=∠CED,再根据等角对等边的性质可得CE=CD,然后利用平行四边形对边相等求出CD、BC的长度,再求出▱ABCD的周长.【解答】解:∵DE平分∠ADC,∴∠ADE=∠CDE,∵▱ABCD中,AD∥BC,∴∠ADE=∠CED,∴∠CDE=∠CED,∵在▱ABCD中,AD=6,BE=2,∴AD=BC=6,∴CE=BC﹣BE=6﹣2=4,∴CD=AB=4,∴▱ABCD的周长=6+6+4+4=20.故答案为:20.【点评】本题考查了平行四边形对边平行,对边相等的性质,角平分线的定义,等角对等边的性质,是基础题,准确识图并熟练掌握性质是解题的关键.17.如图,在Rt△ABC中,∠ACB=90°,点D,E分别是边AB,AC的中点,延长BC到点F,使CF=BC.若AB=10,则EF的长是5.【考点】平行四边形的判定与性质;直角三角形斜边上的中线;三角形中位线定理.【专题】压轴题.【分析】根据三角形中位线的性质,可得DE与BC的关系,根据平行四边形的判定与性质,可得DC与EF的关系,根据直角三角形的性质,可得DC与AB的关系,可得答案.【解答】解:如图,连接DC.DE是△ABC的中位线,∴DE∥BC,DE=,∵CF=BC,∴DE∥CF,DE=CF,∴CDEF是平行四边形,∴EF=DC.∵DC是Rt△ABC斜边上的中线,∴DC==5,∴EF=DC=5,故答案为:5.【点评】本题考查了平行四边形的判定与性质,利用了平行四边形的判定与性质,直角三角形斜边上的中线等于斜边的一半.18.将四根长度相等的细木条首尾相接,用钉子钉成四边形ABCD,转动这个四边形,使它形状改变,当∠B=90°时,如图1,测得AC=2,当∠B=60°时,如图2,AC=.【考点】正方形的性质;菱形的性质.【分析】图1中根据勾股定理即可求得正方形的边长,图2根据有一个角是60°的等腰三角形是等边三角形即可求得.【解答】解:如图1,∵AB=BC=CD=DA,∠B=90°,∴四边形ABCD是正方形,连接AC,则AB2+BC2=AC2,∴AB=BC=,如图2,∠B=60°,连接AC,∴△ABC为等边三角形,∴AC=AB=BC=.故答案为:.【点评】本题考查了正方形的性质,勾股定理以及等边三角形的判定和性质,利用勾股定理得出正方形的边长是关键.三、解答题(本大题共有10小题,共86分.请在答题卡指定区域作答,解答时应写出文字说明、证明过程或演算步骤)19.(1)计算: +()0+|﹣1|;(2)先化简,再求值:(x+2)2+x(2﹣x),其中x=.【考点】实数的运算;整式的混合运算—化简求值;零指数幂.【分析】(1)本题涉及零指数幂、绝对值、二次根式化简三个考点.针对每个考点分别进行计算,然后根据实数的运算法则求得计算结果;(2)根据完全平方公式、单项式成多项式,可化简整式,根据代数式求值,可得答案.【解答】解:(1)原式=3+1+1=5;(2)原式=x2+4x+4+2x﹣x2=6x+4,当x=时,原式=6×+4=2+4=6.【点评】本题考查了实数的运算,熟练掌握零指数幂、绝对值、二次根式的运算.20.(1)解方程:2x2+4x﹣1=0;(2)解不等式:5x﹣2≤3x,并在数轴上表示解集.【考点】解一元二次方程-公式法;在数轴上表示不等式的解集;解一元一次不等式.【专题】计算题.【分析】(1)方程利用公式法求出解即可;(2)不等式移项合并,把x系数化为1,求出解集,表示在数轴上即可.【解答】解:(1)这里a=2,b=4,c=﹣1,∵△=16+8=24,∴x==;(2)不等式移项合并得:2x≤2,解得:x≤1,【点评】此题考查了解一元二次方程﹣公式法,以及解一元一次不等式,熟练掌握运算法则是解本题的关键.21.如图,点E、F在BC上,BE=FC,AB=DC,∠B=∠C.求证:∠A=∠D.【考点】全等三角形的判定与性质.【专题】证明题.【分析】可通过证△ABF≌△DCE,来得出∠A=∠D的结论.【解答】证明:∵BE=FC,∴BE+EF=CF+EF,即BF=CE;又∵AB=DC,∠B=∠C,∴△ABF≌△DCE;(SAS)∴∠A=∠D.【点评】此题考查简单的角相等,可以通过全等三角形来证明,判定两个三角形全等,先根据已知条件或求证的结论确定三角形,然后再根据三角形全等的判定方法,看缺什么条件,再去证什么条件.22.如图,在边长为1个单位长度的小正方形所组成的网格中,△ABC的顶点均在格点上.①sinB的值是;②画出△ABC关于直线l对称的△A1B1C1(A与A1,B与B1,C与C1相对应).连接AA1,BB1,并计算梯形AA1B1B的面积.【考点】作图-轴对称变换;勾股定理;锐角三角函数的定义.【分析】①利用勾股定理得出AB的长,再利用锐角三角函数关系得出答案;②利用关于直线对称的性质得出对应点进而利用梯形面积求法得出答案.【解答】解:①∵AC=3,AB==5,∴sinB的值是: =.故答案为:;②如图所示:△A1B1C1,即为所求,梯形AA1B1B的面积为:×(2+8)×4=20.【点评】此题主要考查了轴对称变换和勾股定理以及锐角三角函数关系,正确掌握梯形面积公式是解题关键.23.设中学生体质健康综合评定成绩为x分,满分为100分,规定:85≤x≤100为A级,75≤x≤85为B级,60≤x≤75为C级,x<60为D级.现随机抽取福海中学部分学生的综合评定成绩,整理绘制成如下两幅不完整的统计图,请根据图中的信息,解答下列问题:(1)在这次调查中,一共抽取了50名学生,α=24%;(2)补全条形统计图;(3)扇形统计图中C级对应的圆心角为72度;(4)若该校共有2000名学生,请你估计该校D级学生有多少名?【考点】条形统计图;用样本估计总体;扇形统计图.【专题】图表型.【分析】(1)根据B级的人数和所占的百分比求出抽取的总人数,再用A级的人数除以总数即可求出a;(2)用抽取的总人数减去A、B、D的人数,求出C级的人数,从而补全统计图;(3)用360度乘以C级所占的百分比即可求出扇形统计图中C级对应的圆心角的度数;(4)用D级所占的百分比乘以该校的总人数,即可得出该校D级的学生数.【解答】解:(1)在这次调查中,一共抽取的学生数是: =50(人),a=×100%=24%;故答案为:50,24;(2)等级为C的人数是:50﹣12﹣24﹣4=10(人),补图如下:(3)扇形统计图中C级对应的圆心角为×360°=72°;故答案为:72;(4)根据题意得:2000×=160(人),答:该校D级学生有160人.【点评】此题考查了是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.24.现有A,B两种商品,买2件A商品和1件B商品用了90元,买3件A商品和2件B商品用了160元.(1)求A,B两种商品每件各是多少元?(2)如果小亮准备购买A,B两种商品共10件,总费用不超过350元,但不低于300元,问有几种购买方案,哪种方案费用最低?【考点】一元一次不等式组的应用;二元一次方程组的应用.【专题】优选方案问题.【分析】(1)设A商品每件x元,B商品每件y元,根据关系式列出二元一次方程组.(2)设小亮准备购买A商品a件,则购买B商品(10﹣a)件,根据关系式列出二元一次不等式方程组.求解再比较两种方案.【解答】解:(1)设A商品每件x元,B商品每件y元,依题意,得,解得.答:A商品每件20元,B商品每件50元.(2)设小亮准备购买A商品a件,则购买B商品(10﹣a)件解得5≤a≤6根据题意,a的值应为整数,所以a=5或a=6.方案一:当a=5时,购买费用为20×5+50×(10﹣5)=350元;方案二:当a=6时,购买费用为20×6+50×(10﹣6)=320元;∵350>320∴购买A商品6件,B商品4件的费用最低.答:有两种购买方案,方案一:购买A商品5件,B商品5件;方案二:购买A商品6件,B商品4件,其中方案二费用最低.【点评】此题主要考查二元一次方程组及二元一次不等式方程组的应用,根据题意得出关系式是解题关键.25.如图,轮船从点A处出发,先航行至位于点A的南偏西15°且与点A相距100km的点B处,再航行至位于点B的北偏东75°且与点B相距200km的点C处.(1)求点C与点A的距离(精确到1km);(2)确定点C相对于点A的方向.(参考数据:≈1.414,≈1.732)【考点】解直角三角形的应用-方向角问题.【专题】几何图形问题.【分析】(1)作辅助线,构造直角三角形,解直角三角形即可;(2)利用勾股定理的逆定理,判定△ABC为直角三角形;然后根据方向角的定义,即可确定点C 相对于点A的方向.【解答】解:(1)如右图,过点A作AD⊥BC于点D,∠ABE=∠BAF=15°,由图得,∠ABC=∠EBC﹣∠ABE=∠EBC﹣∠BAF=75°﹣15°=60°,在Rt△ABD中,∵∠ABC=60°,AB=100,∴BD=50,AD=50,∴CD=BC﹣BD=200﹣50=150,在Rt△ACD中,由勾股定理得:AC==100≈173(km).答:点C与点A的距离约为173km.(2)在△ABC中,∵AB2+AC2=1002+(100)2=40000,BC2=2002=40000,∴AB2+AC2=BC2,∴∠BAC=90°,∴∠CAF=∠BAC﹣∠BAF=90°﹣15°=75°.答:点C位于点A的南偏东75°方向.【点评】考查了解直角三角形的应用﹣方向角问题,关键是熟练掌握勾股定理,体现了数学应用于实际生活的思想.26.如图,在△ABC中,∠B=45°,∠ACB=60°,AB=3,点D为BA延长线上的一点,且∠D=∠ACB,⊙O为△ACD的外接圆.(1)求BC的长;(2)求⊙O的半径.【考点】三角形的外接圆与外心;圆周角定理;解直角三角形.【分析】(1)根据题意得出AE的长,进而得出BE=AE,再利用tan∠ACB=,求出EC的长即可;(2)首先得出AC的长,再利用圆周角定理得出∠D=∠M=60°,进而求出AM的长,即可得出答案.【解答】解:(1)过点A作AE⊥BC,垂足为E,∴∠AEB=∠AEC=90°,在Rt△ABE中,∵sinB=,∴AE=ABsinB=3sin45°=3×=3,∵∠B=45°,∴∠BAE=45°,∴BE=AE=3,在Rt△ACE中,∵tan∠ACB=,∴EC====,∴BC=BE+EC=3+;(2)连接AO并延长到⊙O上一点M,连接CM,由(1)得,在Rt△ACE中,∵∠EAC=30°,EC=,∴AC=2,∵∠D=∠M=60°,∴sin60°===,解得:AM=4,∴⊙O的半径为2.【点评】此题主要考查了解直角三角形以及锐角三角函数关系应用,根据题意正确构造直角三角形是解题关键.27.如图1,点O在线段AB上,AO=2,OB=1,OC为射线,且∠BOC=60°,动点P以每秒2个单位长度的速度从点O出发,沿射线OC做匀速运动,设运动时间为t秒.(1)当t=秒时,则OP=1,S△ABP=;(2)当△ABP是直角三角形时,求t的值;(3)如图2,当AP=AB时,过点A作AQ∥BP,并使得∠QOP=∠B,求证:AQ•BP=3.【考点】相似形综合题.【专题】几何动点问题;压轴题.【分析】(1)如答图1所示,作辅助线,利用三角函数或勾股定理求解;(2)当△ABP是直角三角形时,有三种情形,需要分类讨论;(3)如答图4所示,作辅助线,构造一对相似三角形△OAQ∽△PBO,利用相似关系证明结论.【解答】(1)解:当t=秒时,OP=2t=2×=1.如答图1,过点P作PD⊥AB于点D.在Rt△POD中,PD=OP•sin60°=1×=,∴S△ABP=AB•PD=×(2+1)×=.(2)解:当△ABP是直角三角形时,①若∠A=90°.∵∠BOC=60°且∠BOC>∠A,∴∠A≠90°,故此种情形不存在;②若∠B=90°,如答图2所示:∵∠BOC=60°,∴∠BPO=30°,∴OP=2OB=2,又OP=2t,∴t=1;③若∠APB=90°,如答图3所示:过点P作PD⊥AB于点D,则OD=OP•sin30°=t,PD=OP•sin60°=t,∴AD=OA+OD=2+t,BD=OB﹣OD=1﹣t.在Rt△ABP中,由勾股定理得:PA2+PB2=AB2∴(AD2+PD2)+(BD2+PD2)=AB2,即[(2+t)2+(t)2]+[(1﹣t)2+(t)2]=32解方程得:t=或t=(负值舍去),∴t=.综上所述,当△ABP是直角三角形时,t=1或t=.(3)证明:如答图4,过点O作OE∥AP,交PB于点E,则有,∴PE=PB.∵AP=AB,∴∠APB=∠B,∵OE∥AP,∴∠OEB=∠APB,∴∠OEB=∠B,∴OE=OB=1,∠3+∠B=180°.∵AQ∥PB,∴∠OAQ+∠B=180°,∴∠OAQ=∠3;∵∠AOP=∠1+∠QOP=∠2+∠B,∠QOP=∠B,∴∠1=∠2;∴△OAQ∽△PEO,∴,即,化简得:AQ•PB=3.【点评】本题是运动型综合题,考查了相似三角形的判定与性质、解直角三角形、勾股定理、一元二次方程等多个知识点.第(2)问中,解题关键在于分类讨论思想的运用;第(3)问中,解题关键是构造相似三角形,本问有多种解法,可探究尝试.28.如图,抛物线y=(x﹣3)2﹣1与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,顶点为D.(1)求点A,B,D的坐标;(2)连接CD,过原点O作OE⊥CD,垂足为H,OE与抛物线的对称轴交于点E,连接AE,AD,求证:∠AEO=∠ADC;(3)以(2)中的点E为圆心,1为半径画圆,在对称轴右侧的抛物线上有一动点P,过点P作⊙E 的切线,切点为Q,当PQ的长最小时,求点P的坐标,并直接写出点Q的坐标.【考点】二次函数综合题.【专题】代数几何综合题;压轴题.【分析】(1)根据二次函数性质,求出点A、B、D的坐标;(2)如何证明∠AEO=∠ADC?如答图1所示,我们观察到在△EFH与△ADF中:∠EHF=90°,有一对对顶角相等;因此只需证明∠EAD=90°即可,即△ADE为直角三角形,由此我们联想到勾股定理的逆定理.分别求出△ADE三边的长度,再利用勾股定理的逆定理证明它是直角三角形,由此问题解决;(3)依题意画出图形,如答图2所示.由⊙E的半径为1,根据切线性质及勾股定理,得PQ2=EP2﹣1,要使切线长PQ最小,只需EP长最小,即EP2最小.利用二次函数性质求出EP2最小时点P 的坐标,并进而求出点Q的坐标.【解答】方法一:(1)解:顶点D的坐标为(3,﹣1).令y=0,得(x﹣3)2﹣1=0,解得:x1=3+,x2=3﹣,∵点A在点B的左侧,∴A(3﹣,0),B(3+,0).(2)证明:如答图1,过顶点D作DG⊥y轴于点G,则G(0,﹣1),GD=3.令x=0,得y=,∴C(0,).∴CG=OC+OG=+1=,∴tan∠DCG=.设对称轴交x轴于点M,则OM=3,DM=1,AM=3﹣(3﹣)=.由OE⊥CD,易知∠EOM=∠DCG.∴tan∠EOM=tan∠DCG==,解得EM=2,∴DE=EM+DM=3.在Rt△AEM中,AM=,EM=2,由勾股定理得:AE=;在Rt△ADM中,AM=,DM=1,由勾股定理得:AD=.。
九年级中考语文模拟复习测试题(附答案)

九年级中考语文模拟复习测试题(附答案)一、积累与运用(共26分)1.(6分)阅读下面的文字,完成问题。
狂妄自大的民族不喜欢聆.听,___,贪欲和傲漫..(遮挡/遮盖)了他们的视线;闭关自守....的民族不喜欢聆听,___,浅陋.和愚昧妨.碍了他们的(进攻/进取);急攻近利....的民族不喜欢聆听,___,浮躁..和短视制约了他们的识见。
因此,只有喜欢聆听的民族,才是富有智慧的民族。
(1)文中加点字的注音和字形,全都正确的一项是A.聆.听(líng)傲漫B.妨.碍(fǎng)闭关自守C.浅陋.(lòu)浮躁D.狂妄.(wàng)急攻近利(2)依次选用文中括号里的词语,最恰当的一项是A.遮挡进取B.遮挡进攻C.遮盖进取D.遮盖进攻(3)在文中两处横线上依次填入句子,衔接最恰当的一项是①他们只会穷兵黩武②他们只会坐井观天③他们只会浅尝辄止A.①②③B.②③①C.③①②D.①③②2.(2分)下列各句中,没有语病的一项是()A.5月15日,天问一号探测器成功着陆火星,实现了从地月系到行星际的跨越。
B.我国将采取多种节能减排,力争提前实现2060年二氧化碳“零排放”的承诺。
C.为提高学生审美能力,颖滨中学开设了陶艺、书法等超过30余门美育选修课。
D.社区物业应增强社区管理和服务水平,增加群众的获得感、幸福感、安全感。
3.(2分)下列有关传统文化常识的表述,不正确的一项是()A.《蒹葭》《关雎》均选自《诗经》,《诗经》是我国最早的一部诗歌总集,收录了从西周到春秋时期的诗歌305篇,又称“诗三百”。
B.古时住宅旁常栽桑树、梓树,后人就用“桑梓”指家乡;“长河落日圆”中的“河”指黄河;“晋太元中”的“太元”是年号;《范文正公集》中的“文正”是谥号。
C.古人把山的南面、水的北面称为“阳”,山的北面、水的南面称为“阴”。
如“河阳”指的就是黄河的北岸,“汉阴”指的就是汉水的南岸。
D.“特别想念那东坡的月光,梦想跟随在放翁的身旁。
人教版2022-2023学年第一学期九年级数学期末模拟测试题(附答案)

2022-2023学年第一学期九年级数学期末模拟测试题(附答案)一.选择部分(共30分)1.下列函数中y是x的二次函数的是()A.y=﹣2x2B.y=C.y=ax2+bx+c D.y=(x﹣2)2﹣x22.下列图形中,既是轴对称图形又是中心对称图形的有()A.B.C.D.3.若关于x的一元二次方程(k﹣1)x2+x+1=0有两个实数根,则k的取值范围是()A.k≤B.k>C.k<且k≠1D.k≤且k≠1 4.已知a>1,点A(a﹣1,y1),B(a,y2),C(a+1,y3)都在二次函数y=﹣2x2的图象上,则()A.y1<y2<y3B.y1<y3<y2C.y3<y2<y1D.y2<y1<y35.参加足球联赛的每两支球队之间都要进行两场比赛,共要比赛110场,设参加比赛的球队有x支,根据题意,下面列出的方程正确的是()A.x(x+1)=110B.x(x﹣1)=110C.x(x+1)=110D.x(x﹣1)=1106.某路口的交通信号灯每分钟红灯亮30秒,绿灯亮25秒,黄灯亮5秒,当小明到达该路口时,遇到绿灯的概率是()A.B.C.D.7.如图,⊙O的直径CD=20,AB是⊙O的弦,AB⊥CD,垂足为M,OM:OC=3:5,则AB的长为()A.8B.12C.16D.28.如图,在Rt△ABC中,∠BAC=90°,∠B=50°,AD⊥BC,垂足为D,△ADB与△ADB'关于直线AD对称,点B的对称点是点B',则∠CAB'的度数为()A.10°B.20°C.30°D.40°9.已知抛物线y=ax2+bx+3在坐标系中的位置如图所示,它与x,y轴的交点分别为A,B,P是其对称轴x=1上的动点,根据图中提供的信息,以下结论中不正确的是()A.2a+b=0B.a>﹣C.△P AB周长的最小值是D.x=3是ax2+bx+3=0的一个根10.二次函数y=ax2+bx+c的图象如图所示,其对称轴是直线x=1.下列结论:①abc<0;②a+c>b;③4a+c>0;④a+b≤m(am+b)(m为实数).其中结论正确的个数为()A.4个B.3个C.2个D.1个二.填空题(共33分)11.一个三角形的两边长分别为3和6,第三边长是方程x2﹣10x+21=0的根,则三角形的周长为.12.若x1,x2方程x2﹣4x﹣2021=0的两个实数根,则代数式x12﹣2x1+2x2的值等于.13.把二次函数y=2x2﹣1的图象向左平移1个单位长度,再向下平移2个单位长度,平移后抛物线的解析式为.14.如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△DEC,连接AD,若∠BAC =25°,则∠BAD=.15.如图,将△ABC绕点A逆时针旋转得到△ADE,点C和点E是对应点,若∠CAE=90°,AB=1,则BD=.16.抛物线y=ax2+bx+c(a≠0)的部分图象如图所示,其与x轴的一个交点坐标为(﹣3,0),对称轴为x=﹣1,则当y<0时,x的取值范围是.17.已知点P(x,y)在二次函数y=2(x+1)2﹣3的图象上,当﹣2<x≤1时,y的取值范围是.18.如图,⊙O的半径为2,弦AB=,E为弧AB的中点,OE交AB于点F,则OF 的长为.19.如图,直线a⊥b,垂足为H,点P在直线b上,PH=4cm,O为直线b上一动点,若以1cm为半径的⊙O与直线a相切,则OP的长为.20.若一个圆锥的底面半径为1cm,它的侧面展开图的圆心角为90°,则这个圆锥的母线长为cm.21.如图,二次函数y=ax2+bx+c的图象与x轴的两个交点分别为(﹣1,0),(3,0)对于下列命题:①b﹣2a=0;②abc<0;③a﹣2b+4c<0④8a+c<0,其中正确的有.三.解答题(共57分)22.如图,已知△ABC是锐角三角形(AC<AB).(1)请在图1中用无刻度的直尺和圆规作图:作直线l,使l上的各点到B、C两点的距离相等;设直线l与AB、BC分别交于点M、N,作一个圆,使得圆心O在线段MN上,且与边AB、BC相切;(不写作法,保留作图痕迹)(2)在(1)的条件下,若BM=,BC=2,则⊙O的半径为.23.如图,正方形网格中,每个小正方形的边长都是一个单位长度,在平面直角坐标系内,△ABO的三个顶点坐标分别为A(﹣1,3),B(﹣4,3),O(0,0).(1)画出△ABO关于x轴对称的△A1B1O,并写出点A1的坐标;(2)画出△ABO绕点O顺时针旋转90°后得到的△A2B2O,并写出点A2的坐标;(3)在(2)的条件下,求点A旋转到点A2所经过的路径长(结果保留π).24.已知关于x的一元二次方程x2+(2m﹣1)x+m2﹣1=0(1)若该方程有两个实数根,求m的取值范围.(2)若方程的两个实数根为x1,x2,且(x1﹣x2)2﹣10m=2,求m的值.25.已知:如图,在正方形ABCD中,G是CD上一点,延长BC到E,使CE=CG,连接BG并延长交DE于F.(1)求证:△BCG≌△DCE;(2)将△DCE绕点D顺时针旋转90°得到△DAE′,判断四边形E′BGD是什么特殊四边形,并说明理由.26.已知:如图,A是⊙O上一点,半径OC的延长线与过点A的直线交于B点,OC=BC,AC=OB.(1)求证:AB是⊙O的切线;(2)若∠ACD=45°,OC=2,求弦CD的长.27.山西转型综合改革示范区的一工厂里,生产的某种产品按供需要求分为十个档次.若生产第一档次(最低档次)的产品,一天可生产76件,每件的利润为10元,每提高一个档次,每件的利润增加2元,每天的产量将减少4件.设产品的档次(每天只生产一个档次的产品)为x,请解答下列问题.(1)用含x的代数式表示:一天生产的产品件数为件,每件产品的利润为元;(2)若该产品一天的总利润为1080元,求这天生产产品的档次x的值.28.如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B两点,A点在原点左侧,B点的坐标为(4,0),与y轴交于C(0,﹣4)点,点P是直线BC下方的抛物线上一动点.(1)求这个二次函数的表达式;(2)连接PO、PC,并把△POC沿CO翻折,得到四边形POP′C,那么是否存在点P,使四边形POP′C为菱形?若存在,请求出此时点P的坐标;若不存在,请说明理由.参考答案一.选择部分(共30分)1.解:A、是二次函数,故此选项符合题意;B、不是二次函数,故此选项不合题意;C、a=0时,不是二次函数,故此选项不合题意;D、不是二次函数,故此选项不合题意;故选:A.2.解:A.该图形是轴对称图形,不是中心对称图形,故此选项不合题意;B.该图形是轴对称图形,不是中心对称图形,故此选项不合题意;C.该图形既是轴对称图形,又是中心对称图形,故此选项符合题意;D.该图形是中心对称图形,不是轴对称图形,故此选项不合题意.故选:C.3.解:∵关于x的一元二次方程(k﹣1)x2+x+1=0有两个实数根,∴,解得:k≤且k≠1.故选:D.4.解:∵a>1,∴0<a﹣1<a<a+1,∵y=﹣2x2,﹣2<0,∴当x>0时,y随x值的增大而减少,∴y3<y2<y1.故选:C.5.解:设有x个队参赛,则x(x﹣1)=110.故选:D.6.解:∵每分钟红灯亮30秒,绿灯亮25秒,黄灯亮5秒,∴当小明到达该路口时,遇到绿灯的概率P==,故选:D.7.解:连接OA,∵⊙O的直径CD=20,OM:OC=3:5,∴OC=10,OM=6,∵AB⊥CD,∴AM===8,∴AB=2AM=16.故选:C.8.解:∵∠BAC=90°,∠B=50°,∴∠C=40°,∵△ADB与△ADB'关于直线AD对称,点B的对称点是点B',∴∠AB'B=∠B=50°,∴∠CAB'=∠AB'B﹣∠C=10°,故选:A.9.解:A、根据图象知,对称轴是直线x=﹣=1,则b=﹣2a,即2a+b=0.故A正确;B、根据图象知,点A的坐标是(﹣1,0),对称轴是直线x=1,则根据抛物线关于对称轴对称的性质知,抛物线与x轴的另一个交点的坐标是(3,0),∴x=3时,y=9a+3b+3=0,∴9a﹣6a+3=0,∴3a+3=0,∵抛物线开口向下,则a<0,∴2a+3=﹣a>0,∴a>﹣,故B正确;C,点A关于x=1对称的点是A′为(3,0),即抛物线与x轴的另一个交点.连接BA′与直线x=1的交点即为点P,则△P AB周长的最小值是(BA′+AB)的长度.∵A(﹣1,0),B(0,3),A′(3,0),∴AB=,BA′=3.即△P AB周长的最小值是+3,故C错误;D、根据图象知,点A的坐标是(﹣1,0),对称轴是直线x=1,则根据抛物线关于对称轴对称的性质知,抛物线与x轴的另一个交点的坐标是(3,0),所以x=3是ax2+bx+3=0的一个根,故D正确;故选:C.10.解:∵函数开口方向向上,a>0,∵对称轴为x=1,则﹣=1,∴b=﹣2a<0,∵与y轴交点在y轴负半轴,∴c<0,∴abc>0,故①错;当x=﹣1时,y=a﹣b+c>0,即a+c>b,故②正确;对称轴为x=1,则﹣=1,即b=﹣2a,由上知,a﹣b+c>0,则a+2a+c>0,即3a+c>0,∴4a+c>a>0,故③正确;由图象可得,当x=1时,函数取得最小值,∴对任意m为实数,有am2+bm+c≥a+b+c,∴am2+bm≥a+b,即a+b≤m(am+b),故④正确.综上,正确的个数有三个.故选:B.二.填空题(共33分)11.解:解方程x2﹣10x+21=0得x1=3、x2=7,∵3<第三边的边长<9,∴第三边的边长为7.∴这个三角形的周长是3+6+7=16.故答案为:16.12.解:∵x1,x2是方程x2﹣4x﹣2021=0的两个实数根,∴x1+x2=4,x12﹣4x1﹣2021=0,即x12﹣4x1=2021,则原式=x12﹣4x1+2x1+2x2=x12﹣4x1+2(x1+x2)=2021+2×4=2021+8=2029.故答案为:2029.13.解:由“左加右减”的原则可知,将二次函数y=2x2﹣1的图象向左平移1个单位长度所得抛物线的解析式为:y=2(x+1)2﹣1;由“上加下减”的原则可知,将抛物线y=2(x+1)2﹣1向下平移2个单位长度所得抛物线的解析式为:y=2(x+1)2﹣1﹣2=2(x+1)2﹣3,故答案为:y=2(x+1)2﹣3.14.解:∵Rt△ABC绕其直角顶点C按顺时针方向旋转90°后得到Rt△DEC,∴AC=CD,∴△ACD是等腰直角三角形,∴∠CAD=45°,则∠BAD=∠BAC+∠CAD=25°+45°=70°,故答案为:70°.15.解:∵将△ABC绕点A逆时针旋转的到△ADE,点C和点E是对应点,∴AB=AD=1,∠BAD=∠CAE=90°,∴BD===.故答案为.16.解:∵抛物线y=ax2+bx+c(a≠0)与x轴的一个交点坐标为(﹣3,0),对称轴为直线x=﹣1,∴抛物线与x轴的另一个交点为(1,0),由图象可知,当y<0时,x的取值范围是﹣3<x<1.故答案为:﹣3<x<1.17.解:∵二次函数y=2(x+1)2﹣3,∴该函数对称轴是直线x=﹣1,当x=﹣1时,取得最小值,此时y=﹣3,∵点P(x,y)在二次函数y=2(x+1)2﹣3的图象上,∴当﹣2<x≤1时,y的取值范围是:﹣3≤y≤5,故答案为:﹣3≤y≤5.18.解:∵E为弧AB的中点,∴OE⊥AB于F,∵AB=2,∴AF=BF=,在Rt△OAF中,OA=2,,故答案为:1.19.解:∵直线a⊥b,O为直线b上一动点,∴⊙O与直线a相切时,切点为H,∴OH=1cm,当点O在点H的左侧,⊙O与直线a相切时,如图1所示:OP=PH﹣OH=4﹣1=3(cm);当点O在点H的右侧,⊙O与直线a相切时,如图2所示:OP=PH+OH=4+1=5(cm);∴⊙O与直线a相切,OP的长为3cm或5cm,故答案为:3cm或5cm.20.解:设母线长为lcm,则=2π×1解得:l=4.故答案为:4.21.解:根据图象可得:a>0,c<0,对称轴:x=﹣>0,①∵它与x轴的两个交点分别为(﹣1,0),(3,0),∴对称轴是直线x=1,∴﹣=1,∴b+2a=0,故①错误;②∵a>0,∴b<0,∵c<0,∴abc>0,故②错误;③∵a﹣b+c=0,∴c=b﹣a,∴a﹣2b+4c=a﹣2b+4(b﹣a)=2b﹣3a,又由①得b=﹣2a,∴a﹣2b+4c=﹣7a<0,故此选项正确;④根据图示知,当x=4时,y>0,∴16a+4b+c>0,由①知,b=﹣2a,∴8a+c>0;故④错误;故正确为:③1个.故答案为:③.三.解答题(共57分)22.解:(1)如图直线l,⊙O即为所求.(2)过点O作OE⊥AB于E.设OE=ON=r,∵BM=,BC=2,MN垂直平分线段BC,∴BN=CN=1,∴MN===,∵s△BNM=S△BNO+S△BOM,∴×1×=×1×r+××r,解得,r=.故答案为:.23.解:(1)如图,△A1B1O即为所求,点A1的坐标(﹣1,﹣3);(2)如图,△A2B2O即为所求,点A2的坐标(3,1);(3)点A旋转到点A2所经过的路径长==π24.解:(1)由题意可知:Δ=(2m﹣1)2﹣4(m2﹣1)≥0,∴﹣4m+5≥0,∴m≤;(2)由题意可知:x1+x2=1﹣2m,x1x2=m2﹣1,∵(x1﹣x2)2﹣10m=2,∴(x1+x2)2﹣4x1x2﹣10m=2,∴(1﹣2m)2﹣4(m2﹣1)﹣10m=2,解得:m=;25.(1)证明:∵四边形ABCD是正方形,∴BC=CD,∠BCD=90°.∵∠BCD+∠DCE=180°,∴∠BCD=∠DCE=90°.又∵CG=CE,∴△BCG≌△DCE.(2)解:四边形E′BGD是平行四边形.理由如下:∵△DCE绕D顺时针旋转90°得到△DAE′,∴CE=AE′.∵CE=CG,∴CG=AE′.∵四边形ABCD是正方形,∴BE′∥DG,AB=CD.∴AB﹣AE′=CD﹣CG.即BE′=DG.∴四边形E′BGD是平行四边形.26.(1)证明:如图,连接OA;∵OC=BC,AC=OB,∴OC=BC=AC=OA.∴△ACO是等边三角形.∴∠O=∠OCA=60°,∵AC=BC,∴∠CAB=∠B,又∠OCA为△ACB的外角,∴∠OCA=∠CAB+∠B=2∠B,∴∠B=30°,又∠OAC=60°,∴∠OAB=90°,∴AB是⊙O的切线;(2)解:作AE⊥CD于点E,∵∠O=60°,∴∠D=30°.∵∠ACD=45°,AC=OC=2,∴在Rt△ACE中,CE=AE=;∵∠D=30°,∴AD=2,∴DE=AE=,∴CD=DE+CE=+.27.解(1)一天生产的产品件数为[76﹣4(x﹣1)]=(80﹣4x)件,每件产品的利润为[10+2(x﹣1)]=(8+2x)元,故答案为(80﹣4x),(8+2x);(2)当利润是1080元时,即:[10+2(x﹣1)][76﹣4(x﹣1)]=1080,整理得:﹣8x2+128x+640=1080,解得x1=5,x2=11,因为x=11>10,不符合题意,舍去.因此取x=5,当生产产品的质量档次是在第5档次时,一天的总利润为1080元.28.解:(1)将B、C两点的坐标代入y=x2+bx+c得:,解得:,所以二次函数的表达式为:y=x2﹣3x﹣4;(2)存在点P,使四边形POP′C为菱形;设P点坐标为(x,x2﹣3x﹣4),PP′交CO于E若四边形POP′C是菱形,则有PC=PO;如图,连接PP′,则PE⊥CO于E,∵C(0,﹣4),∴CO=4,又∵OE=EC,∴OE=EC=2∴y=﹣2;∴x2﹣3x﹣4=﹣2,解得:x1=,x2=(不合题意,舍去),∴P点的坐标为(,﹣2).。
人教版九年级英语模拟试题及答案解析

六、选择填空(共15小题;计20分)A)从各题的A、B、C三个选项中选出正确答案。
(共10小题,每小题1分;计10分)31.I want to be engineer when I grow up.A.aB.anC.the32.Mike lost his school ID card this morning.He is looking for now.A.itB.himC.them33.I can’t see Lucy because she is the tree.A.in front ofB.behindC.next to34.Our English teacher wants us English stories out of class.A.readB.readingC.to read35.-----Hi,Amy,you live on Center Street.Can you tell me?-----Sure.There is one called Grandma’s HomeA.where it isB.how I can get thereC.if there is a restaurant on it36.This pair of glasses be Tony’s.He’s the only one who wears glasses.A.mustB.mightC.can’t37.Many people still try to climb Qomolangma every year it is very dangerous.A.whenB.ifC.though38.Jim studies better than Tom,but Tom is and he has more friends.A.friendlyB.more friendlyC.the most friendly39.A kind of shared bike is called bluegogo is getting more and more popular in Chengdu.A.itB.whoC.which40.-----Did you hear someone knock at the door just now?-----Sorry,I to my friend on the phone.A.was talkingB.talkedC.am talkingB)补全对话。
2024-2025学年初中九年级上学期第一次月考数学试题及答案(苏科版)

2024-2025学年度第一学期第一次月考模拟试卷一、单选题1. 下列是一元二次方程的是( )A. 20ax bx c ++=B. 22x x −=C. ()222x x x −=−D. 11x x+= 2. 一元二次方程2310x x −−=的根的情况为( )A. 无实数根B. 有一个实数根C. 有两个相等的实数根D. 有两个不相等的实数根3. 一元二次方程2430x x −+=配方后变形为( )A. ()241x −=B. ()221x −=C. ()241x +=D. ()221x += 4. 若关于x 一元二次方程2690kx x −+=有两个不相等的实数根,则k 的取值范围是( )A. 1k >B. 0k ≠C. 1k <D. 1k <且0k ≠ 5. 将抛物线2y x =先向上平移2个单位长度,再向右平移3个单位长度后,得到的抛物线对应的函数解析式为( )A. ()223y x =−+B. ()232y x =−+ C. ()223y x =++ D. ()232y x =−− 6. 若()()()1232,,1,,2,A y B y C y −是抛物线()221y x a =−+上的三点,则123,,y y y 为的大小关系为( )A 123y y y >> B. 132y y y >> C. 321y y y >> D. 312y y y >> 7. 若抛物线242y kx x =−−与x 轴有两个交点,则k 的取值范围为( )A. 2k >−B. 2k ≥−C. 2k >−且0k ≠D. 2k ≥−且0k ≠ 8. 二次函数2y ax bx c =++图象上部分点的对应值如下表则使0y <的x 的取值范围为( ) x 3− 2− 1− 01 2 3 4 y 60 4− 6− 6− 4− 0 6A. 0x <B. 12x >C. 23x −<<D. 2x <−或3x >的.二、填空题9. 已知m 是方程2520x x −−=的一个根,则22101m m −−=______. 10. 一元二次方程()2110x k x +++=有两个相等的实数根,那么k 的值为_____. 11. 若关于x 的一元二次方程()22240m x mx m −++−=有一个根是0,则m 的值为________ 12. 用一根长22cm 的铁丝围成面积是230cm 的矩形.假设矩形的一边长是cm x ,则可列出方程_____________________13. 如图,已知抛物线2y ax bx c ++与直线y kx m =+交于()3,1A −−、()0,3B 两点,则关于x 的不等式2ax bx c kx m ++≥+的解集是________.14. 抛物线()232y x =−−−的顶点坐标是________ .15. 已知二次函数()214y x =+−,当02x ≤≤时,函数值y 取值范围为__________16. 飞机着陆后滑行的距离(米)关于滑行时间(秒)的函数解析式为260 1.5s t t =−,则飞机着陆后滑行_________秒才停下来.17. 如图所示,,A B 分别为22(2)1y x =−−图象上的两点,且直线AB 垂直于y 轴,若2AB =,则点B 的纵坐标为________.18. 如图,横截面为抛物线的山洞,山洞底部宽为8米,最高处高163米,现要水平放置横截面为正方形的箱子,其中两个顶点在抛物线上的大箱子,在大箱子的两侧各放置一个横截面为正方形的小箱子,则小箱子的正方形的最大边长为______米.三、解答题19. 商场销售某种拖把,已知这种拖把的进价为80元/套,售价为120元/套,商场每天可销售20套、国庆假期临近,该商场决定采取适当的降价措施,经调查:这种拖把的售价每降价1元,平均每天可多售出2套,设这种拖把每套降价x 元.(1)降价后每套拖把盈利______元,平均每天可销售______套(用含x 的代数式表示);(2)为扩大销售量,尽快减少库存,当每套拖把降价多少元时,该商场销售这种拖把平均每天能盈利1242元?(3)该商场销售这种拖把平均每天的盈利能否达到1400元?若能,求出x 的值;若不能,请说明理由. 20. 解方程:(1)2(2x 1)9+=;(2)2x 2﹣4x =1(配方法);(3)22x 5x 10−+=;(4) ()2(x 3)4x 3x 0−−−= 21. 随着科技的发展,某省正加快布局以5G 等为代表的新兴产业.据统计,目前该省5G 基站数量约为1.5万座,计划到今年底,全省5G 基站数是目前的4倍;到后年底,全省5G 基站数量将达到17.34万座.(1)计划在今年底,全省5G 基站数量是多少万座?(2)按照计划,从今年底到后年底,全省5G 基站数量的年平均增长率为多少?22. 如图,老李想用长为70m 的栅栏,再借助房屋的外墙(外墙足够长)围成一个矩形羊圈ABCD ,并在边BC 上留一个2m 宽的门(建在EF 处,另用其他材料).(1)当羊圈的边AB 的长为多少米时,能围成一个面积为2640m 的羊圈?(2)羊圈的面积能达到2650m 吗?如果能,请你给出设计方案;如果不能,请说明理由.23. 已知函数()214y x =−−+.(1)当x =____________时,抛物线有最大值,____________.(2)当x ____________时,y 随x 的增大而增大.(3)该函数可以由函数2y x =−的图象经过怎样的平移得到?(4)该抛物线与x 轴交于点____________,与y 轴交于点____________.(写坐标)(5)在下面的坐标系中画出该抛物线的图象.24. 已知图象的顶点坐标是()2,1,且与x 轴的一个交点坐标是()3,0,求此二次函数的解析式. 25. 已知:二次函数()221y x m x m =−++−. (1)求证:该抛物线与x(2)设抛物线与x 轴的两个交点是A B 、(A 在原点左边,B 在原点右边),且3AB =,求此时抛物线的解析式.26. 若直线5y x =−与y 轴交于点A ,与x 轴交于点B ,二次函数2y ax bx c =++的图象经过点A ,点B ,且与x 轴交于点()1,0C −.(1)求二次函数解析式;(2)若点P 为直线AB 下方抛物线上一点,连接PA ,PB ,求ABP 面积的最大值及此时点P 的坐标;是的2024-2025学年度第一学期第一次月考模拟试卷一、单选题1. 下列是一元二次方程的是( )A. 20ax bx c ++=B. 22x x −=C. ()222x x x −=−D. 11x x += 【答案】B【解析】【分析】本题主要考查了一元二次方程的识别.本题根据一元二次方程的定义解答.【详解】解:A 、当0a ≠时,20ax bx c ++=是一元二次方程,故本选项不符合题意; B 、22x x −=是一元二次方程,故本选项符合题意;C 、变形为22x =不是一元二次方程,故本选项不符合题意;D 、11x x+=含有分式,不是一元二次方程,故本选项不符合题意; 故选:B2. 一元二次方程2310x x −−=的根的情况为( )A. 无实数根B. 有一个实数根C. 有两个相等的实数根D. 有两个不相等的实数根【答案】D【解析】【分析】本题考查一元二次方程根的情况,涉及一元二次方程根的判别式,由题中一元二次方程得到判别式,即可判断答案,熟记一元二次方程根的情况与判别式符号关系是解决问题的关键.【详解】解:一元二次方程2310x x −−=, 3,1,1a b c ==−=−,()()21431∴∆−−××−112=+130=>,∴一元二次方程2310x x −−=的根的情况为有两个不相等的实数根,故选:D .3. 一元二次方程2430x x −+=配方后变形为( )A. ()241x −=B. ()221x −=C. ()241x +=D. ()221x +=【答案】B【解析】【分析】本题考查了解一元二次方程—配方法,掌握配方法是解题的关键.先把常数项移到方程右边,再把方程两边加上4,然后把方程左边写成完全平方形式即可.【详解】解:2430x x −+=,∴243x x −=−,∴24434x x −+=−+,即()221x −=.故选:B4. 若关于x 的一元二次方程2690kx x −+=有两个不相等的实数根,则k 的取值范围是( )A. 1k >B. 0k ≠C. 1k <D. 1k <且0k ≠ 【答案】D【解析】【分析】本题考查了一元二次方程的定义和一元二次方程根的判别式.根据一元二次方程根的判别式,即可求解.【详解】解:∵关于x 的一元二次方程2690kx x −+=有两个不相等的实数根,∴()26490k ∆=−−×>,且0k ≠,解得:1k <且0k ≠,即k 的取值范围是1k <且0k ≠.故选:D5. 将抛物线2y x =先向上平移2个单位长度,再向右平移3个单位长度后,得到的抛物线对应的函数解析式为( )A. ()223y x =−+B. ()232y x =−+ C. ()223y x =++ D. ()232y x =−− 【答案】B【解析】【分析】本题考查函数图象的平移,解题的关键是要熟练掌握函数的平移规律:“左加右减,上加下减”,根据函数图象平移规律即可得到答案.【详解】解:将抛物线2y x =先向上平移2个单位长度,得到22y x =+,再向右平移3个单位长度,得到()232y x =−+, 故选:B .6. 若()()()1232,,1,,2,A y B y C y −是抛物线()221y x a =−+上三点,则123,,y y y 为的大小关系为( )A. 123y y y >>B. 132y y y >>C. 321y y y >>D. 312y y y >>【答案】B【解析】【分析】本题主要考查了二次函数的性质,掌握当抛物线开口方向向上时,离对称轴越远,函数值越大成为解题的关键.先确定抛物线的对称轴,再确定抛物线开口向上,此时离对称轴越远,函数值越大,据此即可解答.【详解】解:∵()221y x a =−+,∴抛物线的对称轴为直线1x =,开口向上,∴离对称轴越远,函数值越大,∵点()12,A y −离对称轴最远,点()21,B y 在对称轴上,∴132y y y >>.故选:B .7. 若抛物线242y kx x =−−与x 轴有两个交点,则k 的取值范围为( )A. 2k >−B. 2k ≥−C. 2k >−且0k ≠D. 2k ≥−且0k ≠ 【答案】C【解析】【分析】本题主要考查了二次函数与一元二次方程之间的关系,二次函数的定义,二次函数与x 轴有两个交点,则与之对应的一元二次方程有两个不相等的实数根,据此利用判别式求出k 的取值范围,再结合二次项系数不为0即可得到答案.【详解】解:∵抛物线242y kx x =−−与x 轴有两个交点, 的∴()()2Δ44200k k =−−×−⋅> ≠ , ∴2k >−且0k ≠,故选:C .8. 二次函数2y ax bx c =++图象上部分点的对应值如下表则使0y <的x 的取值范围为( ) x 3− 2− 1− 01 2 3 4 y 60 4− 6− 6− 4− 0 6A. 0x <B. 12x >C. 23x −<<D. 2x <−或3x >【答案】C【解析】 【分析】本题主要考查了二次函数的性质,先求出二次函数的表达式,再根据与x 轴的交点即可求出0y <的x 的取值范围,解题的关键是求出二次函数2y ax bx c ++的表达式.【详解】解:由表格可知2y ax bx c ++经过()2,0−,()3,0,()0,6−,设解析式为()()23y a x x =+−∴()()02036a +−=−, 解得:1a =,∴抛物线解析式为()()2236y x x x x =+−=−−,∴抛物线图象开口向上,与x 轴的交点为()2,0−,()3,0,∴0y <时x 的取值范围是23x −<<,故选:C .二、填空题9. 已知m 是方程2520x x −−=的一个根,则22101m m −−=______. 【答案】3【解析】【分析】本题考查一元二次方程的根的定义、代数式求值,根据一元二次方程的根的定义,将m 代入2520x x −−=,求出252m m −=,即可求出22101m m −−的值.【详解】解:∵m 是方程2520x x −−=的一个根,∴252m m −=,∴()2221012512213,m m m m −−=−−=×−=故答案为:3. 10. 一元二次方程()2110x k x +++=有两个相等的实数根,那么k 的值为_____. 【答案】1或3−【解析】【分析】本题考查了根的判别式:一元二次方程()200ax bx c a ++=≠的根与24b ac ∆=−有如下关系:当0∆>时,方程有两个不相等的实数根;当Δ0=时,方程有两个相等的实数根;当Δ0<时,方程无实数根.根据判别式的意义得到()2Δ1410k =+−×=,然后解关于k 的方程即可. 【详解】解:由题意得:()2Δ1410k =+−×=,即:()214k +=,解得:1k =或3−,故答案为:1或3−. 11. 若关于x 的一元二次方程()22240m x mx m −++−=有一个根是0,则m 的值为________ 【答案】2−【解析】【分析】此题考查了一元二次方程的定义及方程的解的定义,将0x =代入方程求出2m =±,再根据一元二次方程的定义求出2m ≠,由此得到答案,正确理解一元二次方程的定义及方程的解的定义是解题的关键.【详解】解:将0x =代入()22240m x mx m −++−=,得240m −=, 解得2m =±,∵20m −≠,∴2m ≠,∴2m =−,故答案为2−.12. 用一根长22cm 的铁丝围成面积是230cm 的矩形.假设矩形的一边长是cm x ,则可列出方程_____________________ 【答案】22=302x x −【解析】【分析】本题考查了一元二次方程的运用,要掌握运用长方形的面积计算公式S ab =来解题的方法.本题可根据长方形的周长可以用x 表示另一边长的值,然后根据面积公式即可列出方程.【详解】解:一边长为 c m x ,则另一边长为22cm 2x −, 得22=302x x −. 故答案为:22=302x x −. 13. 如图,已知抛物线2y ax bx c ++与直线y kx m =+交于()3,1A −−、()0,3B 两点,则关于x 的不等式2ax bx c kx m ++≥+的解集是________.【答案】30x −≤≤【解析】【分析】本题考查了二次函数与不等式的关系,主要利用了数形结合的思想,解题关键在于对图象的理解,题目中的不等式的含义为:二次函数的图象在一次函数图象上方时,自变量x 的取值范围.根据图象,写出抛物线在直线上方部分的x 的取值范围即可.【详解】∵抛物线2y ax bx c ++与直线y kx m =+交于()3,1A −−、()0,3B 两点, ∴由函数图象可得,不等式2ax bx c kx m ++≥+的解集是30x ≤≤﹣,故答案为:30x −≤≤.14. 抛物线()232y x =−−−的顶点坐标是________ . 【答案】()3,2− 【解析】【分析】本题考查了二次函数2()y a x h k =−+(a ,h ,k 为常数,0a ≠)性质,2()y a x h k =−+是抛物线的顶点式,a 决定抛物线的形状和开口方向,其顶点是(,)h k ,对称轴是直线x h =. 【详解】解:物线()232y x =−−−的顶点坐标是()3,2−.故答案为:()3,2−.15. 已知二次函数()214y x =+−,当02x ≤≤时,函数值y 的取值范围为__________ 【答案】35y −≤≤##53x ≥≥− 【解析】【分析】本题考查二次函数的图象与性质,根据题意得当1x >−时,y 随x 的增大而增大,求得当0x =时,=3y −;2x =时,5y =,即可求解.【详解】解:由题意得,10a =>,对称轴1x =−, ∴当1x >−时,y 随x 增大而增大, ∵当0x =时,=3y −;2x =时,5y =,∴当02x ≤≤时,函数值y 的取值范围为35y −≤≤, 故答案为:35y −≤≤.16. 飞机着陆后滑行的距离(米)关于滑行时间(秒)的函数解析式为260 1.5s t t =−,则飞机着陆后滑行_________秒才停下来. 【答案】20 【解析】【分析】本题主要考查二次函数的应用,飞机停下时,也就是滑行距离最远时,即在本题中需求出s 最大时对应的t 值,根据顶点坐标的实际意义可得答案. 【详解】∵()2260 1.5 1.520600s t t t =−=−−+, ∴当20t =时,s 取得最大值600, ∴飞机着陆后滑行20秒才停下来.的的故答案:20.17. 如图所示,,A B 分别为22(2)1y x =−−图象上的两点,且直线AB 垂直于y 轴,若2AB =,则点B 的纵坐标为________.【答案】1 【解析】【分析】本题主要考查二次函数图象的对称性,能够熟练运用对称轴求点的横坐标是解题关键.求出对称轴后根据对称性求点B 横坐标,再代入解析式即可解答. 【详解】解:∵()2221y x =−−, ∴抛物线对称轴为直线2x =, ∵2AB =,∴点B 横坐标为213+=,将3x =代入()2221y x =−−得1y =, ∴点B 的纵坐标为1. 故答案为:118. 如图,横截面为抛物线的山洞,山洞底部宽为8米,最高处高163米,现要水平放置横截面为正方形的箱子,其中两个顶点在抛物线上的大箱子,在大箱子的两侧各放置一个横截面为正方形的小箱子,则小箱子正方形的最大边长为______米.【解析】为【分析】本题主要考查了二次函数的实际应用,先建立解析中坐标系,则()4,0A ,设大小正方形的边长分别为2m ,n ,则点B 、C 的坐标分别为:()(),2,m m m n n +,,利用待定系数法求出抛物线解析式为211633y x =−+,再把B 、C 坐标代入求解即可.【详解】解:建立如下平面直角坐标系,则点()4,0A ,设大小正方形的边长分别为2m ,n ,则点B 、C 的坐标分别为:()(),2,m m m n n +,、设抛物线的表达式为:()21603y ax a =+≠, 将点A 的坐标代入上式得:160163a =+,解得13a =−,∴抛物线的表达式为:213y x =− 将点B 、C 的坐标代入上式得:()2211623311633m m n m n =−+ =−++①②,由①得1228m m ==−,(舍去),解得:2m n = = 或2m n = =(舍去),米.. 三、解答题19. 商场销售某种拖把,已知这种拖把的进价为80元/套,售价为120元/套,商场每天可销售20套、国庆假期临近,该商场决定采取适当的降价措施,经调查:这种拖把的售价每降价1元,平均每天可多售出2套,设这种拖把每套降价x 元.(1)降价后每套拖把盈利______元,平均每天可销售______套(用含x 的代数式表示);(2)为扩大销售量,尽快减少库存,当每套拖把降价多少元时,该商场销售这种拖把平均每天能盈利1242元?(3)该商场销售这种拖把平均每天的盈利能否达到1400元?若能,求出x 的值;若不能,请说明理由. 【答案】(1)()40x −,2x(2)每套拖把降价17元时,能让利于顾客并且商家平均每天能赢利1242元; (3)不能,理由见解析 【解析】【分析】此题考查了一元二次方程的实际应用,解题的关键是正确分析题目中的等量关系. (1)设每套拖把降价x 元,根据题意列出代数式即可;(2)设每套拖把降价x 元,则每套的销售利润为()40x −元,平均每天的销售量为()202x +套,根据题意列出一元二次方程求解即可;(3)设每套拖把降价y 元,则每套的销售利润为()12080y −−元,平均每天的销售量为()202y +套,根据题意列出一元二次方程,然后依据判别式求解即可. 【小问1详解】解:设每套拖把降价x 元,则每天销售量增加2x 套,即每天销售()202x +套, 每套拖把盈利()1208040x x −−=−元.故答案为:()40x −,()202x +; 【小问2详解】解:设每套拖把降价x 元,则每套的销售利润为()40x −元,平均每天的销售量为()202x +套,依题意得:()()402021242x x −+=, 整理得:2302210x x −+=,解得:121317x x ==,. 又∵需要尽快减少库存,∴17x =.答:每套拖把降价17元时,能让利于顾客并且商家平均每天能赢利1242元; 【小问3详解】解:商家不能达到平均每天盈利1400元,理由如下:设每套拖把降价y 元,则每套的销售利润为()12080y −−元,平均每天的销售量为()202y +套,依题意得:()()120802021400y y −−+=, 整理得:2303000y y −+=. ∵()22Δ43041300300<0b ac =−=−−××=−, ∴此方程无实数解, 即不可能每天盈利1400元. 20. 解方程:(1)2(2x 1)9+=; (2)2x 2﹣4x =1(配方法); (3)22x 5x 10−+=;(4) ()2(x 3)4x 3x 0−−−=【答案】(1)121,2x x ==−;(2)1211x x ;(3)12x x ;(4)1233,5x x == 【解析】【分析】(1)直接开平方法解方程即可;(2)先方程两边除以2,将二次项系数化为1,再在方程两边同时加上1,配方开平方即可解答; (3)确定a 、b 、c ,求出△值,当判断方程有解时,带入公式求解即可; (4)整理方程,利用因式分解法解方程即可. 【详解】(1)2(2x 1)9+= 开平方,得:2x 13+=±, 解得:121,2x x ==−; (2)22x 41x −=,二次项系数化为1,得:21x 22x −=, 配方,得:21x 2112x −+=+, 即23(x 1)2−=,开方,得:1x −=解得:1211x x (3)22x 5x 10−+= ∵a=2,b=﹣5,c=1,∴△=224(5)42117b ac −=−−××=﹥0,∴x =,解得:12x x =(4)()2(x 3)4x 3x 0−−−= ()2(x 3)4x 30x +−−=(3)(53)0x x −−=∴30x −=或530x −=,解得:1233,5x x ==. 【点睛】本题考查解一元二次方程的方法,熟练掌握一元二次方程的各种解法的步骤和注意点,灵活选用解法是解答的关键.21. 随着科技的发展,某省正加快布局以5G 等为代表的新兴产业.据统计,目前该省5G 基站数量约为1.5万座,计划到今年底,全省5G 基站数是目前的4倍;到后年底,全省5G 基站数量将达到17.34万座.(1)计划在今年底,全省5G 基站数量是多少万座?(2)按照计划,从今年底到后年底,全省5G 基站数量的年平均增长率为多少? 【答案】(1)6万座 (2)70% 【解析】【分析】本题考查有理数乘法的应用,一元二次方程的实际应用:(1)根据计划到今年底,全省5G 基站数是目前的4倍,列出算式计算即可;(2)设全省5G 基站数量的年平均增长率为x ,根据题意,列出一元二次方程,进行求解即可 【小问1详解】解:由题意得:1.546×=(万座); 答:计划在今年底,全省5G 基站数量是6万座. 【小问2详解】解:设全省5G 基站数量的年平均增长率为x ,由题意得:()26117.34x +=,解得:120.7, 2.7x x ==−(不符合题意,舍去); 答:全省5G 基站数量的年平均增长率为70%.22. 如图,老李想用长为70m 的栅栏,再借助房屋的外墙(外墙足够长)围成一个矩形羊圈ABCD ,并在边BC 上留一个2m 宽的门(建在EF 处,另用其他材料).(1)当羊圈的边AB 的长为多少米时,能围成一个面积为2640m 的羊圈?(2)羊圈的面积能达到2650m 吗?如果能,请你给出设计方案;如果不能,请说明理由. 【答案】(1)当羊圈的边AB 的长为16m 或20m 时,能围成一个面积为2640m 的羊圈 (2)羊圈的面积不能达到2650m ,理由见解析 【解析】【分析】本题考查了一元二次方程的应用,根据题意列出一元二次方程,解一元二次方程是解题的关键. (1)设羊圈的边AB 的长为m x ,则边BC 的长为()722m x -根据题意列出一元二次方程,解方程即可求解;(2)同(1)的方法建立方程,根据方程无实根即可求解. 【小问1详解】解:设羊圈的边AB 的长为m x ,则边BC 的长为()722m x -,根据题意,得()722640x x −=,化简,得2363200x x −+=,解方程,得116x =,220x =,当116x =时,72240x −=, 当220x =时,72232x −=.答:当羊圈的边AB 的长为16m 或20m 时,能围成一个面积为2640m 的羊圈. 【小问2详解】不能,理由如下:根据题意,得()722650x x −=, 化简,得2363250x x −+=,()22436432540b ac −=−×=−−< , ∴该方程没有实数根. ∴羊圈的面积不能达到2650m 23. 已知函数()214y x =−−+.(1)当x =____________时,抛物线有最大值,是____________. (2)当x ____________时,y 随x 的增大而增大.(3)该函数可以由函数2y x =−的图象经过怎样的平移得到?(4)该抛物线与x 轴交于点,与y 轴交于点____________.(写坐标) (5)在下面的坐标系中画出该抛物线的图象.【答案】(1)1;4 (2)1<(3)见解析 (4)(1,0)−和(3,0);(0,3) (5)见解析 【解析】【分析】本题考查了二次函数的性质、抛物线与x 轴的交点坐标、二次函数图象与几何变换以及二次函数的最值,熟练掌握二次函数的性质是解题的关键.(1)根据二次函数的顶点式找出抛物线的顶点坐标,再根据二次项系数为1−得出抛物线开口向下,由此即可得出结论;(2)根据抛物线开口方向结合抛物线的对称轴,即可找出单增区间;(3)找出函数2y x =−的顶点坐标,结合函数2(1)4y x =−−+的顶点坐标,即可找出平移的方法; (4)令0y =可得出关于x 的一元二次方程,解方程求出x 值,由此得出抛物线与x 轴的交点坐标;令0x =求出y 值,由此即可得出抛物线与y 轴的交点坐标;(5)列表,描点,连线即可画出该抛物线的图象. 【小问1详解】解: 函数解析式为2(1)4y x =−−+,∴抛物线的开口向下,顶点坐标为(1,4). ∴当1x =时,抛物线有最大值,是4.故答案为:1;4; 【小问2详解】解: 抛物线的开口向下,对称轴为1x =,∴当1x <时,y 随x 的增大而增大.故答案为:1<; 【小问3详解】解: 函数2y x =−的顶点坐标为(0,0),∴将函数2y x =−的图象先向右平移1个单位长度,再向上平移4个单位长度即可得出函数2(1)4y x =−−+的图象.【小问4详解】解:令0y =,则有2(1)40x −−+=, 解得:11x =−,23x =,∴该抛物线与x 轴的交点坐标为(1,0)−和(3,0).当0x =时,2(01)43y =−−+=, ∴该抛物线与y 轴的交点坐标为(0,3).故答案为:(1,0)−和(3,0);(0,3). 【小问5详解】 解:列表:x 1−0 1 2 3 y343描点,连线,该抛物线的图象如图:.24. 已知图象的顶点坐标是()2,1,且与x 轴的一个交点坐标是()3,0,求此二次函数的解析式. 【答案】()221y x =−−+ 【解析】【分析】本题主要考查了求二次函数解析式,先把解析式设顶点式,再利用待定系数法求解即可. 【详解】解:设此二次函数解析式为()()2210y a x a =−+≠,把()3,0代入()()2210y a x a =−+≠中得:()20321a =−+,解得1a =−,∴此二次函数解析式为()221y x =−−+. 25. 已知:二次函数()221y x m x m =−++−.(1)求证:该抛物线与x 轴一定有两个交点;(2)设抛物线与x 轴的两个交点是A B 、(A 在原点左边,B 在原点右边),且3AB =,求此时抛物线的解析式.【答案】(1)见解析 (2)2y x x 2−− 【解析】【分析】(1)根据()()22Δ2418m m m =+−−=+的符号,即可求解,为(2)由根与系数关系,列出()()2224A B A B A B AB x x x x x x =−=+−⋅,即可求解,本题考查了根的判别式,根据系数关系,解题的关键是:熟练掌握根的判别式,根据系数关系.【小问1详解】证明:()()22Δ2418m m m =+−−=+,20m ≥ ,2Δ880m ∴=+≥>,故抛物线与x 轴一定有两个交点,【小问2详解】解:令0y =,得()2210x m x m −++−=, 由(1)知Δ0>,2A B x x m ∴+=+,1A B x x m ⋅=−,()()()()22224241A B A B A B AB x x x x x x m m =−=+−⋅=+−−, ()()22419m m ∴+−−=,解得1m =±,A 在原点左边,B 在原点右边,10A B x x m ∴⋅=−<,1m ∴<,1m ∴=−,故抛物线的表达式为:2y x x 2−−.26. 若直线5y x =−与y 轴交于点A ,与x 轴交于点B ,二次函数2y ax bx c =++的图象经过点A ,点B ,且与x 轴交于点()1,0C −.(1)求二次函数的解析式;(2)若点P 为直线AB 下方抛物线上一点,连接PA ,PB ,求ABP 面积的最大值及此时点P 的坐标;【答案】(1)245y x x =−−(2)当52x =时,ABP S 最大,最大为1258,这时点P 的坐标为535,24 − 【解析】【分析】本题考查二次函数的综合应用,熟练掌握的图像和性质是解题的关键. (1)利用待定系数法求函数解析式即可;(2)过点P 作PQ x ⊥轴交AAAA 于点Q ,设点P 的坐标为()2,45x x x −−,则点Q 的坐标为(),5x x −,则25PQ x x =−+,然后根据ABPS PQ OB =⋅ 计算即可. 【小问1详解】解:当xx =0时,5y =−,∴点A 的坐标为()0,5−, 当0y =时,50x −=,解得5x =,∴点B 的坐标为()5,0,设抛物线的解析式为()()51y a x x =−+,代入()0,5−得:55a −=−,解得:1a =,∴二次函数的解析式为()()25145y x x x x =−+=−−; 【小问2详解】解:过点P 作PQ x ⊥轴交AAAA 于点Q ,设点P 的坐标为()2,45x x x −−,则点Q 的坐标为(),5x x −, ∴225(45)5PQ x x x x x =−−−−=−+, ∴()2211551255522228ABP S PQ OB x x x =⋅=×−+×==−−+ , 当52x =时,ABP S 最大,最大为1258,这时点P 的坐标为535,24 − .。
语文九年级文言文模拟综合试题带答案

语文九年级文言文模拟综合试题带答案一、文言文1.阅读下面的文言文,回答问题【甲】余幼时即嗜学。
家贫,无从致书以观,每假借于藏书之家,手自笔录,计日以还。
天大寒,砚冰坚,手指不可屈伸,弗之怠。
录毕,走送之,不敢稍逾约。
以是人多以书假余,余因得遍观群书。
既加冠,益慕圣贤之道。
又患无硕师名人与游,尝趋百里外,从乡之先达执经叩问。
先达德隆望尊,门人弟子填其室,未尝稍降辞色。
余立侍左右,援疑质理,俯身倾耳以请;或遇其叱咄,色愈恭,礼愈至,不敢出一言以复;俟其欣悦,则又请焉。
故余虽愚,卒获有所闻。
【乙】铨①九龄,母授以《礼记》、《周易》、《毛诗》,皆成诵。
暇更录唐、宋人诗,教之为吟哦声。
母与铨皆弱而多病;铨每病,母即抱铨行一室中,未尝寝;少痊,辄指壁间诗歌,教儿低吟之以为戏。
母有病,铨则坐枕侧不去;母视铨,辄无言而悲,铨亦凄楚依恋。
尝问曰:“母有忧乎?”曰:“然。
”“然则何以解忧?”曰:“儿能背诵所读书,斯解矣。
”铨诵声琅琅然,争药鼎沸②。
母微笑曰:“病少差矣。
”由是母有病,铨即持书诵于侧,而病辄能痊。
选自《鸣机夜课读记》注释:①铨:蒋士铨,清代著名学者。
②:争药鼎沸:读书声琅琅,与药鼎煮沸声争响。
(1)解释下面句子中划线词语的意思。
①录毕,走送之________②俟其欣悦________③少痊________④然则何以解忧________(2)下面各组句子中划线词语的意义和用法都相同的一项是()A.无从致书以观/母授以《礼记》B.从乡之先达执经叩问/益慕圣贤之道C.门人弟子填其室/安陵君其许寡人D.而病辄能愈/由是则生而有不用也(3)将下列句子翻译成现代汉语。
①以是人多以书假余,余因得遍观群书。
②儿能背诵所读书,斯解也。
(4)【甲】【乙】两文所写内容有哪些异同?请简要分析。
2.阅读文言文,回答问题。
【甲】侍中、侍郎郭攸之、费袢、董允等,此皆良实,志虑忠纯,是以先帝简拔以遗陛下。
愚以为宫中之事,事无大小,悉以咨之,然后施行,必能裨补阙漏,有所广益。
人教版2022-2023学年第一学期九年级数学期末模拟测试题(附答案)

2022-2023学年第一学期九年级数学期末模拟测试题(附答案)一、选择题(共计24分)1.已知sinα=,若α是锐角,则α的度数为()A.30°B.45°C.60°D.90°2.如图所示几何体的主视图是()A.B.C.D.3.圆形物体在阳光下的投影可能是()A.三角形B.圆形C.矩形D.梯形4.如图,l1∥l2∥l3,直线AC和DE分别交l1、l2、l3于点A、B、C和点D、B、E,AB=4,BC=8,DB=3,则DE的长为()A.4B.5C.6D.95.反比例函数y=﹣图象上的两点为(x1,y1),(x2,y2),且x1<x2<0,则y1与y2的大小关系是()A.y1>y2B.y1<y2C.y1=y2D.不能确定6.如图,图形甲与图形乙是位似图形,点O是位似中心,点A、B的对应点分别为点A′、B′,若OA'=2OA,则图形乙的面积是图形甲的面积的()A.2倍B.3倍C.4倍D.5倍7.如图,四边形ABCD为菱形,若CE为边AB的垂直平分线,则∠ADB的度数为()A.20°B.25°C.30°D.40°8.已知反比例函数的图象在每个象限内y随x的增大而增大,则关于x的一元二次方程的根的情况是()A.没有实数根B.有两个相等的实数根C.有两个不相等的实数根D.无法确定二、填空题(共计15分)9.若关于x的方程ax2﹣2ax+1=0的一个根是﹣1,则a的值是.10.如图,在正方形网格中,△AOC的顶点均在格点上,则tan∠CAO的值为.11.在一个不透明的盒子中装有黑球和白球共200个,这些球除颜色外其余均相同,将球搅匀后任意摸出一个球,记下颜色后放回,通过大量重复摸球试验后,发现摸到白球的频率稳定在0.2,则盒子中白球有个.12.如图,点A为反比例函数的图象上一点,连接AO并延长交反比例函数的图象于另一点B,过点A、B分别作x轴、y轴的平行线,两平行线交于点C,则△ABC的面积为.13.如图,将矩形ABCD放置在平面直角坐标系的第一象限内,使顶点A,B分别在x轴、y轴上滑动,矩形的形状保持不变,若AB=2,BC=1,则顶点C到坐标原点O的最大距离为.三、解答题(计81分)14.解方程:(2x﹣9)2=5(2x﹣9).15.如图,AD是△ABC的高,cos B=,sin C=,AC=10,求AD及AB的长.16.如图,在四边形ABCD中,AD∥BC,点E在BC上,∠C=∠DEA.(1)求证:△DEC∽△ADE;(2)若CE=2,DE=4,求△DEC与△ADE的周长之比.17.已知反比例函数y=(k为常数).(1)若函数图象在第二、四象限,求k的取值范围;(2)若x>0时,y随x的增大而减小,求k的取值范围.18.如图,在正方形ABCD中,E,F分别为AB,AD上的点,且AE=AF,点M是EF的中,点,连接CM、CF、CE.求证:CM⊥EF.19.《城镇污水处理厂污染物排放标准》中硫化物的排放标准为1.0mg/L.某污水处理厂在自查中发现,所排污水中硫化物浓度超标,因此立即整改,并开始实时监测.据监测,整改开始第60小时时,所排污水中硫化物的浓度为5mg/L;从第60小时开始,所排污水中硫化物的浓度y(mg/L)是监测时间x(小时)的反比例函数,其图象如图所示.(1)求y与x之间的函数关系式;(2)按规定所排污水中硫化物的浓度不超过0.8mg/L时,才能解除实时监测,此次整改实时监测的时间至少要多少小时?20.如图,▱ABCD的对角线AC、BD交于点O,点E在边CB的延长线上,连接AE,且∠EAC=90°,AE2=EB•EC.求证:四边形ABCD是矩形.21.2021年是中国共产党建党100周年,全国各地积极开展以“弘扬红色文化,重走长征路”为主题的教育学习活动,郑州市“二七纪念堂“成为重要的活动基地.据了解,今年3月份该基地接待参观人数10万,5月份接待参观人数增加到12.1万.求这两个月参观人数的月平均增长率.22.一个阳光明媚的午后,王婷和李力两个人去公园游玩,看见公园里有一棵古老的大树,于是,他们想运用所学知识测量这棵树的高度,如图,李力站在大树AB的影子BC的末端C处,同一时刻,王婷在李力的影子CE的末端E处做上标记,随后两人找来米尺测得BC=10米,CE=2米.已知李力的身高CD=1.6米,B、C、E在一条直线上,DC⊥BE,AB⊥BE,请你运用所学知识,帮助王婷和李力求出这棵树的高度AB.23.随着信息技术的迅猛发展,移动支付已成为一种常见的支付方式.在一次购物中,陈老师和陆老师都随机从“微信”、“支付宝”、“银行卡”三种支付方式中选一种方式进行支付.(1)陆老师选择用“微信”支付的概率是;(2)请用画树状图或列表的方法表示所有结果,并求出两位老师恰好一人用“微信”支付,一人用“银行卡”支付的概率.24.晓琳想用所学知识测量塔CD的高度.她找到一栋与塔CD在同一水平面上的楼房,在楼房的A处测得塔CD底部D的俯角为26.6°,测得塔CD顶部C的仰角为45°,AB ⊥BD,CD⊥BD,BD=30m,求塔CD的高度.(参考数据:sin26.6°≈0.45,c0s26.6°≈0.89,tan26.6°≈0.50)25.如图,一次函数y=k1x+b的图象与反比例函数y=的图象相交于A、B两点,其中点A的坐标为(﹣1,4),点B的坐标为(4,n).(1)求这两个函数的表达式;(2)一次函数y=k1x+b的图象交y轴于点C,若点P在反比例函数y=的图象上,使得S△COP=9,求点P的坐标.26.如图,△ABC和△DEF是两个全等的等腰直角三角形,∠BAC=∠EDF=90°,△DEF 的顶点E与△ABC的斜边BC的中点重合,将△DEF绕点E旋转,旋转过程中,线段DE与线段AB相交于点P,线段EF与射线CA相交于点Q.(1)当点Q在线段CA上时,如图1,求证:△BPE∽△CEQ;(2)当点Q在线段CA的延长线上时,如图2,△BPE和△CEQ是否相似?说明理由;(3)在(2)的条件下,若BP=1,CQ=,求PQ的长.参考答案一、选择题(共计24分)1.解:∵sinα=,α是锐角,∴α的度数为:45°.故选:B.2.解:由题意知,几何体的主视图为,故选:D.3.解:∵同一物体的影子的方向和大小可能不同,不同时刻物体在太阳光下的影子的大小在变.∴圆形物体在阳光下的投影可能是圆形、线段和椭圆形,故选:B.4.解:∵l1∥l2∥l3,∴,∵AB=4,BC=8,DB=3,∴,∴BE=6,∴DE=DB+BE=3+6=9,故选:D.5.解:∵反比例函数y=﹣中,k=﹣6<0,∴此函数的图象在二、四象限,在每一象限内y随x的增大而增大,∵x1<x2<0,∴(x1,y1)、(x2,y2)两点均位于第二象限,∴y1<y2.故选:B.6.解:由题意可得,甲乙两图形相似,且相似比为,根据相似图形的面积比是相似比的平方可得,图形乙的面积是图形甲的面积的4倍,故选:C.7.解:如图,连接AC,∵四边形ABCD为菱形,∴AB=BC=AD,∵CE为边AB的垂直平分线,∴AC=BC,∴AB=AC=BC,∴△ABC是等边三角形,∴∠ABC=60°,∴∠ABD=30°,∵AB=AD,∴∠ADB=∠ABD=30°,故选:C.8.解:∵在每一个象限内y随着x增大而增大,∴k<0,∴一元二次方程的判别式Δ=b2﹣4ac=(2k−1)2−4(k2+14)=﹣4k>0,∴方程有两个不相等的实数根,故选:C.二、填空题(共计15分)9.解:∵关于x的方程ax2﹣2ax+1=0的一个根是﹣1,∴a+2a+1=0,∴3a+1=0,解得a=﹣,故答案为:﹣.10.解:∵正方形网格中,△AOC的顶点均在格点上,∴∠ACO=90°,∴,故答案为:.11.解:因为通过大量重复摸球试验后,发现摸到白球的频率稳定在0.2,所以摸到白球的概率约为0.2,所以白球有200×0.2=40,故答案为:40.12.解:设点A的坐标为(﹣a,),根据中心对称的性质知点B的坐标为(a,﹣),∴点C的坐标为(a,),∴AC=2a,BC=,则△ABC的面积为:×2a×=12.故答案为:12.13.解:如图,取AB的中点E,连接CE,OE,∵∠AOB=90°,在Rt△AOB中,OE=AB=1,∵∠ABC=90°,AE=BE=CB=1,∴在Rt△CBE中,CE==,∵OC≤CE+OE=1+,∴OC的最大值为1+,即点C到原点O距离的最大值是1+,故答案为:1+.三、解答题(共计81分)14.解:方程移项得:(2x﹣9)2﹣5(2x﹣9)=0,分解因式得:(2x﹣9)(2x﹣9﹣5)=0,所以2x﹣9=0或2x﹣14=0,解得:x1=4.5,x2=7.15.解:在Rt△ACD中,,∵,∴,∴AD=6.在Rt△ABD中,,∴∠B=60°,∴∠BAD=90°﹣∠B=30°.∴,∴,∴.16.证明:(1)∵AD∥BC,∴∠DEC=∠ADE.又∵∠C=∠DEA,∴△DEC∽△ADE.解:(2)∵△DEC∽△ADE,∴△DEC与△ADE的周长之比===.17.解:(1)∵函数图象在第二、四象限,∴k﹣5<0,解得:k<5,∴k的取值范围是k<5;(2)∵若x>0时,y随x的增大而减小,∴k﹣5>0,解得:k>5,∴k的取值范围是k>5.18.证明:∵四边形ABCD是正方形∴AB=AD=BC=CD,∠B=∠D=90°∵AE=AF,∴BE=DF.在△BCE和△DCF中,,∴△BCE≌△DCF(SAS),∴CE=CF,∵点M是EF的中点,∴CM⊥EF.19.解:(1)设y与x之间的函数关系式为,根据题意,得:k=xy=60×5=300,∴y与x之间的函数关系式为.(2)当y=0.8时,.20.证明:∵AE2=EB•EC,∴,又∵∠AEB=∠CEA,∴△AEB∽△CEA,∴∠EBA=∠EAC而∠EAC=90°,∴∠EBA=∠EAC=90°,又∵∠EBA+∠CBA=180°,∴∠CBA=90°,而四边形ABCD是平行四边形,∴四边形ABCD是矩形.21.解:设这两个月参观人数的月平均增长率为x,根据题意,得:10(1+x)2=12.1,解得:x1=0.1=10%,x2=﹣2.1(舍去),答:这两个月参观人数的月平均增长率为10%.22.解:根据题意可得,AC∥DE,∴∠DEC=∠ACB.又∵DC⊥BE,AB⊥BE,即∠DCE=∠ABC=90°,∴△ABC∽△DCE,∴.∵BC=10米,CE=2米,CD=1.6米.∴,∴AB=8米,即这棵树的高度AB为8米.23.解:(1)陆老师选择用“微信”支付的概率是,故答案为:;(2)将“微信”、“支付宝”、“银行卡”三种支付方式分别记为:A、B、C,画树状图如下:共有9种等可能的结果,其中两位老师恰好一人用“微信”支付,一人用“银行卡”支付的结果有2种,∴两位老师恰好一人用“微信”支付,一人用“银行卡”支付的概率为.24.解:过A点作AE⊥CD于E点,由题意得,四边形ABDE为矩形,∵∠DAE=26.6°,BD=30m,∴,∴DE=tan26.6°⋅AE≈0.50×30=15m,∵∠CAE=45°,∴∠ACE=45°,∴AE=EC=30m,∴CD=CE+ED=30+15=45(m),∴塔CD的高度是45m.25.解:(1)把点A(﹣1,4)代入反比例函数得,,∴k2=﹣4,∴反比例函数的表达式为,将点B(4,n)代入得,,∴B(4,﹣1),将A、B的坐标代入y=k1x+b得,解得∴一次函数的表达式为y=﹣x+3.(2)在y=﹣x+3中,令x=0,则y=3,∴直线AB与y轴的交点C为(0,3),设P(x,y),由题意得,∴|x|=6,∴x=6或x=﹣6,当x=6时,,此时点P的坐标为;当x=﹣6时,,此时点P的坐标为.∴点P的坐标或.26.(1)证明:如图1中,∵△ABC和△DEF是两个全等的等腰直角三角形,∴∠B=∠C=∠DEF=45°,∵∠BEQ=∠BEP+∠DEF=∠EQC+∠C,∴∠BEP+45°=∠EQC+45°,∴∠BEP=∠EQC,∵∠B=∠C,∴△BPE∽△CEQ;(2)解:结论:△BPE∽△CEQ.理由:如图2中,∵∠BEQ=∠EQC+∠C,即∠BEP+∠DEF=∠EQC+∠C,∴∠BEP+45°=∠EQC+45°,∴∠BEP=∠EQC,又∵∠B=∠C,∴△BPE∽△CEQ;(3)解:∵△BPE∽△CEQ,∴,∵BE=CE,∴,解得:BE=CE=,∴BC=,∴AB=AC=,∴AQ=CQ﹣AC=,AP=AB﹣BP=3﹣1=2,在Rt△APQ中,PQ=.。
2023届四川省自贡市蜀光中学高三下学期生物模拟试题(九)(含答案解析)

2023届四川省自贡市蜀光中学高三下学期生物模拟试题(九)学校:___________姓名:___________班级:___________考号:___________一、单选题1.哺乳动物的催产素具有催产和排乳的作用,加压素具有升高血压和减少排尿的作用。
两者结构简式如下图,各氨基酸残基用3个字母缩写表示。
下列叙述正确的是()A.两种激素都是由八肽环和三肽侧链构成的多肽类化合物B.氨基酸之间脱水缩合形成的水分子中氢全部来自氨基C.肽链中游离氨基的数目与参与构成肽链的氨基酸种类无关D.两种激素间因2个氨基酸种类不同导致生理功能不同2.如图为某一植物在不同实验条件下测得的净光合速率,下列假设条件中能使图中结果成立的是()A.横坐标是CO2浓度,甲表示较高温度,乙表示较低温度B.横坐标是温度,甲表示较高CO2浓度,乙表示较低CO2浓度C.横坐标是光波长,甲表示较高温度,乙表示较低温度D.横坐标是光照强度,甲表示较高CO2浓度,乙表示较低CO2浓度3.下列关于特异性免疫及其相关应用的叙述,正确的是()A.效应T细胞都是在胸腺中由造血干细胞分裂分化产生B.细胞免疫和体液免疫的二次免疫应答都与记忆细胞有关C.健康人的T细胞直接移植给肿瘤患者可提高患者的免疫力D.大量制备一种抗体时需要为浆细胞提供足够营养使其大量增殖4.下图为一只果蝇两条染色体上部分基因分布示意图,下列叙述不正确的是()A.朱红眼基因cn、暗栗色眼基因cl为一对等位基因B.在有丝分裂中期,X染色体和常染色体的着丝粒都排列在赤道板上C.在有丝分裂后期,基因cn、cl、v、w会出现在细胞的同一极D.在减数分裂Ⅱ后期,基因cn、cl、v、w可出现在细胞的同一极5.如图是某神经纤维动作电位的模式图,下列叙述正确的是A.K+的大量内流是神经纤维形成静息电位的主要原因B.bc段Na+大量内流,需要载体蛋白的协助,并消耗能量C.cd段Na+通道多处于关闭状态,K+通道多处于开放状态D.动作电位大小随有效刺激的增强而不断加大6.由于农田的存在,某种松鼠被分隔在若干森林斑块中。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《计算机组成原理》本科生期末试卷九一.选择题1六七十年代,在美国的______州,出现了一个地名叫硅谷。
该地主要工业是______它也是______的发源地。
A 马萨诸塞,硅矿产地,通用计算机B 加利福尼亚,微电子工业,通用计算机C加利福尼亚,硅生产基地,小型计算机和微处理机D加利福尼亚,微电子工业,微处理机2若浮点数用补码表示,则判断运算结果是否为规格化数的方法是______。
A 阶符与数符相同为规格化数B 阶符与数符相异为规格化数C 数符与尾数小数点后第一位数字相异为规格化数D数符与尾数小数点后第一位数字相同为规格化数3定点16位字长的字,采用2的补码形式表示时,一个字所能表示的整数范围是______。
A -215 ~ +(215 -1)B -(215 –1)~ +(215 –1)C -(215 +1)~ +215D -215 ~ +2154某SRAM芯片,存储容量为64K×16位,该芯片的地址线和数据线数目为______。
A 64,16B 16,64C 64,8D 16,16 。
5交叉存贮器实质上是一种______存贮器,它能_____执行______独立的读写操作。
A 模块式,并行,多个B 模块式串行,多个C 整体式,并行,一个D 整体式,串行,多个6用某个寄存器中操作数的寻址方式称为______寻址。
A 直接B 间接C 寄存器直接D 寄存器间接7流水CPU 是由一系列叫做“段”的处理线路所组成,和具有m个并行部件的CPU 相比,一个m段流水CPU______。
A 具备同等水平的吞吐能力B不具备同等水平的吞吐能力C 吞吐能力大于前者的吞吐能力D吞吐能力小于前者的吞吐能力8描述PCI总线中基本概念不正确的句子是______。
A HOST 总线不仅连接主存,还可以连接多个CPUB PCI 总线体系中有三种桥,它们都是PCI 设备C 以桥连接实现的PCI总线结构不允许许多条总线并行工作D 桥的作用可使所有的存取都按CPU 的需要出现在总线上9计算机的外围设备是指______。
A 输入/输出设备B 外存储器C 远程通信设备D 除了CPU 和内存以外的其它设备10.CRAY X-MP向量处理机采用了______个CPU。
A. 1B. 4C. 8D.16二. 填空题1 为了运算器的A. _____,采用了B. _____进位,C. _____乘除法和流水线等并行措施。
2 相联存储器不按地址而是按A. ______访问的存储器,在cache中用来存放B. ______,在虚拟存储器中用来存放C. ______。
3 硬布线控制器的设计方法是:先画出A. ______流程图,再利用B. ______写出综合逻辑表达式,然后用C. ______等器件实现。
4 磁表面存储器主要技术指标有A.______,B. ______,C. ______,和数据传输率。
5 DMA 控制器按其A. ______结构,分为B. ______型和C. ______型两种。
6. Origin2000系统是A______系统,采用B ______微处理器。
Cache 一致性采用C______协议。
三. 求证:[X]补+ [ Y ]补 = [ X + Y ]补 (mod 2)四. 某计算机字长32位,有16个通用寄存器,主存容量为1M 字,采用单字长二地址指令,共有64条指令,试采用四种寻址方式(寄存器、直接、变址、相对)设计指令格式。
五. 如图1表示使用快表(页表)的虚实地址转换条件,快表存放在相联存贮器中,其中容量为8个存贮单元。
问:(1) 当CPU 按虚拟地址1去访问主存时,主存的实地址码是多少?(2) 当CPU 按虚拟地址2去访问主存时,主存的实地址码是多少?(3) 当CPU 按虚拟地址3去访问主存时,主存的实地址码是多少?虚拟地址 123图1六. 假设某计算机的运算器框图如图2所示,其中ALU 为16位的加法器,S A 、S B 为16位暂存器,4个通用寄存器由D 触发器组成,Q 端输出,其读写控制如下表所示:要求:(1)设计微指令格式。
(2)画出ADD ,SUB 两条指令微程序流程图。
七. 画出单机系统中采用的三种总线结构。
八.试推导磁盘存贮器读写一块信息所需总时间的公式。
图2九假设使用50台多处理机系统获得加速比40,求原计算程序中串行部分所占的比例是多少?本科生期末试卷九答案一.选择题1. D2. C3. A4. D5. A6. C7. A8. C9. D 10. B二.填空题1. A.高速性 B.先行 C.阵列。
2. A.内容 B.行地址表 C.页表和段表。
3. A.指令周期 B.布尔代数 C.门电路、触发器或可编程逻辑。
4. A.存储密度 B.存储容量C.平均存取时间。
5. A.组成结构 B.选择 C.多路。
6. A. 多处理机 B. R10000 C.写作废三.解:(1)x > 0 , y > 0 , 则x + y > 0[X]补+ [Y ]补= x + y =[ X + Y ]补(mod 2)(2) x > 0 , y < 0 , 则x + y > 0 或x + y < 0因为[X]补= x , [Y ]补= 2 + y所以[X]补+ [Y ]补= x + 2 + y = 2 + (x + y)当x+y>0时,2+(x+y)>2,进位2必丢失,又因(x+y)>0,所以[X]补+ [Y ]补=x+y= [ X + Y ]补(mod 2)当x+y<0时,2+(x+y)<2,又因(x+y)<0,所以[X]补+ [Y ]补=x+y= [ X + Y ]补(mod 2)(3)x < 0 , y > 0 , 则x + y > 0 或x + y < 0这种情况和第2种情况一样,把x和y的位置对调即得证。
(4)x < 0 , y < 0 , 则x + y < 0因为[X]补= 2 + x , [Y ]补= 2 + y所以[X]补+ [Y ]补= 2 + x + 2 + y = 2 + (2 + x + y)上式第二部分一定是小于2大于1 的数,进位2必丢失,又因(x+y)<0所以[X]补+ [Y ]补= 2 + (x + y)= [ X + Y ]补(mod 2)四.解:64条指令需占用操作码字段(OP)6位,源寄存器和目标寄存器各4位,寻址模式(X)2位,形式地址(D)16位,其指令格式如下:寻址模式定义如下:X= 0 0 寄存器寻址操作数由源寄存器号和目标寄存器号指定X= 0 1 直接寻址有效地址E= (D)X= 1 0 变址寻址有效地址E= (R x)+DX= 1 1 相对寻址有效地址E=(PC)+D其中R x为变址寄存器(10位),PC为程序计数器(20位),位移量D可正可负。
该指令格式可以实现RR型,RS型寻址功能。
五.解:(1)用虚拟地址为1的页号15作为快表检索项,查得页号为15的页在主存中的起始地址为80000,故将80000与虚拟地址中的页内地址码0324相加,求得主存实地址码为80324。
(2)主存实地址码= 96000 + 0128 = 96128(3)虚拟地址3的页号为48,当用48作检索项在快表中检索时,没有检索到页号为48的页面,此时操作系统暂停用户作业程序的执行,转去执行查页表程序。
如该页面在主存中,则将该页号及该页在主存中的起始地址写入主存;如该页面不存在,则操作系统要将该页面从外存调入主存,然后将页号及其在主存中的起始地址写入快表。
六.解:微命令字段共12位,微指令格式如下:各字段意义如下:R—通用寄存器读命令W—通用寄存器写命令.RA0RA1—读R0—R3的选择控制。
WA0W A1—写R0—R3的选择控制。
LDS A—打入SA的控制信号。
LDS B—打入SB的控制信号。
S B->ALU—打开非反向三态门的控制信号。
S B->ALU—打开反向三态门的控制信号,并使加法器最低位加1。
CLR-暂存器SB清零信号。
~ ——一段微程序结束,转入取机器指令的控制信号。
(2)ADD、SUB两条指令的微程序流程图见图B2.3所示。
七.三种系统总线结构如图B2.4所示,从上到下为单总线,双总线,三总线:图B2.4八.解:设读写一块信息所需总时间为T ,平均找到时间为T s ,平均等待时间为T L ,读写一块信息的传输时间为T m ,则:T=T s +T L +T m 。
假设磁盘以每秒r 转速率旋转,每条磁道容量为N 个字,则数据传输率=rN 个字/秒。
又假设每块的字数为n ,因而一旦读写头定位在该块始端,就能在T m ≈(n / rN )秒的时间中传输完毕。
T L 是磁盘旋转半周的时间,T L =(1/2r )秒,由此可得:T=T s +1/2r +n/rN 秒九 解:设加速比S p ,可加速部分的比例F e ,理论加速比S e ,根据Amdahl 定律有:ee e P S F F S /)1(1+-= 假设程序只在两种模式下运行:①使用所有处理机的并行程模式;②只用一台处理机的串行模式。
又假设并行模式下的理论加速比S e 即为多处理机的台数,加速部分的比例F e 即并行部分所占的比例, 已知S p =40; S e =50,代入上式有:40=50/)1(1e e F F +- 求得并行部分所占比例 F e =99.49% 串行部分所占比例 1-F e =0.51%。
