前4章习题课
第4章贪心算法习题(免费阅读)

算法实现题4-5 程序存储问题
数据输入:
第一行是2 个正整数,分别表示文件个数n和磁带的长 度L。接下来的1 行中,有n个正整数,表示程序存放在磁 带上的长度。
结果输出: 最多可以存储的程序数。
输入示例
6 50
2 3 13 8 80 20 输出示例
5
i 012345
x 2 3 13 8 80 20 7
3
算法实现题4-5 程序存储问题
问题描述: 设有n 个程序{1,2,…, n }要存放在长度为L的磁带上。
程序i存放在磁带上的长度是 li,1 ≤ i ≤ n。 程序存储问题要求确定这n 个程序在磁带上的一个
存储方案,使得能够在磁带上存储尽可能多的程序。 编程任务:
对于给定的n个程序存放在磁带上的长度,编程计 算磁带上最多可以存储的程序数。
532.00
10
算法实现题4-6 最优服务次序问题
double greedy( vector<int> x) {
int i,n=x.size(); sort(x.begin(),x.end()); for(i=1;i<n;++i)
x[i] += x[i-1]; double t=0; for(i=0;i<n;++i) t+=x[i]; t /= n;
算法实现题4-5 程序存储问题
int greedy( vector<int> x, int m){
int i=0, sum=0, n=x.size();
sort(x.begin(),x.end());
while(i
if(sum <= m) i++;
自动控制原理课后习题第四章答案

G(s)H(s)=
Kr s(s+1)(s+3)
σ根 s=3-K+ω轨r4-3-迹+p4s132ω1-3的+~3ω32分p===s2-离+001K点.p-3r=3:KK~0θrr===012+ωω6021,o=3,=0+±1810.7o
8
jω
1.7
s1
A(s)B'系(s)统=根A'轨(s迹)B(s)
s3 p3
s=sK2±r没=j24有.8.6位×于2K.r根6=×4轨80.迹6=上7,. 舍去。
2
第四章习题课 (4-9)
4-9 已知系统的开环传递函数,(1) 试绘制出
根轨迹图。
G(s)H与(s虚)=轴s交(0点.01s+1K)(系0.统02根s+轨1迹)
jω
70.7
解: GKK(rr=s=)10H5(0s)=ωω2s1,(3=s=0+±17000K.7)r(s+50)
s1
A(s)B'(系s)统=A根'(轨s)迹B(s)
s3 p3
p2
p1
-4
-2
0
((24))ζ阻=尼03.振5s2荡+1响2应s+s的81==K-r0值0.7范+围j1.2
s=s-s10=3=.-80-56.8+50K.7r×=20=s.82-=54×-.631..1155×3.15=3.1
-2.8
450
1080
360
0σ
0σ
第四章习题课 (4-2)
4-2 已知开环传递函数,试用解析法绘制出系
统的根轨迹,并判断点(-2+j0),(0+j1),
第4章怎样求合力与分力(习题课)课件2(沪科版必修1)

•[解析] 本题考查的是如何根据实际效果分解重力,应注意球 与接触面间作用力的特点.
•球1重力分解如图9甲所示,F1=Gtanθ,F2=
;
•球2重力分解如图乙所示,F1′=Gsinθ,F2′=Gcosθ.
•
图9
•
•题后反思:(1)弹力的方向一定与接触面或接触点的切面 垂直.(2)力产生的作用效果是进行力的分解的重要依据,
()
•图14
•解析:参照图14分析:保持F1与F1和F2的夹角α不变,当F2 增至F2′时,F1和F2的合力F变为F′,由图象可直观看出F>F′, 即两分力中一个力增大,合力不一定增大.同理可分析出: 两个力都增大,合力可能增大,可能减小,也可能不变, 故C、D两项正确.
•答案:CD
•
图15
•2.如图15所示,重力为G的物体静止在倾角为α的斜面上, 将那重么力G分解为垂直斜( 面向)下的力F1和平行斜面向下的力F2, •A.F1就是物体对斜面的压力 •B.物体对斜面的压力方向与F1方向相同,大小为Gcosα •C.F2就是物体受到的静摩擦力 •和D.F2共物五体个受力到的重作力用、斜面对物体的支持力、静摩擦力、F1
•∴1 N≤F12≤15 N •而F3在F1、F2合力的范围内, •所以三个力合力的最小值Fmin=0 •∴0 ≤F≤24 N.
•答案:0≤F≤24 N
•题型二 按力的实际作用效果分解力
•图8 •[例2] 如图8所示,光滑斜面的倾角为θ,有两个相同的 小球,分别用光滑挡板A、B挡柱,挡板A沿竖直方 向.挡板B垂直于斜面,则两挡板受到小球压力的大小之 比为__________,斜面受到两个小球压力大小之比为
•如图13所示,质量为m的等边三棱柱静止在水平放置的 斜面上.已知三棱柱
汽车发动机原理第4章 课后习题答案

第四章复习思考题1.说明汽油机燃烧过程各阶段的主要特点。
答:燃烧过程:(1)着火落后期:它对每一循环都可能有变动,有时最大值是最小值的数倍。
要求:为了提高效率,希望尽量缩短着火落后期,为了发动机稳定运行,希望着火落后期保持稳定(2)明显燃烧期:压力升高很快,压力升高率在0.2-0.4MPa/(°)。
希望压力升高率合适(3)后燃期:湍流火焰前锋后面没有完全燃烧掉的燃料,以及附在气缸壁面上的混合气层继续燃烧。
希望后燃期尽可能的短。
2.爆燃燃烧产生的原因是什么?它会带来什么不良后果?答:燃烧室边缘区域混合气也就是末端混合气燃烧前化学反应过于迅速,以至在火焰锋面到达之前即以低温多阶段方式开始自然,引发爆燃爆燃会给柴油机带来很多危害,发生爆燃时,最高燃烧压力和压力升高率都急剧增大,因而相关零部件所受应力大幅增加,机械负荷增大;爆燃时压力冲击波冲击缸壁破坏了油膜层,导致活塞、气缸、活塞环磨损加剧,爆燃时剧烈无序的放热还使气缸内温度明显升高,热负荷及散热损失增加,这种不正常燃烧还使动力性和经济性恶化。
3.爆燃和早燃有什么区别?答:早燃是指在火花塞点火之前,炽热表面点燃混合气的现象。
爆燃是指末端混合气在火焰锋面到达之前即以低温多阶段方式开始自然的现象。
早燃会诱发爆燃,爆燃又会让更多的炽热表面温度升高,促使更加剧烈的表面点火。
两者相互促进,危害更大。
另外,与爆燃不同的时,表面点火即早燃一般是在正常火焰烧到之前由炽热物点燃混合气所致,没有压力冲击波,敲缸声比较沉闷,主要是由活塞、连杆、曲轴等运动件受到冲击负荷产生震动而造成。
4.爆燃的机理是什么?如何避免发动机出现爆燃?答:爆燃着火方式类似于柴油机,同时在较大面积上多点着火,所以放热速率极快,局部区域的温度压力急剧增加,这种类似阶越的压力变化,形成燃烧室内往复传播的激波,猛烈撞击燃烧室壁面,使壁面产生振动,发出高频振音(即敲缸声)。
避免方法:适当提高燃料的辛烷值;适当降低压缩比,控制末端混合气的压力和温度;调整燃烧室形状,缩短火焰前锋传播到末端混合气的时间,如提高火焰传播速度、缩短火焰传播距离。
高等数学_第四章习题课

四种类型分式的不定积分
1. x A adx Aln xaC;2. (x A a)d nx (1n)A x (a)n1C ;
3. x2M pxN xqdxM 2lnx2pxq
NM2parctx anp2 C;
qp24
qp24
4 .( x 2 M p N q x ) x n d M x 2( x ( 2 2 x p p ) d q x ) n x ( x 2 N p M 2 q x ) n p d
即:连续函数一定有原函数.
2、不定积分
(1) 定义
在区间 I内, 函数f(x)的带 有任意 常数项 的 原函 数称 为f(x)在区间 I 内的 不定积 分, 记
为f(x)dx.
f(x)d xF (x)C
函 数 f(x )的 原 函 数 的 图 形 称 为 f(x )的 积 分 曲 线 .
(1)3axdx lan
ln 3 2
dt t2 1
2l1n3(t
1 1 t
1 )dt 1 lnt1C 1 2(ln 3ln2) t1
2
1
3x2x
ln C.
2(l3 nln2) 3x2x
例2 求ex1(1csoixsnx)dx.
ex(12sinxcosx)
解 原式
2 2 dx 2co2sx
2
(ex 1 extanx)dx
高等数学_第四章习题课
1、原函数
定义 如果在区间I内,可导函数F(x)的导函数为 f(x) ,即xI ,都有F(x) f(x) 或 dF(x) f(x)dx,那么函数F(x)就称为f(x)或 f(x)dx在区间I内原函数. 原函数存在定理 如 果 函 数 f(x)在 区 间 I 内 连 续 , 那 么 在 区 间 I内 存 在 可 导 函 数 F (x), 使 x I, 都 有 F (x)f(x).
第2~4章 习题课

解:反应活性为 C > D > A > B ② 将下列烯烃与浓H2SO4反应活性大小排列成序是: 将下列烯烃与浓H 反应活性大小排列成序是: A. CH3CH2-CH=CH2 C. CH2=CH2 B. CH3-CH=CH-CH3 CH=CHD. (CH3)2C=CH2
解:反应活性为 D > B > A > C
六、鉴别题
要求: 要求:
① 方法简单 ② 反应速度快 ③ 现象明显 ④ 简明扼要
P105P105-9- ① 2-甲基丁烷 3-甲基-1-丁烯 甲基3-甲基-1-丁炔 甲基(-) (-) ( + ) 白↓
Br2 / CCl4
Ag(NH3)2NO2
(-) ( + ) 褪色
命名步骤 1. 根据化合物中所含官能团的情况,确定好母体。 根据化合物中所含官能团的情况,确定好母体。 官能团的情况 2. 选取含母体官能团的最长的碳链作为主链。 选取含母体官能团 最长的碳链作为主链。 母体官能团的 的碳链作为主链 当具有相同长度的碳链可作为主链时, (当具有相同长度的碳链可作为主链时,应选择具 有支链最多的碳链作为主链; 有支链最多的碳链作为主链;当主链的长度和支链 数目相同时,应遵循最低系列原则。) 数目相同时,应遵循最低系列原则。) 3. 编号从离母体官能团最近的一端开始,如果母体 编号从离母体官能团最近的一端开始, 支链的一端开始 官能团位于中间, 从靠近支链的一端开始, 官能团位于中间,就从靠近支链的一端开始,尽可 能使取代基具有最低编号 最低编号。 能使取代基具有最低编号。 4. “先小后大,同基合并” 先小后大,同基合并” 烃基大小的次序(大取代基为“较优”基团) 烃基大小的次序(大取代基为“较优”基团): 甲基<乙基<丙基<丁基<戊基<己基<异戊基< 甲基<乙基<丙基<丁基<戊基<己基<异戊基< 异丁基< 异丁基<异丙基
苏教版选择性必修1——第4章 习题课 等差数列前n项和性质的综合问题

习题课 等差数列前n 项和性质的综合问题学习目标 1.掌握总项数为奇数项或偶数项时前n 项和的特点.2.掌握含绝对值的等差数列的前n 项和的求法.一、等差数列中奇、偶项的和问题1 我们知道等差数列前n 项和公式中的n 表示等差数列的项数,你能利用公式表示S 2n ,S 2n -1吗?提示 S 2n =2n (a 1+a 2n )2=n (a 1+a 2n ),S 2n -1=(2n -1)(a 1+a 2n -1)2,由等差数列的性质m +n =p+q ⇒a m +a n =a p +a q 可知,a 1+a 2n =a n +a n +1,a 1+a 2n -1=2a n ,即S 2n =n (a n +a n +1),S 2n -1=(2n -1)a n ,发现总项数为偶数项时,其和可用中间两项表示,总项数为奇数项时,其和可用中间一项表示.问题2 当总项数为2n 项时,其奇数项和S 奇与偶数项和S 偶有何特点? 提示 S 奇=a 1+a 3+…+a 2n -1=n (a 1+a 2n -1)2=na n , S 偶=a 2+a 4+…+a 2n =n (a 2+a 2n )2=na n +1,则有S 偶-S 奇=na n +1-na n =n (a n +1-a n )=nd , S 偶S 奇=na n +1na n=a n +1a n .问题3 当总项数为2n -1项时,其奇数项和S 奇与偶数项和S 偶有何特点? 提示 S 奇=a 1+a 3+…+a 2n -1=n (a 1+a 2n -1)2=na n , S 偶=a 2+a 4+…+a 2n -2=(n -1)(a 2+a 2n -2)2=(n -1)a n ,则有S 奇-S 偶=a n ,S 奇S 偶=nn -1.知识梳理1.若等差数列{a n }的项数为2n ,则S 2n =n (a n +a n +1),S 偶-S 奇=nd ,S 偶S 奇=a n +1a n .2.若等差数列{a n }的项数为2n +1,则S 2n +1=(2n +1)·a n +1,S 偶-S 奇=-a n +1,S 偶S 奇=n n +1. 3.设两个等差数列{a n },{b n }的前n 项和分别为S n ,T n ,则a n b n =S 2n -1T 2n -1.注意点:(1)总项数为奇数时,其中间项的下标是1和总项数的平均数;(2)总项数为偶数时,其中间有两项,中间第一项的下标为总项数的一半.例1 (1)在等差数列{a n }中,S 10=120,且在这10项中,S 奇S 偶=1113,则公差d =________.答案 2 解析 由⎩⎪⎨⎪⎧S 奇+S 偶=120,S奇S偶=1113,得⎩⎪⎨⎪⎧S 奇=55,S 偶=65, 所以S 偶-S 奇=5d =10,所以d =2.(2)有两个等差数列{a n },{b n }满足a 1+a 2+a 3+…+a n b 1+b 2+b 3+…+b n =7n +2n +3,求a 5b 5.解 方法一 设等差数列{a n },{b n }的公差分别为d 1,d 2, 则a 1+a 2+a 3+…+a n b 1+b 2+b 3+…+b n =na 1+n (n -1)2d 1nb 1+n (n -1)2d 2=a 1+n -12d1b 1+n -12d2,则有a 1+n -12d1b 1+n -12d2=7n +2n +3,①又由于a 5b 5=a 1+4d 1b 1+4d 2,②观察①②,可在①中取n =9,得a 1+4d 1b 1+4d 2=7×9+29+3=6512.故a 5b 5=6512.方法二 设{a n },{b n }的前n 项和分别为A n ,B n , 则有A n B n =7n +2n +3,其中A n =(a 1+a n )n 2,由于a 1+a 9=2a 5.即a 1+a 92=a 5,故A 9=(a 1+a 9)·92=a 5×9.同理B 9=b 5×9. 故A 9B 9=a 5×9b 5×9. 故a 5b 5=A 9B 9=7×9+29+3=6512. 方法三 设{a n },{b n }的前n 项和分别为A n ,B n , 因为等差数列的前n 项和为S n =an 2+bn =an ⎝⎛⎭⎫n +b a , 根据已知,可令A n =(7n +2)kn ,B n =(n +3)kn (k ≠0). 所以a 5=A 5-A 4=(7×5+2)k ×5-(7×4+2)k ×4=65k , b 5=B 5-B 4=(5+3)k ×5-(4+3)k ×4=12k . 所以a 5b 5=65k 12k =6512.方法四 设{a n },{b n }的前n 项和分别为A n ,B n ,由A 2n -1B 2n -1=a n b n ,有a 5b 5=A 9B 9=7×9+29+3=6512.反思感悟 一般地,求等差数列奇、偶项的和需注意:如果已知和,能判断它的中间项是哪一项或哪两项;如果已知某一项或某两项,能判断它是多少项和的中间项.跟踪训练1 (1)等差数列共有2n +1项,所有奇数项之和为132,所有偶数项之和为120,则n 等于( )A .6B .8C .10D .12 答案 C解析 ∵S 奇=a 1+a 3+…+a 2n +1=132,S 偶=a 2+a 4+…+a 2n =120, ∴S 奇-S 偶=a 2n +1-nd =a n +1=12, ∴S 2n +1=S 奇+S 偶=252=()2n +1()a 1+a 2n +12=()2n +1an +1=12()2n +1,解得n =10.(2)已知数列{a n }是项数为偶数的等差数列,它的奇数项的和是50,偶数项的和为34,若它的末项比首项小28,则该数列的公差是________. 答案 -4解析 设等差数列{a n }的项数为2m , ∵末项与首项的差为-28, ∴a 2m -a 1=(2m -1)d =-28,① ∵S 奇=50,S 偶=34,∴S 偶-S 奇=34-50=-16=md ,② 由①②得d =-4.(3)若等差数列{}a n ,{}b n 的前n 项和分别为S n ,T n ,a n b n =n +1n ,则S 9T 9=________.答案 65解析 由等差数列前奇数项和性质,得S 9T 9=9a 59b 5=a 5b 5=5+15=65.二、含绝对值的等差数列的前n 项和问题4 已知等差数列a n =2n -9,求{|a n |}的前n 项和. 提示 设{a n }的前n 项和为S n ,{|a n |}的前n 项和为T n . 则当n ≤4时,T n =-S n =-n 2+8n ,当n ≥5时,T n =(-a 1)+(-a 2)+(-a 3)+(-a 4)+a 5+a 6+…+a n =-S 4+(S n -S 4)=S n -2S 4=n 2-8n +32.∴T n =⎩⎪⎨⎪⎧-n 2+8n ,n ≤4,n 2-8n +32,n ≥5.知识梳理1.若一个等差数列a 1<0,d >0,且a k ≤0,a k +1>0,则其绝对值的前n 项和为T n =⎩⎪⎨⎪⎧-S n ,1≤n ≤k ,S n -2S k ,n >k ,n ∈N *. 2.若一个等差数列a 1>0,d <0,且a k ≥0,a k +1<0,则其绝对值的前n 项和为T n =⎩⎪⎨⎪⎧S n ,1≤n ≤k ,-S n +2S k ,n >k ,n ∈N *. 注意点:(1)要先去掉绝对值才能求和;(2)找准分界点是解决此类问题的关键.例2 数列{a n }的前n 项和S n =100n -n 2(n ∈N *). (1)判断{a n }是不是等差数列,若是,求其首项、公差; (2)设b n =|a n |,求数列{b n }的前n 项和T n . 解 (1)当n ≥2时,a n =S n -S n -1=(100n -n 2)-[100(n -1)-(n -1)2]=101-2n . ∵a 1=S 1=100×1-12=99,满足上式, ∴a n =101-2n (n ∈N *). 又a n +1-a n =-2为常数,∴数列{a n }是首项为99,公差为-2的等差数列. (2)令a n =101-2n ≥0,得n ≤50.5, ∵n ∈N *,∴n ≤50(n ∈N *).①当1≤n ≤50时,a n >0,此时b n =|a n |=a n , ∴数列{b n }的前n 项和T n =100n -n 2. ②当n ≥51时,a n <0,此时b n =|a n |=-a n , 由b 51+b 52+…+b n =-(a 51+a 52+…+a n ) =-(S n -S 50)=S 50-S n ,得数列{b n }的前n 项和T n =S 50+(S 50-S n )=2S 50-S n =2×2 500-(100n -n 2)=5 000-100n +n 2.由①②得数列{b n }的前n 项和为T n =⎩⎪⎨⎪⎧100n -n 2,1≤n ≤50,5 000-100n +n 2,n ≥51,n ∈N *.延伸探究 本例中若a n =2n -101,求数列{b n }的前n 项和. 解 由本例可知,当1≤n ≤50时,a n <0,此时b n =-a n , 数列{}b n 的前n 项和T n =-n 2+100n ,当n ≥51时,a n >0,b 51+b 52+…+b n =a 51+a 52+…+a n . 数列{}b n 的前n 项和T n =-S 50+S n -S 50=n 2-100n +5 000,综上,T n =⎩⎪⎨⎪⎧-n 2+100n ,1≤n ≤50,n 2-100n +5 000,n ≥51,n ∈N *.反思感悟 已知等差数列{a n },求绝对值数列{|a n |}的有关问题是一种常见的题型,解决此类问题的核心便是去掉绝对值,此时应从其通项公式入手,分析哪些项是正的,哪些项是负的,即找出正、负项的“分界点”.跟踪训练2 在等差数列{a n }中,a 10=23,a 25=-22. (1)数列{a n }前多少项和最大? (2)求{|a n |}的前n 项和S n .解 (1)由⎩⎪⎨⎪⎧ a 1+9d =23,a 1+24d =-22,得⎩⎪⎨⎪⎧a 1=50,d =-3,∴a n =a 1+(n -1)d =-3n +53.令a n >0,得n <533,∴当n ≤17时,a n >0;当n ≥18时,a n <0,∴数列{a n }的前17项和最大. (2)当n ≤17时,|a 1|+|a 2|+…+|a n |=a 1+a 2+…+a n =na 1+n (n -1)2d =-32n 2+1032n .当n ≥18,n ∈N *时,|a 1|+|a 2|+…+|a n | =a 1+a 2+…+a 17-a 18-a 19-…-a n =2(a 1+a 2+…+a 17)-(a 1+a 2+…+a n ) =2⎝⎛⎭⎫-32×172+1032×17-⎝⎛⎭⎫-32n 2+1032n =32n 2-1032n +884. ∴S n=⎩⎨⎧-32n 2+1032n ,n ≤17,n ∈N *,32n 2-1032n +884,n ≥18,n ∈N *.1.知识清单:(1)等差数列中奇、偶项的和. (2)含绝对值的等差数列的前n 项和.2.方法归纳:公式法、整体代换法、分类讨论法.3.常见误区:求数列{|a n |}的前n 项和时不讨论,最后不用分段函数表示.1.一个等差数列共有10项,其偶数项之和是15,奇数项之和是12.5,则它的首项与公差分别是( ) A .0.5,0.5 B .0.5,1 C .0.5,2 D .1,0.5答案 A解析 由于项数为10,故S 偶-S 奇=15-12.5=5d , ∴d =0.5,由15+12.5=10a 1+10×92×0.5,得a 1=0.5.2.设S n 是等差数列{a n }的前n 项和,若a 5a 3=59,则S 9S 5等于( )A .1B .-1C .2 D.12答案 A解析 由于S 2n -1=(2n -1)a n , 则S 9S 5=9a 55a 3=95×59=1. 3.设等差数列{a n }的前n 项和为S n ,n ∈N *.若S 12>0,S 13<0,则数列{|a n |}的最小项是( ) A .第6项 B .第7项 C .第12项 D .第13项 答案 B解析 由题意得,S 12>0,S 13<0及S 12=6(a 1+a 12)=6(a 6+a 7),S 13=13a 7,得a 6+a 7>0,a 7<0,所以a 6>0,a 6>|a 7|,且公差d <0,所以|a 7|最小.4.记S n 为等差数列{}a n 的前n 项和,已知a 1=-9,S 5=-25,b n =||a n ,{}b n 的前n 项和为T n ,则T 10=________. 答案 50解析 设等差数列{}a n 的公差为d ,∵a 1=-9,S 5=-25.∴-9×5+5×42×d =-25,解得d =2.∴a n =-9+2(n -1)=2n -11. ∵b n =||a n ,所以b n =||2n -11,∴T 10=||-9+||-7+||-5+||-3+||-1+1+3+5+7+9=2()1+3+5+7+9=50.课时对点练1.在等差数列{}a n 中,a 2+a 4+a 6=-3,a 3+a 5+a 7=6,则{}a n 的前8项的和为( ) A .3 B .4 C .5 D .6 答案 B解析 由等差中项的性质可知a 2+a 4+a 6=3a 4=-3,所以a 4=-1,同理a 5=2,所以a 4+a 5=1,S 8=4(a 4+a 5)=4.2.已知等差数列{}a n 的前n 项和为S n ,2()a 1+a 3+a 5+3()a 8+a 10=60,则S 11的值为( ) A .33 B .44 C .55 D .66 答案 C解析 ∵S n 是等差数列{}a n 的前n 项和, 2()a 1+a 3+a 5+3()a 8+a 10=60,∴2()a 1+a 1+2d +a 1+4d +3()a 1+7d +a 1+9d =60,解得a 1+5d =5,∴a 6=5,∴S 11=112()a 1+a 11=112×2a 6=11a 6=55. 3.等差数列{a n },{b n }的前n 项和分别为S n ,T n ,若a n b n =2n 3n +1,则S 21T 21的值为( )A.1315B.2335C.1117D.49 答案 C解析 S 21T 21=21(a 1+a 21)2÷21(b 1+b 21)2=a 1+a 21b 1+b 21=a 11b 11=2×113×11+1=1117.4.已知等差数列{}a n 的通项公式为a n =5-n ,则||a 1+||a 2+…+||a 10等于( )A .24B .25C .26D .27 答案 B解析 因为a n =5-n ,所以当n ≤5时,a n ≥0,当n ≥6时,a n <0; 因此||a 1+||a 2+…+||a 10=()a 1+a 2+a 3+a 4+a 5-()a 6+a 7+a 8+a 9+a 10 =()4+3+2+1+0+()1+2+3+4+5=10+15=25.5.设等差数列{}a n 和{}b n 的前n 项和分别为S n 和T n ,且S n T n =3n -t 5n +3,若a 7b 3+b 11=14,则t 等于( )A .5B .6C .22 D.512答案 A解析 由题意可得a 7=S 1313,b 3+b 11=2b 7=2T 1313,则a 7b 3+b 11=S 132T 13=3×13-t 2×()5×13+3=14,解得t =5.6.(多选)设等差数列{a n }的前n 项和为S n (n ∈N *),当首项a 1和公差d 变化时,若a 1+a 8+a 15是定值,则下列各项中为定值的是( ) A .a 7 B .a 8 C .S 15 D .S 16 答案 BC解析 由于a 1+a 15=2a 8,故a 1+a 8+a 15是定值可得a 8是定值,S 15=12×15×(a 1+a 15)=15a 8,故S 15为定值.7.设项数为奇数的等差数列,奇数项之和为44,偶数项之和为33,则这个数列的中间项是________,项数是________. 答案 11 7解析 设等差数列{a n }的项数为2n +1(n ∈N *), S 奇=a 1+a 3+…+a 2n +1 =(n +1)(a 1+a 2n +1)2=(n +1)a n +1,S 偶=a 2+a 4+a 6+…+a 2n =n (a 2+a 2n )2=na n +1,所以S 奇S 偶=n +1n =4433,解得n =3,所以项数2n +1=7,S 奇-S 偶=a n +1, 即a 4=44-33=11,为所求的中间项.8.已知在等差数列{a n }中,公差d =1,且前100项和为148,则前100项中的所有偶数项的和为________. 答案 99解析 由题意,得S 奇+S 偶=148, S 偶-S 奇=50d =50, 解得S 偶=99.9.设等差数列{a n }的前n 项和为S n ,已知a 3=12,且S 12>0,S 13<0. (1)求公差d 的取值范围;(2)问前几项的和最大,并说明理由. 解 (1)∵a 3=12,∴a 1=12-2d . ∵S 12>0,S 13<0,∴⎩⎪⎨⎪⎧ 12a 1+66d >0,13a 1+78d <0,即⎩⎪⎨⎪⎧24+7d >0,3+d <0,∴-247<d <-3.即d 的取值范围为⎝⎛⎭⎫-247,-3. (2)∵S 12>0,S 13<0,∴⎩⎪⎨⎪⎧ a 1+a 12>0,a 1+a 13<0,∴⎩⎪⎨⎪⎧a 6+a 7>0,a 7<0,∴a 6>0, 又由(1)知d <0.∴数列前6项为正,从第7项起为负. ∴数列前6项和最大.10.在数列{a n }中,a 1=8,a 4=2,且满足a n +2-2a n +1+a n =0(n ∈N *).(1)求数列{a n }的通项公式;(2)设T n =|a 1|+|a 2|+…+|a n |,求T n .解 (1)∵a n +2-2a n +1+a n =0,∴a n +2-a n +1=a n +1-a n ,∴{a n }是等差数列,又∵a 1=8,a 4=2,∴d =-2,a n =a 1+(n -1)d =10-2n ,n ∈N *.(2)设数列{a n }的前n 项和为S n ,则S n =8n +n (n -1)2×(-2)=9n -n 2.∵a n =10-2n ,令a n =0,得n =5.当n >5时,a n <0;当n =5时,a n =0;当n <5时,a n >0.∴当n ≤5时,T n =|a 1|+|a 2|+…+|a n |=a 1+a 2+…+a n =9n -n 2.当n >5时,T n =|a 1|+|a 2|+…+|a n |=a 1+a 2+…+a 5-(a 6+a 7+…+a n )=S 5-(S n -S 5)=2S 5-S n=2×(9×5-25)-9n +n 2=n 2-9n +40,∴T n =⎩⎪⎨⎪⎧ 9n -n 2,n ≤5,n ∈N *,n 2-9n +40,n ≥6,n ∈N *.11.若数列{a n }的前n 项和是S n =n 2-4n +2,则|a 1|+|a 2|+…+|a 10|等于() A .15 B .35 C .66 D .100答案 C解析 易得a n =⎩⎪⎨⎪⎧-1,n =1,2n -5,n ≥2.|a 1|=1,|a 2|=1,|a 3|=1,令a n >0,则2n -5>0,∴n ≥3.∴|a 1|+|a 2|+…+|a 10|=1+1+a 3+…+a 10=2+(S 10-S 2)=2+[(102-4×10+2)-(22-4×2+2)]=66.12.已知等差数列{}a n 和{}b n 的前n 项和分别为S n 和T n ,且满足S n T n =2n +13n +2,则a 6b 4等于( ) A.32 B.23 C.1314D .1 答案 D解析 由题意,令S n =kn (2n +1),T n =kn (3n +2),∴a 6b 4=S 6-S 5T 4-T 3=78k -55k 56k -33k=1. 13.已知S n ,T n 分别是等差数列{a n },{b n }的前n 项和,且S n T n =2n +14n -2(n ∈N *),则a 10b 3+b 18+a 11b 6+b 15=________.答案 4178 解析 因为b 3+b 18=b 6+b 15=b 10+b 11,所以a 10b 3+b 18+a 11b 6+b 15=a 10+a 11b 10+b 11=10(a 10+a 11)10(b 10+b 11)=S 20T 20=2×20+14×20-2=4178. 14.已知一个有11项且各项都不为零的等差数列,那么其奇数项的和与偶数项的和之比为________.答案 65解析 由题意,得等差数列共有11项,所以奇数项的和为S 奇=6(a 1+a 11)2=6a 6,其偶数项的和为S 偶=5(a 2+a 10)2=5a 6, 所以其奇数项的和与偶数项的和之比为65.15.《九章算术》是人类科学史上应用数学的最早巅峰,书中有如下问题:“今有女子善织,日益功疾,初日织六尺,今一月织十一匹三丈(1匹=40尺,一丈=10尺),问日益几何?”其意思为:“有一女子擅长织布,每天比前一天更加用功,织布的速度也越来越快,从第二天起,每天比前一天多织相同量的布,第一天织6尺,一月织了十一匹三丈,问每天增加多少尺布?”若一个月按30天算,记该女子一个月中的第n 天所织布的尺数为a n ,则a 1+a 3+…+a 29a 2+a 4+…+a 30的值为( ) A.1415 B.1617 C.2324 D.23答案 C解析 由题意,得数列{}a n 为等差数列,a 1=6,S 30=11×40+3×10=470,设数列{}a n 的公差为d ,由等差数列前n 项和公式,得S 30=30×6+30×()30-12d =470,解得d =23, 所以a n =6+()n -1×23=23n +163, a 1+a 3+…+a 29=()a 1+a 29×152=15a 15,a 2+a 4+…+a 30=()a 2+a 30×152=15a 16,所以a 1+a 3+…+a 29a 2+a 4+…+a 30=a 15a 16=23×15+16323×16+163=2324. 16.已知数列{}a n 的首项a 1=1,前n 项和为S n ,且数列⎩⎨⎧⎭⎬⎫S n n 是公差为2的等差数列. (1)求数列{}a n 的通项公式;(2)若b n =(-1)n a n ,求数列{}b n 的前n 项和T n .解 (1)因为数列⎩⎨⎧⎭⎬⎫S n n 是公差为2的等差数列,且S 11=a 1=1,所以S n n =1+()n -1×2=2n -1,所以S n =2n 2-n ,又因为a n =S n -S n -1()n ≥2,所以当n ≥2时,a n =S n -S n -1=4n -3, 又因为a 1=1符合n ≥2的情况,所以a n =4n -3.(2)因为b n =()-1n a n =()-1n()4n -3, 当n 为偶数时,T n =()-1+5+()-9+13+…+[-()4n -7]+()4n -3,所以T n =[()-1+5]+[()-9+13]+…+{[-(4n -7)]+(4n -3)}=4×n 2=2n , 当n 为奇数时,T n =T n -1+b n =2()n -1+[-(4n -3)]=1-2n , 综上可知,T n =⎩⎪⎨⎪⎧ 2n ,n 为偶数,1-2n ,n 为奇数.。
实变函数(程其襄版)第一至四章课后习题答案

,再由极限的唯一性,
上下极限还有用交集与并集来表示。
定理3
⑴ ; ⑵
证明我们利用
来证明⑴式.记 , .设 ,则对任意取定的 ,总有 ,使 ,即对任何 ,总有 ,故 .反之,设 ,则对任意的 ,总有 ,即总存在 ,有 ,所以 ,因此 ,即 .
2.集合的包含关系
若集合A和B满足关系:对任意 ∈A,可以得到x∈B,则成A是B的子集,记为A B或B A,若A B但A并不与B相同,则称A是B的真子集.
例7. 若 在R上定义,且在[a,b]上有上界M,即任意对
∈[a,b]有 M.用集合语言表示为:[a,b] { : M}.
用集合语言描述函数性质,是实变函数中的常用方法,请在看下例.
(1)单射:对任意 ,若 ,使得 ;
(2)满射:对任意 ,存在 ,使得 .
则称A和B对等,记为 ,规定 .
例1 我们可给出有限集合的一个不依赖与于元素个数概念的定义:集合A称为有限合,如果 或者A和正整数的某截断 对等。
注:有限集合的一个不依赖与于元素个数概念的定义,例如A的总个数与正整数的某个截断相对应。
⑵式可同样证明.
用定理3,例12中的⑴式和⑵式可分别简写为
,
.
如果 ,则称 收敛,记为 .若极限允许取 ,则单调数列总有极限,在集合论中也有类似的结论.
5.单调系列
如果集列 满足 , ,则称 为增加(减少)系列.增加与减少的集列统称为单调集列.容易证明:单调集列是收敛的.如果 增加,则 ,如果 减少,则 .请读者自证.
第一章 集合
早在中学里我们就已经接触过集合的概念,以及集合的并、交、补的运算,因此这章的前两节具有复习性质,不过,无限多个集合的并和交,是以前没有接触过的,它是本书中常常要用到,是学习实变函数论时的一项基本功。
课程与教学论各章节练习题及答案

《课程与教学论》练习题第一章绪言一、填空1. 课程与教学论的研究对象是课程问题与教学问题,其宗旨或任务是(揭示规律)、(确立价值)和(优化技术)2.人类早期的课程与教学思想,主要是基于(教育者自身的经验)提炼出来的3.《学记》是我国和世界上最早的教育学专著。
4.西方教育史上第一部系统的教学法专著是《雄辩术原理》。
5.教学论学科的形成,大概在(17——19)世纪。
1632年,捷克人夸美纽斯的《大教学论》,是教学论学科诞生的重要标志。
6.1806年赫尔巴特的《普通教育学》的发表,作为教育学和教学论发展成熟的标志。
7.“传统教学论”是指19世纪中期以来流行于世界各地的(赫尔巴特)教学理论;而“现代教学论”则以(杜威)教学理论为代表。
8.人们常把杜威教学理论的特点概括为(儿童中心)、(经验中心)和(活动中心)。
与此相对,赫尔巴特教学理论的特点是(教师中心)、(书本中心)和(课堂中心)。
9.20世纪50、60年代以来,教学论学科进人了一个多元化发展的时代,其中,有代表性的教学论流派有:美国斯金纳的(程序教学理论)、布鲁纳的(结构主义教学理论)、布卢姆的(掌握学习理论)、罗杰斯的(非指导性教学理论)以及新近流行的建构主义教学理论;苏联赞科夫的(发展性教学理论)、巴班斯基的(教学最优化理论)、阿莫纳什维利等人的合作教育学;德国瓦根舍因的(范例教学理论),等等。
10.(20)世纪初期,课程成为一个独立研究领域,课程论应运而生。
一般认为,美国学者(博比特)1918年出版(课程)一书,是课程论作为独立学科诞生的标志。
11. 泰勒总结了“八年研究”的成果,于1949年出版(课程与教学的基本原理),提出了课程编制的四个基本问题,即(如何确定目标)、(如何选择经验)、(如何组织经验)和(如何评价成果),建立起了著名的课程编制的泰勒原理,即课程编制的“目标模式”。
12.被誉为“现代课程理论之父”的是(泰勒)。
二、简答题1.什么是课程与教学论?2.简述课程论与教学论的关系。
第四章 分子轨道理论习题课

4、CF和CF+的键能分别为548kJ/mol和753kJ/mol。试用MOT解释。
CF的键级为2.5、CF+的键级为3 键级越大,键能越大。
5、构成大π键的条件是什么?下列分子生成什么大π键? 醌、苯胺、尿素、丁二烯、苯乙烯、臭氧、三氟化硼、二氧化氮。 醌
8 8
苯胺
8 7
尿素
6 4
丁二烯
键级=2.5,能稳定存在。 rO rO
+ 2
2
2 2 2 2 2 4 3 F2+ (1 σ ) (1 σ ) (2 σ ) (2 σ ) (3 σ ) (1 π ) (1 π ) g u g u g u g
键级=1.5,能稳定存在。 rF rF
+ 2
2
9、用HMO法处理环戊二烯负离子,写出其久期行列式和形成 的离域大π键的符号,并计算键能Eπ和离域能ED。 解:
2 2 2 2 2 0 0 1 0 2
py 和_____ dyz 。 15、在z方向上能与dyz轨道成键的角量子数l≤2 的原子轨道是 _____ 2 2 2 2 3 16、C2+的分子轨道为____________________________ ,键级____ 1.5 ; 1 g 1 u 2 g 2 u 1 u Z 轴。 17、 AB 为双原子分子,若A与B形成型分子轨道,那么分子的键轴为____ 6 6 ;多电子离域键,如 18、离域键可分为正常离域键,如_____ 苯 分子中存在_____ 2 4 氯乙烯 烯丙基正离子 ______分子中存在_____ 3 。 3 ;缺电子离域键,如___________分子中存在_____
二、填空题
σ-π分离 1、HMO法的核心是_________________ 。 2、HMO法是在_________________ 理论基础上进一步简化提出的。 MO py、dxy AO可形成MO。 3、以X 轴为键轴,A原子的Py与B原子的_______ 4、N2与CO分子轨道能级次序和电子排布类似是因为等电子 ______效应。 2 2 2 2 2 B2 的基态。 1 u 2 g 2 u 1 u 5、某分子的电子组态为 1 g ,该组态最可能是___ ˆ E E。 6、变分法处理分子的 H ,关于试探函数Φ的能量 E 体系能量E0间的关系为_____ 0 4 。 7、有四个AO进行线性组合形成的 MO 数目为 ____ 2 2 2 4 4 KK1 g 1 u 2 g 1 u 1,其键级为 8、F2的电子组态为_________________ ____ g 1 。 9、CN-的电子组态为_________________________________ 。 1 2 2 2 3 2 4 21 4 5 2 10、S、p、d等原子轨道中只能形成σ形分子轨道的是______ 。只能形成δ形分子轨 S轨道 道的是______ 。 d轨道 4 3 多 11、SO2分子中离域π键为_____ ,它属于___ 电子离域π键。 6 12、光气的离域π键为________ 。 4 ˆ e e e B-O 近似。 13、H 2 的 H ,此种形式采取了________ 2m 4 R 4 r 4 r 能量相近;__________ 对称性匹配; ________ 最大重叠 。 14、原子轨道有效地形成分子轨道的条件__________
电工与电子技术课后答案习题4(上篇第四章)

习题44-1 在题4-1图所示的电路中,电容元件原未储能。
① 求开关S 闭合后瞬间各元件上的电压、电流的初始值;② 求开关S 闭合后电路达到稳定状态各元件上的电压、电流的值。
解:①由于开关闭合前,电容元件未储能,故由换路定律可知,0)0()0(==-+C C u u 。
开关闭合后,电容元件相当短路,其等效电路如题4-1图(a )所示,则在+=0t 时各电压、电流为A 66//312//)0(21===+R R E i A 46636)0()0(2121=⨯+=+=++i R R R iA 26633)0()0(2112=⨯+=+=++i R R R iV 12)0()0(21===++Eu u② 开关S 闭合后电路达到稳定状态时,电容元件相当于断路,其等效电路如题4-1图(b )所示。
则当S 闭合后∞=t 时各电压、电流为 A 4312)()(11===∞=∞R E i i 0)(2=∞i V 12)(1==∞E u 0)(2=∞uE 题4-1图(a)+)0(2+题4-1图(b))(2∞)(∞CV 12)(==∞E u C4-2 求题4-2图所示电路中标明的各电流、电压的初始值及稳态值。
解: ① 求初始值:在开关S 断开之前电路处于稳定状态,电容相当于断路,电感相当于短路,其等效电路如题4-2图(a )所示。
则-=0t 时电容两端的电压及电感中的电流为V 410406040)0(=⨯+=-C uA 101406010)0(=+=-L i由换路定律可知:V 4)0()0(==-+C C u u,A 101)0()0(==-+L L i i 那么开关S 断开的瞬间即+=0t 时,电容元件相当于恒压源,电感元件相当于恒流源,其等效电路如题4-2(b)所示。
根据节点电压法,A 和B 两点之间的电压为201601)0(20)0(6010+-+=++i u u C ABV 42016011012056010=+-+=则 0204420)0()0(=-=-=++C AB C u u i 题4-2图题4-2图(a)-=0题4-2图(b)+0+BV 2601014)2040()0()0(-=⨯-=+⨯-=++L AB L i u u ② 求稳态值:在开关S 断开后电路达到稳定状态时,电容相当于断路,电感相当于短路,等效电路如题4-2图(c)所示。
第四章 习题课 数列中的构造问题

2.下列说法错误的是 A.任意等差数列{an}和{bn},数列{an+bn}是等差数列 B.存在等差数列{an}和{bn},数列{anbn}是等差数列
√C.任意等比数列{an}和{bn},数列{an+bn}是等比数列
D.存在等比数列{an}ຫໍສະໝຸດ {bn},数列{anbn}是等比数列
1234
解析 A项,若{an}和{bn}都是等差数列,不妨设an=k1n+b1,bn=k2n+b2, 故可得an+bn=(k1+k2)n+b1+b2,则an+1+bn+1=(k1+k2)(n+1)+b1+b2, 则an+1+bn+1-(an+bn)=k1+k2,故数列{an+bn}是等差数列,则A正确; B项,设数列{an}是数列1,1,1;数列{bn}是数列2,2,2,故可得数列{anbn} 是数列2,2,2,是等差数列,故B正确. C 项,若{an}和{bn}是等比数列,设 an=a1qn1,bn=b1qn2,故可得 an+bn= a1qn1+b1qn2,an+1+bn+1=a1qn1+1+b1qn2+1, 则ana+n1++bbnn+1=a1aqn11+ q1n1+ +bb11qq2n2n+1,不是常数,故{an+bn}不是等比数列,故 C 错误;
延伸探究 1.本例中“an=2an-1+2n”变为“an=2an-1+2n+1”,其余不变,求 数列{an}的通项公式.
解 等式两边同时除以 2n,得a2nn=a2nn--11+2,即a2nn-a2nn--11=2, 所以a2nn是以12为首项,以 2 为公差的等差数列, 所以a2nn=12+(n-1)×2,即 an=2n-23×2n.
第四章 §4.3 等比数列
学习目标
1.掌握利用构造法求数列通项公式的方法. 2.会用构造法公式解决一些简单的问题.
人教A版高中数学选择性必修第二册精品课件 第4章 数列 习题课——数列求和

[nx
-(n+1)x
+1],
2
(1-)
(+1)
,
2
= 1,
∴Sn= 0, = 0,
+1
[
-(
+
1)
+ 1], ≠ 0, ≠ 1.
2
(1-)
若若已知数列{(2n-1)an-1}(a≠0,n∈N*),求它的前n项和Sn.
解:当 a=1 时,数列变成 1,3,5,7,…,(2n-1),…,则
2.什么情况下可以用错位相减法求和?
提示:当一个数列的各项是由一个等差数列和一个等比数列的对应项之
积构成时可以用错位相减法求和.
3.已知数列{an}的前n项和为Sn,且an=n·2n,则Sn=
解析:∵an=n·2n,
∴Sn=1×21+2×22+3×23+…+n×2n,①
∴2Sn=1×22+2×23+…+(n-1)×2n+n×2n+1.②
( 1 + )
(-1)
Sn=
=na1+
d
2
2
等比数列{an}的前 n 项和公式是 Sn=
;
1 , = 1,
1 (1- )
,
1-
.
≠1
2.是不是所有的数列求和都可以直接用这两个公式求解?
提示:不是.
3.将数列中的每项分解,然后重新组合,使之能消去一些项,最终达到求和
的目的的方法叫做裂项相消法.
解:设数列的第 n 项为 an,则 an=1+2+2 +…+2
2
1-2
第四章 数列的求和(一)习题课 课件高二上学期数学人教A版(2019)选择性必修第二册

B.33
C.30
√D.27
由 f(x)=x+log228+ -xx,知28+ -xx>0,解得-2<x<8. 所以-2<an<8.又因为an=n-2,所以满足f(an)的an所有的取值为-1, 0,1,2,…,7,即a1,a2,…,a9. 因为 f(6-x)=6-x+log282- +xx,所以 f(x)+f(6-x)=6. 所以数列{f(an)}的各项之和S=f(a1)+f(a2)+…+f(a9)=f(-1)+f(0) +…+f(7).
f
(0)
②
n 1
由① + ②可得 2an n 1 ,an 2
所以数列an 是首项为
1,公差为
1 2
的等差数列,其前
20
项和为 201
20 1 2
115
2
巩固练习
2.
A.36
已知数列{an}的通项公式为an=n-2(n∈N*),设f(x)=x+log228+-xx ,
则数列{f(an)}的各项之和为
Sn
n(a1 an ) 2
或 Sn
n(n 1) na1+ 2 d
2.等比数列前n项和公式(错位相
减法)
Sn
naa1(111,qqqn )1
a1 anq 1 q
,
q 1
3.两类特殊数列的前n项和(二次幂和、三次幂和)
①12+22+32+…+n2=16n(n+1)(2n+1) ②13+23+33+…+n3=14n2(n+1)2
第四章 习题课 数列求和(一)
高二数学备课组
学习目标
1. 熟练掌握等差和等比数列前n项和的结构特点以 及各个符号的意义
2. 掌握分组求和、倒序相加法求和、并项求
大学 机械振动 课后习题和答案(1~4章 总汇)

1.1 试举出振动设计、系统识别和环境预测的实例。
1.2 如果把双轴汽车的质量分别离散到前、后轴上去,在考虑悬架质量和非悬架质量两个离散质量的情况下,画出前轴或后轴垂直振动的振动模型简图,并指出在这种化简情况下,汽车振动有几个自由度?1.3 设有两个刚度分别为1k ,2k 的线性弹簧如图T —1.3所示,试证明:1)它们并联时的总刚度eq k 为:21k k k eq +=2)它们串联时的总刚度eq k 满足:21111k k k eq +=解:1)对系统施加力P ,则两个弹簧的变形相同为x ,但受力不同,分别为:1122P k xP k x=⎧⎨=⎩由力的平衡有:1212()P P P k k x =+=+故等效刚度为:12eq Pk k k x ==+2)对系统施加力P ,则两个弹簧的变形为: 1122Px k Px k ⎧=⎪⎪⎨⎪=⎪⎩,弹簧的总变形为:121211()x x x P k k =+=+故等效刚度为:122112111eq k k P k x k k k k ===++1.4 求图所示扭转系统的总刚度。
两个串联的轴的扭转刚度分别为1t k ,2t k 。
解:对系统施加扭矩T ,则两轴的转角为: 1122t t Tk T k θθ⎧=⎪⎪⎨⎪=⎪⎩系统的总转角为:121211()t t T k k θθθ=+=+,12111()eq t t k T k k θ==+故等效刚度为:12111eq t t k k k =+1.5 两只减振器的粘性阻尼系数分别为1c ,2c ,试计算总粘性阻尼系数eq c1)在两只减振器并联时,2)在两只减振器串联时。
解:1)对系统施加力P ,则两个减振器的速度同为x ,受力分别为:1122P c x P c x =⎧⎨=⎩ 由力的平衡有:1212()P P P c c x =+=+故等效刚度为:12eq P c c c x ==+ 2)对系统施加力P ,则两个减振器的速度为:1122P x c Px c ⎧=⎪⎪⎨⎪=⎪⎩,系统的总速度为:121211()x x x P c c =+=+ 故等效刚度为:1211eq P c x c c ==+1.6 一简谐运动,振幅为0.5cm,周期为0.15s,求最大速度和加速度。
计算机组成原理第四章课后习题和答案-唐朔飞(完整版)

第4章存储器1. 解释概念:主存、辅存、Cache、RAM、SRAM、DRAM、ROM、PROM、EPROM、EEPROM、CDROM、Flash Memory。
答:主存:主存储器,用于存放正在执行的程序和数据。
CPU可以直接进行随机读写,访问速度较高。
辅存:辅助存储器,用于存放当前暂不执行的程序和数据,以及一些需要永久保存的信息。
Cache:高速缓冲存储器,介于CPU和主存之间,用于解决CPU和主存之间速度不匹配问题。
RAM:半导体随机存取存储器,主要用作计算机中的主存。
SRAM:静态半导体随机存取存储器。
DRAM:动态半导体随机存取存储器。
ROM:掩膜式半导体只读存储器。
由芯片制造商在制造时写入容,以后只能读出而不能写入。
PROM:可编程只读存储器,由用户根据需要确定写入容,只能写入一次。
EPROM:紫外线擦写可编程只读存储器。
需要修改容时,现将其全部容擦除,然后再编程。
擦除依靠紫外线使浮动栅极上的电荷泄露而实现。
EEPROM:电擦写可编程只读存储器。
CDROM:只读型光盘。
Flash Memory:闪速存储器。
或称快擦型存储器。
2. 计算机中哪些部件可以用于存储信息?按速度、容量和价格/位排序说明。
答:计算机中寄存器、Cache、主存、硬盘可以用于存储信息。
按速度由高至低排序为:寄存器、Cache、主存、硬盘;按容量由小至大排序为:寄存器、Cache、主存、硬盘;按价格/位由高至低排序为:寄存器、Cache、主存、硬盘。
3. 存储器的层次结构主要体现在什么地方?为什么要分这些层次?计算机如何管理这些层次?答:存储器的层次结构主要体现在Cache-主存和主存-辅存这两个存储层次上。
Cache-主存层次在存储系统中主要对CPU访存起加速作用,即从整体运行的效果分析,CPU访存速度加快,接近于Cache的速度,而寻址空间和位价却接近于主存。
主存-辅存层次在存储系统中主要起扩容作用,即从程序员的角度看,他所使用的存储器其容量和位价接近于辅存,而速度接近于主存。
高中物理必修一第四章习题课等时

【答案】
4.7 m/s2
1.34 N
第四章
牛顿运动定律
尝试应用
3. 如图所示,两个质量相同的物体 A 和 B 紧靠在一起,放在 光滑的水平桌面上,如果它们分别受到水平推力 F1 和 F2 作 用,而且 F1>F2,则 A 施于 B 的作用力大小为( ) A.F1 B.F2 1 1 C. (F1+F2) D. (F1-F2) 2 2
第四章
牛顿运动定律
6.
如图所示,质量为 80 kg 的物体放在安装在小车上的水平磅 秤上,小车沿斜面无摩擦地向下运动,现观察到物体在磅秤 上的读数只有 600 N,求: (1)斜面的倾角 θ 为多少? (2)物体对磅秤的静摩擦力为多少?(g 取 10 m/s2)
第四章
牛顿运动定律
解析:对物体、磅秤和小车组成的整体应用牛顿第二定律得 (M+m)gsin θ=(M+m)a,解得 a=gsin θ 隔离 M,对 M 在竖直方向上应用牛顿第二定律,有 Mg-FN=Masin θ,即 Mg-FN=Mgsin2θ 1 代入数据解得 sin θ= ,故 θ=30° . 2 (2)对 M 在水平方向上应用牛顿第二定律,有 Ff=Macos θ=Mgsin θcos θ=200 3 N 由牛顿第三定律知物体对磅秤的静摩擦力为 200
【答案】
C
第四章
牛顿运动定律
尝试应用 1.如图所示,一物体从竖直平面内的圆环的最高点A处由静
止开始沿光滑弦轨道AB下滑至B点,那么(
A.只要知道弦长,就能求出运动时间 B.只要知道圆半径,就能求出运动时间 C.只要知道倾角θ,就能求出运动时间 D.只要知道弦长和倾角,就能求出运动时间
)
第四章
牛顿运动定律
连接体问题的方法.
自动控制原理第四章习题课

【练习】系统的闭环传递函数为)13()3(3)(23++++++=ΦK s K s s Ks s ,其中,K >0试绘制系统根轨迹,并求出s=-2时的闭环极点和零点。
解: ,得根轨迹方程:由0)13()3(323=+++++K s K s s0)1()3(13=+++s s K0)2)(2(2=+++s s s 2721,23,21js s ±-=-=⇒【练习1】一单位负反馈系统,其开环传递函数为:]4)1[()1(4)(++-=s K s s K s G(1) 试绘制K 从0→+∞时的系统根轨迹; (2) 求系统阶跃响应中含有分量)cos(βωα+-t et时的K 值范围,其中0,0>>ωα;(3) 求系统有一个闭环极点为-2时的闭环传递函数。
解:(1)根轨迹方程为:)4()2(12=+-+s s s K等效开环传递函数为:)4()2()(2+-=s s s K s G实轴上的根轨迹:[-4,0] 分离点:122411-=-=++d d d d,得:由与虚轴交点:劳斯表如下KsK s K K s 404441012-+显然,K=1时,系统处于临界稳定,由辅助方程可解出交点处21,±==ωK由模值条件得分离点处根轨迹增益:313*33*1==d K 系统根轨迹如下图所示:(2)求K值范围尼状态,分量时,系统处于欠阻当系统含有)cos(βωα+-t et系统有一对具有负实部的共轭极点,K值的范围为:131<<K(3)求闭环极点41442221=⨯⨯=-=K K s 值为:其对应的时,由模值条件,当系统具有闭环极点)445()1(]4)1[()1(4)(+-=++-=∴s s s s K s s K s G)2)(4.0()1(8.0)(1)()(++-=+=Φs s s s G s G s 闭环传递函数为:【练习2】负反馈系统的开环传递函数为22*)1)(1()2()(+-+=s s s K s G(1)绘制K 从0→+∞时的系统闭环根轨迹;(2)用根轨迹模值方程确定系统稳定 *K 的取值范围; (3)试证明复平面上的根轨迹不是圆。
第四章 高分子分子量及分布课后习题

第4章分子量及分子量分布一、思考题1.写出四种平均分子量的定义式,它们有什么样的大小顺序?2.利用稀溶液的依数性可测定高聚物的哪种平均分子量?简述测定数均相对分子质量的几种方法的测试原理。
3.用光散射法测定高聚物的质均相对分子质量时,为何对不同尺寸高分子的试样要采用不同的公式?4.黏度法中涉及哪几种黏度概念?它们之中何者与溶液的浓度无关?写出黏度法测黏均相对分子质量的过程及公式。
5.描述高聚物分子量分布有哪些方式?如何作出高聚物的积分质量分布曲线和微分质量分布曲线?6.体积排除理论是如何解释GPC 法的分级原理的?二、选择题1.已知[]1-=KM η,判断以下哪一条正确? ( ) ①n M M =η ②W M M =η ③ηM M M M Z W n ===2.下列哪个溶剂是线型柔性高分子的良溶剂? ( ) ①1χ=1.5 ② 1χ=0.5 ③ 1χ=0.23.已知[]KM =η,判断以下哪一条正确? ( ) ①n M M =η ②W M M =η ③ηM M M M Z W n === ( )4.下列哪种方法可以测定聚合物的绝对相对分子质量? ( ) ①凝胶渗透色谱法 ②光散射法 ③黏度法5.用GPC 测定聚合物试样的相对分子质量分布时,从色谱柱最先分离出来的是 ( ) ①相对分子质量最小的②相对分子质量最大的③依据所用的溶剂不同,其相对分子质量大小的先后次序不同6.高聚物样品的黏均相对分子质量不是唯一确定值的原因是 ( ) ①黏均相对分子质量与Mark-Houwink 方程中的系数K 有关②黏均相对分子质量与Mark-Houwink 方程中的系数α和K 有关 ③样品相对分子质量具有多分散性7.高聚物多分散性越大,其多分散性系数d 值 ( ) ①越大于1 ② 越小于1 ③越接近18.测定同一高聚物样品的相对分子质量,以下哪个结果正确? ( ) ①黏度法的结果大于光散射法的②VPO 法的结果大于黏度法的③黏度法的结果大于端基分析法的三、计算题1. 分别计算出下列两种情况下的M n和M w,并对计算结果进行解释。
数学分析 第四章 习题课
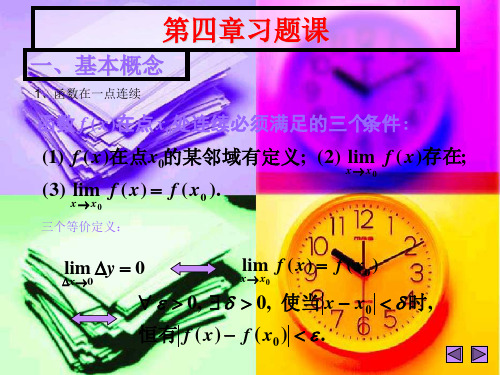
f ( x0 0); f ( x0 0).
第二类:f ( x0 0)不全存在(无穷大间断、振动间断、)
四、连续函数的性质
1、局部性质
有界性,保号性,复合运算性,四则运算性,反函数连续性。
2、整体性质(闭区间上连续函数的性质)
(1)最大最小值定理, (3)介值性定理, (5)一致连续性定理。
(2)有界性定理, (4)根的存在性定理,
第四章习题课
一、基本概念
1、函数在一点连续
函数 f ( x)在点 x0处连续必须满足的三个条件 :
(1)
f ( x)在点x0的某邻域有定义;
(2) lim x x0
f ( x)存在;
(3) lim x x0
f (x)
f ( x0 ).
三个等价定义:
lim y 0
x0
lim
x x0
f (x)
f ( x0 )
证
0,取 ,x, x I ,| x x | ,
L
有 | f ( x) f ( x) |
故f(x)在I上一致连续。
P81. 6, 16
f在[a,)上连续,lim f ( x) A, x
证明f在[a,)上有界且一致连续, 且f在[a,)上必有最大值或最小值。
证
lim f ( x) A,
五、初等函数的连续性
1、基本初等函数在其定义域内连续, 2、初等函数在其定义区间内连续。
五、连续函数作极限运算
连续函数的函数符号可与极限号交换次序。
lim f ( x) f ( lim x),
x x0
x x0
lim f ( g( x)) f ( lim g( x)), 只要f连续,g有极限。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
4 测得某设备的真空度为76mmHg,若当时的大气压强为 1kgf/cm2,则该设备内的绝对压强为 Pa。 A.8.79×103 B.8.79×104 C.8.79×105 . × D.8.79×106
现象的发生, 5 由于离心泵无自吸能力,为避免 启动前先要灌泵。 A.气缚 B.气蚀 C.倒吸 D.叶轮不转 .
局部阻力系数由表1-4查得为 进口突然缩小(入管口) ζ=0.5 90°标准弯头 ζ=0.75 180°回弯头 ζ=1.5 球心阀(全开) ζ=6.4 故
8 (1.04) Σh f = 0.039 × + 0.5 + 2 × 0.75 + 1.5 + 6.4 × 0.032 2
阻力损失
2 l u Σh f = λ + ζ d 2
取管壁绝对粗糙度ε=0.3mm,则:
ε
duρ
0 .3 = = 0.00938 d 32
0.032 × 1.04 × 861 Re = = = 4.46 × 10 4 (湍流) µ 0.643 × 10 −3
由图查得λ=0.039
料液自高位槽流入精馏塔,如附图所示。塔内压强为 1.96×104Pa(表压),输送管道为φ36×2mm无缝钢管,管长 8m。管路中装有90°标准弯头两个,180°回弯头一个,球心 阀(全开)一个。为使料液以3m3/h的流量流入塔中,问高位槽 应安置多高?(即位差Z应为多少米)。料液在操作温度下的物 性:密度ρ=861kg/m3;粘度µ=0.643×10-3Pa·s。
10 随着温度的增加,导热系数的变化趋势是,空气变大 变大,水不确 变大 不确 定先增大后减小,金属 定先增大后减小 不变 。 (A)变大 (B)变小 (C)不变 (D)不确定
11 热流体在换热器中进行无相变逆流传热,换热器用久后形 成污垢层,在同样的操作条件下,与无垢层相比,结垢后的 , 换热器的K 变小∆t m 。 变大 (A)变大 (B)变小 (C)不变 (D)不确定
(3)流量、轴功率及效率 附图中泵的特性曲线与管路特性曲线的交点就是泵的工作点, 从图中点M读得: 泵的流量 Q=27L/s=97.2m3/h 泵的轴功率 N=6.6kW 泵的效率 η=77%
YYY L4-16
在一单壳程单管程列管式换热器内,流量为 在一单壳程单管程列管式换热器内,流量为10000kg/h的某种 的某种 溶液在管束内呈湍流流动,其比热容为4.18kJ/(kgK),由15℃加 溶液在管束内呈湍流流动,其比热容为 由 ℃ 热到100 ℃,管内对流传热系数为 管内对流传热系数为600w/(m2 ℃).温度为 温度为110 ℃ 热到 温度为 的饱和水蒸气在壳方冷凝为同温度的水, 的饱和水蒸气在壳方冷凝为同温度的水,其对流传热系数为 1.2x104w /(m2 ℃).列管换热器由 列管换热器由Φ25x2mm的160根不锈钢管 列管换热器由 的 根不锈钢管 组成,不锈钢导热系数为17w/(m2 ℃)。若污垢热阻和热损失 组成,不锈钢导热系数为 。 可以忽略,试求: 可以忽略,试求: 1) 列管长度 2)若 管数不变,改为双管程时,列管长度多少? ) ) 管数不变,改为双管程时,列管长度多少?
1.局部阻力损失计算式
u hf = ζ 2
2
中的u是指标 。 A.小管中的流速 1 小管中的流速u 小管中的流速 B.大管中的流速u2 C.小管中的流速u1与大管中的流速u2的平均值(u1+ u2)/2 D.与流向有关
2.如图所示,冷热两流体在套管换热器中进行换热 (均无相变化),现冷流体的流量 wsc 减少,则 (A) 总换热量Q减少,冷热流体出口温度 减少, 总换热量 减少
14.同一离心泵分别输送密度为
ρ1
及
ρ2
的两种流体,已知两者体积流量相等,
ρ1
=1.2
ρ2
,则 。 A)扬程H1=H2,轴功率N2=1.2N1 B)扬程H1=1.2H2,轴功率N2=N1 C)扬程H C)扬程H1=H2,轴功率N1=1.2N2 D D)扬程H2=1.2H1,轴功率 H 轴功率N N2=1.2N1
6 热量传递有三种基本方式,其中描述传导传热的定律是 定律。 A.牛顿冷却定律 C.菲克定律 B.傅立叶定律 D.分配定律
7 用120℃饱和蒸汽加热原油,蒸汽冷凝成同温度的冷凝水,此 时两流体的平均温度差,(△tm)并流 (△tm)逆流。 A.小于 B.大于 C.等于 D.不定 .
8 离心泵性能测定过程中,当水的流量从小变大时,泵入口 处的压强 。 A.减小 B.增大 C.先增大后减小 D.先减小后增 . 大 9 在卧式列管式换热器中,用饱和蒸气对空气进行加热(冷凝 液在饱和温度下排出),饱和蒸汽应走 。 A.管程 B.壳程 C.壳程或管程都可以 .
(2)标绘管路特性曲线 根据管路特性方程,可计算不同流量所需的压头值,现将计算结果列表如下:
0.00857Qe2
Qe/L·s-1 He/m
0
4
8
12
16
20
24
28
13
13.14
13.55
14.23
15.2
16.43
17.94
19.72
由上表数据可在4B20型水泵的特性曲线图上标绘出管路特性曲线He-Qe。
12 离心泵的扬程是指单位重量流体经过泵后以下 能量 的增加值。 A.包括内能在内的总能量 B.机械能 C.静压能 . D.位能
13 以下泵中具有自吸能力的是 。 A.往复泵 B.齿轮泵和旋涡泵 C.离心泵 D.旋 . 转泵和旋涡泵
13 某一套管换热器,由管间的饱和蒸气加热管内空气,设饱和 蒸汽温度为100℃,空气进口温度为20℃,出口温度为80℃,则 。 此换热器内管壁温度应是 A.接近空气平均温度 B.接近饱和蒸汽和空气进口温度的平 均温度 C.接近饱和蒸汽温度 D.接近饱和蒸汽和空气出口温度的平 . 均温度
将20℃的清水从贮水池送至水塔,已知塔内水面高于贮水池水 面13m。水塔及贮水池水面恒定不变,且均与大气相通。输水 管为φ140×4.5mm的钢管,总长为200m(包括局部阻力的当 量长度)。现拟选用4B20型水泵,当转速为2900r/min时,其 特性曲线见附图,试分别求泵在运转时的流量、轴功率及效率。 摩擦系数λ可按0.02计算。
解:求泵运转时的流量、轴功率及效率,实际上是求泵的工作 点。 即应先根据本题的管路特性在附图上标绘出管路特性曲线。 (1)管路特性曲线方程 在贮水池水面与水塔水面间列柏努利方程
∆p H e = ∆Z + +Hf ρg
式中∆Z=13m ∆p=0 由于离心泵特性曲线中Q的单位为L/s, 故输送流量Qe的单位也为L/s,输送管内流速为:
Hale Waihona Puke 解:取管出口处的水平面作为基准面。在高位槽液 面1-1与管出口截面2-2间列柏努利方程
2 u12 p2 u2 gZ 1 + + = gZ 2 + + + Σh f 2 2 ρ ρ
p1
式中 Z1=Z Z2=0 p1=0(表压) u1≈0 p2=1.96×104Pa
3 Vs 3600 u2 = = = 1.04 m/s 2 π 2 0.785(0.032 ) d 4
u=
π
4
Qe d × 1000
2
=
1000 ×
π
Qe × (0.131)
2
= 0.0742Qe
4
l + le u 2 200 (0.0742Qe ) H f = λ = 0.02 × × d 2g 0.131 2 × 9.81
=
2
本题的管路特性方程为: 0.00857Qe2 He=13+
=10.6J/kg 所求位差
2
2 2 p 2 − p1 u 2 Σh f 1.96 × 10 4 (1.04 ) 10.6 Z= + + = + + = 3.46m ρg 2g g 861 × 9.81 2 × 9.81 9.81
截面2-2也可取在管出口外端,此时料液流入 塔内,速度u2为零。但局部阻力应计入突然扩 大(流入大容器的出口)损失ζ=1,故两种计算 方法结果相同。
t 2 T2
均上升; 均上升;
(B)总换热量Q不变,冷热流体出口温度 (C)总换热量Q增大,冷热流体出口温度
t 2 T2 也不变;
均下降;
t 2 T2
(D)总传热系数K不变,总换热量Q也不变。
t1 , wsc , C pc
T1 wsh , C ph
T2
t2
3.内径为27mm的自来水管其设计输水能力宜 为 。 (A)0.2m3/h (C)20 m3/h (B)2 m3/h (D)200 m3/h
